ГДЗ Алгебра 7 класс Мордкович, Александрова
В седьмом классе школьники знакомятся с новой дисциплиной — алгеброй. Ее очень трудно назвать простой и ребятам на собственном опыте предстоит в этом убедиться. Проблемы у учащихся могут возникнуть с такими темами, как «Линейная функция», «Многочлены» и манипуляции с ними, а так же некоторым не просто раскладывать многочлены на множители. Решебник к учебнику «Алгебра. Задачник 7 класс» Мордкович, Александрова способен помочь ученикам разобраться со всеми этими недопониманиями.
Что в него включено.
Семь глав заключают в себя множество заданий, которые помогают лучше понять, о чем именно идет речь. В конце пособия представлены задачи для итогового повторения и элементы статистической обработки данных. При заключении очередной темы в ГДЗ по математике 7 класс школьникам предлагается пройти контрольное решение упражнений, которые должны выявить насколько именно подростки усвоили материал.
Нужен ли решебник.
Семиклассникам не так просто преодолеть возникшие препятствия из-за сложности программы, поэтому дополнительная поддержка им явно не помешает. Зачастую финансовые возможности родителей таковы, что нанимать репетитора могут позволить себе далеко не все. Да и не факт, что они окажут долгоиграющую пользу. Решебник к учебнику «Алгебра. Задачник 7 класс» Мордкович может стать именно той палочкой-выручалочкой, которая порой очень сильно требуется ученикам. Главное, им не злоупотреблять, а воспринимать как вспомогательное пособие.
«Мнемозина», 2013 г.
Похожие ГДЗ Алгебра 7 класс
Глава 1. § 1:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
Глава 1. § 2:
1234567891011121314151617181920212223
Глава 1. § 3:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
Глава 1. § 4:
§ 4:
12345678910111213141516171819202122232425262728293031323334353637383940414243
Глава 1. § 5:
123456789101112131415161718192021222324252627282930313233343536373839404142
Глава 1. § 6:
12345678910111213141516171819202122232425262728293031323334353637383940
Глава 2. § 7:
123456789101112131415161718192021222324252627282930313233343536373839
Глава 2. § 8:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
Глава 2. § 9:
12345678910111213141516171819
Глава 2. § 10:
1234567891011121314151617181920212223
Глава 3. § 11:
123456789101112131415161718192021
Глава 3. § 12:
1234567891011121314151617181920212223242526272829
Глава 3. § 13:
§ 13:
123456789101112131415161718
Глава 3. § 14:
1234567891011121314151617181920212223242526272829303132333435363738
Глава 4. § 15:
12345678910111213141516171819202122232425262728293031323334353637
Глава 4. § 16:
1234567891011121314151617181920212223242526
Глава 4. § 17:
123456789101112131415161718192021222324252627282930313233343536373839404142
Глава 4. § 18:
123456789101112131415161718192021222324
Глава 4. § 19:
123456789101112
Глава 5. § 20:
12345678910111213141516171819
Глава 5. § 21:
1234567891011121314151617181920212223242526272829303132333435363738394041
Глава 5. § 22:
12345678910111213141516171819202122232425262728293031323334
Глава 5. § 23:
§ 23:
12345678910111213141516171819
Глава 6. § 24:
12345678910111213141516171819202122232425262728
Глава 6. § 25:
12345678910111213
Глава 6. § 26:
123456789101112131415161718192021222324252627282930313233
Глава 6. § 27:
123456789101112131415161718192021222324252627
Глава 6. § 28:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465
Глава 6. § 29:
1234567891011121314151617
Глава 7. § 30:
123456789101112131415161718
Глава 7. § 31:
12345678910111213141516171819202122232425262728
Глава 7. § 32:
1234567891011121314151617181920212223
Глава 7. § 33:
§ 33:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253
Глава 7. § 34:
1234567891011121314151617181920212223242526272829
Глава 7. § 35:
123456789101112131415161718192021222324252627282930313233343536373839404142
Глава 7. § 36:
12345678910111213141516171819
Глава 8. § 37:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
Глава 8. § 38:
12345678910111213141516
Глава 8. § 39:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
Глава 9. Итоговое повторение:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188
Приложение:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071
Домашние контрольные работы:
№1№2№3№4№5№6№7№8
Предыдущий
Следующий
Название
Условие
Решебник №1
Решебник №2
Решебник №3
Предыдущий
Следующий
ГДЗ Учебник по Алгебре 7 класс Мордкович
«ГДЗ по алгебре 7 класс Учебник Мордкович (Просвещение)» поможет не упустить важную информацию в этом учебном году, и позволит с лёгкостью сдавать все работы на отлично.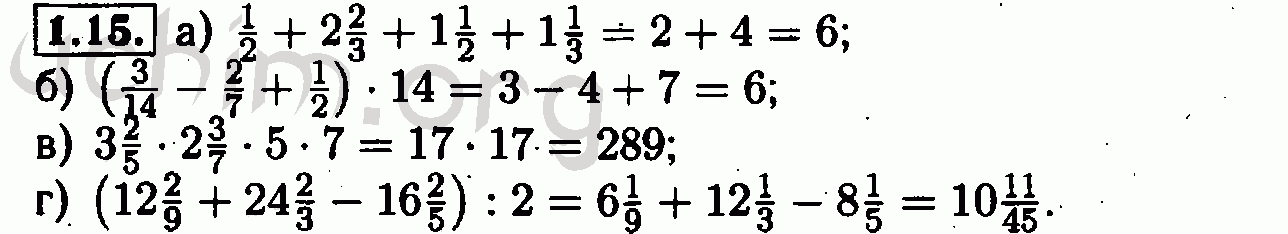 При этом, не нужно часами выполнять задачи, и волноваться перед занятиями. Решебник предоставит возможность ученику проверить свои ответы, и исправить ошибки.
При этом, не нужно часами выполнять задачи, и волноваться перед занятиями. Решебник предоставит возможность ученику проверить свои ответы, и исправить ошибки.
Содержание курса алгебры
Данная дисциплина является важнейшей частью школьной программы семиклассников, ведь в будущем их ожидает экзамен по математике, к которому нужно начинать подготовку уже сейчас. В этом году математика делится на два предмета — алгебру и геометрию. Основными разделами информации из книги можно считать:
- алгебраические и числовые выражения;
- линейные функции, и их графики;
- системы уравнений с двумя переменными;
- таблица основных степеней;
- арифметические операции над многочленами;
- решение уравнений с помощью графиков.
Освоить каждую тему, и достойно отвечать на вопросы у доски поможет онлайн-сборник с готовыми ответами.
В чём заключается польза ГДЗ по алгебре 7 класс Учебник Мордкович
Пособие направлено на тщательное изучение математического языка, и позволяет ученикам:
- Разобраться в попущенных параграфах.

- С лёгкостью справляться с домашней работой.
- Сдавать самостоятельные на высокие баллы.
- Повысить общую успеваемость.
Онлайн-доступ к ресурсу создаёт возможность пользоваться им независимо от времени и местоположения с помощью любого телефона или ноутбука. Кроме того, пособие мотивирует подростков изучать науку, и стремиться к достижению отличных результатов. При этом, нужно помнить, что списывать готовые ответы запрещено, ведь это только ухудшит успеваемость, и создаст пробелы в знаниях ребёнка. Правильный подход к работе с решебником обеспечит высокие баллы за проверочные задания.
Кому пригодится решебник
Не только дети с пользой применяют информацию из ГДЗ. Родители используют помощника для быстрой проверки домашней работы ребёнка, и исправления ошибок. Это позволяет не получать низких оценок за допущенные недочёты. Педагогам также полезен онлайн-сборник. С готовыми решениями гораздо проще оценивать самостоятельные и контрольные работы, и создавать собственную программу обучения. Из вышеперечисленного можно сделать вывод, что «ГДЗ по алгебре 7 класс Учебник Мордкович А. Г., Семенов П. В., Александрова Л. А., Мардахаева Е. Л. (Просвещение)» — незаменимый консультант для всех семиклассников, их родителей и учителей!
Из вышеперечисленного можно сделать вывод, что «ГДЗ по алгебре 7 класс Учебник Мордкович А. Г., Семенов П. В., Александрова Л. А., Мардахаева Е. Л. (Просвещение)» — незаменимый консультант для всех семиклассников, их родителей и учителей!
Ответы из решебника
§1. Числовые и алгебраические выражения
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1. 8
1.9
1.10
1.11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1.19
1.
8
1.9
1.10
1.11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1.19
1.
§2. Понятие о математическом языке
2. 1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.
1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
2.10
2.11
2.12
2.
§3. Свойства степеней с натуральными показателями
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
3.

§4. Понятие о математических моделях
4.1
4.2
4.3
4.4
4.5
4. 6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.16
4.17
4.
6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.16
4.17
4.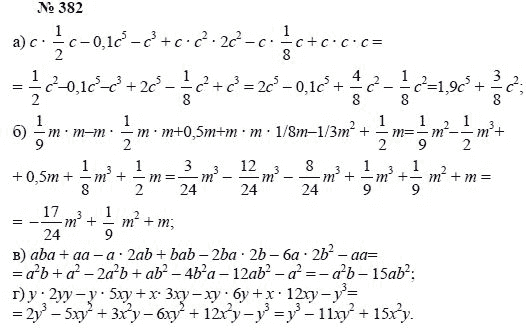 18
4.19
4.20
4.21
4.22
4.23
4.24
4.25
4.26
4.27
18
4.19
4.20
4.21
4.22
4.23
4.24
4.25
4.26
4.27
§5. Линейные уравнения с одной переменной
5.1
5. 2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
5.12
5.13
5.
2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
5.12
5.13
5. 14
5.15
5.16
5.17
5.18
5.19
5.20
5.21
5.22
5.23
5.24
14
5.15
5.16
5.17
5.18
5.19
5.20
5.21
5.22
5.23
5.24
§6. Координатная прямая
6. 1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
6.11
6.12
1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
6.11
6.12
§7.
 Числовые промежутки на координатной прямой
Числовые промежутки на координатной прямой 7.1
7.2
7.3
7.4
7.5
7.6
7.7
7.8
7.9
7.10
7.11
7. 12
7.13
7.14
7.15
7.16
7.17
7.18
7.19
7.20
7.21
12
7.13
7.14
7.15
7.16
7.17
7.18
7.19
7.20
7.21
§8. Координатная плоскость. Координаты точки на плоскости
8. 1
8.2
8.3
8.4
8.5
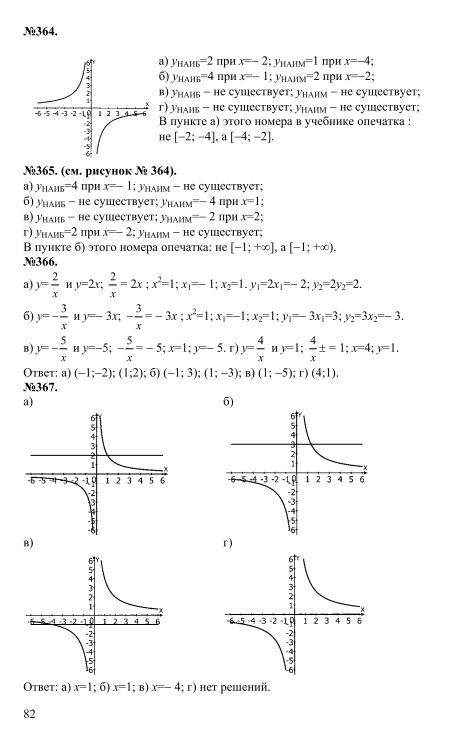
8.6
8.7
8.8
8.9
8.10
8.11
1
8.2
8.3
8.4
8.5
8.6
8.7
8.8
8.9
8.10
8.11
§9.
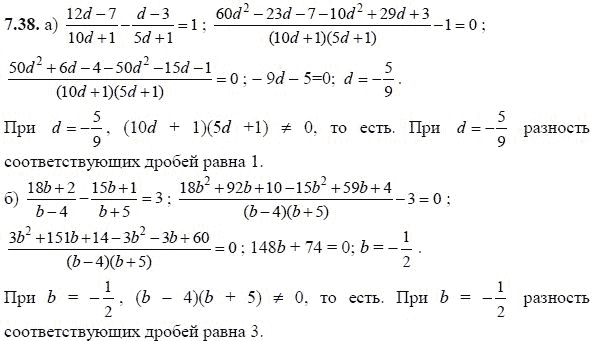 Координатная плоскость. Построение точки на плоскости по заданным координатам
Координатная плоскость. Построение точки на плоскости по заданным координатам 9.1
9.2
9.3
9.4
9.5
9.6
9.7
9.8
9.9
9.10
9.11
9.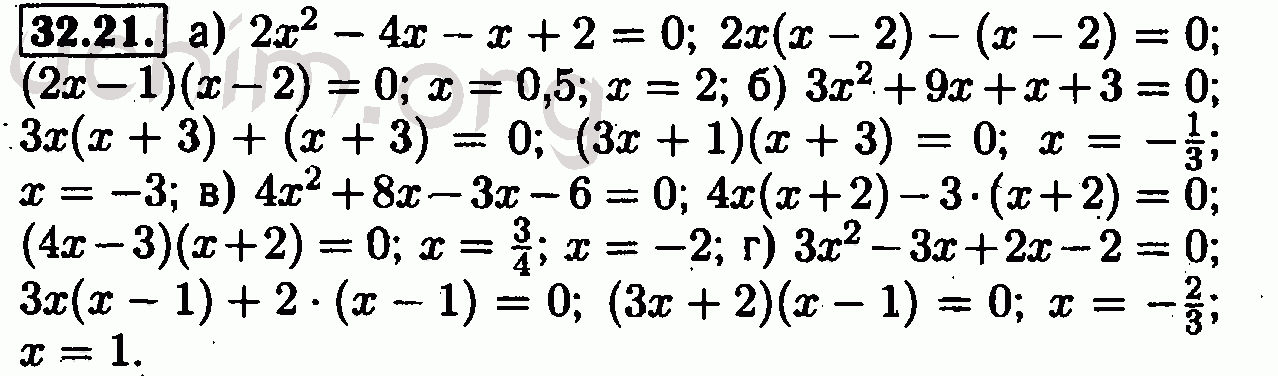 12
9.13
9.14
9.15
12
9.13
9.14
9.15
§10. Линейные уравнения с двумя переменными
10.1
10.2
10.3
10.4
10.5
10.6
10.7
10. 8
10.9
10.10
10.11
10.12
10.13
8
10.9
10.10
10.11
10.12
10.13
§11. График линейного уравнения с двумя переменными
11.1
11.2
11.3
11.4
11.5
11. 6
11.7
11.8
11.9
11.10
11.11
11.12
11.13
11.14
11.15
11.16
6
11.7
11.8
11.9
11.10
11.11
11.12
11.13
11.14
11.15
11.16
ГДЗ Алгебра 7 класс Мордкович, Александрова, Мишустина
- Алгебра 7 класс
- Тип пособия: Сборник задач
- Авторы: Мордкович, Александрова, Мишустина
- Издательство: «Мнемозина»
Глава 1.
 Математический язык. §1. Числовые и алгебраические выражения1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
Математический язык. §1. Числовые и алгебраические выражения1234567891011121314151617181920212223242526272829303132333435363738394041424344454647Глава 1. Математический язык. Домашняя контрольная работа №1
Вариант 1Вариант 2Глава 1. Математический язык. §2. Что такое математический язык
1234567891011121314151617181920212223Глава 1. Математический язык. §3. Что такое математическая модель
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647Глава 1. Математический язык. §4. Линейное уравнение с одной переменной
12345678910111213141516171819202122232425262728293031323334353637383940414243Глава 1. Математический язык. §5. Координатная прямая
123456789101112131415161718192021222324252627282930313233343536373839404142Глава 2. Линейная функция. Домашняя контрольная работа №2
Вариант 1Вариант 2Глава 2. Линейная функция. §6. Координатная плоскость
12345678910111213141516171819202122232425262728293031323334353637383940Глава 2.
 Линейная функция. §7. Линейное уравнение с двумя переменными и его график123456789101112131415161718192021222324252627282930313233343536373839
Линейная функция. §7. Линейное уравнение с двумя переменными и его график123456789101112131415161718192021222324252627282930313233343536373839Глава 2. Линейная функция. §8. Линейная функция и её график
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566Глава 2. Линейная функция. §9. Линейная функция у=кх
12345678910111213141516171819Глава 2. Линейная функция. §10. Взаимное расположение графиков линейных функций
1234567891011121314151617181920212223Глава 3. Системы двух линейных уравнений с двумя переменными. Домашняя контрольная работа №3
Вариант 1Вариант 2Глава 3. Линейная функция. §11. Основные понятия
123456789101112131415161718192021Глава 3. Линейная функция. §12. Метод подстановки
1234567891011121314151617181920212223242526272829Глава 3. Линейная функция. §13. Метод алгебраического сложения
123456789101112131415161718Глава 3.
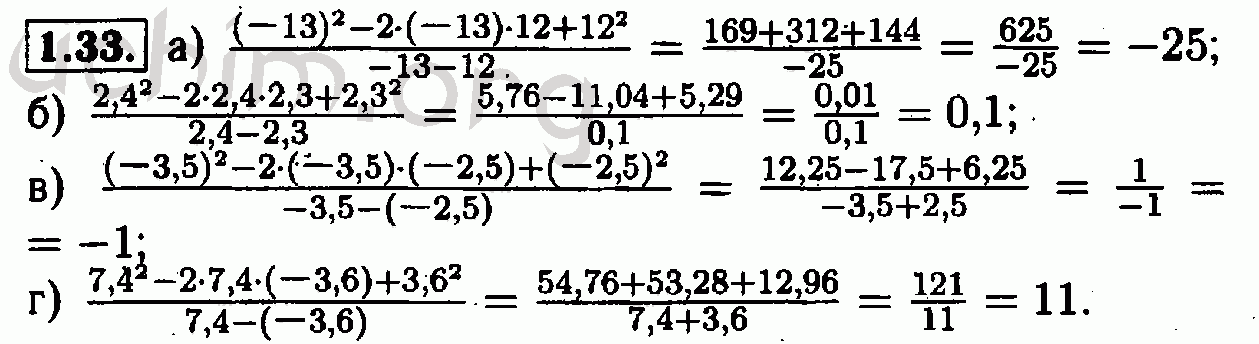 Линейная функция. §14. Системы двух линейных уравнений с двумя переменными как математические модели1234567891011121314151617181920212223242526272829303132333435363738
Линейная функция. §14. Системы двух линейных уравнений с двумя переменными как математические модели1234567891011121314151617181920212223242526272829303132333435363738Глава 4. Степень с натуральным показателем и её свойства. Домашняя контрольная работа №4
Вариант1Вариант2Глава 4. Степень с натуральным показателем и её свойства. §15. Что такое степень с натуральным показателем
12345678910111213141516171819202122232425262728293031323334353637Глава 4. Степень с натуральным показателем и её свойства. §16. Таблица основных степеней
1234567891011121314151617181920212223242526Глава 4. Степень с натуральным показателем и её свойства. §17. Свойства степени с натуральными показателями
123456789101112131415161718192021222324252627282930313233343536373839404142Глава 4. Степень с натуральным показателем и её свойства. §18. Умножение и деление степеней с одинаковыми показателями
123456789101112131415161718192021222324Глава 4.
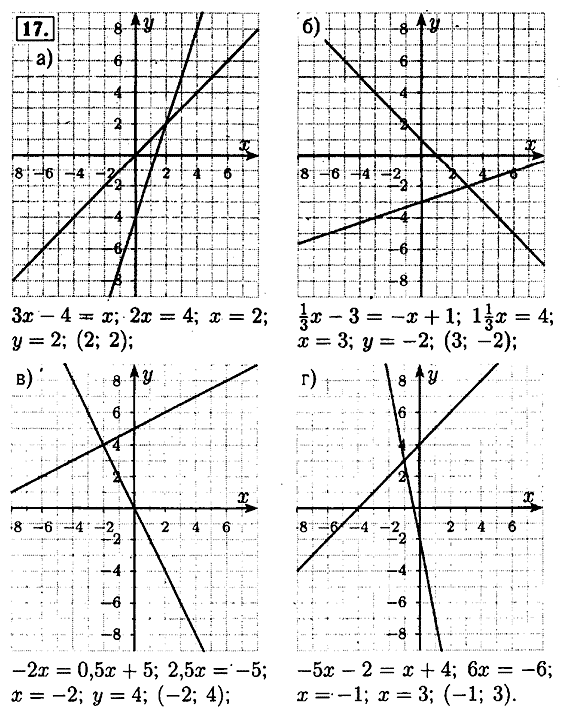 Степень с натуральным показателем и её свойства. §19. Степень с нулевым показателем123456789101112
Степень с натуральным показателем и её свойства. §19. Степень с нулевым показателем123456789101112Глава 5. Одночлены. Арифметические операции над одночленами. Домашняя контрольная работа №5
Вариант1Вариант2Глава 5. Одночлены. Арифметические операции над одночленами. §20. Понятие одночлена. Стандартный вид одночлена
12345678910111213141516171819Глава 5. Одночлены. Арифметические операции над одночленами. §21. Сложение и вычитание одночленов
1234567891011121314151617181920212223242526272829303132333435363738394041Глава 5. Одночлены. Арифметические операции над одночленами. §22. Умножение одночленов. Возведение одночлена в натуральную степень
12345678910111213141516171819202122232425262728293031323334Глава 5. Одночлены. Арифметические операции над одночленами. §23. Деление одночлена на одночлен
12345678910111213141516171819Глава 6. Многочлены. Арифметические операции над многочленами. Домашняя контрольная работа №5
Вариант1Вариант2Глава 6.
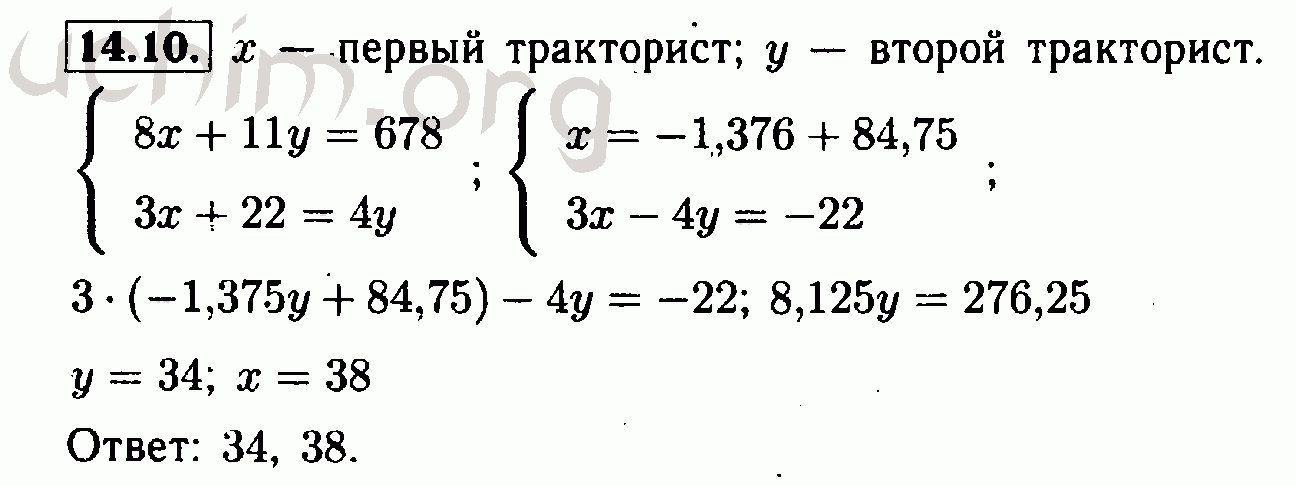 Многочлены. Арифметические операции над многочленами. §24. Основные понятия12345678910111213141516171819202122232425262728
Многочлены. Арифметические операции над многочленами. §24. Основные понятия12345678910111213141516171819202122232425262728Глава 6. Многочлены. Арифметические операции над многочленами. §25. Сложение и вычитание многочленов
12345678910111213Глава 6. Многочлены. Арифметические операции над многочленами. §26. Умножение многочлена на одночлен
123456789101112131415161718192021222324252627282930313233Глава 6. Многочлены. Арифметические операции над многочленами. §27. Умножение многочлена на многочлен
123456789101112131415161718192021222324252627Глава 6. Многочлены. Арифметические операции над многочленами. §28. Формулы сокращенного умножения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465Глава 6. Многочлены. Арифметические операции над многочленами. §29. Деление многочлена на одночлен
1234567891011121314151617Глава 7. Разложение многочленов на множители.
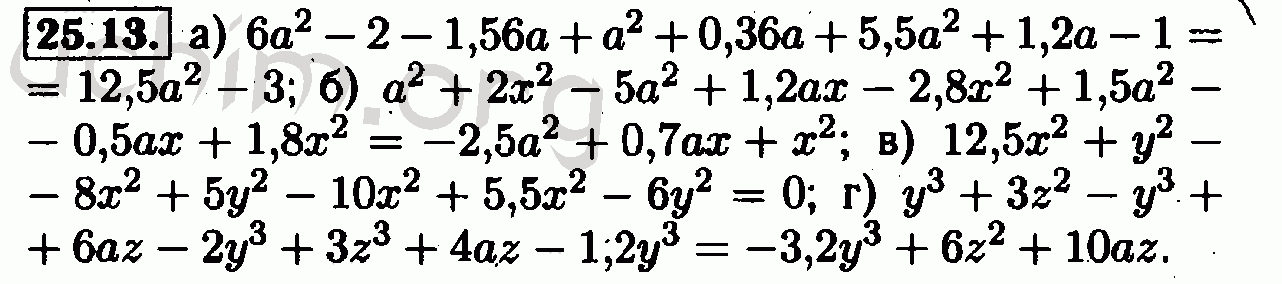 Домашняя контрольная работа №712
Домашняя контрольная работа №712Глава 7. Разложение многочленов на множители. §30. Что такое разложение многочленов на множители и зачем оно нужно
123456789101112131415161718Глава 7. Разложение многочленов на множители. §31. Вынесение общего множителя за скобки
12345678910111213141516171819202122232425262728Глава 7. Разложение многочленов на множители. §32. Способ группировки
1234567891011121314151617181920212223Глава 7. Разложение многочленов на множители. §33. Разложение многочленов на множители с помощью формул сокращенного умножения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253Глава 7. Разложение многочленов на множители. §34. Разложение многочленов на множители с помощью комбинации различных приемов
1234567891011121314151617181920212223242526272829Глава 7. Разложение многочленов на множители. §35. Сокращение алгебраических дробей
123456789101112131415161718192021222324252627282930313233343536373839404142Глава 7.
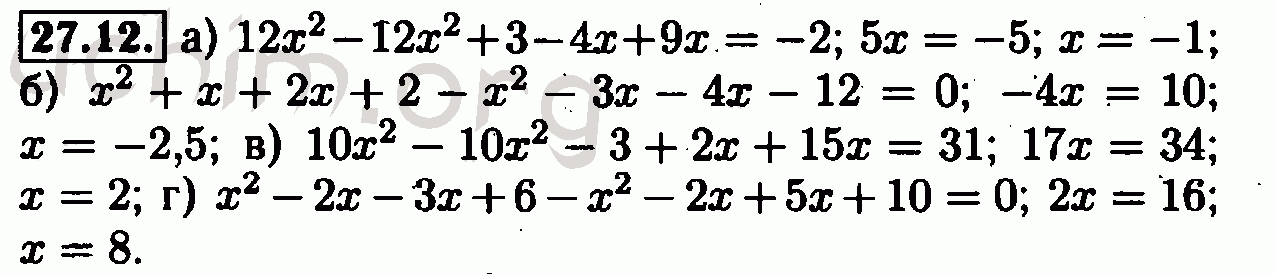 Разложение многочленов на множители. §36. Тождества12345678910111213141516171819
Разложение многочленов на множители. §36. Тождества12345678910111213141516171819Глава 8. Фунции y=x2. Домашняя контрольная работа №8
Вариант1Вариант2Глава 8. Фунции y=x2. §38. Графическое решение уравнений
12345678910111213141516Глава 8. Фунции y=x2. §39. Что означает в математике запись y=f(x)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748Глава 8. Фунции y=x2. §37. Функция y=x2 и её график
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556Глава 9. Итоговое посторение
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188Приложения
123456789101112131416171819202122232526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071Похожие ГДЗ Алгебра 7 класс
- Алгебра 7 класс
- Контрольные и самостоятельные работы
- УМК
- Попов, Мордкович
- Экзамен
- Алгебра 7-9 класс
- Тетрадь для контрольных работ
- Мордкович
- Мнемозина
- Алгебра 7-9 класс
- Тесты
- Мордкович, Тульчинская
- Мнемозина
Глава 1.
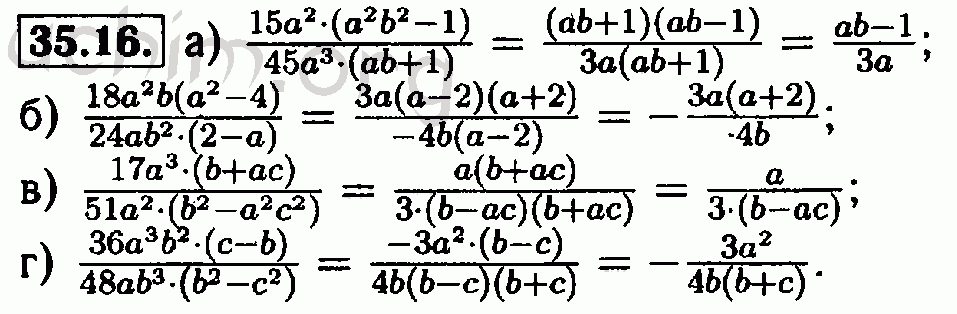 Математический язык. §1. Числовые и алгебраические выражения: 1
Математический язык. §1. Числовые и алгебраические выражения: 1Условие
Решение
Алгебра — трудности продолжаются
Школьники взрослеют и седьмой класс во многом является более трудным для них, чем все остальные. Нагрузка в это время возрастает неимоверно. Кроме того, бередят чуткую детскую душу и ожидания контрольных работ по алгебре, которую многие просто не могут полностью осознать. В наше время повсеместной перестройки системы образования, в учеников пытаются впихнуть объемные знания за минимальное время, поэтому зачастую материал на уроках бывает подан плохо. А это в свою очередь порождает:
- неуверенность в своих силах;
- плохое знание программы;
- нелюбовь к данному предмету.
Вполне естественно, что дети нехотя ходят на уроки и выполняют задания кое-как, лишь бы разделаться. При том они совершенно не стремятся к тому, чтобы вникнуть в суть тематики, так как просто не понимают, как это можно сделать. Чтобы ребенок не терял нить знаний на помощь может прийти решебник к учебнику «Алгебра 7 класс Сборник задач Мордкович, Александрова, Мишутина (Мнемозина)».
Чтобы ребенок не терял нить знаний на помощь может прийти решебник к учебнику «Алгебра 7 класс Сборник задач Мордкович, Александрова, Мишутина (Мнемозина)».
В этом справочнике приведены подробные пояснения ко всем сложным моментам , так что даже сильно отстающие ученики смогут без проблем разобраться в материале. Язык изложения таков, что семиклассникам не придется обращаться за дополнительными пояснениями к родителям. А это означает, что домашние задания они будут выполнять самостоятельно, ища ответы на свои вопросы в проверенном источнике. Главное, сразу предупредить ребенка о тех негативных последствиях, которые могут возникнуть в случае списывания.
Что можно найти в решебнике
Пособие разделено на девять глав, в каждой из которых включены соответствующие тематике параграфы. ГДЗ по Алгебре 7 класс Мордкович можно отнести к наиболее полным руководствам по ответам на школьные задания. Все номера примеров хорошо проработаны авторами и приведены полные решения на все задачи. Поэтому ученики имеют возможность:
Поэтому ученики имеют возможность:
- Подготовиться к предстоящим урокам.
- Проверить правильность своих д/з.
- Повысить уровень знаний.
- Улучшить успеваемость.
И все это можно сделать всего лишь занимаясь под руководством данного сборника, не затрачивая при этом много времени. Учащиеся при должном усердии постепенно перейдут от полнейшего недопонимания предмета к его полному осознанию. Успеваемость начнет выправляться, что несомненно порадует как родителей, так и самих школьников.
Преимущества решебника
Определенно пользование ГДЗ облегчает школьникам жизнь, но в добавок ко всему это реальная возможность не спеша ознакомиться с материалом и разобраться в нем. Сборник доступен онлайн, поэтому пользоваться им можно в любое время и где угодно, достаточно просто зайти на сайт с личного гаджета.
Но некоторые школьники порой начинают злоупотреблять подобной доступностью готовых ответов, и это не идет им на пользу. Ведь, как и все остальные дидактические материалы, ГДЗ требует хорошей проработки представленной информации, а не просто ее списывания. Если пользоваться им правильно, то решебник к учебнику «Алгебра 7 класс Мордкович» хорошо поможет в учебе и станет незаменимым советчиком при преодолении многочисленных препятствий. А делать это лучше так:
Ведь, как и все остальные дидактические материалы, ГДЗ требует хорошей проработки представленной информации, а не просто ее списывания. Если пользоваться им правильно, то решебник к учебнику «Алгебра 7 класс Мордкович» хорошо поможет в учебе и станет незаменимым советчиком при преодолении многочисленных препятствий. А делать это лучше так:
- Изучить теорию из учебника.
- Выполнить все номера самостоятельно.
- Сравнить свои ответы с теми, которые приведены в ГДЗ.
- Исправить допущенные ошибки.
- Закрепить пройденное.
Ответственно отнесясь к учебному процессу, ребята получат полноценные навыки по одному из самых сложных предметов в школьной программе. Многие считают, что знания по алгебре не пригодятся им в будущем, поэтому не особо стараются ее постичь. Однако не стоит забывать о том, что впереди предстоит сдать два серьезных экзамена, не считая многочисленных проверок знаний. Чтобы не испортить себе аттестат, стоит внимательно относиться к каждой дисциплине.
Польза решебника в учебе
Чем старше класс, тем более сложный материал начинают изучать школьники. Времени урока, которого и до этого не хватало, становится катастрофически мало. Учителя просто разрываются между необходимостью разъяснить новую тематику и требованиями программы, которые зачастую этому препятствуют. Ребят нагружают бесконечными контрольными, тестированиями и проверочными, при этом они должны сами разбираться с непростыми параграфами, вникая в суть сложных формул.
В итоге довольно часто у учеников наблюдаются такие проблемы в учебе как:
- ошибки при написании задач и примеров;
- низкие оценки;
- отсутствие реальных знаний.
Все это не добавляет ребятам любви к предмету. Родители на данном этапе тоже мало чем способны помочь, так как просто не помнят всех нюансов того, что когда-то изучали сами. Поэтому единственным выходом для большинства является обращение к репетитору. Однако такой способ весьма дорогостоящ и не обязательно приводит к успеху. Намного прагматичнее начать использовать ГДЗ по алгебре 7 класс Учебник Мордкович (Мнемозина), где дети почерпнут всю необходимую информацию.
Намного прагматичнее начать использовать ГДЗ по алгебре 7 класс Учебник Мордкович (Мнемозина), где дети почерпнут всю необходимую информацию.
Стоит ли использовать ГДЗ
Для многих учащихся решебник становится настоящей палочкой-выручалочкой. В представленных решениях и условиях разберется даже тот человек, который вообще не ориентируется в алгебраических законах. Периодические тренировки под руководством ГДЗ будут намного эффективнее, если не просто списывать информацию, а тщательно изучать все приведенные аспекты. Кроме того, ученикам стоит помнить о том, что сами учителя нередко черпают задания для проверочных испытаний именно в этом сборнике, поэтому лучше работать немного наперед, чтобы не испытывать неудобств во время контрольных.
Лаконичное изложение сведений в справочнике позволяет сократить время, которое дети обычно проводят за учебниками. Таким образом, они смогут не только в кратчайшие сроки выполнить д/з и подготовиться к следующему уроку, но и полноценно отдохнуть перед новым учебным днем, заняться любимым хобби, погулять с друзьями, спокойно посещать дополнительные секции, не переживая о том, что что-то осталось не сделанным.
Мордкович А.Г. Алгебра. 7 класс. В 2 ч. Часть 2. Задачник для учащихся общеобразовательных учреждений
- формат djvu
- размер 2.69 МБ
- добавлен 06 июля 2010 г.
Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч
.2. Задачник для учащихся общеобразовательных учреждений
Автор: А. Г. Мордкович, Л. А Александрова, Т. Н. Мишустина, Е. Е.
Тульчинская
Издательство: Мнемозина
Год: 2009
Страниц: 270
Задачник (13-е изд., испр. ) представляет собой вторую часть
комплекта из двух книг, предназначенных для изучения курса алгебры
в 7-м классе (первая часть — учебник).
Задачник содержит разнообразные системы упражнений, тщательно
выстроенные на четырех уровнях — по степени нарастания трудности.
Выделение в отдельную книгу задачника позволило авторам создать
избыточную по объему систему упражнений, обеспечивающую учителю
более чем достаточный материал для работы в классе и для домашних
заданий без привлечения других источников. Каждая глава
заканчивается разделом «Домашняя контрольная работа» (в двух
вариантах).
Каждая глава
заканчивается разделом «Домашняя контрольная работа» (в двух
вариантах).
Начиная с этого издания, в задачнике имеется Приложение «Элементы
статистической обработки данных» (его автор — П. В. Семенов). Оно
состоит из восьми пунктов, в каждом из которых задачи
сопровождаются небольшими теоретическими комментариями. Первые 5—8
задач каждого пункта Приложения связаны с математической
статистикой, а две последние задачи — с простейшей комбинаторикой
или нахождением простейших вероятностей.
Купить книгу «Алгебра. 7 класс. В 2 ч. Часть 2. Задачник для учащихся общеобразовательных учреждений»
Смотрите также
- формат djvu
- размер 3.3 МБ
- добавлен 06 июля 2010 г.
Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч 1. Учебник для учащихся общеобразовательных учреждений Издательство: Мнемозина Год: 2009 Страниц: 160 Учебник (13-е изд. , испр. ) представляет собой первую часть комплекта из двух книг, предназначенных для изучения курса алгебры в 7-м классе (вторая часть — задачник) Главная особенность учебника состоит в том, что он основан на принципах проблемного, развивающего и опережающего обучения. Книга имеет пов…
, испр. ) представляет собой первую часть комплекта из двух книг, предназначенных для изучения курса алгебры в 7-м классе (вторая часть — задачник) Главная особенность учебника состоит в том, что он основан на принципах проблемного, развивающего и опережающего обучения. Книга имеет пов…
- формат djvu
- размер 2.21 МБ
- добавлен 23 ноября 2010 г.
Мордкович А. Г. Алгебра. 8 класс: учеб. для учащихся общеобразоват. учреждений. Издательство: Мнемозина. Год: 2008. Страниц: 240. ISBN: 978-5-346-01011-1. Это — учебник для классов с повышенным уровнем математической подготовки в общеобразовательных школах. Он написан в русле той концепции, которая использована в соответствующем учебнике А. Г. Мордковича для 8-го класса общеобразовательных учреждений, с соблюдением практически того же порядка сле…
- формат pdf
- размер 1.
 62 МБ
62 МБ - добавлен 08 января 2010 г.
Учебно-практическое пособие. Страниц ч.1. 247 и ч.2. 45. к задачнику «Алгебра. 7 класс: Задачник для общеобразоват. учреждений. — 3-е изд., доработ. » А. Г. Мордкович и др. VI.: «Мнемозина», 2000 г. Часть I и 2.
- формат djvu
- размер 3.01 МБ
- добавлен 18 июня 2010 г.
Мордкович А. Г. и др. Алгебра и начала математического анализа. 10 класс В 2 ч. Ч. 2. Задачник (профильный уровень). Издательство: Мнемозина. Год: 2009. Страниц: 343. Задачник представляет собой вторую часть комплекта из двух книг предназначенных для изучения курса алгебры и начал математического анализа в 10-м классе с профильной подготовкой по математике (первая часть — учебник).
- формат djvu
- размер 2.
 16 МБ
16 МБ - добавлен 06 июля 2010 г.
Мордкович А. Г., Николаев Н. П. Алгебра. 7 класс. В 2 ч. Ч 1. Учебник для учащихся общеобразовательных учреждений. Издательство: Мнемозина Год: 2009 Страниц: 191 Это — первая часть комплекта для изучения алгебры для классов с повышенным уровнем математической подготовки в общеобразовательных школах (вторая часть — задачник). Он написан в русле той концепции, которая использована в соответствующем учебнике А. Г. Мордковича для 7-го класса общеоб…
- формат djvu
- размер 2.08 МБ
- добавлен 06 июля 2010 г.
Мордкович А. Г., Николаев Н. П. Алгебра. 7 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений Издательство: Мнемозина Год: 2009 Страниц: 207 Это — вторая часть комплекта для изучения алгебры-7 для классов с повышенным уровнем математической подготовки в общеобразовательных школах (первая часть — учебник). Данный комплект адресован не специализированным математическим школам или классам с собственными авторскими программами…
Данный комплект адресован не специализированным математическим школам или классам с собственными авторскими программами…
- формат djvu, pdf
- размер 5.01 МБ
- добавлен 08 января 2010 г.
Учебное пособие. Страниц 251+984. к задачнику «Алгебра и начала анализа. Задачник для 10-11 кл. общеобразовательных учреждений Л. Г. Мордкович. Л. О. Депищева. Т. Д. Корешкова. Т. Н. Мишустина, Е. Е. Тульчинская — VI.: «Мнемозина». 2001 г. »
- формат pdf
- размер 1.87 МБ
- добавлен 26 ноября 2009 г.
Предлагаемое учебное пособие содержит подробное решение заданий к задачнику «Алгебра и начала анализа. Задачник для 10-11 кл. общеобразовательных учреждений А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина, Е. Е. Тульчинская — М. : 2001 г. » Пособие адресовано в первую очередь школьникам, испытывающим трудности в решении задач по алгебре, а также их родителям для проверки уровня готовности ученика к контрольным работам. 251 с.
А. Корешкова, Т. Н. Мишустина, Е. Е. Тульчинская — М. : 2001 г. » Пособие адресовано в первую очередь школьникам, испытывающим трудности в решении задач по алгебре, а также их родителям для проверки уровня готовности ученика к контрольным работам. 251 с.
Умножение многочлена на одночлен. Типовые задачи. Видеоурок «Умножение многочлена на одночлен
Если числа обозначаются разными буквами, то можно обозначить только из произведения; пусть, например, надо число а умножить на число b, — мы можно обозначить это либо через a∙b, либо через ab, но не может быть и речи о том, чтобы как-то выполнить это умножение.Однако, когда мы имеем дело с мономами, то, в силу 1) наличия коэффициентов и 2) того, что в эти одночлены могут входить множители, обозначаемые одинаковыми буквами, можно говорить об умножении одночленов, для многочленов эта возможность еще шире.Рассмотрим ряд случаев, когда можно производить умножение, начиная с простейшего
1. Умножение степеней с теми же основаниями . .. Пусть, например, потребуется а 3 ∙ а 5. Зная смысл возведения в степень, запишем то же более подробно:
.. Пусть, например, потребуется а 3 ∙ а 5. Зная смысл возведения в степень, запишем то же более подробно:
а ∙ а ∙ а ∙ а ∙ а ∙ а ∙ а ∙ а
Глядя на эту подробную запись, мы видим, что мы написали а в 8 раз, или, короче, в 8 раз. Итак, а 3 ∙ а 5 = а 8.
Пусть требуется b 42 ∙ b 28. Пришлось бы написать сначала множитель b 42 раза, а потом снова множитель b 28 раз — в общем, мы бы получили, что b берется множителем 70 раз. т. е. b 70. Значит, b 42 ∙ b 28 = b 70. Отсюда уже видно, что при умножении степеней с одинаковыми основаниями основание степени остается неизменным, а показатели степени складываются. Если у нас есть a 8 ∙ a, то мы должны иметь в виду, что множитель a подразумевает показатель степени 1 («a в первой степени»), — следовательно, a 8 ∙ a = a 9.
Примеры: х ∙ х 3 ∙ х 5 = х 9; а 11 ∙ 22 ∙ 33 = 66; 3 5 ∙ 3 6 ∙ 3 = 3 12; (а + б) 3 ∙ (а + б) 4 = (а + б) 7; (3x — 1) 4 ∙ (3x — 1) = (3x — 1) 5 и т. д.
Иногда приходится иметь дело со степенями, показатели степени которых обозначаются буквами, например, xn (x в степени н). К таким выражениям нужно привыкнуть. Вот несколько примеров:
К таким выражениям нужно привыкнуть. Вот несколько примеров:
Поясним некоторые из этих примеров: bn — 3 ∙ b 5 основание b оставить без изменений, а показатели добавить, то есть (n — 3) + (+5) = n — 3+5=n+2. Конечно, такие прибавления надо научиться делать быстро в уме.
Другой пример: x n + 2 ∙ x n — 2, — основание x оставить без изменений, а показатель степени добавить, т.е. (n + 2) + (n — 2) = n + 2 + n — 2 = 2н.
Можно выше найденный порядок, как выполнять умножение степеней с одинаковыми основаниями, теперь можно выразить равенством:
а м ∙ н = а м + n
2. Умножение одночлена на одночлен. Предположим, например, что вы хотите 3a²b³c ∙ 4ab²d². Мы видим, что здесь точкой обозначено одно умножение, но мы знаем, что один и тот же знак умножения имеется в виду между 3 и а², между а² и b³, между b³ и с, между 4 и а, между а и b², между b² и д². Следовательно, мы можем видеть здесь произведение 8 множителей и можем умножать их на любые группы в любом порядке. Переставим их так, чтобы коэффициенты и степени с одинаковыми основаниями стояли рядом друг с другом, т.е.
Переставим их так, чтобы коэффициенты и степени с одинаковыми основаниями стояли рядом друг с другом, т.е.
3 ∙ 4 ∙ а² ∙ а ∙ b³ ∙ b² ∙ с ∙ d².
Тогда мы можем перемножить 1) коэффициенты и 2) степени с одинаковыми основаниями и получить 12a³b5cd².
Итак, при умножении одночлена на одночлен мы можем умножать коэффициенты и степени с теми же основаниями, а остальные множители приходится переписывать без изменений.
Еще примеры:
3. Умножение многочлена на одночлен. Предположим, вы должны сначала какой-нибудь многочлен, например, a — b — c + d умножить на положительное целое число, например, +3. Поскольку положительные числа считаются такими же, как и арифметические числа, то это то же самое, что (a — b — c + d) ∙ 3, т.е. a — b — c + d берется 3 раза как слагаемое, или
(a — b — c + d) ∙ (+3) = a — b — c + d + a — b — c + d + a — b — c + d = 3a — 3b — 3c + 3d,
, то есть в итоге каждый член многочлена пришлось умножать на 3 (или на +3).
Отсюда следует:
(a — b — c + d) ÷ (+3) = a — b — c + d,
, то есть каждый член многочлена надо было разделить на (+3). Также суммируя, получаем:
и т.д.
Теперь пусть надо умножить (a — b — c + d) на положительную дробь, например, на +. Это как умножение на арифметическую дробь, то есть взятие частей (a — b — c + d). Пятую часть этого многочлена взять легко: нужно разделить (a — b — c + d) на 5, и мы уже умеем это делать, — получаем… Осталось повторить полученный результат 3 раз или умножить на 3, т.е.
В итоге мы видим, что нам пришлось умножать каждый член полинома на или на +.
Теперь пусть надо умножить (a — b — c + d) на отрицательное число, целое или дробное,
то есть и в этом случае каждый член многочлена надо было умножить на -.
Таким образом, каким бы ни было число m, всегда (a — b — c + d) ∙ m = am — bm — cm + dm.
Поскольку каждый одночлен является числом, здесь мы видим указание, как умножать многочлен на одночлен — каждый член многочлена надо умножать на этот одночлен.
4. Умножение многочлена на многочлен … Пусть надо (а+b+с)∙(d+e). Так как d и e обозначают числа, то (d + e) также выражает любое одно число.
(a + b + c) ∙ (d + e) = a (d + e) + b (d + e) + c (d + e)
(можно объяснить это образом: мы имеем право временно принять d + e за моном).
Ad+ae+bd+be+cd+ce
В результате можно изменить порядок членов.
(a + b + c) ∙ (d + e) = ad + bd + ed + ae + be + ce,
то есть, чтобы умножить многочлен на многочлен, надо умножить каждый член единицы многочлен от каждого члена другого. Удобно (для этого порядок полученных членов был изменен выше) умножать каждый член первого многочлена сначала на первый член второго (на + d), затем на второй член второго (на + д), то, если бы это было, третьим и т. д. . д.; после этого следует провести кастинг похожих участников.
В этих примерах двучлен умножается на двучлен; в каждом биноме члены расположены в убывающей степени буквы, общей для обоих биномов. Такие умножения легко выполнить в уме и сразу записать конечный результат.
Такие умножения легко выполнить в уме и сразу записать конечный результат.
Из умножения старшего члена первого двучлена на старший член второго, т.е. 4x² на 3x, получаем 12x³ старший член произведения — подобного ему явно не будет. Далее ищем, от умножения каких слагаемых получим слагаемые с меньшей, чем 1 степенью буквы х, то есть с х². Нетрудно видеть, что такие слагаемые будут получены умножением второго члена первого сомножителя на 1-й член второго и умножением 1-го члена первого сомножителя на 2-й член второго (скобки внизу пример указывает на это). Нетрудно произвести эти умножения в уме, а также выполнить приведение этих двух подобных слагаемых (после чего мы получим слагаемое –19х²). Затем замечаем, что следующее слагаемое, содержащее букву х в степени на 1 меньше, то есть х в 1-й степени, получится только от умножения второго слагаемого на второе, и подобных им не будет.
Другой пример: (x² + 3x) (2x — 7) = 2x³ — x² — 21x.
Также несложно мысленно проделать примеры наподобие следующих:
Старший член получается умножением старшего члена на старший, подобных ему членов не будет, и он = 2а³. Затем ищем, какие умножения дадут слагаемые с а² — от умножения 1-го слагаемого (а²) на 2-е (–5) и от умножения второго слагаемого (–3а) на 1-е (2а) – это указывается ниже в скобках; выполняя эти умножения и объединяя полученные слагаемые в одно, мы получаем –11a². Затем ищем, какие умножения дадут термы с а в первой степени — эти умножения отмечены скобками выше. Выполнив их и объединив полученные слагаемые в одно, получим +11а. Наконец, обратите внимание, что наименее значащий член в произведении (+10), который вообще не содержит a, получается путем умножения младшего значащего члена (–2) одного полинома на младший значащий член (–5) многочлена. Другой.
Затем ищем, какие умножения дадут слагаемые с а² — от умножения 1-го слагаемого (а²) на 2-е (–5) и от умножения второго слагаемого (–3а) на 1-е (2а) – это указывается ниже в скобках; выполняя эти умножения и объединяя полученные слагаемые в одно, мы получаем –11a². Затем ищем, какие умножения дадут термы с а в первой степени — эти умножения отмечены скобками выше. Выполнив их и объединив полученные слагаемые в одно, получим +11а. Наконец, обратите внимание, что наименее значащий член в произведении (+10), который вообще не содержит a, получается путем умножения младшего значащего члена (–2) одного полинома на младший значащий член (–5) многочлена. Другой.
Другой пример: (4а 3 + 3а 2 — 2а) ∙ (3а 2 — 5а) = 12а 5 — 11а 4 — 21а 3 + 10а 2.
Из всех предыдущих примеров также получим общий результат: старший член произведения всегда получается умножением старших членов сомножителей, и подобных членов быть не может; также низший член произведения получается путем умножения низших членов множителей, и одинаковых членов быть не может.
Остальные слагаемые, полученные умножением многочлена на многочлен, могут быть подобны, и даже может случиться так, что все эти слагаемые взаимно аннулируются, и останутся только старший и младший.
Вот несколько примеров:
(a² + ab + b²) (a — b) = a³ + a²b + ab² — a²b — ab² — b³ = a³ — b³
(a² — ab + b²) (a — b) = a³ — a²b + ab² + a²b — ab² + b³ = a³ + b³
(a³ + a²b + ab² + b³) (a — b) = a 4 — b 4 (запишите только результат)
(x 4 — x³ + x² — x + 1) (x + 1) = x 5 + 1 и т. д.
Эти результаты заслуживают внимания и их полезно запомнить.
Особенно важен следующий случай умножения:
(a + b) (a — b) = a² + ab — ab — b² = a² — b²
или (x + y) (x — y) = x² + xy — xy — y² = x² — y²
или (x + 3) (x — 3) = x² + 3x — 3x — 9 = x² — 9 и т. д. .
Во всех этих примерах применительно к арифметике мы имеем произведение суммы двух чисел на их разность, а результатом является разность квадратов этих чисел.
Если мы видим подобный случай, то нет необходимости детально выполнять умножение, как это было сделано выше, а можно сразу написать результат.
Например, (3а + 1) ∙ (3а — 1). Здесь первый множитель, с точки зрения арифметики, есть сумма двух чисел: первое число 3а и второе 1, а второй множитель есть разность этих же чисел; следовательно, результат должен быть: квадрат первого числа (т.е. 3a ∙ 3a = 9а²) минус квадрат второго числа (1 ∙ 1 = 1), т.е.
(3а + 1) ∙ (3а — 1) = 9а² — 1.
Также
(аб — 5) ∙ (аб + 5) = a²b² — 25 и т.д.
Итак, запомните
(a + b) (a — b) = a² — b²
то есть произведение суммы двух чисел на их разность равно разность квадратов этих чисел.
При умножении многочлена на одночлен воспользуемся одним из законов умножения. Он получил в математике название распределительного закона умножения. Распределительный закон умножения :
1. (a + b) * c = a * c + b * c
2. (a — b) * c = a * c — b * c
Для умножения моном на многочлен, достаточно каждый из членов многочлена умножить на одночлен. После этого добавьте получившиеся работы.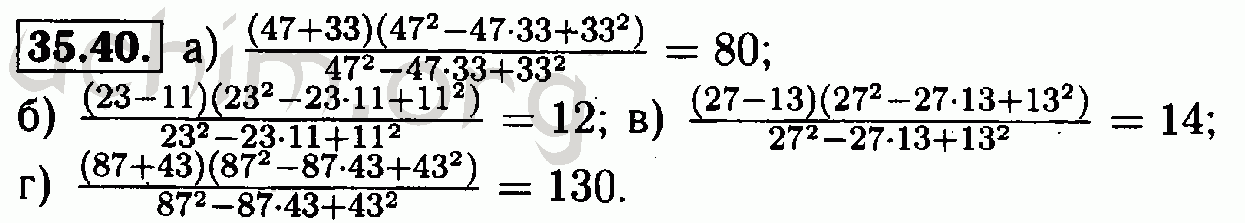 2*у — 4*х*у)*4*х. 92.
2*у — 4*х*у)*4*х. 92.
Задача :
- Обеспечить усвоение начальных знаний по теме «Умножение одночлена на многочлен»;
- Развивать аналитическое и синтезирующее мышление;
- Воспитывать мотивы к обучению и положительное отношение к знаниям.
Тимбилдинг класса.
Задания :
- Ознакомиться с алгоритмом умножения одночлена на многочлен;
- Отработать алгоритм практического использования.
Оборудование : карточки с заданиями, компьютер, интерактивный проектор.
Тип урока : комбинированный.
Во время занятий I. Организационный момент:Здравствуйте ребята, садитесь.
Сегодня мы продолжаем изучение раздела «Многочлены» и темы нашего урока «Умножение одночлена на многочлен». Откройте тетради и запишите номер и тему урока «Умножение одночлена на многочлен».
Задача нашего урока — вывести правило умножения одночлена на многочлен и научиться применять его на практике. Полученные сегодня знания необходимы вам на протяжении всего изучения всего курса алгебры.
Полученные сегодня знания необходимы вам на протяжении всего изучения всего курса алгебры.
У вас на столах лежат бланки, в которые мы будем вносить ваши баллы, набранные в течение урока, и в результате будет выставлена оценка. Точки будем изображать в виде смайликов. ( Приложение 1 )
II. Этап подготовки учащихся к активному и осознанному усвоению нового материала.При изучении новой темы нам понадобятся знания, полученные на предыдущих уроках.
Учащиеся выполняют задания на карточках по теме «Степень и ее свойства». (5-7 минут)
Фронтальная работа:
1) Дано два монома: 12п 3 и 4п 3
а) сумма;
б) разница;
в) произведение;
д) частный;
f) квадрат каждого одночлена.
2) Назовите члены многочлена и определите степень многочлена:
а) 5 аб – 7 а 2 + 2 б – 2,6
б) 6 ху 5 + х 2 у — 2
3) Сегодня нам понадобится распределительное свойство умножения.
Сформулируем это свойство и обозначение в буквальном виде.
III. Этап усвоения новых знаний.Мы повторили правило умножения одночлена на одночлен, распределительное свойство умножения. Теперь усложним задачу.
Разделитесь на 4 группы. В каждой группе на карточках по 4 выражения. Попробуйте восстановить недостающее звено в цепочке и объяснить свою точку зрения.
- 8x 3 (6x 2 — 4x + 3) = …………………. …… = 48x 5 — 32x 4 + 24x 3
- 5а 2 (2а 2 + 3а — 7) = ……………………….. = 10а 4 + 15а 3 — 35а 2
- 3 года (9 лет 3 — 4 года 2 — 6) = ………………………. = 27г 4 — 12г 3 — 18г
- 6б 4 (6б 2 + 4б — 5) = …………. …………… = 36б 6 + 24б 5 — 30б 4
(К экрану подходит один представитель от каждой группы, записывает недостающую часть выражения и поясняет свою точку зрения.)
Попробуйте сформулировать правило (алгоритм) умножения многочлена на одночлен.
Какое выражение получается в результате выполнения этих действий?
Чтобы проверить себя, откройте обучающую страницу 126 и прочитайте правило (вслух читает 1 человек).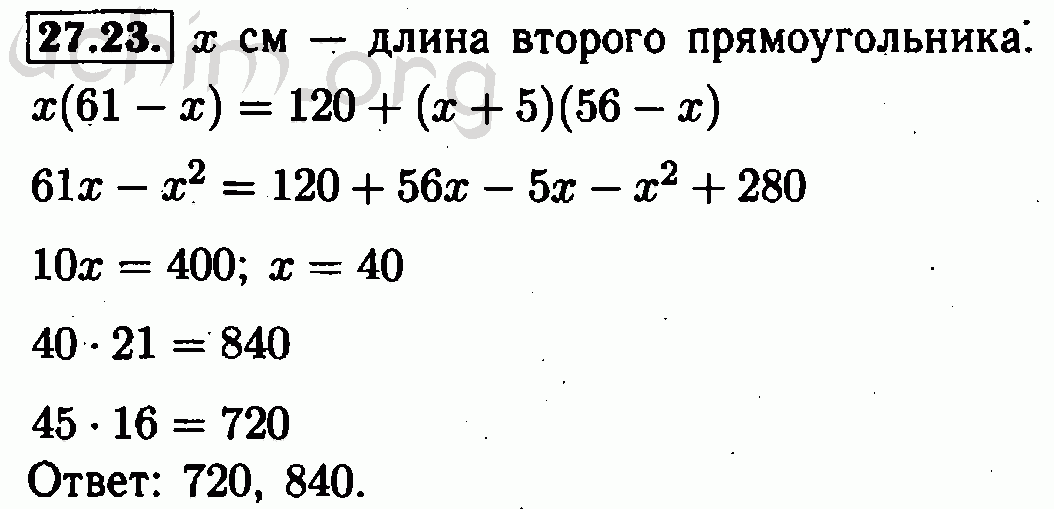
Совпадают ли наши выводы с правилом в учебнике? Запишите в тетрадь правило умножения одночлена на многочлен.
IV. Анкеровка:1. Физкультура:
Ребята, сядьте поудобнее, закройте глаза, расслабьтесь, сейчас мы отдыхаем, мышцы расслаблены, изучаем тему «Умножение одночлена на многочлен».
И так запоминаем правило и повторяем за мной: чтобы умножить одночлен на многочлен, нужно умножить одночлен на каждый член многочлена и записать сумму полученных выражений. Мы открываем глаза.
2. Работа по учебнику № 614 у доски и в тетрадях;
а) 2х (х 2 — 7х — 3) = 2х 3 — 14х 2 — 6х
б) -4в 2 (5в 2 — 3в — 2) = -20в 4 + 12в 3 + 8в 2
в) (3а 3 — а 2 + а) (- 5а 3) = -15а 6 + 5а 5 — 5а 4
г) (у 2 — 2,4у + 6) 1,5у = 1,5у 3 — 3,6у 2 + 9у
д) -0,5 x 2 (-2x 2 — 3x + 4) = x 4 + 1,5x 3 — 2x 2
f) (-3y 2 + 0,6y) (- 1,5y 3) = 4,5y 5 — 0,9y 4
(При выполнении номера анализируются наиболее типичные ошибки)
3.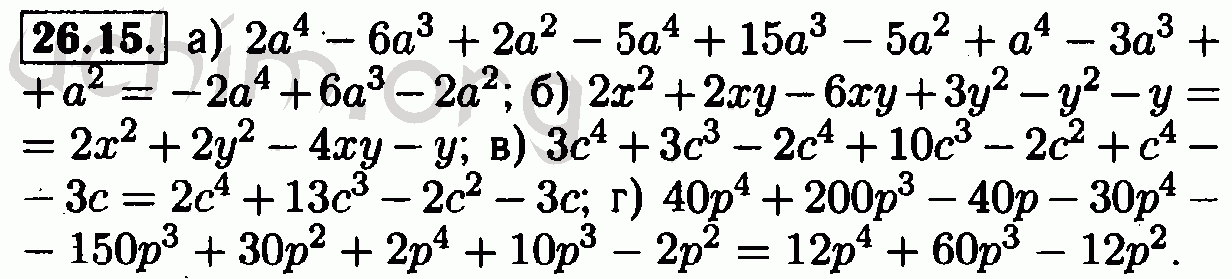 Конкурс по вариантам (расшифровка пиктограммы). (Приложение 2)
Конкурс по вариантам (расшифровка пиктограммы). (Приложение 2)
| Опция 1: | Опция 2: | |
| 1) -3x 2 (- x 3 + x — 5) 2) 14 х (3 ху 2 – х 2 у + 5) 3) -0,2 м 2 н (10 мин 2 – 11 м 3 – 6) 4) (3a 3 — a 2 + 0,1a) (- 5a 2) 5) 1/2 с (6 с 3 d — 10c 2 d 2) 6) 1,4p 3 (3q — pq + 5p) 7) 10x 2 y (5,4xy — 9017 906 9062) — 0,4 3 а б (а 2 — 2аб + б 2) | 1) 3а 4 х (а 2 — 2ах + х 3 — 1) 2) -11а (2а 2 б — а 3 + 5б 2) 3) -0,5 NS 2 Y ( NS Y 3 — 3 NS + Y 2) 4) (6B 4 -B 2 + 0,01) (7B 3) (7B 2) (7B 2) (7B 2) (7B 2) (7B 2) (7B 2) 4. 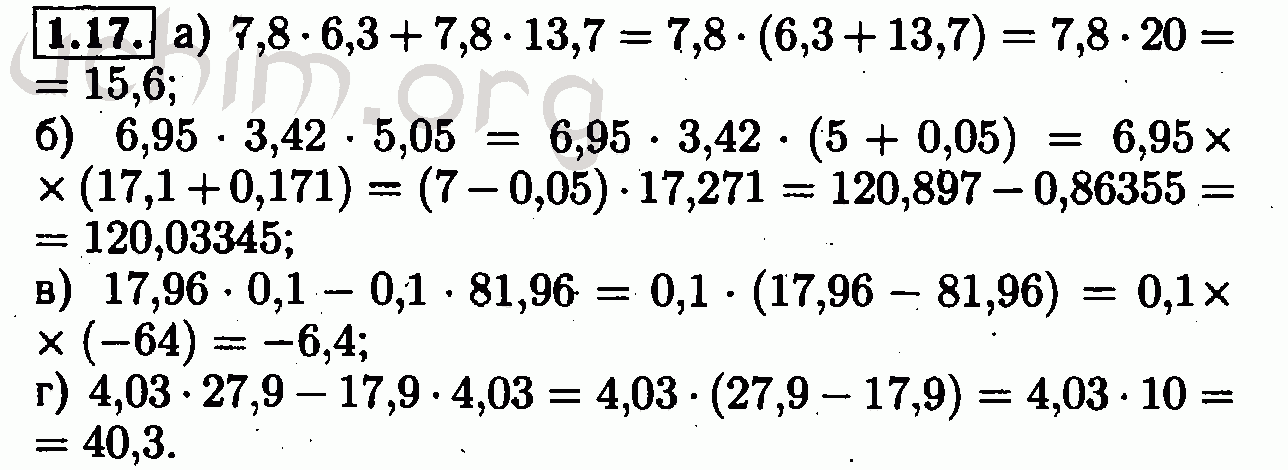 9. 4). 1/3м 2 (9м 3 н 2 — 15мн) 9. 4). 1/3м 2 (9м 3 н 2 — 15мн) 6) 1,6с 4 (2с 2 д — кд + 5д) 7) 10п 4 (0,7пк — 6,1к — 3,6) 7 90) 5xy (x 2 — 3xy + x 3) |
Задания представлены на отдельных карточках и на экране. Каждый ученик выполняет свое задание, находит букву и записывает ее на экране напротив выражения, которое он преобразовал. Если вы получите правильный ответ, вы получите слово: молодец! умники 7а
Частным случаем умножения многочлена на многочлен является умножение многочлена на одночлен. В этой статье мы сформулируем правило выполнения этого действия и разберем теорию на практических примерах.
Правило умножения многочлена на одночлен
Разберемся, что лежит в основе умножения многочлена на одночлен. Это действие основано на распределительном свойстве умножения по отношению к сложению. Буквально это свойство записывается так: (a + b) c = a c + b c (a, b и c — некоторые цифры). В этой записи выражение (a+b)c есть в точности произведение полинома (a+b) и монома c.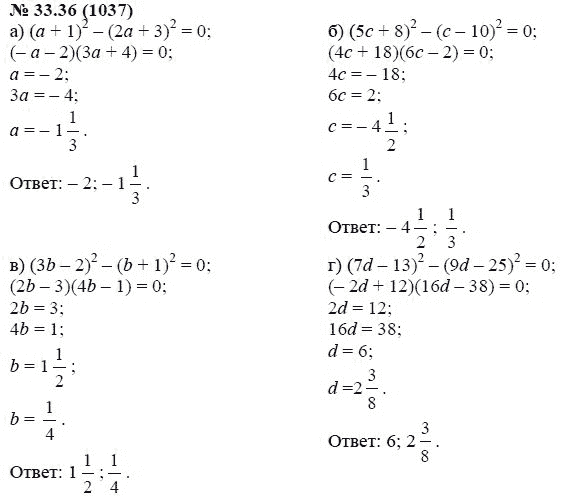 .. Правая часть равенства ac+bc есть сумма произведения одночленов и b на одночлен c .
.. Правая часть равенства ac+bc есть сумма произведения одночленов и b на одночлен c .
Приведенные выше рассуждения позволяют сформулировать правило умножения многочлена на одночлен:
Определение 1
Для выполнения действия умножения многочлена на одночлен необходимо:
- напишите произведение многочлена на одночлен, который надо перемножить;
- умножить каждый член полинома на заданный моном;
- найти сумму полученных произведений.
Поясним дополнительно приведенный выше алгоритм.
Чтобы составить произведение полинома на моном, исходный полином заключают в круглые скобки; далее между ним и данным мономом ставится знак умножения. В случае, когда написание монома начинается со знака минус, его также необходимо заключать в круглые скобки. Например, произведение многочлена — 4 х 2 + х — 2 и одночлен 7 у запишем как (- 4 х 2 + х — 2) 7 у , а произведение многочлена а 5 б — 6 а Ь и одночлен — 3 а 2 составить в виде: (а 5 б — 6 а б) (- 3 а 2) .
Следующим шагом алгоритма является умножение каждого члена полинома на заданный моном. Компоненты многочлена являются мономами, т.е. фактически нам нужно выполнить умножение одночлена на одночлен. Предположим, что после первого шага алгоритма мы получили выражение (2 х 2 + х + 3) 5 х, затем на втором шаге мы умножаем каждый член многочлена 2 х 2 + х + 3 на одночлен 5 х , таким образом, получаем: 2 х 2 5 х = 10 х 3, х 5 х = 5 х 2 и 3 5 х = 15 х … Результатом будут мономы 10 х 3, 5 х 2 и 15 х .
Последним действием по правилу является добавление полученных работ. Из предложенного примера после выполнения этого шага алгоритма получаем: 10 х 3 + 5 х 2 + 15 х .
По умолчанию все шаги записываются в виде цепочки равенств. Например, находя произведение многочлена 2 х 2 + х + 3 и одночлена 5 х запишем так: (2 х 2 + х + 3) 5 х = 2 х 2 5 х + х 5 х + 3 5 х = 10 х 3 + 5 х 2 + 15 х. Исключая промежуточные вычисления второго шага, короткое решение можно расположить следующим образом: (2 х 2 + х + 3) 5 х = 10 х 3 + 5 х 2 + 15 х.
Рассмотренные примеры позволяют заметить важный нюанс: в результате умножения многочлена на одночлен получается многочлен. Это утверждение верно для любого перемноженного многочлена и монома.
По аналогии производится умножение одночлена на многочлен: данный одночлен умножается на каждый член многочлена и полученные произведения суммируются.
Примеры умножения многочлена на одночлен
Пример 1
Необходимо найти произведение: 1, 4 · х 2 — 3, 5 · у · — 2 7 · х.
Решение
Первый шаг правила уже выполнен — произведение записано. Теперь выполняем следующий шаг, умножая каждый член полинома на заданный моном. В этом случае удобно сначала переводить десятичные дроби из обыкновенных. Тогда получаем:
1, 4 х 2 — 3,5 у — 2 7 х = 1, 4 х 2 — 2 7 х — 3,5 у — 2 7 х = = — 1, 4 2 7 х 2 х + 3, 5 2 7 х у = — 7 5 2 7 х 3 + 7 5 2 7 х у = — 2 5 х 3 + х у
Ответ: 1, 4 х 2 — 3,5 у — 2 7 х = — 2 5 х 3 + х у.
Уточним, что когда исходный многочлен и/или моном заданы в нестандартной форме, перед нахождением их произведения желательно привести их к стандартной форме.
Пример 2
Многочлен 3 + а — 2 а 2 + 3 а — 2 и мономиал — 0,5 а б (- 2) а … Надо найти их работу.
Решение
Видим, что исходные данные представлены в нестандартном виде, поэтому для удобства дальнейших расчетов приведем их к стандартному виду:
— 0,5 a b (- 2) a = (- 0,5 ) (- 2) (а а) b = 1 а 2 b = а 2 b 3 + а — 2 а 2 + 3 а — 2 = (3 — 2) + (а + 3 а) — 2 а 2 = 1 + 4 а — 2 а 2
Теперь выполним умножение одночлена a 2 b для каждого члена многочлена 1 + 4 a — 2 a 2
a 2 b (1 + 4 a — 2 a 2) = a 2 b 1 + a 2 b 4 a + a 2 b (- 2 a 2) = = a 2 B + 4 a 3 b — 2 a 4 b
Мы не могли привести исходные данные к стандартному виду: решение было бы более громоздким. В этом случае на последнем этапе возникнет необходимость привлечения таких членов. Для понимания приведем решение по такой схеме:
Для понимания приведем решение по такой схеме:
— 0,5 а б (- 2) а (3 + а — 2 а 2 + 3 а — 2) = = — 0,5 а б (- 2) а 3 — 0,5 a b (- 2) a a — 0,5 a b (- 2) a (- 2 a 2) — 0,5 a b (- 2) a 3 a — 0,5 a b (- 2) a (- 2) = = 3 a 2 b + a 3 б — 2 а 4 б + 3 а 3 б — 2 а 2 б = а 2 б + 4 а 3 б — 2 а 4 б
Ответ: — 0,5 a b (- 2) a (3 + a — 2 a 2 + 3 a — 2) = a 2 b + 4 a 3 b — 2 a 4 b .
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
§ 1 Умножение многочлена на одночлен
При умножении многочленов мы можем иметь дело с операциями двух видов: умножение многочлен на одночлен и умножение многочлена на многочлен. В этом уроке мы научимся умножать многочлен на одночлен.
Основное правило, которое используется при умножении многочлена на одночлен, это распределительное свойство умножения. Давайте вспомним:
Чтобы умножить сумму на число, вы можете умножить каждое слагаемое на это число и сложить полученные произведения.
Это свойство умножения распространяется и на действие вычитания. В буквальном обозначении свойство распределения умножения выглядит так:
(a + b) ∙ c = ac + bc
(a — b) ∙ c = ac — bc
Рассмотрим пример: многочлен (5ab — 3a2) умножается на одночлен 2b.
Введем новые переменные и обозначим 5ab буквой x, 3a2 буквой y, 2b буквой c. Тогда наш пример примет вид:
(5аb — 3а2) ∙ 2b = (x — y) ∙ с
По закону распределения это равно xc — us. Теперь вернемся к исходному значению новых переменных. Получаем:
5аb∙2b — 3а2∙2b
Теперь приведем полученный полином к стандартному виду. Получаем выражение:
Таким образом, мы можем сформулировать правило:
Чтобы умножить многочлен на одночлен, нужно каждый член многочлена умножить на этот одночлен и сложить полученные произведения.
То же правило применяется при умножении одночлена на многочлен.
§ 2 Примеры по теме занятия
При умножении многочленов на практике, во избежание путаницы с определением полученных знаков, рекомендуется сначала определить и сразу записать знак произведения, и только затем найдите и запишите произведение чисел и переменных. Вот как это выглядит на конкретных примерах.
Вот как это выглядит на конкретных примерах.
Пример 1. (4a2b — 2a) ∙ (-5ab).
Здесь моном — 5аb надо умножить на два монома, из которых состоит полином, 4а2b и — 2а. Первая часть будет со знаком «-», а вторая со знаком «+». Следовательно, решение будет выглядеть так:
(4а2b — 2а) ∙ (-5аb) = — 4а2b ∙ 5аb + 2а ∙ 5аb = -20а3b2 + 10а2b
Пример 2.-xy (2x — 3y +5).
Здесь мы должны выполнить три шага умножения, причем знак первого произведения будет «-«, знак второго «+», знак третьего «-«. Решение выглядит так:
Hu (2x — 3y + 5) = -xy ∙ 2x + xy ∙ 3y — xy ∙ 5 = -2x2y + 3xy2 — 5xy.
Список использованной литературы:
- Мордкович А.Г. Алгебра 7 класс в 2 ч. Ч. 1, Учебник для общеобразовательных учреждений / А.Г. Мордкович. — 10-е изд., перераб. — Москва, «Мнемозина», 2007 г.
- Мордкович А.Г., Алгебра 7 класс в 2-х частях, часть 2, Задача для общеобразовательных учреждений / [А.Г. Мордкович и др.]; под редакцией А.Г.
 Мордковича — 10-е издание, переработанное — Москва, «Мнемозина», 2007 г.
Мордковича — 10-е издание, переработанное — Москва, «Мнемозина», 2007 г. - ЕЕ. Тульчинская, Алгебра 7 класс. Блиц-опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, «Мнемозина», 2008
- Александрова Л.А., Алгебра 7 класс. Тематические тесты в новой форме для учащихся общеобразовательных учреждений под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011
- Александрова Л.А. Алгебра 7 класс. Самостоятельная работа для студентов общеобразовательных учреждений под редакцией Мордковича А.Г. — 6-е издание, шаблонное, Москва, «Мнемозина», 2010
как их использовать? Урок й материал по теме Эффективная подготовка к ОГЭ и олимпиадам
Решения и готовые домашние задания (ГДЗ): как ими пользоваться? Урок й материал по теме Эффективная подготовка к ОГЭ и олимпиадам
Изображения обложек учебников размещаются на страницах данного сайта исключительно в качестве иллюстративного материала (пункт 1 статьи 1274 части четвертой Гражданского кодекса Российской Федерации)
- Алгебра 7 класс.
 ФГОС Мерзляк, Полонский, Якир Вентана-Граф
ФГОС Мерзляк, Полонский, Якир Вентана-Граф - Алгебра 7 класс. продвинутый уровень Макарычев, Миндюк Мнемозина
- Алгебра 7 класс. ФГОС Мордкович, Александрова, Мишустин Мнемозина
- Алгебра 7 класс Алимов Просвещение
- Алгебра 7 класс. ФГОС Дорофеева, Суворова Образование
- Алгебра 7 класс. ФГОС Колягин, Ткачева, Федорова Образование
- Алгебра 7 класс. ФГОС Никольский, Потапов, Решетников Образование
- Алгебра 7 класс. ФГОС Макарычев, Миндюк, Нешков Образование
- Мерзляк, Полонский, Рабинович Вентана-Граф
- Дидактические материалы Алгебра 7 класс Феоктистов Мнемозина
- Дидактические материалы по алгебре 7 класс Зив, Гольдич Петроглиф
- Дидактические материалы по алгебре 7 класс, Карфиева 7 класс
- Дидактические материалы по алгебре 7 класс
- Дидактические материалы по алгебре 7 класс Ткачева, Федорова Образование
- Дидактические материалы по алгебре 7 класс. ФГОС Звавич, Кузнецова Образование
- Дидактические материалы по алгебре 7 класс Попов.
 К учебнику Мордковича Экзамен
К учебнику Мордковича Экзамен - Дидактические материалы по алгебре 7 класс Звавич, Дьяконова Экзамен
- Контрольные работы по алгебре 7 класс Мордкович Мнемозина
- Контрольные работы по алгебре 7 класс. ФГОС Александрова Мнемозина
- Алгебра 7 класс контрольные. ФГОС Кузнецова Просвещение
- Контрольная и СРО по алгебре 7 класс. ФГОС Попов, Мордкович Экзамен
- Контрольные и контрольные работы по алгебре 7 класс. ФГОС Глазков, Гаиашвили Экзамен
- Контрольная работа по алгебре 7 класс. ФГОС Александрова Мнемозина
- Самостоятельная работа по алгебре 7 класс. ФГОС Александрова Мнемозина
- Мартышова Вако
- Контрольно-измерительные материалы (КИМ) по алгебре 7 класс. ФГОС Глазков, Гаиашвили Экзамен 9019
Рабочие тетради
- Мерзляк Полонский Якир Вентана-Граф
- Зубарева Мильштейн Мнемозина
- Минаева Рослова Воспитание
- Алгебра рабочая тетрадь 7 класс.0193
- Рабочая тетрадь по алгебре 7 класс.
 Ч.1, 2. ФГОС Миндюк, Шлыкова Просвещение
Ч.1, 2. ФГОС Миндюк, Шлыкова Просвещение - Рабочая тетрадь по алгебре 7 класс. Часть 1, 2. ФГОС Колягин, Ткачева Образование
- Рабочая тетрадь по алгебре 7 класс. ФГОС Журавлева, Перепелкина. К учебнику Никольского Экзамен
- Рабочая тетрадь по алгебре 7 класс. ФГОС Ключников, Комиссаров. К учебнику Мордкович Экзамен
- Рабочая тетрадь по алгебре 7 класс. Часть 1, 2. ФГОС Ерина. К учебнику Макарычева Экзамен
Тесты
- Mordkovich, Tulchinskaya Mnemosyne
- Kuznetsova Enlightenment
- Thematic tests in algebra Grade 7. GEF Dudnitsyn, Krongauz Education
- Thematic tests in algebra Grade 7. GEF Tkachev Enlightenment
- Thematic tests in algebra Grade 7. GEF Chulkov Enlightenment
- Algebra тесты 7 класс. ФГОС Ключников, Комиссаров. К учебнику Мордковича Экзамен
ГДЗ по алгебре 7 класс. ФГОС
- Как быстро и правильно выполнить домашнее задание по алгебре ученику 7 класса без помощи родителей и репетитора? Как сделать так, чтобы уроки были усвоены и осталось время для отдыха на природе? А если очень хочется поиграть на компе, но надо до ночи разбираться с алгеброй? Как раз по всем этим вопросам поможет методическое пособие ГДЗ по алгебре 7 за класс.
 Заботливые авторы-математики уже решили все домашние задания по алгебре за весь год! Неприятные неравенства и уравнения, сложные задачи и примеры. Теперь вам не нужно ломать голову над тем, правильно ли вам удалось решить задачу, вы можете просто проверить ее с помощью книги решений!
Заботливые авторы-математики уже решили все домашние задания по алгебре за весь год! Неприятные неравенства и уравнения, сложные задачи и примеры. Теперь вам не нужно ломать голову над тем, правильно ли вам удалось решить задачу, вы можете просто проверить ее с помощью книги решений! - Всем известно, что даже отличникам иногда не хочется долго сидеть за домашним заданием. Первая любовь, интересные премьеры в кинотеатрах или новые игры на консолях, которые только и ждут, чтобы их приняли — все это зовет и отвлекает семиклассников от уроков. Правильно, ведь во время учебы реальной жизни не увидишь!
- Что делает в этом случае средний студент? Ничего такого. Ходьба. А перед уроками в спешке списывает «домашнюю работу» у одноклассников из тетради с ошибками и без понимания. Родителям достаточно купить и подарить к своему ГДЗ по алгебре 7 класс, все проблемы с решением домашних заданий решатся сами собой.
 Время, отведенное на уроки, сократится в 3 раза, а в тетради за домашнее задание будет гарантирована высокая оценка. Кроме того, в книге решений есть подробное объяснение решения задач и уравнений, необходимые формулы и правила. Таким образом, даже при механическом копировании работы учащийся волей-неволей запоминает правила выполнения заданий и систематизирует эти знания в своей голове.
Время, отведенное на уроки, сократится в 3 раза, а в тетради за домашнее задание будет гарантирована высокая оценка. Кроме того, в книге решений есть подробное объяснение решения задач и уравнений, необходимые формулы и правила. Таким образом, даже при механическом копировании работы учащийся волей-неволей запоминает правила выполнения заданий и систематизирует эти знания в своей голове. - Особо строгие родители могут купить раствор не для ребенка, а для себя. Прошло много времени с тех пор, как вы закончили школу, некоторые знания могут исчезнуть или быть забытыми. Стыдно попасть впросак перед ребенком, показывая свое невежество в каком-то математическом вопросе. Решатель по математике всегда поможет быстро и наглядно проверить задачу, поможет ученику в понимании и решении особо сложных упражнений и освежит его знания.
- В 7 классе традиционная математика в рамках школьного курса делится на два предмета – геометрию и алгебру.
 Семиклассники считают последний более понятным для изучения. Тем не менее обилие новой терминологии, законов и практик требует внимательного, скрупулезного и вдумчивого отношения к дисциплине. Зачастую одного школьного урока для полного усвоения материала недостаточно. В этом случае пригодятся специальные обучающие материалы и решения для них. Но важно помнить, что работая с ГДЗ тогда дает значимые результаты, когда:
Семиклассники считают последний более понятным для изучения. Тем не менее обилие новой терминологии, законов и практик требует внимательного, скрупулезного и вдумчивого отношения к дисциплине. Зачастую одного школьного урока для полного усвоения материала недостаточно. В этом случае пригодятся специальные обучающие материалы и решения для них. Но важно помнить, что работая с ГДЗ тогда дает значимые результаты, когда:
— регулярно;
— на основании специально разработанной схемы, учебного плана;
— с запоминанием и проработкой рассмотренного материала, возвратом к тем темам, заданиям, которые вызвали наибольшие затруднения. - Такая работа полезна еще и тем, что позволяет изучить и запомнить порядок правильной грамотной записи полученных результатов. Это важно для школьников, так как в диагностической работе умение представлять и записывать ответы в соответствии с требованиями стандарта дает учащимся дополнительные баллы. Плюс — все семиклассники — будущие выпускники, а грамотная запись — основа высокого балла на ОГЭ/ЕГЭ.
 В выпускных тестах много алгебраических заданий как для девятиклассников, так и для одиннадцатиклассников, которые в обязательном порядке сдают математику.
В выпускных тестах много алгебраических заданий как для девятиклассников, так и для одиннадцатиклассников, которые в обязательном порядке сдают математику. - Прежде чем выбрать лучший учебник по алгебре для 7 класса, следует оценить:
— начальный уровень собственных знаний;
— УМК, программа, по которой изучается дисциплина в школе. Если школьные знания преподаются качественно, есть смысл подобрать дополнительный учебник по программе, отличной от школьной. Если нет, выберите книгу, которую изучают в классе;
— четкость изложения материала, заданий, ответов на них. - Семиклассники могут разобрать все вышеперечисленные пункты в школе, с учителем-предметником, с репетитором или самостоятельно. Специалисты называют самоподготовку одной из самых эффективных форм работы для средней и старшей школы. Но чтобы оно принесло желаемый результат, нужна настойчивость, регулярность и самоконтроль, объективная оценка собственного прогресса. Вы можете совмещать самоподготовку с посещением специальных курсов.

Лучше вдумчиво списать из формуляра, чем наспех из тетради с ошибками
Родителям с решателями по алгебре легко проверить уроки семиклассника
Изображения обложек учебников размещаются на страницах данного сайта исключительно в качестве иллюстративного материала (пункт 1 статьи 1274 части четвертой Гражданского кодекса Российской Федерации)
- Алгебра 8 класс. ФГОС Мерзляк, Полонский, Якир Вентана-Граф
- Алгебра 8 класс. продвинутый уровень Макарычев, Миндюк Мнемозина
- Алгебра 8 класс. ФГОС Мордкович, Александрова, Мишустин Мнемозина
- Алгебра 8 класс Алимов Просвещение
- Алгебра 8 класс. ФГОС Дорофеева, Суворова Образование
- Алгебра 8 класс. ФГОС Макарычев, Миндюк, Нешков Образование
- Алгебра 8 класс. ФГОС Никольский, Потапов Образование
- Алгебра 8 класс. ФГОС Колягин, Ткачева, Федорова Образование
- Сборник задач по алгебре 8 класс Галицкий, Гольдман Образование
- Мерзляк, Полонский, Рабинович Вентана-Граф
- Дидактические материалы по алгебре 8 класс Феоктистов Мнемозина
- Дидактические материалы по алгебре, 8 класс Зив Гольдич Петроглиф
- Дидактические материалы по алгебре 8 класс Потапов, Шевкин Просвещение
- Дидактические материалы по алгебре 8 класс Евстафьева Карп Образование
- Дидактические материалы по алгебре 8 класс Жохов, Макарычев, Миндюк Образование
- Дидактические материалы по алгебре 8 класс.
 ФГОС Ткачева, Федорова Образование
ФГОС Ткачева, Федорова Образование - Дидактические материалы по алгебре 8 класс Попов. К учебнику Мордковича Экзамен
- Дидактические материалы по алгебре 8 класс Звавич, Дьяконова Экзамен
- Мордкович Мнемозина
- Контрольные работы по алгебре 8 класс. ФГОС Александрова Мнемозина
- Контрольные работы по алгебре 8 класс Кузнецова 9, Минаева Образование Образование0193
- Контрольная и контрольная работа по алгебре 8 класс. ФГОС Попов, Мордкович Экзамен
- Контрольная работа по алгебре 8 класс Дудницын, Кронгауз Экзамен
- Самостоятельная и контрольная работа по алгебре 8 класс Глазков, Гаиашвили Экзамен
- Самостоятельная работа по алгебре 8 класс. ФГОС Александрова Мнемозина
- Черноруцкий Вацо
- Контрольно-измерительные материалы (КИМ) по алгебре 8 класс. ФГОС Глазков, Гаиашвили Экзамен
Рабочие тетради
- Рабочая тетрадь по алгебре 8 класс. Часть 1, 2 Мерзляк, Полонский Вентана-Граф
- Зубарева, Мильштейн Мнемозина
- Алгебра рабочая тетрадь 8 класс.
 Часть 1, 2. ФГОС Миндюк, Шлыкова Просветление
Часть 1, 2. ФГОС Миндюк, Шлыкова Просветление - Алгебра рабочая тетрадь 8 класс. Часть 1, 2. ФГОС Минаева, Рослова Образование
- Алгебра рабочая тетрадь 1, 8 класс. 2. ФГОС Колягина Ткачева Образование
- Эрина. К учебнику Макарычева Экзамен
- Рабочая тетрадь по алгебре 8 класс. ФГОС Журавлева, Перепелкина. К учебнику Никольского Экзамен
- Рабочая тетрадь по алгебре 8 класс. Ч.1, 2. ФГОС Ключников, Комиссаров. К учебнику Мордкович Экзамен
Tests
- Mordkovich, Tulchinskaya Mnemosyne
- Tkachev Enlightenment
- Thematic tests in algebra Grade 8. GEF Dudnitsyn, Krongauz Education
- Thematic tests in algebra Grade 8. GEF Kuznetsova Enlightenment
- Thematic tests in algebra Grade 8. GEF Чулков, Струков Просвещение
- Контрольные по алгебре 8 класс. ФГОС Журавлев, Ермаков. К учебнику Никольского Экзамен
- Тесты по алгебре 8 класс. ФГОС Ключников, Комиссаров.
 К учебнику Мордковича Экзамен
К учебнику Мордковича Экзамен - Тесты по алгебре 8 класс. ФГОС Глазков. К учебнику Макарычева Экзамен
ГДЗ по алгебре 8 класс. ФГОС
Стремительное развитие общества привело к значительному усложнению школьных программ и общеобразовательных реформ. Информационная нагрузка на современного школьника постоянно растет, и сегодня, чтобы усвоить весь необходимый материал, ребенку приходится проводить за партой 8 часов: целый рабочий день, и это без учета времени, затраченного на подготовка домашнего задания. Такая нагрузка приводит к усталости, снижению работоспособности, потере мотивации. Помочь справиться с возрастающим объемом информации, научиться анализировать и логически мыслить, повысить успеваемость поможет ГДЗ — готовые домашние задания.
ГДЗ, или «решебники» — учебные пособия, которые активно используются в качестве учебных пособий, дополняющих образовательную программу по таким предметам, как русский язык, математика (алгебра), химия, физика и ряду других. В настоящее время создано множество ресурсов в помощь школьникам и их родителям: Ставкур, Спиши.Ру, ГДЗ от Путина и другие, но как с их помощью получить настоящие знания?
В настоящее время создано множество ресурсов в помощь школьникам и их родителям: Ставкур, Спиши.Ру, ГДЗ от Путина и другие, но как с их помощью получить настоящие знания?
Решаки для родителей
Методические пособия, называемые ГДЗ, разрабатываются опытными педагогами, прежде всего, в помощь родителям. На протяжении всей школьной жизни многие взрослые стремятся контролировать учебный процесс, чтобы быть в курсе успехов и неудач ребенка, помогать ему в освоении новых знаний. Однако, это не всегда возможно.
Во-первых, потому что современная образовательная программа претерпела значительные изменения — это легко заметить, посетив такой сайт, как Мегаботан, ГДЗ Путина. Во-вторых, не каждый родитель сможет запомнить теоретические знания, заложенные в школе, а значит, проконтролировать правильность выполнения ребенком домашнего задания. В-третьих, у взрослых может просто не хватить времени на то, чтобы самостоятельно с ребенком разобраться с домашними заданиями (особенно в многодетных семьях). Но это не значит, что нужно пускать учебный процесс «на самотек»: иногда помощь родителей просто необходима, чтобы ребенок не потерял интерес к предмету, приобрел знания, понял сложный для него материал. И ГДЗ вполне может в этом помочь. С их помощью:
Но это не значит, что нужно пускать учебный процесс «на самотек»: иногда помощь родителей просто необходима, чтобы ребенок не потерял интерес к предмету, приобрел знания, понял сложный для него материал. И ГДЗ вполне может в этом помочь. С их помощью:
- Родители быстро разберутся, как решить сложную задачу и объяснят ее ребенку;
- Взрослые могут контролировать правильность выполнения домашнего задания учащимся;
- Учащийся средней и старшей школы может самостоятельно проверить себя и при обнаружении ошибок проанализировать причину их возникновения, лучше усвоить материал и предотвратить ошибки в будущем.
Таким образом, использование тетрадей с решениями направлено, прежде всего, на помощь школьникам в усвоении сложного материала.
Дополнение к школьной программе
Как известно, школьная программа ориентирована на «среднего ученика», но что делать тем, кто по каким-то причинам отстал от программы (например, из-за продолжительной болезни) или , наоборот, развиваются быстрее, чем подавляющее большинство их одноклассников? В обоих случаях решатели станут универсальным ответом.
С помощью ГДЗ отстающий ученик сможет понять не усвоенный им материал и «догнать» остальных в классе, а для учащихся, чей уровень выше среднего, ГДЗ станет «волшебным палочка», с которой он сможет двигаться дальше в своем развитии, усваивая материал с опережением школьной программы. Более того, часто такие ресурсы, как Мегаботан и Ответ.Ру, используются родителями для того, чтобы дать ребенку знания, выходящие за рамки школьной программы, расширить кругозор ребенка.
В помощь репетитору
ГДЗ также является уникальным инструментом для репетиторов и учителей. Не секрет, что усложнение школьной программы привело к тому, что почти каждый ученик посещает репетиторов для подготовки к выпускным экзаменам и зачетам. Книжки-решения активно используются учителями, чтобы помочь своим ученикам освоить весь школьный курс, а также для проверки знаний школьников и контроля их успеваемости.
Кстати, поскольку такие ресурсы, как «Скриб онлайн» или «Чит. Ру» изучаются и используются учителями, ученики не могут просто списать домашнюю работу из тетради с решениями — учитель это сразу заметит. Поэтому ГДЗ нельзя использовать таким образом.
Ру» изучаются и используются учителями, ученики не могут просто списать домашнюю работу из тетради с решениями — учитель это сразу заметит. Поэтому ГДЗ нельзя использовать таким образом.
Экспертное заключение
Несмотря на вышеизложенное, мнения экспертов относительно готовых домашних заданий разделились. Некоторые считают, что такие льготы приносят больше вреда, чем пользы. Поэтому были проведены многочисленные исследования влияния ресаков на общеобразовательный процесс. И выводы поражают: американские ученые Стивенс и Лайонсон доказали, что при использовании ГДЗ мозг ребенка работает почти в два раза активнее для анализа изучаемой информации, что увеличивает скорость усвоения материала в 1,4 раза и, соответственно, повышает успеваемость школьника. .
Положительное влияние ГДЗ заключается, прежде всего:
- Развитие аналитических способностей ребенка: готовое домашнее задание учит учащегося анализировать собственное домашнее задание и ответы, данные в методическом пособии, искать ошибки, выбирать оптимальные решения из нескольких вариантов.

- Развитие самостоятельности: ГДЗ способствуют развитию навыка обучения и самостоятельного поиска информации.
- Постоянная стимуляция любознательности: если материал слишком сложен или слишком прост, у ребенка быстро пропадает мотивация к обучению – как правило, это причина того, что даже успешный в прошлом ученик вдруг «скатывается» до двоек. Использование ГДЗ позволяет поддерживать интерес ребенка к процессу обучения, предохраняет его от переутомления, облегчает восприятие сложного материала и не дает ему потерять веру в свои силы.
Именно по этим причинам с каждым годом появляется все больше головоломок, самые популярные из которых собраны для удобства учителей, учеников и их родителей на этом ресурсе.
Уважаемый посетитель нашего сайта! Мы рады предложить вашему вниманию более 1000 бесплатных видеоуроков по всем предметам школьной программы. Особый упор делается на основные школьные предметы: математику, английский язык, русский язык, физику, химию, биологию и историю. Все уроки разбиты по классам и предметам. То есть внутри каждого класса можно выбрать определенный предмет и наоборот. Далее в каждой из категорий есть видеоуроки, конспекты уроков и проверочные работы. Также на нашем образовательном канале много задач с решениями. Уроки готовят квалифицированные педагоги, многие из которых являются педагогами высшей категории с большим опытом педагогической деятельности.
Все уроки разбиты по классам и предметам. То есть внутри каждого класса можно выбрать определенный предмет и наоборот. Далее в каждой из категорий есть видеоуроки, конспекты уроков и проверочные работы. Также на нашем образовательном канале много задач с решениями. Уроки готовят квалифицированные педагоги, многие из которых являются педагогами высшей категории с большим опытом педагогической деятельности.
Воспользоваться нашими учебными материалами могут также репетиторы на дистанционных и очных занятиях. Особенно удобно использовать онлайн-уроки совместно с интерактивной доской, доступной для учителей в меню «Виртуальный кабинет». персональный аккаунт. При проведении урока через Интернет репетитор может загрузить урок прямо в учебную оболочку.
Желаем Вам приятного просмотра, побольше знаний и отличных оценок в школе!
Предварительный просмотр:
Бюджетное учреждение профессионального образования
Ханты-Мансийский автономный округ− Югра
Нижневартовский социально-гуманитарный колледж
Факультет начального общего и дополнительного образования
Урок (русский)
Тема: «Буквы Е Ё Ю И и их функции в словах».
Класс: 1 А
Дата проведения занятия: 12.04.2017
Подготовил:
студентка 215.Н группы
ФИО Мельникова Татьяна Алексеевна,
(Ф.И.О.)
(Ф.И.О.)0003
Преподавание в начальных классах
(шифр Наименование специальности)
Руководитель организации:
учитель начальных классов МБОУ СОШ №3 ФИО Ефременко Зульфия Фанилевна,
(Фамилия Имя Отчество) подпись руководителя
2 колледж
ФИО Майдибор Елена Сергеевна
Тема: Буквы Е, Ё, Ю, И и их функции в словах.
Цель: развивать умение учащихся дифференцировать функции букв
Э, Йо, Ю, Я на разных позициях в слове.
Задачи: совершенствовать знания о гласных звуках;
Провести наблюдение за смысловой функцией
Гласные в слове;
Обучить распознаванию гласных среди других звуков в слове;
Развивать речь, мышление, умение выделять главное, обобщать,
Развивать фантазию;
Воспитывать ответственность, добросовестное отношение к
Выполненная работа.
Во время занятий
И.Орг.момент
Проверка готовности к занятию.
Сегодня, как всегда, необходимо ваше внимание. Вы должны показать знания, полученные на предыдущих уроках.
Ребята, урок мы проведем в сказке, которую расскажем вместе. Вместе с нами в сказке окажется волшебный шар. Итак, начнем! С каких слов обычно начинаются сказки? («В каком-то королевстве, в каком-то государстве», «Жили-были»)
В каком-то царстве, в каком-то штате жили Буквы Е, Е, Ю, И. Но их можно было услышать, потому что они были настоящими певцами. У этих писем были тайные друзья, о которых мы узнаем позже.
Итак, в путь сказочными тропами в страну Знаний!
II. Обновление знаний. Каллиграфия.
Перед нами камень-указатель. (Дети читают надписи на камне). Главные герои обычно идут по одному пути, а мы с волшебным шаром пройдем все пути (гласным, тайным друзьям, секреты раскроем). Ведь для нас каждый путь уже исследован, нужно все рассказать волшебному шару.
Итак, выбираем путь налево — к гласным!
Момент очищения:
Ее
ю и
Возьмите карту №1. Положите ее перед собой.
Упражнение на внимание.
В течение 1 минуты вы должны найти слова среди мешанины букв. Выделите их.
MabanandklpryapplePearcloyoCucumber
Назовите слова, которые вы нашли. (Банан, яблоко, груша, огурец.)
Среди этих слов найдите одно лишнее. (Огурец.)
Почему вы решили, что это слово лишнее? (Это овощ, остальные фрукты.)
Убрать карты. Продолжаем работать дальше с буквами.
Сколько букв в алфавите? (33)
Сколько звуков? (31)
Почему звуков меньше, чем букв? (б и б — не обозначают звуки)
Напишите в тетради буквы, которые я буду диктовать.
(1 ученик у доски записывает, остальные ученики пишут в тетради, я диктую
Буквы: A E E O O U Y Y I Y
Прочитайте написанные вами буквы.
Что вы можете о них сказать? (Эти буквы обозначают гласные звуки)
Сколько гласных букв в алфавите? (десять)
Сколько мы записали? Кто назовет букву, которую мы не записали? (Е) завершить его.
Об этом письме будет отдельный разговор на следующих уроках.
А сегодня мы поговорим о других письмах.
Я разделил все эти буквы на две группы. Как это.
Но сегодня мы будем работать с первой группой гласных e e yu i.
III. Постановка учебной задачи.
Если говорить об этих буквах сегодня на уроке, то вы должны помнить, что это очень хитрые буквы. И почему? Вот о чем мы поговорим.
IV. Работа по теме урока.
Идем дальше с нашим волшебным колобоком вправо — тайные друзья!
Выполним задание, которое написано в карточке №2
1. Наблюдение
СЕЛ ЭЛЬ ИСТРЕБИТЕЛЬСКАЯ СЕМЬЯ
ПОЛЕТ ЁЛКА ПРИЕМ ОБЪЯВЛЕНИЕ
КЛЮВ ЮЖНЫЙ КАБИНА ШИТЬ
МЯСНАЯ ЯМА ПИТЬЕВАЯ
, Ю, Е букв словпервый столбец? (после согласных, в середине слова)
Какую роль они играют? (смягчить предыдущий согласный).
Сколько и какие звуки они обозначают? (Читаем каждое слово и наблюдаем) СЕЛ (Э), КЛЮВ (У), ПОЛЕТ (О), МЯСО (А)
Какой вывод мы делаем? (Значит, эти буквы обозначают один звук, если стоят после мягких согласных). Отличная работа!
Отличная работа!
Прочитайте слова во втором столбце.
Где буквы Е, Йо, Ю, И в словах второго столбца? (В начале слова.)
Посмотрим, какие звуки они обозначают и сколько их? ЭЛЬ (ЕЛЬ), ЁЛКА (ЁЛКА), ЮГ (ЮГ), ЯМА (ЯМА)
Какой вывод делаем? (Так эти буквы обозначают два звука в начале слова.) Молодец! Запишите эти слова.
Посмотрим на слова третьего столбца. Читай слова.
Где буквы Е, Е, Ю, И? (После гласных.)
Посмотрим, какие звуки они обозначают и сколько их? ИСТРЕБИТЕЛЬ (БОЙЕТС), РЕЦЕПЦИЯ (ПРИЕМНАЯ), КАБИНА (КАЮТ) СТЕНДА (СТЕНДА)
Какой вывод делаем? (Значит, эти буквы обозначают два звука после гласных). Отличная работа! Запишите эти слова.
Посмотрим на слова четвертого столбца. Читай слова.
Где буквы Е, Е, Ю, И? (После ь и ъ)
Посмотрим, какие звуки они обозначают и сколько их? СЕМЬЯ (СЕМЬЯ), ОБЪЯВЛЕНИЕ (ОБЪЯВЛЕНИЕ), ШУ (ШЮ), ПЁТ (ПЁТ).
Какой вывод мы делаем? (Значит, эти буквы обозначают два звука в после б и б). Отличная работа! Запишите эти слова.
Отличная работа! Запишите эти слова.
2. Заключение.
Какой вывод мы можем сделать? При каких условиях буквы Е, Е, Ю, Я обозначают два звука? (Если они стоят в начале слова, после гласной и после b и b.)
Молодец!
V. Физическая минута
Дыхательные упражнения:
О, и что-то случилось в городе Гласных Букв! (Дети вместе с воспитателем продолжают рассказывать сказку). Соловей-разбойник письма свистом пугал. Все спрятались. Давайте вместе сделаем зарядку и прогоним Соловья-разбойника. Дуй сильнее, еще сильнее!
Молодец! Соловья-разбойника прогнали.
VI. Закрепление изученного материала.
Бабушка знает весь мир,
Ей всего триста лет.
Ее дом на курьих ножках,
Стоит на тропинках фей
Молодец! Это Баба Яга.
Баба Яга вас пропустит, если вы расскажете ей все секреты «Хитрых Гласных». Дети разговаривают. (Буквы Е Ё Ю у меня два звука: — в начале слова, после гласной и после знаков ь и ъ)
Молодец! Баба Яга теперь пойдем дальше.
VII. Отражение.
А теперь мы идем прямо по дороге и раскрываем секреты.
Подведем итоги.
Какую роль могут играть буквы Е Y Y Z
Учебник стр.60
Задание 6, 7 (устно).
Задание 8: рассмотри картинки, изображение каких предметов ты видишь?
мак, ежик, ерш, шар, деревце.(ель)
Какое слово пропущено? (Мак)
Почему? (Все согласные твердые, а в остальных словах буквы хитрые)
Запишите слова, в которых выделенная буква обозначает гласный звук и указывает на мягкость предшествующего согласного звука.
Бортовой чек:
Шарик, тетка, пос.
Подписи к слайдам:
Сказочное путешествие на гласные Е Е Ю Я
В некое царство, в некое государство… Е Е Ю Я
на гласные, друзья-тайны тайны откроют
на гласные
E Y Y Y A O U I Y Y E
тайные друзья
Ел, дерево, юг, яма. Истребитель, приемная, кабина, стоя. Семья, реклама, шить, пить.
ФИЗМИНУТКА
Бабушка знает весь мир, Ей всего триста лет. Ее дом на курьих ножках Стоит на сказочных дорожках.
Ее дом на курьих ножках Стоит на сказочных дорожках.
раскроем секреты
Шарик, тетка, пос.
определение, примеры Одинаково равные значения следующих выражений a4
Обе части которых являются тождественно равными выражениями. Идентификаторы делятся на буквенные и числовые.
Тождественные выражения
Два алгебраических выражения называются тождественными (или тождественно равными ), если при любых числовых значениях букв они имеют одинаковое числовое значение. Это, например, выражения:
х (5 + х ) и 5 х + х 2
Оба представленных выражения, при любом значении х будут равны между собой, поэтому их можно назвать тождественными или тождественно равными.
Числовые выражения, равные друг другу, также можно назвать идентичными. Например:
20 — 8 и 10 + 2
Тождества букв и цифр
Тождества букв — это равенство, которое справедливо для любых значений входящих в него букв. Другими словами, такое равенство, при котором обе части являются тождественно равными выражениями, например:
Другими словами, такое равенство, при котором обе части являются тождественно равными выражениями, например:
( а + б ) м = ам + бм
( a + b ) 2 = a 2 + 2 ab + b 2
Числовое тождество , состоящее из одних и тех же частей, состоящее только из цифр, выраженное равенством численная величина. Например:
4 + 5 + 2 = 3 + 8
5 (4 + 6) = 50
Преобразования идентичных выражений
Все алгебраические действия представляют собой преобразование одного алгебраического выражения в другое, идентичное первому.
При вычислении значения выражения, раскрытии скобок, вынесении за скобки общего множителя и в ряде других случаев одни выражения заменяются другими, тождественно равными им. Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием выражения или просто преобразованием выражения . Все преобразования выражений производятся на основе свойств действий над числами.
Рассмотрим тождественное преобразование выражения на примере вынесения общего множителя за скобки:
10 х — 7 х + 3 х = (10 — 7 + 3) х = 6 x
После того, как мы разобрались с понятием тождеств, мы можем перейти к изучению тождественно равных выражений. Цель этой статьи — объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равны другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Вот основное определение, взятое из одного учебника:
Определение 1
Тождественно равными друг другу будут такие выражения, значения которых будут одинаковыми при любых возможных значениях переменных, входящих в их состав .
Также тождественно равными считаются такие числовые выражения, которым будут соответствовать одинаковые значения.
Это достаточно широкое определение, которое будет правильным для всех целочисленных выражений, смысл которых не меняется при изменении значений переменных. Однако позже возникает необходимость уточнить это определение, так как помимо целых чисел существуют и другие типы выражений, которые не будут иметь смысла для тех или иных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определения диапазона допустимых значений. Сформулируем более точное определение.
Однако позже возникает необходимость уточнить это определение, так как помимо целых чисел существуют и другие типы выражений, которые не будут иметь смысла для тех или иных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определения диапазона допустимых значений. Сформулируем более точное определение.
Определение 2
Тождественно равные выражения — это такие выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равны друг другу, если они имеют одинаковые значения.
Фраза «для любых допустимых значений переменных» относится ко всем тем значениям переменных, для которых оба выражения будут иметь смысл. Мы объясним это положение позже, когда приведем примеры тождественно равных выражений.
Можно также указать следующее определение:
Определение 3
Равно равные выражения — это выражения, расположенные в одном и том же идентификаторе слева и справа.
Примеры выражений, тождественно равных друг другу
Используя приведенные выше определения, рассмотрим несколько примеров таких выражений.
Начнем с числовых выражений.
Пример 1
Итак, 2 + 4 и 4 + 2 будут тождественно равны друг другу, так как их результаты будут равны (6 и 6).
Пример 2
Точно так же тождественно равны выражения 3 и 30: 10, (2 2) 3 и 2 6 (чтобы вычислить значение последнего выражения, нужно знать свойства степени).
Пример 3
Но выражения 4 — 2 и 9 — 1 не будут равны, так как их значения различны.
Перейдем к примерам литеральных выражений. A+b и b+a будут тождественно равны, и это не зависит от значений переменных (равенство выражений в данном случае определяется свойством смещения сложения).
Пример 4
Например, если a равно 4, а b равно 5, результаты останутся теми же.
Другой пример тождественно равных выражений с буквами — 0 x y z и 0. Какими бы ни были значения переменных в этом случае, при умножении на 0 они дадут 0. Неравные выражения — 6 x и 8 x, так как они не будет равным ни для какого x.
Неравные выражения — 6 x и 8 x, так как они не будет равным ни для какого x.
В случае совпадения диапазонов допустимых значений переменных, например, в выражениях а + 6 и 6 + а или а b 0 и 0, или х 4 и х, и значений сами выражения будут равны для любых переменных, то такие выражения считаются тождественно равными. Итак, a + 8 = 8 + a для любого значения a, и a b 0 тоже = 0, так как умножение любого числа на 0 дает в конце 0. Выражения x 4 и x будут тождественно равны для любого x из интервала [0, +∞).
Но диапазон достоверности одного выражения может отличаться от диапазона другого.
Пример 5
Например, возьмем два выражения: x — 1 и x — 1 x x. Для первого из них диапазоном допустимых значений х будет все множество действительных чисел, а для второго множество всех действительных чисел, за исключением нуля, потому что тогда мы получим 0 в знаменателе , и такое деление не определено. Эти два выражения имеют общий диапазон значений, образованный пересечением двух отдельных областей. Можно сделать вывод, что оба выражения x — 1 x x и x — 1 будут иметь смысл при любых действительных значениях переменных, кроме 0,9.0003
Можно сделать вывод, что оба выражения x — 1 x x и x — 1 будут иметь смысл при любых действительных значениях переменных, кроме 0,9.0003
Основное свойство дроби также позволяет сделать вывод, что х — 1 х х и х — 1 будут равны для любого х, отличного от 0. Это означает, что в общем диапазоне допустимых значений эти выражения будут тождественно равны между собой, и ни для какого действительного х нельзя говорить об тождественном равенстве.
Если заменить одно выражение другим, тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и мы подробно поговорим о нем в отдельной статье.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Говорят, что два выражения тождественно равны на множестве, если они имеют смысл на этом множестве и все их соответствующие значения равны.
Равенство, в котором левая и правая части являются тождественно равными выражениями, называется тождеством.
Замена одного выражения другим, тождественно равным ему на данном множестве, называется идентичное преобразование выражения.
Задача. Найти область выражения.
Раствор. Так как выражение является дробью, то для нахождения его области определения необходимо найти те значения переменной НС , при которых знаменатель обращается в нуль, и исключить их. Решая уравнение НС 2 — 9 = 0, находим, что НС = -3 и НС = 3. Следовательно, область определения этого выражения состоит из всех чисел, кроме -3 и 3. Если обозначить его к NS , то можно написать:
NS = (- ¥; -3) È (-3; 3) È (3; + ¥).
Задача. Выражения и NS — 2 тождественно равны: а) на множестве R ; б) на множестве ненулевых целых чисел?
Раствор. а) На множестве R эти выражения не тождественно равны, так как для NS = 0 выражение неактуально, а выражение NS — 2 имеет значение -2.
б) На множестве ненулевых целых чисел эти выражения тождественно равны, так как = .
Задача. При каких значениях НС следующие равенства являются тождествами:
а) ; б).
Раствор. а) Равенство есть тождество, если;
б) Равенство есть тождество, если.
Получив представление об идентичностях, логично перейти к знакомству с . В этой статье мы ответим на вопрос, что такое тождественно равные выражения, а также на примерах разберемся, какие выражения тождественно равны, а какие нет.
Навигация по страницам.
Что такое тождественно равные выражения?
Определение тождественно равных выражений дается параллельно с определением тождества. Это происходит на уроках алгебры в 7 классе. В учебнике по алгебре для 7 классов автора Ю.Н. Макарычева дана следующая формулировка:
Определение.
Являются выражениями, значения которых равны при любых значениях входящих в них переменных. Числовые выражения, имеющие одинаковые значения, также называются тождественно равными.
Это определение используется до 8 класса, оно справедливо для целочисленных выражений, так как они имеют смысл при любых значениях входящих в них переменных. А в 8 классе уточняется определение тождественно равных выражений. Поясним, с чем это связано.
В 8 классе начинается изучение других видов выражений, которые, в отличие от целочисленных выражений, при некоторых значениях переменных могут не иметь смысла. Это заставляет ввести определения допустимых и недопустимых значений переменных, а также диапазона допустимых значений ОДЗ переменной и, как следствие, уточнить определение тождественно равных выражений.
Определение.
Два выражения, значения которых равны при всех допустимых значениях входящих в них переменных, называются тождественно равными выражениями . Два числовых выражения, имеющих одинаковое значение, также называются тождественно равными.
В этом определении тождественно равных выражений стоит уточнить смысл фразы «для всех допустимых значений входящих в них переменных». Под ним подразумеваются все такие значения переменных, для которых оба тождественно равных выражения имеют смысл одновременно. Мы проясним эту идею в следующем параграфе, рассматривая примеры.
Под ним подразумеваются все такие значения переменных, для которых оба тождественно равных выражения имеют смысл одновременно. Мы проясним эту идею в следующем параграфе, рассматривая примеры.
Определение тождественно равных выражений в учебнике А.Г. Мордковича дано несколько иначе:
Определение.
Тождественно равные выражения Выражения слева и справа от тождества.
Значение этого и предыдущего определений совпадают.
Примеры тождественно равных выражений
Определения, введенные в предыдущем абзаце, позволяют нам привести примеров тождественно равных выражений .
Начнем с тождественно равных числовых выражений. Числовые выражения 1 + 2 и 2 + 1 тождественно равны, так как им соответствуют равные значения 3 и 3. Также тождественно равны выражения 5 и 30:6, как и выражения (2 2) 3 и 2 6 (т.е. значения последних выражений равны по силе). Но числовые выражения 3+2 и 3−2 тождественно не равны, так как им соответствуют значения 5 и 1 соответственно, и они не равны.
Теперь приведем примеры тождественно равных выражений с переменными. Это выражения a + b и b + a. Действительно, при любых значениях переменных a и b написанные выражения принимают одинаковые значения (что следует из цифр). Например, для a = 1 и b = 2 имеем a + b = 1 + 2 = 3 и b + a = 2 + 1 = 3. При любых других значениях переменных a и b также получаем равные значения этих выражений. Выражения 0 x y z и 0 также тождественно равны при любых значениях переменных x, y и z. Но выражения 2 х и 3 х не тождественно равны, так как, например, при х = 1 их значения не равны. Действительно, при x = 1 выражение 2 x равно 2 1 = 2, а выражение 3 x равно 3 1 = 3,
Когда диапазоны допустимых значений переменных в выражениях совпадают, как, например, в выражениях а + 1 и 1 + а, или а б 0 и 0, или и, и значения этих выражений равны для всех значений переменных из этих областей, то тут все ясно — эти выражения тождественно равны для всех допустимых значений переменных, входящих в них. Итак, а + 1≡1 + а для любого а, выражения а · b · 0 и 0 тождественно равны при любых значениях переменных а и b, а выражения и тождественно равны при всех х из; изд. С. А. Теляковский. — 17-е изд. – М.: Просвещение, 2008. – 240 с. : больной. — ИСБН 978-5-09-019315-3.
С. А. Теляковский. — 17-е изд. – М.: Просвещение, 2008. – 240 с. : больной. — ИСБН 978-5-09-019315-3.
Рассмотрим два равенства:
1.a 12 * a 3 = a 7 * a 8
Это равенство будет выполняться при любых значениях переменной a. Диапазоном допустимых значений для этого равенства будет весь набор действительных чисел.
2.а 12: а 3 = а 2 * а 7.
Это неравенство будет выполняться для всех значений переменной а, кроме а равного нулю. Диапазоном допустимых значений этого неравенства будет весь набор действительных чисел, кроме нуля.
Каждое из этих равенств можно считать верным для любых допустимых значений переменных a. Такие равенства в математике называются тождествами .
Понятие тождества
Тождество — это равенство, истинное для любых допустимых значений переменных. Если в это равенство вместо переменных подставить какие-либо допустимые значения, то должно получиться правильное числовое равенство.
Стоит отметить, что истинные числовые равенства также являются тождествами. Тождества, например, будут свойствами действий над числами. 92*б) и -а 3*б 2;
3. ((x 3 * x 8) / x) и x 10.
Мы всегда можем заменить одно выражение любым другим выражением, тождественно равным первому. Такая замена будет тождественной трансформацией.
Примеры тождеств
Пример 1: равны ли следующие равенства:
1.а + 5 = 5 + а;
2.а * (- б) = -а * б;
3,3 * а * 3 * Ь = 9 * а * Ь;
Не все приведенные выше выражения будут тождествами. Из этих равенств только 1, 2 и 3 равенства являются тождествами.


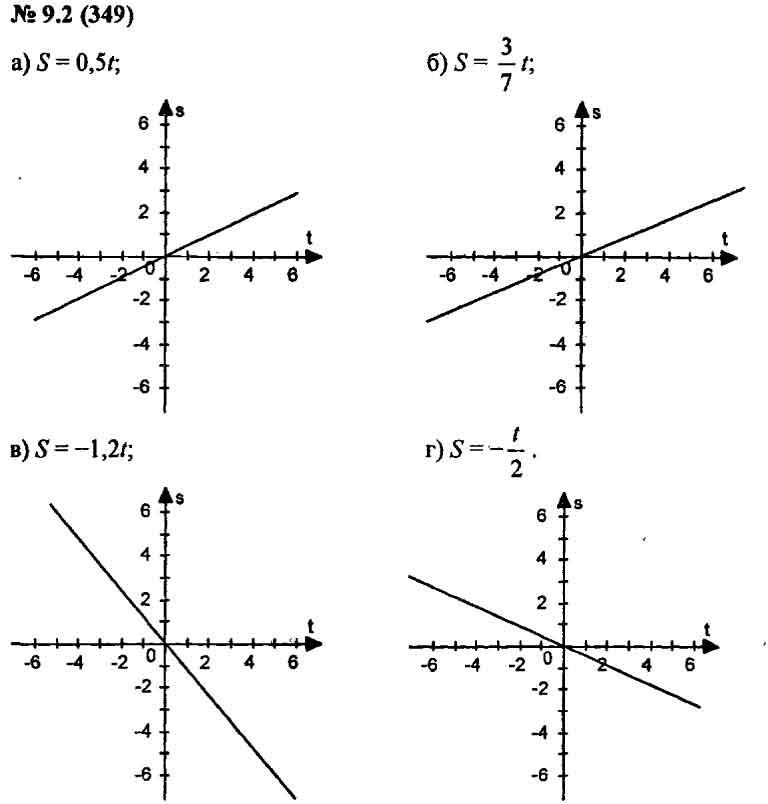
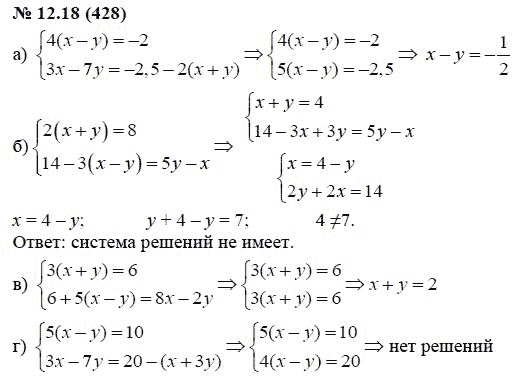 62 МБ
62 МБ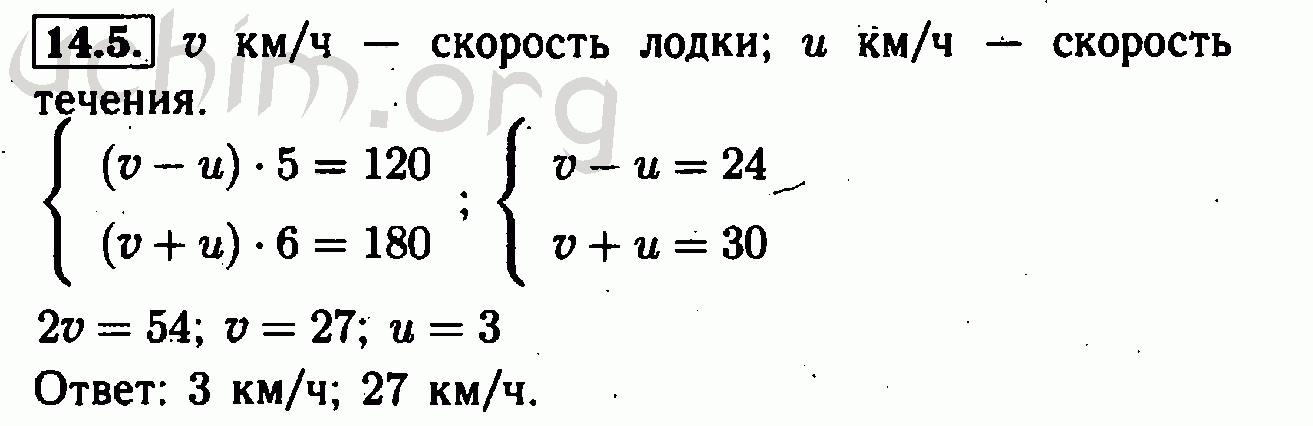 16 МБ
16 МБ