ГДЗ по геометрии 7 класс учебник Мерзляк Полонский Якир
ГДЗ готовые домашние задания учебника по геометрии 7 класс Мерзляк Полонский Якир ФГОС Вентана Граф на русском от Путина. Решебник (ответы на вопросы и задания) учебников и рабочих тетрадей необходим для проверки правильности домашних заданий без скачивания онлайн
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 Задание № 1 Проверьте себя в тестовой форме 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 Задание № 2 Проверьте себя в тестовой форме 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 Задание № 3 Проверьте себя в тестовой форме 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 Задание № 4 Проверьте себя в тестовой форме 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744
ГДЗ по геометрии 7 класс Мерзляк Полонский Якир учебник
ГДЗ учебник Геометрия. 7 класс. ФГОС А. Г. Мерзляка, В. Б. Полонского, М. С. Якира оранжевый. Издательство Вентана — Граф. Серия Математика (Алгоритм успеха). Состоит из одной части со 192 страницами.
7 класс. ФГОС А. Г. Мерзляка, В. Б. Полонского, М. С. Якира оранжевый. Издательство Вентана — Граф. Серия Математика (Алгоритм успеха). Состоит из одной части со 192 страницами.
Начиная изучение геометрии, школьники узнают новые для себя понятия, которые станут основой освоения предмета в следующих классах. Луч, отрезок, прямая, биссектриса, равносторонний треугольник, параллельные и перпендикулярные прямые – расширят математические знания учащихся, станут основой развития логической интуиции, сформируют понимание значения геометрии в повседневной жизни. Решение заданий в группе поможет выработать необходимые навыки работы в коллективе. Настойчивость, целеустремленность, формирование собственного мировоззрения и внутренней дисциплинированности приведут к успеху в изучении предмета. Планирование выполнения работы, выработка необходимого уровня критичности мышления, а также поиск самых рациональных путей решения задач внесут наибольший вклад в удовлетворенность семиклассников процессом учёбы, покажут достигнутый результат.
Выполнение готовых домашних заданий ГДЗ должно осуществляться с соблюдением принципа самоконтроля. Только при этом условии ответы станут приносить положительные оценки. Наш решебник окажет бесценную помощь в проверке выполненных упражнений, при необходимости подскажет верное решение заданий.
Задание: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 Задание № 1 Проверьте себя в тестовой форме 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 Задание № 2 Проверьте себя в тестовой форме 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 Задание № 3 Проверьте себя в тестовой форме 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 Задание № 4 Проверьте себя в тестовой форме 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744
ГДЗ Геометрия 7 класс Мерзляк, Полонский, Рабинович
Геометрия 7 классДидактические материалы
Мерзляк, Полонский, Рабинович
Вентана-Граф
Вполне понятно почему именно школьники упорно изыскивают всевозможные способы избежать заучивания новой информации, ведь освоить подобные объемы и многим взрослым будет далеко не под силу. Однако оставить без внимания такие попытки ребенка — значит, оказать ему медвежью услугу. Лучше сразу же разобрать все непонятные моменты и досконально разъяснить все нюансы сложной темы, чтобы потом ученик чувствовал себя спокойно и уверенно во время уроков. Сделать это, а так же подготовиться к проверочным испытаниям, поможет решебник к учебнику «Геометрия. Дидактические материалы 7 класс» Мерзляк, Полонский.
Однако оставить без внимания такие попытки ребенка — значит, оказать ему медвежью услугу. Лучше сразу же разобрать все непонятные моменты и досконально разъяснить все нюансы сложной темы, чтобы потом ученик чувствовал себя спокойно и уверенно во время уроков. Сделать это, а так же подготовиться к проверочным испытаниям, поможет решебник к учебнику «Геометрия. Дидактические материалы 7 класс» Мерзляк, Полонский.
Параметры данного сборника
В пособии содержится четыре варианта, в каждом из которых сто восемьдесят пять заданий. Помимо этого приведено пять контрольных работ. Для более удобного осуществления подготовки к проверочной части обучения, авторы предоставили подробные решения по всем номерам.
Поможет ли он в учебе
Семиклассники уже достаточно взрослые, чтобы понимать, что за любые свои поступки надо отвечать. В школе любое уклонение от изучения дисциплин карается плохими оценками, а в самом крайнем случае — исключением. Выявить реальные познания учащихся призваны всевозможные самостоятельные и контрольные работы.И если в домашних условиях еще можно воспользоваться готовыми ответами, то вот в классе такое уже не прокатит. Поэтому прежде чем начинать пользоваться шпаргалками вместо того, чтобы хорошо понять и усвоить материал, учащимся следует задуматься о том, справятся ли они с последующими испытаниями. Успешно к ним подготовиться поможет решебник к учебнику «Геометрия. Дидактические материалы 7 класс» Мерзляк.
Выявить реальные познания учащихся призваны всевозможные самостоятельные и контрольные работы.И если в домашних условиях еще можно воспользоваться готовыми ответами, то вот в классе такое уже не прокатит. Поэтому прежде чем начинать пользоваться шпаргалками вместо того, чтобы хорошо понять и усвоить материал, учащимся следует задуматься о том, справятся ли они с последующими испытаниями. Успешно к ним подготовиться поможет решебник к учебнику «Геометрия. Дидактические материалы 7 класс» Мерзляк.
Решебник ⏩ ГДЗ Геометрия 7 класс ⚡ А. Г. Мерзляк, В. Б. Полонский, М. С. Якир 2015
ГДЗ 7 класс Геометрияпоказать обложку
Авторы: А. Г. Мерзляк, В. Б. Полонский, М. С. Якир
Год: 2015
Рейтинг: 4.3Оцените книгуАналоги другого года издания
показать обложку
Авторы:А. Г. Мерзляк, В. Б. Полонский, М. С. Якир
Год:2011
показать обложку
Авторы:А. Г. Мерзляк, В. Б. Полонский, М. С. Якир, Ю. М. Рабинович
Рабинович
Год:2015
Описание:Сборник задач
показать обложку
Авторы:А. Г. Мерзляк, В. Б. Полонский, М. С. Якир
Год:2015
Описание:Сборник задач и контрольных работ
показать обложку
Авторы:А. Г. Мерзляк, В. Б. Полонский, М. С. Якир, Ю. М. Рабинович
Год:2007
Описание:Сборник задач и заданий для тематического оценивания
Самые популярные книги
показать обложку
Авторы:А. Г. Мерзляк, В. Б. Полонский, М. С. Якир, Ю. М. Рабинович
Год:2013
Описание:Сборник задач и контрольных работ
показать обложку
Авторы:В. М. Бойко, И. Л. Дитчук
Год:2017
Описание:Тетрадь для практических работ
показать обложку
Авторы:В. И. Соболь
Год:2015
Описание:Рабочая тетрадь
показать обложку
Авторы:В. Г. Барьяхтар, Ф. Я. Божинова, С. А. Довгий
Год:2015
показать обложку
Авторы:Naomi Simmons
Год:2019
Описание:Family and Friends 4 workbook 2nd edition
показать обложку
Авторы:В. Г. Барьяхтар, Ф. Я. Божинова, Е. А. Кирюхина, С. А. Довгий
Г. Барьяхтар, Ф. Я. Божинова, Е. А. Кирюхина, С. А. Довгий
Год:2016
- ✅ ГДЗ ✅
- ⚡ 7 класс ⚡
- Геометрия ✍
- Мерзляк 2015
ГДЗ по геометрии — зачем это нужно
В седьмом классе школьники как никогда нуждаются в помощи. Именно ГДЗ по геометрии за 7 класс А.Г.Мерзляк М.С.Якир В.Б.Полонский 2015 поможет школьникам разобраться в новых темах и качественно провести срез знаний.
Что в ГДЗ
ГДЗ за 7 класс по геометрии А.Г.Мерзляк М.С.Якир В.Б.Полонский 2015 состоит из 5 частей:
§ 1. Простейшие геометрические фигуры и их свойства
§ 2. Треугольники
§ 3. Параллельные прямые. Сумма углов треугольника
§ 4. Шар и круг
Упражнения для повторения курса геометрии за 7 класс
Почему именно ГДЗ
ГДЗ за 7 класс по геометрии А.Г.Мерзляк М.С.Якир В.Б.Полонский 2015 — это уникальная возможность выучить новый материал во время практических занятий, а не путем зазубривания. Так как подростки легче воспринимают материал в динамике, методика практических занятий дает гораздо лучший результат, чем традиционное зазубривание правил и терминов.
Так как подростки легче воспринимают материал в динамике, методика практических занятий дает гораздо лучший результат, чем традиционное зазубривание правил и терминов.
ГДЗ — почему это работает
Изучение геометрии — это очень сложный процесс. Порой, желая помочь школьнику, родители пытаются объяснить сложный материал «по своему», идя в разрез с объяснениями учителя. В этом случае, взрослые наносят ребенку непоправимый вред, так как окончательно запутывают его. Именно во избежание таких случаев и создали ГДЗ за 7 класс по геометрии А.Г.Мерзляк М.С.Якир В.Б.Полонский 2015. Издание за 7 класс ГДЗ по геометрии А.Г.Мерзляк М.С.Якир В.Б.Полонский 2015 поможет подросткам не только проверить правильность выполнения домашних заданий, но и даст возможность разобраться в сложном материале.
Мерзляк А.Г., Полонский В.Б., Якир М.С
Календарно-тематическое планирование по геометрии
7 класс
в неделю 2 ч, всего 70 ч ;
учебник: «Геометрия:7 класс: учебник для учащихся общеобразовательных организаций», авторы: Мерзляк А. Г., Полонский В.Б., Якир М.С., издательский центр «Вентана-Граф», Москава, 2017г. ФГОС
Г., Полонский В.Б., Якир М.С., издательский центр «Вентана-Граф», Москава, 2017г. ФГОС
Кол-во часов
Кол-во контрольных работ
1 четверть
9 недель – 18 ч
2 четверть
7 недель – 14 ч
3 четверть
10 недель – 20 ч
4 четверть
9 недель – 18 ч
35 недель – 70 ч
РазделТема урока
Сроки
Планируемые результаты
Деятельность обучающихся
МТ база, ЭОРы
Формы организации образовательного процесса
личностные
метапредметные
предметные
Простейшие геометрические фигуры и их свойства (13 ч. )
)
1
§ 1
Точки и прямые
6.09
формировать интерес к изучению геометрии потребность применять приобретенные знания и умения.
формировать первоначальные представления об идеях и о методах геометрии, как об универсальном языке науки и техники, о средстве моделирования явлений и процессов.
сформировать представление о новом школьном предмете геометрии, познакомить учащихся со свойствами точки и прямой, с такими видами математических терминов, как «определение» и «теорема», начать формировать навыки доказательных рассуждений.
Применяют свойства точки и прямой при решении задач, Оперируют терминами «определение» и «теорема».
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
http://easyen.ru/
Фронтальная беседа об истории появления понятий, работа у доски и в тетрадях. Работа у доски, самостоятельная работа
2
§ 1
Точки и прямые
формировать интерес к изучению геометрии потребность применять приобретенные знания и умения.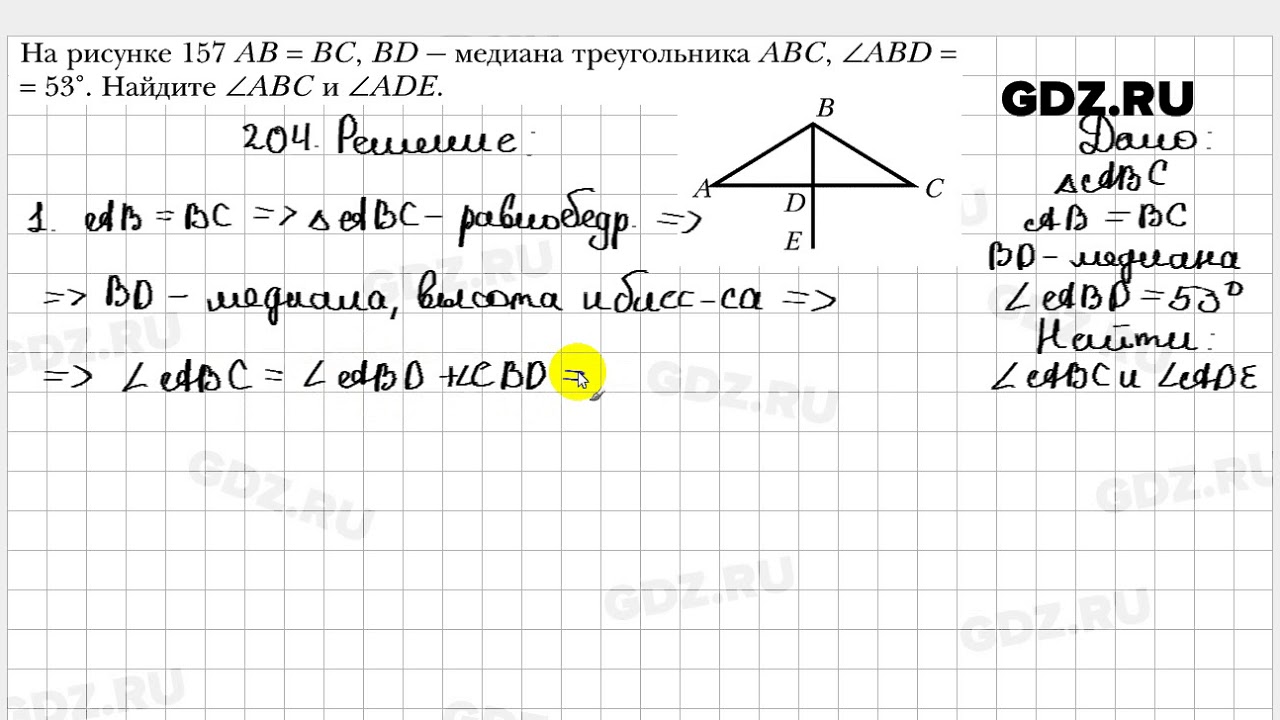
формировать первоначальные представления об идеях и о методах геометрии, как об универсальном языке науки и техники, о средстве моделирования явлений и процессов.
Закрепить навыки применения свойств точки и прямой
Применяют свойства точки и прямой при решении задач
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
3
§ 2
Отрезок и его длина
8.09
формировать умение планировать свои действия в соответствии с учебным заданием.
формировать умение определять понятия, создавать обобщения, устанавливать аналогии.
познакомить учащихся с понятием отрезка, основным свойством отрезка, научить измерять и сравнивать отрезки.
Распознают отрезки на чертежах, строят и сравнивают отрезки
Демонстрационный материал (слайды),
Раб. тетр. №1,
тетр. №1,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
4
§ 2
Отрезок и его длина
12.09
формировать умение планировать свои действия в соответствии с учебным заданием.
формировать умение определять понятия, создавать обобщения, устанавливать аналогии.
закрепить знания учащихся об отрезке, основном свойстве отрезка, навыки сравнения отрезков
Распознают отрезки на чертежах, строят и сравнивают отрезки
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа у доски, индивидуальная работа
5
§ 3
Луч и угол. Измерение углов
14.09
формировать умение работать в коллективе и находить согласованные решения.
формировать умение определять понятия, создавать обобщения, устанавливать аналогии.
познакомить учащихся с понятиями луча, угла, развернутого угла, равных углов, биссектрисы угла, единичного угла, градуса, острого угла, прямого угла, тупого угла, основного свойства величины угла.
Распознают лучи, углы, биссектрису угла, изображают и обозначают лучи и углы
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
6
§ 3
Луч и угол. Измерение углов
19.09
формировать умение работать в коллективе и находить согласованные решения.
формировать умение определять понятия, создавать обобщения, устанавливать аналогии.
закрепить знания учащихся о понятии единичного угла, градуса, острого угла, прямого угла, тупого угла, основного свойства величины угла
Распознают лучи, углы, биссектрису угла, изображают и обозначают лучи и углы
Демонстрационный материал (слайды),
Раб. тетр. №1,
тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
7
§ 4
Смежные углы
22.09
формировать умение соотносить полученный результат с поставленной целью.
формировать умения определять понятия строить логическое рассуждение, умозаключение и делать выводы
познакомить учащихся с понятием смежных углов, изучить свойства смежных углов.
Распознают смежные углы, формулируют и доказывают теорему о свойстве смежных углов.
Строят угол смежный с данным углом
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа у доски, индивидуальная работа
8
§ 4
Вертикальные углы
26.09
формировать умение соотносить полученный результат с поставленной целью.
формировать умения определять понятия строить логическое рассуждение, умозаключение и делать выводы
познакомить учащихся с понятием вертикальных углов, изучить свойства вертикальных углов.
Распознают на чертежах вертикальные углы, строят их. Формулируют и доказывают теорему о свойстве вертикальных углов
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
9
§ 4
Смежные и вертикальные углы
формировать умение планировать свои действия в соответствии с учебным заданием.
формировать умение выдвигать гипотезы при решении задачи и понимание необходимости их проверки.
закрепить знания учащихся о вертикальных и смежных углах, закрепить навыки решения задач.
Распознают на чертежах вертикальные углы, строят их. Формулируют и доказывают теорему о свойстве вертикальных углов
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
10
§ 5
Перпендикуляр-ные прямые.
формировать интерес к изучению темы и желание применять приобретенные знания и умения.
формировать умения определять понятия, создавать обобщения, устанавливать аналогии, строить логическое рассуждение.
познакомить учащихся с определением перпендикулярных прямых, перпен-дикулярных отрезков; ввести понятия угла между прямыми, перпендикуляра, наклонной, расстояния от точки до прямой; изучить свойства прямой, перпенди-кулярной данной и проходящей через точку, лежащую на данной прямой.
Распознают и строят перпендикулярные прямые и отрезки, находят расстояние от точки до прямой, формулируют и доказывают свойство прямой, перпендикулярной данной.
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
11
§ 6
Аксиомы.
формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
формировать первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техники.
сформировать представление учащихся о роли аксиом при построении системы геометрических знаний, разъяснить, что с помощью одних свойств фигуры можно доказывать другие ее свойства.
Получают представление о роли аксиом при построении системы геом. знаний,
понимают, что с помощью одних свойств фигуры можно доказывать другие её свойства
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
12
Повторение и систематизация учебного материала
формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
формировать первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техники.
закрепить знания учащихся по теме «Простейшие геометрические фигуры и их свойства»
Решают заадчи на основные понятия темы: градусная мера угла, острые, тупые, прямые, развернутые, смежные, вертикальные углы; свойства смежных и вертикальных углов, проводят измерительные работы
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
13
Контрольная работа №1 «Простейшие геометрические фигуры и их свойства»
формировать интерес к желанию применять приобретенные знания и умения.
формировать первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техники.
проверить знания учащихся по теме «Простейшие геометрические фигуры и их свойства»
Находят длину отрезка;
используют свойства смежных и вертикальных углов при решении задач,
строят биссектрису угла с помощью транспортира
Дид. матер.
матер.
индивидуальная работа
Треугольники (16ч)
14
§ 7
Равные треугольники.
формировать интерес к изучению темы и желанию применять приобретенные знания и умения.
формировать умения определять понятия, создавать обобщения, устанавливать аналогии, классифицировать
обобщить и углубить знания о треугольнике, ввести понятия периметра треугольника, остроугольного, прямоугольного и тупоугольного треугольников, равных треугольников, изучить основное свойство равенства треугольников и свойство прямой, проходящей через заданную точку, не лежащую на данной прямой, и перпендикулярной данной.
Распознают элементы треугольника, находят периметр треугольника, распознают треугольники по видам углов, доказывают свойства прямой
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
15
§ 7
Высота медиана, биссектриса треугольника
формировать ответственное отношение к получению новой информации, готовность к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
формировать умения определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации.
ввести понятия: высота, медиана, биссектриса треугольника.
Решают прос-тейшие задачи по теме; строят медианы, биссектрисы и высоты треугольника; находят их на чертежах
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
16
§ 8
Первый признак равенства треугольников
формировать умение планировать свои действия в соответствии с учебным заданием.
формировать умения определять понятия, строить логическое рассуждение, умозаключение и делать выводы.
изучить первый признак равенства треугольников, свойство серединного перпендикуляра отрезка, научить учащихся применять признак равенства треугольников при решении задач.
доказывают 1 признак равенства треугольников, применяют его в решении задач.
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
17
§ 8
Второй признак равенства треугольников
формировать умение планировать свои действия в соответствии с учебным заданием.
формировать умение строить логическое рассуждение, умозаключение и делать выводы.
сформировать и доказать второй признак равенства треугольников, научить учащихся применять второй признак равенства треугольников при решении задач.
доказывают 2 признак равенства треугольников, применяют его в решении задач.
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
18
§ 8
Первый и второй признаки равенства треугольников
формировать умение соотносить полученный результат с поставленной целью.
формировать умение выдвигать гипотезы при решении задачи и понимание необходимости их проверки.
закрепить навыки применения первого и второго признаков равенства треугольников при решении задач.
применяют 1 и 2 признаки равенства треугольников при решении задач.
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
19
§ 8
Первый и второй признаки равенства треугольников
формировать умение соотносить полученный результат с поставленной целью.
формировать умение выдвигать гипотезы при решении задачи и понимание необходимости их проверки.
закрепить навыки применения первого и второго признаков равенства треугольников при решении задач.
применяют 1 и 2 признаки равенства треугольников при решении задач.
Демонстрационный материал (слайды),
Раб. тетр. №1,
тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
20
§ 9
Равнобедренный треугольник и его свойства
формировать умения определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации.
формировать ответственное отношение к получению новой информации, готовность к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
познакомить учащихся с понятиями равнобедренного и разностороннего треугольников, элементами равнобедренного треугольника.
Распознают треугольники в зависимости от количества разных сторон, изображают разные виды треугольников, находят элементы равнобедренного тругольника
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
21
§ 9
Равнобедренный треугольник и его свойства
формировать умение контролировать процесс и результат учебной и математической деятельности.
формировать умение строить логическое рассуждение, умозаключение и делать выводы.
сформировать и доказать свойства равнобедренного и равностороннего треугольников, научить учащихся применять эти свойства при решении задач.
Доказывают свойства равноб. Треугольника, применяют эти свойства при решении задач
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
22
§ 9
Равнобедренный треугольник и его свойства
формировать умение представлять результат своей деятельности.
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
закрепить знания свойств равнобедренного и равностороннего треугольников, навыки применения этих свойств при решении задач.
Доказывают свойства равноб. Треугольника, применяют эти свойства при решении задач
Треугольника, применяют эти свойства при решении задач
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
23
§ 10
Признаки р/б треугольника
формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
формировать умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение и делать выводы.
изучить признаки равнобедренного треугольника, научить применять признаки равнобедренного треугольника при решении задач.
Доказывают признаки равнобедренного треугольника
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
24
§ 10
Признаки р/б треугольника
развивать готовность к самообразованию и решению творческих задач.
формировать умение выдвигать гипотезы при решении задачи и понимание необходимости их проверки.
закрепить навыки применения признаков равнобедренного треугольника при решении задач.
Применяют признаки равнобедренного треугольника при решении задач
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
25
§ 11
Третий признак равенства треугольников
формировать умение формулировать собственное мнение.
формировать умение строить логическое рассуждение, умозаключение и делать выводы.
изучить третий признак равенства треугольников, свойство точек, равноудаленных от концов отрезка, научить учащихся применять третий признак равенства треугольников при решении задач.
доказывают 3 признак равенства треугольников, применяют его в решении задач.
Демонстрационный материал (слайды),
Раб. тетр. №1,
тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
26
§ 11
Третий признак равенства треугольников
формировать умение самостоятельно определять цели своего обучения, ставить и формировать для себя новые задачи в учебе и познавательной деятельности.
формировать умение соотносить полученный результат при решении задач.
закрепить знание третьего признака равенства треугольников, навыки применения третьего признака равенства треугольников при решении задач.
доказывают 3 признак равенства треугольников, применяют его в решении задач.
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
27
§ 12
Теоремы
формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики
формировать первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техники.
сформировать представление учащихся о структуре теоремы, познакомить с основными видами теорем, научить распознавать взаимно обратные теоремы, разъяснять, в чем заключается метод доказательства от противного.
Выделяют условие и заключение теоремы, определяют виды теорем, распознают взаимно-обратные теоремы
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
28
Повторение и систематизация учебного материала
формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
формировать первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техники.
закрепить знания учащихся по теме «Треугольники»
Решают простейшие задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №1,
№1,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
29
Контрольная работа №2 «Треугольники»
формировать интерес к желанию применять приобретенные знания и умения.
формировать первоначальные представления об идеях и о методах геометрии как об универсальном языке науки и техники.
проверить знания учащихся по теме «Треугольники»
Применяют при решении задач признаки равенства тре-ков, признаки р/б тр-ка, понятия равнобедр. и равностор. тр-ков; боковые стороны, вершина, углы при основании, периметр р/б тр-ка.
Демонстрационный материал (слайды),
Раб. тетр. №1,
Дид. матер.
индивидуальная работа
Параллельные прямые. Сумма углов треугольника. (15 ч)
30
§ 13
Параллельные прямые
формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
формировать умение использовать приобретенные знания в практической деятельности.
сформировать понятия параллельных прямых, отрезков, лучей, изучить признак параллельности двух прямых, связанный с их перпендикулярностью третьей прямой, познакомить учащихся с аксиомой параллельных прямых и транзитивностью параллельности прямых.
Распознают и строят параллельные прямые, применяют признак параллельности двух прямых при решении заадч
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
31
§ 14
Признаки параллельности прямых
формировать интерес к изучению темы и желание применять приобретенные знания и умения, формировать умение объективно оценивать труд других.
формировать умение строить логическое рассуждение, умозаключение и делать выводы.
познакомить учащихся с понятиями: односторонних углов, накрест лежащих углов, соответственных углов, изучить признаки параллельности двух прямых, научить учащихся применять признаки параллельности двух прямых при решении задач.
применяют признак параллельности двух прямых при решении заадч
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
32
§ 14
Признаки параллельности прямых
развивать готовность к самообразованию и решению творческих задач.
закрепить знания признаков параллельности двух прямых, навыки применения признаков параллельности двух прямых при решении задач.
формировать умение сравнивать, анализировать, обобщать по разным основаниям, моделировать выбор способов деятельности.
применяют признак параллельности двух прямых при решении заадч
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
33
§ 15
Свойства параллельных прямых
формировать ответственное отношение к учению, готовить к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
формировать умение выдвигать гипотезы при решении задач и понимание необходимости их проверки
изучить свойства параллельных прямых, научить учащихся применить свойства параллельных прямых при решении задач.
доказывают признак параллельности двух прямых. и решают простейшие задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
34
§ 15
Свойства параллельных прямых
формировать ответственное отношение к учению, готовить к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
формировать умение выдвигать гипотезы при решении задач и понимание необходимости их проверки
закрепить знание свойств параллельных прямых, навыки применения свойств параллельных прямых при решении задач.
решают простейшие задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
35
§ 15
Свойства параллельных прямых
формировать ответственное отношение к учению, готовить к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
формировать умение выдвигать гипотезы при решении задач и понимание необходимости их проверки
обобщить и систематизировать знания свойств параллельных прямых, умения применять свойства параллельных прямых при решении задач.
решают простейшие задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
36
§ 16
Сумма углов треугольника
формировать ответственное отношение к учению, готовить к саморазвитию на основе мотивации к обучению и познанию.
формировать умение строить логическое рассуждение, умозаключение и делать выводы.
сформировать и доказать теорему о сумме углов треугольника и теорему о свойстве углов треугольника, научить учащихся применять их при решении задач.
доказывают теоремы о сумме углов треугольника, ее следствия, решают задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
37
§ 16
Сумма углов треугольника. Внешний угол треугольника
формировать способность осознанного выбора и построения дальнейшей индивидуальной траектории обучения.
формировать умение определять понятия, строить логическое рассуждение, умозаключение и делать выводы.
ввести понятие внешнего угла, изучить свойства внешнего угла треуголь-ника, научить учащихся применять свойства внешнего угла при решении задач.
доказывают теоремы о сумме углов треугольника, ее следствия, решают задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
38
§ 16
Сумма углов треугольника. Неравенство треугольника
формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
формировать умение строить логическое рассуждение, умозаключение и делать выводы.
изучить неравенство треугольника, соотношение между сторонами и углами треугольника; научить учащихся применять изученные теоремы при решении задач.
доказывают теоремы о сумме углов треугольника, ее следствия, решают задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
39
§ 17
Прямоугольный треугольник
формировать ответственное отношение к учению, готовить к саморазвитию на основе мотивации к обучению и познанию, формировать умение работать в коллективе и находить согласованные решения.
формировать умение определять понятия, строить логическое рассуждение, умозаключение и делать выводы.
познакомить учащихся с понятиями катета и гипотенузы, изучить признаки равенства прямоугольных треугольников, научить учащихся применять признаки рав-ва прямоугольных треугольников для решения задач.
Распознают и строят прямойгольные треугольники, доказывают признаки равенства прямоугольных треугольников, решают задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
40
§ 17
Прямоугольный треугольник
формировать интерес к изучению темы и желание применять приобретенные знания и умения.
формировать умение соотносить свои действия с планируемыми результатами.
закрепить знание признаков равенства прямоугольных треугольников, навыки применения признаков равенства прямоугольных треугольников при решении задач.
решают задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
41
§ 18
Свойства прямоуг. треугольника
формировать способность осознанного выбора и построения дальнейшей индивидуальной траектории обучения.
формировать умение использовать приобретенные знания в практической деятельности.
изучить свойства прямоугольного треугольника, научить учащихся применять свойства прямоугольного треугольника при решении задач.
Доказывают свойчтва прямоуг.треуг., решают задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
42
§ 18
Свойства прямоуг. треугольника
развивать навыки самостоятельной работы, анализа своей работы.
формировать умение самостоятельно определять цели своего обучения, ставить и формировать для себя новые задачи в учебе и познавательной деятельности.
закрепить знание свойств прямоугольного треугольника, навыки применения свойств прямоугольного треугольника при решении задач.
решают задачи по теме
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
43
Повторение и систематизация учебного материала
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания по теме « Параллельные прямые. Сумма углов треугольника».
использовать теоретичес-кие сведения для решения задач
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
44
Контрольная работа №3 «Параллельные прямые. Сумма углов треугольника»
развивать навыки самостоятельной работы, анализа своей работы
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания по теме « Параллельные прямые. Сумма углов треугольника».
Применяют при решении задач формулировку и док-во теоремы о сумме углов тр-ка, признаки равенства прямоуг. тр-ков; признак прямоуг. тр-ка и свойство медианы прямоуг. тр-ка
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
Окружность и круг. Геометрические построения ( 15 ч)
45
§ 19
Геометрическое место точек. Окружность и круг
формировать ответственное отношение к учению, готовность к саморазви-тию и самообразованию на основе мотивации к обучению и познанию.
формировать умение использовать приобретенные знания в практической деятельности.
сформировать представление учащихся о геометрическом месте точек, изучить свойство серединного перпендикуляра, свойство биссектрисы угла, дать понятие окружности, круга и их элементов.
Доказывают свойство серед.перпенд.,распознают и строят элементы окружности и круга, решают задачи
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
46
§ 19
Геометрическое место точек. Окружность и круг
формировать умение соотносить полученный результат с поставленной целью.
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
закрепить представление учащихся о геометрическом месте точек, навыки решения задач на нахождение элементов окружности и круга, научить доказывать что данная фигура является ГМТ.
решают задачи
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
47
§ 20
Некоторые свойства окружности. Касательная к окружности
формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
формировать умения определять понятия, строить логическое рассуждение, умозаключение и делать выводы.
ввести основные свойства окружности, познакомить учащихся с понятием касательной к окружности, ее свойством и признаками.
Применяют при решении заадч определения окружности, круга, их элементов; касательной к окружности; свойства: касательной к окружности; диаметра и хорды; признаки касательной.
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
48
§ 20
Некоторые свойства окружности. Касательная к окружности
формировать умение планировать свои действия в соответствии с учебным заданием.
формировать умение выдвигать гипотезы при решении задачи и понимание необходимости их проверки.
закрепить знания основных свойств окружности, свойства касательной к окружности и ее признаков, развивать навыки решения задач на применение этих свойств и признаков.
Применяют при решении заадч определения окружности, круга, их элементов; касательной к окружности; свойства: касательной к окружности; диаметра и хорды; признаки касательной.
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
49
§ 20
Некоторые свойства окружности. Касательная к окружности
развивать готовность к самообразованию и решению творческих задач.
формировать умение соотносить свои действия с планируемыми результатами, корректировать свои действия в соответствии с изменяющейся ситуацией.
обобщить и систематизировать знания основных свойств окружности, свойства касательной к окружности и ее признаков, углубить навыки решения задач на применение этих свойств и признаков.
Применяют при решении заадч определения окружности, круга, их элементов; касательной к окружности; свойства: касательной к окружности; диаметра и хорды; признаки касательной.
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
50
§ 21
Описанная и вписанная окружности треугольника
формировать интерес к изучению темы и желание применять приобретенные знания и умения.
формировать умение использовать приобретенные знания к практической деятельности.
познакомить учащихся с понятиями вписанной и описанной окружностей треугольника и их свойствами.
Распознают опис.и впис. окружности, доказывают теорему об опис.и впис. окружности
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
51
§ 21
Описанная и вписанная окружности треугольника
умение контролировать процесс и результат учебной и математической деятельности.
формировать умение самостоятельно определять цели своего обучения, ставить и формировать для себя новые задачи в учебной и познавательной деятельности.
закрепить знания о вписанной и описанной окружностях треугольника и их свойствах, закрепить навыки применения этих свойств при решении задач.
Применяют свойства об опис.и впис. окружности при решении задач
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
52
§ 21
Описанная и вписанная окружности треугольника
формировать критичность мышления, инициативу, находчивость, активность при решении задач.
формировать умение осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией.
обобщить и систематизировать знания о вписанной и описанной окружностях треугольника и их свойствах, углубить навыки применения этих свойств при решении задач.
Применяют свойства об опис.и впис. окружности при решении задач
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
53
§ 22
Задачи на построение
формировать интерес к изучению темы и желание применять приобретенные знания и умения.
формировать умение использовать приобретенные знания в практической деятельности.
познакомить учащихся с правилами, по которым решаются задачи на построение, со структурой задач на построение, формировать навыки решения задач на построение.
Строят угол, равный данному, серединный перпендикуляр данного отрезка, середину данного отрезка, прямую, перпендикулярную данной, биссектрису угла.
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
54
§ 22
Задачи на построение
формировать умение контролировать процесс и результат учебной и математической деятельности.
формировать умение определить способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией.
сформировать навыки построения треугольника по заданным элементам, закрепить навыки решения задач на построение.
решают
основные задачи на построение
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
55
§ 22
Задачи на построение
развивать познавательный интерес к математике.
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания о задачах на построение, углубить навыки решения задач на построение.
решают
основные задачи на построение
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
56
§ 23
Метод геометрических мест точек в задачах на построение
формировать интерес к изучению темы и желание применять приобретенные знания и умения.
формировать умение использовать приобретенные знания в практической деятельности.
познакомить учащихся с методом ГМТ в задачах на построение, научить применять этот метод при решении задач.
решают зада-чи на построение методом ГМТ
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
57
§ 23
Метод геометрических мест точек в задачах на построение
формировать умение планировать свои действия в соответствии с учебным заданием.
формировать умение определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией.
закрепить знания учащихся о методе ГМТ в задачах на построение, углубить навыки применения этого метода при решении задач.
решают зада-чи на построение методом ГМТ
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
58
Повторение и систематизация учебного материала
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата
закрепить представление учащихся о геометрическом месте точек, навыки решения задач на нахождение элементов окружности и круга
использовать теоретичес-кие сведения для решения задач
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
59
Контрольная работа №4 «Окружность и круг. Геометрические построения»
развивать навыки самостоятельной работы, анализа своей работы
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания по теме «Окружность и круг. Геометрические построения»
использовать теоретичес-кие сведения для решения задач
Демонстрационный материал (слайды),
Раб. тетр. №2,
Дид. матер.
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
Повторение и систематизация учебного материала. (11 ч.)
60
Повторение по теме «Начальные геометрические сведения
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
http://easyen.ru/
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
61
Повторение по теме «Начальные геометрические сведения
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
62
Повторение по теме «Признаки равенства треугольников. Равнобедренный треугольник»
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
63
Годовая промежу-точная аттестация. Письменная проверка: Тестовая работа
64
Повторение по теме «Признаки равенства треугольников. Равнобедренный треугольник»
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
65
Повторение по теме «Параллельные прямые»
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
66
Повторение по теме «Параллельные прямые»
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
67
Повторение по теме «Соотноше-ния между сто-ронами и углами треугольника»
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
68
Повторение по теме «Соотноше-ния между сто-ронами и углами треугольника»
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
69
Повторение по теме «Задачи на построение»
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
70
Повторение по теме «Задачи на построение»
формировать умение планировать свои действия в соответствии с учебным заданием
формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.
обобщить и систематизировать знания
использовать теоретичес-кие сведения для решения задач
Фронтальный опрос, работа в парах, работа у доски, индивидуальная работа
Описание учебно-методического и материально-технического обеспечения образовательного процесса
«Геометрия:7 класс: учебник для учащихся общеобразовательных организаций», авторы: Мерзляк А.Г., Полонский В.Б., Якир М.С., издательский центр «Вентана-Граф», Москава, 2017г. ФГОС
«Геометрия: 7 класс. Рабочие тетради №1, 2», Мерзляк А.Г, Полонский В. Б., Якир М. С.. издательский центр Вентана – Граф, Москва, 2017г.
«Геометрия: 7 класс. Дидактические материалы: сборник задач и контрольных работ», Мерзляк А.Г., Полонский В. Б., Якир М. С., издательский центр Вентана – Граф, Москва, 2017
«Геометрия: 7 класс: методическое пособие», Буцко Е.В., Мерзляк А.Г., Полонский В. Б., Якир М. С., издательский центр Вентана – Граф, Москва, 2017
Интернет – ресурсы:
Сайты для учащихся:
Сайты для учителя:
▶▷▶ сборник задач по алгебре за 7 класс мерзляк полонский якир
▶▷▶ сборник задач по алгебре за 7 класс мерзляк полонский якир| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 07-11-2018 |
сборник задач по алгебре за 7 класс мерзляк полонский якир — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Сборник задач контрольных Алгебра 7 класс Мерзляк 2015 4bookorg … 7 класс Алгебра Материалы сайта (підручники в pdf, ГДЗ, решебники к робочим зошитам) имеют авторское права и любое копирование возможно только при согласии авторов Скачать Сборник задач по алгебре 7 класс Мерзляк, Полонский uchebniki-onlinenet 7 класс Алгебра Портал школьных учебников онлайн Для любопытных учеников, стремящихся овладеть интересными науками, учиться на отлично и получать высокие баллы в школе, очень важно иметь хороших учителей и иметь в своей домашней ГДЗ по алгебре 7 класс Мерзляк Полонский Якир yagdzcom 7 класс Алгебра ГДЗ по алгебре 7 класс Мерзляк Полонский Якир ГДЗ решебник к учебнику по алгебре 7 класс Мерзляк Полонский Якир синий учебник ФГОС Вентана Граф Сборник Задач По Алгебре За 7 Класс Мерзляк Полонский Якир — Image Results More Сборник Задач По Алгебре За 7 Класс Мерзляк Полонский Якир images ГДЗ по алгебре 7 класс Мерзляк Полонский Якир gdzmaniacom/gdz/70-algebra- 7 -klass-merzlyak-polonskij Cached Она способсвует развитию логического мышления и памяти В помощь ученикам, мы добавили вспомогательное пособие, а именно сборник решений по алгебре за 7 класс Мерзляк, Полонский, Якир Алгебра Сборник задач и контрольных работ 7 класс Мерзляк pidruchnikinet/algebra 7 /1710-algebra-sbornik-zadach-i Cached Алгебра Сборник задач и контрольных работ 7 класс Мерзляк Полонский Рабинович Якир Дата: 27-07-2017, 19:38 Переглядів: 7294 Алгебра 7 класс Мерзляк сборник wwwdomashkainfo/algebra- 7 -klass-merzliak-sbornikhtml Cached Решение задач по алгебре для 7 класса из сборника Мерзляка АГ — хороший способ интересно провести время Скоротать вечерок с пользой можно решая задачи по алгебре для 7 класса из сборника Мерзляка АГ ГДЗ (решебник) к учебнику Мерзляк АГ и др Алгебра 7 класс math-helpernet/reshebniki-po-matematike/gdz-k Cached Домашняя работа по алгебре за 7 класс к учебнику авторов АГ Мерзляк, ВБ Полонский, МС Якир «Алгебра 7 класс : учебник для учащихся общеобразовательных организаций (углубленное изучение)» ГДЗ (решебник) по алгебре 7 класс Мерзляк, Полонский, Якир reshatorru/ 7 -klass/algebra/merzlyak Cached Онлайн решебник и ГДЗ по алгебре 7 класс Мерзляк, Полонский, Якир углублённое изучение (уровень) — Решатор! За счет использования ГДЗ по алгебре 7 класс Мерзляк, успешность изучения дисциплины выходит на новый уровень Решебник (ГДЗ) Алгебра 7 класс АГ Мерзляк, ВБ Полонський vshkolecom … Алгебра Но за классную работу тоже хочется получить 12 баллов Именно поэтому на уроке пригодиться всем школьникам ГДЗ Алгебра 7 клас АГ Мерзляк, ВБ Полонський, МС Якір Просто посещайте этот сайт с Ваших мобильных устройств Учебник Алгебра 7 класс АГ Мерзляк, ВБ Полонский, МС vklasseonline … Алгебра Ваш мобильный телефон для учебы Вы можете скачать Учебник Алгебра 7 класс АГ Мерзляк , ВБ Полонский , МС Якир на свое мобильное устройство Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 30,200 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- ВБ Полонський
- Полонский
- В Б Полонський
Полонский
Якир — Дидактические материалы Вентана-Граф
- а именно сборник решений по алгебре за 7 класс Мерзляк
- Полонский
- Якир reshatorru/ 7 -klass/algebra/merzlyak Cached Онлайн решебник и ГДЗ по алгебре 7 класс Мерзляк
сборник задач по алгебре за 7 класс мерзляк полонский якир — Все результаты ГДЗ по алгебре 7 класс Мерзляк, Полонский, Якир › Алгебра › 7 класс Решебник по алгебре за 7 класс авторы Мерзляк , Полонский , Якир издательство Вентана-Граф Решебник по алгебре 7 класс Мерзляк, Полоньский — ГДЗ › ГДЗ › 7 класс › Алгебра › А Г Мерзляк Похожие Подробные ГДЗ по алгебре за 7 класс , авторов А Г Мерзляк , В Б Полонський, М Ц Якір ГДЗ к учебнику по Алгебре 7 класс Мерзляк , Полонский для Российских школ ГДЗ учебник алгебра 7 класс А Г Мерзляк Номера задач ГДЗ решебник по алгебре 7 класс Мерзляк — Mathcomua wwwmathcomua/gdz-reshebnik/algebra-7-klass/merzlyakhtml Рейтинг: 4,1 — 12 голосов Решебник по алгебре за 7 класс к учебнику Мерзляк , Полонский , Якир с после чего школьники должны научится решать простые задачи с помощью Видео 1:36 ГДЗ по АЛГЕБРЕ 7класс Авторы АГМерзляк, ВБ Полонский, М С Miks er YouTube — 11 сент 2016 г 3:57 Алгебра 7 класс Мерзляк Полонский Якир GDZ Ru YouTube — 25 мая 2018 г 1:04 ГДЗ АЛГЕБРА 7 класс сборник с48 N 76, 79 Мерзляк, Полонский Miks er YouTube — 19 нояб 2016 г Все результаты Скачать Сборник задач по алгебре 7 класс Мерзляк, Полонский › 7 класс › Алгебра Сборник задач Алгебра 7 класс Мерзляк Сборник задач Алгебра 7 класс Мерзляк Год випуска: 2010 Автор: Мерзляк , Полонский , Рабинович, Якир А Г Мерзляк В Б Полонский М С Якир АЛГЕБРА Учебник для 7 А Г Мерзляк В Б Полонский М С Якир АЛГЕБРА Учебник для 7 класса общеобразовательных К каждому пункту подобраны задачи для самостоятельного решения, к которым мы советуем Мельник берет за работу ^ смолотой муки Сборник задач для подготовки к итоговой работе по математике Сборник мерзляк полонский якир по алгебре 10 класс cristinaamermanvacaucom/sbornik_merzlyak_polonskiy_yakir_po_algebre_10_klass/ Сборник задач и Мерзляк АГ, Полонский В по алгебре за 8 класс под 10 класс мерзляк , сборник Полонский ВБ, Якир М гдз по алгебре 7 класс ГДЗ (решебник) Алгебра 7 класс А Г Мерзляк, В Б Полонский, Ю › Моя Школа › ГДЗ › 7 класс › Алгебра Рейтинг: 5 — 3 голоса Учебники: Алгебра 7 класс Сборник задач и контрольных работ А Г по алгебре за 7 класс АГ Мерзляк ВБ Полонский ЮМРабинович МС Якир 2015 Сборник задач мерзляка 7 класс | Nilsaquiroz nilsaquirozhost22com/sbornik-zadach-merzlyaka-7-klass/ ГДЗ 7 класс , полонский якир Мерзляка Мерзляк Сборник задач Алгебра 7 класс ГДЗ к сборнику задач по алгебре за 7 класс для Алгебра 7 клас , збірник Книга: «Алгебра Сборник задач и контрольных работ для 6 класса › › Математика › Математика (5-9 классы) Для учителей средних школ, учащихся 6 классов и их родителей Мерзляк , Рабинович, Полонский , Якир — Алгебра Сборник задач и контрольных работ для Поделитесь с 7 -9 классы Задачи и упражнения на готовых чертежах 7 рец Важно Акции · Главные книги · Бонус за рецензию · Сертификаты Рабочая программа по алгебре 7 класс Мерзляк — Инфоурок › Алгебра 9 янв 2018 г — 5-11 классы / [АГ Мерзляк ВБ Полонский , МС Якир и др] 7 класс : Количество часов за год (34 недели): 136 ч Количество часов в неделю: 4 ч Алгебра : 7 класс : дидактические материалы: сборник задач и Сборник задач и заданий для тематического оценивания по › Экзамены › Экзамены по Алгебре 10 нояб 2011 г — Смотреть, читать и скачать бесплатно pdf, djvu и купить бумажную и электронную книгу по лучшей цене со скидкой: Сборник задач и заданий для по алгебре для 7 класса (авторы А Г Мерзляк , В Б Полонский , М С Якир ) за собой к удивительным открытиям, приключениям и победам Книга: «Алгебра 7 класс Самостоятельные и контрольные работы › › Математика › Математика (5-9 классы) ФГОС» Сборник содержит упражнения для самостоятельных и контрольных работ Мерзляк , Рабинович, Полонский , Якир — Алгебра 7 класс Картинки по запросу сборник задач по алгебре за 7 класс мерзляк полонский якир «cl»:3,»id»:»-orQrhVqRet7pM:»,»ml»:»600″:»bh»:90,»bw»:130,»oh»:720,»ou»:» «,»ow»:1280,»pt»:»iytimgcom/vi/eOH7-iO3k9w/maxresdefaultjpg»,»rh»:»youtubecom»,»rid»:»gAY1OGRwazG7fM»,»rt»:0,»ru»:» \u003deOH7-iO3k9w»,»st»:»YouTube»,»th»:90,»tu»:» \u003dtbn:ANd9GcTXeyXh0QxKX5wYhiVi4s2cd63O4p_murKNO9WWqFc9Xi20-ay4dvWTQY6k»,»tw»:160 «id»:»u53R89bklQEoiM:»,»ml»:»600″:»bh»:90,»bw»:66,»oh»:383,»ou»:» «,»ow»:260,»pt»:»uchebniki-onlinenet/uploads/posts/2014-10/1413617″,»rh»:»uchebniki-onlinenet»,»rid»:»ccIMeuRuc5jrTM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Учебники онлайн»,»th»:101,»tu»:» \u003dtbn:ANd9GcQcNh—D1OMaav7jAWz9tZRk79GoZ8_JfDKFbpAKXDu9tpRQgQ8LmexSoE»,»tw»:69 «id»:»xzPpFJK1aSjUuM:»,»ml»:»600″:»bh»:90,»bw»:130,»oh»:1350,»ou»:» «,»ow»:2048,»pt»:»reshatorru/otvety/7-klass-merzlyak/86png»,»rh»:»reshatorru»,»rid»:»L94JA1zdQPA78M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:90,»tu»:» \u003dtbn:ANd9GcQGq7TrcAU9n4HEk9qF79tLppbOGtBy1ZJ_CkvbBq28OpVuQILdzKsiZZAZ»,»tw»:137 «id»:»DNPv0QabHOn4cM:»,»ml»:»600″:»bh»:90,»bw»:130,»oh»:1257,»ou»:» «,»ow»:2044,»pt»:»reshatorru/otvety/7-klass-merzlyak/83png»,»rh»:»reshatorru»,»rid»:»L94JA1zdQPA78M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:90,»tu»:» \u003dtbn:ANd9GcT0qfoxCuOPTIKmIRmQT9IXPDHm9_PVgpCxU7lnaWoPKLLJAdpixjRKOztt»,»tw»:146 «id»:»NqEqBENpypiUVM:»,»ml»:»600″:»bh»:90,»bw»:128,»oh»:1345,»ou»:» «,»ow»:2025,»pt»:»reshatorru/otvety/7-klass-merzlyak/85png»,»rh»:»reshatorru»,»rid»:»L94JA1zdQPA78M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:90,»tu»:» \u003dtbn:ANd9GcQpBKY0mrSBU49TOxNl3OWLgZgPE8Ht_eZ3057eq8iI17gKj_5o1qGFTM9s»,»tw»:136 Другие картинки по запросу «сборник задач по алгебре за 7 класс мерзляк полонский якир» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Математика 5 класс Мерзляк, Полонский, Якир › Учебники › Математика 5 класс Мерзляк, Полонский, Якир авторы: АГ Мерзляк , ВБ Полонский , МС Якир издательство: Вентана- Граф, 2018 г Посмотреть глоссарий Задачи 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 · 11 ГДЗ по геометрии 7 класс Мерзляк Полонский Якир учебник — Я ГДЗ › 7 класс › Геометрия ГДЗ решебник к учебнику по геометрии 7 класс Мерзляк Полонский Якир ФГОС оранжевый Вентана Граф Ответы и решения на задания на сайте Алгебра Дидактические материалы 7 класс Аркадий Мерзляк , Михаил Якир , Виталий Полонский — 2018 — Study Aids Аркадий Мерзляк , Михаил Якир , Виталий Полонский , Е Рабинович « Алгебра 7 класс » авторов АГ Мерзляка, ВБ Полонского , МС Якира Первая часть варианта по 210 задач в каждом ( задачи , имеющие одинаковые номера, Это сделано намеренно, чтобы можно было использовать сборник как ГДЗ по математике за 5 класс, решебник и ответы онлайн — GDZru › ГДЗ › 5 класс › Математика Математика 5 класс рабочая тетрадь Авторы: АГ Мерзляк , ВБ Полонский , МС Якир издательство: Вентана-граф серия: Алгоритм успеха ГДЗ (решебник) по алгебре 7 класс Мерзляк, Полонский, Якир reshatorru/7-klass/algebra/merzlyak/ Подробный разбор задач по алгебре за 7 класс из учебника Мерзляка, Полонского , Якир ГДЗ по Математике 6 класс: Виленкин, Решебник учебника Решебник по математике для 6 класса Виленкин – это сборник готовых решений и ответов, который составлен на базе учебника по математике для Алгебра 7 класс Дидактические материалы Аркадий Мерзляк Похожие В книжном интернет-магазине OZON можно купить учебник Алгебра 7 класс Аркадий Мерзляк , Виталий Полонский , Ефим Рабинович, Михаил Якир Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (29) Показать скрытые результаты В ответ на официальный запрос мы удалили некоторые результаты (1) с этой страницы Вы можете ознакомиться с запросом на сайте LumenDatabaseorg Вместе с сборник задач по алгебре за 7 класс мерзляк полонский якир часто ищут гдз по алгебре 7 класс мерзляк поляков алгебра 7 класс мерзляк учебник гдз по алгебре 7 класс мерзляк дидактический материал гдз по алгебре 7 класс мерзляк ягдз гдз по геометрии 7 класс мерзляк полонский якир гдз по алгебре 7 класс мерзляк сборник алгебра 7 класс мерзляк поляков гдз по алгебре 7 класс мерзляк углубленный уровень Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Музыка Переводчик Диск Почта Коллекции Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Сборник задач Алгебра 7 класс Мерзляк bookforschoolinua › 357-sbornik-zadach…klasshtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Название учебника: Сборник задач Алгебра 7 класс Автор: Мерзляк АГ, Полонский ВБ, Рабинович ЕМ, Якир МС Скачать учебник Сборник задач Алгебра 7 класс 2 ГДЗ по алгебре 7 класс Мерзляк , Полонский , Якир eurokiorg › gdz…7_klass…merzlyak-polonskii-yakir-89 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ алгебра 7 класс Мерзляк , Полонский , Якир Вентана-Граф Комплекс изучения математических дисциплин «Алгоритм успеха» в рамках школы Применяя сборник для самоподготовки, рекомендуется обратить внимание на решебник к нему Регулярно прорабатывая по ГДЗ то, что вызывает вопросы, можно уже с азов Читать ещё ГДЗ алгебра 7 класс Мерзляк , Полонский , Якир Вентана-Граф Комплекс изучения математических дисциплин «Алгоритм успеха» в рамках школы подразумевает разделение классической математики в 7 -м классе на две самостоятельные дисциплины: геометрию и алгебру Последняя, как правило, более понятна и хорошо усваивается семиклассниками Особенно – если проводить занятия по качественным учебным пособиям, теоретическим и практикумам к ним Применяя сборник для самоподготовки, рекомендуется обратить внимание на решебник к нему Регулярно прорабатывая по ГДЗ то, что вызывает вопросы, можно уже с азов изучения алгебры ( 7 класса ) собрать к выпускным экзаменам обширный и качественный багаж знаний Скрыть 3 Скачать Сборник задач по алгебре 7 класс Мерзляк uchebniki-onlinenet › …sbornik…klass-merzlyakhtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник задач Алгебра 7 класс Мерзляк Наш сайт существенно поможет вам в этом и позволит просмотреть онлайн или скачать на телефон или планшет новые учебники pdf для всех классов и предметов школьной программы Читать ещё Сборник задач Алгебра 7 класс Мерзляк Год випуска: 2010 Автор: Мерзляк , Полонский , Рабинович, Якир Скачать pdf Читать онлайн Наш сайт существенно поможет вам в этом и позволит просмотреть онлайн или скачать на телефон или планшет новые учебники pdf для всех классов и предметов школьной программы Скрыть 4 Решебник и ГДЗ по Алгебре за 7 класс сборник задач gdz-putinanet › 7-klass…sbornik-zadach-merzlyak Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ Алгебра 7 класс А Г Мерзляк Решебник и ГДЗ по Алгебре для 7 класса сборник задач , авторы учебника: А Г Мерзляк , В Б Полонський, Ю М Рабінович, М Ц Якір на 2017-2018 год Читать ещё ГДЗ Алгебра 7 класс А Г Мерзляк ГДЗ по Алгебре 7 класс Сборник задач авторы: А Г Мерзляк , В Б Полонський, Ю М Рабінович, М Ц Якір Решебник и ГДЗ по Алгебре для 7 класса сборник задач , авторы учебника: А Г Мерзляк , В Б Полонський, Ю М Рабінович, М Ц Якір на 2017-2018 год Вариант 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 Скрыть 5 ГДЗ (решебник) к учебнику Мерзляк АГ и др Алгебра math-helpernet › reshebniki-po…k…merzlyak…7-klass… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Домашняя работа по алгебре за 7 класс к учебнику авторов АГ Мерзляк , ВБ Полонский , МС Якир « Алгебра 7 класс : учебник для учащихся общеобразовательных организаций (углубленное изучение)» Читать ещё Домашняя работа по алгебре за 7 класс к учебнику авторов АГ Мерзляк , ВБ Полонский , МС Якир « Алгебра 7 класс : учебник для учащихся общеобразовательных организаций (углубленное изучение)» В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника « Мерзляк АГ Алгебра 7 класс : учебник для учащихся общеобразовательных организаций / АГ Мерзляк , ВM Поляков 3-е изд, стереотип — М, 2019 Скрыть 6 ГДЗ по алгебре 7 класс Мерзляк , Полонский , Якир GDZplusru › 7-klass/algebra/merzlyak…material/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте На GDZpluseru вы найдёте ответы к задачам и контрольным вопросам из учебника по алгебре за 7 класс Мерзляка , Полонского , Якир со всем решением Ответы и решебник к учебнику Мерзляк , Полонский , Якир — Дидактические материалы Вентана-Граф, 2018 Вариант 1 Вариант 1 (Страницы с 4 по 34) Читать ещё На GDZpluseru вы найдёте ответы к задачам и контрольным вопросам из учебника по алгебре за 7 класс Мерзляка , Полонского , Якир со всем решением Ответы и решебник к учебнику Мерзляк , Полонский , Якир — Дидактические материалы Вентана-Граф, 2018 Вариант 1 Вариант 1 (Страницы с 4 по 34) Введение в алгебру : 1; 2; 3; 4; 5; 6; 7 ; 8; Линейное уравнение с одной переменной: 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 23; Решение задач с помощью уравнений: 24; 25; 26; 27; 28; 29; 30; 31; 32; 33; 34; 35; 36; 37; 38; 39; 40; 41; 42; 43; Тождественно равные выражения Скрыть 7 ГДЗ (решебник) по алгебре 7 класс Мерзляк , Полонский reshatorru › 7 класс › Алгебра › Мерзляк Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробный разбор задач по алгебре за 7 класс из учебника Мерзляка , Полонского , Якир А поскольку изучение нового материала по силам не каждому ученику, на помощь приходят решебники, в том числе и ГДЗ по алгебре 7 класс Мерзляк В этой книге содержатся ответы на все математические задачи из Читать ещё Подробный разбор задач по алгебре за 7 класс из учебника Мерзляка , Полонского , Якир А поскольку изучение нового материала по силам не каждому ученику, на помощь приходят решебники, в том числе и ГДЗ по алгебре 7 класс Мерзляк В этой книге содержатся ответы на все математические задачи из соответствующего учебника, благодаря чему школьники могут глубже усваивать полученные знания и получать хорошие оценки без особых усилий Скрыть 8 ГДЗ по Алгебре 7 класс : Мерзляк Решебник заданий gdzputinainfo › Решебники › 7 класс › Алгебра › merzlyak-a-g Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решебник по алгебре для 7 класса Мерзляк – это сборник онлайн-решений по упражнениям одноименного учебника математики, составленного авторитетными российскими учеными – Мерзляком АГ, Полонским ВБ, Якиром МС в 2015 году, который ныне включен в учебную программу многих российских Читать ещё Решебник по алгебре для 7 класса Мерзляк – это сборник онлайн-решений по упражнениям одноименного учебника математики, составленного авторитетными российскими учеными – Мерзляком АГ, Полонским ВБ, Якиром МС в 2015 году, который ныне включен в учебную программу многих российских общеобразовательных школ Онлайн-решебник к алгебре 7 класс Мерзляка – спутник идеальной домашней работы Для того чтобы успевать по предметам школьной программы, качественно выполнять задания на контрольных и экзаменах семиклассникам крайне важно уметь управлять своим временем Скрыть 9 ГДЗ по алгебре для 7 класса сборник задач АГ Мерзляк GdzPutinaru › po-algebre/7-klass/sbornik…merzlyak Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Тут отличные гдз по алгебре сборник задач для 7 класса , АГ Мерзляк , ВБ Полонський, ЮМ Рабінович, МЦ Якір от Путина Очень удобный интерфейс с решениями ГДЗ к учебнику по Алгебре 7 класс Мерзляк , Полонский для 10 Сборник задач по алгебре за 7 класс Мерзляк Полонский Якир — смотрите картинки ЯндексКартинки › сборник задач по алгебре за 7 класс мерзляк Пожаловаться Информация о сайте Ещё картинки АЛГЕБРА Контрольные работы 7 класс Мерзляк контрользнанийрф › algebra-kontrolnye…7-klass/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ОТВЕТЫ: АЛГЕБРА Контрольные работы 7 класс Решения вопросов и задач из пособия для учащихся «Дидактические материалы по алгебре 7 класс ФГОС» (авт АГ Мерзляк , ВБ Полонский , ЕМРабинович, изд-во «Вентана-Граф»), которое используется в комплекте с учебником « Алгебра 7 класс » (авт Читать ещё ОТВЕТЫ: АЛГЕБРА Контрольные работы 7 класс Решения вопросов и задач из пособия для учащихся «Дидактические материалы по алгебре 7 класс ФГОС» (авт АГ Мерзляк , ВБ Полонский , ЕМРабинович, изд-во «Вентана-Граф»), которое используется в комплекте с учебником « Алгебра 7 класс » (авт АГ Мерзляк , ВБ Полонский , МС Якир ) Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания , а в случае необходимости помочь детям в выполнении домашней контрольной работы по математике В начале указана цитата (образец варианта контрольной работ Скрыть Сборник задач по алгебре 7 класс (рурукин А, Гусева Доставка Акции Книги Канцтовары chitai-gorodru › Сборник-задач-по-алг Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Литература для образования Программа бонусов – копите и оплачивайте! Контактная информация +7 (495) 444-84-44 пн-вс 9:00-21:00 Магазин на Маркете 18+ Скачать: учебник алгебра 7 класс / litresru litresru Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Школьные учебники скачивайте онлайн в электронном формате на ЛитРес Контактная информация +7 (800) 333-27-37 круглосуточно Магазин на Маркете 18+ Вместе с « сборник задач по алгебре за 7 класс мерзляк полонский якир » ищут: сборник задач по математике дидактические материалы по алгебре 7 класс решение уравнений сборник заданий по алгебре 9 класс кузнецова ответы и решения 1 2 3 4 5 дальше Bing Google Mailru Нашлось 147 млн результатов Дать объявление Показать все Регистрация Войти 0+ В ЯндексБраузере теперь можно поиграть с Алисой Установить Закрыть Спасибо, что помогаете делать Яндекс лучше! Эта реклама отправилась на дополнительную проверку ОК ЯндексДирект Попробовать еще раз Включить Москва Настройки Клавиатура Помощь Обратная связь Для бизнеса Директ Метрика Касса Телефония Для души Музыка Погода ТВ онлайн Коллекции Яндекс О компании Вакансии Блог Контакты Мобильный поиск © 1997–2018 ООО «Яндекс» Лицензия на поиск Статистика Поиск защищён технологией Protect Попробуйте быстрый Браузер с технологией защиты Протект 0+ Установить
ГДЗ по Математике 6 класс Мерзляк Алгоритм успеха
Одним ученикам точные науки даются проще, другим тяжелее, однако изучать эту непростую дисциплину приходится всем ведь впоследствии ее нужно будет сдавать на экзаменах. «ГДЗ по математике 6 класс учебник Мерзляк (Вентана-граф Алгоритм успеха)» поможет школьникам справиться с трудностями в образовательном процессе и создать базу знаний, достаточную для продвинутого изучения предмета в старшей школе. Нередко сложнее всего учениками воспринимаются такие темы, как:
- обыкновенные дроби;
- отношения и пропорции;
- делимость натуральных чисел.
В пособии есть верные ответы на все задания, а решения расписаны доступно и подробно, что упрощает процесс их понимания. Благодаря постоянным занятиям по решебнику ученики запомнят нужные формулы и алгоритмы намного быстрее, а сэкономленное время смогут потратить на отдых или подготовку по другим дисциплинам.
Содержание решебника
«ГДЗ по математике 6 класс учебник А.Г. Мерзляк, В.Б. Полонский, М.С. Якир (Вентана-граф Алгоритм успеха)» предназначается для использования в паре с основным учебником. Как и соответствующее пособие, решебник содержит в себе четыре главы, разделенные на параграфы – после каждого из них следуют упражнения различных уровней сложности, предназначенные для закрепления в памяти пройденного материала. Пособие полностью выполнено в соответствии с образовательными требованиями и с рабочей программой. В нем изложены не только верные ответы, а и расписанные ходы, и методы их решения. Подробные разъяснения и хорошая подача материала облегчают понимание дисциплины учениками.
Что можно почерпнуть из ГДЗ по математике 6 класс А.Г. Мерзляк,
Лучше всего информация усваивается при самостоятельных занятиях, при которых школьник имеет доступ к опыту профессиональных учителей. Разобравшись в материале, ученик начнет интересоваться предметом и еще больше повышать успеваемость. Оценив удобство ГДЗ и начав заниматься по нему регулярно, ребенок начнет:
- качественно и вовремя сдавать домашние работы;
- хорошо понимать даже самые сложные темы;
- не бояться проверок знаний;
- активно работать на уроках;
- получать высокие оценки.
Сборник принесет пользу как детям, так и взрослым. Родители смогут без особых затрат времени и сил помочь ребенку с домашними заданиями. Учителя же используют его в качестве шаблона или дополнения для собственной программы урока которая будет интересна всем ученикам.
ГДЗ по математике 6 класс рабочая тетрадь Мерзляк (Часть 1, 2, 3) можно посмотреть здесь.
ГДЗ по математике 6 класс дидактические материалы Мерзляк можно посмотреть здесь.
ГДЗ к тестам по математике 6 класс Ерина Т.М. можно посмотреть здесь.
рупий Aggarwal для класса 6 по математике Глава 4
Страница № 63:
Вопрос 1:
Напишите противоположное каждому из следующих пунктов:
(i) Увеличение на 8
(ii) Потеря на 7
рупий (iii) Увеличение веса на 5 кг
(iv) 10 км над уровнем моря
(v) На 5 ° C ниже точки замерзания
(vi) Залог в размере 100
рупий (vii) Заработок 500
рупий (viii) Пройдя 6 м на восток
(ix) 24
(x) −34
Ответ:
(i) Уменьшение на 8
(ii) Прирост на 7
рупий (iii) Потеря веса на 5 кг
(iv) на 10 км ниже уровня моря
(v) 5 o C выше точки замерзания
(vi) Снятие 100 рупий
(vii) Расходы 500 рупий
(viii) Переход на 6 м на запад
(ix) Противоположность 24 — -24.
(x) Противоположность -34 — 34.
Страница № 63:
Вопрос 2:
Укажите следующее, используя знак «+» или «-»:
(i) Прибыль в размере 600 рупий
(ii) Убыток в размере 800 рупий
(iii) На 7 ° C ниже точки замерзания
(iv) Уменьшение на 9
(v) 2 км над уровнем моря
(vi) 3 км ниже уровня моря
(vii) Залог в размере 200
рупий (viii) Снятие 300
Ответ:
(i) + 600
(ii) -Rs 800
(iii) -7 o C
(iv) -9
(v) +2 км
(vi) -3 км
(vii) + Rs 200
(viii) -300
Страница № 64:
Вопрос 3:
Отметьте следующие целые числа в числовой строке:
(i) −5
(ii) −2
(iii) 0
(iv) −7
(v) −13
Страница № 64:
Вопрос 4:
Какое число больше в каждой из следующих пар?
(i) 0, −2
(ii) −3, −5
(iii) −5, 2
(iv) −16, 8
(v) −365, −913
(vi) −888, 8
Ответ:
(i) 0, -2
0> -2
Это потому, что ноль больше любого отрицательного целого числа.
(ii) -3, -5
-3> -5
Поскольку 3 меньше 5, -3 больше -5.
(iii) -5, 2
2> -5
Это потому, что каждое положительное целое число больше любого отрицательного целого числа.
(iv) -16, 8
8> -16
Это потому, что каждое положительное целое число больше любого отрицательного целого числа.
v) -365, -913
-365> -913
Поскольку 365 меньше 913, -365 больше -913.
vi) -888, 8
8> -888
Это потому, что каждое положительное целое число больше любого отрицательного целого числа.
Страница № 64:
Вопрос 5:
Какое число меньше в каждой из следующих пар?
(i) 6, −7
(ii) 0, −1
(iii) −13, −27
(iv) −26, 17
(v) −317, −603
(vi) −777, 7
Ответ:
i) -7 <6
Это потому, что каждое положительное целое число больше любого отрицательного целого числа.
ii) -1 <0
Это потому, что ноль больше любого отрицательного целого числа.
iii) -27 <-13
Поскольку 27 больше 13, -27 меньше -13.
iv) -26 <17
Это потому, что каждое положительное целое число больше любого отрицательного целого числа.
v) -603 <-317
Поскольку 603 больше 317, -603 меньше -317.
vi) -777 <7
Это потому, что каждое положительное целое число больше любого отрицательного целого числа.
Страница № 64:
Вопрос 6:
Запишите все целые числа от
(i) 0 до 6
(ii) −5 и 0
(iii) −3 и 3
(iv) от −7 до −5
Ответ:
i) 1, 2, 3, 4, 5
ii) -4, -3, -2, -1
iii) -2, -1, 0, 1, 2
iv) -6
Страница № 64:
Вопрос 7:
Заполните пропуски соответствующим символом> или <:
(i) 0…… 7
(ii) 0 …… −3
(iii) −5 …… −2
(iv) −15 …… 13
(v) −231 …… −132
(vi) −6 … … 6
Ответ:
i) 0 <7
Это потому, что 0 меньше любого положительного целого числа.
ii) 0> -3
Это потому, что 0 больше любого отрицательного целого числа.
iii) -5 <-2
Поскольку 5 больше 2, -5 меньше -2.
iv) -15 <13
Это потому, что каждое положительное целое число больше любого отрицательного целого числа.
v) -231 <-132
Поскольку 231 больше 132, -231 меньше -132.
vi) -6 <6
Это потому, что каждое положительное целое число больше любого отрицательного целого числа.
Страница № 64:
Вопрос 8:
Запишите следующие целые числа в порядке возрастания:
(i) 5, −7, −2, 0, 8
(ii) −23, 12, 0, −6, −100, −1
(iii) −17 , 15, −363, −501, 165
(iv) 21, −106, −16, 16, 0, −2, −81
Ответ:
i) -7 <-2 <0 <5 <8
ii) -100 <-23 <-6 <-1 <0 <12
iii) -501 <-363 <-17 <15 <165
iv) -106 <-81 <-16 <-2 <0 <16 <21
Страница № 64:
Вопрос 9:
Запишите следующие целые числа в порядке убывания:
(i) 0, 7, −3, −9, −132, 36
(ii) 51, −53, −8, 0, −2
(iii) −71 , −81, 36, 0, −5
(iv) −365, −515, 102, 413, −7
Ответ:
i) 36> 7> 0> -3> -9> -132
ii) 51> 0> -2> -8> -53
iii) 36> 0> -5> -71> -81
iv) 413> 102> -7> -365> -515
Страница № 64:
Вопрос 10:
В числовой строке запишите целое число, равное
(i) 4 больше 6
(ii) 5 больше -6
(iii) 6 меньше 2
(iv) 2 меньше -3
Ответ:
i) 4 больше 6
Нам нужно целое число, которое на 4 больше 6.Итак, мы начнем с 6 и проделаем 4 шага вправо, чтобы получить 10.
ii) 5 больше, чем -6
Нам нужно целое число, которое на 5 больше, чем -6. Итак, мы начнем с -6 и проделаем 5 шагов вправо, чтобы получить -1.
iii) 6 меньше 2
Нам нужно целое число, которое на 6 меньше 2. Итак, мы начнем с 2 и проделаем 6 шагов влево, чтобы получить -4.
iv) 2 меньше -3
Нам нужно целое число, которое на 2 меньше -3. Итак, мы начнем с -3 и проделаем 2 шага влево, чтобы получить -5
Страница № 64:
Вопрос 11:
Для каждого из следующих утверждений напишите (T) для истинного и (F) для ложного:
(i) Наименьшее целое число равно нулю.
(ii) Ноль не является целым числом.
(iii) Нулевой противоположностью является ноль.
(iv) -10 больше -6.
(v) Абсолютное значение целого числа всегда больше целого.
(vi) 0 больше любого отрицательного целого числа.
(vii) Каждое отрицательное целое число меньше любого натурального числа.
(viii) Преемник −187 равен −188.
(ix) Предшественник −215 равен −214.
Ответ:
i) Неверно
Это потому, что 0 больше любого отрицательного целого числа.
ii) Ложь
0 — целое число, поскольку мы знаем, что каждое целое число является целым числом, а 0 — целым числом.
iii) Истинно
0 — целое число, которое не является ни положительным, ни отрицательным. Итак, противоположность нулю — это ноль.
iv) Неверно
Поскольку 10 больше 6, -10 меньше -6.
v) Верно
Это потому, что абсолютное значение является положительным числом. Например, -2 — целое число, но его абсолютное значение равно 2, и оно больше -2.
vi) Верно
Это потому, что все отрицательные целые числа находятся слева от 0.
vii) Истина
Это потому, что натуральные числа положительны, и каждое положительное целое число больше любого отрицательного целого числа.
viii) Неверно
Это потому, что преемник -187 равен -186 (-186 + 1). Последовательно двигаемся слева направо по числовой прямой.
ix) Неверно
Это потому, что предшественником -215 является -216 (-216-1). Чтобы найти предшественника, двигаемся справа налево по числовой прямой.
Страница № 64:
Вопрос 12:
Найдите значение
(i) | −9 |
(ii) | −36 |
(iii) | 0 |
(iv) | 15 |
(в) — | −3 |
(vi) 7 + | −3 |
(vii) | 7−4 |
(viii) 8 — | −7 |
Ответ:
i) Значение | -9 | равно 9
ii) Значение | -36 | равно 36
iii) Значение | 0 | равно 0
iv) Значение | 15 | равно 15
v) Значение | -3 | составляет 3
∴ — | -3 | = -3
vi) 7 + | -3 |
= 7 + 3 (значение | -3 | равно 3)
= 10
vii) | 7 — 4 |
= | 3 |
= 3 (значение | 3 | равно 3)
viii) 8 — | -7 |
= 8-7 (значение | -7 | равно 7)
= 1
Страница № 64:
Вопрос 13:
(i) Запишите пять целых отрицательных чисел больше −7.
(ii) Запишите пять целых отрицательных чисел меньше −20.
Ответ:
i) Каждое отрицательное целое число справа от -7 больше -7.
Итак, пять отрицательных целых чисел, которые больше -7, равны -6, -5, -4, -3, -2 и -1.
ii) Каждое отрицательное целое число слева от -20 меньше -20.
Итак, пять отрицательных целых чисел меньше -20 — это -21, -22, -23, -24 и -25.
Страница № 68:
Вопрос 1:
В числовой строке сложите следующие целые числа:
(i) 9 + (−6)
(ii) (−3) + 7
(iii) 8 + (−8)
(iv) (−1) + (−3)
(v) (−4) + (−7)
(vi) (−2) + (−8)
(vii) 3 + (−2) + (−4)
(viii) ( −1) + (−2) + (−3)
(ix) 5 + (−2) + (−6)
Ответ:
i) На числовой прямой мы начинаем с 0 и перемещаемся на 9 шагов вправо, чтобы достичь точки A.Теперь, начиная с A, мы перемещаемся на 6 шагов влево, чтобы достичь точки B.
B представляет собой целое число 3.
∴ 9 + (−6) = 3
(ii) На числовой прямой мы начинаем с 0 и переместимся на 3 шага влево, чтобы достичь точки A. Теперь, начиная с A, мы переместимся на 7 шагов вправо, чтобы достичь точки B.
B представляет собой целое число 4.
∴ (−3) + 7 = 4
(iii) На числовой прямой мы начинаем с 0 и перемещаемся на 8 шагов вправо, чтобы достичь точки A. Теперь, начиная с A, мы перемещаемся на 8 шагов влево, чтобы достичь точки B.
B представляет собой целое число 0.
∴ 8 + (−8) = 0
(iv) На числовой прямой мы начинаем с 0 и перемещаемся на 1 шаг влево, чтобы достичь точки A. Теперь, начиная с A, мы перемещаемся на 3 шага влево, чтобы достичь точки B.
B представляет собой целое число −4.
∴ (−1) + (−3) = −4
(v) На числовой прямой мы начинаем с 0 и перемещаемся на 4 шага влево, чтобы достичь точки A. Теперь, начиная с A, мы перемещаемся на 7. шаги влево для достижения точки B.
B представляет собой целое число -11.
∴ (−4) + (−7) = −11
(vi) На числовой прямой мы начинаем с 0 и перемещаемся на 2 шага влево, чтобы достичь точки A. Теперь, начиная с A, мы перемещаемся 8 шагов влево для достижения точки B.
B представляет собой целое число -10.
∴ (−2) + (−8) = −10
(vii) На числовой прямой мы начинаем с 0 и перемещаемся на 3 шага вправо, чтобы достичь точки A. Теперь, начиная с A, мы перемещаемся на 2 шаги влево, чтобы достичь точки B. И снова, начиная с точки B, мы перемещаемся на 4 шага влево, чтобы достичь точки C.
C представляет собой целое число −3.
∴ 3 + (−2) + (−4) = −3
(viii) На числовой прямой мы начинаем с 0 и перемещаемся на 1 шаг влево, чтобы достичь точки A. Теперь, начиная с A, мы перемещаемся на 2 шага влево, чтобы достичь точки B. Снова, начиная с B, мы перемещаемся на 3 шага влево, чтобы достичь точки C.
C представляет собой целое число −6.
∴ (−1) + (−2) + (−3) = −6
(ix) На числовой прямой мы начинаем с 0 и перемещаемся на 5 шагов вправо, чтобы достичь точки A.Теперь, начиная с A, мы перемещаемся на 2 шага влево, чтобы достичь точки B. Снова, начиная с B, мы перемещаемся на 6 шагов влево, чтобы достичь точки C.
C представляет собой целое число −3.
∴ 5 + (−2) + (−6) = −3
Страница № 68:
Вопрос 2:
Заполните пропуски:
(i) (−3) + (−9) = …….
(ii) (−7) + (−8) = …….
( iii) (−9) + 16 = …….
(iv) (−13) + 25 =…….
(v) 8 + (−17) = …….
(vi) 2 + (−12) = …….
Ответ:
(i)
(−3) + (−9)
= −3 — 9
= −12
(ii)
(−7) + (−8)
= −7-8
= −15
(iii)
(−9) + 16
= −9 + 16
= 7
(iv)
(−13) + 25
= −13 + 25
= 12
(v)
8 + ( −17)
= 8-17
= −9
(v)
2 + (−12)
= 2-12
= −10
Страница № 68:
Вопрос 3:
Добавить:
(i) -365-87
(ii) -73-687
(iii) -1065-987
(iv) -3596-1089
Ответ:
(i)
−365 −87−452
−365
−365 −87 −365 −87 -365 и -87 — оба отрицательные целые числа.Итак, складываем 365 и 87, а перед суммой ставим знак минус.
(ii)
−687 −73−760
-687 и -73 — оба отрицательные целые числа. Итак, складываем 365 и 87, а перед суммой ставим знак минус.
(iii)
−1065 −987−2052
-1065 и -987 — оба отрицательные целые числа. Итак, складываем 1065 и 987, а перед суммой ставим знак минус.
(iv)
−3596−1089−4685
-3596 и -1089 — оба отрицательные целые числа. Итак, складываем 3596 и 1089, а перед суммой ставим знак минус.
Страница № 68:
Вопрос 4:
Доп. Адрес:
(i) -206 +98
(ii) +178-69
(iii) -103 +312
(iv) -493 +289
Ответ:
i)
−206 + 98−108 Поскольку мы добавляем отрицательное число к положительному, мы вычтем меньшее число, то есть 98, из большего числа, т.е.е. 206206 — 98 = 108 Поскольку большее число отрицательно, знак результата будет отрицательным. Таким образом, ответ будет -108
ii)
178-69 109
Поскольку мы добавляем отрицательное число к положительному, мы вычтем меньшее число, то есть 69, из большего числа, то есть 178178 — 69 = 109 Поскольку большее число положительно, знак результата будет положительным. Таким образом, ответ будет 109
(iii)
312 -103 209
Поскольку мы добавляем отрицательное число к положительному числу
, мы вычтем меньшее число, т.е.е. -103, от большего числа, т.е. 312
312-103 = 209
Поскольку большее число положительно, знак результата будет положительным.
Таким образом, ответ будет 209
(iv) −493 + 289−204
Поскольку мы добавляем отрицательное число к положительному числу
, мы вычтем меньшее число, то есть 289, из большего числа, т.е. 493.
493 — 289 = 204
Поскольку большее число отрицательно, знак результата будет отрицательным.
Итак, ответ будет -204
Страница № 68:
Вопрос 5:
Найдите сумму
(i) 137 и −354
(ii) 1001 и −13
(iii) −3057 и 199
(iv) −36 и 1027
(v) −389 и −1032
(vi) −36 и 100
(vii) 3002 и −888
(viii) −18, + 25 и −37
(ix) −312, 37 и 192
(x) −51, −203, 36 и −28
Ответ:
(i) 137 и −354−354 + 137−217 (ii) 1001 и −131001−13988 (iii) −3057 и 199−3057 199−2858 (iv) −36 и 10273057−363021 (v) −389 и −1032−1032−389−1421 (vi) −36 и 100100−3664 (vii) 3002 и −8883002−8882114
(viii) −18, + 25 и −37
25 + (−18) + (−37)
= 25 — (18 + 37)
= 25 — 55
= –30
(ix) −312, 39 и 192
39 + 192 + (−312)
= 39 + 192 — 312
= 231 −312
= −81
(x) −51, −203, 36 и −28
36 + (−51) + (−203) + (−28)
= 36 — (51 + 203 + 28)
= 36 — 282
= −246
Страница № 68:
Вопрос 6:
Найдите аддитивную обратную величину
(i) −57
(ii) 183
(iii) 0
(iv) −1001
(v) 2054
Ответ:
(i) −57 + 57 = 0
Итак, аддитивная величина, обратная −57, равна 57.
(ii) 183 — 183 = 0
Таким образом, аддитивная величина, обратная 183, равна −183.
(iii) 0 + 0 = 0
Таким образом, аддитивная величина, обратная 0, равна 0.
(iv) −1001 + 1001 = 0
Таким образом, аддитивная величина, обратная −1001, равна 1001.
(v) 2054-2054 = 0
Таким образом, аддитивная величина, обратная 2054, равна -2054
Страница № 68:
Вопрос 7:
Запишите преемника каждого из следующих:
(i) 201
(ii) 70
(iii) −5
(iv) −99
(v) −500
Ответ:
(i) Преемник 201:
201 + 1 = 202
(ii) Преемник 70:
70 + 1 = 71
(iii) Преемник −5:
−5 + 1 = −4
( iv) Преемник −99:
−99 + 1 = −98
(v) Преемник −500:
−500 + 1 = −499
Страница № 68:
Вопрос 8:
Запишите предшественника каждого из следующих:
(i) 120
(ii) 79
(iii) −8
(iv) −141
(v) −300
Ответ:
(i) Предшественник числа 120:
120 — 1 = 119
(ii) Предшественник числа 79:
79-1 = 78
(iii) Предшественник числа -8:
−8-1 = −9
( iv) Предшественник −141:
−141-1 = −142
(v) Предшественник −300:
−300-1 = −301
Стр. № 69:
Вопрос 9:
Упростить:
(i) (−7) + (−9) + 12 + (−16)
(ii) 37 + (−23) + (−65) + 9 + (−12)
(iii) ( −145) + 79 + (−265) + (−41) + 2
(iv) 1056 + (−798) + (−38) + 44 + (−1)
Ответ:
(i) (−7) + (−9) + 12 + (−16)
= 12 — (7 + 9 + 16)
= 12-32
= −20
(ii) 37 + (−23 ) + (−65) + 9 + (−12)
= 37 + 9 — (23 + 65 + 12)
= 46-100
= −54
(iii) (−145) + 79 + (- 265) + (−41) + 2
= 79 +2 — (145 + 265 + 41)
= 81-451
= −370
(iv) 1056 + (−798) + (−38) + 44 + (−1)
= 1056 + 44 — (798 + 38 + 1)
= 1100-837
= −263
Стр. № 69:
Вопрос 10:
Автомобиль проехал 60 км к северу от Патны, а затем 90 км к югу оттуда.Как далеко от Патны наконец оказалась машина?
Ответ:
Пусть расстояние, пройденное в северном направлении, будет положительным, а в южном — отрицательным.
Пройденное расстояние к северу от Патны = 60 км
Пройденное расстояние к югу от Патны = -90 км
Общее расстояние, пройденное на машине = 60 + (-90)
= -30 км
Автомобиль прошел 30 км к югу от Патны.
Стр. № 69:
Вопрос 11:
Мужчина купил несколько карандашей за 30 рупий и несколько ручек за 90 рупий. На следующий день он снова купил несколько карандашей за 25 рупий. Затем он продал все карандаши за 20 рупий и ручки за 70 рупий. прибыль или убыток?
Ответ:
Общая себестоимость = Цена карандашей + Цена ручек
= 30 + 90 + 25
= 145 рупий
Общая проданная сумма = Цена ручки + Цена карандашей
= 20 + 70
= 90
Цена продажи — себестоимость = 90 — 145
= -55
Отрицательный знак означает убыток.
Следовательно, его чистый убыток составил 55.
Стр. № 69:
Вопрос 12:
Для каждого из следующих утверждений напишите (T) для истинного и (F) для ложного:
(i) Сумма двух отрицательных целых чисел всегда является отрицательным целым числом.
(ii) Сумма отрицательного целого числа и положительного целого числа всегда является отрицательным целым числом.
(iii) Сумма целого и отрицательного числа равна нулю.
(iv) Сумма трех разных целых чисел никогда не может быть равна нулю.
(v) | −5 | <| −3 |
(vi) | 8 — 5 | = | 8 | + | −5 |
Ответ:
(i) Верно
Например: — 2 + (-1) = -3
(ii) Неверно
Может быть отрицательным или положительным.
Например: -2 + 3 = 1 дает положительное целое число, но -5 + 2 = -3 дает отрицательное целое число.
(iii) Верно
Например: 100 + (-100) = 0
(iv) Неверно
Например: (-5) + 2 + 3 = 0
(v) Неверно
| -5 | = 5 и | -3 | = 3, 5> 3
(vi) Неверно
| 8 — 5 | = 3
| 8 | + | −5 | = 8 + 5
= 13
∴ | 8 — 5 | ≠ | 8 | + | −5 |
Стр. № 69:
Вопрос 13:
Найдите целое число a такое, что
(i) a + 6 = 0
(ii) 5 + a = 0
(iii) a + (−4) = 0
(iv) — 8 + a = 0
Ответ:
(i) a + 6 = 0
=> a = 0-6
=> a = — 6
(ii) 5 + a = 0
=> a = 0-5
(iii ) a + (−4) = 0
=> a = 0 — (−4)
=> a = 4
(iv) −8 + a = 0
=> a = 0 + 8
=> а = 8
Страница № 70:
Вопрос 1:
Вычтем:
(i) 18 из −34
(ii) −15 из 25
(iii) −28 из −43
(iv) 68 из −37
(v) 219 из 0
(vi) −92 из 0
(vii) −135 от −250
(viii) −2768 от −287
(ix) 6240 от −271
(x) −3012 от 6250
Ответ:
(i) −34 — 18
= −52
(ii) 25 — (−15)
= 25 + 15
= 40
(iii) −28 из −43
= −43 — (−28)
= −43 + 28
= −15
(iv) 68 от −37
= −37-68
= −105
(v) 219 от 0
= 0-219
= −219
(vi ) −92 от 0
= 0 — (−92)
= 0 + 92
= 92
(vii) −135 от −250
= −250 — (−135)
= −250 + 135
= — 115
(viii) −2768 от −287
= −287 — (−2768)
= 2768-287
= 2481
(ix) 6240 от −271
= −271 — (6240)
= — 271 — 6240
= −6511
(x) −3012 из 6250
= 6250 — (−3012)
= 6250 + 3012
= 9262
Страница № 70:
Вопрос 2:
Вычтем сумму −1050 и 813 из −23.
Ответ:
Сумма −1050 и 813:
−1050 + 813
= −237
Вычитание суммы −1050 и 813 из −23:
−23 — (−237)
= −23 +237
= 214
Страница № 70:
Вопрос 3:
Вычтите сумму −250 и 138 из суммы 136 и −272.
Ответ:
Сумма 138 и −250:
138 + (−250)
= 138 — 250
= −112
Сумма 136 и −272:
= 136 + (−272)
= 136 — 272
= −136
Вычитая сумму −250 и 138 из суммы 136 и −272:
−136 — (−112)
= −136 + 112
= −24
Страница № 70:
Вопрос 4:
Из суммы 33 и −47 вычтем −84.
Ответ:
Сложение 33 и −47:
33 + (−47)
= 33-47
= −14
Вычитание −84 из −14:
−14 — (−84)
= −14 + 84
= 70
Страница № 70:
Вопрос 5:
Добавьте −36 к разности −8 и −68.
Ответ:
Разница −8 и −68:
−8 — (−68)
= −8 + 68
= 60
Добавление -36 к 60:
−36 + 60
= 24
Страница № 70:
Вопрос 6:
Упростить:
(i) [37 — (−8)] + [11 — (−30)]
(ii) [−13 — (−17) + [−22 — (−40)]
Ответ:
(i) [37 — (−8)] + [11 — (−30)]
= (37 + 8) + (11 + 30)
= 45 + 41
= 86
(ii) [−13 — (−17) + [−22 — (−40)]
= (−13 +17) + (-22 + 40)
= 4 + 18
= 22
Страница № 70:
Вопрос 7:
Найдите 34 — (−72) и (−72) — 34.Они равны?
Ответ:
Нет, не равны.
34 — (−72)
= 34 + 72
= 106
(−72) — 34
= −72-34
= −106
Поскольку 106 не равно −106, два выражения не равный.
Страница № 70:
Вопрос 8:
Сумма двух целых чисел равна −13. Если одно из чисел 170, найдите другое.
Ответ:
Пусть другое целое число будет x.
Согласно вопросу, мы имеем:
x + 170 = −13
=> x = −13-170
=> x = −183
Таким образом, другое целое число равно −183.
Страница № 70:
Вопрос 9:
Сумма двух целых чисел равна 65. Если одно из целых чисел равно -47, найдите другое.
Ответ:
Пусть другое целое число будет x .
Согласно вопросу, мы имеем:
x + (−47) = 65
=> x — 47 = 65
=> x = 65 + 47
=> x = 112
Таким образом, другое целое число равно 112.
Страница № 70:
Вопрос 10:
Какие из следующих утверждений верны, а какие нет?
(i) Сумма двух целых чисел всегда является целым числом.
(ii) Разница двух целых чисел всегда является целым числом.
(iii) −14> −8 — (−7)
(iv) −5-2> −8
(v) (−7) — 3 = (−3) — (−7)
Ответ:
(i) Истина
Целое число, добавленное к целому, дает целое число.
(ii) Истина
Целое число, вычитаемое из целого числа, дает целое число.
iii) Неверно
−8 — (−7)
= −8 + 7
= −1
Поскольку 14 больше 1, −1 больше −14.
iv) Истинно
−5-2 = −7
Поскольку 8 больше 7, −7 больше −8.
-7> −8
v) Неверно
L.H.S.
(−7) — 3 = −10
R.H.S.
(−3) — (−7)
= (−3) + 7
= 4
∴ L.H.S. ≠ R.H.S.
Страница № 71:
Вопрос 11:
Точка A находится на горе, которая находится на высоте 5700 метров над уровнем моря, а точка B находится в шахте, которая находится на 39600 метров ниже уровня моря.Найдите расстояние по вертикали между A и B .
рисунок
Ответ:
Считаем высоту над уровнем моря положительной, а высоту ниже уровня моря — отрицательной.
∴ Высота точки A от уровня моря = 5700 м
Глубина точки B от уровня моря = -39600 м
Расстояние по вертикали между A и B = Расстояние от точки A до уровня моря — Расстояние от точки B до уровня моря
= 5700 — (-39600)
= 45300 м
Страница № 71:
Вопрос 12:
В день в Сринагаре температура в 6 р.м. было 1 ° C, но в полночь того дня оно упало до -4 ° C. На сколько градусов по Цельсию упала температура?
Ответ:
Начальная температура Сринагара в 18:00. = 1 ° C
Конечная температура Сринагара в полночь = −4 ° C
Изменение температуры = Конечная температура — Начальная температура
= (−4-1) ° C
= −5 ° C
Итак, температура изменилась на −5 ° C.
Знак минус означает, что температура упала.
Итак, температура упала на 5 ° C.
Лист № 72:
Вопрос 1:
Умножить:
(i) 15 на 9
(ii) 18 на −7
(iii) 29 на −11
(iv) −18 на 13
(v) −56 на 16
(vi) 32 на −21
(vii) −57 на 0
(viii) 0 на −31
(ix) −12 на −9
(x) −746 на −8
(xi) 118 на −7
(xii) −238 на — 143
Ответ:
(i) 15 на 9
= 15 × 9
= 135
(ii) 18 на −7
= — (18 × 7)
= –126
(iii) 29 на –11
= — (29 × 11)
= –319
(iv) –18 на 13
= — (18 × 13)
= –234
(v) –56 на 16
= — (56 × 16)
= –896
(vi) 32 на –21
= — (32 × 21)
= –672
(vii) –57 на 0
= — (57 × 0)
= 0
(viii) 0 на –31
= — (0 × 31)
= 0
(ix) –12 на –9
= (–12) × (- 9)
= 108
(x) (- 746) на (–8)
= (–746) × (–8)
= 5968
(xi) 118 на −7
= 118 × (-7)
= –826
(xii) −238 на −143
= (−238 ) × (−143)
= 34034
Страница № 73:
Вопрос 2:
Найдите продукты:
(i) (−2) × 3 × (−4)
(ii) 2 × (−5) × (−6)
(iii) (−8) × 3 × 5
(iv ) 8 × 7 × (−10)
(v) (−3) × (−7) × (−6)
(vi) (−8) × (−3) × (−9)
Ответ:
(i) (–2) × 3 × (–4)
= [(–2) × 3] × (–4)
= (–6) × (–4)
= 24
(ii) 2 × (–5) × (–6)
= [2 × (–5)] × (–6)
= (–10) × (–6)
= 60
(iii) (–8) × 3 × 5
= [(–8) × 3] × 5
= (–24) × 5
= –120
(iv) 8 × 7 × (–10)
= [8 × 7] × (–10)
= 56 × (–10)
= –560
(v) (–3) × (–7) × (–6)
= [(–3) × (–7)] × (–6)
= 21 × (–6)
= –126
(vi) (–8) × (–3) × (–9)
= [(–8) × (–3)] × (–9)
= 24 × (–9)
= –216
Страница № 73:
Вопрос 3:
Используйте удобные группировки и найдите значения
(i) 18 × (−27) × 30
(ii) (−8) × (−63) × 9
(iii) (−17) × (−23) × 41
(iv) (−51) × (−47) × (−19)
Ответ:
(i) 18 × (–27) × 30
= (–27) × [18 × 30]
= (–27) × 540
= –14580
(ii) (–8) × (–63) × 9
= [(–8) × (–63)] × 9
= 504 × 9
= 4536
(iii) (–17) × (–23) × 41
= [(–17) × ( –23)] × 41
= 391 × 41
= 16031
(iv) (–51) × (–47) × (–19)
= [(–51) × (–47)] × (–19 )
= 2397 × (–19)
= — 45543
Страница № 73:
Вопрос 4:
Проверьте следующее:
(i) 18 × [9 + (−7)] = 18 × 9 + 18 × (−7)
(ii) (−13) × [(−6) + (−19)] = (−13) × (−6) + (−13) × (−19)
Ответ:
(i)
Л.H.S .
= 18 × [9 + (–7)]
= 18 × [9–7]
= 18 × 2
= 36
R.H.S .
= 18 × 9 + 18 × (–7)
= 162 — (18 × 7)
= 162 — 126
= 36
∴ L.H.S = R.H.S
Следовательно, проверено.
(ii) (–13) × [(–6) + (–19)] = (–13) × (–6) + (–13) × (–19)
L.H.S.
= (–13) × [(–6) + (–19)]
= (–13) × [–6 — 19]
= (–13) × (–25)
= 325
р.H.S .
= (–13) × (–6) + (–13) × (–19)
= 78 + 247
= 325
∴ L.H.S = R.H.S
Следовательно, проверено.
Страница № 73:
Вопрос 5:
Заполните следующую таблицу умножения:
| x | −3 | -2 | -1 | 0 | 1 | 2 | 3 |
| −3 | |||||||
| -2 | |||||||
| -1 | |||||||
| 0 | |||||||
| 1 | |||||||
| 2 | |||||||
| 3 |
Ответ:
| × | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| –3 | 9 | 6 | 3 | 0 | –3 | –6 | –9 |
| –2 | 6 | 4 | 2 | 0 | –2 | –4 | –6 |
| –1 | 3 | 2 | 1 | 0 | –1 | –2 | –3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| 2 | –6 | –4 | –2 | 0 | 2 | 4 | 6 |
| 3 | –9 | –6 | –3 | 0 | 3 | 6 | 9 |
Страница № 73:
Вопрос 6:
Какие из следующих утверждений верны, а какие — ложны?
(i) Произведение положительного целого числа и отрицательного целого числа отрицательно.
(ii) Произведение двух отрицательных целых чисел является отрицательным целым числом.
(iii) Произведение трех отрицательных целых чисел является отрицательным целым числом.
(iv) Каждое целое число при умножении на −1 дает его мультипликативную обратную величину.
Ответ:
(i) Произведение положительного целого числа и отрицательного целого числа отрицательно.
Истина
(ii) Произведение двух отрицательных целых чисел является отрицательным целым числом.
False
Произведение двух отрицательных целых чисел всегда является положительным целым числом.
(iii) Произведение трех отрицательных целых чисел является отрицательным целым числом.
Истинно
(iv) Каждое целое число, умноженное на (–1), дает его обратное мультипликативное число.
Ложь
Каждое целое число, умноженное на (1), дает его обратное умножение.
Страница № 73:
Вопрос 7:
Упростить:
(i) (−9) × 6 + (−9) × 4
(ii) 8 × (−12) + 7 × (−12)
(iii) 30 × (−22) + 30 × (14)
(iv) (−15) × (−14) + (−15) × (−6)
(v) 43 × (−33) + 43 × (−17)
(vi) (−36 ) × (72) + (−36) × 28
(vii) (−27) × (−16) + (−27) × (−14)
Ответ:
(i) (–9) × 6 + (–9) × 4
Решение:
Используя закон распределения:
(–9) × 6 + (–9) × 4
= (–9) × ( 6 + 9)
= (–9) × 10
= –90
(ii) 8 × (–12) + 7 × (–12)
Решение :
Использование закона распределения:
8 × (- 12) + 7 × (–12)
= (–12) × (8 + 7)
= (–12) × 15
= –180
(iii) 30 × (–22) + 30 × (14)
Решение :
Использование закона распределения:
30 × (–22) + 30 × (14)
= 30 × [(–22) + 14]
= 30 × [–22 + 14]
= 30 × (–8)
= –240
(iv) (–15) × (–14) + (–15) × (–6)
Решение:
(–15) × (–14) + (- 15) × (–6)
Используя закон распределения:
= (–15) × [(–14) + (–6)]
= (–15) × [–14 — 6]
= (–15) × (–20)
= 300
(v) 43 × (–33) + 43 × (–17)
Решение:
43 × (–33) + 43 × (–17)
Использование закона распределения :
= (43) × [- (33) + (–17)]
= (43) × [–33 — 17]
= 43 × (–50)
= –2150
(vi) (–36) × (72) + (–36) × 28
Решение
(–36) × (72) + (- 36) × 28
Используя закон распределения:
= (–36) × (72 + 28)
= (–36) × 100
= –3600
(vii) (–27) × (–16) + ( –27) × (–14)
Решение:
(–27) × (–16) + (–27) × (–14)
Использование закона распределения:
= (–27) × [(–16 ) + (–14)]
= (–27) × [–16 –14]
= (–27) × [–30]
= 810
Стр. № 75:
Вопрос 1:
Разделить:
(i) 85 на −17
(ii) −72 на 18
(iii) −80 на 16
(iv) −121 на 11
(v) 108 на −12
(vi) −161 на 23
(vii) −76 на −19
(viii) −147 на −21
(ix) −639 на −71
(x) −15625 на −125
(xi) 2067 на −1
(xii) 1765 на −1765
(xiii) 0 на −278
(xiv) 3000 на −100
Ответ:
(i) 85 на — 17
= −8517
= –5
(ii) –72 на 18
= −7218
= –4
(iii) –80 на 16
= −8016
= –5
(iv) –121 на 11
= −12111
= –11
(v) 108 на –12
= 108–12
= –9
(vi) –161 на 23
= −16123
= –7
(vii) –76 на –19
= –76–19
= 4
(viii) –147 на –21
= –147–21
= 7
(ix) –639 на –71
= –639–71 = 9
(x) –639 на –71
= –639–71 = 9
(x) –15625 на –125
= –15625–125 = 125
(xi) 2067 на –1
= 2067−1 = −2067
(xii) 1765 на –1765
= 1765−1765 = −1 × 17651765 = -1 × 1 = -1
(xiii) 0 на –278
= 0–278 = 0
(xiv) 3000 на –100
= 3000–100 = –30
Стр. № 75:
Вопрос 2:
Заполните пропуски:
(i) 80 ÷ (……) = −5
(ii) (−84) + (……) = −7
(iii) (……) ÷ (−5) = 25
( iv) (……) ÷ 372 = 0
(v) (……) ÷ 1 = −186
(vi) (……) ÷ 17 = −2
( vii) (……) ÷ 165 = −1
(viii) (……) ÷ (−1) = 73
(ix) 1 ÷ (……) = — 1
Ответ:
(i) 80 ÷ ( –16 ) = –5
(ii) (–84) ÷ ( 12 ) = –7
(iii) ( –125 ) ÷ (–5) = 25
(iv) ( 0 ) ÷ (372) = 0
(v) ( –186 ) ÷ 1 = –186
(vi) ( –34 ) ÷ 17 = –2
(vii) ( –165 ) ÷ 165 = –1
(viii) ( –73 ) ÷ –1 = 73
(ix) 1 ÷ ( –1 ) = –1
Стр. № 75:
Вопрос 3:
Запишите (T) для истинного и (F) для ложного для каждого из следующих утверждений:
(i) 0 ÷ (−6) = 0
(ii) (−8) ÷ 0 = 0
(iii) 15 ÷ (−1) = −15
(iv) (−16) ÷ (−4) = −4
(v) (−7) ÷ (−1) = 7
(vi) (−18) ÷ 9 = — 2
(vii) 20 ÷ (−5) = −4
(viii) (−10) ÷ 1 = −10
(ix) (−1) ÷ (−1) = −1
Ответ:
(i) Верно
(ii) Неверно
Это потому, что мы не можем разделить любое целое число на 0.Если мы это сделаем, мы получим частное как бесконечность.
(iii) Верно
(iv) Неверно
Это потому, что деление любых двух отрицательных целых чисел всегда дает положительное частное.
(v) Верно
(vi) Верно
(vii) Верно
(viii) Верно
(ix) Ложно
Это потому, что деление любых двух отрицательных целых чисел всегда дает положительное частное.
Стр. № 75:
Вопрос 1:
Что из следующего является верным?
(a) −4> −3
(b) −4 <−3
(c) −4 и −3 несопоставимы
Ответ:
(b) –4 <–3
Поскольку 4 больше 3, –4 меньше –3.
Стр. № 75:
Вопрос 2:
2 меньше −3 равно
(а) −1
(б) 1
(в) −5
(г) 5
Ответ:
(c) –5
2 меньше –3 означает следующее:
= –3 — 2
= –5
Страница № 76:
Вопрос 3:
4 больше −5 равно
(а) 9
(б) −9
(в) −1
(г) 1
Ответ:
c) –1
4 больше чем –5 означает следующее:
= –5 + 4
= –1
Страница № 76:
Вопрос 4:
2 меньше −7 равно
(a) −9
(b) −5
(c) 5
(d) ни один из этих
Ответ:
(a) –9
2 меньше −7 означает следующее:
= −7 — 2
= −9
Страница № 76:
Вопрос 5:
7 + | −3 | знак равно
(a) 4
(b) 10
(c) −10
(d) ни один из этих
Ответ:
(б) 10
7 + | -3 |
= 7 + (+ 3) (Абсолютное значение −3 равно 3.)
= 7 + 3
= 10
Страница № 76:
Вопрос 6:
(-42) + (-35) =?
(a) −7
(b) 7
(c) −77
(d) ни один из этих
Ответ:
(в) –77
(–42) + (–35)
= –42 — 35
= –77
Страница № 76:
Вопрос 7:
(-37) + 6 =?
(a) −43
(b) −31
(c) 31
(d) ни один из этих
Ответ:
(б) –31
(−37) + 6
= −37 + 6
= −31
Страница № 76:
Вопрос 8:
49 + (−27) =?
(a) −73
(b) 73
(c) 22
(d) ни один из этих
Ответ:
(в) 22
49 + (−27)
= 49 — 27
= 22
Страница № 76:
Вопрос 9:
Преемником −18 является
(a) −19
(b) 17
(c) −17
(d) 19
Ответ:
(c) –17
Последовательно перемещаемся слева направо от числовой строки.
Страница № 76:
Вопрос 10:
Предшественник −16 —
(a) −15
(b) −17
(c) 15
(d) 17
Ответ:
(b) –17
Чтобы найти предшественника числа, мы перемещаемся справа налево от числовой строки.
Страница № 76:
Вопрос 11:
Аддитивная величина, обратная −5, равна
(a) 5
(b) 0
(c) −4
(d) −6
Ответ:
(a) 5
Если мы добавим аддитивное обратное число к числу, мы получим 0.
−5 + 5 = 0
Страница № 76:
Вопрос 12:
−12 — (−5) =?
(a) −17
(b) −7
(c) 7
(d) ни один из этих
Ответ:
(б) –7
−12 — (−5)
= −12 + 5
= −7
Страница № 76:
Вопрос 13:
−5 — (−8) =?
(a) 3
(b) 13
(c) −3
(d) ни один из этих
Ответ:
б 13.5 — (−8)
= 5 + 8
= 13
Страница № 76:
Вопрос 14:
Сумма двух целых чисел равна −25. Если одному из них 30, то другому
(а) 55
(б) 5
(в) -55
(г) ни один из этих
Ответ:
(c) –55
Пусть x будет другим целым числом.
x + 30 = –25
⇒ x = –25 — 30
⇒ x = –55
Страница № 76:
Вопрос 15:
Сумма двух целых чисел равна 20.Если один из них равен −5, то другой равен
(a) 25
(b) −25
(c) 15
(d) ни один из этих
Ответ:
(a) 25
Пусть другое целое число будет x
x + (-5) = 20
⇒ x — 5 = 20
⇒ x = 25
Страница № 76:
Вопрос 16:
Сумма двух целых чисел равна −13.Если один из них равен 8, то другой равен
(a) −5
(b) −21
(c) 21
(d) ни один из этих
Ответ:
(b) −21
Пусть другое целое число будет x .
x + 8 = −13
=> x = −13-8
=> x = −21
Страница № 76:
Вопрос 17:
При вычитании −8 из 0 получаем
(a) −8
(b) 8
(c) ни один из этих
Ответ:
(б) 8
0 — (−8)
= 0 + 8
= 8
Страница № 76:
Вопрос 18:
8 + (−8) =?
(a) 16
(b) −16
(c) 0
(d) ни один из этих
Ответ:
(в) 0
8 + (−8)
= 8-8
= 0
Страница № 76:
Вопрос 19:
(−6) + 4 — (−3) =?
(a) −5
(b) −1
(c) 1
(d) ни один из этих
Ответ:
(в) 1
(−6) + 4 — (−3)
= −6 + 4 + 3
= −6 + 7
= 1
Страница № 76:
Вопрос 20:
6 — (−4) =?
(а) 2
(б) −10
(в) 10
(г) ни один из этих
Ответ:
(в) 10
6 — (−4)
= 6 + 4
= 10
Страница № 76:
Вопрос 21:
(−7) + (−9) + 12 + (−16) =?
(a) −20
(b) 20
(c) −12
(d) ни один из этих
Ответ:
(а) –20
(−7) + (−9) + 12 + (−16)
= −7 — 9 + 12 −16
= −20
Страница № 76:
Вопрос 22:
При вычитании 8 из −4 получаем
(a) 4
(b) 12
(c) −12
(d) ни один из этих
Ответ:
(в) –12
— 4 — 8
= — 12
Страница № 76:
Вопрос 23:
При вычитании −9 из −6 получаем
(a) −15
(b) −3
(c) 3
(d) ни один из этих
Ответ:
(c) 3
Имеем:
−6 — (−9)
= −6 + 9
= 3
Страница № 76:
Вопрос 24:
При вычитании −5 из 10 получаем
(a) 5
(b) −15
(c) 15
(d) ни один из этих
Ответ:
(c) 15
Имеем:
10 — (−5)
= 10 + 5
= 15
Стр. № 77:
Вопрос 25:
(−6) × 9 =?
(a) 54
(b) −54
(c) ни один из этих
Ответ:
(б) –54
Имеем:
(−6) × 9
= — (6 × 9)
= −54
Стр. № 77:
Вопрос 26:
(−9) × 6 + (−9) × 4 =?
(а) −90
(б) 90
(в) −18
(г) 18
Ответ:
(a) –90
(−9) × 6 + (−9) × 4
Используя распределительный закон:
(−9) × (6 + 4)
= (−9) × (10)
= — 90
Стр. № 77:
Вопрос 27:
36 ÷ (−9) =?
(а) 4
(б) −4
(в) ни один из этих
Ответ:
(б) –4
36 ÷ (−9)
36-9 = 369 × (-1) = 1 (-1) × 369 = -1 × 4 = -4
Страница № 78:
Вопрос 1:
Что такое целые числа? Запишите все целые числа от −5 до 5.
Ответ:
Числа …– 4, –3, –2, –1, 0, 1, 2, 3, 4 … являются целыми числами.
Группа положительных и отрицательных чисел, включающая 0, называется целыми числами.
–5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5
Страница № 78:
Вопрос 2:
Найдите в каждой из пар, представленных ниже, большее целое число.
(i) 0, −3
(ii) −4, −6
(iii) −99, 9
(iv) −385, −615
Ответ:
(i) 0, –3
0
Это потому, что 0 больше любого отрицательного целого числа.
(ii) –4, –6
–4
Поскольку 6 больше 4, –4 больше –6.
(iii) –99, 9
9
Это потому, что каждое положительное целое число больше любого отрицательного целого числа.
(iv) –385, –615
–385
Поскольку 615 больше 385, –385 больше –615.
Страница № 78:
Вопрос 3:
Запишите следующие целые числа в порядке возрастания:
−18, 16, 0, −5, 8, −36, −1, 1
Ответ:
Мы можем расположить данные целые числа в порядке возрастания следующим образом:
–36, –18, –5, –1, 0, 1, 8, 16
Страница № 78:
Вопрос 4:
Найдите значение:
(i) 9 — | −6 |
(ii) 6 + | −4 |
(iii) −8 — | −3 |
Ответ:
(i) 9 — | –6 |
= 9 — (6)
= 9 — 6
= 3
(ii) 6 + | –4 |
= 6 + (4)
= 6 + 4
= 10
(iii) –8 — | –3 |
= –8 — 3
= –11
Страница № 78:
Вопрос 5:
Запишите четыре целых числа меньше −6 и четыре целых числа больше −6.
Ответ:
Четыре целых числа меньше –6 (т. Е. Четыре отрицательных целых числа, которые лежат слева от –6) — это –7, –8, –9 и –10.
Четыре целых числа больше –6 (т. Е. Четыре отрицательных целых числа, которые лежат справа от –6) — это –5, –4, –3 и –2.
Страница № 78:
Вопрос 6:
Вычислите:
(i) 8 + (−16)
(ii) (−5) + (−6)
(iii) (−6) × (−8)
(iv) (−36) ÷ 6
(v) 30 — (−50)
(vi) (−40) ÷ (−10)
(vii) 8 × (−5)
(viii) (−30) — 15
Ответ:
(i) 8 + (–16)
= 8 — 16
= –8
(ii) (–5) + (–6)
= –5 — 6
= –11
(iii) (- 6) × (–8)
= (6 × 8)
= 48
(iv) (–36) ÷ 6
-366 = (-1) × 366 = -6
(v)
30 — (- 50)
= 30 + 50
= 80
(vi) (–40) ÷ (–10)
= -40-10 = (- 1) × 40 (-1) × 10 = 4
(vii) 8 × (–5)
= — (8 × 5)
= –40
(viii) (–30) — 15
= –30 — 15
= –45
Страница № 78:
Вопрос 7:
Сумма двух целых чисел равна −12.Если одному из них 34, найдите другого.
Ответ:
Пусть целое число будет x .
∴ 34 + x = –12
или x = –12 — 34
или x = –46
Следовательно, другое целое число равно –46.
Страница № 78:
Вопрос 8:
Упростить:
(i) (−24) × (68) + (−24) × 32
(ii) (−9) × 18 — (−9) × 8
(iii) (−147) ÷ (- 21)
(iv) 16 ÷ (−1)
Ответ:
(i) (–24) × (68) + (–24) × 32
= — (24) × (68 + 32)
= –24 × 100
= –2400
(ii) (–9) × 18 — (–9) × 8
= — (9) × [18 — 8]
= –9 × 10
= –90
(iii) (–147) ÷ (–21)
= -147 -21 = (- 1) × 147 (-1) × 21 = (- 1) (- 1) × 14721 = 7
(iv) 16 ÷ (–1)
= 16-1 = 16 × (- 1) (- 1) × (-1) = 16 × (-1) = — 16 {Умножение числителя и знаменателя на (–1)}
Страница № 78:
Вопрос 9:
Преемник −89 —
(a) −90
(b) −88
(c) 90
(d) 88
Ответ:
(b) −88
Преемник −89 равен −88.Преемник числа находится справа на числовой прямой.
−88 лежит правее −89.
Страница № 78:
Вопрос 10:
Предшественник −99 —
(a) −98
(b) −100
(c) 98
(d) 100
Ответ:
(b) −100
Предшественник числа находится слева от числа.
−100 лежит слева от -99.Следовательно, −100 является предшественником -99.
Страница № 78:
Вопрос 11:
Аддитив, обратный −23, равен
(a) -123
(b) 123
(c) 23
(d) −23
Ответ:
(c) 23
Аддитивное обратное число, добавленное к числу, дает 0.
−23 + 23 = 0
Следовательно, 23 является аддитивным обратным числом -23.
Страница № 78:
Вопрос 12:
Если (-13 + 6) -25 — (-9), то правильный символ в заполнителе:
(a) <
(b)>
(c) =
(d) ни один из этих
Ответ:
(б)>
Здесь L.H.S. = (−13 + 6)
= −7
R.H.S. = −25 — (−9)
= −25 + 9
= −16
−7> −16
L.H.S. > R.H.S.
Страница № 78:
Вопрос 13:
? + (−8) = 12
(а) −4
(−20)
(в) 20
(г) 4
Ответ:
(c) 20
x + (−8) = 12
=> x — 8 = 12
=> x = 12 + 8
=> x = 20
Страница № 78:
Вопрос 14:
Целое число, которое на 5 больше, чем (−7), равно
(a) −12
(b) 12
(c) −2
(d) 2
Ответ:
(c) -2
5 больше, чем (−7) означает, что 5 добавляется к (−7).
5 + (−7)
= 5-7
= −2
Страница № 78:
Вопрос 15:
Что нужно добавить к 16, чтобы получить (−31)?
(а) 15
(б) −15
(в) 47
(г) −47
Ответ:
(d) −47
Пусть число, которое нужно добавить к 16, будет x .
x + 16 = (−31)
=> x = (−31) −16
=> x = −47
Страница № 78:
Вопрос 16:
Если вычесть 34 из −36, мы получим
(a) 2
(b) −2
(c) 70
(d) −70
Ответ:
(г) −70
−36-34
= −70
Страница № 78:
Вопрос 17:
Заполните пустые поля.
(i) −23 — (?) = 15.
(ii) Наибольшее отрицательное целое число …….
(iii) Наименьшее положительное целое число ….
(iv) (−8) + (−6) — (−3) = …….
(v) Предшественник −200 — …….
Ответ:
(i)
Пусть требуется число x .
−23 — x = 15
=> −23 = 15 + x
=> 15 + x = −23
=> x = −15 −23
=> x = — 38
(ii)
Наибольшее отрицательное целое число равно -1.
(iii)
Наименьшее положительное целое число равно 1.
(iv)
(−8) + (−6) — (−3)
= (−8) + (−6) +3
= −8 −6 + 3
= −11
(v)
Предшественник −200:
(−200 — 1)
= −201
Страница № 79:
Вопрос 18:
Напишите «T» для истинного и «F» для ложного в каждом из следующих случаев:
(i) 0 не является ни положительным, ни отрицательным.
(ii) — (- 36) — 1 = — 37.
(iii) На числовой прямой −10 находится справа от −6.
(iv) 0 — целое число.
(в) — | −15 | = -15.
(vi) | −40 | + 40 = 0.
Ответ:
(i) T
(ii) F
— (- 36) — 1
= 36 — 1
= 35
(iii) F
Это потому, что −10 меньше −6.
(iv) T
(v) T
— | −15 |
= — (15)
= −15
(vi) F
| −40 | + 40
= 40 + 40
= 80
Просмотреть решения NCERT для всех глав класса 6
РешенияNCERT для математики класса 7 Глава 1: Целые числа
Решения NCERTдля математики класса 7, глава 1 — Целые числа доступны здесь.В этой статье вы также можете загрузить PDF-файл учебника NCERT по математике для класса 7, глава 1, Целые числа.
Решения NCERT для математики класса 7 Глава 1: Целые числаУпражнение 1.1 (Страница № 4)
Вопрос1. Следующая числовая строка показывает температуру в градусах Цельсия (° C) в разных местах в определенный день.
(a) Обратите внимание на эту числовую строку и запишите температуру в отмеченных на ней местах.
Решение (а):
Место | Температура |
Бангалор | 22 o С |
Ути | 14 o С |
Шимла | 5 o С |
Сринагар | ‒2 o C |
Лахулспити | ‒8 o C |
(b) Какова разница температур между самыми жаркими и самыми холодными местами среди перечисленных выше?
Решение (b):
Самым жарким местом является Бангалор с температурой 22 o C
.Самым холодным местом является Лахулспити с температурой — 8 o C
.Разница температур = (22 o C) — (- 8 o C) = 30 o C.
(c) Какая разница температур между Лахулспити и Сринагаром?
Решение (c):
Температура Лахулспити = — 8 o C
Температура Сринагара = ‒2 o C
Разница температур = (2 o C) — (- 8 o C) = 6 o C.
(d) Можно ли сказать, что температура Шринагара и Шимлы, вместе взятых, меньше, чем температура в Шимле? Это тоже меньше, чем температура в Сринагаре?
Решение (d):
Температура Шринагара = — 2 o C, температура Шимлы = 5 o C
Температура Шимлы и Сринагара, взятые вместе = (5 o C) + (- 2 o C) = 3 o C
С, температура Сринагара = ‒2 o C
Ясно, что температура в Шринагаре выше.
Вопрос2. В викторине положительные оценки выставляются за правильные Решения, а отрицательные — за неправильные. Если Джек набрал в пяти последовательных раундах 25, — 5, — 10, 15 и 10, каков был его результат в конце?
Решение2:
Тотал Джека будет суммой очков за все раунды, т.е. (25) + (- 5) + (- 10) + (15) + 10 = 35.
Вопрос3. В Сринагаре в понедельник температура была -5 ° C, а во вторник она упала на 2 ° C.Какой была температура в Шринагаре во вторник? В среду она поднялась на 4 ° C. Какая была температура в этот день?
Решение3:
Температура понедельника = -5 ° C
Температура вторника упала на 2 ° C = (- 5 ° C) — (2 ° C) = — 7 ° C
Температура среды = Температура вторника + 4 ° C = -7 ° C + 4 ° C = -3 ° C
Вопрос4. Самолет летит на высоте 5000 м над уровнем моря. В определенной точке он находится точно над подводной лодкой, плавающей на 1200 м ниже уровня моря.Какое расстояние между ними по вертикали?
Решение4:
Высота самолета над уровнем моря = 5000 м
Глубина подводной лодки ниже уровня моря = 1200 м
Расстояние между самолетом и подводной лодкой — это сумма высоты самолета над уровнем моря и глубины подводной лодки ниже уровня моря = 5000 м + 1200 м = 6200 м.
Вопрос 5. Мохан депозиты рупий. 2000 на его банковский счет и снимает рупий.1642 от него, на следующий день. Если снятие суммы со счета представлено отрицательным целым числом, то как вы представите внесенную сумму? Найдите баланс на счету Мохана после вывода средств.
Решение5:
Здесь снятие суммы со счета представлено отрицательным целым числом и показано положительным целым числом.
Сумма депозита = 2000
рупийСнятая сумма = — 1642
рупийОбщий баланс на счете Мохана = Деньги депонированы + Деньги сняты = (2000 рупий) — (- 1642 рупия) = рупии.358.
Вопрос6. Рита идет 20 км на восток от точки A до точки B. От точки B она движется на 30 км на запад по той же дороге. Если расстояние на восток представлено положительным целым числом, тогда как вы представите расстояние, пройденное на запад? Каким целым числом вы представите ее окончательную позицию от A?
Решение4:
Высота самолета над уровнем моря = 5000 м
Глубина подводной лодки ниже уровня моря = 1200 м
Расстояние между самолетом и подводной лодкой — это сумма высоты самолета над уровнем моря и глубины подводной лодки ниже уровня моря = 5000 м + 1200 м = 6200 м.
Вопрос 5. Мохан депозиты рупий. 2000 на его банковский счет и снимает рупий. 1642 от него, на следующий день. Если снятие суммы со счета представлено отрицательным целым числом, то как вы представите внесенную сумму? Найдите баланс на счету Мохана после вывода средств.
Решение5:
Здесь снятие суммы со счета представлено отрицательным целым числом и показано положительным целым числом.
Сумма депозита = 2000
рупийСнятая сумма = — 1642
рупийОбщий баланс на счете Мохана = Деньги депонированы + Деньги сняты = (2000 рупий) — (- 1642 рупия) = рупии. 358.
Вопрос6. Рита идет 20 км на восток от точки A до точки B. От точки B она движется на 30 км на запад по той же дороге. Если расстояние на восток представлено положительным целым числом, тогда как вы представите расстояние, пройденное на запад? Каким целым числом вы представите ее окончательную позицию от A?
Решение6:
Здесь точка A — это исходная точка, и расстояние, пройденное в восточном направлении, принимается положительным, тогда как расстояние, пройденное в западном направлении, принимается как отрицательное.
Пройденное расстояние в восточном направлении = 20 км
Пройденное расстояние в западном направлении = −30 км
Пройденное расстояние от A = 20 + (−30) = −10 км
Расстояние, пройденное Ритой от точки А, составит — 10 км. Положение Риты — западнее или левее А.
.Вопрос7. В магическом квадрате каждая строка, столбец и диагональ имеют одинаковую сумму. Проверьте, что из следующего является магическим квадратом.
(я)
5 | — 1 | — 4 |
— 5 | — 2 | 7 |
0 | 3 | — 3 |
(ii)
1 | -10 | 0 |
— 4 | — 3 | — 2 |
— 6 | 4 | — 7 |
Решение7:
С помощью простых вычислений мы можем заметить, что в квадрате (i) каждая строка и столбец в сумме дают 0, но сумма одной из его диагоналей не равна нулю.Итак, (i) не является магическим квадратом.
Принимая во внимание, что в случае квадрата (ii) каждая строка, столбец и диагональ в сумме дают −9. Следовательно, (ii) — магический квадрат.
Вопрос8. Убедитесь, что a — (- b ) = a + b для следующих значений a и b .
(i) a = 21, b = 18
(ii) a = 118, b = 125
(iii) a = 75, b = 84
(iv) a = 28, b = 11
Решение8:
( i ) a = 21, b = 18
Теперь, a — (- b ) = 21 — (−18) = 21 + 18 = 39
Кроме того, a + b = 21 + 18 = 39
Итак, a — (- b ) = a + b = 39
( ii ) a = 118, b = 125
Теперь, a — (- b ) = 118 — (−125) = 118 + 125 = 243
Также a + b = 118 + 125 = 243
Итак, a — (- b ) = a + b = 243
( iii ) a = 75, b = 84
Теперь, a — (- b ) = 75 — (−84) = 75 + 84 = 159
Также a + b = 75 + 84 = 159
Итак, a — (- b ) = a + b = 159
(iv) a = 28, b = 11
Теперь, a — (- b ) = 28 — (−11) = 28 + 11 = 39
Также a + b = 28 + 11 = 39
Итак, a — (- b ) = a + b = 39.
Вопрос9. Используйте знак>, <или = в поле, чтобы утверждения верны.
(а) (- 8) + (- 4) _ _ _ _ (–8) — (- 4)
(б) (- 3) + 7 — (19) _ _ _ _ 15-8 + (- 9)
(в) 23 — 41 + 11 _ _ _ _ 23 — 41 — 11
(г) 39 + (- 24) — (15) _ _ _ _ 36 + (- 52) — (- 36)
(д) — 231 + 79 + 51 _ _ _ _ — 399 + 159 + 81
Решение9:
(a) (- 8) + (- 4) _ _ _ _ (–8) — (- 4)
⇒ — 8-4 _ _ _ _ — 8 + 4
⇒ — 12 _ _ <_ _ - 4
(б) (- 3) + 7 — (19) _ _ _ _ 15-8 + (- 9)
⇒ — 3 + 7 — 19 _ _ _ _ 15 — 8 — 9
⇒ — 15 _ _ <_ _ - 2
(в) 23 — 41 + 11 _ _ _ _ 23 — 41 — 11
⇒ — 7 _ _> _ _ — 29
(г) 39 + (- 24) — (15) _ _ _ _ 36 + (- 52) — (- 36)
⇒ 39-24-15 _ _ _ _ 36-52 + 36
⇒ 0 _ _ <_ _ 20
e) — 231 + 79 + 51 _ _ _ _ — 399 + 159 + 81
⇒ — 101 _ _> _ _ — 159
Вопрос10.В резервуаре для воды есть ступеньки. Обезьяна сидит на самой верхней ступеньке (то есть на первой ступеньке). Уровень воды на девятой ступени.
(i) Он прыгает на 3 шага вниз, а затем на 2 шага назад вверх. За сколько прыжков он достигнет уровня воды?
(ii) Выпив воды, он хочет вернуться. Для этого он прыгает на 4 шага вверх, а затем отскакивает на 2 шага назад за каждое движение. За сколько прыжков он вернется на верхнюю ступеньку?
(iii) Если количество шагов, перемещенных вниз, представлено отрицательными целыми числами, а количество шагов, перемещенных вверх, положительными целыми числами, представьте его ходы в частях (i) и (ii), выполнив следующие действия;
( a ) — 3 + 2 -… = — 8
( b ) 4 — 2 + … = 8. В (a) сумма (- 8) представляет уменьшение на восемь шагов. Итак, что будет представлять сумма 8 в (b)?
Раствор:
Предположим, что шаг, перемещенный обезьяной вниз, представлен положительными целыми числами, а шаг, перемещенный вверх, представлен отрицательными целыми числами
(i) В начале обезьяна была на шаге = 1, после
• 1-й прыжок, позиция обезьяны будет на шаге = 1 + 3 = 4
• 2-й прыжок, позиция обезьяны будет на шаге = 4 + (−2) = 2
• 3-й прыжок, позиция обезьяны будет на шаге = 2 + 3 = 5
• 4-й прыжок, позиция обезьяны будет на шаге = 5 + (−2) = 3
• 5-й прыжок, позиция обезьяны будет на шаге = 3 + 3 = 6
• 6-й прыжок, позиция обезьяны будет на шаге = 6 + (−2) = 4
• 7-й прыжок, позиция обезьяны будет на шаге = 4 + 3 = 7
• 8-й прыжок, позиция обезьяны будет на шаге = 7 + (−2) = 5
• 9-й прыжок, позиция обезьяны будет на шаге = 5 + 3 = 8
• 10-й прыжок, позиция обезьяны будет на шаге = 8 + (−2) = 6
• 11-й прыжок, позиция обезьяны будет на step = 6 + 3 = 9
Очевидно, обезьяна будет на уровне воды (т.е., 9-й шаг) после 11 прыжков.
(ii) Изначально положение обезьяны было на шаге = 9
.• 1-й прыжок, позиция обезьяны будет на шаге = 9 + (−4) = 5
• 2-й прыжок, позиция обезьяны будет на шаге = 5 + 2 = 7
• 3-й прыжок, позиция обезьяны будет на шаге = 7 + (- 4) = 3
• 4-й прыжок, позиция обезьяны будет на шаге = 3 + 2 = 5
• 5-й прыжок, позиция обезьяны будет на шаге = 5 + (- 4) = 1
Итак, обезьяна вернется на верхнюю ступеньку после 5 прыжков.
(iii)
(a) Если шаги, перемещенные вниз, представлены отрицательными целыми числами, а шаги, перемещенные вверх, представлены положительными целыми числами, то вот подробности его хода
Ходы обезьяны в части (i), — 3 + 2-3 + 2-3 + 2-3 + 2-3 + 2-3 = −8
(b) Ходы обезьяны в части (ii), 4-2 + 4-2 + 4-2 + 4-2 = 8
Итак, движения обезьяны в части (ii) представляют собой подъем на 8 ступеней вверх.
Упражнение 1.2 (стр. 9)
1.Запишите пару целых чисел, из которых:
( a ) сумма составляет –7
( b ) разница –10
( c ) сумма 0
Раствор:
( a ) (+1) + (- 8) = −7
( b ) (- 8) — (- 2) = −10
( с ) 5 + (−5) = 0
2. ( a ) Запишите пару отрицательных целых чисел, разность которых дает 8.
( b ) Запишите отрицательное целое число и положительное целое число, сумма которых равна –5.
( c ) Запишите отрицательное целое число и положительное целое число, разность которых равна –3.
Раствор:
( a ) — 16 — (- 8).
( b ) — 10 + 5 = –5.
( c ) — 5 — (2) = –3.
3. В викторине команда A набрала — 40, 10, 0, а команда B — набрала 10, 0, — 40 в трех последовательных раундах.Какая команда забила больше? Можно ли сказать, что можно складывать целые числа в любом порядке?
Раствор:
Общий балл команды A = — 40 + 10 + 0 = — 30.
Общий балл команды B = 10 + 0 + (- 40) = — 30.
Итак, обе команды имеют равный счет.
Да, мы можем складывать целые числа в любом порядке.
4. Заполните пропуски, чтобы следующие утверждения были верными:
(i) (–5) + (- 8) = (- 8) + (…………)
(ii) –53 + ………… = –53
(iii) 17 + ………… = 0
(iv) [13 + (- 12)] + (…………) = 13 + [(–12) + (–7)]
(v) (- 4) + [15 + (–3)] = [- 4 + 15] + …………
Раствор:
(i) (–5) + (- 8) = (- 8) + (…– 5 …)
(ii) (–53) + ..0 .. = –53
(iii) 17+.. –17 .. = 0
(iv) [13 + (- 12)] + (…..– 7 …..) = 13 + [(–12) + (–7)]
(v) (- 4) + [15 + (–3)] = [- 4 + 15] + …. –3 ……..
Упражнение 1.3 (стр. 21)
1. Найдите каждый из следующих продуктов:
(а) 3 × (–1)
(б) (–1) × 225
(в) (–21) × (–30)
(г) (–316) × (–1)
(д) (–15) × 0 × (–18)
(е) (–12) × (–11) × (10)
(г) 9 × (–3) × (- 6)
(в) (–18) × (–5) × (- 4)
(i) (–1) × (–2) × (–3) × 4
(к) (–3) × (–6) × (–2) × (–1)
Раствор:
(а) 3 × (−1) = −3
(б) (−1) × 225 = −225
(в) (−21) × (−30) = 630
(г) (-316) × (-1) = 316
(е) (−15) × 0 × (−18) = 0
(е) (−12) × (−11) × 10 = 1320
(г) 9 × (−3) × (−6) = 162
(час) (−18) × (−5) × (−4) = −360
(я) (−1) × (−2) × (−3) × 4 = −24
(к) (−3) × (−6) × (−2) × (−1) = 36
2.Проверьте следующее:
(a) 18 × [7 + (–3)] = [18 × 7] + [18 × (–3)]
(b) (–21) × [(- 4) + (- 6)] = [(–21) × (- 4)] + [(–21) × (- 6)]
Раствор:
(а) L.H.S. = 18 × [7 + (–3)] = 72
R.H.S. = [18 × 7] + [18 × (–3)] = 72
Итак, L.H.S. = R.H.S.
(б) L.H.S. = (–21) × [(- 4) + (- 6)] = 210
R.H.S. = [(–21) × (- 4)] + [(–21) × (- 6)] = 210
Так, Л.H.S. = R.H.S.
3. (i) Чему равно (–1) × a для любого целого числа a ?
(ii) Определите целое число, произведение которого с (–1) равно
(а) –22 (б) 37 (в) 0
Раствор:
«а» может быть положительным, нулевым или отрицательным.
(–1) × a = –a (если a положительно)
(–1) × a = a (если a отрицательно)
(–1) × 0 = 0 (a равно нулю)
4.Начиная с (–1) × 5, напишите различные продукты, показывающие некоторый узор, чтобы показать (–1) × (–1) = 1.
Раствор:
-1 × 5 = -5
-1 × 4 = -4
-1 × 3 = -3
-1 × 2 = -2
-1 × 1 = -1
-1 × 0 = 0
-1 × (-1) = 1
Шаблон показывает, что мы движемся влево от числовой прямой с разницей на 1. Ясно, что −1 × (−1) = 1.
5.Найдите продукт, используя подходящие свойства:
(а) 26 × (- 48) + (- 48) × (–36)
(б) 8 × 53 × (–125)
(в) 15 × (–25) × (- 4) × (–10)
(г) (- 41) × 102
(д) 625 × (–35) + (- 625) × 65
(ж) 7 × (50-2)
(г) (–17) × (–29)
(в) (–57) × (–19) + 57
Раствор:
(а) 26 × (−48) + (−48) × (−36)
= (-48) × 26 + (-48) × (-36)
= (−48) [26 — 36]
= (-48) × (-10) = 480
(б) 8 × 53 × (−125) = 8 × [53 × (−125)]
= 8 × [(−125) × 53]
= [8 × (−125)] × 53
= [-1000] × 53 = -53000
(в) 15 × (−25) × (−4) × (−10)
= 15 × [(−25) × (−4)] × (−10)
= 15 × [100] × (−10)
= 15 × (-1000) = -15000
(г) (−41) × 102
= (−41) × (100 + 2)
= (−41) × 100 + (−41) × 2
= — 4100 — 82 = −4182
(д) 625 × (−35) + (−625) × 65
= 625 × [(-35) + (-65)]
= 625 × [−100] = −62500
(ж) 7 × (50-2)
= (7 × 50) — (7 × 2)
= 350 — 14
= 336
(г) (−17) × (−29)
= (−17) × [−30 + 1]
= [(−17) × (−30)] + [(−17) × 1]
= [510] + [−17] = 493
(в) (−57) × (−19) + 57
= 57 × 19 + 57 × 1 [здесь для удобства мы берем 57 x 1]
= 57 [19 + 1]
= 57 × 20 = 1140.
6. Определенный процесс замораживания требует, чтобы комнатная температура понижалась с 40 ° C со скоростью 5 ° C каждый час. Какая будет температура в помещении через 10 часов после начала процесса?
Раствор:
Пусть понижение температуры обозначается целым отрицательным числом.
Температура снижается со скоростью 5 ° C в час, поэтому снижение температуры через 10 часов составит -50 ° C.
Температура в помещении через 10 часов составит 40 ° C + (- 50 ° C) = — 10 o C.
7. В тесте класса, содержащем 10 вопросов, 5 баллов выставляются за каждое правильное Решение и (–2) балла выставляются за каждое неправильное Решение и 0 баллов за вопросы, на которые не пытались ответить.
( i ) Мохан получает четыре правильных и шесть неправильных решений. Какая у него оценка?
( ii ) Решма получает пять правильных решений и пять неправильных решений, каков ее балл?
( iii ) Хина получает два правильных и пять неправильных решений из семи заданных ею вопросов.Какая у нее оценка?
Раствор:
(i) Общая оценка Мохана = [{(4) × (5)} + {(6) × (‒2)}] = 20–12 = 8.
(ii) Всего оценок Решмы = [{(5) × (5)} + {(5) × (‒2)} = 15.
(iii) Оценка Хины = [{(2) × (5)} + {(5) × (-2)} = 0.
8. Цементная компания получает прибыль в размере рупий. 8 за мешок проданного белого цемента и потеря рупий. 5 штук за мешок проданного серого цемента.
(a) Компания продает 3 000 мешков белого цемента и 5 000 мешков серого цемента в месяц.Какая у него прибыль или убыток?
(b) Сколько белых мешков для цемента он должен продать, чтобы не было ни прибыли, ни убытка, если количество проданных серых мешков составляет 6 400 мешков.
Раствор:
Обозначим прибыль положительным целым числом, а убыток — отрицательным целым числом.
(a) Чистая прибыль, полученная при продаже 1 мешка белого цемента = рупий. 8
Прибыль от продажи 3000 мешков белого цемента = рупий.8 × 3000 = рупий. 24000
Чистый убыток от продажи 1 мешка серого цемента = — 5
рупийУбыток от продажи 5000 мешков серого цемента = −5 × 5000 = −25000.
Таким образом, общий убыток составляет рупий. 1000.
б)
Убыток от продажи 1 мешка серого цемента = — 5
рупийУбыток от продажи 6400 мешков серого цемента = рупий. (−5) × 6400 = рупий. −32000
Предположим, что количество продаваемых мешков белого цемента равно x.
Теперь прибыль от продажи 1 мешка белого цемента = 8
рупий.Итак, прибыль, полученная при продаже x мешков белого цемента = x × 8 = 8 x
Без прибыли и убытков
Полученная прибыль = понесенный убыток
⇒ 8x = −32000
⇒ 8x = 32000
⇒ x = 4000
Итак, ни для прибыли, ни для убытка нужно продать 4000 белых мешков для цемента.
9. Замените пробел на целое число, чтобы оно соответствовало действительности.
(а) (–3) × _____ = 27
(б) 5 × _____ = –35
(в) _____ × (- 8) = –56
(г) _____ × (–12) = 132
Раствор:
(а) (–3) × __ (- 9) ___ = 27
(б) 5 × __ (- 7) ___ = –35
(в) __ (7) ___ × (- 8) = –56
(d) __ (- 11) ___ × (–12) = 132
Упражнение 1.4 (стр. 26)
1. Оцените каждое из следующих значений:
(а) (–30) ÷ 10
(б) 50 ÷ (–5)
(в) (–36) ÷ (–9)
(г) (- 49) ÷ (49)
(e) 13 ÷ [(–2) + 1]
(ж) 0 ÷ (–12)
(г) (–31) ÷ [(–30) + (–1)]
(ч) [(–36) ÷ 12] ÷ 3
(i) [(- 6) + 5)] ÷ [(–2) + 1]
Раствор:
(а) (–30) ÷ 10 = — 3
(б) 50 ÷ (–5) = ‒10
(в) (–36) ÷ (–9) = 4
(г) (- 49) ÷ (49) = ‒1
(e) 13 ÷ [(–2) + 1] = 13 ÷ [‒1] = — 13
(ж) 0 ÷ (–12) = 0
(г) (–31) ÷ [(–30) + (–1)] = [−31] ÷ [−31] = 1
(ч) [(–36) ÷ 12] ÷ 3 = [−3] ÷ 3 = −1
(i) [(- 6 + 5)] ÷ [(–2) + 1] = 1
2.Убедитесь, что a ÷ ( b + c ) ≠ ( a ÷ b ) + ( a ÷ c ) для каждого из следующих значений a, b и c.
( a ) a = 12, b = — 4 , c = 2
( b ) a = (–10), b = 1, c = 1
Раствор:
(а)
Л.H.S . = a ÷ ( b + c ) = 12 ÷ (- 4 + 2) = — 6
R.H.S. = (a ÷ b) + (a ÷ c) = [12 ÷ (−4)] + [12 ÷ 2] = — 3 + 6 = 3.
Итак, a ÷ ( b + c ) ≠ ( a ÷ b ) + ( a ÷ c )
( б )
L.H.S. = a ÷ ( b + c ) = (−10) ÷ (1 + 1) = (−10) ÷ 2 = −5
р.H.S. = [(−10) ÷ 1] + [(−10) ÷ 1] = — 10 — 10 = −20
Итак, a ÷ ( b + c ) ≠ ( a ÷ b ) + ( a ÷ c )
3. Заполните пустые поля:
(а) 369 ÷ _____ = 369
(б) (–75) ÷ _____ = –1
(в) (–206) ÷ _____ = 1
(г) — 87 ÷ _____ = 87
(д) _____ ÷ 1 = — 87
(ж) _____ ÷ 48 = –1
(г) 20 ÷ _____ = –2
(час) _____ ÷ (4) = –3
Раствор:
(а) 369 ÷ __ (1) ___ = 369
(б) (–75) ÷ __ (75) ___ = –1
(c) (–206) ÷ __ (- 206) ___ = 1
(г) — 87 ÷ _ (- 1) _ = 87
(е) __ (- 87) ___ ÷ 1 = — 87
(ж) __ (- 48) ___ ÷ 48 = –1
(г) 20 ÷ __ (- 10) ___ = –2
(ч) ___ (- 12) __ ÷ (4) = –3
4.Напишите пять пар целых чисел (a, b) таких, что a ÷ b = –3. Одна такая пара — (6, –2), потому что 6 ÷ (–2) = (–3).
Раствор:
5 других пар:
(- 24, 8), (−18, 6), (−3, 1), (12, −4), (−9, 3)
5. Температура в 12 часов дня была 10 ° C выше нуля. Если она будет снижаться со скоростью 2 ° C в час до полуночи, в какое время температура опустится на 8 ° C ниже нуля? Какая будет температура в полночь?
Раствор:
Температура i.е., в 12 часов дня = 10 ° C
Пусть понижение представлено отрицательной температурой, поэтому изменение температуры за час = −2 ° C
• Температура в 13:00 = (10 ° C) + (−2 ° C) = 8 ° C
• Температура в 14:00 = (8 ° C) + (−2 ° C) = 6 ° C
• Температура в 15:00 = (6 ° C) + (−2 ° C) = 4 ° C
• Температура в 16:00 = (4 ° C) + (−2 ° C) = 2 ° C
• Температура в 17:00 = (2 ° C) + (−2 ° C) = 0 ° C
• Температура в 18:00 = (0 ° C) + (−2 ° C) = −2 ° C
• Температура в 19:00 = (−2 ° C) + (−2 ° C) = −4 ° C
• Температура в 20:00 = (−4 ° C) + (−2 ° C) = −6 ° C
• Температура в 21:00 = (−6 ° C) + (−2 ° C) = −8 ° C
Следовательно, температура в 21:00 будет ниже нуля на 8 ° C.
С 12 полудня до 12 ночи 12 часов, поэтому изменение температуры за 12 часов = −2 ° C × 12 = −24 ° C
В середине ночи температура будет = 10 + (−24) = −14 ° C или на 14 ° C ниже 0.
6. В тесте класса (+ 3) оценки даются за каждое правильное Решение, и (–2) оценки даются за каждое неправильное Решение, и не ставятся оценки за то, что он не пытается ответить на какой-либо вопрос.
(i) Радика набрала 20 баллов. Если у нее есть 12 правильных решений, сколько вопросов она задала неверно?
(ii) Мохини набрала –5 баллов в этом тесте, хотя она получила 7 правильных решений.Сколько вопросов она задала неправильно?
Раствор:
баллов за 1 правильный ответ = +3
баллов за 1 неправильный ответ = −2
(i) Оценка Радхики = 20
баллов за правильные решения = 12 × 3 = 36 баллов
Итак, баллы, полученные за неправильные ответы = Всего баллов — Баллы, полученные за правильные ответы = 20 — 36 = — 16
баллов за 1 неправильный ответ = −2
Итак, количество неправильных ответов = (−16) ÷ (−2) = 8
Следовательно, она попыталась задать 8 неверных вопросов.
(ii)
Всего оценок Мохини = −5
оценок Мохини за 7 правильных ответов = 7 × 3 = 21
Итак, баллы, полученные за неправильные ответы = Общий балл — Баллы, полученные за правильные ответы = — 5 — 21 = −26
As, Оценка за 1 неверный ответ = −2
Итак, количество неправильных ответов = (−26) ÷ (−2) = 13
Следовательно, она попыталась задать 13 неправильных вопросов.
(iii)
Всего оценок Ракеша = 18
Количество вопросов, заданных Ракешем = 16
Согласно вопросу,
(3) × (Количество правильных ответов) + (−2) × (Количество неправильных ответов) = 18
⇒ (3) × (Количество правильных ответов + (−2) × (16 — Количество правильных ответов) = 18
⇒ (3) × (Количество правильных ответов) + (−32) + 2 (Количество правильных ответов) = 18
⇒ (3) × (Количество правильных ответов) + (−32) + 2 (Количество правильных ответов) = 18
⇒ 5 × (Количество правильных ответов) + (−32) = 18
⇒ 5 × (Количество правильных ответов) = 18 + 32 = 50
⇒ 5 × (Количество правильных ответов) = 18 + 32 = 50
⇒ Количество правильных ответов = 10
⇒ Количество правильных ответов = 16 –10 = 6.
Теперь количество правильных и неправильных ответов, полученных Ракешем, составляет 10 и 6 соответственно.
7. Лифт спускается в шахту со скоростью 6 м / мин. Если спуск начинается с 10 м над уровнем земли, сколько времени потребуется на спуск — 350 м.
Раствор:
Позвольте показать, считать, что оно спущено на отрицательное целое число.
Начальная высота от уровня земли = +10 м
Конечная глубина от уровня земли = −350 м
Чистое расстояние спуска на лифте = (−350) — (+10) = −360 м
Время спуска лифта −6 м = 1 мин
Итак, время, затраченное лифтом на спуск −360 м = (−360) ÷ (−6) = 60 минут = 1 час.
Загрузить решения NCERT для математики класса 7 — Глава 1 Целые числа
Математика Авторы / названия «новые»
Новые поступления
Работы получены с пт, 1 октября, 21 октября по пн, 4 октября, 21 октября, объявлено вт, 5 октября,
[всего 503 записей: 1-503 ][отображение до 2000 записей на странице: меньше | подробнее]
Новые заявки на вторник, 5 октября 21
- [1] arXiv: 2110.00594 [pdf, другое]
- [2] arXiv: 2110.00596 [pdf, ps, другое]
- [3] arXiv: 2110.00599 [pdf, ps, другое]
- [4] arXiv: 2110.00600 [pdf, другой]
- [5] arXiv: 2110.00604 [pdf, другой]
- [6] arXiv: 2110.00608 [pdf, ps, другое]
- [7] arXiv: 2110.00611 [pdf, ps, другое]
- [8] arXiv: 2110.00614 [pdf, ps, другое]
- [9] arXiv: 2110.00628 [pdf, другое]
- [10] arXiv: 2110.00638 [pdf, ps, другое]
- [11] arXiv: 2110.00642 [pdf, другой]
- [12] arXiv: 2110.00649 [pdf, другой]
- [13] arXiv: 2110.00655 [pdf, ps, другое]
- [14] arXiv: 2110.00656 [pdf, ps, другое]
- [15] arXiv: 2110.00657 [pdf, ps, другое]
- [16] arXiv: 2110.00663 [pdf, ps, другое]
- [17] arXiv: 2110.00664 [pdf, ps, другое]
- [18] arXiv: 2110.00670 [pdf, ps, другое]
- [19] arXiv: 2110.00689 [pdf]
- [20] arXiv: 2110.00694 [pdf, ps, другое]
- [21] arXiv: 2110.00701 [pdf, другой]
- [22] arXiv: 2110.00702 [pdf, другой]
- [23] arXiv: 2110.00705 [pdf, ps, другое]
- [24] arXiv: 2110.00706 [pdf, ps, другое]
- [25] arXiv: 2110.00709 [pdf, другое]
- [26] arXiv: 2110.00716 [pdf, ps, другое]
- [27] arXiv: 2110.00718 [pdf, ps, другое]
- [28] arXiv: 2110.00721 [pdf, ps, другое]
- [29] arXiv: 2110.00729 [pdf, ps, другое]
- [30] arXiv: 2110.00730 [pdf, другой]
- [31] arXiv: 2110.00738 [pdf, ps, другое]
- [32] arXiv: 2110.00739 [pdf, ps, другое]
- [33] arXiv: 2110.00743 [pdf, ps, другое]
- [34] arXiv: 2110.00746 [pdf, ps, другое]
- [35] arXiv: 2110.00750 [pdf, ps, другое]
- [36] arXiv: 2110.00752 [pdf, ps, другое]
- [37] arXiv: 2110.00753 [pdf, ps, другое]
- [38] arXiv: 2110.00754 [pdf, ps, другое]
- [39] arXiv: 2110.00757 [pdf, ps, другое]
- [40] arXiv: 2110.00763 [pdf, ps, другое]
- [41] arXiv: 2110.00765 [pdf, ps, другое]
- [42] arXiv: 2110.00769 [pdf, ps, другое]
- [43] arXiv: 2110.00774 [pdf, ps, другое]
- [44] arXiv: 2110.00779 [pdf, ps, другое]
- [45] arXiv: 2110.00786 [pdf, ps, другое]
- [46] arXiv: 2110.00787 [pdf, ps, другое]
- [47] arXiv: 2110.00789 [pdf, другое]
- [48] arXiv: 2110.00793 [pdf, ps, другое]
- [49] arXiv: 2110.00798 [pdf, ps, другое]
- [50] arXiv: 2110.00800 [pdf, другой]
- [51] arXiv: 2110.00802 [pdf, ps, другое]
- [52] arXiv: 2110.00805 [pdf, ps, другое]
- [53] arXiv: 2110.00817 [pdf, ps, другое]
- [54] arXiv: 2110.00818 [pdf, ps, другое]
- [55] arXiv: 2110.00820 [pdf, ps, другое]
- [56] arXiv: 2110.00826 [pdf, ps, другое]
- [57] arXiv: 2110.00832 [pdf, ps, другое]
- [58] arXiv: 2110.00833 [pdf, другой]
- [59] arXiv: 2110.00838 [pdf, ps, другое]
- [60] arXiv: 2110.00848 [pdf, ps, другое]
- [61] arXiv: 2110.00849 [pdf, другой]
- [62] arXiv: 2110.00856 [pdf, другой]
- [63] arXiv: 2110.00861 [pdf, ps, другое]
- [64] arXiv: 2110.00862 [pdf, ps, другое]
- [65] arXiv: 2110.00870 [pdf, ps, другое]
- [66] arXiv: 2110.00873 [pdf, ps, другое]
- [67] arXiv: 2110.00875 [pdf, ps, другое]
- [68] arXiv: 2110.00880 [pdf, другой]
- [69] arXiv: 2110.00883 [pdf, ps, другое]
- [70] arXiv: 2110.00885 [pdf]
- [71] arXiv: 2110.00889 [pdf, другое]
- [72] arXiv: 2110.00892 [pdf, ps, другое]
- [73] arXiv: 2110.00900 [pdf, ps, другое]
- [74] arXiv: 2110.00904 [pdf, ps, другое]
- [75] arXiv: 2110.00906 [pdf, другой]
- [76] arXiv: 2110.00912 [pdf, другой]
- [77] arXiv: 2110.00915 [pdf, другой]
- [78] arXiv: 2110.00917 [pdf]
- [79] arXiv: 2110.00922 [pdf, ps, другое]
- [80] arXiv: 2110.00923 [pdf, другой]
- [81] arXiv: 2110.00930 [pdf, ps, другое]
- [82] arXiv: 2110.00935 [pdf, другой]
- [83] arXiv: 2110.00951 [pdf, ps, другое]
- [84] arXiv: 2110.00962 [pdf, другой]
- [85] arXiv: 2110.00963 [pdf, ps, другое]
- [86] arXiv: 2110.00964 [pdf, ps, другое]
- [87] arXiv: 2110.00983 [pdf, ps, другое]
- [88] arXiv: 2110.00985 [pdf, ps, другое]
- [89] arXiv: 2110.00989 [pdf, ps, другое]
- [90] arXiv: 2110.00993 [pdf, другой]
- [91] arXiv: 2110.00994 [pdf, ps, другое]
- [92] arXiv: 2110.00995 [pdf, ps, другое]
- [93] arXiv: 2110.00999 [pdf, ps, другое]
- [94] arXiv: 2110.01000 [pdf, ps, другое]
- [95] arXiv: 2110.01007 [pdf, ps, другое]
- [96] arXiv: 2110.01011 [pdf, ps, другое]
- [97] arXiv: 2110.01020 [pdf, ps, другое]
- [98] arXiv: 2110.01026 [pdf, другой]
- [99] arXiv: 2110.01027 [pdf, другой]
- [100] arXiv: 2110.01036 [pdf, другой]
- [101] arXiv: 2110.01040 [pdf, другой]
- [102] arXiv: 2110.01042 [pdf, ps, другое]
- [103] arXiv: 2110.01043 [pdf, ps, другое]
- [104] arXiv: 2110.01046 [pdf, ps, другое]
- [105] arXiv: 2110.01051 [pdf, ps, другое]
- [106] arXiv: 2110.01055 [pdf, ps, другое]
- [107] arXiv: 2110.01059 [pdf, другой]
- [108] arXiv: 2110.01062 [pdf, ps, другое]
- [109] arXiv: 2110.01064 [pdf, ps, другое]
- [110] arXiv: 2110.01066 [pdf, ps, другое]
- [111] arXiv: 2110.01068 [pdf, другой]
- [112] arXiv: 2110.01069 [pdf, другой]
- [113] arXiv: 2110.01070 [pdf, другой]
- [114] arXiv: 2110.01081 [pdf, ps, другое]
- [115] arXiv: 2110.01082 [pdf, ps, другое]
- [116] arXiv: 2110.01083 [pdf, ps, другое]
- [117] arXiv: 2110.01084 [pdf, ps, другое]
- [118] arXiv: 2110.01087 [pdf, другое]
- [119] arXiv: 2110.01088 [pdf, ps, другое]
- [120] arXiv: 2110.01112 [pdf, ps, другое]
- [121] arXiv: 2110.01116 [pdf, ps, другое]
- [122] arXiv: 2110.01118 [pdf, ps, другое]
- [123] arXiv: 2110.01120 [pdf, ps, другое]
- [124] arXiv: 2110.01129 [pdf, ps, другое]
- [125] arXiv: 2110.01130 [pdf, ps, другое]
- [126] arXiv: 2110.01131 [pdf, ps, другое]
- [127] arXiv: 2110.01132 [pdf, другой]
- [128] arXiv: 2110.01133 [pdf, другой]
- [129] arXiv: 2110.01135 [pdf, ps, другое]
- [130] arXiv: 2110.01138 [pdf, другой]
- [131] arXiv: 2110.01139 [pdf, другой]
- [132] arXiv: 2110.01142 [pdf, ps, другое]
- [133] arXiv: 2110.01149 [pdf, ps, другое]
- [134] arXiv: 2110.01150 [pdf, другой]
- [135] arXiv: 2110.01151 [pdf, ps, другое]
- [136] arXiv: 2110.01153 [pdf, ps, другое]
- [137] arXiv: 2110.01156 [pdf, другой]
- [138] arXiv: 2110.01163 [pdf, ps, другое]
- [139] arXiv: 2110.01180 [pdf, ps, другое]
- [140] arXiv: 2110.01184 [pdf, ps, другое]
- [141] arXiv: 2110.01189 [pdf, другой]
- [142] arXiv: 2110.01190 [pdf, ps, другое]
- [143] arXiv: 2110.01193 [pdf, ps, другое]
- [144] arXiv: 2110.01197 [pdf, ps, другое]
- [145] arXiv: 2110.01201 [pdf, ps, другое]
- [146] arXiv: 2110.01215 [pdf, ps, другое]
- [147] arXiv: 2110.01220 [pdf, ps, другое]
- [148] arXiv: 2110.01222 [pdf, ps, другое]
- [149] arXiv: 2110.01223 [pdf, другой]
- [150] arXiv: 2110.01233 [pdf, ps, другое]
- [151] arXiv: 2110.01234 [pdf, ps, другое]
- [152] arXiv: 2110.01238 [pdf, ps, другое]
- [153] arXiv: 2110.01244 [pdf, ps, другое]
- [154] arXiv: 2110.01248 [pdf, ps, другое]
- [155] arXiv: 2110.01267 [pdf, ps, другое]
- [156] arXiv: 2110.01268 [pdf, другой]
- [157] arXiv: 2110.01270 [pdf, ps, другое]
- [158] arXiv: 2110.01273 [pdf, ps, другое]
- [159] arXiv: 2110.01277 [pdf, ps, другое]
- [160] arXiv: 2110.01281 [pdf, другой]
- [161] arXiv: 2110.01282 [pdf, ps, другое]
- [162] arXiv: 2110.01292 [pdf, ps, другое]
- [163] arXiv: 2110.01297 [pdf, другой]
- [164] arXiv: 2110.01316 [pdf, другой]
- [165] arXiv: 2110.01321 [pdf, другой]
- [166] arXiv: 2110.01327 [pdf, ps, другое]
- [167] arXiv: 2110.01332 [pdf, ps, другое]
- [168] arXiv: 2110.01340 [pdf, ps, другое]
- [169] arXiv: 2110.01342 [pdf, ps, другое]
- [170] arXiv: 2110.01343 [pdf, другой]
- [171] arXiv: 2110.01346 [pdf, ps, другое]
- [172] arXiv: 2110.01348 [pdf, ps, другое]
- [173] arXiv: 2110.01350 [pdf, ps, другое]
- [174] arXiv: 2110.01353 [pdf, ps, другое]
- [175] arXiv: 2110.01355 [pdf, другой]
- [176] arXiv: 2110.01359 [pdf, другое]
- [177] arXiv: 2110.01372 [pdf, другой]
- [178] arXiv: 2110.01373 [pdf, другой]
- [179] arXiv: 2110.01374 [pdf, другой]
- [180] arXiv: 2110.01375 [pdf, ps, другое]
- [181] arXiv: 2110.01376 [pdf, ps, другое]
- [182] arXiv: 2110.01377 [pdf, ps, другое]
- [183] arXiv: 2110.01378 [pdf, другой]
- [184] arXiv: 2110.01386 [pdf, ps, другое]
- [185] arXiv: 2110.01392 [pdf, ps, другое]
- [186] arXiv: 2110.01396 [pdf, другой]
- [187] arXiv: 2110.01400 [pdf, ps, другое]
- [188] arXiv: 2110.01413 [pdf, ps, другое]
- [189] arXiv: 2110.01419 [pdf, ps, другое]
- [190] arXiv: 2110.01420 [pdf, другой]
- [191] arXiv: 2110.01440 [pdf, ps, другое]
- [192] arXiv: 2110.01441 [pdf, ps, другое]
- [193] arXiv: 2110.01453 [pdf, другой]
- [194] arXiv: 2110.01454 [pdf, другой]
- [195] arXiv: 2110.01468 [pdf, ps, другое]
- [196] arXiv: 2110.01473 [pdf, ps, другое]
- [197] arXiv: 2110.01481 [pdf, другой]
- [198] arXiv: 2110.01489 [pdf, другой]
- [199] arXiv: 2110.01492 [pdf, ps, другое]
- [200] arXiv: 2110.01504 [pdf, ps, другое]
- [201] arXiv: 2110.01507 [pdf, ps, другое]
- [202] arXiv: 2110.01508 [pdf, другой]
- [203] arXiv: 2110.01512 [pdf, ps, другое]
- [204] arXiv: 2110.01520 [pdf, ps, другое]
- [205] arXiv: 2110.01527 [pdf, другой]
- [206] arXiv: 2110.01536 [pdf, другое]
- [207] arXiv: 2110.01541 [pdf, ps, другое]
- [208] arXiv: 2110.01545 [pdf, другой]
- [209] arXiv: 2110.01551 [pdf, другой]
- [210] arXiv: 2110.01553 [pdf, ps, другое]
- [211] arXiv: 2110.01558 [pdf, ps, другое]
- [212] arXiv: 2110.01559 [pdf, другой]
- [213] arXiv: 2110.01563 [pdf, ps, другое]
- [214] arXiv: 2110.01566 [pdf, ps, другое]
- [215] arXiv: 2110.01569 [pdf, ps, другое]
- [216] arXiv: 2110.01570 [pdf, ps, другое]
- [217] arXiv: 2110.01574 [pdf, ps, другое]
- [218] arXiv: 2110.01576 [pdf, ps, другое]
- [219] arXiv: 2110.01580 [pdf, ps, другое]
- [220] arXiv: 2110.01588 [pdf, ps, другое]
- [221] arXiv: 2110.01594 [pdf, ps, другое]
- [222] arXiv: 2110.01597 [pdf, ps, другое]
- [223] arXiv: 2110.01600 [pdf, ps, другое]
Перекрестные списки на Вт, 5 окт 21
- [224] arXiv: 1701.04343 (перекрестный список из Physics.flu-dyn) [pdf, другое]
- [225] arXiv: 2110.00618 (перекрестный список из eess.SY) [pdf, другие]
- [226] arXiv: 2110.00625 (перекрестный список из cs.LG) [pdf, ps, другое]
- [227] arXiv: 2110.00629 (перекрестный список из stat.ML) [pdf, другое]
- [228] arXiv: 2110.00667 (перекрестный список из eess.SY) [pdf, другое]
- [229] arXiv: 2110.00675 (перекрестный список из cs.LG) [pdf, другое]
- [230] arXiv: 2110.00683 (перекрестный список из cs.LG) [pdf, другое]
- [231] arXiv: 2110.00693 (перекрестный список из cs.LG) [pdf, другое]
- [232] arXiv: 2110.00715 (перекрестный список из cs.CV) [pdf, другое]
- [233] arXiv: 2110.00725 (перекрестный список из Physics.bio-ph) [pdf, другое]
- [234] arXiv: 2110.00734 (перекрестный список из cs.GT) [pdf, ps, другое]
- [235] arXiv: 2110.00735 (перекрестный список из cs.CL) [pdf, другое]
- [236] arXiv: 2110.00744 (перекрестный список из cs.DS) [pdf, ps, другое]
- [237] arXiv: 2110.00747 (перекрестный список из Quant-ph) [pdf, ps, other]
- [238] arXiv: 2110.00819 (перекрестный список из cs.DC) [pdf, другое]
- [239] arXiv: 2110.00843 (перекрестный список из cs.RO) [pdf, другое]
- [240] arXiv: 2110.00871 (перекрестный список из cs.LG) [pdf, другое]
- [241] arXiv: 2110.00874 (перекрестный список из cs.LG) [pdf, другое]
- [242] arXiv: 2110.00884 (перекрестный список из stat.CO) [pdf, другое]
- [243] arXiv: 2110.00891 (перекрестный список из cs.RO) [pdf, другое]
- [244] arXiv: 2110.00905 (перекрестный список из Quant-ph) [pdf, ps, прочее]
- [245] arXiv: 2110.00926 (перекрестный список из cs.LG) [pdf, другое]
- [246] arXiv: 2110.00932 (перекрестный список из Quant-ph) [pdf, ps, other]
- [247] arXiv: 2110.01093 (перекрестный список из cs.CG) [pdf, ps, другое]
- [248] arXiv: 2110.01114 (перекрестный список из cs.LO) [pdf, ps, другое]
- [249] arXiv: 2110.01165 (перекрестный список из стат.ML) [pdf, другой]
- [250] arXiv: 2110.01195 (перекрестный список из cs.CR) [pdf, другое]
- [251] arXiv: 2110.01231 (перекрестный список из cs.CG) [pdf, другое]
- [252] arXiv: 2110.01278 (перекрестный список из cs.LG) [pdf, другое]
- [253] arXiv: 2110.01317 (перекрестный список из gr-qc) [pdf, ps, other]
- [254] arXiv: 2110.01405 (перекрестный список из Physics.med-ph) [pdf, другое]
- [255] arXiv: 2110.01407 (кросс-лист из cs.DM) [pdf, другое]
- [256] arXiv: 2110.01414 (перекрестный список из cs.DC) [pdf, другое]
- [257] arXiv: 2110.01444 (перекрестный список из cs.DC) [pdf]
- [258] arXiv: 2110.01450 (перекрестный список из cs.LG) [pdf, ps, другое]
- [259] arXiv: 2110.01496 (перекрестный список из q-fin.TR) [pdf, другое]
- [260] arXiv: 2110.01498 (перекрестный список из Quant-ph) [pdf, ps, other]
- [261] arXiv: 2110.01522 (перекрестный список из cond-mat.dis-nn) [pdf, другое]
- [262] arXiv: 2110.01538 (перекрестный список из hep-th) [pdf, другие]
- [263] arXiv: 2110.01539 (перекрестный список из cond-mat.stat-mech) [pdf, другое]
- [264] arXiv: 2110.01543 (перекрестный список из cs.LG) [pdf, другое]
- [265] arXiv: 2110.01581 (перекрестный список из eess.SP) [pdf, другое]
- [266] arXiv: 2110.01593 (перекрестный список из стат.ML) [pdf, другой]
- [267] arXiv: 2110.01598 (перекрестный список из cs.CV) [pdf, другое]
- [268] arXiv: 2110.01601 (перекрестный список из cs.LG) [pdf, другое]
- [269] arXiv: 2110.01602 (перекрестный список из stat.ML) [pdf, другое]
Замены на Вт, 5 окт 21
- [270] arXiv: 1311.6226 (заменено) [pdf, ps, другое]
- [271] arXiv: 1409.3052 (заменено) [pdf, ps, другое]
- [272] arXiv: 1506.04341 (заменено) [pdf, ps, другое]
- [273] arXiv: 1601.07092 (заменено) [pdf, ps, другое]
- [274] arXiv: 1604.00755 (заменено) [pdf, ps, другое]
- [275] arXiv: 1705.01663 (заменено) [pdf, ps, другое]
- [276] arXiv: 1801.08229 (заменено) [pdf, другое]
- [277] arXiv: 1803.03139 (заменено) [pdf, ps, другое]
- [278] arXiv: 1803.06510 (заменено) [pdf, другое]
- [279] arXiv: 1804.10646 (заменено) [pdf, ps, другое]
- [280] arXiv: 1807.02731 (заменено) [pdf, ps, другое]
- [281] arXiv: 1807.10622 (заменено) [pdf, другое]
- [282] arXiv: 1809.01823 (заменено) [pdf, ps, другое]
- [283] arXiv: 1809.06538 (заменено) [pdf, ps, другое]
- [284] arXiv: 1809.08867 (заменено) [pdf, ps, другое]
- [285] arXiv: 1810.08184 (заменено) [pdf, ps, другое]
- [286] arXiv: 1902.04203 (заменено) [pdf, ps, другое]
- [287] arXiv: 1903.11477 (заменено) [pdf, ps, другое]
- [288] arXiv: 1903.12256 (заменено) [pdf, другое]
- [289] arXiv: 1904.03010 (заменено) [pdf, ps, другое]
- [290] arXiv: 1905.07333 (заменено) [pdf, ps, другое]
- [291] arXiv: 1907.01382 (заменено) [pdf, другое]
- [292] arXiv: 1908.08880 (заменено) [pdf, другое]
- [293] arXiv: 1909.08904 (заменено) [pdf, ps, другое]
- [294] arXiv: 1910.01263 (заменено) [pdf, ps, другое]
- [295] arXiv: 1910.05718 (заменено) [pdf, ps, другое]
- [296] arXiv: 1910.06546 (заменено) [pdf, ps, другое]
- [297] arXiv: 1910.07339 (заменено) [pdf, ps, другое]
- [298] arXiv: 1910.08701 (заменено) [pdf, другое]
- [299] arXiv: 1910.11184 (заменено) [pdf]
- [300] arXiv: 1911.11031 (заменено) [pdf, ps, другое]
- [301] arXiv: 1912.02301 (заменено) [pdf, другое]
- [302] arXiv: 1912.13353 (заменено) [pdf, ps, другое]
- [303] arXiv: 2001.03124 (заменено) [pdf, ps, другое]
- [304] arXiv: 2001.06455 (заменено) [pdf, ps, другое]
- [305] arXiv: 2002.03659 (заменено) [pdf, ps, другое]
- [306] arXiv: 2002.04960 (заменено) [pdf, другое]
- [307] arXiv: 2002.06872 (заменено) [pdf, ps, другое]
- [308] arXiv: 2003.00222 (заменено) [pdf, ps, другое]
- [309] arXiv: 2003.01636 (заменено) [pdf, ps, другое]
- [310] arXiv: 2003.04006 (заменено) [pdf, ps, другое]
- [311] arXiv: 2003.04842 (заменено) [pdf, ps, другое]
- [312] arXiv: 2003.05828 (заменено) [pdf, ps, другое]
- [313] arXiv: 2003.06511 (заменено) [pdf, другое]
- [314] arXiv: 2003.08347 (заменено) [pdf, ps, другое]
- [315] arXiv: 2003.08941 (заменено) [pdf, другое]
- [316] arXiv: 2003.10056 (заменено) [pdf, ps, другое]
- [317] arXiv: 2003.14342 (заменено) [pdf, другое]
- [318] arXiv: 2004.00938 (заменено) [pdf, ps, другое]
- [319] arXiv: 2004.06024 (заменено) [pdf, ps, другое]
- [320] arXiv: 2004.12455 (заменено) [pdf, ps, другое]
- [321] arXiv: 2004.14361 (заменено) [pdf, ps, другое]
- [322] arXiv: 2005.01100 (заменено) [pdf, ps, другое]
- [323] arXiv: 2005.01202 (заменено) [src]
- [324] arXiv: 2005.10234 (заменено) [pdf, ps, другое]
- [325] arXiv: 2005.11404 (заменено) [pdf, другое]
- [326] arXiv: 2005.11419 (заменено) [pdf, ps, другое]
- [327] arXiv: 2006.01866 (заменено) [pdf, другое]
- [328] arXiv: 2006.02132 (заменено) [pdf, ps, другое]
- [329] arXiv: 2006.04299 (заменено) [pdf, другое]
- [330] arXiv: 2006.09648 (заменено) [pdf, другое]
- [331] arXiv: 2006.11864 (заменено) [pdf, ps, другое]
- [332] arXiv: 2006.13325 (заменено) [pdf, ps, другое]
- [333] arXiv: 2007.00367 (заменено) [pdf, ps, другое]
- [334] arXiv: 2007.05147 (заменено) [pdf, ps, другое]
- [335] arXiv: 2007.12006 (заменено) [pdf, ps, другое]
- [336] arXiv: 2008.00585 (заменено) [pdf, другое]
- [337] arXiv: 2008.00771 (заменено) [pdf, ps, другое]
- [338] arXiv: 2008.08070 (заменено) [pdf, ps, другое]
- [339] arXiv: 2009.04074 (заменено) [pdf, другое]
- [340] arXiv: 2009.04542 (заменено) [pdf, ps, другое]
- [341] arXiv: 2009.07108 (заменено) [pdf, ps, другое]
- [342] arXiv: 2009.13382 (заменено) [pdf, ps, другое]
- [343] arXiv: 2010.01130 (заменено) [pdf, ps, другое]
- [344] arXiv: 2010.02677 (заменено) [pdf, ps, другое]
- [345] arXiv: 2010.03230 (заменено) [pdf, другое]
- [346] arXiv: 2010.04392 (заменено) [pdf, другое]
- [347] arXiv: 2010.07552 (заменено) [pdf, другое]
- [348] arXiv: 2010.07843 (заменено) [pdf, другое]
- [349] arXiv: 2010.08342 (заменено) [pdf, ps, другое]
- [350] arXiv: 2011.03929 (заменено) [pdf, ps, другое]
- [351] arXiv: 2011.06986 (заменено) [pdf, другое]
- [352] arXiv: 2011.07142 (заменено) [pdf, другое]
- [353] arXiv: 2011.09503 (заменено) [pdf, другое]
- [354] arXiv: 2011.10130 (заменено) [pdf, другое]
- [355] arXiv: 2011.10709 (заменено) [pdf, другое]
- [356] arXiv: 2011.10979 (заменено) [pdf, другое]
- [357] arXiv: 2011.13613 (заменено) [src]
- [358] arXiv: 2011.14453 (заменено) [pdf, ps, другое]
- [359] arXiv: 2011.15085 (заменено) [pdf, другое]
- [360] arXiv: 2012.03503 (заменено) [pdf, другое]
- [361] arXiv: 2012.03792 (заменено) [pdf, ps, другое]
- [362] arXiv: 2012.04068 (заменено) [pdf, ps, другое]
- [363] arXiv: 2012.07793 (заменено) [pdf, другое]
- [364] arXiv: 2012.10665 (заменено) [pdf, ps, другое]
- [365] arXiv: 2012.11053 (заменено) [pdf, другое]
- [366] arXiv: 2012.11314 (заменено) [pdf, ps, другое]
- [367] arXiv: 2012.12783 (заменено) [pdf, ps, другое]
- [368] arXiv: 2012.13549 (заменено) [pdf, ps, другое]
- [369] arXiv: 2012.14157 (заменено) [pdf, другое]
- [370] arXiv: 2012.14658 (заменено) [pdf, ps, другое]
- [371] arXiv: 2101.00473 (заменено) [pdf, другое]
- [372] arXiv: 2101.04044 (заменено) [pdf, ps, другое]
- [373] arXiv: 2101.05480 (заменено) [pdf, другое]
- [374] arXiv: 2101.06501 (заменено) [pdf, ps, другое]
- [375] arXiv: 2101.07445 (заменено) [pdf, другое]
- [376] arXiv: 2101.09692 (заменено) [pdf, ps, другое]
- [377] arXiv: 2101.10666 (заменено) [pdf, ps, другое]
- [378] arXiv: 2102.00421 (заменено) [pdf, другое]
- [379] arXiv: 2102.00660 (заменено) [pdf, ps, другое]
- [380] arXiv: 2102.01855 (заменено) [pdf, другое]
- [381] arXiv: 2102.01942 (заменено) [pdf, ps, другое]
- [382] arXiv: 2102.02045 (заменено) [pdf, ps, другое]
- [383] arXiv: 2102.03918 (заменено) [pdf, ps, другое]
- [384] arXiv: 2102.04979 (заменено) [pdf, ps, другое]
- [385] arXiv: 2102.05738 (заменено) [pdf, другое]
- [386] arXiv: 2102.06927 (заменено) [pdf, ps, другое]
- [387] arXiv: 2102.07732 (заменено) [pdf, другое]
- [388] arXiv: 2102.07754 (заменено) [pdf, другое]
- [389] arXiv: 2102.08855 (заменено) [pdf, другое]
- [390] arXiv: 2102.09976 (заменено) [pdf, ps, другое]
- [391] arXiv: 2102.13475 (заменено) [pdf, ps, другое]
- [392] arXiv: 2103.02987 (заменено) [pdf, другое]
- [393] arXiv: 2103.07481 (заменено) [pdf, другое]
- [394] arXiv: 2103.09902 (заменено) [pdf, другое]
- [395] arXiv: 2103.10586 (заменено) [pdf, ps, другое]
- [396] arXiv: 2103.11142 (заменено) [pdf, другое]
- [397] arXiv: 2103.11653 (заменено) [pdf, ps, другое]
- [398] arXiv: 2103.11914 (заменено) [pdf, ps, другое]
- [399] arXiv: 2103.13466 (заменено) [pdf, ps, другое]
- [400] arXiv: 2103.14975 (заменено) [pdf, другое]
- [401] arXiv: 2103.16077 (заменено) [pdf, ps, другое]
- [402] arXiv: 2103.16502 (заменено) [pdf, другое]
- [403] arXiv: 2104.01322 (заменено) [pdf, другое]
- [404] arXiv: 2104.02268 (заменено) [pdf, другое]
- [405] arXiv: 2104.04882 (заменено) [pdf, другое]
- [406] arXiv: 2104.06932 (заменено) [pdf, ps, другое]
- [407] arXiv: 2104.08101 (заменено) [pdf, другое]
- [408] arXiv: 2104.09755 (заменено) [pdf, другое]
- [409] arXiv: 2104.09763 (заменено) [pdf, другое]
- [410] arXiv: 2104.10836 (заменено) [pdf, ps, другое]
- [411] arXiv: 2104.11268 (заменено) [pdf, другое]
- [412] arXiv: 2104.12062 (заменено) [pdf, другое]
- [413] arXiv: 2105.00018 (заменено) [pdf, другое]
- [414] arXiv: 2105.04586 (заменено) [pdf, ps, другое]
- [415] arXiv: 2105.06078 (заменено) [pdf, ps, другое]
- [416] arXiv: 2105.07374 (заменено) [pdf, другое]
- [417] arXiv: 2105.07978 (заменено) [pdf, ps, другое]
- [418] arXiv: 2105.08160 (заменено) [pdf, ps, другое]
- [419] arXiv: 2105.11922 (заменено) [pdf, ps, другое]
- [420] arXiv: 2105.12845 (заменено) [pdf, ps, другое]
- [421] arXiv: 2105.14308 (заменено) [pdf, ps, другое]
- [422] arXiv: 2106.01206 (заменено) [pdf, другое]
- [423] arXiv: 2106.02073 (заменено) [pdf, другое]
- [424] arXiv: 2106.03222 (заменено) [pdf, ps, другое]
- [425] arXiv: 2106.06956 (заменено) [pdf, другое]
- [426] arXiv: 2106.06982 (заменено) [pdf, ps, другое]
- [427] arXiv: 2106.07108 (заменено) [pdf, другое]
- [428] arXiv: 2106.07274 (заменено) [pdf, ps, другое]
- [429] arXiv: 2106.07746 (заменено) [pdf, ps, другое]
- [430] arXiv: 2106.07764 (заменено) [pdf, ps, другое]
- [431] arXiv: 2106.08119 (заменено) [pdf, ps, другое]
- [432] arXiv: 2106.08926 (заменено) [pdf, другое]
- [433] arXiv: 2106.09518 (заменено) [pdf]
- [434] arXiv: 2106.09978 (заменено) [pdf, ps, другое]
- [435] arXiv: 2106.12361 (заменено) [pdf, ps, другое]
- [436] arXiv: 2106.12935 (заменено) [pdf, ps, другое]
- [437] arXiv: 2106.15511 (заменено) [pdf, ps, другое]
- [438] arXiv: 2107.01874 (заменено) [pdf, ps, другое]
- [439] arXiv: 2107.03264 (заменено) [pdf, другое]
- [440] arXiv: 2107.04017 (заменено) [pdf]
- [441] arXiv: 2107.06220 (заменено) [pdf, другое]
- [442] arXiv: 2107.06740 (заменено) [pdf, другое]
- [443] arXiv: 2107.06792 (заменено) [pdf, ps, другое]
- [444] arXiv: 2107.07152 (заменено) [pdf, другое]
- [445] arXiv: 2107.08698 (заменено) [pdf, другое]
- [446] arXiv: 2107.08901 (заменено) [pdf, ps, другое]
- [447] arXiv: 2107.09673 (заменено) [pdf, другое]
- [448] arXiv: 2107.11086 (заменено) [pdf, ps, другое]
- [449] arXiv: 2107.13125 (заменено) [pdf, ps, другое]
- [450] arXiv: 2108.00332 (заменено) [pdf, другое]
- [451] arXiv: 2108.00565 (заменено) [pdf, ps, другое]
- [452] arXiv: 2108.03179 (заменено) [pdf, ps, другое]
- [453] arXiv: 2108.04433 (заменено) [pdf, другое]
- [454] arXiv: 2108.05291 (заменено) [pdf, ps, другое]
- [455] arXiv: 2108.06416 (заменено) [pdf, ps, другое]
- [456] arXiv: 2108.07671 (заменено) [pdf, другое]
- [457] arXiv: 2108.07746 (заменено) [pdf, ps, другое]
- [458] arXiv: 2108.07850 (заменено) [pdf, другое]
- [459] arXiv: 2108.10011 (заменено) [pdf, другое]
- [460] arXiv: 2108.10100 (заменено) [pdf, ps, другое]
- [461] arXiv: 2108.10650 (заменено) [pdf, ps, другое]
- [462] arXiv: 2108.11019 (заменено) [pdf, другое]
- [463] arXiv: 2108.12775 (заменено) [pdf, ps, другое]
- [464] arXiv: 2108.13014 (заменено) [pdf, ps, другое]
- [465] arXiv: 2108.13762 (заменено) [pdf, ps, другое]
- [466] arXiv: 2108.13999 (заменено) [pdf, другое]
- [467] arXiv: 2109.00935 (заменено) [pdf, ps, другое]
- [468] arXiv: 2109.02101 (заменено) [pdf, ps, другое]
- [469] arXiv: 2109.02180 (заменено) [pdf, ps, другое]
- [470] arXiv: 2109.02455 (заменено) [pdf, ps, другое]
- [471] arXiv: 2109.02766 (заменено) [pdf, ps, другое]
- [472] arXiv: 2109.02818 (заменено) [pdf, ps, другое]
- [473] arXiv: 2109.05247 (заменено) [pdf, другое]
- [474] arXiv: 2109.06106 (заменено) [pdf, другое]
- [475] arXiv: 2109.07233 (заменено) [pdf, ps, другое]
- [476] arXiv: 2109.08911 (заменено) [pdf, ps, другое]
- [477] arXiv: 2109.09006 (заменено) [pdf, ps, другое]
- [478] arXiv: 2109.09018 (заменено) [pdf, другое]
- [479] arXiv: 2109.09204 (заменено) [pdf, другое]
- [480] arXiv: 2109.10008 (заменено) [pdf, другое]
- [481] arXiv: 2109.10113 (заменено) [pdf, ps, другое]
- [482] arXiv: 2109.10117 (заменено) [pdf, ps, другое]
- [483] arXiv: 2109.10520 (заменено) [pdf, другое]
- [484] arXiv: 2109.10611 (заменено) [pdf, ps, другое]
- [485] arXiv: 2109.10845 (заменено) [pdf, ps, другое]
- [486] arXiv: 2109.10913 (заменено) [pdf, ps, другое]
- [487] arXiv: 2109.11581 (заменено) [pdf, ps, другое]
- [488] arXiv: 2109.12015 (заменено) [pdf, ps, другое]
- [489] arXiv: 2109.12313 (заменено) [pdf, другое]
- [490] arXiv: 2109.12353 (заменено) [pdf, другое]
- [491] arXiv: 2109.12486 (заменено) [pdf, ps, другое]
- [492] arXiv: 2109.12687 (заменено) [pdf, ps, другое]
- [493] arXiv: 2109.14079 (заменено) [pdf, другое]
- [494] arXiv: 2109.14607 (заменено) [pdf, ps, другое]
- [495] arXiv: 2109.14756 (заменено) [pdf, другое]
- [496] arXiv: 2109.14851 (заменено) [pdf, другое]
- [497] arXiv: 2109.14893 (заменено) [pdf, ps, другое]
- [498] arXiv: 2109.15016 (заменено) [pdf, ps, другое]
- [499] arXiv: 2109.15137 (заменено) [pdf, ps, другое]
- [500] arXiv: 2109.15245 (заменено) [pdf, ps, другое]
- [501] arXiv: 2109.15280 (заменено) [pdf, другое]
- [502] arXiv: 2110.00088 (заменено) [pdf, другое]
- [503] arXiv: 2110.00285 (заменено) [pdf, ps, другое]
[отображение до 2000 записей на странице: меньше | подробнее]
Отключить MathJax (Что такое MathJax?)
Ссылки на: arXiv, интерфейс формы, найти, математика, недавний, 2110, контакт, помощь (ключ доступа к информации)
NCERT Exemplar Class 7 Maths Глава 1 Целые числа
NCERT Exemplar Class 7 Maths Глава 1 Целые числа являются частью NCERT Exemplar Class 7 Maths.Здесь мы привели NCERT Exemplar Class 7 Maths Solutions Глава 1 Целые числа.
NCERT Exemplar Class 7 Maths Solutions Глава 1 Целые числа
Вопрос 1.
Когда целые числа 10, 0, 5, -5, -7 расположены в порядке убывания или возрастания, выясните, какое из следующих целых чисел всегда остается в середине расположения.
(a) 0
(b) 5
(c) — 7
(d) -5
Решение:
(a): целые числа: 10, 0, 5, -5, -7
По убыванию: 10, 5, 0, — 5, — 7
По возрастанию: -7, — 5,0, 5, 10
Следовательно, 0 — это целое число, которое всегда остается в середине расположения.
Вопрос 2.
Наблюдая за числовой прямой, укажите, какое из следующих утверждений неверно?
(a) B больше -10
(b) A больше 0
(c) B больше A
(d) 6 меньше 0
Решение:
(c): Так как B равно меньше, чем A
Вопрос 3.
Наблюдая за числовой линией выше, укажите, какое из следующих утверждений верно?
(a) B равно 2
(b) A равно — 4
(c) S равно -13
(d) B равно — 4
Решение:
(d): Здесь A равно 7, а B равно -4.
Вопрос 4.
Следующие три последовательных числа в шаблоне 11, 8, 5, 2, ______, __, __ — это
(a) 0, — 3, — 6
(b) -1, -5, -8
(c) — 2, — 5, — 8
(d) -1, -4, -7
Решение:
(d): Здесь шаблон
11-3 = 8, 8-3 = 5, 5 — 3 = 2
Итак, следующие три последовательных числа будут 2 — 3 = -1, -1 — 3 = — 4, -4 — 3 = — 7
то есть, -1, -4, -7
Вопрос 5.
Следующее число в шаблоне — 62, — 37, — 12 _________________.
(a) 25
(b) 13
(c) 0
(d) -13
Решение:
(b): Здесь шаблон -62 + 25 = -37, -37 + 25 = -12
∴ Следующее число в шаблоне будет -12 + 25 = 13
Вопрос 6.
Какое из следующих утверждений неверно? ;
(a) Когда складываются два положительных целых числа, мы всегда получаем положительное целое число.
(b) Когда складываются два отрицательных целых числа, мы всегда получаем отрицательное целое число.
(c) Когда добавляются положительное целое число и отрицательное целое число, мы всегда получаем отрицательное целое число.
(d) Аддитивная инверсия целого числа 2 равна (-2), а аддитивная инверсия (-2) равна 2.
Решение:
(c): Утверждение (c) неверно, потому что когда положительное целое число и отрицательное целое число равны добавлено, мы также можем получить положительное целое число или ноль.
Вопрос 7.
На следующей числовой строке «ноль» показан точкой
(a) X
(b) Y
(c) Z
(d) W
Решение:
(c):
Вопрос 8.
Если и • представляют некоторые целые числа в числовой строке, то порядок убывания этих чисел равен
Решение:
(c) Порядок убывания данных чисел —
Вопрос 9:
На числовой строке значение (-3) x 3 находится справа от
(a) -10
(b) — 4
(c) 0
(d) 9
Решение:
(a):
Так как, (-3) × 3 = — 9
Он лежит справа от -10.
Вопрос 10.
Значение 5 + (- 1) не находится между
(a) 0 и -10
(b) 0 и 10
(c) — 4 и -15
(d) — 6 и 6
Решение:
(b): значение \ (5 \ div (-1) = \ frac {5} {(- 1)} = — 5 \)
∴ -5 не находится между 0 и 10.
Вопрос 11.
Уровень воды в колодце был на 20 м ниже уровня земли. В сезон дождей дождевая вода, собранная в разных резервуарах для воды, сливалась в колодец, и уровень воды поднимался на 5 м выше предыдущего уровня.Стена колодца высотой 20 см, шкив закреплен на высоте 80 см. Рагху хочет набрать воду из колодца. Минимальная длина веревки, которую он может использовать, составляет
Решение:
(a): Высота стенки колодца = 1 м 20 см = 1,20 м
Высота шкива = 80 см = 0,80 м
∴ Требуемая минимальная длина каната
= (20-5 + 1,20 +0,80) м
= (15 + 2) м = 17 м
Вопрос 12.
(-11) × 7 не равно
(a) 11 × (-7)
(b) — (11 × 7)
(c) (- 11) × (- 7)
( d) 7 × (-11)
Решение:
(c): (- 11) × 7 = — (11 × 7)
= 11 × (-7) = 7 × (-11) = -77
∴ ( -11) × 7 ≠ (-11) × (-7) = 77
Вопрос 13.
(- 10) × (- 5) + (- 7) равно
(a) -57
(b) 57
(c) -43
(d) 43
Решение:
(d): (- 10) × (- 5) + (- 7) = 50 + (-7) = 50-7 = 43
Вопрос 14.
Что из следующего не является аддитивным обратным величине a?
(a) — (-a)
(b) a × (-1)
(c) — a
(d) a + (-1)
Решение:
(a): Аддитив, обратный a, равен (- а).
Таким образом, он не может быть аддитивным обратным.
Вопрос 15.
Что из следующего является мультипликативным тождеством для целого числа o?
(a) a
(b) 1
(c) 0
(d) -1
Решение:
(b): мультипликативное тождество для целого числа a равно 1.[∵ a × 1 = a = 1 × a]
Вопрос 16.
[(- 8) × (- 3)] × (- 4)] не равно
(a) (- 8) × [(- 3) × (- 4)]
(b) [(- 8) × (- 4)] × (- 3)
(c) [(- 3) × (- 8)] × (- 4)
(d) (- 8) × (- 3) — (- 8) × (- 4)
Решение:
(d): [(-8) × (-3)] × (-4)
= (-8) × [(3) × (-1)]
= [(-8) × (-4)] × (-3)
= [(-3) — (-8)] × (-4)
Но
[(-8) × (-3)] × (-4) ≠ (-8) × (-3) — (-8) × (-4)
Вопрос 17.
(- 25) × [6 + 4] не то же самое, что
(a) (-25) × 10
(b) (-25) × 6 + (- 25) × 4
(c) -25 × 6 × 4
(d) — 250
Решение:
(c): (- 25) × [6 + 4] ≠ (- 25) × 6 × 4
Вопрос 18.
— 35 × 107 не то же самое, что
(a) — 35 × (100 + 7)
(b) (- 35) × 7 + (- 35) × 100
(c) — 35 × 7 + 100
( d) (-30-5) × 107
Решение:
(c): — 35 × 107 ≠ -35 × 7 + 100
Вопрос 19.
(- 43) × (- 99) + 43 равно
(a) 4300
(b) — 4300
(c) 425
(d) -4214
Решение:
(a): ( — 43) × (- 99) + 43 = 43 × -99) + 43
= 4257 + 43 = 4300
Вопрос 20.
(- 16) ÷ 4 не то же самое, что
(a) (-4) ÷ 16
(b) — (16 ÷ 4)
(c) 16 ÷ (-4)
(d) — 4
Решение:
(a): \ ((- 16) \ div 4 = \ frac {(- 16)} {4} = — 4 \)
Но \ ((- 4) \ div 16 = \ frac { -4} {16} = — \ frac {1} {4} \)
(-16) ÷ 4 не то же самое, что (-4) ÷ 16
Вопрос 21.
Что из следующего не представляет собой целое число?
(a) 0 ÷ (- 7)
(b) 20 ÷ (- 4)
(c) (-9) ÷ 3
(d) (-12) ÷ 5
Решение:
(d):
(a) 0 ÷ (-7) = 0
(b) 20 ÷ (- 4) = -5
(c) (-9) ÷ 3 = -3
(d) \ ((- 12) \ div 5 = \ frac {-12} {5} \)
Следовательно, (-12) ÷ 5 не представляет собой целое число.
Вопрос 22.
Что из перечисленного отличается от других?
(a) 20 + (-25)
(b) (-37) — (-32)
(c) (-5) × (- 1)
(d) 45 ÷ (- 9)
Решение:
(в):
(а) 20 + (- 25) = 20-25 = — 5
(б) (- 37) — (- 32) = — 37 + 32 = — 5
(в) (- 5) × (- 1) = 5
(d) \ ((45) \ div (-9) = — \ frac {45} {9} = — 5 \)
Следовательно, (-5) × (-1) равно разные
Вопрос 23.
Что из перечисленного показывает максимальное повышение температуры?
(a) от 23 ° до 32 °
(b) от -10 ° до 1 °
(c) от -18 ° до -11 °
(d) от -5 ° до 5 °
Раствор:
(b): Поднимитесь внутрь температура,
(а) 32 ° — 23 ° = 9 °
(б) 1 ° — (-10) ° = 1 ° + 10 ° = 11 ° (максимум)
(в) -11 ° — (-18) ° = -11 ° + 18 ° = 7 °
(d) 5 ° — (-5 °) = 5 ° + 5 ° = 10 °
Следовательно, максимальное повышение температуры от -10 ° до + 1 °.
Вопрос 24.
Если a и b — два целых числа, то какое из следующего не может быть целым числом?
(a) a + b
(b) a — b
(c) a × b
(d) a ÷ b
Решение:
(d): если a и b — два целых числа, то
a + b равно всегда целое число.
a — бис всегда целое число.
a × b также является целым числом,
, но a ÷ b может быть или не быть целым числом.
Вопрос 25.
Для ненулевого целого числа a, что из следующего не определено?
(a) a ÷ 0
(b) 0 ÷ a
(c) a ÷ 1
(d) 1 ÷ a
Решение:
(a): \ (a \ div 0 = \ frac {a} {0 } \) Не определено
Указания: обведите нечетное из следующего: (Вопросы с 26 по 30)
Вопрос 26.
(a) (-3, 3)
(b) (-5, 5)
(c) (-6, 1)
(d) (-8, 8)
Решение:
(c ): (А) -3 + 3 = 0
(б) -5 + 5 = 0
(в) -6 + 1 = -5
(г) -8 + 8 = 0
∴ (-6,1) отличается.
Вопрос 27.
(a) (-1, -2)
(b) (-5, 2)
(c) (- 4, 1)
(d) (- 9, 7)
Решение:
( г): (а) -1 — 2 = -3
(б) -5 + 2 = -3
(в) -4 + 1 = -3
(г) -9 + 7 = -2
∴ (- 9, +7) другое.
Вопрос 28.
(a) (- 9) × 5 × 6 × (- 3)
(b) 9 × (-5) × 6 × (-3)
(c) (- 9) × (- 5 ) × (- 6) × 3
(d) 9 × (- 5) × (- 6) × 3
Решение:
(c): (a) (- 9) × 5 × 6 × (- 3) = -810
(б) 9 × (-5) × 6 × (-3) = 810
(в) (- 9) × (- 5) × (- 6) × 3 = -810
(d) 9 × (- 5) × (- 6) × 3 = 810
∴ (- 9) × (- 5) × (- 6) × 3 различается
Вопрос 29.
(a) (-100) ÷ 5
(b) (-81) ÷ 9
(c) (- 75) ÷ 5
(d) (-32) ÷ 9
Решение:
(d):
∴ (-32) ÷ 9 разное
Вопрос 30.
(a) (- 1) × (- l)
(b) (- 1) × (- l) × (- 1)
(c) (-1) × (-1) × ( -1) × (-1)
(d) (-1) × (-1) × (-1) × (-1) × (-1) × (-1)
Решение:
(b):
(а) (-1) × (-1) = 1
(б) (- 1) × (-1) × (-1) = — 1
(в) (- 1) × (- 1) × ( — 1) × (- 1) = 1
(d) (-1) × (-1) × (-1) × (- 1) × (-1) × (-1) = 1
∴ (- 1 ) × (-1) × (-1) отличается
Указания: В вопросах с 31 по 71 заполните пропуски, чтобы утверждения соответствовали действительности.
Вопрос 31.
(- a) + b = b + аддитивная обратная ___.
Решение:
a: (-a) + b = b + (-a)
= b + Аддитив, обратный a.
Вопрос 32.
__________ ÷ (- 10) = 0
Решение:
\ (0: 0 \ div (-10) = — \ frac {0} {10} = 0 \)
Вопрос 33.
(- 157) × (- 19) + 157 = ___________.
Решение:
3140: (-157) × (-19) + 157
= 157 × 19 + 157 × 1
= 157 × [19 + 1] = 157 × 20 = 3140
Вопрос 34.
[(- 8) + ___] + ___ = ___ + [(-3) + ___] = — 3
Решение:
-3, 8, (-8), 8: [(-8) + (-3)] + 8 = -8 + [(- 3) + 8] = -3
Вопрос 35.
На следующей числовой строке (- 4) × 3 обозначено точкой _____.
Решение:
D: (-4) × 3 = — 12
∴ -12 представлено точкой D.
Вопрос 36.
Если x, y и z целые числа, то (x + ____) + z = ____ + (y + ____)
Решение:
y, x, z: (x + y) + z = x + (y + z) [Ассоциативное свойство целых чисел]
Вопрос 37.
(-43) + __________ = (-43)
Решение:
0: (-43) + 0 = — 43
Вопрос 38.
(- 8) + (- 8) + (- 8) = _______ × (- 8)
Решение:
3: (-8) + (-8) + (-8)
= (- 8) × [1 + 1 + 1] = (-8) × 3 = 3 × (-8)
Вопрос 39.
11 × (- 5) = — (_____ x____) = _____
Решение:
11, 5, -55: 11 × (-5) = — (11 × 5) = -55
Вопрос 40.
(- 9) × 20 = _______
Решение:
-180: (-9) × 20 = -180
Вопрос 41.
(- 23) × (42) = (- 42) × ______
Решение:
23: (-23) × (42) = (-42) × 923)
Вопрос 42.
При умножении положительного целого числа и отрицательного целого числа мы умножаем их как ___ числа и ставим знак ___ перед произведением.
Решение:
Целое, отрицательное
Вопрос 43.
Если мы умножим ___ число отрицательных целых чисел, то полученное целое число будет положительным.
Решение:
Даже
Вопрос 44.
Если мы умножим шесть отрицательных целых чисел и шесть положительных целых чисел, то получится целое число ___.
Решение:
Положительное: когда четное число отрицательных целых чисел умножается, они дают положительное целое число, а когда положительные целые числа умножаются, они всегда дают положительное целое число.
Вопрос 45.
Если мы умножим пять положительных целых чисел и одно отрицательное целое число, то получится целое число ___.
Решение:
Отрицательное: умножение нечетного числа отрицательных чисел дает отрицательное целое число. Кроме того, когда отрицательное и положительное целые числа умножаются, они дают отрицательное целое число.
Вопрос 46.
________ — это мультипликативное тождество для целых чисел.
Решение:
1: a × 1 = 1 × a = a
Вопрос 47.
Мы получаем аддитивную инверсию целого числа a, когда умножаем его на ___.
Решение:
(-1): a × (-1) = -a
Вопрос 48.
(- 25) × (- 2) = ______.
Решение:
50: (-25) × (-2) = 25 × 2 = 50
Вопрос 49.
(- 5) × (- 6) × (- 7) = ______.
Решение:
210: (-5) × (-6) × (-7)
= 5 × 6 × (-7) = 30 × (-7) = -210
Вопрос 50.
3 × (- 1) × (- 15) = _______.
Решение:
45: 3 × (-1) × (-15) = (-3) × (- 15) = 45
Вопрос 51.
[12 × (- 7)] × 5 = _____ × [(- 7) × ____]
Решение:
12, 5: [12 × (- 7)] × 5 = 12 × [(- 7) × 5]
Вопрос 52.
23 × (- 99) = ____ × (- 100 + ____) = 23 × ____ + 23 × ____
Решение:
23, 1, -100, 1: 23 × (- 99) = 23 × (- 100 + 1) = 23 × (- 100) + 23 × 1
Вопрос 53.
______ × (- 1) = — 35
Решение:
35: — 35 × (-1) = — 35
Вопрос 54.
____ × (- 1) = 47
Решение:
-47: (- 47) × (- 1) = 47
Вопрос 55.
88 × ____ = — 88
Решение:
-1: 88 × (- 1) = — 88
Вопрос 56.
____ × (- 93) = 93
Решение:
-1: (- 1) × (- 93) = 93
Вопрос 57.
(- 40) × ___ = 80
Решение:
-2: (- 40) × (-2) = 80
Вопрос 58.
____ × (-23) = — 920
Решение:
40: Пусть умножается число x.
x × (-23) = -920
\ (\ Rightarrow x = -920 \ div (-23) = \ frac {920} {23} = 40 \)
Вопрос 59.
Когда мы делим отрицательное целое число на положительное, мы делим их на целые числа и ставим знак ____ перед частным.
Решение:
Минус
Вопрос 60.
Когда (-16) делится на ____, частное получается 4.
Решение:
-4: Делим -16 на x дает частное 4.
\ (\ следовательно \ frac {-16} {x} = 4 \)
\ (\ Rightarrow \ quad x = \ frac {- 16} {4} = — 4 \)
Вопрос 61.
Деление — это операция, обратная ____.
Решение:
Умножение.
Вопрос 62.
65 ÷ (- 13) = _____.
Решение:
\ (- 5: 65 \ div (-13) = — \ frac {65} {13} = — 5 \)
Вопрос 63.
(-100) ÷ (-10) = _____.
Решение:
\ (10: (- 100) \ div (-10) = \ frac {100} {10} = 10 \)
Вопрос 64.
(-225) ÷ 5 = _____.
Решение:
\ (- 45: (- 225) \ div 5 = — \ frac {225} {5} = — 45 \)
Вопрос 65.
_____ ÷ (-1) = (- 83)
Решение:
83: 83 ÷ (-1) = — 83
Вопрос 66.
____ ÷ (-1) = 75
Решение:
\ (- 75: (- 75) \ div (-1) = \ frac {75} {1} = 75 \)
Вопрос 67.
51 ÷ ____ = (- 51)
Решение:
\ (- 1: 51 \ div (-1) = — \ frac {51} {1} = — 51 \)
Вопрос 68.
113 ÷ ____ = (- 1)
Решение:
\ (- 113: 113 \ div (-113) = — \ frac {113} {113} = — 1 \)
Вопрос 69.
-95 ÷ (-1) = 95
Решение:
\ (- 1: (- 95) \ div (-1) = \ frac {95} {1} = 95 \)
Вопрос 70.
(-69) ÷ 69 = _____.
Решение:
\ (- 1: (- 69) \ div (69) = — \ frac {69} {69} = — 1 \)
Вопрос 71.
(-28) ÷ (-28) = _____
Решение:
\ (1: (- 28) \ div (-28) = \ frac {28} {28} = 1 \)
Указания: В вопросах с 72 по 108 укажите, верны ли утверждения или нет.
Вопрос 72.
5 — (-8) совпадает с 5 + 8.
Решение:
True
5 — (-8) = 5 + 8
Вопрос 73.
(-9) + (-11) больше, чем (-9) — (- 11).
Решение:
Ложь
(-9) + (-11) = — 9-11 = -20
и (-9) — (-11) = -9 + 11 = 2
Поскольку, -20 <2⇒ - 9 + (-11) <(-9) - (-11)
Вопрос 74.
Сумма двух отрицательных целых чисел всегда дает число меньше обоих целых чисел.
Решение:
True
Вопрос 75.
Разница двух отрицательных целых чисел не может быть положительным целым числом.
Решение:
Неверно
As -3 — (-5) = -3 + 5 = 2
Вопрос 76.
Мы можем написать пару целых чисел, сумма которых не является целым числом.
Решение:
False
Так как сумма двух целых чисел всегда является целым числом.
Вопрос 77.
Целые числа закрываются вычитанием.
Решение:
Истина
Поскольку вычитание любых двух целых чисел всегда является целым числом.
∴ Целые числа закрываются при вычитании.
Вопрос 78.
(- 23) + 47 совпадает с 47 + (- 23).
Решение:
Истинно
(-23) + 47 = 24
и 47 + (-23) = 47-23 = 24
Вопрос 79.
Когда мы меняем порядок целых чисел, их сумма остается прежней.
Решение:
True
Вопрос 80.
Когда мы меняем порядок целых чисел, их разница остается неизменной.
Решение:
Неверно
Как 2 — 3 — 5 = 2 — 8 = -6
, но 3 — 2 — 5 = 3 — 7 = -4
Вопрос 81.
Пройти сначала 500 м на восток, а затем на 200 м назад, это то же самое, что пойти сначала на 200 м на запад, а затем на 500 м назад.
Решение:
True
В первом случае он находится на расстоянии (500 — 200) м = 300 м к востоку.
Во втором случае он находится на расстоянии (200-500) м = -300 м к западу, т.е. 300 м к востоку.
Вопрос 82.
(-5) × (33) = 5 × (- 33)
Решение:
Истинно
(-5) × (33) = — 165 = 5 × (-33)
Вопрос 83.
(-19) × (-11) = 19 × 11
Решение:
Истинно
(-19) × (-11) = 19 × 11 = 209
Вопрос 84.
(-20) × (5–3) = (-20) × (-2)
Решение:
Неверно
(-20) × (5–3) = (-20) × 2 = ( -40)
, но (-20) × (-2) = 20 × 2 = 40
Вопрос 85.
4 × (-5) = (-10) × (-2)
Решение:
Ложь
4 × (-5) = — 20
, но (-10) × (-2) = 10 × 2 = 20
Вопрос 86.
(-1) × (-2) × (-3) = 1 × 2 × 3
Решение:
Неверно
(-1) × (-2) × (-3) = 1 × 2 × (-3) = 2 × (-3) = (-6)
, но 1 × 2 × 3 = 6
Вопрос 87.
(-3) × 3 = (-12) — (-3)
Решение:
Истинно
Поскольку, (-3) × 3 = (- 9)
и (-12) — (-3 ) = (-12) + 3 = (-9)
Вопрос 88.
Произведение двух отрицательных целых чисел является отрицательным целым числом.
Решение:
False
Поскольку произведение двух отрицательных целых чисел всегда является положительным целым числом.
Вопрос 89.
Произведение трех отрицательных целых чисел — отрицательное целое число.
Решение:
Истина
Так как произведение нечетного числа отрицательных чисел всегда является отрицательным целым числом.
Вопрос 90.
90 Произведение отрицательного целого числа и положительного целого числа является положительным целым числом.
Решение:
False
Как произведение отрицательного целого числа и положительного целого числа является отрицательным целым числом.
Вопрос 91.
Когда мы умножаем два целых числа, их произведение всегда больше, чем оба целых числа.
Решение:
Неверно
Когда мы умножаем два целых числа, их произведение может быть или не быть больше обоих целых чисел.
Вопрос 92.
Целые числа замкнуты при умножении.
Решение:
Истина
Так как умножение двух целых чисел всегда является целым числом.
Целые числа замкнуты при умножении.
Вопрос 93.
(-237) × 0 совпадает с 0 × (-39).
Решение:
Истина
(-237) × 0 = 0
и 0 × (-39) = 0
Вопрос 94.
Умножение не коммутативно для целых чисел.
Решение:
False
As Умножение коммутативно для целых чисел.
Вопрос 95.
(-1) не является мультипликативным тождеством целых чисел.
Решение:
Истина
Поскольку 1 является мультипликативным тождеством для целых чисел.
Вопрос 96.
99 × 101 можно записать как (100 — 1) × (100 + 1).
Решение:
Истина
99 = 100 — 1 и 101 = 100 + 1
Итак, 99 × 101 = (100 — 1) × (100 + 1)
Вопрос 97.
Если a, b и c — целые числа и b ≠ 0, то a × (b — c) = a × b — a × c
Решение:
Истина
a × (b — c) = (a × b) — (a × c)
(Распределительное свойство умножения над вычитанием)
Вопрос 98.
(a + b) × c = a × c + a × b
Решение:
Неверно
a × (b + c) = a × b + a × c
Вопрос 99.
a × b = b × a
Решение:
True
Вопрос 100.
a ÷ b = b ÷ a
Решение:
False
Поскольку деление не коммутативно для целых чисел,
∴ a ÷ b ≠ b ÷ a
Вопрос 101.
a — b = b — a
Решение:
False
Поскольку вычитание не коммутативно для целых чисел.
∴ а — б ≠ б — а
Вопрос 102.
a ÷ (- b) = — (a ÷ b)
Решение:
True
\ (a \ div (-b) = \ frac {a} {- b} = — \ left (\ frac {a} {b} \ right) = — (a \ div b) \)
Вопрос 103.
a ÷ (-l) = — a
Решение:
True
\ (a \ div (-1) = \ frac {a} {- 1} = — a \)
Вопрос 104.
Факт умножения (-8) × (-10) = 80 совпадает с фактом деления 80 ÷ (-8) = (-10).
Решение:
Истина
(-8) × (-10) = 8 × 10 = 80
и \ (80 \ div (-8) = — \ frac {80} {8} = — 10 \)
Вопрос 105.
Целые числа закрываются на деление.
Решение:
Неверно
Поскольку целые числа не закрываются при делении.
Вопрос 106.
[(-32) ÷ 8] ÷ 2 = — 32 ÷ [8 ÷ 2]
Решение:
Неверно
Вопрос 107.
Сумма целого числа и его аддитивного обратного равна нулю (0).
Решение:
Истина
Пусть любое целое число будет a.
Его аддитивная инверсия — -a.
а + (-а) = а — а = 0
Вопрос 108.
Преемник 0 × (-25) равен 1 × (-25).
Решение:
False
0 × (-25) = 0
и 1 × (-25) = -25
Но преемником 0 является 1.
Вопрос 109.
Соблюдайте следующие шаблоны и заполните пропуски, чтобы утверждения верны:
(a) — 5 × 4 = — 20
-5 × 3 = -15 = -20 — (-5)
-5 × 2 = _____ = -15 — (-5)
-5 × 1 = _____ = ______
-5 × 0 = 0 = _______
-5 × -1 = 5 = _____
— 5 × — 2 = __ = ______
(б) 7 × 4 = 28
7 × 3 = ______ = 28 — 7
7 × 2 = ______ = ____ — 7
7 × 1 = 7 = ____ -7
7 × 0 = ______ = ____ -______
7 × — 1 = -7 = __ -______
7 × — 2 = ___ = ______ -_____
7 × — 3_____ = ____ -______
Решение:
(a) -10, -5, 10, -10 — (-5), -5 — (-5), 0 — (-5), 10, 5 — (-5):
-5 × 2 = -15 — (-5)
-5 × 1 = — 5 = — 10 — (-5)
-5 × 0 = 0 = -5 — (-5)
-5 × -1 = 5 = 0 — (-5)
-5 × — 2 = 10 = 5 — (-5)
(б) 21, 14, 21, 14, 0, 7, 7, 0, 7, -14, -7, 7, -21, -14, 7:
7 × 3 = 28-7
7 × 2 = 14 = 21 — 7
7 × 1 = 7 = 14 — 7
7 × 0 = 0 = 7 — 7
7 × (-1) = -7 = 0 — 7
7 × (- 2) = — 14 = -7 — 7
7 × (- 3) = -21 = — 14 — 7
Вопрос 110.
Science Application Атом состоит из заряженных частиц, называемых электронами и протонами. Каждый протон имеет заряд +1, а каждый электрон имеет заряд -1. Помните, что количество электронов равно количеству протонов, отвечая на эти вопросы:
(а) Какой заряд на атоме?
(б) Каким будет заряд у атома, если он потеряет электрон?
(в) каков будет заряд на атоме, если он получит электрон?
Решение:
(a) Полный заряд = + 1-1 = 0
(b) Если атом теряет электрон, то заряд на атоме равен +1.
(c) Заряд атома, если он получает электрон, равен -1.
Вопрос 111:
Атом превращается в заряженную частицу, называемую ионом, если он теряет или приобретает электроны. Заряд иона — это заряд электронов плюс заряд протонов. Теперь запишите недостающую информацию в таблице ниже:
| Имя Иона | Протонный заряд | Электронный заряд | Ионный заряд |
| Ион гидроксида | +9 | – | -1 |
| Ион натрия | +11 | – | +1 |
| Ион алюминия | +13 | -10 | – |
| Ион оксида | +8 | -10 | – |
Решение:
Заряд гидроксид-иона = заряд протона + заряд электрона
⇒ -1 = +9 + заряд электрона
⇒ Заряд электрона = -1-9 = — 10
Заряд иона натрия = заряд протона + заряд электрона
⇒ +1 = +11 + заряд электрона
⇒ Заряд электрона = +1-11 = -10
Заряд иона алюминия = заряд протона + заряд электрона
⇒ +13 + (-10) = +13-10 = +3
Оксид-ион заряд = заряд протона + заряд электрона
⇒ +8 + (-10) = +8-10 = -2
Вопрос 112.
Приложение «Социальные исследования», в котором запоминается, что 1 год нашей эры наступил сразу после 1 года до н.э., при решении следующих задач 1 год до нашей эры равен -1, а 1 год нашей эры — +1.
(a) Греко-римская эра, когда Египтом правили Греция и Рим, началась в 330 году. До н.э. и закончился в 395 году нашей эры. Как долго длилась эта эпоха?
(б) Хаскарачарья родился в 1114 году нашей эры и умер в 1185 году нашей эры. В каком возрасте он умер?
(c) Турки правили Египтом в 1517 году нашей эры, и правила царицей Нефертис. Египет около 2900 лет, до правления турок.В каком году она правила?
(d) Греческий математик Архимед жил между 287 г. и 212 г. до н. Э., А Аристотель — между 380 и 322 г. до н. Э. Кто жил раньше?
Решение:
Принятие 1 г. до н.э. за -1 и 1 г. н.э. как +1
(a) Год начала = 330 г. до н.э. = (-330) г. н.э.
г. Конечный год = 395 г. н.э.
Эра длилась = 395 — (-330)
= 395 + 330 = 725 лет
(b) Год рождения = 1114 г. н.э.
Год смерти = 1185 г. н.э.
∴ Общий возраст = 1185 — 1114 = 71 год
(c) Турки правили Египтом в 1517 году нашей эры.
Царица Нефертис правила Египтом в
(1517-2900) нашей эры = -1383 нашей эры или 1383 году до нашей эры.
г. (г) Архимед жил между 287 г. и 212 г. до н. Э.
Аристотель жил между 380 и 322 годами до нашей эры.
∴ Аристотель жил в более ранний период.
Вопрос 113.
В таблице показаны самые низкие зарегистрированные температуры для каждого континента. Запишите континенты в порядке от самой низкой зарегистрированной температуры до самой высокой зарегистрированной температуры.
| Самые низкие зарегистрированные температуры | |
| Континент | Температура (по Фаренгейту) |
| Африка | -11 ° |
| Антарктида | -129 ° |
| Азия | -90 ° |
| Австралия | -9 ° |
| Европа | -67 ° |
| Северная Америка | -81 ° |
| Южная Америка | -27 ° |
Решение:
С,
-129 ° <-90 ° <-81 ° <-67 ° <-27 ° <-11 ° <-9 °
Следовательно, порядок континентов от низшего к высшему зарегистрированная температура
Антарктида, Азия, Северная Америка, Европа, Южная Америка, Африка, Австралия.
Вопрос 114.
Напишите пару целых чисел, произведение которых равно -12, и между ними лежит семь целых чисел (исключая данные целые числа).
Решение:
Пусть целые числа равны -2 и 6, так что (-2) × 6 = -12
∴ Пара целых чисел равна (-2, 6).
И есть семь целых чисел, то есть
-1, 0, 1, 2, 3, 4, 5, которые лежат между -2 и 6.
Вопрос 115.
Из заданных целых чисел в столбце I сопоставьте целое число столбца II, чтобы их произведение находилось в диапазоне от -19 до -6.
Решение:
-5 → 3; 6 → -2; -7 → 1; 8 → -1;
-5 × 3 = -15 и -19 <-15 <-6
6 × (-2) = -12 и -19 <-12 <-6
-7 × 1 = -7 и -19 <-7 <-6
8 × (-1) = — 8 и -19 <-8 <- 6
Вопрос 116.
Напишите пару целых чисел, произведение которых равно -36, а разность равна 15.
Решение:
Пусть целые числа равны 12 и -3, так что 12 × (-3) = -36
и их разность = 12 — (-3) = 12 + 3 = 15
∴ Пара целых чисел — (-3,12).
Вопрос 117.
Соответствует следующему:
Решение:
Вопрос 118.
В начале месяца на вашем сберегательном счете есть 500 ₹. В приведенной ниже записи показаны все ваши транзакции в течение месяца. Сколько денег остается на вашем счете после этих транзакций?
| Контрольный № | Дата | Описание транзакции | Платеж | Залог |
384102 275146 | 4/9 12/9 | Депозит совета Jal | ₹ 120 | ₹ 200 |
384103 801351 | 22/9 29/9 | LIC Индия Депозит | ₹ 240 | ₹ 150 |
Решение:
Деньги, оставшиеся на счете после данных транзакций
= ₹ (500 + 200 + 150 — 120 — 240)
= ₹ (850 — 360) = 490 ₹
Вопрос 119.
(a) Запишите положительное целое число и отрицательное целое число, сумма которых является отрицательным целым числом.
(b) Запишите положительное целое число и отрицательное целое число, сумма которых является положительным целым числом.
(c) Запишите положительное целое число и отрицательное целое число, разность которых является отрицательным целым числом.
(d) Запишите положительное целое число и отрицательное целое число, разность которых является положительным целым числом.
(e) Запишите два целых числа, которые меньше -5, но их разница равна -5.
(f) Запишите два целых числа, которые больше -10, но их сумма меньше -10.
(g) Запишите два целых числа, которые больше — 4, но их разница меньше — 4.
(h) Запишите два целых числа, которые меньше — 6, но их разность больше — 6.
(i) Запишите два отрицательные целые числа, разность которых равна 7.
(j) Запишите два целых числа так, чтобы одно было меньше -11, а другое больше -11, но их разность была -11.
(k) Напишите два целых числа, произведение которых меньше обоих целых чисел.
(l) Напишите два целых числа, произведение которых больше обоих целых чисел.
Решение:
(a) 2 + (-3) = — l
(b) 3 + (-2) = 1
(c) -1 — (4) = -5
(d) 4 — (-1 ) = 5
(e) -7 <-5, -12 <-5 и -12 - (-7) = -5
(f) -5> -10, -6> -10 и -5 + (- 6) = -11 <-10
(g) 2> -4, -3> -4 и -3-2 = -5 <-4
(h) -7 <-6, -8 <-6 и- 7 - (- 8) = -7 + 8 = 1> -6
(i) -2 — (- 9) = -2 + 9 = 7
(j) -18 <-11; -7> -11 и -18 — (-7) = -18 + 7 = -11
(k) (-1) × (2) = -2. Кроме того, -2 <-1 и -2 <2
(l) 2 × 3 = 6.Также, 2 <6 и 3 <6
Вопрос 120.
В чем ошибка? Раму вычислил выражение — 7 — (-3) и получил ответ — 10. Что Раму сделал не так?
Решение:
7 — (-3) = -7 + 3 = -4
Но -7-3 = -10.
∴ Раму сделал сложение вместо вычитания.
Вопрос 121.
В чем ошибка? Рита оценила -4 + d для d = — 6 и дала ответ 2. Что могла сделать Рита не так?
Решение:
-4 + d, d = -6
∴ -4 + (-6) = -10
Но -4 — (-6) = -4 + 6 = 2
Следовательно, Рита выполнила вычитание на месте сложения.
Вопрос 122.
В таблице, приведенной ниже, показаны отметки относительно уровня моря в четырех местах. Приняв уровень моря за ноль (0), ответьте на следующие вопросы.
| Расположение | Высота (м) |
| А | -180 |
| B | 1600 |
| С | -55 |
| D | 3200 |
(a) Какое место ближе всего к уровню моря? Вопрос 123. Вопрос 124. (ii) (-85) × 43 + 43 × (-15) (iii) 53 × (-9) — (-109) × 53 (iv) 68 × (-17) + (-68) × 3 = 68 × (-17) + 68 × (-3) Вопрос 125. (ii) Теперь положим a = — 6 и b = 2 Вопрос 126. (ii) (-7) Δ (-1) = (-7) × (-1) — 2 × (-7) × (-1) Вопрос 127. Вопрос 128. Вопрос 129. \ (c = \ frac {5} {9} (F-32) \) Вопрос 130. Вопрос 131. Вопрос 132. (ii) Всего правильных ответов = 10 Вопрос 133. Вопрос 134. Вопрос 135. Вопрос 136. Мы надеемся, что NCERT Exemplar Class 7 Maths Chapter 1 Integer вам поможет.Если у вас есть какие-либо вопросы относительно NCERT Exemplar Class 7 Maths Solutions Глава 1 Целые числа, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время. В настоящее время, поскольку потребность в кислороде настолько низка, культивирование hMSC не требует барботажной аэрации (барботирования) для повышения k L a для удовлетворения этого . Тем не менее, он использовался в 1.3 л биореакторы с мешалкой при скорости потока ∼0,04 об / мин с чМСК [75] и ∼0,08 об / мин с ЭСК мыши [30]. Эти скорости потока довольно высоки по сравнению с теми, которые используются в культуре свободной суспензии, и ни в одной из статей не упоминалось использование Плюроника. Обе культуры были успешными с точки зрения плотности жизнеспособных клеток и качественных характеристик. Эти результаты обнадеживают, поскольку при достижении значительного увеличения плотности клеток неизбежно возникнет необходимость в пузырьковой аэрации.Ясно, однако, что если пузырьковая аэрация кажется желательной для удовлетворения потребности в кислороде, необходимо будет исследовать чувствительность к повреждению из-за этого механизма. В нашей работе во вращающихся колбах [31] спиннеры на рис. 3.2A, B имели чешуйки Колмогорова 131 и 183 мкм, соответственно, при соответствующем значении N JS с микроносителями Cytodex 3 175 мкм. Рост был достигнут с обоими типами спиннеров, и в обоих случаях λ K ≥ ∼0.6 d micro . Однако показатели роста были немного лучше у блесен, показанных на рис. 3.2B. Также было показано, что перемешивание голых шариков без клеток в течение 7 дней не приводило к образованию каких-либо пластиковых фрагментов, которые могли бы оказаться проблематичными для терапевтического использования. Наша более поздняя работа с вращающимися колбами типа показанных на рис. 3.2B с пластиковыми микроносителями дала почти идентичные результаты (таблица 3.2) [23,32]. В биореакторе 5 л (рабочий объем 2,5 л) при N JS (75 об / мин), (εT¯) JS = ∼1.6 × 10–3 Вт / кг при условии, что число мощности 1,5 для рабочего колеса с наклонными лопастями [23]. Таким образом, если предположить, что Φ = 30, (εT) max = ∼0,05 Вт / кг и λ K = 118 мкм, снова в ∼0,6 раза больше размера 200 мкм пластиковых микроносителей P102-L, что хорошо согласуется с наше исследование вращающейся колбы [31] и другие более ранние работы [35]. Для DASGIP, с другой стороны, (εT¯) JS было заметно выше, а ( λ K ) JS значительно меньше, примерно на 30% d micro .Наконец, плохая геометрия подвески в ambr привела к гораздо более высокому (εT¯) JS и, как следствие, ( λ K ) JS = ∼0,25 d micro . Даже в этом случае в обоих случаях клетки сохранили желаемые атрибуты качества [76]. Очевидно, эти результаты очень обнадеживают, потому что необходимость работы при N < N JS , безусловно, устранит многие преимущества использования биореакторов с перемешиванием. В целом, кажется, что (εT) JSmax может быть значительно больше и ( λ K ) JS меньше, чем было первоначально предложено, но все еще существует необходимость в дальнейшей работе в этой области, чтобы установить верхние пределы интенсивности перемешивания, которые стволовые клетки на микроносителях могут терпеть.Он почти наверняка будет зависеть от донора (из-за относительных изменений в скорости прикрепления между донорами), и протокол, изложенный здесь, работающий по адресу N JS , кажется, предлагает подходящий; Если комбинация клетки / микроносителя / биореактора не обеспечивает удовлетворительного размножения при N JS , вероятно, не стоит над этим работать. Лигия Кларк (1920-1988).ADAGP, Париж / Фото Алесио де Андраде. Галерист Макс Перлингейро, основатель галереи Pinakotheke, является куратором выставки «Столетие Лигии Кларк (1920-1988)», которая сейчас проходит в Рио-де-Жанейро. В ретроспективе представлены 100 работ за четыре десятилетия карьеры Кларка, включая все семнадцать официальных серий радикального художника в хронологическом порядке. В шоу также представлен 30-минутный документальный фильм «Memória do Corpo» («Память тела», 1984) режиссера Марио Карнейро и снятого художником-концептуалистом Вальтерсио Кальдасом.Фильм фокусируется на сеансах Кларк «Структурирование себя», методе арт-терапии, который она создала и которому она посвятила последнюю треть своей жизни после того, как вернулась на рынок искусства. В середине ноября выставка переместится в Пинакотеку Сан-Паулу, а затем в Пинакотеку MultiArte в Форталезе в начале 2022 года. В 300-страничной книге, изданной галереей для выставки, вступление Перлингейро представляет собой посмертное письмо Кларку. где он сообщает, что ему довелось встретиться с ней дважды, но в обоих случаях он был слишком застенчив, чтобы подойти к легендарному художнику. Лигия Кларк, Superfície modulada (Модулированная поверхность), около 1955 года, промышленная краска по дереву, 114 x 77 см / Фото Хайме Ачиоли. Последняя персональная выставка Кларка в Сан-Паулу при ее жизни, «Лигия Кларк: Десятилетие 1950 года» с кураторским текстом Пауло Сержиу Дуарте, состоялась в 1982 году в Gabinete de Arte Raquel Arnaud (позже переименованной в Galeria Raquel Arnaud). Галерист вспоминает: «Лигия была харизматичной, умной, разговорчивой и обладала сильным и сложным характером. На выставке она решила показать только работы из двух серий: серию середины 1950-х годов Superfície Modulada (Модулированная поверхность), эксперимент с идеей спирали вокруг центральной оси для получения ощущения движения внутри картины, и Casulos ( Cocoons) конца 1950-х годов, структуры из листового металла, указывающие на то, что к тому времени у нее было твердое намерение выйти за пределы «поверхности» геометрической абстракции.Во время выставки она читала лекцию в университете PUC на тему «Структурирование себя», своего арт-терапевтического метода. Ее мысли были интересно сформулированы, студенты были очарованы. Она вдохновила поклонников поп-культуры, ее имя является отсылкой к движению Tropicalia 1970-х годов. Расширяющее границы искусство Лигии сломало барьеры и помогло укрепить современное искусство. Она была выдающейся художницей и женщиной ». Родившись в богатой семье из Белу-Оризонти, ее родного города, Кларк задала новый курс бразильской арт-сцене, создавая работы, не подпадающие под традиционные рубрики художественного творчества.Замужняя, имеет троих детей, она была домохозяйкой, пока нервный срыв не привел ее в поисках убежища в изобразительное искусство, и ее буржуазное существование не было выброшено на свалку. Живя между Рио и Парижем с 1947 года, ее жизнь была полностью посвящена искусству, сначала с Роберто Бурле Марксом, художником и ландшафтным дизайнером, который в качестве учителя познакомил ее с абстрактной геометрией. Деньги не волновали — после развода она переехала в Париж с состоянием из восьмидесяти пяти арендуемых квартир (согласно интервью ее сына, фотографа Эдуардо Кларка в газете Folha de São Paulo), которые она будет продавать одну за другой, чтобы выжить в своей жизни. миссия художника.Она ходила на занятия с коммунистом Фернаном Леже и познакомилась с психоаналитической терапией. В Рио Кларк стал одним из основателей нео-бетонного движения вместе с поэтом Феррейрой Гуллар и художником Элио Оитичикой, ее родственной душой. Эти два любознательных творца были на одном уровне с международным авангардом, радикально переосмыслившим арт-объект в конце 1960-х и 1970-х годах. Кларк и Ойтисика — пионеры Бразилии в области перформанса, инсталляции и концептуального искусства через переживания через взаимодействие зрителя.В случае Кларк ее более поздний опыт арт-терапии привел, как она объяснила в 1965 году, к «исключительному состоянию искусства без искусства». Лигия Кларк, перформанс Arquiteturas biológicas II (Биологические архитектуры), 1969, ADAGP, Париж / фото Алесио де Андраде. С 1953 по 1967 годы ее работы выставлялись во всех выпусках São Paulo Bienal. В 1958 и 1960 годах Фонд Гуггенхайма предоставил ей стипендию и награду. Выставлялась на Венецианской биеннале в 1954, 1960, 1962 и 1968 годах.После этого она эмигрировала в Париж, город, который она больше всего любила, чтобы избежать репрессий со стороны военной диктатуры в Бразилии и ее семьи, наслаждаясь контркультурой шестидесятых и давая уроки рисования в Сорбонне. В 1968 году хваленая выставка на 34-й Венецианской биеннале бросила ее в вихре арт-рынка. Однако, поскольку Лигия была Лигией, она отказалась, заявив, что не уступит цирку арт-рынка, и сбежала от всей суеты, прежде чем ее объектировали и превратили в товар.Вместо денег и славы она выбрала одинокое поле, чтобы пахать, и заново изобрела себя целительницей. В своем известном «Письме к Мондриану» от мая 1959 года измученный Кларк признался умершему голландскому художнику (умершему с 1944 года): «Мондриан, если ваша сила может мне помочь, это будет похоже на сырой бифштекс, положенный на стол. этот болезненный глаз, чтобы он мог видеть снова как можно быстрее и мог столкнуться с этой порой болезненной правдой: «художник — одинокий человек» ». Сложная система противопоставлений пустой / полный, внутренний / внешний является ключом к пониманию наследия работы Кларка.Хотя кажущаяся простота ее работ сбивает с толку ее недоброжелателей, творчество Кларка последовательно, серия за серией (семнадцать из них) развивалось в устойчивое интеллектуальное упражнение большой эстетической глубины и свободы, которое, в свою очередь, привело ее к неконтролируемым перепадам настроения и психическому здоровью. кризисы, но в конечном итоге поставили ее неиссякаемые эксперименты на путь ее конечного поиска: растворения барьера между жизнью и искусством. Или, как она сама выразилась, «экспериментальное проявление свободы» для того, чтобы в полной мере воплотить «искусство в жизнь».Это ясно видно из груд журналов, писем и заметок — Кларк писал обильно, откровенно и был прекрасным писателем — которые послужили кардинальными точками для концептуально хорошо продуманной серии, разработанной этим новаторским художником-интеллектуалом. С середины 1970-х годов до своей смерти она отложила свою жизнь в качестве художника и разработала «Структурирование Я», радикальный арт-терапевтический метод, который включал ее собственное тело и себя, а также тела ее пациентов, используя Objetos Relacionais ( Relational Objects), ряд простых объектов, непритязательных сборок, одежды и сенсорных масок для обоняния, звука и прикосновения, разработанных ею в лечебных целях: «Весь мой процесс был попыткой объединить искусство и жизнь, а иногда сырое восприятие приходит ко мне в жизни, это бездна.» Мы взяли интервью у галериста Макса Перлингейро. Лигия Кларк и Трепанте (Краулер) / Фото Эдуардо Кларка. Associação Cultural Lygia Clark. Макс, расскажите, как вы организовали такую сложную выставку в условиях пандемии. Наша исследовательская группа приступила к работе в середине октября 2020 года, в тот самый день, когда исполнилось 100 лет со дня рождения Лигии Кларк, когда я был назначен организатором праздничной выставки Associação Cultural Lygia Clark, учреждением, которое управляет ее наследием.Я прочитал и перечитал все, что было на Лигии, и связался с тремя ее близкими друзьями, экспертами по ее творчеству, французским историком искусства Ив-Аленом Буа, художником Лучано Фигейредо и философом Марсио Доктором. Затем я связался с Матинас Сузуки, которая в 1986 году дала ей историческое интервью для газеты Folha de São Paulo, через два года до ее смерти. Наконец, я подошел к Джине и Луле Вандерли, чтобы понять, что стоит за «Структурированием Самости», методом исцеления между искусством и терапией, разработанным Лигией, который некоторые считают неоднозначным.Она практиковала революционный метод лечения пациентов в середине 1970-х, на пике жесткой военной диктатуры Бразилии, вплоть до своей смерти в 1988 году. Objeto Relacional (Relational Object) — это имя, которое она дала элементам, очень простым и базовым, она использованные во время этих терапевтических сеансов: камень, вода, нитки и т.д. тогда все молодые люди будут вакцинированы. Молодое поколение бразильских художников почитает Лигию, не так ли? Лигия — главный символ нового поколения бразильских художников из-за ее работ, а также из-за того, что она была тревожным бунтарем, который стал символом движения Тропикалии 1970-х годов. Откровенно говоря, легко понять, почему ее работы так мифологизированы, потому что они фантастические. По сути, он выводит искусство на другой уровень, на уровень концептуального искусства. Лигия Кларк, Бичо (Криттер), 1960, алюминий и петли, 35,8 x 36 x 7 см / Фото Хайме Ачиоли. Какие посмертные выставки вписали ее имя на карту международного мира искусства? Через девять лет после смерти Лигии в 1997 году выставка в Fundació Antoni Tàpies в Барселоне, куратором которой был Мануэль Дж. Борха Виллель, прошла в нескольких европейских учреждениях и завершилась в Paço Imperial в Рио-де-Жанейро. Эта выставка послужила сигналом для международного музейного сообщества о ее расширяющем границы искусстве, и, как следствие, ее работы попали в основные коллекции учреждений по всему миру.Еще одна передвижная выставка, которая расширила ее признание, прошла в 2005 году в Музее изящных искусств в Нанте, Франция, а также была показана в Pinacoteca do Estado в Сан-Паулу. Однако именно всеобъемлющая выставка MoMA 2014 года «Лигия Кларк: если вы держите камень», кураторы которой выступили Луис Перес-Орамас и Конни Батлер, закрепила ее имя в истории искусства двадцатого века. Две другие важные посмертные выставки — «Retrospectiva» в Itaú Cultural в Сан-Паулу, куратор которой — Пауло Серхио Дуарте, и в 2020 году «Лигия Кларк: Живопись как экспериментальное поле, 1948–1958», переосмысление решающих лет становления Кларка.Шоу проходило в Музее Гуггенхайма в Бильбао под кураторством Жеанин Гутьеррес-Гимарайнш с эссе Пауло Мияды. Какое место занимает ее работа на мировом арт-рынке? На протяжении десятилетий она была крупнейшим мировым художником. Лигия — одна из самых ценных женщин-художников всех времен, ее работы высоко ценятся крупными коллекционерами и международными организациями. Она одна из немногих бразильских художников, чья работа оценивается в миллион долларов. Купить Лигию Кларк любого периода практически невозможно; Когда вещь выставляется на продажу, покупатели со всего мира спешат за ней.Ее творчество входит в число наиболее хорошо сформулированных концепций художественных произведений в искусстве двадцатого века. При всем этом Лигия Кларк играет квинтэссенцию в искусстве, которая вызывает как горячие дискуссии, так и восхищение. Лигия Кларк, Caixa Trepante (Crawler Box), 1965, медь, 25,0 x 50,0 x 25,0 см Когда Тарсиле ду Амарал, хронологически первой великой даме бразильского искусства, было за семьдесят, ей было за семьдесят. сказала своей семье, что она предвидела, что ее работа будет очень ценной после ее смерти.Было ли у Лигии такое предчувствие? Отношения Лигии с арт-рынком всегда были очень далекими и трудными, особенно с 1970-х годов, однако она дала понять своей семье и близким друзьям, что ее творчество наверняка достигнет новых высот. Она была права. Ваша галерея превратилась в семейное предприятие в Рио, Форталезе и Сан-Паулу и занимает одно из первых мест в Бразилии на вторичном рынке. Расскажите, чем вы занимались до Пинакотеки. Я родом из штата Рио-де-Жанейро. В 1966 году, когда я изучал химическую технику и технику безопасности в колледже, моя жизнь изменилась, когда галерист Франко Терранова пригласил меня поработать в своей Petite Galerie в Рио-де-Жанейро, одной из первых галерей современного искусства в Бразилии. Десять лет спустя я основал Пинакотеку в Рио, в 1987 году я открыл Multiarte, филиал Пинакотеки в Форталезе, а в 2002 году — Пинакотеку Сан-Паулу. За эти сорок два года мы выиграли несколько наград, я очень горжусь всеми нашими культурные достижения и редакционная деятельность, но в особенности наших образовательных художественных проектов, посвященных детям. Lygia Clark, Bicho (Critter), 1960, алюминий, петли, 37,0 x 30,0 см. Прежде чем мы подведем итоги, знаете ли вы, была ли у Лигии Кларк слабость к какой-либо серии в частности? Лигия гордилась эволюцией своей работы и своими достижениями как в качестве художника, так и в дальнейшем в качестве терапевта, но серия Bichos (на английском языке Creature of Critter, металлические скульптуры из шарнирно соединяющихся пластин) всегда оставалась ею. мягкое место. Сериал, созданный в 1964 году, стал прорывом в том, что он предлагает зрителям подобрать и обработать их, и преодолевает еще один барьер, на этот раз в области семантики.За неимением лучшего слова рынок определяет это как скульптуру, и, по словам Лигии, это не значит, что скульптура. Лигия Кларк, Бичо (Криттер), алюминий и петли. Рекламное фото. Итак, как мы должны называть складные трансформируемые не-скульптуры Кларка начала 1960-х годов? Бичо. Лигия Кларк, ADAGP, Париж, 1970 г. / Фотография Алесио де Андраде. Ниже приведены отредактированные отрывки из двуязычной книги с названием выставки, опубликованной Пинакотекой и написанной экспертами, в том числе французским искусствоведом Ив-Аленом Буа, автором нескольких книг по искусству и профессором истории искусства в Школе исторического искусства. Учится в Институте перспективных исследований в Принстоне.Буа встретил Кларк в Париже после того, как она выставила серию Bichos на 34-й Венецианской биеннале в 1968 году с восторженными отзывами. Некоторые наблюдения французского ученого: При встрече с Лигией Кларк: «Я впервые встретился с Лигией после лета 1968 года, вскоре после вмешательства России в Чехословакию. Она только что вернулась с Венецианской биеннале, где представляла Бразилию с большой ретроспективой своих работ, которая включала в себя ранние вещи, а также различные наряды Máscaras sensoriais (сенсорные маски) и Roupa-corpo-roupa (одежда-тело-одежда). 1967, а также большая инсталляция / среда A casa é o corpo (Дом — это тело). Лигия Кларк, Без названия, серия Quebra da moldura (Разрушение рамы), 1954, холст, масло, 82,7 x 74,8 x 4,7 см О предложении, как Лигия Кларк назвала свои работы: «В этом случае одним из« объектов », которые я запомнил наиболее ярко, был ее Diálogo de mãos (« Диалоги рук ») 1966 года, который она придумала вместе со своей второй половинкой, Элио Ойтисикой. Эта работа, или, скорее, «предложение», как она уже называла свои произведения, состоит почти из ничего, как и многие ее произведения, то есть на самом деле это ничто, если вы не используете его.Он состоит из небольшой ленты Мёбиуса, сделанной из эластичного медицинского бинта, где каждая наша правая рука проходит через одну петлю ленты Мёбиуса в противоположных направлениях. Взявшись за руки или отпустив их, мы испытываем сопротивление материи. Если «диалог» продолжается достаточно долго, зрительные и тактильные ощущения, кажется, расходятся, и наступает момент, когда создается впечатление, что руки танцуют сами по себе, отделенные от тела. Этот момент может быть чрезвычайно тревожным, почти галлюцинаторным. Предложение Лигии Кларк Pedra e ar (Stone and Air, 1966) в действии. Это камень и полиэтиленовый пакет. О движении нео-бетона и вытеснение Макса Билла: «В момент моего первого визита Лигия начала вспоминать зарождение необетонного движения в Бразилии. и преднамеренная атака, которую она спланировала с Ойтисикой (с которой мне никогда не довелось встретиться) против геометрической абстракции, традиции, которой оба были обучены. Она открыла мне важность швейцарского художника Макса Билла для бразильского искусства в начале пятидесятых, особенно после его ретроспективы в MAM / SP (Museu de Arte Moderna of São Paulo) в 1950 году, после чего он был удостоен международной премии в области скульптуры первая биеннале в Сан-Паулу в 1951 году.Энтузиасты «Конкретного искусства» Билла (так он называл свою постановку, в которой все должно было планироваться с помощью арифметических вычислений) внезапно наводнили мир бразильского искусства, который до этого был довольно устойчив к современному искусству. Она привела меня к пониманию того, что ее Диалог 1966 года (Диалоги рук) на самом деле представляет собой завершение долгой битвы с типом искусства Билла. Полоса Мебиуса была одной из любимых геометрических фигур Билла: он поместил ее полированный гранитный образ во многих садах скульптур по всему миру.В то время как Билл заморозил ленту Мебиуса в символ автономии модернистского арт-объекта, Лигия превратила ее в опору для эксперимента, направленного на отмену любой идеи определенной, закрытой идентичности. С Диалогом «скульптурный» объект больше не является священным как автономный и формально совершенный, а ложно симметричные руки, ведущие диалог, становятся как бы автономными исполнителями ». Лигия Кларк, Обра мол, 1964, промышленный каучук, 49,0 x 49,0 см / Фото Хайме Ачиоли Об устранении оппозиций пустой / полный, внутренний / внешний и разрушении рационализма Макса Билла: «Возвращение переехав в Бразилию в 1952 году после года, проведенного в Париже, где она училась у Фернана Леже, Лигия быстро усвоила рационалистический катехизис Билла и вскоре начала разрушать его изнутри.Отметив, что Билл часто заимствовал свои формы из топологии, она решила выйти за рамки его чисто иконографического обращения к этой области науки. Ее первые зрелые картины (1954) были головоломками, часто из дерева, в которых она пыталась придать положительную роль черным промежуткам (пустым стыкам) между цветными блоками и превратить рамку в изобразительный элемент. Как она настаивала в то время, ее цель состояла в том, чтобы устранить противопоставления пустого / полного, внутреннего / внешнего, на которых основана плоская геометрия и рационализм.” Лигия Кларк, перформанс Arquiteturas biológicas II (Биологические архитектуры), 1969, ADAGP, Париж / Фото Алесио де Андраде. О нео-конкретном манифесте: «Другая важная фигура, помимо Лигии, вышедшая из этого движения, ее друг и альтер-эго Элио Ойтичика, сплотившаяся к делу только после публикации манифеста группы, была написана поэт и критик Феррейра Гуллар. Текст был полностью основан на переосмыслении Лигией традиции геометрической абстракции через призму феноменологии восприятия, цитирующей философскую работу Мерло-Понти, которую она недавно обнаружила и которая будет интересовать всю жизнь.Публикация «Необетонного манифеста» совпала с разработкой Лигией серии рельефов 1958–1959 годов, названных Casulo (Кокон) и Contra-релево (Контррельеф), посвященных Татлину ». Лигия Кларк, Estrutura de caixa de fósforo (Структура спичечного короба), 1964 гуашь, клей и деревянная коробка, 6,0 x 6,0 x 8,5 см / Фотография Эдуарда Фрайпона. О серии Bichos, 1960-64: «Тот факт, что у самолета есть объем, и что этот объем можно раскрыть, как кокон, лежат в основе самых знаменитых произведений Лигии, Bichos 1960- 64, отдельно стоящие конструкции из шарнирных металлических пластин, которыми можно манипулировать, чтобы придать скульптуре различные формы, и при хранении Bicho остается совершенно плоским.Артикуляция и расположение Бичо задуманы как организм, который со своими законами и ограничениями реагирует на движения любого, кто им манипулирует, чтобы изменить его конфигурацию. Часто требует определенных жестов или неожиданно выворачивается наизнанку, как перчатка. Диалог между Бичо и «смотрящим» временами радует, временами расстраивает, но он всегда подрывает представление о том, что один может когда-либо контролировать другого. Лигия писала: «Когда меня спрашивают, сколько движений может выполнить Бичо, я отвечаю:« Я не знаю, вы не знаете, но Бичо знает.’” Lygia Clark, Espaço modulado Nº 4 (Модулированное пространство), 1958, промышленная краска, ДСП / Фото Хайме Ачиоли На пассивных объектах X-манипуляция с предложением: « Богатство Bichos остается недоступным. никому, кто не вступает с ними в боевые действия. Изображенные как пассивные объекты на пьедестале, они выглядят как любая другая абстрактная геометрическая скульптура. Лигия всегда настаивала на том, чтобы люди могли манипулировать ими, когда бы они ни выставлялись, и отчасти именно неспособность музейных галерей обеспечить такое тактильное восприятие этих работ уводила ее от подобных учреждений.» Лигия Кларк делает Caminhando (« Ходьба », 1963) с бумагой и ножницами. Об исчезновении арт-объекта: «Из-за того, что ее Bichos слишком легко превращались в арт-объекты и, таким образом, визуально потреблялись, она изобрела Caminhando (Ходьба), которая в 1964 г. ее окончательное прощание с геометрическим искусством и начало направления в ее творчестве — и в творчестве Оитичики, — которое можно охарактеризовать как постепенное исчезновение арт-объекта как такового.Caminhando еще раз вернулся к увлечению Билла лентой Мебиуса, но вместо того, чтобы быть объектом, он задуман как опыт, который необходимо пережить. Сначала вы должны сделать ленту Мебиуса из бумаги, а затем следовать инструкциям Лигии по самостоятельной работе ». Лигия Кларк, Contra-Relief, 1958, промышленная краска, дерево, 56,3 x 56 , 3 см / Фото Хайме Ачиоли На Trepantes (альпинисты или ползунки) и Obras Moles (Soft Works): «Из Каминандо последовала целая серия работ из меди, стали или резины, названных Trepantes for их можно повесить где угодно, на любых объектах, на деревьях или просто бросить на пол.Самые интересные из них, Obras Moles, сделаны из черной промышленной резины и на несколько лет предвосхищают развитие того, что будет называться Antiform в Соединенных Штатах (висит на стене, они напоминают Felt Tangle 1967 года Роберта Морриса). . Но это было направление, в котором она не могла продолжаться очень долго ». Лигия Кларк, Descoberta da linha orgânica (Открытие органической линии), около 1954 г., холст, масло, дерево, 93,2 x 93,2 x 2,0 см / Фотография Хайме Ачиоли. Об интерактивной практике / терапии и о несоответствии искусства и художника: «Опыт Каминхандо стал прорывом, который заставил любой арт-объект выглядеть подозрительно: она перестала резать трепантес в течение года, а затем В течение длительного кризиса она и Оитичика разработали сложную интерактивную практику, которая избегала бы не только рассмотрения объекта как такового, но и любого понятия театральности, и никакого представления, даже в « предложениях », в которых участвовали несколько « участников ». ‘- использовать слова, заменившие объект и смотрящий, соответственно, в их многочисленных текстах.Само понятие художника постепенно теряло актуальность, поскольку искусство Лигии становилось своего рода терапией или социальной работой. Излишне говорить, что этот более поздний период практики Лигии был еще менее подходящим для музеев или художественных галерей, к ее восторгу и гордости. После Венецианской биеннале 1968 года Лигия решительно отключила свою деятельность от рыночной экономики и сохранила лишь ограниченные контакты с миром искусства. Она покинула традиционную землю искусства, чтобы предложить другую модель эстетического общения.Она предпочитала слово «чувственный», но, как я напомнил ей во время одного из наших ежедневных обедов, греческое слово «эстетика» (эстетика, восприятие прекрасного) означает ощущение ». Лигия Кларк (1920-1988) Столетие
(b) Какое место дальше всего от уровня моря?
(c) Расположите места от наименьшего до наибольшего возвышения.
Решение:
(a) C находится ближе всего к уровню моря.
(b) D дальше всего от уровня моря.
(c) Так как, -180 <-55 <1600 <3200.
∴ Расположение от наименьшей до наибольшей отметки A
Вы находитесь на высоте 380 м над уровнем моря, когда начинаете поездку на автомобиле. Во время поездки ваша высота меняется на следующие метры: 540 м, -268 м, 116 м, -152 м, 490 м, -844 м, 94 м. Какова ваша высота по отношению к уровню моря в конце поездки?
Решение:
Высота относительно уровня моря в конце поездки
= [380 + 540 — 268 + 116-152 + 490 — 844 + 94] м
= [380 + 540 + 116 + 490 + 94 — 268 — 152–844] м
= [1620–1264] м = 356 м
Оцените следующее, используя свойство распределения.
(i) -39 × 99
(ii) (-85) × 43 +43 × (-15)
(iii) 53 × (-9) — (-109) × 53
(iv) 68 × (- 17) + (-68) × 3
Решение:
(i) -39 × 99 = -39 × [100-1]
= -39 × 100 + (-39) × (-1)
= -3900 + 39 = -3861
= 43 × (-85) + 43 × (-15)
= 43 × [-85 — 15]
= 43 × [-100] = -4300
= 53 × (-9) — 53 × (-109)
= 53 × [(-9) — (-109)]
= 53 × [-9 + 109] = 53 × 100 = 5300
= 68 × [(-17) + (-3)]
= 68 × (-20) = -1360
Если «*» — это операция have, то есть для целых чисел a и b. Имеем a * b = a × b + (a × a + b × b), затем находим
(i) (-3) * (- 5)
(ii) (-6) * 2
Решение:
(i ) Имеем a * b = a × b + (a × a + b × b)
Теперь положим a = (-3) и b = (-5)
(-3) * (-5) = ( — 3) × (- 5) + [(- 3) × (- 3) + (- 5) × (- 5)]
= 15 + (9 + 25) = 15 + 34 = 49
(-6) * 2 = (-6) × 2 + [(- 6) × (-6) + 2 × 2
= -6 × 2 + (36 + 4) = -12 + 40 = 28
Если Δ — операция такая, что для целых чисел a и b выполняется a Δb = a × b — 2 × a × b + b × b (-a) × b + b × b, то найдите
(i) 4 Δ ( — 3)
(ii) (- 7) Δ (- 1)
Также покажите, что 4 Δ (- 3) ≠ (- 3) Δ 4 и (-7) Δ (-1) ≠ (-1) Δ ( — 7)
Решение:
a Δ b = a × b — 2 × a × b + b × b (-a) × b + b × b
(i) 4 Δ (-3) = 4 × (-3 ) — 2 × 4 × (-3)
+ (-3) × (-3) (- 4) × (-3) + (-3) × (-3) = -12 + 24 + 108 + 9 = -12 + 141 = 129
+ (-1) × (-1) (7) × (-1) + (-1) × (-1) = 7-14-7 + 1 = 8-21 = -13
Итак, (-3) Δ 4 = (-3) × 4-2 × (- 3) × (4) + 4 × 4 (3) × 4 + 4 × 4
= -12 + 24 + 192 + 16 = -12 + 232 = 220
Но 4 Δ (-3) = 129
∴ 4 Δ (-3) ≠ (-3) A 4
А, (-1) Δ (-7) = (-1) × (-7) — 2 × (-1) × (-7) + (-7) × (-7) (1) × (-7) + (-7) × (-7)
= 7-14-343 + 49 = 56-357 = -301
Но (-7) Δ (-1) = -13
∴ (-7) Δ (-1) ≠ (-1) Δ (-7)
Ниже u, v, w и x представляют разные целые числа, где u = (-4) и x ≠ 1. Используя следующие уравнения, найдите каждое из значений
uxv = u
x × w = w
u + x = w
(a) v
(b) w
(c) x
Объясните причину, используя свойства целых чисел
Решение:
(a) Поскольку u × v = u и u = -4 ∴ -4 × v = -4
⇒ v = l (Мультипликативное тождество)
(b) Поскольку x × w = w. Учитывая, что x ≠ 1
∴ x × w = w, возможно только при w = 0
(c) Поскольку u + x = w, положим u = — 4 и w = 0
∴ -4 + x = 0
⇒ x = 4 (перенос -4 в R.H.S.)
Высота населенного пункта А составляет 1800 м над уровнем моря. Другое место B находится на 700 м ниже уровня моря. В чем разница между уровнями этих двух мест?
Решение:
Разница между уровнями мест A и B составляет [1800 — (-700)] m = [1800 + 700] m = 2500 м
В данной таблице показаны точки замерзания в ° F различных газов на уровне моря. Преобразуйте каждый из них в ° C с точностью до ближайшего целого значения, используя соотношение, и заполните таблицу Газ Точка замерзания на уровне моря (° F) Температура замерзания на уровне моря (° C) Водород -435 Криптон -251 Кислород -369 Гелий -458 Аргон -309
Решение:
Сана и Фатима участвовали в яблочной гонке. Гонка проводилась в 6 этапах. В первой части Сана выиграла на 10 секунд. Во второй части она проиграла 1 минуту, затем выиграла на 20 секунд в третьей и проиграла 25 секунд в четвертой, проиграла на 37 секунд в пятой и выиграла 12 секунд в последней части. Кто наконец выиграл гонку?
Решение:
Считать выигрыш по времени положительным целым числом, а проигрыш по времени — отрицательным целым числом.
∴ Общее время Саны (победа / поражение)
= (10 — 60 + 20 — 25 — 37 + 12) секунд
= (42 — 122) секунды = -80 секунд
Следовательно, Сана проиграла гонку на 80 секунд или 1 мин.20 секунд.
, то есть Фатима наконец выиграла гонку.
Зелёный бакалейщик получил прибыль в размере 47 фунтов стерлингов в понедельник, убыток в размере 12 фунтов стерлингов во вторник и убыток в размере 8 фунтов стерлингов в среду. Найдите его чистую прибыль или убыток за 3 дня.
Решение:
Принимая прибыль как положительное целое число и убыток как отрицательное целое число, мы получаем
чистую прибыль или убыток бакалейщика за 3 дня
= ₹ (47-12-8) = 27
Следовательно, бакалейщик имеет прибыль в размере 27.
В тесте за каждый правильный ответ ставится +3 балла и за каждый неправильный ответ — -1 балл.Сона попыталась ответить на все вопросы и набрала +20 баллов, хотя получила 10 правильных ответов.
(i) Сколько неправильных ответов она попыталась ответить?
(ii) Сколько вопросов было задано в тесте?
Решение:
(i) Общее количество баллов, выставленных Соной = 20
Всего правильных ответов = 10
∴ Баллы за правильные ответы = 10 × 3 = 30
, но она получила 20 баллов.
∴ Баллы за неправильные ответы = 20 — 30 = — 10
-1 балл ставится за каждый неправильный ответ.
∴ Всего неверных ответов \ (= \ frac {-10} {- 1} = 10 \)
Всего неправильных ответов = 10 (Из части (i))
∴ Всего вопросов, заданных в тесте = 10 + 10 = 20
В тесте «верно-неверно», содержащем 50 вопросов, учащийся должен получить 2 балла за каждый правильный ответ, -2 за каждый неправильный ответ и 0 за отсутствие ответа. Если Яш набрал 94 балла в тесте, каковы возможности его оценки правильным или неправильным ответом?
Решение:
Яш обеспечен = 94 балла Итак, минимальное количество правильных ответов = 94 ÷ 2 = 47
Теперь есть две возможности:
(1) Он попытался ответить 47 правильных ответов и 3 без попытки.
(2) Он попытался дать 48 правильных ответов, 1 ответ без попытки и 1 неправильный ответ.
Многоэтажное здание имеет 25 этажей над уровнем земли, каждый высотой 5 м. Он также имеет 3 этажа в подвале, каждый высотой 5 метров. Лифт в здании движется со скоростью лм / с. Если человек начинает с 50 м над землей, сколько времени ему потребуется, чтобы добраться до 2-го этажа подвала?
Решение:
Высота каждого этажа = 5 м
∴ Высота под подвалом, который должен быть покрыт
= 2 × 5 м = 10 м
Если человек начинает с 50 м над уровнем земли
и достигает 2 этажа подвала.
∴ Его общее расстояние, которое необходимо преодолеть
= (50 + 10) м = 60 м
Скорость движения лифта = 1 м / с
∴ Человек достигает 2-го этажа подвала за 1 × 60 = 60 секунд или 1 минута.
Принимая сегодня за ноль на числовой прямой, если позавчера 17 января, какова дата через 3 дня после завтрашнего дня?
Решение:
Позавчера 17 января.
∴ Сегодня 19 января.
Через 3 дня послезавтра будет 20 января + 3 дня = 23 января
Самая высокая точка, измеренная над уровнем моря, — это вершина горы Эверест, которая находится на высоте 8 848 м над уровнем моря, а самая низкая точка находится на глубине Марианской впадины, которая находится на 10 911 м ниже уровня моря. Какое расстояние по вертикали между этими двумя точками?
Решение:
Самая высокая точка (над уровнем моря) = 8 848 м
Самая низкая точка (ниже уровня моря) = 10 911 м
∴ Общее расстояние по вертикали между двумя точками
= [8 848 — (-10 911)] м
= [8 848 + 10,911] м = 19,759 м Барботаж — обзор | Темы ScienceDirect
3.3.10.2 Применение к культуре hMSC
Сенсорная эстетика: новая выставка, охватывающая четырехлетнюю карьеру Лигии Кларк
Куратор Макс Перлингейро
Культурная пинакотека / Рио-де-Жанейро
До 23 октября 2021 г.

