Гдз по алгебре 7 класс номер 114: Номер задания №114 - ГДЗ по Алгебре 7 класс: Макарычев Ю.Н.

Содержание

Страница 114 — ГДЗ по Алгебре для 7 класса Учебник Мерзляк А. Г., Якир М. С., Полонский В. Б. (решебник)

Страница 114 — ГДЗ по Алгебре для 7 класса Учебник Мерзляк А. Г., Якир М. С., Полонский В. Б. (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Мерзляк А. Г., Якир М. С., Полонский В. Б.

Издательство: Вентана-Граф

Тип: Учебник

Выберите номер

12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235

Выберите номер
Проверь себя №1

123456789101112

Проверь себя №2

123456789101112

Проверь себя №3

123456789101112

Проверь себя №4

123456789101112

Проверь себя №5

123456789101112

Проверь себя №6

123456789101112

Проверь себя №7

123456789101112

Выберите параграф

§1§2§4§5§6§7§8§10§11§12§14§15§16§18§20§21§22§23§24§25§26

Выберите страницу

67891011151617181921222324252627283334353738394041424346474849505153545556575960616364656667687071727374767778798082838485868788899091939495969899100101103104105106107108109111112113114115116118119120121124125126127128129138139140141142143144145146147149150151152153157158159160161162166167168169170171172173174175176183184185186189190191192193194199200201202203205206207209210211212213214216217218219220221222223224227228229230231232233234235-236

Adblock
detector

ГДЗ Мордкович 7 Повторение (упр.

107 — 188)

ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович (2019). Итоговое повторение: Алгебраические преобразования. ОТВЕТЫ на упражнения 107 — 188). Вернуться в ОГЛАВЛЕНИЕ.

ГДЗ Алгебра 7 класс Мордкович (2019)

ИТОГОВОЕ ПОВТОРЕНИЕ (упр. 107 — 188)

В учебнике 2019 года нет параграфа под номером 48, но для удобства понимания о каком номере задания идет речь мы присвоили главе «Итоговое повторение» параграф 48.
Нажмите на спойлер, чтобы посмотреть ответ на задание:

№ 107.
а) 3⁴ + 2⁵; б) (–1)¹⁰ – 5²; в) 3³ – 17⁰; г) 10³ – 2¹⁰.

Смотреть ответы на № 107

Смотреть ответы на № 108

Смотреть ответы на № 109

Смотреть ответы на № 110

Смотреть ответы на № 111

Смотреть ответы на № 112

№ 113.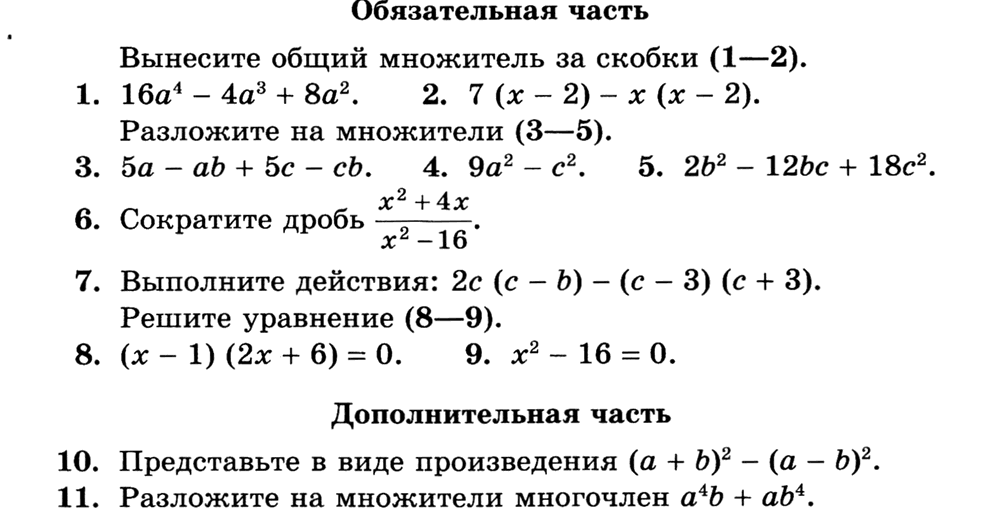
Представьте в виде степени с натуральным показателем: а) 625; б) 196; в) 81; г) 64.

Смотреть ответы на № 113

№ 114.
Представьте число 256 в виде: а) квадрата натурального числа; б) четвёртой степени натурального числа.

Смотреть ответы на № 114

№ 115.
Представьте число 729 в виде: а) куба натурального числа; б) квадрата натурального числа.

Смотреть ответы на № 115

№ 116.
а) Представьте число 100 в виде произведения квадратов двух натуральных чисел.
б) Представьте число 216 в виде произведения кубов двух натуральных чисел.

Смотреть ответы на № 116

Смотреть ответы на № 117

Смотреть ответы на № 118

Смотреть ответы на № 119

Смотреть ответы на № 120

Смотреть ответы на № 121

Смотреть ответы на № 122

Смотреть ответы на № 123

Смотреть ответы на № 124

Смотреть ответы на № 125

Смотреть ответы на № 126

Смотреть ответы на № 127

Смотреть ответы на № 128

Смотреть ответы на № 129

Смотреть ответы на № 130

Смотреть ответы на № 131

№ 132.
Стороны прямоугольника относятся как 4 : 5, а его площадь равна 180 см². Найдите стороны прямоугольника.

Смотреть ответы на № 132

№ 133.
Измерения прямоугольного параллелепипеда относятся как 3 : 4 : 6, а его объём равен 576 см³. Найдите измерения прямоугольного параллелепипеда.

Смотреть ответы на № 133

Смотреть ответы на № 134

Смотреть ответы на № 135

Смотреть ответы на № 136

Смотреть ответы на № 137

Смотреть ответы на № 138

Смотреть ответы на № 139

Смотреть ответы на № 140

Смотреть ответы на № 141

Смотреть ответы на № 142

Смотреть ответы на № 143

Смотреть ответы на № 144

Смотреть ответы на № 145

Смотреть ответы на № 146

Смотреть ответы на № 147

Смотреть ответы на № 148

Смотреть ответы на № 149

Смотреть ответы на № 150

Смотреть ответы на № 151

Смотреть ответы на № 152

Смотреть ответы на № 153

Смотреть ответы на № 154

Смотреть ответы на № 155

Смотреть ответы на № 156

Смотреть ответы на № 157

Смотреть ответы на № 158

Смотреть ответы на № 159

Смотреть ответы на № 160

Смотреть ответы на № 161

Смотреть ответы на № 162

Смотреть ответы на № 163

Смотреть ответы на № 164

Смотреть ответы на № 165

Смотреть ответы на № 166

Смотреть ответы на № 167

Смотреть ответы на № 168

Смотреть ответы на № 169

Смотреть ответы на № 170

Смотреть ответы на № 171

Смотреть ответы на № 172

Смотреть ответы на № 173

Смотреть ответы на № 174

Смотреть ответы на № 175

Смотреть ответы на № 176

Смотреть ответы на № 177

Смотреть ответы на № 178

Смотреть ответы на № 179

Смотреть ответы на № 180

Смотреть ответы на № 181

Смотреть ответы на № 182

Смотреть ответы на № 183

Смотреть ответы на № 184

Смотреть ответы на № 185

Смотреть ответы на № 186

Смотреть ответы на № 187

Смотреть ответы на № 188

Вернуться в ОГЛАВЛЕНИЕ.

ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019). Итоговое повторение. Алгебраические преобразования. ОТВЕТЫ на упражнения 107 — 188.

Математика 114 Дискретная математика

Кларк Каталог Описание курса Math 114: Охватывает математические структуры, которые естественным образом возникают в компьютерных науках. Включает элементарную логику и теорию множеств, отношения эквивалентности, функции, подсчет аргументов, асимптотическую сложность, индуктивно определенные множества, рекурсию, графы и деревья, булеву алгебру и комбинаторные схемы, конечные автоматы, а также аргументы диагонализации и счетности. Уделяет внимание доказательствам и решению проблем.
Требование: Один семестр математических вычислений (MATH 120 или 124), или CSCI 120, или разрешение.
Курсовые цели.
- Дать учащимся хорошее понимание концепций и методы дискретной математики, подробно описанные в программе.
- Разработать формальные методы логических рассуждений путем изучения символической логики в общие и логические доказательства в дискретной математике в частности.
- Ввести и/или пересмотреть комбинаторные принципы и дискретные математические структуры, занимающие центральное место в математике, информатике и статистике
Цели курса. Учащиеся смогут применять конкретные концепции и методы, описанные в программе, — логику, теорию множеств, последовательности и ряды, теорию чисел, комбинаторику, дискретную вероятность и теорию графов. Они смогут решать задачи, используя эти различные концепции и методы, они будут знать ряд приложений дискретной математики и смогут следовать логическим аргументам и разрабатывать скромные логические аргументы. Текст и обсуждение в классе познакомят с понятиями, методами, приложениями и логическими аргументами; студенты будут практиковать их и решать задачи на ежедневных заданиях, а также будут проверяться на викторинах, промежуточных и итоговых.
Учебник. Дискретная математика и ее приложения, шестое издание, Кеннет Х. Розен. (Существует седьмое издание, но шестое издание широко доступно и дешевле. Мы будем использовать шестое издание.)
Часы курса. ПнВ 11:00-11:50. BP 316. Рабочие часы до и после занятий.
Время и учеба
Помимо занятий, вы потратите время на чтение текста, выполнение заданий и подготовку к викторинам и тестам. В среднем это составляет около пяти-девяти часов вне занятий в неделю, фактическое количество варьируется от недели к неделе. Вот краткое изложение 180 часов типичного семестра.
Подробнее об изучении математики см. в разделе Об изучении математики.
Задания и тесты. Будут ежедневные домашние задания, периодические викторины, два теста в течение семестра и двухчасовой выпускной экзамен в течение недели выпускных экзаменов. Вы можете использовать калькулятор при сдаче тестов, но тесты составлены таким образом, что калькуляторы не требуются и даже не приносят пользы. Две даты испытаний еще не определены, но одна будет в феврале, другая во второй половине марта.
Оценка курса. Оценка за курс будет рассчитываться как средневзвешенное значение:
2/9 (домашнее задание, тесты и посещаемость) + 4/9 (промежуточные тесты) + 3/9 (выпускной экзамен)
Несмотря на то, что вы будете получать комментарии к своей домашней работе, все, что будет записано и использовано для оценки курса, — это количество выполненных домашних заданий. Домашнее задание будет собрано в начале часа.
Общение вне занятий. Помимо обновления этой страницы курса, я иногда прибегаю к электронной почте, чтобы сообщить вам о рабочих часах и событиях, которые требуют немедленного сообщения. Вы можете написать мне по электронной почте, позвонить в мой офис или зайти в мой офис.
Общие правила
- Посещение занятий и участие в занятиях обязательны. Во время занятий текст будет дополняться более строгой теорией и специальными темами.
- Сотовые телефоны и ноутбуки должны быть выключены. Могут быть редкие случаи, когда они используются для целей, связанных с классом, в противном случае никаких текстовых сообщений, просмотра или электронной почты. Сотовые телефоны и ноутбуки нельзя использовать во время испытаний.
- Академическая честность . Академическая честность является базовой ценностью для любого высшего образования. Проще говоря, это требует, чтобы представленная работа была полностью собственной и уникальной для этого курса. Все прямые цитаты должны быть идентифицированы по источнику. Академическая честность может быть нарушена разными способами: например, путем подачи чужой работы за свою; списывание на экзамене; подача одной работы более чем в один класс; копирование компьютерной программы; изменение данных в эксперименте; или цитирование опубликованных материалов без надлежащего цитирования ссылок или источников. Попытки изменить официальную академическую запись также будут рассматриваться как нарушение академической честности.
  В целях обеспечения академической честности и защиты прав студентов обо всех предполагаемых нарушениях академической честности сообщается Совету колледжей. Такие отчеты должны быть тщательно задокументированы, а учащиеся, обвиняемые в нарушении, должны быть уведомлены об этом обвинении. В случае доказанной академической нечестности студент получит санкцию, которая может варьироваться от F за задание или курс до отстранения или исключения из Университета. Полная политика академической честности доступна в разделе «Академическое консультирование» по адресу http://www.clarku.edu/offices/aac/integrity.cfm.
- Учащиеся с ограниченными возможностями . Университет Кларка стремится предоставить студентам с подтвержденной инвалидностью равный доступ ко всем университетским программам и возможностям. Если у вас есть инвалидность или вы думаете, что у вас есть инвалидность и вам требуется академическое приспособление, вы должны зарегистрироваться в офисе Службы доступности для студентов (SAS), который находится в комнате 430 на четвертом этаже Библиотеки Годдарда.
  
  Если вы зарегистрированы в SAS и имеете право на приспособления, которые вы хотели бы использовать в этом курсе, пожалуйста, своевременно запросите эти приспособления через SAS. Дополнительные сведения см. в разделе Службы специальных возможностей для учащихся.
- Преподаватели являются ответственными работниками . Управление по гражданским правам требует от преподавателей сообщать обо всех предполагаемых сексуальных преступлениях координатору Университета по Разделу IX Линн Леви, [email protected].
  Единственными исключениями из этой ответственности за сообщение являются члены сообщества, которые были назначены и/или/обучены как «Конфиденциальные источники». Сюда входят профессиональные сотрудники Центра консультирования и личностного роста Кларка, в том числе директор Меган Керстинг, [email protected], и медицинские работники Центра здоровья. Сюда также входят профессор Джеймс Кордова, [email protected], профессор Кэти Палм Рид, kpr.confidential@clarku.
  edu, и профессор Эндрю Стюарт, [email protected].
  Преподаватели Кларка верят в то, что всем учащимся необходимо предоставить образовательную среду, свободную от дискриминации. Сексуальные домогательства к учащимся, в том числе сексуальное насилие, нарушают право учащихся на получение образования без дискриминации и, в случае сексуального насилия, являются преступлением. Преподаватели Кларка стремятся сделать Университет Кларка безопасной и инклюзивной средой для всех.

Силлабус. Не все эти темы будут раскрыты с одинаковой глубиной, и домашние задания будут даны не по всем разделам.

1 Основы: логика и доказательства

Темы главы 1: высказывание, истинностное значение, отрицание, логические операторы, составное высказывание, таблица истинности, дизъюкция, конъюнкция, исключающее или, импликация, обратное, противоположное, бит, логическая переменная, битовая операция, битовая строка, побитовая операция; тавтология, противоречие, случайность, логическая эквивалентность, пропозициональная функция Законы Де Моргана; предикаты, квантор существования, квантор всеобщности; вложенные квантификаторы, свободные и связанные переменные; правила вывода; теорема, гипотеза, доказательство, лемма, следствие, заблуждение, круговое рассуждение (начинающий вопрос), бессодержательное и тривиальное доказательство, прямое и косвенное доказательство; доказательство случаями, контрпример.

2 Основные структуры: наборы, функции, последовательности и суммирование

Темы главы 2: множество, аксиома, парадокс, элемент, пустое множество, равенство множества, подмножество, конечное и бесконечное множество, мощность, множество мощности, произведения множеств; объединение, пересечение, непересекающиеся множества, разность множеств, дополнение множеств, симметричная разность, диаграммы Венна; функция, домен, домен, образ, прообраз, диапазон, функция на, функция 1-1, соответствие 1-1, обратная функция, композиция, пол, потолок; последовательность, строка, нотация суммирования, нотация произведения.

3 Основы: алгоритмы, целые числа и матрицы

Темы главы 3: алгоритм, алгоритм поиска, алгоритм линейного поиска, алгоритм бинарного поиска, временная сложность, пространственная сложность, временная сложность в наихудшем случае, временная сложность в среднем; делимость, простое и составное число, простое число Мерсенна, наибольший общий делитель, относительно простое число, попарно взаимно простые целые числа, наименьшее общее кратное, остаток и модуль, шифрование и дешифрование, двоичное представление, шестнадцатеричное представление, линейная комбинация, обратное по модулю n, линейная конгруэнтность, псевдопростое шифрование, шифрование с закрытым и открытым ключом; Алгоритм Евклида.

4 Индукция и рекурсия

Темы главы 4: математическая индукция; рекурсивно определенные функции, наборы и структуры; рекурсивные алгоритмы; итерация.

5 Подсчет

Темы главы 5: мультипликативные и аддитивные принципы счета, принцип включения и исключения, древовидные диаграммы; базовый и обобщенный принцип группировки; перестановки, r -перестановки, комбинации; биномиальные коэффициенты, треугольник Паскаля.

6 Дискретная вероятность

Темы главы 6: основы вероятности, частотная интерпретация, симметричные ситуации, исходы, события, выборочное пространство, правило сумм, принцип включения и исключения; равномерное распределение, условная вероятность, независимость, испытания Бернулли, биномиальное распределение; определение ожидаемого значения, частотная интерпретация, случайные величины, линейность ожидания, независимые случайные величины, дисперсия.

8 Отношения

Темы главы 8: бинарное отношение, n -арное отношение, симметрия, антисимметрия, рефлексивность, транзитивность, композиция; графы и отношения, матрицы инцидентности; закрытие отношения, транзитивное закрытие; отношение эквивалентности, класс эквивалентности, разбиение; частичный порядок, лексикографический порядок, диаграммы Хассе.

9 графиков

Темы главы 9: определение графов, вершин (узлов), ребер, ориентированных и неориентированных графов, приложений графов; смежность вершин, степень (валентность), изолированные и висячие вершины, теорема рукопожатия, полные графы, циклы, двудольные графы, локальные сети, подграфы.

Конспекты занятий, викторины, тесты, домашние задания Все будущие даты являются предварительными. Разделы часто переполняются предыдущими или последующими днями. Кроме того, каждый раздел будет обсуждаться более одного дня — в один день, когда он будет представлен, позже, когда будут вопросы по нему и упражнения по его назначению.

Среда, 17 января
Добро пожаловать! Обсуждение курса.
Обсудить § 1.1. Введение в символическую логику предложений. Концепции суждение, истинностное значение, составное суждение, логический оператор, таблица истинности, отрицание, союз, дизъюнкция (включающее и исключающее)
Пятница, 19 января
Продолжить обсуждение символической логики. Концепции условного оператора (импликация), обратное, контрапозитивное, обратное, соглашения о приоритете логические операторы.
Понедельник, 22 января
§ 1.1. Упражнения должны: 1-4, 7, 10, 15, 16, 19, 21.
Закончить § 1.1, начать § 1.2. Пропозициональные эквивалентности.
Среда, 24 января
§ 1.1. Упражнения должны: 23, 31a-d, 32ace, 54, 62. Ответы
Продолжить § 1.2. Понятия тавтологии, противоречия, случайности, логическая эквивалентность, законы, такие как законы Де Моргана и распределительные законы
Пятница, 26 января
Обсудить § 1.3. Предикаты и квантификаторы. Понятия предиката (пропозициональная функция), универсальный и экзистенциальный квантор. Логическая эквивалентность предложений с кванторами.
Понедельник, 29 января
§ 1.2. Количество упражнений: 1, 2, 5-7, 12, 14, 17, 20, 27, 35, 46, 48, 50. Ответы
Продолжить § 1.3., Понятия контрпримера, отрицания и двойственности для количественные выражения.
Начало § 1.4 о вложенных квантификаторах. Понятия объема квантификатора, двойника кванторы всеобщности, двойные кванторы существования, смешанные кванторы.
Среда, 31 января
Завершить § 1.4: отрицание вложенных квантификаторов.
Начало § 1.5. Правила вывода. Понятия доказывания, действительности, правило вывода, специальные правила вывода для логики высказываний включая modus ponens (закон отстранения), modus tollens, гипотетический силлогизм, дизъюнктивный силлогизм, союз, разрешение и т. д.
Пятница, 2 февраля
§ 1.3. Количество упражнений: 1-3, 6, 10, 15-16, 35-36, 52-53. Ответы
Подробнее о § 1.5. Правила вывода для логики предикатов: универсальные конкретизация и обобщение, экзистенциальная конкретизация и обобщение.
Начало § 1.6. Введение в доказательства в математике. Теоремы, леммы, и следствия.
Понедельник, 5 февраля
§ 1.4. Количество упражнений: 4-6, 12-13, 19-20, 23, 27-28, 31-32, 45-46. Ответы
Продолжить § 1.6. Прямые доказательства, контрапозитивы, доказательства универсальные теоремы, бессодержательные доказательства, доказательство от противного, доказательства эквивалентность, контрпримеры.
Среда, 7 февраля
§ 1.5. Упражнения должны: 1-4, 7-8, 9abc, 10abc, 15, 23. Ответы
Обсудить § 1.7. Методы и стратегия доказательства. Доказательство случаями. Существование доказательства и неконструктивные доказательства существования. Доказательства уникальности. Вперед и обратное рассуждение. Процесс открытия. Догадки.
Пятница, 9 февраля
§ 1.6. Упражнения должны: 3, 6, 10-11, 39. Ответы
Викторина по разделам 1.4 и 1.5. Ответы
Начните главу 2. Обсудите § 2.1 о множествах. Связь с логикой. Примеры.
Понедельник, 12 февраля
§ 1.7. Упражнения должны: 3, 12, 21-22. Ответы
Продолжить § 1.1. Диаграммы Венна, мощность, бесконечные множества, степенные множества, Декартовы произведения множеств
Обсудить § 2.2. Операции над множествами. Союз, пересечение и т. д., и тождества, относящиеся к ним
Примечания к наборам
Среда, 14 февраля
§ 2. 1. Упражнения должны: 1-2, 17, 26, 27, 29. Ответы
Обсудите § 2.3 о функциях. Функция «один к одному» (инъекция), на функцию (сюръекция), однозначное соответствие (биекция).
Пятница, 16 февраля
§ 2.2. Упражнения должны: 1-4, 6-7, 16, 23, 27, 30, 32, 35-36, 38б, 40. Ответы
Из § 2.3. Композиция и обратные функции. Графики функций.
Обсудить § 2.4. Последовательности, строки, запись суммирования, геометрические серия, обозначение продукта.
Понедельник, 19 февраля
§ 2.3. Упражнения должны: 1-5, 8-11, 19, 28-29, 32, 36, 38, 61а. Ответы
Класс отменен
Среда, 21 февраля
Обзор за первый промежуточный экзамен
Пятница, 23 февраля
Первый промежуточный экзамен по главе 1 и с главы 2 по § 2.3. Вы можете принести калькулятор и лист для заметок.
Две версии: Первая, ответы; Второй, ответы
Понедельник, 26 февраля
§ 3. 1 Алгоритмы. Алгоритмы поиска, алгоритмы сортировки, проблема остановки
Среда, 28 февраля
§ 3.2 Рост функций. Big- O , большая омега, большая тета.
Рост функций.
§ 3.3 Сложность алгоритмов. Временная сложность, худший случай, средний случай
Пятница, 2 марта
§ 3.1. Упражнения должны: 2, 11, 12, 16, 19. Ответы
§ 3.4 Целые числа и деление. Делимость, модульная арифметика, конгруэнтность.
Весенние каникулы, с 5 по 9 марта.
Понедельник, 12 марта
§ 3.2. Упражнения должны: 1-2, 8-9, 19-20 и § 3.3: 5, 7-9. Ответы на 3.2, ответы на 3.3
§ 3.5 Простые числа и наибольшие общие делители. Основная теорема арифметика, доказательство Евклида бесконечности простых чисел, простые числа Мерсенна и совершенные числа, теорема о простых числах, наибольший общий делитель (НОД) и наименьшее общее кратное (НОК), взаимно простые числа
Среда, 14 марта
§ 3. 4. Упражнения должны: 1-2, 6-7, 9а-г, 11, 16, 33 и § 3.5: 3-5, 14, 20, 22. Ответы на 3.4, ответы на 3.5
§ 3.6 Целые числа и алгоритмы: базовое преобразование, эффективный алгоритм для вычислительные мощности, алгоритм Евклида, расширенный алгоритм Евклида, решение одиночных линейных сравнений.
Криптография и теория чисел, стоящая за ней
Пятница, 16 марта
§ 3.6. Упражнения должны: 1-5, 8, 23-24. Ответы
§ 4.1: Математическая индукция. Базовый случай, индуктивный шаг, индуктивная гипотеза
Понедельник, 19 марта.
§ 3.7. Упражнения по желанию: 1abc, 2abc, 6-7, 18-19, 46. Ответы
Еще о математической индукции.
Среда, 21 марта
§ 4.1. Упражнения должны: 9, 10, 14, 16, 21. Ответы
§ 4.2: сильная индукция и правильное упорядочение
Пятница, 23 марта
Викторина по §§ 3.2 и 3.5. Ответы
Заметки по комбинаторике
§ 5. 1. Основные принципы комбинаторики. Мультипликативное и аддитивное принципы счета, принцип включения и исключения, древовидные диаграммы. Перестановки
Понедельник, 26 марта
§ 5.2. Принцип сортировки, обобщенный принцип сортировки
§ 5.3. Перестановки и комбинации. r-перестановки, комбинации
Среда, 28 марта
§ 5.4. Биномиальные коэффициенты. Треугольник Паскаля
Введение в дискретную вероятность.
Пятница, 30 марта
§ 5.1. Количество упражнений: 7-8, 10-12, 16, 23-24, 31, 39, 42. Ответы.
§ 5.2. Упражнения должны: 1-2, 6, 20-21, 30. Ответы.
§ 6.1. Основные принципы вероятности. Равномерная конечная вероятность.
Понедельник, 2 апреля
§ 5.3. Упражнения из-за: 1-2, 6, 8, 10, 15, 20аб, 27-28. Ответы.
§ 5.4. Упражнения должны: 2, 4, 12, 31. Ответы.
§ 6.2. Теория вероятности. Условная вероятность, независимость.
Среда, 4 апреля
Подробнее о § 6.2. Испытания Бернулли, биномиальное распределение, случайные величины.
§ 6.3. Теорема Байеса.
Пятница, 6 апреля
Обзор второго промежуточного экзамена по главам с 3 по 5
Понедельник, 9 апреля
Второй промежуточный экзамен по главам с 3 по 5. Вы можете принести калькулятор и лист для заметок. Ответы
Среда, 11 апреля
§ 6.1. Количество упражнений: 3, 5, 6, 10-12, 25, 30. Ответы.
§ 6.4. Ожидаемое значение.
Пятница, 13 апреля
§ 6.2. Упражнения из-за: 7, 8, 12, 17, 25, 26, 28. Ответы.
Свойства ожидаемого значения.
Понедельник, 16 апреля
§ 6.4. Упражнения должны: 1-6, 12, 16. Ответы.
§ 8.1. Связи. Бинарное отношение на множестве S как подмножество S ² , функции как отношения. Свойства отношений: рефлексивность, симметричный, транзитивный, антисимметричный. Операции над отношениями: союз, пересечение, различие, композиция.
§ 8.3. Представление отношения в виде матрицы и в виде ориентированный граф (орграф).
Среда, 18 апреля
§ 8.5. Отношения эквивалентности, классы эквивалентности, разбиения.
Пятница, 20 апреля
§ 8.1. Упражнения должны: 4, 10, 17, 24. Ответы.
§ 8.3. Количество упражнений: 1-2, 5-6, 11-12, 18-19, 31-32. Ответы.
§ 5.6. Частичные упорядочения (посеты), лексикографический порядок, диаграммы Хассе.
Понедельник, 23 апреля
§ 9.1 Графики и графовые модели. Вершины и ребра, петли, метки. Простые графы против мультиграфов. Ориентированные графы (орграфы) и неориентированные графы. Графовые модели, т. е. приложения.
Среда, 25 апреля
§ 8.5. Упражнения должны: 1-3, 21-23, 26-28. Ответы.
§ 8.6. Упражнения должны: 7, 9-11, 15, 22. Ответы.
§ 9.