ГДЗ самостоятельные работы по алгебре 7 класс Александрова Мнемозина
Взяв за правило регулярно заниматься с помощью гдз по алгебре за 7 класс самостоятельная работа Александрова, школьники смогут не только существенно улучшить свои результаты в изучении этой математической науки, но и повысить оценки и успеваемость, начать или углубить подготовку к специализированным предметным конкурсам. Для достижения наилучших результатов специалисты советуют уделять такой работе минимум один час в день. И – отказаться от длительных, сверх двух недель подряд, перерывов в ней. Более продолжительные пропуски приводят к забыванию части изученного материала, а последующее наверстывание вызывает усталость и потерю интереса к занятиям.
Кто и почему использует онлайн помощники в процессе обучения?
В числе тех, кто часто, постоянно или системно использует подробные решения по алгебре за 7 класс к самостоятельным работам Александровой в своей практике:
- семиклассники, часто отсутствующие на школьных занятиях.

- подростки, переведенные на дистанционную форму обучения. Или самостоятельно избравшие семейный формат образования. Для них этот материал станет альтернативой объяснениям учителя или актуальным дополнением к нему;
- готовящиеся к математическим олимпиадам и иным аналогичным конкурсам. Особенно те ребята, которые не учатся в специализированных инженерных, математических классах и школах, но желают участвовать в конкурсных мероприятиях на равных с теми, кто в них обучается;
- родители семиклассников, стремящиеся быстро и качественно проверить уровень знаний своего ребенка, не вникая глубоко в суть дисциплины, понять, насколько хорошо он готов к проводимым в школе проверочным по предмету;
- сами школьные учителя. В условиях постоянной занятости современного педагога, наличием дополнительных обязанностей по планированию, контролю и составлению отчетности, этот справочник-решебник позволит оперативно проверить большое количество сданных ученических работ без потери качества результата такой проверки.

Очевидные преимущества применения онлайн ответов по алгебре за 7 класс самостоятельные работы (автор Александрова)
И хотя некоторые родители и педагоги еще не оценили пользы и преимуществ справочников, большинство пользователей уже отметили их безусловные плюсы:
- доступность ежедневно, круглосуточно и для всех;
- грамотный и понятный формат поиска, позволяющий в кратчайший срок отыскать нужный ответ и воспользоваться им в условиях ограниченности времени на выполнение задачи;
- соответствие решений и оформления ответов на задания действующим Стандартам образования;
- экономической доступности материалов, возможности отказаться или снизить расходы на привлечение репетиторов, посещение платных математических курсов и кружков.
Регулярно применяя онлайн сборники, подростки учатся грамотно работать с математической, научной и справочной информацией. Это пригодится им и в настоящем, и в будущем.
ГДЗ по Алгебре 7 класс самостоятельные работы Александрова Базовый уровень
В целях повышения уровня знаний у учащихся преподаватели используют в своей практике различные вспомогательные материалы – это и рабочие тетради, и задачники, и дидактики. Но одним из самых эффективных пособий считается методичка с самостоятельными работами. Здесь собрано 44 урока, каждый из которых имеет по четыре варианта. В дополнение к ним были разработаны готовые домашние задания Александровой от издательства «Мнемозина» 2016 года.
Но одним из самых эффективных пособий считается методичка с самостоятельными работами. Здесь собрано 44 урока, каждый из которых имеет по четыре варианта. В дополнение к ним были разработаны готовые домашние задания Александровой от издательства «Мнемозина» 2016 года.
Как и кому пригодятся ГДЗ по алгебре к самостоятельным работам для 7 класса (автор: Александрова Л. А.)
Такие решебники предназначены для:
- Семиклассников, которые без посторонней помощи хотят повысить свою успеваемость посредством выполнения заданий из данной тетради. Как в таком случае поможет сборник? Очень просто. Так как здесь собраны верные ответы ко всем номерам, то ученик может контролировать правильность выполнения, не дожидаясь при этом подмоги со стороны.
- Учителей, которые благодаря учебно-методическому комплексу могут осуществлять контроль знаний, составляя тем самым какие-либо карточки для индивидуальной и групповой работы на уроке или же разрабатывая упражнения для доп.
 занятий.
занятий. - Родителей, которые с помощью пособия могут проверять выполненные ребенком задания и помогать разбирать непонятные случаи, если в этом есть необходимость.
Важно отметить, что все решения достаточно подробно расписаны по действиям и выполнены квалифицированными педагогами страны, имеющими большой опыт, поэтому наличие каких-либо ошибок исключено.
Что включает в себя решебник для самостоятельных работ по алгебре за 7 класс Александровой
ГДЗ имеет абсолютно идентичное содержание тому, что дано в основном учебнике, следовательно, тем самым соблюдены все требования ФГОС (федерального государственного образовательного стандарта):
- Язык и модель математики.
- Линейные функции и их системы.
- Степень с натуральным показателем и ее свойства.
- Одночлены. Многочлены. Арифметические операции над ними.
- Разложение многочл-в на множители.
- Функции.

Помимо тем, которые в полной мере раскрывают важнейшие аспекты школьной программы и курса в частности, в учебно-методическом комплексе есть попутные комментарии к особо сложным номерам.
Главный плюс сборника в том, что он работает в онлайн-режиме круглосуточно и без перебоев. Открыть задачи можно с любого устройства (ноутбук, компьютер, планшет, телефон и т. д.), где имеется доступ к интернету. Также удобный формат поиска поможет без проблем найти нужное упражнение: просто выберете интересующий номер и вариант.
С онлайн-решебником ученики станут увереннее чувствовать себя на уроке, а преподаватели смогут значительно экономить время при разработке плана занятия.
ГДЗ Алгебра 7 класс Александрова
Алгебра 7 класс
Самостоятельные работы (Базовый уровень)
Александрова
Мнемозина
В настоящее время основная нагрузка по подготовке к контрольным и прочим работам ложится на плечи самих школьников, что в некотором роде является неправильным. Нет никаких гарантий, что они осуществят данную процедуру в нужном формате. Однако решебник к учебнику «Алгебра. Самостоятельные работы 7 класс (базовый уровень)» Александрова такие гарантии дать может, именно поэтому он завоевал такую популярность среди учащихся, педагогов и родителей.
Нет никаких гарантий, что они осуществят данную процедуру в нужном формате. Однако решебник к учебнику «Алгебра. Самостоятельные работы 7 класс (базовый уровень)» Александрова такие гарантии дать может, именно поэтому он завоевал такую популярность среди учащихся, педагогов и родителей.
Содержимое данного сборника
Сорок четыре самостоятельных работы рассчитаны на четыре варианта и распределены по тематической направленности. Исчерпывающие решения по всем номерам помогут ребятам лучше систематизировать и осознать учебный курс. ГДЗ по алгебре 7 класс Александрова поможет подготовиться к проверочным испытаниям, не затрачивая при этом много времени и усилий.
Реальную ли помощь можно от него получить
Изучение этого предмета само по себе достаточно непростое, ведь алгебраические формулы необходимо не просто запомнить, но и понять, что каждая из них обозначает и с чем связанна. Сделать это весьма трудно, если во время обучения была пропущена какая-либо тема и школьники не поняли одной из составляющих. Добиться на уроках внятного разъяснения от учителя порой бывает так же трудно, как и связаться напрямую с авторами учебных пособий, поэтому по большей части учащимся приходится осваивать необходимый материал самостоятельно, либо при помощи родителей. Подготовка к различного рода проверочным испытаниям носит в себе и другой смысл — она позволяет систематизировать познания, сделать их более скомпонованными. Решебник к учебнику «Алгебра. Самостоятельные работы 7 класс (базовый уровень)» Александрова станет хорошим советчиком в этом учебном году. «Мнемозина», 2016 г.
Добиться на уроках внятного разъяснения от учителя порой бывает так же трудно, как и связаться напрямую с авторами учебных пособий, поэтому по большей части учащимся приходится осваивать необходимый материал самостоятельно, либо при помощи родителей. Подготовка к различного рода проверочным испытаниям носит в себе и другой смысл — она позволяет систематизировать познания, сделать их более скомпонованными. Решебник к учебнику «Алгебра. Самостоятельные работы 7 класс (базовый уровень)» Александрова станет хорошим советчиком в этом учебном году. «Мнемозина», 2016 г.
Похожие ГДЗ Алгебра 7 класс
Название
Условие
Решение
Александрова Л. А. Алгебра 7 класс. Самостоятельные работы ОНЛАЙН
Александрова Л. А. Алгебра. 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л. А. Александрова ; под ред. А. Г. Мордковича. — 5-е изд., стер. — М., 2009. — 104 с.
Данное пособие предназначено для учеников общеобразовательных классов, изучающих курс алгебры по учебному комплекту А. Г. Мордковича. Пособие содержит учебный материал для проведения самостоятельных работ по каждой теме и может быть использовано учителем для осуществления текущего контроля знаний, умений и навыков школьников, в качестве дополнительных упражнений, а также учащимися в целях самоподготовки.
Г. Мордковича. Пособие содержит учебный материал для проведения самостоятельных работ по каждой теме и может быть использовано учителем для осуществления текущего контроля знаний, умений и навыков школьников, в качестве дополнительных упражнений, а также учащимися в целях самоподготовки.
Самостоятельные работы составлены согласно программе курса алгебры 7-го класса. Они предусматривают проверку знаний, умений и навыков учащихся по каждой теме в соответствии с обязательными результатами обучения. Необязательные задания и задания повышенной сложности отмечены символом #.
В пособии приводится примерное планирование учебного материала из расчета 3 ч в неделю с указанием номеров самостоятельных работ (С-1 …) по всем темам.
ПРИМЕРНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
Тематическое планирование дано в соответствии с параграфами учебника А. Г. Мордковича «Алгебра-7» (М. : Мнемозина, 2007) из расчета 3 ч в неделю.
Тема 1 МАТЕМАТИЧЕСКИЙ ЯЗЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ (13 ч)
1. Числовые и алгебраические выражения 3 ч С-1, 2
Числовые и алгебраические выражения 3 ч С-1, 2
2. Что такое математический язык 2 ч С-3
3. Что такое математическая модель 3 ч С-4
4. Линейное уравнение с одной переменной 2 ч С-5
5. Координатная прямая 2 ч С-6
Контрольная работа № 1 1ч
Тема 2 ЛИНЕЙНАЯ ФУНКЦИЯ (11 ч)
6. Координатная плоскость 2 ч С-7
7. Линейное уравнение с двумя переменными и его график 3 ч С-8
8. Линейная функция и ее график 3 ч С-9, 10
9. Линейная функция у = kx 1 ч С-11
10. Взаимное расположение графиков линейных функций 1ч Контрольная работа №2 1ч
Тема 3
СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ (13 ч)
11. Основные понятия 2 ч С-12
12. Метод подстановки 3 ч С-13, 14
13. Метод алгебраического сложения 3 ч С-15, 16
14. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций 4 ч С-17
Контрольная работа № 3 1ч
Тема 4
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА (6 ч)
15. Что такое степень с натуральным показателем 1ч С-18
16. Таблица основных степеней 1ч С-19
Таблица основных степеней 1ч С-19
17. Свойства степени с натуральным показателем 2 ч С-20
18. Умножение и деление степеней с одинаковыми показателями 1ч С-21
19. Степень с нулевым показателем 1 ч С-21
Тема 5
ОДНОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ (8 ч)
20. Понятие одночлена. Стандартный вид одночлена 1 ч
21. Сложение и вычитание одночленов 2 ч С-22, 23
22. Умножение одночленов. Возведение одночлена в натуральную степень 2 ч С-24
23. Деление одночлена на одночлен 2 ч С-25 Контрольная работа М 4 1ч
Тема 6
МНОГОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ (15 ч)
24. Основные понятия 1ч С-26
25. Сложение и вычитание многочленов 2 ч С-27
26. Умножение многочлена на одночлен 2 ч С-28, 29
27. Умножение многочлена на многочлен 3 ч С-30
28. Формулы сокращенного умножения 5 ч С-31—33
29. Деление многочлена на одночлен 1 ч Контрольная работа М 5 1ч
Тема 7
РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ (18 ч)
30. Что такое разложение многочленов на множители и зачем оно нужно 1 ч
31. Вынесение общего множителя за скобки 2 ч С-34
Вынесение общего множителя за скобки 2 ч С-34
32. Способ группировки 2 ч С-35
33. Разложение многочленов на множители с помощью формул сокращенного умножения 5 ч С-36—38
34. Разложение многочленов на множители с помощью комбинации различных
приемов 3 ч С-39
35. Сокращение алгебраических дробей 3 ч С-40
36. Тождества 1 ч
Контрольная работа №6 1ч
Тема 8 ФУНКЦИЯ у = х² (9 ч)
37. Функция у = х² и ее график 3 ч С-41
38. Графическое решение уравнений 2 ч С-42
39. Что означает в математике запись у = f(x) 3 ч С-43
Контрольная работа №7 1ч
Итоговое повторение 9 ч С-44
ГДЗ к сборнику находится здесь: http://math-helper.ru/izbrannoe/reshebnik-k-sborniku-samostoyatelnyih-rabot-po-algebre-dlya-7-klassa-aleksandrovoy-l-a-onlayn
Алгебра 7 Контрольные Мордкович — Контроль знаний
Контрольные работы по алгебре 7 класс с решениями и ответами в 4-х вариантах по УМК Мордкович. Цитаты заданий из пособия: «Алгебра 7 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г. Мордковича — М.: Мнемозина» использованы в учебных целях. Алгебра 7 Контрольные Мордкович. Представленные ниже работы ориентированы на учебник «Алгебра 7 класс» авторов А.Г. Мордкович и др. Решения и ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Контрольные работы для учащихся общеобразовательных учреждений / Л.А. Александрова; под ред. А.Г. Мордковича — М.: Мнемозина» использованы в учебных целях. Алгебра 7 Контрольные Мордкович. Представленные ниже работы ориентированы на учебник «Алгебра 7 класс» авторов А.Г. Мордкович и др. Решения и ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Нажмите на необходимую вам тему контрольной работы. При постоянном использовании данных контрольных работ рекомендуем КУПИТЬ книгу: Лидия Александрова: Алгебра 7 класс. Контрольные работы. ФГОС. Мнемозина, 2019 (переход по ссылке в интернет-магазин «Лабиринт.Ру»). Вопросы и ответы представлены в учебных целях, а также для ознакомления и покупки учебного пособия.
Алгебра 7 класс (Мордкович)
Контрольные работы с ответами:
Контрольная работа № 1 К-1
Контрольная работа № 2 К-2
Контрольная работа № 3 К-3
Контрольная работа № 4 К-4
Контрольная работа № 5 К-5
Контрольная работа № 6 К-6
Контрольная работа № 7 К-7
Контрольная работа № 8 Итоговая за 7 класс
Вы смотрели страницу «Алгебра 7 Контрольные Мордкович» — ответы на задачи контрольных работ из учебного пособия: «Алгебра 7 класс.
Если Вы считаете, что какой-то пример решен неправильно обязательно напишите нам в поле для Комментариев (ниже) с указанием № контрольной работы, № варианта и № задачи.
Другие контрольные работы по математике в 7 классе:
▶▷▶ алгебра 7 класс контрольные и самостоятельные работы попов гдз
▶▷▶ алгебра 7 класс контрольные и самостоятельные работы попов гдзалгебра 7 класс контрольные и самостоятельные работы попов гдз — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download ГДЗ решебник по алгебре 7 класс контрольные и самостоятельные gdzputinaco 7 класс Алгебра ГДЗ / 7 класс / Алгебра / контрольные и самостоятельные работы Попов Мордкович Онлайн ответы из решебника по алгебре за 7 класс авторов Попова МА, Мордкович АГ 2011 года издания ГДЗ: Контрольные и самостоятельные работы по алгебре 7 класс yougdzcom/exesizephp?id=446 Cached Алгебра 7 класс : Контрольные и самостоятельные работы Авторы: Попов МА Издательство: Экзамен 2017 год Алгебра за 7-ой класс — МА Попов Контрольные и gdzwtf/grade/ 7 /subject/algebra/book/576 Cached ГДЗ → 7 -ой класс → Алгебра → МА Попов Контрольные и самостоятельные работы по алгебре 7 класс к учебнику АГ Мордкович Алгебра 7 -ой класс → Алгебра 7 Класс Контрольные И Самостоятельные Работы Попов Гдз — Image Results More Алгебра 7 Класс Контрольные И Самостоятельные Работы Попов Гдз images ГДЗ по алгебре за 7 класс, решебник и ответы онлайн gdzru/class- 7 /algebra Cached Вот ты и стоишь на самом пороге удивительной дисциплины — алгебры! Именно с 7 класса начинается изучение этой математической науки Попов МА Контрольные и самостоятельные работы по алгебре: 7 edu-libcom/izbrannoe/popov-m-a-kontrolnyie-i Cached алгебра 7 класс , к учебнику Мордковича Алгебра 7 класс , Контрольные и самостоятельные работы по алгебре, контрольные работы по алгебре, Попов , Самостоятельные работы по алгебре, Учебно ГДЗ контрольные и самостоятельные по алгебре 9 класс Попов lovegdzcom … 9 класс Алгебра ГДЗ по алгебре за 9 класс автора Попова МА 2017 года издания Сюда внесены готовые решения на контрольные и самостоятельные работы , рассчитанные на базовый и высокий уровень подготовки Учебник Алгебра 9 класс МА Попов 2011 Контрольные и vklasseonline … Алгебра Подготовка к самостоятельно и контрольной работе Каждый ученик может найти на нашем интернет-ресурсе учебник Алгебра 9 класс МА Попов Контрольные и самостоятельные работы 2011 года Мордкович Попов алгебра 7 класс контрольные и самостоятельные uchebnik-tetradcom/matematika-uchebniki-rabochie-tetra Cached На сайте можно читать, смотреть онлайн и скачать учебники и рабочие тетради по всем предметам за любой класс ГДЗ решебник самостоятельные работы по алгебре 7 класс gdzputinaco 7 класс Алгебра ГДЗ решебник по алгебре 7 класс контрольные и самостоятельные работы Попов Мордкович Контрольные и самостоятельные работы по алгебре, 7 класс nasholcom … Экзамены по Алгебре Контрольные и самостоятельные работы по алгебре, 7 класс , Попов МА, 2011 Данное пособие Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 21,700 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
алгебра 7 класс контрольные и самостоятельные работы попов гдз — Все результаты ГДЗ по алгебре 7 класс контрольные и самостоятельные работы › Алгебра › 7 класс Решебник по алгебре за 7 класс авторы Попов , Мордкович издательство Экзамен ГДЗ по Алгебре за 7 класс дидактические материалы, к учебнику › › 7 класс › Алгебра › дидактические материалы Попов Подробный решебник ( ГДЗ ) по Алгебре для 7 класса дидактические материалы, ГДЗ по алгебре 7 класс дидактические материалы, к учебнику Мордкович Попов МА Самостоятельная работа №7 Контрольная работа №1 Контрольные и самостоятельные работы по алгебре 7 класс К allengorg/d/math/math2004htm Скачать: Контрольные и самостоятельные работы по алгебре 7 класс К учебнику Мордковича АГ Попов МА (pdf) Решебник ГДЗ по алгебре 7 класс дидактические материалы Попов гдз-классрф/load/7_klass/algebra/gdz_po_algebre_7_klasspopov/67-1-0-1484 14 сент 2018 г — Ответы по предмету Алгебра здесь находится ГДЗ по алгебре 7 ГДЗ по алгебре 7 класс контрольные и самостоятельные работы ГДЗ Попов МА 7 класс по Алгебре дидактические материалы, к ГДЗ к учебнику по алгебре за 7 класс Мородкович АГ посмотреть здесь ГДЗ к учебнику по Самостоятельная работа №1 Контрольная работа №1 Решебник дидактические материалы, к учебнику Мордкович (гдз к учебнику Мордкович по Алгебре для 7 класса Попов МА, гдз и ответы к домашнему ГДЗ к учебнику по алгебре за 7 класс Мородкович АГ можно скачать здесь Самостоятельная работа №1 Вариант 1 1 2 3 4 5 6 Вариант 2 1 2 3 4 5 6 Самостоятельная работа №2 Контрольная работа №1 Ответы@MailRu: Мне нужно гдз Контрольные и самостоятельные работы Похожие Контрольные и самостоятельные работы по алгебре 7 класс К учебнику Мордковича А Г Попов М А Контрольные и самостоятельные работы по алгебре 7 класс К obrazbaseru/matematika//1975-kontrolnye-i-samostoyatelnye-raboty-po-algebre-7- Похожие 2 сент 2015 г — Контрольные и самостоятельные работы по алгебре 7 класс К учебнику АГ Мордковича МА Попов Рейтинг: 0 / 5 Звезда не активна Контрольные и самостоятельные работы по алгебре 7 класс — Ozon › › Учителям › Дополнительные методические пособия Похожие 7 класс от издательства Экзамен Кроме этого, в нашем книжном Контрольные и самостоятельные работы по алгебре 7 класс Максим Попов Мегарешеба — ГДЗ по Алгебре за 7 класс Попов МА дидактические ГДЗ по Алгебре за 7 класс Дидактические материалы Попов МА ФГОС ГДЗ по Алгебре за 7 Самостоятельная работа №1 Контрольная работа №1 Контрольные и самостоятельные работы по Алгебре 7 класс к matlikbezru/algebra/item/69 Похожие Контрольные и самостоятельные работы по Алгебре 7 класс к при работе с учебником Мордковича АГ » Алгебра 7 класс » Авторы: ПОПОВ М А Издательство: ЭКЗАМЕН; Город: МОСКВА; Год: 2011; Страниц: 64 стр Контрольные и самостоятельные работы по алгебре 7 класс К 11klasovru › Алгебра Контрольные и самостоятельные работы по алгебре 7 класс К учебнику — Мордковича АГ Попов МА cкачать в PDF Контрольные и самостоятельные Контрольные и самостоятельные работы по алгебре: 7 класс: к › › 7 класс › Алгебра Контрольные и самостоятельные работы по алгебре : 7 класс : к учебнику АГ Купить Попов Михаил Александрович « Контрольные и самостоятельные Попов МА Контрольные и самостоятельные работы по алгебре 7 › › Контроль результатов освоения программы Попов МА Контрольные и самостоятельные работы по алгебре 7 класс : к учебнику АГ Мордковича ‘ Алгебра 7 класс ‘ Файл формата pdf; размером 1 Контрольные и самостоятельные работы по алгебре 7 класс К 50,00 ₽ — В наличии Купить книгу « Контрольные и самостоятельные работы по алгебре 7 класс К учебнику АГ Мордковича » Алгебра 7 класс » ФГОС» ( Попов МА) в Контрольные и самостоятельные работы по алгебре 7 класс К Контрольные и самостоятельные работы по алгебре 7 класс К учебнику АГ Мордковича » Алгебра 7 класс » (М: Мнемозина) Попов М В наличии: 61 ₽ ГДЗ 2819 §28 алгебра 7 класс задачник АГ Мордкович — GDZru › ГДЗ › 7 класс › Алгебра › Мордкович АГ › 2819 Алгебра 7 класс контрольные работы Автор: Александрова ЛА Алгебра 7 класс самостоятельные работы Автор: Попов МА издательство: ГДЗ по алгебре 7 класс АГ Мордкович задачник §28 — 2819, Решебник №3 / §28 / Книга: «Алгебра 7 класс Контрольные и самостоятельные работы › › Математика › Математика (5-9 классы) Книга: Алгебра 7 класс Контрольные и самостоятельные работы к учебнику АГМордковича ФГОС Автор: Максим Попов Аннотация, отзывы М А Попов — новинки — LiveLib Похожие Контрольные и самостоятельные работы к учебнику Н Я Виленкина · М А Попов М А Попов — Домашняя работа по алгебре за 7 класс 000 Купить Картинки по запросу алгебра 7 класс контрольные и самостоятельные работы попов гдз «id»:»tJ_olHeIcadbJM:»,»ml»:»600″:»bh»:90,»bw»:60,»oh»:868,»ou»:» «,»ow»:600,»pt»:»wwweurokiorg/system/books/covers/000/005/039/thu»,»rh»:»eurokiorg»,»rid»:»-cqBFOOPieETsM»,»rt»:0,»ru»:» «,»sc»:1,»th»:100,»tu»:» \u003dtbn:ANd9GcShjKOi578pWKRW9yxa1ddYvqnPYu2Zh203VLHCaohNiQ1bv7ittUc2ulc»,»tw»:69 «id»:»D9W-CWjbu7xjuM:»,»ml»:»600″:»bh»:90,»bw»:59,»oh»:700,»ou»:» «,»ow»:475,»pt»:»ozon-stcdnngenixnet/multimedia/1007048611jpg»,»rh»:»ozonru»,»rid»:»NZ7RKmuJD76BgM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Ozon»,»th»:101,»tu»:» \u003dtbn:ANd9GcT86qcgJhBVV6mAAlJj7ZJk1pxf4cwWaLGxzXIZfvQVQGVDoZYiBGvMa_g»,»tw»:69 «id»:»irNtlgH-UOS3PM:»,»ml»:»600″:»bh»:90,»bw»:58,»oh»:400,»ou»:» \u003d20141127235613″,»ow»:265,»pt»:»cv01twirpxnet/1547/1547225jpg?t\u003d20141127235613″,»rh»:»twirpxcom»,»rid»:»EbBDMdbqvNw5tM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Все для студента»,»th»:103,»tu»:» \u003dtbn:ANd9GcQnYBBzPNh_45DyXmQ53NQkfVyxjKX9-YkKpw1x5KgTIA7oeZ164gMDOA»,»tw»:67 «id»:»UhQkEnDaHo4ZUM:»,»ml»:»600″:»bh»:90,»bw»:50,»oh»:1338,»ou»:» «,»ow»:780,»pt»:»cdneurokiorg/books/gdzs/5039/1543908png»,»rh»:»eurokiorg»,»rid»:»5MJ5FtUo4feoCM»,»rt»:0,»ru»:» «,»sc»:1,»th»:109,»tu»:» \u003dtbn:ANd9GcQv7h-EXjTC37BRUItwYFq5FtWC6hmT2rE-UIw23CkNx_wPtCaUzYzMLQ»,»tw»:63 «id»:»MfujmGwhxbk6-M:»,»ml»:»600″:»bh»:90,»bw»:60,»oh»:870,»ou»:» «,»ow»:595,»pt»:»cdneurokiorg/system/books/covers/000/005/116/thu»,»rh»:»eurokiorg»,»rid»:»7OYOgGZysjY3IM»,»rt»:0,»ru»:» «,»sc»:1,»th»:101,»tu»:» \u003dtbn:ANd9GcQmDO-0zv0fVPpPRgNuCn3WiqgGHsKSXijUFIkUALzgw492Ipt5Ejos7Q»,»tw»:69 «id»:»zouZmyxcxDa-eM:»,»ml»:»600″:»bh»:90,»bw»:57,»oh»:1200,»ou»:» «,»ow»:790,»pt»:»ozon-stcdnngenixnet/multimedia/1017378235jpg»,»rh»:»ozonru»,»rid»:»7X15IJAcHmwbLM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Ozon»,»th»:103,»tu»:» \u003dtbn:ANd9GcTGwJ4sl86aJDTHLY0sixhTR23KpdmyPeapTR_EI2aDnmKpRE04qpt19A»,»tw»:67 «id»:»9-xCbRW05K1FmM:»,»ml»:»600″:»bh»:90,»bw»:102,»oh»:643,»ou»:» \u003d1490367504″,»ow»:747,»pt»:»cdneurokiorg/books/gdzs/5039/1543952png?v\u003d14903″,»rh»:»eurokiorg»,»rid»:»8eh5nZRPKvY3zM»,»rt»:0,»ru»:» «,»sc»:1,»th»:90,»tu»:» \u003dtbn:ANd9GcT4WFfpGZeuU72_coR3yF20ACG8bnZ-TyWUf3AZddJqTGQvz8_a1ZysFQ»,»tw»:105 «id»:»2EhoitVMAeVlaM:»,»ml»:»600″:»bh»:90,»bw»:60,»oh»:1102,»ou»:» \u003d1490367504″,»ow»:755,»pt»:»cdneurokiorg/books/gdzs/5039/1544010png?v\u003d14903″,»rh»:»eurokiorg»,»rid»:»DPjBqfq8YAZW6M»,»rt»:0,»ru»:» \u003dkx-zadanie-variant-1″,»sc»:1,»th»:101,»tu»:» \u003dtbn:ANd9GcQkb9msa9-L4h5zGZ-GMG8En2wl1Id-PLV8YvS4NO5R6O_zFQJ26CqU0mM»,»tw»:69 «id»:»-GZwkEFmHTLVoM:»,»ml»:»600″:»bh»:90,»bw»:62,»oh»:848,»ou»:» «,»ow»:600,»pt»:»cdneurokiorg/system/books/covers/000/005/101/thu»,»rh»:»eurokiorg»,»rid»:»BwID8awUXJb1cM»,»rt»:0,»ru»:» «,»sc»:1,»th»:99,»tu»:» \u003dtbn:ANd9GcQ-gv7rIpD0VMGBDkg9YUqVsiO00VzDIjQtaj0GVsQlKCd1eu4WwQwasCo»,»tw»:70 Другие картинки по запросу «алгебра 7 класс контрольные и самостоятельные работы попов гдз» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты АЛГЕБРА Контрольные работы 7 класс Мерзляк | Контроль знаний контрользнанийрф/algebra-kontrolnye-raboty-7-klass/ 3 апр 2018 г — Самостоятельные и контрольные работы » · Контрольные работы из пособия « Попова : Контрольно-измерительные материалы по алгебре 7 класс ВАКО» · Контрольные работы из пособия «Гаврилова: ГДЗ по алгебре для 7 класс от Путина Похожие Алгебра 7 класс самостоятельные работы Алгебра 7 класс (математика, геометрия), итоговые контрольные работы Гальперина автор: Попов МА Попов Максим Александрович «Контрольные и самостоятельные Книга Попов Максим Александрович » Контрольные и самостоятельные работы по алгебре 7 класс К учебнику АГ Мордковича ФГОС» — купить Гдз по самостоятельным работам по алгебре 7 класс попов 23 сент 2018 г — Контрольные и самостоятельные работы по алгебре , 7 класс , Попов М Данное пособие полностью соответствует новому ГДЗ решебник по алгебре 7 класс дидактические материалы Звавич › 7 класс › Алгебра ГДЗ решебник по алгебре 7 класс дидактические материалы Звавич — лучший онлайн решебник Контрольные работы: Самостоятельные работы : Алгебра дидактические материалы, к учебнику Мордкович Попов Автора: Попов МА Издательство: Экзамен Полные и подробные ответы к упражнениям ГДЗ к учебнику по алгебре за 7 класс Мородкович АГ можно скачать здесь Самостоятельная работа №1 Контрольная работа №1 Алгебра 7 класс: учебники, ГДЗ, учебные пособия, справочная x-unicom/books/18-s7 Похожие ГДЗ по алгебре для 7 класса 2014 к « Контрольные работы по алгебре за 7-9 Контрольные и самостоятельные работы по алгебре , 7 класс , Попов Учебник Алгебра 8 класс МА Попов (2011 год) Контрольные работы › Учебники за 8 класс › Алгебра Учебник Алгебра 8 класс МА Попов (2011 год) Контрольные работы Авторы: МА Попов + САМОСТОЯТЕЛЬНЫЕ РАБОТЫ стр 7 — 36 · К главе 1 ГДЗ ЛОЛ за 7 класс по Алгебре Попов МА дидактические ГДЗ по Алгебре за 7 класс Попов МА дидактические материалы, к учебнику Мордкович Самостоятельная работа № 7 Контрольная работа №1 Мегаботан по Алгебре 7 класс Похожие Алгебра 7 класс самостоятельные и контрольные работы АП Ершова Алгебра 7 класс дидактические материалы, к учебнику Мордкович Попов МА Попов МА Контрольные и самостоятельные работы по алгебре: 7 Попов МА Контрольные и самостоятельные работы по алгебре : 7 класс : к учебнику АГ Мордковича « Алгебра 7 класс » / МА Попов — 4-е изд, 7 класс :: ZUBRILANET zubrilanet/books/algebra/7-klass/ Похожие Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса Ершова АП 7 класс К учебнику Мордковича АГ Попов МА 2011 Контрольные и самостоятельные работы по алгебре для 7 8 апр 2013 г — Учебно-методический материал по алгебре ( 7 класс ) по теме: Контрольные и самостоятельные работы по алгебре для 7 класса ГДЗ по Алгебре за 7 класс — новые решебники с ответами › ГДЗ по алгебре Готовые домашние задания по алгебре за 7 класс — собрано 137 решебников с проверенными ответами на ГДЗ , самостоятельные работы и рабочие Решебник по Алгебре для 7 класса Попов МА ГДЗ дидактические ГДЗ к учебнику по алгебре за 7 класс Мородкович АГ можно скачать здесь ГДЗ к учебнику Самостоятельная работа № 7 Контрольная работа № 7 ГДЗ по алгебре дидактические материалы, к учебнику Мордкович 7 › ГДЗ › 7 класс › Алгебра › дидактические материалы Попов Качественные решения и подробные гдз по алгебре для учеников 7 класса дидактические Алгебра 7 класс дидактические материалы Попов МА ГДЗ по Алгебре для 7 класса дидактические материалы, к — na5ru Решебник ( ГДЗ ) для 7 класса по алгебре дидактические материалы, к учебнику Мордкович ФГОС Авторы учебника: Попов МА Содержит в себе полные и подробные Самостоятельная работа №5 Контрольная работа №1 Решебник по Алгебре 7 класс дидактические материалы, к ГДЗ по Алгебре за 7 класс Попов МА дидактические материалы, к учебнику Мордкович Самостоятельная работа №1 Вариант 1 1 2 3 4 5 6 Вариант 2 1 2 3 4 5 6 Самостоятельная работа №2 Контрольная работа №1 ГДЗ дидактические материалы, к учебнику Мордкович по Алгебре 7 Алгебра 7 класс Попов МА Дидактические материалы Подробные гдз и решебник по Самостоятельная работа №1 Контрольная работа №1 ГДЗ по Алгебре за 7 класс Дидактические материалы УМК Попов М › › 7 класс › Алгебра › дидактические материалы Попов Решебник по Алгебре Дидактические материалы для 7 класса, авторы учебника УМК: Попов МА на 2017-2018 год Алгебра 7 класс Решебник Попов МА Авторы: Самостоятельная работа №1 Контрольная работа №1 ГДЗ по Алгебре за 7 класс решебники, ответы онлайн Гдз по Алгебре 7 класс самостоятельные и контрольные работы АП Ершова Алгебра Алгебра 7 класс дидактические материалы Попов МА Гдз по ГДЗ по Алгебре 7 класс Попов МА дидактические материалы, к ГДЗ по Алгебре 7 класс Попов МА дидактические материалы, к учебнику Мордкович самостоятельная работа №7 контрольная работа №1 Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (50) Показать скрытые результаты В ответ на официальный запрос мы удалили некоторые результаты (1) с этой страницы Вы можете ознакомиться с запросом на сайте LumenDatabaseorg Вместе с алгебра 7 класс контрольные и самостоятельные работы попов гдз часто ищут контрольные и самостоятельные работы по алгебре 7 класс мордкович ответы самостоятельные работы по алгебре 7 класс макарычев самостоятельные работы по алгебре 7 класс колягин самостоятельная работа по алгебре 7 класс линейные уравнения ответы контрольные работы по алгебре 7 класс мордкович контрольная работа по алгебре 7 класс ответы контрольные работы по алгебре 7 класс александрова гдз по алгебре контрольные работы 7 класс кузнецова Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Решебник к сборнику самостоятельных работ по алгебре для 7 класса Александровой ОНЛАЙН
Решения самостоятельных работ по алгебре из сборника для 7 класса Александровой Л. А. Рукопись. — 2014.
А. Рукопись. — 2014.
Настоящее пособие содержит решения самостоятельных работ из сборника «Александрова Л. А. Алгебра. 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л. А. Александрова ; под ред. А. Г. Мордковича. — 5-е изд., стер. — М. : Мнемозина, 2009. — 104 с.»
Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по математике.
Страницы решебника представлены в виде слайдов. Кликните на нужный слайд, чтобы прочитать содержание страницы. Как листать слайды — читайте на странице http://gdz.math-helper.ru/kak-prosmatrivat-slaydyi/
Внимание! Рукопись не проверялась, возможны ошибки!
Содержание
Тема 1. МАТЕМАТИЧЕСКИЙ ЯЗЫК.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
1. Числовые и алгебраические выражения С-1, 2
2. Что такое математический язык С-3
3. Что такое математическая модель С-4
4. Линейное уравнение с одной переменной С-5
5. Координатная прямая С-6
Координатная прямая С-6
Контрольная работа № 1
Тема 2. ЛИНЕЙНАЯ ФУНКЦИЯ
6. Координатная плоскость С-7
7. Линейное уравнение с двумя переменными и его график С-8
8. Линейная функция и ее график С-9, 10
9. Линейная функция у = kx С-11
10. Взаимное расположение графиков линейных функций
Контрольная работа №2
Тема 3. СИСТЕМЫ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
11. Основные понятия С-12
12. Метод подстановки С-13, 14
13. Метод алгебраического сложения С-15, 16
14. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций С-17
Тема 4. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА
15. Что такое степень с натуральным показателем С-18
16. Таблица основных степеней С-19
17. Свойства степени с натуральным показателем С-20
18. Умножение и деление степеней с одинаковыми показателями С-21
19. Степень с нулевым показателем С-21
Тема 5. ОДНОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД ОДНОЧЛЕНАМИ
20. Понятие одночлена. Стандартный вид одночлена
Понятие одночлена. Стандартный вид одночлена
21. Сложение и вычитание одночленов С-22, 23
22. Умножение одночленов. Возведение одночлена в натуральную степень С-24
23. Деление одночлена на одночлен С-25
Тема 6. МНОГОЧЛЕНЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД МНОГОЧЛЕНАМИ
24. Основные понятия С-26
25. Сложение и вычитание многочленов С-27
26. Умножение многочлена на одночлен С-28, 29
27. Умножение многочлена на многочлен С-30
28. Формулы сокращенного умножения С-31—33
29. Деление многочлена на одночлен
Тема 7. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ
30. Что такое разложение многочленов на множители и зачем оно нужно
31. Вынесение общего множителя за скобки С-34
32. Способ группировки С-35
33. Разложение многочленов на множители с помощью формул сокращенного умножения С-36—38
34. Разложение многочленов на множители с помощью комбинации различных приемов С-39
35. Сокращение алгебраических дробей С-40
36. Тождества
Тема 8. ФУНКЦИЯ у = х²
37. Функция у = х² и ее график С-41
38. Графическое решение уравнений С-42
39. Что означает в математике запись у = f(x) 3 С-43
Итоговое повторение С-44
ВНИМАНИЕ! Все права на публикацию рукописей принадлежат сайту gdz.math-helper.ru. Копирование и распространение материалов запрещено!
12 умножение одночлена на многочлен. Видеоурок «Умножение многочлена на одночлен
».На этом уроке будет изучена операция умножения многочлена на одночлен, которая является основой для изучения умножения многочленов. Напомним закон распределения умножения и сформулируем правило умножения любого многочлена на одночлен. Напомним также некоторые свойства степеней. Кроме того, будут сформулированы типичные ошибки при выполнении различных примеров.
Тема: Полиномы. Арифметические операции над одночленами
Урок: Умножение многочлена на одночлен. Типовые задачи
Операция умножения многочлена на одночлен является основой для рассмотрения операции умножения многочлена на многочлен, и вы должны сначала научиться умножать многочлен на одночлен, чтобы понять умножение полиномы.
В основе этой операции лежит закон распределения умножения.Напомним ему:
По сути, мы видим правило умножения многочлена, в данном случае двучлена, на одночлен, и это правило можно сформулировать следующим образом: чтобы умножить многочлен на одночлен, каждый член многочлена должен быть умножен этим мономом. Сложите алгебраически полученные произведения, а затем выполните необходимые действия над многочленом, а именно приведите его к стандартному виду.
Рассмотрим пример:
Комментарий: этот пример решается с точным соблюдением правила: каждый член многочлена умножается на одночлен.Чтобы хорошо понять и усвоить закон распределения, в этом примере члены многочлена были заменены на x и y соответственно, а моном на c, после чего было выполнено элементарное действие в соответствии с законом распределения и произведена замена начальных значений. Будьте осторожны со знаками и правильно умножайте их на минус один.
Давайте рассмотрим пример умножения трехчлена на одночлен и убедимся, что он ничем не отличается от той же операции с двучленом:
Перейдем к решению примеров:
Комментарий: этот пример решается согласно закону распределения и аналогичен предыдущему примеру — каждый член многочлена умножается на одночлен, полученный многочлен уже записан в стандартной форме, поэтому его нельзя упростить.
Пример 2 — выполнить действия и получить многочлен стандартного вида:
Комментарий: для решения этого примера сначала умножим первый и второй бином по закону распределения, затем приведем полученный полином к стандартному виду — приведем аналогичные члены.
Теперь сформулируем основные проблемы, связанные с операцией умножения многочлена на одночлен, и приведем примеры их решения.
Задача1 — упростить выражение:
Комментарий: этот пример решается аналогично предыдущему, а именно, сначала выполняется умножение многочленов на соответствующие одночлены, после чего аналогичные сокращаются.
Задача 2 — упростить и вычислить:
Пример 1:;
Комментарий: этот пример решается так же, как и предыдущий, с той лишь разницей, что после приведения таких членов вам нужно подставить его конкретное значение вместо переменной и вычислить значение полинома. Напомним, чтобы легко умножить десятичную дробь на десять, вам нужно переместить запятую на одну позицию вправо.
Если цифры обозначены разными буквами, то можно только обозначать из произведения; пусть, например, нужно умножить число a на число b, — мы можем обозначить это либо через a ∙ b, либо через ab, но не может быть и речи о том, как как-то выполнить это умножение.Однако, когда мы имеем дело с одночленами, то в силу 1) наличия коэффициентов и 2) того факта, что в состав этих одночленов могут входить множители, обозначаемые одинаковыми буквами, можно говорить об умножении одночленов; эта возможность еще шире для многочленов. Рассмотрим ряд случаев, когда можно выполнить умножение, начиная с самого простого.
1. Умножение степеней с одинаковым основанием … Пусть, например, требуется 3 ∙ a 5.Зная значение возведения в степень, напишем то же самое более подробно:
а ∙ а ∙ а ∙ а ∙ а ∙ а ∙ а ∙ а
Глядя на эту подробную запись, мы видим, что мы написали a в 8 раз, или, короче, в 8. Итак, a 3 ∙ a 5 = a 8.
Пусть требуется b 42 ∙ b 28. Нужно было бы сначала записать множитель b 42 раза, а затем снова множитель b 28 раз — в общем, мы бы получили, что b взято в 70 раз. т.е. b 70. Итак, b 42 ∙ b 28 = b 70. Из этого уже ясно, что при умножении степеней с одинаковыми основаниями основание степени остается неизменным, а показатели степени складываются.Если у нас 8 ∙ a, то мы должны иметь в виду, что множитель a подразумевает показатель степени 1 («a в первой степени»), — следовательно, a 8 ∙ a = a 9.
Примеры: x ∙ x 3 ∙ x 5 = x 9; а 11 ∙ а 22 ∙ а 33 = а 66; 3 5 ∙ 3 6 ∙ 3 = 3 12; (а + б) 3 ∙ (а + б) 4 = (а + б) 7; (3x — 1) 4 ∙ (3x — 1) = (3x — 1) 5 и т. Д.
Иногда приходится иметь дело со степенями, показатели степени которых обозначаются буквами, например, xn (x в степени n). К таким выражениям нужно привыкнуть.Вот несколько примеров:
Поясним некоторые из этих примеров: bn — 3 ∙ b 5 базу b нужно оставить без изменений, а показатели добавить, то есть (n — 3) + (+5) = n — 3 + 5 = п + 2. Конечно, такие дополнения нужно научиться делать быстро в уме.
Другой пример: xn + 2 ∙ xn — 2, — основание x должно быть оставлено без изменений, а показатель степени должен быть добавлен, т.е. (n + 2) + (n — 2) = n + 2 + n — 2 = 2n .
Вы можете найти выше найденный порядок, как выполнить умножение степеней с одинаковыми основаниями, теперь можно выразить равенством:
а м ∙ а п = а м + п
2. Умножение одночлена на одночлен. Предположим, например, вам нужно 3a²b³c ∙ 4ab²d². Мы видим, что здесь одно умножение обозначено точкой, но мы знаем, что один и тот же знак умножения означает между 3 и a², между a² и b³, между b³ и c, между 4 и a, между a и b², между b² и d². Таким образом, мы можем увидеть здесь произведение 8 множителей и умножить их на любые группы в любом порядке. Переставим их так, чтобы коэффициенты и степени с одинаковыми основаниями располагались рядом друг с другом, т.е.е.
3 ∙ 4 ∙ a² ∙ a ∙ b³ ∙ b² ∙ c ∙ d².
Затем мы можем перемножить 1) коэффициенты и 2) степени с одинаковыми основаниями и получить 12a³b5cd².
Итак, умножая одночлен на одночлен, мы можем умножить коэффициенты и степени с одинаковыми основаниями, а остальные множители должны быть переписаны без изменений.
Другие примеры:
3. Умножение многочлена на одночлен. Предположим, вам нужно сначала некоторый многочлен, например, a — b — c + d, умноженный на положительное целое число, например +3.Поскольку положительные числа считаются такими же, как арифметические числа, это то же самое, что и (a — b — c + d) ∙ 3, то есть a — b — c + d является членом 3 раза, или
(a — b — c + d) ∙ (+3) = a — b — c + d + a — b — c + d + a — b — c + d = 3a — 3b — 3c + 3d,
, то есть в результате каждый член полинома нужно было умножить на 3 (или на +3).
Отсюда следует:
(а — б — в + г) ÷ (+3) = а — б — в + г,
, то есть каждый член полинома нужно было разделить на (+3).Также, суммируя, получаем:
и т. Д.
Пусть теперь нужно умножить (a — b — c + d) на положительную дробь, например, на +. Это похоже на умножение на арифметическую дробь, что означает взятие частей (a — b — c + d). Пятую часть этого многочлена взять легко: нужно (a — b — c + d) разделить на 5, а мы уже знаем, как это сделать, — получаем … Осталось повторить полученный результат 3 раз или умножьте на 3, т. е.
В результате мы видим, что нам пришлось умножить каждый член многочлена на или на +.
Предположим, теперь нам нужно (a — b — c + d) умножить на отрицательное число, целое или дробное,
, то есть и в этом случае каждый член полинома нужно было умножить на -.
Таким образом, независимо от числа m всегда (a — b — c + d) ∙ m = am — bm — cm + dm.
Поскольку каждый одночлен является числом, здесь мы видим указание на то, как умножить многочлен на одночлен — каждый член многочлена должен быть умножен на этот одночлен.
4. Умножение многочлена на многочлен … Пусть нужно (a + b + c) ∙ (d + e). Поскольку d и e обозначают числа, то (d + e) также выражает любое одно число.
(a + b + c) ∙ (d + e) = a (d + e) + b (d + e) + c (d + e)
(мы можем объяснить это так: мы имеем право временно принять d + e за моном).
Ad + ae + bd + be + cd + ce
В результате вы можете изменить порядок элементов.
(a + b + c) ∙ (d + e) = ad + bd + ed + ae + be + ce,
, то есть, чтобы умножить многочлен на многочлен, вы должны умножить каждый член одного многочлена на каждый член другого.Удобно (для этого порядок полученных слагаемых был изменен выше) каждый член первого многочлена сначала умножить на первый член второго (на + d), затем на второй член второго (на + д), а если и было, то третьим и т. д. d.; после этого следует произвести кастинг подобных элементов.
В этих примерах бином умножается на бином; в каждом биноме члены расположены в порядке убывания буквы, общей для обоих биномов.Такие умножения легко выполнять в уме и сразу записывать конечный результат.
Умножая главный член первого бинома на старший член второго, то есть 4x² на 3x, мы получаем 12x³ старшего члена произведения — очевидно, не будет ничего похожего на него. Далее мы ищем, умножая какие члены, мы получаем члены с степенью меньше 1 буквы x, то есть с x². Мы легко можем видеть, что такие члены будут получены путем умножения 2-го члена первого множителя на 1-й член второго и умножения 1-го члена первого множителя на 2-й член второго (скобки внизу пример указывает на это).Выполнить эти умножения в уме несложно, а также выполнить редукцию этих двух одинаковых членов (после чего мы получим член –19x²). Затем мы замечаем, что следующий член, содержащий букву x в степени на 1 меньше, то есть x в степени 1, будет получен только умножением второго члена на второй, и подобного ему не будет.
Другой пример: (x² + 3x) (2x — 7) = 2x³ — x² — 21x.
Также легко мысленно воспроизвести такие примеры, как следующий:
Старший срок получается путем умножения старшего члена на старший, с ним не будет похожих членов, и it = 2a³.Затем мы ищем, какие умножения приведут к выражению с a² — умножению 1-го члена (a²) на 2-е (–5) и умножения второго члена (–3a) на 1-е (2a) — это указывается ниже в скобках; выполняя эти умножения и объединяя полученные члены в один, мы получаем –11a². Затем мы ищем, какие умножения приведут к выражениям с первой степенью — эти умножения отмечены круглыми скобками выше. Заполнив их и объединив получившиеся члены в один, мы получим + 11a.Наконец, обратите внимание, что наименее значимый член в произведении (+10), который вообще не содержит a, получается путем умножения наименее значимого члена (–2) одного полинома на наименее значимый член (–5) Другие.
Другой пример: (4a 3 + 3a 2 — 2a) ∙ (3a 2 — 5a) = 12a 5 — 11a 4 — 21a 3 + 10a 2.
Из всех предыдущих примеров мы также получаем общий результат: главный член произведения всегда получается умножением главных членов множителей, и не может быть никаких похожих членов; Кроме того, самый низкий член продукта получается путем умножения самых низких членов множителей, и не может быть подобных членов.
Остальные члены, полученные умножением многочлена на многочлен, могут быть похожими, и может даже случиться так, что все эти члены взаимно аннулируются, и остаются только старший и младший.
Вот несколько примеров:
(a² + ab + b²) (a — b) = a³ + a²b + ab² — a²b — ab² — b³ = a³ — b³
(a² — ab + b²) (a — b) = a³ — a²b + ab² + a²b — ab² + b³ = a³ + b³
(a³ + a²b + ab² + b³) (a — b) = a 4 — b 4 (записать только результат)
(x 4 — x³ + x² — x + 1) (x + 1) = x 5 + 1 и т. Д.
Эти результаты заслуживают внимания и их полезно помнить.
Особенно важен следующий случай умножения:
(a + b) (a — b) = a² + ab — ab — b² = a² — b²
или (x + y) (x — y) = x² + xy — xy — y² = x² — y²
или ( x + 3) (x — 3) = x² + 3x — 3x — 9 = x² — 9 и т. д.
Во всех этих примерах, применительно к арифметике, мы имеем произведение суммы двух чисел на их разность, и результатом является разность квадратов этих чисел.
Если мы увидим подобный случай, то подробно производить умножение, как это было сделано выше, нет необходимости, но можно сразу записать результат.
Например, (3a + 1) ∙ (3a — 1). Здесь первый множитель с точки зрения арифметики представляет собой сумму двух чисел: первое число — 3a, второе — 1, а второе — разность тех же чисел; следовательно, результат должен быть следующим: квадрат первого числа (то есть 3a ∙ 3a = 9a²) минус квадрат второго числа (1 ∙ 1 = 1), то есть
(3a + 1) ∙ (3a — 1) = 9a² — 1.
Также
(ab — 5) ∙ (ab + 5) = a²b² — 25 и т. Д.
Итак, помните
(a + b) (a — b) = a² — b²
, то есть произведение суммы двух чисел на их разность равно разности квадратов этих чисел.
§ 1 Умножение многочлена на одночлен
Когда дело доходит до умножения многочленов, мы можем иметь дело с операциями двух видов: умножение многочлена на одночлен и умножение многочлена на многочлен.В этом уроке мы узнаем, как умножить многочлен на одночлен.
Основное правило, которое используется при умножении многочлена на одночлен, — это свойство распределения умножения. Напомним:
Чтобы умножить сумму на число, вы можете умножить каждый член на это число и сложить полученные произведения.
Это свойство умножения распространяется на действие вычитания. В буквальном обозначении свойство распределения умножения выглядит так:
(a + b) ∙ c = ac + bc
(а — б) ∙ c = ac — bc
Рассмотрим пример: многочлен (5ab — 3a2) умножается на одночлен 2b.
Введем новые переменные и обозначим 5ab буквой x, 3a2 буквой y, 2b буквой c. Тогда наш пример примет вид:
(5аb — 3а2) ∙ 2b = (x — y) ∙ с
По закону распределения это равно xc — us. Теперь вернемся к исходному значению новых переменных. Получаем:
5аb ∙ 2b — 3а2 ∙ 2b
Приведем получившийся многочлен к стандартному виду. Получаем выражение:
Таким образом, мы можем сформулировать правило:
Чтобы умножить многочлен на одночлен, вам нужно умножить каждый член многочлена на этот одночлен и сложить полученные произведения.
То же правило применяется при умножении одночлена на многочлен.
§ 2 Примеры по теме урока
При умножении многочленов на практике во избежание путаницы с определением получаемых знаков рекомендуется сначала определить и сразу записать знак произведения, а уже потом найдите и запишите произведение чисел и переменных. Вот как это выглядит на конкретных примерах.
Пример 1. (4a2b — 2a) ∙ (-5ab).
Здесь одночлен — 5аb нужно умножить на два одночлена, составляющих многочлен, 4а2b и — 2а. Первый кусок будет со знаком «-», а второй со знаком «+». Следовательно, решение будет выглядеть так:
(4а2b — 2а) ∙ (-5аb) = — 4а2b ∙ 5аb + 2а ∙ 5аb = -20а3b2 + 10а2b
Пример 2.-xy (2x — 3y +5).
Здесь мы должны выполнить три шага умножения, и знак первого произведения будет «-», знак второго «+», знак третьего «-».Решение выглядит так:
Hu (2x — 3y + 5) = -xy ∙ 2x + xy ∙ 3y — xy ∙ 5 = -2x2y + 3xy2 — 5xy.
Список использованной литературы:
- Мордкович А.Г., 7 класс Алгебра в 2-х частях, Часть 1, Учебник для общеобразовательных учреждений / А.Г. Мордкович. — 10-е изд., Перераб. — Москва, «Мнемозина», 2007
- Мордкович А.Г., Алгебра 7 класс в 2 ч., 2 ч., Задачник для образовательных учреждений / [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича — 10-е изд., переработанное — Москва, «Мнемозина», 2007
- HER.Тульчинская, 7 класс. Алгебра. Блиц-опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, переработанное и дополненное, Москва, «Мнемозина», 2008 г.
- Александрова Л.А., Алгебра 7 класс. Тематические тесты в новой форме для учащихся образовательных учреждений, под ред. А.Г. Мордковича, Москва, «Мнемозина», 2011
- Александрова Л.А. Алгебра 7 класс. Самостоятельная работа для студентов образовательных учреждений, под ред. А.Г. Мордковича — 6-е издание, стереотипное, Москва, «Мнемозина», 2010 г.
NR МОБУ «Пойковская средняя общеобразовательная школа №1.2 «
Открытый урок алгебры в 7 классе
по теме:
«Умножение одночлена на многочлен»
Учителя математики
Лимар Т.А.
поселок Пойковский, 2014 г.
Методические указания
Тип урока
Урок «открытия» новых знаний
Цели урока (образовательные, развивающие, образовательные)
Цель занятия : формирование у студентов умений к самостоятельному построению новых способов действия по теме «Умножение одночлена на многочлен» на основе метода рефлексивной самоорганизации.
Образовательная : расширение концептуальной базы по теме «Многочлены» за счет включения в нее новых элементов: умножение одночленов на многочлен.
Задачи урока
образовательные:
Разработайте алгоритм умножения одночлена на многочлен, рассмотрите примеры его применения.
развивающие:
Развитие внимания, памяти, способности рассуждать и аргументировать свои действия путем решения проблемной проблемы;
Развитие познавательного интереса к предмету;
Формирование эмоционально положительного отношения учащихся за счет использования активных форм организации урока и использования ИКТ;
Развитие рефлексивных навыков через анализ результатов урока и самоанализ собственных достижений.
образовательная:
Развитие коммуникативных навыков студентов путем организации групповой, парной и фронтальной работы на занятиях.
Используемые методы
Вербальные методы (разговор, чтение),
Визуальные (демонстрация презентации),
Проблемный поисковик,
Рефлексивный метод самоорганизации (метод деятельности),
Формирование личного УУД.
Дидактическое сопровождение урока:
Компьютерная презентация,
Квестовые карточки,
Оценочные карточки для работы на уроке,
Карточки с практическими упражнениями по новой теме.
Этапы урока
Деятельность преподавателя
Деятельность студентов
Организационный этап. (1 минута)
Задачи: обновление знаний учащихся, определение целей урока, разделение класса на группы (разные уровни), выбор руководителя группы.
Психологический настрой, приветствие студентов.
Приветствует учащихся, называет эпиграф урока. Он предлагает занять места в заранее назначенных группах и дает предварительные инструкции.
Здравствуйте, присаживайтесь. Ребята, за тысячи лет до нашего рождения Аристотель сказал, что «… математика … открывает порядок, симметрию и определенность, а это самые важные виды красоты». И после каждого урока в мире математики неопределенность становится меньше. Надеюсь, что сегодня мы откроем для себя что-то новое.
Во время урока вы будете заполнять оценочный лист, который лежит на ваших партах после выполнения каждого задания.
Студенты рассаживаются по заранее разделенным группам.Ознакомился с протоколом.
Устный счет.
Цель: проверить усвоение теоретического материала по теме: «Умножение одночлена на одночлен. Возведение в степень »и умение применять его на практике, развитие у учащихся мыслительных способностей, осознание ценности совместной деятельности, борющейся за успех группы.
а) математический диктант.
Принесите аналогичные мономы.
a) 2x + 4y + 6x =
b) -4a + c-3a =
c) 3c + 2d + 5d =
d) -2d + 4a-3a =
2. Умножьте одночлен на a моном
a) -2x 3x
b) (-4av) (-2c)
d) (-5av) (2z)
e) 2z (x + y)
Учитель предлагает заполнить математический диктант, написанный на доске. Контролирует правильность выполнения, приводит к изучению нового материала.
Вместе со студентами формулирует цель и тему урока
— Какое из номеров диктанта вызвало у вас наибольшие затруднения?
Попробуем найти , где была сложность, а почему?
— Цель нашего урока: научиться выполнять умножение одночлена на многочлен (справедливость вашего решения).
Тема урока: «U умножение одночлена на многочлен».
Учащиеся выполняют задания. Вместе с учителем формулирует цель и тему урока. Запишите тему урока в тетрадях.
(ожидаемый ответ учащегося d)
Разработайте (сформулируйте) правило умножения одночлена на многочлен.
Переход к новой теме
Цель: подготовить учащихся к усвоению нового материала .
Групповая работа.
Группа № 1.
Рассчитать.
15 80 + 15 20 = 1200 + 300 = 1500
15 (80 + 20) = 15100 = 1500
Номер группы. 2
Рассчитать.
20 40 + 20100 = 800 + 2000 = 2800
20 (40 + 100) = 20140 = 2800
Номер группы 3.
Рассчитать .
6 (2a + 3a) = 6 5a = 30a
6 2a + 6 3a = 12a + 18a = 30
Группа No.4
Вычислить
7 (4x + 2x) = 7 6x = 42
7 4x + 7 2x = 28x + 14x = 42x
Учитель дает инструкции. Следит за исполнением.
Каждой группе нужно найти значение двух выражений. Сравните их и запишите результат как равенство или неравенство.
Студенты решают примеры в группах, делают выводы.
По 1 члену от каждой группы пишет заключение на доске.
На доске написано:
15 80 + 15 20 = 15 (80 + 20)
20 40 + 20100 = 20 (40 + 100)
6 (2a + 3a) = 6 2a + 6 3
7 (4x + 2x) = 7 4x + 7 2x
Учащиеся ставят себя в контрольную ведомость.Если заключение сформулировано и написано правильно, то поставьте 5.
«Открытие» студентами нового материала.
Цель: формирование у студентов умений самостоятельно выстраивать новые приемы действий по теме «Умножение одночлена на многочлен» на основе метода рефлексивной самоорганизации.
Завершение задания «Заполнить пробелы»
Слайд 2.
2z ∙ (x + y) = 2z ∙ + 2z ∙
3x (a + b) = a + b
Через минуту, правильное решение отображается на доске.
Учитель дает инструкции.
Проводит опрос. Заключает.
Используя уравнения на классной доске, заполните пропуски в следующих выражениях.
Обратите внимание, что стоит перед круглыми скобками?
Что в скобках?
Какой ответ?
Итак, давайте сделаем вывод, как умножить одночлен на многочлен. Через три минуты представьте их материал классу (используя белую простыню и фломастеры).
Суммирует
Давайте проверим, правильно ли вы сформулировали правило.Для этого откройте руководство на стр.
Ученики работают в группах, каждая группа обсуждает, как заполнить пропуски.
Проверить правильность заполнения зазоров.
Каждая группа выдвигает гипотезу и представляет классу, проводится общее обсуждение и делается вывод.
Прочтите вслух правило из учебника.
Одночлен
Многочлен
Новый многочлен
Первичная привязка.
Цель: отработка навыков умножения одночлена на многочлен, развитие мыслительных навыков учащихся, осознание ценности совместной деятельности, борьба за успех группы, повышение мотивации учебной деятельности.
Групповая работа.
Группа № 1, 3
x ∙ (
м ∙ (n +3) = __________________; 7a ∙ (2b -3c) = _______________;
№ группы2, 4
a ∙ (c-y) = __________________; c ∙ (c + d) = ___________________;
м ∙ (y + 5) = __________________; 6м ∙ (2н-3к) = ______________;
7
Учитель дает указания.
Возьмите на стол номер карты 2 Обязательное условие — при принятии решения о произнесении правила друг другу.
Проведите перекрестную проверку, группа 1 обменивается карточками с группой 3, а группа 2 — с группой 4.Поставьте оценки группам в зачетном листе:
5 правильно выполненных заданий — оценка «5»; 4 — «4»; 3- «3»; менее 3- «2».
Выполняют задание по карточкам, проводят взаимную проверку.
Ответственный член группы № 1 спрашивает любого члена группы № 3. Ставит оценку в протокол.
ответственный член группы №2 спрашивает любого члена группы №4. Ставит оценку в протокол.
6. Математические упражнения.
Цель: повысить или сохранить умственную работоспособность детей в классе;
обеспечивают кратковременный активный отдых учащихся во время урока.
Учитель дает инструкции, показывает карточки, на которых написаны одночлены, многочлены и выражения, которые не являются ни одночленами, ни многочленами.
Студенты выполняют упражнения по командам
«Моном» — руки подняты; «Полином» — руки перед собой; «Другое выражение» — руки в стороны;
Они закрыли глаза, сосчитали до 30, открыли глаза.
Математическое лото
Задача: закрепить алгоритм умножения одночлена на многочлен и стимулировать интерес к математике
Группа № 1.3
s (3a-4b) = 3ac-12vs;
3) 3c (x-3y) = 3cx-9cy;
4) -n (x-m) = — nx + нм;
5) 3z (x-y) = 3zx-3zy.
Карты ответов:
3ac-12vs; 3ac + 12vs; 3ac-4v
zx + 2zy; zx-2zy; zx + 2y;
3cx-9cy; 3cx + 9cy; 3cx-3cy;
Nx + нм; nx + нм; nx-нм;
3zx-3zy; 3zx-y; zx-zy.
Группа № 2, 4
Умножаем одночлен на многочлен
5a (b + 3d) = 5ab + 15ad
A (3b + c) = — 3av-ac;
4x (5c -s) = 20cx -4xs;
a (3c + 2b) = 3ac + 2ba
Карты ответов:
3av-as; 3ср + ас; ты;
20cx -4xs; 20cx + 4xs; 5c -4xs;
3ac + 2ba; 3ac + 6ba; 3ac-2ba;
сп-5см; Ср-5м; р-5см.
5ab + ad; 5ab + 5b; 5ab + 15ad
Раздает конверты.Рассказывает правила игры. Один конверт содержит 5 примеров умножения одночлена на многочлен и 15 карточек с ответами.
Объясняю, как оценивать выполненную работу.
Группа получает оценку «5», если первый правильно выполнил все задания, 4 задания — «4»; 3 задания — «3», меньше трех — «2», группа, завершившая игру во втором лото, при выполнении всех заданий правильно получает оценку «4», третья — «3», последняя — «2».
Получать конверты с заданиями.
Произведено умножение одночлена на одночлен.
Выберите правильные ответы из всех предложенных карточек.
Самотестирование.
Получите карточку самопроверки. Поставьте отметку в протоколе.
8 . Отражение учебной деятельности в уроке (конспект урока).
Цель: самооценка учащимися результатов учебной деятельности, осознание способа построения границ и использования нового метода действий.
Фронтальная беседа по вопросам на слайде:
Какой алгоритм умножения одночлена на многочлен существует в математике?
Каков результат вашей деятельности?
Учитель анализирует оценочные листы (их результаты видны на слайде)
Возвращается к девизу урока, проводит параллель между эпиграфом и алгоритмом, выведенным на уроке.
Раздайте оценочные карточки, которые четко показывают результат вашей деятельности.
Вернемся к девизу нашего урока: «… математика … открывает порядок, симметрию и определенность, а это самые важные виды красоты». Алгоритм, который мы вывели сегодня на уроке, поможет нам сделать новые открытия в будущем: умножение многочлена на многочлен поможет выучить сокращенные формулы умножения, о которых много говорят в алгебре. Впереди нас ждет много интересного и важного.
Спасибо за урок !!!
Учащиеся проводят самоанализ своей работы, вспоминают алгоритм, изученный на уроке, отвечают на вопросы.
ПРИМЕНЕНИЕ.
КАРТА №1.
Группа №1
Рассчитать.
15 80 + 15 20 = ______________________________
15 (80 + 20) = _______________________________
КАРТОЧКА №1.
№ группы 2
Рассчитать.
20 40 + 20 100 = _________________________________
20 (40 + 100) = __________________________________
КАРТА №1.
Номер группы 3.
Вычислить .
6 (2a + 3a) = _____________________________________
6 2a + 6 3a = _____________________________________
КАРТА № 1
Группа № 4
Рассчитать
7 (4x + 2x) = _____________________________________
7 4x + 7 2x = _____________________________________
КАРТА №2.
Группа №3
x ∙ (z + y) = __________________; a ∙ (c + d) = ___________________;
5x ∙ (3a-6a) = _______ -________ = _______.
КАРТОЧКА №4.
Номер группы. 2
7x ∙ (5d -8d) = ______ — ________ = _______.КАРТА №2.
Группа №1
x ∙ (z + y) = __________________; a ∙ (c + d) = ___________________;
м ∙ (n + 3) = __________________; 7a ∙ (2b-3c) = _______________;
5x ∙ (3a-6a) = _______ -________ = _______.
КАРТОЧКА №2.
Номер группы. 2
a ∙ (c -y) = __________________; c ∙ (c + d) = ___________________;
м ∙ (y +5) = __________________; 6м ∙ (2н -3к) = ______________;
7x ∙ (5d -8d) = ______ — ________ = _______.Математическое лото ( две копии)
с (3a-4b)
z (x + 2y)
3c (x-3y)
-н (х-м)
3z (x-y)
-а (3в + с)
4x (5c-s)
а (3c + 2b)
с (п-5м)
5а (б + 3д)
Lotto Answers (две копии)
3ac-12vs
3ac + 12vs
3ac-4v
zx + 2zy;
zx-2zy
zx + 2y
3skh-9su
3cx-3cy
3sx + 3su
Nx + nm
nx + nm
nx-nm
zx3
3zx-3zy
3av-as
3av + ac;
you
20cx -4xs
20cx + 4xs
5c -4xs
3ac + 2ba
3ac + 6ba
3ac-2ba
cp-5cm
m
Wed-5cm
m
Ср.
5ab + объявление
5ab + 5b
Частный случай умножения многочлена на многочлен — это умножение многочлена на одночлен. В этой статье мы сформулируем правило выполнения этого действия и проанализируем теорию на практических примерах.
Правило умножения многочлена на одночлен
Давайте разберемся, на чем основано умножение многочлена на одночлен. Это действие основывается на распределительном свойстве умножения относительно сложения.Дословно это свойство записывается так: (a + b) c = a c + b c (a, b и c — некоторые числа). В этой записи выражение (a + b) c является в точности произведением многочлена (a + b) и одночлена c … Правая часть равенства ac + bc является суммой произведения одночленов a и b на одночлен c .
Приведенные выше рассуждения позволяют сформулировать правило умножения многочлена на одночлен:
Определение 1
Для выполнения действия умножения многочлена на одночлен необходимо:
- запишите произведение многочлена и одночлена, которое нужно умножить;
- умножить каждый член многочлена на данный одночлен;
- находим сумму полученных работ.
Поясним дополнительно описанный выше алгоритм.
Чтобы составить произведение многочлена на одночлен, исходный многочлен заключен в круглые скобки; далее между ним и заданным одночленом ставится знак умножения. В случае, когда написание монома начинается со знака минус, его также необходимо заключить в круглые скобки. Например, произведение полинома — 4 x 2 + x — 2 и одночлена 7 y запишем как (- 4 x 2 + x — 2) 7 y , а произведение полинома a 5 b — 6 ab и одночлен — 3 a 2 составим в виде: (a 5 b — 6 ab) (- 3 a 2) .
Следующим шагом алгоритма является умножение каждого члена многочлена на данный одночлен. Компоненты многочлена являются одночленами, т.е. фактически нам нужно произвести умножение одночлена на одночлен. Предположим, что после первого шага алгоритма мы получили выражение (2 x 2 + x + 3) 5 x, , тогда на втором шаге мы умножаем каждый член полинома 2 x 2 + x + 3 на одночлен 5 x , получая: 2 x 2 5 x = 10 x 3, x 5 x = 5 x 2 и 3 5 x = 15 x … Результатом будут одночлены 10 x 3, 5 x 2 и 15 x .
Последнее действие по правилу — сложение полученных работ. Из предложенного примера, выполнив этот шаг алгоритма, получим: 10 x 3 + 5 x 2 + 15 x .
По умолчанию все шаги записываются в виде цепочки равенств. Например, найдя произведение многочлена 2 x 2 + x + 3 и одночлена 5 x , мы запишем это так: (2 x 2 + x + 3) 5 x = 2 x 2 5 x + x 5 х + 3 5 х = 10 х 3 + 5 х 2 + 15 х. Исключая промежуточные вычисления второго шага, краткое решение можно сформулировать следующим образом: (2 x 2 + x + 3) 5 x = 10 x 3 + 5 x 2 + 15 x.
Рассмотренные примеры позволяют заметить важный нюанс: в результате умножения многочлена на одночлен получается многочлен. Это утверждение верно для любого умножаемого многочлена и монома.
По аналогии выполняется умножение одночлена на многочлен: данный одночлен умножается на каждый член многочлена и полученные произведения суммируются.
Примеры умножения многочлена на одночлен
Пример 1Необходимо найти произведение: 1, 4 · x 2 — 3, 5 · y · — 2 7 · x.
Решение
Первый шаг правила уже выполнен — произведение записано. Теперь мы выполняем следующий шаг, умножая каждый член многочлена на данный одночлен. В этом случае удобно сначала переводить десятичные дроби на обычные. Тогда получаем:
1, 4 x 2 — 3.5 y — 2 7 x = 1, 4 x 2-2 7 x — 3,5 y — 2 7 x = = — 1, 4 2 7 x 2 x + 3, 5 2 7 xy = — 7 5 2 7 x 3 + 7 5 2 7 ху = — 2 5 х 3 + ху
Ответ: 1, 4 x 2 — 3,5 y — 2 7 x = — 2 5 x 3 + x y.
Уточним, что когда исходный многочлен и / или одночлен заданы в нестандартной форме, перед нахождением их произведения желательно привести их к стандартному виду.
Пример 2
Полином 3 + a — 2 a 2 + 3 a — 2 и одночлен — 0.5 а б (- 2) а … Надо их работу найти.
Решение
Мы видим, что исходные данные представлены в нестандартном виде, поэтому для удобства дальнейших расчетов приведем их к стандартному виду:
— 0,5 ab (- 2) a = (- 0,5) (- 2) (aa) b = 1 a 2 b = a 2 b 3 + a — 2 a 2 + 3 a — 2 = (3 — 2) + (а + 3 а) — 2 а 2 = 1 + 4 а — 2 а 2
Теперь произведем умножение одночлена a 2 b для каждого члена многочлена 1 + 4 a — 2 a 2
a 2 b (1 + 4 a — 2 a 2) = a 2 b 1 + a 2 b 4 a + a 2 b (- 2 a 2) = = a 2 B + 4 a 3 b — 2 a 4 б
Привести исходные данные к стандартному виду не удалось: решение было бы более громоздким.В этом случае последним шагом будет необходимость привести таких членов. Для понимания приведем решение по такой схеме:
— 0,5 ab (- 2) a (3 + a — 2 a 2 + 3 a — 2) = = — 0,5 ab (- 2) a 3 — 0,5 ab (- 2) aa — 0,5 ab (- 2) a (- 2 a 2) — 0,5 ab (- 2) a 3 a — 0,5 ab (- 2) a (- 2) = = 3 a 2 b + a 3 b — 2 a 4 b + 3 a 3 b — 2 а 2 б = а 2 б + 4 а 3 б — 2 а 4 б
Ответ: — 0,5 a b (- 2) a (3 + a — 2 a 2 + 3 a — 2) = a 2 b + 4 a 3 b — 2 a 4 b .
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Графика с корневыми примерами. Запланируйте функцию квадратного корня, преобразовывая графики. Производная степенной функции
Основные цели:
1) образуют представление о возможности проведения обобщенного исследования зависимостей реальных значений на примере значений, приведенных к соотношению y =
2) для формирования возможности построения графа y = и его свойств;
3) повторить и закрепить приемы устных и письменных вычислений, построения квадратного корня.
Оборудование, демонстрационный материал: раздаточный материал.
1. Алгоритм:
2. Образец для задания по группам:
3. Образец для самостоятельной работы самопроверки:
4. Карта для фазы отражения:
1) Я понял, как построить график функции y =.
2) Я могу перечислить его свойства по графику.
3) Не допускал ошибок в самостоятельной работе.
4) Допускал ошибки в самостоятельной работе (перечислите эти ошибки и укажите их причину).
На занятиях
1. Самоопределение для учебной деятельности
Назначение сцены:
1) вовлекать обучающихся в учебную деятельность;
2) Определите содержательную структуру урока: мы продолжаем работать с действительными числами.
Организация учебного процесса на шаге 1:
— Что мы изучали на последнем уроке? (Мы изучили множество допустимых чисел, действий с ними, построили алгоритм описания свойств функции, повторили функции, изученные в 7 классе).
— Сегодня мы продолжим работу с множеством действительных чисел, функцией.
2. Актуализация знаний и фиксация трудностей в деятельности
Назначение сцены:
1) обновить содержание обучения, необходимое и достаточное для восприятия нового материала: функция, независимая переменная, зависимая переменная, графики
y = kx + m, y = kx, y = c, y = x 2, y = — x 2,
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) закрепить все повторяющиеся понятия и алгоритмы в виде схем и символов;
4) Зафиксируйте индивидуальную трудность в деятельности, демонстрируя на личностном значении уровень недостаточности имеющихся знаний.
Организация учебного процесса на 2 ступени:
1. Вспомним, как устанавливать зависимости между значениями? (С использованием текста, формул, таблиц, графики)
2. Что называется функцией? (Зависимость между двумя значениями, где каждому значению одной переменной соответствует единственное значение другой переменной y = f (x)).
Что называется х? (Независимая переменная — аргумент)
Как называется? (Зависимая переменная).
3.В 7 классе изучали функции? (y = kx + m, y = kx, y = c, y = x 2, y = — x 2,).
Индивидуальное задание:
Что представляет собой график функций y = kx + m, y = x 2, y =?
3. Определить причины трудностей и цель деятельности
Назначение сцены:
1) организует коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшее затруднение в учебной деятельности;
2) Согласуйте цель и тему урока.
Организация учебного процесса на 3 ступени:
— Что особенного в этой задаче? (Зависимость дается формулой y = с которой мы еще не встречались).
— Какова цель урока? (Для ознакомления с функцией y =, ее свойствами и расписанием. Функции в таблице определяют тип зависимости, строят формулу и график.)
— Можно сформулировать тему урока? (Функция y =, ее свойства и расписание).
— Запишите тему в тетрадь.
4. Выход из трудностей
Назначение сцены:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленной трудности;
2) Закрепить новый способ действия в знаковой, словесной форме и с помощью эталона.
Организация учебного процесса на 4 ступени:
Работу на этапе можно организовать по группам, предлагая группам построить график y =, затем проанализировать полученные результаты.Также группам может быть предложен алгоритм для описания свойств этой функции.
5. Первичная консолидация во внешней речи
Цель этапа: закрепить изученное содержание обучения во внешней речи.
Организация учебного процесса на пятой ступени:
Постройте график y = — и опишите его свойства.
Свойства у = -.
1. Определения функций.
2.Значения функций.
3. у = 0, у> 0, у
y = 0, если x = 0.
г.
4. Станция, уменьшение функции.
Функция убывает в точке x.
Строим граф y =.
Выделяем часть на сегменте. Обратите внимание, что Naim. = 1 при х = 1, а в наиб. = 3 при х = 9.
Ответ: Наим. = 1, наиб. = 3.
6. Самостоятельная работа с самотестированием по стандарту
Цель этапа: Проверить вашу способность применять новый учебный контент в типичных условиях на основе сравнения вашего решения с эталонным стандартом.
Организация учебного процесса на 6 ступени:
Студенты самостоятельно выполняют задание, проводят самотестирование по стандарту, анализируют, исправляют ошибки.
Строим граф y =.
Используя график, найдите наименьшее и наибольшее значения функции на отрезке.
7. Включение в систему знаний и повторения
Цель этапа: отработать навыки использования нового содержания вместе с ранее изученным: 2) повторить учебное содержание, которое потребуется на следующих уроках.
Организация учебного процесса на шаге 7:
Решите графически уравнение: = x — 6.
Один ученик у оставшейся доски в тетрадях.
8. Отражение деятельности
Назначение сцены:
1) исправить новое содержание, изученное на уроке;
2) оценивать собственную активность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) фиксирует нерешенные трудности как направления будущей учебной деятельности;
5) Обсудите и запишите домашнее задание.
Организация учебного процесса на шаге 8:
— Ребята, какая цель была сегодня перед нами? (Изучите функцию y =, ее свойства и график).
— Какие знания помогли нам в достижении цели? (Умение искать закономерности, умение читать графики.)
— Проанализируйте свою деятельность на уроке. (Карты с отражением)
Домашнее задание
п.13 (к Примеру 2) № 13,3, 13,4
Решите уравнение графически.2. Из рисунка видно, что график касается только оси АС, в точке с координатами (0; 0).
Теперь стоит отметить основные свойства этой функции.
Свойства функции y = √x
1. Функция определения функции — балка.
Ответ. D (f) = [-1,4].
А.Г. Мордкович Алгебра 10 класс
Календарь и тематическое планирование по математике, видео по математике онлайн, математика в школе
Задачи урока:
Оборудование:
Компьютер, интерактивная доска, раздаточные материалы.
Презентация к уроку.
ВО ВРЕМЯ ЗАНЯТИЙ
План урока.
Вступительное слово учителя.
Повторение ранее изученного материала.
Изучение нового материала (групповая работа).
Исследовательская функция. Свойства графики.
Обсуждение графика (фасадные работы).
Игральные математические карты.
Результаты урока.
И.Актуализация справочных знаний.
Приветствие учителя.
Учитель :
Зависимость одной переменной от другой называется функцией. Пока что вы изучили функции y = kx + b; y = k / x, y = x 2. Сегодня продолжим изучение функций. На сегодняшнем уроке вы узнаете, как выглядит график функции квадратного корня, научитесь строить диаграммы функции квадратного корня.
Запишите тематический урок ( Slide1).
2. Повторение изучаемого материала.
1. Какие функции задаются формулами:
а) y = 2x + 3; б) у = 5 / х; в) у = -1 / 2х + 4; г) у = 2х; д) у = -6 / х д) у = х 2?
2. Какой у них график? Как оно расположено? Укажите область определения и значение каждой из этих функций (на рис. Изображены графики функций, задаваемых этими формулами, укажите ее вид для каждой функции) ( slide2).
3. Какой график у каждой функции, как эти графики построены?
(Слайды 3, схематично графические функции построены).
3. Изучение нового материала.
Учитель :
Итак, сегодня изучаем функцию
и ее график.
Мы знаем, что график функции y = x 2 представляет собой параболу. Каким будет график функции y = x 2, если взять только x ≥ 0? Это часть параболы — ее правая ветвь.Построим функциональный график
.
Повторяем алгоритм построения графиков функций (слайд 4, с алгоритмом)
Вопрос : Что вы думаете, глядя на аналитический вход функции, можно сказать о том, какие значения h. Допустимо? (Да, x≥0 ). Поскольку выражение
Имеет смысл вообще x большое или равное 0.
Учитель: В явлениях природы, в деятельности человека часто существует связь между двумя ценностями.По какому графику можно представить эту зависимость? (групповая работа)
Класс делится на группы. Каждая группа получает задачу: Составить расписание работы
на миллиметровой бумаге, выполняя все пункты алгоритма. Затем от каждой группы подходит представитель и показывает работу группы. (Открывается , sweet 5, проверяет, потом расписание в тетради встраивается)
4. Исследование функции. (Работа групп продолжается)
Учитель:
найти область определения функции;
найти область значений функции;
,определяют пропуски убывания (возрастания) функции;
> 0, u
Вызов результатов (слайд 6).
Учитель: Разберем график. График функции — это ветвь параболы.
Вопрос : Скажите, а вы раньше где-то встречались с этим расписанием?
Посмотрите график и скажите, прямо ли он пересекает ой? (Не) ОУ? (Не) . Посмотрите расписание и скажите, есть ли в расписании центр симметрии? Ось симметрии?
Подведем итоги:
Атепер поверит, как выучили новую тему и повторили пройденный материал.Игра в математические карты. (Правила игры: каждой группе из 5 человек предлагается набор карточек (25 карточек). Каждый игрок получает 5 карточек, на которых написаны вопросы. Первый ученик дает одну из карточек второму ученику, который должен ответить на вопрос. с карточки … Если ученик отвечает на вопрос, то растровое изображение, если нет, ученик берет карту себе и предает ход и т. д. только 5 ходов. Если у ученика не осталось карточек, то рейтинг — 5, остается 1 карта — счет 4, 2 карты — счет 3, 3 карты — счет — 2)
5.Итоги урока. (объясненные оценки обучаемых на контрольных листах)
Задание на дому.
Изучите стр.8.
Решить №172, №179, №183.
Подготовьте сообщения на тему «Применение функции в различных областях науки и в литературе».
Отражение.
Покажите свое настроение картинками на столе.
Сегодня урок
Мне нравится.
Не понравился.
Материал урока I ( я понял, я не понял).
Линейная функция и ее график (презентация). Презентация «Линейная функция, ее график, свойства». методическая разработка по алгебре (7 класс) по теме Скачать презентацию линейная функция
Задачи урока: сформулировать определение линейной функции, представление о ее графике; определить роль параметров b и k в расположении графика линейной функции; формировать умение строить график линейной функции; развивать умение анализировать, обобщать, делать выводы; развивать логическое мышление; развитие навыков самостоятельной деятельности
Uk-badge uk-margin-small-right «>
Ответы 1.а; б 2.а) 1; 3 б) 2; x y 1. a; в 2. а) 2; 4 б) 1; x y вариант 2 вариант
Uk-badge uk-margin-small-right «>
B k b> 0b0 K 0b0 K «> 0b0 K»> 0b0 K «title =» (! LANG: b k b> 0b0 K «> title = «b k b> 0b0 K»> !}
B kb> 0b0 y = kx I, III четверти Через начало K 0b0 y = kx I, III четверти Через начало K «> 0b0 y = kx I, III четвертей Через начало координат K»> 0b0 y = kx I, III четверти Через происхождение K «title =» (! LANG: bkb> 0b0 y = kx I, III четверти Через происхождение K «> title = «b k b> 0 b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx I, III четвертей Через начало координат K координат «> 0b0 y = kx I, III четвертей Через начало координат K координат»> 0b0 y = kx I, III четвертей Через начало координат K координат «title =» (! LANG: bkb> 0b0 y = kx I, III четверти Через начало координат K «> title = «b k b> 0b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx I, III четвертей Через начало координат K 0b0 y = kx I, III четвертей Через начало K координат «> 0b0 y = kx I, III четвертей Через начало координат K координаты»> 0b0 y = kx I, III четверти Через начало координат K координаты «title =» (! LANG: bkb> 0b0 y = kx I, III четверти Через начало координат K «> title = «b k b> 0b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx I, III четвертей Через начало координат K 0b0 y = kx I, III четвертей Через начало K координат «> 0b0 y = kx I, III четвертей Через начало координат K координаты»> 0b0 y = kx I, III четверти Через начало координат K координаты «title =» (! ЯЗЫК: bkb> 0b0 y = kx I, III четверти Через начало координат K «> title = «b k b> 0b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx I, III четвертей Через начало координат K 0b0 y = kx I, III четвертей Через начало K координат «> 0b0 y = kx I, III четвертей Через начало координат K координаты»> 0b0 y = kx I, III четверти Через начало координат K координаты «title =» (! ЯЗЫК: bkb> 0b0 y = kx I, III четверти Через начало координат K «> title = «b k b> 0b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координаты K 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K координаты «> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через происхождение координаты K «title =» (! ЯЗЫК: bkb> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> title = «bkb> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> !}
B kb> 0b0 y = kx + b (y = 2x + 1) I, III четверть y = kx + b (y = 2x-1) I, III четверть y = kx I, III четверть Через начало координат K 0b0 y = kx + b (y = 2x + 1) I, III четверть y = kx + b (y = 2x-1) I, III четверть y = kx I, III четверть Через начало K-координаты «> 0b0 y = kx + b (y = 2x + 1) I, III четверти.y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> 0b0 y = kx + b (y = 2x + 1) I, III четверти. y = kx + b (y = 2x-1) I, III четверть y = kx I, III четверти Через начало координаты K «title =» (! LANG: bkb> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> title = «bkb> 0b0 y = kx + b (y = 2x + 1) I, III четверть y = kx + b (y = 2x-1) I, III четверть y = kx I, III четверть Через начало координат K «> !}
Полное наименование образовательного учреждения:
Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №Кочубеевское 3, Ставропольский край
Предметная область: математика
Название урока: «Линейная функция, свой график, свойства ».
Возрастная группа: 7 класс
Название презентации: «Линейная функция, ее график, свойства».
Количество слайдов: 37
Среда (редактор), в которой сделана презентация: Power Point 2010
Настоящая презентация
1 слайд — заголовок
2 слайд — актуализация базовых знаний: определение линейного уравнения, устно из предложенных выбрать те, которые являются линейными.
3 слайда — определение линейной функции.
4 слайда распознавания линейной функции предложены.
Вывод на 5 слайдов.
6 скользящих способов установки функции.
7 слайд Я привожу пример, показываю.
8 слайд — пример привожу, показываю.
Задание из 9 слайдов для студентов.
10 слайдов — проверка правильности задания. Обращаю внимание студентов на взаимосвязь между коэффициентами k и b и расположением графиков.
Вывод на 11 слайдов.
12 слайдов — работа с графиком линейной функции.
13 слайд-заданий для самостоятельного решения: построить графики функций (выполнить в блокноте).
Слайды 14-17 — показывают правильное выполнение задания.
18-27 слайдов — задания устного и письменного характера. Я выбираю не все задания, а только те, которые подходят по уровню подготовленности класса при наличии времени.
Задание из 28 слайдов для сильных учеников.
29 слайдов — подвести итоги.
30-31 слайдов — выводы.
32-36 слайдов — историческая справка. (Если есть время)
37 слайдов Использованная литература
Список использованной литературы и Интернет-ресурсы:
1.Мордкович А.Г. и др. Алгебра: учебник для 7-х классов общеобразовательных учреждений — М .: Просвещение, 2010.
2. Звавич Л.И. и другие. Дидактические материалы по алгебре для 7 класса — М .: Просвещение, 2010.
3.Алгебра 7 класс под редакцией Ю.Н. Макарычев и др., Образование, 2010
4. Интернет-ресурсы: www.symbolsbook.ru/Article.aspx% … id% 3D222
Preview:
Чтобы использовать предварительный просмотр презентаций, создайте себе аккаунт (аккаунт) Google и войдите в него: https: // accounts .google.com
Подписи к слайдам:
Линейная функция, ее график, свойства. Кирьянова Марина Владимировна, учитель математики СОШ №3 с. Кочубеевское, Ставропольский край
Задайте линейные уравнения: 1) 5y = x 2) 3y = 0 3) y 2 + 16x 2 = 0 4) + y = 4 5) x + y = 4 6) y = -x + 11 7) + 0.5x — 2 = 0 8) 25d — 2m + 1 = 0 9) y = 3 — 2x 5
Функция вида у = kx + b называется линейной. График функции вида y = kx + b представляет собой прямую линию. Чтобы провести прямую линию, нужны всего две точки, так как единственная прямая линия проходит через две точки.
Найдите уравнения линейных функций y = -x + 0,2; у = 1 2, 4х-5,7; у = — 9 х — 1 8; y = 5,04x; y = — 5,04x; у = 1 26,35 + 8,75x; у = х -0,2; у = х: 8; y = 0,005x; у = 13 3, 13 3 13 3 х; у = 3 — 1.01x; у = 2: х; у = -0,004 9; y = x: 6 2.
y = kx + b — линейная функция х — аргумент (независимая переменная) y — функция (зависимая переменная) k, b — числа (коэффициенты) к ≠ 0
x X 1 X 2 X 3 y Y 1 Y 2 Y 3
y = — 2x + 3 — линейная функция. График линейной функции представляет собой прямую линию; для построения прямой нужно иметь две точки x — независимую переменную, поэтому ее значения мы выберем сами; Y — зависимая переменная, ее значение будет получено в результате подстановки выбранного значения x в функции.Записываем результаты в таблицу: xy 0 2 Если x = 0, то y = — 2 · 0 + 3 = 3. 3 Если x = 2, то y = -2 2 + 3 = — 4 + 3 = -1 . — 1 Отметьте точки (0; 3) и (2; -1) на координатной плоскости и проведите через них прямую линию. xy 0 1 1 Y = — 2x + 3 3 2 — 1 выбираем
Построим график линейной функции y = — 2 x +3 Составим таблицу: xy 03 1 1 Построим точки (0; 3) и (1; 5) на координатной плоскости и провести через них прямую линию x 1 0 1 3 y
Вариант I Вариант II y = x-4 y = — x + 4 Определить взаимосвязь между коэффициентами k и b и расположение прямых линий Построить график линейной функции
y = x-4 y = -x + 4 Вариант I Вариант II xy 1 2 0-4 x 1 2 0 4 y
x 0 yy = kx + m (k> 0) x 0 yy = kx + m (k 0, то линейная функция y = kx + b увеличивается, если k
Используя график линейной функции y = 2x — 6, ответьте на вопросы: a) при каком значении x будет y = 0? б) при каких значениях x y 0? в) при каких значениях x y 0? 1 0 3 y 1 x -6 a) y = 0 для x = 3 b) y 0 для x 3 Если x 3, то линия расположена над осью x, что означает, что ординаты соответствующих точки линии положительны c) y 0 при x 3 Если x 3, то прямая расположена ниже оси x, что означает, что ординаты соответствующих точек прямой отрицательны
Задачи для независимых Решение: построить графики функций (выполнить в записной книжке) 1.y = 2x — 2 2.y = x + 2 3.y = 4 — x 4. y = 1 — 3x Обратите внимание: точки, выбранные вами для построения прямой линии, могут быть разными, но расположение графиков должно обязательно совпадают
Ответ на задание 1
Ответ на задание 2
Ответ на задание 3
Ответ на задание 4
На каком рисунке показан график линейной функции y = kx? Ответ — объяснить. 1 2 3 4 5 x y x y x y x y x y
Учащийся ошибся при построении функции.Какая картинка? 1.y = x + 2 2.y = 1.5x 3.y = -x-1 x y 2 1 x y 3 1 x y 3 3
1 2 3 4 5 x y x y y x y x y На каком рисунке коэффициент k отрицательный? x
Какой знак у коэффициента k для каждой из линейных функций:
На каком рисунке свободный член b в уравнении линейной функции отрицателен? 1 2 3 4 5 xyxyxyxyxy
Выберите линейную функцию, график которой показан на рисунке y = x — 2 y = x + 2 y = 2 — xy = x — 1 y = — x + 1 y = — х — 1 у = 0.5x y = x + 2 y = 2x Молодец! Считать!
xy 1 2 0 1 2 3 -1 -2 -1 -2 xy 1 2 0 1 2 3 -1 -2 -1 -2 y = 2x y = 2x + 1 y = 2x- 1 y = -2x + 1 y = — 2x- 1 y = -2x
y = -0,5x + 2, y = -0,5x, y = -0,5x- 2 xy 1 2 0 1 2 3-1-2-1-2 3 4 5 6-3 xy 1 2 0 2 3-1-2-1-2 3 4 5 6-3 1 y = 0,5x + 2 y = 0,5x- 2 y = 0,5xy = -0,5x + 2 y = -0.5xy = -0, 5x- 2
y = x + 1 y = x- 1, y = xy 1 2 0 1 2 3-1-2-1-2 3 4 5 6-3 xy 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6-3 xy = -xy = -x + 3 y = -x- 3 y = x + 1 y = x- 1 y = x
Нарисуйте уравнение линейной функции согласно следующим условиям:
подвести итог
Записать выводы в тетрадь Мы узнали: * Функция вида y = kx + b называется линейной.* График функции вида y = kx + b представляет собой прямую линию. * Только две точки необходимы, чтобы нарисовать прямую линию, так как есть только одна прямая линия, проходящая через две точки. * Коэффициент k показывает увеличение или уменьшение прямой. * Коэффициент b показывает, в какой точке линия пересекает ось OY. * Условие параллельности двух линий.
Успехов Вам!
Алгебра — это слово происходит от названия работы Мухаммада аль-Хорезми «Аль-джебр и аль-мукабала», в которой алгебра была представлена как самостоятельный предмет.
Роберт Рекорд — английский математик, который в 1556 году.ввел знак равенства и объяснил свой выбор тем, что ничто не может быть равнее двух параллельных отрезков.
Готфрид Лейбниц — немецкий математик (1646-1716), который первым ввел термин «абсцисса» — в 1695 г., «ордината» — в 1684 г., «координаты» — в 1692 г.
Рене Декарт — французский философ и математик (1596-1650), который первым ввел понятие «функция»
Литература 1.Мордкович А.Г. и др. Алгебра: учебник для 7-х классов общеобразовательных учреждений — М.: Образование, 2010. 2. Звавич Л.И. и другие. Дидактические материалы по алгебре для 7 класса — М .: Просвещение, 2010. 3.Алгебра 7 класс под редакцией Ю.Н. Макарычев и др., Образование, 2010 4. Интернет-ресурсы: www.symbolsbook.ru/Article.aspx% … id% 3D222
Информационная карта урока:
Учебный предмет: алгебра
Тема: «Линейная функция и ее график»
Тип урока: объяснение нового материала
Место урока в учебной программе: третий урок в разделе «Функции».Линейная функция изучается после того, как студенты изучат концепции функции и ее графика, смогут ответить на вопросы о предметной области и диапазоне значений, смогут найти значения функции из графика и найти аргумент, который соответствует значение функции. Они знают, как определить функцию. На этом уроке ученики должны выучить определение линейной функции, научиться строить ее график. Определите расположение графа в зависимости от чисел k и b. Основное содержание изучаемого материала устанавливается учебной программой и обязательным минимумом содержания образования по математике.
Аннотация: Урок рассчитан на учащихся 7-х классов с углубленным изучением математики по учебнику «Алгебра 7» авторов Ю.Н. Макарычев, Н. Миндюк, К. Нешков, И. Феоктистов. Урок проходит по сценарию мультимедийной презентации, что экономит время, которое учитель тратит на конструирование на доске. Презентация была оформлена красочными иллюстрациями, анимацией и звуковыми эффектами. При необходимости этап урока, на котором возникли трудности, можно повторить.В уроке использованы материалы, не входящие в обязательные образовательные стандарты.
Цель урока: познакомить с понятием линейной функции и ее графика. Проверьте способность учеников читать график.
Задачи урока:
научить применять полученные знания для решения практических задач;
развивать Творческие способности;
для усиления внимания студентов за счет использования мультимедийных средств;
вызывают интерес к предмету, уверенность в положительном результате обучения.
Оборудование:
Методы:
информационные и развивающие;
визуальный;
репродуктивный;
частично — поисковые системы.
Учебный этап | Время (мин) | ||
Организация времени. | Создание условий для успешной совместной деятельности | ||
Проверка домашнего задания. | Фронтальная и индивидуальная проверка, создание рабочей атмосферы на уроке. Фронтальная проверка теоретического материала. Повторение. | ||
Постановка задачи | Создание математической модели задачи. Формулировка цели урока. | ||
Основная часть урока состоит из нескольких этапов. | Определение линейной функции. График линейной функции. Способы задания линейной функции. | ||
Первый этап | Введение в понятие линейной функции. | ||
Вторая фаза | Построение линейной функции | ||
Третий этап | Расположение графика линейной функции | ||
Подведение итогов | Проверка умений студентов с помощью самостоятельной работы.Отражение. Оценка. | ||
Домашнее задание | Ознакомление студентов с домашними заданиями. |
Во время занятий
Время на организацию
Привет, ребята.Сесть.
Проверка домашнего задания
Дайте определение функции. Как называется независимая переменная? Как вы можете определить функцию? Что такое функциональный график?
3. Постановка задачи. Известный польский математик Гуго Штайнхаус в шутку утверждает, что существует закон, который формулируется следующим образом: математик сделает это лучше. А именно, если вы поручите двум людям, один из которых математик, выполнить любую незнакомую им работу, результат всегда будет следующим: математик сделает ее лучше.Представьте себе проблему: на складе было 500 тонн угля. Ежедневно стали вывозить 30 тонн угля. Сколько тонн угля будет на складе через x дней? Составим математическую модель решения этой задачи. (Слайд №1)
y = 500 — 30x
Рассчитаем значение при x = 2 и x = 5 (Слайд №2)
Составим таблицу значений с шагом 1 для x и y (Слайд № 3)
Дополнительные вопросы: 1) Сколько угля останется на складе, если его вывезут через 7 дней? 2) На 20 дней хватит угля?
Покажем зависимость y от x на координатной плоскости (Слайд № 4) Что мы получили?
Сегодня мы изучим функции, которые можно задать формулой вида y = kx + b, где k и b — некоторые ненулевые числа.Такие функции называются линейными. График линейной функции представляет собой прямую линию.
4. Основная часть урока. Скажите, а функция y = 2x + 1 линейна? Какое у нее будет расписание? Сколько точек нужно, чтобы построить прямую. Подведем итоги: чтобы построить график линейной функции, нужно выбрать два значения аргумента, найти значение функции для этих значений аргумента. Нарисуйте точки на координатной плоскости. Проведите через эти точки прямую линию.Итак, мы строим график функции y = 2x + 1 (Слайд № 6, № 7)
Промежуточное отражение: Выберите линейные функции (Слайд № 8)
Постройте функцию y = 3x-4. Проверьте с номером слайда 9
Давайте познакомим вас с понятием области определения и области значений линейной функции.
Рассмотрим зависимость положения графика линейной функции от чисел k и
b. Рассмотрите графики на слайде 11 и сделайте вывод.
Принципиальные схемы (номер слайда 12)
Reflection : (номер слайда 13)
Какая функция называется линейной? Какой у нее график?
Под каким углом (острым или тупым) наклонена прямая к оси x, если
1) k ˃0 2) k ˂ 0
Какова область определения линейной функции?
Каков диапазон линейной функции?
Самостоятельная работа над опциями с выборочной проверкой.
№1063 (б, г)
Домашнее задание: № 1065 (а, е), № 1066, 1068 (б, г)
Задачи урока: сформулировать определение линейной функции, представление о ее графике; определить роль параметров b и k в расположении графика линейной функции; формировать умение строить график линейной функции; развивать умение анализировать, обобщать, делать выводы; развивать логическое мышление; развитие навыков самостоятельной деятельности
Uk-badge uk-margin-small-right «>
Ответы 1.а; б 2.а) 1; 3 б) 2; x y 1. a; в 2. а) 2; 4 б) 1; x y вариант 2 вариант
Uk-badge uk-margin-small-right «>
B k b> 0b0 K 0b0 K «> 0b0 K»> 0b0 K «title =» (! LANG: b k b> 0b0 K «> title = «b k b> 0b0 K»> !}
B kb> 0b0 y = kx I, III четверти Через начало K 0b0 y = kx I, III четверти Через начало K «> 0b0 y = kx I, III четвертей Через начало координат K»> 0b0 y = kx I, III четверти Через происхождение K «title =» (! LANG: bkb> 0b0 y = kx I, III четверти Через происхождение K «> title = «b k b> 0 b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx I, III четвертей Через начало координат K координат «> 0b0 y = kx I, III четвертей Через начало координат K координат»> 0b0 y = kx I, III четвертей Через начало координат K координат «title =» (! LANG: bkb> 0b0 y = kx I, III четверти Через начало координат K «> title = «b k b> 0b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx I, III четвертей Через начало координат K 0b0 y = kx I, III четвертей Через начало K координат «> 0b0 y = kx I, III четвертей Через начало координат K координаты»> 0b0 y = kx I, III четверти Через начало координат K координаты «title =» (! ЯЗЫК: bkb> 0b0 y = kx I, III четверти Через начало координат K «> title = «b k b> 0b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx I, III четвертей Через начало координат K 0b0 y = kx I, III четвертей Через начало K координат «> 0b0 y = kx I, III четвертей Через начало координат K координаты»> 0b0 y = kx I, III четверти Через начало координат K координаты «title =» (! ЯЗЫК: bkb> 0b0 y = kx I, III четверти Через начало координат K «> title = «b k b> 0b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx I, III четвертей Через начало координат K 0b0 y = kx I, III четвертей Через начало K координат «> 0b0 y = kx I, III четвертей Через начало координат K координаты»> 0b0 y = kx I, III четверти Через начало координат K координаты «title =» (! ЯЗЫК: bkb> 0b0 y = kx I, III четверти Через начало координат K «> title = «b k b> 0b0 y = kx I, III четверти Через начало координат K»> !}
B kb> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координаты K 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K координаты «> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через происхождение координаты K «title =» (! ЯЗЫК: bkb> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> title = «bkb> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> !}
B kb> 0b0 y = kx + b (y = 2x + 1) I, III четверть y = kx + b (y = 2x-1) I, III четверть y = kx I, III четверть Через начало координат K 0b0 y = kx + b (y = 2x + 1) I, III четверть y = kx + b (y = 2x-1) I, III четверть y = kx I, III четверть Через начало K-координаты «> 0b0 y = kx + b (y = 2x + 1) I, III четверти.y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> 0b0 y = kx + b (y = 2x + 1) I, III четверти. y = kx + b (y = 2x-1) I, III четверть y = kx I, III четверти Через начало координаты K «title =» (! LANG: bkb> 0b0 y = kx + b (y = 2x + 1) I, III четверти y = kx + b (y = 2x-1) I, III четверти y = kx I, III четверти Через начало координат K «> title = «bkb> 0b0 y = kx + b (y = 2x + 1) I, III четверть y = kx + b (y = 2x-1) I, III четверть y = kx I, III четверть Через начало координат K «> !}


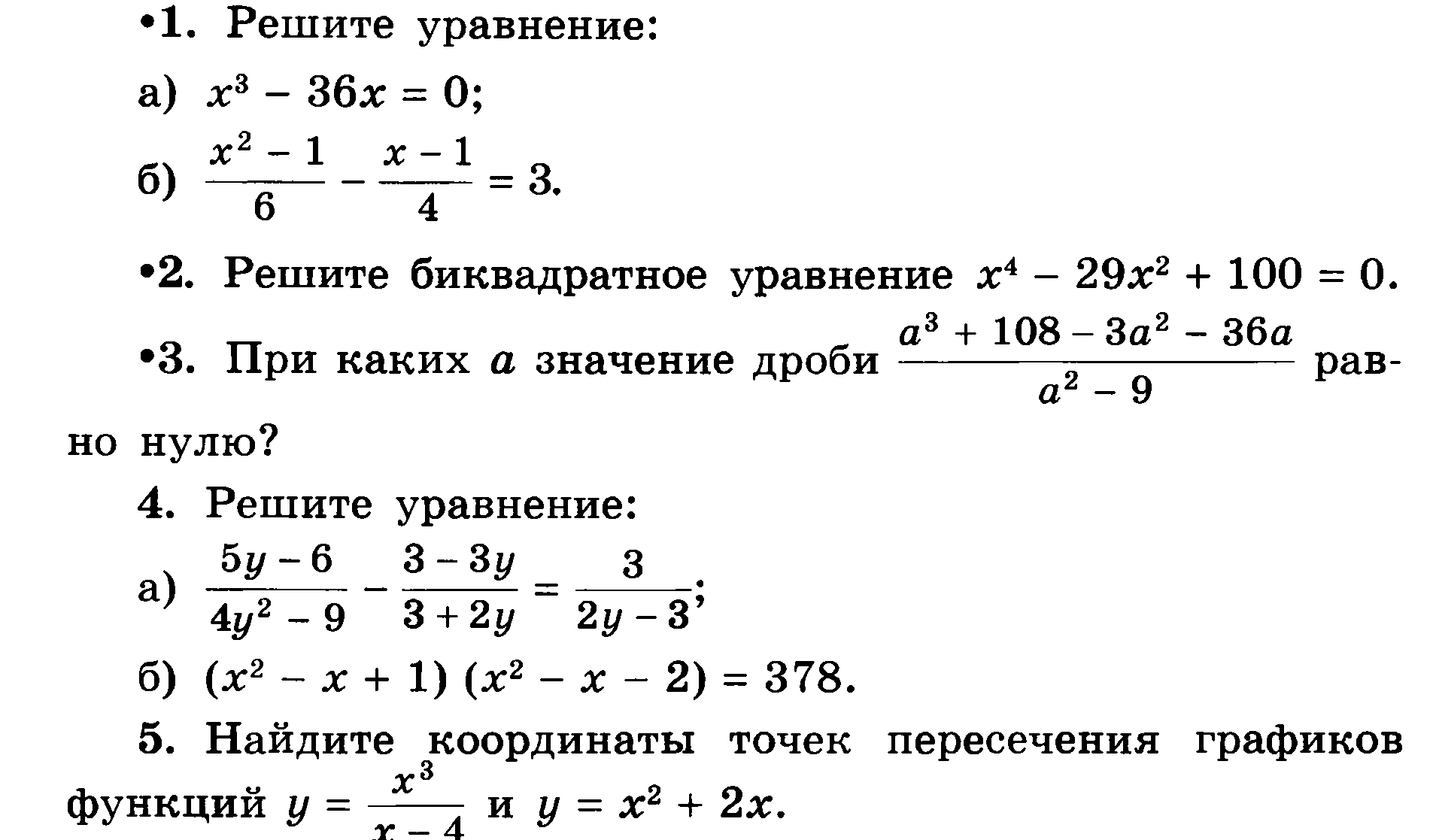

 занятий.
занятий.