Алгебра 7 класс примеры для решения: Как складывать и вычитать многочлены. Алгебра, 7 класс: уроки, тесты, задания.

Основные правила математики с примерами. 7 класс Алгебра.

Основные правила математики с примерами. 7 класс Алгебра.

Содержание

• Уравнения. Равносильные уравнения. Свойства
• Линейное уравнение
• Одночлены и многочлены
• Формулы сокращенного умножения
• Степень. Свойства степени с целым показателем
• Функция. Область определения и область значений функции
• Линейная функция, её график и свойства
• Системы линейных уравнений с двумя переменными
• Графический метод решения системы двух линейных уравнений с двумя переменными
• Решение системы двух линейных уравнений с двумя переменными методом подстановки
• Решение систем линейных уравнений методом сложения

Уравнения. Равносильные уравнения. Свойства

Корень уравнения

• Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство.
• Решить уравнение означает найти все его корни или убедиться, что их вообще нет. Также можно сказать, что решить уравнение — это значит найти множество его корней.

2 x  + 6 =36x = 15 —корень уравнения, поскольку2 · 15  + 6 =3636 = 36 —верное равенство.5x — 5x = 100 —не имеет корней, посколькуx(5 — 5)∥0 = 100  0 = 100  — неверно.

Равносильные уравнения

Два уравнения называют равносильными, если они имеют одно и тоже множество корней.

2x — 5 = 5 ≡равносильно 4x — 10 =10,поскольку x = 5 корень и для 1—го, и для 2—го уравнения.

 

Свойства уравнений

• Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.

2x — 5 = 7 +52x — 5 + 5 = 7 + 52x = 12x = 12 : 2x = 6

• Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.

2x — 5 =+5→ 72x = 7 + 52x =12x = 12 : 2x =6

• Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному

12x = 24  : 1212x :12 = 24 : 12x = 2.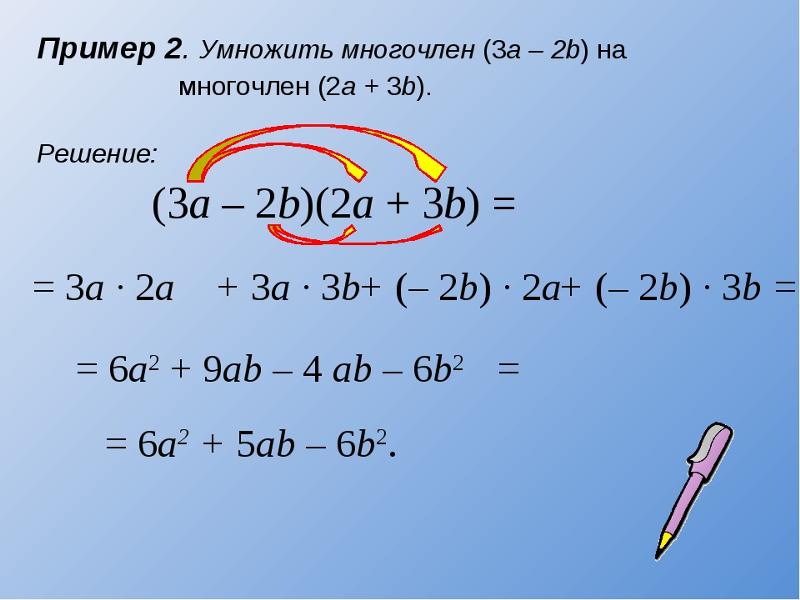

x5 = 3  · 5×5 · 5  = 3 · 5x = 15

Линейное уравнение

Уравнение вида   , где — переменная,  и некоторые числа, называют линейным уравнением с одной переменной.

Значения и
Корни уравнения		-любое число	корней нет

2x = 0, 5y —3 = 12 — линейные уравненияx2 —4 = 0,  5x = 8 —нелинейные уравнения

Одночлены и многочлены

Одночлены

• Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.

2x,  356x2y,  0,2a20,  b, 15 — одночлены.

• Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.

2x,  356x2y,  0,2a20 — одночлены стандартного вида.

• Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.

2x,  356x2y,  0,2a20.2,  356,  0,2 —коэффициенты.

• Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.

2x2y3z ,  —15x2y3z,    0,5x2y3z —подобные.2x2y3z и  2x2y3 — не подобные.

• Нуль-одночлен степени не имеет.

Многочлены

• Выражение, являющееся суммой нескольких одночленов, называют многочленом.

2x + 3x2y

• Одночлены, из которых состоит многочлен, называют членами многочлена.

2x + 3x2y —многочлен;2x и  3x2y — его одночлены

• Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.

 Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Формулы сокращенного умножения

Разность квадратов двух выражений

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:

Произведение разности и суммы двух выражений

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

Квадрат суммы и квадрат разности двух выражений

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражении:

Преобразование многочлена в квадрат суммы или разности двух выражений

Формулы

позволяют «свернуть» трёхчлен в квадрат двучлена.

Трёхчлен, который можно представить в виде квадрата двучлена, называют полным квадратом.

Сумма и разность кубов двух выражений

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:

Многочлен  называют неполным квадратом суммы.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

Многочлен   называют неполным квадратом разности.

Степень. Свойства степени с целым показателем

Свойства степени с целым показателем

Для любого и любых целых  выполняются равенства:

Для любых , и любого целого   выполняются равенства:

Функция. Область определения и область значений функции

Функция

Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной пeременной от другой — функциональной.
Обычно независимую переменную обозначают ,  зависимую обозначают  , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной   называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Способы задания функции

Описательный, табличный, с помощью формулы, графический.

График функции

Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Линейная функция, её график и свойства

• Функцию, которую можно задать формулой вида , где и  — некоторые числа, — независимая переменная, называют линейной.
• Графиком линейной функции является прямая.
• Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными

 Уравнение с двумя переменными

Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.

Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.

Если некоторая фигура является графиком уравнения, то выполняются два условия:

•  все решения уравнения являются координатами точек, принадлежащих графику;
•  координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.

Графический метод решения системы двух линейных уравнений с двумя переменными

Графический метод решения системы уравнений заключается в следующем:

• построить в одной координатной плоскости графики уравнений, входящих в систему;
• найти координаты всех точек пересечения построенных графиков;
• полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

• если прямые пересекаются, то система имеет единственное решение.
• если прямые совпадают, то система имеет бесконечно много решении.
• если прямые параллельны, то система решений не имеет.

Решение системы двух линейных уравнений с двумя переменными методом подстановки

Чтобы решить систему линейных уравнений методом подстановки, следует:

• выразить из любого уравнения системы одну переменную через другую;
• подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
• решить уравнение с одной переменной, полученное на втором шаге;
• подставить найденное значение переменной в выражение, полученное на первом шаге;
• вычислить значение второй переменной;
• записать ответ.

Решение систем линейных уравнений методом сложения

Чтобы решить систему линейных уравнений методом сложения, следует:

• подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
• сложить почленно левые и правые части уравнений, полученных на первом шаге
• решить уравнение с одной переменной, полученной на втором шаге
• подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
• вычислить значение второй переменной;
• записать ответ.

Данная информация взята  из  УМК  А.Г.Мерзляк, В.Б.Полонский, М.С. Якир

Числовые выражения – как решить задачу (алгебра 7 класс) по вычислению значений числового выражения

4.7

Средняя оценка: 4.7

Всего получено оценок: 827.

4.7

Средняя оценка: 4.7

Всего получено оценок: 827.

Одним из понятий алгебры 7 класса являются числовые выражения. Они используются для решения задач. Что собой представляют числовые выражения и как их использовать?

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Определение понятия

Какое же выражение является числовым в алгебре? Так обозначают запись, составленную из чисел, скобок и знаков сложения, вычитания, умножения и деления.

Понятие числового выражения допустимо только в том случае, если запись несет смысловую нагрузку. К примеру, запись 4-) не является числовым выражением, так как она бессмысленна.

Примеры числовых выражений:

• 25 х 13;
• 32 – 4 + 8;
• 12 х (25 – 5).

Характеристики понятия

Числовое выражение имеет несколько свойств, которые используются в решении примеров и задач. Рассмотрим эти свойства подробнее. Для этого возьмем такой пример – 45 + 21 – (6 х 2).

Значение

Так как числовое выражение содержит знаки различных арифметических действий, их можно выполнить и получить в результате какое-то число. Оно называется значением числового выражения. Как производится вычисление значений числового выражения? Оно соответствует правилам выполнения арифметических действий:

• в выражениях без скобок выполняют действия, начиная с высших ступеней – умножение и деление, затем сложение и вычитание;
• если имеется несколько одинаковых действий, их выполняют слева направо;
• если есть скобки, сначала выполняют действия в них;
• при вычислении дробей сначала выполняют действия в числителе и знаменателе, а затем числитель делят на знаменатель.

Применим эти правила к нашему примеру.

Итак, число 54 будет являться значением выражения 45 + 21 – (6 х 2).

Для того, чтобы правильно прочитать числовое выражение нужно определить, какое действие будет являться последним в подсчетах. В выражении 45 + 21 – (6 х 2) последним действием было вычитание. Соответственно, называть это выражение нужно “разность”. Если бы вместо знака “-” стоял знак “+”, выражение называли бы суммой.

Если у выражения невозможно произвести подсчет значения, его называют не имеющим смысла. Например, смысла не имеет такое выражение: 12 : (4 – 4). В скобках разность равна нулю. А по правилам математики на ноль делить нельзя. Значит, найти значение выражения невозможно.

Равенство

Так называют запись, в которой два числовых выражения разделены знаком “=”. Например, 45 + 21 – (6 х 2) = 66 – 12. Обе части записи равны числу 54, а значит, они равны друг другу. Такое равенство называют верным.

Если же написать 45 + 21 – (6 х 2) = 35 + 12, это равенство будет неверным. В левой части равенства значение выражения равно 54, а в правой – 57. эти числа не равны друг другу, значит, и равенство неверное.

Пример задачи

Для того, чтобы лучше понять тему, рассмотрим пример решения задачи. Как решить задачу числовым выражением?

Дано: две машины выезжают из одного пункта в другой. Они поедут по разным дорогам. Одной машине предстоит проехать 35 км, а другой – 42 км. Первая машина едет со скоростью 70 км/ч, а вторая – 84 км/ч Окажутся ли они в конечном пункте в одно и то же время?

Решение: нужно составить два числовых выражения, чтобы найти время в пути у каждой машины. Если они окажутся одинаковыми, значит, машины прибудут в конечный пункт одновременно. Для того, чтобы найти время, нужно расстояние разделить на скорость. 35 км : 70 км/ч = 0,5 ч. 42 км : 84 км/ч = 0,5 ч.

Итак, обе машины приехали в конечный пункт одновременно, через полчаса.

Что мы узнали?

Из темы по алгебре, изучаемой в 7 классе, мы узнали, что числовое выражение – это запись из чисел и знаков арифметических действий. С помощью числовых выражений можно решать задачи. Если последним действием в числовом выражении было вычитание (сложение), то его называют разностью (суммой). Если последним действием было бы умножение (деление), то выражение называлось бы произведением (частным).

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Ольга Кузина

  10/10

• Мария Гаврилова

  10/10

• Александра Веригина

  9/10

• Макс Чупин

  6/10

• Эдик Брага

  10/10

• Наталья Слинькова

  10/10

• Любовь Дружинина

  8/10

• Света Колодий

  10/10

• Джек Кортес

  8/10

• Александра Елисеева

  9/10

Оценка статьи

4.7

Средняя оценка: 4.7

Всего получено оценок: 827.

---

А какая ваша оценка?

Wolfram|Alpha Примеры: Common Core Math: 7 класс

О-о! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

Примеры для

В седьмом классе учащиеся начинают свободно оперировать выражениями и решать уравнения, в том числе с отрицательными числами и числами, выраженными в виде дробей или десятичных дробей. Студенты вычисляют с процентами и отношениями и описывают пропорциональные отношения, используя числовые, графические, алгебраические и словесные представления. Учащиеся анализируют и сравнивают данные из случайных выборок и обобщают, чтобы сделать выводы о популяциях. Учащиеся также работают с вероятностью, проводя вероятностные эксперименты и вычисляя вероятности с помощью вероятностных моделей. Учащиеся вычисляют площади, объемы и площади поверхности правильных и неправильных форм и решают задачи, связанные с углами, в том числе рисуют фигуры, соответствующие заданным геометрическим условиям, и классифицируют типы треугольников.

Стандарты Common Core

Получить информацию об Стандартах Common Core.

Поиск определенного стандарта:

CCSS.Math.Content.7.G.A.1Общий базовый стандарт седьмого класса EE.B.4

Поиск всех стандартов седьмого класса:

Общие базовые стандарты седьмого классаВыражения и уравнения

Работа с выражениями и решение уравнений и неравенства, в том числе с отрицательными числами.

Упрощение выражений (CCSS.Math.Content.7.EE.A.1):

расширенная форма 3.2 (x — 5) — 8x + 4 (2.7 + x) объединять одинаковые члены 1/2x + 2 — 3/4x + 3/2

Факторные выражения (CCSS.Math.Content.7.EE.A.1):

коэффициент 6x + 18

Решить уравнение (CCSS.Math.Content.7.EE.B.4a):

решить 0,5 (x + 3) = -15решить 46,4 = 4x + 11,2

Решить неравенство (CCSS.Math.Content.7.EE.B.4b):

решить 8 — x > 2,2Больше примеровГеометрия

Рисовать фигуры и вычислять геометрические измерения.

Нарисуйте треугольник с заданными длинами сторон, если это возможно (CCSS.

Math.Content.7.G.A.2): треугольник с длинами сторон 2, 6 и 7

Нарисуйте фигуры с заданными условиями (CCSS.Math.Content.7 .Г.А.2):

параллелограмм со всеми прямыми углами

Решение для измерения окружности (CCSS.Math.Content.7.G.B.4):

площадь круга с радиусом = 2

Решение для измерения трехмерных тел (CCSS.Math.Content.7 .G.B.6):

объем цилиндра с радиусом = 2 и высотой = 5Еще примерыСистема счисления

Выполнять арифметические действия с целыми, дробными и десятичными дробями, в том числе с несколькими операциями в одном выражении.

Сложение и вычитание рациональных чисел (CCSS.Math.Content.7.NS.A.1):

-4 + 9/2-5/8 — 1/4

Распознавать закономерности в умножении и делении (CCSS.Math.Content.7.NS.A.2):

отрицательное число * положительное число

Выполнять несколько операций с рациональным числом числа (CCSS.Math.Content.7.NS.A.2c):

(-5)(-2) — (4)(-3)(-1/2 + 3/8 + 1/4 + -3 /2) / 2

Преобразование рационального числа в десятичное (CCSS.

Math.Content.7.NS.A.2d): 5/8 в виде десятичного числаБольше примеровRatios & Proportions

Вычисление с отношениями и процентами в различных контекстах.

Определение удельной скорости, связанной с коэффициентом (CCSS.Math.Content.7.RP.A.1):

0,75 фута за 0,25 часа5 миль на 1/8 галлона

Представлять изменения количества в процентах (CCSS.Math.Content.7.RP.A.3):

5 увеличить на 300%

Определить цены и чаевые, используя проценты (CCSS.Math.Content.7.RP.A.3):

Чаевые 20 % при 38,40 долл. США 80 долл. США со скидкой 30 %Больше примеров Бесплатные неограниченные практические задачи по алгебре

СВЯЗАННЫЕ ПРИМЕРЫ

Алгебра

Базовая математика: 6 класс

Математика: 8 класс

Элементарная математика

Статистика и вероятность

Анализ и сравнение наборов данных, в том числе полученных из вероятностных экспериментов.

Сравните центры двух наборов данных (CCSS.Math.Content.7.SP.B.4):

среднее {2, 1, 4, 8, 2, 1} и среднее {7, 8, 6, 8, 9, 4}медиана {187, 202, 112, 198, 155} и медиана {34, 78, 61, 42, 89}

Сравните изменчивость двух наборов данных (CCSS.

Math.Content.7.SP.B.4 ): IQR {2, 4, 8, 2, 1} по сравнению с IQR {7, 8, 6, 9, 9}

Проведение вероятностных экспериментов (CCSS.Math.Content.7.SP.C.6):

20 бросков монеты вероятность выпадения 7 на двух шестигранных костяхБольше примеров

Что такое алгебра? Определение, основы, примеры, факты

Алгебра — это часть математики, помогающая представлять проблемы или ситуации в виде математических выражений. В алгебре мы используем такие числа, как 2, −7, 0,068 и т. д., которые имеют определенное или фиксированное значение. В алгебре мы используем такие переменные, как x, y и z, наряду с числами.

Знаки, используемые в алгебре 

Математические операции, такие как умножение (×), деление (÷), сложение (+) и вычитание (−), используются для формирования осмысленного математического выражения.

Есть и другие знаки и символы, которые также часто используются в алгебре.

равно (=), не равно (≠), меньше (<), больше (＞), меньше равно (≤), больше равно ( ≥).

Простой пример уравнения в алгебре: x + 5 = 10,

Алгебра Головоломка

Алгебра состоит из головоломок.

Вот тебе.

⬜+ 10 = 13

⬜ плюс 10 равно 13.

Нам нужно найти число в этом поле, и какое число, прибавив его к 10, даст нам 13. Просто, это три ; мы видим, что 3 плюс 10 равняется 13. Головоломка, которую мы здесь видим, состоит только из чисел.

Мы также можем сказать, что x плюс 10 равно 13. Найдите x.

Мы используем букву вместо ящика. Эти буквы также называются переменными, иногда называемыми неизвестными, поскольку их значения нам неизвестны.

Похожие игры

1. Общая стоимость 1 кг яблока и 2 кг гуавы составляет 3 доллара. Если x представляет собой стоимость 1 кг яблока, а y представляет собой стоимость 1 кг гуавы, то это утверждение представляется в виде алгебраического выражения как:

x + 2 y = 3

2. Если площадь прямоугольника 36 см ² . Его длина представлена ​​как l , а ширина представлена ​​как b . Тогда этот оператор представлен как:

l  × b = 36

Решенные примеры

Вопрос 1: У Уильяма было с собой несколько шоколадных конфет. Подошел Джек и забрал пять своих шоколадок. А потом у него осталось всего семь шоколадок. Сколько шоколадок было у него до того, как к нему подошел Джек?

Ответ: Предположим, что у Уильяма было с собой x шоколадок, и Джек забрал у него пять шоколадок.

х — 5 = 7

Итак, вычтем из х пять. Более того, после всего этого у Уильяма осталось семь шоколадок. Тогда вся эта головоломка будет равна семи.

x − 5 + 5 = 7 + 5

x = 12

Вопрос 2: Фокусника пригласили выступить на дне рождения. Фокусник прибыл на вечеринку с 18 воздушными шарами. По дороге сдуло 7 воздушных шаров. Так сколько же шариков было у фокусника вначале?

Ответ: Мы можем решить эту задачу с помощью алгебры, x − 7 = 18.

Итак, мы вычитаем семь из x, и после этого у нас остается 18 шариков.

Теперь все, что нам нужно сделать, это найти x.

x − 7 + 7= 18 + 7

x = 18 + 7

x = 25

Вопрос 3: Амман хочет посетить зоопарк. Входной билет в зоопарк стоил 4 доллара. У него всего 3 доллара. Сколько еще денег ему нужно, чтобы купить билет?

Ответ: Пусть Амману нужно $ у больше, чтобы купить билет.

Итак, решим эту задачу с помощью алгебры, 3 + y = 4

Прибавляем y к 3, чтобы получить 4.

Теперь нам нужно найти значение y .

3 + y — 3 = 4 — 3

y = 4 — 3

y = 1

Практические задачи

1

Напишите Запись. 40.

4 × у = 40

4 + у = 40

4 = y × 40

4 × 40 = y

Правильный ответ: 4 × y = 40
Время здесь означает умножение (×).
Число не указано, поэтому возьмем переменную y и запишем уравнение 4 × y = 40.

2

В магазине было 90 воздушных змеев, а у продавца осталось только 5 воздушных змеев. Сколько воздушных змеев продает продавец?

85

95

80

5

Правильный ответ: 85
Пусть продавец продаст x воздушных змеев.
90 — x = 5
Таким образом, x = 85

3

Оценить выражение 4T + 7,

11

7

4

15

Правильный ответ: 15
4T + 7 = 4 (2 (2 (2 ) + 7 = 8 + 7 = 15

4

На рабочем столе всего 5 книг, а у вас их 14. Сколько книг не хватает на учебном столе?

5

9

4

19

Правильный ответ: 9
Пусть в учебном столе не хватает x книг.
14 − x = 5
Итак, x = 9

Часто задаваемые вопросы

Шесть меньше числа равно двум.