«Детская школа искусств» Мошенского муниципального района

Алгебра 7 класс макарычев 247: Номер задания №247 — ГДЗ по Алгебре 7 класс: Макарычев Ю.Н.

Номер 247 — ГДЗ по алгебре 8 класс Макарычев



Номер 247 — ГДЗ по алгебре 8 класс Макарычев — ГДЗ РЕД

Перейти к содержанию

Search for:

Авторы: Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б.

Издательство: Просвещение

Тип: Учебник

Упражнения

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153

Контрольные вопросы и задания

§1§2§3§4§5§6§7§8§9§10§11§12§13



Adblock
detector

ГДЗ Алгебра 7 класс Макарычев, Миндюк, Нешков

  • Алгебра 7 класс
  • Серия: Углубленный уровень.
  • Тип пособия: Учебник
  • Авторы: Макарычев, Миндюк, Нешков
  • Издательство: «Просвещение»

Задания

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022 1023 1024 1025 1026 1027 1028 1029 1030 1031 1032 1033 1034 1035 1036 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050 1051 1052 1053 1054 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064 1065 1066 1067 1068 1069 1070 1071 1072 1073 1074 1075 1076 1077 1078 1079 1080 1081 1082 1083 1084 1085 1086 1087 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105 1106 1107 1108 1109 1110 1111 1112 1113 1114 1115 1116 1117 1118 1119 1120 1121 1122 1123 1124 1125 1126 1127 1128 1129 1130 1131 1132 1133 1134 1135 1136 1137 1138 1139 1140 1141 1142 1143 1144 1145 1146 1147 1148 1149 1150 1151 1152 1153 1154 1155 1156 1157 1158 1159 1160 1161 1162 1163 1164 1165 1166 1167 1168 1169 1170 1171 1172 1173 1174 1175 1176 1177 1178 1179 1180 1181 1182 1183 1184 1185 1186 1187 1188 1189 1190 1191 1192 1193 1194 1195 1196 1197 1198 1199 1200 1201 1202 1203 1204 1205 1206 1207 1208 1209 1210 1211 1212 1213 1214 1215 1216 1217 1218 1219 1220 1221 1222 1223 1224 1225 1226 1227 1228 1229 1230 1231 1232 1233 1234 1235 1236 1237 1238 1239 1240 1241 1242 1243 1244 1245 1246 1247 1248 1249 1250 1251 1252 1253 1254 1255 1256 1257 1258 1259 1260 1261 1262 1263 1264 1265 1266 1267 1268 1269 1270 1271 1272 1273 1274 1275 1276 1277 1278 1279 1280 1281 1282 1283 1284 1285 1286 1287 1288 1289 1290 1291 1292 1293 1294 1295 1296 1297 1298 1299 1300 1301 1302 1303 1304 1305 1306 1307 1308 1309 1310 1311 1312 1313 1314 1315 1316 1317 1318 1319 1320 1321 1322 1323 1324 1325 1326 1327 1328 1329 1330 1331 1332 1333 1334 1335 1336 1337 1338 1339 1340 1341 1342 1343 1344 1345 1346 1347 1348 1349 1350 1351 1352 1353 1354 1355 1356 1357 1358 1359 1360 1361 1362 1363 1364 1365 1366 1367 1368 1369 1370 1371 1372 1373 1374 1375 1376 1377 1378 1379 1380 1381 1382 1383 1384 1385 1386 1387 1388 1389 1390 1391 1392 1393 1394 1395 1396 1397 1398 1399 1400 1401 1402 1403 1404 1405 1406 1407 1408 1409 1410

Контрольные вопросы с.

61 .Задания

1 2 3 4 5 6 7

Контрольные вопросы с.74 .Задания

1 2 3 4 5

Контрольные вопросы с.108 .Задания

1 2 3 4 5

Контрольные вопросы с.136 .Задания

1 2 3

Контрольные вопросы с.145 .Задания

1 2

Контрольные вопросы с.156 .Задания

1 2

Контрольные вопросы с.174 .Задания

1 2 3 4 5

Контрольные вопросы с.189 .Задания

1 2 3 4 5 6

Контрольные вопросы с.

221 .Задания

1 2 3 4 5 6

Контрольные вопросы с.254 .Задания

1 2 3 4

Контрольные вопросы с.277 .Задания

1 2 3 4

Контрольные вопросы и задания

№ 1 № 2 № 3 № 4 № 5 № 6 № 7 № 8 № 9 № 10 № 11 № 12 № 13 № 14 № 15 № 16

Похожие ГДЗ Алгебра 7 класс

  • Алгебра 7 класс
  • Учебник
  • Макарычев, Миндюк
  • Мнемозина
  • Алгебра 7 класс
  • Учебник
  • Макарычев, Миндюк, Нешков
  • Просвещение

Задания: 1

Условие

Решение

С премудростями алгебры школьники знакомятся в седьмом классе. Основной проблемой этого учебного года становится одновременное появление в программе сразу нескольких сложнейших дисциплин. Поэтому распределять учебное время необходимо таким образом, чтобы успеть подготовиться к занятиям по всем новым и старым предметам. Именно на поддержку ученика в таком сложном вопросе и ориентирован отличный онлайн-репетитор «ГДЗ к учебнику алгебры для 7 класса, Макарычев (Просвещение)».

Закладываем фундамент науки с решебником

Очень многие профессии немыслимы без умения выполнять достаточно сложные расчёты. Поэтому изучение алгебры на углублённом уровне может помочь выпускнику поступить в самые лучшие технические вузы, и главное – без проблем осваивать их программу. Но работать много и кропотливо необходимо с самых первых дней изучения сложнейшей науки. Онлайн-пособие «ГДЗ к учебнику алгебры для 7 класса, Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. (Просвещение)» послужит надёжным персональным наставником, который быстро и понятно объясняет трудную теорию и её применение для решения практических задач.

Что входит в содержание пособия

В издание авторы включили 1410 тематических заданий и контрольные вопросы, которые позволят проанализировать успехи семиклассника в изучении всех тем основного учебника алгебры на углублённом уровне:

  1. Многочлен и его стандартный вид.
  2. Выведение степени за скобку.
  3. Прямая пропорциональность.
  4. Возведение в степень.
  5. Функции и их графики.
  6. Квадратные уравнения.

В решебнике семиклассник сможет найти не только точный ответ, но и подробно изложенный образец верного решения – достаточно внимательно его проработать. И выполнять аналогичные задания школьник сможет по изученному алгоритму.

Чему научит ГДЗ

Если самостоятельно выполнять каждое задание учебника, консультируясь в ГДЗ (а не списывая из него ответ), то ребята смогут уяснить не только детали работы с конкретным заданием, но и общие направления основ курса алгебры:

  • что такое линейное уравнение с одной переменной;
  • как работать с коэффициентом;
  • расчёт пути двух движущихся объектов с заданной скоростью;
  • система линейных уравнений с тремя неизвестными;
  • решение линейных уравнений.

До Государственной итоговой аттестации ещё немало времени, но добросовестная работа с решебником позволит быстро и надёжно освоить выполнение заданий в экзаменационном стиле – формате ГИА и ЕГЭ.

Моментные неравенства для сумм случайных матриц и их применение в оптимизации

  • Ай В., Чжан С.: Сильная двойственность для подзадачи CDT: необходимое и достаточное условие. СИАМ Дж. Оптим. 19 (4), 1735–1756 (2009)

    Артикул MathSciNet МАТЕМАТИКА Google ученый

  • Алон Н., Макарычев К., Макарычев Ю., Наор А.: Квадратичные формы на графах. Изобретать. Мат. 163 (3), 499–522 (2006)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Anstreicher K., Chen X., Wolkowicz H., Yuan Y.X.: Сильная двойственность для релаксации типа доверенной области квадратичной задачи о назначениях. Приложение линейной алгебры. 301 (1–3), 121–136 (1999)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Анстрейхер К., Волкович Х.: О лагранжевой релаксации квадратичных матричных ограничений. СИАМ Дж. Матричный анал. заявл. 22 (1), 41–55 (2000)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Арора С., Ли Дж. Р., Наор А.: Евклидово искажение и синтаксический анализ. Варенье. Мат. соц. 21 (1), 1–21 (2008)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Арора, С., Рао, С., Вазирани, У.: Расширяющие потоки, геометрические вложения и разбиение графов. Дж. АСМ 56 (2): Статья 5 (2009)

  • Барвинок А.И.: Проблемы дистанционной геометрии и выпуклых свойств квадратичных отображений. Дискретный. вычисл. геом. 13 , 189–202 (1995)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Бек А., Эльдар Ю.К.: Сильная двойственность в невыпуклой квадратичной оптимизации с двумя квадратичными ограничениями. СИАМ Дж. Оптим. 17 (3), 844–860 (2006)

    Артикул MathSciNet МАТЕМАТИКА Google ученый

  • Бен-Таль А., Немировский А.: О безопасных податливых аппроксимациях линейных матричных неравенств с ограничениями на случайность. Мат. Опер. Рез. 34 (1), 1–25 (2009)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Бухгольц А.: Операторное неравенство Хинчина в некоммутативной вероятности. Мат. Анна. 319 , 1–16 (2001)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Делаж, Э. , Йе, Ю.: Распределительно-надежная оптимизация в условиях неопределенности момента с применением к задачам, управляемым данными. Чтобы появиться в опер. Рез. (2009)

  • Дупачова, Дж.: Стохастическое программирование: минимаксный подход. В: Floudas, C.A., Pardalos, P.M. Энциклопедия оптимизации, 2-е изд., Springer Science+Business Media, LLC, Нью-Йорк (2009 г.).)

  • Goemans MX: Полуопределенное программирование в комбинаторной оптимизации. Мат. Программа. 79 , 143–161 (1997)

    MathSciNet МАТЕМАТИКА Google ученый

  • Goemans MX, Williamson DP: Улучшенные алгоритмы аппроксимации для задач максимального сокращения и выполнимости с использованием полуопределенного программирования. J. ACM 42 (6), 1115–1145 (1995)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Gower JC, Dijksterhuis GB: Procrustes Problems, Oxford Statistical Science Series, vol. 30. Издательство Оксфордского университета, Нью-Йорк (2004)

    Google ученый

  • Grötschel M., Lovász L., Schrijver A.: Геометрические алгоритмы и комбинаторная оптимизация, Алгоритмы и комбинаторика, том. 2, 2-е исправленное изд. Спрингер, Берлин (1993)

    Google ученый

  • Хорн Р.А., Джонсон К.Р.: Матричный анализ. Издательство Кембриджского университета, Кембридж (1985)

    МАТЕМАТИКА Google ученый

  • Каргер Д., Мотвани Р., Судан М.: Приближенная раскраска графа с помощью полуопределенного программирования. J. ACM 45 (2), 246–265 (1998)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Хинчин А.: Über dyadische brüche. Мат. Цайт. 23 , 109–116 (1923)

    Артикул MathSciNet Google ученый

  • Купманс Т. С., Бекманн М.: Проблемы распределения и местонахождения экономической деятельности. Econometrica 25 (1), 53–76 (1957)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Леду М., Талагран М.: Вероятность в банаховых пространствах: изопериметрия и процессы, Математические расчеты и их расчеты. 3. Folge/A Series of Modern Surveys in Mathematics, vol. 23. Спрингер, Берлин (1991)

    Google ученый

  • Li, W.L., Zhang, Y.J., So, A.M.C., Win, M.Z.: Медленное адаптивное OFDMA через случайное программирование с ограничениями. Препринт (2009)

  • Луо З.К., Сидиропулос Н.Д., Ценг П., Чжан С.: Аппроксимационные оценки для квадратичной оптимизации с однородными квадратичными ограничениями. СИАМ Дж. Оптим. 18 (1), 1–28 (2007)

    MathSciNet МАТЕМАТИКА Google ученый

  • Lust-Piquard F. : Inégalités de Khintchine dans C р (1 <  p  < ∞). Comptes Rendus de l’Académie des Sciences de Paris, Série I 303 (7), 289–292 (1986)

    MathSciNet МАТЕМАТИКА Google ученый

  • Немировский А.: Суммы случайных симметричных матриц и квадратичная оптимизация при ограничениях ортогональности. Мат. Программа. сер. Б 109 (2–3), 283–317 (2007)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Немировский А., Роос К., Терлаки Т.: О максимизации квадратичной формы над пересечением эллипсоидов с общим центром. Мат. Программа. сер. А 86 , 463–473 (1999)

    Артикул MathSciNet МАТЕМАТИКА Google ученый

  • Немировский А., Шапиро А. : Выпуклые аппроксимации случайных программ с ограничениями. СИАМ Дж. Оптим. 17 (4), 969–996 (2006)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Немировский А., Шапиро А.: Сценарные аппроксимации случайных ограничений. В: Калафиоре, Г., Даббене, Ф. Вероятностные и рандомизированные методы проектирования в условиях неопределенности, стр. 3–47. Спрингер, Лондон (2006)

  • Нестеров Ю.: Качество полуопределенной релаксации для невыпуклой квадратичной оптимизации. ОСНОВНОЙ документ для обсуждения 9719, Католический университет Лувена, Бельгия (1997)

  • Пардалос, П.М., Волкович, Х. (ред.): Квадратичные присваивания и связанные с ними проблемы, Серия DIMACS по дискретной математике и теоретической информатике, том. 16. Американское математическое общество, Провиденс, Род-Айленд (1994)

  • Патаки Г. : О ранге экстремальных матриц в полуопределенных программах и кратности оптимальных собственных значений. Мат. Опер. Рез. 23 (2), 339–358 (1998)

    Артикул MathSciNet МАТЕМАТИКА Google ученый

  • Пешкир Г., Ширяев А.Н.: Неравенства Хинчина и мартингал, расширяющий сферу их действия. Русь. Мат. Surv. 50 (5), 849–904 (1995)

    Статья MathSciNet Google ученый

  • Pisier, G.: Некоммутативный вектор со значением L стр. -пробелы и полностью р -суммирующие карты. Asterisque, 247 (1998)

  • Куайн М.П.: основанное на исчислении доказательство формулы Стирлинга для гамма-функции. Междунар. Дж. Матем. Образовательный науч. Технол. 28 (6), 914–917 (1997)

    MathSciNet Google ученый

  • Шарф, Х. : Минимум-макс решение проблемы инвентаризации. В: Эрроу, К.Дж., Карлин, С., Скарф, Х. Исследования по математической теории запасов и производства, стр. 201–209.. Издательство Стэнфордского университета, Стэнфорд (1958)

  • Шапиро А.: Ранговая сводимость симметричной матрицы и теория выборки анализа минимального следового фактора. Психометрика 47 (2), 187–199 (1982)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Шенуда, М.Б., Дэвидсон, Т.Н.: Проекты для многопользовательских приемопередатчиков на основе сбоев. В: Материалы Международной конференции IEEE 2009 г. по акустике, речи и обработке сигналов (ICASSP 2009).), стр. 2389–2392 (2009)

  • Итак, AMC: О характеристиках детекторов MIMO с полуопределенной релаксацией для созвездий QAM. В: Труды Международной конференции IEEE 2009 г. по акустике, речи и обработке сигналов (ICASSP 2009), стр. 2449–2452 (2009 г.)

  • Итак, AMC: Вероятностный анализ детектора полуопределенной релаксации в цифровой связи. Для публикации в Proceedings of the 21st Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2010)

  • So A.M.C., Ye Y., Zhang J.: Единая теорема о снижении ранга SDP. Мат. Опер. Рез. 33 (4), 910–920 (2008)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • So AMC, Zhang J., Ye Y.: Об аппроксимации сложных задач квадратичной оптимизации с помощью релаксации полуопределенного программирования. Мат. Программа. сер. В 110 (1), 93–110 (2007)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Томчак-Ягерманн Н.: Модули гладкости и выпуклости и средние значения Радемахера для классов следов S р (1 ≤ p  < ∞). Стад. Мат. 50 , 163–182 (1974)

    MathSciNet МАТЕМАТИКА Google ученый

  • Тропп Дж. А.: Свойство случайного мощения для равномерно ограниченных матриц. Стад. Мат. 185 (1), 67–82 (2008)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Е. Ю.: Аппроксимация глобальной квадратичной оптимизации с выпуклыми квадратичными ограничениями. Дж. Глобальный оптимум. 15 (1), 1–17 (1999)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Е Ю., Чжан С.: Новые результаты по квадратичной минимизации. СИАМ Дж. Оптим. 14 (1), 245–267 (2003)

    Статья MathSciNet МАТЕМАТИКА Google ученый

  • Чжао К., Кариш С.Э., Рендл Ф., Волкович Х. : Релаксации полуопределенного программирования для квадратичной задачи о назначениях. Дж. Комб. Оптим. 2 (1), 71–109 (1998)

    Статья MathSciNet МАТЕМАТИКА Google ученый

    • Зимний квартал | Магистр вычислительных социальных наук

    Перспективы компьютерного моделирования

    (МАКС 30100). Рик Эванс, П/П 23:30-13:20 и еженедельная лаборатория по средам с 16:30 до 17:20.

    Студенты часто хорошо обучены деталям конкретных моделей, имеющих отношение к их соответствующим областям. Этот курс представляет общее определение модели в социальных науках, а также таксономию широкого спектра различных типов используемых моделей. Затем мы рассмотрим принципы построения моделей, в том числе статические и динамические модели, линейные и нелинейные, простые и сложные, идентификацию и переоснащение. Основные типы моделей, реализованных в этом курсе, включают системы нелинейных уравнений, линейную и нелинейную регрессию, обучение с учителем (деревья решений, случайные леса, машины опорных векторов и т. д.) и обучение без учителя. Мы также изучим широкий спектр вычислительных стратегий, используемых для оценки моделей на основе данных и создания статистических и причинно-следственных выводов. Студенты изучат как хорошие примеры, так и плохие примеры моделирования и оценки.

    Исследовательское обязательство MA

    (МАКС 35000). Джеймс Эванс, по договоренности.

    Студент Инициировал исследование и написание для исследовательского компонента MA. Открыт только для студентов MACSS.

    Структурная оценка

    (MACS 40200). Рик Эванс, П/П 13:30-14:50

    Структурная оценка относится к оценке параметров модели путем непосредственного сопоставления теоретической модели с данными. соответствующую теоретическую модель). На этом занятии будет рассмотрен ряд структурных моделей, а затем обучат студентов подходам к оценке, включая обобщенный метод моментов и оценку максимального правдоподобия. Затем мы рассмотрим сильные и слабые стороны обоих подходов на ряде примеров из областей экономики, политологии и социологии. Мы также изучим симулированный метод приближения моментов. Мы будем изучать приложения в социальных науках.

    Введение в причинно-следственные связи

    (МАКС 51000). Гуанлей Хун, Казуо Ямагучи и Фан Ян, вторник 14:00–16:50 и еженедельная лаборатория по пятницам с 13:30 до 14:50.

    Этот курс предназначен для аспирантов и студентов старших курсов бакалавриата в области социальных наук, образования, общественного здравоохранения, государственной политики, управления социальными службами и статистики, которые участвуют в количественных исследованиях и заинтересованы в изучении причинно-следственных связей. Цель этого курса – дать учащимся базовые знания и аналитические навыки в области причинно-следственных связей. Темы курса будут включать структуру потенциальных результатов для причинно-следственного вывода; экспериментальные и наблюдательные исследования; допущения идентификации для причинных параметров; потенциальные ловушки использования ANCOVA для оценки причинно-следственной связи; методы, основанные на показателе склонности, включая сопоставление, стратификацию, взвешивание по обратной вероятности лечения (IPTW), взвешивание по предельному среднему через стратификацию (MMWS) и двойную надежную оценку; метод инструментальной переменной (IV); регрессионный дизайн разрыва (RDD), включая точный RDD и нечеткий RDD; разность в разнице (DID) и обобщенные методы DID для поперечных и панельных данных, а также модель с фиксированными эффектами. Промежуточная статистика или эквивалент, например, STAT 224, является обязательным условием. Этот курс является предварительным условием для «Продвинутых тем в причинно-следственном выводе» и «Посредничества, модерации и побочных эффектов».

    Вычислительный контент-анализ

    (МАКС 60000). Джеймс Эванс, пятница с 13:30 до 16:20.

    Огромное количество информации о том, что люди делают, знают, думают и чувствуют, заключено в тексте, и больше информации о современном социальном мире живет в электронном тексте, чем когда-либо прежде. Эти текстовые следы варьируются от коллективной активности в Интернете, социальных сетях, обмена мгновенными сообщениями и автоматически расшифрованных видео YouTube до онлайн-транзакций, медицинских карт, оцифрованных библиотек и правительственной разведки. Это предложение текста вызвало спрос на инструменты обработки естественного языка и машинного обучения для фильтрации, поиска и преобразования текста в ценные данные. В ходе курса будут рассмотрены и практически применены многие из самых интересных вычислительных подходов к анализу текста, выделены как методы с учителем, которые расширяют старые теории до новых данных, так и методы без учителя, которые обнаруживают скрытые закономерности, достойные теоретизирования. Они будут рассмотрены и оценены по существу, а также относительно достоверности и надежности классического контент-анализа, интерпретационных проблем качественного контент-анализа и интерактивных проблем анализа разговоров. Мы также рассмотрим, как эти подходы можно адаптировать к нетекстовому контенту, включая аудио, изображения и видео. Мы одновременно рассмотрим недавние исследования, в которых эти подходы используются для развития социального понимания путем изучения (а) коллективного внимания и рассуждений на основе содержания общения; (б) социальные отношения через процесс общения; и (c) социальные состояния, роли и движения, идентифицируемые с помощью разнородных сигналов в рамках коммуникации.

    Курс построен вокруг понимания и экспериментирования с инструментами анализа текста, развертывания этих инструментов и интерпретации их результатов в контексте отдельных исследовательских проектов, а также оценки современных исследований в этой области. Обсуждение в классе и задания будут сосредоточены на том, как использовать, интерпретировать и комбинировать вычислительные методы в контексте убедительных исследований социальных наук.

    Семинар по вычислительной социальной науке

    (МАКС 50000).  Джеймс Эванс, четверг с 23:00 до 12:20. Saieh 247. PQ: студенты, изучающие вычислительные науки, должны зарегистрироваться для получения степени R. Другие преподаватели и аспиранты приветствуются.

    Высокопроизводительные и облачные вычисления, массивные цифровые следы человеческого поведения от вездесущих датчиков и растущий набор инструментов для эффективной оценки моделей, машинного обучения и моделирования не только расширяют классические исследования социальных наук, но и трансформируют их, чтобы ставить новые вопросы в более широком и меньшие масштабы. Семинар по вычислительной социальной науке (CSS) – это еженедельное мероприятие, на котором рассказывается об этой работе, освещаются связанные навыки и данные, а также исследуется использование CSS в мире. Семинар CSS еженедельно чередуется между исследовательскими семинарами и профессиональными семинарами. На исследовательских семинарах представлены новые работы по CSS от ведущих преподавателей и аспирантов из Калифорнийского университета в Чикаго и со всего мира, в то время как профессиональные семинары освещают полезные навыки и данные (например, машинное обучение с помощью Python’s scikit-learn; API Firehose Twitter) и демонстрируют практикующих специалистов, использующих CSS. в правительстве, промышленности и некоммерческом секторе. Каждый квартал на семинаре CSS также проводятся выдающиеся лекции, дебаты и ужин, а также студенческая конференция.

    Информатика с приложениями – 2

    (CAPP 30122). Энн Роджерс, Пн/П/П 9:30–10:20 и еженедельные лабораторные занятия по вторникам в (1) 15–16:20, (2) 16:30–17:50 или (3) 6– 19:20

    Этот курс является вторым в последовательности из трех четвертей, которая обучает вычислительному мышлению и навыкам студентов, изучающих естественные науки, математику, экономику и т.  д. Лекции охватывают темы (1) представления данных, (2) основы реляционных баз данных, (3 ) сценарии оболочки, (4) алгоритмы анализа данных, такие как кластеризация и деревья решений, и (5) структуры данных, такие как хэш-таблицы и кучи. Приложения и наборы данных из самых разных областей служат как примерами в лекциях, так и основой для заданий по программированию. В недавних предложениях студенты написали поисковую систему для курсов и систему для идентификации говорящего. Учащиеся будут программировать на Python и выполнять четвертьдневный проект по программированию.

    Математика для информатики и анализа данных

    (CAPP 30255). Амитабх Чаудхари, П/П/П 14:30-15:20

    Этот курс развивает математические основы дискретной математики и линейной алгебры, которые широко используются в информатике, особенно в алгоритмах, базах данных, машинном обучении и анализе данных. // Темы дискретной математики необходимы для развития вычислительного мышления, особенно для разработки и анализа алгоритмов.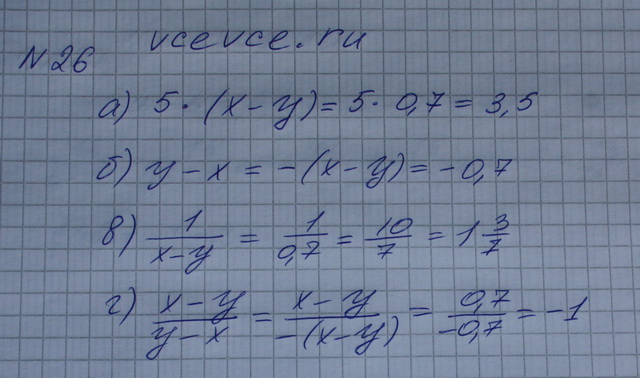 К ним относятся логика, доказательства, нотация с большим O, рекурсия, индукция и подсчет. // В линейной алгебре этот курс охватывает векторы и векторные пространства, то, как матрицы представляют линейное преобразование векторов, и их отношение к решению систем линейных уравнений. Мы изучаем определители, обратные матрицы, проекции и, наконец, то, как собственные векторы и собственные значения позволяют нам разлагать матрицу на более простые матрицы. Эти концепции лежат в основе нескольких методов машинного обучения и анализа данных, таких как уменьшение размерности.

    Статистическая теория и методы — 1

    (СТАТ 24400). Wei Biao Wu, T/Th 9:30–10:50 PQ: Многомерное исчисление. Некоторый предыдущий опыт работы со статистикой и/или вероятностью полезен, но не обязателен.

    Этот курс представляет собой первую четверть двухчетвертного систематического введения в принципы и методы статистики, а также в практические соображения при анализе данных с упором на анализ экспериментальных данных. Этот курс охватывает инструменты теории вероятностей и элементы статистической теории. Темы включают определения вероятности и случайных величин, биномиальные и другие дискретные распределения вероятностей, нормальные и другие непрерывные распределения вероятностей, совместные распределения вероятностей и преобразование случайных величин, принципы вывода (включая байесовский вывод), оценку максимального правдоподобия, проверку гипотез и доверительные интервалы, тесты отношения правдоподобия, мультиномиальные распределения и тесты хи-квадрат. Примеры взяты из социальных, физических и биологических наук. Охват тем по вероятности ограничен и краток, поэтому студенты, прошедшие курс по вероятности, находят подкрепление, а не избыточность. Учащиеся, которые уже сдали STAT 25100, могут выбрать STAT 24410 (если предлагается) вместо STAT 24400.

    Статистическая теория и методы — 2

    (СТАТ 24500). Chao Gao, T/Th 9:30–10:50 PQ: Многомерное исчисление и линейная алгебра и STAT 24400 или STAT 24410.

    Этот курс представляет собой вторую четверть двухчетвертного систематического введения в принципы и методы статистики, а также в практические аспекты анализа данных с упором на анализ экспериментальных данных. Этот курс продолжается от STAT 24400 или STAT 24410 и охватывает статистическую методологию, включая дисперсионный анализ, регрессию, корреляцию и некоторые виды многомерного анализа. Вводятся некоторые принципы анализа данных и делается попытка представить дисперсионный и регрессионный анализ в единой структуре. Используется статистическое программное обеспечение. 9n включая теоремы Больцано-Вейерштрасса и Гейне-Бореля, а также подробное рассмотрение абстрактных метрических пространств, включая сходимость и полноту, компактные множества, непрерывные отображения и многое другое.

    Анализ в Rn II

    (МАТЕМАТИКА 20400). Инструктор подлежит уточнению, М/Ж/П Секция 31: 10:30–11:20, Секция 41: 23:30–12:20 или Секция 51: 12:30–13:20 PQ: MATH 20700 ИЛИ MATH 20300 И MATH 20250 или STAT 24300. n, включая частные производные, градиенты, полную производную, цепное правило, задачи оптимизации, векторнозначные функции, а также теоремы об обратной и неявной функциях. .

    Методы вычислительной нейронауки

    (КПНС 34231). Silvan Bensmaia, M/W 15:30–16:50, пятница 13:30–14:50 и еженедельная лаборатория по средам 9:30–11:20  PQ: PSYC 36210 и PSYC 36211, которые должны приниматься одновременно или с согласия инструктора.

    Темы включают (но не ограничиваются): уравнения Ходжкина-Хаксли, теорию кабелей, модели одиночных нейронов, теорию информации, теорию обнаружения сигналов, обратную корреляцию, связь нейронных реакций с поведением и скорость и временные коды.

    Основы вычислительного анализа данных

    (МПКС 53110). Джеральдин Брейди, дней/времени TBD.  PQ: Основное программирование. B или выше MPCS 50103 или проходной балл на вступительном экзамене по математике. Учащийся, не являющийся участником программы MPCS, должен выполнить предварительные требования и заполнить заполненную форму запроса на курс.

    Этот курс охватывает базовую статистику и линейную алгебру, а также программирование в R. Темы статистики включают дискретные и непрерывные случайные величины, дискретные и непрерывные распределения вероятностей, дисперсию, ковариацию, корреляцию, выборку и распределение среднего и стандартного отклонения выборки, центральная предельная теорема, доверительные интервалы, оценки максимального правдоподобия, проверка гипотез, линейная и множественная регрессия. Темы линейной алгебры включают исключение Гаусса, транспонирование матрицы и обратную матрицу, собственные векторы и собственные значения, разложение по сингулярным числам.

    Теоретическая нейронаука: сетевая динамика и вычисления

    (КПНС 35520). Николя Брюнель, дней/времени TBD.

    Этот курс является второй частью цикла из трех четвертей по теоретической/вычислительной нейронауке. Основное внимание будет уделено математическим моделям сетей нейронов. Темы будут включать: модели скорости возбуждения для популяций нейронов; пространственно расширенные модели скорострельности; модели зрительной коры; модели сетей мозга на разных уровнях; характеристика свойств конкретных сетей мозга; модели сетей бинарных нейронов, средние скорости, корреляции, редукции к моделям скоростей; обучение в сетях бинарных нейронов, модели ассоциативной памяти; модели сетей спайковых нейронов: асинхронные и синхронные состояния; колебания в сетях спайковых нейронов; обучение в сетях спайковых нейронов; модели оперативной памяти; модели принятия решений.

    Машинное обучение

    (PLSC 43502). Джастин Гриммер, М/З 23:30-13:20

    Этот курс знакомит с методами сбора, анализа и использования больших коллекций данных для выводов в социальных науках. Конечная цель курса — познакомить студентов с современными методами машинного обучения и дать навыки, необходимые для широкого применения этих методов. Для достижения этой конечной цели учащиеся также: 1) Узнают об основных концепциях машинного обучения и статистики, разовьют навыки, применимые к другим типам данных и задачам логического вывода. 2) Развивать свои навыки программирования в R и знакомиться с Python. 3) Познакомьтесь с существенными проблемами.

    Продвинутые темы биологической психологии

    (ПСИК 40300). Лесли Кей, по четвергам с 14:00 до 16:50.

    Каковы отношения между разумом и мозгом? Как мозг регулирует психические, поведенческие и гормональные процессы; и как они влияют на организацию и активность мозга? Этот курс представляет собой введение в анатомию, физиологию и химию мозга; их изменения в ответ на эмпирическую и социокультурную среду; и их отношение к восприятию, вниманию, поведению, действию, мотивации и эмоциям. PQ: Высшее образование и некоторая сложность в биологических темах, включая неврологию 9.0350 .

    Математические методы в биологических науках — 2

    (PSYC 36211). Дмитрий Кондрашов, Т/Чт 14-15:20 и еженедельная лаборатория по пятницам с 15:30 до 17:20. PQ: PSYC 36210.

    Этот курс является продолжением PSYC 36210. Темы начинаются с задач оптимизации, таких как нелинейная аппроксимация методом наименьших квадратов, анализ основных компонентов и выравнивание последовательностей. Вводятся стохастические модели, такие как цепи Маркова, процессы рождения-смерти и процессы диффузии, с приложениями, включая скрытые модели Маркова, моделирование популяции опухолей и сети химических реакций. В компьютерных классах студенты изучают методы оптимизации и стохастические алгоритмы, например, цепь Маркова, алгоритм Монте-Карло и алгоритм Гиллеспи. Учащиеся выполняют самостоятельный проект по интересующей их теме.

    Алгоритмы

    (CMSC 37000). Юрий Макарычев, Т/Чт 9:30-10:50

    Это курс для выпускников по алгоритмам с акцентом на вычислительные проблемы, которые являются центральными как для теории, так и для практики, а также на разработку методов проектирования и тщательного анализа алгоритмов и структур данных для таких задач.

    Сетевой анализ

    (PLSC 57200). Джон Пэджетт, 9 лет0351 По понедельникам с 13:30 до 16:20.

    На этом семинаре исследуется социологическая полезность сети как единицы анализа. Каким образом модели социальных связей, в которые вовлечены люди, по-разному влияют на их способность справляться с кризисами, на их решения о переезде или смене работы, на их готовность принять новые установки и модели поведения? Группа семинара рассмотрит (а) чем сеть отличается от других единиц анализа, (б) структурные свойства сетей, последствия потоков (или контента) в сетевых связях и (в) динамику этих связей.

    Теория игр II

    (PLSC 31000). Джон   Пэтти, Т/Чт 15:30–16:50

    Это курс для аспирантов по политическим наукам. Он знакомит учащихся с играми с неполной информацией посредством решения наборов задач. Мы рассмотрим концепции байесовского равновесия по Нэшу, идеального байесовского равновесия и равновесия с квантовым откликом. Что касается приложений, курс расширит темы, изучаемые в предварительных требованиях, PLSC 309.01. Теория игр I, чтобы допустить неполную информацию, с акцентом на конкурирующие проблемы морального риска и неблагоприятного отбора в этих условиях.

    Теория социального выбора

    (PLSC 40801). Мэгги Пенн, T/Th 14-15:20

    Этот курс познакомит вас с теорией социального выбора, исследованием объединения индивидуальных предпочтений в «коллективное предпочтение». Основное внимание будет уделено классическим теоремам и методам доказательства с целью изучения свойств различных процедур коллективного выбора и описания процедур, дающих желаемые результаты.

    Добавить комментарий