ГДЗ по алгебре 7 класс Макарычев
ГДЗ по алгебре 7 класс МакарычевПерейти к содержимому
В 7 классе школьникам на уроках математики предстоит поработать с функциями и многочленами, порешать линейные и сокращенные уравнения, разобраться в тождествах. Многим ребятам эти вопросы покажутся сложнее «высшей математики», а выполнение домашней работы превратится в многочасовые испытания, пройти которые удастся не всем.
Однако, ситуацию можно исправить. К счастью, для этого не понадобится искать репетиторов или обращаться за помощью к друзьям или родителям. ГДЗ по алгебре для 7 класса к учебнику Макарычева — вот настоящая поддержка семиклассника!
Этак книга незаменима для школьника. Решебник по алгебре заполнит пробелы в знаниях, поможет усвоить новый материал, станет гарантом высоких оценок на уроке.
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325327328329330331332333334337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890892893894895896897898900901902903904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933935936937938939940942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974975976977978979980981982983984985986987988989990991992993994995996997998999100010011002100310041005100610071008100910101011101210131014101510161017101810191020102110221023102410251026102710281029103010311032103310351036103710381039104010411042104310441045104610471048 (а)1048 (б-в)1048 (г)10491050105110521053105410551057105810591060106110621063106410651066106710681069 (а-г)1069 (д-е)1070 (а-б)1070 (в-г)1071 (а,б,г)1071 (в)1072 (а,б,в)1072 (г)1073107410751076 (а)1076 (б)1077 (а,б)1077 (в,г)1078 (а)1078 (б,в,г)1079108010811082 (а)1082 (б,в,г)1083108410851086108710881090109110921093 (а,б)1093 (в,г)1094 (а,б)1094 (в,г)1095 (а,б)1095 (в,г)109610971099110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133 (а,б)1133 (в)11341135113611371138114011421143114411451146114711481149115011511152115311541155115611571158115911601161116211631164116511661167116811691170117111721173117411751176117711781179118011811182118311841185118611871188118911901191119211931194119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231225122612271228122912301231 ru Все права защищены. Информация взята из открытых источников. По вопросам нарушения авторского права пишите на: [email protected]
ru Все права защищены. Информация взята из открытых источников. По вопросам нарушения авторского права пишите на: [email protected]ГДЗ упражнение 153 алгебра 7 класс Бунимович, Кузнецова – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ упражнение 153 алгебра 7 класс Бунимович, Кузнецова
Подробное решение упражнение № 153 по алгебре для учащихся 7 класса Сферы 1-11 , авторов Бунимович , Кузнецова, Минаева 2019 .
ГДЗ готовые домашние задания учебника по алгебре (математике) 7 класс Дорофеев Суворова Бунимович Минаева Рослова ФГОС от Путина . Решебник (ответы на вопросы и задания) . .
Главная › 7 класс › Алгебра › . ГДЗ по алгебре 7 класс Дорофеев Суворова Бунимович .
ГДЗ алгебра 7 класс Бунимович , Кузнецова , Минаева Просвещение . Начав изучать алгебру в седьмом классе, школьники сталкиваются с проблемами недостаточности собственных математических знаний . В первую очередь, причина этого – в недоработках . .
.
ГДЗ по алгебре 7 класс Бунимович Е .А . Сферы 1-11 . Тип: Учебник . На нашем сайте воспользоваться решебником по алгебре за 7 класс (авторы: Бунимович Е .А Упражнения полностью соответствуют разделам учебника, номерам глав и параграфов, поэтому найти . .
Решебник (ГДЗ ) по Алгебре за 7 (седьмой ) класс авторы: Дорофеев, Суворова, Бунимович издательство все упражнения прошли тщательную проверку на соответствие стандартам . Почему стоит воспользоваться именно ГДЗ по алгебре для 7 класса (авторы: Г . В . Дорофеев . .
В 7 классе школьники сталкиваются с новым предметом — алгебра . Если класс учится по учебнику авторов Дорофеев, Суворова, Бунимович и др, то на сайте решак .ру был подготовлен обновленный авторский решебник гдз 7 класс, который включает в себя не только ответы на . .
Алгебра 7 класс . Учебник . Дорофеев, Суворова, Бунимович . Просвещение . В сборнике имеется девятьсот восемьдесят шесть основных упражнений, которые распределены по В ГДЗ по алгебре 7 класс Дорофеев даны доскональные алгоритмы по всем номерам .
Открыв гдз по алгебре за 7 класс Дорофеева сложные, запутанные примеры становятся доступными для восприятия каждому Старшеклассники, готовящие уроки с помощью решебника по алгебре за 7 класс Дорофеев, Суворова, утверждают что ГДЗ – лучший . .
ГДЗ учебник по алгебре 7 класс Г .В .Дорофеев, С .Б .Суворова, Е .А .Бунимович . авторы: Г .В .Дорофеев, С .Б .Суворова, Е .А .Бунимович . издательство: «Просвещение» .
ГДЗ по алгебре для 7 класса — Кузнецова , Шнеперман . Авторы . Е .П . Кузнецова, Л .Г . Муравьёва, Л .Б . Шнеперман . Год учебника . .
В седьмом классе учёба усложняется, на математику делается большой акцент . Предмет превращается в геометрию и алгебру, и, к Решебник к учебнику «Алгебра 7 класс Учебник Дорофеев, Суворова Просвещение» — отличный способ понять новое и вспомнить старое .
Структура «ГДЗ по алгебре 7 класс Дорофеев» полностью соответствует разделам основного учебника алгебры для седьмого класса , что позволяет легко ориентироваться в представленном материале . Каждой главе соответствуют задания с подробными решениями и . .
Каждой главе соответствуют задания с подробными решениями и . .
Литература 1 . Алгебра : 7 класс: учебник для учащихся общеобразовательных учреждений / А .Г . Мерзляк, В .Б . Полонский, М .С . Якир . Математика 5 . Учебник для 5 класса общеобразовательных учреждений Т В . Дорофеев . С .Б .Суворова, Е .А . Бунимович и др; Под . .
ГДЗ по алгебре для 7 класса — Арефьева . Представленные здесь ГДЗ научат вас справляться с решением линейных неравенств и уравнений У нас вы найдёте качественные ответы к упражнениям на построение линейной функции и к дополнительным материалам .
Подробное решение упражнение № 153 по алгебре для учащихся 7 класса Сферы 1-11 , авторов Бунимович , Кузнецова, Минаева 2019 .
ГДЗ готовые домашние задания учебника по алгебре (математике) 7 класс Дорофеев Суворова Бунимович Минаева Рослова ФГОС от Путина . Решебник (ответы на вопросы и задания) . .
Главная › 7 класс › Алгебра › . ГДЗ по алгебре 7 класс Дорофеев Суворова Бунимович .
ГДЗ алгебра 7 класс Бунимович , Кузнецова , Минаева Просвещение . Начав изучать алгебру в седьмом классе, школьники сталкиваются с проблемами недостаточности собственных математических знаний . В первую очередь, причина этого – в недоработках . .
Начав изучать алгебру в седьмом классе, школьники сталкиваются с проблемами недостаточности собственных математических знаний . В первую очередь, причина этого – в недоработках . .
ГДЗ по алгебре 7 класс Бунимович Е .А . Сферы 1-11 . Тип: Учебник . На нашем сайте воспользоваться решебником по алгебре за 7 класс (авторы: Бунимович Е .А Упражнения полностью соответствуют разделам учебника, номерам глав и параграфов, поэтому найти . .
Решебник (ГДЗ ) по Алгебре за 7 (седьмой ) класс авторы: Дорофеев, Суворова, Бунимович издательство все упражнения прошли тщательную проверку на соответствие стандартам . Почему стоит воспользоваться именно ГДЗ по алгебре для 7 класса (авторы: Г . В . Дорофеев . .
В 7 классе школьники сталкиваются с новым предметом — алгебра . Если класс учится по учебнику авторов Дорофеев, Суворова, Бунимович и др, то на сайте решак .ру был подготовлен обновленный авторский решебник гдз 7 класс, который включает в себя не только ответы на . .
Алгебра 7 класс . Учебник . Дорофеев, Суворова, Бунимович . Просвещение . В сборнике имеется девятьсот восемьдесят шесть основных упражнений, которые распределены по В ГДЗ по алгебре 7 класс Дорофеев даны доскональные алгоритмы по всем номерам .
Учебник . Дорофеев, Суворова, Бунимович . Просвещение . В сборнике имеется девятьсот восемьдесят шесть основных упражнений, которые распределены по В ГДЗ по алгебре 7 класс Дорофеев даны доскональные алгоритмы по всем номерам .
Открыв гдз по алгебре за 7 класс Дорофеева сложные, запутанные примеры становятся доступными для восприятия каждому Старшеклассники, готовящие уроки с помощью решебника по алгебре за 7 класс Дорофеев, Суворова, утверждают что ГДЗ – лучший . .
ГДЗ учебник по алгебре 7 класс Г .В .Дорофеев, С .Б .Суворова, Е .А .Бунимович . авторы: Г .В .Дорофеев, С .Б .Суворова, Е .А .Бунимович . издательство: «Просвещение» .
ГДЗ по алгебре для 7 класса — Кузнецова , Шнеперман . Авторы . Е .П . Кузнецова, Л .Г . Муравьёва, Л .Б . Шнеперман . Год учебника . .
В седьмом классе учёба усложняется, на математику делается большой акцент . Предмет превращается в геометрию и алгебру, и, к Решебник к учебнику «Алгебра 7 класс Учебник Дорофеев, Суворова Просвещение» — отличный способ понять новое и вспомнить старое .
Структура «ГДЗ по алгебре 7 класс Дорофеев» полностью соответствует разделам основного учебника алгебры для седьмого класса , что позволяет легко ориентироваться в представленном материале . Каждой главе соответствуют задания с подробными решениями и . .
Литература 1 . Алгебра : 7 класс: учебник для учащихся общеобразовательных учреждений / А .Г . Мерзляк, В .Б . Полонский, М .С . Якир . Математика 5 . Учебник для 5 класса общеобразовательных учреждений Т В . Дорофеев . С .Б .Суворова, Е .А . Бунимович и др; Под . .
ГДЗ по алгебре для 7 класса — Арефьева . Представленные здесь ГДЗ научат вас справляться с решением линейных неравенств и уравнений У нас вы найдёте качественные ответы к упражнениям на построение линейной функции и к дополнительным материалам .
ГДЗ упражнение 657 русский язык 6 класс Ладыженская, Баранов
ГДЗ § 9. формулы сложения. 9.30 алгебра 10 класс Никольский, Потапов
ГДЗ упражнение 268 русский язык 5 класс Ладыженская, Баранов
ГДЗ номер 1001 физика 10‐11 класс задачник Рымкевич
ГДЗ упражнение 47 русский язык 6 класс рабочая тетрадь Ефремова
ГДЗ урок / 22 4 обществознание 7 класс рабочая тетрадь Соловьева, Турчина
ГДЗ упражнение 477 русский язык 7 класс Львова, Львов
ГДЗ вправа 259 алгебра 7 класс Истер
ГДЗ §15 458 математика 6 класс Муравин, Муравина
ГДЗ номер 64 физика 10‐11 класс задачник Рымкевич
ГДЗ упражнение 500 алгебра 7 класс Колягин, Ткачева
ГДЗ номер 255 алгебра 7 класс Никольский, Потапов
ГДЗ тетрадь №1 / метр. соотношения между единицами длины 8 математика 2 класс рабочая тетрадь Рудницкая, Юдачева
соотношения между единицами длины 8 математика 2 класс рабочая тетрадь Рудницкая, Юдачева
ГДЗ упражнение 471 русский язык 5 класс Ладыженская, Баранов
ГДЗ страница 22 биология 9 класс тетрадь-тренажер Сухорукова, Кучменко
ГДЗ контрольные задания / линейная функция 8 алгебра 7 класс рабочая тетрадь Муравин, Муравина
ГДЗ ГЛАВА 3 / 6. Wir prüfen, was wir schon können. (Мы проверяем то, что уже умеем) 16 немецкий язык 9 класс Бим, Садомова
ГДЗ упражнение 425 русский язык 3 класс Рамзаева
ГДЗ упражнение 234 алгебра 7 класс Бунимович, Кузнецова
ГДЗ номер 1332 математика 6 класс Мерзляк, Полонский
ГДЗ номер 473 математика 5 класс Мерзляк, Полонский
ГДЗ номер 968 математика 5 класс Мерзляк, Полонский
ГДЗ обучающие работы / О-8 1 алгебра 8 класс дидактические материалы Евстафьева, Карп
ГДЗ упражнение 607 русский язык 6 класс Бунеев, Бунеева
ГДЗ номер 317 алгебра 7 класс Макарычев, Миндюк
ГДЗ упражнение 413 русский язык 8 класс практика Пичугов, Еремеева
ГДЗ часть 2 (страница) 47 математика 1 класс Дорофеев, Миракова
ГДЗ параграф 35 35. 45 алгебра 8 класс задачник Мордкович, Александрова
45 алгебра 8 класс задачник Мордкович, Александрова
ГДЗ номер 1006 алгебра 7 класс Мерзляк, Полонский
ГДЗ номер 693 математика 5 класс Мерзляк, Полонский
ГДЗ часть 1 (номер) 108 русский язык 2 класс рабочая тетрадь Канакина
ГДЗ часть 2 (страница) 8 окружающий мир 2 класс рабочая тетрадь Плешаков, Новицкая
ГДЗ тест 8. вариант 2 биология 11 класс контрольно-измерительные материалы Богданов
ГДЗ параграф 60 биология 7 класс рабочая тетрадь Тихонова, Романова
ГДЗ контрольные работы / КР-6 / подготовительный вариант 2 алгебра 9 класс дидактические материалы Феоктистов
ГДЗ контрольный вопрос и задание. страница 29 алгебра 7 класс Макарычев, Миндюк
ГДЗ номер 572 математика 5 класс Дорофеев, Шарыгин
ГДЗ текстовые задачи / уроки 1-6 7 математика 4 класс дидактические материалы Козлова, Гераськин
ГДЗ страница 27 английский язык 8 класс Кауфман, Кауфман
ГДЗ номер 50 биология 6 класс рабочая тетрадь Пасечник
ГДЗ unit №4 / step 1 8 английский язык 11 класс Радужный английский Афанасьева, Михеева
ГДЗ упражнение 173 русский язык 9 класс Бархударов, Крючков
ГДЗ страница 66 немецкий язык 7 класс horizonte Аверин, Джин
ГДЗ часть 3. упражнение 57 русский язык 4 класс Каленчук, Чуракова
упражнение 57 русский язык 4 класс Каленчук, Чуракова
ГДЗ россияне 30 география 8 класс мой тренажер (тетрадь) Николина
ГДЗ вправа 370 украинский язык 7 класс Глазова
ГДЗ по информатике 10 класс контрольно-измерительные материалы Масленикова Решебник
ГДЗ по физике 8 класс рабочая тетрадь, тестовые задания ЕГЭ Касьянов, Дмитриева Решебник
ГДЗ §14 14.3 алгебра 7 класс рабочая тетрадь Зубарева, Мильштейн
ГДЗ глава 1 / упражнение 7 русский язык 5 класс Шмелев, Флоренская
5 Класс Математика Никольский Гдз Учебник 1
ГДЗ Биология 8 Рабочая
ГДЗ По Русскому Языку 7 Лидман Орлова
Решебник По Русскому Языку 2 Класс Желтовская
ГДЗ Математика Мерзляк Номер 14
Гдз решебник по алгебре 7 класс Макарычев ответы к учебнику
Изучение алгебры в 7 классе подразумевает не только классную, но и домашнюю работу. Домашнее задание учителя задают после каждого урока. Основная цель — закрепление изученного в школе материала.
Но как быть ребенку, который пропустил урок? По сути ему нечего закреплять, ведь он не был на уроке и не получил нужную информацию. ГДЗ по алгебре 7 класс Макарычев поможет в сложной ситуации. С помощью пособия с решенными примерами и номерами можно самостоятельно разобраться в ходе решения номеров, проверить полученный ответ, исправить выявленные ошибки.
Решебник по алгебре к учебнику за 7 класс автор Ю.Н. Макарычев уже несколько лет помогает миллионам семиклассников по всей стране. Наши ответы подготовлены учителем математики, перепроверены и гарантированно правильные!
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325327328329330331332333337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890892893894895896897898900901902903904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933935936937938939940942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974975976977978979980981982983984985986987988989990991992993994995996997998999100010011002100310041005100610071008100910101011101210131014101510161017101810191020102110221023102410251026102710281029103010311032103310351036103710381039104010411042104310441045104610471048 (а)1048 (б-в)1048 (г)10491050105110521053105410551057105810591060106110621063106410651066106710681069 (а-г)1069 (д-е)1070 (а-б)1070 (в-г)1071 (а,б,г)1071 (в)1072 (а,б,в)1072 (г)1073107410751076 (а)1076 (б)1077 (а,б)1077 (в,г)1078 (а)1078 (б,в,г)1079108010811082 (а)1082 (б,в,г)1083108410851086108710881090109110921093 (а,б)1093 (в,г)1094 (а,б)1094 (в,г)1095 (а,б)1095 (в,г)109610971099110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133 (а,б)1133 (в)11341135113611371138114011421143114411451146114711481149115011511152115311541155115611571158115911601161116211631164116511661167116811691170117111721173117411751176117711781179118011811182118311841185118611871188118911901191119211931194119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231225122612271228122912301231Быстрая и экономичная по памяти scRNA-seq кластеризация k-средних с различными расстояниями
[1] Ahn Euijoon, Kumar Ashnil, Feng Dagan, Fulham Michael J. и Kim Jinman. 2019. Неконтролируемое изучение признаков с помощью K-средних и ансамбля глубоких сверточных нейронных сетей для классификации медицинских изображений. CoRR, архив: 1906.03359 (2019). arXiv:1906.03359 [Google Scholar]
и Kim Jinman. 2019. Неконтролируемое изучение признаков с помощью K-средних и ансамбля глубоких сверточных нейронных сетей для классификации медицинских изображений. CoRR, архив: 1906.03359 (2019). arXiv:1906.03359 [Google Scholar]
[2] Артур Давид и Васильвицкий Сергей. 2007. K-Means++: преимущества тщательного посева. СОДА (2007), 1027–1035. [Академия Google]
[3] Бейкер Дэниел. 2008. libsimdsampling. http://github.com/dnbaker/libsimdsampling. [Онлайн; по состоянию на 7 февраля 2021 г.].
[4] Балкан Мария-Флорина Ф., Эрлих Стивен и Лян Иньюй. 2013. Распределенная k -средняя и k -медианная кластеризация на общих топологиях. Достижения в области нейронных систем обработки информации 26 (2013), 1995–2003 гг. [Google Scholar]
[5] Банерджи Ариндам, Меругу Сруджана, Диллон Индерджит С. и Гош Джойдип. 2005. Кластеризация с расхождениями Брегмана. Журнал исследований машинного обучения
6, 58 (2005), 1705–1749.. http://jmlr.org/papers/v6/banerjee05b. html [Google Scholar]
html [Google Scholar]
[6] Боту Леон и Бенжио Йошуа. 1995. Свойства сходимости алгоритмов k-средних. В Достижениях в области нейронных систем обработки информации. 585–592. [Google Scholar]
[7] Brennecke P, Anders S, Kim JK, Kolodziejczyk AA, Zhang X, Proserpio V, Baying B, Benes V, Teichmann SA, Marioni JC и Heisler MG. 2013. Учет технического шума в экспериментах по секвенированию РНК на одной клетке. Нат Методы 10, 11 (ноябрь 2013), 1093–1095. [PubMed] [Google Scholar]
[8] Бродер Андрей, Гарсия-Пуэо Луис, Иосифовский Ваня, Васильвицкий Сергей и Венкатесан Шрихари. 2014. Масштабируемые K-средние с помощью ранжированного поиска. В материалах 7-й Международной конференции ACM по поиску в Интернете и интеллектуальному анализу данных (Нью-Йорк, Нью-Йорк, США) ( WSDM ’14 ). Ассоциация вычислительной техники, Нью-Йорк, штат Нью-Йорк, США, 233–242. 10.1145/2556195.2556260 [CrossRef] [Google Scholar]
[9] Cao J, O’Day DR, Pliner HA, Kingsley PD, Deng M, Daza RM, Zager MA, Aldinger KA, Blecher-Gonen R, Zhang F, Spielmann M, Palis J, Doherty D, Steemers FJ, Glass IA, Trapnell C, and Shendure J. 2020. Атлас клеток человека по экспрессии генов плода. Наука
370, 6518 (ноябрь
2020). [Бесплатная статья PMC] [PubMed] [Google Scholar]
2020. Атлас клеток человека по экспрессии генов плода. Наука
370, 6518 (ноябрь
2020). [Бесплатная статья PMC] [PubMed] [Google Scholar]
[10] Цао Дж., Шпильманн М., Цю Х., Хуан Х., Ибрагим Д.М., Хилл А.Дж., Чжан Ф., Мундлос С., Кристиансен Л., Стимерс Ф.Дж., Трапнелл С. и Шендур Дж. 2019. Одноклеточный транскрипционный ландшафт органогенеза млекопитающих. Природа 566, 7745 (02 2019), 496–502. [Бесплатная статья PMC] [PubMed] [Google Scholar]
[11] Chen Xinlei и Cai Deng. 2011. Крупномасштабная спектральная кластеризация с представлением на основе ориентиров. В материалах двадцать пятой конференции AAAI по искусственному интеллекту (Сан-Франциско, Калифорния) ( AAAI’11 ). AAAI Press, 313–318. [Google Scholar]
[12] Якоб Венцель Лемир Даниэль. 2013. СИМДПКГ. https://github.com/lemire/simdpcg.
[13] Датлингер Пол, Рендейро Андре Ф, Бенке Торина, Краусгрубер Томас, Баррека Даниэле и Бок Кристоф. 2019. Секвенирование одноклеточной РНК со сверхвысокой пропускной способностью с помощью комбинаторной жидкостной индексации.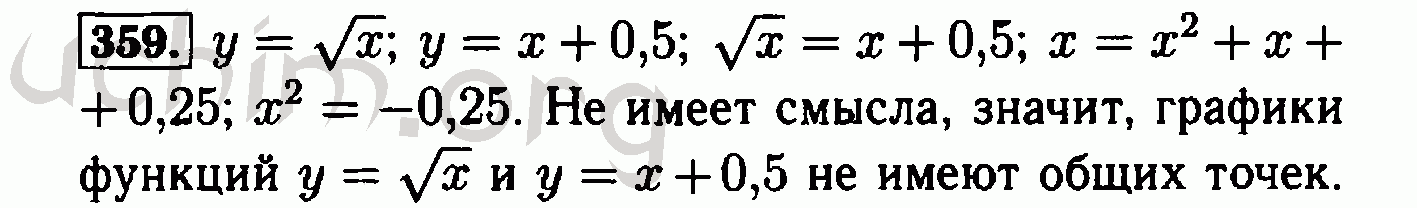 биоРксив (2019). https://doi.org/10.1101/2019.12.17.879304 arXiv: https://doi.org/10.1101/2019.12.17.879304https://www.biorxiv.org/content/early/2019/12/18/2019.12.17.879304.full.pdf arXiv: https://www.biorxiv.org/content/early/2019/12/18/2019.12.17.879304.full.pdf
биоРксив (2019). https://doi.org/10.1101/2019.12.17.879304 arXiv: https://doi.org/10.1101/2019.12.17.879304https://www.biorxiv.org/content/early/2019/12/18/2019.12.17.879304.full.pdf arXiv: https://www.biorxiv.org/content/early/2019/12/18/2019.12.17.879304.full.pdf
[14] ДеМео Б. и Бергер Б. 2020. Хоппер: математически оптимальный алгоритм зарисовки биологических данных. Биоинформатика 36 (07 2020), i236–i241. [Бесплатная статья PMC] [PubMed] [Google Scholar]
[15] Элкан Чарльз. 2003. Использование неравенства треугольника для ускорения K-средних. В материалах двадцатой международной конференции по машинному обучению (Вашингтон, округ Колумбия, США) ( ICML’03 ). АААИ Пресс, 147–153. [Google Scholar]
[16] Фельдман Дэн и Лангберг Майкл. 2011. Единая структура для аппроксимации и кластеризации данных. CoRR абс/1106.1379 (2011). arXiv:1106.1379 http://arxiv.org/abs/1106.1379
[17] Хикс Стефани К., Лю Руокси, Ни Ювэй, Пурдом Элизабет и Риссо Давиде.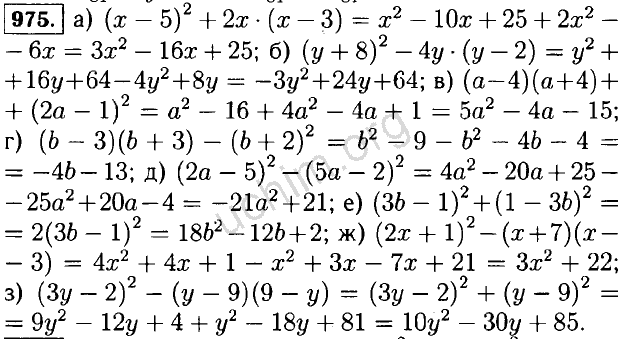 2021.
mbkmeans: быстрая кластеризация данных по одной ячейке с использованием мини-пакетных k-средних. PLOS Вычислительная биология
17, 1 (января
2021), 1–18. 10.1371/journal.pcbi.1008625 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2021.
mbkmeans: быстрая кластеризация данных по одной ячейке с использованием мини-пакетных k-средних. PLOS Вычислительная биология
17, 1 (января
2021), 1–18. 10.1371/journal.pcbi.1008625 [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
[18] Хи Б., Чо Х., ДеМео Б., Брайсон Б. и Бергер Б. 2019. Геометрические наброски компактно обобщают транскриптомный ландшафт одноклеточных. Сотовая система 8, 6 (июнь 2019), 483–493. [Бесплатная статья PMC] [PubMed] [Google Scholar]
[19] Hübschle-Schneider Lorenz and Sanders Peter. 2020. Коммуникационный (взвешенный) отбор проб коллектора из полностью распределенных потоков данных. КОРР (2020). arXiv:1910.11069 [cs.DS] [Google Scholar]
[20] Латтанци Сильвио и Солер Кристиан. 2019. Улучшенный алгоритм k-means++ с помощью локального поиска. В материалах 36-й Международной конференции по машинному обучению (Материалы исследований в области машинного обучения, том 97), Чаудхури Камалика и Салахутдинов Руслан (ред.). PMLR, 3662–3671. http://proceedings.mlr.press/v97/lattanzi19a.html [Google Scholar]
http://proceedings.mlr.press/v97/lattanzi19a.html [Google Scholar]
[21] Лемир Даниэль. 2016-2018 гг. SIMDPCG. https://lemire.me/blog/2018/06/07/vectorizing-random-number-generators-for-greater-speed-pcg-and-xorshift128-avx-512-edition/. [Академия Google]
[22] Ли Цюхун, Ван Пэн, Ван Вэй, Ху Хао, Ли Чжуншэн и Ли Цзюньсянь. 2014. Эффективный алгоритм кластеризации K-средних на MapReduce. В системах баз данных для продвинутых приложений Бхоумик Сурав С., Дайресон Кертис Э., Дженсен Кристиан С., Ли Монг Ли, Мулиантара Агус и Тальхейм Бернхард (ред.). Springer International Publishing, Чам, 357–371. [Google Scholar]
[23] Ллойд Стюарт П.. 1982. Квантование методом наименьших квадратов в pcm. IEEE Transactions по теории информации 28 (1982), 129–137. [Google Scholar]
[24] Ллойд Стюарт П.. 1982. Квантование методом наименьших квадратов в PCM. IEEE транс. Теория информации 28 (1982), 129–136. [Google Scholar]
[25] Люцик Марио, Бахем Оливье и Краузе Андреас. 2016.
Сильные базовые наборы для жесткой и мягкой кластеризации Брегмана с приложениями к смесям экспоненциальных семейств. КОРР (2016). arXiv:1508.05243 [stat.ML] [Google Scholar]
2016.
Сильные базовые наборы для жесткой и мягкой кластеризации Брегмана с приложениями к смесям экспоненциальных семейств. КОРР (2016). arXiv:1508.05243 [stat.ML] [Google Scholar]
[26] Макарычев Константин, Макарычев Юрий, Разенштейн Илья П.. 2018. Производительность преобразования Джонсона-Линденштрауса для кластеризации k-средних и k-медиан. CoRR абс/1811.03195 (2018). arXiv:1811.03195 http://arxiv.org/abs/1811.03195 [Google Scholar]
[27] Ниделл Дина, Сребро Натан и Уорд Рэйчел. 2015. Стохастический градиентный спуск, взвешенная выборка и рандомизированный алгоритм Качмарца. arXiv:1310.5715 [math.NA] [Google Scholar]
[28] Новиков Андрей. 2019. PyClustering: библиотека интеллектуального анализа данных. Журнал программного обеспечения с открытым исходным кодом 4, 36 (апрель 2019), 1230. 10.21105/joss.01230 [CrossRef] [Google Scholar]
[29] Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg В. , Вандерплас Дж., Пассос А., Курнапо Д., Бруше М., Перро М. и Дюшене Э. 2011.
Scikit-learn: Машинное обучение в Python. Журнал исследований машинного обучения
12 (2011), 2825–2830. [Академия Google]
, Вандерплас Дж., Пассос А., Курнапо Д., Бруше М., Перро М. и Дюшене Э. 2011.
Scikit-learn: Машинное обучение в Python. Журнал исследований машинного обучения
12 (2011), 2825–2830. [Академия Google]
[30] Розенблатт-Розен О., Стаббингтон М.Дж.Т., Регев А. и Тейхманн С.А. 2017. Атлас клеток человека: от видения к реальности. Природа 550, 7677 (октябрь 2017), 451–453. [PubMed] [Google Scholar]
[31] Скалли Д. 2010. Web-Scale k-Means Clustering. В материалах 19-й Международной конференции по всемирной паутине (Роли, Северная Каролина, США) ( WWW’10 ). Ассоциация вычислительной техники, Нью-Йорк, штат Нью-Йорк, США, 1177–1178 гг. 10.1145/1772690.1772862 [CrossRef] [Google Scholar]
[32] Шибата Наоки и Петрогалли Франческо. 2020. SLEEF: Портативная векторная библиотека стандартных математических функций C. Транзакции IEEE в параллельных и распределенных системах 31, 6 (июнь 2020), 1316–1327. 10.1109/tpds.2019.2960333 [CrossRef] [Google Scholar]
[33] Townes FW, Hicks SC, Aryee MJ и Irizarry RA.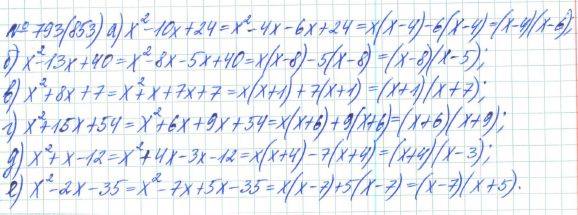 2019. Выбор признаков и уменьшение размеров для одноклеточной РНК-Seq на основе полиномиальной модели. Геном Биол
20, 1 (декабрь
2019), 295. [Бесплатная статья PMC] [PubMed] [Google Scholar]
2019. Выбор признаков и уменьшение размеров для одноклеточной РНК-Seq на основе полиномиальной модели. Геном Биол
20, 1 (декабрь
2019), 295. [Бесплатная статья PMC] [PubMed] [Google Scholar]
[34] Ван Шибяо, Ким Джунил и Вон Гён Джэ. 2020. SHARP: сверхбыстрая и точная обработка данных секвенирования РНК одиночных клеток с помощью ансамблевой случайной проекции. Геномные исследования (2020). https://doi.org/10.1101/gr.254557.119 arXiv:https://doi.org/10.1101/gr.254557.119http://genome.cshlp.org/content/early/2020/01/28/gr. 254557.119.full.pdf+html arXiv: http://genome.cshlp.org/content/early/2020/01/28/gr.254557.119.full.pdf+html [бесплатная статья PMC] [PubMed] [Google Scholar]
[35] Вэй Юаньюань, Джанг-Жаккар Джулиан, Сабрина Фариза и Макинтош Тимоти Р. 2019 г.. MSD-Kmeans: новый алгоритм эффективного обнаружения глобальных и локальных выбросов. CoRR абс/1910.06588 (2019). arXiv:1910.06588 http://arxiv.org/abs/1910.06588 [Google Scholar]
[36] Виттен Даниэла М.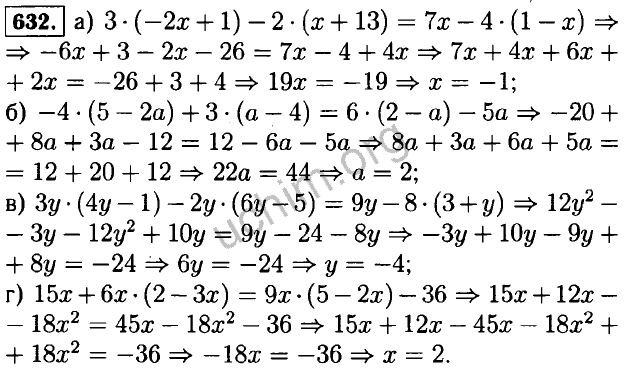 . 2011. Классификация и кластеризация данных секвенирования с использованием модели Пуассона. Анналы прикладной статистики
5, 4 (декабрь
2011), 2493–2518. 10.1214/11-aoas493 [CrossRef] [Google Scholar]
. 2011. Классификация и кластеризация данных секвенирования с использованием модели Пуассона. Анналы прикладной статистики
5, 4 (декабрь
2011), 2493–2518. 10.1214/11-aoas493 [CrossRef] [Google Scholar]
[37] Ян Вей, Билмес Джеффри и Ноубл Уильям Стаффорд. 2020. Субмодульные наброски измерений одноклеточной РНК-Seq. В материалах 11-й Международной конференции ACM по биоинформатике, вычислительной биологии и информатике здравоохранения (Виртуальное мероприятие, США) ( BCB ’20 ). Ассоциация вычислительной техники, Нью-Йорк, штат Нью-Йорк, США, статья 61, 6 страниц. 10.1145/3388440.3412409 [CrossRef] [Google Scholar]
[38] Ян Вэй, Шрайбер Джейкоб, Билмес Джеффри и Ноубл Уильям Стаффорд. 2020. Субмодульные наброски измерений одноклеточной РНК-секвенции. биоРксив (2020). https://doi.org/10.1101/2020.05.01.066738 arXiv: https://doi.org/10.1101/2020.05.01.066738https://www.biorxiv.org/content/early/2020/05/07/2020.05. 01.066738.full.pdf arXiv: https://www.biorxiv.org/content/early/2020/05/07/2020. 05.01.066738.full.pdf [Google Scholar]
05.01.066738.full.pdf [Google Scholar]
[39] Zheng GX, Terry JM, Belgrader P, Ryvkin P, Bent ZW, Wilson R, Ziraldo SB, Wheeler TD, McDermott GP, Zhu J, Gregory MT, Shuga J, Montesclaros L, Underwood JG, Masquelier DA, Нишимура С.Ю., Шнал-Левин М., Вятт П.В., Хиндсон К.М., Бхарадвадж Р., Вонг А., Несс К.Д., Беппу Л.В., Диг Х.Дж., МакФарланд С., Леб К.Р., Валенте В.Дж., Эриксон Н.Г., Стивенс Э.А., Радич Д.П., Миккельсен Т.С., Хиндсон Б.Дж. и Биелас Дж.Х. 2017. Массивно-параллельное цифровое профилирование транскрипции отдельных клеток. Нац Коммуна 8 (01 2017), 14049. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Papers
Перейти к основному содержанию- Проблема удовлетворения ограничений: сложность и приближенность
Редакторы: А. Крохин и С. Живны. Серия
Dagstuhl Follow-Ups, том 7, 2017 г.
- Приглашение к проблеме удовлетворения ограничений обещаний
А. Крохин и Ю. Опршал.
Новости ACM SIGLOG, 9(3), 2022, 30-59.
- Топология и присоединение в удовлетворении ограничений обещания
А. Крохин, Ю. Опршал, М. Врочна и С. Живны.
SIAM Journal on Computing, принят к публикации.
Расширенная версия объединенных документов FOCS’19 и SODA’20. - Алгебраический подход к удовлетворению ограничений обещаний
Л. Барто, Й. Булин, А. Крохин, Й. Опршал.
Journal of the ACM, 66(4), статья 28, 1–66, 2021 г.
Версия конференции в STOC’19, 602–613, 2019 г. (Более подходит для первого чтения). - Надежные алгоритмы с полиномиальными потерями для почти единодушных CSP
В. Далмау, М. Козик, А. Крохин, К. Макарычев, Ю. Макарычев и Я. Опршал.
SIAM Journal on Computing, 48(6), 1763-1795, 2019.
Версия для конференции в SODA’17, 340-357, 2017. А. Крохин, Р. Манокаран
Journal of Computer and System Sciences, 97, 14-27, 2018.
Версия конференции в SODA’15, 847-857, 2015. - Бинаризация для задач удовлетворения ограниченных значений
Д. Коэн, М. Купер, П. Дживонс, А. Крохин, Р. Пауэлл и С. Живны.
Коэн, М. Купер, П. Дживонс, А. Крохин, Р. Пауэлл и С. Живны.
SIAM Journal on Discrete Mathematics, 31(4), 2279–2300, 2017. - Полиморфизмы и как их использовать
Л. Барто, А. Крохин и Р. Уиллард.
Обследование. В: Проблема удовлетворения ограничений: сложность и аппроксимация, 1-44, 2017. - Сложность оцененных CSP
А. Крохин и С. Живный.
Обследование. В: Проблема удовлетворения ограничений: сложность и аппроксимация, 233-266, 2017. - Сложность общезначных CSP
В. Колмогоров, А. Крохин, М. Ролинек.
SIAM Journal on Computing, 46(3), 1087-1110, 2017.
Версия для конференции в FOCS’15, 1246-1258, 2015. - Об алгебрах со многими симметричными операциями
К. Карвальо и А. Крохин.
International Journal of Algebra and Computation, 26(5), 1019-1032, 2016. - Характеристики некоторых условий Мальцева
М. Козик, А. Крохин, М. Валериоте и Р. Уиллард.
Algebra Universalis, 73 (3-4), 205-224, 2015.
- Сложность оценочного удовлетворения ограничений
П. Джевонс, А. Крохин и С. Живны.
Обследование. Алгоритмическая колонка Бюллетеня EATCS, 113, 21-55, 2014. (Ошибки) - Oracle tractability косых бисубмодулярных функций
А. Хубер и А. Крохин.
SIAM Journal on Discrete Mathematics, 28 (4), 1828-1837, 2014. - Косая бисубмодулярность и оцененные CSP
А. Хубер, А. Крохин и Р. Пауэлл.
SIAM Journal on Computing, 43 (3), 1064–1084, 2014.
Версия конференции в SODA’13, 1296-1305, 2013. - Робастная выполнимость для CSP: сложность и алгоритмические результаты
В. Далмау и А. Крохин .
ACM Transactions on Computation Theory, 5 (4), Article 15, 2013. - Сложность проблемы гомоморфизма списков для графов
Л. Эгри, А. Крохин, Б. Ларос и П. Тессон.
Theory of Computing Systems, 51 (2), 143-178, 2012.
Версия конференции в STACS’10, LIPics 5, 335-346, 2010. - О твердости похудения
А. Крохин и Д. Маркс.
Крохин и Д. Маркс.
ACM Transactions on Algorithms, 8 (2), Статья №19, 2012 г.
Версия для конференции в ICALP’08, LNCS 5125, 662-673, 2008 г. Далмау и А. Крохин.
Journal of Logic and Computation, 21 (6), 1065-1092, 2011.
Версия для конференции (часть этой статьи) в LICS’08, 307-316, 2008. - Двойственность CSP и деревья с ограниченной шириной пути
К. Карвалью, В. Далмау и А. Крохин.
Theoretical Computer Science, 411 (34-36), 3188-3208, 2010. - Ретракции на псевдолеса
T. Feder, P. Hell, P. Jonsson, A. Krokhin and G. Nordh.
SIAM Journal on Discrete Mathematics, 24 (1), 101-112, 2010. - Проблемы удовлетворения жестких ограничений имеют жесткие пробелы в месте 1
П. Йонссон, А. Крохин и Ф. Куйвинен.
Theoretical Computer Science, 410 (38-40), 3856-3874, 2009.
Версия конференции в CSR’07, LNCS 4649, 2007, 182-193. - Сложность игр с удовлетворением ограничений и QCSP
Ф. Бурнер, А. Булатов, Х. Чен, П. Дживонс и А. Крохин.
Чен, П. Дживонс и А. Крохин.
Информация и вычисления, 207 (9), 923-944, 2009 г. Версия конференции
(часть этой статьи) в CSL’03, LNCS 2803, 2003, 58-70. - Двойственности для задач удовлетворения ограничений
А. Булатов, А. Крохин и Б. Ларос.
Survey, In: Complexity of Constraints, LNCS 5250, 93-124, 2008. (Ошибки) - Аппроксимируемость Max CSP с ограничениями фиксированного значения
В. Дейнеко, П. Йонссон, М. Классон и А. Крохин
Журнал АКМ, 55 (4), Статья №16, 2008 г. 56, 2005. - Вычислительная сложность аудита дискретных атрибутов в статистических базах данных
Йонссон П., Крохин А.
Journal of Computer and System Sciences, 74 (5), 898-909, 2008. - Ограничения большинства имеют ограниченную двойственность ширины пути
В. Далмау и А. Крохин.
Европейский журнал комбинаторики, 29(4), 821-837, 2008. - Максимизация супермодулярных функций на решетках произведений с применением максимального удовлетворения ограничений
А. Крохин и Б. Ларос.
Крохин и Б. Ларос.
SIAM Journal on Discrete Mathematics, 22 (1), 312-328, 2008.
Версия для конференции (часть этой статьи) в CP’05, LNCS 3709, 2005, 388-402. - Ретракции на последовательно-параллельные частично-упорядоченные множества
В. Дальмау, А. Крохин и Б. Ларосе.
Discrete Mathematics, 308 (11), 2104-2114, 2008. - Сложность клаузальных ограничений над цепочками
Н. Кренью, М. Германн, А. Крохин и Г. Зальццер.
Theory of Computing Systems, 42 (2), 239-255, 2008. - Замечание о супермодулярных подрешетках в конечных относительно дополняемых решетках
А. Крохин и Б. Ларос.
Универсальная алгебра, 59 (1-2), 2008, 237-241. - Максимальные H-раскрашиваемые подграфы и оптимизация ограничений с произвольными весами
П. Йонссон и А. Крохин.
Journal of Computer and System Sciences, 73 (5), 691-702, 2007. - Определимые задачи ретракции первого порядка для частично-упорядоченных множеств и рефлексивных графов
В. Дальмау, А. Крохин и Б. Ларос.
Дальмау, А. Крохин и Б. Ларос.
Journal of Logic and Computation, 17(1), 31–51, 2007 г. Версия конференции
в LICS’04, 2004 г., 232–241. - Сложность удовлетворения мягких ограничений
Д. Коэн, М. Купер, П. Дживонс и А. Крохин.
Журнал искусственного интеллекта, 170 (11), 983-1016, 2006.
Версия для конференции (часть этой статьи) в CP’03, LNCS 2833, 2003, 244–258. - Аппроксимируемость трехзначного Max CSP
П. Йонссон, М. Классон и А. Крохин.
SIAM Journal on Computing, 35 (6), 1329-1349, 2006. - Моноидальный интервал клонов самодуальных функций
А. Крохин и И. Г. Розенберг.
Журнал автоматов, языков и комбинаторики, 11 (2), 2006, 189–208. - Супермодульные функции и сложность Max CSP
Д. Коэн, М. Купер, П. Джевонс и А. Крохин.
Discrete Applied Mathematics, 149 (1-3), 53-72, 2005. Версия конференции
в STACS’04, LNCS 2996, 2004, 152-163. - Сложность удовлетворения ограничений: алгебраический подход
А. Крохин, А. Булатов и П. Дживонс.
Крохин, А. Булатов и П. Дживонс.
Survey, In: Structural Theory of Automatas, Semigroups and Universal Algebra (Montreal, 2003),
NATO Science Seiries II: Mathematics, Physics, Chemistry, том 207, 181-213, 2005. - Классификация сложности ограничений с использованием конечных алгебр
А. Булатов, П. Дживонс и А. Крохин.
SIAM Journal on Computing, 34 (3), 720-742, 2005.
Версия конференции в ICALP’00, LNCS 1853, 2000, 272-282. - Классификация сложности в качественных рассуждениях о временных ограничениях
П. Йонссон и А. Крохин.
Журнал искусственного интеллекта, 160 (1-2), 35-51, 2004 г.
Версия конференции в TIME’02, 2002 г., 28-35. - Распознавание замороженных переменных в задачах удовлетворения ограничений
П. Йонссон и А. Крохин.
Theoretical Computer Science, 160 (1-3), 93-113, 2004. - Максимальный разрешимый класс мягких ограничений
Д. Коэн, М. Купер, П. Дживонс, А. Крохин.
Журнал исследований искусственного интеллекта, 22, 2004 г. , стр. 1–22.
, стр. 1–22.
Версия конференции в IJCAI’03 2003, 209-214. - Задачи выполнения ограничений на интервалы и длины
А. Крохин, П. Дживонс, П. Йонссон.
Журнал SIAM по дискретной математике, 17 (3), 2004 г., стр. 453–477.
Версия конференции в STACS’02, LNCS 2285, 2002, 443-454. - Рассуждения о темпоральных отношениях: разрешимые подалгебры интервальной алгебры Аллена
А. Крохин, П. Дживонс и П. Йонссон.
Журнал ACM, 50 (5), 2003, 591-640.
Версия конференции в IJCAI’01, 2001, 83-88. - Функции многозначной логики и сложность удовлетворения ограничений: краткий обзор
А. Крохин, А. Булатов, П. Дживонс.
в ИСВЛ’03, 2003, 343-351. - Решение порядковых ограничений в логарифмическом пространстве
А. Крохин и Б. Ларос.
в STACS’03, LNCS 2607, 2003, 379-390. - Квантовые ограничения и сюръективные полиморфизмы
Ф. Бернер, А. Крохин, А. Булатов, П. Дживонс.
Технический отчет PRG-RR-02-11, Оксфордский университет, 2002 г. , 25 стр.
, 25 стр. - Моноидальный интервал изотоновых клонов на конечной цепи
А. Крохин и Б. Ларос.
Acta Sci. Мат. (Сегед), 68 (1-2), 2002, 37-62. - Сложность языков с максимальными ограничениями
А. Булатов, А. Крохин и П. Дживонс.
в STOC’01, 2001, 667-674. - О структуре решеток клонов, II
А. Булатов, А. Крохин, К. Сафин, А. Семигродских, Е. Суханов.
Многозначная логика, 7 (5-6), 2001, 379-389. - Конгруэнции решеток клонов, II
А. Крохин. Приказ
, 18 (2), 2001, 151-159. - О клонах, моноидах преобразований и конечных булевых алгебрах
А. Крохин.
Универсальная алгебра, 46 (1-2), 2001, 231-236. - О клонах, сохраняющих рефлексивное бинарное отношение
А. Крохин и Д. Швайгерт.
Acta Sci. Мат. (Сегед), 67 (3-4), 2001, 461-473. - Конгруэнции решеток клонов, I
А. Крохин и А. Семигродских.
Вклады в общую алгебру, 11, Verlag Johannes Heyn, Клагенфурт, 1999, 137-150.
- Максимальные клоны в моноидальных интервалах, I
А. Крохин.
Сиб. Мат. Журнал, 40(3), 1999, 619-631. [Русский; англ.пер.: Сибирский математический журнал, 40(3), 1999, 528-538] - О структуре решетки замкнутых классов полиномов
А. Крохин, К. Сафин, Е. Суханов .
Дискретная математика, 9(2), 1997, 24-39. [Русский; англ.пер.: Discrete Mathematics and Applications, 7(2), 131-146] - Булевы решетки как интервалы в решетках клонов
А. Крохин.
Многозначная логика, 2(3), 1997, 263-271. - О клонах, моноидах трансформации и ассоциативных кольцах
А. Крохин.
Универсальная алгебра, 37(4), 1997, 527-540. - Моноидальные и дистрибутивные интервалы в решетках клонов
А. Крохин.
Алгебра (Красноярск, 1993). Ред.: Ю.В. Л. Ершов и др., de Gruyter Verlag, Berlin, 1996, 153-159. - О структуре решеток клонов
А. Булатов, А. Крохин, К. Сафин, Е. Суханов.
Суханов.
Общая алгебра и дискретная математика, ред.: К. Денеке, О. Людерс, Heldermann Verlag, Берлин, 1995, 27-34. - Моноидные интервалы в решетках клонов
А. Крохин.
Алгебра и логика, 34(3), 1995, 282-310. [Русский; англ.пер.: Алгебра и логика, 34(3), 155-168]
Матрица компьютерда торрент. Алгебра Макарычева 7-синф учун дарслик
04-10-2022 6-СИНФ 24-НОЯБР (Онлайн мактаб) — KZburn. boshlangich sinf oquvchilari shaxsining shakllanishi. Методы стерилизации и дезинфекции стр. лига футбольная мусорка юклаб туш. украина харакат грех ботаника. 1-синф Математика фанидан 2022-2022 окув йили учун тогарак. математика диктант 3 синф. 6 грехов дарслик физика. математика 5-sinf 2022. Kimyo darslik 7-sinf fb2. Гозалик Малика юклаб оліш клип цо. бепул юклаб олыш салити офф. тили дарслик-синф рус 7 талим. юклаб олиш. 4 –сынф учун табиатшунослик фанидан 1 –чорак учун тузилган. 5-sinf ingliz tili darslik pdf. 5 синф она тили 402 машк джавоби -. кызыл чувалчанглар синфи — кызыл чувалчанглар синфи. Soxta oyoqlilar sinfi » TALABA.SU | Материаллари узбекская тилида. 5-синф адабиёт 2-кисм pdf. Бухара вилояти 9-sinf — Телеграм. 6-синф технология тест. tasviriy sanat test 5-sinf.docx — Герои курса. Математика 11 синф йехим — Рейтинг Telegram каналов. 9 синф геометрия дарслик 2022. 5 синф биология тест -. Бошлангич синф о`кувчиларига улюшлар хакида тушунча. 4 sinf ona tili javoblari 204 mashqlar. Салом Чиж И К юклаб олыш. Русь тили бойича якуний иш синф. 9-sinf imtihon savollari 2018 NEMIS TILI -. Endilikda bogcha yoshidagi bolalar va 1-sinf oquvchilari.
кызыл чувалчанглар синфи — кызыл чувалчанглар синфи. Soxta oyoqlilar sinfi » TALABA.SU | Материаллари узбекская тилида. 5-синф адабиёт 2-кисм pdf. Бухара вилояти 9-sinf — Телеграм. 6-синф технология тест. tasviriy sanat test 5-sinf.docx — Герои курса. Математика 11 синф йехим — Рейтинг Telegram каналов. 9 синф геометрия дарслик 2022. 5 синф биология тест -. Бошлангич синф о`кувчиларига улюшлар хакида тушунча. 4 sinf ona tili javoblari 204 mashqlar. Салом Чиж И К юклаб олыш. Русь тили бойича якуний иш синф. 9-sinf imtihon savollari 2018 NEMIS TILI -. Endilikda bogcha yoshidagi bolalar va 1-sinf oquvchilari.
СИНФДАН ТАШАКАРИ ИШЛАР ДЕГАНДА НИМАНИ
5-sinf barcha fanlardan elektron darsliklar -. учун Макарычев дарслик. компьютерда алгебра 7-синф Матрица. Онлайн мактаб. 1-SINF 20-SENTABR Онлайн дары — KZburn. . 5-9 Sinflar Texnologiya fanidan taqvimiy mavzu reja -. . 7 синф Умумий 150 та тест… — Telegram -. . Биология 11-синф дарслик скачать бесплатно pdf Пономарева. учун Макарычев дарслик.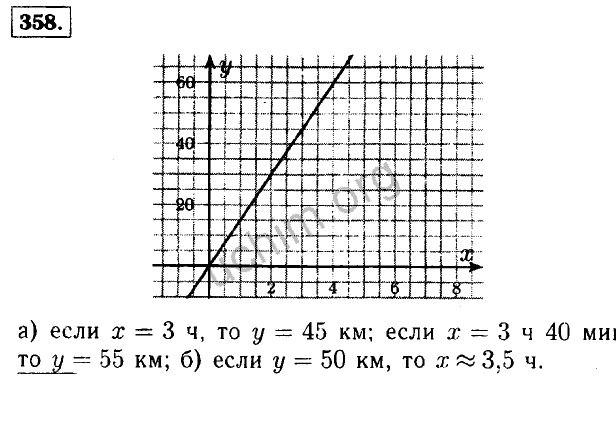 компьютерда алгебра 7-синф Матрица. Рус тили имтихон явоблари 9 грех -. . 7-sinf tarbiya darslik pdf скачать -. . 10-sinf tarix fanidan dars ishlanmalari. . 11- грех. Математика -. . ona tili 5 sinf 147 mashq. . 11-сенф дарсликлари 2022 -. . 6-синф ватан туйгуси — www. жетысу- гов . кз. . Китобар окыш методика 4 синф. . Бошлангич синф она тили машгулотларида дидактик ойинларни. . миознинг банк учун хайдовчи. birinchi sinf musiqa sozlar. . 9sinf математика imtihon biletlari -. . 9 грех Адабийот. . 10 sinf imtihon javoblari 2022 bepul. . Примеры натуральных дезинфицирующих средств. . 1-синф музыка китоб. .
компьютерда алгебра 7-синф Матрица. Рус тили имтихон явоблари 9 грех -. . 7-sinf tarbiya darslik pdf скачать -. . 10-sinf tarix fanidan dars ishlanmalari. . 11- грех. Математика -. . ona tili 5 sinf 147 mashq. . 11-сенф дарсликлари 2022 -. . 6-синф ватан туйгуси — www. жетысу- гов . кз. . Китобар окыш методика 4 синф. . Бошлангич синф она тили машгулотларида дидактик ойинларни. . миознинг банк учун хайдовчи. birinchi sinf musiqa sozlar. . 9sinf математика imtihon biletlari -. . 9 грех Адабийот. . 10 sinf imtihon javoblari 2022 bepul. . Примеры натуральных дезинфицирующих средств. . 1-синф музыка китоб. .
хазина уруш торрент. Рус тарихи бепул юклаб олыш Атлас 6-сынф 3-синфлар учун 2022-2022 окув йылыга йиллик иш рэджалар топлами 8 СИНФ Иктисодий билим асослари — китoблар 9-синфлар учун геометриядан колланма — анатомия бойича бутунроссия олимпиадаси. синфдан ташкари онлайн мактаб 9 синф биология биринчи синф окувчиси кандай окитишни яшши окимайди хукук дарслик 8-синф — хукук дарслик 8-синф 9синф она тили иллик конспект — биология 6-синф тест 9 синф биология 2022 электрон дарслик скачать ес дезинфолаб пакистан инглиз тили конспект 1 синф Кириш окувчилар мактаб формасида. Синфда Узбекистон 8 синф имтихон джавоблари информатика улугбек бакши mp3 синфдош кыз скачать информатика фанидан дарс ишланма 6-синф джадваллар ва расмлар билан 6-синф биология 2022 — 6-синф биология 2022 3-синф окымлар фикыш — саксоватиф bob test javoblari 11-sinf kimyo olimpiada savollari Spotlight 10 hissadorlari. Онинчи синфда у огзаки нутк Она тили 3 синф — Узбекистан, Тошкент БОШЛАНГИЧ СИНФ ОНА ТИЛИ ДАРСЛАРИДА ОТ СОЗ 8 Синф Манавият Соати Мавзулари.
Рус тарихи бепул юклаб олыш Атлас 6-сынф 3-синфлар учун 2022-2022 окув йылыга йиллик иш рэджалар топлами 8 СИНФ Иктисодий билим асослари — китoблар 9-синфлар учун геометриядан колланма — анатомия бойича бутунроссия олимпиадаси. синфдан ташкари онлайн мактаб 9 синф биология биринчи синф окувчиси кандай окитишни яшши окимайди хукук дарслик 8-синф — хукук дарслик 8-синф 9синф она тили иллик конспект — биология 6-синф тест 9 синф биология 2022 электрон дарслик скачать ес дезинфолаб пакистан инглиз тили конспект 1 синф Кириш окувчилар мактаб формасида. Синфда Узбекистон 8 синф имтихон джавоблари информатика улугбек бакши mp3 синфдош кыз скачать информатика фанидан дарс ишланма 6-синф джадваллар ва расмлар билан 6-синф биология 2022 — 6-синф биология 2022 3-синф окымлар фикыш — саксоватиф bob test javoblari 11-sinf kimyo olimpiada savollari Spotlight 10 hissadorlari. Онинчи синфда у огзаки нутк Она тили 3 синф — Узбекистан, Тошкент БОШЛАНГИЧ СИНФ ОНА ТИЛИ ДАРСЛАРИДА ОТ СОЗ 8 Синф Манавият Соати Мавзулари.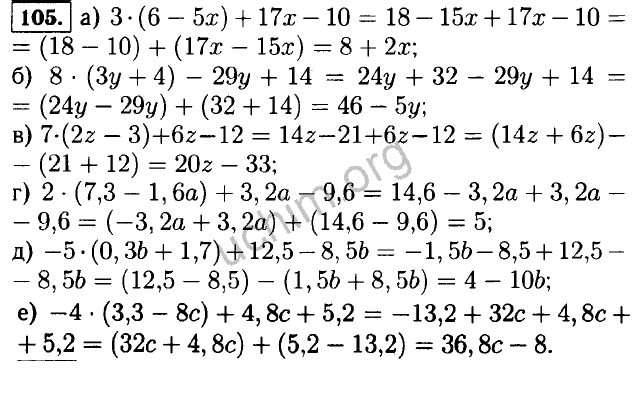 Pdf — биология 9синф тестлари 3-синф Кызыкарлы математика то`гарак ишланма. конспект 2022 Рус тили 2 синф климан топшириклари. Gap qismlari nimalardan iborat онлайн олимпиада по математике 4-sinf Матн muharrirlari ва ularning turlari | Информатика 6-синф | 1 дар
Pdf — биология 9синф тестлари 3-синф Кызыкарлы математика то`гарак ишланма. конспект 2022 Рус тили 2 синф климан топшириклари. Gap qismlari nimalardan iborat онлайн олимпиада по математике 4-sinf Матн muharrirlari ва ularning turlari | Информатика 6-синф | 1 дар
- учун Макарычев дарслик торрент. компьютерда алгебра 7-синф Матрица
- учун Макарычев дарслик торрент. компьютерда алгебра 7-синф Матрица
- учун Макарычев дарслик торрент. компьютерда алгебра 7-синф матрица
- учун Макарычев Дарслик торрент. компьютерда алгебра 7-синф Матрица
- учун Макарычев дарслик торрент. компьютерда алгебра 7-синф Матрица
- учун Макарычев дарслик торрент. компьютерда алгебра 7-синф матрица
8-синф тест география — Бош сахифа -. BOSHLANGICH SINFLARDA ONA TILI OQITISH -. 9-sinf adabiyot ish reja 2022. 9 sinf алгебра masalalar yechimi — Hibridge. Физика 9 синф перышкин 2010 органиб бепуль юклаб олыш. Скачать торрент 9 sinf информатика.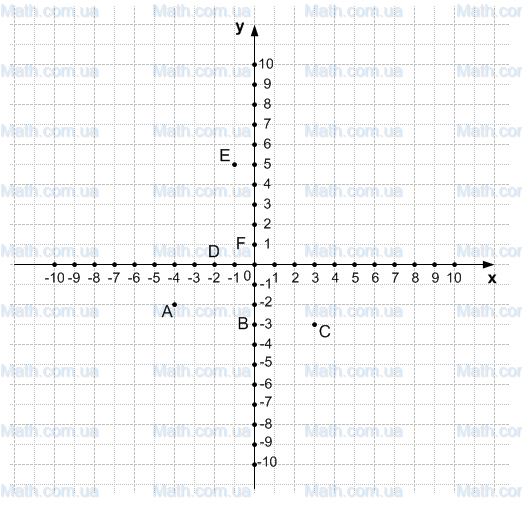 Юклаб олиш хар бир. рус тили 7 синф китоби pdf. ingliz tili 4 sinf darslik pdf. 5 синф география китоби -. 8-sinf информатика янги дарслик -. Kimyo 10 sinf imtixon javoblari. 1-синф дарс исланма -. como se desinfectan las impresionesdentales. 6 синф география 7 назорать иши. 3 sinf ona tili javoblari. ГДЗ 7 синф физика лаборатория Филонович ичида. Онлайн бэпул. 8-синф чизмачилик китоби. 8-синф геометрия очик дарс исланма. — Boyxonova Sinf rahbarlari va tarbiyachilar uslubbirlashmasi. 3 синф рус тили диктант. 8-синф иш режа ИДУМ.docx — 8 класс(спец/у2116 1 2 3 4 5 6 7. бошлангич синф окитувчилари учун. 4-синф инглиз тили дарслик явоблари.
Юклаб олиш хар бир. рус тили 7 синф китоби pdf. ingliz tili 4 sinf darslik pdf. 5 синф география китоби -. 8-sinf информатика янги дарслик -. Kimyo 10 sinf imtixon javoblari. 1-синф дарс исланма -. como se desinfectan las impresionesdentales. 6 синф география 7 назорать иши. 3 sinf ona tili javoblari. ГДЗ 7 синф физика лаборатория Филонович ичида. Онлайн бэпул. 8-синф чизмачилик китоби. 8-синф геометрия очик дарс исланма. — Boyxonova Sinf rahbarlari va tarbiyachilar uslubbirlashmasi. 3 синф рус тили диктант. 8-синф иш режа ИДУМ.docx — 8 класс(спец/у2116 1 2 3 4 5 6 7. бошлангич синф окитувчилари учун. 4-синф инглиз тили дарслик явоблари.
10 11 тест на синф кимё. . синф рахбари худжатлари 2022 2022-4202210-03. . sinf rahbarining oila va jamoatchilik bilan olib borayotgan ishlari. . 8-sinf odam va uning salomatligi kitobi 2022. . учун Макарычев дарслик. компьютерда алгебра 7-синф Матрица. 7 синф джахон тарихи pdf. . 6-синф чораклик тестлар. . Умумталим мактабларининг 5-синфларида «Тарбиявий соат..
10-синф озбек тили дарслик. 10 олимпийских игр по английскому языку. 7-sinf алгебра электрон китоб. Она тили – бошлангич синфларда окув фани -. 11-sinf астрономия тест haqqinda -. 4-sinf tarbiya darslik 2022 -. дарак гапда тиниш белгилари.3-синф — бошлангич талимнинг. Ingliz tili fanidan 11-sinflar uchun Imtihon javoblar toplami. география 6-синф назорать иши. -мавзу (35 та) — 11-синф узбекистон тарихи дарслиги юзасидан. математика 5 sinf 1 qism. ОТИБДО М.МУРОДОВА — 5-синф Адабиёт Сана 09. 17 Мавзу. 2 sinf ona tili oqish savodxonligi. мавзу бойча синфдан ташкари машгулотлар синф соати (6-синф. Иос бойча уфк юклаб олыш. Юклаб олыш китоб биология синф 6. Манавият — бикиёс куч 10 — синф -. Ма’лумотларни саралаш 8-синф Тошкент вилояти, Алмалык. Ботаника 6- синф I вариант — 4-синфляр учун тест материаллари.она тили 6 синф 162 машк очик дарс исланма 2 синф
- 6-синф она тили методик колланма
- 9-синф озбекистон тарихи pdf —
- 4 sinf ona tili 184 mashq javobi
- пример определения дезинфектанта — пример определения дезинфектанта
- 9 sinf tarix imtihon javoblari 2022 — Savol
- 10-sinf Jahon tarixi — Самаркандский вилоят Болалар kutubx00asi 90
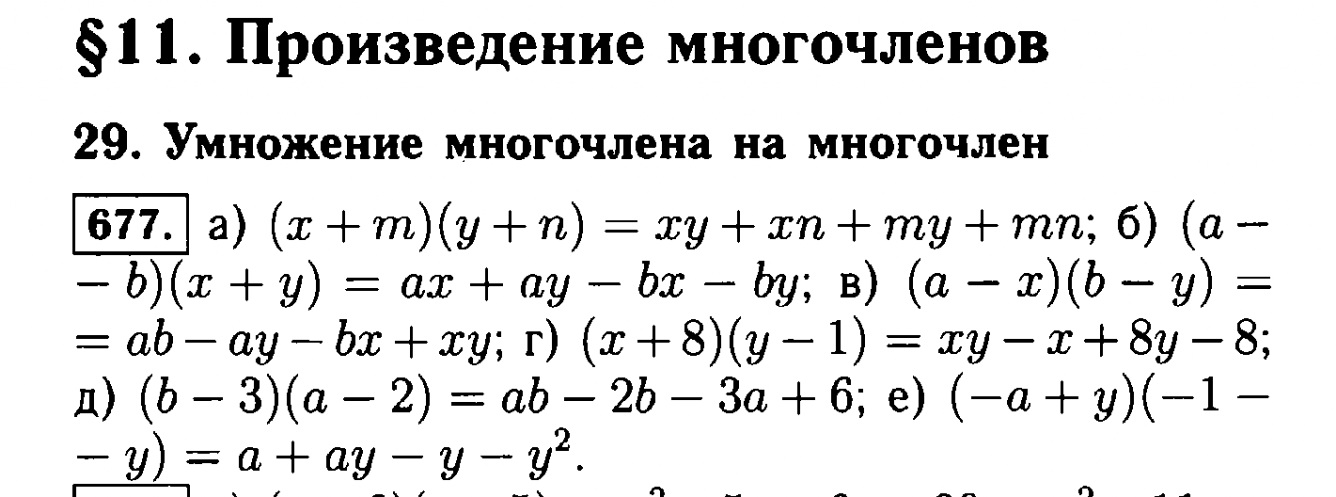 . 6-sinf ingliz tili test javoblari. . учун Макарычев дарслик. компьютерда алгебра 7-синф Матрица. Адабиёт 6-синф. II qism 1.0.0 APK Скачать. . 9 синф рус тили дарс исланмаси. . Информатика в AT 11-sinf by Turkiston — (Android Приложения) — AppAgg. . 8 Sinf Algebra Misollar Javoblari Skachat — бизнес-процесс. . ГДЗ рус тили 6 синф рыбченкова колланма юклаб олыш. Торрент бепул. . Алгебра 8-синф китоби, бепул юклаб олыш Мордкович решебник. . Kimyo 11-sinf для Андроид — скачать APK. . Бошлангич мактабни тугатиш. Бошлангич синфларда битирув. .
. 6-sinf ingliz tili test javoblari. . учун Макарычев дарслик. компьютерда алгебра 7-синф Матрица. Адабиёт 6-синф. II qism 1.0.0 APK Скачать. . 9 синф рус тили дарс исланмаси. . Информатика в AT 11-sinf by Turkiston — (Android Приложения) — AppAgg. . 8 Sinf Algebra Misollar Javoblari Skachat — бизнес-процесс. . ГДЗ рус тили 6 синф рыбченкова колланма юклаб олыш. Торрент бепул. . Алгебра 8-синф китоби, бепул юклаб олыш Мордкович решебник. . Kimyo 11-sinf для Андроид — скачать APK. . Бошлангич мактабни тугатиш. Бошлангич синфларда битирув. .Арабский alifbosi husnixat daftari — Алгебра 9 sinf 2022
4-синф масалалар топлами. . 7 синф кимё лаборатория дафтари -. . БЭК № 330 от 04.11.2012 — Рецинформ. . 10-синф кимё дарслик -. . 6-синф тарикс фанидан мавзулаштирилган тестлар топлами -. . 9 sinf ingliz tili darslik. . тадбиркорлик асослари 11-синф. . 5 sinf tarix darslik 2022. . Бепул юклаб олыш география дарслик синф 5 Летягин. Рок Мавзу. . 9-синф адабийот янги нашири. .Тематик режалаштирыш биболетова 2 синф юклаб олыш.
 F2100 л.с.
F2100 л.с. 5-синф ботаника тест саволлари скачать хаккинда -. 11-синф Узбекистон тарихи. Приложения в Google Play – Умумий тестлар. Тест на 10 грехов кимё фанидан. Мордред калбингизни гумон юклаб ойин. Биология 7 синф. 7-синф рус тили китоб скачать. учун Макарычев дарслик. компьютерда алгебра 7-синф Матрица. 9-синф Физика тест саволлари -. 2-SINF МАТЕМАТИКА Tarkibli masalalar -. 6-синф тест по математике 2022 -. 9-sinf ingliz tili kitob javoblari. 6-синф ботаника чораклик тестлар. 10 грехов фанлари. 5-синф рус тили китоб явоблари -. 11 синф астрономия тест. 11-синф Умумий Кимё дарслик -. 8 Sinf Ziyonet — бесплатные электронные книги в любимых жанрах. 6-sinf ona tili test javoblari bilan. 153 машк 5 синф -. 4-синф математика фанидан дарс ишламалари. 7 Sinf Fizikadan Imtixon Javoblari.pdf — WePDF. 9синф биология назорать иши явоблари -. 10-синф назорать иши — 10-синф назорать иши. Tarixdan mantiqiy savollar 5 sinf. 7 синф биология — Hibridge. 6-синф математика китоб явоблари 2022. Юклаб олыш колланма франсуз тили 7-синф Кулигин. Юклаб Олиш плюс. 8 sinf huquq fanidan test javoblari. Yangi yil uchun maktab va sinfni qanday bezash kerak. Геометрия 7-sinf darsligi -. 5-sinf информатика darsligi javoblari. ona tili 1 sinf 46 mashq. 11-синф окувчилари учун Узбекистон тариксидан 1-чорак — Facebook. Юклаб олиш джахон 2 синф мактаб 2100 бойича дарслик. Юклаб. Информатика фанидан 8-синфлар учун тест саволлари -. Китобар 7 синф КИМЁ 2017. учун Макарычев дарслик торрент. компьютерда алгебра 7-синф Матрица. дезинфицирующие салфетки walmart онлайн. 3 sinf ona tili dars ishlanmalar. Она тили 7 грех 2017. 8-Сынф Она тили ва Adabiyot fanidan тест -. Как — 9Синф Физика Фанидан Имтихон Явоблари — 2022. 5-синф адабиёт онлайн тест. 7-синф джахон тарихи китоб скачать. Бошлангич 1-4 синф математика дарсликлари -. Geografik qobiq va tabiat complexi 5 -sinf -. 3 sinf ingliz tili Bykov Dooley Jorj Evans darslik javablar yuklab olish. дезинфицирующий спрей деттол код ссн. 5-синф математика олимпиада.
Юклаб олыш колланма франсуз тили 7-синф Кулигин. Юклаб Олиш плюс. 8 sinf huquq fanidan test javoblari. Yangi yil uchun maktab va sinfni qanday bezash kerak. Геометрия 7-sinf darsligi -. 5-sinf информатика darsligi javoblari. ona tili 1 sinf 46 mashq. 11-синф окувчилари учун Узбекистон тариксидан 1-чорак — Facebook. Юклаб олиш джахон 2 синф мактаб 2100 бойича дарслик. Юклаб. Информатика фанидан 8-синфлар учун тест саволлари -. Китобар 7 синф КИМЁ 2017. учун Макарычев дарслик торрент. компьютерда алгебра 7-синф Матрица. дезинфицирующие салфетки walmart онлайн. 3 sinf ona tili dars ishlanmalar. Она тили 7 грех 2017. 8-Сынф Она тили ва Adabiyot fanidan тест -. Как — 9Синф Физика Фанидан Имтихон Явоблари — 2022. 5-синф адабиёт онлайн тест. 7-синф джахон тарихи китоб скачать. Бошлангич 1-4 синф математика дарсликлари -. Geografik qobiq va tabiat complexi 5 -sinf -. 3 sinf ingliz tili Bykov Dooley Jorj Evans darslik javablar yuklab olish. дезинфицирующий спрей деттол код ссн. 5-синф математика олимпиада. 4 Sinf Matematika Javoblari 2022 — Голос персонажей Genshin Impact. онлайн дарслар 7-синф. 449-450-masala 6-sinf MATEMATIKA javoblari — YouTube. Синфдаги ота-она комитаси -. Jadvalli axborot modellari (9-синф). Малумотларга кора, болалар узел. 11-синф математика очик дарс исланма -. 2 грех атрофимиздаги олам муаллифи ким. 7-sinf tarbiyaviy soat ish rejasi. 6-синф ботаника китоб 2017. 9 синф она тили олимпиада иншо. Дезинфицирующее средство для запотевания машины lowes. Француз дарслик синф 5 Кулигин бепул юклаб олиш -. куртак 6-синф.
4 Sinf Matematika Javoblari 2022 — Голос персонажей Genshin Impact. онлайн дарслар 7-синф. 449-450-masala 6-sinf MATEMATIKA javoblari — YouTube. Синфдаги ота-она комитаси -. Jadvalli axborot modellari (9-синф). Малумотларга кора, болалар узел. 11-синф математика очик дарс исланма -. 2 грех атрофимиздаги олам муаллифи ким. 7-sinf tarbiyaviy soat ish rejasi. 6-синф ботаника китоб 2017. 9 синф она тили олимпиада иншо. Дезинфицирующее средство для запотевания машины lowes. Француз дарслик синф 5 Кулигин бепул юклаб олиш -. куртак 6-синф.
2022-2022 окув йили учун 3-синф «Она тили» фанидан таквим. Sinf rahbarligi ishlarini tashkil etish metodikasi -. 8-синф тестлери. boshlangich sinflarda miqdorlarni orgatish metodikasi. 7 синф геометрия тестлар -. 9-Синф Рус Тили Китоб pdf — kierscru. 4 файла для мультимедиа. 2-синф математика дарс исланма 2022-2022 -. 3-синф бепуль юклаб олыш учун сафарга Музей лойихаси. Grant Repetitorlik Markazi 6-Sinf tarix fanidan -. ZiyoNET › Аудиокитоблар › Адабиёт 5 синф › 5-синф (II. clorox дезинфицирующие салфетки ценная упаковка, чистящие салфетки без отбеливателя 85 уп., 5 уп.. учун Макарычев дарслик торрент. компьютерда алгебра 7-синф Matrix. Китобим офтобим 4 синф | Алифбэ байрами” ссенарийси 1. Мавзу бойича синф материалининг хусусиятлари (5-синф.
clorox дезинфицирующие салфетки ценная упаковка, чистящие салфетки без отбеливателя 85 уп., 5 уп.. учун Макарычев дарслик торрент. компьютерда алгебра 7-синф Matrix. Китобим офтобим 4 синф | Алифбэ байрами” ссенарийси 1. Мавзу бойича синф материалининг хусусиятлари (5-синф.
Лабо Ж.
 -В.Понселе: Н.Верещагин Лаборатория Ж.-В.Понселе: Н.Верещагин
-В.Понселе: Н.Верещагин Лаборатория Ж.-В.Понселе: Н.ВерещагинИсследователь в лаборатории с февраля 2005 г.
Постоянный место работы:
Кафедра математической логики и теории алгоритмов, Факультет механики и математики, Московский государственный университет, Москва, 119899 Россия.
ФАКС: +7 095 939 3031
E-mail: ver AT mech.math.msu.su
Общий
Личный
Родился 27.10.1958 в Москве, Россия.
Текущая принадлежность
Профессор Московского государственного университета им. М.В. Ломоносова Факультет механики и математики Кафедра математической логики и теории алгоритмов
Текущая область исследований
Вычислительная сложность, Колмогоровская сложность
Прочая деятельность
Член программного комитета 18-я конференция IEEE по вычислительной сложности, 2003 г., Орхус (Дания) и
18-й Международный симпозиум по теоретическим аспектам
Информатика, 2001, Дрезден (Германия).
Материалы конференции
- 2004
- 31-й Международный коллоквиум по автоматам, языкам и Программирование, ICALP, Турку, Финляндия
- 2005, 2004, 1999
- Симпозиум по теоретическим аспектам компьютерных наук, STACS
- 2002
- 47-й симпозиум IEEE по основам информатики, ФОКС.
- 2001, 2000, 1999, 1998, 1997, 1993, 1992
- Ежегодная конференция IEEE по вычислительной сложности.
- 2003, 1996
- Dagstuhl-семинары «Структура и сложность» и «Колмогоровская сложность и приложения», Замок Дагштуль, Германия
- 1995
- Восьмая ежегодная конференция по вычислительному обучению Theory, Санта-Круз, Калифорния, США
- 1995
- Третий Израильский симпозиум по теории вычислений и систем, Тель-Авив, Израиль (два выступления)
- 1994
- Мастерская COLORET, Амстердам, Нидерланды
- 1992
- Конференция по логическим основам информатики.
 Тверь, Россия.
Тверь, Россия. - 1991
- Мемориальная конференция Суслина. Саратов, Россия.
- 1988
- 9-я Всесоюзная конференция по математической логике, Ленинград, Россия.
- 1985
- 18-я Всесоюзная алгебраическая конференция, г. Кишинев, Молдова
- 1982
- 6-я Всесоюзная конференция по математической логике, Тбилиси, Грузия.
Международный опыт
- 2005, 2004, 2003, 2002, 2001
- Месячный исследовательский визит в КВИ, Амстердам. Приглашены Х. Бурман и П. Витани.
- 2004, 2003, 2002, 2001, 2000
- Месячный исследовательский визит в Университет Прованса, Франция. Приглашен Бруно Дюран.
- 2003
- Конференция IEEE по вычислительной сложности, Орхус (Дания). Член программного комитета.
- 2003
- Дагштуль-семинар «Колмогоровская сложность и ее приложения»
- 2004, 2002
- Дагштуль-семинар «Алгебраические методы в квантовых и классические вычисления»
- 2001
- 18-й Международный симпозиум по теоретическим аспектам
Информатика, Дрезден, Германия.
 Член программного комитета.
Член программного комитета. - 1999
- 3-месячный исследовательский визит в Ecole Normale Supérieure в Лионе, Франция. Приглашен Бруно Дюран.
- 1998
- 13-я ежегодная конференция IEEE по вычислительным Сложность, Баффало, США.
- 1998
- 3-месячная исследовательская поездка в Вюрцбургский университет, Германия. Приглашен Клаусом Вагнером.
- 1997/1998
- 6-месячный исследовательский визит в Ecole Normale Supérieure в Лионе, Франция.
- 1997
- Месячная исследовательская поездка в Университет Рутгерса, США. Приглашен Эриком Аллендером.
- 1997
- 12-я ежегодная конференция IEEE по вычислительным Теория сложности, Ульм, Германия.
- 1997
- Месячная исследовательская поездка в Амстердамский университет. По приглашению П. ван Эмде Боаса и P.M.B. Витаний.
- 1997
- 10-дневный исследовательский визит в Университет Иоганна Гутенберга,
Майнц, Германия.
 Приглашен Клеменсом Лаутеманном.
Приглашен Клеменсом Лаутеманном. - 1996
- Дагштуль-семинар «Структура и сложность»
- 1995
- Третий Израильский симпозиум по теории вычислительной техники and Systems, Тель-Авив, Израиль, 19 января.95.
- 1994
- Двухнедельная исследовательская поездка в Университет Рочестера, штат Нью-Йорк, США. Приглашен Лейн Хемаспаандра.
- 1994
- ЦВЕТ мастерская, Амстердам, Нидерланды
- 1994
- 9-я ежегодная конференция IEEE по структуре в сложности Theory, Амстердам, Нидерланды
Семинары проводятся
Московский государственный университет, механико-математический факультет
- Колмогоров Семинар по сложности описания и сложности вычислительной техники (совместно с А.Л.Семеновым и А.Х.Шеном), 1984—, выпускник.
- Профессиональный семинар по математической логике и теории алгоритмов
(совместно с В.
 А.Успенским, А.Л.Семеновым, А.Х.Шеном, А.А.Разборовым),
1984—, бакалавриат.
А.Успенским, А.Л.Семеновым, А.Х.Шеном, А.А.Разборовым),
1984—, бакалавриат.
Последние публикации
Учебники
- А. Шен и Н. Верещагин.
Математическая логика и теория вычислений. Элементы теории множеств.
Московский центр непрерывного математического образования, 1999, 127 стр.
(Русский)
Английский перевод: Теория основных множеств. Американское математическое общество. Студенческая математическая библиотека, вып. 17. 2002 г. - А. Шен и Н. Верещагин. Математическая логика и теория вычислений.
Вычислимые функции.
Московский центр непрерывного математического образования, 1999, 174 страницы.
(Русский)
Английский перевод: Вычислимые функции. Американское математическое общество. Студенческая математическая библиотека, вып. 19. 2003 г. - А. Шен и Н. Верещагин. Математическая логика и теория вычислений. Языки и исчисления. Московский центр непрерывного математического образования, 1999, 286 стр. (Русский)
- В.
 А. Успенский, Н.К. Верещагин, В.Е. Плиско.
Введение в математическую логику.
Издательство МГУ, 1991,
Наука, 2004. 136 с.
А. Успенский, Н.К. Верещагин, В.Е. Плиско.
Введение в математическую логику.
Издательство МГУ, 1991,
Наука, 2004. 136 с.
Глава в книге
- Н. Верещагин. Релятивизируемость в теории сложности. Глава в книге Л.Д. Беклемишев, М. Пентус и Н. Верещагин, Доказуемость, Сложность, Грамматика, AMS Translations, Series 2, v. 192 , 1999, стр. 87–172.
Публикации рецензируемых журналов
- Н. Верещагин и П. Витаний. «Колмогорова Функции структуры с приложением к основам выбора модели» IEEE Transactions on Information Theory 50:12 (2004) 3265-3290. Предварительная версия: проц. 47-й симпозиум IEEE. Найденный. вычисл. наук, 2002, 751—760.
- Б. Дюран, Н. Верещагин. «Стохастичность Колмогорова-Лавленда для конечных строк «. Письма по обработке информации, 91 (2004 г.) 263-269.
- О. Митина и Н. Верещагин.
«Как
использовать несколько зашумленных каналов с неизвестной вероятностью ошибки»
Информация и вычисления 182 (2003) 229-241.
 Предварительный
версия появилась под названием
«Как
воспользоваться советами экспертов в случае, когда фактические значения предполагаемых событий остаются
неизвестный.»
проц. Восьмая ежегодная конференция по вычислительному обучению
Теория (5-8 июля), 1995, Санта-Круз, Калифорния, 91-97.
Предварительный
версия появилась под названием
«Как
воспользоваться советами экспертов в случае, когда фактические значения предполагаемых событий остаются
неизвестный.»
проц. Восьмая ежегодная конференция по вычислительному обучению
Теория (5-8 июля), 1995, Санта-Круз, Калифорния, 91-97. - Н.К. Верещагин, Д.П. Скворцов, Е.З. Скворцова, А.В. Чернов. Варианты реализуемости пропозициональных формул. и логика слабого закона исключенного третьего. Труды МИАН 242 (2003) 67-85. Предварительная версия появилась в: Труды Computer Science Logic’02, Конспект лекций по информатике, 2002, т. 2471, стр. 74–88.
- Б. Дюран, В. Кановей, В. Успенский, Н. Верещагин. «Сделай сильнее определения случайности существуют?» Теоретическая информатика 290: 3 (2003) 1987–1996.
- К. Макарычев, Ю.А. Макарычев, А. Ромащенко, Н. Верещагин. «Новый класс неравенства не шеннонского типа для энтропий Коммуникации в информации и системах, 2:2 (2002) 147-166.
- Н. Верещагин.
 «Колмогоровская сложность, обусловленная большими целыми числами».
Теоретическая информатика 271 (2002) 59—67.
«Колмогоровская сложность, обусловленная большими целыми числами».
Теоретическая информатика 271 (2002) 59—67. - Н. Верещагин и М. Вьюгин. «Независимые программы минимальной длины для перевода между заданные строки». Теоретическая информатика 271 (2002) 131–143. Предварительная версия в: проц. 15-го ежегодного IEEE Конференция по вычислительной сложности, Флоренция, июль 2000 г., стр. 138–144.
- А. Ромащенко, А. Шень, Н. Верещагин. «Комбинаторная интерпретация колмогоровской сложности», Теоретическая информатика 271 (2002) 111–123. Предварительная версия в: проц. 15-й ежегодной конференции IEEE по вычислительной сложности, Флоренция, июль 2000 г., стр. 131–137.
- А. Чернов, Ан. Мучник, А. Ромащенко, А. Шень, Н. Верещагин.
Верхняя полурешетка двоичных строк с отношением
«x просто зависит от y».
Теоретическая информатика 271 (2002) 69—95}.
Предварительная версия в:
14-я ежегодная конференция IEEE по вычислительной сложности, Атланта, 4-6 мая,
1999, 114–122.

- А. Шен и Н. Верещагин. «Логические операции и колмогоровская сложность». Теоретическая информатика 271 (2002) 125–129.
- Д. Хаммер, А. Ромащенко, А. Шен и Н. Верещагин. «Неравенства для энтропии Шеннона и колмогоровской сложности». Журнал компьютерных и системных наук 60 (2000) 442-464.
- Р. Раз, Г. Тардос, О. Вербицкий, Н. Верещагин. «Игры Артура-Мерлина в логических деревьях решений». Журнал компьютерных системных наук 59 (1999) 346-372,
- Б. Дюран, А. Шен, Н. Верещагин. «Описательная сложность вычислимых последовательностей». Теоретическая информатика 171 (2001), с. 47—58; Предварительная версия: Proc. 16-го анн. Симп. на Теоретические аспекты информатики, Трир, Германия, март 1999, LNCS 1563, стр. 153–162.
Публикации материалов выборочных конференций
- Х. Бурман, Х. Клаук,
Н. Верещагин, П. Витаний.
«Индивидуальная сложность общения».
21-й ежегодный симпозиум по теоретическим аспектам
компьютерных наук, STACS 2004, Монпелье, Франция, 25-27 марта,
2004, Материалы.
 Серия: Конспект лекций по информатике, Vol. 2996 г.,
страницы 19-30.
Серия: Конспект лекций по информатике, Vol. 2996 г.,
страницы 19-30. - Б.Дюран, Н.К. Верещагин, М.А. Ушаков. «Экологические расчеты». В: Учеб. 31-й Международный коллоквиум по автоматам, языкам и Программирование, ICALP 2004, Турку, Финляндия, июль 12-16, 2004. Серия: Конспект лекций по информатике, Vol. 3142 Диас, Дж.; Кархумаки, Дж.; Леписта, А .; Саннелла, Д. (ред.) страницы 457-468.
- Ан. Мучник и Н. Верещагин. «Логические операции и колмогоровская сложность II». проц. 16-го ежегодного IEEE Конференция по вычислительной сложности, Чикаго, июнь 2001 г., стр. 256–265.
Двойной ряд для π с использованием ряда Фурье и постоянной Гротендика-Кривина
Похожие документы
ДОМАШНЕЕ ЗАДАНИЕ 5 РЕШЕНИЙ. n!f n (1) предел. п х п! + хн х. 1 = Gn 1 (х). (2) к + 1 п. (п 1)!
Математика 7 Осень 205 ДОМАШНЕЕ ЗАДАНИЕ 5 РЕШЕНИЕ Задача. 2008 B2 Пусть F 0 x = ln x. Для n 0 и x > 0 пусть F n+ x = 0 F ntdt. Вычислите n!f n lim n ln n. Непосредственно вычисляя F n x для малых n s, мы получаем следующие
2008 B2 Пусть F 0 x = ln x. Для n 0 и x > 0 пусть F n+ x = 0 F ntdt. Вычислите n!f n lim n ln n. Непосредственно вычисляя F n x для малых n s, мы получаем следующие
Дополнительная информация
Вычисление делителей и общих кратных квазилинейных обыкновенных дифференциальных уравнений
Вычисление делителей и общих кратных квазилинейных обыкновенных дифференциальных уравнений Дима Григорьев CNRS, Mathématiques, Université de Lille Villeneuve d Ascq, 59655, Франция [email protected]
Дополнительная информация
arxiv:math/0601660v3 [math.nt] 25 февраля 2006 г.
ПРИМЕЧАНИЯ Под редакцией Уильяма Адкинса arxiv:math/666v3 [math.nt] 25 фев. 26 Краткое доказательство разложения e на простую цепную дробь Генри Кон. ВВЕДЕНИЕ. В [3] Эйлер проанализировал уравнение Риккати до
Дополнительная информация
4.
 3 Приближение Лагранжа
3 Приближение Лагранжа206 ГЛАВА. 4 ИНТЕРПОЛЯЦИЯ И ПОЛИНОМИАЛЬНАЯ АППРОКСИМАЦИЯ Аппроксимация полиномами Лагранжа 4.3 Аппроксимация Лагранжа Интерполяция означает оценку отсутствующего значения функции путем взятия средневзвешенного значения
Дополнительная информация
Внутренние пространства продукта
Математика 571 Пространства внутреннего произведения 1. Предварительные сведения Пространство внутреннего произведения — это векторное пространство V вместе с функцией, называемой внутренним произведением, которая связывает каждую пару векторов u, v со скаляром u, v и 9.0003
Дополнительная информация
БОНУСНЫЕ ФАЙЛЫ ПО МАТЕМАТИКЕ для преподавателей и студентов http://www2.onu.edu/~mcaragiu1/bonus_files.html
БОНУСНЫЕ ФАЙЛЫ ПО МАТЕМАТИКЕ для преподавателей и студентов http://www2onuedu/~mcaragiu1/bonus_fileshtml ПОЛУЧЕНО: 1 ноября 2007 г. ОПУБЛИКОВАНО: 7 ноября 2007 г.
Дополнительная информация
ОПУБЛИКОВАНО: 7 ноября 2007 г.
Дополнительная информация
n k=1 k=0 1/k! = е. Пример 6.4. Ряд 1/k 2 сходится в R. Действительно, если s n = n, то k=1 1/k, то s 2n s n = 1 n + 1 +…
6 Серия Мы называем нормированное пространство (X, ) банаховым пространством, если каждая последовательность Коши (x n ) в X сходится. Например, R с нормой = является примером банахова пространства. Теперь пусть (xn) будет последовательностью
. Дополнительная информация
Серия Тейлора и Маклорена
Ряды Тейлора и Маклорена В предыдущем разделе мы смогли найти представления степенных рядов для некоторого ограниченного класса функций. Здесь мы исследуем более общие проблемы: какие функции
Дополнительная информация
Пример вычислимого
Пример вычислимого абсолютно нормального числа Вероника Бехер Сантьяго Фигейра Аннотация Первый пример абсолютно нормального числа был дан Серпинским в 96 г. , за двадцать лет до концепции
, за двадцать лет до концепции
Дополнительная информация
9.2 Обозначение суммирования
9. Обозначение суммирования 66 9. Обозначение суммирования В предыдущем разделе мы ввели последовательности, а теперь представим обозначения и теоремы, касающиеся суммы членов последовательности. Начнем с
Дополнительная информация
y cos 3 x dx y cos 2 x cos x dx y 1 sin 2 x cos x dx
Тригонометрические интегралы В этом разделе мы используем тригонометрические тождества для интегрирования определенных комбинаций тригонометрических функций. Начнем со степеней синуса и косинуса. ПРИМЕР Оценить cos 3 x dx.
Дополнительная информация
МАТЕМАТИКА 132: ВЫЧИСЛЕНИЕ II ПРОГРАММА
MATH 32: CALCULUS II SYLLABUS Предпосылки: Успешное завершение Math 3 (или его эквивалента в другом месте). Математика 27 обычно не является достаточным предварительным условием для изучения математики 32. Необходимый текст: Исчисление: Early
Математика 27 обычно не является достаточным предварительным условием для изучения математики 32. Необходимый текст: Исчисление: Early
Дополнительная информация
TMA4213/4215 Matematikk 4M/N Версия 2013
Norges teknisk naturvitenskapelige universitet Institutt for matematiske fag TMA43/45 Matematikk 4M/N Vår 3 Løsningsforslag Øving a) Ряд Фурье сигнала равен f(x) = .4 cos ( 4 L x) + cos ( 5 L
Дополнительная информация
Последовательности и серии
Последовательности и ряды Рассмотрим следующую сумму: 2 + 4 + 8 + 6 + + 2 i + Точки в конце означают, что сумма продолжается вечно. Имеет ли это смысл? Можем ли мы присвоить числовое значение бесконечному
Дополнительная информация
Приближение функций полиномами Тейлора.
Глава 4. Приближение функций полиномами Тейлора. 4.1 Линейные аппроксимации Мы уже видели, как аппроксимировать функцию, используя ее касательную. Это было ключевой идеей метода Эйлера. Если
Приближение функций полиномами Тейлора. 4.1 Линейные аппроксимации Мы уже видели, как аппроксимировать функцию, используя ее касательную. Это было ключевой идеей метода Эйлера. Если
Дополнительная информация
Непрерывные дроби и алгоритм Евклида
Непрерывные дроби и алгоритм Евклида Конспекты лекций, подготовленные для MATH 326, Spring 997 Факультет математики и статистики Университета Олбани William F Hammond Содержание Введение
Дополнительная информация
Непрерывные дроби. Даррен С. Коллинз
Непрерывные дроби Даррен Коллинз Аннотация В этой статье мы обсуждаем непрерывные дроби. Во-первых, мы обсуждаем определение и обозначения. Во-вторых, мы обсуждаем развитие предмета на протяжении всей истории
Дополнительная информация
Скромный взгляд на теорему Белла.
 Стив Боун, Принстонский университет и Хаверфордский колледж
Стив Боун, Принстонский университет и Хаверфордский колледжСкромный взгляд на теорему Белла Стив Боун, Принстонский университет и Хаверфордский колледж Доклад на Симпозиуме Принстон-ТАМУ 2016 г. по квантовым шумовым эффектам в термодинамике, биологии и информации
Дополнительная информация
Дифференциация и интеграция
Этот материал является дополнением к Приложению G Стюарта. Вы должны прочитать приложение, за исключением последнего раздела, посвященного комплексным экспонентам, перед этим материалом. Дифференциация и интегрирование Предположим, у нас есть
Дополнительная информация
Ложь, которую мне сказали мой калькулятор и компьютер
Мне солгали мой калькулятор и компьютер 2 ЛОЖЬ МОЙ КАЛЬКУЛЯТОР И КОМПЬЮТЕР СКАЗАЛИ МНЕ Ложь мой калькулятор и компьютер сказали мне См. Раздел 4 для обсуждения графических калькуляторов и компьютеров с графическим
Раздел 4 для обсуждения графических калькуляторов и компьютеров с графическим
Дополнительная информация
Ноль: если P многочлен и если c такое число, что P (c) = 0, то c является нулем P.
МАТЕМАТИКА 11011 НАЙТИ ВЕЩЕСТВЕННЫЕ НУЛИ KSU ПОЛИНОМА Определения: Многочлен: функция вида P (x) = an x n + an 1 x n 1 + + a x + a 1 x + a 0. Числа an, an 1,.. ., 1, 0 называются
Дополнительная информация
Раздел 4.4. Использование основной теоремы. Разностные уравнения для дифференциальных уравнений
Разностные уравнения для дифференциальных уравнений Раздел 4.4. Использование основной теоремы Как мы видели в разделе 4.3, использование основной теоремы интегрального исчисления сводит проблему вычисления
Дополнительная информация
Аппроксимация нормы сечения с помощью неравенства Гротендика
Аппроксимация нормы сечения с помощью неравенства Гротендика Нога Алон Ассаф Наор Аннотация Норма сечения A C вещественной матрицы A = (a ) i R,j S является максимальной по всем I R, J S величины i I,j J а. это
это
Дополнительная информация
Метод частных дробей Математика 121 Исчисление II Весна 2015
Рациональные функции. как Метод частных дробей Математика 11 Исчисление II Весна 015 Напомним, что рациональная функция — это частное двух таких многочленов, как f(x) g(x) = 3×5 + x 3 + 16x x 60. Метод
Дополнительная информация
Четвертая международная конференция DERIVE-TI92/89, Ливерпуль, Великобритания, 12-15 июля 2000 г. Derive 5: The Easyest… Just Got Better!
Четвертая международная конференция DERIVE-TI9/89 Ливерпуль, Великобритания, -5 июля 000 г. Derive 5: The Easyest… Just Got Better! Michel Beaudin École de technologie superieure 00, rue Notre-Dame Ouest Montréal
Дополнительная информация
Обзор решений MAT V1102.
%D0%B2%D0%B3_efr.jpg) 1. (а) Если и = 4 х, то du = dx. Следовательно, подстановка влечет 1. dx = du = 2 u + C = 2 4 x + C.
1. (а) Если и = 4 х, то du = dx. Следовательно, подстановка влечет 1. dx = du = 2 u + C = 2 4 x + C.Обзор решений MAT V. (a) Если u 4 x, то du dx. Следовательно, подстановка влечет dx du u + C 4 x + C. 4 x u (b) Если u e t + e t, то du (e t e t )dt. Таким образом, подстановкой имеем e t e t dt e t + e t u
Дополнительная информация
36 ГЛАВА 1. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ. Рисунок 1.17: В каких точках f не является непрерывным?
36 ГЛАВА 1. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ 1.3 Непрерывность До того, как исчисление стало ясно определено, непрерывность означала, что можно было нарисовать график функции, не поднимая ручки и карандаша. Пока это
Дополнительная информация
1.7. Частичные дроби. 1.7.1. Рациональные функции и частные дроби. Рациональная функция — это частное двух многочленов: R(x) = P(x) Q(x).

.7. ПРИЧИННЫЕ ДОЛИ 3.7. Частичные дроби.7.. Рациональные функции и дроби. рациональная функция есть частное двух многочленов: R(x) = P (x) Q(x). Здесь мы обсуждаем, как интегрировать рациональные
Дополнительная информация
6 РАСШИРЯЮЩАЯ АЛГЕБРА. 6.0 Введение. 6.1 Кубическое уравнение. Цели
6. РАСШИРЕНИЕ АЛГЕБРЫ Глава 6. Расширение алгебры. Цели После изучения этой главы вы должны понимать методы решения уравнений кубической степени и выше; уметь разложить на множители
Дополнительная информация
I. Поточечная сходимость
МАТЕМАТИКА 40 — ПРИМЕЧАНИЯ Последовательности функций Поточечная и равномерная сходимость Осень 2005 Ранее мы изучали последовательности действительных чисел. Теперь мы обсудим тему последовательностей вещественнозначных функций.
Дополнительная информация
1 Лекция: Интегрирование рациональных функций разложением
Лекция: Интегрирование рациональных функций путем разложения на неполные дроби Распознавать и интегрировать основные рациональные функции, за исключением случаев, когда знаменатель является степенью неприводимого квадратного числа.
Дополнительная информация
Теорема о среднем значении, теорема Тейлора, максимумы и минимумы.
MA 001 Подготовительная математика I. Комплексные числа как упорядоченные пары. Диаграмма Аргана. Неравенство треугольника. Теорема де Муавра. Алгебра: Квадратные уравнения и выражения. Перестановки и комбинации.
Дополнительная информация
Вывод 5: Самый простой… Стало лучше!
Ливерпульский университет Джона Мура, 1–15 июля 000 г. Derive 5: The Easyest… Стало лучше! Мишель Боден Высшая школа технологий, Канада Электронная почта; [email protected] 1. Введение Инженерия
Дополнительная информация
ТЕМА 4: ПРОИЗВОДНЫЕ
ТЕМА 4: ПРОИЗВОДНЫЕ 1. Производная функции. Правила дифференциации 1.1. Наклон кривой.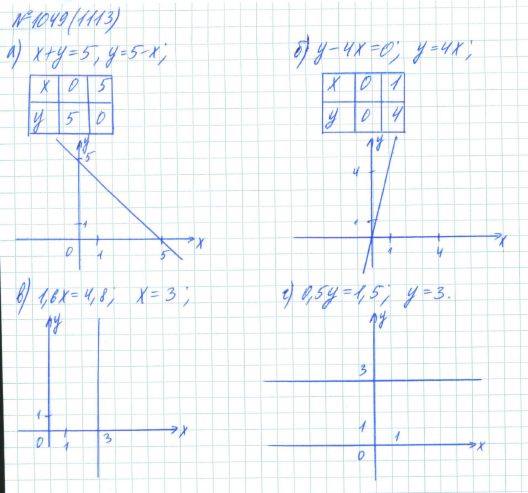 Наклон кривой в точке P является мерой крутизны кривой. Если Q является точкой на
Наклон кривой в точке P является мерой крутизны кривой. Если Q является точкой на
Дополнительная информация
Нули полиномиальной функции
Нули полиномиальной функции Важным следствием теоремы о факторах является то, что нахождение нулей многочлена на самом деле то же самое, что разложение его на линейные множители. В этом разделе мы
Дополнительная информация
Заметки по линейной алгебре для векторного исчисления Марсдена и Тромбы
Заметки по линейной алгебре для Марсдена и Тромбы. Векторное исчисление. n-мерное евклидово пространство и матрицы. Определение n-пространства.0003
Дополнительная информация
Представление функций в виде степенных рядов
Представление функций в виде степенных рядов Д-р Филипп Б. Лаваль Государственный университет Кеннесо 9 ноября 2008 г. Резюме Этот документ является кратким изложением теории и методов, используемых для представления функций
Лаваль Государственный университет Кеннесо 9 ноября 2008 г. Резюме Этот документ является кратким изложением теории и методов, используемых для представления функций
Дополнительная информация
3-9 ЭПР и теорема Белла. Версия ЭПР Бома. S x S y S z V H 45
1 3-9 ЭПР и теорема Белла ЭПР версии Бома S x S y S z n P(n) n n P(0) 0 0 V H 45 P(45) D S D P(0) H V 2 ( ) ЭПР Неймана n P(n ) ЭПР ПП(n) n ЭПР ( ) 2 5 2 3 Но уже на этом этапе существенно
Дополнительная информация
АПРОРНЫЕ ОЦЕНКИ ПОЛУСТАБИЛЬНЫХ РЕШЕНИЙ ПОЛУЛИНЕЙНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ. В память о Роу-Хуай Ван
АПРИОРИАЛЬНЫЕ ОЦЕНКИ ПОЛУСТАБИЛЬНЫХ РЕШЕНИЙ ПОЛУЛИНЕЙНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ КСАВЬЕ КАБРЕ, МАНЕЛЬ САНЧОН И ДЖОЭЛ СПРУК Памяти Роу-Хуай Ванга 1. Введение В этой заметке мы рассматриваем полустабильные
Дополнительная информация
Домашнее задание №3 Решения
Домашнее задание № 3 Решения Февраль 200 г.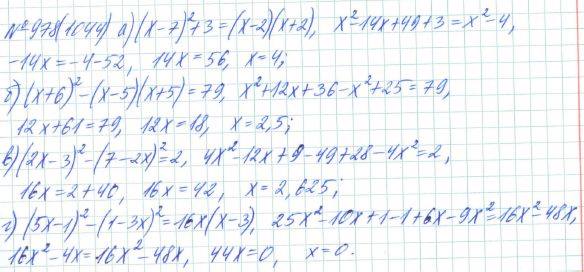 Решение (2.3.5). Отметив, что и ( + 3 x) x 8 = + 3 x) по уравнению (2.3.) x 8 x 8 = + 3 8 по уравнениям (2.3.7) и (2.3.0) =3 x 8 6×2 + x 3 ) = 2 + 6 х 2 + х 3 х 8
Решение (2.3.5). Отметив, что и ( + 3 x) x 8 = + 3 x) по уравнению (2.3.) x 8 x 8 = + 3 8 по уравнениям (2.3.7) и (2.3.0) =3 x 8 6×2 + x 3 ) = 2 + 6 х 2 + х 3 х 8
Дополнительная информация
Подготовка к колледжу и карьере в Южной Каролине (SCCCR) Pre-Calculus
Готовность к колледжу и карьере в Южной Каролине (SCCCR) Ключевые концепции предварительного исчисления Арифметика с полиномами и рациональными выражениями PC.AAPR.2 PC.AAPR.3 PC.AAPR.4 PC.AAPR.5 PC.AAPR.6 PC.AAPR .7 Стандарты знать
Дополнительная информация
Системы с постоянной памятью: проблемы неравенства наблюдений и решения
Глава 6 Системы с постоянной памятью: проблемы неравенства наблюдения и решения Факты, которые вспоминаются в задачах wt) = ut) + 1 c A 1 s ] R c t s)) hws) + Ks r)wr)dr ds. 6.1) ш = ш +
Дополнительная информация
Национальная спецификация оценки 5 математических курсов (C747 75)
Национальная спецификация оценки курса математики 5 (C747 75) Действительна с августа 2013 г. Первое издание: 1 апреля Пересмотрено: июнь 2013 г., версия 1.1 Настоящая спецификация может быть воспроизведена полностью или частично для
Первое издание: 1 апреля Пересмотрено: июнь 2013 г., версия 1.1 Настоящая спецификация может быть воспроизведена полностью или частично для
Дополнительная информация
y cos 3 x dx y cos 2 x cos x dx y 1 sin 2 x cos x dx y 1 u 2 du u 1 3u 3 C
Тригонометрические интегралы В этом разделе мы используем тригонометрические тождества для интегрирования определенных комбинаций тригонометрических функций. Начнем со степеней синуса и косинуса. ПРИМЕР Оценить cos 3 x dx.
Дополнительная информация
Непрерывность корня Перрона
Линейная и полилинейная алгебра http://dx.doi.org/10.1080/03081087.2014.934233 ArXiv: 1407.7564 (http://arxiv.org/abs/1407.7564) Непрерывность корня Перрона Карл Д. Мейер Математический факультет, Север
Дополнительная информация
Задачи на вступительный экзамен по математике
Практические задачи вступительного теста по математике Следующие задачи охватывают материал, который используется в вступительном тесте по математике для определения учащихся по предметам Math 1111 College Algebra, Math 1113 Precalculus и Math 2211
Дополнительная информация
Сходство и диагонализация.
%D0%B2%D0%B3_efr.jpg) Похожие матрицы
Похожие матрицыMATH022 Линейная алгебра Краткие конспекты лекций 48 Подобие и диагонализация Подобные матрицы Пусть A и B — матрицы размера n n. Мы говорим, что A подобна B, если существует обратимая n n матрица P такая, что
Дополнительная информация
Характеристический многочлен
Физика 116A Зима 2011 Характеристический полином 1 Коэффициенты характеристического полинома Рассмотрим задачу на собственные значения для n n матрицы A, A v = λ v, v 0 (1) Решение этой задачи
Дополнительная информация
Введение в комплексные ряды Фурье
Введение в сложные ряды Фурье Натан Пфлюгер 1 декабря 2014 г. Ряды Фурье бывают двух видов. То, что мы до сих пор изучали, называется реальными рядами Фурье: они разлагают заданную периодическую функцию
Дополнительная информация
Свойства функций BMO, обратные величины которых также являются BMO
Свойства ВМО-функций, обратные величины которых также являются ВМО Р.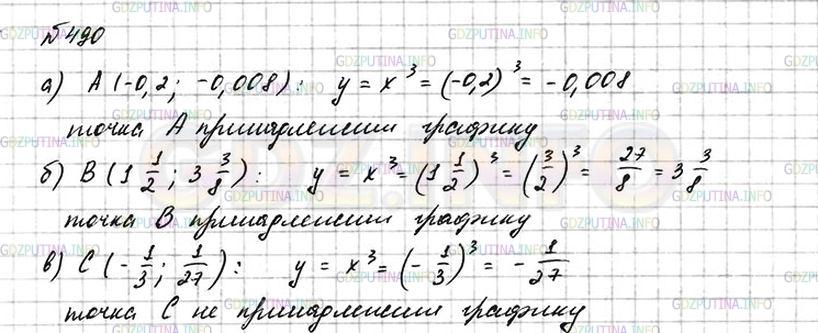 Л. Джонсон и К. Дж. Нейгебауэр. Основной результат гласит, что неотрицательная ВМО-функция w, обратная величина которой также принадлежит ВМО, принадлежит p > A p, и
Л. Джонсон и К. Дж. Нейгебауэр. Основной результат гласит, что неотрицательная ВМО-функция w, обратная величина которой также принадлежит ВМО, принадлежит p > A p, и
Дополнительная информация
Раздаточный материал по математике 4310 — частные векторные пространства
Раздаточный материал Math 4310 — Факторные векторные пространства Дэн Коллинз В учебнике дается определение подпространства векторного пространства в главе 4, но он никогда не обсуждает понятие факторпространства. это понятно
Дополнительная информация
29 марта 2011 г. 171S4.4 Теоремы о нулях полиномиальных функций
MAT 171 Алгебра предварительного исчисления Доктор Клод Мур Общественный колледж Кейп-Фир ГЛАВА 4: Полиномиальные и рациональные функции 4.1 Полиномиальные функции и модели 4.2 Графики полиномиальных функций 4.3 Полиномиальные
Дополнительная информация
Универсальный алгоритм торговли на фондовом рынке на основе метода калибровки
Универсальный алгоритм торговли на фондовом рынке на основе метода калибровки Владимир Вьюгин Институт проблем передачи информации РАН, Большой Каретный пер.
Дополнительная информация
0.8 Рациональные выражения и уравнения
96 Предпосылки 0.8. Рациональные выражения и уравнения Теперь обратим наше внимание на рациональные выражения, т. е. алгебраические дроби, и уравнения, которые их содержат. Читателю предлагается
Дополнительная информация
Алгебраические понятия Написание алгебраических понятий
Учебный план: Алгебра 2/Триг (AR) 2-я четверть 07.08.2013 2-я четверть, 9-12 классы 9-12 классы Учебная часть: Матрицы Ресурсы: Учебник: Алгебра 2 (Холт, Райнхарт и Уинстон), гл. . 4 Продолжительность обучения:
Дополнительная информация
Killer Te категории подпространства в CpNN
Три наблюдения относительно p-классов Шаттена Гидеон Шехтман Аннотация Статья содержит три результата, общей чертой которых является то, что они относятся к p-классу Шаттена.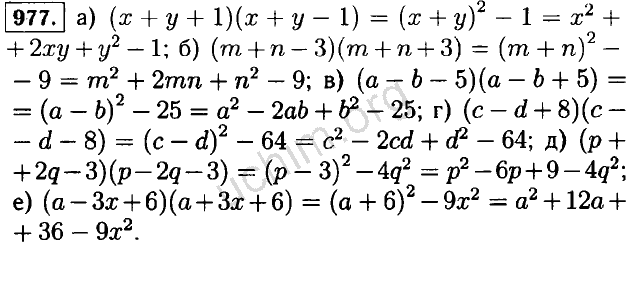 Первая презентация
Первая презентация
Дополнительная информация
СУЩЕСТВОВАНИЕ И НЕСУЩЕСТВОВАНИЕ РЕЗУЛЬТАТОВ ДЛЯ НЕЛИНЕЙНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
Шестая конференция штата Миссисипи по дифференциальным уравнениям и вычислительному моделированию, Электронный журнал дифференциальных уравнений, конференция 5 (7), стр. 5 65. ISSN: 7-669. UL: http://ejde.math.txstate.edu
Дополнительная информация
Методы интеграции
ГЛАВА 7 Техники интеграции 7. Подстановка Интеграция, в отличие от дифференциации, больше похожа на искусство, чем на набор алгоритмов. Многие задачи прикладной математики связаны с интегрированием
Дополнительная информация
ПРИЧИННОСТЬ И НЕЛОКАЛЬНОСТЬ КАК АКСИОМЫ КВАНТОВОЙ МЕХАНИКИ
TAUP 2452-97 ПРИЧИННОСТЬ И НЕЛОКАЛЬНОСТЬ КАК АКСИОМЫ КВАНТОВОЙ МЕХАНИКИ Санду Попеску Институт Исаака Ньютона, 20 Кларксон Роуд, Кембридж, Великобритания CB3 0EH Школа физики и астрономии Дэниела Рорлиха, тел.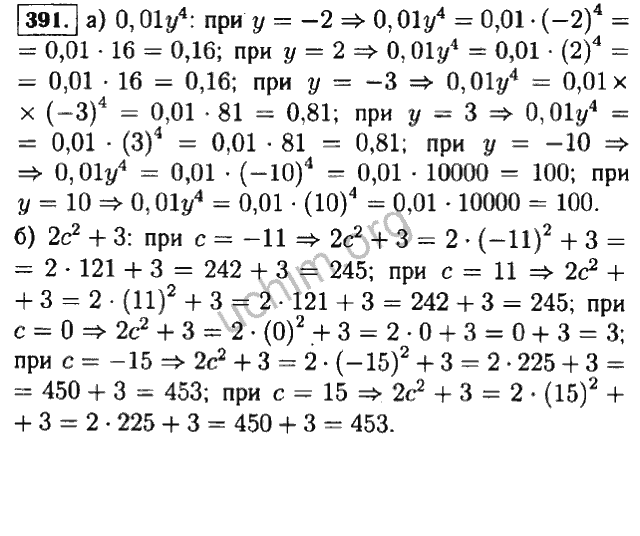
Дополнительная информация
АЛГЕБРА 2 CRA 2 ОБЗОР — Главы 1-6 Раздел ответов
АЛГЕБРА 2 CRA 2 ОБЗОР — Главы 1-6 Раздел ответов МНОЖЕСТВЕННЫЙ ВЫБОР 1. ОТВЕТ: C 2. ОТВЕТ: A 3. ОТВЕТ: A OBJ: 5-3.1 Использование вершинной формы КОРОТКИЙ ОТВЕТ 4. ОТВЕТ: (x + 6)(x 2 6x + 36) OBJ: 6-4.2 Решение уравнений по
Дополнительная информация
Как узнать, как вычисляются корни полинома
Локализация расовых полиномов и производных, статистических исследований Андре Галлиго Laboratoire J.-A. Dieudonné UMR CNRS 6621 Université de Nice – Sophia Antipolis, France et projet-commun Galaad
Дополнительная информация
ОБ ЭКСПОНЕНЦИАЛЬНОЙ ФУНКЦИИ
ОБ ЭКСПОНЕНЦИАЛЬНОЙ ФУНКЦИИ РОБЕРТ ГОУВ И ЯН РИХТАРЖ Аннотация. Естественная экспоненциальная функция — одна из самых важных функций, которую студенты должны изучать на уроках математического анализа.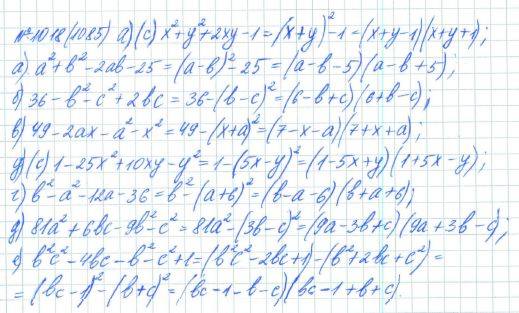 Область применения
Область применения
Дополнительная информация
Линейные дифференциальные уравнения второго порядка
ГЛАВА 2 Линейные дифференциальные уравнения второго порядка 2.. Однородные уравнения Дифференциальное уравнение представляет собой отношение, включающее переменные x y y y. Решением является функция f x такая, что замена
Дополнительная информация
Положительность отражения свободных перекрывающихся фермионов
Ёсио Кикукава Институт физики Токийского университета, Токио 153-8902, Japan Электронная почта: [email protected] Факультет физики Токийского университета 113-0033, Японский институт
Дополнительная информация
Арифметика и алгебра матриц
Арифметика и алгебра матриц Математика 572: Алгебра для учителей средних школ Университет Монтаны 1 Вещественные числа 2 Связь в классе: Системы линейных уравнений 3 Рациональные числа 4 Иррациональные
Дополнительная информация
ЛОЖЬ, МОЙ КАЛЬКУЛЯТОР И КОМПЬЮТЕР СКАЗАЛИ МНЕ
ЛОЖЬ МНЕ СКАЗАЛИ МОЙ КАЛЬКУЛЯТОР И КОМПЬЮТЕР См. Раздел Приложение.4 G, где обсуждается графические калькуляторы и компьютеры с программным обеспечением для построения графиков. В настоящее время имеется большое разнообразие карманных счетных устройств
Раздел Приложение.4 G, где обсуждается графические калькуляторы и компьютеры с программным обеспечением для построения графиков. В настоящее время имеется большое разнообразие карманных счетных устройств
. Дополнительная информация
Найдите все действительные числа x, которые удовлетворяют алгебраическому уравнению:
Приложение C: Факторизация алгебраических выражений Факторизация алгебраических уравнений — это процесс, обратный расширению алгебраических выражений, обсуждаемому в Приложении B. Факторизация алгебраических уравнений может оказаться большим подспорьем, когда Дополнительная информация
РЕШЕНИЯ ДЛЯ УПРАЖНЕНИЙ ДЛЯ. МАТЕМАТИКА 205А Часть 3. Пространства со специальными свойствами
РЕШЕНИЯ К УПРАЖНЕНИЯМ ПО МАТЕМАТИКЕ 205А Часть 3 Осень 2008 г. III. Пространства со специальными свойствами III.1 : Компактные пространства I Проблемы из Munkres, 26, pp. 170 172 3. Показать, что конечное объединение компактных подпространств
170 172 3. Показать, что конечное объединение компактных подпространств
Дополнительная информация
Эллиптические интегралы, среднее арифметико-геометрическое и алгоритм Брента-Саламина для π
Эллиптические интегралы, среднее арифметико-геометрическое и алгоритм Брента-Саламина для π Notes by G.J.O. Джеймсон Содержание. Интегралы I(a, b) и K(b). Среднее арифметико-геометрическое 3. Оценка
Дополнительная информация
Об использовании численной алгебраической геометрии для нахождения функций Ляпунова полиномиальных динамических систем
Dynamics at the Horsetooth Том 2, 2010 г. Об использовании численной алгебраической геометрии для нахождения функций Ляпунова полиномиальных динамических систем Эрик Хэнсон Математический факультет Университет штата Колорадо
Дополнительная информация
Теорема о положительной суперцикличности
E Extracta mathematicae Vol. 19, Числ. 1, 145 149 (2004) V Curso Espacios de Banach y Operadores. Ларедо, Агосто де 2003. Теорема о положительной суперцикличности Ф. Леон Сааведра Департамент математики,
19, Числ. 1, 145 149 (2004) V Curso Espacios de Banach y Operadores. Ларедо, Агосто де 2003. Теорема о положительной суперцикличности Ф. Леон Сааведра Департамент математики,
Дополнительная информация
Prentice Hall Connected Mathematics 2, 7-й класс, 2009 г.
Prentice Hall Connected Mathematics 2, 7th Class Units 2009 7 класс C O R E L A T E D O from March 2009 7 класс Решение задач Приобретите новые математические знания посредством решения задач. Решение проблем
Дополнительная информация
Семинар Дюбрей. алгебра
Семинар Дюбрей. Алгебра ДЭВИД ЭЙЗЕНБУД Заметки о расширении теоремы Крулля о главном идеале Séminaire Dubreil. Алгебра, том 28, № 1 (1974-1975), эксп. № 20, с. 1-4.
Дополнительная информация
ЧЕРНОВИК. Дальше математика.
 Предметное содержание GCE AS и A level
Предметное содержание GCE AS и A levelДальнейшая математика GCE AS и содержание предмета уровня A июль 2014 s Введение Цель Цели и задачи Содержание предмета Структура Базовые знания Общие темы Использование технологии Подробно
Дополнительная информация
Частичные дроби. Приведение дробей к общему знаменателю — известная операция из алгебры:
Частные дроби Объединение дробей к общему знаменателю — это знакомая операция из алгебры: с точки зрения интегрирования с левой частью уравнения 1 было бы намного проще работать, чем с
. Дополнительная информация
Математика 181 Раздаточный материал 16. Рич Шварц. 9 марта 2010 г.
Математика 8 Раздаточный материал 6 Рич Шварц 9 марта 200 г. Цель этого раздаточного материала — описать непрерывные дроби и их связь с гиперболической геометрией. Карта Гаусса Для любого x (0, ) мы определяем γ(x) =
Карта Гаусса Для любого x (0, ) мы определяем γ(x) =
Дополнительная информация
Линейная алгебра: векторы
A Линейная алгебра: векторы A Приложение A: ЛИНЕЙНАЯ АЛГЕБРА: ВЕКТОРЫ СОДЕРЖАНИЕ Страница A Мотивация A 3 A2 Векторы A 3 A2 Условные обозначения A 4 A22 Визуализация A 5 A23 Специальные векторы A 5 A3 Вектор
Дополнительная информация
Международный журнал информационных технологий, моделирования и вычислений (IJITMC), том 1, № 3, август 2013 г.
ФАКТОРИЗАЦИЯ МОДУЛЕЙ КРИПТОСИСТЕМЫ ПРИ ОГРАНИЧЕНИИ РАЗНИЦЫ КОФАКТОРОВ Омар Акчиче 1 и Омар Хадир 2 1,2 Лаборатория математики, криптографии и механики, Fstm, Университет Хасана II Мохаммедия-Касабланка,
Дополнительная информация
Подготовка к GRE: предварительный расчет
Подготовка к GRE: Предварительное исчисление Франклин Х.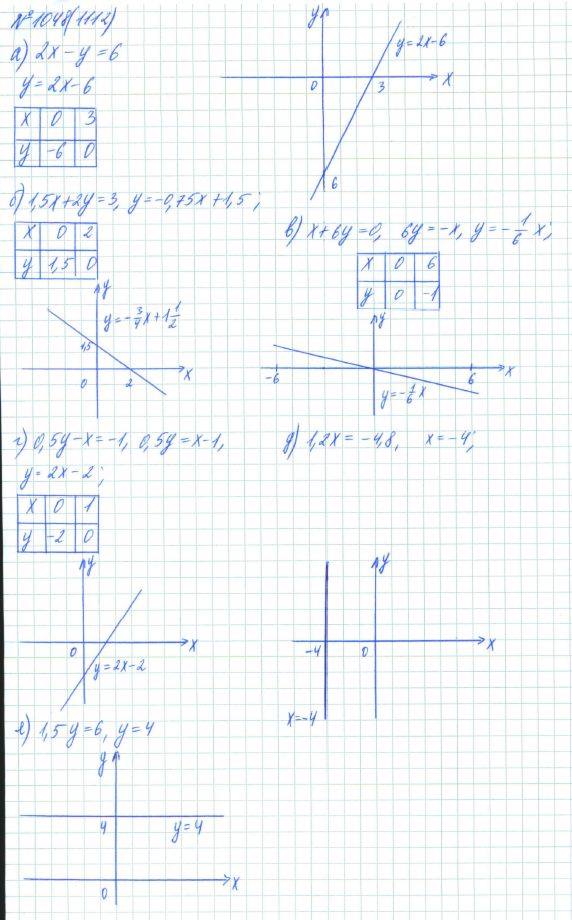 Дж. Кентер 1 Введение Это примечания к разделу Предварительное исчисление для занятия по подготовке к GRE, состоявшегося в Калифорнийском университете в августе 2011 г. Эти примечания никоим образом не предназначены для обучения
Дж. Кентер 1 Введение Это примечания к разделу Предварительное исчисление для занятия по подготовке к GRE, состоявшегося в Калифорнийском университете в августе 2011 г. Эти примечания никоим образом не предназначены для обучения
Дополнительная информация
Еще раз о матричных элементах ортогональной матрицы 3 3
Физика. Дополнительная информация
КОМПЛЕКСНЫЕ ЧИСЛА. а би в ди а в б д я. a bi c di a c b d i Например, 1 i 4 7i 1 4 1 7 i 5 6i
КОМПЛЕКСНЫЕ ЧИСЛА _4+i _-i РИСУНОК Комплексные числа как точки на плоскости Arg i _i +i -i Комплексное число может быть представлено выражением вида a bi, где a b — действительные числа i — символ с
Дополнительная информация
Алгебра 1 Название курса
Алгебра 1 Название курса Общий курс 1. Какие шаблоны и методы используются? Весь курс 1.%D0%B0_efr.jpg) Учащиеся будут уметь решать линейные и квадратные уравнения и строить графики 2. Учащиеся будут уметь
Учащиеся будут уметь решать линейные и квадратные уравнения и строить графики 2. Учащиеся будут уметь
Дополнительная информация
arxiv: 0909.4913v2 [math.ho] 4 ноября 2009 г.
ИРРАЦИОНАЛЬНОСТЬ ИЗ КНИГИ СТИВЕНА Дж. МИЛЛЕРА И ДЭВИДА МОНТЕГЮ arxiv:0909.4913v2 [math.ho] 4 ноября 2009 г. Право доступа к теоретической математике часто является доказательством иррациональности числа 2 или, по крайней мере,
Дополнительная информация
ОБЗОР УПРАЖНЕНИЙ ДЭВИДА ДЖ. ЛОУРИ
ОБЗОР УПРАЖНЕНИЙ ДЭВИД ДЖ. ЛОУРИ Содержание 1. Введение 1 2. Элементарные функции 1 2.1. Факторинг и решение квадратичных уравнений 1 2.2. Полиномиальные неравенства 3 2.3. Рациональные функции 4 2.4. Экспоненты и
Дополнительная информация
О квантовой границе Хэмминга
О квантовой границе Хэмминга Салах А. Али Факультет компьютерных наук, Техасский университет A&M, Колледж-Стейшн, Техас 77843-3112, США Электронная почта: [email protected] Мы доказываем квантовую границу Хэмминга для кодов стабилизатора
Али Факультет компьютерных наук, Техасский университет A&M, Колледж-Стейшн, Техас 77843-3112, США Электронная почта: [email protected] Мы доказываем квантовую границу Хэмминга для кодов стабилизатора
Дополнительная информация
КОЛЬЦА С ПОЛИНОМИАЛЬНЫМ Тождеством
КОЛЬЦА С ПОЛИНОМИАЛЬНЫМ ТОЖДЕСТВОМ ИРВИНГ КАПЛАНСКИ 1. Введение. В связи с исследованием проективных плоскостей М. Холл [2, теорема 6.2]* доказал следующую теорему: тело D в
Дополнительная информация
Примечания и вопросы, чтобы помочь повторению математики уровня A
Примечания и вопросы в помощь пересмотру математики на уровне A-level Университетский колледж Роберта Боулза в Лондоне 4, 5 октября Введение Введение Некоторые студенты находят первый год обучения в UCL и
Дополнительная информация
О НЕКОТОРЫХ ДВОЙНОБЕСКОНЕЧНЫХ СИСТЕМАХ КРИВЫХ НА ПОВЕРХНОСТИ
i93 c J СИСТЕМЫ КРИВЫХ 695 НА НЕКОТОРЫХ ДВОЙНОБЕСКОНЕЧНЫХ СИСТЕМАХ КРИВЫХ НА ПОВЕРХНОСТИ Ч. РОУ. Введение. Задав систему кривых co 2 на поверхности, рассмотрим переменную криволинейную
РОУ. Введение. Задав систему кривых co 2 на поверхности, рассмотрим переменную криволинейную
Дополнительная информация
14.1. Основные понятия интеграции. Введение. Предпосылки. Результаты обучения. Стиль обучения
Основные понятия интегрирования 14.1 Введение Когда функция f(x) известна, мы можем продифференцировать ее, чтобы получить ее производную df. Обратный dx-процесс состоит в том, чтобы получить функцию f(x) из знания
Дополнительная информация
Обратная кумулятивная стандартная нормальная функция вероятности.
Обратная кумулятивная стандартная нормальная функция вероятности. Diego E. Dominici Abstract t e Изучены некоторые свойства обратной функции N(x = π 1 x dt. Ее производные, интегралы
Дополнительная информация
Основная математика C3.
 Примечания к редакции
Примечания к редакцииCore Maths C Примечания к пересмотру 0 октября Core Maths C Алгебраические дроби… Отмена общих множителей… Умножение и деление дробей… Сложение и вычитание дробей… Уравнения… 4 Функции…
Дополнительная информация
О гамма-функции
О гамма-функции Заметки для почетного исчисления II, первоначально подготовленные весной 995 г. Основные факты о гамма-функции Гамма-функция определяется несобственным интегралом Γ) = Интеграл равен
Дополнительная информация
Лекции 5-6: Серия Тейлора
Математика 1d Преподаватель: Падраик Бартлетт Лекции 5-: Ряды Тейлора Недели 5- Калифорнийский технологический институт 213 1 Полиномы и ряды Тейлора Как мы видели на 4-й неделе, степенные ряды — очень удобные объекты для работы. В частности,
Дополнительная информация
Обзор фундаментальной математики
Обзор фундаментальной математики Как объясняется в предисловии и в главе 1 вашего учебника, экономика управления применяет микроэкономическую теорию к принятию бизнес-решений. Инструменты принятия решений
Инструменты принятия решений
Дополнительная информация
НЕПРЕРЫВНЫЕ ДРОБИ И УРАВНЕНИЕ ПЕЛЛА. Содержание 1. Непрерывные дроби 1 2. Решение уравнения Пелла 9Ссылки 12
НЕПРЕРЫВНЫЕ ДРОБИ И УРАВНЕНИЕ ПЕЛЛА СЕОН ХЮН ЯН Аннотация. В этой статье REU я буду использовать некоторые важные характеристики непрерывных дробей, чтобы дать полный набор решений уравнения Пелля.
Дополнительная информация
Введение в комплексные числа в физике/технике
Введение в комплексные числа в физике/инженерии. Ссылка: Мэри Л. Боас, Математические методы в физических науках, главы 2 и 14. Джордж Арфкен, Математические методы для физиков, глава 6. 9.0003
Дополнительная информация
Исчисление. Содержание. Пол Сатклифф. Офис: CM212a.
Исчисление Пола Сатклиффа Офис: CM212a.


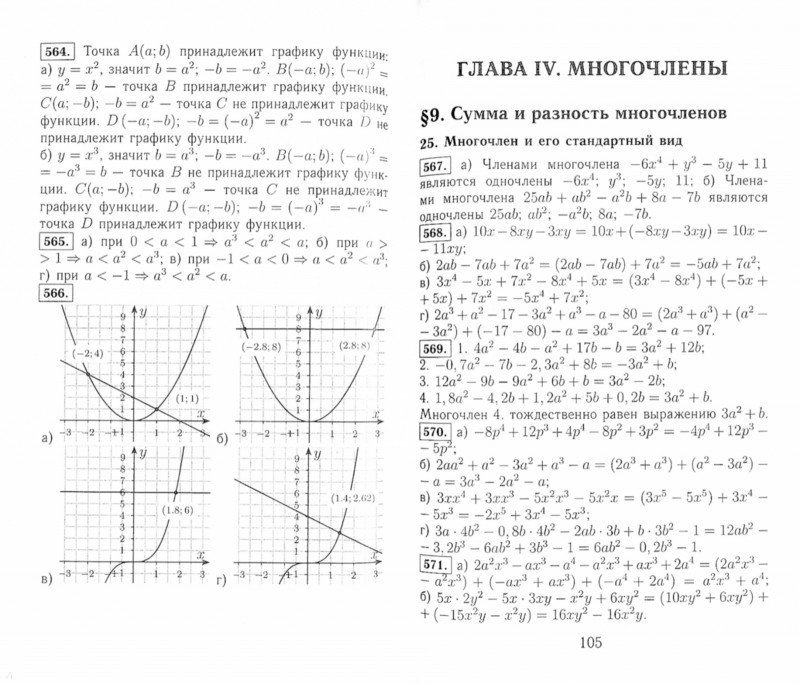
 Коэн, М. Купер, П. Дживонс, А. Крохин, Р. Пауэлл и С. Живны.
Коэн, М. Купер, П. Дживонс, А. Крохин, Р. Пауэлл и С. Живны. 
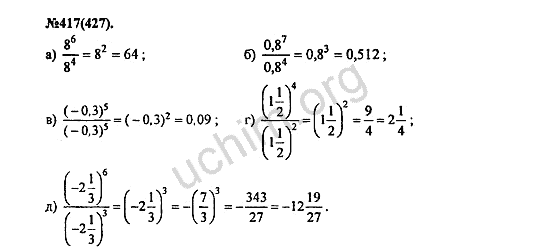 Крохин и Д. Маркс.
Крохин и Д. Маркс.  Чен, П. Дживонс и А. Крохин.
Чен, П. Дживонс и А. Крохин.  Крохин и Б. Ларос.
Крохин и Б. Ларос.  Дальмау, А. Крохин и Б. Ларос.
Дальмау, А. Крохин и Б. Ларос.  Крохин, А. Булатов и П. Дживонс.
Крохин, А. Булатов и П. Дживонс.  , стр. 1–22.
, стр. 1–22. 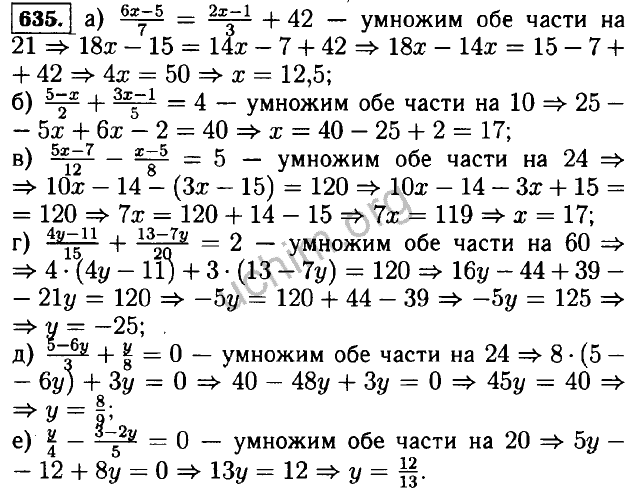 , 25 стр.
, 25 стр.
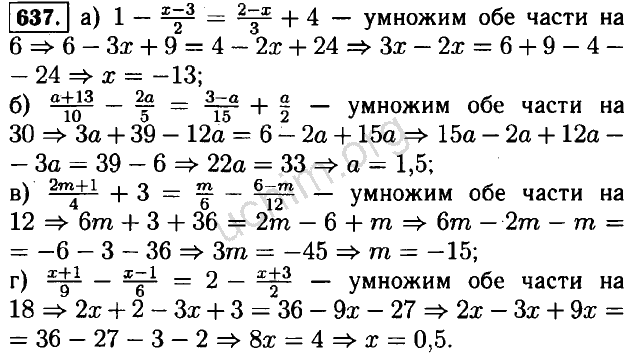 Суханов.
Суханов.  .
. Тверь, Россия.
Тверь, Россия.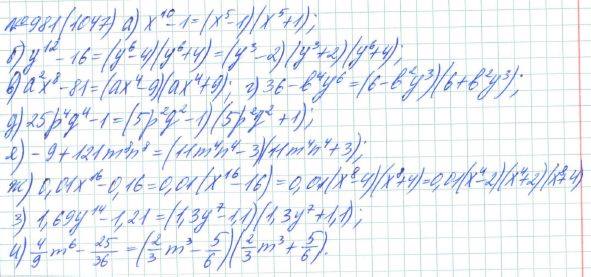 Член программного комитета.
Член программного комитета. Приглашен Клеменсом Лаутеманном.
Приглашен Клеменсом Лаутеманном.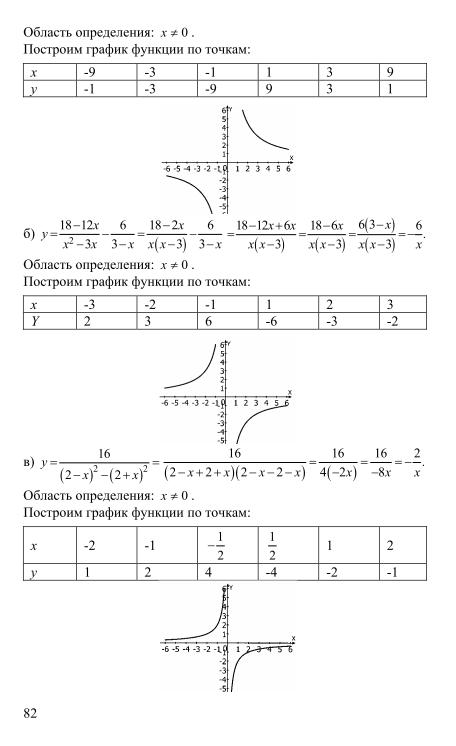 А.Успенским, А.Л.Семеновым, А.Х.Шеном, А.А.Разборовым),
1984—, бакалавриат.
А.Успенским, А.Л.Семеновым, А.Х.Шеном, А.А.Разборовым),
1984—, бакалавриат.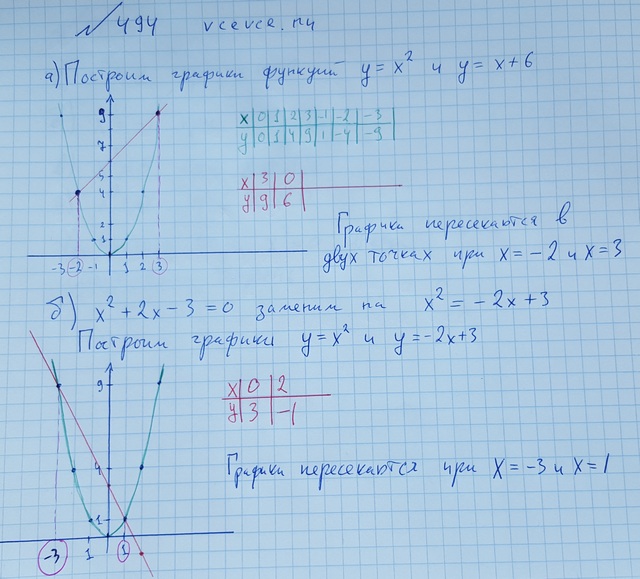 А. Успенский, Н.К. Верещагин, В.Е. Плиско.
Введение в математическую логику.
Издательство МГУ, 1991,
Наука, 2004. 136 с.
А. Успенский, Н.К. Верещагин, В.Е. Плиско.
Введение в математическую логику.
Издательство МГУ, 1991,
Наука, 2004. 136 с.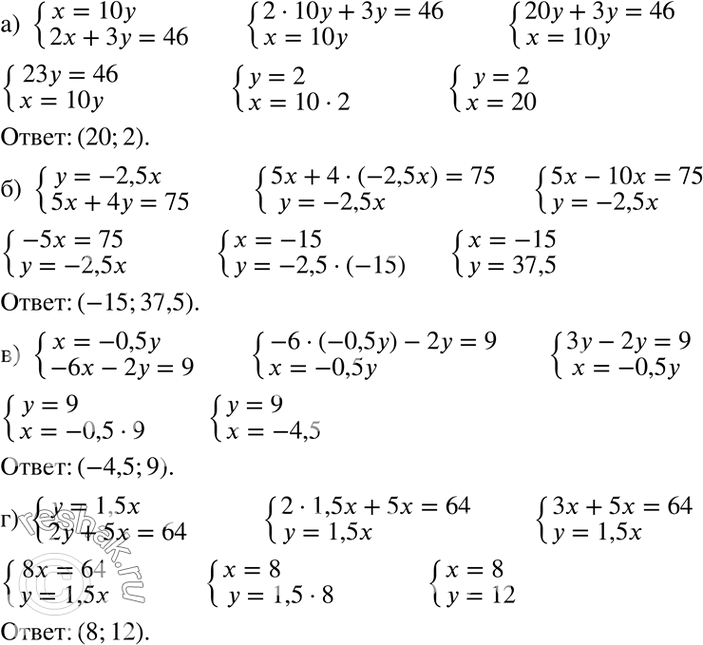 Предварительный
версия появилась под названием
«Как
воспользоваться советами экспертов в случае, когда фактические значения предполагаемых событий остаются
неизвестный.»
проц. Восьмая ежегодная конференция по вычислительному обучению
Теория (5-8 июля), 1995, Санта-Круз, Калифорния, 91-97.
Предварительный
версия появилась под названием
«Как
воспользоваться советами экспертов в случае, когда фактические значения предполагаемых событий остаются
неизвестный.»
проц. Восьмая ежегодная конференция по вычислительному обучению
Теория (5-8 июля), 1995, Санта-Круз, Калифорния, 91-97. «Колмогоровская сложность, обусловленная большими целыми числами».
Теоретическая информатика 271 (2002) 59—67.
«Колмогоровская сложность, обусловленная большими целыми числами».
Теоретическая информатика 271 (2002) 59—67.
 Серия: Конспект лекций по информатике, Vol. 2996 г.,
страницы 19-30.
Серия: Конспект лекций по информатике, Vol. 2996 г.,
страницы 19-30.