ГДЗ решебник по алгебре 7 класс Мордкович, Александрова, Мишустина учебник Мнемозина
К сожалению, ряд предметов обладает настолько высоким уровнем сложности, что с первого дня изучения помощь родителей сводится к минимуму. В первую очередь, это относится к точным наукам. Помочь выполнить задания по алгебре сумеет только профессионал. В этом нет ничего удивительного – без постоянной практики знание этого предмета слишком быстро улетучивается из памяти любого человека.
Нередко родители вынуждены прибегать к помощи профессионального репетитора, чтобы поддерживать успеваемость своего ребенка на должном уровне. Но, помимо серьезных материальных затрат, этот способ имеет еще один существенный недостаток: огромный расход времени, которое ученик вынужден отнимать у работы с другими предметами. Для поддержки школьника в этой сложной ситуации и разработана великолепная учебная литература — решебник к пособию «Алгебра 7 класс Учебник Мордкович, Александрова, Мишустина (Мнемозина)».
Регулярная работа с пособием позволит ученикам с минимальными затратами времени разобраться в алгебре с самых первых дней ее изучения, не допуская пробелы в знаниях по всем ее разнообразным темам:
Решебник поможет семикласснику надежно подготовиться к любой контрольной проверке в классе.
Глава 1. Математический язык. §1. Числовые и алгебраические выражения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
Глава 1. Математический язык. Домашняя контрольная работа №1
Вариант 1Вариант 2
Глава 1. Математический язык. §2. Что такое математический язык
1234567891011121314151617181920212223
Глава 1. Математический язык. §3. Что такое математическая модель
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
Глава 1.
Математический язык. §4. Линейное уравнение с одной переменной12345678910111213141516171819202122232425262728293031323334353637383940414243
Глава 1. Математический язык. §5. Координатная прямая
123456789101112131415161718192021222324252627282930313233343536373839404142
Глава 2. Линейная функция. Домашняя контрольная работа №2
Вариант 1Вариант 2
Глава 2. Линейная функция. §6. Координатная плоскость
12345678910111213141516171819202122232425262728293031323334353637383940
Глава 2. Линейная функция. §7. Линейное уравнение с двумя переменными и его график
123456789101112131415161718192021222324252627282930313233343536373839
Глава 2. Линейная функция. §8. Линейная функция и её график
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
Глава 2.
Линейная функция. §9. Линейная функция у=кх12345678910111213141516171819
Глава 2. Линейная функция. §10. Взаимное расположение графиков линейных функций
1234567891011121314151617181920212223
Глава 3. Системы двух линейных уравнений с двумя переменными. Домашняя контрольная работа №3
Вариант 1Вариант 2
Глава 3. Линейная функция. §11. Основные понятия
123456789101112131415161718192021
Глава 3. Линейная функция. §12. Метод подстановки
1234567891011121314151617181920212223242526272829
Глава 3. Линейная функция. §13. Метод алгебраического сложения
123456789101112131415161718
Глава 3. Линейная функция. §14. Системы двух линейных уравнений с двумя переменными как математические модели
1234567891011121314151617181920212223242526272829303132333435363738
Глава 4.
Степень с натуральным показателем и её свойства. Домашняя контрольная работа №4Вариант1Вариант2
Глава 4. Степень с натуральным показателем и её свойства. §15. Что такое степень с натуральным показателем
12345678910111213141516171819202122232425262728293031323334353637
Глава 4. Степень с натуральным показателем и её свойства. §16. Таблица основных степеней
1234567891011121314151617181920212223242526
Глава 4. Степень с натуральным показателем и её свойства. §17. Свойства степени с натуральными показателями
123456789101112131415161718192021222324252627282930313233343536373839404142
Глава 4. Степень с натуральным показателем и её свойства. §18. Умножение и деление степеней с одинаковыми показателями
123456789101112131415161718192021222324
Глава 4. Степень с натуральным показателем и её свойства.
§19. Степень с нулевым показателем123456789101112
Глава 5. Одночлены. Арифметические операции над одночленами. Домашняя контрольная работа №5
Вариант1Вариант2
Глава 5. Одночлены. Арифметические операции над одночленами. §20. Понятие одночлена. Стандартный вид одночлена
12345678910111213141516171819
Глава 5. Одночлены. Арифметические операции над одночленами. §21. Сложение и вычитание одночленов
1234567891011121314151617181920212223242526272829303132333435363738394041
Глава 5. Одночлены. Арифметические операции над одночленами. §22. Умножение одночленов. Возведение одночлена в натуральную степень
12345678910111213141516171819202122232425262728293031323334
Глава 5. Одночлены. Арифметические операции над одночленами. §23. Деление одночлена на одночлен
12345678910111213141516171819
Глава 6.
Многочлены. Арифметические операции над многочленами. Домашняя контрольная работа №5Вариант1Вариант2
Глава 6. Многочлены. Арифметические операции над многочленами. §24. Основные понятия
12345678910111213141516171819202122232425262728
Глава 6. Многочлены. Арифметические операции над многочленами. §25. Сложение и вычитание многочленов
12345678910111213
Глава 6. Многочлены. Арифметические операции над многочленами. §26. Умножение многочлена на одночлен
123456789101112131415161718192021222324252627282930313233
Глава 6. Многочлены. Арифметические операции над многочленами. §27. Умножение многочлена на многочлен
123456789101112131415161718192021222324252627
Глава 6. Многочлены. Арифметические операции над многочленами. §28. Формулы сокращенного умножения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465
Глава 6.
Многочлены. Арифметические операции над многочленами. §29. Деление многочлена на одночлен1234567891011121314151617
Глава 7. Разложение многочленов на множители. Домашняя контрольная работа №7
12
Глава 7. Разложение многочленов на множители. §30. Что такое разложение многочленов на множители и зачем оно нужно
123456789101112131415161718
Глава 7. Разложение многочленов на множители. §31. Вынесение общего множителя за скобки
12345678910111213141516171819202122232425262728
Глава 7. Разложение многочленов на множители. §32. Способ группировки
1234567891011121314151617181920212223
Глава 7. Разложение многочленов на множители. §33. Разложение многочленов на множители с помощью формул сокращенного умножения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253
Глава 7.
Разложение многочленов на множители. §34. Разложение многочленов на множители с помощью комбинации различных приемов1234567891011121314151617181920212223242526272829
Глава 7. Разложение многочленов на множители. §35. Сокращение алгебраических дробей
123456789101112131415161718192021222324252627282930313233343536373839404142
Глава 7. Разложение многочленов на множители. §36. Тождества
12345678910111213141516171819
Глава 8. Фунции y=x2. Домашняя контрольная работа №8
Вариант1Вариант2
Глава 8. Фунции y=x2. §38. Графическое решение уравнений
12345678910111213141516
Глава 8. Фунции y=x2. §39. Что означает в математике запись y=f(x)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
Глава 8.
Фунции y=x2. §37. Функция y=x2 и её график1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
Глава 9. Итоговое посторение
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188
Приложения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071
Метод решения системы уравнений методом сложения. Решение сложных систем уравнений
Разберем два вида решения систем уравнений:
1.
Решение системы методом подстановки.
2. Решение системы почленным сложением (вычитанием) уравнений системы.
Для того чтобы решить систему уравнений методом подстановки нужно следовать простому алгоритму:
1. Выражаем. Из любого уравнения мы выражаем одну переменную.
2. Замена. Подставляем в другое уравнение вместо выражаемой переменной полученное значение.
3. Решаем полученное уравнение с одной переменной. Находим решение системы.
Для решения системы методом почленного сложения (вычитания) необходимо:
1. Выбрать переменную, для которой будем делать одинаковые коэффициенты.
2. Складываем или вычитаем уравнения, в результате получаем уравнение с одной переменной.
3. Решаем полученное линейное уравнение. Находим решение системы.
Решением системы являются точки пересечения графиков функции.
Рассмотрим подробно решение систем на примерах.
Пример №1:
Решим методом подстановки
Решение системы уравнений методом подстановки
2x+5y=1 (1 уравнение)
x-10y=3 (2-е уравнение)
1.
Выразить
Видно, что во втором уравнении стоит переменная х с коэффициентом 1, отсюда и получается, что проще всего выразить переменную х из второго уравнения.
x=3+10y
2. После выражения подставляем в первое уравнение вместо переменной x 3 + 10y.
2(3+10y)+5y=1
3. Решаем полученное уравнение с одной переменной.
2(3+10y)+5y=1 (открытые скобки)
6+20y+5y=1
25y=1-6
25y=-5 |: (25)
y=-5:25
y=- 0.2
Решением системы уравнений являются точки пересечения графиков, поэтому нужно найти x и y, т.к. точка пересечения состоит из x и y. Найдем x, в первый абзац, где мы выражались, подставим туда y.
x=3+10y
x=3+10*(-0.2)=1
Принято писать точки на первом месте, пишем переменную x, а на втором месте переменную y.
Ответ: (1; -0,2)
Пример #2:
Решим почленным сложением (вычитанием).
Решение системы уравнений методом сложения
3x-2y=1 (1 уравнение)
2x-3y=-10 (2-е уравнение)
1.
Выбираем переменную, допустим, выбираем x. В первом уравнении переменная x имеет коэффициент 3, во втором — 2. Нам нужно сделать коэффициенты одинаковыми, для этого мы имеем право умножать уравнения или делить на любое число. Умножаем первое уравнение на 2, а второе на 3 и получаем суммарный коэффициент 6.
3x-2y=1 |*2
6x-4y=2
2x-3y=-10 |*3
6x-9y=-30
2. Из первого уравнения вычтите второе, чтобы избавиться от переменная х. Решите линейное уравнение.
__6x-4y=2
5y=32 | :5
y=6,4
3. Найдите x. Подставляем найденное y в любое из уравнений, допустим в первое уравнение.
3x-2y=1
3x-2*6,4=1
3x-12,8=1
3x=1+12,8
3x=13,8 |:3
x=4,6
Точка пересечения будет x=4,6; у=6,4
Ответ: (4.6; 6.4)
Хотите бесплатно подготовиться к экзаменам? Репетитор онлайн бесплатно . Без шуток.
Метод алгебраического сложения
Решить систему уравнений с двумя неизвестными можно различными способами — графическим методом или методом замены переменных.
В этом уроке мы познакомимся с еще одним способом решения систем, который вам наверняка понравится — это метод алгебраического сложения.
А откуда пришла идея — поставить что-то в системы? При решении систем основной проблемой является наличие двух переменных, потому что мы не можем решать уравнения с двумя переменными. Значит, необходимо каким-то законным способом исключить одну из них. И такими законными способами являются математические правила и свойства.
Одно из этих свойств звучит так: сумма противоположных чисел равна нулю. Это означает, что если у одной из переменных есть противоположные коэффициенты, то их сумма будет равна нулю и мы сможем исключить эту переменную из уравнения. Понятно, что мы не имеем права добавлять только термы с нужной нам переменной. Нужно складывать уравнения целиком, т.е. отдельно добавлять одинаковые члены то в левую часть, то в правую. В результате мы получим новое уравнение, содержащее только одну переменную. Давайте рассмотрим конкретные примеры.
Мы видим, что в первом уравнении стоит переменная y, а во втором противоположное число y. Значит, это уравнение можно решить методом сложения.
Одно из уравнений оставить как есть. Любой, который вам нравится больше всего.
Но второе уравнение будет получено путем сложения этих двух уравнений почленно. Те. Прибавляем 3x к 2x, прибавляем y к -y, прибавляем 8 к 7.
Получаем систему уравнений
Второе уравнение этой системы представляет собой простое уравнение с одной переменной. Из него находим х = 3. Подставляя найденное значение в первое уравнение, находим у = -1.
Ответ: (3; — 1).
Образец решения:
Решите систему уравнений алгебраическим сложением
В этой системе нет переменных с противоположными коэффициентами. Но мы знаем, что обе части уравнения можно умножить на одно и то же число. Умножим первое уравнение системы на 2.
Тогда первое уравнение примет вид:
Теперь мы видим, что при переменной x стоят противоположные коэффициенты.
Итак, поступим так же, как и в первом примере: оставим одно из уравнений без изменений. Например, 2у + 2х = 10. А второе получаем сложением.
Теперь у нас есть система уравнений:
Из второго уравнения легко находим y=1, а затем из первого уравнения x=4. как решать системы двух линейных уравнений с двумя неизвестными методом алгебраического сложения. Таким образом, теперь мы знаем три основных метода решения таких систем: графический метод, метод замены переменной и метод сложения. Этими методами можно решить почти любую систему. В более сложных случаях используется комбинация этих методик.
Список использованной литературы:
- Мордкович А.Г., Алгебра 7 класс в 2-х частях, ч.1, Учебник для общеобразовательных учреждений / А.Г. Мордкович. — 10-е изд., перераб. — М., «Мнемозина», 2007.
- Мордкович А.Г., Алгебра 7 класс в 2-х частях, часть 2, Задание для общеобразовательных учреждений / [А.Г. Мордкович и др.]; под редакцией А.Г. Мордковича — Издание 10-е, переработанное — М.
, Мнемозина, 2007. - ЕЕ. Тульчинская, Алгебра 7 класс. Блиц-опрос: пособие для учащихся общеобразовательных учреждений, 4-е издание, исправленное и дополненное, Москва, Мнемозина, 2008.
- Александрова Л.А., Алгебра 7 класс. Тематические контрольные работы в новой форме для учащихся общеобразовательных учреждений под редакцией А.Г. Мордковича, Москва, «Мнемозина», 2011.
- Александрова Л.А. Алгебра 7 класс. Самостоятельная работа для учащихся общеобразовательных учреждений под редакцией Мордковича А.Г. — 6-е издание, стереотипное, Москва, «Мнемозина», 2010.
, Мнемозина, 2007.Системы уравнений широко используются в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнений применяются не только в области математики, но и в физике, химии и биологии при решении задач нахождения численности популяции.
Система линейных уравнений — это термин, обозначающий два или более уравнений с несколькими переменными, для которых необходимо найти общее решение. Такая последовательность чисел, для которой все уравнения становятся истинными равенствами или доказывают, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называются линейными. Обозначения x, y – неизвестные, значение которых необходимо найти, b, a – коэффициенты при переменных, c – свободный член уравнения.
Решение уравнения путем построения его графика будет иметь вид прямой линии, все точки которой являются решением многочлена.
Типы систем линейных уравнений
Наиболее простыми являются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — функциональные переменные.
Решить систему уравнений — означает найти такие значения (х, у), при которых система становится истинным равенством, или установить, что подходящих значений х и у нет.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или не имеют решения, они называются эквивалентными.
Однородные системы линейных уравнений — это системы, правая часть которых равна нулю. Если правая часть после знака «равно» имеет значение или выражается функцией, такая система не является однородной.
Количество переменных может быть намного больше двух, тогда следует говорить о примере системы линейных уравнений с тремя и более переменными.
Столкнувшись с системами, школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Общего аналитического способа решения таких систем не существует, все методы основаны на численных решениях.
В школьном курсе математики подробно описаны такие методы, как перестановка, алгебраическое сложение, подстановка, а также графический и матричный метод, решение методом Гаусса.
Основная задача в обучении методам решения — научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не запомнить систему правил и действий по каждому методу, а понять принципы применения того или иного метода.
Решение примеров систем линейных уравнений 7 класса общеобразовательной школьной программы довольно простое и очень подробно объясняется. В любом учебнике по математике этому разделу уделяется достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучается на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем приводится к однопеременной форме.
Действие повторяется в зависимости от количества неизвестных в системе
Приведем пример системы линейных уравнений 7-го класса методом подстановки:
Как видно из примера, переменная x была выражается через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы вместо X, позволило получить одну переменную Y во 2-м уравнении. Решение этого примера не вызывает затруднений и позволяет получить значение Y. Последним шагом является проверка полученных значений.
Не всегда возможно решить пример системы линейных уравнений подстановкой. Уравнения могут быть сложными и выражение переменной через вторую неизвестную будет слишком громоздким для дальнейших вычислений. Когда в системе более 3 неизвестных, решение подстановки также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение методом алгебраического сложения
При поиске решения систем методом сложения выполняются почленное сложение и умножение уравнений на различные числа.
Конечной целью математических операций является уравнение с одной переменной.
Применение этого метода требует практики и наблюдения. Непросто решить систему линейных уравнений методом сложения с числом переменных 3 и более. Алгебраическое сложение полезно, когда уравнения содержат дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некоторое число. В результате арифметического действия один из коэффициентов переменной должен стать равным 1.
- Сложите полученное выражение почленно и найдите одно из неизвестных.
- Подставьте полученное значение во второе уравнение системы, чтобы найти оставшуюся переменную.
Метод решения путем введения новой переменной
Введение новой переменной допускается, если системе необходимо найти решение не более двух уравнений, число неизвестных также должно быть не более двух.
Метод используется для упрощения одного из уравнений путем введения новой переменной.
Новое уравнение решается относительно введенного неизвестного, и полученное значение используется для определения исходной переменной.
Из примера видно, что введением новой переменной t удалось привести 1-е уравнение системы к стандартному квадратному трехчлену. Вы можете решить многочлен, найдя дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В данном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то есть два решения: t = -b±√D/2*a, если дискриминант меньше нуля, то решение только одно: x= -b/2*a.
Решение для полученных систем находится методом сложения.
Визуальный метод решения систем
Подходит для систем с 3 уравнениями. Метод заключается в построении графиков каждого уравнения, входящего в систему, на оси координат. Координаты точек пересечения кривых и будут общим решением системы.
Графический метод имеет ряд нюансов.
Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой построено по две точки, значения переменной x выбраны произвольно: 0 и 3. На основании значений x получены значения для y: 3 и 0. На графике отмечены точки с координатами (0, 3) и (3, 0), которые соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.
Как видно из примера, система не имеет решений, так как графики параллельны и не пересекаются по всей длине.
Системы из примеров 2 и 3 похожи, но при построении становится очевидным, что их решения различны. Следует помнить, что не всегда можно сказать, имеет система решение или нет, всегда необходимо строить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений.
Матрица — это особый тип таблицы, заполненной числами. n*m имеет n строк и m столбцов.
Матрица является квадратной, если количество столбцов и строк равно. Матрица-вектор — это одностолбцовая матрица с бесконечно возможным числом строк. Матрица с единицами вдоль одной из диагоналей и нулевыми остальными элементами называется единичной.
Обратная матрица — это такая матрица, при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений коэффициенты и свободные члены уравнений записываются в виде чисел матрицы, одно уравнение — это одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому, если в каком-либо из уравнений количество переменных отличается, то необходимо вместо отсутствующих неизвестных ввести ноль.
Столбцы матрицы должны строго соответствовать переменным.
Это означает, что коэффициенты при переменной х можно записывать только в один столбец, например первый, коэффициент при неизвестной у — только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы достаточно проста: K -1 = 1 / |K|, где K -1 — обратная матрица, а |K| — определитель матрицы. |К| не должен быть равен нулю, то система имеет решение.
Определитель легко вычисляется для матрицы два на два, нужно только перемножить элементы по диагонали друг на друга. Для варианта «три на три» существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + а 3 б 2 в 1 . Можно воспользоваться формулой, а можно запомнить, что нужно брать по одному элементу из каждой строки и каждого столбца, чтобы номера столбцов и строк элементов не повторялись в произведении.
Решение примеров систем линейных уравнений матричным методом
Матричный метод поиска решения позволяет уменьшить громоздкость обозначений при решении систем с большим количеством переменных и уравнений.
В примере a nm — коэффициенты уравнений, матрица — вектор, x n — переменные, b n — свободные члены.
Решение систем методом Гаусса
В высшей математике метод Гаусса изучается вместе с методом Крамера, а процесс нахождения решения систем называется методом решения Гаусса-Крамера. Эти методы используются для нахождения переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения подстановки и алгебраического сложения, но более систематичен. В школьном курсе решение Гаусса используется для систем из 3 и 4 уравнений. Цель метода — привести систему к форме перевернутой трапеции. Путем алгебраических преобразований и подстановок значение одной переменной находится в одном из уравнений системы. Второе уравнение представляет собой выражение с 2 неизвестными, а 3 и 4 — с 3 и 4 переменными соответственно.
После приведения системы к описанному виду дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.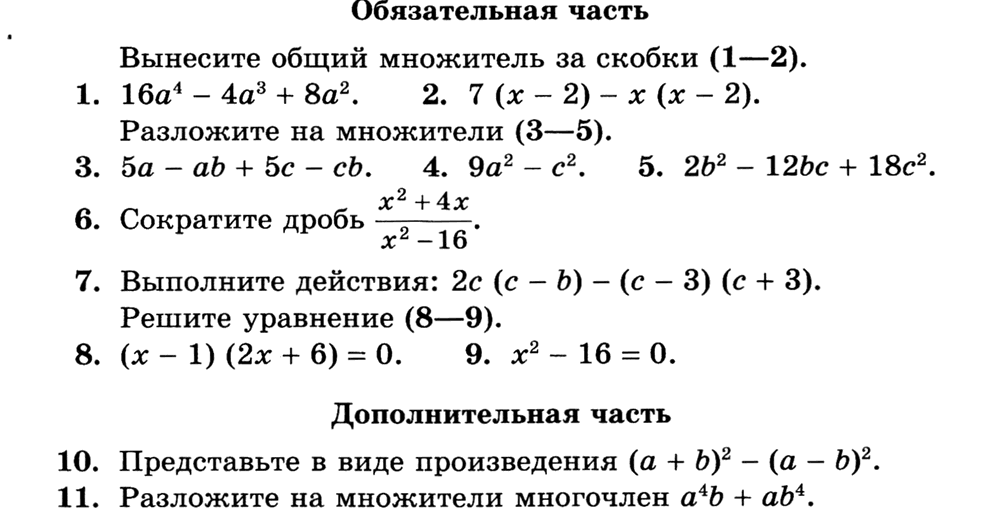
В школьных учебниках для 7 класса пример решения Гаусса описан так:
Как видно из примера, на шаге (3) были получены два уравнения 3х 3 -2х 4 =11 и 3х 3 + 2x 4 = 7. Решение любого из уравнений позволит узнать одну из переменных x n.
Теорема 5, упоминаемая в тексте, утверждает, что если одно из уравнений системы заменить эквивалентным, то полученная система также будет эквивалентна исходной.
Метод Гаусса сложен для понимания учениками средней школы, но это один из самых интересных способов развития изобретательности детей, обучающихся по программе углубленного изучения на уроках математики и физики.
Для удобства записи расчетов принято делать следующее:
Коэффициенты уравнения и свободные члены записываются в виде матрицы, где каждой строке матрицы соответствует одно из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначены номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия, проводимые с одной из строк.
Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические операции до достижения результата.
В результате должна получиться матрица, у которой одна из диагоналей равна 1, а все остальные коэффициенты равны нулю, то есть матрица приведена к единому виду. Нельзя забывать производить расчеты с числами обеих частей уравнения.
Эта запись менее громоздка и позволяет не отвлекаться на перечисление множества неизвестных.
Бесплатное применение любого метода решения потребует осторожности и определенного опыта. Применяются не все методы. Одни способы поиска решений более предпочтительны в той или иной области человеческой деятельности, а другие существуют с целью обучения.
Система линейных уравнений с двумя неизвестными — это два или более линейных уравнения, для которых необходимо найти все их общие решения. Будем рассматривать системы двух линейных уравнений с двумя неизвестными. Общий вид системы двух линейных уравнений с двумя неизвестными показан на рисунке ниже:
( a1*x + b1*y = c1,
( a2*x + b2*y = c2
Здесь x и y — неизвестные переменные, a1, a2, b1, b2, c1, c2 — некоторые действительные числа.
Решением системы двух линейных уравнений с двумя неизвестными является пара чисел (x, y) такая, что если эти числа подставить в уравнения системы, то каждое из уравнений системы превращается в истинное равенство.Существует несколько способов решения системы линейных уравнений.Рассмотрим один из способов решения системы линейных уравнений, а именно метод сложения.
Алгоритм решения методом сложения
Алгоритм решения системы линейных уравнений с двумя неизвестными методами сложения.
1. При необходимости с помощью эквивалентных преобразований уравнять коэффициенты при одной из неизвестных в обоих уравнениях.
2. Сложить или вычесть полученные уравнения, чтобы получить линейное уравнение с одним неизвестным
3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив вторую переменную.
5. Проверьте решение.
Пример решения методом сложения
Для большей наглядности решим следующую систему линейных уравнений с двумя неизвестными методом сложения:
(3*x + 2*y = 10;
(5* x + 3*y = 12;
Так как ни одна из переменных не имеет одинаковых коэффициентов, приравняем коэффициенты переменной y.
Для этого умножим первое уравнение на три, а второе уравнение на два.
(3*x+2*y=10 |*3
(5*x + 3*y = 12 |*2
) Получите следующую систему уравнений:
(9*x+6*y = 30;
(10*x+6*y=24;
Теперь из второго уравнения вычтем первое. Представим одинаковые члены и решим полученное линейное уравнение.
10*x+6*y — (9* x+6*y) = 24-30; x=-6;
Подставляем полученное значение в первое уравнение исходной системы и решаем полученное уравнение
(3*(-6) + 2*y =10;
(2*y=28; y=14;
Получится пара чисел x=6 и y=14. Проверяем. Делаем подстановку.
(3*x + 2*y = 10 ;
(5*x + 3*y = 12;
{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;
{10 = 10;
{12=12;
Как видите, у нас получилось два верных равенства, следовательно, мы нашли правильное решение
Очень часто учащиеся затрудняются с выбором метода решения систем уравнений
В данной статье мы рассмотрим один из способов решения систем — метод подстановки.
Если найдено общее решение двух уравнений, то говорят, что эти уравнения образуют систему. В системе уравнений каждое неизвестное представляет одно и то же число во всех уравнениях. Чтобы показать, что эти уравнения образуют систему, их обычно записывают одно под другим и объединяют фигурной скобкой, например
. Заметим, что при x = 15 и y = 5 оба уравнения системы верны. Эта пара чисел является решением системы уравнений. Каждая пара неизвестных величин, одновременно удовлетворяющая обоим уравнениям системы, называется решением системы.
Система может иметь одно решение (как в нашем примере), бесконечно много решений и не иметь решений.
Как решать системы методом подстановки? Если коэффициенты при каком-то неизвестном в обоих уравнениях равны по абсолютной величине (если не равны, то уравниваем), то сложив оба уравнения (или вычитая одно из другого), можно получить уравнение с одним неизвестным. Затем решаем это уравнение. Определим одно неизвестное. Подставляем полученное значение неизвестного в одно из уравнений системы (в первое или во второе).
Пример 1 Решить систему уравнений
Здесь коэффициенты при y равны по модулю, но противоположны по знаку. Попробуем почленно сложить уравнения системы.
Полученное значение x = 4 подставляем в какое-нибудь уравнение системы (например, в первое) и находим значение y:
2 * 4 + y = 11, y = 11 — 8, y = 3.
Наша система имеет решение x = 4, y = 3. Или ответ можно записать в скобках, как координаты точки, на первом месте x, на втором y .
Ответ: (4; 3)
Пример 2 . Решаем систему уравнений
Приравниваем коэффициенты при переменной x, для этого первое уравнение умножаем на 3, а второе на (-2), получаем
Будьте внимательны при сложении уравнений
Тогда y = — 2. Подставляем число (-2) вместо y в первое уравнение, получаем
4x + 3 (-2) = — 4. Решаем это уравнение 4x = — 4 + 6, 4х = 2, х = ½.