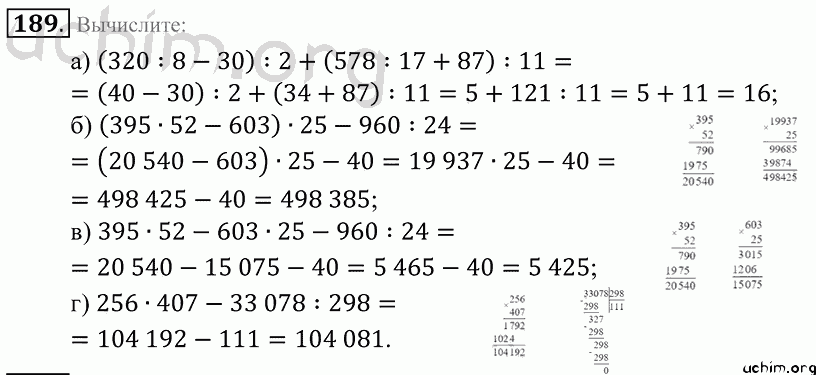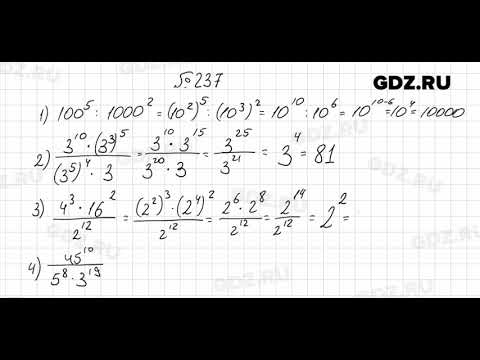Ответы Задание 210 . ГДЗ по алгебре 7 класс Дорофеев Суворова Бунимович Минаева Рослова
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141.. Это надо уметь141141. Проверьте себя (тест)142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228.. Это надо уметь228228. Проверьте себя (тест)229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335.
. Это надо уметь633633. Проверьте себя (тест)634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810.. Это надо уметь810810. Проверьте себя (тест)811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897898899900901902903904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933934935936937.
Страница 72 ГДЗ к учебнику «Алгебра» 7 класс Дорофеев, Суворова, Бунимович
ГДЗ 1 класс
ГДЗ 10 класс
- Категория: ГДЗ Алгебра учебник 7 класс Дорофеев, Суворова, Бунимович ✔
Задание 6. Автомобиль, двигаясь с постоянной скоростью, за определенной время проехал $\frac{1}{3}$ всего расстояния до пункта назначения. Какую часть этого расстояния можно было бы проехать за это же время со скоростью, в 1,2 раза большей?
Решение
При постоянном времени движения скорость движения и пройденный путь являются прямо пропорциональными зависимостями, поэтому, увеличив скорость в 1,2 раза, автомобиль проедет расстояние в 1,2 раза больше.
$1,2 * \frac{1}{3} = 0,4$ (расстояния) − проедет автомобиль.
Ответ: 0,4 расстояния.
Задание 7. Для школы купили 6 одинаковых компьютеров. Сколько компьютеров, стоимость которых в 1,5 раза меньше, можно было бы купить на эту же сумму?
1) 4;
2) 8;
3) 9;
4) для ответа не хватает данных.
Решение
Обратная пропорциональность.
6 * 1,5 = 9 (компьютеров) − можно было бы купить.
Ответ: 3) 9 компьютеров.
Задание 8. Из каких отношений нельзя составить пропорцию?
2) $\frac{1}{3} : \frac{1}{4}$ и $2 : \frac{1}{2}$;
3) 0,1 : 7 и 0,5 : 35;
4) 0,02 : 0,1 и 2 : 10.
Решение
1) 2 : 7 и 11 : 33
2 * 33 = 66
7 * 11 = 77
66 ≠ 77 − пропорцию составить нельзя.2) $\frac{1}{3} : \frac{1}{4}$ и $2 : \frac{1}{2}$
$\frac{1}{3} * \frac{1}{2} = \frac{1}{6}$;
$\frac{1}{4} * 2 = \frac{1}{2}$;
$\frac{1}{6} ≠ \frac{1}{2}$ − пропорцию составить нельзя.3) 0,1 : 7 и 0,5 : 35
0,1 * 35 = 3,5;
7 * 0,5 = 3,5;
3,5 = 3,5 − составить пропорцию можно.4) 0,02 : 0,1 и 2 : 10
0,02 * 10 = 0,2;
0,1 * 2 = 0,2;
0,2 = 0,2 − составить пропорцию можно.Ответ: пропорцию нельзя составить из соотношений 1) и 2)
Задание 9. Дана пропорция 5 : a = 6 : b. Какое из следующих равенств пропорцией не является?
1) a : b = 5 : 6;
3) a : b = 6 : 5;
4) a : 5 = b : 6.
Ответ 7 гуру
Пропорцией не является равенство 3) a : b = 6 : 5.
Задание 10. Как можно найти неизвестный член пропорции $\frac{x}{1,2} = \frac{5}{8}$?
1) $x = \frac{8 * 1,2}{5}$;
2) $x = \frac{1,2 * 5}{8}$;
3) $x = \frac{8 * 5}{1,2}$;
4) $x = \frac{8}{1,2 * 5}$.
Решение
$\frac{x}{1,2} = \frac{5}{8}$
$x = \frac{1,2 * 5}{8}$
$x = \frac{6}{8}$
$x = \frac{3}{4}$
x = 0,75
Ответ: вариант 2)
Задание 11.
Одна машинистка печатает страницу за 6 мин, а другая − за 10 мин. Первая за некоторое время напечатала 40 страниц. Сколько страниц за это же время напечатает вторая?
Установите, какая пропорция соответствует условию задачи (x − число страниц, которое напечатает вторая машинистка).
2) $\frac{6}{10} = \frac{40}{x}$;
3) $\frac{6}{40} = \frac{x}{10}$;
4) $\frac{6}{40} = \frac{10}{x}$.
Решение
6 мин − 40 страниц
10 мин − x страниц
Обратная пропорциональность.
$\frac{6}{10} = \frac{x}{40}$
$x = \frac{6 * 40}{10}$
x = 6 * 4 = 24 (страницы) − напечатает вторая машинистка.
Ответ: 24 страницы; условию задачи соответствует пропорция 1)
Задание 12. Отрезок AB, длина которого равна 21 см, точками C и D разделен на три части в отношении 2 : 3 : 5. Чему равна длина отрезка CB?
Решение
1) 21 : (2 + 3 + 5) = 21 : 10 = 2,1 (см) − приходится на одну часть;
2) 2,1 * (3 + 5) = 2,1 * 8 = 16,8 (см) − длина отрезка CB.
Ответ: 16,8 см.
- Назад
- Вперед
умножить наподелить на
- ГДЗ
- ГДЗ по математике
- ГДЗ Алгебра учебник 7 класс Дорофеев, Суворова, Бунимович
Вам может пригодиться:
АМС 210 | Прикладная математика и статистика
AMS 210, Прикладная линейная алгебра
Описание по каталогу : Введение в теорию и использование векторов и матриц.
Теория матриц, включая
системы линейных уравнений. Теория евклидовых и абстрактных векторных пространств. собственные значения
и собственные векторы. Линейные преобразования. Не может быть взято в кредит в дополнение к
МАТ 211.
Предпосылки : AMS 151, или MAT 131, или 141, или сопутствующий MAT 126, или уровень 7 или выше по математике экзамен по размещению.
SBC: STEM+
3 кредита
Учебник для летней сессии 2022 г. (онлайн) с профессором Хёнкён Лим:
Требуется: «Введение в линейную алгебру: модели, методы и теория», Алан Такер, XanEdu
Издательство, 1995; ISBN: 9781506696720
Учебник на осенний семестр 2022 г.
ТОЛЬКО для лекции 02 с профессором Дэвидом Грином :
Требуется: «Введение в линейную алгебру» Гилберта Стрэнга, 5-е издание, Уэлсли-Кембридж. Пресс, 2016; ISBN: 978-009802327-6
Требуется: «Введение в линейную алгебру: модели, методы и теория», Алан Такер, XanEdu
Издательская, 1995; ISBN: 9781506696720
Темы
1.
Введение в модели (глава 1) – 4 академических часа
2. Матрицы: матричные операции, матричная алгебра, матричные нормы, собственные значения и собственные векторы
(Глава 2) – 9 аудиторных часов
3. Решение систем линейных уравнений: исключение Гаусса, обратные, определители,
итерационные методы, числа условий и связанный с ними численный анализ (глава 3) – 10
класс часов
4. Приложения: регрессия, цепи Маркова, модели роста (гл. 4) – 6 академических часов
5. Теория систем линейных уравнений: линейная независимость, основания, ранг, нулевое пространство
и диапазон, ортогональные басы, псевдоинверсия (гл. 5) – 8 акад. часов
6. Экзамены и повторение – 5 акад. часов.
Результаты обучения для AMS 210, Прикладная линейная алгебра
1.) Ознакомьтесь с разнообразным набором линейных моделей и используйте их для интерпретации
теория и методики на протяжении всего курса:
* система из 3-х линейных уравнений с 3-мя неизвестными;
* модель цепи Маркова
* динамическая (итерационная) линейная система уравнений
* модель общего равновесия.
2.) Вычислить и применить основные векторно-матричные операции:
* скалярные произведения;
* произведения матрицы-вектора;
* умножение матриц.
3.) Продемонстрировать разнообразие использования скалярных и векторных мер матрицы:
* нормы матрицы;
* доминирующее собственное значение и доминирующий собственный вектор.
4.) Решите систему линейных уравнений, используя:
* Исключение Гаусса;
* определители;
* обратная матрица;
* итерационные методы,
* приближенные решения методом наименьших квадратов с использованием псевдообратных методов.
5.) Продемонстрируйте, как метод исключения Гаусса определяет, является ли система линейных уравнений
равно:
* переопределено;
* недоопределено — и как определить семейство решений;
* определяется однозначно — и найдите решение.
6.) Применять основные идеи числовой линейной алгебры:
* вычислительная сложность матричных операций;
* Разложение LU;
* использование секционирования для упрощения матричных операций;
* плохо обусловленные матрицы и номер обусловленности матрицы.
7.) Изучите и используйте основы теории векторных пространств, связанных с линейным преобразованием:
* линейная независимость;
* пустое пространство;
* пространство диапазона;
* ортонормированные пространства.
8.) Изучите выборку линейных моделей, выбранных из линейной регрессии, компьютерной графики, цепи Маркова и линейное программирование.
9.) Улучшить навыки общения и перевода математических понятий,
модели для реальных условий:
* представлять решения проблем в ясной, хорошо изложенной форме;
* объясните ключевые понятия урока на письменном английском языке;
*преобразование задач, описанных в письменной форме на английском языке, в соответствующий математический
форма;
* преобразовать математические решения в письменный ответ.
Математика 210A: Современная алгебра
Математика 210A: Современная алгебра Лекции: Вторник и Четверг 11-12:15 в Rm. 380 Вт.Время работы: в 380-383М (третий этаж математического корпуса). Вторник и четверг 2:30-3:30. Дайте мне знать, если это не удобно. У нас с Покманом будут дополнительные рабочие часы перед промежуточным и финальным экзаменами.
Учебник: Ротмана Современная современная алгебра . Книжный магазин может быть уже закрыт; если это так, пожалуйста дай мне знать. Я благодарен Ставросу Тумпису за указание что опечатки для книги доступны по адресу Домашняя страница Ротмана.
Схема классификации:
Ассистент курса: Покман Чунг,
[email protected].
У Покмана будут проблемные сессии (например, рабочие часы)
в своем кабинете, 380-р по понедельникам с 4:30 до 5:30 (обратите внимание на изменение!) и среда 2-3.
Наборы задач: Наборы задач будут приходить по вторникам в 15:30 на почтовый ящик Пьера. (на первом этаже 380-го матматкорпуса, табличка «Альбин»). Оценщик — Пьер Альбин, [email protected].
Это первый курс в последовательности из трех частей со следующими описание из учебника: «Группы, кольца и поля, Галуа теория, идеальная теория. Введение в алгебраическую геометрию и алгебраическая теория чисел. Представления групп и некоммутативные алгебры, полилинейная алгебра. Требование: 120 или эквивалент.»
Мы сосредоточимся на группах, кольцах и полях (включая теорию Галуа). примерно до конца главы 5 в книге Ротмана Advanced Modern. Алгебра , хотя и не обязательно по порядку.
Для получения информации о квалификации нажмите здесь.
Бейл Шанкс любезно создал веб-сайт с некоторыми из своих заметок из конечно здесь.
Курс на данный момент: Ниже представлены раздаточные материалы в форматах dvi, ps и pdf.
Я подозреваю, что способы создания PDF-файлов зависят от устройства (т.
они могут выглядеть забавно на вашей машине), поэтому я попробовал два разных
способами (pdfA и pdfB).
Если вы попробуете оба и один лучше другого, пожалуйста, дайте мне знать.
Я думаю, что pdfB может быть лучше на некоторых машинах.
Глава 2.
Глава 3 (3.7 предполагается линейная алгебра), за исключением частей
из 3.8, чтобы сделать с конечными полями. Глава 5.1. Глава 6.1 и
6.2. (Мы сделали части 6.3 и 6.4, но вы не несете ответственности
для них.) Вот промежуточные решения:
(дви,
пс,
pdfA,
pdfB,
pdfС).