Основные задачи по геометрии 7 класс. УМК Атанасян Л.С. | Учебно-методический материал по геометрии (7 класс) по теме:
Опубликовано 09.08.2013 — 18:37 — Губина Клара Владимировна
В данном документе собраны задачи по всему курсу геометрии 7 класса. Эти задачи в нашей школе используются при подготовки к устному экзамену по геометрии за курс 7 класса.
Скачать:
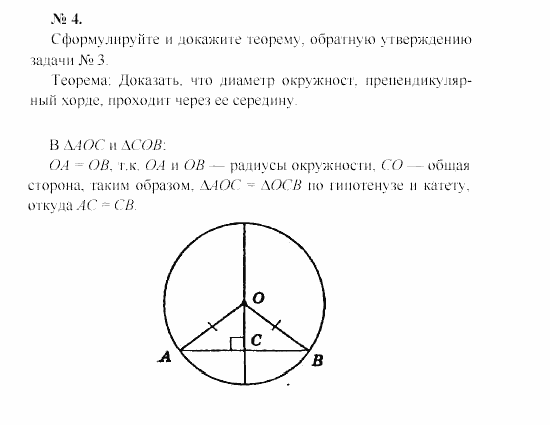
Предварительный просмотр:
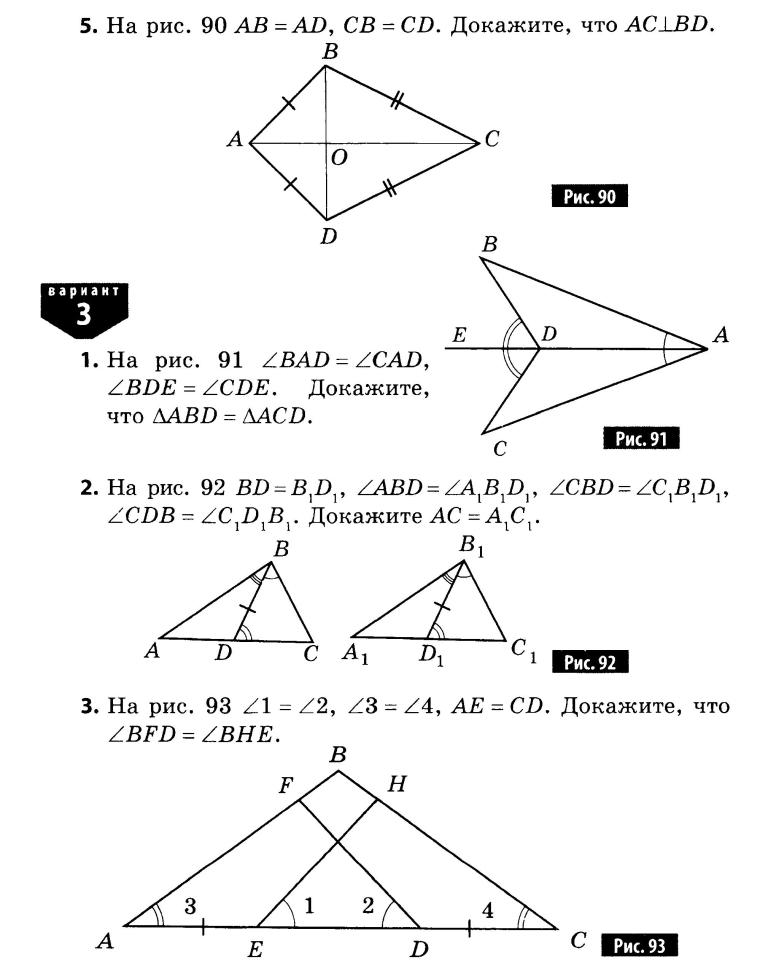
Задачи по геометрии за курс 7 класса (для итогового повторения).
- На прямой a расположены точки A, B, C, причем A B = 5см, BC = 7 см. Какой может быть длина отрезка AC.
- На прямой a отмечены точки A, B, M. Найдите длину AM и MB, если AB = 6 см, MA + MB = 9 см.
- Прямой угол ADB разделен лучом DC на два угла, причем один угол на 90 больше другого. Найдите градусные меры этих углов.
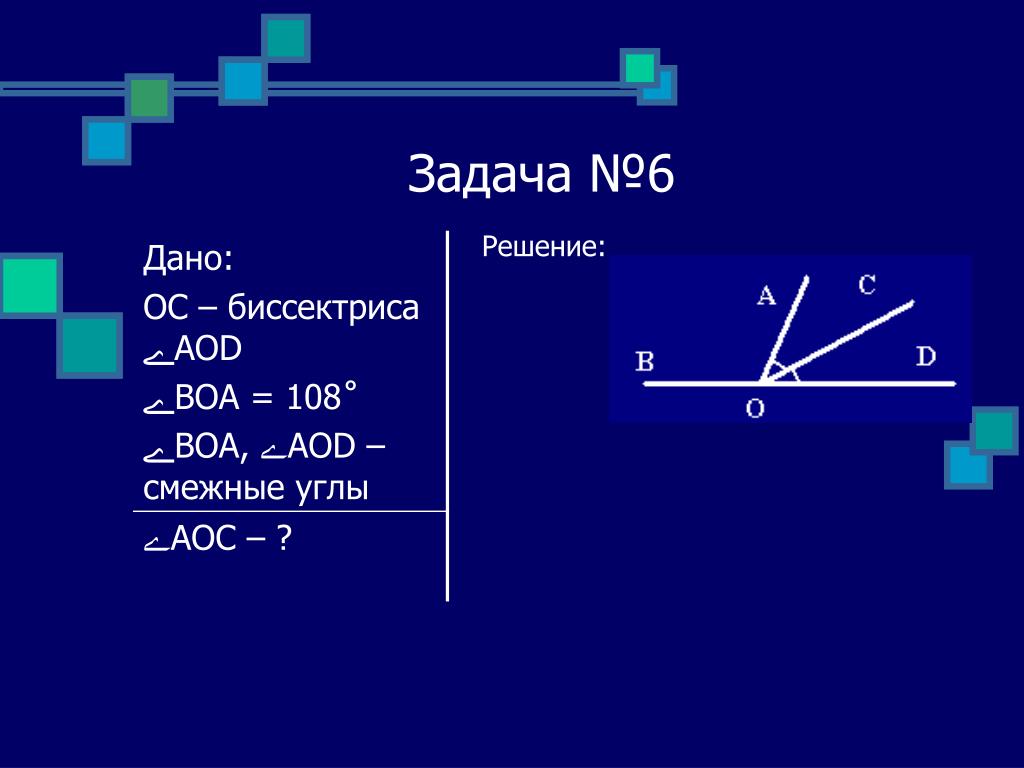
- Угол AOB, равный 1240, лучом OC разделен на два угла, разность которых равна 340. Найдите эти углы. Чему равен угол, образованный лучом OC и биссектрисой угла AOB.

- Угол AOB, равный 1360, лучом OC разделен на два угла, градусные меры которых относятся как 3:1. Найдите эти углы. Чему равен угол, образованный лучом OC и биссектрисой угла AOB.
- Луч BM делит развернутый угол ABC в отношении 5:1, считая от луча BA. Найдите угол ABK, если BK – биссектриса угла MBC.
- Один из смежных углов на 500 больше другого. Найдите эти углы.
- Разность двух смежных углов равна 540. Найдите эти углы.
- Прямая ВК перпендикулярна прямым МВ и КТ. Докажите, что треугольники МВО и ОКТ равны. Найдите углы ОМВ, ВОМ, ОТК, если известно, что МВ=КТ, а угол ТОК=400. (Обязательно доказательство равенства треугольников)
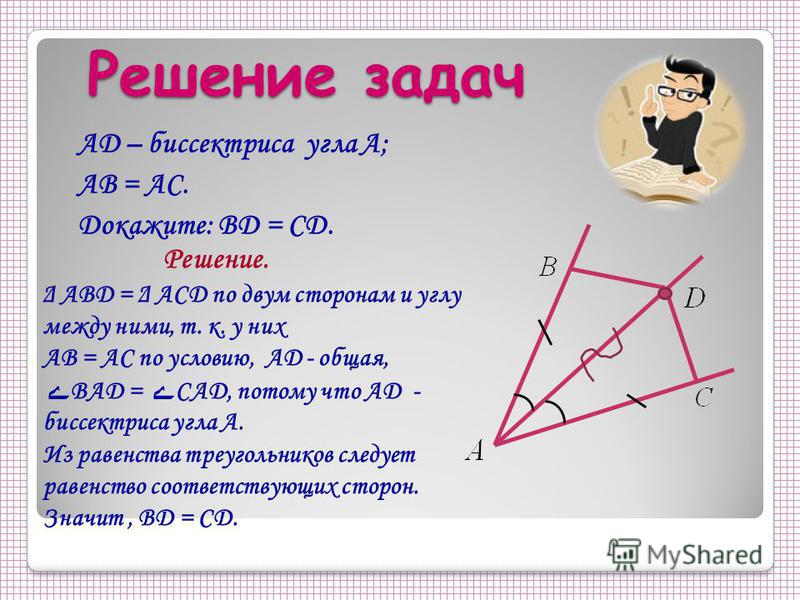
- Отрезки АС и ВD пересекаются в точке О. ВD = АС, ОВ=ОС. а) Докажите, что ∆ АОВ = ∆ СОD;
б) Найдите периметр ∆ СОD, если АВ=9см, ВО=5см, ОD=7см.
- В ∆АВС АВ = ВС, ВЕ – медиана треугольника АВС, Угол АВЕ =41˚. Найдите углы АВС и СЕВ.

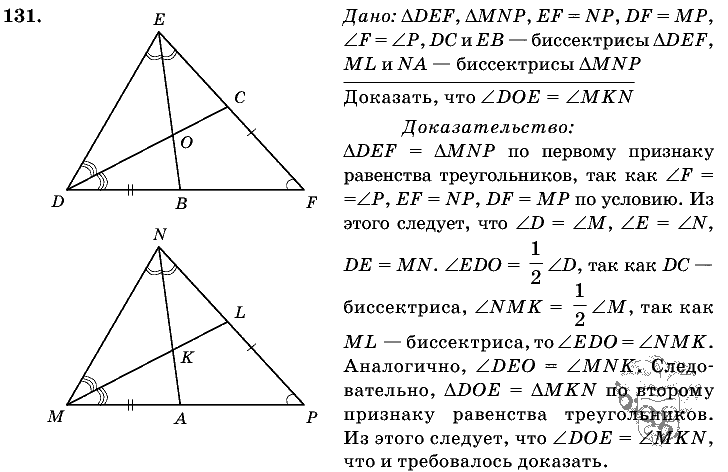
- В ∆АВС и ∆А1В1С1 медианы ВМ и В1М1 равны, АВ=А1В1 , АМ=А1М1. Докажите, что ∆АВС = ∆А1В1С1.
- Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма трех из них равна 3070.
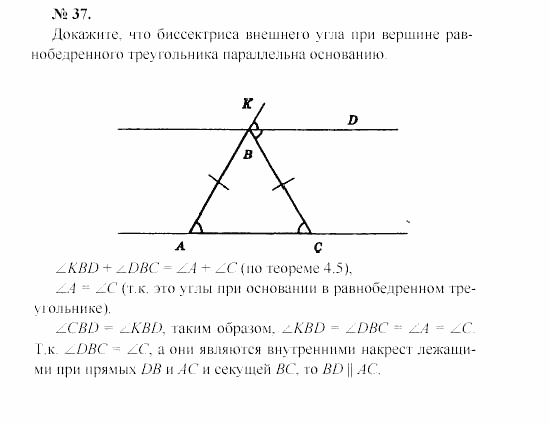
- Равнобедренные треугольники ABC и ADC имеют общее основание AC. Докажите, что BAD = BCD.
- На медиане CM равнобедренного треугольника ABC с основанием AB взята точка О.Докажите, что треугольник AOB равнобедренный.
- Один из внешних углов равнобедренного треугольника равен 126˚. Найдите углы треугольника.
- AD и CE – биссектрисы равнобедренного треугольника с основанием AC. Докажите, что AEC = CDA.
- Точки C и D расположены по разные стороны от прямой AB так, что AD = AC, BD = DC. Докажите, что AB – биссектриса угла DAC.
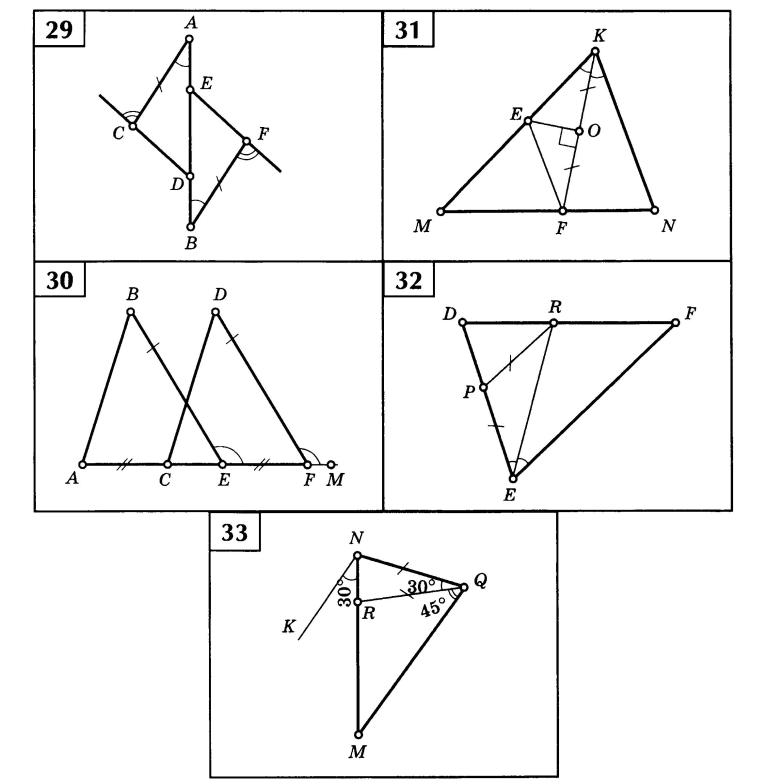
- Какими являются перечисленные углы? Обозначьте равные углы:
Углы 1 и 2 — | |
Углы 2 и 3 — | |
Углы 1 и 4 — | |
Углы 3 и 4 — | |
Углы 3 и 5 — | |
Углы 4 и 5 — |
- Найдите все неразвернутые углы, образованные при пересечении двух прямых, если сумма трех из них равна 3070.

- Определите углы: МРО, РВО, ОВТ, ХКО, АКО, КОА, ОАК, ОАС, ВОА, РОК, если известно, что угол ОРВ=520, а угол РОВ=1020, РВ параллельно АК.
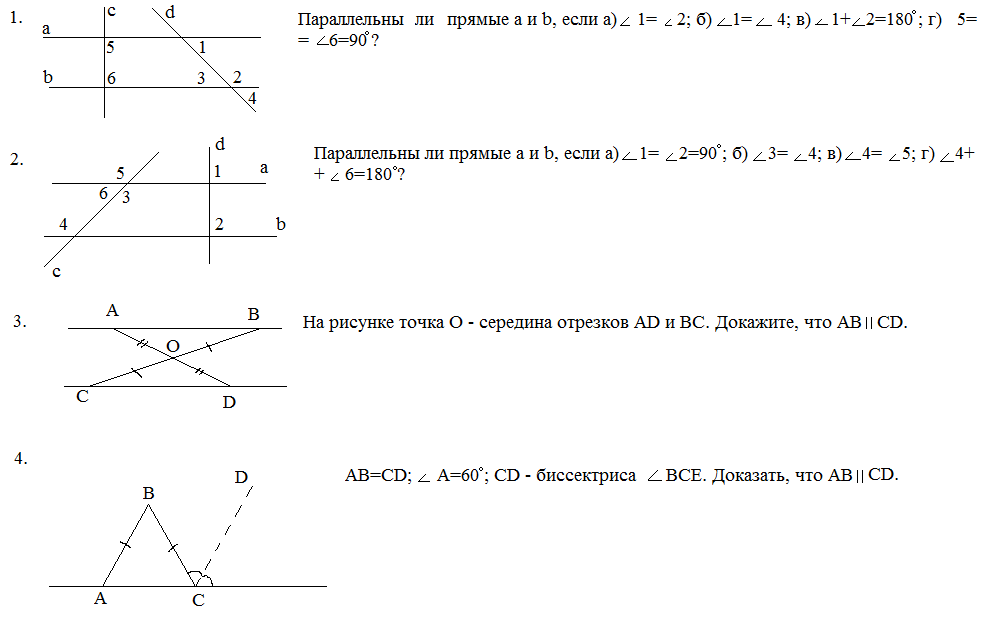
- Найдите все углы, образованные при пересечении двух параллельных прямых f и d секущей c, если один из углов на 50˚ больше другого.
- В треугольнике АВС
- Один из внешних углов равнобедренного треугольника равен 126˚. Найдите углы треугольника.
- В треугольнике ABC угол A равен 700, внешний угол при вершине B равен 790. Найдите угол C. Ответ дайте в градусах.
- В треугольнике ABC угол A равен 390, АС=ВС. Найдите угол C. Ответ дайте в градусах.
- В треугольнике ABC угол C равен 1300,АС=ВС. Найдите угол A. Ответ дайте в градусах.
- В треугольнике ABC АС=ВС. Внешний угол при вершине B равен 1520. Найдите угол C. Ответ дайте в градусах.
- Сумма двух углов треугольника и внешнего угла к третьему равна 1200. Найдите этот третий угол. Ответ дайте в градусах.
- В треугольнике ABC угол C равен 900, CH — высота, угол A равен 60.
 Найдите угол BCH. Ответ дайте в градусах.
Найдите угол BCH. Ответ дайте в градусах. - Один острый угол прямоугольного треугольника на 420 больше другого. Найдите больший острый угол. Ответ дайте в градусах
- Дан прямоугольный треугольник АВС с прямым углом С. Угол В равен 300. Гипотенуза равна 12, а катет СВ равен 10. Определите периметр треугольника и угол А.
- В треугольнике АВС угол А больше угла В в 9 раз, а угол С меньше угла А на 100. Определите углы треугольника и укажите, каким этот треугольник является.
- Угол при основании равнобедренного треугольника равен 700, чему равен внешний угол при при основании треугольника, не смежный с данным углом?
- Внешний угол при основании равнобедренного треугольника на 200 больше одного из углов при основании треугольника. Найдите углы треугольника.
- В треугольнике ABC точка D лежит на стороне BC, причем AD = DC.Сумма внешних углов при вершине A равна 1600. Найдите угол C, если AD – биссектриса угла BAC.
- Один из углов прямоугольного треугольника равен 30˚, а сумма гипотенузы и меньшего катета равна 12,6 см.
 Найдите длину гипотенузы.
Найдите длину гипотенузы. - Дан квадрат со стороной 16 см. Точка М лежит на стороне и делит эту сторону в отношении 3:5 от вершины . Прямая, проходящая через точку М пересекает сторону в точке Т, таким образом, что угол ВТМ равен 1200. Из вершины к прямой ТМ проведен перпендикуляр . Определите длину этого перпендикуляра.
- Даны две параллельные прямые и секущая, которая пересекает прямые в точках А и В. Биссектрисы углов А и В пересекаются в точке О. Найдите периметр треугольника АВО, если известно, что АВ равно 8, угол ВАО в 2 раза меньше угла ОВА, а АК равно 12,6 см, где точка К – точка пересечения прямой АО и одной из параллельных прямых.
- Один из внешних углов прямоугольного треугольника равен 1200. Найдите большую и меньшую стороны треугольника, если их сумма равна 18 см.
- В прямоугольном треугольнике ABC с гипотенузой BC и углом B равным 600, проведена высота AD. Найдите DC, если DB = 2 см.
- В прямоугольном треугольнике ABC с гипотенузой AC, равной 12 см проведена высота BD.
 Найдите CD, DA если
Найдите CD, DA если
По теме: методические разработки, презентации и конспекты
Рабочая программа по геометрии 8 класс к учебнику «Геометрия 7-9» /Атанасян Л.С./
Основой для рабочей программы по геометрии в 8 классе является Примерная программа основного общего образования по математике составленная на основе федерального компонента государственного стандарта …
Планирование по геометрии 7 класс. (Учебник «Геометрия 7-9» Атанасян Л.С. и др.)
Данное планирование асчитано на 68 учебных часов (2 часа в неделю, 34 учебных недели)…
Календарно-тематическое планирование. Геометрия 7 класс. Базовый учебник Геометрия 7-9 класс.Авторы : Атанасян Л.С. и др.
Календарно-тематическое планирование. Геометрия 7 класс. Базовый учебник Атанасян Л.С. и др. Геометрия 7-9 класс….
Календарно-тематическое планирование. Геометрия 8 класс. Базовый учебник Геометрия 7-9 класс.Авторы : Атанасян Л.С. и др.
Календарно-тематическое планирование.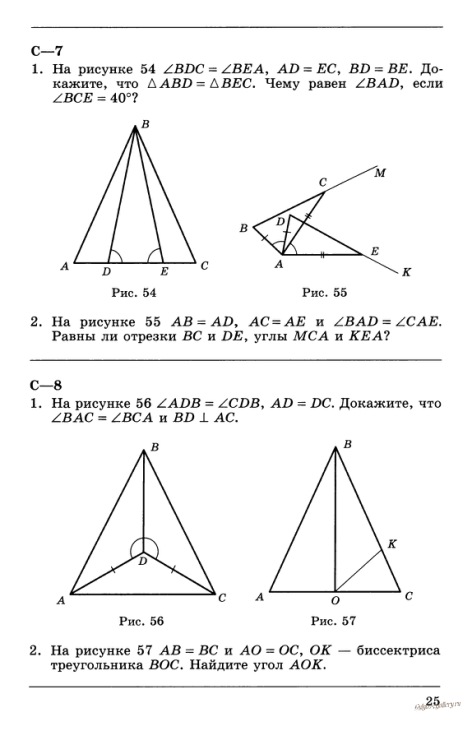 Геометрия 8 класс. Базовый учебник Геометрия 7-9 класс.Авторы : Атанасян Л.С. и др….
Геометрия 8 класс. Базовый учебник Геометрия 7-9 класс.Авторы : Атанасян Л.С. и др….
Календарно-тематическое планирование. Геометрия 9 класс. Базовый учебник Геометрия 7-9 класс.Авторы : Атанасян Л.С. и др.
Календарно-тематическое планирование. Геометрия 9 класс. Базовый учебник Геометрия 7-9 класс.Авторы : Атанасян Л.С. и др….
Календарно-тематическое планирование. Геометрия 10 класс. Базовый учебник Геометрия 10-11 класс.Авторы : Атанасян Л.С. и др.
Календарно-тематическое планирование. Геометрия 10 класс. Базовый учебник Геометрия 10-11 класс.Авторы : Атанасян Л.С. и др….
Календарно-тематическое планирование. Геометрия 11 класс. Базовый учебник Геометрия 10-11 класс.Авторы : Атанасян Л.С. и др.
Календарно-тематическое планирование. Геометрия 11 класс. Базовый учебник Геометрия 10-11 класс.Авторы : Атанасян Л.С. и др….
Поделиться:
Тесты по геометрии для 7 класса онлайн
Окружность
-
Тест по теме «Смежные и вертикальные углы»
30.
 07.2018
11342
07.2018
11342
Тест направлен на проверку знаний учащихся по теме «Смежные и вертикальные углы»
-
Начальные сведения из геометрии
вопросы содержат теоретический материал, служат проверкой первоначальных знаний по предмету
-
7 класс. Геометрия. Прямая и отрезок. Луч и угол.
27.02.2022 1780 0
Данный тест предназначен для повторения темы: «Прямая и отрезок. Луч и угол»
-
7 класс Глава 1 Начальные геометрические сведения
04.
0 10.2020
12361
10.2020
123617 класс геометрия учебник Л.С.Атанасян.
-
Прямая, луч, отрезок. Геометрия 7 класс.
01.11.2021 255 0
Тест по теме «Прямая, луч, отрезок» проверяет умение находить длины отрезков, устанавливать пересекаются ли прямые, отрезки и лучи на рисунке.
-
углы и их виды
10.02.2020 5509
Определение угла. Виды углов. Измерение углов. Сравнение углов.Построение углов.
-
7 класс.
 Геометрия. Смежные и вертикальные углы №6
Геометрия. Смежные и вертикальные углы №6
14.10.2016 5320
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Смежные и вертикальные углы».
-
Итоговый тест по геометрии для 7 класса
13.05.2020 9334
Итоговый тест по геометрии 7 класса за 2019/2020 учебный год по всем темам учебной программы
-
Медиана, биссектриса и высота треугольника
12.11.2020 351 0
Проверочный тест по теме «Медианы биссектрисы и высоты треугольника»
-
Итоги знаний за 7 классов.

25.09.2022 8
Данный тест предназначен для оценки знаний учащихся 7 и 8 классов. Состоит из 25 вопросов базового уровня. Целесообразно тестировать учащихся в конце учебного года 7 класса или вначале 8 класса, при повторении изученного материала.
-
7 класс. Геометрия. Смежные углы. (диктант)
09.01.2016 1648
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Смежные углы.»
-
Треугольники. Обобщение 7 класс
19.07.2019 4751 0
Данный тест предназначен для проверки знаний учащихся по темам «Треугольники», «Равнобедренный треугольник и его свойства», «Прямоугольный треугольник»
-
7 класс.
 Геометрия. Прямоугольный треугольник. Углы и их свойства.
Геометрия. Прямоугольный треугольник. Углы и их свойства.
20.02.2016 6749 0
Тест предназначен для учащихся 8 классов при отработке навыков решения задач по теме «Прямоугольный треугольник. Углы и их свойства.»
-
ТЕСТ ПО ТЕМЕ: «ПРИЗНАКИ ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ»
01.06.2020 962 0
С помощью этого теста можно проверить кругозор семиклассников по теме: «Признаки параллельности прямых»
-
Первый признак равенства треугольников.
21.10.2020 3021
Тест седержит несколько интересных теоретических и практических вопросов по теме «Первый признак равенства теругольников».

-
Итоговый тест 7 класс геометрия ТЕОРИЯ тренировочный
12.05.2021 8619 0
7 класс геометрия учебник Л.С.Атанасян. Данный тест предназначен для повторения теории по курсу геометрии 7 класса. В тесте 40 вопросов, которые выбираются случайным образом из общей базы заданий 80 вопросов. По завершении выставляется оценка. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%.
-
7 класс. Геометрия. Параллельные прямые.
07.01.2016 24831
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Параллельные прямые.
«.
-
7 класс. Геометрия. Смежные и вертикальные углы № 4 (диктант).
09.01.2016 1120
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Смежные и вертикальные углы.»
-
7 класс. Геометрия. Смежные углы № 1 (диктант).
08.10.2016 1938
Тест предназначен для учащихся 7 классов при отработке навыков устного счёта при решении задач по теме «Смежные углы».
-
7 класс. Геометрия. Смежные и вертикальные углы №5
14.
 10.2016
8863
10.2016
8863
Тест предназначен для учащихся 7 классов при отработке навыков устного счёта при решении задач по теме «Смежные и вертикальные углы».
-
Тест по теме «Окружность» (геометрия, 7-8 класс)
16.11.2016 16501
Тест предназначен для проверки знаний учащихся после изучения темы «Окружность». Основные тестируемые понятия: окружность, радиус, хорда, касательная
-
7 класс Геометрия
14.03.2019 25095
Данный тест предназначен для определения знания предмета «Геометрия» за курс 7 класса.

-
Треугольники.Сумма углов треугольника.
08.05.2020 104 0
Данный тест предназначен для проверки знаний учащихся 7 класса по темам «Треугольники», «Равнобедренный треугольник и его свойства», «Прямоугольный треугольник»
-
25.10.2020 9087
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
Окружность.
 Начальные сведения.
Начальные сведения.
22.11.2020 255 0
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
Итоговый тест 7 класс геометрия ТЕОРИЯ
25.04.2021 1274 0
В тесте 30 вопросов, которые выбираются случайным образом из общей базы заданий. По завершении выставляется оценка. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%.
-
7 класс. Геометрия. Прямые на плоскости.
11.04.2015 1027 0
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Прямые на плоскости.
 «.
«. -
7 класс. Геометрия. Равнобедренный и равносторонний треугольники.
16.01.2016 9890
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Равнобедренный и равносторонний треугольники.»
-
Прямоугольные треугольники
16.04.2020 20573
Тест по теме «Прямоугольные треугольники» для 7 класса. Содержит 10 вопросов, расположенных в последовательности от простых к более сложным
-
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
22.
 04.2020
1896
0
04.2020
1896
0
Тест по теме «Прямоугольный треугольник. Элементы, признаки равенства»
-
Геометрия. Итоговый тест.
04.05.2020 23071
Геометрия. 7 класс. Итоговый тест по геометрии за 2019 — 2020 учебный год.
-
Геометрия 7 класс
14.05.2020 82 0
Тестовая работа к ГЛАВЕ 1. Начальные геометрические сведения. Прямая. Отрезок. Измерение углов
-
Построение треугольника по трем элементам (проверочная работа)
24.
 05.2020
769
0
05.2020
769
0
Обобщающий тест по теме «Построение треугольника по трем элементам». Состоит из 6 вопросов с выбором ответа и заполнением пропусков.
-
Годовая контрольная работа по геометрии 7 класс
10.07.2020 2663
Годовая контрольная работа по геометрии состоит из 11 заданий. с 1 по 5 — тестовые задания (от 1 до 4 правильных), с 6 по 7 нужно установить соответствие (1-4:А-Д), с 8 по 9 нужно вписать ответ (число), с 10 по 11 — вписать ответ. Время на контрольную – 60 мин.
-
Входной тест Геометрия 7
21.07.2020 18 0
Входной тест по геометрии контролирующий освоение учениками темы измерение отрезков и углов.

-
Равнобедренный треугольник и его свойства
18.11.2020 8810
Проверочный тест по теме «Равнобедренный треугольник». Геометрия 7 класс.
-
Окружность и ее элементы — 7 класс
16.12.2020 859 0
Тест предназначен для проверки усвоения учащимися 7 класса тем «Окружность», «Элементы окружности».
-
ГЕОМЕТРИЯ выбор верных утверждений 7 класс
12.04.2021 2643 0
Тест содержит 20 заданий.
 Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста. -
Решение задач по теме «Параллельные прямые»
07.02.2022 436 0
Тест предназначен для проверки заний по 3 главе. Удачи в прохождении!!!
-
7 класс. Геометрия. Свойства углов, образованных при пересечении параллельных прямых секущей. (диктант)
09.01.2016 4291 0
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Свойства углов, образованных при пересечении параллельных прямых секущей.
 «.
«. -
7 класс. Геометрия. Треугольники.
09.01.2016 2280
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Треугольники.»
-
7 класс. Геометрия. Признаки равенства треугольников.
10.01.2016 11093
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Признаки равенства треугольников.»
-
7 класс. Геометрия. Сумма углов треугольника. Внешний угол треугольника.

16.01.2016 23138
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Сумма углов треугольника. Внешний угол треугольника.»
-
7 класс. Геометрия. Смежные углы № 2 (диктант).
08.10.2016 891
Тест предназначен для учащихся 7 классов при отработке навыков устного счёта при решении задач по теме «Смежные углы».
-
7 класс. Геометрия. Смежные и вертикальные углы №3
14.10.2016 3028
Тест предназначен для учащихся 7 классов при отработке навыков устного счёта при решении задач по теме «Смежные и вертикальные углы».

-
Геаметрыя 7 клас. Трохвугольнікі.
28.11.2019 6 0
Тэст прызначаны для навучэнцаў 7 класаў пры адпрацоўцы навыкаў рашэня задач па тэме .
-
Геометрия 7 класс. Некоторые свойства прямоугольных треугольников
02.04.2020 1912 0
Тест по теме «Некоторые свойства прямоугольных треугольников»
-
7 класс. Признаки равенства прямоугольных треугольников
10.04.2020 5324 0
Тест — тренинг на применение признаков равенства прямоугольных треугольников.
 Тест содержит 5 задач на готовых чертежах.
Тест содержит 5 задач на готовых чертежах.
-
Неравенство треугольника 7 класс
15.04.2020 7451 0
Данный тест предназначен для закрепления материала по теме «Неравенство треугольника». Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!!
-
ГЕОМЕТРИЯ 7. Окружность.
16.04.2020 5886 0
Тест по геометрии рассчитан на учащихся 7 классов для проверки знаний по теме: «Окружность». Время прохождения теста ограничено 30 минутами.
-
Прямоугольные треугольники.
 Вариант 2
Вариант 2
16.04.2020 2463 0
Тест по теме «Прямоугольные треугольники» для 7 класса. Содержит 10 вопросов, расположенных в последовательности от простых к более сложным
-
Геометрия 7 класс (теоретический материал)
24.04.2020 9364
Тест на знание теоретического материала по геометрии 7 класса
-
Повторение. Геометрия 7 класс
10.05.2020 866 0
Данный тест можно использовать на последних уроках геометрии.
 Обучающиеся выбирают верные ответы на каждый вопрос, по окончании тестирования получают оценку
Обучающиеся выбирают верные ответы на каждый вопрос, по окончании тестирования получают оценку -
Контрольный тест по теме «Окружность и круг. Геометрические построения» Вариант 1 (7 класс)
11.05.2020 389 0
Контрольная работа по теме «ОКружноть и круг. Геометрические построения», вариант 1. Всего вопросов 8. С выбором ответа — 4 вопроса; с кратким ответом — 3 вопроса; заполнить пропуски в тексте — 1 вопрос. Максимальное количестко баллов — 22 балла. Пятибальная система оценивания.
-
Контрольный тест по теме «Окружность и круг. Геометрические построения» Вариант 2 (7 класс)
11.05.2020 342 0
Контрольная работа по теме «ОКружноть и круг.
 Геометрические построения», вариант 2.
Всего вопросов 8. С выбором ответа — 4 вопроса; с кратким ответом — 3 вопроса; заполнить пропуски в тексте — 1 вопрос.
Максимальное количестко баллов — 22 балла. Пятибальная система оценивания.
Геометрические построения», вариант 2.
Всего вопросов 8. С выбором ответа — 4 вопроса; с кратким ответом — 3 вопроса; заполнить пропуски в тексте — 1 вопрос.
Максимальное количестко баллов — 22 балла. Пятибальная система оценивания. -
Математика 7 класс. Итоговая контрольная работа.
13.05.2020 423
Данный тест предназначен для проверки знаний по математике учащихся 7-х классов. Тест состоит из 16 заданий, рассчитан на 40 минут выполнения.
-
Геометрия 7 класс. Итоговый тест №2
20.05.2020 204 0
Итоговый тест по теме «Признаки равенства треугольников.
 Медиана, биссектриса и высота треугольника»
Медиана, биссектриса и высота треугольника» -
Сумма углов треугольника (I вариант)
27.05.2020 1952 0
Тест по теме «Сумма углов треугольника» предназначен для учащихся 7 класса , содержит 10 задний с чертежами, по которым надо решить и записать ответ в окно теста.
-
Сумма углов в треугольнике
09.08.2020 56 0
Геометрия, 7 класс. Тест предназначен для закрепления материала «Сумма углов в треугольнике».
-
7 класс Глава 2 Треугольники
18.
 10.2020
9168
0
10.2020
9168
0
7 класс геометрия учебник Л.С.Атанасян. Данный тест предназначен для повторения Главы 2 «Труегольники». Вопросы двух типов — по теории и практические задания. В тест случайным образом выбираются 5 теоретических вопросов и 5 практических.
-
7 класс Медианы биссектрисы и высоты треугольника. Равнобедренный треугольник. ТЕОРИЯ
19.10.2020 1850 0
7 класс геометрия учебник Л.С.Атанасян. Тест предназначени для повторения и закрепления теоретического материала по теме «Медианы, биссектрисы и высоты треугольника». Содержит 17 заданий.
-
Свойства равнобедренного треугольника.

25.10.2020 2786 0
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
Основные утверждения по геометрии. 7 класс.
05.11.2020 165 0
Тест предназначен для проверки теоретических знаний по геометрии 7 класса. Ориентирован на учебник Л. С. Атанасяна и др. «Геометрия 7-9 классы». Может быть использован для подготовки к ОГЭ по математике.
-
Равные треугольники. Высота, медиана, биссектриса треугольника
26.
 11.2020
196
0
11.2020
196
0
Тест составлен на основе учебника по геометрии за 7 класс авторы Мерзляк А.Г., Полонский В. Б., Якир М. С.
-
Признаки равенства треугольников
26.11.2020 191 0
Тест предназначен для учащихся 7 классов при отработке навыков решения задач по теме «Признаки равенства треугольников.»
-
Остроугольный, прямоугольный и тупоугольный треугольники. 7 класс
20.12.2020 197
Ребята! Я предлагаю вам ответить на вопросы теста по теме «Виды треугольников». Будьте внимательны!
-
Геометрия 7 класс
02.
 03.2021
1986
0
03.2021
1986
0
Теоретический тест по теме «Параллельные прямые» 7 класс.Для урока обобщения изученного материала.
-
Параллельные прямые
27.03.2021 54 0
Тест по геометрии «Свойства параллельных прямых» состоит из десяти заданий с выбором правильного варианта ответа из числа предложенных. Он поможет семиклассникам вспомнить все изученное по этой важной теме, а старшеклассникам – повторить материал при подготовке к экзамену. Решить тест можно на нашем сайте онлайн.
-
Треугольники и элементы. Признаки равенства треугольников (7 класс. Повторение)
27.
 10.2021
451
0
10.2021
451
0
Тест на знание теоретического материала по теме «Треугольники» для 7 класса
-
Кері байланыс
04.11.2021 25
Рефлексия ______________________________________________________________________________________________________
-
Итоговый тест по геометрии за курс 7 класса
17.12.2021 229 0
Тест состоит из пяти вопросов. В каждом вопросе один правильный ответ
-
Тест по теме «Свойства параллельных прямых.
 Сумма внутренних углов треугольника.» (геометрии 7 класс)
Сумма внутренних углов треугольника.» (геометрии 7 класс)
31.01.2022 191
Тест по теме «Свойства параллельных прямых. Сумма внутренних углов треугольника.» (геометрии 7 класс)
Геометрия 7 Атанасян Задачи 1-23
Практические задания и задачи №№ 1 — 23 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе 1 «Начальные геометрические сведения». Геометрия Атанасян Задачи 1-23 к:
- § 1. Прямая и отрезок (1. Точки, прямые, отрезки. 2. Провешивание прямой на местности)
- § 2. Луч и угол. (3. Луч. 4. Угол)
- § 3. Сравнение отрезков и углов. (5. Равенство геометрических фигур. 6. Сравнение отрезков и углов)
Вернуться в ОГЛАВЛЕНИЕ Смотреть задачи 24-40
Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
Цитаты из учебника представлены в учебных целях.
Практические задания №№ 1-7
Практические задания №№ 8-17
Задачи №№ 18-23
Геометрия 7 класс (УМК Атанасян)
к § 1. «Измерение отрезков»:
Практические задания №№ 1-7№ 1. Проведите прямую, обозначьте её буквой а и отметьте точки А и В, лежащие на этой прямой, и точки Р, Q и R, не лежащие на ней. Опишите взаимное расположение точек А, В, Р, Q, R и прямой а, используя символы ∈ и ∉.
Смотреть РЕШЕНИЕ упражнения 1 в тетради
№ 2. □ Отметьте три точки А, В и С, не лежащие на одной прямой, и проведите прямые АВ, ВС и СА.
Смотреть РЕШЕНИЕ упражнения 2 в тетради
№ 3. Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Смотреть РЕШЕНИЕ упражнения 3 в тетради
№ 4. Отметьте точки А, В, С, D так, чтобы точки А, В, С лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?
Отметьте точки А, В, С, D так, чтобы точки А, В, С лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?
Смотреть РЕШЕНИЕ упражнения 4 в тетради
№ 5. Проведите прямую а и отметьте на ней точки А и В. Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.
Смотреть РЕШЕНИЕ упражнения 5 в тетради
№ 6. Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой?
Смотреть РЕШЕНИЕ упражнения 6 в тетради
№ 7. □ На рисунке 10 изображена прямая, на ней отмечены точки А, В, С и D. Назовите все отрезки: а) на которых лежит точка С; б) на которых не лежит точка В.
Смотреть РЕШЕНИЕ упражнения 7 в тетради
к § 2 «Луч и угол»
Практические задания №№ 8-17№ 8. Проведите прямую, отметьте на ней точки А и В и на отрезке АВ отметьте точку С. а) Среди лучей АВ, ВС, СА, АС и ВА назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА.
Проведите прямую, отметьте на ней точки А и В и на отрезке АВ отметьте точку С. а) Среди лучей АВ, ВС, СА, АС и ВА назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 9. Начертите три неразвёрнутых угла и обозначьте их так: ∠AOB, ∠hk, ∠M.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 10. Начертите два развёрнутых угла и обозначьте их буквами.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 11. Начертите три луча h, k и I с общим началом. Назовите все углы, образованные данными лучами.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 12. Начертите неразвёрнутый угол hk. Отметьте две точки внутри этого угла, две точки вне этого угла и две точки на сторонах угла.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 13. Начертите неразвёрнутый угол. Отметьте точки А, В, М и N так, чтобы все точки отрезка АВ лежали внутри угла, а все точки отрезка MN лежали вне угла.
Отметьте точки А, В, М и N так, чтобы все точки отрезка АВ лежали внутри угла, а все точки отрезка MN лежали вне угла.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 14. Начертите неразвёрнутый угол АОВ и проведите: а) луч ОС, который делит угол АОВ на два угла; б) луч OD, который не делит угол АОС на два угла.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 15. □ Сколько неразвёрнутых углов образуется при пересечении двух прямых?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 16. □ Какие из точек, изображённых на рисунке № 17, лежат внутри угла hk, а какие — вне этого угла?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 17. Какие из лучей, изображённых на рисунке № 18, делят угол АОВ на два угла?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
к § 3 «Сравнение отрезков и углов»
Задачи №№ 18-23№ 18. На луче с началом О отмечены точки А, В и С так, что точка В лежит между точками О и А, а точка А — между точками О и С. Сравните отрезки ОВ и ОА, ОС и О А, ОВ и ОС.
На луче с началом О отмечены точки А, В и С так, что точка В лежит между точками О и А, а точка А — между точками О и С. Сравните отрезки ОВ и ОА, ОС и О А, ОВ и ОС.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 19. Точка О является серединой отрезка АВ. Можно ли совместить наложением отрезки: а) ОА и ОВ; б) ОА и АВ?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 20. □ На рисунке 25 отрезки АВ, ВС, CD и DE равны. Укажите: а) середины отрезков АС, АЕ и СЕ; б) отрезок, серединой которого является точка D; в) отрезки, серединой которых является точка С.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 21. Луч ОС делит угол АОВ на два угла. Сравните углы АОВ и АОС.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 22. □ Луч l — биссектриса угла hk. Можно ли наложением совместить углы: a) hl и lk; б) hl и hk?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 23. □ На рисунке 26 углы, обозначенные цифрами, равны. Укажите: а) биссектрису каждого из углов АОС, BOF, АОЕ; б) все углы, биссектрисой которых является луч ОС.
□ На рисунке 26 углы, обозначенные цифрами, равны. Укажите: а) биссектрису каждого из углов АОС, BOF, АОЕ; б) все углы, биссектрисой которых является луч ОС.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
Вы смотрели: Практические задания и задачи №№ 1 — 23 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе 1 «Начальные геометрические сведения»: § 1. Прямая и отрезок; § 2. Луч и угол; § 3. Сравнение отрезков и углов. Геометрия Атанасян Задачи к Главе 1 задачи 1-23.
Вернуться в ОГЛАВЛЕНИЕ учебника Смотреть задачи 24-40
Седьмой класс (7 класс) Вопросы по геометрии и измерениям для тестов и рабочих листов
Выбрать все вопросыЕсли площадь треугольника 15 см в квадрате, а основание 2 см, то чему равна высота?
- 45 см
- 30 см
- 9 см
- 15 см
Два угла, сумма мер которых равна 180°?
- Тупой угол
- Прямой угол
- Внешний угол
- Дополнительный
- Внутренний угол
- Дополнительный
[математика]mangDBC = x[/математика]
[математика]mangCBA = 2x[/math]
- [математика]2x — x = 90[/математика]
- [математика]2x + x = 90[/математика]
- [математика]2x — x = 180[/математика]
- [математика]2x + x = 180[/математика]
Два угла являются углами, если сумма их мер равна 180 градусам
- дополнительный
- дополнительный
- прямой
- Правильно
Используя показанную диаграмму, [math]ang[/math]1 и [math]ang[/math]4 являются дополнительными углами.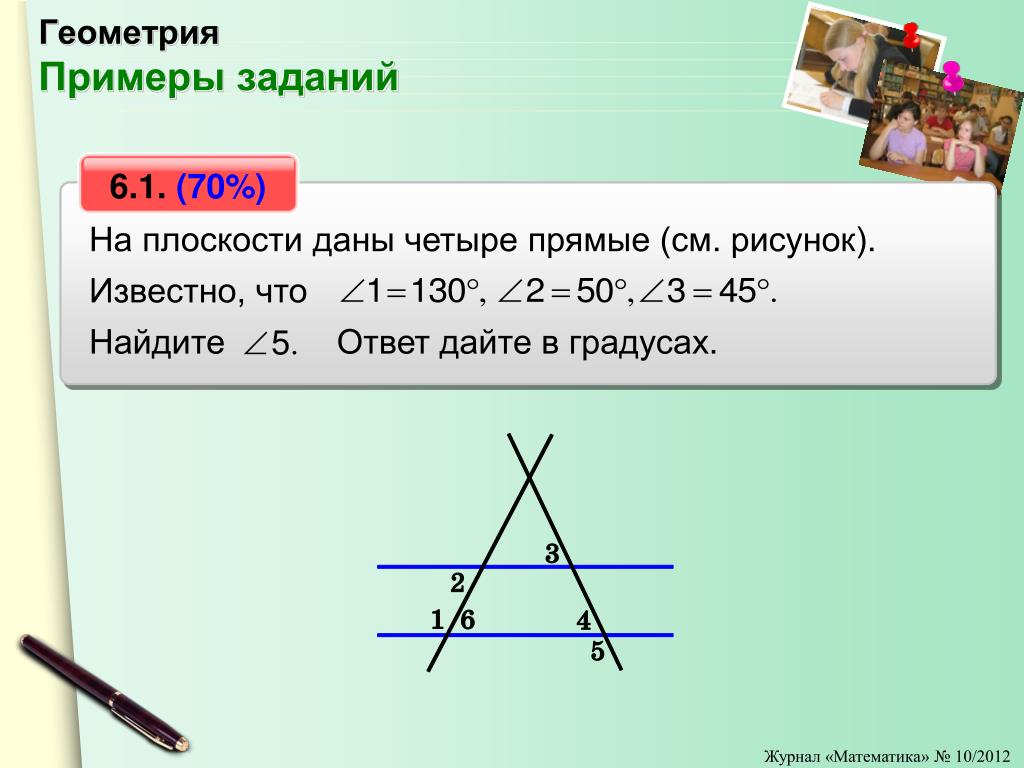 Если [math]ang[/math]4 = 70[math]градусов[/math], какова мера [math]ang[/math]1?
Если [math]ang[/math]4 = 70[math]градусов[/math], какова мера [math]ang[/math]1?
- 180[математика]градус[/математика]
- 20[математика]градус[/математика]
- 110[математика]градус[/математика] 92[/математика]
Два угла являются углами, если сумма их мер равна 90 градусам.
- дополнительный
- дополнительный 92[/математика]
Как называются два угла, сумма мер которых равна 90 градусов?
- Дополнительные углы
- Прямые углы
- Тупые углы
- Дополнительные углы
Площадь показанной фигуры равна 144 см в квадрате. Чему равна сторона BC?
Чему равна сторона BC?
- 144 см
- 12 см
- 48 см
Если угол 1 равен 55 градусам, то угол 3 равен градусов.
- 125
- 35
- 55
- 90
;[математика]80 градусов[/математика];[математика]22 градуса[/математика]
- [математика]258 градусов[/математика]
- [математика]129 градусов[/математика]
- [математика]32 градуса[/математика]
- [математика]78 градусов[/математика]
Шестиугольник, треугольник, десятиугольник, пятиугольник
- Десятиугольник, шестиугольник, пятиугольник, треугольник
- Треугольник, шестиугольник, пятиугольник, десятиугольник
- Шестиугольник, треугольник, десятиугольник, пятиугольник
- Треугольник, пятиугольник, шестиугольник, десятиугольник
Сколько будет стоить укладка ковра в комнате размером 25 на 13 футов, если укладка ковра стоит 15,50 долларов за квадратный ярд?
- 5037,50 долларов США
- $559,72
- 419,79 долларов США
- 1679 долларов США.
 17
17
Если радиус круга 5 дюймов, каков диаметр?
- 5 дюймов
- 10 дюймов
- 25 дюймов
- 2 дюйма
Мера [math]ang 1 [/math] равна [math]150deg[/math]. Каковы меры [math]ang4, ang3 и ang2[/math]?
- [математика]30 градусов, 150 градусов, 30 градусов[/математика]
- [математика]45 градусов, 120 градусов, 30 градусов[/математика]
- [математика]60 градусов, 150 градусов, 45 градусов[/математика]
- [математика]90 градусов, 135 градусов, 30 градусов[/математика]
Найдите длину окружности радиусом 10 м.
- 6,28 м
- 62,8 м
- 628 м
- 6280 м
Стол для пинг-понга Мэгги имеет длину 9 футов и ширину 5 футов. Какова площадь прямоугольной игровой поверхности стола для пинг-понга?
- 28 квадратных футов
- 36 квадратных футов
- 45 квадратных футов
- 54 квадратных фута
Слово равносторонний означает
- конгруэнтные стороны.

- равные углы.
- совпадающие точки.
- конгруэнтная фигура.
Если стороны треугольника составляют основание, равное 4 дюймам, высоте, равной 3 дюймам, и другой стороне, равной 5 дюймам, какова площадь этого треугольника?
- 6 квадратных дюймов
- 4 квадратных дюйма
- 2 квадратных дюйма
- 1 квадратный дюйм
Рабочие листы по геометрии для 7-го класса | Бесплатные рабочие листы по геометрии для 7 класса
- Рабочие листы для печати
Понимание расстояния и положения геометрических структур
Рабочие листы по геометрии для 7-го класса сосредоточены на вычислении площади и периметра различных форм и размеров. Это может помочь проанализировать свойства форм, с которыми мы действительно сталкиваемся в повседневной жизни.
Это может помочь проанализировать свойства форм, с которыми мы действительно сталкиваемся в повседневной жизни.
Например, измерение площади поля или его периметра может рассказать нам о покрытии поверхности поля и о том, сколько места оно занимает.
Практическое выполнение геометрических измерений
Некоторые из стандартных рабочих листов по геометрии знакомят с практическим применением измерений и углов, которые очень широко используются.
Нахождение длин и углов фигуры путем сравнения их с другими сторонами этой фигуры помогает учащимся понять, как создается полная геометрическая структура. Профессионалы, работающие в таких областях, как строительство, должны ежедневно реализовывать эти концепции.
Понятия об основных формах вокруг нас
Рабочие листы по геометрии для 7-го класса могут помочь учащимся понять основные характеристики различных фигур, таких как линии и углы конгруэнтных треугольников.
Объяснение геометрии для 7-го класса: Онлайн-рабочие листы по геометрии были разработаны, чтобы сделать процесс изучения геометрии более доступным и увлекательным.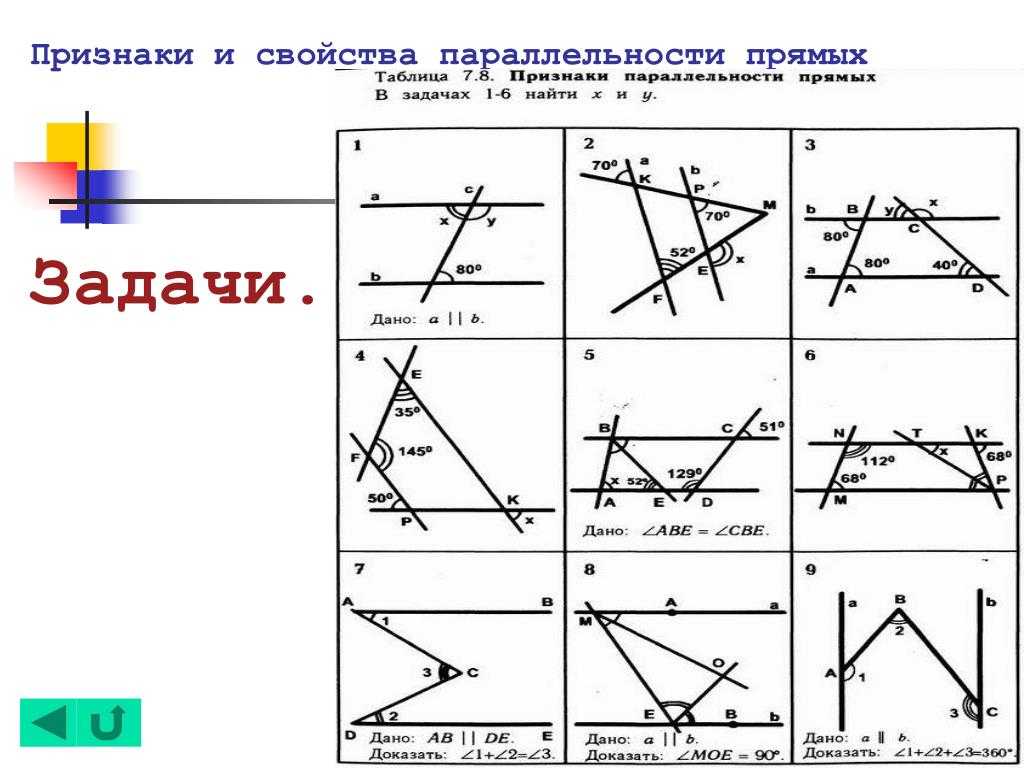 Очень важно изучать геометрию, поскольку она создает прочную основу для более продвинутых уровней математики. Рабочие листы по геометрии для 7 класса представляют собой захватывающий и увлекательный метод изучения основных понятий для учащихся. Студенты могут практиковать эти рабочие листы в своем собственном темпе, преодолевая различные уровни сложности и укрепляя уверенность в себе.
Очень важно изучать геометрию, поскольку она создает прочную основу для более продвинутых уровней математики. Рабочие листы по геометрии для 7 класса представляют собой захватывающий и увлекательный метод изучения основных понятий для учащихся. Студенты могут практиковать эти рабочие листы в своем собственном темпе, преодолевая различные уровни сложности и укрепляя уверенность в себе.
Понятия, рассматриваемые в рабочем листе по геометрии для 7-го класса, включают:
Линии и углы:
Линия — это удлиненный отрезок, не имеющий концов. Отрезки линий — это две конечные точки.
При пересечении двух отрезков образуется угол. Другими словами, углы образуются в результате пересечения двух прямых или отрезков прямых.
Конгруэнтные треугольники:
Конгруэнтные треугольники — это два одинаковых треугольника. Этот рабочий лист по геометрии раскрывает концепцию конгруэнтных треугольников с помощью красочных графических примеров и иллюстраций.
Существуют различные методы определения треугольников одинакового размера, все они описаны в Рабочих листах по геометрии для 7 класса: Сторона гипотенузы
Практическая геометрия:
Рабочие листы по геометрии для 7-го класса также охватывают практические реализации геометрии, такие как рисование правильных углов и размеров фигур по отношению к другим линиям и фигурам. Это концепции геометрии, используемые во многих профессиональных областях, таких как архитектура, планирование инфраструктуры и дизайн.
Площадь и периметр:
Площадь и периметр — две самые важные формулы, которые ученики изучают в 7-м классе геометрии. Площадь и периметр вычисляют размеры поверхности.
Этот расчет обычно используется для различных повседневных целей, таких как расчет расстояния или измерение дома при планировании ремонта или просто при покупке новой мебели.
Геометрия необходима детям для распознавания пространственных связей. Помогая учащимся научиться определять геометрические фигуры, которые можно найти в окружающем нас мире, они могут помочь им увидеть геометрию в своей повседневной жизни. Рабочие листы по геометрии для 7 класса дополняют то, чему учат в классе, и помогают установить связь с реальным миром, что делает основы геометрии более запоминающимися. Рабочие листы по геометрии для 7-го класса помогут учащимся изучить геометрию и понять, зачем она нужна и как она поможет им за пределами класса.
Помогая учащимся научиться определять геометрические фигуры, которые можно найти в окружающем нас мире, они могут помочь им увидеть геометрию в своей повседневной жизни. Рабочие листы по геометрии для 7 класса дополняют то, чему учат в классе, и помогают установить связь с реальным миром, что делает основы геометрии более запоминающимися. Рабочие листы по геометрии для 7-го класса помогут учащимся изучить геометрию и понять, зачем она нужна и как она поможет им за пределами класса.
Часто задаваемые вопросы
Какие преимущества дают учащимся рабочие листы по геометрии для 7 класса?
Одной из первых областей математики является геометрия. Геометрия невероятно практична, потому что она имеет дело с размерами, положениями, углами и формами всего, что нас окружает. В этом мире геометрия — это все. Мы живем на сферической планете с эллиптической орбитой, которая является домом для многих народов и народов, проживающих в определенных географических точках.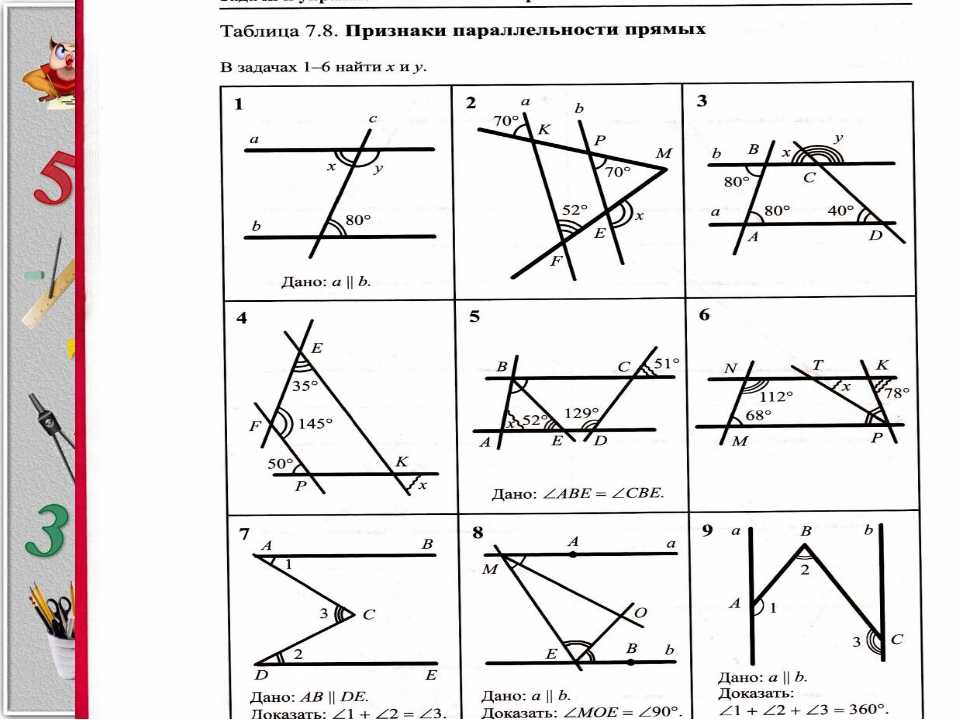 Как нам это понять? посредством геометрии. Рабочие листы по геометрии для 7-го класса расширяют предыдущие знания учащегося по геометрии, охватывая более сложные темы.
Как нам это понять? посредством геометрии. Рабочие листы по геометрии для 7-го класса расширяют предыдущие знания учащегося по геометрии, охватывая более сложные темы.
Как рабочие тетради по геометрии в седьмом классе помогают вам в учебе?
Учащиеся могут связать концепции картирования, изученные в классе, с обстоятельствами, где важны местоположение и направление. Функция пространственных связей в решении проблем и навыках мышления более высокого порядка также считается решающей. Практикуя рабочие листы по геометрии для 7 класса, вы улучшите аналитические и мыслительные навыки.
Как можно использовать геометрию в реальном мире?
Супермодели и актеры являются идеальными примерами этого. Почки, легкие и мозг — еще один пример человеческой симметрии. Эти органы имеют зеркальные отражения друг друга, если разделить их пополам или провести через них линию. Лепестки, чашелистики, тычинки и листья у цветов очень похожи.
Каких целей преследуют рабочие листы по геометрии в седьмом классе?
Учеников будут обучать основам геометрии, в том числе тому, как использовать индуктивные рассуждения, как измерять отрезки и углы, как делить отрезок или угол на две равные половины, а также отношения между отдельными парами углов.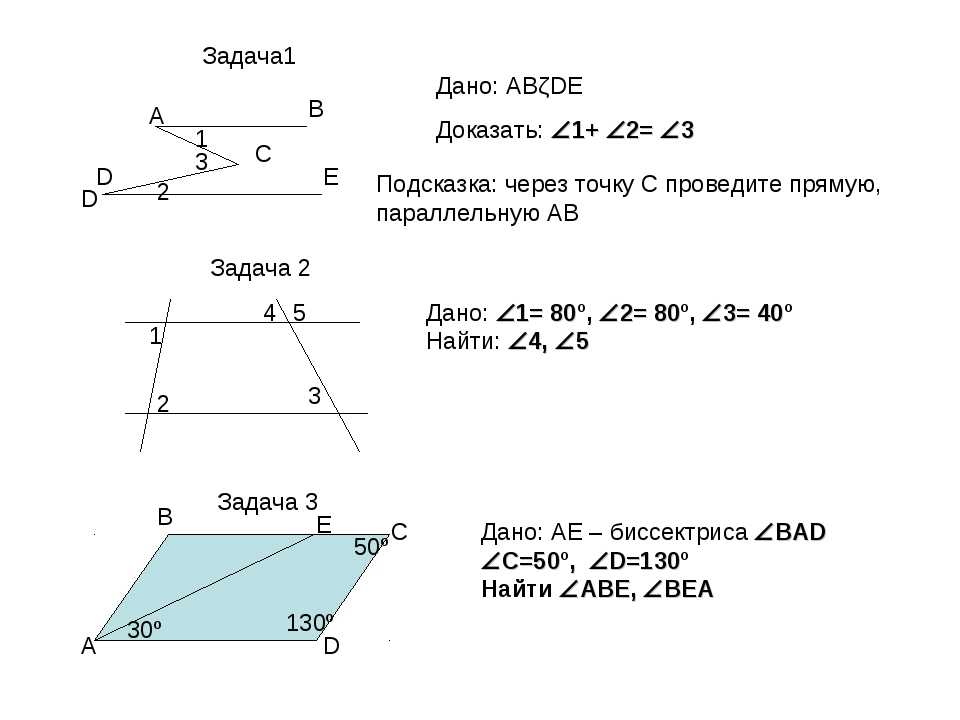 Определяя, деконструируя и формулируя логические аргументы, учащиеся смогут решать трудности.
Определяя, деконструируя и формулируя логические аргументы, учащиеся смогут решать трудности.
Почему геометрия такой более простой предмет, чем алгебра?
По сравнению с алгеброй, геометрия требует меньше математики, а необходимая математика проще. С другой стороны, геометрия требует запоминания нескольких правил и формул, что для некоторых учащихся может оказаться более сложным, чем фундаментальная алгебра.
Заблуждения в геометрии и варианты их решения для учащихся 7-х классов Текст научной работы на тему «Педагогические науки»
Доступно в Интернете по адресу www.sciendirect.com
Sciverse ScienceDirect
Процедура — Социальные и поведенческие науки 55 (2012) 720 — 729
Международная конференция по новым горизонтам в образовании
. Для
Учащиеся седьмого класса
Айсен Озерем
Педагогический факультет Ближневосточного университета PhD. Студент
Реферат
Основной целью данного исследования является выявление слабостей учащихся средней школы в вопросах геометрии мер, углов и фигур, преобразований и построения и трехмерных форм. Учебная программа 7 класса содержит 4 темы по геометрии из 17 тем по математике. В дополнение к этому, это исследование направлено на выявление ошибок, допущенных 28 учениками 7-го класса на последних 4 экзаменах, включая два промежуточных и два выпускных экзамена. Для сбора данных учащиеся были протестированы на двух промежуточных и двух выпускных экзаменах с использованием открытых вопросов по геометрии, чтобы проанализировать их навыки решения задач и проверить, сколько они приобрели в течение года. При анализе данных использовались таблицы частот. Для достижения этой цели на первом промежуточном экзамене были протестированы предметные показатели. На первом выпускном экзамене, который следовал за первым промежуточным экзаменом, в дополнение к мерам и углам также проверялись навыки форм. После этих тестов во втором промежуточном семестре мы проверили учащихся на трансформацию и построение. Для анализа и интерпретации результатов в исследовании использовались описательная методология и интервью со студентами.
Учебная программа 7 класса содержит 4 темы по геометрии из 17 тем по математике. В дополнение к этому, это исследование направлено на выявление ошибок, допущенных 28 учениками 7-го класса на последних 4 экзаменах, включая два промежуточных и два выпускных экзамена. Для сбора данных учащиеся были протестированы на двух промежуточных и двух выпускных экзаменах с использованием открытых вопросов по геометрии, чтобы проанализировать их навыки решения задач и проверить, сколько они приобрели в течение года. При анализе данных использовались таблицы частот. Для достижения этой цели на первом промежуточном экзамене были протестированы предметные показатели. На первом выпускном экзамене, который следовал за первым промежуточным экзаменом, в дополнение к мерам и углам также проверялись навыки форм. После этих тестов во втором промежуточном семестре мы проверили учащихся на трансформацию и построение. Для анализа и интерпретации результатов в исследовании использовались описательная методология и интервью со студентами.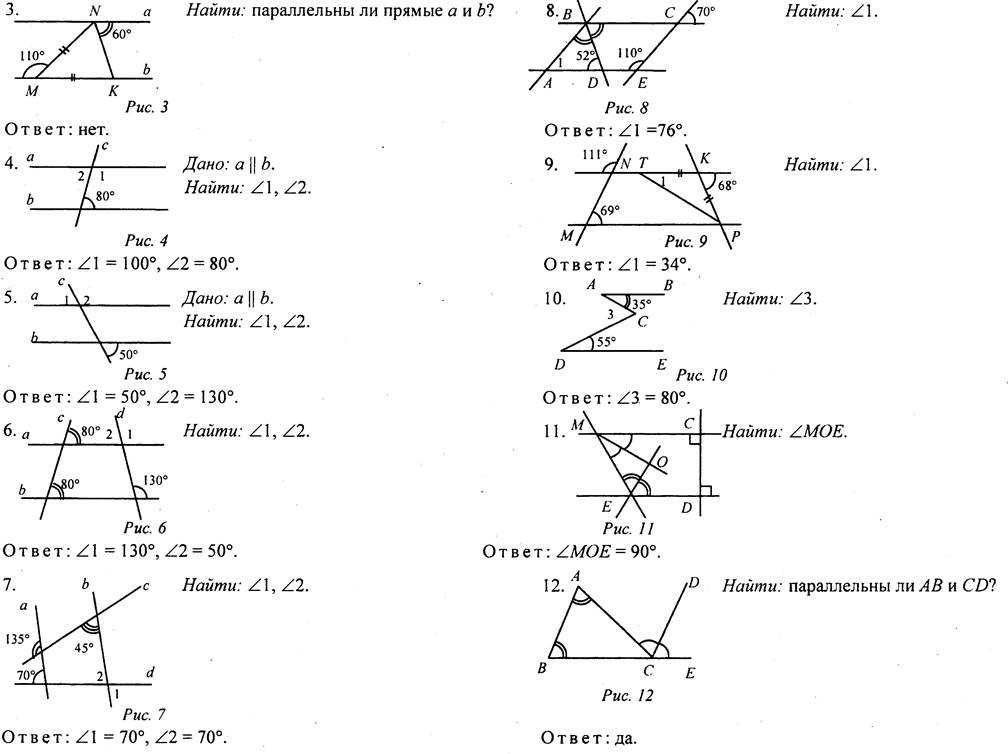 Результаты этого исследования показали, что учащиеся 7-х классов средней школы имеют ряд неправильных представлений, отсутствие фоновых знаний, ошибок в рассуждениях и основных действиях по темам, упомянутым выше
Результаты этого исследования показали, что учащиеся 7-х классов средней школы имеют ряд неправильных представлений, отсутствие фоновых знаний, ошибок в рассуждениях и основных действиях по темам, упомянутым выше
Ключевые слова: математическое образование; студенческие трудности; вопросы по геометрии; заблуждения; геометрические ошибки; обучающие предложения по геометрии.
ВВЕДЕНИЕ
Общая цель математики сформулирована так: научить человека приобретать математические знания, необходимые в повседневной жизни, научить решать задачи, научить его/ее методу решения задач и овладеть методами рассуждений (Алтун, 2008) .Для этого, чтобы усвоить математические понятия, нужно уметь визуализировать диаграммы. Другими словами, математика является областью, в которой предварительные условия имеют решающее значение, поэтому перед началом учебного процесса необходимо проверить знания учащихся по этому предмету (Байкул, 1987). Ганье разделил понятия на два: конкретные и абстрактные понятия.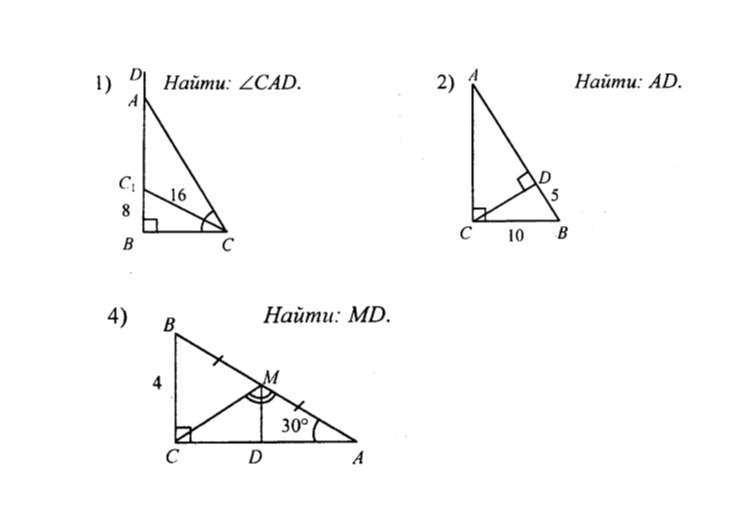
1877-0428 © 2012 г. Опубликовано Elsevier Ltd. Отбор и/или экспертная оценка под ответственностью Ассоциации науки, образования и технологий doi:10.1016/j.sbspro.2012.09.557
Конкретные концепции изучаются, начиная с начало жизни самим человеком. Однако изучение абстрактных понятий, которым иногда обучают другие, необходимо (Сенемоглу, 2000). В этом контексте обучение на основе математики должно осуществляться в соответствии с тремя целями, перечисленными выше (Байкул, 2002).
• Для овладения учащимися математическими понятиями.
• Понимать математические операции.
• Чтобы помочь учащимся установить связи с понятиями и операциями.
Согласно Пиаже и Инхельдеру (1956), существуют определенные этапы обучения, начиная с рождения. Эти этапы:
Стадия 0: каракули (менее 2)
Стадия 1: топологическая — неправильные замкнутые кривые для представления кругов, квадратов и т. д. (2-4 года) Стадия 2: проективно-прогрессивная дифференциация евклидовых форм (4-4 года). 7 лет) 3 этап: Евклидово умение рисовать евклидовы фигуры (7-8 лет)
7 лет) 3 этап: Евклидово умение рисовать евклидовы фигуры (7-8 лет)
Хотя в этом есть определенные возрастные группы, это не получило широкого признания. Было высказано предположение, что даже младшие дети иногда могут оперировать некоторыми евклидовыми понятиями. Вполне вероятно, что топологические, проективные и евклидовы понятия со временем развиваются, и их использование становится все более интегрированным.
Пиаже предположил, что дети смотрят на мир совсем с другой точки зрения, чем взрослые. Поэтому ученые начали исследовать причины этого, внимательно слушая, что студенты говорят и делают по различным предметным заданиям. Они обнаружили удивительные факты, что учащиеся усваивают идеи, которые часто довольно эффективно дополняются концепциями, представленными в классе. У них было мощное развитие представлений, но они иногда не согласовывались с общепринятыми математическими и научными представлениями.
Модель Ван Хиле (1986 г.) по-прежнему остается самым известным теоретическим описанием того, как учащиеся изучают формы. Модель предполагает, что дети должны пройти последовательность уровней в фиксированном порядке при изучении формы. Первые три уровня в модели следующие:
Модель предполагает, что дети должны пройти последовательность уровней в фиксированном порядке при изучении формы. Первые три уровня в модели следующие:
уровень визуализации (уровень 1, также известный как уровень распознавания), на котором учащиеся узнают и учатся называть определенные геометрические фигуры, но обычно знают только формы в целом, а не их свойств или их компонентов;
На уровне анализа (уровень 2, также известный как описательный) учащиеся начинают распознавать формы по их свойствам.
На уровне абстракции (уровень 3, также известный как реляционный) учащиеся начинают формировать определения форм на основе их общих свойств и понимать некоторые доказательства.
Многие учителя заметили, что у многих маленьких детей возникают многочисленные неправильные представления о геометрии, когда учитель обсуждает задачу на доказательство геометрии в классе, это обычно включает устное представление формального доказательства и движения тела, указывающие на разные части фигуры задачи. Студенты должны смотреть, слушать, делать заметки и думать по ходу лекции. Они должны обращаться ко многим элементам инструкции и включать их в свою память (Свеллер, 19 лет).88). Это часто вызывает когнитивную перегрузку и отрицательно сказывается на обучении учащихся. Многочисленные исследователи экспериментировали с различными способами обучения и обнаружили серьезные проблемы у изучающих геометрию: неполное понимание задачи и математических символов, получение доказательств на основе прямых визуальных элементов (например, Chazan, 1993; Healy & Hoyles, 2000), отсутствие стратегических знаний в получение доказательств и т. д. Обращаясь к трудностям в изучении геометрии, Дюваль (1998) и Хили и Хойлс (1998) объяснил, что обучение геометрии часто бывает более сложным, чем обучение числовым операциям или элементарной алгебре. Поэтому более важно, чтобы инструкции по геометрии включали в себя новые и проверенные подходы, такие как использование визуальных и мультимедийных инструментов в классе.
Студенты должны смотреть, слушать, делать заметки и думать по ходу лекции. Они должны обращаться ко многим элементам инструкции и включать их в свою память (Свеллер, 19 лет).88). Это часто вызывает когнитивную перегрузку и отрицательно сказывается на обучении учащихся. Многочисленные исследователи экспериментировали с различными способами обучения и обнаружили серьезные проблемы у изучающих геометрию: неполное понимание задачи и математических символов, получение доказательств на основе прямых визуальных элементов (например, Chazan, 1993; Healy & Hoyles, 2000), отсутствие стратегических знаний в получение доказательств и т. д. Обращаясь к трудностям в изучении геометрии, Дюваль (1998) и Хили и Хойлс (1998) объяснил, что обучение геометрии часто бывает более сложным, чем обучение числовым операциям или элементарной алгебре. Поэтому более важно, чтобы инструкции по геометрии включали в себя новые и проверенные подходы, такие как использование визуальных и мультимедийных инструментов в классе.
Изучение геометрии является важным компонентом изучения математики, поскольку оно позволяет учащимся анализировать и интерпретировать мир, в котором они живут, а также вооружает их инструментами, которые они могут применять в других областях математики. Поэтому учащимся необходимо развивать понимание геометрических понятий
, а также получение соответствующих навыков, связанных с геометрией. В этом проекте анализируется развитие геометрических навыков и использование инструментов, воспроизведение конструкций, проверка свойств, предположения и исследования. Можно сказать, что геометрия не используется учащимися с самого начала из-за их предыдущего статического опыта обучения. Еще одна трудность, с которой сталкиваются некоторые студенты, связана с пониманием геометрического языка. После этого опроса учитель седьмого класса может проанализировать геометрические ошибки учащихся и помочь им улучшить свои геометрические знания. В данной статье мы описываем некоторые приемы управляемого исследования для учителей седьмого класса на уроке геометрии. Эта статья дает методы о преподавании.
Эта статья дает методы о преподавании.
В нашем учебном классе, когда используются строительные задания, они включают разработку новых идей и их соединение с существующими идеями учащихся. Если учащиеся не находятся на определенном уровне модели Ван Хиле, они могут быть не в состоянии понять то, что учитель видит в геометрической ситуации, поэтому требуется более высокий уровень понимания. Заблуждения возникают часто, если учащиеся обходят или пропускают уровень модели. Учитель должен заставить учащихся объяснить, как они приходят к своим ответам или правилам, чтобы он/она мог проанализировать неправильное взаимодействие между существующими идеями учащихся и новой концепцией. Таким образом, учитель может понять причину неправильных представлений и исправить их, оспаривая или противопоставляя их правильному представлению. Предварительное обучение учащихся иногда вызывает неверные представления либо в классе, либо в результате их взаимодействия с социальным и физическим миром. Однако поиск истоков этих заблуждений не может уходить в корень образовательной проблемы.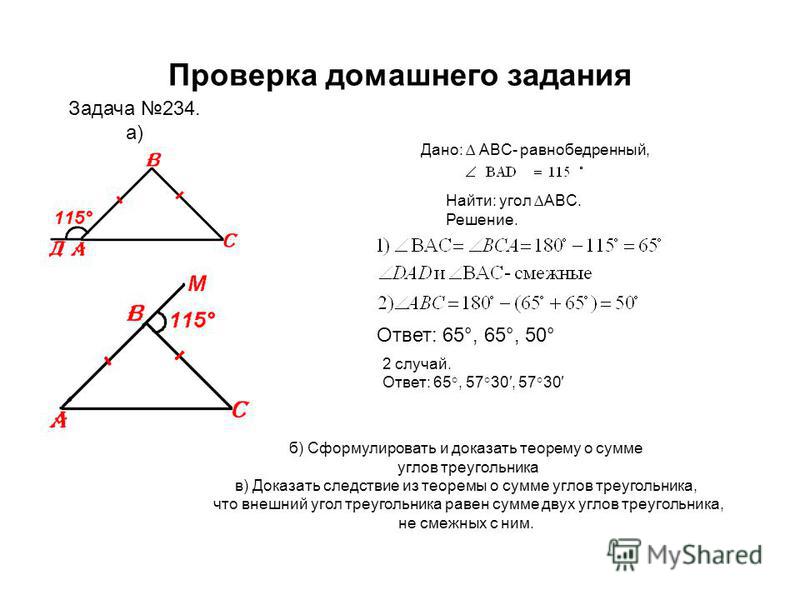 Если заблуждения устойчивы и устойчивы к изменениям, это означает, что они имеют прочную эмпирическую основу.
Если заблуждения устойчивы и устойчивы к изменениям, это означает, что они имеют прочную эмпирическую основу.
ЦЕЛЬ ИССЛЕДОВАНИЯ:
Целью данного исследования является выявить успеваемость учащихся 7-х классов по геометрии и показать концептуальные трудности, с которыми они сталкиваются во время обучения. Делая это, исследование пыталось выявить неправильные представления, которые возникают в процессе изучения геометрии.
SAMPLE
28 учеников седьмого класса, состоящих из 12 мальчиков и 16 девочек, в Turk Maarif Koleji на Кипре. МЕТОД
Целью данного исследования является выявление неверных представлений студентов колледжей о предмете геометрии. Для анализа и интерпретации результатов в исследовании использовались описательная методология и интервью со студентами. Описательный метод был использован, так как основная цель этого исследования — прояснить существующую ситуацию. В этом описательном исследовании были проанализированы точки зрения и опыт экзаменационных работ 28 студентов (два промежуточных и два выпускных экзамена).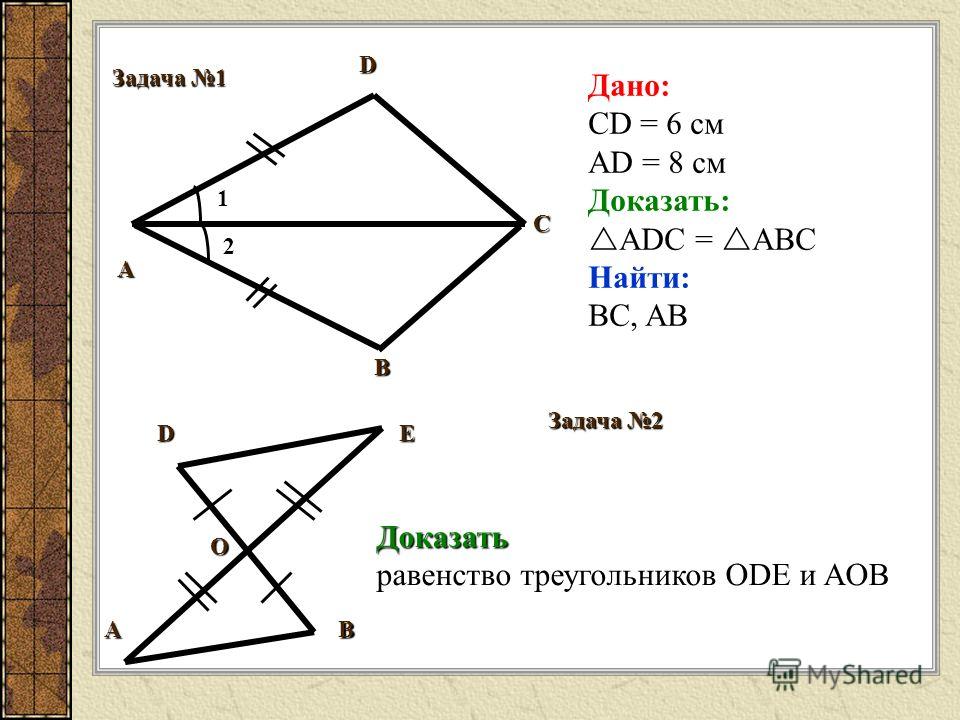
ВАЖНОСТЬ ТЕХНОЛОГИЙ НА КЛАССЕ ГЕОМЕТРИИ:
Технологии позволяют как учащимся, так и учителям получить доступ к широкому спектру инструментов для использования в математике. Перкинс (1995) предложил три стадии процесса понимания в контексте информационных и коммуникационных технологий. Это
• Они предлагают учащимся объяснения
• Делают доступными реляционные знания
• Учащиеся могут иметь пересматриваемые и подробные веб-объяснения
ПРОБЛЕМА
Главной проблемой, решаемой данным исследованием, является реальность заблуждений, которые учащиеся уже проходят или приобретают на уроках геометрии. Эти заблуждения часто связаны с восприятием формы и трех измерений.
ЧАСТЬ ИНТЕРВЬЮ СТУДЕНТОВ:
Учащиеся проходят собеседование и задают четыре вопроса, чтобы узнать их мнение. Исследователь записывал интервью лицом к лицу, делая заметки. Чтобы не создавать тревожной обстановки, записывающая машина не использовалась. В приведенных выше заявлениях студентов имена студентов представлены числами в скобках.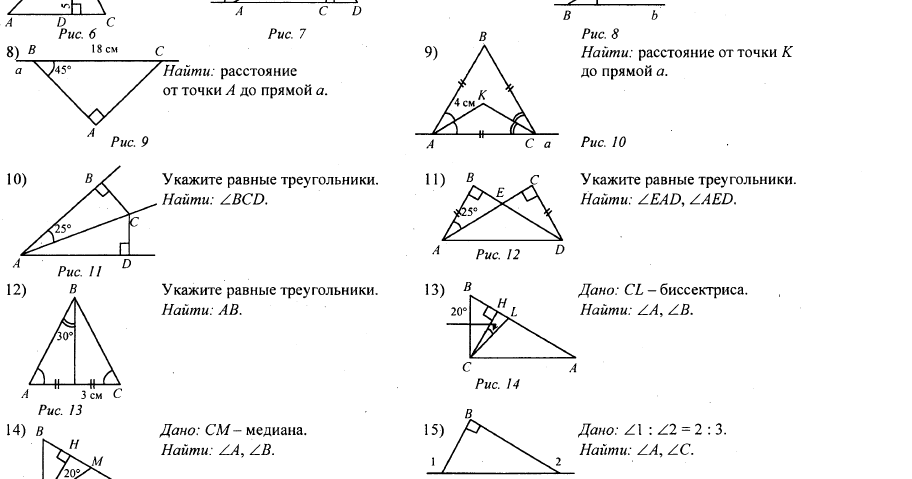 Основными предметами исследования и данными 10 учащихся, которые оказались выше случайно выбранных учащихся 7-х классов, в конце семестра являются:
Основными предметами исследования и данными 10 учащихся, которые оказались выше случайно выбранных учащихся 7-х классов, в конце семестра являются:
1. Что вы думаете об уроках геометрии? Вы находите это интересным?
Восемь из десяти учеников любят уроки геометрии и интересуются уроком. Одному из этих десяти учеников нравятся уроки геометрии, однако он/она находит предмет измерения сложным. Он/она предпочитает предметы, которые включают логику и операции. Другой 1 принимает тот факт, что геометрия необходима, но поскольку она требует очень много времени, она не интересна. Согласно этим данным, 80 процентов учеников сказали, что им нравятся уроки геометрии. Несмотря на то, что учащимся нравится урок, они делают ошибки, поэтому в результате может быть проведено больше тестов, а неправильные представления учащихся должны быть более подчеркнуты после викторин, и в дополнение к этому следует выбрать более наводящие на размышления вопросы, а темы должны быть связаны с реальная жизнь.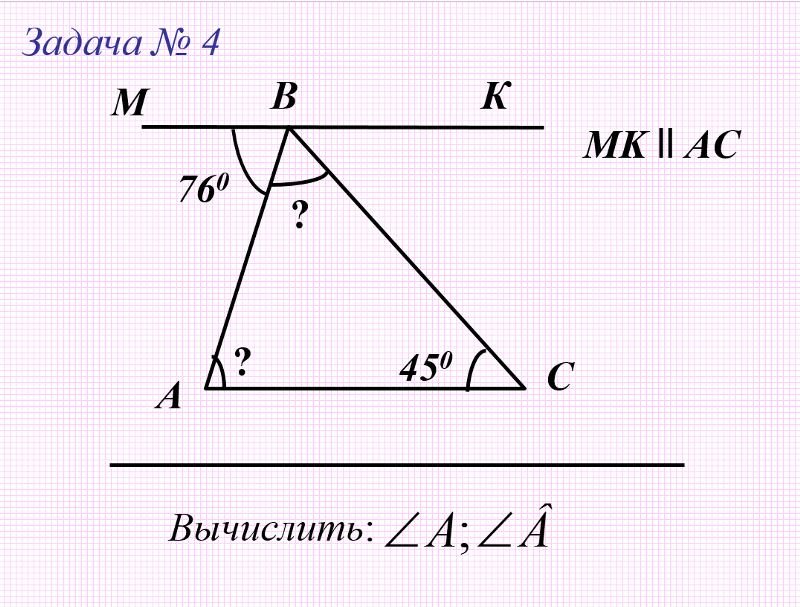
2. Вы хотите превратить уроки геометрии в нечто более наглядное с помощью компьютеров?
Девять учеников сказали, что использование компьютера может сделать уроки более интересными. Считалось, что использование компьютеров позволяет им визуализировать, и это помогает им постоянно учиться. Один из студентов считает, что пользоваться компьютерами не обязательно. Он/она считает, что рисование учителем на доске более полезно. Согласно этим данным, девяносто процентов опрошенных школьников считают, что использование компьютера на уроках геометрии помогает им лучше учиться и запоминать.
3. Как вы изучаете и запоминаете правила и формулы?
Двое студентов сказали, что учат их на письме. Один из них сказал наизусть. Четыре из них сказали письменно и визуализируя. Один сказал это, написав и нарисовав. Один сказал, читая вслух и записывая. Те, кто учится визуализацией, утверждают, что когда они пишут и приклеивают бумажки к некоторым местам в доме, таким как кабинет или двери шкафа, им легче выучить правила и формулы. Последний ученик сказал, что он/она учится, устанавливая с ними логические связи, чтобы потом лучше запоминать с помощью созданной им логики. Согласно данным, учителя должны предоставить учащимся возможность выбора правил и формул обучения, чтобы учащиеся могли выбрать для себя наилучшие.
Последний ученик сказал, что он/она учится, устанавливая с ними логические связи, чтобы потом лучше запоминать с помощью созданной им логики. Согласно данным, учителя должны предоставить учащимся возможность выбора правил и формул обучения, чтобы учащиеся могли выбрать для себя наилучшие.
4. Как вы думаете, почему на экзаменах делаются геометрические ошибки?
Семеро учеников считают причиной ошибок поспешность и небрежность. Один из учеников сказал, что классы переполнены, поэтому ученики не могут получить достаточно внимания от учителей. Один из них сказал, что он/она недооценивал рисунки, поэтому, когда он/она увидел их на экзамене, он/она запаниковал и не смог сделать их должным образом. Последний считает, что недостаточно учился, поэтому запутался на экзамене. Согласно данным, поскольку семьдесят процентов учащихся считают причиной своих ошибок небрежность и опрометчивость, преподаватели могут подсказать им методы избавления от своих привычек.
Данные, полученные после опроса студентов, цитируются напрямую. В ходе интервью было установлено, что учащиеся довольны используемым методом, однако учителя могут использовать компьютеры и уделять больше внимания рисованию.
В ходе интервью было установлено, что учащиеся довольны используемым методом, однако учителя могут использовать компьютеры и уделять больше внимания рисованию.
ПРЯМОЕ МНЕНИЕ УЧАЩИХСЯ:
Ученик (1): ‘….Я нахожу уроки геометрии интересными, однако больше внимания следует уделять рисункам
и давать больше заданий. У меня больше всего трудностей было в теме расширения…..’
Ученик (2): ‘….У меня не было трудностей по геометрии. После математической темы алгебры это дало мне мотивацию. Мне нравилось рисовать, пользуясь циркулем и транспортиром. Я изучаю формулы, записывая их на бумаге и на доске…»
Учебную программу 7-го класса можно разделить на четыре основные категории: меры, углы, преобразования и построение, а также трехмерные формы.
Первый промежуточный экзамен:
. Первый промежуточный экзамен состоял из 25 вопросов. 3 из 25 вопросов были на субъектах геометрии
Таблица 1: Первое промежуточное экзамен. Геометрия Геометрия
Ошибка сделала
возможные причины
В то время как. площадь треугольника была найдена, студент забыл разделить число на два, которое было в формуле площади. (Формула площади треугольника равна основанию, умноженному на высоту два, и студент забыл разделить его на два)
площадь треугольника была найдена, студент забыл разделить число на два, которое было в формуле площади. (Формула площади треугольника равна основанию, умноженному на высоту два, и студент забыл разделить его на два)
-Только запомнил формулу
-Не могу визуализировать изображение
-Отсутствие рассуждений
-Мало достоверности в начальных классах
-Больше упражнений по теме -Частое использование изображений при более интерактивном обучении -Больше зрительно-предметное использование -Вывод формулы площади в классе
Ошибки при нахождении заштрихованной области из общего числа
-Отсутствие пространственного мышления -Отсутствие идеи построения -Отсутствие фонового образования по операциям
-Больше упражнений -Больше домашних заданий
-Практика той же процедуры на бумаге для облегчения понимания -Больше практики в операциях в начальной школе
Неправильное или отсутствующее использование формул. (Пример: площадь параллелограмма равна основанию, умноженному на высоту. Учащийся разделил основание, умноженное на высоту, на два)
Учащийся разделил основание, умноженное на высоту, на два)
-неполное понимание
-нет концентрации
-недостаточно практики по теме
-компьютерное обучение может быть использовано для демонстрации студенты формулы в более веселой и красочной форме, чтобы облегчить их запоминание.
РЕЗУЛЬТАТЫ ПЕРВОГО ПРОМЕЖУТОЧНОГО ЗАКЛЮЧИТЕЛЬНОГО ЭКЗАМЕНА
Первый промежуточный выпускной экзамен состоит из 25 вопросов, из которых 8 по предметам геометрии. ТАБЛИЦА 2: Заблуждения на первом промежуточном итоговом экзамене
Допущенные ошибки
Возможная причина
Предложения
Неправильное использование формулы (треугольник площади, параллелограмм… и т. д.)
of -Не могу понять термин площадь.
— нет правильного понимания формул.
— Дополнительная разминка перед обучением формам
-Попросите учеников найти фигуры в их реальной жизни. Например, квадратный журнальный столик, прямоугольный блокнот, треугольная пепельница, чтобы они лучше понимали формы.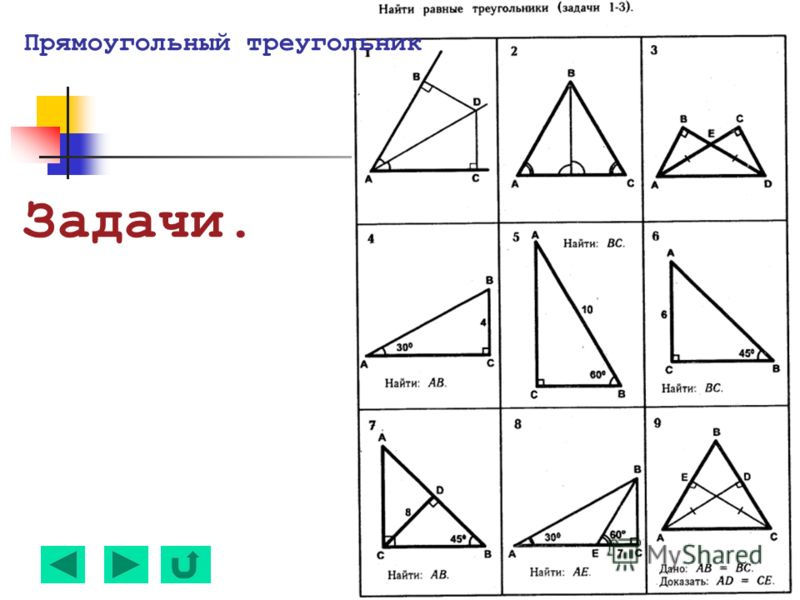
Нет причин для ответов
-Проблемы в использовании второго языка(не могу выразить себя на языке)
-Не могу объяснить свои ответы
-Больше математических терминов в классе -Больше практики
-Больше стресса при объяснениях в классе.
Отсутствие усвоения углов в параллельных линиях, таких как чередующиеся и соответствующие углы
— Игнорирование важных углов в параллельных линиях
of — Важность рассмотрения углов следует больше подчеркивать в классе
— Красочные изображения может использоваться для отображения альтернативных и соответствующих углов.
— Недостаток узнавания и — Не может визуализировать свойства восприятия — Не может усвоить
— Больше внимания свойствам четырехугольников и
четырехугольники
-Не различают типы четырехугольников
свойства четырехугольников -Студенты прилагают мало усилий.
сходства и различия во время обучения —
учащиеся должны быть более вовлечены в
сходство и различие этапов обучения
Неправильное преобразование метрических единиц измерения (например, перевод миллиметра в метр) жизнь
-Недостаточно практики в обучении
— В классе можно использовать различные виды деятельности, чтобы показать их применение в реальной жизни (например, показать метрическую систему на собственных линейках)
Неправильное определение углов в равнобедренном треугольнике
— Не удается связать фоновые данные учился в начальных классах новому материалу.
-Спонтанно отвечать на вопросы, не читая рубрику вопроса.
-Отсутствие пространственного мышления
-Больше разнообразия вопросов по разным типам треугольников
Операционные ошибки (во время области -Отсутствие концентрации -Лекции могут быть даны
вычислений, умножения и -Недооценка -студент советует по оплате
сложения, вычитания или деления важности операций внимание методы
ошибок). -Больше практики в операциях
Ошибки, сделанные на углах, сторонах и -Недостаточная практика и свойства параллелизма при специальном обучении четырехугольников -Не могу усвоить свойства
четырехугольников
Не может различать понятия уравнений и выражений (например, когда длины сторон даны в алгебраических выражениях, учащиеся не могут найти площадь)
— Тема уравнений и алгебраических выражений изучена недостаточно хорошо.
— цветные материалы могут быть использованы при обучении свойствам четырехугольников для демонстрации равенства углов и сторон и параллелизма (равные углы могут быть показаны красным цветом, а равные стороны зеленым, чтобы подчеркнуть разницу)
— Вместо того, чтобы использовать x, y, z (которые пугают учащихся, буквы a, b, c могут использоваться больше, чтобы показать неизвестное)
Таблица 3: Неправильные представления второго промежуточного экзамена
Допущенная ошибка
— В то время как студент делал увеличение он/она не написал координату центра увеличения
Возможная причина_
-Студент небрежно прочитал вопрос
-Студент не внимательно выполнил инструкции вопроса
Suggestions_
-Учитель должен подчеркнуть важность более внимательного прочтения вопросов, чтобы дать соответствующие ответы.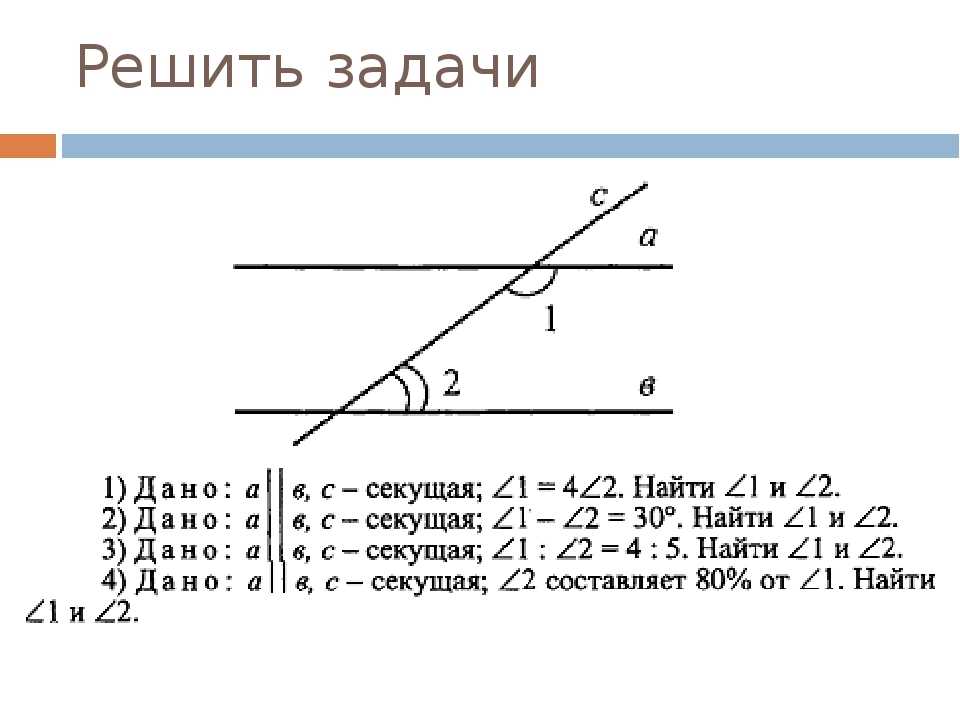
-Учитель должен обобщить тему, чтобы улучшить понимание учащихся_
-Учащиеся перепутали названия -Основная ошибка в словарном запасе -Должны быть показаны детали
трехмерных объектов. Учащийся явно начал с неправильного в классе
Например: вместо того, чтобы написать шаг, чтобы он/она не смог закончить -Пересмотры и дополнительная практика
прямоугольный, студент написал кубический. правильно. должно быть сделано
-Студент нашел сумму -Учебные формулы и -Студенты должны быть
внутренние углы неправильно определены неадекватно. рекомендуется изучать и практиковать
, а также найти размер каждого -Студенты не знают, что сложнее
внутренние и внешние углы делать правильно. неправильно
-Ученик сместил линии -Ученик не может использовать кальку -Использование кальки должно при правильном применении отражения и бумаги и подсчете быть показано подробно с помощью вращения. квадраты на бумаге неправильно. обучение на компьютере
ТАБЛИЦА 4 Заблуждения на итоговом экзамене второго семестра:
Всего 20 вопросов, 8 из них по геометрии.
Допущенные ошибки
Возможные причины
Предложения
Отсутствие информации в описательных вопросах (например, когда учащегося попросили описать преобразование, он/она не использовал определенные слова, такие как перевод, вращение)
— Недостаток знаний -Забудьте детали темы
-Студенты должны быть более внимательными на экзаменах, описывая трансформацию -Учитель должен повторять трансформацию более подробно от начала до конца, используя наглядные пособия.
Ученик допустил ошибки при увеличении объектов и неправильном использовании координат
-Не понял процесс увеличения. — Перепутаны координаты при увеличении объектов
— Можно выполнять компьютерные упражнения, чтобы учащиеся лучше усвоили тему увеличения. -Опишите положение и движение более подробно. — Чтобы учащиеся могли визуализировать изображения, следует использовать 2-х и 3-х мерные объекты._
Учащийся умножил число на 2 вместо 3 при вычислении объема куба
-Не знал формулы -Спутал формулу куба с формулой площади
-Обучать учащихся объему, использовать изображения трехмерных объектов с разных точек зрения и анализировать идею объема
Неправильное использование словарного запаса (например, учащийся использовал слово «перевод» вместо «преобразование»
— Непонимание формальных терминов
— При обучении и практике следует уделять больше внимания формальным математическим терминам
Измерения были неправильными в
— Неправильное использование транспортира
— Заставить учащихся использовать настоящие
вопросы о подшипниках — Неправильное применение угловых правил жизни объектов в классе, чтобы они могли лучше визуализировать и учиться
Вопросы о многоугольниках и квадратах, ученик рассмотрел только один угол многоугольников и игнорировал квадрат — Не может анализировать составные фигуры — Использовать геометрические изображения, чтобы дать учащимся представление о комбинировании объектов
Не мог нарисовать биссектрису угла (например, ученик должен был нарисовать биссектрису заданного угла, но он/она построил только угол )
-Неправильно понял -Больше разнообразия вопросов
Вопросы на похожие темы следует
практиковать, чтобы избежать недоразумений
Площадь поверхности куба была рассчитана неправильно из-за неправильного измерения длины
-Связь между вычислением длины и площади поверхности не была установлена должным образом поняты
— Необходимо разработать стратегии обучения учащихся восприятию куба и прямоугольного параллелепипеда, такие как использование связанных визуальных примеров для ответов на вопросы о площади поверхности и объеме
Неправильное вращение изображений
— Неправильное использование кальки
— Заставить учащихся распознавать позиции и направления.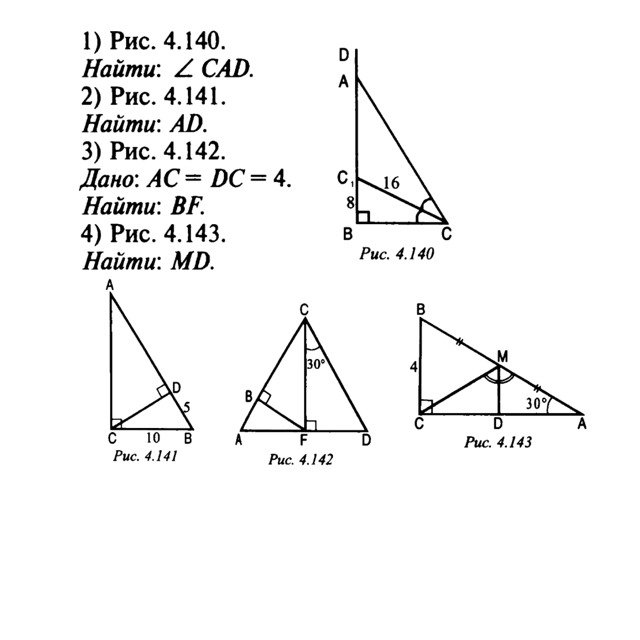 -Используйте красочные изображения, чтобы научить учащихся вращать объекты. -Предложите учащимся нарисовать фигуры в своих тетрадях и попросите их интерпретировать вращение.
-Используйте красочные изображения, чтобы научить учащихся вращать объекты. -Предложите учащимся нарисовать фигуры в своих тетрадях и попросите их интерпретировать вращение.
Неправильное расположение в вопросах перевода
— Недостаточная концентрация — Неверное измерение
— Больше практики в своем собственном темпе
— Учитель должен предоставить больше практических вопросов (Moodle можно использовать чаще и эффективнее)_
В процессе обучения студентов есть несколько ключевых факторов, таких как сеть, изображения, слова, анекдоты, примеры, формальные принципы и, наконец, структуры объяснения.
ЗАКЛЮЧЕНИЕ
Согласно моему исследованию, можно сделать вывод, что учащиеся 7-го класса преуспели в достижении целей учебной программы. Мое исследование направлено на то, чтобы учителя знали о заблуждениях учащихся и общеобразовательных проблемах. В результате исследования выявлено, что у учащихся седьмого класса общеобразовательной школы имеется ряд заблуждений и недостаточных знаний по предмету геометрия.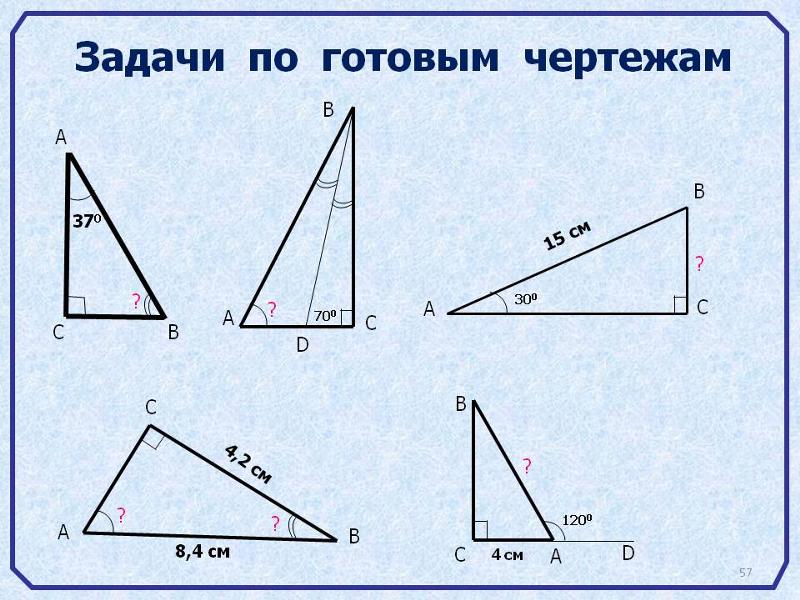
ПРЕДЛОЖЕНИЯ:
Основные проблемы в математике — недостаточные способности мышления и рассуждения. Роль учителя очень важна для преодоления этой проблемы.
Учитель должен подробно объяснить учащимся, на что им следует обращать внимание в вопросах, основанных на изображениях. В математике обучение должно проводиться с использованием наглядных пособий. Выяснилось, что учащиеся не могут понять и оценить математику, для улучшения понимания следует использовать наглядные материалы и методы, направленные на пять органов чувств учащихся. Чтобы преуспеть в изучении геометрии, очень важно давать определения объектам и их определениям. Учащиеся путаются, узнавая фигуры. Причиной этого является человеческое восприятие. Чтобы устранить эту проблему, учитель должен сначала заставить учащихся распознавать формы, а затем научить мысленно вращать объекты, чтобы воспринимать их более четко. В зависимости от уровня геометрического мышления учащихся методы могут различаться. Учитель должен постоянно напоминать учащимся, что вращение объекта не меняет его форму.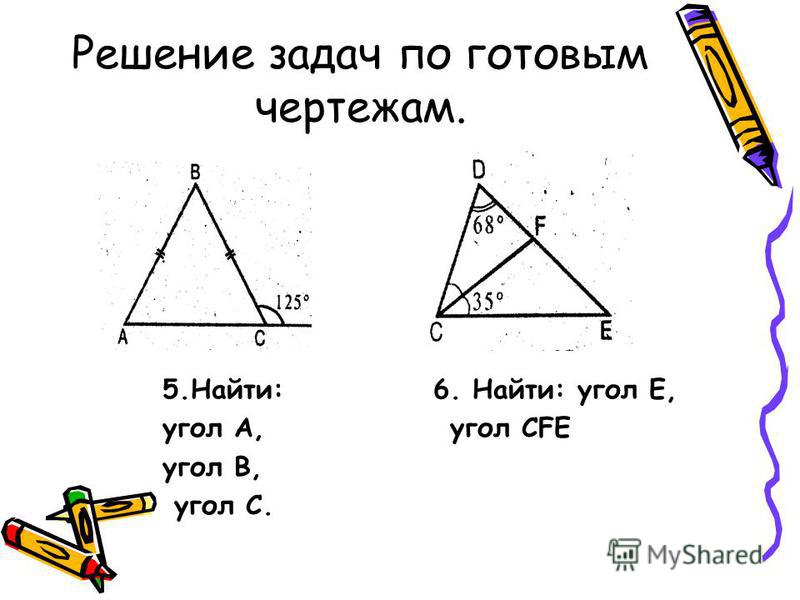
Новые приемы на уроке геометрии Общие рекомендации
Для обучения учащихся названиям различных фигур можно использовать телевизор, книги и компьютерные игры. Их понимание концепции должно быть улучшено. Их метакогнитивные способности должны быть усилены.
• Учителя должны использовать соответствующую лексику для описания соответствующих геометрических утверждений и их взаимосвязей.
• Чтобы оценить правильность геометрических аргументов, учитель должен применить логику. Один из способов сделать это — проанализировать последствия использования альтернативных определений геометрических объектов.
• Чтобы облегчить учащимся запоминание формул, формулы можно показывать с доказательствами, используя разные подходы.
Свойства геометрических фигур и математическое мышление следует применять для выполнения и обоснования основных геометрических построений. Простые построения линейки и компаса должны быть выполнены и объяснены. Для повышения эффективности и достижения целей на основе компьютера необходимы визуальные методы. Для проверки или создания предположений о геометрических свойствах или отношениях можно использовать геометрический компьютер или пакеты калькуляторов.
Для проверки или создания предположений о геометрических свойствах или отношениях можно использовать геометрический компьютер или пакеты калькуляторов.
• Блокнот для рисования геометрии — это программа, которую можно использовать для построения основных геометрических фигур. Это также позволяет вам редактировать, а с помощью меню отображения вы можете добавлять фигуры и анимировать их. Его настраиваемые инструменты позволяют воспроизводить сложные геометрические конструкции одним простым способом.
• Схема работы: Подробная схема, какие темы и в каком порядке должны быть освещены.
• Учебник: Они предоставляют учащимся множество упражнений, основанных на содержании разделов.
• Представления в Powerpoint
ССЫЛКИ
Алтун, М. (2008). Ilkogretim ikinci Kademe (6, 7 ve 8. Siniflarda) Matematik Ogretimi, 5. Baski, Bursa: Aktuel Yayinlari.
Байкул Ю. (1987). Математика Ogretimi Yonunden Okullarimizdaki Durum, Hacettepe Universitesi Egitim Fakultesi Dergisi. 2, 154-168.
2, 154-168.
Байкул Ю. (2002). ilkogretimde Matematik Огретимы 6.-8. Siniflar igin, Анкара: Pegem AYayincilik Boekaerts, M. (1992). Адаптивный процесс обучения: инициирование и поддержание поведенческих изменений.
Журнал прикладной психологии: международный обзор, 41, 377-397.
Букартс, М. (1995). Интерфейс между интеллектом и личностью как детерминанты обучения в классе. В DH Saklofske & M. Zeidner (Eds.),
Handbook of Personality and Intelligence (стр. 161-183). Нью-Йорк: Пленум Пресс. Бокертс, М. (1997). Способности, склонность и чувствительность к математике. Тревога, стресс и преодоление, 10, 5-33
Чазан, Д. (1993). Обоснование учащимися средней школы геометрии своих взглядов на эмпирические данные и математические доказательства. Образовательные исследования по математике, 24 (4), 359.-387.
Клементс и Баттиста, 1992 Д.Х. Клементс, М.Т. Баттиста Геометрия и пространственное мышление Д.А. Гроувс (ред.), Справочник по исследованиям в области преподавания и обучения математике, MacMillan, New York, NY (1992), стр. 420-464
420-464
Duval, R. (1998). Геометрия с познавательной точки зрения. В C. Mammana & V. Villani (Eds.),
Перспективы преподавания геометрии в 21 веке: исследование ICMI (стр. 37–52), Дордрехт: Kluwer.
Эркус А. (2005). Билимсел Арастирма Сармали, Сегкин Яинлари, Анкара.
Хили, Л. и Хойлс, К. (1998). Обоснование и доказательство в школьной математике. Технический отчет по общенациональному исследованию, Лондон: Институт образования, Лондонский университет.
Хили, Л. и Хойлс, К. (2000). Изучение концепций доказательства в алгебре. Журнал исследований в области математического образования, 31 (4), 396–428.
Инзунза, С. (2006 г.). Ошибки и трудности студентов при решении задач выборочного распределения средствами компьютерного моделирования, ICOTS-7.
Jeavans, A.C., почему программное обеспечение для динамической геометрии является таким эффективным инструментом в математическом образовании, Chichester, UK
Klein, A.S. (1998). Гибкость стратегий ментальной арифметики на другой базе знаний. Утрехт: Институт Фройденталя
Утрехт: Институт Фройденталя
Лим, К.С., и Хва, Т.Ю. (2007). Содействие математическому мышлению в малайзийском классе: проблемы и проблемы. Центр исследований международного сотрудничества в области развития образования (CRICED), Университет Цукуба
Монтегю, М. Эпплгейт, Б. и Маргард, К. (1993). Обучение когнитивной стратегии и
Решение математических задач учащимися с ограниченными возможностями обучения.
Национальный совет учителей математики (NCTM). (2004). Обучение детей математике.
Получено 16 октября 2004 г. с http://my.nctm.org/eresources/article_summary.asp?URI=TCM2005-04-
3a&from=B.
Национальный совет учителей математики (NCTM). (1989). Учебный план и стандарты оценки школьной математики, Рестон, Вирджиния: автор.
Национальный совет учителей математики (NCTM). (1991). Учебный план и стандарты оценки школьной математики, Рестон, Вирджиния: автор.
Портер, А. (1989). Несбалансированная учебная программа: пример математики в начальной школе.



 Найдите угол BCH. Ответ дайте в градусах.
Найдите угол BCH. Ответ дайте в градусах. Найдите длину гипотенузы.
Найдите длину гипотенузы. Найдите CD, DA если
Найдите CD, DA если 07.2018
11342
07.2018
11342
 10.2020
12361
10.2020
12361 Геометрия. Смежные и вертикальные углы №6
Геометрия. Смежные и вертикальные углы №6
 Геометрия. Прямоугольный треугольник. Углы и их свойства.
Геометрия. Прямоугольный треугольник. Углы и их свойства.


 10.2016
8863
10.2016
8863
 Начальные сведения.
Начальные сведения.
 «.
«. 04.2020
1896
0
04.2020
1896
0
 05.2020
769
0
05.2020
769
0
 Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.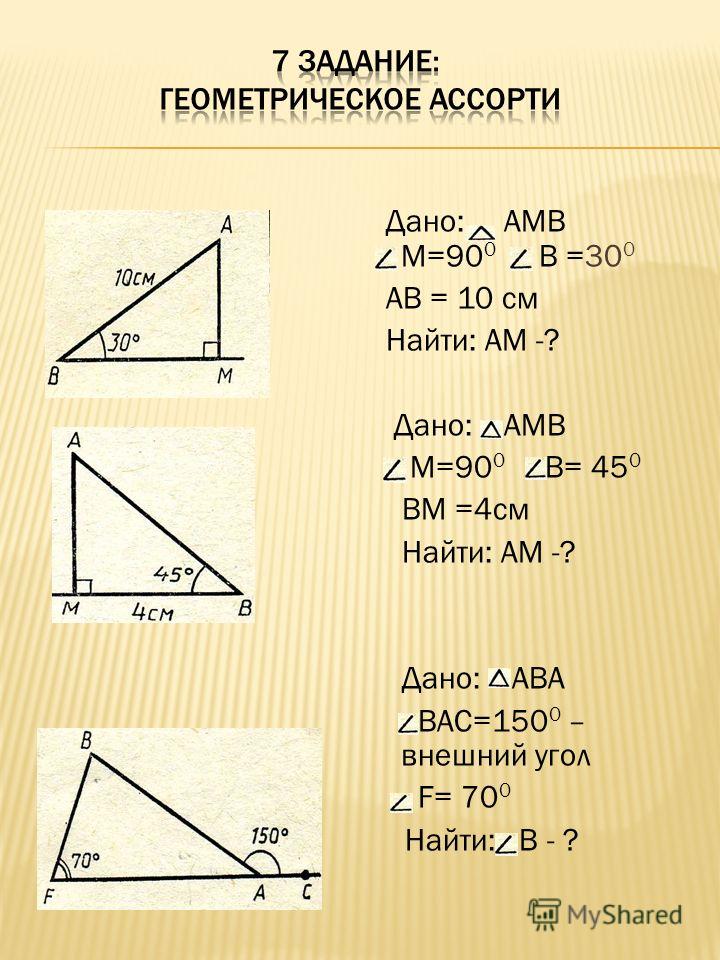 «.
«.

 Тест содержит 5 задач на готовых чертежах.
Тест содержит 5 задач на готовых чертежах. Вариант 2
Вариант 2
 Обучающиеся выбирают верные ответы на каждый вопрос, по окончании тестирования получают оценку
Обучающиеся выбирают верные ответы на каждый вопрос, по окончании тестирования получают оценку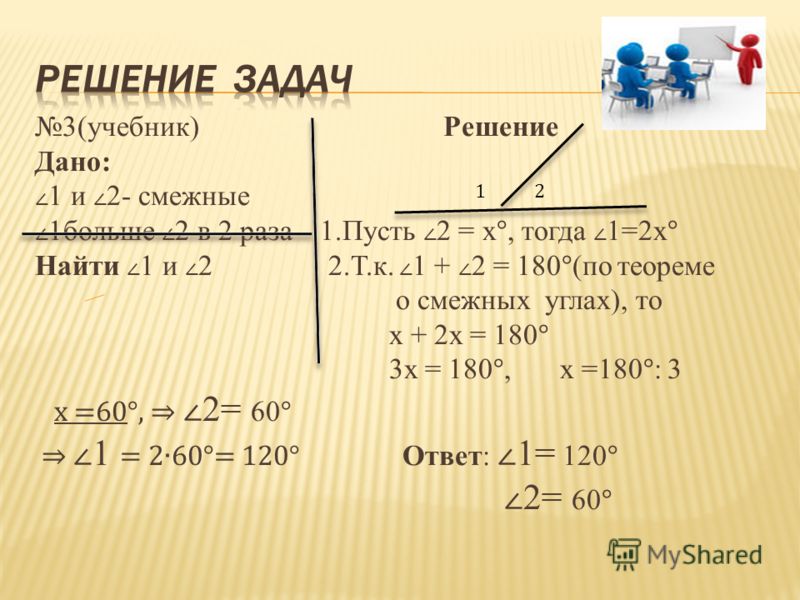 Геометрические построения», вариант 2.
Всего вопросов 8. С выбором ответа — 4 вопроса; с кратким ответом — 3 вопроса; заполнить пропуски в тексте — 1 вопрос.
Максимальное количестко баллов — 22 балла. Пятибальная система оценивания.
Геометрические построения», вариант 2.
Всего вопросов 8. С выбором ответа — 4 вопроса; с кратким ответом — 3 вопроса; заполнить пропуски в тексте — 1 вопрос.
Максимальное количестко баллов — 22 балла. Пятибальная система оценивания. Медиана, биссектриса и высота треугольника»
Медиана, биссектриса и высота треугольника» 10.2020
9168
0
10.2020
9168
0
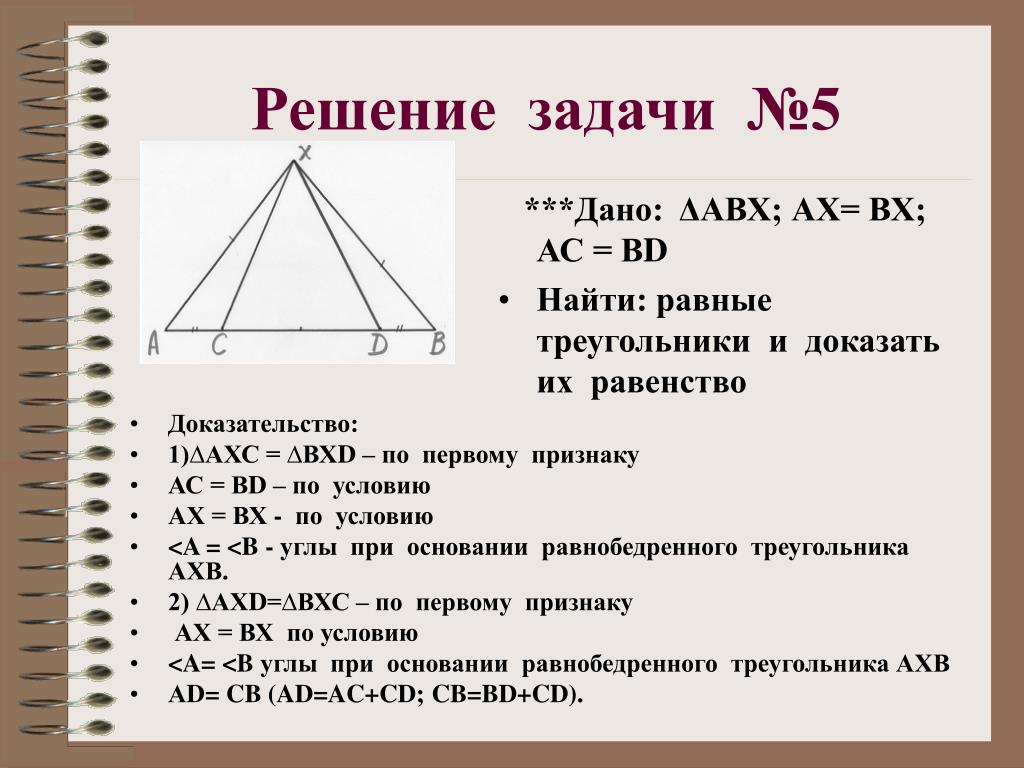
 11.2020
196
0
11.2020
196
0
 03.2021
1986
0
03.2021
1986
0
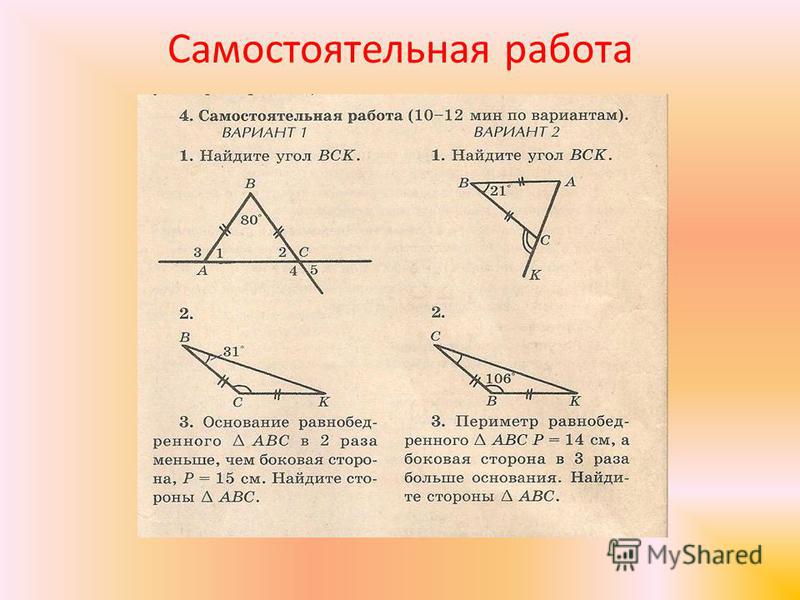 10.2021
451
0
10.2021
451
0
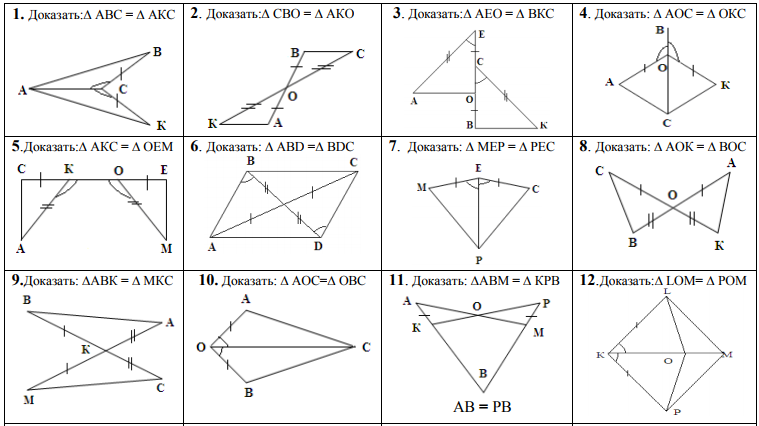 Сумма внутренних углов треугольника.» (геометрии 7 класс)
Сумма внутренних углов треугольника.» (геометрии 7 класс)
 17
17