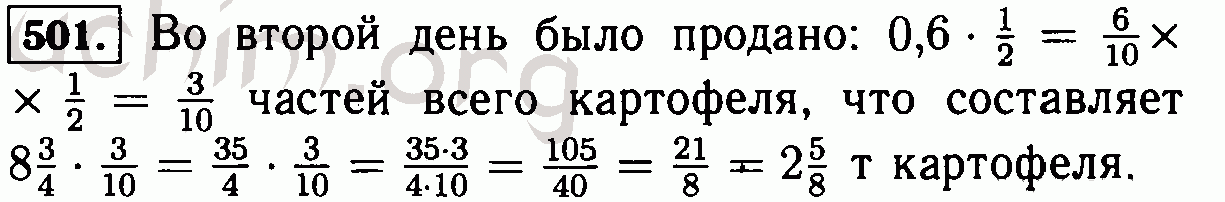ГДЗ по Математике 6 класс Виленкин, Решебник заданий
ГДЗ по математике за 6 класс Виленкин – это онлайн-сборник готовых ответов (из решебника) на задания одноименного учебника по математике, составленного Виленкиным Н.Я., Жоховым В.И., Чесноковым А.С., Шварцбурдом С.И. Он позволяет школьникам проверять правильность выполнения домашних заданий и разбираться со сложными задачами, а родителям – оказывать своим детям посильную помощь в деле подготовки домашних работ по математике.
Помощник в изучении математики в 6 классе — решебник Виленкин Н.Я. 2013 года
Курс математики для 6-го класса общеобразовательных школ РФ включает в себя широкий комплекс тем, связанных с натуральными и дробными числами. Высокий уровень сложности отдельных задач зачастую не позволят ребенку в классе разобраться с алгоритмом решения примера.
Решением этой проблемы может стать решебник по математике 6 класс Виленкин Н.Я., который представлен на нашем сайте в онлайн доступе. В чем его преимущества?
- Благодаря удобному интерфейсу достаточно вбить в строку поиска номер домашнего задания или условие примера (на выбор) – и система предложит список задачек с подобными условиями;
- Для каждого примера приводится не только готовый ответ, но и развернутый алгоритм его решения.

Такие опции позволяют школьникам самостоятельно разобраться в решении той или иной задачи, а родителям – адекватно проверить домашнюю работу учеников. Кроме того, таким способом можно сэкономить немало времени.
Что включено в решебник по математике для 6 класса: Виленкин, Жохов, Чесноков, Шварцдурд?
Представленный на сайте решебник составлен на основе учебника по математике за 6 класс под редакцией Виленкина Н.Я. в его 30-м издании (2013). Но это вовсе не означает, что здесь нельзя найти решения для более ранних и поздних изданий: на деле в поисковую строку необходимо вбить условия примера – и система найдет нужную задачу.
Учебник Виленкина Н.Я. включает в себя две основные главы:
- Обыкновенные дроби – их понятие, свойства, операции с ними;
- Рациональные числа – сущность, роль в осуществлении расчетов, математические действия с ними.
В первой части учебного пособия детально расписаны понятие и признаки делимости чисел, механизм расчета наименьшего общего краткого (НОК) и наибольшего общего делителя (НОД), а также алгоритм составления и решения пропорций.
Во второй части подробно расписаны правила осуществления математических действий с положительными и отрицательными числами, а также порядок решения уравнений с учетом расположения координат на плоскости.
Наш сайт готовых домашних заданий – это не только помощь в решении домашних заданий для учеников 6 классов и их родителей, но и полноценное практическое руководство, позволяющее постигать основы математики самостоятельно.
класс «Решение задач на движение с помощью уравнения», 6 класс, УМК Н. Я. Виленкина
Мастер — класс
Решение задач на движение с помощью уравнения (6 класс)
Цель: Создание условий для передачи опыта по формированию умения у учащихся по решению задач на движение с помощью уравнения.
Задачи: 1. показать способ решения задач на движение с помощью уравнения;
2. оценить эффективность мастер – класса через рефлексию участников.
Форма проведения: урок — импровизация.
Оборудование: рабочие листы с заданиями, «Билет на выход» для проведения рефлексии.
Ход мастера -класса:
Если человека постоянно приучать усваивать знания и умения в готовом виде, можно и притупить его природные творческие способности — «разучить» думать самостоятельно. В максимальной степени процесс мышления проявляется и развивается при решении проблемных задач.
К сожалению, очень часто мы с вами не предоставляет свободы ученику, когда он пытается ответить на вопрос. Не ждём, а сразу же задаём наводящий вопрос. Можно ли учить так, чтобы каждый ребёнок рассуждал над проблемой своим путём, своим темпом, но при необходимости мог сопоставить свою точку зрения с одноклассниками, может даже изменить её? Конечно же, можно.
Помочь ученику раскрыться, лучше использовать свой творческий потенциал помогает создание проблемных ситуаций на уроке.
Проблемное обучение основывается на теоретических положениях американского философа, психолога, педагога Дж. Дьюи (1859-1952). В России дидактику проблемного обучения разработал И.Я. Лернер.
Дьюи (1859-1952). В России дидактику проблемного обучения разработал И.Я. Лернер.
Сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей.
Как же создавать проблемные ситуации?
Вот проблемная ситуация на сегодня.
Эмблема урока: 28k + 30n + 31m = 365
Комментарий учителя к уравнению: Говорят, уравнение вызывает сомнение, но итогом сомнения может быть озарение!
Задание: Найти хотя бы одно решение уравнения.
(Уравнение, красочно оформленное, вывешивается сверху, в центре доски, к концу занятия будет найдено его решение)
Существует множество приёмов создания проблемных ситуаций. Вот некоторые из них:
Создание проблемных ситуаций через
умышленно допущенные учителем ошибки;
формулирование задания в занимательной форме;
выполнение практических заданий;
решение задач на внимание и сравнение;
противоречие нового материала старому, уже известному;
различные способы решения одной задачи;
выполнение небольших исследовательских заданий;
решение задач, связанных с жизнью.
Участникам мастер класса предлагается выбрать задачи на движение из предложенного списка задач.
Задание 1. Выберите задачу на движение и обоснуйте свой ответ.
Задача №1.
Лыжник прошел 900 м за 3 минуты, двигаясь с одинаковой скоростью. С какой скоростью двигался лыжник?
Задача №2.
Рабочий за 10 часов изготовил 300 деталей. Сколько деталей изготовит рабочий за 40 часов?
Задача №3.
Длина прямоугольника 6 м, а ширина в 3 раза меньше. Чему равен периметр и площадь прямоугольника?
Задача №4.
Биатлонист пробежал последний круг дистанции за 3 минуты со скоростью, равной 220 м/м. Чему равно данное расстояние?
После выполнения задания предлагается вопрос:
По каким признакам вы определили, что это задачи на движение?
(Ответ: время, скорость, расстояние).
Задача
Двое детей одновременно начали есть кашу. Через некоторое время первый ребенок кашу съел, а второй нет, хотя порции были одинаковые. Почему это произошло?
(Ответ: Скорость первого ребенка больше, чем скорость второго).
А эта задача на движение?
Почему нет, ведь в ней присутствуют время и скорость?
(Ответ: Нет такой величины как расстояние).
Данный этап урока (актуализация знаний) помогает определить вид задачи, выделить ее существенные признаки. Но при этом учащимся предлагается задача, которая направлена на то, чтобы ребенок мог увидеть, что не всегда то, на что он привык опираться, ведет по верному пути. В данном случае есть скорость, время, но задача не на движение, так как отсутствуют другие величины.
Задание № 2. Фронтальная работа
Расстояние между двумя пунктами катер прошел по течению реки за 5 часов, а против течения — за 6 часов. Найдите расстояние между этими пунктами, если скорость течения реки 3 км/ч.
Найдите расстояние между этими пунктами, если скорость течения реки 3 км/ч.
К какому виду задач относится данная задача? (задача на движение)
1.2. Какие величины характеризуют движение? (Ответ: время, скорость, расстояние).
1.3. Построим таблицуВремя (ч) | Скорость (км/ч) | Расстояние (км) | |
по течению реки | 5 | х+3 | 5(х+3) |
против течения | 6 | Х-3 | 6(х-3) |
1. 4.В верхней строке занесем величины, характеризующие движение.
4.В верхней строке занесем величины, характеризующие движение.
1.5. Определим этапы движения. (по течению реки, против течения)
1.6. Занесем этапы движения в 1-й столбик.
1.7. Определим известную величину на каждом этапе (время) и занесем в таблицу.
1.8. Определим величину, которую примем за х: собственная скорость катера. Тогда скорость по течению (х+3), а против течения (х-3).
1.9. Заполнили два столбца, а третий заполним, исходя из правила нахождения расстояния.
1.10 Что знаем про расстояние из условия задачи. (На обоих этапах пройдено одинаковое расстояние)
1.11 Составим и решим уравнение.
5(х+3)= 6(х-3)
5х+15=6х-18
х=33
33 (км/ч) собственная скорость катера
33-3=30(км/ч) скорость катера против течения
30х6 -180 (км) прошёл катер
Ответ: 180 км
Половину пути мотоциклист ехал с намеченной скоростью 45 км /ч , затем задержался на 10 мин.
К какому виду задач относится данная задача? (задача на движение)
2.2. Какие величины характеризуют движение? (Ответ: время, скорость, расстояние).
2.3. Построим таблицу
Время (ч) | Скорость (км/ч) | Расстояние (км) | |
Первая половина пути | х | 45 | 45х |
Вторая половина пути | Х-1/6 | 45+15=60 | 60(х-1/6) |
2. 4.В верхней строке занесем величины, характеризующие движение.
4.В верхней строке занесем величины, характеризующие движение.
2.5. Определим этапы движения. (Первая половина пути, вторая половина пути)
2.6. Занесем этапы движения в 1-й столбик.
2.7. Определим известную величину на каждом этапе (скорость) и занесем в таблицу.
2.8. Определим величину, которую примем за х: время до увеличения скорости. 10 мин=1/6ч
2.9. Заполнили два столбца, а третий заполним, исходя из правила нахождения расстояния.
2.10 Что знаем про расстояние из условия задачи. (На обоих этапах пройдено одинаковое расстояние)
2.11 Составим и решим уравнение.
45х=60(х-1/6)
45х=60х-10
15х=10
Х=2/3
1)2/3 (ч) проехал мотоциклист первую половину пути
2)45х2/3х2=60(км) путь
Ответ: 60 км
Задание № 3. Работа в группах
Участники мастер-класса разбиваются на 6 групп и каждой группе предлагается решить задачи.
Из пункта А в пункт В выехал велосипедист со скоростью 12км/ч. После того, как велосипедист проехал 3 км, из пункта А со скоростью 4 км /ч вышел пешеход, который пришёл в пункт В на 5/4 ч позже велосипедиста. Найдите расстояние между пунктами. (12х=4(х+5/4)+3)
Расстояние между двумя пунктами катер прошел по течению реки за 7 часов, а против течения — за 8 часов. Найдите расстояние между этими пунктами, если скорость течения реки 2,5 км/ч.(7(х+2,5)=8(х+2,5))
Турист 3 ч ехал на велосипеде, и 2 часа шел пешком, причем пешком он шел на 6 км/ч медленнее, чем ехал на велосипеде. С какой скоростью шел турист, если всего он преодолел 38 км? (2х+3(х+6)=38)
4.Из двух пунктов реки на встречу друг другу движутся две моторные лодки, собственные скорости которых равны. До встречи лодка, идущая по течению, прошла1 ,1 ч., а лодка, идущая против течения, 1,5 часа. Найдите собственную скорость лодок, если лодка , идущая по течению по течению до встречи прошла на 1 км больше другой лодки . Скорость течения реки 3 км /ч .
Скорость течения реки 3 км /ч .
[1,1(х+3) – 1,5(х-3) =1]
5.Из двух пунктов реки , расстояние между которыми 51 км , на встречу друг другу движутся две моторные лодки , собственные скорости которых равны . Скорость течения реки 3 км/ч. Лодка , идущая по течению , до встречи прошла 1,5 ч., а лодка , идущая против течения , 2 ч.Найдите собственную скорость лодок.
[1,5(х+3) + 2(х-3) = 51]
Из Москвы в Ростов – на – Дону вышел пассажирский поезд со скоростью 60 км/ч. Спустя 2 ч. 10 мин. Из Ростова- на- Дону в Москву вышел пассажирский поезд со скоростью 80 км/x . На коком расстоянии от Москвы поезда встретятся , если расстояние между городами считать равным 1250 км ?
[ 60х +80(х-21/6=1250]
Работа ведется маркерами на листах, листы вывешиваются.
Вернемся к эмблеме занятия.
28k + 30n + 31m = 365
Слова учителя: Озарило?!
Ответ: 365 – это количество дней в году, 28 – количество дней в феврале, 30 – количество дней имеют 4 месяца в году, 31 – количество дней имеют 7 месяцев в году. Тогда: 28 ·1 + 30 · 4 + 31 · 7 = 365.
Тогда: 28 ·1 + 30 · 4 + 31 · 7 = 365.
Меняется мир непрерывно, неспешно,
Меняется всё – от концепций до слов.
И тот лишь сумеет остаться успешным,
Кто сам вместе с миром меняться готов!
П. Калита
Рефлексия.
Участникам мастер – класса предлагается заполнить «Билет на выход».
Уважаемые участники мастер – класса, пожалуйста, выскажите свое мнение, закончив предложение.
Положительным моментом в данном мастер – классе является
__________________________________________________________________________________________________________________________
Я считаю, что такие приёмы работы
____________________________________________________________________________________________________________________________________
3. Думаю надо продумать
____________________________________________________________________________________________________________________________________
Мое настроение
Источники:
https://nsportal. ru/shkola/algebra/library/2015/12/03/metapredmet-problema-na-urokah-matematiki
ru/shkola/algebra/library/2015/12/03/metapredmet-problema-na-urokah-matematiki
https://yandex.ru/images/search?text=картинки
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ «КРУГОВ ЭЙЛЕРА»
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ «КРУГОВ ЭЙЛЕРА»
Рыбина Ангелина
Класс 5 «Д», МОУ «СОШ № 59 с УИП», РФ, г. Саратов
Багаева Ирина Викторовна
научный руководитель, педагог высшей категории, преподаватель математики, МОУ «СОШ № 59 с УИП», РФ, г. Саратов
«… круги очень подходят для того, чтобы облегчить наши размышления»
Леонард Эйлер
Нет ученого, имя которого упоминалось бы в учебной математической литературе столь же часто, как имя Эйлера. Даже в средней школе логарифмы и тригонометрию изучают до сих пор в значительной степени «по Эйлеру».
В 1741 году Эйлер пишет «Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе…», где появились впервые «круги Эйлера». Эйлер писал тогда, что «круги очень подходят для того, чтобы облегчить наши размышления».
При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».
С помощью этих кругов Эйлер изобразил и множество всех действительных чисел:
· N — множество натуральных чисел,
· Z — множество целых чисел,
· Q — множество рациональных чисел,
· R — множество всех действительных чисел.
Рисунок 1. Изображение множества действительных чисел
Что такое множество?
В математике нет точного определения этого понятия. Понятие «множество» не определяется, оно поясняется примерами: множество яблок в корзине; множество точек отрезка прямой. Множество состоит из элементов. В приведенных примерах — это яблоки, буквы, точки.
Понятие «множество» не определяется, оно поясняется примерами: множество яблок в корзине; множество точек отрезка прямой. Множество состоит из элементов. В приведенных примерах — это яблоки, буквы, точки.
Множества обозначаются заглавными буквами латинского алфавита: А, В, С, … K, M, N … Х, …; элементы множества — строчными буквами алфавита: а, в, с, … k, m, n … х, у, …. А={а; в; с; d} — множество А состоит из элементов а, в, с, d, или, говорят, что элемент а принадлежит множеству А, записывается: аА (знак читается: «принадлежит»). Элемент 5 не входит в множество А, говорят, что «5 не принадлежит А»: 5 А, или . Если множество В не содержит ни одного элемента, то говорят, что оно пустое, обозначается: В=.
Под множеством можно понимать совокупность каких-либо объектов, называемых элементами множества [1, с. 18]. Примерами множеств могут быть и дома на нашей улице, и алфавит — совокупность букв, и наш 5 «Д» класс — множество учеников.
Множества могут быть:
· Конечное (элементы которого можно пересчитать; например — множество цифр)
· Бесконечное (пересчитать нельзя; например — песчинки в пустыне)
· Пустое (не содержащее ни одного элемента; например — множество зайцев, которые учатся в нашем классе).
Множество K называется подмножеством множества N, если каждый элемент множества K является элементом множества N. Обозначается: KÍN. Говорят, что множество K включается в множество N.
Подмножества можно проиллюстрировать кругами Эйлера.
Рисунок 2. Изображение подмножества
Действия с множествами
В математике существуют несколько операций над множествами. Мы разберем два из них: пересечение и объединение.
1. Пересечение множеств
Пересечением множеств M и N называется множество, состоящее из элементов, одновременно принадлежащих M и N. Пересечение множеств M и N обозначается [1, с. 23].
Пересечение множеств M и N обозначается [1, с. 23].
Пример. Множество N = { А Н Д Р Е Й };
множество K = { А Л Е К С Е Й }; множество M = { Д М И Т Р И Й }
Рисунок 3. Пример пересечения множеств
2. Объединение множеств
Объединение множеств — это множество, содержащее в себе все элементы исходных множеств. Объединение множеств M и N обозначается .
Пример ; 2) объединение множества всех пород собак и множества мопсов есть множество всех собак.
Операции объединения и пересечения множеств очень удобно показывать с помощью кругов Эйлера.
По определению в пересечение двух множеств M и N входят элементы, принадлежащие множествам M и N одновременно
Пример. Пусть D — множество из 12 самых хороших девочек, M — множество из 12 самых умных мальчиков. Получили наш класс.
Получили наш класс.
Рисунок 4. Пример объединения множеств
3. Вложенные множества.
Пример. Имеется три множества: «дети», «школьники», «учащиеся начальной школы». Мы видим, что эти 3 множества находятся одно внутри другого. Про множество, находящееся внутри другого множества, говорят, что оно вложенное.
Рисунок 5. Пример вложенных множеств
Задачи, которые можно решить с помощью диаграмм Эйлера
Задача № 1
На стол бросили две салфетки 10 см х 10 см. Они покрыли площадь стола, равную 168. Какова площадь перекрытия?
Решение
1)168 – 10 х 10 = 68;
2)10 х 10 – 68 = 32.
Ответ: 32 см
Рисунок 6. Рисунок к задаче № 1
Рисунок к задаче № 1
Задача № 2
В поход ходили 80 % учеников класса, а на экскурсии было 60 %, причем каждый был в походе или на экскурсии. Сколько процентов класса были и там, и там?
Решение
А — множество учеников, которые ходили в поход
В — множество учеников, которые были на экскурсии
100 % – 80 % = 20 %
60 % – 20 % = 40 %
Ответ: 40 %
Рисунок 7. Рисунок к задаче № 2
Задача № 3
В нашем классе 24 ученика. Все они хорошо провели зимние каникулы.10 человек катались на лыжах, 16 ездили на каток, а 12 — лепили снеговиков. Сколько учеников смогли покататься и на лыжах, и на коньках, и слепить снеговика?
А — множество ребят, катающихся на лыжах
В — множество ребят, катающихся на коньках
С — множество ребят, лепивших снеговиков
Решение
Пусть х — число ребят,
которые успели за эти каникулы всё!
(12 — х) + (16 — х) + (10 — х) + х = 24
Ответ: 7 ребят
Рисунок 8. Рисунок к задаче № 3
Рисунок к задаче № 3
Задача № 4
9 моих друзей любят бананы, 8 – апельсины, а 7 – сливы, 5 – бананы и апельсины, 3 – бананы и сливы, 4 – апельсины и сливы, 2 – бананы, апельсины и сливы. Сколько у меня друзей?
Решение
5 – 2 = 3 3 – 2 = 1 4 – 2 = 2
9 – 6 = 3 8 – 7 = 1 7 – 5 = 2
3 + 1 + 2 + 3 + 2 + 1 + 2 = 14
Ответ: 14 друзей
Рисунок 9. Рисунок к задаче № 4
Задача № 5
В пионерском лагере «Дубки» в смене актива отдыхали: 30 отличников, 28 победителей олимпиад и 42 спортсмена. 10 человек были и отличниками и победителями олимпиад, 5 — отличниками и спортсменами, 8 — спортсменами и победителями олимпиад, 3 — и отличники, и спортсмены, и победители олимпиад.
Сколько ребят отдыхали в лагере?
А — множество отличников
В — множество победителей олимпиад
С — множество спортсменов
Решение
10 – 3 = 7 5 – 3 = 2 8 – 3 = 5
30 – 12 = 18 28 – 15 = 13 42 – 10 = 32
18 + 13 + 32 + 7 + 2 + 5 + 3 = 80
Ответ: 80 ребят
Рисунок 10. Рисунок к задаче № 5
3. Заключение
Диаграммы Эйлера — это общее название целого ряда способов графической иллюстрации , широко используемых в различных областях математики: теория множеств, теория вероятностей, логика, статистика, компьютерные науки, и др. Применение кругов Эйлера позволяет даже пятикласснику легко решать задачи, которые обычным путем решаются только в старших классах.
Список литературы:
1. Александрова Р.А., Потапов А.М. Элементы теории множеств и математической логики. Практикум / Калининград. 1997. — 66 с.
Александрова Р.А., Потапов А.М. Элементы теории множеств и математической логики. Практикум / Калининград. 1997. — 66 с.
2.Депман И.Я., Виленкин Н.Я. За страницами учебника математики. Пособие для учащихся 5—6 кл. М.: Просвещение, 1999. с. 189—191, 231.
3.Задачи для внеклассной работы по математике в V—VI классах: Пособие для учителей / Сост. В.Ю. Сафонова. Под ред. Д.Б. Фукса, А.Л. Гавронского. М.: МИРОС, 1993. — с. 42.
4.Занимательная математика. 5—11 классы. Как сделать уроки нескучными / Авт. сост. Т.Д. Гаврилова. Волгоград: Учитель, 2005. — с. 32—38.
5.Смыкалова Е.В. Дополнительные главы по математике для учащихся 5 класса. СПб: СМИО Пресс, 2009. — с. 14—20.
6.Энциклопедия для детей. Т. 11. Математика Глав.ред. М.Д. Аксёнова. М.: Аванта +, 2001. — с. 537—542.
Математика как язык символов
Обучая своих студентов по предварительному исчислению и AP-исчислению, я понял, что использование математических символов для создания алгебраических выражений и решения текстовых задач обычно является для них большой проблемой. Им трудно перевести словесную постановку проблемы в символические математические выражения и уравнения.
Им трудно перевести словесную постановку проблемы в символические математические выражения и уравнения.
Допустим, студенты должны решить следующую задачу: «Найдите площадь поверхности сферы в момент, когда скорость увеличения объема сферы в девять раз превышает скорость увеличения радиуса. 1 (На самом деле, эта постановка задачи не очень удачная. В задаче упоминается «сфера», но речь идет не об одной сфере. Это о семействе сфер, радиус которых варьируется, в каком направлении или в зависимости от к какой переменной не поясняется.) Как видите, в этой задаче нет ни одного математического символа. Это всего лишь одно предложение, написанное на английском языке. Студенты должны уметь «переводить» его на математический язык с помощью формул и создавать модели на основе полученных данных.Для моих учеников это чрезвычайно сложная задача. Большинство из них готовы сдаться, даже не пытаясь.
Истоки этой борьбы восходят к арифметике и простой алгебре. Их нужно было научить писать алгебраические выражения и создавать математические модели задачи со словами. Эти навыки необходимы для их успеха в математике, физике и химии высшего уровня. К сожалению, у большинства из них есть очень скромные навыки такого рода. Итак, моя цель при разработке этого модуля — помочь учителям и ученикам заполнить этот пробел.
Эти навыки необходимы для их успеха в математике, физике и химии высшего уровня. К сожалению, у большинства из них есть очень скромные навыки такого рода. Итак, моя цель при разработке этого модуля — помочь учителям и ученикам заполнить этот пробел.
Страх перед математикой похож на страх говорить на иностранном языке. Некоторые слова на иностранном языке мы просто не знаем и поэтому боремся с переводом. Чтобы добиться успеха в математике, мы должны уметь «переводить» задачу с английского на математический язык. Частично это знание того, что означает каждое слово. Более глубокая трудность состоит в том, что перевод не может быть дословным. Он должен передавать общий смысл.
Возвращаясь к вышеупомянутой связанной задаче скорости, студенты узнают, что словосочетание «скорость увеличения объема» переводится на математический язык очень просто: dV / dt .Анализируя задачу, студенты должны прийти к выводу, что объем изменяется во времени. Они должны ввести переменную t (время) и подчеркнуть, что t была неопределенной переменной из-за неполноты задачи. Акт введения переменной t должен быть явным. Аналогичным образом «скорость увеличения радиуса» составляет др / дт .
Акт введения переменной t должен быть явным. Аналогичным образом «скорость увеличения радиуса» составляет др / дт .
Чтобы перевести его дальше, нам нужно будет создать алгебраическое выражение:
dV / dt = 9 dr / dt
Это выражение кажется изучающим алгебру сложным и «полностью греческим».Однако концепция, которую мы использовали при написании этого выражения, такая же, как и при написании очень простого алгебраического выражения «число A в девять раз больше, чем число B ».
A = 9 B
Итак, студентов нужно научить писать алгебраические выражения как можно раньше.
Я преподаю в небольшой средней школе, куда дети должны подать заявление, чтобы их приняли. Большая часть политики приема — это привлечение студентов с самым разным опытом.Поэтому студенческий состав очень разнообразен. У нас есть дети из элитных частных школ, а также дети из действительно неблагополучных городских средних школ. В результате навыки студентов сильно различаются. Я должен соответствующим образом скорректировать свой стиль преподавания и подойти к своим ученикам индивидуально. Хотя некоторые из них берут самые строгие классы AP, многие из них испытывают трудности с простыми математическими концепциями. Моя цель как учителя — удовлетворить потребности каждого ученика и дать им возможность добиться успеха.
В результате навыки студентов сильно различаются. Я должен соответствующим образом скорректировать свой стиль преподавания и подойти к своим ученикам индивидуально. Хотя некоторые из них берут самые строгие классы AP, многие из них испытывают трудности с простыми математическими концепциями. Моя цель как учителя — удовлетворить потребности каждого ученика и дать им возможность добиться успеха.
Англо-математический «словарь»
В первый день в школе я всегда говорю своим ученикам-математикам, что математика — это язык. И одна из его ключевых особенностей — очень лаконичный. Компактность символьных выражений — важная особенность, позволяющая нам эффективно с ними работать. Компромисс заключается в увеличении трудозатрат на перевод между символическими и словесными выражениями. Цифры и буквы, а также некоторые специальные символы представляют собой «слова» этого удивительного языка.Когда мы соединяем «слова» с помощью знаков <,>, +, -, = и т.д., мы пишем предложения на математическом языке.
Большинство из них выглядит сбитым с толку. Затем я прошу их перевести несколько случайных английских слов на испанский или французский. Делают это легко и с удовольствием. Следующее задание — перевести слова «сложить», «вычесть», «равно» на математический язык символов. Важно отметить, что существуют разные способы выражения на английском языке вещей, которые в конечном итоге будут одинаковыми символами.Например, «сумма a и b », «возьмите a и добавьте его к b » и « a плюс b » все приведут к выражению a + б . Это отправная точка их путешествия в чудесный мир математических символов. Мое заявление о математике как о языке становится для них ясным.
Теперь очередь моих учеников привести свои собственные примеры. Они очень взволнованы. Мы создаем наш первый англо-математический «словарь».Вот как это может выглядеть:
Английский | Математика |
добавить | + |
вычесть | – |
умножить | × |
делить | ÷ |
равно | = |
примерно равно | ≈ |
корень квадратный | √ |
больше или равно | ≥ |
меньше или равно | ≤ |
Мое любимое слово, к которому я всегда подхожу особым образом, — это слово «ноль». Ноль означает «ничего».
Ноль означает «ничего».
Я обращаю особое внимание на 0, потому что учащиеся не чувствуют себя уверенно с этим числом, особенно когда они решают уравнения, и ни одна из сторон уравнения не остается. Они очень сбиты с толку и не могут решить задачу. «0» — очень важная и значимая цифра для математиков. Само открытие этой цифры дало нам возможность записывать числа, используя таблицу разрядов. Это также важная концепция при написании алгебраических выражений.Иногда я говорю, что важность ничего была большим математическим открытием.
Еще одна глава в этом разговоре — надстрочные и подстрочные индексы. Надстрочные символы — это маленькие символы, которые располагаются немного выше линии; нижние индексы находятся под нормальной строкой текста. Верхний или нижний индекс может быть числом, буквой или специальным математическим символом.
Традиционно учащиеся знают следующие надстрочные индексы:
градусов (45 градусов) | 45 ° |
процентов | % |
число в квадрате (показатель степени) | x 2 |
Обычно используемый нижний индекс обозначает базовые системы, например, log 2 10 (логарифм по основанию 2 числа 10).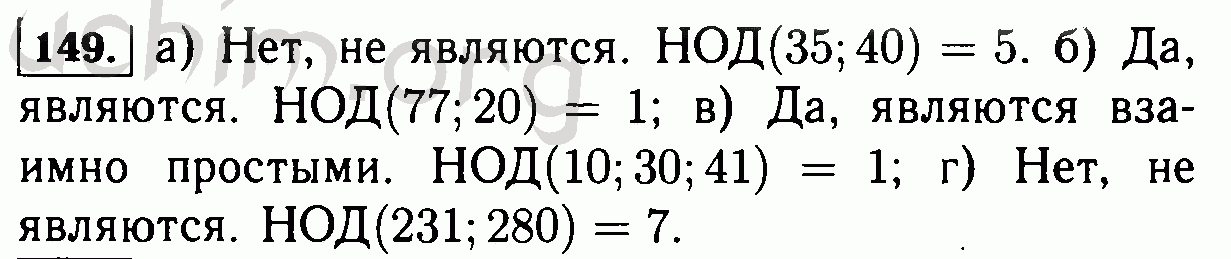 В какой-то момент учащиеся также встречают индексы, обозначающие термины в последовательности.
В какой-то момент учащиеся также встречают индексы, обозначающие термины в последовательности.
Следующие логические вопросы будут: «Можно ли использовать, например, другой символ для сложения? Зачем нужны символы? Почему бы нам просто не описать словами методы решения некоторых математических задач? » Кроме того, какова ценность согласования фиксированного символа для конкретной идеи, например объединения чисел путем сложения?
Алгебра обобщенная Арифметика
Это хорошее время, чтобы вернуться в доисторические времена и кратко проследить по стопам человечества в его попытке разработать эффективный инструмент для описания вычислений и измерений.
«Современный способ записи чисел, простой и удобный, европейцы позаимствовали у арабов. В свою очередь арабы позаимствовали эту систему у индейцев. Поэтому европейцы называют современные цифры «арабскими», а арабы — «индийскими». Интересно, что арабская и индийская версии этих символов несколько отличаются от стандартных европейских.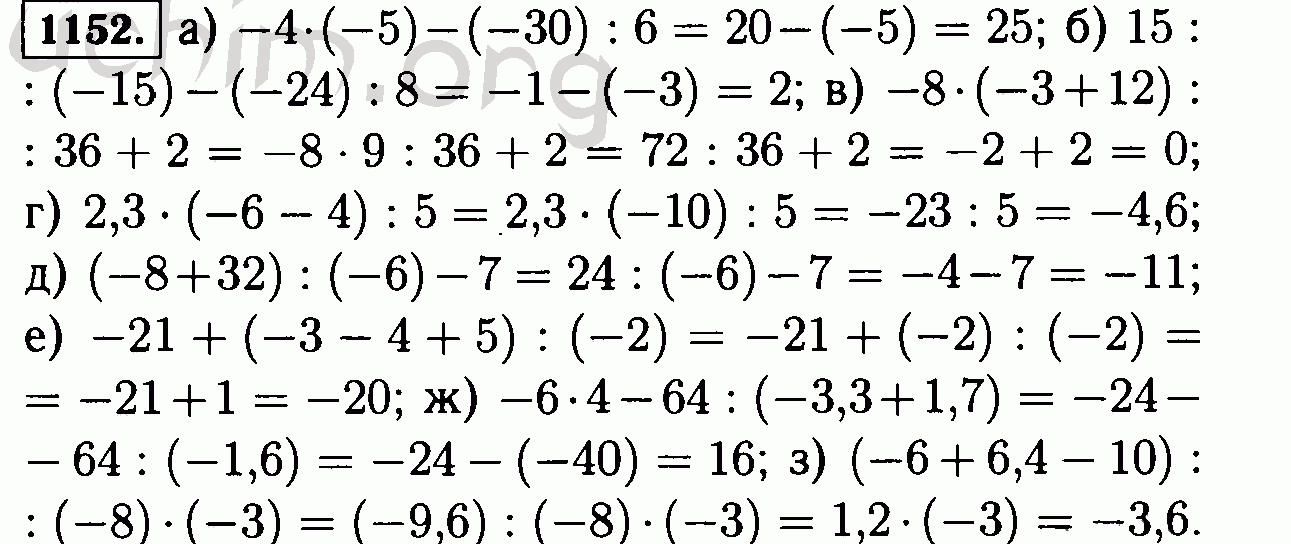 Английский ученый и путешественник Аделард представил европейцам эту систему примерно в 1120 году.Подавляющее большинство стран приняло его только к 1600 году ». 2 Фибоначчи (Леонардо Пизанский) также следует упомянуть в этом развитии. Итак, человечеству потребовалось довольно много времени, чтобы даже символизировать числа, которые мы используем для счета.
Английский ученый и путешественник Аделард представил европейцам эту систему примерно в 1120 году.Подавляющее большинство стран приняло его только к 1600 году ». 2 Фибоначчи (Леонардо Пизанский) также следует упомянуть в этом развитии. Итак, человечеству потребовалось довольно много времени, чтобы даже символизировать числа, которые мы используем для счета.
Следующая длинная цитата очень хорошо передает идею моего устройства:
«Хотя то, что мы сейчас называем« задачами алгебры слов », изучались и решались со времен Древнего Египта и Вавилонии, около 4000 лет назад, а может, и больше, символическая алгебра — гораздо более позднее изобретение, впервые примененное Франсуа Виете незадолго до этого. 1600 и развивалась в течение следующих 50 лет.(Использование x для неизвестного было популяризировано Декартом.) Символическая алгебра, в свою очередь, была главным двигателем научной революции, в частности, математического анализа. Представьте себе науку без формул. Представьте, что вы пытаетесь даже говорить о производных, не говоря уже о том, чтобы их вычислить, без компактной записи для выражения разностного коэффициента.
Представьте, что вы пытаетесь даже говорить о производных, не говоря уже о том, чтобы их вычислить, без компактной записи для выражения разностного коэффициента.
Упор в последнем предложении должен быть сделан на «компактный». Придумайте простое выражение, например 3 x +2. По сути, это рецепт вычисления.Он неявно говорит: возьмите число x , умножьте его на 3 и прибавьте 2 к результату. Однако он существенно короче! Составное выражение, например 4 y (3 x + 2) — 7, можно перевести как: возьмите число x , умножьте его на 3 и прибавьте 2 к результату. Возьмите другое число y и умножьте его на 4. Умножьте первый результат на второй, а затем вычтите 7.
По мере того, как выражения становятся более сложными, резко возрастает контраст между длиной полного набора словесных инструкций, необходимых для перефразирования символического выражения, и краткостью самого выражения.Компактность символической формы вместе с компактным и элегантным набором правил (правил арифметики) для преобразования (часто в целях упрощения) выражений позволяет практикующему составить и управлять выражениями, словесные переводы которых были бы неуправляемыми. Такое сочетание краткости и формальности делает символическую алгебру мощным инструментом.
Такое сочетание краткости и формальности делает символическую алгебру мощным инструментом.
Однако, как и в случае с другими предметами математики, компактность, которая делает символические обозначения мощными, также усложняет преподавание.Студенты, особенно студенты, которые могут приходить к алгебре, не будучи уверенными в значениях числовой записи и с ограниченным пониманием операций, не сразу адаптируются к символической алгебраической записи или осознают возможности, которые она предлагает ». 3
«Основная задача начинающих студентов алгебры — научиться работать с переменными и, в частности, работать с символьными выражениями — их интерпретировать, создавать, манипулировать ими и использовать их для формулирования и решения уравнений, а также для интерпретации решения.” 4
Основная посылка этого модуля заключается в том, что «преподавание символической алгебры и ее использование при решении словесных задач может быть полезно с лингвистической точки зрения; чтобы учащиеся могли увидеть, изучить, обсудить и проработать перевод на алгебру многих примеров словесно сформулированных ситуаций, включая работу по решению этих задач как с алгеброй, так и без нее, а также сравнение алгебраических и арифметических решений этих задач. Делая это, они могут постепенно познакомиться с языком алгебраической нотации, словарем и грамматикой полиномиальных выражений, а также с правилами, позволяющими перефразировать в пределах этого языка (т.е., принципы преобразования выражений и уравнений). Кроме того, они могут попрактиковаться в переводе арифметики в алгебру и алгебру в арифметику. Испытывая сильную связь между ними, они могут прийти к пониманию изречения о том, что «алгебра — это обобщенная арифметика», вместо того, чтобы думать о них как о далеких странах, разделенных огромным океаном, что является ситуацией слишком многих американских студентов (см. например, Ли и Уиллер (1989)) ». 5
Делая это, они могут постепенно познакомиться с языком алгебраической нотации, словарем и грамматикой полиномиальных выражений, а также с правилами, позволяющими перефразировать в пределах этого языка (т.е., принципы преобразования выражений и уравнений). Кроме того, они могут попрактиковаться в переводе арифметики в алгебру и алгебру в арифметику. Испытывая сильную связь между ними, они могут прийти к пониманию изречения о том, что «алгебра — это обобщенная арифметика», вместо того, чтобы думать о них как о далеких странах, разделенных огромным океаном, что является ситуацией слишком многих американских студентов (см. например, Ли и Уиллер (1989)) ». 5
Чем раньше мы, учителя, приступим к этой работе, тем лучших результатов достигнут ученики.
Набор прогрессивных задач
Для этого модуля я написал набор задач, которые развиваются от очень простых одношаговых арифметических задач, подходящих для первоклассников и второклассников, до более сложных алгебраических задач, содержащих переменные.
Числовые и алгебраические выражения.
Задача I. Буханка хлеба стоит 2 доллара. Большая пицца стоит 20 долларов. Для каждого вопроса ниже напишите числовое выражение, которое дает ответ на вопрос.Затем вычислите значение каждого выражения.
- На сколько долларов буханка хлеба дешевле большой пиццы?
- Во сколько раз пицца дороже буханки хлеба?
- Сколько стоит пицца и буханка хлеба вместе?
- Сколько стоят две большие пиццы?
- Сколько стоят пять буханок хлеба?
- Сколько стоят две большие пиццы и пять буханок хлеба вместе?
- На сколько долларов две большие пиццы дороже пяти буханок хлеба?
- Во сколько раз дороже две большие пиццы, чем пять буханок хлеба?
Задачи I 1) с по I 5) представляют собой одноэтапные задачи для сложения / вычитания и умножения / деления.Здесь важно, чтобы студенты сначала записали выражение, а не просто вычислили ответ. Например, в задаче I 3) выражение должно выглядеть так:
Например, в задаче I 3) выражение должно выглядеть так:
Цена на пиццу и хлеб вместе: 20 долларов +2 доллара = 22 доллара. Важно потребовать, чтобы учащиеся выражали окончательный ответ в правильных единицах, и они должны знать единицы, прикрепленные к каждому числу, которое они используют. Все члены в уравнении сложения должны относиться к одной и той же единице.
Проблемы 6) с по 8) представляют собой трехэтапные задачи. Например, выражение для Задача I 6) :
Цена двух больших пицц и пяти буханок хлеба в долларах = 2 (20) + 5 (2) = 50.
Студенты должны заметить, что все эти выражения содержат только числа и символы арифметических операций. Такие выражения называются числовыми выражениями .
Следующий шаг — дать студентам ту же задачу, но заменить числовые значения цен буквами.
Проблема II. Буханка хлеба — х долларов. Большая пицца стоит и долларов. Для каждого вопроса ниже напишите алгебраическое выражение, которое дает ответ на вопрос.
Для каждого вопроса ниже напишите алгебраическое выражение, которое дает ответ на вопрос.
- На сколько долларов буханка хлеба дешевле большой пиццы?
- Во сколько раз пицца дороже буханки хлеба?
- Сколько стоит пицца и буханка хлеба вместе?
- Сколько стоят две большие пиццы?
- Сколько стоят пять буханок хлеба?
- Сколько стоят две большие пиццы и пять буханок хлеба вместе?
- На сколько долларов две большие пиццы дороже пяти буханок хлеба?
- Во сколько раз дороже две большие пиццы, чем пять буханок хлеба?
Например, решение проблемы II 1) :
Буханка хлеба на у-х долларов дешевле большой пиццы.
Здесь важно научить детей, что эту задачу можно сформулировать по-другому. Мы можем спросить: насколько большая пицца в долларах дороже буханки хлеба? Студенты должны заметить, что решение проблемы остается неизменным.
Задача II 7) посложнее.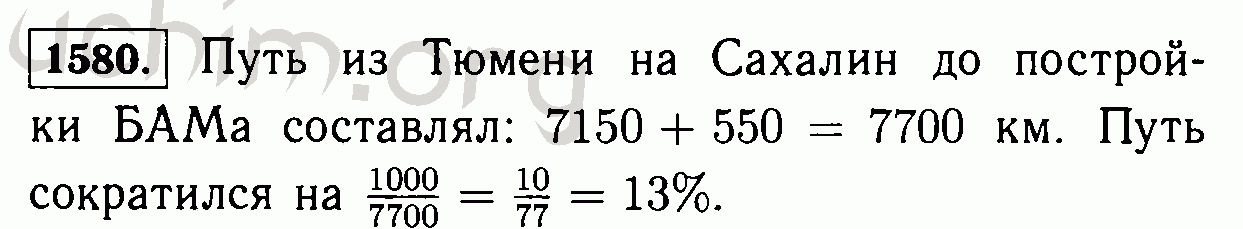 Студенты должны усвоить, что термин, обозначающий более дорогой продукт, всегда является первым членом выражения.
Студенты должны усвоить, что термин, обозначающий более дорогой продукт, всегда является первым членом выражения.
Две большие пиццы дороже пяти буханок хлеба.2 y -5 x представляет разницу в цене. Опять же, дети должны иметь возможность изменить задачу, заменив «дороже» на «дешевле». Таким образом, проблема будет в следующем: насколько в долларах пять буханок хлеба дешевле двух больших пицц?
Как и в Задача II 1) , решение не изменится.
Студенты должны ответить на вопрос: В чем разница между задачей I и задачей II ? Они должны указать, что выражения в Задача II содержат не только числа и символы арифметических операций, но также буквы, которые представляют числа, то есть переменные.Такие выражения называются алгебраическими выражениями .
Проблема III . Напишите алгебраическое выражение, а затем найдите его значение по значению каждой переменной.
- В три раза больше разницы между a и b .
 Найдите значение, если a = 5 и b = 4.
Найдите значение, если a = 5 и b = 4. - Частное 25 на сумму чисел x и y . Найдите значение, если x = 3 и y = 2.
- Тройное число a и прибавьте его к b . Найдите значение, если a = 6 и b = 10.
- Разница 72 и дважды c . Найдите значение, если c = 20.
Проблема III повторяет Проблема II , но на этот раз нет реальных сценариев. Студенты должны «перевести» каждое алгебраическое выражение с английского языка с помощью математических символов, а затем оценить их. Решение проблемы III 3) может выглядеть так:
3 а + б
3 (6) + 10 = 18 + 10 = 28
Важно, чтобы наборы задач включали разные сценарии, например, Problems IV и V ниже.Дети могут представить себя в этой реальной жизненной ситуации, что делает саму идею решения словесных задач более актуальной для них.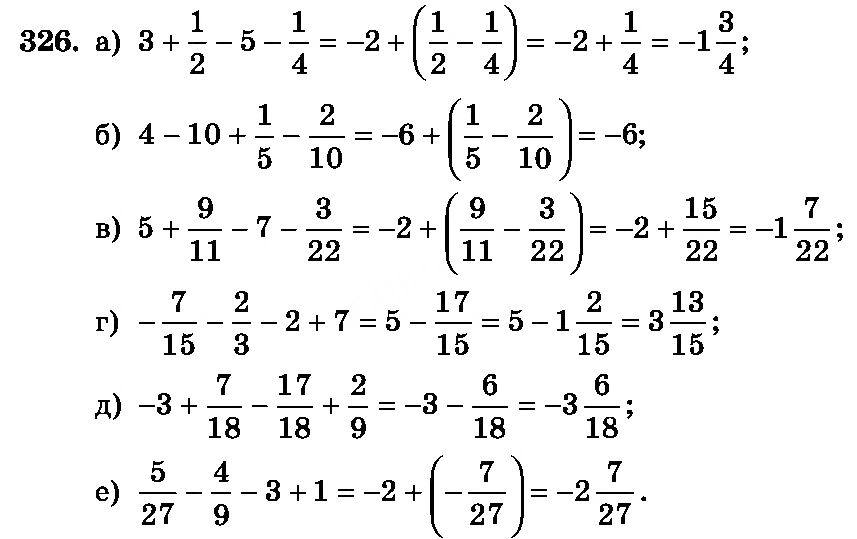 Эти две задачи также дают учителю возможность подчеркнуть, что математика — это также язык науки. Физика учит, что для определения расстояния нужно умножать скорость на время. Если мы заменим каждое слово в этом правиле буквами, мы сможем описать его математическим языком. «Равенство, которое представляет собой правило для вычисления значения некоторой переменной, называется формулой .” 6
Эти две задачи также дают учителю возможность подчеркнуть, что математика — это также язык науки. Физика учит, что для определения расстояния нужно умножать скорость на время. Если мы заменим каждое слово в этом правиле буквами, мы сможем описать его математическим языком. «Равенство, которое представляет собой правило для вычисления значения некоторой переменной, называется формулой .” 6
Проблема IV . Автомобиль и велосипед стартуют в одной точке, но движутся в противоположных направлениях. Скорость автомобиля 60 миль / ч. Скорость велосипеда — 10 миль / ч. Для каждого вопроса ниже напишите числовое выражение, которое дает ответ на вопрос. Затем вычислите значение каждого выражения.
- Какое расстояние между автомобилем и велосипедом через час после трогания с места?
- С какой скоростью они удаляются друг от друга?
- Какое расстояние между автомобилем и велосипедом через два часа после трогания с места?
- Какое расстояние проехала машина за два часа?
- Какое расстояние проехал велосипед за два часа?
- Насколько больше расстояние, пройденное автомобилем, превышает расстояние, пройденное велосипедом за 2 часа?
- Во сколько раз расстояние, пройденное автомобилем, превышает расстояние, пройденное велосипедом за 2 часа?
Проблема V . Автомобиль и велосипед стартуют в одной точке, но движутся в противоположных направлениях. Скорость автомобиля составляет х миль / ч. Скорость велосипеда — y миль / ч. Для каждого вопроса ниже напишите алгебраическое выражение, которое дает ответ на вопрос.
Автомобиль и велосипед стартуют в одной точке, но движутся в противоположных направлениях. Скорость автомобиля составляет х миль / ч. Скорость велосипеда — y миль / ч. Для каждого вопроса ниже напишите алгебраическое выражение, которое дает ответ на вопрос.
- Какое расстояние между автомобилем и велосипедом через час после трогания с места?
- С какой скоростью они удаляются друг от друга?
- Какое расстояние между автомобилем и велосипедом через два часа после трогания с места?
- Какое расстояние проехала машина за два часа?
- Какое расстояние проехал велосипед за два часа?
- Насколько больше расстояние, пройденное автомобилем, превышает расстояние, пройденное велосипедом за 2 часа?
- Во сколько раз расстояние, пройденное автомобилем, превышает расстояние, пройденное велосипедом за 2 часа?
Числовое и алгебраическое выражение, записанное цифрами, буквами и символами арифметических операций, является «переводом» реальных событий с английского на математический язык. Как вы видели, несколько различных сценариев могут быть описаны с использованием одних и тех же математических моделей. По этой причине математика используется в строительстве, сельском хозяйстве, медицине, машиностроении и многих других областях жизни человека. Следующие две задачи подчеркивают эту важную особенность математики.
Как вы видели, несколько различных сценариев могут быть описаны с использованием одних и тех же математических моделей. По этой причине математика используется в строительстве, сельском хозяйстве, медицине, машиностроении и многих других областях жизни человека. Следующие две задачи подчеркивают эту важную особенность математики.
Проблема VI. Автомобиль преодолевает расстояние в 180 км за 2 часа, а грузовик — за 3 часа. Когда встретятся машина и грузовик, если расстояние между ними 300 км и они начнут движение навстречу друг другу?
Проблема VII. Первая бригада трактористов вспахивает 180 акров за 2 дня. Вторая команда может проделать ту же работу за 3 дня. Сколько дней потребуется, чтобы вспахать 300 акров, если две команды будут работать вместе?
Для решения задач VI и VII студенты должны установить и найти значение того же алгебраического выражения:
300 ÷ (180 ÷ 2 + 180 ÷ 3)
Эти две задачи подчеркнут идею о том, что совершенно разные ситуации из реальной жизни могут быть описаны одинаково, используя математический язык. Это единственное числовое выражение представляет собой математическую модель обеих этих реальных жизненных ситуаций. Однако обратите внимание, что в Задаче VI единицы измерения — часы, а в Задаче VII — дни.
Это единственное числовое выражение представляет собой математическую модель обеих этих реальных жизненных ситуаций. Однако обратите внимание, что в Задаче VI единицы измерения — часы, а в Задаче VII — дни.
Обратный перевод.
Для студентов чрезвычайно важно уметь делать обратный «перевод». Они должны понимать, какую реальную жизненную ситуацию описывает данная математическая модель.
Задача VIII. Посмотрите на таблицу ниже. Объясните, как вы это понимаете.
Учитывая | Математическая модель | Перевод |
В миске есть апельсины и b бананов. | a + b = 30 | Общее количество плодов 30. |
a = 2 b | Количество апельсинов в два раза превышает количество бананов. | |
a = b + 10 | Апельсинов на 10 больше, чем бананов. |
В качестве примера студенты должны указать, что в первом столбце есть некоторые данные. Во втором столбце представлены математические модели, основанные на данных и некоторой новой информации. Третий столбец дает нам представление о том, как алгебраические выражения из второго столбца следует «переводить» на английский язык.
Проблема IX. Создайте сценарии, которые можно описать следующими числовыми выражениями:
- 2 × 94 + 17.
- 25 ÷ (18 ÷ 6 + 18 ÷ 9).
Задачи этого типа важны для развития навыков математического моделирования. Сценарии будут разными. Студенты могут бороться с этими проблемами. Я планирую провести в классе обсуждение такого рода проблем и приведу несколько примеров, прежде чем предлагать своим ученикам создавать свои собственные сценарии для выражений. После этого я попрошу добровольцев поделиться своими сценариями со всем классом.
Связанные ставки.
Задачи этого раздела предназначены для студентов, изучающих математику. Чтобы преуспеть в этой теме, они должны легко «переводить» текстовые задачи с английского на математический «язык», уверенно настраивать и оценивать алгебраические выражения и работать с формулами. Это высший уровень математики, доступный школьникам. Что касается этой темы, мои студенты всегда упоминают, что это помогает им понять, почему они тратят так много времени на овладение своими навыками алгебраических выражений.«Вся математика» теперь имеет для них смысл.
Чтобы преуспеть в этой теме, они должны легко «переводить» текстовые задачи с английского на математический «язык», уверенно настраивать и оценивать алгебраические выражения и работать с формулами. Это высший уровень математики, доступный школьникам. Что касается этой темы, мои студенты всегда упоминают, что это помогает им понять, почему они тратят так много времени на овладение своими навыками алгебраических выражений.«Вся математика» теперь имеет для них смысл.
В качестве примера рассмотрим эту относительно простую задачу:
Задача X. «Точка движется по окружности радиусом 6 дюймов, закон ее движения равен
.Ɵ = т 3 -6 т 2 +9 т , (10)
, где t (время) измеряется в секундах, а Ɵ (угол против часовой стрелки, который радиус точки образует с осью x) в радианах.Найдите (а) угловую скорость ω , когда t = 4 секунды. Решение. (а) Из (10) получаем
ω = dƟ / dt = 3 т 2 -12 т +9.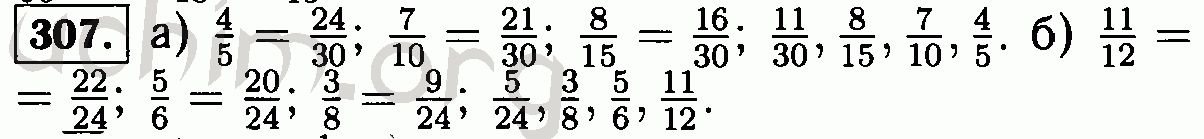 (11)
(11)
Следовательно,… угловая скорость при t = 4 секунды равна
ω 1 = 3 × 4 2 -12 × 4 + 9 = 9 радиан в секунду ». 7
Игнорировать вопрос вычисления производной; студенты должны уметь оценивать выражение (11).Эта задача — хороший пример, чтобы подчеркнуть важность обучения алгебраическим выражениям в средней и начальной школе.
Следующая задача более серьезная.
Проблема XI. «Точка движется по прямой таким образом, что пройденное расстояние (означает расстояние от положения, когда t = 0) изменяется как куб времени. Если точка находится на расстоянии 3 фута от начальной точки в конце 2 секунд, каким будет ее расстояние от начальной точки и ее скорость в конце 6 секунд?
Решение.Общий закон движения, сформулированный в виде уравнения, становится
.s = k × т 3 , (3)
, где k — некоторая константа, а s — пройденное расстояние. Более того, по гипотезе s = 3, когда t = 2.
Более того, по гипотезе s = 3, когда t = 2.
Следовательно (3) дает 3 = k × 8, так что k = 3/8 фут / сек 3 . Таким образом, точный закон движения равен
.S = (3 ̸8) × т 3 (4)
Таким образом, желаемое расстояние от начальной точки в конце 6 секунд будет
.S 1 = 3/8 × 6 3 = 81 фут.
Что касается скорости, то из (4)
dS / dt = 9/8 × т 2 ,
Так что, в соответствии с пояснениями к этой статье, желаемая скорость по истечении 6 секунд будет
V 1 = 9/8 × 6 2 = 40 ½ футов в секунду ”. 8
Примечание : Фактически, вам не нужно вычислять k. Если расстояние от начала пропорционально t 3 , то, поскольку 6 = 3×2, точка будет на расстоянии 3 3 x 3 = 81 фут.
Как видите, на самом первом этапе ученики должны «перевести» первое предложение задачи с английского на математический язык. Соотношение между расстоянием и временем должно быть выражено формулой. Если этот навык не был развит, они сразу же провалиют задачу. Эта проблема ясно иллюстрирует важность обучения студентов тому, как переводить текстовые задачи в математические модели, начиная с того момента, как это возможно.
Соотношение между расстоянием и временем должно быть выражено формулой. Если этот навык не был развит, они сразу же провалиют задачу. Эта проблема ясно иллюстрирует важность обучения студентов тому, как переводить текстовые задачи в математические модели, начиная с того момента, как это возможно.
В этом разделе я хотел бы обсудить, как я планирую использовать задачи, подобные упомянутым выше, чтобы помочь моим ученикам улучшить свои навыки перевода и решения.
Урок 1.
Цель: Студенты будут практиковаться в написании числовых и алгебраических выражений, чтобы переводить текстовые задачи в математические модели.
Проблемы в модуле разработаны таким образом, чтобы постепенно повышать строгость, начиная с Задачи I , что относительно просто. Таким образом, Задача I может быть приведена в классе в качестве примера. Я планирую провести обсуждение в группе и помочь студентам записывать числовые выражения. Студенты должны найти значение каждого выражения без использования калькулятора.
Проблема II основана на проблеме Проблема I . Студенты должны выполнить ее самостоятельно, используя идеи, изложенные в задаче I . Студенты могут по очереди написать ответ на каждое утверждение на доске, чтобы проверить решения.
Я решу, какие еще задачи использовать для работы в классе, и поставлю аналогичные для домашнего задания. Однако я не планирую делать больше пяти или семи за первый урок. Я также считаю, что должно быть несколько уроков с одной и той же целью.
Урок 2.
.Цель: Студенты будут практиковаться в интерпретации каждой математической модели в терминах заданных сценариев.
Проблемы этого типа традиционно сложны. Студентам сложно «расшифровать» математические модели. Начну, наверное, с Проблема VIII. В начале третий столбец «Перевод» должен быть пустым. Учитель поможет ученикам проанализировать математические модели для каждого сценария и заполнить столбец. Учащиеся могут самостоятельно работать над другими задачами в парах или группах с последующим обсуждением в группе.
Опять же, в зависимости от целей, навыков учащихся и сроков обучения, я буду корректировать конкретные классные и домашние задания.
Урок 3.
.Задача: учащиеся решат связанные с курсом задачи.
Тема сложная. Мой подход будет заключаться в том, чтобы начать с Задача X постепенно прогрессировать с точностью. Учащиеся могут работать над задачами X и XI самостоятельно или в группах с последующим обсуждением в группе.Особо обращу внимание на агрегаты. Это поможет студентам понять проблему физически.
Примечание : Вопрос о единицах в Задаче X даже сложнее, чем в XI. Цифры «3», «12» и «9» имеют разные единицы измерения.
Набор задач
Задача I. Фунт клубники стоит x долларов. Фунт вишни стоит y долларов. Напишите алгебраическое выражение для каждой фразы или вопроса ниже.
- Цена за 2 фунта клубники.
- Цена за 3 фунта вишни.
- На сколько денег фунт вишни дороже фунта клубники?
- Во сколько раз фунт вишни дороже фунта клубники?
- Цена 1 фунта клубники и 1 фунта вишни вместе.

- Цена 2 фунта вишни и 3 фунта клубники.
- На сколько денег 2 фунта вишни дороже 3 фунтов клубники?
- Сколько раз 2 фунта.вишни дороже, чем 3 фунта клубники?
Чтобы найти значения алгебраических выражений, мы должны знать значение каждой переменной. Если нам известна цена 1 фунта клубники и вишни, мы можем найти значение каждого выражения в Задаче II .
Проблема II . Пусть в задаче I 1 фунт клубники равен 2 долларам, а 1 фунт вишни равен 6 долларам.
Теперь найдите значение каждого созданного вами выражения для задачи Задача I .
Проблема III. Напишите числовое выражение для каждой фразы и найдите ее значение:
- Произведение числа 100 и суммы чисел 8 и 7.
- Произведение разности чисел 57 и 42 и числа 1000.
- Отношение суммы чисел 32 и 24 к числу 7.
- Частное числа 81 на разность чисел 77 и 68.
Проблема IV.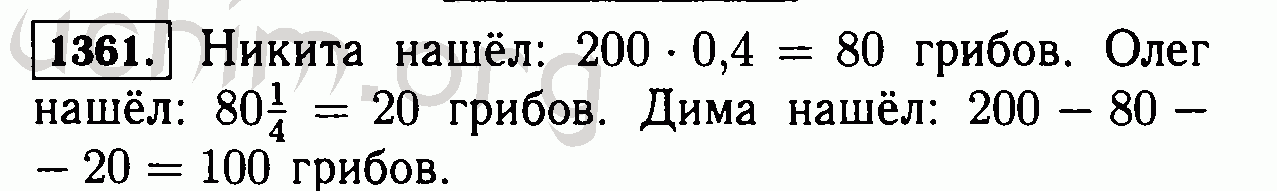 Напишите алгебраическое выражение для каждой фразы:
Напишите алгебраическое выражение для каждой фразы:
- Произведение числа x и суммы чисел y и z .
- Произведение разности чисел a и b и числа c .
- Частное от суммы чисел t и w и числа q .
- Частное числа f и разности чисел g и h .
Задача V. Напишите числовое выражение для каждой фразы и найдите ее значение:
- Сумма произведения чисел 15 и 2 и частного числа 42 на 6.
- Разница частного числа 270 на 3 и произведения чисел 25 и 3.
- Сумма произведения чисел 17 и 3 и произведения чисел 4 и 13.
- Разница частного числа 45 на 3 и частного числа 64 на 32.
Проблема VI. Автомобиль и автобус отправились в путь из одной точки в противоположных направлениях. Скорость автомобиля 60 миль / ч. Скорость автобуса — 50 миль / ч. Для каждого вопроса ниже напишите числовое выражение, которое дает ответ на вопрос. Затем вычислите значение каждого выражения.
Затем вычислите значение каждого выражения.
- Какое расстояние между автомобилем и автобусом через час?
- С какой скоростью они удаляются друг от друга?
- Какое расстояние между автомобилем и автобусом через 2 часа?
- Какое расстояние проезжает машина за два часа?
- Какое расстояние проезжает автобус за два часа?
- Насколько больше расстояние, пройденное автомобилем, превышает расстояние, пройденное автобусом за 2 часа?
- Во сколько раз расстояние, пройденное автомобилем, превышает расстояние, пройденное автобусом за 2 часа?
Проблема VII. Автомобиль и автобус начали движение из одной точки в противоположных направлениях. Скорость автомобиля x миль / ч. Скорость автобуса y миль / ч. Машина едет быстрее, чем автобус. Для каждого вопроса ниже напишите алгебраическое выражение, которое дает ответ на вопрос.
- Какое расстояние между автомобилем и автобусом через час?
- С какой скоростью они удаляются друг от друга?
- Какое расстояние между автомобилем и автобусом через 2 часа?
- Какое расстояние проезжает машина за два часа?
- Какое расстояние проезжает автобус за два часа?
- Насколько больше расстояние, пройденное автомобилем, превышает расстояние, пройденное автобусом за 2 часа?
- Во сколько раз расстояние, пройденное автомобилем, превышает расстояние, пройденное автобусом за 2 часа?
- Что означают выражения x-y и 2 x -3 y ?
Задача VIII. Цена одного тюльпана x долларов, роза на y долларов дороже. Напишите алгебраическое выражение для каждой фразы:
Цена одного тюльпана x долларов, роза на y долларов дороже. Напишите алгебраическое выражение для каждой фразы:
- Стоимость букета из 5 тюльпанов и 4 роз составляет 25 долларов.
- Три розы на 10 долларов дороже пяти тюльпанов.
- Цена семи тюльпанов меньше 20 долларов.
- Цена семи роз больше 20 долларов.
- Что означают выражения 7 x +3 ( x + y ) и 12 ( x + y ) — 8 x ?
Примечание : Я попрошу своих студентов упростить эти выражения и указать, что означают эти упрощенные выражения, и имеет ли это смысл в контексте проблемы; то есть ясно, что упрощенные выражения должны иметь те же значения, что и исходные?
Проблема IX. Фунт яблок стоит м долларов; фунт груш на 4 доллара дороже. Напишите алгебраическое выражение для каждой фразы:
- Цена 2 фунта. яблок и 3 фунта. груш 17 долларов.
- Цена 7 фунтов.
 груш на 30 долларов больше, чем цена 5 фунтов. яблок.
груш на 30 долларов больше, чем цена 5 фунтов. яблок. - Цена 2 фунта. груш меньше 12 долларов.
- Цена 4 фунта. яблок стоит более 3 долларов.
- Что означают выражения 3 m +2 ( m +4) и 4 ( m +4) -3 m ?
Проблема X. Объясните следующие математические модели, связанные с данными:
Учитывая | Математическая модель |
В ресторане a стульев и b столов. | 1) a = 4 b 2) a = b +30 |
Проблема XI. Интерпретировать каждую математическую модель в соответствии с заданными сценариями.
Сценарий | Математическая модель |
В стаде a коров и b лошадей. | 1) a + b = 30 2) a = 3 b 3) a = b +15 4) а-б = 17 5) a : 5 = b |
Путешественник прошел – миль и проплыл – миль. | |
Человек заплатил a долларов за яблоки и b долларов за апельсины. | |
В классе a девочек и b мальчиков. |
Примечание : Студенты должны интерпретировать все пять математических моделей для каждого сценария.
Проблема XII. Создайте сценарии, которые можно описать следующими математическими моделями.
- 100 — 3 × 15.
- 48 ÷ (10 ÷ 2 + 24 ÷ 8).
Проблемы, связанные с тарифами.
Список проблем, связанных с тарифами, и их решений предлагается KhanAcademy (см. Ресурсы). Здесь учителя и ученики могут найти все основные типы задач, которые появляются в тесте AP Calculus AB. Интернет-репетитор проведет вас через весь процесс решения проблемы.
Проблемы, связанные с тарифами
https://www.khanacademy.org/math/ap-calculus-ab/derivative-applications-ab/related-rates-ab/e/related-rates
Внедрение стандартов обучения математике в государственных школах Вирджинии
Четвертый класс
Расчет и оценка
4. 4 Студент
4 Студент
e) создавать и решать одношаговые и многоступенчатые практические задачи, связанные со сложением, вычитанием и умножением, и одношаговые практические задачи, связанные с делением целых чисел.
Пятый класс
Паттерны, функции и алгебра
5.19 Студент будет
а) исследовать и описывать понятие переменной;
b) написать уравнение для представления заданной математической зависимости, используя переменную;
c) использовать выражение с переменной для представления данного словесного выражения, включающего одну операцию; и
г) создать проблемную ситуацию на основе заданного уравнения, используя одну переменную и одну операцию.
Шесть классов
Паттерны, функции и алгебра
6.14 Студент
а) представляют практическую ситуацию с линейным неравенством по одной переменной; и
b) решить одношаговые линейные неравенства с одной переменной, включая сложение или вычитание, и построить график решения на числовой прямой.
Седьмой класс
Паттерны, функции и алгебра
7.11 Учащийся оценит алгебраические выражения для заданных значений замены переменных.
восьмой класс
Паттерны, функции и алгебра
8.14 Студент
a) вычислить алгебраическое выражение для заданных значений замены переменных; и
б) упростить алгебраические выражения с одной переменной.
Выражения и операции
A.1 Студент будет
а) представлять словесные количественные ситуации алгебраически; и
b) вычислить алгебраические выражения для заданных значений замены переменных.
Выше я перечислил соответствующие стандарты. Как видите, начиная с четвертого класса учащиеся должны уметь переводить практическую ситуацию в математическую модель, которая включает запись числового или алгебраического выражения и оценивать его. Они также должны быть компетентными в написании и решении уравнений, представляющих данную математическую зависимость. Таким образом, учителя начальной и средней школы смогут использовать задачи из моего раздела в своих классах. После того, как студенты усвоят содержание моего модуля, они будут лучше подготовлены к математике и физике высшего уровня, где им придется переводить текстовые задачи в математические модели, используя математический язык.В моем классе это устройство поможет мне исправить положение моих учеников, которые планируют сдавать AP Calculus в будущем.
Таким образом, учителя начальной и средней школы смогут использовать задачи из моего раздела в своих классах. После того, как студенты усвоят содержание моего модуля, они будут лучше подготовлены к математике и физике высшего уровня, где им придется переводить текстовые задачи в математические модели, используя математический язык.В моем классе это устройство поможет мне исправить положение моих учеников, которые планируют сдавать AP Calculus в будущем.
Башмакова, Изабелла, Галина Смирнова Начало и развитие алгебры. Кембридж: Издательство Кембриджского университета, 2000.
Блюман, Алан . Демистификация математических словесных задач. Нью-Йорк: McGrawHill, авторское право 2005.
Форд, Уолтер Бертон. Первый курс дифференциального и интегрального исчисления. Нью-Йорк: Генри Холт и компания, авторское право 1928.
Лам, Лай Йонг, Тиан Се Анг . Мимолетные шаги: прослеживание концепции арифметики и алгебры в Древнем Китае. Сингапур: World Scientific, авторское право 2004 г.
Сингапур: World Scientific, авторское право 2004 г.
Ма, Уильям. 5 шагов к 5 AP Calculus AB 2017. Нью-Йорк: McGrawHill, 2016 .
Роджер Хоу, От арифметики к алгебре. Пекин: математический бюллетень, 2010.
Виленкин, Наум. Математика 5 класс. Москва: Мнемозина, 1997 .
Зубарева Ирина Александровна Мордкович, Математика 5 класс. Москва: Мнемозина, 2004.
Зубарева Ирина Александровна Мордкович, Математика 6 класс. Москва: Мнемозина, 2004.
- William Ma, 5 шагов до 5 AP Calculus AB 2017 , 178.
- Наум Виленкин, Математика 5 класс , 44 (перевел с русского).
- Роджер Хоу, От арифметики к алгебре , 1.
- Роджер Хоу, От арифметики к алгебре , 2.

- Роджер Хоу, От арифметики к алгебре , 2.
- Ирина Зубарева, Александр Мордкович, Математика 6 класс , 62 (перевел с русского).
- Уолтер Бертон Форд, Первый курс дифференциального и интегрального исчисления , 107.
- Walter Burton Ford, Первый курс дифференциального и интегрального исчисления , 105.
109 Математические рассуждения
109 Математические рассуждения Инструктор: Дэвид А. МЕЙЕР
Часы работы: AP&M 7218, WF 11:05-11:45 или по предварительной записи
Лекция A: Pepper Canyon Hall 122, MWF 10:00 am-10:50
Лекция C: Pepper Canyon Hall 122 , MWF 12: 00nn-12: 50pm
Электронная почта: dmeyer «at» math «dot» ucsd «dot» edu
Ассистент преподавателя: Yucheng TU
Часы работы: AP&M 5720, чт 14: 00–15: 00, или по предварительной записи
Секция A01: AP&M B412, Вт 16: 00–16: 50; раздел не будет встречаться вт 3 апр
Электронная почта: y7tu «at» ucsd «dot» edu
Ассистент преподавателя: Zihao LI
Часы работы: AP&M 5801, Вт 16: 00–18: 00 или по предварительной записи
Секция A02: AP&M B412, Вт 17: 00–17: 50; секция не будет проходить вт 3 апр
Секция A03: AP&M B412, Вт 18: 00-18: 50; раздел не будет встречаться вт 3 апр
Электронная почта: zil108 «at» ucsd «dot» edu
Ассистент преподавателя: Yiwei SANG
Часы работы: AP&M 5218, Вт 14: 00-16: 00, или по предварительной записи
Секция C01: AP&M B402A, Вт 19: 00-19: 50; раздел не будет соответствовать Вт 3 апр
Электронная почта: yisang «at» ucsd «dot» edu
Ассистент преподавателя: Рошил ПАУДИАЛЬ
Часы работы: AP&M 6414, Пн. 13: 00–14: 00, Вт. 15: 00–16: 00, или по предварительной записи
13: 00–14: 00, Вт. 15: 00–16: 00, или по предварительной записи
Раздел C02: AP&M B402A, Вт. 17: 00–17: 50; секция не будет проходить вт 3 апр,
Секция C03: AP&M B402A, Вт 18: 00-18: 50; раздел не будет встречаться вт 3 апр
Электронная почта: ropaudya «at» ucsd «dot» edu
Описание курса
Этот курс представляет собой введение в математические рассуждения.Для кого угодно, возможно
наиболее полезным последствием изучения математики является повышенная способность
анализировать проблемы, математические или иные, логически. В продвинутых
курсы математики, и в исследованиях математики эта способность используется
в первую очередь доказывают, что верны конкретные утверждения. Цель
этот курс предназначен для студентов, чтобы узнать, что значит сделать математики,
помимо простых вычислений. Это включает в себя изучение того, какие
утверждения нуждаются в доказательстве, что составляет доказательство, и как читать и писать доказательства.
Предварительные условия для прохождения этого курса: математика 18 / 20F / 31AH и Math 20C или согласие инструктора. Учебник — P. J. Eccles, An Introduction to Математическое мышление (Кембридж: издательство Кембриджского университета 1997). Её копии находятся в резерве в Научно-технической библиотеке.
Домашние задания будут выполняться еженедельно по вторникам в секции. Пожалуйста следуйте рекомендациям по форматированию. Студенты разрешено обсуждать домашнее задание между собой, но ожидается, что они сдадут свои собственные работы — копирование чужих недопустимо.Оценки за домашнее задание внесет 20% в итоговую оценку.
Будет два промежуточных семестра, в третью и седьмую недели квартала. Финал лекции назначен на понедельник, 11 июня; финал лекции C запланировано на среду, 13 июня. Результаты двух промежуточных и final будет составлять 20%, 25% и 35% итоговой оценки соответственно. Тестов на макияж не будет.
Связанные события
Syllabus (может быть изменен)
| 2 апреля | обзор курса гл.  1. Язык математики 1. Язык математики логические элементы и булева алгебра [приложение] |
| 4 апреля | Глава. 2. Импликации неопределенных терминов, аксиом / постулатов, предложений [1, гл. 4] HWK (до вторника, 10 апреля). Пр. 1.2, 2.1, 2.4, 2.6, 3.1, 3.2, 3.3, 3.7 |
| 6 апреля | Глава. 3. Доказательства свойств целых чисел [1, гл. 8] Пятничная математическая игра [2] |
| 9 апреля | Глава.4. Доказательство от противного задач разбиения [3] |
| 11 апреля | фон о хроматическом номере плоскости [4] Гл. 5. Индукционный принцип HWK (до вторника 17 апреля). Пр. 4.1, 4.2, 4.4, 4.7, 5.1, 5.4, 5.6, 5.7 |
| 13 апреля | Глава.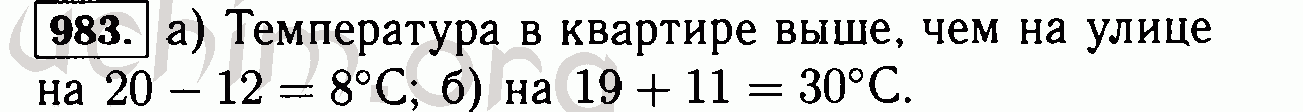 5. Принцип индукции 5. Принцип индукции выводов по индукции [примечания] Пятничная математическая забава [5] |
| 16 апреля | принцип сильной индукции Обзор обзор курса [практические экзаменационные задачи] [практические решения] |
| 18 апреля | Промежуточный семестр 1, охватывающий главы 1-5 Пожалуйста, возьмите с собой синие книги и студенческий билет.Вы можете принести страницу рукописных заметок, но ничего больше. [назначение мест лекции A] [назначение мест лекции C] [экзамен лекции A] [решения] [результаты] [экзамен лекции C] [решения] [результаты] |
| 20 апреля | Глава. 6. Язык теории множеств HWK (ожидается во вторник, 24 апреля). Пр. 6.2, 6.3, 6.4, 6.6, 7.3, 7.4, 7.5, 7. 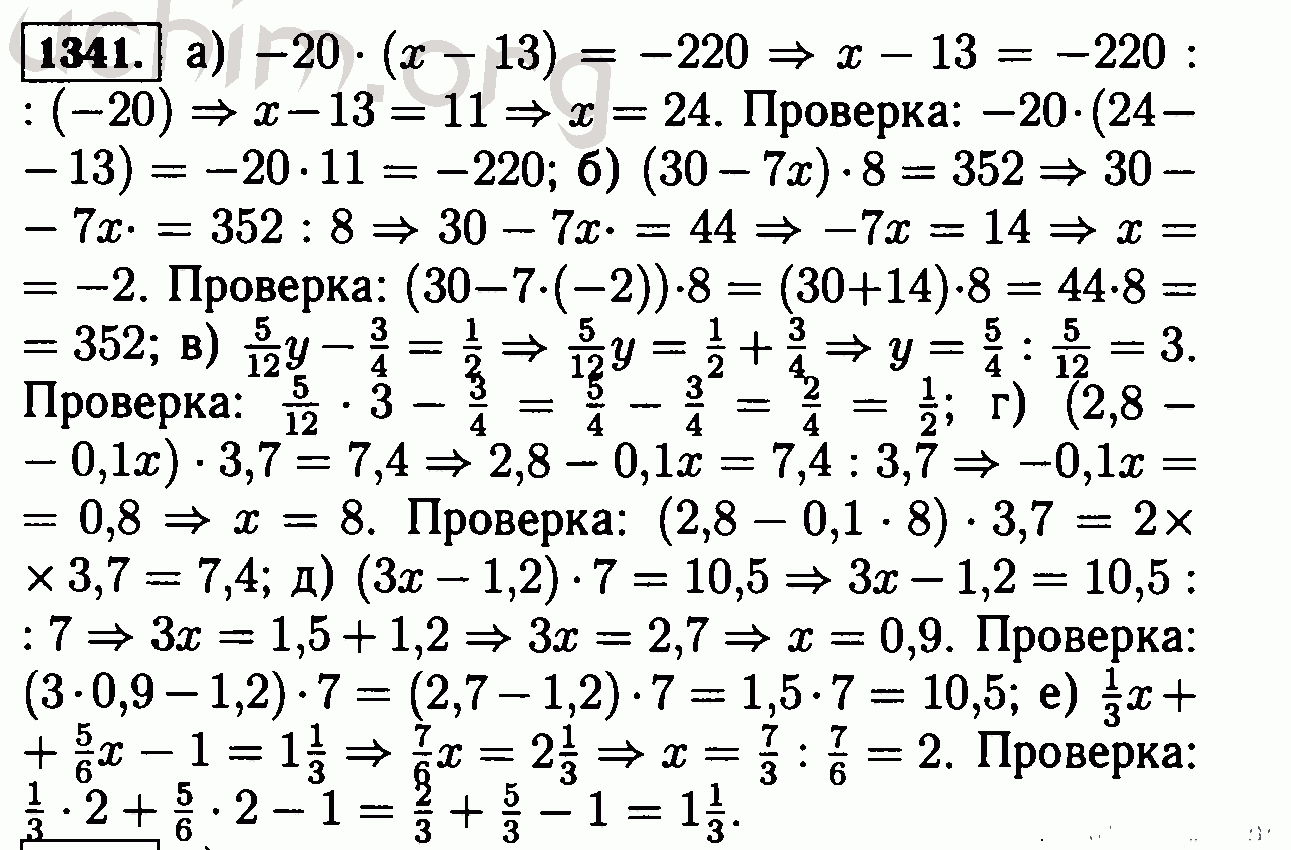 8 8 Пятничная математическая забава [6] |
| 23 апреля | информация о хроматическом номере самолета [7] Гл.7. Кванторы определение предела последовательности утверждений и доказательств о пределах последовательностей [примечания] |
| 25 апреля | Глава. 8. Функции HWK (до вторника, 1 мая). Пр. 8.1, 8.2, 8.3; упражнения в конце заметок о лимитах |
| 27 апреля | Глава. 8. Функции Пятничная математика [8] |
| 30 апреля | Глава.9. Уколы, сюръекции и биинъекции |
| 2 мая | Глава. 10. Подсчет HWK (до вторника, 8 мая). 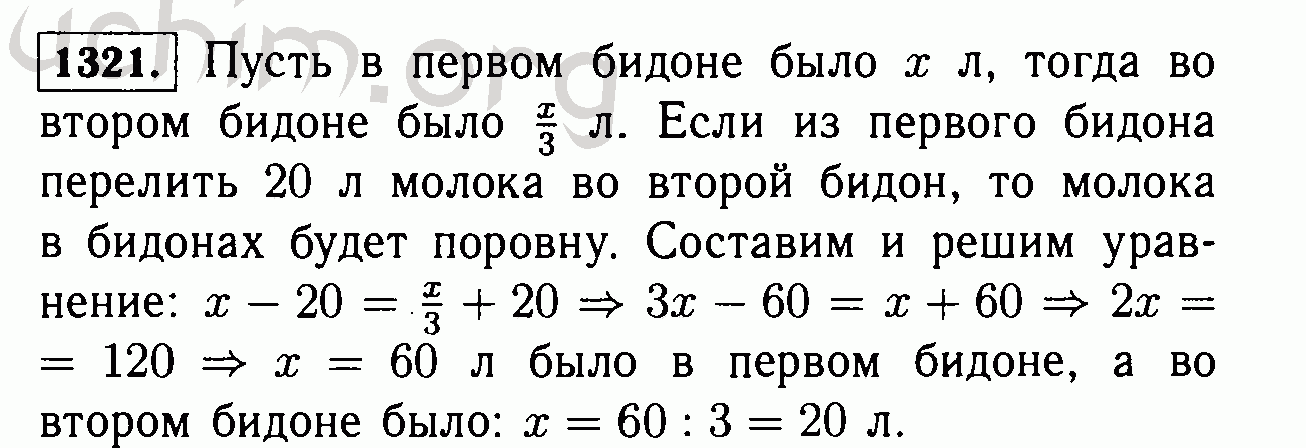 Пр. 9.1, 9.3, 9.5, 9.7, 10.1, 10.3, 10.4 |
| 4 мая | Глава. 11. Свойства конечных множеств Пятничная математическая забава [9] |
| 7 мая | Глава. 11. Свойства конечных множеств |
| 9 мая | Глава.12. Подсчет функций и подмножеств HWK (до вторника, 15 мая). Пр. 11,2, 11,3, 11,4, 11,6, 12,3, 12,5, 12,6 |
| 11 мая | Нет лекции [практические экзаменационные задачи] [практические решения] |
| 14 мая | счетные функции Обзор обзор курса |
| 16 мая | Промежуточный семестр 2, охватывающий главы 1-12 Пожалуйста, принесите с собой учебники и студенческий билет.  Вы можете принести страницу рукописных заметок, но ничего больше. Вы можете принести страницу рукописных заметок, но ничего больше. [назначение мест лекции A] [назначение мест лекции C] [экзамен лекции A] [решения] [результаты] [экзамен лекции C] [решения] [результаты] |
| 18 мая | подсчет подмножеств Гл. 13. Система счисления HWK (до вторника, 22 мая). Пр. 13.1, 13.2, 13.3, 13.4, 13.5 Пятничная математическая забава [10] |
| 21 мая | иррациональность квадратного корня из 2 [11] [графика] |
| 23 мая | Глава.14. Подсчет бесконечных множеств HWK (до вторника, 29 мая). Пр. 14.1, 14.2, 14.3, 14.4, 15.2, 15.3, 15.4, 15.5 |
| 25 мая | кардинальные числа в сравнении с порядковыми Гл.  15. Алгоритм деления 15. Алгоритм деления Пятничная математическая забава [12] |
| 28 мая | Нет лекции; День памяти |
| 30 мая | Глава. 16. Алгоритм Евклида HWK (до вторника, 5 июня). Пр. 16.1, 16.2, 16.3, Проб. IV.1, IV.2, IV.3, IV.7 |
| 1 июня | Нет лекции |
| 4 июня | Глава. 19. Сравнение целых чисел гл. 21. Классы сравнения и арифметика остатков |
| 6 июня | правила разделения пределы функций [примечания] HWK (не сдавать). Пр. 19.2, 19,3, 19,4, 21,3, 21,4, 21,6 |
| 8 июн | непрерывность функций производных функций обзор / обзор курса [практические экзаменационные задачи] [практические решения] |
| 11 июн | Заключительный экзамен по лекции А в 8:00.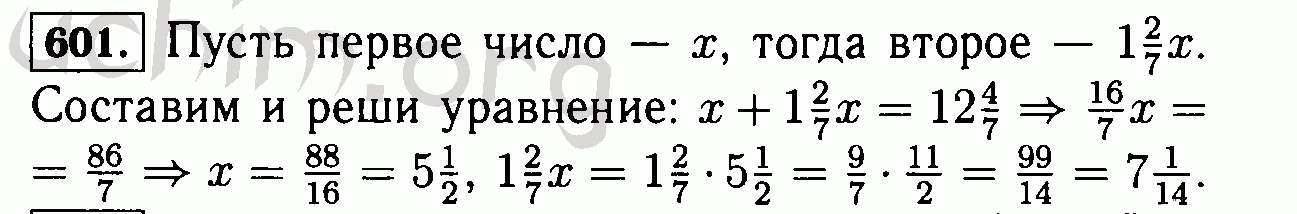 Будет всесторонним. Будет всесторонним. Пожалуйста, принесите синие книги и студенческий билет. Вы можете принести страницу рукописных заметок, но ничего больше. [лекция A назначение мест] [лекция A экзамен] [решения] |
| 13 июн | Заключительный экзамен по лекции C в 11:30. Будет всесторонним. Пожалуйста, принесите синие книги и студенческий билет. Вы можете принести страницу рукописных заметок, но ничего больше. [назначение мест на лекции C] [экзамен на лекцию C] [решения] |
Рекомендуемое чтение
| [1] | Д.Р. Хофштадтер, Гёдель, Эшер, Бах: вечная золотая коса (Нью-Йорк: Основные книги 1979). |
| [2] | И. Тепер,
«Секретный номер», Strange Horizons (20 ноября 2000 г.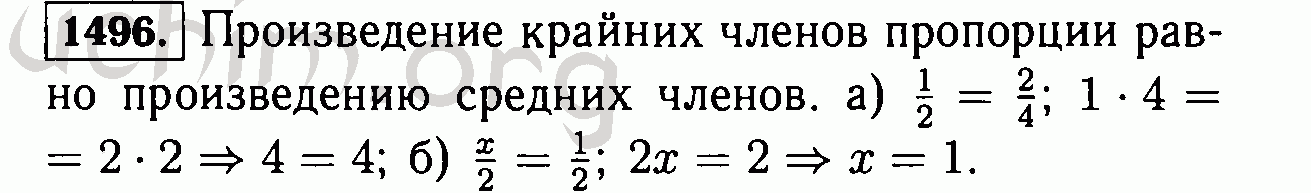 ) [рассказ]; ) [рассказ]; К. Леви, «Тайный номер» (2012) [короткометражный фильм]. |
| [3] | М. Блэк, Критическое мышление. Введение в логику и научный метод (Нью-Йорк: Prentice Hall 1946). |
| [4] | А. Д. Н. Дж. Де Грей, «Хроматическое число плоскости не менее 5», arXiv: 1804.02385v2 [math.CO] (2018). |
| [5] | К. Фитцджеральд, «Хлеб и поцелуи» (2010) [короткометражный фильм]. |
| [6] | Д. Клифтон, «Расчет любви» (2011) [короткометражный фильм]. |
| [7] | Д. Г. Миксон,
«Polymath26, второй поток: что нужно, чтобы быть 5-хроматическим?» (22 апреля 2018 г. ). ). |
| [8] | В. Харт, «Рисование в классе математики: слоны бесконечности» (2 декабря 2010 г.) [видео]. |
| [9] | К. Ягнемма, «Теорема Жилковского», Zoetrope: All-Story 5 No. 3 (осень 2001 г.). |
| [10] | А. Конан Дойл, Мемуары Шерлока Холмса , Приключение XI, «Последняя проблема» (Лондон: Джордж Ньюнес, Ltd.1894) 234-252. |
| [11] | С. Дж. Миллер и Д. Монтегю, «Иррациональность из книги», arXiv: 0909.4913 [math.HO]. |
| [12] | Н.Я. Виленкин,
«Необычный отель, или тысячное первое путешествие Иона Тихого»
в В поисках бесконечности , пер.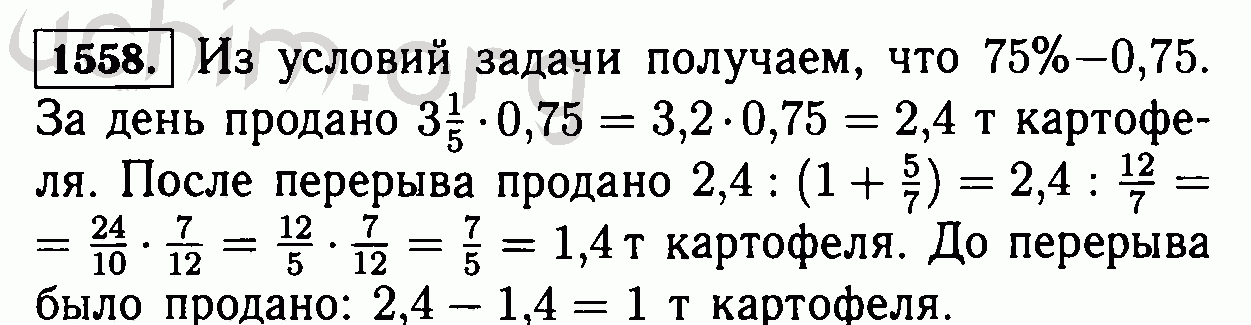 А. Шеницера при редакции Х. Гранта и С. Микитюка.
(Бостон: Birkh & aumlaut; пользователь 1995). А. Шеницера при редакции Х. Гранта и С. Микитюка.
(Бостон: Birkh & aumlaut; пользователь 1995). |
| [13] | Г. Поля, Как решить: новый аспект математического метода (Принстон, Нью-Джерси: Princeton University Press, 1945). |
| [14] | Д. Солоу, Как читать и делать доказательства: Введение в процессы математического мышления , 4-е издание (Хобокен, Нью-Джерси: Wiley 2005). |
Последнее изменение: 14 июня 2018 г.
Почему математика скучна | Кафе n-Category
Уважаемый профессор Баэз,
Меня зовут Паоло Биццарри, и я следую вашему приглашению на поделитесь своим мнением по теме «Почему математика скучна?»
Разрешите представиться: мне 37 лет, я дипломированный специалист.
Наука в 1994 г. За последние четыре-пять лет я начал учиться
математика для развлечения и увлечения.
За последние четыре-пять лет я начал учиться
математика для развлечения и увлечения.
Поскольку моя работа отличается от других, у меня есть ограниченное время, чтобы посвятить страсть. Даже если я нахожу математику чрезвычайно интересной, у меня часто считал изучение математики скучным, трудным и трудным для себя. Так что я немного поразмышлял над тем, почему мне сложно и скучно то, к чему я все равно испытываю страсть.
Мои выводы следующие:
- математика преподается неестественным образом;
- математика — практическая дисциплина, но преподается как абстрактная один;
- есть много неявных знаний, которые недоступны через книги.
Я постараюсь расширить каждое из этих предложений следующим образом.
Математика преподается неестественным образом.
Моя точка зрения здесь в основном относится к учебникам и их типичным структура определения / леммы / теоремы / определения.
Где проблема? Проблема в том, что такой подход неестественен. Не так математики рассуждают и производят свои
работай.
Не так математики рассуждают и производят свои
работай.
Если вы видите демонстрацию, она настолько кратка и важна, насколько это необходимо. быть.Каждый отрывок прекрасно связан с предыдущими отрывками. Каждая гипотеза делается именно тогда, когда это было необходимо, и это абсолютно минимальный.
Вопрос (мой вопрос) такой: да, все работает отлично, но это не наука. Это больше похоже на голливудский фильм, где все происходит по определенной причине.
Но математики так не работают (или, по крайней мере, это моя понимание). Настоящая проблема математики часто не в том, чтобы продемонстрировать теорему: найти хороший объект для изучения.В определение приходит ПОСЛЕ того, как была продемонстрирована теорема. В сама демонстрация уточняется много раз, чтобы получить «Отлично», демонстрация по учебнику. Это единственная демонстрация вам видите, и я нашел их совершенно неестественными именно потому, что они были идеально.
Дело в том, что учебник математики должен обеспечивать
контекст, причина, ПОЧЕМУ они что-то изучают, и что они собой представляют
пытаюсь учиться. Это подводит нас ко второму пункту.
Это подводит нас ко второму пункту.
Математика — это практическая дисциплина, но преподается как абстрактная.
Опять же, это основано на моем ограниченном опыте и может быть довольно типично итальянский. Но, в любом случае, это единственный опыт, который я могу предоставлять.
Один из главных аспектов математики — то, что она «абстрактна», «Чистый», не привязанный к какой-либо практической проблеме.
Что неверно с исторической точки зрения. Но это тоже ложь по более конкретному, повседневному, практическому вопросу.
Математика скучна для математиков, не работающих полный рабочий день, потому что они не знать «инструменты торговли».Они не используются для манипулирования умственными такие объекты, как группы или векторные пространства. Когда я прочитал в первый раз время о группах, мне было трудно понять многие вещи о них и их важности. Когда я начал видеть их используемыми, они стали мне намного понятнее.
Возможно, математики не очень-то чувствуют эту проблему, потому что они
используются для работы с абстрактными объектами. Это та же проблема, что и
непрофессионал в области информационных технологий, когда ему приходится использовать компьютерную программу,
ИТ-специалист.
Это та же проблема, что и
непрофессионал в области информационных технологий, когда ему приходится использовать компьютерную программу,
ИТ-специалист.
Это разделение является сильным еще и потому, что вы не должны использовать инструменты, которые вы изучаете сами: демонстрации уже предоставлены, и улучшать их не нужно (все равно не получится…). Вы должны использовать их в некоторых сфабрикованных ситуациях, но, опять же, есть мало понимания, что это делается по определенной причине. Который Подведите нас к третьему и, возможно, последнему аргументу.
Существует множество неявных знаний, недоступных из книг.
Это одна из самых поразительных вещей, которые я видел: здесь много вещь о математике, которая явно не выражена в учебники по математике.
Один — это то, что вся математика называет «элегантностью». Это нечеткое понятие,
но это принципиально. Я не видел ни одной явной ссылки на
это (кроме, пожалуй, разделов по алгебре). Но это фундаментальный
критерий для создания и оценки математических теорий, а также сильное руководство
о том, какую структуру вы ожидаете.
Второй касается «стилей» демонстрации, которые вы применяете.Учитывая определенного домена довольно часто можно увидеть демонстрации, использующие ограниченный набор методов, которые необходимо выполнить, но эти методы никогда не явно назначены или указаны.
Но без имени трудно эффективно обучить этим вещи. Мы даже не можем о них толком говорить.
Выводы.
Хорошо. Если вам не показались скучными эти мои сочинения, я должен вам пицца в Пизе, если вы когда-нибудь приедете в мой город.
С уважением.
Паоло Биззарри
Обобщенный дробный порядок функций Чебышева в нелинейных краевых задачах в полубесконечной области
Новый метод коллокации, а именно обобщенный дробный порядок коллокации ортогональных функций Чебышева (GFCF), дается для решения некоторой нелинейной границы. задачи в полубесконечной области, такие как уравнения нестационарного изотермического течения газа, жидкости третьего сорта, уравнение Блазиуса и уравнение поля, определяющее профиль вихря.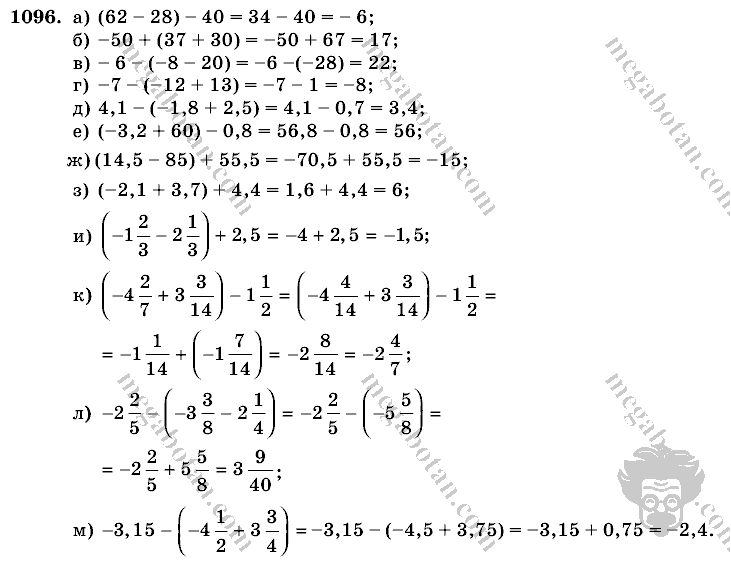 Метод сводит решение задачи к решению нелинейной системы алгебраических уравнений. Чтобы проиллюстрировать надежность метода, численные результаты настоящего метода сравниваются с несколькими численными результатами.
Метод сводит решение задачи к решению нелинейной системы алгебраических уравнений. Чтобы проиллюстрировать надежность метода, численные результаты настоящего метода сравниваются с несколькими численными результатами.
3 примера
Многие проблемы, возникающие в гидродинамике, квантовой механике, астрофизике и других областях, определены в бесконечных или полубесконечных областях. Существуют различные подходы к решению этого типа уравнений, такие как численные, аналитические и полуаналитические методы.В этом разделе мы попытаемся ввести численный метод, основанный на обобщенном дробном порядке ортогональных функций Чебышева, для решения этого типа уравнений.
3.1 Неустановившееся изотермическое течение газа
Одним из важных нелинейных обыкновенных дифференциальных уравнений, возникающих в полубесконечной области, является уравнение нестационарного газа:
d 2 у d т 2 + 2 т 1 — β у ( т ) d у d т знак равно 0 , т ∈ [ 0 , ∞ ) , (9)
где 0 ⩽ β ⩽ 1 — действительная константа, а граничные условия таковы: у
(
0
)
знак равно
1
,
Lim
т
→
∞
у
(
т
)
знак равно
0. (10)
(10)
До сих пор в эту модель был вложен значительный объем численных и аналитических работ [17]. Основная причина такого интереса в том, что это приближение можно использовать для многих инженерных целей. Как было сказано ранее, проблема уравнения. Уравнение (9) было обработано Киддером [17], в котором используется метод возмущения для включения членов второго порядка. Вазваз [18] решил это уравнение нелинейно, изменив метод разложения и приближение Паде.Parand et al. [19, 20], и Taghavi et al. [21] также применили рациональные функции Якоби, метод коллокации функций Бесселя и модифицированные обобщенные полиномы Лагерра для решения этого уравнения. Rezaei et al. [22] применили два численных метода, основанные на функциях Sinc и рациональных функциях Лежандра, для решения проблемы потока газа через микронанопористую среду. Rad et al. [23] решили это уравнение с помощью двух численных и аналитических решений, основанных на методе гомотопического анализа и методе коллокации функций Эрмита. (
т
)
знак равно
λ
т
2
+
λ
+
т
е
—
2
т
у
м
(
т
)
,
(11)
(
т
)
знак равно
λ
т
2
+
λ
+
т
е
—
2
т
у
м
(
т
)
,
(11)
Уравнения для получения коэффициента { а я } я знак равно 0 м — 1 возникают в результате уравнивания Res ( t ) до нуля на m точек совмещения:
р
е
s
(
т
я
)
знак равно
0
,
я
знак равно
0
,
1
,
. (
т
)
.
(
т
)
.
Таблица 1 показывает значение y ′ (0) по настоящему методу и сравнивает его со значениями коллокации функции Бесселя (BFC) [20], метода съемки [24] и RBF [24] для β = 0,25, 0,50, 0,75 при м = 35 и α = 0,50.
Таблица 1Сравнение полученных значений y ′ (0) для β = 0,25, 0.50, 0,75 настоящим методом, методом стрельбы [24], BFC [20] и RBF [24], с м = 35 и α = 0,50
| β | λ | Настоящее время | BFC | RBF | Стрельба | Абс.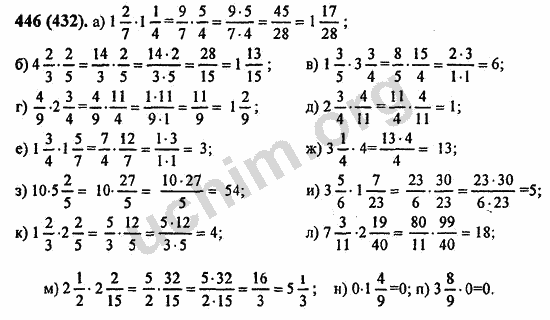 Err. Err. | |
|---|---|---|---|---|---|---|---|
| 0,25 | 0,1754 | -1,156572055 | -1.156275 | -1,156557 | -1,156572 | 5.514e-8 | |
| 0,50 | 0,1755 | -1,1917 | -1,1 | -1,1 | -1,1 | 5.078e-7 | |
| 0,75 | 0,0167 | -1,239760055 | -1,239760 | -1,239671 | -1.239760 | 5.565e-8 |
Таблица 2 показывает полученные значения y ’(0) и
∥
р
е
s
∥
ш
2
по настоящему способу для различных значений м , β = 0,50 и α = 0,50.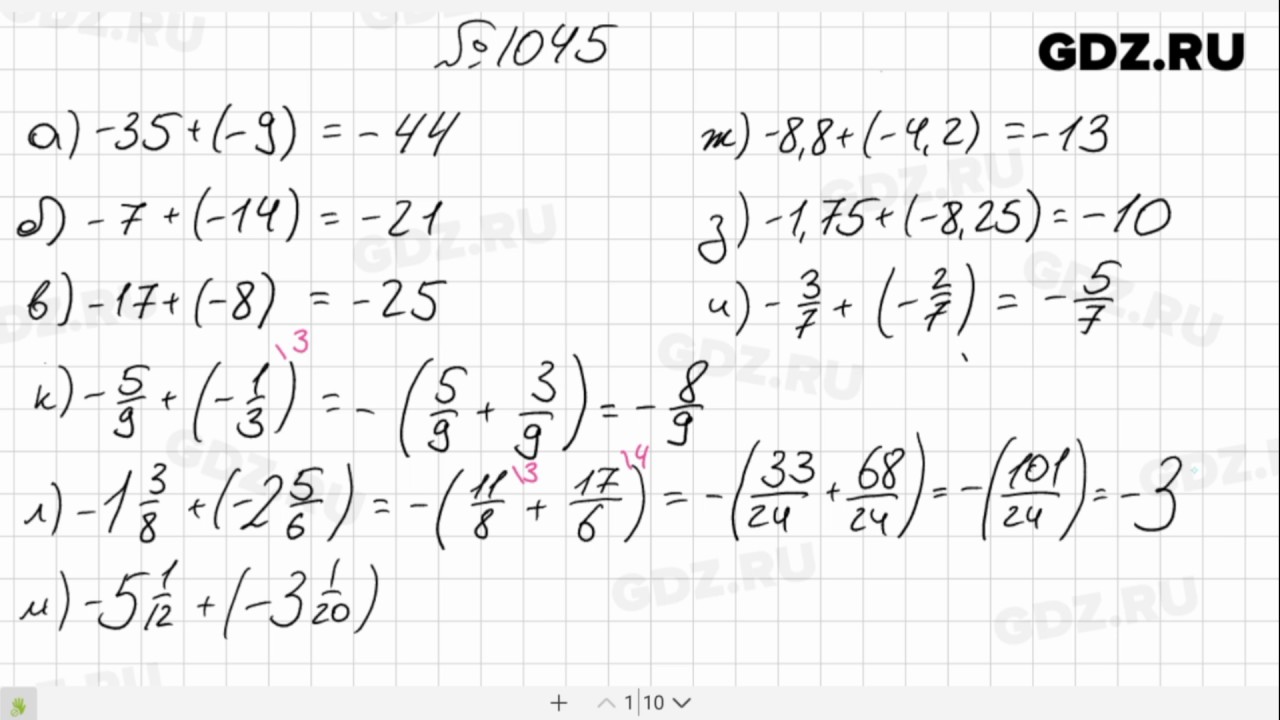
Полученные значения y ′ (0) данным методом для различных значений m , β = 0.50 и α = 0,50
| м | λ | y ′ (0) | ∥ р е s ∥ ш 2 |
|---|---|---|---|
| 15 | 0,3005 | -1,1097 | 2. 2591e-02 2591e-02 |
| 25 | 0,1788 | -1,1 | 1559.2586e-05 |
| 35 | 0,1755 | -1,1917 | 1.0379e-05 |
Таблица 3 показывает значения y ( t ) для различных значений t по настоящему методу и сравнивает их со значениями возмущения (PB) [17], коллокации функций Бесселя (BFC) [20] , модифицированный обобщенный метод Лагерра (MGL) [21], метод Рунге-Кутта (RK) [24], RBF [24] и метод конечных разностей (FD) [25], с м = 35 и α = 0.50.
Таблица 3Полученные значения y ( t ) для β = 0,5, α = 0,5, м = 35 и λ = 0,1755, сравнение настоящего метода, BFC [20], RBF [24], FD [25], PB [17], RK [24] и MGL [21]
- 873
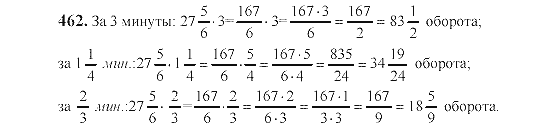 3
3- 678
- 99
На рис. 2 показаны графики y ( t ) и y ′ ( t ) из решения уравнения нестационарного газа для β = 0.25, 0,50 и 0,75 при м = 35, α = 0,5 и η = 10.
Рис.2
Полученные графики уравнения нестационарного газа для β = 0,25, 0,50, 0,75
На рис. 3 показаны графики остаточных ошибок уравнения. (12) и логарифм коэффициентов | a i | для β = 0,50, 0,75, при м = 35 и α = 0.50, чтобы показать сходимость метода.
Рис.3
Графики остаточных ошибок и журнала (| a i | для β = 0,50 (синий) и β = 0,75 (красный)
3,2 Жидкость третьего сорта в пористом полупространстве
Краевая задача, моделирующая установившееся течение жидкости третьего сорта в пористом полупространстве на полубесконечной области, выглядит следующим образом:
d 2 у d т 2 1 + б 1 ( d у d т ) 2 — б 1 б 2 3 у d у d т 2 — б 2 у знак равно 0 , т ∈ [ 0 , ∞ ) , (13)
где б 1 и б 2 — действительные константы и граничные условия для этого уравнения:у ( 0 ) знак равно 1 , Lim т → ∞ у ( т ) знак равно 0.(14)
Некоторые исследователи аппроксимируют уравнения жидкости третьего класса в пористом полупространстве; например, Ахмад [26], применив метод гомотопического анализа, Kazem et al. [27] с применением метода коллокации радиальных базисных функций, Паранда и Хаджизаде [28] с применением модифицированного метода коллокации рациональных функций Христова, Бахарифард и др. [29] с применением рационального и экспоненциального метода Лежандра Тау.
Для удовлетворения граничных условий, мы удовлетворяем уравнению.( т ) знак равно λ т 2 + λ + т е — 2 т у м ( т ) , (15)
, где λ — произвольная действительная постоянная, а y m ( t ) определено в уравнении. .( т ) .
Таблица 4 показывает полученные значения y ′ (0) с помощью настоящего метода и сравнивает их со значениями гауссова RBF (G-RBF) [27], рациональных функций Христова (RCF) [28], метода стрельбы [ 29], рациональный метод Тау Лежандра (RLT) [29] и экспоненциальный метод Тау Лежандра (ELT) [29] для различных значений b 1 и b 2 , при m = 20 и α = 0.50.
Таблица 4Сравнение полученных значений y ′ (0) для различных значений b 1 и b 2 по настоящему способу, способу съемки, RLT, ELT, RCF и G-RBF
| б 1 | б 2 | λ | Настоящее время | Стрельба | RLT [29] | ELT [29] | RCF [28] | G-RBF [27] |
|---|---|---|---|---|---|---|---|---|
| 0.3 | 0,5 | 0,80 | -0,636 | -0,6 | -0,6 | -0,6 | ||
| 0,6 | 0,80 | -0,67830298 | -0,678301 | -0,678511 | -0,678302 | -0,6783017 | -0,6783013 | |
| 0.9 | 0,80 | -0,66732796 | -0,667327 | -0,667528 | -0,667327 | |||
| 1,2 | 0,80 | -0,65783825 | -0,657838 | -0,658029 | -0,657837 | |||
| 0,6 | 0.3 | 0,81 | -0,5333 1017 | -0,533303 | -0,533545 | -0,533302 | ||
| 0,6 | 0,81 | -0,73800824 | -0,738008 | -0,738116 | -0,738007 | |||
| 0,9 | 0.81 | -0,88746913 | -0,887467 | -0,887350 | -0,887467 | |||
| 1,2 | 0,81 | -1,00865474 | -1,008653 | -1,008516 | -1,008653 |
В таблице 5 приведены полученные значения y ′ (0) и ∥ р е s ∥ ш 2 данным способом для различных значений м , b 1 = 0.60, b 2 = 0,50 и α = 0,50.
Таблица 5Полученные значения y ′ (0) данным методом для различных значений м и α = 0,50
| м | λ | y ′ (0) | ∥ р е s ∥ ш 2 |
|---|---|---|---|
| 10 | 0.4 | -0,6757266461 | 6.098e-03 |
| 15 | 0,7 | -0,6782 | |
| 5.147e-05 | |||
| 20 | 0,8 | -0,6783029829 | 1.198e-05 |
В таблице 6 приведены полученные значения y ′ (0) и ∥ р е s ∥ ш 2 данным способом для различных значений α , b 1 = 0.60, b 2 = 0,50 и м = 20.
Таблица 6Полученные значения y ′ (0) данным методом для различных значений α и м = 20
| α | λ | y ′ (0) | ∥ р е s ∥ ш 2 |
|---|---|---|---|
| 0.25 | 0,4 | -0,67827627 | 9.6011e-04 |
| 0,50 | 0,8 | -0,67830298 | 1.1986e-05 |
| 0,75 | 1,0 | -0,67844196 | 1.1074e-06 |
| 1,00 | 1,8 | -0,67830171 | 2,7556e-08 |
Таблица 7 показывает полученные значения y ( t ) для различных значений t по настоящему методу и сравнение их со значениями метода гомотопического анализа (HAM) [26], Gaussian RBF (G-RBF ) [27], рациональные функции Христова (RCF) [28], рациональный метод Лежандра Тау (RLT) [29] и экспоненциальный метод Лежандра (ELT) [29], при м = 20 и α = 0 .50.
Таблица 7Сравнение полученных значений y ( t ) для различных значений t по данной методике, RLT, ELT, RCF, G-RBF и HAM
| т | Настоящее время | RLT [29] | ELT [29] | RCF [28] | G-RBF [27] | HAM [26] |
|---|---|---|---|---|---|---|
| 0,2 | 0.87261020 | 0,87261 | 0,87261 | 0,872608596 | 0,87265264 | 0,87220 |
| 0,4 | 0,76062562 | 0,76063 | 0,76063 | 0,760626805 | 0,76074843 | 0,76010 |
| 0,6 | 0,66243220 | 0,66243 | 0.66243 | 0,662431176 | 0,66261488 | 0,66190 |
| 0,8 | 0,57650340 | 0,57650 | 0,57650 | 0,576502298 | 0,57671495 | 0,57600 |
| 1,0 | 0,50143723 | 0,50143 | 0,50144 | 0,501436165 | 0.50164542 | 0,50100 |
| 1,2 | 0,43595139 | 0,43595 | 0,43595 | 0,435950397 | 0,43613322 | 0,43560 |
| 1,6 | 0,32 | |||||
| 0,32920 | 0,32920 | 0,3252 | 0,329 | 0,32890 | ||
| 2.0 | 0,24838691 | 0,24837 | 0,24838 | 0,248384348 | 0,24842702 | 0,24820 |
| 2,5 | 0,17455143 | 0,17455 | 0,17455 | 0,174547634 | 0,17456033 | 0,17440 |
| 3,0 | 0,12261790 | 0.12264 | 0,12261 | 0,122612386 | 0,12262652 | 0,12250 |
| 3,5 | 0,08612124 | 0,08617 | 0,08611 | – | – | – |
| 4,0 | 0,06048471 | 0,06054 | 0,06047 | 0,060473418 | 0.06049038 | 0,06042 |
| 4,5 | 0,04248174 | 0,04252 | 0,04247 | – | – | – |
| 5,0 | 0,02984241 | 0,02984 | 0,02982 | 0,029819128 | 0,02982446 | 0,02979 |
На рисунке 4 показаны графики остаточной ошибки уравнения.(16) и логарифм коэффициентов | a i | для b 1 = 0,60, b 2 = 0,50, при м = 20 и α = 0,50, чтобы показать сходимость метода.
Фиг.4
Полученные графики остаточной ошибки и логарифма коэффициентов | a i для b 1 = 0.60 и b 2 = 0,50, чтобы показать сходимость метода.
3.3 Уравнение Блазиуса
Еще одним важным нелинейным обыкновенным дифференциальным уравнением третьего порядка, возникающим в полубесконечной области, является уравнение Блазиуса:
2 d 3 у d т 3 + у d 2 у d т 2 знак равно 0 , т ∈ [ 0 , ∞ ) , (17)
, где граничные условия для этого уравнения следующие:у ( 0 ) знак равно 0 , у ′ ( 0 ) знак равно 0 , Lim т → ∞ у ′ ( т ) знак равно 1.(18)
В последние годы для решения уравнения Блазиуса использовались разные методы. Например, Ляо [30], применив метод гомотопического анализа (HAM), Ю и Чен [31], применив метод дифференциального преобразования, Ван [32], применив метод разложения Адомиана (ADM), Хашим [33], применив подход ADM Pade, Cortell [34] с применением алгоритма Рунге-Кутта, Wazwaz [35] с применением модифицированного метода разложения Адомиана, Parand et al.( т ) знак равно т 3 ( т + λ ) 2 + т 2 е — 2 т — 2 у м ( т ) , (19)
где λ — произвольная действительная постоянная и л м ( т ) определяется в Уравнение′ ( т ) знак равно 1 когда t стремится к ∞, а граничные условия ( 18) довольны всем λ > 0, и определяется в полубесконечной области. d т 2 .(20)Таблица 8 показывает значение y ″ (0) по настоящему методу с м = 20, α = 0,50 и λ = 0,9859 и сравнивает его со значениями Liao [30], Parand et al. al. [3, 36] и Бойд [38].
Таблица 8Сравнение полученных значений y ″ (0) по настоящему методу, Boyd [38], Parand et al. [3, 36] и Ляо [30]
| Настоящее время | Бойд [38] | Parand [36] | Parand [3] | Ляо [30] |
|---|---|---|---|---|
| 0.3320573049 | 0,33205733621519630 | 0,33205733621519542 | 0,33205733 | 0,33206 |
Таблица 9 показывает полученные значения y ″ (0) и ∥ р е s ∥ ш 2 данным методом для различных значений м и α = 0.50.
Таблица 9Полученные значения y ″ (0) данным методом для различных значений м и α = 0,50
| м | λ | y ′ (0) | ∥ р е s ∥ ш 2 |
|---|---|---|---|
| 10 | 0.77 | 0,33238931 | 2.0196e-01 |
| 15 | 1,09 | 0,33213594 | 1.0365e-03 |
| 20 | 0,98 | 0,33205367 | 2.8918e-08 |
Таблица 10 показывает полученные значения y ″ (0) и ∥ р е s ∥ ш 2 данным методом для различных значений α и м = 20.
Таблица 10Полученные значения y ″ (0) данным методом для различных значений α и м = 20
| α | λ | y ″ (0) | ∥ р е s ∥ ш 2 |
|---|---|---|---|
| 0.25 | 1.0164 | 0,3320600170 | 1.1698e-02 |
| 0,50 | 0,9859 | 0,3320573049 | 2.8930e-08 |
| 0,75 | 1,7191 | 0,3320718355 | 3.4739e-08 |
| 1,00 | 0,9168 | 0,3320573541 | 1.5661e-06 |
Таблицы 11-13 показывают значения y ( t ), y ′ ( t ) и y ″ ( t ) для различных значений t с помощью настоящего метода и сравнения. это со значениями Parand et al. [3, 36], Кортелл [34] и Ховарт [39], при м = 20, α = 0,50 и λ = 0,9859.
Таблица 11Сравнение полученных значений y ( t ) для различных значений t по данной методике, Parand et al.[3, 36], Ховарт [39] и Кортелл [34]
| т | Настоящее время | Parand [36] | Ховарт [39] | Кортелл [34] | Parand [3] |
|---|---|---|---|---|---|
| 1,0 | 0,1655717346 | 0,1655717 | 0,16557 | 0,16557 | 0,1655724 |
| 2,0 | 0.6500244189 | 0,6500243 | 0,65003 | 0: 65003 | 0,6500351 |
| 3,0 | 1,3968083309 | 1,3968082 | 1,39682 | 1,39682 | 1,3968223 |
| 4,0 | 2.3057465742 | 2,3057464 | 2,30576 | 2,30576 | 2.3057618 |
| 5,0 | 3,2832738023 | 3,2832736 | 3,28329 | 3,28330 | 3,2832910 |
Сравнение полученных значений y ′ ( t ) для различных значений t с помощью настоящего метода, Parand et al. [3, 36], Howarth [39] и Cortell [34]
| т | Настоящее время | Parand [36] | Ховарт [39] | Кортелл [34] | Parand [3] |
|---|---|---|---|---|---|
| 1.0 | 0,3297800807 | 0,32978003 | 0,32979 | 0,32978 | 0,3297963 |
| 2,0 | 0,6297657868 | 0,62976573 | 0,62977 | 0,62977 | 0,6297763 |
| 3,0 | 0,8460444987 | 0,84604444 | 0,84605 | 0.84605 | 0,8460595 |
| 4,0 | 0,9555182849 | 0,95551823 | 0,95552 | 0,95552 | 0,9555236 |
| 5,0 | 0,9 3606 | 0,9 90 | 0,99155 | 0,99155 | 0,9 | 6
Сравнение полученных значений y ″ ( t ) для различных значений t по настоящему методу, Parand et al.[3, 36], Ховарт [39] и Кортелл [34]
| т | Настоящее время | Parand [36] | Ховарт [39] | Кортелл [34] | Parand [3] |
|---|---|---|---|---|---|
| 0,0 | 0,3320573049 | 0,3320573362 | 0,33206 | 0,33206 | 0,3320571 |
| 1.0 | 0,3230074062 | 0,3230071168 | 0,32301 | 0,32301 | 0,3230136 |
| 2,0 | 0,2667515144 | 0,2667515456 | 0,26675 | 0,26675 | 0,2667557 |
| 3,0 | 0,1613603185 | 0,1613603194 | 0,16136 | 0.16136 | 0,1613637 |
| 4,0 | 0,0642341187 | 0,0642341209 | 0,06424 | 0,06423 | 0,0642411 |
| 5,0 | 0,01575 | 0,015 85 | 0,01591 | 0,01591 | 0,0159134 |
На рис. 5 показан график остаточной ошибки уравнения.(20) и график полученного решения для уравнения Блазиуса по данной методике при м = 20 и α = 0,50.
Фиг.5
Получены графики остаточной ошибки и решение Блазиуса.
3.4 Уравнение поля, определяющее профиль вихря
Наконец, рассмотрим уравнение поля, определяющее профиль вихря:
d 2 у d т 2 + 1 т d у d т + 1 — п 2 т 2 у ( т ) — у 3 ( т ) знак равно 0 , т ∈ [ 0 , ∞ ) , (21)
, где граничные условия для этого уравнения следующие:Lim т → 0 у ( т ) знак равно k п т п + О ( т п + 2 ) , Lim т → ∞ у ( т ) знак равно 1.(22)
где л ( t ) является реальной функцией и n ∈ Z .Основная проблема этих граничных условий состоит в том, чтобы найти значение (я) свободного параметра, k n , чтобы обеспечить граничные условия (22) y ( t ) при т = ∞.
Это уравнение исследуется в статическом вращательно-симметричном глобальном вихре в эффективной теории Гинзбурга-Ландау [40], которая имеет множество приложений, начиная от конденсированного вещества и заканчивая космическими струнами [41].Некоторые исследователи аппроксимируют уравнение поля, определяющее профиль вихря; например, Boisseau et al. [42], применяя аналитический метод, основанный на замене исходных ОДУ последовательностью вспомогательных полиномиальных ОДУ первого порядка с постоянными коэффициентами, и Аморе и Фернандес [43], применяя метод Паде-Ханкеля.
Для удовлетворения граничных условий, мы удовлетворяем уравнению. ( т ) знак равно т п т п + λ + т п е — 2 т — 2 у м ( т ) , (23)
где λ — произвольная действительная постоянная и л м ( т ) укладывается в Уравнение3 ( т ) . (24)Таблица 14 показывает значения k n по настоящему методу с m = 40 и α = 0,50, и сравнивает их со значениями метода Shooting [42], Boisseau et al. [42] и Аморе и Фернандес [43].
Таблица 14Сравнение полученных значений k n между настоящим методом, методом съемки [42], Boisseau et al.[42] и Аморе и Фернандес [43].
| к н | λ | Настоящее время | Стрельба [42] | Буассо [42] | Аморе [43] |
|---|---|---|---|---|---|
| к 1 | 0,1 | 0,583189717489 | 0,5831894959 | 0,5831894936 | 0.5831894958601 |
| к 2 | 2 | 0,15309 29 | 0,15309 | 0,15309 | 0,15309 6 |
| к 3 | 23 | 0,026183420209 | 0,02618342072 | 0,026185 | 0,0261834207 |
| к 4 | 45 | 0.003327173339 | 0,00332717340 | 0,0033 | 0,0033271734 |
В таблице 15 показаны полученные значения k 2 и ∥ р е s ∥ ш 2 по настоящему способу для различных значений м и α = 0,50.
Таблица 15Полученные значения k 2 данным методом для различных значений m и α = 0.50
| м | λ | к 2 | ∥ р е s ∥ ш 2 |
|---|---|---|---|
| 10 | 2 | 0,152 | 73004.3939e-05 |
| 20 | 2 | 0,1530970 | 3.5332e-10 |
| 30 | 2 | 0,15309 | 7.3141e-13 |
| 40 | 2 | 0,15309 29 | 1.5483e-16 |
В таблице 16 показаны полученные значения k 2 и ∥ р е s ∥ ш 2 данным методом для различных значений α и м = 40.Как видно, результаты для α = 0,50 и α = 1,00 практически идентичны.
Таблица 16Полученные значения k 2 данным методом для различных значений α и м = 40
| α | λ | к 2 | ∥ р е s ∥ ш 2 |
|---|---|---|---|
| 0.25 | 2 | 0,1530254 | 2,7708e-04 |
| 0,50 | 2 | 0,15309 29 | 1.5483e-16 |
| 0,75 | 2 | 0,153068774773 | 6.7629e-08 |
| 1,00 | 2 | 0,1530972 | 8.0842e-16 |
| 1.25 | 1 | 0,151696304817 | 8.8242e-05 |
| 1,50 | 1 | 0,137087413881 | 7.2232e-04 |
Таблица 17 показывает полученные значения y ( t ) по настоящему способу для различных значений n и t с m = 40 и α = 0,50.
Таблица 17Получены значения y ( t ) данным способом для различных значений n и t .
| т | n = 1 | n = 2 | n = 3 | n = 4 | |
|---|---|---|---|---|---|
| 0,5 | 0,28282173 | 0,03748381 | 0,00322210 | 0,00020535 | |
| 1,0 | 0,52005163 | 0.14078358 | 0,02458744 | 0,00316426 | |
| 1,5 | 0,6 35 | 0,28531419 | 0,07662991 | 0,01503527 | |
| 2,0 | 0.80495682 | 0,44008751 | 0,16224506 | 0,04343598 | |
| 2,5 | 0,87497019 | 0.57972330 | 0,27383162 | 0,0 07 | |
| 3,0 | 0, | 0,6 | 54 | 0,39661914 | 0,16 |
| 3,5 | 0,703 | 0,77435581 | 0,51495766 | 0,26313174 | |
| 4,0 | 0,95946829 | 0.83300459 | 0,61788070 | 0,36737260 | |
| 6,0 | 0,98473111 | 0,460 | 0,84845320 | 0,71026581 | |
| 8,0 | 0,9 33 | 0,96681821 | 0, | 713 | 0,85614939 |
| 10. | 0,99487378 | 0.97 | 90,95265849 | 0, 234 |
На рисунке 6 показаны графики остаточных ошибок уравнения. (24) и графики полученных решений для уравнения поля по данной методике при м = 40 и α = 0,50.
Фиг.6
Полученные графики остаточных ошибок и полученные решения для различных значений n .
На рисунке 7 показаны графики 1 п ! у ( п ) ( т ) для n = 1, 2, 3 и 4, и графики log (| a i |) для n = 2, 3 и 4, чтобы показать сходимость метода.
Фиг.7
(а) Графики 1 п ! у ( п ) ( т ) для n = 1, 2, 3, 4 (б) Графики log (| a i |) для n = 2, 3, 4, чтобы показать сходимость.
Литература
[1] М.Р. Эслахчи, М. Дехган, С. Амани, Полиномы Чебышева и наилучшее приближение некоторых классов функций, J.Numer. Матем., 23 (1) (2015) 41-50. Искать в Google Scholar
[2] J.A. Рад, С. Казем, М. Шабан, К. Паранд, А. Йилдирим, Численное решение дробных дифференциальных уравнений методом Тау на основе полиномов Лежандра и Бернштейна, Math. Метод. Appl. Наук, 37 (3) (2014) 329-342. Искать в Google Scholar
[3] K.Паранд, А. Тагави, М. Шахини, Сравнение рациональных псевдоспектральных методов Чебышева и модифицированных обобщенных функций Лагерра для решения уравнений Лейна-Эмдена и нестационарного газа, Acta Phys. Pol. В, 40 (12) (2009) 1749-1763. Искать в Google Scholar
[4] К. Паранд, Х. Юсефи, М. Делкхош, А. Гадери, Новый численный метод получения точного решения уравнения Томаса-Ферми, Eur. Phys. J. Plus, 131 (2016) 228. Поиск в Google Scholar
[5] М. Делхош, Введение в производные и интегралы дробного порядка и их приложения, Appl.Математика. Phys., 1 (4) (2013) 103-119. Искать в Google Scholar
[6] С. Казем, С. Аббасбанди, С. Кумар, Функции Лежандра дробного порядка для решения дифференциальных уравнений дробного порядка, Прил. Математика. Модель., 37 (2013) 5498-5510. Искать в Google Scholar
[7] К. Паранд, М. Никария, Дж. А. Рад, Решение нелинейных уравнений типа Лейна-Эмдена с использованием метода коллокации ортогональных функций Бесселя, Селест. Мех. Дин. Astr., 116 (1) (2013) 97-107. Искать в Google Scholar
[8] J.Эшаги, Х. Адиби, С. Казем, Решение нелинейных слабо сингулярных интегральных уравнений Вольтерра с использованием функций Лежандра дробного порядка и псевдоспектрального метода, Матем. Метод. Appl. Наук, 39 (12) (2016) 3411-3425. Искать в Google Scholar
[9] К. Паранд, А. Гадери, Х. Юсефи, М. Делкхош, Новый подход к решению нелинейного уравнения Томаса-Ферми, основанный на дробном порядке рациональных функций Бесселя, Electronic J.Differential Equations, 2016 (2016) 331: 1-18. Искать в Google Scholar
[10] A.H. Bhrawy, M.A. Zaky, Сдвинутые ортогональные функции Якоби дробного порядка: приложение к системе дробных дифференциальных уравнений, Appl. Математика. Modell. 40 (2016) 832-845. Искать в Google Scholar
[11] К. Паранд, П. Мазахери, Х. Юсефи, М. Делкхош, Дробный порядок рациональных функций Якоби для решения нелинейного сингулярного уравнения Томаса-Ферми, Eur. Phys. J. Plus, 132 (2) (2017) 77. Поиск в Google Scholar
[12] К. Паранд, Х. Юсефи, М. Делкхош, Численный подход к решению уравнений типа Лейна-Эмдена с помощью дробного порядка рациональных функций Бернулли, Румынский J.Phys. 62 (2017) 104: 1-24. Искать в Google Scholar
[13] З. Одибат, С. Момани, Алгоритм численного решения дифференциальных уравнений дробного порядка, J. Appl. Математика. Информ. 26 (2008) 15-27. Искать в Google Scholar
[14] К. Паранд, М. Делхош, Точное решение уравнения Томаса-Ферми с использованием дробного порядка рациональных функций Чебышева, J. Comput. Appl. Матем., 317 (2017) 624-642. Искать в Google Scholar
[15] E.B. Бейкер, Применение статистической модели Ферми-Томаса к вычислению распределения потенциала в положительных ионах, Quart.Appl. Матем., 36 (1930) 630-647. Искать в Google Scholar
[16] М.А. Дарани, М. Насири, Дробный тип полиномов Чебышева для приближения решения дробно-линейных дифференциальных уравнений, Comp. Meth. Diff. Equ., 1 (2013) 96-107. Искать в Google Scholar
[17] R.E. Киддер, Нестационарное течение газа через полубесконечную пористую среду, J. Appl. Мех. 24 (1957) 329-332. Искать в Google Scholar
[18] А.М. Вазваз, Модифицированный метод разложения применительно к нестационарному течению газа через пористую среду, Прил.Математика. 118 (2001) 123-132. Искать в Google Scholar
[19] К. Паранд, П. Мазахери, М. Делхош, А. Гадери, Новые численные решения для решения уравнения Киддера с использованием рациональных функций Якоби, SeMA J., (2017) 10.1007 / s40324- 016-0103-з. Искать в Google Scholar
[20] К. Паранд, М. Никария, Решение проблемы нестационарного изотермического газа через микронано-пористую среду с помощью метода коллокации функций Бесселя, J. Comput. Теор. Нано-наука, 11 (2014) 1-6. Искать в Google Scholar
[21] A.Тагави, К. Паранд, Х. Фани, метод Лагранжа для решения уравнения нестационарного газа, Мировая Акад. Sci. Англ. Техн., 3 (2009) 11-23. Искать в Google Scholar
[22] A.R. Резаи, К. Паранд и А. Пирхедри, Численное исследование потока газа через микронано-пористую среду на основе специальных функций, J. Comput. Теор. NanoSci., 8 (2010) 282-288. Искать в Google Scholar
[23] J.A. Рад, С. Гадери, К. Паранд, Численное и аналитическое решение потока газа через микронано-пористую среду: сравнение, J.Comput. Теор. Нанонаука, 8 (2011) 2033-2041. Искать в Google Scholar
[24] С. Казем, Дж. А. Рад, К. Паранд, М. Шабан и Х. Сабери, Численное исследование нестационарного течения газа в полубесконечной пористой среде с использованием метода коллокации RBF , Int. J. Comput. Матем., 89 (16) (2012) 2240-2258. Искать в Google Scholar
[25] С. Аббасбанди, Численное исследование потока газа через микронано-пористую среду, Acta Phy. Pol. А, 121 (2012) 581-585. Искать в Google Scholar
[26] F.Ахмад, Простое аналитическое решение для устойчивого течения жидкости третьего сорта в пористом полупространстве, Коммунал. Нелинейные науки. Нумер. Simul., 14 (2009) 2848-2852. Искать в Google Scholar
[27] S. Kazem, J.A. Рад, К. Паранд, С. Аббасбанди, Новый метод решения установившегося течения жидкости третьего сорта в пористом полупространстве, основанный на радиальных базисных функциях, З. Натурфорш. А, 66 (2011) 591-598. Искать в Google Scholar
[28] К. Паранд, Э. Хаджизаде, Решение задачи устойчивого течения жидкости третьего сорта в пористом полупространстве с помощью нормальных и модифицированных рациональных методов совмещения функций Христова, З.Naturforsch. А, 69 (2014) 188-194. Искать в Google Scholar
[29] Ф. Бахарифард, С.Казем, К. Паранд, Рациональный и экспоненциальный метод Лежандра Тау для устойчивого течения жидкости третьего сорта в пористом полупространстве, Int. J. Appl. Comput. Математика, 10.1007 / s40819-015-0096-9, (2015) 1-20. Поиск в Google Scholar
[30] С. Ляо, Явное, полностью аналитическое приближенное решение для задач вязкого течения Блазиуса, Int. J. Nonlin. Мех. 34 (1999) 759-778. Искать в Google Scholar
[31] L.Т.Ю. и К.К. Чен, Решение уравнения Блазиуса методом дифференциального преобразования, Матем. Comput. Модель. 28 (1998) 101-111. Поиск в Google Scholar
[32] Л. Ван, Новый алгоритм решения классического уравнения Блазиуса, Прил. Математика. Comput. 157 (2004) 1-9. Искать в Google Scholar
[33] И. Хашим, Комментарии к «Новому алгоритму решения классического уравнения Блазиуса» Л. Ванга, Прил. Математика. Comput. 176 (2006) 700-703. Искать в Google Scholar
[34] R.Кортелл, Численные решения классической задачи Блазиуса о плоской пластине, Appl. Математика. Comput. 170 (2005) 706-710. Искать в Google Scholar
[35] A.M. Wazwaz, Модифицированный метод декомпозиции и аппроксимации Паде для уравнения пограничного слоя в неограниченной области, Прил. Математика. Comput. 177 (2006) 737-744. Искать в Google Scholar
[36] K. Parand, M. Nikarya, J.A. Рад, Ф. Бахарифард, Новый надежный численный алгоритм, основанный на первом виде функций Бесселя для решения ламинарного вязкого течения Прандтля-Блазиуса над полубесконечной плоской пластиной, Z.Naturforsch. А, 67 (12) (2012) 665-673. Искать в Google Scholar
[37] К. Паранд, М. Шахини, М. Дехан, Решение ламинарного течения в пограничном слое численным методом, Commun. Нелинейные науки. Нумер. Simul., 15 (2) (2010) 360-367. Поиск в Google Scholar
[38] Дж. П. Бойд, Функция Блазиуса: вычисления перед компьютерами, ценность уловок, студенческие проекты и проблемы открытых исследований, SIAM. Ред. 50 (4) (2008) 791-804. Искать в Google Scholar
[39] L.Ховарт, О расчете установившегося течения в пограничном слое у поверхности цилиндра в потоке, Aero Res. Counc. Лондон. РМ, 164 (1935) 16-32. Искать в Google Scholar
[40] В.Л. Гинзбург, Л.П. Питаевский, К теории сверхтекучести, Докл. Phys. ЖЭТФ, 7 (5) (1958) 858-861. Искать в Google Scholar
[41] А. Виленкин, Е.П.С. Шеллард, Космические струны и другие топологические дефекты, Кембридж: Издательство Кембриджского университета, (1994). Искать в Google Scholar
[42] B.Boisseau, P. Forgacs, H. Giacomini, Аналитическая схема аппроксимации двухточечных краевых задач обыкновенных дифференциальных уравнений, J. Phys. A: Математика. Теор., 40 (2007) F215-F221. Искать в Google Scholar
[43] P. Amore, F.M. Фернандес, Рациональная аппроксимация решений двухточечных краевых задач, Acta Poly., 51 (4) (2011) 9-13. Искать в Google Scholar
Старая новая математика | JD2718
В начале 70-х все выучили немного математики в начальной школе.Наборы, диаграммы Венна, разные основы… Мы мало знали, мало ли нам было дела до того, откуда это взялось, или что это не всегда было частью учебной программы…
(* Вы можете прочитать немного больше о Новой математике в конце этого сообщения.)
(Продолжение: обсуждение того, какие темы добавить и удалить из учебной программы прямо здесь.)
Я знаю, что этому перестали учить. Дети больше не знают, что такое набор. И все же одно дело знать, другое — видеть пустые выражения на их лицах.Странный.
, четверг. Я планировал учить своих первокурсников комплексному неравенству. В моем (превосходном) тексте по алгебре (Дольчиани и др.) Есть небольшая боковая единица по объединению и пересечению. Поэтому я решил втиснуть свой урок в последние 5-10 минут и вместо этого преподать старую новую математику.
Я начал с того, что поставил на доску большой и большой. Я спросил, знает ли кто-нибудь, что это за символы.
В моей школе дети учатся в самых разных средних школах, и многие из них учатся по программам с отличием или по ускоренным программам.Так что шанс был. Я ожидал, что поднимется около трети рук. Только трое сделали. Я спросил, кто готов поставить несколько очков в следующем тесте, который им действительно известен.
Сделают ли они ставки? Все руки опустились.
Потом поговорили. Их время для веселья. Холодная война. Кто потерял Китай. Нацистские ученые. Спутник. Лайка. Гагарин. Новая математика.
Тогда настала моя очередь повеселиться. Быстрый и грязный набор я определил. Приводил несколько примеров. Определенная мощность, поскольку им нравится думать, что они учат громкие слова.Определил пустой набор. Определенное подмножество (и немного позже различие между правильными и неправильными подмножествами). Услышал, как ребенок сказал, что это «меньше чем», и улыбнулся; Я вернулся к этому позже.
Высшая точка произошла после того, как я поставил это на доску:
Я спросил их, истинно это утверждение или нет, и записал их ответ и их объяснение. У нас было оживленное небольшое обсуждение, но большинство из них следовали модели (поскольку нет доказательств того, что V не является подмножеством R, это подмножество R)
Наконец, мы немного поговорили о пересечении и объединении, их отношении к «или» и «и», к умножению и сложению.Я пообещал им, что если они возьмут с собой логику, когда они юниоры или старшие… но на урок почти не оставалось времени.
(Новая математика была попыткой добавить некоторую раннюю теорию, в основном аксиоматику, для детей младшего возраста. Идея заключалась в том, что когда они стали старше и перешли на продвинутые темы, они уже могли справиться с некоторой строгостью. Это был ответ Sputnik Они утверждали, что это произошло потому, что у Советов было больше и лучше инженеров, и потому что маленькие советские дети изучали теорию множеств.Хммм)
(New Math запутался из-за того, что относился к себе слишком серьезно. Немного наборов, диаграмм Венна и баз было бы круто. Но они слишком много вложили в большинство студентов, и стали слишком сложными, слишком молодыми для большинства студентов)
В статьеВикипедии о Новой математике говорилось, что она возвращается. Жаль, что в более умеренной форме было ценно то, что дети знакомились с наборами и некоторыми связанными с ними концепциями. Но нет, это не так, не возвращаясь в первоначальном виде, не возвращаясь более скромно.
Нравится:
Нравится Загрузка …
СвязанныеНарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей (Технический отчет)
Холм Д. Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей . США: Н. П., 1976.
Интернет. DOI: 10,2172 / 7348957.
Холм, Д. Д. Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей . Соединенные Штаты. https://doi.org/10.2172/7348957
Holm, D D. Thu.
«Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей». Соединенные Штаты. https://doi.org/10.2172/7348957. https://www.osti.gov/servlets/purl/7348957.
@article {osti_7348957,
title = {Нарушение симметрии в гидродинамике: приводимые движения группы Ли для реальных жидкостей},
author = {Holm, D D},
abstractNote = {Физика жидкостей основана на определенных принципах кинематической инвариантности, которые относятся к системам координат, размерам и системе отсчета Галилея.Другие, термодинамические, принципы симметрии вводятся в описании материала. В настоящей работе взаимодействие между этими двумя типами принципов инвариантности используется для решения классов одномерных нестационарных изэнтропических движений жидкости, уравнение состояния которой относится к типу Ми-Грюнайзена. Также на уровне приближения Бюргерса изучается изменение профиля и затухание слабых ударных волн в диссипативной среде с точки зрения лежащей в основе структуры симметрии.Математический метод подхода основан на теории бесконечно малых групп Ли. Движения жидкости охарактеризованы в соответствии с неэквивалентными подгруппами группы полной инвариантности описания течения и представлены точные групповые приводимые решения.},
doi = {10.2172 / 7348957},
url = {https://www.osti.gov/biblio/7348957},
journal = {},
number =,
объем =,
place = {United States},
год = {1976},
месяц = {7}
}
Мои поиски непревзойденной природы реальности Макс Тегмарк
Дикая поездка с Безумным МаксомАльфред Норт Уайтхед сказал, что философия — это серия сносок к Платону.Добро пожаловать в еще одну сноску, поскольку тезис этой книги, по словам автора, « можно рассматривать как форму радикального платонизма, утверждающего, что все математические структуры в« царстве идей »Платона существуют« где-то там »в физический смысл. »Другими словами, физической реальности нет, есть чистая математика.
Эта книга — увлекательная поездка для тех, кто хорошо разбирается в физике, при условии, что развлечение означает стимулирование вашего мышления, не воспринимая все это слишком серьезно.Что касается остальных из нас, имейте в виду, что сам автор явно оценивает свои собственные главы как «мейнстримные», «противоречивые» и «чрезвычайно противоречивые». И некоторые из якобы мейнстримных вещей тоже следует назвать спорными.
Объективная реальность требует объективной математики
Давайте начнем с самого начала, с предположения, что позволяет заниматься наукой: « Существует внешняя физическая реальность, полностью независимая от нас, людей. »Но затем Тегмарк следует за этим следствием, о котором я действительно не думал:
« Если мы предположим, что реальность существует независимо от нас, людей, то для того, чтобы описание было полным, оно также должно быть хорошо определено в соответствии с нечеловеческими сущности — скажем, инопланетяне или суперкомпьютеры — которым не хватает понимания человеческих концепций.Такое описание должно быть выражено в форме, лишенной какого-либо человеческого багажа, такого как «частица», «наблюдение» или других человеческих слов. ”
Математика — единственный язык, который соответствует этим требованиям. Вопрос о том, действительно ли наша математика свободна от человеческого багажа, на самом деле не рассматривается, но давайте предположим, что такая математика где-то существует. Таким образом, целью науки должно быть устранение такого субъективного человеческого багажа. Все идет нормально.
Иллюзия эквивалентности
Мы узнаем, что наши нынешние описания реальности на самом базовом уровне становятся все более абстрактными и математическими.Да, но теперь начинается самое интересное. Нам говорят, что принцип эквивалентности означает, что два описания эквивалентны, если между ними существует соответствие, сохраняющее все отношения. Следовательно, если внешняя реальность может быть описана математикой, на самом деле это должна быть математическая структура. И если известная нам реальность — это не что иное, как математика, тогда все мыслимые формы математики в равной степени достоверные описания других реальностей.
Здесь у нас есть произвольное предположение, что поскольку могут быть эквивалентные описания реальности, из этого следует, что эти описания эквивалентны самой реальности.Затем мы получаем то самое основное логическое заблуждение, что если одна математическая структура описывает реальность, то все такие структуры должны определять реальность. Эта логика ведет нас от единой объективной реальности к выводу, что все возможные реальности истинны, что означает, что реальность произвольна и, следовательно, субъективна.
Скользкая субъективность
Тот же вид словесной игры используется для введения концепции субъективности в теорию квантовой мультивселенной Хью Эверетта.По иронии судьбы, эта теория была построена, чтобы избежать субъективности стандартной Копенгагенской интерпретации. Логика такая: когда вы подбрасываете квантовую монету, в одной вселенной оказывается решка, а в другой — решка. Затем он заявляет: « В конце этого эксперимента (на любой выбор) будут две разные версии вас, каждая из которых субъективно ощущается такой же реальной, как и другая, но совершенно не осознает существования друг друга. »
Это злоупотребление термином« субъективный ».Каждая версия вас (при условии, что они существуют) имеет полное право объективно чувствовать себя реальным, поскольку нет возможности взаимодействия с другой предполагаемой вселенной. На самом деле он делает абсурдное заявление: «Работа Эверетта показала, что понимание процесса наблюдения требует, чтобы мы также включали третью часть нашей Вселенной: ваше психическое состояние как наблюдателя. «Не верьте мне на слово, что это неправильно. Позже в книге, когда он снова станет физиком, он говорит:
« Вам нужен человек-наблюдатель, чтобы коллапсировать волновую функцию? Теперь я убежден, что сознание не имеет к этому никакого отношения, поскольку даже одна частица может сделать это дело.Я понял, что квантовое наблюдение касается не сознания, а просто передачи информации. ”
Превращение энтропии в субъективную кашу
Теперь мы переходим от плохой философии к откровенной ошибке, связанной с хорошо обоснованной научной концепцией энтропии. Хотя я немного слаб в его математическом обосновании, все, что мне нужно знать, это то, что он имеет математическое основание, чтобы знать, что следующее — чушь:
« Энтропия — это количественная мера отсутствия информации о системе … .Если объект взаимодействует с вами, вы получите больше информации о нем, и его энтропия уменьшится. Если объект взаимодействует с окружающей средой, вы теряете информацию о нем, поэтому его энтропия увеличивается… Традиционная формулировка закона просто соответствует игнорированию субъекта. ”
Субъект игнорируется по той веской причине, что энтропия касается информационного содержания системы, а не наблюдателя. Позвольте мне попробовать эту простую аналогию: если вы не убираете свой стол, он имеет тенденцию становиться беспорядочным, то есть более беспорядочным, что приводит к увеличению энтропии.Даже если вы думаете, что знаете, где все находится, стол все равно в таком же беспорядке. Ваши знания описывают энтропию вашего разума, а не стола. Если вы аккуратно сложите бумаги, стол станет более упорядоченным, с меньшей энтропией, даже если вы больше не знаете, где что-то находится.
Как может выдающийся физик взять такое стандартное понятие, как энтропия, и превратить его в субъективную кашу?
Природа реальности
Пока мы говорим о философии, давайте обратимся к вопросу о том, как мы можем что-либо знать, как это пытался сделать Платон очень давно.Это блестящая трактовка в книге «Начало бесконечности: объяснения, преобразующие мир». У меня есть более простое объяснение. Мы не философы, живущие в пещере Платона; мы должны выжить в реальном мире. Если наша субъективная модель не соответствует внешней реальности, мы становимся чьим-то обедом.
Но решение Макс для связи между нашим внутренним субъективным восприятием и внешней реальностью состоит в том, чтобы вставить между ними слой, называемый «согласованной реальностью». Это довольно неожиданный шаг для того, кто гордится тем, что бросает вызов консенсусу и осуждает его стадный менталитет, но нам следует ожидать сюрпризов.Вот как он это формулирует: « Задача физики — вывести согласованную реальность из внешней реальности, а задача когнитивной науки — вывести внутреннюю реальность из согласованной реальности. ”
Хотя с практической точки зрения реальность консенсуса важна (но, конечно, не безошибочна), она ни в коем случае не является фундаментальной.
Инфляционная мультивселенная
Большая часть книги посвящена идее мультивселенной. Но одного недостаточно; Нововведение Безумного Макса состоит в том, чтобы постулировать четыре слоя различных типов мультивселенных.
Она начинается с главы о космической инфляции, которая действительно должна иметь скорее «спорную», чем «мейнстримную» классификацию. Идея состоит в том, что наша наблюдаемая Вселенная — лишь часть бесконечного пространства, созданного инфляционной силой. Каким-то образом общая теория относительности создает бесконечное пространство внутри конечного пространства размером меньше атома. Поскольку это пространство бесконечно велико, очевидно, что все, что может случиться, где-то происходит, поэтому должно быть бесконечно много других миров, точно таких же, как этот.Это мультивселенная уровня I.
Не уверен во всем этом? Нет проблем, просто перейдите к следующему пункту книги:
« [Инфляция] предсказала бесконечно много наблюдателей, измеряющих разные вещи с вероятностями в зависимости от неизвестной нам меры. Что, в свою очередь, означает, что инфляция, строго говоря, вообще ничего не предсказывает относительно того, что должны увидеть типичные наблюдатели. Все прогнозы отменяются, в том числе те, прогнозы которых заставили нас серьезно отнестись к инфляции! Самоуничтожение полное. ”
Другими словами, это операция приманки и переключения. Первоначальная теория инфляции якобы объясняла некоторые особенности ранней Вселенной, но с дальнейшим развитием она превратилась в «вечную инфляцию», и теперь все возможно. Поэтому, по его словам, все прогнозы отменяются.
У меня тоже было подозрение на использование бесконечности. То же самое и с Максом:
«. В основе современной физики лежит фундаментально ошибочное предположение. Вот мой главный подозреваемый: бесконечность.На самом деле у меня есть два подозреваемых: «бесконечно большой» и «бесконечно маленький». Под бесконечно большим я подразумеваю идею о том, что пространство может иметь бесконечный объем, что время может продолжаться вечно и что может быть бесконечно много физических объектов. Под бесконечно малым я подразумеваю континуум: идею о том, что даже литр пространства содержит бесконечное количество точек, что пространство может растягиваться бесконечно без каких-либо неприятностей, и что в природе есть количества, которые могут непрерывно меняться. Эти два явления тесно связаны: инфляция создала бесконечный объем за счет неограниченного растяжения непрерывного пространства. ”
Все это сносит два из четырех уровней мультивселенной. Третий — квантовая мультивселенная. Помните принцип эквивалентности? Это действительно применимо здесь. Существует только одно математическое выражение квантовой теории поля, поэтому все интерпретации эквивалентны. Итак, квантовая мультивселенная — законная, но непроверяемая интерпретация. Последний уровень — это математическая вселенная, в которой все, что мы можем вообразить, одинаково верно. Я оставлю оценку этой идеи читателю.500 вариантов теории струн по определению верны. Раньше считалось, что теория, предсказывающая все и вся, ничего не предсказывала. Это еще одно свидетельство существования мультивселенной.
Дело в том, что мне очень понравилось читать эту книгу. Большая часть информации хорошо представлена, и есть много идей, которыми можно стимулировать воображение. Есть некоторые курьезы.



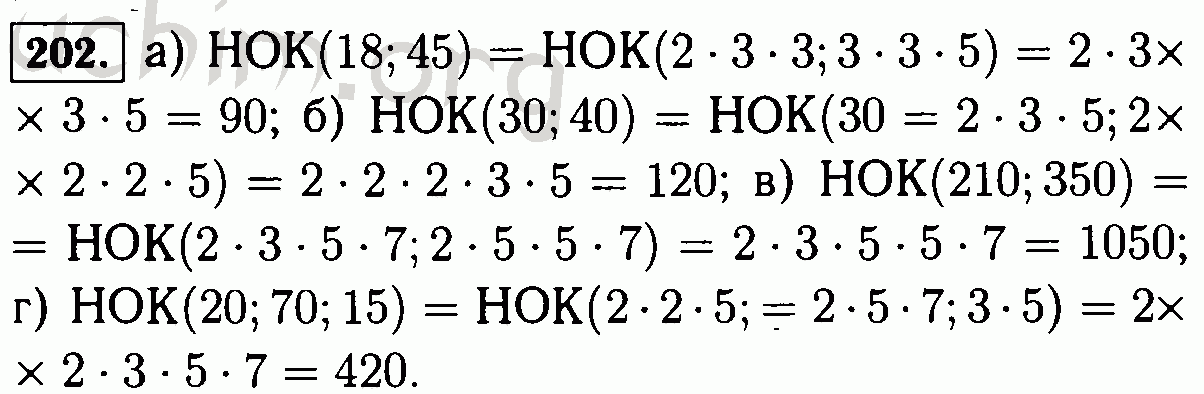 Найдите значение, если a = 5 и b = 4.
Найдите значение, если a = 5 и b = 4.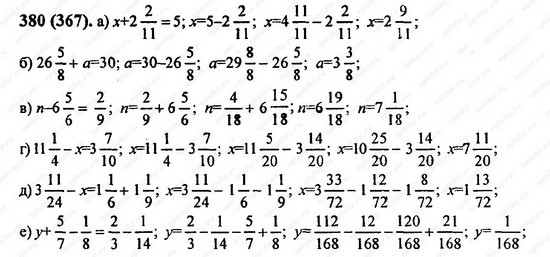
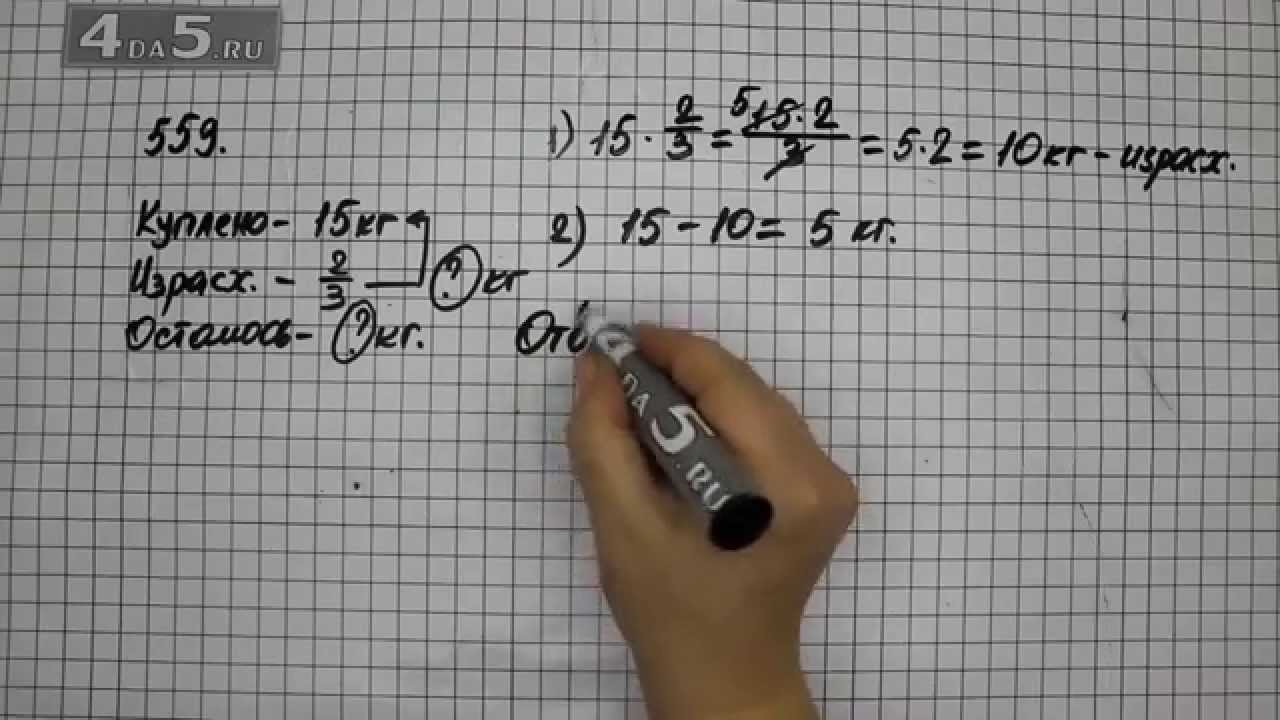
 груш на 30 долларов больше, чем цена 5 фунтов. яблок.
груш на 30 долларов больше, чем цена 5 фунтов. яблок.