Задача по математике 6 класс 115 виленкин: Задача 115 — Виленкин Математика 6 класс

Такой страницы нет !!!

• Популярные запросы
  • Обстоятельство
  • Дополнение
  • Определение
  • Деление дробей
  • Математика 6 класс
  • Русский язык 6 класс
  • Русский язык 5 класс
  • Алгебра 8 класс
  • Математика 5 класс
  • Русский язык 7 класс
  • Алгебра 7 класс
  • Наименьшее общее кратное
  • Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
  • Деление и дроби
  • Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
  • Наибольший общий делитель. Взаимно простые числа
  • Доли. Обыкновенные дроби
  • Квадратный корень из неотрицательного числа
  • Окружность и круг
  • Антонимы. Синонимы
  • Десятичная запись дробных чисел
  • Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)

Математика 6 Самостоятельная № 19 Пропорции + Ответы

Самостоятельная работа по математике в 6 классе «Пропорции» по УМК Мерзляк с ОТВЕТАМИ.  Цитаты из пособия «Математика 6 класс. Дидактические материалы / Мерзляк и др.» использованы в учебных целях. СР-19 Пропорции + ответы. Используется в комплекте с учебником «Математика 6 класс» авторов: Мерзляк, Полонский, Якир.

Самостоятельная работа № 19.

Математика 6 класс (Мерзляк)

Тексты заданий самостоятельной работы

СР-19.

110. Решите уравнение: 1) 6 : 5 = х: 75; 2) а : 1 ⁷/₅₀ = 5/57 : 1/2; 3) х : 0,8 = 15/4; 4) (5-у)/4 = 3/7.
111. Используя числа 24, 3, 18 и 4, составьте пропорцию.
112. Для изготовления 6 одинаковых приборов нужно 14 кг металла. Сколько металла требуется для изготовления 15 таких приборов?
113. Из 300 кг семян льна получают 144 кг масла. Сколько масла получат из 225 кг семян льна? Сколько семян льна требуется, чтобы получить 420 кг масла?
114. Площадь поля равна 520 га. За первый день собрали урожай с 15 % площади поля. С какой площади (в гектарах) собрали урожай?
115. Расстояние между городами А и В на карте равно 4,8 см, а на местности — 120 км. Каково расстояние между городами C и D на этой карте, если расстояние между ними на местности равно 160 км?

СР-19. Вариант 2.

110. Решите уравнение: 1) 7 : 8 = х : 96; 2) у : 1 ⁵/₃₁ = 7 ¾ : 1/3; 3) а : 0,6 = 25/3; 4) (2+х)/5 = 4/9.
111. Используя числа 32, 5, 4 и 40, составьте пропорцию.
112. Масса восьми одинаковых деталей равна 18 кг. Найдите массу 28 таких деталей.
113. В 400 кг сплава содержится 176 кг меди. Сколько килограммов меди содержится в 325 кг сплава? Найдите массу сплава, если в нём содержится 308 кг меди.
114. Строители должны были проложить 480 м путепровода. За первую неделю они выполнили 35 % работы. Сколько метров путепровода проложили строители за первую неделю?
115. Расстояние между сёлами М и К на карте равно 5,6 см, а на местности — 420 км. Каково расстояние между сёлами С и D на местности, если на этой карте расстояние между ними равно 3,6 см?

ОТВЕТЫ на самостоятельную работу

Вариант 1. Ответы:

№110. 1) 90; 2) 1/5; 3) 3; 4) 3 2/7.
№111. 24:4 = 18:3
№112. 35 кг.
№113. 108 кг; 875 кг.
№114. 78 га.
№115. 6,4 см.

Вариант 2. Ответы:

№110. 1) 84; 2) 27; 3) 5; 4) 2/9.
№111. 32:4 = 40:5.
№112. 63 кг.
№113. 143 кг; 700 кг.
№114. 168 м.
№115. 270 км.

Вариант 3. Ответы:

№110. 1) 65; 2) 28; 3) 4,6; 4) 1 4/11.
№111. 72:8 = 63:7
№112. 104 кг.
№113. 143 кг; 350 кг.
№114. 84 кг.
№115. 8 см.

Вариант 4. Ответы:

№110. 1) 64; 2) 3; 3) 8,5; 4) 3 1/3.
№111. 48:6 = 56:7
№112. 30 кг.
№113. 135 кг; 250 кг.
№114. 141 кг.
№115. 360 км.

Вы смотрели «СР-19 Пропорции». Цитаты самостоятельных работ из пособия для учащихся «Математика 6 класс. Дидактические материалы / Мерзляк и др.», которое используется в комплекте с учебником «Математика 6 класс» авторов: Мерзляк и др.

Вернуться к Списку самостоятельных работ по математике в 6 классе (УМК Мерзляк)

4 СТРОКИ МАТЕМАТИЧЕСКИХ ЗНАНИЙ | Сложим: помощь детям в изучении математики

Fuson, K.C., & Burghardt, B.H. (1993). Групповые тематические исследования второклассников, изобретающих многозначные процедуры сложения десятичных блоков и письменных оценок. В J.R.Becker & B.J.Pence (Eds.), Proceedings of the пятнадцатого ежегодного собрания Североамериканского отделения Международной группы психологии математического образования (стр. 240–246).Сан-Хосе, Калифорния: Государственный университет Сан-Хосе. (Услуга размножения документов ERIC № ED 372 917).

Fuson, K.C., Carroll, W.M., & Landis, J. (1996). Уровни осмысления и решения сложения и вычитания сравнивают словесные задачи. Познание и обучение , 14 , 345– 371.

Гири, округ Колумбия (1995). Отражения эволюции и культуры в детском познании. Американский психолог , 50 (1), 24–37.

Грино Дж. Г., Пирсон П. Д. и Шонфельд А. Х. (1997). Последствия для NAEP исследований в области обучения и познания. В: Р. Линн, Р. Глейзер и Г. Борнштедт (редакторы), Оценка в переходный период: мониторинг национального прогресса в области образования (Справочные исследования, стр. 151–215). Стэнфорд, Калифорния: Национальная академия образования.

Hagarty, M., Mayer, R.E., & Monk, C.A. (1995). Понимание арифметических словесных задач: сравнение успешных и неудачных решателей задач. Журнал педагогической психологии , 87 , 18–32.

Хатано, Г. (1988, осень). Социальные и мотивационные основы математического понимания. Новые направления развития ребенка , 41 , 55–70.

Хиберт, Дж. (Ред.). (1986). Концептуальные и процедурные знания: пример математики . Хиллсдейл, Нью-Джерси: Эрлбаум.

Хиберт, Дж., И Карпентер, Т.П. (1992). Учиться и преподавать с пониманием. В Д. А. Гроуза (ред.), Справочник по исследованиям в области преподавания и обучения математике (стр. 65–97). Нью-Йорк: Макмиллан.

Хиберт, Дж., Карпентер, Т.П., Феннема, Э., Фусон, К.С., Вирн, Д., Мюррей, Х., Оливье, А., и Хумэн, П. (1997). Осмысление: преподавание и изучение математики с пониманием . Портсмут, Нью-Хэмпшир: Heinemann.

Хиберт Дж. И Уирн Д. (1986). Процедуры над понятиями: приобретение знаний о десятичных числах.В J.Hiebert (Ed.), Концептуальные и процедурные знания: случай математики (стр. 199–223). Хиллсдейл, Нью-Джерси: Эрлбаум.

Хиберт Дж. И Уирн Д. (1996). Обучение, понимание и навыки сложения и вычитания многозначных чисел. Познание и обучение , 14 , 251–283.

Хилгард, Э. Р. (1957). Введение в психологию (2-е изд.). Нью-Йорк: Харкорт Брейс.

Инелдер, Б., И Пиаже Дж. (1958). Развитие логического мышления с детства до подросткового возраста . Нью-Йорк: Основные книги.

Катона, Г. (1940). Организация и запоминание . Нью-Йорк: издательство Колумбийского университета.

Килпатрик Дж. (1985). Заниматься математикой, не понимая ее: комментарий к Хигби и Кунихире. Психолог-педагог , 20 (2), 65–68.

Кнапп, М.С., Шилдс П.М. и Тернбулл Б.Дж. (1995). Академическая задача в классах с высоким уровнем бедности. Дельта Фи Каппан , 76 , 770–776.

Куба В.Л., Карпентер Т.П. и Сваффорд Дж. (1989). Количество и операции. В М. М. Линдквисте (ред.), Результаты четвертой математической оценки Национальной системы оценки успеваемости (стр. 64–93). Рестон, Вирджиния: Национальный совет учителей математики.

Как легко привести дробь к общему знаменателю.Как привести к общему знаменателю? Как привести дробь к наименьшему общему знаменателю

Приведение дробей к общему знаменателю

Фрой и имеют одинаковые знаменатели. Скажем, у них есть общий знаменатель 25. Дроби и имеют разные знаменатели, но их можно привести к общему знаменателю, используя основное свойство дробей. Для этого находим число, которое делим на 8 и 3, например 24. Приводим дроби в знаменатель 24, для этого умножаем числитель и знаменатель дроби на , дополнительный множитель 3.Слева над числителем обычно записывается дополнительный множитель:

Умножьте числитель и знаменатель дроби на дополнительный множитель 8:

Приводим дроби и к общему знаменателю. Чаще всего дроби приводят к наименьшему общему знаменателю, который является наименьшим общим кратным знаменателем этих дробей. Поскольку НОК (8, 12) = 24, то дробь можно привести к знаменателю 24. Найдем дополнительные погрешности дроби: 24: 8 = 3, 24:12 = 2.затем

К общему знаменателю можно привести несколько дробей.

Пример. Приводим дроби к общему знаменателю. Так как 25 = 5 2, 10 = 2 5, 6 = 2 3, то NOC (25, 10, 6) = 2 3 5 2 = 150.

Найдем дополнительные дроби неисправностей и дадим их к знаменателю 150:

Сравнить дроби

На рис. 4.7 изображен отрезок АВ длиной 1. Он разделен на 7 равных частей. Речь AU имеет длину, а длина AD — длину.

Длина отрезка AD больше длины топора. E. Фракция больше фракции

Из двух дробей с общим знаменателем, у большей из которых числитель больше, то есть

Например, или

Чтобы сравнить любые две дроби, они приводят к общему знаменателю, а затем применяют правило сравнения с общим знаменателем.

Пример. Сравнить дроби

Решение.NOK (8, 14) = 56. Тогда как 21> 20, потом

Если первая дробь меньше второй, а вторая меньше третьей, то первая меньше третьей.

Доказательства. Пусть даны три дроби. Приводим их к общему знаменателю. Пусть после этого они будут выглядеть как первая дробь за вычетом

второй, тогда r

Дробь называется правая , если ее числитель меньше знаменателя.

Дробь ошибочно называется , если ее числитель больше знаменателя или равен ему.

Например, дробилки правильные, и фракции пленки.

Правильная дробь меньше 1, а неправильная дробь больше или равна 1.

Как привести алгебраические (рациональные) дроби к общему знаменателю?

1) Если в знаменателях есть многочлены, нужно попробовать один из известных способов.

2) наименьший общий знаменатель (н.у.) состоит из всего множители взяты в high градуса.

Наименьший общий знаменатель чисел устно ищется как наименьшее число, которое делится на другие числа.

3) Чтобы найти дополнительный множитель к каждой дроби, вам нужен новый знаменатель, чтобы разделить на старый.

4) Числитель и знаменатель исходной дроби умножаются на дополнительный множитель.

Рассмотрим примеры приведения алгебраических дробей к общему знаменателю.

Чтобы найти общий знаменатель чисел, выберите большее число и проверьте, делится ли оно на меньшие.15 на 9 не делятся. Умножьте 15 на 2 и проверьте, делится ли полученное число на 9. От 30 до 9 не делится. Умножаем 15 на 3 и проверяем, делится ли полученное число на 9.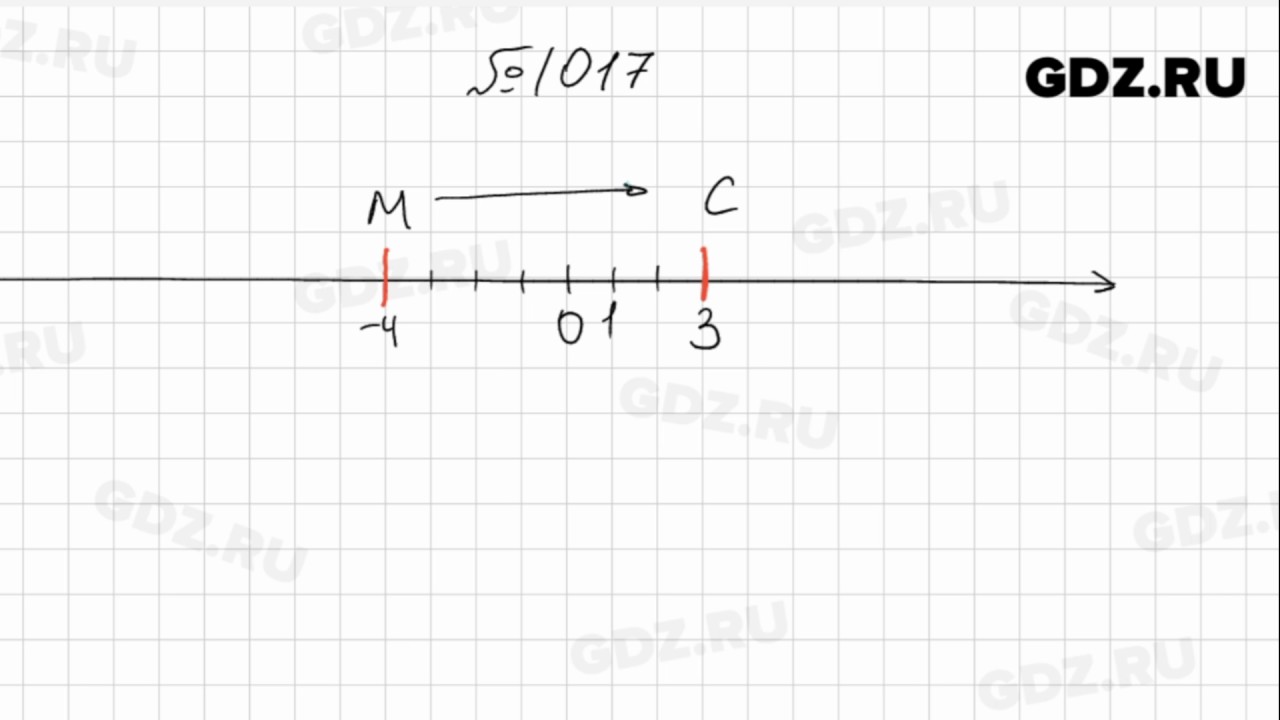 Делится 45 на 9, значит общий знаменатель чисел равен 45.

Наименьший общий знаменатель состоит из всех множителей, взятых в наибольшей степени. Таким образом, общий знаменатель этих дробей равен 45 г. до н.э. (буквы принимаются в алфавитном порядке).

Чтобы найти дополнительный множитель для каждой дроби, вам нужен новый знаменатель, чтобы разделить на старый.45BC: (15B) = 3C, 45BC: (9C) = 5B. Умножаем числитель и знаменатель каждой дроби на дополнительный множитель:

Сначала ищем общий знаменатель для чисел: 8 на 6 не делится, 8 ∙ 2 = 16 на 6 не делится, 8 ∙ 3 = 24 на 6 делится. Каждую из переменных необходимо один раз включить в общий знаменатель. Из степеней мы берем степень с отличной фигурой.

Таким образом, общий знаменатель этих дробей равен 24a³BC.

Чтобы найти дополнительный множитель к каждой дроби, вам понадобится новый знаменатель, чтобы разделить на старый: 24a³BC: (6a³c) = 4B, 24a³BC: (8a²bc) = 3A.

Дополнительный множитель умножается на числитель и знаменатель:

Многовинаты в знаменателях этих фракций нужны.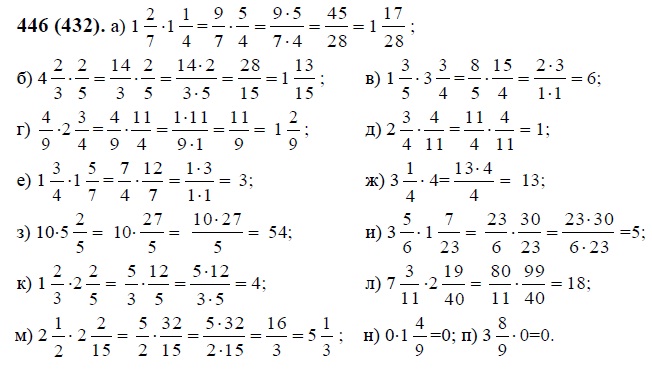 В знаменателе первой дроби — полный квадрат разности: x²-18x + 81 = (x-9) ²; В знаменателе вторая — разность квадратов: x²-81 = (x-9) (x + 9):

Общий знаменатель состоит из всех множителей, сделанных в наибольшей степени, то есть равных (x-9) ² (x + 9).Находим дополнительные множители и умножаем их на числитель и знаменатель каждой дроби:

В этом уроке мы рассмотрим приведение дробей к общему знаменателю и решим задачу по этой теме. Дадим определение понятию общего знаменателя и дополнительного множителя, запомним взаимно простые числа. Дадим определение понятию наименьшего общего знаменателя (Nos) и решим ряд задач для его нахождения.

Тема: Сложение и вычитание дробей с разными знаменателями

Урок: приведение дробей к общему знаменателю

Повторение. Главное свойство фракции.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то дробь равна ему.

Например, числитель и знаменатель дроби можно разделить на 2.Получим дробь. Эта операция называется нарезкой дроби. Вы также можете выполнить обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае говорят, что мы привели к новому знаменателю. Число 2 называется дополнительным фактором.

Выход. Дробь может быть сведена к любому знаменателю и кратному знаменателю этой дроби. Чтобы получить новый знаменатель, его числитель и знаменатель умножаются на дополнительный множитель.

1. Подвести дробь к знаменателю 35.

Число 35 умноженное на 7, то есть 35 делится на 7 без остатка. Так что это преобразование возможно. Найдите дополнительный фактор. Для этого делим 35 на 7. Получаем 5. Умножаем на 5 число и знаменатель исходной дроби.

2. Подвести дробь к знаменателю 18.

Найдите дополнительный фактор. Для этого делим новый знаменатель на исходный.Получаем 3. Умножаем на 3 числитель и знаменатель этой дроби.

3. Подставим дробь в знаменатель 60.

Разделив 60 на 15, мы получим дополнительный множитель. Он равен 4. Умножьте числитель и знаменатель на 4.

4. Подвести дробь к знаменателю 24

В простых случаях приведение к новому знаменателю выполняется в уме. Он применяется только для указания дополнительного коэффициента за небольшой правой скобкой и над исходной дробью.

Дробь можно довести до знаменателя 15, а дробь — до знаменателя 15. Дроби и общий знаменатель 15.

Общим знаменателем может быть любое общее кратное их знаменателя. Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему знаменателю кратного знаменателя.

Пример. Приведите дроби и к наименьшему общему знаменателю.

Найдем наименьшие знаменатели общего кратного знаменателя.Это число 12. Мы находим дополнительный множитель для первой и для второй дроби. Для этого 12 разделите на 4 и на 6. Три являются дополнительным множителем для первой дроби, а два — для второй. Приводим дроби в знаменатель 12.

Мы привели дробь и к общему знаменателю, то есть нашли равные им дроби, которые имеют одинаковый знаменатель.

Правило. Чтобы привести дробь к наименьшему общему знаменателю, необходимо

Сначала найдите наименьший общий кратный знаменатель этих дробей, это будет их наименьший общий знаменатель;

Во-вторых, разделите наименьший общий знаменатель на знаменатели данных дробей, т.е.е., найти для каждой дроби дополнительный множитель.

В-третьих, умножьте числитель и знаменатель каждой дроби на ее дополнительный множитель.

а) приводят к общему знаменателю и.

Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби равен 4, для второй — 3. Приведите дробь в знаменатель 24.

б) приводят к общему знаменателю и.

Наименьший общий знаменатель — 45. Подбирая 45 к 9 к 15, получаем соответственно 5 и 3. Доли дроби приводим к знаменателю 45.

c) приводят к общему знаменателю и.

Общий знаменатель — 24. Дополнительные множители соответственно — 2 и 3.

Иногда бывает сложно выбрать устно наименьший суммарный множитель для знаменателей этих дробей. Затем общий знаменатель и дополнительные множители находятся с помощью разложения на простые множители.

привести к общему знаменателю и.

Делает числа 60 и 168 на простые множители. Отталкиваем разложение числа 60 и добавляем недостающие множители 2 и 7 из второго разложения. Умножив 60 на 14, мы получим общий знаменатель 840. Дополнительный множитель для первой дроби равен 14. Дополнительный множитель для второй дроби — 5. Приводим дроби к общему знаменателю 840.

Библиография

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и другие. Математика 6. — М .: Мнемозина, 2012.

2. Мерзляк А. Г., Полонский В.В., Якир М.С. Математика 6 класс — Гимназия, 2006.

3. Депима И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.

4. Рурукин А.Н., Чайковский И.В. Задания по курсу математики 5-6 класс. — Ж МИПИ, 2011.

5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Учебное пособие для учащихся 6-х классов заочной школы МИФИ.- Ж МИПИ, 2011.

6. Шеврин Л.Н., Гаин А.Г., Коряков И.О. и другие. Математика: Учебник — Собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.

Вы можете скачать книги, указанные в п. 1.2. Это урок.

Домашнее задание

Виленкин Н.Я., Жохов В.И., Чесноков А.С. и другие. Математика 6. — М .: Мнемозина, 2012. (См. Ссылку 1.2)

Домашнее задание: №297, №298, №300.

Прочие задачи: №270, №290

Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации было столько, а важность ее настолько велика (ведь общие знаменатели не только в числовых дробях), что этот вопрос лучше изучить отдельно.

Итак, у нас есть две дроби с разными знаменателями. И мы хотим, чтобы знаменатели стали такими же. На помощь приходит главное свойство дроби, которое, напомним, звучит так:

Дробь не изменится, если ее числитель и знаменатель умножат одно и то же число, кроме нуля.

Таким образом, при правильном подборе множителей знаменатели в фразах равны — этот процесс называется приведением к общему знаменателю. А искусственные числа, «выравнивающие» знаменатели, называются дополнительными фабриками.

Зачем нужно приводить дробь к общему знаменателю? Вот всего несколько причин:

1. Сложение и вычитание дробей с разными знаменателями. По-другому эта операция не выполняется;
2. Сравнение дробей.Иногда приведение к общему знаменателю значительно упрощает эту задачу;
3. Решение задач на акции и проценты. Коэффициенты процента — это, по сути, обычные выражения, содержащие дроби.

Есть много способов найти числа, при умножении на которые знаменатели станут равными. Мы рассмотрим только три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «кросс-лоу»

Самый простой и надежный способ, гарантирующий знаменатели.Будем действовать «поперёк»: первую дробь умножаем на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:

В качестве дополнительных факторов рассмотрим знаменатели соседних дробей. Получаем:

Да так все просто. Если вы только начинаете изучать дробь, лучше работать именно этим методом — так вы напрягитесь от множества ошибок и гарантированно получите результат.

Единственный недостаток этого метода — много считать, потому что знаменатели умножаются, и в результате могут получиться очень большие числа. Такова плата за надежность.

Метод общих делителей

Этот прием очень помогает сократить объем вычислений, но, к сожалению, применяется редко. Метод выглядит следующим образом:

1. Прежде чем действовать «Инсульт» (то есть методом кросс-кросс-времени), взгляните на знаменатели. Возможно, один из них (тот, что больше) разделяется на другой.
2. Число, полученное в результате этого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем ничего умножать не нужно — это экономия. При этом резко снижается вероятность ошибки.

Задача. Найдите значения выражений:

Обратите внимание, что 84: 21 = 4; 72: 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, воспользуемся методом общих множителей.У нас:

Обратите внимание, что вторая дробь вообще никуда не умножалась. Фактически мы сократили объем вычислений вдвое!

Кстати, дробь в данном примере я взял не случайно. Если интересно, попробуйте посчитать их методом «перекрестного пересечения». После вырезания ответы получатся такими же, но работы будет намного больше.

В этом сила метода общих делителей, но, повторяю, его можно применить только тогда, когда один из знаменателей делится на другой без остатка.Что бывает довольно редко.

Метод наименьшего общего кратного

Когда мы приводим дробь к общему знаменателю, мы, по сути, пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приведите к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них не обязательно будет равно прямому произведению знаменателей исходных дробей, как это предполагается в методе «Перекресток».

Например, для знаменателей 8 и 12 вполне подойдет число 24, так как 24: 8 = 3; 24: 12 = 2. Это число намного меньше работы 8 · 12 = 96.

Наименьшее число, которое делится на каждый знаменатель, называется их наименьшим общим кратным (НОК).

Обозначение: Наименьшие общие кратные числа A и B обозначаются NOC (A; B). Например, NOC (16; 24) = 48; NOC (8; 12) = 24.

Если вам удастся найти такое число, окончательный объем вычислений будет минимальным.Посмотрите на примеры:

Задача. Найдите значения выражений:

Отметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно простые (не имеют общих делителей, кроме 1), а множитель 117 общий. Следовательно, NOK (234; 351) = 117 · 2 · 3 = 702.

Аналогично 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно простые, а множитель 5 общий. Следовательно, NOK (15; 20) = 5 · 3 · 4 = 60.

Теперь представим дроби для общих знаменателей:

Обратите внимание, насколько хорошо было разложить начальный знаменатель на множители:

1. Обнаружив одинаковые множители, мы сразу перешли к малейшей общей боли, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения вы можете узнать, каких факторов «недостаточно» для каждой из фракций. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, как огромные выигрыши дают метод наименьшего общего кратного, попробуйте вычислить те же примеры методом Креста. Конечно, без калькулятора. Думаю, после этого комментарии будут излишними.

Не думайте, что в этих примерах не будет таких сложных дробей. Они постоянно встречаются, и вышеперечисленные задачи не предел!

Проблема только в том, как найти эту церковь. Иногда все происходит за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения.Здесь мы не будем его трогать.

Часто оказывается, что действия с дробями не вызывают затруднений у студентов. Основной проблемой становится основание общего знаменателя. Чтобы разобраться с этим вопросом, нужно запомнить правило приведения дробей к общему знаменателю и понимать, зачем нужен этот общий знаменатель.

Что такое дробь?

В 5 классе ученики объясняют, что дробь делится на части. Более того, знаменатель обозначает количество частей, на которые был разделен предмет, и количество этих частей в числителе, которое было взято для расчета.

Но в математике есть другое определение: дробь называется операцией неполного деления. Это означает, что обе дроби можно превратить в деление, а любое деление можно превратить в дробь. Например:

$$ (5 \ OVER (7)) = 5: 7 $$

$$ 7: 13 = (7 \ OVER (13)) $$

$$ 12: 9 = (12 \ OVER (9)) $$

Вы можете бесконечное количество примеров, но смысл от этого не изменится: дробь заменит знак деления.

Зачем нужно искать общий знаменатель?

Чтобы сложить или вычесть две дроби, вам нужно превратить две операции деления в одну. Это возможно только при условии наличия такого же делителя. В виде формулы это выглядит так:

a: BC: E = (A * E): (V * E) — (C * B) 🙁 B * E) = ((A * E) — (C * B)) 🙁 B * E)

То есть для того, чтобы складывать или вычитать дроби, нужно будет привести их к общему знаменателю. В противном случае решить пример будет непросто.

Для умножения и деления дробей не требуется приводить дробь к общему знаменателю. Для этих операций есть еще одно теоретическое обоснование, предполагающее другую процедуру.

Как найти общий знаменатель

Чтобы найти общий знаменатель дробей, вам нужно найти наибольшие общие кратные знаменатели. Приведем пример, решим маленькое выражение:

$$ (3 \\ OVER (5)) + (7 \\ Over (15)) $$

Находим NOC знаменателей.Число 15 делится на число 5, это означает, что

$$ (3 \ OVER (5)) + (7 \ OVER (15)) = ((3 * 3) \ OVER (15)) + (7 \ OVER (15)) = ( 9 \ OVER (15)) + (7 \ OVER (15)) = (16 \ OVER (15)) = 1 (1 \ OVER (15)) $$ — Обратите внимание, что при увеличении числитель, знаменатель тоже увеличился. В конце решения примера с дробями по возможности необходимо выделить целую часть выражения.

Привести дробь к общему знаменателю можно только с помощью основного свойства дроби.Формулировка этого свойства звучит так: если числитель и знаменатель дроби умножить на одно и то же число, значение дроби не изменится. Это значит, что при приведении дроби к общему знаменателю требуется учитывать увеличение числа.

Нок можно найти аналитически, как мы это сделали в примере. Но чаще всего приходится прибегать к разложению на простые факторы. Для того, чтобы найти НОК из двух чисел, следует:

• Разложите эти числа на простые множители
• Проверить, каких простых факторов недостаточно для разложения.
• Число берется с наименьшим числом множителей, и его разложение складывает числа, которые есть в других разложениях, но в основном их нет. При этом учитывается количество цифр. Это означает, что если в основном разложение — это одно число 3, а в других разложениях два числа 3, то вам нужно умножить основное разложение на два-три.

Что мы знали?

Мы говорили о приведении дробей к общему знаменателю. Рассказали, зачем это нужно, и какие операции с дробями можно производить, не приводя к общему знаменателю.Они привели пример и рассказали, как меняется числитель, когда она приводила дроби к общему знаменателю.

Тест по теме

Оценка статьи

Средняя оценка: 4,7. Всего получено оценок: 115.

Предыдущая статья: Положительный эффект адреналина Следующая статья: Тестирование от психолога

Презентация на тему атрибутивных местоимений. Урок-презентация на тему «Определительные местоимения» Презентация к уроку русского языка (6 класс) по теме.На каждый рот шарф не надеть

Чтобы использовать предварительный просмотр презентаций, создайте себе аккаунт (аккаунт) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Трошенкова Света, 41 группа История номеров.

История появления чисел У древних людей, кроме каменного топора и шкуры вместо одежды, ничего не было, поэтому им было нечего считать. Постепенно стали приручать скот, обрабатывать поля; торговля появилась, и здесь без счета не обойтись.Сначала посчитали по пальцам. Когда кончались пальцы на одной руке, переключались на другую, а если на двух руках не хватало, переключались на ноги.

История чисел Древние шумеры первыми изобрели числа. Они использовали только два числа. Вертикальная полоса представляет собой одну единицу, а угол двух лежачих брусьев — десять. Они получили эти линии в виде клиньев, потому что писали острой палочкой на сырых глиняных табличках, которые затем сушили и сжигали.Вот как выглядели эти доски.

История появления чисел Древние майя вместо самих чисел рисовали страшные головы, как у пришельцев, и отличить одну голову — фигуру от другой было очень сложно.

История появления чисел Индейцы и народы Древней Азии при счете завязывали узлы на шнурках разной длины и цвета. Некоторые богатые люди накопили несколько метров этой веревочной «счетной книжки», попробуйте, вспомните через год, что означают четыре узла на красной веревке! Поэтому того, кто связал себя узами брака, называли реклером.

История появления чисел Древние египтяне писали очень сложные, громоздкие знаки вместо чисел на очень длинных и дорогих папирусах. Например, вот как выглядело число 5656.

История происхождения чисел Хранить глиняные таблички, веревки с узлами и свитки папируса было очень неудобно. И так продолжалось до тех пор, пока древние индейцы не изобрели для каждого числа свой знак. Так они выглядели

История чисел Арабы первыми позаимствовали числа у индейцев и принесли их в Европу.Чуть позже арабы упростили эти значки, они стали выглядеть так. Они похожи на многие наши числа. Арабы называли ноль, или «пустой», «сифра». С тех пор и появилось слово «цифра». Правда, сейчас все десять символов для записи чисел, которые мы используем, называются числами.

История появления чисел Из пальцевого счета пошла пятеричная система счисления (одна рука), десятичная (две руки) и десятичная (пальцы рук и ног). В древности не было единой системы счета для всех стран.Одни системы исчисления основывались на 12, другие — на 60, третьи — на 20, 2, 5, 8.

История происхождения чисел Римляне ввели десятичную систему счисления. Римские цифры до сих пор используются в часах и для оглавления книг, но эта система чисел также была слишком сложной для счета. Предки русского народа славяне использовали буквы для обозначения чисел. Такой способ обозначения чисел называется цифрами.

История появления чисел Для обозначения больших чисел славяне придумали свой оригинальный способ: десять тысяч — тьма, десять тем — легион, десять легионов — леодр, десять леодр — вороны, десять воронов — колода.Такой способ именования номеров был очень неудобным. Поэтому Петр I ввел в Россию знакомые нам десять чисел, которые мы используем до сих пор.

Значение чисел согласно Пифагору Пифагор, его ученики и последователи сократили все числа до чисел от 1 до 9 включительно, поскольку они являются исходными числами, из которых могут быть получены все остальные. Знаменитый Корнелиус Агриппа в своей работе «Оккультная философия», опубликованной в 1533 году, назвал эти числа и их значения.

Значение чисел по Пифагору Число 1 — это число цели, которое проявляется в форме агрессивности и амбиций. Цифра 2 — это число с крайностями. Он поддерживает баланс, сочетая положительные и отрицательные качества. Цифра 3 — означает нестабильность. Он сочетает в себе талант и веселье и символизирует приспособляемость.

Значение чисел по Пифагору Число 4 — число означает стабильность и силу. Цифра 5 символизирует риск. Это число одновременно и самое счастливое, и самое непредсказуемое.Цифра 6 — символ надежности. Он находится в гармонии с природой. Это идеальный номер.

Значение чисел по Пифагору Число 7 — число символизирует тайну, а также учебу и знания. Число 8 — это число материального успеха. Это надежность, доведенная до совершенства, сбалансированность. Число 9 — символ всеобщего успеха. Он объединяет черты всей группы.

Информационные ресурсы числа судьбы: пифагорейская, индийская и китайская нумерология.-Сборник, предисловие Андрея Костенко. С.-Пб., «Экслибрис», 2003 г. И.Я. Депман Мир чисел: рассказы о математике: Дет. лит., 1982 А. Ликум Все обо всем. Популярная энциклопедия для детей — М .: Филологическое общество «Слово», 1993, том 1,7,9. А. Лопатина Хорошая математика. М: «Амрита Рус» 2004 Интернет-ресурсы.

История номеров. «Основное число» человека. Образовательно-исследовательский проект 900igr.net

Фундаментальный вопрос «Кто бросил в мир сетку чисел?»

История появления чисел У древних людей, кроме каменного топора и шкуры вместо одежды, ничего не было, поэтому им было нечего считать.Постепенно стали приручать скот, обрабатывать поля; торговля появилась, и здесь без счета не обойтись. Сначала посчитали по пальцам. Когда кончались пальцы на одной руке, переключались на другую, а если на двух руках не хватало, переключались на ноги.

История чисел Древние шумеры первыми изобрели числа. Они использовали только два числа. Вертикальная полоса представляет собой одну единицу, а угол двух лежачих брусьев — десять. Они получили эти линии в виде клиньев, потому что писали острой палочкой на сырых глиняных табличках, которые затем сушили и сжигали.Вот как выглядели эти доски.

История появления чисел Древние майя вместо самих чисел рисовали страшные головы, как у пришельцев, и отличить одну голову — фигуру от другой было очень сложно.

История появления чисел Индейцы и народы Древней Азии при счете завязывали узлы на шнурках разной длины и цвета. Некоторые богатые люди накопили несколько метров этой веревочной «счетной книжки», попробуйте, вспомните через год, что означают четыре узла на красной веревке! Поэтому того, кто связал себя узами брака, называли реклером.

История появления чисел Древние египтяне писали очень сложные, громоздкие знаки вместо чисел на очень длинных и дорогих папирусах. Например, вот как выглядело число 5656.

История происхождения чисел Хранить глиняные таблички, веревки с узлами и свитки папируса было очень неудобно. И так продолжалось до тех пор, пока древние индейцы не изобрели для каждого числа свой знак. Так они выглядели

История чисел Арабы первыми позаимствовали числа у индейцев и принесли их в Европу.Чуть позже арабы упростили эти значки, они стали выглядеть так. Они похожи на многие наши числа. Арабы называли ноль, или «пустой», «сифра». С тех пор и появилось слово «цифра». Правда, сейчас все десять символов для записи чисел, которые мы используем, называются числами.

История появления чисел Из пальцевого счета пошла пятеричная система счисления (одна рука), десятичная (две руки) и десятичная (пальцы рук и ног). В древности не было единой системы счета для всех стран.Одни системы счисления основывались на 12, другие — на 60, третьи — на 20, 2, 5, 8. 8 60 12 2 20 10 5 Система счисления

История происхождения чисел Римляне ввели десятичную систему счисления. Римские цифры до сих пор используются в часах и для оглавления книг, но эта система чисел также была слишком сложной для счета. Предки русского народа славяне использовали буквы для обозначения чисел. Такой способ обозначения чисел называется цифрами.

История появления чисел Для обозначения больших чисел славяне придумали свой оригинальный способ: десять тысяч — тьма, десять тем — легион, десять легионов — леодр, десять леодр — вороны, десять воронов — колода.Такой способ именования номеров был очень неудобным. Поэтому Петр I ввел в Россию знакомые нам десять чисел, которые мы используем до сих пор.

Мы узнали «главное число» человека: древние ученые считали, что числа имеют загадочное, магическое значение и влияют на человека. Согласно поверьям древних, у каждого человека есть определенное число, обладающее мистической силой, влияющей на характер и привычки. В нумерологии, науке о числах, используются первые 9 чисел от 1 до 9.1, 2, 3, 4, 5, 6, 7, 8, 9.

Значение чисел согласно Пифагору Пифагор, его ученики и последователи сократили все числа до чисел от 1 до 9 включительно, поскольку они являются исходными числа, из которых могут быть получены все остальные. Знаменитый Корнелиус Агриппа в своей работе «Оккультная философия», опубликованной в 1533 году, назвал эти числа и их значения.

Значение чисел по Пифагору Число 1 — это число цели, которое проявляется в форме агрессивности и амбиций.Цифра 2 — это число с крайностями. Он поддерживает баланс, сочетая положительные и отрицательные качества. Цифра 3 — означает нестабильность. Он сочетает в себе талант и веселье и символизирует приспособляемость.

Значение чисел по Пифагору Число 4 — число означает стабильность и силу. Цифра 5 символизирует риск. Это число одновременно и самое счастливое, и самое непредсказуемое. Цифра 6 — символ надежности. Он находится в гармонии с природой. Это идеальный номер.

Значение чисел по Пифагору Число 7 — число символизирует тайну, а также учебу и знания.Число 8 — это число материального успеха. Это надежность, доведенная до совершенства, сбалансированность. Число 9 — символ всеобщего успеха. Он объединяет черты всей группы.

Исследование У каждого человека есть свой основной номер. ВАША ЗАДАЧА: Подсчитайте «количество голов» для всех учеников в вашем классе. Я Вика Папа Мама

Наше исследование Вы можете рассчитать свое «основное число» по дню, месяцу и году вашего рождения. Например, вы родились 5 августа 1998 года (05.08.1998). Складываем все эти числа вместе: 5 + 8 + 1 + 9 + 9 + 8 = 40 и получаем 40.Эти два числа тоже нужно сложить: 4 + 0 = 4. «Четыре» — мое основное число. Так что можете посчитать «основные числа» наших одноклассников.

Наше исследование для одноклассников

Наше исследование для одноклассников

Наше исследование для одноклассников

Информационные ресурсы Число Судьбы: пифагорейская, индийская и китайская нумерология.-Сборник, предисловие Андрея Костенко. С.-Пб., «Экслибрис», 2003 г. И.Я. Депман Мир чисел: рассказы о математике: Дет.лит., 1982 А. Ликум Все обо всем. Популярная энциклопедия для детей — М .: Филологическое общество «Слово», 1993, том 1,7,9. А. Лопатина Хорошая математика. М: «Амрита Рус» 2004 Интернет-ресурсы.

Числа — вечные спутники людей. Их влияние на человеческую жизнь настолько сильно, что люди называют его волшебным.

«Математическая игра» — Конкурс болельщиков. Для болельщиков проводятся конкурсы. + 5. Век. 12. Вертикальный. 7. Весенний месяц. 8. Устройство для расчетов.14. 13. Вопрос для решения. 21. Мера длины. 17. Ход игры: Станция № 3. Работа со «спичками». Разделение. тринадцать.

«Сравнение чисел 5 класс» — Какие лучи называются дополнительными? 10) В чем разница между координатным лучом и лучом? Длина Волги — 3520 км; Дон — 1870 м; Дунай — 2850 км. Задание 2. I. Повторение теоретического материала. Запишите числа как двойное неравенство. Учитель 5 класса: Седина Н.С. Задание 3. Есть ли у прямой концы? Я ЯРешение задач Задача 1. Сравнение чисел.

«Деление остатка урока» — 9 (остальные 7). Цель урока: Неполное частное. Каждый хочет получить только пятерку. Может ли остаток быть больше делителя? Как найти дивиденд по неполному частному, делителю и остатку? Разделите и сравните результат: Divisor. 100: 8 = 79: 8 = 144: 8 = 115: 8 = 213: 8 =. В вазе было 23 конфеты. Остаток.

«Делитесь уроком» — обыкновенные дроби.Акции. Умение читать и записывать обыкновенные дроби числителем и знаменателем. Урок математики в 5 классе. Учитель: Щетинина О.Г. Задачи урока:

«Вычислительные цепочки» — 37. Вычислительные цепочки. 25. Заполните таблицы. 15. 20. 40. Н.Я. Виленкин «Математика 5». 5 класс. 29.17.10.18.

ИЗ ИСТОРИИ НОМЕРОВ Денисенко Алла Петровна

Слайд 2

: 1. Какие числа для 2. Как люди научились записывать числа 3.Цифры Древнего Египта 4. Цифры древних римлян 5. Цифры Китая 6. Цифры индейцев майя 7. Современные числа

Слайд 3

Задача: Познакомить с историей возникновения числа и его ролью. Актуальность темы: Современный мир, ведь человеку без воздуха не обойтись без цифр. Ведь даже звук или картинка записываются комбинацией цифр.

Слайд 4

Почти все люди на Земле знают, что такое числа.Даже если мы берем иностранную книгу и не понимаем ни слова, мы все равно можем читать на языке чисел. Но так было не всегда

Слайд 5

Люди начали учиться счету с незапамятных времен, и их учителем была сама жизнь. Чтобы жертва не улетела, ее нужно было окружить, ну хотя бы так: пять человек справа, семь сзади, четверо слева. Здесь без счета не обойтись! И вождь первобытного племени справился с этой задачей.Даже в те времена, когда человек не знал таких слов, как «пять» или «семь», он мог показывать числа на пальцах.

Слайд 6

Как люди научились писать числа Прошло много-много лет. Человеческая жизнь менялась. Постепенно знания людей росли, и чем дальше, тем больше возрастала потребность в умении считать и измерять. Скотоводы должны были считать свои стада, и в то же время счет мог исчисляться сотнями и тысячами. Для фермера отсчет времени по лунным месяцам уже не годился.Нужен был точный календарь. Кроме того, людям все чаще приходилось иметь дело с большими числами … Пришлось придумать, как их записывать!

Слайд 7

В разных странах и в разное время это делалось по разному. Очень разные, а иногда даже забавные, эти «числа» у разных народов … В Древнем Египте числа первой десятки записывались соответствующим количеством палочек. Вместо цифры «3» — три палочки. Но у десятков есть другой знак — как подкова.

Слайд 8

У древних римлян были разные номера. Мы до сих пор иногда используем римские цифры. Их можно увидеть как на циферблате часов, так и в книге, где указан номер главы. Если присмотреться, римские цифры похожи на пальцы. Один — это один палец; два — два пальца; пять — это палец с большим пальцем наружу; шесть — это палец и еще один палец. Автограф Б.Н. Ельцин (первый президент России) 10 ноября 1988 года. Месяц указан римскими цифрами.

Слайд 9

Так выглядели древние китайские числа. Майя умели писать любые числа, используя только точку, линию и круг.

«Как появились числа и числа?»

Лис Марина Николаевна,

учитель математики

МОУ «Школа № 3 г. Черемхово»

«Мир построен на силе чисел» Пифагор

Можете ли вы представить мир без чисел?

Покупки;

Определение времени;

Номера телефонов и т. Д.

Люди так часто используют числа и счет, что трудно даже представить, что они не всегда существовали, а были изобретены человеком.

Очень интересно найти исторические корни чисел !

Как появились числа и числа

Числа были всегда 4 и 5 тысяч лет назад, только правила их изображения были разными. Но смысл был тот же: числа изображались с помощью определенных знаков — цифр.

Цифра — это символ, участвующий в написании числа.

Число — это значение, состоящее из чисел в соответствии с определенными правилами. Эти правила называются системами счисления.

Еще раньше, в древности, когда человек хотел показать, сколько у него овец или коз, он насыпал в мешок столько камней, сколько у него животных. Чем больше животных, тем больше камешков. Затем человек научился использовать символы для разных расчетных единиц. Он нарисовал черточку или другую отметку для любого объекта, на который рассчитывал, но у него все еще не было слов для обозначения чисел.

В этой системе счисления для записи чисел используется только одна цифра.

Такая система счисления использовалась и до сих пор используется в основном людьми, не имеющими письменности.

Номера начинают получать имена

В древние времена, когда человек хотел показать, сколько у него животных, он клал в большой мешок столько же камешков, сколько у него было животных. Чем больше животных, тем больше камешков. Отсюда и возникло слово «калькулятор», «исчисление» в переводе с латыни означает «камень».

Названия номеров впервые были показаны на пальцах. Так они начали учиться считать, пользуясь тем, что дала им сама природа — собственным пальцем. Когда кончались пальцы на одной руке, переключались на другую, а если на двух руках не хватало, переключались на ноги.

то, что дала им сама природа — своими руками.

Надо было знать, хватило ли улова до следующей охоты, сколько рыбы было поймано. Жизнь требовала обучения счету

Индейцы и народы древней Азии при счете завязывались узлы на шнурках разной длины и цвета.Некоторые богатые люди накопили несколько метров этой веревочной «счетной книжки», попробуйте, вспомните через год, что означают четыре узла на красной веревке! Поэтому того, кто связал себя узами брака, называли реклером.

Древние шумеры первыми изобрели числа

Они использовали только два числа. Вертикальная полоса представляет собой одну единицу, а угол между двумя лежащими брусьями — десять. Они получили эти линии в виде клиньев, потому что писали острой палочкой на сырых глиняных табличках, которые затем сушили и сжигали.Так выглядели эти платы

Египетская нумерация и I

AT Древнеегипетская нумерация , возникшая более 5000 лет назад, существовали специальные знаки (иероглифы) для записи чисел 1, 10, 100, 1000,…: (рис. 3). В Древнем Египте около 5000-4000 лет до нашей эры. использовали следующие обозначения чисел: одну обозначали палкой, сотню — пальмовым листом, а сто тысяч — лягушкой (лягушек в дельте Нила было много, поэтому у людей сложилась такая ассоциация: одна сто тысяч — много, как лягушки в Ниле).

Индийская нумерация

Хранить глиняные таблички, завязанные узлами веревки и свитки папируса было очень неудобно. И так продолжалось до тех пор, пока древние индейцы не изобрели для каждого числа свой знак.

С Индии на арабский номер

Однако Индия была отрезана от других стран — тысячи километров пути и высокие горы лежали на пути. Арабы были первыми «чужаками», которые позаимствовали числа у индейцев и привезли их в Европу.Чуть позже арабы упростили эти значки, они стали выглядеть так

Латинская (римская) нумерация

Достоверных сведений о его происхождении нет. В языке римлян нет следов пятичленной системы. Следовательно, эти числа были заимствованы римлянами у другого народа (скорее всего, у этрусков).

Эта нумерация возникла в Древнем Риме.

I V X L C D M

1 5 10 50100500 1000

CCXXXVII = 100 + 100 + 10 + 10 + 10 + 5 + 1 + 1 = 237

Но XXXIX = 10 + 10 + 10 — 1 + 10 = 39

Такая нумерация преобладала в Италии до XIII века, а в других странах Западной Европы — до 16 века.