Номер №283 — ГДЗ по Математике 6 класс: Виленкин Н.Я.
войтирегистрация
- Ответкин
- Решебники
- 6 класс
- Математика
- Виленкин
- Номер №283
НАЗАД К СОДЕРЖАНИЮ
2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №283 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.
2019г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №283 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
Условие 20132019г.
Cменить на 2013 г.
Cменить на 2019 г.
Приведите к наименьшему общему знаменателю дроби:
а) 1/6 и 3/8; г) 8/15 и 11/12; ж) 11/30 и 8/45; к) 9/98 и 5/56;
б) 4/9 и 7/15; д) 9/10 и 5/12; з) 11/20 и 9/16; л) 13/750 и 7/450;
в) 5/12 и 1/8; е) 13/12 и 13/18; и) 8/33 и 9/77; м) 10/297 и 14/363.
Сократите дроби 5/15, 13/26, 15/40, 24/32, а потом приведите их к знаменателю 24.
Решение 1
Решение 1
Решение 2
Решение 2
Решение 3
Решение 3
ГДЗ по Математике 6 класс: Виленкин Н.Я.
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А. С. Шварцбурд С.И. 2013/2019г.
С. Шварцбурд С.И. 2013/2019г.
ГДЗ по Математике 6 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.
ГДЗ по Математике 6 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018
ГДЗ по Математике 6 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.
ГДЗ по Математике 6 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.
Сообщить об ошибке
Выберите тип ошибки:
Решено неверно
Опечатка
Плохое качество картинки
Опишите подробнее
в каком месте ошибка
Ваше сообщение отправлено
и скоро будет рассмотрено
ОК, СПАСИБО
[email protected]
© OTVETKIN.INFO
Классы
Предметы
Математика 6 класс Виленкин Номер 283
авторы: Виленкин, Жохов, Чесноков, Шварцбурд.
издательство: Мнемозина 2012 год
- Предыдущее
- Следующее
Приведите к наименьшему общему знаменателю дроби:
а)
16
и
38
;
б)
49
и
715
;
в)
512
и
18
;
г)
и
1112
;
д)
910
и
212
;
е)
1312
и
1318
;
ж)
1130
и
845
;
з)
1120
и
916
;
и)
833
и
977
;
к)
998
и
556
;
л)
13750
и
7450
;
м)
10297
и
14363
.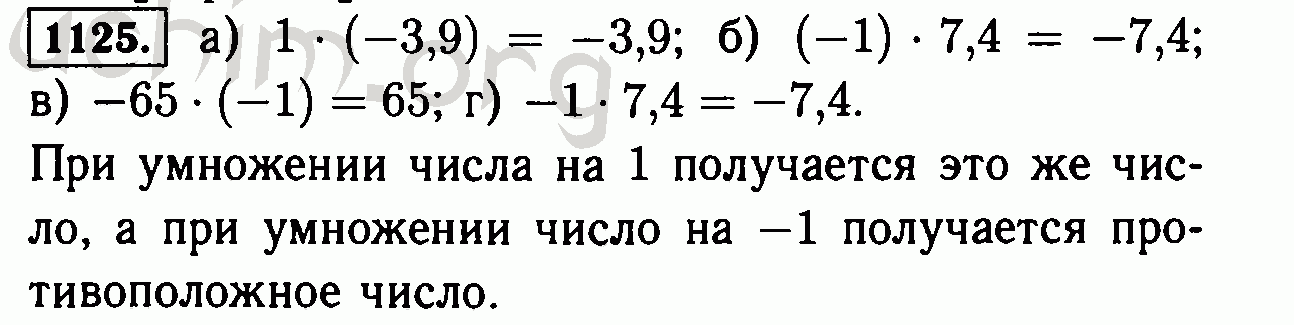
reshalka.com
Решение а
Яркие футболки в нашем магазине reshalkashop.ru
16=424
;
38=924
.
Решение б
49=2045
;
715=2445
.
Решение в
512=1024
;
18=324
.
Решение г
815=3260
;
1112=5560
.
Решение д
910=5460
;
512=2560
.
Решение е
1312=3936
;
1318=2636
.
Решение ж
1130=3390
;
845=1660
Решение з
1120=4480
;
916=4580
.
Решение и
833=56231
;
977=27231
.
Решение к
998=36392
;
556=35392
.
Решение л
13750=392250
;
7450=352250
.
Решение м
10297=1103267
;
14363=1263267
.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Частные суммы рядов Виленкина-Фурье в пространствах Лебега
Г. Агаев, Н. Виленкин, Г. Джафарли, А. Рубинштейн, Мультипликативные системы функций и гармонический анализ на нульмерных группах. (Русский) Баку, Вяз (1981)
Google ученый
Н.Ю. Антонов, Сходимость рядов Фурье. Восток Дж. Прибл. 2 (2), 187–196 (1996)
MathSciNet МАТЕМАТИКА Google ученый
С. Асташкин, Е. Семенов, Константы Лебега системы Уолша и банаховы пределы. Сибирская математика. J. 57 (3), 398–410 (2016)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
М. Авдиспахич, Н. Мемич, О признаке Лебега сходимости рядов Фурье на неограниченных группах Виленкина. Акта Математика. Венгрия.
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Л. Барамидзе, Равномерная сходимость двойных рядов Виленкина-Фурье. Дж. Контемп. Мат. Анальный. 54 (3), 147–156 (2019)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
И. Благота, Л.-Э. Перссон, Г. Тефнадзе, Двусторонние оценки констант Лебега относительно систем Виленкина и приложений. Глазг. Мат. J. 60 (1), 17–34 (2018)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Г. Бредон, Новая трактовка интеграла Хаара. Мичиганская математика. J. 10 , 365–373 (1963)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
А. Эскеназис, П. Иванисвили, Полиномиальные неравенства на кубе Хэмминга, Вероятность. Теория отн. Поля 178 (1–2), 235–287 (2020)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Н. Дж. Файн, О функциях Уолша. Транс. амер. Мат. соц. 65 , 372–414 (1949)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
С. Фридли, Аппроксимация суммами Виленкина-Фурье. Акта Математика. Венгрия. 47 (1–2), 33–44 (1986)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Г. Гат, Ортонормированные системы на группах Виленкина. Акта Математика. Венгрия.
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Г. Гат, Наилучшее приближение системами типа Виленкина. Акта Математика. акад. Педагог. Ньи Хази. (н.с.) 17 (3), 161–169 (2001)
Google ученый
Г. Гат, Ю. Гогинава, Униформа и L — сходимость средних логарифмических рядов Уолша-Фурье. Акта Математика. Грех. (англ. сер.) 22 (2), 497–506 (2006)
Google ученый
Гогинава Ю. О равномерной сходимости рядов Уолша-Фурье. Акта Математика. Венгрия. 93 (1–2), 59–70 (2001)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Гогинава Ю. О аппроксимативных свойствах частных сумм рядов Уолша-Фурье. Acta Sci. Мат. (Сегед) 72 (3–4), 569–579 (2006)
Google ученый
У. Гогинава, Г. Ткебучава, Сходимость подпоследовательностей частных сумм и средних логарифмических рядов Уолша-Фурье. Acta Sci. Мат. (Сегед) 72 (1–2), 159–177 (2006)
Google ученый
Б. Голубов, А. Ефимов, В. Скворцов, Теория и приложения рядов и преобразований Уолша . Теория и приложения (Киев, Ин-т мат. АН Украины, 1992), с. 18–26
Google ученый
Н. Гуличев, Приближение непрерывных функций суммами Уолша-Фурье. Анальный. Мат.
CrossRef MathSciNet Google ученый
Э. Хьюитт, К.А. Росс, Абстрактный гармонический анализ. Структура топологических групп. Теория интеграции. Представления группы , том. I (Спрингер, Берлин, 2013 г.)
Google ученый
П. Иванисвили, А. Вольберг, От дискретного потока Бекнера к непрерывному потоку Янсона в сложной гиперконтракции. Дж. Функц. Анальный. 276 (9), 2716–2730 (2019)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
П. Иванисвили, Р. ван Гендель, А. Вольберг, тип Радемахера и тип Энфло совпадают. Анна. Мат. 192 (2), 665–678 (2020)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
А. Куфнер, Л.-Э. Перссон, Н. Самко, Взвешенные неравенства типа Харди , 2-е изд. (World Scientific, Хакенсак, 2017 г.)
CrossRef МАТЕМАТИКА Google ученый
Л. Ларссон, Л. Малигранда, Л.-Э. Перссон, Дж. Пекарик, Мультипликативные неравенства типа Карлсона и интерполяция (World Scientific, Hackensack, 2006)
CrossRef МАТЕМАТИКА Google ученый
С. Лукомский. Константы Лебега для характеров компактной нульмерной абелевой группы. Восток Дж. Прибл. 15 (2), 219–231 (2009)
MathSciNet МАТЕМАТИКА Google ученый
О. Лукьяненко, О константах Лебега для системы Виленкина. Мат. мех. Саратовский гос. 7 , 70–73 (2005)
Google ученый
Ю. Малыхин, С. Теляковский, Н. Холщевникова, Интегрируемость суммы модулей блоков ряда Фурье-Уолша для функций ограниченной вариации. проц. Стеклова Мат. 290 (1), 306–317 (2015)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Н. Мемич, И. Симон, Г. Тефнадзе, Сильная сходимость двумерных рядов Виленкина-Фурье. Мат. Нахр. 289 (4), 485–500 (2016)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
К. Никулеску, Л.-Э. Перссон, Выпуклые функции и их приложения . Книги CMS по математике, 2-е изд. (Спрингер, Берлин, 2018 г.)
Google ученый
К. Онневер, Равномерная сходимость рядов Фурье по группам. Скалистая гора Дж. Математика. 1 (4), 623–631 (1971)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
C. Онневера, Он L 1 -сходимость рядов Уолша-Фурье. Международный Дж. Матем. Мат. науч. 1 (1), 47–56 (1978)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
К. Онневер, Д. Уотерман, Равномерная сходимость рядов Фурье по группам. I. Мичиганская математика. Дж. 18 , 265–273 (1971)
MathSciNet МАТЕМАТИКА Google ученый
Л.-Э. Перссон, Соотношения между регулярностью периодических функций и их рядами Фурье. Кандидат наук. Диссертация, факультет математики, Университет Умео (1974)
Google ученый
Л.-Э. Перссон, Соотношения между суммируемостью функций и их рядами Фурье. Акта Математика. акад. науч. Венгрия. 27 (3–4), 267–280 (1976)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Л.-Э. Перссон, Lecture Notes, PL. Lions Seminar (Колледж де Франс, Париж, 2015)
Google ученый
Л.-Э. Перссон, Н. Самко, Неравенства и выпуклость, в Теория операторов, операторные алгебры и приложения . Теория операторов: достижения и приложения, том. 242 (Birkhäuser/Springer, Берлин, 2014 г.), стр. 279.–306
Google ученый
Л.-Э. Перссон, Ф. Шипп, Г. Тефнадзе, Ф. Вайс, Аналогия теоремы Карлесона-Ханта относительно систем Виленкина. Ж. Анал Фурье. заявл. 28 (3), 48 (2022)
Google ученый
Л. Понтрягин, Топологические группы , 2-е изд. (Гордон и Брич, Нью-Йорк, 1966)
Google ученый
В. Рудин, Анализ Фурье по группам . Интернет-библиотека Wiley (Wiley, Hoboken, 1962)
Интернет-библиотека Wiley (Wiley, Hoboken, 1962)
Google ученый
В. Рудин, Основы математического анализа . Международная серия по чистой и прикладной математике, том. 3 (Макгроу-Хилл, Нью-Йорк, 1964)
Google ученый
F. Schipp, Über gewissen maximaloperatoren. Анна. ун-т науч. Будапешт. Разд. Мат. 18 , 189–195 (1975)
MathSciNet МАТЕМАТИКА Google ученый
Ф. Шипп, Поточечная сходимость разложений по некоторым системам произведений. Анальный. Мат. 2 (1), 65–76 (1976)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Ф. Шипп, В. Уэйд, П. Саймон, Серия Уолша: Введение в диадический гармонический анализ (Тейлор и Фиансис, Милтон Парк, 1990)
Google ученый
А. Шнайдер, О рядах по функциям Уолша с монотонными коэффициентами. Известия АН СССР, сер. Матем. 12 , 179–192 (1948)
Google ученый
А. Шнайдер, О сходимости рядов Фурье функций Уолша. Мат. сб. 76 (3), 441–472 (1954)
MathSciNet Google ученый
Симон П. О сходимости рядов Виленкина-Фурье. Акта Математика. акад. науч. Венгрия. 33 (1–2), 189–196 (1979)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
П. Саймон, О равенстве Парсеваля и условии Дини-Липшица по отношению к системе Виленкина. Анальный. Мат. 10 (2), 151–161 (1984)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
П. Шелин, Сходимость почти всюду некоторых сингулярных интегралов и кратных рядов Фурье. Ковчег мат. 9 , 65–90 (1971)
Ковчег мат. 9 , 65–90 (1971)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Э. Штейн, Р. Шакарчи, Анализ Фурье. Введение . Принстонские лекции по анализу, том. 2 (издательство Принстонского университета, Принстон, 2003 г.)
Google ученый
G. Szegö, Über die Lebesgueschen konstanten bei den Fourierschen reihen. Мат. Z. 9 (1–2), 163–166 (1921)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Г. Тефнадзе, Замечание о сходимости по норме средними Виленкина–Фейера. Грузинская математика. Дж. 21 (4), 511–517 (2014)
CrossRef MathSciNet МАТЕМАТИКА Google ученый
Р. Толедо, Местные персонажи в группах Виленкина. Акта акад. Паед. Ньиредьхаза 13 , 25–34 (1992)
Акта акад. Паед. Ньиредьхаза 13 , 25–34 (1992)
МАТЕМАТИКА Google ученый
А. Торчинский, Методы действительных переменных в гармоническом анализе . Чистая и прикладная математика, виолончель. 123 (Академическое издательство, Кембридж, 1986)
Google ученый
Н. Виленкин, Об одном классе полных ортонормированных систем. Известия Акад. наук. Сер. СССР. Мат. 11 , 363–400 (1947)
MathSciNet МАТЕМАТИКА Google ученый
Виленкин Н. К теории лакунарных ортогональных систем. Известия Акад. наук. Сер. СССР. Мат. 13 , 245–252 (1949)
MathSciNet Google ученый
Н. Виленкин, К теории интегралов Фурье на топологических группах. Мат. сб. 30 (72), 233–244 (1952)
Мат. сб. 30 (72), 233–244 (1952)
MathSciNet Google ученый
Ф. Вайс, Сходимость и суммируемость преобразований Фурье и пространств Харди . Прикладной и численный гармонический анализ (Springer, Cham, 2017)
Google ученый
В.-С. Янг, На п.в. сходимость рядов Уолша-Качмарца-Фурье. проц. амер. Мат. соц. 44 (2), 353–358 (1974)
Google ученый
А. Зигмунд, Тригонометрический ряд , тт. I и II вместе взятые, 3-е изд. (издательство Кембриджского университета, Кембридж, 2003 г.)
Google ученый
Специальные функции и теория представлений групп
Базовый код продукта Список ключевых слов: ммоно; ММОНО; мммоно/22; ММОНО/22; ммоно-22; MMONO-22
Распечатать код продукта: MMONO/22
Онлайн-код продукта:
MMONO/22.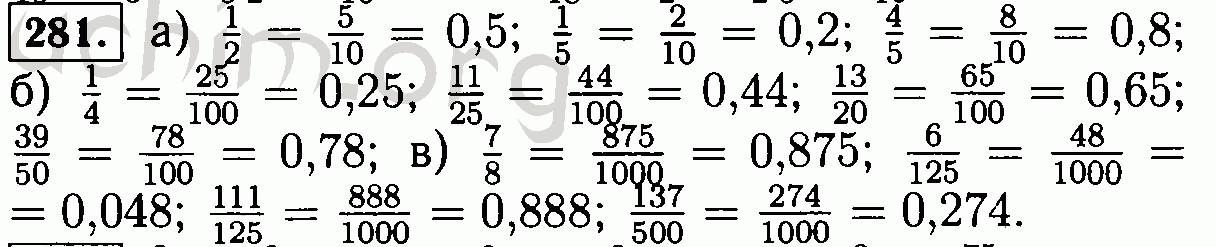 E
E
Название (HTML): Специальные функции и теория представлений групп
Автор(ы) (Отображение продукта): Н. Я. Виленкин
Абстрактный:
Стандартная схема отношений между специальные функции и теория представлений групп: некоторые классы специальных функций интерпретируются как матричные элементы неприводимых представлений некоторой группы Ли, и тогда свойства специальных функций связаны с (и получены из) простые общеизвестные факты теории представлений. Книга сочетает в себе большинство известных результатов в этом направлении. В частности, автор описывает связи между экспоненциальными функциями и аддитивная группа действительных чисел (анализ Фурье), Лежандр и Якоби полиномы и представления группы \(SU(2)\), а также гипергеометрическая функция и представления группы \(SL(2,R)\), а также многие другие классы специальных функции.
Название серии книг: Переводы математических монографий
Месяц и год публикации: 1968-12-31
Год авторского права: 1968
Количество страниц: 613
Тип крышки: Мягкая обложка
Печать ISBN-13: 978-0-8218-1572-4
Интернет ISBN 13: 978-1-4704-4439-6
Распечатать ISSN: 0065-9282
Интернет-ISSN: 0065-9282
Основной MSC: 33
Вторичный MSC: 22
Учебник?: false
Прикладная математика?: ложь
Книга МАА?: false
Обучение на основе запросов?: false
Электронные носители?: false
Одежда или подарок: ложь
SXG Тема: AN
Цена онлайн 1 этикетка: Список
Цена онлайн 1:
135. 00
00
Цена печати 1 Этикетка: Список
Цена печати 1: 135.00
Цена онлайн 2 Этикетка: Участник AMS
Цена онлайн 2: 108.00
Цена печати 2 Этикетка: Участник AMS
Цена печати 2: 108.00
Цена онлайн 3 Этикетка: Член МАА
Цена онлайн 3: 121.50
Цена печати 3 Этикетка: Член MAA
Цена печати 3: 121.50
Цена комплекта 1 Этикетка: Список
Цена комплекта 1: 202.50
Цена комплекта 2 Этикетка: Участник AMS
Цена пакета 2: 162.00
Цена комплекта 3: 182.25
Цена комплекта 3 Этикетка: Член MAA
Распечатать Добавить в корзину URL: /some/url/at/AMS/MMONO-22
Электронный адрес Добавить в корзину: /some/url/at/AMS/MMONO-22.E
Распечатать Доступно для заказа: правда
Копия обзора:
https://www.ams.org/exam-desk-review-request?&eisbn=978-1-4704-4439-6&pisbn=978-0-8218-1572-4&epc=MMONO/22.E&ppc=MMONO/22&title= Special%20Functions%20and%20the%20Theory%20of%20Group%20Representations&author=N.

