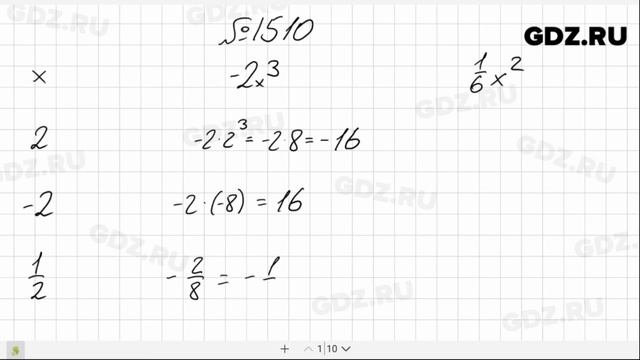Виленкин 6 класс номер 297: Номер №297 - ГДЗ по Математике 6 класс: Виленкин Н.Я.

Содержание

Номер №297 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

войтирегистрация

Ответкин
Решебники
6 класс
Математика
Виленкин
Номер №297

НАЗАД К СОДЕРЖАНИЮ

2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №297 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №297 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.

Условие 20132019г.

Cменить на 2013 г.

Cменить на 2019 г.

Приведите дробь:
а) 5/6 к знаменателю 24;
б) 12/13 к знаменателю 65;
в) 11/19 к знаменателю 57;
г) 12/13 к знаменателю 78.

Космический корабль «Вега-1» двигался к комете Галлея со скоростью 34 км/с, а сама комета двигалась ему навстречу со скоростью 46 км/с. Какое расстояние было между ними за 15 мин до встречи?

Решение 1

Решение 2

Решение 3

ГДЗ по Математике 6 класс: Виленкин Н.Я.

Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.

ГДЗ по Математике 6 класс: Мерзляк А.Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.

ГДЗ по Математике 6 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018

ГДЗ по Математике 6 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.

ГДЗ по Математике 6 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

Классы

Предметы

Номер 297 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020.

Часть 1 (решебник)Номер 297 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая версия

Старая версия

ЧАСТЬ 1
Выберите номер упражнения

ЧАСТЬ 2
Выберите номер упражнения

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595

Adblock
detector

Н.

Виленкин, “Об одном классе полных ортонормированных систем”, Изв. акад. АН СССР Сер. мат., 11:4 (1947), 363–400

	Общая информация
	Последний выпуск
	Предстоящие документы
	Архив
	Импакт-фактор
	Подписка
	Руководство для авторов
	Лицензионное соглашение
	Подать рукопись

	Поисковые документы
	Поиск ссылок

	RSS
	Последний выпуск
	Текущие выпуски
	Выпуски архива
	Что такое RSS

Личный кабинет:
Логин:
Пароль:
	Сохранить пароль
	Введите
	Забыли пароль?
	Регистр

Известия Академии Наук СССР. Серия Математическая, 1947, Том 11, Выпуск 4, Страницы 363–400 (ми им3004)

Эта статья цитируется в 33 научных статьях (всего в 33 статьях)

По классу полной ортонормированные системы

Н. Виленкин

Полный текст PDF (2338 кБ)

Поступила в редакцию: 25.07.1946

Библиографические базы данных:

Язык: Русский

Ссылка:

Н. Виленкин, “Об одном классе полных ортонормированные системы”, Изв. акад. АН СССР Сер. Мат., 11:4 (1947), 363–400

Цитирование в формате AMSBIB

\RBibitem{Vil47} \by Н.~Виленкин \paper Об одном классе полных ортонормированные системы \jour Изв. акад. АН СССР Сер. Мат. \год 1947 \том 11 \выпуск 4 \страниц 363--400 \mathnet{http://mi.mathnet.ru/im3004} \mathscinet{http://www.ams.org/mathscinet -getitem?mr=22560} \zmath{https://zbmath.org/?q=an:0125.34304|0036.35601}

Варианты соединения:

https://www.mathnet.ru/eng/im3004

https://www.mathnet.ru/eng/im/v11/i4/p363

Эта публикация цитируется в следующих статьях:

А. М. Зубакин, “К теории полных мультипликативных периодических ортонормированных систем”, УМН, 24:6(150) (1969), 187–188
С. Л. Блюмин, Б. Д. Котляр, “Операторы Гильберта–Шмидта и абсолютная сходимость рядов Фурье”, Матем. СССР-Изв., 4:1 (1970), 215–223
Г. А. Акишев, С. Т. Махашев, “Об абсолютной сходимости рядов Фурье по обобщенной системе Хаара”, Изв. (Из. ВУЗ), 44:3 (2000), 6–14
А. И. Рубинштейн, “О наилучшей сходимости”, Матем. Math., 192:2 (2001), 277–297
В. С. Выхованец, В. Д. Малюгин, “Мультипликативная алгебра и ее применение в логической обработке данных”, Пробл. управл., 3 (2004), 67–77
Г. А. Акишев, “О порядках приближения классов функций многочленами по обобщенной системе Хаара”, Изв. (Из. ВУЗ), 2005, вып. 3, 11–20

С. С. Волосивец, “Сходимость рядов Фурье по мультипликативным системам и модуль непрерывности $p$-флуктуаций”, Сиб. матем. J., 47:2 (2006), 193–208
Г. А. Акишев, “О порядках приближения классов полиномами по общей системе Хаара”, Сиб. электрон. матем. изв., 3 (2006), 92–105
В. С. Выхованец, “Алгебраическое разложение дискретных функций”, Автомат. Пульт дистанционного управления, 67: 3 (2006), 361–39.2
М. Г. Плотников, “О множествах единственности кратных рядов Уолша”, Матем. Notes, 81:2 (2007), 234–246
Г. А. Акишев, “Абсолютная сходимость рядов Фурье суперпозиций функций”, Изв. (Из. ВУЗ), 53:11 (2009), 1–8
Казарян М.Л., “Оптимальное зонное кодирование цифровых липшицевых сигналов посредством класса системы модифицированных преобразований хаара”, Телекоммуникации, 2011, №1. 1, 2–10 9r$ по системе Виленкина”, Изв. (Из. ВУЗ), 57:2 (2013), 25–33

М. Г. Плотников, “Кратные ряды Уолша и множества Зигмунда”, Матем. Notes, 95:5 (2014), 686–696
Волосивец С.С., “Теоремы типа Винера для рядов Фурье–Виленикина с неотрицательными коэффициентами и полнотелыми пространствами”, Матем. Неравный. Appl., 17:4 (2014), 1415–1425
М. С. Беспалов, “Производящий оператор для дискретных функций Крестенсона”, Пробл. Передача, 51:1 (2015), 37–48
В. И. Щербаков, “Расходимость рядов Фурье по обобщенным системам Хаара в точках непрерывности функции”, Изв. (Из. ВУЗ), 60:1 (2016), 42–59
С. А. Саргсян, “О константах Лебега систем Виленкина”, Уч. записки ЕГУ, сер. Физика и математика, 2016, № 1, с. 2, 63–66

В. И. Щербаков, “Признак Дини–Липшица для обобщенных систем Хаара”, Изв. Сарат. ун-та. нояб. сер. Сер.: Математика. Механика. Информатика, 16:4 (2016), 435–448
В. И. Щербаков, “Майоранты ядер Дирихле и поточечные признаки Дини для обобщенных систем Хаара”, Матем. Notes, 101:3 (2017), 542–565
Сагателян Т.М., “О поточечной универсальности частных сумм рядов Фурье классов l-P,P >= 1 по системе Крестенсона — Леви”, Матем. Монтиснигри, 40 (2017), 24–35
Г. Г. Геворкян, К. А. Навасардян, “Теоремы единственности для обобщенных систем Хаара”, Матем. Примечания, 104:1 (2018), 10–21
Григорян М.Г., Саркисян С.А., “Сходимость почти всюду жадного алгоритма по системе Виленкина”, Журн. контемп. Мат. Анал.-Арм. акад., 53:6 (2018), 331–345
Ю. А. Фарков, “Дискретные вейвлет-преобразования в анализе Уолша”, Фундамент. науч. (Нью-Йорк), 257:1 (2021), 127–137
В. И. Щербаков, “Сравнение V- и S-тестов Дини. Контрпримеры на симметричные критерии Дини по системам типа Хаара и Уолша”, Изв. (Из. ВУЗ), 63:9(2019), 63–83
С. М. Воронов, “Некоторые признаки сходимости рядов Фурье по системе Виленкина в случае неограниченного $p_k$”, Вестник Московского государственного университета, 74:5 (2019), 195–197
Холщевникова Н., “Проблема объединения и проблема категорий множеств единственности в теории ортогональных рядов”, Real Anal. Exch., 44:1 (2019), 65–76
С. М. Воронов, “Аналог критерия Харди–Литтлвуда для рядов Фурье по системе Виленкина в случае неограниченного $p_k$”, Вестник Московского университета по математике, 75:2 (2020), 80–82
А. С. Целищев, “Неравенство Литтлвуда–Пэли–Рубио де Франсиа для ограниченных систем Виленкина”, Матем. Math., 212:10 (2021), 1491–1502
Ю. А. Фарков, “Фреймы в анализе Уолша, матрицы Адамара и равномерно распределенные множества”, Материалы 20 Международной Саратовской зимней школы «Современные проблемы теории функций и их приложений», Саратов, 28 января — 1 февраля 2020 г. Часть 1, Итоги науки и техн. сер. соврем. мат. я ее прил. Темат. обз., 199, ВИНИТИ РАН, М., 2021, 17–30
С. М. Воронов, “О равномерной сходимости рядов Fure по системе Виленкина в случае неограниченных $p_k$”, Вестн. Моск. ун-та. сер. 1. Матем., мех., 2022, №1. 1, 61–65
Г. Г. Ониани, “О множествах расходимости рядов Фурье по системам характеров компактных абелевых групп”, Матем. Примечания, 112:1 (2022), 100–108

Ссылки на статьи в Google Scholar: русские цитаты, английские цитаты
Статьи по теме в Google Scholar: русские статьи, Английские статьи

QR-?

(открытый доступ) Специальные функции и теория представлений групп (1968) | Наум Я.

Виленкин

Наум Я. Виленкин

31 декабря 1968-

Аннотация: Стандартная схема связи специальных функций с теорией представлений групп такова: некоторые классы специальных функций интерпретируются как матричные элементы неприводимых представлений некоторой группы Ли, а затем свойства специальных функций связаны (и выведены) с простыми хорошо известными фактами теории представлений. В книге объединено большинство известных результатов в этом направлении. В частности, автор описывает связи экспоненциальных функций с аддитивной группой действительных чисел (анализ Фурье), полиномами Лежандра и Якоби и представлениями группы $SU(2)$, а также гипергеометрической функцией и представлениями группы $SL (2,R)$, а также многие другие классы специальных функций.

Citations

PDF

Open Access

More filters

Convex bodies : the Brunn-Minkowski theory

[. ..]

Rolf Schneider ¹ •Institutions (1 )

University of Freiburg ¹

01 Feb 1993

Abstract: 1. Основная выпуклость 2. Граничная структура 3. Сложение Минковского 4. Мера кривизны и интегралы квермассы 5. Смешанные объемы 6. Неравенства для смешанных объемов 7. Выбранные объемы Приложения Приложение.

…читать дальшеЧитать меньше

3,685 цитирований

Журнальная статья•DOI•

Разложение функций Харди на интегрируемые с квадратом вейвлеты постоянной формы

[…]

А. Гроссманн, Дж. Морле

92 01 июля 1984-Siam Journal on Mathematical Analysis

Аннотация: Произвольную интегрируемую с квадратом вещественную функцию (или, что то же самое, связанную с ней функцию Харди) можно удобно проанализировать в подходящее семейство интегрируемых с квадратом вейвлетов постоянной формы (т. е. получить сдвигами и расширениями от любого из них.) Результирующее интегральное преобразование является изометричным и самообратным, если вейвлеты удовлетворяют приведенному здесь «условию допустимости». Получены явные выражения в случае конкретного анализирующего семейства, играющего роль, аналогичную роли когерентных состояний (вейвлетов Габора) в обычной $L_2$-теории. Они записываются в терминах модифицированной $\Gamma $-функции, которая вводится и изучается. С точки зрения теории групп, эта работа посвящена суммируемым с квадратом коэффициентам неприводимого представления неунимодулярной $ax + b$-группы.

… Прочитайте Moreread Less

3165 Цитаты

Журнал.

Журнальная статья•DOI•

Когерентные состояния для произвольной группы Ли

[…]

Аскольд Переломов

01 сентября 1972 г.-Communications in Mathematical Physics

Аннотация: Концепция когерентных состояний изначально тесно связана с нильпотентной группа Вейля обобщается на произвольную группу Ли. Для простейших групп Ли построена система когерентных состояний и исследованы ее особенности.

…читать дальшечитать меньше

1 123 цитирования

Представление групп Ли и специальные функции

[…]

А. Ю. Климык, Н.Я. Виленкин

01 января 1991 г.

Аннотация: Сначала в математическом анализе изучались только элементарные функции. Затем были введены новые функции для вычисления интегралов. Их назвали специальными функциями: интегральный синус, логарифмы, показательная функция, интеграл вероятности и так далее. Наиболее важными оказались эллиптические интегралы. Они связаны с выпрямлением дуг определенных кривых. Замечательная идея Абеля заменить эти интегралы соответствующими обратными функциями привела к созданию теории эллиптических функций.

…read moreread less

991 citations

Collapse

Related Papers (5)

Higher Transcendental Functions