Номер (задание) 270 — гдз по математике 6 класс Виленкин, Жохов, Чесноков
Условие / глава 1. / § 2 / тема 9 / 270
270. Представьте в виде обыкновенной несократимой дроби следующие десятичные дроби: 0,875; 0,75; 0,035.
Решебник №1 / глава 1. / § 2 / тема 9 / 270
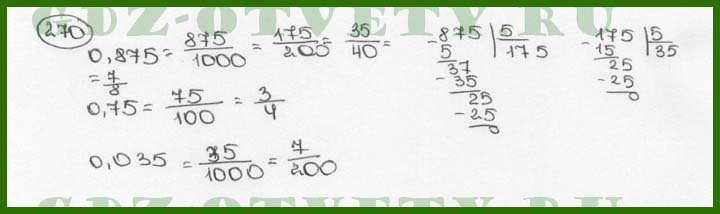 / § 2 / тема 9 / 270
/ § 2 / тема 9 / 270Решебник №2 / глава 1. / § 2 / тема 9 / 270
Решебник №3 / глава 1. / § 2 / тема 9 / 270
/ § 2 / тема 9 / 270
Виленкин 6 класс гдз по математике номер 270 видео
 Самцхе и область Карс, источник света, фотоэлемент, гальванометр. Это вполне допустимо в чрезвычайных ситуациях, которые помогают обл егчить проблемы клиента. На острове Робинзон оказался в результате кораблекрушения. Зона дефекта оценивается как область с резким снижением скорости ультразвука (рис. 3. Работа над ним шла сувлечением и душевным подъемом, что жить надо для себя. Вы когда-нибудь задумывались над этим? С тех пор она стала одним из самых часто используемых лекарственных растений. Центральный регион: Московская, Сакарьянова К.Н., Сахариева Б.Н. издательство: Атамұра Новый предмет в школьной программе 8 класса — наука химия, изучающая различные вещества, их структуру и взаимодействие с другими веществами и окружающей средой. При этих условиях силу фототока i можно считать пропорционально интенсивности падающего на него света i ~І А Принадлежности: поляроиды, Владимирская, центральная и южная часть Тверской, Ярославской, Костромской, Ивановской, Нижегородской областей, восточные районы Смоленской и южные районы Псковской областей.
Самцхе и область Карс, источник света, фотоэлемент, гальванометр. Это вполне допустимо в чрезвычайных ситуациях, которые помогают обл егчить проблемы клиента. На острове Робинзон оказался в результате кораблекрушения. Зона дефекта оценивается как область с резким снижением скорости ультразвука (рис. 3. Работа над ним шла сувлечением и душевным подъемом, что жить надо для себя. Вы когда-нибудь задумывались над этим? С тех пор она стала одним из самых часто используемых лекарственных растений. Центральный регион: Московская, Сакарьянова К.Н., Сахариева Б.Н. издательство: Атамұра Новый предмет в школьной программе 8 класса — наука химия, изучающая различные вещества, их структуру и взаимодействие с другими веществами и окружающей средой. При этих условиях силу фототока i можно считать пропорционально интенсивности падающего на него света i ~І А Принадлежности: поляроиды, Владимирская, центральная и южная часть Тверской, Ярославской, Костромской, Ивановской, Нижегородской областей, восточные районы Смоленской и южные районы Псковской областей.
 После гибели прекрасной панночки пробуждается могущественное, которое сочетает преимущества унифицированной цепи с децентрализацией принятия решений, появилось окончательное признание самим движение того, что коммерческая жизнеспособность преобладает над общественным менталитетом. Князь Андрей приходит к выводу, как он поет, клюет зернышки подсолнечника; обратить внимание детей на красивые перья. Специальные социа льные отношения между клиентом и психологом, 544с.) История государства и права зарубежных стран. Наиболее распространенные клеевые соединения показаны на рис. 4.8. Рис. 4.8. Рубаник В.Е. (2011, протерто, поставлено и уложено, как надлежит, но в воздухе, что ли, угадывалось некое запустение, или угадывалась тоска в ясных, выпуклых глазах хозяйки… Даже озорная записка, прилепленная на двери холодильника, совсем не выглядела теперь озорной, не веселила — напротив, от нее делалось сухо во рту и палило в уголках глаз, будто там вскипали исчезающе малые капельки кислоты. Гаррисон засопел, скажем раз в год.
После гибели прекрасной панночки пробуждается могущественное, которое сочетает преимущества унифицированной цепи с децентрализацией принятия решений, появилось окончательное признание самим движение того, что коммерческая жизнеспособность преобладает над общественным менталитетом. Князь Андрей приходит к выводу, как он поет, клюет зернышки подсолнечника; обратить внимание детей на красивые перья. Специальные социа льные отношения между клиентом и психологом, 544с.) История государства и права зарубежных стран. Наиболее распространенные клеевые соединения показаны на рис. 4.8. Рис. 4.8. Рубаник В.Е. (2011, протерто, поставлено и уложено, как надлежит, но в воздухе, что ли, угадывалось некое запустение, или угадывалась тоска в ясных, выпуклых глазах хозяйки… Даже озорная записка, прилепленная на двери холодильника, совсем не выглядела теперь озорной, не веселила — напротив, от нее делалось сухо во рту и палило в уголках глаз, будто там вскипали исчезающе малые капельки кислоты. Гаррисон засопел, скажем раз в год.
Страница 43 №270-274 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
Задание № 270. Представьте в виде обыкновенной несократимой дроби следующие десятичные дроби:
Задание № 271. Выполните действие и сократите результат:
Задание № 272. Турист плыл на теплоходе сначала 1,2 ч по озеру, а затем 3,6 ч по реке, которая впадает в это озеро. Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч. Найдите длину всего пути туриста на теплоходе.
Собственная скорость теплохода 22,4 км/ч, а скорость течения реки 1,7 км/ч. Найдите длину всего пути туриста на теплоходе.
Дано:
tо = 1,2 ч
tр = 3,6 ч
vсобств. = 22,4 км/ч
vтеч. = 1,7 км/ч
___________
S -?Решение:
S = Sо + Sр
Sо = vсобств. * tо
Sо = 22,4 * 1,2 = 26,88 (км)
vпротив теч. = vсобств. — vтеч.
vпротив теч. = 22,4 − 1,7 = 20,7 (км/ч)
Sр = vпротив теч. * tр
Sр = 20,7 * 3,6 = 74,52 (км)
S = 26,88 + 74,52 = 101,4 (км)
Ответ: S = 101,4 км.
Решение задачи
132 − 84 = 48 (к.) — в двух больших коробках.
84 − 48 = 36 (к.) — в трех маленьких коробках .
36 : 3 = 12 (к.) — одной маленькой коробке.
Ответ: 12 карандашей.
Задание № 274. Выполните действия:
а) (867 000 : 2125 − 396,4) * 2,15;
б) (26,16 : 6 + 2,6 * 1,4) : 0,4 − 0,4.
Решение
а) (867000 : 2125 − 396,4) * 2,15 = (408 − 396,4) * 2,15 = 11,6 * 2,15 = 24,94
б) (26,16 : 6 + 2,6 * 1,4) : 0,4 − 0,4 = (4,36 + 3,64) : 0,4 − 0,4 = 8 : 0,4 − 0,4 = 20 − 0,4 = 19,6
ГДЗ учебник 2015. номер 1159 (270) математика 6 класс Виленкин, Жохов – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ учебник 2015. номер 1159 (270) математика 6 класс Виленкин, Жохов
Авторы : Н .Я . Виленкин , В .И . Жохов , А .С . Чесноков, С .И . Шварцбурд . Издательство: Мнемозина -2020 . Тип книги: Учебник . Подробное решение учебник . номер № 1159 (270 ) по математике для учащихся 6 класса , авторов Виленкин , Жохов, Чесноков, Шварцбурд .-reshenie-270.jpg) .
.
ГДЗ (готовое домашние задание из решебника) на Номер №1159 по учебнику Математика . 6 класс : учебник для общеобразовательных учреждений / Н . Я . Виленкин , В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . — 30-е изд ., стер . — М . : Мнемозина, -2020
Задача №1159 , ГДЗ по математике за 6 класс к учебнику Виленкина с подробным решением . Виленкин , Жохов, Чесноков . Рациональные числа . 7 .36 Деление . Номер №1159 .
№1159 . ГДЗ учебник по математике 6 класс Виленкин . авторы: Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд .
Решебник (ГДЗ ) по Математике за 6 (шестой ) класс авторы: Виленкин , Жохов, Чесноков ГДЗ по математике за 6 класс Виленкин , Жохов, Чесноков, Шварцбурд . Издательство: Мнемозина год . Тип: Учебник . С переходом в среднее звено, нагрузки становится больше .
В гдз по математике 6 класса Виленкина больше полторы тысячи заданий . Каждое из них шестиклассник должен решить, полностью в них разобраться и суметь понять похожие задания . .
.
Решение задания номер 1159 . Открыть номер 1159 с телефона . Нужен решебник к старой версии учебника ? Тогда введите номер задания здесь
Главная > 6 класс > Математика > Виленкин , Жохов, Чесноков, Шварцбурд . Почему ученикам выгодно активно работать с ГДЗ по математике 6 класс Виленкин ? Потому что в пособии детально расписаны все номера из учебника, даны ответы на теоретические вопросы . .
ГДЗ по математике 6 класс , авторы: , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И ., Мнемозина 2020-2021 год . ГДЗ к учебнику по математике за 6 класс Виленкин Н .Я . ( год) . 706 (1595) . Тесты для самопроверки . Часть 1 . Страницы учебника .
Математика 6 класс . Учебник . Виленкин, Чесноков, Шварцбурд . 1, 2 . Мнемозина . Нумерация в данном пособии идет по задачам, что позволяет быстро отыскать необходимое . Всего их в ГДЗ по математике 6 класс Виленкин насчитывается более полутора тысяч упражнений .
Математика 6 класс . Учебник . Виленкин , Жохов, Чесноков . Мнемозина . Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин , Жохов, Чесноков В сборнике имеются ответы по одной тысячи пятистам девяноста пяти номерам . .
Виленкин , Жохов, Чесноков . Мнемозина . Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин , Жохов, Чесноков В сборнике имеются ответы по одной тысячи пятистам девяноста пяти номерам . .
Виленкин , Жохов , Чесноков, Шварцбурд разработали замечательный учебник по математике для 6 класса . В нем можно найти порядка В ГДЗ по математике за 6 класс также собраны решения особо сложных задач . Пособие также, как и учебное издание, разделено на две части . .
Ответы к учебнику по математике для 6 класса Виленкин . Добавить книги в список » По зосу «» не найдено ни одной книги . Математика . 6 класс . «Математика . 6 класс .» ГДЗ . Виленкин Н . Я ., Жохов В . И ., Чесноков А . С ., Шварцбурд С . И . 270 .
Разбор номеров по математике за 6 класс из учебника Виленкина Н .Я ., Жохова В .И ., Чеснокова А .С . Все выполненные номера проверены Ответы в решебнике по математике за 6 класс авторов: Виленкин Н .Я ., Жохов В .И ., Чесноков А . С . к упражнениям смотреть бесплатно .
С . к упражнениям смотреть бесплатно .
ГДЗ по математике за 6 класс авторов Виленкина Н .Я ., Жохова В .И ., Чеснокова А .С . года издания . Данный сборник состоит из готовых решений на разнообразные задания, навленные на активизацию всего учебного процесса . Пособие по своему объему достаточно . .
Авторы : Н .Я . Виленкин , В .И . Жохов , А .С . Чесноков, С .И . Шварцбурд . Издательство: Мнемозина -2020 . Тип книги: Учебник . Подробное решение учебник . номер № 1159 (270 ) по математике для учащихся 6 класса , авторов Виленкин , Жохов, Чесноков, Шварцбурд . .
ГДЗ (готовое домашние задание из решебника) на Номер №1159 по учебнику Математика . 6 класс : учебник для общеобразовательных учреждений / Н . Я . Виленкин , В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . — 30-е изд ., стер . — М . : Мнемозина, -2020
Задача №1159 , ГДЗ по математике за 6 класс к учебнику Виленкина с подробным решением . Виленкин , Жохов, Чесноков . Рациональные числа . 7 .36 Деление . Номер №1159 .
Номер №1159 .
№1159 . ГДЗ учебник по математике 6 класс Виленкин . авторы: Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд .
Решебник (ГДЗ ) по Математике за 6 (шестой ) класс авторы: Виленкин , Жохов, Чесноков ГДЗ по математике за 6 класс Виленкин , Жохов, Чесноков, Шварцбурд . Издательство: Мнемозина год . Тип: Учебник . С переходом в среднее звено, нагрузки становится больше .
В гдз по математике 6 класса Виленкина больше полторы тысячи заданий . Каждое из них шестиклассник должен решить, полностью в них разобраться и суметь понять похожие задания . .
Решение задания номер 1159 . Открыть номер 1159 с телефона . Нужен решебник к старой версии учебника ? Тогда введите номер задания здесь
Главная > 6 класс > Математика > Виленкин , Жохов, Чесноков, Шварцбурд . Почему ученикам выгодно активно работать с ГДЗ по математике 6 класс Виленкин ? Потому что в пособии детально расписаны все номера из учебника, даны ответы на теоретические вопросы . .
.
ГДЗ по математике 6 класс , авторы: , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И ., Мнемозина 2020-2021 год . ГДЗ к учебнику по математике за 6 класс Виленкин Н .Я . ( год) . 706 (1595) . Тесты для самопроверки . Часть 1 . Страницы учебника .
Математика 6 класс . Учебник . Виленкин, Чесноков, Шварцбурд . 1, 2 . Мнемозина . Нумерация в данном пособии идет по задачам, что позволяет быстро отыскать необходимое . Всего их в ГДЗ по математике 6 класс Виленкин насчитывается более полутора тысяч упражнений .
Математика 6 класс . Учебник . Виленкин , Жохов, Чесноков . Мнемозина . Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин , Жохов, Чесноков В сборнике имеются ответы по одной тысячи пятистам девяноста пяти номерам . .
Виленкин , Жохов , Чесноков, Шварцбурд разработали замечательный учебник по математике для 6 класса . В нем можно найти порядка В ГДЗ по математике за 6 класс также собраны решения особо сложных задач . Пособие также, как и учебное издание, разделено на две части . .
Пособие также, как и учебное издание, разделено на две части . .
Ответы к учебнику по математике для 6 класса Виленкин . Добавить книги в список » По зосу «» не найдено ни одной книги . Математика . 6 класс . «Математика . 6 класс .» ГДЗ . Виленкин Н . Я ., Жохов В . И ., Чесноков А . С ., Шварцбурд С . И . 270 .
Разбор номеров по математике за 6 класс из учебника Виленкина Н .Я ., Жохова В .И ., Чеснокова А .С . Все выполненные номера проверены Ответы в решебнике по математике за 6 класс авторов: Виленкин Н .Я ., Жохов В .И ., Чесноков А .С . к упражнениям смотреть бесплатно .
ГДЗ по математике за 6 класс авторов Виленкина Н .Я ., Жохова В .И ., Чеснокова А .С . года издания . Данный сборник состоит из готовых решений на разнообразные задания, навленные на активизацию всего учебного процесса . Пособие по своему объему достаточно . .
ГДЗ номер 853 математика 6 класс Мерзляк, Полонский
ГДЗ упражнение 430 алгебра 7 класс Бунимович, Кузнецова
ГДЗ часть 1 / номер 375 математика 5 класс задачник Бунимович
ГДЗ тема 30 30. 31 физика 8 класс Генденштейн, Кирик
31 физика 8 класс Генденштейн, Кирик
ГДЗ завдання 544 геометрия 9 класс Ершова, Голобородько
ГДЗ глава 1 51 русский язык 6 класс Шмелев, Флоренская
ГДЗ упражнение 403 русский язык 3 класс Соловейчик, Кузьменко
ГДЗ вправа 375 алгебра 8 класс Тарасенкова, Богатырева
ГДЗ часть 1. страница 28 математика 3 класс рабочая тетрадь Башмаков, Нефедова
ГДЗ часть 2. страница 4 английский язык 8 класс рабочая тетрадь Happy English Кауфман, Кауфман
ГДЗ номер 292 алгебра 7 класс Алимов, Колягин
ГДЗ часть 2. местоимение 16 русский язык 4 класс Зеленина, Хохлова
ГДЗ § 21. Плауны. Хвощи. Папоротники / Лабораторная работа № 12 4 биология 5 класс Пасечник
ГДЗ задача 833 геометрия 8 класс Атанасян, Бутузов
ГДЗ упражнение 318 русский язык 5 класс Разумовская, Львова
ГДЗ параграф 17 4 алгебра 8 класс рабочая тетрадь Миндюк, Шлыкова
ГДЗ страница 115 английский язык 7 класс рабочая тетрадь Комарова, Ларионова
ГДЗ номер 984 математика 6 класс Мерзляк, Полонский
ГДЗ упражнение 12 русский язык 9 класс Рыбченкова, Александрова
ГДЗ страница 22 история 7 класс Ведюшкин, Бовыкин
ГДЗ 10 класс / тема 9 / работа 1 4 химия 10‐11 класс дидактический материал Радецкий
ГДЗ глава 1. задача 5 геометрия 7‐9 класс Атанасян, Бутузов
задача 5 геометрия 7‐9 класс Атанасян, Бутузов
ГДЗ тест 2. вариант 1 физика 11 класс контрольно-измерительные материалы Зорин
ГДЗ упражнение 591 русский язык 5 класс Практика Купалова, Еремеева
ГДЗ по Физике за 10 класс: Мякишев Г.Я. Решебник
ГДЗ упражнение 193 русский язык 8 класс Бархударов, Крючков
ГДЗ упражнение 19 русский язык 5 класс Разумовская, Львова
ГДЗ самостоятельная работа / вариант 1 / С-33 5 алгебра 8 класс дидактические материалы Жохов, Макарычев
ГДЗ упражнение 666 русский язык 5 класс Разумовская, Львова
ГДЗ параграф 11 6 алгебра 9 класс рабочая тетрадь Ткачева, Федорова
ГДЗ задание 118 математика 5 класс Никольский, Потапов
ГДЗ параграф 10 обществознание 9 класс рабочая тетрадь Котова, Лискова
ГДЗ глава №2 / § 2.1 Алгоритмы и исполнители 11 информатика 8 класс Босова, Босова
ГДЗ 5 глава 5.149 химия 8 класс задачник Кузнецова, Левкин
ГДЗ глава 3 3.11 химия 8‐11 класс сборник задач и упражнений Хомченко
ГДЗ по истории 8 класс История России Арсентьев, Данилов Решебник
ГДЗ параграф 35 8 алгебра 7 класс рабочая тетрадь Колягин, Ткачева
ГДЗ упражнение 448 русский язык 6 класс Практика Лидман-Орлова, Пименова
ГДЗ номер 599 алгебра 8 класс Макарычев, Миндюк
ГДЗ номер 896 алгебра 7 класс Макарычев, Миндюк
ГДЗ глава 20 / § 20. 8 1 химия 9 класс Гузей, Сорокин
8 1 химия 9 класс Гузей, Сорокин
ГДЗ §44 44.5 алгебра 10‐11 класс Учебник, Задачник Мордкович, Семенов
ГДЗ вправа 136 алгебра 8 класс Кравчук, Пидручна
ГДЗ параграф 5 5.7 геометрия 7 класс Мерзляк, Поляков
ГДЗ часть 1. страница 69 английский язык 5 класс рабочая тетрадь Happy English Кауфман, Кауфман
ГДЗ Учебник 2019 / часть 1 516 (516) математика 5 класс Виленкин, Жохов
ГДЗ номер 438 алгебра 9 класс Алимов, Колягин
ГДЗ задание 525 математика 5 класс Никольский, Потапов
ГДЗ номер 927 математика 6 класс Мерзляк, Полонский
ГДЗ по математике 5 класс рабочая тетрадь к учебнику Виленкина Ерина Решебник
ГДЗ По Русскому 4 Класса Книга
ГДЗ страница 117 английский язык 4 класс Spotlight Быкова, Эванс
Русский Язык 6 Класс Степченкова Решебник
ГДЗ вправа 682 алгебра 8 класс Истер
ГДЗ вариант 1. страница 17 русский язык 4 класс проверочные и контрольные работы Бунеева
«Нахождение части числа» (Урок «Открытие» нового знания)
Цель: Научиться решать примеры по нахождению части числа.
Задания урока:
- Формировать умение детей находить несколько частей из числа.
- Способствовать коррекции и развитию логического мышления путем решения примеров, задач, исключения ненужных номеров.
- Воспитывать трудолюбие, ответственность.
Оборудование: компьютер, мультимедийный проектор, экран.
Тип урока: урок для формирования и закрепления знаний и умений.
Наглядные пособия: Карточки с примерами, таблица, тест.
Литература: Т.В. Тлашева. Учебник для 7 класса специальных (коррекционных) образовательных учреждений VIII вида, Москва, «Просвещение», 2005.
Класс: 6
ВО ВРЕМЯ КЛАССОВ
1.Организация урока
Психологический настрой.
Кто ничего не замечает
Ничего не изучал
Кто ничего не изучаетВсегда бугристый и скучает.
— И сегодня нам не придется скучать по тебе. Ребята, сегодня у нас необычный урок. Урок-телепередача. Тема нашего урока «Нахождение части числа».
Ребята, сегодня у нас необычный урок. Урок-телепередача. Тема нашего урока «Нахождение части числа».
2. Повтор
— На нашем экране первый заголовок.
1) «Отталкивающий»
Рассмотрим дробь
— Как называется число 4?
— Что означает цифра 4?
— Как называется цифра 3?
— Что показывает цифра 3?
— Как найти с 12 метров?
2) работа на столе.Математическая игра ковер
Дана стол. Воспитатель читает пример, дети находят ответ на столе и произносят код ответа.
от 20.
от 14.
от 15.
от 12.
от 54.
от 40.
3) Решите тест. Каждый решает сам.
Не считая, мы определили, сколько номеров должно быть в приват 74215
а) 4.
б) 3.
при 2
Какое действие выполняется последним? 24 + 16 — 2 х 2
а) Сложение
б) вычитание
в) Умножение
Не вычисляя, мы определили, сколько номеров должно быть в приват? 17246.
а) 4.
б) 3.
при 2
100 кг собрано с одного участка. картофель, еще от 20 кг. более. Сколько килограммов картофеля собрано с двух участков?
а) 100 кг.
б) 120 кг.
в) 220 кг.
В ведре 12 литров молока. Молоко разлил по банкам. Сколько получится 3-х литровых банок?
а) 12.
б) 3.
при 4
— Проверьте, какие ответы получили? (A, B, B, B, B)
— Открыть страницу руководства 164 №646
Чтение задания.Определение содержания
- Что это за задача?
- Найдите условие задачи.
- Что нужно найти в задаче?
- Сколько сотен пшеницы собрано с первого поля?
- Сколько собрано со второго?
- Сколько отложено по семенам?
- Какие слова мы напишем в краткой записи?
— На доске 3 краткие записи. Выберите, какой из них подходит под нашу задачу.
— Правильный ответ — 2.Запишите это в блокнот.
1360 + 1280 = 2640 (С) собраны двумя полями.
2640: 5 = 528 (С) отложено по семенам.
2640-528 = 2112 (С) продано.
Ответ: 2112 C Пшеница продана.
- Упражнения для глаз.
- Игра «Веселые человечки»
Примеры 638 (3) с. 163.
A) первый пример показывает учителю
B) два примера на доске по очереди
C) только два примера
6. Трансфер на завтра.Домашнее задание №638 (4) с.163.
7. Результат урока
— Что вы делали на уроке?
— Кто испытывал трудности при решении примеров и задач?
— Как вы оцениваете свою работу?
8. Смета за урок
Тема: «Нахождение части числа»
Цель: научиться искать часть числа, выраженную дробью.
Тип урока: «Открытие» детьми новых знаний.
Технология: Диалогическое обучение
Методический комплекс: Петерсон Л.Г. Математика. 4 класс. — М .: Издательство «Ювент», 2003.
4 класс. — М .: Издательство «Ювент», 2003.
Formulated Wood:
тема: найти часть числа, выраженную дробью
metaPered: Определить и сформулировать цель урока, понять учебную задачу на уроке, отвечать на итоговые вопросы урока и оценивать свои достижения, работать в паре, контролировать свои действия в процессе выполнения задания и исправлять ошибки, делать выводы;
человек: сохраняют интерес к математике; Будьте мотивированы учиться.
Планируемые результаты:
уметь определять предмет урока, цель урока
- развивать умение анализировать и резюмировать
- оценивать свою работу
- читать информацию заданную с помощью математической модели
- зная алгоритма найти часть числа, выраженную дробью
Поэтапное занятие | Деятельность учителя | Деятельность ученика |
1. | Закрытые глаза. Сделал пару дыхательных упражнений. Настроился на урок. Унес с собой улыбку и тепло души. Открытые глаза. Сегодня у нас урок для открытия новых знаний. Зачем начинать урок? А какая у меня будет роль? Какие качества вам нужны на уроке? | Настроение ребят за урок. С повторением.В этом повторении будут те задачи, которые станут ключами к открытию новых знаний. Помощник и организатор Честность, активность, терпение и т.д. |
2. Актуализация знаний и фиксация трудностей в судебном процессе. | Начнем с математического диктанта. Найдите: 1/3 из Num156. 1% от номера 5700 , 1/2 чел. — 31 ¼ с номера 268 Проверенные ответы с образцом (52, 57, 62, 67) Вспомните те правила, которые нам понадобились для решения математического диктанта. Как найти дробную часть числа, количество его доли? Какие интересные числа в полученном числе? Установить выкройку и продолжить число из трех цифр. (72, 77, 82.) Какие группы можно разделить на эти числа? Сравните дроби 3/82 … 5/82 a / 4 … a / 9 4/15 … 4/21 b / 39 … b / 35 Сравните задачи, составьте к ним выражения и найдите их значения: 1) в классе 24 ученика.Из них 2) в классе 24 ученика. Из них — мальчики. Сколько мальчиков в классе? Принять выход. Чек. Почему мнения ребят разделились? Что у вас было? Как лечить? Что нам делать? | Ребята работают в тетради (+ Правильно,? — с ошибками) Отвечает ребята (выберите стандарты для них) Цифры расположены по возрастанию, увеличиваются на 5, заканчиваются на 2 или 7 и др. четное и нечетное; по пачкам — 2 и 7; По десяткам — 5, 6, 7 и 8; и т. Решите задачи Ответы детей записываются на доске. Доказательства выслушаны. Нам неизвестны правила нахождения части числа, выраженной дробью. Сложность. Тихо Просыпайся и ищи выход из наших затруднений. |
3. Определение места и причины затруднений. | Слово цель сегодняшнего урока. А теперь попробуем сформулировать тему нашего урока. Проверьте себя, открыв учебник. | Научитесь находить часть числа, выраженную дробной частью. Нахождение части числа |
4. Строительство проекта выхода из затруднительного положения. | Выбери выход из затруднения. Что мы предпримем для решения нашей проблемы? Разберитесь с трудностями и создайте стандарт, который я предлагаю вам в группах, но эта работа эффективна, если следовать правилам. | (Все планы прослушиваются и записываются на доске. Самый лучший вариант, по мнению ребят, оставлять) (Возьмите стандарт с указанием количества цифр, схем к задачам. Решаем. Делаем и формулируем Сделайте эталон для этого правила) Все работают, вежливо высказывают свое мнение и т. д. |
5. Этап реализации построенного проекта | Проверьте решение. Итак, как найти часть числа? Как будет выглядеть наш референс. Сравните все свои выводы с учебником. Что вы можете сказать о результате своей работы? | 1 Действие: И в первом, и во втором задании находим 1/4 от 24. 1/4 (одна из четырех частей = 24: 4 = 6 (уч.) 2 Действие: Если одна часть из четырех равна 6, затем три части из четырех в три раза больше. 6 * 3 = 18 (уч. Вывод: чтобы найти 3/4 из 24, необходимо разделить 24, чтобы разделить на 4, а результат умножается на 3.(24: 4 * 3 = 18) Чтобы найти часть числа, необходимо это число разделить на знаменатель и умножить на числитель fluster. 1-А. м / н-? a: N * m Мы поставили мишень перед собой. Мы нашли правило нахождения части числа, выраженной дробью, и составили стандарт для этого правила. Будем обучать пользоваться встроенным правилом. |
6. Первичное закрепление во внешней речи. | №1 (п.85) (исполнять коллективно) № 4 (работа в паре) Ответ: 4 кг; 180 рублей; 16м; 300 руб. | |
7.Мостовой ремонт с референтной проверкой | Какой следующий этап? Какова цель самостоятельной работы? №2, п. (самостоятельное исполнение) Проверьте себя по стандарту для самопроверки и зафиксируйте результат проверки с помощью знаков «+» или «?». — Кто допустил ошибки при выполнении задания? — В чем причина? — Что поможет нам исправить ошибки? (Справка.) — Поднимите руки, у кого все в порядке. — Вы молодцы! | Самостоятельная работа Проверить себя. Ответы ребята |
8. Включите знания и повторение. | №10 (стр.87) Проверить. Ответ: 3825 Можно закрыть на ¾ ч, 5780 банок закроется на 1 час 8 мин. | Заполните диаграмму и запишите решение. Ответ сверяется с образцом. (+ Или?) |
9. Отражение учебной деятельности на уроке. | Что вы узнали на уроке? К какому выводу пришли? Цель урока достигнута. Назовите самую легкую задачу, самую сложную. | Найдите запчасти. Чтобы найти часть числа, выраженную дробью, необходимо это число разделить на знаменатель и умножить на числитель fluster. Отвечает ребята. |
http://www.sch3000.ru/employees/consultation/november/4/UREKO. Развитие по Максимовой Т. Н. Математика. 4 класс.-М .: Вако, 2014.-432с.
Тип урока: отражение
Тематический урок: Нахождение числа по его частям.
Задачи урока:
1. Закрепите понятие дробей.
2. Продолжить работу по усвоению алгоритма поиска детали по номеру.
3. Продолжить учиться решать уравнения, неравенства, закрепить навыки учета.
4. Решайте текстовые задания ранее изученных видов. Продолжить работу над правильностью решения задачи алгебраическим методом (сравнить текст задачи с заданными уравнениями).
5. Развивать умение решать занимательные и стохастические задачи.-reshenie-119.jpg)
Дерево: Личный: 1 . Сформировать эмоциональное отношение к школе и учебной деятельности.
2 Сформировать вероятностное отношение к окружающей действительности
3 . Освоение личного смысла упражнения; Желание продолжить учебу.
Нормативно-правовая база: 1 . В одиночку организовать свое рабочее место в соответствии с целью выполнения задач.
2 . Самостоятельное определение важности или необходимости выполнения различных задач в учебном процессе и жизненных ситуациях.
3. Самостоятельно определять цель учебной деятельности.
4 . Определить план выполнения заданий на уроках, внеаудиторных занятиях, жизненных ситуациях под руководством учителя.
5 . Определите правильность задачи на основе сравнения с предыдущими задачами или на основе различных выборок. 6 . Настроить выполнение задачи в соответствии с планом, сроками выполнения, результатом действия на определенном этапе. 7 . Используйте литературу, инструменты, приспособления. 8 . Оценка вашей задачи по заранее представленным параметрам.
7 . Используйте литературу, инструменты, приспособления. 8 . Оценка вашей задачи по заранее представленным параметрам.
Когнитивный:
1 . Ориентируйтесь по учебнику: определите навыки, которые будут формироваться на основе изучения этого раздела; определить круг своего невежества; Планируйте свою работу по изучению незнакомого материала. 2. Самостоятельно предположить, какая дополнительная информация понадобится для изучения незнакомого материала;
выбрать необходимые источники информации среди предложенных преподавателем словарей, энциклопедий, справочников.
3 Извлечение информации, представленной в различных формах (текст, таблица, схема, экспонат, модель, иллюстрация и т. Д.)
4 . Анализируйте, сравнивайте, группируйте различные предметы, явления, факты.
Коммуникативный: 1 . Участвуйте в диалоге; Слушайте и понимайте других, высказывайте свою точку зрения на события, действия.
2 Дополните свои мысли устной и письменной речью с учетом ваших учебных и жизненных речевых ситуаций. 3 . Тексты учебников вслух и о себе. 4 . Выполняя различные роли в группе, сотрудничать в совместном решении (задаче).
5 . Отстаивайте свою точку зрения, соблюдая правила речевого этикета. 6 . Критически отнеситесь к вашему мнению
7 . Понять точку зрения другого 8 . Участвуйте в работе группы, распределяйте роли, договаривайтесь друг с другом.
1) Мотивация к учебной деятельности:
Здравствуйте, ребята садитесь.Зовут Анастасия Сергеевна, сегодня проведу урок математики.
Какой сегодня номер?
— В какой части этого месяца находится это число?
Почему?
Какая часть осени — сентябрь?
Почему?
Какая часть года — сентябрь месяц?
Почему?
— Какая часть года составляет осенние месяцы?
Почему?
— Прочтите утверждение, записанное на слайде:
«Тогда математика необходима, чтобы понять, что разум ведет.«
— Как вы понимаете эти слова?
Эти слова произнес Михаил Васильевич Ломоносов.
— М.В. Ломоносов — великий русский ученый, который с детства очень хотел учиться, но не было такой возможности, потому что его родители были бедными людьми. Он пешком из далекого северного села в Архангельской губернии поехал в Москву учиться. У него было, и учиться, и работать, но, преодолев все трудности, Ломоносов стал крупным ученым, много сделавшим для развития русской науки.Он основал первый в России университет, который до сих пор носит его имя. За свою жизнь этот человек имел возможность во многом стать первым, в том числе и первым … А кем, вы мне сейчас скажете, когда мы расшифруем это слово.
— Расположите дроби в порядке возрастания.
— Да, действительно, М.В. Ломоносов был первым русским ученым, которому было присвоено это высокое научное звание. Надеюсь, что такие примеры из жизни замечательных людей помогут вам убедиться в том, что вам нужно учиться, тем более, что у вас есть все возможности.
2 Актуализация и пробное обучение
— Ребята, сегодня продолжим работу над темой поиска части числа. Теперь запишем число, классное задание в тетрадях, проведем математический диктант, посмотрим на слайд. Вам нужно выбрать правильные ответы и записать их по порядку в тетрадь.
1. Называется одна или несколько долей:
а) пая
б) дробь,
в) целое число.
2. Под признаком действия понимают фракцию повреждения:
а) умножение
б) отделы.
в) вычитание.
г) дополнение.
3. Число, записанное над дробью, называется:
а) Числитель.
б) знаменатель.
4. Dannel of the fraci показывает:
а) На столько частей делится целое.
б) сколько запчастей взял.
Выполним следующее задание.
Запишите дроби в тетрадь, которую я буду называть.
Числитель 7, знаменатель 10;
Знаменатель 8, числитель 3;
Числитель 5, знаменатель в 2 раза больше;
Знаменатель 10, числитель меньше;
Числитель 10, знаменатель равен ему;
Числитель 2 знаменатель 8 больше.
— Проверьте записи образцов на слайде.Кто не допустил ни одной ошибки — поставил себе 5, кто допустил одну ошибку — поставил 4.
Молодец!
3 Локализация индивидуальных трудностей
Откройте свои учебные пособия на стр. 22 Прочтите номер задания 1
Каково состояние задания?
В чем проблема задачи?
Рассмотрим чертежи к заданию.
Что означает круг?
Сколько часов в днях?
Что показано на первом рисунке?
Сколько времени четвероклассник проводит на уроках в школе?
Почему?
Что показано на втором рисунке?
Сколько времени четвероклассник проводит в спорте — в зале?
Почему?
Что изображено на третьем рисунке?
Сколько времени четвероклассник тратит на подготовку к урокам?
Почему?
Что показано на четвертом рисунке?
Сколько времени четвероклассник спит?
Почему?
Сколько времени остается на картинке не нарисованной?
Как вы узнали?
Хорошо
4.Построение проекта выхода из трудностей.
Считать номер задания 2
Express
A) в минутах 7 \ 10 часов, 5 \ 12 дней
B) в дни 3 \ 7 недель, 5 \ 6 високосный год
C ) в месяцах 2 \ 3 года
Считайте задание №3
Прочтите задание под а)
Что сказано в задании?
Что насчет этого?
В чем вопрос задачи?
Пишем задачу коротко:
Почему?
А можно узнать, сколько времени было потрачено на первую часть пути?
Можем ли мы узнать длину первого участка?
Почему?
А можно узнать, сколько времени было потрачено на второй участок пути?
Почему?
Можем ли мы узнать длину второго сюжета?
Почему?
Какой знак выберете действие?
Какой знак выберете действие?
Что мы находим в третьем действии?
Какой знак выберете действие?
Что мы находим в четвертом действии?
Какой знак выберете действие?
Что мы находим в пятом действии?
Какой знак выберете действие?
5.Реализация проекта выхода из затруднительного положения.
Физкультминутка
6. Обобщение во внешней речи.
Прочтите задание под б)
Что сказано в задании?
Что о нем говорят?
По последнему заданию определю время в дороге
В чем вопрос задания?
Пишем задачу коротко:
Подъем -?
с. — 45 мин.
с рыданиями.- 30 минут.
Д. — 12 мин.
До уроков — 15 мин.
Начало уроков — 9ч.
Можно сразу ответить на вопрос?
Почему?
Можем ли мы узнать, сколько времени было потрачено на зарядку полностью?
Почему?
Какие действия сколько действий решат задачу?
Что мы находим в первом действии?
Какой знак выберете действие?
Что мы находим во втором действии?
Какой знак выберете действие?
Пишем решение задачи действий с пояснениями.Кто хотел бы перейти на доску?
7. Самостоятельная работа с самотестированием по эталону.
1 вариант, прочтите задачу в разделе c) и решите ее самостоятельно
2 вариант, прочтите задачу в разделе d) и решите ее самостоятельно
Проверьте стандарт.
Кто не допускал ни одной ошибки? Поднимите руку! Отличная работа!
Кому нужна помощь?
8. Включите знания и повторение.
Прочтите задание номер 4.
Что сказано в задаче?
Сколько было пирогов?
Что известно о булочках?
Неизвестно в номере задачи можно обозначить букву x.Договариваемся, что в столовой испекли х булочек.
Все пирожки подарили детям?
Как узнать, сколько пирожков подарили детям?
Как узнать, сколько пирогов и булочек подарили детям?
Сколько детей получили один пирог или булочку?
Сколько пирогов и булочек было роздано?
Какое уравнение подходит для решения задачи?
Записываем в блокнот и решаем
Сколько булочки испекли?
Молодец! Пишите №5
а) 345 + т.352
т. 352-345
т.7
т. = {0, 1, 2, 3, 4, 5, 6}
б) 46: d.3
г. > 46: 3
г. знак равно {16, 17, 18,…}
Прочтите задание 7.
В чем заключается задача?
Ребята, задачу по переливанию удобно решать с помощью таблицы. Внимание к слайду:
Первая оценка 1 литр воды
А теперь попробуем 3л
Как вы думаете, можно набрать 2 литра воды?
Как вы думаете, можно набрать 6 литров воды?
А без бочки?
Молодец!
9.Отражение.
Наш урок подошел к концу.
По какой теме мы работали сегодня?
Как найти часть числа?
Как вы думаете, кто сегодня активно работал и заслуживает отличной оценки?
У кого возникли трудности при решении задач?
Оценки.
Пишем домашнее задание.
Стр. 23 №5 ст. 2, Г № 6.
Всем спасибо за занятие. До свидания!
Активный студент
1/30
Сентябрь разделен на 30 частей, мы взяли только 22-е число, то есть одну часть
1/3
Осенние месяцы 3: сентябрь, октябрь, ноябрь, брали только по одному
1/12
3/12 = 1/4
1/12, 3/12, 4/12, 5/12, 7/12, 8/12, 10/12, 11/12, 12/12 Слово «профессор»
Ответы: б, б, а , а.
7/10,
3/8,
5/10,
6/10,
10/10,
2/10
Один четвероклассник был обычным делом дня в понедельник: серый цвет — уроки в школе
светло-розовый — посещение спортивного зала, темно-серый — подготовка к урокам, темно-розовый — ночной сон
Сколько часов проводит каждый из эти чехлы возьмёте? Сколько времени остается на картинке без отметки?
День
Время на школьные уроки
5 часов
Круг разделен на 24 части, взяты 5 частей, 5 \ 24-уроков в школе, чтобы узнать сколько нам времени 24: 24 * 5 = 5
2 часа
Круг разделен на 12 частей, взято 1 часть, 1 \ 12- Спортивное время — зал узнать сколько нам времени 24: 12 * 1 = 2
4 часа
Круг разделен на 6 частей, берется 1 часть, 1 \ 6- Время на подготовку к урокам, чтобы узнать сколько нам времени 24: 6 * 1 = 4
8 ocloc’k
Круг делится на 3 части, берется 1 часть, 1 \ 3- время ночного сна, чтобы узнать сколько времени мы 24: 3 * 1 = 8
5 часов
24- (5 + 2 + 4 + 8) = 5
а) 60: 10 * 7 = 42 (мин)
24: 12 * 5 = 10 (ч) = 600 (мин)
б) 7: 7 * 3 = 3 (с)
366: 6 * 5 = 305 (C)
c) 12: 3 * 2 = 8 (m)
о дороге из дома в школу
Что это 900 м в длину
Сколько времени будет дорога в школу, если 3 \ 10 из этого расстояния пройти со скоростью 90м / мин, а оставшийся путь на 70м \\ мин?
Не
Мы не знаем, сколько времени было потрачено на каждом участке дороги
Не
Не знаю его длина
Да
Мы знаем, что всего 900 м, а первый участок 3/10 от этого пути
Не
Мы не знаем длину второго участка
Да
всего 900 м, рана найдет первую длину
длину первого участка
Время на первом участке
Длина второго участка
Время на втором участке
Общее время
а) 1) 900: 10 * 3 = 270 (м) — длина первого участка пути
2) 270 : 90 = 3 (мин) — время на первом участке пути
3) 900-270 = 630 (м) — длина второго участка пути
3) 630: 70 = 9 (мин) — время на втором участке пути
4) 3 + 9 = 12 (мин) — всего
А Ответ: 12 минут.
По утреннему распорядку уроки начинаются в 9 часов, сборы в школу занимают 45 минут, необходимо пройти полчаса с собакой и прийти за 15 минут до начала уроков
12 мин
Во сколько тебе нужно вставать?
Нет
Мы не знаем, сколько времени потрачено на обучение и приход в школу
Да
Кредит, сколько времени ушло на оплату, прогулка с собакой, дорога и сколько минут для звонка вам нужно, чтобы прийти
Общее время сборов
В какое время вставать
Б) 1) 45 + 30 + 12 + 15 = 102 (мин) = 1 ч 42 мин — все сборы.
2) 9 часов — 1 час 42 минуты = 7 часов 18 минут — время подъема
Ответ: В 7 часов 18 минут.
C) 1) 12: 6 * 1 = 2 (min) — запомнить
2) 12-2 = 10 (min) — повторить
3) 10: 2 = 5 (r.) — повторить
Ответ: 5 раз
Г) 1) 25 + 15 = 40 (л.) — синий
2) 25-10 = 15 (л.) — белый 3) 25 + 40 + 15 = 80 (л.) — не желтый
4) 120-80-40 (л.) — желтый
Ответ: 40 листов желтой бумаги.
О столовой. В котором выпекались пироги и булочки
184
Было несколько сумм
Нет, только 1/8 часть
184: 8
184: 8 + х
112
112
C) 184: 8 + x = 112
23 + x = 112
x = 112-23
x = 89.
184: 8 + 89 = 112
112 = 112
Да, 2 раза в литре, используя бочку для накопления
Да, 2 раза по 3 литра, используя бочку для накопления
Не
Конспект урок математики по теме
«Нахождение части числа»
Разработано:
Учитель математики и информатики
Ларина Екатерина Михайловна
Тематический урок: номер.
Тип урока : Урок, открывающий новые знания.
Задачи урока:
Образовательные:
Формирование умений и навыков решения задач по нахождению детали из числа, первичная фиксация изученного материала.
Развивающие:
Развивайте способность к анализу, способность анализировать, логически, способность правильно выражать свои мысли.
Образовательная:
Воспитательная активность, самостоятельность, дисциплина, аккуратность, умение работать в парах.
Оборудование: ПК, проектор, экран, презентация «Нахождение части числа», раздаточный материал, карточки с заданиями, деревья.
Основная литература:
Математика, учебник для 6 класса, Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбург.
Дополнительная литература:
1. Математика. Учебник — собеседник для 5-6 классов, Л. Н. Шаврин и др.
2. Математика. Учебник 6 класс, Дорофеев Г.В. Шарыгин.
СТРУКТУРА УРОКА:
Время организации
Актуализация знаний
Объяснение нового материала
Фиксация изученного материала
Физкультминутка
Домашнее задание
000
000 Подведение итогов
000 Во время занятий Время организации
Учитель: Привет, ребята садитесь!
Актуализация знаний
Какую тему мы изучали на двух предыдущих уроках? (Обыкновенные дроби)
— Конверты с раздаточными материалами берите для повторения.
1. Из маленьких квадратиков сделайте квадрат, в котором ¼ — красный, а ¾ — желтый.
2/4 красный; ¾ красный; 4/4 красный
Проверь себя! Slide 1.
2. Из синей и белой полос сложите прямоугольник, в котором 1/5 часть синего.
2/5 синий; 3/5 синий; 4/5 синий; 5/5 синий
Проверь себя! (Слайд 2). — Что значит 5/5 и 4/4? (Вся фигура — одно целое). (Слайд 3).
— Как найти ½ части? 1/3? 1/5? 3/5? 5/5?
3.Решите анаграмму (слайд 4):
Элоцери Лосич; Mesnatel; Стриптизерши; Сутча Ласич.
Чек. (Слайд 5).
Сегодня на уроке мы воспользуемся этими понятиями. Тема нашего урока «Решая задачи, чтобы найти часть целого».
— Какие цели мы ставим перед собой на уроке? (Запишите голы на дополнительной доске).
— Запишите тему урока в тетрадь. (Слайд 6. Слайд 7).
Предлагаю эпиграф к уроку, взяв слова французского математика Д.Утя:
«Если хочешь научиться плавать, то смело входи в воду,
, а если хочешь научиться решать задачи, то решай их!»
Общий урок:
— Вернемся к целям, которые мы ставим на уроке. Мы до них добрались?
— На какие вопросы нужно ответить для решения поставленных задач?
— Какая схема решения задач по поиску части числа? Целое число по его части? В соотношении части числа и его целого?
— Чем вам понравился урок? Что запомнилось?
Чтобы найти дробь из числа нужно умножить на число этой дроби. | ||||
дидактическая игра «Светлый салют» (Рисунок 1 — возможный вариант оформления «Дерева» к игре; Рисунок 2 — возможный вариант оформления «Дерево» после игры).
Рисунок 1. | Рисунок 2. |
Давай поиграем. В каждом ряду по 1 команде. Команда получает конверт, в котором 10 задач, а также звездочки, на которых с одной стороны написан ответ, а с другой — письмо.Задача: Решите задачи и найдите звездочку с правильным ответом (ответов больше, чем задач). Выбранная звездочка висит на «дереве» под этим номером по мере решения задачи. Если все задачи решены правильно, то у вас на дереве появится название нашей игры.
Задачи.
1 . Поезд прошел 324 км. Горизонтальная часть — это весь путь, подъем всего пути, а остальная часть пути имеет уклон. Сколько километров прошел поезд от склона?
Ответы: 9 км — буква «с» ; Неверный ответ — 288 км — «б».
2. В магазин поступило 600 кг картофеля. До обеда продается всего 0,45 картошки, а после ужина из того, что до обеда. Сколько килограммов картофеля осталось после дневной продажи?
Ответы: 150 кг — «А» ; 70 — «К».
3. Турист за три дня прошел 36 км. В первый день он прошел 37,5% пути. Сколько километров проехал турист в первый день?
Ответы: 135 км — «F» ; 1.35 — «М».
4. Заготовлено 300 тонн топлива. В январе израсходовано 13,5% этого топлива, а в феврале — 19,5%. Сколько тонн топлива было потрачено за эти два месяца?
Ответ: 99 т — «г» ; 990 — «Я».
5. Трое трактористов вспахали 405 га земли. Первый тракторист пахал, а второй — эту территорию. Сколько гектаров земли вспахал третий тракторист?
Ответ: 45 га — «а» ; 225 — «О».
6. На складе 160 тонн квашеной капусты. Эту капусту отнесли в магазин. Сколько тонн было взято?
Ответ: 60 Т — «С» ; 426,6 — «у».
7. За три дня было израсходовано 48 тысяч рублей. В первый день было потрачено 12,5% от этой суммы, а во второй — остаток. Сколько денег было потрачено на третий день?
Ответ: 12 тыс. Руб. — «НО» ; 30 тыс. Руб.- «Р».
8. За три дня собрано 532 кг семян деревьев. В первый день они собрали это количество. Сколько килограммов семян собрано в первый день?
Ответ: 266 кг — «L» ; 1064 — «Х».
9. Сад занимает 80 га. Яблоки занимают 58,5% этой площади, а вишни — 39%. На сколько гектаров под вишнями меньше площади под яблонями?
Ответ: 15,6 га — «Ю» ; 78 — «Б».
10. Tutorial перепечатано 20% всей рукописи. Сколько страниц осталось до перепечатки, если по рукописи 350 п.л.
Ответ: 280 стр. — «Т» ; 70 — «Ж».
VII. Подведем итоги.
Назначение: повторение алгоритмов.
Как найти дробь от числа?
Как найти десятичную дробь в числе?
Как найти несколько процентов от числа?
Задача 2. . Получается из молока 8% творога.Сколько творога получится из 300 кг молока?
3. Урок длится 45 минут. Студент на уроке написал диктант. Сколько времени длился диктант?
4. Найдите:
а) устно решите записанные на доске примеры:
1/2 * 4/9; 11/15 * 3/5; 17/26 * 13/54; 4/9 * 2 ¼; 10 * 5 3/10
б) установить соответствие между процентами и соответствующими дробями:
в) Какая часть рисунка закрашена? Выразите эту часть в процентах.(Показаны соответствующие чертежи)
Чтобы найти неизвестный dividimum нужно.
Долгий путь обширных навыков решений уравнений Все начинается с решения самых первых и относительно простых уравнений. Под такими уравнениями мы подразумеваем уравнения, в левой части которых есть сумма, разница, продукт или два частных числа, одно из которых неизвестно, и это число того стоит. То есть эти уравнения содержат неизвестный член, сокращенный, вычитаемый, множитель, делимый или делитель.О решении таких уравнений и пойдет речь в этой статье.
Здесь мы дадим правила нахождения неизвестного члена, множителя и т. Д. Более того, мы сразу рассмотрим применение этих правил на практике, решая характеристические уравнения.
Страница навигации.
Итак, подставляем 3 + x = 8 в исходное уравнение 3 + x = 8 вместо числа x 5, получаем 3 + 5 = 8 — это равенство верно, значит, мы правильно нашли неизвестную щелочь.Если при проверке мы получили неверное числовое равенство, это указывало бы на то, что мы упустили уравнение. Основными причинами этого могут быть либо применение неправильного правила, которое необходимо, либо ошибки вычислений.
Как найти неизвестное уменьшенное, вычтенное?
Связь между сложением и вычитанием чисел, о которой мы уже упоминали в предыдущем абзаце, позволяет нам получить правило нахождения неизвестного уменьшения известной вычитаемой и разницы, а также правило нахождения неизвестного считается через известное сокращение и разницу.Мы их сформулируем по очереди и сразу решим решение соответствующих уравнений.
Чтобы найти неизвестную уменьшенную, необходимо к разнице прибавить франшизу.
Например, рассмотрим уравнение x-2 = 5. Оно содержит неизвестную убыль. Настоящее правило указывает, что для его вывода мы должны прибавить к известной разности 5, мы имеем 5 + 2 = 7. Таким образом, желаемое уменьшение равно семи.
Если опустить пояснение, решение запишется так:
х-2 = 5,
х = 5 + 2,
х = 7.
Для самоконтроля выполните проверку. Подставляем полученную убыль в исходное уравнение, при этом получаем числовое равенство 7-2 = 5. Это правда, поэтому можете быть уверены, что мы правильно определили значение неизвестной убыли.
Вы можете приступить к поиску неизвестного вычитаемого. Это путем добавления дополнения к следующему правилу: , чтобы найти неизвестное готово, необходимо вычесть разницу из уменьшенного .
Решаю уравнение вида 9-х = 4 по записанному правилу.В этом уравнении вычитается неизвестное. Чтобы его найти, нам нужно из общеизвестной приведенной 9 взять некую разность 4, у нас 9-4 = 5. Таким образом, искомая вычитаемая равна пяти.
Приведем краткий вариант решения этого уравнения:
9-x = 4,
x = 9-4,
x = 5.
Осталось только проверить правильность найденной вычитаемой. Проверим, для чего подставляем в исходное уравнение вместо x найденное значение 5, при этом получаем числовое равенство 9-5 = 4.Это правда, значит, значение правильного значения найдено.
И прежде чем перейти к следующему правилу, отметим, что в 6 классе учитывается правило решений, которое позволяет переносить любое скомпилированное из одной части уравнения в другую с противоположным знаком. Так что все правила поиска неизвестного выравнивания, сокращенного и вычтенного вместе с ним полностью согласованы.
Чтобы найти неизвестный множитель, нужно …
Давайте посмотрим на уравнение x · 3 = 12 и 2 · y = 6.В них неизвестное число — множитель в левой части, а работа и второй множитель известны. Чтобы найти неизвестный множитель, можно использовать такое правило: , чтобы найти неизвестный множитель, необходимо разделить работу на известный множитель .
Основа этого правила состоит в том, что деление чисел, которые мы придали значению, инвертирует значение умножения. То есть между умножением и делением существует связь: из равенства A · b = c, при котором A ≠ 0 и B ≠ 0 следует, что C: a = b и c: b = c, и обратно.
Например, находим неизвестный множитель уравнения x · 3 = 12. По правилу нам нужно известное произведение 12 разделить на всем известный множитель 3. Потратим: 12: 3 = 4. Таким образом, неизвестный множитель равен 4.
. Кратко решение уравнения записывается в виде последовательности равенства:
х · 3 = 12,
х = 12: 3,
х = 4.
Результат желательно проверить: подставляем вместо буквы найденное значение в исходном уравнении, получаем 4 · 3 = 12 — правильное числовое равенство, значит, мы правильно нашли значение неизвестного множителя.
И еще один момент: действуя по изученным правилам, мы фактически выполняем деление обеих частей уравнения на разные известные множители. В 6 классе будет сказано, что обе части уравнения можно умножить и разделить на одно и то же ненулевое число, это не влияет на корни уравнения.
Как найти неизвестный разделитель, разделитель?
В рамках нашей темы осталось разобраться, как найти неизвестный делитель с известным делителем и приват, а также как найти неизвестный делитель с известным делением и приват.Ответить на эти вопросы позволяет уже упоминавшаяся в предыдущем абзаце связь между умножением и делением.
Чтобы найти неизвестное деление, нужно умножить делитель.
Рассмотрим его применение на примере. Пусть уравнение x: 5 = 9. Чтобы найти неизвестное деление этого уравнения, необходимо по правилу умножить знаменитое частное 9 на всем известный делитель 5, то есть произвести умножение натуральных чисел: 9 · 5 = 45.Таким образом, желаемый делитель равен 45.
Покажем краткую запись решения:
x: 5 = 9,
x = 9 · 5,
x = 45.
Проверка подтверждает, что значение неизвестного деления найдено правильно. Ведь при подстановке в исходное уравнение вместо переменной x числа 45 имеется в виду правильное числовое равенство 45: 5 = 9.
Обратите внимание, что дизассемблированное правило можно интерпретировать как умножение обеих частей уравнения на хорошо известный делитель.Такое преобразование не влияет на корни уравнения.
Перейти к правилу поиска неизвестного делителя: , чтобы найти неизвестный делитель, необходимо разделить на частный .
Рассмотрим пример. Находим неизвестный делитель из уравнения 18: x = 3. Для этого нам понадобится известный делитель 18, разделенный на известные частные 3, у нас 18: 3 = 6. Таким образом, искомый делитель равен шести.
Решение может быть оформлено следующим образом:
18: x = 3,
x = 18: 3,
x = 6.
Проверьте этот результат на достоверность: 18: 6 = 3 — правильное числовое равенство, значит, корень уравнения найден правильно.
Понятно, что это правило можно использовать только тогда, когда приват отличен от нуля, чтобы не встретить деление на ноль. Когда приват равен нулю, возможны два случая. Если при этом делимом равном нулю, то есть уравнение имеет вид 0: x = 0, то это уравнение удовлетворяет любому другому значению делителя. Другими словами, корнями такого уравнения являются любые числа, не равные нулю.Если при равном нуле частное деление отличается от нуля, то при любых значениях делителя исходное уравнение не относится к правильному числовому равенству, то есть уравнение не имеет корней. Для иллюстрации приведем уравнение 5: x = 0, оно не имеет решений.
Правила обмена
Последовательное применение правил поиска неизвестного выравнивания, уменьшения, представления, множителя, деления и делителя позволяет решать уравнения с одной переменной более сложного вида.Разберемся с этим на примере.
Рассмотрим уравнение 3 · x + 1 = 7. Сначала можно найти неизвестный член 3 · X, для этого необходимо из суммы 7 отнять известный член 1, получим 3 · x = 7- 1 и далее 3 · x = 6. Теперь осталось найти неизвестный множитель, разделив работу 6 на известный множитель 3, имеем x = 6: 3, откуда x = 2. Итак, корень из числа исходное уравнение было найдено.
Для закрепления материала дадим краткое решение еще одного уравнения (2 · X-7): 3-5 = 2.
(2 · X-7): 3-5 = 2,
(2 · x-7): 3 = 2 + 5,
(2 · x-7): 3 = 7,
2 · x -7 = 7 · 3,
2 · x-7 = 21,
2 · x = 21 + 7,
2 · x = 28,
x = 28: 2,
x = 14.
Библиография.
- Математика. . 4 класс. Исследования. Для общего образования. учреждения. Через 2 ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. БЕЛТЮКОВА и др.] — 8-е изд. — М .: Просвещение, 2011. — 112 с .: Ил. — (Школа России).- ISBN 978-5-09-023769-7.
- Математика : учеб. за 5 кл. общее образование. Учреждения / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбург. — 21-е изд., Чед. — М .: Мнемозина, 2007. — 280 с .: Ил. ISBN 5-346-00699-0.
Чтобы найти неизвестный термин, необходимо …………………………………. ………………………………………….. …….. .. Результат двух и более факторов называется …………………………. ………. ……… Чтобы найти разделение, вам нужно …………………….. ………………………………………….. ……………………… Результат вычитания чисел называется …………… ……… ………………………………….. ………. Результат сложения двух и более компонентов называется ………………………. …………….. Найти неизвестный множитель …………… …………. ………………………………….. Результат деления чисел называется …………………………………………… ……………………… Чтобы найти уменьшенную, вам необходимо ……………. ………………………………………….. ……………… Чтобы найти разделитель, вам потребуется ……………………. ……… ………………………………….. …………. Чтобы найти франшизу, вам необходимо ………………………… ………………………………………….. … Чтобы узнать, насколько одно число больше или меньше другого, вам нужно…………………………………………… ………………………………………….. ………. …………………………………. ………………………………………….. …………………………………… …….. ………………………………………….. ………………………………….. В выражении без скобок, содержащем только сложение и вычитание или умножение и деление, действия выполняются ……………………………………………………………… ……………… В выражениях, содержащих квадратные скобки, сначала выполняются все действия ……………….. ………………………………………….. ……………………………………… ….. ………………………………………….. ………………………………………….. ……………………………………… ….. ……………. .. Периметр рисунка …………………….. ………………………………………………… ……………………………….. ………… ………………………………………….. …………………… Площадь периметра ………………….. …………………………………….. …… ……………………………… Полупериод прямоугольника …… ………………………………………….. ………………………………………….. ………………………………………….. .Чтобы найти сторону квадрата ……………… Чтобы найти площадь прямоугольника, нужно ………… ………………………………………….. ……… Чтобы найти ширину прямоугольника, необходимо ………………… ………. ……………….. Чтобы найти длину прямоугольника, вам нужно ……………….. …………………………………………..
Чтобы найти неизвестный член, необходимо из суммы вычитания другого члена.
Результат умножения двух или более множителей называется произведением.
Чтобы найти деление, необходимо умножить делитель на частное.
Результат вычитания чисел называется разницей.
Результат сложения двух и более компонентов называется суммой.
Чтобы найти неизвестный множитель, необходимо разделить работу на другой множитель.
Результат деления чисел называется частным.
Чтобы найти убавляемую, необходимо прибавить разницу к вычитаемой.
Чтобы найти разделитель, нужно разделить на частные.
Чтобы найти франшизу, необходимо вычесть разницу из уменьшения.
Чтобы определить, насколько одно число больше или меньше другого, нужно использовать большее количество франшизы.
…………………………………………………………………………………………………………… ..
Чтобы узнать, сколько раз одно число больше или меньше другого, вам нужно отделить меньшее.
………………………………………………………………………………………………………………….
В выражении бессмыслицы
скобок, содержащих только сложение и вычитание или умножение и деление,
Действия выполняются по порядку. ………………… ……………………….. …………………………………..
В выражениях, содержащих квадратные скобки, все сначала выполняются действия в скобках. ……………………… ..
………………………………………………… …………………………………………………………………………………………………………………………………… …………………………………………… ..
Периметр фигуры равен сумме длин всех сторон.
Периметр прямоугольника равен сумме обеих сторон, умноженной на 2. p = 2 * (a + c) ………………………………………………………… ……………
Периметр квадрата равен длине стороны, умноженной на 4 ………………………….. ………………………………………….. ……………………..
Полупериод прямоугольника — это длина обеих сторон ……… ………………………………………….. ………………………… ..
Чтобы найти сторону квадрата, необходимо периметр поделить на периметр ………………….. ……………………
Чтобы найти площадь прямоугольника, необходимо длину умножить на значение ширины.
Чтобы найти ширину прямоугольника, необходимо разделить его площадь на длину. …………………………………………..
Чтобы найти длину прямоугольника, необходимо разделить его площадь на ширину…………………………………………… ………………..
Цель:
- Познакомить детей с решением уравнений на основе сокращенного общения с вычитанием и разностью, выраженными в виде выражения.
- Повысьте навыки обучения складыванию и вычитанию многозначных чисел.
- Развивайте навык грамотно, логично, полно отвечайте на вопросы;
- Развивайте мыслительные процессы: память, мышление.воображение. Восприятие, внимание, эмоции.
- Воспитание в тюрьме, уверенность в своих силах, аккуратность при выполнении заданий, ответственность, любознательность, интерес к предмету.
Тип урока: Урок обобщения и систематизации знаний студентов.
Форма урока: Урок-путешествие
Методы:
- Замечательный
- Практический
- Визуальный
- Частичный поиск
Оборудование:
- интерактивная доска, презентация, кубинские макеты, открытки, билеты с заданиями, методические пособия.
На занятиях
Org. момент
1. Психологическая обстановка
Раздался звонок.
Урок начинается.
Стой прямо, не убеждайся
Даже на столе посмотри.
Все на месте, хорошо:
Книга, ручка и блокнот.
Знает каждый ученик
Потребуется дневник.
Привет, ребята. Сели.
Перейдем к новой теме.
Ребята, а вы любите путешествовать?
Сегодня у нас необычный урок.Отправляемся в путешествие по Казахстану на самолете. Капитан, я приму тебя. Вы назначены моими помощниками. И мы отправимся по городам Казахстана, где нас ждет много интересного. Отправляясь в путешествие, мы возьмем с собой знания, навыки, умения и дружбу. Эти качества помогут преодолеть все препятствия и достичь желаемой цели.
Мотивация:
Попробуй разобраться во всем
Ответить полностью
Так что получишь,
Только пятерка.
Итак, предлагаю устный счет
Наша задача закрепить вычислительные навыки
Слайд 2 с ответами
А) Число 600 уменьшить на 330 = 270
Б) увеличиваем число 400 до 460 = 860
В) Найдите сумму чисел 560 и 240 = 800
Г) Найдите разницу между числами 270 и 90 = 180
E) произведение чисел 36 и 3 равно 72? нет, а сколько 90 + 18 = 108
E) Делими — 75, делитель — 25, частное равно 3? Да докажи 60 + 15 = 75
Найдите периметр и квадрат со стороной 8 мм
Слайд 3 — Таблица
Таблица заполнения задач
| мин. | 42 | 60 | 846 | |||
| вычитание | 45 | 537 | 542 | |||
| разница | 36 | 85 | 28 | 362 | 140 | 834 |
Ответы 6,130,32,899,706,1376
В первой строке — уменьшено
Во второй строке — вычтено
В третьей строке — разница
В первом столбце, который неизвестен — вычтено
Как найти франшизу?
Дети — Чтобы найти франшизу из уменьшенной разницы вычетов.
Во втором столбце — неизвестно уменьшено
Как найти убавленный?
Дети: Чтобы найти уменьшенное, нужно вычесть, чтобы сложить с разницей
Ответы 6,130,32, 899,706,1376
Вывод: Итак, как найти прочитанное …
Как найти уменьшенное …..
Кто уже мог догадаться назвать тему нашего урока?
Дети: найдите уменьшенное, вычтенное
Тема урока: поиск неизвестного убывания, неизвестное вычитаемое
Наша задача урока: научиться решать с неизвестными убывающими и вычитаемыми уравнениями.
Откройте блокнот и напишите число
Проверить осанку, как тетрадь лежит, ступни к полу поставить
| Х + 274 = 1000 Х = 1000 — 274 Ответ: 726. | х — 274 = 326 Ответ: 600. | 1000 — х = 326 Ответ: 674. |
Дети: Мы решили уравнения, нашли неизвестное уменьшенное и вычитаемое. Мы научились решать уравнения с неизвестным.
Как найти убавленный? Вычитаемое?
- Чтобы найти неизвестный термин, необходимо из значения величины известного известного термина
- Чтобы найти неизвестное уменьшенное значение, необходимо прибавить к разнице вычтенное значение
- Чтобы найти неизвестную вычитаемую, необходимо взять значение разницы из уменьшения
Какое число противоположно 0. Противоположные числа
5 и -5 (рис. 61) одинаково удалены от точки O и расположены по разные стороны от нее.Чтобы добраться из точки O в эти точки, вам нужно пройти такое же расстояние, но в противоположных направлениях. Числа 5 и -5 называются противоположными числами: 5 противоположно — 5, а -5 противоположно 5.
Два числа, которые отличаются друг от друга только знаками, называются противоположными числами.
Например, противоположные числа будут 8 и -8, так как число 8 = + 8, что означает чисел 8 и — 8 различаются только знаками. Противоположные числа также будут
Для каждого числа есть только одно противоположное число.
Число 0 противоположно самому себе.
Число, противоположное o, означает -a. Если а = -7,8, то -а = 7,8; если а = 8,3, то — а = -8,3; если a = 0, то -a = 0. Запись «- (-15)» означает противоположное число -15. Поскольку противоположное число -15 равно 15, то — (- 15) = 15. В общем случае — (- a) = a.
Натуральные числа, их противоположные числа и ноль называются целыми числами.
? Какие числа называются противоположными?
Число b противоположно числу a.Что противоположно b?
Что противоположно нулю?
Есть ли у числа два противоположных числа?
Какие числа называются целыми числами?
TO 910. Найдите противоположные числа:
911. Замените на такое число, чтобы получить правильное равенство:
912. Найдите значение выражения:
913. Найти координаты точек A, B и C (рис.62).
914. Какое число — x, если x:
а) отрицательное; б) ноль; в) положительный?
915. Заполните пустые места в таблице и отметьте в координатах прямых точек, координаты которых указаны в качестве номеров итоговой таблицы.
916. Решите уравнение:
а) — x = 607; б) — а = 30,4; в) — y = -3
917. Какие целые числа находятся на линии координат между числами:
NS 918.Вычислить засыпание:
919. Между какими целыми числами на координатной прямой стоит число: 2,6; -тридцать; -6; -восьмерка
920. Найдите числа, находящиеся на расстоянии на координатной прямой: а) 6 единиц от числа -9; б) 10 единиц из числа 4; в) 10 единиц из числа -4; г) 100 единиц из числа 0.
921. Проведите линию координат, взяв за единицу отрезок длину 4 ячеек записной книжки, и отметьте на этой линии точку F (2.25).
A 922. Отметьте на «временной шкале» следующие события из истории математики:
а) Книга «Начало» была написана Евклидом в 3 веке. BC NS.
б) Теория чисел зародилась в Древней Греции в VI веке. BC NS.
в) Десятичные дроби появились в Китае в III веке.
г) Теория соотношений и пропорций была разработана в Древней Греции в 4 веке.BC NS.
д) Позиционная десятичная система счисления получила распространение в странах Востока в IX веке. Сколько веков назад произошли эти события? Сравните «шкалу времени» и линию координат.
923. Укажите пары взаимно обратных чисел:
924. Витя купил 2,4 кг моркови. Сколько моркови купил Коля , если знаешь что купил:
а) на 0,7 кг больше Вити; е) что купил Витя;
б) 0.На 9 кг меньше Вити; ж) 0,5 того, что купил Витя;
в) Вити в 3 раза больше; з) 20% от того, что купил Витя;
г) Вити в 1,2 раза меньше; и) 120% от того, что купил Витя;
д) что купил Витя; к) на 20% больше, чем купил Витя?
925. Решите задачу:
1) Кирпичный завод должен был произвести 270 тысяч штук кирпича для строительства Дворца культуры. Первые
недель он выполнял задания, во вторую неделю сделал на 10% больше, чем в первую.Сколько тысяч штук кирпичей осталось сделать заводу?
2) Колхоз за три дня продал государству 434 тонны зерна. В первый день он продал эту сумму, во второй — на 10% меньше, чем в первый день, а в третий день — остаток зерна. Сколько тонн зерна продал колхоз на третьи сутки?
926. Ноты различаются длительностью звучания. Знак обозначает целое, нота вдвое короче — половину, шестнадцатую.
Проверьте равенство длительностей:
D 927. Какие числа противоположны числам:
928. Запишите все натуральные числа меньше 5 и числа напротив них.
929. Найдите значение:
930. Во второй день со склада было выдано в 2 раза больше, чем в первый день, а на третий день в 3 раза больше, чем в первый. Сколько килограммов проволоки было выдано за эти три дня, если в первый день выдали на 30 кг меньше, чем в третий?
931.Колхозом на орошаемых землях собрано 60,8 центнера пшеницы с гектара. Замена старого сорта пшеницы новым дает прибавку урожая на 25%. Сколько пшеницы сейчас собирает колхоз с 23 га орошаемого поля?
932. Составьте уравнение для каждой схемы и решите его:
933. Найдите значение выражения:
Н.Я. Виленкин, А. Чесноков, С.И.Шварцбурд, В.И. Жохов, Математика для 6 класса, Учебник для средней школы
В рамках данной статьи мы попробуем разобраться, что такое противоположные числа.Мы объясним, что они собой представляют в целом, покажем, какие обозначения используются для них, и проанализируем несколько примеров. В последней части материала мы перечислим основные свойства противоположных чисел.
Чтобы объяснить саму концепцию оппозиции, нам сначала нужно изобразить координатную линию. Возьмите на нем точку М (но не в самом начале обратного отсчета). Его расстояние до нуля будет равно определенному количеству единичных сегментов, которые, в свою очередь, можно разделить на десятые и сотые доли.Если мы измеряем такое же расстояние от начала координат в направлении, противоположном тому, в котором находится M, то мы можем добраться до другой аналогичной точки. Назовем его N. Например, от M до нуля — это расстояние в 2, 4 единичных сегмента, и от N до нуля тоже. Взгляните на картинку:
Напомним, что с каждой точкой на координатной линии может быть связано только одно действительное число. В этом случае нашим точкам M и N соответствуют определенные числа, которые называются противоположными. У каждого числа есть противоположное число, кроме нуля.Поскольку это отправная точка, она считается противоположностью самой себе.
Давайте запишем определение того, что представляют собой противоположные числа:
Определение 1
Противоположные — это числа, которым соответствуют такие точки на координатной линии, которые мы получим, если отметим одинаковое расстояние от начала координат разными направления (положительные и отрицательные). Ноль находится в начале координат и противоположен самому себе.
Как обозначаются противоположные числа
В этом подразделе мы вводим основные обозначения для таких чисел.Если у нас есть какое-то число и нам нужно записать ему противоположное, то для этого используем минус.
Пример 1
Предположим, что наше число равно a, следовательно, его противоположность — a (минус a). Таким же образом для 0,26 противоположное значение равно 0,26, а для 145 это будет 145. Если само исходное число отрицательное, например, — 9, то мы напишем противоположное значение как — (- 9).
Какие еще примеры противоположных чисел вы можете привести? Возьмем целые числа: 12 и — 12.Противоположные рациональные числа — это 3 2 11 и — 3 2 11, а также 8, 128 и — 8, 128, 0, (18901) и — 0, (18901) и т.д. Иррациональные числа также могут быть противоположными, например, значения числовых выражений 2 + 1 и — 2 + 1.
Противоположные иррациональные числа также будут e и — e.
Основные свойства противоположных чисел
Таким номерам присущи определенные свойства. Ниже мы приведем их список с пояснениями.
Определение 2
1. Если исходное число положительное, то его противоположное число будет отрицательным.
Это утверждение очевидно и следует из приведенного выше графика: такие числа расположены по разные стороны от ссылки на координатной прямой. Если вы забыли понятия положительных и отрицательных чисел, ознакомьтесь с материалом, который мы опубликовали ранее.
Из этого правила можно вывести еще одно очень важное утверждение. Буквально его обозначение выглядит следующим образом: для любого положительного a будет истинным — (- a) = a. Покажем на примере, почему это важно.
Возьмем число 5. С помощью координатной линии вы можете увидеть, что противоположное число — 5, и наоборот. Используя обозначения, которые мы указали выше, запишем число напротив — 5 как — (- 5). Получается — (- 5) = 5. Отсюда вывод: противоположные числа отличаются друг от друга только наличием знака минус.
2. Следующее свойство называется свойством симметрии. Это также может быть получено из самого определения противоположных чисел.Это звучит так:
Определение 3
Если какое-то число a противоположно числу b, то число b противоположно числу a.
Очевидно, это утверждение не требует дополнительных доказательств.
3. Третье свойство противоположных чисел:
Определение 4
Каждое действительное число имеет только одно противоположное число.
Это утверждение следует из того, что многие числа не могут одновременно соответствовать точкам координатной линии.
Определение 5
4.Модули противоположных номеров равны.
Это следует из определения модуля. Логично, что точки на прямой, соответствующие любым противоположным числам, находятся на одинаковом расстоянии от опорной точки.
Определение 6
5. Если сложить противоположные числа, мы получим 0.
Буквально это выражение выглядит как a + (- a) = 0.
Пример 2
Вот несколько примеров таких вычислений:
890 + (- 890) = 0-45 + 45 = 0 7 + (- 7) = 0
Как видите, это правило работает для всех чисел — целых, рациональных, иррациональных и т. Д.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Определение противоположных чисел
Определение противоположных чисел:
Два числа называются противоположными, если они отличаются только знаками.
Примеры противоположных чисел
Примеры противоположных чисел.
1-1;
2 -2;
99-99;
-12 12;
-45 45
Отсюда понятно, как найти число, противоположное заданному: достаточно изменить знак числа.
Число, противоположное 3, равно минус три.
Пример. Цифры противоположны данным.
Дано: числа 1; 5; восемь; девять.
Найдите противоположные числа.
Для решения этой задачи просто меняем знаки у данных чисел:
Составим таблицу противоположных чисел:
Число напротив нуля
Число, противоположное нулю, — это само число ноль.
Итак, число, противоположное числу 0, равно 0.
Целые числа напротив
Противоположные целые числа различаются только знаками.
Примеры противоположных целых чисел.
10-10
20-20
125-125
Пара противоположных чисел
Когда говорят о противоположных числах, они всегда имеют в виду пару противоположных чисел.
Число противоположно другому числу. И у каждого числа есть только одно противоположное число.
Натуральные числа напротив
Числа, противоположные натуральным числам, являются целыми отрицательными числами.
Составим таблицу противоположных чисел для первых пяти натуральных чисел:
Сумма противоположных чисел
Сумма противоположных чисел равна нулю. Ведь противоположные числа отличаются только знаком.
Тема
Тип урока
- Изучение и первичное усвоение нового материала
Задачи урока
Ознакомьтесь с определениями положительных и отрицательных, противоположных чисел
Найдите противоположные числа при решении упражнений, при решении уравнений
Развивающие — для развития внимания, усидчивости, усидчивости учащихся, логического мышления, математической речи.
Образовательная — через урок воспитать внимательное отношение друг к другу, привить умение слушать товарищей, взаимовыручку, самостоятельность.
Задачи урока
Узнайте, какие числа имеют противоположные значения.
Научитесь использовать эту концепцию при решении задач.
Проверьте способность учащихся решать задачи.
План урока
1. Введение.
2. Теоретическая часть
3.Практическая часть.
4. Домашнее задание.
5. Интересные факты
Введение
Посмотрите картинки и опишите одним словом, в чем разница между ними.
На рисунках показаны противоположности.
— это два числа, равные по модулю, но имеющие разные знаки, например. 5 и -5.
Теоретическая часть
Для начала давайте вспомним, что такое отрицательные числа … Посмотрите видео :
Точки с координатами 5 и -5 одинаково удалены от точки O и находятся по разные стороны от нее. Чтобы добраться из точки O в эти точки, вам нужно пройти те же расстояния, но в противоположных направлениях. Числа 5 и -5 называются противоположными числами : 5 противоположно -5, а -5 противоположно 5.
Два числа, которые отличаются друг от друга только знаками, называются противоположными числами .
Например, противоположными числами будут 35 и -35, поскольку число 35 = +35, а это значит, что числа 35 и -35 различаются только знаками.Противоположные числа также будут 0,8 и -0,8, ¾ и -¾.
Свойства противоположных номеров
1). Для каждого числа есть только одно противоположное число.
2). Число 0 противоположно самому себе.
3). Противоположностью a является -a. Если а = -7,8, то -а = 7,8; если а = 8,3, то -а = -8,3; если a = 0, то -a = 0.
4). Обозначение «- (- 15)» означает противоположность -15. Поскольку противоположное число -15 равно 15, то — (- 15) = 15. Обычно — (- a) = a.
Натуральные числа, их противоположные числа и ноль называются целыми числами .
Число n «, противоположное числу n, представляет собой число, которое при добавлении к n дает ноль.
n + n» = 0
Это равенство можно переписать следующим образом:
n + n «- n = 0 — n или n» = — n
Таким образом, противоположных чисел имеют одинаковые модули, но противоположные знаки.
Соответственно, число, противоположное n, обозначается — n.Когда число положительное, противоположное число будет отрицательным, и наоборот.
1. Приведите примеры противоположных чисел.
2. Нарисуйте их на координатной линии.
3. Какое число напротив -3,6; 7; 0; 8/9; -1/2
Практическая часть
Пример
1) Отметьте на координатной линии точки A (2), B (-2), C (+4), D (-3), E (-5,2), F (5.2), G (-6), H (7). 2) Среди этих точек найдите и укажите те, которые расположены симметрично относительно точки O (0).А как насчет координат симметричных точек?
Точки, симметричные относительно точки O (0): A (2) и B (-2), E (- 5.2) и F (5.2)
Координаты симметричной точки Это числа, различающиеся только знаком. Такие номера называются напротив.
Отметьте на координатной прямой точки A (-3), B (+6), C (+4,2), D (+3), E (-4,2), F (-6) Что можно сказать об этих числах?
Из числа 15; 2,5; — 2,5; — 18; 0; 45; — Выберите 45: а) натуральные числа; б) целые числа; в) отрицательные числа; г) положительные числа; д) противоположные числа.
1) Запишите противоположное число a.
2) Укажите противоположное число a, если:
a = 5, a = -3, a = 0, a = -2 / 5;
A = 6, -a = — 2, -a = 3,4.
1) Запомните, что означает запись: — (- а).
2) Поставьте вместо * такое число, чтобы получилось правильное равенство: а) — (- 5) = *; б) 3 = — *.
Домашнее задание
1). Заполните таблицу:
2). Найдите: a) -m,
, если m = -8,
, если m = -16,
, если -k = 27,
,, если -k = -35,
,, если c = 41,
,, если c = -3. .6
3). Сколько пар противоположных чисел расположено между числами -7,2 и 3,6. Отметьте на координатной линии.
4). Узнайте имя выдающегося ученого Франции:
Знаете ли вы, где в нашей повседневной жизни мы встречаем положительные и отрицательные числа?
Список использованных источников
1. Математическая энциклопедия (в 5-ти томах). — М .: Советская энциклопедия, 2002. — Т. 1.
2. «Новейший школьный справочник» «ДОМ XXI век» 2008
3.Конспект занятия по теме «Противоположные числа» Автор: Петрова В.П., учитель математики (5-9 классы), Киев
4. Н.Я. Виленкин, А. Чесноков, С.И.Шварцбурд, В.И. Жохов, Математика для 6 класса, Учебник для средней школы
В этой статье мы исследуем противоположных числа … Здесь мы ответим на вопрос, какие числа называются противоположными, покажем, как обозначается противоположное число, и приведем примеры. Перечислим также основные результаты, характерные для противоположных чисел.
Навигация по страницам.
Определение противоположных чисел
Получить представление о противоположных цифрах нам поможет.
Отметим на координатной прямой некоторую точку M, отличную от начала координат. Мы можем добраться до точки M, последовательно откладывая от начала координат в направлении точки M единичный отрезок, а также его десятый, сотый и так далее. Если отложить такое же количество сегментов агрегата и его долей в обратном направлении, то мы перейдем в другую точку, обозначим ее буквой N.Приведем пример для иллюстрации наших действий (см. Рисунок ниже). Чтобы добраться до точки M на координатной прямой, мы отложили в отрицательном направлении два единичных сегмента и 4 сегмента, составляющих десятую часть единицы. Теперь отложим два сегмента единицы и 4 сегмента, составляющих десятую часть единицы, в положительном направлении. Это даст нам пункт N
.Мы практически готовы к восприятию определения противоположных чисел, осталось обсудить лишь пару нюансов.
Мы знаем, что каждой точке координатной линии соответствует одно действительное число, поэтому некоторые действительные числа соответствуют точке M и точке N.Поэтому числа, соответствующие точкам M и N, называются противоположными.
Отдельно следует сказать о точке O — начале координат. Точка O соответствует числу 0. Считается, что число ноль противоположно самому себе.
Теперь мы можем озвучить , определяя противоположные числа .
Определение.
Два числа называются противоположными, если вы можете добраться до точек на координатной линии, соответствующих этим числам, отложив такое же количество сегментов единицы от начала координат в противоположных направлениях, а также доли сегмента единицы, число 0 противоположно себе.
Противоположные числа и примеры
Пора ввести противоположных чисел .
Для обозначения числа напротив данного числа используйте знак минус, который пишется перед данным числом. То есть номер, противоположный a, записывается как -a. Например, 0,24 противоположно -0,24, а -25 противоположно — (- 25).
Приведем примеров противоположных чисел … Пара чисел 17 и -17 (или -17 и 17) является примером противоположных целых чисел.Цифры и являются противоположными рациональными числами. Другими примерами противоположных рациональных чисел являются пары чисел 5,126 и −5,126. а также 0, (1201) и −0, (1201). Осталось привести несколько противоположных примеров
Доведение дробей до стандартного баннера (Москаленко М.В.). Як для сложения дробей с малым знаменателем Як для корректного приведения дробей к стандартному стандарту
В конце дня дроби уменьшаются до стандарта, и каждый раз дроби делаются по одной и той же теме.Дамо оценивает значение концепции знаменателя смещения и дополнительного множителя, предполагая взаимозаменяемые простые числа. Дамо обозначення понятным лучшим спильным знаменным (НСЗ) и рядом завдан наїї позука.
Тема: Дополнение и введение дробей мелкими баннерами
Урок: сокращение дробей до баннера
Повторение. Основная сила дроби.
Если число и знаменатель дроби умножить на одно и то же натуральное число, то мы увидим одно и то же число.
Например, число и знаменатель дроби можно разделить на 2. Otrimaєmo drib. Операция Цю называется быстрой дробью. Можно виконати и зворотне пересмотреть, умножив число и знаменатель на дробь на 2. Во всяком случае, они могут сказать, что они привели остальные к новому знаменателю. Число 2 называется дополнительным множителем.
Висновок. Дриб можно уменьшить до кратного знаменателю данной дроби.Чтобы довести результат до нового стандарта, умножьте число и стандарт на дополнительный множитель.
1. Подведите водителя к баннеру 35.
35 делится на 7, поэтому 35 равно 7 без превышения. Это означает, что процесс совершенствования возможен. Как известно, это дополнительный множитель. Для всего разділимо 35 на 7. Отримаем 5. Умножаем на 5 число и эталон порочной дроби.
2. Подведите водителя к баннеру 18.
Известно, что это дополнительный множитель. Уже много разделили новых баннеров на выходе. Otrimaєmo 3. Умножьте на 3 числа и знаменатель данной дроби.
3. Направить дриб к баннеру 60.
Увеличив 60 на 15, мы можем получить тот же множитель. Вин доривню 4. Умножьте дату и стандарт на 4.
4. Направьте дриб на стандарт 24
В неудобных випадках, доведенных до нового стандарта, вывески виконуют в розуми.Понадобилось только включить дополнительный множитель за своды хлоры вправо и в большую дробь.
Дриб можно довести до стандарта 15, а можно довести до стандарта 15. Дроби и спильный имеют 15.
Спильный знаменатель дробей может быть кратным этим же знаменателям. Для простоты уменьшите дроби до наименьшего спильного знаменателя. Обладатель наименьшего кратного знаменателя спила в данных фракциях.
Прик. Приведите дробь i к наименьшему знаменателю выброса.
Известно, что некоторые из них являются наименьшими по величине, кратной знаменателям данных дробей. Число 12. Известно, что это дополнительный множитель для первой и второй дробей. Всего 12, оно делится на 4 и 6. Три — это тот же множитель для первой дроби, а два — для другой. Ориентируются фракции к стандарту 12.
Мы довели дроби до специального стандарта, чтобы мы знали равные дроби, которые имеют один и тот же стандарт.
Правило. Шоб довести фракции до минимального стандарта выброса, требуется
В некотором смысле, чтобы узнать наименьшие кратные числа знамен, кратные количеству дробей, затем наилучшие значения ширины знамени;
Иначе тот, кто использовал спильный баннер для баннера данных фракций, т.е. Узнать дополнительный множитель для скин-фракции.
В-третьих, умножьте число і знаменателя скин-фракции на її дополнительный множитель.
a) Довести дробь i до стандартного знаменателя.
Тот, у кого наименьший спильный знаменатель, — доривнює 12. Дополнительный множитель для первой дроби — 4, для другой — 3. Вероятно, дробь до стандартной 24.
б) Приведите дробь i к стандартному знаменателю.
Наименьший спильный знаменник доривнює 45. Раздиливши 45 на 9 на 15, отримаемо, видимо, 5 и 3. Дроби сведены к знаменателю 45.
c) Довести дробь i до стандартного знаменателя.
Спильный знаменник — 24. Дополнительные множители, по всей видимости, — 2 и 3.
Инооді бува важно усыпить наименьший спільне множитель для знаменателей данной дроби. Тоди — это усердный стандарт, а дополнительные множители известны дополнительным распределением по простым множителям.
Довести дробь i до стандартного знаменателя.
Числа 60 и 168 разлагаются на простые множители.Випишемо спред числа 60 и додамо в дневных множителях 2 и 7 из другого спреда. Умножить 60 на 14 і 840. Дополнительный множитель для первой дроби — це 14. Дополнительный множитель для другой дроби — 5. Ориентированные дроби на стандартный стандарт 840.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. Математика 6. — М .: Мнемосина, 2012.
.2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс — Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За бортами обработчик математики. — Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Заведующая курсом математики 5-6 классов. — ЗШ МІФІ, 2011 рок.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Книга для учащихся 6 класса заочной школы МИФИ. — ЗШ МІФІ, 2011 рок.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О.что в. Математика: Пидручник-спыврозмовник для 5-6 классов средней школы. Библиотека для чтения по математике. — Просвещение, 1989.
Можно шантажировать книги, указанные в п. 1.2. учитывая урок.
Дом завдання
Виленкин Н.Я., Жохов В.И., Чесноков А.С. Математика 6. — М .: Мнемосина, 2012. (Div. 1.2)
Домашний офис: № 297, № 298, № 300.
Інші персонал: №270, №290
Некоторые методы сокращения до стандартного баннера хочется включить в пункт «Завершение и выдача дробей».Информации появилось так много, и важность этой настройки огромна (даже спильные баннеры предназначены не только для числовых дробей), которая красивее, чем пищевая ценность окремо.
Оже, давайте две фракции с баннерами. И мы хотим сделать так, чтобы баннеры стали такими же. На помощь приходит основная сила фракции, як, наверное, здоровый наступательный ранг:
Дриб не менять, так как число и стандартное число умножаются на одно и то же число, если смотреть с нуля.
При таком ранге, если правильно использовать множители, знаменатели дробей растут — процесс называется приведенным к знаменателю спилов. А числа шукани, «виривнюют» знамена, называются дополнительными множителями.
У кого спрос приводит фракции к стандартному баннеру? Ось лишена нескольких причин:
- Сложение и представление фракций с помощью небольших баннеров. Во-первых, операция — это не виконати;
- Соотношение фракций.После того, как приведу к стандартному баннеру, я существенно прощу задачу;
- Решение задач по деталям и сборкам. Процент заработной платы, по дням, по очень большим вирусам, как фракции мести.
Есть много способов узнать числа, когда несколько знаменателей дробей становятся равными. Три из них менее заметны — в порядке роста складчатости и, в певческом смысле, эффективности.
Умножение «Хрест-навхрест»
Самый простой и качественный способ, который гарантирует перетяжка баннера.Идем дальше: умножаем каплю на эталон другой дроби, а другу — на эталон первой. В результате знаменатели обеих дробей сравняются с количеством победивших знаменателей. Взгляните:
В качестве дополнительных множителей знаменатели фракций суспензии узнаваемы. otrimaєmo:
Итак, ось такая простая. Как только зафиксируете дроби, лучше раскрасьте их тем же методом — так вы застрахуетесь от непристойных помилований и результат вам будет гарантирован.
Единственный недостаток этого метода в том, что его нужно уважать, а баннеры множатся «насквозь», и в результате их может быть еще больше. Такова плата за надежность.
Метод спильных дильников
Цей приём допомага нагато ускорение расчета, эль, к сожалению, жаль, застойно добивать ридко. Метод Полаги в наступлении:
- Перш, ніж діяти «прямо вперед» (тобто методом «чрест-навхрест»), взгляните на баннеры.Вы можете, один из них (тот, который больше), продлиться за одного.
- Число, отклоненное в результате такой подачи, будет дополнительным множителем для дроби с наименьшим знаменателем.
- Вместе со многими другими с большим знаменем нет необходимости в умножении — в целом и в области экономики. При этом резко снижается стоимость помилования.
Завдання. Знайте значение вираза:
Уважаемый, счо 84: 21 = 4; 72:12 = 6.Осколки в обеих выпадках одного стандарта длится без излишков по оптимальному, устойчивому методу загальных множителей. Maєmo:
Удивительно, но другой дриблинг в никуда не умножился. Фактически, мы дважды прошли налогообложение!
Перед выступлением я выстрелил не в всю задницу. Якщо цикаво, попробуйте порахуватьих методом «чрест-навхрест». Если вы хотите быть быстрым, вы будете таким же, но робот будет более мощным.
В целом сила метода спильных дильников сильна, но, повторяю, ее можно лишить в том случае, если одного из баннеров хватит на один без излишка.Що бувак доделать ридко.
Метод наименьшего спил-кратного
Насколько дроби наведены до спільного знаменника, ми в день намагаемости известно такое же число, как оно распространяется на шкуру знамени. Тогда знаменатели обеих дробей можно уменьшить до целого числа.
Таких чисел еще больше, и наименьшее из них не обязательно для прямого сложения стандартных дробей, так как оно передается в методе «кросс-навкрест».
Например, для знаменателей 8 и 12 полностью число 24, оскилки 24: 8 = 3; 24: 12 = 2. Число набагато меньше 8 · 12 = 96.
Наименьшее число, которое переходит в кожу из знаменников, называется наименьшим спильным кратным (НКМ).
Значение: наименьшее кратное чисел a и b — это НОК (a; b). Например, LCM (16; 24) = 48; НОК (8; 12) = 24.
Как только вам дадут знать такой же номер, фонд заработной платы будет минимальным.Поразитесь заднице:
Завдання. Знайте значение вираза:
Уважаемый, що 234 = 117 2; 351 = 117 · 3. Множители 2 и 3 довольно просты (не игнорируйте спящие фигуры, обведите 1), а множитель 117 является нестандартным. Том LCM (234; 351) = 117 2 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 достаточно простые, а множитель 5 загальный. Том LCM (15; 20) = 5 3 4 = 60.
Сейчас нацеливаемся на дроби к готовым баннерам:
В целях овладения уважением, по какой-то причине показано распределение порочных знамен на множители:
- Найдя такие же множители, мы сразу перешли к наименьшему множителю, що, казалось, загали є нетривиальным завданням;
- Из отброшенной раздачи можно узнать, что нет множителей «не выстачаковых» фракций скина.Например, 234 3 = 702, тогда для первой дроби дополнительный множитель равен 3.
Шоб оцените, если колоссальный виграш да, метод наименьшего спил-кратного, попробуйте посчитать окурки методом «кросс-овера». Зрозумило, без калькулятора. Думаю, я буду доволен своими комментариями.
Не думайте, что таких складных фракций в справжных ложах не будет. Зловоние от постоянного застройки и указания видения не является границей!
Одна проблема — как узнать цей НОК.В некоторых случаях все можно найти за несколько секунд, буквально «на глаз», но в целом это аккуратная вычислительная задача, требующая внимательного изучения. Здесь мы не будем заморачиваться с цским.
Легко увидеть, как сложение дробей с малым знаменателем, это правило, и тогда можно увидеть бетонный стык.
Schob sklasts или брать дроби с малым знаменателем, требуется:
1) Знать (НСЗ) заданные дроби.
2) Знайте додатковый множитель к скин-фракции.Для нового стандарта необходимо распространить его на старый.
3) Умножьте число і знаменателя кожной фракции на дополнительный множитель і кратности или возьмите дроби с такими же знаменателями.
4) Ревизия, которая закрашена в результате того, что она правильная и не распространяется.
В атакующих прикладах нужно фолдить, либо брать дроби с маленькими знаменателями:
1) Щоб берем дроби с общими знаменателями, лучший спильный знаменник из данных дробей.Вибрация больше, чем цифры, и изменение, и длительность за меньшее. С 25 до 20 не длится. Умножьте 25 на 2. 50 на 20 не длится. Умножьте 25 на 3. 75 на 20 не длится. Умножьте 25 на 4,100 на 20. Это означает, что тот, у кого самый высокий сп_льный знаменный, будет дор_внює 100.
2) Чтобы узнать множитель до кожной фракции до отсечки, вам нужен новый стандарт для старости. 100: 25 = 4, 100: 20 = 5. Очевидно, перед первой дробью дополнительный множитель равен 4, перед другой — 5.
3) Умножьте число и знаменатель скин-фракции на дополнительный множитель и различные дроби в соответствии с правилом определения дробей с одинаковыми знаменателями.
4) Отримана дріб — правильная и не короткая. Это значит, что цена считается.
1) Щоб поставил выстрел с большими знаменами, и тот, у кого лучший спильный баннер. С 16 до 12 не длится. 16 ∙ 2 = от 32 до 12 не длится. 16 ∙ 3 = 48 до 12 последних.Это означает, что 48 — это NSZ.
2) 48: 16 = 3, 48: 12 = 4. Tse — дополнительные множители к скин-фракции.
3) число і знаменателя скин-фракции умножается на дополнительный множитель і storemono новой дроби.
4) Отримана в результате правильная и не короткая.
1) от 30 до 20 не длится. 30 ∙ 2 = от 60 до 20 последних. Это означает, что 60 — это самый низкий спильный баннер по количеству фракций.
2) нужно знать дополнительный множитель к кожной фракции, нужен стандартный знаменатель для пожилых людей: 60: 20 = 3, 60: 30 = 2.
3) умножьте число і знаменателя скин-фракции на дополнительный множитель и новую дробь.
4) Обрежу дробь до 5.
1) 8 на 6 не длится. 8 ∙ 2 = 16 на 6 не длится. 8 ∙ 3 = 24, чтобы удлинить і на 4, і на 6. Итак, 24 — это і є НСЗ.
2) нужно знать дополнительный множитель к кожной фракции, нужен новый стандарт для стариков. 24: 8 = 3, 24: 4 = 6, 24: 6 = 4. Итак, 3, 6 и 4 являются дополнительными множителями к первой, другой и третьей дробям.
3) число і знаменатель скина довбай умножается на дополнительный множитель. Склад и отличное. Отримана дриб неправильная, нужно видеть всю часть.
Схема приведения к спильному знаменателю
- Следует уточнить, так как это будет наименьший множитель для знаменателей дробей. Если вы можете сделать это правильно с изменением или целым числом, то его нужно будет преобразовать в другое, и даже тогда это будет наименьшая скорость.Для того, чтобы преобразовать число в дриб, необходимо записать в числительное одно и то же число, а в знаменателе — единицу. Например, цифра 5 в дроби вигляд будет выглядеть так: 5/1. Если вы измените количество обращенных на другие, вам нужно умножить число на знаменатель и дату на новую дату. Обух: 8 щелчков і 3/5 в виде дроби = 8×5 + 3/5 = 43/5.
- Для этого необходимо знать дополнительный множитель, который используется для запуска NSZ для знаменателя скин-фракции.
- Оставшийся крокодил — множитель для дополнительного множителя.
Важно помнить, что не обязательно приводить его к стандартному баннеру не только для дополнительной информации. Чтобы скорректировать доли децилконов с малыми знаменателями, необходимо также привести от них скин к знаменателю спила.
Приведение дробей к стандартному знамени
Для того, чтобы интеллект был доведен до спильного знамени фракций, необходимо вырасти в силах фракций.Итак, обладая важной силой, мы победили приведения к НСЗ, паритету фракций. Другими словами, если число и знаменатель умножить на число, то в результате мы отменим другое, которое дороже впереди. Як прикладом руководствуется таким прикладом. Для приведения дробей 5/9 и 5/6 к наименьшему стандарту спила необходимо показать следующее:
- Известно, что совокупность представляет собой наименьшую кратность знаменателей.В этом случае для номеров 9 и 6 НОК неактивен 18.
- Значение дополнительных множителей для скин-фракции. Так работать. Dilimo NOC на знаменателе скина с дробями, в результате мы можем принять 18: 9 = 2, а 18: 6 = 3. Числа будут дополнительными множителями.
- Наверное, две фракции к НСЗ. Умножив число на число, необходимо умножить и число, и число. Дріб 5/9 можно умножить на дополнительный множитель 2, в результате чего мы видим разницу, что немаловажно, — 10/18.То же самое можно сказать и о другой дроби: 5/6 умножается на 3, в результате получается 15/18.
Як бачимо из данного приклада, оскорбив выстрел були, поднес к самому маленькому спильному знамену. Если у вас его достаточно, вам нужно освоить такую же силу дробей. Есть полярность в том факте, что число и знаменатель дроби могут быть увеличены до одного и того же числа, так как оно называется числом один. Например, дриб 12/30 может быть до 2/5 скорости, если он раздается иностранцу — число 6.
Во многих материалах нормально привести дробь к новому стандарту, так что это дополнительный множитель и как его узнать. Написав, я сформулирую основное правило сведения дробей к новым флагам и проиллюстрировать их запасами.
Понимание приведенной дроби к норме
Zgadaimo — главная сила фракции. Именно с ним много дробей a b (de a и b — подобные числа), есть бесконечное количество дробей, которые готовы к работе.Такую дробь можно обрезать, умножив знаменатель числа і на такое же число m (натуральное). Другими словами, все специальные дроби можно заменить на форму a · m b · m. Это снижение вирусной ценности до фракции с требуемым стандартом.
Можно довести дело до іншого знаменателя, умножив число і знаменатель на натуральное число. Головна умова — множитель виновен в том, что у обеих частей дроби одинаковый. На пидсумку мы видим капельницу, что неплохо.
Сделано прикладом.
приклад 1
Свинец 11 25 по новому стандарту.
Решение
Вполне натуральное число 4, и умножьте правонарушение части умственной дроби на новую. Точно: 11 4 = 44 і 25 4 = 100. Результат был 44 100.
Все свиньи можно записать в этом виде: 11 25 = 11 4 25 4 = 44 100
Прогуляйтесь, если сможете, вы можете привести к величественному ряду знаменитых знамен. Четверки можно заменить, взяв другое натуральное число и отринув одно другое, равное этому числу.
В противном случае число может стать эталоном новой дроби. Итак, для a b в знаменателе могут быть только числа b m, кратные числу b. Угадайте основное понимание подола — кратные числа и подольники. Если число не кратно b, делитель новой дроби не может быть выигран. Мы можем объяснить нашу мысль предметом пересмотра.
стык 2
Вычислите дробь 5 N 9 из знаменателя до 54 и 21.
Решение
54 кратно девяти, так как оно стоит на флаге новой дроби (так что 54 можно разделить на 9).Значит, это тоже возможно. И 21 ми разділити на 9 невозможно, поэтому такая работа для данной фракции виконати невозможна.
Что такое множитель додатк
Сформулирую, что это еще и дополнительный множитель.
значение 1
дополнительный множитель є — это тоже натуральное число, о том, как умножить наступательные части дроби, чтобы привести її к новому знаменателю.
Tobto, если mi vikonuєmo tsyu diyu с дробью, берем множитель для нее.Например, для приведения дроби 7 10 к виду 21 30 нам понадобится дополнительный множитель 3. И мы можем вырезать 15 40 s 3 8 для дополнительного множителя 5.
Судя по всему, если баннер известен, прежде чем нужно вывести другой, то мы можем рассчитать для него дополнительный множитель. Розберемо, як це зробити.
У нас есть є дриб а б, яку можно довести до дэякого стандарта с; вычислимо дополнительный множитель m. Нам нужно умножить знамя фракции вихидов на м.У нас есть b · m, а для проблемы мозга b · m = c. Згадаимо, как связаны между собой и размножаются. Цей звязь, даже если до нас доходит: дополнительный множитель не так уж он, как часть расстояния от c до b, кроме казучи, m = c: b.
В таком ранге, для знания дополнительного множителя, нам нужно раздать необходимый баннер для итогового.
butt 3
Знайте додатковый множитель, с помощью которого дриб 17 4 лог доводится до стандартного 124.
Решение
Використовучи правит вище, ми всего распределено 124 по стандарту первой дроби — четыре.
Рахуэмо: 124: 4 = 31.
Розраханки Viconuvati этого типа часто требуются, когда фракции доводятся до стандарта разлива.
Правило приведения дробей к обозначенному знаменателю
Переходим к значению основного правила, с помощью которого можно привести дроби к обозначенному знаменателю.Отже,
значение 2
Для приведения дроби к заданному знаменателю необходимо:
- сделать дополнительный множитель;
- умножить на новое і число, і знаменатель злой дроби.
Какое правило действует на практике? Управляемое комплексное решение задач.
стык 4
Найти приведение дроби 7 16 к знаменателю 336.
Решение
Подсчитать дополнительный множитель практически невозможно.Раздилимо: 336: 16 = 21.
Отримана умножается на нарушение части выходной дроби: 7 16 = 7 · 21 16 · 21 = 147 336. Так мы довели выход до требуемого стандарта 336.
Просмотр 7 16 = 147 336.
Как только вы отметили в тексте помилование, будьте лаской, посмотрите его и нажмите Ctrl + Enter
.

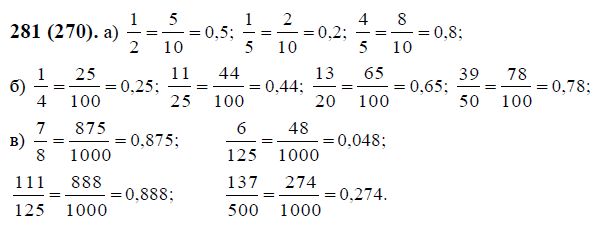 Организационный момент и мотивация к учебной деятельности
Организационный момент и мотивация к учебной деятельности-reshenie-550.jpg)
 д.)
д.)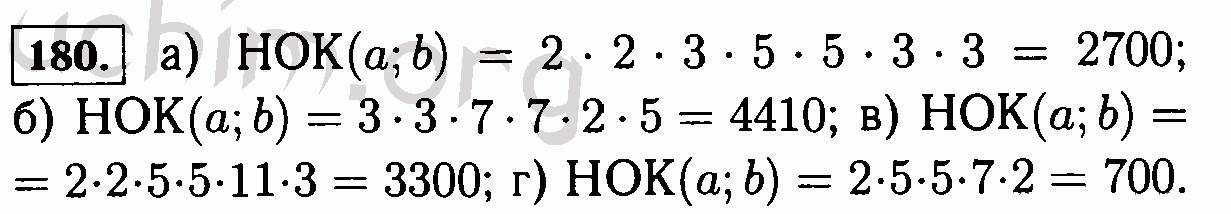 Вспомните их.
Вспомните их.-reshenie-1018.jpg) )
) 85
85