Номер №124 — ГДЗ по Математике 6 класс: Виленкин Н.Я.
войтирегистрация
- Ответкин
- Решебники
- 6 класс
- Математика
- Виленкин
- Номер №124
НАЗАД К СОДЕРЖАНИЮ
2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №124 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.
2019г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №124 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
Условие 20132019г.
Cменить на 2013 г.
Cменить на 2019 г.
Выясните, делится ли число а на число b без остатка, если:
а) а = 2 * 2 * 2 * 3 * 5 * 7 и b = 2 * 3 * 7;
б) а = 3 * 3 * 5 * 5 * 11 и b = 3 * 3 * 5;
в) а = 3 * 3 * 5 * 7 * 13 и b = 3 * 5 * 5 * 13;
г) a = 2 * 3 * 3 * 7 * 7 и b = 21;
д) а = 2 * 2 * 3 * 3 * 3 * 5 * 7 и b = 135;
е) а = 2 * 2 * 2 * 3 * 3 * 5 * 5 и b = 1000.
В случае, когда а делится на b, найдите частное.
Найдите значение выражения: (15,964 : 5,2 — 1,2) * 0,1.
Решение 1
Решение 1
Решение 2
Решение 2
Решение 3
Решение 3
ГДЗ по Математике 6 класс: Виленкин Н. Я.
Я.
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.
ГДЗ по Математике 6 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.
ГДЗ по Математике 6 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018
ГДЗ по Математике 6 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.
ГДЗ по Математике 6 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.
Сообщить об ошибке
Выберите тип ошибки:
Решено неверно
Опечатка
Плохое качество картинки
Опишите подробнее
в каком месте ошибка
Ваше сообщение отправлено
и скоро будет рассмотрено
ОК, СПАСИБО
[email protected]
© OTVETKIN. INFO
INFO
Классы
Предметы
Номер 124 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник)
Номер 124 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
CZ — Чешская цифровая математическая библиотека: О средних Нёрлунда рядов Виленкина-Фурье
[1] Благота, И. : О неравенстве нормы по отношению к системам типа Виленкина . Акта Математика. Повесили. 89 (2000), 15-27. DOI 10.1023/A:1026769207159 | MR 1912235 | Zbl 0973.42020
: О неравенстве нормы по отношению к системам типа Виленкина . Акта Математика. Повесили. 89 (2000), 15-27. DOI 10.1023/A:1026769207159 | MR 1912235 | Zbl 0973.42020
[2] Благота, И.: Связь между ядрами Дирихле относительно виленкиноподобных систем . Акта акад. Педагог. Агриенсис, Секта. Мат. (NS) 22 (1994), 109-114. Збл 0882.42017
[3] Благота, И., Гат, Г.: Суммируемость по норме логарифмических средних Нёрлунда на неограниченных группах Виленкина . Анальный. Теория прил. 24 (2008), 1-17. DOI 10.1007/s10496-008-0001-z | МР 2422455 | Zbl 1164.42022
[4] Благота И., Тефнадзе Г.: О {$(C,\alpha)$}-средних по системе Уолша . Анальный. Мат. 40 (2014), 161-174. DOI 10.1007/s10476-014-0301-9 | МР 3240221 | Zbl 1313.42083
[5] Благота И., Тефнадзе Г.: Теорема сильной сходимости для средних Виленкина-Фейера 91$}-функции на обобщенной группе Уолша-Пэли . проц. Являюсь. Мат. соц. 77 (1979), 111-116. MR 0539641
[7] G{á}t, G. : Средние Чезаро интегрируемых функций по неограниченным системам Виленкина . Дж. Прибл. Теория 124 (2003), 25-43. DOI 10.1016/S0021-9045(03)00075-3 | МР 2010779 | Збл 1032.43003
: Средние Чезаро интегрируемых функций по неограниченным системам Виленкина . Дж. Прибл. Теория 124 (2003), 25-43. DOI 10.1016/S0021-9045(03)00075-3 | МР 2010779 | Збл 1032.43003
[8] Г{а}т, Г.: Исследования некоторых операторов по системе Виленкина . Акта Математика. Повесили. 61 (1993), 131-149. DOI 10.1007/BF01872107 | MR 1200968 | Zbl 0805.42019
[9] Гат Г., Гогинава Ю.: Сходимость почти всюду {$(C,\alpha)$}-средних квадратичных частичных сумм двойных рядов Виленкина-Фурье . Грузинская математика. Журнал 13 (2006), 447-462. МР 2271060 | Zbl 1107.42006
[10] Гат Г., Гогинава Ю.: Равномерная и {$L$}-сходимость логарифмических средних рядов Уолша-Фурье . Акта Математика. син., англ. сер. 22 (2006), 497-506. DOI 10.1007/s10114-005-0648-8 | MR 2214371
[11] Гат Г., Надь К.: О логарифмической суммируемости ряда Фурье . Грузинская математика. Журнал 18 (2011), 237-248. MR 2805978 | Zbl 1221.42049
[12] Гогинава Ю. : Неравенство слабого типа для максимального оператора средних {$(C,\alpha)$} двумерных рядов Уолша-Фурье . Анальный. Мат. 36 (2010), 1-31. DOI 10.1007/s10476-010-0101-9 | MR 2606574
: Неравенство слабого типа для максимального оператора средних {$(C,\alpha)$} двумерных рядов Уолша-Фурье . Анальный. Мат. 36 (2010), 1-31. DOI 10.1007/s10476-010-0101-9 | MR 2606574
[13] Гогинава, У.: Максимальные операторы средних Фейера-Уолша . Acta Sci. Мат. 74 (2008), 615-624. MR 2487936 | Збл 1199.42127
[14] Гогинава У.: Максимальный оператор средних Марцинкевича-Фейера {$d$}-мерного ряда Уолша-Фурье . Восток Дж. Прибл. 12 (2006), 295-302. MR 2252557
[15] Гогинава, Ю.: Максимальный оператор средних {$(C,\alpha)$} ряда Уолша-Фурье . Анна. ун-т науч. Будапешт. Роландо Этвёш, Sect. вычисл. 26 (2006), 127-135. MR 2388683 | Zbl 1121.42020
[16] Гогинава, Ю.: Сходимость почти всюду подпоследовательности логарифмических средних рядов Уолша-Фурье . Акта Математика. акад. Педагог. Нихази. (NS) (только в электронном виде) 21 (2005), 169-175. МР 2162613 | Збл 1093.42018
[17] Гогинава Ю.: Об аппроксимативных свойствах чезаро-средних отрицательного порядка рядов Уолша-Фурье . Дж. Прибл. Теория 115 (2002), 9-20. DOI 10.1006/jath.2001.3632 | MR 1888974 | Zbl 0998.42018
Дж. Прибл. Теория 115 (2002), 9-20. DOI 10.1006/jath.2001.3632 | MR 1888974 | Zbl 0998.42018
[18] Мур, К. Н.: Суммируемые ряды и коэффициенты сходимости . Dover Publications, Нью-Йорк (1966). МР 0201863 | Збл 0142.30704
[19] Мориц Ф., Сиддики А.Х.: Аппроксимация средними Нёрлунда ряда Уолша-Фурье . Дж. Прибл. Теория 70 (1992), 375-389. DOI 10.1016/0021-9045(92)-X | MR 1178380 | Zbl 0757.42009
[20] Nagy, K.: Аппроксимация средними Нёрлунда двойных рядов Уолша-Фурье для липшицевых функций . Мат. Неравный. заявл. 15 (2012), 301-322. МР 2962234 | Zbl 1243.42038
[21] Nagy, K.: Аппроксимация средними Нёрлунда ряда Уолша-Качмарца-Фурье . Грузинская математика. Журнал 18 (2011), 147-162. MR 2787349 | Zbl 1210.42043
[22] Nagy, K.: Аппроксимация средними Чезаро отрицательного порядка ряда Уолша-Качмарца-Фурье . Восток Дж. Прибл. 16 (2010), 297-311. MR 2789336 | Zbl 1216.42006
[23] Nagy, K.: Аппроксимация средними Нёрлунда квадратичных частичных сумм двойного ряда Уолша-Фурье . Анальный. Мат. 36 (2010), 299-319. DOI 10.1007/s10476-010-0404-x | MR 2738323 | Zbl 1240.42133
Анальный. Мат. 36 (2010), 299-319. DOI 10.1007/s10476-010-0404-x | MR 2738323 | Zbl 1240.42133
[24] Пал, Дж., Саймон, П.: Об обобщении понятия производной . Акта Математика. акад. науч. Повесили. 29 (1977), 155-164. DOI 10.1007/BF01896477 | МР 0450884 | Zbl 0345.42011
[25] Schipp, F.: Перестановки рядов в системе Уолша . Мат. Notes 18 (1976), 701-706 перевод с \kern 3sp Матем. заметки 18 (1975), 193-201. MR 0390633
[26] Simon, P.: Суммируемость по Чезаро относительно двухпараметрических систем Уолша . Монац. Мат. 131 (2000), 321-334. DOI 10.1007/s006050070004 | МР 1813992
[27] Simon, P.: Теорема сильной сходимости для рядов Виленкина-Фурье . Дж. Матем. Анальный. заявл. 245 (2000), 52-68. DOI 10.1006/jmaa.2000.6732 | MR 1756576 | Zbl 0987.42022
[28] Simon, P.: Исследования по системе Виленкина . Анна. ун-т науч. Будапешт. Роландо Этвёш, Sect. Мат. 27 (1984), 87-101. МР 0823096 | Zbl 0586.43001
[29] Simon, P. , Weisz, F.: Слабые неравенства для суммирования по Чезаро и Риссу ряда Уолша-Фурье . Дж. Прибл. Теория 151 (2008), 1-19. DOI 10.1016/j.jat.2007.05.004 | MR 2403893 | Zbl 1143.42032
, Weisz, F.: Слабые неравенства для суммирования по Чезаро и Риссу ряда Уолша-Фурье . Дж. Прибл. Теория 151 (2008), 1-19. DOI 10.1016/j.jat.2007.05.004 | MR 2403893 | Zbl 1143.42032
[30] Тефнадзе Г.: О максимальных операторах логарифмических средних Рисса ряда Виленкина-Фурье . Стад. науч. Мат. Повесили. 51 (2014), 105-120. MR 3188506 | Zbl 1299.42098
[31] Тефнадзе Г.: О частных суммах ряда Виленкина-Фурье . Дж. Контемп. Мат. Анальный. 49 23-32 русский (2014). DOI 10.3103/S1068362314010038 | MR 3237573
[32] Тефнадзе Г.: Теоремы сильной сходимости для средних Уолша-Фейера . Акта Математика. Повесили. 142 (2014), 244-259. DOI 10.1007/s10474-013-0361-5 | MR 3158862 | Zbl 1313.42086
[33] Тефнадзе Г.: О максимальных операторах средних Виленкина-Фейера на пространствах Харди . Мат. Неравный. заявл. 16 (2013), 301-312. MR 3060398 | Zbl 1263.42008
[34] Тефнадзе Г.: О максимальных операторах средних Виленкина-Фейера . Турок. Дж. Матем. 37 (2013), 308-318. MR 3040854 | Збл 1278.42037
Турок. Дж. Матем. 37 (2013), 308-318. MR 3040854 | Збл 1278.42037
[35] Тефнадзе Г.: Замечание о коэффициентах Фурье и частных суммах рядов Виленкина-Фурье . Акта Математика. акад. Педагог. Нихази. (NS) (только в электронном виде) 28 (2012), 167-176. MR 3048092 | Zbl 1289.42084
[36] Тефнадзе Г.: Средства Фейера ряда Виленкина-Фурье . Стад. науч. Мат. Повесили. 49 (2012), 79-90. MR 3059789 | Zbl 1265.42099
[37] Тефнадзе Г.: Максимальные операторы логарифмических средних одномерных рядов Виленкина-Фурье . Акта Математика. акад. Педагог. Нихази. (NS) (только в электронном виде) 27 (2011), 245-256. MR 2880697 | Zbl 1265.42100
[38] Виленкин Н. Дж.: Об одном классе полных ортонормированных систем . Являюсь. Мат. соц. Перевод сер. (2), 28 (1963), 1-35 перевод с \kern 3sp Изв. акад. АН СССР, сер. Мат. 11 (1947), 363-400. МР 0154042 | Zbl 0036.35601
[39] Weisz, F.: $\theta$-суммируемость ряда Фурье . Акта Математика. Повесили. 103 (2004), 139-176. DOI 10.1023/B:AMHU.0000028241.87331.c5 | MR 2047878 | Збл 1060.42021
Повесили. 103 (2004), 139-176. DOI 10.1023/B:AMHU.0000028241.87331.c5 | MR 2047878 | Збл 1060.42021
[40] Weisz, F.: {$(C,\alpha)$} суммируемость рядов Уолша-Фурье . Анальный. Мат. 27 (2001), 141-155. DOI 10.1023/A:1014364010470 | MR 1834858 | Zbl 0992.42016
[41] Weisz, F.: Суммирование по Чезаро одномерных и двумерных рядов Уолша-Фурье . Анальный. Мат. 22 (1996), 229-242. DOI 10.1007/BF02205221 | MR 1627638 | Zbl 0866.42020
[42] Weisz, F.: Мартингальные пространства Харди и их приложения в анализе Фурье . Конспект лекций по математике 1568 Springer, Берлин (1994). DOI 10.1007/BFb0073448 | МР 1320508 | Zbl 0796.60049
О максимальных операторах средних Виленкина-Фейера
Основная цель данной статьи – доказать, что максимальный оператор \overset{\sim}{s}\astf:=\underset{n \in P} \ sup\frac{|s nf|}{\log2 (n+1)} ограничен из пространства Харди h2/2 в пространство L1/2, где s nf — средние Фейера ограниченных рядов Виленкина–Фурье.
Анахтар Келимелер:
Основная цель этой статьи — доказать, что максимальный оператор \overset{\sim}{s}\astf:=\underset{n \in P} \sup\frac{|s nf|}{\log2 ( n+1)} ограничен из пространства Харди h2/2 в пространство L1/2, где s nf — средние Фейера ограниченных рядов Виленкина–Фурье.
Ключевые слова:
Там Метин
___
- [1] Агаев Г.Н., Виленкин Н.Я., Джафарлы Г.М., Рубинштейн А.И. Мультипликативные системы функций и гармонический анализ на нульмерных группах, Баку, Эхим, 1981 (в кн. Русский).
- [2] Благота И., Гаат Г., Гогинава У. Максимальные операторы средних Фейера двойных рядов Виленкина-Фурье // Сб. Мат. 107, нет. 2, 287–296, (2007).
- [3] Благота И., Гат Г., Гогинава У. Максимальные операторы средних Фейера рядов Виленкина-Фурье, JIPAM. Дж. Неравный. Чистое приложение Мат. 7, 1–7, (2006).
- [4] Fujii, N.J.: Максимальное неравенство для функций h2 на обобщенной группе Уолша-Пэли, Proc. амер. Мат. соц.
 77, (1979), 111–116.
77, (1979), 111–116. - [5] G´at, G.: Средние Чезаро интегрируемых функций относительно неограниченных систем Виленкина, J. Approx. Теория 124, вып. 1, 25–43, (2003).
- [6] Гогинава, У.: Максимальные операторы средних Фейера-Уолша, Acta Sci. Мат. (Сегед) 74, вып. 3–4, 615–624, (2008).
- [7] Гогинава, У.: Максимальный оператор средних Фейера системы характеров поля p-серии в перестановке Качмарца, Опубл. Мат. Дебрецен 71, нет. 1–2, 43–55, (2007).
- [8] Гогинава, У.: Максимальные операторы средних Фейера двойных рядов Уолша-Фурье, Acta Math. Венгрия. 115, нет. 4, 333–340, (2007).
- [9] Гогинава, У., Надь, К.: О максимальном операторе средних Уолша-Качмарца-Фейера, Чехословацкая математика. Дж. (появляется).
- [10] Пал, Дж., Саймон, Дж.: Об обобщении понятия производной, Acta Math. Hung., 29, 155–164, (1977).
- [11] Шипп, Ф.: Некоторые перестановки рядов в рядах Уолша, Матем. Заметки, 18, 193–201, (1975).
- [12] Саймон, П.
 : Желание суммирования по Чезаро относительно двухпараметрических систем Уолша, Monatsh. Матем., 131, 321–334, (2000).
: Желание суммирования по Чезаро относительно двухпараметрических систем Уолша, Monatsh. Матем., 131, 321–334, (2000). - [13] Саймон, П.: Исследования в отношении системы Виленкина, Annales Univ. науч. Будапешт Эотв., Разд. Матем., 28, 87–101, (1985).
- [14] Виленкин Н.Я. Об одном классе полных ортонормированных систем // Изв. акад. наук. СССР, сер. мат., 11, 363–400, (1947).
- [15] Weisz, F.: Мартингальные пространства Харди и их приложения в анализе Фурье, Springer, Berlin-Heidelberg-New York, 19.94.
- [16] Weisz, F.: Суммирование Чезро одномерных и двумерных рядов Фурье, Anal. Мат. 5 (1996), 353-367.re Appl. Мат. 7, 1–7, (2006).
- [17] Weisz, F.: Суммарность многомерных рядов Фурье и пространство Харди, Kluwer Academic, Dordrecht, 2002.
- [18] Weisz, F.: Неравенства слабого типа для систем Уолша и ограниченных систем Цизельского. Анальный. Мат. 30, нет. 2, 147–160, (2004).
- [19] Zygmund, A.: Trigonometric Series, Vol.
 1, Кембриджский унив. Пресса, 1959.
1, Кембриджский унив. Пресса, 1959.
___
| Бибтекс | @ {tbtkmath245758, журнал = {Турецкий математический журнал}, иссн = {1300-0098}, эйссн = {1303-6149}, адрес = {}, издатель = {TÜBİTAK}, год = {2013}, громкость = {37}, число = {2}, страницы = {308 — 318}, дои = {10,3906/мат-1010-438}, title = {О максимальных операторах средних Виленкина-Фейера}, ключ = {цитировать}, автор = {Тефнадзе, Георгий} } |
| АПА | Тефнадзе Г. (2013). О максимальных операторах средних Виленкина-Фейера . Турецкий математический журнал , 37 (2) , 308-318 . ДОИ: 10.3906/мат-1010-438 |
| ГНД | Тефнадзе, Г.
«О максимальных операторах средних Виленкина-Фейера»
. Турецкий математический журнал 37 (2013 г.)
): 308-318 Турецкий математический журнал 37 (2013 г.)
): 308-318 |
| Чикаго | Тефнадзе, Г. «О максимальных операторах средних Виленкина-Фейера». Турецкий математический журнал 37 (2013 г.) ): 308-318 |
| РИС | ТЫ — ДЖУР T1 — О максимальных операторах средних Виленкина-Фейера AU — Георгий Тепнадзе 1 год – 2013 г. ПГ — 2013 N1 — дои: 10.3906/mat-1010-438 DO — 10.3906/mat-1010-438 T2 — Турецкий математический журнал JF — Журнал ДЖО — ДЖОР СП — 308 ЭП — 318 ВЛ — 37 ИС — 2 СН — 1300-0098-1303-6149 M3 — doi: 10.3906/mat-1010-438 UR — Y2 — 2022 Скорая помощь — |
| Примечание | %0 Turkish Journal of Mathematics О максимальных операторах средних значений Виленкина-Фейера
%A Георгий Тефнадзе
%T О максимальных операторах средних Виленкина-Фейера
%D 2013 г.
%J Турецкий математический журнал
%Р 1300-0098-1303-6149
%V 37
%N 2
%R дои: 10,3906/мат-1010-438 %U 10. |


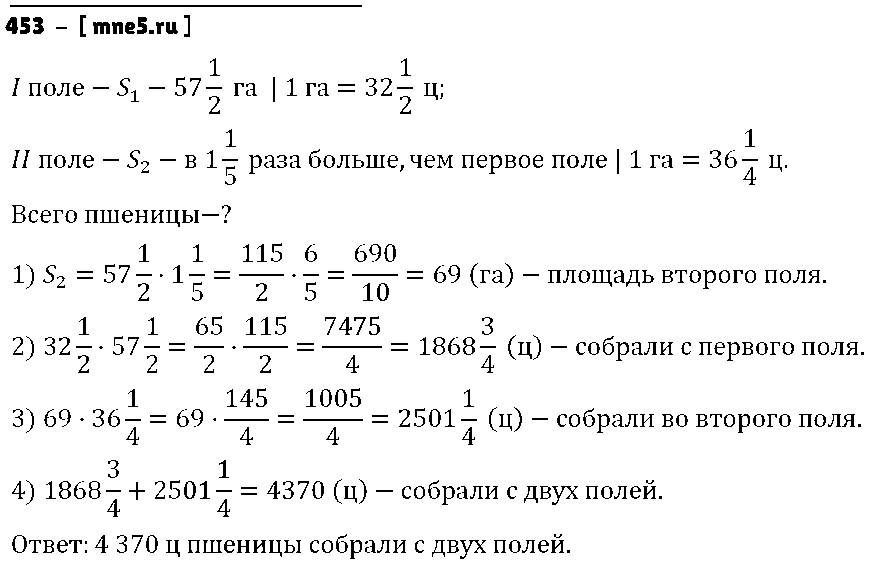 77, (1979), 111–116.
77, (1979), 111–116.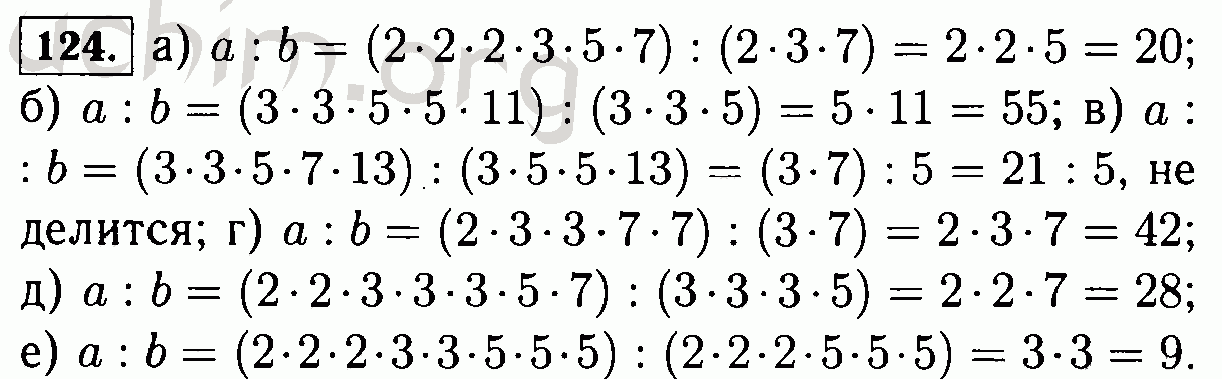 : Желание суммирования по Чезаро относительно двухпараметрических систем Уолша, Monatsh. Матем., 131, 321–334, (2000).
: Желание суммирования по Чезаро относительно двухпараметрических систем Уолша, Monatsh. Матем., 131, 321–334, (2000). 1, Кембриджский унив. Пресса, 1959.
1, Кембриджский унив. Пресса, 1959.