|
||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| И ЕЩЁ… | ||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
| gif»> | ||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
Этапы урока | Цель этапа | Деятельность учителя | Деятельность обучающихся | Универсальные учебные действия |
Организационный момент | Создание благоприятного психологического настроя на работу | Приветствует учащихся, | Взаимное приветствие, настраиваются на работу | Коммуникативные: |
Актуализация знаний | Актуализация опорных знаний и способов действий | Демонстрирует слайд 2 и предлагает выполнить устные вычисления | Выполняют вычисления с подробными объяснениями, при необходимости исправляют и дополняют ответы одноклассников | Коммуникативные: взаимодействие с учителем и сверстниками; |
Демонстрирует слайды 3, 4 и предлагает решить два уравнения. | Один учащийся проговаривает алгоритм решения уравнения, остальные – внимательно слушают, при необходимости дополняют или исправляют ответ. | Коммуникативные: взаимодействие с учителем и сверстниками; умение выражать мысли | ||
Постановка учебной задачи | Обеспечение мотивации учения детьми, принятие ими цели урока | Демонстрирует слайды 5, 6 и предлагает решить две задачи: первая задача решается арифметическим способом, вторая – алгебраическим (с помощью уравнения). Учитель задает вопросы, приводящие к пониманию о недостаточности знаний для решения второй задачи. В ходе беседы помогает определить связь между изученной темой «Уравнения» и новой задачей, подводит к формулированию темы урока (слайд 8) | Решают первую задачу.
Формулируют цель и тему урока | Коммуникативные: взаимодействие с учителем и сверстниками; умение выражать мысли |
«Открытие» учащимися новых знаний | Обеспечение восприятия и осмысления и первичного запоминания детьми новой темы | Демонстрирует слайд 9, объясняет решение задачи | Отвечают на вопросы учителя, записывают решение в тетрадь | Коммуникативные: взаимодействие с учителем и сверстниками; умение выражать мысли |
Физкультминутка | Смена деятельности. | Демонстрирует слайды 10-15 | Учащиеся выполняют упражнения |
|
Первичное закрепление | Установление правильности и осознанности изучения темы. | Слайды 16-18. Вместе с учащимися разбирает задачи по плану: — О чем задача? — Какие слова будут в краткой записи? — Что обозначим за х? — Как будут записаны остальные данные? — Какое уравнение можно составить? | Учащиеся вместе с учителем разбирают условия предложенных задач, выбирают данные для краткой записи, определяются с обозначением неизвестной и составляют уравнения | Коммуникативные: взаимодействие с учителем и сверстниками; умение выражать мысли |
Самостоятельная работа с самопроверкой по эталону | Установление правильности и осознанности изучения темы. | Предлагает учащимся самостоятельно решить задачу (слайд 19). После завершения работы открывает слайд 20 с готовым образцом решения. | Самостоятельно решают задачу, затем сверяют с образцом решения на экране (слайд 20). Оценивают свою работу (слайд 21) | Регулятивные: составление плана и последовательности действий; сличение способа действия и его результата с заданным эталоном, в случае необходимости – коррекция |
Подведение итогов | Самооценка результатов своей деятельности и всего класса | Учитель предлагает ответить на вопросы (слайд 22) | Учащиеся отвечают на вопросы | Регулятивные: |
Постановка домашнего задания |
| Домашнее задание: выучить признаки § 42, № 1174, 1176 | Записывают домашнее задание в дневник |
|
Решение нескольких текстовых задач КДР по математике.
 6 класс.
6 класс. Завтра шестиклассники пишут КДР по математике. Понимаю, насколько трудно собраться после праздников и написать итоговую годовую работу хорошо. Тем более хочется заострить внимание детей и их родителей, которые, возможно, сегодня помогают ребятам в подготовке, на задачах. Не всегда за текстовые задачи ученики берутся, а зря. Давайте рассмотрим решения нескольких задач, условия которых я взяла из вариантов КДР 2011-2012 годов.
ЗАДАЧА 1. Моторная лодка прошла 31,8 км против течения реки, затратив на этот путь 2 часа. Найдите собственную скорость моторной лодки, если скорость течения реки-1,7км/ч. Решение. Зная путь, пройденный лодкой против течения и затраченное на этот путь время, найдем скорость против течения реки. 1. 31,8:2=15,9 (км/ч) – скорость против течения реки. Так как течение реки препятствует движению лодки против течения, то для нахождения собственной скорости необходимо к скорости против течения прибавить скорость самого течения.
 2. 15,9+1,7=17,6 (км/ч) – собственная
скорость лодки. Ответ:
17,6 км/ч. ЗАДАЧА 2. В двух аудиториях стояло в общей сложности 92 стола. Когда из первой
аудитории переместили во вторую 16 столов, то в аудиториях столов стало
поровну. Сколько столов стояло в каждой аудитории первоначально? Решение. Пусть в первой аудитории – x столов, тогда во второй – (92-x). После проделанных перемещений, в
первой аудитории осталось x-16
столов, а во второй стало – (92-x)+16 столов. Составим и решим уравнение, учитывая, что
после перемещений, столов в помещениях стало поровну: 1. x-16=(92-x)+16. Решая, находим, что x=62 (шт.) – в первой аудитории. 2. Тогда
92-62=30 (шт.) – во второй аудитории. Ответ:
30 и 62 штуки первоначально. ЗАДАЧА 3. В двух коробках лежат 240 карандашей.
Когда из первой коробки переложили во вторую 18 карандашей, то карандашей в
коробках стало поровну. Сколько карандашей лежало в каждой коробке
первоначально? Решение.
2. 15,9+1,7=17,6 (км/ч) – собственная
скорость лодки. Ответ:
17,6 км/ч. ЗАДАЧА 2. В двух аудиториях стояло в общей сложности 92 стола. Когда из первой
аудитории переместили во вторую 16 столов, то в аудиториях столов стало
поровну. Сколько столов стояло в каждой аудитории первоначально? Решение. Пусть в первой аудитории – x столов, тогда во второй – (92-x). После проделанных перемещений, в
первой аудитории осталось x-16
столов, а во второй стало – (92-x)+16 столов. Составим и решим уравнение, учитывая, что
после перемещений, столов в помещениях стало поровну: 1. x-16=(92-x)+16. Решая, находим, что x=62 (шт.) – в первой аудитории. 2. Тогда
92-62=30 (шт.) – во второй аудитории. Ответ:
30 и 62 штуки первоначально. ЗАДАЧА 3. В двух коробках лежат 240 карандашей.
Когда из первой коробки переложили во вторую 18 карандашей, то карандашей в
коробках стало поровну. Сколько карандашей лежало в каждой коробке
первоначально? Решение. Задача решается,
аналогично предыдущей. Пусть в первой коробке x карандашей, тогда во второй – 240-x. После того, как карандаши переложили,
в первой осталось x-18
карандашей, во второй прибавилось и стало – (240-x)+18 штук. Составим и решим уравнение. 1. x-18=(240-x)+18. Находим, что x=138 (шт.) – в первой коробке. 2. Тогда 240-138=102 (шт.) – во второй
коробке. Ответ:
102 и 138 штук первоначально. ЗАДАЧА 4. Из села в город выехал велосипедист со
скоростью 11,5 км/ч. Через 2,4 ч вслед за ним выехал мотоциклист со скоростью
46 км/ч. Через какое время после своего выезда мотоциклист догонит
велосипедиста? Решение. При решении таких
задач советую включать воображение и никогда не использовать только лишь
формулы движения – запутаетесь. Итак. 1. Велосипедист выехал раньше
мотоциклиста и за 2,4 часа успел проделать путь, равный: 11,5 × 2,4= 27,6 (км.). 2. Скорость выехавшего мотоциклиста
больше, чем скорость велосипедиста, именно эта разница в скоростях и позволит
мотоциклу в конечном итоге догнать велосипед:
46-11,5=34,5 (км/ч) – скорость вдогонку.
Задача решается,
аналогично предыдущей. Пусть в первой коробке x карандашей, тогда во второй – 240-x. После того, как карандаши переложили,
в первой осталось x-18
карандашей, во второй прибавилось и стало – (240-x)+18 штук. Составим и решим уравнение. 1. x-18=(240-x)+18. Находим, что x=138 (шт.) – в первой коробке. 2. Тогда 240-138=102 (шт.) – во второй
коробке. Ответ:
102 и 138 штук первоначально. ЗАДАЧА 4. Из села в город выехал велосипедист со
скоростью 11,5 км/ч. Через 2,4 ч вслед за ним выехал мотоциклист со скоростью
46 км/ч. Через какое время после своего выезда мотоциклист догонит
велосипедиста? Решение. При решении таких
задач советую включать воображение и никогда не использовать только лишь
формулы движения – запутаетесь. Итак. 1. Велосипедист выехал раньше
мотоциклиста и за 2,4 часа успел проделать путь, равный: 11,5 × 2,4= 27,6 (км.). 2. Скорость выехавшего мотоциклиста
больше, чем скорость велосипедиста, именно эта разница в скоростях и позволит
мотоциклу в конечном итоге догнать велосипед:
46-11,5=34,5 (км/ч) – скорость вдогонку. 3. Зная скорость вдогонку и расстояние между
транспортными средствами, найдем время, за которое это расстояние с указанной
скоростью будет преодолено: 27,6:34,5=0,8 (ч.) – искомое время. Ответ:
через 0,8 часа. ЗАДАЧА 5. Моторная лодка прошла 47,6 км против
течения реки и 107,2 км по течению реки. Известно, что её собственная скорость
равна 25,3 км/ч, а скорость течения реки 1,5 км /ч. Сколько часов лодка
затратила на весь путь? Решение. Решим задачу по
действиям. 1. Найдем скорость по течению:
25,3+1,5=26,8 (км/ч). 2. Определим скорость против течения: 25,3
– 1,5= 23,8 (км/ч). 3. Найдем время, затраченное на путь
против течения реки: 47,6:23,8=2 (ч.). 4. Время по течению: 107,2:26,8=4 (ч.). 5. Время в пути 4+2=6 (ч.). Ответ:
6 часов. Желаю успехов в
завтрашней работе!
3. Зная скорость вдогонку и расстояние между
транспортными средствами, найдем время, за которое это расстояние с указанной
скоростью будет преодолено: 27,6:34,5=0,8 (ч.) – искомое время. Ответ:
через 0,8 часа. ЗАДАЧА 5. Моторная лодка прошла 47,6 км против
течения реки и 107,2 км по течению реки. Известно, что её собственная скорость
равна 25,3 км/ч, а скорость течения реки 1,5 км /ч. Сколько часов лодка
затратила на весь путь? Решение. Решим задачу по
действиям. 1. Найдем скорость по течению:
25,3+1,5=26,8 (км/ч). 2. Определим скорость против течения: 25,3
– 1,5= 23,8 (км/ч). 3. Найдем время, затраченное на путь
против течения реки: 47,6:23,8=2 (ч.). 4. Время по течению: 107,2:26,8=4 (ч.). 5. Время в пути 4+2=6 (ч.). Ответ:
6 часов. Желаю успехов в
завтрашней работе!Уравнение на… право! Методические рекомендации к интегрированному уроку математика-химия по теме “Решение задач с химическим содержанием”
План
1) Вступительное слово: “Математика и химия, общие точки соприкосновения” (Учителя математики и химии).
2) Решение задач на сплавы и смеси с помощью уравнений и систем уравнений. (Учитель математики).
3) Решение задач на сплавы и смеси с использованием “конверта Пирсона”. (Учитель химии).
4) Проверка усвоенного материала: самостоятельная работа.
5) Игровая ситуация, интеллектуальная разминка.
6) Способы решения систем уравнений в задачах с химическим содержанием. (Учитель математики).
7) Подведение итогов. (Учителя математики и химии).
Организация урока
Решение задач по математике с химическим содержанием вызывает затруднение у ребят. Очень важно разобраться в самом тексте задачи, вникнуть в условия, составить алгоритм решения. На спаренном уроке математика-химии можно не только научить ребят решать задачи такого содержания, но и расширить диапазон восприятия и понимания. Ознакомившись на уроке с различными способами решения одной и той же задачи, ребята будут подходить к решению подобных задач более осознанно, более осмысленно. А это значит, что учителя выполнили свою миссию.
Решение задач на сплавы и смеси с помощью уравнений и систем уравнений
Учитель математики читает условие первой задачи (желательно прочитать наизусть) 2-3 раза и начинает с ребятами искать решение, то есть рассуждать. Когда решение найдено, учитель включает кодоскоп с решенной задачей N 1 на кодопозитиве и поясняет ее решение. Необязательно записывать или конспектировать, чтобы не отвлекать ребят от творческого мышления, то есть необходим максимум внимания без каких-либо записей. После некоторого закрепления материала учитель отключает кодоскоп, и ребята устно проговаривают решение.
Решение задач на смеси и сплавы с использованием “конверта Пирсона”.
Учитель химии повторяет процедуру решения той же задачи, используя “конверт Пирсона”.
Следующую задачу N 2 поясняет учитель математики, а затем учитель химии. Следовательно, были разобраны четыре решения двух задач математическим и химическим способами.
На пояснение и решение задач затрачивается 30-40 минут.
Проверка усвоенного материала: самостоятельная работа.
После пояснения задач ребятам предлагается самостоятельная работа на 20-25 минут в двух вариантах по две задачи (варианты прилагаются). Одну задачу надо решить, используя математический способ, а вторую – химический способ. Но если две задачи решены математически или две задачи решены химически, то за это оценка не снижается. Главное, чтобы две задачи были решены правильно.
После самостоятельной работы учитель химии начинает проверять работы, а учитель математики начинает интеллектуальную разминку.
Игровая ситуация, интеллектуальная разминка
На разминке оба учителя предлагают различные виды логических задач: ребусы, вопросы, задачи и так далее.
Например:
Задача
Дается 100 монет в 10 столбцах по 10 монет. Одна из стопок состоит из фальшивых монет. Настоящая монета весит 5 граммов, а фальшивая – на 0,5 грамма меньше настоящей. Нужно одним взвешиванием определить столбец из фальшивых монет.
Решение
Из 1-й стопки берем одну монету, из 2-й две и т.д. Имеем: 1+2+3+4 …+10 = 55 монет. Вес этих монет без фальшивых должен быть: 5х55 = 275 г. На одну чашку весов ставим эти монеты и взвешиваем. Допустим, получили 274 г – значит две монеты фальшивые, следовательно, вторая стопка – из фальшивых монет.
Вес этих монет без фальшивых должен быть: 5х55 = 275 г. На одну чашку весов ставим эти монеты и взвешиваем. Допустим, получили 274 г – значит две монеты фальшивые, следовательно, вторая стопка – из фальшивых монет.
Способы решения систем уравнений в задачах с химическим содержанием
Пока еще проверяются работы, учитель математики показывает, как более рационально надо решать системы уравнений в химических задачах, где в основном встречаются большие числа, а еще чаще – десятичные дроби.
Вот одна из систем уравнений.
65x + 56y = 2,33
22,4x + 22,4y = 0,896.
На уроках химии часто учитель применяет метод подстановки, то есть из первого уравнения имеем:
65x = 2,33 – 56y
x = (2,33 – 56y)/65,
данное значение x подставляется во второе уравнение и находят y, это есть решение, но не рациональное. А желательно решать так: а) разделить каждый член второго уравнения на 22,4, имеем x+y= 0,04, а затем подставить x = 0,04 – y в первое уравнение. Но лучше полученное уравнение x+y = 0,04 умножить на 65. Имеем 65x+65y = 2,6
Имеем 65x+65y = 2,6
65x+56y = 2,33
65x+65y = 2,6
Вычитая из второго уравнения первое, получим
9y = 0,27
y = 0,03,
а x находим из уравнения x+y = 0,04, x = 0,04-y, x = 0,01.
Следовательно, решение исходной системы x = 0,01, y = 0,03.
А вот другая система уравнений
x+y = 600,
0,3x+0,1y = 90
y = 600 – x,
0,3x + 0,1y = 90.
Если не применять подстановку, то можно решить более рационально:
а) умножим II на 10, имеем
x+y = 600
3x+y = 900.
б) вычитаем из II уравнения I, имеем
2x = 300
x = 150,
y = 450.
Или можно так
x+y = 600,
3x+y = 900,
x+y = 600,
2x+x+y = 900,
x+y = 600,
2x+600 = 900,
x+y = 600,
2x = 300,
x = 150,
y = 450.
Следовательно, решение исходной системы x = 150, y = 450.
Следовательно, при решении систем уравнений можно применять более рациональное решение, меньше производить сложные вычислительные операции.
P.S. Учительница по химии была очень благодарна за эти решения.
Подведение итогов
Проверяющий зачитывает результаты самостоятельной работы.
Результаты бывают всегда хорошими: качество 80% – 100%, а успеваемость почти всегда 100%. (Есть маленький нюанс, классы у меня усиленные, то есть работают по расширенной авторской программе. Но такие уроки проводили и в обыкновенных классах, и результаты были хорошими).
Роберт БАГИЕВ
поселок Нефтегорск,
Апшеронский район,
Краснодарский край
Загадки на логику с подвохом | Развивающие игры для детей — онлайн занятия для детей
Решение различных задач и загадок, способствующих развитию логического мышления, само по себе сложное и затягивающее в «омут знаний» занятие. А когда задачки еще и с подвохом, думать тяжелее вдвойне: ответ на вопрос может оказаться предельно простым и ввести в «ступор» даже бывалого математика.
Не нервничайте раньше времени и подключите к решению загадок детей, а еще лучше – зайдите с ними на сайт Умназии и составьте индивидуальную программу. Развивайте пять навыков мышления вместе с нами и будьте уверены в том, что ваш ребенок справится с любой логической (и даже алогической) школьной задачей.
Развивайте пять навыков мышления вместе с нами и будьте уверены в том, что ваш ребенок справится с любой логической (и даже алогической) школьной задачей.
Загадки с подвохом. В чем суть?
Вопросы с «подковыркой» содержат «тайну», которую нужно разгадать и детям, и взрослым. Здесь нет очевидных ответов, «прозрачных» решений и скучных алгоритмов. Верный ответ порой переворачивает сознание с ног на голову и заставляет взглянуть на мир по-другому. Дети учатся мыслить нестандартно и расширяют кругозор, взрослые смеются и (или) хватаются за голову в бесконечных попытках найти правильное решение.
Зачем это нужно?
Когда ребенок решает обычную задачу, он ищет самый «логичный» ответ на нее. Учится думать и анализировать, обрабатывать информацию, оценивать факты и делать выводы. При решении загадок с подвохом ему приходится менять алгоритм и подключать к работе не только левое «аналитическое» полушарие, но и «творческое» правое, которое оперирует вдохновением и фантазией. Найти правильный ответ помогает и то, и другое: в загадках с подвохом важно не только соотнести аргументы, посылки и выводы, но и предугадать неоднозначность самой отгадки.
Найти правильный ответ помогает и то, и другое: в загадках с подвохом важно не только соотнести аргументы, посылки и выводы, но и предугадать неоднозначность самой отгадки.
Загадки с подвохом для детей
Начнем с малого и решим 5 загадок для самых маленьких. Взрослым ответ покажется очевидным, а вот ребятам придется подумать (но может быть и наоборот). Чур, не подсказывать!
Загадка №1
Что ты никогда не сможешь съесть на завтрак?
Показать ответ
Ответ: Обед и/или ужин.
Загадка №2.
Что может путешествовать по свету, оставаясь в одном и том же углу?
Показать ответ
Ответ: Почтовая марка.
Загадка №3
В одноэтажном розовом доме жил розовый человек, розовый кот, розовая рыбка, был розовый компьютер, розовое кресло, розовый стол, розовый телефон, розовая душевая кабина – все было розовым! Какого цвета была лестница?
Показать ответ
Ответ: В этом доме не было лестницы, потому что это был одноэтажный дом.
Загадка №4
Что настолько же огромное, как слон, но ничего не весит?
Показать ответ
Ответ: Тень слона.
Загадка №5
Какое слово в словаре написано неправильно?
Показать ответ
Ответ: Это слово «неправильно».
Мы знаем, что вам и вашим детям, как минимум, было интересно. А как максимум – вы серьезно задумались и хотите идти дальше!
СМЕШНЫЕ ЗАГАДКИ НА ЛОГИКУ
Подойдут для всех возрастных категорий и потребуют максимально нестандартных решений. Не заставят скучать, рассмешат и научат мыслить логически даже самого нелогичного человека. Переходим к изучению и поиску правильного ответа!
Загадка №1
У каких волос есть сходство с океаном?
Показать ответ
Ответ: У волнистых.
Загадка №2
Мужчина гулял в парке, когда на улице пошел дождь. У мужчины не было зонтика, и он не мог накинуть на себя плащ или накрыться шляпой. На нем не осталось сухой одежды, однако ни один волос на его голове не промок. Как это могло произойти?
На нем не осталось сухой одежды, однако ни один волос на его голове не промок. Как это могло произойти?
Показать ответ
Ответ: Мужчина был лысый.
Загадка №3
Какой рукой удобнее размешивать сахар в стакане с чаем?
Показать ответ
Ответ: Рукой, которая держит ложку.
Загадка №4
На что больше всего похожа половинка яблока?
Показать ответ
Ответ: На вторую половинку этого же яблока.
Загадка №5
Какое изобретение позволяет смотреть сквозь стены?
Показать ответ
Ответ: Ничего сверхъестественного. Сквозь стены мы смотрим через окно.
Посмеялись? Если да, мы вас поздравляем: ученые утверждают, что смех продлевает жизнь. Если нет, не грустите – попробуйте еще раз вчитаться в условие и соотнести его с правильным ответом. Даже если после этого на вашем лице нет и намека на улыбку, будьте уверены, вы старались не зря: развитое логическое мышление непременно пригодится в повседневной жизни вам и вашему ребенку.
Трудные загадки с подвохом
Нет, мы еще не закончили. Последние пять загадок будут особенно сложными: здесь детям понадобится помощь взрослых. Опять придется мобилизовать оба полушария мозга, немного понервничать и вспомнить кое-что из школьного курса обществознания. Поразмышляйте над ответом, «пораскиньте» мозгами и найдите то самое решение!
Загадка №1
Человек выпрыгнул из самолёта без парашюта. Он приземлился на твёрдый грунт, но остался невредимым. Почему?
Показать ответ
Ответ: Самолёт стоял на земле.
Загадка №2
«Мой брат – адвокат», — говорит бухгалтер. Адвокат говорит, что у него нет брата. Кто из них лжет?
Показать ответ
Ответ: Никто, потому что бухгалтер – сестра адвоката.
Загадка №3
Мужчина ехал по дороге на своем грузовике. Фары не были включены. Луна не светила. Перед грузовиком женщина в черной одежде переходила дорогу. Догадайтесь, как мужчина ее увидел.
Догадайтесь, как мужчина ее увидел.
Показать ответ
Ответ: Женщину было отчетливо видно, потому что это происходило днем, а не ночью.
Загадка №4
Однажды за завтраком девушка уронила кольцо в чашку с кофе. Однако кольцо осталось сухим. Почему?
Показать ответ
Ответ: Кофе не был напитком: он был в зернах. Если вы ответили, что кофе был молотый или растворимый, вы тоже правы.
Загадка №5
Что все время приходит, но никак не придет?
Показать ответ
Ответ: Завтра.
Ура! Мы с вами поработали на отлично и стали чуть-чуть умнее.
Хотите еще?
Приводите ребенка в Умназию и развивайтесь вместе с нами.
В вашем распоряжении более 4000 авторских задач, выбор траектории обучения, игровой формат и формирование каждого из пяти навыков. Логика, эрудиция, внимание, память и обучаемость – настраивайте и выбирайте наиболее интересные для ребенка задания, получайте награды и вместе радуйтесь новым победам.
Начните заниматься в Умназии уже сегодня!
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнееЧитайте также:
6 класс по математике
1. Учащиеся свяжут соотношение и коэффициент с умножением и делением целых чисел и будут использовать понятия коэффициента и коэффициента для решения задач.
2. Студенты завершат понимание деления дробей и распространят понятие числа на систему рациональных чисел, которая включает отрицательные числа.
3. Учащиеся будут писать, интерпретировать и использовать выражения и уравнения.
4.Студенты разовьют понимание статистического мышления.
Больше заниматься математикой дома
Две важные цели для всех учащихся: 1) они научатся ценить математику и 2) обрести уверенность в своих способностях. Родители могут помочь детям развить в себе склонность к математике, взращивая в них естественное любопытство и обеспечивая поддержку и поддержку.
Родители могут помочь детям развить в себе склонность к математике, взращивая в них естественное любопытство и обеспечивая поддержку и поддержку.
Математика повсюду, но многие дети ее не замечают.Ищите способы подчеркнуть и закрепить математические навыки дома. Например:
· Расскажите о том, как вы используете математику на работе или дома
· Вовлекайте детей в задачи, требующие вычислений, измерения, оценки, построения, следования указаниям, решения проблем и рассуждений
· Ищите занятия, которые требуют от детей использования их математических навыков, таких как построение масштабных моделей, приготовление пищи, планирование поездок и игра в логические игры.
Ищите игры и упражнения, которые учат и / или укрепляют математику и мышление.Например, ищите игры, которые:
· требуют и развивают навыки умственного вычисления и оценки
· требуют от игроков использования математических навыков
· включают разработку стратегий
· требуется игроки должны думать о вероятности наступления определенных событий
· требовать использования навыков пространственной визуализации
· требовать логического мышления
Когда вы видите статьи, содержащие данные, которые могут заинтересовать ваших детей (например,g. , спортивная статистика, данные о курении среди подростков, факты о стихийных бедствиях), поделитесь ими и поговорите о том, что означают цифры.
, спортивная статистика, данные о курении среди подростков, факты о стихийных бедствиях), поделитесь ими и поговорите о том, что означают цифры.
Поделитесь своими стратегиями и методами решения проблем, стратегиями мысленных вычислений и стратегиями оценки. Пусть ваши дети научат вас чему-нибудь. Поработайте над одной и той же проблемой, а затем сравните стратегии и ответы.
Предложите детям объяснить, что было изучено на уроке математики, или попросите их научить вас этому. Это дает детям возможность помочь прояснить свое мышление, отработать новые навыки и попрактиковаться в математическом общении.
Если у ваших детей есть доступ к технологиям, ищите программное обеспечение и приложения, которые укрепляют и обучают математическим понятиям. Помогите своим детям научиться использовать математические утилиты, такие как электронные таблицы и программы для построения графиков.
Обзор 6-го класса
Соотношение и пропорциональные отношения
· Понять концепцию соотношений и использовать рассуждения о соотношении для решения проблем.
· Словарь
o Соотношение — сравнение двух величин, выраженных как 3/5, 3: 5 или 3-5.
o Ставка единицы — ставка с одним из чисел равна 1 или количеством 1.
o Процент — из 100.
o Доход — сумма полученных денег.
o Прибыль — сумма, на которую доход больше расходов.
Система счисления
· Применяйте и расширяйте предыдущие представления об умножении и делении для деления дробей на дроби
· Умножайте и делите многозначные числа и находите общие множители и кратные.
· Примените и расширите предыдущее понимание чисел на систему рациональных чисел.
· Словарь
o Фактор — одно или несколько целых чисел, которые умножаются вместе, чтобы получить произведение.
o Кратное — произведение заданного целого числа на другое целое число.
o Простое число — число с двумя множителями, единицей и самим собой.
o Составной — число с более чем двумя факторами.
o Факторизация на простые числа — произведение простых чисел, возможно с некоторыми повторениями, в результате чего получается желаемое число. БЫВШИЙ. 27 = 3 x 3 x 3 или 30 = 2 x 3 x 5
o Квадратное число — число, которое является результатом произведения числа, умноженного на само себя.
o Наименьшее общее кратное (НОК) — наименьшее кратное, общее для двух или более чисел.
o Наибольший общий фактор (GCF) — наибольший фактор, который разделяют два или более числа.
o Экспонента — небольшое повышенное число, показывающее, сколько раз используется коэффициент.
o Повторяющееся десятичное число — десятичное число с шаблоном фиксированного количества цифр, которое повторяется бесконечно.
o Завершающее десятичное число — десятичное число, которое заканчивается или завершается.
Выражения и уравнения
· Применяйте и расширяйте предыдущие представления об арифметике для алгебраических выражений.
· Обдумайте и решите уравнения и выражения с одной переменной.
· Представьте и проанализируйте количественные отношения между зависимыми и независимыми переменными.
· Словарь
o Распределительное свойство — математическое свойство, используемое для перезаписи выражений, включающих сложение и умножение. БЫВШИЙ. 4 (5 + x) = 4 (5) + 4 (x) = 20 + 4x
o Порядок операций — установленное соглашение для выполнения расчетов с одной или несколькими операциями. (Круглые скобки, экспоненты, умножение / деление (перемещение слева направо), сложение / вычитание (перемещение слева направо)
o Эквивалент — равно по значению
o Неравенство — утверждение, которое сравнивает две величины. <,>, <И> используются для обозначения неравенства.
<,>, <И> используются для обозначения неравенства.
o Выражение — математическая фраза, содержащая числа, переменные и символы операций.
o Переменная — величина, которая может изменяться, часто обозначается буквой
o Коэффициент — число, которое умножается на переменную в уравнении или выражении.
Геометрия
· Решение реальных и математических задач, касающихся площади, площади поверхности и объема.
· Словарь
o Площадь — мера площади, заключенной в границу фигуры, количество квадратных единиц в фигуре.
o Периметр — мера расстояния вокруг двухмерной фигуры.
o Объем — объем пространства, занимаемого трехмерной фигурой, количество единичных кубов, которые вписываются в форму.
o Площадь поверхности — площадь, необходимая для покрытия трехмерной формы.
o Координаты X и Y — числа в паре координат, используемые для определения точки на координатном графике.
Статистика и вероятность
· Развивайте понимание статистической изменчивости.
· Обобщите и опишите распределения.
· Словарь
o Среднее — значение, найденное, когда все данные объединены, а затем распределены равномерно (среднее значение)
o Медиана — число, которое является средней точкой упорядоченного набора данных.
o Режим — число, которое чаще всего встречается в заданном наборе данных.
o Диапазон — разница между максимальным и минимальным значением в распределении.
o Линейный график — способ упорядочить данные по числовой прямой, где X (или другие символы) над числом обозначают частоту упоминания каждого значения.
o Таблица частот —
o Коробчатая диаграмма — отображение, которое показывает распределение значений в наборе данных, разделенных на 4 группы равного размера, построенное на основе 5-значной сводки данных (минимальное значение, нижний квартиль, медиана, верхний квартиль и максимальное значение)
o Верхний квартиль — медиана данных слева от медианы.
o Нижний квартиль — медиана данных справа от медианы.
o Выбросы — значение, которое находится далеко от центра распределения данных и не похоже на другие значения.
МАТЕМАТИКА G6: 6 класс по математике
Описание
По математике в шестом классе около
— Связь соотношения и скорости с умножением и делением целых чисел и использование концепций соотношения и скорости для решения задач
— Завершение понимания деления дробей и расширение понятия числа до системы рациональных чисел
— Написание, интерпретация и использование выражений и уравнений
— Развитие понимания статистического мышления.
О загружаемых ресурсах
История соотношений, карта учебного плана и обзор для 6-8 классов : Карта учебного плана и обзор истории соотношений предоставляют учителям четкое представление о модулях на каждом уровне с 6 по 8 класс.
Контрольный список CCLS для истории соотношений : Контрольный список CCLS для истории соотношений включает в себя диаграммы уровней классов, позволяющие быстро определить, когда выполняется каждый стандарт.
Поддержка беглости речи по математике для 6–8 классов : Общие основные стандарты по математике призывают учащихся получить и продемонстрировать не только концептуальное понимание и решение задач, но также процедурные навыки и беглость.
Scaffolding Instruction for ELLs: Resource Guide for Mathematics : предоставить преподавателям инструкции по использованию учебных материалов на EngageNY и предоставить дополнительные строительные леса для студентов ELL в соответствии с их уровнем владения английским языком.
Загрузки
Могут быть случаи, когда наши загружаемые ресурсы содержат гиперссылки на другие сайты. Эти гиперссылки ведут на веб-сайты, опубликованные или управляемые третьими сторонами. UnboundEd и EngageNY не несут ответственности за содержание, доступность или политику конфиденциальности этих веб-сайтов.
Теги
- Нет тегов для этого ресурса.
Кредиты
от EngageNY.org Департамента образования штата Нью-Йорк. 6 класс по математике. Доступно на сайте engageny.org/resource/grade-6-mat Mathematics; доступ 2015-05-29.
Авторские права © 2015 Great Minds. UnboundEd не связан с правообладателем этой работы.
Добро пожаловать в Space Math @ NASA!
Решение проблем
Задача 564: Исследование звезд Ориона — Безумие светового года
Студенты изучают световой год и его связь со временем путешествия света для наблюдения за событиями в различных частях космоса.-reshenie-614.jpg) Когда колонисты в разных местах увидят, что звезда Бетельгейзе стала сверхновой?
[Оценка: 6-8 | Темы: временные рамки; расчет временных интервалов; время = расстояние / скорость]
[Кликните сюда]
Когда колонисты в разных местах увидят, что звезда Бетельгейзе стала сверхновой?
[Оценка: 6-8 | Темы: временные рамки; расчет временных интервалов; время = расстояние / скорость]
[Кликните сюда]
Задача 507: Исследование запуска Falcon 9
Учащиеся используют данные о запуске ракеты-носителя Falcon 9 для определения ее скорости и ускорения.
[Оценка: 6-8 | Темы: скорость = расстояние / время; Расчет времени]
[Кликните сюда]
Проблема 505: SDO видит корональный дождь — оценка скорости плазмы
Студенты оценивают скорость плазменных стримеров у поверхности Солнца, используя изображения, полученные в обсерватории солнечной динамики.[Оценка: 6-8 | Темы: масштабные модели; скорость = расстояние / время; пропорции]
[Кликните сюда]
Задача 488: RBSP и расположение хора рассвета — II
Учащиеся используют гипотетическую информацию от космического корабля-близнеца RBSP для триангуляции местоположения сигнала Chorus вблизи Земли с помощью угловых измерений, построения графиков и транспортира для определения точки пересечения сигналов CHorus. [Оценка: 6-8 | Темы: Углы; построение графиков; транспортиры]
[Кликните сюда]
[Оценка: 6-8 | Темы: Углы; построение графиков; транспортиры]
[Кликните сюда]
Задача 452: Ближайшее сближение астероида 2005YU55 — I
Учащиеся работают с масштабным рисунком орбиты Луны и траектории астероида, чтобы предсказать, где астероид будет относительно Земли и орбиты Луны.[Оценка: 6-8 | Темы: время = расстояние / скорость; масштабные модели; метрическая математика]
[Кликните сюда]
Задача 451: Эффектная планетарная туманность Кошачий глаз
Студенты измеряют диаметр туманности и используют информацию о скорости, чтобы оценить возраст туманности.
[Оценка: 6-8 | Темы: время = расстояние / скорость; масштабные модели; метрическая математика]
[Кликните сюда]
Задача 445: LRO — Относительный возраст лунных поверхностей
Студенты исследуют две зоны приземления Аполлона, используя изображения с космического корабля LRO, чтобы оценить относительный возраст двух регионов с использованием
подсчет кратеров. [Оценка: 6-8 | Темы: масштаб; гистограмма]
[Кликните сюда]
[Оценка: 6-8 | Темы: масштаб; гистограмма]
[Кликните сюда]
Задача 438: Последний полет космического корабля «Индевор»
Студенты используют табличные данные и графики для определения скорости запуска и ускорения космического челнока со стартовой площадки. [Оценка: 6-8 | Темы: табличные данные, графики, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 437: Скорость и высота старта ракеты Сатурн V.
Учащиеся используют табличные данные для определения скорости запуска ракеты Сатурн V со стартовой площадки.[Оценка: 6-8 | Темы: табличные данные, графики, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 436: Спейс шаттл Challenger развертывает спутник INSAT-1B
Учащиеся используют последовательность изображений, чтобы определить скорость запуска спутника из грузового отсека космического корабля «Шаттл».
[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 435: Запуск Аполлона-17 с поверхности Луны
Студенты используют последовательность изображений для определения скорости подъема капсулы Аполлона-17 с поверхности Луны. [Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 434: Космический корабль «Рассвет» видит вблизи астероид Веста!
Студенты используют изображение астероида для определения диаметра кратеров
и горы с помощью миллиметровой линейки и масштаба изображения в метрах на миллиметр.
[Оценка: 6-8 | Темы: шкала, метрические измерения]
[Кликните сюда]
Задача 433: космический шаттл «Атлантис» — скорость шлейфа
Учащиеся используют последовательность изображений из видеозаписи запуска, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения.[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Проблема 432: Спейс Шаттл Атлантис — Скорость выхлопа
Учащиеся используют последовательность изображений из видеозаписи запуска, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения. [Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 431: космический корабль «Атлантис» — скорость запуска
Учащиеся используют последовательность изображений из видеозаписи запуска, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения.[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 430: Спейс шаттл «Атлантис» — восхождение на орбиту
Учащиеся используют последовательность изображений из видеозаписи запуска, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения.
[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 429: Отслеживание морской черепахи из космоса
Широта, долгота, прошедшее время и пройденное расстояние представлены в таблице. Учащиеся используют эти данные для определения суточной и почасовой скорости кожистой черепахи, когда она путешествует из Новой Зеландии в Калифорнию через Тихий океан.
[Оценка: 4-6 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Учащиеся используют эти данные для определения суточной и почасовой скорости кожистой черепахи, когда она путешествует из Новой Зеландии в Калифорнию через Тихий океан.
[Оценка: 4-6 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 404: Космический аппарат STEREO дает 360-градусный обзор Солнца Учащиеся используют спутниковые изображения STEREO, чтобы определить, какие объекты можно увидеть с Земли, а какие нет. Они учатся о расположении и изменении положения спутников относительно орбиты Земли.[Оценка: 6-8 | Темы: угловая мера, экстраполяция; расстояние = скорость x время] [Кликните сюда]
Задача 267: Определение материалов по их отражательной способности Отражательная способность материала может использоваться для его идентификации. Это важно при съемке лунной поверхности на предмет минералов, а также в создании «зеленой» среды обитания на Земле. [Оценка: 6-8 | Темы: процент, интерпретация табличных данных, площадь] [Нажмите здесь]
Задача 237: Марсианские пыльные дьяволы Учащиеся определяют скорость и ускорение марсианского пылевого дьявола на основе изображений временных кругов и информации о масштабе изображения. [Оценка: 6-8 | Темы: весы; Определение скорости из последовательных изображений; V = D / T] [Нажмите здесь]
[Оценка: 6-8 | Темы: весы; Определение скорости из последовательных изображений; V = D / T] [Нажмите здесь]
Задача 247: Космическая мобильная головоломка Учащиеся рассчитывают недостающие массы и длины в мобильном телефоне, используя основное уравнение баланса m1 x r1 = m2 x r2 для солнечная система мобильная. [Оценка: 6-8 | Темы: метрическая мера, алгебра 1, геометрия] [Нажмите здесь]
Задача 245: Твердотопливные ракетные ускорители Студенты узнают, как SRB на самом деле создают тягу, и изучают ускоритель Ares-V, чтобы оценить его тягу.[Оценка: 6-8 | Темы: объем, площадь, преобразование единиц] [Нажмите здесь]
Задача 238: Спутник и космический телескоп Хаббла Спутники увлекаются атмосферой, что в конечном итоге приводит к их сгоранию в атмосфере. Студенты учатся
различные прогнозы высоты космического телескопа Хаббла, чтобы оценить год его возвращения в атмосферу. [Оценка: 6-8 | Темы: интерпретация графических данных; прогнозирование тенденций] [Нажмите здесь]
[Оценка: 6-8 | Темы: интерпретация графических данных; прогнозирование тенденций] [Нажмите здесь]
Задача 211: Куда делись все звезды? — Студенты узнают, почему на фотографиях НАСА часто не видны звезды из-за того, как камеры снимают яркие и тусклые объекты.[Оценка: 6-8 | Темы: умножение; разделение; десятичные числа.] [Щелкните здесь]
Задача 209: Как выделить тусклые предметы в ярком мире! — Учащиеся узнают, что сложение изображений вместе часто улучшает слабые вещи, которые не видны только на одном изображении; мощность усреднения данных. [Оценка: 6-8 | Темы: умножение; разделение; десятичные числа.] [Щелкните здесь]
Задача 148 Исследование умирающей звезды Учащиеся используют данные спутника Spitzer для вычисления массы планетарной туманности по умирающей звезде.[Класс: 9 — 11 | Темы: Научная нотация; преобразование единиц измерения; объем сферы] [Нажмите здесь]
Задача 141
Изучение пыльной молодой звезды Учащиеся используют спутниковые данные Spitzer, чтобы узнать, как пыль излучает инфракрасный свет и
рассчитать массу пылинок от молодой звезды в туманности NGC-7129. [Оценка: 4–7 | Темы: Алгебра I; умножение, деление; научная нотация] [Щелкните здесь]
[Оценка: 4–7 | Темы: Алгебра I; умножение, деление; научная нотация] [Щелкните здесь]
Задача 134 Последнее полное солнечное затмение — когда-либо! Студенты изучают геометрию, необходимую для полное солнечное затмение и оцените, на сколько лет в будущем произойдет последнее полное солнечное затмение. затмение произойдет, когда Луна будет медленно удаляться от Земли на 3 сантиметра в год.[Класс: 7–10 | Темы: Простые линейные уравнения] [Щелкните здесь]
Задача 124 Атмосфера Луны Студенты узнают об очень тонкой атмосфере Луны, вычисляя ее общую массу в килограммах, используя объем сферической оболочки и измеренную плотность. [Оценка: 8-10 | Темы: объем шара, оболочки; плотность-масса-объем; преобразование единиц] [Нажмите здесь]
Задача 115
Математическая модель Солнца Студенты будут использовать формулу для сферы и оболочки, чтобы вычислить массу
солнце для различных вариантов его плотности. Цель состоит в том, чтобы воспроизвести измеренную массу и радиус Солнца с помощью
тщательный подбор его плотности в области ядра и области оболочки. Учащиеся будут изменять значения плотности и размера оболочки, чтобы
достичь правильной общей массы. Это можно сделать вручную или с помощью программирования.
электронную таблицу Excel.
[Оценка: 8-10 | Темы: научная нотация; объем шара и сферической оболочки; плотность, масса и объем.] [Щелкните здесь]
Цель состоит в том, чтобы воспроизвести измеренную массу и радиус Солнца с помощью
тщательный подбор его плотности в области ядра и области оболочки. Учащиеся будут изменять значения плотности и размера оболочки, чтобы
достичь правильной общей массы. Это можно сделать вручную или с помощью программирования.
электронную таблицу Excel.
[Оценка: 8-10 | Темы: научная нотация; объем шара и сферической оболочки; плотность, масса и объем.] [Щелкните здесь]
Задача 95 Исследование доз облучения космонавтов в космосе — Студенты изучат график доз облучения космонавтов для полетов космических шаттлов и оценят общие дозировки для космонавтов, работающих на Международной космической станции.[Уровень обучения: 9-11 | Темы: анализ графиков, интерполяция, преобразование единиц измерения] [Щелкните здесь]
Задача 83
Риски падения метеорита на Лунер — В 2006 году ученые идентифицировали 12 вспышек света на Луне, которые, вероятно, были падением метеорита. По их оценкам, эти метеориты, вероятно, были размером с грейпфрут.
Как долго лунным колонистам придется ждать, чтобы увидеть такую вспышку на своем горизонте? Ученики
будет использовать вычисление площади и вероятности, чтобы определить среднее время ожидания.[Уровень оценки: 8-10 | Темы: арифметика; преобразование единиц измерения; площадь поверхности сферы] [Нажмите здесь]
По их оценкам, эти метеориты, вероятно, были размером с грейпфрут.
Как долго лунным колонистам придется ждать, чтобы увидеть такую вспышку на своем горизонте? Ученики
будет использовать вычисление площади и вероятности, чтобы определить среднее время ожидания.[Уровень оценки: 8-10 | Темы: арифметика; преобразование единиц измерения; площадь поверхности сферы] [Нажмите здесь]
Задача 74 Жаркое время на Марсе — Эксперимент NASA Mars Radiation Environment (MARIE) создал карту поверхности Марса и измерил радиационный фон на уровне земли, которому будут подвергаться астронавты. Эта математическая задача позволяет студентам изучить общую дозу радиации, которую эти исследователи получат в серии 1000-километровых путешествий по марсианскому региону. поверхность.Студенты будут сравнивать эту дозировку с типичными фоновыми условиями на Земле и на Международной космической станции, чтобы получить представление о перспективе. [Уровень обучения: 6-8 | Темы: десятичные дроби, преобразование единиц измерения, построение графиков и анализ] [Нажмите здесь]
Задача 71
Действительно ли пояса Ван Аллена смертельно опасны? — В этой задаче исследуются дозы радиации, которые космонавты получат во время путешествий. через пояс Ван Аллена по пути к Луне.Учащиеся будут использовать данные, чтобы рассчитать продолжительность поездки через ремни и общую полученную дозу, и сравнить ее со смертельной дозой с
противостоять заблуждению о том, что астронавты «Аполлона» мгновенно погибли бы во время полета на Луну.
[Уровень оценки: 8-10 | Темы: десятичные дроби, площадь прямоугольника, анализ графиков] [Нажмите здесь]
через пояс Ван Аллена по пути к Луне.Учащиеся будут использовать данные, чтобы рассчитать продолжительность поездки через ремни и общую полученную дозу, и сравнить ее со смертельной дозой с
противостоять заблуждению о том, что астронавты «Аполлона» мгновенно погибли бы во время полета на Луну.
[Уровень оценки: 8-10 | Темы: десятичные дроби, площадь прямоугольника, анализ графиков] [Нажмите здесь]
Задача 68 Введение в космическое излучение — Прочтите о дозах естественного фонового излучения, узнайте о Ремс и Рад, а также разница между дозировками низкого и высокого уровня.Студенты используют основные математические операции для расчета общих доз на основе дозировки и расчета риска рака. [Уровень обучения: 6-8 | Темы: Чтение для получения информации; десятичные дроби, дроби, квадратные корни] [Нажмите здесь]
Задача 66
Фоновое излучение и образ жизни — Живя на Земле, вы будете подвергаться воздействию множества различных излучений. среды. Эта задача следует за одним человеком через четыре различных возможных варианта будущего и сравнивает
кумулятивные дозировки за всю жизнь.[Уровень обучения: 6-8 | Темы: дроби, десятичные дроби, преобразование единиц] [Нажмите здесь]
среды. Эта задача следует за одним человеком через четыре различных возможных варианта будущего и сравнивает
кумулятивные дозировки за всю жизнь.[Уровень обучения: 6-8 | Темы: дроби, десятичные дроби, преобразование единиц] [Нажмите здесь]
Задача 54 Изучение далеких галактик — Астрономы определяют красные смещения далеких галактик, используя спектры и измеряя сдвиги длин волн для знакомых атомные линии. Чем больше красное смещение, обозначенное буквой Z, тем дальше галактика. В этом упражнении учащиеся будут использовать реальное изображение далекого уголка Вселенной с красными смещениями. идентифицированных галактик.После гистограммы распределения красного смещения они будут использовать онлайн-калькулятор космологии для определения времени «оглядки назад» для галактик и найдите самую древнюю галактику в этой области. Могут ли студенты найти только сформированную галактику? 500 миллионов лет после Большого взрыва? [Уровень обучения: 6-8 | Темы: Десятичная математика; с помощью онлайн-калькулятора; Данные гистограммы] [Нажмите здесь]
Задача 49
Спиральная галактика крупным планом. — Астрономы могут многому научиться, изучая фотографии галактик.В
в этом упражнении учащиеся вычисляют масштаб изображения (световых лет на миллиметр) в
сфотографируйте ближайшую спиральную галактику и исследуйте размеры деталей, обнаруженных на изображении. Они
будет также использовать Интернет или другие ресурсы, чтобы заполнить недостающую справочную информацию об этой галактике.
[Уровень обучения: 6-8 | Темы: Интернет-исследования; Определение масштаба изображения; метрическое измерение; десятичная математика] [Нажмите здесь]
— Астрономы могут многому научиться, изучая фотографии галактик.В
в этом упражнении учащиеся вычисляют масштаб изображения (световых лет на миллиметр) в
сфотографируйте ближайшую спиральную галактику и исследуйте размеры деталей, обнаруженных на изображении. Они
будет также использовать Интернет или другие ресурсы, чтобы заполнить недостающую справочную информацию об этой галактике.
[Уровень обучения: 6-8 | Темы: Интернет-исследования; Определение масштаба изображения; метрическое измерение; десятичная математика] [Нажмите здесь]
Задача 41 Солнечная энергия в космосе Студенты рассчитают площадь поверхности спутника. используется для солнечных батарей из реальной фотографии спутника IMAGE.Они рассчитают электрическую мощность, обеспечиваемую этой панелью. Ученики Придется вычислить площадь неправильной области, используя вложенные прямоугольники. [Уровень оценки: 7-10 | Темы: Площадь неправильного многоугольника; десятичная математика] [Нажмите здесь]
Задача 36
Распад орбиты космической станции и космос
Погода Студенты узнают о
продолжающийся распад орбиты Международной космической станции из-за
изучение графика зависимости высоты станции от времени. Они будут
рассчитать скорость затухания орбиты и выяснить, почему это может быть
происходит. [Класс: 5 — 8 | Темы: интерпретация графических данных; десятичная математика] [Нажмите здесь]
Они будут
рассчитать скорость затухания орбиты и выяснить, почему это может быть
происходит. [Класс: 5 — 8 | Темы: интерпретация графических данных; десятичная математика] [Нажмите здесь]
Задача 31 Авиарейсы и космическая погода Студенты прочитают отрывок из книги «Космическая погода» книгу доктора Стена Оденвальда «23-й цикл» и ответьте на вопросы о авиаперелеты во время солнечных бурь. Они узнают о естественном радиационный фон, которому они подвергаются каждый день, и сравните это с дозы радиации во время путешествия на реактивном самолете.[Класс: 6 — 8 | Темы: Чтение, чтобы быть в курсе; десятичная математика] [Нажмите здесь]
Задача 10 Жизненный цикл полярного сияния Студенты изучают описания двух очевидцев полярное сияние и определите общие элементы, чтобы они могли извлечь общие картина изменений. [Оценка: 4–6 | Темы: Создание хронологии из повествования; упорядочивание событий по дате и времени] [Нажмите здесь]
Эван Мур | Учебные материалы и планы уроков: Ежедневные задания Эвана-Мура 6 класс
Полностью переработанный в 2019 году с учетом стандартов на уровне класса Daily Word Problems — идеальный ресурс для улучшения навыков учащихся в решении проблем. Абсолютно НОВЫЕ текстовые задачи написаны для поддержки текущих математических стандартов и ожиданий и обеспечивают последовательный спиральный обзор математических понятий. Навыки решения проблем учащиеся улучшаются по мере того, как они участвуют в содержательной, реальной математической практике.
Абсолютно НОВЫЕ текстовые задачи написаны для поддержки текущих математических стандартов и ожиданий и обеспечивают последовательный спиральный обзор математических понятий. Навыки решения проблем учащиеся улучшаются по мере того, как они участвуют в содержательной, реальной математической практике.
36 недель занятий дают возможность попрактиковаться в математических понятиях на уровне класса, таких как сложение, умножение, дроби, логика, алгебра и многое другое.
Каждую неделю посвящается теме и предлагается ежедневная словесная задача в контексте реальной жизненной ситуации.
- Занятия с понедельника по четверг включают одно- или двухэтапную задачу.
- Пятничный формат более обширен и требует нескольких шагов. Многоступенчатые задачи требуют, чтобы учащиеся использовали навыки мышления более высокого порядка, применяя свое понимание в другом контексте.
- Воспроизводимые страницы предоставляют студентам достаточно места для решения, используя стратегию по своему выбору.

Что нового в обновленном издании Daily Word Problems ?
- Совершенно новые задачи Word для поддержки текущих стандартов.
- Новые еженедельные темы, которые представляют проблемы в контексте реальной жизни
- Ежедневный список навыков, помогающий учителям определять применяемые навыки
Практика математических навыков 6-го класса включает:
- положительные и отрицательные числа
- сложение и вычитание
- умножение и деление
- множители и кратные
- дроби
- десятичные дроби
- проценты
- отношения и скорости
- неравенства
- время и температура
- линейное измерение
- площадь поверхности и площадь
- площадь и объем
- статистика
- координатная плоскость
- графики, диаграммы и карты
- логическое мышление
- пространственное мышление
- выражений и уравнений
Включает в себя диаграмму области действия и последовательности и ключ ответа.
6 класс по математике | Государственные школы Гринфилда
6 класс MATH — Ms. Boosahda
Математика — это язык чисел и символов
используется для анализа данных, расчета денег, создания инженерных проектов, проверки прочности конструкций, заказа продуктов, планирования мероприятий …
наших ЦЕЛЕЙ в этом году:
· Беглость с дробями, десятичными знаками, процентами
· Гибкость в решении задач — учащиеся должны уметь объяснить КАК они пришли к своему ответу И уметь решать проблему другим методом
· Знакомство с «грамматикой» алгебры — использование переменных для представления ситуаций, которые могут измениться
наш ИНСТРУМЕНТЫ:
· учебник: Pre-Algebra Prentice Hall В каждой главе есть примеры! Просмотрите примеры при выполнении домашнего задания. Посмотрите видео-репетитор по домашнему заданию, указанный в вашей книге.
Посмотрите видео-репетитор по домашнему заданию, указанный в вашей книге.
на сайте www.pearsonsuccessnet.com Имя пользователя: Имя Фамилия пароль: MSA2015
· MobyMax — это сайт, предназначенный для практики беглости речи. Каждому ученику будут назначены новые задания в зависимости от их успеха в каждом предыдущем задании.
Пожалуйста, используйте этот сайт ЧАСТО !! www.mobymax.com код школы: ma711
НАШИ ТЕМЫ (из MASSACHUSETTSCURRICULUM FRAMEWORK FOR MATHEMATICS http: // www.doe.mass.edu/frameworks/math/0311.pdf)
Обзор 6-го класса
Коэффициенты и пропорциональные отношения
• Понять концепции соотношений и использовать рассуждения о соотношении для решения проблем.
Система счисления
• Применяйте и расширяйте предыдущие представления об умножении и делении для деления дробей на дроби.
• Быстро вычисляйте многозначные числа и находите общие и кратные множители.
• Применяйте и расширяйте предыдущие представления о числах в системе рациональных чисел.
Выражения и уравнения
• Применяйте и расширяйте предыдущие представления об арифметике для алгебраических выражений.
• Обсудите и решите уравнения и неравенства с одной переменной.
• Представлять и анализировать количественные отношения между зависимыми и независимыми переменными.
Геометрия
• Решение реальных и математических задач, касающихся площади, площади поверхности и объема.
Статистика и вероятность
• Развивайте понимание статистической изменчивости.
• Обобщите и опишите распределения.
6 класс | Математика | Iowa Core
В 6 классе учебное время должно быть сосредоточено на четырех критических областях: (1) связь соотношения и скорости с умножением и делением целых чисел и использование концепций соотношения и скорости для решения задач; (2) завершение понимания деления дробей и распространение понятия числа на систему рациональных чисел, которая включает отрицательные числа; (3) написание, интерпретация и использование выражений и уравнений; и (4) развитие понимания статистического мышления.
- Учащиеся используют рассуждения об умножении и делении для решения задач о соотношении и соотношении количеств. Рассматривая эквивалентные соотношения и коэффициенты как производные и расширяющие пары строк (или столбцов) в таблице умножения, а также анализируя простые рисунки, на которых указывается относительный размер величин, учащиеся связывают свое понимание умножения и деления с соотношениями и коэффициентами. . Таким образом, учащиеся расширяют круг задач, для решения которых они могут использовать умножение и деление, и соединяют отношения и дроби.Студенты решают самые разные задачи, связанные с соотношениями и ставками.
- Учащиеся используют значение дробей, значение умножения и деления и взаимосвязь между умножением и делением, чтобы понять и объяснить, почему процедуры деления дробей имеют смысл. Студенты используют эти операции для решения задач. Студенты расширяют свои предыдущие представления о числах и порядке чисел до полной системы рациональных чисел, которая включает отрицательные рациональные числа и, в частности, отрицательные целые числа.
 Они рассуждают о порядке и абсолютном значении рациональных чисел и о расположении точек во всех четырех квадрантах координатной плоскости.
Они рассуждают о порядке и абсолютном значении рациональных чисел и о расположении точек во всех четырех квадрантах координатной плоскости. - Студенты понимают использование переменных в математических выражениях. Они пишут выражения и уравнения, соответствующие заданным ситуациям, оценивают выражения и используют выражения и формулы для решения проблем. Студенты понимают, что выражения в разных формах могут быть эквивалентными, и они используют свойства операций для переписывания выражений в эквивалентных формах.Студенты знают, что решения уравнения — это значения переменных, которые делают уравнение истинным. Учащиеся используют свойства операций и идею сохранения равенства обеих сторон уравнения для решения простых одношаговых уравнений. Учащиеся составляют и анализируют таблицы, такие как таблицы величин в эквивалентных соотношениях, и используют уравнения (например, 3 x = y ) для описания отношений между величинами.
- Опираясь на свое понимание чисел и укрепляя его, учащиеся начинают развивать свою способность мыслить статистически.
 Студенты признают, что распределение данных может не иметь определенного центра и что разные способы измерения центра дают разные значения. Медиана измеряет центр в том смысле, что это примерно среднее значение. Средние меры имеют центральное значение в том смысле, что это значение, которое каждая точка данных приняла бы, если бы сумма значений данных была перераспределена равномерно, а также в том смысле, что это точка баланса. Студенты признают, что мера изменчивости (межквартильный размах или среднее абсолютное отклонение) также может быть полезной для обобщения данных, потому что два очень разных набора данных могут иметь одинаковое среднее и медианное значение, но различаться по своей изменчивости.Студенты учатся описывать и резюмировать наборы числовых данных, идентифицируя кластеры, пики, пробелы и симметрию, учитывая контекст, в котором были собраны данные.
Студенты признают, что распределение данных может не иметь определенного центра и что разные способы измерения центра дают разные значения. Медиана измеряет центр в том смысле, что это примерно среднее значение. Средние меры имеют центральное значение в том смысле, что это значение, которое каждая точка данных приняла бы, если бы сумма значений данных была перераспределена равномерно, а также в том смысле, что это точка баланса. Студенты признают, что мера изменчивости (межквартильный размах или среднее абсолютное отклонение) также может быть полезной для обобщения данных, потому что два очень разных набора данных могут иметь одинаковое среднее и медианное значение, но различаться по своей изменчивости.Студенты учатся описывать и резюмировать наборы числовых данных, идентифицируя кластеры, пики, пробелы и симметрию, учитывая контекст, в котором были собраны данные.Учащиеся 6-го класса также опираются на свою работу с площадью в начальной школе, рассуждая о взаимосвязях между формами, чтобы определить площадь, площадь поверхности и объем.
 Они находят области прямоугольных треугольников, других треугольников и специальных четырехугольников, разлагая эти формы, переставляя или удаляя части и соотнося формы с прямоугольниками.Используя эти методы, студенты обсуждают, разрабатывают и обосновывают формулы для площадей треугольников и параллелограммов. Учащиеся находят области многоугольников и площади призм и пирамид, разбивая их на части, площадь которых они могут определить. Они рассуждают о правильных прямоугольных призмах с дробными длинами сторон, чтобы расширить формулы для объема правой прямоугольной призмы до дробных сторон. Они готовятся к работе над масштабными чертежами и конструкциями в 7 классе, рисуя многоугольники в координатной плоскости.
Они находят области прямоугольных треугольников, других треугольников и специальных четырехугольников, разлагая эти формы, переставляя или удаляя части и соотнося формы с прямоугольниками.Используя эти методы, студенты обсуждают, разрабатывают и обосновывают формулы для площадей треугольников и параллелограммов. Учащиеся находят области многоугольников и площади призм и пирамид, разбивая их на части, площадь которых они могут определить. Они рассуждают о правильных прямоугольных призмах с дробными длинами сторон, чтобы расширить формулы для объема правой прямоугольной призмы до дробных сторон. Они готовятся к работе над масштабными чертежами и конструкциями в 7 классе, рисуя многоугольники в координатной плоскости.



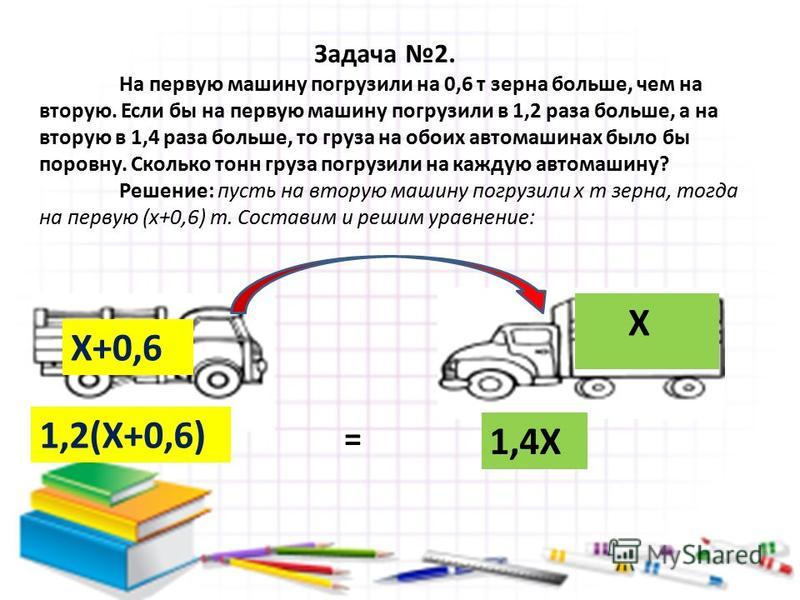
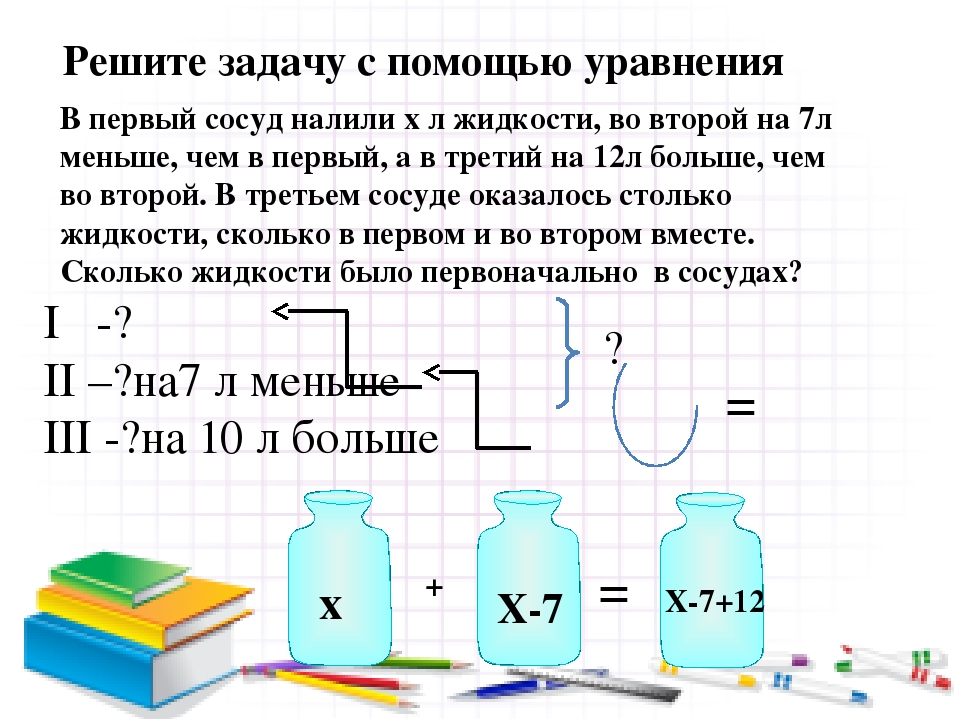
 Основное
свойство дроби.
Основное
свойство дроби.





















 ..
.. 6-й класс
6-й класс Каждое задание выполняется одним учащимся. Учитель открывает последующую строчку только после того, как обучающийся правильно проговорил ее
Каждое задание выполняется одним учащимся. Учитель открывает последующую строчку только после того, как обучающийся правильно проговорил ее Слайд 7.
Слайд 7.
 Выявление первичного осмысления изучаемого материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу
Выявление первичного осмысления изучаемого материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу
 Они рассуждают о порядке и абсолютном значении рациональных чисел и о расположении точек во всех четырех квадрантах координатной плоскости.
Они рассуждают о порядке и абсолютном значении рациональных чисел и о расположении точек во всех четырех квадрантах координатной плоскости.  Студенты признают, что распределение данных может не иметь определенного центра и что разные способы измерения центра дают разные значения. Медиана измеряет центр в том смысле, что это примерно среднее значение. Средние меры имеют центральное значение в том смысле, что это значение, которое каждая точка данных приняла бы, если бы сумма значений данных была перераспределена равномерно, а также в том смысле, что это точка баланса. Студенты признают, что мера изменчивости (межквартильный размах или среднее абсолютное отклонение) также может быть полезной для обобщения данных, потому что два очень разных набора данных могут иметь одинаковое среднее и медианное значение, но различаться по своей изменчивости.Студенты учатся описывать и резюмировать наборы числовых данных, идентифицируя кластеры, пики, пробелы и симметрию, учитывая контекст, в котором были собраны данные.
Студенты признают, что распределение данных может не иметь определенного центра и что разные способы измерения центра дают разные значения. Медиана измеряет центр в том смысле, что это примерно среднее значение. Средние меры имеют центральное значение в том смысле, что это значение, которое каждая точка данных приняла бы, если бы сумма значений данных была перераспределена равномерно, а также в том смысле, что это точка баланса. Студенты признают, что мера изменчивости (межквартильный размах или среднее абсолютное отклонение) также может быть полезной для обобщения данных, потому что два очень разных набора данных могут иметь одинаковое среднее и медианное значение, но различаться по своей изменчивости.Студенты учатся описывать и резюмировать наборы числовых данных, идентифицируя кластеры, пики, пробелы и симметрию, учитывая контекст, в котором были собраны данные. Они находят области прямоугольных треугольников, других треугольников и специальных четырехугольников, разлагая эти формы, переставляя или удаляя части и соотнося формы с прямоугольниками.Используя эти методы, студенты обсуждают, разрабатывают и обосновывают формулы для площадей треугольников и параллелограммов. Учащиеся находят области многоугольников и площади призм и пирамид, разбивая их на части, площадь которых они могут определить. Они рассуждают о правильных прямоугольных призмах с дробными длинами сторон, чтобы расширить формулы для объема правой прямоугольной призмы до дробных сторон. Они готовятся к работе над масштабными чертежами и конструкциями в 7 классе, рисуя многоугольники в координатной плоскости.
Они находят области прямоугольных треугольников, других треугольников и специальных четырехугольников, разлагая эти формы, переставляя или удаляя части и соотнося формы с прямоугольниками.Используя эти методы, студенты обсуждают, разрабатывают и обосновывают формулы для площадей треугольников и параллелограммов. Учащиеся находят области многоугольников и площади призм и пирамид, разбивая их на части, площадь которых они могут определить. Они рассуждают о правильных прямоугольных призмах с дробными длинами сторон, чтобы расширить формулы для объема правой прямоугольной призмы до дробных сторон. Они готовятся к работе над масштабными чертежами и конструкциями в 7 классе, рисуя многоугольники в координатной плоскости.