ГДЗ Математика 6 класс Чесноков, Нешков
Шестой класс является преддверием более сложных направлений в учебе, особенно по математике. Поэтому упускать что-либо крайне нежелательно, так как иначе будет очень сложно справиться с дальнейшей школьной программой. Но бывают и такие случаи, когда объяснения учителя звучат крайне невразумительно и учащимся бывает трудно разобраться в изучаемом материале. Но на выручку всегда готов прийти решебник к учебнику «Математика. Дидактические материалы 6 класс» Чесноков, Нешков.
Что в него включено.
Пособие поделено на самостоятельные и контрольные работы. В первом случае, школьникам предлагается четыре варианта, которые полностью раскрывают все изучаемые на уроках темы. Во втором случае, в ГДЗ по математике 6 класс представлены проверочные работы двух авторов. Досконально приведенные решения должны помочь ученикам лучше усвоить все темы и с честью пройти любое тестирование.
Нужен ли решебник.

Порой, сидя над домашним заданием, не хватает малейшего толчка, чтобы осознать все, что нужно сделать. Редко у каких родителей в бесконечной череде житейских дел хватает времени на то, чтобы сидеть рядом с ребенком и доходчиво ему объяснять что, как и почему следует сделать. Решебник к учебнику «Математика. Дидактические материалы 6 класс» Чесноков могут прекрасно сделать это вместо них. Но ребенок должен четко понимать, что лишь вдумчивый и аналитический подход способен повысить общий уровень знаний. «Скатывание» д/з такого эффекта не произведет.
«Академкнига», 2014 г.
Похожие ГДЗ Математика 6 класс
Самостоятельные работы
Вариант 1:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349
Самостоятельные работы
Вариант 2:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349
Самостоятельные работы
Вариант 3:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349
Самостоятельные работы
Вариант 4:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349
Проверочная работа стр.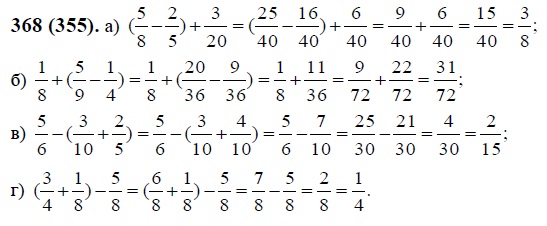 29:
29:
упр.1упр.2упр.3упр.4упр.5упр.6упр.7упр.8упр.9упр.10упр.11упр.12упр.13упр.14
Проверочная работа стр. 57:
упр.1упр.2упр.3упр.4упр.5упр.6упр.7упр.8упр.9упр.10упр.11упр.12упр.13упр.14
Проверочная работа стр. 85:
упр.1упр.2упр.3упр.4упр.5упр.6упр.7упр.8упр.9упр.10упр.11упр.12упр.13упр.14
Проверочная работа стр. 113:
упр.1упр.2упр.3упр.4упр.5упр.6упр.7упр.8упр.9упр.10упр.11упр.12упр.13упр.14
Контрольная работа №1 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №1 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №2 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №2 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №3 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №3 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №4 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №4 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №5 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №5 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №6 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №6 (Нурк):
Вариант1
Контрольная работа №7 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №7 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №8 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №8 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №9 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №9 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №10 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №10 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №11 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №11 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №12 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №12 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №13 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №13 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №14 (Виленкин):
Вариант1Вариант2Вариант3Вариант4
Контрольная работа №14 (Нурк):
Вариант1Вариант2Вариант3Вариант4
Предыдущий
Следующий
Название
Условие
Решебник №1
Решебник №2
Решебник №3
Решебник №4
Предыдущий
Следующий
Зачетные дз по математике 6 класс
Домашние зачётные работы
по математике
Класс: 6
УМК: А. Г.
Мерзляк и др.
Г.
Мерзляк и др.
Темы домашних зачётных работ:
№1. Делимость чисел
№2. Все действия с обыкновенными дробями
№3. Отношения и пропорции
№4. Все действия с рациональными числами
№ 5. Примеры на порядок действий
№6. Упрощение выражений
№7. Решение линейных уравнений
Зачётная работа
№1. по теме «Делимость чисел»
по теме «Делимость чисел»
1. Разложение числа на простые множители
1). 24 2). 42 3). 32 4). 27 5). 36
6). 138 7). 144 8). 126 9). 256 10). 2661120 и сколько 2 участвует в разложении?
2. Вычислить НОД чисел
1). НОД (21;42)= 2). НОД (24 , 10)= 3). НОД (6 , 39)=
4). НОД (39 , 18)= 5). НОД (6 , 36)= 6). НОД (27 , 24)=
7). НОД (10 , 16)= 8). НОД (24 , 16)= 9). НОД (27 , 12)=
10). НОД (36 и 42)=
3. Вычислить НОК чисел
1). НОК (30 , 42)= 2). НОК (36 , 9)= 3). НОК (12 , 20)=
4). НОК (22 , 30)=
5). НОК (15
, 27)=
6). НОК (12 , 27)=
НОК (12 , 27)=
7). НОК (45 , 33)= 8). НОК (30 , 21)= 9). НОК (42 , 18)=
10). НОК (3 ; 6 и 8)=
4. Признаки делимости
1). Из чисел 2736; 4582; 5271; 3456; 96432; 28719; 43644; 9870030 выпишите те, которые делятся нацело:
1) на 2; 2) на 5; 3) на 10; 4) на 3; 5) на 9
2). Вместо звёздочки поставьте такую цифру, чтобы получилось число, кратное 3 (рассмотрите все возможное случаи):
1) 286*1 2) 58*481 3) 5*62
3). а) Запишите все нечетные значения х, при которых будет верным неравенство 709 ˂ х ˂ 720
б) Запишите все четные значения у, при которых будет верным неравенство 845 ˂ у ˂ 856
4). Найдите все значения а, кратных числу 9, при которых будет верным неравенство 145 ˂ а ˂ 180
Зачётная работа №2.
по теме «Все действия с обыкновенными дробями».
1. Сложение и вычитание дробей с разными знаменателями
1). 2). 3). 4).
5). 6). 7).
8). 9). 10).
2. Сложение и вычитание смешанных чисел с разными знаменателями
1). 2). 3). 4).
5). 6). 7).
8). 9). 10). =
3. Умножение и деление обыкновенных дробей
1). 2). 3). 4).
5). 6). 7). 8).
6). 7). 8).
9). 10).
4. Умножение и деление смешанных чисел
1). 2). 3). 4).
5). 6). = 7). = 8). =
9). = 10). =
5. Все действия с обыкновенными дробями
1). = 2). = 3). =
4). 5).
6). 7).
8). 9).
10).
Зачётная работа №3. по теме «Отношения и пропорции»
1. Найти
неизвестный член пропорции
Найти
неизвестный член пропорции
1). 6 : 5 = х : 75 2). 3).
4). 5). 7 : 8 = у : 96 6).
7). 8). 9). 8 : 7 = а : 56
10).
2. Деление числа в данном отношении
1). Разделите число на две части в отношении:
1) 56 в отношении 3 : 4 2) 64 в отношении 3 : 5
3) 72 в отношении 2 : 7 4) 114 в отношении 7 : 12
2). Разделите число на три части в отношении:
1) 480 в отношении 3 : 4 : 5 2) 490 в отношении 2 : 5 : 7
3) 525 в отношении 5 : 7 : 9 4) 420 в отношении 2 : 3 : 7
3). Сплав состоит из 5 частей меди и 8 частей цинка. Сколько
надо взять кг цинка, чтобы получить 520 кг сплава?
4). Периметр
треугольника равен 114 см, а длины его сторон
Периметр
треугольника равен 114 см, а длины его сторон
относятся как 5 : 6 : 8. Найдите стороны треугольника.
5). Сахарный сироп состоит из 11 частей воды и 3 частей сахара.
Сколько сахара надо взять, чтобы получить 280 г сиропа?
6). Периметр треугольника равен 123 см, а длины его сторон
относятся как 10 : 12 : 19. Найдите стороны треугольника.
7). Раствор содержит 5 частей кислоты и 8 частей воды. Сколько
кислоты надо взять, чтобы получилось 442г раствора?
8). Периметр треугольника равен 144 см, а длины его сторон
относятся как 9 : 11 : 16. Найдите стороны треугольника.
9). Развёрнутый угол разделён лучом на два угла в отношении 5 : 7.
Сколько градусов содержит каждый угол?
10). Прямой
угол разделён лучом на два угла в отношении 7 : 11.
Сколько градусов содержит каждый угол?
Зачётная работа №4.
по теме «Все действия с рациональными числами»
1. Сложение и вычитание рациональных чисел
1). 32 – 41 + 54 – 73 2). 18 – 92 + 108 – 9
3). 91 – 108 + 13 − 49 4). 37 – 29 + 159 – 86
5). – 190 + 39 – 84 + 235 6). – 73 + 24 – 58 + 96
7). 23 – 32 – 24 + 68 8). 97 – 88 – 39 + 42
2. Умножение и деление рациональных чисел
1). −2 · (54 − 129) 2). 4 · (43 − 150)
3). (31 − 12) · (32 − 62) 4). (13 − 44) · (27 − 47)
5). (63 − 75) · (110 − 115) 6). (54 − 75) : 7
7). 81 : (76
– 67) 8). 49 : (84 – 91)
49 : (84 – 91)
9). – 54 : (66 – 84) 10). (39 − 57) : (27 − 18)
11). (63 − 84) : (14 − 21) 12). (87 – 68 – 22) : 3
13). (12 + 63 – 36) : (− 13) 14). (84 − 120) : 36
15). (53 − 27 – 14) : (41 − 29) 16). – 96 : (54 – 62)
17). (123 − 49 – 83) : (186 − 195) 18). (7 − 13) · (192 − 184)
19). 5 · (74 − 93) 20). −3 · (72 − 138)
Зачётная работа №5.
по теме «Примеры на порядок действий»
1). 2).
3). 4).
5). 6).
7). 8).
9). 10).
11). 12).
13). 14).
15). 16).
Зачётная работа №6. по теме «Упрощение выражений»
1. Приведение подобных слагаемых
1). 8а + 19а – 28а + 3а = 2). — 4х + 11х + 35х – 38х =
3). 14а – а + в – 26в = 4). 1,6с – 1,2 – 3,1с + 0,8 =
5). 2,6а – 5,4с – а + 2с = 6). — 9у + 12у — 41у — 17у =
7). 8х – 17х — 19 + 21х = 8). — 5,6к + 4,8 + 8,2к – 9,1=
9). — 8х + 16х – 23х + 17х = 10). 5х – 5 – 4х – 8 + 3х =
2. Раскрытие скобок
1). 3(х + у + с) = 2). (х + у + с) · 4 = 3). 3(2х -3у + 4с) =
4). —3·(-3х + 5у – 4к + с) = 5). (5х + 2у — с) · (-2) =
6). 5(2а
+ в – 8с) = 7). – 4(- х + 3у – 4к) = 8). 8(6х — 7) – 17а
=
8(6х — 7) – 17а
=
9). 9у – 5(12 — х) = 10). – 4(5х + 9у — к) =
3. Упрощение выражений
1). 3(х + 6) – х – 2(х + 9) = 2). 6 – 3(х + 1) – (7 – х) =
3). (8х + 3) – (10х — 6) – 9 = 4). 5 – 2(х — 1) – ( — 4 – х )=
5). (7х +1) – (9х + 3) + 5 = 6). (3,4 + 2у) — 7(у – 2,3) =
7). 4(5х + 2) — 10(3х — 3) + 15 = 8). 4(х — 1) — 2(2х — 8) + 12 =
9). 5,6 – 3(2 – 0,4х) — 0,4(4х — 1) =
10). 5(х — 12) + 6(х — 10) – (х — 1) =
Зачётная работа №7. по теме «Решение линейных уравнений»
1. Вычисление неизвестного множителя
1). — 8х = 72 2). 0,9х = — 5,4 3). – 1,7х = — 5,1
4). 1/9
· х = — 8/9 5). — 2/7· х = — 1/6 6). — 6у = 48
1/9
· х = — 8/9 5). — 2/7· х = — 1/6 6). — 6у = 48
7). 0,8х = — 3,2 8). – 1,6х = — 6,4 9). 1/7· х = — 3/4
10). – 4/9 · х = — 1/7
2. Решение уравнений без скобок
1). х + 16 = 7 2). х + 5,8 = — 4,7 3). 5,5 – х = 12,9
4). – 8,8 – х = — 3,7 5). х – 9,21 = — 4,3 6). х – 4,7 = — 2,34
7). 4,8 – х = 16,3 8). х + 12 = 5 9). – 5,4 – х = — 3,5
10). х + 6,2 = — 7,8 11). 2х = 18 — х 12). 7х + 3 = 30 – 2х
13). 7 – 2х = 3х – 18 14). 0,2х + 2,7 = 1,4 – 1,1х
15). 5,4 – 1,5х = 0,3х – 3,6 16). 11х = 36 – х
17). 9х + 4 = 48 – 2х 18). 8 – 4х =
2х — 16
8 – 4х =
2х — 16
19). 0,4х + 3,8 = 2,6 – 0,8х 20). 6,8 – 1,3х = 0,6х – 2,7
3. Решение уравнений со скобками
1). 4(х — 6) = х — 9 2). 6 – 3(х + 1) = 7 – х
3). (8х + 3) – (10х + 6) = 9 4). 14х – 14 = 7(2х — 3) +7
5). 3(х — 2) = х + 2 6). 5 – 2(х — 1) = 4 – х
7). (7х +1) – (9х + 3) = 5 8). 3,4 + 2у = 7(у – 2,3)
9). 4(5х + 2) = 10(3х — 3) + 15 10). 2(7х — 7) = 7(2х — 3) + 7
11). 5,6 – 3(2 – 0,4х) = 0,4(4х — 1) 12). 5(х — 12) = 6(х — 10) – х
13). 0,3(8 – 3у) = 3,2 – 0,8(у — 7) 14). 4(х — 1) = 2(2х — 8) + 12
15). 8(5 – 3х) = 6(2 – 4х) + 7 16). 7(4х — 1) = 6 – 2(3 – 14х)
17). 4 — 6(х + 2) = 3 – 5х 18). (5х + 8) – (8х + 14) = 9
19). -7(х
+ 3) + 9 = 5 – 6х 20). –(11х — 7) + (7х + 9) = 8
-7(х
+ 3) + 9 = 5 – 6х 20). –(11х — 7) + (7х + 9) = 8
ОТВЕТЫ, ОТВЕТЫ, ОТВЕТЫ:
Зачётная работа №1.
по теме «Делимость чисел»
1. Разложение числа на простые множители
1). 2·2·2·3 2). 2·3·7 3). 2·2·2·2·2 4). 3·3·3 5). 2·2·3·3
6). 2·3·23 7). 2·2·2·2·3·3 8). 2·3·3·7 9). 2·2·2·2·2·2·2·2
10). 2·2·2·2·2·2·2·2·5·3·3·3·7·11 (2-восемь)
2. Вычислить НОД чисел
1). 21 2). 2 3). 3 4). 3 5). 6 6). 3 7). 2 8). 8 9). 3 10). 6
3. Вычислить НОК чисел
1). 210
2). 36 3). 60 4). 330 5). 135 6). 108 7). 495 8). 210
60 4). 330 5). 135 6). 108 7). 495 8). 210
9). 378 10). 48
4. Признаки делимости
1). 1) 2736; 4582; 3456; 96432; 43644; 9870030. 2) 9870030.
3) 9870030. 4) 2736; 5271; 3456; 96432; 28719; 43644; 9870030.
5) 2736; 3456; 28719; 9870030.
2). 1) 1; 4; 7. 2) 1; 4; 7. 3) 2; 5; 8
3). а) 711; 713; 715; 717; 719. б)846; 848; 850; 852; 854.
4). 153; 162; 171.
Зачётная работа №2.
по теме «Все действия с обыкновенными дробями».
1. Сложение и вычитание дробей с разными знаменателями.
1). ; 2). 5/24 3). 1/16 4). 33/70 5). 6/15 = 2/5 6). 23/24
7). 15/30 = ½ 8). 24/36 = 2/3 9). 7/18 10). 39/48
2. Сложение
и вычитание смешанных чисел с разными знаменателями
Сложение
и вычитание смешанных чисел с разными знаменателями
1). 2). 3). 4). 5). 6).
7). 8). 9). 10).
3. Умножение и деление обыкновенных дробей
1). 1/8 2). 18/77 3). 5/13 4). ¼ 5). 5/11 6). 35/72 7). 1/45
8). 10 9). 1 10). 1
4. Умножение и деление смешанных чисел
1). 2). 3). 4). 5).
6). 7). 8). 9).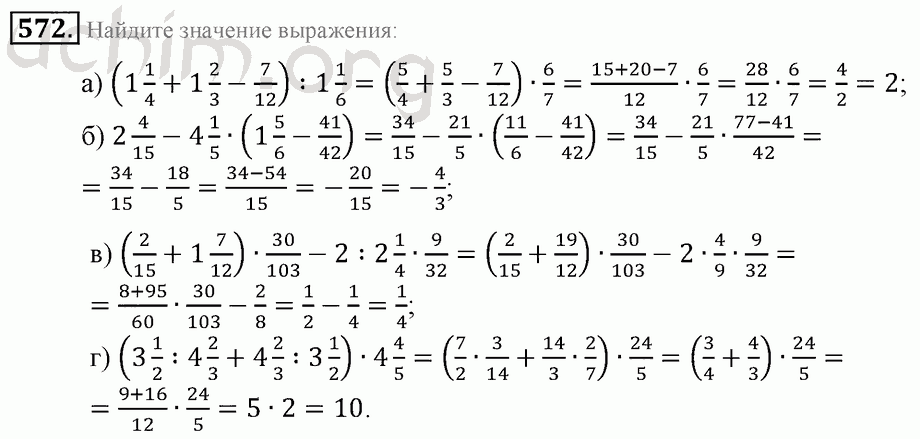 10). 8/9
10). 8/9
5. Все действия с обыкновенными дробями
1). 4/3 =? 2). 5/4=? 3). 10/12=5/6 4). 3,4 5). 63/100
6). 1 (55/81) 7). 7/10 8). 11(1/7) 9). 1,5 10). 13,25
Зачётная работа №3.
по теме «Отношения и пропорции»
1. Найти неизвестный член пропорции
1). 90 2). 1/10 3). 3 4). 3(2/7) 5). 84 6). 27 7). 5 8). 2/9
9). 64 10). 8,5
2. Деление числа в данном отношении
1). 1) 24 и 32 2) 24 и 40 3) 16 и 56 4) 42 и 72
2). 1) 120; 160; 200 2) 70; 175; 245 3) 125; 175; 225
4) 70; 105; 245
3). 320
кг 4). 30см; 36см; 48см 5). 60г
320
кг 4). 30см; 36см; 48см 5). 60г
6). 30см; 36см; 57см 7). 170 г 8). 36см; 44см; 64см
9). 75˚ и 105˚ 10). 35˚ и 55˚
Зачётная работа №4.
по теме «Все действия с рациональными числами»
1. Сложение и вычитание рациональных чисел
1). — 28 2). 25 3). — 53 4). 81 5). 0 6). — 11 7). 35 8). 12
2. Умножение и деление рациональных чисел
1). 150 2). – 428 3). – 570 4). 620 5). 60 6). — 3 7). 9
8). — 7 9). 3 10). — 2 11). 3 12). – 1 13). – 3 14). – 1
15). 1 16). 12 17). 1 18). – 40 19). — 95 20). 198
1 16). 12 17). 1 18). – 40 19). — 95 20). 198
Зачётная работа №5.
по теме «Примеры на порядок действий»
1). -4 2). 1 3). 2,25 4). 4/21 5). 48/35 6). -7
7). 33/8 8). 78/7 9). 7/16 10). -4 11). -3 12). 18/5
13). 6 14). 53/4 15). -9 16). 17
Зачётная работа №6.
по теме «Упрощение выражений»
1. Приведение подобных слагаемых
1). 2а 2). 4х 3). 13а-25в 4). -1,5с – 0,4 5). 1,6а — 3,4с
6). -55у 7). 12х — 19 8). 2,6к – 4,3 9). 2х 10). 4х — 13
2. Раскрытие скобок
1). 3х+3у+3с
2). 4х+4у+4с 3). 6х-9у+12с 4). 9х-15у+12к-3с
3х+3у+3с
2). 4х+4у+4с 3). 6х-9у+12с 4). 9х-15у+12к-3с
5). -10х -4у+2с 6). 10а+5в-40с 7). 4х -12у+16к
8). 48х-56-17а 9). 9у -60 +5х 10). -20х-36у+4к
3. Упрощение выражений
1) = 3х + 18 – х – 2х – 18 = 0 |
2) = 6 – 3х – 3 – 7 + х = — 2х — 4 |
3) = 8х + 3 – 10х + 6 – 9 = — 2х |
4) = 5 – 2х + 2 + 4 + х = — х + 11 |
5) = 7х + 1 – 9х – 3 + 5 = — 2х + 3 |
6) = 3,4 + 2у – 7у + 2,3 = 5,7 – 5у |
7) = 20х + 8 – 30х + 30 + 15 = — 10х + 53 |
8) = 4х – 4 – 4х + 16 + 12 = 24 |
9) = 5,6 – 6 + 1,2х – 1,6х + 0,4 = — 0,4х |
10) = 5х – 60 + 6х – 60 – х + 1 = 10х — 119 |
Зачётная работа №7.
по теме «Решение линейных уравнений»
1. Вычисление неизвестного множителя
1). -9 2). -6 3). 3 4). -8 5). 7/12 6). -8 7). -4 8). 4
9). -5,25 10). 9/28
2. Решение уравнений без скобок
1). 9 2). -10,5 3). -7,4 4). -5,1 5). 4,91 6). 2,36 7). -11,5
8). -7 9). – 1,9 10). -14 11). 6 12). 3 13). 5 14). -1
15). 5 16). 3 17). 4 18). 4 19). -1 20). 5
3. Решение уравнений со скобками
1). 5 2). -2 3). -6 4). нет реш. 5). 4 6). 3 7). -3,5 8). 3,9
9). 2,3
10). нет реш. 11). 0 12). нет реш. 13). -64
нет реш. 11). 0 12). нет реш. 13). -64
14). любое число 15). нет реш. 16). нет реш.
17). — 11 18). — 5 19). – 17 20). 2
Используемые ресурсы:
Картинка/ http://www.playcast.ru/uploads/2017/03/09/21951359.png
· А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Математика: 6 класс: учебник для учащихся общеобразовательных организаций, — 2-е изд., перераб. – М.:Вентана-Граф, 2016
· А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир. Сборник задач и заданий для тематического оценивания по математике для 6 класса.- Харьков: Гимназия,2005
· А.П. Ершов, В.В. Голобородько. Самостоятельные и контрольные работы по математике для 6 класса.- М.:ИЛЕКСА, 2008
·
Н.Я.
Виленкин и др. Математика: учеб. для 6 кл. общеобразоват. учреждений -4-е изд.
испр. и доп. – М.: Мнемозина, 1996
и доп. – М.: Мнемозина, 1996
· А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир. Математика: 6 класс: дидактические материалы: пособие для учащихся общеобразовательных учреждений. – М.: Вентана-Граф, 2017.
· М.А. Максимовская, Ф.А. Пчелинцев, А.Б. Уединов, П.В.Чулков. Тесты. Математика. 5-11 кл. –М.: «Олимп»; «Издательство Астрель», 1999г.
Добро пожаловать в космическую математику НАСА!
Задача 564: Изучение звезд в Орионе — Безумие светового года
Учащиеся изучают световой год и его связь со временем прохождения света для наблюдения за событиями в разных частях космоса. Когда колонисты в разных местах увидят, как звезда Бетельгейзе станет сверхновой?
[Класс: 6-8 | Темы: линии времени; расчеты временных интервалов; время = расстояние/скорость]
[Кликните сюда]
Задача 507: Изучение запуска Falcon 9
Учащиеся используют данные о запуске ракеты-носителя Falcon 9, чтобы определить ее скорость и ускорение. [Класс: 6-8 | Темы: скорость = расстояние/время; Расчеты времени]
[Кликните сюда]
[Класс: 6-8 | Темы: скорость = расстояние/время; Расчеты времени]
[Кликните сюда]
Задача 505: SDO видит корональный дождь — оценка скорости плазмы
Учащиеся оценивают скорость плазменных стримеров у поверхности Солнца, используя изображения из Обсерватории солнечной динамики.
[Класс: 6-8 | Темы: масштабные модели; скорость = расстояние/время; пропорции]
[Кликните сюда]
Задача 488: RBSP и расположение Dawn Chorus — II
Учащиеся используют гипотетическую информацию от двойного космического корабля RBSP для триангуляции местоположения сигнала Chorus вблизи Земли, используя угловые измерения, графики и транспортиры, чтобы определить точку пересечения сигналов CHorus.
[Класс: 6-8 | Темы: Углы; графическое изображение; транспортиры]
[Кликните сюда]
Задача 452: Ближайшее сближение астероида 2005YU55 — I
Учащиеся работают с масштабным рисунком орбиты Луны и траектории астероида, чтобы предсказать, где астероид будет находиться относительно Земли и орбиты Луны. [Класс: 6-8 | Темы: время=расстояние/скорость; масштабные модели; метрическая математика]
[Кликните сюда]
[Класс: 6-8 | Темы: время=расстояние/скорость; масштабные модели; метрическая математика]
[Кликните сюда]
Задача 451: Впечатляющая планетарная туманность Кошачий глаз
Студенты измеряют диаметр туманности и используют информацию о скорости, чтобы оценить возраст туманности.
[Класс: 6-8 | Темы: время=расстояние/скорость; масштабные модели; метрическая математика]
[Кликните сюда]
Задача 445: LRO — Относительный возраст лунных поверхностей
Учащиеся исследуют два района посадки Аполлона, используя изображения космического корабля LRO, чтобы оценить относительный возраст двух регионов, используя
подсчет кратеров. [Класс: 6-8 | Темы: масштаб; гистограмма]
[Кликните сюда]
Задача 438: Последний полет космического корабля «Индевор»
Учащиеся используют табличные данные и графики, чтобы определить скорость запуска и ускорение космического корабля «Шаттл» со стартовой площадки. [Класс: 6-8 | Темы: табличные данные, графики, метрические измерения, скорость=расстояние/время]
[Кликните сюда]
Задача 437: Скорость и высота старта ракеты Сатурн V
Учащиеся используют табличные данные для определения скорости старта ракеты «Сатурн-5» со стартовой площадки. [Класс: 6-8 | Темы: табличные данные, графики, метрические измерения, скорость=расстояние/время]
[Кликните сюда]
[Класс: 6-8 | Темы: табличные данные, графики, метрические измерения, скорость=расстояние/время]
[Кликните сюда]
Проблема 436: космический шаттл «Челленджер» запускает спутник INSAT-1B
Учащиеся используют серию изображений, чтобы определить скорость запуска спутника из грузового отсека космического корабля «Шаттл».
[Класс: 6-8 | Темы: масштаб, метрическое измерение, скорость=расстояние/время]
[Кликните сюда]
Задача 435: Запуск Аполлона-17 с поверхности Луны
Студенты используют серию изображений для определения скорости подъема капсулы Аполлон-17 с поверхности Луны.
[Класс: 6-8 | Темы: масштаб, метрическое измерение, скорость=расстояние/время]
[Кликните сюда]
Задача 434: Космический корабль Dawn видит астероид Веста с близкого расстояния!
Студенты используют изображение астероида для определения диаметра кратеров
и горы с помощью миллиметровой линейки и масштаба изображения в метрах на миллиметр. [Класс: 6-8 | Темы: шкала, метрические измерения]
[Кликните сюда]
[Класс: 6-8 | Темы: шкала, метрические измерения]
[Кликните сюда]
Задача 433: космический корабль «Атлантис» — скорость шлейфа
Учащиеся используют последовательность изображений из видеоролика о запуске, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения.
[Класс: 6-8 | Темы: масштаб, метрическое измерение, скорость=расстояние/время]
[Кликните сюда]
Задача 432: космический корабль «Атлантис» — скорость выхлопа
Учащиеся используют последовательность изображений из видеоролика о запуске, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения.
[Класс: 6-8 | Темы: масштаб, метрическое измерение, скорость=расстояние/время]
[Кликните сюда]
Задача 431: космический корабль «Атлантис» — скорость запуска
Учащиеся используют последовательность изображений из видеоролика о запуске, чтобы определить скорость по времени. интервал между изображениями и масштаб каждого изображения.
[Класс: 6-8 | Темы: масштаб, метрическое измерение, скорость=расстояние/время]
[Кликните сюда]
интервал между изображениями и масштаб каждого изображения.
[Класс: 6-8 | Темы: масштаб, метрическое измерение, скорость=расстояние/время]
[Кликните сюда]
Задача 430: космический корабль «Атлантис» — восхождение на орбиту
Учащиеся используют последовательность изображений из видеоролика о запуске, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения.
[Класс: 6-8 | Темы: масштаб, метрическое измерение, скорость=расстояние/время]
[Кликните сюда]
Задача 429: Отслеживание морской черепахи из космоса
Широта, долгота, истекшее время и пройденное расстояние представлены в таблице. Студенты используют данные для определения дневной и часовой скорости кожистой черепахи, когда она путешествует из Новой Зеландии в Калифорнию через Тихий океан.
[Класс: 4-6| Темы: масштаб, метрическое измерение, скорость=расстояние/время]
[Кликните сюда]
Задача 404: Космический аппарат STEREO дает 360-градусный обзор Солнца Учащиеся используют спутниковые снимки STEREO, чтобы определить, какие объекты можно увидеть с Земли, а какие нет. Они учатся
о местоположении и изменении положения спутников относительно орбиты Земли.
[Класс: 6-8 | Темы: угловая мера, экстраполяция; расстояние = скорость х время]
[Кликните сюда]
Они учатся
о местоположении и изменении положения спутников относительно орбиты Земли.
[Класс: 6-8 | Темы: угловая мера, экстраполяция; расстояние = скорость х время]
[Кликните сюда]
Задача 267. Определение материалов по их отражательной способности Отражательная способность материала может быть использована для его идентификации. Это важно при съемке лунной поверхности на предмет полезных ископаемых, а также в создании «зеленой» среды обитания на Земле. [Класс: 6-8 | Темы: процент, интерпретация табличных данных, площадь ] [Нажмите здесь]
Задача 237: Марсианские пылевые дьяволы Учащиеся определяют скорость и ускорение марсианского пылевого вихря по изображениям временных интервалов и информации о масштабе изображения. [Класс: 6-8 | Темы: весы; Определение скорости по последовательным изображениям; V = D/T] [Нажмите здесь]
Задача 247: космическая мобильная головоломка Учащиеся вычисляют недостающие массы и длины мобильного телефона, используя базовое уравнение баланса m1 x r1 = m2 x r2 для мобильного телефона. мобильная солнечная система.
[Класс: 6-8 | Темы: метрическая мера, алгебра 1, геометрия] [Нажмите здесь]
мобильная солнечная система.
[Класс: 6-8 | Темы: метрическая мера, алгебра 1, геометрия] [Нажмите здесь]
Задача 245: Твердотопливные ускорители Учащиеся узнают, как SRB фактически создают тягу, и изучают ускоритель Ares-V, чтобы оценить его тягу. [Класс: 6-8 | Темы: объем, площадь, преобразование единиц измерения] [Нажмите здесь]
Задача 238: Перетаскивание спутника и космический телескоп Хаббла Спутники сталкиваются с атмосферой, что в конечном итоге приводит к их сгоранию в атмосфере. Студенты учатся различные прогнозы высоты космического телескопа Хаббла для оценки года его входа в атмосферу. [Класс: 6-8 | Темы: интерпретация графических данных; прогнозирование тенденций] [Нажмите здесь]
Задача 211: Куда делись все звезды? — Учащиеся узнают, почему на фотографиях НАСА часто не видно звезд из-за того, как камеры снимают яркие и тусклые объекты.
[Класс: 6-8| Темы: умножение; разделение; десятичные числа. ] [Нажмите здесь]
] [Нажмите здесь]
Задача 209: Как выделить тусклые вещи в ярком мире!- Учащиеся узнают, что совмещение изображений часто усиливает тусклые вещи, которых нет только на одном изображении; мощность усреднения данных. [Класс: 6-8| Темы: умножение; разделение; десятичные числа.] [Нажмите здесь]
Проблема 148 Исследование умирающей звезды Студенты используют данные со спутника Spitzer для расчета массы планетарной туманности умирающей звезды. [Класс: 9–11 | Темы: Научная нотация; преобразование единиц измерения; объем сферы ] [Нажмите здесь]
Проблема 141 Изучение пыльной молодой звезды Студенты используют данные спутника Spitzer, чтобы узнать, как пыль излучает инфракрасный свет и рассчитать массу пылинки молодой звезды в туманности NGC-7129. [Класс: 4–7 | Темы: Алгебра I; умножение, деление; научное обозначение] [Нажмите здесь]
Проблема 134
Последнее полное солнечное затмение в истории! Учащиеся изучают геометрию, необходимую для
полного солнечного затмения и оценить, через сколько лет в будущем произойдет последнее полное солнечное затмение. затмение произойдет, когда Луна будет медленно удаляться от Земли на 3 сантиметра в год.
[Класс: 7–10 | Темы: Простые линейные уравнения] [Нажмите здесь]
затмение произойдет, когда Луна будет медленно удаляться от Земли на 3 сантиметра в год.
[Класс: 7–10 | Темы: Простые линейные уравнения] [Нажмите здесь]
Проблема 124 Атмосфера Луны Учащиеся узнают об очень тонкой атмосфере Луны, вычислив ее общую массу в килограммах, используя объем сферической оболочки и измеренную плотность. [Класс: 8-10 | Темы: объем шара, оболочка; плотность-масса-объем; единиц измерения] [Нажмите здесь]
Проблема 115
Математическая модель Солнца Учащиеся используют формулу сферы и оболочки для вычисления массы тела.
солнце для различных вариантов его плотности. Цель состоит в том, чтобы воспроизвести измеренную массу и радиус Солнца путем
тщательный подбор его плотности в области ядра и области оболочки. Учащиеся будут манипулировать значениями плотности и размера раковины, чтобы
добиться правильной общей массы. Это можно сделать вручную или с помощью программы
электронную таблицу Excel. [Класс: 8-10 | Темы: научные обозначения; объем сферы и сферической оболочки; плотность, масса и объем.] [Нажмите здесь]
[Класс: 8-10 | Темы: научные обозначения; объем сферы и сферической оболочки; плотность, масса и объем.] [Нажмите здесь]
Проблема 95 Исследование доз радиации астронавтов в космосе — Учащиеся изучат график доз облучения космонавтов во время полетов космического корабля «Шаттл» и оценят суммарные дозы для космонавтов, работающих на Международной космической станции. [Уровень: 9-11 | Темы:Анализ графиков, интерполяция, преобразование единиц измерения] [Нажмите здесь]
Проблема 83 Риски столкновения с метеоритом Лунер — В 2006 году ученые выявили 12 вспышек света на Луне, которые, вероятно, были ударами метеоритов. По их оценкам, эти метеориты, вероятно, были размером с грейпфрут. Сколько времени придется ждать лунным колонистам, прежде чем они увидят такую вспышку на своем горизонте? Студенты будет использовать расчет площади и вероятности, чтобы определить среднее время ожидания. [Уровень: 8-10 | Темы: арифметика; преобразование единиц измерения; площадь поверхности сферы ] [Нажмите здесь]
Проблема 74
Жаркое время на Марсе — В ходе эксперимента NASA Mars Radiation Environment (MARIE) была создана карта поверхности Марса и измерен радиационный фон на уровне земли, которому будут подвергаться астронавты. Эта математическая задача позволяет учащимся определить общую дозу радиации, которую эти исследователи получат во время серии 1000-километровых путешествий по Марсу.
поверхность. Студенты будут сравнивать эту дозировку с типичными фоновыми условиями на Земле и на Международной космической станции, чтобы получить представление о перспективе.
[Уровень: 6-8 | Темы: десятичные дроби, преобразование единиц измерения, графики и анализ ] [Нажмите здесь]
Эта математическая задача позволяет учащимся определить общую дозу радиации, которую эти исследователи получат во время серии 1000-километровых путешествий по Марсу.
поверхность. Студенты будут сравнивать эту дозировку с типичными фоновыми условиями на Земле и на Международной космической станции, чтобы получить представление о перспективе.
[Уровень: 6-8 | Темы: десятичные дроби, преобразование единиц измерения, графики и анализ ] [Нажмите здесь]
Проблема 71 Ремни Ван Аллена действительно смертельны? — Эта задача исследует дозы радиации, которые космонавты получат во время путешествия. через пояса Ван Аллена на пути к Луне. Студенты будут использовать данные, чтобы рассчитать продолжительность поездки через ремни и общую полученную дозу, и сравнить это со смертельной дозой для противостоять ошибочному представлению о том, что астронавты Аполлона мгновенно погибли бы во время своего полета на Луну. [Уровень: 8-10 | Темы: десятичные числа, площадь прямоугольника, анализ графика] [Нажмите здесь]
Проблема 68
Введение в космическую радиацию — Прочтите о своих дозах естественного радиационного фона, узнайте о
Rems и Rads, а также разница между дозировками низкого уровня и дозами высокого уровня.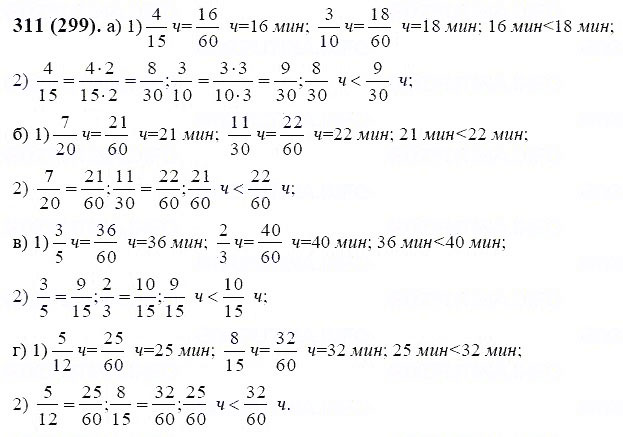 Студенты используют
основные математические операции для расчета общей дозировки на основе дозировки и расчета риска развития рака.
[Уровень: 6-8 | Темы: Чтение, чтобы быть в курсе; десятичные дроби, квадратные корни] [Нажмите здесь]
Студенты используют
основные математические операции для расчета общей дозировки на основе дозировки и расчета риска развития рака.
[Уровень: 6-8 | Темы: Чтение, чтобы быть в курсе; десятичные дроби, квадратные корни] [Нажмите здесь]
Проблема 66 Радиационный фон и образ жизни — Живя на Земле, вы будете подвергаться множеству различных излучений среды. Эта задача следует за одним человеком через четыре различных возможных будущего и сравнивает кумулятивные пожизненные дозы. [Уровень: 6-8 | Темы: дроби, десятичные числа, перевод единиц [Нажмите здесь]
Задача 54
Изучение далеких галактик — Астрономы определили красное смещение далеких
галактик, используя спектры и измеряя сдвиги длин волн для знакомых
атомные линии. Чем больше красное смещение, обозначаемое буквой Z, тем дальше галактика.
В этом упражнении учащиеся будут использовать реальное изображение отдаленного уголка Вселенной с красным смещением. обнаруженных галактик. После построения гистограммы распределения красного смещения они будут использовать
он-лайн космологический калькулятор для определения времени «оглядывания назад» для галактик и
найти ту, которая является самой древней галактикой в этой области. Смогут ли студенты найти галактику, образованную только
500 миллионов лет после Большого Взрыва?
[Уровень: 6-8 | Темы: Десятичная математика; с помощью онлайн-калькулятора; Данные гистограммы] [Нажмите здесь]
обнаруженных галактик. После построения гистограммы распределения красного смещения они будут использовать
он-лайн космологический калькулятор для определения времени «оглядывания назад» для галактик и
найти ту, которая является самой древней галактикой в этой области. Смогут ли студенты найти галактику, образованную только
500 миллионов лет после Большого Взрыва?
[Уровень: 6-8 | Темы: Десятичная математика; с помощью онлайн-калькулятора; Данные гистограммы] [Нажмите здесь]
Проблема 49 Спиральная галактика вблизи. — Астрономы могут многому научиться, изучая фотографии галактик. В В этом упражнении учащиеся вычислят масштаб изображения (световые годы на миллиметр) в фотография ближайшей спиральной галактики и изучить размеры элементов, обнаруженных на изображении. Они также будет использовать Интернет или другие ресурсы, чтобы заполнить недостающую справочную информацию об этой галактике. [Уровень: 6-8 | Темы: Интернет-исследования; Нахождение масштаба изображения; метрическое измерение; десятичная математика] [Нажмите здесь]
Проблема 41
Солнечная энергия в космосе Учащиеся вычисляют площадь поверхности спутника. используется для солнечных батарей из реальной фотографии спутника IMAGE.
Они рассчитают электрическую мощность, обеспечиваемую этой одной панелью. Студенты
придется вычислить площадь неправильной области, используя вложенные прямоугольники.
[Уровень: 7-10 | Темы: Площадь неправильного многоугольника; десятичная математика] [Нажмите здесь]
используется для солнечных батарей из реальной фотографии спутника IMAGE.
Они рассчитают электрическую мощность, обеспечиваемую этой одной панелью. Студенты
придется вычислить площадь неправильной области, используя вложенные прямоугольники.
[Уровень: 7-10 | Темы: Площадь неправильного многоугольника; десятичная математика] [Нажмите здесь]
Проблема 36 Затухание орбиты космической станции и космос Погода Учащиеся узнают о продолжающееся снижение орбиты Международной космической станции из-за изучение графика зависимости высоты станции от времени. Они будут рассчитать скорость затухания орбиты и выяснить, почему это может быть происходит. [Класс: 5–8 | Темы: Интерпретация графических данных; десятичная математика] [Нажмите здесь]
Проблема 31
Авиаперелеты и космическая погода Школьники прочитают отрывок из Космической погоды
книгу «23-й цикл» доктора Стена Оденвальда и ответить на вопросы о
авиаперелеты во время солнечных бурь. Они узнают о природе
фоновое излучение, которому они подвергаются каждый день, и сравните его с
доз радиации во время полета на реактивном самолете. [Класс: 6–8 | Темы: Чтение, чтобы быть в курсе; десятичная математика] [Нажмите здесь]
Они узнают о природе
фоновое излучение, которому они подвергаются каждый день, и сравните его с
доз радиации во время полета на реактивном самолете. [Класс: 6–8 | Темы: Чтение, чтобы быть в курсе; десятичная математика] [Нажмите здесь]
Проблема 10 Жизненный цикл авроры Студенты изучают описания двух очевидцев северное сияние и определить общие элементы, чтобы они могли извлечь общие закономерность изменений. [Класс: 4–6 | Темы: Создание временной шкалы из повествования; упорядочивание событий по дате и времени] [Нажмите здесь]
6 класс | Математика (основные элементы)
Примечание: Iowa Core Essential Elements предназначены только для учащихся со значительными когнитивными нарушениями, которые участвуют в альтернативных экзаменах.
Соотношения и отношения пропорциональности (EE.6.RP)
Понимание концепций соотношений и использование рассуждений о соотношениях для решения задач.
 (EE.6.RP.A)
(EE.6.RP.A)- Продемонстрируйте отношение простого соотношения. (EE.6.RP.A.1)
- Не применимо. См. EE.7.RP.1-3. (EE.6.RP.A.2)
- Не применимо. См. EE.8.F.1-3. (EE.6.RP.A.3)
Система счисления (EE.6.NS)
Применение и расширение предыдущего понимания умножения и деления для деления дробей на дроби. (EE.6.NS.A)
- Сравните соотношения между двумя долями единиц. (EE.6.NS.A.1)
Свободно вычисляйте многозначные числа и находите общие делители и кратные. (EE.6.NS.B)
- Применить концепцию справедливой доли и равных долей для разделения. (EE.6.NS.B.2)
- Решите задачи на двухфакторное умножение с произведениями до 50, используя конкретные объекты и/или калькулятор. (EE.6.NS.B.3)
- Не применимо. (EE.6.NS.B.4)
Применить и расширить предыдущее понимание чисел на систему рациональных чисел. (EE.6.NS.C)
- Поймите, что положительные и отрицательные числа используются вместе для описания величин, имеющих противоположные направления или значения (например, температура выше/ниже нуля).
 (EE.6.NS.C.5)
(EE.6.NS.C.5) - Поймите, что положительные и отрицательные числа используются вместе для описания величин, имеющих противоположные направления или значения (например, температура выше/ниже нуля). (EE.6.NS.C.6)
- Поймите, что положительные и отрицательные числа используются вместе для описания величин, имеющих противоположные направления или значения (например, температура выше/ниже нуля). (EE.6.NS.C.7)
- Поймите, что положительные и отрицательные числа используются вместе для описания величин, имеющих противоположные направления или значения (например, температура выше/ниже нуля). (EE.6.NS.C.8)
Выражения и уравнения (EE.6.EE)
Применение и расширение предыдущего понимания арифметики на алгебраические выражения. (ЕЕ.6.ЕЕ.А)
- Найдите эквивалентные числовые предложения. (EE.6.EE.A.1)
- Определите предложения с эквивалентными числами. (EE.6.EE.A.2)
- Применить свойства сложения для определения эквивалентных числовых выражений.
 (EE.6.EE.A.3)
(EE.6.EE.A.3) - Не применимо. (EE.6.EE.A.4)
Рассуждать и решать уравнения и неравенства с одной переменной. (EE.6.EE.B)
- Сопоставьте уравнение с реальной задачей, в которой переменные используются для представления чисел. (EE.6.EE.B.5)
- Сопоставьте уравнение с реальной задачей, в которой переменные используются для представления чисел. (EE.6.EE.B.6)
- Сопоставьте уравнение с реальной задачей, в которой переменные используются для представления чисел. (EE.6.EE.B.7)
- Не применимо. (EE.6.EE.B.8)
Представление и анализ количественных взаимосвязей между зависимыми и независимыми переменными. (EE.6.EE.C)
- Неприменимо. (EE.6.EE.C.9)
Геометрия (EE.6.G)
Решение реальных и математических задач на площадь, площадь поверхности и объем. (EE.6.G.A)
- Решайте реальные и математические задачи на площади, используя единичные квадраты. (EE.



 (EE.6.NS.C.5)
(EE.6.NS.C.5) (EE.6.EE.A.3)
(EE.6.EE.A.3)