решение задач за 5 — 6 класс — Колпаков Александр Николаевич
На этой странице публикуются решения задач по математике для 5 и 6 класса: части, проценты, пропорции, вычисления, простые текстовые задачи на движение, на работу, не требующие применения никаких уравнений кроме линейных. Помните о том, что виртуальный репетитор по математике не знает по какой программе учится Ваш ребенок и поэтому возможны расхождения со школой. Часто одну и ту же задачу на дроби можно решить по разному: средствами 5 класса (при помощи отдельных действий с числителями и знаменателями), а можно, например, средствами 6 класса, выполняя умножение или деление на соответствующие дроби. Для того, чтобы помочь репетитору математики выбрать оптимальный способ оформления номера, указывайте ссылки на авторов школьных учебников и Ваш класс. Пожалуйста, не заваливайте репетитора целыми списками номеров. Ориентировочное ограничение: 1-2 номера для каждого посетителя. Если Вам понравилась эта страница — нажмите на кнопку +1:
Это поможет другим ученикам найти сайт в интернете.
Виртуальный репетитор по математике (5-6 класс). Решения ваших задач.
Вопрос от Вовы: Из пункта М в пункт N выехал почтальон со скоростью 23 км/ч, и одновременно с ним из N в M выехал второй почтальон со скоростью 19 км/ч. Когда первый почтальон прибыл N, второму еще оставалось до М проехать 24 км. Каково расстояние между М и N?
Репетитор по математике о задаче про почтальона (А.Н. Колпаков)
Обозначим буквой t время, за которое первый почтальон прибыл в N, тогда 23t — путь, пройденный первым, а 19t — путь, пройденный вторым почтальоном за это же время. Так как второму езе оставалось 24 км, то он прошел за это время расстояние на 24 км меньшее, чем первый, поэтому 23t-19t=24. Решим это простенькое уравнение и получим в ответе t=6 часов. В итоге (км) — пусть первого, равный всему расстоянию от M до N.
Ответ: 138 км.
Вопрос репетитору по математике от Оксаны:
Помогите с задачей. Она элементарная, но нам надо ее решить без использования дробей!!! У квадрата одну его сторону увеличили на 9 см, а другую сторону уменьшили в 5 раз.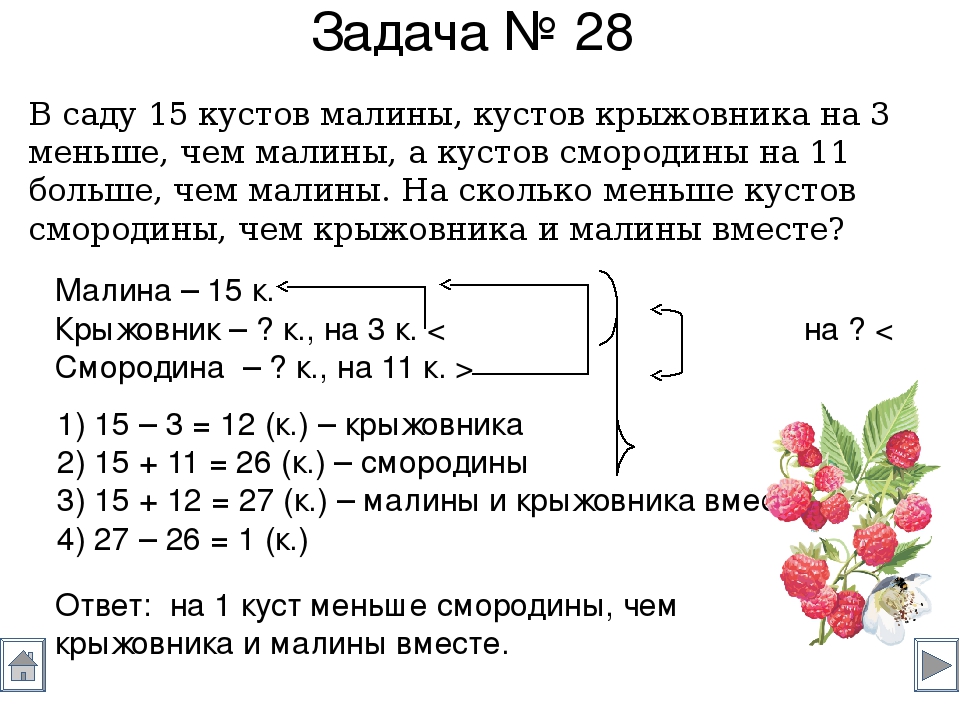 В результате этого получилcя прямоугольник с периметром равным 66 см. У какой фигуры — у прямоугольника или у квадрата — получилась больше площадь и на сколько?
В результате этого получилcя прямоугольник с периметром равным 66 см. У какой фигуры — у прямоугольника или у квадрата — получилась больше площадь и на сколько?Репетитор по математике о задаче c квадратом:
Если Вы хотите решить эту задачу без применения каких-либо дробей, не выходя за рамка программы 5 класса, то буквой икс необходимо обозначить наименьшую из величин, то есть ширину прямоугольника. Итак, пусть AK=x, тогда AD=AB=5x. Поскольку сторону AB увеличили на 9 см, то длина полученного прямоугольника выражается как 5x+9. Принимая во внимание условие с периметром, получаем простенькое уравнение без дробей:
x+x+5x+9+5x+9=66
Решая его получим, что x=4. Теперь легко найти интересующие нас площади: кв.см., кв.см.
Вопрос от Анны: Помогите решить задачу.
Отец и сын, работая вместе, покрасили забор за 12 ч. Если бы отец красил забор один, он выполнил бы эту работу за 21 ч. За сколько часов покрасил бы этот забор сын?
За сколько часов покрасил бы этот забор сын?
Репетитор по математике, Тимур Розугнов
Примем весь объем работы (забор) за единицу и воспользуемся тем, что совместная скорость равна сумме отдельных скоростей отца и сына. Следить за решением удобно при помощи табличного метода оформления:
1) (заб/час) — совместная скорость
2) (заб/час) — скорость отца
3) (заб/час) — скорость сына
4) (часов) — время работы сына
Ответ: 28 часов
Вопрос от Марины:
Редактор прочитал две пятых рукописи, что составило 80 страниц. На другой день он прочитал четверть оставшихся страниц. ВОПРОСЫ: 1) Сколько страниц в рукописи? 2) Сколько страниц осталось не прочитано?
Репетитор по математике, Никита Афанасьевич
Для лучшего усвоения решения полезно сделать краткую запись. Выглядеть она будет следующим образом:
Решение:
1) (страниц) в рукописи.
2) (рукописи) — составляет остаток.
3) (страниц) — остаток.
4) (страниц) — прочитано во второй день.
5) (страниц) не прочитано.
Ответ: 90 страниц.
Задача от Наташи:
Мотоциклист в первый час проехал 3/8 всего пути ,во второй час 3/5 остатка,а в третий час остальные 40 км. Найдите весь путь. Помогите решить!
Репетитор по математике, Александр Колпаков
Старайтесь указывать для какого класса и по какой программе репетитору оформлять решение !!! будем считать, что что вы в 6 классе. Оформим краткую запись ровно так, как я это рекомендую делать своим ученикам: (в вертикальную рамку я выделяю доли, связанные законом сложения)
1) (остатка) — проехал мотоциклист за третий час
2) (км) — остаток
3) (всего пути) — остаток после пройденного мотоциклистом пусти за I час.
4) (км) — составляет весь путь
Ответ: 160 км
Вопрос от Оксаны: Объясните, пожалуйста, как правильно решить задачу: поезд проходит расстояние АВ за 10,5 ч. На сколько процентов следует увеличить его скорость, чтобы то же расстояние он преодолел за 8 ч? Решение нужно СРОЧНО к 1 сентября! Пыталась сама решить ее через уравнение, но не знаю правильно ли.
Репетитор по математике, Григорий Александров: Не нужно никаких уравнений. Они только Вас запутают. Вот мое решение: поскольку прирост любой вличины в процентах не зависит от ее единицы измерения, то примем за единицу полное расстояние от А до В. Тогда скорости будут такими: и Тогда прирост по скорости составит
Осталось эту часть перевести в проценты умножением на 100. Получим в итоге %
Задача от Арины:
У Шынар в копилке 80 монет достоинством 20 и 50 тенге Всего 2590 тенге. Сколько монет в копилке у Шынар достоинством 20 тенге? достоинством 50 тенге? Заранее спасибо очень надеюсь на вашу помощь.
Репетитор по математике, Колпаков А.Н.
Если бы все монеты были по 50 тенге, то Шынар имела бы всего 4000 тенге. Замена одной монеты в 50 тенге на одну монету достоинство в 20 тенге приводит к снижению капитала ровно на 30 тенге. На сколько тенге нам необходимо уменьшить общий капитал Шынар с 4000 до 2590? Ровно на 4000—2590=1410 тенге. Тогда сколько раз необходимо произвести замену? 1410:30=47 раз. Поэтому 47 монет нужно поменять на двадцатитенговые. Останется 80-47=33 монеты по 50 тенге.
Тогда сколько раз необходимо произвести замену? 1410:30=47 раз. Поэтому 47 монет нужно поменять на двадцатитенговые. Останется 80-47=33 монеты по 50 тенге.
Вопрос от Татьяны: нужно решить задачу:
В первый день садовод вскопал на 40% своего участка, а во второй — 40% оставшейся части. На третий день он закончил работу, вскопав 180 кв.м. Определить площадь всего участка?
Репетитор по математике и физике, Галкин Р.А.
Можно предложить 3 способа решения. Остановлюсь на том, который ориентирован на 5 класс. В целях лучшего восприятия задачи составим схему (краткую запись) условия:Здесь все проценты переведены в дроби . Найдем какую часть (или сколько процентов) составляет вскопанная часть в 3 день от того, что осталось вскопать после 1-го дня:
1) %(остатка) -вскопали в 3 день.
По известному значению 180кв.м дроби найдем целую величину, то есть остаток:
2) (кв.
Найдем какую часть остаток составляет от всего участка:
3) %(всего участка) — осталось
По известному значению 300 кв.м дроби найдем целую величину, то есть весь участок:
4) (кв.м) — площадь всего участка.
Ответ: 500 кв.м.
Вопрос от Ангелины:
У меня возник вопрос с решением задачи. Помогите пожалуйста. Можно ли из какого угодно кол-ва троек получить в ответе 100, при помощи действий сложение, вычитание и умножение?
Репетитор по математике, Файгойз М.Ю.
Не очень понял вопрос. Что значит из «какого-угодно»? Угодно нам или угодно составителю задачи? Эх … не математик условие писал. Если на нас спускается количество троек как приказ, то не из любого. Ведь из двух троек никак нельзя составить 100. А если мы сами вправе выбирать количество троек, то можно так: . Конечно, условие должно быть переписано: можно ли из какого-нибудь количества троек получить 100?
Pages: 1 2 3
Как решать задачи на проценты в 6 классе
Предлагаю вашему вниманию легкий способ разобраться, как решать задачи на проценты в 6 классе.
При решении задачи на проценты первым делом нужно определить вид задачи. Задачи на проценты в 6 классе можно подразделить на три вида:
1) Нахождение процентов от числа.
2) Нахождение числа по его процентам.
3) Нахождение процентного отношения двух чисел.
Определить вид задачи на проценты можно по записи ее условия. Если напротив 100% стоит число, то это — задача на нахождение процентов от числа. Если число напротив 100% неизвестно, то это — задача на нахождение числа по его процентам. Если же неизвестное значение стоит в колонке процентов, то это — задача на нахождение процентного отношения двух чисел.
Рассмотрим на примерах, как научиться определять вид задачи на проценты.
1. Из картофеля выходит 20% крахмала. Сколько крахмала выйдет из 45 т картофеля?
| тонны | % | |
| Картофель | 45т | 100% |
| Крахмал | ? | 20% |
Это задача на нахождение процентов от числа (так как напротив 100% стоит число).
2. Руда содержит 67% железа. Сколько нужно руды для получения 13,4 т железа?
| % | ||
| Руда | ? | 100% |
| Железо | 13,4т | 67% |
Это задача на нахождение числа по его процентам (так как напротив 100% стоит ?)
3. Из 400 зерен пшеницы взошло 360. Определить процент всхожести семян.
| Зерна | % | |
| Всего посеяли | 400 | 100% |
| Взошло | 360 | ? |
Это задача на процентное отношение (так как в колонке процентов стоит ?).
Страница 72 — ГДЗ Математика 3 класс. Моро, Бантова. Учебник часть 1
Вернуться к содержанию учебника
Площадь. Единицы площади
Вопрос
1. Составь по таблице три задачи и реши их.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
2. На каждое детское пальто пришивают 3 пуговицы. Сколько пуговиц нужно пришить на 8 таких пальто? на 9 пальто? на 10 пальто?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
3. В куске 25 м ткани. Хватит ли этой ткани, чтобы сшить 6 платьев, расходуя на каждое по 3 м ткани? Сколько метров ткани останется, если расходовать на каждое по 4 м?
В куске 25 м ткани. Хватит ли этой ткани, чтобы сшить 6 платьев, расходуя на каждое по 3 м ткани? Сколько метров ткани останется, если расходовать на каждое по 4 м?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
4.
| 72 — 32 : 4 | 64 — 16 : 8 + 8 | 9 • (13 — 6) |
| 36 — 18 : 2 | 64 — 16 : (8 + 8) | 6 • (27 — 20) |
| 48 — 24 : 3 | (64 — 16) : 8 + 8 | 40 : (30 — 25) |
Ответ
Поделись с друзьями в социальных сетях:
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
6. У входа в парк были две цветочные клумбы. Одна клумба имела форму квадрата, длина стороны которого 3 м, а другая — форму прямоугольника, длины сторон которого 4 м и 2 м. У какой клумбы площадь больше? Что можно сказать про их периметры?
У входа в парк были две цветочные клумбы. Одна клумба имела форму квадрата, длина стороны которого 3 м, а другая — форму прямоугольника, длины сторон которого 4 м и 2 м. У какой клумбы площадь больше? Что можно сказать про их периметры?
Подсказка
Периметр многоугольника — это сумма длин всех его сторон. У квадрата все стороны равны, поэтому мы можем длину умножить на 4 и вычислить периметр.
Площадь прямоугольника равна произведению его длины и ширины. У квадрата длина равна ширине.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
7. Расставь скобки так, чтобы равенства были верными.
Расставь скобки так, чтобы равенства были верными.
16 + 20 : 4 = 9
9 • 10 — 7 = 27
15 + 36 : 9 — 3 = 21
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
В овощную палатку привезли 8 ящиков огурцов, по 10 кг в каждом. До обеденного перерыва продали 54 кг. Сколько килограммов огурцов осталось?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Магические квадраты:
Подсказка
Сложи числа в каждом квадрате по строкам, по столбцам, из угла в угол. Если суммы равны, то такой квадрат называется магическим.
Если суммы равны, то такой квадрат называется магическим.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
© budu5.com, 2021
Пользовательское соглашение
Copyright
Рабочие листы задач по математике для 6-го класса с ответами
Важные факты о решении и оценивании текстовых задач для 6-го класса
В значительной степени наши потрясающие рабочие листы для решения проблем и оценки помогут вашим юным ученикам, изучающим математику, быстро понять важность навыков оценки в математических концепциях и реальной жизни.
Следует отметить, что эти навыки решения задач и оценки являются не только ключевой частью математических концепций, но и не менее важным методом, позволяющим похвастаться умственными математическими навыками, способностями логического и творческого мышления вашего ребенка.
Как навыки оценивания могут повысить точность детей и повысить их знатоков математики?
Если ваши дети могут живо оценивать и разумно, то не будет сомнений, что их точность в математике повысится, в том числе и в экспертах по математике.
Более того, обладая оценочными навыками, они могут быстро определить, находится ли их ответ в разумных пределах или нет.
Учитывая, что умение оценивать повышает умственные способности ребенка к математике, ваш классник 6 – сможет прийти к разумным или конкретным ответам в мгновение ока.
Что наиболее важно, эти навыки решения задач и оценки не только укрепят навыки детей в основных математических операциях, но и подготовят их к таким областям продвинутой математики, как вероятность, статистика, геометрия и алгебра. На этом этапе от них потребуется применить навыки логического мышления и оценки.
На этом этапе от них потребуется применить навыки логического мышления и оценки.
Как навыки оценки актуальны в нашей повседневной жизни?
Дома, на рынке, на улице или среди друзей, наша деятельность всегда будет окружена оценкой.Это правда, поскольку мы продолжаем использовать фразу «Скажем …….».
Итак, навыки решения проблем и оценки помогут вашим детям легко;
- Смета рецептов при приготовлении, выпечке и т. Д.
- Оцените стоимость товаров в продуктовом магазине, т. Е. Если вы хотите остаться в рамках бюджета
- Оцените количество людей, которых вы пригласите на предстоящее мероприятие, в зависимости от имеющегося бюджета.
- Оценивайте и умейте распоряжаться своим драгоценным временем или тратить его.Это предотвратит небрежное отвлечение внимания, а также побудит вас выполнить свою задачу.
Основные стратегии, наилучшие для решения задач оценивания слов для 6
-го класса Наши рабочие листы математических словесных задач для 6-го класса с ответами являются прекрасным примером для детей, чтобы овладеть жизненно важными стратегиями, которые лучше всего подходят для решения задач оценивания слов для 6 -го -го класса .
Каковы же тогда эти специфические стратегии, которые следует учитывать при столкновении с ситуациями решения проблем и оценки?
В большинстве случаев математические задачи со словами требуют выполнения пошаговой процедуры решения .Это относится к нашему упражнению с задачами, состоящими из нескольких шагов. Но прежде чем мы начнем решать эти словесные задачи, нам нужно;
- Внимательно прочтите всю задачу дважды, чтобы лучше понять ее ключевые слова.
- Хорошо разобравшись в проблеме, постарайтесь оценить ответ, прежде чем решать.
- При решении покажите пошаговый расчет, сделав видимыми различные знаки операции там, где это необходимо.
Наконец, проверьте правильность своего ответа, сравнив его с тем, который вы оценили выше.
Коэффициенты преподавания и ставки по математике
Суть математики в средней школе и ключевая часть готовности к алгебре — это понимание соотношений и оценок. Обзор и уроки, представленные ниже, представляют собой инструменты для подготовки учащихся, обычно учащихся 6-х классов и выше, к изучению этих концепций. Приведенные ниже уроки обычно занимают два дня обучения.
Приведенные ниже уроки обычно занимают два дня обучения.
Коэффициенты и ставки
Коэффициент — это сравнение двух чисел или измерений.Сравниваемые числа или измерения иногда называют членами отношения. Например, если в магазине продается 6 красных рубашек и 8 зеленых рубашек, соотношение красных и зеленых рубашек составляет 6 к 8. Вы можете записать это соотношение как 6 красных / 8 зеленых, 6 красных: 8 зеленых — или при быстром письме или пытаясь доказать свою точку зрения — просто 6/8 или 6: 8. Оба выражения означают, что на каждые 8 зеленых футболок приходится 6 красных футболок. Обратите внимание, как вы можете переписать 6/8 как 3/4, ничем не отличается от любого другого случая, когда математическая концепция может отображаться в виде дроби.
Коэффициент — это особое соотношение, в котором два члена указаны в разных единицах измерения. Например, если банка кукурузы объемом 12 унций стоит 69 центов, то ставка составит 69 центов за 12 унций. Это не соотношение двух одинаковых единиц, например рубашки. Это соотношение двух разных единиц: центов и унций. Первый член отношения (69 ¢) измеряется в центах , а второй член (12) в унциях . Вы можете записать эту ставку как 69 ¢ / 12 унций или 69: 12 унций. Оба выражения означают, что вы платите 69 центов за каждые 12 унций кукурузы, и аналогично коэффициенту рубашки можно ввести в расчетах как дробь 69/12.Но обратите внимание, что на этот раз создается новая единица: цент в час .
Это не соотношение двух одинаковых единиц, например рубашки. Это соотношение двух разных единиц: центов и унций. Первый член отношения (69 ¢) измеряется в центах , а второй член (12) в унциях . Вы можете записать эту ставку как 69 ¢ / 12 унций или 69: 12 унций. Оба выражения означают, что вы платите 69 центов за каждые 12 унций кукурузы, и аналогично коэффициенту рубашки можно ввести в расчетах как дробь 69/12.Но обратите внимание, что на этот раз создается новая единица: цент в час .
Ставки используются людьми каждый день, например, когда они работают 40 часов в неделю или зарабатывают процентов каждый год в банке. Когда скорость выражается как количество, равное 1, например 2 фута в секунду (то есть за 1 секунду) или 5 миль в час (то есть за 1 час), они могут быть определены как единицы скорости . Вы можете записать любую ставку как единицу, уменьшив дробь так, чтобы знаменатель или второй член имел 1.В качестве примера расчетной ставки вы можете показать, что расчетная ставка для 120 студентов на каждые 3 автобуса составляет 40 студентов на автобус.
120/3 = 40/1
Вы также можете найти единичную ставку, разделив первый член отношения на второй член.
120 ÷ 3 = 40
Когда цена выражается как количество, равное 1, например 25 долларов за билет или 0,89 доллара за банку, это называется ценой за единицу . Если у вас не единичная цена, например 5 долларов.50 за 5 фунтов картофеля, и хотите найти цену за единицу, разделите условия отношения.
5,50 доллара США ÷ 5 фунтов = 1,10 доллара США за фунт
Цена за единицу картофеля, который стоит 5,50 доллара за 5 фунтов, составляет 1,10 доллара за фунт.
Тарифы в реальном мире
Скорость и удельная скорость используются для решения многих реальных проблем. Взгляните на следующую проблему. «Тоня работает по 60 часов каждые 3 недели. При такой скорости, сколько часов она проработает за 12 недель? » Проблема говорит вам, что Тоня работает по 60 часов каждые 3 недели. Чтобы найти количество часов, которое она проработает за 12 недель, запишите соотношение, равное 60/3, при втором семестре 12.
Чтобы найти количество часов, которое она проработает за 12 недель, запишите соотношение, равное 60/3, при втором семестре 12.
60/3 =? / 12
60/3 = 240/12
Удаление единиц облегчает просмотр расчетов. Однако при интерпретации нового соотношения важно помнить об этих единицах измерения.
Тоня проработает 240 часов за 12 недель.
Вы также можете решить эту проблему, сначала найдя удельный вес и умножив его на 12.
60/3 = 20/1
20 × 12 = 240
Когда вы находите равные отношения, важно помнить, что если вы умножаете или делите один член отношения на число, тогда вам нужно умножить или разделить другой член на это же число.
Давайте рассмотрим проблему, связанную с ценой за единицу. «Вывеска в магазине гласит:« 3 ручки за 2,70 доллара ». Сколько будут стоить 10 ручек? » Чтобы решить эту проблему, найдите цену ручки, затем умножьте ее на 10.
2 доллара.70 ÷ 3 ручки = 0,90 доллара США за ручку
0,90 доллара США × 10 ручек = 9,00 долларов США
Определение стоимости одной единицы позволяет определить стоимость любого количества единиц.
Стратегии решения математических задач, которые заставляют учащихся говорить: «Я понял!»
Даже ученики, которые быстро усваивают математические факты, могут застрять, когда дело доходит до решения задач.
Как только концепция переводится в словесную задачу или простое математическое предложение содержит неизвестное, они попадают в тупик.
Это потому, что решение проблем требует от нас сознательного выбора стратегии, наиболее подходящей для решения проблемы под рукой . И не все студенты обладают этой метакогнитивной способностью.
Но вы можете научить этим стратегиям решения проблем. Просто нужно знать, что они из себя представляют.
Мы собрали их здесь и разделили на четыре категории:
- Стратегии понимания проблемы
- Стратегии решения проблемы
- Стратегии тренировки
- Стратегии проверки решения
Познакомьтесь с этими стратегиями, а затем явным образом смоделируйте их для своих учеников.В следующий раз, когда они погрузятся в сложную задачу, они заполнят рабочий документ быстрее, чем когда-либо!
Стратегии понимания проблемы
Прежде чем учащиеся смогут решить проблему, они должны знать, о чем их спрашивают. Часто это первое препятствие для задач со словами, в которых не указывается конкретная математическая операция.
Поощряйте своих студентов:
Прочтите и перечитайте вопрос
Они говорят, что читали, но действительно ли ? Иногда учащиеся пропускают вперед, как только заметили какую-то знакомую информацию, или прекращают попытки понять ее, если на первый взгляд проблема не имеет смысла.
Научите студентов интерпретировать вопрос, используя стратегии самоконтроля, например:
- Медленнее перечитывать вопрос, если в первый раз он не имеет смысла
- Обращение за помощью
- Выделение или подчеркивание важной информации.
Обозначьте важную и постороннюю информацию
Джон собирает деньги на день рождения своего друга Ари. Он начинает с собственных 5 долларов, затем Маркус дает ему еще 5 долларов.Сколько у него сейчас?
Как взрослые, глядя на вышеуказанную задачу, мы можем мгновенно взглянуть за пределы имен и сценария дня рождения и увидеть простую задачу сложения. Студенты, однако, могут с трудом определить, что имеет отношение к информации, которая им была предоставлена.
Научите студентов сортировать и анализировать информацию в задаче, чтобы найти то, что имеет отношение к делу. Хороший способ сделать это — попросить их обмениваться информацией, чтобы увидеть, изменится ли решение. Если изменение названий, предметов или сценариев не повлияет на конечный результат, они поймут, что при решении проблемы это необязательно.
Если изменение названий, предметов или сценариев не повлияет на конечный результат, они поймут, что при решении проблемы это необязательно.
Схема подхода
Это стратегия вмешательства в математику, которая может облегчить решение задач для всех учащихся, независимо от способностей.
Сравните разные словесные задачи одного типа и создайте формулу или математическую основу предложения, которая применима ко всем. Например, простая задача на вычитание может быть выражена как:
[Число / количество A] с удаленным [Число / количество B] становится [конечным результатом].
Это основная процедура или схема , которую просят использовать студентов.Получив список схем для различных математических операций (сложение, умножение и т. Д.), Они могут по очереди применить их к проблеме с незнакомыми словами и посмотреть, какая из них подходит.
Бесплатные рабочие листы для решения проблем
Стратегии решения проблемы
Учащиеся, испытывающие трудности, часто считают, что математика — это то, что вы делаете автоматически или не делаете вообще. Но это неправда. Помогите своим ученикам понять, что у них есть выбор из стратегий решения проблем, и, если одна из них не работает, они могут попробовать другую.
Но это неправда. Помогите своим ученикам понять, что у них есть выбор из стратегий решения проблем, и, если одна из них не работает, они могут попробовать другую.
Вот четыре распространенных стратегии, которые студенты могут использовать для решения проблем.
Визуализация
Визуализация абстрактной проблемы часто упрощает ее решение. Студенты могли нарисовать картинку или просто нарисовать отметки на рабочем листе.
Поощряйте визуализацию, моделируя ее на доске и предоставляя графические органайзеры, в которых учащиеся могут рисовать, прежде чем они запишут окончательное число.
Угадай и проверь
Покажите студентам, как сделать обоснованное предположение, а затем снова вставьте этот ответ в исходную задачу.Если это не сработает, они могут соответственно изменить свое первоначальное предположение выше или ниже.
Найдите выкройку
Чтобы найти закономерности, покажите учащимся, как извлечь и составить список всех важных фактов в задаче, чтобы их можно было легко сравнить. Если они найдут закономерность, они смогут найти недостающую информацию.
Если они найдут закономерность, они смогут найти недостающую информацию.
Назад
Работа в обратном направлении полезна, если учащимся нужно найти неизвестное число в задаче или математическом предложении. Например, если задача 8 + x = 12, учащиеся могут найти x по:
- Начиная с 12
- Взятие восьмерки из 12
- Остался с 4
- Проверка того, что 4 работает при использовании вместо x
Стратегии развития
Теперь студенты поняли проблему и сформулировали стратегию, пора применить ее на практике.Но если они просто начнут и сделают это, они могут усложнить себе задачу. Покажите им, как эффективно решать проблему:
Документирующая разработка
Смоделируйте процесс записи каждого шага, который вы делаете для решения математической задачи, и предоставьте рабочий документ, когда учащиеся решают задачу. Это позволит учащимся отслеживать свои мысли и выявлять ошибки, прежде чем они придут к окончательному решению.
Это позволит учащимся отслеживать свои мысли и выявлять ошибки, прежде чем они придут к окончательному решению.
Проверка в пути
Проверка работы на ходу — еще одна важная стратегия самоконтроля для изучающих математику.Смоделируйте это, задав им вслух вопросы, например:
- Последний шаг выглядит правильным?
- Это следует из предыдущего шага?
- Выполнял ли я какие-либо «меньшие» суммы в рамках более крупной задачи, требующей проверки?
Стратегии проверки решения
Студенты часто ошибаются, думая, что скорость — это все в математике, поэтому они спешат получить ответ и идут дальше, не проверяя.
Но проверка тоже важна.Это позволяет им точно определять проблемные области по мере их возникновения, а также позволяет решать более сложные проблемы, требующие многократных проверок , прежде чем придет окончательный ответ.
Вот несколько проверочных стратегий, которые вы можете продвигать:
Проверить у партнера
Сравнение ответов с коллегами — это более рефлексивный процесс, чем просто получение галочки от учителя. Если у учащихся есть два разных ответа, предложите им рассказать о том, как они к ним пришли, и сравнить методы работы.Они точно поймут, где они пошли не так, а что сделали правильно.
Перечитайте проблему своим решением
В большинстве случаев учащиеся смогут определить, верен ли их ответ, вернув его в исходную задачу. Если это не работает или просто «выглядит неправильно», пора вернуться и исправить.
Исправление ошибок
Покажите студентам, как вернуться к выполнению своей работы, чтобы найти точную точку, в которой они сделали ошибку.Подчеркните, что они не могут этого сделать, если не все записали с самого начала — поэтому один-единственный ответ без работы не так впечатляет, как они могли бы подумать!
Нужна дополнительная помощь в развитии навыков решения проблем?
Прочтите, как задать задачу по решению задач и рассуждению, или изучите Mathseeds и Mathletics, наши отмеченные наградами онлайн-математические программы. Они предложили учителям более 900 упражнений по решению проблем!
Они предложили учителям более 900 упражнений по решению проблем!
Решение задач: Составьте таблицу
Составьте таблицу — это стратегия решения задач, которую учащиеся могут использовать для решения математических текстовых задач, записывая информацию в более организованном формате.
Решение проблем: составление таблицы
Что это такое?
«Составить таблицу» — это стратегия решения задач, которую учащиеся могут использовать для решения математических текстовых задач, записывая информацию в более организованном формате. Вот пример проблемы, которую можно решить, составив таблицу:
Хуанита извлекла книгу из библиотеки, и теперь она просрочена на 7 дней. Если книга просрочена на 1 день, штраф составляет 10, за просрочку на 2 дня, 20, за просрочку на 3 дня, 30 ¢ и так далее. Насколько она в порядке?
Почему это важно?
Эта стратегия решения задач позволяет учащимся обнаруживать взаимосвязи и закономерности между данными. Он побуждает студентов систематизировать информацию логическим образом и критически относиться к данным, чтобы найти закономерности и разработать решение.
Он побуждает студентов систематизировать информацию логическим образом и критически относиться к данным, чтобы найти закономерности и разработать решение.
Как это сделать?
Предложите ученикам задачу, которая потребует от них составить таблицу для решения задачи. Например:
Сколько часов потребуется автомобилю, движущемуся со скоростью 65 миль в час, чтобы догнать автомобиль, движущийся со скоростью 55 миль в час, если более медленный автомобиль заводится на час раньше, чем более быстрый?
Разберитесь в проблеме
Продемонстрируйте, что первым шагом является понимание проблемы.Это включает в себя определение ключевой информации, необходимой для поиска ответа. Это может потребовать от студентов прочитать задачу несколько раз или изложить ее своими словами.
В этой задаче учащиеся должны понимать, что есть более медленная машина, едущая со скоростью 55 миль в час, и более быстрая машина, едущая со скоростью 65 миль в час.
 Более медленная машина заводится на час раньше более быстрой. Учащимся нужно определить, сколько часов потребуется более быстрой машине, чтобы догнать более медленную.
Более медленная машина заводится на час раньше более быстрой. Учащимся нужно определить, сколько часов потребуется более быстрой машине, чтобы догнать более медленную.Выберите стратегию
Поскольку необходимо организовать три набора данных, вам следует использовать стратегию «Создать таблицу».Как правило, если есть данные, связанные с определенной категорией, их можно легко организовать, составив таблицу. Эта стратегия также пересекается со стратегией «Найти шаблон», потому что часто легче найти шаблон, когда данные организованы в виде таблицы.
Решение проблемы
Создайте таблицу для организации данных. В этом примере создайте строку для более медленной машины, строку для более быстрой машины и столбец для каждого часа. Найдите расстояние, пройденное за каждый час, просмотрев расстояния, указанные в каждом столбце.Расстояние более быстрой машины было больше, чем расстояние более медленной машины в седьмом часе. Более быстрая машина ехала шесть часов, чтобы догнать более медленную.

Час 1 2 3 4 5 4 9037 55
110 165 220 275 330 385 Faster Car 0 65 130 195 260 392 Проверить
Прочтите проблему еще раз, чтобы убедиться, что на вопрос дан ответ.
Вы узнали, сколько часов потребовалось более быстрой машине, чтобы ее догнать? Да, прошло 6 часов.
Проверьте математику, чтобы убедиться, что она верна.
55 x 2 = 110, 55 x 3 = 165, 55 x 4 = 220, 55 x 5 = 275, 55 x 6 = 330, 55 x 7 = 385
65 x 2 = 130, 65 x 3 = 195, 65 x 4 = 260, 65 x 5 = 325, 65 x 6 = 390Определите, была ли выбрана лучшая стратегия для этой проблемы или существовал другой способ решения проблемы.

Изготовление стола — хороший способ решить эту проблему.
- Объясните
Последний шаг — объяснить, как вы нашли ответ. Продемонстрируйте, как написать абзац, описывающий шаги, которые вы предприняли, и то, как вы принимали решения на протяжении всего процесса.
Я составил таблицу миль, которые проехала каждая машина за каждый час. Я продолжал добавлять столбцы, пока более быстрая машина не догнала более медленную. К концу седьмого часа более быстрая машина прошла 390 миль, что больше, чем расстояние, пройденное более медленной машиной, — 385 миль.Поскольку более быстрая машина ехала не в первый час, она ехала шесть часов.
- Практика с инструкциями
Предложите учащимся попробовать решить следующую задачу, используя стратегию «Составить стол».
Принтер в медиацентре может печатать 1 страницу каждые 30 секунд. Принтер в офисе может печатать 4 страницы каждые 30 секунд.
 Если оба принтера печатают, сколько страниц распечатает офисный принтер к тому моменту, когда принтер медиацентра напечатает 5 страниц?
Если оба принтера печатают, сколько страниц распечатает офисный принтер к тому моменту, когда принтер медиацентра напечатает 5 страниц?Попросите учащихся поработать в парах, группах или индивидуально, чтобы решить эту задачу.Они должны уметь рассказать или написать о том, как они нашли ответ, и обосновать свои рассуждения.
Как развить мышление студентов?
Эта стратегия может быть расширена в сочетании с другими стратегиями, такими как поиск закономерностей или рисование изображения. Комбинируя эту стратегию с другими, учащиеся могут анализировать данные, чтобы найти более сложные взаимосвязи.
Стратегии решения задач — математика для учителей начальной школы
Вернитесь к первой задаче в этой главе — проблеме ABC.Что вы сделали, чтобы решить эту проблему? Даже если вы не разобрались с этим полностью самостоятельно, вы, вероятно, работали над решением и выяснили, что не работает.
В отличие от упражнений, простых рецептов решения проблемы не бывает.
 Вы можете становиться все лучше и лучше в решении проблем, как наращивая свои базовые знания, так и просто практикуясь. По мере того, как вы решаете больше проблем (и узнаете, как их решали другие люди), вы изучаете стратегии и методы, которые могут быть полезны.Но ни одна стратегия не работает каждый раз.
Вы можете становиться все лучше и лучше в решении проблем, как наращивая свои базовые знания, так и просто практикуясь. По мере того, как вы решаете больше проблем (и узнаете, как их решали другие люди), вы изучаете стратегии и методы, которые могут быть полезны.Но ни одна стратегия не работает каждый раз.Джордж Полиа был великим чемпионом в области , обучая навыкам эффективного решения проблем. Он родился в Венгрии в 1887 году, получил степень доктора философии. в Университете Будапешта и был профессором Стэнфордского университета (среди других университетов). Он написал множество математических статей и три книги, самая известная из которых — «Как это решить». Полиа умерла в 1985 году в возрасте 98 лет.
Джордж Полиа, около 1973 г.В 1945 году Полиа опубликовал короткую книгу How to Solve It , в которой был дан четырехэтапный метод решения математических задач:
- Во-первых, вы должны понять проблему.
- Разобравшись, составьте план.

- Осуществить план.
- Оглянитесь на свою работу. Как могло быть лучше?
Это все хорошо, но как на самом деле сделать эти шаги?!?! Шаги 1 и 2 особенно загадочны! Как вы «составляете план»? Вот где вам понадобятся некоторые инструменты в вашем наборе инструментов и некоторый опыт, на который можно опираться.
С 1945 года было написано много, чтобы объяснить эти шаги более подробно, но правда в том, что они больше искусство, чем наука.Вот где математика становится творческим занятием (и становится таким увлекательным). Мы сформулируем некоторые полезные стратегии решения проблем, но такой список никогда не будет полным. Это действительно только начало, которое поможет вам на вашем пути. Лучший способ научиться решать проблемы — хорошо выучить справочный материал, а затем решить множество проблем!
Мы уже видели одну стратегию решения проблем, которую мы называем «желаемое за действительное». Не бойтесь менять проблему! Задайте себе вопросы «а что, если»:
- Что, если бы картинка была другой?
- Что, если бы числа были попроще?
- Что, если я просто придумал какие-то числа?
Вам нужно обязательно вернуться к исходной проблеме в конце, но принятие желаемого за действительное может быть мощной стратегией для начала.
Это подводит нас к самой важной стратегии решения проблем:
Стратегия решения проблем 2 (Попробуйте что-нибудь!). Если вы действительно пытаетесь решить проблему, все дело в том, что вы не знаете, что делать прямо на старте. Вам нужно просто что-то попробовать! Приложите карандаш к бумаге (или стилус к экрану, или мел к доске, или что-то еще!) И попробуйте что-нибудь. Часто это важный шаг в понимании проблемы; просто немного повозитесь с этим, чтобы понять ситуацию и выяснить, что происходит.
И не менее важно: если то, что вы попробовали сначала, не работает, попробуйте что-нибудь другое! Поиграйте с проблемой, пока не почувствуете, что происходит.
Задача 2 (Окупаемость)На прошлой неделе Алекс занял деньги у нескольких своих друзей. В конце концов, ему заплатили на работе, поэтому он принес в школу наличные, чтобы выплатить долги. Сначала он увидел Брианну и отдал ей четверть денег, которые принес в школу. Затем Алекс увидел Криса и отдал ему 1/3 того, что у него осталось после того, как он заплатил Брианне.Наконец, Алекс увидел Дэвида и отдал ему половину того, что у него осталось. Кто получил больше всего денег от Алекса?
Думать / Пара / ПоделитьсяПосле того, как вы некоторое время поработали над проблемой самостоятельно, обсудите свои идеи с партнером (даже если вы еще не решили ее). Что ты пробовал? Что вы узнали о проблеме?
Эта проблема поддается двум конкретным стратегиям. Пробовали ли вы что-нибудь из этого, когда работали над проблемой? Если нет, прочтите о стратегии, а затем попробуйте ее перед просмотром решения.
Стратегия решения проблем 3 (Нарисуйте картинку). Некоторые задачи, очевидно, связаны с геометрической ситуацией, и ясно, что вы хотите нарисовать картинку и пометить всю данную информацию, прежде чем пытаться ее решить. Но даже для не геометрической задачи, как эта, может помочь визуальное мышление! Можете ли вы изобразить что-то в ситуации картинкой?
Нарисуйте квадрат, представляющий все деньги Алекса. Затем заштрихуйте 1/4 квадрата — вот что он отдал Брианне.Как картинка может помочь вам решить проблему?
После того, как вы поработали над проблемой самостоятельно, используя эту стратегию (или если вы полностью застряли), вы можете посмотреть решение кого-то другого.
Стратегия решения проблем 4 (Сводные числа). Отчасти эта проблема усложняется тем, что она связана с деньгами, но цифры не приводятся. Это означает, что числа не должны иметь значения. Так что просто придумайте их!
Вы можете работать наперед: предположим, у Алекса была определенная сумма денег, когда он пришел в школу, скажем, 100 долларов.Затем выясните, сколько он дает каждому человеку. Или вы можете работать в обратном порядке: предположим, у него в конце осталась какая-то определенная сумма, например, 10 долларов. Поскольку он отдал Крису половину того, что у него осталось, это означает, что у него было 20 долларов, прежде чем он столкнулся с Крисом. Теперь поработайте в обратном направлении и выясните, сколько получил каждый человек.
Следите за решением только после того, как попробуете эту стратегию на себе.
Если вы используете стратегию «Прибавить числа», действительно важно помнить, о чем спрашивала исходная проблема! Не стоит отвечать примерно так: «У всех по 10 долларов.«Это не так в исходной задаче; это артефакт чисел, которые вы составили. Так что после того, как вы все проработаете, обязательно перечитайте задачу и ответьте на вопрос!
Задача 3 (Квадраты на шахматной доске)Сколько квадратов любого возможного размера на шахматной доске 8 × 8? (Ответ — не 64… Это намного больше!)
Помните, что первый шаг Поли — это понять проблему. Если вы не уверены, о чем спрашивают, или почему ответ не 64, обязательно спросите кого-нибудь!
Думать / Пара / ПоделитьсяПосле того, как вы некоторое время поработали над проблемой самостоятельно, обсудите свои идеи с партнером (даже если вы еще не решили ее).Что ты пробовал? Что вы узнали о проблеме, даже если не решили ее полностью?
Понятно, что вы хотите нарисовать картинку для этой проблемы, но даже с картинкой может быть трудно понять, нашли ли вы правильный ответ. Цифры становятся большими, и может быть трудно отслеживать свою работу. Ваша цель в конце — быть абсолютно уверенным в том, что вы нашли правильный ответ. Вы никогда не должны спрашивать учителя: «Это правильно?» Вместо этого вы должны заявить: «Вот мой ответ, и вот почему я знаю, что он правильный!»
Стратегия решения проблем 5 (Попробуйте более простую задачу). Полиа предложил такую стратегию: «Если вы не можете решить проблему, то есть более простая проблема, которую вы можете решить: найти ее». Он также сказал: «Если вы не можете решить предложенную проблему, попробуйте сначала решить какую-нибудь связанную проблему. Можете ли вы представить себе более доступную связанную проблему? » В этом случае шахматная доска 8 × 8 довольно большая. Сможете ли вы решить проблему с платами меньшего размера? Как 1 × 1? 2 × 2? 3 × 3?
Конечно, конечная цель — решить исходную проблему. Но работа с досками меньшего размера может дать вам некоторое представление и помочь разработать план (это шаг (2) Полии).
Стратегия решения проблем 6 (Работайте систематически). Если вы работаете над более простыми проблемами, полезно отслеживать, что вы выяснили и что меняется по мере усложнения проблемы.
Например, в этой задаче вы можете отслеживать, сколько квадратов 1 × 1 на каждой доске, сколько квадратов 2 × 2 на каждой доске, сколько квадратов 3 × 3 на каждой доске и т. Д. . Вы можете отслеживать информацию в таблице:
размер платы Количество квадратов 1 × 1 Количество квадратов 2 × 2 Количество квадратов 3 × 3 Число квадратов 4 × 4 … 1 по 1 1 0 0 0 2 на 2 4 1 0 0 3 на 3 9 4 1 0 … Стратегия решения проблем 7 (Используйте манипуляторы, чтобы помочь вам в расследовании). Иногда даже нарисовать картинку может быть недостаточно, чтобы помочь вам разобраться в проблеме. Наличие реальных материалов, которые вы перемещаете, иногда может очень помочь!
Например, в этой задаче может быть сложно отследить, какие клетки вы уже подсчитали. Вы можете вырезать квадраты 1 × 1, 2 × 2, 3 × 3 и так далее. На самом деле вы можете систематически перемещать меньшие клетки по шахматной доске, убедившись, что вы посчитаете все один раз и ничего не посчитаете дважды.
Стратегия решения проблем 8 (поиск и объяснение закономерностей). Иногда числа в задаче настолько велики, что вы не можете сосчитать все вручную. Например, если бы задача в этом разделе касалась шахматной доски 100 × 100, вы бы не захотели пересчитывать все клетки вручную! Было бы гораздо более привлекательно найти узор на меньших досках, а затем расширить этот узор, чтобы решить проблему для шахматной доски 100 × 100, просто вычислив.
Думать / Пара / ПоделитьсяЕсли вы еще этого не сделали, расширьте таблицу вверху до шахматной доски 8 × 8, заполнив все строки и столбцы. Используйте свою таблицу, чтобы найти общее количество квадратов на шахматной доске 8 × 8. Тогда:
- Опишите все шаблоны, которые вы видите в таблице.
- Можете ли вы объяснить и оправдать любую из наблюдаемых закономерностей? Как вы можете быть уверены, что они продолжатся?
- Какой расчет вы бы сделали, чтобы найти общее количество клеток на шахматной доске 100 × 100?
(Мы скоро вернемся к этому вопросу.Так что, если вы прямо сейчас не уверены, как объяснить и обосновать обнаруженные вами закономерности, это нормально.)
Проблема 4 (Часы сломаны)Эти часы разбиты на три части. Если вы сложите числа в каждой части, суммы будут последовательными числами. ( Последовательные числа — это целые числа, которые появляются одно за другим, например 1, 2, 3, 4 или 13, 14, 15.)
Можете ли вы разбить другие часы на другое количество частей, чтобы суммы были последовательными числами? Предположим, что на каждой части есть как минимум два номера и ни один из них не поврежден (например,грамм. 12 не делится на две цифры 1 и 2.)
Помните, что ваш первый шаг — понять проблему. Разберитесь, что здесь происходит. Каковы суммы чисел на каждой фигуре? Они последовательные?
Думать / Пара / ПоделитьсяПосле того, как вы некоторое время поработали над проблемой самостоятельно, обсудите свои идеи с партнером (даже если вы еще не решили ее). Что ты пробовал? Какого прогресса вы достигли?
Стратегия решения проблем 9 (Найдите математику, удалите контекст). Иногда проблема состоит из множества деталей, которые не важны или, по крайней мере, не важны для начала работы. Цель состоит в том, чтобы найти основную математическую задачу, затем вернуться к исходному вопросу и посмотреть, сможете ли вы решить ее с помощью математики.
В этом случае беспокоиться о часах и о том, как именно ломаются части, менее важно, чем беспокоиться о поиске последовательных чисел, суммирующих правильную сумму. Спросите себя:
- Какова сумма всех цифр на циферблате?
- Могу ли я найти два последовательных числа, дающих правильную сумму? Или четыре последовательных числа? Или какую-то другую сумму?
- Как мне узнать, что я закончил? Когда мне перестать искать?
Конечно, решение вопроса о последовательных числах — это не то же самое, что решение исходной задачи.Вы должны вернуться и посмотреть, могут ли часы действительно разойтись, чтобы каждая часть давала вам одно из этих последовательных чисел. Возможно, вам удастся решить математическую задачу, но это не приведет к решению проблемы с часами.
Стратегия решения проблем 10 (проверьте свои предположения). При решении проблем легко ограничить свое мышление, добавив дополнительные предположения, которых нет в проблеме. Обязательно спросите себя: не слишком ли я ограничиваю свое мышление?
В задаче о часах, поскольку в первом решении часы сломаны радиально (все три части встречаются в центре, так что это похоже на разрезание пирога), многие люди предполагают, что именно так часы должны ломаться.Но проблема не в том, чтобы часы ломались радиально. Он может разбиться на такие части:
Вы предполагали, что часы сломаются определенным образом? Попробуйте решить проблему сейчас, если вы еще этого не сделали.
Решение математических задач со словами
Мы обучили систему, которая решает математические задачи начальной школы с почти вдвое большей точностью, чем точная модель GPT-3. Он решает примерно на 90% больше проблем, чем настоящие дети: небольшая выборка детей от 9 до 12 лет набрала 60% на тесте из нашего набора данных, в то время как наша система набрала 55% по тем же задачам.Это важно, потому что сегодняшний ИИ все еще довольно слаб в здравом смысле многоэтапных рассуждений, что легко даже для школьников. Мы достигли этих результатов, обучая нашу модель распознавать свои ошибки, чтобы она могла повторять попытки многократно, пока не найдет работающее решение.
Читать статьюПросмотреть образцыСкачать набор данныхВведение
Большие языковые модели, такие как GPT-3, обладают множеством впечатляющих навыков, в том числе способностью имитировать множество стилей письма, а также обширными фактическими знаниями.Однако им сложно выполнять задачи, требующие точного многоэтапного мышления, например, решение словесных задач по математике в начальной школе. Хотя модель может имитировать последовательность правильных решений, она регулярно приводит к критическим ошибкам в логике.
Чтобы соответствовать возможностям человека в сложных логических областях, наши модели должны научиться распознавать свои ошибки и тщательно выбирать шаги. С этой целью мы обучаем верификаторов оценивать правильность предлагаемого решения. Чтобы решить новую проблему, мы используем верификаторы, чтобы выбрать лучшее среди множества предложенных решений.Мы собрали новый набор данных GSM8K, чтобы оценить наши методы, и выпускаем этот набор данных для облегчения исследования.
В десяти примерах ниже мы показываем решения, созданные с помощью нашего нового метода проверки и нашего базового метода точной настройки.
GSM8K Набор данных
GSM8K состоит из 8,5 тыс. Высококачественных задач по математике для начальной школы. Для решения каждой проблемы требуется от 2 до 8 шагов, а решения в первую очередь включают выполнение последовательности элементарных вычислений с использованием основных арифметических операций (+ — × ÷) для достижения окончательного ответа.Тонко настроенные современные языковые модели плохо работают с этим набором данных, в первую очередь из-за большого разнообразия проблем. В то же время решения GSM8K зависят только от элементарных концепций, поэтому достижение высоких результатов тестирования — задача достижимая.
Решения в GSM8K записываются на естественном языке, а не в виде чисто математических выражений. Придерживаясь естественного языка, решения, созданные на основе моделей, легче интерпретируются людьми, а наши методы остаются относительно независимыми от предметной области.
Обучение верификаторов: модели, которые учатся на своих ошибках
Одной из серьезных проблем математических рассуждений является высокая чувствительность к индивидуальным ошибкам. В моделях авторегрессии, которые генерируют каждый токен решения по токену, нет механизма для исправления собственных ошибок. Решения, отклоняющиеся от курса, быстро становятся невосстановимыми, как видно из приведенных примеров.
Мы решаем эту проблему, обучая верификаторов оценивать правильность решений, созданных на основе моделей.Верификаторам предоставляется множество возможных решений, все они написаны самой моделью, и они обучаются решать, какие из них верны, если таковые имеются.
Чтобы решить новую проблему во время тестирования, мы генерируем 100 возможных решений, а затем выбираем решение, получившее наивысший рейтинг проверяющей стороны. Верификаторы извлекают выгоду из этой неотъемлемой опциональности, а также из того факта, что проверка часто оказывается более простой задачей, чем генерация.
Мы обнаружили, что мы получаем значительный прирост производительности от проверки, если набор данных достаточно велик.С слишком маленькими наборами данных мы полагаем, что верификаторы переоснащаются, запоминая окончательные ответы в обучающем наборе, вместо того, чтобы изучать какие-либо другие полезные свойства математических рассуждений.
На полном обучающем наборе проверка параметров 6B немного превосходит точно настроенную модель параметров 175B, обеспечивая прирост производительности, который приблизительно эквивалентен увеличению размера модели в 30 раз. Более того, проверка, похоже, более эффективно масштабируется с дополнительными данными, если мы экстраполируем на основе текущих результатов.
Заключение
Приведение правильных аргументов и распознавание неправильных — ключевые проблемы в разработке более общего ИИ. Математика в начальной школе — идеальный полигон для проверки этих способностей. Проблемы в GSM8K концептуально просты, но одной тонкой ошибки достаточно, чтобы сорвать все решение. Выявление и предотвращение таких ошибок — важнейший навык для развития наших моделей. Обучая верификаторов, мы учим наши модели отделять хорошие решения от тех, которые не совсем сработали.Мы ожидаем, что эти навыки будут становиться все более актуальными по мере того, как мы пытаемся применить наши модели к более логически сложным областям.
задач 6-го класса
задач 6-го класса1)
- Дядя Генри ехал в Галифакс, когда заметил большую лужайку.
горилла на обочине дороги. Он с криком остановился, выпрыгнул из
его машина. Он увидел цифру на горилле. Он не мог совсем
видел номер, но он знал, что это четырехзначное число.И:
- 1) Он вспомнил, что видел число 1.
2) Вместо сотни он помнит, что число в 3 раза больше число в разряде тысяч.
3) Он сказал, что число на одном месте в 4 раза больше числа на десятку.
4) Наконец, он сказал, что число 2 стоит на месте тысячи.
Нужна подсказка?
Ответ
2)
- Элмер Фадд решил вырастить сад, чтобы делать салат.Он хочет
сделать его длиной 10,1 м и шириной 4,2 м. Однако во избежание ошибок
Зайчик, чтобы войти в свой сад, он должен сделать забор вокруг сада.
Он решает сделать забор длиной 11,2 м и шириной 5,0 м. Какая площадь
между забором и садом?
Ответ
3)
- Дженни купила 7 футболок, по одной для каждого из семи своих братьев, для
9 долларов.95 каждый. Кассир взимает с нее дополнительный налог с продаж в размере 13,07 доллара.
Она вышла из магазина с скромными 7,28 доллара. Сколько денег начинала Дженни
с участием?
Ответ
4)
- Дэйв отдал Шарлотте половину своего погона. Шарлотта отдала Джонни половину
о погонах, которые она получила от Дэйва. Джонни сохранил 8 таких погонов и дал
оставшиеся 10 — Дане. Сколько погов Дэйв устроил Шарлотте?
Ответ
5)
- В среднем канадцы тратят 958904 доллара в день.00 покупка видеоигр.
Из этой суммы 767123,00 долларов потрачены на игры Nintendo. За одну неделю сколько
тратят ли канадцы на игры Nintendo. Сколько они тратят на другое видео
игры через неделю?
Ответ
6)
- Среднемесячное количество осадков за 6 месяцев составило 28,5 мм. Если бы это было
каждый месяц выпадало на 1 мм больше дождя, каков был бы средний показатель? На сколько
увеличилась бы общая сумма за шесть месяцев и на сколько
в среднем были увеличены за месяц?
Ответ
7)
- Я атроном, объектив моей камеры 1.372 м в поперечнике. Мой друг
Джордж — шпион, и у него есть объектив камеры диаметром 2,9 см. Моя тетя мари
хирург, и у нее линза диаметром 1,5 см.
- 1) На сколько метров диаметр объектива моей камеры больше, чем у Мари?
2) На сколько метров меньше в поперечнике линза камеры Мари, чем у Джорджа?
3) Сколько линз камеры Джорджа поместится на моей?
Ответ
8)
- Если вам задают следующие вопросы: Сколько российских рублей
Вы можете купить за 300 долларов.00 канадский? Какая еще информация вам нужна
чтобы решить проблему?
Вам необходимо знать курс обмена. Сколько рублей можно получить за один канадский доллар?
Итак, если теперь вопрос гласит: «Сколько российских рублей вы можете купить? с канадскими $ 300.00 зная обменный курс 20 рублей / канадский доллар. Что бы вы ответили?
Ответ
9)
Нужна подсказка?Ответ
10)
- Джилл получила 3 красных леденца, 2 синих и 2 желтых.Используйте несколько соотношений, чтобы описать конфеты, которые есть у Джилл.
Ответ
11)
- а) Мистер Мейсон попросил детей открыть свои учебники по математике.
разворачивающиеся страницы, чьи номера страниц в сумме достигают 85. К каким страницам следует
дети превращаются?
Марк случайно вырвал страницу из своего учебника по математике. Мистер Мейсон спросил ему какая это была страница.Марк сказал, что сумма номеров страниц на обращенных страниц было 127. Каковы номера страниц на страницах, которые разорвал Марк? из книги?
Ответ
12)
ПРОДАЖА Кельтская распродажа хлебобулочных изделий Белый хлеб - 2 шт. По $ 1,25 Ржаной хлеб - 2 по 1,35 доллара Луковые рулетики - 6 по 1 доллар.00 Булочки для гамбургеров - 6 за 0,85 доллара Булочки для хот-догов - 6 за 0,69 доллара
Мелани и Кевин идут за мамой в пекарню Celtic Bakery. Им сказали купить 15 луковых булочек, 10 булочек для гамбургеров и 2 буханки ржаной хлеб. Во сколько им это будет стоить? Нужна подсказка?Ответ
13)
- a) Если вы сэкономили 2 доллара 1 января, то 4 доллара.00:00 1 февраля, $ 6,00 в
1 марта, 8 долларов США 1 апреля и т. Д., Сколько денег вы бы сэкономили
один год?
б) Если вы сэкономили 2 доллара 1 января, 4 доллара 1 февраля, 8 долларов 1 марта, 1 апреля — 16 долларов и т. Д. Сколько денег вы бы сэкономили в один год?
Ответ
14)
- Числовая прямая от 0 до 2 разделена на семь равных сегментов.Какая фракция называет точку А? Какая фракция называет точку B?
Ответ
15)
- Деннис-Угроза думает о двух числах. Их самый большой общий
Фактор равен 6. Их наименьшее общее кратное — 36. Одно из чисел — 12.
Какой другой номер?
Ответ
16)
Нужна подсказка?Ответ
17)
Нужна подсказка?Ответ
18)
- Этель составила список всех целых чисел от 1 до 100.Как
много раз она писала цифру 2?
Ответ
19)
- Сколько треугольников на этом рисунке?
Ответ
20)
- Можете ли вы решить этот магический квадрат?
Поместите оставшиеся числа от 0 до 15 в 16 маленьких квадратов.В сумма четырех чисел в каждой строке, столбце и двух диагоналях должна быть 30.
15 | | | 12 ---- + ---- + ---- + ---- | 10 | 9 | ---- + ---- + ---- + ---- | | | 11 ---- + ---- + ---- + ---- 3 | | | 0
Нужна подсказка?Ответ
21)
- Мэри и Джейсон изготавливали пропеллеры для своих деревянных вертолетов.Мэри поставила номер на свой пропеллер и заметила, что, когда она повернула
пропеллер у нее был такой же номер.
Джейсон пытался придумать число, которое он мог бы поставить на свой имел ту же вращательную синметрию (выглядит так же в перевернутом виде). Какие следующее большее число, обладающее этим свойством?
Ответ
22)
- а) Мистери миссис Каллахан и их трое детей заплатили 7 долларов за билеты.
Какую игру они планируют посмотреть?
СОФТБОЛ: Взрослые 2 доллара США Дети 1 доллар США БАСКЕТБОЛ: Взрослые 3,00 доллара США Дети 1,50 доллара США ФУТБОЛ: Взрослые 5,00 $ Дети 2,50 $
б) Сколько сдачи получили бы мистер и миссис Каллахан, если бы взяли свои дети посмотрели баскетбольный матч и заплатили за это купюрой в 20 долларов? Нужна подсказка?Ответ
23)
- Фермер Том поставил квадратный забор вокруг своего огорода, чтобы сохранить
олень от еды его кукурузы.Одна сторона была 10 метров в длину. Если сообщения
были размещены на расстоянии 2 м друг от друга, сколько столбов он использовал?
Ответ
24)
- Амми передала находившимся у нее девочкам корзину с клубникой.
вечеринка. Перед вечеринкой она съела 5 ягод клубники и подарила другу 3. Восемь.
на вечеринку приехали девушки. Первая девочка взяла клубнику, вторая
девочка взяла 3 клубники, третья девочка — 5 клубники и так далее.После того, как последняя девочка взяла клубнику, корзина опустела. Как много
клубника была в корзине вначале?
Ответ
25)
- Роб хотел пособие. Его отец дал ему выбор получить
это еженедельно или ежедневно. Он сказал, что либо заплатит ему 1,25 доллара.
в неделю или заплатить ему за неделю следующим образом: в понедельник он
дать ему 0 долларов.01; Во вторник 0,02 доллара США; В среду 0,04 доллара США и по воскресенье.
Что бы вы посоветовали сделать Робу, чтобы он мог получать больше денег?
Ответ
26)
- Сторона квадрата B в четыре раза больше длины стороны квадрата
A. Во сколько раз площадь квадрата B больше площади квадрата
А?
Ответ
27)
- Улитка Шейн вздрогнула.На какой стороне он будет, когда
он прополз 13/20 расстояния вокруг правильного пятиугольника, равного
стороны?
Ответ
28)
- Количество оставшихся в сутках часов составляло одну треть от
количество часов уже прошло. Сколько часов осталось в дне?
Ответ
29)
- Прямоугольный кухонный стол в три раза больше его ширины.
Если бы он был на 3 м короче и на 3 м шире, это был бы квадрат.
Какие размеры у прямоугольного стола?
Ответ
30)
- Производитель утверждает, что новое моторное масло экономит 5 процентов
бензин, используемый автомобилем. Если вы проезжаете 24000 километров в год, и он получает
32 километра галлона бензина, сколько галлонов бензина может
вы экономите за 1 год?
Ответ
31)
- Какой начальный номер (?)?
Ответ
32)
- Ковровое покрытие продается и Mrs.Дойл ищет ковер для
ее гостиная. Размер ее гостиной 4х5м. Сколько это будет ей стоить
сделать это по продажной цене?
ПРОДАЖА КОВРОВ Обычный квадратный метр стоимостью 9,99 долларов США. Сейчас в продаже для Скидка 20%
Нужна подсказка?Ответ
33)
- Дерек завел машину (автомат) проехал 9 км и проехал 3 минуты
ожидание на светофоре.Примерно сколько бензина использовала машина Дерека?
ДАННАЯ ДИАГРАММА:
АВТОМОБИЛЬНОЕ ИСПОЛЬЗОВАНИЕ ТОПЛИВА Начальный 0,015 литра На холостом ходу в течение 1 минуты 0,047 литра Движущийся Ручное переключение передач 30 км 3,0 литра Автоматическое переключение передач 27 км 3,0 литра
Нужна подсказка?Ответ
34)
- Паром Pictou Ferryboat заполнен, когда на борту десять автомобилей.это
также полный, когда на борту шесть грузовиков. Паром никогда не везет
легковые и грузовые автомобили одновременно.
Паром совершил пять переходов через реку и на каждом был загружен. поездка. Он перевез через реку 42 легковых и грузовых автомобиля.
Сколько машин всего перевез паром за пять рейсов?
Ответ
35)
- Джереми столкнулся с этой проблемой на первом экзамене по математике.Он
возникли большие проблемы с ответом на вопрос. Заменить каждую букву
с другим номером. Идентичные буквы следует заменить на
такое же количество.
SPART х 4 ---------- ЛОВУШКИ
Вы можете ему помочь? Нужна подсказка?Ответ
36)
- В доме Порки было 100 м 2 жилой площади.Затем он добавил
Комната была 4м на 5м. Какое было дробное увеличение жилплощади?
Какой был процент увеличения жилплощади?
Ответ
37)
- Шери, Бет и Хасинта — дочери г-на Салливана, г-на Маршана.
и г-н Бенуа. Четверо из этих людей играют в теннис в парном разряде. Г-на Бенуа
дочь и мистер Салливан — партнеры.Отец Шери и мистер Маршан
дочь тоже партнеры. Никаких комбинаций отца и дочери не существует.
Кто отец Чери?
Ответ
38)
- Маг сказал: «Среднее из семи чисел равно 49. Если 1 — это
прибавляется к первому числу, ко второму числу прибавляется 2, прибавляется 3
до третьего числа и так до седьмого числа », что нового
в среднем?
Ответ
39)
- Стоимость проезда на автобусе составила 2 доллара.10. Какое расстояние было пройдено, когда
стоимость проезда составляет 0,90 доллара США за первую 1/3 км и 0,10 доллара США за каждую дополнительную 1/8 километра.
километр?
Ответ
40)
- Вот вам вопрос !!!
Одна из этих вещей здесь не принадлежит, одна из этих вещей не то же самое. Вы можете сказать, какой куб?
Ответ
41)
- Наибольший общий делитель двух чисел равен 30.Их наименее распространенные
кратное 420. Одно из чисел — 210. Сможете ли вы найти другое число?
Ответ
42)
- Кожура банана весит около 1/8 от общего веса банана.


 Более медленная машина заводится на час раньше более быстрой. Учащимся нужно определить, сколько часов потребуется более быстрой машине, чтобы догнать более медленную.
Более медленная машина заводится на час раньше более быстрой. Учащимся нужно определить, сколько часов потребуется более быстрой машине, чтобы догнать более медленную.

 Если оба принтера печатают, сколько страниц распечатает офисный принтер к тому моменту, когда принтер медиацентра напечатает 5 страниц?
Если оба принтера печатают, сколько страниц распечатает офисный принтер к тому моменту, когда принтер медиацентра напечатает 5 страниц? Вы можете становиться все лучше и лучше в решении проблем, как наращивая свои базовые знания, так и просто практикуясь. По мере того, как вы решаете больше проблем (и узнаете, как их решали другие люди), вы изучаете стратегии и методы, которые могут быть полезны.Но ни одна стратегия не работает каждый раз.
Вы можете становиться все лучше и лучше в решении проблем, как наращивая свои базовые знания, так и просто практикуясь. По мере того, как вы решаете больше проблем (и узнаете, как их решали другие люди), вы изучаете стратегии и методы, которые могут быть полезны.Но ни одна стратегия не работает каждый раз.