ГДЗ учебник 2015. номер 361 (366) математика 6 класс Виленкин, Жохов
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Литература
- Окружающий мир
- Технология
- 3 класс
ГДЗ учебник 2019 / часть 1. упражнение 361 (357) математика 6 класс Виленкин, Жохов
упражнение 361 (357) математика 6 класс Виленкин, Жохов
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Окружающий мир
- Технология
ГДЗ учебник 2019 / часть 2. упражнение 361 (1251) математика 6 класс Виленкин, Жохов
упражнение 361 (1251) математика 6 класс Виленкин, Жохов
Решение есть!- 1 класс
- Математика
- Английский язык
- Русский язык
- Музыка
- Литература
- Окружающий мир
- 2 класс
- Математика
- Английский язык
- Русский язык
- Немецкий язык
- Информатика
- Музыка
- Литература
- Технология
Контрольные работы по математике 6 класс (Виленкин Н. Я.) | Материал (6 класс) на тему:
Я.) | Материал (6 класс) на тему:
Преподавание математики в 5-6 классах: Методические рекомендации
для учителей к учебнику Н.Я.Виленкина, В.И. Жохова, А.С.Чеснокова,
С.И.Шварцбурда. – М.: Вербум – М, 2000.
Согласовано: заместитель директора
по УВР МКОУ «Покровская СОШ»
Косогор Евгения Николаевна
«___»_____________________
Утверждаю: директор
МКОУ «Покровская СОШ»
Иванова Светлана Анатольевна
Приказ №________от________
Контрольные работы
Математика
6 класс
2014
Контрольная работа №1
Вариант I
1.Найдите:
а) наибольший общий делитель чисел 24 и 18;
б) наименьшее общее кратное чисел 12 и 15.
2. Разложите на простые множители число 546.
3. Какую цифру можно записать вместо звездочки в числе 681*, чтобы оно:
а) делилось на 9;
б) делилось на 5;
в) было кратно 6?
4. Выполните действия:
а) 7 – 2,35 + 0,435;
б) 1,763 : 0,086 – 0,34 ∙ 16.
5. Найдите произведение чисел a и b, если их наименьшее общее кратное равно 420, а наибольший общий делитель равен 30.
Вариант II
1. Найдите:
а) наибольший общий делитель чисел 28 и 42;
б) наименьшее общее кратное чисел 20 и 35.
2. Разложите на простые множители число 510.
3. Какую цифру можно записать вместо звездочки в числе 497*, чтобы оно:
а) делилось на 3;
б) делилось на 10;
в) было кратно 9.
4. Выполните действия:
а) 9 – 3,46 +0,535;
б) 2,867 : 0,094 + 0,31 ∙ 15.
5. Найдите наименьшее общее кратное чисел m и n, если их произведение равно 67200, а наибольший общий делитель равен 40.
Критерии оценки:
«5» — верно выполнены все задания;
«4» — верно выполнены 4 задания;
«3» — верно выполнены 3 задания.
Контрольная работа №2
Вариант I
1. Сократите: .
2. Выполните действия:
а) ; б) ; в) .
3. Решите уравнение:
а) ; б) 5,86m + 1,4m = 76,23.
4. В первые сутки теплоход прошёл всего пути, во вторые сутки – на пути больше, чем в первые. Какую часть всего пути теплоход прошел за эти двое суток?
5. Найдите четыре дроби, каждая из которых больше и меньше .
Вариант II
1. Сократите: .
2. Выполните действия:
а) ; б) ; в) .
3. Решите уравнение:
а) ; б) 6,28n – 2,8n = 36,54.
4. В первый день засеяли всего поля, во второй день засеяли на поля меньше, чем в первый. Какую часть поля засеяли за эти два дня?
5. Найдите четыре дроби, каждая из которых больше и меньше .
Критерии оценки:
«5» — верно выполнены все задания;
«4» — верно выполнены 4 задания;
«3» — верно выполнены 3 задания.
Контрольная работа №3
Вариант I
1. Сравните числа:
а) и ; б) и ; в) 0,48 и .
2. Найдите значение выражения:
а) ; б) ; в) ; г) .
3. На автомашине планировали перевезти сначала т груза, а потом ещё т.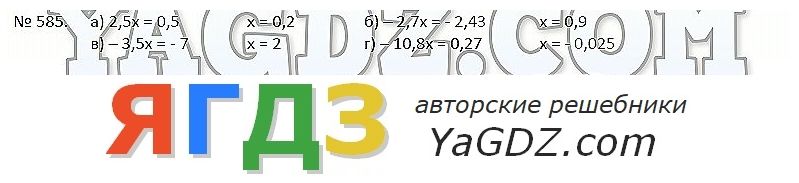 Однако перевезли на т меньше, чем предполагали. Сколько всего тонн груза перевезли на автомашине?
Однако перевезли на т меньше, чем предполагали. Сколько всего тонн груза перевезли на автомашине?
4. Решите уравнение:
а) ; б) 3,45∙(2,08 – k) = 6,21.
5. Представьте дробь в виде суммы трех дробей, у каждой из которых числитель
равен 1.
Вариант II
1. Сравните числа:
а) и ; б) и ; в) и 0,72.
2. Найдите значения выражения:
а) 7 — ; б) ; в) ; г) .
3. С одного опытного участка рассчитывали собрать т пшеницы, а с другого т. Однако с них собрали на т пшеницы больше. Сколько тонн пшеницы собрали с этих двух участков?
4. Решите уравнение:
а) ; б) 2,65∙(n – 3,06) = 4,24.
5. Представьте дробь в виде суммы трех дробей, у каждой из которых числитель равен 1.
Критерии оценки:
«5» — верно выполнены все задания;
«4» — верно выполнены 4 задания;
«3» — верно выполнены 3 задания.
Контрольная работа №4
Вариант I
1. Найдите произведение:
Найдите произведение:
а) ; б) ; в); г); д) .
2. Выполните действия:
а) ; б) (4,2:1,2 – 1,05)∙1,6.
3. В один пакет насыпали кг пшена, а в другой этого количества. На сколько меньше пшена насыпали во второй пакет, чем в первый?
4. Упростите выражение и найдите его значение при m = .
5. В овощехранилище привезли 320 т овощей. 75% привезенных овощей составлял картофель, а остатка – капуста. Сколько тонн капусты привезли в овощехранилище?
Вариант II
1. Найдите произведение:
а) ; б) ; в) ; г) ; д) .
2. Выполните действия:
а) ; б) (6,3:1,4 – 2,05)∙1,8.
3. Площадь одного участка земли га, а другого – в раза больше. На сколько гектаров площадь первого участка меньше площади второго?
4. Упростите выражение и найдите его значение при k =.
5. В книге 240 страниц. Повесть занимает 60% книги, а рассказы остатка. Сколько страниц в книге занимают рассказы?
Сколько страниц в книге занимают рассказы?
Критерии оценки:
«5» — верно выполнены все задания;
«4» — верно выполнены 4 задания;
«3» — верно выполнены 3 задания.
Контрольная работа №5
Вариант I
1. Выполните действия:
а) ; б) ; в) ; г) ; д) .
2. За кг конфет заплатили 15р. Сколько стоит 1кг этих конфет?
3. Решите уравнение:
а) ; б) (3,1х + х):0,8 = 2,05.
4. У Сережи и Пети всего 69 марок. У Пети марок в раза больше, чем у Сережи. Сколько марок у каждого из мальчиков?
5. Сравните числа р и k, если числа р равны 35% числа k (числа p и k не равны нулю).
Вариант II
1. Выполните действия:
а) ; б) ; в) ; г) ; д) .
2. За кг печенья заплатили 6р. Сколько стоит 1кг этого печенья?
3. Решите уравнение:
а) ; б) (7,1у – у):0,6 = 3,05.
4. В два железнодорожных вагона погрузили 91 т угля. Во втором вагоне угля оказалось в раза больше. Сколько угля погрузили в каждый из этих вагонов?
Во втором вагоне угля оказалось в раза больше. Сколько угля погрузили в каждый из этих вагонов?
5. Сравните числа m и n, если числа m равны 15% числа n (числа m и n не равны нулю).
Критерии оценки:
«5» — верно выполнены все задания;
«4» — верно выполнены 4 задания;
«3» — верно выполнены 3 задания.
Контрольная работа №6
Вариант I
1. Найдите значение выражения:
а) ; б) ; в) .
2. Решите уравнение
3. Вспахали поля, что составило 210 га. Какова площадь всего поля?
4. Заасфальтировали 35% дороги, после чего осталось заасфальтировать ещё 13 км. Какова длина всей дороги?
5. 0,9 от 20% числа р равны 5,49. Найдите число р.
Вариант II
1. Найдите значение выражения:
а) ; б) ; в) .
2. Решите уравнение
3. Заасфальтировали дороги, что составило 45 км. Какова длина всей дороги?
4. Вспахали 45% поля, после чего осталось вспахать ещё 165 га.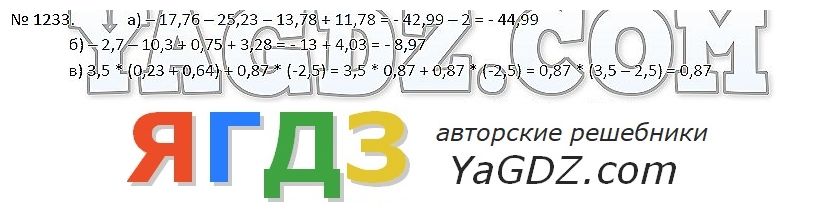 Какова площадь всего поля?
Какова площадь всего поля?
5. 0,7 от 40% числа d равны 2,94. Найдите число d.
Критерии оценки:
«5» — верно выполнены все задания;
«4» — верно выполнены 4 задания;
«3» — верно выполнены 3 задания.
Контрольная работа №7
Вариант I
1. Решите уравнение .
2. Автомобиль первую часть пути прошёл за 2,8 ч, а вторую – за 1,2 ч. Во сколько раз меньше времени израсходовано на вторую часть пути, чем на первую? Сколько процентов всего времени движения затрачено на первую часть пути?
3. В 8 кг картофеля содержится 1,4 кг крахмала. Сколько крахмала содержится в 28 кг картофеля?
4. Поезд путь от одной станции до другой прошёл за 3,5 ч со скоростью 70 км/ч. С какой скоростью должен был бы идти поезд, чтобы пройти этот путь за 4,9 ч?
5. 40% от 30% числа х равны 7,8. Найдите число х.
Вариант II
1. Решите уравнение .
2. Трубу разрезали на две части длиной 3,6 м и 4,4 м. Во сколько раз первая часть трубы короче второй? Сколько процентов длины всей трубы составляет длина первой её части?
3. Из 6 кг льняного семени получается 2,7 кг масла. Сколько масла получится из 34 кг семян льна?
Из 6 кг льняного семени получается 2,7 кг масла. Сколько масла получится из 34 кг семян льна?
4. Теплоход прошел расстояние между двумя пристанями со скоростью 40 км/ч за 4,5 ч. С какой скоростью должен идти теплоход, чтобы пройти это расстояние за 3,6 ч?
5. 60% от 40% числа у равны 8,4. Найдите число у.
Критерии оценки:
«5» — верно выполнены все задания;
«4» — верно выполнены 4 задания;
«3» — верно выполнены 3 задания.
Контрольная работа №8
Вариант I
1. Найдите длину окружности, если её диаметр равен 25 см. Число округлите до десятых.
2. Расстояние между двумя пунктами на карте равно 3,8 см. Определите расстояние между этими пунктами на местности, если масштаб карты 1:100 000.
3. Найдите площадь круга, радиус которого равен 6 м. Число округлите до десятых.
4. Цена товара понизилась с 42,5 р. до 37,4 р. На сколько процентов понизилась цена товара?
5. Прямоугольный земельный участок изображен на плане в масштабе 1:300. Какова площадь земельного участка, если площадь его изображения на плане 18 см2.
Какова площадь земельного участка, если площадь его изображения на плане 18 см2.
Вариант II
1. Найдите длину окружности, если её диаметр равен 15 дм. Число округлите до десятых.
2. Расстояние между двумя пунктами на карте равно 8,2 см. Определите расстояние между этими пунктами на местности, если масштаб карты 1:10 000.
3. Найдите площадь круга, радиус которого равен 8 см. Число округлите до десятых.
4. Цена товара понизилась с 57,5 до 48,3 р. На сколько процентов понизилась цена товара?
5. Прямоугольный земельный участок изображен на плане в масштабе 1:400. Какова площадь земельного участка, если площадь его изображения на плане 16 см2?
Критерии оценки:
«5» — верно выполнены все задания;
«4» — верно выполнены 4 задания;
«3» — верно выполнены 3 задания.
Контрольная работа №9
Вариант I
1. Отметьте на координатной прямой точки А(-5), С(3), Е(4,5), К(-3), N(-0,5), S(6).
а) Какие из точек имеют противоположные координаты?
б) В какую точку пере
Курс: Математика • 6 класс
Содержание
- номер
- Квадратные числа
- Числа куба
- Простые множители
- Простая факторизация с экспонентами
- Линейные последовательности
- Наборы
- Пересечение множеств
- Пересечение множеств с помощью диаграмм Венна
- Союз множеств
- Объединение множеств с использованием диаграмм Венна
- Подмножества набора
- Подмножество множеств с использованием диаграмм Венна
- Набор натуральных чисел
- Умножение и деление на целые числа
- Умножение целых чисел
- Деление целых чисел
- Деление на дроби
- Деление дробей на целые числа
- Деление правильных дробей на целые числа
- Деление целых чисел на единичные дроби
- Деление целых чисел на правильные дроби
- Многоступенчатые задачи с дробями
- Деление с десятичными знаками
- Деление десятичных знаков на 10, 100 и 1000
- Деление десятичных знаков на степень десяти
- Целочисленное деление с десятичными частными
- Деление десятичных дробей на однозначные числа с использованием моделей
- Деление десятичных знаков на однозначные числа
- Деление десятичных дробей на двузначные числа
- Оценка десятичных частных
- Деление десятичных знаков: целые частные числа
- Использование числового значения для деления десятичных чисел
- Деление десятичных знаков: десятичные частные
- Многоступенчатые задачи с десятичными знаками
- Проценты
- Введение в проценты
- Процент сумм
- Составные проценты от сумм
- Процентное соотношение сумм: поиск недостающих значений
- Моделирование процентного изменения
- Эквивалентные дроби, десятичные дроби и проценты
- Соотношение
- Коэффициенты моделирования
- Соотношения: часть к части и часть к целому
- Чертежи в масштабе
- Коэффициенты масштабирования
- Площадь и периметр
- Площадь квадратов и прямоугольников
- Площадь составных прямолинейных форм
- Площадь параллелограмма
- Площадь треугольника
- Площадь составных фигур
- Объем
- Измерение объема с помощью единичных кубов
- Объем прямоугольной призмы: единичные кубы
- Объем прямоугольной призмы
- Объем составных фигур
- Оценка емкости ящиков
- Геометрия
- Многогранники и неполиэдры
- Круги
- Тесселяция многоугольников
- Углы рисования
- Точное рисование 2D-форм с помощью линейок и транспортиров
Решения NCERT для математики класса 6, глава 2 Целые числа в PDF
Решения NCERT для математики класса 6, глава 2
| Class: 6 | Maths (English and Hindi Medium) |
| Целые числа |
6 Математика Глава 2 Решения
Математика класса 6 Глава 2 на английском языке Medium
Математика класса 6 Глава 2 на хинди
Класс 6 Математика Глава 2 Упражнение 2.1 Решение и объяснение Математика для класса 6 Глава 2 Упражнение 2.1 Объяснение Математика для класса 6 Глава 2 Упражнение 2.1 РешенияМатематика для класса 6 Глава 2 Упражнение 2.2 Решение и пояснение
Математика для класса 6 Глава 2 Упражнение 2.2 Математика для класса 6 Глава 2 Упражнение 2.2 РешенияМатематика для класса 6 Глава 2 Упражнение 2.3 Решение и объяснение
Математика для класса 6 Глава 2 Упражнение 2.3 Объяснение Класс 6 Математика Глава 2 Упражнение 2.3 РешенияВ 6 Математике Глава 2 Целые числа (Натуральные числа вместе с нулем образуют совокупность целых чисел.), Мы будем изучать свойства целых чисел, используя предшественник и последователь данные числа. Дополнительная информация:
Все натуральные числа также целые.
Все целые числа, кроме 0, также являются натуральными числами.
Ноль — наименьшее целое число.
Мы не можем найти наибольшее целое число.
Свойства целых чисел:
Целые числа замкнуты как при сложении, так и при умножении.
Целые числа не закрываются на вычитание и деление.
Деление целого числа на 0 не определено.
Сложение и умножение являются коммутативными для целых чисел.
При отображении числа на числовой прямой сложение соответствует перемещению вправо на числовой прямой, тогда как умножение соответствует прыжкам на равное расстояние, начиная с нуля.Справка и поддержка
Если у кого-то возникнут трудности с получением всего содержимого, сообщите нам об этом. Мы постараемся исправить ошибку как можно скорее, чтобы содержание было удобным.
Мы работаем в секции хинди среднего уровня по другим предметам 6 класса. Очень скоро он будет доступен для всех студентов, использующих книги NCERT среднего уровня на хинди. Мы всегда вносим изменения в соответствии с вашими предложениями, чтобы принести вам пользу.Важные вопросы по математике Глава 2
Напишите следующие три натуральных числа после 10999.
10,999 + 1 = 11,000
11,000 + 1 = 11,001
11,001 + 1 = 11,002उपयुक्त क्रम में लगाकर ज्ञात कीजिए: 837 + 208 + 363
837 + 208 + 363
= (837 + 363) + 208
= 1200 + 208
= 1408Запишите три целых числа непосредственно перед 10001.
10 001 — 1 = 10 000
10 000 — 1 = 9 999
9 999 — 1 = 9 998Какое наименьшее целое число?
«0» (ноль) — наименьшее целое число.
Сколько целых чисел от 32 до 53?
53 — 32 — 1 = 20
Есть 20 целых чисел от 32 до 53.किसी टैक्सी-ड्राइवर ने अपनी गाड़ी की में सोमवार को 40 लीटर पेट्रोल भरवाया। अगले दिन, उसने टंकी में 50 लीटर पेट्रोल भरवाया। यदि पेट्रोल का मूल्य ₹ 44 प्रति लीटर था, तो उसने पेट्रोल पर कुल कितना व्यय किया?
सोमवार को भरवाया गया पेट्रोल = 40 लीटर
अगले दिन भरवाया गया पेट्रोल = 50 लीटर
कुल भरवाया गया पेट्रोल = 90 लीटरअब,
1 लीटर पेट्रोल का मूल्य = ₹ 44
इसलिए, 90 लीटर पेट्रोल का मूल्य = 44 x 90
= 44 x (100 — 10)
= 44 x 100 — 44 x 10
= 4400 — 440
= ₹ 3960अतः, उसने पेट्रोल पर कुल ₹ 3960 व्यय किया।
कोई दूधवाला एक होटल को सुबह 32 लीटर दूध देता है और शाम को 68 लीटर दूध देता है। यदि दूध का मूल्य ₹ 15 प्रति लीटर है, तो दूधवाले को प्रतिदिन कितनी धनराशि प्राप्त होगी?
सुबह के समय दिया गया दूध = 32 लीटर
शाम के समय दिया गया दूध = 68 लीटर
कुल दूध = 32 + 68 = 100 लीटरअब,
1 लीटर दूध से प्राप्त धनराशि धनराशि = ₹ 15
इसलिए, 100 लीटर दूध से प्राप्त धनराशि
= 15 x 100
= ₹ 1500अतः, दूधवाले को प्रतिदिन ₹ 1500 प्राप्त होंगे।
Запишите преемника 2440701.
Преемник 2440701 равен 2440701 + 1 = 2440702.
Запишите предшественника 94.
Предшественником 94 является 94 — 1 = 93.
Если произведение двух целых чисел равно нулю, мы можем сказать, что или их обоих будет ноль? Обоснуйте примеры.
Да, если мы умножим любое число на ноль, получится ноль.Примеры:
2 x 0 = 0,
5 x 0 = 0,
9 x 0 = 0Если оба числа равны нулю, то результат также будет нулевым.
0 x 0 = 0Если произведение двух целых чисел равно 1, можем ли мы сказать, что одно или оба из них будут 1? Обоснуйте примеры.
Если только одно число равно 1, то произведение не может быть 1.Примеры:
5 x 1 = 5,
4 x 1 = 4,
8 x 1 = 8Если оба числа равны 1, то произведение равно 1
1 x 1 = 1Рациональные числа Математика — оценка ppt видео онлайн скачать
Презентация на тему: «Математика рациональных чисел — 7 класс.»- стенограмма презентации:
1 Математика рациональных чисел — 7 класс
2 Цели модуля Знать значение, стандартную форму и эквиваленты рациональных чисел, Развивать навык представления рациональных чисел на числовой прямой, Знать сравнение рациональных чисел, находить рациональные числа между любыми двумя рациональными числами, Знать операции с рациональными числами, Знать метод записи рациональных чисел в десятичной форме Знать умножение, операции деления десятичных чисел и решение задач на их основе.Изучите метод преобразования единиц измерения.
3 Введение Натуральные числа N = {1,2,3,4…} Целые числа W = {0,1,2,3,…}
Целые числа Z = {…, -4, -3, -2, -1 , 0,1,2,3,4…} Рациональные числа имеют вид где и a, b — целые числа. Примеры: Вот несколько видеороликов, которые помогут объяснить тему: Ознакомительное видео 1 Ознакомительное видео 24 Мы можем записать все целые числа, натуральные числа и целые числа как целые числа.Пример: 1,5 — рациональное число, потому что 1,5 = 3/2 (его можно записать в виде дроби)
5 В рациональном числе, если и a, и b являются положительными или отрицательными целыми числами, то это положительное рациональное число. Пример: если (a или b) любой является отрицательным целым числом, то это отрицательное рациональное число.
6 Стандартная форма (простейшая форма) рационального числа
Рациональное число называется стандартным, если его числитель и знаменатель не имеют общего делителя, кроме 1, а его знаменатель — положительное целое число.Рассмотрим. Разделив числитель и знаменатель на 2, мы получим стандартную форму. Аналогично стандартной форме (при делении на 5) стандартной форме7 Эквивалентные рациональные числа
Эквивалентные рациональные числа могут быть получены путем умножения или деления числителя и знаменателя рационального числа на одно и то же целое число, отличное от нуля. Пример: напишите 4 эквивалентных рациональных числа. Пример: напишите 4 рациональных числа, эквивалентных8 Представление рациональных чисел на числовой прямой
Разделите единицу длины на числовой прямой на количество частей, как в знаменателе рационального числа.Затем отметьте количество частей как в числителе рационального числа. Вот ссылка на видео по теме. Пример: обозначение 3/5 на числовой строке Пример: обозначение -7/4 на числовой строке9 Сравнение рациональных чисел
Если знаменатели двух дробей одинаковы, то дробь с большим числителем является наибольшей; то же самое и с рациональными числами. Примеры:10 Чтобы сравнить рациональные числа с разными знаменателями, преобразуйте их с помощью НОК, чтобы иметь одинаковый знаменатель, а затем сравните их в дробях.Пример: Что больше от 2/3 до 3/5? Пример: Что больше между -7/4 и -5/3?
11 Рациональные числа между двумя рациональными числами
Мы можем легко найти целые числа между любыми двумя целыми числами. Пример: целые числа от -2 до 4 равны -1,0,1,2,3.


 упражнение 361 (357) математика 6 класс Виленкин, Жохов
упражнение 361 (357) математика 6 класс Виленкин, Жохов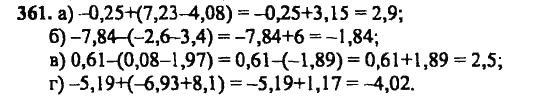 упражнение 361 (1251) математика 6 класс Виленкин, Жохов
упражнение 361 (1251) математика 6 класс Виленкин, Жохов Я.) | Материал (6 класс) на тему:
Я.) | Материал (6 класс) на тему: