Номер 207 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник)
Номер 207 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwowПерейти к содержаниюSearch for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
Старая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
Помогите найти проценты от числа.
№ 207 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. – Рамблер/класс Помогите найти проценты от числа. № 207 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?Найди 75% от числа:
ответы
Ответ: 42.
0,8 · 0,75 = 0,6.
Ответ: 0,6.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
похожие вопросы 5
Приветик! Кто решил? № 411 Математика 6 класс Виленкин.
Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)
ГДЗМатематика6 классВиленкин Н.Я.
Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Вырежи из бумаги № 694 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.Вырежи из бумаги 20 одинаковых произвольных треугольников и составь
из них паркет. Всегда ли это можно сделать? Почему?
ГДЗМатематика6 классДорофеев Г.
В.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Курс математического анализа — Хинчин
В этом посте мы увидим книгу «Курс математического анализа» А.Я. Хинчин.
Данный курс математического анализа является учебным пособием для студентов механико-математических и физико-математических факультетов наших университетов (а отчасти и пединститутов); он задуман как основной учебник по изучению науки, которая фигурирует в учебной программе под заголовком математический анализ и посвящена теории пределов, бесконечных рядов и дифференциальному исчислению с простыми приложениями этих предметов.
Книга была переведена с русского языка, опубликована в 1957 году.
Кредиты автору оригинала.
Книгу можно получить здесь.
Следите за нами в Интернет-архиве: https://archive.org/details/@mirtitles
Следуйте за нами в Twitter: https://twitter.com/MirTitles
Пишите нам: [email protected]
Разветвите нас в GitLab: https://gitlab.com/mirtitles/
Добавьте новые записи в подробный каталог книг здесь.
Глава 1. ФУНКЦИИ 1
§ 1. Переменные 1
§ 2. Функции 3
§ 3. Область определения функции 6
§ 4. Функции и формулы 7
§ 5. Геометрическое представление функций 11
§ 6. Элементарные функции 13
Глава 2. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПРЕДЕЛОВ 18
§ 7. Бесконечно малые величины 18
§ 8. Операции с бесконечно малыми величинами 23
§ 9. Бесконечно большие величины 26
§ 10. Величины, стремящиеся к пределам 29 9 0029 § 11. Операции с количествами, стремящимися к пределам 33
§ 12. Бесконечно малые и бесконечно большие величины различных порядков 39
Глава 3. РАЗВИТИЕ ТОЧНОЙ ТЕОРИИ ПРЕДЕЛЬНЫХ ПЕРЕХОДОВ 45
§ 13.
Математическое определение процесса 45
§ 14. Точное понятие пределов 47
§ 15. Развитие понятия предельных переходов 52
Глава 4. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА 56
§ 16. Необходимость создания общей теории действительных чисел 56
§ 17. Построение континуума 59
§ 18. Основные леммы 69
§ 19. Заключительные пункты в связи с теорией пределов 74
Глава 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ 79
§ 20. Определение непрерывности 79
§ 21. Операции с непрерывными функциями 84 900 29 § 22 Непрерывность сложной функции 85
§ 23. Основные свойства непрерывных функций 87
§ 24. Непрерывность элементарных функций 94
Глава 6. ПРОИЗВОДНЫЕ 98
§ 25. Равномерная и неравномерная вариация функций 98
§ 26. Мгновенная скорость неравномерного движения 101
§ 27. Локальная плотность неоднородного стержня 106
§ 28. Определение производной 108
§ 29. Законы дифференцирования 110
§ 30. Существование функций и их геометрическая иллюстрация 123
Глава 7.
ДИФФЕРЕНЦИАЛЫ 128 § 31. Определение и связь с производными 128
§ 32. Геометрическая иллюстрация и законы вычисления 132
§ 33. Инвариантный характер связи между производной и дифференциалом 134
Глава 8. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 136
§ 34. Производные высших порядков 136
§ 35. Дифференциалы высших порядков и их связь с производными 139
Глава 9. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ 142
§ 36. Теорема о конечных приращениях 142
§ 37. Вычисление пределов отношений бесконечно малых и бесконечно больших величин 147
§ 38. Формула Тейлора 154
§ 39. Последний член в формуле Тейлора 158
Глава 10. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ВЫЧИСЛЕНИЯ К АНАЛИЗУ ФУНКЦИЙ 164
§ 40. Возрастание и убывание функций 164
§ 4л. Экстремумы 167
Глава 11. ОБРАТНАЯ ДИФФЕРЕНЦИАЦИЯ 175
§ 42. Понятие о примитивах 175
§ 43. Простые общие методы интегрирования 182
Глава 12. ИНТЕГРАЛ 193
9000 2 § 44.
Площадь криволинейной трапеции 193 § 45. Работа переменной силы 198
§ 46. Общее понятие интеграла 201
§ 47. Верхние и нижние суммы 204
§ 48. Интегрируемость функций 207
Глава 13. СВЯЗЬ МЕЖДУ ИНТЕГРАЛОМ И ПРИМИТИВОМ 213
§ 49. Простые свойства интегралов 213
§ 50 , Связь между интегралом и примитив 218
§ 51. Другие свойства интегралов 223
Глава 14. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИМЕНЕНИЯ ИНТЕГРАЛОВ 230
§ 52. Длина дуги плоской кривой 230
§ 53. Длины дуг кривых в пространстве 24 1
§ 54. Масса, центр тяжести и моменты инерции материальной плоской кривой 242
§ 55. Емкости геометрических тел 247
Глава 15. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ 254
§ 56. Проблемная постановка 254
§ 57 .Метод трапеций 257
§ 58. Метод парабол 262
Глава 16. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 265
§ 59. Алгебраическое введение 265
§ 60. Интегрирование простых дробей 274 9002 9 § 61.
Метод Остроградского 277 9{2}+ bx +c}) 284
§ 64. Примитивы биномиальных дифференциалов 287
§ 65. Интегрирование тригонометрических дифференциалов 289
§ 66. Интегрирование дифференциалов, содержащих показательные
функции 294
Глава 18. ЧИСЛЕННЫЕ БЕСКОНЕЧНЫЕ СЕР ИЭС 297
§ 67. Основные понятия 297
§ 68. Ряды с постоянными знаками 305
§ 69. Ряды с переменными знаками 316
§ 70. Операции с рядами 320
§ 71. Бесконечные произведения 326
Глава 19. БЕСКОНЕЧНЫЕ S РЯД ФУНКЦИЙ 333
§ 72. Область сходимости ряда функций 333
§ 73. Равномерная сходимость 335
§ 74. Непрерывность суммы функционального ряда 340
§ 75. Почленное интегрирование и дифференцирование ряда 344
Глава 20 СТЕПЕННЫЕ РЯДЫ И РЯДЫ ПОЛИНОМОВ 351
§ 76. Область сходимости степенного ряда 351
§ 77. Равномерная сходимость и ее следствия 357
§ 78. Разложение функций в степенные ряды 361 9002 9 § 79. Серия многочленов 369
§ 80.
Теорема Вейерштрасса 372
Глава 21. Тригонометрические ряды 377
§ 81. Коэффициенты Фурье 377
§ 82. Среднее приближение 383
§ 83. Теорема Дирихле — Ляпунова о замкнутом треугольнике гонометрические системы 388
§ 84. Сходимость Ряды Фурье 394
§ 85. Обобщенные тригонометрические ряды 396
Глава 22. ДИФФЕРЕНЦИИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 400
§ 86. Непрерывность функций нескольких независимых переменных 400 9
§ 88. Свойства непрерывных функций 408
§ 89. Частные производные 410
§ 90. Дифференциалы 413
§ 91. Производные по произвольным направлениям 419
§ 92. неявные функции 422
§ 93. Однородные функции и теорема Эйлера 427
§ 94. Частные производные высших порядков 429
§ 95. Формула Тейлора для функций двух переменных 433
§ 96. Экстремумы 438
Глава 23. НЕКОТОРАЯ ПРОСТАЯ ГЕОМЕТРИЯ ИСКУССТВЕННЫЕ ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ ВЫЧИСЛЕНИЕ 443
§ 97. Уравнения касательной и нормали к плоской кривой 443
§ 98.
Касательная и нормаль к кривой в пространстве 446
§ 99. Касательные и нормальные плоскости к поверхности 448
§ 100. Направление выпуклости и вогнутость кривой 451
§ 101. Кривизна плоской кривой 453
§ 102. Касательная окружность 458
Глава 24. НЕЯВНЫЕ ФУНКЦИИ 462
§ 103. Простейшая задача 462
§ 1 04. Общая задача 469
§ 105 Определитель Остроградского 475
§ 106. Условный экстремум. 26. ИНТЕГРАЛЫ ПАРАМЕТРИЧЕСКИХ ФУНКЦИЙ 514
§ 109. Интегралы с конечными пределами 514
§ 110. Интегралы с бесконечными пределами 526
§ 111. Примеры 535
§ 112. Интегралы Эйлера 541
§ 113. Формула Стирлинга 548
Глава 27. ДВОЙНОЕ И ТРОЙНОЕ В ТЕГРАЛ 557
§ 114. Измеримые плоские фигуры 557
§ 115. Объемы цилиндрических тел 567
§ 116. Двойной интеграл 571
§ 117. Вычисление двойных интегралов с помощью двух простых интегрирований 576
§ 118. Подстановка переменных в двойных интегралах 584
§ 119.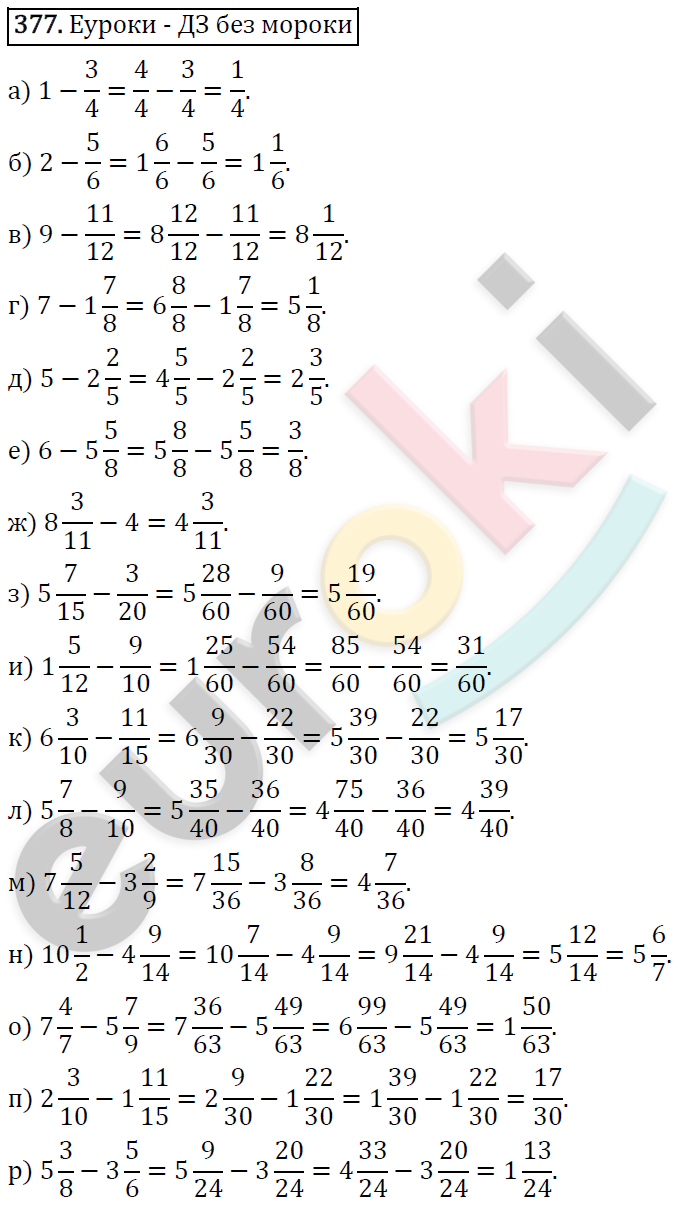
Тройные интегралы 590
§ 120. Приложения 593
Глава 28. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ 602
§ 121. Определение плоского криволинейного интеграла 602
§ 122. плоское силовое поле 610
§ 123. Формула Грина. 626
§ 127. Общее определение поверхностных интегралов 630
§ 128. Формула Остроградского 637
§ 129. Формула Стокса 642
§ 130. Элементы теории поля 647
ЗАКЛЮЧЕНИЕ. 5
Нравится:
Нравится Загрузка…
Эта запись была размещена в рубрике: книги, математика, советский анализ, приложения интегралов, приближенное вычисление интегралов, непрерывные функции, производные, дифференциалы, двойные интегралы, функции, неявные функции , бесконечные ряды, интегрирование, пределы, математика, теоремы о среднем значении, степенные ряды, примитивы, действительные числа, советские, поверхностные интегралы, тройные интегралы. Добавьте постоянную ссылку в закладки.
Гравитационное поле глобального монополя — arXiv Vanity
Синь Ши и Синь-чжоу Ли
Шанхайский объединенный центр астрофизики, Шанхай
Педагогический университет, 100 Guilin Road,
Шанхай 200234, Китай
Abstract
Приведено точное решение нелинейного уравнения, которое
описывает глобальный монополь в плоском пространстве.
Мы повторно изучаем
метрика и геодезические вне глобального монополя. Посмотрим
что глобальный монополь создает отталкивающее гравитационное поле
вне ядра в дополнение к солидному угловому дефициту. Линзы
собственность глобального монополиста и глобального монополия-антимонополя
изучается механизм аннигиляции.
(Эта статья опубликована в Class. Quantum Garv. 8 (1991) 761-767)
1 Введение
Идея о том, что магнитные монополи должны существовать, доказана
быть удивительно прочным. Сначала был приведен убедительный аргумент
вперед Дираком [1]. Много лет спустя, еще один очень хороший аргумент
появился. Монопольное решение ’т Хофта-Полякова представляет собой синтез
монополь Дирака в неабелевых калибровочных теориях [2],[3].
монопольные решения реалистических моделей великого объединения, основанные на
калибровочные группы SU(5) и SO(10) рассматривались в [4]
и [5]. Обширный список монопольной литературы Калуцы-Клейна.
сделано в [6]–[11]. Удивительные и качественные явления возникают
если рассматривать квантовую механику электрически заряженных
фермионы, взаимодействующие с магнитными монополями [12]–[16].
Недавно Барриола и Виленкин [17] показали приближенное решение уравнения Эйнштейна. уравнения для метрики вне глобального монополя, возникающие в результате нарушения глобальной симметрии. Такой монополь имеет поля Голдстоуна с плотностью энергии, уменьшающейся с расстоянием только как r−2, так что полная энергия линейно расходится на большом расстоянии. Пренебрегая массой Термин монопольная метрика описывает пространство с недостаточным телесным углом. Площадь сферы радиуса r не 4πr2, а 4π(1−8πGη2)r2. Требуя, чтобы плотность массы в таком монополе не превышала значительно критической плотность означает, что существует не более одного глобального монополя в местной группе галактик. Столь же строгие ограничения также полученные, не зависящие от космологических предположений, с использованием большие приливные гравитационные силы, связанные с глобальным монополь [18].
В этой статье мы представляем точное решение нелинейной
уравнение, описывающее глобальный монополь в плоском пространстве.
Мы пересматриваем метрику вне глобального монополиста. мы увидим
отталкивающее гравитационное поле вне ядра в дополнение к
солидный угловой дефицит. Мы исследуем геодезические и находим, что
угол отклонения небольшой. Для ультрарелятивистских частиц
угол отклонения также зависит от прицельного параметра. Если
прицельный параметр имеет масштаб галактики, а δ имеет большое
шкале унификации член с прицельным параметром может быть
пренебрегают. Однако, если срок имеет масштаб мини
солитонная звезда [19], этот термин важен. Объективное свойство
глобального монополя, как и другие классические эффекты,
изучал. Покажем, что отталкивающая сила гравитации между
глобальный монополь и антимонополь (M¯¯¯¯¯¯M) не изменяет
М¯¯¯¯¯¯М
аннигиляции, предложенной Барриолой и Виленкиным [17].
2 Точное решение глобального монополя в плоском пространстве
Простейшая модель, порождающая глобальный монополист описывается лагранжианом
| L=12∂μϕa∂μϕa−14λ(ϕaϕa−η2)2 | (1) |
где ϕa — тройка скалярных полей, a=1,2,3.
Модель имеет глобальную симметрию O(3), которая
самопроизвольно ломается
к U(1). Конфигурация поля, описывающая монополь, равна
| . | ϕa=ηf(r)xar | (2) |
Уравнения поля для ϕa в плоской метрике сводятся к одному уравнению для f(r)
| f′′+2rf′−2r2f−f(f2−1)δ2=0 | (3) |
где δ=(η√λ)−1 — радиус ядра монополя. Функция f(r) линейно растет, когда r<δ и экспоненциально стремится к единице, как только r≥δ. Барриола и Виленкин [17] взяли ф=1 вне ядра что является приближением к точному решению.
С другой стороны, Лан и Ван [20] обсудили точное солитонное решение льдоподобной структуры в виде ряд гиперболических функций. Аналогичным образом мы дадим точное решение глобального монополя. Кроме того, мы также обсуждаем сходимость решений этих рядов.
Настройка x=r/δ в уравнении (3) получаем
| x2f′′+2xf′−x2f3+(x2−2)f=0 | (4) |
удовлетворяющий граничным условиям
| f(0)=0 , | (5) | ||
f(∞)=1. | (6) |
Эту задачу можно решить в явном виде методом гиперболического функции, в виде
| f(x)=∞∑n=0cntanh3n+1x√2 | (7) |
, удовлетворяющее граничному условию при х→∞
| ∞∑n=0cn=1. | (8) |
По формуле
| х=√2tanhx√2∞∑n=0tanh3nx√2(2n+1)−1, | (9) |
у нас есть
| x2=2tanh3x√2∞∑n=0(1n+1∞∑l=012l+1)tanh3nx√2. | (10) |
Для определения cn сначала подставим уравнения (7), (8) и (10) в уравнение (4). Мы показать, что формула рекурсии коэффициентов cn может быть выражается следующим образом:
| н(2н+3)сп | = | ∑l+k=n−1(2(2k+1)(2l+1)(2l+3)+4k(k+1)dl−(2k+1)kdl−1 | (11) | ||
| −(k+1)(2k+1)dl−1)ck+∑i+j+k+l=n−2dlcicjck, |
где
dl=⎧⎪⎨⎪⎩0if \quadl=−11l+1l∑i=012i+1ifl=0,1,2,3,…. | (12) |
Уравнения (8) и (11) приводят к простому методу определить сп.
Используя уравнение (8), мы имеем |f(x)|<1 для x≥0. Ряд гиперболических функций (7) сходится равномерно в область x≥0. Таким образом, считаем, что функциональный ряд (7) показывает точное решение уравнения (4).
Далее рассмотрим приближенное решение N-го порядка
| f(N)=N∑n=0c(N)ntanh3n+1x√2 | (13) |
, удовлетворяющий бесконечному граничному условию,
| N∑n=0c(N)n=1. | (14) |
Приближенное решение нулевого порядка
| f(0)=tanhx√2. | (15) |
Приближенное решение 10-го порядка:
| ф10(х) | = | 0,7539tanhx√2+0,1005tanh4x√2+0,0414tanh5x√2+ | (16) | ||
| +0,0249tanh7x√2+0,0178tanh9x√2+0,0141tanh21x√2+ | |||||
| +0,0118tanh23x√2+0,0103tanh25x√2+0,0092tanh27x√2+ | |||||
| +0,0084tanh29x√2+0,0078tanh31x√2 |
Для N≥10 соответствующая ошибка составляет менее 0,5%.
Когда Н
увеличивается, соответствующая ошибка будет уменьшаться. можно в принципе
достичь произвольной точности, если сохранить достаточные члены в
уравнения (13) и (14) .
В области x≫1 решение (7) можно записать в виде
| f(x)=1−be−√2x+o(e−√2x) | (17) |
где
| b=∞∑n=02(2n+1)cn=limN→∞N∑n=02(2n+1)c(N)n. | (18) |
3 Метрика вокруг глобального монополя
Наиболее общая статическая метрика со сферической симметрией можно записать как
| ds2=B(r)dt2−A(r)dr2−r2(dθ2+sinθ2dφ2). | (19) |
Ненулевые компоненты тензора Риччи для этой метрики равны
| Rtt=-B»2A+B’4A(A’A+B’B)-1rB’A , | (20) | ||
| Rrr=B»2B-B’4B(A’A+B’B)-1rA’A , | (21) | ||
| Rθθ=−1+r2A(−A′A+B′B)+1A, | (22) | ||
Rφφ=sin2θRθθ. | (23) |
Тензор энергии-импульса монополя равен
| Ttt=η2f′22A+η2f2r2+14λη4(f2−1)2 , | (24) | ||
| Trr=-η2f′22A+η2f2r2+14λη4(f2−1)2 , | (25) | ||
| Tθθ=Tφφ=η2f′22A+14λη4(f2−1)2. | (26) |
В плоском пространстве сердечник монополя имеет размер δ∼(η√λ)−1. При η≪mp, где mp — масса планка, ожидаем, что гравитация существенно не меняет структуру монополя на малом расстоянии, так что оценка δ в плоском пространстве все еще применяется.
Полезные уравнения Эйнштейна задаются как
| 1A(1r2−1rA′A)−1r2=8πGTtt, | (27) |
| 1A(1r2+1rB′B)−1r2=8πGTrr. | (28) |
Из уравнения (27) получаем общее соотношение для A(r):
| A−1(r)=1−8πGr∫r0Tttr2dr | (29) |
и из уравнения (28) получаем общее соотношение для B(r):
B(r)=A−1(r)exp(−8µ∫r0f2rdr). | (30) |
Подставляя решение f(r) в (29) и (30), получаем решения для A(r) и B(r). В линейном аппроксимации, т. е. в предположении, что и A(r), и B(r) очень близко к единице, результат равен
| A(r)=1+8μ+Gmr, | (31) | ||
| B(r)=1−8(1+β)μ−Gmr. | (32) |
где μ=πGη2, и
| m=8πη2∫∞0(f′2+f2−1r2+14λη2(f2−1)2)r2dr | (33) | ||
| β=∫∞0f′2dr. | (34) |
Используя уравнение (16), мы получаем численный результат для m,
| м=-46,99η2δ. | (35) |
В плоском пространстве ядро глобального монополя имеет размер δ∼λ−12η−1.
Мы ожидаем, что гравитация не
заметно меняют структуру монополя на малых расстояниях, поэтому
что,
| |м|∼10η2δ. | (36) |
Существует крошечный гравитационный потенциал отталкивания из-за массовый срок. Свободно движущаяся частица вблизи ядра испытывает внешнее собственное ускорение:
| ¨r=−Gmr2=G|m|r2. | (37) |
Поскольку |m|∼10η2δ, массовый член ∼10η2δ/r. Когда r ≫ δ, массовый член может быть незначительный. Пренебрегая массовым членом и масштабируя переменные r и t, мы можем переписать метрику как
| ds2=dt2−dr2−(1−8µ)r2(dθ2+sinθ2dφ2). | (38) |
Метрика (38) описывает пространство с телесным ангелом дефицита.
4 Геодезические
Давайте теперь запишем уравнения для геодезических в
метрика (19).
Из
| d2xμdp2+Γμνλdxνdpdxλdp=0 | (39) |
у нас есть
| A(r)(drdp)2=1B(r)−J2r2−E, | (40) | ||
| r2dφdp=J, | (41) | ||
| dtdp=1B(r). | (42) |
Здесь J и E — интегральные константы. J представляет угловой момент траектории, а E12 – отношение собственного времени на траектории к аффинному параметр p, то есть ds2=-Edp2.
Из уравнений (???)−(???) формы пути, r=r(φ), можно найти. Это
| ∣∣∣dφdr∣∣∣≡△(r)=1r2A1/2(r)[1JB(r)−EJ2−1r2]−1/2 | (43) |
И мы можем параметризовать траекторию с точки зрения расстояния
наибольшего приближения к ядру, r0, вместо углового
импульс J.
Форма
drdφ|r0=0, имеем
| J=r0(1/B(r0)−E)1/2. | (44) |
Тогда уравнение (43) сокращается до
| |dφdr|≡△(r)=r0rA1/2(r)[B(r0)B(r)1−EB(r)1−EB(r0)−(r0r)2]−1/2 | (45) |
Рассмотрим траекторию, начинающуюся с расстояния L≫r0, и со скоростью V такой, что V2≫µ. Большая часть отклонения отпечатывается на траектории гравитационным полем в области r≈r0, где
| △(r)≈r0r1[1−(r0/r)2]1/2[1+4µ+Gm2r−Gm4V21r011+r0/r] | (46) |
до первого порядка μ и μ/V2. Также от E=1−V2 до этот заказ . Угол отклонения
| ε=π−Δφ | (47) |
где
| Δφ=2∫∞r0△(r)др. | (48) |
Уравнения (???)−(???) дают
| ε=−4πμ−(1−12V2)Gmr0 | (49) |
В нашем порядке аппроксимации r0 совпадает с воздействием
параметр траектории.
Аналогичный результат уравнению
(49) для калибровочной струны есть ε=−4πµ с µ
энергия струны на единицу длины. Случай монополя отличается от
калибровочной струны по зависимости ε от обоих
прицельный параметр и скорость траектории.
В случае ультрарелятивистских частиц (V≈1) угол отклонения
| ε=−4πμ[1+Gm8μδδr0] | (50) |
, где Gm/8μδ=O(1). Мы утверждаем, что световые лучи отклоняются различными ангелами, в зависимости от прицельного параметра р0. Если r0 — масштаб галактики, а δ порядка масштаба великого объединения, второй член в уравнении (50) можно пренебречь. В этом случае угол отклонения не зависит прицельного параметра. Однако, если прицельный параметр масштаб мини-солитонной звезды, второй член в уравнении (50) нельзя пренебрегать. Такой объект может быть сформирован, если глобальный монополь поглощается мини-солитонной звездой.
Существует пороговая скорость V0, выше которой монополь
действует как собирающая линза, ниже которой монополь действует как
рассеивающая линза.
Полагая ε=0 в уравнении (49), можно
получает
| V20=[2(1+4πμδGmr0δ)]−1. | (51) |
Если r0 и δ имеют масштаб мини солитонной звезды, V0 составляет примерно половину скорости света. Когда частица движется на скорость V0 нет чистого отклонения.
5 обсуждение
Ключевой вопрос сейчас заключается в том, какова ожидаемая плотность мировых монополий. Барриола и Виленкин [17] предложили глобальная монопольно-антимонопольная аннигиляция как возможная чрезвычайно действенный механизм сокращения их количества. Энергия пара (M¯¯¯¯¯¯M) есть E∼η2R, где R — M¯¯¯¯¯¯M расстояние. Сила притяжения, действующая на Mand ¯¯¯¯¯¯M, равна F и не зависит от расстояния. Отталкивающий гравитационная сила Frep оказывает максимальное влияние при расстояние R∼δ, где оно равно
| Fреп∼Gm2δ2∼103μη2 | (52) |
Поскольку μ∼10−6 в типичном масштабе великого объединения
1016 ГэВ, сила отталкивания Frep может быть
пренебречь согласно большой силе притяжения F.
Большая
сила притяжения между глобальным монополистом и антимонополем предполагает
что M¯¯¯¯¯¯M аннигиляция очень эффективна и что
проблема монопольного перепроизводства может и не существовать.
Каталожные номера
- [1] Дирак ПАМ 1931 проц. Р. Соц. А 133 60
- [2] Поляков А М 1974 Письма в ЖЭТФ. 20 194
- [3] т, Hooft G 1974 Nucl. физ. Б 79 276
- [4] Докос С. и Томарас Т. 1980 Phys. Ред. D 21 2940
- [5] Li X, Wang K и Zhang J 1984 Phys. лат. 140Б 209
- [6] Соркин Р Д 1983 Физ. Преподобный Летт. 51 87
- [7] Гросс Д. Дж. и Перри М. Дж. 1983 Nucl. физ. Б 226 29
- [8] Li X, Yu F и Zhang J 1986 Phys. Ред. D 34 1124
- [9] Ли Х 1988 физ. лат. 205Б 451
- [10] Xu J и Li X 1988 Phys. лат. 207Б 391
- [11] Xu J и Li X Phys. Ред. D 40 1101
- [12] т, Hooft G 1976 Phys. Преподобный Летт. 37 8
- [13] Гроссман Б. 1983 г., Phys. Преподобный Летт. 50 464
- [14]
Kazama Y, Yang CN и Goldhaber AS 1977 Phys.
