Номер 101 — ГДЗ Математика 6 класс. Мерзляк, Полонский. Учебник. Страница 18
- Главная
- ГДЗ
- 6 класс
- Математика
- Мерзляк, Полонский. Учебник
- Делимость натуральных чисел
- Упражнения § 3
- Номер 101
- ← Предыдущее
- Следующее →
Вернуться к содержанию учебника
Делимость натуральных чисел. Упражнения § 3. Страница 18
Вопрос
Найдите значение выражения:
1) 25;
2) 72;
3) 0,62;
4) 0,53;
6) 1,23;
7) 06;
8) 112.
Подсказка
Вспомните:
- Степень числа.
- Умножение десятичных дробей.
- Умножение натуральных чисел.
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
- ← Предыдущее
- Следующее →
© budu5.com, 2021
Пользовательское соглашение
Copyright
Нашли ошибку?
Связаться с нами
ГДЗ по математике для 6 класса А.
 Г. Мерзляк, В.Б. Полонский, М.С. Якир
Г. Мерзляк, В.Б. Полонский, М.С. ЯкирИздательство: Вентана-граф
Авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир
«ГДЗ по математике 6 класс Учебник Мерзляк (Вентана-граф)» очень пригодится школьникам, которые испытывают периодические проблемы с предметом. А таких ребят, к сожалению, очень много, ведь не все из них обладают математическим складом ума. Кроме того, некоторые дети проявляют элементарную невнимательность, что мешает им правильно понять текущий материал. Не зная теорию, и, главное, не поняв ее, весьма трудно:
- Правильно выполнять практические упражнения.
- Писать тесты и контрольные работы.
- Принимать участие в олимпиадах и других испытаниях.
Кроме того, хорошее знание математики позволит ребятам легче перейти к изучению алгебры и геометрии, а также успешно сдать предстоящие экзамены.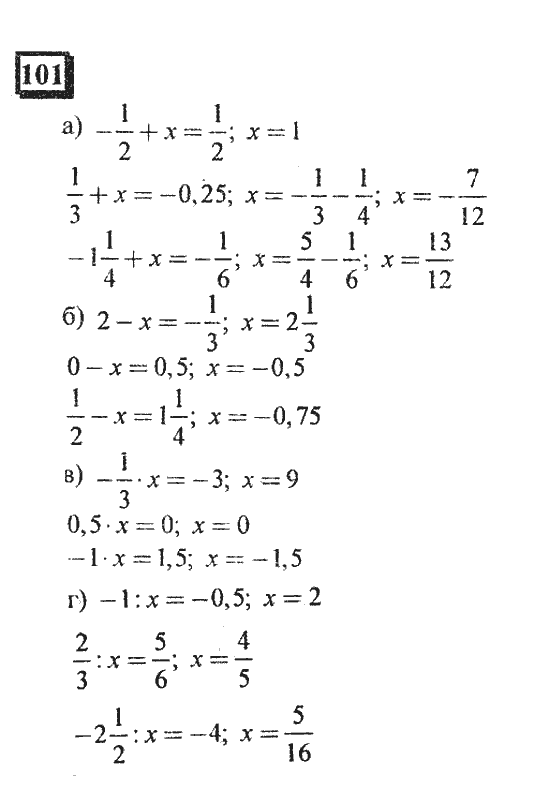 Но трудно ожидать от шестиклассников такой дальновидности, поэтому у многих из них к старшим классам наблюдается довольно низкая успеваемость и весьма посредственные навыки. Решебник способен в значительной мере улучшить ситуацию, но только при условии тщательного подхода к работе с ним.
Но трудно ожидать от шестиклассников такой дальновидности, поэтому у многих из них к старшим классам наблюдается довольно низкая успеваемость и весьма посредственные навыки. Решебник способен в значительной мере улучшить ситуацию, но только при условии тщательного подхода к работе с ним.
Содержимое онлайн-издания ГДЗ по математике для 6 класса Мерзляк
В сборнике представлены упражнения по 47 параграфам, которые распределены по четырем тематическим разделам. Все номера досконально проработаны авторами, поэтому вниманию школьников предоставлены обширные ответы и пояснения, что позволит:
- досконально проверить д/з;
- выявить малейшие неточности и ошибки в решениях;
- повторить материал и подготовиться к тестам.
Используя задачник, ученики могут в значительной степени улучшить свои познания, чтобы выработать все необходимые навыки. Это поможет улучшить успеваемость и не испытывать затруднений с учебой.
Онлайн-решебник — для чего он нужен
Математика относится к точным наукам, которые школьники начинают постигать с самого начала обучения. Но и в шестом классе многие из них продолжают испытывать сложности с ее освоением. Поэтому зачастую учащимся требуется помощь, которую не так уж просто получить. Учителя редко дополнительно что-то разъясняют, поэтому на них уже практически никто не рассчитывает. Родители тоже мало чем могут посодействовать своим детям, ведь у них нет ни соответствующего времени, ни познаний.
Но и в шестом классе многие из них продолжают испытывать сложности с ее освоением. Поэтому зачастую учащимся требуется помощь, которую не так уж просто получить. Учителя редко дополнительно что-то разъясняют, поэтому на них уже практически никто не рассчитывает. Родители тоже мало чем могут посодействовать своим детям, ведь у них нет ни соответствующего времени, ни познаний.
Поэтому многие ребята прибегают к помощи
ГДЗ Математика 6 класс Потапов, Шевкин
Математика 6 класс
Тип пособия: Рабочая тетрадь
Авторы: Потапов, Шевкин
Издательство: «Просвещение»
Похожие ГДЗ Математика 6 класс
Задания: стр. 3
Предыдущее
Следующее
Предыдущее
Следующее
Сложно, но нужно!
В математике как нигде нужна точность. А со стороны учеников — усидчивость, вдумчивость и понимание предмета. И родители уже далеко не всегда могут помочь. Потому что чем дальше, тем сложнее изучение. Но и здесь об учащихся позаботились. Созданы различные пособия, решебники, которые являются настоящей палочкой-выручалочкой.
А со стороны учеников — усидчивость, вдумчивость и понимание предмета. И родители уже далеко не всегда могут помочь. Потому что чем дальше, тем сложнее изучение. Но и здесь об учащихся позаботились. Созданы различные пособия, решебники, которые являются настоящей палочкой-выручалочкой.
Кто спешит на помощь?
Рабочая тетрадь по математике за 6 класс авторов Потапова, Шевкина, издательства «Просвещение». Эта тетрадь была составлена к учебнику математика 6 класс Никольского, где 5 глав, и 253 страницы. В конце книги — задания для закрепления, ответы почти ко всем номерам задач и примеров.
Огромная работа составителей пособия
- Здорово то, что авторы проделали большую работу и сумели собрать в одном месте огромный материал, что изучается на уроках. Они это сделали настолько великолепно, что все темы стали просты и понятны для понимания. Даже такие сложные темы, как «дроби», рациональные уравнения — просто пристают!
- Но совсем, играючи, не стоит к ним относиться.
 Нужно понимать всю серьезность предмета. И что еще немаловажно, так это то, что теперь даже родители проявят интерес и смогут поддержать в сложных решениях. ГДЗ рабочая тетрадь по математике 6 класс Потапов, Шевкин — 327 заданий и их подробный разбор содержаться на 109 страницах.
Нужно понимать всю серьезность предмета. И что еще немаловажно, так это то, что теперь даже родители проявят интерес и смогут поддержать в сложных решениях. ГДЗ рабочая тетрадь по математике 6 класс Потапов, Шевкин — 327 заданий и их подробный разбор содержаться на 109 страницах. - Присутствие картинок. Именно они делают учебник нескучным для восприятия.
- Еще один плюс. Есть возможность пользоваться онлайн версией, конечно при наличии интернета. Есть даже портал. А кто-то любит листать страницы в учебнике. Здесь уж кто что предпочитает. В обоих случаях предлагается решить задачи на логическое мышление. Мыслить логично — важно.
Все преподаватели поддерживают обращение к этому решебнику. Пользуемся и получаем удовольствие!
MathPractice101 Homework Answer Keys
Что такое Common Core
The Common Core — это набор высококачественных академических стандартов по математике и английскому языку искусств / грамотности (ELA).
Эти учебные цели определяют, что ученик должен знать и уметь делать в конце каждого класса.
Подробнее »
Что должны знать родители
Сегодняшние студенты готовятся войти в мир, в котором колледжи и предприятия требуют больше, чем когда-либо прежде.
Чтобы все учащиеся были готовы к успеху после окончания средней школы, Общие основные государственные стандарты устанавливают четкие и последовательные рекомендации в отношении того, что каждый учащийся должен знать и уметь по математике и искусству английского языка от детского сада до 12-го класса.
Подробнее »
Общее ядро - Типичные ошибки
Используйте стратегию повторного сложения, чтобы решить 5×3.
Если вы ответите на вопрос с помощью 5 + 5 + 5 = 15, вы ошибетесь.
Правильный ответ: 3 + 3 + 3 + 3 + 3.
Математически оба верны. Но в Common Core вы должны читать 5×3 как «пять групп по три». Итак, «три группы по пять» — это неправильно.
Начало работы
Подробнее »
Получить дополнительные дидактические материалы
Мы предлагаем школьные учебники, библиотечные книги, контрольные и практические задания, которые помогут вам отточить свои математические навыки.
Подробнее »
Бесплатный онлайн-репетитор
Как зарегистрированный участник, у вас есть доступ к нашим онлайн-преподавателям, которые помогут вам с любыми вопросами, которые могут у вас возникнуть.
Подробнее »
Набор «Понимание математики» для 6 классов
В этом учебнике в твердом переплете 170 уроков, в которых анализируются и расширяются навыки, полученные в предыдущих классах. Повторение в каждом уроке поддерживает актуальность предыдущих навыков. Новые концепции включают следующие области.
Повторение в каждом уроке поддерживает актуальность предыдущих навыков. Новые концепции включают следующие области.
- Числа —Наибольший общий множитель, наименьшее общее кратное, умственные сокращения в вычислениях.
- Дроби — эквиваленты десятичных дробей.
- Десятичные знаки —Множение и деление.
- Проценты —Скидки, комиссии, проценты.
- Меры —Преобразование английских единиц измерения в метрические единицы, часовые пояса.
- Геометрия —Периметр и площадь треугольников и параллелограммов, окружность и площадь кругов, измерение углов с помощью транспортира.
- Графики —Построение круговых графтов.
Тесты и тесты скорости представлены в отдельном буклете с отрывными листами.
Глава тестов также находится в отдельном буклете.
Пособие для учителя состоит из двух томов. На каждом уроке ученики показывали полноразмерные страницы с заполненными ответами. Дополнительные страницы помогают учителю в подготовке урока. Ключи для ответов на викторины, тесты скорости и тесты глав включены.
Дополнительные страницы помогают учителю в подготовке урока. Ключи для ответов на викторины, тесты скорости и тесты глав включены.
Содержание пособия для учителя
- Материалы для этого курса
Учителю
- Основная философия
- План курса
- Тетрадь ученика
- Пособие для учителя
- Процедура общего класса
- Викторины и тесты скорости
- Глава Тесты
Глава 1. Работа с числами
- 1.Работа с большими числами
- 2. Местная система ценностей
- 3. Округление чисел
- 4. Римские цифры
- 5. Добавление столбца
- 6. Горизонтальное сложение
- 7. Ментальное прибавление
- 8. Вычитание
- 9. Горизонтальное вычитание
- 10. Ментальное вычитание
- 11.
Работа с графиками: графическое изображение
- 12. Проблемы с чтением: поиск нужной информации
- 13. Обзор главы 1
- 14.Глава 1 Тест (в тестовом буклете)
Глава 2: Умножение и деление
- 15. Умножение с однозначным множителем
- 16. Умножение с помощью двух- и трехзначных множителей
- 17. Проверка умножения путем исключения девяток
- 18. Умножение с четырехзначным множителем
- 19. Умножение на десять
- 20. Сокращение двойного и разделения
- 21. Работа с Подразделением
- 22.Короткий дивизион
- 23. Работа с двузначными делителями
- 24. Работа с трехзначными делителями
- 25. Более сложные трехзначные делители
- 26. Ярлыки дивизии
- 27. Расчет средних значений
- 28. Проблемы с чтением: выбор правильной операции
- 29. Обзор главы 2
- 30. Глава 2 Тест (в тестовом буклете)
Глава 3.
Работа с мерами
- 31. Введение в меры
- 32.Единицы линейной меры
- 33. Единицы веса
- 34. Единицы мощности
- 35. Мысленное преобразование мер
- 36. Площадь
- 37. Единицы времени
- 38. Часовые пояса
- 39. Сложение и вычитание сложных английских мер
- 40. Умножение сложных английских мер
- 41. Делящие сложные английские меры
- 42. Проблемы с чтением: поиск нужной информации
- 43. Обзор главы 3
- 44.Глава 3 Тест (в тестовом буклете)
Глава 4. Работа с дробями
- 45. Простые и составные числа
- 46. Нахождение основных факторов составных чисел
- 47. Наибольшие общие факторы
- 48. Наименьшее общее кратное
- 49. Введение в дроби
- 50. Неправильные дроби и смешанные числа
- 51. Сравнение дробей
- 52. Сложение правильных дробей
- 53.
Вычитание правильных дробей
- 54.Сложение смешанных чисел
- 55. Сложение трех или более смешанных чисел
- 56. Вычитание смешанных чисел
- 57. Обзор главы 4
- 58. Глава 4 Тест (в тестовом буклете)
Глава 5: Умножение и деление на дроби
- 59. Нахождение дробных частей делением и умножением
- 60. Умножение целого числа на дробь
- 61. Умножение дроби на дробь
- 62. Умножение дроби на смешанное число
- 63.Умножение целого числа на смешанное
- 64. Умножение смешанных чисел
- 65. Деление целого числа на правильную дробь
- 66. Деление дроби на дробь
- 67. Деление смешанных чисел
- 68. Умножение сложных величин как смешанных чисел
- 69. Проблемы с чтением: оценка в повседневной жизни
- 70. Обзор главы 5
- 71. Глава 5 Тест (в тестовом буклете)
Глава 6. Работа с десятичными знаками
- 72.
Знакомство с десятичными знаками
- 73. Преобразование дробей в десятичные
- 74. Преобразование десятичных дробей в дроби
- 75. Сравнение десятичных знаков
- 76. Сложение и вычитание десятичных знаков
- 77. Вычитание более сложных десятичных знаков
- 78. Умножение десятичных знаков на 10, 100 и 1 000
- 79. Умножение десятичных знаков
- 80. Умножение более сложных десятичных знаков
- 81. Обзор семестра I
- 82. Обзор семестра II
- 83.Семестровый тест (в тестовом буклете)
- Викторины и тесты скорости
- Глава Тесты
- Индекс
- Символы
- Формулы
- Таблицы показателей
Глава 7. Десятичные дроби и пропорции
- 84. Деление десятичных знаков на 10, 100 и 1 000
- 85. Деление десятичной дроби на целое число
- 86. Деление на десятичную дробь
- 87.
Более сложные десятичные делители
- 88.Округление десятичных знаков
- 89. Работа с бесконечными десятичными знаками
- 90. Использование дробных эквивалентов для умножения мысленно
- 91. Выбор разумного десятичного ответа
- 92. Использование соотношений для сравнения чисел
- 93. Пропорции письма
- 94. Проблемы с чтением: использование пропорций
- 95. Обзор главы 7
- 96. Глава 7 Тест (в тестовом буклете)
Глава 8: Использование метрической системы
- 97.Использование метрической линейки
- 98. Метрические единицы линейной меры
- 99. Единицы измерения веса
- 100. Единицы измерения вместимости
- 101. Метрические единицы площади
- 102. Метрические меры в задачах чтения
- 103. Преобразование между метрическими и английскими единицами измерения: линейная мера и вес
- 104. Преобразование между метрическими и английскими единицами измерения: вместимость и площадь
- 105.
Работа с расстоянием, скоростью и временем
- 106.Расстояние, скорость и время в задачах чтения
- 107. По шкале миль
- 108. Чтение чертежа
- 109. Работа с гистограммами
- 110. Обзор главы 8
- 111. Глава 8 Тест (в тестовом буклете)
Глава 9: Работа с процентами
- 112. Знакомство с процентами
- 113. Выражение десятичных и дробных чисел в процентах
- 114. Выражение дробей в процентах
- 115. Выражение процентов в виде десятичных и дробных чисел
- 116.Вычитание процентов от 100%
- 117. Нахождение числа в процентах
- 118. Решение более сложных проблем в процентах
- 119. Нахождение процента больше или меньше числа
- 120. Расчет цен со скидкой
- 121. Расчет комиссионных с продаж
- 122. Как определить процентное соотношение одного числа к другому
- 123. Как определить процентное соотношение одного числа к другому
- 124.
Умножение мысленно путем изменения процента на дробь
- 125.Глава 9 Обзор
- 126. Глава 9 Тест (в тестовом буклете)
Глава 10. Работа с деньгами
- 127. Подсчет сдачи
- 128. Ведение учета расходов
- 129. Доходы, расходы и прибыль
- 130. Расчет цен за единицу продукции
- 131. Расчет процентов
- 132. Расчет процентов за часть года
- 133. Проверка интересов
- 134. Проблемы чтения: решение многоэтапных задач
- 135.Глава 10 Обзор
- 136. Глава 10 Тест (в тестовом буклете)
Глава 11: Геометрия: периметр и площадь
- 137. Введение в геометрию
- 138. Работа с периметром
- 139. Нахождение периметра прямоугольников и треугольников
- 140. Работа с площадью
- 141. Определение площади квадрата
- 142. Определение площади параллелограмма
- 143. Определение площади треугольника
- 144.
Работа с графиками: линейный график
- 145. Проблемы чтения: Использование параллельных задач
- 146. Глава 11 Обзор
- 147. Глава 11 Тест (в тестовом буклете)
Глава 12: Геометрия: круги, углы и объем
- 148. Работа с кругами
- 149. Определение окружности круга
- 150. Определение площади круга
- 151. Введение в Том
- 152. Определение объема куба
- 153.Метрические единицы объема
- 154. Работа с углами
- 155. Использование транспортира для измерения углов
- 156. Работа с треугольниками
- 157. Работа с графами: круговой график
- 158. Работа с графами: построение круговых графов
- 159. Проблемы с чтением: использование эскизов
- 160. Обзор главы 12
- 161. Глава 12 Тест (в тестовом буклете)
Глава 13: Числовые предложения и обзор на конец года
- 162.Работа с числовыми предложениями
- 163.
Использование числовых предложений для решения проблем с чтением
- 164. Обзор глав 1 и 2
- 165. Обзор глав 3 и 8
- 166. Обзор глав 4 и 5
- 167. Обзор глав 6 и 7
- 168. Обзор глав 9 и 10
- 169. Обзор глав 11 и 12
- 170. Итоговый тест (в тестовом буклете)
- Викторины и тесты скорости
- …
- 89.Тест: умножение и деление десятичных знаков
- …
- 148. Тест на скорость: места поиска
- …
- Глава Тесты
- Индекс
- Символы
- Формулы
- Таблицы показателей
Стандарты данных PEIMS 300 ДАННЫЕ РАЗДЕЛА КУРСА — CAMPUS
Стандарты данных PEIMS 300 ДАННЫЕ РАЗДЕЛА КУРСА — CAMPUS 300 ДАННЫЕ РАЗДЕЛА КУРСА — КАМПУС Ниже представлены предлагаемые курсы для первого и шестого классов начальной школы Техаса (111-111-101) на 2010-2011 учебный год. В Texas Elementary есть 2 класса для первого класса и 2 класса для шестого класса.
В Texas Elementary есть 2 класса для первого класса и 2 класса для шестого класса.
02620010 — Чтение, 1 класс 02640010 — Математика, 1 класс 02630010 — Искусство английского языка, 1 класс 02650100 — Наука, 1 класс 02660010 — Обществознание, 1 класс 02510004 — Искусство 1 марка 02520005 — Музыка, 1 класс 02530003 — Физическая культура, 1-6 классы | 03200510 — Английский язык, искусство и чтение, 6 класс 02640060 — Математика, 6 класс 02800000 — Искусство английского языка, 6 класс 03060600 — Естественные науки, 6 класс 02660060 — Обществознание, 6 класс 02510009 — Искусство 6 марка 02520010 — Музыка, 6 класс 02850000 — Физическая культура, 6 класс |
|---|
О курсах, предлагаемых Texas Elementary, будет сообщаться следующим образом:
Входная запись | Район ID | Campus ID | Идентификационный номер класса | Идентификатор услуги | Период занятий | Код последовательности курса | Код обучения вне кампуса | Наполнитель |
|---|---|---|---|---|---|---|---|---|
E0755 | E0212 | E0782 | E1056 | E0724 | E1074 | E0948 | E1072 | |
C042 | C022 | C135 | C182 | |||||
Колонны | Колонны | Колонны | Колонны | Колонны | Колонны | Колонна | Колонны | Колонны |
ПЕРВЫЙ | МАРКА | |||||||
300 | 111111 | 111111101 | 00000000000001 | 02620010 | 01 | А | 00 | |
300 | 111111 | 111111101 | 00000000000002 | 02620010 | 01 | А | 00 | |
300 | 111111 | 111111101 | 00000000000003 | 02640010 | 02 | А | 00 | |
300 | 111111 | 111111101 | 00000000000004 | 02640010 | 02 | А | 00 | |
300 | 111111 | 111111101 | 00000000000005 | 02630010 | 03 | А | 00 | |
300 | 111111 | 111111101 | 00000000000006 | 02630010 | 03 | А | 00 | |
300 | 111111 | 111111101 | 00000000000007 | 02650100 | 04 | А | 00 | |
300 | 111111 | 111111101 | 00000000000008 | 02650100 | 04 | А | 00 | |
300 | 111111 | 111111101 | 00000000000009 | 02660010 | 05 | А | 00 | |
300 | 111111 | 111111101 | 00000000000010 | 02660010 | 05 | А | 00 | |
300 | 111111 | 111111101 | 00000000000011 | 02510004 | 06 | А | 00 | |
300 | 111111 | 111111101 | 00000000000012 | 02510004 | 06 | А | 00 | |
300 | 111111 | 111111101 | 00000000000013 | 02520005 | 07 | А | 00 | |
300 | 111111 | 111111101 | 00000000000014 | 02520005 | 07 | А | 00 | |
300 | 111111 | 111111101 | 00000000000015 | 02530003 | 08 | А | 00 | |
300 | 111111 | 111111101 | 00000000000016 | 02530003 | 08 | А | 00 | |
ШЕСТОЙ | МАРКА | |||||||
300 | 111111 | 111111101 | 00000000000017 | 03200510 | 01 | А | 00 | |
300 | 111111 | 111111101 | 00000000000018 | 03200510 | 01 | А | 00 | |
300 | 111111 | 111111101 | 00000000000019 | 02640060 | 02 | А | 00 | |
300 | 111111 | 111111101 | 00000000000020 | 02640060 | 02 | А | 00 | |
300 | 111111 | 111111101 | 00000000000021 | 02800000 | 03 | А | 00 | |
300 | 111111 | 111111101 | 00000000000022 | 02800000 | 03 | А | 00 | |
300 | 111111 | 111111101 | 00000000000023 | 03060600 | 04 | А | 00 | |
300 | 111111 | 111111101 | 00000000000024 | 03060600 | 04 | А | 00 | |
300 | 111111 | 111111101 | 00000000000025 | 02660060 | 05 | А | 00 | |
300 | 111111 | 111111101 | 00000000000026 | 02660060 | 05 | А | 00 | |
300 | 111111 | 111111101 | 00000000000027 | 02510009 | 06 | А | 00 | |
300 | 111111 | 111111101 | 00000000000028 | 02510009 | 06 | А | 00 | |
300 | 111111 | 111111101 | 00000000000029 | 02520010 | 07 | А | 00 | |
300 | 111111 | 111111101 | 00000000000030 | 02520010 | 07 | А | 00 | |
300 | 111111 | 111111101 | 00000000000031 | 02850000 | 08 | А | 00 | |
300 | 111111 | 111111101 | 00000000000032 | 02850000 | 08 | А | 00 |
Объяснение 300 Campus — Макет записи раздела курса
НОМЕРА КЛАССА 00000000000001 — 00000000000032 указывают уникальные номера, присвоенные каждому курсу, который предлагается студентам в кампусе.
ПЕРИОДЫ КЛАССА 01–08 указывают момент времени в расписании занятий, когда курс был предложен студентам в кампусе.
КОД ПОСЛЕДОВАТЕЛЬНОСТИ КУРСОВ A указывает, что эти курсы не для старшей школы преподаются в годичном формате.
КОД ИНСТРУКЦИИ, НЕ ОСНОВАННЫЙ НА КАМПУСЕ 00 означает, что курс преподавался в кампусе школьного округа нанятыми или нанятыми учителями школьным округом.
Эта версия стандартов данных PEIMS представляет собой программно преобразованную HTML-версию стандартов данных PEIMS. Он предназначен в качестве вспомогательного средства для облегчения навигации по документации стандартов данных PEIMS и не должен использоваться для представления данных PEIMS или для получения окончательных выводов об отдельных государственных школах. Вся предоставленная информация проверяется на точность и достоверность; однако TEA не несет ответственности за какие-либо ошибки, появляющиеся в HTML-версии Стандартов данных PEIMS.
101 Глупые математические шутки и шутки, заставляющие школьников смеяться как сумасшедшие
Почему книга по геометрии была такой очаровательной? Потому что у него было острых углов.
Хорошо … Я признаю, что это было банально, но все мы знаем, что математика — не всегда самый увлекательный предмет для преподавания. Это означает, что вам нужно найти стратегии, чтобы сделать уроки увлекательными, например, геймификация в классе, математические головоломки или — в данном случае — математических анекдота, которые поднимут настроение и оживят атмосферу в вашем классе.
И, кроме того, лучшие математические анекдоты действительно могут помочь в обучении концепциям на уроках математики. Только подумайте о возможностях: ученики могут использовать эти шутки как устройства, чтобы запомнить, как решать различные математические задачи!
Вот 101 математическая шутка для детей, которые сделают ваши уроки более увлекательными.
Кредит: Andertoons
- Вчера я видел своего учителя математики с миллиметровой бумагой. Я думаю, он что-то замышляет.
- Что треугольник сказал кругу? «Ты бессмысленен».
- Как математик вспахивает поля? С протрактором.
- Какое дерево больше всего нравится учителю математики? Геометрия.
- У параллельных линий так много общего … Жаль, что они никогда не встретятся.
- Как вы называете более одной L? Параллель!
- Почему в школе не учили геометрию? Потому что она растянула угол.
- У меня был аргумент с углом 90 °. Оказывается, это было правильно.
- Слышали ли вы о чрезмерно образованном круге? Имеет 360 °!
- Какая форма обычно ждет вас в Starbucks? Линия.

- Почему никто не общается с кругами? Потому что в этом нет смысла.
- Почему всегда расстраивался тупой треугольник? Потому что это никогда не бывает.
- Что учителя геометрии украшают свой пол? Коврики!
- Что делают математики после метели? Делайте снежные углы!
- Почему математик вылил всю еду в духовку? В инструкции было сказано: «Поставить в духовку на 180 °».
- Почему уроки математики были такими длинными? Учитель продолжал сбиваться с пути.
Кредит: Неправильные руки
- Почему ученик выполнял задачи умножения на полу? Учитель сказал ему не пользоваться таблицами.
- Вы слышали о математике, который боится отрицательных чисел? Он ни перед чем не остановится, чтобы избежать их.
- Как решить любое уравнение? Умножьте обе стороны на ноль.

- Какие таблицы вам не нужно учить? Обеденные столы!
- Хирург: Медсестра, у меня так много пациентов.Над кем я работаю в первую очередь? Медсестра: Просто, соблюдайте порядок действий.
- Я встретил учителя математики, у которого было 12 детей. Она действительно умеет размножаться!
- Почему ученик был сбит с толку, когда перешел с английского на математический? Потому что его учили, что двойное отрицание в английском — плохо, а в математике — положительное.
- Какой инструмент лучше всего подходит для математики? Клещи.
- Почему класс мистера Гилсона был таким шумным? Он любил практиковать деление гонга!
- Почему девочка носила очки на уроке математики? Улучшено ди-зрение.
- Отец заметил, что его сын однажды вернулся домой из школы грустно. «Что случилось?» — спросил отец.
 «Я действительно не люблю деление в столбик, — ответил сын, — мне всегда жаль остаток».
«Я действительно не люблю деление в столбик, — ответил сын, — мне всегда жаль остаток». - Какой вид математики у пловцов самый любимый? Dive-ision!
- Знаете, что мне кажется странным? Числа, которые не делятся на два.
- Знаете, в чем странность? Любой другой номер!
- Почему шестеро боялись семерых? Потому что семь, восемь, девять!
- Говорящая овчарка загоняет всех овец в загон для своего фермера.Он возвращается и говорит: «Хорошо, вождь, учтены все 40 овец». Фермер говорит: «Но я их посчитал, и у меня их всего 36!» Овчарка отвечает: «Я знаю, но я поймала их».
- Я нанял случайного человека, который сделал для меня восемь работ. Когда я вернулся, он выполнял только работу первый, третий, пятый и седьмой.
- На какие десять вещей вы всегда можете рассчитывать? Твои пальцы.

- Монстры хорошо разбираются в математике? Нет, если вы не граф Дракула.
Кредит: Каталог мыслей
- В этом мире есть три типа людей. Те, кто умеют считать, и те, кто не умеет.
- Почему квартал не скатился с холма с никелем? Потому что центов было больше!
- Что орфографическая книга сказала математике? «Я знаю, что могу на тебя рассчитывать!»
- Почему подростки всегда путешествуют группами по три, пять или семь человек? Потому что даже не умеют!
- Что вы получите, если скрестите собаку и калькулятор? Друг, на которого можно положиться.
- Почему две четверки пропустили обед? Их уже восемь!
- Как сделать семь четным числом? Удалите S.
- Какой король любил дроби? Генрих ⅛.

- Между числителем и знаменателем есть тонкая грань… Но только дробь поймет.
- Чем похож доллар и луна? У них обоих по четыре четверти!
- Почему ⅕ пошла к массажистке? Потому что было две десятых!
- Как мы узнаем, что дроби x / c, y / c и z / c находятся в Европе? Они повсюду!
Кредит: Neatorama
- Вы слышали анекдот про статистиков? Наверное.
- Статист промок насквозь, пытаясь перейти реку. Он думал, что сможет перейти, потому что в среднем он был в один фут глубиной.
- Почему ученица расстроилась, когда учитель назвал ее средним? Это было «подло» сказать.
- Был учитель статистики, который всегда резко ускорялся при проезде перекрестков, а затем замедлялся после проезда. Однажды он отвез на работу коллегу, которому было заметно неудобно за рулем.
 Коллега спросил: «Почему вы всегда так быстро проезжаете перекрестки?» На что учитель статистики ответил: «Ну, со статистической точки зрения, у вас больше шансов попасть в аварию на перекрестке, поэтому я стараюсь проехать через них как можно быстрее!»
Коллега спросил: «Почему вы всегда так быстро проезжаете перекрестки?» На что учитель статистики ответил: «Ну, со статистической точки зрения, у вас больше шансов попасть в аварию на перекрестке, поэтому я стараюсь проехать через них как можно быстрее!» - Профессор статистики и профессор математики вместе работали над кулинарной книгой. Они назвали это «Pi A La Mode».
- Математик видит, как три человека входят в здание. Позже она видит, как уходят четыре человека.Когда ее спрашивают, сколько людей в доме, она отвечает: «Ну, если один человек войдет в дом, он будет пустым».
- Почему статистика никогда не бывает чьим-либо любимым предметом? Это просто среднее.
Кредит: Каталог мыслей
- Почему у Pi отозвали водительские права? Потому что он не знал, когда остановиться.
- Никогда не начинайте разговор с Пи.
 Это будет продолжаться и продолжаться вечно.
Это будет продолжаться и продолжаться вечно.
- Что вы получите, если разделите окружность фонаря из тыквы на его диаметр? Тыквенный пи.
- Математик: πr2 (Pi r в квадрате). Бейкер: Нет! Пироги круглые, а торты квадратные!
- Кто был самым круглым рыцарем за столом короля Артура? Sir Cumference. Как он так рассердился? Он съел слишком много π.
- Какое официальное животное в день Пи? Пи-тон!
Кредит: ClassHook
- Как вы называете двух друзей, любящих математику? Algebros.
- Что вы называете 3 в выражении x3? X-компонент
- В выражении 𝑦2, как вы называете 2? А-компонент.
- Вы знаете, почему семь восемь девять? Потому что вы должны есть трижды в день!
- Почему мальчик отказался пить воду с восемью кубиками льда? Потому что он слишком кубовидный!
- Почему у атеистов проблемы с экспонентами? Они не верят в высшие силы!
- Учитель: Что такое 2n плюс 2n? Студент: Я не уверен.
 Для меня это звучит как 4n.
Для меня это звучит как 4n. - Почему растения ненавидят математику? Потому что это дает им квадратные корни.
- Почему алгебра помогает лучше танцевать? Потому что можно использовать алгоритм-ритм!
Кредит: Teepublic
- Почему учебник по математике был таким грустным? Потому что у него было так много проблем.
- Какой математический вид больше всего нравится птицам? Сова-гебра.
- Какие змеи хорошо разбираются в математике? Сумматоры.
- Почему нос не может быть 12 дюймов в длину? Потому что тогда это будет фут.
- Кто король пенала? Правитель.
- Ученик спросил своего учителя, не возникнут ли у него проблемы на предстоящем тесте. Учитель ответил: «Думаю, на тесте у вас будет много проблем».
- Всегда полезно взять с собой математика в поход.
 Они поставляются с парой осей.
Они поставляются с парой осей. - Какой формы нужно всегда остерегаться? Ловушка-азоид!
- Я не понимаю десятичных дробей. Я более неравнодушен к дробям.
- Я знал математика, который не мог позволить себе обед. Он мог биномы.
- Что одна книга по алгебре сказала другой? «Не беспокойте меня, у меня свои проблемы».
- Когда вы все время пропускаете урок по математике, он начинает складываться по-настоящему.
- Что сказала пчела, когда решила проблему? «Улей получил!»
- Какое любимое время года у учителя математики? ЛЕТО!
- Почему математика считается созависимой? Он полагается на других в решении своих проблем.
- На какую математическую задачу немецкие студенты не могут ответить? Знаете ли вы, что такое квадратный корень из 81? 9!
- Как позвонить по номеру, который не может сидеть на месте? Бродячая цифра!
- Что студентка сказала об уравнении, которое не могла решить? «Это сводит меня с ума!»
Занятия не должны быть скучными для учащихся.-reshenie-303.jpg) Есть много способов оживить уроки, кроме банальных математических анекдотов.
Есть много способов оживить уроки, кроме банальных математических анекдотов.
Вот три обучающих стратегии, которые вы можете попробовать, чтобы сделать класс интересным!
1. Обучение на основе игрНе секрет, что многие дети любят видеоигры. Используйте игровое обучение в классе, чтобы оживить уроки и помочь обучению в классе соответствовать потребностям обучения различных детей.
Prodigy — это форма обучения на основе игр, которая уже используется миллионами учителей и учеников по всему миру!
Студенты могут насладиться волшебным миром с захватывающим игровым процессом и одновременно изучать математику.В большинстве случаев ваш класс даже не осознает, что принимает участие в уроках. Все это часть захватывающего мира игры!
Prodigy Интуитивно понятный дизайн позволяет мгновенно отмечать, оставлять отзывы и создавать индивидуальные условия обучения для каждого из ваших учеников. Это увлекательный инструмент для преподавателей, а весь образовательный контент в игре бесплатен для учащихся!
Оцените Prodigy сегодня, чтобы узнать, подходит ли он для вашего класса!
2. Перевернутый класс
Перевернутый класс Перевернутый класс — это индивидуальная стратегия обучения, в которой время выполнения домашних заданий и уроков меняется.Учащиеся проводят время дома, просматривая такие материалы, как видео или записи уроков. Затем они приходят в класс, чтобы работать над заданиями и воплощать идеи в жизнь!
Это означает, что ученики приходят в школу подготовленными, чтобы задавать вопросы и получать помощь от учителей во время уроков.
Это дает студентам возможность учиться в удобном для них темпе. Классное время тратится на улучшение знаний, а не на объяснение основных понятий студентам для самостоятельной работы.
3. Час генияКонцепция «Часа гения» дает учащимся возможность изучить интересующие их темы.Студенты несут ответственность за исследование темы, придумывают проект по ней и затем представляют его классу.
Как учитель, вы можете выделить для своих учеников разное количество времени для работы над своими увлеченными проектами: от пары часов в месяц до свободного времени в течение недели.
Сроки не сдвигаются, и творческий потенциал расцветает, когда учащиеся начинают заниматься своими собственными проектами. Во время «Часа гения» учащимся предоставляется возможность выразить свои увлечения и взять под контроль свое образование.
Заключение: математические шутки для детейМатематика не должна быть скучной. Использование лучших математических шуток в ваших уроках может сделать их более увлекательными и запоминающимися!
Исследование Национальной ассоциации независимых школ показывает, что «к старшей школе от 40 до 60 процентов молодежи не вовлечены». Что еще более важно, «вовлечение студентов все чаще рассматривается как один из ключей к решению таких проблем, как низкая успеваемость, скука и отчуждение, а также высокий процент отсева.”
Используйте наш список из 101 математической шутки, чтобы помочь ученикам увлечься уроками … или, по крайней мере, рассмешить их!
Создайте или войдите в свою бесплатную учетную запись учителя на Prodigy — игровой платформе для обучения математике, которую легко использовать как преподавателям, так и студентам. Он согласован с учебными планами англоязычного мира, его используют миллионы учителей и студентов.
Он согласован с учебными планами англоязычного мира, его используют миллионы учителей и студентов.
6-1 Prime Time — концепции и объяснения
Порядок операций
Общепринятый порядок решения математических задач.Аббревиатура PEMDAS используется, чтобы помочь запомнить порядок шагов.
Пример
- Вычислить любое выражение с скобками .
- Вычислить любую экспоненту .
- Выполните все умножение и деление слева направо.
- Выполните все , сложение, и , вычитание, в порядке слева направо.
(4 + 6) x 2 = (10) x 2
= 20
Распределительная собственность
Свойство распределения показывает, как число может быть записано в виде двух эквивалентных выражений.Число может быть выражено как произведением, так и суммой. Умножение распределяется поверх сложения.-(Modul-chisla)-reshenie-64.jpg) Это может быть полезно для понимания структуры многозначного умножения.
Это может быть полезно для понимания структуры многозначного умножения.
Пример
Prime
Число ровно с двумя множителями: 1 и само число.
Пример
Примеры простых чисел: 11, 17, 53 и 101. Число 1 не является простым числом, так как оно имеет только один делитель.
Все множители числа 11 равны 1 и 11. Все множители числа 17 равны 1 и 17.
Композитный
Целое число с множителями, отличными от него самого, и 1 или целым числом, которое не является простым.
Пример
Некоторые составные числа — 6, 12, 20 и 1001. Каждое из этих чисел имеет более двух факторов.
Все множители 6 равны 1, 2, 3, 6. Все множители 1001 равны 1, 7, 11, 13, 77, 91, 142 и 1001.
Общее кратное
Кратное, общее для двух или более чисел. Наименьшее общее кратное (НОК) 12 и 18 равно 36.
Пример
Первые несколько кратных 5: 5, 10, 15, 20, 25, 30, 35 , 40, 45, 50, 55, 60, 65 и 70 .
Первые несколько чисел, кратных 7: 7, 14, 21, 28, 35 , 42, 49, 56, 63, 70 , 77, 84 и 91.
Из этих списков вы можете видеть, что два общих кратных 5 и 7 — это 35 и 70. Есть и более общие кратные, которые можно найти.
Общие факторы
Фактор, общий для двух или более чисел.Наибольший общий множитель (CGF) 12 и 18 равен 6.
Пример
Число 7 является общим делителем 14 и 35, потому что 7 — это коэффициент 14 (14 = 7 x 2), а 7 — коэффициент 35 (35 = 7 x 5).
Основная факторизация
Произведение простых чисел, дающее желаемое число. Факторизация числа на простые множители уникальна, за исключением порядка множителей. Это основная арифметическая теорема .
Пример
Разложение 360 на простые множители равно 2 x 2 x2 x3 x5.
Хотя вы можете изменить порядок множителей, каждая строка простого продукта для 360 будет иметь три двойки, две тройки и одну 5.
5 математических игр, в которые нужно играть в каждом классе
Гостевой пост Ли Лэнгтон
Привет, ребята! Это Ли из «Пытливого учителя»! Я очень рад вести сегодня блог на Corkboard Connections. Я делюсь практикой, которую использую, чтобы помочь моим ученикам повысить вовлеченность и чувство числа во время блока математики.
Я делюсь практикой, которую использую, чтобы помочь моим ученикам повысить вовлеченность и чувство числа во время блока математики.
Вы играете в игры в классе? Чего ждать?! Нет времени? Что ж … ты должен найти время! Особенно во время занятий математикой.Для меня математика и игры идут рука об руку, как нутелла и крендели. Вкусно по отдельности, но вместе потрясающе.
Как учитель третьего класса, я знаю, насколько ограниченным может быть наше время, поэтому я здесь, чтобы поделиться с вами 5 математическими играми, в которые вы должны найти время, чтобы поиграть в этом году! Все эти игры веселые, легкие и практически не требуют подготовки. Это математические игры, в которые я много лет играл со второклассниками. Когда я поднялся на третье место, я смог легко модифицировать эти игры для моих новых «больших детей».
В эту игру можно играть в классе k-5.Он идеально подходит для развития чувства числа, и единственное необходимое условие — это умение учеников. Для игры не требуется никаких принадлежностей, и моим детям нравилось играть в эту игру, как на «передышку» перед математикой.-(Raskrytie-skobok)-reshenie-544.jpg)
Вот как играть…
Пусть ваш класс встанет в круг. Двигаясь по часовой стрелке, попросите учеников считать вслух, пока они не дойдут до ста. Человек, который говорит «100», садится. Последний выживший, ВЫИГРЫВАЕТ!
Идея проста, но ее можно изменить для ваших учеников.Во втором классе мы будем считать по 5, 10 и 25 (чтобы помочь с деньгами позже в этом году). В-третьих, мы считаем кратные числа. Для чисел, не кратных 100, я выбираю последнее число в последовательности 12 в качестве «конечного числа».
Другие варианты
Учащиеся садятся на определенное число, кратное 7 (например, на число, кратное 7). Ученики не говорят, что число кратное. Студенты могут считать от единиц до ста, но все, кратные, например, 4, «запрещены».«Если студент говорит их, они садятся. Вы также можете изменить его на «Студент не говорит делители» (идеально подходит для тех 4-5-х классов, которым нужно больше практики с их фактами!)
101 и Out…
Эта игра с бумагой и карандашом хорошо работает в классах со второго по пятый класс, и в нее можно играть как командами учеников (например, мальчики против девочек), так и парами.-(Proporcionalnost-velichin)-reshenie-1046.jpg) Для игры вам понадобятся лист бумаги, карандаш и один кубик.Цель игры — набрать как можно ближе к 101, не выходя за рамки или не выходя за пределы поля.
Для игры вам понадобятся лист бумаги, карандаш и один кубик.Цель игры — набрать как можно ближе к 101, не выходя за рамки или не выходя за пределы поля.
Чтобы играть, ученики по очереди бросают кости. Во время броска они могут принять число либо как единицу, либо как десятку. Например, если ученик выбрасывает 5, он может принять это как 5 или 50. Ученики ведут текущий учет своей суммы во время игры.
Мне нравится, как дети начинают формировать стратегию выбора чисел, которые они хотят выпустить в следующий раз. Это отличный способ построить умственные математические стратегии. Чтобы представить эту игру, я обычно играю в нее как «Учитель vs.Класс». Это дает время на моделирование, в то время как дети остаются в процессе. Какой класс не любит бить учителя? Они всегда хотят играть снова, если я выиграю раунд.
Эта игра лучше всего работает на длинных отрезках, поэтому можно играть в несколько раундов. Обычно я люблю использовать ее в начале года как классную игру перед математическими центрами. Тогда это становится легкой и увлекательной игрой для детей в математических центрах.
Назад 2 Назад
Серьезно, без сомнения, любимая игра в моем классе! Эта игра идеально подходит для внутреннего перерыва, так как весь класс может играть одновременно, и все рады игре.
Эта игра требует некоторого «мозгового пота», поэтому она хорошо подходит для 2–5 классов. Есть две разные версии этой игры. Необходимые материалы минимальны: поверхность для письма, письменные принадлежности и кто-то, кто быстро расчитывает математические факты для «звонящего».
Цель игры — угадать номер другого игрока, прежде чем он угадает ваш. Чтобы играть, два ученика подходят к доске и встают спиной друг к другу (отсюда и название). Это позволяет учащимся писать на доске, но не позволяет им видеть номер другого человека.
«Абонент» сообщает: «Нумерация увеличивается». Это означает, что два ученика напишут на доске число по своему выбору. Я обычно играю числами 2–9, чтобы дети не сели в легкий поезд с нулями и единицами, но вы можете играть с числами настолько высокими или низкими, насколько это необходимо для вашей группы детей.
Затем вызывающий абонент называет сумму (для младших школьников) или произведение (3-5-е) двух чисел. Учащиеся используют свое понимание математических фактов, чтобы выяснить, какое число у другого человека складывается или умножается на его число.Первый игрок, который назовет номер другого человека, побеждает в раунде. «Проигравший» выбирает следующего человека, который выйдет за доску.
Пожалуйста, имейте в виду … эта игра может стать немного шумной, так как ученики выигрывают и проигрывают раунды, и почему-то учителя всегда подтягивают, чтобы «очистить» игрока, который слишком долго просидел … Но это очень весело и хорошо стоит 10-20 минут! Лучше повторять упражнения с карточками!
Угадай мой номер
Эта следующая игра очень универсальна и может быть изменена множеством способов! В нее можно играть в детском саду на протяжении всего 5-го класса.Для игры вам понадобится числовая таблица и маркер сухого стирания. В эту игру можно играть всей группой, парами или небольшими группами по 3-4 человека.
Для начала один ученик выбирает номер. Остальные игроки пытаются угадать число, задавая серию вопросов. Учащийся вычеркивает числа, которых не может быть, и обводит числа, которые могли бы быть. Человек, который угадает правильное число, выигрывает и получает возможность выбрать следующее число.
Лучшая часть этой игры — то, что в нее можно играть с ламинированными личными таблицами сотен в небольших группах.
В нее также можно играть как в групповую игру, используя большую таблицу.
Для третьего класса я рекомендую использовать ответы на вопросы, например: «Множится ли оно на 5? Или больше 70? » Чтобы представить игру, я обычно моделирую вычеркивание чисел, когда ученики задают вопросы о числах и помогают связать подсказки, чтобы найти правильное число.
Для детского сада или первого класса вы можете поиграть числовой линией с числами от 1 до 20.Затем ученики могут спросить, больше или меньше число, чем числа в этом диапазоне. В 4–5 классе можно дополнить игру ответами на вопросы вроде: «Делится ли оно на 3?» или «Это кратно 5?» Возможности безграничны! Диапазон времени для игры может составлять от 5 минут до 20 минут, и это можно использовать как игру в перерыве или как быстрый перерыв до или после урока.
Математический факт.
Эта последняя игра хорошо работает в классах с 1 по 5 класс, и лучше всего в нее играть в группах по 2-4 ученика.Все, что нужно для игры, — это карточки с математическими фактами. Вы можете использовать карты сложения, вычитания, умножения или деления. Это просто зависит от того, на каком уровне математических навыков находятся ваши ученики. Мне нравится думать об этой игре как о «Войне за класс», поскольку к этой версии математических фактов применяются правила традиционной карточной игры.
Для игры ученики равномерно распределяют флеш-карты между всеми игроками. Затем на счет «три» все ученики бросают карточки. Карта с наибольшей суммой или произведением выигрывает все карты в игре.Это может быть изменено на наименьшую разницу или частное. Если ученики дают одинаковый ответ, они снова играют друг с другом, и победитель забирает все карты в игре. Студенты играют до тех пор, пока не будут выиграны все карты. Ученик в зависимости от используемых вами карточек. с наибольшим количеством карт в конце — победа. Я считаю, что эта игра лучше всего работает в математических центрах и дает учащимся возможность практиковать математические факты новым и уникальным способом!
Скачать бесплатно с инструкциями по игре
Так что вперед и играйте! Вовлеките своих учеников в обучение в новом году! Если вы не уверены, что запомните все игры, которыми я поделился сегодня, я собрал для вас все инструкции в одном файле.Он доступен в моем магазине TpT!
Ли — жена, мать и учительница из второго класса, а потом из третьего. В настоящее время она проживает в Центральной Флориде, где преподает 7 лет. Когда Ли не преподает и не пишет для своего блога для учителей «Применимый учитель», ей нравится прижиматься к хорошей книге, пробегать несколько миль или проводить время со своей семьей.
MATHS 6 класс, часть 2 страницы школьной тетради 101–150 — Flip PDF Download
БЛОК 26: ДИАГРАММЫ ДИАГРАММЫ В этом блоке вы узнаете о: • сборе данных.• представление данных в виде трех типов диаграмм: пиктограмма, гистограмма и круговая диаграмма • анализ диаграмм. Мы используем диаграммы, такие как пиктограммы, гистограммы и круговые диаграммы, для представления, анализа и интерпретации информации. Они позволяют нам понять, как вещи различаются, и мы можем проводить сравнения. Фрукты Предпочтение Владение домашними животными Фрукты Количество детей кошки птицы Виноград Бананы Обозначение: 2 ребенка 1350 450 Апельсины Личис 1800 Яблоки собаки Покупатели в супермаркете Предпочтение напитков Чай 300 275 Молоко 250 Газированные напитки 225 Напитки 200 Сок 175 0 5 10 15 20 25 30 35 40 45 50 150 125 Количество детей 100 Напитки 75 50 Количество посетителей 25 0 Понедельник Вторник Среда Четверг Пятница Суббота Воскресенье Дни ataМы можем собирать данные разными способами.Например: (i) мы можем бросить кубик и отметить, сколько раз мы получаем числа 1, 2, 3, 4, 5 и 6. (ii) Мы можем провести опрос в нашем классе, чтобы выяснить, какого цвета ученики нравится больше или меньше. (iii) Мы можем собирать данные об окружающей среде, например, количество осадков за неделю. 95
ДИАГРАММЫ Напоминание Пиктограмма использует изображения для представления информации.Пример: количество учеников в каждом классе небольшой школы показано в таблице ниже. Класс № учеников 1 35 2 40 3 35 4 30 5 20 6 25 Мы можем изобразить вышеуказанную информацию в виде пиктограммы, выбрав подходящий ключ. Например, мы можем использовать символ для обозначения 10 учеников. Таким образом, представляет 5 детей. Класс № учеников 1 2 3 4 5 6 (a) Чем таблица отличается от пиктограммы? (б) Какую информацию вы можете получить с помощью пиктограммы? большинство, минимум, меньше, больше, сколько / намного больше, сколько / много меньше, то же самое, что и 96
ДИАГРАММЫ1.Масса рыбы, продаваемой торговцем рыбой в течение недели, составляет: понедельник: 40 кг, вторник: 24 кг, среда: 12 кг, четверг: 32 кг, пятница: 16 кг. (A) Используйте приведенную выше информацию, чтобы приготовить таблица. (b) Используйте таблицу, чтобы нарисовать пиктограмму. Обозначение: используйте для обозначения 4 кг рыбы 2. Г-н Радж провел эксперимент, чтобы выяснить, в какой день недели выпадает больше всего осадков. Он записал свою информацию в пиктограмме ниже. Условное обозначение: = 5 мм осадков Дни Осадки Понедельник Вторник Среда Четверг Пятница Суббота (a) В какой день выпало больше всего осадков? (B) В какой день было меньше всего осадков? (C) Насколько больше осадков выпало в субботу, чем в понедельник? (D ) В воскресенье выпало на 10% больше осадков, чем во вторник.Изобразите эту информацию на пиктограмме. 97
ГРАФИКИ 3. В 2012 году в Гранд-Бэй открылся новый отель. Пиктограмма ниже показывает количество клиентов, которых он принимал каждый год с момента открытия. Условное обозначение: = 500 гостей Год Гости 2012 2013 2014 2015 2016 (a) Сколько клиентов было у отеля в 2013 году? (B) На сколько клиентов было больше в 2013 году, чем в 2012 году? (C) В каком году отель принимает 3250 клиентов? (d) Сколько клиентов посетили отель с 2013 по 2015 год? 4.В таблице ниже указана сумма, сэкономленная пятью людьми. Имя Пол Мэри Радж Чанг Сам Сумма денег (Rs) 375 150 100 425 500 Используйте подходящий ключ, чтобы представить вышеуказанные данные на пиктограмме. В таблице ниже указано количество рыб в большом аквариуме. Тип рыбы Золотая рыбка Гуппи Длинный хвост Кошка-рыба Platis Number 25 45 30 15 10 Используйте клавишу = 5 рыбок, чтобы отобразить вышеуказанную информацию в виде пиктограммы.IT Corner www.topmarks.co.uk/Flash aspx? F = pictograms98
ДИАГРАММЫ Интерпретация информации на гистограмме В таблице ниже показано количество оценок, полученных Майклом на экзаменах для 6-го уровня. Предмет Математика Английский Французский Естествознание Hist / Geo Оценка 65 90 80 65 85 Информация в таблице представлена в виде столбчатой диаграммы, как показано на рис. 1. Оценки, полученные Майклом Матсом English Subjects French Science Hist / Geo 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95100 Маркировка Рис.1 Внимательно изучите рис. 1 и ответьте на следующие вопросы. (А) По какому предмету Майкл показал себя лучше всего? (Б) На сколько больше оценок он набрал по Hist / Geo, чем по математике? (C) Найдите соотношение оценок (d) Каково общее количество баллов, которые Майкл получил за все? (e) Найдите среднее количество баллов, которые Майкл получил на экзаменах. 99
ДИАГРАММЫ Когда вы рисуете гистограмму: (i) дайте название (ii) пометьте оси (iii) выберите подходящий масштаб (iv) начертите полосы одинаковой ширины (v) оставьте одинаковое пространство между последовательными полосами.6. Группа учеников провела опрос о количестве автомобилей, проезжающих мимо их школы в течение трех часов. Они записали информацию ниже. Транспортные средства Легковые автомобили Фургоны Автобусы Велосипеды Мотоциклы Номер 125 75 50 100 175 Используйте подходящий масштаб и нарисуйте столбчатую диаграмму, чтобы представить вышеуказанную информацию. Четыре ученицы в классе миссис Саманты сажали семена фасоли. Через две недели они измерили высоту своих бобовых растений и занесли свои результаты в таблицу ниже. Ученики Фил Сами Бен Лам Высота растений в см 10 8 4 6 Нарисуйте столбчатую диаграмму, чтобы представить информацию и ответить на следующие вопросы.(а) Насколько выше растение Лама вырастало, чем растение Бена? (б) Насколько короче растение Бена, чем растение Сами? (в) Если бы растение Фила выросло вдвое меньше, чем оно есть на самом деле, какой бы была его высота? ( г) Фил сказал Бену: «Мое растение в два раза выше твоего». Он прав? Объясните, почему.100
ДИАГРАММЫ 8. Изучите гистограмму ниже и ответьте на следующие вопросы. Посетители в Best Restaurant 300 275 250 225 Количество посетителей 200 175 150 125 100 75 50 25 0 Понедельник Вторник Среда Четверг Пятница Суббота Воскресенье Дни (a) Что представляет собой столбчатая диаграмма выше? (B) 300 человек пошли в Best Restaurant в воскресенье.Изобразите эту информацию на столбчатой диаграмме. (C) В какой день ресторан посетило наименьшее количество посетителей? (D) В какие два дня такое же количество людей посетило лучший ресторан? (E) В какой день ресторан посетил получить вдвое больше посетителей, чем в среду? (е) Сформулируйте вопрос, на который можно было бы ответить с помощью графика. (ж) Лучший ресторан всегда привлекает больше посетителей в воскресенье. Вы можете найти этому объяснение? 101
НапиткиКАРТЫ 9.Гистограмма на рис. 2 показывает напитки, предпочитаемые группой детей. Напитки Предпочтение Чай Молоко Газированные напитки Сок 0 5 10 15 20 25 30 35 40 45 50 Количество детей Рис. 2 (а) Какой напиток предпочитает большинство детей? б) Сколько детей предпочитают молоко? в) Сколько еще детей предпочли сок чаю? (d) Выразите количество детей, предпочитающих чай, в процентах от числа детей, предпочитающих газированные напитки.(e) Найдите отношение количества детей, предпочитающих молоко, к количеству детей, предпочитающих сок. (f) Сколько детей было в группе? 102
ТАБЛИЦЫ10. На гистограмме ниже показано количество учеников в 5 секциях 6 класса в школе. Количество учеников в каждом разделе 6-го класса Количество учеников 45 40 35 30 25 20 15 10 5 Красный Синий Желтый Зеленый Белый Разделы (а) В каких двух разделах обучается одинаковое количество учеников? (Б) Сколько учеников в разделе Желтый ? (c) Насколько больше учеников в разделе «Синий», чем в разделе «Белый»? (г) Учитывая, что в разделе «Оранжевый» 26 учеников, добавьте шестой столбец к таблице.(e) Рассчитайте среднее количество учеников в классе. (f) Еще четыре ученика присоединяются к секции Red. Изобразите эту информацию на гистограмме. IT Corner www.topmarks.co.uk/Flash.aspx?=barchartv 103
ДИАГРАММА Круговая диаграмма Найла, Хлоя и Ким-Си делят пиццу, как показано на рис. 3. Пицца разделена на 8 равных частей. Хлоя Наиля Ким — см. Рис.3 8 долей 1 целое 8 долей 3600 1 доля 3600 = 450 Кол-во частей 8 1 ученик Фракция пиццы Угловая Наиля 3450 Хлоя 1 Ким-Си 4 8 3 x 450 = 1350 4 x 450 = 1800 3 8 4 или 1 8 2Мы также можем рассчитать угол Например: Naila: 1 x 3600 = 450 Chloe Naila 8 1350 450 Chloe: 3 x 3600 = 1350 8 1800 4 8 Kim-SeeKim-See: x 3600 = 1800 Рис.4 Диаграмма, показанная на рис. 4, называется круговой диаграммой. Это позволяет нам сравнить доли троих детей.104
ДИАГРАММЫ Остановить и подумать Типы мороженого, предпочитаемые группой из 100 детей, показаны в таблице ниже: Тип Количество детей Ванильное 25% Шоколадное Более 50% Мятное очень small number Strawberry 10 childrenМы можем представить информацию в таблице в виде круговой диаграммы.Сопоставьте виды мороженого с частями круговой диаграммы. Интерпретация информации на круговой диаграмме • Сумма углов на круговой диаграмме равна 3600. • Круговую диаграмму можно понять с точки зрения долей. • Мы используем пропорции для сравнения углов и соответствующих долей. • Мы можем представить каждую акцию в виде дроби или процента. • Мы можем сравнить доли на круговой диаграмме, используя соотношение. Пример: круговая диаграмма на рис. 5 показывает, как Дираджен потратил свои деньги на покупку канцелярских принадлежностей (линейка, ручка, ластик и карандаш).Он потратил 15 рупий на покупку линейки. (а) Рассчитайте угол x. б) Сколько он потратил на покупку карандаша? в) Сколько денег он вообще потратил? г) Какую часть своих денег он тратит на правителя? д) Какой процент своих денег он тратит на ручку? (е) Найдите соотношение денег, потраченных на ластик, к деньгам, потраченным на карандаш. 105
ДИАГРАММЫ (a) Сумма углов на круговой диаграмме равна 3600.ластик Сумма известных углов = 900 + 1800 + 600 = 3300 карандашей x = 3600 — 3300 = 300 x 600 (b) Мы используем пропорцию для сравнения углов 900 линейки и соответствующих долей. Угол, соответствующий карандашу, равен 600. 1800. Сначала мы находим соотношение между углом и долей. Угол, соответствующий линейке, равен 900. ручка Сумма, соответствующая линейке, составляет 15 рупий.Следовательно, Рис.5 900 рупий 15 10 15 рупий 90 600 рупий 15 x 60 = 10 рупий 90 (c) Сумма денег, которую Дираджен потратил в целом, соответствует 3600. 10 15 90 рупий 3600 рупий 15 x 360 = 60 рупий 90 (d) Метод 1 Метод 2 Общая сумма потраченных денег: 60 рупий Сумма углов = 3600 Угол, представляющий линейку = 900 Сумма денег, потраченных на линейку: 15 рупий Доля = 900 = 1 Доля денег, потраченных на линейку: 15 = 1 3600 4 60 4 (e) Общая сумма потраченных денег: 60 рупий Сумма денег, потраченных на ручку: 30 рупий Процент денег, потраченных на ручку: 30 x 100% = 50% 60 (f) Деньги, потраченные на ластик: 5 рупий, деньги потрачено на карандаш: 10 рупий Соотношение денег, потраченных на ластик, к деньгам, потраченным на карандаш, составляет 5: 10 = 1: 2.106
ДИАГРАММЫ 11. На круговой диаграмме показаны фрукты, которые предпочитает группа из 120 детей. (A) Какие фрукты нравятся детям (i) больше всего (ii) меньше всего? (B) Сколько детей предпочитают клубнику? (C) Сколько детей предпочитают груши ? Манго 1500 (d) Сколько детей предпочитают яблоки манго? 1200 Яблоки (д) Какая часть детей предпочитает яблоки? 300 600 груш клубника 12.На круговой диаграмме показан выбор напитков группой из 54 учеников. (A) Найдите угол y. (B) Какая часть группы предпочитает чай? (C) Сколько детей предпочитают воду молоку? Вода Фруктовый сок y 1000 800 600 Чай с молоком 13.В зале 540 человек. На круговой диаграмме показано количество взрослых и детей в зале. (A) Рассчитайте угол x. (B) Каково соотношение взрослых и детей? Дети 1200 x Взрослые 14. 36 учеников 4-х классов спросили, какие предметы они предпочитают.Информация представлена на круговой диаграмме ниже. Hist / Geo Science 1200 600 300 600 Французский математик Английский 107
ДИАГРАММЫ Ответьте на следующие вопросы: (a) Найдите количество учеников, которые предпочитают математику.б) Сколько еще учеников предпочитают хист / гео математике? (c) Учитывая, что французский и английский языки предпочитает одно и то же количество учеников, найдите, какая часть класса предпочитает французский язык? (d) Укажите количество учеников, предпочитающих английский язык, в процентах от общего числа учеников. (e) Найдите отношение количества учеников, предпочитающих естественные науки, к количеству учеников, предпочитающих Hist / Geo. 15. На круговой диаграмме ниже показано, как г-н Пол потратил свои деньги в декабре прошлого года. Транспортировка y Подарки 720 1440 Аренда еды x Одежда Ответьте на следующие вопросы: (a) Учитывая, что Mr.Пол потратил на еду 7 500 рупий, подсчитайте общую сумму денег, которую он потратил в декабре. б) на одежду он потратил вдвое больше, чем на транспорт. Рассчитайте угол x и угол y. в) Сколько денег он потратил на подарки? (d) Выразите сумму, потраченную на транспорт, как долю суммы, потраченной на питание, уменьшенную до минимального значения. IT Corner www.mathplayground.com/piechart.html108
ДИАГРАММЫ Непрерывная оценка1. В таблице ниже показано количество денег, потраченных Ашвини на овощи.Овощи Помидоры Огурец Морковь Тыква Количество (Rs) 100 50 25 75 Используя подходящий масштаб, нарисуйте столбчатую диаграмму, чтобы представить вышеуказанную информацию. В супермаркете был проведен опрос, чтобы выяснить, какие вкусы мороженого предпочитают дети в возрасте 5-11 лет. Предпочтение мороженого 50 45 Количество детей 40 35 30 25 20 15 10 5 0 Kulfi Strawberry Dame Blanche Шоколад со вкусом мороженого (a) Сколько детей предпочитают Dame Blanche? (B) На сколько меньше детей предпочитают шоколад Kulfi? (C) Какие большинство детей предпочитали вкус? (г) Найдите отношение количества детей, которые предпочли шоколад, к количеству детей Дам Бланш.(e) Сколько детей участвовало в опросе? (f) Если бы вы были владельцем супермаркета и хотели бы продавать мороженое только двух разных вкусов, какие два вкуса вы бы выбрали? Обосновать ответ. 109
ДИАГРАММЫ 3. Пиктограмма ниже показывает количество тыкв, собранных пятью фермерами. Ключ: = 50 тыкв Имя Кол-во тыкв Раджен Салим Бернард Ах Тонг Джоэл (a) Кто собрал наибольшее количество тыкв? (B) Сколько тыкв собрал Салим? (C) Кто собрал 250 тыкв? (D) Назовите фермеров кто собрал столько же тыкв.(e) Найдите среднее количество собранных тыкв. 4. Круговая диаграмма представляет количество шариков, которые есть у Бена, Тома и Кришны, у Кришны — 20 шариков, у Бена — 24 шарика, у Тома — 16 шариков. Криш Бен (a) Какую долю от общего количества шариков c b представляют шарики Тома? (b) Найдите угол a, угол b и угол c. Том5.На круговой диаграмме показано количество денег, потраченных четырьмя людьми в воскресенье. (A) Ширли потратила 720 рупий. Сколько потратил Пол? (B) Найдите угол p. Ширли (c) Сколько денег они всего потратили? (D) Выразите потраченные Полом деньги как процент Vimla 600 от общей суммы потраченных денег. 1200 720 Paul p Raj110
БЛОК 27: COCOORODRINDIANTAETESSAANNDD LLIINNEEGGRARPAHPSHS В этом блоке вы научитесь: • определять точки на графике.• рисовать и интерпретировать линейные графики. В истории и географии мы используем сетку для определения местоположения таких объектов, как реки, сахарные заводы или больницы. Задание 1: Расположение объекта на сетке. Помогите пирату Джонасу найти свое сокровище и распознать различные объекты. объекты на карте (рис. 1). 3 2 1 A B C D Рис. 11. В каком квадрате изображены следующие элементы: (i) флаг (ii) кит (iii) камни? 2.Где находится клад? 3. Нарисуйте звезду в A2. Задание 2: Нарисуйте карту сокровищ. Нарисуйте карту сокровищ, используя сетку, предоставленную вашим учителем. Опишите, где расположены различные объекты. 111
КООРДИНАТЫ И ЛИНИЙНЫЕ ГРАФИКИ Задача 3: Найдите объект в рядах и столбцах. Схема рассадки ниже показывает расположение учеников в классе 6. Ясин Дан Зара Эша Гаэль Строка 4 Фредерик Бала Лим Уджала Вайса Строка 3 Амина Веда Сунил Реаз Джейн Строка 2 Наваз Седрик Юшрин Пегги Том Строка 1 Колонка 1 Колонка 2 Колонка 3 Колонка 4 Колонка 5 Рис.2 Можете ли вы описать положение Сунила в терминах столбцов и строк? Сунил сидит в столбце 3 и строке 2. Таким образом, его положение можно описать в следующем порядке: (3, 2). Точно так же мы можем определить положение других учеников. Имя учеников Столбец Строка Позиция Сунил 3 2 (3, 2) Том Бала Джейн Седрик Наваз Остановитесь и подумайте. Сравните местоположения Сунила и Балы.Положение Сунила — (__, __), а Бала — (__, __). В обоих случаях у нас есть числа ___ и ___, но в разном порядке. способ изобразить расположение учеников в упражнении 3 (рис. 2) — использовать квадрат / миллиметровую бумагу. Квадратная бумага состоит из горизонтальных линий, обозначающих строки, и вертикальных линий, обозначающих столбцы. Ось y 654321 0 1 2 3 4 56 Ось x происхождение Рис.3 Синяя горизонтальная линия на рис. 3 называется осью X. Красная вертикальная линия на рис. 3 называется осью Y. Точка пересечения обеих линий называется началом координат. Мы используем первую букву имен в Рис. 2 для изображения учеников. Например, Nawaz представлен буквой Ny-axis6543B (3, 2) 2 SJ1 NC T 0 1 2 3 4 56 x-axisorigin Рис. , 2).На сетке было представлено местоположение Сунила точкой (3, 2). 3 — координата x, а 2 — координата y точки S. Постройте координаты для других зрачков на рис. 4. 113
КООРДИНАТЫ И ЛИНИЙНЫЕ ГРАФИКИ 1. Запишите координаты точек A, B, C, D, E, F и O. Ось y 5 4E F 3B 2 1C A 0 1 2 D 56 Начало координат оси x 342.(a) Постройте точки P (4, 0), Q (2, 4), R (4, 6) и S (6, 4). Соедините точки P, Q, R и S. (b) Какую форму имеет фигура PQRS? (c) Проведите линию симметрии фигуры. y 5 4 3 2 1 0 1 2 3 4 56 x начало координат 3. (a) Используя квадратную бумагу, нанесите точки A (2, 1), B (3, 4), C (4, 7), D (5 , 4) и E (6, 1). Соедините A с C, C с E и B с D. (b) Какой алфавит вы получите? 4. (a) Используя бумагу в квадрате, нанесите точки K (2, 2), L (8, 2), M (10, 5) и N (4, 5).(b) Нарисуйте фигуру KLMN. (c) Какой формы фигура KLMN? 5. (a) Нарисуйте точки C (3, 9), D (1, 6), E (3, 1) и F (5, 6) на бумаге в квадрате. (b) Нарисуйте фигуру CDEF.114
КООРДИНАТЫ И ЛИНИЙНЫЕ ГРАФИКИ6. PQRS представляет собой ромб с P (5, 1), Q (0, 4) и R (5, 7). (а) Изобразите точки P, Q и R на бумаге в квадрате. (b) Отметьте точку S и запишите ее координаты. (c) Проведите линии PQ, QR, RS и SP. (d) Проведите линии симметрии ромба. (e) Линии симметрии пересекаются в T.Запишите координаты T. (f) Найдите площадь ромба. Линия графика Изучите следующий пример: Rapid Motorsports выпустила новую модель спортивного автомобиля. Расход топлива автомобиля показан в таблице ниже. ) 1 2 3 4 5 Расстояние (км) 10 20 30 40 50 Мы можем отобразить вышеуказанную информацию в виде линейного графика. (I) Запишем соответствующие значения в таблице в виде координат: (1, 10), (2, 20), (3, 30), (4, 40) и (5, 50). (Ii) Мы наносим точки на миллиметровую бумагу. (Iii) Мы проводим линию через точки и получаем прямую линию.Полученный график называется линейным. Расстояние (км) (5, 50) (4, 40) (3, 30) (2, 20) (1, 10) Расход топлива (л) 115
Стоимость (рупий) КООРДИНАТЫ И ЛИНИЙНЫЙ ГРАФИК Стоимость (Rs) Интерпретация линейного графика Пример: На линейном графике ниже показана стоимость муки в супермаркете ABC.40 30 20 10 01 2 34 Масса муки (кг) 1 Используйте линейный график, чтобы найти (i) стоимость 2 2 кг муки, (ii) массу муки, которую можно купить за 35 рупий, (iii) стоимость 8 кг муки.40 PQ 30 DC 20 10 0 1 2 B 3 R4 Масса муки (кг) 116
КООРДИНАТЫ И ЛИНИЙНЫЕ ГРАФИКИ (i) На оси абсцисс находится масса, представляющая 21 кг (обозначена буквой B). 2 Мы рисуем вертикальную линию, параллельную оси Y, чтобы разрезать линейный график в точке C.В точке C мы проводим горизонтальную линию, параллельную оси x, чтобы разрезать ось y в точке D. В точке D мы принимали стоимость 25 рупий, стоимость 21 кг муки составляет 25 рупий. мы находим 2 (ii) Аналогичным образом мы проводим линии PQ и QR и считываем массу в R. 1 Таким образом, за 35 рупий мы можем купить 3–2 кг муки. (iii) Мы не можем найти стоимость 8 кг муки. прямо из графика, а вот стоимость 1 кг муки можно узнать из графика.1 кг муки стоит 10,8 рупий. Кг муки стоит 10 x 8 = 80,7 рупий. График показывает почасовую оплату заводского рабочего. 400 300 Заработная плата (рупии) 200 100 01 2 34 часа (h) Используйте график, чтобы ответить на вопросы ниже. (A) Сколько он зарабатывает, если работает 4 часа? (B) Сколько он получает за 2 1 h работы? (c) h 2 работы. Подсчитайте его заработную плату в размере 7 1 2 из (d) Как долго он будет работать в субботу, если получит 350 рупий? 117
КООРДИНАТЫ И ЛИНИЙНЫЕ ГРАФИКИ 8.На линейном графике ниже показана цена на фасоль. Используйте график, чтобы ответить на вопросы ниже. Стоимость (Rs) 80 70 60 50 40 30 20 10 01 2 34 Масса фасоли (кг) (a) Сколько стоят 3 кг фасоли? (B) Сколько килограммов бобы можно купить за (i) 32 рупия (ii) 128 рупий? (c) Найдите стоимость 13 1 кг бобов.2 1 (d) Амрита купила 8 2 кг бобов и заплатила банкнотой в 200 рупий. Сколько сдачи она получила? 9. (а) Заполните таблицу. Длина 1 стороны (см) 23456 Периметр квадрата (см) 8 12 20 (b) Нарисуйте линейный график на бумаге в квадрате, чтобы показать взаимосвязь между периметром квадратов (по оси Y) и их сторонами (по оси x). -оси) .118
КООРДИНАТЫ И ЛИНИЙНЫЕ ГРАФИКИ Непрерывная оценка 1.ABCD — прямоугольник. Координаты A, B и C равны (3, 2), (3, 6) и (10, 6) соответственно. (a) Изобразите точки A, B и C на бумаге в квадрате. (b) Отметьте точку D и запишите ее координаты. 2. Нарисуйте на бумаге квадраты точки A (2, 3), B (4, 8), C (9, 6) и D (7, 1). (a) Проведите прямые AB, BC, CD и DA. (б) Какой формы фигура ABCD? (c) Сколько линий симметрии у ABCD? (d) Найдите площадь рисунка ABCD.3. Линейный график показывает соотношение между количеством купленных апельсинов и их стоимостью.Стоимость (рупий) 40 35 30 25 20 15 10 5 0 1 2 34 56 7 8 Количество апельсинов (a) Используйте линейный график, чтобы заполнить приведенную ниже таблицу. Количество апельсинов 1 4 Стоимость (Rs) 15 (b) Найдите стоимость 7 апельсинов. (C) Сколько апельсинов можно купить за (i) 45 рупий (ii) 125 рупий? 119
КООРДИНАТЫ И ЛИНИЙНЫЕ ГРАФИКИ 4.На линейном графике ниже показаны цены на груши в супермаркете. Стоимость (Rs) 200 175 150 125 100 75 50 25 0 12 3 4 Масса груш (кг) (a) Сколько стоит 1 кг груш? 2 (b) Сколько килограммов груш можно купить за 125 рупий? (C) Сколько стоит 7.5 кг груш? (Г) Рина купила 4,5 кг груш и получила 275 рупий в качестве сдачи. Она использовала записку для оплаты. Какой купюрой она использовала для оплаты? 5. В течение определенного периода года 1 евро (1 евро) обменивался на 40 рупий. Заполните приведенную ниже таблицу. Евро (€) 135 рупий (Rs) 80 160 (a) Нарисуйте линейный график для представления вышеуказанной информации. (B) Используйте линейный график, чтобы найти эквивалент (i) 360 рупий (ii) 400 рупий (iii) 7 € (iv) 12 €.120
БЛОК 28: ОБЪЕМ ОБЪЕМ В этом блоке вы узнаете: • об объеме кубов и кубоидов. • о решении задач, связанных с объемом. Объем объекта — это объем пространства, которое он занимает. 4 м 3 м 5 м Резервуар Mare aux Vacoas Объем бетона = 6 м3 Объем контейнера = 60 м3 Объем воды = 26 миллионов м3 В блоке 19 для измерения площади 2D-поверхности мы подсчитали количество единичных квадратов (например.г., см2, м2), которые помещаются на нем. Аналогично, чтобы измерить объем трехмерного объекта, мы подсчитываем количество единичных кубов, которые в него помещаются. Единичные кубы Есть 2 типа единичных кубов: 1-см куб (1 см3) и куб длиной 1 м (1 м3). Куб длиной 1 см называется кубом размером 1 см, а куб длиной 1 м — кубом размером 1 м. 1м 1 см1 см 1 см 1м 1м Объем куба с ребром 1 см составляет 1 кубический сантиметр или 1 см3.Объем куба с ребром 1 м составляет 1 кубический метр или 1 м3. Мы используем куб размером 1 см для измерения пространства, занимаемого мелкими объектами. Мы используем куб размером 1 м для измерения пространства, занимаемого большими объектами. 121
ТОМ1. Найдите объем каждого из следующих твердых тел. Каждый занимает пространство в 1 см3, то есть объем каждого куба равен 1 см3. (A) Количество кубиков = Объем = см3 (b) Количество кубиков = Объем = см3 (c) Количество кубиков = Объем = см3 Остановитесь и подумайте, нужно отправить другу две посылки (рис.1 и 2) по почте. 10 см 20 см 30 см 30 см 40 см 80 см Рис. 1 Рис. 2 Сравните пространство, занимаемое двумя участками.122
ОБЪЕМНОСТЬ 1: Измерение пространства, занимаемого кубом1. Вырежьте шаблон в Приложении (A2 (ii)) и приклейте его на бристольскую бумагу. 2. Вырежьте по красным линиям 3.Сложите и приклейте шаблон в виде куба (рис. 3) 4. Аналогичным образом вырежьте шаблон в Приложении (A1), чтобы сделать кубики длиной 1 см (рис. 4). 5. Поместите кубики размером 1 см в большой куб, чтобы сформировать первый слой (рис. 5). кубиков по ширине рис. 5? (c) Сколько кубиков в первом слое? 6. Положите еще кубики размером 1 см, чтобы сформировать второй и третий слой.(г) Сколько кубиков по высоте? (д) Сколько кубиков размером 1 см заполняют пространство в кубе на рис. 5? Объем куба — это объем пространства, которое он занимает. В этом примере 27 единичных кубов (1 см3) занимают все пространство (большого) куба. Мы говорим, что куб имеет объем 27 см3 (рис. 6). Объем куба = длина x ширина x высота = 3 см x 3 см x 3 см = 27 см3 Рис. 6 123
ОБЪЕМ 2: Измерение занимаемого пространства кубоидом Повторите шаги действия 1, чтобы построить кубоид, используя шаблон, приведенный в Приложении (A2 (ii)).Кубоид имеет размеры 3 см на 4 см на 2 см. 1. Поместите кубики диаметром 1 см в кубоид, чтобы образовался первый слой (рис. 7). а) Сколько кубиков по длине кубоида? б) Сколько кубиков по ширине кубоида? (c) Сколько кубиков в первом слое? Рис. 72. Поместите кубики диаметром 1 см в кубоид, чтобы сформировать второй слой (Рис. 8). а) Сколько кубиков по высоте? б) Сколько всего кубиков? Инжир.8 Объем кубоида — это объем занимаемого пространства. В этом примере в него помещается 24 единичных куба (1 см3). Кубоид имеет объем 24 см3. Объем кубовида = длина x ширина x высота = 4 см x 3 см x 2 см = 24 см3. Пример 1 Сколько кубов размером 1 см необходимо, чтобы сделать кубоид длиной 6 см и шириной 3 см. и высотой 2 см? Количество необходимых кубиков размером 1 см: По длине = 6 По ширине = 3 По высоте = 2 Количество необходимых кубиков диаметром 1 см = 6 × 3 × 2 = 36 Объем куба = 36 × 1 см3 = 36 см3 или Объем куба = длина × ширина × высота = 6 см × 3 см × 2 см = 36 см 3124
ОБЪЕМ 2.Сколько кубиков размером 1 см нужно, чтобы получился реберный куб: а) 5 см, б) 9 см? 3. Заполните таблицу. Край куба Количество кубиков размером 1 см Объем куба 3 см 27 3 см x 3 см x 3 см = 27 см3 4 см 6 см 10 см4. Найдите объем ребра куба в м3: (a) 7 м (b) 2,5 м (c) 3 14 м. 5. Найдите объем кубоида длиной 10 см, шириной 6 см и высотой 4 см. 6. Найдите объем коробки длиной 2 м, шириной 1,5 м и высотой 0,5 м. 7. Заполнить таблицу.Длина кубоида Ширина кубоида Высота кубоида Объем кубоида 4 см 3 см 2 см 9 см 7 см 315 см3 12 см 10 см 1680 см3 8 см 4 см 224 см38. Объем прямоугольного металлического блока длиной 40 см и шириной 30 см составляет 9600 см3. Найдите высоту металлического блока.9. Объем пластикового контейнера высотой 12 см и длиной 52 см составляет 12480 см3. Найдите его ширину 10. Найдите объем куба с ребром 0,4 м в см3. 11. Заполните таблицу.Длина кубоида Ширина кубоида Высота кубоида Объем куба 3м 2,5 м 0,5 м м3 4 м 300 см м м 0,5 м 8 м 40 м3 90 м3 125
ОБЪЕМ 12.Объем кубоида высотой 8 см составляет 1 440 см3. Ширина кубоида равна 1 из 5 его длины. Вычислите длину кубоида 13. Кубовид имеет объем 2 430 см3. Его высота 10 см. Отношение его длины к его ширине составляет 3: 1. Вычислите длину кубоида. 14. Длина одного края куба 8 см. Объем куба длиной 32 см и шириной 20 см в 4 раза больше куба. Найдите высоту кубоида.15. Вычислите объем в см3 кубоида длиной 0,9 м, шириной 0,4 м и высотой 0,3 м. 16. Объем воды в бассейне длиной 7,5 м и шириной 4,5 м составляет 50,625 м3. Рассчитайте его глубину 17. Мишель находит два аквариума в зоомагазине. Бак А имеет размеры 30 см на 22 см на 18 см. Бак B 25 см на 20 см на 15 см. (i) Если Мишель хочет купить бак большего объема, какой бак ей следует купить? (ii) Найдите разницу между объемами двух резервуаров. Отношение ширины кубоида к его высоте 5: 4.Его высота 16 см. Отношение высоты к длине 2: 7. Найдите объем кубовида.19. Из бруска вынимается кусок дерева в форме куба. Какой объем древесины остался? 2,2 м 0,8 м 2 м 3 м 4m126
ОБЪЕМ 1-см куб 2-см куб 3-см куб 4-см куб Куб длиной 2 см называется 2-сантиметровым кубом.Куб длиной 3 см называется кубом 3 см. Куб длиной 4 см называется кубом 4 см. Установка кубиков в ящик Пример 1: Кубики с ребром 5 см помещаются в ящик размером 25 см на 20 см. на 15 см (рис.9). 15 см 5 см 5 см 5 см 25 см 20 см Рис. 9 Сколько 5-сантиметровых кубиков поместится точно в коробку? кубиков по длине = 25 = 5 5 кубиков по ширине = 20 = 4 5 шт.кубиков по высоте = 15 = 3 5 Общее количество 5-сантиметровых кубиков = 5 x 4 x 3 = 60 127
ОБЪЕМ 20. Сколько кубиков размером 3 см нужно, чтобы получился куб с ребром 12 см? 21. Сколько кубиков ребра 2 см нужно, чтобы построить куб 10 см на 8 см на 6 см? 22. Сколько кубиков кромки 5 см точно поместится в прямоугольной коробке 30 см на 25 см на 10 см? 23. Прямоугольный металлический блок размером 24 см на 15 см на 9 см расплавляют, чтобы получить кубики с ребром 3 см каждый.Сколько получается таких кубиков? 24. Ящики размером 25 см на 15 см на 12 см помещают в контейнер размером 4,5 м на 3 м на 2,4 м. Подсчитайте максимальное количество ящиков, которое может точно поместиться в контейнере. Пример 2: Кубики с краем 3 см помещают в коробку 18 см на 12 см на 10 см. Рис. 10 Рассчитайте (а) наибольшее количество кубиков, которое может быть помещено в коробку, (б) объем оставшегося незанятого места. Количество кубиков по длине = 18 ÷ 3 = 6 (6 кубиков поместятся точно) Количество кубиков по ширине = 12 ÷ 3 = 4 (уместится ровно 4 кубика) Нет.кубиков по высоте = 10 ÷ 3 = 3 1 (3 куба умещаются по высоте и остается 1 см) 3 (a) Наибольшее количество кубиков, которое может быть помещено в коробку = 6 x 4 x 3 = 72 (b) Объем незанятого пространства = 18 см x 12 см x 1 см = 216 см3 Рис. 11128
ОБЪЕМ 25. Куб с гранью 5 см кладут внутрь кубической коробки с гранью 8 см. Подсчитайте объем оставшейся незанятой площади 26. (а) Сколько кубиков ребра 0,3 м можно поместить в ящик 3.5 м в длину, 2,4 м в ширину и 1,5 м в высоту? (b) Найдите объем свободного пространства. Пример 3: Кубоиды размером 5 см на 4 см на 3 см помещены в коробку шириной 16 см, длиной 25 см и высотой 14 см. Найдите (а) наибольшее количество кубоидов. кубоидов, которые могут быть помещены в коробку, (б) объем, оставшийся незанятым. (а) Чтобы найти наибольшее количество кубоидов, которые могут поместиться в коробке, мы рассматриваем размеры кубоида и коробки, которые точно делятся: Размеры Размер коробки: 16 см x 25 см x 14 см Размеры кубоида: 5 см x 4 см x 3 см16 точно делится на 425 точно делится на 514 не делится на 3, 4 или 5.Кол-во кубов по длине = 25 ÷ 5 = 5 кубоидов по ширине = 16 ÷ 4 = 4 шт. кубоидов по высоте = 14 ÷ 3 = 4 2 (4 кубоида умещаются по высоте и 3 остается 2 см) Наибольшее количество кубоидов, которое может быть помещено в коробку = 5 x 4 x 4 = 80 (b) Объем осталось незанятым = 25 х 16 х 2 = 800 см 327. Ящики размером 40 см на 30 см на 20 см помещают в контейнер длиной 2,1 м, шириной 1,6 м и высотой 1,3 м. (а) Рассчитайте максимальное количество ящиков, которое можно поместить в контейнер.(b) Рассчитайте объем, оставшийся незанятым. 129
ОБЪЕМ Отношение между емкостью и объемом Цилиндр, содержащий 1 мл жидкости, может полностью заполнить куб размером 1 см. 1 мл эквивалентен 1 см3. x 1000 мл 5 1 мл = 1 см3 L ÷ 1000 см3 4 1 L = 1000 мл 3 Следовательно, 1000 мл = 1000 см3 2 1 L = 1000 см3 1 1 см 1 см 1 см x 1000 л м31000 L = 1000 x 1000 см3 = 100 см x 100 см x 100 см ÷ 1000 = 1 м x 1 м x 1 м 1000 L = 1 м3 или 1 м3 = 1000 контейнер LA, 1 м на 1 м на 1 м, вмещает 1000 л воды.28. Заполните таблицу. Объем (л) 7 2 3 4 Объем (см3) 500 1229. Из емкости, содержащей 25 л воды, откачивается 15 500 см3. Сколько литров воды осталось? 30. В ведре 20 л сока. Сколько бутылок объемом 250 см3 можно налить от всего сока? 31. Прямоугольный резервуар размером 50 на 40 на 30 см наполовину заполнен водой.Вся вода наливается в 6 ведер одинаковой вместимости. Найдите вместимость одного ведра в L.32. Заполните таблицу Объем (м3) 2 3,25 5,035 Объем (л) 2500 3750130
ОБЪЕМ 33. Наполовину полный бак вмещает 120 л воды. Рассчитайте высоту бака 80 см 60 см 34. Прямоугольный контейнер длиной 60 см, шириной 40 см и высотой 80 см наполнен соком.Каким образом можно наполнить соком из емкости 4 бутылки объемом 1,5 л? 35. Для полного заполнения бака используется 7 ведер с водой, каждое объемом 5 л. Найдите длину резервуара. 25 см 5L 20 см 236.Аквариум размером 80 см на 60 см на 50 см заполнен водой на 3 штуки. Вся вода сливается во вторую емкость длиной 1 м и шириной 50 см. Второй бак полностью заполнен. Найдите высоту второго резервуара 37. Контейнер длиной 1,4 м, шириной 0,8 м и глубиной 0,5 м наполнен водой. Утечка воды составляет 40 мл в минуту. Через сколько времени бак будет пустым? Дайте ответ в час. 38. Рита наливает 15 л воды из ведра в резервуар длиной 50 см, шириной 30 см и высотой 25 см, который уже был заполнен на глубину 5 см.(i) Какова новая глубина воды в аквариуме? (ii) Сколько воды необходимо для полного заполнения бака? Ответьте буквой L. • Внимательно прочтите задачу, прежде чем производить вычисления. 131
ОБЪЕМ Непрерывная оценка 1. Найдите объем куба с ребром 7 см. 2. Найдите объем кубоида длиной 12 см, шириной 10 см и высотой 8 см. 3. Сколько нужно 7-сантиметровых кубиков, чтобы получился куб с гранью 21 см? 4.Ящик длиной 15 см и шириной 10 см имеет объем 750 см³. Рассчитайте его высоту 5. Резервуар для воды имеет длину 120 см, ширину 100 см и высоту 60 см. Рассчитайте вместимость бака в литрах 6. Общая площадь куба составляет 486 см². Рассчитайте объем куба 7. Куб и кубоид имеют одинаковый объем. Общая площадь куба составляет 600 см². Вычислите (а) длину куба, (б) объем куба и (в) высоту кубоида. 10 см 20 см 8.Прямоугольный деревянный брусок имеет длину 40 см, ширину 28 см и высоту 20 см. Из него вырезаются кубики ребром 4 см. Найдите количество полученных кубиков 9. Танк имеет длину 50 см, ширину 30 см и высоту 20 см. В емкость наливают 24 литра воды. Рассчитайте уровень воды в баке 10. Контейнер длиной 12 см, шириной 10 см и высотой 45 см был заполнен на четверть. После того, как вы вылили сок из бутылки в емкость, она наполнилась на две трети. Найдите объем сока, налитого из бутылки в емкость, в сантилитрах.11. Прямоугольный резервуар длиной 8 м и шириной 5 м был заполнен водой на 25%. Когда Бен налил в бак еще 70 м3 воды, бак наполнился водой на 60%. Найдите высоту цистерны в метрах.132
БЛОК 29: СКОРОСТЬ СКОРОСТЬ В этом блоке вы узнаете о: • скорости (км / ч, м / с). • решении текстовых задач, связанных со скоростью. Вы когда-нибудь видели знак показано на рис. 1 во время путешествия? Что это значит? Автомобиль B Автомобиль A Автомобиль B Автомобиль A Рис.1 Две машины, A и B, едут по дороге (как показано на рисунке выше). Какой автомобиль движется в пределах установленной скорости? Остановитесь и подумайте, если автомобиль C преодолевает 38 км за 30 минут, а автомобиль D — 25 км за 20 минут. , какие тележки едут быстрее? Почему? Скорость в реальной жизни. Скорость этих самолетов Скорость спорткаров больше 150 км / ч. более 500 км / ч. Скорость спортсмена IV класса предупреждения о циклонах составляет 10 м / с.Порыв ветра: 120 км / ч 133
СКОРОСТЬ Скорость — это расстояние, пройденное за единицу времени. Он показывает, насколько быстро что-то движется. Обычно для измерения скорости используется км / ч (километр в час) или м / с (метр в секунду). Расчет скорости, когда указаны расстояние и время Пример 1: Майкл может проплыть 50 метров за 25 секунд Какова его скорость в м / с? Метод 1:25 с 50 м 1 с 50 м = 2 м 25 Майкл преодолевает 2 м за 1 с.Его скорость составляет 2 метра в секунду или 2 м / с. Метод 2: Скорость = D istance = 50 = 2 м / с. Время 25 Простой способ запомнить соотношение между скоростью (S), расстоянием (D) и временем (T). показано на схеме ниже. D ST Пример 2: Микроавтобус едет за 2 часа и преодолевает расстояние 140 км. Какова скорость фургона в км / ч? 2 часа 140 км1 час 140 км = 70 км 2 Микроавтобус преодолевает 70 км за 1 час.Его скорость составляет 70 км в час или 70 км / ч. Или Скорость = Дистанс = 140 = 70 км / ч. Время 2 1. Алан участвует в гонке. Он пробегает дистанцию 100 м за 10 с. Найдите его среднюю скорость в м / с. 2. Автобус преодолевает расстояние 150 км за 3 часа. Найдите его среднюю скорость. 3. Симран пробежал 500 метров за 100 секунд. Найдите ее среднюю скорость в метрах в секунду. 4. За 11 часов самолет пролетает 750 км. Найдите его среднюю скорость. 4 5.Грузовик преодолевает расстояние 35 км от Порт-Луи до Флик-ан-Флак за 50 минут. Найдите его среднюю скорость в км / ч. 6. В гонке Maiden Cup лошадь пробегает 2400 м за 3 минуты. Найдите его среднюю скорость в м / с. 134
СКОРОСТЬ Расчет времени, затрачиваемого с учетом расстояния и скорости Пример: автобус проехал расстояние 120 км со средней скоростью 60 км / ч. Рассчитайте время, затраченное на поездку. 60 км 1 час 2 км 1 60 час 220 км 1 x 120 = 2 часа 60 Затраченное время = Расстояние D Скорость S T = 120 = 2 часа 607.Тина бежит 400 м со средней скоростью 8 м / с. Сколько времени ей понадобится, чтобы преодолеть дистанцию? 8. Найдите время, затрачиваемое поездом, который проезжает 250 км со средней скоростью 75 км / ч. 9. Остров A находится в 600 км от острова B. Корабль движется со средней скоростью 25 км / ч от острова A до острова B. Сколько времени требуется кораблю, чтобы добраться до острова B? Расчет расстояния, когда указаны скорость и время Пример: Среднее скорость велосипедиста 20 км / ч. Найдите общее расстояние, которое он преодолевает за 3 часа. Скорость = 20 км / ч2 ч 20 км3 ч (20 x 3) км = 60 км или Расстояние = Скорость x Время D = 20 x 3 ST = 60 км10.Соня едет со средней скоростью 8 км / ч. Как далеко она уедет, если ездит на велосипеде 1 час? 411. Автомобиль двигался со средней скоростью 75 км / ч. Какое расстояние он прошел за 1 (a) 4h (b) 4 2 h? 12. Велосипедист едет со средней скоростью 20 км / ч. Как далеко он уедет за 45 минут? 135
СКОРОСТЬ 13.Салим покинул Rose Belle в 09:30 и поехал на велосипеде в Bassin Blanc со средней скоростью 40 км / ч. Он достиг Бассен Блан в 10.15. Вычислите расстояние, которое он проехал на велосипеде. Первые 2 часа своего путешествия Рахул едет со средней скоростью 60 км / ч, а остальные 3 часа — со средней скоростью 45 км / ч. а) Какое общее расстояние проделал Рахул за свое путешествие? б) Найдите среднюю скорость Рахула на протяжении всего пути. Заполните следующую таблицу: Средняя скорость Пройденное расстояние Пройденное время 90 км / ч 360 км 50 км / ч 3 1 ч 120 км 4 9 м / с 270 м 100 м / с 450 м 1 1 ч 2 15 с 45 с 16.На соревнованиях спортсмен бросил летающий диск на 140 метров в воздух. В полете диск двигался со средней скоростью 15 м / с. Как долго диск оставался в воздухе? 17. В 05:30 рыбак отправляется на своей лодке из мыса Малерё на остров Габриэль. Он преодолевает расстояние 12 км со средней скоростью 15 км / ч. В какое время он прибывает на остров Габриэль? 18. Автомобиль едет на расстояние 210 км. Первые 112 км он проезжает со средней скоростью 32 км / ч.Остальной путь проходит со средней скоростью 42 км / ч. (а) Найдите общее затраченное время. (б) Найдите среднюю скорость для всего пути. 19. Радж вышел из дома в 8:00 и пошел в школу со средней скоростью 5 км / ч. Его сестра Шалини вышла из дома через 10 минут и поехала в школу на велосипеде. Они оба пришли в школу в 08:30. Вычислите среднюю скорость Шалини.136
SPEED20. Автомобиль, движущийся со скоростью 80 км / ч, преодолевает определенное расстояние за 1 час. Автомобиль возвращается на 2 таким же образом и снижает скорость на 20 км / ч.Сколько еще времени займет машина на обратный путь? 21. Автомобиль преодолевает 60 км за 1 час, а автобус — 24 000 м за 45 2 минут. Найдите соотношение их средних скоростей 22. Отношение средней скорости грузового автомобиля к средней скорости автомобиля составляет 2: 3. Грузовик преодолевает 14 км за 15 минут. Найдите среднюю скорость автомобиля. 23. Расстояние от Cap Malheureux до Souillac составляет 72 км. Рейчел ехала из Cap Malheureux в Souillac со средней скоростью 80 км / ч.Такси также покинуло Кап-Мальерё в то же время и по тому же маршруту до Суйяка ехало со средней скоростью 65 км / ч. Когда Рэйчел подъезжает к Суйяку, насколько далеко отстает такси? Непрерывная оценка1. Обведите правильный ответ. (I) Яшика бежит трусцой со средней скоростью 12 м / с на расстояние 400 м. Сколько времени ей нужно, чтобы преодолеть это расстояние? A 33 1 с B 4 800 с C 0,03 с D 1,8 с 3 (ii) Автомобиль преодолевает расстояние 175 км со средней скоростью 50 км / ч.Найдите время, за которое машина проехала это расстояние. A 2 ч. B 3,5 ч. C 1,5 ч. D 3 ч. (Iii) Эмили катается на роликовых коньках со средней скоростью 6 км / ч. Как далеко она сможет проехать за 2 часа? A 3 км B 12 км C 10 км D 18 км2. Найдите расстояние, которое преодолел самолет, который двигался со средней скоростью 960 км / ч, учитывая, что продолжительность полета составляла 1 час 50 минут. 3. Учитель просит Орели пройти в офис, который находится в 90 метрах от класса. Она добирается до офиса через 45 секунд.Как быстро она бежала? 137
СКОРОСТЬ 4. Ясин дважды пробегает путь длиной 480 м за 8 мин. Рассчитайте его среднюю скорость в м / с. 5. Бен едет из города А в город Б. Два пути он проезжает со скоростью 40 км / ч, а оставшиеся 180 км преодолевает за 3 часа. а) Какое расстояние между городом А и городом Б? б) Какова средняя скорость Бена за все время путешествия? 6.Дев и Бринда хотят ехать на велосипедах из своего района в школу, которая находится в 14,4 км. Бринда добирается до школы за 40 минут. Дев приходит через 20 минут после Бринды. Насколько выше, в м / с, средняя скорость Бринды за всю поездку? 7. Отец Зайны поехал из города А в город Б. Такси также выехало из города А в то же время и ехало по тому же маршруту в город Б. Отец Зайны ехал на 30 км / ч быстрее, чем такси. По прошествии 4 часов отцу Рэйчел оставалось преодолеть 40 км, в то время как такси преодолело только 3 пути.Какая скорость была у такси? 5138
БЛОК 30: РЕШЕНИЕ ПРОБЛЕМ VRINOGBLE2M В этом блоке вы узнаете о: • стратегиях решения проблем. • различные типы задач со словами. В части 1 (блок 15) нашей книги мы проиллюстрировали 5 стратегий решения проблем, а именно: 1. Используйте блоки мышления 2. Нарисуйте диаграмму 3. Угадайте и проверьте4. Работа в обратном направлении 5. Составьте таблицу Теперь мы проиллюстрируем еще 3 стратегии: 6. Найдите шаблон 7. Составьте список 8. Рассмотрим более простой случай Стратегия 6: Найдите шаблон Проблема: 3 августа 2016 года была среда.Какой это был день 18 сентября 2016 года? Разница между двумя последовательными средами составляет 7 дней. Мы можем установить следующую схему: 3, 10, 17, 24, 31, 7, 14, 21 августа, сентябрь, 14 сентября — среда. Поэтому 18 сентября — воскресенье. Стратегия 7: Составьте список Проблема: Площадь прямоугольника составляет 120 см2. Его длина и ширина являются целыми числами. (I) Каковы возможные значения длины и ширины? (Ii) Какая возможность дает наименьший периметр? Мы знаем, что: площадь прямоугольника = длина x ширина Нам нужно найти 2 числа, произведение которых равно 120.То есть нам нужно найти множители 120. (i) Возможны следующие варианты: Ширина (см) Длина (см) Периметр (см) 1 120 242 2 60 124 3 40 86 4 30 98 5 24 58 6 20 52 8 15 46 10 12 44 (ii) Длина 12 см и ширина 10 см дают наименьший периметр в 44 см. 139
РЕШЕНИЕ ПРОБЛЕМ Стратегия 8: Возьмем более простой случай Проблема: у Джоша 9 500 рупий в его ящике для сбережений.Каждую неделю он снимает 450 рупий. Через сколько недель в его ящике для сбережений останется 4 100 рупий? Начнем с более простого случая: предположим, что у Джоша было 100 рупий в его ящике для сбережений, и он снимает 20 рупий каждую неделю. Через сколько недель останется 40 рупий? Если у него осталось 40 рупий, он удалил (100 — 40 рупий) = 60 рупий в целом. Таким образом, количество недель = 60 рупий ÷ 20 рупий = 3. наша исходная задача и используйте те же рассуждения: Более простой случай: 100-40 = 60 60 ÷ 20 = 3 Фактическая задача: 9 500 — 4 100 = 5400 5400 ÷ 450 = 12 Таким образом, количество недель = 12 Если вы хотите научиться плаванию , вы должны погрузиться в воду, и если вы хотите научиться решать проблемы, вы должны решать проблемы.Джордж Поля (известный венгерский математик и профессор математики) 140
РЕШЕНИЕ ПРОБЛЕМ Прямоугольник имеет площадь 72 см2. Его длина и ширина — целые числа. Каковы возможности длины и ширины? Какая возможность дает наименьший периметр? 2. Прямоугольник имеет периметр 28 см. Его длина и ширина — целые числа. Каковы возможности длины и ширины? Какая возможность дает наибольшую площадь? 3. Последняя пятница февраля была 26-го числа.В какой день недели было 1 февраля? 4. Если сегодня четверг, то какой день недели будет через 40 дней? Учитель рисует на доске рисунок, как показано ниже, и просит Жан-Марка продолжить рисунок. Сколько квадратов будет в 7-м дизайне? 6. Бутылка концентрированного апельсинового сока объемом 750 мл смешивается с водой, чтобы получить пятнадцать стаканов по 250 мл разбавленного апельсинового напитка. Сколько воды нужно для приготовления 10 л разбавленного апельсинового напитка? 7. На столе 256 печенек. Первый человек, который приходит, забирает 1 из числа файлов cookie.Второй человек затем 1 из того, что 2 продолжается, как берет 2 осталось. Если этот шаблон, многие люди смогут принимать файлы cookie, пока не останется только один файл cookie? 8. 15 000 рабочих построили корабль «Титаник» за 26 месяцев. Сколько рабочих понадобилось бы, если бы корабль построили за 1 год? То, что что-то сложно, не означает, что вам не следует ПЫТАТЬСЯ. Значит, стоит попробовать ПОТЕРЯ.Автор неизвестен 141
РЕШЕНИЕ ПРОБЛЕМ Практические задачи 2. Сколько шестых в 12? 4. Перевести 250 мл в литры. 1. — 247 = 153 6. 2 x 0 x 152 = 3. Отрезок ленты длиной 8 м. Его разрезают на 16 частей одинаковой длины. Найдите длину одного куска. 5. 8 = 27. Часы Аджива отстают на 2 минуты.Что такое 8. Выразите 450 мл как долю 1 л. Точное время, когда его часы показывают 10:58? 10. На распродаже часы продаются за 3 500 рупий со скидкой 9. Запишите триста тысяч 450 рупий по первоначальной цене. Что было и семьдесят цифр. Первоначальная цена часов? 11. Сейчас 10.15. Который был час 12. Сколько дней осталось на 27 минут раньше? С 5 октября по 31 октября 2016 г.? 13.Элоди родилась в мае 2013 года. Геркузен Николас на 11 месяцев старше 14. Школьный фургон вмещает 15 учеников, чем она. В каком месяце и году было Сколько таких фургонов нужно, чтобы родился Николай? возить 65 учеников? 15. Запишите недостающее число: 16. 2,5 x 7 = 17,5 Найдите значение 250 x 70. 89 x 28 = ____ x 28 + 2817. Запишите семь десятков и восемь десятых 18. Запишите название фигуры цифрами.который не имеет линии симметрии. 19. Сколько дней было с 23-го 20. В классе вдвое больше с февраля 2012 г. по 19 марта 2012 г.? мальчики как девочки. Если в классе 24 ученика, сколько мальчиков и девочек142 в классе?
РЕШЕНИЕ ПРОБЛЕМ 21. Запишите квадратное число от 22. Запишите простые числа 500 и 600.от 80 до 90,23. Запишите дробь от 2 до 24. Сколько полных витков составляет 9. 7 в 15 прямых углах? 14 26. 7 7 1 425. Стрелка, показанная на диаграмме, — 27. 1 л 56 мл 1 x 3 перевернуто через 2 2 вправо углы в направлении против часовой стрелки. Какое новое положение стрелки? Северо-Северо-Запад Северо-ВостокЗапад Восток 28.12 лет 6 месяцев — 8 лет 9 месяцев Юго-запад Юго-Восток Юг 39. Автобус отправляется с автобусной остановки A в 08 46 и 30. Какова общая длина в метрах, прибывает на автобусную остановку B в 11 23. Какую длину из 3 кусков ленты 5,3 м, 3 000 мм было в пути? и 395 см? 31. Рост Мелины 1 м 31 см. 32. Расположите так, чтобы стартовая Мелина была на 8 см выше Симы.Найдите с наименьшим ростом. 1, 0,45, 4, 0,1533. В каждом случае запишите 45 наименование формы: (а) Я — двухмерная фигура. У меня 4 равно 34. Найдите периметр shape.sides, 2 пары параллельных сторон и 2 линии симметрии по 6 см. Кто я? (Б) Я трехмерная фигура. У меня одно квадратное лицо размером 10 см и 12 см и 4 одинаковых треугольных лица. Кто я? 143
РЕШЕНИЕ ПРОБЛЕМ 35.Собака в 3 раза тяжелее кошки. 36. Танк прямоугольной формы, длиной 80 см, длиной 60 см. Собака весит 12 кг. На сколько килограмм собака тяжелее кошки? шириной и высотой 40 см, 4 заполнены водой. а) Сколько литров воды в баке? б) Какой будет новая высота уровня воды, если в резервуар добавить еще 24 л воды? 2 38.Магазин канцелярских товаров продает разные товары37. Екатерина потратила 5 своих денег. цветные ручки. В январе магазин продает 2 шт., То есть 1 282 синих ручки, 3 450 черных ручек, 233 Затем она дала 5 зеленых ручек и несколько красных ручек. 60% от общего количества проданных ручек в январе осталось ее брату. Осталось 36 рупий. Как были черными. Найдите количество красных ручек, проданных в январе.много денег было у Екатерины сначала? 39. Разделив 3 своих денег с 40-летним Иджазом. Торговец купил 240 ананасов 4. У Наваза осталось 60 рупий. Сколько денег за 1600 рупий. Он продал 4 из них по 10 рупий сначала у Наваза? каждый, а остальные по 3 за 25 рупий. Найдите его процентную прибыль.41. Кену 12 лет 4 месяца. Бену 42 года. Копировальный аппарат может печатать на 7 месяцев моложе Кена.Том на 10 1500 копий на 30 мин. Месяцев старше Кена. Найдите сумму: (а) Сколько времени потребуется, чтобы вывести 18 000 возрастов трех детей. копии? (б) Сколько копий он может напечатать за 1 час 45 43. Ученик сидит за 5 минут теста по математике? и должен получить средний балл 90, чтобы иметь оценку A. У ученика средний балл 44. Автобус отправляется из Деревни X в 09 30 и получает 92 балла в первых трех тестах. Что едет со средней скоростью 48 км / ч.это среднее количество баллов, которое он достигает деревни Y в 11:00. После того, как 15 нужно сдать другие 2 теста, чтобы иметь минутку, он покидает деревню Y, чтобы вернуться в класс A? деревня X по тому же маршруту, но увеличивает свою среднюю скорость на 6 км / ч. В какое время 45. В классе из 45 учеников, какова доля автобуса до деревни Y? мальчики к девочкам было 5: 4.


 Нужно понимать всю серьезность предмета. И что еще немаловажно, так это то, что теперь даже родители проявят интерес и смогут поддержать в сложных решениях. ГДЗ рабочая тетрадь по математике 6 класс Потапов, Шевкин — 327 заданий и их подробный разбор содержаться на 109 страницах.
Нужно понимать всю серьезность предмета. И что еще немаловажно, так это то, что теперь даже родители проявят интерес и смогут поддержать в сложных решениях. ГДЗ рабочая тетрадь по математике 6 класс Потапов, Шевкин — 327 заданий и их подробный разбор содержаться на 109 страницах. Работа с графиками: графическое изображение
Работа с графиками: графическое изображение Работа с мерами
Работа с мерами-(Krug-Ploshhad-kruga)-reshenie-681.jpg) Вычитание правильных дробей
Вычитание правильных дробей Знакомство с десятичными знаками
Знакомство с десятичными знаками Более сложные десятичные делители
Более сложные десятичные делители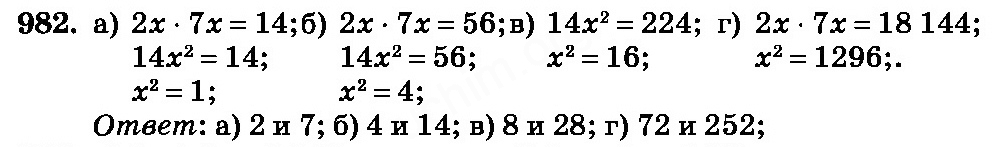 Работа с расстоянием, скоростью и временем
Работа с расстоянием, скоростью и временем-(Delimost-proizvedenija)-reshenie-740.jpg) Умножение мысленно путем изменения процента на дробь
Умножение мысленно путем изменения процента на дробь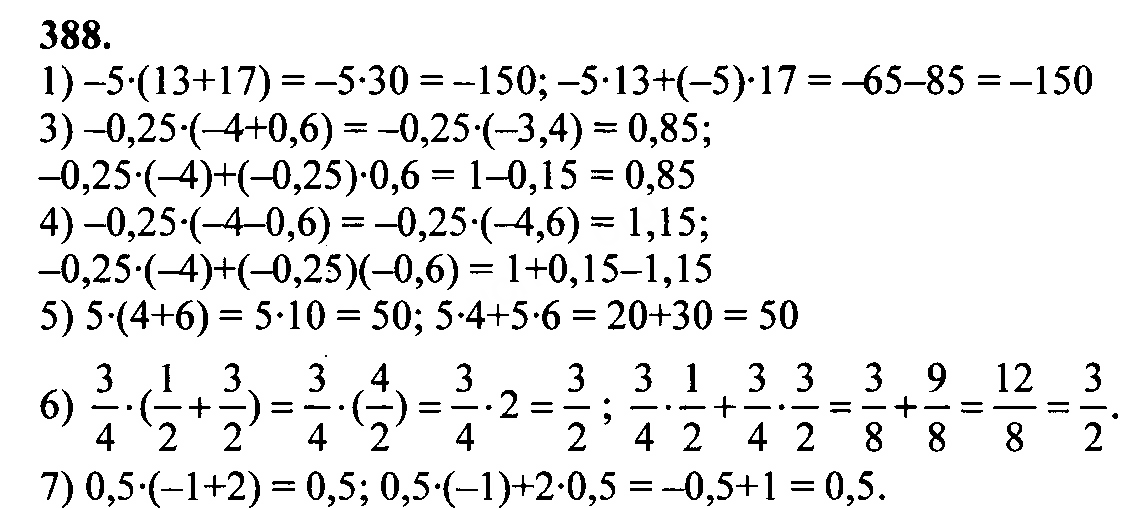 Работа с графиками: линейный график
Работа с графиками: линейный график Использование числовых предложений для решения проблем с чтением
Использование числовых предложений для решения проблем с чтением
-(Umnozhenie-i-delenie-polozhitelnyh-i-otricatelnyh-chisel)-reshenie-387.jpg)
 «Я действительно не люблю деление в столбик, — ответил сын, — мне всегда жаль остаток».
«Я действительно не люблю деление в столбик, — ответил сын, — мне всегда жаль остаток».-(Deliteli-i-kratnye)-reshenie-717.jpg)

 Коллега спросил: «Почему вы всегда так быстро проезжаете перекрестки?» На что учитель статистики ответил: «Ну, со статистической точки зрения, у вас больше шансов попасть в аварию на перекрестке, поэтому я стараюсь проехать через них как можно быстрее!»
Коллега спросил: «Почему вы всегда так быстро проезжаете перекрестки?» На что учитель статистики ответил: «Ну, со статистической точки зрения, у вас больше шансов попасть в аварию на перекрестке, поэтому я стараюсь проехать через них как можно быстрее!»-reshenie-1029.jpg) Это будет продолжаться и продолжаться вечно.
Это будет продолжаться и продолжаться вечно.-reshenie-679.jpg) Для меня это звучит как 4n.
Для меня это звучит как 4n.-(Pravilo-vychislenija-znachenija-algebraicheskoj-summy-dvuh-chisel)-reshenie-273.jpg) Они поставляются с парой осей.
Они поставляются с парой осей.