Математика виленкин 6 класс номер 266: Номер №266 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

Номер 266 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник)

Номер 266 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая версия

Старая версия

ЧАСТЬ 1
Выберите номер упражнения

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897

ЧАСТЬ 2
Выберите номер упражнения

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595

Adblock
detector

ГДЗ учебник 2015.

номер 787 (793) математика 6 класс Виленкин, Жохов – Telegraph

>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<

ГДЗ учебник 2015. номер 787 (793) математика 6 класс Виленкин, Жохов

ГДЗ по математике 6 класс Виленкин учебник . номер — 787 (793 ) . Авторы : Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд . 

Решебник (ГДЗ ) по Математике за 6 (шестой ) класс авторы: Виленкин , Жохов , Чесноков, Шварцбурд издательство Мнемозина, год .  ГДЗ по математике за 6 класс Виленкин , Жохов , Чесноков, Шварцбурд . Учебник Мнемозина (ответы к старому и новому изданию) . 

ГДЗ (готовое домашние задание из решебника) на Номер №787 по учебнику Математика . 6 класс : учебник для общеобразовательных учреждений / Н . Я . Виленкин , В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . — 30-е изд ., стер . — М . : Мнемозина, -2020 

В гдз по математике 6 класса Виленкина больше полторы тысячи заданий . Каждое из них шестиклассник должен решить, полностью в них разобраться и суметь понять похожие задания . .
Решение задачи(задания) номер 787 к учебнику по математике за 6 класс авторов Виленкин , Жохов .  ГДЗ (готовые домашние задания ), решебник онлайн по математике за 6 класс авторов Виленкин , Жохов задание(номер ) 787 — вариант решения упражнения 787 . 

Решение задания номер 787 .  Нужен решебник к старой версии учебника ? Тогда введите номер задания здесь 

Математика 6 класс . Учебник . Виленкин , Жохов, Чесноков . Мнемозина .  Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин , Жохов, Чесноков  В сборнике имеются ответы по одной тысячи пятистам девяноста пяти номерам . . 

Задача №787 , ГДЗ по математике за 6 класс к учебнику Виленкина с подробным решением . Виленкин , Жохов, Чесноков .  Обыкновенные дроби . 4 .22 Пря и обратная пропорциональные зависимости . Номер №787 . 

Математика 6 класс . Учебник . Виленкин, Чесноков, Шварцбурд . 1, 2 . Мнемозина .  Нумерация в данном пособии идет по задачам, что позволяет быстро отыскать необходимое . Всего их в ГДЗ по математике 6 класс Виленкин насчитывается более полутора тысяч упражнений . 

ГДЗ по математике 6 класс , авторы: , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И ., Мнемозина 2020-2021 год . 

Подробное решение задач по математике для учащихся 6 класса , авторы: Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд .  авторы: Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд . издательство: Мнемозина год . 

В решебнике к пособию «Математика 6 класс Учебник Виленкин , Жохов , Чесноков, Шварцбурд Мнемозина» представлены все темы, изучение которых предусмотрено программой для 6 класса по предмету математика . Сборник поделен на главы, номера заданий соответствуют . . 

ГДЗ (домашнее задание ) по математике за 6 класс к учебнику Виленкина , Жохова, Чеснокова, Шварцбурд .  На «Решатор» размещен бесплатный решебник по математике за 6 класс Виленкин . Чтобы воспользоваться ГДЗ , надо просто щелкнуть по номеру задания . . 

ГДЗ математика 6 класс Виленкин , Жохов , Чесноков, Шварцбурд Мнемозина . Математика в 6 классе включает в себя большой объем знаний .  В качестве полезного и интересного базового источника многие педагоги, репетиторы и сами шестиклассники называют учебник Виленкина . . 

Разбор номеров по математике за 6 класс из учебника Виленкина Н .Я ., Жохова В .И ., Чеснокова А .С . Все выполненные номера проверены  Ответы в решебнике по математике за 6 класс авторов: Виленкин Н .Я ., Жохов В .И ., Чесноков А .С . к упражнениям смотреть бесплатно . 

ГДЗ по математике 6 класс Виленкин учебник . номер — 787 (793 ) . Авторы : Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд . 

Решебник (ГДЗ ) по Математике за 6 (шестой ) класс авторы: Виленкин , Жохов , Чесноков, Шварцбурд издательство Мнемозина, год .  ГДЗ по математике за 6 класс Виленкин , Жохов , Чесноков, Шварцбурд . Учебник Мнемозина (ответы к старому и новому изданию) . 

ГДЗ (готовое домашние задание из решебника) на Номер №787 по учебнику Математика . 6 класс : учебник для общеобразовательных учреждений / Н . Я . Виленкин , В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . — 30-е изд ., стер . — М . : Мнемозина, -2020 

В гдз по математике 6 класса Виленкина больше полторы тысячи заданий . Каждое из них шестиклассник должен решить, полностью в них разобраться и суметь понять похожие задания . .
Решение задачи(задания) номер 787 к учебнику по математике за 6 класс авторов Виленкин , Жохов .  ГДЗ (готовые домашние задания ), решебник онлайн по математике за 6 класс авторов Виленкин , Жохов задание(номер ) 787 — вариант решения упражнения 787 . 

Решение задания номер 787 .  Нужен решебник к старой версии учебника ? Тогда введите номер задания здесь 

Математика 6 класс . Учебник . Виленкин , Жохов, Чесноков . Мнемозина .  Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин , Жохов, Чесноков  В сборнике имеются ответы по одной тысячи пятистам девяноста пяти номерам . . 

Задача №787 , ГДЗ по математике за 6 класс к учебнику Виленкина с подробным решением . Виленкин , Жохов, Чесноков .  Обыкновенные дроби . 4 .22 Пря и обратная пропорциональные зависимости . Номер №787 . 

Математика 6 класс . Учебник . Виленкин, Чесноков, Шварцбурд . 1, 2 . Мнемозина .  Нумерация в данном пособии идет по задачам, что позволяет быстро отыскать необходимое . Всего их в ГДЗ по математике 6 класс Виленкин насчитывается более полутора тысяч упражнений . 

ГДЗ по математике 6 класс , авторы: , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И ., Мнемозина 2020-2021 год . 

Подробное решение задач по математике для учащихся 6 класса , авторы: Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд .  авторы: Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд . издательство: Мнемозина год . 

В решебнике к пособию «Математика 6 класс Учебник Виленкин , Жохов , Чесноков, Шварцбурд Мнемозина» представлены все темы, изучение которых предусмотрено программой для 6 класса по предмету математика . Сборник поделен на главы, номера заданий соответствуют . . 

ГДЗ (домашнее задание ) по математике за 6 класс к учебнику Виленкина , Жохова, Чеснокова, Шварцбурд .  На «Решатор» размещен бесплатный решебник по математике за 6 класс Виленкин . Чтобы воспользоваться ГДЗ , надо просто щелкнуть по номеру задания . . 

ГДЗ математика 6 класс Виленкин , Жохов , Чесноков, Шварцбурд Мнемозина . Математика в 6 классе включает в себя большой объем знаний .  В качестве полезного и интересного базового источника многие педагоги, репетиторы и сами шестиклассники называют учебник Виленкина . . 

Разбор номеров по математике за 6 класс из учебника Виленкина Н .Я ., Жохова В .И ., Чеснокова А .С . Все выполненные номера проверены  Ответы в решебнике по математике за 6 класс авторов: Виленкин Н .Я ., Жохов В .И ., Чесноков А .С . к упражнениям смотреть бесплатно . 

ГДЗ по алгебре 9 класс Учебник, Задачник (2018) Мордкович, Семенов Решебник
ГДЗ глава 4 / упражнение 99 русский язык 5 класс Шмелев, Флоренская
ГДЗ повторение курса алгебры 7-9 классов / подготовка к экзамену 7 алгебра 10 класс дидактические материалы Шабунин, Ткачева
ГДЗ учебник 2015. упражнение 78 (78) математика 5 класс Виленкин, Жохов
ГДЗ самостоятельная работа / вариант 1 228 математика 6 класс дидактические материалы Чесноков, Нешков
ГДЗ номер 68 математика 5 класс Мерзляк, Полонский
ГДЗ упражнение 696 математика 6 класс Истомина
ГДЗ номер 167 физика 10‐11 класс задачник Рымкевич
ГДЗ номер 1046 алгебра 7 класс Макарычев, Миндюк
ГДЗ упражнения для работы дома / часть 2. страница 107 русский язык 4 класс Бунеев, Бунеева
ГДЗ номер 1373 физика 7‐9 класс Сборник задач Перышкин
ГДЗ вариант 1 159 геометрия 7 класс дидактические материалы Мерзляк, Полонский
ГДЗ самостоятельные работы / СР-20 / вариант 1 5 алгебра 9 класс дидактические материалы Феоктистов
ГДЗ глава 1 / § 4 / вариант 2 10 алгебра 10 класс дидактические материалы Шабунин, Ткачева
ГДЗ упражнение 186 математика 4 класс Аргинская, Ивановская
ГДЗ упражнение 166 русский язык 5 класс Ладыженская, Баранов
ГДЗ упражнение 110 русский язык 5 класс Ладыженская, Баранов
ГДЗ §43. Природа Сибири / Вопросы и задания 5 география 9 класс Алексеев, Низовцев
ГДЗ часть 2 / § 47-48 6 история 5 класс рабочая тетрадь Чернова
ГДЗ номер 198 алгебра 9 класс Никольский, Потапов
ГДЗ страница 75 русский язык 1 класс рабочая тетрадь Тихомирова
ГДЗ тетрадь №1. страница 62 литература 2 класс рабочая тетрадь Ефросинина
ГДЗ упражнение 156 русский язык 9 класс рабочая тетрадь Литвинова
ГДЗ вариант 3 157 алгебра 8 класс дидактические материалы Мерзляк, Полонский
ГДЗ упражнение 560 русский язык 7 класс Львова, Львов
ГДЗ тексты 9 русский язык 6 класс рабочая тетрадь Малюшкин
ГДЗ § 10 6 алгебра 9 класс Мерзляк, Поляков
ГДЗ часть 1. страница 108 математика 2 класс Дорофеев, Миракова
ГДЗ § 4 2 обществознание 8 класс рабочая тетрадь Котова, Лискова
ГДЗ упражнение 60 русский язык 4 класс Рамзаева
ГДЗ страница 177 английский язык 10 класс New Millenium Гроза, Дворецкая
ГДЗ часть №1 / сложение двузначных чисел (общий случай) 22 математика 2 класс Рудницкая, Юдачева
ГДЗ номер 266 физика 7‐9 класс Сборник задач Перышкин
ГДЗ страница 55 английский язык 6 класс рабочая тетрадь Тер-Минасова, Кутьина
ГДЗ часть 1. страница 85 английский язык 2 класс Happy English Кауфман, Кауфман
ГДЗ вариант 2 59 математика 6 класс дидактические материалы Мерзляк, Полонский
ГДЗ параграф 9 обществознание 6 класс рабочая тетрадь Королькова, Федоров
ГДЗ упражнение 92 алгебра 7 класс Бунимович, Кузнецова
ГДЗ задача 83 алгебра 10‐11 класс Колмогоров, Абрамов
ГДЗ §10 7 химия 10 класс Рудзитис, Фельдман
ГДЗ параграф 22 9 алгебра 7 класс рабочая тетрадь Колягин, Ткачева
ГДЗ тест 16. вариант 2 русский язык 7 класс контрольные измерительные материалы Потапова
ГДЗ страница 67 английский язык 7 класс лексико-грамматический практикум rainbow Афанасьева, Михеева
ГДЗ номер 282 математика 5 класс Дорофеев, Шарыгин
ГДЗ контрольный вопрос §17 математика 6 класс Зубарева, Мордкович
ГДЗ параграф 10 10.6 геометрия 9 класс Мерзляк, Поляков
ГДЗ часть 2 (страница) 4 окружающий мир 3 класс рабочая тетрадь Ивченкова, Потапов
ГДЗ Учебник 2019 / часть 1 785 (782) математика 5 класс Виленкин, Жохов
ГДЗ страница 148 английский язык 11 класс spotlight Эванс, Дули
ГДЗ часть 2. страница 124 русский язык 3 класс Зеленина, Хохлова

ГДЗ часть №1 / упражнение 85 русский язык 2 класс Климанова, Бабушкина

ГДЗ Учебники По Биологии Пономарева

Решебник По Русскому Языку 4 Пронина

ГДЗ Зубарева 5

ГДЗ Математика 3 Планета Знаний Учебник

Ответы Задание 266 . ГДЗ по математике 6 класс Виленкин Жохов Чесноков Шварцбурд учебник ответы

12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614471448144914501451145214531454145514561457145814591460146114621463146414651466146714681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595

100 лет математической космологии: Модели, теории и проблемы, часть Б

1. Старобинский А.А. 1980. Новый тип изотропных космологических моделей без сингулярности. физ. лат. Б 91 , 99-102. ( 10.1016/0370-2693(80)-X) [CrossRef] [Google Scholar]

2. Казанас Д. 1980. Динамика Вселенной и спонтанное нарушение симметрии. Ап. Дж. Летт. 241 , Л59. ( 10.1086/183361) [CrossRef] [Google Scholar]

3. Guth AH. 1981. Инфляционная вселенная: возможное решение проблем горизонта и плоскостности. физ. Преподобный Д 23 , 347-356. ( 10.1103/PhysRevD.23.347) [CrossRef] [Google Scholar]

4. Steinhardt PJ. 1982. Естественная инфляция. В The Very Early Universe (под редакцией GW Gibbons, SW Hawking, STC Siklos), Proc. Семинар Наффилда, 21 июня — 9 июля г., стр. 251–266. Кембридж, Великобритания: Издательство Кембриджского университета.

5. Вайнберг С.В. 1972. Гравитация и космология. Нью-Йорк, штат Нью-Йорк: Аддисон-Уэсли. [Google Scholar]

6. Brandenberger RH. 1985. Методы квантовой теории поля и инфляционные модели Вселенной. Преподобный Мод. физ. 57 , 1-60. ( 10.1103/RevModPhys.57.1) [CrossRef] [Google Scholar]

7. Колб Э.В., Тернер М.С. 1990. Ранняя Вселенная. Нью-Йорк, штат Нью-Йорк: Аддисон-Уэсли. [Google Scholar]

8. Вайнберг С.В. 2007. Космология. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar]

9. Аде ПАР и др. Сотрудничество BICEP/Keck, 2021 г. Улучшены ограничения на первичные гравитационные волны с использованием наблюдений

Planck , WMAP и BICEP/ Keck в течение сезона наблюдений 2018 года. физ. Преподобный Летт. 127 , 151301. ( 10.1103/PhysRevLett.127.151301) [PubMed] [CrossRef] [Google Scholar]

10. Виленкин А. 1983. Рождение инфляционных вселенных. физ. Преподобный Д 27 , 2848-2855. ( 10.1103/PhysRevD.27.2848) [CrossRef] [Google Scholar]

11. Linde AD. 1986 год. Вечно существующая самовоспроизводящаяся хаотическая инфляционная вселенная.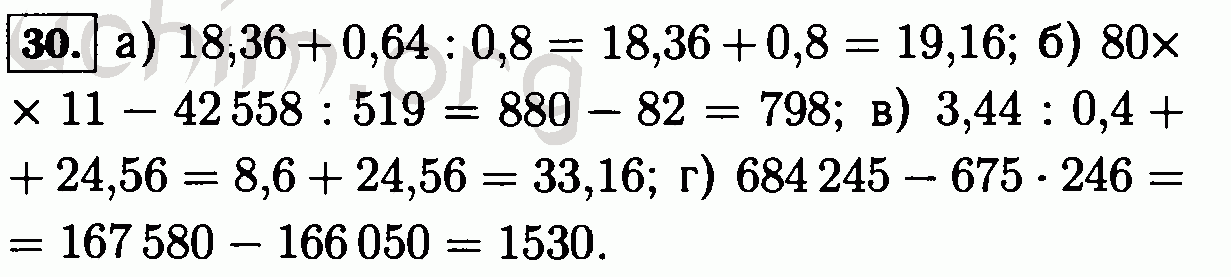 физ. лат. Б 175 , 395-400. ( 10.1016/0370-2693(86)

-8) [CrossRef] [Google Scholar]

12. Linde AD. 1995. Квантовая космология и структура инфляционной Вселенной. В PASCOS / HOPKINS 1995 (Совместное собрание Международного симпозиума по частицам, струнам и космологии и 19-го семинара Джона Хопкинса по текущим проблемам теории частиц

), стр. 349–394.

13. Виленкин А. 2004. Вечная инфляция и хаотичная терминология. (http://arxiv.org/abs/gr-qc/0409055 [gr-qc])

14. Кофман Л., Линде А.Д., Муханов В.Ф. 2002. Инфляционная теория и альтернативная космология. J. Физика высоких энергий. 2002 , 057. ( 10.1088/1126-6708/2002/10/057) [CrossRef] [Google Scholar]

15. Холландс С., Уолд Р.М. 2002. Эссе: альтернатива инфляции. Генерал Отн. Грав. 34 , 2043-2055. ( 10.1023/A:1021175216055) [CrossRef] [Google Scholar]

16. Linde AD. 1990. Физика элементарных частиц и инфляционная космология. Швейцария: Harwood Academic Publishers. [Google Scholar]

17. Борде А., Гут А.Х., Виленкин А. 2003. Инфляционное пространство-время неполно в прошлых направлениях. физ. Преподобный Летт.

90 , 151301. ( 10.1103/PhysRevLett.90.151301) [PubMed] [CrossRef] [Google Scholar]

18. Агирре А., Граттон С. 2003. Инфляция без начала: предложение нулевой границы. физ. Преподобный Д 67 , 083515. ( 10.1103/PhysRevD.67.083515) [CrossRef] [Google Scholar]

19. DeWitt BS. 1967. Квантовая теория гравитации. I. Каноническая теория. физ. преп. 160 , 1113-1148. ( 10.1103/PhysRev.160.1113) [CrossRef] [Google Scholar]

20. Wheeler JA. 1968 год. Суперпространство и природа квантовой геометродинамики. В Battelle Rencontres (редакторы CM DeWitt, JA Wheeler), Лекции по математике и физике. Нью-Йорк, штат Нью-Йорк: В. А. Бенджамин.

21. Хартл Дж.Б., Хокинг С.В. 1983. Волновая функция Вселенной. физ. Преподобный Д 28 , 2960-2975. ( 10.1103/PhysRevD.28.2960) [CrossRef] [Google Scholar]

22. Виленкин А. 1985. Граничные условия в квантовой космологии. физ. Преподобный Д 33 , 3560-3569. ( 10.1103/PhysRevD.33.3560) [PubMed] [CrossRef] [Google Scholar]

23. Виленкин А. 1987. Квантовая космология и начальное состояние Вселенной. физ. Преподобный Д 37 , 888-897. ( 10.1103/PhysRevD.37.888) [PubMed] [CrossRef] [Google Scholar]

24. Гиббонс Г.В., Грищук Л.П. 1989. Какова типичная волновая функция Вселенной? Нукл. физ. Б 313 , 736-748. ( 10.1016/0550-3213(89)-7) [CrossRef] [Google Scholar]

25. Halliwell JJ. 1991 Вводные лекции по квантовой космологии. В Квантовая космология и детские вселенные (редакторы С. Коулман, Дж. Б. Хартл, Т. Пиран, С. Вайнберг). Сингапур: Мировой научный.

26. Аштекар А. 2021. Краткий обзор петлевой квантовой гравитации. Представитель прог. физ. 84 , 042001. (10.1088/1361-6633/abed91) [PubMed] [CrossRef] [Google Scholar]

27. Bojowald M. 2008. Петлевая квантовая космология. Живой преподобный отн. 11 , 044025. ( 10.12942/lrr-2008-4) [PMC free article] [PubMed] [CrossRef] [Google Scholar]

28. Белинский В.А., Грищук Л.П., Зельдович Ю.Б., Халатников И.М. 1985. Инфляционные стадии в космологических моделях со скалярным полем. сов. физ. Дж. Эксп. Теор. физ. 62 , 195. [Google Scholar]

29. Halliwell JJ. 1987. Скалярные поля в космологии с экспоненциальным потенциалом. физ. лат. Б 185 , 341-344. ( 10.1016/0370-2693(87)91011-2) [CrossRef] [Google Scholar]

30. Henneaux M. 1983. Производство энтропии Гиббса в общей теории относительности. Нуово Сим. лат. 38 , 609-614. ( 10.1007/BF02782751) [CrossRef] [Google Scholar]

31. Гиббонс Г.В., Хокинг С.В., Стюарт Дж.М. 1987. Естественная мера на множестве всех вселенных. Нукл. физ. Б 281 , 736-751. ( 10.1016/0550-3213(87)-1) [CrossRef] [Google Scholar]

32.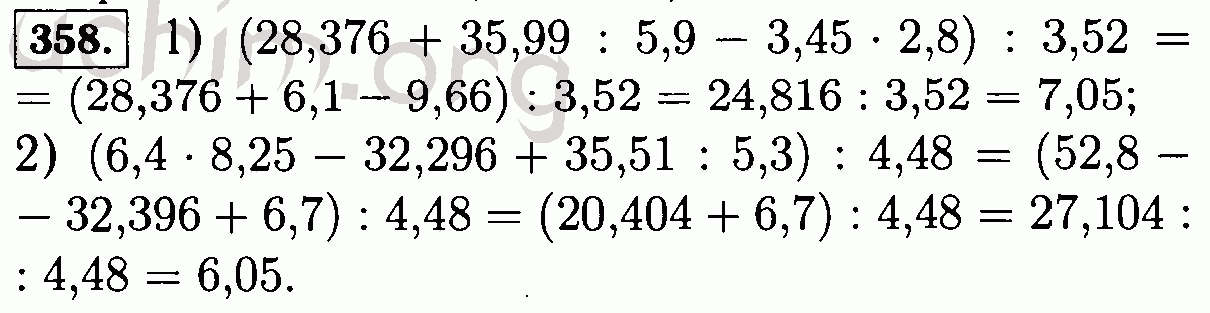 Hawking SW, Page DN. 1988 год. Насколько вероятна инфляция? Нукл. физ. Б 298 , 789-809. ( 10.1016/0550-3213(88)-9) [CrossRef] [Google Scholar]

33. DN страницы. 1987. Вероятность инфляции R2. физ. Преподобный Д 36 , 1607-1624. ( 10.1103/PhysRevD.36.1607) [PubMed] [CrossRef] [Google Scholar]

34. Chmielowski P, Page DN. 1988 год. Вероятность инфляции типа Бьянки I. физ. Преподобный Д 38 , 2392. (10.1103/PhysRevD.38.2392) [PubMed] [CrossRef] [Google Scholar]

35. Gibbons GW, Turok N. 2008. Проблема меры в космологии. физ. Преподобный Д 77 , 063516. (10.1103/PhysRevD.77.063516) [CrossRef] [Google Scholar]

36. Страница DN. 2011. Конечная каноническая мера для неособых космологий. Дж. Космол. Астропарт. физ. 1106 , 038. (10.1088/1475-7516/2011/06/038) [CrossRef] [Google Scholar]

37. Schiffrin JS, Wald RM. 2012. Мера и вероятность в космологии. физ. Преподобный Д 86 , 023521. (10.1103/PhysRevD.86.023521) [CrossRef] [Google Scholar]

38. Линде А., Нурбала М. 2010. Проблема меры для вечной и невечной инфляции. Дж. Космол. Астропарт. физ. 09 , 008. (10.1088/1475-7516/2010/09/008) [CrossRef] [Google Scholar]

39. Ellis GFR, Maartens R, MacCallum MAH. 2012. Релятивистская космология. Кембридж, Великобритания: Издательство Кембриджского университета. [Google Scholar]

40. Хокинг С.В. 1988 год. Червоточины в пространстве-времени. физ. Преподобный Д 37 , 904-910. ( 10.1103/PhysRevD.37.904) [PubMed] [CrossRef] [Google Scholar]

41. Coleman S. 1988. Почему нет ничего, а не что-то: теория космологической постоянной. Нукл. физ. Б 310 , 643-668. ( 10.1016/0550-3213(88)-1) [CrossRef] [Google Scholar]

42. Fischler W, Susskind L. 1989. Катастрофа червоточины. физ. лат. Б 217 , 48-54. ( 10.1016/0370-2693(89)91514-1) [CrossRef] [Google Scholar]

43. Коулман С., Хартл Дж. Б., Пиран Т., Вайнберг С. (ред.). 1991. Квантовая космология и детские вселенные. Сингапур: Мировой научный. [Google Scholar]

44. Моррис М.С., Торн К.С. 1988 год. Червоточины в пространстве-времени и их использование для межзвездных путешествий: инструмент для обучения общей теории относительности. Являюсь. Дж. Физ. 56 , 395-412. ( 10.1119/1.15620) [CrossRef] [Google Scholar]

45. Моррис М.С., Торн К.С., Юрцевер Ю. 1988. Червоточины, машины времени и слабое энергетическое состояние. физ. Преподобный Летт. 61 , 1446-1449. ( 10.1103/PhysRevLett.61.1446) [PubMed] [CrossRef] [Google Scholar]

46. Бронников К.А., Мельников В.Н., Денен Х. 2003. Общий класс черных дыр мира браны. физ. Преподобный Д 68 , 024025. ( 10.1103/PhysRevD.68.024025) [CrossRef] [Google Scholar]

47. Бронников К.А., Скворцова М.В., Старобинский А.А. 2010. Заметки о существовании червоточин в скалярно-тензорной и F(R) гравитации. Грав. Космол. 16 , 216-222. ( 10.1134/S0202289310030047) [CrossRef] [Google Scholar]

48. Бронников К.А., Lemos JPS. 2009. Цилиндрические червоточины. физ. Преподобный Д 79 , 104019. (10.1103/PhysRevD.79.104019) [CrossRef] [Google Scholar]

49. Visser M. 1995. Лоренцевы червоточины — от Эйнштейна до Хокинга. Нью-Йорк, штат Нью-Йорк: AIP Press. [Google Scholar]

50. Molina-Paris C, Visser M. 1999. Минимальные условия для создания вселенной Фридмана-Робертсона-Уокера из «отскока». физ. лат. Б 455 , 90-95. ( 10.1016/S0370-2693(99)00469-4) [CrossRef] [Google Scholar]

51. Freund PGO. 1982. Космологии Калуцы-Клейна. Нукл. физ. Б 209 , 146-156. ( 10.1016/0550-3213(82)-7) [CrossRef] [Google Scholar]

52. Abbott RB, Barr SM, Ellis SD. 1984. Космологии Калуцы-Клейна и инфляция. физ. Преподобный Д 30 , 720-727. ( 10.1103/PhysRevD.30.720) [PubMed] [CrossRef] [Google Scholar]

53. Okada Y. 1982. Эволюция вселенной Калуцы-Клейна. Нукл. физ. Б 264 , 197-220. ( 10.1016/0550-3213(86)-7) [CrossRef] [Google Scholar]

54. Overduin JM, Wesson PS. 1997. Калуца-Кляйн Гравитация. физ. Представитель 283 , 303-378. ( 10.1016/S0370-1573(96)00046-4) [CrossRef] [Google Scholar]

55. Furusawa T, Hosoya A. 1985. Хаотична ли анизотропная модель Калуцы-Клейна Вселенной? прог. Теор. физ. 73 , 467-475. ( 10.1143/PTP.73.467) [CrossRef] [Google Scholar]

56. Барроу Дж.Д., Стейн Шабес Дж.А. 1985. Миксмастерские вселенные Калуцы-Кляйна. физ. Преподобный Д 32 , 1595-1596. ( 10.1103/PhysRevD.32.1595) [PubMed] [CrossRef] [Google Scholar]

57. Демаре Дж., Хенно М., Шпиндель П. 1985. Неколебательное поведение в космологии Калуцы-Клейна в вакууме. физ. лат. Б 164 , 27-30. ( 10.1016/0370-2693(85)-3) [CrossRef] [Google Scholar]

58. Demaret J, Hanquin JL, Henneaux M, Spindel P, Taormina A. 1986. Судьба миксмастерского поведения в неоднородных космологических моделях Калуцы-Клейна в вакууме. физ. лат. Б 175 , 129-132. ( 10.1016/0370-2693(86)

-X) [CrossRef] [Google Scholar]

59. Демаре Дж., де Роп Ю., Хенно М. 1988. Хаос в недиагональных пространственно-однородных космологических моделях в пространственно-временных размерностях ≤10. физ. лат. Б 211 , 37-41. ( 10.1016/0370-2693(88)

-9) [CrossRef] [Google Scholar]

60. Хосоя А., Дженсен Л.Г., Стейн Шабес Дж.А. 1987. Критическое измерение для хаотической космологии. Нукл. физ. Б 283 , 657-668. ( 10.1016/0550-3213(87)-4) [CrossRef] [Google Scholar]

61. Гасперини М. 2007. Элементы струнной космологии. Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. [Академия Google]

62. Питер П., Узан Дж.-П. 2009. Первичная космология. Оксфорд, Великобритания: Издательство Оксфордского университета. [Google Scholar]

63. Гасперини М., Венециано Г. 1993. До большого взрыва в струнной космологии. Астропарт. физ. 1 , 317-339. ( 10.1016/0927-6505(93)-8) [CrossRef] [Google Scholar]

64. Billyard AP, Coley AA, Lidsey JE. 2000. Циклическое поведение в космологиях ранней Вселенной. Дж. Матем. физ. 41 , 6277-6283. ( 10.1063/1.1286878) [CrossRef] [Google Scholar]

65. Барроу Д.Д., Кунце К.Е. 1997. Пространственно однородные струнные космологии. физ. Преподобный Д 55 , 623-629. ( 10.1103/PhysRevD.55.623) [CrossRef] [Google Scholar]

66. Барроу Д.Д., Кунце К.Е. 1997. Неоднородные струнные космологии. физ. Преподобный Д 56 , 741-752. ( 10.1103/PhysRevD.56.741) [CrossRef] [Google Scholar]

67. Lidsey JE, Wands D, Copeland EJ. 2000. Суперструнная космология. физ. Представитель 337 , 343-492. ( 10.1016/S0370-1573(00)00064-8) [CrossRef] [Google Scholar]

68. Ланцош К. 1957. Электричество и общая теория относительности. Преподобный Мод. физ. 19 , 337-350. ( 10.1103/RevModPhys.29.337) [CrossRef] [Google Scholar]

69. Lanczos C. 1957. Расщепление тензора Римана. Преподобный Мод. физ. 34 , 379-389. ( 10.1103/RevModPhys.34.379) [CrossRef] [Google Scholar]

70. Buchdahl HA. 1970. Нелинейные лагранжианы и космологическая теория. Пн. Нет. Р. Астрон. соц. 150 , 1-8. ( 10.1093/mnras/150.1.1) [CrossRef] [Google Scholar]

71. Гурович В.Т. 1971. Нелинейная поправка к лагранжевой плотности гравитационного поля и космологические решения без сингулярности. сов. физ. Доклады 15 , 1105. [Google Scholar]

72. Нариай Х. 1973. Гравитационная неустойчивость регулярных моделей вселенных в модифицированной общей теории относительности. прог. Теор. физ. 49 , 165-180. ( 10.1143/PTP.49.165) [CrossRef] [Google Scholar]

73. Кернер Р. 1982. Космология без сингулярности и нелинейные гравитационные лагранжианы. Генерал Отн. Грав. 14 , 453-469. ( 10.1007/BF00756329) [CrossRef] [Google Scholar]

74. Барроу Д.Д., Оттевилл А.С. 1983. Устойчивость общей релятивистской космологической теории. Дж. Физ. А 16 , 2757-2776. (10.1088/0305-4470/16/12/022) [CrossRef] [Google Scholar]

75. Барроу Дж. Д., Коцакис С. 1988. Инфляция и конформная структура теорий гравитации высшего порядка. физ. лат. Б 214 , 515-518. ( 10.1016/0370-2693(88)-4) [CrossRef] [Google Scholar]

76. Мангейм П.Д., Казанас Д. 1989. Точное вакуумное решение конформной гравитации Вейля и кривых вращения галактики. Астрофиз. Дж. 342 , 635-638. ( 10.1086/167623) [CrossRef] [Google Scholar]

77. Cotsakis S, Miritzis J, Querella L. 1999. Вариационная и конформная структура нелинейных метрически-связных гравитационных лагранжианов. Дж. Матем. физ. 40 , 3063-3071. ( 10.1063/1.532744) [CrossRef] [Google Scholar]

78. Барроу Дж. Д., Коцакис С. 2020. Инфляция без следа лямбды. Евро. физ. Дж. С. 80 , 839. ( 10.1140/epjc/s10052-020-8428-2) [CrossRef] [Google Scholar]

79. Harrison ER. 1967. Нормальные моды колебаний Вселенной. Преподобный Мод. физ. 39 , 862-882. ( 10.1103/RevModPhys.39.862) [CrossRef] [Google Scholar]

80. Гиббонс Г.В. 1988 год. Энтропия и стабильность Вселенной. Нукл. физ. Б 292 , 784-792. ( 10.1016/0550-3213(87)-5) [CrossRef] [Google Scholar]

81. Гиббонс Г.В. 1988 год. Неравенство Соболева, теорема Йенсена и масса и энтропия Вселенной. Нукл. физ. Б 310 , 636-642. ( 10.1016/0550-3213(88)

-X) [CrossRef] [Google Scholar]

82. Ellis GFR, Maartens R. 2004. Эмерджентная Вселенная: инфляционная космология без сингулярности. Учебный класс. Квант. Грав. 21 , 223-232. ( 10.1088/0264-9381/21/1/015) [CrossRef] [Google Scholar]

83. Барроу Д.Д., Эллис Г. Ф.Р., Мартенс Р., Цагас К.Г. 2003. Об устойчивости статической Вселенной Эйнштейна. Учебный класс. Квант. Грав. 20 , L155-L164. (10.1088/0264-9381/20/11/102) [CrossRef] [Google Scholar]

84. Барроу Дж. Д., Ямамото К. 2012. Неустойчивости статических вселенных Эйнштейна типа IX Бьянки. физ. Преподобный Д 85 , 083505. ( 10.1103/PhysRevD.85.083505) [CrossRef] [Google Scholar]

85. Барроу Д.Д. 2020. Пересмотрен принцип конечного действия. физ. Преподобный Д 101 , 023527. (10.1103/PhysRevD.101.023527) [CrossRef] [Google Scholar]

86. Wainwright J, Ellis GFR. 1993. Динамические системы в космологии. Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета. [Академия Google]

87. Барроу Д.Д., Сонода Д.Х. 1985. Асимптотическая устойчивость вселенных типа Бьянки. физ. Респ. 139 , 1-49. ( 10.1016/0370-1573(86)

-6) [CrossRef] [Google Scholar]

88. Вальд Р.М. 1983. Асимптотика однородных космологических моделей при наличии положительной космологической постоянной. физ. Преподобный Д 28 , 2118-2120. ( 10.1103/PhysRevD.28.2118) [CrossRef] [Google Scholar]

89. Cotsakis S, Flessas G. 1993. Обобщенные космические теоремы об отсутствии волос. физ. лат. Б 319 , 69-73. ( 10.1016/0370-2693(93)

-E) [CrossRef] [Google Scholar]

90. Cotsakis S, Miritzis J. 1998. Доказательство космической гипотезы об отсутствии волос для некоторых квадратичных однородных космологий. Учебный класс. Квант. Грав. 15 , 2795-2801. ( 10.1088/0264-9381/15/9/024) [CrossRef] [Google Scholar]

91. Yokoyama J, Maeda K. 1990. Квантовый космологический подход к космической гипотезе об отсутствии волос в пространстве-времени Бьянки типа IX. физ. Преподобный Д 41 , 1047-1053. ( 10.1103/PhysRevD.41.1047) [PubMed] [CrossRef] [Google Scholar]

92. Уэйнрайт Дж., Эллис ГФР. 1989. Динамический системный подход к космологии Бьянки: ортогональные модели класса А. Класс. Квант. Грав. 6 , 1409-1431. ( 10.1088/0264-9381/6/10/011) [CrossRef] [Google Scholar]

93. Богоявленский О.И. 1985. Методы качественной теории динамических систем в астрофизике и газовой динамике. Нью-Йорк, штат Нью-Йорк: Спрингер. [Google Scholar]

94. Александр С., Бранденбергер Р.Х., Иссон Д.А. 2000. Бранные газы в ранней Вселенной. физ. Преподобный Д 62 , 103509. (10.1103/PhysRevD.62.103509) [CrossRef] [Google Scholar]

95. Barrow JD, Dabrowski MP. 1998. Струнная космология и хаос. физ. Преподобный Д 57 , 7204. [Google Scholar]

96. Damour T, Henneaux M. 2000. Хаос в суперструнной космологии. физ. Преподобный Летт. 85 , 920-923. ( 10.1103/PhysRevLett.85.920) [PubMed] [CrossRef] [Google Scholar]

97. Damour T, de Buyl S. 2008. Описание общих космологических особенностей переменных Ивасавы. физ. Преподобный Д 77 , 043520. (10.1103/PhysRevD.77.043520) [CrossRef] [Google Scholar]

98. Damour T, Николай. 2008. Симметрии, сингулярности и исчезновение пространства. Междунар. Дж. Мод. физ. Д 17 , 525-531. ( 10.1142/S0218271808012206) [CrossRef] [Google Scholar]

99. Лукас А., Оврут Б.А., Уолдрам Д. 1997. Струнная и М-теория космологических решений с формами Рамона. Нукл. физ. Б 495 , 365-399. ( 10.1016/S0550-3213(97)00194-6) [CrossRef] [Google Scholar]

100. Лукас А., Оврут Б.А., Уолдрам Д. 1998 Космология и М-теория суперструн типа II. (http://arxiv.org/abs/hep-th/9802041)

101. Billyard AP, Coley AA, Lidsey JE, Nilsson US. 2000. Динамика космологии М-теории. физ. Преподобный Д 61 , 043504. (10.1103/PhysRevD.61.043504) [CrossRef] [Google Scholar]

102. Таунсенд П. 2003 Космическое ускорение и М-теория. (http://arxiv.org/abs/hep-th/0308149 [hep-th])

103. Андерссон Л., Марк Хайнцле Дж. 2007. Вечное ускорение из М-теории. Доп. Теор. Мат. физ. 11 , 371-398. ( 10.4310/ATMP.2007. v11.n3.a2) [CrossRef] [Google Scholar]

104. Townsend P, Wohlfarth MNR. 2004. Космология как геодезическое движение. Учебный класс. Квант. Грав. 21 , 5375-5396. ( 10.1088/0264-9381/21/23/006) [CrossRef] [Google Scholar]

105. Марольф Д. Струны/М-браны для релятивистов, 1999. (http://arxiv.org/abs/gr-qc/9

5)

106. Антониадис И. 1990. Возможное новое измерение в несколько ТэВ. физ. лат. Б 246 , 377-384. ( 10.1016/0370-2693(90)-F) [CrossRef] [Google Scholar]

107. Антониадис И. 2006. Физика дополнительных измерений. Дж. Физ. конф. сер. 33 , 170-181. (10.1088/1742-6596/33/1/015) [CrossRef] [Google Scholar]

108. Randall L, Sundrum R. 1999. Альтернатива компактификации. физ. Преподобный Летт. 83 , 4690-4693. ( 10.1103/PhysRevLett.83.4690) [CrossRef] [Google Scholar]

109. Maartens R. 2004. Космологическая динамика на бране. Живой преподобный отн. 7 , 7. (10.12942/lrr-2004-7) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

110. Langlois D. 2003. Космология браны: введение. прог. Теор. физ. Доп. 148 , 181-212. ( 10.1143/PTPS.148.181) [CrossRef] [Google Scholar]

111. Khoury J, Ovrut BA, Steinhardt PJ, Turok N. 2001. Экпиротическая Вселенная: сталкивающиеся браны и происхождение горячего Большого взрыва. физ. Преподобный Д 64 , 123522. ( 10.1103/PhysRevD.64.123522) [CrossRef] [Google Scholar]

112. Ленерс Дж.Л. 2008. Экпиротическая и циклическая космология. физ. Представитель 465 , 223-263. ( 10.1016/j.physrep.2008.06.001) [CrossRef] [Google Scholar]

113. Brandenberger RH, Patrick P. 2017. Отскакивающие космологии: прогресс и проблемы. Найденный. физ. 47 , 797-850. ( 10.1007/s10701-016-0057-0) [CrossRef] [Google Scholar]

114. Антониадис И., Коцакис С., Клаудату И. 2021. Регулярные бранные миры с нелинейными объемными жидкостями. Евро. физ. Дж. С. 81 , 771. (10.1140/epjc/s10052-021-09558-y) [CrossRef] [Google Scholar]

115. Witten E. 1998. Антиде Ситтеровское пространство и голография. Доп. Теор. Мат. физ. 2 , 253-291. ( 10.4310/ATMP.1998.v2.n2.a2) [CrossRef] [Google Scholar]

116. Антониадис I, Коцакис С. 2015. Образование Σ(1385)± и Ξ(1530)0 в протонно-протонных столкновениях при s=7 ТэВ. Евро. физ. Дж. С. 75 , 1-12. ( 10.1140/epjc/s10052-014-3191-x) [CrossRef] [Google Scholar]

117. Susskind L. 2003 Антропный ландшафт теории струн. (http://arxiv.org/abs/hep-th/0302219[геп-й])

118. Гут А.Х. 2007. Вечная инфляция и ее последствия. Дж. Физ. А 40 , 6811-6826. ( 10.1088/1751-8113/40/25/S25) [CrossRef] [Google Scholar]

119. Hawking SW, Hertog T. 2006. Население ландшафта: нисходящий подход. физ. Преподобный Д 73 , 123527. (10.1103/PhysRevD.73.123527) [CrossRef] [Google Scholar]

120. Hartle JB, Hawking SW, Hertog T. 2008. Безграничная мера Вселенной. физ. Преподобный Летт. 100 , 201301. см. также (10.1103/PhysRevLett.100.201301) [PubMed] [CrossRef] [Google Scholar]

121. Тегмарк М. Параллельные вселенные. (http://arxiv.org/abs/astro-ph/0302131 [astro-ph])

122. Трион Э. 1973. Является ли Вселенная вакуумной флуктуацией? Природа 246 , 396-397. ( 10.1038/246396a0) [CrossRef] [Google Scholar]

123. Соколов ДД, Шварцман ВФ. 1974. Оценка размера Вселенной с топологической точки зрения. сов. физ. ЖЭТФ 39 , 196-200. [Google Scholar]

124. Gott JR. 1980. Хаотические космологии и топология Вселенной. Пн. Нет. Р. Астрон. соц. 193 , 153-169. ( 10.1093/mnras/193.1.153) [CrossRef] [Google Scholar]

125. Зельдович Ю.Б., Старобинский А.А. 1984. Квантовое создание Вселенной с нетривиальной топологией. Сов Астрон. лат. 10 , 135-137. [Google Scholar]

126. Luminet J-P. 2008. Круглая вселенная. Уэлсли, Массачусетс: А.К. Питерс. [Google Scholar]

127. Бэрроу Д.Д. 2014. Космология: поиск двадцати четырех (или более) функций. физ. Преподобный Д 89 , 064022. ( 10.1103/PhysRevD.89.064022) [CrossRef] [Google Scholar]

128. Fagundes HV. 1985. Релятивистские космологии с замкнутыми, локально однородными пространственными сечениями. физ. Преподобный Летт. 54 , 1200-1202. ( 10.1103/PhysRevLett.54.1200) [PubMed] [CrossRef] [Google Scholar]

129. Ashtekar A, Samuel J. 1991. Космологии Бьянки: роль пространственной топологии. Учебный класс. Квантовая Грав. 8 , 2191-2215. ( 10.1088/0264-9381/8/12/005) [CrossRef] [Google Scholar]

130. Койке Т., Танимото М., Хосоя А. 1993. Компактные однородные вселенные. Дж. Матем. физ. 35 , 4855-4888. ( 10.1063/1.530819) [CrossRef] [Google Scholar]

131. Танимото М., Койке Т., Хосоя А. 1997. Динамика компактных однородных вселенных. Дж. Матем. физ. 38 , 350-368. ( 10.1063/1.531853) [CrossRef] [Google Scholar]

132. Кодама Х. 1998. Каноническое строение локально однородных систем на компактных замкнутых трехмерных многообразиях типов E3, Nil и Sol. прог. Теор. физ. 99 , 173-236. ( 10.1143/ПТР.99.173) [CrossRef] [Google Scholar]

133. Барроу Дж. Д., Кодама Х. 2001. Изотропия компактных вселенных. Учебный класс. Квант. Грав. 18 , 1753-1766. ( 10.1088/0264-9381/18/9/310) [CrossRef] [Google Scholar]

134. Барроу Дж. Д., Кодама Х. 2001. Все вселенные большие и малые. Междунар. Дж. Мод. физ. Д 10 , 785-790. ( 10.1142/S0218271801001554) [CrossRef] [Google Scholar]

135. Фишер А.Е., Монкриф В. 1996. Структура квантового конформного суперпространства. В Глобальная структура и эволюция в общей теории относительности (ред. С. Коцакис, Г. В. Гиббонс), том. 460, стр. 111–173. Конспекты лекций по физике. Берлин, Германия: Springer.

136. Фишер А.Е., Монкриф В. 2000. Приведенный гамильтониан общей теории относительности и сигма-константа конформной геометрии. В (ред. С. Коцакис, Г. Гиббонс), Proc. 2-я Самосская встреча. Космология, геометрия и теория относительности, математические и квантовые аспекты теории относительности и космологии . Конспект лекций по физике, том. 537, стр. 70–101. Берлин, Германия: Springer.

137. Фишер А.Е., Монкриф В. 2006. Гамильтонова редукция уравнений Эйнштейна. Энциклопедия математической физики, стр. 607-623. Нью-Йорк, штат Нью-Йорк: Academic Press. [Google Scholar]

138. Moncrief V, Mondal P. 2019. Может ли Вселенная иметь экзотическую топологию? Чистое приложение Мат. кв. 15 , 921-966. ( 10.4310/PAMQ.2019.v15.n3.a7) [CrossRef] [Google Scholar]

139. Collins CB, Ellis GFR. 1979. Сингулярности в космологиях Бьянки. физ. Представитель 56 , 65-105. ( 10.1016/0370-1573(79)-6) [CrossRef] [Google Scholar]

140. Wald RM. 1990. Доказательство гипотезы повторного коллапса замкнутой вселенной для общих космологий Бьянки типа IX. физ. Преподобный Д 41 , 2444-2448. (10.1103/PhysRevD.41.2444) [PubMed] [CrossRef] [Google Scholar]

141. Choquet-Bruhat Y, Cotsakis S. 2002. Глобальная гиперболичность и полнота. Дж. Геом. физ. 43 , 345-350. ( 10.1016/S0393-0440(02)00028-1) [CrossRef] [Google Scholar]

142. Шоке-Брюа Ю. 2009. Общая теория относительности и уравнения Эйнштейна. Нью-Йорк, штат Нью-Йорк: Издательство Оксфордского университета. [Google Scholar]

143. Коцакис С., Клаудату И. 2005. Будущие особенности изотропных космологий. Дж. Геом. физ. 55 , 306-315. ( 10.1016/j.geomphys.2004.12.012) [CrossRef] [Google Scholar]

144. Cotsakis S, Klaoudatou I. 2007. Космологические сингулярности и энергия Бела–Робинсона. Дж. Геом. физ. 57 , 1303-1312. ( 10.1016/j.geomphys.2006.10.007) [CrossRef] [Google Scholar]

145. Нодзири С., Одинцов С.Д., Цудзикава С. 2005. Свойства сингулярностей в (фантомной) вселенной темной энергии. физ. Преподобный Д 71 , 063004. (10.1103/PhysRevD.71.063004) [CrossRef] [Google Scholar]

146. Cotsakis S. 2013. Структура бесконечности в космологии. Междунар. Дж. Мод. физ. Д 23 , 1330003. (10.1142/S0218271813300036) [CrossRef] [Google Scholar]

147. Fernandez-Jambrina L, Lazkoz R. 2006. Классификация космологических вех. физ. Преподобный Д 74 , 064030. (10.1103/PhysRevD.74.064030) [CrossRef] [Google Scholar]

148. Cattoen C, Visser M. 2005. Необходимые и достаточные условия для больших взрывов, отскоков, схлопываний, разрывов, внезапных сингулярностей и экстремальных событий. Учебный класс. Квант. Грав. 22 , 4913-4930. ( 10.1088/0264-9381/22/23/001) [CrossRef] [Google Scholar]

149. Cotsakis S, Barrow JD. 2007. Доминирующий баланс в космологических сингулярностях. Дж. Физ. конф. сер. 68 , 012004. ( 10.1088/1742-65968.06.01.012004) [CrossRef] [Google Scholar]

150. Белинский В.А., Халатников И.М., Лифшиц Е.М. 1963 год. Исследования по релятивистской космологии. Доп. физ. 12 , 185-249. ( 10.1080/00018736300101283) [CrossRef] [Google Scholar]

151. Старобинский А.А. 1983. Изотропизация произвольного космологического расширения при заданной эффективной космологической постоянной. сов. физ. ЖЭТФ лат. 37 , 66-69. [Google Scholar]

152. Барроу Дж. Д., Коцакис С., Цокарос А. 2010. Общая внезапная космологическая сингулярность. Учебный класс. Квант. Грав. 27 , 165017. (10.1088/0264-9381/27/16/165017) [CrossRef] [Google Scholar]

153. Барроу Дж. Д., Коцакис С., Трачилис Д. 2020. Общая внезапная особенность в теории Бранса – Дикке. Евро. физ. Дж. С. 80 , 11-97. ( 10.1140/epjc/s10052-020-08771-5) [CrossRef] [Google Scholar]

154. Марк Хайнцле Дж., Сандин П. 2012. Исходная сингулярность ультражестких идеально-жидких пространств-времен без симметрий. Комм. Мат. физ. 313 , 385-403. ( 10.1007/s00220-012-1496-x) [CrossRef] [Google Scholar]

155. Ландау Л., Лифшиц Э.М. 1975 год. Классическая теория поля, 4-е исправленное изд. Нью-Йорк, штат Нью-Йорк: Пергамон. [Google Scholar]

156. Халатников И.М., Лифшиц Е.М. 1961. Об особенностях космологических решений уравнений гравитации. И. Сов. физ. ЖЭТФ 12 , 108. [Google Scholar]

157. Халатников И.М., Лифшиц Е.М. 1964. Проблемы релятивистской космологии. сов. физ. Усп. 6 , 495-522. ( 10.1070/ПУ1964v006n04ABEH003585) [CrossRef] [Google Scholar]

158. Халатников И.М., Каменщик А.Ю., Мартеллини М., Старобинский А.А. 2003. Квазиизотропное решение уравнений Эйнштейна вблизи космологической сингулярности для двухжидкостной космологической модели. Дж. Космол. Астропарт. физ. 03 , 001. ( 10.1088/1475-7516/2003/03/001) [CrossRef] [Google Scholar]

159. Халатников И.М., Каменщик А.Ю., Старобинский А.А. 2002. Комментарий о квазиизотропном решении уравнений Эйнштейна вблизи космологической сингулярности. Учебный класс. Квантовая Грав. 19 , 3845-3849. ( 10.1088/0264-9381/19/14/322) [CrossRef] [Google Scholar]

160. Derouelle N, langlois D. 1995. Длинноволновая итерация уравнений Эйнштейна вблизи пространственно-временной сингулярности. физ. Преподобный Д 52 , 2007-2019. (10.1103/PhysRevD.52.2007) [PubMed] [CrossRef] [Google Scholar]

161. Томита К. 1993. Усреднение неоднородных космологических моделей. физ. Преподобный Д 48 , 5634-5641. ( 10.1103/PhysRevD.48.5634) [PubMed] [CrossRef] [Google Scholar]

162. Riess A, et al. 1998. Свидетельства наблюдений сверхновых для ускоряющейся Вселенной и космологической постоянной. Астрон. Дж. 116 , 1009-1038. ( 10.1086/300499) [CrossRef] [Google Scholar]

163. Perlmutter S, et al. 1999. Измерения Ω и Λ 42 сверхновых с большим красным смещением. Астрофиз. Дж. 517 , 565-586. ( 10.1086/307221) [CrossRef] [Google Scholar]

164. Peebles PJE. 2020. Век космологии. Принстон, Нью-Джерси: Издательство Принстонского университета. [Академия Google]

165. Коупленд Э.Дж., Сами М., Цудзикава С. 2006. Динамика темной энергии. Междунар. Дж. Мод. физ. Д 15 , 1753-1935. ( 10.1142/S021827180600942X) [CrossRef] [Google Scholar]

166. Clifton T, Ferreira PG, Padilla A, Skordis C. 2012. Модифицированная гравитация и космология. физ. Представитель 513 , 1-189. ( 10.1016/j.physrep.2012.01.001) [CrossRef] [Google Scholar]

167. Capozziello S, De Laurentis M. 2011. Расширенные теории гравитации. физ. Представитель 509 , 167-321. ( 10.1016/j.physrep.2011.09.003) [CrossRef] [Google Scholar]

168. Джойс А., Джейн Б., Хури Дж. 2015. За пределами космологической стандартной модели. Представитель физ. 568 , 1-98. ( 10.1016/j.physrep.2014.12.002) [CrossRef] [Google Scholar]

169. Jiménez JB, Heisenberg L, Olmo GJ, Rubiera-Garcia D. 2018. Борн-Инфельд вдохновил модификации гравитации. Физический отчет 727 , 1-129. ( 10.1016/j.physrep.2017.11.001) [CrossRef] [Google Scholar]

170. Кобаяши Т. 2019. Теория Хорндески и не только: обзор. Представитель прог. физ. 82 , 086901. ( 10.1088/1361-6633/ab2429) [PubMed] [CrossRef] [Google Scholar]

171. Фрушанте Н. 2020. Теория эффективного поля темной энергии: обзор. физ. Представитель 857 , 1-63. ( 10.1016/j.physrep.2020.02.004) [CrossRef] [Google Scholar]

172. Ван С., Ван И, Ли М. 2017. Голографическая темная энергия. физ. Представитель 696 , 1-57. ( 10.1016/j.physrep.2017.06.003) [CrossRef] [Google Scholar]

173. Бранденбергер Р. 2022. Ограничения эффективной теории поля для космологии ранней Вселенной. Фил. Транс. Р. Соц. А 380 , 20210178. ( 10.1098/rsta.2021.0178) [CrossRef] [Google Scholar]

174. Гасперини М. 2022. От до и после большого взрыва: (почти) самодвойственная космологическая история. Фил. Транс. Р. Соц. А 380 , 20210179. ( 10.1098/rsta.2021.0179) [CrossRef] [Google Scholar]

175. Антониадис И., Коцакис С., Клаудату И. 2022. Особенности бранного мира и асимптотика объемных пятимерных жидкостей. Фил. Транс. Р. Соц. А 380 , 20210180. ( 10.1098/rsta.2021.0180) [CrossRef] [Google Scholar]

176. Vanhove P. 2022. S -матричный подход к физике гравитационных волн. Фил. Транс. Р. Соц. А 380 , 20210181. ( 10.1098/rsta.2021.0181) [CrossRef] [Google Scholar]

177. Solà Peracaula J. 2022. Проблема космологической постоянной и бегущий вакуум в расширяющейся Вселенной. Фил. Транс. Р. Соц. А 380 , 20210182. ( 10.1098/rsta.2021.0182) [CrossRef] [Google Scholar]

178. Эриксон К.В., Леунг Р., Стелле К.С. 2022. Эффект Хиггса без обеда. Фил. Транс. Р. Соц. А 380 , 20210184. (10.1098/rsta.2021.0184) [CrossRef] [Google Scholar]

179. Таунсенд П.К. 2022. Эфир, темная энергия и струнные компактификации. Фил. Транс. Р. Соц. А 380 , 20210185. (10.1098/rsta.2021.0185) [PubMed] [CrossRef] [Google Scholar]

180. Tan L, Tsamis NC, Woodard RP. 2022. Как инфляционные гравитоны влияют на гравитационное излучение. Фил. Транс. Р. Соц. А 380 , 20210187. (10.1098/rsta.2021.0187) [CrossRef] [Google Scholar]

181. Казанас Д., Пападопулос Д., Христодулу Д. 2022. Гравитация выше Эйнштейна? Да, но в каком направлении? Фил. Транс. Р. Соц. А 380 , 20210367. ( 10.1098/rsta.2021.0367) [CrossRef][Google Scholar]

182. Дадхич Н. 2022. О пространственно-временной структуре и Вселенной: некоторые вопросы концепции и принципа. Фил. Транс. Р. Соц. А 380 , 20210405. ( 10.1098/rsta.2021.0405) [CrossRef] [Google Scholar]

DLMF: Библиография V ‣ Библиография

• Г. Валент (1986) Интегральное преобразование, включающее функции Гойна и связанную с ним проблему собственных значений. СИАМ Дж. Матем. Анальный. 17 (3), стр. 688–703.
• О. Валле и М. Соарес (2010) Функции Эйри и приложения к физике. Второе издание, Imperial College Press, Лондон.
• А. Л. Ван Бюрен, Р. В. Байер, С. Ханиш и Б. Дж. Кинг (1972) Расчет сфероидальных волновых функций. Дж. Акус. соц. амер. 51, стр. 414–416. 907:00
• А. Л. Ван Бурен, Р. В. Байер и С. Ханиш (1970) Компьютерная программа на Фортране для вычисления сплюснутых сфероидальных радиальных функций первого и второго рода и их первых производных. Отчет НРЛ № 6959 Военно-морской рез. лаборатория Вашингтон, округ Колумбия.
• А. Л. Ван Бюрен, Б. Дж. Кинг, Р. В. Байер и С. Ханиш (1975) Таблицы угловых сфероидальных волновых функций, Vol. 1, вытянутый, m=0; Том. 2, сплющенный, m=0. Военно-морской рез. лаборатория Отчеты, Вашингтон, округ Колумбия. 907:00
• А. Л. Ван Бюрен и Дж. Э. Бойсверт (2002) Точное вычисление вытянутых сфероидальных радиальных функций первого рода и их первых производных. кв. заявл. Мат. 60 (3), стр. 589–599.
• А. Л. Ван Бюрен и Дж. Э. Бойсверт (2004) Улучшен расчет вытянутых сфероидальных радиальных функций второго рода и их первых производных. кв. заявл. Мат. 62 (3), стр. 493–507.
• А. Л. Ван Бюрен и Дж. Э. Бойсверт (2007) Точное вычисление модифицированных функций Матье целого порядка. кв. заявл. Мат. 65 (1), стр. 1–23. 907:00
• Ван Бюрен (веб-сайт) Матье и сфероидальные волновые функции: программы на Фортране для их точного расчета
• ХК ван де Хюльст (1957) Рассеяние света мелкими частицами. Джон Уайли и сыновья. Inc., Нью-Йорк.
• ХК ван де Хюльст (1980) Многократное рассеяние света. Том. 1, Академик Пресс, Нью-Йорк.
• Дж. ван де Лун, Х. Дж. Дж. Те Риле и Д. Т. Винтер (1986) О нулях дзета-функции Римана в критической полосе. IV. Мат. Комп. 46 (174), стр. 667–681. 907:00
• Х. Ван де Вель (1969) О методе разложения в ряд для вычисления неполных эллиптических интегралов первого и второго рода. Мат. Комп. 23 (105), стр. 61–69.
• К. Г. ван дер Лаан и Н. М. Темме (1984) Вычисление специальных функций: гамма-функция, экспоненциальные интегралы и функции, подобные ошибкам. Трактат CWI, Vol. 10, Математический центр Stichting, Centrum voor Wiskunde en Информатика, Амстердам.
• Эй Джей ван дер Поортен (1980) Некоторые замечательные формулы… Введение в полилогарифмы. В материалах конференции по теории чисел королевы, 1979 (Кингстон, Онтарио, 1979), Р. Рибенбойм (ред.), Бумаги королевы в Pure и Appl. Матем., Том. 54, Кингстон, Онтарио, стр. 269–286.
• Б. Л. ван дер Варден (1951) О методе седловых точек. заявл. науч. Исследование Б. 2, стр. 33–45.
• Дж. Ван Деун и Р. Кулс (2008) Интегрирование произведений функций Бесселя с дополнительным экспоненциальным или рациональным множителем. вычисл. физ. Комм. 178 (8), стр. 578–590.
• Дж. Ф. Ван Диен и В. П. Спиридонов (2001) Модульные гипергеометрические суммы вычетов эллиптических интегралов Сельберга. лат. Мат. физ. 58 (3), стр. 223–238. 907:00
• К. Ван Лоан (1992) Вычислительные основы для быстрого преобразования Фурье. Границы прикладной математики, Vol. 10, Общество промышленной и прикладной математики (SIAM), Филадельфия, Пенсильвания.
• Б. Ф. ван Миллиген и А. Лопес Фрагуас (1994) Разложение вакуумных магнитных полей по тороидальным гармоникам. вычисл. физ. Комм. 81 (1-2), стр. 74–90.
• А. ван Вейнгаарден (1953) О коэффициентах модулярного инварианта J⁢(τ). Недерл. акад. Ветенш. проц. сер. A. 56 = Indagationes Мат. 15 56, стр. 389–400.
• А. Н. Варченко (1976) Многогранники Ньютона и оценки осциллирующих интегралов. Функциональный. Анальный. я приложен. 10 (3), стр. 13–38 (рус.).
• Р. С. Варма (1941) Бесконечный ряд функций параболического цилиндра Вебера. проц. Бенарес Математика. соц. (NS) 3, стр. 37.
• Д. А. Варшалович, А. Н. Москалев, В. К. Херсонский (1988) Квантовая теория углового момента. World Scientific Publishing Co. Inc., Сингапур.
• А. Н. Ваврек и В. Томпсон (1984) Некоторые новые бесконечные серии сферических функций Бесселя. кв. заявл. Мат. 42 (3), стр. 321–324.
• Г. Веделер (1950) Уравнение Матье для кораблей, катящихся среди волн. я, II. Norske Vid. Сельск. Forh., Trondheim 22 (25–26), стр. 113–123.
• Р. Вейн и П. Дейл (1999) Детерминанты и их приложения в математической физике. Прикладные математические науки, Vol. 134, Спрингер-Верлаг, Нью-Йорк.
• Дж. Венециано (1968) Построение кросс-симметричной редже-амплитуды для линейно возрастающих траекторий. Il Nuovo Cimento A 57 (1), стр. 190–197.

• П. Вербек (1970) Рациональные аппроксимации экспоненциальных интегралов En⁢(x). акад. Рой. бельг. Бык. Кл. науч. (5) 56, стр. 1064–1072.
• А. Верма и В. К. Джайн (1983) Некоторые формулы суммирования q-рядов. Дж. Индийская математика. соц. (NS) 47 (1–4), стр. 71–85 (1986).
• Р. Видунас и Н. М. Темме (2002) Символическое вычисление коэффициентов в асимптотических разложениях типа Эйри. Дж. Матем. Анальный. заявл. 269 ​​(1), стр. 317–331.
• Р. Видунас (2005) Преобразования некоторых гипергеометрических функций Гаусса. Дж. Вычисл. заявл. Мат. 178 (1-2), стр. 473–487. 907:00
• Л. Виеторис (1983) Dritter Beweis der die unvollständige Gammafunktion betreffenden Lochsschen Ungleichungen. Австрия. акад. Висс. Матем.-натур. Кл. Ситцунгсбер. II 192 (1–3), стр. 83–91 (немецкий).
• Н. Я. Виленкин и А.Ю. Климык (1991) Представление групп Ли и специальные функции. Том 1: Простейшие группы Ли, специальные функции и интегральные преобразования. Математика и ее приложения (советская серия), Vol. 72, Kluwer Academic Publishers Group, Дордрехт. 907:00
• Н. Я. Виленкин и А.Ю. Климык (1992) Представление групп Ли и специальные функции. Том 3: Классические и квантовые группы и специальные функции. Математика и ее приложения (советская серия), Vol. 75, Kluwer Academic Publishers Group, Дордрехт.
• Н. Я. Виленкин и А.Ю. Климык (1993) Представление групп Ли и специальные функции. Том 2: Представления класса I, специальные функции и интегральные преобразования. Математика и ее приложения (советская серия), Vol. 74, Kluwer Academic Publishers Group, Дордрехт. 907:00
• Н. Я. Виленкин (1968) Специальные функции и теория представлений групп. Американское математическое общество, Провиденс, Род-Айленд.
• И. М. Виноградов (1937) Представление нечетного числа в виде суммы трех простых (рус.). Докл. акад. Наук СССР 15, стр. 169–172 (рус.).
• И. М. Виноградов (1958) Новая оценка функции ζ⁢(1+i⁢t). Изв. акад. наук СССР. сер. Мат. 22, стр. 161–164 (рус.).
• Н. Вирченко и И. Федотова (2001 г. ) Обобщенные ассоциированные функции Лежандра и их приложения. World Scientific Publishing Co. Inc., Сингапур. 907:00
• Х. Фолькмер (1999) Разложения по произведениям полиномов Гейне-Стилтьеса. Констр. прибл. 15 (4), стр. 467–480.
• Х. Фолькмер и Джей Джей Вуд (2014) Замечание об асимптотическом разложении обобщенных гипергеометрических функций. Анальный. заявл. (Сингап.) 12 (1), стр. 107–115.
• Х. Фолькмер (1982) Интегральные соотношения для функций Ламе. СИАМ Дж. Матем. Анальный. 13 (6), стр. 978–987.
• Х. Фолькмер (1983) Integralgleichungen für Periodische Lösungen Hill’scher Differentialgleichungen. Анализ 3 (1–4), стр. 189.–203 (немецкий).
• Х. Фолькмер (1984) Интегральные представления произведений функций Ламе с помощью фундаментальных решений. СИАМ Дж. Матем. Анальный. 15 (3), стр. 559–569.
• Х. Фолькмер (1998) О росте радиусов сходимости собственных значений уравнения Матье. Мат. Нахр. 192, стр. 239–253.
• Х. Фолькмер (2004a) Оценки погрешности аппроксимаций Рэлея-Ритца собственных значений и собственных функций уравнения Матье и сфероидального волнового уравнения. Констр. прибл. 20 (1), стр. 39–54.
• Х. Фолькмер (2004b) Четыре замечания о собственных значениях уравнения Ламе. Анальный. заявл. (Сингап.) 2 (2), стр. 161–175.
• Х. Фолькмер (2008) Приближение собственных значений некоторых дифференциальных уравнений нулями ортогональных многочленов. Дж. Вычисл. заявл. Мат. 213 (2), стр. 488–500.
• Х. Фолькмер (2021) Представление в ряд Фурье функции Феррера P.
• Х. фон Кох (1901) Über die Riemann’sche Primzahlfunction. Мат. Анна. 55, стр. 441–464 (немецкий). 907:00
• А. П. Воробьев (1965) О рациональных решениях второго уравнения Пенлеве. Отличаться. Уравн. 1 (1), стр. 79–81 (рус.).
• М. Н. Врахатис, Т. Н. Грапса, О. Рагос и Ф. А. Зафиропулос (1997a) О локализации и вычислении нулей функций Бесселя. З. Энгью. Мат. мех. 77 (6), стр. 467–475.
• М. Н. Врахатис, О. Рагос, Т. Скиниотис, Ф. А. Зафиропулос и Т. Н. Грапса (1995) RFSFNS: Портативный пакет для численного определения числа и вычисления корней функций Бесселя. вычисл. физ. Комм. 92 (2-3), стр. 252–266.
• М. Н. Врахатис, О. Рагос, Т. Скиниотис, Ф. А. Зафиропулос и Т. Н. Грапса (1997b) Теория топологической степени для локализации и вычисления комплексных нулей функций Бесселя. Число. Функц. Анальный. Оптим. 18 (1-2), стр. 227–234.

Lp-сходимость жадного алгоритма по обобщенной системе Уолша

%PDF-1.7 % 1 0 объект > >> эндообъект 9 0 объект /Заголовок (Lp-сходимость жадного алгоритма по обобщенной системе Уолша) /В ловушке /Ложь /дои (10.1016/j.jmaa.2012.01.014) /роботы (без индекса) >> эндообъект 2 0 объект > ручей приложение/pdfdoi:10.1016/j.jmaa.2012.01.014

Lp-сходимость жадного алгоритма по обобщенной системе Уолша

С.А. Епископосян

М.Г. Григорян

Обобщенная система Уолша

Монотонные коэффициенты

Жадный

Журнал математического анализа и приложений, 389 (2012) 1374–1379. 10.1016/j.jmaa.2012.01.014

Эльзевир Инк

журналJournal of Mathematical Analysis and ApplicationsАвторские права ©2012 Elsevier Inc. Все права защищены.0022-247X38921374-13791374137910.1016/j.jmaa.2012.01.014http://dx.doi.org/10.1016/j.jmaa.2012.01.0142012-05-1515 май 2012 г.2010-04-23true10.1016/j.jmaa.20129 9 elsevier.com

sciencedirect.com

6.210.1016/j.jmaa.2012.01.014noindex2010-04-23true

sciencedirect.com

elsevier.com

Elsevier2012-01-26T13:31:12+02:002012-01-26T13:31:12+02:002012-01-26T13:31:12+02:00TrueAcrobat Distiller 9.4.6 (Windows)Falseuid:65643409-c62a-4d60-8c26-9151a43fa642uuid:4d547d18-004f-4c6b-b550-1c92e0ea15e5 конечный поток эндообъект 3 0 объект > эндообъект 4 0 объект > /Шрифт > /ProcSet [/PDF /текст /ImageC] /XОбъект > >> /Повернуть 0 /TrimBox [8,504 8,504 552,756 751,181] /Тип /Страница >> эндообъект 5 0 объект > эндообъект 6 0 объект > эндообъект 7 0 объект > эндообъект 8 0 объект > >> эндообъект 10 0 объект > эндообъект 11 0 объект > эндообъект 12 0 объект > /Граница [0 0 0] /С [1 1 1] /ЗДРАВСТВУЙ /Rect [217,682 7090,393 346,824 717,254] /Подтип /Ссылка /Тип /Аннот >> эндообъект 13 0 объект > /Граница [0 0 0] /С [1 1 1] /ЗДРАВСТВУЙ /Rect [289,269 681,926 375,768 691,455] /Подтип /Ссылка /Тип /Аннот >> эндообъект 14 0 объект > /Граница [0 0 0] /С [1 1 1] /ЗДРАВСТВУЙ /Rect [225,494 626,126 341,352 635,655] /Подтип /Ссылка /Тип /Аннот >> эндообъект 15 0 объект > /Граница [0 0 0] /С [1 1 1] /ЗДРАВСТВУЙ /прямо [105,38 82,0209 154,908 89,8823] /Подтип /Ссылка /Тип /Аннот >> эндообъект 16 0 объект > /Граница [0 0 0] /С [1 1 1] /ЗДРАВСТВУЙ /прямо [48.