ГДЗ: Математика 6 класс Зубарева, Мордкович
Математика 6 класс
Тип: Учебник
Авторы: Зубарева, Мордкович
Издательство: Мнемозина
Существует множество предметов согласно общеобразовательной программе, которые дети изо дня в день изучают. Но сколько детей, столько и мнений. Кому-то из детей ближе гуманитарные дисциплины, кто-то восхищается точными науками, кто-то искусством и физической культурой. Предрасположенность учащегося к определенному предмету определяет его будущее и оценки по предмету. Но что делать если предмет не лежит к душе и его не получается понять. В современном мире давно нашли выход из этой ситуации. Родители понимают, что не всегда могут прийти на помощь своему ребенку, поэтому пользуются решебниками.
МАТЕМАТИКА В СОВРЕМЕННОМ МИРЕ
Какую бы дисциплину не выбрал для себя школьник в качестве своего приоритетного обучения, ему потребуется математика.
ПРОБЛЕМАТИКА ИЗУЧЕНИЯ ПРЕДМЕТА
Основными проблемами изучения являются:
- Отсутствие предрасположенности к изучению точных наук.
- Большой объем изучаемого материала.
- Необходимость постоянного повторения и построения логических цепочек.
КОРОТКО О ГЛАВНОМ
Решебник к учебнику «Математика 6 класс Учебник Зубарева, Мордкович Мнемозина» является прекрасным пособием для помощи школьнику. Авторы очень доступно для понимания детей объясняют задания с арифметическими манипуляциями чисел. Представляют прекрасное объяснение правильной работы с координатными плоскостями. Объясняют материал о делимости чисел, изучают пропорции, учат находить максимальный общий делитель, минимальное общее кратное.
Авторы очень доступно для понимания детей объясняют задания с арифметическими манипуляциями чисел. Представляют прекрасное объяснение правильной работы с координатными плоскостями. Объясняют материал о делимости чисел, изучают пропорции, учат находить максимальный общий делитель, минимальное общее кратное.
ДОСТОИНСТВА
Чтобы учащиеся не «спотыкались» в линейных уравнениях и координатных плоскостях следует пользоваться ГДЗ для проверки домашнего задания или самостоятельного обучения дома. Пособие по «Математике 6 класс Зубарева позволит сформировать пространственное мышление у школьника, закрепить и проверить полученные знания по пропорциям, делимости чисел и т.д.
ГДЗ от Путина по математике 6 класс Зубарева, Мордкович
Точные науки считаются одними из самых сложных во всей школьной программе, именно поэтому для того, чтобы справиться с задаваемые в школе примерами и задачами, вашему ребенку могут понадобиться ответы по математике для 6 класса Зубарева, Мордкович. ГДЗ не просто позволяют разобрать то или иное упражнение, но и понять, как теория применяется на практике.
ГДЗ не просто позволяют разобрать то или иное упражнение, но и понять, как теория применяется на практике.
Школьная книга уже готовых заданий содержит в себе как ответы на разнообразные теоретические вопросы тестового характера, так и подробные авторские решения примеров и задач. Все представленные ГДЗ-материалы поделены на соответствующие тематические блоки, разделы и подразделы, благодаря чему удается довольно быстро найти нужное упражнение. Также, подобная классификация позволяет ознакомиться сразу с серией задач на определенную математическую тематику.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 415 416 417 418 419 420 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 463 464 465 466 467 468 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 704 705 706 707 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 810 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 839 840 841 842 843 844 845 846 847 848 849 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 923 924 925 926 927 928 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 958 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022 1023 1024 1025 1026 1027 1028 1029 1030 1031 1032 1033 1034 1035 1036 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050 1051 1053 1054 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064 1065 1066 1067 1068 1069 1070 1071 1072 1073 1074 1075 1076 1077 1078 1079 1080 1081 1082 1083 1084 1085 1086 1087 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105 1107 1108 1109 1110 1111 1112 1113 1114
Домашние контрольные работы Раздел 1
1. 11.21.31.4
11.21.31.4
Раздел 2
2.12.22.32.4
Раздел 3
3.13.23.33.43.5
Раздел 4
4.14.24.34.4
Раздел 5
5.15.25.35.4
Раздел 6
6.16.26.36.4
Раздел 7
7.17.27.37.4
Раздел 8
8.18.28.38.4
ГДЗ номер 265 математика 6 класс Зубарева, Мордкович – Telegraph
➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!
ГДЗ номер 265 математика 6 класс Зубарева, Мордкович
Решебник, математика , 6 класс — Зубарева , Мордкович поможет в выполнении и проверке . Вы открыли задание номер 265 из решебника на uchim .org .
ГДЗ (готовое домашние задание из решебника) на Номер №265 по учебнику Математика . 6 класс . Учебник для общеобразовательных организаций / И .И . Зубарева , А .Г . Мордкович .
Ответы из задачника . Зубарева , Мордкович . Номер №265 .
ГДЗ по математике 6 класс Зубарева номер — 265 . Авторы : Зубарева И .И ., Мордкович А .Г . Издательство: Мнемозина 2019 . Подробное решение номер № 265 по математике для учащихся 6 класса , авторов Зубарева , Мордкович 2019 .
Математика шестой класс Зубарева ГДЗ : 265 . суммы: Найдите значение выражения устно, используя правило вычисления алгебраической а) -78 + 20 + 26 — 46 — 100 . . ГДЗ (решебники) -> 6 класс -> Зубарева И .И ., Мордкович А .Г . «Математика » 6 класс .
Подробный решебник (ГДЗ ) по Математике за 6 (шестой ) класс — готовый ответ номер — 265 . Авторы учебника: Зубарева , Мордкович . Авторы: Зубарева И .И ., Мордкович А .Г . Издательство: Мнемозина 2019 год . Тип: Учебник .
авторы: Зубарева И .И ., Мордкович А .Г . Решебник для учащихся 6 класса под редакцией Зубаревой И .И УМК по математике от данных методистов соответствует всем стандартам ФГОС, он принят для Каждый номер имеет поэтапный алгоритм прорешивания, который не . .
Подробный разбор решения задачи номер 265 из учебника по математике за 6 класс авторов: Зубарева И .И ., Мордкович А .Г . Решебник к номеру №265 — математика 6 класс Зубарева .
Подробное решение номер 265 ГДЗ !Математика 6 класс ФГОС !Зубарева , Мордкович номер 265 Решебник . Класс : 6 класс . Автор: !Зубарева , Мордкович . Загрузи своё решение домашки и заработай на этом отметки!
Класс : 6 класс . Автор: !Зубарева , Мордкович . Загрузи своё решение домашки и заработай на этом отметки!
ГДЗ 6 класс Математика Зубарева И .И . Помимо ответов к номерам и полные решений задач здесь имеются ключи к контрольным вопросам после каждого раздела . Данная книга дуэта методистов Зубарева И .И ., Мордкович А .Г . — отличное подспорье для любого умысла . 265 .
Авторы: Зубарева И .И ., Мордкович А .Г . Онлайн решебник по Математике для 6 класса Зубарева И .И ., Мордкович А .Г ., гдз и ответы к домашнему заданию . ГДЗ к рабочей тетради по математике за 6 класс Ерина Т .М . можно скачать здесь . ГДЗ к номерам задач .
Учебник по математике под авторством Зубарева Мордкович 6 класс ориентирован на классные занятия и работу дома и является достаточно популярным в Многих школьникам приходится прибегать к использованию авторского ГДЗ решебника Зубарева 6 класс, который . .
Зубарева , Мордкович . «Мнемозина» . год . ГДЗ по математике 6 класс Зубарева , Мордкович ответы к учебнику . Шестиклассникам приходится выполнять действия с обыкновенными дробями, работать с координатной прямой, решать задачи на отношения и . .
Шестиклассникам приходится выполнять действия с обыкновенными дробями, работать с координатной прямой, решать задачи на отношения и . .
Математика 6 класс . Учебник . Зубарева , Мордкович . Практично составленное пособие прекрасно поможет детям освоиться с предметом . «ГДЗ по Математике 6 класс Зубарева » поделены на пять тематических глав, с полным набором заданий, которые помогут не только . .
Зубарева , Мордкович . Мнемозина . год . ГДЗ по математике 6 класс Зубарева , Мордкович (учебник) . Шестиклассники решают примеры с отрицательными числами, работают с координатной плоскостью, изучают признаки делимости, знакомятся с основами теории . .
Решебник, математика , 6 класс — Зубарева , Мордкович поможет в выполнении и проверке . Вы открыли задание номер 265 из решебника на uchim .org .
ГДЗ (готовое домашние задание из решебника) на Номер №265 по учебнику Математика . 6 класс . Учебник для общеобразовательных организаций / И .И . Зубарева , А .Г . Мордкович .
Ответы из задачника . Зубарева , Мордкович . Номер №265 .
ГДЗ по математике 6 класс Зубарева номер — 265 . Авторы : Зубарева И .И ., Мордкович А .Г . Издательство: Мнемозина 2019 . Подробное решение номер № 265 по математике для учащихся 6 класса , авторов Зубарева , Мордкович 2019 .
Математика шестой класс Зубарева ГДЗ : 265 . суммы: Найдите значение выражения устно, используя правило вычисления алгебраической а) -78 + 20 + 26 — 46 — 100 . . ГДЗ (решебники) -> 6 класс -> Зубарева И .И ., Мордкович А .Г . «Математика » 6 класс .
Подробный решебник (ГДЗ ) по Математике за 6 (шестой ) класс — готовый ответ номер — 265 . Авторы учебника: Зубарева , Мордкович . Авторы: Зубарева И .И ., Мордкович А .Г . Издательство: Мнемозина 2019 год . Тип: Учебник .
авторы: Зубарева И .И ., Мордкович А .Г . Решебник для учащихся 6 класса под редакцией Зубаревой И .И УМК по математике от данных методистов соответствует всем стандартам ФГОС, он принят для Каждый номер имеет поэтапный алгоритм прорешивания, который не . .
.
Подробный разбор решения задачи номер 265 из учебника по математике за 6 класс авторов: Зубарева И .И ., Мордкович А .Г . Решебник к номеру №265 — математика 6 класс Зубарева .
Подробное решение номер 265 ГДЗ !Математика 6 класс ФГОС !Зубарева , Мордкович номер 265 Решебник . Класс : 6 класс . Автор: !Зубарева , Мордкович . Загрузи своё решение домашки и заработай на этом отметки!
ГДЗ 6 класс Математика Зубарева И .И . Помимо ответов к номерам и полные решений задач здесь имеются ключи к контрольным вопросам после каждого раздела . Данная книга дуэта методистов Зубарева И .И ., Мордкович А .Г . — отличное подспорье для любого умысла . 265 .
Авторы: Зубарева И .И ., Мордкович А .Г . Онлайн решебник по Математике для 6 класса Зубарева И .И ., Мордкович А .Г ., гдз и ответы к домашнему заданию . ГДЗ к рабочей тетради по математике за 6 класс Ерина Т .М . можно скачать здесь . ГДЗ к номерам задач .
Учебник по математике под авторством Зубарева Мордкович 6 класс ориентирован на классные занятия и работу дома и является достаточно популярным в Многих школьникам приходится прибегать к использованию авторского ГДЗ решебника Зубарева 6 класс, который . .
.
Зубарева , Мордкович . «Мнемозина» . год . ГДЗ по математике 6 класс Зубарева , Мордкович ответы к учебнику . Шестиклассникам приходится выполнять действия с обыкновенными дробями, работать с координатной прямой, решать задачи на отношения и . .
Математика 6 класс . Учебник . Зубарева , Мордкович . Практично составленное пособие прекрасно поможет детям освоиться с предметом . «ГДЗ по Математике 6 класс Зубарева » поделены на пять тематических глав, с полным набором заданий, которые помогут не только . .
Зубарева , Мордкович . Мнемозина . год . ГДЗ по математике 6 класс Зубарева , Мордкович (учебник) . Шестиклассники решают примеры с отрицательными числами, работают с координатной плоскостью, изучают признаки делимости, знакомятся с основами теории . .
ГДЗ часть 1 64 русский язык 3 класс Каленчук, Чуракова
ГДЗ глава 3. задача 209 геометрия 7‐9 класс Атанасян, Бутузов
ГДЗ номер 421 физика 7‐9 класс сборник задач Лукашик, Иванова
ГДЗ учебник 2015. упражнение 1333 (484) математика 5 класс Виленкин, Жохов
упражнение 1333 (484) математика 5 класс Виленкин, Жохов
ГДЗ упражнение 135 русский язык 10‐11 класс Гольцова, Шамшин
ГДЗ по английскому языку 6 класс рабочая тетрадь Happy English Кауфман, Кауфман Решебник
ГДЗ страница 43 английский язык 8 класс рабочая тетрадь Кузовлев, Перегудова
ГДЗ самостоятельная работа / самостоятельная работа №7 / вариант 2 6 алгебра 7 класс дидактические материалы Феоктистов
ГДЗ к учебнику Погорелова / самостоятельные работы / СП-10 В2 геометрия 10 класс самостоятельные и контрольные работы Ершова, Голобородько
ГДЗ параграф 25 6 алгебра 7 класс рабочая тетрадь Миндюк, Шлыкова
ГДЗ номер 679 алгебра 9 класс Алимов, Колягин
ГДЗ номер 179 математика 6 класс Дорофеев, Шарыгин
ГДЗ параграф 28 2 алгебра 9 класс рабочая тетрадь Миндюк, Шлыкова
ГДЗ номер 50 алгебра 9 класс Алимов, Колягин
ГДЗ § 26 6 история 8 класс рабочая тетрадь Юдовская, Ванюшкина
ГДЗ страница 201 английский язык 7 класс новый курс (3-ий год обучения) Афанасьева, Михеева
ГДЗ часть 2. местоимение 15 русский язык 4 класс Зеленина, Хохлова
местоимение 15 русский язык 4 класс Зеленина, Хохлова
ГДЗ Учебник 2019 / часть 2 167 (1016) математика 5 класс Виленкин, Жохов
ГДЗ учебник 2015. упражнение 1662 (815) математика 5 класс Виленкин, Жохов
ГДЗ учебник 2015. номер 431 (436) математика 6 класс Виленкин, Жохов
ГДЗ часть №3 3 математика 6 класс Петерсон, Дорофеев
ГДЗ вариант 2. тест 1 математика 5 класс тематические тесты Чулков, Шершнев
ГДЗ тема 9 9.21 физика 8 класс Генденштейн, Кирик
ГДЗ часть №1 / 4 63 химия 8‐9 класс задачник с помощником Гара, Габрусева
ГДЗ параграф 5 5.1 геометрия 7 класс Мерзляк, Поляков
ГДЗ страница 27 география 7 класс тетрадь-экзаменатор Барабанов, Дюкова
ГДЗ номер 265 алгебра 9 класс Дорофеев, Суворова
ГДЗ § / § 14 17 математика 4 класс Муравин, Муравина
ГДЗ часть 1 617 математика 6 класс задачник Бунимович, Кузнецова
ГДЗ § 18 18.49 алгебра 11 класс учебник, задачник Мордкович, Денищева
ГДЗ тест 9. вариант 1 алгебра 7 класс контрольно-измерительные материалы Мартышова
ГДЗ упражнения / упражнение 18 4 физика 7 класс Перышкин
ГДЗ номер 69 математика 5 класс Дорофеев, Шарыгин
ГДЗ часть 2 / страница 13 1 математика 2 класс Моро, Бантова
ГДЗ упражнение 1056 алгебра 10‐11 класс Алимов, Колягин
ГДЗ страница 92 английский язык 8 класс Пахомова, Бондар
ГДЗ вариант 3 135 алгебра 8 класс дидактические материалы Мерзляк, Полонский
ГДЗ страница 74 история 7 класс тетрадь-тренажёр Данилов, Лукутин
ГДЗ номер 108 математика 6 класс Мерзляк, Полонский
ГДЗ часть 1. страница 50 математика 3 класс рабочая тетрадь Моро, Волкова
страница 50 математика 3 класс рабочая тетрадь Моро, Волкова
ГДЗ учебник 2015. упражнение 318 (318) математика 5 класс Виленкин, Жохов
ГДЗ номер 549 алгебра 8 класс Никольский, Потапов
ГДЗ по русскому языку 4 класс Полякова Решебник
ГДЗ самостоятельная работа / С-3 / вариант 3 5 алгебра 7 класс дидактические материалы Потапов, Шевкин
ГДЗ задание 913 математика 5 класс Никольский, Потапов
ГДЗ самостоятельная работа №3 / вариант 1 1 алгебра 7 класс дидактические материалы, к учебнику Мордкович Попов
ГДЗ § 23 25 алгебра 7 класс Мерзляк, Поляков
ГДЗ № 102 математика 5 класс Зубарева, Мордкович
ГДЗ задача 886 геометрия 8 класс Атанасян, Бутузов
ГДЗ тест 9. вариант 4 математика 6 класс тематические тесты Кузнецова, Минаева
ГДЗ § 23 15 алгебра 7 класс Мерзляк, Поляков
ГДЗ задание 160 информатика 9 класс рабочая тетрадь Босова, Босова
ГДЗ Математика 5 Класс Жохов 1 Часть
ГДЗ Математика 6 Класс Просвещение 2020
Дорофеев Математика 2 Класс Учебник Решебник
| ||||||||||||||
| Другой наш проект Сказки Хитрого Кота | ||||||||||||||
Контактный Email: | ||||||||||||||
| Контент опубликованный на сайте vcevce.ru защищен законом об авторском праве. Любое частичное или полное копирование опубликованной информации запрещено. © | ||||||||||||||
ГДЗ Математика 6 класс Зубарева
Вперед за новым
В 6 классе учащиеся познакомятся с алгеброй, с чего она начинается, на чем основывается. Узнают о наибольшем общем делителе и наименьшем общем кратном. Будут учиться складывать и вычитать дроби, у которых разные знаменатели. Научатся их множить и делить. Самой главной считается тема линейных уравнений с неизвестной. Придется сосредоточиться, потому что все темы требуют ответственного подхода.
Научатся их множить и делить. Самой главной считается тема линейных уравнений с неизвестной. Придется сосредоточиться, потому что все темы требуют ответственного подхода.
Авторы всегда рядом
Математик и автор Зубарева составила вместе с Мордкович учебник математики за 6 класс, по которому ведется обучение. Параллельно было разработано пособие к этому учебнику, решебник к учебнику «Математика 6 класс рабочая тетрадь Зубарева», издательства Мнемозина. Тетрадь согласована с учебником и состоит из двух частей. В первой – 16 заданий. Во второй – с номера 17 по 39. И в заключении – познавательный раздел о математике в целом и частности.
Используем с умом
С каждым годом все сложнее учебный материал и требуется больше сил и времени для изучения предмета. Но преподаватели стараются использовать разные способы, чтобы донести до учеников все знания. Одним из таких является решебник «ГДЗ Математика 6 класс рабочая тетрадь Зубарева Мнемозина», где автором Зубаревой собраны задания для тренировки и занимательного выполнения. Выстроено очень последовательно. Но решебник ГДЗ нужно использовать разумно:
Выстроено очень последовательно. Но решебник ГДЗ нужно использовать разумно:
- Не переписывать готовое, а вдумчиво разбирать представленные решения.
- Выбирать более подходящее.
- Сравнивать ответы и еще раз проверять свое выполнение.
Если использовать онлайн версию, тогда можно еще и обсудить в интернете с одноклассниками, поинтересоваться, какой вариант решения был ими выбран и почему. Поэтому используйте этот решебник как настольную книгу! Он ваш настоящий помощник и наставник.
Учебное пособие по математике для 6-го классаSpectrum — умножение и деление дробей и десятичных знаков, геометрия с примерами, тесты, ключ ответа для домашнего обучения или классной комнаты (160 стр.): Spectrum: 9781483808741: Amazon.com: Книги
ОСОБЕННОСТИ УПРАЖНЕНИЯ:
• Возраст 11–12, 6 класс
• 160 страниц, 8 дюймов x 11 дюймов
• Охватывает умножение и деление дробей и десятичных знаков, соотношения, уравнения и т. Д.
Д.
• Предварительные тесты, последующие тесты, промежуточное тестирование и заключительный тест
• Включен ключ ответа
ЦЕЛЕВАЯ ПРАКТИКА: Учебное пособие по математике Spectrum для шестого класса обеспечивает целенаправленную практику в овладении математикой для детей в возрасте 11 и 12 лет.Эта 160-страничная рабочая тетрадь из семи глав помогает детям оставаться на вершине своей математической игры, используя прогрессивные практики, математику в повседневных условиях и тесты для отслеживания прогресса.
СООТВЕТСТВУЕТ ТЕКУЩИМ ГОСУДАРСТВЕННЫМ СТАНДАРТАМ: Эта увлекательная рабочая тетрадь охватывает умножение и деление дробей и десятичных знаков, соотношений, коэффициентов, процентов, уравнений и неравенств, решение задач в координатной плоскости, вероятность и статистику, комплексные измерения и начальную алгебру.
ЧТО ВНУТРИ: Включает уроки и упражнения, которые помогают учащимся понять сложный предмет, а также предварительные, итоговые, промежуточные и заключительные тесты. Ключ ответа предоставляется для измерения успеваемости учащегося.
Ключ ответа предоставляется для измерения успеваемости учащегося.
РАБОТАЕМ ВМЕСТЕ: Серия Spectrum Math Workbooks, любимая учителем и родителями, помогает детям оставаться впереди в математике, предлагая систематические и заставляющие задуматься упражнения, предназначенные для повышения сложности.
ПОЧЕМУ SPECTRUM: Уже более 20 лет Spectrum предоставляет решения для родителей, которые хотят помочь своим детям добиться успеха, а также для учителей, которые хотят, чтобы их ученики достигли поставленных целей обучения и превзошли их; Рабочие тетради также являются отличным ресурсом для домашнего обучения.Spectrum вместе с вами поддерживает образовательный путь вашего ребенка на каждом этапе его пути.
Расчет всей детали. Нахождение целого по его части
Основные типы запроса процентов
I. Нахождение части целого
Чтобы найти часть (%) от целого, необходимо умножить это число на часть (процент переведен в десятичную дробь).
ПРИМЕР: Учащийся 32 класса. Во время тестовой работы не было 12.5% студентов. Узнайте, сколько студентов отсутствовало?
Решение 1: Inteid в этой задаче — общее количество студентов (32).
12,5% = 0,125
32 · 0,125 = 4
Решение 2:
от общего количества учеников (100%), то
32 ученика — 100%
x Ученики — 12,5%
ОТВЕТ: В классе не было 4 учеников.
II. Нахождение целого по его части
Чтобы найти целое число в его части (%), необходимо число разделить на части (проценты переводятся в десятичную дробь).
ПРИМЕР: Коль I потратил в парке развлечений 120 крон, что составило 75% всех его карманных денег. Сколько денег на карманные расходы у Коля до прихода в парк развлечений?
Решение 1: В этой задаче вам нужно найти целое число, если эта часть и значение известны.
данной части.
75% = 0,75
120: 0,75 = 160
Решение 2: Пусть x коронок было в корпусе, то есть 100%. Если он потратил 120 крон, что составило 75%, то
x крон — 100%
ОТВЕТ: У Коли было 160 крон.
III. Выражение в процентах от отношения двух чисел
Типичный вопрос:
Сколько% одно значение от другого?
ПРИМЕР: Ширина прямоугольника 20 м, длина 32 м. Сколько% составляет ширина длины? (Длина является основой для сравнения)
Решение 1:
Решение 2: В этой задаче длина прямоугольника 32 м равна 100%, тогда ширина 20 м равна x%.Составим и решим пропорцию:
20 метров — x%
32 метра — 100%
ОТВЕТ: Ширина от длины 62,5%.
NB! Обратите внимание на то, как меняется решение в зависимости от изменения вопроса.
ПРИМЕР: Ширина прямоугольника 20 м, длина 32 м. Сколько% составляет длина от ширины? (Ширина является основой для сравнения)
Решение 1:
Решение 2: В этой задаче ширина прямоугольника 20 м равна 100%, тогда длина 32 м равна x%.
20 метров — 100%
32 метра — x%
ОТВЕТ: Длина от ширины 160%.
IV. Выражение в процентах от изменения звездной величины
Типичный вопрос:
Насколько изменилось (увеличилось, уменьшилось) начальное значение?
Чтобы найти изменение в% в%:
1) Найдите столько же, сколько значение (без%)
2) разделите полученное значение из утверждения 1) на значение, которое является основой для сравнения
3) Переведите результат в% (путем умножения на 100%)
ПРИМЕР: Цена платья упала с 1250 крон до 1000 крон.Узнайте, на сколько процентов снизилась цена платья?
Решение 1:
2) базой для сравнения является 1250 крон (то есть то, что было изначально)
3)
Ответ: Цена платья снизилась на 20%.
NB! Обратите внимание на то, как меняется решение в зависимости от изменения вопроса.
ПРИМЕР: Цена платья выросла с 1000 до 1250 крон. Найдите, на сколько процентов выросла цена платья?
Найдите, на сколько процентов выросла цена платья?
Раствор 1:
1) 1250 -1000 = 250 (кр) настолько изменилась цена
2) базой для сравнения здесь является 1000 крон (т.е. что было изначально)
3)
Решение проблемы одним действием:
Решение 2:
1250 -1000 = 250 (CR) настолько изменилась цена
В этой задаче начальная цена 1000 крон 100%, то изменение цены 250 крон — x%. Составим и решим пропорцию:
1000 CZK — 100%
250 крон — x%
x =
ОТВЕТ: Цена платья увеличена на 25%.
V. Последовательное изменение размера (числа)
ПРИМЕР: Число было уменьшено на 15%, а затем увеличено на 20%.Найдите, на сколько процентов изменилось число?
Самая частая ошибка: число увеличилось на 5%.
Решение 1:
1) хотя начальное число не указано, для простоты его можно принять за 100 (т.е. один или 1)
2) Если число уменьшилось на 15%, итоговое число будет 85%, или из 100 было бы 85.
3) теперь полученный результат нужно увеличить на 20%, т.е.
85 — 100%
новое число x — 120% (потому что увеличилось на 20%)
x \ u003d
4) Таким образом, в результате изменений число 100 (начальное) изменилось и стало 102, а это значит, что начальное число увеличилось на 2%
Решение 2:
1) Пусть начальное число number x
2) если число уменьшилось на 15%, результирующее число будет 85% от x, т.е.е. 0,85x.
3) теперь получившееся число нужно увеличить на 20%, т.е.
0,85х — 100%
и новое число? — 120% (потому что увеличилось на 20%)
? =
ОТВЕТ: Число увеличилось на 2%.
§ 1 Правила поиска части целого и целого его части
В этом уроке мы формулируем правила нахождения части целого и целого в его части, а также рассматриваем решение задач с использованием этих правил. .
.
Рассмотрим две задачи:
Сколько километров прошли туристы в первый день, если весь туристический маршрут составляет 20 км.?
Найдите длину всего пути туриста.
Сравните эти задачи — в обоих случаях принимается весь путь. В первом задании известно все — 20 км, а во втором — неизвестно. В первом задании необходимо найти часть целого, а во втором — целое число в его части. В первом задании известно значение 20 км, во втором задании неизвестно, а во втором задании известно — 8 км, в первом нужно найти.Такие задачи называются взаимно обратными, так как они известны и нужные значения меняются местами.
Рассмотрим первую задачу:
Знаменатель 5 показывает, на сколько частей было разделено, т.е. если целые 20 разделить на 5, мы узнаем, сколько километров составляет одна часть, 20: 5 = 4 км. Числитель 2 показывает, что туристы прошли 2 участка пути, значит 4 нужно умножить на 2, получится 8 км. В первый день туристы прошли 8 км.
Получилось выражение 20: 5 ∙ 2 = 8.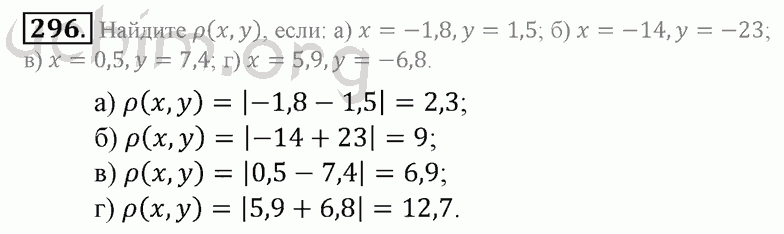
Переходим ко второму заданию.
Следовательно, одна часть будет равна частным 8 и 2, это будет 4, знаменатель 5, что означает все части 5.
4 Умножаем на 5, получится 20. Ответ 20 км — длина всего пути.
Запишем выражение: 8: 2 ∙ 5 = 20
Используя смысл умножения и деления числа на дробь, правила нахождения части из целого и целой его части можно сформулировать следующим образом:
Чтобы найти часть целого, число, соответствующее целому, умножьте на дробь, соответствующую этой части;
, чтобы найти целое число в его части, необходимо число, соответствующее этой части, разделить на соответствующую часть дроби.
Соответственно, решение задачи теперь можно записать иначе:
на первое задание 20 ∙ 2/5 = 8 (км),
для второго задания 8: 2/5 = 20 (км).
Чтобы не было затруднений, решение таких задач пишется так:
По порядку: до конца известно — 20 км.
Ответ: 8 км.
Целом: до конца неизвестно.
Ответ: 20 км.
§ 2 Алгоритм решения задач по нахождению целого по его части и части целого
Составим алгоритм решения таких задач.
Сначала мы анализируем состояние и вопрос задачи: выясняем, что такое целое, известно это или нет, затем выясняем, как представлена часть целого и что нужно найти.
Если необходимо найти часть целого, то целое умножьте на дробь, соответствующую этой части, если вам нужно найти целое число в его части, то число, соответствующее части, разделится на дробь, соответствующую этой части. часть. В результате получаем выражение. Далее находим значение выражения и записываем ответ, читая перед ним еще раз выпуск задачи.
Итак, прежде чем решать подобные задачи, вам необходимо ответить на следующие вопросы:
Какая величина приятного для всего?
Известна ли эта величина?
Что требуется, чтобы найти: часть целого или целое число по частям?
Подведем итоги: В этом уроке вы познакомились с правилами нахождения части целого и целой его части, а также научились решать задачи по этим правилам.
Список литературы:
- Математика.6 класс: Заготовка планов по учебнику И.И. Зубарева, А.Г. Мордкович // Автор-составитель Л.А. Топиль. Мнемозина, 2009.
- Математика. 6 класс: Учебник для учащихся общеобразовательных учреждений. И. Зубарева, А.Г. Мордкович. — М .: Мнемозина, 2013. .
- Математика. 6 класс: Учебник для общеобразовательных учреждений / Г.В. Дорофеев, И.Ф. Шарыгин, С. Суворов и др. / Под редакцией Г.В. Дорофеева, И.Ф. Шарыгин; Рос. Акад. Наук, Росакадемия, М .: Образование, 2010.
- Математика. 6 класс: этюд. Для общего образования. Учреждения / Н. Виленкин, В. Жохов, А. Чесноков, С.И.Шварцборд. — М .: Мнемозина, 2013. .
- Математика. 6 кл .: Учебник / Г.К. Муравин, О. Моравин. — М .: Падение, 2014. .
Цель: Систематизировать, расширить, обобщить и закрепить знания, полученные по теме «Нахождение части целого и целой части. Информатика среди нас»
Задачи:
Усилить знания студентов о понятиях дробь, решение задач на дробь.
Научить школьников решать задачи по теме, уметь различать способы решения задач.
Использование полученных теоретических знаний при решении практических задач.
Расширьте кругозор студентов в области информатики.
Этапы урока.
Вратарь — 2 мин.
Актуализация справочных знаний — 8 мин.
Крепление и обобщение материала. — 23 мин.
Подведение итогов урока и постановка домашнего задания. — 5 минут.
Ожидаемые результаты: Студенты должны научиться применять необходимые методы. Решения для конкретной задачи должны уметь решать задачи, уметь выполнять дроби.
Во время занятий:
Организационное время. — 2 минуты.
Приветствую студентов.
Гол — 2 мин.
Угадай ребус.
Какое слово здесь зашифровано? Верно, в Интернете.
Какую тему мы изучаем с вами сейчас? (справа, «Нахождение части целого и целой его части»)
Как Интернет будет связан с этой темой? (Задачи по этой теме будем решать на знании Интернета 0
Кто сможет сформулировать тему сегодняшнего урока? (Интернет среди нас)
Вы знаете, что такое Интернет? (Откажитесь от своих версий)
Интернет — (от лат. .Inter-between и Net-network), глобальная компьютерная сеть, объединяющая как пользователей компьютерных сетей, так и пользователей индивидуальных (в том числе домашних) компьютеров.
.Inter-between и Net-network), глобальная компьютерная сеть, объединяющая как пользователей компьютерных сетей, так и пользователей индивидуальных (в том числе домашних) компьютеров.
Актуализация справочных знаний — 8 мин.
Выполнить устно:
А) Найдите запчасть из числа:
3/4 из 16;
2/5 из 80;
7/10 из 120;
3/5 из 150;
6/11 из 121;
5/6 из 108.
B) Найдите число, если:
3/8 оно равно 15;
2/5 из него равно 30;
5/8 из 45;
4/9 равно 36;
7/10 равно 42;
2/11 Равно 99.
Крепление и обобщение материала . — 23 мин.
Как вы думаете, где и когда появился Интернет? (выражать мнение)
В 1957 году, после запуска Советским Союзом первого искусственного спутника Земли, Министерство обороны США посчитало, что в случае войны США мне понадобится надежная система передачи информации. Агентство перспективных оборонных исследований и разработок США предложило разработать для этого компьютерную сеть.
Теперь решим несколько задач.
На личную страничку Алены Н. На сайт «Одноклассники» скачано 140 фото. 2/7 количества всех фотографий загружено в альбом «Личные фото», 1/4 — в альбом «Хобби», 3/35 — в альбом «Отдых», 5/28 — в альбом «Семья». », а остальное -« Фото друзей ». Сколько фотографий Алены в каждом альбоме?
140: 7 * 2 = 40 (f) «Личные фото»
140: 4 * 1 = 35 (f) «Хобби»
140: 35 * 3 = 12 (f) «Отдых»
140: 28 * 5 = 25 (е) «Семья»
140-40-35-12-25 = 28 (е) «На фото друзей»
Миша Б.электронная почта 276 писем, что составляет 3/5 от количества писем в электронной почте. На сколько букв у Миши больше?
276: 3 * 5 = 460
460 — 276 = 184.
На флеш-карте, рассчитанной на 4гбайт (1гбайт = 1024мбайт) есть различные файлы. Фото занимают 3/16 всей памяти, фильмы — на 1/8 части (из всей памяти) больше фотографии, текстовые документы — на 5/64 части (из всей памяти) больше фотографии. Сколько m байтов приходится на каждый из файлов?
4 * 1024 = 4096
4096: 16 * 3 = 768 (м байт) на фото
4096: 8 * 1 = 512
768 + 512 = 1280 (м байт) на фильмах
4096: 64 * 5 = 320
320 +768 = 1088 (м байт) в текстовых документах.
Ребят, а зачем вам интернет?
Связь;
Информация;
Games.
Какие вам известны социальные сети? (выскажите свое мнение)
Назовем «плюсы» и «минусы» социальных сетей:
«Плюсы»:
Общение;
Информация.
«Минусы»:
Отрицательное влияние на здоровье;
Интернет — зависимость;
Погружение в виртуальный мир;
Опасность от посторонних.
Решим следующую задачу.
Среди учащихся 5 классов одна из школ прошла анкетирование на тему «Социальные школы и дети».На вопрос «Сколько времени в день вы проводите в Интернете» 3/10 из числа всех опрошенных школьников ответили «5-6 часов». Сколько школьников ежедневно проводят это время в Интернете, если в опросе участвовало 150 детей?
150: 10 * 3 = 45 (дети).
45 детей! Это очень большое число! Ведь каждый день они проводят столько времени зря, сидя за компьютером.
Ребята, как вы думаете, насколько навредить здоровью может длительное времяпрепровождение в Интернете?
Возможные ответы студентов:
Обесценение;
Снижение двигательной активности;
Психологическое перенапряжение;
Человек теряет способность к общению;
Рахиокампсис;
Головные боли;
Нарушение сна.
Вот видите, сколько негатива можно заработать, посидев несколько часов в интернете!
5. Подведение итогов урока и ведение домашнего хозяйства . — 5 минут.
Что нового вы узнали сегодня в классе?
Как вы думаете, что лучше всего тратить в Интернете ежедневно?
Что вы в основном будете использовать в Интернете?
Считаете ли вы, что 5-6 часов в Интернете каждый день — это норма?
Домашнее задание : Подготовьте сообщение на тему «История возникновения Интернета»
Объявление сметы.
Спасибо за урок!
§ 20. Говорят о частях от целого и от целого, а его часть — это учебник по математике 5 класс (Зубарева, Мордкович)
Краткое описание:
Бывает, что нам нужно найти какую-то часть числа, например, из определенного количества картошки, только чтобы почистить об этом. Или, наоборот, когда нам говорят, что на экскурсию пришла только четверть класса, нам нужно выяснить, каково общее количество учеников класса.Зная целое, вы можете найти из него какую-то определенную часть, точно так же, зная часть, вы можете определить, какое было целое число. Об этом сегодня вы узнаете из этого абзаца учебника.
Определение части целого, и наоборот, имеет прямое отношение к простым дробям, которые вы уже изучили. Действия в этом случае происходят не с двумя обозначенными числами, а с одной дробью и одним целым числом. Например, найти 1/2 из 16 будет означать умножение 16 на 1/2, в этом случае знаменатель числа 16 = 1 и выражение можно записать как: 1/2 16/1 = 16/2 = 8.
Чтобы найти целое число в его части, мы используем обратный метод и умножаем известное число на обратную дробь (то есть делим его). В противном случае это можно объяснить следующим образом: чтобы найти целое число из его части, необходимо, чтобы известное число, которое соответствует его части, разделилось на числитель и умножилось на знаменатель, который обозначает эту часть (т.е. действие дробей, или умножение на обратную дробь — вы можете вспомнить наиболее удобный для вас способ решения таких задач).Таким образом, чтобы найти целое число, 3/4 которого равно 12, вам потребуется 12: 3/4 = 12 4/3 = 48/3 = 16. Или метод №2, убирающий лишние математические действия — число х, 2/5 откуда 20: х = 20: 2 5 = 50.
Проверяйте себя при выполнении заданий из учебника и не забывайте просматривать материал, чтобы лучше его усвоить и запомнить!
§ 20. Говорят о частях от целого и от целого, а его часть — это учебник по математике 5 класс (Зубарева, Мордкович)
Краткое описание:
Бывает, что нам нужно найти какую-то часть числа, например, из определенного количества картошки, только чтобы почистить об этом.Или, наоборот, когда нам говорят, что на экскурсию пришла только четверть класса, нам нужно выяснить, каково общее количество учеников класса. Зная целое, вы можете найти из него какую-то определенную часть, точно так же, зная часть, вы можете определить, какое было целое число. Об этом сегодня вы узнаете из этого абзаца учебника.Определение части целого, и наоборот, напрямую связано с простыми дробями, которые вы уже изучили.Действия в этом случае происходят не с двумя обозначенными числами, а с одной дробью и одним целым числом. Например, найти 1/2 из 16 будет означать умножение 16 на 1/2, в этом случае знаменатель числа 16 = 1 и выражение можно записать как: 1/2 16/1 = 16/2 = 8.
Чтобы найти целое число в его части, воспользуемся обратным методом, а известное число умножим на обратную дробь (то есть делим). В противном случае это можно объяснить следующим образом: чтобы найти целое число из его части, необходимо, чтобы известное число, которое соответствует его части, разделилось на числитель и умножилось на знаменатель, который обозначает эту часть (т.е. действие дробей, или умножение на обратную дробь — вы можете вспомнить наиболее удобный для вас способ решения таких задач).Таким образом, чтобы найти целое число, 3/4 которого равно 12, вам потребуется 12: 3/4 = 12 4/3 = 48/3 = 16. Или метод №2, убирающий лишние математические действия — число х, 2/5 откуда 20: х = 20: 2 5 = 50.
Проверяйте себя при выполнении заданий из учебника и не забывайте просматривать материал, чтобы лучше его усвоить и запомнить!
Как найти часть целого. Нахождение целого по его частям.Vi. Обеспечение нового материала
§ 1 Правила поиска части из целого и целого в его части
В этом уроке мы сформулируем правила нахождения части целого и целого в его части, а также рассмотрим решение задач с использованием этих правил. .
Рассмотрим две задачи:
Сколько километров прошли туристы в первый день, если весь туристический маршрут составлял 20 км?
Найдите длину всего пути туриста.
Сравним эти задачи — в обоих весь путь взят как единое целое.В первой задаче все известно — 20 км, а во второй — неизвестно. В первом задании нужно найти часть целого, а во втором целое по его частям. Известное в первой задаче значение 20 км неизвестно во второй задаче, и наоборот, известное во второй задаче — 8 км, в первой должно быть найдено. Такие задачи называются взаимно обратными, так как в них известные и искомые величины меняются местами.
Рассмотрим первую задачу:
Знаменатель 5 показывает, на сколько частей было разделено целое, т.е.е. если целые 20 разделить на 5, мы узнаем, сколько километров в одной части, 20: 5 = 4 км. Числитель 2 показывает, что туристы преодолели 2 части пути, поэтому 4 нужно умножить на 2, получится 8 км. В первый день туристы прошли 8 км.
Получилось выражение 20: 5 ∙ 2 = 8.
Перейдем ко второй задаче.
Следовательно, одна часть будет равна частному 8 и 2, получится 4, знаменатель 5, что означает всего 5 частей.
4 умножить на 5, получится 20. Ответ 20 км длины всего пути.
Запишем выражение: 8: 2 ∙ 5 = 20
Используя значение умножения и деления числа на дробь, правила нахождения части целого и целого в его части можно сформулировать следующим образом:
Чтобы найти часть целого, нужно умножить число, соответствующее целому, на дробь, соответствующую этой части;
, чтобы найти целое число по его части, необходимо число, соответствующее этой части, разделить на соответствующие части дроби.
Соответственно решение задач теперь можно записать иначе:
для первой задачи 20 ∙ 2/5 = 8 (км),
для второй задачи 8: 2/5 = 20 (км).
Во избежание затруднений записываем решение таких задач следующим образом:
Целом: всю дорогу, как известно — 20 км.
Ответ: 8 км.
Целый: весь путь неизвестен.
Ответ: 20 км.
§ 2 Алгоритм решения задач нахождения целого по его части и части целого
Составим алгоритм решения таких задач.
Сначала давайте проанализируем состояние и вопрос проблемы: выясним, что такое целое, известно оно или нет, затем мы выясним, как представлена часть целого и что необходимо найти.
Если необходимо найти часть целого, то мы умножаем целое на дробь, соответствующую этой части, если нам нужно найти целое на его часть, то число, соответствующее части, делится на дробь, соответствующую этой части. к этой части. В результате получаем выражение.Далее найдем значение выражения и запишем ответ, предварительно прочитав проблемный вопрос еще раз.
Итак, прежде чем решать такие задачи, вам необходимо ответить на следующие вопросы:
Какая стоимость принимается за целое?
Известно ли это значение?
Что вам нужно найти: часть целого или целое в своей части?
Подведем итоги: на этом уроке вы познакомились с правилами нахождения части из целого и целого в своей части, а также научились решать задачи по этим правилам.
Список использованной литературы:
- Математика. 6 класс: планы уроков по учебнику И.И. Зубарева, А.Г. Мордкович // Составитель Л.А. Топилин. Мнемосина, 2009.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И. Зубарева, А.Г. Мордкович. — М .: Мнемосина, 2013. .
- Математика. 6 класс: учебник для общеобразовательных учреждений / Г.В. Дорофеев, И.Ф. Шарыгин, С. Суворов и др. / Под ред. Г.В. Дорофеева, И.Ф. Шарыгин; Российская академия наук, Российская академия образования, Москва: Просвещение, 2010.
- Математика. 6 класс: учебник. для общего образования. учреждения / Н.Я. Виленкин, В.И. Жохов, А. Чесноков, С.И.Шварцбурд. — М .: Мнемосина, 2013. .
- Математика. 6 класс: учебник / Г.К. Муравин, О.В. Муравина. — М .: Дрофа, 2014. .
ОСНОВНЫЕ ВИДЫ ПРОЦЕНТНОГО РЕШЕНИЯ
I. ПОИСК ЧАСТИ ВСЕГО
Чтобы найти часть (%) целого, вам нужно умножить число на часть (процент, преобразованный в десятичную форму).
ПРИМЕР: В классе 32 ученика. Во время тестирования отсутствовали 12,5% студентов. Найдите, сколько студентов пропало?
РЕШЕНИЕ 1: Целое число в этой задаче — общее количество студентов (32).
12,5% = 0,125
32 0,125 = 4
РЕШЕНИЕ 2: Пусть отсутствовали x студентов, что составляет 12,5%. Если 32 студента —
от общего количества студентов (100%), то
32 студента — 100%
x студентов — 12.5%
ОТВЕТ: На занятиях отсутствовали 4 ученика.
II. ПОИСК ВСЕГО ПО ЧАСТИ
Чтобы найти целое число по его части (%), вам нужно разделить число на часть (процент преобразован в десятичную дробь).
ПРИМЕР: Коля потратил в парке аттракционов 120 крон, что составляло 75% всех его карманных денег. Сколько карманных денег было у Коли до прихода в парк развлечений?
РЕШЕНИЕ 1: В этой задаче вам нужно найти целое число, если данная часть и значение известны
этой части.
75% = 0,75
120: 0,75 = 160
РЕШЕНИЕ 2: Пусть у Коли было x корон, то есть целое, то есть 100%. Если он потратил 120 крон, что составляет 75%, то
120 крон — 75%
x крон — 100%
ОТВЕТ: У Коли было 160 крон.
III. ВЫРАЖЕНИЕ В ПРОЦЕНТРАХ ДВУХ НОМЕРОВ
ТИПИЧНЫЙ ВОПРОС:
СКОЛЬКО% ОДНА ЗНАЧЕНИЕ ОТ ДРУГОГО?
ПРИМЕР: Прямоугольник имеет ширину 20 м и длину 32 м.Сколько% составляет ширина длины? (Длина является основой для сравнения)
РЕШЕНИЕ 1:
РЕШЕНИЕ 2: В этой задаче длина прямоугольника 32 м равна 100%, тогда ширина 20 м равна x%. Составим и решим пропорцию:
20 метров — x%
32 метра — 100%
ОТВЕТ: Ширина составляет 62,5% от длины.
NB! Обратите внимание, как меняется решение по мере изменения вопроса.
ПРИМЕР: Прямоугольник имеет ширину 20 м и длину 32 м.Сколько% составляет длина от ширины? (Ширина — основа для сравнения)
РЕШЕНИЕ 1:
РЕШЕНИЕ 2: В этой задаче ширина прямоугольника 20 м равна 100%, тогда длина 32 м равна x%. Составим и решим пропорцию:
20 метров — 100%
32 метра — x%
ОТВЕТ: Длина составляет 160% от ширины.
IV. ВЫРАЖЕНИЕ В ПРОЦЕНТАХ ИЗМЕНЕНИЯ СТОИМОСТИ
ТИПИЧНЫЙ ВОПРОС:
НАСКОЛЬКО НА% ИЗМЕНЕНО (УВЕЛИЧИЛОСЬ, УМЕНЬШЕНО) ИСХОДНАЯ СТОИМОСТЬ?
Чтобы найти изменение значения в%, вам необходимо:
1) найти, насколько изменилось значение (без%)
2) разделить полученное значение из пункта 1) на значение, являющееся базовым для сравнения
3) преобразовать результат в% (умножив на 100%)
ПРИМЕР: Цена платья упала с 1250 CZK до 1000 CZK.Узнайте, насколько упала цена платья?
РЕШЕНИЕ 1:
2) Базой для сравнения является 1250 крон (т.е. то, что было изначально)
3)
ОТВЕТ: Цена платья снизилась на 20%.
NB! Обратите внимание, как меняется решение по мере изменения вопроса.
ПРИМЕР: Цена платья увеличилась с 1000 CZK до 1250 CZK. Найдите процент увеличения цены платья?
РЕШЕНИЕ 1:
1) 1250 -1000 = 250 (kr) насколько изменилась цена
2) Базой для сравнения здесь является 1000 CZK (т.е.е. что было изначально)
3)
Решение проблемы за один шаг:
РЕШЕНИЕ 2:
1250 -1000 = 250 (кр) насколько изменилась цена
В этой задаче начальная цена 1000 крон составляет 100 %, то изменение цены на 250 крон составляет x%. Составим и решим пропорцию:
1000 CZK — 100%
250 CZK — x%
x =
ОТВЕТ: Цена платья выросла на 25%.
V. КОСВЕННОЕ ЗНАЧЕНИЕ (НОМЕР)
ПРИМЕР: Число было уменьшено на 15%, а затем увеличено на 20%.Найдите процентное изменение числа?
Наиболее частая ошибка: число увеличилось на 5%.
РЕШЕНИЕ 1:
1) Хотя исходное число не указано, для простоты его можно принять как 100 (т.е. одно целое число или 1).
2) Если число уменьшилось на 15%, то результирующее число будет 85%, или из 100 это будет 85.
3) Теперь полученный результат должен быть увеличен на 20%, т.е.
85 — 100%
и новое число x равно 120% (так как оно увеличилось на 20%). %)
x =
4) Таким образом, в результате изменений число 100 (исходное) изменилось и стало 102, а это значит, что исходное число увеличилось на 2%
РЕШЕНИЕ 2:
1) Пусть исходное число X
2) Если число уменьшилось на 15%, то полученное число будет 85% от X, т.е.е. 0,85X.
3) Теперь получившееся число нужно увеличить на 20%, т.е.
0,85X — 100%
и новое число? — 120% (при увеличении на 20%)
? =
4) Таким образом, в результате изменений число X (начальное) является базой для сравнения, а число 1.02X (получено), (см. IV тип решения задачи), затем
ОТВЕТ: Число увеличилось на 2%.
Открытый урок математики в 5б классе.
Учитель: Бамбутова М.И.
Тема: Как найти часть целого и целое в своей части.
Цель: научиться решать задачи по нахождению части из целого и целого в своей части.
Образовательные: вывести правило поиска части из целого и целого в его части,
решить задачи поиска части из целого и целого в своей части.
Развивающие: развивать память и математическую речь
Образовательные: развивать коммуникативные навыки.
План урока:
1) Вводно-мотивационный этап.
1.Орг. Момент
2. Обновление базовых знаний
Ответьте на вопросы (слайд)
1) Что означает дробь?
2) Что означает дробь?
3)
Постановка задачи:
1 задача:
2 задачи на слайд
1) нарисуйте прямоугольник со сторонами 2 см и 5 см. Какая у него площадь?
Решаем задачу
1) Площадь прямоугольника 10 см 2.Заштрихованные части прямоугольной области. Какова площадь залитой части прямоугольника?
2) Заштрихованная часть прямоугольника составляет 4 см 2, что составляет часть всего прямоугольника. Какая площадь у прямоугольника?
Ответьте на вопросы: ()
часть целого и в чем целиком по частям ?
Что мы находим в задаче 1 (целое по частям), что мы находим в задаче 2 (часть целого)
2 задание: Прочтите задания и ответьте на вопросы:
1) Площадь поля — 50 га.Днем бригада трактористов вспахивала поля. Сколько гектаров бригада за день вспахала?
2) За сутки бригада вспахала 20 гектаров, что составляло площадь всего поля. Какая площадь поля?
Ответьте на вопросы: ( раздать задания в виде карточки )
Какое целочисленное значение у каждой задачи?
В каких задачах это значение известно, а в каких нет?
В какой из задач вы хотите найти часть целого и в чем целиком по частям ?
Что это за задачи? (взаимно)
Что общего у этих задач? Что мы искали в этих задачах?
-часть целого и целиком по частям.
Итак, что наша тема сегодня? ?
Тема: Как найти часть целого и целое в его части . (Слайд)
Правильное решение двух последних задач можно найти в учебнике на странице 95.
Итак мы решили 4 задачи, суммировали все проблемы и вывели правило для нахождения части из целого и целого в своей части.
Ученики стараются, чтобы помочь им разбросав фразу, нужно собрать ее в логически правильное предложение, что и будет правилом.
, который выражает эту часть.
соответствует целому,
Чтобы найти часть целого
разделите на знаменатель
и умножьте результат на числитель дроби
нужно число
Чтобы найти часть целого, вам нужно разделить число, соответствующее целому, на знаменатель и умножить результат на числитель дроби, выражающей эту часть.
и умножьте результат на знаменатель дроби,
нужно число
разделите на числитель
, который выражает эту часть.
Чтобы найти целое на его части,
, соответствующее этой части,
Чтобы найти целое число на его части, вам нужно разделить число, соответствующее этой части, на числитель и умножить результат знаменателем дроби, выражающей эту часть.
Соберите это правило на доске.
Студенты повторяют это правило друг другу.
3. Первичная анкеровка. Игра «Сортировка задач».
Мастер-класс по решению проблем. Вариант 1 решает проблему поиска части целого, Вариант 2 решает проблему поиска целого по его частям.
1 . В хоре 80 учеников, из них ¼ юноши. Сколько мальчиков в хоре?
2. В хоре 20 мальчиков, что составляет всех учащихся хора.Сколько учеников в хоре?
3. Небольшой лиственный лес очищает воздух от 70 тонн пыли в год. А хвойный лес составляет ½ этой суммы. Сколько пыли фильтрует хвойный лес за год?
4. Из бочки вылилось 7/12 керосина. Сколько литров керосина было в бочке, если из нее налили 84 литра?
5. Девушка прошла 300 м, что составляет 3/8 всей дистанции. Какое расстояние?
6.От снега очищено 2/5 площади катка, а это 200 кв.м. Найти площадь всего катка?
7. Девушка прочитала ¾ книги, это 120 страниц. Сколько страниц в книге?
8. Белка приготовила всего 600 орехов. В первую неделю она собрала 20% всех орехов. Сколько белка вы собрали за первую неделю?
9. Найдите число x , 1/8 которого равна 1/24.
10. Девушка собрала 40 слив, что составляет 1/3 всех слив.Сколько всего слив было собрано?
11. Мама купила 6 кг конфет. Витя сразу съел 2/3 всех конфет и почувствовал себя плохо. После скольких сладостей у Вити заболел живот?
12. Мальчик собрал 80 орехов, что составляет 2/3 всех собранных орехов. Сколько орехов было собрано?
13. В курятнике было 40 кур. За неделю лиса украла 3/8 всех цыплят. Сколько цыплят унесла лиса?
14. Алиса упала в сказочный колодец и за 1 минуту пролетела 90 м.Какова глубина колодца, если за 1 минуту Алиса пролетела ¾ всей дистанции?
15. Перед балом мачеха дала Золушке много работы. У Золушки ушло 6 часов, чтобы выполнить 3/5 этой работы. Сколько времени потребуется Золушке, чтобы сделать всю работу?
4. Отражение. Правило — произносить.
5. Домашнее задание: выучите правило, составьте карточку с заданиями, чтобы найти часть целого и целое за его часть (по 3 задания на каждое правило).
Правило нахождения числа по дроби :
Чтобы найти число по заданному значению его дроби, вам нужно разделить это значение на дробь.
Рассмотрим, как найти число по дроби, на конкретных примерах.
Примеры.
1) Найдите число 3/4, из которого 12.
Чтобы найти число по дроби, разделите это число на эту дробь. Чтобы, вам нужно умножить данное число на обратную дробь (то есть на обратную дробь). Чтобы, вам нужно умножить числитель на это число, а знаменатель оставить неизменным. 12 и 3 на 3. Поскольку знаменатель равен единице, ответ будет целым.
2) Найдите число, если 9/10 равно 3/5.


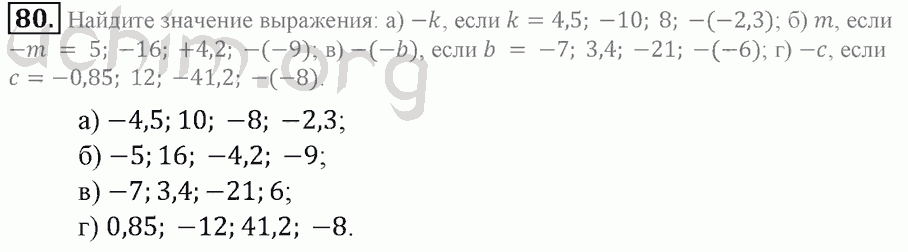 Взаимно простые числа.».
Взаимно простые числа.».