Номер №23 — ГДЗ по Математике 6 класс: Виленкин Н.Я.
войтирегистрация
- Ответкин
- Решебники
- 6 класс
- Математика
- Виленкин
- Номер №23
НАЗАД К СОДЕРЖАНИЮ
2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №23 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.
2019г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №23 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
Условие 20132019г.
Cменить на 2013 г.
Cменить на 2019 г.
Государственные флаги многих стран состоят из горизонтальных или вертикальных полос разных цветов. Сколько могло бы быть различных государственных флагов, состоящих из двух горизонтальных полос одинаковой ширины и разного цвета — белого, красного и синего?
Решите задачу:
1) В первом мешке было 54,4 кг крупы, во втором — в 1,7 раза меньше, чем в первом, а в третьем — на 2,6 кг больше, чем во втором. Сколько килограммов крупы было в трёх мешках вместе?
2) На первую машину погрузили 4,5 т картофеля, на вторую — в 1,4 раза больше, чем на первую, а на третью — на 1,6 т меньше, чем на вторую. Сколько тонн картофеля погрузили на все три машины вместе?
Решение 1
Решение 1
Решение 2
Решение 2
Решение 3
Решение 3
ГДЗ по Математике 6 класс: Виленкин Н. Я.
Я.
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.
ГДЗ по Математике 6 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.
ГДЗ по Математике 6 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018
ГДЗ по Математике 6 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.
ГДЗ по Математике 6 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.
Сообщить об ошибке
Выберите тип ошибки:
Решено неверно
Опечатка
Плохое качество картинки
Опишите подробнее
в каком месте ошибка
Ваше сообщение отправлено
и скоро будет рассмотрено
ОК, СПАСИБО
[email protected]
© OTVETKIN. INFO
INFO
Классы
Предметы
Номер 23 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021. Часть 2 (решебник)
Номер 23 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2021. Часть 2 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
1 ЧАСТЬ
Выберите номер
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684686687688689690691692693694695696697698698699701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793793794795797798799800801802803804805806807808809810811812813814815816817817819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852
2 ЧАСТЬ
Выберите номер
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744845045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231224122512261227122812291230123112321233123412351236123712381239124012411242124312441245124612471248124912501251125212531254125512561257125812591260126112621263126412651266126712681269127012711272127312741275127612771278127912801281128212831284128512861287128812891290129112921293129412951296129712981299130013011302130313041305130613071308130913101311131213131314131513161317131813191320132113221323132413251326132713281329133013311332133313341335133613371338133913401341134213431344134513461347134813491350135113521353135413551356135713581359136013611362136313641365136613671368136913701371137213731374137513761377137813791380138113821383138413851386138713881389139013911392139313941395139613971398139914001401140214031404140514061407140814091410141114121413141414151416141714181419142014211422142314241425142614271428142914301431143214331434143514361437143814391440144114421443144414451446144714481449145014511452145314541455145614571458145914601461146214631464146514661467146814691470147114721473147414751476147714781479148014811482148314841485148614871488148914901491149214931494149514961497149814991500150115021503150415051506150715081509151015111512151315141515151615171518151915201521152215231524152515261527152815291530153115321533153415351536153715381539154015411542154315441545154615471548154915501551155215531554155515561557155815591560156115621563156415651566156715681569157015711572157315741575157615771578157915801581158215831584158515861587158815891590159115921593159415951596159715981599160016011602160316041605160616071608160916101611161216131614161516161617161816191620162116221623162416251626162716281629163016311632163316341635163616371638163916401641164216431644164516461647164816491650165116521653165416551656165716581659166016611662166316641665166616671668166916701671167216731674167516761677167816791680168116821683168416851686168716881689169016911692169316941695169616971698169917001701170217031704170517061707170817091710171117121713171417151716171717181719172017211722172317241725172617271728172917301731173217331734173517361737173817391740174117421743174417451746174717481749175017511752175317541756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849
Adblockdetector
Много миров в одном: поиски других вселенных Алекса Виленкина
Алекса Виленкина
Оцените эту книгу
Ведущая фигура в развитии новой космологии объясняет, что все это значит Среди своих коллег Алекс Виленкин пользуется уважением как один из самых изобретательных и творческих космологов нашего времени. Его вклад в наше нынешнее понимание Вселенной включает ряд новых идей, две из которых — вечная космическая инфляция и квантовое создание Вселенной из ничего — обеспечили научную основу для возможного существования множественных вселенных. С этой книгой — своей первой для широкого читателя — Виленкин присоединяется к другой избранной группе: горстке первоклассных ученых, которые одинаково хорошо умеют объяснять свою работу неспециалистам. С увлекательным, динамичным повествованием, забавным чувством юмора и щедрым количеством полезных мультфильмов он вызывает в воображении причудливое и увлекательное новое мировоззрение, которое, перефразируя Нильса Бора, может быть достаточно безумным, чтобы быть правдой.
Его вклад в наше нынешнее понимание Вселенной включает ряд новых идей, две из которых — вечная космическая инфляция и квантовое создание Вселенной из ничего — обеспечили научную основу для возможного существования множественных вселенных. С этой книгой — своей первой для широкого читателя — Виленкин присоединяется к другой избранной группе: горстке первоклассных ученых, которые одинаково хорошо умеют объяснять свою работу неспециалистам. С увлекательным, динамичным повествованием, забавным чувством юмора и щедрым количеством полезных мультфильмов он вызывает в воображении причудливое и увлекательное новое мировоззрение, которое, перефразируя Нильса Бора, может быть достаточно безумным, чтобы быть правдой.
248 страниц, Мягкая обложка
Впервые опубликовано 1 января 2006 г.
Об авторе
Алекс Виленкин — физик, известный своими работами по космологии ранней Вселенной. Он известен, в частности, своими исследованиями топологических дефектов, вечной космической инфляции, квантовой космологии и теорией хиральных магнитных и хиральных вихревых эффектов.
Он известен, в частности, своими исследованиями топологических дефектов, вечной космической инфляции, квантовой космологии и теорией хиральных магнитных и хиральных вихревых эффектов.
Виленкин родился в городе Харькове (бывший Советский Союз) и окончил Харьковский государственный университет в 1971 по специальности физик. Он иммигрировал в США в 1976 году и получил докторскую степень. от SUNY Buffalo в следующем году. Проработав год постдоком в Университете Кейс Вестерн Резерв, он присоединился к факультету Университета Тафтса, где в настоящее время является профессором эволюционных наук Л. и Дж. Бернштейнов. Он также является директором Института космологии Тафтса. Виленкин — член Американского физического общества и член Национальной академии наук.
Чем занимаетесь вы думаете?
Оцените эту книгу
Поиск по тексту отзыва
Показано 1–21 из 21 отзыва
4 августа 2022 г.
Чертовски круто. Для меня это первая книга по квантовой космологии. Большую часть времени мы относимся к космологии как к чему-то, что связано с пространством-временем или чем-то «большим», например, с самим космосом, и со всем, что с этим связано, в отношении теорий Эйнштейна, евклидовой геометрии или пространства ДеСиттера, но в данном случае космология рассматривается с квантовая перспектива: все, что связано как с планковским временем, так и с длиной. Это не что-то связанное с Мультивселенной Человека-паука или чем-то подобным: это научная книга, и вам может понадобиться некоторая предыстория, чтобы глубоко понять такие концепции, особенно то, что мы называем «вакуумом».
Определенно, это будет не последняя моя книга на эту тему, но я понимаю, что достать такие книги мне немного сложно.
29 февраля 2016 г.
Я не уверен, кто лучший ученый, но с точки зрения прозы, необходимой для решения этой проблемы мультивселенной, из тех, что я читал, преимущество следующее: Грин>Виленкин>Тегмарк . Этот текст был ценным дополнением к Грину, потому что я не думаю, что какой-то один набор аналогий может правильно концептуализировать этот сложный материал, и действительно, для неспециалистов все, что мы действительно ищем, — это какой-то способ понять по аналогии. Рекомендуется в качестве дополнения к мультивселенному тексту Грина «СКРЫТАЯ РЕАЛЬНОСТЬ».
Этот текст был ценным дополнением к Грину, потому что я не думаю, что какой-то один набор аналогий может правильно концептуализировать этот сложный материал, и действительно, для неспециалистов все, что мы действительно ищем, — это какой-то способ понять по аналогии. Рекомендуется в качестве дополнения к мультивселенному тексту Грина «СКРЫТАЯ РЕАЛЬНОСТЬ».
- документальная литература
3 мая 2009 г.
Интересная книга, но совсем не то, что я ожидал. Основываясь на названии и рецензиях, я подумал, что это будет глубокое погружение в многомировую интерпретацию квантовой механики. Но никаких упоминаний о мультивселенных не встречается до последнего отрывка книги, да и то только в связи с обсуждением автором его последней статьи, описывающей теорию вселенной, возникающей из ничего. Здесь обсуждение сопоставляется с древними мифами о сотворении мира. Действительно ли вселенная больше похожа на космическое яйцо, возникающее из ничего, или больше на танец Шивы, находящегося в постоянном состоянии созидания и разрушения? Существует ли вселенная, отображающая все возможные математические структуры, и если да, то любит ли Бог математику так сильно, что готов тратить ее на вселенные, которые никогда не смогут поддерживать себя достаточно долго, чтобы создать разумную жизнь, которая сможет ее оценить? Кроме того, если математика является продуктом разума, может ли разум каким-то образом предшествовать сотворению вселенной? Все вопросы интересные, но поскольку основная часть книги посвящена более формальному обсуждению Стандартной модели физики элементарных частиц, последние мимолетные мысли возникают из ниоткуда, необоснованны и остаются повиснуть в воздухе без ответа.
Ричард
Автор 6 книг88 подписчиков
26 ноября 2013 г.Свежий обзор того, что открывается с вершины горы под названием «Теория космической инфляции». Сказать, что вид огромен, было бы все равно, что назвать
Войну и мир длинной историей — и жаль, что через поколение после монументальных открытий Алана Гута более ошеломляющие последствия инфляционной космологии не дошли до более не ученые. Но это в лучшем случае весьма неоднозначный успех: Виленкин пишет с замечательной легкостью и ясностью, на уровне предложения, но плохо понимает, как сократить математику и при этом адекватно объяснить понятия. Ложный вакуум, например, является основной концепцией, и Виленкин, кажется, просто не понимает, что можно прочитать всю эту книгу с десятками упоминаний о ложном вакууме (ложном вакууме?), не имея ни малейшего представления о том, что такое ф. в.
в.
.
В каком-то смысле гораздо сложнее и технически более емко, но все же лучше объясняя непрофессионалу собственную оригинальную популяризацию Гутом своей «Захватывающей реализации», книги 1990-х годов под названием Инфляционная Вселенная .
Адам
18 отзывов7 подписчиков
17 февраля 2009 г.Удивительный исторический обзор развития теории космологической инфляции, который с каждой главой становится все более умопомрачительным. Очаровательно и доходчиво написано, с интригующими историческими отступлениями, которые мало отстают от череды изумлений.
22 июля 2022
алекс виленкин так красноречиво пишет и формулирует сложные понятия (по крайней мере мне, т.к. я не очень разбираюсь в квантовой физике). мне нравилось узнавать о космосе и о «сотворении» нашей вселенной/пространства-времени.
21 апреля 2018 г.

Красивое разоблачительное изложение идей и результатов исследований Алексея Вилекина в понятном и увлекательном стиле. Ее стоит прочитать, чтобы узнать о больших идеях, лежащих в основе квантовой космологии.
- owned-eng физика
7 декабря 2020
Читать Виленкин был там во время холодной войны 1970-х, разрабатывая модели инфляции. У меня есть бумажная копия этого где-то в моем книжном шкафу. Я должен взять его снова и дать ему достойный обзор.
14 февраля 2022 г.
Исследование космологии и квантовой физики, особое внимание уделено различным теориям, которые, вероятно, можно охарактеризовать как «многомировые». Я не нашел эту книгу впечатляющей ни в каком аспекте, краткое изложение основных идей не было чем-то невероятным, и ее было нелегко читать и понимать с общей точки зрения. Я действительно думал, что примерно на четверти пути произошел довольно хороший переход от общих знаний к основам теории многих миров, но помимо этого я, вероятно, порекомендовал бы другую книгу для того же типа информации.
Voyt
215 отзывов13 подписчиков
3 ноября 2022 г. Виленкин «Хотите верьте, хотите нет»
РАЗМЕЩЕНО МНОЙ НА AMAZON 2006
Вот у нас еще одна настоящая научно-популярная книга. На этот раз речь пойдет о моделях Вселенной, увиденных сквозь призму злободневной темы вакуума и скалярных полей.
Чрезвычайно хорошо написанный и полный предположений текст объясняет различия между моделями: Единой Вечно Раздувающейся Вселенной, Циклической Вселенной, Пузырящейся Вселенной, Мультивселенных (включая математические структуры Тегемарка) и Параллельных Вселенных. Особое внимание уделяется доказательству того, что было начало из ничего либо в результате квантового туннелирования, либо в результате квантового происхождения, называемого «отсутствием границ». Только необходимые факты, мало времени автор тратит на повторение банальных тем относительности Эйнштейна, избегая сложности и подробностей физики частиц/струн (хорошо!). Завершая свою книгу, Виленкин затрагивает деликатные вопросы антропного начала и творения. И делает это с большой чувствительностью. То, что «ничто не может быть создано из ничего» — это не исключает возможности существования Разума, предшествовавшего Вселенной. Он заключает: возможно, математика — это Закон, который мы постоянно открываем (а не создаем).
И делает это с большой чувствительностью. То, что «ничто не может быть создано из ничего» — это не исключает возможности существования Разума, предшествовавшего Вселенной. Он заключает: возможно, математика — это Закон, который мы постоянно открываем (а не создаем).
Верить всему тому, что здесь читается, или просто воспринимать это как «с-ф» — решать читателю. Тем не менее, книга эффектная и провоцирующая, настоятельно рекомендуется всем любителям космологии.
5 апреля 2023
Я недостаточно умен, чтобы полностью понять эту книгу
Рама Рао
725 рецензий103 подписчика слабонервный; для этого требуются базовые знания физики и космологии. Параллельные вселенные, также известные как мультивселенные, представляют собой набор вселенных, включающих в себя всю физическую и квантовую реальность. Наша Вселенная — очень маленький остров в огромном океане многочисленных вселенных, разделенных ложным вакуумом; по сути, это набор несвязанных пространственно-временных доменов, и наш доступ к другой вселенной в мультивселенной ограничен специальной теорией относительности. Параллельные вселенные были теоретически предсказаны несколькими космологами, и структура вселенной и отношения с другими вселенными зависят от теории.
Параллельные вселенные были теоретически предсказаны несколькими космологами, и структура вселенной и отношения с другими вселенными зависят от теории.
Главы 1-4 книги знакомят с теорией относительности и космологией, а в главах 5-11 обсуждаются основные идеи вечной космической инфляции: Эйнштейн использовал антигравитацию вакуума во Вселенной, чтобы уравновесить гравитационное притяжение материи, чтобы сохранить вселенную статической, и назвал эту космологическую постоянную. Есть два типа вакуума; ложный вакуум и истинный вакуум. Согласно современным теориям элементарных частиц, вакуум является физическим объектом и может быть только заряжен энергией и может находиться в различных состояниях. Самый низкий энергетический вакуум — это настоящий вакуум. Состояние вакуума с высокой энергией называется ложным вакуумом, и, поскольку оно нестабильно, оно распадается на истинный вакуум; высвобождение избыточной энергии в огненном взрыве (Большом взрыве) элементарных частиц. Есть два состояния ложного вакуума; электрослабый и великий объединенный вакуум, и оба имеют большую симметрию и меньшее разнообразие среди частиц и их взаимодействий. Например, в электрослабом вакууме электроны безмассовы и подобны нейтрино, кроме того электромагнитные, а слабые взаимодействия имеют такую же силу и проявляются как единая сила. В великом объединенном вакууме все три типа взаимодействия частиц унифицированы, а электроны, нейтроны и кварки взаимозаменяемы. Для ложного вакуума отталкивание в три раза сильнее гравитации. В раннюю эпоху, когда Вселенная находилась в состоянии ложного вакуума, плотность материи была недостаточной, чтобы сбалансировать Вселенную в статическом состоянии, в это время, возможно, преобладала отталкивающая гравитация ложного вакуума, приводящая Вселенную к бешеному расширению с большей частью пространство, занимаемое ложным вакуумом. Одно из требований заключается в том, что ложный вакуум должен распадаться плавно, по крайней мере, через несколько сотен периодов удвоения, чтобы Вселенная расширилась за пределы текущей наблюдаемой части и тем самым предотвратила коллапс Вселенной до того, как она получила возможность расшириться.
Например, в электрослабом вакууме электроны безмассовы и подобны нейтрино, кроме того электромагнитные, а слабые взаимодействия имеют такую же силу и проявляются как единая сила. В великом объединенном вакууме все три типа взаимодействия частиц унифицированы, а электроны, нейтроны и кварки взаимозаменяемы. Для ложного вакуума отталкивание в три раза сильнее гравитации. В раннюю эпоху, когда Вселенная находилась в состоянии ложного вакуума, плотность материи была недостаточной, чтобы сбалансировать Вселенную в статическом состоянии, в это время, возможно, преобладала отталкивающая гравитация ложного вакуума, приводящая Вселенную к бешеному расширению с большей частью пространство, занимаемое ложным вакуумом. Одно из требований заключается в том, что ложный вакуум должен распадаться плавно, по крайней мере, через несколько сотен периодов удвоения, чтобы Вселенная расширилась за пределы текущей наблюдаемой части и тем самым предотвратила коллапс Вселенной до того, как она получила возможность расшириться. Во время инфляции происходили два конкурирующих процесса; ложный вакуум-распад характеризуется периодом полураспада, а ложный вакуум-пространство-размножение (расширение) характеризуется временем его удвоения. Области ложного вакуума размножаются (расширяются) гораздо быстрее, чем распадаются. Это означает, что инфляция никогда не заканчивается в мультивселенной, а объем инфляционных регионов продолжает неуклонно расти, что приводит к вечной инфляции. Согласно этой теории, в любой данный момент некоторые отдаленные части мультивселенной заполнены ложным вакуумом и подвергаются экспоненциальному инфляционному расширению, но в таких областях, как наша, инфляция закончилась (инфляцию не следует путать с нормальным расширением вселенной). Из-за инфляции пространство между этими островами (индивидуальная вселенная) быстро расширяется, освобождая место для формирования новых островных вселенных; эта инфляция становится неуправляемым процессом. Распад последнего ложного вакуума в любой конкретной области мультивселенной приводит к Большому взрыву, высвобождающему огромное количество энергии в форме фундаментальных частиц.
Во время инфляции происходили два конкурирующих процесса; ложный вакуум-распад характеризуется периодом полураспада, а ложный вакуум-пространство-размножение (расширение) характеризуется временем его удвоения. Области ложного вакуума размножаются (расширяются) гораздо быстрее, чем распадаются. Это означает, что инфляция никогда не заканчивается в мультивселенной, а объем инфляционных регионов продолжает неуклонно расти, что приводит к вечной инфляции. Согласно этой теории, в любой данный момент некоторые отдаленные части мультивселенной заполнены ложным вакуумом и подвергаются экспоненциальному инфляционному расширению, но в таких областях, как наша, инфляция закончилась (инфляцию не следует путать с нормальным расширением вселенной). Из-за инфляции пространство между этими островами (индивидуальная вселенная) быстро расширяется, освобождая место для формирования новых островных вселенных; эта инфляция становится неуправляемым процессом. Распад последнего ложного вакуума в любой конкретной области мультивселенной приводит к Большому взрыву, высвобождающему огромное количество энергии в форме фундаментальных частиц. Это единовременное событие для одной вселенной, но Большой взрыв не является единовременным событием в мультивселенной.
Это единовременное событие для одной вселенной, но Большой взрыв не является единовременным событием в мультивселенной.
Автору известно, что физические доказательства существования параллельных вселенных (мультивселенных) невозможно получить из-за ограничений, накладываемых специальной теорией относительности. В эпоху современной космологии и теории струн строгие требования к экспериментальным доказательствам в поддержку математических расчетов были сильно нарушены. Многие издатели и авторы злоупотребили этой ситуацией в своих интересах, чтобы продать продукт, который является скорее научной фантастикой, чем научной реальностью.
- физика физической реальности
23 февраля 2017 г.
Не самая замечательная книга по космологии, которую я когда-либо читал, но она была достаточно хороша. Это было несколько упрощенно по сравнению с книгой Стейнхардта об Экпиросисе и особенно с книгой Пенроуза о конформной циклической космологии. Я полагаю, что это либо преимущество, либо недостаток, в зависимости от вашей точки зрения. Я думаю, что Виленкин преувеличивает проблему энтропии в этих циклических моделях, но, конечно, у него не было места, чтобы полностью объяснить свои рассуждения в этой книге, и это увело бы его далеко в сторону от основного акцента. Это первая книга, которую я прочитал о Вечной Инфляции, и я, конечно, вышел из этой книги с чувством, что понимаю ее намного лучше, чем когда начинал.
Я думаю, что Виленкин преувеличивает проблему энтропии в этих циклических моделях, но, конечно, у него не было места, чтобы полностью объяснить свои рассуждения в этой книге, и это увело бы его далеко в сторону от основного акцента. Это первая книга, которую я прочитал о Вечной Инфляции, и я, конечно, вышел из этой книги с чувством, что понимаю ее намного лучше, чем когда начинал.
- наука
январь
487 отзывов11 подписчиков
16 июля 2015 г.Мне понравилась эта книга, какой бы сложной она ни была. Я прочитала ее по рекомендации моего любящего науку мужа, и одной из радостей книги было то, что он произвел на него впечатление моей способностью прочитать ее от начала до конца. (Он назвал меня Девушка-физик, пока я читал ее — НЕ оскорбление, исходившее от него — или от кого?? Но точно НЕ его обычное для меня прозвище!)
Я процитирую автора с форзаца книги : «Предполагаемый читатель этой книги — тот, кто, глядя вверх на звездное небо, время от времени задается вопросом, откуда все это взялось и как наша маленькая Земля и наша цивилизация вписываются в великую схему вещей. Моя цель — рассказать этому читателю о новой картине мироздания, поначалу сопротивлявшейся подавляющему большинству физиков, которая постепенно складывалась в течение последних двух десятилетий и теперь становится общепринятой космологической парадигмой Я постараюсь сделать книгу легкой для чтения и максимально занимательной , используя историю моих личных поисков как фон для обсуждения научных идей». Я не мог понять ВСЮ концепцию в этой книге (и это меня не беспокоило), но спасибо Алексу Виленкину за то, что я понял НИЧЕГО из нее — и действительно получил удовольствие от чтения.
Моя цель — рассказать этому читателю о новой картине мироздания, поначалу сопротивлявшейся подавляющему большинству физиков, которая постепенно складывалась в течение последних двух десятилетий и теперь становится общепринятой космологической парадигмой Я постараюсь сделать книгу легкой для чтения и максимально занимательной , используя историю моих личных поисков как фон для обсуждения научных идей». Я не мог понять ВСЮ концепцию в этой книге (и это меня не беспокоило), но спасибо Алексу Виленкину за то, что я понял НИЧЕГО из нее — и действительно получил удовольствие от чтения.
Также на форзаце издатель пишет: «С этой книгой — своей первой для широкого читателя — Виленкин присоединяется к другой избранной группе: горстке первоклассных ученых, умеющих объяснять свою работу не- С увлекательным, динамичным повествованием, забавным чувством юмора и обилием полезных карикатур он вызывает в воображении причудливое и увлекательное новое мировоззрение, которое, перефразируя Нильса Бора, может быть достаточно безумным, чтобы будь настоящим. »
»
Я не рекомендую эту книгу всем подряд. В конце концов, не у каждого будет сильное стремление получить прозвище «Девушка-физик» или «Мальчик-физик». Но… это читабельно, и мой взгляд на вселенную абсолютно обогатился, когда я занял гостевое место на этой увлекательной лекции о «поиске других вселенных».
- 2015
Huyen
142 отзыва186 подписчиков
29 марта 2009 Моя проблема с такими книгами в том, что из них нельзя многому научиться. Либо вы работаете в поле, знаете всю математику и физику за этим, тогда читать эту книгу бесполезно. Или вы не работаете в поле и пытаетесь понять слишком упрощенную версию, которую он пытается объяснить, но она все равно не имеет смысла.
Например: Если вы сжимаете объект, его сила тяжести увеличивается, а если вы растягиваете его, сила тяжести уменьшается. если бы вы могли продолжать растягивать объект, не ломая его, вы могли бы, в принципе, уменьшить гравитацию до такой степени, что полностью нейтрализовали бы ее или даже сделали бы ее отталкивающей. Отталкивающей гравитации вакуумного напряжения более чем достаточно, чтобы преодолеть притяжение его массы.
Отталкивающей гравитации вакуумного напряжения более чем достаточно, чтобы преодолеть притяжение его массы.
или: если ложный вакуум окружен истинным вакуумом, напряжение внутри не уравновешивается какой-либо внешней силой и заставляет кусок ложного вакуума сжиматься, потому что гравитационное отталкивание является чисто внутренним.
Я думал, что читаю на древнегреческом. Но нет, эта книга полна «объяснений» такого рода. Я мог бы притвориться, что понимаю, о чем говорят эти слова, но нет, честно говоря, я совершенно не понимаю его теории. Дайте мне немного времени, чтобы изучить общую теорию относительности и, возможно, еще много лет, чтобы изучить теорию инфляции из ее математики, и это может иметь смысл. И я также не согласен с его логикой, что «если теория инфляции подтверждается данными в наблюдаемой части Вселенной, не должны ли мы также верить ее выводам о частях, которые мы не можем наблюдать?». Я имею в виду, разве это не смешно? Теория инфляции еще не высечена на камне, все еще есть много проблем с объяснением крупномасштабной структуры и темной материи. Это догадки, распространять их на ненаблюдаемое просто слишком надуманно, слишком спекулятивно и бессмысленно. Если это ненаблюдаемо, это означает, что у него не будет никакой причинно-следственной связи с нами, так зачем вообще беспокоиться?
Это догадки, распространять их на ненаблюдаемое просто слишком надуманно, слишком спекулятивно и бессмысленно. Если это ненаблюдаемо, это означает, что у него не будет никакой причинно-следственной связи с нами, так зачем вообще беспокоиться?
- наука-математика-физика
Прочитать
94 отзыва4 подписчика
24 августа 2014 г.Интересная книга, я твердо верю в теорию инфляции. Г-н Виленкин проделал замечательную работу, описав, кто его товарищи, такие как Андре Линде, Алан Гут и Стивен Хокинг, а также продемонстрировал заметное соперничество с Полом Стейнхардтом и Princeton Boys. Похоже, Стейнахардт любит задеть некоторых людей.
В книге Виленкин прекрасно описывает, что такое истинный вакуум, ложный вакуум, отрицательный вакуум, скалярное поле, возмущения плотности, инфляционный процесс и т. д.
Мне нравятся его беседы со Стефаном Хокингсом и в начале 1980-х годов, когда Хокинг пригласил лучших физиков на свой выездной семинар для обсуждения астрофизики.
Он взял за правило читать российские журналы по физике, так как многие великие идеи остаются незамеченными.
Разговоры об островных вселенных, откатах, нашей вселенной, параллельных вселенных и многих других темах.
Очень хорошая книга.
29 июля 2016 г.
Это одна из самых вдохновляющих книг по космологии, когда-либо написанных. Она требует базовых (хотя и не огромных) познаний в космологии, но очень вознаграждает терпеливого читателя. В некотором смысле она даже яснее объясняет идею «вселенной из ничего», чем книга Лоуренса Краусса. Настоятельно рекомендуется.
- научное чтение
16 сентября 2013 г.
Довольно крутая версия книги по космологии. Предлагает разные взгляды и точки зрения по сравнению с другими книгами.
Хочу прочитать
12 декабря 2020 г. ПОТРЯСАЮЩЕЕ И ЗАХВАТЫВАЮЩЕЕ ЧТЕНИЕ ОБ ИСТОРИИ АСТРОФИЗИКИ И КОСМОЛОГИИ, ПОСЛЕДНИХ ДОСТИЖЕНИЯХ В КОСМОЛОГИИ И КВАНТОВОЙ МЕХАНИКЕ. ИССЛЕДУЕТ ВОЗМОЖНОСТЬ МУЛЬТИВСЕЛЕННОЙ.
ИССЛЕДУЕТ ВОЗМОЖНОСТЬ МУЛЬТИВСЕЛЕННОЙ.
3 июля 2018 г.
Это хорошая, относительно легкая для чтения книга о космологии. Язык довольно прост, и эту книгу можно рекомендовать тем, кто ищет общий обзор современных космологических концепций и теорий. Никакой математики или каких-то сложных мыслей, но иногда требуется поломать голову, чтобы понять идеи, лежащие за кулисами нашей Вселенной.
Показано 1 — 21 из 21 отзывов
Некоторые неравенства для средних Чезаро двойных рядов Виленкина–Фурье
- Список журналов
- Открытый выбор Спрингера
- PMC6300583
Являясь библиотекой, NLM предоставляет доступ к научной литературе. Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения. Узнайте больше о нашем отказе от ответственности.
Узнайте больше о нашем отказе от ответственности.
Журнал неравенств и приложений
J Неравное приложение 2018; 2018 (1): 352.
Опубликовано онлайн 2018 декабрь 19. DOI: 10.1186/S13660-018-1929-Y
и
Информация Авторская информация Примечания. Статья и лицензионная информация. мы формулируем и доказываем некоторые новые неравенства, связанные со скоростью аппроксимации Lp средними Чезаро квадратичных частных сумм двойных рядов Виленкина–Фурье функций из Lp.
Ключевые слова: Неравенства, Аппроксимация, Система Виленкина, Ряды Виленкина–Фурье, Средние Чезаро, Сходимость по норме
Пусть N+ обозначает множество натуральных чисел, и пусть N:=N+∪{0}. Пусть m:=(m0,m1,…) — последовательность натуральных чисел не менее 2. Обозначим через Zmk:={0,1,…,mk−1} аддитивную группу целых чисел по модулю mk. Определим группу Gm как полное прямое произведение групп Zmj на произведение дискретных топологий Zmj.
Прямой продукт мер
µk({j}):=1mk(j∈Zmk)
— мера Хаара на Gm с µ(Gm)=1. Если последовательность m ограничена, то Gm называется ограниченной группой Виленкина. В данной работе мы рассматриваем только ограниченные группы Виленкина. Элементы Gm могут быть представлены последовательностями x:=(x0,x1,…,xj,…) (xj∈Zmj). Групповая операция + в Gm задается выражением
x+y=((x0+y0)modm0,…,(xk+yk)modmk,…)
для x:=(x0,…,xk,…) и y:=(y0,…,yk ,…)∈Gm. Обратное + будет обозначаться -.
Легко дать базу для окрестностей Gm:
I0(x):=Gm,In(x):={y∈Gm|y0=x0,…,yn−1=xn−1}
для x∈Gm и n∈N. Определить In:=In(0) для n∈N+. Положим en:=(0,…,0,1,0,…)∈Gm, где n -я координата которого равна 1, а остальные нули (n∈N).
Определим так называемую обобщенную систему счисления, основанную на m , следующим образом: M0:=1, Mk+1:=mkMk (k∈N). Тогда каждое n∈N однозначно выражается как n=∑j=0∞njMj, где nj∈Zmj (j∈N+), и только конечное число nj отличны от нуля. Далее введем на Gm ортонормированную систему, называемую системой Виленкина. Сначала определим комплекснозначные функции rk(x):Gm→C, обобщенные функции Радемахера, следующим образом: rk(x):=exp2πixkmk(i2=−1,x∈Gm,k∈N). Теперь определим систему Виленкина ψ:=(ψn:n∈N) на Gm как ψn(x):=∏k=0∞rknk(x)(n∈N). В частности, если m=2, то мы называем эту систему системой Уолша–Пэли. Каждый ψn является характером Gm, и все характеры Gm имеют эту норму. Более того, ψn(−x)=ψ¯n(x). Ядра Дирихле определяются формулой Dn:=∑k=0n−1ψk(n∈N+). Напомним, что (см. [20] или [23]) DMn(x)={Mnif x∈In,0if x∉In. 1 Система Виленкина ортонормирована и полна в L1(Gm) (см. [1]). Далее введем некоторые обозначения из теории двумерной системы Виленкина. Пусть m̃ будет последовательностью, подобной m . Норма пространства Lp(Gm2) определяется формулой ∥f∥p:=(∫Gm2|f(x,y)|pdµ(x,y))1/p(1≤p<∞). Обозначим через C(Gm2) класс непрерывных функций на группе Gm2, снабженных супремум-нормой. Для краткости обозначений мы пишем L∞(Gm2) вместо C(Gm2). Двумерные коэффициенты Фурье, прямоугольные частичные суммы рядов Фурье и ядра Дирихле по двумерной системе Виленкина определяются следующим образом: fˆ(n1,n2):=∫Gm2f(x,y)ψ¯n1(x)ψ¯n2(y)dµ(x,y),Sn1,n2(x,y,f):=∑k1 =0n1−1∑k2=0n2−1fˆ(k1,k2)ψk1(x)ψk2(y),Dn1,n2(x,y):=Dn1(x)Dn2(y), Обозначим Sn(1)(x,y,f):=∑l=0n−1fˆ(l,y)ψ¯l(x),Sm(2)(x,y,f):=∑r=0m −1fˆ(x,r)ψ¯r(y), , где fˆ(l,y)=∫Gmf(x,y)ψl(x)dµ(x) и fˆ(x,r)=∫Gmf(x,y)ψr(y)dµ(y). Средние (C,−α) двойного ряда Виленкина–Фурье определяются следующим образом: σn−α(f,x,y)=1An−1−α∑j=1nAn−j−α−1Sj,j(f,x,y), где A0α=1,Anα=(α+1)⋯(α+n)n!. Хорошо известно, что (см. [28]) Anα=∑k=0nAkα−1, 2 Anα−An−1α=Anα−1, 3 и c1(α)nα≤Anα≤c2(α)nα, 4 где положительные константы c1 и c2 зависят от α . Диадические частичные модули непрерывности функции f∈Lp(Gm2) в Lp-норме определяются соотношениями ω1(f,1Mn)p=supu∈In∥f(⋅+u,⋅)−f(⋅,⋅)∥p и ω2(f,1Mn)p=supv∈In∥f(⋅,⋅+v)−f(⋅,⋅)∥p, , тогда как диадический смешанный модуль непрерывности определяется следующим образом: ω1,2(f,1Mn,1Mm)p=sup(u,v)∈In×Im∥f(⋅+u,⋅+v)−f(⋅+u,⋅)−f(⋅,⋅ +v)+f(⋅,⋅)∥p. Понятно, что ω1,2(f,1Mn,1Mm)p≤ω1(f,1Mn)p+ω2(f,1Mm)p. Диадический полный модуль непрерывности определяется выражением ω(f,1Mn)p=sup(u,v)∈In×In∥f(⋅+u,⋅+v)−f(⋅,⋅)∥p. Проблемы суммирования частных сумм и чезаровских средних для рядов Уолша–Фурье изучались в [2, 13–19, 21, 22, 25, 26]. Вопрос сходимости средних Фейера (и Чезаро) на группах Уолша и Виленкина для неограниченного случая изучался в [3–11]. В своей монографии [27] Жижинашвили подробно исследовал поведение чезаровских (C,α)-средних для двойных тригонометрических рядов Фурье. Гогинава [18] изучала аналогичный вопрос в случае системы Уолша. В частности, были доказаны следующие теоремы. Пусть ф ∥σ2k−α(f)−f∥p≤c(α){2kαω1(f,1/2k−1)p+2kαω2(f,1/2k−1)p+∑r=0k−22r−kω1 (f,1/2r)p+∑s=0k−22s−kω2(f,1/2s)p}. Пусть ф принадлежат Lp(G2) для некоторых p∈[1,∞] и α∈(0,1). ∥σn−α(f)−f∥p≤c(α){2kαkω1(f,1/2k−1)p+2kαkω2(f,1/2k−1)p+∑r=0k−22r−kω1 (f,1/2r)p+∑s=0k−22s−kω2(f,1/2s)p}. В настоящей работе мы формулируем и доказываем аналогичные результаты в случае двойных рядов Виленкина–Фурье. Нашими основными результатами являются следующие теоремы. Пусть ф принадлежат Lp(Gm2) для некоторых 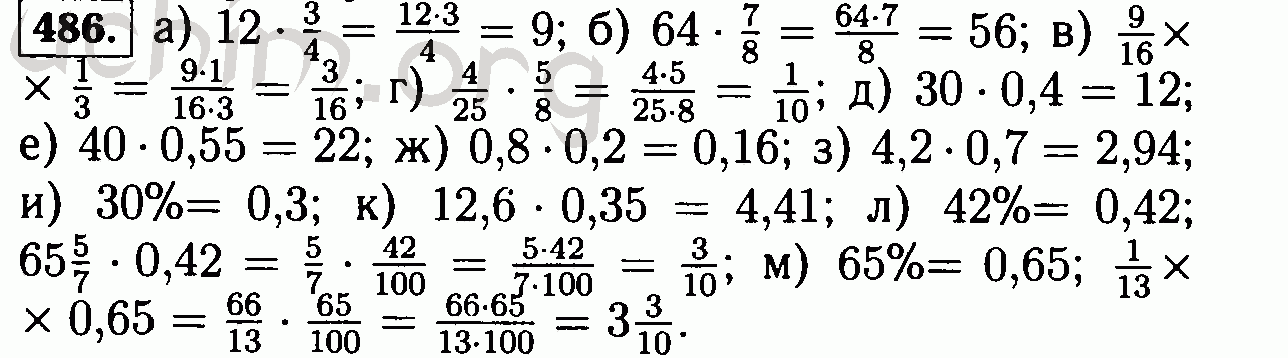 Мы также используем следующие обозначения: |n|:=max{k∈N:nk≠0} (т. е. M|n|≤n
Мы также используем следующие обозначения: |n|:=max{k∈N:nk≠0} (т. е. M|n|≤n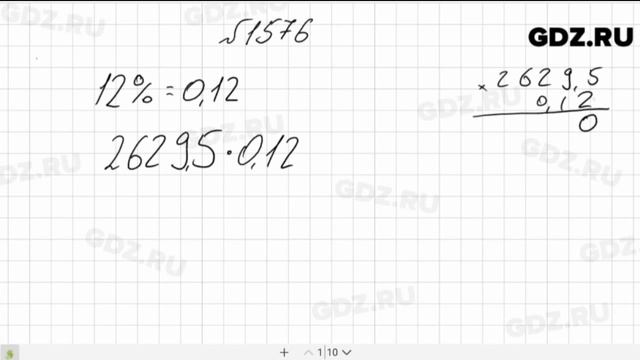 Связь между последовательностями (m˜n) и (M˜n) такая же, как между последовательностями (mn) и (Mn). Группа Gm×Gm˜ называется двумерной группой Виленкина. Нормализованная мера Хаара обозначается μ , как и в одномерном случае. Мы также предполагаем, что m=m˜ и Gm×Gm˜=Gm2.
Связь между последовательностями (m˜n) и (M˜n) такая же, как между последовательностями (mn) и (Mn). Группа Gm×Gm˜ называется двумерной группой Виленкина. Нормализованная мера Хаара обозначается μ , как и в одномерном случае. Мы также предполагаем, что m=m˜ и Gm×Gm˜=Gm2.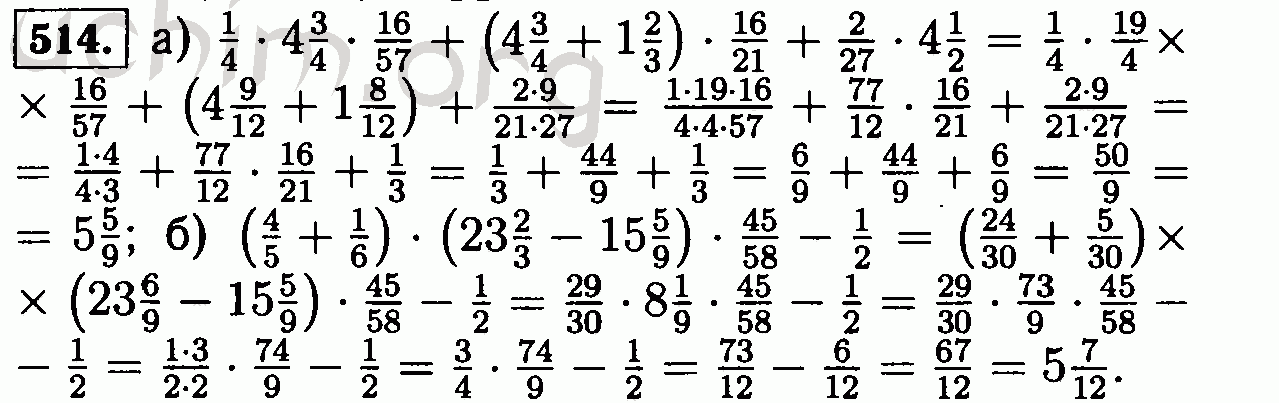
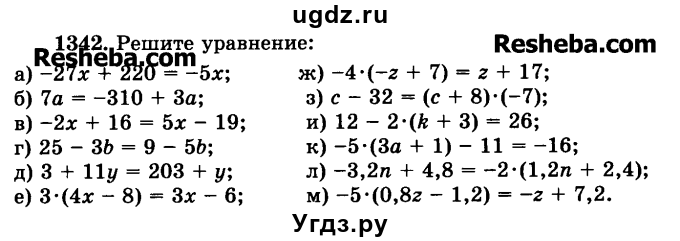
Теорема А
Теорема B
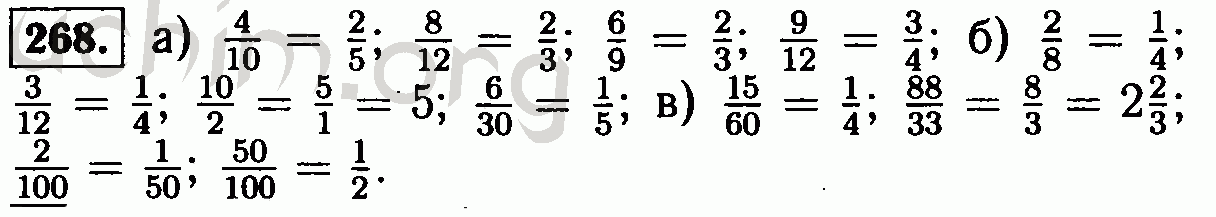 Затем , для любых 2k≤n<2k+1 (k,n∈N), имеем неравенство
Затем , для любых 2k≤n<2k+1 (k,n∈N), имеем неравенство Теорема 1
∥σMk−α(f)−f∥p≤c(α)(ω1(f,1/Mk−1)pMkα+ω2(f,1/Ml−1)pMkα+∑r=0k−2MrMkω1( f,1/Mr)p+∑s=0k−2MsMkω2(f,1/Ms)p).
Теорема 2
Пусть ф принадлежат Lp(Gm2) для некоторых p∈[1,∞] и α∈(0,1). Затем , для любого Mk≤n
∥σn−α(f)−f∥p≤c(α)(ω1(f,1/Mk−1)pMkαlogn+ω2(f,1/Ml−1)pMkαlogn+∑r=0k−2MrMkω1(f ,1/Mr)p+∑s=0k−2MsMkω2(f,1/Ms)p).
Чтобы сделать доказательства этих теорем более ясными, мы сформулируем некоторые вспомогательные леммы в разд. 2. Некоторые из этих лемм являются новыми и представляют самостоятельный интерес. Подробные доказательства можно найти в разд. 3.
Для доказательства теорем 1 и 2 нам понадобятся следующие три леммы (см. [1, 12] и [8] соответственно)
Лемма 1
Пусть α1,α2,…,αn — действительные числа . Затем
1n∫G|∑k=1nαkDk(x)|dµ(x)≤cn(∑k=1nαk2)1/2.
Лемма 2
Пусть α1,α2,…,αn — действительные числа . Затем
1n∫Gm2|∑k=1nαkDk(x)Dk(y)|dµ(x,y)≤cn(∑k=1nαk2)1/2.
Лемма 3
Пусть 0≤j
DnsMs-j=DnsMs-ψnsMs-1D¯j.
Нам также понадобятся следующие новые неммы, представляющие самостоятельный интерес.
Лемма 4
Пусть ф принадлежат Lp(Gm2) для некоторых p∈[1,∞]. Затем , на каждые α∈(0,1), имеем неравенство
Затем , на каждые α∈(0,1), имеем неравенство
I:=1An−α∥∫Gm2∑i=1Mk−1An−i−α−1Di(u)Di(v)[f(⋅−u,⋅−)−f(⋅,⋅)]dµ( u,v)∥p≤∑r=0k−2MrMkω1(f,1/Mr)p+∑s=0k−2MsMkω2(f,1/Ms)p,
где Мк≤n<Мк+1.
Лемма 5
Пусть α∈(0,1) и р=Мк,Мк+1,… . Затем
II:=∫Gm2|∑i=1MkAp−i−α−1Di(u)Di(v)|dµ(u,v)≤c(α)<∞,k=1,2,….
Лемма 6
Имеем неравенство
III:=∫Gm2|∑i=1nAn−i−α−1Di(u)Di(v)|dµ(u,v)≤c(α)logn
Доказательство леммы 3
Применяя преобразование Абеля, из (2) получаем
I≤1An−α∥∫Gm2∑i=1Mk−1−1An−i−α−2∑l=1iDi(u)Di(v)[f(⋅−u,⋅−v)−f(⋅ ,⋅)]dµ(u,v)∥p+1An−α∥∫Gm2An−Mk−1−α−1∑i=1Mk−1Di(u)Di(v)[f(⋅−u,⋅−v )−f(⋅,⋅)]dµ(u,v)∥p:=I1+I2,
5
где первое и второе слагаемые в правой части неравенства (5) обозначены I1 и I2, соответственно.
Для I2 имеем оценку
I2≤1An−α∥∫Gm2An−Mk−1−α−1∑r=1k−2∑i=MrMr+1−1Di(u)Di(v)×[f(⋅−u,⋅−v )−f(⋅,⋅)]∥pdµ(u,v)≤1An−α∥∫Gm2An−Mk−1−α−1∑r=1k−2∑i=MrMr+1−1Di(u)Di( v)×[f(⋅−u,⋅−v)−SMr,Mr(⋅−u,⋅−v,f)]dµ(u,v)∥p+1An−α∥∫Gm2An−Mk−1− α−1∑r=1k−2∑i=MrMr+1−1Di(u)Di(v)×[SMr,Mr(⋅−u,⋅−v,f)−SMr,Mr(⋅,⋅,f )]dµ(u,v)∥p+1An−α∥∫Gm2An−Mk−1−α−1∑r=1k−2∑i=MrMr+1−1Di(u)Di(v)×[SMr, Mr(⋅,⋅,f)−f(⋅,⋅)]dµ(u,v)∥p:=I21+I22+I23,
6
где первый, второй и третий члены в правой части неравенства (6) обозначаются I21, I22 и I23 соответственно.
Очевидно, что
∫Gm2∑i=MrMr+1−1Di(u)Di(v)[SMr,Mr(⋅−u,⋅−v,f)−SMr,Mr(⋅,⋅,f)]dµ(u, v)=∑i=MrMr+1−1(∫Gm2Di(u)Di(v)SMr,Mr(⋅−u,⋅−v,f)dµ(u,v)−SMr,Mr(⋅,⋅, f))=∑i=MrMr+1−1(Si(⋅,⋅,SMr,Mr(f))−SMr,Mr(⋅,⋅,f))=∑i=MrMr+1−1(SMr, Mr(⋅,⋅,f)−SMr,Mr(⋅,⋅,f))=0.
Отсюда
I22=0.
7
Кроме того, в силу обобщенного неравенства Минковского, леммы 2 и в силу (1) и (4) получаем
I21≤1An−α|An−Mk−1−α−1|∑r=1k−2∫Gm2|∑i=MrMr+1−1Di(u)Di(v)|×∥f(⋅−u ,⋅−v)−SMr,Mr(⋅−u,⋅−v,f)∥pdµ(u,v)≤c(α)Mk∑r=1k−2(ω1(f,1/Mr)p+ ω2(f,1/Mr)p)×∫Gm2|∑i=MrMr+1−1Di(x)Di(y)|dµ(u,v)≤c(α)∑r=1k−2MrMk(ω1( f,1/Mr)p+ω2(f,1/Mr)p).
8
Оценка I23 аналогична оценке I21:
I23≤c(α)∑r=1k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p).
9
Аналогично можно оценить I1 следующим образом:
I1≤1An−α∑r=1k−2∥∫Gm2∑i=MrMr+1−1An−i−α−2∑l=1iDl(u)Dl(v)×[f(⋅−u,⋅ −v)−SMr,Mr(⋅−u,⋅−v,f)]dµ(u,v)∥p+1An−α∑r=1k−2∥∫Gm2∑i=MrMr+1−1An−i −α−2∑l=1iDl(u)Dl(v)×[SMr,Mr(⋅−u,⋅−v,f)−SMr,Mr(⋅,⋅,f)]∥pdµ(u,v) +1An−α∑r=1k−2∥∫Gm2∑i=MrMr+1−1An−i−α−2∑l=1iDl(u)Dl(v)×[SMr,Mr(⋅,⋅,f) −f(⋅,⋅)]dµ(u,v)∥p≤1An−α∑r=1k−2∫Gm2|∑i=MrMr+1−1An−i−α−2∑l=1iDl(u) Dl(v)|×∥f(⋅−u,⋅−v)−SMr,Mr(⋅−u,⋅−v,f)∥pdµ(u,v)+1An−α∑r=1k−2∫ Gm2|∑i=MrMr+1−1An−i−α−2∑l=1iDl(u)Dl(v)|×∥SMr,Mr(⋅,⋅,f)−f(⋅,⋅)∥pdµ( u,v)≤c(α)Mkα∑r=1k−2∑i=MrMr+1−1(n−i)−α−2i(ω1(f,1/Mr)p+ω2(f,1/ Mr)p)≤c(α)Mkα∑r=1k−2∑i=MrMr+1−1(n−Mr+1−1)−α−2i(ω1(f,1/Mr)p+ω2( f,1/Mr)p)≤c(α)∑r=0k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p).
10
Комбинируя (7)–(9) с (10) для I , мы находим, что
I≤c(α)∑r=0k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p).
11
Лемма 3 доказана. □
Доказательство леммы 4
Очевидно, что
II≤∫Gm2|∑i=1Mk−1Ap−Mk+i−α−1DMk−i(u)DMk−i(v)|dµ(u,v)+|Ap−Mk−α−1|∫ Gm2DMk(u)DMk(v)dµ(u,v):=II1+II2,
12
где первое и второе слагаемые в правой части неравенства (12) обозначены через II1 и II2 соответственно.
Из (1) через |Ap−Mk−α−1|≤1 получаем, что
II2≤1.
13
Более того, по лемме 3 имеем
II1≤∫Gm2|∑i=1Mk−1Ap−Mk+i−α−1D¯i(u)D¯i(v)|dµ(u,v)+∫Gm2DMk(u)|∑i=1Mk −1Ap−Mk+i−α−1D¯i(v)|dµ(u,v)+∫Gm2DMk(v)|∑i=1Mk−1Ap−Mk+i−α−1D¯i(u)|dµ (u,v)+|∑i=1Mk−1Ap−Mk+i−α−1|∫Gm2DMk(u)DMk(v)dµ(u,v):=II11+II12+II13+II14,
14
где первое, второе, третье и четвертое слагаемые в правой части неравенства (14) обозначены соответственно II11, II12, II13 и II14.
Из (1) и (4) следует, что
II14≤c(α)∑v=1∞v−α−1<∞.
15
Применяя преобразование Абеля, с учетом леммы 2 имеем, что
II11≤∫Gm2|∑i=1Mk−2Ap−Mk+i−α−2∑l=1iD¯l(u)D¯l(v)|dµ(u,v)+∫Gm2|Ap−1 −α−1∑i=1Mk−1D¯i(u)D¯i(v)|dµ(u,v)≤c(α){∑v=1Mk−2(p−Mk+i)−α− 2i+(p−1)−α−1Mk}≤c(α){∑i=1∞i−α−1+Mk−α}<∞.
16
Оценка II12 и II13 аналогична оценке II11. Применяя преобразование Абеля, с учетом леммы 1 находим, что
II12≤∫Gm2DMk(u)|∑i=1Mk−2Ap−Mk+i−α−2∑l=1iD¯l(v)|dµ(u,v)+∫Gm2DMk(u)|Ap−1 −α−1∑i=1Mk−1D¯i(v)|dµ(u,v)≤c(α){∑v=1Mk−2(p−Mk+i)−α−2i+(p−1) −α−1Mk}≤c(α){∑i=1∞i−α−1+Mk−α}<∞
17
и
III12≤∫Gm2DMk(v)|∑i=1Mk−2Ap−Mk+i−α−2∑l=1iD¯l(u)|dµ(u,v)+∫Gm2DMk(v)|Ap−1 −α−1∑i=1Mk−1D¯i(u)|dµ(u,v)≤c(α){∑v=1Mk−2(p−Mk+i)−α−2i+(p−1) −α−1Mk}≤c(α){∑i=1∞i−α−1+Mk−α}<∞.
18
Доказательство завершается комбинацией (12)–(18). □
Доказательство леммы 5
Пусть
n=nk1Mk1+⋯+nksMks,k1>⋯>ks≥0.
Обозначение
n(i)=nkiMki+⋯+nksMks,i=1,2,…,s.
С (см. [20])
Dj+nAMA=DnAMA+ψnAMADj,
19
находим, что
III≤∫Gm2|∑i=1nk1Mk1An−i−α−1Di(u)Di(v)|dµ(u,v)+∫Gm2|∑i=1n(2)An(2)−i−α −1Di(u)Di(v)|dµ(u,v)+∫Gm2Dnk1Mk1(u)Dnk1Mk1(v)|∑i=1n(2)An(2)−i−α−1|dµ(u,v )+∫Gm2Dnk1Mk1(u)|∑i=1n(2)An(2)−i−α−1Di(v)|dµ(u,v)+∫Gm2Dnk1Mk1(v)|∑i=1n(2)An (2)−i−α−1Di(u)|dµ(u,v):=III1+III2+III3+III4+III5,
20
где первое, второе, третье, четвертое и пятое слагаемые в правой части неравенства (20) обозначены символами III1, III2, III3, III4 и III5 соответственно.
По (1) имеем, что
III3≤c(α).
21
Кроме того, поскольку (см. [24])
|∑i=1nAn−i−α−1Di(u)|=O(|u|α−1),
22
для III4, получаем, что
III4≤∫Gm2Dnk1Mk1(u)|v|α−1dµ(u,v)≤∫Gm|v|α−1dµ(v)=1α<∞.
23
Аналогично находим, что
III5≤∫Gm2Dnk1Mk1(v)|u|α−1dµ(u,v)≤∫Gm|u|α−1dµ(v)=1α<∞.
24
Для r∈{0,…mA−1} и 0≤j Dj+rMA=(∑q=0r−1ψMAq)DMA+ψMArDj. Таким образом, мы имеем ∫Gm2∑i=1nk1Mk1−1An−i−α−1Di(u)Di(v)dµ(u,v)≤∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α −1Di+rMk1(u)Di+rMk1(v)dµ(u,v)≤∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α−1(∑q=0r−1ψMk1q) DMk1(u)×(∑q=0r−1ψMk1q)DMk1(v)dµ(u,v)+∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α−1(∑q= 0r−1ψMk1q)DMk1(u)ψMArDi(v)dµ(u,v)+∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α−1ψMArDi(u)(∑q=0r− 1ψMk1q)DMk1(v)dµ(u,v)+∫Gm2∑r=0nk1−1∑i=0Mk1−1An−i−rMk1−α−1ψMArDi(u)ψMArDi(v)dµ(u,v). С другой стороны, в силу (1) и (4) получаем, что ∫Gm2An−nk1Mk1−α−1Dnk1Mk1(u)Dnk1Mk1(v)dµ(u,v)≤c(α). Следовательно, для III1 имеем оценку III1≤∫Gm2DMk1(u)DMk1(v)|∑r=0nk1−1∑i=1Mk1An−i−rMk1−α−1|dµ(u,v)+∫Gm2DMk1(u)|∑r=0nk1 −1∑i=1Mk1An−i−rMk1−α−1Di(v)|dµ(u,v)+∫Gm2DMk1(v)|∑r=0nk1−1∑i=1Mk1An−i−rMk1−α−1Di( u)|dµ(u,v)+∫Gm2|∑r=0nk1−1∑i=1Mk1An−i−rMk1−α−1Di(u)Di(v)|dµ(u,v)+c(α) :=III11+III12+III13+III14+c(α), 25 где первое, второе, третье и четвертое слагаемые в правой части неравенства (25) обозначены через III11, III12, III13 и III14 соответственно. Из леммы 4 получаем, что III14≤c(α). 26 Оценка III11 аналогична оценке III3, и мы находим, что III11≤c(α). 27 Оценка III12 и III13 аналогична оценке III4, и мы получаем, что III12<∞ 28 и III13<∞. 29 После подстановки (21) и (23)–(29) в (20) заключаем, что ∫Gm2|∑i=1nAn−i−α−1Di(u)Di(v)|dµ(u,v)≤∫Gm2|∑i=1n(2)An(2)−i−α−1Di (u)Di(v)|dµ(u,v)+c(α)≤⋯≤∫Gm2|∑i=1n(s)An(s)−i−α−1Di(u)Di(v)| dµ(u,v)+c(α)s≤c(α)+c(α)s≤c(α)logn. Доказательство завершено. □ Теперь мы готовы доказать основные результаты. Очевидно, что ∥σMk−α(f)−f∥p≤1AMk−1−α∥∫Gm2∑i=1Mk−1AMk−i−α−1Di(u)Di(v)[f(⋅−u,⋅− v)−f(⋅,⋅)]dµ(u,v)∥p+1AMk−1−α∥∫Gm2∑i=Mk−1+1MkAMk−i−α−1Di(u)Di(v)[f (⋅−u,⋅−v)−f(⋅,⋅)]dµ(u,v)∥p:=I+II. 30 Из леммы 5 следует, что I≤c(α)∑r=0k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p). 31 Кроме того, для II , у нас есть оценка II≤1AMk−1−α∥∫Gm2∑i=Mk−1+1MkAMk−i−α−1Di(u)Di(v)×[f(⋅−u,⋅−v)−SMk−1( 1)(⋅−u,⋅−v,f)]dµ(u,v)∥p+1AMk−1−α∥∫Gm2∑i=Mk−1+1MkAMk−i−α−1Di(u)Di( v)×[SMk−1(1)(⋅−u,⋅−v,f)−f(⋅,⋅)]dµ(u,v)∥p:=II1+II2, 32 , где первое и второе слагаемые в правой части неравенства (32) обозначены соответственно II1 и II2. С учетом обобщенного неравенства Минковского в силу (4) и леммы 5 получаем, что II1≤1AMk−1−α∫Gm2|∑i=Mk−1+1MkAMk−i−α−1Di(u)Di(v)|×∥f(⋅−u,⋅−v)−SMk−1 (1)(⋅−u,⋅−v,f)∥pdµ(u,v)≤c(α)Mkαω1(f,1/Mk−1)p. 33 Оценка II2 аналогична оценке II1, и мы находим, что II2≤c(α)Mkαω2(f,1/Mk−1)p. 34 Объединяя (30)–(34), получаем доказательство теоремы 1. □ Очевидно, что ∥σn−α(f)−f∥p≤1An−1−α∥∫Gm2∑i=1Mk−1An−i−α−1Di(u)Di(v)[f(⋅−u,⋅− v)−f(⋅,⋅)]dµ(u,v)∥p+1An−1−α∥∫Gm2∑i=Mk−1+1MkAn−i−α−1Di(u)Di(v)[f (⋅−u,⋅−v)−f(⋅,⋅)]dµ(u,v)∥p+1An−1−α∥∫Gm2∑i=Mk+1nAn−i−α−1Di(u)Di (v)[f(⋅−u,⋅−v)−f(⋅,⋅)]dµ(u,v)∥p:=I+II+III, 35 где первый, второй и третий члены правой части неравенства (35) обозначены I , II и III соответственно. Из леммы 4 следует, что I≤c(α)∑r=0k−2MrMk(ω1(f,1/Mr)p+ω2(f,1/Mr)p). 36 Далее, повторяя рассуждения так же, как при доказательстве теоремы 1, получаем, что II≤c(α)Mkα(ω1(f,1/Mk−1)p+ω2(f,1/Mk−1)p). 37 С другой стороны, для III имеем III≤1An−1−α∥∫Gm2∑i=Mk+1nAn−i−α−1Di(u)Di(v)×[f(⋅−u,⋅−v)−f(⋅,⋅) ]∥pdµ(u,v)≤1An−α∥∫Gm2∑i=Mk+1nAn−i−α−1Di(u)Di(v)×[f(⋅−u,⋅−v)−SMk,Mk (⋅−u,⋅−v,f)]dµ(u,v)∥p≤1An−α∥∫Gm2∑i=Mk+1nAn−i−α−1Di(u)Di(v)×[SMk, Mk(⋅−u,⋅−v,f)−SMk,Mk(⋅,⋅,f)]dµ(u,v)∥p≤1An−α∥∫Gm2∑i=Mk+1nAn−i−α− где первое, второе и третье слагаемые в правой части неравенства (38) обозначаются через III1, III2 и III3 соответственно. Легко показать, что III2=0. 39 В силу обобщенного неравенства Минковского и леммы 5 для III1 получаем, что III1≤1An−α∫Gm2|∑i=Mk+1nAn−i−α−1Di(u)Di(v)|×∥f(⋅−u,⋅−v)−SMr,Mr(⋅−u ,⋅−v,f)∥pdµ(u,v)≤c(α)Mkα(ω1(f,1/Mk−1)p+ω2(f,1/Mk−1)p)×∫Gm2|∑ v=Mk+1nAn−v−α−1Dv(u)Dv(v)|dµ(u,v)≤c(α)Mkαlogn(ω1(f,1/Mk−1)p+ω2(f,1/ Мк-1)р). 40 Оценка III3 аналогична оценке III2, и мы находим, что III3≤c(α)Mkαlogn(ω1(f,1/Mk−1)p+ω2(f,1/Mk−1)p). 41 После подстановки (36)–(37) и (41) в (35) получаем доказательство теоремы 2. □ Авторы благодарят рецензентов за полезные советы. Авторы внесли равный вклад в написание этой статьи. Оба автора одобрили окончательный вариант рукописи. Неприменимо. Авторы заявляют об отсутствии конкурирующих интересов. Примечание издателя Springer Nature сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности. Т. Тепнадзе, Email: moc.liamg@ezdanfetonist. Л. Э. Перссон, электронная почта: moc.liamg@srep6kiresral. 1. Агаев Г.Н., Виленкин Н.Я., Джафарли Г.М., Рубинштейн А.И. Мультипликативные системы функций и гармонический анализ на нульмерных группах. Баку: Эльм; 1981. [Google Scholar] 2. Файн Н. Дж. Чезаро суммируемость рядов Уолша–Фурье. проц. Натл. акад. науч. США. 1995;41:558–591. [PMC free article] [PubMed] [Google Scholar] 3. Гат Г. О поточечной сходимости чезаро-средних функций двух переменных по неограниченным системам Виленкина. Дж. Прибл. Теория. 2004;128(1):69–99. doi: 10.1016/j.jat.2004.04.003. [CrossRef] [Google Scholar] 4. Гат Г. Сходимость почти всюду средних Фейера функций L1 на редко неограниченных группах Виленкина. Акта Математика. Грех. англ. сер. 2007;23(12):2269–2294. doi: 10.1007/s10114-007-0961-5. [Перекрестная ссылка] [Академия Google] 5. Гат Г. О сходимости почти всюду рядов Фурье на неограниченных группах Виленкина. 6. Гат Г. Некоторые результаты сходимости и расходимости в отношении суммирования рядов Фурье на одномерных и двумерных неограниченных группах Виленкина. Анна. ун-т науч. бп. Роландо Этвёш Nomin., Sect. вычисл. 2010; 33: 157–173. [Google Scholar] 7. Гат Г., Блахота И. Нормовая суммируемость логарифмических средних Нёрлунда на неограниченных группах Виленкина. Анальный. Теория прил. 2008;24(1):1–17. дои: 10.1007/s10496-008-0001-з. [CrossRef] [Google Scholar] 8. Гат Г., Гогинава Ю. Сходимость почти всюду (C,α)-средних квадратичных частных сумм двойных рядов Виленкина–Фурье. Грузинская математика. Дж. 2006;13(3):447–462. [Google Scholar] 9. Гат Г., Гогинава Ю. Неравенство слабого типа для максимального оператора (C,α)-средних рядов Фурье по системе Уолша–Качмарца. Акта Математика. Висела. 2009; 125(1–2):65–83. doi: 10.1007/s10474-009-8217-8. [CrossRef] [Академия Google] 10. Гат Г., Гогинава Ю. 11. Гат Г., Гогинава Ю. Нормовая сходимость логарифмических средних на неограниченных группах Виленкина. Банах Дж. Матем. Анальный. 2018;12(2):422–438. doi: 10.1215/17358787-2017-0031. [CrossRef] [Google Scholar] 12. Глухов В.А. О суммировании кратных рядов Фурье по мультипликативным системам. Мат. Заметки. 1986;39:665–673. [Google Scholar] 13. Гогинава Ю. О равномерной сходимости рядов Уолша–Фурье. Акта Математика. Висела. 2001;93(1–2):59–70. doi: 10.1023/A:1013865315680. [CrossRef] [Google Scholar] 14. Гогинава Ю. Об аппроксимативных свойствах чезаровских средних отрицательного порядка рядов Уолша–Фурье. Дж. Прибл. Теория. 2002;115(1):9–20. doi: 10.1006/jath.2001.3632. [CrossRef] [Google Scholar] 15. Гогинава Ю. Равномерная сходимость чезаровских средних отрицательного порядка двойных рядов Уолша–Фурье. 16. Гогинава Ю. О средних Чезаро двойных тригонометрических рядов Фурье. Мат. Заметки. 2003;74(4):502–507. doi: 10.4213/mzm285. [CrossRef] [Google Scholar] 17. Гогинава У. Средние Чезаро двойных рядов Уолша–Фурье. Анальный. Мат. 2004;30(4):289–304. doi: 10.1007/s10476-005-0516-x. [CrossRef] [Google Scholar] 18. Гогинава Ю. Аппроксимационные свойства (C,α) средних двойных рядов Уолша–Фурье. Анальный. Теория прил. 2004; 20(1):77–9.8. doi: 10.1007/BF02835261. [CrossRef] [Google Scholar] 19. Гогинава Ю., Надь К. О максимальном операторе средних Уолша–Качмарца–Фейера. Чехослов. Мат. Дж. 2011;61(3):673–686. doi: 10.1007/s10587-011-0038-6. [CrossRef] [Google Scholar] 20. Голубов Б.И., Ефимов А.В., Скворцов В.А. Ряды Уолша и преобразования. Москва: Наука; 1987. [Google Scholar] 21. Надь К. Аппроксимация средними Чезаро отрицательного порядка рядов Уолша–Качмарца–Фурье. 22. Schipp F. Über gewisse Maximaloperatoren. Анна. ун-т науч. бп. Роландо Этвёш Nomin., Sect. Мат. 1975; 18: 189–195. [Google Scholar] 23. Шипп Ф., Уэйд В.Р., Саймон П. Уолш. Серия «Введение в диадический гармонический анализ». Бристоль: Хильгер; 1990. [Google Scholar] 24.
Шаварденидзе Г.: О сходимости чезаро-средних отрицательного порядка рядов Виленкина–Фурье. arXiv:1811.08367 25. Саймон П., Вайс Ф. Слабые неравенства для суммирования по Чезаро и Риссу рядов Уолша–Фурье. Дж. Прибл. Теория. 2008; 151(1):1–19. doi: 10.1016/j.jat.2007.05.004. [CrossRef] [Google Scholar] 26. Тевзадзе В.И. Равномерная (C,α)(−1≤α≤0) суммируемость рядов Фурье по системе Уолша–Пэли. Акта Математика. акад. Педагог. Нихази. 2006;22(1):41–61. [Google Scholar] 27. Жижиашвили Л.В. Тригонометрические ряды Фурье и их сопряженные. Дордрехт: Kluwer Academic; 1996. [Google Scholar] 28. Зигмунд А. Тригонометрические ряды.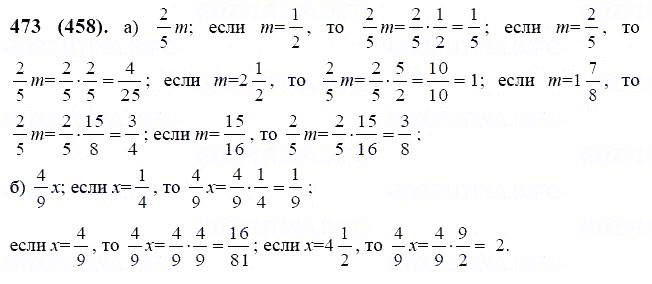

Доказательство теоремы 1

Доказательство теоремы 2
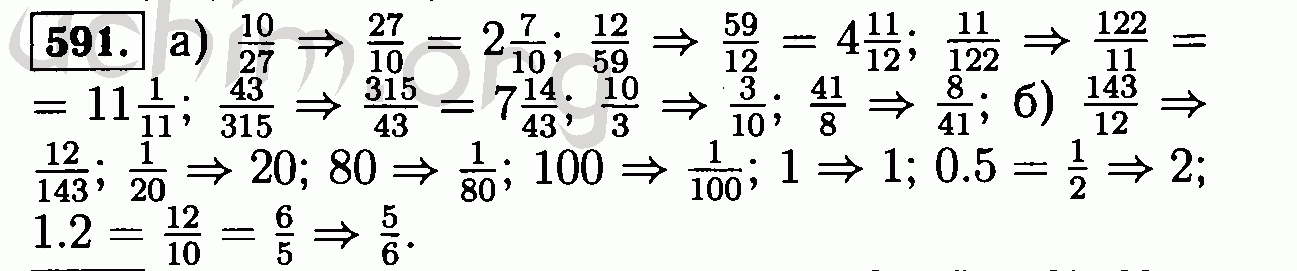
Конкурирующие интересы

 Опубл. Мат. (Дебр.) 2009;75(1–2):85–94. [Google Scholar]
Опубл. Мат. (Дебр.) 2009;75(1–2):85–94. [Google Scholar] Сходимость по норме двойных рядов Фурье на неограниченных группах Виленкина. Акта Математика. Висела. 2017;152(1):201–216. doi: 10.1007/s10474-017-0703-9. [CrossRef] [Google Scholar]
Сходимость по норме двойных рядов Фурье на неограниченных группах Виленкина. Акта Математика. Висела. 2017;152(1):201–216. doi: 10.1007/s10474-017-0703-9. [CrossRef] [Google Scholar] Дж. Прибл. Теория. 2003;124(1):96–108. doi: 10.1016/S0021-9045(03)00134-5. [CrossRef] [Google Scholar]
Дж. Прибл. Теория. 2003;124(1):96–108. doi: 10.1016/S0021-9045(03)00134-5. [CrossRef] [Google Scholar] Восток Дж. Прибл. 2010;16(3):297–311. [Google Scholar]
Восток Дж. Прибл. 2010;16(3):297–311. [Google Scholar]

