Номер 651 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник)
Номер 651 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
Старая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
ГДЗ учебник 2015.
 номер 229 (234) математика 6 класс Виленкин, Жохов – Telegraph
номер 229 (234) математика 6 класс Виленкин, Жохов – Telegraph>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ учебник 2015. номер 229 (234) математика 6 класс Виленкин, Жохов
ГДЗ по математике 6 класс Виленкин учебник . номер — 229 (234 ) . Авторы : Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд .
Решебник (ГДЗ ) по Математике за 6 (шестой ) класс авторы: Виленкин , Жохов , Чесноков, Шварцбурд издательство Мнемозина, год . ГДЗ по математике за 6 класс Виленкин , Жохов , Чесноков, Шварцбурд . Учебник Мнемозина (ответы к старому и новому изданию) .
6 класс : учебник для общеобразовательных учреждений / Н . Я . Виленкин , В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . Решебник по математике для 6 класса к Виленкину – это сборник Издатель: С .М . Никольский, М .К, Потапов, Н .Н . Решетников, А .В . Шевкин . -2019 .
Задача №234 , ГДЗ по математике за 6 класс к учебнику Виленкина с подробным решением .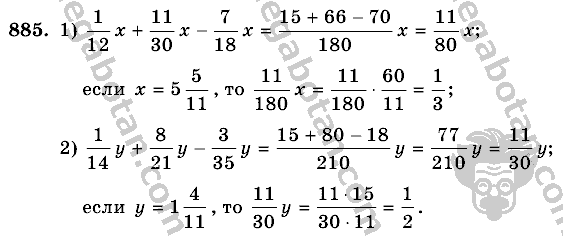 Виленкин , Жохов, Чесноков . 2 .8 Основное свойство дроби . Номер №234 .
Виленкин , Жохов, Чесноков . 2 .8 Основное свойство дроби . Номер №234 .
В гдз по математике 6 класса Виленкина больше полторы тысячи заданий . Каждое из них шестиклассник должен решить, полностью в них разобраться и суметь понять похожие задания . .
ГДЗ Виленкин Жохов 6 класс В 2х частях (математика) . Часть 1 . Ученики 6 класса переходят от простых математических упражнений к более сложным . Чтобы самостоятельно справиться с материалом, есть решебник по математике за 6 класс Виленкин , Жохов . .
ГДЗ > Математика > 6 класс > Учебник Виленкин > Номер 229 . Ответы к учебнику по математике за 6 класс Виленкин , Жохов , Чесноков, Шварцбурд — номер 229 .
Решение задачи(задания) номер 229 к учебнику по математике за 6 класс авторов Виленкин , Жохов . ГДЗ (готовые домашние задания ), решебник онлайн по математике за 6 класс авторов Виленкин , Жохов задание(номер ) 229 — вариант решения упражнения 229 .
ГДЗ по математике 6 класс , авторы: , Виленкин Н . Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И ., Мнемозина 2020-2021 год .
Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И ., Мнемозина 2020-2021 год .
Математика 6 класс . Учебник . Виленкин, Чесноков, Шварцбурд . 1, 2 . Мнемозина . Нумерация в данном пособии идет по задачам, что позволяет быстро отыскать необходимое . Всего их в ГДЗ по математике 6 класс Виленкин насчитывается более полутора тысяч упражнений .
Главная > 6 класс > Математика > Виленкин , Жохов, Чесноков, Шварцбурд . Почему ученикам выгодно активно работать с ГДЗ по математике 6 класс Виленкин ? Потому что в пособии детально расписаны все номера из учебника, даны ответы на теоретические вопросы . .
Математика 6 класс . Учебник . Виленкин , Жохов, Чесноков . Мнемозина . Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин , Жохов, Чесноков В сборнике имеются ответы по одной тысячи пятистам девяноста пяти номерам . .
ГДЗ к учебнику по математике за 6 класс Виленкин Н .Я . (2019 год) можно скачать здесь . ГДЗ к математическому тренажёру за 6 класс Жохов В .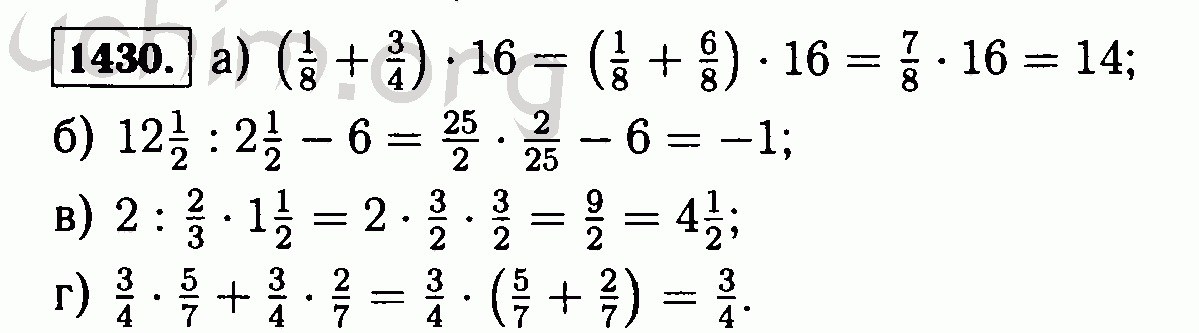 И . можно скачать здесь . ГДЗ к номерам задач .
И . можно скачать здесь . ГДЗ к номерам задач .
Разбор номеров по математике за 6 класс из учебника Виленкина Н .Я ., Жохова В .И ., Чеснокова А .С . Все выполненные номера проверены Ответы в решебнике по математике за 6 класс авторов: Виленкин Н .Я ., Жохов В .И ., Чесноков А .С . к упражнениям смотреть бесплатно .
ГДЗ решебник и ответы 6 класс , Математика , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбург С .И ., Учебник , год, 2019 год, 2019 год, 2019 год, 2020 год, 2020 год . Готовые домашние задания с подробными ответами .
ГДЗ по математике 6 класс Виленкин учебник . номер — 229 (234 ) . Авторы : Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд .
Решебник (ГДЗ ) по Математике за 6 (шестой ) класс авторы: Виленкин , Жохов , Чесноков, Шварцбурд издательство Мнемозина, год . ГДЗ по математике за 6 класс Виленкин , Жохов , Чесноков, Шварцбурд . Учебник Мнемозина (ответы к старому и новому изданию) .
6 класс : учебник для общеобразовательных учреждений / Н . Я . Виленкин , В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . Решебник по математике для 6 класса к Виленкину – это сборник Издатель: С .М . Никольский, М .К, Потапов, Н .Н . Решетников, А .В . Шевкин . -2019 .
Я . Виленкин , В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . Решебник по математике для 6 класса к Виленкину – это сборник Издатель: С .М . Никольский, М .К, Потапов, Н .Н . Решетников, А .В . Шевкин . -2019 .
Задача №234 , ГДЗ по математике за 6 класс к учебнику Виленкина с подробным решением . Виленкин , Жохов, Чесноков . 2 .8 Основное свойство дроби . Номер №234 .
В гдз по математике 6 класса Виленкина больше полторы тысячи заданий . Каждое из них шестиклассник должен решить, полностью в них разобраться и суметь понять похожие задания . .
ГДЗ Виленкин Жохов 6 класс В 2х частях (математика) . Часть 1 . Ученики 6 класса переходят от простых математических упражнений к более сложным . Чтобы самостоятельно справиться с материалом, есть решебник по математике за 6 класс Виленкин , Жохов . .
ГДЗ > Математика > 6 класс > Учебник Виленкин > Номер 229 . Ответы к учебнику по математике за 6 класс Виленкин , Жохов , Чесноков, Шварцбурд — номер 229 .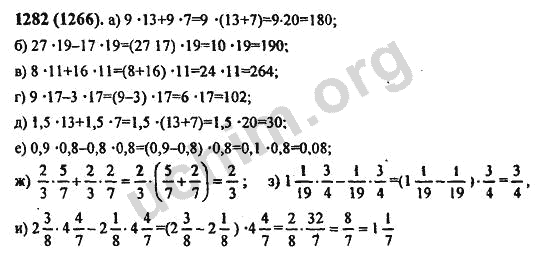
Решение задачи(задания) номер 229 к учебнику по математике за 6 класс авторов Виленкин , Жохов . ГДЗ (готовые домашние задания ), решебник онлайн по математике за 6 класс авторов Виленкин , Жохов задание(номер ) 229 — вариант решения упражнения 229 .
ГДЗ по математике 6 класс , авторы: , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И ., Мнемозина 2020-2021 год .
Математика 6 класс . Учебник . Виленкин, Чесноков, Шварцбурд . 1, 2 . Мнемозина . Нумерация в данном пособии идет по задачам, что позволяет быстро отыскать необходимое . Всего их в ГДЗ по математике 6 класс Виленкин насчитывается более полутора тысяч упражнений .
Главная > 6 класс > Математика > Виленкин , Жохов, Чесноков, Шварцбурд . Почему ученикам выгодно активно работать с ГДЗ по математике 6 класс Виленкин ? Потому что в пособии детально расписаны все номера из учебника, даны ответы на теоретические вопросы . .
Математика 6 класс . Учебник . Виленкин , Жохов, Чесноков . Мнемозина . Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин , Жохов, Чесноков В сборнике имеются ответы по одной тысячи пятистам девяноста пяти номерам . .
Мнемозина . Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин , Жохов, Чесноков В сборнике имеются ответы по одной тысячи пятистам девяноста пяти номерам . .
ГДЗ к учебнику по математике за 6 класс Виленкин Н .Я . (2019 год) можно скачать здесь . ГДЗ к математическому тренажёру за 6 класс Жохов В .И . можно скачать здесь . ГДЗ к номерам задач .
Разбор номеров по математике за 6 класс из учебника Виленкина Н .Я ., Жохова В .И ., Чеснокова А .С . Все выполненные номера проверены Ответы в решебнике по математике за 6 класс авторов: Виленкин Н .Я ., Жохов В .И ., Чесноков А .С . к упражнениям смотреть бесплатно .
ГДЗ решебник и ответы 6 класс , Математика , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбург С .И ., Учебник , год, 2019 год, 2019 год, 2019 год, 2020 год, 2020 год . Готовые домашние задания с подробными ответами .
ГДЗ номер 510 алгебра 9 класс Макарычев, Миндюк
ГДЗ §20 40 алгебра 8 класс Задачник Мордкович, Александрова
ГДЗ часть 1 258 математика 6 класс задачник Бунимович, Кузнецова
ГДЗ упражнение 898 алгебра 7 класс Макарычев, Миндюк
ГДЗ часть №1 233 математика 6 класс Петерсон, Дорофеев
ГДЗ страница 56 английский язык 6 класс Комарова, Ларионова
ГДЗ часть 2 / упражнение 268 русский язык 4 класс Желтовская, Калинина
ГДЗ упражнение 155 русский язык 5 класс Разумовская, Львова
ГДЗ номер 435 геометрия 8 класс Мерзляк, Полонский
ГДЗ страница 12 геометрия 7 класс рабочая тетрадь Глазков, Камаев
ГДЗ номер 116 математика 5 класс рабочая тетрадь Мерзляк, Полонский
ГДЗ глава 1 17 русский язык 6 класс Шмелев, Флоренская
ГДЗ §87 А1 физика 11 класс Мякишев, Буховцев
ГДЗ по английскому языку 3 класс Enjoy English Биболетова, Денисенко Решебник
ГДЗ глава 3 132 русский язык 8 класс Шмелев, Флоренская
ГДЗ часть 2 445 русский язык 6 класс Рыбченкова, Александрова
ГДЗ Учебник 2019 / часть 1 768 (765) математика 5 класс Виленкин, Жохов
ГДЗ страница 116 немецкий язык 7 класс рабочая тетрадь Wunderkinder Радченко, Глушак
ГДЗ урок 31 6 русский язык 1 класс Иванов, Евдокимова
ГДЗ вправа 236 алгебра 8 класс Кравчук, Пидручна
ГДЗ контрольная работа / К-2 / вариант 2 5 алгебра 8 класс дидактические материалы Звавич, Дьяконова
ГДЗ страница 39 английский язык 9 класс starlight Баранова, Дули
ГДЗ задача 93 геометрия 8 класс рабочая тетрадь Дудницын
ГДЗ упражнение 976 алгебра 9 класс Мерзляк, Полонский
ГДЗ упражнение 456 русский язык 6 класс Разумовская, Львова
ГДЗ задание 40 алгебра 7 класс рабочая тетрадь Потапов, Шевкин
ГДЗ С-5. вариант 2 алгебра 9 класс самостоятельные работы Александрова
вариант 2 алгебра 9 класс самостоятельные работы Александрова
ГДЗ вариант 1 157 геометрия 7 класс дидактические материалы Мерзляк, Полонский
ГДЗ номер 212 биология 8 класс рабочая тетрадь Сонин, Агафонова
ГДЗ часть №1 / номер 187 русский язык 2 класс Канакина, Горецкий
ГДЗ упражнение 611 алгебра 9 класс Мерзляк, Полонский
ГДЗ часть 1 5 история 5 класс рабочая тетрадь Годер
ГДЗ упражнение 280 русский язык 6 класс Разумовская, Львова
ГДЗ упражнение 521 русский язык 8 класс Бархударов, Крючков
ГДЗ урок 76 литература 5 класс рабочая тетрадь Соловьева
ГДЗ практическая работа 2 химия 10 класс Еремин, Кузьменко
ГДЗ упражнение 314 русский язык 3 класс Нечаева, Яковлева
ГДЗ unit 3 / homework 8 английский язык 7 класс Enjoy English Биболетова, Трубанева
ГДЗ часть 1. задание 197 математика 3 класс рабочая тетрадь Захарова, Юдина
ГДЗ учебник 2015. номер 754 (760) математика 6 класс Виленкин, Жохов
ГДЗ обучающие работы / О-13 7 алгебра 7 класс дидактические материалы Евстафьева,, Карп
ГДЗ часть 2 (страница) 96 литература 2 класс Кац
ГДЗ страница 92 обществознание 5 класс рабочая тетрадь Болотина, Мишина
ГДЗ самостоятельные работы / С-13. вариант А2 алгебра 10‐11 класс самостоятельные и контрольные работы Ершова, Голобородько
вариант А2 алгебра 10‐11 класс самостоятельные и контрольные работы Ершова, Голобородько
ГДЗ часть 1. страница 39 английский язык 3 класс Happy English Кауфман, Кауфман
ГДЗ часть 2. страница 13 математика 5 класс рабочая тетрадь Рудницкая
ГДЗ параграф 15 15.27 алгебра 8 класс задачник Мордкович, Александрова
ГДЗ вариант 3 19 алгебра 8 класс дидактические материалы Мерзляк, Полонский
ГДЗ страница 80 английский язык 4 класс Цуканова, Фатнева
ГДЗ страница 6 русский язык 1 класс рабочая тетрадь Соловейчик, Кузьменко
Решебник По Русскому Языку 2 Класс Евдокимова
ГДЗ По Биологии 6 Класс Учебник Ответы
Гдз По Биологии 6 Класс Учебник
ГДЗ Чтение 3 Класс Учебник 2 Часть
Решебник По Алгебре 9 Класс Пирютко
Средние Уолша-Марцинкевича и пространства Харди
Карой Надь; Георгий Тефнадзе
Открытая математика (2014)
- Том: 12, Выпуск: 8, стр.
 1214-1228
1214-1228 - ISSN: 2391-5455
Доступ к полной статье
topДоступ к полному тексту
Полный (PDF)
Аннотация
вершина Основная цель этой статьи — исследовать средние Уолша-Марцинкевича на пространстве Харди H p, когда 0 < p < 2/3. Мы определяем взвешенный максимальный оператор средних Уолша-Марцинкевича и устанавливаем некоторые его свойства. С его помощью мы даем необходимое и достаточное условие сходимости средних Уолша-Марцинкевича по модулю непрерывности на пространстве Харди H p и доказываем сильную теорему сходимости для средних Уолша-Марцинкевича.Как цитировать
топ- MLA
- БибТекс
- РИС
Карой Надь и Георгий Тефнадзе. «Средства Уолша-Марцинкевича и пространства Харди». Открытая математика 12. 8 (2014): 1214-1228.
8 (2014): 1214-1228.
@article{KárolyNagy2014,
abstract = {Основной целью этой статьи является исследование средних значений Уолша-Марцинкевича в пространстве Харди H p, когда 0 < p < 2/3. Мы определяем взвешенный максимальный оператор средних Уолша-Марцинкевича и устанавливаем некоторые его свойства. С его помощью мы даем необходимое и достаточное условие сходимости средних Уолша-Марцинкевича по модулю непрерывности на пространстве Харди H p и доказываем сильную теорему сходимости для средних Уолша-Марцинкевича.},
автор = {Карой Надь, Георгий Тефнадзе},
ключевые слова = {система Уолша; Марцинкевич означает; Максимальный оператор; Двумерная система; выносливое пространство; Сильная сходимость; модуль непрерывности; двумерная система Уолша; максимальный оператор; диадическое пространство Харди; сильная сходимость; модуль непрерывности},
language = {eng},
number = {8},
pages = {1214-1228},
title = {средства Уолша-Марцинкевича и пространства Харди},
url = {http://eudml .
 org/doc/269327},
org/doc/269327}, том = {12},
год = {2014},
}
TY — JOUR
AU — Карой Надь
AU — Джордж Тефнадзе
TI — средние Уолша-Марцинкевича и пространства Харди
JO 9034 Математика PY — 2014
VL — 12
IS — 8
SP — 1214
EP — 1228
AB — Основной целью данной работы является исследование средних Уолша-Марцинкевича на пространстве Харди H p, когда 0 < p < 2/ 3. Мы определяем взвешенный максимальный оператор средних Уолша-Марцинкевича и устанавливаем некоторые его свойства. С его помощью мы даем необходимое и достаточное условие сходимости средних Уолша-Марцинкевича по модулю непрерывности на пространстве Харди H p и доказываем сильную теорему сходимости для средних Уолша-Марцинкевича.
KW — Система Уолша; Марцинкевич означает; Максимальный оператор; Двумерная система; выносливое пространство; Сильная сходимость; модуль непрерывности; двумерная система Уолша; максимальный оператор; диадическое пространство Харди; сильная сходимость; модуль непрерывности
UR — http://eudml.
 org/doc/269327
org/doc/269327 ER —
Ссылки
top- [1] Блахота И., О неравенстве по норме относительно виленкиноподобных систем, Acta Math. Венгрия, 2000, 89(1–2), 15–27 http://dx.doi.org/10.1023/A:1026769207159 Zbl0973.42020
- [2] Благота И., Гат Г., Гогинава Ю., Максимальные операторы средних Фейера рядов Виленкина-Фурье, JIPAM. Дж. Неравный. Чистое приложение Матем., 2006, 7(4), #149 Збл1232.42024
- [3] Благота И., Гат Г., Гогинава Ю., Максимальные операторы средних Фейера двойных рядов Виленкина-Фурье, Сб. Матем., 2007, 107(2), 287–296 http://dx.doi.org/10.4064/cm107-2-8 Zbl1117.42006
- [4] Fine NJ, Суммируемость по Чезаро рядов Уолша-Фурье, Proc. Нац. акад. науч. США, 1955, 41(8), 588–591 http://dx.doi.org/10.1073/pnas.41.8.588 Zbl0065.05303
- [5] Fujii N.
 , Максимальное неравенство для H
1-функции на обобщенной группе Уолша-Пэли, Proc. амер. Мат. соц., 1979, 77(1), 111–116
, Максимальное неравенство для H
1-функции на обобщенной группе Уолша-Пэли, Proc. амер. Мат. соц., 1979, 77(1), 111–116 - [6] Гат Г., Исследования некоторых операторов по отношению к системе Виленкина, Acta Math. Венгрия, 1993, 61(1–2), 131–149 http://dx.doi.org/10.1007/BF01872107
- [7] Глухов В.А., Суммирование кратных рядов Фурье по мультипликативным системам, Матем. заметки, 1986, 39(5), 665–673 (на русском языке) Zbl0607.42020
- [8] Гогинава Ю., Максимальный оператор средних Марцинкевича-Фейера d-мерного ряда Уолша-Фурье, East J. Approx., 2006, 12(3), 295–302
- [9] Гогинава Ю., Максимальные операторы средних Фейера-Уолша, Acta Sci. Мат. (Сегед), 2008, 74(3–4), 615–624 Zbl1199.42127
- [10] Гогинава Ю., Неравенство слабого типа для максимального оператора средних Марцинкевича-Фейера двумерного ряда Уолша-Фурье, J.
 Approx. Теория, 2008, 154(2), 161–180 http://dx.doi.org/10.1016/j.jat.2008.03.012 Zbl1183.42028
Approx. Теория, 2008, 154(2), 161–180 http://dx.doi.org/10.1016/j.jat.2008.03.012 Zbl1183.42028 - [11] Гогинава Ю., Неравенство слабого типа для системы Уолша, Studia Math., 2008, 185(1), 35–48 http://dx.doi.org/10.4064/sm185-1-2 Zbl1213. 42098
- [12] Гогинава Ю., Мартингальное неравенство типа Харди для средних Марцинкевича-Фейера двумерных сопряженных рядов Уолша-Фурье, Acta Math. Грех. (англ. сер.), 2011, 27(10), 1949–1958 http://dx.doi.org/10.1007/s10114-011-9551-7
- [13] Nagy K., Некоторые свойства сходимости системы Уолша-Качмарца по отношению к средним Марцинкевича, Rend. Цирк. Мат. Палермо (2) Приложение, 2005, 76, 503–516 Zbl1214.42056
- [14] Надь К., О максимальном операторе средних Уолша-Марцинкевича, Опубл. Мат. Дебрецен., 2011, 78(3–4), 633–646 http://dx.doi.org/10.5486/PMD.2011.4829Збл1249.42013
- [15] Пал Дж.
 , Саймон П., Об обобщении понятия производной, Acta Math. акад. науч. Hungar., 1977, 29(1–2), 155–164 http://dx.doi.org/10.1007/BF01896477 Zbl0345.42011
, Саймон П., Об обобщении понятия производной, Acta Math. акад. науч. Hungar., 1977, 29(1–2), 155–164 http://dx.doi.org/10.1007/BF01896477 Zbl0345.42011 - [16] Шипп Ф., Некоторые перестановки рядов по системе Уолша, Матем. заметки, 1975, 18(2), 193–201 (на русском языке)
- [17] Шипп Ф., Уэйд В.Р., Саймон П., Серия Уолша, Адам Хилгер, Бристоль, 1990
- [18] Саймон П., Исследования по системе Виленкина, Ann. ун-т науч. Будапешт. Секта Этвёш. матем., 1985, 27, 87–101 Zbl0586.43001
- [19] Саймон П., Сильная сходимость некоторых средних относительно ряда Уолша-Фурье, Acta Math. Hungar., 1987, 49(3-4), 425–431 http://dx.doi.org/10.1007/BF01951006
- [20] Саймон П., Суммируемость по Чезаро относительно двухпараметрических систем Уолша, Monatsh. Матем., 2000, 131(4), 321–334 http://dx.doi.org/10.1007/s006050070004 Zbl0976.
 42014
42014 - [21] Саймон П., Замечания о сильной сходимости по системе Уолша, East J. Approx., 2000, 6, 261–276 Zbl1084.42513
- [22] Тефнадзе Г., Средние Фейера ряда Виленкина-Фурье, Stud. науч. Мат. Hungar., 2012, 49(1), 79–90 Zbl1265.42099
- [23] Тефнадзе Г., О максимальном операторе средних Виленкина-Фейера, Турецкая математика, 2013, 37(2), 308–318 Zbl1278.42037
- [24] Тефнадзе Г., О максимальных операторах средних Виленкина-Фейера на пространствах Харди, Матем. Неравный. заявл., 2013, 16(1), 301–312 Zbl1263.42008
- [26] Тефнадзе Г., Замечание о сходимости по норме средних Виленкина-Фейера, Грузин.
 матем. J. (в печати) Zbl1303.42012
матем. J. (в печати) Zbl1303.42012 - [27] Вайс Ф., Мартингальные пространства Харди и их приложения в анализе Фурье, Lecture Notes in Math., 1568, Springer, Berlin, 1994 Zbl0796.60049
- [28] Weisz F., Суммируемость по Чезаро одномерных и двумерных рядов Уолша-Фурье, Anal. Матем., 1996, 22(3), 229–242 http://dx.doi.org/10.1007/BF02205221 Zbl0866.42020
- [29] Вейс Ф., Пространства Харди и средние Чезаро двумерных рядов Фурье, В сб.: Теория приближений и функциональные ряды, Будапешт, 21–25 августа, 19.95, Бойяи Соц. Мат. Исследования, 5, Математическое общество Яноша Бойяи, Будапешт, 1996, 353–367
- [30] Вайс Ф., Сходимость двойных рядов Уолша-Фурье и пространства Харди, Approx. Теория прил. (н.с.), 2001, 17(2), 32–44
- [31] Вайс Ф., Суммируемость многомерных рядов Фурье и пространство Харди, Матем. Appl.
 , 541, Kluwer, Dordrecht, 2002 http://dx.doi.org/10.1007/978-94-017-3183-6
, 541, Kluwer, Dordrecht, 2002 http://dx.doi.org/10.1007/978-94-017-3183-6
Вы должны войти, чтобы оставлять комментарии.
ПО МАКСИМАЛЬНОЙ ФУНКЦИИ И V-СОПРЯЖЕНИЮ | Садикович
Главная > Vol 31, No 5 (2016) > Sadikovic
ON MAXIMAL FUNCTION AND V-CONJUGATION
Samra Sadikovic
DOI Number
10.22190/FUMI1605999S
First page
999
Последняя страница
1009
Abstract
В этой статье мы доказываем, что на 3-й серии поле h2 не может быть определено с помощью V-сопряжения. Другими словами, нормы kfkh2 и k ˜ fkL1 не эквивалентны в случае поля 3-й серии. Это дает новое доказательство результата Мемича [7], отвечающего на вопрос, поставленный П. Саймоном [13]. Кроме того, мы доказываем, что среднее значение функции f ∈ L1(G) на смежном классе IN−1(x) мажорируется либо MN−1, либо MN на каком-то сдвинутом элементе.
Саймоном [13]. Кроме того, мы доказываем, что среднее значение функции f ∈ L1(G) на смежном классе IN−1(x) мажорируется либо MN−1, либо MN на каком-то сдвинутом элементе.
Ключевые слова
Максимальная функция; V-сопряжение; Группы Виленкина
Ключевые слова
V-сопряжение, максимальная функция, группы Виленкина
Полный текст:
PDFЛитература
М. Авдиспахич, Н. Мемич и Ф. Вайс: Максимальные функции, пространства Харди и теоремы Фурье о множителях для неограниченных групп Виленкина. Дж. Матем. Анальный. заявл. 390 (2012), 68–73.
И. Благота, Г. Гат и Ю. Гогинава: Максимальные операторы на средних Фейера рядов Виленкина-Фурье. Дж. Неэкв. Чистый и Appl. Мат. 7(4), статья 149, (2006).
Н. Фуджи: Максимальное неравенство для функций h2 на обобщенной группе Уолша-Пэли. проц. амер. Мат. соц. 77 (1979), 111–116.
Г. Гат: Средние Чезаро интегрируемых функций по неограниченным системам Виленкина. Дж. Прибл. Теория 124 (2003), вып. 1, 25–43.
Дж. Прибл. Теория 124 (2003), вып. 1, 25–43.
Г. Гат: На п.в. сходимость рядов Фурье по неограниченным группам Виленкина. Акта Математика. акад. Паед. Nyıregyhásiensis 15 (1999), 27–34.
У. Гогинава: Максимальный оператор средних Марцинкевича-Фейера d-мерного ряда Уолша-Фурье. Ист Дж. Около 12 (3) (2006), 295–302.
Н. Мемич: Об ограниченности оператора V-сопряжения в пространствах Харди. NZJMath. Том 42 (2012), 121–129.
Й. Пал — П. Саймон: Об обобщении понятия производной. Акта Математика. акад. науч. Висела. 29(1-2) (1977), 155–164.
Дж. Дж. Прайс: Некоторые группы ортонормированных ступенчатых функций. Канада. Дж. Матем. 9 (1957), 413–425.
Ф. Шипп: Некоторые перестановки рядов в ряду Уолша. Мат. заметки 18 (1975), 193–201.
Ф. Шипп, В. Р. Уэйд, П. Саймон и Дж. Пал: Серия Уолша: Введение в диадический гармонический анализ. Адам Хилгер, Бристоль и Нью-Йорк, 19 лет90.
П. Саймон: Суммируемость по Чезаро относительно двухпараметрических систем Уолша.


 1214-1228
1214-1228 , Максимальное неравенство для H
1-функции на обобщенной группе Уолша-Пэли, Proc. амер. Мат. соц., 1979, 77(1), 111–116
, Максимальное неравенство для H
1-функции на обобщенной группе Уолша-Пэли, Proc. амер. Мат. соц., 1979, 77(1), 111–116 Approx. Теория, 2008, 154(2), 161–180 http://dx.doi.org/10.1016/j.jat.2008.03.012 Zbl1183.42028
Approx. Теория, 2008, 154(2), 161–180 http://dx.doi.org/10.1016/j.jat.2008.03.012 Zbl1183.42028 , Саймон П., Об обобщении понятия производной, Acta Math. акад. науч. Hungar., 1977, 29(1–2), 155–164 http://dx.doi.org/10.1007/BF01896477 Zbl0345.42011
, Саймон П., Об обобщении понятия производной, Acta Math. акад. науч. Hungar., 1977, 29(1–2), 155–164 http://dx.doi.org/10.1007/BF01896477 Zbl0345.42011 42014
42014 матем. J. (в печати) Zbl1303.42012
матем. J. (в печати) Zbl1303.42012 , 541, Kluwer, Dordrecht, 2002 http://dx.doi.org/10.1007/978-94-017-3183-6
, 541, Kluwer, Dordrecht, 2002 http://dx.doi.org/10.1007/978-94-017-3183-6