№ 120 Математика 6 класс Виленкин. Найдите значение выражения – Рамблер/класс
№ 120 Математика 6 класс Виленкин. Найдите значение выражения – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Помогите посчитать!
Найдите значение выражения: (15,964 : 5,2 — 1,2) • 0,1.
ответы
(15,964 : 5,2 — 1,2) • 0,1 = (3,07 – 1,2) • 0,1 = 1,87 • 0,1 = 0,187.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
3 класс
5 класс
Репетитор
похожие вопросы 5
Приветик! Кто решил? № 411 Математика 6 класс Виленкин.
Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)
ГДЗМатематика6 классВиленкин Н.Я.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N.
ЕГЭЭкзаменыМатематикаЯщенко И.В.
На каком расстоянии № 776 ГДЗ Математика 6 класс Дорофеев Г.В. Часть3.
Из города к озеру вышел турист со скоростью 5 км/ч, а через 15 мин вслед за
ним выехал велосипедист со скоростью 20 км/ч. Через (Подробнее…)
ГДЗМатематика6 классДорофеев Г. В.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Номер 120 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник)
Номер 120 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
| Табличка на дверь |
Нахождение целого по его части.
 Образцы решения типовых задач на интерес
Образцы решения типовых задач на интересПравило нахождения числа по его дроби :
Чтобы найти число по этому значению его дроби, нужно это значение разделить на дробь.
Рассмотрим, как найти число по его дроби, на конкретных примерах.
Примеры.
1) Найдите число, 3/4 которого равно 12.
Чтобы найти число по его дроби, разделите это число на эту дробь. К, нужно умножить заданное число на обратную дробь (то есть на перевернутую дробь). То есть надо числитель умножить на это число, а знаменатель оставить без изменений. 12 и 3 на 3. Поскольку знаменатель равен единице, ответ — целое число.
2) Найдите число, если 9/10 равно 3/5.
Чтобы найти число для данного значения его дроби, разделите это значение на эту дробь. Чтобы разделить дробь на дробь, умножьте первую дробь на величину, обратную второй (перевернутую). Чтобы умножить дробь на дробь, умножьте числитель на числитель, а знаменатель на знаменатель. Сократите 10 и 5 на 5, 3 и 9 — на 3.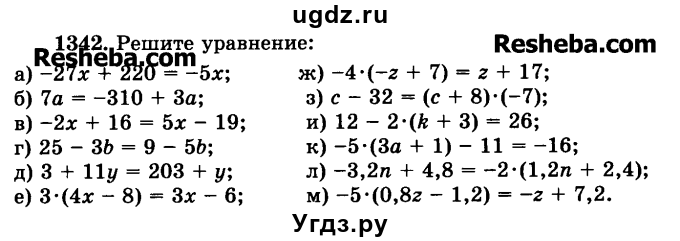 В итоге мы получили правильную несократимую дробь, а значит, это и есть окончательный результат.
В итоге мы получили правильную несократимую дробь, а значит, это и есть окончательный результат.
3) Найдите число, 9/7 которого равны
Чтобы найти число по значению его дроби, разделите это значение на эту дробь. Смешать число и умножить его на обратную вторую (перевернутую дробь). 99 и 9 уменьшите на 9, 7 и 14 — на 7. Так как мы получили неправильную дробь, то необходимо выделить из нее целую часть.
Тема урока: «Нахождение части целого и целого по его части».
Цель урока:
- Научитесь находить дробь числа и число по его дроби.
- Обобщить понятие обыкновенная дробь и действия с обыкновенными дробями.
Оборудование: Мультимедийный проектор, Power Presentation Point ( Приложение ).
ВО ВРЕМЯ ЗАНЯТИЙ
I. Организационный момент
Учащиеся рассаживаются группами (5-6 человек). Можно предложить провести диагностику своего настроения на этапах урока.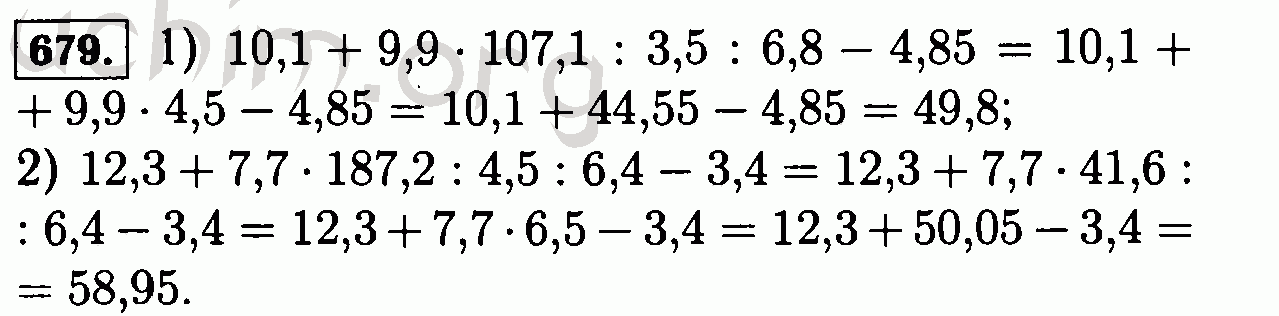 Каждому ученику выдается карточка, на которой он выделяет «характер» своего настроения.
Каждому ученику выдается карточка, на которой он выделяет «характер» своего настроения.
II. Обновление знаний
Мы уже знакомы с понятием обыкновенной дроби.
— Что показывает числитель дроби? (На сколько частей было разделено целое).
— Что показывает знаменатель дроби? (Сколько деталей было взято).
— Рассмотрите рисунок и ответьте на вопросы:
Учащимся предлагается воспроизвести его.
III. Вербальный счет. (Лучший счетчик)
Каждой команде предлагается задание на экране. Команды по очереди выполняют задание.
1-я команда
2-я команда
3-я команда
4-я команда
Суммирует, какая команда лучше всех противостоит.
IV. Диктант
Диктант проводится с последующей самопроверкой. Возможно выполнение под копирку, один экземпляр студенты сдают преподавателю для сверки.
1. Вставить вместо х пропущенное число:
2. Сократить дробь:
Сократить дробь:
3. Расставить дроби в порядке убывания:
4. Выполнить действия:
5. На островах живут тихоокеанские черепахи — гиганты. Они настолько велики, что дети могут кататься, сидя на их раковине. Следующее задание поможет нам узнать имя самой большой в мире черепахи.
После прохождения решения учащиеся проверяют ответы.
V. Новый материал
Учитель предлагает решить задачи (на обдумывание дается 5-7 минут)
1. На ветке сидело 12 птиц. Потом они улетели. Сколько птиц улетело?
2. В вашем классе математики за третью четверть 6 человек получили оценку «5». Это соответствует количеству всех учеников в классе. Сколько учеников в классе?
Затем решение проверяется и показывается на слайде.
1 способ: 12: 3 2 = 8 (птицы)
Способ 2: 12 = 8 (птиц)
2 задание. 6:=6=34 (чел.)
Воспитатель обращает внимание на то, что можно выделить два типа заданий:
1. Чтобы найти часть числа , выраженную дробью, нужно это число умножьте на заданную дробь.
2. Чтобы найти число по его частоте и, выраженное в виде дроби, нужно разделить на эту дробь на соответствующее ей число.
Студентам предлагается запомнить это правило прямо в классе и пересказать друг другу в парах.
Учитель акцентирует внимание на следующем: для тех, кто затрудняется определить тип задачи, советую обратить внимание на предлоги что , это … Эти предлоги встречаются в задачах на нахождение чисел по его дроби .
Ви. Закрепление нового материала
На слайде условия шести задач и учащимся предлагается рассортировать их в две колонки по типам.
1. Магазин принял на продажу 156 кг рыбы. 1/3 всей рыбы составлял карп. Сколько кг карпа получил магазин?
2. Проведено 18 опытов, это 2/9 всей серии опытов. Сколько экспериментов нужно провести?
3. Учитель проверил 20 тетрадей. Это составило 4/5 всех тетрадей. Сколько тетрадей должен проверить учитель?
4.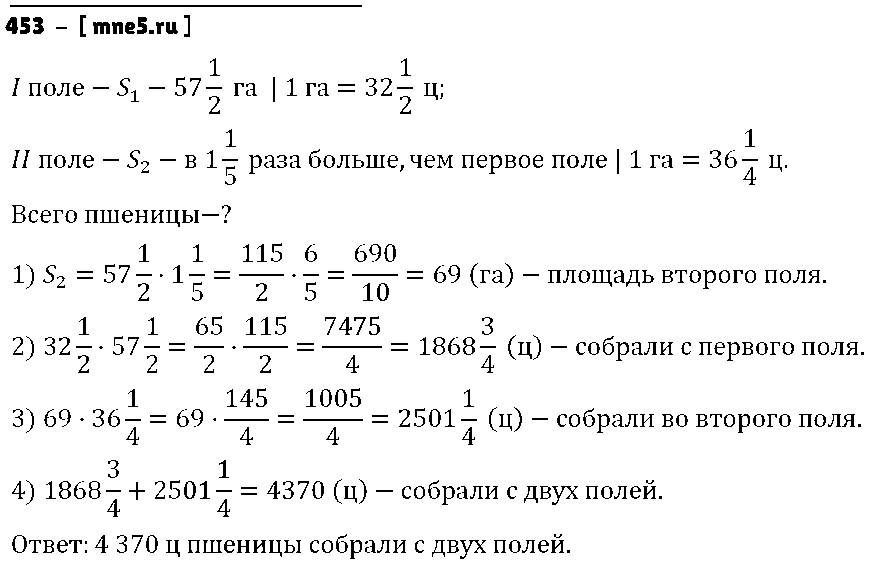 Из 72 пятиклассников 3/8 занимаются легкой атлетикой. Сколько школьников занимается этим видом спорта?
Из 72 пятиклассников 3/8 занимаются легкой атлетикой. Сколько школьников занимается этим видом спорта?
5. Для выставки отобрано 30 картин. Это составило 2/3 картин в музее. Сколько картин вошло в экспозицию?
6. 3/4 его длины вырезано из веревки длиной 18 м. Сколько метров веревки осталось?
VII. Конспект урока
Учитель возвращает учащихся к цели урока, предлагает выделить два типа задач на дроби и алгоритмы их решения. Бумаги с диагностикой настроения собираются.
VIII. Домашнее задание: стр. 9.6, № 1050, 1058, 1060.
§ 1 Правила нахождения части из целого и целого в его части
На этом занятии сформулируем правила нахождения части в целое и целое в его части, а также рассмотреть решение задач с использованием этих правил.
Рассмотрим две задачи:
Сколько километров прошли туристы в первый день, если весь туристический маршрут составляет 20 км?
Найдите длину всего пути туристов.
Давайте сравним эти задания — в обоих весь путь взят как единое целое.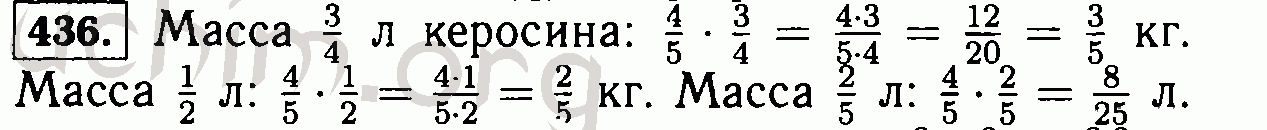 В первой задаче известно целое число — 20 км, а во второй неизвестное. В первом задании нужно найти часть целого, а во втором — целое по его части. Значение, известное в первой задаче, 20 км, неизвестно во второй задаче, и наоборот, известное во второй задаче — 8 км, в первой нужно найти. Такие задачи называются взаимно обратными, так как в них известные и искомые величины меняются местами.
В первой задаче известно целое число — 20 км, а во второй неизвестное. В первом задании нужно найти часть целого, а во втором — целое по его части. Значение, известное в первой задаче, 20 км, неизвестно во второй задаче, и наоборот, известное во второй задаче — 8 км, в первой нужно найти. Такие задачи называются взаимно обратными, так как в них известные и искомые величины меняются местами.
Рассмотрим первую задачу:
Знаменатель 5 показывает, на сколько частей разделили целое, т.е. если все 20 разделить на 5, то узнаем, сколько километров составляет одна часть, 20:5=4 км . Числитель 2 показывает, что туристы преодолели 2 части пути, поэтому 4 надо умножить на 2, получится 8 км. В первый день туристы прошли 8 км.
Получилось выражение 20: 5∙2 = 8.
Перейдем ко второй задаче.
Следовательно, одна часть будет равна частному 8 и 2, получится 4, знаменатель равен 5, значит всего 5 частей.
4 умножить на 5, получится 20. Ответ: 20 км длина всего пути.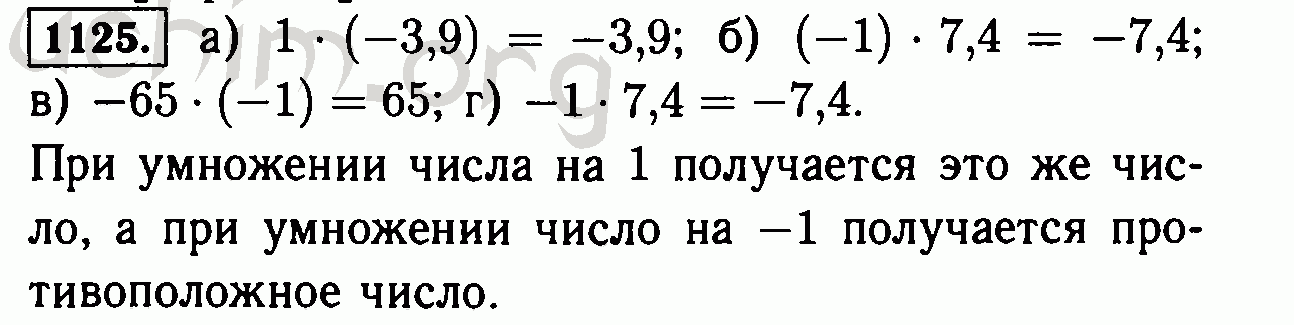
Запишем выражение: 8:2 ∙ 5 = 20
Используя смысл умножения и деления числа на дробь, правила нахождения части целого и целого в его части можно сформулировать следующим образом:
Чтобы найти часть целого, нужно число, соответствующее целому, умножить на дробь, соответствующую этой части;
чтобы найти целое число по его части, нужно число, соответствующее этой части, разделить на соответствующие части дроби.
Соответственно, решение задач теперь можно записать иначе:
для первой задачи 20 ∙ 2/5 = 8 (км),
для второй задачи 8: 2/5 = 20 (км).
Во избежание каких-либо затруднений запишем решение таких задач так:
Всего: весь путь, известно — 20 км.
Ответ: 8 км.
Целое: весь путь неизвестен.
Ответ: 20 км.
§ 2 Алгоритм решения задач на нахождение целого по его части и части целого
Составим алгоритм решения подобных задач.
Сначала разберем условие и вопрос задачи: выясним, что есть целое, известно оно или нет, затем узнаем, как представлена часть целого и что нужно найти.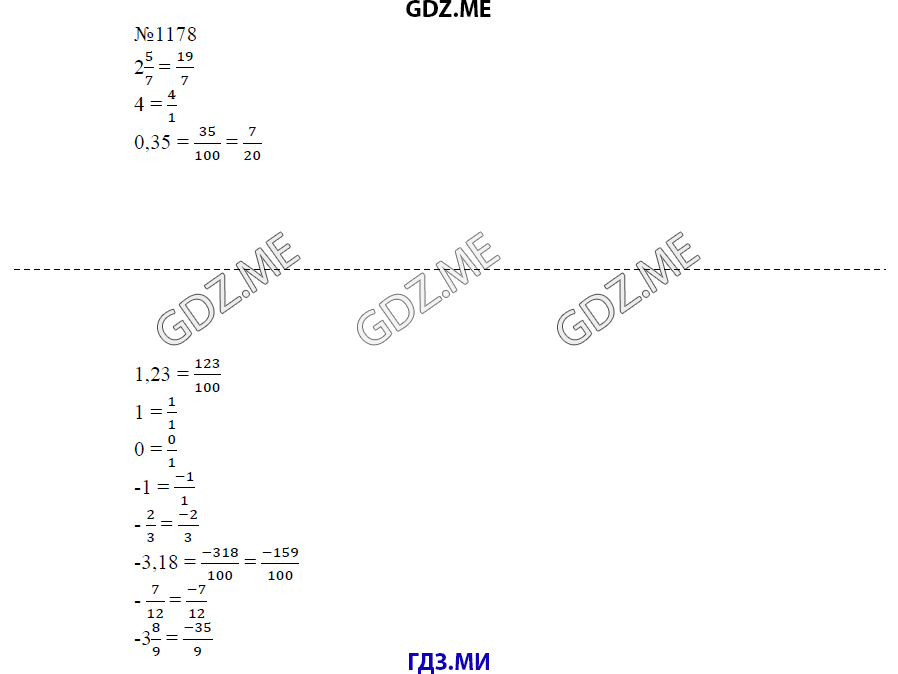
Если необходимо найти часть целого, то целое умножается на соответствующую этой части дробь, если необходимо найти целое на его часть, то число, соответствующее части, делится на дробь, соответствующая этой части. В результате получаем выражение. Далее найдем значение выражения и запишем ответ, предварительно прочитав еще раз вопрос задачи.
Итак, прежде чем решать подобные задачи, нужно ответить на следующие вопросы:
Какое значение принимается в целом?
Известно ли это значение?
Что нужно найти: часть целого или целое в его части?
Подведем итоги: на этом уроке вы познакомились с правилами нахождения части из целого и целого в его части, а также научились решать задачи по этим правилам.
Список использованной литературы:
- Математика. 6 класс: планы уроков по учебнику И.И. Зубарева, А.Г. Мордкович // Составитель Л.А. Топилина. Мнемозина, 2009 г..
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений.
 .. И.И. Зубарева, А.Г. Мордкович. — М.: Мнемосина, 2013.
.. И.И. Зубарева, А.Г. Мордкович. — М.: Мнемосина, 2013. - Математика. 6 класс: учебник для общеобразовательных учреждений / Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворов и др. / Под редакцией Г.В. Дорофеева, И.Ф. Шарыгин; Российская академия наук, Российская академия образования, Москва: Просвещение, 2010. .
- Математика. 6 класс: учеб. для общего образования. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. — М.: Мнемосина, 2013.
- Математика. 6 класс: учебник / Г.К. Муравин, О. В. Муравина. — М.: Дрофа, 2014.
ОСНОВНЫЕ ВИДЫ РЕШЕНИЯ ПРОЦЕНТНЫХ ЗАДАЧ
I. НАХОЖДЕНИЕ ЧАСТИ ЦЕЛОГО
Чтобы найти часть (%) целого, нужно число умножить на часть (проценты переводятся в десятичную).
ПРИМЕР: В классе 32 ученика. Во время контрольной работы отсутствовали 12,5 % учащихся. Найдите, сколько учеников пропало?
РЕШЕНИЕ 1: Всего в этой задаче всего учащихся (32).
12,5% = 0,125
32 0,125 = 4
РЕШЕНИЕ 2: Пусть x учеников отсутствует, что составляет 12,5%.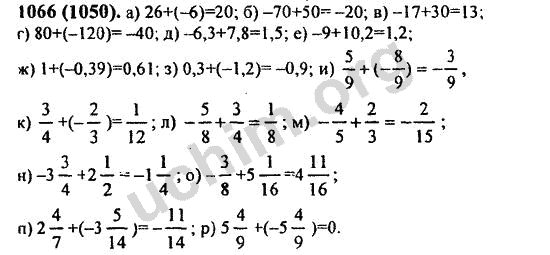 Если 32 ученика —
Если 32 ученика —
общее количество учеников (100%), то
32 ученика — 100%
x учеников — 12,5%
ОТВЕТ: В классе отсутствовали 4 ученика.
II. НАЙТИ ЦЕЛОЕ ПО ЧАСТИ
Чтобы найти целое по его части (%), число должно быть разделено на часть (проценты переведены в десятичную форму).
ПРИМЕР: Коля потратил в парке развлечений 120 крон, что составляет 75% всех его карманных денег. Сколько карманных денег было у Коли до прихода в парк развлечений?
РЕШЕНИЕ 1: В этой задаче нужно найти целое число, если заданная часть и значение известны
этой части.
75% = 0,75
120 : 0,75 = 160
РЕШЕНИЕ 2: Пусть у Коли было x корон, что есть целое, то есть 100%. Если он потратил 120 крон, что составляет 75%, то
120 крон — 75%
x крон — 100%
ОТВЕТ: У Коли было 160 крон.
III. ВЫРАЖЕНИЕ В ПРОЦЕНТАХ ОТ ДВУХ ЧИСЕЛ
ТИПИЧНЫЙ ВОПРОС:
НАСКОЛЬКО % ОТЛИЧАЕТСЯ ОДНО ЗНАЧЕНИЕ ОТ ДРУГОГО?
ПРИМЕР: Прямоугольник имеет ширину 20 м и длину 32 м. Сколько % составляет ширина длины? (Длина является основой для сравнения)
Сколько % составляет ширина длины? (Длина является основой для сравнения)
РЕШЕНИЕ 1:
РЕШЕНИЕ 2: В этой задаче длина прямоугольника 32м равна 100%, тогда ширина 20м равна x%. Составим и решим пропорцию:
20 метров — х%
32 метра — 100%
ОТВЕТ: Ширина составляет 62,5% от длины.
Внимание! Обратите внимание, как меняется решение по мере изменения вопроса.
ПРИМЕР: Прямоугольник имеет ширину 20 м и длину 32 м. Каков % длины от ширины? (Ширина является основой для сравнения)
РЕШЕНИЕ 1:
РЕШЕНИЕ 2: В этой задаче ширина прямоугольника 20м равна 100%, тогда длина 32м равна x%. Составим и решим пропорцию:
20 метров — 100%
32 метра — х%
ОТВЕТ: Длина составляет 160% от ширины.
IV. ВЫРАЖЕНИЕ В ПРОЦЕНТАХ ИЗМЕНЕНИЯ ЗНАЧЕНИЯ
ТИПИЧНЫЙ ВОПРОС:
НАСКОЛЬКО% ИЗМЕНИЛОСЬ (УВЕЛИЧИЛОСЬ, УМЕНЬШИЛСЯ) ИСХОДНОЕ ЗНАЧЕНИЕ?
Чтобы найти изменение значения в %, нужно:
1) найти насколько изменилось значение (без %)
2) разделить полученное значение из п. 1) на значение, которое является базой для сравнения
1) на значение, которое является базой для сравнения
3) преобразовать результат в % (умножив на 100%)
ПРИМЕР: Цена платья упала с 1250 крон до 1000 крон. Узнай, насколько подешевело платье?
РЕШЕНИЕ 1:
2) База для сравнения здесь 1250 CZK (т.е. то, что было изначально)
3)
ОТВЕТ: Цена платья уменьшилась на 20%.
Внимание! Обратите внимание, как меняется решение по мере изменения вопроса.
ПРИМЕР: Цена платья увеличилась с 1000 крон до 1250 крон. Найдите процент увеличения цены платья?
РЕШЕНИЕ 1:
1) 1250 -1000 = 250 (кр) насколько изменилась цена
2) База для сравнения здесь 1000 крон (т.е. то, что было изначально)
3)
Решение задачи в одном шаг:
РЕШЕНИЕ 2:
1250 -1000 = 250 (cr) насколько изменилась цена
В этой задаче начальная цена 1000 крон равна 100%, тогда изменение цены 250 крон равно x%. Составим и решим пропорцию:
1000 крон — 100%
250 крон — x%
x =
ОТВЕТ: Цена платья увеличилась на 25%.
V. ПОСЛЕДУЮЩЕЕ ИЗМЕНЕНИЕ ЗНАЧЕНИЯ (НОМЕРА)
ПРИМЕР: Число было уменьшено на 15%, а затем увеличено на 20%. Найдите процент изменения числа?
Самая распространенная ошибка: число увеличилось на 5%.
РЕШЕНИЕ 1:
1) Хотя исходное число не указано, для простоты решение можно принять равным 100 (т. е. одно целое число или 1)
2) Если число уменьшилось на 15%, то результирующее число будет 85%, или из 100 было бы 85.
3) Теперь полученный результат нужно увеличить на 20%, т.е.
85 – 100%
а новое число х равно 120% (поскольку оно увеличилось на 20%)
х =
4) Таким образом, в результате изменений число 100 (исходное) изменилось и стало 102, значит исходное число увеличилось на 2%
РЕШЕНИЕ 2:
1) Пусть исходное число Х
2) Если число уменьшилось на 15%, то полученное число будет 85% от Х, т.е. 0,85Х.
3) Теперь полученное число нужно увеличить на 20%, т.е.
0,85Х — 100%
и новое число? — 120% (увеличение на 20%)
? =
4) Таким образом, в результате изменений число Х (исходное) является базой для сравнения, а число 1,02Х (получено), (см.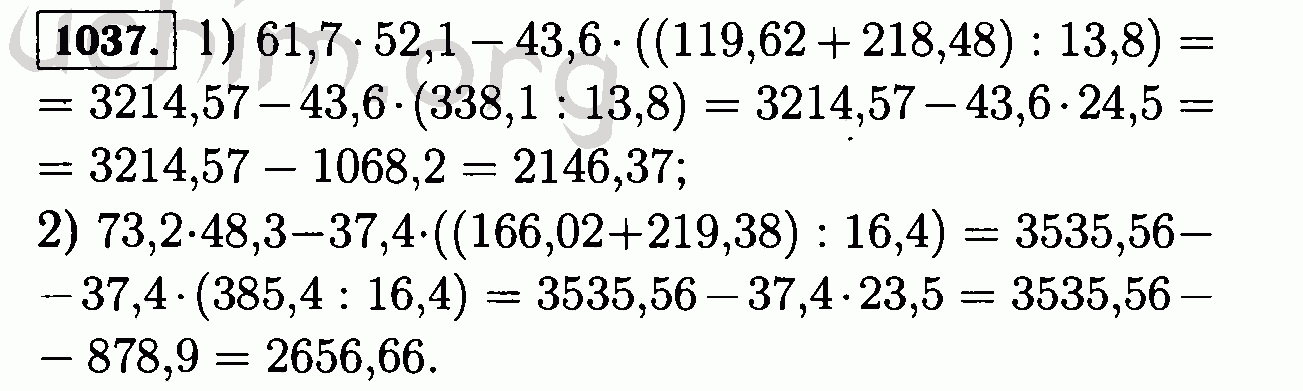 IV тип решения задачи), тогда
IV тип решения задачи), тогда
ОТВЕТ: Количество увеличилось на 2%.
Тема урока: Нахождение целого по его части.
Задача : развивать навык устного счета, развивать логическое мышление,
развивать умение работать самостоятельно и в группе,
воспитывать интерес к математике, воспитывать чувство дружбы и
взаимопонимания, воспитывать любовь к родному краю.
Во время занятий.
1. Организационный момент. (Слайд №1, 2)
Раздается долгожданный звонок
Урок начинается.
2. Устный счет.
Давайте подумаем!
а) Люда и Надя купили в буфете булочку, а Лена забыла взять с собой деньги. Тогда Люда и Надя дали Лене по 1/2 буханки. У кого больше роллов? (Лене достался целый батон, а Люде и Наде по половинке) (Слайд №3)
б) У ежика 3 целых яблока, 10 половинок, 8 четвертинок. Сколько яблок у ежика? (У ежика 10 яблок) (Слайд №4)
в) Улитка движется по вертикальному столбу высотой 6 м. Днем она поднимается на 4 м, а ночью опускается на 3 м. За сколько дней улитка доберется до вершины? (3 дня) (Слайд №5)
Днем она поднимается на 4 м, а ночью опускается на 3 м. За сколько дней улитка доберется до вершины? (3 дня) (Слайд №5)
г) Сколько сантиметров:
1/4 м, 3/5 м, 6/10м. (25 см, 60 см, 60 см)
Сколько метров:
1/5 км, 4/5 км, 7/10 км. (200м, 800м, 700м) (Горка №6)
e) Какая часть сегмента AB является сегментом SD. Найдите длину отрезка АВ, если отрезок CD равен 5см (А
(Слайд №7)
3.Работа с новой темой.
а) 1/8 отрезка АВ — 8 мм. Нарисуйте отрезок АВ.
8 * 8 = 64 мм = 6 см 4 мм (слайд номер 8)
д) Торт стоит 160 руб. Его разрезали на 4 части. Сколько будет стоить 1/4 часть. Ты и двое твоих друзей пришли в кафе. Сколько денег вы заплатите, если каждый съест один кусок торта?
Решение (160 : 4 = 40 (р.) Стоимость 1 шт, 40 * 3 = 120 (р.) Необходимо оплатить (Слайд № 9, 10)
Физминутка (Слайд №11)
в) М. Д. 1/2 часа, 1/3 часа, 1/4 часа, 1/10 часа. (30мин, 20мин, 15мин, 6мин) (Слайд №12)
Д. 1/2 часа, 1/3 часа, 1/4 часа, 1/10 часа. (30мин, 20мин, 15мин, 6мин) (Слайд №12)
г) Решение задачи
Длина реки Дон в Воронежской области 530 км. Это 1/3 всей длины реки Дон. Найдите длину реки Дон.
Решение: (530 * 3 = 1590 (км) длины реки Дон) (Слайд №13, 14)
Береза живет 240 лет. Это составляет 1/5 жизни голубой ели. Сколько лет живет ель голубая.
240 * 5 = 1200 (л) ф — ель голубая живет (Слайд № 15, 16, 17 )
Физминутка (Слайд №18)
4. Закрепление изученного.
Задача № 227. (Слайд № 19)
Купил 5 мотков электропровода по 56 метров. Израсходовано 2/7 всей проволоки. Сколько метров провода осталось?
Решение: (56*5=280м — всего проводов, 280:7*2=80м — израсходовано, 280-80=200(м) — проводов осталось)
5) Обзор прошлого
а ) Задача № 231. (самостоятельная работа) (Слайд № 20)
Лимоны раскладывали в корзины по 100 шт. Сколько лимонов было, если было заполнено 15 корзин и осталось еще 30 лимонов?
Сколько лимонов было, если было заполнено 15 корзин и осталось еще 30 лимонов?
Решение: (100*15+30=1530(л) — было)
б) Деление с остатком. №229 (чек) (Слайд №21)
76: 8 = 9 (остальные 4) 8 * 9 + 4 = 76,
54: 11 = 4 (остальные 10) 4 * 11 + 10 = 54
612: 7 = 87 (остальные 3) 87 * 7 + 3 = 612
793: 6 = 132 (остальные 1) 132 * 6 + 1 = 793
939: 4 = 234 (остальные 3) 234 * 4 + 3 = 939
в) Задача № 228. (Слайд №22)
За 3 часа работы бульдозер выровнял 234 квадратных метра дороги. сколько квадратных метров дороги выровняет бульдозер за 10 часов, если он будет работать с такой же производительностью?
Решение: (234:3=78- за 1 час, 78*10=780- за 10 часов)
6. Групповая работа по рангам
Решение задачи (по карточкам)
6 конфет составляют 1/7 всех конфет. Сколько конфет?
8 конфет составляют 1/3 всех конфет. Сколько конфет?
3 конфеты составляют 1/8 всех конфет.


 Расширение скобки
Расширение скобки .. » [Википедия, «Апории Зенона»]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
.. » [Википедия, «Апории Зенона»]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман. Если применить к этой ситуации понятие «бесконечность», то правильно будет сказать «Ахиллес бесконечно быстро догонит черепаху».
Если применить к этой ситуации понятие «бесконечность», то правильно будет сказать «Ахиллес бесконечно быстро догонит черепаху».

 ..
..
 Что мы наделали? Мы преобразовали число в числовой графический символ. Это не математическая операция.
Что мы наделали? Мы преобразовали число в числовой графический символ. Это не математическая операция. Посмотрим на результат.
Посмотрим на результат.
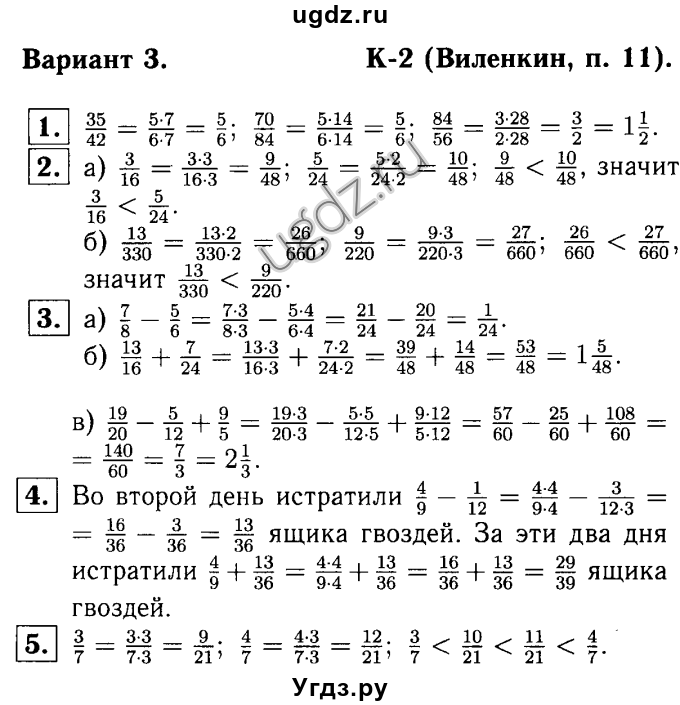 И математики учат нас этому все время. Вот пример.
И математики учат нас этому все время. Вот пример.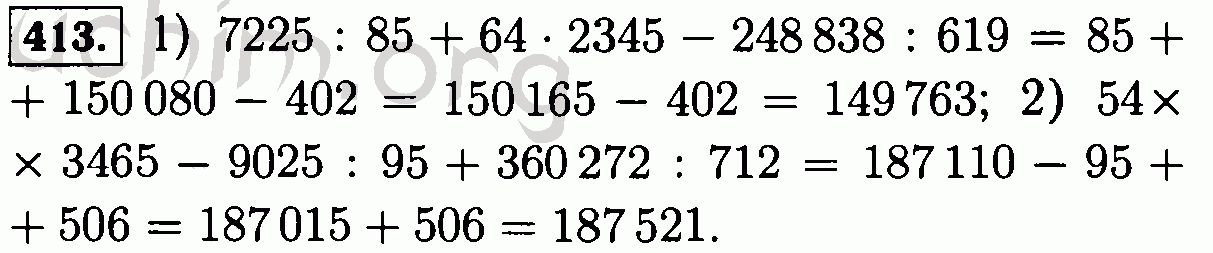
 Раскрыть скобки означает избавиться от лишних символов. Например: (-15)+3=-15+3=-12, 18+(-16)=18-16=2. Вы помните распределительное свойство умножения по отношению к сложению? Ведь в том примере мы тоже избавились от скобок для упрощения вычислений. Названное свойство умножения можно применить и к четырем, трем, пяти и более терминам. Например: 15*(3+8+9+6)=15*3+15*8+15*9+15*6=390. Вы замечали, что при раскрытии скобок числа в них не меняют знак, если число перед скобками положительное? Ведь пятнадцать — положительное число. А если решить этот пример: -15*(3+8+9+6)=-15*3+(-15)*8+(-15)*9+(-15)*6=-45+( — 120)+(-135)+(-90)=-45-120-135-90=-390. Перед скобками у нас стояло отрицательное число минус пятнадцать, когда мы раскрывали скобки все числа начинали менять свой знак на другой — противоположный — с плюса на минус.
Раскрыть скобки означает избавиться от лишних символов. Например: (-15)+3=-15+3=-12, 18+(-16)=18-16=2. Вы помните распределительное свойство умножения по отношению к сложению? Ведь в том примере мы тоже избавились от скобок для упрощения вычислений. Названное свойство умножения можно применить и к четырем, трем, пяти и более терминам. Например: 15*(3+8+9+6)=15*3+15*8+15*9+15*6=390. Вы замечали, что при раскрытии скобок числа в них не меняют знак, если число перед скобками положительное? Ведь пятнадцать — положительное число. А если решить этот пример: -15*(3+8+9+6)=-15*3+(-15)*8+(-15)*9+(-15)*6=-45+( — 120)+(-135)+(-90)=-45-120-135-90=-390. Перед скобками у нас стояло отрицательное число минус пятнадцать, когда мы раскрывали скобки все числа начинали менять свой знак на другой — противоположный — с плюса на минус. 
 к. если перед скобками стоит знак сложения, то при раскрытии скобок знаки внутри них не меняются. Пример:
к. если перед скобками стоит знак сложения, то при раскрытии скобок знаки внутри них не меняются. Пример: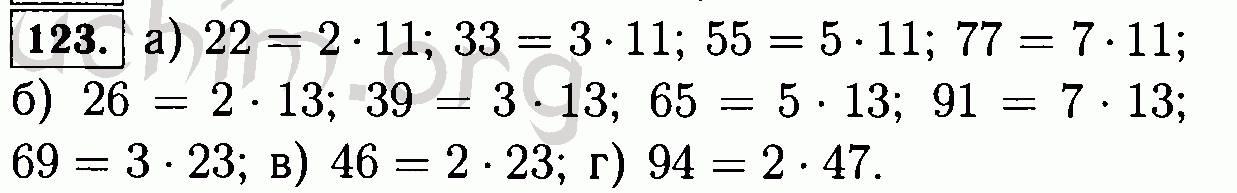 Пример: 92) * 12 = 1728.
Пример: 92) * 12 = 1728.
 Раскрыв скобки, мы изменим порядок действий и значительно упростим расчеты.
Раскрыв скобки, мы изменим порядок действий и значительно упростим расчеты.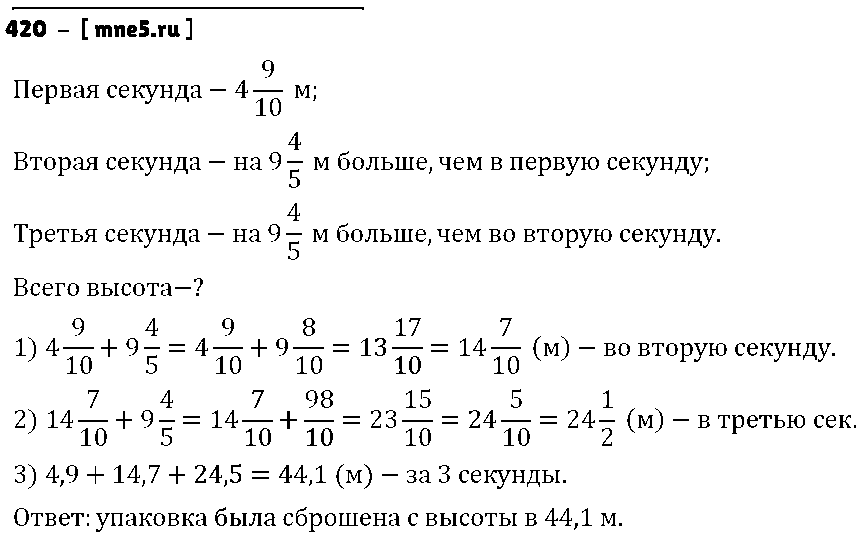 Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: 6. — Математика. Мнемозина, 2012.
Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: 6. — Математика. Мнемозина, 2012. .. И.И. Зубарева, А.Г. Мордкович. — М.: Мнемосина, 2013.
.. И.И. Зубарева, А.Г. Мордкович. — М.: Мнемосина, 2013.