Бунимович Математика Учебник (Сферы) | Частная школа. 6 класс
Математика. Арифметика. Геометрия. 6 класс : учеб, для общеобразоват. организаций с прил. на электрон, носителе / [Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева и др.]. — М. : Просвещение (Сферы). В двух частях (учебник + задачник).
Данный учебник продолжает линию учебно-методических комплектов «Сферы» по математике. Издание подготовлено в соответствии с новым образовательным стандартом и освещает вопросы курса математики 6 класса. Содержательно материал учебника направлен на продолжение формирования центральных математических понятий (число, величина, геометрическая фигура), обеспечивающих преемственность и перспективность математического образования школьников.
При его создании использованы концептуальные идеи учебника «Математика, 6» под редакцией Г.В. Дорофеева и И.Ф. Шарыгина. Главными особенностями данного учебника являются: фиксированный в тематических разворотах формат, лаконичность и жёсткая структурированность текста, разнообразный иллюстративный ряд.
Использование электронного приложения к учебнику позволит значительно расширить информацию (текстовую и визуальную) и научиться применять её при решении разнообразных математических задач.
Бунимович Математика Учебник. ОГЛАВЛЕНИЕ:
ВВЕДЕНИЕ 5
Глава 1. ДРОБИ И ПРОЦЕНТЫ
1. Что мы знаем о дробях 8
2. Вычисления с дробями 12
3. Основные задачи на дроби 16
4. Что такое процент 20
5. Столбчатые и круговые диаграммы 24
Подведём итоги 28
Глава 2. ПРЯМЫЕ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
6. Пересекающиеся прямые 30
7. Параллельные прямые 34
8. Расстояние 38
Подведём итоги 42
Глава 3. ДЕСЯТИЧНЫЕ ДРОБИ
9. Какие дроби называют десятичными 44
10. Перевод обыкновенной дроби в десятичную 50
11. Сравнение десятичных дробей 54
Подведём итоги 58
Глава 4. ДЕЙСТВИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ
12. Сложение и вычитание десятичных дробей 60
13. Умножение и деление десятичной дроби на 10, 100, 1000 , 64
14.
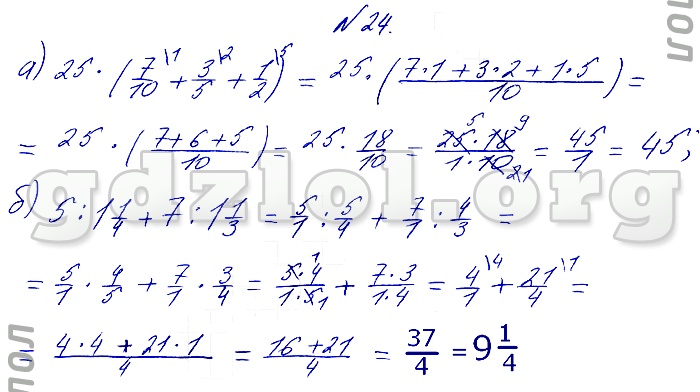Умножение десятичных дробей 68
15. Деление десятичных дробей 72
16. Округление десятичных дробей 80
Подведём итоги 84
Глава 5. ОКРУЖНОСТЬ
17. Прямая и окружность 86
18. Две окружности на плоскости 90
19. Построение треугольника 94
20. Круглые тела 98
Подведём итоги 102
Глава 6. ОТНОШЕНИЯ И ПРОЦЕНТЫ
21. Что такое отношение 104
22. Отношение величин. Масштаб 108
23. Проценты и десятичные дроби 112
24. «Главная» задача на проценты 116
25. Выражение отношения в процентах 120
Подведём итоги 124
Глава 7. ВЫРАЖЕНИЯ, ФОРМУЛЫ, УРАВНЕНИЯ
26. О математическом языке 126
27. Буквенные выражения и числовые подстановки 130
28. Составление формул и вычисление по формулам 134
29. Формулы длины окружности, площади круга и объёма шара 138
30. Что такое уравнение 142
Подведём итоги 146
Глава 8. СИММЕТРИЯ
31. Осевая симметрия 148
32.
Ось симметрии фигуры 152
33. Центральная симметрия 156
Подведём итоги 160
Глава 9. ЦЕЛЫЕ ЧИСЛА
34. Какие числа называют целыми 162
35. Сравнение целых чисел 166
36. Сложение целых чисел 170
37. Вычитание целых чисел 174
38. Умножение и деление целых чисел 178
Подведём итоги 182
Глава 10. РАЦИОНАЛЬНЫЕ ЧИСЛА
39. Какие числа называют рациональными 184
40. Сравнение рациональных чисел. Модуль числа 188
41. Сложение и вычитание рациональных чисел 192
42. Умножение и деление рациональных чисел 196
43. Координаты 200
Подведём итоги 204
Глава 11. МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
44. Параллелограмм 206
45. Правильные многоугольники 210
46. Площади 214
47. Призма 218
Подведём итоги 222
Глава 12. МНОЖЕСТВА. КОМБИНАТОРИКА
48. Понятие множества 224
49. Операции над множествами 228
50. Решение комбинаторных задач 232
Подведём итоги 236
ОТВЕТЫ 237
Фрагменты учебника для ознакомления
По библейскому преданию, Вавилонскую башню людям так и не удалось достроить, потому что они говорили на разных языках и не понимали друг друга. И сегодня в мире тысячи разных языков, и люди часто не могут понять друг друга, найти общий язык. Но есть один особый язык, на котором должны уметь говорить все люди, в любой стране, который учат во всех школах мира, — это язык математики.
Чем бы вы ни решили заниматься в жизни, какую бы профессию ни выбрали, вам не обойтись без математики, её языка, правил и методов. Но ещё важнее то, что математика учит умению рассуждать, анализировать, доказывать, отличать истинное от ложного, искать пути решения и делать выводы, развивает ум, логику, мышление. Не случайно великий художник, учёный, изобретатель Леонардо да Винчи утверждал, что «никакой достоверности нет в том, что не имеет связи с математикой».
Математику, математический язык, строгий и красивый, мы и продолжим изучать в 6 классе. Вы узнаете, из чего состоит алфавит математического языка, как строятся в нём слова и предложения, как осуществляется перевод с русского языка на математический и обратно. Вы узнаете много нового, интересного и полезного и о том, с чем вы уже знакомились на уроках математики, — о целых и дробных числах, геометрических фигурах и их свойствах, и о многом другом.
Надёжным помощником в изучении математики в 6 классе станет для вас учебный комплекс «Сферы». Вы знакомы с этим комплексом по 5 классу и уже хорошо знаете, как он устроен, как выделяется в учебнике самое важное, то, что необходимо запомнить, как обозначены задачки попроще и посложнее, где найти образцы решений и как подводить итоги изучения каждой главы, как узнать, хорошо ли вы всё усвоили, поняли, осмыслили и запомнили. Поупражняться в решении задач вам помогут «Задачник» и «Тетрадь-тренажёр», а проверить ваши знания поможет «Тетрадь-экзаменатор». Электронное приложение к учебнику позволит использовать все возможности компьютера для того, чтобы освоение математики стало ещё ярче, интересней, разнообразней и увлекательней.
Просмотров: 6 414
Страница 58. Подведем итоги. ГДЗ к учебнику «Математика» 6 класс Бунимович, Кузнецова, Минаева
ГДЗ 1 класс
ГДЗ 10 класс
- Категория: ГДЗ Математика учебник 6 класс Бунимович, Кузнецова, Минаева ✔
Задание 1. Запишите какую−нибудь десятичную дробь с четырьмя знаками после запятой и прочитайте ее.
Ответ
8,26523 − восемь целых двадцать шесть тысяч пятьсот двадцать три стотысячных.
Задание 2. Запишите в виде суммы разрядных слагаемых:
а) натуральное число 3205;
б) десятичную дробь 0,3205.
Ответ
а) 3205 = 3000 + 200 + 5
б) 0,3205 = 0 + 0,3 + 0,002 + 0,0005
а) $\frac{9}{10}$;
б) $1\frac{3}{100}$;
в) $\frac{549}{100}$.
Ответ
а) $\frac{9}{10} = 0,9$
б) $1\frac{3}{100} = 1,03$
в) $\frac{549}{100} = 5\frac{49}{100} = 5,49$
Задание 4. 1) Чему равен знаменатель обыкновенной дроби, если в ее десятичной записи содержится 2 знака после запятой? 4 знака после запятой?
2) Представьте в виде обыкновенной дроби число:
а) 0,7;
б) 0,091;
в) 1,203.
Ответ
1) Если в десятичной записи обыкновенной дроби содержится 2 знака после запятой, то знаменатель этой дроби равен 100.
Если в десятичной записи обыкновенной дроби содержится 4 знака после запятой, то знаменатель этой дроби равен 10000.2)
а) а) $0,7 = \frac{7}{10}$;
б) $0,091 = \frac{91}{1000}$;
в) $1,203 = 1\frac{203}{1000}$.
Задание 5. Запишите числа, соответствующие точками, отмеченным на координатной прямой.
Ответ
0,02; 0,05; 0,11; 0,18; 0,23; 0,29.
Задание 6. Начертите координатную прямую, приняв за единичный отрезок 10 клеток. Отметьте на прямой число:
а) 0,1;
б) 0,5;
в) 1,8;
г) 2,2.
Решение
Задание 7. 1) Ответьте на вопросы и проиллюстрируйте свои ответы примерами.
а) Какую обыкновенную дробь можно записать в виде десятичной?
б) В каком случае несократимую обыкновенную дробь нельзя представить в виде десятичной. 3} = \frac{875}{1000} = 0,875$;
$\frac{1}{5} = \frac{1 * 2}{5 * 2} = \frac{2}{10} = 0,2$.
б) Если знаменатель обыкновенной дроби имеет хотя бы один простой делитель, отличный от 2 и 5, и эта дробь несократима, то ее нельзя представить в виде десятичной.
Примеры:
$\frac{1}{9} = \frac{1}{3 * 3}$;
2) а) $\frac{1}{2} = \frac{5}{10} = 0,5$;
б) $\frac{3}{4} = \frac{75}{100} = 0,75$;
в) $\frac{1}{8} = \frac{125}{1000} = 0,125$;
г) $\frac{2}{5} = \frac{4}{10} = 0,4$;
д) $\frac{7}{20} = \frac{35}{100} = 0,35$;
е) $\frac{4}{25} = \frac{16}{100} = 0,16$.
Задание 8. Как записать десятичную дробь, равную данной десятичной дроби? Запишите три десятичной дроби, равные числу 5,070.
Ответ 7 гуру
Чтобы записать десятичную дробь, равную десятичной дроби, надо приписать к данной дроби любое количество нулей справа.
5,070 = 5,07 = 5,0700 = 5,07000000.
Задание 9. Сравните числа:
а) 1,001 и 0,9999;
б) 8,455 и 8,54;
в) 0,305 и 0,3050.
Ответ
Задание 10. Между какими последовательными натуральными числами заключено число:а) 1,001 > 0,9999
б) 8,455 < 8,54
в) 0,305 = 0,3050
а) 9,8; б) 15,03?
Отвечая на вопрос, запишите соответствующее двойное неравенство и покажите примерное положение числа на координатной прямой.
Решение
а) Число 9,8 заключено между последовательными натуральными числами 9 и 10.
9 < 9,8 < 10б) Число 15,03 заключено между последовательными натуральными числами 15 и 16.
15 < 15,03 < 16
Задание 11. а) Выразите в метрах: 3 см; 70 см; 3 м 48 см.
б) Выразите в тоннах: 20 кг; 200 кг; 1 т 500 кг.
в) Выразите в рублях: 2 к.; 90 к.; 10 р. 25 к.
Решение
а) 3 см = $\frac{3}{100} = 0,03$ м;
70 см = $\frac{70}{100} = 0,7$ м;
3 м 48 см = $3\frac{48}{100} = 3,48$ м.