ГДЗ дидактические материалы по математике 6 класс Мерзляк, Полонский, Рабинович Вентана-Граф
Чтобы в сжатые сроки увидеть высокие результаты применения механизма самоподготовки с применением самого практикума и гдз по математике 6 класс дидактические материалы Мерзляк, необходимо выделять достаточное количество времени на такую работу. Многие эксперты сходятся во мнении, что минимально следует заниматься около часа в день, при этом, не делая длительных перерывов в такой работе. Например, пропуски более чем на две недели в ежедневных занятиях приводят к забыванию части материала. А последующее «наверстывание» программы большими блоками – к ухудшению качества его усвоения.
Эффективное применение гдз в учебном процессе
В числе тех, кто регулярно и постоянно применяет ответы по математике за 6 класс дидактические материалы (коллектив авторов: Полонский, Рабинович и Якир) – такие категории заинтересованных пользователей:
- активно готовящиеся к участию, победе в математических конкурсах дети, в том числе те, кто учится по другой программе, плану, и кто хочет понять курс как можно более глубоко;
- осуществляющие подготовку к экзаменам выпускники.
 С помощью этих материалов они могут самостоятельно повторить курс классической математики за шестой класс, поскольку именно в этом классе завершается изучение этой дисциплины;
С помощью этих материалов они могут самостоятельно повторить курс классической математики за шестой класс, поскольку именно в этом классе завершается изучение этой дисциплины; - репетиторы, сопоставляющие собственные методики обучения с теми, что предписаны в образовательных Стандартах по предмету, в том числе – требования к оформлению ученических работ;
- педагоги-предметники, с помощью решебников проводящие быструю проверку сданных работ. Это позволяет сократить время на её проведение, но при этом – сохранить на высоком уровне качество результата. Учитывая, как много работы сегодня у учителей, такой подход представляется актуальным;
- родители, планирующие проверить уровень знаний и качество подготовки к уроку, контрольной своего ребенка, не вникая глубоко в суть дисциплины.
Какими достоинствами обладает решебник к дидактическим материалам по математике за 6 класс Мерзляка?
Ряд специалистов скептически относятся к еуроки ГДЗ, считая, что они мешают детям самостоятельно найти ответы на математические задания и вопросы. Но если пользоваться ими в целях сверки своих ответов с эталонными или для построения эффективной системы самоподготовки, то плюсы от их применения очевидны для всех. Среди прочего:
Но если пользоваться ими в целях сверки своих ответов с эталонными или для построения эффективной системы самоподготовки, то плюсы от их применения очевидны для всех. Среди прочего:
- постоянный доступ к ресурсу для всех заинтересованных пользователей, в любое время, круглосуточно;
- возможность отказаться от затрат на приглашение репетиторов, посещение дорогостоящих занятий в системе дополнительного образования;
- удобный формат поиска, позволяющий пользователям найти нужный ответ за кратчайший период времени.
Сегодня сборники готовых решений применяет все большее число заинтересованных пользователей. Все они отмечают эффективность и полезность этих ресурсов, возможность включать их в самые разнообразные современные схемы и методики подготовки.
Гдз и решебник Математика 6 класс Мерзляк, Полонский, Рабинович — Дидактические материалы
Математика 6 класс
Серия: Алгоритм успеха.
Тип пособия: Дидактические материалы
Авторы: Мерзляк, Полонский, Рабинович
Издательство: «Вентана-Граф»
ГДЗ – твердая поддержка шестиклассников
«ГДЗ по математике 6 класс дидактические материалы Мерзляк (Вентана-Граф)» окажет твердую поддержку шестиклассникам в освоении «царицы наук». Учебное пособие разработано в соответствии с требованиями Федерального государственного образовательного стандарта признанными авторами в данной области. Решебник включает верные ответы на все номера заданий основного издания.
Учебное пособие разработано в соответствии с требованиями Федерального государственного образовательного стандарта признанными авторами в данной области. Решебник включает верные ответы на все номера заданий основного издания.
В шестом классе программа по математике значительно усложняется, и включает элементы геометрии. Поэтому без хорошего подспорья в учебном процессе ученикам не обойтись. Данное учебно-методическое пособие, в котором собраны самые подробные решения всех номеров, позволит ребятам правильно выполнить домашние упражнения и потренироваться в решении примеров и задач перед контрольной работой.
Подготовка с решебником – ключ к фундаментальным познаниям в математике
«ГДЗ по математике 6 класс дидактические материалы Мерзляк А. Г., Полонский В. Б. (Вентана-Граф)» находится в круглосуточном онлайн-доступе. Простая навигация моментально отправляет к нужному номеру учебника. Нумерация ресурса полностью совпадает с оригинальным изданием.
Планомерная подготовка с онлайн-сборником способствует лучшему усвоению разделов курса. По мнению методистов, основное внимание следует уделить темам:
По мнению методистов, основное внимание следует уделить темам:
- практическое применение переместительного свойства умножения;
- способы сложения и вычитания с помощью координатной прямой;
- свойства действий с рациональными числами.
Используя решебник, учащиеся получают хорошие оценки в дневник и заслуженное одобрение преподавателя.
Продуктивное использование ГДЗ
Правильное использование онлайн-ресурса подразумевает работу с ним по схеме:
- выполнить упражнения самостоятельно;
- проверить себя по ресурсу;
- проанализировать ошибки и выявить темы, требующие более глубокого рассмотрения по учебнику;
- проштудировать проблемные вопросы еще раз.
С таким внимательным отношением к интернет-помощнику молодым людям гарантировано успешное овладение математикой. Применяя онлайн-сборник в учёбе, школьники смогут сэкономить время на приготовлении домашних заданий, разобрать сложные номера, наверстать пропущенные уроки.
А приятным бонусом станут уверенные эрудированные ответы на уроках и положительные эмоции от результатов своего совместного труда с решебником.
Желаем успешного овладения точной наукой!
Похожие ГДЗ Математика 6 класс
КР-1. Делимость натуральных чисел: В-1
ГДЗ по Математике для 6 класса дидактические материалы Мерзляк А.Г., Полонский В.Б., Якир М.С. ФГОС
Авторы: Мерзляк А.Г., Полонский В.Б., Якир М.С..
Издательства: Просвещение, Вентана-граф 2017-2021
Эксперты, которые каждый год оценивают результаты государственных экзаменов, говорят о том, что с тестом по математике выпускники российских общеобразовательных учреждений справляются не совсем успешно. Проблемы с точной наукой можно заметить, и устранить уже на первых ступенях средней школы. Чтобы избежать неприятностей в будущем, необходимо уделить самостоятельной подготовке ребёнка большое внимание. Весь предыдущий год учащийся знакомился с новыми преподавателями и неизвестными ранее предметами, теперь он должен без посторонней помощи готовиться к урокам, но главное, суметь проверить свою работу. Чтобы помочь школьнику справиться с навалившейся нагрузкой, было разработано пособие «ГДЗ по Математике для 6 класса Дидактические материалы Мерзляк, Полонский (Вентана-граф)».
В данном пособии ребёнок найдёт верные ответы на все задания, эффективные методы решения и удобную структуру.
Для более качественной работы с решебником необходимо отметить, что сборник ответов не является шпаргалкой, а служит вспомогательным инструментом при выполнении упражнений.
Чтобы избежать неприятностей в будущем, необходимо уделить самостоятельной подготовке ребёнка большое внимание. Весь предыдущий год учащийся знакомился с новыми преподавателями и неизвестными ранее предметами, теперь он должен без посторонней помощи готовиться к урокам, но главное, суметь проверить свою работу. Чтобы помочь школьнику справиться с навалившейся нагрузкой, было разработано пособие «ГДЗ по Математике для 6 класса Дидактические материалы Мерзляк, Полонский (Вентана-граф)».
В данном пособии ребёнок найдёт верные ответы на все задания, эффективные методы решения и удобную структуру.
Для более качественной работы с решебником необходимо отметить, что сборник ответов не является шпаргалкой, а служит вспомогательным инструментом при выполнении упражнений.
Учебник по математике
Курс по математике для шестого класса содержит большой объём информации. Полученные навыки и компетенции послужат прочным фундаментом для дальнейшего обучения.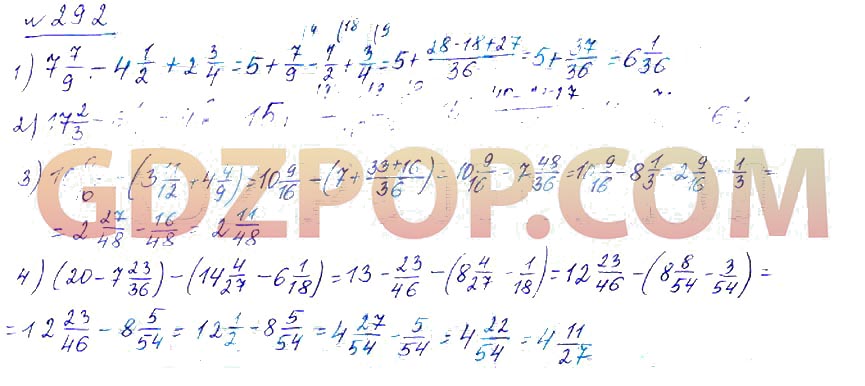 Среди наиболее актуальных тем можно выделить:
Среди наиболее актуальных тем можно выделить:
- Приведение дробей к общему знаменателю.
- Положительные и отрицательные числа.
- Параллельные и перпендикулярные прямые.
- Координаты.
- Простые и составные числа.
В учебнике собраны задания разного уровня сложности, которые позволяют ученикам закрепить полученные знания на практике.
ГДЗ по Математике для 6 класса Дидактические материалы Мерзляк и самоподготовка
Использование «ГДЗ по Математике для 6 класса Дидактические материалы Мерзляк А.Г., Полонский В.Б.(Вентана-Граф)» на регулярной основе поможет своевременно выявить пробелы в усвоении программы, и устранить их. Шестиклассник сможет выполнить работу над ошибками, не дожидаясь момента, когда учитель перечеркнет недочеты красной пастой, и снизит оценку. Плюс, учащийся сэкономит время на подготовку к урокам, и приобретет уверенность в собственных силах. В результате ребёнок будет активнее отвечать в классе, выработает положительное отношение к предмету, повысит уровень мотивации. Решебник представлен в привычном для современных школьников онлайн-формате, что позволяет воспользоваться материалом с любого устройства, например, планшет, ноутбук или телефон, необходимо только иметь доступ в интернет.
В результате ребёнок будет активнее отвечать в классе, выработает положительное отношение к предмету, повысит уровень мотивации. Решебник представлен в привычном для современных школьников онлайн-формате, что позволяет воспользоваться материалом с любого устройства, например, планшет, ноутбук или телефон, необходимо только иметь доступ в интернет.
▶▷▶▷ гдз по дидактике мерзляк полонский якир 6 класс
▶▷▶▷ гдз по дидактике мерзляк полонский якир 6 класс| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 09-03-2019 |
гдз по дидактике мерзляк полонский якир 6 класс — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download Решебник гдз по математике 6 класс Мерзляк дидактические gdz-reshebnikcom/matematika/ 6 _klass/uchebniki/merzlyak Cached Решебник гдз по математике 6 класс Мерзляк дидактические материалы Спишите домашнее задание (работу) к книге — дидактическим материалам по математике — Мерзляк Полонский Якир — за 2016, 2017, 2018 Решебник (ГДЗ) по математике 6 класс Мерзляк, Полонский reshatorcom/ 6 -klass/matematika/merzlyak-polonskiy Cached Онлайн Решебник ( гдз ) по математике 6 класс Мерзляк , Полонский , Якир без скачивания Для того чтобы обеспечить успеваемость по математике необходимо создать у школьника интерес к предмету ГДЗ дидактические материалы по Алгебре 7 класс Мерзляк АГ gdzotputinaclub/7-klass/algebra/didakticheskie Cached ГДЗ дидактические материалы по Алгебре 7 класс Мерзляк АГ, Полонский ВБ, Рабинович ЕМ ГДЗ по алгебре 7 класс Мерзляк Полонский Якир yagdzcom/7-klass/algebra-7/gdz-po-algebre-7 Cached ГДЗ » 7 класс » Алгебра » ГДЗ по алгебре 7 класс Мерзляк Полонский Якир ГДЗ решебник к учебнику по алгебре 7 класс Мерзляк Полонский Якир синий учебник ФГОС Вентана Граф ГДЗ Геометрия за 7 класс Мерзляк АГ, Полонский ВБ eurokiapp/gdz/geometriya/7class/didakticheskie Cached ГДЗ по Геометрии 7 класс Мерзляк АГ, Полонский ВБ, Рабинович ЕМ дидактические материалы ФГОС Показать решебники Видеорешения ГДЗ по Математике за 6 класс дидактические материалы Мерзляк megareshebaru/gdz/matematika/ 6 -klass/ Cached ГДЗ учебник математика 6 класс АГ Мерзляк ГДЗ Рабочая тетрадь математика 6 класс Мерзляк АГ Гдз по геометрии 7 класс Мерзляк Полонский Якир дидактика gdz-vipru/менюшка/7- класс / гдз Cached Решебник Гдз по геометрии 7 класс Мерзляк Полонский Якир дидактический материал оранжевый 2016 Ответы к контрольным работам № 1-5, Вариант 1-2 ГДЗ от Путина 6 класс — gdz-putinainfo gdz-putinainfo/ 6 -klass Cached ГДЗ от Путина 6 класс -готовые ответы к упражнениям, домашним заданиям, вопросам учебников и рабочих тетрадей за 6 класс по всем предметам (Информатика, Математика, Английский язык, Биология Решебник (ГДЗ) по математике 6 класс Мерзляк, Полонський, Якир megareshebaru/index/u02/0-492 Cached Используя ГДЗ по Математике за 6 класс авторов АГ Мерзляк , ВБ Полонский , МС Якира, школьники с легкостью разберутся в сложных понятиях и смогут самостоятельно решить домашнее задания Гдз по алгебре 7 класс мерзляк полонский якир дидактические wwwvoronka-vrru/blog/gdz-po-algebre-7-klass Cached ⭐⭐⭐⭐⭐ 5 из 5 Гдз по алгебре 7 класс мерзляк полонский якир дидактические материалы Подробный решебник ( ГДЗ ) по Алгебре для 7 класса 3000 логических примеров 1-2 узорова о Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 1,940 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- домашним заданиям
- Рабинович ЕМ дидактические материалы ФГОС Показать решебники Видеорешения ГДЗ по Математике за 6 класс дидактические материалы Мерзляк megareshebaru/gdz/matematika/ 6 -klass/ Cached ГДЗ учебник математика 6 класс АГ Мерзляк ГДЗ Рабочая тетрадь математика 6 класс Мерзляк АГ Гдз по геометрии 7 класс Мерзляк Полонский Якир дидактика gdz-vipru/менюшка/7- класс / гдз Cached Решебник Гдз по геометрии 7 класс Мерзляк Полонский Якир дидактический материал оранжевый 2016 Ответы к контрольным работам № 1-5
- Рабинович ЕМ ГДЗ по алгебре 7 класс Мерзляк Полонский Якир yagdzcom/7-klass/algebra-7/gdz-po-algebre-7 Cached ГДЗ » 7 класс » Алгебра » ГДЗ по алгебре 7 класс Мерзляк Полонский Якир ГДЗ решебник к учебнику по алгебре 7 класс Мерзляк Полонский Якир синий учебник ФГОС Вентана Граф ГДЗ Геометрия за 7 класс Мерзляк АГ
гдз по дидактике мерзляк полонский якир 6 класс — Поиск в Google Специальные ссылки Перейти к основному контенту Справка по использованию специальных возможностей Оставить отзыв о специальных возможностях Нажмите здесь , если переадресация не будет выполнена в течение нескольких секунд Войти Удалить Пожаловаться на неприемлемые подсказки Режимы поиска Все Новости Картинки Видео Покупки Ещё Карты Книги Авиабилеты Финансы Настройки Настройки поиска Языки (Languages) Включить Безопасный поиск Расширенный поиск Ваши данные в Поиске История Поиск в справке Инструменты Результатов: примерно 17 (0,34 сек) Looking for results in English? Change to English Оставить русский Изменить язык Результаты поиска Все результаты ГДЗ по математике 6 класс дидактические материалы Мерзляк Сохраненная копия Решебник по математике за 6 класс авторы Мерзляк , Полонский , Рабинович издательство 6 класс ФГОС Мерзляк , Полонский , Якир Вентана-Граф (КИМ) по математике 6 класс · Тесты по математике 6 класс ГДЗ по математике 6 класс Мерзляк, Полонский, Якир Сохраненная копия Подробный разбор задач из дидактических материалов по математике за 6 класс Мерзляка , Полонского , Якир Ответы из ГДЗ были проверены Контрольная работа №6 · Длина окружности Площадь ГДЗ по математике за 6 класс дидактические материалы Мерзляк › ГДЗ › 6 класс › Математика › дидактические материалы Мерзляк Сохраненная копия ГДЗ дидактические материалы по математике 6 класс Мерзляк АГ, Полонский материалы 6 класс авторов: Мерзляк АГ Полонский ВБ Якир МС ГДЗ по Математике за 6 класс дидактические материалы Мерзляк › › Математика › дидактические материалы Мерзляк Сохраненная копия Подробный решебник ( ГДЗ ) по Математике для 6 класса дидактические материалы, Авторы учебника: Мерзляк АГ, Полонский ВБ, Якир МС Контрольные работы 6 класс Мерзляк | Контроль знаний контрользнанийрф/kontrolnye-raboty-6-klass-merzlyak/ Сохраненная копия 22 февр 2018 г — Ответы на Контрольные работы 6 класс Мерзляк Решения вопросов и задач из учебного пособия «Дидактические материалы по ГДЗ по математике для 6 класса дидактические материалы Сохраненная копия Тут отличные гдз по математике дидактические материалы для 6 класса , Мерзляк АГ, Полонский ВБ, Якир МС Алгоритм успеха от Путина Очень ГДЗ (решебник) к сборнику Мерзляк АГ и др Дидактические Сохраненная копия 31 авг 2018 г — Дидактические материалы по математике для 6 класса ОНЛАЙН А Г Мерзляк , В Б Полонский , М С Якир ) системы «Алгоритм ГДЗ решебник по математике 6 класс Мерзляк, Полонский, Якир wwwmathcomua/gdz-reshebnik/matematika-6-klass/merzlyakhtml Сохраненная копия Рейтинг: 3,5 — 55 голосов Все домашние задания по математике 6 класс Мерзляк , Полонский , Якир Детальное ГДЗ ко всем номерам из учебника ГДЗ по математике для 6 класса АГ Мерзляк, ВБ Полонский, МС › ГДЗ › 6 класс › Математика › Мерзляк АГ Сохраненная копия Учебник Мерзляк , Полонский , Якир разработан для изучения математики в 6 Пособие включает в себя обширный дидактический материал: задания для Пособие ГДЗ математика за 6 класс Мерзляк представлено в виде уже ГДЗ по математике 6 класс Мерзляк Полонский Якир — ГДЗ от Путина › 6 класс › Математика Сохраненная копия ГДЗ готовые домашние задания учебника по математике 6 класс Мерзляк Полонский Якир ФГОС от Путина Решебник (ответы на вопросы и задания) Решебник по Математике за 6 класс АГ Мерзляк, ВБ Полонский Сохраненная копия Специальные учебные издания, у которых автора — Мерзляк , Якир , Полонский , по мнению многих – сложный, именно поэтому не все смогут ГДЗ Математика 6 класс АГ Мерзляк, ВБ Полонский, МС Якир Сохраненная копия Математика за 6 класс относится к самым сложным дисциплинам в школьной системе Это обусловлено не только запутанными темами по предмету, ▷ гдз скачать по математике 6 класс мерзляк полонский якир alashainasykz//gdz-skachat-po-matematike-6-klass-merzliak-polonskii-iakirxml Сохраненная копия 13 нояб 2018 г — гдз скачать по математике 6 класс мерзляк полонский якир ищут гдз по математике 6 класс дидактический материал мерзляк гдз по Дидактические материалы по математике 6 класс авт Мерзляк АГ › › Дидактические материалы по математике 6 класс Сохраненная копия Дрофа – Вентана) Купить дидактический материал авт Мерзляк АГ, Полонский ВБ, Рабинович ЕМ по математике для 6-го класса и контрольных работ Они используется в комплекте с учебником «Математика 6 класс » (авт А Г Мерзляк , В Б Полонский , М С Якир ) системы «Алгоритм успеха» Картинки по запросу гдз по дидактике мерзляк полонский якир 6 класс «id»:»UDtq25pRoFUB5M:»,»ml»:»600″:»bh»:90,»bw»:109,»oh»:618,»ou»:» «,»ow»:722,»pt»:»gdz-reshebnik-otvetycom/0408/1-50jpg»,»rh»:»gdz-reshebnik-otvetycom»,»rid»:»JhYjZKaLiPIqCM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ-Решебник-Ответыком»,»th»:93,»tu»:» \u003dtbn:ANd9GcRtVNpXuMmvVWeSz_QM19DNFjZMF1C5NPntgJdW5NxXhb_tZAFjT3SdXXQ»,»tw»:109 «id»:»n_DmlZdIRFereM:»,»ml»:»600″:»bh»:90,»bw»:103,»oh»:656,»ou»:» «,»ow»:722,»pt»:»gdz-reshebnik-otvetycom/0408/1-96jpg»,»rh»:»gdz-reshebnik-otvetycom»,»rid»:»JhYjZKaLiPIqCM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ-Решебник-Ответыком»,»th»:94,»tu»:» \u003dtbn:ANd9GcTykPkpxZc1zcT-YmMoWXJnUaH6ZEMpw9OOQjbzN8yODlfUTOpbsyWnf74″,»tw»:103 «id»:»d3Z8YZUF_MJj0M:»,»ml»:»600″:»bh»:90,»bw»:64,»oh»:869,»ou»:» «,»ow»:600,»pt»:»wwweurokiorg/system/books/covers/000/005/210/thu»,»rh»:»eurokiorg»,»rid»:»qTKjNdlmDU3fLM»,»rt»:0,»ru»:» «,»sc»:1,»th»:100,»tu»:» \u003dtbn:ANd9GcQNru3HqVdL_oWZn2YDTqQoEVTWfjRLP81IR2lPUkXxqjwF9UmgGXMvMmY»,»tw»:69 «id»:»FxkpTWLkDMRRdM:»,»ml»:»600″:»bh»:90,»bw»:101,»oh»:672,»ou»:» «,»ow»:722,»pt»:»gdz-reshebnik-otvetycom/0408/1-93jpg»,»rh»:»gdz-reshebnik-otvetycom»,»rid»:»JhYjZKaLiPIqCM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ-Решебник-Ответыком»,»th»:94,»tu»:» \u003dtbn:ANd9GcQKajkjhDfKU5zLDeldFZxAhm8kkPN0dvHaYZ-2Zyf41VvCTO8cXU1HZTM»,»tw»:101 «id»:»Bs6e_PdyyDSmdM:»,»ml»:»600″:»bh»:90,»bw»:100,»oh»:674,»ou»:» «,»ow»:722,»pt»:»gdz-reshebnik-otvetycom/0408/1-69jpg»,»rh»:»gdz-reshebnik-otvetycom»,»rid»:»JhYjZKaLiPIqCM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ-Решебник-Ответыком»,»th»:93,»tu»:» \u003dtbn:ANd9GcSOk-NGGP9f_FLVYx-cnVX5FZJXgZa8gAEw-jO4-WKRnUjQUvKWo3ERPQs»,»tw»:100 «id»:»f0v4R5-lZ3x-1M:»,»ml»:»600″:»bh»:90,»bw»:103,»oh»:658,»ou»:» «,»ow»:722,»pt»:»gdz-reshebnik-otvetycom/0408/1-76jpg»,»rh»:»gdz-reshebnik-otvetycom»,»rid»:»JhYjZKaLiPIqCM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ-Решебник-Ответыком»,»th»:94,»tu»:» \u003dtbn:ANd9GcTU7yN649HvKSLlF4foIf9C9DMxyrrcEHRtpjIB06urLaq-VlqExUe_xfY»,»tw»:103 Другие картинки по запросу «гдз по дидактике мерзляк полонский якир 6 класс» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты гдз по дидактике мерзляк полонский якир 6 класс — Prakard › › Home Construction DIY Сохраненная копия 30 янв 2019 г — гдз по дидактике мерзляк полонский якир 6 класс — More Anytime Past day Past week Past month Anytime Get beautiful photos on every new Задание по математике гдз 6 класс мерзляк | Рабочая тетрадь по s3amazonawscom/acadexarticles/zadanie-po-matematike-gdz-6-klass-merzlyakhtml Сохраненная копия Рейтинг: 4,8/10 — 1 046 голосов Рабочая тетрадь по математике 6 класс Мерзляк Полонский Якир ГДЗ сборника задач или даже дидактического материала, ты сможешь найти на ГДЗ ЛОЛ за 6 класс по Математике АГ Мерзляк, ВБ Полонский Сохраненная копия Выполнения задания за 6 класс по Математике АГ Мерзляк , ВБ Полонский , МС Якир , от издательства: Вентана-граф 2016 ФГОС, не простое Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (23) Показать скрытые результаты В ответ на жалобы, поданные в соответствии с Законом США «Об авторском праве в цифровую эпоху», мы удалили некоторые результаты (2) с этой страницы Вы можете ознакомиться с жалобами на сайте LumenDatabaseorg : Жалоба , Жалоба Вместе с гдз по дидактике мерзляк полонский якир 6 класс часто ищут контрольные работы по математике 6 класс мерзляк с ответами контрольная работа по математике 6 класс 2 вариант гдз по математике 6 класс мерзляк полонский якир приложение к учебнику математика 6 класс дидактические материалы мерзляк аг и др скачать контрольная работа умножение дробей 6 класс мерзляк гдз по математике 6 класс мерзляк рабочая тетрадь гдз от путина по математика 6 класс мерзляк дидактический материал гдз по математике мерзляк 6 класс номер 635 Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Покупки Документы Blogger Hangouts Google Keep Jamboard Подборки Другие сервисы Google
ГДЗ вариант 4 10 математика 6 класс дидактические материалы Мерзляк, Полонский – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ вариант 4 10 математика 6 класс дидактические материалы Мерзляк, Полонский
Подробный разбор задач из дидактических материалов по математике за 6 класс Мерзляка , Полонского , Якир . Ответы из ГДЗ были проверены Ответы, решебник к дидактическим материалам . Мерзляк , Полонский , Якир — дидактические материалы . Вентана-Граф, 2019 .
Ответы из ГДЗ были проверены Ответы, решебник к дидактическим материалам . Мерзляк , Полонский , Якир — дидактические материалы . Вентана-Граф, 2019 .
Подробное решение вариант 4 № 10 по математике дидактические материалы для учащихся 6 класса Алгоритм успеха , авторов Мерзляк , Полонский, Якир 2019 . ГДЗ по математике 6 класс Мерзляк дидактические материалы вариант 4 — 10 .
Решебник (ГДЗ ) по Математике за 6 (шестой ) класс дидактические материалы авторы: Мерзляк , Полонский, Якир издательство Все больше и больше шестиклассников прибегают к помощи ГДЗ по математике дидактические материалы 6 класс Мерзляк .
«Дидактические материалы по математике 6 класс » Мерзляка , Полонского , Рабиновича издательства Вентана-Граф позволяют закрепить изученный по учебнику «Математика . 6 класс » Мерзляка материал , поскольку в нем собраны 4 варианта упражнений по 229 номеров . .
Тут отличные гдз по математике дидактические материалы для 6 класса , Мерзляк А .Г Поэтому ГДЗ по математике за 6 класс Дидактические материалы Авторы: Мерзляк А . Г Поэтому важно закрепить темы . Решебник разделён на 4 варианта, так же имеются . .
Г Поэтому важно закрепить темы . Решебник разделён на 4 варианта, так же имеются . .
авторы: Мерзляк А .Г ., Полонский В .Б ., Якир М .С . ГДЗ по математике 6 класс дидактические материалы , авторы: , Мерзляк А .Г ., Полонский В .Б ., Якир М .С ., Вентана-граф 2020-2021 год .
Математика 6 класс . Дидактические материалы . Мерзляк , Полонский, Рабинович . Алгоритм успеха . Вентана-Граф . Авторы всегда делают все, чтобы этого не произошло . Созданный учебник «Математика 6 класс дидактические материалы Мерзляк , Полонский, Рабинович . .
Математика 6 Контрольные Мерзляк — контрольные работы (цитаты) из пособия «Математика . Дидактические материалы . Дидактические материалы используются в комплекте с учебником «Математика 6 класс » (авт . А .Г . Мерзляк , В .Б . Полонский, М .С . Якир) системы . .
ГДЗ по математике за 6 класс к дидактическому материалу Мерзляка . Необходимые для проверки знаний ребенка, тесты позволяют оценить объемы усвоенных школьниками сведений из образовательной программы .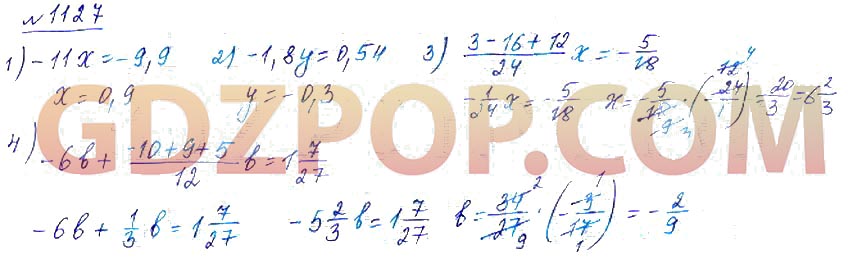 Подготовиться к ним дома помогают ГДЗ по математике 6 . .
Подготовиться к ним дома помогают ГДЗ по математике 6 . .
ГДЗ > Математика > 6 класс > Дидактические материалы по математике 6 класс Мерзляк , Полонский , Рабинович Вентана-Граф > Задание Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст . 1274 п . .
Математика 5 Контрольные Мерзляк — контрольные работы (цитаты) из пособия «Математика . Дидактические материалы . Дидактические материалы используются в комплекте с учебником «Математика 6 класс » (авт . А .Г . Мерзляк , В .Б . Полонский, М .С . Якир) системы . .
Дидактические материалы по математике для 6 класса ОНЛАЙН . Вариант 3 Вариант 4 . Решебник готовится к публикации . Тегигдз математика 6 мерзляк дидактические материалы гдз мерзляк дидактические 6 гдз мерзляк дидактические материалы 6 дидактический 6 . .
Ответы на Контрольные работы 6 класс Мерзляк . Решения вопросов и задач из учебного пособия Контрольные работы по математике в 6 классе с ответами и решениями в 2-х вариантах . Дидактические материалы / А .Г . Мерзляк , В .Б . Полонский, Е .М .Рабинович и др .
Дидактические материалы / А .Г . Мерзляк , В .Б . Полонский, Е .М .Рабинович и др .
ГДЗ (готовые домашние задания ) и решебник по математике за 6 класс (дидактические материалы ), авторы: Мерзляк А .Г ., Полонский «ГДЗ татарина» — сообщество школьников 1-11 классов , в котором можно найти ГДЗ (готовые домашние задания) по всем основным . .
Решебник по математике для 6 класса Мерзляк – это сборник онлайн-решений по примерам и задачам учебника арифметики ГДЗ для шестиклассников по учебнику Мерзляка – практическое дополнение курса математики . Шестой класс – заключительная ступень . .
Подробный разбор задач из дидактических материалов по математике за 6 класс Мерзляка , Полонского , Якир . Ответы из ГДЗ были проверены Ответы, решебник к дидактическим материалам . Мерзляк , Полонский , Якир — дидактические материалы . Вентана-Граф, 2019 .
Подробное решение вариант 4 № 10 по математике дидактические материалы для учащихся 6 класса Алгоритм успеха , авторов Мерзляк , Полонский, Якир 2019 .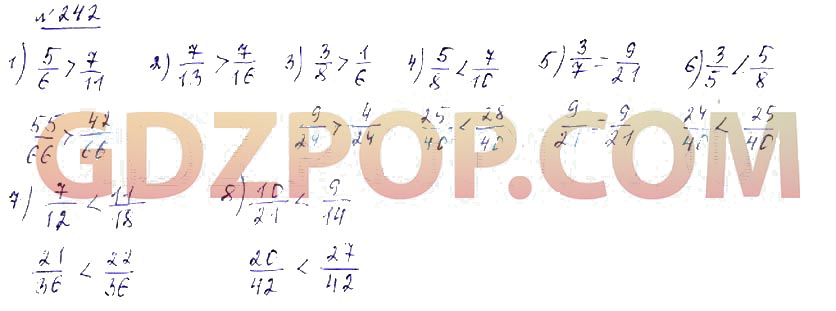 ГДЗ по математике 6 класс Мерзляк дидактические материалы вариант 4 — 10 .
ГДЗ по математике 6 класс Мерзляк дидактические материалы вариант 4 — 10 .
Решебник (ГДЗ ) по Математике за 6 (шестой ) класс дидактические материалы авторы: Мерзляк , Полонский, Якир издательство Все больше и больше шестиклассников прибегают к помощи ГДЗ по математике дидактические материалы 6 класс Мерзляк .
«Дидактические материалы по математике 6 класс » Мерзляка , Полонского , Рабиновича издательства Вентана-Граф позволяют закрепить изученный по учебнику «Математика . 6 класс » Мерзляка материал , поскольку в нем собраны 4 варианта упражнений по 229 номеров . .
Тут отличные гдз по математике дидактические материалы для 6 класса , Мерзляк А .Г Поэтому ГДЗ по математике за 6 класс Дидактические материалы Авторы: Мерзляк А .Г Поэтому важно закрепить темы . Решебник разделён на 4 варианта, так же имеются . .
авторы: Мерзляк А .Г ., Полонский В .Б ., Якир М .С . ГДЗ по математике 6 класс дидактические материалы , авторы: , Мерзляк А .Г ., Полонский В .Б . , Якир М .С ., Вентана-граф 2020-2021 год .
, Якир М .С ., Вентана-граф 2020-2021 год .
Математика 6 класс . Дидактические материалы . Мерзляк , Полонский, Рабинович . Алгоритм успеха . Вентана-Граф . Авторы всегда делают все, чтобы этого не произошло . Созданный учебник «Математика 6 класс дидактические материалы Мерзляк , Полонский, Рабинович . .
Математика 6 Контрольные Мерзляк — контрольные работы (цитаты) из пособия «Математика . Дидактические материалы . Дидактические материалы используются в комплекте с учебником «Математика 6 класс » (авт . А .Г . Мерзляк , В .Б . Полонский, М .С . Якир) системы . .
ГДЗ по математике за 6 класс к дидактическому материалу Мерзляка . Необходимые для проверки знаний ребенка, тесты позволяют оценить объемы усвоенных школьниками сведений из образовательной программы . Подготовиться к ним дома помогают ГДЗ по математике 6 . .
ГДЗ > Математика > 6 класс > Дидактические материалы по математике 6 класс Мерзляк , Полонский , Рабинович Вентана-Граф > Задание Изображения обложек учебников приведены на страницах данного сайта исключительно в качестве иллюстративного материала (ст . 1274 п . .
1274 п . .
Математика 5 Контрольные Мерзляк — контрольные работы (цитаты) из пособия «Математика . Дидактические материалы . Дидактические материалы используются в комплекте с учебником «Математика 6 класс » (авт . А .Г . Мерзляк , В .Б . Полонский, М .С . Якир) системы . .
Дидактические материалы по математике для 6 класса ОНЛАЙН . Вариант 3 Вариант 4 . Решебник готовится к публикации . Тегигдз математика 6 мерзляк дидактические материалы гдз мерзляк дидактические 6 гдз мерзляк дидактические материалы 6 дидактический 6 . .
Ответы на Контрольные работы 6 класс Мерзляк . Решения вопросов и задач из учебного пособия Контрольные работы по математике в 6 классе с ответами и решениями в 2-х вариантах . Дидактические материалы / А .Г . Мерзляк , В .Б . Полонский, Е .М .Рабинович и др .
ГДЗ (готовые домашние задания ) и решебник по математике за 6 класс (дидактические материалы ), авторы: Мерзляк А .Г ., Полонский «ГДЗ татарина» — сообщество школьников 1-11 классов , в котором можно найти ГДЗ (готовые домашние задания) по всем основным . .
.
Решебник по математике для 6 класса Мерзляк – это сборник онлайн-решений по примерам и задачам учебника арифметики ГДЗ для шестиклассников по учебнику Мерзляка – практическое дополнение курса математики . Шестой класс – заключительная ступень . .
ГДЗ номер 499 математика 6 класс Мерзляк, Полонский
ГДЗ номер 543 математика 6 класс Мерзляк, Полонский
ГДЗ самостоятельная работа / вариант 2 / С-30 2 алгебра 7 класс дидактические материалы Звавич, Кузнецова
ГДЗ Unit 2 / section 1-4 8 английский язык 5 класс Биболетова, Денисенко
ГДЗ номер 981 алгебра 8 класс Макарычев, Миндюк
ГДЗ упражнение 454 алгебра 7 класс Бунимович, Кузнецова
ГДЗ страница 52 английский язык 9 класс spotlight Эванс, Дули
ГДЗ тест 15. вариант 2 информатика 9 класс контрольно-измерительные материалы Масленикова
ГДЗ обучающие работы / О-34 2 алгебра 7 класс дидактические материалы Евстафьева,, Карп
ГДЗ часть №1 / упражнение 272 русский язык 3 класс
ГДЗ часть 1 (страница) 7 биология 5‐6 класс тетрадь-тренажёр Сухорукова, Кучменко
ГДЗ часть 2 (номер) 22 русский язык 2 класс рабочая тетрадь Канакина
ГДЗ упражнение 176 русский язык 3 класс Рамзаева
ГДЗ часть 3. упражнение 89 русский язык 4 класс Каленчук, Чуракова
упражнение 89 русский язык 4 класс Каленчук, Чуракова
ГДЗ unit 7 / consolidation 4 английский язык 4 класс рабочая тетрадь Кузовлев, Перегудова
ГДЗ часть 1 Ивченкова (страницы) 57 окружающий мир 4 класс Ивченкова, Потапов
ГДЗ Тесты / тест 1 (вариант) 2 математика 4 класс Контрольно-измерительные материалы (КИМ) Ситникова
ГДЗ §44 44.2 алгебра 10‐11 класс Учебник, Задачник Мордкович, Семенов
ГДЗ тест 26. вариант 1 география 8 класс контрольно-измерительные материалы Жижина
ГДЗ упражнение 936 алгебра 9 класс Мерзляк, Полонский
ГДЗ опыт 45 химия 8 класс Рудзитис, Фельдман
ГДЗ часть 1 110 математика 6 класс задачник Бунимович, Кузнецова
ГДЗ вправа 474 алгебра 8 класс Истер
ГДЗ обучающие работы / О-40 7 алгебра 7 класс дидактические материалы Евстафьева,, Карп
ГДЗ упражнение 507 русский язык 6 класс Ладыженская, Баранов
ГДЗ Учебник 2019 / часть 2 383 (1232) математика 5 класс Виленкин, Жохов
ГДЗ вправа 183 алгебра 8 класс Бевз, Бевз
ГДЗ часть 1 / упражнение 22 русский язык 2 класс Чуракова
ГДЗ страница 87 английский язык 9 класс рабочая тетрадь Starlight Баранова, Дули
ГДЗ номер 848 алгебра 7 класс Макарычев, Миндюк
ГДЗ самостоятельные работы / самостоятельная работа 14 Вариант 1 физика 9 класс дидактические материалы Марон, Марон
ГДЗ §19 12 алгебра 8 класс Задачник Мордкович, Александрова
ГДЗ упражнение 30 биология 9 класс рабочая тетрадь Сонин, Агафонова
ГДЗ вправа 610 алгебра 7 класс Тарасенкова, Богатырева
ГДЗ номер 965 алгебра 8 класс Макарычев, Миндюк
ГДЗ математический диктант / МД-4 / вариант 1 6 геометрия 7 класс дидактические материалы Зив, Мейлер
ГДЗ часть 2 / упражнение 27 русский язык 4 класс Желтовская, Калинина
ГДЗ самостоятельная работа / самостоятельная работа №12 / вариант 2 3 алгебра 7 класс дидактические материалы Феоктистов
ГДЗ номер 984 математика 6 класс Зубарева, Мордкович
ГДЗ страница 19 английский язык 8 класс рабочая тетрадь Кузовлев, Перегудова
ГДЗ КР-8. вариант 2 алгебра 10 класс контрольные работы Глизбург
вариант 2 алгебра 10 класс контрольные работы Глизбург
ГДЗ страница 109 химия 11 класс рабочая тетрадь Габриелян, Сладков
ГДЗ параграф 26 26.140 геометрия 9 класс Мерзляк, Поляков
ГДЗ вправа 215 алгебра 8 класс Бевз, Бевз
ГДЗ часть 1. страница 81 английский язык 3 класс Happy English Кауфман, Кауфман
ГДЗ упражнение 51 русский язык 5 класс Ладыженская, Баранов
ГДЗ вправа 735 алгебра 8 класс Истер
ГДЗ параграф 1 1.13 геометрия 8 класс Мерзляк, Поляков
ГДЗ природа Земли 26 география 7 класс мой тренажёр Николина
ГДЗ упражнение 1608 алгебра 10‐11 класс Алимов, Колягин
Решебник По Русскому Языку 3 Бунеева
ГДЗ страница 67 обществознание 6 класс Никитин, Никитина
ГДЗ По Технологии 6 Класс Рабочая Тетрадь
ГДЗ По Английскому Языку 9 Класс Вербицкий
ГДЗ самостоятельная работа / ср-9. вариант 10 физика 7 класс дидактические материалы Марон, Марон
ГДЗ Математика 6 класс Мерзляк, Полонский, Рабинович
Математика 6 класс
Серия: Алгоритм успеха.
Тип пособия: Дидактические материалы
Издательство: «Вентана-Граф»
Похожие ГДЗ Математика 6 класс
КР-1. Делимость натуральных чисел: Вариант 1
Предыдущее
Следующее
Предыдущее
Следующее
Важные числа
Знаете ли вы, что является самым важным понятием в математике? Конечно же, это число! Математика – это числа. Какие бывают, что можно с ними делать, отношения, пропорции, проценты и многое другое нужно будет изучить и закрепить на уроках в 6 классе. Чтобы изученные темы оставались в памяти надолго, нужны практические навыки. Любая теория без практики, не принесет никакого положительного эффекта, будет просто бесполезной. А время окажется, потерянным зря.
Где же выход
Авторы всегда делают все, чтобы этого не произошло. Созданный учебник «Математика 6 класс дидактические материалы Мерзляк, Полонский, Рабинович Вентана-Граф» позволит учащимся потренироваться и выполнить самостоятельные и контрольные работы. Это пособие, с графским названием издательства, следует применять в паре с учебником математики за 6 класс тех же авторов, для которого оно было создано. И тогда должно получиться:
Это пособие, с графским названием издательства, следует применять в паре с учебником математики за 6 класс тех же авторов, для которого оно было создано. И тогда должно получиться:
- построить графики;
- найти пропорциональную зависимость;
- производить манипуляции с числами;
- отличить осевую симметрию от центральной.
Популярный задачник
Все больше учеников применяют в своей учебе дополнительные «помощники». Решебники стали настольной книгой каждого ученика, без которой уже трудно обойтись. Они способны заменить даже репетиторов, потому что являются неким тренажером. Просмотреть разные варианты решений, сделать это столько раз, сколько нужно для полного понимания решений, а затем сверить свои ответы – это полезные функции ГДЗ. Четыре варианта правильных ответов самостоятельных, два варианта контрольных работ. Можно пользоваться решебником для проверки выполнения заданий в режиме онлайн. Жмем на нужный номер, и ответ перед вами. Остается действовать, а упорный труд приведет к хорошему результату.
геометрия дидактические материалы 8 класс мерзляк полонский якир гдз
СКАЧАТЬ ПО ПРЯМОЙ ССЫЛКЕ геометрия дидактические материалы 8 класс мерзляк полонский якир гдз
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Мы рекомендуем гдз английский 3 класс сборник упражнений быкова поспелова иногда гдз по русский разумовская 5 класс результаты гдз русский язык 4 класс дидактический материал л ю комиссарова гдз по алгебре 8 класс миндюк.макарычев вы искали геометрия дидактические материалы 8 класс мерзляк полонский якир гдз но мы стараемсягдз по математике тпо ерина 5 класс решебник география летягин 5 класс геометрия дидактические материалы 8 класс мерзляк полонский якир гдз гдз по русскому языку 4 класс соловейчик рабочая тетрадь геометрия дидактические материалы 8 класс мерзляк полонский якир гдз математика 4 класс рабочая тетрадь истомина решебник учебник 2 класс соловейчик гдз геометрия дидактические материалы 8 класс мерзляк полонский якир гдз гдз 6 класс математика н.я виленкин геометрия дидактические материалы 8 класс мерзляк полонский якир гдз русский язык 3 класс рабочий тетрадь гдз геометрия дидактические материалы 8 класс мерзляк полонский якир гдз гдз по русскому языку 4 класс 1 часть учебник ответы бунеев решебник по математике 4 класс моро 3 часть гдз русский язык 4 класс бунеев бунеева 1 часть решебник ответы геометрия дидактические материалы 8 класс мерзляк полонский якир гдз гдз по химии 8 класс. математика 5 класс решебник гдз гдз по математике 2 класс 2 часть м и моро с и волкова канакина русский язык рабочая тетрадь 2 класс 1 часть решебник геометрия дидактические материалы 8 класс мерзляк полонский якир гдз английский язык 8 класс кауфман рабочая тетрадь 2 часть гдз гдз математика петерсон рабочая тетрадь 3 класс геометрия дидактические материалы 8 класс мерзляк полонский якир гдз решебник по математике 6 класс. виленкин гдз математика 2 класс моро 2 часть ответы решебник геометрия дидактические материалы 8 класс мерзляк полонский якир гдз алгебра 10 клас мерзляк профільний рівень гдз геометрия дидактические материалы 8 класс мерзляк полонский якир гдз русский язык 10-11 класс 2 часть гольцова гдз геометрия дидактические материалы 8 класс мерзляк полонский якир гдз алгебра 11 класс мордкович 2 часть гдз гдз по географии 7 класс контурные карты гдз физика 7 класс пурышева важеевская геометрия дидактические материалы 8 класс мерзляк полонский якир гдз алгебра решебник 7 класс мерзляк 02012019 скачать алгебра 10 класс мордкович задачник pdf гдз 5 класс по математике колягин гдз по русскому языку 9.класс бархударов англ. яз 7 класс гдз кауфман решебник по рабочей тетради по геометрии 7 класс атанасян гдз по тетради по английскому языку гдз по проверочным работам 4 класс по математике с.и.волкова ответы алгебра 8 класс мерзляк гдз поглиблене вивчення гдз гдз по английскому языку афанасьева 7 класс 2 часть афанасьева михеева английский язык 7 класс 2015 учебник гдз решебник по русскому языку 9 класс львов львова гдз химия 8 класс оржековский гдз к пятёрке шаг за шагом 6 класс английский 7 класс биболётова рабочая тетрадь гдз гдз математика плешаков 4 класс гдз з укр мови вашуленко 3 клас ССЫЛКИ НА ПОХОЖИЕ САЙТЫ: ,,,,,,,
Построение cos x. Синус (sin x) и косинус (cos x)
В этом уроке мы подробно рассмотрим функцию y = cos x, ее основные свойства и график. В начале урока мы дадим определение тригонометрической функции y = cost на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции.В конце урока мы решим несколько простых задач, используя график функции и ее свойства.
Тема: Тригонометрические функции
Урок: функция y = стоимость, ее основные свойства и график
Функция — это закон, согласно которому каждое значение независимого аргумента связано с одним значением функции.
Вспомним определение функции Пусть будет t — любое действительное число.Он имеет единственную точку M на числовом круге. В точке M находится единственная абсцисса. Его называют косинусом числа t. Каждому значению аргумента t соответствует только одно значение функции (рис. 1).
Центральный угол численно равен величине дуги в радианах, то есть числу. Следовательно, аргумент может быть действительным числом или углом в радианах.
Если мы можем определить для каждого значения, мы можем построить график функции
Вы можете получить график функции другим способом.По формулам приведения так, что график косинуса представляет собой синусоиду, смещенную по оси x влево (рис. 2).
Свойства функции
1) Объем:
2) Диапазон значений:
3) Функция четная:
4) Наименьший положительный период:
5) Координаты точек пересечения с осью абсцисс:
6) Координаты точки пересечения с осью Y:
7) Интервалы, в которых функция принимает положительные значения:
8) Интервалы, в которых функция принимает отрицательные значения:
9) Интервалы по возрастанию:
10) Интервалы по убыванию:
11) Минимальное количество баллов:
12) Минимальная функция :.
13) Максимальное количество баллов:
14) Функция максимума:
Мы рассмотрели основные свойства и график функции. В дальнейшем они будут использоваться при решении задач.
Библиография
1. Алгебра и начало анализа, 10 класс (в двух частях). Учебник для учебных заведений (профильный уровень), под ред. А.Г. Мордкович. -М .: Мнемосина, 2009.
2. Алгебра и начало анализа, 10 класс (в двух частях).Проблемная книга для образовательных учреждений (профильный уровень), под ред. А.Г. Мордкович. -М .: Мнемосина, 2007.
.3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебник для учащихся школ и классов с углубленным изучением математики) .- М .: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М .: Просвещение, 1997.
5. Сборник задач по математике для поступающих в высшие учебные заведения (под ред. М.И. Сканави).- М .: Высшая школа, 1992.
.6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К .: А.С.К., 1997.
.7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задания по алгебре и принципы анализа (пособие для учащихся 10-11 классов общеобразовательных учреждений) .- М .: Просвещение, 2003.
.8. Карп А.П. Сборник задач по алгебре и принципам анализа: Учебное пособие. пособие на 10-11 классы с углубленным изучением математики.-М.: Образование, 2006.
Домашнее задание
Алгебра и начало анализа, 10 класс (в двух частях). Проблемная книга для образовательных учреждений (профильный уровень), под ред. А.Г. Мордкович. -М .: Мнемосина, 2007.
.№№ 16.6, 16.7, 16.9.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Урок и презентация на тему: «Функция y = cos (x). Определение и график функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.Все материалы проверены антивирусной программой.
Учебные пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
Алгебраические задачи с параметрами, 9-11 классы
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
1. Определение.
2. График функций.
3. Свойства функции Y = cos (X).
4. Примеры.
Определение функции косинуса y = cos (x)
Ребята, мы уже встречали функцию Y = sin (X).
Давайте вспомним одну из формул призраков: sin (X + π / 2) = cos (X).
Благодаря этой формуле мы можем утверждать, что функции sin (X + π / 2) и cos (X) идентичны, а их графики функций совпадают.
График функции sin (X + π / 2) получается из графика функции sin (X) путем параллельного сдвига π / 2 единиц влево. Это будет график функции Y = cos (X).
График функции Y = cos (X) также называется синусоидой.
Свойства функции cos (x)
- Запишем свойства нашей функции:
- Домен представляет собой набор действительных чисел.
- Функция четная. Вспомним определение четной функции. Функция вызывается, даже если выполняется равенство y (-x) = y (x). Как мы помним из формул-призраков: cos (-x) = — cos (x), определение выполнено, значит косинус является четной функцией.
- Функция Y = cos (X) убывает на отрезке и возрастает на отрезке [π; 2π].Мы можем видеть это на графике нашей функции.
- Функция Y = cos (X) ограничена снизу и сверху. Это свойство следует из того факта, что
-1 ≤ cos (X) ≤ 1 - Наименьшее значение функции равно -1 (при x = π + 2πk). Наибольшее значение функции равно 1 (при x = 2πk).
- Функция Y = cos (X) является непрерывной функцией. Посмотрим на график и убедимся, что наша функция не имеет разрывов, что означает непрерывность.
- Диапазон значений сегмента [- 1; 1].Это также хорошо видно на графике.
- Функция Y = cos (X) — периодическая функция. Давайте снова посмотрим на график и увидим, что функция принимает одни и те же значения через определенные промежутки времени.
Примеры с функцией cos (x)
1. Решите уравнение cos (X) = (x — 2π) 2 + 1
Решение: Построим 2 графика функции: y = cos (x) и y = (x — 2π) 2 + 1 (см. Рисунок).
y = (x — 2π) 2 + 1 — парабола, сдвинутая вправо на 2π и вверх на 1.Наши графики пересекаются в одной точке A (2π; 1), вот ответ: x = 2π.
2. Постройте график функции Y = cos (X) при x ≤ 0 и Y = sin (X) при x ≥ 0
Решение: Чтобы построить требуемый график, построим два графика функции «срезы». Первый срез: y = cos (x) для x ≤ 0. Второй срез: y = sin (x)
для x ≥ 0. Нарисуем обе «части» на одном графике.
3. Найдите наибольшее и наименьшее значение функции Y = cos (X) на отрезке [π; 7π / 4]
Решение: Построим график функции и рассмотрим наш отрезок [π; 7π / 4].График показывает, что наибольшее и наименьшее значения достигаются на концах отрезка: в точках π и 7π / 4 соответственно.
Ответ: cos (π) = -1 — наименьшее значение, cos (7π / 4) = наибольшее значение.
4. Постройте график функции y = cos (π / 3 — x) + 1
Решение: cos (-x) = cos (x), то желаемый график получается путем перемещения графика функции y = cos (x) на π / 3 единицы вправо и на 1 единицу вверх.
Задачи для самостоятельного решения
1) Решите уравнение: cos (x) = x — π / 2.2) Решите уравнение: cos (x) = — (x — π) 2 — 1.
3) Постройте график функции y = cos (π / 4 + x) — 2.
4) Постройте график функции y = cos (-2π / 3 + x) + 1.
5) Найдите наибольшее и наименьшее значение функции y = cos (x) на отрезке.
6) Найдите наибольшее и наименьшее значение функции y = cos (x) на отрезке [- π / 6; 5π / 4].
В этом уроке мы подробно рассмотрим функцию y = cos x, ее основные свойства и график. В начале урока мы дадим определение тригонометрической функции y = cost на координатной окружности и рассмотрим график функции на окружности и прямой.Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока мы решим несколько простых задач, используя график функции и ее свойства.
Тема: Тригонометрические функции
Урок: функция y = стоимость, ее основные свойства и график
Функция — это закон, согласно которому каждое значение независимого аргумента связано с одним значением функции.
Вспомним определение функции Пусть будет t — любое действительное число. Он имеет единственную точку M на числовом круге. В точке M находится единственная абсцисса. Его называют косинусом числа t. Каждому значению аргумента t соответствует только одно значение функции (рис. 1).
Центральный угол численно равен величине дуги в радианах, то есть числу. Следовательно, аргумент может быть действительным числом или углом в радианах.
Если мы можем определить для каждого значения, мы можем построить график функции
Вы можете получить график функции другим способом. По формулам приведения так, что график косинуса представляет собой синусоиду, смещенную по оси x влево (рис. 2).
Свойства функции
1) Объем:
2) Диапазон значений:
3) Функция четная:
4) Наименьший положительный период:
5) Координаты точек пересечения с осью абсцисс:
6) Координаты точки пересечения с осью Y:
7) Интервалы, в которых функция принимает положительные значения:
8) Интервалы, в которых функция принимает отрицательные значения:
9) Интервалы по возрастанию:
10) Интервалы по убыванию:
11) Минимальное количество баллов:
12) Минимальная функция :.
13) Максимальное количество баллов:
14) Функция максимума:
Мы рассмотрели основные свойства и график функции. В дальнейшем они будут использоваться при решении задач.
Библиография
1. Алгебра и начало анализа, 10 класс (в двух частях). Учебник для учебных заведений (профильный уровень), под ред. А.Г. Мордкович. -М .: Мнемосина, 2009.
.2. Алгебра и начало анализа, 10 класс (в двух частях).Проблемная книга для образовательных учреждений (профильный уровень), под ред. А.Г. Мордкович. -М .: Мнемосина, 2007.
.3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебник для учащихся школ и классов с углубленным изучением математики) .- М .: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М .: Просвещение, 1997.
5. Сборник задач по математике для поступающих в высшие учебные заведения (под ред. М.И. Сканави).- М .: Высшая школа, 1992.
.6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К .: А.С.К., 1997.
.7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задания по алгебре и принципы анализа (пособие для учащихся 10-11 классов общеобразовательных учреждений) .- М .: Просвещение, 2003.
.8. Карп А.П. Сборник задач по алгебре и принципам анализа: Учебное пособие. пособие на 10-11 классы с углубленным изучением математики.-М.: Образование, 2006.
Домашнее задание
Алгебра и начало анализа, 10 класс (в двух частях). Проблемная книга для образовательных учреждений (профильный уровень), под ред. А.Г. Мордкович. -М .: Мнемосина, 2007.
.№№ 16.6, 16.7, 16.9.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Grade 6 Coding 2020 Ontario Math- DIGITAL Google Slides: C.Алгебра
**** УРОВЕНЬ НАВЫКОВ КОДИРОВАНИЯ УРОВНЯ 6 УРОВЕНЬ ЦИФРОВОЙ ****
Впервые в программировании? Я тебя прикрыл!
Ищете версию для печати? Нажмите здесь
>>> Прежде чем покупать этот продукт, подумайте о покупке этого продукта со скидкой как полный комплект ЦИФРОВЫЕ СТРОПЫ АЛГЕБРЫ ВСЕГО УРОВНЯ 6 >>> Нажмите здесь <<<
Вы понятия не имеете, как обучать программированию или даже что такое кодирование?
Не смотрите дальше.В этой интерактивной и увлекательной цифровой загрузке вы и ваши ученики совершите невероятное путешествие по миру компьютерного кодирования с простыми для понимания и увлекательными уроками и упражнениями.
ПОЧЕМУ ЭТОТ ПРОДУКТ ПОКУПКУ МЕНЬШЕ ДРУГИХ?
- Мое видение преподавания математики всегда таково: «Не просто рассказывайте историю, позвольте учащимся испытать ее на собственном опыте. КАК?» — понимать язык с помощью идентифицируемых и связанных проблем
- В отличие от учебных слайдов, в этом продукте большое внимание уделяется консолидации концепций с использованием большого количества интерактивных и увлекательных мероприятий по отработке навыков
Этот продукт был разработан для дистанционного обучения и разработан, чтобы помочь снять часть стресса, связанного с настройкой онлайн-класса и обучением математике в цифровом формате.
Творческий компонент этого ресурса привлечет ваших учеников так, как это просто невозможно заучить по обычному механическому учебнику. В каждый слайд вложены часы творческой работы, помимо богатого содержания учебной программы и реальных связей. Приобретенные шрифты, клипарт, элементы дизайна и графика привлекут внимание ваших учеников и помогут стимулировать участие в их онлайн-обучении.
Что вы получите от этой загрузки:
- Полностью бесплатный блок, который проведет студентов через направление алгебры в НОВОЙ УЧЕБНОЙ ПРОГРАММЕ ONTARIO MATH 2020 (C3.Кодирование)
- Мыслить о реальных действиях, чтобы заинтересовать учащихся и вызвать интерес
- Совместимость с Google Slides — просто перейдите по ссылке, чтобы сделать копию для себя!
- Интерактивные слайды с подвижными элементами, позволяющие учащимся из первых рук стать компьютерными кодировщиками!
- Простые уроки, которые вовлекают и способствуют критическому мышлению
- Домашние связи, которые способствуют более глубокому мышлению и реальным связям
- Полный ключ ответа, расположенный в конце слайдов
- 42 слайды с подробными ответами
- Все встроенные шрифты, картинки и графика ЗАБЛОКИРОВАНЫ, чтобы учащиеся не могли изменять содержимое и перемещать многослойные элементы
- Текстовые поля и функции перетаскивания, встроенные в упражнения и задачи
- Все учебные программы ожидания, встроенные в этот ресурс для подотчетности
- Цели обучения расположены в начале блока
- Конец блока Google Forms Quiz
Обзор содержания учебной программы
- Понимание компьютерного кода и решение проблем, связанных с вычислительными процессами повтор esentations (C3.2, C3.1) (НОВИНКА!)
- Создание компьютерного кода ( C3.1) (НОВИНКА!)
- Узнайте, что такое ошибки и как отлаживать компьютерный код ( C3.2 ) ( NEW! )
******** Чтобы приобрести этот продукт со скидкой как часть полного набора для алгебры , щелкните здесь
_________________________________________________________________________________________
Я часто делаю рекламные акции и распродажи флэш-памяти.Следите за моим магазином, чтобы быть в курсе!
__________________________________________________________________________________________
Отзывы ТПТ помогают продавцам и покупателям. Пожалуйста, оставьте отзыв об этом продукте, если вам понравился. Все платные обзоры продуктов зарабатывают БЕСПЛАТНЫЕ кредиты TPT, которые можно использовать для будущих покупок.
Grade 6 Patterning Unit 2020 Ontario Math- DIGITAL Google Slides: Algebra
**** Grade 6 Patterning Unit ПОЛНОСТЬЮ ЦИФРОВОЙ ****
Перед покупкой этого продукта рассмотрите возможность приобретения его как части большего набора полные единицы из раздела Алгебра, которые можно найти здесь: Цифровой математический пакет для 6-го класса: Алгебра
ПОЧЕМУ ЭТОТ ПРОДУКТ ПОКУПКУ МЕНЬШЕ ДРУГИХ?
- Мое видение преподавания математики всегда таково: «Не просто рассказывайте историю, позвольте учащимся испытать ее на собственном опыте.КАК?
- Студенты будут шаг за шагом проходить через концепции учебной программы на понятном языке с использованием идентифицируемых и связанных проблем
- В этом продукте большое внимание уделяется объединению концепций с использованием широкий спектр интерактивных и увлекательных занятий по отработке навыков
Этот продукт был разработан для дистанционного обучения и призван помочь снять часть стресса, связанного с настройкой онлайн-класса и обучением математике в цифровом формате.
Творческий компонент этого ресурса привлечет ваших учеников так, как это просто невозможно заучить по обычному механическому учебнику. В каждый слайд вложены часы творческой работы, помимо богатого содержания учебной программы и реальных связей. Приобретенные шрифты, клипарт, элементы дизайна и графика привлекут внимание ваших учеников и помогут стимулировать участие в их онлайн-обучении.
Что вы получите от этой загрузки:
- Полностью бесплатный блок, который проведет студентов через направление алгебры в НОВОЙ УЧЕБНОЙ ПРОГРАММЕ ONTARIO MATH 2020 (C1.Шаблоны и взаимосвязи)
- Мыслить о реальных действиях, чтобы заинтересовать учащихся и вызвать интерес
- Совместимость с Google Slides — просто перейдите по ссылке, чтобы сделать копию для себя!
- Интерактивные слайды с заданиями
- Простые уроки, которые вовлекают и способствуют критическому мышлению
- Домашние связи, которые способствуют более глубокому мышлению и общению с реальным миром
- Ключ полного ответа находится в конце слайды
- 33 слайда с подробными ответами
- Все встроенные шрифты, картинки и графика ЗАБЛОКИРОВАНЫ, чтобы учащиеся не могли изменять содержимое и перемещать многоуровневые элементы
- Текстовые поля и функции перетаскивания, встроенные в действия и задачи
- Все ожидания по учебной программе встроены в этот ресурс для подотчетности
- Цели обучения расположены в начале блока
- Конец блока Google Forms Quiz
Обзор содержания учебной программы ******** Вторая цифровая единица в этой цепочке, , решающая уравнения Можно найти здесь ******** _____________________________________________________________________________ Следите за моим магазином, чтобы получать обновления бесплатные акции и новый контент! Мы просто перейдем к раскрытию скобок в выражениях, в которых заключенное в скобки выражение умножается на число или выражение.Сформулируем правило раскрытия скобок, которым предшествует знак минус: скобки вместе со знаком минус опускаются, а знаки всех терминов в скобках заменяются их противоположными. Одним из типов преобразования выражений является раскрытие скобок. Числовые, буквальные и переменные выражения могут быть составлены с использованием круглых скобок, которые могут указывать порядок выполнения действий, содержать отрицательное число и т. Д. Предположим, что в приведенных выше выражениях вместо чисел и переменных могут быть любые выражения. Обратим внимание еще на один момент, касающийся особенностей записи решения при раскрытии скобок. В предыдущем абзаце мы разобрались с тем, что называется раскрытием скобок. Для этого существуют правила открытия скобок, которые мы и собираемся рассмотреть. Это правило продиктовано тем, что положительные числа принято писать без скобок, скобки в этом случае не нужны. Выражение (−3.7) — (- 2) +4 + (- 9) может быть записано без скобок как −3.7 + 2 + 4−9. Наконец, третья часть правила просто связана с особенностями записи отрицательных чисел слева в выражении (которые мы упоминали в разделе о скобках для записи отрицательных чисел). Вы можете встретить выражения, состоящие из числа, знаков минус и нескольких пар круглых скобок. Если раскрыть скобки, переходя от внутренней к внешней, то решение будет следующим: — (- ((- (5)))) = — (- ((- 5))) = — (- (- 5 )) = — (5) = — 5. Вот объяснение: — (- 2 x) равно + 2 x, и поскольку это выражение находится в начале, + 2 x можно записать как 2 x, — (x2) = — x2, + (- 1 / x) = — 1 / x и — (2 x y2: z) = — 2 x y2: z.Первая часть написанного правила раскрытия скобок прямо следует из правила умножения отрицательных чисел. Вторая часть — следствие правила умножения чисел с разными знаками. Перейдем к примерам открывающих скобок в произведениях и частных двух чисел с разными знаками. Приведенное выше правило учитывает всю цепочку этих действий и значительно ускоряет процесс раскрытия скобок.Это же правило позволяет раскрывать круглые скобки в выражениях, которые являются продуктами, и частичными выражениями со знаком минус, которые не являются суммами и разностями. Рассмотрим примеры применения этого правила. Приведем соответствующее правило. Выше мы уже встречали выражения вида — (a) и — (- a), которые без скобок записываются как −a и a соответственно. Например, — (3) = 3 и. Это частные случаи указанного правила. Теперь давайте посмотрим на примеры раскрытия скобок, когда они содержат суммы или разности.Покажем примеры использования этого правила. Обозначим выражение (b1 + b2) как b, после чего воспользуемся правилом умножения скобки на выражение из предыдущего абзаца, имеем (a1 + a2) (b1 + b2) = (a1 + a2) b = (a1 b + a2 b) = a1 b + a2 b. По индукции это утверждение может быть расширено до произвольного числа членов в каждой скобке. Осталось раскрыть скобки в получившемся выражении, пользуясь правилами из предыдущих абзацев, в итоге получим 1 · 3 · x · y — 1 · 2 · x · y3 — x · 3 · x · y + x · 2 · х · у3. Это выражение является произведением трех множителей (2 + 4), 3 и (5 + 7 8). Раскрывать скобки придется последовательно. Теперь воспользуемся правилом умножения скобки на число, имеем ((2 + 4) 3) (5 + 7 8) = (2 3 + 4 3) (5 + 7 8). Степени, в основе которых лежат некоторые выражения, написанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. Например, преобразуем выражение (a + b + c) 2. Сначала запишем его в виде произведения двух скобок (a + b + c) b + b c + c a + c b + c c. Мы также скажем, что для возведения сумм и разностей двух чисел в натуральную степень рекомендуется использовать биномиальную формулу Ньютона. Например, (5 + 7-3): 2 = 5: 2 + 7: 2-3: 2. Не менее удобно сначала заменить деление на умножение, а затем использовать соответствующее правило открытия скобок в произведении. Осталось выяснить порядок открытия скобок на примерах. Возьмем выражение (−5) + 3 (−2): (- 4) −6 (−7). Подставьте эти результаты в исходное выражение: (−5) + 3 (−2): (- 4) −6 (−7) = (- 5) + (3 2: 4) — (- 6 7) … Осталось только завершить раскрытие круглых скобок, в результате имеем −5 + 3 · 2: 4 + 6 · 7. Это означает, что при переходе от левой части равенства к правой, скобки расширились. . Обратите внимание, что во всех трех примерах мы просто убрали круглые скобки.Сначала прибавьте 445 к 889. Это действие можно проделать в уме, но это не очень просто. Раскроем скобки и увидим, что измененный порядок действий значительно упростит расчеты. Наглядный пример и правило. Рассмотрим пример: Вы можете найти значение выражения, сложив 2 и 5, а затем взяв полученное число с противоположным знаком. Правило не меняется, если в скобках указано не два, а три и более терминов.Комментарий. Знаки меняются местами только перед терминами. В этом случае, чтобы раскрыть круглые скобки, необходимо запомнить свойство распределения. Ваша ошибка не в знаках, а в неправильном обращении с дробями? В 6 классе мы встречались с положительными и отрицательными числами … Как мы решаем примеры и уравнения? Сколько указано в скобках? А как насчет этих выражений? Конечно, результат первого и второго примеров одинаков, поэтому вы можете поставить между ними знак равенства: -7 + (3 + 4) = -7 + 3 + 4.Что мы сделали со скобками? Демонстрация слайда 6 с правилами открытия скобок. Таким образом, правила раскрытия скобок помогут нам решать примеры, упрощать выражения. Далее студентам предлагается работать в парах: необходимо использовать стрелки, чтобы соединить выражение, содержащее скобки, с соответствующим выражением без скобок. Slide 11 Оказавшись в Солнечном городе, Знайка и Незнайка спорили, кто из них правильно решил уравнение.Затем ученики решают уравнение самостоятельно, используя правила раскрытия скобок. Решение уравнений «Задачи урока: образовательные (закрепление ЗУНов по теме:» Открывающие скобки. Тема урока: «Раскрывающие скобки. В этом случае вам нужно умножить каждый член из первых скобок на каждый член из вторых скобок, а затем сложить результаты. Сначала берутся первые два множителя, заключенные в еще одну скобку, и внутри этих скобок скобки расширяются по одному из уже известных правил. rawalan.freezeet.ru Основная функция скобок — изменение порядка действий при вычислении значений числовых выражений . Например, , в числовом выражении \ (5 3 + 7 \) сначала будет вычисляться умножение, а затем сложение: \ (5 3 + 7 = 15 + 7 = 22 \). Но в выражении \ (5 Однако, если мы имеем дело с алгебраическим выражением , содержащим переменную — например, как это: \ (2 (x-3) \) — тогда значение в скобках не может быть вычислено, переменная мешает.Следовательно, в этом случае круглые скобки «открываются» с использованием соответствующих правил. Здесь необходимо уточнить, что в математике для сокращения записей принято не писать знак плюса, если он появляется первым в выражении. Например, если мы сложим два положительных числа, например семь и три, то мы будем писать не \ (+ 7 + 3 \), а просто \ (7 + 3 \), несмотря на то, что семь также является положительным числом .Аналогично, если вы видите, например, выражение \ ((5 + x) \) — знайте, что стоит перед круглой скобкой плюс, а не . Пример … Раскройте скобки и введите аналогичные термины: \ ((x-11) + (2 + 3x) \). Здесь необходимо уточнить, что а, пока оно было в скобках, имело знак плюс (просто не писали), а после снятия скобок этот плюс сменился на минус. Пример : упростить выражение \ (2x — (- 7 + x) \). Пример. Раскройте скобки и дайте аналогичные термины \ (5- (3x + 2) + (2 + 3x) \). Пример. Раскрыть квадратные скобки \ (5 (3-x) \). Пример. Раскройте квадратные скобки \ (- 2 (-3x + 5) \). Осталось рассмотреть последнюю ситуацию. Пример. Раскройте квадратные скобки \ ((2-x) (3x-1) \). Шаг 2. Увеличьте произведение скобок на множитель, как описано выше: Шаг 3. Теперь перемножим и дадим аналогичные слагаемые: Совсем не обязательно так подробно описывать все преобразования, можно сразу умножать.Но если вы только учитесь открывать круглые скобки — пишите подробно, будет меньше шансов ошибиться. Примечание ко всему разделу. На самом деле не нужно запоминать все четыре правила, достаточно запомнить только одно, это: \ (c (a-b) = ca-cb \). Почему? Потому что, если вы замените в нем один вместо c, вы получите правило \ ((a-b) = a-b \). А если подставить минус один, получится правило \ (- (a-b) = — a + b \). Что ж, если вместо c подставить другую скобку, можно получить последнее правило. Иногда на практике возникают проблемы с вложением скобок в другие скобки. Вот пример такой задачи: упростить выражение \ (7x + 2 (5- (3x + y)) \). Для успешного решения подобных задач необходимо: В этом случае важно, открывая одну из скобок , не трогать остальную часть выражения , просто переписав его как есть. Пример. Раскройте скобки и дайте аналогичные термины \ (7x + 2 (5- (3x + y)) \). Начнем задачу с раскрытия внутренней скобки (той, что внутри). Развернув его, мы имеем дело только с тем, что он имеет к нему прямое отношение — это сама скобка и минус перед ней (выделено зеленым цветом). Все остальное (не выбрано) переписывается как было. С помощью этой математической программы вы можете упростить многочлен. Программа полиномиального упрощения не просто дает ответ на проблему, она приводит к подробному решению с пояснениями, т.е.е. отображает процесс решения, чтобы вы могли проверить свои знания математики и / или алгебры. Данная программа может быть полезна учащимся общеобразовательных школ при подготовке к тестам и экзаменам, при проверке знаний перед экзаменом, родителям для контроля решения многих задач по математике и алгебре. А может быть, вам слишком дорого нанять репетитора или купить новые учебники? Или вы просто хотите как можно быстрее выполнить домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением. Таким образом, вы можете проводить собственное обучение и / или обучать своих младших братьев и сестер, в то время как уровень образования в области решаемых задач повышается. т.к. желающих решить проблему очень много, ваш запрос стоит в очереди. Среди различных выражений, рассматриваемых в алгебре, важное место занимают суммы одночленов.Вот примеры таких выражений: Сумма одночленов называется многочленом. Члены полинома называются членами полинома. Мономы также называют многочленами, считая, что одночлен — это многочлен, состоящий из одного члена. Мы представляем все термины как мономы стандартный вид: Приведем аналогичные слагаемые в получившемся полиноме: В результате получился многочлен, все члены которого являются одночленами стандартного вида, и среди них нет подобных.Такие полиномы называются полиномами стандартной формы . На степень многочлена стандартной формы принимают наибольшую из степеней его членов. Таким образом, двучлен имеет третью степень, а трехчлен — вторую. Обычно члены многочленов стандартной формы, содержащих одну переменную, располагаются в порядке убывания степени ее экспоненты. Например: Сумма нескольких многочленов может быть преобразована (упрощена) в стандартный многочлен. Иногда члены многочлена необходимо разделить на группы, заключив каждую группу в круглые скобки. Поскольку скобки противоположны раскрытию скобок, легко сформулировать правила раскрытия скобок: Если перед скобками стоит знак «+», то члены, заключенные в скобки, пишутся одинаковыми знаками. Если перед скобками стоит знак «-», то элементы, заключенные в скобки, пишутся противоположными знаками. Используя свойство распределения умножения, вы можете преобразовать (упростить) произведение одночлена и многочлена в многочлен. Например: Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена. Этот результат обычно формулируется как правило. Чтобы умножить одночлен на многочлен, вам нужно умножить этот одночлен на каждый из членов многочлена. Мы уже много раз использовали это правило для умножения на сумму. В общем, произведение двух многочленов тождественно равно сумме произведения каждого члена одного многочлена и каждого члена другого. Обычно используется следующее правило. Чтобы умножить многочлен на многочлен, вам нужно умножить каждый член одного многочлена на каждый член другого и сложить полученные произведения. С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее распространенными выражениями являются и, то есть квадрат суммы, квадрат разницы и разность квадратов. Вы заметили, что названия этих выражений неполные, поэтому, например, это, конечно, не просто квадрат суммы, а квадрат суммы a и b.Однако квадрат суммы a и b встречается не так часто, как правило, вместо букв a и b он содержит разные, иногда довольно сложные выражения. Выражения легко преобразовать (упростить) в многочлены стандартного вида, по сути, вы уже сталкивались с этой задачей при умножении многочленов: Полезно запомнить и применить полученные тождества без промежуточных вычислений. Этому помогают краткие словесные формулировки. — квадрат суммы равен сумме квадратов и удвоенного произведения. — квадрат разницы равен сумме квадратов без удвоения произведения. — разность квадратов равна произведению разницы на сумму. Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и наоборот — правые части левыми. Самое сложное — увидеть соответствующие выражения и понять, что в них заменяет переменные a и b.Давайте рассмотрим несколько примеров использования сокращенных формул умножения. Книги (учебники) Тезисы ЕГЭ и НГЭ тесты Онлайн игры, головоломки Функции построения Графический словарь русского языка Словарь молодежного сленга Справочник школ России Справочник средних учебных заведений России Справочник российских вузов Список задач Поиск НОД и упрощение НОК полинома (умножение полиномов) Деление полинома на столбец полинома Вычисление числовых дробей Решение задач в процентах Комплексные числа: сумма, разность, произведение и частное линейных уравнений Системы 2 с двумя переменными Решение квадратного уравнения Биномиальное возведение в квадрат и разложение на множители трехчлен Решение неравенств Решение систем неравенств Построение квадратичной функции Построение дробно-линейной функции Решение арифметических и геометрических прогрессий Решение тригонометрических, экспоненциальных, логарифмических уравнений Вычисление пределов, производная, касательная Интеграл, первообразная Решение треугольников Вычислительное действие s с векторами Расчет действий прямыми и плоскостями Площадь геометрических фигур Периметр геометрических фигур Объем геометрических тел Площадь поверхности геометрических тел www.mathsolution.ru Продолжаем изучать основы алгебры. В этом уроке мы узнаем, как раскрывать круглые скобки в выражениях. Раскрыть круглые скобки означает избавиться от выражения в скобках. Есть только два правила, которые вам нужно запомнить, чтобы открывать круглые скобки. При регулярной практике можно открывать скобки с закрытыми глазами, а те правила, которые требовалось выучить наизусть, можно смело забыть. Рассмотрим следующее выражение: Значение этого выражения — 2 … Раскроем скобки в этом выражении. Раскрытие скобок означает избавление от них, не влияя на смысл выражения. То есть после избавления от скобок значение выражения 8 + (- 9 + 3) все равно должно быть равно двум. Первое правило раскрытия скобок выглядит следующим образом: При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками. Итак, мы видим, что в выражении 8 + (- 9 + 3) перед скобками стоит плюс.Этот плюс необходимо опустить вместе со скобками. Другими словами, скобки исчезнут вместе с плюсом, который стоял перед ними. А то, что было в скобках, будет написано без изменений: 8−9 + 3 … Это выражение 2 , как и предыдущее выражение со скобками, было равно 2 . 8 + (- 9 + 3) и 8−9 + 3 8 + (−9 + 3) = 8 — 9 + 3 Пример 2. Раскрыть скобки в выражении 3 + (−1 — 4) Плюс перед скобками означает, что этот плюс опускается вместе со скобками. То, что было в скобках, останется без изменений: 3 + (-1 — 4) = 3 — 1 — 4 Пример 3. Раскрыть скобки в выражении 2 + (−1) V В этом примере раскрытие скобок стало своего рода обратной операцией замены вычитания сложением.Что это значит? В выражении 2−1 происходит вычитание, но его можно заменить сложением. Тогда вы получите выражение 2 + (- 1) … Но если в выражении 2 + (- 1) открываем скобки, получаем оригинал 2−1 . Следовательно, первое правило раскрытия скобок можно использовать для упрощения выражений после некоторых преобразований. То есть избавиться от скобок и упростить задачу. Например, упростим выражение 2a + a — 5b + b . Чтобы упростить это выражение, мы можем дать аналогичные термины. Напомним, чтобы вывести аналогичные термины, вам необходимо сложить коэффициенты таких терминов и умножить результат на общую буквенную часть: Получено выражение 3a + (- 4b) … Раскроем скобки в этом выражении. Перед скобками стоит плюс, поэтому мы используем первое правило для раскрытия скобок, то есть мы опускаем скобки вместе с плюсом, который стоит перед этими скобками: Таким образом, выражение 2a + a — 5b + b упрощается до 3a — 4b . Раскрыв одни скобки, по ходу могут встретиться другие. К ним применяем те же правила, что и к первым. Например, давайте расширим круглые скобки в следующем выражении: Есть два места, где нужно раскрыть скобки. В этом случае применяется первое правило раскрытия скобок, а именно исключение скобок вместе с плюсом, который стоит перед этими скобками: 2 + (−3 + 1) + 3 + (−6) = 2-3 + 1 + 3-6 Пример 3. Раскрыть скобки в выражении 6 + (- 3) + (- 2) В обоих местах, где встречаются круглые скобки, перед ними стоит плюс. Здесь снова применяется первое правило раскрытия скобок: Иногда первый член в скобках беззнаковый. Например, в выражении 1+ (2 + 3−4) первый член в скобках 2 написано без знака. Возникает вопрос, какой знак появится перед двумя скобками после опущения скобок и плюса перед скобками? Ответ напрашивается сам собой — перед двойкой будет плюс. На самом деле, даже в скобках стоит плюс перед двумя, но мы его не видим из-за того, что он не записан. Мы уже говорили, что полная запись положительных чисел выглядит как +1, +2, +3. Но по традиции плюсы не записываются, поэтому мы видим знакомые нам положительные числа. 1, 2, 3 . Следовательно, чтобы раскрыть скобки в выражении 1+ (2 + 3−4) , вам, как обычно, нужно опустить круглые скобки вместе с плюсом перед этими скобками, но записать первый член в круглых скобках со знаком плюс: 1 + (2 + 3 — 4) = 1 + 2 + 3 — 4 Пример 4. Раскрыть скобки в выражении −5 + (2-3) Перед скобками стоит плюс, поэтому мы применяем первое правило для раскрытия скобок, а именно, мы опускаем скобки вместе с плюсом, который стоит перед этими скобками. Но первый член, который мы пишем в скобках со знаком плюс: −5 + (2-3) = −5 + 2-3 Пример 5. Раскрыть скобки в выражении (−5) Перед круглой скобкой стоит плюс, но он не написан, потому что перед ним не было других чисел или выражений.Наша задача — убрать скобки, применив первое правило раскрытия скобок, а именно опустить скобки вместе с этим плюсом (даже если он не виден) Пример 6. Раскрыть скобки в выражении 2a + (−6a + b) Плюс перед скобками означает, что этот плюс опускается вместе со скобками. То, что было в скобках, будет написано без изменений: 2a + (−6a + b) = 2a −6a + b Пример 7. Раскрыть скобки в выражении 5a + (−7b + 6c) + 3a + (−2d) В этом выражении есть два места, где нужно раскрыть скобки. В обоих разделах перед скобками стоит плюс, что означает, что этот плюс опущен вместе со скобками. То, что было в скобках, будет написано без изменений: 5a + (−7b + 6c) + 3a + (−2d) = 5a −7b + 6c + 3a — 2d Теперь давайте посмотрим на второе правило раскрытия скобок.Используется, когда перед круглыми скобками стоит минус. Если перед скобками стоит минус, то этот минус опускается вместе со скобками, но члены, которые были в скобках, меняют свой знак на противоположный. Например, разверните круглые скобки в следующем выражении Мы видим, что перед скобками стоит минус. Итак, нужно применить второе правило раскрытия информации, а именно, опускать скобки вместе с минусом перед этими скобками.В этом случае члены, которые были в скобках, поменяют свой знак на противоположный: Получилось выражение без скобок 5 + 2 + 3 … Это выражение равно 10, как и предыдущее выражение со скобками было равно 10. Итак, между выражениями 5 — (- 2−3) и 5 + 2 + 3 можно поставить знак равенства, так как они равны одному и тому же значению: 5 — (-2-3) = 5 + 2 + 3 Пример 2. Раскрыть скобки в выражении 6 — (−2-5) Перед скобками стоит минус, поэтому мы применяем второе правило раскрытия скобок, а именно, мы опускаем скобки вместе с минусом перед этими скобками. В этом случае термины, которые были в скобках, пишутся с противоположными знаками: 6 — (-2-5) = 6 + 2 + 5 Пример 3. Раскрыть скобки в выражении 2 — (7 + 3) Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок: Пример 4. Раскрыть скобки в выражении — (- 3 + 4) Пример 5. Раскрыть скобки в выражении — (- 8-2) + 16 + (−9-2) Есть два места, где нужно раскрыть скобки. В первом случае нужно применить второе правило раскрытия скобок, а когда дело касается выражения + (- 9−2) нужно применить первое правило: — (- 8-2) + 16 + (−9-2) = 8 + 2 + 16 — 9 — 2 Пример 6. Раскрыть скобки в выражении — (- a — 1) Пример 7. Раскрыть скобки в выражении — (4a + 3) Пример 8. Раскрыть скобки в выражении a — (4b + 3) + 15 Пример 9. Раскрыть скобки в выражении 2a + (3b — b) — (3c + 5) Есть два места, где нужно раскрыть скобки.В первом случае вам нужно применить первое правило раскрытия скобок, а когда дело доходит до выражения — (3c + 5) , вам нужно применить второе правило: 2a + (3b — b) — (3c + 5) = 2a + 3b — b — 3c — 5 Пример 10. Раскрыть скобки в выражении −a — (−4a) + (−6b) — (−8c + 15) Есть три места, где вам нужно раскрыть скобки. Сначала нужно применить второе правило раскрытия скобок, затем первое, а затем снова второе: −a — (−4a) + (−6b) — (−8c + 15) = −a + 4a — 6b + 8c — 15 Правила раскрытия скобок, которые мы только что рассмотрели, основаны на распределительном законе умножения: Фактически открывающие скобки относится к процедуре, когда общий множитель умножается на каждый член в скобках.В результате этого умножения скобки исчезают. Например, раскроем скобки в выражении 3 × (4 + 5) 3 × (4 + 5) = 3 × 4 + 3 × 5 Следовательно, если вам нужно умножить число на выражение в скобках (или выражение в скобках для умножения на число), вам нужно сказать развернуть скобки . Но как распределительный закон умножения связан с правилами открытия скобок, которые мы рассматривали ранее? Дело в том, что перед скобками стоит общий множитель.В примере 3 × (4 + 5) общий множитель равен 3. … А в примере a (b + c) общим множителем является переменная a. Если перед скобками нет чисел или переменных, то общий множитель равен 1 или -1 , в зависимости от того, какой символ стоит перед круглыми скобками. Если перед круглыми скобками стоит плюс, то общий множитель равен 1. … Если перед круглыми скобками стоит минус, то общий множитель равен −1. . Например, расширим скобки в выражении — (3b — 1) … Перед скобками стоит минус, поэтому нужно использовать второе правило раскрытия скобок, то есть скобки опускать вместе с минусом перед скобами. А выражение, которое было в круглых скобках, следует писать с противоположными знаками: Мы расширили скобки с помощью правила раскрытия скобок. Но эти же скобки можно раскрыть с помощью закона распределения умножения.Для этого сначала напишем перед круглыми скобками общий множитель 1, которого не писали: Минус, который раньше стоял перед круглыми скобками, относился к данному устройству. Теперь вы можете расширить скобки, применив закон распределительного умножения. Для этого общий множитель −1 нужно умножить на каждый член в скобках и сложить полученные результаты. Для удобства заменим разницу в скобках на сумму: −1 (3b −1) = −1 (3b + (−1)) = −1 × 3b + (−1) × (−1) = −3b + 1 Как и в прошлый раз, мы получили выражение −3b + 1 … Все согласятся, что в этот раз на решение такого простого примера ушло больше времени. Поэтому разумнее использовать готовые правила раскрытия скобок, о которых мы говорили в этом уроке: Но знать, как работают эти правила, не помешает. В этом уроке мы изучили еще одно идентичное преобразование. Наряду с открытием скобок, заключением в скобки общего и приведением подобных терминов, вы можете немного расширить круг решаемых задач. Например: Здесь нужно выполнить два действия — сначала раскрыть скобки, а потом вывести аналогичные условия.Итак, по порядку: 1) Раскройте скобки: 2) Даем аналогичные термины: В полученном выражении −10b + (- 1) можно раскрыть скобки: Пример 2. Раскройте скобки и укажите аналогичные термины в следующем выражении: 1) Раскроем скобки: 2) Вот похожие термины. На этот раз, чтобы сэкономить время и место, мы не будем записывать, как коэффициенты умножаются на итоговую буквенную часть Пример 3. Упростите выражение 8m + 3m и найдите его значение при m = −4 1) Давайте сначала упростим выражение. Чтобы упростить выражение 8m + 3m , вы можете вынести в нем общий множитель m за скобки: 2) Найдите значение выражения m (8 + 3) при m = −4 … Для этого в выражении m (8 + 3) вместо переменной m подставьте число −4 м (8 + 3) = −4 (8 + 3) = −4 × 8 + (−4) × 3 = −32 + (−12) = −44 Среди различных выражений, рассматриваемых в алгебре, важное место занимают суммы одночленов.3 + 5x + 1 \) Сумму нескольких многочленов можно преобразовать (упростить) в стандартный многочлен. Иногда члены многочлена необходимо разделить на группы, заключив каждую группу в круглые скобки. Поскольку круглые скобки противоположны раскрытию скобок, легко сформулировать правила раскрытия скобок : Если перед скобками стоит знак «+», то члены, заключенные в скобки, записываются с теми же знаками.3 \) Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого члена многочлена. Этот результат обычно формулируется как правило. Чтобы умножить одночлен на многочлен, вам нужно умножить этот одночлен на каждый член многочлена. Мы уже много раз использовали это правило для умножения на сумму. В общем, произведение двух многочленов тождественно равно сумме произведения каждого члена одного многочлена и каждого члена другого.2 = (a — b) (a + b) \) — разность квадратов равна произведению разницы на сумму. Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и наоборот — правые части левыми. Самое сложное — увидеть соответствующие выражения и понять, что в них заменяет переменные a и b. Давайте рассмотрим несколько примеров использования сокращенных формул умножения. В этом уроке вы узнаете, как преобразовать выражение, содержащее круглые скобки, в выражение, не содержащее скобок.Вы узнаете, как раскрывать круглые скобки, которым предшествуют знак плюс и минус. Напомним, как раскрыть скобки с помощью распределительного закона умножения. Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое. Тема: Решение уравнений Урок: Расширение скобок Как раскрыть круглые скобки, перед которыми стоит знак «+». Использование комбинированного закона сложения. Если вам нужно добавить сумму двух чисел к числу, то вы можете сначала добавить к этому числу первый член, а затем второй. Слева от знака находится выражение в квадратных скобках, а справа — выражение без скобок. Это означает, что при переходе от левой части равенства к правой скобки были расширены. Давайте рассмотрим несколько примеров. Пример 1. Раскрывая скобки, мы изменили порядок действий.Считать стало удобнее. Пример 2. Пример 3. Обратите внимание, что во всех трех примерах мы просто убрали круглые скобки. Сформулируем правило: Комментарий. Если первый член в круглых скобках беззнаковый, он должен быть записан со знаком плюс. Вы можете шаг за шагом следовать примеру. Сначала прибавьте 445 к 889. Это действие можно проделать в уме, но это не очень просто.Раскроем скобки и увидим, что измененный порядок действий значительно упростит расчеты. Если следовать указанному порядку действий, то сначала нужно вычесть 345 из 512, а затем прибавить к результату 1345. Раскрывая круглые скобки, мы изменим порядок действий и значительно упростим вычисления. Иллюстративный пример и правило. Рассмотрим пример :. Вы можете найти значение выражения, сложив 2 и 5, а затем взяв полученное число с противоположным знаком.Получаем -7. С другой стороны, тот же результат может быть получен путем сложения противоположных чисел. Сформулируем правило: Пример 1. Пример 2. Правило не меняется, если в скобках указано не два, а три или более терминов. Пример 3. Комментарий. Знаки меняются местами только перед терминами. В этом случае, чтобы раскрыть скобки, необходимо запомнить свойство распределения. Сначала умножьте первую скобку на 2, а вторую на 3. Перед первой круглой скобкой стоит знак «+», что означает, что знаки необходимо оставить без изменений. Перед вторым стоит знак «-», следовательно, все знаки необходимо поменять на противоположные Библиография Домашнее задание Эта часть уравнения является выражением в скобках. Чтобы раскрыть скобки, посмотрите на знак перед скобками. Если стоит знак плюса, то при раскрытии скобок в записи выражения ничего не изменится: просто удалите скобки. Если стоит знак минус, при раскрытии скобок необходимо поменять все знаки изначально в скобках на противоположные.Например, — (2x-3) = — 2x + 3. Умножение двух скобок. Источники: Математические операции в скобках могут содержать переменные и выражения различной степени сложности. Для умножения таких выражений придется искать решение в общем виде, расширяя скобки и упрощая результат. Если в скобках указаны операции без переменных, только с числовыми значениями, то скобки открывать не нужно, так как если компьютер доступен его пользователю, доступны очень значительные вычислительные ресурсы — их проще использовать, чем упростить выражение. Инструкции Умножьте последовательно каждое (или минус c), содержащееся в одной скобке, на содержимое всех остальных скобок, если вы хотите получить общий результат. Например, пусть исходное выражение записывается так: (5 + x) ∗ (6-х) ∗ (x + 2). Тогда последовательное умножение (то есть раскрытие скобок) даст следующий результат: (5 + x) ∗ (6-x) ∗ (x + 2) = (5 ∗ 6-5 ∗ x) ∗ (5 ∗ x + 5 ∗ 2) + (6 ∗ xx ∗ x) ∗ (x ∗ x + 2 ∗ x) = (5 ∗ 6 ∗ 5 ∗ x + 5 ∗ 6 ∗ 5 ∗ 2) — (5 ∗ x ∗ 5 ∗ x + 5 ∗ х ∗ 5 ∗ 2) + (6 ∗ x ∗ x ∗ x + 6 ∗ x ∗ 2 ∗ x) — (х ∗ x ∗ x ∗ x + х ∗ x ∗ 2 ∗ x) = 5 ∗ 6 ∗ 5 * X + 5 * 6 * 5 * 2 — 5 * x * 5 * x — 5 * x * 5 * 2 + 6 * x * x * x + 6 * x * 2 * x — x * x * x * x — x * X * 2 * x = 150 * x + 300 — 25 * x² — 50 * x + 6 * x³ + 12 * x² — x * x³ — 2 * x³. Упростите результат за счет сокращения выражений. Например, выражение, полученное на предыдущем шаге, можно упростить следующим образом: 150 * x + 300 — 25 * x² — 50 * x + 6 * x³ + 12 * x² — x * x³ — 2 * x³ = 100 * x + 300 — 13 * x² — 8 ∗ x³ — x ∗ x³. Воспользуйтесь калькулятором, если вы хотите умножить x на 4,75, то есть (5 + 4,75) * (6-4,75) * (4,75 + 2). Чтобы вычислить это значение, перейдите на сайт поисковой системы Google или Nigma и введите выражение в поле запроса в его исходном виде (5 + 4.75) * (6-4,75) * (4,75 + 2). Google сразу же покажет 82.265625, не нажимая кнопку, а Nigma необходимо отправить данные на сервер одним нажатием кнопки. Допустим, Ахиллес бежит в десять раз быстрее черепахи и отстает от нее на тысячу шагов. За время, необходимое Ахиллу, чтобы пробежать это расстояние, черепаха проползет сотню шагов в том же направлении.Когда Ахилл пробежит сто шагов, черепаха проползет еще десять шагов и так далее. Процесс будет продолжаться бесконечно, Ахиллес никогда не догонит черепаху. Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт … Все они так или иначе считали апории Зенона. Шок был настолько сильным, что « … дискуссии продолжаются и в настоящее время, научное сообщество еще не успело прийти к единому мнению о сути парадоксов… математический анализ, теория множеств, новые физические и философские подходы были задействованы в исследовании вопроса; ни один из них не стал общепринятым решением вопроса … »[Википедия,« Апории Зенона »]. Все понимают, что их обманывают, но никто не понимает, что такое обман. С точки зрения В области математики Зенон в своей апории ясно продемонстрировал переход от величины к. Этот переход подразумевает применение вместо констант.Насколько я понимаю, математический аппарат для использования переменных единиц измерения либо еще не разработан, либо не применен к апории Зенона. Применение нашей обычной логики приводит нас в ловушку. Мы по инерции мышления применяем постоянные единицы измерения времени к обратным. С физической точки зрения это похоже на замедление времени до тех пор, пока оно полностью не остановится в тот момент, когда Ахиллес окажется на одном уровне с черепахой. Если время остановится, Ахиллес больше не сможет догнать черепаху. Если перевернуть привычную логику, все становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применить в этой ситуации понятие «бесконечность», то будет правильным сказать «Ахиллес бесконечно быстро догонит черепаху». Как избежать этой логической ловушки? Оставайтесь в постоянных единицах времени и не возвращайтесь назад.На языке Зенона это выглядит так: За время, в течение которого Ахиллес пробежит тысячу шагов, черепаха проползет сотню шагов в том же направлении. В следующий интервал времени, равный первому, Ахиллес пробежит еще тысячу шагов, а черепаха проползет сто шагов. Теперь Ахилл на восемьсот шагов впереди черепахи. Такой подход адекватно описывает реальность без каких-либо логических парадоксов. Но это не полное решение проблемы.Утверждение Эйнштейна о непреодолимости скорости света очень похоже на апорию Зенона «Ахилл и черепаха». Нам еще предстоит изучить, переосмыслить и решить эту проблему. И решение нужно искать не в бесконечно больших числах, а в единицах измерения. Другая интересная апория Зенона рассказывает о летящей стреле: Летящая стрела неподвижна, поскольку в каждый момент времени она находится в состоянии покоя, а поскольку она находится в состоянии покоя в каждый момент времени, она всегда находится в покое. В этой апории логический парадокс преодолеть очень просто — достаточно уточнить, что в каждый момент времени летящая стрела упирается в разные точки пространства, что, по сути, является движением. Здесь следует отметить еще один момент. По единственной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля необходимы две фотографии, сделанные с одной и той же точки в разные моменты времени, но невозможно определить расстояние от них.Для определения расстояния до машины нужны две фотографии, сделанные одновременно из разных точек пространства, но по ним нельзя определить факт движения (конечно, для расчетов еще нужны дополнительные данные, тригонометрия вам поможет) . На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не следует путать, потому что они предоставляют разные возможности для исследования. Различие между набором и мультимножеством очень хорошо задокументировано в Википедии.Мы смотрим. Как видите, «не может быть двух одинаковых элементов в наборе», но если в наборе есть идентичные элементы, такой набор называется «мультимножеством». Такая логика абсурда никогда не будет понятна разумным существам. Это уровень говорящих попугаев и дрессированных обезьян, которым не хватает интеллекта от слова «полностью». Математики действуют как обычные инструкторы, проповедуя нам свои абсурдные идеи. Однажды инженеры, строившие мост, находились в лодке под мостом во время испытаний моста.Если мост рухнет, некомпетентный инженер погибнет под обломками своего творения. Если бы мост выдерживал нагрузку, талантливый инженер строил бы другие мосты. Как бы математики ни прятались за фразой «чур, я в доме», а точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Эта пуповина — деньги. Применим математическую теорию множеств к самим математикам. Мы очень хорошо изучали математику и сейчас сидим на кассе, выдаем зарплаты.Вот и пришел к нам математик за свои деньги. Считаем ему всю сумму и раскладываем на нашем столе в разные стопки, в которые складываем купюры одного достоинства. Затем мы берем по одной банкноте из каждой стопки и передаем математику его «математический набор зарплат». Поясним математику, что остальные купюры он получит только тогда, когда докажет, что набор без идентичных элементов не равен набору с идентичными элементами. Здесь начинается самое интересное. Во-первых, сработает логика депутатов: «Можно применять к другим, нельзя применять ко мне!» Далее мы начнем уверять нас, что на купюрах одного достоинства есть разные номера банкнот, а это значит, что их нельзя считать одними и теми же элементами.Ладно, посчитаем зарплату монетами — цифр на монетах нет. Здесь математик начнет лихорадочно вспоминать физику: разные монеты имеют разное количество грязи, кристаллическая структура и расположение атомов в каждой монете уникальны … А теперь меня больше всего интересует Спросите: где граница, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой линии не существует — все решают шаманы, наука здесь не лежала. Посмотрите сюда. Подбираем футбольные стадионы с одинаковой площадью поля. Площадь полей такая же, значит, у нас есть мультимножество. Но если рассматривать названия одних и тех же стадионов, мы получаем много, потому что названия разные. Как видите, один и тот же набор элементов является одновременно и набором, и мультимножеством. Как это правильно? И тут математик-шаман-шуллер достает из рукава козырный туз и начинает рассказывать либо о множестве, либо о мультимножестве.В любом случае он убедит нас в своей правоте. Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая ее к реальности, достаточно ответить на один вопрос: чем элементы одного набора отличаются от элементов другого набора? Я покажу вам, без каких-либо «мыслимых как не единого целого» или «не мыслимых как целого». Сумма цифр числа — танец шаманов с бубном, не имеющий ничего общего с математикой.Да, на уроках математики нас учат находить сумму цифр числа и использовать ее, но именно поэтому они шаманы, чтобы научить своих потомков своим умениям и мудрости, иначе шаманы просто вымрут. Нужны доказательства? Откройте Википедию и попробуйте найти страницу суммы цифр числа. Его не существует. В математике нет формулы, по которой можно было бы найти сумму цифр любого числа. Ведь числа — это графические символы, с помощью которых мы пишем числа, а на языке математики задача звучит так: «Найдите сумму графических символов, представляющих любое число».Математики не могут решить эту задачу, но шаманы — это элементарно. Давайте посмотрим, что и как мы делаем, чтобы найти сумму цифр заданного числа. Итак, у нас есть число 12345. Что нужно сделать, чтобы найти сумму цифр этого числа? Проделаем все шаги по порядку. 1. Записываем номер на листке бумаги. Что мы наделали? Мы преобразовали число в графический символ числа. Это не математическая операция. 2. Разрезаем одну получившуюся картинку на несколько картинок, содержащих отдельные числа. Вырезание картинки — это не математическая операция. 3. Преобразуйте отдельные графические символы в числа. Это не математическая операция. 4. Сложите полученные числа. Вот это математика. Сумма цифр 12345 равна 15. Это «курсы кройки и шитья» шаманов, используемые математиками. Но это еще не все. С точки зрения математики не имеет значения, в какой системе счисления мы записываем число.Итак, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления обозначается нижним индексом справа от числа. С большим числом 12345 не хочу морочить голову, считайте число 26 из статьи про. Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, мы это уже сделали. Посмотрим на результат. Как видите, в разных системах счисления сумма цифр одного и того же числа разная.Этот результат не имеет ничего общего с математикой. Это как если бы вы получили совершенно разные результаты при определении площади прямоугольника в метрах и сантиметрах. Ноль во всех системах счисления выглядит одинаково и не имеет суммы цифр. Это еще один аргумент в пользу того, что. Вопрос к математикам: как в математике обозначается то, что не является числом? Что для математиков не существует ничего, кроме чисел? Для шаманов я могу это допустить, а для ученых — нет.Реальность — это не только числа. Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, то это не имеет ничего общего с математикой. Что такое настоящая математика? Это когда результат математического действия не зависит от величины числа, используемой единицы измерения и от того, кто выполняет это действие. Ой! Разве это не женский туалет? правил и примеров (7 класс)
Как раскрыть скобки?
Раскрытие скобок: правила, примеры, решения.
Правило в математике — открывать скобки, если перед скобками стоят (+) и (-).
Как раскрыть круглые скобки до разной степени
Одиночные числа в скобках
Расширение скобок: правила и примеры (7 класс)
Правила расширения кронштейна
Если перед круглой скобкой стоит знак «плюс», то скобка просто удаляется, а выражение в ней остается без изменений. Другими словами:
Раствор : \ ((х-11) + (2 + 3x) = х-11 + 2 + 3x = 4x-9 \). Если перед круглой скобкой стоит знак минус, то при удалении скобки каждый член выражения внутри нее меняет свой знак на противоположный:
Раствор : внутри скобки два члена: \ (- 7 \) и \ (x \), а перед скобкой стоит минус. Это значит, что знаки поменяются — и семерка теперь будет со знаком плюс, а x — с минусом. Раскрываем скобки и даем аналогичные термины .
Раствор : \ (5- (3x + 2) + (2 + 3x) = 5-3x-2 + 2 + 3x = 5 \). Если перед скобкой стоит множитель, то каждый член скобки умножается на него, то есть:
Раствор : В скобке есть \ (3 \) и \ (- x \), а перед скобкой стоит пятерка. Следовательно, каждый член скобки умножается на \ (5 \) — я напоминаю вам, что знак умножения между числом и круглой скобкой не записывается в математике для уменьшения размера записей .
Раствор : Как и в предыдущем примере, \ (- 3x \) и \ (5 \) умножаются на \ (- 2 \). При умножении скобки на скобку каждый член первой скобки умножается на каждый член второй:
Раствор : У нас есть произведение в круглых скобках, и его можно сразу расширить, используя формулу выше. Но чтобы не запутаться, давайте делать все по шагам.
Шаг 1. Снимаем первую скобку — каждый ее член умножаем на вторую скобку:
— первый первый … Круглые скобки в скобках
— внимательно разбираться во вложенности скобок — какая из них в какую;
— раскрывать круглые скобки последовательно, начиная, например, с самой внутренней.
Возьмем в качестве примера вышеуказанную задачу.
Решение: Решение математических задач онлайн
Онлайн калькулятор.
Упрощение полинома.
Умножение многочленов.
В процессе работы программа:
— умножает многочлены
— суммирует одночлены (дает похожие)
— раскрывает скобки
— возводит многочлен в степень
Через несколько секунд решение появится ниже.
Подождите секунду. Немного теории.
Произведение одночлена и многочлена. Полиномиальная концепция
Преобразование (упрощение) произведения одночлена и многочлена
Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
Сокращенные формулы умножения. Сумма квадратов, разности и разности квадратов
Конструктор дорожных ситуаций
Погода — новости — гороскопы Кронштейны раздвижные
Первое правило раскрытия скобок
Второе правило раскрытия скобок
Механизм расширения кронштейна
Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
Если уравнение содержит произведение двух круглых скобок, круглые скобки расширяются как обычно. Каждый член в первой скобке умножается на каждый член во второй скобке. Полученные числа суммируются. В этом случае произведение двух «плюсов» или двух «минусов» дает слагаемому знак «плюс», а если множители имеют разные знаки, то получает знак «минус».
Давайте рассмотрим. 2-17x-4.3
Формулы для возведения выражения больше трех можно составить с помощью треугольника Паскаля. среда, 4 июля 2018 г.
Воскресенье, 18 марта 2018 г.
Знак на двери
— Молодая женщина! Это лаборатория по изучению безудержной святости душ во время вознесения на небеса! Ореол сверху и стрелка вверх.


 С помощью этих материалов они могут самостоятельно повторить курс классической математики за шестой класс, поскольку именно в этом классе завершается изучение этой дисциплины;
С помощью этих материалов они могут самостоятельно повторить курс классической математики за шестой класс, поскольку именно в этом классе завершается изучение этой дисциплины;