6 класс виленкин жохов: Номер №373 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

Номер №419 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

войтирегистрация

1. Ответкин
2. Решебники
3. 6 класс
4. Математика
5. Виленкин
6. Номер №419

НАЗАД К СОДЕРЖАНИЮ

2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №419 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №419 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.

Условие 20132019г.

Cменить на 2013 г.

Cменить на 2019 г.

Бочки горючего хватает для работы одного двигателя на 7 ч, а другого — на 5 ч. Какая часть горючего останется от полной бочки после 2 ч работы первого двигателя и 3 ч работы второго двигателя?

Выполните действие:
а) 91 1/6 + 3 5/18; г) 39 5/6 + 12 5/9; ж) 4 + 3 3/7;
б) 1 4/15 + 2 3/20; д) 36 5/7 + 12 7/8; з) 8 7/9 + 3.
в) 5 1/8 + 41 7/12; е) 5 2/3 + 3/4;

Решение 1

Решение 1

Решение 2

Решение 2

Решение 3

Решение 3

ГДЗ по Математике 6 класс: Виленкин Н.Я.

Издатель: Виленкин Н.Я. Жохов В. И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.

ГДЗ по Математике 6 класс: Мерзляк А.Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.

ГДЗ по Математике 6 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018

ГДЗ по Математике 6 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.

ГДЗ по Математике 6 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

© OTVETKIN.INFO

Классы

Предметы

Номер №420 — ГДЗ по Математике 6 класс: Виленкин Н.

Я.

войтирегистрация

1. Ответкин
2. Решебники
3. 6 класс
4. Математика
5. Виленкин
6. Номер №420

НАЗАД К СОДЕРЖАНИЮ

2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №420 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №420 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.

Условие 20132019г.

Cменить на 2013 г.

Cменить на 2019 г.

Для экспедиции, работающей в тайге, сбросили с вертолёта упаковку с продуктами, которая упала на землю через 3 с. С какой высоты была сброшена эта упаковка, если в первую секунду она пролетела 4 9/10 м, а в каждую следующую секунду она пролетала на 9 4/5 м больше, чем в предыдущую?

Найдите значение разности:
а) 1 — 8/15;  г) 7 3/8 — 5;         ж) 10 3/23 — 7 19/46;
б) 3 — 2/11;  д) 45 — 44 3/8;     з) 16 2/5 — 4 3/7;
в) 4 — 3 4/9; е) 6 7/15 — 3 1/5; и) 19 5/12 — 8 17/18.

Решение 1

Решение 1

Решение 2

Решение 2

Решение 3

Решение 3

ГДЗ по Математике 6 класс: Виленкин Н. Я.

Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.

ГДЗ по Математике 6 класс: Мерзляк А.Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.

ГДЗ по Математике 6 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018

ГДЗ по Математике 6 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.

ГДЗ по Математике 6 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

© OTVETKIN. INFO

Классы

Предметы

Делители и кратные. Делители и кратные, определения и примеры

§ 1 Делитель и кратное — определение понятий

На этом уроке вы узнаете, что такое делитель и что такое кратное натуральных чисел, и научитесь их находить.

Давайте вспомним, какие числа называются натуральными числами? Это числа, которые используются при счете, например: 1, 2, 3, 4…

Решим задачу:

Летом три мальчика пошли на рыбалку и поймали 9щуки. Весь свой улов они складывали в одно ведро. Пайк решил поделить поровну. Сколько рыбок достанется каждому мальчику?

Таким образом, каждый мальчик получит по 3 рыбки.

3 называется делителем 9, потому что 9 делится на 3 без остатка.

А теперь посмотрим, что будет, если мальчиков будет не три, а четыре.

В этом случае всю рыбу нужно разделить на четыре

9:4=2 (1 в остатке), т.е. каждый мальчик получит по 2 щуки и одна рыба останется в ведре. Это означает, что число 4 не является делителем числа 9., так как 9 не делится на 4 без остатка.

делитель натурального числа а — это натуральное число, на которое а делится без остатка.

Обратите также внимание, что любое натуральное число делится на единицу без остатка, поэтому 1 является наименьшим делителем для всех натуральных чисел. А наибольшим делителем любого натурального числа является само число.

Следовательно, натуральное число 9 имеет три делителя: 1, 3, 9.

Именно на эти числа 9 делится без остатка. 9:1=9, 9:3=3, 9:9=1.

Теперь вернемся к нашей задаче:

Три парня поделили между собой поровну 9 щук, каждый получил по 3 рыбы.

9 считается кратным 3, потому что 9 делится на 3 без остатка.

Немного изменим условия задачи:

А если поймали 10 щук? Сколько рыбы досталось каждому?

10:3=3 (осталась 1)

В этом случае каждый мальчик получил бы по 3 рыбки, а в ведре осталась бы 1 щука. Число 10 не кратно 3, потому что 10 не делится на 3 без остатка.

Кратное натурального числа а — это натуральное число, которое делится на а без остатка.

§ 2 Нахождение делителя и кратного

Необходимо правильно употреблять слова кратный и кратный.

Обычно говорят: число девять кратно трем, или девять кратно трем.

При использовании слова «несколько»: число девять кратно трем, или девять кратно трем.

Существует много натуральных чисел, которые делятся на 3 без остатка, например: 3, 12, 39, 96 и т. д. Все эти числа кратны 3.

Получить их очень просто, нужно умножить 3 на 1, 2, 3, 4 и т. д.

Например: 3*1=3 , 3*2=6, 3*3=9, 3*4=12 и т. д.

Таким образом, любое натуральное число имеет бесконечное число кратных. Обратите внимание, что наименьшим кратным любого натурального числа является само число.

Но при этом число 3 для чисел 3, 6, 9, 12 и т.д. будет делителем. Числа, являющиеся также делителями некоторых чисел, называются их общими делителями.

Итак, на уроке мы познакомились с понятиями делитель и кратное натуральных чисел и научились их находить.

Список использованной литературы:

1. Матем. 6 класс. Учебник. Виленкин Н.Я., Жохов В.И. и др., 2013. — 288 с.
2. Считаем без ошибок. Работа с самопроверкой по математике 5-6 классы. Минаева С.С. — 2014.
3. Матем. 6 класс. И.И. Зубарева, А.Г. Мордкович. 2009.

Эта статья о делителях и кратных. Здесь мы разъясняем эти понятия, формулируем определения, приводим примеры делителей и различных кратных (мы пока будем рассматривать только целые числа). Отдельно остановимся на делителях 1 и -1, а также делителях и кратных 0.

Основные определения

Сначала сформулируем определения для целого числа.

Определение 1

Делителем целого числа а называется число b, на которое а делится без остатка.

Если вспомнить такое понятие, как делимость, то эту формулировку можно немного изменить.

Определение 2

Делителем целого числа a является такое число b, которое в сочетании с некоторым числом q дает равенство a = b q .

Когда мы говорим о том, что число b является делителем целого числа a , это означает, что b делит a , что можно кратко записать как b | а или б \ а .

Согласно определению целых чисел, а также свойствам умножения целых чисел любое целое число можно разделить на единицу и само на себя, то есть на а = а 1 и а = 1 а . Зная свойства умножения, мы также можем вывести равенства a = (− a) (− 1) и a = (− 1) (− a) . Из них следует, что у a будет еще два делителя, равные −a и −1. Следовательно, мы всегда можем разделить целое число a на a , − a , 1 и − 1. . Например, число 12 делится на 12, -12, 1 и -1.

Остановимся на делителях таких чисел, как ноль, единица и минус один. Так как мы знакомы со свойствами делимости, то можем сделать вывод, что любое целое число (включая сам 0) может стать делителем 0, а единица и минус единица имеют только делители, равные 1 и — 1 соответственно.

Таким образом, 0 всегда будет иметь бесконечное количество делителей в виде целых чисел (включая ноль), а 1 и − 1 будут иметь только 2 делителя — единицу и минус единицу. Минимальное количество делителей для любого целого числа a равно четырем. Они включают a , − a , 1 и − 1 .

Какие еще примеры делителей можно привести в случае целых чисел?

Пример 1

Итак, 8 можно разделить на — 2, потому что равенство 8 = (− 2) (− 4) верно (при необходимости повторить материал об умножении целых чисел). Мы также можем разделить восьмерку на — 8, — 4, — 1, 1, 2, 4, 8, но — 3 не входит в состав делителей, так как числа q, для которых выполняется равенство

8 = (− 3) q было бы верно, но не существует. То есть мы можем разделить 8 на — 3 только с остатком. Кроме указанных делителей, мы не можем делить восьмерку ни на какие целые числа без остатка.

Рассмотренные выше примеры говорят нам о том, что не только положительные, но и отрицательные целые числа могут выступать в качестве делителей целого числа. Эта возможность обосновывается одним из свойств делимости: если b является делителем целого числа a, то противоположное ему число — b также будет его делителем. Поэтому можно рассматривать только случаи с положительными делителями и просто распространять полученные результаты на отрицательные.

Напомним также еще одно свойство делимости, которое гласит, что если целое число b является делителем a , то a делится на — b , следовательно, наборы делителей для положительного и отрицательного a будут одинаковыми. Это правило еще раз подтверждает возможность работы только с положительными числами для простоты и краткости вычислений.

У единицы есть только один положительный делитель — сама единица. Это отличает 1 от других натуральных чисел, так как другие имеют как минимум 2 делителя: кроме одного, они могут делиться на равные сами себе числа. В зависимости от того, есть ли делители, отличные от самого числа и единицы, различают простые и составные числа.

Наименьшим положительным делителем числа а является единица (если само число а не равно 1),
и число а является наибольшим положительным делителем самого себя (подробнее о сравнении трех и более натуральных чисел мы писали в отдельная статья). Таким образом, для любого натурального числа a положительный делитель b будет удовлетворять условию 1 ≤ b ≤ a . Важную роль здесь также играет наибольший общий делитель (НОД), о котором мы поговорим отдельно.

Понятие кратности

Начнем, как всегда, с определения.

Определение 3

Число a называется кратным b, если оно делится на b без остатка.

Другими словами, кратным b является некоторое число a, для которого будет верно равенство a = b q (здесь q — некоторое целое число). Если у нас есть a, кратное b, мы говорим, что a кратно b. Вы можете написать это так: a ⋮ b .

Между множественным и делимым существует совершенно определенная связь. На самом деле, если a кратно b, то b будет делителем этого числа, и наоборот.

Возьмем несколько примеров кратных.

Пример 2

Значит — 12 будет кратно 3, потому что — 12 = 3 (- 4) . Тройка имеет много других кратных, например, 0, 3, − 3, 6, − 6, 9, − 9 и т. д. И 5 не будет кратным 3, так как не существует такого q, для которого выполняется равенство было бы верно 7 = 3 q .

Согласно определению кратности, 0 будет кратным любому b , включая ноль. Доказательством является равенство 0 = b 0 Потому что умножение любого числа на ноль дает ноль.

Уточняем также, что для любого целого числа b бесконечно много кратных, и любое целое число, соответствующее произведению b q , где q – любое целое число, будет кратно b .

Наименьшим положительным кратным положительного числа является само число. Обратите внимание, что наименьшее кратное в этом случае не следует путать с наименьшим общим кратным кратных чисел (НОК).

Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl+Enter

В этой статье мы обсудим делители и кратные . Здесь мы даем определения делителя и кратного. Эти определения позволят нам привести примеры делителей и кратных различных целых чисел. Мы отдельно рассмотрим делители единицы и минус один, а также поговорим о делителях и кратных нулю.

Навигация по страницам.

Числовые делители – определение, примеры

Сначала давайте определение делителя целого числа.

Определение.

делитель целое число a называется целым числом b , на которое a делится без остатка.

Натуральное число 1 имеет только один положительный делитель — это число 1. Этот факт отличает единицу от других натуральных чисел, так как натуральные числа, отличные от единицы, имеют по крайней мере два делителя, а именно само себя и 1. В зависимости от отсутствия или наличия делителей, отличных от самого натурального числа, и от единицы различают простые и составные числа.

Единица — наименьший положительный делитель натурального числа a, отличного от 1, а само число a — наибольший положительный делитель (о наибольшем и наименьшем числе мы говорили в разделе). То есть для любого натурального числа a любой его положительный делитель b удовлетворяет условию .

Множители — определение, примеры

Дадим множественное определение .

Определение.

Несколько целых чисел b — это целое число a , которое без остатка делится на b.

Другими словами, кратным целому числу b является целое число a , которое может быть представлено в виде a=b·q , где q — некоторое целое число.

Если a кратно целому числу b , то говорят, что a кратно b . В этом случае используется обозначение ab.

Определение кратного и делимого ясно указывает на связь между ними. Действительно, по определению, если а кратно b, то b кратно а, и наоборот, если b кратно а, то а кратно b.

Приведем примера кратных . Например, целое число -12 кратно 3, потому что -12=3·(-4) . Другими числами, кратными 3, являются целые числа 0, 3, −3, 6, −6, 9, −9 и так далее. Но число 7 не кратно целому числу 3, так как 7 не делится на 3 без остатка, то есть не существует такого целого числа q, при котором выполняется равенство 7=3 q.

Из определения кратного видно, что ноль кратен любому целому числу b, включая ноль. Равенство 0=b 0 в этом случае выглядит очень убедительно.

Обратите внимание, что существует бесконечно много кратных любому целому числу b , поскольку существует бесконечно много целых чисел, и любое целое число, равное произведению b q , где q — произвольное целое число, кратно b .

Наименьшее положительное кратное данного положительного числа а есть само число а. Здесь стоит обратить внимание на то, что наименьшее положительное кратное не следует путать с наименьшим общим кратным (НОК) нескольких чисел.

Далее можно рассматривать только натуральные кратные целых положительных чисел. Мы можем сделать это по тем же причинам, которые были упомянуты в первом абзаце этой статьи, при этом не будет нарушена общность изложения.

Библиография.

• Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
• Виноградов И.М. Основы теории чисел.
• Михелович Ш.Х. Теория чисел.
• Куликов Л.Я. и другие. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физико-математических факультетов. специальности педагогических институтов.

«Дивизоры и кратные» — Учебник по математике 6 класс (Виленкин)

Краткое описание:

В этом разделе вы узнаете, какое число называется кратным, а какое делителем. Вам нужно хорошо выучить эти определения, потому что потом вы будете постоянно ими пользоваться.
Но сначала повторим, какие числа мы называем натуральными числами. Натуральные числа — это числа, с помощью которых мы можем подсчитать количество различных объектов. Например, на столе пять бананов. Как мы их считаем: один банан, два, три, четыре, пять. Подсчитав бананы, мы получили цифру 5, что естественно. Сразу возникает вопрос: является ли число ноль натуральным? Нет, это не так. Мы не стали считать бананы с нуля: ноль бананов, раз, два. Следовательно, натуральные числа начинаются с единицы.
А какое число можно назвать делителем натурального числа? По определению делитель натурального числа (назовем его Большим) — это натуральное число, на которое Большое делится полностью, то есть целиком, то есть без остатка, абсолютно, совершенно без остатка.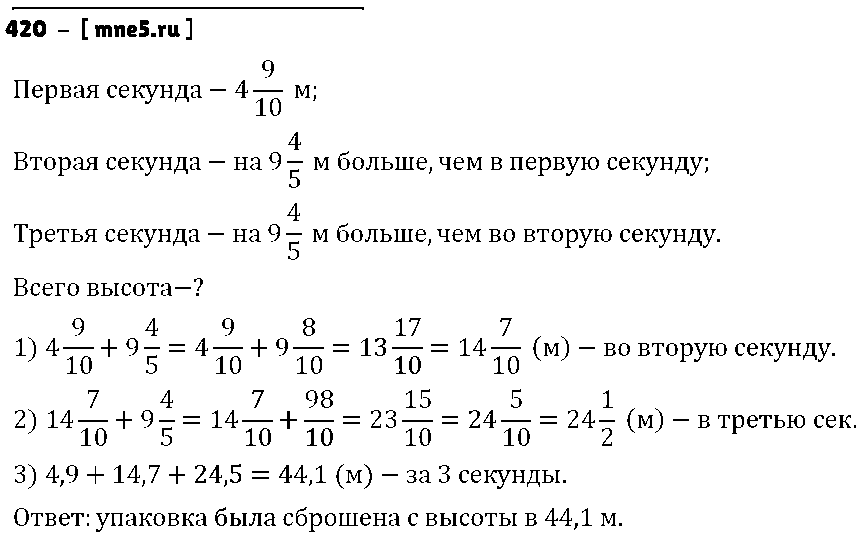 Например, на бальные танцы ходят 10 девочек и 9 мальчиков. Можно ли разделить мальчиков так, чтобы у каждой девочки был партнер? Нет, мальчики не делят партии, поэтому 1 мальчик может танцевать только с 1 девушкой за раз. У всех ли девушек есть партнер? Нет, одна девушка останется без партнера — она ​​останется. А если придет еще один мальчик и их будет 10, то 10 мальчиков и 10 девочек прекрасно спарятся, то есть девочки не останется и мальчиков не надо будет делить на части. То есть 10 делится на 10 без остатка, получается, что число 10 является делителем числа 10. Как запомнить это определение. Все просто. Делитель — это число, которое делит что-то.
Немного сложнее с кратными. Кратное — это наше Большое число, которое готово делить на делитель, но только без остатка. Например, в каждой упаковке «Баунти» содержится 2 конфеты. Мама разрешила брать их в школу, но с одним условием: конфеты должны быть в упаковке. Вы хотите взять 5 конфет, чтобы угостить друзей, но вы не можете взять конфету без обертки в школу и поэтому вам нужно взять 3 упаковки, то есть 6 конфет.