6 класс номер 30 виленкин: Номер №30, Часть 2 - ГДЗ по Математике 6 класс: Виленкин Н.Я.

Содержание

Номер №30 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

войтирегистрация

Ответкин
Решебники
6 класс
Математика
Виленкин
Номер №30

НАЗАД К СОДЕРЖАНИЮ

2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №30 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №30 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.

Условие 20132019г.

Cменить на 2013 г.

Cменить на 2019 г.

Выполните действия:
а) 18,36 + 0,64 : 0,8; в) 3,44 : 0,4 + 24,56;
б) 80 * 11 — 42 558 : 519; г) 684 * 245 — 675 * 246.

Решение 1

Решение 2

Решение 3

ГДЗ по Математике 6 класс: Виленкин Н.Я.

Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.

ГДЗ по Математике 6 класс: Мерзляк А.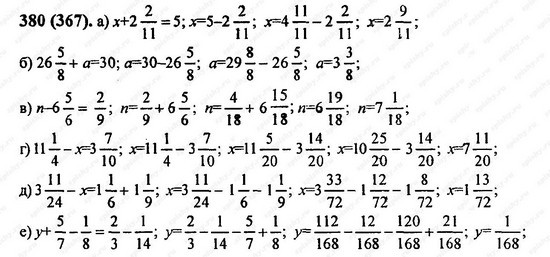 Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.

ГДЗ по Математике 6 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018

ГДЗ по Математике 6 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.

ГДЗ по Математике 6 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

Классы

Предметы

Номер 30 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020.

Часть 1 (решебник)Номер 30 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая/Старая версия

ЧАСТЬ 1
Выберите номер упражнения

ЧАСТЬ 2
Выберите номер упражнения

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595

Adblock
detector

[PDF] Голографическая мультивселенная и проблема меры

1ГолографическаяМА, title={Голографическая мультивселенная и проблема меры}, автор={Александр Виленкин}, journal={Журнал космологии и физики астрочастиц}, год = {2011}, том={2011}, страницы = {032-032} }
- А.
  Виленкин
- Опубликовано 6 марта 2011 г.
- Математика
- Журнал космологии и физики астрочастиц
Мы обсуждаем предполагаемую в более ранней работе двойственность между волновой функцией мультивселенной и трехмерной евклидовой теорией на будущей границе пространства-времени. В частности, мы обсуждаем выбор граничной метрики и связь между УФ-масштабом обрезания ξ на границе и гиперповерхностью Σ, на которой волновая функция определена в объеме. Мы предлагаем в пределе ξ → 0 использовать эту гиперповерхность в качестве поверхности среза в мере мультивселенной. Более того, мы утверждаем…
Посмотреть PDF на arXiv
Голографическая безграничная мера
- Т. Хертог, Дж. Хартл
- Математика
- 2012
A аннотацияМы показываем, что комплексные седловые точки безграничной волновой функции с положительная космологическая постоянная и положительный скалярный потенциал имеют представление, в котором геометрия…

голографическая безграничная мера
Мы показываем, что комплексные седловые точки безграничной волновой функции с положительной космологической постоянной и положительным скалярным потенциалом иметь представление, в котором геометрия состоит из…
Голографическая инфляция и сохранение ζ
- Дж. Гаррига, Ю. Уракава
- Физика
- 2014
Краткое изложение голографического описания инфляции , космологическая временная эволюция в балке должна соответствовать поток группы реномализации (РГ) в теории двойных границ. Здесь мы анализируем…
δN формализм из суперпотенциала и голографии
- Дж. Гаррига, Ю. Уракава, Ф. Верницци
- Физика
- 2015
Мы рассматриваем формализм суперпотенциала для описания эволюции D-скалярных полей во время инфляции, обобщая его на случай с неканоническими кинетическими членами. Мы предоставляем…
Феноменология меры CAH+
- Michael P. Salem, A. Vilenkin
- Математика
- 2011
CAH+ мера регулирует бесконечный пространственно-временной объем мультивселенной, создавая поверхность постоянной сопутствующего видимого горизонта (CAH) и последующего удаления будущих световых конусов всех точек…
Реликтовое излучение и мера мультивселенной
В контексте вечной инфляции космологические предсказания зависят от выбора меры для регулирования расходящегося пространственно-временного объема.
Спектр инфляционных возмущений не является исключением,…
Реликтовое излучение и мера мультивселенной
- Майкл П. Салем
- Физика
- 2012
A bs тракта В контексте вечной инфляции космологические предсказания зависят от выбор меры регулирования расходящегося пространственно-временного объема. Спектр инфляционных возмущений не…
CERN-PH-TH-2015-231 δN-формализм из суперпотенциала и голографии
- Дж. Гаррига, Ю. Уракава, Ф. Верницци
- Физика
- 2015 900 04
Мы рассматриваем формализм суперпотенциала для описания эволюцию скалярных полей D во время инфляции, обобщив ее на случай с неканоническими кинетическими членами. Мы предоставляем…
Наблюдатели мультивселенной
- Жауме Гаррига, Александр Виленкин
- Информатика
- 2013
В этой работе рассматривается мера, основанная на зондирующей геодезической, которая проходит бесконечное число проходов через хрусты, которую можно рассматривать как мировую линию вечного «наблюдателя», собирающего данные.
Столкновения пузырей и измерения мультивселенной
- Майкл П. Салем
- Физика
- 2011
наблюдатель в вечно расширяющейся мультивселенной, необходимо выбрать меру расходящегося объема пространства-времени, в том числе выбрать «начальный»…
Граничное определение меры мультивселенной
- Р. Буссо, Бен Фрайвогель, Штефан Лейхенауэр, В. Розенхаус
- Физика
- 2010
9002 0 Мы предлагаем регулировать бесконечность вечной инфляции, связывая поздний предел времени в массе до ближней отсечки на будущей границе. Время светового конуса события определяется в…

Голографическая мультивселенная и конформная инвариантность
- Дж. Гаррига, А. Виленкин
- Математика
- 2009
Рассмотрим голографическое описание инфляционной мультивселенной, согласно которому волновая функция Вселенной интерпретируется как производящий функционал для более низкой размерности…
Голографическая мультивселенная
9 0010
Дж. Гаррига, А. Виленкин
Математика
2008

Мы исследуем идею о том, что динамика инфляционной мультивселенной закодирована в ее будущей границе, где она описывается теорией более низкого измерения, конформно инвариантной в УФ .…

Дополнительность в мультивселенной

Р. Буссо
Физика
2009

В мультивселенной, как и в пространстве AdS, световые конусы связывают объемные точки с граничным масштабом с. Эта голографическая УФ-ИК связь определяет предпочтительную глобальную временную отсечку, которая регулирует расхождения… 007

Недавно было предложено Малдасена утверждает, что большие $N$ пределы некоторых конформных теорий поля в $d$ измерениях могут быть описаны в терминах супергравитации (и теории струн) на произведении…

Голографическое описание вакуумных пузырей

Дж. Гаррига
Физика
2011

Описание мультивселенной. В частности, мы подробно остановимся на недавнем наблюдении Малдасены,…

Голографическая граница в пространстве анти-де Ситтера

Л. Сасскинд, Э. Виттен
Физика
1998

Соответствие между теорией струн в пространстве Анти-де Ситтера и супертеорией Янга-Миллса является примером голографического принципа, согласно которому квантовая теория с гравитацией должна быть…

Соответствие dS/CFT

A Строминджер
Математика, Физика
2001

Предлагается голографическая двойственность, связывающая квантовую гравитацию на dSD (D-мерном пространстве де Ситтера) с конформной теорией поля на одном SD−1 ((D-1)- сфера), в которой объемные корреляторы де Ситтера с…

Вероятности в инфляционной мультивселенной

Дж. Гаррига, Делия Шварц-Перлов, А. Виленкин, С. Виницки
Математика
2006

Инфляционная космология приводит к картине «мультивселенной», включающей бесконечное количество (пространственно бесконечных) постинфляционных термализованных регионов, называемых карманными вселенными.

В контексте…

Освобождение границ в AdS/CFT

G. Compère, D. Marolf
Физика
2008

Описан новый класс граничных условий для AdSd+1, при которых граничная метрика становится динамическим полем. Ключевой технический момент заключается в том, чтобы показать, что вклады граничных контрчленов…

Доводы в пользу параллельных вселенных

Примечание редактора: В августовском номере Scientific American космолог Джордж Эллис описывает, почему он скептически относится к концепции параллельных вселенных. вселенные. Здесь сторонники мультивселенной Александр Виленкин и Макс Тегмарк предлагают контраргументы, объясняя, почему мультивселенная объясняет так много особенностей нашей Вселенной и как ее можно проверить.

Добро пожаловать в Мультивселенную
Александр Виленкин

Вселенная, какой мы ее знаем, возникла в результате великого взрыва, который мы называем Большим взрывом. Почти столетие космологи изучали последствия этого взрыва: как Вселенная расширялась и охлаждалась, и как галактики постепенно стягивались под действием гравитации. На природу самого взрыва обратили внимание сравнительно недавно. Это предмет теории инфляции, которая была разработана в начале 19 века.80-х годов Алана Гута, Андрея Линде и других, и привело к радикально новому глобальному взгляду на вселенную.

Инфляция — это период сверхбыстрого, ускоренного расширения в ранней космической истории. Это так быстро, что за долю секунды крошечная субатомная частица пространства раздувается до размеров, намного превышающих всю наблюдаемую в настоящее время область. В конце инфляции энергия, вызвавшая расширение, воспламеняет горячий огненный шар из частиц и излучения. Это то, что мы называем большим взрывом.

Конец инфляции спровоцирован квантовыми, вероятностными процессами и не происходит везде одновременно. В нашем космическом соседстве инфляция закончилась 13,7 миллиарда лет назад, но она все еще продолжается в отдаленных частях Вселенной, и постоянно формируются другие «нормальные» области, подобные нашей. Новые области появляются в виде крошечных микроскопических пузырьков и сразу же начинают расти. Пузыри продолжают расти без ограничений; тем временем инфляционное расширение раздвигает их, освобождая место для образования новых пузырей. Этот бесконечный процесс называется вечной инфляцией. Мы живем в одном из пузырей и можем наблюдать лишь небольшую его часть. Независимо от того, насколько быстро мы путешествуем, мы не можем догнать расширяющиеся границы нашего пузыря, поэтому для всех практических целей мы живем в замкнутой вселенной пузыря.

Теория инфляции объяснила некоторые загадочные особенности Большого взрыва, которые раньше просто нужно было постулировать. Он также сделал ряд проверяемых предсказаний, которые затем были убедительно подтверждены наблюдениями. К настоящему времени инфляция стала ведущей космологической парадигмой.

Другой ключевой аспект нового мировоззрения проистекает из теории струн, которая в настоящее время является нашим лучшим кандидатом на роль фундаментальной теории природы. Теория струн допускает огромное количество решений, описывающих пузырьковые вселенные с различными физическими свойствами. Величины, которые мы называем константами природы, такие как массы элементарных частиц, гравитационная постоянная Ньютона и т. д., принимают разные значения в разных типах пузырей. Теперь соедините это с теорией инфляции. Каждый тип пузырьков имеет определенную вероятность образования в надувном пространстве. Так неизбежно в ходе вечного надувания будет образовываться неограниченное количество пузырей всех возможных типов.

Эта картина Вселенной, или мультивселенная , как ее называют, объясняет давнюю загадку того, почему константы природы кажутся точно настроенными для возникновения жизни. Причина в том, что разумные наблюдатели существуют только в тех редких пузырях, в которых по чистой случайности константы оказываются как раз подходящими для развития жизни. Остальная часть мультивселенной остается бесплодной, но никто не может пожаловаться на это.

Некоторые из моих коллег-физиков находят теорию мультивселенной тревожной. Любая теория в физике стоит или рушится в зависимости от того, согласуются ли ее предсказания с данными. Но как мы можем проверить существование других пузырьковых вселенных? Пол Стейнхардт и Джордж Эллис утверждали, например, что теория мультивселенной ненаучна, поскольку ее невозможно проверить даже в принципе.

Удивительно, но наблюдательные проверки картины мультивселенной на самом деле могут быть возможны. Энтони Агирре, Мэтт Джонсон, Мэтт Клебан и другие указывали, что столкновение нашего расширяющегося пузыря с другим пузырем в мультивселенной оставило бы отпечаток в космическом фоновом излучении — круглое пятно с большей или меньшей интенсивностью излучения. Обнаружение такого пятна с предсказанным профилем интенсивности предоставило бы прямое свидетельство существования других вселенных-пузырей. Сейчас поиск продолжается, но, к сожалению, нет никакой гарантии, что столкновение пузырей произошло в пределах нашего космического горизонта.

Существует и другой подход, которому можно следовать. Идея состоит в том, чтобы использовать нашу теоретическую модель мультивселенной для предсказания констант природы, которые мы можем ожидать измерить в нашем локальном регионе. Если константы варьируются от одной пузырьковой вселенной к другой, их локальные значения нельзя предсказать с уверенностью, но мы все же можем сделать 90 287 статистических 90 288 предсказаний. Мы можем вывести из теории, какие значения констант, скорее всего, будут измерены типичным наблюдателем в мультивселенной. Предполагая, что мы типичны — предположение, которое я назвал принцип посредственности — тогда мы можем предсказать вероятные значения констант в нашем пузыре.

Эта стратегия была применена к плотности энергии вакуума, также известной как «темная энергия». Стивен Вайнберг заметил, что в регионах, где темная энергия велика, Вселенная очень быстро расширяется, не позволяя материи слипаться в галактики и звезды. Наблюдатели вряд ли будут развиваться в таких регионах. Расчеты показали, что большинство галактик (а значит, и большинство наблюдателей) находятся в областях, где темная энергия примерно равна плотности вещества в эпоху образования галактик. Таким образом, предсказание состоит в том, что подобное значение должно наблюдаться в нашей части Вселенной.

По большей части физики не воспринимали эти идеи всерьез, но, к их большому удивлению, темная энергия примерно ожидаемой величины была обнаружена в ходе астрономических наблюдений в конце 1990-х годов. Это может быть нашим первым свидетельством того, что действительно существует огромная мультивселенная. Это изменило многие взгляды.

Теория мультивселенной все еще находится в зачаточном состоянии, и некоторые концептуальные проблемы еще предстоит решить. Но, как писал Леонард Засскинд, «держу пари, что на рубеже 22-го века философы и физики с ностальгией посмотрят на настоящее и вспомнят золотой век, когда узкое провинциальное представление о Вселенной 20-го века уступило место более широкому и лучшему. [мультивселенная] … умопомрачительных размеров».

Мультивселенная наносит ответный удар
Макс Тегмарк

Вы действительно живете в мультивселенной или это понятие выходит за рамки науки?

Вдохновленный интересной критикой мультивселенных в августовском номере Scientific American, , написанной пионером теории теории относительности Джорджем Ф. Р. Эллисом, позвольте отдать вам свои пять копеек.

Идеи мультивселенной традиционно подвергались расправе со стороны истеблишмента: Джордано Бруно с его мультивселенной бесконечного пространства сгорел на костре в 1600 году, а Хью Эверетт с его квантовой мультивселенной сгорел на рынке труда физика в 1957. Я даже испытал на себе некоторый жар, когда старшие коллеги предположили, что мои публикации, связанные с мультивселенной, были чушью и разрушили бы мою карьеру. Однако в последние годы произошли кардинальные изменения. Параллельные вселенные сейчас в моде, они появляются в книгах, фильмах и даже в шутках: «Вы сдали экзамен во многих параллельных вселенных, но не в этой».

Обнародование идей, конечно же, не привело к консенсусу среди ученых, но сделало дебаты о мультивселенной гораздо более тонкими и, на мой взгляд, более интересными, когда ученые выходят за рамки выкрикивания звуковых фрагментов мимо друг друга и искренне пытаются понять противоположные точки зрения. Новая статья Джорджа Эллиса — отличный тому пример, и я очень рекомендую ее прочитать, если вы еще этого не сделали.

Под нашей вселенной я подразумеваю сферическую область пространства, из которой свет успел достичь нас в течение 13,7 миллиардов лет, прошедших с момента нашего Большого взрыва. Говоря о параллельных вселенных, я считаю полезным различать четыре разных уровня: Уровень I (другие подобные регионы далеко в космосе, где кажущиеся законы физики одинаковы, но где история развивалась по-другому, потому что все начиналось по-другому), Уровень II (области пространства, где даже кажущиеся законы физики различны), Уровень III (параллельные миры где-то в так называемом гильбертовом пространстве, где разыгрывается квантовая реальность) и Уровень IV (полностью несвязанные реальности, управляемые разными математическими уравнениями) .

В своей критике Джордж классифицирует многие аргументы в пользу этих уровней мультивселенной и утверждает, что все они имеют проблемы. Вот мое резюме его основных аргументов против мультивселенной:

1) Инфляция может быть ошибочной (или не вечной)

2) Квантовая механика может быть ошибочной (или не унитарной)

3) Теория струн может быть ошибочной (или не иметь несколько решений)

4) Мультивселенные могут быть нефальсифицируемыми

5) Некоторые заявления о мультивселенной сомнительны

6) Аргументы тонкой настройки могут потребовать слишком многого

7) Это скользкий путь к еще большим мультивселенным

(Джордж на самом деле не упомянул (2) в статье, но я добавляю это здесь, потому что я думаю он бы это сделал, если бы редактор разрешил ему больше шести страниц.)

Каково мое отношение к этой критике? Интересно, что я согласен со всеми этими семью утверждениями — и, тем не менее, я с радостью поставлю свои сбережения на существование мультивселенной!

Начнем с первых четырех. Инфляция естественным образом порождает мультивселенную уровня I, и если вы добавите теорию струн к ландшафту возможных решений, вы также получите уровень II. Квантовая механика в ее математически простейшей («унитарной») форме дает вам Уровень III. Так что, если эти теории исключаются, то рушится ключевое свидетельство этих мультивселенных.

Помните: параллельные вселенные — это не теория, а предсказания некоторых теорий.

Для меня ключевым моментом является то, что если теории научны, то законной наукой является разработка и обсуждение всех их следствий, даже если они связаны с ненаблюдаемыми объектами. Чтобы теорию можно было опровергнуть, нам не обязательно иметь возможность наблюдать и проверять все ее предсказания, достаточно хотя бы одного из них. Таким образом, мой ответ на (4) состоит в том, что с научной точки зрения можно проверить наши математические теории, а не обязательно их следствия, и это вполне нормально. Например, поскольку общая теория относительности Эйнштейна успешно предсказала многие вещи, которые мы можем наблюдать, мы также серьезно относимся к ее предсказаниям для вещей, которые мы не можем наблюдать, например, что происходит внутри черных дыр.

Точно так же, если нас впечатлили успешные предсказания инфляции или квантовой механики, то нам нужно серьезно отнестись и к другим их предсказаниям, включая мультивселенную Уровня I и Уровня III. Джордж даже упоминает возможность того, что однажды вечную инфляцию можно будет исключить — для меня это просто аргумент в пользу того, что вечная инфляция — это научная теория.

Теория струн, безусловно, не дошла до инфляции и квантовой механики в плане утверждения себя в качестве поддающейся проверке научной теории. Однако я подозреваю, что мы застрянем на мультивселенной уровня II, даже если теория струн окажется отвлекающим маневром. Довольно часто математические уравнения имеют несколько решений, и до тех пор, пока они есть у фундаментальных уравнений, описывающих нашу реальность, вечная инфляция обычно создает огромные области пространства, которые физически реализуют каждое из этих решений. Например, уравнения, управляющие молекулами воды, которые не имеют ничего общего с теорией струн, допускают три решения, соответствующие парам, жидкой воде и льду, и если само пространство может аналогичным образом существовать в разных фазах, инфляция будет стремиться реализовать их все.

Джордж перечисляет ряд наблюдений, предположительно подтверждающих теории мультивселенной, которые в лучшем случае сомнительны, например, доказательства того, что некоторые константы природы на самом деле не постоянны, свидетельства в космическом микроволновом фоновом излучении столкновений с другими вселенными или странным образом связанным пространством и т. д. Я полностью разделяю его скептицизм в отношении этих утверждений. Однако во всех этих случаях разногласия касались анализа данных, как и в случае фиаско с холодным синтезом. Для меня сам факт, что ученые проводят эти измерения и спорят о деталях данных, является еще одним свидетельством того, что это находится в пределах науки: именно это отличает научную полемику от ненаучной!

Наша Вселенная удивительно точно приспособлена для жизни в том смысле, что если бы вы изменили многие из наших констант природы лишь на крошечную величину, жизнь, какой мы ее знаем, была бы невозможна. Почему? Если существует мультивселенная уровня II, где эти «константы» принимают все возможные значения, неудивительно, что мы оказываемся в одной из редких обитаемых вселенных, так же как неудивительно, что мы живем на Земле, а не на Меркурии или Нептуне. . Джордж возражает против того факта, что вам нужно принять теорию мультивселенной, чтобы сделать этот вывод, но именно так мы проверяем любую научную теорию: мы предполагаем, что она верна, прорабатываем последствия и отбрасываем теорию, если предсказания не совпадают с наблюдениями. . Некоторые точные настройки кажутся достаточно экстремальными, чтобы смущать — например, нам нужно настроить темную энергию примерно до 123 знаков после запятой, чтобы сделать галактики пригодными для жизни. Для меня необъяснимое совпадение может быть красноречивым признаком пробела в нашем научном понимании. Отвергнуть его, сказав: «Нам просто повезло — хватит искать объяснение!» не только неудовлетворительна, но также равносильна игнорированию потенциально важной подсказки.

Джордж утверждает, что если мы серьезно относимся к тому, что все, что может произойти, происходит, мы скатываемся по скользкой дорожке к еще более крупным мультивселенным, таким как мультивселенная уровня IV. Поскольку это мой любимый уровень мультивселенной, и я один из очень немногих его сторонников, я с удовольствием скатываюсь по этому склону!

Джордж также упоминает, что мультивселенные могут противоречить бритве Оккама, вводя ненужные сложности. Как физик-теоретик я сужу об элегантности и простоте теории не по ее онтологии, а по элегантности и простоте ее математических уравнений — и меня весьма поразительно, что математически простейшие теории склонны давать нам мультиверсы. Доказано, что написать теорию, которая порождает именно ту вселенную, которую мы видим, и ничего более, оказалось чрезвычайно сложно.

Наконец, есть аргумент против мультивселенной, которого я рекомендую Джорджу избегать, но который, на мой взгляд, является наиболее убедительным для большинства людей: параллельные вселенные кажутся слишком странными, чтобы быть правдой.

Рассмотрев аргументы против мультивселенной, давайте теперь более внимательно проанализируем аргумент в пользу мультивселенной. Я собираюсь доказать, что все спорные вопросы исчезнут, если мы примем Гипотезу Внешней Реальности: существует внешняя физическая реальность, полностью независимая от нас, людей. Предположим, что эта гипотеза верна. Тогда большая часть критики мультивселенной основывается на некоторой комбинации следующих трех сомнительных предположений:

1) Предположение всевидения: физическая реальность должна быть такой, чтобы хотя бы один наблюдатель в принципе мог наблюдать ее всю.

2) Допущение педагогической реальности: физическая реальность должна быть такой, чтобы все разумно информированные люди-наблюдатели чувствовали, что они интуитивно ее понимают.

3) Предположение об отсутствии копирования: никакой физический процесс не может копировать наблюдателей или создавать субъективно неразличимые наблюдатели.

(1) и (2), по-видимому, мотивированы не более чем человеческим высокомерием. Предположение о всевидении эффективно переопределяет слово «существует», чтобы оно стало синонимом того, что можно наблюдать для нас, людей, сродни страусу, засунувшему голову в песок. Санта-Клаус, местный реализм, Зубная фея и креационизм — но действительно ли они достаточно усердно работали, чтобы освободиться от утешительно знакомых представлений, которые имеют более глубокие корни? мир устроен, а не указывать ему, как работать, основываясь на наших философских предубеждениях.

Если предположение о всевидении ложно, то существуют ненаблюдаемые вещи, и мы живем в мультивселенной.

Если предположение о педагогической реальности ложно, то возражение о том, что мультиверсы слишком странны, не имеет логического смысла.

Если предположение об отсутствии копий ложно, то нет фундаментальной причины, по которой ваши копии не могут существовать где-либо еще во внешней реальности — ведь и вечная инфляция, и единая квантовая механика обеспечивают механизмы для их создания.

Мы, люди, имеем хорошо задокументированную склонность к высокомерию, высокомерно воображая себя в центре внимания, когда все вращается вокруг нас. Мы постепенно узнали, что вместо этого мы вращаемся вокруг Солнца, которое само вращается вокруг одной галактики среди бесчисленного множества других. Благодаря прорывам в физике мы можем получить еще более глубокое понимание самой природы реальности.

Цена, которую мы должны заплатить, становится все скромнее — что, вероятно, пойдет нам на пользу, — но взамен мы можем оказаться в реальности более грандиозной, чем наши предки мечтали в своих самых смелых мечтах.