Номер (задание) 231 — гдз по математике 6 класс Виленкин, Жохов, Чесноков
Условие / глава 1. / § 2 / тема 8 / 231
231. Найдите наибольший общий делитель и наименьшее общее кратное чисел: 1) 2450 и 3500; 2) 792 и 2178.
Решебник №1 / глава 1. / § 2 / тема 8 / 231
 / § 2 / тема 8 / 231
/ § 2 / тема 8 / 231Решебник №2 / глава 1. / § 2 / тема 8 / 231
Решебник №3 / глава 1. / § 2 / тема 8 / 231
/ § 2 / тема 8 / 231
Страница 30 №179-184 ГДЗ к учебнику «Математика» 6 класс Виленкин, Жохов, Чесноков
а) а = 3 * 5, b = 7 * 5;
б) а = 2 * 2 * 3 * 3 * 5, b = 2 * 2 * 3 * 7.
Решение
а) Обозначим наименьшее общее кратное чисел а и b НОК(а;b).
НОК(а;b) = НОК(3 * 5; 7 * 5) = 3 * 5 * 7 = 105
б) Обозначим наименьшее общее кратное чисел а и b НОК(а;b).
НОК(а;b) = НОК(2 * 2 * 3 * 3 * 5; 2 * 2 * 3 * 7) = 2 * 2 * 3 * 3 * 5 * 7 = 1260
Задание № 180. Найдите наименьшее общее кратное чисел а и b, если:
Найдите наименьшее общее кратное чисел а и b, если:
б) а = 3 * 3 * 7 * 7 и b = 2 * 3 * 3 * 5 * 7 * 7;
в) а = 2 * 2 * 5 * 5 * 11 и b = 2 * 2 * 3 * 5 * 11;
г) а = 2 * 5 * 5 * 7 и b = 2 * 2 * 5 * 5 * 7.
Решение
а) НОК(а;b) = 2 * 2 * 3 * 5 * 5 * 3 * 3 = 2700
б) НОК(а;b) = 3 * 3 * 7 * 7 * 2 * 5 = 4410
в) НОК(а;b) = 2 * 2 * 5 * 5 * 11 * 3 = 3300
г) НОК(а;b) = 2 * 5 * 5 * 7 * 2 = 700
Задание № 181. Найдите наименьшее общее кратное чисел:
а) 6 и 8;
б) 12 и 16;
в) 72 и 99;
г) 396 и 180;
д) 34, 51 и 68;
е) 168, 231 и 60.
Решение
а) 6 = 2 * 3; 8 = 2 * 2 * 2; HOK(6; 8) = 2 * 3 * 2 * 2 = 24
б) 12 = 2 * 2 * 3; 16 = 2 * 2 * 2 * 2; НОК(12; 16) = 2 * 2 * 3 * 2 * 2 = 48
в) 72 = 2 * 2 * 2 * 3 * 3; 99 = 3 * 3 * 11; НОК(72; 99) = 2 * 2 * 2 * 3 * 3 * 11 = 792
г) 396 = 2 * 2 * 3 * 3 * 11; 180 = 2 * 2 * 3 * 3 * 5; НОК(396; 180) = 2 * 2 * 3 * 3 * 11 * 5 = 1980
д) 34 = 2 * 17; 51 = 3 * 17; 68 = 2 * 2 * 17; НОК(34; 51; 68) = 2 * 17 * 3 * 2 = 204
е) 168 = 2 * 2 * 2 * 3 * 7; 231 = 3 * 7 * 11; 60 = 2 * 2 * 3 * 5; НОК(168; 231; 60) = 9240
Задание № 182.-reshenie-231.jpg) Являются ли числа 54 и 65 взаимно простыми? Найдите наименьшее общее кратное чисел 54 и 65. Равно ли оно произведению 54 и 65? Запишите какие−нибудь два взаимно простых числа. Найдите наименьшее общее кратное этих чисел. Сделайте вывод.
Являются ли числа 54 и 65 взаимно простыми? Найдите наименьшее общее кратное чисел 54 и 65. Равно ли оно произведению 54 и 65? Запишите какие−нибудь два взаимно простых числа. Найдите наименьшее общее кратное этих чисел. Сделайте вывод.
Решение
НОД(54; 65) = НОК(2 * 3 * 3 * 3; 5 * 13) = 1. Эти числа взаимно простые.
Вывод: НОК двух взаимно простых чисел равно их произведению.
НОК(54; 65) = 2 * 3 * 3 * 3 * 5 * 13 = (2 * 3 * 3 * 3) * (5 * 13) = 54 * 65 = 3510.
НОК чисел 54 и 65 равно их произведению. Возьмём числа 6 и 35. Это взаимно простые числа.
6 = 2 * 3; 35 = 5 * 7. НОК(6; 35) = 2 * 3 * 5 * 7 = (2 * 3) * (5 * 7) = 6 * 35 = 210.
Задание № 183. Найдите наименьшее общее кратное чисел:
а) 45 и 135;
б) 34 и 170.
Равно ли оно одному из данных чисел?
Ответы 7 гуру
а) Да равно. НОК(45; 135) = НОК(3 * 3 * 5; 3 * 3 * 3 * 5) = 3 * 3 * 5 * 3 = 135
б) Да равно.НОК(34; 170) = НОК(2 * 17; 2 * 5 * 17) = 2 * 5 * 17 = 170
Задание № 184. Вдоль дороги от пункта А поставлены столбы через каждые 45 м. Эти столбы решили заменить другими, поставив их на расстоянии 60 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который будет стоять на месте старого, кроме столба в точке А.
Решение
Необходимо найти НОК(45;60) = НОК(3 * 3 * 5; 2 * 2 * 3 * 5) = 3 * 3 * 5 * 2 * 2 = 180 м.
Математика 6 Виленкин Контрольная 1 (Попова) + ОТВЕТЫ
Математика 6 Виленкин Контрольная 1 (Попова). Контрольная работа по математике 6 класс с ответами. Цитаты из пособия «Контрольно-измерительные материалы по математике 6 класс» (составитель вопросов — Л.П.Попова, издательство ВАКО) использованы в учебных целях. Контрольные работы составлены по УМК Виленкин и др. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.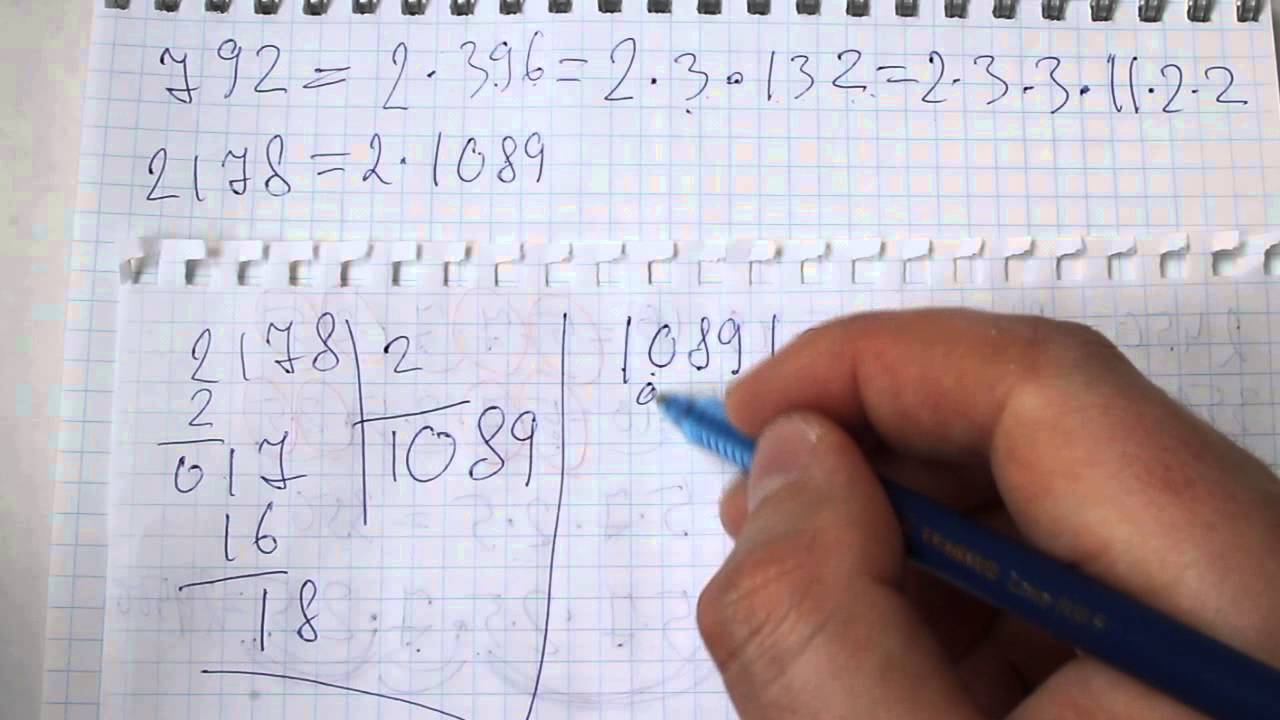
Математика 6 класс (Виленкин)
Контрольная работа № 1
КР-1. Вариант 1 (транскрипт)
- Разложите на простые множители числа 300 и 9828.
- Найдите наибольший общий делитель и наименьшее общее кратное чисел 1512 и 1008.
- Докажите, что: а) числа 189 и 1905 не взаимно простые; б) числа 231 и 676 взаимно простые.
- Выполните действия: 273,6 : 0,76 + 7,24 – 16.
- Найдите произведение чисел, если их наименьшее общее кратное равно 420, а наибольший общий делитель равен 30.
КР-1. Вариант 2 (транскрипт)
- Разложите на простые множители числа 700 и 8316.
- Найдите наибольший общий делитель и наименьшее общее кратное чисел 936 и 1404.
- Докажите, что: а) числа 483 и 366 не взаимно простые; б) числа 455 и 968 взаимно простые.
- Выполните действия: 268,8 : 0,56 + 6,44 – 12.
- Найдите наименьшее общее кратное чисел, если их произведение равно 67 200, а наибольший общий делитель равен 40.

ОТВЕТЫ на контрольную работу:
КР-01. Вариант 1. ОТВЕТЫ:
№1. 300=2*2*5*5*3, 9828=2*2*3*3*3*91.
№2. НОД (1512; 1008)= 2*2*2*3*3*7= 504, НОК(1512; 1008) = 2*2*2*2*3*3*3*7= 3024.
№3. а) 189=3*3*3*7 и 1905 = 3*5*127 у этих чисел есть одинаковый простой множитель 3 значит это не взаимно простые числа.
№4. Ответ: 475,84
№5. Ответ: 12600
КР-01. Вариант 2. ОТВЕТЫ:
№1. 700 = 2*2*5*5*7, 8316 = 2*2*3*3*3*7*11.
№2. НОД(936;1404) = 2*2*3*3*13 = 468. НОК(936;1404) = 2*2*2*3*3*3*13 = 2808
№3. а) НОД(483, 366)=3 не взаимно простые, потому, что у них два общих делителей 1 и 3.
б) НОД(455, 968)=1 эти числа взаимно простые, потому, что у них только один общий делитель 1
№4.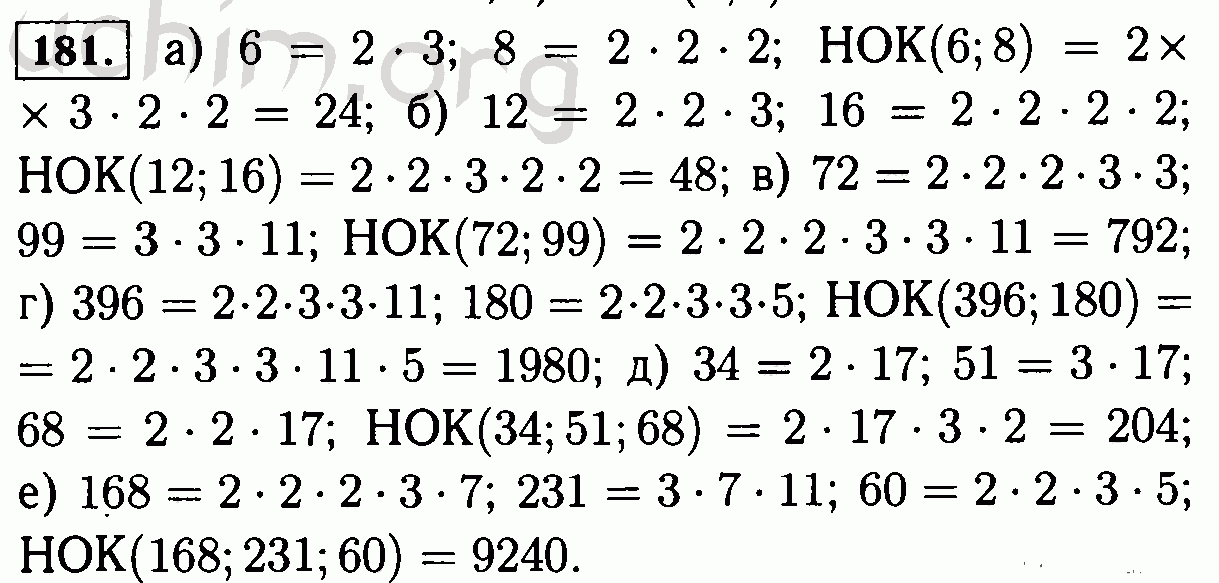 Ответ: 557,28
Ответ: 557,28
№5. Подсказка: НОД*НОК=равно произведение этих двух чисел. Ответ: 1680
Вы смотрели: Математика 6 Виленкин Контрольная 1. Контрольная работа по математике 6 класс с ответами. Цитаты из пособия «Контрольно-измерительные материалы по математике 6 класс» (автор вопросов — Людмила Павловна Попова) использованы в учебных целях. Контрольные работы составлены по УМК Виленкин и др.
Вернуться к Списку контрольных работ по математике 6 класс (Виленкин)
Решебник (ГДЗ) по математике 6 класс Чесноков, Нешков
Онлайн решебник (ГДЗ) по математике 6 класс Чесноков, Нешков дидактические материалы
Математика – это один из наиболее сложных предметов, который многим ученикам может казаться сухим и неинтересным. К тому же, для его изучения необходимо заучивать множество правил, которые необходимо постоянно помнить. Между тем, если ученик в 6 классе перестал понимать математику, то это означает, что алгебра и геометрия, которые ему придется изучать в последующих классах, станут для него скоплением непонятных формул и теорем, которые нужно зазубривать для того чтобы получить положительную оценку. В итоге, ученик не только потеряет мотивацию к обучению, но и перестанет даже пытаться понять предмет.
В итоге, ученик не только потеряет мотивацию к обучению, но и перестанет даже пытаться понять предмет.
Для того чтобы этого не случилось можно использовать различные учебно-методические пособия, в числе которых и ГДЗ по математике за 6 класс Чеснакова (дидактические материалы).
Как правильно использовать гдз — готовые ответы по математике в 6-том классе из учебника Чеснакова
На первый взгляд, кажется, что ГДЗ могут только навредить отстающему ученику. Ведь он просто скатится к элементарному списыванию с решебника. Если пустить этот процесс на самотек, то так может и случится. Совсем по-другому может решиться ситуация в том случае, если родители интересуются успеваемостью ученика и уделяют ему внимание.
Советы родителям:
- Никогда не упрекайте ребенка за плохую отметку по математике и не требуйте исправить ее любой ценой. Многие родители лишают детей привычного для них досуга, например, компьютерных игр, в расчете на то, что это подстегнет их мотивацию к обучению.
 Практика показывает, что таким способом можно добиться результатов, обратных к ожидаемым.
Практика показывает, что таким способом можно добиться результатов, обратных к ожидаемым. - Уделяйте время своим детям в процессе выполнения ими домашних работ. При этом вы не должны заниматься мелочной опекой, но и полностью покидать ребенка на самого себя не следует.
- Самый эффективный вариант – «точечный» контроль. Проверяйте с ребенком каждую выполненную работу с гдз. Очень хорошим способом контроля может стать решебник по математике за 6 класс Чеснакова.
- При обнаружении ошибок проведите вместе с ребенком работу по их устранению используя решебник Чеснакова по математике за 6 класс. Если возникла такая необходимость – попросите ребенка повторить те или иные правила.
На решаторе можно найти все решебники для всех классов в режиме онлайн. Поэтому, если вам необходимы ответы по математике за 6 класс Чеснакова и другие дидактические материалы – заходите на наш ресурс с гдз и получайте всю необходимую информацию совершено бесплатно.
Контрольная работа № 1 Вариант – 1
а) 255 и 338 не взаимно простые; б) 392 и 675 взаимно простые
6* Может ли разность двух простых чисел быть простым числом? Приведите пример. | Контрольная работа № 1 Вариант – 2
а) 266 и 285 не взаимно простые; б) 301 и 585 взаимно простые
6* Может ли сумма двух простых чисел быть простым числом? Приведите пример. |
Контрольная работа № 1 Вариант – 3
а) 390 и 231 не взаимно простые; б) 864 и 875 взаимно простые
6* Может ли произведение двух простых чисел быть простым числом? Ответ объясните. | Контрольная работа № 1 Вариант – 4
а) 231 и 280 не взаимно простые; б) 130 и 231 взаимно простые
6* Может ли частное двух простых чисел быть простым числом? Ответ объясните. |
Контрольная работа № 1 Вариант – 1
а) 255 и 338 не взаимно простые; б) 392 и 675 взаимно простые
6* Может ли разность двух простых чисел быть простым числом? Приведите пример. | Контрольная работа № 1 Вариант – 2
а) 266 и 285 не взаимно простые; б) 301 и 585 взаимно простые
6* Может ли сумма двух простых чисел быть простым числом? Приведите пример. |
Контрольная работа № 1 Вариант – 3
а) 390 и 231 не взаимно простые; б) 864 и 875 взаимно простые
6* Может ли произведение двух простых чисел быть простым числом? Ответ объясните. | Контрольная работа № 1 Вариант – 4
а) 231 и 280 не взаимно простые; б) 130 и 231 взаимно простые
6* Может ли частное двух простых чисел быть простым числом? Ответ объясните. |
5 класс. Математика. Виленкин. Учебник. Ответы к стр. 14
Натуральные числа
Натуральные числа и шкалы
Отрезок. Длина отрезка. ТреугольникОтветы к стр. 14
51. Прочитайте числа: 6008; 5 231 154; 9 055 007; 60 080 015.
6008 — шесть тысяч восемь;
5 231 154 — пять миллионов двести тридцать одна тысяча сто пятьдесят четыре;
9 055 007 — девять миллионов пятьдесят пять тысяч семь;
60 080 015 — шестьдесят миллионов восемьдесят тысяч пятнадцать.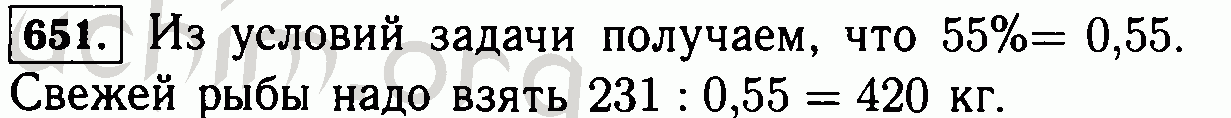
52. Запишите цифрами числа:
десять миллионов пять тысяч двадцать три;
три миллиарда восемьдесят две тысячи триста пять;
десять миллиардов два миллиона шестьдесят четыре тысячи;
пятнадцать миллиардов два миллиона двести восемьдесят тысяч семь;
пятьсот четыре миллиарда восемьдесят девять;
один миллиард один миллион восемьсот;
один миллион одна тысяча двадцать.
десять миллионов пять тысяч двадцать три — 10 005 023;
три миллиарда восемьдесят две тысячи триста пять — 3 000 082 305;
десять миллиардов два миллиона шестьдесят четыре тысячи — 10 002 064 000;
пятнадцать миллиардов два миллиона двести восемьдесят тысяч семь — 15 002 280 007;
пятьсот четыре миллиарда восемьдесят девять — 504 000 000 089;
один миллиард один миллион восемьсот — 1 001 000 800;
один миллион одна тысяча двадцать — 1 001 020.
53. Вычислите устно:
а) 8 + 7; б) 11 — 3; в) 9 • 8; г) 45 : 9;
16 + 9; 16 — 7; 8 • 7; 64 : 8;
28 + 6; 12 — 5; 9 • 9; 49 : 7;
19 + 5; 15 — 9; 6 • 8; 30 : 6;
37 + 0; 21 — 0; 7 • 0; 48 : 8.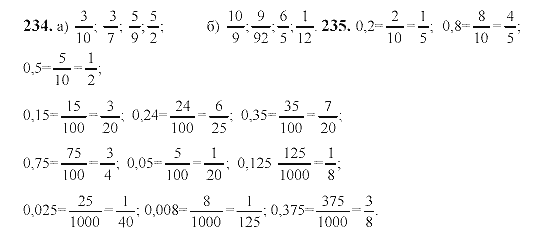
а) 8 + 7; б) 11 — 3;
16 + 9; 16 — 7;
28 + 6; 12 — 5;
19 + 5; 15 — 9;
37 + 0; 21 — 0;
в) 9 • 8; г) 45 : 9;
8 • 7; 64 : 8;
9 • 9; 49 : 7;
6 • 8; 30 : 6;
7 • 0; 48 : 8.
54. Заполните таблицу:
| Слагаемое | 15 | 30 | 17 | 29 | 42 | 19 | 17 | 26 |
| Слагаемое | 10 | 10 | 8 | 18 | 28 | 24 | 27 | 38 |
| Сумма | 25 | 40 | 25 | 47 | 70 | 42 | 44 | 64 |
55. Вычислите устно, используя приём округления:
Вычислите устно, используя приём округления:
а) 97 + 49; б) 398 + 435; в) 237 + 48.
а) 97 + 49 = (100 — 3) + (50 — 1) = (100 + 50) — (3 + 1) = 150 — 4 = 146;
б) 398 + 435 = (400 — 2) + 435 = (400 + 435) — 2 = 835 — 2 = 833;
в) 237 + 48 = (240 — 3) + (50 — 2) = (240 + 50) — (3 + 2) = 290 — 5 = 285.
56. Какое число надо вписать в последнюю клетку цепочки?
а) [40] →:5→ (8) →•3→ (24) →:6→ (4) →+46→ [50]
б) [72] →:8→ (9) →+11→ (20) →:5→ (4) →•9→ [36]
в) [28] →:7→ (4) →•8→ (32) →+8→ (40) →:10→ [4]
г) [56] →:8→ (7) →+13→ (20) →:4→ (5) →•8→ [40]
57. Подумайте, какие математические знания вам могут потребоваться, если вы собрались пойти: а) в бассейн; б) в магазин.
а) ширина, длина и глубина бассейна; расстояние от бассейна до дома; время сеанса по плаванию;
б) стоимость покупки; расстояние от магазина до дома; время работы магазина.
58. Какие двузначные числа можно записать с помощью цифр:
а) 6 и 0; б) 1, 5 и 0; в) 3 и 5?
а) 60, 66;
б) 11, 15, 10, 55, 51, 50;
в) 33, 35, 55, 53.
Ответы по математике. 5 класс. Учебник. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И
Математика. 5 класс
5 класс. Математика. Виленкин. Учебник. Ответы к стр. 14
Оцените и поделитесь с друзьями!Решебник дидактические материалы по Математике за 6 класс А.С. Чесноков, К.И. Нешков на Гитем ми
авторы: А.С. Чесноков, К.И. Нешков.
Данное пособие содержит решебник (ГДЗ) дидактические материалы по Математике за 6 класс . Автора: А.С. Чесноков, К.И. Нешков Издательство: Академкнига. Полные и подробные ответы к упражнениям на Гитем
ГДЗ к контрольным работам по математике за 6 класс Жохов В. И. можно скачать
здесь.
И. можно скачать
здесь.
ГДЗ к рабочей тетради по математике за 6 класс Рудницкая В.Н. можно скачать здесь.
ГДЗ к учебнику по математике за 6 класс Виленкин Н.Я. (2015 год) можно скачать здесь.
ГДЗ к дидактическим материалам по математике за 6 класс Попов М.А. можно скачать здесь.
ГДЗ к учебнику по математике за 6 класс Виленкин Н.Я. (2017 год) можно скачать здесь.
ГДЗ к рабочей тетради по математике за 6 класс Ерина Т.М. можно скачать
здесь.
ГДЗ к рабочей тетради по математике за 6 класс Ерина Т.М. можно скачать здесь.
ГДЗ к контрольным измерительным материалам по математике за 6 класс Глазков Ю.А. можно скачать здесь.
Космическое видение Виленкина: обзорный очерк множества миров в одном: поиск других вселенных
Задача научной популяризации — сложная. Слишком многие авторы думают, что это может быть достигнуто путем частого обращения к объяснительно бессмысленным и запутывающим метафорам, которые оставляют читателя в недоумении относительно того, что именно утверждает конкретная теория. Одно из больших достоинств книги Александра Виленкина состоит в том, что он избегает этого пути в пользу прямых, простых объяснений ключевых терминов и идей.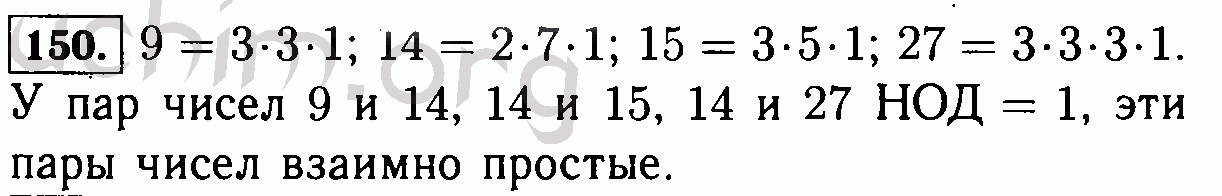 Соедините это с удивительно ясным стилем письма, и вы получите одну из лучших популяризаций современной физической космологии, доступную от одного из ведущих ее практиков.
Соедините это с удивительно ясным стилем письма, и вы получите одну из лучших популяризаций современной физической космологии, доступную от одного из ведущих ее практиков.
Виленкин решительно отстаивает идею о том, что мы живем в мультивселенной, то есть причинно связанная вселенная — это всего лишь одна область в гораздо более обширном космосе, который включает бесконечное количество таких областей. Более того, каждая причинно связанная область подразделяется на бесконечное количество подобластей, каждая из которых составляет наблюдаемую вселенную, ограниченную горизонтом событий.Как будто этого было недостаточно, Виленкин также поддерживает интерпретацию многих миров квантовой физики Эверетта, так что даже бесконечная мультивселенная является лишь одним из бесконечно большого класса различных мультивселенных. Результатом является захватывающее дух видение физической реальности.
В основе мировоззрения Виленкина лежит теория будущей вечной или вечной инфляции (Виленкин ошибочно называет ее вечной инфляцией, хотя и считает, что инфляционная мультивселенная имеет только конечное прошлое). Согласно общей теории инфляции, наша Вселенная существует в состоянии истинного вакуума с плотностью энергии, которая почти равна нулю, но раньше она существовала в состоянии ложного вакуума с очень высокой плотностью энергии. Плотность энергии ложного вакуума подавляет даже интенсивное гравитационное притяжение, порожденное чрезвычайно высокой плотностью материи ранней Вселенной, вызывая сверхбыстрое или инфляционное расширение, во время которого Вселенная выросла с атомных пропорций до размеров больше, чем наблюдаемая Вселенная за одну тридцатую микросекунду.Виленкин прекрасно объясняет эмпирические данные, подтверждающие факт наступления такой ранней инфляционной эры.
Согласно общей теории инфляции, наша Вселенная существует в состоянии истинного вакуума с плотностью энергии, которая почти равна нулю, но раньше она существовала в состоянии ложного вакуума с очень высокой плотностью энергии. Плотность энергии ложного вакуума подавляет даже интенсивное гравитационное притяжение, порожденное чрезвычайно высокой плотностью материи ранней Вселенной, вызывая сверхбыстрое или инфляционное расширение, во время которого Вселенная выросла с атомных пропорций до размеров больше, чем наблюдаемая Вселенная за одну тридцатую микросекунду.Виленкин прекрасно объясняет эмпирические данные, подтверждающие факт наступления такой ранней инфляционной эры.
Но Виленкину нужно нечто большее, чем общая теория инфляции. Чтобы обеспечить вечную инфляцию, Виленкин выдвигает гипотезу о том, что скалярные поля, определяющие плотность энергии и эволюцию состояния ложного вакуума, характеризуются определенным наклоном, который проявляется в ложном вакууме, расширяющемся так быстро, что, распадаясь на карманы настоящего вакуума «островные вселенные», создаваемые таким образом в этом море ложного вакуума, хотя сами расширяются с огромной скоростью, не могут угнаться за расширением ложного вакуума и поэтому оказываются все более разделенными со временем. Новые очаги истинного вакуума будут продолжать формироваться в промежутках между островными вселенными и сами станут изолированными мирами. Несмотря на то, что мультивселенная конечна и геометрически замкнута, Виленкин утверждает, что ложный вакуум будет продолжать расширяться бесконечно. Он не объясняет, как это согласуется, помимо особых возражений, со Вторым законом термодинамики.
Новые очаги истинного вакуума будут продолжать формироваться в промежутках между островными вселенными и сами станут изолированными мирами. Несмотря на то, что мультивселенная конечна и геометрически замкнута, Виленкин утверждает, что ложный вакуум будет продолжать расширяться бесконечно. Он не объясняет, как это согласуется, помимо особых возражений, со Вторым законом термодинамики.
В этот момент Виленкин выполняет изящную лекцию. По мере того, как островные вселенные расширяются, их центральные области в конечном итоге становятся темными и бесплодными, в то время как звезды формируются по их постоянно расширяющимся периметрам.Мы должны думать о распаде ложного вакуума в истинный вакуум, происходящем на расширяющихся границах островов, как о множественных Больших взрывах. С глобальной точки зрения раздувающейся мультивселенной, эти большие взрывы происходят последовательно, поскольку границы островов со временем растут. В глобальном времени мультивселенной каждый остров в любое время имеет конечную протяженность, хотя и растет. Теперь наступает ловкость рук. Когда мы рассматриваем внутреннее космическое время каждой островной вселенной, каждый из них можно проследить до начального события Большого взрыва.Теперь мы можем связать эти различные события Большого взрыва, как происходящие одновременно. Большие взрывы, которые произойдут в глобальном будущем, теперь следует рассматривать как настоящее. В результате бесконечный временной ряд последовательных Больших взрывов превращается в бесконечный пространственный массив одновременных Больших взрывов. Следовательно, с внутренней точки зрения каждая островная вселенная бесконечна.
Теперь наступает ловкость рук. Когда мы рассматриваем внутреннее космическое время каждой островной вселенной, каждый из них можно проследить до начального события Большого взрыва.Теперь мы можем связать эти различные события Большого взрыва, как происходящие одновременно. Большие взрывы, которые произойдут в глобальном будущем, теперь следует рассматривать как настоящее. В результате бесконечный временной ряд последовательных Больших взрывов превращается в бесконечный пространственный массив одновременных Больших взрывов. Следовательно, с внутренней точки зрения каждая островная вселенная бесконечна.
Это смешение внешнего вида и реальности приводит Виленкина к странным выводам. Поскольку каждый остров-вселенная считается ее обитателями бесконечной, ее можно разделить на бесконечное количество наблюдаемых областей (или O-областей), каждая размером с нашу наблюдаемую Вселенную.Квантовая механика подразумевает, что существует только конечное число историй от Большого взрыва до любого момента в любой О-области. Отсюда следует, что для бесконечного числа О-регионов каждая история повторяется бесконечное количество раз. Таким образом, наш собственный мир в мельчайших деталях дублируется бесконечное количество раз в О-регионах нашего острова. В самом деле, «всевозможные вариации» истории нашего мира будут появляться бесконечное количество раз в ансамбле О-регионов.
Отсюда следует, что для бесконечного числа О-регионов каждая история повторяется бесконечное количество раз. Таким образом, наш собственный мир в мельчайших деталях дублируется бесконечное количество раз в О-регионах нашего острова. В самом деле, «всевозможные вариации» истории нашего мира будут появляться бесконечное количество раз в ансамбле О-регионов.
Обратите внимание, что этот вывод предполагает, что физический мир может быть полностью описан уравнениями квантовой механики.Как таковая, она подрывается присутствием в мире агентов, наделенных свободой воли, действия которых категорически не случайны. Нет никаких оснований полагать, что в каком-то О-регионе Адольф Гитлер (или его коллега) произнесет свой нюрнбергский адрес, стоя на голове, не говоря уже о том, что он (или они) решат сделать что-то настолько глупое бесконечное количество раз. . Но не бери в голову; более фундаментальная ошибка со стороны Виленкина — его ловкое преобразование бесконечной временной последовательности будущих O-областей в бесконечный пространственный массив одновременных O-областей. Мы видим переключатель, когда он говорит: «Любая история с ненулевой вероятностью произойдет — или, вернее, произошла — в бесконечном количестве О-регионов!» (стр.112). Если смотреть глобально, эти О-регионы находятся в будущем, и их будет бесконечное число только в том смысле, что остров будет существовать вечно. Еще более фундаментально заключение Виленкина, кажется, предполагает пространственно-временной реализм или, как его иногда называют, четырехмерность, поскольку, если напряжение и временное становление являются объективными характеристиками реальности, тогда будущее потенциально бесконечно, а будущие О-области не в любом смысле существуют.Если есть глобальная волна становления, тогда в конце концов не существует бесконечного набора О-регионов.
Мы видим переключатель, когда он говорит: «Любая история с ненулевой вероятностью произойдет — или, вернее, произошла — в бесконечном количестве О-регионов!» (стр.112). Если смотреть глобально, эти О-регионы находятся в будущем, и их будет бесконечное число только в том смысле, что остров будет существовать вечно. Еще более фундаментально заключение Виленкина, кажется, предполагает пространственно-временной реализм или, как его иногда называют, четырехмерность, поскольку, если напряжение и временное становление являются объективными характеристиками реальности, тогда будущее потенциально бесконечно, а будущие О-области не в любом смысле существуют.Если есть глобальная волна становления, тогда в конце концов не существует бесконечного набора О-регионов.
Этот рецензент не может не задаться вопросом о психологии людей, которые, кажется, находят определенную радость в перспективе бесконечных дубликатов нашего мира. (Мне сказали, что Виленкин изначально находил эту идею удручающей; но если так, то он, кажется, преодолел ее. ) Почему некоторым людям эта идея кажется такой привлекательной? Думаю, ключ к разгадке есть в «Прощании с уникальностью» Виленкина, где он пишет:
) Почему некоторым людям эта идея кажется такой привлекательной? Думаю, ключ к разгадке есть в «Прощании с уникальностью» Виленкина, где он пишет:
В мировоззрении, возникшем в результате вечной инфляции, наша Земля и наша цивилизация совсем не уникальны.Вместо этого бесчисленные идентичные цивилизации разбросаны по бескрайним просторам космоса. Когда человечество сведено к абсолютной космической незначительности, наше нисхождение из центра вселенной теперь завершено (стр. 117).
Не говоря уже о странном предположении, что значение человечества следует оценивать с точки зрения его редкости в космосе; Меня поражает примечание празднования, которое сопровождает это предполагаемое понижение в должности.
Большая часть интереса Виленкина к постулированию множества миров в одном состоит в том, чтобы найти поддержку Антропному Принципу, чтобы объяснить тонкую настройку Вселенной.Квантовые флуктуации в скалярных полях определяют, какой вакуум распадется из ложного вакуума, каждый из которых связан с различным набором значений для констант природы. Постулируя бесконечное множество островных вселенных, случайным образом меняющих свои константы, Виленкин может обратиться к Антропному принципу, чтобы объяснить наблюдаемую тонкую настройку: наши наблюдения ограничены эффектом отбора, навязанным нашим собственным существованием. Постулирование множества миров позволяет избежать вывода о замысле, который можно было бы сделать, чтобы поместить homo sapiens (самая сложная структура в мире) в центр вселенной.Удовольствие от дублированных миров проистекает из последующего свержения человечества как венца творения.
Постулируя бесконечное множество островных вселенных, случайным образом меняющих свои константы, Виленкин может обратиться к Антропному принципу, чтобы объяснить наблюдаемую тонкую настройку: наши наблюдения ограничены эффектом отбора, навязанным нашим собственным существованием. Постулирование множества миров позволяет избежать вывода о замысле, который можно было бы сделать, чтобы поместить homo sapiens (самая сложная структура в мире) в центр вселенной.Удовольствие от дублированных миров проистекает из последующего свержения человечества как венца творения.
Но если бесконечный ансамбль одновременных островных вселенных на самом деле не существует, попытка Виленкина объяснить тонкую настройку вселенной для разумной жизни терпит крах. Ведь если на самом деле бесконечное множество островных вселенных еще не существует, если большинство из них лежат в потенциально бесконечном будущем и, следовательно, нереальны, то на самом деле существует лишь столько вселенных, сколько могло образоваться в ложном вакууме с тех пор, как зарождение мультивселенной на ее границе в конечном прошлом. Учитывая непостижимую маловероятность того, что все константы случайным образом попадают в допустимый для жизни диапазон, вполне может быть крайне маловероятным, чтобы разрешающая жизнь островная вселенная так скоро распалась из ложного вакуума. В этом случае жало тонкой настройки не уменьшилось.
Учитывая непостижимую маловероятность того, что все константы случайным образом попадают в допустимый для жизни диапазон, вполне может быть крайне маловероятным, чтобы разрешающая жизнь островная вселенная так скоро распалась из ложного вакуума. В этом случае жало тонкой настройки не уменьшилось.
Напомним, что весь сценарий мультивселенной Виленкина зависит от гипотезы вечной инфляции, которая, в свою очередь, основана на существовании определенных изначальных скалярных полей, управляющих инфляцией.Хотя Виленкин замечает, что «инфляция вечна практически во всех предложенных до сих пор моделях» (стр. 214), он также признает: «Другой важный вопрос заключается в том, действительно ли такие скалярные поля существуют в природе. К сожалению, мы не знаем. Прямых доказательств их существования нет »(с. 61). Можно было бы подумать, что это отсутствие доказательств умерило бы уверенность, с которой Виленкин продвигает гипотезу мультивселенной.
Однако совершенно независимо от своей спекулятивной природы гипотеза мультивселенной сталкивается с потенциально смертельной проблемой, о которой Виленкин даже не упоминает. Проще говоря, если наша Вселенная является всего лишь одним из членов бесконечного набора случайно изменяющихся вселенных, то в подавляющем большинстве случаев более вероятно, что мы должны наблюдать совершенно иную вселенную, чем та, которую мы наблюдаем на самом деле. Эта же проблема оказалась разрушительной для обращения Людвига Больцмана к гипотезе мультивселенной в классической физике, чтобы объяснить, почему, если она существовала вечно, Вселенная сейчас не находится в состоянии термодинамического равновесия или тепловой смерти. Больцман сделал смелое предположение о том, что Вселенная в целом действительно существует в состоянии тепловой смерти, но что здесь и там случайные колебания создают очаги дисбаланса, которые Больцман называл «мирами».«Наша гипотеза — одна из них, и мы не должны удивляться, наблюдая наш мир в таком крайне маловероятном неравновесном состоянии, поскольку наблюдатели не могут существовать где-либо еще. Смелая гипотеза Больцмана была повсеместно отвергнута современной физикой на том основании, что это была наша Вселенная, но один такой мир в мультивселенной, гораздо более вероятно, что мы должны наблюдать гораздо меньшую область неравновесия — даже такую, в которой одна только наша солнечная система возникла в мгновение ока в результате случайных колебаний, — чем то, что мы наблюдаем , поскольку это несравнимо более вероятно, чем постепенное формирование всей Вселенной за счет уменьшения энтропии из состояния равновесия.
Проще говоря, если наша Вселенная является всего лишь одним из членов бесконечного набора случайно изменяющихся вселенных, то в подавляющем большинстве случаев более вероятно, что мы должны наблюдать совершенно иную вселенную, чем та, которую мы наблюдаем на самом деле. Эта же проблема оказалась разрушительной для обращения Людвига Больцмана к гипотезе мультивселенной в классической физике, чтобы объяснить, почему, если она существовала вечно, Вселенная сейчас не находится в состоянии термодинамического равновесия или тепловой смерти. Больцман сделал смелое предположение о том, что Вселенная в целом действительно существует в состоянии тепловой смерти, но что здесь и там случайные колебания создают очаги дисбаланса, которые Больцман называл «мирами».«Наша гипотеза — одна из них, и мы не должны удивляться, наблюдая наш мир в таком крайне маловероятном неравновесном состоянии, поскольку наблюдатели не могут существовать где-либо еще. Смелая гипотеза Больцмана была повсеместно отвергнута современной физикой на том основании, что это была наша Вселенная, но один такой мир в мультивселенной, гораздо более вероятно, что мы должны наблюдать гораздо меньшую область неравновесия — даже такую, в которой одна только наша солнечная система возникла в мгновение ока в результате случайных колебаний, — чем то, что мы наблюдаем , поскольку это несравнимо более вероятно, чем постепенное формирование всей Вселенной за счет уменьшения энтропии из состояния равновесия.
Теперь аналогичная проблема затрагивает современные обращения к мультивселенной с просьбой объяснить тонкую настройку. Роджер Пенроуз подсчитал, что вероятность того, что условие низкой энтропии в нашей Вселенной будет получено случайно, составляет порядка 1:10 10 (123) , что немыслимо. Если бы наша Вселенная была всего лишь одним из членов мультивселенной случайно упорядоченных миров, то гораздо более вероятно, что мы наблюдали бы гораздо меньшую упорядоченную Вселенную. Вероятность мгновенного образования нашей Солнечной системы в результате случайных столкновений частиц, согласно Пенроузу, составляет примерно 1:10 10 (60) , огромное число, но немыслимо меньше, чем 10 10 (123) .Или, опять же, если наша Вселенная является всего лишь одним из членов мультивселенной, тогда мы должны наблюдать весьма необычные события, такие как появление и исчезновение лошадей в результате случайных столкновений или вечные двигатели, поскольку они гораздо более вероятны, чем все остальные. константы и количества природы случайно попадают в практически бесконечно малый допустимый для жизни диапазон. Наблюдаемые вселенные, подобные этим, гораздо более многочисленны в ансамбле вселенных, чем миры, подобные нашему, и поэтому должны были бы наблюдаться нами, если бы Вселенная была всего лишь одним из членов мультивселенной миров.Поскольку у нас нет таких наблюдений, этот факт сильно опровергает гипотезу мультивселенной. По крайней мере, с точки зрения натурализма, поэтому весьма вероятно, что мультивселенной не существует.
константы и количества природы случайно попадают в практически бесконечно малый допустимый для жизни диапазон. Наблюдаемые вселенные, подобные этим, гораздо более многочисленны в ансамбле вселенных, чем миры, подобные нашему, и поэтому должны были бы наблюдаться нами, если бы Вселенная была всего лишь одним из членов мультивселенной миров.Поскольку у нас нет таких наблюдений, этот факт сильно опровергает гипотезу мультивселенной. По крайней мере, с точки зрения натурализма, поэтому весьма вероятно, что мультивселенной не существует.
Но Виленкин еще не закончил. Признавая, что большинство физиков агностически относятся к физической интерпретации квантовой механики, Виленкин чувствует себя обязанным принять «Интерпретацию многих миров» Эверетта. В копенгагенской интерпретации это измерение наблюдателем, которое сводит квантовую неопределенность к точному состоянию.«Ортодоксальная копенгагенская интерпретация, которая требует внешнего наблюдателя для проведения измерений в системе, не может быть даже сформулирована в этом случае [, т. Е. , квантовая космология]: нет внешних наблюдателей по отношению к Вселенной» (стр. 115) . Однако такое утверждение, похоже, предполагает атеизм. Более того, он игнорирует тот факт, что «Копенгаген» и «Многие миры» не исчерпывают наш выбор: существует множество альтернатив.
Е. , квантовая космология]: нет внешних наблюдателей по отношению к Вселенной» (стр. 115) . Однако такое утверждение, похоже, предполагает атеизм. Более того, он игнорирует тот факт, что «Копенгаген» и «Многие миры» не исчерпывают наш выбор: существует множество альтернатив.
Что характерно, Виленкин позже утверждает, что его собственная теория квантового творения предполагает в качестве необходимого условия Интерпретацию многих миров:
Если принять копенгагенскую интерпретацию, то сотворение мира было одноразовым событием, когда единственная вселенная возникла из ничего.Однако это приводит к проблеме. Скорее всего, из ничего выскочит крошечная Вселенная размером с Планк, которая не будет туннелировать, а мгновенно схлопнется и исчезнет. Туннелирование большего размера имеет небольшую вероятность и, следовательно, требует большого количества испытаний. Похоже, это согласуется только с интерпретацией Эверетта (стр. 187).
Виленкин лучше надеялся, что это не так, поскольку большинство философов и физиков сочли бы это reductio ad absurdum его рассказом о сотворении.
Это подводит нас к другому великому космологическому вопросу, которым Виленкин занимается в книге: имела ли Вселенная — или, скорее, мультивселенная — абсолютное начало. Пересказав предсказание об абсолютном начале стандартной модели Большого взрыва и каталогизируя различные попытки предотвратить его, Виленкин объясняет свою формулировку с Арвиндом Бордом и Аланом Гутом в 2003 году теоремы, которая устанавливает, что любая вселенная, которая в среднем имела в своей прошлой истории находящийся в состоянии расширения не может быть бесконечным в прошлом, но должен иметь границу пространства-времени.Это теорема великой силы, которая применима как к инфляционным моделям, так и к текущим космологическим моделям бран более высоких измерений, основанным на теории струн, а также к типичным моделям расширения. Виленкин не любит ударов: «Говорят, что аргумент — это то, что убеждает разумных людей, а доказательство — это то, что нужно, чтобы убедить даже неразумного человека. Имея доказательство, космологи больше не могут прятаться за возможностью прошлого. вечная вселенная. Выхода нет, им предстоит столкнуться с проблемой космического начала »(стр.176).
вечная вселенная. Выхода нет, им предстоит столкнуться с проблемой космического начала »(стр.176).
Признавая, что теологи часто приветствовали свидетельства о начале Вселенной как свидетельство существования Бога, Виленкин отвергает такой взгляд как «слишком упрощенный» (стр. 177). Как так? Виленкин цитирует джайнского поэта Джинасена, который спросил: «Если Бог создал мир, был ли Он до творения?» и «Как мог Бог создать мир без какого-либо сырья?» (стр.170). Поскольку Виленкин отвергает джайнскую точку зрения о несотворенности и вечности мира, он знает, что подобные «парадоксы» встречаются и с ним (стр.177). Следовательно, если теизм является упрощенным, то не потому, что он сталкивается со специфическими проблемами, а потому, что он не позволяет решить эти проблемы. Виленкин, кажется, полагает, что теист ошеломлен подобными вопросами. Но это не так. Первый вопрос Дзинасены касается действующей причины вселенной, а второй — материальной причины. На первый вопрос нетрудно ответить: «Нигде», поскольку пространство и время возникают при творении, так что нет «до» и «где» до начала. Второй вопрос более загадочный; но если теория квантового туннелирования Виленкина дает представление о том, как Вселенная может возникнуть без материальной причины, то теист также может свободно ею воспользоваться. Преимущество теизма перед натуралистическими учениями состоит в том, что теизм обеспечивает действенную причину возникновения Вселенной, тогда как натурализм не может.
Второй вопрос более загадочный; но если теория квантового туннелирования Виленкина дает представление о том, как Вселенная может возникнуть без материальной причины, то теист также может свободно ею воспользоваться. Преимущество теизма перед натуралистическими учениями состоит в том, что теизм обеспечивает действенную причину возникновения Вселенной, тогда как натурализм не может.
Поэтому натуралист вынужден сказать, что вселенная возникла без какой-либо действенной или материальной причины. Теория квантового творения Виленкина как раз и является попыткой сделать такую точку зрения правдоподобной.Его изложение своей модели настолько ясно и просто, что метафизику легко увидеть, где Виленкин неверно истолковал ее онтологическое значение. Он предлагает нам представить себе маленькую замкнутую сферическую вселенную, заполненную ложным вакуумом и содержащую некоторую обычную материю. Если радиус такой Вселенной мал, классическая физика предсказывает, что она схлопнется в точку; но квантовая физика позволяет ему «туннелировать» в состояние инфляции. (Напомним, что такое событие, тем не менее, настолько маловероятно, что для сохранения учетной записи необходимо вызвать Интерпретацию многих миров.) Если мы позволим радиусу полностью сузиться до нуля, все равно останется некоторая положительная вероятность туннелирования Вселенной к инфляции. Теперь Виленкин объяснительно приравнивает начальное состояние вселенной до туннелирования к небытию: «То, что у меня было, было математическим описанием туннелирования вселенной от нулевого размера — из ничего! — до конечного радиуса и начала раздувания» (стр. 180) . Эта эквивалентность явно ошибочна. Как показывает диаграмма Виленкина на той же странице, квантовое туннелирование в каждой точке является функцией от чего-то к чему-то.Чтобы квантовое туннелирование действительно происходило из ничего, функция должна иметь единственный член, апостериорный член. Другой способ увидеть суть дела — подумать о том, что «не иметь радиуса» (как в случае с небытием) не означает «иметь радиус, мера которого равна нулю».
(Напомним, что такое событие, тем не менее, настолько маловероятно, что для сохранения учетной записи необходимо вызвать Интерпретацию многих миров.) Если мы позволим радиусу полностью сузиться до нуля, все равно останется некоторая положительная вероятность туннелирования Вселенной к инфляции. Теперь Виленкин объяснительно приравнивает начальное состояние вселенной до туннелирования к небытию: «То, что у меня было, было математическим описанием туннелирования вселенной от нулевого размера — из ничего! — до конечного радиуса и начала раздувания» (стр. 180) . Эта эквивалентность явно ошибочна. Как показывает диаграмма Виленкина на той же странице, квантовое туннелирование в каждой точке является функцией от чего-то к чему-то.Чтобы квантовое туннелирование действительно происходило из ничего, функция должна иметь единственный член, апостериорный член. Другой способ увидеть суть дела — подумать о том, что «не иметь радиуса» (как в случае с небытием) не означает «иметь радиус, мера которого равна нулю».
Сам Виленкин, кажется, понимает, что на самом деле он не описал туннелирование вселенной буквально из ничего, поскольку он допускает: «И все же состояние« ничто »не может быть отождествлено с абсолютным небытием .Туннелирование описывается законами квантовой механики, и поэтому «ничто» не должно подчиняться этим законам »(стр. 181). Отсюда следует, что Вселенная, описываемая этими законами, не есть ничто. К сожалению, Виленкин делает ошибочный вывод, что «Законы физики должны были существовать, даже если вселенной не было» (стр. 181). Даже если кто-то принимает платонический взгляд на законы природы, они, в лучшем случае, являются либо математическими объектами, либо предложениями, абстрактными сущностями, которые не имеют воздействовать на что угодно.(Интересно, что Виленкин придерживается концептуалистской точки зрения, согласно которой законы существуют в разуме, предшествующем Вселенной [стр. 205], наиболее близкий к теизму — Виленкин). Если эти законы действительно описательны, то, очевидно, не может быть правдой, что «вселенной не было». Конечно, законы могли существовать и быть ложными, и в этом случае они не являются описательными; но тогда теория Виленкина окажется ложной.
Конечно, законы могли существовать и быть ложными, и в этом случае они не являются описательными; но тогда теория Виленкина окажется ложной.
То, что Виленкин по-настоящему не осознал, насколько радикальным является происхождение существа из небытия, очевидно из его недоверия к утверждению модели Хартла-Хокинга о том, что бесконечная вселенная должна возникать из ничего.Он восклицает: «Тогда наиболее вероятно, что из ничего может выскочить бесконечное, пустое, плоское пространство. Мне очень трудно в это поверить!» (с. 191). Виленкину легче поверить, что крошечная вселенная должна возникнуть из ничего. Тем самым он демонстрирует непонимание метафизической пропасти, отделяющей бытие от небытия. Как указывал А.Н.Прайор, если что-то может возникнуть из ничего, тогда становится необъяснимым, почему все и вся, включая бесконечную вселенную, не возникает из ничего.
Таким образом, Виленкин не может ответить на парадоксы творения так же хорошо, как теист. Фактически, соединение теизма с моделью Виленкина было бы подходящим объяснением творения. Мы могли бы получить полное научное описание Вселенной до ее начала, когда Бог создал начальное состояние Вселенной. Но натурализм сам по себе не справится. Если эффективная причинность в отрыве от материальной причинно-следственной связи кажется трудной, то происхождение Вселенной без эффективной или материальной причинности является еще более трудным.
Мы могли бы получить полное научное описание Вселенной до ее начала, когда Бог создал начальное состояние Вселенной. Но натурализм сам по себе не справится. Если эффективная причинность в отрыве от материальной причинно-следственной связи кажется трудной, то происхождение Вселенной без эффективной или материальной причинности является еще более трудным.
Можно попытаться спасти натуралистическое описание квантового туннелирования, предоставив его математическое описание в терминах евклидова, или того, что Хокинг называет мнимым временем. В этом случае Вселенная вообще не возникает, а существует вне времени как неособое четырехмерное многообразие, имеющее форму, аналогичную форме волана. По крайней мере, Хокинг, как известно, использовал это, чтобы исключить необходимость в Создателе. Но интересно, что у Виленкина не будет грузовика со столь реалистичным построением евклидова четырехмерного пространства.Он введен «только для удобства вычислений» (стр. 182). Предложение Хартла-Хокинга об отсутствии границ «потеряло большую часть своей интуитивной привлекательности» после перехода на евклидово время; фактически, «он учит нас суммировать истории, которые, безусловно, невозможны, потому что мы не живем в евклидовом времени» (стр. 190-1). Это разумная метафизика; но это исключает обращение к воображаемому времени как способ избежать так называемых парадоксов творения.
190-1). Это разумная метафизика; но это исключает обращение к воображаемому времени как способ избежать так называемых парадоксов творения.
Виленкин может сказать интересные вещи по другим темам — например, по физической эсхатологии, — но его трактовка центральных тем тонкой настройки и космического происхождения, обсуждаемых в этом обзоре, будет особенно интересна философам религии, интересующимся космологией и наукой. телеологические аргументы в пользу Создателя и Создателя Вселенной.
| 31 марта 2009 г. По словам физика Александра Виленкина, директора Института космологии Университета Тафтса, если вы видели один Большой взрыв, вы определенно не видели их всех.Виленкин — приглашенный спикер на лекцию Хофштадтера в этом году, спонсируемую Стэнфордским физическим факультетом. Согласно Виленкину, Большой взрыв, породивший нашу Вселенную, — всего лишь одна из бесконечного числа вселенных, которые появляются из ниоткуда, просто пузыри в большей вселенной вселенных, которая сама расширяется с невообразимой скоростью. И этот сценарий, по словам Виленкина, приводит к удивительному выводу. В бесконечном количестве вселенных все возможные устройства пространства, материи и времени будут происходить бесконечное количество раз. «Поразительным следствием новой картины мира является то, что должно появиться бесконечное количество регионов с историей, абсолютно идентичной нашей», — писал Виленкин. «Верно, десятки ваших дубликатов сейчас читают копии этой статьи. Они живут на планетах, точно таких же, как Земля, со всеми ее горами, городами, деревьями и бабочками. Также должны быть регионы, история которых несколько отличается от нашей, со всеми возможные варианты «. Например, должно быть бесчисленное множество регионов, в которых Эл Гор стал президентом США. По словам физика, значение этих открытий может быть удручающим. Homo sapiens не особенный во вселенной; на самом деле мы даже не уникальны. Это большой шаг назад по сравнению с теми днями, когда люди считали себя буквально центром Вселенной. Родился в бывшем Советском Союзе, Виленкин получил степень бакалавра в 1971 году в Харьковском государственном университете. Его призвали в армию, а затем он работал на разных должностях, в том числе в ночном стороже в зоопарке, а в свободное время занимался физическими исследованиями.Он иммигрировал в Соединенные Штаты в 1976 году как еврейский беженец. Он является авторитетом в так называемой теории инфляции ранней вселенной и автором популярной книги Многие миры в одном: поиск других вселенных . Он утверждает, что вселенные возникают из пустоты, а затем расширяются так быстро, что за крошечную долю секунды область размером с атом раздувается до размеров, намного превышающих размеры всей наблюдаемой Вселенной. Наш галактический дом, Млечный Путь, в конечном итоге встретит свою гибель одним из двух способов, сказал Виленкин в интервью Stanford Report . Скорее всего, это столкновение Млечного Пути с галактикой Андромеды, которое должно произойти через несколько миллиардов лет.Но также возможно, что до этого наша собственная пузырьковая вселенная столкнется с другим пузырем. «Если это столкновение произойдет в нашем районе, мы никогда его не увидим», — сказал Виленкин. Это был бы очень внезапный, катастрофический конец. Такое столкновение выглядело бы как небольшая рябь на чрезвычайно однородном фоне космического излучения.«На этом фоне это будет выглядеть как горячее или холодное пятно», — сказал он. «Там будет небольшое круглое пятно, где плотность излучения будет немного слабее, чем где-либо еще». По его словам, наблюдатели уже заметили неожиданное холодное пятно: «Итак, кто знает, это может быть следом столкновения». По мере того, как космологи исследуют самые ранние микромоменты Большого взрыва, неизбежно возникает вопрос: «Что существовало до Большого взрыва?» Обычно ответ — «ничего», поскольку до начала не было ни пространства, ни времени. Но у Виленкина есть более тонкий ответ. Если законы природы диктуют, как Вселенная может спонтанно возникать из небытия, и если существует элегантное математическое описание этих законов, то, возможно, законы и уравнения существовали до самого творения. Это пересмотр учеными старого вопроса: «Где был Бог до того, как Бог создал вселенную?» Лекция Виленкина «Множество миров в одном» запланирована на 20:00. Понедельник, 6 апреля, в учебном центре Hewlett, 370 Serra Mall, комната 200.Это бесплатно и открыто для всех. Он также выступит на более техническом коллоквиуме «Меры Мультивселенной» в 16:15. Вторник, 7 апреля, в 201 кабинете учебного центра. Лекция Хофштадтера посвящена памяти покойного лауреата Нобелевской премии физика Роберта Хофштадтера, который был членом факультета Стэнфорда с 1950 года до своей смерти в 1990 году. -30- |
В начале было началом
К настоящему времени существует научный консенсус в отношении того, что наша Вселенная возникла почти 14 миллиардов лет назад в результате события, известного как Большой взрыв.Но эта теория поднимает больше вопросов о происхождении Вселенной, чем дает ответов, включая самый простой: что произошло в г. до Большого взрыва г.? Некоторые космологи утверждали, что у Вселенной не могло быть начала, но всегда было.
до Большого взрыва г.? Некоторые космологи утверждали, что у Вселенной не могло быть начала, но всегда было.
В 2003 году космолог Тафтса Александр Виленкин и его коллеги Арвинд Борд, ныне старший профессор математики в Университете Лонг-Айленда, и Алан Гут, профессор физики в Массачусетском технологическом институте, доказали математическую теорему, показывающую, что при очень общих предположениях На самом деле вселенная должна была иметь начало.
После этого открытия другие специалисты в этой области выступили против альтернативных теорий, описывающих другие типы вселенных, к которым теорема Борде-Гута-Виленкина, как ее называют, неприменима. Виленкин, профессор физики и астрономии, и аспирант Одри Митани, G15, с помощью математики исследовали три потенциальных логистических лазейки в теореме 2003 года, укрепив их первоначальную предпосылку о том, что Вселенная действительно возникла. Первые две лазейки уже были устранены в теореме.Целью статьи было устранение третьей лазейки. Статья, размещенная на онлайн-форуме по математике и науке, организованном Корнельским университетом под названием arXive , получила освещение в ненаучных публикациях, включая британский Daily Mail и веб-сайт Fox News, и вызвала новые дискуссии по поводу начало начала.
Статья, размещенная на онлайн-форуме по математике и науке, организованном Корнельским университетом под названием arXive , получила освещение в ненаучных публикациях, включая британский Daily Mail и веб-сайт Fox News, и вызвала новые дискуссии по поводу начало начала.
Tufts Now: Какие основные теории Вселенной вы рассматривали?
Александр Виленкин : Мы рассмотрели три возможных сценария — все они, кстати, были предложены древними индусами 3000 лет назад.
В одном сценарии, который индусы назвали «вечной вселенной», в разных местах происходят множественные начала. В научной космологии это более или менее соответствует идее, называемой вечной инфляцией. В этом случае Вселенная расширяется очень быстро, а затем то тут, то там случаются Большие Взрывы. Эти большие взрывы локализованы в пузырьках. По мере того, как эти пузыри — каждый из которых содержит дискретную вселенную — раздвигаются, между ними открывается пространство, где создаются новые пузыри. Мы живем в одном таком пузыре.[Все эти пузырьки, содержащие вселенную, составляют то, что космологи называют мультивселенной.]
Мы живем в одном таком пузыре.[Все эти пузырьки, содержащие вселенную, составляют то, что космологи называют мультивселенной.]
Другая идея — это циклическая вселенная, которая расширяется, сжимается и затем начинается заново.
Третья возможность и основная цель этой статьи, которую я написал вместе со своей ученицей Одри Митани, — это возникающая вселенная, статическая вселенная, которая существует вечно, а затем каким-то образом распахивается и начинает расширяться. Индусы называли это «космическим яйцом». Вам нужен какой-то механизм, который вызовет это событие, но это выполнимо.
Как вам удалось исключить первые два сценария?
Для модели вечной инфляции математически мы можем показать, что этому процессу нет конца. Некоторые люди думали, что, может быть, ты тоже можешь избежать начала. Но наша теорема 2003 года показывает, что [избежать начала] для этого сценария невозможно. Хотя инфляция может быть вечной в будущем, ее нельзя бесконечно распространять на прошлое. Вот и все.
Вот и все.
Циклическая Вселенная подчиняется второму закону термодинамики, который гласит, что любая система, предоставленная самой себе, в конечном итоге достигает состояния максимального беспорядка, называемого тепловым равновесием.Итак, если бы Вселенная была цикличной, то в каждом цикле беспорядок во Вселенной увеличивался бы. В конце концов Вселенная достигнет этого состояния теплового равновесия, которое представляет собой смесь всего без каких-либо особенностей — это не то, что мы видим вокруг.
Однако одна гипотеза о циклической Вселенной позволяет избежать этой проблемы термодинамики. Существуют модели циклической Вселенной, в которой объем увеличивается с каждым циклом. Таким образом, Вселенная расширяется и сжимается, но сжимается до большего объема, чем в предыдущем цикле.Таким образом, даже если беспорядок увеличивается, беспорядок на единицу объема не меняется.
Это возможно, но наша теорема 2003 года создает проблему, потому что если объем Вселенной увеличивается, то должно быть начало.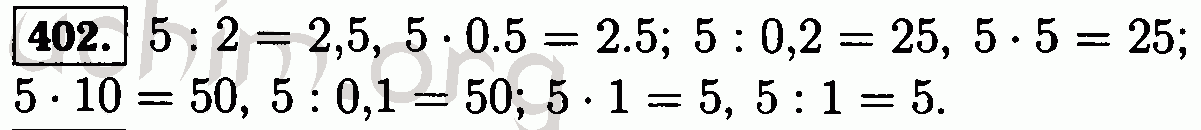 Таким образом, сценарий циклической вселенной также не избегает начала.
Таким образом, сценарий циклической вселенной также не избегает начала.
А космическое яйцо?
Существуют модели классической физики, согласно которым эта статическая Вселенная будет оставаться там вечно, а затем внезапно начать расширяться. Но мы показали, что квантово-механически эта Вселенная нестабильна.[Квантовая механика — это раздел физики, который описывает поведение субатомных частиц и приписывает событиям вероятность.]
Например, в классической или ньютоновской физике, если вы поместите мяч в чашку, он не вылезет. Он будет сидеть там вечно. Но с точки зрения квантовой механики объекты могут проходить сквозь них. Если я посижу здесь достаточно долго, есть некоторая вероятность, что я пройду через эту стену, и тогда я окажусь в коридоре. Конечно, вероятность очень мала, но она «не нулевая».”
Мы показали [в статье], что эта замкнутая статическая Вселенная также имеет вероятность квантово-механического коллапса. Вероятность его коллапса отлична от нуля, и поэтому он не мог существовать вечно. Итак, этот сценарий возникающего яйца, если включить квантовую механику — а мы должны это сделать — тоже нежизнеспособен.
Итак, этот сценарий возникающего яйца, если включить квантовую механику — а мы должны это сделать — тоже нежизнеспособен.
Есть ли у вашей теоремы недоброжелатели?
По этому поводу было много споров. Совсем недавно Леонард Сасскинд из Стэнфорда разместил статью по адресу arXiv , в которой он сказал, что, хотя теорема математически верна, если вечная инфляция продолжается вечно, насколько вероятно, что мы живем в самом начале? Если инфляция вечна для будущего, мы, скорее всего, будем очень и очень далеки от начала.И если мы живем очень-очень далеко в будущем от начала, то почти все следы начала стираются из нашего окружения. Итак, говорит Сасскинд, на самом деле мы не можем обнаружить ничего о происхождении Вселенной с помощью наблюдений.
С тех пор у нас было несколько обсуждений, и он [Сасскинд] отправил вторую заметку на arXive , в которой говорилось, что на самом деле не вся информация о начале Вселенной стерта. Есть некоторые признаки того, что в принципе свидетельство начала можно наблюдать.
Некоторые люди утверждают, что ваша работа доказывает существование Бога или, по крайней мере, божественный момент творения. Что вы думаете?
Не думаю, что это что-то так или иначе доказывает.
Я был на собрании богословов и космологов. По сути, я понял, что у этих богословов та же проблема с Богом. Что Он делал до того, как создал вселенную? Почему Он внезапно решил создать вселенную?
Для многих физиков начало Вселенной неудобно, потому что оно предполагает, что что-то должно было послужить причиной начала, что должна быть какая-то причина за пределами Вселенной.Фактически, теперь у нас есть модели, где в этом нет необходимости — Вселенная возникает спонтанно, квантово-механически.
В квантовой физике события не обязательно имеют причину, только некоторую вероятность.
Таким образом, существует некоторая вероятность того, что Вселенная выскочит из «ничего». Вы можете найти относительную вероятность того, что он будет того или иного размера и будет обладать различными свойствами, но не будет конкретной причины для любого из них, только вероятности.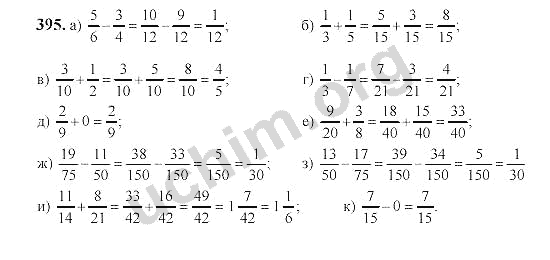
Я говорю «ничего» в цитатах, потому что то «ничто», о котором мы здесь говорим, — это отсутствие материи, пространства и времени.Это почти ничего, но все, что здесь требуется, — это законы физики. Так что законы физики все еще должны действовать, и они определенно не ничто.
Итак, как вы думаете, как возникла Вселенная?
Я не могу утверждать, что понимаю начало Вселенной. У нас есть логичная картина, и я считаю ее достижением. Потому что, если вы подумаете об этом, вы спросите: «Хорошо, а что было до Большого взрыва, до инфляции?» Кажется, вы можете продолжать задавать эти вопросы, и ответить на них невозможно.
Но это квантовое творение «из ничего», кажется, позволяет избежать этих вопросов. У него красивое математическое описание, а не просто слова. Но есть кое-что интересное; Описание создания Вселенной из ничего дается в терминах законов физики. Это заставляет задуматься, а где же эти законы? Если законы описывают создание Вселенной, это предполагает, что они существовали до Вселенной. Вопрос, на который никто не понимает, как ответить, — это откуда эти законы и почему именно эти законы? Так что есть много загадок, которые заставляют нас работать.
Вопрос, на который никто не понимает, как ответить, — это откуда эти законы и почему именно эти законы? Так что есть много загадок, которые заставляют нас работать.
Жаклин Митчелл можно позвонить по телефону [email protected] .
Добро пожаловать в Space Math @ NASA!
Решение проблем
Задача 564: Исследование звезд Ориона — Безумие светового года
Учащиеся изучают световой год и его связь со временем путешествия света для наблюдения за событиями в различных частях космоса. Когда колонисты в разных местах увидят, что звезда Бетельгейзе стала сверхновой?
[Оценка: 6-8 | Темы: временные рамки; расчет временных интервалов; время = расстояние / скорость]
[Кликните сюда]
Задача 507: Исследование запуска Falcon 9
Учащиеся используют данные о запуске ракеты-носителя Falcon 9 для определения ее скорости и ускорения.[Оценка: 6-8 | Темы: скорость = расстояние / время; Расчет времени]
[Кликните сюда]
Проблема 505: SDO видит корональный дождь — оценка скорости плазмы
Студенты оценивают скорость плазменных стримеров у поверхности Солнца, используя изображения, полученные в обсерватории солнечной динамики. [Оценка: 6-8 | Темы: масштабные модели; скорость = расстояние / время; пропорции]
[Кликните сюда]
[Оценка: 6-8 | Темы: масштабные модели; скорость = расстояние / время; пропорции]
[Кликните сюда]
Задача 488: RBSP и расположение хора рассвета — II
Учащиеся используют гипотетическую информацию от космического корабля-близнеца RBSP для триангуляции местоположения сигнала Chorus вблизи Земли с помощью угловых измерений, построения графиков и транспортира для определения точки пересечения сигналов CHorus.[Оценка: 6-8 | Темы: Углы; построение графиков; транспортиры]
[Кликните сюда]
Задача 452: Ближайшее сближение астероида 2005YU55 — I
Учащиеся работают с масштабным рисунком орбиты Луны и траектории астероида, чтобы предсказать, где астероид будет относительно Земли и орбиты Луны.
[Оценка: 6-8 | Темы: время = расстояние / скорость; масштабные модели; метрическая математика]
[Кликните сюда]
Задача 451: Эффектная планетарная туманность Кошачий глаз
Студенты измеряют диаметр туманности и используют информацию о скорости, чтобы оценить возраст туманности.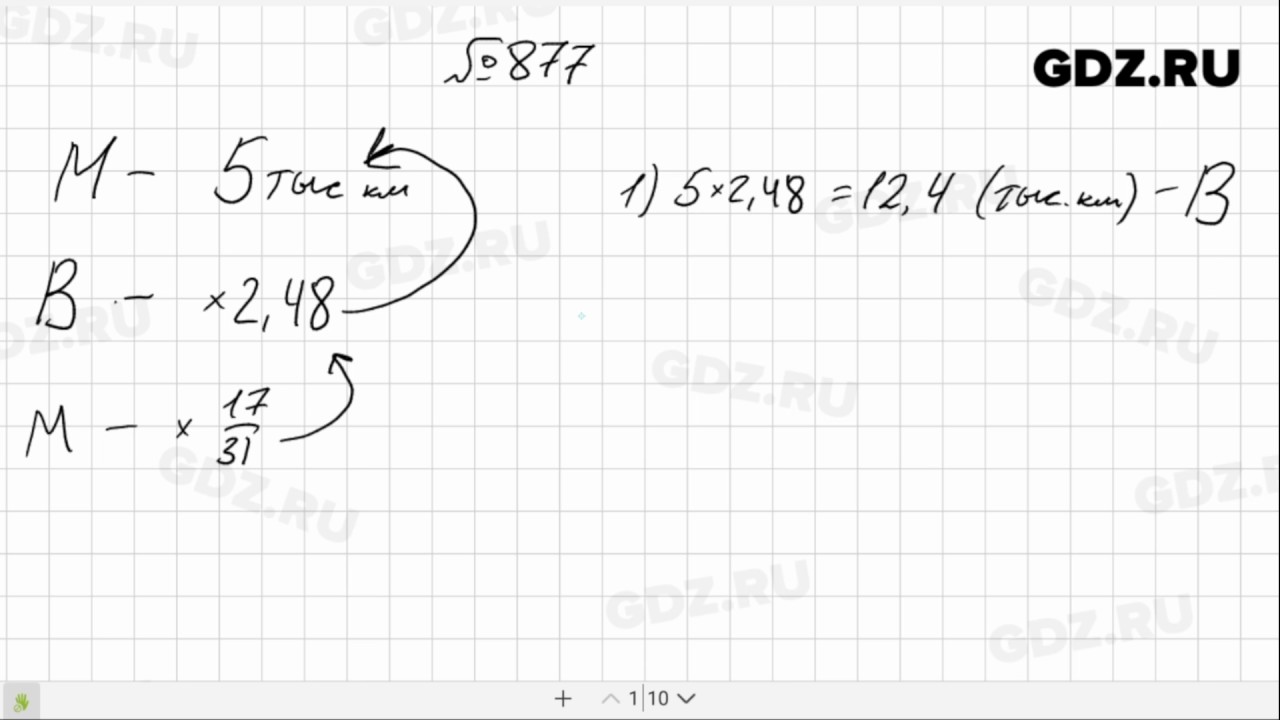 [Оценка: 6-8 | Темы: время = расстояние / скорость; масштабные модели; метрическая математика]
[Кликните сюда]
[Оценка: 6-8 | Темы: время = расстояние / скорость; масштабные модели; метрическая математика]
[Кликните сюда]
Задача 445: LRO — Относительный возраст лунных поверхностей
Учащиеся исследуют две зоны приземления Аполлона, используя изображения с космического корабля LRO, чтобы оценить относительный возраст двух регионов с использованием
подсчет кратеров.[Оценка: 6-8 | Темы: масштаб; гистограмма]
[Кликните сюда]
Задача 438: Последний полет космического корабля «Индевор»
Учащиеся используют табличные данные и графики для определения скорости запуска и ускорения космического челнока со стартовой площадки. [Оценка: 6-8 | Темы: табличные данные, графики, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 437: Скорость и высота старта ракеты Сатурн V
Учащиеся используют табличные данные для определения скорости запуска ракеты Сатурн V со стартовой площадки.[Оценка: 6-8 | Темы: табличные данные, графики, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 436: Спейс шаттл Challenger развертывает спутник INSAT-1B
Учащиеся используют последовательность изображений, чтобы определить скорость запуска спутника из грузового отсека космического шаттла. [Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 435: Запуск Аполлона-17 с поверхности Луны
Учащиеся используют последовательность изображений для определения скорости подъема капсулы Аполлона-17 с поверхности Луны.[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 434: Космический корабль «Рассвет» видит вблизи астероид Веста!
Студенты используют изображение астероида для определения диаметра кратеров
и горы, используя миллиметровую линейку и масштаб изображения в метрах на миллиметр.
[Оценка: 6-8 | Темы: шкала, метрические измерения]
[Кликните сюда]
Задача 433: космический шаттл «Атлантис» — скорость шлейфа
Учащиеся используют последовательность изображений из видеозаписи запуска, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения. [Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Проблема 432: Спейс Шаттл Атлантис — Скорость выхлопа
Учащиеся используют последовательность изображений из видеозаписи запуска, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения.
[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 431: космический шаттл «Атлантис» — скорость запуска
Учащиеся используют последовательность изображений из видеозаписи запуска, чтобы определить скорость по времени.
интервал между изображениями и масштаб каждого изображения.[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 430: Спейс шаттл «Атлантис» — восхождение на орбиту
Учащиеся используют последовательность изображений из видеозаписи запуска, чтобы определить скорость по времени. интервал между изображениями и масштаб каждого изображения.
[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
интервал между изображениями и масштаб каждого изображения.
[Оценка: 6-8 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 429: Отслеживание морской черепахи из космоса
Широта, долгота, прошедшее время и пройденное расстояние представлены в таблице.Учащиеся используют эти данные для определения суточной и почасовой скорости кожистой черепахи, когда она путешествует из Новой Зеландии в Калифорнию через Тихий океан.
[Оценка: 4-6 | Темы: шкала, метрические измерения, скорость = расстояние / время]
[Кликните сюда]
Задача 404: Космический аппарат STEREO дает 360-градусный обзор Солнца Студенты используют спутниковые изображения STEREO, чтобы определить, какие объекты можно увидеть с Земли, а какие нет. Они учатся о расположении и изменении положения спутников относительно орбиты Земли.[Оценка: 6-8 | Темы: угловая мера, экстраполяция; расстояние = скорость x время] [Кликните сюда]
Задача 267: Определение материалов по их отражательной способности Отражательная способность материала может использоваться для его идентификации.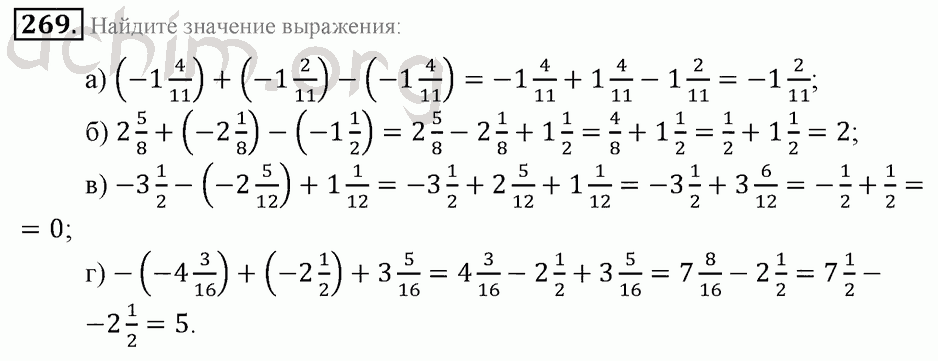 Это важно при съемке лунной поверхности на предмет
минералов, а также в создании «зеленой» среды обитания на Земле.
[Оценка: 6-8 | Темы: процент, интерпретация табличных данных, площадь] [Нажмите здесь]
Это важно при съемке лунной поверхности на предмет
минералов, а также в создании «зеленой» среды обитания на Земле.
[Оценка: 6-8 | Темы: процент, интерпретация табличных данных, площадь] [Нажмите здесь]
Задача 237: Марсианские пыльные дьяволы Учащиеся определяют скорость и ускорение марсианского пылевого дьявола на основе изображений временных кругов и информации о масштабе изображения.[Оценка: 6-8 | Темы: весы; Определение скорости из последовательных изображений; V = D / T] [Нажмите здесь]
Задача 247: Космическая мобильная головоломка Учащиеся вычисляют недостающие массы и длины в мобильном телефоне, используя основное уравнение баланса m1 x r1 = m2 x r2 для солнечная система мобильная. [Оценка: 6-8 | Темы: метрическая мера, алгебра 1, геометрия] [Нажмите здесь]
Задача 245: Твердотопливные ракетные ускорители Студенты узнают, как SRB на самом деле создают тягу, и изучают ускоритель Ares-V, чтобы оценить его тягу. [Оценка: 6-8 | Темы: объем, площадь, преобразование единиц] [Нажмите здесь]
[Оценка: 6-8 | Темы: объем, площадь, преобразование единиц] [Нажмите здесь]
Задача 238: Спутник и космический телескоп Хаббла Спутники увлекаются атмосферой, что в конечном итоге приводит к их сгоранию в атмосфере. Студенты учатся различные прогнозы высоты космического телескопа Хаббла, чтобы оценить год его возвращения в атмосферу. [Оценка: 6-8 | Темы: интерпретация графических данных; прогнозирование тенденций] [Нажмите здесь]
Задача 211: Куда делись все звезды? — Студенты узнают, почему на фотографиях НАСА часто не видны звезды из-за того, как камеры снимают яркие и тусклые объекты.[Оценка: 6-8 | Темы: умножение; разделение; десятичные числа.] [Щелкните здесь]
Задача 209: Как выделить тусклые предметы в ярком мире! — Студенты узнают, что сложение изображений вместе часто усиливает слабые вещи, которые не видны на одном изображении; мощность усреднения данных.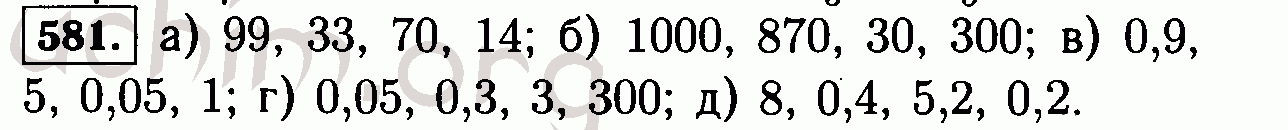 [Оценка: 6-8 | Темы: умножение; разделение; десятичные числа.] [Щелкните здесь]
[Оценка: 6-8 | Темы: умножение; разделение; десятичные числа.] [Щелкните здесь]
Задача 148 Изучение умирающей звезды Учащиеся используют данные спутника Spitzer для вычисления массы планетарной туманности по умирающей звезде.[Класс: 9 — 11 | Темы: Научная нотация; преобразование единиц измерения; объем сферы] [Нажмите здесь]
Задача 141 Изучение пыльной молодой звезды Учащиеся используют спутниковые данные Spitzer, чтобы узнать, как пыль излучает инфракрасный свет и рассчитать массу пылинок от молодой звезды в туманности NGC-7129. [Оценка: 4–7 | Темы: Алгебра I; умножение, деление; научная нотация] [Щелкните здесь]
Задача 134
Последнее полное солнечное затмение — когда-либо! Студенты изучают геометрию, необходимую для
полное солнечное затмение и оцените, сколько лет в будущем последнее полное солнечное затмение
затмение произойдет, когда Луна будет медленно удаляться от Земли на 3 сантиметра в год. [Класс: 7–10 | Темы: Простые линейные уравнения] [Щелкните здесь]
[Класс: 7–10 | Темы: Простые линейные уравнения] [Щелкните здесь]
Задача 124 Атмосфера Луны Студенты узнают об очень тонкой атмосфере Луны, вычисляя ее общую массу в килограммах, используя объем сферической оболочки и измеренную плотность. [Оценка: 8-10 | Темы: объем шара, оболочки; плотность-масса-объем; преобразование единиц] [Нажмите здесь]
Задача 115
Математическая модель Солнца Студенты будут использовать формулу для сферы и оболочки, чтобы вычислить массу
солнце для различных вариантов его плотности.Цель состоит в том, чтобы воспроизвести измеренную массу и радиус Солнца с помощью
тщательный подбор его плотности в области ядра и области оболочки. Учащиеся будут изменять значения плотности и размера оболочки, чтобы
достичь правильной общей массы. Это можно сделать вручную или с помощью программирования.
электронную таблицу Excel.
[Оценка: 8-10 | Темы: научная нотация; объем шара и сферической оболочки; плотность, масса и объем. ] [Щелкните здесь]
] [Щелкните здесь]
Задача 95 Исследование доз облучения космонавтов в космосе — Студенты изучат график доз облучения космонавтов для полетов космических шаттлов и оценят общие дозировки для космонавтов, работающих на Международной космической станции.[Уровень обучения: 9-11 | Темы: анализ графиков, интерполяция, преобразование единиц] [Нажмите здесь]
Задача 83 Риски падения метеорита на Лунер — В 2006 году ученые идентифицировали 12 вспышек света на Луне, которые, вероятно, были падением метеорита. По их оценкам, эти метеориты, вероятно, были размером с грейпфрут. Как долго лунным колонистам придется ждать, чтобы увидеть такую вспышку на своем горизонте? Студенты будет использовать вычисление площади и вероятности для определения среднего времени ожидания.[Уровень оценки: 8-10 | Темы: арифметика; преобразование единиц измерения; площадь поверхности сферы] [Нажмите здесь]
Задача 74
Жаркое время на Марсе — Эксперимент NASA Mars Radiation Environment (MARIE) создал карту поверхности Марса и измерил радиационный фон на уровне земли, которому будут подвергаться астронавты. Эта математическая задача позволяет студентам изучить общую дозу радиации, которую эти исследователи получат в серии 1000-километровых путешествий по марсианскому региону.
поверхность.Студенты будут сравнивать эту дозировку с типичными фоновыми условиями на Земле и на Международной космической станции, чтобы получить представление о перспективе.
[Уровень обучения: 6-8 | Темы: десятичные дроби, преобразование единиц измерения, построение графиков и анализ] [Нажмите здесь]
Эта математическая задача позволяет студентам изучить общую дозу радиации, которую эти исследователи получат в серии 1000-километровых путешествий по марсианскому региону.
поверхность.Студенты будут сравнивать эту дозировку с типичными фоновыми условиями на Земле и на Международной космической станции, чтобы получить представление о перспективе.
[Уровень обучения: 6-8 | Темы: десятичные дроби, преобразование единиц измерения, построение графиков и анализ] [Нажмите здесь]
Задача 71 Действительно ли пояса Ван Аллена смертельно опасны? — В этой задаче исследуются дозы радиации, которые космонавты получат во время путешествия. через пояс Ван Аллена по пути к Луне.Учащиеся будут использовать данные, чтобы рассчитать продолжительность поездки через ремни и общую полученную дозу, и сравнить это со смертельной дозой с противостоять заблуждению о том, что астронавты «Аполлона» мгновенно погибли бы во время полета на Луну. [Уровень оценки: 8-10 | Темы: десятичные дроби, площадь прямоугольника, анализ графиков] [Нажмите здесь]
Задача 68
Введение в космическое излучение — Прочтите о дозах естественного фонового излучения, узнайте о
Ремс и Рад, а также разница между дозировками низкого и высокого уровня. Студенты используют
основные математические операции для расчета общих дозировок на основе дозировки и расчета риска рака.
[Уровень обучения: 6-8 | Темы: Чтение для получения информации; десятичные дроби, дроби, квадратные корни] [Нажмите здесь]
Студенты используют
основные математические операции для расчета общих дозировок на основе дозировки и расчета риска рака.
[Уровень обучения: 6-8 | Темы: Чтение для получения информации; десятичные дроби, дроби, квадратные корни] [Нажмите здесь]
Задача 66 Фоновое излучение и образ жизни — Живя на Земле, вы будете подвергаться воздействию множества различных излучений. среды. Эта задача следует за одним человеком через четыре различных возможных варианта будущего и сравнивает кумулятивные дозировки за всю жизнь.[Уровень обучения: 6-8 | Темы: дроби, десятичные дроби, преобразование единиц] [Нажмите здесь]
Задача 54
Изучение далеких галактик — Астрономы определяют красные смещения далеких
галактик, используя спектры и измеряя сдвиги длин волн для знакомых
атомные линии. Чем больше красное смещение, обозначенное буквой Z, тем дальше галактика.
В этом упражнении учащиеся будут использовать реальное изображение далекого уголка Вселенной с красными смещениями. идентифицированных галактик.После гистограммы распределения красного смещения они будут использовать
онлайн-калькулятор космологии для определения времени «оглядки назад» для галактик и
найдите самую древнюю галактику в этой области. Могут ли студенты найти только сформированную галактику?
500 миллионов лет после Большого взрыва?
[Уровень обучения: 6-8 | Темы: Десятичная математика; с помощью онлайн-калькулятора; Данные гистограммы] [Нажмите здесь]
идентифицированных галактик.После гистограммы распределения красного смещения они будут использовать
онлайн-калькулятор космологии для определения времени «оглядки назад» для галактик и
найдите самую древнюю галактику в этой области. Могут ли студенты найти только сформированную галактику?
500 миллионов лет после Большого взрыва?
[Уровень обучения: 6-8 | Темы: Десятичная математика; с помощью онлайн-калькулятора; Данные гистограммы] [Нажмите здесь]
Задача 49 Спиральная галактика крупным планом. — Астрономы могут многому научиться, изучая фотографии галактик.В в этом упражнении учащиеся вычисляют масштаб изображения (световых лет на миллиметр) в сфотографируйте ближайшую спиральную галактику и исследуйте размеры деталей, обнаруженных на изображении. Они будет также использовать Интернет или другие ресурсы, чтобы заполнить недостающую справочную информацию об этой галактике. [Уровень обучения: 6-8 | Темы: Интернет-исследования; Нахождение масштаба изображения; метрическое измерение; десятичная математика] [Нажмите здесь]
Задача 41
Солнечная энергия в космосе Студенты рассчитают площадь поверхности спутника. используется для солнечных батарей из реальной фотографии спутника IMAGE.Они рассчитают электрическую мощность, обеспечиваемую этой панелью. Студенты
Придется вычислить площадь неправильной области, используя вложенные прямоугольники.
[Уровень оценки: 7-10 | Темы: Площадь неправильного многоугольника; десятичная математика] [Нажмите здесь]
используется для солнечных батарей из реальной фотографии спутника IMAGE.Они рассчитают электрическую мощность, обеспечиваемую этой панелью. Студенты
Придется вычислить площадь неправильной области, используя вложенные прямоугольники.
[Уровень оценки: 7-10 | Темы: Площадь неправильного многоугольника; десятичная математика] [Нажмите здесь]
Задача 36 Распад орбиты космической станции и космос Погода Студенты узнают о продолжающийся распад орбиты Международной космической станции из-за изучение графика зависимости высоты станции от времени.Они будут рассчитать скорость затухания орбиты и выяснить, почему это может быть происходит. [Оценка: 5 — 8 | Темы: интерпретация графических данных; десятичная математика] [Нажмите здесь]
Задача 31
Авиарейсы и космическая погода Студенты прочитают отрывок из книги «Космическая погода»
книгу доктора Стена Оденвальда «23-й цикл» и ответьте на вопросы о
авиаперелеты во время солнечных бурь. Они узнают о естественном
радиационный фон, которому они подвергаются каждый день, и сравните это с
дозы радиации во время путешествия на самолете.[Класс: 6 — 8 | Темы: Чтение, чтобы быть в курсе; десятичная математика] [Нажмите здесь]
Они узнают о естественном
радиационный фон, которому они подвергаются каждый день, и сравните это с
дозы радиации во время путешествия на самолете.[Класс: 6 — 8 | Темы: Чтение, чтобы быть в курсе; десятичная математика] [Нажмите здесь]
Задача 10 Жизненный цикл полярного сияния Студенты изучают описания двух очевидцев полярное сияние и определите общие элементы, чтобы они могли извлечь общие картина изменений. [Оценка: 4–6 | Темы: Создание хронологии из повествования; упорядочивание событий по дате и времени] [Нажмите здесь]
тестов по математике на делители и кратные.Математические тесты на делители и кратные. Тестовые работы на делители и кратные
Экзамен по математике Делители и кратные. Делимость на 10, 5 и 2. Делимость на 9 и 3. Простые и составные числа. Простые множители. Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное для 6 класса с ответами. Тест включает 4 варианта по 5 заданий в каждом.
Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное для 6 класса с ответами. Тест включает 4 варианта по 5 заданий в каждом.
Вариант 1
1. Запишите все делители числа 28.
2.
а) 125 и 150
б) 39 и 520
3.
а) 13 и 26
б) 2, 5 и 12
4. Какую цифру нужно поставить в 26 *, чтобы полученное число делилось на 2 и 3 одновременно?
5. Найдите сумму всех трехзначных чисел, которые одновременно кратны 112 и 3.
6. Сколько четных пятизначных чисел можно составить из 1, 2, 3?
Вариант 2
1. Запишите все делители числа 34.
2. Найдите наибольший общий делитель чисел:
а) 46 и 69
б) 34 и 680
3. Найдите наименьшее общее кратное чисел:
а) 32 и 48
б) 4, 7 и 12
4. Какую цифру нужно поставить в запись 34 *, чтобы полученное число делилось на 3 и 5 одновременно?
5. Найдите сумму всех трехзначных чисел, кратных 77 и 5 одновременно.
Найдите сумму всех трехзначных чисел, кратных 77 и 5 одновременно.
6. Сколько четных пятизначных чисел можно составить из цифр 0, 4, 5?
Вариант 3
1. Запишите все делители числа 42.
2. Найдите наибольший общий делитель чисел:
а) 32 и 84
б) 51 и 170
3. Найдите наименьшее общее кратное чисел:
а) 24 и 18
б) 3, 8 и 12
4. Какую цифру нужно поставить в записи 28 *, чтобы полученное число делилось на 2 и 5 одновременно?
5. Найдите сумму всех трехзначных чисел, кратных 49 и 9.
6. Сколько нечетных пятизначных чисел может состоять из 3, 5, 6?
Вариант 4
1. Запишите все делители числа 56.
2. Найдите наибольший общий делитель чисел:
а) 26 и 130
б) 48 и 66
3. Найдите наименьшее общее кратное чисел:
а) 35 и 14
б) 4, 5 и 12
4.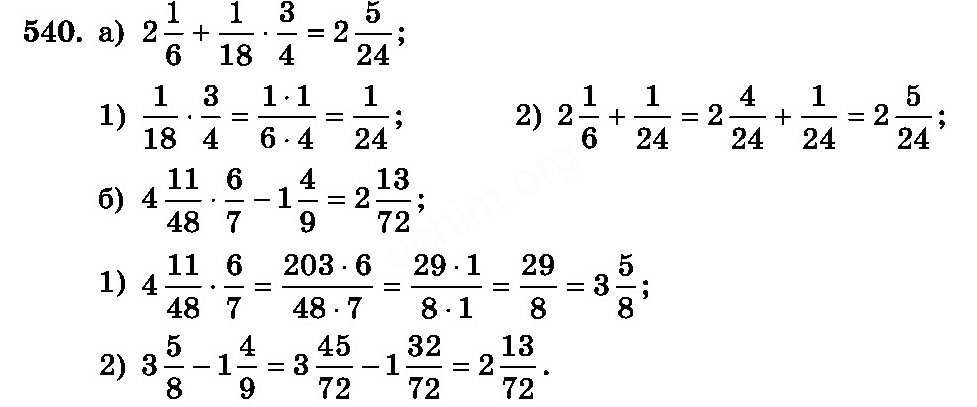 Какую цифру нужно поставить в записи числа 3 * 8, чтобы полученное число делилось на 9?
Какую цифру нужно поставить в записи числа 3 * 8, чтобы полученное число делилось на 9?
5. Найдите наибольшее трехзначное число, кратное 2, 5 и 17 одновременно.
6. Сколько нечетных пятизначных чисел можно составить из цифр 0, 3, 4?
Ответы на контрольную работу по математике Делители и кратные. Делимость на 10, 5 и 2. Делимость на 9 и 3. Простые и составные числа. Простые множители.Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное степени 6
Вариант 1
1. 1, 2, 4, 7, 14, 28
2.
a) 25
b) 13
3.
a) 26
b) 60
4. 4
5. 1008
6. 81
Вариант 2
1. 1, 2, 17, 34
2.
a) 23
b) 34
3.a) 96
b) 84
4. 5
5. 1155
6. 108
Вариант 3
1. 1, 2, 3, 6, 7, 14, 21, 42
2.
a) 4
6) 17
3.а) 72
б) 24
4. 0
5. 1323
6. 162
Вариант 4
1. 1, 2, 4, 7, 8, 14, 28, 56
1, 2, 4, 7, 8, 14, 28, 56
2.
а) 26
б) 6
3.
а) 70
б) 60
4. 7
5. 850
6. 54
Прежде чем договориться с репетитором по математике о начале реальных занятий, вы можете самостоятельно протестировать своего ребенка по основным разделам программы 6-го класса (учебник Виленкина). Эта страница содержит тест на тему «делители и кратные». Уровень представленных заданий соответствует основным требованиям к знаниям шестиклассника и предназначен для тематической (продолжительной) работы репетитора по математике с умным (средним) учеником.Решай и сравни свой уровень! Онлайн-математика для шестиклассника. Проблемы можно использовать для совместного обсуждения их решений и проверки всего диапазона навыков решения проблем на предмет свойств делимости.
Математика 6 класс. Делители и кратные
Варианты ответов были выбраны таким образом, чтобы уловить невнимательного или недостаточно знающего математику ученика на наиболее типичных ошибках по заданной теме. Часто вместо наибольшего общего делителя дети ищут наименьшее общее кратное, и наоборот.Последняя цифра обычно используется для определения делимости на 9. Если репетитор по математике сможет найти задания, которые провоцируют учащегося на эти ошибки, и уточнить каждую из них, это поможет значительно улучшить общую успеваемость. Главное — обсуждать ошибки, а не просто их исправлять!
Часто вместо наибольшего общего делителя дети ищут наименьшее общее кратное, и наоборот.Последняя цифра обычно используется для определения делимости на 9. Если репетитор по математике сможет найти задания, которые провоцируют учащегося на эти ошибки, и уточнить каждую из них, это поможет значительно улучшить общую успеваемость. Главное — обсуждать ошибки, а не просто их исправлять!
Приложение № 2
Тест делителей и кратных
Опция I
A1. Какое из чисел 5, 6, 7 и 31 делит число 93?
1) 5; 2) 6; 3) 7; 4) 31.
A2. Какое из чисел 2, 6, 24 и 50 делится на 12?
1) 2; 2) 6; 3) 24; 4) 50.
A3. В пачках по 7 стаканов. Сколько чашек можно взять, не открывая упаковку?
1) 64; 2) 48; 3) 56; 4) 90.
A4. Верно ли утверждение: сумма двух натуральных чисел кратна каждому из членов?
IN 1. Запишите все делители числа 24.
IN 2. Запишите все двузначные числа, кратные 36.
Опция II
A1.Какое из чисел 2, 4, 6 и 34 делит число 68?
1) 2; 2) 4; 3) 6; 4) 34.
A2. Какое из чисел 6, 12, 36 и 72 делится на 72?
1) 6; 2) 12; 3) 26; 4) 72.
A3. В пачках по 8 книг. Сколько книг я могу взять, не открывая упаковку?
1) 35; 2) 29; 3) 96; 4) 83.
A4. Верно ли утверждение: произведение двух натуральных чисел является кратным каждому из множителей?
1) да; 2) нет; 3) Затрудняюсь ответить.
IN 1. Запишите все делители числа 36.
____________________________________________________________________________
IN 2. Запишите все двузначные числа, кратные 24.
_____________________________________________________________________________
Тест
Вариант 1
1) 3 делитель 26; 2) 37 делитель 814;
3) 23 делитель 943; 4) 67 делитель 3350;
5) 4 делитель 4; 6) 0 делитель 5.
а) 1 и 6; б) 1, 4 и 6; в) 1, 5 и 6; г) ваш ответ.
33 делится на 11; 2) 565 делится на 15;
3) 67 кратно 67; 4) 672 делится на 1;
5) 17 делится на 0; 6) 45 делится на 2.
а андба> б?
а) а + б; б) а-б; в) а б; г) 2а-2б.
Какая из этих сумм кратна 5:
1) 7316 + 97564; 2) 4523 + 7415;
3) 678 + 991 + 31; 4) 230 + 179.
а) 1 и 3; б) 1 и 4; в 1; г) их нет.
Какое из этих чисел не кратно 3:
1) 1706; 2) 12364; 3) 40215;
4) 131421; 5) 18279.
а) 1 и 5; б) 1 и 2; в) 1 и 4; г) ваш ответ.
Найдите остаток от 78567, деленный на 5.
а) 1; Би 2; в 3; г) ваш ответ.
Фактор 420.
а) 420 = 2 · 2 · 3 · 5 · 7; б) 420 = 1 · 2 · 2 · 3 · 5 · 7; в) 420 = 4 · 3 · 5 · 7;
г) ваш ответ.
Какая из предложенных пар чисел имеет НОД, равный 4:
4) 18 и 32; 5) 4 и 16.
а) 2, 3, 5; б) 1, 5; в) 1, 3, 5; г) все.
НОК какой из предложенных пар чисел равен 24:
1) 24 и 2; 2) 18 и 12; 3) 3 и 8;
4) 12 и 32; 5) 4 и 6.
а) 1 и 3; б) 1 и 5; в 1; г) ваш ответ.
Сколько двузначных чисел кратно 11, но не кратно 33?
а) 6; б) 5; в 4; г) ваш ответ.
Тест :
Вариант 2
7 делитель 85; 2) 73 делитель 876;
3) 16 делитель 849; 4) 23 делитель 1288;
5) 1 делитель 4; 6) делитель 0 5.
а) 1, 2, 5; б) 1, 4 и 5; в) 1, 5; г) ваш ответ.
56 делится на 14; 2) 765 делится на 15;
3) 11 кратно 11; 4) 78 делится на 1;
5) 7 делится на 0; 6) 85 раз 9.
а) 1, 3, 4; б) 1, 2, 3; в) 1, 2, 3, 4; г) ваш ответ.
Какое из этих выражений принимает только четные значения ifa andb — натуральные нечетные числа anda> б?
а) а б; б) б + 2; в) а + 2б; г) а-б.
Какая из этих сумм не кратна 5:
1) 7314 + 454; 2) 45232 + 74158;
3) 378 + 981 + 31; 4) 260 + 149.
а) 1 и 5; б) 1 и 2; в) 1 и 4; г) их нет.
Какое из этих чисел кратно 3:
1) 3366; 2) 37564; 3) 23415;
4) 678991; 5) 23179.
а) 1 и 5; б) 1 и 3; в) 1 и 4; г) нет
Найдите остаток от 87656, деленный на 9.
а) 3; б) 5; в 1; г) ваш ответ.
Разделите 280 на простые множители.
а) 280 = 2 2 2 5 7; б) 280 = 1 2 2 2 5 7; в) 280 = 8 5 7;
г) ваш ответ.
1) 24 и 20; 2) 24 и 30; 3) 24 и 32;
4) 18 и 30; 5) 6 и 200.
а) 2, 4; б) 1, 3; в) 1, 2, 4, 5; г) все.
НОК какой из предложенных пар чисел равен 60:
1) 30 и 2; 2) 18 и 15; 3) 4 и 15;
4) 12 и 60; 5) 10 и 6.
а) 2, 3, 4; б) 3 и 4; в) 2, 4; г) все
Сколько существует двузначных чисел, кратных 12, но не кратных 24?
а) 5; б) 3; в 4; г) ваш ответ.
Тест: Делимость чисел. Критерии делимости.
Вариант 3
17 делитель 635; 2) 4 делитель 43;
Какое из этих утверждений не соответствует действительности:
3) 26 делитель 494; 4) 98 делитель 1078;
5) 5 делитель 5; 6) 0 делитель 31.
а) 1, 4, 5; б) 5 и 6; в) 1, 3, 5; г) ваш ответ.
2. Какие из этих утверждений верны?
55 делится на 5; 2) 167 делится на 12;
3) 236 делится на 6; 4) 41 делится на 41;
5) 324 делится на 1; 6) 13 делится на 0.
а) 1, 4, 5, 6; б) 1, 5, 3; в) 1, 5, 4; г) ваш ответ.
3. Какое из приведенных выражений принимает только нечетные значения, если a — четное и b — нечетные натуральные числа и a> 2 б?
а) а + б; б) 3а-2б; в) а б; г) 2а-2б.
4. Какая из этих сумм кратна 10:
1) 221 + 346 + 123; 2) 3654 + 2136;
3) 7231 + 231; 4) 451 + 458.
а) 3, 4; б) 1 и 3; в) 1 и 2; г) их нет.
Какое из этих чисел не кратно 9:
1) 3453; 2) 4347; 3) 123030;
4) 697211; 5) 3591954.
а) 1 и 2; б) 4 и 2; в) 1, 3 и 4; г) ваш ответ.
Найдите остаток от деления 94587 на 6.
а) 2; б) 9; в 3; г) ваш ответ.
Фактор 884.
а) 884 = 4 * 13 * 17; б) 884 = 1 2 2 13 17; в) 884 = 2 2221;
г) ваш ответ.
Какая из предложенных пар чисел имеет НОД, равный 6:
1) 48 и 72; 2) 24 и 30; 3) 42 и 54;
4) 24 и 16; 5) 6 и 8.
а) 1, 2, 3; б) 2, 3, 4; в) 2, 3; г) все.
НОК какой из предложенных пар чисел равен 36:
1) 6 и 6; 2) 6 и 36; 3) 12 и 3;
4) 9 и 4; 5) 18 и 2.
а) 1, 2 и 3; б) 2 и 4; в) 2, 4, 5; г) ваш ответ.
Сколько двузначных чисел кратно 7, но не кратно 21?
а) 10; б) 11; в 9; г) ваш ответ.
Тест: Делимость чисел. Критерии делимости.
Вариант 4
1. Какие из этих утверждений верны:
1 делитель 35; 2) 8 делитель 999;
3) 4 делитель 4; 4) делитель 0 1799;
5) 9 делитель 81; 6) 17 делитель 985.
а) 2, 3, 4; б) 3, 5; в) 1, 5 и 3; г) ваш ответ.
31 делится на 2; 2) 565 делится на 5;
Какое из этих утверждений не соответствует действительности?
3) 121 делится на 1; 4) 17 делится на 0;
5) 8 делится на 2; 6) 74 раза по 8.
а) 4; б) 1, 4, 6; в) 3, 4; г) ваш ответ.
Какое из приведенных выражений принимает только нечетные значения ifa andb — четные натуральные числа anda> б?
a) 3a b; b) 2a + b + 1; in) a + 3b; r) 3a-b.
Какая из этих сумм не кратна 10:
1) 1526 + 344; 2) 78901 + 43281;
3) 527 + 343 + 81; 4) 380 + 120.
а) 1 и 5; б) 2 и 3; в) 1 и 4; г) их нет.
Какое из этих чисел кратно 9:
1) 89946; 2) 25215; 3) 46827;
4) 789002; 5) 5607.
а) 1, 3 и 5; б) 1 и 5; в) 3 и 4; г) их нет.
Найдите остаток от деления 43278 на 7.
а) 8; б) 4; в 3; г) ваш ответ.
Фактор 490.
а) 490 = 2 · 5 · 49; б) 490 = 1 2 5 7 7; в) 490 = 2 2 5 7;
г) ваш ответ.
Какая из предложенных пар чисел имеет НОД, равный 8:
1) 24 и 40; 2) 48 и 64; 3) 8 и 234;
4) 24 и 16; 5) 24 и 32.
а) 1, 4, 5; б) 1, 2; в) 1, 4; г) ваш ответ
НОК какой из предложенных пар чисел равен 72:
1) 8 и 9; 2) 36 и 2; 3) 21 и 3;
4) 18 и 4; 5) 72 и 2.
а) 1, 3, 5; б) 2, 3, 4; в) 1, 5; г) все.
Сколько существует двузначных чисел, кратных 9, но не кратных 36?
а) 9; б) 10; в 11; г) ваш ответ.
.

 НОК(34; 170) = НОК(2 * 17; 2 * 5 * 17) = 2 * 5 * 17 = 170
НОК(34; 170) = НОК(2 * 17; 2 * 5 * 17) = 2 * 5 * 17 = 170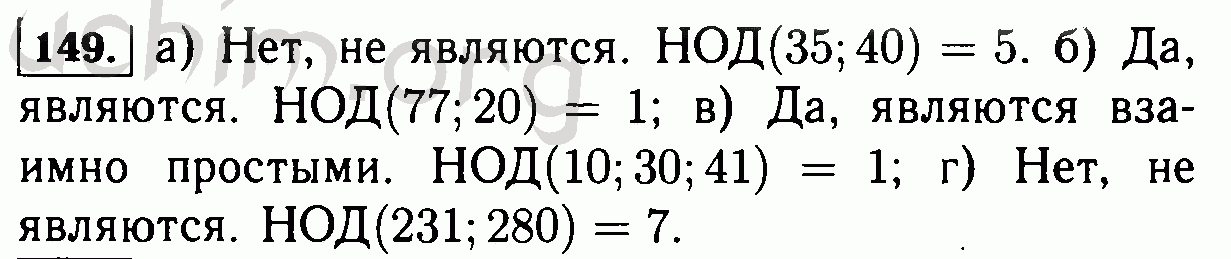
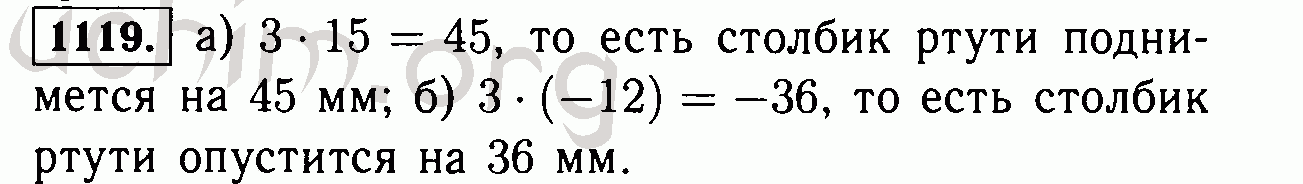 Практика показывает, что таким способом можно добиться результатов, обратных к ожидаемым.
Практика показывает, что таким способом можно добиться результатов, обратных к ожидаемым.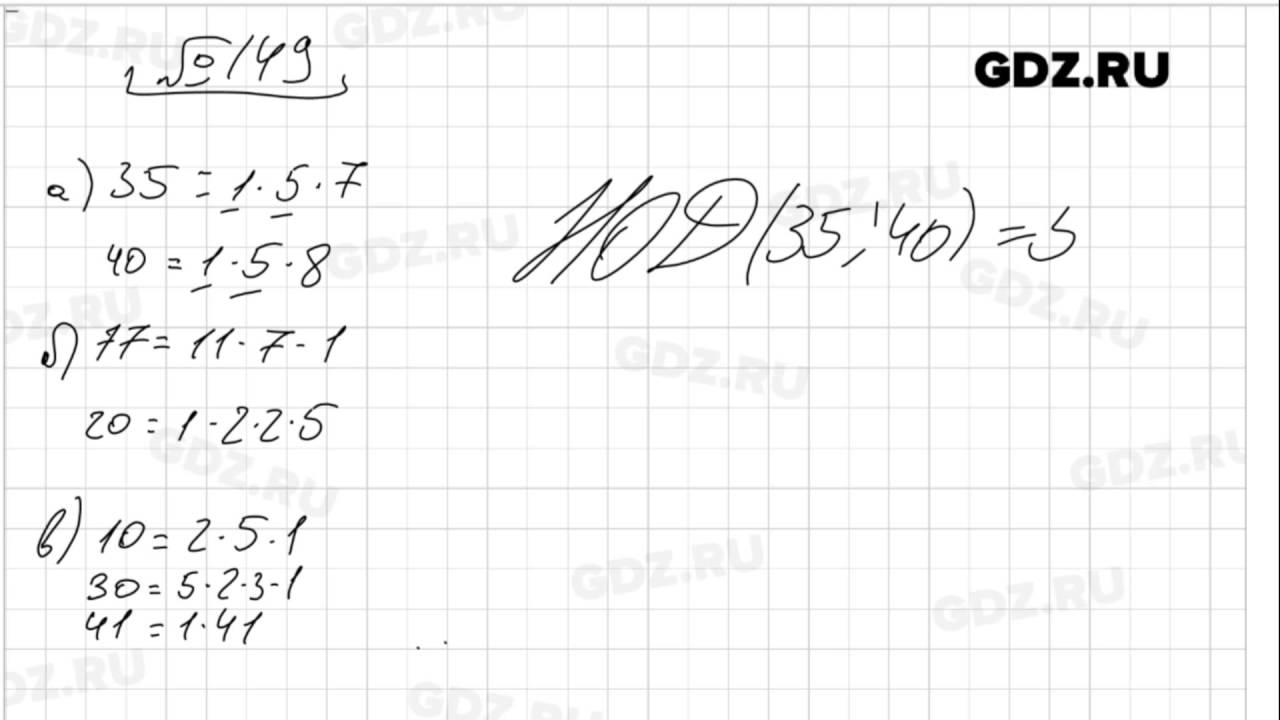




 Он выступит 6 апреля.
Он выступит 6 апреля.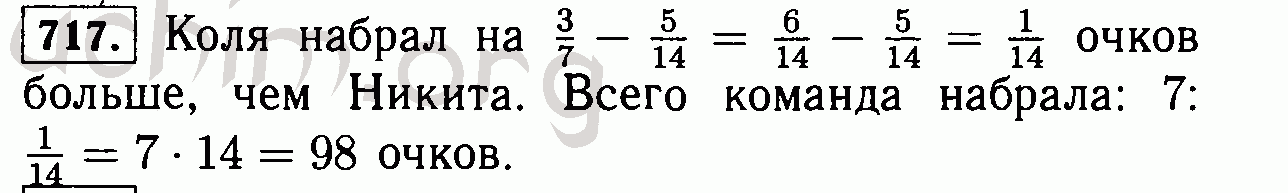
 В нашей локальной вселенной эта «инфляция» закончилась около 14 миллиардов лет назад, и энергия, вызвавшая расширение, пошла на воспламенение горячего огненного шара из частиц и излучения, который мы называем Большим взрывом.По мере того, как огненный шар расширялся (со скоростью, намного меньшей, чем инфляция, но фантастической по земным меркам), он охлаждался, позволяя формироваться звездам. Затем гравитация соединила звезды в галактики, которые все еще сияют в нашем ночном небе.
В нашей локальной вселенной эта «инфляция» закончилась около 14 миллиардов лет назад, и энергия, вызвавшая расширение, пошла на воспламенение горячего огненного шара из частиц и излучения, который мы называем Большим взрывом.По мере того, как огненный шар расширялся (со скоростью, намного меньшей, чем инфляция, но фантастической по земным меркам), он охлаждался, позволяя формироваться звездам. Затем гравитация соединила звезды в галактики, которые все еще сияют в нашем ночном небе. С другой стороны, столкновение пузырей в дальних уголках нашей Вселенной может не причинить нам вреда. Мы даже можем заметить, что одна из этих пузырьковых вселенных сталкивается с нашей на космическом расстоянии. Но, как говорит Виленкин, «на много не похоже».
С другой стороны, столкновение пузырей в дальних уголках нашей Вселенной может не причинить нам вреда. Мы даже можем заметить, что одна из этих пузырьковых вселенных сталкивается с нашей на космическом расстоянии. Но, как говорит Виленкин, «на много не похоже».