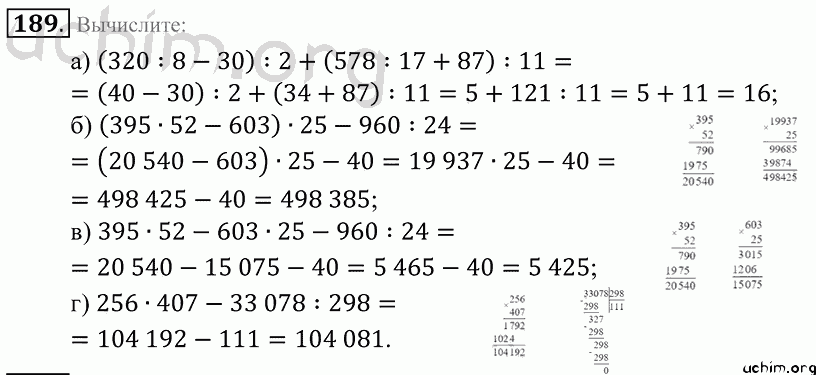Решения математика 5 класс: ГДЗ по Математике 5 класс от Путина: решебники

Содержание

Основные правила математики с примерами. 5 класс

Содержание

Натуральные числа
Сравнение натуральных чисел
Свойства сложения
Формула пути
Корень уравнения
Правила решения уравнений
Отрезок, прямая, луч
Угол, биссектриса угла
Углы: развернутый, прямой, острый, тупой
Многоугольники. Равные фигуры
Треугольники: остроугольный, прямоугольный, тупоугольный
Треугольники: равнобедренный, равносторонний, разносторонний

Прямоугольник. Квадрат. Периметр
Умножение. Свойства умножения
Деление. Деление с остатком
Площадь. Площадь квадрата, прямоугольника
Объем. Объем прямоугольного параллелепипеда, куба
Дроби: правильная, неправильная, сравнение дробей
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Преобразование неправильной дроби в смешанное число

Преобразование смешанного числа в неправильную дробь
Десятичные дроби: свойства, сравнение, округление
Десятичные дроби: сложение, вычитание
Десятичные дроби: умножение, деление
Среднее арифметическое
Процент

Натуральные числа

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.

Сравнение натуральных чисел

Число 0 меньше любого натурального числа.

0<1, 0<100

Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.

4352⏟4>999⏟3

Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр

3561>3559

Свойства сложения

Переместительный закон:

15+10=10+15

Сочетательный закон:

(23+15)+25=23+(15+25)

Формула пути

S=V·t,где S — пройденный путь, V — скорость движения, t — время, за которое пройден путь S

= 50км, = 2ч, = 25км/ч

, 50км = 25км/ч· 2ч

, 25км/ч = 50км : 2ч

, 2ч = 50км : 25км/ч

Корень уравнения

Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.

2·x+10=16

x = 3 — корень, так как 2·3+10=16

Что значит «Решить уравнение»

Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.

Правила решения уравнений

Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.

20слагаемое+xслагаемое=100суммаx = 100 — 20x = 80

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

xуменьшаемое—10вычитаемое=40разностьx = 40 + 10x = 50

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

50уменьшаемое—xвычитаемое=40разностьx = 50 — 40x = 10

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

xмножитель·7множитель=56произведениеx = 56 : 7x = 8

Чтобы найти неизвестное делимое, надо делитель умножить на частное.

xделимое:8делитель=9частноеx = 9 · 8x = 72

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

42делимое:xделитель=7частноеx = 42 : 7x = 6

Отрезок, прямая, луч

Отрезок

Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)

Свойство длины отрезка

Если на отрезке отметить точку , то длина отрезка равна сумме длин отрезков и .

Равные отрезки

Два отрезка называют равными, если они совмещаются при наложении.

Свойство прямой

Через две точки проходит только одна прямая.

Измерить отрезок

Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается

Ломаная

Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом

Луч

Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, . Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

Угол, биссектриса угла

Угол

Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.

Равные углы

Два угла называют равными, если они совмещаются при наложении.

Свойство величины угла

Если между сторонами угла ∠ провести луч , то градусная мера ∠ равна сумме градусных мер углов ∠ и ∠, то есть ∠ = ∠+ ∠.

Биссектриса угла

Луч, который делит угол на два равных угла, называется биссектрисой угла.

Углы: развернутый, прямой, острый, тупой

Развернутый угол

Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.

Прямой угол

Угол, градусная мера которого равна 90°, называют прямым.

Острый угол

Угол, градусная мера которого меньше 90°, называют острым.

Тупой угол

Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.

Многоугольники.

Равные фигуры

Равные многоугольники

Два многоугольники называют равными, если они совмещаются при наложении.

Равные фигуры

Две фигуры называют равными, если они совмещаются при наложении.

Треугольники: остроугольный, прямоугольный, тупоугольный

Остроугольный треугольник

Если все углы треугольника острые, то его называют остроугольным треугольником.

Прямоугольный треугольник

Если один из углов треугольника прямой, то его называют прямоугольным треугольником.

Тупоугольный треугольник

Если один из углов треугольника тупой, то его называют тупоугольным треугольником.

Треугольники: равнобедренный, равносторонний, разносторонний

Равнобедренный треугольник

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

Равносторонний треугольник

Если три стороны треугольника равны, то его называют равносторонним треугольником.

Периметр равностороннего треугольника

Если сторона равностороннего треугольника равна , то его периметр вычисляют по формуле

Разносторонний треугольник

Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.

Прямоугольник. Квадрат. Периметр

Прямоугольник

Если в четырехугольнике все углы прямые, то его называют прямоугольником.

Свойство прямоугольника

Противоположные стороны прямоугольника равны.

Периметр прямоугольника

Если соседние стороны прямоугольника равны и , то его периметр вычисляют по формуле

Квадрат

Прямоугольник, у которого все стороны равны, называют квадратом.

Периметр квадрата

Если сторона квадрата равна , то его периметр вычисляют по формуле .

Умножение. Свойства умножения

Умножение

Произведением числа на натуральное число , которое не равно 1, называют сумму, состоящую из слагаемых, каждый из которых равен . В равенства числа и называют множителями, а число и запись — произведением.

Если один из двух множителей равен 1, то произведение равно второму множителю.

Если один из множителей равен нулю, то произведение равно нулю.

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

Свойства умножения

Переместительный закон умножения:

Сочетательный закон умножения:

Распределительное свойство умножения относительно сложения:

2·(3+10) = 2·3 + 2·103·11 + 3·4 = 3·(11 + 4)

Распределительное свойство умножения относительно вычитания:

2·(15—7) = 2·15 — 2·73·10 — 3·4 = 3·(10 — 4)

Деление. Деление с остатком

Деление

Для натуральных чисел равенство является правильным, если является правильным равенство

15 : 5 = 3 -правильное равенство, так как равенство 5 · 3 = 15 верное

В равенстве число называют делимым, число — делителем, число и запись — частным от деления, отношением, долей.

На ноль делить нельзя.

Для любого натурального числа правильными являются равенства:

Деление с остатком

, где — делимое, — делитель, — неполное частное, — остаток, .

154делимое=50делитель · 3неполное частное + 4остаток, 4<50

Если остаток равен нулю, то говорят, что число делится нацело на число .

Площадь. Площадь квадрата, прямоугольника

Свойства площади фигуры

Равные фигуры имеют равные площади;

Площадь фигуры равна сумме площадей фигур, из которых она состоит.

Площадь прямоугольника

Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.

Площадь квадрата

где — площадь квадрата, — длина его стороны.

Объем. Объем прямоугольного параллелепипеда, куба

Свойства объема фигуры

Равные фигуры имеют равные объемы;
Объем фигуры равен сумме объемов фигур, из которых она состоит.

Объем прямоугольного параллелепипеда

где — объем параллелепипеда, , и — его измерения, выраженные в одних и тех же единицах;

, где — площадь поверхности прямоугольного параллелепипеда.

где — площадь основания параллелепипеда, — его высота.

Объем куба

где — объем куба, — длина его ребра.

Дроби: правильная, неправильная, сравнение дробей

Правильная дробь

Дробь, числитель которой меньше знаменателя, называют правильной

Неправильная дробь

Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.

Из двух дробей с одинаковыми числителями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.

Все правильные дроби меньше единицы, а неправильные — больше или равны единице.

Любая неправильная дробь больше любой правильной дроби.

Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.

Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.

Сложение и вычитание смешанных чисел

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.

Преобразование неправильной дроби в смешанное число

Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно

числитель разделить на знаменатель;
полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

227= смешанное число? 7322—211 227=317

Преобразование смешанного числа в неправильную дробь

Чтобы преобразовать смешанное число в неправильную дробь нужно

целую часть числа умножить на знаменатель дробной части;
к полученному произведению прибавить числитель дробной части;
эту сумму записать как числитель неправильной дроби;
в его знаменателе записать знаменатель дробной части смешанного числа.

523= неправильная дробь?523=5*3+23=15+23=173

Десятичные дроби: свойства, сравнение, округление

Свойства десятичной дроби

Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.

Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.

2,23 = 2,230 = 2,230000005,50000=5,50000=5,5

Сравнение десятичных дробей

Из двух десятичных дробей больше та, у которой целая часть больше.

Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо

с помощью приписывания нулей справа уравнять количество цифр в дробных частях,
после чего сравнить полученные дроби поразрядно.

Сравнить 5,03 и 5,0375.5,03⏟2=5,0300⏟4 и 5,0375⏟4 ; 5,0300 < 5,0375.

Округление десятичных дробей

Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо

все следующие за этим разрядом цифры отбросить.
если при этом первая из цифр, которые отбрасывают равна 0,1, 2, 3, 4, то последнюю из цифр, которые оставляют, не меняют;
если же первая из цифр, которые отбрасывют, равна 5, 6, 7, 8, 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.

Округлить 5,248 и 3,952:а) до десятых:5,248≈5,2; 3,952≈4,0;б) до сотых:5,248≈5,25;3,952≈3,95.

Десятичные дроби: сложение, вычитание

Сложение десятичных дробей

Чтобы найти сумму двух десятичных дробей, нужно:

уравнять количество цифр после запятых;

записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
сложить полученные числа так, как складывают натуральные числа;
поставить в полученной сумме запятую под запятыми.

Сложить 2,5 и 3,623.2,500⏟3 и 3,263⏟3;2,500+3,2635,763

Вычитание десятичных дробей

Чтобы найти разность двух десятичных дробей, нужно:

уравнять количество цифр после запятых;
записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
выполнить вычитание так, как вычитают натуральные числа;
поставить в полученной разности запятую под запятыми.

Вычесть 3,27 и 3,009.3,270⏟3 и 3,009⏟3;3,270—3,0090,261

Десятичные дроби: умножение, деление

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:

перемножить их как натуральные числа, не обращая внимания на запятые;
в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.

Умножить 1,5 и 2,25.2×2,2511,5+1125225·33,375 —количество цифр после запятой

Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.

Умножить 1,235 на 10, 100, 1000.а) на 10:1,235 ×10⏟1=12,35б) на 100:1,235 ×100⏟2 = 123,5в) на 1000:1,235 ×1000⏟3=1235,0 = 1235

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.

Умножить 512,3 на 0,1, 0,01 и 0,001.а) на 0,1:512,3 ×0,1⏟1=51,23б) на 0,01:512,3 ×0,01⏟2=5,123в) на 0,001:512,3 ×0,001⏟3=0,5123

Деление десятичных дробей

Чтобы разделить десятичную дробь на десятичную, надо:

перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;

выполнить деление на натуральное число.

Разделить 24,2 на 0,02.24,2 : 0,02⏟ 2= 2420,0 : 2 = 2420 : 2 = 1210.

Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Разделить 25,5 на 10, 100, 1000.а) на 10:25,5 : 10⏟1=2,55;б) на 100:25,5 : 100⏟2=0,255;в) на 1000:25,5 : 1000⏟3=0,0255;

Среднее арифметическое

Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.

Найти среднее арифметическое чисел 15, 25 и 20.

15+25+20⏞сумма чисел3⏟количество чисел = 603= 20

Примечание:

Задача. Автомобиль 200 км ехал со скоростью 50 км/ч. Затем 120 км он ехал со скоростью 30 км/ч. Найти среднюю скорость.

Здесь

Vсредняя =Sобщtобщ .

1) 200 + 120 = 320(км) -весь путь;

2) 200 : 50 = 4(ч) — время, затраченное на 1-ую часть пути;

3) 120 : 30 = 4(ч) — время, затраченное на 2-ую часть пути;

4) 4 + 4 = 8(ч) — все время;

5) 320 : 8 = 40(км/ч) — средняя скорость.

Ответ: 40 км/ч.

Процент

Процентом называют сотую часть величины или числа 1%=

Найти 4% от числа 20.20 : 100 = 0,2 (0,2 —это 1% от числа 20);0,2 × 4 =0,8( 0,8—искомое число).Или 4% = 4100 = 0,04;0,04 ×20 = 0,8.

Математика, 5 класс — обучающая программа

Образовательный комплекс (ОК) содержит все основные темы, включенные в школьную программу по математике. Материалы ОК поддерживают все виды учебной деятельности и предназначены как для самостоятельной работы дома, так и для использования в классе под руководством учителя. Для изучения выбранной темы предполагается линейное прохождения материала в том порядке, в каком он представлен в комплексе, с возвратом к лекциям и слайдам при необходимости.

Лекция

Анимация, в которой новая тема объясняется в доступной и наглядной форме.

Слайд-резюме

Содержит краткое описание нового материала и может использоваться для быстрого его повторения и самоконтроля.

Закрепление материала

Содержит решения типовых задач по данной теме с пропусками для заполнения учеником.

Математический диктант

Служит для промежуточной проверки усвоенного материала.

Проблема-упражнение

Содержит задачи по данной теме с проверкой правильности решения.

Опрос

Несколько вопросов, на которые ученик должен уметь быстро ответить; проверка не производится.

Самостоятельная работа (базовая)

Содержит пять заданий для проверки усвоения материала; ответы проверяются, результат заносится в журнал.

Самостоятельная работа (повышенной сложности)

Содержит одно задание повышенной сложности, которым можно заменить выполнение базовой самостоятельной работы; ответ проверяется, результат заносится в журнал.

Ученику позволяет:
• самостоятельно изучить новый материал;
• обрести повышенный интерес к предмету за счет мультимедийного способа представления информации;
• развить исследовательские навыки и аналитические способности при работе с интерактивными моделями и играми.

Учителю дает возможность:
• повысить заинтересованность учащихся в предмете;
• подобрать иллюстративный материал к уроку;
• разнообразить каждый урок современными формами представления материала.

1. Точка. Отрезок. Луч. Прямая. Числовая прямая

2. Чтение и запись больших натуральных чисел

3. Десятичные дроби

4. Сравнение десятичных дробей

5. Изображение десятичных дробей на числовой прямой

6. Сложение и вычитание десятичных дробей

7. Уравнения. Решение уравнений

8. Округление

9. Прикидка

10. Умножение и деление десятичных дробей на 10, 100, 1000 и т. д.

11. Умножение десятичных дробей

12. Распределительный закон умножения относительно сложения

13. Деление десятичной дроби на натуральное число. Среднее арифметическое

14. Деление на десятичную дробь

15. Буквенные выражения. Значения буквенных выражений

16. Упрощение записи произведений, содержащих буквенные множители

17. Решение задач с помощью уравнений

18. Обыкновенные дроби. Дроби правильные и неправильные

19. Сравнение, сложение и вычитание дробей с одинаковыми знаменателями

20. Сравнение, сложение, вычитание дроби и натурального числа

21. Смешанные числа

22. Сложение и вычитание смешанных чисел, дробные части которых имеют одинаковые знаменатели

23. Деление и дроби

24. Три задачи на дроби

25. Проценты

26. Квадрат числа

27. Прямоугольный параллелепипед. Куб

28. Объем прямоугольного параллелепипеда и куба. Куб числа

29. Натуральная степень числа

30. Длина окружности и площадь круга

Операционная система Microsoft Windows 2000/XP/7;
Требует наличие Flash-плеер! (см. https://obr.1c.ru/read/info/rabota-adobe-flash-v-2021-godu/)
Pentium III 700 МГц;
память 256 Мб;
Видеокарта, поддерживающая разрешение 1024х768, true color;
устройство воспроизведения DVD/CD-ROM;
да 2 Гб на выбранном для установки диске
не менее 400 Мб на системном диске
звуковая карта;
колонки или наушники;
мышь.

Дата выхода продукта: 29.08.2009
Разработчик: ООО «1С-Паблишинг»
Адрес техподдержки: [email protected]
Штрих-код: 4601546066848
Серии: 1С:Школа
Возрастная категория: 0+

Классные уроки 4-5 | Решения по математике

4–5 классы

Подробнее о датах

Материалы Коллекция монет, датированных до 1990 года, помещенная в прозрачный пластиковый пакет Обзор урока Мэрилин всегда ищет способы дать учащимся опыт вычислений в уме. . Ее коллега Джейн Кроуфорд подала ей идею поставить перед старшеклассниками задачу определения возраста монет. В…

Просмотреть урок

4–5 классы

Отрезки линий на геодоске

Геометрия оживает на этом уроке, так как Расти Брессер предлагает четвероклассникам использовать геодоски для создания пар отрезков, которые касаются ровно девяти колышков, записывают их на точечной бумаге и обозначают как параллельны, пересекаются или перпендикулярны. Расти — автор новой книги «Математика и литература, 4–6 классы, второе издание…»

Просмотреть урок

4–5 классы

Больше или меньше половины

На этом уроке Мэрилин Бернс показывает пятиклассникам дробь, и они решают, больше она или меньше половины, а затем объясняют свои рассуждения. Этот акцент на половине помогает сделать ее важным и полезным эталоном. Урок также предлагает практику вычисления целых чисел в уме, когда учащиеся сравнивают числители и знаменатели.…

Просмотр урока

4–5 классы

Связь литературы и математики — День рождения Мойры

Собирайте и используйте данные для решения задачи . Используйте собранные данные для разработки статистических концепций среднего, медианы и режима. Отсылки: «День рождения Мойры», Роберт Мунш (Анник, 19 лет).92) Книга с материалами: День рождения Мойры Маленькие квадратные стикеры (2 на 2 дюйма), по крайней мере 1 на каждого ученика Кубики с картинками — примерно 100–150 (может быть больше, если в вашем классе больше 25 человек) Большие листы…

Просмотр урока

4–5 классы

Очистить доску

Это задание взято из мини-уроков для математической практики для 3–5 классов, проведенных Расти Брессером и Карен Хольцман (Math Solutions Publications, 2006). Эми Джексон представила этот урок своим ученикам в начальной школе Флоренции в Сан-Диего, Калифорния. В этом упражнении с кубиками класс работает вместе, чтобы составить числа от одного до двенадцати по порядку. Очистить…

Просмотреть урок

4–5 классы

Теория чисел: дифференцирование в единице Урок с пятиклассниками

Этот учитель пятого класса знает, что установление связей между понятиями и представлениями — важная идея в математике. Она хочет, чтобы все ее ученики могли представлять и связывать идеи теории чисел. Например, она хочет, чтобы ее ученики визуально представляли квадратные числа, рисуя квадраты на миллиметровой бумаге, а также соединяли…

Просмотреть урок

Классы 4–5

Марта Бла Бла

В этом уроке, взятом из «Помесячного руководства: Математика для четвертого класса» (Math Solutions, 2009), Лэйни Шустер дает старт своим четвероклассникам учебный год с исследованием, которое предлагает им возможность работать в парах для сбора, представления и анализа данных. Она использует детскую книгу «Марта Бла Бла» Сьюзан Меддо (Houghton Mifflin Company, 1996),…

View Lesson

4–5 классы

Day-by-Day Math. — и предлагаемые ими математические исследования, задачи или виды деятельности. Каждый день в году, с 1 января по 31 декабря, перечисляет исторические события, каждое из которых является беззаботным или серьезным моментом. Вот некоторые предложения для занятий в классе:

Посмотреть урок

4–5 классы

Одна пицца, один пенни

Я был чуть меньше половины чтения книги К. Т. Хао «Одна пицца, один пенни» для четвероклассников Робина Гордона, когда прочитал, что думает Бен Беар: «Если Крис Крок сможет продать свой торт, моя пицца может принести мне состояние! Если каждый кусочек будет продаваться за одну золотую монету, и если я смогу продать…

Просмотр урока

4–5 классы

Игра Николая

Я написал ¾ на доске и спросил класс: «Кто может придумать дробь, у которой числитель больше числителя дроби, которую я написал на доске, а также знаменатель больше знаменателя на доске?» Поднялось несколько рук. Я подозревал, что некоторые не слышали…

Просмотр урока

4–5 классы

Вычисление площадей

Недавно просматривая раздел «О преподавании математики», я наткнулся на задание «Площадь и периметр», которое когда-то было одним из моих любимых, но не было учил довольно давно. Я решил использовать его с пятиклассниками иначе, чем предложено в книге, и описал ниже то, что я…

Просмотреть урок

Классы 4–5

Одна загадка, один ответ

«Кто может объяснить, что такое загадка?» — спросила Даниэль Гиллиган своих пятиклассников. «Это похоже на тайну, которую нужно разгадать», — сказала Джилл. «В нем есть подсказки, которые помогут вам решить эту проблему», — добавил Рамон. — У меня есть книга о загадке, — сказала Даниэлла. «Я буду читать рассказ и остановлюсь на определенном месте…

Просмотр урока

4–5 классы

Численные отношения

Вопрос: Вот набор чисел: {2, 3, 5, 7, 11, 13, 17}. Чем похожи эти числа? Учащиеся могут предположить, что все числа меньше 20. Примите это, но подтолкните учащихся к размышлению о множителях чисел. Ниже приведены несколько возможных ответов: Все имеют коэффициент один. Все…

Просмотреть урок

4–5 классы

Игра в мишень 300

На этом уроке учащиеся четвертого и пятого классов получают опыт, умноженный на десять и кратный десяти, поскольку они выбирают числа, которые нужно использовать для достижения цели. Целевая сумма триста. Я начал урок: «Сегодня я хотел бы поделиться с вами игрой. В этой игре вы будете умножать на десять,…

Посмотреть урок

4–5 классы

Только один раз

Учащиеся старших классов получают пользу от занятий, которые помогают укрепить их понимание множителей, кратных и простых чисел. В этой игре для двух человек учащиеся по очереди определяют множители последовательных чисел, продолжая до тех пор, пока один из них больше не сможет вводить новое число. Указания по игре Игрок 1 записывает число больше единицы…

Просмотр урока

4–5 классы

Объем прямоугольных призм

На предыдущих уроках учащиеся построили прямоугольные призмы, используя кубические единицы, и определили объем призм, считая кубы. Студенты начали разрабатывать методы нахождения объема любой прямоугольной призмы без счета. На этом уроке учащиеся продолжают работу по разработке метода определения объема любой прямоугольной призмы. Они…

Просмотреть урок

Классы 4–5

Великие оценки

На этом уроке шарики и бобы вместе с книгой Брюса Голдстоуна «Великие оценки» используются для того, чтобы дать учащимся возможность исследовать и применять стратегии для оценки. Кроме того, коллекции клеточной бумаги с сетками разного размера, мерные стаканчики разных размеров, несколько кубиков unifix, весы и гири обеспечивают увлекательное занятие…

Посмотреть урок

4–5 классы

Задания после оценивания для 3–5 классов

Задачи с открытым ответом могут стать отличным средством после оценивания. Хотите знать, как вы можете разработать эффективные задачи после оценивания для ваших студентов? Этот урок предлагает план из четырех шагов, включая 3–5 примеров заданий и соответствующие аутентичные ответы учащихся. Урок адаптирован из книги Линды Дейси и Джейн Бэмфорд Линч «Математика для всех: дифференцированное обучение для 3–5 классов». Посетите www.mathsolutions.com…

Посмотреть урок

4–5 классы

Остаток единицы

Я начал урок, написав на доске: 48 ÷ 3. «Что это значит?» Я спросил. «Меня интересуют все ваши идеи». У студентов были разные идеи. — Здесь сорок восемь разделить на три, — сказал Мейсон. — Это означает, сколько раз три могут составить сорок восемь, — добавила Ноэль. Эмма предложила…

Посмотреть урок

4–5 классы

«Угадай мой номер» 3–5

«Угадай мой номер» предлагает детям рассмотреть структуру системы счисления, участвуя в логической игре. Студенты пытаются угадать секретное число из заданного диапазона возможностей. Угадай мое число также дает возможность усилить математические символы, такие как знаки «больше» и «меньше». Благодаря этому…

View Lesson

4–5 классы

Задача о трех магазинах

Человек заходит в магазин и говорит владельцу: «Дайте мне столько денег, сколько у меня есть, и я потрачу 10 долларов. ” Это сделано, и человек делает то же самое во втором и третьем магазине, после чего у него не остается денег. С чего он начал?…

Посмотреть урок

4–5 классы

Спагетти и фрикадельки для всех!

Шерил начала урок с чтения «Спагетти и фрикадельки для всех»! вслух к классу. По сюжету мистер и миссис Комфорт приглашают 32 члена семьи и друзей на встречу и накрывают восемь квадратных столов, за каждым из которых могут разместиться по четыре человека, по одному с каждой стороны. Когда приходят гости, у каждого из них есть свои идеи…

Просмотр урока

4–5 классы

В ближайшие три секунды . . .

Предсказания на тысячелетие

Роуленд Морган В следующие три секунды . . . Predictions for the Millennium (New York: Puffin, 1997) — сборник предсказаний о повседневных и не очень повседневных событиях, которые произойдут в следующие три секунды, следующие три минуты, следующие три часа, дни, недели. . . до…

Просмотр урока

4–5 классы

Верные, ложные и открытые предложения

В этом начальном уроке учащиеся сначала изучают арифметические предложения, чтобы решить, истинны они или ложны. Затем урок знакомит учащихся с предложениями, которые не являются ни истинными, ни ложными, но являются алгебраическими уравнениями, также называемыми открытыми предложениями, такими как x + 3 = 7 или 2 x = 12. Упражнение появляется в Maryann Wickett,…

View Lesson

Классы 4–5

Соотношение

Золотое сечение представляет собой отношение длины к ширине и составляет примерно 1:1,618. Это соотношение проявляется не только в искусстве и архитектуре, но также может наблюдаться в природе и в человеческом теле. Золотое сечение — это отношение общего роста человека к высоте от ступней до пупка. Как…

Просмотр урока

Классы 4–5

Обучение на письме учащихся

В предыдущем выпуске информационного бюллетеня Math Solutions (номер 23, весна/лето 1998 г.) я описал урок «Приведение в порядок», который я преподавал чтобы помочь пятиклассникам научиться сравнивать и упорядочивать дроби. В течение года я продолжал помогать классу учиться сравнивать дроби. Как всегда, я многому научился у…

Просмотреть урок

4–5 классы

Использование транспортиров в средней школе

Из своего прошлого опыта преподавания углов ученикам средней школы Кэти Хамфрис знала, что ученикам часто бывает трудно научиться пользоваться транспортирами. Часто они не видят необходимости в инструменте, поэтому Кэти не вводит транспортиры до тех пор, пока учащиеся не получат конкретный опыт измерения углов несколькими способами. Когда Кэти раздавала транспортиры…

Просмотреть урок

4–5 классы

Division Partner Game

В этой партнерской игре учащиеся четвертого класса делятся на однозначные числа, чтобы определить, есть ли остаток в частном. Ключом к изучению математики является понимание «почему» за «как». HMH Into Math подчеркивает важность установления концептуального понимания и укрепляет это понимание процедурной практикой. Модель обучения предлагает учащимся сначала разработать…

Просмотр урока

4–5 классы

Задача о лобстере

Деньги — полезная модель, помогающая учащимся разобраться в десятых и сотых долях, но учащиеся часто испытывают трудности с расширением своих знаний, чтобы понять тысячные и десятитысячные доли. Задача «Лобстер» дает учащимся опыт решения задач, который помогает им узнать о расширении десятичных дробей за пределы сотых и дает им возможность попрактиковаться в определении десятичных дробей…

Посмотреть урок

4–5 классы

Диаграммы Венна и проценты

Я нарисовал на доске большую диаграмму Венна и обозначил каждый из трех пересекающихся кругов: Брал уроки игры на музыкальных инструментах, Не любит папайю, В почтовом адресе ровно три цифры. Интерес учеников пробудился, когда я написал свои инициалы на стикере размером 1 на 2 дюйма и поместил его на пересечение всех трех…

В этой партнерской игре пятиклассники учатся складывать и вычитать десятичные дроби. Ключом к изучению математики является понимание «почему» за «как». HMH Into Math подчеркивает важность установления концептуального понимания и укрепляет это понимание процедурной практикой. Модель обучения предлагает учащимся сначала развить свои рассуждения, прежде чем связывать свое понимание с…

View Lesson

4–5 классы

Знакомство с умножением дробей

Обучение умножению дробей с одной стороны просто — правило умножения на числители и студенты учиться. Однако преподавание, направленное на то, чтобы учащиеся также развивали понимание, является более требовательным, и Мэрилин Бернс решает эту проблему в своей новой книге «Обучение арифметике: уроки умножения и…»

View Lesson

4–5 классы

Когда дробь стоит половину?

После того, как класс сравнил две дроби, используя половину в качестве эталона, я написал на доске: 6/12 «Поднимите руку, если вы можете объяснить, почему эта дробь эквивалентна половине», — сказал я. . Я подождал, пока все ученики не поднимут руку. Хотя вопрос был тривиальным для большинства учеников, я планировал…

Посмотреть урок

4–5 классы

Остатки с 100

Новая книга Мэриэнн Уикетт и Мэрилин Бернс «Преподавание арифметики: уроки для расширения дивизиона, классы 4–5» (публикации Math Solutions Publications, 2003 г.) основана на концепциях и навыках, представленных в книге «Преподавание арифметики: уроки для введения в дивизион, классы 3–5». 4 (Публикации математических решений, 2002 г.). Их новая книга помогает учащимся вычислять многозначные делители и дивиденды (используя метод, который делает…

View Lesson

Классы 4–5

Делящие пирожные

В этом отрывке из урока учащиеся делят «пирожные» на половинки, используя либо пространственный подход (сосредоточив внимание на формах дробных частей), либо численный подход (вычисляя количество квадратных единиц в фигурах, которые они создают). В полнометражном уроке «Деление пирожных», который появляется в книге Мэрилин Бернс «Обучение арифметике: уроки для расширения…»

Просмотреть урок

Классы 4–5

Домашнее задание по математике, которое имеет значение

Домашнее задание: если 3 равно 5% от число, что составляет 30% от этого числа? Это задание, на первый взгляд, не кажется очень сложным. Но когда я попросил своих шестиклассников решить эту задачу в качестве домашнего задания, я также попросил их сделать заметки о том, как они ее решили. Когда мы поделились нашими подходами, я был…

Просмотреть урок

Классы 4–5

Игра в множители

Игра в множители представляет собой увлекательный формат, в котором учащиеся могут познакомиться с множителями чисел от двух до тридцати, играя в настольную игру для двух человек. Чтобы играть в факторную игру, каждый игрок выбирает число, а другой игрок находит сумму доступных факторов этого числа. Во время игры…

Просмотр урока

4–5 классы

Задача измерения

На этом уроке я планировал, чтобы учащиеся работали индивидуально над решением задачи измерения с использованием дробей. Перед началом урока я начертил на доске отрезок длиной 22 1/2 дюйма. Кроме того, я положил тридцать три кубика Unix в пластиковый пакет. «Когда я соединяю эти кубики вместе, — сказал я, — вы…

Просмотр урока

Классы 4–5

Урок дробей для пятого класса

Чтобы познакомить моих учеников с задачами на деление с дроби, я использую проблемные ситуации, которые опираются на знакомые контексты. Я продолжаю фокусировать их работу на осмыслении ситуации и объяснении их стратегий и решений. Некоторые из задач, которые я использую, не требуют, чтобы учащиеся обязательно приходили к…

Просмотреть урок

Классы 4–5

Миллионы

За почти два месяца до визита Дэвида Шварца наша школа взяла на себя задачу собрать 1 000 000 пенни. интересный вызов. За семь недель мы собрали 250 000 пенни, и мы планируем продолжить как минимум до конца года, чтобы увидеть, насколько мы близки…0006

Прежде чем приступить к этому уроку, я заглянул в местный ресторан, где подают гамбургеры, и узнал, что в одной порции около сорока картофелин фри. Я спросил класс: «Если в одной порции картофеля фри сорок картофелин фри, сколько друзей можно накормить тысячей картофеля фри?» Я дал им несколько минут, чтобы…

Просмотр урока

Решения NCERT для математики класса 5

Решения NCERT для математики класса 5 | Обновлено для сессии 2023–2024 гг.

Обновлено Ракеш
от 4 февраля 2023 г. | Время чтения: < 1 минуты

Учебник: 0426 Режим содержания: Текст и изображения Сессия: CBSE 2023-2024 Средний: Английский и хинди средний

Класс V Математические решения на хинди Medium полезны для тех, кто хочет учиться на языке хинди. Все решения представлены здесь бесплатно для скачивания без какой-либо регистрации. Учебные материалы 5-го стандарта по математике доступны здесь для использования в Интернете или загрузки для использования в автономном режиме.

Класс 5 Математика легко понять и решить. Чтобы быть уверенным в себе, необходима регулярная практика. В противном случае вы можете столкнуться с такими проблемами, как страх перед математикой или паника из-за математики, или вы можете не любить этот предмет как бремя на всю свою жизнь. Многие из вас, студенты, увлекаются инженерией и хотят стать успешными инженерами. Без математики учащийся не может мечтать о технике и многих других областях. Но теперь не нужно бояться, потому что мы здесь, чтобы помочь вам. Академия Тивари предоставляет математические решения NCERT 5-го класса для всех глав. Математические решения NCERT Class 5 подготовлены нашими самыми надежными и опытными экспертами в данной области.

Правильный способ подготовки к экзаменам по математике для 5 класса

Математика для 5 класса Решения NCERT проходят тщательную проверку и перепроверку для вашей безопасности и гарантируют отличные результаты. Студентам будет очень легко, если вы хорошо изучите основы формул. Вы должны практиковать несколько вопросов ежедневно и проводить самооценку через регулярные промежутки времени, чтобы узнать свой прогресс или снижение, если таковое имеется. Решения NCERT для математики класса 5 Основаны на рекомендациях, которым следует CBSE, и их недавних, а также прошлых вопросах.

Математика для 5-го класса, простое решение по главам

После изучения основ математики и формул для 5-го класса, представленных в NCERT, дети должны выполнить упражнения, приведенные в каждой главе. Это важный шаг, потому что когда вы это сделаете, вы увидите все типы вопросов, которые могут быть показаны на экзамене. При этом вам может быть трудно решать различные проблемы, в основном вопросы, основанные на концепциях. Приложение Tiwari Academy NCERT Class 5 Maths Chapter Solution в формате PDF, содержащее решения всех вопросов, рассмотренных в различных упражнениях по главам. Решения решаются очень простыми шагами, а также включают объяснение каждого шага, так что все шаги легко усваиваются учащимися любого типа.

NCERT Решения по математике по главам для класса 5

Бесплатная загрузка в формате PDF При изучении такого предмета, как математика, если вы сможете следовать правильным методам обучения, математика станет очень приятным и увлекательным предметом. Здесь мы следуем всем этим методам, чтобы сделать ваше обучение приятным и приятным. Таким образом, математические решения NCERT 5th Class Math Solutions состоят в общей сложности из 14 глав.

Вы также можете скачать файл PDF для каждой главы по ссылке, указанной ниже. Из-за этого они смогут понять сложные концепции позже, когда перейдут на уровень среднего и высшего среднего образования. Вы можете скачать математические решения NCERT для 5-го класса в формате PDF и распечатать их, чтобы помочь ребенку хорошо учиться.

Роль родителей в повышении уровня знаний по математике для его учащегося 5 класса

Вас, как родителя, это может беспокоить, когда ваш ребенок переходит из младшего класса в более высокий. Мы хотим сделать все возможное, чтобы помочь вашему ребенку, и для этого вы также можете найти академический PDF-файл с учебными материалами. Однако не факт, что только это даст вашему ребенку необходимую поддержку и помощь. В этом возрасте важна направленность на личностное развитие для подготовки к будущим занятиям. Когда ученик достигает пятого класса, его учебная программа становится более специализированной, чем у его предыдущих классов. На этом этапе важно иметь прочную основу. Начиная с 5 класса школьная программа занятий ученика станет более конкретной. Следовательно, как родитель, вы должны помочь им следовать определенному предметному подходу к подготовке к экзамену.

Основные темы математических решений NCERT для класса 5

Эти решения NCERT для класса 5 по математике включают в себя все основные принципы, такие как множители, большие числа, HCF и LCM, дроби, десятичные дроби, проценты, средние значения, тест на делимость, простые проценты, время, Прибыли и убытки, метрические измерения, метод единиц, геометрия, температура и многое другое охватывают больше. Мы предоставили учащимся решения по главам для более глубокого понимания всех концепций. Студенты могут легко загружать PDF-решения всех глав без входа в систему.

Учебным материалом номер один, который помогает учащимся выполнить учебный план путем глубокого понимания концепций, должны быть книги NCERT. Благодаря этим книгам у вас будет доступ к исчерпывающей информации, которая укрепит ваши основы и поможет вам создать прочную основу для ваших старших классов. Всем учащимся CBSE и государственных советов рекомендуется следовать книгам NCERT по всем предметам в своем классе.

Более разумный способ математических решений NCERT класса 5

В начальных и старших классах школьная программа становится очень конкретной. В математических решениях NCERT для 5-го класса Академии Тивари вы найдете конкретные решения для различных глав и упражнений. Решения NCERT по математике для класса 5 доступны для всех сумм, приведенных в главах учебника по математике для класса 5 NCERT. Вы можете легко загрузить решения для определенной главы, а затем следовать приведенным там решениям проблем. Например, в учебнике для 5 класса есть глава, посвященная стандартным единицам. В этой главе рассматриваются понятия расстояния, высоты, веса и меры.

Почему математические решения 5-го класса важны?

Хотя 5-й класс является самым базовым уровнем, эти понятия очень важны для предметов среднего, среднего и высшего среднего образования. Вот почему необходимо, чтобы учащиеся полностью понимали и могли применять концепции класса V. Все упражнения в главах предназначены для проверки знаний учащегося после окончания главы. Однако, если вы хотите полностью понять новую концепцию, вам может понадобиться помощь ключей ответов. Узнайте здесь, как решить математику в классе 5 простыми шагами. Нередко учащиеся проверяют свои ответы после решения задачи. На самом деле, почти все книги по математике заканчиваются решениями. Но они дают только ответ, а не объяснение концепции.

Легко ли решить математические задачи 5 класса NCERT?

Вы знаете, что такое математика? Это сложный или легкий предмет? Возможно, вы слышали, как люди случайным образом говорят, что они хороши в математике, но другие недостаточно хороши в ней. Кстати, скажем вам, что математика — очень сложный предмет. Да, потому что либо вы будете хороши в этом, либо вы будете средними, вы можете столкнуться с множеством проблем, проходя через это. Но еще не поздно, так как вы учитесь в пятом классе и можете построить фундамент для математики и делать это очень усердно. В противном случае вы можете столкнуться с массой серьезных проблем в будущем из-за отсутствия базовых понятий, которые вы знаете. Практика — единственный способ облегчить математику.

Как проще решать задания NCERT по математике для 5 класса?

Чтобы убедиться, что книга NCERT для математики 5-го класса имеет правильный подход к проблемам учащихся, мы подготовили лучшие решения NCERT для математики 5-го класса. В подготовке этих математических решений NCERT 5th Class Math Solutions участвуют только лучшие эксперты в этой области, которые дают ответы на задачи с подробным объяснением. Эти решения очень эффективны для укрепления ваших представлений и устранения сомнений. Благодаря математическим решениям NCERT 5th Class Math Solutions от Tiwari Academy учащиеся смогут легко справляться со своими заданиями и хорошо готовиться к экзаменам.

Как подготовить все главы по математике для 5 класса к экзаменам?

Мы, лучшая бесплатная образовательная академия в Индии, предлагаем всем учащимся полностью сосредоточиться на всех главах учебника NCERT по математике для 5 класса, успешно сдать экзамен и получить хорошие оценки.