| Пройти тест | 2-3 классы. Умножение и деление | Гилмуллина Ильсояр Габдраисовна, МБОУ «Бехтеревская СОШ», Татарстан. |
| Пройти тест | 2-3 классы. Задачи на движение | Сорокина Любовь Анатольевна, Средняя школа № 17, с. Шира, Республика Хакасия |
| Пройти тест | 4 класс. Курс математики начальной школы | Смыкалова Елена Владимировна, ФМЛ № 366, Санкт-Петербург |
| Пройти тест | 4 класс. Математика, I полугодие | Староверова Валентина Васильевна, ГБОУ школа № 212 г. Санкт-Петербург |
| Пройти тест | 4 класс. Единицы измерения | |
| Пройти тест | 5 класс. Курс математики | Смыкалова Елена Владимировна, ФМЛ № 366, Санкт-Петербург |
| Пройти тест | 5 класс. Нумерация натуральных чисел | Ямашева Лариса Николаевна, МБОУ «Верхнешипкинская СОШ», Татарстан |
| Пройти тест | 5 класс. Десятичные дроби | Рогожникова Анна Ивановна, Заинская СОШ № 6, Татарстан |
| Пройти тест | 5 класс. Сложение и вычитание натуральных чисел | Ямашева Лариса Николаевна, МБОУ «Верхнешипкинская СОШ», Татарстан |
| Пройти тест | 5 класс. Обыкновенные дроби | Суханова Татьяна Николаевна, Барабо-Юдинская средняя школа, Новосибирская область. |
| Пройти тест | 5 класс. Умножение и деление натуральных чисел | Цыгер Ольга Викторовна, МБОУ «СОШ № 87», Томская обл. |
| Пройти тест | 5 класс. Смешанные числа | Золотова Ольга Александровна, средняя школа № 30 г. Тамбова |
| Пройти тест | 5 класс. Уравнения | Васина Галина Александровна, Болдовская средняя школа, Республика Мордовия |
| Пройти тест | 5 класс. Задачи на сложение и вычитание натуральных чисел | Новикова Ольга Александровна, «Щеколдинская ООШ», д. Щеколдино Тверской области. |
| Пройти тест | 5-6 классы. Проценты | Мирончук Ирина Степановна, СОШ № 230, г. Санкт-Петербург |
| Пройти тест | 5-6 классы. Сложение и вычитание десятичных дробей | Савельева Марина Эдуардовна, СОШ № 76, г. Санкт-Петербург |
| Пройти тест | 5-6 классы. Умножение и деление десятичных дробей | Гаврилова Лариса Альбертовна, СОШ им. К. Иванова, Башкортостан. |
| Пройти тест | 5-6 классы. Умножение и деление обыкновенных дробей | Перевалова Елена Валентиновна, МБОУ «ООШ № 5», г. Краснотурьинск |
| Пройти тест | 5-6 классы. Сложение и вычитание рациональных чисел | Гаврилова Лариса Альбертовна, СОШ им. К. Иванова, Башкортостан |
| Пройти тест | 5-6 классы. Периметр и площадь | Лукьянченко Людмила Рудольфовна, средняя школа № 7, Адыгея. |
| Пройти тест | 5-6 классы. Десятичныe дроби. Перевод, сравнение | Сащенко Лада Анатольевна. СОШ № 559, Санкт-Петербург |
| Пройти тест | 5-6 классы. Умножение и деление обыкновенных, смешанных и десятичных дробей | Костюк Юлия Исфандияровна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 5-6 классы. Математический язык. Язык и логика. | 5-6 класс, Кучеренко Александра Дмитриевна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 5-6 классы. Целые числа. | Гаус Надежда Павловна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 5-9 классы. Круги Эйлера-Венна | Щербина Полина Алексеевна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 5-10 классы. Логические задачи. Часть 1 | Гаврилова Лариса Альбертовна, средняя школа 519, г. Санкт-Петербург. |
| Пройти тест | 5-10 классы. Логические задачи. Часть 2 | Гаврилова Лариса Альбертовна, средняя школа 519, г. Санкт-Петербург |
| Пройти тест | 6 класс. Курс математики | Смыкалова Елена Владимировна, ФМЛ № 366, Санкт-Петербург |
| Пройти тест | 6 класс. Делимость чисел | Ямашева Лариса Николаевна, МБОУ «Верхнешипкинская СОШ», Татарстан |
| Пройти тест | 6 класс. Сложение и вычитание обыкновенных дробей | Ямашева Лариса Николаевна, МБОУ «Верхнешипкинская СОШ», Татарстан |
| Пройти тест | 6 класс. Сравнение обыкновенных дробей | Антропова Эльза Валерьевна, ГБОУ СОШ № 539, г. Санкт-Петербург |
| Пройти тест | Тюлюкина Оксана Александровна, МК ОУ СОШ № 24, Иркутская область. | |
| Пройти тест | 6 класс. Рациональные числа | Сычева Оксана Ивановна, МБОУ СОШ № 9 г. Усть-Илимска, Иркутской обл. |
| Пройти тест | 6 класс. Смешанные числа. Сложение и вычитание смешанных чисел | Елисеева Ольга Борисовна, ГБОУ СШ № 242, г. Санкт-Петербург. |
| Пройти тест | 6 класс. Наибольший общий делитель и наименьшее общее кратное | Бугаева Марина Владиславовна, СОШ № 62, г. Санкт-Петербург |
| Пройти тест | 6 класс. Координаты на плоскости | Некрасова Светлана Юрьевна, средняя школа с. Козьмино, Архангельская область. |
| Пройти тест | 6 класс. Уравнения с одним неизвестным | Рослякова Ирина Анатольевна, Средняя школа № 14, г. Братск |
| Пройти тест | 6 класс. Диаграммы и графики | Белова Ирина Александровна. Гимназия № 13, г. Алексин Тульской области. |
| Пройти тест | 6 класс. Положительные и отрицательные числа. Координатная прямая | Раджабова Рамзия Джураевна, МБОУ Поручиковская ООШ Заинского муниципального района Республики Татарстан |
| Пройти тест | 6-9 классы. Отношения и пропорции | Иванова Ирина Леонидовна, школа № 149, Санкт-Петербург |
| Пройти тест | 7 класс. Одночлены и многочлены | Колесова Алла Олеговна, МОУ СОШ «Основная общеобразовательная школа № 9», г. Междуреченск |
| Пройти тест | 7 класс. Разложение многочленов на множители | Удалова Елена Михайловна, ГБОУ СОШ № 579, Санкт-Петербург |
| Пройти тест | 7 класс. Соотношения между сторонами и углами треугольника | Пономарева Елена Владимировна, ГБОУ СОШ № 156 с углубленным изучением информатики Калининского района г. Санкт-Петербурга |
| Пройти тест | 7 класс. Свойства степени с натуральным показателем | Шелест Екатерина Юльевна, Андреевская общеобразовательная школа, Днепропетровская область |
| Пройти тест | 7 класс. Линейная функция и ее график | Соколова Ольга Евгеньевна, г. Кашира Московской области |
| Пройти тест | 7 класс. Треугольники | Нуранеева Гульшат Касимовна, «Чистопольская СОШ № 5», Татарстан |
| Пройти тест | 7 класс. Параллельные прямые | Толкачева Елена Сергеевна, Гимназия № 13 г. Алексина Тульской области |
| Пройти тест | 7 класс. Начальные геометрические сведения | Напалкова Татьяна Львовна, СОШ № 4 Алтайского края, г. Горняк |
| Пройти тест | 7 класс. Формулы сокращенного умножения | Рогожникова Анна Ивановна, школа № 6, г. Заинск |
| Пройти тест | 7 класс. Алгебра. Итоговый тест | Бугаева Марина Владиславовна, СОШ № 62, г. Санкт-Петербург |
| Пройти тест | 7 класс. Формулы сокращенного умножения, разложение многочленов на множители | Ишмакова Ирина Евгеньевна. Гимназия «Альма Матер», Санкт-Петербург |
| Пройти тест | 7 класс. Формулы сокращенного умножения. | Бильчугова Татьяна Сергеевна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 7-9 классы. Уравнения с одним неизвестным, сводящиеся к линейным | Иванова Ирина Леонидовна, школа № 149, Санкт-Петербург |
| Пройти тест | 7-9 классы. Уравнения с одним неизвестным | Павлова Наталия Николаевна, СОШ № 43, г. Санкт-Петербург |
| Пройти тест | 7-9 классы. Системы двух линейных уравнений с двумя неизвестными | Гаврилова Лариса Альбертовна, СОШ им. К. Иванова, Башкортостан. |
| Пройти тест | 7-9 классы. Треугольники | Букина Олеся Алексеевна, Мешалкина Ольга Геннадьевна, МБОУ Лицей № 2, г. Барнаул |
| Пройти тест | 7-9 классы. Формулы сокращенного умножения | Бажанова Ирина Леонидовна, «Рассветовская общеобразовательная школа», п. Рассвет, Лодейнопольский район |
| Пройти тест | 7-9 классы. Простейшие квадратные уравнения | Трофимова Дарья Юрьевна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 8 класс. Квадратные корни | Чикрин Евгений Александрович, лицей № 83 г. Казани |
| Пройти тест | 8 класс. Квадратные уравнения | Семенова Виктория Викторовна, ГБОУ Лицей № 226, Санкт-Петербург |
| Пройти тест | 8 класс. Четырехугольники | Осипова Алла Владимировна, ГБОУ лицей № 373 «Экономический лицей», Санкт-Петербург |
| Пройти тест | 8 класс. Окружность | Афанасьева Валентина Николаевна, «Альшеевская СОШ», Татарстан |
| Пройти тест | 8 класс. Числовые неравенства и их свойства | Середа Светлана Петровна, Верх-Чуманская школа, Алтайский край |
| Пройти тест | 8 класс. Соотношения между сторонами и углами прямоугольного треугольника | Цыбульская Татьяна Дмитриевна, ГБОУ СОШ № 47, г. Санкт-Петербург |
| Пройти тест | 8 класс. Теорема Пифагора | Цыбульская Татьяна Дмитриевна, средняя школа N 47, Санкт-Петербург. |
| Пройти тест | 8 класс. Площадь | Баталова Оксана Владимировна, «Сингапайская СОШ», г. Сингапай, Ханты-Мансийский автономный округ |
| Пройти тест | 8 класс. Подобные треугольники | Ладыгина Елена Арсеньевна, средняя школа № 164, г. Санкт-Петербург. |
| Пройти тест | 8 класс. Модуль действительного числа | Григорьева Ольга Васильевна, Судиславская СОШ Судиславского муниципального района Костромской области |
| Пройти тест | 8 класс. Степень с целым показателем. Стандартный вид числа. | Мамонова Виктория Викторовна, МБОУ ООШ № 6 н/п Щукозеро Мурманской обл. |
| Пройти тест | 8 класс. Площадь многоугольников | Джавадян Рузанна Рубеновна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 8 класс. Теорема Виета. | Николаева Алина Дмитриевна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 8 класс. Линейные неравенства. | Удалова Елена Михайловна, ГБОУ СОШ 579 г. Санкт-Петербург |
| Пройти тест | 8-9 классы. Алгебраические дроби | Иванова Ирина Леонидовна, школа № 149, Санкт-Петербург |
| Пройти тест | 8-9 классы. Квадратичная функция | Шишорик Елена Сергеевна, МОУ «Сертоловская СОШ № 2», Ленинградская область |
| Пройти тест | 8-9 классы. Площади четырехугольников | Ковалева Ольга Александровна, КГУ Комплекс школа — детский сад № 33 города Караганды Казахстан |
| Пройти тест | 8-9 классы. Квадратные корни | Нестеренко Галина Ивановна, СОШ № 603, г. Санкт-Петербург |
| Пройти тест | 8-9 классы. Квадратные неравенства | Данилович Татьяна Александровна, СОШ № 18, г. Апшеронск |
| Пройти тест | 8-11 классы. Центральные и вписанные углы | Тихомирова Татьяна Борисовна, СОШ № 277, г. Санкт-Петербург |
| Пройти тест | 8-11 классы. Вычисление площадей фигур на клетчатой бумаге | Туранова Ирина Николаевна, ГБОУ гимназия № 628, г. Санкт-Петербург |
| Пройти тест | 9 класс. Неравенства | Воробьёв Василий Васильевич, лицей г. Калачинск Омской области |
| Пройти тест | 9 класс. Геометрическая прогрессия | Гриценко Давид, школа № 147 г. Еревана |
| Пройти тест | 9 класс. Свойства степени с рациональным показателем | Карасёва Вера Васильевна, МБОУ «СОШ № 38» г. Чебоксары |
| Пройти тест | 9 класс. Координатный метод | Мелихова Анна Геннадьевна, школа № 671, Санкт-Петербург |
| Пройти тест | 9 класс. Элементы теории вероятностей | Любимова Виктория Сергеевна, ГБОУ школа № 454, Санкт-Петербург |
| Пройти тест | 9 класс. Площадь | Букина Олеся Алексеевна, Мешалкина Ольга Геннадьевна, МБОУ Лицей № 2, г. Барнаул |
| Пройти тест | 9 класс. Площади фигур | Попова Лариса Георгиевна, гимназия № 17, г. Кемерово |
| Пройти тест | 9 класс. Скалярное произведение векторов | Шелест Екатерина Юльевна, Андреевская общеобразовательная школа, Днепропетровская область |
| Пройти тест | 9 класс. Правильные многоугольники | Прокофьева Юлия Викторовна, школа № 326, г. Санкт-Петербург |
| Пройти тест | 9 класс. Cтепенная функция | Новожилова Марина Алексеевна, «Невский колледж имени А. Г. Неболсина», г. Санкт-Петербург. |
| Пройти тест | 9 класс. Алгебраические уравнения (повышенной сложности) | Кузнецова Наталья Викторовна, Первомайская средняя школа, п. Первомайский Воронежской области |
| Пройти тест | 9 класс. Подобные треугольники | Кузнецова Наталья Викторовна, Первомайская средняя школа, п. Первомайский Воронежской области |
| Пройти тест | 9 класс. Векторы на плоскости | Грищенко Игорь Михайлович, Областная специализированная школа-лицей для одарённых детей ЛОРД, г. Петропавловск, Республика Казахстан |
| Пройти тест | 9 класс. Длина окружности и площадь круга | Павленко Ольга Юрьевна, г. Санкт-Петербург, средняя общеобразовательная школа при Посольстве России в Румынии |
| Пройти тест | 9 класс. Решение треугольников | Арчибасова Елена Михайловна, гимназия № 1 г. Новосибирска |
| Пройти тест | 9 класс. Арифметическая прогрессия | Михалева Елена Александровна, гимназия № 13, г. Алексин, Тульская область |
| Пройти тест | 9 класс. Краткое повторение курса математики 9 класса | Рогожникова Анна Ивановна, МБОУ Заинская средняя общеобразовательная школа № 6 |
| Пройти тест | 9 класс. Векторы. | Лыс Анна Николаевна, средняя школа № 22 г. Коврова |
| Пройти тест | 9 класс. Векторы. Сложение и вычитание векторов | Данькова Валентина Николаевна, средняя школа № 2 г. Азова Ростовской области |
| Пройти тест | 9 класс. Углы в планиметрии. | Симоненко Яна Викторовна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 9 класс. Вычисления и алгебраические выражения | Напрушкина Елена Сергеевна, Средняя школа № 136, г. Санкт-Петербург |
| Пройти тест | 9-11 классы. Проценты. Подготовка к ОГЭ и ЕГЭ | Букина Олеся Алексеевна, Мешалкина Ольга Геннадьевна, МБОУ Лицей № 2, г. Барнаул |
| Пройти тест | 9-11 классы. Элементы комбинаторики | Судакова Анна Григорьевна, магистрант РГПУ им. А. И. Герцена, Санкт-Петербург |
| Пройти тест | 10-11 классы. Преобразование выражений, содержащих тригонометрические и обратные тригонометрические функции | Воеводина Ольга Анатольевна, МАОУ «Лицей № 62», г. Саратов |
| Пройти тест | 10-11 классы. Метод координат в пространстве. Часть 1 | Бударина Анна Юрьевна, Волкова Виктория Александровна, МБОУ СОШ им. А. М. Горького, МБОУ СОШ им. С. М. Кирова, г. Карачев, Брянская обл. |
| Пройти тест | 10-11 классы. Метод координат в пространстве. Часть 2 | Бударина Анна Юрьевна, Волкова Виктория Александровна, МБОУ СОШ им. А. М. Горького, МБОУ СОШ им. С. М. Кирова, г. Карачев, Брянская обл. |
| Пройти тест | 10-11 классы. Логарифмы. Свойства логарифма. | Волчкова Татьяна Николаевна, МБОУ Краснополянская СОШ № 32, с. Красная Поляна Ростовской области |
| Пройти тест | 10-11 классы. Решение неравенств методом интервалов | Возная Оксана Анатольевна, Урожайновская школа, Симферопольский район, Республика Крым |
| Пройти тест | 11 класс. Итоговый тест | Викулина Елена Владимировна, Колледж «Красносельский», Санкт-Петербург |
| Пройти тест | 11 класс. Логарифмы и их свойства | Воеводина Ольга Анатольевна, МАОУ «Лицей № 62» г. Саратов |
| Пройти тест | 11 класс. Исследование логарифмических функций | Михалева Елена Александровна, гимназия № 13, г. Алексин, Тульская область |
| Пройти тест | 11 класс. Дифференцирование степенной и линейной функций | Мирончук Ирина Степановна, ГБОУ СОШ № 230, г. Санкт-Петербург |
metaschool.ru
Решение задач по математике онлайн
Данный сайт обращён к учащимся в том или ином объеме изучающим математику и/или геометрию и призван помочь школьникам и
студентам в изучении курса математики, освободить их от многих рутинных вычислений, и подсказать метод решения.
Основу сайта составляют математические программы (калькуляторы) для решения задач онлайн.
Все вычисления производятся на сайте, программы не нужно скачивать и устанавливать на компьютер.
На каждую задачу приводится поэтапный процесс получения ответа, т.е. подробное решение с объяснениями этапов решения данной задачи.
Решение задач приводится в виде, принятом в большинстве школ и вузов, некоторые задачи решаются двумя способами.
Все математические программы (калькуляторы) бесплатные.
Полный список математических и геометрических задач для решения вы можете найти в меню справа.
| Промежуточные результаты: |
| $$2\frac{3}{4}-1\frac{3}{8} = \frac{2\cdot(2\cdot4+3)-1\cdot8-3}{8} = \frac{11}{8}$$ |
Вычислим дискриминант.
$$D = b^2-4ac = 8$$ $$x_{1,2}= \frac{-b\pm\sqrt{D}}{2a} = \frac{-2\pm\sqrt{8}}{2} = \frac{-2\pm2\sqrt{2}}{2} $$ Ответ: $$ x_1 = -1+\sqrt{2},\; x_2 = -1-\sqrt{2} $$ Решить неравенство: $$\frac{4 x^2-7 x+3}{3 x-1} \geq x-1$$ Решение: $$\frac{4 x^2-7 x+3}{3 x-1} \geq x-1\Rightarrow $$ $$\frac{4 x^2-7 x+3- \left( x-1 \right) \left( 3 x-1 \right) }{3 x-1} \geq 0$$Упрощение выражения \(4 x^2-7 x+3- \left( x-1 \right) \left( 3 x-1 \right) \)
$$4 x^2-7 x+3- \left( x-1 \right) \left( 3 x-1 \right) = $$ Раскрытие скобок: $$4 x^2-7 x+3+ \left( -x+1 \right) \left( 3 x-1 \right) = $$ Раскрытие скобок: $$4 x^2-7 x+3-3 x^2+x+3 x-1= $$ $$x^2-3 x+2$$ Ответ: \( x^2-3 x+2 \) Решим квадратное уравнение \( x^2-3 x+2= 0 \)Решение квадратного уравнения \( x^2-3 x+2= 0 \)
Вычислим дискриминант. $$D = b^2-4ac = 1$$ $$x_{1,2}= \frac{-b\pm\sqrt{D}}{2a} = \frac{3\pm\sqrt{1}}{2} = \frac{3\pm1}{2} $$ Ответ: \( x_1 = 2,\; x_2 = 1 \)
Решение по теореме Виета
Т.к. \( \left| a \right|=1 \), то можно воспользоваться теоремой Виета: $$x^2+px+q=0 \Rightarrow \left\{\begin{array}{l} x_1+x_2=-p \\ x_1 \cdot x_2=q \end{array}\right.$$ $$\left\{\begin{array}{l} x_1+x_2=3 \\ x_1 \cdot x_2=2 \end{array}\right. \Rightarrow \left\{\begin{array}{l} x_1=2 \\ x_2=1 \end{array}\right.$$ Ответ: \( x_1= 2,\; x_2= 1 \) Корни квадратного уравнения: $$ x_1 = 1 ;\; x_2 = 2 $$ Решим линейное уравнение \( 3 x-1= 0 \) Корень линейного уравнения: \( x = \frac{1}{3}\)| $$ \frac{1}{3} $$ | $$ 1 $$ | $$ 2 $$ |
Нахождение производной функции
Найти производную функции $$ f(x) = \left( 1+sin \left( 2 \cdot x\right) \right) ^{2}$$ Решение $$ f'(x) = \left( \left( 1+sin \left( 2 \cdot x\right) \right) ^{2}\right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot \left( 1+sin \left( 2 \cdot x\right) \right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot \left( sin \left( 2 \cdot x\right) \right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) \cdot \left( 2 \cdot x\right) ‘= $$ $$ = 2 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) \cdot 2= $$ $$ = 4 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) $$ Ответ: $$ f'(x) = 4 \cdot \left( 1+sin \left( 2 \cdot x\right) \right) \cdot cos \left( 2 \cdot x\right) $$В разделе Книги вы найдете большой список книг, учебников, решебников, ГДЗ, тестов и контрольных работ с ответами по математике
и геометрии для всех классов общеобразовательных школ.
Все книги в электронном виде и доступны для скачивания бесплатно.
Отдельно стоит упомянуть программу для построения графиков функций онлайн.
Программа работает в вашем браузере, её не нужно устанавливать на компьютер.
Для её работы нужен только установленный Adobe Flash Player.
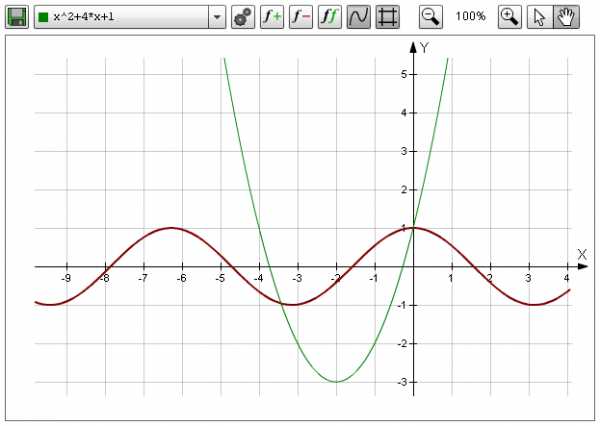
Возможности программы:
— можно строить несколько графиков в одном окне
— можно менять цвет и толщину линии постоения графика
— можно скрывать и отображать как сетку так и графики
— можно изменять масштаб отображения
— можно трассировать графики
— можно сохранять построение графиков в виде картинки
www.mathsolution.ru
Математика онлайн: Обучение и практика бесплатно
Математика онлайн для начальной школы
Наш проект Математика онлайн поможет Вашему ребенку лучше усвоить а укрепить знания по математике. Математика Онлайн разработана для учеников начальных школ.
Задачи и примеры по математике расчитаны на ученико срених школ начальных классов. Задачи включают в себя счет до 100, таблицу умножения и деления, задачи с картинками и основы действий с дробями.
Математика онлайн состоит из 5 уровней сложности по 9 виду задач в каждом уровне. Каждый вид задач генерируется случайным образом.
После практики решения задач и примеров, можете проверить свои знания посетив раздел тестов.
После прохождения теста по математике, Вам будет выставлена оценка.
Тест пророка
Попробуйте пройти наш тест а узнайте больше о своих способностях!
Определите уровень Вашего интеллекта
Определите уровень Вашего интеллекта. IQ тест длится 30 минут и содержит 40 простых вопросов
Тест по ПДД
База данных содержит 285 дорожных знаков РФ, утвержденных правилами дорожного движения (ПДД)
Тест памяти
Предлагаем Вам бесплатное тестирование Вашей памяти, способом запоминания картинок
Тест по Флагам стран
Пройдите тест на знание флагов стран, укрепите свои знания по географии
Тест по географии
Тест на знание государств мира по флагам, расположению, площади, рекам, горам, морям, столицам, городам, населению, валютам
Тест: граничащие страны
База данных содержит подробную информацию о 199 странах мира!
Материки и континенты
Чем больше количесво вопросов, тем выше точность результата теста!
IQ тест бесплатно онлайн
Средний IQ выпускников ВУЗов составляет 115, отличников — 135—140. А как насчет вас?
Free games online · Eng · CZ Hry · Игры онлайн бесплатно ·
Иконка на Ваш Web · Книга посетителей
Copyright (c) 2019 by Topglobus.ru. Все права защищены!
www.topglobus.ru
Как решать Задачи по Математике 5 класс (2017) + Примеры, Таблицы
Editor choiceСохранитьSavedRemoved 8

Существует много причин, по которым ребёнок не может решить задачу по математике 5 класс. В большинстве из них он не виноват, поэтому стоит ему помочь разобраться с проблемой. Задачи не такие трудные, но в связи с появлением дробей и уравнений иногда сложно определить способ и верный путь их решения.
Почему инструкция лучше решебника?
В этой инструкции вы сможете найти типовые задачи, которые встречаются в курсах математики за 5 класс и разобранное, подробное, пошаговое решение. Это значительно полезнее книг, так как в них собраны далеко не все задачи, а те решения, которые есть, сжаты до минимума. Поэтому пользоваться решебником — порой не самый лучший выход.

Решебник по математике не всегда может дать исчерпывающую информацию
Как правило, при составлении ответов на свои задачи авторы не расписывают подробности и дают решения не ко всем номерам. Возможно, в расчёт идёт тот факт, что ученик способен справиться самостоятельно. Но вдруг ребёнок пропустил тему, что же тогда делать?
Лучший вариант — посмотреть решение типовых задач с пояснениями каждого действия. В этой инструкции собраны самые распространённые примеры, которые вызывают трудности у детей при решении, а также родителей при попытке объяснить задачу.
вернуться к меню ↑Почему важно уметь решать задачи по математике?
Математика — точная дисциплина, связанная с вычислениями. Но её часто называют царицей всех наук. Это не просто так. Основное, чему учатся дети — решение конкретно поставленных задач. Это самое важное для развития любого человека.
Для построения правильного ответа на задачу нужно выделить:
- главную мысль;
- заданное условие;
- что требуется найти;
- связь между искомым и данным.

Математика — один из самых важных предметов в школьной программе
На основе этого строится логичное решение с использованием условий для получения требуемого результата. Вместе с этим развивается познавательная активность, логические мышление.
вернуться к меню ↑Какие бывают задачи по математике в 5-ом классе?
В 5-ом классе по математике встречается несколько разновидностей задач. Этот год самый важный для ученика, потому что здесь собраны все базовые условия, которые углублённо решаются в следующие годы обучения. Здесь представлен список самых распространённых задач:
- на базовые арифметические действия;
- на скорость, время и расстояние;
- на движение;
- решаемые алгебраическим способом — проценты, дроби, уравнения;
- решаемые геометрическим способом — площадь, длина.

Существует немало различных задач и путей их решения
Для грамотного решения всех типов задач можно составить единый алгоритм:
- Прочитайте вдумчиво, не торопясь полный текст задачи;
- Определите к какому типу она относится;
- На основе этого составьте краткое условие или таблицу;
- Начните читать каждое предложение отдельно, заполняя таблицу или краткое условие;
- Определите вопросом то, что нужно найти;
- Выберите вариант решения и составьте выражение, в результате которого получится ответ;
- Проверьте правильность и соответствие условию;
- Запишите полученный ответ.
Этот алгоритм можно применять ко всем типам задач. В разных заданиях отличаться будут только числа и способ решения.
Далее представлены все типы задач, которые могут встретить пятиклассники в учебниках и задачниках по математике. Все они будут разобраны на двух примерах с подробным разъяснением.
вернуться к меню ↑Задачи на сложение, вычитание, умножение и деление
вернуться к меню ↑Пример 1
На кухне лежит пакет, в котором 3000 грамм муки. Повар для выпечки из него брал 4 раза муку. В первый раз 250 грамм, во второй 320 грамм, в третий 140 грамм, в четвёртый 690 грамм. Найдите сколько муки осталось в пакете.
Решение
Таблица 1 — Краткое условие
| Условие | Количество |
|---|---|
| Было | 3000 |
| Первый раз | 250 |
| Второй раз | 320 |
| Третий раз | 140 |
| Четвёртый раз | 690 |
| Осталось | ? |
- Сделанная таблица наглядно показывает, что для расчёта остатка нужно из 3000 вычесть количество, которое повар забрал всего;
- Для этого сложим количество муки, которое повар израсходовал за четыре раза. Получается такое выражение: 250+320+140+690=1400 грамм;
- Теперь найдём остаток. Для этого из того, что было, вычтем полученное значение — 1400. Получим выражение: 3000-1400=1600 грамм. Это то, что от нас требовалось — найти сколько осталось муки;
- Записываем это в ответ к задаче.
Пример 2
В пассажирском поезде 12 вагонов. В каждом из них по 40 мест. Сколько осталось свободных мест, при условии, что в поездку отправились 352 пассажира?
Решение
Таблица 2 — Условие задачи
| Места в вагоне | Количество |
|---|---|
| Кол-во вагонов | 12 |
| Кол-во мест в вагоне | 40 |
| Кол-во пассажиров | 352 |
| Осталось мест | ? |
- Теперь приступаем к вычислениям. Для начала нам нужно узнать сколько всего свободных мест было в вагонах. Для этого умножим количество вагоном на количество свободных мест в каждом. Получается выражение: 40×12=480;
- Для того, чтобы найти сколько осталось свободных мест нужно, из полученного значения вычесть занятые места. Получим выражение: 480-352=128;
- Полученное число — это ответ на вопрос из условия задачи. Записываем его.
Эти задачи самые простые и встречаются в начале учебного года. Используют их авторы учебников для того, чтобы ученик мог вспомнить алгоритм решения и базовые правила.
вернуться к меню ↑Задачи на скорость, время, расстояние
вернуться к меню ↑Пример 1
За 7 часов теплоход проделал путь в 210 км. Поезд за 4 часа преодолел 420 км. Во сколько раз скорость поезда больше скорости теплохода?
Решение
Таблица 3 — Краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| Теплоход | ? | 7 | 210 |
| Поезд | ? | 3 | 360 |
- Приступим к поиску неизвестных. Нам нужно узнать скорость у теплохода и поезда. Для этого используется формула — скорость равна результату деления расстояния на время. Математически записывается так — V=S:T;
- Подставив числа из условия, получаем выражение для скорости теплохода. 210:7=30 км/ч;
- Также поступаем и для расчёта скорости поезда. 360:3=120 км/ч;
- Мы нашли все неизвестные и теперь возвращаемся к главному вопросу задачи. Нам нужно определить во сколько раз скорость поезда превышает скорость теплохода;
- Для этого делим большее значение на меньшее. Получается: 120:30=4;
- В ответ пишем, что скорость теплохода и поезда отличается в 4 раза.
Пример 2
Автомобилист за 4 часа проехал 320 километров. Какой путь проделает автомобиль за 8 часов с той же скоростью?
Решение
Таблица 4 — краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| Автомобиль | ? | 4 | 320 |
- Ищем неизвестные. В нашем случае нужно найти скорость. Для этого воспользуемся формулой V=S:T. Подставляем числа и получаем: 320:4=80 км/ч;
- После того, как стали известны все значения, переходим к главному вопросу задачи — сколько проедет автобус за 8 часов с той же скоростью;
- Для расчёта используем формулу S=VT. Подставляем числа и получаем: 80×8=640 км;
- Записываем полученное значение в ответ к задаче.
Решение этих задач требует знать основную формулу S=VT. Расшифровывается она так: расстояние равно произведению скорости на время. Из неё вытекают все решения для нахождения неизвестных. Также для упрощения задачи можно рисовать схему.
вернуться к меню ↑Задачи на движение
вернуться к меню ↑Пример 1
Расстояние между двумя городами 125 километров. В одно и то же время выезжают два велосипедиста навстречу. Скорость первого велосипедиста 10 км/ч. Второй едет со скоростью 15 км/ч. Через какое время они встретятся?
Решение
Таблица 5 — краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| 1 велосипедист | 10 | ? | 125 |
| 2 велосипедист | 15 | ? | 125 |
- Теперь переходим к расчётам. Логично, что для встречи велосипедисты должны проехать в сумме весь путь. Необязательно одинаковое расстояние, так как оно зависит от скорости каждого из них;
- Нам нужно посчитать какое расстояние они преодолевают в час. Для этого сложим скорости первого и второго. Получаем выражение: 10+15=25 км/ч;
- Для расчёта времени через которое они встретятся нужно воспользоваться формулой T=S:V. Подставляем числа и получаем выражение: 125:25=5 ч;
- Соответственно, велосипедисты пересекутся между собой через 5 часов. Записываем это в ответ.
Пример 2
Расстояние, на котором между собой находятся два города — 600 км. Из них одновременно на встречу друг другу выехали два автомобиля. В пути они встретились через 5 часов. Найдите скорость первого автомобиля, если известно, что второй ехал со скоростью 80 км/ч.
Решение
Таблица 6 — краткое условие
| Скорость | Время | Расстояние | |
|---|---|---|---|
| 1 автомобиль | ? | 5 | 600 |
| 2 автомобиль | 80 | 5 | 600 |
- Переходим к расчётам. Для нахождения скорости первого автомобиля нам нужно знать, сколько километров он проехал. Найти это можно, вычтя из общего пути расстояние, которое проехал второй до их встречи;
- Используем формулу S=VT. Подставляем числа из таблицы, получаем выражение: 80×5=400 км. Это расстояние прошёл второй автомобиль до встречи с первым. Значит, первый проехал всего: 600-400=200 км;
- Теперь можно найти скорость первого автомобиля. Используем формулу V=S:T. Подставляем числа: 200:5=40 км/ч;
- Полученное значение — ответ на главный вопрос задачи. Записываем его.
Если вас смущает время, которое написано один раз для всех объектов, то можно поступить следующим образом. Записывайте его отдельно к каждой строке и рядом нарисуйте отрезок, который снизу отмечен расстоянием, а сверху подписан временем.
вернуться к меню ↑Задачи, решаемые алгебраическим способом
вернуться к меню ↑Пример 1
Из цистерны отлили 80 литров молока, в нем осталось на 240 литров больше, чем отлили. Сколько литров молока было в цистерне с самого начала?
Решение
Таблица 7 — краткое условие задачи
| Было | Х |
|---|---|
| Отлили | 80 |
| Осталось | 240+80 |
- Приступаем к расчётам. Нам нужно узнать, сколько было молока изначально. Для этого составляем уравнение. От начального количества вычитаем отлитое и получаем остаток;
- Математически получаем такую запись: x-80=240+80;
- Начинаем решение с того, что считаем всё, что можно посчитать. В данном случае складываем правую часть уравнения. 240+80=320. Теперь уравнение имеет вид: x-80=320;
- Теперь находим «x». Используем базовое правило математики и получаем следующее: x=320+80. Считаем правую часть и получаем: x=400;
- Возвращаемся к началу и смотрим, что мы обозначили за «x». В этом примере за икс мы взяли объём молока, который был изначально. То есть, изначально было 400 литров молока;
- Записываем полученное значение в ответ.
Пример 2
Первое слагаемое на 52 больше второго слагаемого, а второе слагаемое на 14 меньше третьего слагаемого. Сумма трех слагаемых равна 327. Найдите каждое слагаемое.
Решение
- Записываем краткое условие в виде таблицы;
- Потребуется четыре строки, так как нам дали три слагаемых и их сумму;
- Заполняем таблицу числами, обозначив за икс последнее слагаемое. Выбираем третье, потому что от него зависят все остальные;
Таблица 8 — краткое условие задачи
| 1 слагаемое | (x-14)+52 |
|---|---|
| 2 слагаемое | x-14 |
| 3 слагаемое | x |
| Сумма | 327 |
- Приступаем к расчётам. Для нахождения слагаемых нужно решить уравнение, после чего число подставить в выражения из таблицы.
- Уравнение составляется исходя из условия – три слагаемых и сумма – складываем значения из второго столбца таблицы и приравниваем это к сумме.
- Получится такое выражение: (x-14)+52+(x-14)+x=327.
- Открываем скобки и упрощаем выражение: 3x+24=327.
- Переносим числа в правую часть: 3x=303
- Считаем икс: 303:3=101.
- Теперь подставляем число 101 в таблицу вместо икса.
- Получается третье слагаемое равно 101; второе: 101-14=87; первое: 87+52=139.
- Эти числа записываем в ответ. Легко проверить правильность решения просто сложив эти значения. Если пример получается правильный, то и решено всё верно.
Для правильного решения этих типовых задач необходимо ничего не напутать с иксом. Лучше потратить больше времени и сразу всё проверить, чем переделывать задание сначала. Неправильное обозначение повлечёт за собой ошибку на протяжении всего решения
вернуться к меню ↑Задачи, решаемые геометрическим способом
вернуться к меню ↑Пример 1
В доме 4 двери. Ширина каждой 1 метр, высота — 2 метра. Сколько нужно белил, чтобы покрасить их с обеих сторон, при условии, что на 1 квадратный метр поверхности требуется 100 грамм белил? Ответ дайте в граммах.
Решение
Пример 2
Площадь прямоугольника 192 квадратных сантиметра, длина одной из сторон — 16 см. Найдите периметр прямоугольника.
Решение
Для решения геометрических задач нужно знать наизусть все формулы площадей и периметров. Без этого не получится даже приступить к решению задания.
вернуться к меню ↑Нужен ли ребёнку репетитор по математике в пятом классе?
После перехода в средний этап школы у ребёнка может упасть успеваемость по некоторым предметам, в том числе и по математике. Более того математика — самый проблематичный предмет для детей. Некоторые родители сразу бьют тревогу и ищут репетиторов, чтобы исправить эту ситуацию.
На самом деле, не стоит делать поспешных выводов. Для начала нужно определить причину падения успеваемости. Возможно, некоторые из новых учителей просто халатно относятся к преподнесению нового учебного материала. Другие преподаватели не могут найти особый подход к ребёнку в связи с ограничением по времени.

У многих детей в школе возникают сложности с изучением математики
Это не значит, что ваш ребёнок неспособный к определённым дисциплинам. Попробуйте объяснить ему материал самостоятельно, ведь именно вы знаете своё чадо лучше других. Если и это не помогло, то обращайтесь к помощи репетитора.
Главная задача специалиста — найти персональный подход к каждому ученику. Они смогут максимально эффективно и просто объяснить ребёнку тему в зависимости от особенностей его восприятия и склада ума.
Перед обращением убедитесь, что ухудшение оценок произошло только по нескольким взаимосвязанным предметам, а не в целом. Если успеваемость сильно упала в общем плане, то скорее всего ребёнок ленится. Связано это может быть со скукой на уроках и утратой интереса к учёбе. В таком случае, поговорите с ним, объясните, что это очень важно и пригодится в жизни, приводя аргументы и наглядные примеры.
Конечно, если это связано, например, с пропуском занятий по причине болезни, или в школе неправильно преподносится материал, то стоит задуматься о найме репетитора. Он поможет в кратчайшие сроки улучшить результаты ребёнка.
вернуться к меню ↑Как решить проблемы с математикой
Как только у ребёнка появляются проблемы с математикой родители почему-то начинают думать, что причина заключается в плохой предрасположенности к точным наукам. Потому что формулы вроде бы знает, простые примеры решить тоже может, но каждая контрольная и самостоятельная работа превращается в целое испытание для всей семьи. Все сидят в ожидании результатов. Никогда нельзя сказать точно какую оценку получит ребёнок — четвёрку или двойку.
Дети часто получают плохие отметки именно по математике
Также много жалоб по типу: занимаемся все выходные напролёт, учим эту математику, учим, а в итоге всё равно результат прежний. На самом деле, причина такого плохого восприятия — отсутствие адекватных причин заниматься всеми этими цифрами. Большинство родителей сходятся во мнении, что ребёнок просто гуманитарий, главное — литература, история, обществознание, а математика неважна.
вернуться к меню ↑Гуманитариям математика не нужна?
Это огромная ошибка, ведь для лучшего восприятия точных наук этому самому «гуманитарию» нужно лишь вдохновение и цель. Отлично будет, если ребёнку объяснить, что математика — это такая же наука, как и любая другая, и она не ограничивается уравнениями и задачами. Это нечто большее. Математика позволяет изменить мышление, воспринимать старые вещи по-новому.
Главная проблема всех гуманитариев, которые имели проблемы с математикой — это логика. Для составления, например, грамотной и структурированной статьи нужно руководствоваться не только правилами русского языка, но и логикой изложения мысли. Все части должны быть связаны между собой, в то же время, должны легко читаться отдельные фрагменты.
Именно логическое мышление в первую очередь развивает математика и воспринимать это нужно, как возможность расширения кругозора и свежего взгляда на старое. Также точные науки помогают дисциплинировать свой ум и комплексно подходить к решению поставленных задач.
вернуться к меню ↑Математика — сложный предмет
Самая популярная отговорка заключается в том, что математика — самый сложный предмет из всех. Нет, на самом деле это одна из самых простых и понятных дисциплин. Для сравнения, возьмите наш богатый русский язык.
Мало того, что в нём существует немало правил орфографии, пунктуации, стилистики, так ещё и исключения есть почти в каждом правиле. Вот уж где нужно запоминать «тонну» информации.
В то же время в математике существуют базовые правила, на которых строятся все остальные. То есть, более сложное всегда можно привести к простому. Всё построено на железной логике, и, следуя этим правилам, вы сможете решить задачи, которые казались на первый взгляд непосильными.
Вспомните, как учат всех детей. Для того, чтобы научить их писать, сначала нужно выводить палочки, точки, изгибы. Потом уже буквы, а из букв — простые слова, из слов — предложения.
Начните изучать математику с самых простых уравнений
В математике с самого начала всё объясняется на пальцах или предметах. При этом, за то же самое время, потраченное на русский язык и на математику, прогресс в изучении второй будет больше. Например, считать учатся дети на яблоках, конфетках.
Используйте это и для решения более сложных задач. В пятом классе аналогии привести не составит труда. Это поможет ребёнку ассоциировать вычисления не с сухими числами, а, например, с мандаринами.
вернуться к меню ↑Формула спокойствия
Часто плохие оценки становятся причиной ссор между родителями и детьми. Это категорически неправильно. Вместо того, чтобы высказывать ребёнку, что он «ленится», «не думает о будущем» да и в общем «туго соображает», следует отвести от неудачи или помочь исправиться с ней.
Но под помощью подразумевается не «вдалбливание» и «зубрёжка» неинтересных формул и правил. Следует возбудить интерес к теме, которая была плохо воспринята. Да и к тому же поставить правильную цель ребёнку. Не нужно говорить, что от оценок зависит его будущее. Вообще не зацикливайте внимание на оценках.
По исследованиям российских психологов дети, которые хотели стать врачами, инженерами и просто хорошими людьми, быстро повышали свою успеваемость. А те ученики, которым с первого класса «вдалбливают» в голову знания, думали только о том, как не стать худшим в классе, и уделяли своим отметкам слишком большое внимание.
Лучшим вариантом по-прежнему остаются занятия с репетитором. Он сохранит нервы, и вам, и ребёнку. Обеспечивая нужное количество времени на обучение и выбрав правильный подход, ученик станет показывать результаты лучше прежнего. Но, моментально отличником вашего ребёнка это не сделает.
Надеемся, что вы смогли найти решение задач, которое искали. Также для понимания темы рекомендуем посмотреть видео по этой теме от организаторов специальной математической школы федерального уровня «Аристотель».
8.5 Общий Балл
Некоторые ученики, как пятых, так и других классов, часто сталкиваются с проблемами в изучении математики. В этом случае родителям не стоит впадать в панику. Следует уделить больше внимания детальному разбору примеров и задач. Если это не улучшит успеваемость, есть смысл обратиться за помощью к репетитору.
Плюсы
- Подробные инструкции помогут разобраться в решении задач и примеров
- Для изучения математики можно пользоваться решебниками
Минусы
- Полученных знаний в школе не всегда достаточно для понимания предмета
slovami.net

