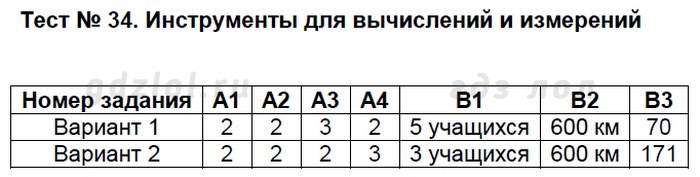
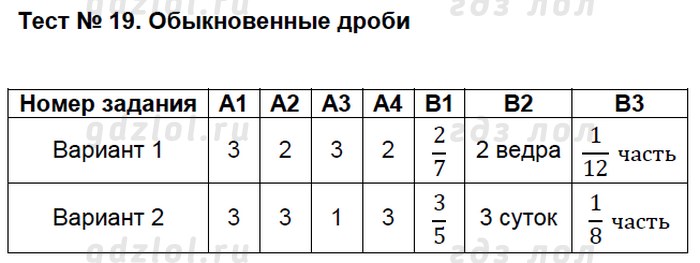
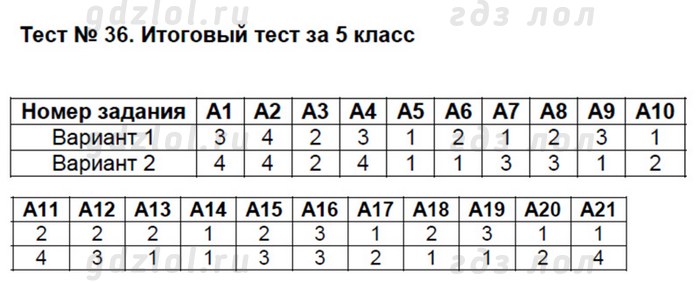
Попова контрольно измерительные материалы математика 5 класс: ГДЗ по Математике для 5 класса контрольно-измерительные материалы Попова Л.П. на 5

Pre-K–2 Ожидания:  В подготовительном классе до 2 класса каждый ученик должен –

• измерение нескольких копий единиц одного размера, таких как скрепки, уложенные встык;
• использовать повторение одной единицы для измерения чего-то большего, чем единица, например, для измерения длины комнаты с помощью одной метровой палки;
• использовать инструменты для измерения;
• разработать общие референсы для измерений для проведения сравнений и оценок.

3–5 классы Ожидания:  В 3–5 классах каждый ученик должен –

• разработать стратегии оценки периметров, площадей и объемов неправильных форм;
• выбрать и применить соответствующие стандартные единицы и инструменты для измерения длины, площади, объема, веса, времени, температуры и величины углов;
• выбирать и использовать контрольные точки для оценки измерений;
• разрабатывать, понимать и использовать формулы для нахождения площади прямоугольников и связанных с ними треугольников и параллелограммов;
• разработка стратегий для определения площади поверхности и объема прямоугольных тел.

6–8 классы Ожидания:  В 6–8 классах каждый ученик должен –

• использовать общие ориентиры для выбора подходящих методов оценки измерений;
• выбирать и применять методы и инструменты для точного определения длины, площади, объема и углов с соответствующим уровнем точности;
• разрабатывать и использовать формулы для определения длины окружности и площади треугольников, параллелограммов, трапеций и окружностей, а также разрабатывать стратегии для нахождения площади более сложных фигур;
• разработать стратегии для определения площади поверхности и объема выбранных призм, пирамид и цилиндров;
• решать задачи, связанные с масштабными факторами, используя отношение и пропорцию;
• решают простые задачи, связанные с расходами и производными измерениями таких атрибутов, как скорость и плотность.

9–12 классы Ожидания:  В 9–12 классах каждый ученик должен –

• анализ точности, правильности и приблизительной погрешности в ситуациях измерения;
• понимать и использовать формулы площади, площади поверхности и объема геометрических фигур, включая конусы, сферы и цилиндры;
• применяют неформальные концепции последовательного приближения, верхних и нижних границ и предела в ситуациях измерения;
• использовать модульный анализ для проверки расчетов измерений.

---

Измерение – группа изучения уроков

Обычно обучение и изучение каждого атрибута измерения состоит из четырех этапов: (1) прямое сравнение; (2) косвенное сравнение; (3) измерение в произвольных (нестандартных) единицах; и (4) измерение в стандартных единицах. В CCSS эти этапы четко описаны в преподавании и изучении линейных измерений от детского сада до 2-го класса. Однако учащиеся должны пройти эти этапы со всеми измеримыми атрибутами, даже если они могут тратить меньше времени на некоторые этапы, поскольку они приобретают больше опыта в измерениях. . Например, когда учащиеся узнают об объеме твердых тел в пятом классе, они, скорее всего, потратят гораздо меньше времени на первые три этапа по сравнению с тем, что они сделали, когда узнали о длине. Тем не менее, для студентов по-прежнему важно пройти эти этапы, чтобы они могли понять, что такое объем, процесс его измерения и как использовать инструменты для этого.

Итак, почему важно следовать этим четырем стадиям, когда мы начинаем наши инструкции по измерению? Основное внимание на первых двух этапах уделяется тому, чтобы помочь учащимся понять измеряемые атрибуты. В конце концов, прежде чем мы сможем что-то измерить, нам действительно нужно понять, что именно мы хотим измерить. Например, прежде чем мы сможем измерить длину, нам нужно понять, что такое длина. Поставив рядом два предмета (прямое сравнение), учащиеся могут определить, какой из них длиннее, а какой короче. Благодаря такому опыту учащиеся понимают, что длина — это расстояние между двумя концами объекта.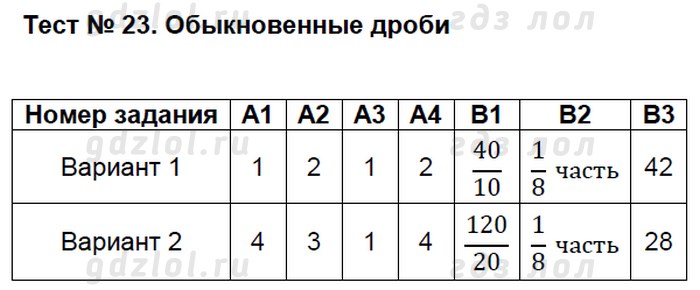 (Хотя мы можем использовать разные слова, «высота» на самом деле не является атрибутом. Ее можно рассматривать как длину в вертикальной ориентации.) Конечно, посредством прямого сравнения учащиеся получают некоторое фундаментальное понимание того, как измерять объект. также. Например, при сравнении длин двух объектов важно, чтобы один конец объектов был выровнен.

Нельзя сказать, что верхний сегмент на рисунке ниже длиннее только потому, что он «выпирает» дальше вправо.

Учащиеся также узнают, что интересующее нас «пространство» находится на прямой траектории. Таким образом, мы не можем просто сравнить положения конечных точек, как показано на рисунке ниже.

Прежде чем мы сможем сравнить эти два объекта, конечные точки второго объекта должны быть расположены по прямой линии. Эти знания имеют основополагающее значение для понимания ребенком измерения.

Стадия

К сожалению, не всегда возможно прямое сравнение двух объектов. В ситуациях, когда это не так, иногда полезно использовать третий объект, который можно сравнивать непосредственно с каждым из двух объектов и действовать как ссылка между ними. Например, если один дверной проем шире размаха ваших рук, а другой уже, чем размах рук, вы знаете, что первый шире второго. Косвенное сравнение обеспечивает большую гибкость при сравнении двух объектов. Это также дает детям возможность испытать важное математическое свойство отношений, называемое транзитивностью. Это свойство утверждает, что если a > b и b > c, то a > c. Конечно, формальное изучение такого свойства произойдет гораздо позже.

Возможно, более важной причиной обучения и изучения непрямого сравнения является то, что оно готовит почву для самой фундаментальной идеи о процессе измерения: использование единицы измерения . При использовании третьего объекта для косвенного сравнения его количество не всегда может быть промежуточным между количеством исходных двух объектов. Например, деревянная палка может быть намного короче обоих дверных проемов. Однако в этих случаях можно определить, что один дверной проем выше трех (одних и тех же) деревянных палочек, поставленных встык, а другой короче трех деревянных палочек. Теперь мы можем сказать, что первый дверной проем выше (длиннее), чем второй.

Нетрудно заметить, что такие переживания становятся основанием для идеи выражения признака через число третьего предмета, единицы, необходимой для его «покрытия». Когда мы переходим на эту стадию, мы теперь действительно «измеряем» в том смысле, что мы присваиваем номер объекту с точки зрения того, сколько атрибутов он имеет. Есть много преимуществ для выражения количества атрибута с помощью чисел. Ясно, что это упрощает процесс сравнения, поскольку нам больше не нужно находить разные объекты для использования в качестве эталона — сравнение нескольких объектов можно легко выполнить, просто сравнив числа одной установленной единицы. Еще одним важным преимуществом присвоения атрибутам чисел является то, что мы можем ответить не только на вопрос «что длиннее?» но и «на сколько?» В общем, как только мы выражаем количество атрибута числами, арифметические операции могут использоваться для ответа на более сложные вопросы. Несмотря на то, что CCSS прямо не заявляет об этих достоинствах, я надеюсь, что учителя помогут учащимся испытать и понять их.

Зачем

Некоторые люди могут возразить, что, как только мы дойдем до этого этапа, мы должны просто использовать стандартные единицы. Этот аргумент, возможно, имеет смысл позже, в начальных классах, когда учащиеся узнают об измерении трех или четырех различных атрибутов.   Однако на уровне начального класса важно помнить, что учащиеся все еще изучают процесс измерения: выберите единицу измерения, затем определите, сколько итераций единицы необходимо, чтобы сравняться с атрибутом объекта, который вы измеряют. Для нас это так очевидно, а с детьми не так. Введение стандартных единиц на этом этапе потребует от детей одновременного изучения двух новых идей — новых единиц и нового процесса.  Есть и другие соображения. Во-первых, некоторые единицы могут быть слишком маленькими или слишком большими, так что размер полученных чисел может не подходить для детей в данное время. Используя нестандартные единицы измерения, учителя могут контролировать диапазон чисел, которые могут получить учащиеся. Кроме того, важно отметить, что измерение в стандартных единицах обычно означает измерение с помощью различных инструментов. Например, если вы измеряете в дюймах, скорее всего, вы будете измерять линейкой. Однако обучение использованию линейки или любого измерительного инструмента также является сложной задачей само по себе — это может быть третьей новой идеей, с которой придется столкнуться учащимся, если мы будем вводить стандартные единицы без обучения нестандартным единицам .

Этап

Хотя это может показаться немного парадоксальным, использование нестандартных единиц полезно для детей, чтобы понять необходимость наличия стандартных единиц. Например, если два ученика измерят ширину одного и того же дверного проема карандашами, они могут получить разные результаты. Этот тип опыта позволит им увидеть, что они не могут сравнивать числа, если их единицы измерения не совпадают.