Номер 364 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд. Часть 2
Номер 364 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд. Часть 2 — ГДЗ РЕДПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
Часть 1
Выберите номер
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684686687688689690691692693694695696697698698699701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793793794795797798799800801802803804805806807808809810811812813814815816817817819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852
Часть 2
Выберите номер
123456789101112131415161718192122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744845045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786887087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231224122512261227122812291230123112321233123412351236123712381239124012411242124312441245124612471248124912501251125212531254125512561257125812591260126112621263126412651266126712681269127012711272127312741275127612771278127912801281128212831284128512861287128812891290129112921293129412951296129712981299130013011302130313041305130613071308130913101311131213131314131513161317131813191320132113221323132413251326132713281329133013311332133313341335133613371338133913401341134213431344134513461347134813491350135113521353135413551356135713581359136013611362136313641365136613671368136913701371137213731374137513761377137813791380138113821383138413851386138713881389139013911392139313941395139613971398139914001401140214031404140514061407140814091410141114121413141414151416141714181419142014211422142314241425142614271428142914301431143214331434143514361437143814391440144114421443144414451446144714481449145014511452145314541455145614571458145914601461146214631464146514661467146814691470147114721473147414751476147714781479148014811482148314841485148614871488148914901491149214931494149514961497149814991500150115021503150415051506150715081509151015111512151315141515151615171518151915201521152215231524152515261527152815291530153115321533153415351536153715381539154015411542154315441545154615471548154915501551155215531554155515561557155815591560156115621563156415651566156715681569157015711572157315741575157615771578157915801581158215831584158515861587158815891590159115921593159415951596159715981599160016011602160316041605160616071608160916101611161216131614161516161617161816191620162116221623162416251626162716281629163016311632163316341635163616371638163916401641164216431644164516461647164816491650165116521653165416551656165716581659166016611662166316641665166616671668166916701671167216731674167516761677167816791680168116821683168416851686168716881689169016911692169316941695169616971698169917001701170217031704170517061707170817091710171117121713171417151716171717181719172017211722172317241725172617271728172917301731173217331734173517361737173817391740174117421743174417451746174717481749175017511752175317541756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849
Старая версия
Выберите страницу
678911121314151617181920212324252627282930313235363738394041434445464748495051525354555657586061626364656768697071727375767778798081828384868788899091929495969798100101102103104105106107108109110111112113115116117118119120121122123124127128129130131134135136137138140141142143144145147148149150152153154155156157158159160161162163164165166167169170171172173175176177178179181182183184186187188189190192193194195196197198200201202203205206207208210211212213214215216217218219220221222223224225226227228229230231233234235236237238239240241242243245246247248249251252253254255256257258259261262263264265266267268269270271272273274260
Adblockdetector
дайын үй жұмыстары Математика Абылкасымова 5 класс 2017 Упражнение 364 2020
Глава 1.
 НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ§ 1. Запись натуральных чисел
12345678910111213
§ 2. Координатный луч
14151617181920212223242526
§ 3. Сравнение натуральных чисел
2728293031323334353637383940
§ 4. Арифметические действия е натуральными числами
4142434445464748495051525354555657585960
§ 5. Числовые и буквенные выражения. Упрощение выражений
61626364656667686970717273747576777879
§ 6. Уравнения
808182838485868788899091
§ 7. Формулы. Вычисления по формулам
9293949596979899100101102
§ 8. Решение текстовых задач
103104105106107108109110111112113114115116117118119
120121122
§ 9. Последовательность из натуральных чисел
123124125126127128129130131132
Глава 2.
 ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ
ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ§ 10. Делители и кратные натуральных чисел. Простые и составные числа
133134135136137138139140141142143144145146147148149150151152153
§11. Основные свойства делимости
154155156157158159160161162163164165166167168169170
§ 12. Признаки делимости на числа 2. 3, 5, 9.
171172173174175176177178179180181182183184185186187188189190191192193194
§13. Степень
195196197198199200201202203204205206207208209210211212
§14. Разложение натурального числа на простые множители
213214215216217218219220221222223224225226227228229230231232233
§15. Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)
234235236237238239
240241242243244245246247248249250251252253254255256257258259
Глава 3.
 ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ
ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ§ 16. Обыкновенная дробь. Чтение и запись обыкновенных дробей
260261262263264265266267268269270271272273274275276277278279280281282283284285286
§ 17. Основное свойство обыкновенной дроби
287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325
§ 18. Правильные и неправильные обыкновенные дроби. Смешанные числа
326327328329330331332333334335336337338339340341342343344345
§19. Перевод неправильной обыкновенной дроби в смешанное число и смешанного числа в неправильную обыкновенную дробь
346347348349350351352353354355356357358359
360361362363364
§ 20. Изображение обыкновенных дробен и смешанных чисел на координатном луче
365366367368369370371372373374375376377378379380381
§ 21.
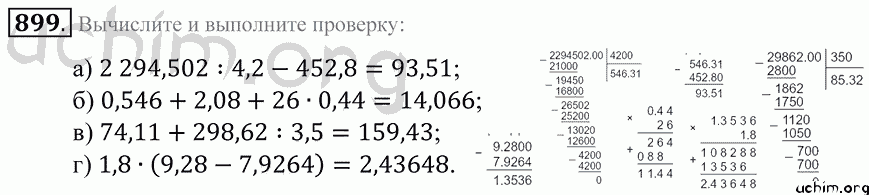 Приведение обыкновенных дробей к общему знаменателю
Приведение обыкновенных дробей к общему знаменателю382383385386387388389390391392393394395396397398
§ 22. Сравнение обыкновенных дробей и смешанных чисел
399400401402403404405406407408409410411412413414415416417418419420
§ 23. Сложение и вычитание обыкновенных дробей
421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454
§ 24. Сложение смешанных чисел
455456457458459460461462463464465466467468469470471472473474475476477478
§ 25. Вычитание смешанных чисел
479480
481482483484485486487488489490491492493494495496497498499500501502503
§ 26. Умножение обыкновенных дробей и смешанных чисел
504505506507508509510511512513514515516517518519
§ 27.
 Деление обыкновенных дробей и смешанных чисел
Деление обыкновенных дробей и смешанных чисел520521522523524525526527528529530531532533534535536537
§ 28. Действия с обыкновенными дробями, нулем, натуральными и смешанными числами
538539540541542543544545546547548549550551552553554555556
Глава 4. ТЕКСТОВЫЕ ЗАДАЧИ
§ 29. Нахождение дроби от числа и числа по его дроби
557558559560561562563564565566567568569570571572573574575576577578
§ 30. Задачи на совместную работу
579580581582583584585586587588589590591592593
Глава 5. ДЕСЯТИЧНЫЕ ДРОБИ II ДЕЙСТВИЯ НАД НИМИ
§ 31. Десятичная дробь. Чтение и запись десятичных дробей
594595596597598599600
601602603604606607
§ 32. Перевод десятичной дроби в обыкновенную дробь
608609610611612613614615616617
§ 33.
 Изображение десятичных дробей на координатном луче. Сравнение десятичных дробей
Изображение десятичных дробей на координатном луче. Сравнение десятичных дробей618619620621622623624625626627628629630631632633
§ 34. Сложение и вычитание десятичных дробей
634635636637638639640641642643644645646647648649650
§ 35. Умножение десятичной дроби на натуральное число
651652653654655656657658659660661662663664665666667668669
§ 36. Умножение десятичных дробей
670671672673674675676677678679680681682683684685
§ 37. Деление десятичной дроби на натуральное число
686687688689690691692693694695696697698699700701
§ 38. Деление десятичных дробей
702703704705706707708709710711712713714715716717718719720
§ 39. Умножение и деление десятичных дробей на 10. 100. 1000. … и на 0.1. 0,01, 0,001
721
722723724725726727728729730731732733734735736
§ 40.
 Действия с десятичными и обыкновенными дробями
Действия с десятичными и обыкновенными дробями737738739740741742743744745746747748749750751752753754755756757
§41. Округление чисел
758759760761762763764765
§ 42. Решение текстовых задач
766767768769770771772773774775776777778779
Глава 6. МНОЖЕСТВА
§ 43. Множество. Элементы множества. Изображение множеств
780781782783784785787
§ 44. Отношения между множествами. Подмножества
788789790791792793794795
§ 45. Объединение и пересечение множеств
796797798799800
§ 46. Решение текстовых задач
801802803804805806807808
Глава 7. ПРОЦЕНТЫ
§ 47. Процент
809810811812813815816817818819820821822823824825826828829830831
§ 48. Нахождение процентов от числа и числа по его процентам
832833834835836837838839840841842843
§ 49.
 Решение текстовых задач
Решение текстовых задач844
845846847848849850851852853854855856857858859860861862863864865866867868869
Глава 8. УГЛЫ. МНОГОУГОЛЬНИКИ
§ 50. Угол
870871872873874875876877878880881
§ 51. Многоугольники
882883884885886887888889890
Глава 9. ДИАГРАММЫ
§ 52. Окружность. Крут
891892893894895896897898899901902
§ 53. Диаграмма. Представление статистических данных с помощью диаграмм
903904906907908909910911912913915916917919920921
Глава 10. РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР
§ 54. Прямоугольный параллелепипед (куб) и его развертка
922923924926
§ 55. Задачи на разрезание фигур. Задачи на складывание фигур
929930931932933934
Глава 11.
 УПРАЖНЕНИЯ ДЛЯ ПОВТОРНЕИЯ
УПРАЖНЕНИЯ ДЛЯ ПОВТОРНЕИЯ937938939940941942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974
975976977978979980
Калькулятор НОД и НОК с решением онлайн
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
При помощи данного калькулятора вы можете легко найти наибольший общий делитель НОД и наименьшее общее кратное НОК благодаря подробно расписанному решению.
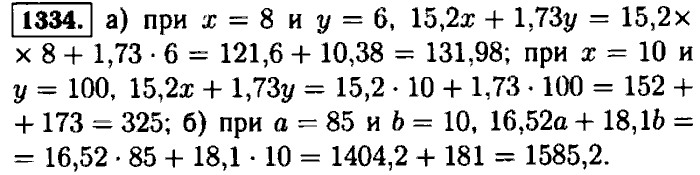 Вы можете найти НОД и НОК для двух, трех и четырех чисел
Вы можете найти НОД и НОК для двух, трех и четырех чиселВыберите количество чисел для НОД и НОК
| 2 числа | 3 числа | 4 числа |
Вы так же можете воспользоваться:
калькулятором нахождения НОД и НОК по алгоритму Евклида калькулятором нахождения НОД и НОК для любого количества чисел
Наибольший общий делитель НОД
Наибольший общий делитель НОД(a, b) – это наибольшее натуральной число, на которое можно разделить без остатка числа a и b.
Если числа имеют только один общий делитель – единицу, то такие числа называют взаимно простыми.
Наибольший общий делитель НОД обозначают: НОД(a, b), (a, b), gcd(a, b), hcf(a, b).
Свойства НОД
- Наибольший общий делитель чисел a и b делится на любой общий делитель этих чисел.
Данное свойство означает, что если найти все общие делители чисел a и b, то НОД(a, b) будет делится на любой из этих делителей.
Например, возьмём два числа 15 и 30 и найдем все общие делители этих чисел: 1, 3, 5, 15. Наибольший из этих делителей – число 15. Тогда число 15 делится на 1, 3, 5, 15. - Если число a делится на b, то НОД(a, b) = b.
Например, число 20 делится на число 10, тогда НОД(20, 10) = 10. - При помощи наибольшего общего делителя можно привести дроби к несократимому виду.
Например, дробь 5/30 можно привести к несократимому виду, если найти НОД(30, 5). НОД(30, 5) = 5, следовательно число 5 – самое больше число из возможных делителей числа 30 и 5 на которое можно разделить эти числа, тогда 30:5 = 6, 5:5 = 1. Получаем дробь 5/30 = 1/6.
Любые действия с дробями и развернутое поэтапное решение можно вычислить, используя калькулятор дробей.
Как найти наибольший общий делитель НОД
Чтобы найти наибольший общий делитель НОД двух, трех и более чисел, необходимо:
- Разложить числа на простые множители.

- Найти общие множители чисел – такие числа, которые есть в разложении всех чисел и вычеркнуть их.
- Перемножить оставшиеся множители.
Приведем пример, найдем наибольший общий делитель двух чисел 24 и 58.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
58 — составное число
Разложим число 24 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
24 : 2 = 12 — делится на простое число 2
12 : 2 = 6 — делится на простое число 2
6 : 2 = 3 — делится на простое число 2.
Завершаем деление, так как 3 простое числоРазложим число 58 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
58 : 2 = 29 — делится на простое число 2.

Завершаем деление, так как 29 простое число - Выделим синим цветом и выпишем общие множители.
24 = 2 ⋅ 2 ⋅ 2 ⋅ 3
58 = 2 ⋅ 29У чисел (24, 58) только один общий множитель — 2 и он и будет наибольшим общим делителем этих чисел
Ответ: НОД (24, 58) = 2
Способ №2
- Найдем все возможные делители чисел (24, 58). Для этого поочередно разделим число 24 на делители от 1 до 24, число 58 на делители от 1 до 58. Если число делится без остатка, то делитель запишем в список делителей.
Для числа 24 выпишем все случаи, когда оно делится без остатка:
24 : 1 = 24;
24 : 2 = 12;
24 : 3 = 8;
24 : 4 = 6;
24 : 6 = 4;
24 : 12 = 2;
24 : 24 = 1;Для числа 58 выпишем все случаи, когда оно делится без остатка:
58 : 1 = 58;
58 : 2 = 29;
58 : 29 = 2;
58 : 58 = 1; - Выпишем все общие делители чисел (24, 58) и выделим зеленым цветом самый большой, это и будет наибольший общий делитель НОД чисел (24, 58)
Общие делители чисел (24, 58): 1, 2
Ответ: НОД (24, 58) = 2
Наименьшее общее кратное НОК
Наименьшее общее кратное НОК(a, b) – это наименьшее число, которое можно разделить на числа a и b без остатка.
Наименьшее общее кратное НОК обозначается: НОК(a, b), [a, b], LCM(a, b), lcm(a, b).
Как найти наименьшее общее кратное НОК
Чтобы найти НОК двух, трех и более чисел необходимо:
- Разложить эти числа на простые множители.
- Выписать множители одного из чисел и добавить к ним множители из разложения остальных чисел, которых нет в разложении.
- Умножить получившиеся множители.
Приведем пример, найдем наименьшее общее кратное НОК для чисел 30 и 225.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
225 — составное число
30 — составное числоРазложим число 225 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
225 : 3 = 75 — делится на простое число 3
75 : 3 = 25 — делится на простое число 3
25 : 5 = 5 — делится на простое число 5.
Завершаем деление, так как 5 простое числоРазложим число 30 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
30 : 2 = 15 — делится на простое число 2
Завершаем деление, так как 5 простое число - Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители, выделим синим цветом в разложении меньшего числа множители, которые не вошли в разложение большего числа.
225 = 3 ∙ 3 ∙ 5 ∙ 5
30 = 2 ∙ 3 ∙ 53) Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями, которые выделены синим цветом
НОК (225 ; 30) = 3 ∙ 3 ∙ 5 ∙ 5 ∙ 2 = 450
Способ №2
- Найдем все возможные кратные чисел (225 ; 30). Для этого поочередно умножим число 225 на числа от 1 до 30, число 30 на числа от 1 до 225.

Выделим все кратные числа 225 зеленым цветом: зеленым цветом:
225 ∙ 1 = 225; 225 ∙ 2 = 450; 225 ∙ 3 = 675; 225 ∙ 4 = 900;
225 ∙ 5 = 1125; 225 ∙ 6 = 1350; 225 ∙ 7 = 1575; 225 ∙ 8 = 1800;
225 ∙ 9 = 2025; 225 ∙ 10 = 2250; 225 ∙ 11 = 2475; 225 ∙ 12 = 2700;
225 ∙ 13 = 2925; 225 ∙ 14 = 3150; 225 ∙ 15 = 3375; 225 ∙ 16 = 3600;
225 ∙ 17 = 3825; 225 ∙ 18 = 4050; 225 ∙ 19 = 4275; 225 ∙ 20 = 4500;
225 ∙ 21 = 4725; 225 ∙ 22 = 4950; 225 ∙ 23 = 5175; 225 ∙ 24 = 5400;
225 ∙ 25 = 5625; 225 ∙ 26 = 5850; 225 ∙ 27 = 6075; 225 ∙ 28 = 6300;
225 ∙ 29 = 6525; 225 ∙ 30 = 6750;Выделим все кратные числа 30 зеленым цветом:
30 ∙ 1 = 30; 30 ∙ 2 = 60; 30 ∙ 3 = 90; 30 ∙ 4 = 120;
30 ∙ 5 = 150; 30 ∙ 6 = 180; 30 ∙ 7 = 210; 30 ∙ 8 = 240;
30 ∙ 9 = 270; 30 ∙ 10 = 300; 30 ∙ 11 = 330; 30 ∙ 12 = 360;
30 ∙ 13 = 390; 30 ∙ 14 = 420; 30 ∙ 15 = 450; 30 ∙ 16 = 480;
30 ∙ 17 = 510; 30 ∙ 18 = 540; 30 ∙ 19 = 570; 30 ∙ 20 = 600;
30 ∙ 21 = 630; 30 ∙ 22 = 660; 30 ∙ 23 = 690; 30 ∙ 24 = 720;
30 ∙ 29 = 870; 30 ∙ 30 = 900; 30 ∙ 31 = 930; 30 ∙ 32 = 960;
30 ∙ 33 = 990; 30 ∙ 34 = 1020; 30 ∙ 35 = 1050; 30 ∙ 36 = 1080;
30 ∙ 37 = 1110; 30 ∙ 38 = 1140; 30 ∙ 39 = 1170; 30 ∙ 40 = 1200;
30 ∙ 41 = 1230; 30 ∙ 42 = 1260; 30 ∙ 43 = 1290; 30 ∙ 44 = 1320;
30 ∙ 45 = 1350; 30 ∙ 46 = 1380; 30 ∙ 47 = 1410; 30 ∙ 48 = 1440;
30 ∙ 49 = 1470; 30 ∙ 50 = 1500; 30 ∙ 51 = 1530; 30 ∙ 52 = 1560;
30 ∙ 53 = 1590; 30 ∙ 54 = 1620; 30 ∙ 55 = 1650; 30 ∙ 56 = 1680;
30 ∙ 57 = 1710; 30 ∙ 58 = 1740; 30 ∙ 59 = 1770; 30 ∙ 60 = 1800;
30 ∙ 61 = 1830; 30 ∙ 62 = 1860; 30 ∙ 63 = 1890; 30 ∙ 64 = 1920;
30 ∙ 65 = 1950; 30 ∙ 66 = 1980; 30 ∙ 67 = 2010; 30 ∙ 68 = 2040;
30 ∙ 69 = 2070; 30 ∙ 70 = 2100; 30 ∙ 71 = 2130; 30 ∙ 72 = 2160;
30 ∙ 73 = 2190; 30 ∙ 74 = 2220; 30 ∙ 75 = 2250; 30 ∙ 76 = 2280;
30 ∙ 77 = 2310; 30 ∙ 78 = 2340; 30 ∙ 79 = 2370; 30 ∙ 80 = 2400;
30 ∙ 81 = 2430; 30 ∙ 82 = 2460; 30 ∙ 83 = 2490; 30 ∙ 84 = 2520;
30 ∙ 85 = 2550; 30 ∙ 86 = 2580; 30 ∙ 87 = 2610; 30 ∙ 88 = 2640;
30 ∙ 89 = 2670; 30 ∙ 90 = 2700; 30 ∙ 91 = 2730; 30 ∙ 92 = 2760;
30 ∙ 93 = 2790; 30 ∙ 94 = 2820; 30 ∙ 95 = 2850; 30 ∙ 96 = 2880;
30 ∙ 97 = 2910; 30 ∙ 98 = 2940; 30 ∙ 99 = 2970; 30 ∙ 100 = 3000;
30 ∙ 101 = 3030; 30 ∙ 102 = 3060; 30 ∙ 103 = 3090; 30 ∙ 104 = 3120;
30 ∙ 105 = 3150; 30 ∙ 106 = 3180; 30 ∙ 107 = 3210; 30 ∙ 108 = 3240;
30 ∙ 109 = 3270; 30 ∙ 110 = 3300; 30 ∙ 111 = 3330; 30 ∙ 112 = 3360;
30 ∙ 113 = 3390; 30 ∙ 114 = 3420; 30 ∙ 115 = 3450; 30 ∙ 116 = 3480;
30 ∙ 117 = 3510; 30 ∙ 118 = 3540; 30 ∙ 119 = 3570; 30 ∙ 120 = 3600;
30 ∙ 121 = 3630; 30 ∙ 122 = 3660; 30 ∙ 123 = 3690; 30 ∙ 124 = 3720;
30 ∙ 125 = 3750; 30 ∙ 126 = 3780; 30 ∙ 127 = 3810; 30 ∙ 128 = 3840;
30 ∙ 129 = 3870; 30 ∙ 130 = 3900; 30 ∙ 131 = 3930; 30 ∙ 132 = 3960;
30 ∙ 137 = 4110; 30 ∙ 138 = 4140; 30 ∙ 139 = 4170; 30 ∙ 140 = 4200;
30 ∙ 141 = 4230; 30 ∙ 142 = 4260; 30 ∙ 143 = 4290; 30 ∙ 144 = 4320;
30 ∙ 145 = 4350; 30 ∙ 146 = 4380; 30 ∙ 147 = 4410; 30 ∙ 148 = 4440;
30 ∙ 149 = 4470; 30 ∙ 150 = 4500; 30 ∙ 151 = 4530; 30 ∙ 152 = 4560;
30 ∙ 153 = 4590; 30 ∙ 154 = 4620; 30 ∙ 155 = 4650; 30 ∙ 156 = 4680;
30 ∙ 157 = 4710; 30 ∙ 158 = 4740; 30 ∙ 159 = 4770; 30 ∙ 160 = 4800;
30 ∙ 161 = 4830; 30 ∙ 162 = 4860; 30 ∙ 163 = 4890; 30 ∙ 164 = 4920;
30 ∙ 165 = 4950; 30 ∙ 166 = 4980; 30 ∙ 167 = 5010; 30 ∙ 168 = 5040;
30 ∙ 169 = 5070; 30 ∙ 170 = 5100; 30 ∙ 171 = 5130; 30 ∙ 172 = 5160;
30 ∙ 173 = 5190; 30 ∙ 174 = 5220; 30 ∙ 175 = 5250; 30 ∙ 176 = 5280;
30 ∙ 177 = 5310; 30 ∙ 178 = 5340; 30 ∙ 179 = 5370; 30 ∙ 180 = 5400;
30 ∙ 181 = 5430; 30 ∙ 182 = 5460; 30 ∙ 183 = 5490; 30 ∙ 184 = 5520;
30 ∙ 185 = 5550; 30 ∙ 186 = 5580; 30 ∙ 187 = 5610; 30 ∙ 188 = 5640;
30 ∙ 189 = 5670; 30 ∙ 190 = 5700; 30 ∙ 191 = 5730; 30 ∙ 192 = 5760;
30 ∙ 193 = 5790; 30 ∙ 194 = 5820; 30 ∙ 195 = 5850; 30 ∙ 196 = 5880;
30 ∙ 197 = 5910; 30 ∙ 198 = 5940; 30 ∙ 199 = 5970; 30 ∙ 200 = 6000;
30 ∙ 201 = 6030; 30 ∙ 202 = 6060; 30 ∙ 203 = 6090; 30 ∙ 204 = 6120;
30 ∙ 205 = 6150; 30 ∙ 206 = 6180; 30 ∙ 207 = 6210; 30 ∙ 208 = 6240;
30 ∙ 209 = 6270; 30 ∙ 210 = 6300; 30 ∙ 211 = 6330; 30 ∙ 212 = 6360;
30 ∙ 213 = 6390; 30 ∙ 214 = 6420; 30 ∙ 215 = 6450; 30 ∙ 216 = 6480;
30 ∙ 217 = 6510; 30 ∙ 218 = 6540; 30 ∙ 219 = 6570; 30 ∙ 220 = 6600;
30 ∙ 221 = 6630; 30 ∙ 222 = 6660; 30 ∙ 223 = 6690; 30 ∙ 224 = 6720;
30 ∙ 225 = 6750; - Выпишем все общие кратные чисел (225 ; 30) и выделим зеленым цветом самое маленькое, это и будет наименьшим общим кратным чисел (225 ; 30).

Общие кратные чисел (225 ; 30): 450, 900, 1350, 1800, 2250, 2700, 3150, 3600, 4050, 4500, 4950, 5400, 5850, 6300, 6750
Ответ: НОК (225 ; 30) = 450
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
| Инструктор, грейдер, книга… | |||||||||||||||||||||||||||||||||||
| Инструктор : Мойра Час, офис 3-119 Math Tower, e-mail: moira.chas»at»stonybrook.edu Часы работы инструктора: Понедельник 1:30:00-3:30
(в 3-119, Математическая башня), среда с 11:00 до 12:00 или до
деловое свидание, встреча. Классные собрания: MWF 10:00–10:53 Earth&Space 183 Класс : Xuntao Hu xuntao.hu»at»stonybrook.edu Часы работы оценщика: Вторник с 10 до 11 утра в его Учебник : Топология поверхностей, Л. Кристин Kinsey Материалы курса (слайды, заметки и т. д.) находятся здесь (Включая слайды первого дня, которые также являются частью учебный план). | |||||||||||||||||||||||||||||||||||
| Об этом курсе | |||||||||||||||||||||||||||||||||||
(из бюллетеня для студентов)
введение в топологию и геометрию, математические теории
формы, формы и жесткой конструкции. Темы включают интуитивный узел
теория, решетки и тайлинги, неевклидова геометрия, гладкая
кривые и поверхности в трехмерном евклидовом пространстве, открытые множества и
непрерывность, комбинаторные и алгебраические инварианты пространств,
пространства более высокой размерности. Мы рассмотрим главы с 1 по 5 из учебника, возможно пропустив пару разделов и добавив пару тем. Расписание будет обновляться по мере прохождения курса. | |||||||||||||||||||||||||||||||||||
| Экзамены и оценки | |||||||||||||||||||||||||||||||||||
| Будет два промежуточных экзамена (в классе) и итоговый итоговый экзамен. Даты указаны ниже. Успех на экзаменах будет требуют правильных и эффективных решений более сложных проблемы с домашним заданием. Убедитесь, что вы можете присутствовать на экзаменах в назначенное время;
косметику не дадут. Если пропущен один промежуточный экзамен
из-за серьезного (документально подтвержденного) заболевания или чрезвычайной ситуации,
Семестровая оценка будет определяться на основе баланса работы
в ходе. Студенты, посещающие мероприятия, спонсируемые университетом, или
в случае необходимости отсутствовать на религиозные праздники следует обратиться в
инструктором на первых двух неделях занятий, чтобы обсудить
соответствующий план.
| |||||||||||||||||||||||||||||||||||
| Домашнее задание | |||||||||||||||||||||||||||||||||||
| Домашнее задание будет задаваться еженедельно и должно быть выполнено в среду до учебный класс. Домашнее задание является обязательным, поскольку оно является неотъемлемой частью курс: Почти невозможно выучить математику без работа над проблемами
Рубрика для оценивания проблемы (адаптировано из Emert — Приходская книга и это сайт)
| |||||||||||||||||||||||||||||||||||
| Письменные домашние задания всегда можно нашел ЗДЕСЬ. Единственная рука в подчеркнутая проблемы. | |||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||
| Рецепт успеха на этом курсе | |||||||||||||||||||||||||||||||||||
Помните: математика, как правило, хорошо себя ведет с людьми, которые «лечить ее» хорошо, то есть с людьми, которые вкладывают время и силы в понимании. Очень редко можно провести рабочую сессию на математику, ничего не поняв. Мы все учимся в разными способами и с разной скоростью, но мы все можем учиться. Как и в любом курсе математики, не расстраивайтесь, если вы обнаружите вы часами боретесь с проблемой или концепцией. Ты необходимо провести расчеты, чтобы понять материал, но не тратьте время на бездумное заучивание методы. Конструктивная обратная связь с вашим инструктором будет всегда добро пожаловать. | |||||||||||||||||||||||||||||||||||
Заявление Центра поддержки доступности для учащихсяЕсли у вас есть физические, психологические, медицинские или учебные инвалидность, которая может повлиять на вашу курсовую работу, пожалуйста, свяжитесь с Центр поддержки доступности для учащихся, ECC (Образовательный узел связи) корпус, комн. 128, (631)632-6748. Они
определит с вами, какие приспособления, если таковые имеются, необходимы
и уместно. Вся информация и документация
конфиденциально. 128, (631)632-6748. Они
определит с вами, какие приспособления, если таковые имеются, необходимы
и уместно. Вся информация и документация
конфиденциально.Студенты, которым требуется помощь во время экстренной эвакуации, рекомендуется обсуждать свои потребности со своими профессорами и Центр поддержки доступности для учащихся. Для процедур и информацию перейти на следующий веб-сайт: ЗДЕСЬ. Заявление об академической честностиКаждый студент должен честно преследовать свои академические цели и быть несет личную ответственность за все представленные работы. Представляя работа другого человека как ваша собственная всегда неправильна. Факультет обязаны сообщать о любых подозреваемых случаях академической нечестности в академический суд. Факультет Центра медицинских наук (Школа медицинских технологий и менеджмента, сестринского дела, социальных Социальное обеспечение, Стоматологическая медицина) и Школа медицины обязаны следовать своим школьным процедурам.  Для более полного
сведения об академической честности, включая категории
академическая нечестность, пожалуйста, обратитесь к веб-сайту академической судебной системы
в Для более полного
сведения об академической честности, включая категории
академическая нечестность, пожалуйста, обратитесь к веб-сайту академической судебной системы
в http://www.stonybrook.edu/commcms/academic_integrity/index.html Управление критическими инцидентамиУниверситет Стоуни-Брук ожидает от студентов уважения прав, привилегии и имущество других людей. Факультет обязан сообщать в Управление общественных стандартов университета о любых разрушительное поведение, которое прерывает их способность к обучению, ставит под угрозу безопасность среды обучения или препятствует способность учащихся к обучению. Факультет в школах HSC и Медицинские школы обязаны следовать своим школьным правилам. процедуры. Дополнительную информацию по большинству академических вопросов можно получить можно найти в бюллетене бакалавриата, класс бакалавриата Расписание и Справочник преподавателей и сотрудников. | |||||||||||||||||||||||||||||||||||
Math464AAWinter2018
Math464AAWinter2018 МАТЕМАТИКА 364 / МАТЕМАТИКА 626, Осень 2018раздел А
Преподаватель: д-р Павел Гора,
ЛБ-901-17, тел.: 848-2424, доб.
3257
электронная почта: [email protected]
Офис часы работы: уточняется
или по
деловое свидание, встреча.
Книга: Заметки о реальном анализе Л. Ларсона.
Доступно в Интернете: http://www.math.louisville.edu/~lee/RealAnalysis/IntroRealAnal.pdf
Вспомогательный
учебник, который будет доступен в Moodle:
Introductoy
Реальный анализ Фрэнка
Данжелло и Майкл Сейфрид, изданный
Брукс/Коул.
Тест класса: Будет класс тест запланирован на 7-й или 8-й неделе занятий.
Задания: Выдаются еженедельно на веб-странице http://www.mathstat.concordia.ca/faculty/pgora/m364/ . Решения будут представлены на следующей неделе в классе. Просроченных заданий не будет принято. Вы должны предоставить полный аргументы в вашем домашнем задании. Решения для назначенные проблемы будут размещены на том же веб-страница. Некоторые проблемы могут быть не отмечены.
Другие материалы, связанные с курсом, также будут разместил там.
90% баллов за выпускной экзамен + 10% заданий или
комбинация: 60 % итоговый экзамен + 30 % тест +
10% заданий, в зависимости от того, что больше.
Задания делают важным
часть курса, как принято считать
что единственный способ выучить математику — это
работать самостоятельно над проблемами.
Решения будут размещены в формате pdf на
Moodle и на http://www.mathstat.concordia.ca/faculty/pgora/m364/
Промежуточный тест: Есть
будет промежуточный тест, запланированный на 7-й или на 8-й неделе
классы.
точная дата экзамена будет объявлена
в классе не менее чем за неделю. Макияжа в середине срока не будет
экзамен.
Темы: Элементы
доказательств и теории множеств.  Набор реальных чисел
Набор реальных чисел Последовательности Ограничения функций
и Непрерывность Производные 12 5 Элементы
Топология
Обзор
Номера в разных обозначения
Назначения: #1 , #2 , #3 , #4
, #5 , #6 , #7 , #8 , #9 , #10 , #11
Решения: №1
, #2 , № 3 , № 4 , #5, #6 , #7, #8 , #9 , № 10
, #11
Пример для задач 4,5 в задании 1.

Старые промежуточные результаты упражнение. Ненужные проблемы убраны. Некоторые решения.
Последний окончание семестра
Чтобы получить дополнительные 5% к своей оценке, вам необходимо:
Изучите доказательство теоремы Шредера-Бернштейна.
Предъявите мне доказательство без каких-либо заметок или помощи.
Ответь на мои вопросы, чтобы убедить меня, что Ты
понять доказательство.
Если я убеждён, Вы получите 5%.
Крайний срок — один день до финала.
(Это не значит, что я буду доступен.)
MASSA создала опрос для получения обратной связи
об их серии Lunch & Learn:
Обед & Learn Feedback
У SIAM есть веб-страница о карьере открыты для выпускников математических факультетов:
https://www.
 maa.org/programs/faculty-and-departments/pic-math/solving-real-world-problems
maa.org/programs/faculty-and-departments/pic-math/solving-real-world-problems Старые промежуточные экзамены по упражнениям. Некоторые решения.
Вот несколько старых финалов, некоторые решения здесь.
Примечания: Доказательство «лимсапа» теорема. Только для смелых.
Примечания о непрерывности и равномерной непрерывности. (обновлено 15 ноября 2015 г.)
Краткие заметки для нескольких первых классов, незаконченных и неполных, но возможно полезно.
Заметки на разные темы (любезно предоставленные д-ром Бертолой): 90 007 Последующие ограничения , Плотность последовательности sin(n) , Мощность
Некоторые интересные ограничения.
Результаты заданий
и тесты
(пожалуйста
отчет любые ошибки по телефону [email protected])
Вернуться к главная страница математики и статистики
Треугольник Паскаля
Одной из самых интересных числовых моделей является треугольник Паскаля (названный в честь Блеза Паскаля , известного французского математика и философа).
Чтобы построить треугольник, начните с «1» вверху, затем продолжайте размещать цифры под ним в виде треугольника.
Каждое число представляет собой сложенные числа непосредственно над ним.
(Здесь я подчеркнул, что 1+3 = 4)
Узоры внутри треугольника
Диагонали
Первая диагональ — это, конечно, просто «1»
На следующей диагонали находятся Счетные числа (1,2,3 и т. д.).
д.).
Третья диагональ имеет треугольные числа
(Четвертая диагональ, не выделенная, имеет четырехгранные числа.)
Симметричный
Треугольник также симметричен. Числа на левой стороне имеют одинаковые совпадающие числа на правой стороне, как зеркальное отражение.
Горизонтальные суммы
Что вы заметили в горизонтальных суммах?
Есть шаблон?
Они удваивают каждый раз (степень двойки).
Экспоненты числа 11
Каждая строка также представляет собой степени (показатели) числа 11:
- 11 0 =1 (первая строка просто «1»)
- 11 1 =11 (вторая строка «1» и «1»)
- 11 2 =121 (третья строка «1», «2», «1»)
- и т.д.!
Но что происходит с 11 5 ? Простой! Цифры просто перекрываются, вот так:
То же самое происходит с 11 6 и т. д.
д.
квадратов
Для второй диагонали квадрат числа равен сумме чисел рядом с ним и под обоими из них.
Примеры:
- 3 2 = 3 + 6 = 9,
- 4 2 = 6 + 10 = 16,
- 5 2 = 10 + 15 = 25,
- …
Есть и веская причина… ты можешь ее придумать? (Подсказка: 4 2 =6+10, 6=3+2+1 и 10=4+3+2+1)
Последовательность Фибоначчи
Попробуйте следующее: создайте фигуру, двигаясь вверх и вниз, затем сложите значения (как показано на рисунке)… вы получите последовательность Фибоначчи.
(Последовательность Фибоначчи начинается с «0, 1», а затем продолжается добавлением двух предыдущих чисел, например, 3+5=8, затем 5+8=13 и т. д.)
Шансы и четы
Если мы раскрасим нечетные и четные числа, мы получим узор, аналогичный треугольнику Серпинского
Пути
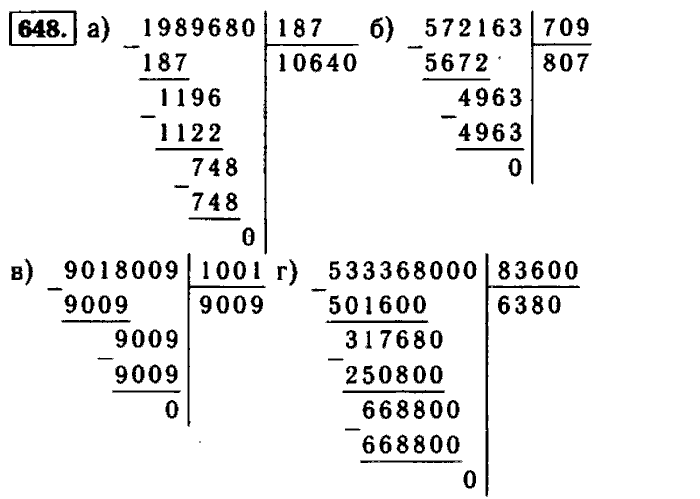
Каждая запись также является числом различных путей сверху вниз.
Пример: существует только один путь сверху вниз к любой «1»
И мы видим, что есть 2 разных пути к «2»
То же самое вверх, есть 3 разных пути от 3:
Ваша очередь, посмотрите, сможете ли вы найти все пути вниз к «6»:
Использование треугольника Паскаля
Орел и решка
Треугольник Паскаля показывает нам, сколько способов может сочетаться орел и решка. Затем это может показать нам вероятность любой комбинации.
Например, если вы подбросите монету три раза, только одна комбинация даст три орла (HHH), но есть три комбинации, которые дадут два орла и одну решку (HHT, HTH, THH), а также три комбинации, которые дадут одна голова и две решки (HTT, THT, TTH) и одна для всех решек (TTT). Это паттерн «1,3,3,1» в треугольнике Паскаля.
| Подбрасывает | Возможные результаты (сгруппированные) | Треугольник Паскаля |
|---|---|---|
| 1 | Х Т | 1, 1 |
| 2 | HH HT TH TT | 1, 2, 1 |
| 3 | HHH HHT, HTH, THH HTT, THT, TTH TTT | 1, 3, 3, 1 |
| 4 | HHHH HHHT, HHTH, HTHH, THHH HHTT, HTHT, HTTH, THHT, THTH, TTHH HTTT, THTT, TTHT, TTTH TTTT | 1, 4, 6, 4, 1 |
.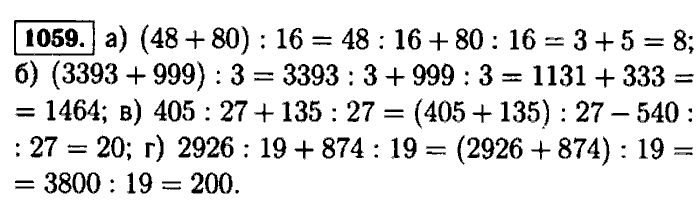 .. и т. д. … .. и т. д. … |
Пример. Какова вероятность того, что при 4 подбрасываниях монеты выпадет ровно два орла?
Существует 1+4+6+4+1 = 16 (или 2 4 = 16) возможных результатов, и 6 из них дают ровно два орла. Таким образом, вероятность равна 6/16, или 37,5%
.Комбинации
Треугольник также показывает нам, сколько комбинаций объектов возможно.
Пример: У вас есть 16 шаров для пула. Сколькими способами можно выбрать только 3 из них (игнорируя порядок их выбора)?
Ответ: спуститесь в начало 16 ряда (верхний ряд 0), а затем по 3 местам (первое место 0) и значение там будет вашим ответом, 560 .
Вот выдержка из строки 16:
1 14 91 364 ... 1 15 105 455 1365 ... 1 16 120 560 1820 4368 ...
Формула для любого входа в треугольник
На самом деле существует формула из Комбинаций для определения значения в любом месте треугольника Паскаля:
Это обычно называется «n select k» и пишется так: | н! к!(н-к)! = ( n к ) |
Обозначение: «n выбирает k» также может быть записано как C(n,k) , n C k или n C k 9,0059
| ! | «!» является «факториалом» и означает умножение ряда убывающих натуральных чисел.
|
Таким образом, Треугольник Паскаля также может быть
треугольником «n выбрать k» , подобным этому.
(Обратите внимание, что верхняя строка — это нулевая строка
, а также крайний левый столбец — ноль)
Пример: Строка 4, член 2 в треугольнике Паскаля равен «6» …
… посмотрим, работает ли формула:
( 4 2 ) = 4! 2!(4−2)! = 4! 2!2! = 4×3×2×1 2×1×2×1 = 6
Да, это работает! Попробуйте другое значение для себя.
Это может быть очень полезно… теперь мы можем найти любое значение в Треугольнике Паскаля непосредственно (без вычисления всего треугольника над ним).
Многочлены
Треугольник Паскаля также показывает нам коэффициенты в биномиальном разложении:
| Мощность | Биномиальное расширение | Треугольник Паскаля |
|---|---|---|
| 2 | (х + 1) 2 = 1 х 2 + 2 х + 1 | 1, 2, 1 |
| 3 | (x + 1) 3 = 1 x 3 + 3 x 2 + 3 x + 1 | 1, 3, 3, 1 |
| 4 | (x + 1) 4 = 1 x 4 + 4 x 3 + 6 x 2 + 4 .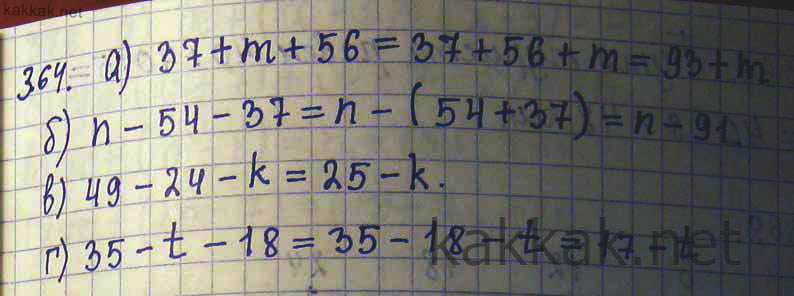 0009 0009 | 1, 4, 6, 4, 1 |
| … и т. д. … |
Первые 15 строк
Для справки я включил строки с 0 по 14 треугольника Паскаля
.1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35
35
21
7
1
1
8
28
56
70
56
28
8
1
9
36
84
126
126
84
169
6
1
10
45
120
210
252
210
120
45
10
6
1
11
55
165
330
462
462
330
165
55
11
1
1
12
66
220
495
792
924
792
495
220
495
220
495
220
495
220
495
495
495
900166
12
1
1
13
78
286
715
1287
1716
1716
1287
715
286
78
13
1
1
14
91
364
1001
2002
3003
3432
3003
2002
1001
364
91
14
1
Китайцы знали об этом
Этот рисунок озаглавлен «Таблица старого метода семи умножающих квадратов».






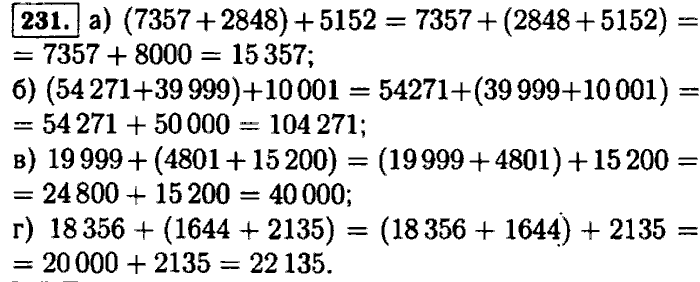

 (да, это
надо сказать)
(да, это
надо сказать) (да! я имею в виду
что математические рассуждения должны быть написаны полностью
предложение.)
(да! я имею в виду
что математические рассуждения должны быть написаны полностью
предложение.)
 Примеры:
Примеры: