Контрольные работы по математике 5 класс, Н.Я. Виленкин и др. | Методическая разработка по алгебре (5 класс) по теме:
Контрольная работа №2
Вариант I
№1 Выполнить действия:
а) (829-239)*75
б) 8991:111:3
№2 Задача. Периметр треугольника 36 см, а периметр прямоугольника в 3 раза меньше. На сколько сантиметров периметр треугольника больше периметра прямоугольника?
№3 Вычислить:
4кг – 80гр
№4
а) На сколько число 59345 больше числа 53568?
б) На сколько число 59345 меньше числа 69965?
№5 Задача. Вдоль аллеи (по прямой) высадили 15 кустов. Расстояние между любыми двумя соседними кустами одинаковое. Найдите это расстояние, если между крайними кустами 210дм.
Контрольная работа №2
Вариант II
№1 Выполнить действия:
а) 2000 – (859+1085):243
б) 3969:(305 – 158)
№2 Задача. Туристы в первый день ехали на велосипедах 6 часов со скоростью 12 км/ч, во — второй день они проехали с одинаковой скоростью такой же путь за 4 часа. С какой же скоростью ехали туристы во – второй день?
С какой же скоростью ехали туристы во – второй день?
№3 Вычислить:
2кг – 60гр
№4
а) на сколько число 38954 больше числа 22359
б) На сколько число 38954 меньше числа 48234.
№5 Задача. Вдоль шоссе (по прямой) высадили 20 деревьев. Расстояние между любыми двумя соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 380м.
Контрольная работа №1
Вариант I
№1 Найдите сумму:
а) 3000000+5000+7
б) 654+765
№2 Выполнить действия:
(60+40):2 – 30:5
№3 Сравните числа и поставьте вместо звездочки знак
а) 63001 * 63002
б) 41527 * 42326
№4 Задача. От туристского лагеря до города 84 км. Турист ехал на велосипеде из лагеря в город со скоростью 12 км/ч., а возвращался по той же дороге со скоростью 14 км/ч. На какой путь турист затратил больше времени и на сколько часов.
Контрольная работа №1
Вариант II
№1 Найдите сумму:
а) 2000000+7000+300+2
б) 763+448
№2 Выполнить действия:
(70-50)∙5:20+55
№3 Сравните числа и поставьте вместо звездочки знак
а) 20850 * 20860
б) 31255 * 32254
№4 Задача. Игорь живет на расстоянии48 км от районного центра. Путь от дома до райцентра он проехал на велосипеде со скоростью 16 км/ч, а обратный путь по той же дороге он проехал со скоростью 12 км/ч. На какой путь Игорь затратил меньше времени и насколько часов.
Игорь живет на расстоянии48 км от районного центра. Путь от дома до райцентра он проехал на велосипеде со скоростью 16 км/ч, а обратный путь по той же дороге он проехал со скоростью 12 км/ч. На какой путь Игорь затратил меньше времени и насколько часов.
Контрольная работа №3
Вариант I
№1 Решите уравнение:
а) 21+х=56
б) у-89=90
№2 Найти значение выражения:
260+в – 160, если в=93
№3 Вычислите, выбирая удобный порядок действий
а) 5+1977+1515
б) 863 – (163+387)
№4 Решить задачу с помощью уравнения.
В автобусе было 78 пассажиров. После того, как на остановке из него несколько человек вышли, в автобусе осталось 59 пассажиров. Сколько человек вышли из автобуса на остановке.
№5
На отрезке MN =19, отметили точку К такую, что МК=15 и точку F такую, что FN=13. Найти длину отрезка KF.
Контрольная работа №3
Вариант II
№1 Решите уравнение:
а) х+32=68
б) 76 – у=24
№2 Найти значение выражения:
340+к – 240, если к=87
№3 Вычислите, выбирая удобный порядок действий
а) 7231+1437+563
б) (964+479) – 264
№4 Решить задачу с помощью уравнения.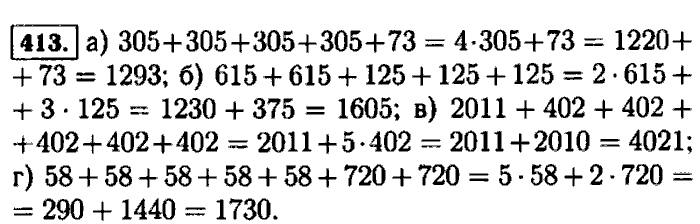
В санатории было 97 отдыхающих. После того, как несколько человек уехали на экскурсию, в санатории осталось 78 отдыхающих. Сколько отдыхающих уехали на экскурсию.
№5
На отрезке DE=25 отметили точку L такую, что DL=19, и точку Р такую, что РЕ=17. Найдите длину отрезка LP.
Контрольная работа №4
Вариант I
№1 Найдите значение выражения:
а) 58∙196
б) 405∙208
в) 36490:178
№2 Решите уравнение
а) х∙14=112
б) 133:у=19
в) m:15=90
№3 Вычислите, выбирая удобный порядок действий.
а) 4∙289∙25
б) 50∙97∙20
№4 Задача. Коля задумал число, умножил его на 3 и от произведения отнял 7. Он получил 50. Какое число задумал Коля?
№5 Угадайте корень уравнения и сделайте проверку:
х+х – 20=х+5
Контрольная работа №4
Вариант II
№1 Найдите значение выражения:
а) 67∙189
б) 306∙805
в) 38130:186
№2 Решите уравнение
а) х∙13=182
б) 187:у=17
в) n:14=98
№3 Вычислите, выбирая удобный порядок действий.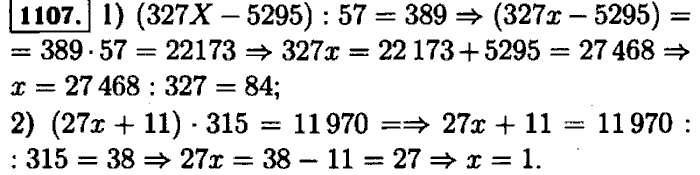
а) 25∙197∙4
б) 50∙23∙40
№4 Задача. Света задумала число, умножила его на 4 и к произведению прибавила 8. Получила 60. Какое число задумала Света?
№5 Угадайте корень уравнения и сделайте проверку:
у+у – 25=у+10
Контрольная работа №5
Вариант I
№1 Найдите значение выражения:
а) 684∙397 — 584∙397
б) 39∙58 – 9720:27+33
в) 23 + 32
№2 Решите уравнение:
а) 7у – 39=717
б) х+3х=76
№3 Упростите выражение:
а) 24а+16+13а
б) 25∙m∙16
№4 Задача. В книге напечатаны 2 сказки. Первая занимает в 4 раза больше страниц, чем вторая, а обе они занимают 30 стр. Сколько страниц занимает каждая сказка?
№5 Имеет ли корни уравнение:
х2=х:х
Контрольная работа №5
Вариант II
№1 Найдите значение выражения:
а) 798∙349-798∙249
б) 57∙38-8640:24+66
в) 52+33
№2 Решите уравнение:
а) 8х+14=870
б) 5у-у=68
№3 Упростите выражение:
а) 37к+13+22к
б) 50∙n∙12
№4 Задача. В двух корзинах 98 яблок. В первой яблок в шесть раз меньше, чем во второй. Сколько яблок в каждой корзине?
В двух корзинах 98 яблок. В первой яблок в шесть раз меньше, чем во второй. Сколько яблок в каждой корзине?
№5 Имеет ли корни уравнение:
у3=у∙у
Контрольная работа №6
Вариант I
1. Вычислите:
а) (53+132):21
б) 180∙94-47700:45+4946
2. Задача. Длина прямоугольного участка земли 125м, а ширина 96м. Найдите площадь поля и выразите её в арах.
3. Задача. Найдите объем прямоугольного параллелепипеда, измерения которого равны 4м, 3м и 5 дм.
4. Используя формулу пути s=v∙t, найдите:
а) путь, пройденный автомашиной за 3 ч, если её скорость 80 км/ч,
б) время движения катера, прошедшего 90 км со скоростью 15 км/ч
5. Задача. Найдите площадь поверхности и объем куба, ребро которого равно 6 дм. Во сколько раз уменьшится площадь поверхности и во сколько раз – объем куба, если ребро уменьшить вдвое?
Контрольная работа №6
Вариант II
1. Вычислите:
а) (63+122):15
б) 86∙170-5793+72800:35
2. Задача. Ширина прямоугольного поля 375м, а длина 1600м. Найдите площадь поля и выразите её в гектарах.
Ширина прямоугольного поля 375м, а длина 1600м. Найдите площадь поля и выразите её в гектарах.
3. Задача. Найдите объем прямоугольного параллелепипеда, измерения которого равны 2дм, 6дм и 5 см.
4. Используя формулу пути s=v∙t, найдите:
а) путь, пройденный моторной лодкой за 2 часа, если её скорость 18 км/ч
б) скорость движения автомобиля, за 3 ч прошедшего 150 км.
5. Задача. Ребро куба равно 5см. Найдите площадь поверхности и объем этого куба. Во сколько раз увеличится площадь поверхности и во сколько раз – объем куба, если его ребро увеличить вдвое?
Контрольная работа №7
Вариант I
1. Примите за единичный отрезок длину 8 клеток тетради и отметьте на координатном луче точки А(), М(), К(), Т(), Р()
2. Сравните числа:
а) и , б) и , в) 1 и , г) и
3. Сложите числа 30 и числа 14.
4. Какую часть составляют:
а) 9 см2 от квадратного дециметра,
б) 17 дм3 от кубического метра,
в) 13 кг от 2 ц?
5.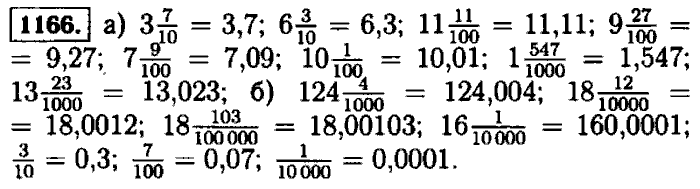 Задача. Ширина прямоугольника 48 см, что составляет его периметра. Найдите длину этого прямоугольника.
Задача. Ширина прямоугольника 48 см, что составляет его периметра. Найдите длину этого прямоугольника.
Контрольная работа №7
Вариант II
1. Примите за единичный отрезок длину 12 клеток тетради и отметьте на координатном луче точки В(), С(), Е(), О(), Н()
2. Сравните числа:
а) и , б) и , в) 1 и , г) и
3. Сложите числа 18 и числа 40.
4. Какую часть составляют:
а) 7 дм2 от квадратного метра,
б) 19 см3 от кубического дециметра,
в) 9ц от 4 т?
5. Задача. Длина прямоугольника составляет его периметра. Найдите ширину этого прямоугольника, если его длина равна 80 см.
Контрольная работа №8
Вариант I
1. Выполните действия:
а) б)
в) г)
2. Задача. Турист шел с постоянной скоростью и за 3 часа прошел 14 км. С како скоростью он шел?
3. Задача. В гараже 45 автомобилей. Из них — легковые. Сколько легковых автомобилей в гараже.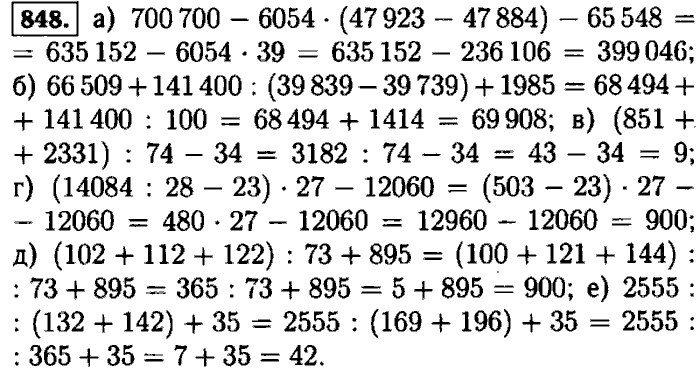
4. Решите уравнение:
а) б)
5. Какое число надо разделить на 8, чтобы частное равнялось ?
Контрольная работа №8
Вариант II
1. Выполните действия:
а) б)
в) г)
2. Задача. Автомобиль, двигаясь с постоянной скоростью, прошел 14 км за 9 мин. Какова скорость автомобиля?
3. Задача. В классе 40 учеников. Из них занимаются в спортивных секциях. Сколько учеников класса занимаются спортом?
4. Решите уравнение:
а) б)
5. Какое число надо разделить на 6, чтобы частное равнялось ?
Контрольная работа №9
Вариант I
1. Сравните числа: 7,195 и 12,1; 8,276 и 8,3; 0,76 и 0,7598
2. Выполните действия:
а) 12,3 + 5,26 в) 79,1-6,08
б) 0,48 + 0,057 г) 5-1,63
3.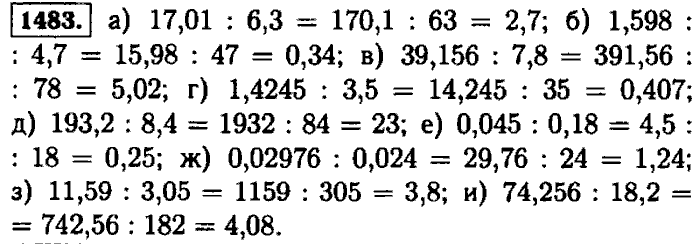 Округлите:
Округлите:
а) 3,18; 30,625; 257,51; 0,28 до единиц
б) 0,531; 12,467; 8,5452 и 0,009 до сотых
4. Задача. Собственная скорость лодки 3,4 км/ч. Скорость лодки против течения реки 0,8 км/ч. Найдите скорость лодки по течению.
5. Запишите четыре значения m, при которых верно неравенство 0,71
Контрольная работа №9
Вариант II
1. Сравните числа: 8,2 и 6,984; 7,6 и 7,596; 0,6387 и 0,64
2. Выполните действия:
а) 15,4+3,18 в) 86,3 – 5,07
в) 0,068+0,39 г) 7 – 2,78
3. Округлите:
а) 8,72; 40,198; 164,53 и 0,61 до единиц
б) 0,834; 19,471; 6,352 и 0,08 до десятых.
4. Задача. Собственная скорость катера 32,8 км/ч. Скорость катера по течению реки 34,2 км/ч. Найдите скорость катера против течения.
5. Запишите четыре значения n, при которых верно неравенство 0,65
Контрольная работа №10
Вариант I
1. Вычислите:
а) 4,35∙18 г) 53,3:26
б) 6,25∙108 д) 6:24
в) 126,385∙10 е) 126,385:100
2.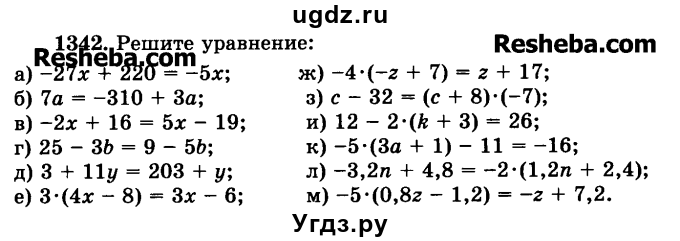 Решить уравнение:
Решить уравнение:
7у+2,6=27,8
3. Найдите значение выражения
90-16,2:9+0,08
4. Задача. На автомобиль погрузили 6 контейнеров и 8 одинаковых ящиков по 0,28т каждый. Какова масса одного ящика, если масса всего груза 2,4т?
5. Задача. Как изменится произведение двух десятичных дробей, если в одном множителе перенести запятую вправо через две цифры, а в другом – влево через четыре цифры?
Контрольная работа №10
Вариант II
1. Вычислите:
а) 3,85∙24; г) 35,7:34
б) 4,75∙116; д) 7:28
в) 234,166∙100 е) 234,166:10
2. Решить уравнение:
6х+3,8=20,6
3. Найдите значение выражения
40-23,2:8+0,07
4. Задача. Из 7,7м ткани сшили 7 платьев для кукол и 9 одинаковых полотенец. Сколько ткани пошло на одно полотенце, если на каждое платье потребовалось 0,65 м ткани?
5. Задача. Как изменится произведение двух десятичных дробей, если в одном множителе перенести запятую влево через четыре цифры, а в другом — вправо через две цифры?
Контрольная работа №11
Вариант I
1. Выполните действия:
Выполните действия:
а) 0,872∙6,3 г) 30,42:7,8
б) 1,6∙7,625 д) 0,702:0,065
в) 0,045∙0,1 е) 0,026:0,01
2. Найдите среднее арифметическое чисел 32,4; 41; 27,95; 46,9; 55,75.
3. Найдите значение выражения 296,2 – 2,7∙6,6 + 6:0,15.
4. Задача. Поезд 3ч шел со скоростью 63,2 км/ч и 4ч со скоростью 76,5 км/ч. Найдите среднюю скорость поезда на всем пути.
5. Задача. Сумма трех чисел 10,23, а среднее арифметическое шести других чисел 2,9. Найти среднее арифметическое всех этих девяти чисел.
Контрольная работа №11
Вариант II
1. Выполните действия:
а) 0,964∙7,4 г) 25,23:8,7
б) 2,4∙7,375 д) 0,0918:0,0085
в) 0,72∙0,01 е) 0,39:0,1
2. Найдите среднее арифметическое чисел 63; 40,63; 70,4; 67,97
3. Найдите значение выражения 398,6 – 3,8∙7,7 + 3:0,06
4. Задача. Легковой автомобиль шел 2ч со скоростью 55,4 км/ч и ещё 4ч со скоростью 63,5 км/ч. Найдите среднюю скорость автомобиля на всем пути.
Задача. Легковой автомобиль шел 2ч со скоростью 55,4 км/ч и ещё 4ч со скоростью 63,5 км/ч. Найдите среднюю скорость автомобиля на всем пути.
5. Задача. Среднее арифметическое пяти чисел 4,7, а сумма других трех чисел 25,14. Найдите среднее арифметическое всех этих восьми чисел.
Контрольная работа №12
Вариант I
1. Задача. Площадь поля 260 га. Горохом засеяно 35% поля. Какую площадь занимают посевы гороха?
2. Найдите значение выражения 201 – (176,4:16,8+9,68)∙2,5.
3. Задача. В библиотеке 12% всех книг – словари. Сколько книг в библиотеке, если словарей в ней 900?
4. Решите уравнение 12+8,3х+1,5х = 95,3
5. Задача. От мотка провода отрезали сначала 30%, а затем ещё 60% остатка. После этого в мотке осталось 42 м провода. Сколько метров провода было в мотке первоначально?
Контрольная работа №12
Вариант II
1. Задача. В железной руде содержится 45% железа. Сколько тонн железа содержится в 380 т руды?
2. Найдите значение выражения (299,3:14,6 – 9,62)∙3,5+72,2
3.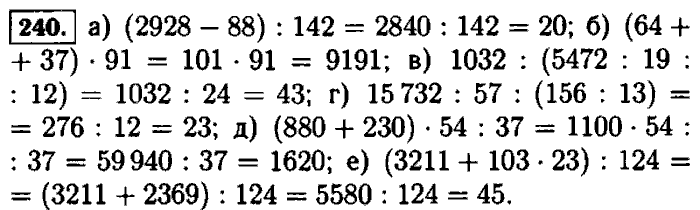 Задача. За день вспахали 18% поля. Какова площадь всего поля, если вспахали 1170 га?
Задача. За день вспахали 18% поля. Какова площадь всего поля, если вспахали 1170 га?
4. Решите уравнение 6,7у+13+3,1у=86,5
5. Задача. Израсходовали сначала 40% имевшихся денег, а затем ещё 30% оставшихся. После этого осталось 105р. Сколько было денег первоначально?
Контрольная работа №13
Вариант I
1. Постройте углы, если:
а)
2. Начертите треугольник AKN такой, чтобы
3. Луч ОК делит прямой угол DOS на два угла так, что угол DOK составляет 0,7 угла DOS. Найдите градусную меру угла KOS.
4. Развернутый угол AMF разделен лучом МС на два угла АМС и CMF. Найдите градусные меры этих углов, если угол АМС вдвое больше угла CMF.
5. Из вершины развернутого угла DKP проведены его биссектриса КВ и луч КМ так, что
Контрольная работа №13
Вариант II
1. Постройте углы, если:
а)
2. Начертите треугольник BCF такой, чтобы
3. Луч АР делит прямой угол CAN на два угла так, что угол NAP составляет 0,3 угла CAN. Найдите градусную меру угла РАС.
4. Развернутый угол ВОЕ разделен лучом ОТ на два угла ВОТ и ТОЕ. Найдите градусные меры этих углов, если угол ВОТ втрое меньше угла ТОЕ.
5. Из вершины развернутого угла MNR проведены его биссектриса NB и луч NP так, что
Контрольная работа №14
Вариант I
1. Вычислите: 2,66:3,8 – 0,81∙0,12 + 0,0372
2. В магазине 240 кг фруктов. За день продали 65% фруктов. Сколько килограммов фруктов осталось.
3. Найдите высоту прямоугольного параллелепипеда, объем которого равен 25,2 дм3, длина 3,5 дм и ширина 16 см.
4. Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь прошел теплоход за все это время?
5. Постройте углы МОК и КОС, если
Контрольная работа №14
Вариант II
1. Вычислите: 7,8∙0,26 – 2,32:2,9 + 0,672.
2. В цистерне 850 л молока. 48% молока разлили в бидоны. Сколько литров молока осталось в цистерне?
3. Объем прямоугольного параллелепипеда равен 1,35 м3, высота 2,25 м и длина 8 дм. Найдите его ширину.
Найдите его ширину.
4. Катер плыл 3,5 ч по течению реки и 0,6 ч по озеру. Найдите путь, пройденный катером за все это время, если собственная скорость катера 16,5 км/ч, а скорость течения реки 2,1 км/ч.
5. Постройте углы AND и NDB, если
5 класс
Итоговая контрольная работа
Вариант I
1. Вычислите: 8,45 + (346 – 83,6):12,8
2. Вычислите площадь прямоугольника, если его ширина 1,9 дм, а длина вдвое больше.
3. Катер шел 3ч против течения реки и 2ч по течению. Какой путь прошел катер за эти 5ч, если собственная скорость катера 18,6 км/ч, а скорость течения реки 1,3 км/ч?
4. Начертите треугольник АОВ, в котором угол АОВ равен 75о.
5. В классе 30 учеников. Оценку «5» на экзамене получили 30% учеников. Сколько учеников получили на экзамене пятерки?
5 класс
Итоговая контрольная работа
Вариант II
1. Вычислите 6,35 + (359 – 63,8):14,4.
2. Длина прямоугольника 12,6 см, а ширина втрое меньше. Найдите площадь этого прямоугольника.
3. Собственная скорость моторной лодки 6,7 км/ч. Скорость течения реки 1,2 км/ч. Лодка шла 2ч против течения и 2ч по течению реки. Какой путь прошла моторная лодка за эти 4ч?
4. Начертите треугольник ВСК, в котором угол ВСК равен 110о.
5. Площадь поля 120 га. Тракторист вспахал 70% поля. Сколько гектаров земли вспахал тракторист?
Итоговая работа по математике 5 класс (к учебнику Н.Я.Виленкина и др.)
Промежуточная аттестация (II этап)
Аттестационная работа по математике для 5-х классов
(по учебнику «Математика 5» автор Н. Я. Виленкин и др., М.: Дрофа, 2014.)
Цель: контроль освоения обучающимися образовательной программы, уровня сформированности умений и навыков по изученным темам «Арифметические действия с десятичными дробями и натуральными числами», «Проценты», «Угол.Транспортир», «Площади и объемы», «Среднее арифметическое».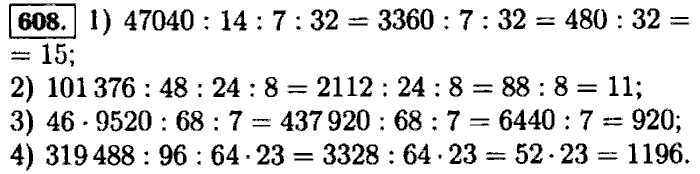
Контрольная работа составлена с использованием следующих методических пособий:
Попов М.А. Контрольные и самостоятельные работы по математике: 5 класс: к учебнику Н.Я. Виленкина и др. «Математика. 5 класс». – 7-е изд., стереотип. – М.: Издательство «Экзамен», 2012.
Чесноков А.С., Нешков К.И. Дидактические материалы по математике: 5 класс:практикум. – 4-е изд. – М.: Академкнига / Учебник, 2012.
Контрольная работа содержит 6 заданийи представлена в двух вариантах.
На выполнение работы отводится 45 минут.
Критерий оценивания
№ п/п | Количество выполненных заданий | Школьная оценка |
1 | 5-6 | «5» |
2 | 4 | «4» |
3 | 3 | «3» |
Менее 3х | «2» |
«ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА» | «ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА» |
| ВАРИАНТ 1 1. 2. В магазине 240 кг фруктов. За день продали 65 % фруктов. Сколько килограммов фруктов продали? 3. Найдите среднее арифметическое чисел 11,2; 14,8; 15,6 и 14,4. 4. Найдите высоту прямоугольного параллелепипеда, объем которого равен 25,2 дм3, длина 3,5 дм и ширина 16 см. 5. Постройте углы МОК и КОС, если МОК = 110, КОС = 46. Какой может быть градусная мера угла СОМ ? 6. Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь прошел теплоход за все это время? | ВАРИАНТ 2 1. Вычислите: а) 2,32 : 2,9 б) 7,8 * 0,26 в) 3,095 — 0,4 г) 1, 348 + 0,552. 2. В цистерне 850 л молока. 48 % молока разлили в бидоны. Сколько молока разлили в бидоны? 3. 4. Объем прямоугольного параллелепипеда 1,35 м3, высота 2,25 м и длина 8 дм. Найдите его ширину. 5. Постройте углы ADN и NDB, если ADN = 34, 6. Катер плыл 3,5 ч по течению реки и 0,6 ч по озеру. Найдите путь, пройденный катером за все это время, если собственная скорость катера 16,5 км/ч, а скорость течения реки 2,1 км/ч. |
«ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА» | «ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА» |
| ВАРИАНТ 1 1. Вычислите: а) 2,66 : 3,8 б) 0,81 * 0,12 в) 0,6 — 0,0864 г) 0,5247 + 0,0353. 2. В магазине 240 кг фруктов. За день продали 65 % фруктов. Сколько килограммов фруктов продали? 3. 4. Найдите высоту прямоугольного параллелепипеда, объем которого равен 25,2 дм3, длина 3,5 дм и ширина 16 см. 5. Постройте углы МОК и КОС, если МОК = 110, КОС = 46. Какой может быть градусная мера угла СОМ ? 6. Собственная скорость теплохода 24,5 км/ч, скорость течения реки 1,3 км/ч. Сначала теплоход 0,4 ч плыл по озеру, а затем 3,5 ч по реке против течения. Какой путь прошел теплоход за все это время? | ВАРИАНТ 2 1. Вычислите: а) 2,32 : 2,9 б) 7,8 * 0,26 в) 3,095 — 0,4 г) 1, 348 + 0, 552. 2. В цистерне 850 л молока. 48 % молока разлили в бидоны. Сколько молока разлили в бидоны? 3. Найдите среднее арифметическое чисел 3,9; 6,1;7,8 и 6,2. 4. Объем прямоугольного параллелепипеда 1,35 м3, высота 2,25 м и длина 8 дм. Найдите его ширину. 5. 6. Катер плыл 3,5 ч по течению реки и 0,6 ч по озеру. Найдите путь, пройденный катером за все это время, если собственная скорость катера 16,5 км/ч, а скорость течения реки 2,1 км/ч. |
Ответы к итоговой работе по математике за курс 5 класса.
№ задания | 1 | 2 | 3 | 4 | 5 | 6 |
Вариант 1 | а) 0,7 б) 0,0972 в) 0,5136 г) 0,56 | 156 | 14 | 4,5 | 640 или 1560 | 91 км |
Вариант 2 | а) 0,8 б) 2,028 в) 2,695 г) 1,9 | 408 | 6 | 0,75 | 860 или 1540 | 75 км |
ГДЗ Математика 5 класс Виленкин, Жохов, Чесноков, Шварцбурд
- Математика 5 класс
- Тип пособия: Учебник
- Авторы: Виленкин, Жохов, Чесноков, Шварцбурд
- Издательство: «Мнемозина»
Часть 1.
 Задания123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852
Задания123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852Часть 2.
 Задания1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057
Задания1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057Часть 1.
 Тесты1234
Тесты1234Часть 2. Тесты
123456Похожие ГДЗ Математика 5 класс
- Математика 5 класс
- Рабочая тетрадь
- Алгоритм успеха
- Ерина
- Экзамен
- Математика 5 класс
- Рабочая тетрадь
- Универсальные учебные действия
- Ерина
- Экзамен
Часть 1. Задания: 1
Условие
Решебник №1
Решебник №2
Решебник №3
Математические дисциплины почти всегда вызывают определенные сложности у школьников, а многие ребята, видя проблему, начинают не любить сам предмет. Чтобы не допустить разочарование относительно предмета и школы в целом, рекомендуется попробовать решебник к учебнику 5 класс математика, созданный под авторством Виленкина.
Особенности решебника
Разбит решебник к учебнику «Математика 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд Мнемозина» на отдельно взятые главы, каждая из которых соответствует конкретной теме в математике за данный период времени. К примеру, дается четкое пояснение вопросов, связанных с дробями, а также началом элементарной алгебры. Несмотря на то, что последняя тема начинается несколько позже, в пятом классе дается ознакомительный курс по этому направлению.
Обратите внимание
Пособие предлагает много интересного материала, оформленного и подготовленного в рамках соответствия со школьной программой и адаптированного под индивидуальное развитие ребенка. Пособие предоставляется в режиме онлайн, каждый родитель сможет контролировать занятия ребенка, не отходя от экрана монитора, помогать ему в освоении предмета. Очень скоро это даст отличные плоды такой совместной деятельности.
Что представляет собой пособие
Издание чрезвычайно объемное: в решебнике ребятам предлагаются тысяча восемьсот сорок девять упражнений различного уровня сложности по всему курсу основного учебника математики для пятого класса:
- Определение площади поверхности и объема прямоугольного параллелепипеда.

- Измерение величины угла.
- Задачи с процентами.
Все задания снабжены подробными и понятными ответами, графиками и чертежами. Изучив любое решение внимательно, ученик сможет уверенно выполнять аналогичные задания на любых контрольных проверках в классе.
Преимущества ГДЗ
Пятый класс означает, что ребята уже сдали первый в жизни школьников настоящий экзамен: Всероссийские проверочные работы. Теперь это ученики со стажем, которые умеют правильно пользоваться учебно-вспомогательной литературой. Если они будут работать с ГДЗ как с персональным репетитором, а не копировать из него ответ так, как будто это шпаргалка, то решебник предоставит ученикам великолепные возможности:
- стабильно высокую успеваемость;
- надежную подготовку к контрольным работам;
- быстрое и качественное приготовление домашних заданий.
Родителям решебник поможет находиться в курсе успехов своего ребенка и в случае необходимости прийти на помощь.
принцип посредственности | Астрономия и геофизика
T Вселенная, какой мы ее знаем, возникла в результате великого взрыва, который мы называем Большим взрывом. Почти столетие космологи изучали последствия этого взрыва: как Вселенная расширялась и охлаждалась, как галактики постепенно стягивались под действием гравитации и т. д. Природа самого Большого взрыва стала известна лишь сравнительно недавно. Это предмет теории инфляции, которая была разработана в начале 19 века.80-х годов Алана Гута, Андрея Линде и других и привела к радикально новой глобальной картине мироздания. Согласно этой новой картине, отдаленные регионы за нашим горизонтом разительно отличаются от того, что мы наблюдаем здесь, и могут даже подчиняться другим законам физики. Здесь я буду обсуждать происхождение нового мировоззрения, его возможные наблюдательные проверки и его значение для начала и конца Вселенной.
Начну с краткого обзора теории инфляции. Ключевую роль в этой теории играет своеобразная сущность под названием «ложный вакуум». Вакуум — это просто пустое пространство, но, согласно современной физике элементарных частиц, он сильно отличается от «ничто». Это физический объект, наделенный плотностью энергии и давлением, и может находиться в различных состояниях. Физики элементарных частиц называют эти состояния различными вакуумами. Свойства и типы элементарных частиц отличаются от одного вакуума к другому. Гравитационная сила, создаваемая ложным вакуумом, весьма своеобразна: она отталкивающая. Чем выше энергия вакуума, тем сильнее отталкивание. Слово «ложный» относится к тому факту, что этот вид вакуума нестабилен. Он распадается на низкоэнергетический вакуум, подобный нашему, и избыточная энергия идет на создание горячего огненного шара из частиц и излучения. Я должен подчеркнуть, что ложный вакуум с этими странными свойствами не был придуман для целей инфляции: их существование следует из физики элементарных частиц и общей теории относительности.
Вакуум — это просто пустое пространство, но, согласно современной физике элементарных частиц, он сильно отличается от «ничто». Это физический объект, наделенный плотностью энергии и давлением, и может находиться в различных состояниях. Физики элементарных частиц называют эти состояния различными вакуумами. Свойства и типы элементарных частиц отличаются от одного вакуума к другому. Гравитационная сила, создаваемая ложным вакуумом, весьма своеобразна: она отталкивающая. Чем выше энергия вакуума, тем сильнее отталкивание. Слово «ложный» относится к тому факту, что этот вид вакуума нестабилен. Он распадается на низкоэнергетический вакуум, подобный нашему, и избыточная энергия идет на создание горячего огненного шара из частиц и излучения. Я должен подчеркнуть, что ложный вакуум с этими странными свойствами не был придуман для целей инфляции: их существование следует из физики элементарных частиц и общей теории относительности.
Теория инфляции предполагает, что в какой-то ранний период своей истории Вселенная находилась в состоянии высокоэнергетического ложного вакуума.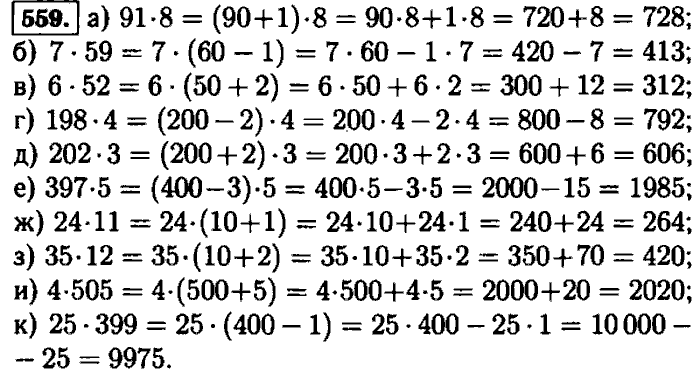 Почему так должно быть — хороший вопрос, и я еще кое-что скажу об этом позже в этой статье. Отталкивающая гравитационная сила, создаваемая этим вакуумом, вызовет сверхбыстрое экспоненциальное расширение Вселенной. Существует характерное время — время удвоения, — в течение которого размер Вселенной удвоился бы. Это похоже на экономическую инфляцию: если уровень инфляции постоянен, цены будут удваиваться, скажем, каждые 10 лет. Космическая инфляция происходит намного быстрее: в зависимости от модели время удвоения может составлять всего 10 −37 секунд. Примерно через 330 удвоений размер Вселенной увеличится в 10 100 раз. Каков бы ни был ее первоначальный размер, Вселенная очень быстро станет огромной. Поскольку ложный вакуум нестабилен, он в конце концов распадается, образуя горячий огненный шар, и на этом инфляция заканчивается. Огненный шар продолжает расширяться по инерции и развивается в соответствии со стандартной космологией Большого Взрыва. Распад ложного вакуума играет в этом сценарии роль Большого Взрыва.
Почему так должно быть — хороший вопрос, и я еще кое-что скажу об этом позже в этой статье. Отталкивающая гравитационная сила, создаваемая этим вакуумом, вызовет сверхбыстрое экспоненциальное расширение Вселенной. Существует характерное время — время удвоения, — в течение которого размер Вселенной удвоился бы. Это похоже на экономическую инфляцию: если уровень инфляции постоянен, цены будут удваиваться, скажем, каждые 10 лет. Космическая инфляция происходит намного быстрее: в зависимости от модели время удвоения может составлять всего 10 −37 секунд. Примерно через 330 удвоений размер Вселенной увеличится в 10 100 раз. Каков бы ни был ее первоначальный размер, Вселенная очень быстро станет огромной. Поскольку ложный вакуум нестабилен, он в конце концов распадается, образуя горячий огненный шар, и на этом инфляция заканчивается. Огненный шар продолжает расширяться по инерции и развивается в соответствии со стандартной космологией Большого Взрыва. Распад ложного вакуума играет в этом сценарии роль Большого Взрыва.
Теория инфляции объяснила некоторые загадочные особенности Большого Взрыва, которые раньше просто нужно было постулировать. Она объяснила расширение Вселенной (это связано с отталкивающей гравитацией ложного вакуума), ее высокую температуру (из-за высокой плотности энергии ложного вакуума) и ее наблюдаемую однородность (ложный вакуум очень однороден: кроме квантовые флуктуации, имеет постоянную плотность энергии). Теория также сделала ряд проверяемых предсказаний. Он предсказывал, что в самых больших наблюдаемых масштабах Вселенная должна точно описываться плоской евклидовой геометрией. Он также предсказал почти масштабно-инвариантный спектр малых гауссовских возмущений плотности. Эти предсказания были эффектно подтверждены наблюдениями. К настоящему времени инфляция стала ведущей космологической парадигмой.
Вечная инфляция
Теперь, когда теория инфляции подтверждается данными в нашей наблюдаемой области, мы должны доверять тому, что она говорит нам об общей картине — структуре Вселенной за пределами нашего космического горизонта.
Конец инфляции спровоцирован квантовыми, вероятностными процессами и не происходит везде одновременно. Области, где ложный вакуум распадается несколько позже, «вознаграждаются» большим инфляционным расширением, поэтому области ложного вакуума имеют тенденцию размножаться быстрее, чем они распадаются. В нашем космическом соседстве инфляция закончилась 13,7 миллиарда лет назад, но, вероятно, она все еще продолжается в отдаленных частях Вселенной, и постоянно формируются другие «нормальные» области, подобные нашей. Этот бесконечный процесс называется вечной инфляцией. Вечная природа инфляции не автоматична, но очень универсальна. Практически все модели инфляции, которые обсуждались до сих пор, предсказывают вечную инфляцию.
Детали распада ложного вакуума зависят от модели; здесь я сосредоточусь на моделях, в которых это происходит посредством зарождения пузырьков. Затем низкоэнергетические области появляются в виде крошечных микроскопических пузырьков и сразу же начинают расти со скоростью, быстро приближающейся к скорости света. Пузыри продолжают расти без ограничений; тем временем инфляционное расширение раздвигает их, освобождая место для образования новых пузырей. Мы живем в одном из пузырей и можем наблюдать лишь небольшую его часть. Независимо от того, насколько быстро мы путешествуем, мы не можем догнать расширяющиеся границы нашего пузыря, поэтому для всех практических целей мы живем в замкнутой вселенной пузыря. В ходе вечного надувания будет образовываться неограниченное количество пузырей. (Обзор инфляции, включая вечную инфляцию, см., например, в Guth and Kaiser 2005.)
Пузыри продолжают расти без ограничений; тем временем инфляционное расширение раздвигает их, освобождая место для образования новых пузырей. Мы живем в одном из пузырей и можем наблюдать лишь небольшую его часть. Независимо от того, насколько быстро мы путешествуем, мы не можем догнать расширяющиеся границы нашего пузыря, поэтому для всех практических целей мы живем в замкнутой вселенной пузыря. В ходе вечного надувания будет образовываться неограниченное количество пузырей. (Обзор инфляции, включая вечную инфляцию, см., например, в Guth and Kaiser 2005.)
The Whitrow Lectures
The Whitrow Lectures были основаны благодаря наследию Джеральда Уитроу, который умер в 2000 году. Карьера профессора Уитроу охватила астрофизику, космологию, историю и философию времени, и он упорно трудился, чтобы наука охватил как можно более широкую аудиторию. Лекции Уитроу охватывают темы космологии, обычно с особым упором на философские аспекты предмета. Обычно их дают раз в два года.
Обычно их дают раз в два года.
Метафизическая интермедия
Здесь я хотел бы отметить замечательное и, на мой взгляд, несколько тревожное следствие этой картины Вселенной (Гаррига и Виленкин, 2001). Поскольку число пузырьковых вселенных неограниченно, и каждая из них безгранично расширяется, они будут содержать неограниченное количество областей размером с наш горизонт. В каждой из этих областей начальные условия при Большом взрыве задаются случайными квантовыми процессами при инфляции, поэтому все возможные начальные условия будут реализованы с некоторой вероятностью.
Ключевым моментом является то, что число различных состояний, в которых может находиться любая такая область, конечно. Как это возможно? Я могу, например, сдвинуть свой стул на один сантиметр, на полсантиметра, на четверть сантиметра и т. д., и, по-видимому, у меня тут же бесконечное число возможных состояний — потому что я могу сдвинуть его на бесконечное число возможных состояний. количество возможных перемещений, которые становятся все меньше и меньше. Однако слишком близкие друг к другу состояния нельзя различить даже в принципе из-за квантовой неопределенности. Итак, квантовая механика говорит нам, что количество различных состояний (в конечном объеме) конечно. Число квантовых состояний в нашей наблюдаемой области оценивается как 9.0033 N ∼ ехр(10 122 ). Это невообразимо большое число. Но важно то, что она не бесконечна.
количество возможных перемещений, которые становятся все меньше и меньше. Однако слишком близкие друг к другу состояния нельзя различить даже в принципе из-за квантовой неопределенности. Итак, квантовая механика говорит нам, что количество различных состояний (в конечном объеме) конечно. Число квантовых состояний в нашей наблюдаемой области оценивается как 9.0033 N ∼ ехр(10 122 ). Это невообразимо большое число. Но важно то, что она не бесконечна.
Таким образом, у нас есть конечное число состояний, встречающихся в бесконечном числе регионов. Неизбежный вывод состоит в том, что каждое состояние, имеющее ненулевую вероятность, возникает бесконечное число раз. В частности, существует бесконечное количество Земель, идентичных нашей. Это означает, что десятки ваших точных дубликатов сейчас читают это предложение. Также должны быть регионы со всеми возможными вариациями. Например, есть регионы, где имя вашей собаки другое, а есть регионы, где по Земле все еще бродят динозавры. Теперь вам может быть интересно, происходит ли все это одновременно. На этот вопрос нет однозначного ответа, потому что время и одновременность не определены однозначно в общей теории относительности. Если, например, мы используем плотность материи в качестве временной переменной во вселенной-пузыре, то в каждый момент времени внутренняя часть пузыря представляет собой бесконечное гиперболическое пространство, и у каждого из нас есть бесконечное число дубликатов, живущих в настоящее время в нашем пузыре.
Теперь вам может быть интересно, происходит ли все это одновременно. На этот вопрос нет однозначного ответа, потому что время и одновременность не определены однозначно в общей теории относительности. Если, например, мы используем плотность материи в качестве временной переменной во вселенной-пузыре, то в каждый момент времени внутренняя часть пузыря представляет собой бесконечное гиперболическое пространство, и у каждого из нас есть бесконечное число дубликатов, живущих в настоящее время в нашем пузыре.
Обратите внимание, что бесконечность пространства (или времени) сама по себе недостаточна для обоснования таких выводов. Мы могли бы, например, бесконечно повторять одну и ту же галактику в бесконечном пространстве. Поэтому нам нужен некий «рандомизатор», стохастический механизм, который выбирал бы начальные состояния для разных областей из множества всех возможных состояний. Даже в этом случае весь набор может быть не исчерпан, если общее число состояний бесконечно. Таким образом, конечность N важна для рассуждения. В случае вечной инфляции конечность N и случайность начальных условий гарантируется квантовой механикой.
В случае вечной инфляции конечность N и случайность начальных условий гарантируется квантовой механикой.
Мультивселенная
До сих пор я предполагал, что другие пузырьковые вселенные подобны нашей с точки зрения их физических свойств. Но это не обязательно так. Теория струн, которая в настоящее время является нашим лучшим кандидатом на роль фундаментальной теории Природы, допускает огромное количество решений, описывающих вакуум с различными физическими свойствами. Эти решения характеризуются различной компактификацией дополнительных измерений, различными способами наматывания бран на дополнительные измерения и т. д. Число возможностей является комбинаторным и может достигать 10 500 (Lerche и др. 1987, Bousso and Polchinski 2000). Каждому решению соответствует вакуум со своими типами элементарных частиц и своими значениями констант Природы.
Теперь соедините это с теорией инфляции. Где бы они ни возникали во Вселенной, высокоэнергетический вакуум будет вызывать экспоненциальное инфляционное расширение. Переходы между различными вакуумами будут происходить посредством зарождения пузырьков, поэтому будут пузырьки внутри пузырьков внутри пузырьков. Каждый тип пузырьков имеет определенную вероятность образования в надувном пространстве. Так что неизбежно в процессе вечного надувания будет образовываться неограниченное количество пузырей всех возможных типов.
Где бы они ни возникали во Вселенной, высокоэнергетический вакуум будет вызывать экспоненциальное инфляционное расширение. Переходы между различными вакуумами будут происходить посредством зарождения пузырьков, поэтому будут пузырьки внутри пузырьков внутри пузырьков. Каждый тип пузырьков имеет определенную вероятность образования в надувном пространстве. Так что неизбежно в процессе вечного надувания будет образовываться неограниченное количество пузырей всех возможных типов.
Эта картина Вселенной, или мультивселенной, как ее называют, объясняет давнюю загадку того, почему константы Природы кажутся точно настроенными для возникновения жизни (см., например, Linde 1990). Я приведу вам только один пример: масса нейтрона. В нашей Вселенной нейтроны немного тяжелее протонов. Изолированный нейтрон распадается на протон, электрон и антинейтрино, но нейтроны, связанные в атомных ядрах, стабилизируются ядерными силами. Предположим теперь, что мы уменьшили массу нейтрона на 1%. Тогда нейтроны станут легче протонов, и это позволит протонам распадаться на нейтроны и более легкие частицы. В результате атомные ядра потеряют свой электрический заряд. Так нечем будет держать электроны в атомах, и они улетят. Таким образом, если массу нейтрона уменьшить на 1%, мы окажемся во Вселенной без атомов, и трудно представить, как в таком месте могла существовать жизнь, хоть что-то подобная нашей.
В результате атомные ядра потеряют свой электрический заряд. Так нечем будет держать электроны в атомах, и они улетят. Таким образом, если массу нейтрона уменьшить на 1%, мы окажемся во Вселенной без атомов, и трудно представить, как в таком месте могла существовать жизнь, хоть что-то подобная нашей.
Теперь, если мы увеличим массу нейтрона на 1%, он станет настолько массивным, что распадется даже внутри ядра, превратившись в протон. Тогда электрическое отталкивание между протонами разорвет ядро на части, и единственным возможным атомом будет одиночный протон в сочетании с электроном, которым является водород. Опять же, трудно понять, как может быть возможна жизнь во Вселенной без каких-либо химических элементов, кроме водорода.
Аналогичная ситуация с другими константами. Если вы измените их относительно небольшими количествами, вы получите вселенную, непригодную для жизни. Это, кажется, предполагает, что константы были точно настроены Творцом, чтобы сделать вселенную, благоприятную для жизни, в которой мы могли бы жить – именно то, что все время твердили нам сторонники разумного замысла!
Картина мультивселенной предлагает другое объяснение. Константы Природы принимают широкий диапазон значений, варьирующихся от одного пузыря к другому. Разумные наблюдатели существуют только в тех редких пузырях, в которых по чистой случайности константы оказываются как раз подходящими для развития жизни. Остальная часть Мультивселенной остается бесплодной, но никто не может пожаловаться на это. (Нетехнический обзор идей мультивселенной см. в Vilenkin 2006, Susskind 2006, Greene 2011.)
Константы Природы принимают широкий диапазон значений, варьирующихся от одного пузыря к другому. Разумные наблюдатели существуют только в тех редких пузырях, в которых по чистой случайности константы оказываются как раз подходящими для развития жизни. Остальная часть Мультивселенной остается бесплодной, но никто не может пожаловаться на это. (Нетехнический обзор идей мультивселенной см. в Vilenkin 2006, Susskind 2006, Greene 2011.)
Некоторые из моих коллег находят теорию мультивселенной тревожной. Любая теория в физике стоит или рушится в зависимости от того, согласуются ли ее предсказания с данными. Но как мы можем проверить существование других пузырьковых вселенных? Некоторые выдающиеся космологи, такие как Пол Стейнхардт и Джордж Эллис, даже утверждали, что теория мультивселенной ненаучна, поскольку ее невозможно проверить даже в принципе.
«Константы Природы принимают широкий диапазон значений, меняющихся от одного пузыря к другому»
Удивительно, но наблюдательные проверки картины мультивселенной на самом деле могут быть возможны. Одна из возможностей состоит в том, чтобы искать наблюдательные признаки столкновений пузырей. По мере расширения наш пузырь будет время от времени сталкиваться с другими пузырьками. На самом деле он испытает бесконечное количество столкновений в ходе своей истории. Каждое такое столкновение оставляет на космическом микроволновом фоне (CMB) отпечаток в виде круглого пятна с большей или меньшей интенсивностью излучения (Агирре и Джонсон, 2011, Клебан, 2011). Поляризация реликтового излучения в пятнах также предсказывает характерную картину (Czech и др. 2011). Обнаружение пятна, обладающего предсказанными характеристиками и значительно возвышающегося над фоном, могло бы предоставить прямое свидетельство существования других пузырьковых вселенных. Сейчас идет поиск (Фини и др. 2011), но, к сожалению, нет гарантии, что столкновение пузырей произошло в пределах нашего космического горизонта. Следовательно, неспособность найти признаки столкновений пузырей на микроволновом небе не может рассматриваться как свидетельство против вечной инфляции.
Одна из возможностей состоит в том, чтобы искать наблюдательные признаки столкновений пузырей. По мере расширения наш пузырь будет время от времени сталкиваться с другими пузырьками. На самом деле он испытает бесконечное количество столкновений в ходе своей истории. Каждое такое столкновение оставляет на космическом микроволновом фоне (CMB) отпечаток в виде круглого пятна с большей или меньшей интенсивностью излучения (Агирре и Джонсон, 2011, Клебан, 2011). Поляризация реликтового излучения в пятнах также предсказывает характерную картину (Czech и др. 2011). Обнаружение пятна, обладающего предсказанными характеристиками и значительно возвышающегося над фоном, могло бы предоставить прямое свидетельство существования других пузырьковых вселенных. Сейчас идет поиск (Фини и др. 2011), но, к сожалению, нет гарантии, что столкновение пузырей произошло в пределах нашего космического горизонта. Следовательно, неспособность найти признаки столкновений пузырей на микроволновом небе не может рассматриваться как свидетельство против вечной инфляции.
Еще одна интересная возможность заключается в том, что наша вселенная-пузырь могла образоваться из расширяющегося вакуума, где некоторые из наших трех пространственных измерений были уплотнены. Тогда можно надеяться обнаружить некоторую остаточную асимметрию в скорости расширения или в спектре флуктуаций температуры реликтового излучения. В простой модели с одним изначально компактным размером этот эффект кажется слишком малым, чтобы его можно было обнаружить (Blanco-Pillado and Salem 2010, Graham et al. 2010), но в других моделях ситуация может быть более благоприятной.
Принцип бездарности
Как и в уголовном процессе, при отсутствии прямых доказательств мультивселенной можно искать косвенные, или косвенные улики. Идея состоит в том, чтобы использовать нашу теоретическую модель мультивселенной для предсказания констант Природы, которые мы можем ожидать измерить в нашем локальном регионе. Одним из критериев отбора является так называемый антропный принцип, впервые введенный Брэндоном Картером (1974). В литературе встречается множество различных формулировок этого принципа, но большинство понимает его как констатацию очевидного факта, что мы можем ожидать измерения только таких значений констант, которые согласуются с существованием жизни. Однако этот «принцип» гарантированно верен, поэтому он не очень полезен для проверки теории.
В литературе встречается множество различных формулировок этого принципа, но большинство понимает его как констатацию очевидного факта, что мы можем ожидать измерения только таких значений констант, которые согласуются с существованием жизни. Однако этот «принцип» гарантированно верен, поэтому он не очень полезен для проверки теории.
Чтобы делать проверяемые предсказания, мы должны использовать несколько иной подход (Виленкин, 1995). Мы можем использовать теорию, чтобы вывести распределение вероятностей для констант, измеренных случайно выбранным наблюдателем в мультивселенной. Предполагая, что мы типичные наблюдатели — предположение, которое я назвал принципом посредственности, — мы можем предсказать ожидаемый диапазон значений констант в нашем пузыре. Ширина этого диапазона будет зависеть от уровня достоверности, при котором мы хотим сделать прогноз. Например, если желаемый уровень достоверности равен 95%, мы должны отбросить 2,5% на обоих концах распределения. Подобные идеи были предложены Gott (1993), Leslie (1989), Page (1996) и Bostrom (2002); на самом деле собственная интерпретация Картером антропного принципа была близка к принципу посредственности.
Эта стратегия была применена к плотности энергии нашего вакуума ρ ν , также известной как «темная энергия». Стивен Вайнберг (1987) (см. также Линде, 1987) отметил, что в областях, где ρν велико, Вселенная расширяется очень быстро, не позволяя материи слипаться в галактики и звезды. Наблюдатели вряд ли будут развиваться в таких регионах. Значения ρν, намного меньшие, чем необходимо для образования галактик, требуют ненужной тонкой настройки и также довольно маловероятны. Расчеты показали, что большинство галактик (а значит, и большинство наблюдателей) находятся в областях, где плотность темной энергии примерно такая же, как плотность вещества в эпоху образования галактик. Поэтому прогноз состоит в том, что подобное значение должно наблюдаться в нашей части Вселенной (обзор и ссылки см. Виленкин, 2007).
По большей части физики не воспринимали эти идеи всерьез, но, к их большому удивлению, темная энергия примерно ожидаемой величины была обнаружена в ходе астрономических наблюдений в конце 1990-х годов. На данный момент нет альтернативных объяснений наблюдаемого значения ρν. Это может быть нашим первым свидетельством того, что действительно существует огромная мультивселенная. Это изменило многие взгляды.
На данный момент нет альтернативных объяснений наблюдаемого значения ρν. Это может быть нашим первым свидетельством того, что действительно существует огромная мультивселенная. Это изменило многие взгляды.
Действительно ли мы типичны?
Принцип посредственности был предметом многочисленных споров. Он утверждает, что мы типичные наблюдатели, но в мультивселенной всегда найдутся несчастные существа, которые будут измерять нетипичные значения констант. Как мы можем быть уверены, что мы не являемся ими? Хартл и Средницкий (2007) утверждали, например, что мы никогда не должны считать себя типичными для какого-либо класса наблюдателей, если у нас нет доказательств, подтверждающих это предположение. Принцип посредственности утверждает обратное: мы должны считать себя типичными для любого класса, к которому мы принадлежим, если нет доказательств обратного (Гаррига и Виленкин, 2008).
На самом деле, я удивлен, что этот вопрос вызывает такие споры, ведь можно легко убедить себя, что принцип посредственности обеспечивает выигрышную стратегию ставок. Я проиллюстрирую это на простом примере. Представьте, что когда вы приходите на собрание Королевского общества, организаторы надевают на вас белую или черную шляпу. Они убрали все зеркала, так что ты не знаешь, какого цвета твоя шляпа. Однако вы замечаете, что 80% людей вокруг вас носят белые шляпы, а 20% — черные. Может быть, а может и не быть какой-то системы распределения головных уборов. Например, цвет может быть связан с вашим полом, возрастом, ростом и т. д., но вы этого не знаете.
Я проиллюстрирую это на простом примере. Представьте, что когда вы приходите на собрание Королевского общества, организаторы надевают на вас белую или черную шляпу. Они убрали все зеркала, так что ты не знаешь, какого цвета твоя шляпа. Однако вы замечаете, что 80% людей вокруг вас носят белые шляпы, а 20% — черные. Может быть, а может и не быть какой-то системы распределения головных уборов. Например, цвет может быть связан с вашим полом, возрастом, ростом и т. д., но вы этого не знаете.
Теперь, чтобы зарегистрироваться на встречу, вы должны поставить 100 фунтов стерлингов на цвет вашей шляпы. Как вы собираетесь делать ставки? Одна из стратегий состоит в том, чтобы предположить, что вы типичны среди участников, и поспорить, что ваша шляпа белая. Другой подход состоит в том, чтобы сказать, что вы на самом деле не знаете, типичны вы или нет. Затем вы бросаете монету и делаете ставку наугад. При первом выборе выиграют 80% людей, а при втором — только 50%. Ясно, что принцип посредственности обеспечивает лучшую стратегию ставок. Имея больше информации, вы можете улучшить свои шансы, соответствующим образом сузив свой эталонный класс. Например, если вы женщина и заметили, что большинство женщин носят черные шляпы, вы должны поспорить, что ваша шляпа черная.
Имея больше информации, вы можете улучшить свои шансы, соответствующим образом сузив свой эталонный класс. Например, если вы женщина и заметили, что большинство женщин носят черные шляпы, вы должны поспорить, что ваша шляпа черная.
Проблема меры
Более серьезной проблемой для теории мультивселенной является так называемая проблема меры. Как обсуждалось выше, любое событие, имеющее ненулевую вероятность, произойдет в ходе вечной инфляции, и произойдет это бесконечное число раз. Статистические прогнозы основаны на относительных частотах событий в пределах t →∞. Однако обнаруживается, что результат чувствительно зависит от ограничивающей процедуры. Точнее, это зависит от того, какую переменную мы используем в качестве времени т . Одним из возможных вариантов является «собственное время», измеряемое часами движущихся вместе с ним наблюдателей. Другим естественным выбором является коэффициент расширения (или масштабный коэффициент) Вселенной. Суть проблемы в том, что объем расширяющейся Вселенной экспоненциально растет со временем, и соответственно растет число всевозможных событий. В результате большинство событий всегда будет находиться вблизи времени отсечки, поэтому неудивительно, что результирующая мера вероятности зависит от того, как именно вводится отсечка.
Суть проблемы в том, что объем расширяющейся Вселенной экспоненциально растет со временем, и соответственно растет число всевозможных событий. В результате большинство событий всегда будет находиться вблизи времени отсечки, поэтому неудивительно, что результирующая мера вероятности зависит от того, как именно вводится отсечка.
Положительным моментом является то, что предсказания мультиполей реликтового излучения и темной энергии не очень чувствительны к выбору меры. Но в принципе теория останется неполной, пока не будет полностью определена мера.
Проблема измерения существует уже почти два десятилетия. За это время было предложено несколько различных мер и исследованы их свойства (недавний обзор см. в Freivogel 2011). Эта работа показала, что некоторые предложения приводят к парадоксам или к конфликту с данными и поэтому должны быть отвергнуты. Например, мера собственного времени работала довольно плохо, в то время как мера коэффициента масштабирования все еще находится в работе. Однако маловероятно, что такого рода феноменологический анализ даст однозначное определение меры. Это говорит о том, что в нашем понимании космической инфляции может отсутствовать какой-то важный элемент.
Однако маловероятно, что такого рода феноменологический анализ даст однозначное определение меры. Это говорит о том, что в нашем понимании космической инфляции может отсутствовать какой-то важный элемент.
Некоторые люди считают, что проблема настолько серьезна, что ставит под серьезное сомнение правильность теории инфляции (например, Steinhardt 2011). Но это мнение лишь незначительного меньшинства космологов. Лично я думаю, что ситуация с теорией инфляции аналогична ситуации с теорией эволюции Дарвина около 100 лет назад. Обе теории значительно расширили диапазон научных исследований, предложив объяснение того, что раньше считалось невозможным. В обоих случаях объяснение было убедительным, и не было предложено никаких жизнеспособных альтернатив. Теория Дарвина получила широкое признание, хотя некоторые важные аспекты оставались неясными до открытия генетического кода. Теория инфляции также может быть неполной и может потребовать дополнительных новых идей. Но в нем также присутствует такая же неизбежность.
Начало и конец вселенной
Если инфляция не имеет конца, может ли она не иметь и начала? Это позволило бы нам избежать многих запутанных вопросов, связанных с началом Вселенной. Когда у вас есть вселенная, ее эволюция описывается законами физики, но как вы описываете начало? Что стало причиной появления Вселенной? А кто задает начальные условия Вселенной? Было бы привлекательным решением, если бы мы могли сказать, что Вселенная всегда находилась в состоянии вечной инфляции, без начала и без конца.
Однако эта идея наталкивается на неожиданное препятствие. Арвинд Борде, Алан Гут и я (2003) доказали теорему, которая гласит, что хотя инфляция вечна для будущего, она не может быть вечной для прошлого. Точнее, теорема говорит, что все геодезические в инфляционном пространстве-времени, кроме множества нулевой меры, неполны в прошлое. Это означает, что у инфляции должно было быть какое-то начало. Затем мы сталкиваемся с вопросом о том, что происходило до инфляции. И каким бы ни был ответ, мы можем продолжать спрашивать: «А что было до этого?» Таким образом, кажется, что на один из самых основных вопросов космологии — «Что было началом Вселенной?» — нет удовлетворительного ответа.
И каким бы ни был ответ, мы можем продолжать спрашивать: «А что было до этого?» Таким образом, кажется, что на один из самых основных вопросов космологии — «Что было началом Вселенной?» — нет удовлетворительного ответа.
Единственный предложенный до сих пор способ решения проблемы бесконечного регресса — это идея о том, что Вселенная может быть спонтанно создана из ничего. Мы часто слышим, что ничто не может возникнуть из ничего. В самом деле, материя обладает положительной энергией, и закон сохранения энергии требует, чтобы любое начальное состояние имело одинаковую энергию. Однако математическим фактом является то, что энергия замкнутой Вселенной равна нулю. В такой вселенной положительная энергия материи в точности компенсируется отрицательной энергией гравитационного поля, поэтому полная энергия равна нулю. Другой сохраняющейся величиной является электрический заряд, но опять оказывается, что в замкнутой Вселенной полный заряд должен обращаться в нуль. Это нетрудно понять. Предположим, Вселенная имеет форму трехмерной сферы, и представьте, что положительный заряд находится на «южном полюсе» этой сферы. Силовые линии, исходящие от заряда, затем сойдутся на северном полюсе, указывая на то, что там должен быть равный отрицательный заряд. Таким образом, вы не можете добавить электрический заряд где-либо в замкнутой вселенной, не добавив противоположный заряд где-то еще.
Силовые линии, исходящие от заряда, затем сойдутся на северном полюсе, указывая на то, что там должен быть равный отрицательный заряд. Таким образом, вы не можете добавить электрический заряд где-либо в замкнутой вселенной, не добавив противоположный заряд где-то еще.
Если все сохраняющиеся числа замкнутой вселенной равны нулю, то ничто не препятствует спонтанному созданию такой вселенной из ничего. В квантовой механике с некоторой вероятностью произойдет любой процесс, не запрещенный строго законами сохранения.
Новорожденные вселенные могут иметь различные размеры и могут быть заполнены различными типами вакуума. Анализ показывает, что наиболее вероятными являются вселенные, имеющие наименьший начальный размер и наибольшую энергию вакуума (подробнее см. Виленкин 2006, глава 17). Как только Вселенная сформирована, она начинает быстро расширяться из-за высокой энергии вакуума. Это обеспечивает запуск сценария вечной инфляции.
Вы можете спросить: «Почему Вселенная возникла из ничего?» Удивительно, но причина не нужна. Если у вас есть радиоактивный атом, он распадется, а квантовая механика дает вероятность распада за заданный интервал времени. Но если вы спросите, почему атом распался именно в этот момент, а не в другой, ответ таков: причины нет: процесс совершенно случайный. Точно так же для квантового сотворения Вселенной не нужна причина.
Если у вас есть радиоактивный атом, он распадется, а квантовая механика дает вероятность распада за заданный интервал времени. Но если вы спросите, почему атом распался именно в этот момент, а не в другой, ответ таков: причины нет: процесс совершенно случайный. Точно так же для квантового сотворения Вселенной не нужна причина.
Я хотел бы закрыть этот раздел важной новостью о конце света. Часто говорят, что если темная энергия является космологической константой, то Вселенная будет продолжать расширяться вечно. Это верно для нашей пузырьковой вселенной в целом, но не для нашего локального региона. В мультивселенной должно быть большое количество вакуумов с отрицательной энергией, и пузырьки таких вакуумов неизбежно будут формироваться в нашем (почти нулевом) вакууме. В какой-то момент, вероятно, в очень отдаленном будущем, наш район будет поглощен пузырем отрицательной энергии. Тогда расширение локально превратится в сжатие, и наш регион рухнет до большого хруста. Пузырь прибудет без предупреждения, так как он расширяется почти со скоростью света. На самом деле, он может мчаться к нам в этот самый момент.
На самом деле, он может мчаться к нам в этот самый момент.
Outlook
Подводя итог, я описал новое мировоззрение, возникшее из инфляционной космологии. Согласно этой точке зрения, инфляция — это бесконечный процесс, постоянно создающий новые «пузырьковые вселенные» с разнообразными свойствами. Эту картину мультивселенной можно проверить как прямым наблюдением за столкновениями пузырей, так и косвенно, используя принцип посредственности. Предсказание для темной энергии, основанное на этом принципе, уже подтвердилось. Здесь я упомяну некоторые другие наблюдательные тесты, предложенные в литературе.
Потенциально проверяемой характеристикой вселенных-пузырей является их отрицательная пространственная кривизна. Параметр кривизны Ω k различен для разных пузырьков в зависимости от величины надувания внутри пузырька. Распределение вероятностей для Ω k было изучено Freivogel et al. (2006 г.) и Де Симона и Салема (2010 г.). Они обнаружили, что обнаруживаемый диапазон значений кривизны (|Ω k |≳ 10 −4 ) имеет незначительную вероятность, но в то же время широкий хвост распределения распространяется на значения, которые слишком малы, чтобы их можно было обнаружить. Помимо кривизны, квантовые флуктуации в родительском вакууме также могут давать характерную особенность в спектре гравитационных волн внутри пузыря. Обнаружение любого из этих эффектов предоставило бы дополнительные доказательства вечной инфляции.
(2006 г.) и Де Симона и Салема (2010 г.). Они обнаружили, что обнаруживаемый диапазон значений кривизны (|Ω k |≳ 10 −4 ) имеет незначительную вероятность, но в то же время широкий хвост распределения распространяется на значения, которые слишком малы, чтобы их можно было обнаружить. Помимо кривизны, квантовые флуктуации в родительском вакууме также могут давать характерную особенность в спектре гравитационных волн внутри пузыря. Обнаружение любого из этих эффектов предоставило бы дополнительные доказательства вечной инфляции.
Принцип посредственности также применялся для объяснения количества темной материи во Вселенной. Состав темной материи неизвестен, и одна из наиболее обоснованных гипотез состоит в том, что она состоит из очень легких частиц, называемых аксионами. Плотность аксионной темной материи определяется квантовыми флуктуациями во время инфляции и варьируется от одного места во Вселенной к другому. Его значение влияет на формирование галактик; следовательно, существует эффект антропного отбора. Тегмарк и др. (2006) (см. более раннюю работу Линде, 1988) рассчитали результирующее распределение вероятностей и обнаружили, что наблюдаемое значение плотности темной материи близко к пику распределения. Если действительно темная материя окажется аксионной, это можно будет считать успехом теории.
Тегмарк и др. (2006) (см. более раннюю работу Линде, 1988) рассчитали результирующее распределение вероятностей и обнаружили, что наблюдаемое значение плотности темной материи близко к пику распределения. Если действительно темная материя окажется аксионной, это можно будет считать успехом теории.
Предсказания масс нейтрино в Мультивселенной были разработаны Тегмарком и др. (2005) и Погосян и др. (2004), с выводом, что сумма масс нейтрино должна быть ∼1 эВ. Интересно отметить, что недавние эксперименты с нейтринными осцилляциями, а также космологические данные указывают на существование стерильных нейтрино с m ∼ 1 эВ (например, Hamann и др. 2010).
Основной нерешенной проблемой инфляционной космологии является проблема меры. Ее решение может потребовать радикально новых идей. Одна возможность, которая была недавно предложена (Гаррига и Виленкин, 2009), состоит в том, что динамика инфляционной мультивселенной имеет двойственное, «голографическое» описание в форме квантовой теории поля, определенной на будущей границе пространства-времени. Затем мера мультивселенной может быть связана с ограничением коротких расстояний в этой теории. Эта и другие возможности сейчас изучаются.
Затем мера мультивселенной может быть связана с ограничением коротких расстояний в этой теории. Эта и другие возможности сейчас изучаются.
Благодарность
Эта работа была частично поддержана грантом PHY-0855447 Национального научного фонда.
В Уитроу-лекции РАН 2011 года Александр Виленкин обсуждает новое космологическое мировоззрение, согласно которому большая часть Вселенной находится в состоянии постоянного ускоренного расширения, называемого инфляцией, и мы живем в одном из многочисленных пузырей с различными свойствами, которые постоянно меняются. сформировался. Каково происхождение этого мировоззрения, его возможные наблюдательные проверки и его последствия для начала и конца Вселенной?
Ссылка
Агирре
A
,
Джонсон
M
. ,
Респ. прог. физ.
,
2011
, том.
74
стр.
074901
Бланко-Пилладо
J J
,
Салем
MP
. ,
JCAP
,
2010
, том.
1007
стр.
7
Бордовый
A
, и др. ,
Физ. Преподобный Летт.
,
2003
, том.
90
стр.
151301
Бостром
N
. ,
Антропное смещение: эффекты отбора наблюдений
,
2002
Нью -Йорк
Routledge
Bousso
R
,
Polchinski
R
,
Polchinski
,
. 0005
0005
Дж
. ,
JHEP
,
2000
, том.
6
стр.
6
Картер
Б
.
Лонгэйр
M S
. ,
Сопоставление космологических теорий с данными
,
1974
Дордрехт
Рейдель
Чехия
B
5 , etal. ,
JCAP
,
2010
, том.
12
стр.
23
Де Симон
A
,
Салем
MP
. ,
Физ. Ред. D
D
,
2010
, том.
81
стр.
083527
Freivogel
B
, и др. ,
JHEP
,
2006
, том.
603
стр.
039
Гаррига
Дж
,
Виленкин
А
. ,
Физ. Ред. D
,
2001
, том.
64
стр.
023507
Гаррига
Дж
,
Виленкин
А
. ,
,
Физ. Ред. D
,
2008
, том.
77
стр.
043526
Гаррига
Дж
,
Виленкин
А
. ,
JCAP
,
2009
, том.
901
стр.
21
Гот
JR
. ,
Природа
,
1993
, том.
363
(стр.
315
—
319
)
Graham
P W
, и др. ,
,
Физ. Ред. D
,
2010
, том.
82
стр.
063524
Зеленый
B
. ,
Скрытая реальность: параллельные вселенные и скрытые законы космоса
,
2011
Кнопф
Гут
A H
,
Кайзер
Д И
. ,
Наука
,
2005
, том.
307
(стр.
884
—
890
)
Hamann
, и др. ,
Физ. Преподобный Летт.
,
2010
, том.
105
стр.
181301
Хартл
J
,
Среднецкий
М
. ,
Физ. Ред. D
,
2007
, том.
75
(стр.
123
—
523
)
Lerche
W
2 et al. ,
Нукл. физ. Б
,
1987
, том.
287
стр.
477
Лесли
Дж
. ,
Вселенные
,
1989
Нью-Йорк
Routledge
Linde
A
.
Hawking
S W
,
Израиль
W
. ,
300 лет гравитации
,
1987
Cambridge
Cambridge University Press
Linde
A
. ,
Физ. лат. Б
,
1988
, том.
201
стр.
437
Linde
A D
. ,
Физика элементарных частиц и инфляционная космология
,
1990
Чур
Harwood Academic
Страница
D N
. ,
Междунар. Дж. Мод. физ.
,
1996
, том.
D5
стр.
583
Погосян
Л
и др. ,
JCAP
,
2004
, том.
407
стр.
5
Steinhardt
P
. ,
Scientific American
,
2011
Susskind
L
. ,
Космический ландшафт: теория струн и иллюзия разумного замысла
,
2006
Back Bay Books
Тегмарк
M
и др. ,
Физ. Ред. D
,
2005
, том.
71
(стр.
103
—
523
)
Tegmark
M
2 и др. ,
Физ. Ред. D
,
2006
, том.
73
стр.
023505
Виленкин
А
. ,
Физ. Преподобный Летт.
,
1995
, том.
74
(стр.
846
—
849
)
Виленкин
А
2 . ,
Много миров в одном: поиск других вселенных
,
2006
Нью-Йорк
Хилл и Ван
Виленкин
А
2
2 .
Карр
Б Дж
. ,
Вселенная или Мультивселенная
,
2007
Кембридж
Издательство Кембриджского университета
Вайнберг
S
. ,
Физ. Преподобный Летт.
,
1987
, том.
59
стр.
2607
Примечания автора
Первоначально эта лекция была прочитана на Национальном астрономическом собрании РАН 19 апреля 2011 г.
Обоснование параллельных вселенных
0034 Scientific American, космолог Джордж Эллис объясняет, почему он скептически относится к концепции параллельных вселенных. Здесь сторонники мультивселенной Александр Виленкин и Макс Тегмарк предлагают контраргументы, объясняя, почему мультивселенная объясняет так много особенностей нашей Вселенной и как ее можно проверить.
Добро пожаловать в Мультивселенную
Александр Виленкин
Вселенная, какой мы ее знаем, возникла в результате великого взрыва, который мы называем Большим взрывом. Почти столетие космологи изучали последствия этого взрыва: как Вселенная расширялась и охлаждалась, и как галактики постепенно стягивались под действием гравитации. На природу самого взрыва обратили внимание сравнительно недавно. Это предмет теории инфляции, которая была разработана в начале 19 века.80-х годов Алана Гута, Андрея Линде и других, и привело к радикально новому глобальному взгляду на вселенную.
Инфляция — это период сверхбыстрого, ускоренного расширения в ранней космической истории. Это так быстро, что за долю секунды крошечная субатомная частица пространства раздувается до размеров, намного превышающих всю наблюдаемую в настоящее время область. В конце инфляции энергия, вызвавшая расширение, воспламеняет горячий огненный шар из частиц и излучения. Это то, что мы называем большим взрывом.
Это то, что мы называем большим взрывом.
Конец инфляции спровоцирован квантовыми, вероятностными процессами и не происходит везде одновременно. В нашем космическом соседстве инфляция закончилась 13,7 миллиарда лет назад, но она все еще продолжается в отдаленных частях Вселенной, и постоянно формируются другие «нормальные» области, подобные нашей. Новые области появляются в виде крошечных микроскопических пузырьков и сразу же начинают расти. Пузыри продолжают расти без ограничений; тем временем инфляционное расширение раздвигает их, освобождая место для образования новых пузырей. Этот бесконечный процесс называется вечной инфляцией. Мы живем в одном из пузырей и можем наблюдать лишь небольшую его часть. Независимо от того, насколько быстро мы путешествуем, мы не можем догнать расширяющиеся границы нашего пузыря, поэтому для всех практических целей мы живем в замкнутой вселенной пузыря.
Теория инфляции объяснила некоторые загадочные особенности Большого взрыва, которые раньше просто нужно было постулировать. Он также сделал ряд проверяемых предсказаний, которые затем были убедительно подтверждены наблюдениями. К настоящему времени инфляция стала ведущей космологической парадигмой.
Он также сделал ряд проверяемых предсказаний, которые затем были убедительно подтверждены наблюдениями. К настоящему времени инфляция стала ведущей космологической парадигмой.
Другой ключевой аспект нового мировоззрения проистекает из теории струн, которая в настоящее время является нашим лучшим кандидатом на роль фундаментальной теории природы. Теория струн допускает огромное количество решений, описывающих пузырьковые вселенные с различными физическими свойствами. Величины, которые мы называем константами природы, такие как массы элементарных частиц, гравитационная постоянная Ньютона и т. д., принимают разные значения в разных типах пузырей. Теперь соедините это с теорией инфляции. Каждый тип пузырьков имеет определенную вероятность образования в надувном пространстве. Так неизбежно в ходе вечного надувания будет образовываться неограниченное количество пузырей всех возможных типов.
Эта картина вселенной, или мультивселенная , как ее называют, объясняет давнюю загадку того, почему константы природы кажутся точно настроенными для возникновения жизни. Причина в том, что разумные наблюдатели существуют только в тех редких пузырях, в которых по чистой случайности константы оказываются как раз подходящими для развития жизни. Остальная часть мультивселенной остается бесплодной, но никто не может пожаловаться на это.
Причина в том, что разумные наблюдатели существуют только в тех редких пузырях, в которых по чистой случайности константы оказываются как раз подходящими для развития жизни. Остальная часть мультивселенной остается бесплодной, но никто не может пожаловаться на это.
Некоторые из моих коллег-физиков находят теорию мультивселенной тревожной. Любая теория в физике стоит или рушится в зависимости от того, согласуются ли ее предсказания с данными. Но как мы можем проверить существование других пузырьковых вселенных? Пол Стейнхардт и Джордж Эллис утверждали, например, что теория мультивселенной ненаучна, поскольку ее невозможно проверить даже в принципе.
Удивительно, но наблюдательные проверки картины мультивселенной на самом деле возможны. Энтони Агирре, Мэтт Джонсон, Мэтт Клебан и другие указывали, что столкновение нашего расширяющегося пузыря с другим пузырем в мультивселенной оставило бы отпечаток в космическом фоновом излучении — круглое пятно с большей или меньшей интенсивностью излучения. Обнаружение такого пятна с предсказанным профилем интенсивности предоставило бы прямое свидетельство существования других вселенных-пузырей. Сейчас поиск продолжается, но, к сожалению, нет никакой гарантии, что столкновение пузырей произошло в пределах нашего космического горизонта.
Обнаружение такого пятна с предсказанным профилем интенсивности предоставило бы прямое свидетельство существования других вселенных-пузырей. Сейчас поиск продолжается, но, к сожалению, нет никакой гарантии, что столкновение пузырей произошло в пределах нашего космического горизонта.
Есть и другой подход, которому можно следовать. Идея состоит в том, чтобы использовать нашу теоретическую модель мультивселенной для предсказания констант природы, которые мы можем ожидать измерить в нашем локальном регионе. Если константы варьируются от одной пузырьковой вселенной к другой, их локальные значения нельзя предсказать с уверенностью, но мы все же можем сделать статистических предсказания. Мы можем вывести из теории, какие значения констант, скорее всего, будут измерены типичным наблюдателем в мультивселенной. Предполагая, что мы типичны — предположение, которое я назвал принцип посредственности — тогда мы можем предсказать вероятные значения констант в нашем пузыре.
Эта стратегия была применена к плотности энергии вакуума, также известной как «темная энергия». Стивен Вайнберг заметил, что в регионах, где темная энергия велика, Вселенная очень быстро расширяется, не позволяя материи слипаться в галактики и звезды. Наблюдатели вряд ли будут развиваться в таких регионах. Расчеты показали, что большинство галактик (а значит, и большинство наблюдателей) находятся в областях, где темная энергия примерно равна плотности вещества в эпоху образования галактик. Таким образом, предсказание состоит в том, что подобное значение должно наблюдаться в нашей части Вселенной.
По большей части физики не воспринимали эти идеи всерьез, но, к их большому удивлению, темная энергия примерно ожидаемой величины была обнаружена в ходе астрономических наблюдений в конце 1990-х годов. Это может быть нашим первым свидетельством того, что действительно существует огромная мультивселенная. Это изменило многие взгляды.
Теория мультивселенной все еще находится в зачаточном состоянии, и некоторые концептуальные проблемы еще предстоит решить.
Мультивселенная наносит ответный удар
Макс Тегмарк
Вы действительно живете в мультивселенной или это понятие выходит за рамки науки?
Вдохновленный интересной критикой мультивселенных в августовском номере Scientific American, , написанной пионером теории теории относительности Джорджем Ф. Р. Эллисом, позвольте мне отдать вам свои пять центов.
Идеи мультивселенной традиционно подвергались расправе со стороны истеблишмента: Джордано Бруно с его мультивселенной бесконечного пространства сгорел на костре в 1600 году, а Хью Эверетт с его квантовой мультивселенной сгорел на рынке труда физика в 1957. Я даже испытал на себе некоторый жар, когда старшие коллеги предположили, что мои публикации, связанные с мультивселенной, были чушью и разрушили бы мою карьеру.
Это разглашение идей, конечно, не привело к консенсусу среди ученых, но сделало дебаты о мультивселенной гораздо более тонкими и, на мой взгляд, более интересными, поскольку ученые выходят за рамки выкрикивания звуковых фрагментов мимо друг друга и искренне пытаются понять противоположные точки зрения. Новая статья Джорджа Эллиса — отличный тому пример, и я очень рекомендую ее прочитать, если вы еще этого не сделали.
Под нашей вселенной я подразумеваю сферическую область пространства, из которой свет успел достичь нас в течение 13,7 миллиардов лет, прошедших после нашего Большого взрыва. Говоря о параллельных вселенных, я считаю полезным различать четыре разных уровня: Уровень I (другие подобные регионы далеко в космосе, где кажущиеся законы физики одинаковы, но где история развивалась по-другому, потому что все начиналось по-другому), Уровень II (области пространства, где даже кажущиеся законы физики различны), Уровень III (параллельные миры где-то в так называемом гильбертовом пространстве, где разыгрывается квантовая реальность) и Уровень IV (полностью несвязанные реальности, управляемые разными математическими уравнениями) .
В своей критике Джордж классифицирует многие аргументы в пользу этих уровней мультивселенной и утверждает, что все они имеют проблемы. Вот мое резюме его основных аргументов против мультивселенной:
1) Инфляция может быть ошибочной (или не вечной)
2) Квантовая механика может быть ошибочной (или не унитарной)
3) Теория струн может быть ошибочной (или не иметь несколько решений)
4) Мультивселенные могут быть нефальсифицируемыми
5) Некоторые заявления о мультивселенной сомнительны
6) Аргументы тонкой настройки могут потребовать слишком многого
7) Это скользкий путь к еще большим мультивселенным
(Джордж на самом деле не упомянул (2) в статье, но я добавляю это здесь, потому что я думаю он бы это сделал, если бы редактор разрешил ему больше шести страниц.)
Каково мое отношение к этой критике? Интересно, что я согласен со всеми этими семью утверждениями — и, тем не менее, я с радостью поставлю свои сбережения на существование мультивселенной!
Начнем с первых четырех. Инфляция естественным образом порождает мультивселенную уровня I, и если вы добавите теорию струн к ландшафту возможных решений, вы также получите уровень II. Квантовая механика в ее математически простейшей («унитарной») форме дает вам Уровень III. Так что, если эти теории исключаются, то рушится ключевое свидетельство этих мультивселенных.
Инфляция естественным образом порождает мультивселенную уровня I, и если вы добавите теорию струн к ландшафту возможных решений, вы также получите уровень II. Квантовая механика в ее математически простейшей («унитарной») форме дает вам Уровень III. Так что, если эти теории исключаются, то рушится ключевое свидетельство этих мультивселенных.
Помните: параллельные вселенные — это не теория, а предсказания некоторых теорий.
Для меня ключевым моментом является то, что если теории научны, то законной наукой является разработка и обсуждение всех их следствий, даже если они связаны с ненаблюдаемыми объектами. Чтобы теорию можно было опровергнуть, нам не обязательно иметь возможность наблюдать и проверять все ее предсказания, достаточно хотя бы одного из них. Таким образом, мой ответ на (4) состоит в том, что с научной точки зрения можно проверить наши математические теории, а не обязательно их следствия, и это вполне нормально. Например, поскольку общая теория относительности Эйнштейна успешно предсказала многие вещи, которые мы можем наблюдать, мы также серьезно относимся к ее предсказаниям для вещей, которые мы не можем наблюдать, например, что происходит внутри черных дыр.
Точно так же, если нас впечатлили успешные предсказания инфляции или квантовой механики, то нам нужно серьезно отнестись и к другим их предсказаниям, включая мультивселенную Уровня I и Уровня III. Джордж даже упоминает возможность того, что однажды вечную инфляцию можно будет исключить — для меня это просто аргумент в пользу того, что вечная инфляция — это научная теория.
Теория струн, безусловно, не дошла до инфляции и квантовой механики в плане утверждения себя в качестве поддающейся проверке научной теории. Однако я подозреваю, что мы застрянем на мультивселенной уровня II, даже если теория струн окажется отвлекающим маневром. Довольно часто математические уравнения имеют несколько решений, и до тех пор, пока они есть у фундаментальных уравнений, описывающих нашу реальность, вечная инфляция обычно создает огромные области пространства, которые физически реализуют каждое из этих решений. Например, уравнения, управляющие молекулами воды, которые не имеют ничего общего с теорией струн, допускают три решения, соответствующие парам, жидкой воде и льду, и если само пространство может аналогичным образом существовать в разных фазах, инфляция будет стремиться реализовать их все.
Джордж перечисляет ряд наблюдений, предположительно подтверждающих теории мультивселенной, которые в лучшем случае сомнительны, например, доказательства того, что некоторые константы природы на самом деле не постоянны, свидетельства в космическом микроволновом фоновом излучении столкновений с другими вселенными или странным образом связанным пространством и т. д. Я полностью разделяю его скептицизм в отношении этих утверждений. Однако во всех этих случаях разногласия касались анализа данных, как и в случае фиаско с холодным синтезом. Для меня сам факт, что ученые проводят эти измерения и спорят о деталях данных, является еще одним свидетельством того, что это находится в пределах науки: именно это отличает научную полемику от ненаучной!
Наша Вселенная удивительно точно приспособлена для жизни в том смысле, что если бы вы изменили многие из наших констант природы лишь на крошечную величину, жизнь, какой мы ее знаем, была бы невозможна. Почему? Если существует мультивселенная уровня II, где эти «константы» принимают все возможные значения, неудивительно, что мы оказываемся в одной из редких обитаемых вселенных, так же как неудивительно, что мы живем на Земле, а не на Меркурии или Нептуне. . Джордж возражает против того факта, что вам нужно принять теорию мультивселенной, чтобы сделать этот вывод, но именно так мы проверяем любую научную теорию: мы предполагаем, что она верна, прорабатываем последствия и отбрасываем теорию, если предсказания не совпадают с наблюдениями. . Некоторые точные настройки кажутся достаточно экстремальными, чтобы смущать — например, нам нужно настроить темную энергию примерно до 123 знаков после запятой, чтобы сделать галактики пригодными для жизни. Для меня необъяснимое совпадение может быть красноречивым признаком пробела в нашем научном понимании. Отвергнуть его, сказав: «Нам просто повезло — хватит искать объяснение!» не только неудовлетворительна, но также равносильна игнорированию потенциально важной подсказки.
. Джордж возражает против того факта, что вам нужно принять теорию мультивселенной, чтобы сделать этот вывод, но именно так мы проверяем любую научную теорию: мы предполагаем, что она верна, прорабатываем последствия и отбрасываем теорию, если предсказания не совпадают с наблюдениями. . Некоторые точные настройки кажутся достаточно экстремальными, чтобы смущать — например, нам нужно настроить темную энергию примерно до 123 знаков после запятой, чтобы сделать галактики пригодными для жизни. Для меня необъяснимое совпадение может быть красноречивым признаком пробела в нашем научном понимании. Отвергнуть его, сказав: «Нам просто повезло — хватит искать объяснение!» не только неудовлетворительна, но также равносильна игнорированию потенциально важной подсказки.
Джордж утверждает, что если мы серьезно относимся к тому, что все, что может произойти, происходит, мы скатываемся по скользкой дорожке к еще более крупным мультивселенным, таким как мультивселенная уровня IV. Поскольку это мой любимый уровень мультивселенной, и я один из очень немногих его сторонников, я с удовольствием скатываюсь по этому склону!
Джордж также упоминает, что мультивселенные могут противоречить бритве Оккама, вводя ненужные сложности. Как физик-теоретик я сужу об элегантности и простоте теории не по ее онтологии, а по элегантности и простоте ее математических уравнений — и меня весьма поразительно, что математически простейшие теории склонны давать нам мультиверсы. Доказано, что написать теорию, которая порождает именно ту вселенную, которую мы видим, и ничего более, оказалось чрезвычайно сложно.
Как физик-теоретик я сужу об элегантности и простоте теории не по ее онтологии, а по элегантности и простоте ее математических уравнений — и меня весьма поразительно, что математически простейшие теории склонны давать нам мультиверсы. Доказано, что написать теорию, которая порождает именно ту вселенную, которую мы видим, и ничего более, оказалось чрезвычайно сложно.
Наконец, есть аргумент против мультивселенной, которого я рекомендую Джорджу избегать, но который, на мой взгляд, является наиболее убедительным для большинства людей: параллельные вселенные кажутся слишком странными, чтобы быть правдой.
Рассмотрев аргументы против мультивселенной, давайте теперь более внимательно проанализируем аргумент в пользу мультивселенной. Я собираюсь доказать, что все спорные вопросы исчезнут, если мы примем Гипотезу Внешней Реальности: существует внешняя физическая реальность, полностью независимая от нас, людей. Предположим, что эта гипотеза верна. Тогда большая часть критики мультивселенной основывается на некоторой комбинации следующих трех сомнительных предположений:
1) Предположение всевидения: физическая реальность должна быть такой, чтобы хотя бы один наблюдатель в принципе мог наблюдать ее всю.
2) Допущение педагогической реальности: физическая реальность должна быть такой, чтобы все разумно информированные люди-наблюдатели чувствовали, что интуитивно ее понимают.
3) Предположение об отсутствии копирования: никакой физический процесс не может копировать наблюдателей или создавать субъективно неразличимые наблюдатели.
(1) и (2), по-видимому, мотивированы не более чем человеческим высокомерием. Предположение о всевидении эффективно переопределяет слово «существует», чтобы оно стало синонимом того, что можно наблюдать для нас, людей, сродни страусу, засунувшему голову в песок. Санта-Клаус, местный реализм, Зубная фея и креационизм — но действительно ли они достаточно усердно работали, чтобы освободиться от утешительно знакомых представлений, которые имеют более глубокие корни? мир устроен, а не указывать ему, как работать, основываясь на наших философских предубеждениях.
Если предположение о всевидении ложно, то существуют ненаблюдаемые вещи, и мы живем в мультивселенной.
Если предположение о педагогической реальности ложно, то возражение о том, что мультиверсы слишком странны, не имеет логического смысла.
Если предположение об отсутствии копий ложно, то нет фундаментальной причины, по которой ваши копии не могут существовать где-либо еще во внешней реальности — ведь и вечная инфляция, и единая квантовая механика обеспечивают механизмы для их создания.
Мы, люди, имеем хорошо задокументированную склонность к высокомерию, высокомерно воображая себя в центре внимания, когда все вращается вокруг нас. Мы постепенно узнали, что вместо этого мы вращаемся вокруг Солнца, которое само вращается вокруг одной галактики среди бесчисленного множества других. Благодаря прорывам в физике мы можем получить еще более глубокое понимание самой природы реальности.
Цена, которую мы должны заплатить, становится все скромнее — что, вероятно, пойдет нам на пользу — но взамен мы можем оказаться в реальности более величественной, чем наши предки мечтали в своих самых смелых мечтах.
Дополнительная литература:
Множество миров в одном: поиск других вселенных. Алексей Виленкин. Hill and Wang, 2006.
Космический ландшафт: теория струн и иллюзия разумного замысла . Леонард Сасскинд. Back Bay Books, 2006.
Скрытая реальность: параллельные вселенные и скрытые законы космоса. Брайан Грин. Knopf, 2011.
ОБ АВТОРЕ(АХ)
Недавние статьи Александра Виленкина
- Космические струны
Известный как «Безумный Макс» за свои неортодоксальные идеи и страсть к приключениям, Макс Тегмарк занимается научными исследованиями в диапазоне от точной космологии до конечной природы реальности. новая популярная книга «Наша математическая Вселенная». Он профессор физики Массачусетского технологического института, на его счету более 200 технических статей, и он снялся в десятках научных документальных фильмов. Его работа с коллаборацией SDSS по кластеризации галактик разделила первую премию в 9Журнал 1093 Science «Прорыв года: 2003».
Его работа с коллаборацией SDSS по кластеризации галактик разделила первую премию в 9Журнал 1093 Science «Прорыв года: 2003».
| | |
Бакалавр наук, Бомбейский университет, 19 лет.76 Электронная почта: Арвинд Дот Борд и Лю Дот Эду Текущие классы:
Административные должности
Другие академические должности
ИнтересыМатематические аспекты общей теории относительности, дизайн компьютерных программ, цифровая типографика и цифровой дизайн документов, веб-программирование и дизайн, современный дизайн, крикет, кулинария. Текущая работа: Награды
Выбранная пресса
Избранные работы, Дизайн
Избранное произведение, Относительность
Избранные работы, Компьютеры
Курсы, преподаваемые в прошломЛИУ-Почта:
В другом месте:
|


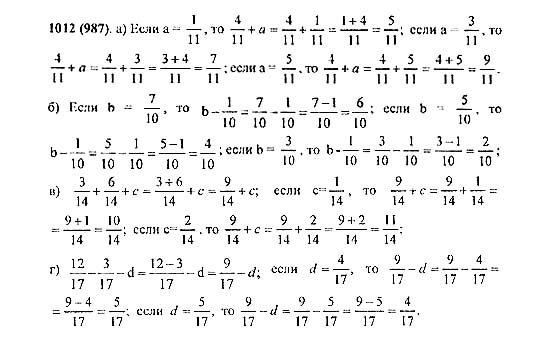 Вычислите: а) 2,66 : 3,8 б) 0,81 * 0,12 в) 0,6 — 0,0864 г) 0,5247 + 0,0353.
Вычислите: а) 2,66 : 3,8 б) 0,81 * 0,12 в) 0,6 — 0,0864 г) 0,5247 + 0,0353. Найдите среднее арифметическое чисел 3,9; 6,1;7,8 и 6,2.
Найдите среднее арифметическое чисел 3,9; 6,1;7,8 и 6,2.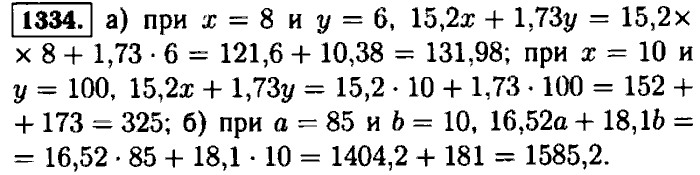 Найдите среднее арифметическое чисел 11,2; 14,8; 15,6 и 14,4.
Найдите среднее арифметическое чисел 11,2; 14,8; 15,6 и 14,4.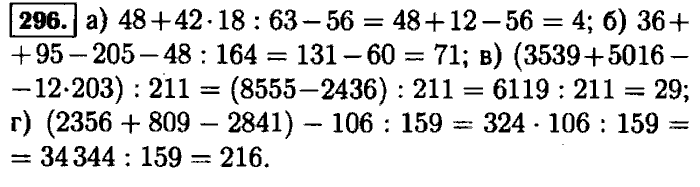 Постройте углы ADN и NDB, если ADN = 34,
Постройте углы ADN и NDB, если ADN = 34,