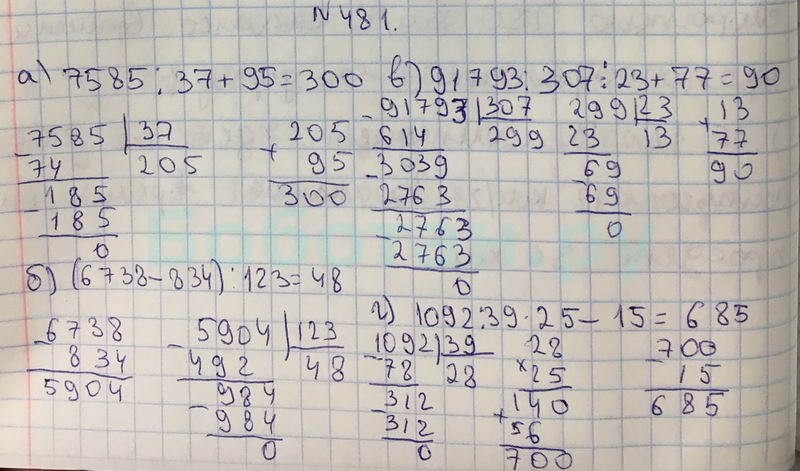Математика 5 класс упр 23: Номер 23 — ГДЗ Математика 5 класс. Мерзляк учебник

Номер №23 — ГДЗ по Математике 5 класс: Виленкин Н.Я.

войтирегистрация

1. Ответкин
2. Решебники
3. 5 класс
4. Математика
5. Виленкин
6. Номер №23

НАЗАД К СОДЕРЖАНИЮ

2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №23 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 31 издание 2013г.

2019г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №23 по учебнику Математика. 5 класс : учебник для учащихся общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 37 издание 2019г.

Условие 20132019г.

Cменить на 2013 г.

Cменить на 2019 г.

Запишите натуральное число:
а) следующее за числом 999;
б) на 1 меньшее 1000;
в) предшествующее числу 1 000 000;
г) на 1 большее числа 999 999 999;
д) на 1 меньшее числа 56 300.

Запишите натуральное число:
а) следующее за числом 999;
б) на 1 меньшее 1000;
в) предшествующее числу 1 000 000;
г) на 1 большее числа 999 999 999;
д) на 1 меньшее числа 56 300.

Решение 1

Решение 1

Решение 2

Решение 2

Решение 3

Решение 3

ГДЗ по Математике 5 класс: Виленкин Н.Я.

Издатель: Виленкин Н.Я. Жохов В. И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.

ГДЗ по Математике 5 класс: Мерзляк А.Г.

Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014-2018г.

ГДЗ по Математике 5 класс: Никольский С.М.

Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников А.В. Шевкин. 2015-2021г

ГДЗ по Математике 5 класс: Дорофеев Г.В.

Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2017-2019г.

ГДЗ по Математике 5 класс: Зубарева, Мордкович

Издатель: И.И. Зубарева, А.Г. Мордкович. 2013-2019г.

Сообщить об ошибке

Выберите тип ошибки:

Решено неверно

Опечатка

Плохое качество картинки

Опишите подробнее
в каком месте ошибка

Ваше сообщение отправлено
и скоро будет рассмотрено

ОК, СПАСИБО

[email protected]

© OTVETKIN.INFO

Классы

Предметы

Математика Алдамуратова 5 класс 2017 Упражнение 23 ГДЗ(дүж) решебник KZGDZ.

COM

Глава I. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ 1.2. Координатный луч. Изображение натуральных чисел и числа нуль на координатном луче Упражнение 23

← Предыдущий Следующий →

Глава I. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ

1.1. Натуральные числа и нуль

Упражнение

134567891011121314151617

1.2. Координатный луч. Изображение натуральных чисел и числа нуль на координатном луче

Упражнение

18192021222324252627

1.3. Сравнение натуральных чисел. Двойное неравенство

Упражнение

282930313233343536373839

1.4. Сложение и вычитание натуральных чисел

Упражнение

4041424344454647484950

1.5. Умножение и деление натуральных чисел. Основное свойство частного

Упражнение

5152535455565758596061

1.

6. Свойства арифметических действий

Упражнение

6263646566676869707172

1.7. Арифметические действия над натуральными числами

Упражнение

73747576777879

1.8. Числовые выражения. Буквенные выражения

Упражнение

80

81828384858687888990

1.9. Упрощение выражений

Упражнение

919293949596979899100101102103

1.10. Уравнение

Упражнение

104105106107108109110111112113114115116117118119120121

1.11. Формулы. Вычисление по формулам

Упражнение

122123124125126127128129130131132133134135136137138139140

1.12. Числовые последовательности

Упражнение

141142143144145146147148149150

Упражнения для повторения главы I

Упражнение

151152153154155156157158159160

161162163164165166

2.

1. Делители натурального числа. Кратные натурального числа

Упражнение

167168169170171172173174175176177178179180181182183184185186187188

Глава II. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ

2.2. Простые числа. Составные числа

Упражнение

189190191192193194195196197198199200

2.3. Основные свойства делимости

Упражнение

201202203204205206207208209210211212213214

2.4. Признаки делимости натуральных чисел на 2, 5 и 10

Упражнение

215216217218219220221222223224225226227

2.5. Признаки делимости натуральных чисел на 3 и на 9

Упражнение

228229230231232233234235236237238239

2.6. Степень числа

Упражнение

240

241242243244245246247248249250251252253254255256257258259260261262

2.

7. Разложение составных чисел на простые множители

Упражнение

263264265266267268269270271272273274275

2.8. Наибольший общий делитель. Взаимно простые числа.

Упражнение

276277278279280281282283284285286287288290291292293294295

2.9. Наименьшее общее кратное

Упражнение

296297298299300301302303304305306307308309310311312313314315

Упражнения для повторения главы II

Упражнение

316317318319320321

322323324325326327

2.10. Движение по реке

Упражнение

328329330331332333334335336337338339340341342343344345346347348

Глава III. ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ

3.1. Обыкновенная дробь. Чтение и запись обыкновенных дробей

Упражнение

349350351352353354355356357358359360361362363364365366367368369370371373374

3.

2. Основное свойство дроби. Сокращение дробей

Упражнение

375376377378379380381382383384385386387388389390391392393394395

3.3. Правильные дроби. Неправильные дроби

Упражнение

396397398399400401402

403404405406407408409410411412413414

3.4. Смешанные числа

Упражнение

415416417418419420421422423424425426427428429430431432433434435436

3.5. Изображение обыкновенных дробей и смешанных чисел на координатном луче

Упражнение

437438439440441442443444445446447448449450451452453454455456

3.6. Приведение обыкновенных дробей и смешанных чисел к наименьшему общему знаменателю

Упражнение

457458459460461462463464465466467468469470471472473474475476477

3.7. Сравнение обыкновенных дробей. Сравнение смешанных чисел

Упражнение

478479480481482

483484485486487488489490491492493494495496497498499

3.

8. Сложение и вычитание обыкновенных дробей

Упражнение

500501502503504506507508509510511512513514515516517518519520521522523524525526527528529530531

3.9. Сложение и вычитание смешанных чисел

Упражнение

532533534535536537538539540541542543544545546547548549550551552553554555556557558559

3.10. Аликвотные дроби

Упражнение

560561562563

564565566567568569570571572

3.11. Умножение обыкновенных дробей и смешанных чисел

Упражнение

573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602

3.12. Взаимно обратные числа

Упражнение

603604605

3.13. Деление обыкновенных дробей и смешанных чисел

Упражнение

606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643

644645646647648649650651652653654655656657658659660661662663664665

3.

14. Нахождение дроби от числа. Нахождение числа по его дроби

Упражнение

666667668669670671672673674675676677678679680681682683684685686687688689690691692693

3.15. Задачи на совместную работу

Упражнение

694695696697698699700701702703704705706707708709710711712713714

Глава IV. ДЕСЯТИЧНЫЕ ДРОБИ. ДЕЙСТВИЯ НАД ДЕСЯТИЧНЫМИ ДРОБЯМИ

4.1. Десятичная дробь. Чтение и запись десятичных дробей.

Упражнение

715716717718719720721722723

724725726727728729730731732733734

4.2. Перевод десятичной дроби в обыкновенную, обыкновенной дроби — в десятичную

Упражнение

735736737738739740741742743744745746747748749750751752753754

4.3. Изображение десятичной дроби на координатном луче. Сравнение десятичных дробей

Упражнение

755756757758759760761762763764765766767768769770771772773774775776777

4.

4. Сложение и вычитание десятичных дробей

Упражнение

778779780781782783784785786787788789790791792793794795796797798799800801802803

804805806807808809810

4.5. Умножение десятичной дроби на натуральное число

Упражнение

811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840

4.6. Умножение десятичных дробей

Упражнение

841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872

4.7. Деление десятичной дроби на натуральное число

Упражнение

873874875876877878879880881882883

884885886887888889890891892893894895896897898899900901902903

4.8. Деление десятичной дроби на десятичную дробь

Упражнение

904905906907908909910911912913914915916917918919920921922923924925926927928929930931932933934

4.

9. Умножение и деление десятичной дроби на 10, 100, 1000 и на 0,1; 0,01; 0,001;

Упражнение

935936937938939940941942943944945946947948949950951952953954955

4.10. Арифметические действия над обыкновенными и десятичными дробями.

Упражнение

956957958959960961962963

964965966967968969970971972973974975976977978979980981

4.11. Округление десятичных дробей

Упражнение

98298398498598698798898999099199299399499599699799899910001001100210031004

4.12. Числовые последовательности, составленные из дробей.

Упражнение

1005100610071008100910101011101210131014

Глава V. МНОЖЕСТВА

5.1. Множество. Элементы множества. Изображения множеств

Упражнение

101510161017101810191020102110221023102410251026102710281029103010311032

5.

2. Подмножество

Упражнение

10331034103510361037103810391040104110421043

1044104510461047104810491050

5.3. Пересечение множеств. Объединение множеств

Упражнение

105110521053105410551056105710581059106010611062106310641065106610671068

5.4. Задачи на множества

Упражнение

1069107010711072107310741075107610771078107910801081108210831084

Глава VI. ПРОЦЕНТЫ

6.1. Проценты

Упражнение

10851086108710881089109010911092109310941095109610971098109911001101110211031104110511061107110811091110111111121113

6.2. Нахождение процентов от данного числа

Упражнение

1114111511161117111811191120112111221123

112411251126112711281129113011311132113311341135113611371138113911401141

6.

3. Нахождение числа по его процентам

Упражнение

1142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169

Упражнения для повторения главы VI.

Упражнение

117011711172117311741175117611771178117911801181118211831184

Глава VII. УГЛЫ. МНОГОУГОЛЬНИКИ

7.1. Угол. Градусная мера угла Краткие сведения о градусе

Упражнение

118511861187118811891190119111921193119411951196119711981199

7.2. Транспортир. Измерение и построение углов

Упражнение

1200120112021203

120412051206120712081209121012111212121312141215

7.3. Сравнение углов. Виды углов. Чертежный треугольник

Упражнение

121612171218121912201221122212231224122512261227122812291230

7.4. Многоугольники

Упражнение

12311232123312341235123612371238123912401241124212431244124512461247

Упражнения для повторения главы VII

Упражнение

1248124912501251125212531254

Глава VIII.

ДИАГРАММЫ

8.1. Окружность. Круг

Упражнение

125512561257125812591260126112621263126412651266126712681269127012711272127312741275

8.2 Круговой сектор

Упражнение

12761277127812791280128112821283

128412851286128712881289

8.3.Способы представления статистических данных. Столбчатые, линейные, круговые и графические диаграммы. Таблицы

Упражнение

129012911292129312941295129612971298129913001301

Глава IX. РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР

9.1. Прямоугольный параллелепипед и его развертка

Упражнение

13021303130413051306130713081309131013111312

9.2. Задачи на разрезание фигур Задачи на склеивание фигур

Упражнение

1313131413151316

Упражнения для повторения пройденного за год

1. Натуральные числа и нуль

Упражнение

13171318131913201321132213231324132513261327

2.

Делимость натуральных чисел

Упражнение

1328132913301331133213331334

3. Обыкновенные дроби и действия над ними

Упражнение

133513361337133813391340134113421343

4. Десятичные дроби и действия над ними

Упражнение

1344134513461347134813491350

5. Множества

Упражнение

1351135213531354

6. Проценты

Упражнение

13551356135713581359

7. Углы. Многоугольники

Упражнение

136013611362

8. Диаграммы. Развертка прямоугольного параллелепипеда

Упражнение

1363

13641365

Класс 5 Время – основы, задачи и примеры решений

• Время – это период, который измеряется в минутах, днях, годах и т. д.
  60 секунд = 1 минута
  60 минут = 1 час
  
  24 часа = 1 день
  365 дней = 1 год
• Время также можно определить как функцию, которая принимает три числа: день (от 1 до 31), месяц (от 1 до 12) и год (скажем, 2004) и возвращает целое число.
  Например,
  Рассмотрим 23.01.2018, эта функция имеет 3 числа: день (23), месяц (01) и год (2018). Когда время определяется таким образом, оно также называется датой.
• Когда мы переводим высшие единицы времени в младшие, мы умножаем. Когда мы переводим младшие единицы времени в высшие, мы делим.

ПРИМЕР 1: Запишите 4 часа 5 минут 60 секунд в секундах.

РЕШЕНИЕ:

Преобразовывая часы и минуты в секунды, мы получаем:

4 часа = 4×60 минут = 4x60x60 секунд = 14400 секунд

5 минут = 5×60 секунд = 300 секунд получить:
= (14400+300+60) секунд
=14760 секунд

Следовательно, 4 часа 5 минут 60 секунд в секундах составляют 14760 секунд.

ПРИМЕР 2: Дата рождения Нехи — тридцатый день восьмого месяца тысяча девятьсот девяносто шестого года. Запишите в формате даты.

Решение:

. имеет 365 дней. Но в некоторых годах 366 дней. Эти годы называются високосными. Дополнительный день приходится на февраль. Високосные годы происходят с интервалом в 4 года.
Как узнать, является ли год високосным? Если конкретный год можно разделить на 4, оставив нулевой остаток, то год является високосным. Например, 1996÷4=499
с остатком 0. Значит, 1996 год високосный.

Всего 12 месяцев. Это январь (1), февраль (2), март (3), апрель (4), май (5), июнь (6), июль (7), август (8), сентябрь (9), октябрь ( 10), ноябрь(11), декабрь(12).

В январе, марте, мае, июле, августе, октябре и декабре 31 день. Апрель, июнь, сентябрь и ноябрь имеют 30 дней. В феврале 28 дней, а в високосный год их 29.дней.

Например,
В 1996 году
В феврале 29 дней
, потому что 1996 год високосный.

Общая информация. Простой способ запомнить, в каких месяцах 31 день, а в каких 30 дней. : 1 23 30 дней

В сентябре 30 дней.
Количество дней, оставшихся до конца Сентябрь= (30-23) дней= 7 дней
Рассматриваем первую декаду октября.
Следовательно, общее количество дней между 23 сентября и 10 октября = (7+10) дней
= 17 дней [ANS]

ПРИМЕР 2: Прибавьте 4 года 5 месяцев прибавьте 7 лет 8 месяцев.
Из 7 лет 2 месяцев вычесть 4 года 5 месяцев

РЕШЕНИЕ: Сложение:

• Сложите цифры в позиции месяцев.
• Здесь 8+5= 13 месяцев.
• Но всего 12 месяцев.
• Итак, будем считать 13 месяцев = (12 месяцев + 1 месяц) = (1 год + 1 месяц)
• Запишите 1 месяц в позиции месяцев и добавьте оставшийся 1 год к (7+4) годам в позиции лет.

	4 года	5 месяцев
	7 лет	8 месяцев
+	= 11 лет	13 месяцев (недействительно)
	+1 год(дополнительные 12 месяцев от позиции месяцев)	-12 месяцев (переведено на лет)
	12 лет	1 месяц

Ответ: 12 лет 1 месяц

Вычитание:

• Вычитание цифры в позиции месяца
• Здесь 2-5=-3. Но, -3 месяца не имеет смысла
• Итак, мы возьмем 12 месяцев (1 год) заимствования из года позиции.
• Теперь -3+12(заимствованные месяцы) = 9 месяцев.
• В позиции лет 7-4=3 года. Но мы взяли 1 год (12 месяцев) брать из летнего положения. Итак, мы должны вычесть 1 год из позиции лет. Таким образом, 3-1= 2 года

	7 лет	2 месяца
	4 года	5 месяцев
—	= 3 года	-3 месяца (недействительно)
	-1 год(компенсация за заимствованные 12 месяцев)	+12 месяцев(взял)
	2 года	9 месяцев

Ответ: 2 года 9месяца

Примечание.

В дополнение к датам 12 месяцев создают перенос 1 года, который добавляется к позиции
года. При вычитании 1 год заимствования из позиции лет добавляется как 12 месяцев в позиции месяцев

• Время может быть представлено в двух форматах: 24-часовом формате и 12-часовом формате.
  24-часовой формат: 00 час, 01 час, 02 час, 03 час, 04 час, 05 час, 06 час, 07 час, 08 час, 09 час, 10 час, 11 час……………., 22 час , 23 часа
  12-часовой формат: 12:00, 1:00, 2:00, 3:00, 4:00, 5:00, 6:00, 7:00, 8:00, 9утра, 10:00, 11:00, 12:00, 13:00, 14:00………….9 вечера, 22:00, 23:00.
• В 12-часовом формате am означает «anti meridiem», что в переводе с латыни означает «до полудня».
  pm означает «post meridiem», что в переводе с латыни означает «после полудня».
• Сравнение 12-часового и 24-часового форматов времени.

• ПРИМЕР 2: Напишите 13:23 в 24-часовом формате. Напишите 4:56 часов в 12-часовом формате.

РЕШЕНИЕ:

Если мы добавим 12 часов, т. е. 12:00 к 12-часовому формату времени (только pm.am будет таким же), то результат будет в 24-часовом формате. Следовательно, 1:23+12= 13:23 в 24-часовом формате.

4:56 часов в 12-часовом формате = 4:56 утра

Примечание:

• Время в формате утра в 12-часовом формате будет равно 24-часовому формату.
• Чтобы преобразовать pm в 24-часовой формат, добавьте 12:00 ко времени, указанному в pm.
• Чтобы преобразовать время больше 12 в 24-часовой формат, вычтите из него 12, чтобы получить такое же время в 12-часовом формате

Q1) Арьян начал делать уроки в 13:23. Он закончил в 14:34. Сколько времени он делал домашнее задание?

Q2) Бани требуется 3 часа 45 минут, чтобы добраться до аэропорта от своего дома. Если она хочет добраться до аэропорта к 10:00, во сколько она должна выйти из дома?

Q3) Поезд едет из города A в город B. Поезд отправляется в 17:06. Поезду требуется 78 часов 19 минут, чтобы добраться до города B. Когда поезд прибудет в город B?

Q4) Чинмаю требуется 2 часа 30 минут, чтобы добраться до города B из города A. Сегодня он добрался до города B через 45 минут. Сколько времени ему потребовалось сегодня, чтобы добраться до города B?

Q5) Запишите прошедшее время для следующего времени начала и окончания.

Q6) Запишите 6 часов 7 минут 8 секунд в виде минут и секунд.

Q7) Запишите дату следующего високосного дня в формате дд/мм/гггг.

Q8) Сколько дней проходит между 9 ^th февраля 2016 г. и 10 ^th марта 2016 г.

Q9) Добавить/вычесть 2 года 3 месяца и/или из 4 лет 10 месяцев.

Q10) Напишите 17:01 и 6:07 в 24-часовом формате. Напишите 13:08 часов и 8 часов 9минут в 12-часовом формате.

• Когда мы переводим более высокие единицы времени в его более низкие единицы, мы умножаем.
• Когда мы переводим младшие единицы времени в его высшие единицы, мы делим.
• Високосный год — это год, который делится на 4.
• В високосном году 366 дней вместо 365.
• В високосный год к февралю добавляется дополнительный день. Он имеет 29 дней вместо 28 дней.
• В часах AB:CD AB стоит на месте часов, а CD — на месте минут.
• В 24-часовом формате диапазон от 00 до 23 часов
• В 12-часовом формате есть два периода по 12 часов, каждый в диапазоне от 01:00 до 00:00.
• Перенос 60 минут в минимальной позиции = Добавляется как 1 час в часовой позиции
  Заем 60 минут вычитается как 1 час из часовой позиции.

20+ упражнений для быстрой разминки по математике в классе — %%sitename%%

Ежедневные разминки по математике предназначены для того, чтобы быстро размять мозг учащегося. Они не предназначены для того, чтобы быть чем-то, что займет много времени, чтобы организовать или спланировать. Но то, что можно быстро использовать для всего класса!

Разминка по математике предназначена для того, чтобы учащиеся могли попрактиковаться в понятиях, которые они изучили на предыдущих уроках, но которым, возможно, все еще нужно будет поработать, например, по счету, сложению, вычитанию, разряду и т. д.

Нужна разминка по математике. можно распечатать прямо сейчас? Перейти к нашей коллекции упражнений по математике !

Важность математической разминки

Вы бы не попросили спортсмена пробежать забег или певца выйти на сцену без предварительной разминки! Кто-то может сказать, что разминка математических мозгов ваших учеников в начале урока — самая важная часть занятия. Разминка пробуждает интерес учащихся перед тем, как погрузиться в ваш контент, отрабатывая известную связанную информацию.

Просмотр знакомых материалов по математике может помочь учащимся практиковать свои базовые знания, доводя это понимание до их сознания, чтобы они были готовы к доступу, когда они погружаются в более новые и сложные предметы, которые вы собираетесь преподавать.

Идеи для разминки по математике для начальной школы

Мы начнем с разминки, которую вы можете выполнять прямо на доске, а затем погрузимся в разговоры о числах, игры в круг и многое другое, чтобы заставить их математические мысли работать.

Математические разминки на доске

Зарегистрируйте это в разделе «Быстро и легко»: использование классной доски и написание быстрых математических задач на доске может стать отличным способом потренировать эти маленькие умственные способности, и для этого не потребуется ничего, кроме маркера и нескольких идей. К счастью, у нашей команды учителей есть много таких для вас …

 

Играйте в «Кто я», используя числа

Я число. У меня 4 цифры. 3 и 5 — 2 из моих многих факторов. Под каким номером я могу быть?

Разберись – ответ… в чем вопрос?

Ответ 3/4. В чем вопрос?

Используйте цифры, чтобы получить ответ.

Ответ 345. Используйте эти числа, чтобы решить ряд вопросов – 10, 3, 4, 5, 2, 1, 100.

Уравняйте четную группу чисел, используя сложение.

Используйте сложение, чтобы сбалансировать эти числа так, чтобы обе стороны были равны – 56, 38, 22, 16, 6, 40, 24, 27, 19, 32.

Составьте число, используя разные методы и предоставленные числа.

Сделайте 126. Используйте все числа (200, 5, 4, 2, 6), чтобы получить ответ 126. Вы можете использовать сложение, вычитание, умножение или деление, но каждое число можно использовать только один раз. .

Угадай число 

Это увлекательная математическая разминка, в которую можно играть всем классом или группами по 3 человека. Учащиеся встают и, не глядя на номера других игроков, пишут число от 2 до 9. , Третий игрок называет сумму чисел, и побеждает тот, кто первым угадает, какой номер у другого игрока. Для учащихся это можно дифференцировать, увеличивая или уменьшая числа, или предлагая третьему игроку найти произведение вместо суммы.

Номер дня

Каждый день записывайте на доске новое число и сделайте так, чтобы учащиеся ежедневно взаимодействовали с числом различными способами — вы можете использовать флип-стики и вызывать учащихся по одному, один, чтобы дать вам число, которое «больше» или «меньше», чем число дня. Вы также можете попросить одного учащегося определить, является ли число дня нечетным или четным, а затем позвонить другим учащимся, чтобы назвать вам другое число, которое является четным или нечетным!

Действия по номеру телефона

Number Talks – это короткие ежедневные занятия , которые позволяют учащимся вести содержательные и увлекательные разговоры о математике. Покажите учащимся лицевую сторону карточки и спросите подсказки на обратной стороне. Эти обмены приведут к разработке более точных, эффективных и гибких стратегий для студентов!

Изучите любимые ресурсы нашей команды преподавателей – от объема до измерений и не только!

Игра «Вокруг света»

«Вокруг света» — это простая и быстрая разминка по математике для вашего класса, которую можно изменить в соответствии с тем, что вы изучаете в классе. Кроме того, если вы чувствуете, что вашим ученикам нужно немного свежего воздуха на свежем воздухе, вы можете легко провести эту математическую разминку на улице!

Вот как играть вокруг света:

• Учащиеся садятся в круг.
• Выбирается один учащийся, который будет стоять за соседним учеником (эти два учащегося будут играть первыми).
• Учитель задает вопрос, например, что такое двойная 5?
• Ученик, ответивший правильно первым, перемещается «по всему миру».
• Если победителем становится стоящий ученик, он просто переходит к следующему сидящему ученику.
• Если победителем становится сидящий ученик, он встает и двигается за пределами круга.

Плакат для разминки по математике

Работаете над умножением? Эти плакаты с наполнителем для живота с умножением — это очень весело и простой способ заставить детей задуматься о том, как умножение помогает нам увеличивать числа!

Выберите шаблон плаката с изображением гориллы, панды или монстра для печати. Количество сделанных копий будет зависеть от обсуждаемого предложения с числом умножения. Например, если бы числовое предложение было 3 х 4, можно было бы отобразить три копии гориллы.

Затем учащиеся прикрепляют по четыре бетонных предмета к животику каждой гориллы. Конкретные объекты, которые можно прикрепить липкой лентой, могут включать в себя соединительные кубики, спички, жетоны и т. д. Эти объекты представляют собой количество вещей, съеденных персонажем. Напишите под каждой гориллой подходящее предложение с повторяющимся сложением, например, 4 + 4 + 4 — на доске!

---

Упражнение «Большая лестница из палочек»

Эта идея для разминки по математике просто золотая! Да, первоначальное создание активности занимает немного времени, однако нет времени на ее настройку после ее создания.

Если можете, составьте классный набор, чтобы каждый ученик каждый раз имел свой или мог работать в парах.

Основная концепция заключается в том, что учащиеся получают полный набор и начинают с палочки для рукоделия со знаком «старт». Они должны найти совпадающие ответы на математические вопросы, пока все палочки не будут в порядке.

---

Разминка по математике в формате PowerPoint

Использование различных методов для ежедневной разминки по математике делает ее интересной для учащихся. Наличие банка различных интерактивных презентаций PowerPoint (или слайдов Google) — еще один фантастический способ заставить эти маленькие умы мыслить математически!

У нас есть множество математических интерактивных презентаций PowerPoint, охватывающих целый ряд тем, в том числе; стоимость места, деньги, умножение и деление.

Разминка с номером дня PowerPoint — прекрасное дополнение к вашей коллекции разминки по математике. Все, что вам нужно, это выбранный номер, и в PowerPoint включено более 20 различных действий. Легко изменить уровень этой математической разминки, изменив используемое число.

Ознакомьтесь также с этими презентациями PowerPoint по умножению!

---

Упражнения на сопоставление

Заламинированные и готовые к использованию карточки с заданиями на сопоставление также являются еще одной быстрой и простой идеей для разминки по математике.

Мне нравилось использовать доску для этих занятий, когда я был в классе — когда мои ученики входили в класс, они сопоставляли один набор карточек. Пока я следил за посещаемостью, это сделало меня отличным звонарем.

Вот несколько замечательных математических заданий, которые вы можете использовать:

---

Математическая разминка «У меня есть, у кого есть»

Существует множество различных вариантов этой разминочной игры, и вы можете следить за тем, как быстро класс выполняет карточки, чтобы у детей возникало желание еще — они продолжали хотят побить свой рекорд времени.

Учащийся, у которого есть предложение «Я начинаю», начинает игру, вставая и читая свою карточку. Прочитав свою подсказку, ученик, у которого на карточке есть совпадающее число, встает и читает то, что написано на его карточке. Игра продолжается до тех пор, пока последний человек не прочитает «Я последний номер!»

Самое приятное в этом то, что однажды распечатав и заламинировав эти игровые карточки, вы сможете использовать их снова и снова! Идеальный!

 

У нас есть огромная коллекция игровых карточек «У меня есть, у кого есть». Кроме того, редактируемая словесная версия игровых карточек «У меня есть, у кого есть», которые вы можете использовать для создания своих собственных, в зависимости от темы, которую вы хотите осветить.

Вот наша коллекция карт «У меня есть, у кого есть»:

---

Используйте колоду карт

Старую верную колоду карт можно использовать множеством способов! Вот лишь один простой способ использовать колоду карт в качестве математической разминки. Проект наш для печати поместите коврик на интерактивную доску, затем случайным образом вытащите четыре карты из колоды карт.

Вот что вы можете предложить своим ученикам с четырьмя карточками:

• Учащиеся составляют наибольшее число, которое они могут, используя четыре числа.
• Составьте из четырех чисел наименьшее число, которое они могут.
• Предложите учащимся сложить четыре числа.
• Учащиеся выбирают два числа, чтобы составить генеалогическое древо фактов.

---

Числовые диаграммы для победы

Использование сотен диаграмм и числовых диаграмм — еще один простой способ активизировать математический мозг ваших учеников!

Используйте наши таблицы Numbers 21-130 различными способами.