«Детская школа искусств» Мошенского муниципального района

Математика 5 класс автор с м никольский: Номер №1028 — ГДЗ по Математике 5 класс: Никольский С.М.

Содержание

С. М. Никольский, “Еще о приближении целыми функциями экспоненциального типа и полиномами”, Исследования по теории дифференцируемых функций многих переменных и ее приложениям. Ч. 16, Труды мат. Инст. Стеклов., 204, Наука, Москва, 1993, 201–225; проц. Стеклова матем., 204 (1994), 173–192

Общая информация
Последний выпуск
Предстоящие документы
Архив
Импакт-фактор
Руководство для авторов
Лицензионное соглашение

Поисковые документы
Поиск ссылок

RSS
Последний выпуск
Текущие выпуски
Выпуски архива
Что такое RSS






Личный кабинет:
Логин:
Пароль:
Сохранить пароль
Введите
Забыли пароль?
Регистр

Труды Математического Института им. В. А. Стеклова, 1993, том 204, страницы 201–225 (Ми тм1269)  
Эта статья цитируется в 5 научных статьях (всего в 6 статьях)

Еще о приближении целыми функциями экспоненциального типа и многочленами

С. М. Никольский

Полный текст PDF (1866 кБ)

Поступила в редакцию октября 1992 г.

Библиографические базы данных:

Тип документа: Артикул

УДК: 517.5

Язык: Русский

Ссылка: С. М. Никольский, “Еще о приближении целыми функциями экспоненциального типа и полиномами”, Исследования по теории дифференцируемых функций многих переменных и ее приложениям. Ч. 16, Труды мат. Инст. Стеклов., 204, Наука, Москва, 1993, 201–225; проц. Стеклова Матем., 204 (1994), 173–19. 2

Цитирование в формате AMSBIB

\RBibitem{Nik93}
\by С.~М.~Никольский
\paper Еще о приближении целыми функциями экспоненциального типа и полиномами \inbook Исследования
в теории дифференцируемых функций многих переменных и ее приложениях. Часть~16
\serial Тр. Матем. Инст. Стеклов.
\год 1993
\том 204

\страниц 201--225
\публ Наука
\пуладдр Москва
\mathnet{http://mi.mathnet.ru/tm1269}
\mathscinet{http://mathscinet.ams.org/mathscinet-getitem?mr=1320026}
\zmath{https://zbmath.org/?q=an:0845.41016}
\transl
\jour Proc. Стеклова Мат.
\год 1994
\об 204
\страниц 173--192

Варианты соединения:

  • https://www.mathnet.ru/rus/tm1269
  • https://www.mathnet.ru/rus/tm/v204/p201

    • Эта публикация цитируется в следующих статьях:

    1. Никольский С. М., “Аппроксимация полиномами функций класса H–P(R) (гамма)”, ДАН, 337:2 (1994), 165–167    
    2. Никольский С.М., “Неравенства Бернштейна для алгебраических многочленов на многообразиях”, ДАН, 335:2 (1994), 146–149      
    3. С. М. Никольский, “Несколько слов о себе”, Тр. Стеклова матем., 232 (2001), 2–12      
    4. С. М. Никольский, “Еще об одной краевой задаче с многочленами”, Тр. Стеклова Матем., 232 (2001), 278–280      
    5. «Список С.М. Никольского», Тр. Стеклова матем., 248 (2005), 2–20      
    6. М. К. Керимов, “К 100-летию со дня рождения академика Сергея Михайловича Никольского”, Ж. вычисл. Мат. Мат. Phys., 46:3 (2006), 345–353        

    Ссылки на статьи в Google Scholar: русские цитаты, английские цитаты
    Статьи по теме в Google Scholar: русские статьи, Английские статьи

    QR-?

    Курс математического анализа (Том 1 и 2) – Никольский

    Опубликовано 18 декабря 2021 г. автором The Mitr

    В этом посте мы увидим двухтомник Курс математики
    Анализ С. М. Никольского.

    Большая часть этого двухтомного учебника восходит к

    курсу математического анализа, который автор читал на протяжении многих
    лет в Московском физико-техническом институте.

    Первый том, состоящий из одиннадцати глав, включает
    введение (глава 1), в котором рассматриваются основные понятия
    математический анализ с использованием интуитивного понятия предела. С помощью
    визуальной интерпретации и некоторых соображений физического характера
    устанавливается связь между производной
    и интегралом и даются некоторые элементы методов дифференцирования и интегрирования, необходимые тем читателям, которые одновременно изучают физику.

    Понятие действительного числа интерпретируется в первом томе
    (глава 2) на основе его представления в виде бесконечного десятичного числа. Главы 3–11 содержат следующие темы: предел последовательности, предел функции, функции одной переменной, функции нескольких переменных, неопределенный интеграл, определенный интеграл, некоторые приложения интегралов, ряды.

    Том 2 содержит кратные интегралы, теорию поля. ряды и интегралы Фурье, дифференциальные многообразия и дифференциальные формы, интеграл Лебега.

    Книги переведены с русского В. М. Волосовым. Книга
    была издана первым издательством «Мир» в 1977 году с переизданиями
    в 1981, 1985 и 1987 годах.

    Примечание. Том 2 имеет гораздо лучшее разрешение сканирования. В предыдущем посте мы видели только Vol. 2, в этом посте были мертвые ссылки. В этом посте с обоими томами были очищены сканы и обновлены ссылки. Предыдущий пост обновлен.

    Кредиты оригинальным загрузчикам .

    Вы можете получить

    Том 1 Здесь

    Том 2 Здесь

    ПРЕДИСЛОВИЕ К ВЕСЕДА.

    Глава 4. Предел функции 90

    Глава 5.

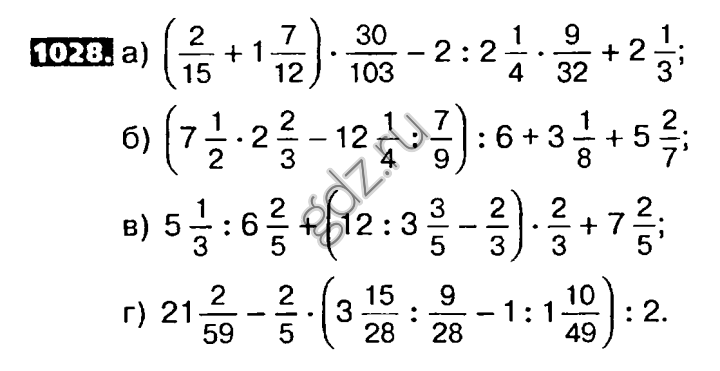    Дифференциальное исчисление. Функции одной переменной 127

    Глава 6. n-мерное пространство. Геометрические свойства кривых 180

    Глава 7. Дифференциальное исчисление. Функции многих переменных 215

    Глава 8. Неопределенный интеграл. Свойства многочленов 314

    Глава 9. Определенный интеграл 351

    Глава 10. Некоторые применения интеграла. Приближенные методы. Дифференциация и интеграция


    интеграла по параметру. Несобственные интегралы 80

    Глава 14. Нормированные линейные пространства. Ортогональные системы 147

    Глава 15. Ряды Фурье. Приближение функций многочленами 188

    Глава 16. Интеграл Фурье. Обобщенные функции.1 Тематический указатель  438

     

    Нравится:

    Нравится Загрузка…

    Эта запись была размещена в книги, математика, мир книги, мир издательства, советский и помеченный анализ, определенный интеграл, дифференцируемые многообразия, дифференциальные формы, поле теория, интеграл Фурье, ряд Фурье, функции одной переменной, функции многих переменных, основы математического анализа, неопределенный интеграл, интеграл Лебега, предел функции, математика, мир издательства, множественные интегралы, предел последовательности действительных чисел, ряд, некоторые Приложения интегралов, советских, векторного поля.

    Добавить комментарий