Математика. 5 класс. Учебник в 2 частях (комплект из 2 книг) (Наум Виленкин)
1 951 ₽
+ до 292 баллов
Бонусная программа
Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.
Офлайн
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
В наличии в 31 магазине. Смотреть на карте
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Проверенный временем учебник полностью соответствует Примерной основной образовательной программе по математике и ФГОС ООО. Разработан с учётом возрастных и гендерных особенностей восприятия материала учащимися. Глубоко продуманная последовательность подачи теоретического и практического материала эффективно развивает мышление, память и речь учащихся.
Первая часть учебника посвящена изучению натуральных чисел и основ геометрии.
Вторая часть учебника посвящена изучению дробных чисел и основ теории множеств, знакомству с инструментами вычислений .и измерений.
Описание
Характеристики
Проверенный временем учебник полностью соответствует Примерной основной образовательной программе по математике и ФГОС ООО. Разработан с учётом возрастных и гендерных особенностей восприятия материала учащимися. Глубоко продуманная последовательность подачи теоретического и практического материала эффективно развивает мышление, память и речь учащихся.
Первая часть учебника посвящена изучению натуральных чисел и основ геометрии.
Вторая часть учебника посвящена изучению дробных чисел и основ теории множеств, знакомству с инструментами вычислений
.и измерений.
Мнемозина
На товар пока нет отзывов
Поделитесь своим мнением раньше всех
Как получить бонусы за отзыв о товаре
1
Сделайте заказ в интернет-магазине
2
Напишите развёрнутый отзыв от 300 символов только на то, что вы купили
3
Дождитесь, пока отзыв опубликуют.
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусов
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусов
Книга «Математика. 5 класс. Учебник в 2 частях (комплект из 2 книг)» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Наум Виленкин
«Математика. 5 класс. Учебник в 2 частях (комплект из 2 книг)» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.
5 класс. Учебник в 2 частях (комплект из 2 книг)» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.
О средствах Нёрлунда Виленкина-Фурье серии
Иштван Благота; Ларс-Эрик Перссон; Георгий Тефнадзе
Чехословацкий математический журнал (2015)
- Том: 65, выпуск: 4, стр. 983-1002
- ISSN: 0011-4642
Доступ к полной статье
топДоступ к полному тексту
Полный (PDF)
Аннотация
вершина Доказываются и обсуждаются некоторые новые неравенства типа (Hp,Lp) взвешенных максимальных операторов средних Виленкина-Нёрлунда с невозрастающими коэффициентами {qk:k≥0}. Эти результаты являются наилучшими в определенном смысле. В качестве приложений указываются некоторые известные, а также новые результаты теории сильной сходимости таких средних Виленкина-Нёрлунда. Для достижения наших основных целей мы также докажем некоторые новые оценки, представляющие независимый интерес, для ядер этих результатов суммирования. В частных случаях общих средних Нёрлунда tn с невозрастающими коэффициентами аналогичные результаты могут быть получены для средних Фейера и Чезаро путем выбора подходящим образом порождающей последовательности {qk:k≥0}.
Эти результаты являются наилучшими в определенном смысле. В качестве приложений указываются некоторые известные, а также новые результаты теории сильной сходимости таких средних Виленкина-Нёрлунда. Для достижения наших основных целей мы также докажем некоторые новые оценки, представляющие независимый интерес, для ядер этих результатов суммирования. В частных случаях общих средних Нёрлунда tn с невозрастающими коэффициентами аналогичные результаты могут быть получены для средних Фейера и Чезаро путем выбора подходящим образом порождающей последовательности {qk:k≥0}.Как цитировать
топ- MLA
- БибТекс
- РИС
Благота, Иштван, Перссон, Ларс-Эрик и Тефнадзе, Георгий. «О средних Нёрлунда ряда Виленкина-Фурье». Чехословацкий математический журнал 65.4 (2015): 983-1002.
@article{Blahota2015,
abstract = {Мы доказываем и обсуждаем некоторые новые неравенства типа $(H_\{p\},L_\{p\})$ взвешенных максимальных операторов средних Виленкина-Нёрлунда с невозрастающими коэффициенты $\lbrace q_\{k\}\colon k\ge 0\rbrace $.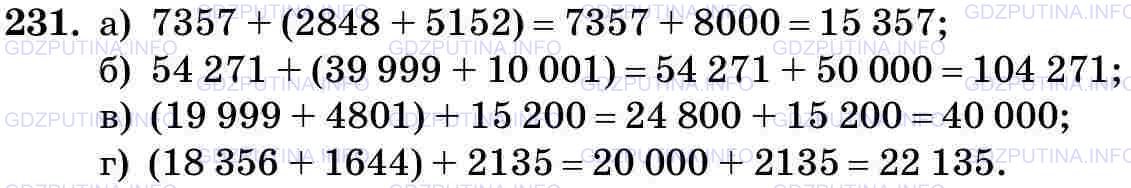
автор = {Блахота, Иштван, Перссон, Ларс-Эрик, Тефнадзе, Гиорги},
журнал = {Чехословацкий математический журнал},
ключевые слова = {система Виленкина; группа Виленкина; Норлунд означает; мартингальное пространство Харди; максимальный оператор; ряды Виленкина-Фурье; сильная сходимость; неравенство},
язык = {eng},
номер = {4},
издатель = {Институт математики Академии наук Чешской Республики},
title = {О Нерлунде средними рядами Виленкина-Фурье},
url = {http://eudml.
 org/doc/276158},
org/doc/276158}, volume = {65},
year = {2015},
}
TY — JOUR
AU — Благота, Иштван
AU — Перссон, Ларс -Эрик
AU — Тефнадзе, Георгий
TI — О средних Нёрлунда рядов Виленкина-Фурье
JO — Чехословацкий математический журнал
PY — 2015
PB — Институт математики АН Чешской Республики
VL — 65
IS — 4
SP — 983
EP — 1002
AB — Доказаны и обсуждены некоторые новые неравенства типа $(H_{p},L_{p})$ взвешенных максимальных операторов средних Виленкина-Нёрлунда с невозрастающими коэффициентами $ \lbrace q_{k}\двоеточие k\ge 0\rbrace $. Эти результаты являются наилучшими в определенном смысле. В качестве приложений указываются некоторые известные, а также новые результаты теории сильной сходимости таких средних Виленкина-Нёрлунда. Для достижения наших основных целей мы также докажем некоторые новые оценки, представляющие независимый интерес, для ядер этих результатов суммирования. В частных случаях общих средних Нёрлунда $t_{n}$ с невозрастающими коэффициентами аналогичные результаты можно получить для средних Фейера и Чезаро, выбирая порождающую последовательность $\lbrace q_{k}\colon k\ge 0\rbrace $ соответствующим образом.
LA — eng
KW — Система Виленкина; группа Виленкина; Норлунд означает; мартингальное пространство Харди; максимальный оператор; ряды Виленкина-Фурье; сильная сходимость; неравенство
UR — http://eudml.org/doc/276158
ER —
Ссылки
наверх- Благота, И., 10.1023/A:1026769207159, Acta Math. Висела. 89 (2000), 15-27. (2000) Zbl0973.42020MR1912235DOI10.1023/A:1026769207159
- Блахота, И., Связь между ядрами Дирихле по отношению к системам типа Виленкина, Acta Acad. Педагог. Агриенсис, Секта. Мат. (Н.С.) 22 (1994), 109-114. (1994) Zbl0882.42017
- Благота И., Гат Г., 10.1007/s10496-008-0001-z, Анал. Теория прил. 24 (2008), 1-17. (2008) Zbl1164.42022MR2422455DOI10.1007/s10496-008-0001-z
- Благота И., Тефнадзе Г., 10.1007/с10476-014-0301-9, Анал. Мат. 40 (2014), 161-174. (2014) Zbl1313.42083MR3240221DOI10.
 1007/s10476-014-0301-9
1007/s10476-014-0301-9 - Благота И., Тефнадзе Г., 10.5486/PMD.2014.5896, Опубл. Мат. Дебрецен 85 (2014), 181-196. (2014) MR3231514DOI10.5486/PMD.2014.5896
- Fujii, N., Максимальное неравенство для h2-функций на обобщенной группе Уолша-Пэли, Proc. Являюсь. Мат. соц. 77 (1979), 111-116. (1979) MR0539641
- Г{а}т, Г., 10.1016/С0021-9045(03)00075-3, Ж. Прим. Теория 124 (2003), 25-43. (2003) Zbl1032.43003MR2010779DOI10.1016/S0021-9045(03)00075-3
- G{á}t, G., 10.1007/BF01872107, Acta Math. Висела. 61 (1993), 131-149. (1993) Zbl0805.42019MR1200968DOI10.1007/BF01872107
- Гат Г., Гогинава У. Сходимость почти всюду (C,α)-средних квадратичных частичных сумм двойных рядов Виленкина-Фурье // Грузин. матем. Журнал 13 (2006), 447-462. (2006) Zbl1107.42006MR2271060
- Гат Г., Гогинава Ю.
 , 10.1007/s10114-005-0648-8, Acta Math. син., англ. сер. 22 (2006), 497-506. (2006) MR2214371DOI10.1007/s10114-005-0648-8
, 10.1007/s10114-005-0648-8, Acta Math. син., англ. сер. 22 (2006), 497-506. (2006) MR2214371DOI10.1007/s10114-005-0648-8 - Гат, Г., Надь, К., О логарифмической суммируемости рядов Фурье, Georgian Math. Журнал 18 (2011), 237-248. (2011) Zbl1221.42049MR2805978
- Гогинава У., 10.1007/с10476-010-0101-9, Анал. Мат. 36 (2010), 1-31. (2010) MR2606574DOI10.1007/s10476-010-0101-9
- Гогинава У., Максимальные операторы средних Фейера-Уолша, Acta Sci. Мат. 74 (2008), 615-624. (2008) Zbl1199.42127MR2487936
- Гогинава У., Максимальный оператор средних Марцинкевича-Фейера d-мерного ряда Уолша-Фурье, East J. Approx. 12 (2006), 295-302. (2006) MR2252557
- Гогинава Ю., Максимальный оператор (C, α) средних рядов Уолша-Фурье, Ann. ун-т науч. Будапешт. Роландо Этвёш, Sect. вычисл. 26 (2006), 127-135. (2006) Zbl1121.42020MR2388683
- Гогинава Ю.
 Сходимость почти всюду подпоследовательности логарифмических средних рядов Уолша-Фурье // Acta Math. акад. Педагог. Нихази. (NS) (только в электронном виде) 21 (2005), 169-175. (2005) Zbl1093.42018MR2162613
Сходимость почти всюду подпоследовательности логарифмических средних рядов Уолша-Фурье // Acta Math. акад. Педагог. Нихази. (NS) (только в электронном виде) 21 (2005), 169-175. (2005) Zbl1093.42018MR2162613 - Гогинава, У., 10.1006/jath.2001.3632, Ж. Прибл. Теория 115 (2002), 9-20. (2002) Zbl0998.42018MR1888974DOI10.1006/jath.2001.3632
- Мур, К. Н., Суммируемые ряды и факторы сходимости, Dover Publications, Нью-Йорк (1966). (1966) Zbl0142.30704MR0201863
- Мориц Ф., Сиддики А. Х., 10.1016/0021-9045(92)
-X, J. Прибл. Теория 70 (1992), 375-389. (1992) Zbl0757.42009MR1178380DOI10.1016/0021-9045(92)
-X
- Надь, К., Аппроксимация средними Нёрлунда двойных рядов Уолша-Фурье для липшицевых функций, Math. Неравный. заявл. 15 (2012), 301-322. (2012) Zbl1243.42038MR2962234
- Надь, К., Аппроксимация средними Нёрлунда рядов Уолша-Качмарца-Фурье, Грузинская математика.
 Журнал 18 (2011), 147-162. (2011) Zbl1210.42043MR2787349
Журнал 18 (2011), 147-162. (2011) Zbl1210.42043MR2787349 - Надь, К., Аппроксимация средними Чезаро отрицательного порядка рядов Уолша-Качмарца-Фурье, East J. Approx. 16 (2010), 297-311. (2010) Zbl1216.42006MR2789336
- Надь К., 10.1007/с10476-010-0404-х, Анал. Мат. 36 (2010), 299-319. (2010) Zbl1240.42133MR2738323DOI10.1007/s10476-010-0404-x
- Пал, Дж., Саймон, П., 10.1007/BF01896477, Acta Math. акад. науч. Висела. 29 (1977), 155-164. (1977) Zbl0345.42011MR0450884DOI10.1007/BF01896477
- Шипп, Ф., Перестановки рядов в системе Уолша, Math. Примечания 18 (1976), 701-706 перевод с мат. заметки 18 (1975), 193-201. (1975) MR03
- Симон П., 10.1007/с006050070004, Монац. Мат. 131 (2000), 321-334. (2000) MR1813992DOI10.1007/s006050070004
- Саймон, П., 10.1006/jmaa.2000.
 6732, J. Math. Анальный. заявл. 245 (2000), 52-68. (2000) Zbl0987.42022MR1756576DOI10.1006/jmaa.2000.6732
6732, J. Math. Анальный. заявл. 245 (2000), 52-68. (2000) Zbl0987.42022MR1756576DOI10.1006/jmaa.2000.6732 - Саймон, П., Исследования в отношении системы Виленкина, Ann. ун-т науч. Будапешт. Роландо Этвёш, Sect. Мат. 27 (1984), 87-101. (1984) Zbl0586.43001MR0823096
- Саймон П., Вайс Ф., 10.1016/j.jat.2007.05.004, J. Прибл. Теория 151 (2008), 1-19. (2008) Zbl1143.42032MR2403893DOI10.1016/j.jat.2007.05.004
- Тефнадзе Г., О максимальных операторах логарифмических средних Рисса рядов Виленкина-Фурье, Stud. науч. Мат. Висела. 51 (2014), 105-120. (2014) Zbl1299.42098MR3188506
- Тефнадзе Г., 10.3103/S1068362314010038, J. Contemp. Мат. Анальный. 4923-32 русский (2014). (2014) MR3237573DOI10.3103/S1068362314010038
- Тефнадзе Г., 10.1007/с10474-013-0361-5, Acta Math. Висела. 142 (2014), 244-259. (2014) Zbl1313.
 42086MR3158862DOI10.1007/s10474-013-0361-5
42086MR3158862DOI10.1007/s10474-013-0361-5 - Тефнадзе Г., О максимальных операторах средних Виленкина-Фейера на пространствах Харди, Матем. Неравный. заявл. 16 (2013), 301-312. (2013) Zbl1263.42008MR3060398
- Тефнадзе Г. О максимальных операторах средних Виленкина-Фейера // Тюрк. Дж. Матем. 37 (2013), 308-318. (2013) Zbl1278.42037MR3040854
- Тефнадзе Г., Замечание о коэффициентах Фурье и частных суммах рядов Виленкина-Фурье, Acta Math. акад. Педагог. Нихази. (NS) (только в электронном виде) 28 (2012), 167-176. (2012) Zbl1289.42084MR3048092
- Тефнадзе Г., Средние Фейера ряда Виленкина-Фурье, Stud. науч. Мат. Висела. 49 (2012), 79-90. (2012) Zbl1265.42099MR3059789
- Тефнадзе Г., Максимальные операторы логарифмических средних одномерных рядов Виленкина-Фурье, Acta Math. акад. Педагог. Нихази. (NS) (только в электронном виде) 27 (2011), 245-256.
 (2011) Zbl1265.42100MR2880697
(2011) Zbl1265.42100MR2880697 - Виленкин, Н. Дж., Об одном классе полных ортонормированных систем, Am. Мат. соц. Перевод сер. (2), 28 (1963), 1-35 перевод из Изв. акад. АН СССР, сер. Мат. 11 (1947), 363-400. (1947) Zbl0036.35601MR0154042
- Weisz, F., 10.1023/B:AMHU.0000028241.87331.c5, Acta Math. Висела. 103 (2004), 139-176. (2004) Zbl1060.42021MR2047878DOI10.1023/B:AMHU.0000028241.87331.c5
- Weisz, F., 10.1023/A:1014364010470, Анал. Мат. 27 (2001), 141-155. (2001) Zbl0992.42016MR1834858DOI10.1023/A:1014364010470
- Weisz, F., 10.1007/BF02205221, Анал. Мат. 22 (1996), 229-242. (1996) Zbl0866.42020MR1627638DOI10.1007/BF02205221
- Weisz, F., 10.1007/BFb0073448, Lecture Notes in Mathematics 1568 Springer, Berlin (1994). (1994) Zbl0796.60049MR1320508DOI10.1007/BFb0073448
Вы должны войти, чтобы оставлять комментарии.
Научная деятельность Г. Гата.
Научная деятельность Г. Гата.Научная деятельность Г. Гата. Это html-файл, и следовательно, математические формулы не в лучшей форме.
| Gyrgy Gt |
| Научная деятельность |
Появились некоторые результаты в статьях
1. Гат Г. Одно из приложений
быстрое преобразование Фурье,
Бюллетени по прикладной математике 41 (1986), 102-105
ZBL
613.65146.
2. Гат Г. О вычислении
обобщенный быстрый дискретный Фурье
преобразование, Бюллетени по прикладной математике 45 (1987), 123-134
ЗБЛ 636.65040.
В статьях [3,4,5] я ввожу новую систему ортонормированных функций,
как общее обобщение некоторых известных, таких как
Уолш,
системы Виленкина, системы продуктов УДМД (представлены Ф. Шипп).
Шипп).
В [5] я показываю, что эти системы дают
новый инструмент в исследовании
предельных периодических почти четных арифметических функций.
Этим
новый метод я решаю некоторые задачи, касающиеся арифметических
функции. В основном, суть метода
в том, что
арифметические функции такого рода могут быть распространены на Виленкин
групп., и система расширения
эта функция
воля
быть системами типа Виленкина. Итак, процедуры, известные в теории
гармонический анализ на группах Виленкина
может быть принят для
исследование арифметических функций.
3. Гат Г. Виленкин Ряды Фурье и предельные периодические
арифметические функции, Colloq Soc. Дж. Боляи 58 Прибл. теория,
Kecskemet,
(Венгрия) (1990), 315332 ZBL 760.42013, MR 94g:42042.
4. Гат Г. Ортонормированные системы на группах Виленкина // Acta Math.
Венгрия. 58(1-2) (1991), 193198 ZBL 753. 11027, MR 93e:42039.
11027, MR 93e:42039.
5. Гат Г. О почти четных арифметических функциях через ортонормированные функции.
системы на группах Виленкина, Acta Arith. 49(2) (1991), 105123
ЗБЛ
725.11049, MR 92j:11083.
В [6] я доказал еще несколько задач, касающихся неограниченных функций Виленкина.
системы и пространства Харди. Я упоминаю, что дал необходимое и
достаточное условие верхней ограниченности так называемого
Оператор Суноути
То есть для ||Tf|| 1 \leq C||f|| Х .
Для
сейчас
я знаю 21
ссылки на эту статью.
6. Гат Г. Исследование некоторых операторов относительно
Система Виленкина, Acta Math. Венгрия. 61(1-2) (1993), 131149
ЗБЛ
805.42019, MR 94d:42035.
В [7] Gyrgy Gt доказывает, что системы типа Виленкина
введенная им, а обычная система Виленкина не
эквивалент
базы в пространстве L p (1 < p
< \infty).
7. Гат Г. О неэквивалентности виленкиноподобных систем // Acta. Мат. акад. Паед. Ньиредьх. 13 (1993), 87-95 ЗБЛ 913.42022.
8. Гат Г. Исследование некоторых операторов относительно
Виленкиноподобные системы, Annales Univ. науч. Будапештиенсис 14
(1994), 61-70 ZBL 923.42018, MR 96a:42034.
9. Гат Г. Об одной теореме сходимости по норме по Виленкину.
система в пространствах Харди, Acta Acad. Паед.
Агриенсис Сектио
Matematicae 22 (1994), 101–107 ZBL 882.42016.
В [11] Gyrgy Gt и Rodolfo Toledo доказали некоторые
аппроксимационные теоремы относительно средних Фейра
интегрируемых функций на неабелевых компактах, полностью несвязных
группы. Среди прочего, они доказали, что известная норма
теорема о сходимости S n f f \in L p (1 < p < \ infti)
не. Кроме того, они доказали
что если один
взять
Вместо этого Fejr означает частичные суммы ряда Фурье, тогда
имеет место сходимость по норме.
В [10] Gyrgy Gt доказал, что теорема Карлесона не имеет места.
в неабелевом случае, т. е. существует
некоммутативной группы Виленкина и p > 1, f \in
L p , например, частичные суммы Фурье
серии
не сходятся на функции почти везде.
10. Гат Г. Поточечная сходимость средних Фейера на компактных
полностью несвязанные группы, Acta Sci. Мат.
(Сегед) 60 (1995),
311-319 ЗБЛ 835.43008, МР 96i:43007.
11. Гат Г., Толедо Р., Lp-нормальная сходимость рядов в компактах.
полностью несвязанные группы, Analysis Math. 22
(1996), 13-24 ЗБЛ
856.42017, MR 97f:42043.
12. Гат Г. Сходимость и суммирование по
Виленкиноподобные системы в: Последние разработки в
Abstract Harmonic
Анализ с приложениями в обработке сигналов, Наука, Белград
и Электронный факультет,
Ниш, 1996, стр. 137-146.
В [13] Gyrgy Gt доказано для всех двумерных
интегрируемая функция, которую средние по Фейру двухпараметрического
Ряды Фурье сходятся к функции почти всюду,
при условии, что отношение индексов остается в некотором конусе.
Тот же результат доказал Ф. Вайс. Его статья появилась в тот же год.
13. Гат Г. Поточечная сходимость двойных средних Уолша-Фейера.
Анналы унив. науч. Budapestiensis, Sect. Комп. 16
(1996), 173-184
ZBL 891.42014, MR 99b:42033.
В [14] Gyrgy Gt доказывает, что более 25 лет
гипотеза М.Х. Taibleson Анализ Фурье на локальном
поля
(издательство Принстонского университета). А именно, он доказывает, что
Теорема Фейра-Лебега относительно системы характеров
группа 2-адических целых чисел. Он также доказывает, что
максимальный оператор средних Фейра имеет тип (H,L).
14. Гат Г. О сходимости почти всюду средних Фейера.
функций на группе 2-адических целых чисел, Journal of Approx.
Theory vol 90 (1) (1997), 88-96 ZBL 883.42021, MR 98m:42042.
В [15] Gyrgy Gt доказал так называемую основную теорему
двумерного диадического производного. А именно, если f \in
L 1 ([0,1) 2 ),
затем
А именно, если f \in
L 1 ([0,1) 2 ),
затем
|
почти везде, где (n 1 ,n 2 )
N 2 , |n 1 -n 2 |
б (б
— некоторый параметр), d (н 1 ,н 2 ) ,
и я
двумерная диадическая разность
и интеграл соответственно.
15. Гат Г. О двумерном точечно-диадическом исчислении. Журнал ок. Теория 92 (2) (1998), 191-215
Журнал ок. Теория 92 (2) (1998), 191-215
ЗБЛ 897.42017, МР
99с:42049.
Определить оператор T Г.И. Суноути В [16] можно найти:
Теорема. Пусть f : G m \to R , f \in L 1 (Г м ) , E 0 f=0. Если некоторые условия удовлетворенный затем
|
Результатом Gt является тот самый во-первых, по нижним границам этого оператора. Ничего не известно
до этого. Также представляет интерес, что так как эта статья появилась в газете
Дейли, Дж., Филлипс, К., Множители Уолша и квадратичные функции
для Hardy Space h2, Acta Math. Венгрия. 79 (4) (1998),
311-328.
Венгрия. 79 (4) (1998),
311-328.
можно прочитать доказательство теоремы относительно Уолша
система. То есть теорема доказана, если m j =2
для всех j и
также в случае достаточно быстрого роста m. Итак, осталось
разрыв. Это довольно необычно в теории двоичной гармоники.
анализ. Обычная процедура выглядит следующим образом. Теорема доказана
для системы Уолша, во-первых. Тогда для ограниченного Виленкина
систем, а потом долгий перерыв… Наконец-то есть
«что-то» по отношению к неограниченным системам Виленкина.
метода относительно систем Уолша и ограниченных систем Виленкина
очень похожи. С другой стороны, обсуждение
не ограничено
Системы Виленкина нуждаются в более мощных методах. Трудности
увеличить еще раз….
16. Гат Г. О нижней границе оператора Суноути с
по системе Виленкина, Analysis Math. 23 (1997),
259-272 ЗБЛ 888. 42017, МР 99ф:42057.
42017, МР 99ф:42057.
17. Гат Г. О ядерных функциях Фейера относительно
Система Уолша-Пэли, Acta Acad. Паед. Agriensis Section
Matematicae
24 (1997), 105-110 ЗБЛ 888.42015.
18. Гат Г. Об одной теореме типа Харди-Литтлвуда относительно виленкиноподобные системы // Acta Acad. Паед. Агриенсис
Раздел Matematicae 25 (1998), 83-89 ZBL 929.42018, MR 1 728 604.Пусть k будет так называемым Система Уолша-Качмарца. Это не что иное, как перестройку системы Уолша-Пэли, которую мы говорил о.
В [19] cikkben можно найти следующие результаты Gt: по системе Уолш-Качмарц:
Теорема. с к н ф \ к ф (н) почти везде для всех ф\в Л 1 (И).
Теорема. Оператор с * имеет
тип (р,р)
для каждого 1 < p \leq \infty,
и он слабого типа (1,1). Более того, ||s * f|| 1 \leq
с|||е||| Н 1 .
Более того, ||s * f|| 1 \leq
с|||е||| Н 1 .
Последний результат (H,L) Gt и Nagy улучшили [32]. Они доказано c||f|| Х 1 , вместо c|||f||| Н 1 .
19. Гат Г. О суммируемости (С; 1) суммируемых функций с относительно системы Уолша-Качмарца, Studia Math. 130 (2)
(1998 г.), 135-148 ЗБЛ 905.42-016, МР 99е:42043.
20. Гат Г. О лемме Кальдерона–Зигмунда о разложении Группа Уолша-Пэли, Acta Math. акад. Паед. Ньиредьх. 14
(1998 г.), 25-30 ЗБЛ 908.42011, МР 1 712 506.
В [21] n Nagy и я проверили результат из [15] для ограниченных группы Виленкина. То есть основная теорема диадического
Расчет. Это читается как: lim мин(n 1 ,n 2 ) d (n 1 ,n 2 ) Если
«=»
f п.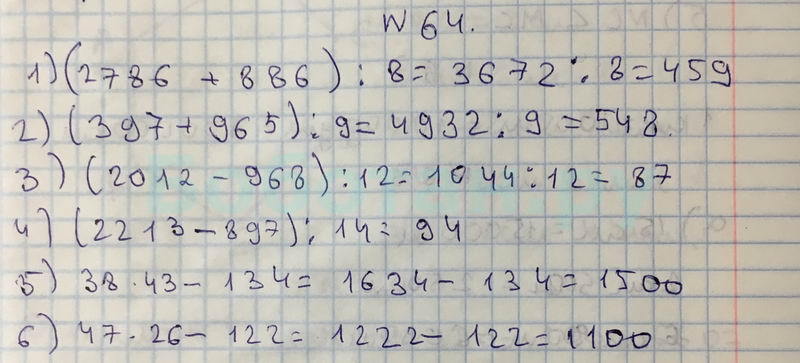 в., где (n 1 ,n 2 ) \in
N 2 ,
|n 1 -n 2 | \leq
б
(b некоторая заданная
параметр).
в., где (n 1 ,n 2 ) \in
N 2 ,
|n 1 -n 2 | \leq
б
(b некоторая заданная
параметр).
21. Гат Г., Надь К. Основная теорема двухпараметрической
поточечное производное по группам Виленкина, Analysis Math.
25 (1999),
33-55 ЗБЛ 0932.42020, МР 1 678 505.
В [22] Gt доказывает: Пусть G m — любая группа Виленкина
(ограниченный
или нет), 1 < p и f \in
Л р (Г м ). Затем s n f
\к ф
э.э.
Раньше ничего не было известно в отношении
почти всюду сходимость средних фейр на
неограниченные
группы Виленкина. Эта статья объемом 36 страниц состоит из
доказательство этой теоремы.
22. Гат Г. Поточечная сходимость фейеровских средних функций.
о неограниченных группах Виленкина, Журнал Прибл.
Теория 101 (1)
ноябрь (1999 г. ), 1-36 ZBL 0972.42019, MR 1 724 023.
), 1-36 ZBL 0972.42019, MR 1 724 023.
23. Гат Г., Толедо Р., Коэффициенты Фурье и абсолютные значения.
сходимость на компактных вполне несвязных группах, Math.
Pannonica 10/2 (1999), 223-233 ZBL 0932.43010, MR 1 704 611.
В [24] я доказал применением элементарных диадных методов
(без мартингальной теоремы о сходимости) a
Кальдерон-Зигмунд
лемма о разложении для неограниченных групп Виленкина.
24. Гат Г. О а.е. сходимость ряда Фурье по
неограниченные группы Виленкина, Acta Math. акад. Паед. Ньиредьх.
15
(1999), 27-34 ЗБЛ 0980.42019, МР 1 706 915.
В [25] доказано Gt Если нет ограничения на индексы,
то наибольшее пространство сходимости двумерного
s n,m f Уолш-Пэли-Фейр означает L
log L. Это
для произвольной измеримой функции d
исчезает в
плюс бесконечность, мы
имеют функцию в LlogL d(L),
такой
та, с н,м ж
может сходится к f в смысле
Прингшейма только на множестве нулевой меры.
25. Гат Г. О расходимости средних (С; 1) двойных
Ряд Уолша-Фурье, Proc. амер. Мат. соц. 128 (2000),
1711-1720
ЗБЛ 0976.42016, МР 1 657 751.
В [26] Блахота и я доказали для двумерных ограниченных
да
системы (эта система является общим обобщением
Виленкина, системы УДМД), что так называемая коническая Фейр
средние интегрируемых функций сходятся к функции
почти
повсюду. Это обобщение результатов работы [13].
26. Благота И., Гат Г. Поточечная сходимость двойных
Виленкин-Фейер означает, Stud. науч. Мат. Венгрия. 36 (2000),
49-63
ZBL 0973.42021, MR 2001h:42041.
В [27]:
Пусть Т к ф
является
оператор Суноути по системе Уолша-Качмарца.
Мы
доказал, что Т к gyengn слабого типа (1,1),
тип (H 1 , L 1 ) и (p, p)
для всех 1 < p \leq
2.
27. Гат Г., Надь К. Об операторе Суноути относительно
система Уолша-Качмарца, Acta Math. Венгрия.
том 89 (1-2)
(2000), 93-101 ZBL 0973.42022, MR 2003e:42040.
В [28] я доказал (одномерный случай)
теорема для систем типа Виленкина. Этих систем
общий
обобщения Уолша, Виленкина, системы характеров
m-адические целые числа, UDMD, системы UCP product
(и многие другие…).
28. Гат Г. О суммируемости (С, 1) для систем типа Виленкина.
Студия математики. 144 (2) (2001), 101-120 ЗБЛ 0974.42020,
МР
2001к:42033.
29. Гат Г. О ядерных функциях Фейера относительно
Система Уолша-Качмарца, Acta Math. акад. Паед.
Ньиредьх. 17(2)
(2001), 121-126 MR 2002m:42030.
30. Гат Г. Расходимость средних (С; 1) d-мерных
Ряды Уолша-Фурье, Analysis Math. 27 (2001),
157171 ЗБЛ
0996.40002, MR 2002j:42005.
31. Гат Г. Наилучшее приближение системами типа Виленкина // Acta.
Мат. акад. Паед. Ньиредьх. 17(3) (2001), 161-169
ЗБЛ 0992.42011,
МР 2002k:42057.
В [32] мы доказали теорему Фейра–Лебега для
перестановка системы персонажей
группа р-серии. Мы
также доказал, что максимальный оператор средних Фейра имеет вид
тип (H,L).
32. Гат Г., Надь К., Чезаро суммируемость системы символов
поля p-ряда в перегруппировке Качмажа,
Analysis Math
28 (2002), 1–36 MR 2003c:42011.
В [33] Gt дал наибольшее пространство сходимости относительно
А именно, в 1989 году Шипп и Уэйд доказали, что если
двухпараметрических
функция принадлежит LlogL, то ее двоичный интеграл равен
почти всюду дифференцируемы, а 9Производная 0034 равна
функция п.в. Если доказано, эта теорема точна, т. е. для
произвольная измеримая величина
плюс бесконечно исчезающая функция d
у нас есть функция в LlogLd(L)такая
что его двоичный интеграл может быть дифференцируем
на
множество нулевой меры, самое большее. В классическом случае (обычный
интеграл и производная) этот результат принадлежит Саксу.
В классическом случае (обычный
интеграл и производная) этот результат принадлежит Саксу.
Он доказал это
в 1935 г.
33. Гат Г. О расходимости двумерного диадического
разность двоичных интегралов, Журнал
Теория приближения
116 (1) (2002), 1-27 ЗБЛ 0999.42016, МР 1 909 010.
В 1996 г. Вайс представил двумерный
Оператор Суноути T имеет
введите (p,p) для всех 1 < p < \infty
и слабого типа (L 1 log + Л, Л 1 ).
В [34] Gt доказал, что теорему нельзя улучшить:
Теорема: пусть d:[0,+\infty) \to
[0,+\infty) , lim t\to\infty d(t)=0
измеримый. То есть
существует
f такое, что f \in L log + Ld(L)
и Tf(x) = +\infty
э.э.
34. Гат Г. Об операторе Суноути относительно
двумерная система Уолша-Пэли, Функция, Серия,
Операторы —
Мемориальная конференция Алексита, Будапешт (Венгрия), Colloq Soc.


 1007/s10476-014-0301-9
1007/s10476-014-0301-9 , 10.1007/s10114-005-0648-8, Acta Math. син., англ. сер. 22 (2006), 497-506. (2006) MR2214371DOI10.1007/s10114-005-0648-8
, 10.1007/s10114-005-0648-8, Acta Math. син., англ. сер. 22 (2006), 497-506. (2006) MR2214371DOI10.1007/s10114-005-0648-8 Сходимость почти всюду подпоследовательности логарифмических средних рядов Уолша-Фурье // Acta Math. акад. Педагог. Нихази. (NS) (только в электронном виде) 21 (2005), 169-175. (2005) Zbl1093.42018MR2162613
Сходимость почти всюду подпоследовательности логарифмических средних рядов Уолша-Фурье // Acta Math. акад. Педагог. Нихази. (NS) (только в электронном виде) 21 (2005), 169-175. (2005) Zbl1093.42018MR2162613 Журнал 18 (2011), 147-162. (2011) Zbl1210.42043MR2787349
Журнал 18 (2011), 147-162. (2011) Zbl1210.42043MR2787349 6732, J. Math. Анальный. заявл. 245 (2000), 52-68. (2000) Zbl0987.42022MR1756576DOI10.1006/jmaa.2000.6732
6732, J. Math. Анальный. заявл. 245 (2000), 52-68. (2000) Zbl0987.42022MR1756576DOI10.1006/jmaa.2000.6732 42086MR3158862DOI10.1007/s10474-013-0361-5
42086MR3158862DOI10.1007/s10474-013-0361-5 (2011) Zbl1265.42100MR2880697
(2011) Zbl1265.42100MR2880697