Виленкин Н.Я. и др. Математика 5 класс + решебник
- формат pdf
- размер 42.3 МБ
- добавлен 03 мая 2010 г.
Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 5 класс, учебник, 2008, 280 с. (+ решебник 2001, 195 с. )
Учебник для общеобразовательных учреждений. Глава 1 — натуральные числа; глава 2 — дробные числа.
Решебник составлен для учебника 2000 г., но задачи не изменились,
только добавлен ряд новых задач. Например, соответствие номеров
учебника и решебника:
в учебнике 137 — в решебнике 134,
в учебнике 1484 — в решебнике 1457.
Смотрите также
- формат djvu
- размер 1.28 МБ
- добавлен
01 декабря 2010 г.
3-я часть решебника по геометрии 7-9 класс. (7 класс. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, И. И. Юдина) даёт правильные решения по данному предмету. Помогает ученикам 9го класса, которые не знаю данный предмет.
- формат djvu
- размер 1.89 МБ
- добавлен 16 декабря 2009 г.
Геометрия, 10-11 класс, Атанасян, решебник 10кл, 1-399.
- формат djvu, pdf
- размер 4.9 МБ
- добавлен 03 мая 2010 г.
Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 6 класс, учебник, 1994, 256 с. (+ решебник 2001, 104 с. ) Учебник для 6-го класса средней школы. Глава 1 — обыкновенные дроби; глава 2 — рациональные числа.
- формат pdf
- размер 8.82 МБ
- добавлен 24 апреля 2011 г.
Домашняя работа (ГДЗ) (решебник) по алгебре за 9 класс к задачнику «Алгебра 9 кл. А. Г. Мордкович и др. М.: «Мнемозина», 2008-2010 годов издания. «
- формат exe
- размер 3.11 МБ
- добавлен 30 ноября 2010 г.
Решебник даёт правильные решения по данному предмету. Помогает ученикам 9-го класса, которые не знают данный предмет.rn
- формат pdf
- размер 25.43 МБ
- добавлен 10 апреля 2011 г.
Математика. 7 класс (Алгебра, Геометрия) (Решения с комментариями к итоговым контрольным работам) Сост.
Гальперина А. Р. — 2011. На русском языке
- формат exe
- размер 4.42 МБ
- добавлен 30 ноября 2010 г.
Решебник по Алгебре 8 класс Мордкович — даёт правильные решения по данному предмету. Помогает ученикам 7го класса, которые не знаю данный предмет.rn
- формат pdf
- размер 2.93 МБ
- добавлен 28 апреля 2009 г.
Решебник на все задачи из сборника «дидактические материалы по геометрии 11 класс Зив 2002 год» в хорошем качестве.
- формат pdf
- размер 2.32 МБ
- добавлен 02 января 2011 г.
4-е изд. учебно-методическое пособие.
— Экзамен, 2009. — 129 с. Серия: Решебник Качество: Отсканированные страницы В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Математика: 5 кл.: учеб. для общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 8-е изд. стер. — М.: Мнемозина, 2006». Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости…
ГДЗ по математике за 5 класс к учебнику С.М. Никольского ОНЛАЙН
Перейти к содержимому
Избранное / Решебники (ГДЗ) для школьников
Домашняя работа по математике за 5 класс: к учебнику С.М. Никольского и др. «Математика. 5 класс: учебник для общеобразовательных учреждений» / М.А. Попов. — М., 2012. — 222 с.
Пособие содержит выполнение всех заданий из учебного издания «Математика.
5 класс: учеб. для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. — 9-е изд. — М.: Просвещение, 2010».
Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по математике.
ОГЛАВЛЕНИЕ
Глава 1. Натуральные числа и нуль………………………………6
1.1. Ряд натуральных чисел………………………………….6
1.2. Десятичная система записи натуральных чисел……………..6
1.3. Сравнение натуральных чисел……………………………8
1.4. Сложение. Законы сложения…………………………..8
1.5. Вычитание………………………………………9
1.6. Решение текстовых задач с помощью сложения и вычитания… 11
1.7. Умножение. Законы умножения…………………………..13
1.8. Распределительный закон……………………………..15
1.9. Сложение и вычитание чисел столбиком.
…………………16
1.10. Умножение чисел столбиком…………………………..18
1.11. Степень с натуральным показателем…………………..21
1.12. Деление нацело…………………………………..22
1.13. Решение текстовых задач с помощью умножения и деления… 23
1.14. Задачи «на части»…………………………………27
1.15. Деление с остатком……………………………….31
1.16. Числовые выражения……………………………….35
1.17. Задачи на нахождение двух чисел по их сумме и разности……38
Дополнения к главе 1……………………………41
1. Вычисления с помощью калькулятора…………………..41
2. Исторические сведения……………………………..42
3. Занимательные задачи………………………………43
Глава 2. Измерение величин………………………………52
2.1. Прямая. Луч. Отрезок……………………………..52
2.2. Измерение отрезков.
………………………………53
2.3. Метрические единицы длины…………………………55
2.4. Представление натуральных чисел на координатном луче….56
2.5. Окружность и круг. Сфера и шар……………………..57
2.6. Углы. Измерение углов…………………………….59
2.7. Треугольники…………………………………..63
2.8. Четырехугольники………………………………..66
2.9. Площадь прямоугольника. Единицы площади……………69
2.10. Прямоугольный параллелепипед…………………….71
2.11. Объем прямоугольного паралеллепипеда. Единицы объема …73
2.12. Единицы массы……………………………………75
2.13. Единицы времени………………………..75
2.14. Задачи на движение……………………………..76
Дополнения к главе 2………………………………….81
1. Многоугольники………………………………………81
3. Занимательные задачи……
…………………………..83
Глава 3. Делимость натуральных чисел……………………85
3.1. Свойства делимости……………………………85
3.2. Признаки делимости…………………………….86
3.3. Простые и составные числа……………………….89
3.4. Делители натурального числа……………………..89
3.5. Наибольший общий делитель………………………93
3.6. Наименьшее общее кратное……………………….96
Дополнения к главе 3………………………………….98
1. Использование четности при решении задач……………..98
3. Занимательные задачи……………………………….99
Глава 4. Обыкновенные дроби…………………………..102
4.1. Понятие дроби………………………………..102
4.2. Равенство дробей……………………………..105
4.3. Задачи на дроби………………………………109
4.4. Приведение дробей к общему знаменателю…….
……113
4.5. Сравнение дробей……………………………..117
4.6. Сложение дробей………………………………121
4.7. Законы сложения………………………………126
4.8. Вычитание дробей……………………………..130
4.9. Умножение дробей……………………………..135
4.10. Законы умножения. Распределительный закон……….141
4.11. Деление дробей……………………………….142
4.12. Нахождение части целого и целого по его части……148
4.13. Задачи на совместную работу……………………151
4.14. Понятие смешанной дроби………………………156
4.15. Сложение смешанных дробей…………………….159
4.16. Вычитание смешанных дробей………………….. 162
4.17. Умножение и деление смешанных дробей…………..166
4.18. Представление дробей на координатном луче………171
4.19. Площадь прямоугольника. Объем прямоугольного параллелепипеда…..174
Дополнения к главе 4.
…………………………………178
1. Сложные задачи на движение по реке…………………..178
3. Занимательные задачи……………………………….182
Задачи для повторения…………………………………191
Средняя линия трапеции атанасяна предлежания. Срединная линия трапеции
Тема «Средняя линия трапеции» относится к одной из важных тем курса геометрии. Эта фигура довольно часто встречается в различных задачах, как и ее средняя линия. Задания, содержащие данные по этой теме, часто встречаются в итоговых контрольно-аттестационных работах. Знания по этой теме также могут пригодиться при обучении в средних и высших учебных заведениях.
Хотя в теме заявлена фигура трапеции, рассмотрение данной темы может проходить в ходе изучения темы «Векторы» и «Использование векторов при решении задач».
Это можно понять, взглянув на слайд презентации.
Здесь автор определяет срединную линию как отрезок, соединяющий середины сторон. Причем здесь также отмечается, что срединная линия трапеции параллельна ее основаниям, а также равна их полусумме. Именно в ходе доказательства этого утверждения пригодятся знания, связанные с векторами. Применяя правила сложения векторов по рисунку, приведенному в качестве иллюстрации условия, получаются равенства. У этих равенств одна и та же левая сторона, и она является средней линией трапеции, заданной в виде вектора. Складывая эти равенства, мы получаем большое выражение в правой части равенства.
слайды 1-2 (Тема презентации «Средняя линия трапеции», определение средней линии трапеции)
Если внимательно рассмотреть, то в двух случаях получается сложение противоположных векторов, в результате чего получается ноль . Тогда остается, что двойной вектор, содержащий среднюю линию трапеции, равен сумме векторов, содержащих основания.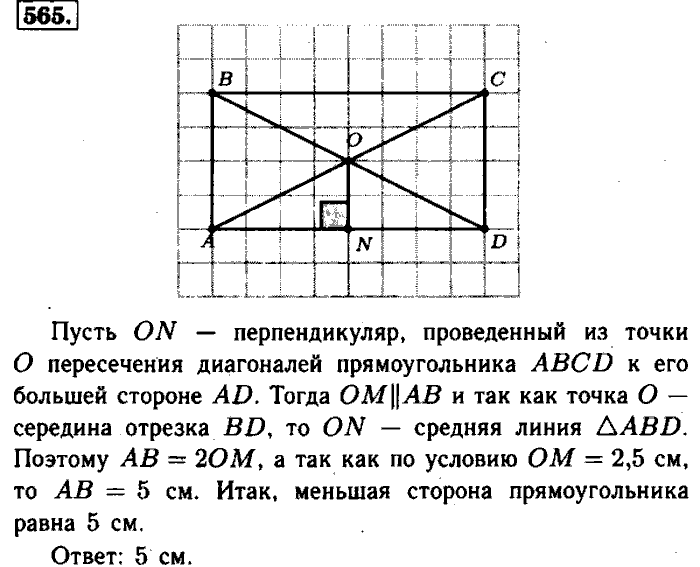
Разделив это равенство на 2, получается, что вектор, содержащий среднюю линию, равен половине суммы векторов, содержащих основания. Теперь идет сравнение векторов. Получается, что все эти векторы одинаково направлены. Это означает, что знаки векторов можно смело опускать. И тогда получается, что средняя линия самой трапеции равна половине суммы оснований.
Презентация содержит один слайд, содержащий большой объем информации. Здесь дано определение средней линии трапеции, а также указано ее основное свойство. В курсе геометрии это свойство является теоремой. Итак, здесь теорема доказывается с использованием знания понятия векторов и действий над ними.
Преподаватель может дополнить эту презентацию своими примерами и заданиями, но здесь публикуется все, что требуется для среднего уровня знаний по данному предмету. При этом автор оставил возможность учителю пофантазировать, доработать то, что он сам хочет, чтобы создать соответствующую атмосферу на уроке. Не забывайте и о самом настроении на урок.
Тогда с помощью этой презентации вы точно сможете добиться желаемого результата.
«Урок площади трапеции» — В основании прямоугольная трапеция 5см. и 17см., а меньшая сторона 10см. Учитель подводит итоги, задавая вопросы: Кто набрал 5, 4, 3 балла? В каждом случае формулируется теорема, которая доказана. Решение задачи. Как рассчитать площадь трапеции? Какие элементы плоских фигур используются в формулах площади?
«Задачи по теореме Пифагора» — № 21 Находка: X. № 18 Находка: X. № 27 Находка: X. Задания по готовым рисункам («Теорема Пифагора»). #23 Найти: X. #25 Найти: X. #26 Найти: X. #13 Найти: X. #20 Найти: X. #19Находка: X. #14 Находка: X. Вы выполнили все предложенные задания. #29 Находка: X. #28 Находка: X. #30 Находка: X. #22 Находка: X.
«Теорема Фалеса» — Фалес широко известен как геометр. Астрономия. Милетский материалист. Проведем через точку B2 прямую EF, параллельную прямой A1A3. Из равенства треугольников следует равенство сторон В1В2=В2В3. Теорема Фалеса.
Считается, что Фалес первым изучил движение солнца по небесной сфере. Треугольники B2B1F и B2B1E равны по второму знаку равенства треугольников.
«Теорема синусов» — Стороны треугольника пропорциональны синусам противоположных углов. Решение: Устная работа: Ответы на задания по рисункам: Проверка домашнего задания. Тема урока: Теорема синусов. Теорема синусов:
«Урок теоремы Пифагора» — Определить вид треугольника: Знакомство с теоремой. Доказательство теоремы. Разогревать. Теорема Пифагора. И найти лестницу длиной 125 футов. План урока: Исторический экскурс. Показ картинок. Решение простых задач. Вычислите высоту CF трапеции ABCD. Доказательство. Определить тип четырехугольника КМНП.
«Теорема Пифагора 8 класс» — ЦИФРЫ. Деление чисел на четные и нечетные, простые и составные. Дано: прямоугольный треугольник a,b катеты c — гипотенуза. Высота. Доказательство Бхаскари. Пифагорейские открытия в математике. Дано: Прямоугольный треугольник, a, b — катеты, c — гипотенуза.
Докажите: c2 = a2 + b2. Меньшая сторона прямоугольного треугольника.
Определение: Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. АК = КС БЭ = СЕ КЭ — средняя линия АВС Определение: средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон. A BC K N E AN = HB KE = CE NOT — средняя линия ABSK A B C K E Сколько средних линий в треугольнике? Сколько средних линий в трапеции?
Срединная линия треугольника Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. А В М К Дано: АВС, МК — средняя линия Доказательство: Так как по условию МК средняя линия, то АМ = МБ = ½ АВ, СК = КВ = ½ ВС, Отсюда, ВМ АВ ВК ВС 1 2 В — общий для АВС и МВК, значит, АВС и МВК подобны по второму признаку сходства, следовательно, ВМС = А, значит МС АС. Докажите: MK AS, MK = ½ AS MK AS 1 2 Из подобия треугольников также следует, что, т. е. MK = ½ AS.
Решить проблему F R N ? А Б
Доказательство: Проведем A 1 B 1 A B C A1A1 B1B1 O C1C1 По условию AA 1, BB 1 медианы, значит BA 1 = CA 1, AB 1 = CB 1, то есть A 1 B 1 есть средняя линия.
Отсюда А 1 В 1 АВ, следовательно, 1 = 2, 3 = 4. Следовательно, треугольники АОВ и А 1 ОВ 1 подобны в двух углах. Следовательно, их стороны пропорциональны: АО БО АВ А1ОА1О В1ОВ1О А1В1А1В1 По свойству средней линии треугольника АВ = 2 А 1 В 1 , т.е. АО БО АВ А1ОА1О В1ОВ1О А1В1А1В1 2 1 Аналогично, СО С1ОС1О 2 1 Получаем: C1OC1O АОБОКО A1OA1OB1OB1O 2 1
Срединная линия трапеции Теорема. Средняя линия трапеции параллельна основаниям и равна половине их суммы. А Б В К М Р Дано: АБСК — трапеция МП — средняя линия Доказать: МП АК, МП ВС МП = Доказательство: О , тогда ВС АК, а, следовательно, ВС МЕ АК Так как МП — средняя линия, то АМ = МБ, КР = СР E Следовательно, MP лежит на ME, что означает MP AK, MP BC. Заходим в ВК. По теореме Фалеса О — середина ВК, значит МО — средняя линия АВК, ОР — средняя линия ВСК МП = МО + ИЛИ = ½ АК + ½ ВС = ½ (АК + ВС ) = т.е. в точке P.
Чтобы использовать предварительный просмотр презентаций, создайте учетную запись Google (аккаунт) и войдите в нее: https://accounts.
google.com
Подписи к слайдам:
Средняя строка (8 класс)
Средняя строка треугольник
Средняя линия треугольника. Определение: Отрезок, соединяющий середины двух сторон треугольника, называется СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.
Теорема Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. то есть: KM ║ AC KM = ½ AC A B C K M
Решите задачу устно: A B C K M 7 см Дано: M K — ср. линия Найти: AC?
Работаем в парах:
Решим задачу: Дано: MN — ср. линия Найти: P ∆ ABC M N A B C 3 4 3, 5
Работать в парах:
Срединная линия трапеции
Напомним: Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны A D B C BC || AD — основания AB łł CD — стороны
Срединная линия трапеции. Определение: Средняя линия трапеции — это отрезок, соединяющий середины ее сторон. A D B C M N MN — средняя линия трапеции ABCD
Теорема о средней линии трапеции Средняя линия трапеции параллельна ее основаниям и равна половине их суммы.
то есть: M N ║BC║A D M N = ½ (BC+A D) M N A D B C
Решить устно: M N A D B C 6,3 см 18,7 см?
Решите устно в парах: Дано: АВ = 16 см; CD = 18 см; М Н = 15 см. Найти: Р ABCD = ? M N A D B C
Самостоятельная работа Задача: Средняя линия трапеции 5см. Найдите основания трапеции, если известно, что нижнее основание в 1,5 раза больше верхнего. Решение: A D B C 5 см Пусть BC = X см, тогда AD = 1,5X см BC+AD = 10 см X + 1,5X = 10 X = 4 Итак: BC = 4 см AD = 6 см
СПАСИБО ЗА УРОК!!!
Презентация разработана учителем математики ГБОУ СОШ № 467 г. Санкт-Петербурга Колпинского района Лугвиной Натальей Анатольевной
На тему: методические разработки, презентации и конспекты
Занятие по обобщению и закреплению знаний на тему «Средняя линия треугольника. Срединная линия трапеции» в 8 классе с применением ИКТ….
Рабочая тетрадь — индивидуальное творческое задание для учащегося. который предполагает самостоятельную работу с текстом по теме «Трапеция.
Срединная линия трапеции», применение знаний при решении задач. …
резюме другие презентации
«Построение правильных многоугольников» — ?=60?. 180?. Геометрия. знак равно н. n — 2. Работа выполнена учителем математики МОУ «Гимназия № 11» Лисицыной Е.Ф.
«Теорема Фалеса» — Теорема Фалеса. Геометрическая теорема названа в честь Фалеса. Астрономия. Проведем через точку B2 прямую EF, параллельную прямой A1A3. Считается, что Фалес первым изучил движение Солнца по небесной сфере. Презентация по геометрии Ученики 9Класс «А» Сорогина Полина. Милетский материалист. Геометрия. По свойству параллелограмма A1A2=FB2, A2A3=B2E. Фалес широко известен как геометр. А так как A1A2=A2A3, то FB2=B2E.
«Разложение вектора на два неколлинеарных» — Пусть p коллинеарно b. Доказательство: Разложение вектора на два неколлинеарных вектора. Доказательство. Пусть a и b — неколлинеарные векторы. Лемма: Если векторы a и b коллинеарны и a? 0, то существует число k такое, что b = ka.
Докажем, что любой вектор p можно разложить на векторы a и b. Геометрия 9 класс. Тогда р = уb, где у — некоторое число.
«Правильные многоугольники 9 класс» — Урок геометрии в 9 классе. Луковникова Н.М., учитель математики. Построение правильного пятиугольника 1 способ. МОУ гимназия № 56, Томск-2007. Правильные многоугольники.
«Симметрия фигур» — Прямая а называется осью симметрии фигуры. Г. Одна фигура получается из другой преобразованием. Оглавление. Преобразование, обратное движению, также является движением. А1. Выполнил: Пантюков Е. А. Видов симметрии много. М1. Трансформация формы.
«Симметрия относительно линии» — Фигура может иметь одну или несколько осей симметрии. Симметрия в природе. Савченко Миша, 9Б класс. Угол. Кто на исходном фото? Л.С. Атанасяна «Геометрия 7-9». Равнобедренная трапеция. Постройте отрезок A1B1, симметричный отрезку AB относительно прямой. Сколько осей симметрии имеет каждая фигура? Прямоугольник.
Русское математическое образование
СЕРИЯ ПО МАТЕМАТИЧЕСКОМУ ОБРАЗОВАНИЮ
Редакторы серии: Могенс Нисс (Университет Роскилле, Дания)
Lee Peng Yee (Наньянский технологический университет, Сингапур)
Джереми Килпатрик (Университет Джорджии, США)
Опубликовано
Том.
1
Как китайцы изучают математику
Мнения инсайдеров
Под редакцией: Л. Фан, Н.-Ю. Вонг, Дж. Кай и С. Ли
Том. 2
Математическое образование
Путешествие в Сингапур
Под редакцией: К. Ю. Вонг, П. Я. Ли, Б. Каур, П. Я. Фунг и С. Ф. Нг
Том. 4
Россия Математическое образование
История и мировое значение
Под редакцией: А. Карпа и Б. Р. Вогели
Том. 5
Российская математика Образование
Программы и практики
Под редакцией А. Карпа и Б. Р. Вогели
ZhangJi — Русское математическое образование — Programs.pmd
05.04.2011, 9:51
1
N E W J E R S E Y
•
Л О Н Д О Н
•
С И Н Г А П О Р Е
•
БЭИ ДЖИ Н Г
•
С Х А Н Г Х А И
•
ХО Н Г К О Н Г
•
ТА И П Е И
•
Ч Е Н Н А И
Мировой научный
Серия по математическому образованию, том.
5
Александр Карп
Брюс Р. Фогели
Колумбийский университет, США
Под редакцией
РУССКИЙ
МАТЕМАТИКА
ОБРАЗОВАНИЕ
Программы и практики
7892 tp.new.indd 2
24.02.11 9:11
Данные каталогизации публикаций Британской библиотеки
Запись в каталоге для этой книги имеется в Британской библиотеке.
Для ксерокопирования материалов в этом томе, пожалуйста, заплатите плату за копирование через авторское право.
Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, США. В этом случае разрешение на
фотокопию от издателя не требуется.
ISBN-13 978-981-4322-70-6
ISBN-10 981-4322-70-9
Набрано Stallion Press
Электронная почта: [email protected]
Все права защищены. Запрещается воспроизводить эту книгу или ее части в какой бы то ни было форме и любыми средствами,
электронные или механические, включая фотокопирование, запись или любое хранение и поиск информации
система, которая уже известна или будет изобретена без письменного разрешения Издателя.