Зубарева И. И., Мордкович А.Г. Математика 5 класс : учебник ОНЛАЙН
Математика / Математика для учителей и преподавателей / Математика для школьников / Учебники, пособия, рабочие тетради по математике
Зубарева И. И., Мордкович А.Г. Математика. 5 класс : учеб. для учащихся общеобразоват. учреждений. — 9-е изд., стер. — М., 2009. — 270 с. : ил.
Теоретический материал в учебнике изложен таким образом, чтобы преподаватель смог применить проблемный подход в обучении. С помощью системы обозначений выделяются упражнения четырех уровней сложности. В каждом параграфе сформулированы контрольные задания, исходя из того, что должны знать и уметь учащиеся для достижения ими уровня стандарта математического образования. В конце учебника даны домашние контрольные работы и ответы. Цветные иллюстрации (рисунки и схемы) обеспечивают высокий уровень наглядности учебного материала.
Учебник можно использовать в качестве продолжения любого курса начальной школы: как традиционного, так и развивающего направления.
ОГЛАВЛЕНИЕ
Предисловие для учителя………………………….4
Глава I. Натуральные числа
§ 1. Десятичная система счисления …………………….5
§ 2. Числовые и буквенные выражения……………….12
§ 3. Язык геометрических рисунков ……………18
§ 4. Прямая. Отрезок. Луч…………………23
§ 5. Сравнение отрезков. Длина отрезка………………..29
§ 6. Ломаная…………………….33
§ 7. Координатный луч…………………..36
§ 8. Округление натуральных чисел…………………42
§ 9. Прикидка результата действия ………………….47
§ 10. Вычисления с многозначными числами ……….52
§ 11. Прямоугольник………………..57
§ 12. Формулы……………………61
§ 13. Законы арифметических действий…………………64
§ 14. Уравнения . ………………………….69
………………………….69
§ 15. Упрощение выражений ……………..71
§ 16. Математический язык……………………75
§ 17. Математическая модель ……………………79
Глава II. Обыкновенные дроби
§ 18. Деление с остатком…………………..82
§ 19. Обыкновенные дроби…………………86
§ 20. Отыскание части от целого и целого по его части…………………93
§ 21. Основное свойство дроби…………………………99
§ 22. Правильные и неправильные дроби. Смешанные числа………………..106
§ 23. Окружность и круг……………………..113
§ 24. Сложение и вычитание обыкновенных дробей…………………118
§ 25. Сложение и вычитание смешанных чисел ………………..126
§ 26. Умножение и деление обыкновенной дроби на натуральное число………..128
Глава III. Геометрические фигуры
§ 27. Определение угла. Развернутый угол ……………………135
§ 28. Сравнение углов наложением. ……………………..140
……………………..140
§ 29. Измерение углов…………………………142
§ 30. Биссектриса угла…………………………….146
§ 31. Треугольник……………………………….150
§ 32. Площадь треугольника………………….155
§ 33. Свойство углов треугольника ……………….159
§ 34. Расстояние между двумя точками. Масштаб………………….164
§ 35. Расстояние от точки до прямой. Перпендикулярные прямые……………167
§ 36. Серединный перпендикуляр………………………..172
§ 37. Свойство биссектрисы угла……………………176
Главы IV. Десятичные дроби
§ 38. Понятие десятичной дроби. Чтение и запись десятичных дробей ………179
§ 39. Умножение и деление десятичной дроби на 10, 100, 1000 и т. д……….185
§ 40. Перевод величин в другие единицы измерения ………………………..190
§ 41. Сравнение десятичных дробей………………………………..192
§ 42. Сложение и вычитание десятичных дробей. ………………..195
………………..195
§ 43. Умножение десятичных дробей…………………..202
§ 44. Степень числа ………………………….206
§ 45. Среднее арифметическое. Деление десятичной дроби на натуральное число……………….210
§ 46. Деление десятичной дроби на десятичную дробь……………………….216
§ 47. Понятие процента………………………..222
§ 48. Задачи на проценты…………………………224
§ 49. Микрокалькулятор ……………………….228
Глава V. Геометрические тела
§ 50. Прямоугольный параллелепипед……………………….233
§ 51. Развертка прямоугольного параллелепипеда…………………..236
§ 52. Объем прямоугольного параллелепипеда……………………243
Глава VI. Введение в вероятность
§ 53. Достоверные, невозможные и случайные события………………249
§ 54. Комбинаторные задачи………………….251
Домашние контрольные работы ………………………258
Ответы . ………………….263
………………….263
§ Учебники по математике. Электронная библиотека по математике
Учебники по математике Учебники по геометрии
Важно!
К сожалению, новые издания учебников нельзя скачать на нашем сайте из-за требований издательств.
Купить новое издание учебника можно по ссылкам ниже. Учебник будет доставлен на дом в кратчайшие сроки.
Начальная школа
Алышева 2 класс
Издательство: Просвещение, 2000 г.
Серия: Просвещение- 7. Обучающиеся с интеллектуальными нарушениями. ФГОС ОВЗ. (Просвещение)
Автор: Алышева Т.В. и др.
Части 1, 2.
Моро 2 класс
Издательство: Просвещение, 2019 г.
Серия: Школа России, Математика, (1-4 кл.), Моро М. И.
И.
Автор: Моро М.И., Бантова М.А. и др.
Части 1, 2.
Башмаков 3 класс
Издательство: ВЕНТАНА-ГРАФ, 2019 г.
Серия: Линия УМК Башмакова. Математика (1-4)
Автор: Башмаков Марк Иванович Нефедова М. Г. и др.
Части 1, 2.
Моро 3 класс
Издательство: Просвещение, 2019 г.
Серия: Школа России
Автор: Моро М.И., Бантова М.А. и др.
Части 1, 2.
Петерсон 3 класс
Издательство: Бином, 2019 г.
Серия: Математика
Автор: Петерсон Л.Г. и др.
Части 1, 2, 3.
Моро 4 класс
Издательство: Просвещение, 2019 г.
Серия: Школа России
Автор: Моро М.И., Бантова М.А. и др.
Части 1, 2.
Петерсон 4 класс
Издательство: Бином, 2017 г.
Серия: Учусь учиться
Автор: Петерсон Л. Г. и др.
Г. и др.
Части 1, 2, 3.
Рудницкая 4 класс
Издательство: ВЕНТАНА-ГРАФ, 2019 г.
Серия: Линия УМК Рудницкой. Математика (1-4)
Автор: Рудницкая и др.
Части 1, 2.
Средняя школа
Виленкин 5 класс
Издательство: Мнемозина, 2018 г.
Серия: Математика
Автор: Виленкин Н.Я. и др.
Части 1, 2.
Дорофеев 5 класс
Издательство: Просвещение, 2019 г.
Серия: Математика 5-9 классы
Автор: Дорофеев и др.
Зубарева, Мордкович 5 класс
Издательство: Мнемозина, 2016 г.
Серия: Математика
Автор: Зубарева И.И., Мордкович А.Г. и др.
Мерзляк 5 класс
Издательство: ВЕНТАНА-ГРАФ, 2017 г.
Серия: Линия УМК Мерзляка. Математика (5-6)
Автор: Мерзляк Аркадий Григорьевич

Никольский 5 класс
Издательство: Просвещение, 2019 г.
Серия: Математика 5-9 классы
Автор: Никольский С.М. и др.
Виленкин 6 класс
Издательство: Мнемозина, 2011 г.
Серия: Математика
Автор: Виленкин Н.Я. и др.
Дорофеев 6 класс
Издательство: Просвещение, 2019 г.
Серия: Дорофеев Г.В. (5-6)
Автор: Дорофеев и др.
Мерзляк 6 класс
Издательство: Мнемозина, 2019 г.
Серия: Линия УМК Мерзляка. Математика (5-6)
Автор: Мерзляк и др.
Никольский 6 класс
Издательство: Мнемозина, 2019 г.
Серия: Математика 5-9 классы
Автор: Никольский и др.
Колягин, Алимов 7 класс
Издательство: Просвещение, 2019 г.
Серия: 7кл ФГОС
Автор: Колягин Ю. М., Алимов Ш. А. и др.
М., Алимов Ш. А. и др.
Макарычев 7 класс
Издательство: Просвещение, 2019 г.
Серия: Математика 5-9 классы
Автор: Макарычев и др.
Мерзляк 7 класс
Издательство: ВЕНТАНА-ГРАФ, 2019 г.
Серия: Математика 5-9 классы
Автор: Мерзляк и др.
Никольский 7 класс
Издательство: Просвещение, 2019 г.
Серия: Математика 5-9 классы
Автор: Никольский и др.
Колягин, Алимов 8 класс
Издательство: Просвещение, 2019 г.
Серия: 8 кл ФГОС
Автор:
Макарычев 8 класс
Издательство: Просвещение, 2019 г.
Серия: Математика 5-9 классы
Автор: Макарычев и др.
Мерзляк 8 класс
Издательство: ВЕНТАНА-ГРАФ, 2019 г.
Серия: Линия УМК Мерзляка. Алгебра (7-9) (Б)
Алгебра (7-9) (Б)
Автор: Мерзляк и др.
Никольский 8 класс
Издательство: Просвещение, 2020 г.
Серия: Никольский С.М. (7-9)
Автор: Никольский и др.
Колягин, Алимов 9 класс
Издательство: Просвещение, 2019 г.
Серия: Математика 5-9 классы
Автор: Колягин Ю.М., Алимов Ш. А. и др.
Макарычев 9 класс
Издательство: Просвещение, 2020 г.
Серия: Математика 5-9 классы
Автор: Макарычев и др.
Мерзляк 9 класс
Издательство: ВЕНТАНА-ГРАФ, 2019 г.
Серия: Математика 5-9 классы
Автор: Мерзляк и др.
Никольский 9 класс
Издательство: Просвещение, 2019 г.
Серия: Никольский С.М. (7-9)
Автор: Никольский и др.
Старшая школа
Никольский 10 класс
Издательство: Просвещение, 2019 г.
Серия: Математика 10-11 классы
Автор: Никольский и др.
Алимов 10–11 класс
Издательство: Просвещение, 2020 г.
Серия: Математика и информатика
Автор: Колягин Ю.М., Алимов Ш. А. и др.
Никольский 11 класс
Издательство: Мнемозина, 2019 г.
Серия: Алгебра и начала математического анализа. Никольский С.М. (10-11) (Базовый/Углублённый) МГУ-Школе
Автор: Никольский и др.
Учебники за школьный курс математики с 2 по 11 класс. .
Все учебники по математике расставлены в порядке возрастания.
По вашим просьбам на нашем математическом сайте создана библиотека учебников по математике.
В данном разделе сможете найти учебники по математике для начальной (1–4 класс), средней (5–9 класс) и старшей школы.
В перспективе мы планируем рассматривать не только учебники по математике, но и другие
дидактические и методические материалы, которые, как мы надеемся, помогут вам в
освоении школьного курса математики.
Учитывая, что в настоящее время учебники часто переиздаются, мы будем стараться подбирать издания разных лет выпуска.
Учебники по математике Учебники по геометрии
5-6 кл Математика Виленкин вне закона. Что вместо?
- Форум
- Архив
- Школы, Олимпиады, Вузы
Московская школа. В прошлом году в нашей школе в 5 классах математика шла по Виленкину. В этом году распоряжением Минобразования учебник снят с московских школ. Теперь у нас Никольский. Но, курс Никольского рассчитан на 5-6 классы. И некоторые темы нашими не пройдены, проходим их сейчас в быстром темпе по учебнику 5 класса. А какие учебники по математике у ваших детей в 6 ом классе? И напишите город, где живете.
6 класс — продолжаем по Виленкину. Никто ничего не менял. Школа в Москве.
Дорофеев, Химки.
По-моему неплохой учебник.
А что за школа, если не секрет? номер?
В новой школе Виленкин и Никольский сразу.
В прежней школе Дорофеев
Сразу, это одновременно? не совсем поняла, извините
У нас по жизни тоже несколько учебников и пособий сразу используется. В 5-м были Виленкин, Петерсон, Сканави, еще пара каких-то.
Да, сразу. Выдали два учебника и дают задания из обоих. Смысла этого я пока не поняла, на надеюсь, что будущее покажет.
А какой Сканави?
Мне известен только для поступающих в ВУЗы
Он и есть. Уже в 5-м классе оттуда какие-то задания решали. И все последующие годы тоже его использовали.
Никольский, Москва
о как. спасибо!
Спасибо за наводку. Помню такой задачник. Надо тоже купить своему.
Да вы что? Неужели этот убогий учебник отменили? Никольский-то гораздо лучше.
У нас Петерсон. Москва.
Не Москва. В пятом классе вместо Виленкина (это было два года назад) часть школ перешла на Никольского, а часть (с углублённым изучением математики) на Мерзляка. Сейчас в 7 классе в нашей физматшколе школе рейтинговые классы изучают алгебру по Мерзляку, остальные учатся по Макарычеву.
хм…нашим в 10-м Виленкина раздали «Алгебра и начала анализа»
Москва. В 5 классе был Виленкин, в 6-ом Мерзляк, школа языковая. ..
..
Никольский, 5 класс. Школа языковая
Виленкин 6 класс Москва
Мерзляк
6 класс, Зубарева, Мордкович математика. Москва
Расскажите, в чем разница учебников Виленкин и Мордкович?
Подмосковье. Старший учился в 5-6 классах по Виленкину, у младшего в 5-6 был Мерзляк, сейчас в 7 классе алгебра Мерзляк и геометрия тоже Мерзляк.
Москва, учебник Петерсон, Дорофеев.
Не очень поняла, Никольский это хорошо? сыну выдали учебники, и там Никольский. Сын настроен на тех.вуз
Это очень хорошо. Виленкин — для тех, кому математика не нужна. Очень слабый учебник.
У нас тоже Дорофеев. В том году сын стал призёром олимпиады , обскакал многих гимназистов ( Мерзляк). В этом году, решили подгрузить его математикой, репетитора взяли. Решает спокойно за 7-8-9 классы некоторые темы. Школа обычная , правда учитель его ведёт по особому маршруту, только контрольные с классом пишет.
5 класс Виленкин, Мерзляк
Мерзляк
Эх, хорошо когда такой учитель!
Хорошо. Класс какой у вас? Мой тоже скорее технарь.
Класс какой у вас? Мой тоже скорее технарь.
Саратов. Мерзляк с 5го класса. сейчас 7й. по мне так в наглую перекатан виленкина
Виленкин слабый учебник?
Это вы по Бунимовичу не учились! Хорошо, что вот это вот все кончилось с окончанием 6 класса.
Вы -учитель?
И на что перешли после Бунимовича?
Мне только вчера это сказала учитель по математике наша.
Наивные родители. Виленкина запретили уже года три как. Но школы менять учебники не хотели. И учителя не хотели, не потому, что Виленкин лучше других, а просто потому, что у них давно все расписано под Виленкина. Только постепенно учебники приходят совсем в негодность, а новых уже закупать не позволяют.
Разницы между тем, по Виленкину учить или по Никольскому, по Бунимовичу или Петерсон, на самом деле, нет никакой. Вся разница только в квалификации учителя.
Обычный учебник Виленкин — самый обычный. О какой вообще сложности можно говорить в 5-6 классах? Там главное аккуратно научить всем базовым действиям с дробями и 5-7 типам задач. По какому учебнику это делать — вообще роли не играет. В любом что-то лучше, что-то хуже. Любой приходится так или иначе корректировать за счет дополнительных материалов.
По какому учебнику это делать — вообще роли не играет. В любом что-то лучше, что-то хуже. Любой приходится так или иначе корректировать за счет дополнительных материалов.
Алгебра Макарычев, геометрия Атанасян.
Открыть тему в окнах
Знаменитости в тренде
Почему важно обращать внимание на форму лица при выборе стрижки?
СМИ: Джонни Депп закрутил роман с замужней правозащитницей Джоэль Рич
Как правильно ухаживать за стопами ног
Константин Макарычев
- Устойчивость к возмущениям
- Константин Макарычев и Юрий Макарычев
- Помимо наихудшего анализа алгоритмов. Монтажер: Тим Рафгарден. Издательство Кембриджского университета.
 2020.
2020.
- Алгоритмы приближения для CSP (обзор результатов)
- Константин Макарычев и Юрий Макарычев
- Проблема удовлетворения ограничений: сложность и приближенность. Редакторы: Андрей Крохин и Станислав Живный. Продолжение Дагштуля. 2017.
- Bilu-Linial Stability (обзор по Bilu-Linial устойчивости и устойчивости к возмущениям)
- Константин Макарычев и Юрий Макарычев
- Расширенный структурированный прогноз. Редакторы: Т. Хазан, Г. Папандреу, Д. Тарлоу. Массачусетский технологический институт Пресс. 2016.
- Объяснимое k-средних. Не жадничайте, сажайте большие деревья!
- Константин Макарычев и Лижэнь Шань
- СТОК 2022
- Почти оптимальные алгоритмы для объяснимых k-медиан и k-средних
- Константин Макарычев и Лижэнь Шань
- ICML 2021
- Локальная корреляционная кластеризация с ошибками асимметричной классификации
- Джафар Джафаров, Санчит Калхан, Константин Макарычев, Юрий Макарычев
- ICML 2021
- Пакетная оптимизация для синтеза ДНК
- Константин Макарычев,
Миклош З.
 Рач,
Сайрус Ращян,
Сергей Еханин
Рач,
Сайрус Ращян,
Сергей Еханин - ИСИТ 2021
- Константин Макарычев,
Миклош З.
- Двусторонняя теорема Киршбрауна
- Артурс Бакурс, Сепидех Махабади, Константин Макарычев, Юрий Макарычев
- СКГ 2021
- Улучшенные гарантии для k-means++ и k-means++ Parallel
- Константин Макарычев, Аравинд Редди, Лижэнь Шань
- НейрИПС 2020
- Корреляционная кластеризация с ошибками асимметричной классификации
- Джафар Джафаров, Санчит Калхан, Константин Макарычев, Юрий Макарычев
- ICML 2020
- Bisect and Conquer: Иерархическая кластеризация с помощью Max-Uncut Bisection
- Сара Ахмадян, Ваггос Хациафратис, Алессандро Эпасто, Эйвунг Ли, Мохаммад Махдиан, Константин Макарычев, Григорий Ярославцев
- АИСТАТ 2020
Сертифицированные алгоритмы - : анализ наихудшего случая и не только
- Константин Макарычев и Юрий Макарычев
- ИТКС 2020
- Корреляционная кластеризация с локальными целями
- Санчит Калхан, Константин Макарычев, Тимоти Чжоу
- НейрИПС 2019
- Производительность преобразования Джонсона-Линденштрауса для кластеризации k-средних и k-медиан
- Константин Макарычев, Юрий Макарычев, Илья Разенштейн
- СТОЦ 2019
Сборка ДНК - для считывания данных хранения нанопор
- с
Карин Штраус,
Луис Сезе,
и другие.

- Nature Communications 10, Артикул: 2933 (2019)
- с
Карин Штраус,
Луис Сезе,
и другие.
- Увеличение масштабов хранения данных ДНК и поиск с произвольным доступом
- с Карин Штраус, Луис Сезе, и другие.
- Природа Биотехнология 36, стр. 242-248, 2018
- Нелинейное уменьшение размерности с помощью внешних билипшицевых расширений
- Сепиде Махабади, Константин Макарычев, Юрий Макарычев, Илья Разенштейн
- СТОК 2018
- Кластеризация миллиардов операций чтения для хранения данных ДНК
- Кир Ращян, Константин Макарычев, Миклош З. Рач, Сиена Дюма Анг, Джордже Евджич, Сергей Еханин, Луис Сезе, Карин Штраус
- NeurIPS 2017 (презентация в центре внимания)
- Алгоритмы для устойчивых и устойчивых к возмущениям задач
- Харис Ангелидакис, Константин Макарычев, Юрий Макарычев
- СТОК 2017
- Первая часть документа доступна по адресу https://arxiv.
 org/abs/1607.06442. Полная версия статьи скоро будет размещена на arxiv.
org/abs/1607.06442. Полная версия статьи скоро будет размещена на arxiv.
- Надежные алгоритмы с полиномиальными потерями для почти единодушных CSP
- Виктор Далмау, Марчин Козик, Андрей Крохин, Константин Макарычев, Юрий Макарычев, Якуб Опршал
- СОДА 2017
- Обучающиеся сообщества при наличии ошибок
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- КОЛЬТ 2016
- Объединение евклидовых метрических пространств является евклидовым
- Константин Макарычев и Юрий Макарычев
- Дискретный анализ 2016
- Алгоритм двухкритериальной аппроксимации для k-Means
- Константин Макарычев, Юрий Макарычев, Максим Свириденко, Джастин Уорд
- ПРИБЛИЗИТЕЛЬНО 2016
- Выполнимость заказа CSP выше среднего
- Константин Макарычев, Юрий Макарычев, Юань Чжоу
- ФОКС 2015
- Корреляционная кластеризация с зашумленной частичной информацией
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- КОЛЬТ 2015
- Почти оптимальный алгоритм округления LP для корреляционной кластеризации на полных графиках
- Шучи Чавла, Константин Макарычев, Целил Шрамм, Григорий Ярославцев
- СТОК 2015
- Планирование с учетом сети для заданий с параллельными данными: планируйте, когда сможете
- Вираджит Джалапарти, Питер Бодик, Ишай Менахе, Шрирам Рао, Константин Макарычев, Мэтью Цезарь
- SIGCOMM 2015
- Решение задач оптимизации с отрицательным эффектом масштаба
- Константин Макарычев и Максим Свириденко
- ФОКС 2014
- Журнал АКМ, том 65, выпуск 6, ноябрь 2018 г.
 , статья № 42.
, статья № 42.
- Неравномерное разбиение графа с несвязанными весами
- Константин Макарычев и Юрий Макарычев
- ИКАЛП 2014
- Сборник: Математика (Российская академия наук), вып. 208
- Черновик версии журнала доступен здесь.
- Ограниченное приоритетом планирование гибких заданий с вытеснением
- Константин Макарычев и Дембалья Паниграхи
- ИКАЛП 2014
- Аппроксимация постоянного фактора для сбалансированного разреза в модели PIE
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагаван
- СТОК 2014
- билу-линиальных стабильных экземпляра Max Cut
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- СОДА 2014
- Алгоритм аппроксимации для разреженного k-разбиения
- Ананд Луи и Константин Макарычев
- СОДА 2014
- Регуляризация скорости и оптимизация в классификации слов
- Джеффри Цвейг и Константин Макарычев
- ICASSP 2013
- Локальный поиск лучше, чем случайное назначение для k-CSP с ограниченным упорядочением вхождения
- Константин Макарычев
- СТАКС 2013
- Сортировка зашумленных данных с частичной информацией
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- ITCS 2013 – Инновации в теоретической информатике
- Алгоритм аппроксимации для небулева MAX k-CSP
- Константин Макарычев и Юрий Макарычев
- ПРИБЛИЗИТЕЛЬНО 2012
- Алгоритмы аппроксимации для задач полуслучайного разбиения графа
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- СТОК 2012
- Неравенства концентрации для нелинейного матроидного пересечения
- Константин Макарычев, Уоррен Шуди, Максим Свириденко
- СОДА 2012
- Случайные структуры и алгоритмы, том.
 46, нет. 3, 2015
46, нет. 3, 2015
- Постоянная Гротендика строго меньше границы Кривина
- Марк Браверман, Константин Макарычев, Юрий Макарычев, Ассаф Наор
- ФОКС 2011; препринт arXiv:1103.6161 [math.FA]
- Математический форум, Π, том 1, 2013 г.
- Как играть в уникальные игры против полуслучайного противника
- Александра Колла, Константин Макарычев, Юрий Макарычев
- ФОКС 2011
- Min-Max Разбиение графа на разделы и расширение малых наборов
- Нихил Бансал, Уриэль Файги, Роберт Краутгеймер, Константин Макарычев, Вишванат Нагараджан, Джозеф (Сеффи) Наор, Рой Шварц
- ФОКС 2011
- Специальный выпуск SIAM Journal of Computing (SICOMP), vol. 43, нет. 2, 2014
- Версия журнала доступна здесь.
- Улучшенная аппроксимация задачи направленного гаечного ключа
- Петр Берман, Арнаб Бхаттачарья, Константин Макарычев, Софья Расходникова, Григорий Ярославцев
- ИКАЛП 2011
- Специальный выпуск информации и вычислений, том.
 222, стр. 93-107, 2013.
222, стр. 93-107, 2013.
- Максимизация многочленов с учетом ограничений присваивания
- Константин Макарычев и Максим Свириденко
- ИКАЛП 2011
- О бережливых объяснениях двумерных древовидных и линейно упорядоченных данных
- Ховард Карлофф, Флип Корн, Константин Макарычев, Юваль Рабани
- СТАКС 2011
- Сборка кольцевых геномов
- Константин Макарычев и Аланта Ньюман
- ИТКС 2011
- . Операторы расширения метрик, разрыхлители вершин и липшицева расширяемость
- Константин Макарычев и Юрий Макарычев
- ФОКС 2010;
- Израильский математический журнал, том. 212 (2), май 2016 г.
- Задача о максимальном квадратичном присваивании
- Константин Макарычев, Раджсекар Манокаран, Максим Свириденко
- ИКАЛП 2010
- ACM Transactions on Algorithms, vol.
 10, нет. 4, статья 18, август 2014 г.
10, нет. 4, статья 18, август 2014 г.
- Как играть в уникальные игры на расширителях
- Константин Макарычев и Юрий Макарычев
- ВАОА 2010
- О сложности ценообразования для целеустремленных участников торгов
- Рохит Хандекар, Трейси Кимбрел, Константин Макарычев, Максим Свириденко
- ПРИБЛИЗИТЕЛЬНО 2009 (см. хорошую запись о проблеме в блоге Ричарда Липтона).
- Пробелы целостности для релаксаций Шерали-Адамса
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СТОК 2009
- Индексация геномных последовательностей на IBM Blue Gene
- Амол Готинг и Константин Макарычев
- СК 2009
- Финалист премии Гордона Белла ACM
- Последовательные и параллельные методы построения эффективного дерева суффиксов ввода-вывода
- Амол Готинг и Константин Макарычев
- SIGMOD 2009
- Транзакции ACM в системах баз данных (TODS), том.
 35(4), стр. 25:1-25:37
35(4), стр. 25:1-25:37 - Премия IBM Pat Goldberg Best Paper Award
- Онлайн-модель совместного пополнения запасов на заказ: первичные двойные конкурентные алгоритмы
- Нив Бухбиндер, Трейси Кимбрел, Рецеф Леви, Константин Макарычев, Максим Свириденко
- СОДА 2008
- Локальные глобальные компромиссы в метрических вложениях
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- ФОКС 2007
- Специальный выпуск SIAM Journal of Computing (SICOMP), vol. 39, нет. 6, стр. 2487-2512, 2010
- О преимуществе перед Random для максимального ациклического подграфа
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- ФОКС 2007
- Почти оптимальные алгоритмы для задач максимального удовлетворения ограничений
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СОДА 2007;
- Специальный выпуск ACM Transactions on Algorithms, vol.
 5, нет. 3, статья 32, июль 2009a
5, нет. 3, статья 32, июль 2009a
- Алгоритм «разделяй и властвуй» для d-мерной линейной компоновки
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СОДА 2007
- Как играть в уникальные игры, используя вложения
- Эден Хламтак, Константин Макарычев, Юрий Макарычев
- ФОКС 2006
- почти оптимальных алгоритма для уникальных игр
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СТОК 2006
- Проблемы с направленными метриками и ориентированными графами
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СОДА 2006
- Алгоритмы аппроксимации квадратного корня log n для задач Min UnCut, Min 2CNF Deletion и задач направленного разреза
- Амит Агарвал, Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СТОК 2005
- Квадратичные формы на графиках
- Нога Алон, Константин Макарычев, Юрий Макарычев, Ассаф Наор
- СТОК 2005
- Inventiones Mathematicae, vol.
 163, нет. 3, стр. 499-522, март 2006 г.
163, нет. 3, стр. 499-522, март 2006 г.
- Независимость цепи и общая информация
- Константин Макарычев и Юрий Макарычев
- IEEE Transactions on Information Theory, 58(8), стр. 5279-5286, 2012 г.
- Новый класс неравенств не Шеннонского типа для энтропий
- Константин Макарычев, Юрий Макарычев, Андрей Ромащенко, Николай Верещагин
- Коммуникации в области информации и систем, том. 2, нет. 2, стр. 147-166, декабрь 2002 г.
- Важность формальности
- Константин Макарычев и Юрий Макарычев
- The Mathematical Intelligencer, vol. 23 нет. 1, 2001
- Доказательство гипотезы Пака о мозаиках Т-тетромино (на русском языке)
- Константин Макарычев и Юрий Макарычев
- рукопись
Опросы (3)
- Устойчивость к возмущениям
- Константин Макарычев и Юрий Макарычев
- Помимо наихудшего анализа алгоритмов.
 Монтажер: Тим Рафгарден. Издательство Кембриджского университета. 2020.
Монтажер: Тим Рафгарден. Издательство Кембриджского университета. 2020.
- Алгоритмы приближения для CSP (обзор результатов)
- Константин Макарычев и Юрий Макарычев
- Проблема удовлетворения ограничений: сложность и приближенность. Редакторы: Андрей Крохин и Станислав Живный. Продолжение Дагштуля. 2017.
- Bilu-Linial Stability (обзор по Bilu-Linial устойчивости и устойчивости к возмущениям)
- Константин Макарычев и Юрий Макарычев
- Расширенный структурированный прогноз. Редакторы: Т. Хазан, Г. Папандреу, Д. Тарлоу. Массачусетский технологический институт Пресс. 2016.
STOC (11)
- Объяснимые k-средние. Не жадничайте, сажайте большие деревья!
- Константин Макарычев и Лижэнь Шань
- СТОЦ 2022
- Производительность преобразования Джонсона-Линденштрауса для кластеризации k-средних и k-медиан
- Константин Макарычев, Юрий Макарычев, Илья Разенштейн
- СТОЦ 2019
- Нелинейное уменьшение размерности с помощью внешних билипшицевых расширений
- Сепидех Махабади, Константин Макарычев, Юрий Макарычев, Илья Разенштейн
- СТОК 2018
- Алгоритмы для устойчивых и устойчивых к возмущениям задач
- Харис Ангелидакис, Константин Макарычев, Юрий Макарычев
- СТОК 2017
- Первая часть документа доступна по адресу https://arxiv.
 org/abs/1607.06442. Полная версия статьи скоро будет размещена на arxiv.
org/abs/1607.06442. Полная версия статьи скоро будет размещена на arxiv.
- Почти оптимальный алгоритм округления LP для корреляционной кластеризации на полных графиках
- Шучи Чавла, Константин Макарычев, Целил Шрамм, Григорий Ярославцев
- СТОК 2015
- Аппроксимация постоянного фактора для сбалансированного разреза в модели PIE
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- СТОК 2014
- Алгоритмы аппроксимации для задач полуслучайного разбиения графа
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- СТОК 2012
- Пробелы целостности для релаксаций Шерали-Адамса
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СТОК 2009
- почти оптимальных алгоритма для уникальных игр
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СТОК 2006
- Алгоритмы аппроксимации квадратного корня log n для задач Min UnCut, Min 2CNF Deletion и задач направленного разреза
- Амит Агарвал, Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СТОК 2005
- Квадратичные формы на графиках
- Нога Алон, Константин Макарычев, Юрий Макарычев, Ассаф Наор
- СТОК 2005
- Математические изобретения, том.
 163, нет. 3, стр. 499-522, март 2006 г.
163, нет. 3, стр. 499-522, март 2006 г.
FOCS (9)
- Выполнимость заказа CSP выше среднего
- Константин Макарычев, Юрий Макарычев, Юань Чжоу
- ФОКС 2015
- Решение задач оптимизации с отрицательным эффектом масштаба
- Константин Макарычев и Максим Свириденко
- ФОКС 2014
- Журнал ACM, том 65, выпуск 6, ноябрь 2018 г., статья № 42.
- Постоянная Гротендика строго меньше границы Кривина
- Марк Браверман, Константин Макарычев, Юрий Макарычев, Ассаф Наор
- ФОКС 2011; препринт arXiv:1103.6161 [math.FA]
- Математический форум, Π, том 1, 2013 г.
- Как играть в уникальные игры против полуслучайного противника
- Александра Колла, Константин Макарычев, Юрий Макарычев
- ФОКС 2011
- Min-Max Разбиение графа на разделы и расширение малых наборов
- Нихил Бансал, Уриэль Файги, Роберт Краутгеймер, Константин Макарычев, Вишванат Нагараджан, Джозеф (Сеффи) Наор, Рой Шварц
- ФОКС 2011
- Специальный выпуск SIAM Journal of Computing (SICOMP), vol.
 43, нет. 2, 2014
43, нет. 2, 2014 - Версия журнала доступна здесь.
- . Операторы расширения метрик, разрыхлители вершин и липшицева расширяемость
- Константин Макарычев и Юрий Макарычев
- ФОКС 2010;
- Израильский математический журнал, том. 212 (2), май 2016 г.
- Локальные глобальные компромиссы в метрических вложениях
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- ФОКС 2007
- Специальный выпуск SIAM Journal of Computing (SICOMP), vol. 39, нет. 6, стр. 2487-2512, 2010
- О преимуществе перед Random для максимального ациклического подграфа
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- ФОКС 2007
- Как играть в уникальные игры, используя вложения
- Эден Хламтак, Константин Макарычев, Юрий Макарычев
- ФОКС 2006
SODA (8)
- Надежные алгоритмы с полиномиальными потерями для почти единодушных CSP
- Виктор Далмау, Марчин Козик, Андрей Крохин, Константин Макарычев, Юрий Макарычев, Якуб Опршал
- СОДА 2017
- билу-линиальных стабильных экземпляра Max Cut
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- СОДА 2014
- Алгоритм аппроксимации для разреженного k-разбиения
- Ананд Луи и Константин Макарычев
- СОДА 2014
- Неравенства концентрации для нелинейного матроидного пересечения
- Константин Макарычев, Уоррен Шуди, Максим Свириденко
- СОДА 2012
- Случайные структуры и алгоритмы, том.
 46, нет. 3, 2015
46, нет. 3, 2015
- Онлайн-модель совместного пополнения запасов на заказ: первичные двойные конкурентные алгоритмы
- Нив Бухбиндер, Трейси Кимбрел, Рецеф Леви, Константин Макарычев, Максим Свириденко
- СОДА 2008
- Почти оптимальные алгоритмы для задач максимального удовлетворения ограничений
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СОДА 2007;
- Специальный выпуск ACM Transactions on Algorithms, vol. 5, нет. 3, статья 32, июль 2009a
- Алгоритм «разделяй и властвуй» для d-мерной линейной компоновки
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- СОДА 2007
- Проблемы с направленными метриками и ориентированными графами
- Моисей Чарикар, Константин Макарычев, Юрий Макарычев
- SODA 2006
ICALP (5)
- Неравномерное разбиение графа с несвязанными весами
- Константин Макарычев и Юрий Макарычев
- ИКАЛП 2014
- Сборник: Математика (Российская академия наук), вып.
 208
208 - Черновик версии журнала доступен здесь.
- Ограниченное приоритетом планирование гибких заданий с вытеснением
- Константин Макарычев и Дембалья Паниграхи
- ИКАЛП 2014
- Улучшенная аппроксимация задачи направленного гаечного ключа
- Петр Берман, Арнаб Бхаттачарья, Константин Макарычев, Софья Расходникова, Григорий Ярославцев
- ИКАЛП 2011
- Специальный выпуск информации и вычислений, том. 222, стр. 93-107, 2013.
- Максимизация многочленов с учетом ограничений присваивания
- Константин Макарычев и Максим Свириденко
- ИКАЛП 2011
- Задача о максимальном квадратичном присваивании
- Константин Макарычев, Раджсекар Манокаран, Максим Свириденко
- ИКАЛП 2010
- ACM Transactions on Algorithms, vol.
 10, нет. 4, статья 18, август 2014 г.
10, нет. 4, статья 18, август 2014 г.
NeurIPS (3)
- Улучшенные гарантии для k-means++ и k-means++ Parallel
- Константин Макарычев, Аравинд Редди, Лижэнь Шань
- НейрИПС 2020
- Корреляционная кластеризация с локальными целями
- Санчит Калхан, Константин Макарычев, Тимоти Чжоу
- НейрИПС 2019
- Кластеризация миллиардов операций чтения для хранения данных ДНК
- Кир Ращян, Константин Макарычев, Миклош З. Рач, Сиена Дюма Анг, Джордже Евджич, Сергей Еханин, Луис Сезе, Карин Штраус
- NeurIPS 2017 (презентация в центре внимания)
ICML (3)
- Алгоритмы, близкие к оптимальным, для объяснимых k-медиан и k-средних
- Константин Макарычев и Лижэнь Шань
- ICML 2021
- Локальная корреляционная кластеризация с ошибками асимметричной классификации
- Джафар Джафаров, Санчит Калхан, Константин Макарычев, Юрий Макарычев
- ICML 2021
- Корреляционная кластеризация с ошибками асимметричной классификации
- Джафар Джафаров, Санчит Калхан, Константин Макарычев, Юрий Макарычев
- ICML 2020
COLT (2)
- Обучающие сообщества при наличии ошибок
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- КОЛЬТ 2016
- Корреляционная кластеризация с зашумленной частичной информацией
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагаван
- COLT 2015
AISTATS (1)
- Bisect and Conquer: Иерархическая кластеризация с помощью Max-Uncut Bisection
- Сара Ахмадян, Ваггос Хациафратис, Алессандро Эпасто, Эйвунг Ли, Мохаммад Махдиан, Константин Макарычев, Григорий Ярославцев
- AISTATS 2020
ПРИБЛИЗИТЕЛЬНО (3)
- Алгоритм двухкритериальной аппроксимации для k-средних
- Константин Макарычев, Юрий Макарычев, Максим Свириденко, Джастин Уорд
- ПРИБЛИЗИТЕЛЬНО 2016
- Алгоритм аппроксимации для небулева MAX k-CSP
- Константин Макарычев и Юрий Макарычев
- ПРИБЛИЗИТЕЛЬНО 2012
- О сложности ценообразования для целеустремленных участников торгов
- Рохит Хандекар, Трейси Кимбрел, Константин Макарычев, Максим Свириденко
- ПРИБЛИЗИТЕЛЬНО 2009 (см.
 хорошую запись о проблеме в блоге Ричарда Липтона).
хорошую запись о проблеме в блоге Ричарда Липтона).
ITCS (3)
- Сертифицированные алгоритмы: анализ наихудшего случая и не только
- Константин Макарычев и Юрий Макарычев
- ИТКС 2020
- Сортировка зашумленных данных с частичной информацией
- Константин Макарычев, Юрий Макарычев, Аравиндан Виджаярагхаван
- ITCS 2013 – Инновации в теоретической информатике
- Сборка кольцевых геномов
- Константин Макарычев и Аланта Ньюман
- ITCS 2011
ISIT (1)
- Пакетная оптимизация для синтеза ДНК
- Константин Макарычев, Миклош З. Рач, Сайрус Ращян, Сергей Еханин
- ISIT 2021
STACS (2)
- Локальный поиск лучше, чем случайное назначение для k-CSP с упорядочением по вхождению
- Константин Макарычев
- СТАКС 2013
- О бережливых объяснениях двумерных древовидных и линейно упорядоченных данных
- Ховард Карлофф, Флип Корн, Константин Макарычев, Юваль Рабани
- STACS 2011
ICASSP (1)
- Регуляризация скорости и оптимизация в классификации слов
- Джеффри Цвейг и Константин Макарычев
- ICASSP 2013
SC (1)
- Индексирование геномных последовательностей на IBM Blue Gene
- Амол Готинг и Константин Макарычев
- СК 2009
- Финалист премии Гордона Белла ACM
SIGCOMM (1)
- Планирование с учетом сети для параллельных данных: планируйте, когда сможете
- Вираджит Джалапарти, Питер Бодик, Ишай Менахе, Шрирам Рао, Константин Макарычев, Мэтью Цезарь
- SIGCOMM 2015
SIGMOD (1)
- Последовательные и параллельные методы для эффективного построения дерева суффиксов ввода/вывода
- Амол Готинг и Константин Макарычев
- SIGMOD 2009
- Транзакции ACM в системах баз данных (TODS), том.
 35(4), стр. 25:1-25:37
35(4), стр. 25:1-25:37 - Премия IBM Pat Goldberg Best Paper Award
SoCG (1)
- Двусторонняя теорема Киршбрауна
- Артурс Бакурс, Сепидех Махабади, Константин Макарычев, Юрий Макарычев
- SoCG 2021
WAOA (1)
- Как играть в уникальные игры на расширителях
- Константин Макарычев и Юрий Макарычев
- WAOA 2010
Журналы* (6)
- Сборка ДНК для считывания данных хранения нанопор
- с Карин Штраус, Луис Сезе, и другие.
- Nature Communications 10, Номер статьи: 2933 (2019)
- Увеличение масштабов хранения данных ДНК и поиск с произвольным доступом
- с Карин Штраус, Луис Сезе, и другие.
- Природа Биотехнология 36, стр. 242-248, 2018
- Объединение евклидовых метрических пространств является евклидовым
- Константин Макарычев и Юрий Макарычев
- Дискретный анализ 2016
- Независимость цепи и общая информация
- Константин Макарычев и Юрий Макарычев
- IEEE Transactions on Information Theory, 58(8), стр.
 5279-5286, 2012 г.
5279-5286, 2012 г.
- Новый класс неравенств не Шеннонского типа для энтропий
- Константин Макарычев, Юрий Макарычев, Андрей Ромащенко, Николай Верещагин
- Коммуникации в области информации и систем, том. 2, нет. 2, стр. 147-166, декабрь 2002 г.
- Важность формальности
- Константин Макарычев и Юрий Макарычев
- The Mathematical Intelligencer, vol. 23 нет. 1, 2001
Введение в линейную алгебру, 5-е издание
Введение в линейную алгебру, 5-е изданиеГилберт Странг ([email protected]) ISBN : 978-09802327-7-6
Wellesley-Cambridge Press
Заказ книги в Wellesley-Cambridge Press
Заказ книги для членов SIAM
Заказ книги от Американского математического общества
Заказ книги от Cambridge University Press (за пределами Северной Америки)
Введение в линейную алгебру, индийское издание, доступно в Wellesley Publishers
Обзор 5-го издания Профессор Фареник для Международного общества линейной алгебры
Рецензия на книгу InsideBIGDATA (2016)
Связанные веб-сайты:
Линейная алгебра для всех (новый учебник, сентябрь 2020 г. ) СМ. ПРИМЕЧАНИЕ НИЖЕ
) СМ. ПРИМЕЧАНИЕ НИЖЕ
Другие книги Гилберта Стрэнга
OpenCourseWare
Домашняя страница Гилберта Стрэнга
Я надеюсь, что этот сайт станет ценным ресурсом для всех изучение и выполнение линейной алгебры. Вот основные ссылки:
- Содержание
- Предисловие
- Раздел 1.3 книги: Матрицы
- Раздел 2.5 книги: Обратные матрицы
- Раздел 3.5 книги: Измерения четырех подпространств
- Раздел 6.1 книги: Введение в собственные значения
- Раздел 7.1 книги: Обработка изображений с помощью линейной алгебры
- Раздел 12.1 книги: Среднее значение, дисперсия и вероятность
- Матричные факторизации
- Индекс
- 6 великих теорем
- Транспонирование производной
- Eigshow в MATLAB
- 18.
 06 Сайт OpenCourseWare с видеолекциями 18.06 по OCW
06 Сайт OpenCourseWare с видеолекциями 18.06 по OCW - Сайт издателя учебника www.wellesleycambridge.com
- Руководство по решению для учебника (обновлено в сентябре 2020 г.)
- Глава 1
- Глава 2
- Глава 3
- Глава 4
- Глава 5
- Глава 6
- Глава 7
- Глава 8
- Глава 9
- Глава 10
- Глава 11
- Глава 12
- Мир матриц: картина всех матриц, Кендзи Хиранабэ
- LU и CR Исключение (появится в разделе «Образование» SIAM Review)
** Каждый раздел в оглавлении содержит ссылки на наборы задач, решения,
** другие веб-сайты и все материалы, относящиеся к теме этого раздела.
** Читателям предлагается предлагать возможные ссылки.
Содержание для введения в линейную алгебру (5-е издание, 2016 г.)
- 1 Введение в векторы
- 1.1 Векторы и линейные комбинации
- 1.2 Длины и скалярные произведения
- 1.3 Матрицы
- 2 Решение линейных уравнений
- 2.1 Векторы и линейные уравнения
- 2.2 Идея ликвидации
- 2.3 Исключение с использованием матриц
- 2.4 Правила матричных операций
- 2.5 Обратные матрицы
- 2.6 Исключение = Факторизация: A = LU
- 2.7 Транспонирование и перестановки
- 3 векторных пространства и подпространства
- 3.
 1 Пространства векторов
1 Пространства векторов - 3.2 Пустое пространство A : Решение Ax = 0 и Rx = 0
- 3.3 Полное решение Ax = b
- 3.4 Независимость, основа и измерение
- 3.5 Измерения четырех подпространств
- 3.
- 4 Ортогональность
- 4.1 Ортогональность четырех подпространств
- 4.2 Проекции
- 4.3 Метод наименьших квадратов
- 4.4 Ортонормированные базисы и Грам-Шмидт
- 5 Детерминанты
- 5.1 Свойства определителей
- 5.2 Перестановки и кофакторы
- 5.3 Правило Крамера, инверсии и объемы
- 6 Собственные значения и собственные векторы
- 6.
 1 Введение в собственные значения
1 Введение в собственные значения - 6.2 Диагонализация матрицы
- 6.3 Системы дифференциальных уравнений
- 6.4 Симметричные матрицы
- 6.5 Положительно определенные матрицы
- 6.
- 7 Разложение по сингулярным числам (SVD)
- 7.1 Обработка изображений с помощью линейной алгебры
- 7.2 Базы и матрицы в СВД
- 7.3 Анализ главных компонентов (PCA по SVD)
- 7.4 Геометрия СВД
- 8 линейных преобразований
- 8.1 Идея линейного преобразования
- 8.2 Матрица линейного преобразования
- 8.3 Поиск хорошей основы
- 9 Комплексные векторы и матрицы
- 9.
 1 Комплексные числа
1 Комплексные числа - 9.2 Эрмитовы и унитарные матрицы
- 9.3 Быстрое преобразование Фурье
- 9.
- 10 приложений
- 10.1 Графики и сети
- 10.2 Матрицы в технике
- 10.3 Марковские матрицы, население и экономика
- 10.4 Линейное программирование
- 10.5 Ряды Фурье: линейная алгебра функций
- 10.6 Компьютерная графика
- 10.7 Линейная алгебра для криптографии
- 11 Числовая линейная алгебра
- 11.1 Исключение Гаусса на практике
- 11.2 Номера норм и условий
- 11.3 Итерационные методы и предварительные условия
- 12 Линейная алгебра в теории вероятностей и статистике
- 12.
 1 Среднее значение, дисперсия и вероятность
1 Среднее значение, дисперсия и вероятность - 12.2 Ковариационные матрицы и совместные вероятности
- 12.3 Многомерный метод Гаусса и взвешенный метод наименьших квадратов
- 12.
- Матричные факторизации
- Индекс
- Шесть великих теорем / Линейная алгебра в двух словах
[верх]
В каждом разделе книги есть набор задач.
В следующих видеороликах щелкните значок «Воспроизвести» ►
Во время воспроизведения щелкните слово «YouTube»
, чтобы просмотреть увеличенное видео на отдельной вкладке
Загрузка выбранных решений (небольшие отличия от приведенных выше решений)
Практические экзаменационные вопросы
- Экзамен 1 (1997-2009)
- Экзамен 1 (2010-2015)
- Экзамен 2 (1997-2009)
- Экзамен 2 (2010-2015)
- Экзамен 3 (1997-2009)
- Экзамен 3 (2010-2015)
- Финал (1998-2009)
- Финал (2010-2015)
Задачи по линейной алгебре в лемме
Мой друг Павел Гринфельд из Drexel прислал мне коллекцию интересных задач — в основном элементарных, но каждая с небольшими особенностями. Они являются частью его более крупного обучающего сайта под названием LEM.MA, и он создал страницу http://lem.ma/LAProb/ специально для этого веб-сайта, связанного с 5-м изданием.
Они являются частью его более крупного обучающего сайта под названием LEM.MA, и он создал страницу http://lem.ma/LAProb/ специально для этого веб-сайта, связанного с 5-м изданием.
Видеостандарт H.264 (обещано в разделе 7.1 книги)
Этот видеостандарт описывает систему кодирования и декодирования («Кодек»), которую инженеры определили для таких приложений, как ТВ высокой четкости. Не ожидается, что вы будете знать значение каждого слова — этого не знает и автор вашей книги. Суть в том, чтобы увидеть важный пример «стандарта», созданного отраслью после многих лет разработки, чтобы все компании знали, какой системе кодирования должна соответствовать их продукция.
Слова «компенсация движения» относятся к способу оценки каждого видеоизображения по сравнению с предыдущим. Проще всего было бы предположить, что последовательные видеоизображения одинаковы. Тогда нам понадобятся только изменения между кадрами — надеюсь, небольшие. Но если камера следит за действием, вся сцена немного сдвинется и потребует коррекции. Идея получше — увидеть, в каком направлении движется сцена, и встроить это изменение в следующую сцену. Это КОМПЕНСАЦИЯ ДВИЖЕНИЯ. На самом деле движение может быть разным в разных частях экрана.
Идея получше — увидеть, в каком направлении движется сцена, и встроить это изменение в следующую сцену. Это КОМПЕНСАЦИЯ ДВИЖЕНИЯ. На самом деле движение может быть разным в разных частях экрана.
Именно такие идеи, о которых легко говорить, но для совершенствования которых требуются годы усилий, делают видеотехнологии и другие технологии возможными и успешными. Инженеры делают свою работу. Я надеюсь, что эти ссылки дают представление о необходимых деталях.
- http://www.h364info.com/h364.html
- http://en.wikipedia.org/wiki/H.264/MPEG-4_AVC
- http://www.axis.com/files/whitepaper/wp_h364_31669_en_0803_lo.pdf
Заметки по линейной алгебре
Доказательство теоремы Шура
Разложение действительных матриц по сингулярным числам (проф. Джугал Верма, ИИТ Бомбея, март 2020 г.)
Наш последний учебник «Линейная алгебра для всех» начинается с идеи независимых столбцов
.
Это приводит к факторизации
A = CR , где C содержит те независимые столбцы из AМатрица
R говорит, как объединить эти столбцы из C для производства всех столбцов AЗатем в Разделе 3.2 объясняется, как решить
Rx = 0 . Это дает нулевое пространство A !!К этой странице обращались по крайней мере раз с января 2009 г.
Доступность
Количественная геометрия — ПМК
1. Громов М. (1981) Группы полиномиального роста и расширяющиеся отображения. Inst Hautes Études Sci Publ Math 53:53–73.
2. Громов М. (1993) Асимптотические инварианты бесконечных групп. Геометрическая теория групп, Том 2, Сассекс, 1991 , London Math Soc Lecture Note Ser (Cambridge University Press, Кембридж, Великобритания), том 182, стр. 1–295.
3. Брейяр Э., Ле Донн Э. О скорости сходимости к асимптотическому конусу для нильпотентных групп и субфинслеровой геометрии. Proc Natl Acad Sci USA. 2012;110(48):19220–19226. [Google Scholar]
Proc Natl Acad Sci USA. 2012;110(48):19220–19226. [Google Scholar]
4. Абрамс А., Брэди Н., Дэни П., Янг Р. Гомологическая и гомотопическая функции Дена различны. Proc Natl Acad Sci USA. 2013;110(48):19206–19212. [Google Scholar]
5. Ю.Г. Грубая гипотеза Баума-Конна для пространств, допускающих равномерное вложение в гильбертово пространство. Изобретите математику. 2000;139(1):201–240. [Google Scholar]
6. де Корнюлье Ю., Тессера Р., Валетт А. Изометрические групповые действия на гильбертовых пространствах: рост коциклов. Geom Funct Anal. 2007;17(3):770–792. [Google Scholar]
7. Матушек Ю. О вложении деревьев в равномерно выпуклые банаховы пространства. Израиль Дж. Матем. 1999; 114: 221–237. [Академия Google]
8. Остин Т., Наор А., Тессера Р. Точная количественная невложимость группы Гейзенберга в суперрефлексивные банаховы пространства. Группы Геом Дин. 2013;7(3):497–522. [Google Scholar]
9. Cheeger J, Kleiner B, Naor A. Границы сжатия для липшицевых отображений из группы Гейзенберга в L 1. Acta Math. 2011;207(2):291–373. [Google Scholar]
Acta Math. 2011;207(2):291–373. [Google Scholar]
10. Гентнер Э., Каминкер Дж. Точность и равномерная вложимость дискретных групп. J Lond Math Soc. 2004;70(3):703–718. [Академия Google]
11. Громов М.И. Количественная теория гомотопий. В: Росси Х, редактор. Перспективы в математике: приглашенные беседы по случаю 250-летия Принстонского университета. Род-Айленд: Американское математическое общество, Провиденс; 1999. С. 45–49. [Google Scholar]
12. Ферри С., Вайнбергер С. Количественная алгебраическая топология и гомотопия Липшица. Proc Natl Acad Sci USA. 2013;110(48):19246–19250. [Google Scholar]
13. Колдинг Т.Х., Миникоцци В.П. Монотонность и ее аналитические и геометрические следствия. Proc Natl Acad Sci USA. 2012;110(48):19233–19236. [Google Scholar]
14. Фреше М. Сборник монографий по теории функций. Том 12. Париж: Готье-Вилларс; 1928. Les Espaces Abstraits et leur Théorie Considérée Comme Introduction à l’Analyse Générale. Французский. [Google Scholar]
15. Банах С. Моногра Математика. Том 1. Варшава: PWN — Польское научное издательство; 1932. Теория линейных операций. [Google Scholar]
Банах С. Моногра Математика. Том 1. Варшава: PWN — Польское научное издательство; 1932. Теория линейных операций. [Google Scholar]
16. Кадец М.И. Доказательство топологической эквивалентности всех сепарабельных бесконечномерных банаховых пространств. Функциональный . Анальный приложен. 1967; 1: 61–70. [Google Scholar]
17. Рибе М. О равномерно гомеоморфных нормированных пространствах. Ковчег мат. 1976;14(2):237–244. [Google Scholar]
18. Мильман В.Д., Шехтман Г. Конспект лекций по математике. Том 1200. Берлин: Springer; 1986. Асимптотическая теория конечномерных нормированных пространств. [Google Scholar]
19. Pisier G. Cambridge Tracts in Mathematics. Том 94. Кембридж, Великобритания: Cambridge Univ Press; 1989. Объем выпуклых тел и геометрия банахова пространства. [Академия Google]
20. Дадуш Д., Вемпала С.С. Близкие к оптимальным детерминированные алгоритмы вычисления объема с помощью М-эллипсоидов. Proc Natl Acad Sci USA. 2013;110(48):19237–19245. [Google Scholar]
[Google Scholar]
21. Джонсон В. Б., Озава Н., Шехтман Г. Количественная версия теоремы о коммутаторе для матриц с нулевым следом. Proc Natl Acad Sci USA. 2012;110(48):19251–19255. [Google Scholar]
22. Бургейн Дж. Метрическая интерпретация сверхрефлексивности в банаховых пространствах. Израиль Дж. Матем. 1986;56(2):222–230. [Академия Google]
23. Ball K (2012) Программа Ribe. Семинар Бурбаки, разоблачение 1047 .
24. Наор А. Введение в программу Рибе. Японская математика. 2012;7(2):167–233. [Google Scholar]
25. Мендель М., Наор А. Ультраметрические скелеты. Proc Natl Acad Sci USA. 2012;110(48):19256–19262. [Google Scholar]
26. Хот С. Материалы тридцать четвертого ежегодного симпозиума ACM по теории вычислений. Нью-Йорк: ACM; 2002. О мощности уникальных 2-доказательных 1-раундовых игр; стр. 767–775. [Академия Google]
27. Хот С (2010) Неаппроксимируемость NP-полных задач, дискретный анализ Фурье и геометрия. Труды Международного конгресса математиков (Индостанское книжное агентство, Нью-Дели), том 4, стр. 2676–2697.
2676–2697.
28. Ловаш Л. О шенноновской емкости графа. IEEE Trans Inf Theory. 1979; 25(1):1–7. [Google Scholar]
29. Алон Н., Макарычев К., Макарычев Ю., Наор А. Квадратичные формы на графах. Изобретите математику. 2006;163(3):499–522. [Академия Google]
30. Briet J, Burman H, Gijswijt D. Нарушение пропускной способности Шеннона метрических графов с запутанностью. Proc Natl Acad Sci USA. 2012;110(48):19227–19232. [Бесплатная статья PMC] [PubMed] [Google Scholar]
31. Барак Б., Двир З., Вигдерсон А., Йегудаёв А. Дробные теоремы Сильвестра–Галлаи. Proc Natl Acad Sci USA. 2012;110(48):19213–19219. [Google Scholar]
32. Ай А., Двир З., Сараф С., Вигдерсон А. (2012) Теоремы типа Сильвестра-Галлаи для приближенной коллинеарности. архив: 1211.0331v1.
33. Pansu P. Croissance des boules et des géodésiques fermées dans les nilvariétés. Эргодическая теория динамических систем. 1983;3(3):415–445. [Google Scholar]
34. Grötschel M, Lovász L, Schrijver A. Алгоритмы и комбинаторика. 2-е изд. Том 2. Берлин: Springer; 1993. Геометрические алгоритмы и комбинаторная оптимизация. [Google Scholar]
Алгоритмы и комбинаторика. 2-е изд. Том 2. Берлин: Springer; 1993. Геометрические алгоритмы и комбинаторная оптимизация. [Google Scholar]
35. Барани И., Фюреди З. Аппроксимация сферы многогранниками, имеющими мало вершин. Proc Am Math Soc. 1988;102(3):651–659. [Академия Google]
36. Мильман В.Д. Inégalité de Brunn-Minkowski inverse и приложения à la théorie locale des espaces normés. C R Acad Sci, Ser 1 Math. 1986;302(1):25–28. [Google Scholar]
37. Бургейн Дж., Цафрири Л. Об одной проблеме Кадисона и Зингера. J Reine Angew Math. 1991; 420:1–43. [Google Scholar]
38. Маркус А., Спилман Д.А., Сривастава Н. (2013) Переплетающиеся семейства II: смешанные характеристические полиномы и проблема Кадисона-Зингера. архив: 1306.3969v3.
39. Талагранд М. Закономерность гауссовских процессов. Акта Математика. 1987;159(1-2):99–149. [Google Scholar]
40. Келети Т., Мате А., Зиндулка О. (2012) Хаусдорфова размерность метрических пространств и липшицевы отображения на кубы. архив: 1203.0686v2.
архив: 1203.0686v2.
41. Бартал Ю., Линиал Н., Мендель М., Наор А. О метрических явлениях типа Рамсея. Энн Мат. 2005;162(2):643–709. [Google Scholar]
42. Бартал Ю., Боллобас Б., Мендель М. Теоремы типа Рамсея для метрических пространств с приложениями к онлайн-задачам. J Comput Syst Sci. 2006;72(5):890–921. [Google Академия]
43. Мендель М., Наор А. Рэмси, разделы и структуры данных близости. J Eur Math Soc. 2007;9(2):253–275. [Google Scholar]
44. Чечик С. (2013) Оракул приблизительного расстояния с постоянным временем запроса. архив: 1305.3314v1.
45. Дворецкий А. Труды Международного симпозиума по линейным пространствам, Иерусалим, 1960. Иерусалим: Иерусалимское академическое издательство; 1961. Некоторые результаты о выпуклых телах и банаховых пространствах; стр. 123–160. [Google Scholar]
46. Bourgain J, Figiel T, Milman V. О гильбертовых подмножествах конечных метрических пространств. Израиль Дж. Матем. 1986;55(2):147–152. [Google Scholar]
47. Мендель М., Наор А. Ультраметрические подмножества с большой хаусдорфовой размерностью. Изобретите математику. 2013;192(1):1–54. [Google Scholar]
Мендель М., Наор А. Ультраметрические подмножества с большой хаусдорфовой размерностью. Изобретите математику. 2013;192(1):1–54. [Google Scholar]
48. Мильман В.Д. Почти евклидовы факторпространства подпространств конечномерного нормированного пространства. Proc Am Math Soc. 1985; 94(3):445–449. [Google Scholar]
49. Мендель М., Наор А. Евклидовы частные конечных метрических пространств. Adv Math 189(2):451–494. 2004 [Google Scholar]
50. Мильман В.Д. Явления, происходящие в высоких измерениях. Успехи мат наук. 2004; 59(1): 157–168. [Google Scholar]
Скачать презентацию на тему линейная функция. Презентация «Линейная функция, ее график, свойства»
Полное наименование образовательного учреждения:
Муниципальное общеобразовательное учреждение Средняя общеобразовательная школа №3 села Кочубеевское Ставропольского края
Предмет: Математика
Название урока: «Линейная функция , ее расписание, свойства.
Возрастная группа: 7 класс
Название презентации: «Линейная функция, ее график, свойства».
Количество слайдов: 37
Среда (редактор), на которой сделана презентация: POWER POINT 2010
Данная презентация
1 Слайд — Капитал
2 Слайд-актуализация опорных знаний: определение линейного уравнения, устно из из предложенных выбирают те, которые являются линейными.
3 Функция Slide-Definition Linear.
4 Слайд-распознавание линейной функции из предложенных.
Вывод 5 слайдов.
6 Слайды функции настройки функции.
7 Слайд-привожу пример, показывающий.
8 Слайд- Привожу пример, показывающий.
9 Слайд-задача для учащихся.
10 Слайд- проверка правильности выполнения задания. Обращаю внимание учащихся на взаимосвязь коэффициентов К и В и расположение графиков.
11 Вывод слайдов.
12 Слайд-работа с графиком линейной функции.
13 Слайд-задания для самостоятельного решения: построить графики функций (выполнить в тетрадях).
14-17 Слайды — показывают правильное выполнение задания.
18-27 Слайды устные и письменные. Я выбираю задания не все, а только те, которые подходят по уровню подготовленности класса при наличии времени.
28 Слайд-задание для сильных учеников.
29 Слайды подведут итоги.
30-31 Слайды-выводы.
32-36 Слайды-историческая справка. (При наличии времени)
37 Слайд-использованная литература
Список использованной литературы и Интернет-ресурсов:
1.Мордкович. и другие. Алгебра: учебник для 7 класса общеобразовательных учреждений — М.: Просвещение, 2010.
2.Свавич Л.И. и другие. Дидактические материалы по алгебре для 7 класса – М.: Просвещение, 2010.
3. Алгебра 7 класс, под редакцией Макарычева Ю.Н. и др., Просвещение, 2010
4. Интернет-ресурсы: www.symbolsbook.ru/article.aspx%…ID%3D222.
Предварительный просмотр:
Чтобы насладиться предварительным просмотром презентаций, создайте себе учетную запись (аккаунт) Google и войдите в нее: https://accounts. google.com
google.com
Линейная функция, ее график, свойства. Кирьянова Марина Владимировна, учитель математики МОУ СОШ №3 с. Кочубеевский Ставропольский край
Укажите линейные уравнения: 1) 5У = х 2) 3У = 0 3) У 2 + 16х 2 = 0 4) + у = 4 5) х + у = 4 6) у \ u003d -x + 11 7) + 0,5x — 2 = 0 8) 25D — 2m + 1 = 0 9) Y = 3 — 2x 5
Функция вида y = kx + B называется линейной . График функции вида y = kx + b прямой. Для построения прямой нужны всего две точки, так как единственная прямая проходит через две точки.
Найти уравнения линейных функций y = -x + 0,2; у = 1 2, 4х-5,7; у = — 9 х- 1 8; у = 5, 04х; у = — 5, 04х; у = 1 26, 35 + 8, 75х; у = х -0, 2; у = х:8; у = 0, 00 5х; у = 13 3, 13 3 13 3 х; у = 3 — 1 0, 01х; у = 2: х; у = 0, 004 9; y = x: 6 2.
y = kx + b — линейная функция x — аргумент (независимая переменная) y — функция (зависимая переменная) k, b — числа (коэффициенты) до ≠ 0
x x 1 x 2 х 3 в 1 у 2 у 3
у = — 2х + 3 — линейная функция. График линейной функции прямой, для построения прямого нужно иметь две точки x — независимая переменная, поэтому выбираем ее значения; Y — зависимая переменная, ее значение будет получено в результате подстановки выбранного значения x в функцию. Результаты запишем в таблицу: х в 0 2 если х = 0, то у = — 2 · 0 + 3 = 3. 3 Если х = 2, то у = -2 · 2 + 3\ u003d — 4 + 3 = -1. — 1 точки (0;3) и (2;-1) отмечаем на координатной плоскости и проводим прямо через них. х в 0 1 1 у = — 2х + 3 3 2 — 1 выбирают сами
Результаты запишем в таблицу: х в 0 2 если х = 0, то у = — 2 · 0 + 3 = 3. 3 Если х = 2, то у = -2 · 2 + 3\ u003d — 4 + 3 = -1. — 1 точки (0;3) и (2;-1) отмечаем на координатной плоскости и проводим прямо через них. х в 0 1 1 у = — 2х + 3 3 2 — 1 выбирают сами
Для построения графика линейной функции у = — 2 х +3 составить таблицу: х в 03 1 1 строим на координатной плоскости точки (0; 3) и (1; 5) и проводим непосредственно x 1 0 1 3 через них
I Вариант II вариант y = x-4 y = — x + 4 определяют связь коэффициентов K и B и место прямого построения графика линейной функции
y = x-4 y = -x + 4 i Вариант II вариант x y 1 2 0 -4 x 1 2 0 4 y
x 0 y y = kx + m (k > 0) x 0 y y \ u003d kx + m (k 0, то линейная функция y = kx + b возрастает, если K
Пользуясь графиком линейной функции у = 2х — 6, ответьте на вопросы: а) при каком значении х будет = 0? б) при каких значениях будет 0? в) при каких значениях х будет равно 0? 1 0 3 в 1 х -6 а) у = 0 при х = 3 б) у 0 при х 3 Если х 3, то прямая проходит над осью х, значит, орденты соответствующие точки прямые положительны в) при 0 при х 3 если х 3, то прямая ниже оси х, значит ординаты соответствующих точек отрицательные
Задания для самостоятельного решения: построить графики функций (выполняется в тетрадях) 1. у = 2х — 2 2. у = х + 2 3. у = 4 — х 4. у = 1 — 3х о БРИТТИН ВНИМАНИЕ: выбранные Вами точки для построения прямой линии могут быть разными, но расположение графиков обязательно должно совпадать 4
у = 2х — 2 2. у = х + 2 3. у = 4 — х 4. у = 1 — 3х о БРИТТИН ВНИМАНИЕ: выбранные Вами точки для построения прямой линии могут быть разными, но расположение графиков обязательно должно совпадать 4
Какой картинкой является график линейной функции y = kx? Ответ, чтобы объяснить. 1 2 3 4 5 х у х у х у х у х у
Учащийся допустил ошибку при построении функциональной графики. Какая картинка? 1. Y = x + 2 2. y = 1,5x 3. y = -x-1 x y 2 1 x y 3 1 x y 3 3
1 2 3 4 5 x Y x y y x y x y На каком рисунке коэффициент K равен отрицательный? X.
Назовите знак K для каждой из линейных функций:
На каком рисунке свободный элемент b в уравнении линейной функции отрицателен? 1 2 3 4 5 x y x y x y x y x y
Выберите линейную функцию, график которой изображен на рисунке y = x — 2 y = x + 2 y = 2 — x = x — 1 y = — x + 1 у = — х — 1 у = 0,5х у = х + 2 у = 2х молодец! Считать!
ху 1 2 0 1 2 3 -1 -2 -1 -2 ху 1 2 0 1 2 3 -1 -2 -1 -2 у = 2х у = 2х + 1 у = 2х- 1 у \ u003d -2x + 1 y = — 2x- 1 y = -2x
y = -0,5x + 2, y = -0,5x, y = -0,5x- 2 xy 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6 -3 ху 1 2 0 2 3 -1 -2 -1 -2 3 4 5 6 -3 1 у = 0,5х + 2 у = 0,5х- 2 у = 0,5х у = -0,5х + 2 у = -0,5х у = -0 , 5х — 2.
у = х + 1 у = х — 1, у = ху 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6 -3 ху 1 2 0 1 2 3 -1 -2 -1 -2 3 4 5 6 -3 ху = -ху = -х + 3 у = -х- 3 у = х + 1 у = х- 1 у = х
Составьте уравнение линейной функции по следующим условиям:
суммируйте
Выводы Запишите в тетрадь Мы узнали: * Функция вида y = kx + B называется линейной. * График функциональной функции y = kx + b прямой. * Для построения прямой нужны только две точки, так как единственная прямая проходит через две точки. * Коэффициент K показывает, что он увеличивается или уменьшается прямолинейно. * Коэффициент B показывает, в какой точке прямая пересекает ось OY. * Условие параллельности двух прямых.
Желаю успехов!
Алгебра — это слово произошло от названия сочинения Мухаммеда аль-Хорезми «Аль-Джебре и Аль-Мукабала», в котором алгебра изложена как самостоятельный предмет
Роберт Рекорд — английский математик, который в 1556 г. Доверили знаку равенства и объяснили тем, что нет ничего более равного, чем два параллельных отрезка.
Готфрид Лейбниц — немецкий математик (1646 — 1716), впервые введший термин «абсцисса» — в 169 г.5, «Ордината» — в 1684 г., «Координаты» — в 1692 г.
Рене Декарт — французский философ и математик (1596 — 1650), впервые введший понятие «функция»
Употреблено 1.Литературой Мордковича. и другие. Алгебра: учебник для 7 класса общеобразовательных учреждений — М.: Просвещение, 2010. 2.Свавич Л.И. и другие. Дидактические материалы по алгебре для 7 класса – М.: Просвещение, 2010. 3. Алгебра 7 класс, под редакцией Макарычева Ю.Н. и др., Просвещение, 2010 4. Итемнересурс: www.symbolsbook.ru/article.aspx%…ID%3D222
Задачи занятия: сформулировать определение линейной функции, представление о ее графике; выявить роль параметров В и К в расположении графика линейной функции; Формирование умения строить график линейной функции; развивать умение анализировать, обобщать, делать выводы; развивать логическое мышление; Формирование навыков самоконтроля
UK-Значок UK-Margin-Small-Right»>
Ответы 1. А; б 2. а) 1; 3 б) 2; х у 1. А; в 2. а) 2; 4 б) 1; х у вариант 2 вариант
А; б 2. а) 1; 3 б) 2; х у 1. А; в 2. а) 2; 4 б) 1; х у вариант 2 вариант
UK-Значок UK-Margin-Small-Right»>
B k b > 0b0 k 0b0 k «> 0b0 k» > 0b0 k «title =» (!Lang: B k b > 0b0 k»> title=»б к б > 0b0 к»> !}
B k b > 0b0 y = kx i, iii четверть через начало координат 0b0 y = KX i, III четверть через начало координат K» > 0B0 Y = KX I, III четверть через начало координат начало К» > 0B0 Y = KX I, III четверть через начало К «Название =» (!Lang: BKB > 0b0 y = KX i, III четверть через начало К»> title=»b k b > 0b0 y = kx i, iii четверть через начало координат»> !}
B k b > 0B0 Y = KX i, III квартал через начало Коорда K» > 0B0 Y = KX I, III квартал через начало координационного K» > 0B0 Y = KX i , III квартал через начало К»Название=»коорд(!язык: БКБ > 0b0 у = КХ I, III квартал через начало коорд»> title=»b k b > 0b0 y = KX I, III квартал через начало координаты»> !}
B k b > 0 y = KX I, III квартал через начало координаты 0B0 Y = KX i, III квартал через начало координат K» > 0B0 Y = KX I, III квартала через начало координаты К» > 0В0 У = КХ i, III четверти через начало К «Название =» согласования (!язык: БКБ > 0b0 у = КХ I, III четверти через начало координат»> title=»b k b > 0b0 y = KX I, III квартал через начало координаты»> !}
B k b > 0b0 y = KX I, III квартал через начало координат 0B0 Y = KX i, III квартал через начало координат K» > 0B0 Y = KX I, III квартал через начало согласования К» > 0В0 У = КХ i, III квартал через начало К «Название =» согласование (!язык: БКБ > 0b0 у = КХ I, III квартал через начало координата»> title=»b k b > 0b0 y = KX I, III квартал через начало координаты»> !}
B k b > 0b0 y = KX I, III квартал через начало координат 0B0 Y = KX i, III квартал через начало координат K» > 0B0 Y = KX I, III квартал через начало согласования К» > 0В0 У = КХ i, III квартал через начало К «Название =» согласование (!язык: БКБ > 0b0 у = КХ I, III квартал через начало координата»> title=»b k b > 0b0 y = KX I, III квартал через начало координаты»> !}
B k b > 0b0 y = kx + b (y = 2x + 1) i, iii квартал y = kx + b (y = 2x-1) i, iii квартал y = kx i, третий квартал через начало координат 0b0 y = kx + b (y = 2x + 1) i, iii квартал y = kx + b (y = 2x-1) i, iii квартал y = kx i, третья четверть через начало согласования k»>0b0 y = kx + b (y = 2x + 1) i, iii четверть y = kx + b (y = 2x-1) i, iii четверть y = kx i, iii четверти через начало k»>0 y = kx + b (y = 2x + 1) i, iii четверти y = kx + b (y = 2x-1) i , iii квартал y = kx i, iii квартал через начало координаты k»название=»(!язык: bkb > 0b0 y = kx + b (y = 2x + 1)i, iii квартал y = kx + b (y = 2x-1) i, третья четверть y = kx i, iii четверть через начало координат»> title=»b k b > 0 y = kx + b (y = 2x + 1) i, iii четверть y = kx + b (y = 2x-1) i, iii четверть y = kx i, треть квартал до начала координат»> !}
B k b > 0b0 y = kx + b (y = 2x + 1) I, III ерунды. Y = KX + B (Y = 2X-1) I, III из четверки. Y = KX I, III четверти через начало координаты 0b0 y = kx + b (y = 2x + 1) I, III четверки. Y = KX + B (Y = 2X-1) I, III из четверки. У = КХ I, III четверти через начало Коорда К» > 0В0 У = КХ + В (У = 2Х + 1) I, III Че + В (У = 2Х-1) I , III четта.У = КХ I, III четверти через начало Коорда К» > 0В0 У = КХ + В (У = 2Х + 1) I, III четта. Y = KX + B (Y = 2X-1) I, III из четверки. У = КХ I, III четверти через начало сочинения к «название =» (!яз.: бкб > 0b y = кх + b (у = 2х + 1) i, III Четв. у = kx + b (y = 2x-1 ) I, III Chetve.Y = KX I, III четверть через начало координат»>
title=»b k b > 0 y = kx + b (y = 2x + 1) I, III из абсурда. Y = KX + B (Y = 2X-1) I, III из четырех. Y = КХ I, III четверти через начало координат»>
!}
Y = KX + B (Y = 2X-1) I, III из четверки. Y = KX I, III четверти через начало координаты 0b0 y = kx + b (y = 2x + 1) I, III четверки. Y = KX + B (Y = 2X-1) I, III из четверки. У = КХ I, III четверти через начало Коорда К» > 0В0 У = КХ + В (У = 2Х + 1) I, III Че + В (У = 2Х-1) I , III четта.У = КХ I, III четверти через начало Коорда К» > 0В0 У = КХ + В (У = 2Х + 1) I, III четта. Y = KX + B (Y = 2X-1) I, III из четверки. У = КХ I, III четверти через начало сочинения к «название =» (!яз.: бкб > 0b y = кх + b (у = 2х + 1) i, III Четв. у = kx + b (y = 2x-1 ) I, III Chetve.Y = KX I, III четверть через начало координат»>
title=»b k b > 0 y = kx + b (y = 2x + 1) I, III из абсурда. Y = KX + B (Y = 2X-1) I, III из четырех. Y = КХ I, III четверти через начало координат»>
!}
Задачи урока: сформулировать определение линейной функции, представление о ее графике; выявить роль параметров В и К в расположении графика линейной функции; Формирование умения строить график линейной функции; развивать умение анализировать, обобщать, делать выводы; развивать логическое мышление; Формирование навыков самоконтроля
UK-Значок UK-Margin-Small-Right»>
Ответы 1. А; б 2. а) 1; 3 б) 2; х у 1. А; в 2. а) 2; 4 б) 1; х у вариант 2 вариант
А; б 2. а) 1; 3 б) 2; х у 1. А; в 2. а) 2; 4 б) 1; х у вариант 2 вариант
UK-Значок UK-Margin-Small-Right»>
B k b > 0b0 k 0b0 k «> 0b0 k» > 0b0 k «title =» (!Lang: B k b > 0b0 k»> title=»б к б > 0b0 к»> !}
B k b > 0b0 y = kx i, iii четверть через начало координат 0b0 y = KX i, III четверть через начало координат K» > 0B0 Y = KX I, III четверть через начало координат начало К» > 0B0 Y = KX I, III четверть через начало К «Название =» (!Lang: BKB > 0b0 y = KX i, III четверть через начало К»> title=»b k b > 0b0 y = kx i, iii четверть через начало координат»> !}
B k b > 0B0 Y = KX i, III квартал через начало Коорда K» > 0B0 Y = KX I, III квартал через начало координационного K» > 0B0 Y = KX i , III квартал через начало К»Название=»коорд(!язык: БКБ > 0b0 у = КХ I, III квартал через начало коорд»> title=»b k b > 0b0 y = KX I, III квартал через начало координаты»> !}
B k b > 0 y = KX I, III квартал через начало координаты 0B0 Y = KX i, III квартал через начало координат K» > 0B0 Y = KX I, III квартала через начало координаты К» > 0В0 У = КХ i, III четверти через начало К «Название =» согласования (!язык: БКБ > 0b0 у = КХ I, III четверти через начало координат»> title=»b k b > 0b0 y = KX I, III квартал через начало координаты»> !}
B k b > 0b0 y = KX I, III квартал через начало координат 0B0 Y = KX i, III квартал через начало координат K» > 0B0 Y = KX I, III квартал через начало согласования К» > 0В0 У = КХ i, III квартал через начало К «Название =» согласование (!язык: БКБ > 0b0 у = КХ I, III квартал через начало координата»> title=»b k b > 0b0 y = KX I, III квартал через начало координаты»> !}
B k b > 0b0 y = KX I, III квартал через начало координат 0B0 Y = KX i, III квартал через начало координат K» > 0B0 Y = KX I, III квартал через начало согласования К» > 0В0 У = КХ i, III квартал через начало К «Название =» согласование (!язык: БКБ > 0b0 у = КХ I, III квартал через начало координата»> title=»b k b > 0b0 y = KX I, III квартал через начало координаты»> !}
B k b > 0b0 y = kx + b (y = 2x + 1) i, iii квартал y = kx + b (y = 2x-1) i, iii квартал y = kx i, третий квартал через начало координат 0b0 y = kx + b (y = 2x + 1) i, iii квартал y = kx + b (y = 2x-1) i, iii квартал y = kx i, третья четверть через начало согласования k»>0b0 y = kx + b (y = 2x + 1) i, iii четверть y = kx + b (y = 2x-1) i, iii четверть y = kx i, iii четверти через начало k»>0 y = kx + b (y = 2x + 1) i, iii четверти y = kx + b (y = 2x-1) i , iii квартал y = kx i, iii квартал через начало координаты k»название=»(!язык: bkb > 0b0 y = kx + b (y = 2x + 1)i, iii квартал y = kx + b (y = 2x-1) i, третья четверть y = kx i, iii четверть через начало координат»> title=»b k b > 0 y = kx + b (y = 2x + 1) i, iii четверть y = kx + b (y = 2x-1) i, iii четверть y = kx i, треть квартал до начала координат»> !}
B k b > 0b0 y = kx + b (y = 2x + 1) I, III ерунды. Y = KX + B (Y = 2X-1) I, III из четверки. Y = KX I, III четверти через начало координаты 0b0 y = kx + b (y = 2x + 1) I, III четверки. Y = KX + B (Y = 2X-1) I, III из четверки. У = КХ I, III четверти через начало Коорда К» > 0В0 У = КХ + В (У = 2Х + 1) I, III Че + В (У = 2Х-1) I , III четта.У = КХ I, III четверти через начало Коорда К» > 0В0 У = КХ + В (У = 2Х + 1) I, III четта. Y = KX + B (Y = 2X-1) I, III из четверки. У = КХ I, III четверти через начало сочинения к «название =» (!яз.: бкб > 0b y = кх + b (у = 2х + 1) i, III Четв. у = kx + b (y = 2x-1 ) I, III Chetve.Y = KX I, III четверть через начало координат»>
title=»b k b > 0 y = kx + b (y = 2x + 1) I, III из абсурда. Y = KX + B (Y = 2X-1) I, III из четырех. Y = КХ I, III четверти через начало координат»>
!}
Y = KX + B (Y = 2X-1) I, III из четверки. Y = KX I, III четверти через начало координаты 0b0 y = kx + b (y = 2x + 1) I, III четверки. Y = KX + B (Y = 2X-1) I, III из четверки. У = КХ I, III четверти через начало Коорда К» > 0В0 У = КХ + В (У = 2Х + 1) I, III Че + В (У = 2Х-1) I , III четта.У = КХ I, III четверти через начало Коорда К» > 0В0 У = КХ + В (У = 2Х + 1) I, III четта. Y = KX + B (Y = 2X-1) I, III из четверки. У = КХ I, III четверти через начало сочинения к «название =» (!яз.: бкб > 0b y = кх + b (у = 2х + 1) i, III Четв. у = kx + b (y = 2x-1 ) I, III Chetve.Y = KX I, III четверть через начало координат»>
title=»b k b > 0 y = kx + b (y = 2x + 1) I, III из абсурда. Y = KX + B (Y = 2X-1) I, III из четырех. Y = КХ I, III четверти через начало координат»>
!}
Заместитель директора УВР,
учитель математики
МОУ «СОШ № 65 им.Б.П.Агапитова Випмез»
г. Магнитогорск
Магнитогорск
у = кх. + б.
График уравнения y = kx + b прямой. При B = 0 уравнение принимает вид y = kx, его график проходит через начало координат.
1.Y = 3x-7 и y = -6x + 2
3 не равно -6, то графики пересекаются.
2. Проведите уравнение:
3х-7 = -6х + 2
1-абсцисса точка пересечения.
3. Идем по ординате:
Y = 3x-7 = -6x + 2 = 3-7 = -4
-4 0 ордината 5 точки пересечения0874 4. A (1;-4) координаты точки пересечения.
Геометрический смысл коэффициента k
От значений К зависит угол наклона прямой к оси X.
Y = 0,5x + 3
Y = 0,5X-3,3
По мере увеличения /k/ увеличивается угол наклона к оси x в прямой.
k равны 0,5 и угол наклона к оси x такой же в прямой
Коэффициент К называется угловым коэффициентом
От значения b. ордината точек пересечения с осью зависит от Y. .
ордината точек пересечения с осью зависит от Y. .
b = 4, (0,4) — точка
Пересечение с осью Y ось
1. Функции задаются формулами: Y = х-4, Y = 2x-3,
Y = -x-4, Y = 2x, X-0,0,0,0090 Найдите пары параллельных прямых. Ответы:
а) у = Х- 4 и у = 2х. б) у = х-4 и у = Х-0,5
в) у = 0809 90 и9
у = Х-0,5 г) у = 2х. и у = 2х-3
Слайд 1.
К уроку алгебры в 7 классе «Линейная функция и ее график» подготовил Татчин Ю.В. Учитель математики МБОУ СОШ №3 г. Сургут
Клада 2.
Цель: Формирование понятия «линейная функция», умение строить ее график по алгоритму задачи: обучающая: — изучить определение линейной функции — познакомить и изучить алгоритм построения линейной функции, отработать навык распознавания линейной функции по заданной формуле, графике, словесному описанию. Развивающие: — развивать зрительную память, математически грамотную речь, аккуратность, аккуратность в построении, умение анализировать. Воспитательная: — воспитывать ответственное отношение к учебе, аккуратность, дисциплинированность, совершенство. — формировать навыки самоконтроля и взаимосвязи
Развивающие: — развивать зрительную память, математически грамотную речь, аккуратность, аккуратность в построении, умение анализировать. Воспитательная: — воспитывать ответственное отношение к учебе, аккуратность, дисциплинированность, совершенство. — формировать навыки самоконтроля и взаимосвязи
Слайд 3.
План урока: I. Организация времени II. Актуализация эталонных знаний III. Изучение новой темы IV. Закрепление: Устные упражнения, задания на построение графов V. Решение занимательных заданий VI. Подведение итогов урока, запись домашних заданий VII. Отражение
Слайд 4.
I. Организационный момент решается словом горизонтально, вы узнаете ключевое слово 1. Точный свод инструкций, описывающий порядок действий Исполнителя для достижения результата решения задачи для окончательного время 2. Одна из координат точки 3. Зависимость одной переменной от другой, при которой каждому значению аргумента соответствует единственное значение зависимой переменной 4. Французский математик, введший прямоугольную систему координат 5. Угол, сигид мера, которая больше 900, но меньше 1800 6. Независимая переменная 7. Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям аргумента функция 8. Путь, который мы выбираем ал г о р и т м а б с ц и с с а ф н к з и м д е к арт т о п о й и р к у м е н т р и ф и к п р и м
Французский математик, введший прямоугольную систему координат 5. Угол, сигид мера, которая больше 900, но меньше 1800 6. Независимая переменная 7. Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям аргумента функция 8. Путь, который мы выбираем ал г о р и т м а б с ц и с с а ф н к з и м д е к арт т о п о й и р к у м е н т р и ф и к п р и м
Слайд 5.
1. Точный набор инструкций, описывающий порядок действий Исполнителя Достичь результата решения задачи в окончательный раз 2. Одна из координат точки 3. Зависимость одной переменной от другой, в котором каждому значению аргумента соответствует единственное значение зависимой переменной 4. Французский математик, введший прямоугольную систему координат 5. Угол, степень которого больше 900, но меньше 1800 6. Независимая переменная 7. Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям аргумента функция 8. Дорога, которую мы выбираем и л. Р и т м и б ц исс и ф ун к з и д е к а рт т т о н о й а р й е н т р а ф и к п р и м
Дорога, которую мы выбираем и л. Р и т м и б ц исс и ф ун к з и д е к а рт т т о н о й а р й е н т р а ф и к п р и м
Слайд 6.
II. Актуализация эталонных знаний Многие реальные ситуации описываются математическими моделями, представляющими линейные функции. Приведем пример. Турист проехал на автобусе 15 км из пункта А в пункт В, а затем продолжил движение из пункта В в том же направлении в пункт с, но уже пешком, со скоростью 4 км/ч. На каком расстоянии от точки и будет находиться турист через 2 часа, через 4 часа, через 5 часов ходьбы? Математической моделью ситуации является выражение у = 15 + 4х, где Х — время ходьбы в часах, у — расстояние от А (километров). Данной моделью мы отвечаем на вопрос задачи: если х = 2, то у = 15 + 4 ∙ 2 = 23, если х = 4, то у = 15 + 4 ∙ 4 = 31, если х = 6, тогда у = 15 + 4∙6 = 39Математическая модель Y = 15 + 4X является линейной функцией. А в С.
Слайд 7.
III. Изучение новой темы. Уравнение вида y = k x + m, где k и m — числа (коэффициенты), называют линейной функцией. Для построения графика линейной функции необходимо, задав конкретное значение X, вычислить соответствующее значение y. Обычно эти результаты оформляются в виде таблицы. Говорят, что X — независимая переменная (или аргумент), Y — зависимая переменная. 2 1 1 2 х х х х у х
Изучение новой темы. Уравнение вида y = k x + m, где k и m — числа (коэффициенты), называют линейной функцией. Для построения графика линейной функции необходимо, задав конкретное значение X, вычислить соответствующее значение y. Обычно эти результаты оформляются в виде таблицы. Говорят, что X — независимая переменная (или аргумент), Y — зависимая переменная. 2 1 1 2 х х х х у х
Слайд 8.
Алгоритм построения линейной функции 1) составить таблицу линейной функции (каждое значение независимой переменной поставить в соответствие со значением зависимой переменной) 2) построить на координатной плоскости точки Xoy 3) через них прямые — график линейной функции по теореме график линейной функции y = kx + M прямой.
Слайд 9.
Рассмотрим использование алгоритма построения графика линейной функции Пример 1 Построить график линейной функции Y = 2X + 3 1) составить таблицу 2) построить в координатной плоскости XoY очко (0; 3) и (1; 5) 3) потратить напрямую
Клада 10.
Если линейную функцию y = k x + m рассматривать не при всех значениях x x, а только для значений x из некоторого числового множества x, то пишут: y = k x + m, где X x (- признак принадлежности) вернется к задаче в нашей ситуации независимой Переменная может принимать любое неотрицательное значение, но почти турист не может шагать с постоянной скоростью без сна и отдыха как много времени. Так что пришлось ввести разумные ограничения на Х, скажем, турист идет не более 6 часов. Теперь запишем более точную математическую модель: у = 15 + 4х, х 0; 6.
Клада 11.
Рассмотрим следующий пример Пример 2 Построить график линейной функции а) Y = -2x + 1, -3; 2; б) у = -2х + 1, (-3; 2) 1) составляем таблицу для линейной функции у = -2х + 1 2) строим на координатной плоскости Хой точки (-3; 7) и ( 2;-3) и провести через них прямую линию. Это график уравнения Y = -2X + + 1. Далее выбираем отрезок, соединяющий построенные точки. х -3 2 у 7 -3
х -3 2 у 7 -3
Слайд 12.
Слайд 13.
Выполняем построение функции Y = -2X + 1 функция, (-3; 2) Чем отличается этот пример от предыдущего?
Слайд 14.
Слайд 15.
IV. Закрепление изучаемой темы Выберите, какая функция является линейной функцией
Слайд 16.
Слайд 17.
Слайд 18.
Выполните следующую задачу Линейная функция задается формулой Y = -3X — 5. Найдите ее значение при x = 23, x = — 5, х = 0
Слайд 19.
Проверка решения если х = 23, то у = -3 23 — 5 = -69 — 5 = -74 если х = -5, то у = -3 (- 5) — 5 = 15-5 = 10 если х = 0 , то у = -3 0- 5 = 0 — 5 = -5
Слайд 20.
Найдите значение аргумента, при котором линейная функция у = -2х + 2,4 принимает значение равное 20,4? Проверка решения при х = -9 Значение функции 20,4 20,4 = — 2х + 2,4 2х = 2,4 — 20,4 2х = -18 х = -18: 2 х = -9
Клада 21.
Ответ на следующую задачу без выполнения построения: график какой функции принадлежит A (1; 0)?
Клада 22.
Слайд 23.
Слайд 24.
Слайд 25.
Назовите координаты точек пересечения графика этой функции с осями координат с осью oh: (-3; 0) Проверьте себя: с осью ОУ: (0; 3)
Исследовательские публикации Венкатесана Гурусвами.
Исследовательские публикации Венкатесана Гурусвами.Исследовательские публикации
| СПИСОК РАСШИФРОВКИ КОДОВ ИСПРАВЛЕНИЯ ОШИБОК Конспект лекций по информатике, Vol. 3282 Springer-Verlag 2005, 350 стр., ISBN: 3-540-24051-9 Проверить цены и наличие на Amazon; Книгамиллион. |
АЛГОРИТМИЧЕСКИЙ
РЕЗУЛЬТАТЫ В СПИСКОВОЙ РАСШИФРОВКЕ , Foundations and Trends® в
Теоретическая информатика , Том 2, Выпуск 2, 2007. Вы можете загрузите бесплатную копию книги (только для личного пользования ) здесь. Печатная и переплетенная версия этой статьи доступна по адресу 40% скидка от Now Publishers. |
Подписка представляет собой список статей (в соавторстве) со мной, составленный тема/категория. Недавние статьи (начиная с 2005 г. или около того) (пока) не классифицированы по темам. Внутри каждой темы статьи упорядочены более или менее в задний ход хронологическом порядке даты первой публикации. я тоже обычно стараюсь сделать только самую последнюю версию (например, журнал вариант/представление, если таковое существует) имеющейся статьи.
- публикаций (с 2006 г.)
- Опросы
- Теория кодирования
- Алгоритмы приближения, твердость Приближения и PCP
- Прочие теоретические работы
- Тезисы
- Алгоритмический и структурный граф Теория
Список DBLP публикаций Академия Google страница Цифровая библиотека ACM страница автора
Документы (с 2006 г.
 по настоящее время)
по настоящее время)- Алгоритмы и сертификаты для Boolean CSP Опровержение: «Сглаживание не сложнее, чем случайное» , STOC 2022 , появиться. (совместно с П. Котари и П. Манохаром)
- Беспроцентный тр\ eshold для враждебных битовых удалений меньше 1/2 , ФОКС 2021 \ . (совместно с Х. Хе и Р. Ли)
- Приблизительный гипер\ граф Vertex Cover и обобщенная гипотеза Тузы , СОДА 2022 . (совместно с С. Сандипом)
- Помимо кодов исправления одиночного удаления: замены и транспозиции , arXiv:2112.09971 . (совместно с Р. Габрисом, Х. Рибейро, К. Ву)
- Пересмотр нижней границы избыточности линейных пакетных кодов , ECCC TR21-145 . (совместно с О. Альрабиа)
- $\ell_p$-спред свойства разреженных матриц , arXiv:2108.13578 , 2021 . (совместно с П. Манохаром и Дж. Мошейффом)
- Улучшенные максимально восстанавливаемые LRC с использованием косых полиномов , ECCC TR21-025 , 2021 г.
 (совместно с С. Гопи)
(совместно с С. Гопи) - Видимый ранг и коды с местоположением , RANDOM 2021 . (совместно с О. Альрабиа)
- Выполнимость КНФ в подпространстве и связанные с ней проблемы , ИПЕК 2021 . (совместно с В. Арвиндом)
- AC-DC: диагностика кривой усиления для группового тестирования Covid-19 , arxiv:2011.05223 , 2021. (совместно с Р. Габрисом, С. Паттабираманом, В. Рана, Дж. Рибейро, М. Черагчи, О. Миленкович )
- Условная дихотомия логических упорядоченных обещаний CSP , ИКАЛП 2021 . (совместно с Дж. Бракензиком и С. Сандипом)
- Линейная мощность Шеннона графов Кэли , ISIT 2021 . (совместно с А. Рязановым)
- Границы линейного программирования для почти сбалансированных двоичных кодов , ИСИТ 2021 . (совместно с А. Рязановым)
- Локальная линза для кодированных вычислений , ИСИТ 2021 .
 (совместно с М. Рудовым и К.В. Рашми)
(совместно с М. Рудовым и К.В. Рашми) - Строгое опровержение всех полуслучайных логических CSP , SODA 2021 . (совместно с Дж. Абаскалем и П. Котари)
- Явные коды с двумя удалениями с избыточностью, соответствующей границе существования , SODA 2021 . (совместно с Дж. Харингстадом)
- Эффективные линейные и аффинные коды для исправления вставок/удалений , SODA 2021 . (совместно с К. Ченгом, Б. Хэуплером и К. Ли)
- Псевдобиномиальность липкого случайного блуждания , ITCS 2021 . (совместно с В. Кумаром)
- Пороговые скорости Sharp для случайных кодов , ITCS 2021 . (совместно с Дж. Мошейфом, Н. Решем, С. Силасом, М. Вуттерсом)
- Арикан встречает Шеннона: полярные коды с почти оптимальной сходимостью к пропускной способности канала , STOC 2020 . (совместно с А. Рязановым и Мин Е)
- Оптимально устойчивые коды для декодирования списка из вставок и удалений , STOC 2020 .
 (совместно с Б. Хеуплером и А. Шахрасби)
(совместно с Б. Хеуплером и А. Шахрасби) - d-to-1 Твердость окрашивания 3-раскрашиваемые графики с O(1) цветами , ICALP 2020 . (совместно с С. Сандипом)
- Границы для списочного декодирования и списочного восстановления случайных линейных кодов , RANDOM 2020 . (совместно с Р. Ли, Дж. Мошейффом, Н. Решем, С. Силасом, М. Вуттерсом)
- Пересмотр сокращения алфавита в PCP Динура , ПРИБЛИЗИТЕЛЬНО 2020 . (совместно с Дж. Опрасалом и С. Сандипом)
- Устойчивое к утечке совместное использование секрета в неразделенных моделях , ITC 2020 . (совместно с Ф. Линь, М. Черагчи, Р. Сафави-Наини, Х. Ван)
- Симметричные полиморфизмы и эффективная разрешимость обещаний CSP , SODA 2020 . (совместно с Дж. Бракензиком)
- Твердость радужной окраски за счет полиморфизмов низкой чувствительности , ПРИБЛИЗИТЕЛЬНО 2019 .
 (С Саем Сандипом)
(С Саем Сандипом) - Уровень потоковой передачи уникальных игр , ПРИБЛИЗИТЕЛЬНО 2019 . (совместно с Р. Тао)
- Построение максимально восстанавливаемых кодов локальной реконструкции через функциональные поля . ИКАЛП 2019 . (совместно с Л. Джин и К. Син)
- Победить Фредмана-Комлоса в идеальном k-хешировании , ICALP 2019 . (совместно с А. Рязановым)
- Почти оптимальное восстановление кодов Рида-Соломона с низкой субпакетностью , ИСИТ 2019 . (совместно с Х. Цзяном)
- Экспоненциальная нижняя граница подпакетизации кодов MSR , STOC 2019 . (совместно с О. Альрабиа)
- Связь между 0/1 и линейным программированием с помощью случайных блужданий , STOC 2019 . (совместно с Дж. Бракензиком)
- CSP с глобальными модульными ограничениями: алгоритмы и жесткость через полиномиальные представления , STOC 2019 .
 (совместно с Дж. Бракензиком и С. Гопи)
(совместно с Дж. Бракензиком и С. Гопи) - Алгоритмическая поляризация для скрытых марковских моделей , ITCS 2019 . (совместно с П. Наккиран и М. Судан)
- Обмен секретами с бинарными общими папками , ITCS 2019 . (совместно с Ф. Линь, М. Черагчи, Р. Сафави-Наини и Х. Ван)
- Алгоритмическая смесь LP и кольцевых уравнений для Promise CSP , СОДА 2019 . (совместно с Дж. Бракензиком)
- Максимально восстанавливаемые LRC: нижняя граница размера поля и конструкции для нескольких тяжелых четностей , СОДА 2019 . (совместно с С. Гопи и С. Еханиным)
- Аппроксимация матричных норм p->q: обобщенное кривинское округление и гиперконтракционная твердость , СОДА 2019 . (совместно с В. Бхаттипролу, Э. Ли, М. Гошем, М. Тулсиани). Это объединенный расширенный реферат, содержащий результаты следующих двух статей:
- Аппроксимация операторных норм с помощью обобщенного кривинского округления , arXiv:1804.
 03644 , 2018.
03644 , 2018. - Неприближимость матричных p-to-q норм , ECCC TR18-037 , 2018.
- Аппроксимация операторных норм с помощью обобщенного кривинского округления , arXiv:1804.
- Полярные коды с экспоненциально малой ошибкой при конечной длине блока , СЛУЧАЙНО 2018 . (совместно с Дж. Бласиоком и М. Суданом)
- Какой длины могут быть оптимальные локально восстанавливаемые коды? , СЛУЧАЙНО 2018 . (С К. Син и К. Юань)
- Явные локально восстанавливаемые коды расстояния оптимальной длины 5 , Allerton 2018 . (совместно с А. Бимером, Р. Котни, Х. Лопесом, Ф. Пиньеро)
- Расширители размерности без потерь с помощью линеаризованных полиномов и планов подпространств , ССС 2018 . (совместно с Н. Решем и К. Син)
- Общая сильная поляризация , STOC 2018 . (совместно с Дж. Бласиоком, П. Наккираном, А. Рудрой и М. Суданом)
- Коды epsilon-MSR: контакт с меньшим количеством блоков кода для точного восстановления , ISIT 2018 .
 (совместно с С. Локам и С. Викнешвар)
(совместно с С. Локам и С. Викнешвар) - О списочной декодируемости случайных линейных ранг-метрических кодов , ИСИТ 2018 . (совместно с Н. Решем)
- Удовлетворение ограничения обещания: алгебраическая структура и симметричная логическая дихотомия , SODA 2018 . (совместно с Дж. Бракензиком)
- Кодирование против удалений в забывчивых и онлайн моделях , SODA 2018 . (с Рэем Ли)
- Семейство тестов диктатуры с идеальной полнотой для обложки этикетки 2-к-2 , Технический отчет ECCC TR17-141 , 2017. (совместно с Дж. Бракензиком)
- Декодирование списка оптимальной скорости по ограниченным алфавитам с использованием алгебро-геометрических кодов , Представление журнала , 2017 г. (совместно с К. Син)
- Кодовые конструкции MDS с малой субпакетностью и почти оптимальной пропускной способностью восстановления , Представление в журнал , 2017 г.
 (совместно с А. Раватом, И. Тамо и К. Ефременко))
(совместно с А. Раватом, И. Тамо и К. Ефременко)) - Гиперграфы жесткости радужной раскраски , FSTTCS 2017 , появиться. (совместно с Р. Сакетом)
- Слабое разделение, полиномиальные складки и приближенная оптимизация над сферой , ФОКС 2017 . (совместно с В. Бхаттипролу, М. Гошем, Э. Ли и М. Тулсиани)
- Стремление к сильной неаппроксимации приводит к идеальной полноте , APPROX 2017 и ECCC TR17-080 . (совместно с Дж. Бракензиком)
- Потоковая сложность аппроксимации Max 2CSP и Max Acyclo Subgraph , ПРИБЛИЗИТЕЛЬНО 2017 . (совместно с А. Велингкером и С. Велусами)
- Населенный пункт через частично поднятые коды , RANDOM 2017 . (совместно с С. Л. Франк-Фишером и М. Вуттерсом)
- Эффективно декодируемые коды для двоичного канала удаления , СЛУЧАЙНОЕ 2017 . (с Рэем Ли)
- Сертификаты суммы квадратов для максимумов случайных тензоров на сфере , RANDOM 2017 .
 (совместно с В. Бхаттипролу и Э. Ли)
(совместно с В. Бхаттипролу и Э. Ли) - Проекты подпространств на основе полей алгебраических функций , ICALP 2017 . (С К. Син и К. Юань)
- Улучшенная граница декодирования списка нулевых ошибок канала 4/3 , ИСИТ 2017 . (совместно с М. Далай и Дж. Радхакришнаном)
- коды epsilon-MSR с малой подпакетностью , ИСИТ 2017 . (совместно с А. Раватом, И. Тамо и К. Ефременко)
- Коды MDS с небольшой подпакетностью и почти оптимальной пропускной способностью восстановления , SODA 2017 . (совместно с А. Раватом)
- Надежная аппроксимация Фурье и полиномиальной кривой , FOCS 2016 . (совместно с Д. Цукерманом)
- Эффективно декодируемые коды вставки/удаления для шумовых и высокоскоростных режимов , ИСИТ 2016 . (с Рэем Ли)
- Новые результаты твердости для раскрасок графов и гиперграфов , CCC 2016 .
 (совместно с Дж. Бракензиком)
(совместно с Дж. Бракензиком) - Жесткие рамки для уточнения соглашения с помощью связи , CCC 2016 . (совместно с Дж. Радхакришнаном)
- Восстановление кодов Рида-Соломона , STOC 2016 . (совместно с М. Вуттерсом)
- Эффективное списочное декодирование проколотых кодов Рида-Мюллера , IEEE Trans. Информация. Теория, 2017 (с Л. Джин и К. Син)
- Улучшенная оценка доли исправимых делеций , SODA’16 и IEEE Trans. Информация. Theory , 2017. (совместно с Б. Бухом и Дж. Харингстадом)
- Эффективные малоизбыточные коды для исправления множественных удалений , SODA 2016 . (совместно с Ю. Бракензиком и С. Збарским)
- Почти оптимальная NP-твердость Unique Coverage , SODA 2016 . (с Э. Ли)
- Простое доказательство устойчивости набора вершин обратной связи , Теория вычислений , 12(6), 2016, 1-11.
 (совместно с Э. Ли)
(совместно с Э. Ли)
- К характеристике сопротивления аппроксимации симметричных CSP , ПРИБЛИЗИТЕЛЬНО 2015 . (совместно с Ыйвуном Ли)
- Приблизительная окраска гиперграфа при низком расхождении и связанных обещаниях , ПРИБЛИЗИТЕЛЬНО 2015 . (совместно с В. Бхаттипролу и Э. Ли)
- Расширители размеров через рядные конденсаторы , RANDOM 2015 . (с Майклом Форбсом)
- Неаппроксимируемость H-образной поперечной/упаковки , ПРИБЛИЗИТЕЛЬНО 2015 . (совместно с Ыйвуном Ли).
- Коды удаления в шумовом и высокоскоростном режимах , RANDOM 2015 . (совместно с Кэрол Ван)
- Неравенство энтропийной суммы и полиномиальная сходимость к емкости Шеннона для всех алфавитов , ССС 2015 . (совместно с А. Велингкером)
- Связь с несовершенно разделенной случайностью . ИТКС 2015 .
 (совместно с К. Канонном, Р. Мекой и М. Суданом)
(совместно с К. Канонном, Р. Мекой и М. Суданом) - Результаты сильной неаппроксимации на сбалансированных раскрашиваемых радугой гиперграфах , SODA 2015 . (совместно с Ыйвуном Ли)
- Ограничения на проверяемые аффинно-инвариантные коды в высокоскоростном режиме , SODA 2015 . (совместно с М. Суданом, А. Велингкером и К. Вангом)
- (2+eps)-SAT является NP-жестким , FOCS 2014 . (совместно с П. Острином и Дж. Харингстадом).
- Явные ранг-метрические коды, декодируемые списком с оптимальной избыточностью , RANDOM 2014 . (совместно с Кэрол Ван)
- Наборы попаданий для полиномов низкой степени с оптимальной плотностью , CCC 2014 . (совместно с К. Син)
- Твердость окраски суперполилогарифмического гиперграфа с помощью длинных кодов низкой степени , STOC 2014 . (совместно с П.
 Харшей, Дж. Харингстадом, С. Шринивасаном и Г. Вармой)
Харшей, Дж. Харингстадом, С. Шринивасаном и Г. Вармой) - Неизменяемое кодирование против подделки побитовых данных и разделенных состояний , TCC 2014 . (совместно с М. Черагчи)
- Емкость негибких кодов , ITCS 2014 . (совместно с М. Черагчи)
- Сложность аппроксимации CSP с Балансовыми/Жесткими ограничениями , ITCS 2014 . (совместно с Э. Ли)
- Округление SDP Лассера с использованием схем выбора столбца и спектральной аппроксимации для разбиения графа и квадратичных IP-адресов , arXiv:1312.3024 . (совместно с А. К. Синопом)
- Декодирование списков с оптимальной скоростью свернутых алгебро-геометрических кодов над алфавитами постоянного размера , СОДА 2014 . (совместно с К. Син)
- Связанная версия Декодирование алгебраического списка с оптимальной скоростью с использованием полей класса узкого луча.
- Полярные коды:
Скорость поляризации и полиномиальная щель на полную мощность , FOCS 2013 .
 (совместно с П. Ся)
(совместно с П. Ся) - PCP с помощью длинного кода низкой степени и жесткости для раскраски гиперграфа с ограничениями , ФОКС 2013 . (совместно с И. Динуром)
- Явный подпространственные конструкции , ФОКС 2013 . (совместно с С. Коппарти)
- Комбинаторные ограничения декодирования списка среднего радиуса , RANDOM 2013 . (совместно с С. Нараянаном)
- Суперлинейные нижние границы для многопроходной обработки графов , CCC 2013 . (совместно с К. Онак)
- Список декодирования субкодов Рида-Соломона, алгебро-геометрических и Габидулина до границы Сингетона , STOC 2013 . (совместно с К. Син)
- Неаппроксимируемость минимального вершинного покрытия на k-однородных k-дольных гиперграфах г., ECCC TR13-071, 2013 г. (совместно с С. Сачдевой и Р. Сакетом)
- CopyCatch: Прекращение групповых атак путем обнаружения поведения Lockstep в социальных сетях , WWW 2013 .
 (совместно с А. Бейтелем, В. Сюй, К. Палоу и К. Фалуцосом)
(совместно с А. Бейтелем, В. Сюй, К. Палоу и К. Фалуцосом) - Ограниченная изометрия матриц Фурье и списочная декодируемость случайных линейных кодов , СОДА 2013 . (совместно с М. Черагчи и А. Велингкером)
- Аппроксимация неравномерного разреженного разреза с помощью обобщенных спектров , СОДА 2013 . (совместно с А. К. Синопом)
- Линейно-алгебраическое списочное декодирование вариантов кодов Рида-Соломона , IEEE Trans. Информация. Theory , 59(6): 3257-3268, 2013 г. (совместно с К. Ван)
- Пробелы целостности Лассера с постоянным коэффициентом для задач разбиения графов , Рукопись , 2012 г. (совместно с А. К. Синопом и Ю. Чжоу)
- Более быстрые решатели иерархии SDP для алгоритмов локального округления , ФОКС 2012 . (совместно с А. К. Синоп.)
- Аппроксимация ограниченного упорядочения вхождений CSP , ПРИБЛИЗИТЕЛЬНО 2012 .
 (совместно с Ю. Чжоу)
(совместно с Ю. Чжоу) - Свернутые коды из башен функциональных полей и улучшенное декодирование списка оптимальных скоростей , STOC 2012 . (совместно с К. Син)
- Список кодов декодирования подпространств из вставок и удалений , ITCS 2012. (совместно с С. Нараянаном и К. Вангом)
- Оптимальная реконструкция низкоранговой матрицы на основе столбцов , SODA 2012. (совместно с А. К. Синопом)
- Полиномиальные разрывы целочисленности для сильных SDP-релаксаций самого плотного k-подграфа , SODA 2012. (Совместно с А. Бхаскара, М. Чарикар, А. Виджаярагхаван и Ю. Чжоу)
- Обход UGC из некоторых оптимальных результатов геометрической неаппроксимации , SODA 2012. (совместно с П. Рагхавендрой, Р. Сакетом и Ю. Ву)
- Иерархия Лассера, высшие собственные значения и схемы аппроксимации для квадратично-целочисленного программирования с целями PSD , FOCS 2011.
 (совместно с А. К. Синопом)
(совместно с А. К. Синопом) - Декодирование списка оптимальных скоростей через производные коды , RANDOM 2011 . (совместно с К. Ван)
- Линейно-алгебраическое списочное декодирование свернутых кодов Рида-Соломона , CCC 2011 .
- Нахождение почти идеальных делений графа пополам , ICS 2011 . (совместно с Ю. Макарычевым, П. Рагхавендрой, Д. Штёрером и Ю. Чжоу)
- Превзойти случайный порядок сложно: каждый упорядочивающий CSP устойчив к аппроксимации
- Сложность нахождения независимых множеств в графах ограниченных степеней (гипер) низкого хроматического числа , СОДА 2011 . (совместно с А. К. Синопом)
- Жесткие границы неаппроксимируемости для почти выполнимого Horn SAT и набора точных попаданий , SODA 2011 . (совместно с Ю. Чжоу)
- Коды для вычислительно простых каналов: явные конструкции с оптимальной скоростью , FOCS 2010 .
 (совместно с А. Смитом)
(совместно с А. Смитом) - Соединение Шеннона и Хэмминга: список исправлений ошибок с оптимальной скоростью , ICM 2010 (приглашенный опрос)
- О неаппроксимируемости вершинного покрытия на k-дольных k-однородных гиперграфах , ICALP 2010 . (совместно с Р. Сакетом)
- Зазоры SDP для 2-к-1 и других вариантов Label-Cover , ICALP 2010 . (совместно с С. Хотом, Р. О’Доннеллом, П. Попатом, М. Тулсиани и Ю. Ву)
- По списку-декодируемости Случайные линейные коды , СТОК 2010 . (С Дж. Харингстад и С. Коппати)
- Агностик изучение мономов по полупространствам сложно , FOCS 2009 . (совместно с В. Фельдманом, П. Рагхавендрой и Йи Ву)
- Улучшены результаты неаппроксимации для максимального k-раскрашиваемого подграфа . ПРИБЛИЗИТЕЛЬНО 2009 .
 (совместно с А. К. Синоп)
(совместно с А. К. Синоп) - Каждая CSP перестановки арности 3 устойчива к аппроксимации , ССС 2009 . (совместно с М. Чарикар и Р. Манокараном)
- Коды для локального тестирования требуют резервных тестеров , CCC 2009 . (совместно с Э. Бен-Сассоном, Т. Кауфманом, М. Суданом и М. Видерманом)
- Исправление ошибок до теоретико-информационного предела . html-версия; Более красочное цифровое издание. Сообщения ACM , март 2009 г. (совместно с А. Рудрой)
- Циклотомическая функция
поля, автоморфизмы Артина-Фробениуса и ошибка списка
коррекция с оптимальным курсом , Алгебра и теория чисел , Vol. 4 (2010), № 4, 433-463.
- Расширенный реферат «Автоморфизмы Артина, циклотомические
функциональные поля и декодируемые коды со свернутым списком »появились в STOC 2009 .
Вот arxiv версия.
- Расширенный реферат «Автоморфизмы Артина, циклотомические
функциональные поля и декодируемые коды со свернутым списком »появились в STOC 2009 .
- Список тензорных произведений декодирования и чередующихся кодов .
 Расширенный аннотация в STOC 2009 . (совместно с П. Гопаланом и П. Рагхавендрой)
Расширенный аннотация в STOC 2009 . (совместно с П. Гопаланом и П. Рагхавендрой) - Распределение Max-Min через разветвления с нижней границей степени , Труды STOC 2009 . (совместно с М. Х. Батени и М. Чарикар)
- Черновик полной версии
- Превзойти случайный порядок сложно: неаппроксимируемость максимального ациклического подграфа , FOCS 2008 . (совместно с Р. Манокараном и П. Рагхавендрой)
- Евклидовы сечения с сублинейной случайностью и исправлением ошибок по вещественным числам , СЛУЧАЙНО 2008 . (с Дж. Ли и А. Вигдерсоном)
- Удовлетворение ограничений в небулевой области: алгоритмы аппроксимации и сложность уникальных игр , ПРИБЛИЗИТЕЛЬНО 2008 . Также Отчет ECCC TR08-08 . (совместно с П. Рагхавендрой)
- Явные перемежители для построения кода повторения с накоплением и накоплением (RAA) , ISIT 2008 .
 (совместно с В. Махмучи)
(совместно с В. Махмучи) - Мягкое декодирование, двойные коды BCH и улучшенные коды , IEEE Trans. Информация. Теория, 2010 . Версия конференции CCC 2008 . (совместно с А. Рудрой)
- Усиление жесткости в NP по сравнению с детерминированными алгоритмами , J. Компьютерные и системные науки , специальный выпуск Киотской премии Карпа. (совместно с П. Гопаланом)
- Версия для конференций в CCC 2008 . 9N через коды расширителей , Принимается к Combinatorica , 2009. Конф. версия SODA 2008 . (С Дж. Ли и А. Разборов)
- Неприближимость путей с непересекающимися ребрами и маршрутизации с низкой перегрузкой на ненаправленных графики , Комбинаторика . (совместно с М. Эндрюсом, Дж. Чужой, С. Ханной, К. Талвар и Л. Чжан)
- Улучшенные коды, декодируемые двоичным списком, благодаря многоуровневой конкатенации, СЛУЧАЙНЫЙ 2007 ; Журнальная версия в IEEE Trans.
 Информация. Теория . (совместно с А. Рудрой)
Информация. Теория . (совместно с А. Рудрой) - Несбалансированные расширители и экстракторы случайности из кодов Парвареша-Варди , Journal of the ACM , 56(4), 2009 г. (совместно с К. Умансом и С. Вадханом)
- Первоначально Экстракторы и конденсаторы из одномерных многочленов , Отчет ECCC TR06-134.
- Версия для конференций: Несбалансированные расширители и экстракторы случайности из кодов Парвареш-Варди , CCC’07 (получил награду за лучшую статью ).
- Сложность решения разреженных переопределенных линейных систем: PCP с 3 запросами над целыми числами , ACM Transactions on Computation Theory , 1(2): (2009). Версия конференции в STOC 2007 . (совместно с П. Рагхавендрой)
- Сложность маршрутизации с перегрузкой в направлены графы , СТОК 2007 . (совместно с Дж. Чужой, С. Ханной и К.
 Талваром)
Талваром)- Более ранняя версия: Сложность маршрутизации с низкой перегрузкой в ориентированных графах , Отчет ECCC TR06-141. (с К. Талваром)
- Итеративное декодирование кодов проверки четности с низкой плотностью , (обзор) , выпуск 90 бюллетеня EATCS.
- Достижение способности декодирования списка с использованием свернутых кодов Рида-Соломона , Приглашенный доклад по адресу Allerton 2006 . (совместно с А. Рудрой)
- Сложность изучения полупространств с шумом , Приглашен на SIAM J. Computing ; Предварительная версия FOCS 2006 . (совместно с П. Рагхавендрой)
- Коррелированные алгебро-геометрические коды: улучшенное декодирование списков по ограниченным алфавитам , Математика вычислений , 77 (2008), 447-473. Расширенная аннотация появилась в ФОКС 2006 . (совместно с А. Паттаком)
- О тестировании кодовых слов с двумя запросами с почти идеальной полнотой , ISAAC 2006 .

- Явные коды, достигающие способности декодирования списка: исправление ошибок с оптимальной избыточностью , IEEE Trans. в информации. Theory, 54(1), январь 2008 г. (совместно с А. Рудрой)
- Первоначально Явные коды для достижения пропускной способности, декодируемые по списку , STOC 2006 . (совместно с А. Рудрой)
- Алгебраико-геометрические обобщения кодов Парвареша-Варди , Отчет ECCC TR05-132 (входит в состав статьи о коррелированных кодах AG выше)
- Декодирование списка в средней сложности и псевдослучайности . Приглашенный мини-опрос, ITW 2006 .
- Усиление твердости с помощью компактных прямых произведений , Вычислительная сложность . (совместно с В. Кабанец)
- Алгоритмы модульного подсчета корней многочленов от многих переменных . LATIN 2006 , Приглашен на Algorithmica . (совместно с П.
 Гопаланом и Р. Липтоном)
Гопаланом и Р. Липтоном) - Корреляция Кластеризация с фиксированным количеством кластеров , Теория вычислительной техники , 2(13) (2006). Версия для конференций SODA 2006 . (совместно с И. Джотисом)
- Объединение Шеннона и Хэмминга: список исправлений ошибок с оптимальной скоростью , Proceedings of ICM 2010 (приглашенный опрос), август 2010 г.
- Исправление ошибок до теоретико-информационного предела . html-версия; Более красочное цифровое издание. Сообщения ACM , март 2009 г. (совместно с А. Рудрой)
- Расшифровка списка двоичных кодов , Краткий обзор, 2009.
- Итеративное декодирование кодов проверки четности с низкой плотностью , выпуск 90 бюллетеня EATCS.
- Расшифровка списка и псевдослучайные построения , AAECC 2007 .
- Алгоритмические результаты в декодировании списка , Foundations and Trends® в
Теоретическая информатика , Том 2, Выпуск 2, 2007.

- Декодирование списка в средней сложности и псевдослучайности . Мини-опрос, ITW 2006 .
- Коды исправления ошибок и
Расширитель графов Новости SIGACT , 35(3): 25-41,
Сентябрь 2004 г.
- Размышления об «Улучшенном
Расшифровка Рида-Соломона и
Алгебраико-геометрические коды» Информационный бюллетень IEEE по теории информации , 2002 г. (совместно с М. Суданом)
- Быстро
Смешивание цепей Маркова: сравнение методов , Неопубликовано , 2000.
- Показания на квартиру,
ускоряющая Вселенная и
модель $\Lambda$CDM , , неопубликованная , 2000.
- В. Гурусвами и С. Вадхан.
Нижняя граница размера списка для декодирования списка
Материалы RANDOM 2005 . - В.
 Гурусвами и А. Рудра.
Гурусвами и А. Рудра.
Толерантные локально тестируемые коды
Материалы RANDOM 2005 . - В. Гурусвами и А. Рудра.
Ограничения для списка декодирования кодов Рида-Соломона
IEEE Trans. Информация. Theory, август 2006 г. Предварительная версия в STOC 2005 . - В. Гурусвами и А. Варди.
Декодирование по методу максимального правдоподобия Рида-Соломона Codes is NP-hard
IEEE Transactions on Information Theory 51(7): 2249-2256 (2005).
Версия конференции в SODA 2005. - В. Гурусвами.
Коды исправления ошибок и Расширяющие графики
Новости SIGACT , 35(3): 25-41, Сентябрь 2004 г. - В.
Гурусвами и П. Индик.
Декодирование линейного списка времени в безошибочных настройках
Материалы ICALP 2004 . - В.
Гурусвами, Д. Мичиансио и О. Регев.
г. Сложность покрытия Радиус Задача о решетках и кодах
Вычислительная сложность , 14(2):90-121, 2005.
Предварительная версия на конференции по вычислительной сложности (CCC), 2004 . - Венкатесан
Гурусвами.
Лучшие экстракторы для лучших кодов?
Материалы STOC 2004 . - Венкатесан Гурусвами и Петр Индик.
Эффективно декодируемые коды встреча с Гилбертом-Варшавовым, направляющимся в Низкие тарифы
Материалы СОДА 2004 . - Венкатесан Гурусвами.
Список Расшифровка с дополнительной информацией
Труды Сложность 2003 . - Венкатесан Гурусвами и Петр Индик.
Линейное время, кодируемое и перечисляемое декодируемые коды
Материалы STOC 2003 . - Венкатесан Гурусвами и Игорь Шпарлински.
Безусловное доказательство Плотность Johnson Bound
Материалы СОДА 2003. - В. Гурусвами.
Пределы для перечисления декодируемости линейные коды
Материалы STOC 2002 .
- В. Гурусвами и П. Индик.
Линейное время, кодируемое/декодируемое коды с почти оптимальными оценка
IEEE Trans. в информации. Теория , октябрь 2005 г. - В. Гурусвами и П. Индик.
Почти оптимальные линейные временные коды для уникального декодирования и нового списка декодируемые коды в меньших алфавитах
Материалы STOC 2002 . - Нога Алон, Венкатесан Гурусвами, Тали Кауфман и Мадху Судан.
Эффективное угадывание секретов через расшифровку списка
Материалы СОДА 2002 . Появился в специальном выпуске ACM Transactions on Algorithms для документов SODA’02. - В. Гурусвами и П. Индик.
Линейные временные коды для коррекции максимально возможная доля ошибок .
Приглашен на Allerton 2001 . - Венкатесан Гурусвами и Мадху Судан.
Декодирование составных кодов с использованием программная информация
Труды Сложность 2002 .
- В. Гурусвами и Мадху Судан.
Размышления об «Улучшенном Расшифровка Рида-Соломона и Алгебраико-геометрические коды»
Информационный бюллетень IEEE по теории информации, март 2002 г. . - В. Гурусвами и П. Индик.
На основе расширителя Конструкции эффективно декодируемых кодов
Материалы FOCS 2001 . - В. Гурусвами.
Расшифровка списка из Erasures: Границы и код Конструкции
IEEE Trans. в информации. Теория , ноябрь 2003. - В. Гурусвами.
Конструкции кодов из числовых полей
IEEE Trans. в информации. Теория , 2003.
(Вот 2 стр. резюме.) - В. Гурусвами.
Список Расшифровка кодов исправления ошибок
Кандидатская диссертация, Массачусетский технологический институт, август 2001. - В. Гурусвами и М. Судан.
расширений Джонсона Переплет
Рукопись , февраль 2001 г.
- В. Гурусвами, Дж. Харингстад, М. Судан и Д. Цукерман.
Комбинаторный Границы для декодирования списка
IEEE Trans. по информации Theory , май 2002 г.
Приглашена предварительная версия на 38-й ежегодный Allerton Конференция по связи, управлению и вычислительной технике . - В. Гурусвами, А. Сахай и М. Судан.
Мягкое решение Расшифровка китайских остаточных кодов
Материалы FOCS 2000 . - В. Гурусвами и Мадху
Судан.
О представительствах Алгебраико-геометрические коды для декодирования списка
IEEE Труды по теории информации , май 2001 г. - В. Гурусвами и М.
Судан.
Список алгоритмы декодирования некоторых составных кодов
Материалы СТОК 2000 . - Венкатесан Гурусвами и Мадху Судан.
Улучшенный Декодирование кодов Рида-Соломона и алгебро-геометрических кодов
IEEE Transactions on Теория информации , 45 (1999), стр. 1757-1767.
1757-1767. - В. Гурусвами и Л. Тревизан.
Сложность уникального выбора: примерно 1-in-kSAT
Труды ПРИБЛИЗИТЕЛЬНО 2005. - В. Гурусвами и С. Хот.
Твердость Max 3SAT без смешанных пунктов
Труды КТС 2005. - В. Гурусвами, Дж. Д. Хартлайн, А. Карлин, Д. Кемпе, К. Кеньон и Ф. Макшерри.
Включено Максимизация прибыли Ценообразование без зависти
Труды СОДА 2005. - В.
Гурусвами, Д. Мичиансио и О. Регев.
Сложность покрытия Радиус Задача о решетках и кодах
Материалы CCC 2004 ; Журнальная версия в спецвыпуске Вычислительная сложность . - Моисей
Чарикар, Венкатесан Гурусвами и Энтони Вирт.
Кластеризация с качественными Информация
ССПС, октябрь 2005 г. (Специальный выпуск). Предварительная версия FOCS 2003 .
Предварительная версия FOCS 2003 . - И.
Динур, В. Гурусвами, С. Хот и О. Регев.
Новый многослойный PCP и твердость вершинного покрытия гиперграфа
СИАМ Дж. Вычисл. 34(5): 1129-1146 (2005)
Версия для конференций в STOC 2003. - И.
Динур, В. Гурусвами и С. Хот.
Vertex Cover на k — однородные гиперграфы трудно аппроксимировать с коэффициентом (k-3-eps)
Технический отчет ECCC TR02-027. - В.
Гурусвами и П. Индик.
Вложения и неаппроксимируемость геометрических задач
Материалы СОДА 2003. - л.
Энгебрецен и В. Гурусвами.
Удовлетворение ограничений закончилось две переменные всегда легко?
Случайные структуры и алгоритмы , 2004 г. Предварительная версия в проц. RANDOM 2002. - В.
Гурусвами, Дж. Хастад
и М. Судан.
Твердость приблизительной раскраски гиперграфа
СИАМ Дж. Вычисл. 31(6): 1663-1686 (2002)
Вычисл. 31(6): 1663-1686 (2002)
Предварительный версия появилась в FOCS 2000 (журнальная версия является значимой ревизия). - М.
Чарикар,
В. Гурусвами, Р. Кумар, С. Раджагопалан и А. Сахай.
Комбинаторный Проблемы выбора признаков
Proc. ФОКС 2000 . - В.
Гурусвами и С. Кханна
На твердость 4-раскраски трехцветного графа
SIAM J. Disc. Math , 2004. (Предварительная версия в Proc. из Сложность 2000 , стр. 188-197.) - В.
Гурусвами.
Неприближимость результатов для множества Проблемы расщепления и выполнимости без смешанных предложений
Algorithmica , 2003 г. (специальный выпуск для избранных статей ПРИБЛИЗИТЕЛЬНО 2000 г.) - В.
Гурусвами, С. Кханна,
Р. Раджараман, Ф.Б. Пасти,
М.
Яннакакис.
Почти оптимальный Результаты твердости и алгоритмы аппроксимации для путей с непересекающимися краями и сопутствующие проблемы .
JCSS , 67(3):473-496, 2003 г. (предварительный версия Proc. СТОЦ 1999 .) - Евгений Додис,
Венкатесан Гурусвами и Санджив
Khanna
Сегментация на 2 каталога Проблема
Материалы СОДА 1999 . - Венкатесан
Гурусвами, Дэниел Левин,
Мадху Судан и Лука Тревизан
А точная характеристика NP с 3 запросами PCP
Материалы ФОКС 1998 . Также доступен как ECCC Technical Отчет TR98-034 .
[Техническое содержание этой статьи (даже версия ECCC) довольно сложно читать без знакомства с бумагой Хастада. Более автономная версия можно найти ниже в форме моей магистерской диссертации.] - В.
Гурусвами.
Эффективная проверка запросов Доказательства и улучшенные характеристики PCP NP
Магистерская диссертация, Массачусетский технологический институт, май 1999 г. Вот HTML Аннотация. - В.
Гурусвами и К. Панду Ранган.
Естественная семья Задачи оптимизации со сколь угодно малой аппроксимацией пороги
Письма обработки информации , 68 (1998), стр. 241-248.
241-248. - В.
Гурусвами и Ч.Панду Ранган.
Примерная трехцветная окраска для Регистрация Распределение
Письма об обработке информации , Vol. 60, 1996. - М. Чарикар, Р. Фагин,
В. Гурусвами, Дж. Клейнберг,
П. Рагхаван и А. Сахаи.
Запрос Стратегии ценовой информации
JCSS 64(4):785-819, 2002. (Предварительная версия в Proc. СТОЦ 2000 .) - В.
Гурусвами и А. Сахаи.
Мультикласс Коды обучения, повышения и исправления ошибок
Труды COLT’99 . - Список декодирования кодов, исправляющих ошибки , к.т.н. диссертация, Массачусетский технологический институт, 2001.
- Эффективный запрос
Проверка доказательств и улучшенных характеристик PCP NP ,
Магистерская диссертация, Массачусетский технологический институт, май 1999 г.
Вот HTML автореферат диссертации.
- Результаты трудоемкости для некоторых теоретико-графовых оптимизаций и Проблемы аппроксимации, Старшая диссертация, Индийский институт Технологии, Мадрас, 19 мая.97.
- В. Гурусвами. Перечислительный Аспекты некоторых классов совершенных графов , Дискретные Математика , 205 (1999), стр. 97-117.
- В. Гурусвами, У.Ротикс, М.С.Маданлал, Дж.А.Маковски и C.Pandu Rangan, Ограничения задач минимального гаечного ключа , Информация и вычисления , 97 августа.
- В. Гурусвами и К. Панду Ранган. Алгоритмические аспекты клико-трансверсальные и кликонезависимые множества , Дискретные Прикладная математика , 100 (2000), стр. 183-202.
- В. Гурусвами. Максимальная отсечка на линейных и общих графиках , Дискретный Прикладная математика , 92 (1999), стр. 217-221.
- В.
Гурусвами, К.
 Панду Ранган, М.С. Чанг, Г.Дж. Чанг и
С.К. Вонг, г.
Задача треугольников с непересекающимися вершинами г., Материалы WG’98,
Замок Смоленице, Словакия, июнь 1998 г. Версия журнала в Computing .
Панду Ранган, М.С. Чанг, Г.Дж. Чанг и
С.К. Вонг, г.
Задача треугольников с непересекающимися вершинами г., Материалы WG’98,
Замок Смоленице, Словакия, июнь 1998 г. Версия журнала в Computing . - В. Гурусвами и К. Панду Ранган. Сложность графа Проблемы с упаковкой . Неопубликованная рукопись .
- В. Гурусвами и К. Панду Ранган. Алгоритмические аспекты Edge Доминирующие наборы . Неопубликованная рукопись .
- В. Гурусвами, Г. Мохан и К. Шива Рама Мурти, 9 лет1795 Вероятностная маршрутизация на многокаскадных, с маршрутизацией по длине волны, Hypercube и Debruijn Networks , Proc. Четвертого Международная конференция по высокопроизводительным вычислениям (HiPC ’97).
- М.С.Маданлал,
В. Гурусвами и Ч. Панду Ранган, Дерево
3-гаечные ключи на интервальных, перестановочных и регулярных двудольных графах , Информация
Обработка писем , Vol. 59, 1996.

- [ Бакалавриат
Тезис ] Результаты неподатливости
для некоторой теоретико-графовой оптимизации
а также
Аппроксимационные задачи , Индийский технологический институт,
Мадрас, май 1997 г.
- Постдок: вакансия открыта. Вышли мне электронное письмо.
- PhD: отметьте это и подайте заявку здесь.
- Стажировка: пришлите мне письмо.
- AI/ML/DB/DM/Stat конференции: AAAI , AISTATS, ICDE, ICML , KDD, NeurIPS , OPT@NeurIPS, VLDB.
- Конференции TCS: APPROX, CCC, ICALP, PODC, RANDOM, SAT, SODA , SOSA@SODA, STOC .
- Журналы: Algorithmica, Combinatorica, I&C, IPL, PNAS , TODS.
- AI/ML: AAAI (’23 – ’20), AISTATS (’23 – ’19), NeurIPS (’22 – ’16), IJCAI (’21), ICML (‘ 22–18), ICLR (23–18), UAI (22–19).
- TCS: СОДА 21 , ПРИБЛИЗИТЕЛЬНО 18, BeyondMR 18, КОКОН 17, SODA 17 , ESA 16, SOFSEM 15.
- Последние тенденции в кластеризации и классификации: 3-дневный семинар в TTI-Chicago, ’19.
- Линейный скетчинг как универсальный инструмент: однодневный семинар на FOCS’17.

- 67-й День теории Среднего Запада: двухдневный семинар в Университете Индианы, Блумингтон, 2017.
- Большие данные через призму сублинейных алгоритмов: двухдневный семинар в Rutgers DIMACS, ’15.
- Алгоритмические границы современных массивно-параллельных вычислений: однодневный семинар на ACM FCRC ’15.
- День сублинейных алгоритмов и больших данных: Сублинейный день № 1 (коричневый ’14), Сублинейный день № 2 (MIT ’15).
- 29.10. Доклад «Иерархическая кластеризация для всех» в Мэрилендском университете, Колледж-Парк, Мэриленд.
- 28 сентября: Доклад в NeurIPS 2021 «Избавление от седловых точек с помощью сжатого SGD».
- 23.08: Начало новой преподавательской работы в Университете Джорджа Мейсона! Снова в академии после года работы в Lunchclub.
- 02/12: Статья в AAAI 2021: «Целенаправленная иерархическая кластеризация векторов глубокого встраивания».
- 14 мая: Доклад «Иерархическая кластеризация для всех» в Калифорнийском университете, Дэвис, Калифорния.

- 13/05: Доклад «Достижения в методах градиентного спуска для невыпуклой оптимизации» в Университете Висконсин-Мэдисон.
- 27 февраля: Доклад «Иерархическая кластеризация для всех» в Университете Брауна, Провиденс, Род-Айленд.
- 26 февраля: я вхожу в состав программного комитета SODA 2021 (32-й ежегодный симпозиум ACM-SIAM по дискретным алгоритмам).
- 03 февраля: Доклад «Иерархическая кластеризация для всех» в Университете Джорджа Мейсона, Фэрфакс, Вирджиния.
- 29 января: Доклад «Иерархическая кластеризация для всех» в Калифорнийском университете, Дэвис, Калифорния.
- 06.01: Две статьи в AISTATS 2020: «Принеси свой собственный жадный» + Макс: почти оптимальные 1/2-аппроксимации для субмодульного ранца» и «Раздели пополам и властвуй: Иерархическая кластеризация с помощью максимального неразрезанного деления пополам».
- 24.
 10: Доклад «Достижения в области иерархической кластеризации векторных данных» в Университете Иллинойса, Урбана-Шампейн, семинар CSL.
10: Доклад «Достижения в области иерархической кластеризации векторных данных» в Университете Иллинойса, Урбана-Шампейн, семинар CSL. - 18.10: Коллоквиум кафедры «Достижения в области иерархической кластеризации векторных данных» в Калифорнийском университете, Риверсайд, Калифорния.
- 16/10: Доклад в OPT@NeurIPS 2019: «Уход от седловых точек с ограничениями неравенства с помощью зашумленного липкого проецируемого градиентного спуска»
- 16.10: Семинар CMI «Достижения в линейном построении эскизов над конечными полями» в Калифорнийском технологическом институте, Пасадена, Калифорния.
- 14/10: Теоретический семинар «Достижения в области иерархической кластеризации векторных данных» в Калифорнийском университете, Сан-Диего, Калифорния.
- 10/10: Теоретический обед «Достижения в области иерархической кластеризации векторных данных» в Университете Южной Калифорнии, Лос-Анджелес, Калифорния.

- 04.10: Статья в SOSA@SODA 2020: «Быстрое тестирование разреженности Фурье».
- 18–09/20: Организация семинара «Последние тенденции в кластеризации и классификации» в TTI-Chicago.
- 15 августа: Доклад «Достижения в области иерархической кластеризации векторных данных» в Google Research, Маунтин-Вью, Калифорния.
- 21/06: Статья в RANDOM 2019: «Приблизительный F 2 — Набросок функций оценки».
- 06/06: Доклад «Достижения в области иерархической кластеризации векторных данных» на семинаре по дискретной математике и приложениям, Уорикский университет, Уорик, Великобритания.
- 30.05: Доклад «Достижения в области иерархической кластеризации векторных данных» на семинаре «Алгоритмы и сложность», Оксфордский университет, Оксфорд, Великобритания.
- 30.04: Документ в CCC 2019: «Оптимальность линейного эскиза при модульных обновлениях».

- 29/04: Статья в KDD 2019: «Состязательная робастная субмодульная максимизация при ограничениях рюкзака» в виде устной презентации (коэффициент одобрения 9,2%).
- 15.03: Статья в VLDB 2019: «Разбиение многомерного сбалансированного графа с помощью прогнозируемого градиентного спуска».
- 11 марта: доклад «Достижения в области иерархической кластеризации векторных данных» на Facebook Core Data Science, Менло-Парк, Калифорния.
- 06.03: Доклад «Достижения в области иерархической кластеризации векторных данных» на семинаре по алгоритмам и сложности, Университет Джона Хопкинса, Балтимор, Мэриленд.
- 01.03: Доклад «Достижения в области иерархической кластеризации векторных данных» на семинаре по компьютерным наукам, Северо-Западный университет, Эванстон, Иллинойс.
- 02/10: Препринт «Разбиение многомерного сбалансированного графа с помощью прогнозируемого градиентного спуска».

- 22.12.18: Статья в AISTATS 2019: «Иерархическая кластеризация для евклидовых данных».
- 16.10.18: Доклад «Достижения в области линейных зарисовок над конечными полями в Институте теории вычислений Саймонса, семинар по интерактивной сложности. Беркли, Калифорния.
- 24.09.18: Препринт «Оптимальность линейного скетчинга при модульных обновлениях».
- 14.09.18: Доклад «Линейный набросок функций над логическим гиперкубом» на семинаре по теории, Мичиганский университет, Анн-Арбор, Мичиган.
- 07.08.18: Доклад «Массово-параллельные алгоритмы и сложность кластеризации с одной связью на ℓ p -Расстояния» в IBM Research Almaden, Сан-Хосе, Калифорния.
- 12.07.18: Доклад «Массово-параллельные алгоритмы и сложность кластеризации с одной связью на ℓ p -Расстояния» на 35-й Международной конференции по машинному обучению (ICML’18).

- 22.06.18: Доклад «Линейный набросок функций над булевым гиперкубом» на 33-й конференции по вычислительной сложности (CCC’18).
- 14.06.18: Доклад «Badger Rampage: многомерное сбалансированное разбиение графов масштаба Facebook» на 2-м -м -м семинаре по локальным алгоритмам в Массачусетском технологическом институте, Кембридж, Массачусетс.
- 17.05.18: Доклад «Массивно-параллельные алгоритмы и сложность кластеризации с одной связью при ℓ p -Расстояния» на семинаре по теории в Стэнфорде.
- 11.05.18: Статья в ICML’18: Массивно-параллельные алгоритмы и сложность кластеризации с одной связью до ℓ p -Расстояния как длинный разговор (коэффициент приема 8,6%) .
- 13.04.18: Доклад «Линейный набросок функций над булевым гиперкубом» на 68-м семинаре по теории Среднего Запада, Технологический институт Тойота, Чикаго, Иллинойс.
- 04.
 04.18: Статья в CCC’18: Linear Sketching over F 2 .
04.18: Статья в CCC’18: Linear Sketching over F 2 . - 20.03.18: Доклад «Массово-параллельные алгоритмы и сложность кластеризации с одной связью до ℓ p -Расстояния» на семинаре по обобщению данных, Уорикский университет, Великобритания.
- 09.03.18: Официально открыт Центр алгоритмов и машинного обучения (CAML) в IU !
- 19.12.17: Я вхожу в состав программного комитета из ПРИБЛИЗИТЕЛЬНО 2018 (21-й международный семинар по алгоритмам аппроксимации для задач комбинаторной оптимизации).
- 22.11.17: Спасибо Facebook за поддержку с наградой факультета исследований Facebook !
- 19.10.17: Я вхожу в программный комитет BeyondMR 2018 (5-й семинар по алгоритмам и системам для MapReduce и не только на SIGMOD/PODS’18).
- 14.10.17: Доклад «Линейный скетчинг для функций над булевым гиперкубом» на семинаре FOCS’17 «Линейный скетчинг как инструмент для всего».

- 14.10.17: Совместная организация семинара Linear Sketching as a Tool for Everything на IEEE FOCS 2017.
- 13.10.17: Доклад «Кластеризация на кластерах 2049: массивно-параллельные алгоритмы кластеризации графов и векторов» на Facebook, Менло-Парк, Калифорния.
- 05.10.17: Препринт «Массивно-параллельные алгоритмы и сложность кластеризации с одной связью» под ℓ p -Distances .
- 15.06.17: Ведомственный коллоквиум «Вычислительная и коммуникационная сложность в массово-параллельных вычислениях» в Университете ИТМО, Санкт-Петербург, Россия.
- 14.06.17: Доклад «Вычислительная и коммуникационная сложность в массово-параллельных вычислениях» в Высшей школе экономики, Москва, Россия. Семинар по сложности вычислений, связи, описаний и доказательств.
- 03.06.17 – 04.06.17: Ускоренный курс «Современные алгоритмы параллельной, потоковой и запросовной обработки данных» в Клубе компьютерных наук, Санкт-Петербург, Россия.

- 02.06.17: Беседа о линейных зарисовках с паритетами на Санкт-Петербургском отделении Математического института им. ВА Стеклова, Санкт-Петербург, Россия.
- 23.05.17: Talk Linear Sketching with Parities на Колмогоровском семинаре, МГУ, Россия.
- 15.04.17 – 16.04.17: Соорганизация 67-го Дня теории Среднего Запада в Университете Индианы.
- 21.03.17: Talk Linear Sketching with Parities at Banff Workshop on Communication Complex and Applications.
- 09.02.17: Доклад «Кластеризация на кластерах: массивно-параллельные алгоритмы кластеризации графов и векторов» на Facebook, Менло-Парк, Калифорния.
- 24.01.17: Награда NSF CRII «Алгоритмы тестирования функций, устойчивых к шуму, с приложениями для глубокого обучения» в качестве единственного PI.
- 21.11.16: Talk Linear Sketching with Parities в Колумбийском университете, Нью-Йорк, штат Нью-Йорк.

- 07.11.16: Препринт Линейный набросок над F 2 . См. также соответствующую запись в блоге.
- 21.10.16: Talk Linear Sketching with Parities в Университете Пенсильвании, Филадельфия, Пенсильвания.
- 09.09.16: Talk Linear Sketching with Parities в Университете Юты, Солт-Лейк-Сити, Юта.
- 12.08.16: Talk Linear Sketching with Parities в Университете Иллинойса, Урбана, Иллинойс.
- 29.06.16: Talk Linear Sketching with Parities в Microsoft Research, Редмонд, Вашингтон.
- 26.06.16 — 02.07.16: Я посещаю теоретическую группу Microsoft Research, Редмонд.
- 30.05.16: Я состою в программном комитете COCOON 2017 (23-я Международная конференция по вычислительной технике и комбинаторике).
- 09.03.16: Ведомственный коллоквиум «Что нового в теории больших данных?» в Университете Дрекселя, Филадельфия, Пенсильвания.

- 05.03.16: Обзорная статья «Баланс между безопасностью и конфиденциальностью в сетевом анализе» на первой странице Penn.
- 29.02.16: Ведомственный коллоквиум «Что нового в теории больших данных?» в Бостонском университете, Бостон, Массачусетс.
- 25.02.16: Ведомственный коллоквиум «Что нового в теории больших данных?» в Университете Колорадо, Боулдер, Колорадо.
- 22.02.16: Ведомственный коллоквиум «Что нового в теории больших данных?» в Университете Индианы, Блумингтон, Индиана.
- 18.02.16: Ведомственный коллоквиум «Что нового в теории больших данных?» в Джорджтаунском университете, Вашингтон, округ Колумбия.
- 08.02.16: Ведомственный коллоквиум «Что нового в теории больших данных?» в Колледже Уильяма и Мэри, Вильямсбург, Вирджиния.
- 08.01.16: Доклад «L p — Тестирование» на семинаре Университета Джонса Хопкинса по сублинейным алгоритмам.
 См. также открытые проблемы.
См. также открытые проблемы. - 22.12.15: Я вхожу в состав программного комитета SODA 2017 (28-й ежегодный симпозиум ACM-SIAM по дискретным алгоритмам).
- 24.11.15: Статья «Конфиденциальность для защищенных (только)» принята в PNAS (Труды Национальной академии наук) путем прямой подачи.
- 19.10.15: Алгоритмы для MapReduce и выше : учебник на CIKM’15 в Мельбурне.
- 11.09.15: Статья в SODA’16: Точные границы линейных набросков приближенных паросочетаний.
- 27.08.15 — 28.08.15: Соорганизация семинара «Большие данные через призму сублинейных алгоритмов» в Университете Рутгерса, DIMACS.
- 26.08.15: Я преподаю CIS 700: алгоритмы для больших данных в Пенсильванском университете осенью 2015 года.
- 22.08.15: Я на программный комитет из ESA 2016, трек A (24-й Европейский симпозиум по алгоритмам).

- 06.08.15: Доклад «Быстрое тестирование разреженности Фурье над логическим гиперкубом» в Университете Висконсина, Мэдисон.
- 15.07.15: Доклад «Параллельные алгоритмы для задач с геометрическими графами» на ISMP 2015 (22-й Международный симпозиум по математическому программированию).
- 14.06.15: Совместная организация семинара «Алгоритмические границы современных массивно-параллельных вычислений» на FCRC 2015 (Конференция по федеративным вычислениям).
- 01.06.15: Препринт: Конфиденциальность для защищенных (только).
- 06.05.15: Препринт: Точные границы линейных эскизов приближенных паросочетаний.
- 04.05.15: Доклад «Почти оптимальное округление LP для корреляционной кластеризации» в Корнельском университете, Итака, Нью-Йорк.
- 14.04.15: Статья в ICALP’15: Усиление сложности односторонней информации с помощью кодов и чувствительности к шуму.

- 10.04.15: Второй «День сублинейных алгоритмов и больших данных» в Массачусетском технологическом институте.
- 09.04.15: Доклад «Почти оптимальное округление LP для корреляционной кластеризации» в Массачусетском технологическом институте, Бостон, Массачусетс.
- 12.03.15: Доклад «Почти оптимальное округление LP для корреляционной кластеризации» в Microsoft Research, Редмонд, Вашингтон.
- 06.03.15: Препринт: Усиление сложности односторонней информации с помощью кодов и чувствительности к шуму.
- 17 февраля 2015 г.: Google Tech Talk «Почти оптимальное округление LP для корреляционной кластеризации» в Google, Нью-Йорк.
- 03.02.15: Статья в STOC’15: Почти оптимальный алгоритм округления LP для корреляционной кластеризации на полных и полных k-дольных графах.
- 28.01.15: Доклад «Почти оптимальное LP округление для корреляционной кластеризации» в Университете Рутгерса, Нью-Брансуик, Нью-Джерси.

- 21 января 2015 г.: Доклад «Почти оптимальное округление LP для корреляционной кластеризации» в Университете Карнеги-Меллона, Питтсбург, Пенсильвания.
- 20.01.15: Доклад «Почти оптимальное LP округление для корреляционной кластеризации» в Университете штата Пенсильвания, Государственный колледж, Пенсильвания.
- 02/12/14: Препринт: Почти оптимальный алгоритм округления LP для корреляционной кластеризации на полных и полных k-дольных графах.
- 19.11.14: Доклад «Параллельные алгоритмы для задач с геометрическими графами» в Университете Джона Хопкинса, Балтимор, Мэриленд.
- 30.10.14: Доклад «Параллельные алгоритмы для задач с геометрическими графами» в Университете Мэриленда, Колледж-Парк, Мэриленд.
- 24.10.14: Беседа «L p — Тестирование» в Колумбийском университете, Нью-Йорк, штат Нью-Йорк.
- 12.10.14: Я начала вести блог The Big Data Theory, в котором буду рассказывать об алгоритмах обработки больших данных.

- 12.09.14: Я организую группу по чтению больших данных в Пенсильванском университете.
- 29.08.14: Доклад «Параллельные алгоритмы для задач с геометрическими графами» в Пенсильванском университете, Филадельфия, Пенсильвания.
- 15.08.14: Я организую семинар по теории компьютерных и информационных наук в Пенсильванском университете.
- 28.07.14 — 01.08.14: Я вел 15-часовой ускоренный курс «Сублинейные алгоритмы для больших данных» в 28-й Международной школе информатики ECI 2014 в Университете Буэнос-Айреса, Аргентина.
- 30.07.14: Препринт: Стремление к скорости: сублинейные алгоритмы для плотных r-CSP.
- 16.07.14: Доклад «За пределами множественной непересекаемости: коммуникационная сложность поиска пересечения» на 33-м ежегодном симпозиуме ACM SIGACT-SIGOPS по принципам распределенных вычислений (PODC 2014), Париж, Франция.
- 13.
 06.14: Доклад «Нижние границы для проверки свойств функций в гиперсетях» на 29-й конференции IEEE по вычислительной сложности (CCC 2014), Ванкувер, Британская Колумбия.
06.14: Доклад «Нижние границы для проверки свойств функций в гиперсетях» на 29-й конференции IEEE по вычислительной сложности (CCC 2014), Ванкувер, Британская Колумбия. - 06.06.14: Статья в RANDOM’14: Подтверждение равенства с ограниченным взаимодействием.
- 01.06.14: Доклад «L p — Тестирование» на 46-м симпозиуме ACM по теории вычислений (STOC 2014), Нью-Йорк, штат Нью-Йорк.
- 19.05.14: Доклад «Параллельные алгоритмы для задач с геометрическими графами» в Массачусетском университете, Амхерст, Массачусетс.
- 16 мая 2014 г.: Доклад «За пределами множества непересекающихся: коммуникационная сложность поиска пересечения» на семинаре Массачусетского технологического института по теории распределенных систем, Бостон, Массачусетс.
- 28.04.14: Я на ПК на 41-й Международной конференции по актуальным тенденциям в теории и практике компьютерных наук (SOFSEM’15), направление «Основы компьютерных наук» (председатель: Роджер Ваттенхофер).
 Сроки здесь.
Сроки здесь. - 20.04.14: Статья в PODC’14: Непересекаемость множества: коммуникационная сложность поиска пересечения.
- 18.04.14: Я организовал День сублинейных алгоритмов и больших данных в Brown ICERM.
- 03.04.14: Google Tech Talk «Параллельные алгоритмы для задач с геометрическими графами» в Google Research, Нью-Йорк.
- 27.03.14: Доклад «Параллельные алгоритмы для задач с геометрическими графами» в Стэнфордском университете, Стэнфорд, Калифорния.
- 25.03.14: Доклад «Параллельные алгоритмы для задач с геометрическими графами» в Sandia Labs, Ливермор, Калифорния.
- 05.03.14: Доклад «Теория больших данных и рандомизированные алгоритмы» в Технологическом институте Джорджии, Атланта.
- 25.02.14: Доклад «Аппроксимация графических задач: старые и новые» на Yahoo! Исследования, Нью-Йорк.
- 19.02.14: Доклад «Аппроксимация задач с графами: старые и новые» на семинаре Массачусетского технологического института по алгоритмам и сложности.

- 17.02.14: Доклад «Аппроксимация графических задач: старые и новые» в Технологическом институте Toyota в Чикаго.
- 09.02.14: Я буду вести ускоренный курс «Сублинейные алгоритмы для больших наборов данных» в Университете Буэнос-Айреса (28 июля – 1 августа)
- 04.02.14: 2 статьи в STOC’14, 1 статья в CCC’14:
- Первая статья «MapReduce» в STOC/FOCS.
- Первая бумага для проверки свойств зашумленных вещественных данных.
- Первая статья с нижними границами сложности связи для проверки свойств функций на гиперсетях.
- ’21 — .
 Ассистент , ГМУ КН.
Ассистент , ГМУ КН. - 16-20 гг. Ассистент , IUB CS.
- S’19. Институт Алана Тьюринга, Лондон, Великобритания.
- ’14 – ’16. Научный сотрудник Центра Уоррена , UPenn CIS и Wharton Statistics.
- ’13 – ’14. Член института , Браун ICERM.
- ’10 – ’13. Кандидат наук , CSE штата Пенсильвания.
- S’13 Междунар. Microsoft Research, Вашингтон.
- F’12 Интерн. Microsoft Research, Калифорния.
- S’12 Междунар. IBM Research, Калифорния.
- S’11 Междунар. AT&T Research, Нью-Джерси.
- Премия факультета Facebook за исследования, ’17.
- Премия NSF CRII, 17.
- Научный сотрудник Центра Уоррена, Университет Пенсильвании, 14-16 гг.
- Научный сотрудник Института ICERM, Браун, 13-14.
- Награда за научные исследования, Penn St.
 CSE, ’12.
CSE, ’12. - Колледж инженеров. Товарищ, Пенн-стрит, 10-13 гг.
- Выпускник университета, Пенн-стрит, 10-11.
- Открытый алгоритм TopCoder (Top-24), ’10.
- Самсон Чжоу (постдок, ’18–’19 → Постдок, Университет Карнеги-Меллона)
- Дмитрий Авдюхин (аспирант, ’17 – )
- Фарид Арто, ENS Paris (стажер, S’19)
- Якуб Богута, У. Варшава (стажер, S’19)
- Станислав Наумов, СПб ИТМО У. (стажер, F’19)
- F’22: CS583 Анализ алгоритмов @ GMU
- S’22: Расширенные алгоритмы CS630 @ GMU
- F’21: CS583 Анализ алгоритмов @ GMU
- S’20: прикладные алгоритмы B505 @ IUB
- F’19: прикладные алгоритмы B505 @ IUB
- S’19: структуры данных h443 (с отличием) @ IUB
- F’18: Структуры данных C343 @ IUB
- S’18: структуры данных h443 (с отличием) @ IUB
- F’17: B505 Applied Algorithms @ IUB (совместно с Funda Ergun)
- F’17: B609 Основы науки о данных @ IUB
- F’16: B609 Основы науки о данных @ IUB
- F’15: Алгоритмы CIS 700 для больших данных @ Penn
- S’15: CIS 625 Computational Learning Theory @ Penn (с Майклом Кернсом)
Выход из седловой точки со сжатым SGD
Д.
 Авдюхин, Г. Ярославцев
Авдюхин, Г. ЯрославцевNeurIPS 2021 (35-я конференция по системам обработки нейронной информации).
Объективная иерархическая кластеризация векторов глубокого вложения
Наумов С., Ярославцев Г. * , Авдюхин Д.
AAAI 2021 (35-я конференция AAAI по искусственному интеллекту).
Разбиение многомерного сбалансированного графа методом прогнозируемого градиентного спуска
Д. Авдюхин, С. Пупырев, Г. Ярославцев
ВЛДБ 2019, Research track (45-я Международная конференция по очень большим базам данных).
Массивно-параллельные алгоритмы и сложность кластеризации с одной связью при ℓ
p -DistancesГ. Ярославцев * , А. Вадапалли
ICML 2018 (35-я Международная конференция по машинному обучению).
 Долгий разговор (скорость приема 8,6%). Код на Github (автор Adithya Vadapalli).
Долгий разговор (скорость приема 8,6%). Код на Github (автор Adithya Vadapalli).Linear Sketching над F
2С. Каннан, Э. Моссель, С. Саньял, Г. Ярославцев
CCC 2018 (33-я конференция по вычислительной сложности).
Запись в блоге на тему «Теория больших данных».Частные алгоритмы для защищенного поиска в социальных сетях
М. Кернс, А. Рот, С. Ву, Г. Ярославцев
PNAS 2016 (Труды Национальной академии наук), путем прямой подачи.
В центре внимания на первой полосе Penn: Баланс между конфиденциальностью и безопасностью в сетевом анализе. Алгоритм округления, близкий к оптимальному, для корреляционной кластеризации на полных и полных k-дольных графах
С. Чавла, К. Макарычев, Т. Шрамм, Г. Ярославцев
STOC 2015 (47-й симпозиум ACM по теории вычислений).
Дополнительные сведения см. в статье Википедии о корреляционной кластеризации. Л
р -ТестированиеП. Берман, С. Расходникова, Г. Ярославцев
STOC 2014 (46-й симпозиум ACM по теории вычислений).
Простое введение Софьи Расходниковой в Энциклопедии алгоритмов (Springer). Параллельные алгоритмы для задач с геометрическими графами
А. Андони, А. Николов, К. Онак, Г. Ярославцев
STOC 2014 (46-й симпозиум ACM по теории вычислений).
Заметки Томаса Стейнке из курса Джелани Нельсона «Алгоритмы для больших данных» в Гарварде Частный анализ структуры графа
В. Карва, С. Расходникова, А. Смит, Г. Ярославцев
VLDB 2011, Research track (37-я Международная конференция по очень большим базам данных).
Полная версия в транзакциях ACM в системах баз данных.Аппроксимационные алгоритмы для задач Шпаннера и направленного леса Штейнера
П.
 Берман,
А. Бхаттачарья,
К. Макарычев,
С. Расходникова,
Г. Ярославцев
Берман,
А. Бхаттачарья,
К. Макарычев,
С. Расходникова,
Г. ЯрославцевICALP 2011, Track A (38-й Международный коллоквиум по автоматам, языкам и программированию), специальный выпуск «Информация и вычисления» .
Второе место в номинации «Лучшая бумага». Поиск эффективных схем с помощью SAT-решателей
А. Кожевников, А. Куликов, Г. Ярославцев
SAT 2009 (12-я Международная конференция по теории и приложениям тестирования на выполнимость).
Многократно цитируется в томе 4B книги Дональда Э. Кнута «Искусство компьютерного программирования». - Bisect and Conquer: Иерархическая кластеризация с помощью Max-Uncut Bisection
С. Ахмадян, В. Хациафратис, А. Эпасто, Э. Ли, М. Махдиан, К. Макарычев, Г. Ярославцев
AISTATS 2020 (23-я Международная конференция по искусственному интеллекту и статистике).
- «Принеси свой собственный жадный» + Макс: почти оптимальные 1/2-аппроксимации для субмодульного ранца
Ярославцев Г. * , Чжоу С., Авдюхин Д.,
AISTATS 2020 (23-я Международная конференция по искусственному интеллекту и статистике).
- Быстрое тестирование разреженности Фурье
Г. Ярославцев, С. Чжоу
SOSA@SODA 2020 (3-й симпозиум SIAM по простоте алгоритмов).
- Выход из седловых точек с ограничениями неравенства с помощью зашумленного липкого прогнозируемого градиентного спуска
Д.
 Авдюхин, К. Джин, Г. Ярославцев
Авдюхин, К. Джин, Г. ЯрославцевOPT@NeurIPS 2019 (11-й семинар OPT по оптимизации для машинного обучения)
- Приблизительный F 2 -Набросок функций оценки г.
Г. Ярославцев, С. Чжоу
RANDOM 2019 (23-й международный семинар по рандомизации и вычислениям).
- Оптимальность линейного эскиза при модульных обновлениях
К. Хоссейни, С. Ловетт, Г. Ярославцев
CCC 2019 (34-я конференция по вычислительной сложности).
- Субмодульная максимизация состязательной защиты при ограничениях рюкзака г.
Д. Авдюхин, С. Митрович, Г. Ярославцев, С. Чжоу
KDD 2019, направление исследований (25-я конференция ACM SIGKDD по обнаружению знаний и интеллектуальному анализу данных). Устная презентация (процент одобрения 9,2%)
- Максимальное количество совпадений в потоках динамических графов и модели одновременной связи
С.
 Асади,
С. Ханна,
Ю. Ли,
Г. Ярославцев
Асади,
С. Ханна,
Ю. Ли,
Г. ЯрославцевSODA 2016 (27-й ежегодный симпозиум ACM-SIAM по дискретным алгоритмам).
- Усиление сложности однонаправленной информации с помощью кодов и чувствительности к шуму
М. Молинаро, Д. Вудрафф, Г. Ярославцев
ICALP 2015, трек A (42-й международный коллоквиум по автоматам, языкам и программированию).
- Сертификация равенства с ограниченным взаимодействием г.
Дж. Броди, А. Чакрабарти, Р. Кондапалли, Д. Вудрафф, Г. Ярославцев
RANDOM 2014 (18-й международный семинар по рандомизации и вычислениям).
- Полная версия в спецвыпуске Algorithmica «Информационная сложность и приложения»
- За пределами множественной непересекаемости: коммуникационная сложность поиска пересечения
Дж. Броди, А. Чакрабарти, Р. Кондапалли, Д. Вудрафф, Г. Ярославцев
PODC 2014 (33-й ежегодный симпозиум ACM SIGACT-SIGOPS по принципам распределенных вычислений).

- Нижние границы для проверки свойств функций над областями гиперсетки
Э. Блейс, С. Расходникова, Г. Ярославцев
CCC 2014 (29-я конференция IEEE по вычислительной сложности).
- Преодоление теоремы о прямой сумме в сложности коммуникации с приложениями к рисованию эскизов
М. Молинаро, Д. Вудрафф, Г. Ярославцев
SODA 2013 (24-й ежегодный симпозиум ACM-SIAM по дискретным алгоритмам).
- Изучение псевдобулевых k-DNF и субмодульных функций
С. Расходникова, Г. Ярославцев
SODA 2013 (24-й ежегодный симпозиум ACM-SIAM по дискретным алгоритмам).
- Точный и эффективный частный выпуск кубов данных и таблиц непредвиденных обстоятельств
Г. Ярославцев * , Г. Кормод, К. М. Прокопюк, Д. Шривастава
ICDE 2013 (29-я Международная конференция IEEE по инженерии данных).

- Первично-двойственные алгоритмы для взвешенного по узлам проектирования сети в планарных графах
П. Берман, Г. Ярославцев
ПРИБЛИЗИТЕЛЬНО 2012 (15-й Международный семинар по алгоритмам аппроксимации для задач комбинаторной оптимизации).
- Гаечные ключи Штейнера с переходным замыканием для d-мерных положений
П. Берман, А. Бхаттачарья, Э. Григореску, С. Расходникова, Д. Вудрафф, Г. Ярославцев
ICALP 2011, трек A (38-й международный коллоквиум по автоматам, языкам и программированию).
- Полная версия на Combinatorica.
- Стремление к скорости: сублинейные алгоритмы для плотных r-CSP
Г. Ярославцев
- Онлайн-алгоритмы для минимизации машин [Препринт на arXiv].

Н. Деванур, К. Макарычев, Д. Паниграхи, Г. Ярославцев
- Достижения в методах градиентного спуска для невыпуклой оптимизации
- Университет Висконсин-Мэдисон, Мэдисон, Висконсин. Семинар СИЛ. 13 мая 2021 г. (виртуальный)
- Иерархическая кластеризация для всех г.
- Техасский университет, Остин, Техас. Теоретический семинар. 28 апреля 2022 г.
- Мэрилендский университет, Колледж-Парк, Мэриленд. Семинар по теории столичных территорий. 29 октября 2021 г.
- Калифорнийский университет, Дэвис, Калифорния. Коллоквиум по информатике. 14 мая 2020 г. (Виртуально)
- Университет Брауна, Провиденс, Род-Айленд. Коллоквиум по информатике. 27 февраля 2020 г.
- Университет Джорджа Мейсона, Фэрфакс, Вирджиния. Коллоквиум по информатике. 03 февраля 2020 г.
- Калифорнийский университет, Дэвис, Калифорния. Математический коллоквиум. 29 января 2020 г.
- Достижения в области иерархической кластеризации векторных данных [ Видео с Северо-Запада (ссылка)] [Слайды: (pptx), (pdf)]
- Университет Иллинойса, Урбана-Шампейн, Иллинойс.
 Семинар ЦСЛ. 24 октября 2019 г.
Семинар ЦСЛ. 24 октября 2019 г. - Калифорнийский университет, Риверсайд, Калифорния. Ведомственный коллоквиум CSE. 18 октября 2019 г..
- Калифорнийский университет, Сан-Диего, Калифорния. Теоретический семинар. 14 октября 2019 г.
- Университет Южной Калифорнии, Лос-Анджелес, Калифорния. Теоретический обед. 10 октября 2019 г.
- Исследования Google, Маунтин-Вью, Калифорния. Технический разговор. 15 августа 2019 г.
- Уорикский университет, Уорик, Великобритания. Семинар по дискретной математике и приложениям. 06 июня 2019 г.
- Оксфордский университет, Оксфорд, Великобритания. Семинар по алгоритмам и сложности. 30 мая 2019 г..
- Facebook Core Data Science, Менло-Парк, Калифорния. Технический разговор. 11 марта 2019 г.
- Университет Джона Хопкинса, Балтимор, Мэриленд. Семинар по алгоритмам и сложности. 06 марта 2019 г.
- Северо-западный университет, Эванстон, Иллинойс. Семинар по информатике.
 01 марта 2019 г.
01 марта 2019 г.
- Университет Иллинойса, Урбана-Шампейн, Иллинойс.
- Достижения в линейном построении эскизов над конечными полями [ Видео от Саймонса (ссылка)][Слайды: (pptx), (pdf)]
- Калифорнийский технологический институт, Пасадена, Калифорния. Семинар КМИ. 15 октября 2019 г.
- Институт теории вычислительной техники Саймонса. Интерактивный мастер-класс по сложности. Беркли, Калифорния. 16 октября 2018 г.
- Badger Rampage: многомерное сбалансированное разбиение графиков масштаба Facebook [Слайды: (pptx), (pdf)]
- Массачусетский технологический институт, Кембридж, Массачусетс. 2 -й Семинар по локальным алгоритмам. 14 июня 2018 г.
- Massively Parallel Algorithms and Hardness for Single Linkage Clustering Under ℓ p -Distances [ Видео из ICML’18 (ссылка)] [Слайды: (pptx), (pdf)]
- IBM Research Almaden, Сан-Хосе, Калифорния. Теоретический семинар. 07 августа 2018 г.

- 35-я Международная конференция по машинному обучению (ICML’18), Стокгольм, Швеция. 12 июля 2018 г.
- Стэнфордский университет, Стэнфорд, Калифорния. Теоретический семинар. 17 мая 2018 г.
- Уорикский университет, Уорик, Великобритания. «Семинар по обобщению данных». 20 марта 2018 г.
- IBM Research Almaden, Сан-Хосе, Калифорния. Теоретический семинар. 07 августа 2018 г.
- Линейный набросок для функций над булевым гиперкубом [Слайды: (pptx), (pdf)]
- Мичиганский университет, Анн-Арбор, Мичиган. Теоретический семинар. 14 сентября 2018 г.
- Технологический институт Тойота. 68-й День теории Среднего Запада. Чикаго, Иллинойс. 13 апреля 2018 г.
- 58-й ежегодный симпозиум по основам информатики (FOCS 2017). Семинар «Линейный скетчинг как инструмент для всего», Беркли, Калифорния. 14 октября 2017 г.
- Кластеризация на кластерах 2049: Массивно-параллельные алгоритмы для кластеризации графов и векторов [Слайды: (pptx), (pdf)]
- Facebook, Менло-Парк, Калифорния.
 Технический разговор. 13 октября 2017 г.
Технический разговор. 13 октября 2017 г.
- Facebook, Менло-Парк, Калифорния.
- Вычислительная и коммуникационная сложность в массивно-параллельных вычислениях [Слайды: (pptx), (pdf)]
- Университет ИТМО, Санкт-Петербург, Россия. Ведомственный коллоквиум. 15 июня 2017 г.
- Высшая школа экономики, Москва, Россия. Семинар по сложности вычислений, связи, описаний и доказательств. 14 июня 2017 г.
- Кластеризация на кластерах: массивно-параллельные алгоритмы для кластеризации графов и векторов [Слайды: (pptx), (pdf)]
- Facebook, Менло-Парк, Калифорния. Технический разговор. 09 февраля 2017 г.
- Линейный набросок с четностью [ Видео из Банфа (ссылка)][Слайды: (pptx), (pdf)]
- 33-я конференция по вычислительной сложности (CCC’18), Сан-Диего, Калифорния. 22 июня 2018 г.
- Санкт-Петербургское отделение Математического института им. ВА Стеклова РАН. Теоретический семинар.
 02 июня 2017 г.
02 июня 2017 г. - Московский государственный университет, Москва, Россия. Колмогоровский семинар по теоретической информатике. 22 мая 2017 г.
- Международная исследовательская станция Банф, Банф, Канада. Семинар по сложности связи и приложений. 20 марта 2017 г.
- Колумбийский университет, Нью-Йорк, штат Нью-Йорк. Теоретический семинар. 21 ноября 2016 г.
- Пенсильванский университет, Филадельфия, Пенсильвания. Теоретический семинар. 21 октября 2016 г.
- Университет Юты, Солт-Лейк-Сити, Юта. Теоретический семинар. 09 сентября 2016 г.
- Университет штата Иллинойс. Урбана, Иллинойс. Теоретический семинар. 12 августа 2016 г.
- Исследования Microsoft. Редмонд, Вашингтон. Теоретический семинар. 29 июня 2016 г.
- Что нового в «Теории больших данных»?
- Университет Дрекселя, Филадельфия, Пенсильвания. Ведомственный коллоквиум. 09 марта 2016 г.
- Бостонский университет, Бостон, Массачусетс.
 Ведомственный коллоквиум. 29 февраля 2016 г.
Ведомственный коллоквиум. 29 февраля 2016 г. - Университет Колорадо, Боулдер, Коллоквиум. Ведомственный коллоквиум. 25 февраля 2016 г.
- Университет Индианы, Блумингтон, Индиана. Ведомственный коллоквиум. 22 февраля 2016 г.
- Джорджтаунский университет, Вашингтон, округ Колумбия. Ведомственный коллоквиум. 18 февраля 2016 г.
- Колледж Уильяма и Мэри, Вильямсбург, Вирджиния. Ведомственный коллоквиум. 08 февраля 2016 г.
- Быстрое тестирование разреженности Фурье над булевым гиперкубом [Слайды: (pptx), (pdf)]
- Университет Висконсина, Мэдисон. Теоретический семинар. 06 августа 2015 г.
- Почти оптимальное округление LP для корреляционной кластеризации [ Видео из MSR (ссылка)] [Слайды: (pptx), (pdf)]
- Корнельский университет, Итака, Нью-Йорк. Теоретический семинар. 04 мая 2015 г.
- Массачусетский технологический институт, Бостон, Массачусетс.
 Семинар по алгоритмам и сложности. 09 апреля 2015 г.
Семинар по алгоритмам и сложности. 09 апреля 2015 г. - Microsoft Research, Редмонд, Вашингтон. 12 марта 2015 г.
- Google Research, Нью-Йорк. Обсуждение технологий Google. 17 февраля 2015 г.
- Университет Рутгерса, Нью-Брансуик, Нью-Джерси. Теоретический семинар. 28 января 2015 г.
- Университет Карнеги-Меллона, Питтсбург, Пенсильвания. Теоретический обед. 21 января 2015 г.
- Университет штата Пенсильвания, Государственный колледж, Пенсильвания. Ведомственный коллоквиум. 20 января 2015 г.
- Нижние границы для проверки свойств функций над гиперсетками [Слайды: (pptx), (pdf)]
- 29-я конференция IEEE по вычислительной сложности (CCC 2014), Ванкувер, Британская Колумбия. 13 июня 2014 г.
- За пределами множественной непересекаемости: коммуникационная сложность поиска пересечения [Слайды: (pptx), (pdf)]
- 33-й ежегодный симпозиум ACM SIGACT-SIGOPS по принципам распределенных вычислений (PODC 2014), Париж, Франция.

- Массачусетский технологический институт, Бостон, Массачусетс. Семинар по теории распределенных систем. 16 мая 2014 г.
- 33-й ежегодный симпозиум ACM SIGACT-SIGOPS по принципам распределенных вычислений (PODC 2014), Париж, Франция.
- «Теория больших данных» и рандомизированные алгоритмы
- Технологический институт Джорджии, Атланта, Джорджия. 05 марта 2014 г.
- Аппроксимирующие задачи с графами: старые и новые
- Yahoo! Исследования, Нью-Йорк. 25 февраля 2014 г.
- Массачусетский технологический институт, Бостон, Массачусетс. Семинар по алгоритмам и сложности. 19 февраля 2014 г.
- Технологический институт Toyota, Чикаго, Иллинойс. 17 февраля 2014 г.
- Университет Брауна, Провиденс, Род-Айленд. Семинар по теории ICERM. 31 января 2014 г.
- л р -Тестирование [Слайды: (pptm), (pdf))]
- Университет Джонса Хопкинса, Семинар по сублинейным алгоритмам. 08 января 2016 г.
- Колумбийский университет, теоретический семинар.
 24 октября 2014 г.
24 октября 2014 г. - 46-й симпозиум ACM по теории вычислений (STOC 2014). 01 июня 2014 г.
- Microsoft Research, Редмонд, теоретический обед. 08 января 2014 г.
- Гарвардский университет, теоретический семинар. 12 ноября 2013 г.
- Университет Брауна, Провиденс, Род-Айленд. Теоретический семинар. 1 ноября 2013.
- Исследовательский центр IBM Almaden, Сан-Хосе, Калифорния. Теоретический семинар. 25 октября 2013 г.
- Сложность тестирования и связи [Слайды: (pptx), (pdf)]
- Массачусетский технологический институт, Бостон, Массачусетс. Семинар по алгоритмам и сложности. 11 сентября 2013 г.
- Точный и эффективный частный выпуск кубов данных и таблиц непредвиденных обстоятельств г.
- Корнельский университет, проектная встреча CDI. 07 мая 2013 г. [Слайды: (pptx), (pdf)]
- 29-я Международная конференция IEEE по обработке данных (ICDE 2013). 10 апреля 2013 г.
 [Слайдов: (pdf)]
[Слайдов: (pdf)]
- Преодоление теоремы о прямой сумме в сложности коммуникации
- Орхусский университет, Дания. Теоретический семинар. 22 мая 2013 г.
- Массачусетский технологический институт, Бостон, Массачусетс. Семинар «Алгоритмы и сложности». 13 декабря 2012 г.
- Принстонский университет, Принстон, Нью-Джерси. Теоретический обед. 16 ноября 2012 г.
- Перекрывающаяся кластеризация с качественной информацией
- 53-й симпозиум IEEE по основам информатики (FOCS 2012). Постерная сессия. 22 октября 2012 г.
- Параллельные алгоритмы для геометрических задач [Слайды: (pptx), (pdf)]
- 22-й Международный симпозиум по математическому программированию (ISMP 2015). 15 июля 2015 г.
- Университет Джона Хопкинса, Балтимор, Мэриленд. Семинар по алгоритмам и сложности. 19 ноября 2014 г.
- Мэрилендский университет, Колледж-Парк, Мэриленд.
 Семинар по теории столичных территорий. 30 октября 2014 г.
Семинар по теории столичных территорий. 30 октября 2014 г. - Пенсильванский университет, Филадельфия, Пенсильвания. Теоретический семинар. 29 августа 2014 г.
- Массачусетский университет, Амхерст, Массачусетс. Теоретический семинар. 19 мая 2014 г.
- Google Research, Нью-Йорк. Обсуждение технологий Google. 04 апреля 2014 г.
- Sandia Labs, Ливермор, Калифорния. 27 марта 2014 г.
- Стэнфордский университет, Стэнфорд, Калифорния. 25 марта 2014 г.
- Microsoft Research, SVC, Маунтин-Вью, Калифорния. Лабораторное совещание. 17 октября 2012 г.
- Изучение и тестирование субмодульных функций [ Видео из MSR (ссылка)][Слайды: (pptx), (pdf)]
- Microsoft Research, Редмонд. Теоретический семинар. 11 июня 2013 г.
- Университет Мельбурна, Австралия. Теоретический семинар. 19 апреля 2013 г.
- Калифорнийский университет в Лос-Анджелесе, Калифорния. Теоретический семинар. 04 февраля 2013 г.

- 24-й симпозиум ACM-SIAM по дискретным алгоритмам (SODA 2013). 08 января 2013 г.
- Научный институт Вейцмана, Реховот, Израиль. 30 декабря 2012 г.
- Гарвардский университет, Бостон, Массачусетс. Семинар по теории вычислительной техники. 10 декабря 2012 г.
- Университет Карнеги-Меллона, Питтсбург, Пенсильвания. Теоретический обед. 05 декабря 2012 г.
- Университет Карнеги-Меллона, Питтсбург, Пенсильвания. Школа бизнеса Теппера, семинар по исследованию операций. 07 декабря 2012 г.
- День компьютерных наук и экономики в Нью-Йорке, 2012 г., постерная сессия. 3 декабря 2012 г.
- IBM Т.Дж. Watson Research Cetner, Йорктаун-Хайтс, Нью-Йорк. ИП на обед. 14 ноября 2012 г.
- Колумбийский университет, Нью-Йорк. Теоретический семинар. 26 октября 2012 г.
- 53-й симпозиум IEEE по основам информатики (FOCS 2012). Постерная сессия. 22 октября 2012 г.
- Microsoft Research, Силиконовая долина. Теоретический семинар.
 10 октября 2012 г.
10 октября 2012 г. - EPFL, Лозанна, Швейцария. Algorithmic Frontiers Workshop, постерная сессия. июнь 2012 г.
- Исследовательский центр IBM Almaden, Сан-Хосе, Калифорния. Теоретический семинар. май 2012 г.
- 44-й симпозиум ACM по теории вычислений (STOC 2012). Постерная сессия. май 2012 г.
- Первично-двойственные алгоритмы для взвешенного по узлам проектирования сети в планарных графах [Слайды: (pptx), (pdf)]
- 15-й Международный семинар по алгоритмам аппроксимации для задач комбинаторной оптимизации (APPROX 2012). август 2012 г.
- Улучшения в гаечных ключах [Слайды: (pdf)].
- Сиднейский университет, Австралия. Теоретический семинар. 9 апреля, 2013.
- Университет Карнеги-Меллона, теоретический обед, ноябрь 2011 г.
- Мэрилендский университет, семинар по теории столичного региона, ноябрь 2011 г.
- Частный анализ структуры графа [Слайды: (pptx), (pdf)]
- EPFL, Лозанна, Швейцария.
 Algorithmic Frontiers Workshop, постерная сессия. Июнь 2012 г. [Постер: (pdf)]
Algorithmic Frontiers Workshop, постерная сессия. Июнь 2012 г. [Постер: (pdf)] - AT&T Labs — Research, Florham Park, NJ. август 2011 г.
- 37-я Международная конференция по очень большим базам данных (VLDB 2011), исследовательский трек. август 2011 г.
- EPFL, Лозанна, Швейцария.
- Улучшенная аппроксимация задачи направленного гаечного ключа [Слайды: (pptx), (pdf)]
- 38-й Международный коллоквиум по автоматам, языкам и программированию (ICALP 2011), трек A. Июль 2011 г. [Слайды: (pptx)]
- AT&T Labs — Research, Florham Park, NJ. Коллоквиум по математическим исследованиям и неформальный семинар. июнь 2011 г.
- 43-й симпозиум ACM по теории вычислений (STOC 2011). Постерная сессия. Июнь 2011 г. [Плакат: (pdf)]
- Московский государственный университет им. Семинар по комбинаторной оптимизации. май 2011 г.
- IBM Т.Дж. Исследовательский центр Уотсона, Йорктаун-Хайтс, Нью-Йорк. ИП на обед.
 апрель 2011 г.
апрель 2011 г. - Санкт-Петербургский институт точной механики и оптики. Теоретический семинар. декабрь 2010 г.
- Переходные гаечные ключи Steiner для низкоразмерных Posets [Слайды: (ppsx), (pdf)]
- 38-й Международный коллоквиум по автоматам, языкам и программированию (ICALP 2011), трек A. июль 2011 г.
- Линейные границы сложности схем и слабо односторонних перестановок [Слайды: (pdf)]
- Университет штата Пенсильвания. Теоретический семинар. апрель 2010 г.
- Я преподавал CSCI-h443 (Структуры данных, диплом с отличием) в Университете Индианы, Блумингтон, весной 2018 года.
- Осенью 2017 года я преподавал CSCI-B505 (Прикладные алгоритмы) в Университете Индианы, Блумингтон.
- Краткое руководство Кластеризация на кластерах: массивно-параллельные алгоритмы для кластеризации графов и векторов на Facebook, Менло-Парк, Калифорния, весна 2017 г.

- Я разработал CSCI-B609, Основы науки о данных (выпускник) в Университете Индианы, Блумингтон, осенью 2016 и осенью 2017.
- Приглашенный лектор CIS 399, Основы науки о данных (бакалавриат) Пенсильванского университета, весна 2016 г.
- Массивно-параллельные алгоритмы. Слайды (pdf).
- Разработал CIS 700, Алгоритмы для работы с большими данными г. (выпускник) Пенсильванского университета, осень 2015 г.
- Совместное преподавание CIS 625, Computational Learning Theory (выпускник вместе с Майклом Кернсом) в Пенсильванском университете, весна 2015 г.
- Лекция 1: Анализ Фурье и обучение, часть 1. Слайды (pdf).
- Лекция 2: Анализ Фурье и обучение, часть 2. Слайды (pdf).
- Лекция 3: Изучение субмодульных функций. Слайды (pdf).
- Лекция 4: Л с -Тестирование. Слайды (pdf).
- Я разработал сублинейные алгоритмы для больших данных : 15-часовой ускоренный курс в Университете Буэнос-Айреса, июль 2014 г.

- Приглашенный лектор CMPSC 464, Введение в теорию вычислений (бакалавриат) Университета штата Пенсильвания, осень 2010 г.
Триатлон и дуатлон
Я подхватил триатлон во время стажировки в IBM и Microsoft Research в районе залива в 2012 году. С тех пор, если я не работаю, то, вероятно, тренируюсь в следующем году ( старых фотографий ). На данный момент 5xIM: Вудлендс, Техас (2013 г.), Лейк-Тахо, Калифорния (2014 г. отменен -> 2015 г.), Лейк-Плэсид, Нью-Йорк (2016 г.), Санта-Роза, Калифорния (2017 г.), Кэрнс, Австралия (2018 г.). Давай сделаем это вместе! 😉
В 2017 году я представлял Team USA в возрастной группе M30-34 на 9-м1795 Чемпионат мира по дуатлону на стандартной дистанции ITU в Пентиктоне, Канада. В 2019 году я представлял сборную США в возрастной группе M30-34 на чемпионате мира по триатлону на длинные дистанции ITU в Понтеведре, Испания.
Соревнования по алгоритмам
Я участвовал в соревнованиях ACM ICPC и TopCoder (под именем griffon ), соревнуясь и ставя задачи в финалах открытых алгоритмов TopCoder.

После участия в финале TopCoder Algorithms Finals 2010 в Лас-Вегасе (24 лучших в мире по отдельности) я ушел из соревновательного программирования, чтобы сосредоточиться на исследованиях и триатлоне.
Алгоритмы обучения старшеклассников
Я вел продвинутые курсы по алгоритмам для старшеклассников в течение ~ 5 лет, тренировал команды для алгоритмических соревнований. Участвовал в подготовке сборов и конкурсов к Российской олимпиаде по информатике и Международной олимпиаде по информатике (как в России, так и в США).
Больше всего я горжусь достижениями в качестве тренера, которые привели мою школьную команду к победе на олимпиаде в Санкт-Петербурге по информатике в 2008-2009 годах и тот факт, что наш небрежный тренерский состав не помешал сборной США заработать кучу медалей в 2011 году.
Некоммерческая организация в сфере образования для старшеклассников:
Домашняя страница , Группа ВКонтактеВ 2009 году я стал соучредителем некоммерческой организации, занимающейся углубленным внешкольным обучением алгоритмам для старшеклассников (5-10 классы) в Санкт-Петербурге, Россия.
 В 2013 году он был расширен до Москвы и Екатеринбурга.
В 2013 году он был расширен до Москвы и Екатеринбурга.В первые дни нас поддерживали , и . Пожертвования приветствуются!
Разработка программного обеспечения
В 2007–2008 годах мне посчастливилось быть частью команды FBReader . Это бесплатный проект для чтения электронных книг с открытым исходным кодом.
Мы разработали первую версию FBReader для Android (сейчас > 10 миллионов загрузок по всему миру на Google play ).
Очень занудно!
Есть вещи, которые я не могу доказать, а просто верю в них. этот логотип я разработал и предложил для веб-сайта CSTheory .
Образование
Санкт-Петербургский академический университет — уникальный центр непрерывного образования в области физики и техники, которым руководит Жорес Алферов , лауреат Нобелевской премии по физике.
 В 8 лет там я закончил среднюю школу, Б.С. и М.С. (пилотный класс по теоретической информатике, где я был первым учеником). Я бесконечно благодарна всем своим учителям за эти счастливые годы!
В 8 лет там я закончил среднюю школу, Б.С. и М.С. (пилотный класс по теоретической информатике, где я был первым учеником). Я бесконечно благодарна всем своим учителям за эти счастливые годы!Вот недавнее видео (на русском языке) о новых программах бакалавриата в Академическом университете.
- Заявление в аспирантуру:
- Как поступить в аспирантуру в США (Эндрю Нг).
- Подача заявления на получение докторской степени. Программы по информатике (автор Мор Хархол-Балтер)
- Поиск работы:
- Советы по процессу собеседования (Джанетт Винг, CMU/Microsoft Research)
- Успех в поиске работы, см. также «Как получить работу на факультете» (часть 1a, часть 1b, часть 2 и часть 3) (автор Мэтт Уэлш, Гарвард/Google)
- Планирование карьеры в исследовательской лаборатории (Лаура Хаас, IBM Research)
- Получение работы в промышленной лаборатории (Мэри Фернандес, AT&T Labs – Research/MentorNet)
- Размышления о поиске работы ассистентом профессора в моем штатном расписании (Филип Гуо, Университет Рочестера)
- Получение научной стажировки (запись в моем блоге)
- Слайды с семинаров CRA по карьерному наставничеству (см.
 , например, слайды Жанетт Винг от 2012 г.)
, например, слайды Жанетт Винг от 2012 г.)
- Финансирование:
- Подписка на обновление NSF
- Слайды с Дня предложения DARPA, 2015 г.
- Консультации по написанию заявки на исследовательский грант (автор Санджив Арора)
- КАРЬЕРА Примеры предложений + комментарии (Адам Кливанс, Джеймс Ли, Мозес Чарикар, Петр Индик, Салил Вадхан и Сариэль Хар-Пелед)
- Советы по вопросам мудрости и карьеры:
- Вы и ваши исследования (Ричард Хэмминг)
- Совет начинающему аспиранту (Мануэль Блюм)
- эссе и мнений (Одед Гольдрейх)
- Консультации по карьере и написанию текстов (Терри Тао)
- Принципы эффективных исследований (Майкл Нильсен)
- Лекция о том, как разбогатеть (путем написания книги) (Джефф Ульман)
- Советы для аспирантов и преподавателей (от Мэтта Майта, см. соответствующие темы, например, «Высшая школа», «Производительность», «Письмо», «Проведение презентаций» и т.
 д.).
д.). - Какие качества характеризуют отличного аспиранта? (на Quora см. ответ Дэвида Каргера).
- Несколько слов об исследованиях для аспирантов (Фан Чанг Грэм)
- Руководство по выживанию для доктора наук (Андрей Карпати)
- Решение задач: Решение математических задач (Терри Тао).
- Архивы проблем (если исследовательских задач недостаточно): IMO, IOI, ACM-ICPC Live Archive, TopCoder, Kaggle.
- Онлайн-семинары по теоретической информатике: TCS+.
- Семинары: Dagstuhl, BIRS, Bertinoro, Simons Center, ICERM, IPAM, MSRI, Shonan Center, Barbados, Fields Institute, Cargese, Oberwolfach, New York Area Theory Day.
- Социальные сети: сообщество TCS в Google+.
- Блоги: Агрегатор блогов TCS, список математических блогов.
- Вопросы и ответы: CSTheory, MathOverflow. См. также популярные вопросы по CSTheory и MathOverflow, в том числе «Какие статьи должен прочитать каждый», «Какие книги должен прочитать каждый», «Какие конспекты лекций должен прочитать каждый», «Советы по надлежащей исследовательской практике», «Развернутые основные алгоритмы», « Алгоритмы из книги», «Примеры распространенных ложных представлений о математике», «Рецензирование статьи» и др.

- Ричард Фейнман: «Вы, конечно, шутите, мистер Фейнман!» и «Какое вам дело до того, что думают другие люди?» (оба Ральфа Лейтона). ИМХО, вам лучше прочитать это, когда вы подросток, и не относиться к этому слишком серьезно, но это так весело! 😉
- Комиксы и другие забавные вещи (я их не читаю, но знаю, что они нравятся многим моим друзьям): XKCD, Abstruse Goose, Ph.D. Комиксы, исследования в процессе.
- Как член SIAM я поддерживаю и следую его заявлению об инклюзивности: «Как профессиональное сообщество, SIAM стремится обеспечить инклюзивный климат, который поощряет открытое выражение и обмен идеями, свободный от всех форм дискриминации, притеснений и возмездия, и это приятно и удобно для всех членов и для тех, кто участвует в его деятельности. Следуя этому обязательству, SIAM придерживается философии равенства возможностей и обращения со всеми участниками, независимо от пола, гендерной идентичности или самовыражения, сексуальной ориентации, расы, цвета кожи, национального или этнического происхождения, религии или религиозных убеждений, возраста, семейного положения.

опросов
г.Теория кодирования
(статьи 2006 г. и далее см. выше)
Алгоритмы аппроксимации, твердость Приближения, ПКП
(документы за 2006 г. и далее см. выше)
Прочее Теоретические документы
Тезисы
Алгоритмический и структурный граф Теория
Уведомление об авторских правах: Документы, распространяемые этим сервером, был как средство обеспечения своевременного распространения научных и технические работы на некоммерческой основе. Copyright © и все права на них сохраняются за авторами или другими авторскими правами владельцев, несмотря на то, что они предложили свои работы здесь в электронном виде. Понятно, что все лица, копирующие это информация будет соответствовать условиям и ограничениям, установленным каждым авторское право. Эти работы нельзя репостить без явное разрешение правообладателей. Опубликованные документы ACM © Авторские права 199x принадлежат ACM, Inc.; Опубликованные документы Springer-Verlag © Спрингер-Верлаг; и опубликованные документы IEEE © 199x IEEE, под эти условия.

Григорий Ярославцев
| Я доцент кафедры компьютерных наук в Университете Джорджа Мейсона, базирующемся в Вашингтоне, округ Колумбия. Если вы интересуетесь алгоритмами и основами ML/AI и хотите присоединиться к: |
Предыдущий Следующий
Массивно-параллельные вычисления
Теоретическая модель Модель для вычислений, подобных MapReduce/Spark. | Односвязная кластеризацияМасштабируемые массивно-параллельные алгоритмы для кластеризации векторных данных с одной связью. |
Иерархическая кластеризация
Разделение графаАлгоритмы разделения многомерных сбалансированных графов для графов Facebook с использованием прогнозируемого градиентного спуска. | Кластеризация векторных данныхАлгоритмы на основе проекций для иерархической кластеризации многомерных векторных данных. |
Анализ частных данных
Частный целевой поискАлгоритмы поиска целевых лиц в сетях с гарантиями конфиденциальности для защищенных субпопуляций. | Частная статистика графика Алгоритмы выпуска статистики подграфов о больших сетях при сохранении конфиденциальности отношений. |
Публикации :
Программные комитеты :
Организатор :
| [email protected] г. Википедия Блог Ученый Гитхаб Фейсбук Твиттер Куора Канал YouTube Скачать резюме |
Достижения и награды
Группа и выпускники
Обучение
Избранные публикации
Освещение во внешних СМИ: PBS Newshour, ACM Tech News / The Daily Pennsylvanian, Schneier on Security, AAU, Quartz, Pacific Standard, Wired (немецкий), подкаст The Naked Scientists и Vice Motherboard.

Для приложений в области интеллектуального анализа данных см. Yahoo! Учебник KDD’14 от Франческо Бончи, Дэвида Гарсиа-Сориано и Эдо Либерти.
Открытые задачи семинара JHU по сублинейным алгоритмам [pptx, pdf].
Отзыв Одеда Гольдрейха о «Мой выбор».
 Пост 1, пост 2. Обзор тестирования свойств.
Пост 1, пост 2. Обзор тестирования свойств.Заметки Куи Танга из курса Алекса Андони «Алгоритмические методы работы с массивными данными» в Колумбийском университете.
Открытая задача № 2 из Принстонского семинара по алгоритмам аппроксимации. Смотрите также мои слайды.
Заметки Райана Уильямса из его курса «Темы сложности цепей» в Стэнфорде.
Расширение в письмах по обработке информации как Е.Деменков, А.Кожевников, А.
 Куликов,
Г.Ярославцев г. Новые верхние границы сложности симметричных функций логической схемы »
[Полный текст: (pdf)]
Куликов,
Г.Ярославцев г. Новые верхние границы сложности симметричных функций логической схемы »
[Полный текст: (pdf)]Прочие публикации
* Указывает на статьи с неалфавитным порядком авторов.


 2020.
2020.  Рач,
Сайрус Ращян,
Сергей Еханин
Рач,
Сайрус Ращян,
Сергей Еханин
 org/abs/1607.06442. Полная версия статьи скоро будет размещена на arxiv.
org/abs/1607.06442. Полная версия статьи скоро будет размещена на arxiv.  , статья № 42.
, статья № 42.  46, нет. 3, 2015
46, нет. 3, 2015  222, стр. 93-107, 2013.
222, стр. 93-107, 2013.  10, нет. 4, статья 18, август 2014 г.
10, нет. 4, статья 18, август 2014 г.  35(4), стр. 25:1-25:37
35(4), стр. 25:1-25:37  5, нет. 3, статья 32, июль 2009a
5, нет. 3, статья 32, июль 2009a  163, нет. 3, стр. 499-522, март 2006 г.
163, нет. 3, стр. 499-522, март 2006 г.  Монтажер: Тим Рафгарден. Издательство Кембриджского университета. 2020.
Монтажер: Тим Рафгарден. Издательство Кембриджского университета. 2020.  org/abs/1607.06442. Полная версия статьи скоро будет размещена на arxiv.
org/abs/1607.06442. Полная версия статьи скоро будет размещена на arxiv.  163, нет. 3, стр. 499-522, март 2006 г.
163, нет. 3, стр. 499-522, март 2006 г. 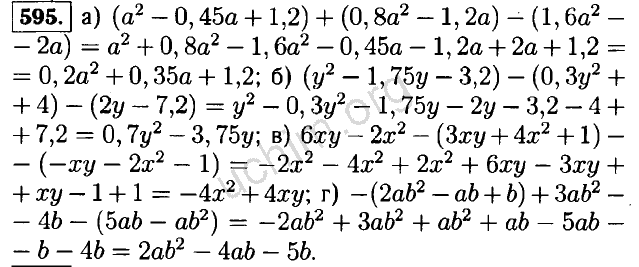 43, нет. 2, 2014
43, нет. 2, 2014 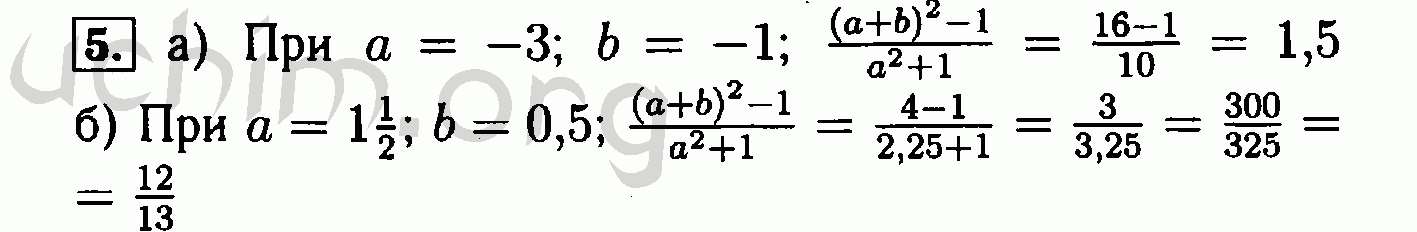 46, нет. 3, 2015
46, нет. 3, 2015  208
208  10, нет. 4, статья 18, август 2014 г.
10, нет. 4, статья 18, август 2014 г.  хорошую запись о проблеме в блоге Ричарда Липтона).
хорошую запись о проблеме в блоге Ричарда Липтона).  35(4), стр. 25:1-25:37
35(4), стр. 25:1-25:37  5279-5286, 2012 г.
5279-5286, 2012 г.  06 Сайт OpenCourseWare с видеолекциями 18.06 по OCW
06 Сайт OpenCourseWare с видеолекциями 18.06 по OCW 1 Пространства векторов
1 Пространства векторов 1 Введение в собственные значения
1 Введение в собственные значения 1 Комплексные числа
1 Комплексные числа 1 Среднее значение, дисперсия и вероятность
1 Среднее значение, дисперсия и вероятность