Задачи с решением по математике для 4 класса: Задачи с ответами. Математика 4 класс.

Тест: Решение задач для 4 класса

Тест: Решение задач для 4 класса — Математика 4 класс

Английский язык

Астрономия

Белорусский язык

Биология

География

ИЗО

Информатика

История

Итальянский язык

Краеведение

Литература

Математика

Музыка

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

ОРКСЭ

Русский язык

Технология

Физика

Физкультура

Химия

Черчение

Для учителей

Дошкольникам

VIP — доступ

• Предметы
»
• Математика
»
• 4 класс
»
• Решение задач для 4 класса

Решение задач для 4 класса

Решение задач с выбором одного ответа на движение, на порпорциональное деление, меру времени.

Математика 4 класс | Автор: Степанова Татьяна Николаевна | ID: 1288 | Дата: 14.2.2014

+138 -77

Помещать страницу в закладки могут только зарегистрированные пользователи

Зарегистрироваться

Вопрос № 1

Путешественнику до места назначения надо преодолеть 820000 м. На автобусе он проехал 230 км, проплыл по реке на катере на 100000 м больше, чем проехал на автобусе, а на поезде проехал 200 км. Остальное расстояние он должен проехать на велосипеде. Сколько км путешественник должен проехать на велосипеде?

10
130
70
60
230
10000
25

Вопрос № 2

На ферме было 15 пятнистых и 12 рыжих коров. От каждой пятнистой коровы получали по 500 литров молока в месяц, а от каждой рыжей коровы — по 513 литров. Сколько литров молока надоили от коров за два месяца?

13656
27312
48564

Вопрос № 3

Люда и Света — сестры. Мама старше Люды на 240 месяцев, а Свету — на 25 лет. Свете — 10 лет. Сколько лет Люде?

10
12
15
20

Вопрос № 4

Из двух поселков навстречу друг другу вышли бабушка и внук. Внук шел со скоростью 5000 м/ч, а бабушка — 2 км/ч. Расстояние между поселками — 14 км. Через какое время встретятся бабушка и внук?

1 час
2 часа
полчаса

Вопрос № 5

В швейной мастерской сшили 360 наволочек за 30 дней. За сколько дней сошьют такое же колличество наволочек, если каждий день будут шить на 6 наволочек больше, чем раньше?

14
16
18
20

Вопрос № 6

Из двух городов навстречу друг другу выехали две машины. Скорость первой машины 60 км/ч, скорость второй 80 км/ч. Через сколько часов машины встретятся, если расстояние между городами 280 км.

1 ч
2 ч
3 ч
30 мин
45 мин
100 сек
5 ч

Вопрос № 7

Миша живет на 11 этаже. В доме не работает лифт, поэтому ему приходится подниматься пешком по лестнице. чтобы попасть на каждый следующий этаж, надо преодолеть 4 ступеньки, а затем — еще 2 раза по 3 ступеньки. Сколько всего ступенек нужно преодолеть Мише, чтобы добраться домой?

100

105
110

Вопрос № 8

Ире было 7 лет 24 месяца назад. Саше исполнится 15 через 60 месяцев. Кто из ребят старше?

Ира
Саша
Они ровестники

Вопрос № 9

Из двух городов навстречу друг другу выехали два автомобиля. Скорость первого автомобиля была 60 км/ч, второго — 80 км/ч. Через 3 часа они встретелись. Найдите расстояние между городами.

320 км
420 км
520 км

Показать ответы

Получение сертификата
о прохождении теста

Доступно только зарегистрированным пользователям

© TestEdu. ru 2013-2022

E-mail администратора: [email protected]

Задачи на время

Подготовка к заданию №4 для четвероклассников.

Занятия в музыкальной школе длятся по 30 минут каждое, а перемены между ними – по 10 минут. В 14:00 началось первое занятие. Во сколько закончится третье занятие?

 

Решение:

Кинотеатр начинает работать с 10 часов. Каждый сеанс длится 1 час 30 минут. После каждого сеанса делается перерыв 20 минут. Во сколько закончится второй сеанс?

 

Решение:

Сегодня в школе четыре урока. Уроки в школе начинаются с 9 часов. Каждый урок длится 40 минут, а перемена – 10 минут. Во сколько заканчивается последний урок?

 

Решение:

20 марта в 2009 году пришлось на пятницу. На какой день недели пришлось 6 апреля в 2009 году? В марте 31 день.

 

Решение:

19 сентября в 2010 году пришлось на воскресенье. На какой день недели пришлось 5 октября в 2010 году? В сентябре 30 дней.

 

Решение:

23 апреля в 2012 году пришлось на понедельник. На какой день недели пришлось 9 мая в 2012 году? В апреле 30 дней.

 

Ответ:

Дядя Федор взглянул на часы. Часы показывали 8 ч 30 мин. Если он сейчас же отправится на вокзал, то, потратив на дорогу 40 мин, опоздает на поезд на 8 мин. В котором часу отправляется поезд?

 

Ответ:

Занятия в школе начинаются в 8 ч 30 мин. Мишка опоздал к первому уроку на 7 мин. Сколько времени ему придется ждать, чтобы попасть на второй урок, который начинается в 9 ч 25 мин?

 

Ответ:

Братец Кролик вышел из своего дома в 8 ч 40 мин. Братец Медведь, выйдя из дома на 17 мин позже, встретился с братцем Кроликом в 9 ч 15 мин. Сколько минут находился в пути Братец Медведь до встречи с Братцем Кроликом?

 

Ответ:

Когда в Ростове 13 часов, в Уфе в это время 15 часов.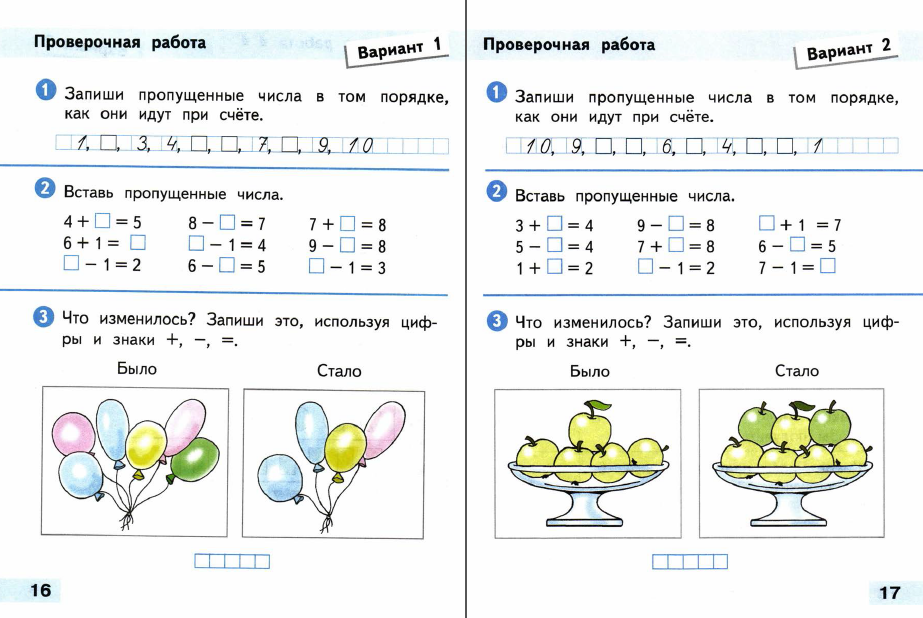 Когда в Уфе 15 часов, в Красноярске в это время 17 часов. Сколько времени в Ростове, когда в Красноярске 20 часов?

 

Ответ:

Когда в Калининграде 14 часов, в Самаре в это время 16 часов. Когда в Самаре 16 часов, в Омске в это время 19 часов. Сколько времени в Калининграде, когда в Омске 23 часа?

 

Ответ:

Когда в Санкт-Петербурге 12 часов, в Новосибирске в это время 15 часов. Когда в Новосибирске 15 часов, в Иркутске в это время 17 часов. Сколько времени в Санкт-Петербурге, когда в Иркутске 21 час?

 

Ответ:

Папе дяди Федора 36 лет. Дядя Федор в 3 раза моложе своего папы. Сколько лет было папе дяди Федора, когда родился дядя Федор?

 

Ответ:

Таймер в часах поставили так, что он подаёт один сигнал через каждые полчаса. В первый раз таймер просигналил в 13:30. Во сколько он просигналит в седьмой раз?

 

Ответ:

Таймер в часах поставили так, что он подаёт один сигнал через каждые полчаса. В первый раз таймер просигналил в 17:30. Во сколько он просигналит в девятый раз?

 

Ответ:

Таймер в часах поставили так, что он подаёт один сигнал через каждые полчаса. В первый раз таймер просигналил в 11:00. Во сколько он просигналит в восьмой раз?

 

Ответ:

Тренировка бегунов началась в 17.35 и закончилась через 2 час 45 минут. Во сколько закончилась тренировка бегунов?

 

Ответ:

Занятия в кружке начались в 14.10 и завершились в 16.35 минут. Сколько минут продолжались занятия в кружке?

 

Ответ:

Кафе открывается в 9.30 и закрывается в 22.15. Перерыв с 14.00 до 15.00. Сколько часов и минут работает кафе?

 

Ответ:

Коля вышел из школы в 15.20 и пошел домой. По пути он на 15 минут зашел в магазин и купил хлебаю. Домой он пришел в 16.10. Сколько минут Коля шел домой?

 

Ответ:

Автобус выехал из города в 10. 35 минут. Доехал до конечной и ждал там 20 минут. Обратно в город автобус приехал в 12. 55. Сколько минут автобус был в пути?

 

Ответ:

Братец Кролик вышел из своего дома в 8 ч 40 мин. Братец Медведь, выйдя из дома на 17 мин позже, встретился с братцем Кроликом в 9 ч 15 мин. Сколько минут находился в пути Братец Медведь до встречи с Братцем Кроликом?

 

Ответ:

Ярмарка в школе началась в 11 утра и продолжалась до 5.30 вечера. Сколько времени длилась ярмарка в школе?

 

Ответ:

Обоснование решения

На уроках математики учителям следует побуждать учащихся концентрироваться не только на правильном ответе; учащиеся должны понимать процесс и лежащие в его основе понятия, чтобы получить правильный ответ (Johnson & Watson, 2011). Другими словами, учащиеся должны найти и обосновать свои решения.

Чтобы обосновать решение, учащиеся должны уметь использовать соответствующий математический язык, чтобы обосновать конкретный подход, используемый для решения проблемы. Каждый раз, когда учащийся предлагает «решение» в попытке решить проблему, это «решение» необходимо обосновать. То есть учащийся должен объяснить, откуда он знает, что его «решение» правильное.

Обоснование решения также может возникнуть в контексте обсуждения математики в классе, когда учащиеся должны будут устно объяснить свои решения.

Чтобы помочь учащимся обосновать свои решения, учитель может:

• есть класс обсуждение того, что значит обосновать решение

Учитель может попросить некоторых учащихся обрисовать в общих чертах, как они могут обосновать конкретное решение из предыдущего урока.

Может быть полезно обсудить ключевую терминологию, связанную с изучаемой математической темой, чтобы стимулировать студентов к их обсуждению. Эти ключевые термины можно найти в классе и записать на доске.

• предложите учащимся задачу и попросите их решить ее, записав свои обоснования
  

• попросите учащихся работать в парах, чтобы обосновать свои решения

• попросите пары поделиться и дать конструктивную обратную связь относительно обоснований друг друга.
  

В приведенном ниже примере показано, как эту стратегию можно применить к классу 10-го класса по линейным уравнениям.

Сценарий: оплата за выполнение задания

Сравните следующие два расчета оплаты за услугу, где C означает стоимость (в долларах) выполнения задачи, а t — время, затраченное (в часах) на выполнение задачи:

Определите, когда первое уравнение дешевле второго

C = 25t + 200
C = 30t +150

Разработка решения

Учащиеся будут работать над решением задачи. Либо графически, либо путем решения одновременных уравнений время, для которого затраты равны, составляет 10 часов.

Примечание. Время, в течение которого первая скорость меньше второй, считается временем, превышающим 10 часов.

Обсуждение в классе

Обсудите в классе, что значит обосновывать решение. Попросите некоторых студентов обрисовать, как они могли бы обосновать свое конкретное решение.

Ключевые термины для обсуждения могут быть фиксированными затратами, переменными затратами, почасовой ставкой и т. д.

Обоснование решения

Попросите учащихся работать в парах, чтобы обосновать свои решения.

Учащиеся обмениваются решениями с другой парой и добавляют предложения по улучшению решений.

Обоснование решения может включать следующее:

• проверку решения уравнений, возможно путем замены
• объяснение с использованием графиков или числовых примеров того, почему решение t >10 часов

Приведенный выше пример ссылается на VCMNA335 и также является частью Математическое умение Рассуждение, когда учащиеся «обосновывают стратегии и сделанные выводы» (VCAA, n.d.)

Видео о грамотности на практике: Математика

В этом видео Эндрю Витт рассказывает о том, как дать учащимся навыки решения сформулированных задач и прикладных задач по математике.

Введение. Выводы из заданий TIMSS 2019 «Решение проблем и исследование» ответы могут быть включены в TIMSS. Гол был

, а не для определения новых конструкций решения проблем и исследования, а для сбора информации, которая поможет улучшить и расширить широту оценки TIMSS, чтобы обеспечить более полный охват решения проблем и исследования, как уже описано в рамках оценки.

Переход TIMSS 2019 на цифровое оценивание

В 2019 году TIMSS перешел на цифровое оценивание по математике и естественным наукам в четвертом и восьмом классах. Половина из почти 70 стран, участвующих в TIMSS 2019провела новую цифровую оценку eTIMSS, способствуя ее разработке посредством пилотных исследований и полевых испытаний, а другая половина продолжила работу с paperTIMSS. Тщательно управляя тем, как компьютеризация элементов eTIMSS была введена в TIMSS 2019, внося некоторые очевидные улучшения (например, щелкая ответ на элемент с множественным выбором, а не заполняя круг), но по-прежнему уделяя большое внимание отражению paperTIMSS, большинство элементы в eTIMSS и paperTIMSS имели схожие психометрические свойства.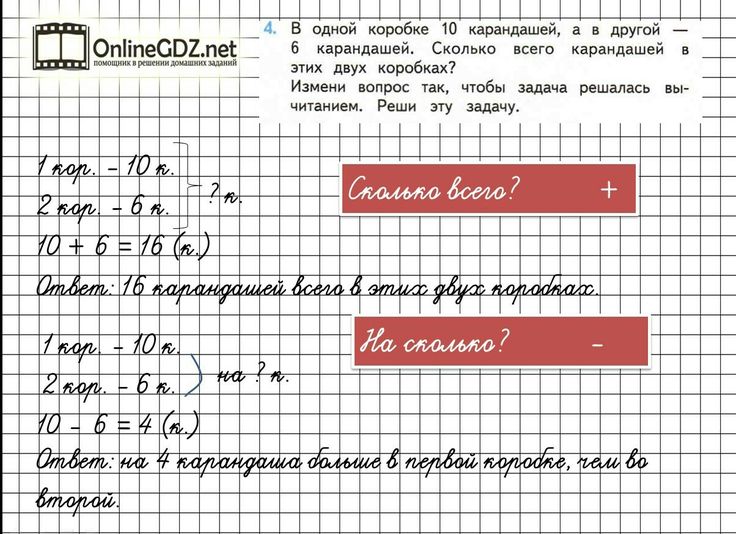 Как указано в Методы и процедуры: TIMSS 2019 Технический отчет , ¹ Сложный пошаговый процесс масштабирования позволил связать eTIMSS и paperTIMSS со шкалами достижений TIMSS по математике и естественным наукам. Публикация

TIMSS 2019 International Results in Mathematics and Science ² , сообщающая о результатах всех стран-участниц по шкалам TIMSS 2019 по математике и естественным наукам, свидетельствует о том, что переход завершен.

В качестве важной особенности перехода eTIMSS создала возможность для разработки инновационных мер оценки, которые расширили бы охват процессов решения проблем и запросов. Было очевидно, что компьютеризированный TIMSS обладает потенциалом для улучшения качества показателей TIMSS навыков более высокого порядка (например, большей глубины концепций, динамических характеристик и обработки данных), и в то же время делает сбор данных более эффективным. выполнение сложных задач. Оценка TIMSS 2019фреймворки с увлекательными компьютеризированными задачами оценки, основанными на самых последних исследованиях, стали явной целью разработки TIMSS 2019.

Начиная с 2017 года, Международный учебный центр TIMSS & PIRLS начал разработку задач «Решение проблем и исследование TIMSS 2019». В итоге было разработано восемь задач — две по математике и две по естественным наукам для четвертого и восьмого классов. Восемь заданий были собраны в два специальных электронных буклета на класс, которые оценивались вместе с eTIMSS в странах eTIMSS в соответствии с чередующимся дизайном (см. Приложение A). Таким образом, все страны eTIMSS (но не страны paperTIMSS) участвовали в оценке TIMSS 2019.Задачи решения проблем и исследования, включая 30 стран и 6 систем сравнительного анализа с участием около 22 000 учащихся четвертого класса и 22 страны и 5 систем сравнительного анализа с примерно 20 000 учащихся восьмого класса.

В этом отчете представлены четыре задачи по решению проблем и расследованию вместе с результатами достижений по странам, с акцентом на сильные и слабые стороны самих задач.

• School Party — четвертый класс математика:  Учащиеся планируют вечеринку для своей школы (продажа билетов, украшения, еда и напитки).
   
• Исследование фермы — Наука четвертого класса:   Мальчик выясняет, какое сельскохозяйственное животное съело растения в его саду.
   
• Building — восьмой класс математика:   Учащиеся строят навес с дождевой бочкой.
   
• Растения перца — восьмой класс науки:   Учащиеся проводят эксперимент, чтобы определить наиболее эффективное удобрение.

eTIMSS 2019 также позволил собрать ценные данные о том, как учащиеся проходят сеансы оценивания. Это включало в себя обширные технологические данные о времени событий, навигации от экрана к экрану, прокрутке и использовании калькуляторов и линеек. Эти данные позволяют воссоздать прогресс учащегося в выполнении заданий и были особенно полезны при анализе данных об отсутствии ответов; различать студентов, у которых не хватило времени, и тех, кто перестал отвечать до того, как время истекло. Прежде чем ошибочно предположить, что учащимся требуется дополнительное время для оценивания заданий PSI, важно было понять, что «нехватка времени» встречается реже, чем «остановка» при наличии достаточного количества времени (см. Приложение B). Понимание причин их прекращения требует дальнейших исследований, но, вероятно, некоторые из них были усталыми или разочарованными. Еще раз подчеркивая свой исследовательский потенциал, TIMSS 2019данные процесса также использовались для анализа неправильных ответов и получения дополнительной информации о том, как учащиеся справляются с интерактивными функциями, чтобы помочь объяснить, почему иногда производительность была ниже ожидаемой. После обнаружения значительного отсутствия ответов на некоторые задачи PSI, особенно по сравнению с почти незначительным отсутствием ответов на «обычный» элемент eTIMSS, данные о времени были использованы для исследования низких показателей выполнения.

Наконец, как побочный продукт задач PSI, один элемент в Building попросил студентов показать, как они вырезают стены из доски. Эти ответы были использованы для изучения возможностей TIMSS с использованием автоматической оценки в будущем (см. Приложение C). Оглядываясь назад на переход TIMSS 2019 к цифровой оценке, решение двигаться вперед и использовать преимущества технологий и новых психометрических исследований будет признано началом кардинальных изменений в методах и процедурах оценки TIMSS.
 

Краткая история TIMSS и задач решения проблем и запросов

Инновационные тесты для оценки навыков более высокого порядка были частью TIMSS с момента его создания. Первый TIMSS 1995 года включал в себя то, что в то время считалось «современной» оценкой успеваемости, которая давалась ученикам четвертого класса в 10 странах и ученикам восьмого класса в 21 стране. Как поясняется в отчете о результатах TIMSS 1995 г., оценка успеваемости основывалась на интегрированных практических задачах с использованием инструментов и оборудования в качестве средства оценки содержания и процедурных знаний учащихся, а также их способности использовать эти знания в рассуждениях и решениях задач. решение (см. Оценка эффективности TIMSS 1995 ³ ). Оценка эффективности была сочтена особенно полезной для оценки науки как процесса исследования (помимо просто совокупности знаний). Из 12 заданий, данных учащимся четвертого и восьмого классов, 11 были одинаковыми для разных классов, а одно было уникальным. Было пять математических задач: «Кости», «Калькулятор», «Складывание и разрезание», «За поворотом» и «Упаковка»; и пять научных задач — «Импульс», «Магниты», «Батарейки», «Резиновая лента» и «Контейнеры» (четвертый класс) или «Решения» (восьмой класс). Значительные усилия были затрачены на оценку структуры «ожиданий эффективности», которая включала решение проблем, планирование расследования, анализ и интерпретацию результатов, а также формулирование выводов.

Оценка успеваемости проводилась в формате «цирк-ринг», когда студенты посещали три из пяти станций, расположенных вокруг комнаты, каждая из которых состояла из собранного оборудования для одного или двух заданий. Оборудование для выполнения задач весило около 100 фунтов, и его нужно было установить в большой комнате. Таким образом, было возможно дать эту очень трудоемкую и ресурсоемкую оценку только подвыборкам студентов, которые участвовали в основной оценке.

Когда TIMSS 2003 ввел регулярно проводимые оценки в четвертом и восьмом классах каждые четыре года для отслеживания тенденций, Национальный научный фонд США (NSF) предоставил Бостонскому колледжу грант для поддержки разработки структуры и оценки. Идея заключалась в том, чтобы разработать расширенные задачи по решению проблем и исследованию, но с использованием только инструментов бумаги и карандаша. Был достигнут прогресс в разработке целей оценки содержания, адаптированных специально для четвертого или восьмого класса, но математики, ученые и сообщество, занимающееся измерениями, изо всех сил пытались сделать бумажные и карандашные задачи доступными для учащихся, а также увлекательными. Оценка производительности была другой и «забавной», например, в задании о влиянии физических упражнений на организм ученики должны были прыгать вверх и вниз, чтобы увеличить частоту сердечных сокращений. В качестве недостатка учащиеся в странах-участницах TIMSS 2003 столкнулись с незнакомой идеей — тестом, который давал вам много времени на проработку серии заданий по теме (например, пищевая цепь в океане или почему разные цвета света могут изменить цвет рубашки). В целом, первые бумажно-карандашные задачи PSI 2003 года не очень мотивировали, поэтому эти более длительные задачи были постепенно исключены из предстоящих оценок.

Тем не менее, было широко признано, что навыки решения проблем и исследования имеют основополагающее значение для оценочных рамок TIMSS. Для TIMSS 2007 Национальный центр статистики образования США (NCES) организовал инициативу для стран по финансированию TIMSS для разработки целей как познавательной, так и содержательной оценки. Это привело к тому, что три когнитивных области — знание, применение и рассуждение — стали постоянным измерением оценок по математике и естественным наукам как в четвертом, так и в восьмом классах. В очередной раз для TIMSS 2015 Международный исследовательский центр TIMSS и PIRLS в Бостонском колледже работал с Национальным центром статистики образования, чтобы получить дополнительное финансирование от NSF для разработки инновационных предметов, тем более что TIMSS 2015 также включал оценку тенденций в TIMSS Advanced. Однако эти усилия по обеспечению финансирования не увенчались успехом, поэтому навыки рассуждения, связанные с решением проблем и исследованием, остались в рамках оценки, а разработке более длительных задач оценки уделялось мало внимания. Несколько целей оценки решения проблем и запросов, показанные ниже, были взяты из Система оценки TIMSS 2019 . ⁴

• Математические основы
• Математические рассуждения включают в себя логическое, систематическое мышление. Он включает в себя интуитивные и индуктивные рассуждения, основанные на шаблонах и закономерностях, которые можно использовать для решения проблем, возникающих в… реальных условиях.
   
• Определить эффективные/соответствующие операции, стратегии и инструменты для решения проблем, для которых существуют обычно используемые методы решения.
   
• Реализовать стратегии и операции для решения задач, связанных со знакомыми математическими понятиями и процедурами.
   
• Связывайте различные элементы знаний, связанные представления и процедуры для решения проблем.

• Научные основы
• Ученые занимаются научными исследованиями, следуя ключевым научным практикам, которые позволяют им исследовать мир природы и отвечать на вопросы о нем. Студенты, изучающие естественные науки, должны овладеть этими практиками…
   
• Используйте диаграмму или другую модель, чтобы продемонстрировать знание научных концепций, проиллюстрировать процесс, цикл, взаимосвязь или систему или найти решения научных проблем.
   
• Предоставьте или определите объяснение наблюдения или природного явления, используя научную концепцию или принцип.
   
• Планировать исследования или процедуры, подходящие для ответов на научные вопросы или проверки гипотез; и описывать или признавать характеристики хорошо спланированных исследований с точки зрения переменных, которые необходимо измерять и контролировать, а также причинно-следственных связей.

Задания TIMSS 2019 для решения проблем и исследования (PSI)

Задания PSI, переосмысленные для TIMSS 2019, представляют собой визуально привлекательные интерактивные сценарии, которые предлагают учащимся адаптивные и реагирующие способы выполнения ряда шагов (элементов оценки) для достижения решение или цель. Ответы учащихся предоставляются с помощью сочетания элементов выбора и составления ответов, а также с помощью различных инновационных форматов для захвата ответов учащихся (например, цифровой клавиатуры, перетаскивания, графических инструментов и бесплатных рисунков).

Существует множество различных способов создания экземпляра задачи PSI. Например, задание PSI может быть:

• Интерактивный научный эксперимент, в котором учащиеся настраивают и проводят эксперимент, регулируя настройки и наблюдая за результатами (см. Pepper Plants —Наука, восьмой класс).
   
• Задача по математике, в которой учащиеся работают от визуализации до готового продукта, включающего несколько этапов и оценку промежуточных результатов (см. Building — Математика, восьмой класс).
   
• Математическая или научная модель, которой учащиеся могут манипулировать (например, отношения хищник-жертва, решения или силы и движение).
   
• Систематическое исследование атрибутов объекта, места или живого организма, реализация процесса или рассмотрение причинно-следственных связей, встроенных в сценарий, который является убедительным и нацелен на темы в рамках (см. School Party и Farm Investigation). , Математика и естественные науки, соответственно, четвертый класс).

Как правило,

• Каждое задание PSI должно быть расположено в реальном мире, проблеме, расследовании или деятельности, которая обеспечивает основное повествование или тему для элементов. Проблема или ситуация должны быть достаточно широкими, чтобы охватить ряд содержательных и познавательных областей в рамках математики или естественных наук. Насколько это возможно, задачи PSI должны включать элементы, посвященные различным темам содержания и ряду когнитивных требований.
   
• Повествование должно обеспечивать логическое или хронологическое развитие от первого пункта к финалу.
   
• Поскольку задачи PSI с единым повествованием от начала до конца трудновыполнимы, задачи PSI также могут быть написаны без большого повествования, при условии, что есть общая тема, связывающая элементы вместе. Тематический тип задания PSI дает учащимся возможность взаимодействовать с различными аспектами сценария без влияния порядка взаимодействий. Элементы могут быть независимыми, но при этом оставаться связными и привлекательными.

В любой задаче PSI важно, чтобы элементы были независимы друг от друга. Правильно ли учащийся ответит на один вопрос, не должно влиять на то, правильно ли учащийся ответит на другой вопрос. То есть в целом ответ на вопрос не должен давать учащимся подсказки, чтобы они могли вернуться и изменить ответ на предыдущий вопрос. Или задание не должно основываться на правильном ответе на предыдущий вопрос, потому что не все учащиеся дали правильный ответ. Различные неправильные ответы могут повлиять на сложность второго пункта или даже сделать невозможным ответ. С другой стороны, при правильном проектировании данные обработки можно использовать для исследования поведения «оглядывающихся назад» в рамках стратегии студентов при сдаче тестов.

Разработка задач по решению проблем и исследованию для eTIMSS 2019

Разработка задач TIMSS 2019 PSI для четвертого и восьмого классов соответствовала стандартным процедурам TIMSS для обеспечения достоверных показателей математических и научных достижений, описанных в Системах оценки TIMSS 2019 . ⁵ Однако для разработки новых и увлекательных проблемных контекстов со связными наборами элементов достижений потребовалось гораздо больше раундов экспертной оценки, чем обычно, поэтому сотрудники Международного исследовательского центра TIMSS & PIRLS сотрудничали с участниками TIMSS 2019.Комитет по рассмотрению предметов науки и математики (SMIRC) в августе 2015 года, чтобы начать разработку задач PSI. Это было почти за два года до того, как началось написание заданий для остальных заданий полевого тестирования TIMSS 2019 (апрель 2017 г.), и потребовалось пять дополнительных личных встреч в Бостонском колледже и многочисленные онлайн-обзоры.

Когнитивные лаборатории с участием 34 студентов в США (август 2015 г.) предоставили важную информацию об удобстве использования интерфейса eTIMSS и различных инновационных типах элементов. SMIRC в целом сосредоточил свой первый углубленный обзор задач PSI на согласовании между задачами и структурами, степени, в которой технология в задачах поддерживала предполагаемые процессы реагирования, и межкультурной уместности сценариев проблем. . Небольшие пилотные испытания в нескольких странах eTIMSS предоставили ключевую информацию на разных этапах процесса разработки.

Предварительный пилотный тест eTIMSS, включающий в общей сложности 12 заданий PSI, был проведен в сентябре 2016 г. в трех англоязычных странах, имеющих опыт проведения цифровых оценок: Австралии, Канаде и Сингапуре. В каждой стране участвовали учащиеся с различными способностями к математике и естественным наукам в PrePilot, что дало примерно 100 ответов на вопрос как в четвертом, так и в восьмом классе. PrePilot предоставил дополнительную информацию об удобстве использования недавно разработанных типов элементов и успехах учащихся в использовании интерфейса eTIMSS, а также оценки количества времени, которое потребовалось учащимся для выполнения каждого задания, и приблизительную сложность задания.

Национальные координаторы исследований (NRC) рассмотрели задачи PSI на своем заседании NRC 3 ^rd TIMSS 2019, которое было проведено до проведения полевых испытаний (март 2017 г.), а затем снова рассмотрели их после полевых испытаний (август 2018 г.), чтобы выбрать задачи, которые будут включены в оценку eTIMSS 2019. NRC выбрали восемь задач PSI (четыре в четвертом классе с 50 элементами и четыре в восьмом классе с 55 элементами) для основного сбора данных. Восемь заданий охватывали ряд тем предметной области математики и естественных наук, и в соответствии с целью заданий PSI по оценке навыков более высокого порядка большинство заданий PSI включали применение и рассуждение.

Приложение A содержит обзор параллельных схем оценивания для paperTIMSS 2019 и eTIMSS 2019. В схеме eTIMSS также указано чередующееся расположение восьми заданий PSI — двух по математике и двух по естественным наукам в каждом классе. И четвертый, и восьмой классы включали два отдельных буклета с элементами PSI.
 

Включение пунктов PSI в шкалы успеваемости по математике и естественным наукам TIMSS 2019 в четвертом и восьмом классах

Приложения с 1 по 4 для сравнения TIMSS 2019оценка достижений с учетом и без учета данных PSI для стран eTIMSS (по одному экспонату по математике в четвертом классе, естественным наукам в четвертом классе, математике в восьмом классе и естественным наукам в восьмом классе соответственно). В первом столбце каждого приложения представлены средние результаты успеваемости, опубликованные в TIMSS 2019 International Results in Mathematics and Science ⁶ для стран, которые администрировали цифровую версию TIMSS (eTIMSS). Во втором столбце представлены средние результаты достижений для eTIMSS, включая TIMSS 2019.PSI (подробности о процедурах масштабирования см. в главе 17 документа «Методы и процедуры: Технический отчет TIMSS 2019 ⁷ »). Для каждого класса практически не было различий (в среднем 0 баллов по шкале) между средними достижениями eTIMSS, исключая учащихся PSI, и средними достижениями, включая учащихся PSI, по математике или естественным наукам.
 

4 класс Математика 4 класс Естествознание 8 класс Математика 8 класс Естествознание

 

Важная информация для будущего развития

Следует отметить, что концепция эффективной задачи PSI будет продолжать развиваться, поскольку после публикации этого отчета в конце октября МЭА опубликует данные процесса для задач PSI TIMSS 2019, что позволит провести ряд дальнейших исследований. -глубинный анализ. Основные критерии, которые были важны в TIMSS 2019, остаются, однако появились дополнительные соображения:

• Задача PSI должна затрагивать темы в рамках TIMSS по математике или естественным наукам.
   
• Задания PSI могут быть полными в восьмом классе (блок из 10-15 заданий) или «мини» примерно из 5-8 заданий. В четвертом классе в TIMSS 2023 будут только задания mini-PSI.
  
  • Показатели завершения, представленные в Приложении A для элементов оценки eTIMSS по сравнению с заданиями PSI, показывают, что задания PSI четвертого класса имели сравнительно низкие показатели завершения.
     
• Никакая задача или элементы PSI не должны требовать чрезмерного чтения, настойчивости или специальных знаний.
   
• Как правило, первый экран представляет тему, а следующие экраны представляют элементы (без конечного экрана).
   
• Каждое задание PSI должно включать элементы определенного уровня сложности. Обычно задача должна начинаться с более простых элементов и заканчиваться более сложными элементами.
   
Элементы
• PSI не должны зависеть от других элементов (за исключением запланированных исследовательских целей).
   
Элементы
• PSI должны использовать преимущества цифровой среды, используя интерактивные или адаптивные функции, но не безвозмездно.
   
• Режим записи ответов учащихся должен помогать учащимся демонстрировать свои знания в области математики или естественных наук, а не отвлекать внимание.
   
• Задачи и элементы PSI должны быть разработаны таким образом, чтобы использовать потенциал данных процесса.
   
Предметы
• PSI должны соответствовать Руководству по написанию предметов TIMSS 2019 . ⁸
   
• К каждому пункту PSI, оцениваемому человеком, должно прилагаться руководство по подсчету очков. (Частичный кредит может быть присужден, если это оправдано. Для этой цели могут использоваться данные процесса.)

Примечания

---

¹ Фой, П., Фишбейн, Б., фон Давье, М., и Инь, Л. (2020). Внедрение методологии масштабирования TIMSS 2019. В MO Martin, M. von Davier и IVS Mullis (Eds.), Методы и процедуры : Технический отчет TIMSS 2019 (стр. 12.1–12.146). Получено с веб-сайта Бостонского колледжа, Международного исследовательского центра TIMSS и PIRLS: https://timssandpirls.bc.edu/timss2019/methods/chapter-12.html

²  Муллис, И.В.С., Мартин, М.О., Фой, П., Келли, Д.Л., и Фишбейн, Б. (2020). Международные результаты TIMSS 2019 по математике и естественным наукам . Получено с веб-сайта Международного исследовательского центра TIMSS & PIRLS Бостонского колледжа: https://timssandpirls.bc.edu/timss2019/international-results/

³ Хармон Э., Смит Т. А., Мартин М. О., Келли Д. Л. , Битон, А.Е., Маллис, И.В.С., Гонсалес, Э.Дж., и Орпвуд, Г. (1997). Оценка эффективности в Третьем международном исследовании МЭА по математике и естественным наукам (TIMSS) . Получено с веб-сайта Международного исследовательского центра TIMSS и PIRLS Бостонского колледжа: https://timss. bc.edu/timss1995i/PAreport.html

⁴ Mullis, I. V. S., & Martin, M. O. (Eds.). (2017). Система оценки TIMSS 2019 . Получено с веб-сайта Бостонского колледжа, Международного исследовательского центра TIMSS и PIRLS: https://timssandpirls.bc.edu/timss2019/frameworks/

9.0002 ⁵ Там же.

⁶  Муллис, И.В.С., Мартин, М.О., Фой, П., Келли, Д.Л., и Фишбейн, Б. (2020). Международные результаты TIMSS 2019 по математике и естественным наукам . Получено с веб-сайта Бостонского колледжа, Международного исследовательского центра TIMSS и PIRLS: https://timssandpirls.bc.edu/timss2019/international-results/

⁷ Fishbein, B., & Foy, P. (2021). Масштабирование данных решения задач и запросов TIMSS 2019. В MO Martin, M. von Davier и IVS Mullis (Eds.), Методы и процедуры: Технический отчет TIMSS 2019 (стр. 17.1–17.51). Получено с веб-сайта Международного исследовательского центра TIMSS и PIRLS Бостонского колледжа: https://timssandpirls.