Задача №10 — гдз и решебник по математике за 4 класс Моро
Умножение и деление на однозначное число
Задачи-расчеты:
1 2 3Странички для любознательных:
1 2 3 4Умножение на числа, оканчивающиеся нулями
Странички для любознательных:
1 2 3 4 5 6Страница 23, Проверочные работы:
1 2Странички для любознательных:
1 2 3 4 5 6 7 8 9 10 11 12Деление на числа, оканчивающиеся нулям
Страница 37, Проверочные работы:
1 2Математика вокруг нас:
1 2 3 4 5 6Умножение на двузначное и трехзначное число
Странички для любознательных:
1 2 3 4 5Страница 56, Проверочные работы:
1 2Деление на двузначное число
Странички для любознательных:
1 2 3 4 5 6Деление на трехзначное число
Странички для любознательных:
1 2 3 4 5 6 7Страница 86, Нумерация:
Страница 89, Выражения и уравнения:
Страница 90, Сложение и вычитание:
Страница 92, Умножение и деление:
Страница 94, Правила о порядке выполнения действий:
Страница 95, Величины:
Страница 96, Геометрические фигуры:
Страница 97, Задачи:
Страница 6, Странички для любознательных:
1 2 3 4 5 6 7 8 9 10 11 12 13 14Страница 104, Доли:
Страница 105, Единицы площади — ар и гектар:
Страница 108, Диагонали прямоугольника(квадрата), и их свойства:
Страница 110, Куб:
Страница 111, Прямоугольный параллелепипед:
Страница 112, Пирамида:
Страница 113, Цилиндр:
Страница 113, Шар:
Тексты для контрольных работ
Страница 114, Задания базового уровня:
1 2 3 4 5 6 7 8Страница 115, Задания повышенного уровня сложности:
1 2 3 4 5 6 7 8 9gdzplus.ru
Задача №10 — гдз и решебник по математике за 4 класс Моро
Умножение и деление на однозначное число
Задачи-расчеты:
1 2 3Странички для любознательных:
1 2 3 4Умножение на числа, оканчивающиеся нулями
Странички для любознательных:
1 2 3 4 5 6Страница 23, Проверочные работы:
1 2Странички для любознательных:
1 2 3 4 5 6 7 8 9 10 11 12Деление на числа, оканчивающиеся нулям
Страница 37, Проверочные работы:
1 2Математика вокруг нас:
1 2 3 4 5 6Умножение на двузначное и трехзначное число
Странички для любознательных:
1 2 3 4 5Деление на двузначное число
Странички для любознательных:
1 2 3 4 5 6Деление на трехзначное число
Странички для любознательных:
1 2 3 4 5 6 7Страница 86, Нумерация:
Страница 89, Выражения и уравнения:
Страница 90, Сложение и вычитание:
Страница 92, Умножение и деление:
Страница 94, Правила о порядке выполнения действий:
Страница 95, Величины:
Страница 96, Геометрические фигуры:
Страница 97, Задачи:
Страница 6, Странички для любознательных:
1 2 3 4 5 6 7 8 9 10 11 12 13 14Страница 104, Доли:
Страница 105, Единицы площади — ар и гектар:
Страница 108, Диагонали прямоугольника(квадрата), и их свойства:
Страница 110, Куб:
Страница 111, Прямоугольный параллелепипед:
Страница 112, Пирамида:
Страница 113, Цилиндр:
Страница 113, Шар:
Тексты для контрольных работ
Страница 114, Задания базового уровня:
1 2 3 4 5 6 7 8Страница 115, Задания повышенного уровня сложности:
1 2 3 4 5 6 7 8 9gdzplus.ru
Задача №10 — гдз и решебник по математике за 4 класс Петерсон
Урок 1. Деление и дроби:
Урок 2. Нахождение части, которую одно число составляет от другого:
Урок 3. Сложение дробей:
Урок 4. Вычитание дробей:
Урок 5. Правильные и неправильные дроби:
Урок 6. Правильные и неправильные части величин:
Урок 7. Задачи на части:
Урок 8. Смешанные числа:
Урок 9. Выделение целой части из неправильной дроби:
Урок 10. Запись смешанного числа в виде неправильной дроби:
Урок 11. Сложение и вычитание смешанных чисел:
Урок 12. Сложение и вычитание смешанных чисел:
Урок 13. Сложение и вычитание смешанных чисел:
Урок 14. Сложение и вычитание смешанных чисел:
Урок 15. Сложение и вычитание смешанных чисел:
Урок 16. Сложение и вычитание смешанных чисел:
Урок 17. Шкалы:
Урок 18. Числовой луч:
Урок 19. Координаты на луче:
Урок 20. Расстояние между точками числового луча:
Урок 21. Движение по числовому лучу:
Урок 22.
Движение по числовому лучу:Урок 23. Одновременное движение по числовому лучу:
Урок 24. Скорость сближения и скорость удаления:
Урок 25. Скорость сближения и скорость удаления:
Урок 26. Встречное движение:
Урок 27. Движение в противоположных направлениях:
Урок 28. Движение вдогонку:
Урок 29. Движение с отставанием:
Урок 30. Формула одновременного движения:
Урок 31. Формула одновременного движения:
Урок 32. Формула одновременного движения:
Урок 33. Формула одновременного движения:
Урок 34. Формула одновременного движения:
Урок 35. Действия над составными именованными величинами:
Урок 36. Новые единицы площади:
Математика 4 класс Моро
Страница 5.Задание 4.
999 + 1 = 1000.
900 − 1 = 899.
700 + 80 + 9 = 780 + 9 = 789.
347 − 7 − 40 = 340 − 40 = 300.
570 + 30 − 330 = 600 − 330 = 270.
950 + 50 − 660 = 1000 − 660 = 340.
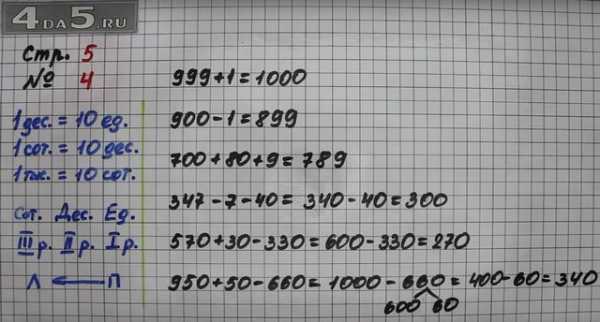
Задание 5.
(Устно). В классе 19 человек, из них 9 мальчиков. Сколько в этом классе девочек?
Составь и реши две задачи, обратные данной.
Найдем сколько девочек в классе:
19 — 9 = 10 (девочек).
Составим задачу самостоятельно: В классе 10 девочек и 9 мальчиков, сколько всего в классе учеников?
Решение: 9 + 10 = 19 (всего учеников).
Составим вторую задачу самостоятельно: В классе 19 человек, из них 10 девочек. Сколько в этом классе мальчиков?
Решение: 19 — 10 = 9 (мальчиков).

Задание 6.
Мише 10 лет. Его дедушка в 6 раз старше Миши, а бабушка на 4 года моложе дедушки.
Сколько лет Мишиной бабушке?
Составь похожую задачу о своих родных.
Умножим возраст Миши на 6:
1) 10 * 6 = 60 (лет) − возраст дедушки;
Вычтем из возраста дедушки 4 года:
2) 60 − 4 = 56 (лет) − возраст бабушки.
Ответ: Мишиной бабушке 56 лет.
Составим задачу самостоятельно: Мне 10 лет. Мой папа старше меня в 4 раза, а мама на 2 года моложе папы. Сколько лет моей маме?
Умножим мой возраст на 4:
1) 10 * 4 = 40 (лет) − возраст папы;
Вычтем из возраста папы 2 года:
2) 40 − 2 = 38 (лет) − возраст мамы.
Ответ: моей маме 38 лет.

Задание 7.
980 − 80 − 100 = 900 − 100 = 800;
640 − 40 + 200 = 600 + 200 = 800;
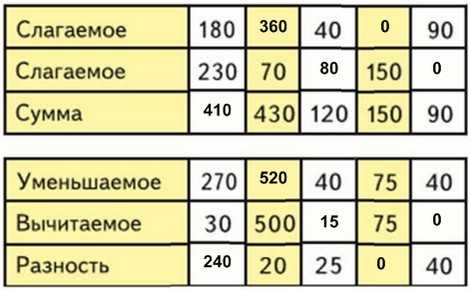
290 + 70 = 360;
680 + 50 = 730;
140 * 6 = 840;
260 * 3 = 780;
480 : 6 = 80;
360 : 9 = 40.

Задание 8.
В книге 180 страниц. В первый день ученик прочитал 52 страницы, во второй − 28 страниц. Сколько страниц ему осталось прочитать?
Реши задачу разными способами.
Способ 1.
Сложим число страниц, прочитанное в первый и второй дни:
1) 52 + 28 = 80 (страниц) − прочитал ученик;
Вычтем из общего числа страниц число прочитанных:
2) 180 − 80 = 100 (страниц) − осталось прочитать.
Способ 2.
Вычтем из общего числа страниц число страниц, прочитанное в первый день:
1) 180 − 52 = 128 (страниц) − осталось прочитать после первого дня;
Вычтем из этого результата число страниц, прочитанное во второй день:
2) 128 − 28 = 100 (страниц) − осталось прочитать.
Способ 3.
Вычтем из общего числа страниц число страниц, прочитанное во второй день:
1) 180 − 28 = 152 (страницы) — страницы книги, кроме прочитанных во второй день;
Вычтем из этого результата число страниц, прочитанное в первый день день:
2) 152 − 52 = 100 (страниц) − осталось прочитать.
Ответ: ученику осталось прочитать 100 страниц.

Задание 9.


Задание 10.
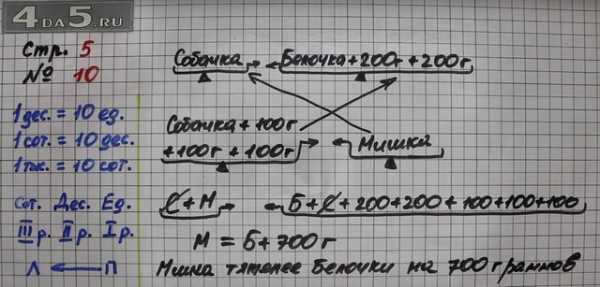
Кто тяжелее: мишка или белочка − и на сколько граммов?
Посмотрим на первые весы. По ним можно сказать, что белочка легче собачки на:
200 + 200 = 400 г.
Посмотрим на вторые весы. По ним можно сказать, что собачка легче мишки на:
100 + 100 + 100 = 300 г.
Получается, что белочка легче собачки на 400 г, а собачка легче мишки на 300 г, значит, белочка легче мишки на:
400 + 300 = 700 г.
Ответ: мишка тяжелее на 700 г.
Задание проверь себя
396 529 748
Задание на полях

vcevce.ru
Задача №20 — гдз и решебник по математике за 4 класс Моро
Умножение и деление на однозначное число
Задачи-расчеты:
1 2 3Странички для любознательных:
1 2 3 4Умножение на числа, оканчивающиеся нулями
Странички для любознательных:
1 2 3 4 5 6Страница 23, Проверочные работы:
1 2Странички для любознательных:
1 2 3 4 5 6 7 8 9 10 11 12Деление на числа, оканчивающиеся нулям
Страница 37, Проверочные работы:
1 2Математика вокруг нас:
1 2 3 4 5 6Умножение на двузначное и трехзначное число
Странички для любознательных:
1 2 3 4 5Страница 56, Проверочные работы:
1 2Деление на двузначное число
Странички для любознательных:
1 2 3 4 5 6Деление на трехзначное число
Странички для любознательных:
1 2 3 4 5 6 7Страница 86, Нумерация:
Страница 89, Выражения и уравнения:
Страница 90, Сложение и вычитание:
Страница 92, Умножение и деление:
Страница 94, Правила о порядке выполнения действий:
Страница 95, Величины:
Страница 96, Геометрические фигуры:
Страница 97, Задачи:
Страница 6, Странички для любознательных:
1 2 3 4 5 6 7 8 9 10 11 12 13 14Страница 104, Доли:
Страница 105, Единицы площади — ар и гектар:
Страница 108, Диагонали прямоугольника(квадрата), и их свойства:
Страница 110, Куб:
Страница 111, Прямоугольный параллелепипед:
Страница 112, Пирамида:
Страница 113, Цилиндр:
Страница 113, Шар:
Тексты для контрольных работ
Страница 114, Задания базового уровня:
1 2 3 4 5 6 7 8Страница 115, Задания повышенного уровня сложности:
1 2 3 4 5 6 7 8 9gdzplus.ru
Задачи по математике 4 класс с ответами. Зачёт 10
1948) Туристы шли до привала 4 ч со скоростью
5 км/ч. Отдохнув, они шли ещё 3 ч. Какова была их скорость после привала, если весь путь равен 32 км?
1949) Путь между двумя деревнями мальчик проезжает на велосипеде за 2 ч со скоростью 10 км/ч. За какое время он пройдет этот путь пешком со скоростью 4 км/ч?
1950) Расстояние от деревни до посёлка 40 км, а от посёлка до города — 200 км. За какое время можно доехать от деревни до города со скоростью 60 км/ч?
1951) Автомобиль проехал 210 км со скоростью 70 км/ч и еще 240 км со скоростью 60 км/ч. Какое время он затратил на всю дорогу?
1952) В первый день туристы за 6 ч прошли 30 км. Во второй день они шли с прежней скоростью и были в пути 7 ч. Какой путь прошли туристы за два дня?
1953) Катер прошёл 96 км за 3 ч. За какое время он пройдёт тот же путь, если его скорость уменьшится на 8 км/ч?
1954) Самолет пролетел 1260 км за 3 ч. Какой путь он пролетит за 4 ч, если увеличит свою скорость на 60 км/ч?
1955) Велосипедист ехал 2 ч со скоростью 10 км/ч. После этого ему осталось проехать в 2 раза больше того, что он проехал. Сколько всего километров он должен проехать?
1956) Лыжник за 3 ч прошёл 36 км, пешеход за 4 ч прошёл 16 км. Во сколько раз скорость лыжника больше скорости пешехода?
1957) Туристы ехали на автобусе 3 ч со скоростью 60 км/ч и шли пешком 5 ч со скоростью 6 км/ч. На сколько больше их путь на автобусе, чем пешком?
1958) Поезд прошёл 250 км со скоростью 50 км/ч. За то же время автомобиль проехал 300 км. Какова скорость автомобиля?
1959) От дома до школы девочка прошла
2 квартала по 300 м и еще 200 м. Сколько ей осталось пройти, если расстояние до школы 1200 м?
Вариант 2
1960) Расстояние между городами 260 км. Часть пути автобус проехал за 3 ч со скоростью 32 км/ч, остальной путь он проехал за 4 ч. Какова скорость автобуса на второй части пути?
1961) Путь между двумя городами можно проехать на поезде за 12 ч со скоростью 80 км/ч. За какое время пролетит этот путь самолёт со скоростью 320 км/ч?
1962) Путь от посёлка до реки лесом 1500 м и ещё полем 1700 м. За какое время можно дойти от посёлка до реки со скоростью 80 м/мин?
1963) Самолёт пролетел до посадки 960 км за
3 ч. После заправки он летел с той же скоростью еще 4 ч. Сколько всего пролетел самолёт?
1964) До станции поезд шёл со скоростью 60 км/ч и прошёл 180 км. До следующей остановки он шёл со скоростью 70 км/ч ещё 280 км. За какое время он прошёл весь путь?
1965) Автобус проехал 240 км за 4 ч. За какое время проедет этот путь автомобиль, скорость которого на 20 км/ч больше?
1966) Автобус проезжает 180 км за 4 ч. Какое расстояние он проедет за 3 ч, если увеличит свою скорость на 10 км/ч?
1967) В первый день туристы шли 6 ч со скоростью 5 км/ч. После этого им осталось пройти в 3 раза больше того, что они прошли. Чему равен весь путь туристов?
1968) Самолет за 4 ч пролетел 1280 км, а автомобиль за 5 ч проехал 400 км. Во сколько раз скорость автомобиля меньше скорости самолета?
1969) Теплоход шёл по озеру 2 ч со скоростью 42 км/ч, затем 3 ч вверх по реке со скоростью 40 км/ч. Какой путь прошёл теплоход?
1970) Велосипедист проехал 30 км со скоростью 10 км/ч. За это же время пешеход прошёл 12 км. С какой скоростью шёл пешеход?
1971) Бегун пробежал 2 круга по 600 м, потом ещё 500 м. Сколько ему осталось пробежать, если вся дистанция равна 2 км?
Вариант 3
1972) От дома до школы а м. Часть пути до поворота ученик прошёл за Ь мин со скоростью d м/мин. Остальной путь он прошёл за п мин. Какова его скорость на пути после поворота?
1973) Пешеход шёл р ч со скоростью k км/ч. За какое время он сможет пройти этот путь на лыжах со скоростью п км/ч?
1974) Расстояние между первым и вторым городами Ь км, между вторым и третим — d км. За какое время поезд со скоростью f км/ч пройдет расстояние между первым и третьим городами?
1975) Расстояние между пристанями m км катер проплывает за Ь ч. До следующей пристани он плыл d ч с той же скоростью. Чему равен весь путь, пройденный катером?
1976) Половину пути до города, равную d км, автобус ехал со скоростью m км/ч. Вторую половину пути он ехал со скоростью п км/ч. За какое время автобус проехал весь путь?
1977) Велосипедист проехал Ь км за m ч. За какое время проедет этот путь мотоцикл, скорость которого на п км/ч больше?
1978) Пешеход проходит a км за Ь ч. Какое расстояние он проедет на велосипеде за k ч, если его скорость увеличится на d км/ч?
1979) Плот проплыл по течению реки Ь км за m ч, а лодка проплыла d км за п ч. Во сколько раз скорость лодки больше, чем скорость плота?
1980) Мальчик шёл до школы a мин со скоростью a м/мин, потом бежал бегом Ь мин со скоростью q м/мин. Каков путь до школы?
1981) Автомобиль проехал m км со скоростью Ь км/ч. За это же время мотоцикл проехал п км. Какова скорость мотоцикла?
1982) Автомобиль проехал первую часть пути за в ч со скоростью Ь км/ч. Вторая часть пути в п раз длиннее. Сколько всего километров должен проехать автомобиль?
1983) Туристы проходили за в дней по Ь км в день, потом еще q км. Сколько им осталось пройти, если весь путь d км?
Вариант 4
1984) Длина лыжной дистанции f км. Часть пути лыжник прошёл за m ч со скоростью a км/ч, остальной путь он прошёл за Ь ч. Какова его скорость на второй части пути?
1985) Лодка плыла f ч со скоростью q км/ч. За какое время пройдет этот путь катер со скоростью j км/ч?
1986) От города до поселка h км, а от поселка до турбазы g км. За какое время туристы дойдут от города до турбазы, если их скорость г км/ч?
1987) Пешеход прошёл от деревни до леса u км за l ч, затем по лесу он шёл еще d ч с той же скоростью. Каков общий путь пешехода?
1988) Путь w км от города до поселка мотоциклист ехал со скоростью p км/ч, а d км от поселка до второго города он ехал со скоростью q км/ч. За какое время он доехал от первого города до второго?
1989) Автомобиль проехал за t ч w км. За какое время проедет этот путь автобус, скорость которого на k км/ч меньше?
1990) Пассажирский поезд проехал m км за u ч. Скорость товарного поезда на t км/ч меньше. Какой путь проедет товарный поезд за k ч?
1991) Когда лодка проплыла от одной пристани до другой f ч со скоростью d км/ч, ей осталось проплыть в в раз меньше того, что она проплыла. Какое расстояние должна проплыть лодка?
1992) Грузовик за d ч прошёл т км, а автобус прошёл за кч п км. На сколько скорость грузовика меньше скорости автобуса?
1993) Лыжник шёл в гору п ч со скоростью j км/ч, потом с горы т ч со скоростью h км/ч. Каков весь путь, пройденный лыжником?
1994) Автобус проехал f км со скоростью w км/ч. За это же время велосипедист проехал к км. Чему равна скорость велосипедиста?
1995) Катер сделал д рейсов по р км и еще проплыл Ь км. Сколько ему осталось плыть, если весь путь составляет а км?
Ответы

referat5vip.ru
Математика 4 класс Богданович. Решебник. ГДЗ. Шестизначные числа. Задание 234 – 258.
Категория: —>> Математика 4 класс Богданович
Задание: —>> 194 – 213 214 – 233 234 – 258
наверхЗадание 234.
Рассмотри записи.
сколько нулей надо отбросить в записи числа, чтооы получить результат деления этого числа на 10; на 100; на 1000?
Решение:
На 10 — один ноль, на 100 2 нуля, на 1000 — 3 нуля.
Задание 235.
- Уменьши в 100 раз числа: 500; 6000; 3800.
- Увеличь в 10 раз числа: 500; 10; 9000.
Решение:
- 1) 500 : 100 = 5; 6000 : 100 = 60; 3800 : 100 = 38;
- 2) 500 * 10 = 5000; 10 * 10 = 100; 9000 * 10 = 90000.
Задание 236.
Реши примеры.
Решение:
- 36000 : 100 * 10 = 3600
- 800 * 10 : 100 = 80
- 600 * 10 * 10 = 60000
- 180 * 100 : 10 = 1800
- (260 + 140) : 100 = 4
- (860 − 50) : 10 = 8100
Задание 237.
Реши примеры.
Решение:
- 260000 : 100 = 2600
- 36000⋅10 : 1000 = 360
- 80000 * 10 = 800000
- 8100 * 100 : 100 = 810
- (100 + 300) * 4 = 1600
- 8400 − 80000 : 10 = 8400 − 8000 = 400
Задание 238.
За день в саду собрали 740 кг яблок. Часть яблок разложили в 26 ящиков, по 10 кг в каждый, а остальные разложили в большие ящики, по 12 кг в каждый. Сколько всего ящиков использовали?
Решение:
- 1) 26 * 10 = 260 (кг) — масса яблок в ящиках по 10 кг;
- 2) 740 − 260 = 480 (кг) — масса яблок в ящиках по 12 кг;
- 3) 480 : 12 = 40 (ящ.) — по 12 кг;
- 4) 26 + 40 = 66 (ящ.).
- Выражение: 26 + (740 − 26 * 10) : 12 = 66 (ящ.).
- Ответ: использовали 66 ящиков.
Задание 239.
- 1) Сколько единиц первого класса в каждом числе: 217 533; 20 705; 7037; 57 009; 300 001; 680 000?
- 2) Сколько всего единиц обозначает цифра 2 в записи каждого из чисел: 245; 320; 127 300; 844 002?
Решение:
- 1) 3, 5, 7, 9, 1, 0.
- 2) 200, 20, 20 000, 2.
Задание 240.
- Увеличь в 1000 раз числа: 7; 75; 700; 705.
- Уменьши в 100 раз числа: 1 000 000; 8000; 380 000.
Решение:
- 7000, 75 000, 700 000, 705 000
- 10 000, 80, 3800
Задание 241.
В числе 230 758 всего 23 075 десятков. Как узнать, сколько всего десятков в числе?
Чтобы узнать, сколько всего десятков в числе, надо отбросить последнюю цифру справа. Оставшееся число покажет, сколько всего десятков в числе.
Задание 242.
Сколько всего сотен в числе 578 445? Сколько всего тысяч? Сколько всего десятков тысяч? Объясни, как узнать, сколькр всего сотен, всего тысяч, всего десятков тысяч, всего сотен тысяч содержится в числе.
Решение:
578445: 578 тысяч, 57 десятков тисяч.
Чтобы узнать, сколько всего сотен в числе, надо отбросить последние две цифры справа, тысяч 3 цифры справа, десятков тысяч 4, сотен тысяч 5 цифр справа.
Задание 243.
Реши примеры.
Решение:
- 1) 702 − 384 + 75 = 318 + 75 = 393 ;
- 2) (140 + 350) : 7 = 490 : 7 = 70 ;
- 3) 78 : 13 = 6 ;
- 4) 7 * 0 = 0 .
Задание 244.
Буратино получил от Мальвины задание решить 240 примеров за 10 дней. Но он решал ежедневно на 2 примера меньше, чем запланировала Мальвина. Сколько примеров решил Буратино за 10 дней?
Решение:
1) 240 : 10 = 24 (пр.) — должен решать Буратино за 1 день;- 2) 24 − 2 = 22 (пр.) — решал Буратино за 1 день;
- 3) 22 * 10 = 220 (пр.).
- Выражение: (240 : 10 − 2) * 10 = 220 (пр.).
- Ответ: Буратино решил за 20 дней 220 примеров.
Задание 245.
3 кг ячменя по питательности заменяют 4 кг овса. Сколько надо килограммов ячменя, чтобы заменить 120 кг овса?
Образец рассуждения. Каждые 4 кг овса можно заменить, взяв 3 кг ячменя. Следовательно, надо узнать, сколько раз по 4 кг содержится в 120 кг. Потом столько раз надо будет взять по 3 кг. Первый вопрос можно сформулировать и так: «Во сколько раз 120 кг больше, чем 4 кг?». Устно составь полный план решения, запиши решение задачи.
Решение:
- 1)Во сколько раз 120 кг больше, чем 4 кг?
120 : 4 = 30 (раз.). - 2) Сколько нужно ячменя?
30 * 3 = 90 (кг). - Выражение: 120 : 4 * 3 = 90 (кг)
- Ответ: нужно 90 кг ячменя.
Задание 246.
Рассмотри рисунок. Сколько на рисунке четырёхугольников; прямоугольников; треугольников? Назови все углы с вершиной в точке А.
Решение:
- 1) 3 четырехугольника, 1 прямоугольник, 3 треугольника.
- ∠KAD , ∠BAK , ∠BAD .
Задание 247.
5 кг лугового сена по питательности заменяют 7 кг овсяной соломы. Сколько потребуется килограммов овсяной соломы, чтобы заменить 15 000 кг лугового сена?
Решение:
- 1)Во сколько раз 15000 кг больше, чем 5 кг?
15000:5 = 3000 (раз.). - 2) Сколько нужно овсяной соломы?
300 * 7 = 21000 (кг). - Выражение: 15000 : 5 * 7 = 21000 (кг).
- Ответ: потребуется 21000 кг овсяной соломы.
Задание 248.
Бригада сантехников должна была установить 160 счётчиков воды, по 8 счётчиков в день, но устанавливала по 10. На сколько дней раньше срока бригада выполнила работу?
Объясни, как составили выражение для решения задачи, и вычисли его значение.
Решение:
- 160 : 8 − 160 : 10 = 20 − 16 = 4 (дня).
- Ответ: на 4 дня раньше срока бригада выполнила работу.
Задание 249.
На платье идёт 5 м ткани, на сорочку 2 м. Из 114 м ткани пошили платья и сорочки. Платьев пошили 18. Сколько пошили сорочек?
Решение:
- 1) 18 * 5 = 90 (м) — потратили на 18 платьев;
- 2) 114 − 90 = 24 (м) — потратили на рубашки;
- 24 : 2 = 12 (рубашек) — пошили.
- Выражение: (114 − 18 * 5) : 2 = 12 (рубашек).
- Ответ: 12 рубашек пошили.
Задание 250.
Прочитай числа, запиши их.
| 340 505 | 6006 | 502 620 | 345 500 | 4025 |
Решение:
340 тысяч 505, 6 тысяч 6, 502 тысячи 620, 345 тысяч 500, 4 тысячи 25.
Задание 251.
Прочитай объяснение о десятичной системе счисления. Пересчитывая какие-либо предметы, называют числа: один, два, три, четыре, пять, шесть, семь и т. д. Это натуральные числа. Если записать их так, что за каждым натуральным числом будет следовать число, большее на единицу, то получим натуральный ряд чисел. В нём наименьшее число — единица, а наибольшего числа не существует.
Сначала каждому новому ч^слу давали отдельное название. Но постепенно начали применять специальные способы для называния и обозначения чисел. Каким бы большим ни было число, его можно записать с помощью лишь десяти числовых знаков — цифр: 1, 2, 3, 4, 5, в, 7, 8, 9, 0. Записывая и читая «мела, группируем их по 10: десять единиц — десяток; десять десятков — сотня; десять сотен — тысяча десять тысяч — десяток тысяч и т. д. Такой спосо( счёта группами по 10 характерен для десятичное системы счисления, или десятичной нумерации. Десятичное группирование чисел обусловило появ ление понятия о разряде, разрядных числах, разряд ных единицах.
В устной нумерации, кроме разрядного счёта, при меняют способ группирования разрядов в классы Чтобы прочитать многозначное число, его запио разбивают на группы, по три цифры в каждой. Tpi первые цифры справа образуют класс единиц, тр> следующие — класс тысяч. Так же образуют клаесь для чисел, больше миллиона.
В каждом классе есть своя счётная единица. Един* цей первого класса является единица. Во второ: классе счётной единицей является тысяча. При чт( нии чисел называют число единиц каждого класса название класса. Письменная нумерация основы нас) ся на позиционном принципе, то есть значение циф|» в записи числа зависит от того, какое место (по:» цию) она занимает. Если цифру переставить на одн место влево, её значение увеличится в 10 рай, а если же переставить на одно место вправо, то ее значение уменьшится в 10 раз.
Можно сказать, что нумерация основывается ещё и на принципе сложения, поскольку число является ничем иным, как записью суммы его разрядных слагаемых. Например:
Решение:
Задание 252.
Прочитай число 723 574. Сколько в этом числе единиц в классе тысяч; в классе единиц?
Решение:
- 723574
- 3 единицы в классе тысяч.
- 4 единицы в классе единиц.
Задание 253.
- 1) Сравни числа в каждом столбце.
Во сколько раз увеличится число, если к нему справа приписать один нуль; два нуля; три нуля? - 2) Как изменится число 9000, если отбросить в его записи один нуль; два нуля; три нуля?
Решение:
- 1) Если справа приписать 1 ноль — число увеличится в десять раз, 2 нуля в 100 раз, 3 нуля в 1000 раз.
- 2) 900, 90, 9.
Задание 254.
(Устно.) Реши уравнения с неизвестным делимым.
| x — 4 = 24 | x : 4 = 24 | x * 4 = 24 | x : 7 = 14 |
Решение:
|
|
|
|
Задание 255.
В саду собрали 428 кг слив. Все сливы разложили в 20 ббльших и 12 меньших ящиков. В больший ящик клали по 16 кг слив. Сколько килограммов слив клали в меньший ящик?
Решение:
- 1) 16 * 20 = 320 (кг) — масса слив в больших ящиках;
- 2) 428 − 320 = 108 (кг) — масса слив в маленьких ящиках;
- 108 : 12 = 9 (кг).
- Выражение: (428 − 16 * 20) : 12 = 9 (кг).
- Ответ: 9 кг яблок ложили в маленький ящик.
Задание 256.
Ученик записал все четырёхзначные числа, в каждом из которых сумма цифр равна трём:
| 3000 | 2100 | 2010 | 2001 | 1101 |
| 1110 | 1200 | 1020 | 1002 | 1011 |
Запиши все четырёхзначные числа, в каждом из которых сумма цифр равна двум.
Решение:
1001, 1010, 1100, 2000
Задание 257.
1 ц 80 кг огурцов разложили в 12 одинаковых ящиков. Сколько потребуется таких ящиков, чтобы разложить 3 ц огурцов?
Решение:
- 1) 1 ц 80 кг = 180 кг;
180 : 12 = 15 (кг) — огурцов в одном ящике; - 2) 3 ц = 300 кг;
300 : 15 = 20 (ящ.). - Выражение: 300 : (180 : 12) = 20 (ящ.).
- Ответ: нужно 20 ящиков.
Задание 258.
Реши примеры.
Решение:
- 753 − 187 * 3 = 753 − 561 = 192
- (442 − 294) * 4 = 148 * 4 = 592
- 8 * 109 − 618 = 872 − 618 = 254
Задание: —>> 194 – 213 214 – 233 234 – 258
reshebniki-uchebniki.ru

