Задачи на встречное движение. Математика 4 класс.
Математика 4 класс
- Математические диктанты
- Тесты
- Нестандартные задачи
- Логические задачи
- Задачи с ответами
- Примеры
Контрольные работы
- Числа, которые больше 1000. Нумерация
- Итоговая контрольная работа за 1 четверть
- 1 четверть
- 2 четверть
- Итоговая контрольная работа 1
- 3 четверть
- Контрольная работа 1
- 4 четверть
- Деление на двузначное число
- Итоговые контрольные работы за курс начальной школы
- Контрольная работа 1
Задача 1.
Из поселка и города навстречу друг другу, одновременно выехали два автобуса. Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.
Один автобус до встречи проехал 100 км со скоростью 25 км/час. Сколько километров до встречи проехал второй автобус, если его скорость 50 км/час.
Решение:
- 1) 100 : 25 = 4 (часа ехал один автобус)
- 2) 50 * 4 = 200
- Выражение: 50 * (100 : 25) = 200
- Ответ: второй автобус проехал до встречи 200 км.
Задача 2.
Расстояние между двумя пристанями 90 км. От каждой из них одновременно навстречу друг другу вышли два теплохода. Сколько часов им понадобится чтобы встретиться, если скорость первого 20 км/час, а второго 25 км/час?
Решение:
- 1) 25 + 20 = 45 (сумма скоростей теплоходов)
- 2) 90 : 45 = 2
- Выражение: 90 : (20 + 25) = 2
- Ответ: теплоходы встретятся через 2 часа.
Задача 3.

От двух станций, расстояние между которыми 564 км., одновременно навстречу друг другу вышли два поезда. Скорость одного из них 63 км/час. Какова скорость второго, если поезда встретились через 4 часа?
Решение:
- 1) 63 * 4 = 252 (прошел 1 поезд)
- 2) 564 — 252 =312 (прошел 2 поезд)
- 3) 312 : 4 = 78
- Выражение: (63 * 4 — 252) : 4 = 78
- Ответ: скорость второго поезда 78 км/час.
Задача 4.
Через сколько секунд встретятся две ласточки, летящие на встречу друг другу, если скорость каждой из них 23 метра в секунду, а расстояние между ними 920 м.
Решение:
- 1) 23 * 2 = 46 (сумма скоростей ласточек)
- 2) 920 : 46 = 20
- Выражение: 920 : (23 * 2) = 20
- Ответ: ласточки встретятся через 20 секунд.
Задача 5
С двух поселков, навстречу друг другу выехали одновременно велосипедист и мотоциклист. Скорость мотоциклиста 54 км/час, велосипедиста 16 км/час. Сколько километров проехал мотоциклист до встречи, если велосипедист проехал 48 км?
Решение:
- 1) 48 : 16 = 3 (часа потратил велосипедист)
- 2) 54 * 3 = 162
- Выражение: 54 * (48 : 16) = 162
- Ответ: мотоциклист проехал 162 км.
Задача 6
Две лодки, расстояние между которыми 90 км, начали движение на встречу друг другу. Скорость одной из лодок 10 км /час, другой 8 км/час. Сколько часов понадобится лодкам, чтобы встретится?
Решение:
- 1) 10 + 8 = 18 (скорость двух лодок вместе)
- 2) 90 : 18 = 5
- Выражение: 90 : (10 + 8) = 5
- Ответ: лодки встретятся через 5 часов.
Задача 7
По дорожке, длинна которой 200 метров, навстречу друг другу побежали два мальчика. Один из них бежал со скоростью 5 м/сек. Какова скорость второго мальчика, если встретились они через 20 сек?
Решение:
- 1) 20 * 5 = 100 (метров пробежал первый мальчик)
- 2) 200 — 100 = 100 (метров пробежал второй мальчик)
- 3) 100 : 20 = 5
- Выражение: (200 — 5 * 20) : 20 = 5
- Ответ: скорость второго мальчика 5 км/сек.
Задача 8
Два поезда выехали навстречу друг другу. Скорость одного из них 35 км/час, другого 29 км/час. Какое расстояние между поездами было сначала, если встретились они через 5 часов?
Решение:
- 1) 35 + 29 = 64 (скорсть двух поездов вместе)
- 2) 64 * 5 = 320
- Выражение: (35 + 29) * 5 = 320
- Ответ: расстояние между поездами было 320 км.
Задача 9
Из двух поселков навстречу друг другу выехали два всадника. Скорость одного из них 13 км/час, встретились они через 4 часа. С какой скоростью двигался второй всадник, если расстояние между поселками 100 км.
Решение:
- 1) 13 * 4 = 52 (проехал первый всадник)
- 2) 100 — 52 = 48 (проехал второй всадник)
- 3) 48 : 4 = 12
- Выражение: (100 — 13 * 4) : 4 = 12
- Ответ: скорость второго всадника 12 км/час.
Простые задачи
- Простые задачи на движение
Составные задачи
- Задачи на встречное движение
- Задачи на движение в одном направлении
- Задачи на противоположное движение
- Задачи на нахождение неизвестного по двум разностям
- Задачи на нахождение числа по доле и доли по числу
- Задачи на нахождение площади
- Задачи на сложение и вычитание многозначных чисел
- Задачи на умножение и деление многозначных чисел
- Задачи на приведение к единице и пропорциональное деление
- Задачи на определение цены, количества, стоимости
Как решать задачи на движение в 4, 5 классе.
 Скорость сближения.
Скорость сближения.Главная » Задания » Домашка
Автор Admin На чтение 3 мин. Просмотров 29.5k. Обновлено
Схемы задач на движение очень просто нарисовать. Они помогают представить наглядно условие задачи и найти верное решение. В дополнение к схеме в сложных случаях или когда ученик затрудняется с решением рекомендуется рисовать таблицу, где в шапке параметры скорости, времени и расстояния. Об этом подробнее ниже.
Узнайте также, как составить схемы к задачам по математике для 2 класса
Содержание
- Простые задачи на движение
- Решение
- Обратные задачи на движение
- Как найти скорость, если известно время и расстояние
- Как найти время, когда известны скорость и расстояние
- Схемы задач на встречное движение
- Решение
- Задачи на движение в одном направлении
- Шпаргалка по решению задач на скорость, время и расстояние
Простые задачи на движение
Простые задачи про путников, лыжников, мотоциклистов и другие движущиеся объекты (встречаются даже задачки про черепах) начинают решать еще в начальных классах. Именно на этих примерах удобно разбирать составление схем.
Именно на этих примерах удобно разбирать составление схем.
Задача 1. Пешеход вышел из пункта А в пункт Б со скоростью 5 км/ч. Через 3 часа он добрался до пункта Б. Какое расстояние между этими двумя пунктами?
Рисуем схему к задаче: прямая линия, соединяющая точки А и Б — это весь путь. Стрелкой обозначаем направление движения путника. Над стрелкой отмечаем скорость, если известна. Время или расстояние отмечаем под (или над) отрезком:
Если со схемой вы не смогли решить задачу, то предлагаю вам воспользоваться таблицей:
| скорость | время | расстояние |
| 5 км/ч | 3 ч | ? км |
Чтобы решать с помощью таблицы, запомните правила:
- Чтобы найти расстояние, нужно скорость умножить на время: S = V x t
- Чтобы найти скорость, нужно расстояние разделить на время, (это производное из первой формулы:
V = S : t ) - чтобы найти время, необходимо расстояние разделить на скорость.
 (также просто вывести из первой формулы:
(также просто вывести из первой формулы:
t = S : t
Решение
5 х 3 = 15 км — расстояние между пунктами А и Б
Обратные задачи на движение
Как найти скорость, если известно время и расстояние
Чтобы не путать вас разными условиями задачи состав задачу, обратную первому примеру:
Задача 2. Расстояние между пунктами А и Б равно 15 км. Путник преодолел это расстояние за 3 часа. С какой скоростью шел пешеход?
| скорость | время | расстояние |
| ? км/ч | 3 ч | 15 км |
Решение
15 : 3 = 5 км/ч
Как найти время, когда известны скорость и расстояние
Задача 3. Расстояние между пунктами 15 км. Пешеход шел со скоростью 5 км/ч. За какое время пешеход преодолеет весь путь?
| Скорость | время | расстояние |
| 5 км/ч | ? ч | 15 км |
Решение
15 : 5 = 3 часа
Схемы задач на встречное движение
Чтобы начертить встречное движение, мы рисуем стрелочки из двух пунктов навстречу. Флажком обозначаем место встречи
Флажком обозначаем место встречи
Когда задачи со встречным или удаляющимся движением — это задачи на общую скорость. Скоро будет подробный урок о них на моем сайте.
Задача 4. Два пешехода вышли одновременно из пунктов А и Б навстречу друг другу. Скорость одного — 5 км/ч, другого — 3 км/ч. Через какое время они встретятся, если известно, что расстояние между пунктами 24 км?
Решение
1 способ:
5 + 3 =8 км/ч — общая скорость
24 : 8 = 3 часа
Задачи на движение в одном направлении
Задача 5. Два пешехода вышли из пунктов А и Б одновременно в одном направлении. Пешеход, который шел впереди, двигался со скоростью 3 км/ч, а второй — со скоростью 5 км/ч. Через какое время второй пешеход догонит первого, если расстояние между пунктами 2 км?
Здесь нужно выяснить скорость сближения. Так как один пешеход шел быстрее второго, то расстояние между ними сокращалось на 2 км/ч (мы посчитали так: 5 — 3 = 2 км/ч). Так как первоначальное расстояние между пунктами 2 км, то найдем время:
Так как первоначальное расстояние между пунктами 2 км, то найдем время:
2км : 2 км/ч = 1 час.
Через 1 час пешеходы встретятся.
Шпаргалка по решению задач на скорость, время и расстояние
Вы можете воспользоваться данной памяткой при решении этого типа задач. Кликните для просмотра в полном размере и распечатайте, нажав на клавиатуре клавиши CTRL + P.
Учимся решать задачи 4 класс, разными способами, логические задачи, на скорость, на время, взаимосвязанные задачи. Математика 4 класс как научиться решать задачи
В четвертом классе на голову детей, а в основном их родителей сваливается много забот. Выпускной в начальной школе, подготовка к переходу в старшие классы, и самое главное-экзамены.
За четыре года дети учатся читать, писать, считать и решать различные математические задачи. Задачи включены в любой экзамен по математике. Умение справляться с такими заданиями показывает, что логические мышление и вычислительные навыки ребенка правильно развиваются.
Содержание статьи
- Учимся решать задачи разными способами 4 класс, просто и ясно для детей
- Решаем логические задачи 4 класс
- Как решать задачи на скорость 4 класс
- Как решать задачи на время 4 класс
- Как решать обратные задачи 4 класс
- Как решать взаимосвязанные задачи 4 класс
- Решаем нестандартные задачи 4 класс
- Видео как правильно решать задачи 4 класс
- Как придумать и решить задачу
- Учимся решать комбинаторные задачи 4 класс
Учимся решать задачи разными способами 4 класс, просто и ясно для детей
Родителям стоит приложить усилия, чтобы их маленький школьник научился хорошо решать задачи в начальных классах. Математика устроена так, что каждая следующая новая тема требует наличия знаний и умений от уже изученной. Также связаны и школьные предметы. Научившись решать задачки в младших классах, ребенок будет с легкостью с ними справляться и дальше, и не только на математике, но и в физике, химии и информатике.
Очень важно запомнить, что перед тем, как приступить к решению задачи, ее нужно внимательно прочитать и представить, о чем идет речь. Дальше составить краткую запись или схему. Определить главный вопрос в задаче и найди те значения, которых не хватает, чтобы на него ответить.
Можно выделить несколько способов решения задач.
В основном мы используем арифметический и алгебраический способы, но и геометрический также применяется не редко. Лучше всего разобраться в способах решения задач на конкретных примерах.
В чем же разница между алгебраическим и арифметическим способами решения? Все просто. При решении задачи алгебраически, неизвестную величину обозначают буквой и составляют уравнение, с помощью которого и решается задача. При решении арифметическим способом, уравнение не составляют, задачу решают по действиям.
Графический или геометрический метод, позволяет нам решать задачи используя только рисунок или чертеж.
Десять яблок разложили по два на несколько тарелок.
Первый способ-арифметический.
Решить задачу можно в одно действие: 10 : 2 = 5 тарелок. Ответ: 5 тарелок.
Второй способ-алгебраический.
Так как мы не знаем, сколько нужно тарелок, обозначим их количество буквой х. В каждую тарелку кладут по два яблока, следовательно число всех яблок на тарелках это 2 • х. По условию яблок 10, значит можно составить уравнение: 2 • х = 10. Чтобы найти х, нужно 10 : 2 = 5. Х = 5. Ответ: 5 тарелок.
Третий и четвертый способы-графический и практический.
Маша читает книгу в которой 150 страниц. В первый день она прочитала 42 страницы, а во второй 25 страниц. Сколько Маше осталось прочитать страниц?
Составим краткую запись.
Арифметический способ. Первым действием найдем сколько прочитано за первый и второй день. Вторым действием из общего числа страниц вычтем уже прочитанные.
- 42 + 25 = 67 — страниц прочитано за 1-ый и 2-ой день
- 150 — 67 = 83 — страницы осталось прочитать
Ответ: 83 страницы осталось прочитать Маше.
Алгебраический способ. Неизвестная величина, это оставшиеся страницы, обозначим их буквой Х. Тогда 42+25+Х, это количество всех страниц в книге. Мы можем составить уравнение.
42 + 25 + Х = 150
67 + Х = 150
Х = 150 — 67
Х = 83.
За Х мы брали оставшиеся непрочитанные страницы, значит осталось прочитать 83 страницы.
Ответ: 83 страницы.
Также есть еще табличный способ решения задач. Его удобно применять при решении задач на логику.
Мама купила Оле, Саше и Паше по — мороженому: пломбир, шоколадное и клубничное. Оля ест не клубничное и не пломбир. Саша не пломбир и не шоколадное, Паша не любит шоколад и клубничное мороженое. Какое мороженое ест каждый ребенок?
Начертим таблицу и заполним ее данными. Чертим таблицу 4х3. Не подходящее по условию значение обозначим <<->> , подходящее <<+>>.
Не подходящее по условию значение обозначим <<->> , подходящее <<+>>.
Так как Оля ест не клубничное и не пломбир, в эти графы ставим минус. Получается, что для Оли подходит шоколадное, там ставим плюс. Саша ест не пломбир и не шоколадное, ставим там минус. Для нее подходящее значение клубничное. Так как Паша не любит шоколад, то и мороженное шоколадное он есть не будет, ставим минус, и на клубничное тоже. Паша ест пломбир.
Ответ: Оля-шоколадное, Саша-клубничное, Паша-пломбир.
Решаем логические задачи 4 класс
Логические задачи встречаются совершенно разные. Это может быть простая классика в виде текстовых задач, могут быть задачи на смекалку. Также ребусы, алгоритмы, определение истины и лжи, комбинаторные и еще множество различных задач на логику.
Текстовые задачи типа <<Считаем ноги и головы>> очень популярны в математических олимпиадах и в заданиях со звездочкой в учебнике.
На ферме живут гуси и овцы. В сумме у них 40 голов и 94 ноги. Сколько на ферме проживает гусей? и сколько овец?
В сумме у них 40 голов и 94 ноги. Сколько на ферме проживает гусей? и сколько овец?
Разберемся для начала со всеми ногами. Мы знаем, что у овцы их четыре, а гуся две. Давайте посчитаем так, если у всех по две ноги. Так как голов 40, то получается:
40 • 2 = 80 ног.
По условию в задаче всего 94 ноги, найдем так называемые <<лишние>> ноги:
94 — 80 = 14.
Если эти 14 ног лишние, значит они принадлежат четвероногим овцам, и теперь мы сможем определить количество овец:
14 : 2 = 7 овец.
Теперь осталось вычислить сколько на ферме гусей. Для этого просто вычтем из общего числа голов те, которые принадлежат овцам:
40 — 7 = 33 гуся.
Ответ: 7 овец и 33 гуся.
Еще одна не менее популярная задача на <<рукопожатия>>.
Ваня на детской площадке встретил своих друзей Петю, Машу и Колю. При встрече они все обменялись рукопожатиями. Сколько всего было рукопожатий при встрече?
В четвертом классе такие задачи удобнее всего решать с помощью схемы. Каждого человека обозначаем точкой. Потом от каждой точки проводим отрезки к тем, с которыми нужно пожать руки. Считаем количество отрезков, оно и будет ответом в задаче.
Каждого человека обозначаем точкой. Потом от каждой точки проводим отрезки к тем, с которыми нужно пожать руки. Считаем количество отрезков, оно и будет ответом в задаче.
Ответ: шесть рукопожатий.
Построен новый пяти подъездный дом, в котором 10 этажей. На каждом этаже расположено по четыре квартиры. На каждую дверь квартиры повесили номер. Сколько потребуется цифры 2 для всех номеров квартир?
Сначала вычислим сколько всего в доме квартир:
10 • 5 • 4 = 200.
Посчитаем, сколько раз встречается цифра два до сотни: 2, 12, 22, 32, 42, 52, 62, 72, 82, 92. Итого десять раз. От ста до 199 также еще десять раз встретится цифра 2. Всего получается 20 раз.
В разряде десятков 10 раз до 100 и еще 10 до 199, и одна двойка в 200. Получаем:
20 + 20 + 1 = 41 цифра.
Ответ: потребуется 41 цифра.
У сороконожки 80 ножек. К зиме она прикупила 12 пар сапожек. Все равно 14 ножек остались без сапожек. Сколько у сороконожки было пар старых сапожек до того, как она купила новые?
- 12 • 2 = 24 ноги в новых сапожках
- 80 — 24 = 56 ног босые и в старых сапогах
- 56 — 14 = 42 ноги в старых сапожках
- 42 : 2 = 21 пара старых сапог.

Ответ: у сороконожки была 21 пара старых сапожек.
Как решать задачи на скорость 4 класс
Задачи на нахождение скорости объекта, требуют знания определенных формул. Чтобы вычислить скорость, требуется разделить пройденное расстояние на затраченное время.
Если в задаче рассматривается движение по воде, то обязательно нужно учитывать скорость течения. Если мы плывем по течению, то скорость увеличивается, если против, то уменьшается.
Рассмотрим совсем простую задачку:
При решении задач на движение удобно нарисовать схему, в этом случае краткую запись можно не составлять. Мы знаем, что для нахождения скорости нужно разделить расстояние на время. Расстояние и время у нас известны: S = 15 м, t = 3 мин.
V = 15 : 3 = 5 м/мин.
Ответ: 5 м/мин.
Есть и более сложные задачи, составные. Движение на встречу друг другу или в противоположных направлениях.
Для того, чтобы ответить на первый вопрос, нужно применить формулу скорости удаления.
Vуд. = 15 + 12 = 27 км/ч.
Чтобы найти расстояние через 3 часа, умножаем скорость удаления на данное время.
S = 27 • 3 = 81 км.
Ответ: 27 км/ч; 81 км.
Скорость сближения равна сумме скоростей велосипедистов: 13 + 11 = 24 км/ч.
За одни час они сблизятся: S = 24 • 1 = 24 км.
За два часа: S = 24 • 2 = 48 км.
Используем известные нам формулы.
Для того, чтобы вычислить скорость катера по реке, находим сумму его собственной скорости и скорости течения реки: 40 + 6 = 46 км/ч.
Против течения наоборот разность: 40 — 6 = 34 км/ч.
Ответ: 46 км/ч и 34 км/ч.
Как решать задачи на время 4 класс
Чтобы вычислить время движения, нужно расстояние разделить на скорость t = S : V.
По формуле 36 км : 12 км/ч = 3 часа.
Пешеход идет со скоростью 6 км/ч. С этой скоростью он двигался 30 км. С какой скоростью идет лыжник, если за такое же время он проходит 50 км? Сколько времени в пути находится лыжник?
Составим краткую запись:
Чтобы узнать скорость лыжника, сначала мы должны узнать время в пути. Для этого используем данные пешехода, так как время в пути у них одинаковое.
Для этого используем данные пешехода, так как время в пути у них одинаковое.
- t п. = 30 : 6 = 5 часов.
- V л. = 50 : 5 = 10 км/ч.
Ответ: 10 км/ч; 5 ч.
Так же в четвертом классе решают задачи на время, не связанные с движением.
Как решать обратные задачи 4 класс
Чтобы научиться решать обратные задачи, нужно внимательно их прочитать и ответить на два вопроса: Чем задачи похожи? Чем они отличаются? Разберемся на примере простых задач на сложение и вычитание.
Света купила 9 фломастеров, а Оля 8. Сколько всего купили фломастеров девочки?
Такая задача называется прямой.
Чтобы получилась обратная ей задача, достаточно сделать неизвестной одну из данных величин. Пусть неизвестно сколько купила фломастеров Оля.
Света и Оля покупали фломастеры, всего 17. Света купила 9 фломастеров. Сколько купила Оля ?
В первой прямой задаче мы должны были узнать общее количество фломастеров, а в обратной задаче эта величина нам уже известна. Наоборот, требуется найти сколько купила фломастеров одна из девочек. Можно составить еще одну обратную задачу, взяв за неизвестное покупку Светы.
Наоборот, требуется найти сколько купила фломастеров одна из девочек. Можно составить еще одну обратную задачу, взяв за неизвестное покупку Светы.
Как решать взаимосвязанные задачи 4 класс
Многие путают обратные и взаимосвязанные задачи. Во взаимосвязанных задачах решение следующей зависит от известных данных предыдущей задачи. Разберемся на примере.
Пояснение: на один костюм уходит 1 метр ткани. Не забудем это при решении второй задачи.
Задача 1.
- 13 • 2 = 26 костюмов жуков
- 13 — 5 = 8 костюмов бож.коровок.
- 13 + 26 + 8 = 47 костюмов всего.
На один костюм требуется 1 метр ткани, значит на все понадобится 47 метров.
Задача 2.
47 метров ткани на костюмы, это четверть всего материала для задника сцены. Чтобы найти количество материала для сцены, нужно умножить ткань для костюмов на 4. Получается 47 • 4 = 188 метров.
Ответ: 188 метров.
Решаем нестандартные задачи 4 класс
Видео как правильно решать задачи 4 класс
youtube.com/embed/MkvaOvrJxF4″ frameborder=»0″ type=»text/html»/>Как придумать и решить задачу
Для того, чтобы придумать задачу надо понимать, что у нее должен быть смысл. Чтобы задача решалась, условие и данные должны быть сформулированы верно.
В задаче должно быть минимум два данных (переменных). У Маши 4 груши, а у Тани 5.
Дальше составляется конкретное условие. Петя взял у Маши 2 груши, а у Тани 3.
После этого обязательно следует главный вопрос задачи, что именно нужно найти. Сколько груш осталось у девочек? И сколько груш стало у Пети?
Соберем все части нашей придуманной задачи, вот что получилось:
<<У Маши 4 груши, а у Тани 5. Петя взял у Маши 2 груши, а у Тани 3. Сколько груш осталось у девочек? И сколько груш стало у Пети?>>.
Иногда дается задание в виде рисунка по которому нужно придумать собственную задачу и решить ее.
Решение:
Задачу можно решить алгебраически, с помощью уравнения.
Пусть вторая полка равна Х книг. Тогда на первой полке 2•Х книг. Всего их 150. Получается уравнение:
Х + 2•Х = 150
3•Х = 150
Х = 150 : 3
Х = 50, следовательно на первой полке 50 книг, на второй 2•Х = 2•50=100 книг.
Учимся решать комбинаторные задачи 4 класс
Комбинаторные задачи — от слова <<комбинировать>>. Решая такие задачи мы подбираем все возможные способы и варианты.
Такие задачи можно решать:
- Перебором
- Построить дерево возможных варинатов
- С помощью таблицы
Задача 2.
Составьте все возможные трехзначные числа из цифр 0, 2, 4?
Ответ: 28.
Решите многошаговые словесные задачи, поставленные с целыми числами и имеющие целочисленные ответы, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину.
 Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление.
Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление.Связанные ресурсы
Проверенные ресурсы, которые преподаватели могут использовать для обучения концепциям и навыкам в этом тесте.
Уроки STEM — Активность по моделированию
Планировщик воздушных шаров на день рождения:
Учащиеся разработают модель для выбора планировщика вечеринок с воздушными шарами и ранжируют их от лучшего к худшему.
Учащиеся смогут использовать предварительные знания о сложении многозначных целых чисел, фактах и понятиях умножения и деления, математических вычислениях с деньгами и временем, понимании дробей и навыках решения задач для решения нестандартных МПС (Модель Выявление деятельности), которая требует реального применения математических навыков.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Cookies and Treats:
Четвероклассники помогут Cookies and Treats найти экономичную и экологически чистую упаковку для своего печенья. Студенты будут систематизировать данные и сравнивать цены, используя десятичную систему счисления, чтобы разработать процедуру выбора упаковки для печенья. Студенты будут использовать умножение и деление целых чисел, чтобы планировать, сколько упаковок заказывать.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Рыба Ахой Рыба:
Учащиеся будут работать в группах, чтобы помочь клиенту купить разную рыбу для рыбного пруда. Из таблицы данных им нужно будет решить, какой тип рыбы и сколько рыбы покупать в зависимости от размера каждого пруда. После этого им нужно будет вернуться к исправленной таблице данных, чтобы сделать другой выбор рыбы и рассчитать затраты на покупку рыбы.
После этого им нужно будет вернуться к исправленной таблице данных, чтобы сделать другой выбор рыбы и рассчитать затраты на покупку рыбы.
Новый слой краски:
В этом MEA учащиеся будут работать в совместных группах над решением многоэтапных задач с целыми числами и десятичными знаками, используя различные математические операции, такие как сложение, вычитание, умножение и деление. Студентов попросят помочь владельцу недвижимости, который планирует отремонтировать свою новую собственность, в покупке подходящей краски для наружных работ. Им нужно будет прочитать таблицу данных, ранжировать краски от самой высокой до самой низкой, рассчитать необходимое количество галлонов в зависимости от площади поверхности и общую стоимость каждой краски. К проблеме добавляется изюминка, когда одной из красок нет в наличии, но добавляются две другие, а также хозяин хочет покрасить перегородки снаружи.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Планирование парка:
Учащихся просят спланировать игровую площадку для нового парка в рамках заданного бюджета и ограниченной площади. Они проанализируют наилучшее использование оборудования для игровых площадок, используя таблицу данных о требованиях к площади и стоимости. Учащиеся будут преобразовывать единицы в рамках единой системы измерения, вычислять площадь прямоугольника и выполнять вычисления сложения/вычитания с использованием денег с использованием десятичной системы счисления.
Требуются планировщики вечеринок:
В этом MEA учащиеся будут работать в совместных группах над решением многоэтапных задач с целыми и десятичными числами, используя различные математические операции, такие как сложение, вычитание, умножение и деление. Студентов попросят помочь бизнесмену, который планирует вечеринку для своих сотрудников. Им нужно будет прочитать несколько объявлений и решить, какая компания предлагает лучшее предложение по аренде столов, стульев и скатертей для клиента. Они должны будут принять во внимание количество гостей, посещающих вечеринку, и разрешенный бюджет. К проблеме добавляется изюминка, когда студентов просят рассмотреть дополнительное объявление и тот факт, что список гостей теперь немного больше.
Им нужно будет прочитать несколько объявлений и решить, какая компания предлагает лучшее предложение по аренде столов, стульев и скатертей для клиента. Они должны будут принять во внимание количество гостей, посещающих вечеринку, и разрешенный бюджет. К проблеме добавляется изюминка, когда студентов просят рассмотреть дополнительное объявление и тот факт, что список гостей теперь немного больше.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Pickle Pick:
Эта модель опроса (MEA) предлагает учащимся разработать процедуру выбора марки маринада для магазина сэндвичей. Учащимся необходимо будет учитывать внешний вид, текстуру, цену, вкус, срок годности и стоимость доставки. Во второй части формулировки задачи учащиеся должны будут обменять то, что они рассматривали ранее, и придать большее значение расчетным затратам на доставку, а также добавить еще три бренда для рассмотрения. Учащиеся выполнят кульминационную работу по созданию рекламного ролика для рекламы выбранного ими бренда. Учащиеся должны будут работать вместе и использовать стандартные правила письма, чтобы написать и показать свою рекламу для других групп.
Учащиеся выполнят кульминационную работу по созданию рекламного ролика для рекламы выбранного ими бренда. Учащиеся должны будут работать вместе и использовать стандартные правила письма, чтобы написать и показать свою рекламу для других групп.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Робототехника с ограниченным бюджетом:
P.T.A. Президенту ABC Elementary нужна помощь ваших учеников в выборе модели робототехники, которая соответствует потребностям учащихся и программе дополнительного образования после школы. Студенты должны придерживаться бюджета в размере 2000 долларов. Студентам будет предложено оценить модели 4 на основе предоставленных им критериев и бюджета. Студентам будет предоставлен набор данных, который поможет им разработать процедуру для этого. В своих командах они напишут письмо президенту PTA с изложением своих процедур и объяснением стратегии, которую они использовали. Студенты будут практиковаться в сложении, вычитании и умножении чисел до тысяч, чтобы рассчитать количество моделей, которые можно купить для определенной модели, не выходя за рамки бюджета. Рубрики включены, чтобы помочь учащимся оценивать.
В своих командах они напишут письмо президенту PTA с изложением своих процедур и объяснением стратегии, которую они использовали. Студенты будут практиковаться в сложении, вычитании и умножении чисел до тысяч, чтобы рассчитать количество моделей, которые можно купить для определенной модели, не выходя за рамки бюджета. Рубрики включены, чтобы помочь учащимся оценивать.
Talented Divas MEA:
Эта модель задания (MEA) написана для 5-го класса. В этом MEA учащимся предлагается выбрать футболку для талантов, которая обеспечит Талантливым Дивам наилучшее соотношение цены и качества. Студентов просят ранжировать Talent Shirt Company от лучшего к худшему. Учащиеся должны предоставить Талантливым дивам рубашки талантов «Лучшая цена» и объяснить, как они пришли к своему решению.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Путешествия и многое другое MEA:
В этом учебном задании (MEA) учащиеся должны будут помочь туристическому агенту подобрать лучший пакет для отдыха в отеле для семьи из четырех человек. Они должны учитывать все удобства, цены, льготы и отзывы. Изюминка возникает, когда турагенту необходимо предоставить пакеты отелей для отдыха для семей из 5 человек.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Walk This Way:
Учащимся будет предложено ранжировать различные напольные плитки для игровых комнат в центрах деятельности в общественных парках. При составлении рейтинга им необходимо будет учитывать определенные факторы. Им также необходимо будет рассчитать затраты на укладку напольной плитки, используя заданные размеры игровой комнаты и напольной плитки. «Изюминка» будет заключаться в том, что теперь клиенту необходимо включить кладовую для некоторого оборудования игровой комнаты. Им нужно будет решить, использовать ли ту же напольную плитку или другую, что и в игровой комнате, а также дополнительные расходы на кладовую. После этого они добавят общую стоимость игровой комнаты и кладовки. Они сообщат о своих выводах и причинах, написав письмо клиенту.
Им также необходимо будет рассчитать затраты на укладку напольной плитки, используя заданные размеры игровой комнаты и напольной плитки. «Изюминка» будет заключаться в том, что теперь клиенту необходимо включить кладовую для некоторого оборудования игровой комнаты. Им нужно будет решить, использовать ли ту же напольную плитку или другую, что и в игровой комнате, а также дополнительные расходы на кладовую. После этого они добавят общую стоимость игровой комнаты и кладовки. Они сообщат о своих выводах и причинах, написав письмо клиенту.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Ярды в ярды:
В этом MEA учащиеся будут работать в совместных группах над решением многошаговых текстовых задач с целыми числами. Студентов попросят помочь ландшафтной компании решить, какие живые изгороди лучше всего использовать для замены существующих живых изгородей, которые в настоящее время не процветают из-за заражения насекомыми. Им нужно будет принять во внимание такие факторы, как высота, холодостойкость, засухоустойчивость, цена и комментарии клиента. К проблеме добавляется изюминка, когда студентов просят подумать, не лучше ли обработать существующую изгородь, а не заменить ее.
Студентов попросят помочь ландшафтной компании решить, какие живые изгороди лучше всего использовать для замены существующих живых изгородей, которые в настоящее время не процветают из-за заражения насекомыми. Им нужно будет принять во внимание такие факторы, как высота, холодостойкость, засухоустойчивость, цена и комментарии клиента. К проблеме добавляется изюминка, когда студентов просят подумать, не лучше ли обработать существующую изгородь, а не заменить ее.
Упражнения по выявлению моделей, MEA, являются открытыми, междисциплинарными действиями по решению проблем, которые предназначены для выявления мыслей учащихся о концепциях, встроенных в реалистичные ситуации. Нажмите здесь, чтобы узнать больше о MEA и о том, как они могут изменить ваш класс.
Оригинальные учебники для учащихся по математике — классы K-5
Полевое безумие (Часть 1):
Совершите экскурсию, изучая, как интерпретировать остатки в многошаговых задачах на деление.
Это первая часть серии интерактивных руководств, состоящей из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Часть 1
- Часть 2
- Часть 3
- Часть 4
Экскурсионное безумие (часть 2):
В этом интерактивном учебном пособии вы узнаете, как интерпретировать остатки в многоэтапных задачах на деление, связанных с экскурсией.
Это руководство является второй частью серии из четырех статей об остатках. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Часть 1
- Часть 2
- Часть 3
- Часть 4
Безумная экскурсия (часть 3):
В этом интерактивном учебном пособии вы узнаете, как интерпретировать остатки в многошаговых задачах на деление. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Часть 1
- Часть 2
- Часть 3
- Часть 4
Field Trip Frenzy (Part 4):
В этом интерактивном учебном пособии вы узнаете, когда записывать остаток многошагового процесса деления в виде дроби или десятичной дроби.
Это последнее руководство из серии Field Trip Frenzy, посвященное остаткам. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Часть 1
- Часть 2
- Часть 3
- Часть 4
Примечание. В этом учебном пособии рассматривается не только частное целого числа с целым остатком, но и частное целого числа с дробным или десятичным остатком.
Ресурсы для учащихся
Проверенные ресурсы, которые учащиеся могут использовать для изучения концепций и навыков в этом эталонном тесте.
Оригинальные учебные пособия для студентов
Безумное путешествие (часть 4):
Из этого интерактивного руководства вы узнаете, когда записывать остаток многошагового процесса деления в виде дроби или десятичной дроби.
Это последнее руководство из серии Field Trip Frenzy, посвященное остаткам. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Часть 1
- Часть 2
- Часть 3
- Часть 4
Примечание. В этом учебном пособии рассматривается не только частное целого числа с целым остатком, но и частное целого числа с дробным или десятичным остатком.
Тип: Оригинальное учебное пособие для учащихся
Веселая экскурсия (часть 3):
В этом интерактивном учебном пособии вы узнаете, как интерпретировать остатки в многоэтапных задачах на деление. Нажмите ниже, чтобы открыть другие руководства из этой серии.
Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Часть 1
- Часть 2
- Часть 3
- Часть 4
Тип: Оригинальное учебное пособие для учащихся
Экскурсионное безумие (часть 2):
В этом интерактивном учебном пособии вы узнаете, как интерпретировать остатки в многошаговых задачах на деление, связанных с экскурсией.
Это руководство является второй частью серии из четырех статей об остатках. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Часть 1
- Часть 2
- Часть 3
- Часть 4
Тип: Оригинальное учебное пособие для учащихся
Экскурсионное безумие (часть 1):
Совершите экскурсию, изучая, как интерпретировать остатки в многошаговых задачах на деление.
Это первая часть серии интерактивных руководств, состоящей из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Часть 1
- Часть 2
- Часть 3
- Часть 4
Тип: Оригинальный учебник для учащихся
Задачи решения проблем
Карнавальные билеты:
Целью этого задания является решение учащимися многоступенчатых задач в контексте концепции, поддерживающей финансовую грамотность, а именно инфляции. Инфляция – это устойчивый рост среднего уровня цен. В этом задании учащиеся видят, что если уровень цен растет, а доходы людей не растут, они не могут покупать столько товаров и услуг; другими словами, их покупательная способность снижается.
Тип: Задание на решение задач
Сад Карла:
Цель задания состоит в том, чтобы учащиеся решили многоступенчатую задачу на умножение в контексте, включающем площадь. Кроме того, числа были выбраны, чтобы определить, есть ли у учащихся распространенное заблуждение, связанное с умножением. Поскольку сложение является одновременно коммутативным и ассоциативным, мы можем переупорядочивать или перегруппировывать слагаемые как угодно. Студенты часто считают, что то же самое верно и для умножения.
Кроме того, числа были выбраны, чтобы определить, есть ли у учащихся распространенное заблуждение, связанное с умножением. Поскольку сложение является одновременно коммутативным и ассоциативным, мы можем переупорядочивать или перегруппировывать слагаемые как угодно. Студенты часто считают, что то же самое верно и для умножения.
Тип: Задача решения проблем
Что такое 23 ÷ 5?:
Когда задача на деление, включающая целые числа, не приводит к целочисленному частному, важно, чтобы учащиеся могли решить, требует ли контекст, чтобы результат был представлен как целое число с остатком (как в части (b)) или смешанным числом/десятичным числом (как в части (c)). Часть (а) представляет два варианта контекста, которые требуют, чтобы эти два разных ответа подчеркивали различие между ними.
Тип: Задача решения проблем
Преобразование дробей в более мелкие единицы:
Цель этого задания — помочь учащимся лучше понять дроби и преобразование дробей в более мелкие единицы.
Тип: Задача решения проблем
Руководство
Дивизия: Знакомство с остатками:
В этом видеоуроке от Академии Хана вы познакомитесь со значением остатков.
Тип: Учебное пособие
Ресурсы для родителей
Проверенные ресурсы, которые воспитатели могут использовать, чтобы помочь учащимся освоить концепции и навыки в этом эталонном тесте.
Задачи решения проблем
Карнавальные билеты:
Целью этого задания является решение учащимися многоступенчатых задач в контексте концепции, поддерживающей финансовую грамотность, а именно инфляции. Инфляция – это устойчивый рост среднего уровня цен. В этом задании учащиеся видят, что если уровень цен растет, а доходы людей не растут, они не могут покупать столько товаров и услуг; другими словами, их покупательная способность снижается.
Тип: Задание на решение задач
Сад Карла:
Цель задания состоит в том, чтобы учащиеся решили многоступенчатую задачу на умножение в контексте, включающем площадь. Кроме того, числа были выбраны, чтобы определить, есть ли у учащихся распространенное заблуждение, связанное с умножением. Поскольку сложение является одновременно коммутативным и ассоциативным, мы можем переупорядочивать или перегруппировывать слагаемые как угодно. Студенты часто считают, что то же самое верно и для умножения.
Тип: Задача решения проблем
Что такое 23 ÷ 5?:
Когда задача на деление, включающая целые числа, не приводит к целочисленному частному, важно, чтобы учащиеся могли решить, требует ли контекст, чтобы результат был представлен как целое число с остатком (как в части (b)) или смешанным числом/десятичным числом (как в части (c)). Часть (а) представляет два варианта контекста, которые требуют, чтобы эти два разных ответа подчеркивали различие между ними.
Тип: Задача решения проблем
Преобразование дробей в более мелкие единицы:
Цель этого задания — помочь учащимся лучше понять дроби и преобразование дробей в более мелкие единицы.
Тип: Задача решения проблем
Руководство
Дивизия: Знакомство с остатками:
В этом видеоуроке от Академии Хана вы познакомитесь со значением остатков.
Тип: Учебное пособие
Элементарная математическая задача Ключевые слова и их ограничения — Класс без помех
Когда вы говорите своим ученикам, что будете работать над задачами, вы слышите хор стонов? Если так, то ты не одинок! Обучение учащихся тому, как решать математические задачи со словами, как правило, не является самым захватывающим математическим упражнением в начальной программе по математике (особенно если не изучать ключевые слова задач со словами и то, как их можно использовать для решения задач). Они также, как правило, очень сложны для студентов. Неудивительно, что многие студенты не любят их!
Они также, как правило, очень сложны для студентов. Неудивительно, что многие студенты не любят их!
Однако для того, чтобы учащиеся овладели математикой, им необходимо применить свои математические знания в реальных жизненных ситуациях, чего можно достичь с помощью текстовых задач. Этот опыт не должен заключаться в следовании механическим процедурам и вычислению правильных ответов. При решении задач такого типа важно, чтобы учащиеся применяли несколько стратегий, чтобы разобраться в проблеме и решить ее. Этот опыт должен основываться на применении стратегии и решении проблем, а не просто на вычислениях.
Выявление ключевых слов словесных задач — одна из многих стратегий, которые учащиеся начальной школы могут использовать для решения одноэтапных и многоэтапных текстовых задач. Кроме того, учащимся необходим доступ к якорным диаграммам, инструментам и манипуляторам, которые снабдят их ресурсами, необходимыми для решения этих проблем. Использование ключевых слов для задач по математике — это только одна часть головоломки!
Этот пост в блоге ответит на следующие вопросы:
- Что такое ключевые слова для задач со словами?
- Какие есть примеры ключевых слов для задач на сложение слов?
- Можете ли вы поделиться несколькими примерами ключевых слов для задач на вычитание?
- Какие есть примеры ключевых слов для задач на умножение?
- Можете ли вы поделиться несколькими примерами ключевых слов для задач на деление слов?
- Каковы ограничения использования ключевых слов для решения текстовых задач?
- Является ли использование ключевых слов для решения задач эффективной стратегией?
Что такое ключевые слова задач Word?
Ключевые слова словесной задачи — это слова или фразы, указывающие, какие операции (сложение, вычитание, умножение или деление) необходимы для решения математической текстовой задачи.
Использование ключевых слов для решения математических задач (часто называемых словами-подсказками и фразами) — это стратегия, позволяющая понять и решить задачи со словами. Идея состоит в том, чтобы научить мозг искать определенные слова и фразы, чтобы определить, какие математические операции необходимы. Вот пример этой стратегии на практике:
Эрин читает задачу: У Пэт 3 красные рубашки. У него 2 синие рубашки. Сколько всего у него красных и синих рубашек? Прочитав задачу один раз, Эрин перечитывает задачу, но на этот раз она ищет ключевые слова и фразы, которые она выучила. Она выделяет или подчеркивает фразу «во всем». В классе она узнала, что «во всем» сигнализирует читателю, что им нужно добавить. Эта стратегия помогла ей разобраться в задаче (что в данном случае означает необходимость операции сложения), составить уравнение (3 + 2 = ?) и найти ответ (5 рубашек).
Ключевые слова и фразы для общей математической задачи
Ниже приведен список ключевых слов и фраз, которые учащиеся могут использовать для решения задач на сложение, вычитание, умножение и деление. Если вы учите младшие классы, вам будет полезен список ключевых слов сложения и вычитания. Если вы учите старшие классы, вам пригодятся эти слова, а также ключевые слова умножения и деления.
Если вы учите младшие классы, вам будет полезен список ключевых слов сложения и вычитания. Если вы учите старшие классы, вам пригодятся эти слова, а также ключевые слова умножения и деления.
Дополнительные ключевые слова
Вот несколько примеров дополнительных ключевых слов :
- add
- altogether
- both
- combine
- in all
- increase
- increased by
- larger
- larger than
- longer
- longer than
- more
- more than
- perimeter
- плюс
- сумма
- вместе
- всего
Ключевые слова вычитания
Вот несколько примеров ключевых слов вычитания :
- изменить
- уменьшить
- разницу
- меньше
- отдать
- Сколько еще…?
- На сколько меньше…?
- Слева
- Свева более
- Меньше
- Меньше
- Остаться
- Строки
- Меньше
- УВИЖИТЬ
 :
:- area
- cubed
- double
- each
- groups
- per
- product
- quadruple
- rows
- squared
- times
- triple
Division Key Words
Here are some examples of деление ключевые слова :
- среднее
- разделить
- каждый
- равная группа
- четвертая
- половина
- четверть
- частное
- отношение
- доля
- отдельно
- разделение
- третье
Ограничения использования ключевых слов для решения словесных задач
, непосредственное обучение и практика с ключевыми словами (также иногда записываются как ключевые слова для задач со словами или ключевые слова для задач по математике). Однако учащиеся должны понимать, что проблемы можно решать разными способами. Это всего лишь один из инструментов в их арсенале. Это не всегда самая эффективная стратегия для решения данной проблемы со словами. Например, учащихся не следует приучать всегда вычитать, когда они видят слово меньше, потому что они могут использовать отсутствующее сложение в сложении для решения. Эту стратегию следует использовать вместе с другими стратегиями (например, визуализацией). По мере того как учащиеся продвигаются по математическому образованию и сталкиваются с более сложными текстовыми задачами, эта стратегия становится менее эффективной. В результате ваши ученики должны быть оснащены множеством разнообразных стратегий.
Это не всегда самая эффективная стратегия для решения данной проблемы со словами. Например, учащихся не следует приучать всегда вычитать, когда они видят слово меньше, потому что они могут использовать отсутствующее сложение в сложении для решения. Эту стратегию следует использовать вместе с другими стратегиями (например, визуализацией). По мере того как учащиеся продвигаются по математическому образованию и сталкиваются с более сложными текстовыми задачами, эта стратегия становится менее эффективной. В результате ваши ученики должны быть оснащены множеством разнообразных стратегий.
Математические ресурсы для учителей 1-5 классов
Если вам нужны печатные и цифровые математические ресурсы для вашего класса, ознакомьтесь с моими математическими коллекциями, которые помогут вам сэкономить время и деньги!
Бесплатные ресурсы по элементарной математике
Мы будем рады, если вы опробуете эти ресурсы для решения текстовых задач со своими учениками. Он предлагает им возможность попрактиковаться в применении стратегий ключевых слов для текстовых задач, а также других стратегий решения проблем. Вы можете загрузить рабочие листы с текстовыми задачами для своего уровня (наряду с множеством других бесплатных материалов по математике) в нашем наборе бесплатных математических ресурсов для печати по этой ссылке: бесплатные математические задания для учителей начальных классов.
Вы можете загрузить рабочие листы с текстовыми задачами для своего уровня (наряду с множеством других бесплатных материалов по математике) в нашем наборе бесплатных математических ресурсов для печати по этой ссылке: бесплатные математические задания для учителей начальных классов.
Посмотрите мои ежемесячные ресурсы по решению текстовых задач!
- 1 -й класс. Проблемы с словом
- 2 -й класс. Проблемы слов
- 3 -го класса. как «вербальные описания проблемных ситуаций, в которых возникает один или несколько вопросов, ответ на которые можно получить путем применения математических операций к числовым данным, доступным в постановке задачи» (Verschaffel, Greer, & De Corte, 2000). Решение текстовых задач включает в себя:
- Хорошо организованное и гибкое использование как концептуальных, так и процедурных знаний
- Стратегии и метапознание
- Положительные эмоции и убеждения (De Corte, Greer, & Verschaffel, 1996; Schoenfeld, 1992)
Является ли решение текстовых задач таким же, как математическое моделирование?
Решение текстовых задач , а не считается тем же, что и математическое моделирование.
 Математическое моделирование, как правило, является более сложным процессом, включающим определение вопросов, на которые необходимо ответить о реальном мире, создание предположений, определение переменных, преобразование явления в математическую модель, оценку решения и повторение процесса для уточнения и расширения модели (COMAP). и СИАМ, 2016 г.). Процесс решения словесной задачи не обязательно такой сложный, так как сама задача обычно дает читателю вопрос, на который нужно ответить, и информацию, необходимую для ответа на него, и не требует моделирования уровня осмысления и интерпретации. Однако эти различия относительны и зависят от способностей учащегося и характера решения, необходимого для решения задачи.
Математическое моделирование, как правило, является более сложным процессом, включающим определение вопросов, на которые необходимо ответить о реальном мире, создание предположений, определение переменных, преобразование явления в математическую модель, оценку решения и повторение процесса для уточнения и расширения модели (COMAP). и СИАМ, 2016 г.). Процесс решения словесной задачи не обязательно такой сложный, так как сама задача обычно дает читателю вопрос, на который нужно ответить, и информацию, необходимую для ответа на него, и не требует моделирования уровня осмысления и интерпретации. Однако эти различия относительны и зависят от способностей учащегося и характера решения, необходимого для решения задачи.Понимание задачи
Что затрудняет решение задач для учащихся?
Основные трудности учащихся при решении текстовых задач объясняются их «приостановкой осмысления» (Schoenfeld, 1991; Verschaffel, Greer, & De Corte). Вместо того, чтобы обдумывать контекст словесной задачи, чтобы понять ее, многие студенты просто ищут простое применение арифметики, необходимое для получения ответа, независимо от того, имеет ли он смысл или нет.
 В следующем видео Каплинский (2013) воспроизводит результат начала 19Исследование 80-х годов, проведенное в Институте исследований математики во Франции.
В следующем видео Каплинский (2013) воспроизводит результат начала 19Исследование 80-х годов, проведенное в Институте исследований математики во Франции.Учителя математики часто беспокоятся о способности учащихся перенести полученные в классе знания в мир за пределами классной комнаты, но эта «приостановка осмысления» показывает, что обратное также затруднено – учащиеся с трудом применяют свои знания и понимание мира. снова в кабинете математики. Выученные годами арифметики, почти всегда включающей очевидные операции и ожидание, что каждая задача имеет правильный ответ, у учащихся развивается «навязчивое стремление к вычислениям» (Stacey & MacGregor, 19).99), которые могут помешать развитию алгебраического мышления, которое обычно необходимо для решения текстовых задач. Некоторые (но не все) результаты исследований показывают, что «принуждение к вычислениям» усиливается по мере того, как учащиеся стареют и у них формируется представление о том, что математика представляет собой набор правил (Radatz, 1983; Stern, 1992, оба цитируются в Verschaffel, Greer, & De Corte, 2000, стр.
 5).
5).Учащиеся также могут испытывать затруднения при решении текстовых задач, потому что у них есть проблемы с академической лексикой, математической лексикой или и тем, и другим. Из-за этих трудностей изучающие английский язык и учащиеся с низким социально-экономическим статусом получают более низкие баллы по стандартным оценочным пунктам, чем те, кто хорошо владеет английским языком (Abedi & Lord, 2001).
Что усложняет задачу учителям?
Некоторые учителя игнорируют или изо всех сил пытаются применить свои реальные знания при решении текстовых задач, как и ученики (Verschaffel, De Corte, & Borghart, 1997). Во время обучения учителя часто пытаются помочь учащимся «убрать то, что нам на самом деле не нужно» (Chapman, 2006, стр. 219) и свести проблему к числам, ключевым словам или фразам, обозначающим операции или отношения. Это игнорирование реальных аспектов текстовых задач может способствовать приостановке осмысления учащимися и их принуждению к вычислениям.
Большинство учителей считают или предполагают, что учащимся будет труднее решить задачу со словами, чем решить алгебраическое уравнение, представляющее ту же математику без слов.
 Из-за этого они верят в преподавание текстовых задач только после того, как учащиеся освоят решение подобных задач в виде уравнений. Традиционные учебники по математике подкрепляют это убеждение, помещая текстовые задачи в конце практических наборов. Это убеждение или предположение оказалось ложным , по крайней мере, при некоторых условиях. При тестировании учащиеся показали, что они могут добиться большего успеха в решении словесных или вербальных задач, чем в эквивалентных чисто символических задачах (Nathan & Koedinger, 2000a, 2000b). Другие исследования показывают, что навыки алгоритмических вычислений могут не соответствовать способности учащихся концептуализировать взаимосвязь между числами в текстовых задачах (Fuchs et al., 2006).
Из-за этого они верят в преподавание текстовых задач только после того, как учащиеся освоят решение подобных задач в виде уравнений. Традиционные учебники по математике подкрепляют это убеждение, помещая текстовые задачи в конце практических наборов. Это убеждение или предположение оказалось ложным , по крайней мере, при некоторых условиях. При тестировании учащиеся показали, что они могут добиться большего успеха в решении словесных или вербальных задач, чем в эквивалентных чисто символических задачах (Nathan & Koedinger, 2000a, 2000b). Другие исследования показывают, что навыки алгоритмических вычислений могут не соответствовать способности учащихся концептуализировать взаимосвязь между числами в текстовых задачах (Fuchs et al., 2006).Рекомендации
Использование текстовых задач для обучения студентов математике
Словесные задачи предназначены не только для приложений уже известной математики. На самом деле, самый действенный способ использования текстовых задач в классе — это помощь учащимся в изучении математики.
 Помещая математику в контекст, понятный учащимся, текстовые задачи побуждают учащихся следовать стратегиям решения, которые имеют для них смысл и чаще приводят к правильным ответам (Koedinger & Nathan, 2004). Затем эти стратегии можно сделать более формальными и символическими с помощью дополнительных инструкций.
Помещая математику в контекст, понятный учащимся, текстовые задачи побуждают учащихся следовать стратегиям решения, которые имеют для них смысл и чаще приводят к правильным ответам (Koedinger & Nathan, 2004). Затем эти стратегии можно сделать более формальными и символическими с помощью дополнительных инструкций.Это очевидно для воспитателей маленьких детей. В ранней математике задачи почти всегда помещаются в реалистичные контексты, понятные детям. Нет причин, чтобы это заканчивалось в раннем детстве. Учащиеся всех уровней должны заниматься математикой в разумном контексте, прежде чем она станет формальной и символической.
Привлекайте учащихся к рассуждениям
Вместо того, чтобы игнорировать контекст текстовых задач, учителя должны проводить время со студентами, чтобы разобраться в текстовых задачах и вспомогательном контексте. Учителя должны сопротивляться принуждению учащихся к вычислениям, сосредоточив внимание на отношениях между известными и неизвестными в текстовых задачах, а не спешить с поиском ответа (Kieran, 2014).
 Некоторые типы текстовых задач могут быть особенно полезны для развития рассуждений, потому что в них либо отсутствует очевидная стратегия, либо нет одного правильного ответа, либо они могут быть «сложными» для учащихся, которые предполагают, что проблема проста. Некоторые примеры:
Некоторые типы текстовых задач могут быть особенно полезны для развития рассуждений, потому что в них либо отсутствует очевидная стратегия, либо нет одного правильного ответа, либо они могут быть «сложными» для учащихся, которые предполагают, что проблема проста. Некоторые примеры:- Пит организовал вечеринку по случаю своего десятого дня рождения. Он пригласил 8 друзей-мальчиков и 4 подруг. Сколько друзей Пит пригласил на свой день рождения?
- У Карла 5 друзей, а у Жоржа 6 друзей. Карл и Жорж решают вместе устроить вечеринку. Они приглашают всех своих друзей. Все друзья присутствуют. Сколько друзей на вечеринке?
- Кэти, Ингрид, Ганс и Том получили от дедушки коробку с 14 плитками шоколада, которые они поделили между собой поровну. Сколько плиток шоколада получил каждый внук?
- Дедушка дает своим 4 внукам коробку с 18 воздушными шарами, которые они делят поровну. Сколько шариков получит каждый внук?
- У лавочника есть два контейнера для яблок.
 В первом контейнере 60 яблок, во втором 90 яблок. Он кладет все яблоки в новый, больший контейнер. Сколько яблок в этом новом контейнере?
В первом контейнере 60 яблок, во втором 90 яблок. Он кладет все яблоки в новый, больший контейнер. Сколько яблок в этом новом контейнере? - Какой будет температура воды в сосуде, если в него налить 1 кувшин воды температурой 80 градусов по Фаренгейту и 1 кувшин воды температурой 40 градусов по Фаренгейту? (Нешер, 1980)
Verschaffel, De Corte и Lasure (1994) использовали эти текстовые задачи, чтобы увидеть, будут ли ученики рассуждать по-разному с нечетными и четными элементами. Их исследования и последующие исследования показали, что подавляющее большинство учащихся — иногда более 90 % — будут вычислять и давать ответы на вопросы с четными номерами так же, как и на вопросы с нечетными номерами, без каких-либо дополнительных рассуждений о реальном мире. соображения. Дайте учащимся общее предупреждение, например, «эти задачи не так просты, как кажутся» 9.0088 существенно не помог ученикам . Вместо этого учителя могут способствовать рассуждению учащихся, предоставляя поддержку, характерную для каждой проблемы, например, поощряя учащихся объяснять свой ответ и объяснять, почему он имеет смысл, рисовать изображение своего решения или рассматривать гипотетическое, но контрастирующее решение другого ученика.
 Хотя эти стратегии могут увеличить число студентов, правильно рассуждающих об этих проблемах, во многих исследованиях они редко давали правильные ответы гораздо более чем 50 % студентов (см. главу 3, Verschaffel, Greer, De Corte). Другими словами, эти стратегии полезны, но вряд ли сами по себе гарантируют успех всем учащимся.
Хотя эти стратегии могут увеличить число студентов, правильно рассуждающих об этих проблемах, во многих исследованиях они редко давали правильные ответы гораздо более чем 50 % студентов (см. главу 3, Verschaffel, Greer, De Corte). Другими словами, эти стратегии полезны, но вряд ли сами по себе гарантируют успех всем учащимся.Бесчисленные словесные задачи
Возможно, самый прямой способ противостоять принуждению учащихся к вычислениям — дать им словесные задачи без чисел. Брайан Бушарт, учитель начальных классов и координатор учебной программы по математике из Техаса, популяризировал идею «бесчисленных задач со словами» после того, как его коллега опробовал этот подход на некоторых учениках третьего класса. Задачи на бесчисленное количество слов не совсем новы, как в книге « Задачи без рисунков » (Гиллан, 1909 г.) представил нечто отдаленно похожее в начале 20 века. Подход Бушарта идет гораздо дальше, сосредоточив внимание на учебных шагах и возможностях для студенческого дискурса, которых не было в подходах вековой давности.
 Сообщение в блоге Бушарта (2014 г.) и последующий сборник ресурсов (без даты) описывают как его процесс решения бесчисленных текстовых задач, так и многочисленные примеры для различного содержания и уровней обучения.
Сообщение в блоге Бушарта (2014 г.) и последующий сборник ресурсов (без даты) описывают как его процесс решения бесчисленных текстовых задач, так и многочисленные примеры для различного содержания и уровней обучения.Пример 1: Одношаговая задача со словами
В качестве примера задачи с бесчисленными словами рассмотрим этот элемент, вышедший из теста PARCC 4-го уровня (PARCC, 2016a):
Кувшин содержит 2 литра сока. Стакан наполнен 180 миллилитрами сока из кувшина. Сколько миллилитров сока осталось в кувшине после наполнения стакана?
Вместо того, чтобы давать учащимся эту задачу в письменном виде, учителя могут представить бесчисленные варианты этой задачи на серии слайдов:
Слайд 1 : В кувшине есть немного сока.
Слайд 2 : В кувшине есть немного сока. Стакан наполняется соком из кувшина.
Слайд 3 : В кувшине есть немного сока. Стакан наполняется соком из кувшина.
 Сколько сока осталось в кувшине после наполнения стакана?
Сколько сока осталось в кувшине после наполнения стакана?Слайд 4 : Кувшин содержит 2 литра сока. Стакан наполняется соком из кувшина. Сколько сока осталось в кувшине после наполнения стакана?
Слайд 5 : Кувшин содержит 2 литра сока. Стакан наполнен 180 миллилитрами сока из кувшина. Сколько сока осталось в кувшине после наполнения стакана?
Слайд 6 : Кувшин содержит 2 литра сока. Стакан наполнен 180 миллилитрами сока из кувшина. Сколько миллилитров сока осталось в кувшине после наполнения стакана?
Учителя могут регулировать количество слайдов в зависимости от способностей учащихся, сложности задачи и количества времени, которое учитель желает посвятить формированию и обмену мнениями учащихся. В этом примере учитель может остановиться после слайда 1, чтобы убедиться, что учащиеся знают, что такое кувшин, и чтобы учащиеся оценили вместимость кувшина. После слайда 2 учитель может попросить учащихся объяснить, что произойдет с количеством сока в кувшине, а также взаимосвязь между соком в кувшине и соком в стакане.
 С каждым последующим слайдом учитель может продолжать исследовать смыслообразование учащихся и понимание взаимосвязей между величинами, описываемыми задачей.
С каждым последующим слайдом учитель может продолжать исследовать смыслообразование учащихся и понимание взаимосвязей между величинами, описываемыми задачей.Пример 2: Многошаговая текстовая задача
Учителя также могут использовать бесчисленные словесные задачи с многошаговыми словесными задачами. Рассмотрим этот многоэтапный вопрос, полученный из теста PARCC 5-го класса (PARCC, 2016b):
Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на 10 порций и использует 3/4 фунта бобов. Сколько всего фунтов фасоли ей нужно, чтобы приготовить 5 порций супа? У нее 1/16 фунта бобов в одном контейнере и 1/4 фунта бобов в другом контейнере. Сколько еще фунтов фасоли нужно Дане, чтобы приготовить 5 порций супа?
Как и в примере 1, учитель может представить бесчисленное количество вариантов этой текстовой задачи на серии слайдов.
Слайд 1 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на несколько порций и использует определенное количество бобов.

Учитель может использовать слайд 1, чтобы убедиться, что учащиеся понимают основной контекст. Студенты могут заметить, что «Если она хочет сварить больше супа, ей понадобится больше бобов», или прийти к другим выводам, которые помогут установить взаимосвязь между количеством супа и количеством бобов.
Слайд 2 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на несколько порций и использует определенное количество бобов. Какое количество фасоли ей нужно, чтобы приготовить меньшее количество порций супа?
На слайде 2 учащиеся должны заметить, что для меньшего количества супа требуется меньше бобов. Учащиеся могут начать строить предположения, например: «Если она хочет в два раза меньше супа, ей понадобится в два раза меньше бобов».
Слайд 3 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на несколько порций и использует определенное количество бобов. Какое количество фасоли ей нужно, чтобы приготовить меньшее количество порций супа? У нее уже есть небольшое количество бобов.
 Сколько еще фасоли нужно Дане, чтобы сварить суп?
Сколько еще фасоли нужно Дане, чтобы сварить суп?Увидев слайд 3, учащиеся должны столкнуться с еще более сложной взаимосвязью: Дане не только нужно меньше бобов, потому что она готовит меньше супа, чем предусмотрено рецептом, но у нее уже есть несколько бобов, которые ей понадобятся. . Наблюдения и предположения учащихся на этом этапе должны предложить две операции, такие как первый шаг, включающий деление, чтобы найти количество бобов, необходимых в сокращенном рецепте, и второй шаг, чтобы вычесть количество бобов, которое уже есть у Даны. Учитывая эту многоступенчатую сложность, учащимся было бы полезно нарисовать или иным образом проиллюстрировать свое мышление.
Слайд 4 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на 10 порций и использует определенное количество бобов. Сколько фасоли ей нужно, чтобы приготовить 5 порций супа? У нее уже есть небольшое количество бобов. Сколько еще фасоли нужно Дане, чтобы приготовить 5 порций супа?
На слайде 4 указано количество порций, но не бобов.
 Имея эту информацию, учащиеся могут пересмотреть свои наблюдения, чтобы прояснить, что количество бобов, указанное в рецепте, нужно разделить на 2 с вычитанием дополнительного количества, чтобы найти, сколько еще бобов нужно Дане.
Имея эту информацию, учащиеся могут пересмотреть свои наблюдения, чтобы прояснить, что количество бобов, указанное в рецепте, нужно разделить на 2 с вычитанием дополнительного количества, чтобы найти, сколько еще бобов нужно Дане.Слайд 5 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на 10 порций и использует 3/4 фунта бобов. Сколько всего фунтов фасоли ей нужно, чтобы приготовить 5 порций супа? У нее уже есть небольшое количество бобов. Сколько еще фунтов фасоли нужно Дане, чтобы приготовить 5 порций супа?
На слайде 5 учащиеся уже должны были решить, что количество фасоли в рецепте нужно разделить на 2, и теперь они могут сосредоточиться на нахождении 3/4 ÷ 2. Учащиеся также могут заметить, что теперь в задаче становится ясно, что все измерения фасоли в фунтах.
Слайд 6 : Дана готовит суп из фасоли. Рецепт, который у нее есть, рассчитан на 10 порций и использует 3/4 фунта бобов. Сколько всего фунтов фасоли ей нужно, чтобы приготовить 5 порций супа? У нее 1/16 фунта бобов в одном контейнере и 1/4 фунта бобов в другом контейнере.
 Сколько еще фунтов фасоли нужно Дане, чтобы приготовить 5 порций супа?
Сколько еще фунтов фасоли нужно Дане, чтобы приготовить 5 порций супа?На слайде 6 задача со словами представлена в ее исходной форме, и учащиеся могут быть удивлены тем, что небольшое количество бобов, которое уже было у Даны, представлено как два количества, которые необходимо рассматривать вместе. Из-за сложности этой задачи может быть не самое подходящее время для введения этой информации, но пятиклассник, который обдумал задачу и дошел до нее, должен быть в состоянии рассуждать с двумя небольшими количествами бобов, либо добавляя сначала их, а затем вычитая сумму из 3/8 или выполняя два вычитания.
Добавление аутентичности
Учащиеся успешнее справляются со словесными задачами, когда от них требуется аутентичный подход к контексту. Например, DeFranco and Curcio (1997, цит. по Verschaffel, Greer, De Corte) дали группе из 20 учеников шестого класса следующую текстовую задачу: «328 пожилых людей собираются в путешествие. Автобус вмещает 40 человек. Сколько нужно автобусов, чтобы все пожилые люди смогли поехать?» Позже исследователи дали студентам аналогичную задачу, но они представили ее в виде таблицы фактов с количеством людей и размером фургонов, а также инструкциями по совершению телефонного звонка, имитирующего размещение реального заказа на определенное количество автомобилей.
 требуемые транспортные средства. В первом сценарии только 2 из 20 студентов ответили правильно и правильно рассуждали, а остальные остались за делением. Во втором сценарии, используя более аутентичную обстановку, 16 из 20 студентов ответили правильно и аргументировали оставшихся, либо округлив до следующего целого фургона, либо попросив «например, машину или что-то в этом роде» для перевозки небольшого количества оставшихся. пассажиры.
требуемые транспортные средства. В первом сценарии только 2 из 20 студентов ответили правильно и правильно рассуждали, а остальные остались за делением. Во втором сценарии, используя более аутентичную обстановку, 16 из 20 студентов ответили правильно и аргументировали оставшихся, либо округлив до следующего целого фургона, либо попросив «например, машину или что-то в этом роде» для перевозки небольшого количества оставшихся. пассажиры.Устранение языковой сложности
Сложная языковая сложность может быть решена путем уменьшения сложности или предоставления учащимся дополнительной поддержки. Учащимся, которые борются с языком текстовых задач, может быть полезно переписать задачу, используя более простой, знакомый язык или родной язык учащегося (Бернардо, 1999). Подобные модификации, как правило, помогают учащимся, изучающим английский язык, и учащимся с низким уровнем SES больше, чем их сверстникам, владеющим английским языком и имеющим более высокий уровень SES, а это означает, что эта стратегия может помочь сократить разрыв в успеваемости (Abedi & Lord, 2001).

Учителя также могут оказать дополнительную поддержку. Рекомендации по обучению изучающих английский язык включают сосредоточение внимания на рассуждениях и дискурсе учащихся, а не на правильности использования языка, и использование знаний и опыта изучающих язык в качестве ресурсов (Moschkovich, 2012). Веб-сайт Understanding Language (ell.stanford.edu) является рекомендуемым ресурсом для понимания того, как помочь изучающим язык в математике.
Ссылки
Abedi, J., & Lord, C. (2001). Языковой фактор в тестах по математике. Прикладные измерения в образовании, 14(3), 219–234. https://doi.org/10.1207/S15324818AME1403_2
Бернардо, ABI (1999). Преодоление препятствий к пониманию и решению текстовых задач по математике. Педагогическая психология, 19 (2), 149–163. https://doi.org/10.1080/01443419203
Бушарт, Б. (без даты). Бесчисленные словесные задачи. Получено 16 ноября 2017 г. с https://bstockus.wordpress.com/numberless-word-problems/
Bushart, B.
 (6 октября 2014 г.). Бесчисленные текстовые задачи [сообщение в блоге]. Получено 16 ноября 2017 г. с https://bstockus.wordpress.com/2014/10/06/numberless-word-problems/ 9.0005
(6 октября 2014 г.). Бесчисленные текстовые задачи [сообщение в блоге]. Получено 16 ноября 2017 г. с https://bstockus.wordpress.com/2014/10/06/numberless-word-problems/ 9.0005Чепмен, О. (2006). Практика в классе для контекста задач по математике. Образовательные исследования по математике, 62 (2), 211–230. https://doi.org/10.1007/s10649-006-7834-1
COMAP и SIAM. (2016). GAIMME: Руководство по оценке и обучению математическому моделированию. Бедфорд, Массачусетс. Получено с http://www.comap.com/Free/GAIMME/index.html
De Corte, E., Greer, B., & Verschaffel, L. (1996). Преподавание математики и обучение. В DC Berliner & RC Calfee (Eds.), Справочник по педагогической психологии (стр. 49).1–549). Нью-Йорк, штат Нью-Йорк: Lawrence Erlbaum Associates.
ДеФранко, Т.С., и Курсио, Ф.Р. (1997). Проблема деления с остатком в двух контекстах: детские решения в ограничительных и реальных условиях. Сосредоточьтесь на проблемах обучения по математике, 19 (2), 58–72.
Фукс, Л.
 С., Фукс, Д., Комптон, Д. Л., Пауэлл, С. Р., Ситалер, П. М., Капицци, А. М., … Флетчер, Дж. М. (2006). Когнитивные корреляты навыков третьего класса в арифметике, алгоритмических вычислениях и арифметических текстовых задачах. Журнал педагогической психологии, 98(1), 29–43. https://doi.org/10.1037/0022-0663.98.1.29
С., Фукс, Д., Комптон, Д. Л., Пауэлл, С. Р., Ситалер, П. М., Капицци, А. М., … Флетчер, Дж. М. (2006). Когнитивные корреляты навыков третьего класса в арифметике, алгоритмических вычислениях и арифметических текстовых задачах. Журнал педагогической психологии, 98(1), 29–43. https://doi.org/10.1037/0022-0663.98.1.29Gillan, SY (1909). Задачи без фигур. Милуоки, Висконсин: SY Gillan & Company. Получено с http://www.schoolinfosystem.org/pdf/2008/10/problemswithoutfigures.pdf
Каплинский, Р. (2013). Сколько лет пастуху? Получено 3 ноября 2017 г. с https://www.youtube.com/watch?v=kibaFBgaPx4
Киран, К. (2014). Что говорят нам исследования о развитии алгебраических рассуждений в школьной алгебре? Рестон, Вирджиния. Получено с http://www.nctm.org/Research-and-Advocacy/Research-Brief-and-Clips/Algebraic-Reasoning-in-School-Algebra/
Koedinger, KR, & Nathan, MJ (2004). Настоящая история, стоящая за задачами истории: влияние представлений на количественные рассуждения.
 Журнал наук об обучении, 13 (2), 129–164. https://doi.org/10.1207/s15327809jls1302_1
Журнал наук об обучении, 13 (2), 129–164. https://doi.org/10.1207/s15327809jls1302_1Мошкович, Дж. Н. (2012). Математика, Common Core и язык. Понимание языка: язык, грамотность и обучение в предметных областях. Получено с http://ell.stanford.edu/publication/mathematics-common-core-and-language
Натан, М.Дж., и Кёдингер, К.Р. (2000a). Исследование взглядов учителей на развитие алгебры учащихся. Познание и обучение, 18 (2), 209–237. https://doi.org/10.1207/S1532690XCI1802_03
Nathan, MJ, & Koedinger, KR (2000b). Представления учителей и исследователей о развитии алгебраического мышления. Журнал исследований в области математического образования, 31 (2), 168–190. https://doi.org/10.2307/749750
Нешер, П. (1980). Стереотипный характер школьных текстовых задач. Для изучения математики, 1 (1), 41–48. Получено с http://flm-journal.org/Articles/flm_1-1_Nesher.pdf
ПАРКЦ. (2016а). Math Spring Operational 2016 Grade 4 Выпущенные элементы. Партнерство по оценке готовности к колледжу и карьере.
 Получено с https://parcc-assessment.org/content/uploads/released_materials/05/Grade_04_Math_Item_Set.pdf
Получено с https://parcc-assessment.org/content/uploads/released_materials/05/Grade_04_Math_Item_Set.pdfPARCC. (2016б). Math Spring Operational 2016 Grade 5 Выпущенные элементы. Партнерство по оценке готовности к колледжу и карьере. Получено с https://parcc-assessment.org/content/uploads/released_materials/05/Grade_05_Math_Item_Set.pdf 9.0005
Радац, Х. (1983). Untersuchungen zum Lösen eingekleideter Aufgaben. Zeitschrift Fur Mathematic-Didaktik, 4 (2), 205–2017. https://doi.org/10.1007/BF03339231
Schoenfeld, AH (1991). О математике как осмыслении: неформальная атака на неудачный развод формальной и неформальной математики. В Дж. Ф. Воссе, Д. Н. Перкинсе и Дж. В. Сигале (ред.), Неформальное мышление и образование (стр. 311–343). Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates.
Шенфельд, А. Х. (1992). Обучение математическому мышлению: решение проблем, метапознание и осмысление математики. В Д. А. Гроувс (ред.), Справочник по исследованиям в области преподавания и обучения математике (стр.





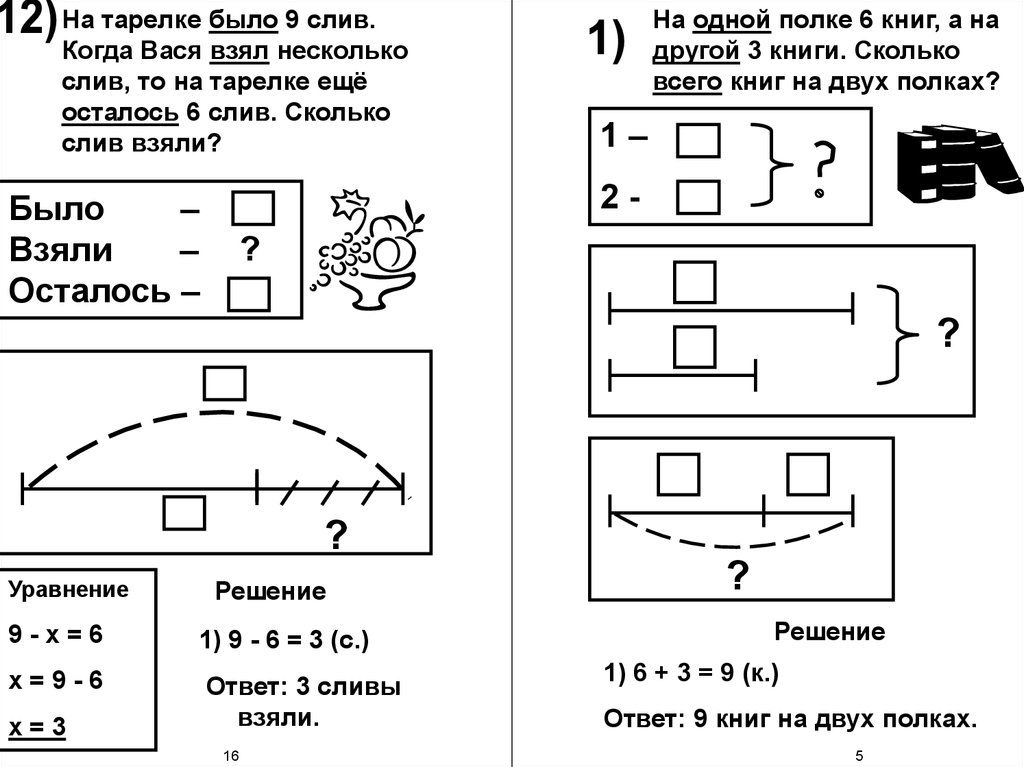
 (также просто вывести из первой формулы:
(также просто вывести из первой формулы:
 Математическое моделирование, как правило, является более сложным процессом, включающим определение вопросов, на которые необходимо ответить о реальном мире, создание предположений, определение переменных, преобразование явления в математическую модель, оценку решения и повторение процесса для уточнения и расширения модели (COMAP). и СИАМ, 2016 г.). Процесс решения словесной задачи не обязательно такой сложный, так как сама задача обычно дает читателю вопрос, на который нужно ответить, и информацию, необходимую для ответа на него, и не требует моделирования уровня осмысления и интерпретации. Однако эти различия относительны и зависят от способностей учащегося и характера решения, необходимого для решения задачи.
Математическое моделирование, как правило, является более сложным процессом, включающим определение вопросов, на которые необходимо ответить о реальном мире, создание предположений, определение переменных, преобразование явления в математическую модель, оценку решения и повторение процесса для уточнения и расширения модели (COMAP). и СИАМ, 2016 г.). Процесс решения словесной задачи не обязательно такой сложный, так как сама задача обычно дает читателю вопрос, на который нужно ответить, и информацию, необходимую для ответа на него, и не требует моделирования уровня осмысления и интерпретации. Однако эти различия относительны и зависят от способностей учащегося и характера решения, необходимого для решения задачи.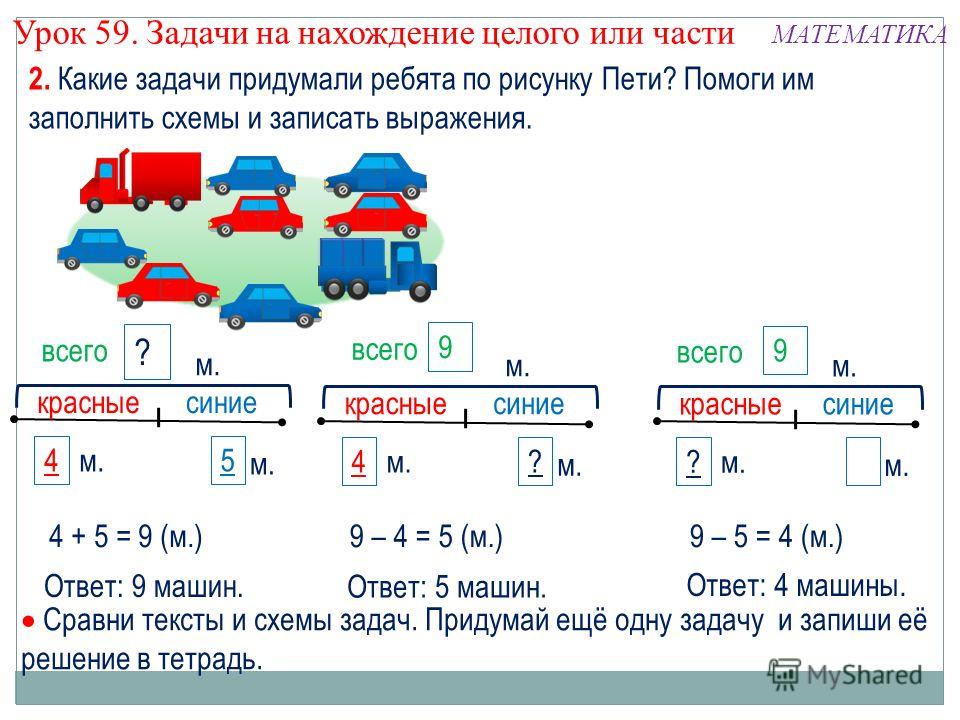 В следующем видео Каплинский (2013) воспроизводит результат начала 19Исследование 80-х годов, проведенное в Институте исследований математики во Франции.
В следующем видео Каплинский (2013) воспроизводит результат начала 19Исследование 80-х годов, проведенное в Институте исследований математики во Франции.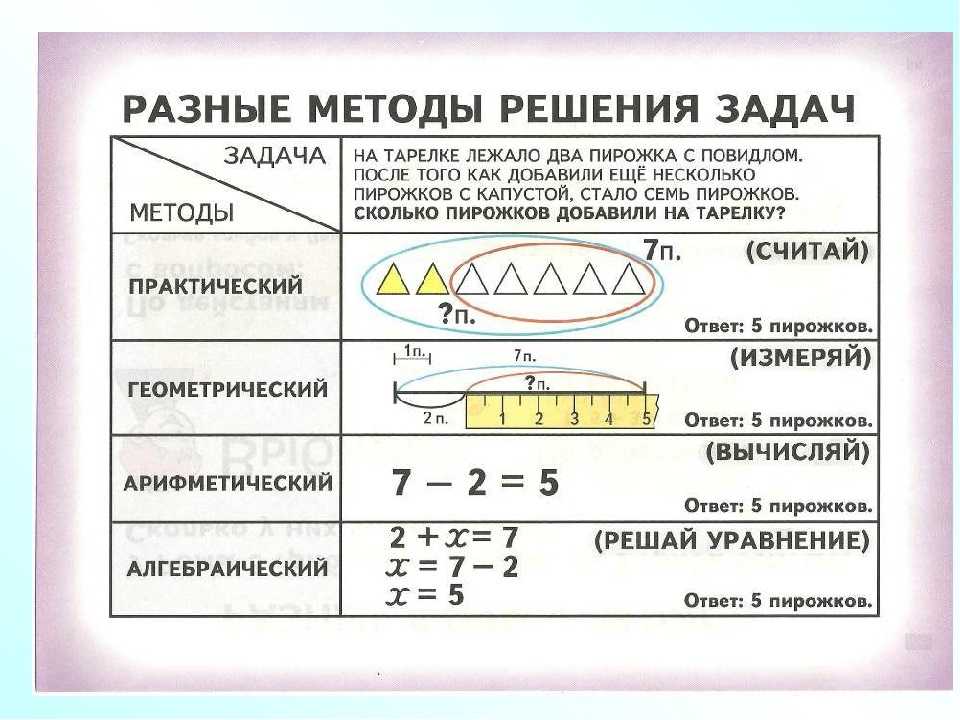 5).
5). Из-за этого они верят в преподавание текстовых задач только после того, как учащиеся освоят решение подобных задач в виде уравнений. Традиционные учебники по математике подкрепляют это убеждение, помещая текстовые задачи в конце практических наборов. Это убеждение или предположение оказалось ложным , по крайней мере, при некоторых условиях. При тестировании учащиеся показали, что они могут добиться большего успеха в решении словесных или вербальных задач, чем в эквивалентных чисто символических задачах (Nathan & Koedinger, 2000a, 2000b). Другие исследования показывают, что навыки алгоритмических вычислений могут не соответствовать способности учащихся концептуализировать взаимосвязь между числами в текстовых задачах (Fuchs et al., 2006).
Из-за этого они верят в преподавание текстовых задач только после того, как учащиеся освоят решение подобных задач в виде уравнений. Традиционные учебники по математике подкрепляют это убеждение, помещая текстовые задачи в конце практических наборов. Это убеждение или предположение оказалось ложным , по крайней мере, при некоторых условиях. При тестировании учащиеся показали, что они могут добиться большего успеха в решении словесных или вербальных задач, чем в эквивалентных чисто символических задачах (Nathan & Koedinger, 2000a, 2000b). Другие исследования показывают, что навыки алгоритмических вычислений могут не соответствовать способности учащихся концептуализировать взаимосвязь между числами в текстовых задачах (Fuchs et al., 2006).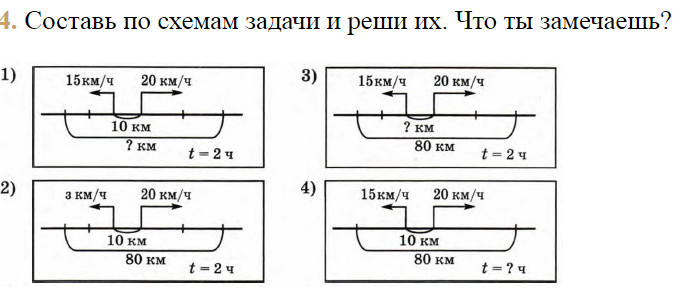 Помещая математику в контекст, понятный учащимся, текстовые задачи побуждают учащихся следовать стратегиям решения, которые имеют для них смысл и чаще приводят к правильным ответам (Koedinger & Nathan, 2004). Затем эти стратегии можно сделать более формальными и символическими с помощью дополнительных инструкций.
Помещая математику в контекст, понятный учащимся, текстовые задачи побуждают учащихся следовать стратегиям решения, которые имеют для них смысл и чаще приводят к правильным ответам (Koedinger & Nathan, 2004). Затем эти стратегии можно сделать более формальными и символическими с помощью дополнительных инструкций. Некоторые типы текстовых задач могут быть особенно полезны для развития рассуждений, потому что в них либо отсутствует очевидная стратегия, либо нет одного правильного ответа, либо они могут быть «сложными» для учащихся, которые предполагают, что проблема проста. Некоторые примеры:
Некоторые типы текстовых задач могут быть особенно полезны для развития рассуждений, потому что в них либо отсутствует очевидная стратегия, либо нет одного правильного ответа, либо они могут быть «сложными» для учащихся, которые предполагают, что проблема проста. Некоторые примеры: В первом контейнере 60 яблок, во втором 90 яблок. Он кладет все яблоки в новый, больший контейнер. Сколько яблок в этом новом контейнере?
В первом контейнере 60 яблок, во втором 90 яблок. Он кладет все яблоки в новый, больший контейнер. Сколько яблок в этом новом контейнере? Хотя эти стратегии могут увеличить число студентов, правильно рассуждающих об этих проблемах, во многих исследованиях они редко давали правильные ответы гораздо более чем 50 % студентов (см. главу 3, Verschaffel, Greer, De Corte). Другими словами, эти стратегии полезны, но вряд ли сами по себе гарантируют успех всем учащимся.
Хотя эти стратегии могут увеличить число студентов, правильно рассуждающих об этих проблемах, во многих исследованиях они редко давали правильные ответы гораздо более чем 50 % студентов (см. главу 3, Verschaffel, Greer, De Corte). Другими словами, эти стратегии полезны, но вряд ли сами по себе гарантируют успех всем учащимся.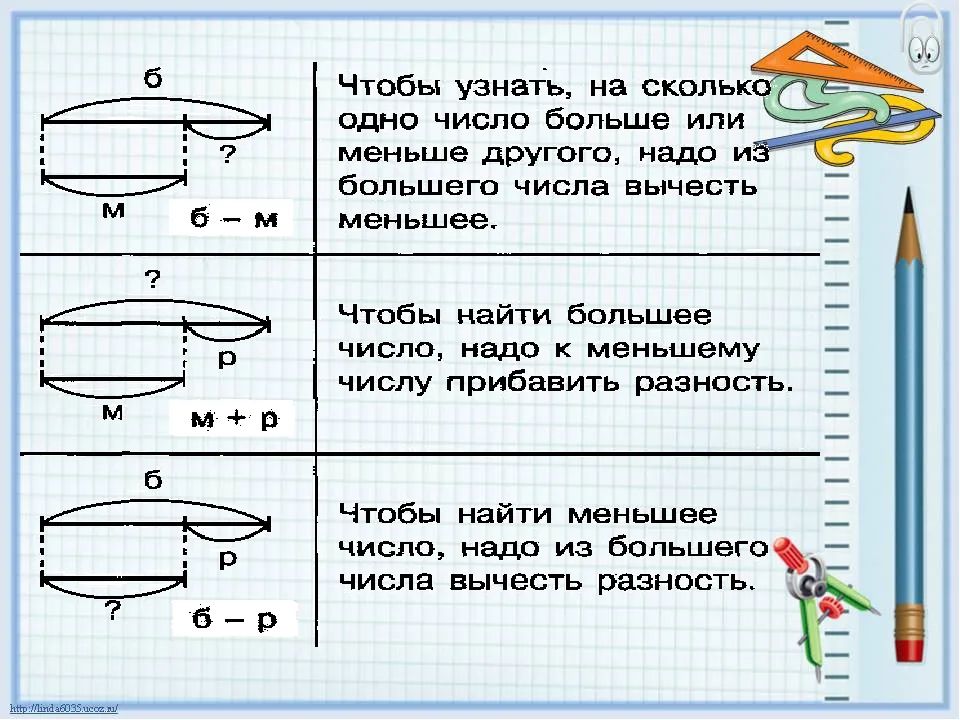 Сообщение в блоге Бушарта (2014 г.) и последующий сборник ресурсов (без даты) описывают как его процесс решения бесчисленных текстовых задач, так и многочисленные примеры для различного содержания и уровней обучения.
Сообщение в блоге Бушарта (2014 г.) и последующий сборник ресурсов (без даты) описывают как его процесс решения бесчисленных текстовых задач, так и многочисленные примеры для различного содержания и уровней обучения. Сколько сока осталось в кувшине после наполнения стакана?
Сколько сока осталось в кувшине после наполнения стакана? С каждым последующим слайдом учитель может продолжать исследовать смыслообразование учащихся и понимание взаимосвязей между величинами, описываемыми задачей.
С каждым последующим слайдом учитель может продолжать исследовать смыслообразование учащихся и понимание взаимосвязей между величинами, описываемыми задачей.
 Сколько еще фасоли нужно Дане, чтобы сварить суп?
Сколько еще фасоли нужно Дане, чтобы сварить суп? Имея эту информацию, учащиеся могут пересмотреть свои наблюдения, чтобы прояснить, что количество бобов, указанное в рецепте, нужно разделить на 2 с вычитанием дополнительного количества, чтобы найти, сколько еще бобов нужно Дане.
Имея эту информацию, учащиеся могут пересмотреть свои наблюдения, чтобы прояснить, что количество бобов, указанное в рецепте, нужно разделить на 2 с вычитанием дополнительного количества, чтобы найти, сколько еще бобов нужно Дане. Сколько еще фунтов фасоли нужно Дане, чтобы приготовить 5 порций супа?
Сколько еще фунтов фасоли нужно Дане, чтобы приготовить 5 порций супа? требуемые транспортные средства. В первом сценарии только 2 из 20 студентов ответили правильно и правильно рассуждали, а остальные остались за делением. Во втором сценарии, используя более аутентичную обстановку, 16 из 20 студентов ответили правильно и аргументировали оставшихся, либо округлив до следующего целого фургона, либо попросив «например, машину или что-то в этом роде» для перевозки небольшого количества оставшихся. пассажиры.
требуемые транспортные средства. В первом сценарии только 2 из 20 студентов ответили правильно и правильно рассуждали, а остальные остались за делением. Во втором сценарии, используя более аутентичную обстановку, 16 из 20 студентов ответили правильно и аргументировали оставшихся, либо округлив до следующего целого фургона, либо попросив «например, машину или что-то в этом роде» для перевозки небольшого количества оставшихся. пассажиры.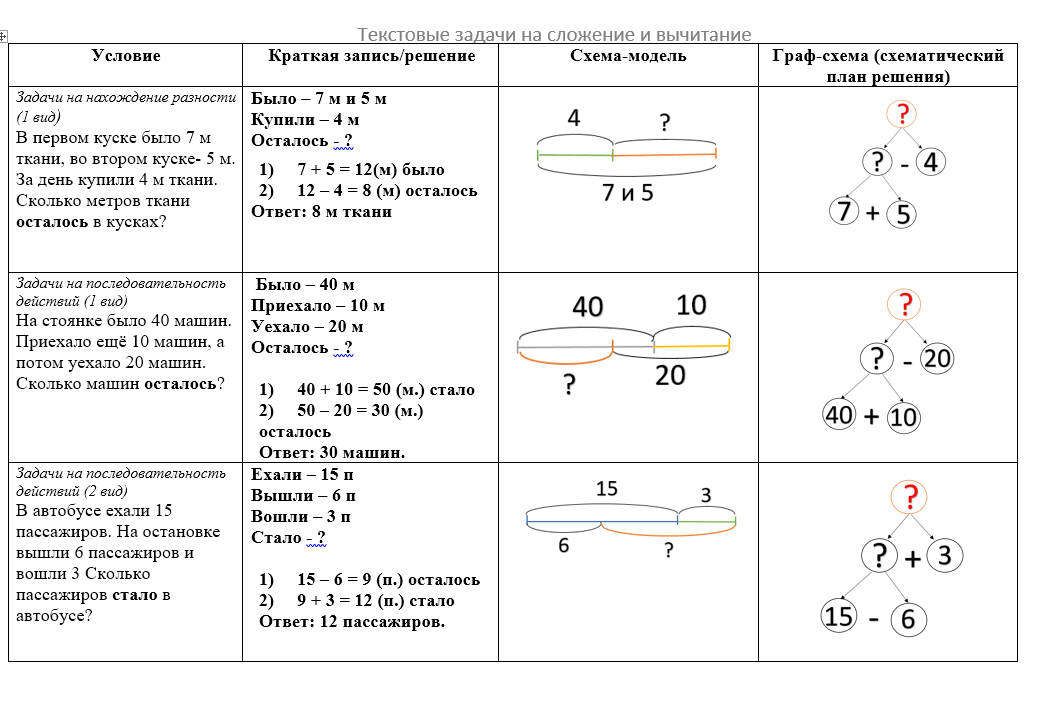
 (6 октября 2014 г.). Бесчисленные текстовые задачи [сообщение в блоге]. Получено 16 ноября 2017 г. с https://bstockus.wordpress.com/2014/10/06/numberless-word-problems/ 9.0005
(6 октября 2014 г.). Бесчисленные текстовые задачи [сообщение в блоге]. Получено 16 ноября 2017 г. с https://bstockus.wordpress.com/2014/10/06/numberless-word-problems/ 9.0005 С., Фукс, Д., Комптон, Д. Л., Пауэлл, С. Р., Ситалер, П. М., Капицци, А. М., … Флетчер, Дж. М. (2006). Когнитивные корреляты навыков третьего класса в арифметике, алгоритмических вычислениях и арифметических текстовых задачах. Журнал педагогической психологии, 98(1), 29–43. https://doi.org/10.1037/0022-0663.98.1.29
С., Фукс, Д., Комптон, Д. Л., Пауэлл, С. Р., Ситалер, П. М., Капицци, А. М., … Флетчер, Дж. М. (2006). Когнитивные корреляты навыков третьего класса в арифметике, алгоритмических вычислениях и арифметических текстовых задачах. Журнал педагогической психологии, 98(1), 29–43. https://doi.org/10.1037/0022-0663.98.1.29 Журнал наук об обучении, 13 (2), 129–164. https://doi.org/10.1207/s15327809jls1302_1
Журнал наук об обучении, 13 (2), 129–164. https://doi.org/10.1207/s15327809jls1302_1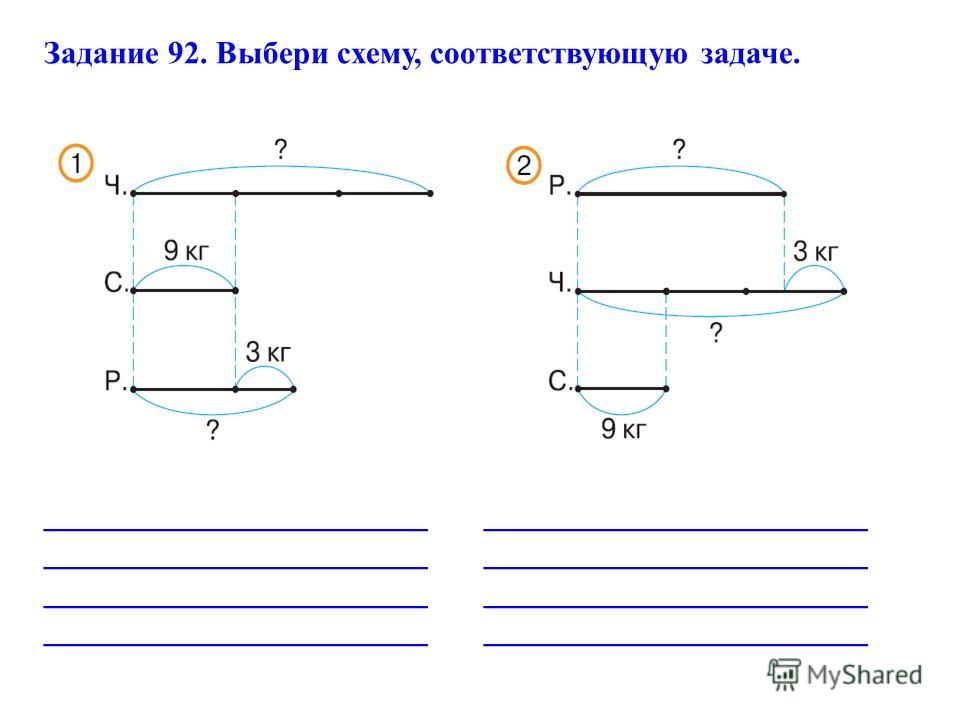 Получено с https://parcc-assessment.org/content/uploads/released_materials/05/Grade_04_Math_Item_Set.pdf
Получено с https://parcc-assessment.org/content/uploads/released_materials/05/Grade_04_Math_Item_Set.pdf