Итоговая контрольная работа (4 кл. матем. сист. ЗАНКОВА) — Математика 4 класс — 4 класс
Ирэн Аргинская;
Елена Вороницына
Итоговые контрольные и проверочные работы
Если в задании два пункта, то пункт а) отражает уровень базовых требований к знаниям, умениям и навыкам учеников и оценивается отдельно от пункта б), который является заданием повышенной трудности и оценивается только в случае его успешного выполнения.
Работы учеников, выполненные без ошибок или с ошибками, полностью исправленными при первоначальной проверке сразу после завершения работы, оцениваются с точки зрения сформированности самоконтроля высшим уровнем.
Предлагаются два варианта контрольной работы. Учитель может выбрать один из вариантов, может из двух предложенных составить свой вариант работы, ориентируясь на уровень подготовки своего класса.
Если работу составляет завуч, то необходимо предварительно показать ее учителю.
4-й класс
Вариант 1
Задание 1
а) Реши задачу.
Самолет пролетел в 6 590 км. 4 часа он летел со скоростью 920 км/ч, а остальной путь со скоростью 970 км/ч. Сколько часов самолет был в пути?
б) Измени вопрос задачи так, чтобы количество действий уменьшилось.
Задание 2
а) Укажи порядок выполнения действий и найди значение выражения.
38 . (9045 : 27 – 8472 : 353)
б) Измени одно из числе так, чтобы значение выражения уменьшилось в 2 раза.
Задание 3
Заполни пропуски так, чтобы получились верные равенства.
7 ч 25 мин = … мин
1 374 дм2 = … м2 .
438 ц = … т … ц.. дм2
3 м … дм 7 см = … 6 … см
Задание 4
Реши уравнение, содержащее три действия. Выполни его проверку.
6 .p – (468 + 9 . 7) = 405
875 : n + 194 = 219
(537 – 129 . 4) . t = 15 414
Задание 5
Площадь прямоугольного треугольника равна 16 см2. Подбери длины сторон, образующих прямой угол. Постарайся найти несколько решений.
Вариант 2
Задание 1
а) Реши задачу.
В магазин привезли 2400 пар обуви. В первый
день продали 3/8 всей привезенной
обуви, а во второй день
б) Измени вопрос задачи так, чтобы
количество действий увеличилось.
Задание 2
Укажи порядок выполнения действий и найди значения выражений.
(479 484 + 113 796) : 72 – 146 . 18
8 ч 36 мин . 475 – 364 ч 48 мин : 24
Задание 3
Вырази данные величины в разных единицах измерения.
80 006 дм 6798 коп. 239 час. 704 см2
Задание 4
Найди корни уравнений. Выполни проверку.
15 т + 30 – 12 т = 42
2 . к – 391 = 73 . 5 + 108
Задание 5
а) Начерти какой-либо
прямоугольник, периметр которого равен
периметру треугольника со сторонами 10 см, 4 см, 8
см. (Сумма длин сторон прямоугольника – целое
число сантиметров. ) Найди площадь этого
прямоугольника.
) Найди площадь этого
прямоугольника.
б) Начерти прямоугольник, периметр которого в 2 раза больше. На сколько изменилась при этом площадь прямоугольника?
Самостоятельная работа 4 класс «Задачи на движение»
Самостоятельная работа
4 класс
Задачи на движение
1вариант
1.Эскимосская собака бежала 60 с со скоростью 15 м/с. За какое время может пробежать этот путь гончая собака, двигаясь со скоростью 30 м/с?
2.Майский жук, двигаясь со скоростью 12 км/ч , был в пути 2 ч. С какой скоростью должна лететь комнатная муха, чтобы преодолеть это расстояние за 4 ч?
3. Рыба-меч, двигаясь со скоростью 70 км/ч, была в пути 2 ч. За какое время может проплыть этот путь скумбрия, двигаясь со скоростью 20 км/ч?
4. Вёсельная лодка, двигаясь со скоростью 8 км/ч , была в пути 8 ч. С какой скоростью должен плыть катер, чтобы преодолеть это расстояние за 2 ч?
Вёсельная лодка, двигаясь со скоростью 8 км/ч , была в пути 8 ч. С какой скоростью должен плыть катер, чтобы преодолеть это расстояние за 2 ч?
5. Плот, двигаясь со скоростью 2 км/ч, был в пути 6 ч. За какое время можно проплыть это расстояние на лодке, двигаясь со скоростью 4 км/ч?
Задачи на движение
- вариант
1.Самолёт летел 2 ч со скоростью 700 км/ч. Вертолёт такое же расстояние пролетит за 4 ч. С какой скоростью должен лететь вертолёт?
2. Рыба-меч, двигаясь со скоростью 70 км/ч, была в пути 2 ч. За какое время может проплыть этот путь скумбрия, двигаясь со скоростью 20 км/ч?
3.Товарный поезд, двигаясь со скоростью 40 км/ч , был в пути 3 ч. С какой скоростью должен ехать пассажирский поезд, чтобы преодолеть это расстояние за 2 ч?
4. Слепень, двигаясь со скоростью 20 км/ч, был в пути 2 ч. С какой скоростью должна лететь бабочка капустница, чтобы преодолеть это расстояние за 5 ч?
Слепень, двигаясь со скоростью 20 км/ч, был в пути 2 ч. С какой скоростью должна лететь бабочка капустница, чтобы преодолеть это расстояние за 5 ч?
5.Трактор, двигаясь со скоростью 10 км/ч, был в пути 4 ч. За какое время можно проехать этот путь на лошади, двигаясь со скоростью 8 км/ч?
10 тыс изображений найдено в Яндекс.Картинках — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Мы гимназисты — Самостоятельные работы по математике. 4 класс
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
Самостоятельная работа «Повторяем все, что знаем»
Самостоятельная работа «Нумерация чисел в пределах 1000″
Самостоятельная работа «Сложение и вычитание в пределах 1000″
Самостоятельная работа «Компоненты сложения, вычитания»
Самостоятельная работа «Решаем задачи»
Самостоятельная работа «Решаем примеры»
Самостоятельная работа «Письменные приемы умножения и деления на однозначное число в пределах 100″
Самостоятельная работа «Компоненты умножения, деления»
Самостоятельная работа «Порядок выполнения действий»
Самостоятельная работа «Уравнения.
Самостоятельная работа «Решаем задачи» — 1
Самостоятельная работа «Решаем задачи» — 2
Самостоятельная работа «Решаем примеры»
Самостоятельная работа «Нумерация чисел, которые больше 1000″
Самостоятельная работа «Сложение многозначных чисел»
Самостоятельная работа «Вычитание многозначных чисел»
Самостоятельная работа «Действия с величинами»
Самостоятельная работа «Решаем задачи»
Самостоятельная работа «Решаем примеры»
Самостоятельная работа «Увеличение и уменьшение чисел в 100, 1000, 10 000 раз»
Самостоятельная работа «Класс миллионов и класс миллиардов»
Самостоятельная работа «Умножение и деление чисел, оканчивающихся нулями»
Самостоятельная работа «Умножение многозначных чисел на однозначное число»
Самостоятельная работа «Решаем задачи»
Самостоятельная работа «Деление многозначных чисел на однозначное число»
Самостоятельная работа «Умножение и деление на числа, оканчивающиеся нулями»
Самостоятельная работа «Умножение и деление на двузначное число»
Самостоятельная работа «Умножение и деление на трехзначное число»
Самостоятельная работа «Решение задач»
Самостоятельная работа «Доли»
Самостоятельная работа «Проценты»
Самостоятельная работа «Единицы длины»
Самостоятельная работа «Единицы времени»
Самостоятельная работа «Единицы массы»
Самостоятельная работа «Единицы площади»
Самостоятельная работа «Угол»
Самостоятельная работа «Периметр и площадь»
Самостоятельная работа «Окружность»
- Просмотров: 4990
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 1331
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1494
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1071
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 939
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1047
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1294
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1288
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 905
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 903
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 788
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 787
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 722
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 660
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 812
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 622
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 742
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 1053
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 773
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 695
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1124
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 909
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 935
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1605
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 862
- Подробности
- Категория: Самостоятельные работы по математике.
 4 класс
4 класс
- Просмотров: 1920
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1632
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 1183
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 981
- Подробности
- Категория: Самостоятельные работы по математике. 4 класс
- Просмотров: 926
Умножение на двузначное число. Математика 4 класс Богданович.
Категория: —>> Математика 4 класс Богданович
Задание: —>>
73 — 92 93 — 106
наверхЗадание 73.
Рассмотри запись письменного умножения на двузначное число и прочитай объяснение.
Объяснение. При письменном умножении на двузначное число сначала умножают на единицы, а потом на десятки. 36 умножить на 7 будет 252 — это первое неполное произведение. Его записывают так, чтобы цифра единиц находилась под единицами. 36 умножить на 2, будет 72 (десятки) — это второе неполное произведение. Его записывают так, чтобы цифра 2 находилась под десятками. Потом складывают неполные произведения и получают окончательный результат 972.
Его записывают так, чтобы цифра единиц находилась под единицами. 36 умножить на 2, будет 72 (десятки) — это второе неполное произведение. Его записывают так, чтобы цифра 2 находилась под десятками. Потом складывают неполные произведения и получают окончательный результат 972.
Задание 74.
Выполни умножение с объяснением.
| 45 * 22 | 51 * 18 | 32 * 25 | 19 * 18 |
Решение:
Задание 75.
Посеяли 15 кг озимой пшеницы, а собрали в 23 раза больше. Сколько килограммов пшеницы собрали?
Решение:
- 1) 15 * 23 = 345 (кг озимой пшеницы собрали)
- Ответ: озимой пшеницы собрали 345 кг.
Задание 76.
1) На 7 грн. 84 к. мама купила 8 ручек по 54 к. и 8 карандашей. Сколько стоит карандаш?
Решение:
- 1) 7 грн. 84 к = 784 к
- 2) 8 * 54 = 432 (копейки мама потратила на ручки)
- 3) 784 — 432 = 352 (копейки мама потратила на карандаши)
- 4) 352 : 8 = 44 (копейки стоит карандаш)
- Выражение: (784 — 8 * 54) : 8 = 44
- Ответ: один карандаш стоит 44 копейки.

Задание 77.
К каждому неравенству подбери по два значения буквы 6, при которых неравенство будет верным.
Решение:
| 25 — b > 20 | b = 1, b = 4 |
| b * 4 < 36 | b = 2, b = 8 |
| b : 4 > 8 | b = 40, b = 36 |
Задание 78.
Даны три числа: 30, 20, 5. Найди все возможные произведения суммы двух чисел и третьего числа.
Решение:
- (30 + 5) * 20 = 35 * 20 = 700
- (20 + 5) * 30 = 25 * 30 = 750
- (30 + 20) * 5 = 50 * 5 = 250
Задание 79.
| 33 * 26 | 42 * 17 | 35 * 25 | 26 * 26 |
Решение:
Задание 80.
От своего дома мальчик проехал на велосипеде в одном направлении 300 м. Потом он развернулся и в противоположном направлении проехал в 3 раза меньшее расстояние. На каком расстоянии от своего дома оказался мальчик?
Решение:
- 1) 300 : 3 = 100 (метров проехал мальчик в обратном направлении)
- 2) 300 — 100 = 200 (расстояние от дома, на котором оказался мальчик)
- Выражение: 300 — 300 : 3 = 200
- Ответ: мальчик оказался от дома на расстоянии 200 метров.

Задание 81.
- Запиши выражения и вычисли их значения.
- 1) Уменьшаемое 85, вычитаемое — произведение чисел 7 и 8.
- 2) Делимое 56, делитель — разность чисел 14 и 6.
Решение:
- 1) 85 — 7 * 8 = 85 — 56 = 29
- 2) 56 : (14 — 6) = 7
Задание 82.
Древесину лучше всего склеивать, если она содержит девятую часть воды. Сколько воды содержит древесина массой 18 кг, готовая к склеиванию?
Решение:
- 1) 18 : 9 = 2 (кг воды содержит 18 кг древесины)
- Ответ: 18 кг древесины, готовой для склейки содержит 2 кг воды.
Задание 83.
Выполни умножение с объяснением.
| 42 * 21 | 31 * 12 | 23 * 23 | 17 * 38 |
Решение:
Задание 84.
Рассмотри рисунок и запиши ответы на вопросы. Какова масса одного ящика масла; трёх ящиков масла; двух ящиков масла?
Решение:
- 1) 40 : 5 = 8 (масса одного ящика масла)
- 2) 8 * 3 = 24 (масса 3-х ящиков масла)
- 3) 8 * 2 = 16 (масса 2-х ящиков масла
Задание 85.
Отец может доехать к месту работы на автобусе за 56 мин или на метро за 28 мин. На сколько меньше времени потратит отец на дорогу к месту работы и обратно за 7 дней, если будет ездить только на метро?
Решение:
- 1) 56 — 28 = 28 (на 28 минут в день меньше отец затрачивает на дорогу на работу, если на метро)
- 2) 28 * 2 = 56 (минт в день экономит отец на дорогу с работы и на работу, если на метро)
- 3) 56 * 7 = 392 (за неделю)
- Выражение: (56 − 28) * 2 * 7 = 392 (минут).
- Ответ: на 392 минуты в неделю меньше.
Задание 86.
Вычисли результат и подели его на подчёркнутое число.
Образец. 8 — 5 + 3 = 43, 43 : 8 = 5 (ост. 3).
Решение:
| 7 * 4 + 5 = 33 | 33 : 7 = 4 (ост 5) |
| 6 * 3 + 2 = 20 | 20 : 6 = 3 (ост 2) |
| 7 * 8 + 4 = 60 | 60 : 7 = 8 (ост 4) |
| 9 * 3 + 3 = 30 | 30 : 9 = 3 (ост 3) |
Задание 87.

В 6 мешках 480 кг зерна, в 9 мешках 450 кг картофеля, поровну в каждом. На сколько килограммов масса мешка картофеля меньше массы мешка зерна?
Решение:
- 1) 480 : 6 = 80 (масса мешка зерна)
- 2) 450 : 9 = 50 (кг картофеля в одном мешке)
- 3) 80 — 50 = 30
- Выражение: 480 : 6 — 450 : 9 = 30
- Ответ: масса мешка картофеля на 30 кг меньше, чем масса мешка зерна.
Задание 88.
Открыли кран, из которого в течение минуты вытекает 20 л воды, и за 8 мин наполнили ванну. Потом кран закрыли и открыли сливное отверстие, через которое вся вода вытекла за 4 мин. Сколько литров воды вытекало за минуту?
Решение:
- 1) 20 * 8 = 160 (литров воды набрали в ванну)
- 2) 160 : 4 = 40 (литров в минуту)
- Выражение: 20 * 8 : 4 = 40
- Ответ: за 1 минуту из ванны вытекало 40 литров воды.
Задание 89.
Реши примеры.
Решение:
| 48 : 6 = 8 | 6 * 7 = 42 | 7 * 9 = 63 | 72 : 12 = 6 |
| 42 : 6 = 7 | 8 * 9 = 72 | 63 — 51 = 12 | 12 * 4 = 3 |
Задание 90.

| 625 : 5 = | 748 : 4 = | 726 : 3 = | 126 : 2 = |
Решение:
Задание 91.
Рассмотри записи и прочитай объяснение, как находили частное чисел 144 и 24.
Объяснение. 14 меньше 24. В частноном будет одна цифра. Частное ищем способом подбора. Первую пробную цифру можно найти, если поделить число всех десятков делимого на число десятков делителя: 14 : 2 = 7. Проверим устно цифру 7: 20 — 7 = 140, 4 * 7 = 28, 140 + 28 = 168, 168 > 144. Цифра 7 не подходит. Проверим цифру 6: 20 • 6 = 120, 4 • 6 = 24, 120 + 24 = 144. Следовательно, цифра 6 подобрана правильно.
Задание 92.
Найди частное 196 : 28 с объяснением.
Решение:
Задание: —>> 73 — 92 93 — 106
ГДЗ самостоятельные работы к учебнику Моро по математике за 4 класс Самсонова ФГОС часть 1, 2
Юным выпускникам приходится нелегко, ведь, хоть они по-прежнему остаются детьми, запросы к их интеллектуальному уровню стали значительно выше. Являясь самыми старшими в начальном звене, они несут определенный груз ответственности. Им постоянно приходится доказывать свои знания при проведении текущего контроля учителем. В конце года малышам предстоит пройти финальную, и потому важнейшую проверку – Государственную итоговую аттестацию, которая должна определить, достаточно ли подготовлен отдельно взятый ученик к переходу на следующей ступень школьного образования. Один из трех предметов, бланки с вопросами по которым будут ожидать детей на ВПР, – это математика. Готовиться к этому непростому испытанию нужно начинать заранее, и желательно подобрать для такого дела самых надежных помощников. В числе лучших представителей жанра готовых домашних заданий по этой дисциплине является «ГДЗ по математике 4 класс самостоятельные работы Самсонова (Экзамен)». Данное онлайн-пособие вобрало в себя всё положительное, что есть у учебно-вспомогательной литературы.
Являясь самыми старшими в начальном звене, они несут определенный груз ответственности. Им постоянно приходится доказывать свои знания при проведении текущего контроля учителем. В конце года малышам предстоит пройти финальную, и потому важнейшую проверку – Государственную итоговую аттестацию, которая должна определить, достаточно ли подготовлен отдельно взятый ученик к переходу на следующей ступень школьного образования. Один из трех предметов, бланки с вопросами по которым будут ожидать детей на ВПР, – это математика. Готовиться к этому непростому испытанию нужно начинать заранее, и желательно подобрать для такого дела самых надежных помощников. В числе лучших представителей жанра готовых домашних заданий по этой дисциплине является «ГДЗ по математике 4 класс самостоятельные работы Самсонова (Экзамен)». Данное онлайн-пособие вобрало в себя всё положительное, что есть у учебно-вспомогательной литературы.
Чем именно будет полезен решебник к СР по математике для 4 класса от Самсоновой?
Во-первых, конечно, следует отметить, что информация, предложенная в нем, исключительно достоверна. Авторы всех предложенных решений – опытные методисты, прекрасно знакомые с материалом и требованиями ГИА. Во-вторых, каждый выполненный номер подкреплен развернутыми авторскими объяснениями. А в-третьих, нельзя не упомянуть главную цель создания таких пособий – это предоставление учащимся возможности самоподготовки. Кто из нас не волновался при написании проходных испытаний? Ребята не всегда уверены в собственных силах, но с помощью ГДЗ к самостоятельным работам по математике за 4 класс от Самсоновой Л. Ю. (Экзамен) они смогут загодя подготовиться ко всем из них.
Авторы всех предложенных решений – опытные методисты, прекрасно знакомые с материалом и требованиями ГИА. Во-вторых, каждый выполненный номер подкреплен развернутыми авторскими объяснениями. А в-третьих, нельзя не упомянуть главную цель создания таких пособий – это предоставление учащимся возможности самоподготовки. Кто из нас не волновался при написании проходных испытаний? Ребята не всегда уверены в собственных силах, но с помощью ГДЗ к самостоятельным работам по математике за 4 класс от Самсоновой Л. Ю. (Экзамен) они смогут загодя подготовиться ко всем из них.
Однако, взаимодействуя с такой лит-рой, обязательно придерживайтесь алгоритма:
- Завершите упражнение самостоятельно.
- Проверьте себя через онлайн-задачник.
- Исправьте ошибки.
Помните, что бездумное списывание верных ответов – это не выход из трудной ситуации. Старайтесь вникать в то, что вы пишете, иначе такой недальновидный подход отрицательно скажется как на качестве вашего образования, так и на успеваемости.
Проверка деления и умножения
Здравствуйте, ребята!
Вы знаете, мне стали приходить письма, в которых ребята пишут о том, что, вроде бы, правильно выполняли деление многозначных чисел, а когда получали проверенные тетради, оказывалось, что там были ошибки. И отметки в тетрадях стояли совсем не те, которые они ожидали. Как же быть? Что необходимо делать, чтобы самим находить ошибки, вовремя их исправлять и получать хорошие отметки?
Ребята, вы ведь знаете, что проверку деления можно выполнить обратным действием – умножением.
Вот посмотрите, как решал пример мой хороший знакомый Витя Считалкин.
Ему надо было сто двадцать девять тысяч восемьсот шестьдесят один разделить на четыреста двадцать три.
Витя определил первое
неполное делимое – тысяча двести девяносто восемь. И для того, чтобы легче было
найти цифру частного, делил на четыреста. Пробная цифра частного
– три. Затем, как и положено, Витя перемножил четыреста двадцать три и три.
Получилось число тысяча двести шестьдесят девять. Оно меньше неполного
делимого, поэтому Витя выполнил вычитание. Остаток равен двадцати девяти. Второе
неполное делимое у Вити – две тысячи девятьсот шестьдесят один. Витя
разделил его на четыреста. Пробная цифра семь. Проверил умножением.
Две тысячи девятьсот шестьдесят один. Вот и найдено значение числового
выражения.
Затем, как и положено, Витя перемножил четыреста двадцать три и три.
Получилось число тысяча двести шестьдесят девять. Оно меньше неполного
делимого, поэтому Витя выполнил вычитание. Остаток равен двадцати девяти. Второе
неполное делимое у Вити – две тысячи девятьсот шестьдесят один. Витя
разделил его на четыреста. Пробная цифра семь. Проверил умножением.
Две тысячи девятьсот шестьдесят один. Вот и найдено значение числового
выражения.
Ах, Витя, Витя. Как ему надо было проверить решение? Конечно, умножением.
Надо перемножить делитель и частное.При этом должно получиться делимое. Ну что, проверяем?
Умножаем четыреста двадцать три
на тридцать семь. Сначала на семь единиц, а потом – на три десятка. Складываем
неполные произведения. Ответ – пятнадцать тысяч шестьсот пятьдесят один. Ну
конечно, это совсем не то число, которое должно было получиться. Значит, в
делении мы допустили ошибку. Ну-ка, ну-ка… Первую цифру нашли правильно.
Вторую… А, вот в чём дело! После остатка во втором неполном делимом
записаны сразу две цифры. Витя забыл, что перед тем, как перенести из
делимого вторую цифру, в частное надо поставить нуль. Ну что, попробуем
ещё раз выполнить проверку умножением. Только теперь вторым множителем будет
число триста семь. Сначала умножаем на семь единиц, а потом – на три сотни. Записывать
неполное произведение начнём под сотнями. Складываем неполные произведения.
Ответ – сто двадцать девять тысяч восемьсот шестьдесят один.
Ну-ка, ну-ка… Первую цифру нашли правильно.
Вторую… А, вот в чём дело! После остатка во втором неполном делимом
записаны сразу две цифры. Витя забыл, что перед тем, как перенести из
делимого вторую цифру, в частное надо поставить нуль. Ну что, попробуем
ещё раз выполнить проверку умножением. Только теперь вторым множителем будет
число триста семь. Сначала умножаем на семь единиц, а потом – на три сотни. Записывать
неполное произведение начнём под сотнями. Складываем неполные произведения.
Ответ – сто двадцать девять тысяч восемьсот шестьдесят один.
Видите, проверка показала, что теперь деление выполнено верно. Если бы Витя сразу проверил деление умножением, он сам смог бы найти ошибку.
Кстати, что ещё забыл Витя,
когда выполнял деление? Догадались? Перед тем, как начать деление, он не
определил количество цифр в частном. И это тоже сыграло с Витей злую шутку. Если
бы он это сделал, то сразу заметил бы, что цифр в частном меньше, чем должно
быть.
Ребята, а как проверить, правильно ли Витя Считалкин решил вот такой пример?
И в этом случае тоже необходимо перемножить делитель и частное. А потом к полученному произведению прибавить остаток. Вот видите, у нас получилось число, которое было в делимом. Значит, этот пример был решён верно.
Друзья, а если надо проверить результат умножения, как вы это сделаете? Ну конечно, делением. К примеру, надо умножить четыреста тридцать девять на семьсот шесть. Умножаем четыреста тридцать девять на шесть, и на семь. Складываем неполные произведения. Получилось тридцать три тысячи триста шестьдесят четыре.
Выполняем проверку делением. Полученное произведение будет делимым, а любой из сомножителей может стать делителем. Мне захотелось в качестве делителя взять число семьсот шесть. Первое неполное делимое – три тысячи триста тридцать шесть. И в частном две цифры… Стоп!
Уже что-то не так. Ведь их
должно быть три, так как другой множитель – число четыреста тридцать девять.
Значит, при умножении была допущена ошибка. Какая? А, вот она! Я умножала
на сотни, а неполное произведение начала записывать под десятками. Нужно
исправить. И ответ, конечно, изменить! Теперь произведение равно трёмстам
девяти тысячам девятистам тридцати четырём.
Ведь их
должно быть три, так как другой множитель – число четыреста тридцать девять.
Значит, при умножении была допущена ошибка. Какая? А, вот она! Я умножала
на сотни, а неполное произведение начала записывать под десятками. Нужно
исправить. И ответ, конечно, изменить! Теперь произведение равно трёмстам
девяти тысячам девятистам тридцати четырём.
Проверяем его делением. Первое
неполное делимое – три тысячи девяносто девять. В частном три цифры. Уже
хорошо. Делим три тысячи девяносто девять на семьсот. Пробная цифра
– четыре. Перемножаем семьсот шесть и четыре. Получилось две тысячи восемьсот
двадцать четыре. Вычитаем. Остаток – двести семьдесят пять. Он меньше делителя.
В частном четыре сотни. Следующее неполное делимое – две тысячи семьсот пятьдесят
три. Делим его на семьсот. Пробная цифра – три. Перемножаем
семьсот шесть и три, получается две тысячи сто восемнадцать. Это число меньше
неполного делимого. Вычитаем. Остаток равен шестистам тридцати пяти. Немаленький
остаток, но всё-таки меньше делителя. В частное пишу три десятка. Делим третье
неполное делимое, шесть тысяч триста пятьдесят четыре, на семьсот. Пробная
цифра – девять. Перемножаем семьсот шесть и девять. Получилось шесть
тысяч триста пятьдесят четыре. Так что в частном девять единиц. И ответ –
четыреста тридцать девять. Именно таким был первый множитель. А это значит, что
деление (и умножение) мы выполнили верно.
Вычитаем. Остаток равен шестистам тридцати пяти. Немаленький
остаток, но всё-таки меньше делителя. В частное пишу три десятка. Делим третье
неполное делимое, шесть тысяч триста пятьдесят четыре, на семьсот. Пробная
цифра – девять. Перемножаем семьсот шесть и девять. Получилось шесть
тысяч триста пятьдесят четыре. Так что в частном девять единиц. И ответ –
четыреста тридцать девять. Именно таким был первый множитель. А это значит, что
деление (и умножение) мы выполнили верно.
Ну а теперь подведём итог:
Чтобы проверить действие деления, мы перемножаем делитель и частное. Если в результате получилось делимое, значит, деление было выполнено верно.
Если деление выполнено с остатком, то сначала перемножаются делитель и частное, а потом к полученному произведению прибавляется остаток.
Чтобы проверить действие
умножения, надо произведение разделить на один из
множителей. Если в результате получится второй множитель, значит, умножение
было выполнено верно.
Если в результате получится второй множитель, значит, умножение
было выполнено верно.
Ну вот и подошло к концу время, отведённое на эту тему, и я должна попрощаться с вами. Успехов вам, друзья мои!
3000 примеров по математике с ответами и методическими рекомендациями. Устный счет. Табличное и внетабличное умножение и деление. Сложение и вычитание в пределах 1000. 4 класс. — Узорова О.В. | 978-5-17-117927-4
Стоимость товара может отличаться от указанной на сайте!Наличие товара уточняйте в магазине или по телефону указанному ниже.
г. Воронеж, площадь Ленина, д.4
8 (473) 277-16-90
г. Липецк, проспект Победы, 19А
8 (4742) 22-00-28
г. Липецк, пл.Плеханова, д. 7
8 (4742) 47-02-53
г. Богучар, ул. Дзержинского, д. 4
8 (47366) 2-12-90
г.Поворино, ул.Советская, 87
8 (47376) 4-28-43
г. Воронеж, ул. Плехановская, д. 33
8 (473) 252-57-43
г. Нововоронеж, ул. Ленина, д.8
8 (47364) 92-350
г. Воронеж, ул. Хользунова, д. 35
Воронеж, ул. Хользунова, д. 35
8 (473) 246-21-08
г. Лиски, ул. Коммунистическая, д.7
8 (47391) 2-22-01
г. Белгород, Бульвар Народный, 80б
8 (4722) 42-48-42
г. Курск, пр. Хрущева, д. 5А
8 (4712) 51-91-15
г. Старый Оскол, мкр Олимпийский, д. 62
8 (4725) 39-00-10
Страница 83 — ГДЗ Математика 2 класс. Моро, Бантова, Бельтюкова, Волкова, Степанова. Учебник часть 2
Вернуться к содержанию учебника
Табличное умножение и деление
Вопрос
1. Рассмотри записи под каждым рисунком.
Спиши, заполняя пропуски, и объясни, как получено каждое следующее равенство из первого.
Подсказка
Повтори принцип деления на однозначное число.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
2.
| 12 : 6 | 18 : 2 | 16 : 8 | 14 : 7 | 8 : 2 |
| 12 : 2 | 18 : 9 | 16 : 2 | 14 : 2 | 8 : 4 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
3. За партами сидели 18 учеников, по 2 ученика за каждой партой. Сколько парт заняли эти ученики?
За партами сидели 18 учеников, по 2 ученика за каждой партой. Сколько парт заняли эти ученики?
Подсказка
Если к задаче есть схематический рисунок или чертёж, краткую запись писать не нужно.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
4. Саша купил ручку за 8 р., ластик за 5 р., и у него осталось 2 р. Что узнаешь, вычислив:
8 — 5?
8 + 5?
8 + 5 + 2?
Подсказка
Повтори, из каких частей состоит задача.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
5. Какое число больше на 9, чем 25? 36? 47?
Какое число меньше на 8, чем 51? 62? 73?
Подсказка
Если в задаче есть слова «на… больше», то задача решается сложением, а если « на… меньше», то задача решается вычитанием.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
6. 1) Измерь каждое звено ломаной и найди её длину.
1) Измерь каждое звено ломаной и найди её длину.
2) Начерти квадрат, периметр которого равен длине этой ломаной.
Подсказка
Чтобы найти длину ломаной линии, нужно сложить длины всех её звеньев.
Периметр многоугольника — это сумма длин всех его сторон. У квадрата все стороны равны, поэтому мы можем длину умножить на 4 и вычислить периметр.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Для игры 12 детей разделились на 2 команды поровну. Сколько детей в каждой команде?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Ребусы:
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
© budu5.com, 2021
Пользовательское соглашение
Copyright
Как объяснить ребенку дроби? — Блог и все письма Ренаты Кирилиной и «Обучение с удовольствием»
Мы делили апельсин. Много нас, а он один
Много нас, а он один
Эта долька для ежа, эта долька для чижа…
А для волка — кожура.
В Школе умных детей Любовь Стрекаловская рассказала, как ввести эту тему и сделать так, чтобы ребенок понял тему и научился решать дроби.
Давайте начнем с самого-самого начала. Представьте себе ребенка, который никогда не видел (а если видел, то не понимает смысла) записи дроби. Он не знает даже этого слова.
Как объснить ему тему и перейти к более сложной части -действию с дробями и решению задач? Как не отбить желание к этой теме? Как связать ее с жизнью?
В школьной программе объяснить дроби предлагается так:
1 Взять яблоко и предложить съесть его двум детям сразу. Они ответят, что это невозможно. Далее необходимо разрезать фрукт и вновь предложить детям. Каждому достанется по одинаковой половине. Таким образом, половинка яблока является частью от целого яблока. А само яблоко состоит из двух частей.
2 Вводим запись. И показываем, что одна половинка — это часть от целого, или 1/2. Значит дробь — это число, которое является частью предмета, меньше, чем один. Также дробь — это количество частей от какой-то вещи.
Значит дробь — это число, которое является частью предмета, меньше, чем один. Также дробь — это количество частей от какой-то вещи.
Далее детям на дом задается выучить определение, и когда введено понятие, начинается период практики.
Однако, по опросам родителей, эта тема является одной из самых трудных для усвоения детьми. Когда обучение происходит по принципу — вот правило — учи — применяй, эффект намного ниже, чем при подходе, который предлагает Любовь Стрекаловская в Школе умных детей.
Ребенок может знать правило, но не понимать, почему это так работает? Почему так записывается?
А отсюда будут ошибки в сравнении 3/11 и 3/17 частей, ошибки в сравнии 2/5 и 1/5 частей
Согласно методике, представленной в школе умных детей, ребенок подводится к новым знаниям и умениям, но все выводы делает самостоятельно. И основной упор при объяснении дел делается на понимание ребенком смысла той или иной темы.
Как эффективно объяснить ребенку дроби?
Шаг первый — Ввести понятие «доли».

Детям показывают апельсин и предлагают разделить его на доли.
Один апельсин — это целый предмет. И состоит он из долей.
Мы делили апельсин. Много нас, а он один
Эта долька для ежа, эта долька для чижа…
А для волка — кожура.
На доли можно поделить многое: арбуз, яблоко, шоколад и даже квартиру (комната, кухня, коридор — все это доли квартиры)
Будет замечательно, если ребенок и вы возьмете и физически разделите шоколадку на доли, апельсинку на доли, мандаринку на доли.
Именно на этом шаге мы обращаем внимание на то, что один апельсин — это целый предмет, и его можно обозначить цифрой 1.
Шоколадка — целый предмет, или 1 шоколадка.
Вторым шагом необходимо ввести понятие «дробь».
Ведь мы шоколадку «разделили» или «раздробили» на части! Апельсин разделили или «раздробили» на доли!
Хорошим подспорьем являются детали ЛЕГО, из которых можно собрать целый прямоугольник и «раздробить» его на части.
На этом шаге можно нарисовать прямоугольник, разделить его на 4 равные части, например, и попросить ребенка закрасить (или отделить) одну часть, две части.
Нарисовать квадрат, раздробить его на 4 части. И попросить закрасить 2 части.
Шаг три — научить ребенка записывать часть
Передаем инициативу думать и делать выводы ребенку и задаем ему вопрос.
— Кто догадается, сколько всего частей в этом предмете?
— На сколько частей мы его раздробли? Разделили?
На четыре!
Вспоминаем, что деление (при делении в столбик, записывается чертой)
Так же и в дробях. Черта обозначает деление! На сколько частей мы разделили данный прямоугольник?
Так и напишем, делили на 4
А теперь сколько частей мы взяли? Закрасили?
А давай возьмем две части? Как закрасим? Как напишем?
Далее необходимо разделить прямоугольник на другое количество частей, и предожить взять две части. Спросите ребенка, как это показать?
Как записать, что взяли 2 части из 5?
Вспоминаем, что надо поставить черту (разделить), на 5 частей. И взять 2 части
И взять 2 части
Шаг 4 Переходим к записи целой части через дробь
Для этого шага пригодится шоколадка.
Можно спросить, сколько шоколадок? Одна.
— На сколько долек мы раздробили шоколадку? — На 8 долек.
— Как записать шоколадку, но с помощью дроби? На сколько разделили?
— На 8 частей.
— А в целой сколько частей?
8 частей или 8/8 целая шоколадка.
Далее возвращаемся и записываем целым предметом другие разделенные до этого предметы.
Шаг 5. Практика
Отломите три кусочка, дайте ребенку. Сколько дали? 3. От скольки? от 8!
Запишем полученную дробь 3/8!
Детали лего, полоски, прямоугольники, шоколад, конфеты, жвачки с дольками и т.п
В ход идет любой подручный материал.
Но одно условие — дробить надо на равные части.
Дети очень любят играть с дольками из пачки жвачки.
10/10 — это целая упаковка жвачки
2/10 — как в рекламе
6/10 — 6 долек из пачки жвачки
Шаг 6. Разбираемся в терминологии
И снова задаем ребенку вопросы и помогаем найти ответы.
— В числе 3/8 что обозначает число 8?
— На сколько поделили!
— Что означает число 3?
— Сколько взяли!
— Правильно, число долек, которое взяли. Его еще называют числитель.
Шаг 7. Задачки с подвохом
Предложите ребенку две дроби:
И поставить знак > в ту сторону, какая дробь больше
Для выполнения задания лучше взять шоколадку, в которой есть 20 долек.
И взять 2 дольки (приложить к дроби 2/20) и 4 дольки (приложить к дроби 4/20). Спросить, где больше. Глядя куда ворона откроет рот?
Техника ворона, благодаря которой детям можно объяснить тему сравнения чисел представлена в видео ниже:
Когда ребенок справится с этим заданием и подобными, усложняем задачу.
Пишем другой пример:
Вспоминаем шоколадку.
Взяли и там и там по две части. Но в первом случае, раздробили шоколадку на 20 долек, а во втором — эту же шоколадку, на 10 долек.
Конечно, лучше всего проделать это на практике.
Подобные сравнения — самая сложная тема для детей на этапе знакомства с темой дроби. Им кажется, что если число 20 больше, то и дробь тоже.
И именно здесь скрывается подводный булыжник.
Попробуйте и практикуйте с шоколадкой такие примеры.
Ребенок, при соблюдении последовательности шагов при объяснении темы, а так же, если вы не будете давать готовые решения и ответы, схватит тему и поймет ее.
А именно это является самым ценным.
Такой подход называется — проблемным обучением, или развитием в ребенке критического мышления. Когда мы ребенку не даем правило или ответ, но помогаем вывести его самому.
Ведь ребенок сам назвал, что шоколадку «раздробили», а значит узнал слово «дробь».
Сам вспомнил, как записывать деление чертой.
Сам ответил, что в примере 3/8, тройка — это число долек, которые «Взяли», числитель
Сам понял, что 8 — это на сколько поделили.
Практика в сочетании с правильной методикой обучения творит чудеса!
В школе умных детей вы найдете простые и понятные видео-ответы на все темы, получите уникальный опыт учителя и пошаговую инструкцию, как и что объяснить ребенку.
Чтобы дети, которые не понимают ту или иную тему или которым не повезло с учителем, имели возможность полюбить обучение, учиться у лучших учителей (в том числе по английскому у носителей языка)
Чтобы родители, которые совсем не педагоги, и не знают методик преподавания, имели инструмент, позволяющий легко и просто учить ребенка на семейном обучении или стать ребенку грамотным помощником дома, не тратя бюджет семьи на репетиторов.
Школа умных детей — это инвестиция, которая окупится уже в первые месяцы обучения ребенка.
Что вы получите?
Уроки по русскому и математике на 4-6 минут, это объяснение для родителей, как объяснить ребенку ту или иную тему, с какими сложностями можно столкнуться. Но многие наши родитетели напрямую включают уроки деткам (3-4 класс смело), а в 1-2 классе вместе смотрят и потом выполняют задания.
Уроки по английскому языку — это напрямую уроки для детей с отдельными поясняющими уроками и материалами для родителей.
Так же в школе открыта база знаний с техниками эффективного обучения: как учить стихотворения, определения, пересказывать текст, повысить скорость чтения и другие инструменты
И многое, много другое.
Сейчас в школе около 500 уроков на все сферы школьной жизни.
Доступ октрывается ко всем урокам начальных классов (1-4 классы) до мая 2019 года (1.5 учебных года вместо 1) при оплате в ноябре-декабре 2017 года
Получить объяснение всех тем начальной школы простым и эффективным языком
Получить объяснение всех тем начальной школы простым и эффективным языком
Наша система позволит вам отыскать самую короткую дорогу на пути к воспитанию умного, счастливого, успешного, талантливого ребенка, верящего в себя.
Вы получите четкую систему действий, которая заиграет ярко, живо и с любовью.
Станьте участником Школы умных детей уже сегодня и получите эффективную систему обучения ребенка.
Стать участником школы умных детей
Вам понравилась статья? Сохраните себе на стену, чтобы не потерять
Похожеестратегий умножения для 4-х и 5-х классов
Испытывают ли ваши ученики трудности с фактами умножения? Несмотря на то, что я думал в первые годы преподавания, им не нужно больше карточек. Им определенно не нужны тренировки или тесты по времени. Вместо этого им нужны стратегии, которые помогут им использовать то, что они действительно знают (более простые факты умножения или сложения), для решения любой проблемы. Прочтите этот пост, чтобы прочитать о 6 стратегиях умножения, которым я обучаю своих 4 -х -х и 5 -х -х классников, и получите бесплатные плакаты для печати, которые помогут вам обучить этим стратегиям своих учеников.
Им определенно не нужны тренировки или тесты по времени. Вместо этого им нужны стратегии, которые помогут им использовать то, что они действительно знают (более простые факты умножения или сложения), для решения любой проблемы. Прочтите этот пост, чтобы прочитать о 6 стратегиях умножения, которым я обучаю своих 4 -х -х и 5 -х -х классников, и получите бесплатные плакаты для печати, которые помогут вам обучить этим стратегиям своих учеников.
Обучение стратегиям умножения
Я пытаюсь научить стратегиям, которые можно применить к любой задаче умножения. Я никогда не добивался успеха в том, чтобы давать своим ученикам конкретные стратегии для использования с конкретными математическими фактами. Как правило, если ученик может вспомнить, чтобы удваивать, а затем удваивать, а затем удваивать для восьмерок, он действительно может запомнить математические факты.
Вместо этого я предпочитаю использовать стратегии умножения, которые являются концептуальными по своей природе и работают с любой задачей умножения (хотя некоторые из них определенно более эффективны с конкретными фактами умножения). Это не только имеет смысл, но и углубляет их понимание умножения, что приводит к большему успеху в решении словесных задач и деления.
Это не только имеет смысл, но и углубляет их понимание умножения, что приводит к большему успеху в решении словесных задач и деления.
Когда вы обучаете этим стратегиям?
Поскольку мое время ограничено учениками 4 и 5 классов, я обучаю этим стратегиям во время числовых бесед или небольших групп со студентами, которым это необходимо. Я стараюсь один день в неделю работать со своими учениками специально над их математическими навыками. Хотелось бы, чтобы у меня было больше времени, но, честно говоря, с учетом требований темпа и уровня знаний, которые нависают над нашими головами, один день в неделю иногда становится проблемой.
После введения и моделирования стратегии умножения я хотел бы предложить своим ученикам немедленную практику использования этого набора карточек задач стратегии умножения. Я использую эти карточки с заданиями в математическом центре или как часть урока интервенции в небольшой группе. Цель ознакомления с этими стратегиями, а затем их практики (с помощью карточек задач) — познакомить моих учеников с использованием различных стратегий. Мы надеемся, что это в конечном итоге приведет к тому, что они выберут наиболее эффективные для них и для конкретной проблемы, которую они решают.
Мы надеемся, что это в конечном итоге приведет к тому, что они выберут наиболее эффективные для них и для конкретной проблемы, которую они решают.
Стратегия умножения №1 — Повторное сложение
Это типичная стратегия, с которой начинают большинство студентов. Мне нравится поощрять своих учеников складывать быстрее (комбинируя) и складывать мысленно. Эта стратегия является основополагающей, которая поможет учащимся понять другие. Вот почему этому так много внимания уделяется в 3-м классе.
Если ваши ученики не могут выполнять повторное сложение, они могут столкнуться с трудностями при использовании более продвинутых стратегий умножения.Таким образом, даже если это может показаться утомительным и трудоемким, это важная основополагающая стратегия, которая приводит к более эффективным стратегиям (и помогает с концептуальным пониманием).
Стратегия умножения №2 — Массивы
Эта стратегия умножения для меня нова, и я использую ее особым образом. Я не призываю своих учеников обязательно рисовать массивы. Вместо этого я использую визуальные эффекты различных массивов, чтобы помочь им увидеть связи и известные факты «внутри» более сложного факта.
Я не призываю своих учеников обязательно рисовать массивы. Вместо этого я использую визуальные эффекты различных массивов, чтобы помочь им увидеть связи и известные факты «внутри» более сложного факта.
Как вы можете видеть из этого примера, 4 x 4 можно визуально разложить на 2 x 4 и 2 x 4. Это помогает студентам решить для 4 x 4. При использовании этой стратегии я предлагаю студентам поделиться как можно большим количеством разложения, как они могут найти, и мы записываем задачи умножения, которые совпадают.
Эта стратегия специально помогает студентам «разложить» более сложную задачу умножения на более мелкие задачи, которые они знают автоматически. Использование массивов — отличный способ помочь студентам визуализировать декомпозиции.Это поможет ученикам понять более сложные стратегии умножения.
Стратегия умножения №3 — Использование единиц, двоек и пятерок
Стратегия декомпозированного массива ведет прямо к следующей стратегии. В этой стратегии учащиеся используют свои известные факты (обычно 1, 2 и 5) для решения неизвестных фактов.
Здесь вы можете увидеть, что 8 x 4 можно решить, разложив 8 на 5, 2 и 1 и решив (некоторые ученики могут сделать 5 и 3). И 6 x 7 можно разложить на 5 x 7 и 1 x 7, чтобы найти произведение.Это отличный способ научить учеников решать более сложные математические факты и подготовить их к умножению частичных произведений.
Щелкните здесь, чтобы прочитать более подробный пост об этой стратегии умножения и взять еще несколько печатных форм.
Стратегия умножения №4 — Подсчет пропусков с поворотом
Как и при повторном сложении, подсчет пропусков — еще одна основополагающая стратегия, которую учащиеся изучают в 3-м классе. Мне нравится расширять это, предлагая учащимся использовать свои навыки подсчета пропусков для решения неизвестных фактов умножения, для которых они не могут пропустить счет (например, 4s, 6s, 8s).
Как видно из примера, учащиеся могут использовать свой счет пропусков по 5 и 2 секунды для решения семерки. Это не моя любимая стратегия, и она работает не со всеми учениками, но некоторые действительно тяготеют к ней.
Стратегия умножения №5 — Добавить группу
Стратегия «Добавить группу» такая же, как следует из названия. Учащиеся используют факт умножения на одну группу меньше (и более простой или известный факт), чтобы помочь им вывести неизвестный факт.
Как видно из примера на изображении, учащиеся могут использовать 5 x 6, чтобы решить 6 x 6, добавив еще одну группу от 6 до 30.Или они могут решить 3 x 8, добавив еще одну группу из 8 к решению 2 x 8.
Как я уже упоминал выше, я предпочитаю использовать стратегии умножения, которые работают независимо от того, в чем проблема. Однако в этой (и в следующей) стратегии есть конкретные факты умножения, с которыми они лучше всего работают.
Стратегия «Добавить группу» (по моему опыту) лучше всего работает при решении 3, 4 и 6 (с использованием 2, 3 и 5 соответственно).
Стратегия умножения №6 — Уберите группу
Подобно описанной выше стратегии, в этой стратегии учащиеся «уводят группу».Стратегия «Убери группу» (по моему опыту) лучше всего работает при решении 4 и 9 (используя 5 и 10 соответственно).
Возьмите здесь плакаты со стратегиями умножения!
Надеюсь, этот пост был информативным, и вы сможете использовать эти стратегии со своими учениками. Щелкните здесь, чтобы получить распечатанные плакаты со стратегиями умножения, показанные в этом посте.
Советы для успеха
- Представляйте каждую стратегию по отдельности и позволяйте непосредственно целенаправленно практиковаться с этой стратегией.В конечном итоге студенты будут стремиться к стратегиям, которые лучше всего подходят для них (или для конкретных задач, которые они решают). Однако мы хотим убедиться, что обеспечиваем столь необходимую практику в каждой стратегии. Щелкните здесь, чтобы увидеть карточки задач стратегий умножения, которые я использую, чтобы помочь в этой практике.
- Назовите стратегии. Присвоение названий стратегиям помогает учащимся поделиться ими, а также помогает, когда учащиеся застряли и нуждаются в предлагаемой стратегии.
- Поощряйте учащихся использовать свои стратегии при решении задач умножения, особенно когда они решают работу на уровне своего класса со встроенными фактами умножения.

- Повесьте плакаты или раздайте учащимся копии стратегий. Это соответствует приведенному выше совету. Поощряя студентов использовать стратегии, им может потребоваться поддержка и напоминания о доступных им стратегиях.
- Помните о сохранении концептуального понимания.Известно, что я сам использую уловки, но я всегда очень стараюсь сохранить концептуальное понимание и избегаю уловок до тех пор, пока это абсолютно необходимо (если вообще возможно). Концептуальное понимание умножения является ключевым для учащихся, когда они используют эти стратегии (и когда они решают словесные задачи).
Понимают ли ваши ученики умножение концептуально?
Если ваши 4–5-классники все еще испытывают трудности с концептуальным пониманием умножения, они могут столкнуться с трудностями при использовании этих стратегий по мере того, как они выстраивают свое понимание.Стратегии концептуальны, поэтому их использование поможет. Однако, если вашим ученикам нужно исправить концептуальное умножение, ознакомьтесь с моими карточками задач «Умножение», щелкнув здесь или на изображение ниже.
БОЛЬШЕ Free Multiplication Facts Деятельность и ресурсы
Предварительный тест на концептуальное понимание умножения БЕСПЛАТНО
Бесплатный набор фактов об умножении и делении на дом
Бесплатные игры на умножение и деление. Факты — партнеры
Ваш четвероклассник и математика в соответствии со стандартами Common Core
Математика для четвертого класса хороша тем, что идеально подходит для игр.Помогите ребенку измерить скорость на скейтборде. Испеките два пирога и сделайте несколько воображаемых кусочков и кубиков, чтобы помочь вашему ребенку найти эквивалентные дроби или вычесть дроби с разными знаменателями (нижнее число). Занятия математикой действительно помогут вашему ребенку в долгосрочной перспективе.
Вот 12 математических навыков, которые ваш ребенок должен освоить к концу четвертого класса:
- Решение многоступенчатых задач со словами с использованием сложения, вычитания, умножения и деления.
- Понимание факторов числа и способы их определения.

- Понимание разницы в 1000000.
- Умножение и деление двух двузначных чисел и умножение четырехзначного числа на однозначное число.
- Решение задач деления с остатком в ответе.
- Нахождение общих знаменателей (нижние числа) двух и более дробей.
- Умножение дроби на целое число.
- Сложение и вычитание смешанных чисел с одинаковым знаменателем (например, 3 1 ⁄ 2 + 1 ⁄ 2 ).
- Сравнение дробей с разными числителями (верхнее число) или знаменателями (нижнее число) или сравнение дробей с единичной дробью, например 1 ⁄ 2 .
- Сравнение двух десятичных знаков с точностью до сотых.
- Понимание взаимосвязи различных единиц измерения, например, 12 дюймов = 1 фут.
- Изучение свойств различных форм, включая измерение их углов.
Нам нужно работать
Четвероклассники достаточно опытны, чтобы решать многоступенчатые задачи со словами, используя любую из четырех операций — сложение, вычитание, умножение и деление — с уравнениями.
Например: у Кейли 272 бусинки. Она покупает еще 38 бусин. Из 85 бусинок она сделает браслеты, а из остальных — ожерелья. Ей нужно 9 бусинок на каждое ожерелье. Сколько ожерелий может сделать Кейли?
272 + 38 = 310. 310 — 85 = 225. 225 ÷ 9 = 25 ожерелий
Ваш ребенок научится находить пары множителей для целых чисел до 100. Это два числа, которые при умножении равно исходному целому числу.
Например: 88 имеет 4 пары факторов: 2 x 44; 4 х 22; 8 х 11; и 88 x 1
Один на миллион
Четвероклассники учатся читать, писать и понимать числовые значения вплоть до 1 000 000.Начиная с единиц, каждое место слева в 10 раз больше.
Например: 987 654 = 900 000 + 80 000 + 7 000 + 600 + 50 + 4.
С таким пониманием разряда ваш ребенок начнет работать с большими числами, включая сложение и вычитание целых чисел до 1 000 000, умножение два двузначных числа и умножение четырехзначного числа на однозначное число.
Например, :
Четвероклассники также учатся делить четырехзначное число на однозначное число с поворотом.В этом году они научатся делить на остатки, когда делимое (число, которое делится) нельзя разделить на равные части.
Например: 9,375 ÷ 7 = 1339 остаток 2 или 1339 R2.
Расчет дробей
Четвероклассники получают более глубокое понимание дробей. Они складывают и вычитают дроби с одинаковым знаменателем (нижнее число).
Например:
Они также складывают и вычитают смешанные числа с тем же знаменателем.
Например: 5 1 ⁄ 3 + 8 1 ⁄ 3 = 13 2 ⁄ 3
10 4 ⁄ 5 — 5 5 — 5 5 = 5 2 ⁄ 5
Четвероклассники учатся находить общие знаменатели, когда эти числа разные. Это помогает научить студентов об эквивалентных дробях — дробях, имеющих одинаковое значение, — даже если их числители (верхние числа) и знаменатели (нижние числа) различаются.
Например: 1 ⁄ 2 эквивалентно 4 ⁄ 8 .
Студенты также учатся умножать дроби на целые числа и понимать, почему произведение (ответ) меньше целого числа.
Например: 7 x 1 ⁄ 8 = 7 ⁄ 8 . Его также можно записать как 7 ⁄ 1 x 1 ⁄ 8 .
Ваш ребенок будет решать задачи со словами, которые требуют сложения, вычитания или умножения целых чисел на дроби.
Например: Райан делает рюкзаки. Он использует ярда ткани, чтобы сделать каждую. Какое общее количество ткани в ярдах Райан использует для изготовления 6 рюкзаков? 6 x 3 ⁄ 4 = 6 ⁄ 1 x 3 ⁄ 4 = 18 ⁄ 4 = 4 1 ⁄ 2 ярдов.
Четвероклассники также учатся переводить дроби со знаменателем 10 или 100 в десятичные и отображать их в числовой строке.
Например: 91 ⁄ 100 = 0,91
По любым меркам
Как долго эта игуана находится в вашей ванне? Один ярд? Три фута? 36 дюймов? Да, да и да: это все вышеперечисленное. Четвероклассники изучают взаимосвязь между различными единицами измерения в каждой системе. В США 12 дюймов равны одному футу, а три фута равны одному ярду. В метрической системе, основанной на 10, требуется 10 миллиметров, чтобы равняться одному сантиметру, и 100 сантиметрам, равным одному метру.
В четвертом классе ваш ребенок будет использовать сложение, вычитание, умножение и деление для решения мировых задач, связанных со временем, расстоянием, объемом, массой и деньгами. Вопросы часто включают дроби и десятичные дроби, и от студентов требуется проиллюстрировать проблему на диаграмме или числовой прямой.
Например: Сара едет со скоростью 60 миль в час до Сент-Луиса, что в 100 милях отсюда. Сколько минут нужно, чтобы добраться туда? Сколько часов?
Куда делась эта сторона?
Четвероклассники учатся решать реальные задачи по определению периметра или площади фигуры, даже если длина одной стороны неизвестна. Они будут применять сложение, вычитание, умножение и деление к формулам для площади и периметра.
Они будут применять сложение, вычитание, умножение и деление к формулам для площади и периметра.
Например: Площадь = длина x ширина
Периметр = сумма длин всех сторон.
Четвероклассник изучит еще несколько свойств, используемых для классификации форм, например, имеет ли форма перпендикулярные или параллельные линии. Дети также работают с углами фигур. Вы можете ожидать, что ваш ребенок будет использовать транспортир для измерения углов, определять прямой угол, когда он его видит, и знать, что сумма углов в треугольнике всегда составляет 180 градусов, а в прямоугольнике — всегда 360 градусов.
Правда, здесь есть несколько более сложных концепций. Если домашнее задание вашего ребенка по математике кажется вам немного сложнее, чем то, что вы помните, наберитесь духа. Сохраняйте позитивное отношение к математике и постарайтесь развлечься, помогая своему ребенку с математикой в этом году.
Посмотрите, как выглядят четвероклассники, работающие на уровне класса с дробями, в наших видеороликах «Вехи»:
• Сравнение дробей
• Дроби в задачах со словами
Поделиться в Pinterest
Обновлено: 2 декабря 2019 г.
Соединение фактов умножения и деления — элементарная математика
Назначение
Для идентификации и предоставления связанных фактов умножения и деления
Материалы
Нет
Обзор
Дайте учащимся два множителя (например, 3 x 7), попросите учащихся дать произведение (21), а затем попросите одного учащегося указать связанный факт деления (например, 21 ÷ 7 = 3).Чтобы учащиеся были внимательны, укажите факторы и попросите учащихся отреагировать на продукт, прежде чем выбрать учащегося, чтобы сообщить соответствующий факт. Чтобы не терять темп, вы можете случайным образом выбирать учеников, используя колоду именных карточек.
О последовательности
Часть 1 просит студентов представить произведение двух факторов, за которым следует частное соответствующего факта деления, используя коэффициенты, меньшие или равные 5. В части 2 используются коэффициенты до 10, а в расширении предлагается практика с коэффициентами до 12.
Часть 1
Давайте попробуем наши факты умножения. Я приведу набор факторов, и вместе мы назовем продукт. Затем доброволец предоставит один связанный факт деления. Например, если я скажу 2 x 4, произведение равно 8, и один связанный факт деления будет 8 ÷ 4 = 2 (или 8 ÷ 2 = 4). Вот так!
Примеры:
- 2 × 5 (10, связанный факт деления 10 ÷ 5 = 2 или 10 ÷ 2 = 5)
- 3 × 2 (6, связанный факт деления 6 ÷ 3 = 2 или 6 ÷ 2 = 3
- 3 × 3 (9, связанный факт деления 9 ÷ 3 = 3)
- 2 × 2 (4, связанный факт деления 4 ÷ 2 = 2)
- 4 × 3 (12, связанный факт деления 12 ÷ 3 = 4 или 12 ÷ 4 = 3)
- 4 × 4 (16, связанный факт деления 16 ÷ 4 = 4)
- 5 × 3 (15, связанный факт деления 15 ÷ 5 = 3 или 15 ÷ 3 = 5)
- 5 × 4 (20, связанный факт деления 20 ÷ 4 = 5 или 20 ÷ 5 = 4)
Пока дети наслаждаются развитием мастерства, не стесняйтесь повторять.Когда дети хотят большего, попробуйте Часть 2.
Часть 2
Давайте продолжим работать над нашими связанными фактами умножения и деления, но на этот раз мы пойдем еще быстрее. (В какой-то момент вы можете позволить студентам вести это задание.)
(В какой-то момент вы можете позволить студентам вести это задание.)
Примеры:
- 5 × 8 (40, связанный факт деления 40 ÷ 8 = 5 или 40 ÷ 5 = 8)
- 9 × 5 (45, связанный факт деления 45 ÷ 9 = 5 или 45 ÷ 5 = 9)
- 7 × 6 (42, связанный факт деления 42 ÷ 6 = 7 или 42 ÷ 7 = 6)
- 6 × 10 (60, связанный факт деления 60 ÷ 6 = 10 или 60 ÷ 10 = 6)
- 10 × 10 (100, связанный факт деления 100 ÷ 10 = 10)
- 6 × 8 (48, связанный факт деления 48 ÷ 8 = 6 или 48 ÷ 6 = 8)
- 9 × 4 (36, связанный факт деления 36 ÷ 4 = 9 или 36 ÷ 9 = 4)
- 9 × 9 (81, связанный факт деления 81 ÷ 9 = 9)
Как всегда, когда кажется, что дети взволнованы новой задачей, двигайтесь дальше.
добавочный номер
Теперь давайте найдем еще несколько продуктов и связанных с ними фактов о подразделениях.
Примеры:
- 11 × 10 (110, связанный факт деления 110 ÷ 10 = 11 или 110 ÷ 11 = 10)
- 11 × 8 (88, связанный факт деления 88 ÷ 8 = 11 или 88 ÷ 11 = 8)
- 11 × 5 (55, связанный факт деления 55 ÷ 5 = 11 или 55 ÷ 11 = 5)
- 12 × 8 (48, связанный факт деления 48 ÷ 8 = 12 или 48 ÷ 12 = 8)
- 11 × 3 (33, связанный факт деления 33 ÷ 3 = 11 или 33 ÷ 11 = 3)
- 12 × 5 (60, связанный факт деления 60 ÷ 5 = 12 или 60 ÷ 12 = 5)
- 12 × 7 (84, связанный факт деления 84 ÷ 7 = 12 или 84 ÷ 12 = 7)
- 11 × 9 (99, связанный факт деления 99 ÷ 9 = 11 или 99 ÷ 11 = 9)
- 12 × 3 (36, связанный факт деления 36 ÷ 3 = 12 или 36 ÷ 12 = 3)
Объединенные школы Уоррена
Математика для четвертого класса
Блок 2: Шаблоны и отношения деления умножения
Что будет изучать ваш ребенок в Блоке 1?
В Блоке 2 четвероклассники рассмотрят основные стратегии обоснования фактов для умножения и деления. Они проанализируют закономерности в продуктах фактов умножения и рассмотрят взаимосвязь между умножением и делением. Свойства умножения будут рассмотрены в Блоке 2. Эти свойства помогут учащимся решать задачи многозначного умножения и деления в Блоке 3. В таблице ниже перечислены свойства умножения.
Они проанализируют закономерности в продуктах фактов умножения и рассмотрят взаимосвязь между умножением и делением. Свойства умножения будут рассмотрены в Блоке 2. Эти свойства помогут учащимся решать задачи многозначного умножения и деления в Блоке 3. В таблице ниже перечислены свойства умножения.
В 3-м классе ученики изучали умножение равными группами и повторное сложение.В четвертом классе ученики познакомятся с умножением как сравнением. В задачах мультипликативного сравнения сравниваются два разных набора. Первый набор содержит определенное количество предметов. Второй набор содержит несколько копий первого набора. Любые два фактора и их произведение можно рассматривать как сравнение. Студенты будут решать задачи со словами, чтобы понимать умножение как сравнение. В приведенной ниже таблице показаны различные типы задач для умножения и деления.Задачи сравнения находятся в центре внимания четвертого класса.
Кроме того, четвероклассники будут генерировать и анализировать числовые модели. Шаблоны чисел позволяют учащимся закрепить факты и развить свободное владение операциями. Паттерн — это последовательность, которая повторяет один и тот же процесс снова и снова. Правило диктует
как будет выглядеть этот процесс. Учащиеся исследуют различные шаблоны, чтобы найти правила, определить особенности в шаблонах и обосновать причину этих особенностей.См. Пример ниже.
Шаблоны чисел позволяют учащимся закрепить факты и развить свободное владение операциями. Паттерн — это последовательность, которая повторяет один и тот же процесс снова и снова. Правило диктует
как будет выглядеть этот процесс. Учащиеся исследуют различные шаблоны, чтобы найти правила, определить особенности в шаблонах и обосновать причину этих особенностей.См. Пример ниже.
Какие математические стратегии будет использовать ваш ребенок в Блоке 2?
Ваш ребенок усвоил в третьем классе различные стратегии для решения основных задач умножения и деления. В раздаточном материале ниже дается объяснение различных типов стратегий.
Посмотрите видео ниже, чтобы увидеть некоторые математические стратегии в действии.
Некоторые объяснения от школьников нашего района. Спасибо студентам за то, что они добровольно объяснили свои мысли!
Стратегии умножения:Как вы можете поддержать своего ребенка дома, чтобы закрепить концепции, изложенные в Блоке 2?
Есть несколько способов заставить вашего ребенка практиковать математические понятия дома. Попробуйте следующие задания:
Попробуйте следующие задания:
- Попросите вашего ребенка создать задачу-рассказ, в которой для решения задачи используется умножение или деление.Предложите ему или ей создать различные типы сюжетных задач.
- Дайте ребенку карточку с задачей на деление. Попросите ребенка найти карточку умножения, которую можно использовать для решения задачи деления. Например, для 12 ÷ 3 ваш ребенок найдет 3 x 4.
- Посетите веб-сайт Exploring Number Patterns , чтобы предложить вашему ребенку изучить числовые шаблоны.
- Посетите Rectangle Division , чтобы ваш ребенок представил любое двузначное число как произведение двух чисел.
- Попросите вашего ребенка выполнить Умножение как задачи сравнения .
- Математические игры для дома : Распечатайте раздаточные материалы, чтобы практиковать концепции в играх.
Задачи на умножение слов 4 класс
Добро пожаловать в наши задачи на умножение слов для 4-го класса.
Здесь вы найдете наш диапазон печатных задач умножения. которые помогут вашему ребенку применять и практиковать свои навыки умножения и умножения для решения ряда «реальных» проблем. на уровне 4-го класса.
Здесь вы найдете ряд рабочих листов для решения задач, связанных с умножением.
Каждый лист включает в себя решение ряда письменных задач на умножение.
Для каждого рабочего листа ниже есть 3 уровня сложности: A, B и C.
Рабочий лист A — самый простой уровень, подходящий для детей в начале их класса.
Рабочий лист B — это рабочий лист среднего уровня для детей, которые работают на ожидаемом уровне в своем классе.
Рабочий лист C задан на более сложном уровне, подходящем для более способных математиков.
Задачи на каждом листе похожи по формулировке, но их числа усложняются по мере того, как уровень становится сложнее.
Чтобы способствовать развитию навыков тщательной проверки и мышления, на каждом листе есть один «хитрый» вопрос, который не является проблемой умножения. Детям необходимо определить эту словесную проблему и решить, какую операцию им необходимо решить.
Детям необходимо определить эту словесную проблему и решить, какую операцию им необходимо решить.
Использование этих листов поможет вашему ребенку:
- применить свои навыки умножения и умножения на 4-м классе;
- применять свои знания таблицы умножения для выяснения связанных фактов;
- распознает проблемы с умножением и пытается обнаружить «хитрые» проблемы;
- решить ряд проблем «реальной жизни».
Некоторые листы имеют версию для Великобритании с орфографическими символами и символами валюты, установленными для Великобритании.
В нашей области задачи умножения слов для 3-го класса вы найдете ряд задач на умножение, предназначенных для учеников 3-го класса.
Охватываются следующие области:
- основные информационные бюллетени по умножению;
- фактов умножения до 10х10;
- 2 цифры x 1 цифра
В нашей области задач умножения слов для 5-х классов вы найдете ряд задач на умножение, предназначенных для 5-х классов.
Охватываются следующие области:
- информационные бюллетени по умножению;
- фактов, связанных с умножением на 10х10, например 6 х 70, 8 х 0,6 и т. Д .;
- задач, для решения которых требуются письменные методы умножения, например: 2 цифры x 2 цифры, десятичное умножение
Взгляните на еще несколько наших рабочих листов, похожих на эти.
Вот наш набор математических задач для 4-го класса, который поможет вашему ребенку научиться решать проблемы.
Каждый лист проблем поставляется с ответами и доступен как в стандартных, так и в метрических единицах измерения, где это возможно.
Многие из проблем основаны на «реальных» проблемах и данных, например о самых тяжелых животных в мире.
Использование этих листов поможет вашему ребенку:
- применяют свои навыки сложения, вычитания и решения задач;
- применяют свои знания в области округления и разметки;
- решает ряд «реальных» проблем;
- пытается решить более сложные и длинные задачи.

Использование задач из этого раздела поможет вашему ребенку развить навыки решения проблем и рассуждения.
Здесь вы найдете подборку таблиц времени умножения. до 10×10 или 12×12, чтобы помочь вашему ребенку в изучении Факты умножения.
Существует широкий выбор таблиц умножения, в том числе цветные и черно-белые, диаграммы меньшего размера, диаграммы с заливкой и пустые диаграммы.
Использование этих таблиц поможет вашему ребенку:
- Узнайте их факты умножения на 10х10 или 12х12;
- Попрактикуйтесь в их таблице умножения.
Все бесплатные печатные математические таблицы в этом разделе основаны на тестах Elementary Math Benchmarks.
Здесь вы найдете ряд бесплатных печатных игр на умножение.
Следующие игры развивают математические навыки умножения в увлекательной и мотивирующей форме.
Использование этих листов поможет вашему ребенку:
- узнать их факты умножения;
- попрактикуйтесь и улучшите отзыв своей таблицы умножения;
- развивают навыки стратегического мышления.

Саламандры-математики надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
БЕСПЛАТНЫХ заданий по математике для 4-го класса
Помогите своим детям получить дополнительные практических занятий по математике с помощью этих бесплатных распечатываемых листов по математике для 4-го класса. Эти бесплатные распечатанные рабочие листы для 4-го класса не требуют подготовки, скачайте файл в формате pdf… распечатайте… .go! Эти бесплатные рабочие листы домашнего обучения идеально подходят для летнего обучения, математических центров и дополнительной практики с по математике для 4 класса , а также для того, чтобы помочь детям овладеть математикой в четвертом классе.
Задания по математике для 4-го класса
Мы всегда ищем забавные способы для наших учеников 4-х классов практиковать математику. Это настолько важно не только для более продвинутой математики, но и для их жизни, что они получают много практики, чтобы сформировать прочную основу и достичь беглости в математике. Поэтому мы стараемся сделать это увлекательным, чтобы они с нетерпением ждали и получали удовольствие от занятий математикой. Эти рабочие листы по математике для 4-го класса можно использовать как бесплатные задания по математике или превратить в бесплатную математическую игру для отработки сложения, вычитания, умножения, деления, дроби, задач со словами и многого другого.
Это настолько важно не только для более продвинутой математики, но и для их жизни, что они получают много практики, чтобы сформировать прочную основу и достичь беглости в математике. Поэтому мы стараемся сделать это увлекательным, чтобы они с нетерпением ждали и получали удовольствие от занятий математикой. Эти рабочие листы по математике для 4-го класса можно использовать как бесплатные задания по математике или превратить в бесплатную математическую игру для отработки сложения, вычитания, умножения, деления, дроби, задач со словами и многого другого.
Рабочие листы 4-го класса
Родителям, учителям или ученикам на дому — вам понравится, что эти распечатанные математические листы помогают детям практиковать различные навыки, такие как сложение (включая трехзначное сложение), вычитание (включая трехзначное вычитание), умножение, деление , дроби, задачи со словом, счет денег и многое другое по математике для четвертого класса.Используйте их в математическом центре в качестве дополнительной практики, работы с сиденьями, математической игры для четвертого класса или летнего обучения, чтобы помочь детям избежать потери учебы летом.
Получите эту бесплатную услугу, прокрутив до конца сообщения, в соответствии с условиями использования, и щелкнув текстовую ссылку, которая гласит >> Загрузить
Ищете другие из наших бесплатных рабочих листов по математике ? Попробуйте эти:
Бесплатные задания по математике для 4-го класса
Это математическое задание БЕЗ ПОДГОТОВКИ отлично подходит для превращения заданий по математике в математическую игру. Просто дайте учащимся один из заданий (они идут в порядке сложности), и вы готовы к 4-му классу математики.
Хотя вы, безусловно, можете использовать эти математические рабочие листы традиционным способом — раздайте их детям, а дети решают математические уравнения, а затем вы их проверяете… Мы предпочитаем развлекать их с помощью MAD MINUTES !
4-й класс по математике
Бесплатные рабочие листы по математике для 4-го класса делают занятия по математике увлекательными, увлекательными и запоминающимися для учеников 4-го класса не только заниматься математикой , но и улучшать запоминание и беглость по математике . Студенты будут лучше запоминать их, повторяя одни и те же задачи изо дня в день, пока им не станет лучше — и они вернутся, чтобы исправить свою работу, чтобы повысить точность.
Студенты будут лучше запоминать их, повторяя одни и те же задачи изо дня в день, пока им не станет лучше — и они вернутся, чтобы исправить свою работу, чтобы повысить точность.
Задания по математике для 4-го класса
Полные инструкции для этих бесплатных рабочих листов по математике для 4-го класса включены в загрузку, но вот суть. Вы даете своему четверокласснику лист «Безумные минуты» лицевой стороной вниз. Установите таймер на 3-5 минут, и когда вы скажете «ИДТИ», они перевернут Рабочий лист «Безумные минуты» и начнут решать математические задачи. Напомните им, что цель — это не только скорость, но и точность.
Рабочие листы для печати по математике
Когда таймер подает звуковой сигнал, они останавливаются. Теперь перейдите к правильным ответам. ( В конце рабочего листа есть ключи для ответов). Сколько они закончили? Сколько они получили права?
Продолжайте использовать те же рабочие листы, пока они не заполнят не менее 90% с точностью 90% за 3-5 минут.
Вам понравится, что в каждый рабочий лист включен ключ с ответом!
Умножение Факты Игры
Деятельность отдела
Ищете еще веселые бесплатные распечатанные игры на деление для детей, чтобы они могли практиковать математику и научиться бегло говорить? Вам понравятся эти листы деления, распечатанные игры на деление и многое другое!
Рабочие листы 4-го класса
Скачивая с моего сайта, вы соглашаетесь со следующим:
- Это только для личного пользования (учителя, пожалуйста, смотрите мой магазин TPT)
- Запрещается продавать, размещать, воспроизводить или хранить на любом другом сайте (включая блог, Facebook, Dropbox и т. Д.))
- Все загруженные материалы защищены авторским правом. См. Условия использования.
- Я предлагаю бесплатные печатные издания, чтобы благословить моих читателей И обеспечить свою семью. Ваши частые посещения моего блога и поддержка покупок по партнерским ссылкам и рекламе заставляют светиться, так сказать.
 Спасибо!
Спасибо!
>> Скачать Минуты безумия 4-го класса
Go math Распределительная собственность 3-го класса
19 февраля 2019 · Мы закончили пятничную работу над распределительной собственностью.Было довольно интересно работать — предстоит еще многому научиться. Мы снова рассмотрели, что такое термины и как перемножать переменные. Я работал над временем ожидания и пытался найти хорошее во всех их ответах, продолжая продвигать их вперед.
Списки словаря математики 3-го класса основаны на Общих математических стандартах. VocabularySpellingCity выбрал академическую лексику, относящуюся к ключевым математическим концепциям 3-го класса, с содержательными примерами предложений и определениями, написанными в соответствии с уровнем математики для третьего класса.
Таблицы функций Рабочие листы Входящие и исходящие ящики Рабочие листы. Вот графический предварительный просмотр всех рабочих листов таблицы функций и рабочих листов входных и исходящих ящиков. Вы можете выбрать различные переменные, чтобы настроить эти рабочие листы таблицы функций и рабочие листы входных и исходящих ящиков в соответствии с вашими потребностями.
Вы можете выбрать различные переменные, чтобы настроить эти рабочие листы таблицы функций и рабочие листы входных и исходящих ящиков в соответствии с вашими потребностями.
Экзамен по математике для четвертого класса Common Core, который в вашем штате используется для оценки усвоения учебной программы Common Core, оценивает учащихся по ряду связанных с математикой концепций, которыми должны владеть четвероклассники, включая умножение, числовые значения до 1000000, сложение и вычитание дробей и более сложная геометрия.
Свойство распределения позволяет вам «распределить» число по каждому слагаемому в круглых скобках. Он предлагает другой способ решения проблемы. Запишем свойство как a x (b + c) = (a x b) + (a x c). Несмотря на свою мощь, свойство распределения может быть сложным. Вот пример. Этот массив показывает 3 x 6.
Умножение, массивы и свойство распределения ВСЕ ЗДЕСЬ! Мы включили: концептуальные плакаты (1-умножение, 1-массив, 1-распределительное свойство) Словарные карточки (для изучения или использования в играх, таких как запоминание или ловля рыбы) Страницы практики (3) Викторина: на уровне И с изменениями, оба с и без t
Привет всем, скоро у меня будет очень важный тест по математике, и я был бы очень признателен, если бы кто-нибудь из вас помог мне решить некоторые вопросы в калькуляторе распределительных свойств упрощенных выражений. В остальном я неплохо разбираюсь в математике, но проблемы, по крайней мере, общие, сбивают меня с толку, и я в растерянности.
В остальном я неплохо разбираюсь в математике, но проблемы, по крайней мере, общие, сбивают меня с толку, и я в растерянности.
1 августа 2016 г. · Используйте математические вычисления для завершения шаблона. x x x x x x 30 Урок АЛГЕБРЫ 1.5 ОБЩИЙ ОСНОВНОЙ СТАНДАРТ CC.5.NBT.2 Разберитесь в системе разметки. 3. 27 270 2700 27000 16 1 (8 xx 101 — (8 x 3) x 102 — (8 x 3) x 103 — 240 2400 24000 2. 5.
Тригонометрический круг. Основные значения тригонометрических функций
Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг:
Мы же здесь будем все подробно разбирать шаг за шагом + показать
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул, чему равен синус, скажем, градусов, или .
Никак?.. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – .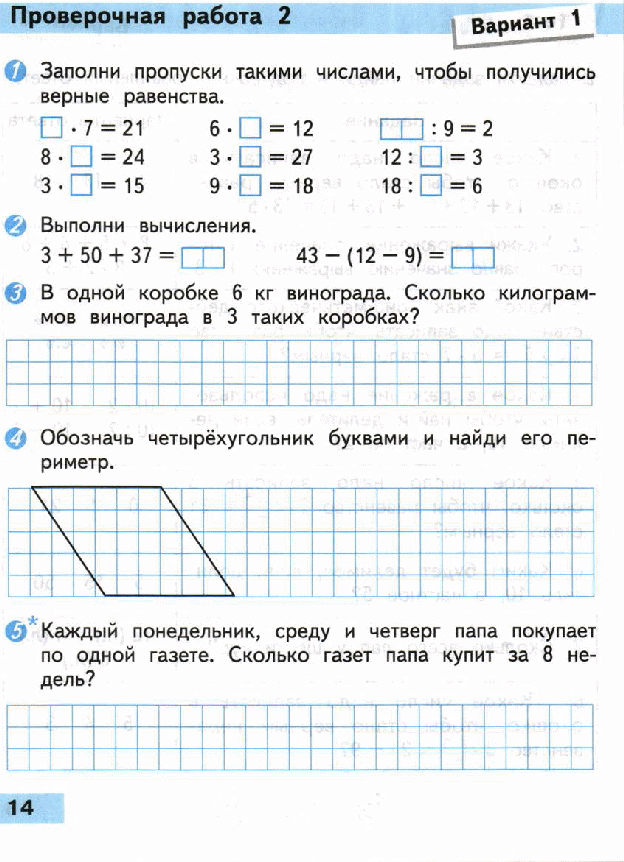 То есть нас будет больше интересовать цепочка .
То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть ).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Наконец, что такое синус, косинус в прямоугольном треугольнике?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов, а ось (oy) – осью синусов. Про тангенс и котангенс позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг, без которого никуда в тригонометрии.
А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.
Планирование: 4 класс по математике
4 класс
Планирование
Перейти к содержанию Щиток приборовАвторизоваться
Панель приборов
Календарь
Входящие
История
Помощь
- Мой Dashboard
- Класс 4
- Страницы
- Планирование
- Home
- Routines
- Closure
- Resource Bank
- Grade 3 Course
- Grade 4 G / T
- Grade 5 Course
- Grade 4 Curriculum Community
- Grade 4 Family and Community
- Collaborations
- Google Drive
- HCPSS.
 мне
мне
Как сделать ваших детей независимыми в математических центрах
Представьте себе это. Ваши ученики, работающие в независимых математических центрах, выполняют значимую математическую работу, в то время как вы делаете свою небольшую группу под руководством учителя. Как бы это было? Отлично, правда? Это может стать вашей реальностью.
Math center time — отличный способ удовлетворить потребности всех ваших учеников, но одна из самых больших проблем, из-за которых математические центры терпят неудачу, — это отсутствие последовательности.
Это может выглядеть по-разному … Студенты тихо сидят за столом и не работают над заданием, студенты говорят о том, что они делали на прошлых выходных, вместо того, чтобы участвовать в разговоре по математике, или студенты постоянно прерывают ваш урок в небольшой группе и заявляют, что они не делают этого. не знаю что делать.
За время своего многолетнего преподавания я обнаружил, что лучший способ сделать студентов независимыми во время обучения в математических центрах — это включить эти 7 ключевых компонентов во время обучения в центрах.
СОВЕТ №1: Всегда сначала моделируйте
Прежде чем я даже помещаю новое задание или игру в ротацию математического центра, я обязательно моделирую, как играть в нее перед всем классом. Это знакомит учащихся с ожиданиями и сокращает количество высказываний учащихся о том, что они не знают, что им делать, когда они находятся в центрах без учителя. Это можно сделать двумя способами:
- Модель «Учитель-ученик» — Вы притворяетесь учеником.Выберите одного ученика из вашего класса и затем подумайте вслух. (Пример: «Теперь я буду вращать вертушку, потому что сейчас моя очередь»).
- Модель «студент-студент» — Выберите 2–3 учащихся для выполнения задания. Направляйте их и задавайте вопросы студентам, которые наблюдают за студентами, моделирующими деятельность. (Пример: «Что ему делать дальше?»)
Познакомьтесь с процедурами и процедурами этих бесплатных математических игр, центров и моделей для ваших учеников уже завтра.
Ищете математические центры, соответствующие стандартам? Нажмите на свой уровень обучения ниже:
СОВЕТ № 2: Создание фото-маршрутов
Итак, теперь вы смоделировали, но мы знаем наших детей, не так ли? Существует высокая вероятность того, что после того, как вы отправите своих детей на их рабочие места, кто-то все равно скажет: «Что мы должны делать?» Устраните это, следуя простым указаниям на фотографиях.
Фото-инструкции помогают, потому что учащиеся могут видеть шаги в действии.Постарайтесь, чтобы формулировка была короткой и приятной. Не усложняйте вещи слишком сильно. Это нормально, потому что у вас есть фотографии для напоминаний.
СОВЕТ № 3: Обеспечьте платформу для обсуждения математики
Обсуждение математики очень важно во время занятий в математическом центре. Однако наши дети могут настолько сосредоточиться на процессе «игры», что единственные слова, которые вы слышите, — это такие вещи, как «Твоя работа» или «Я выиграл». Итак, как мы можем сделать так, чтобы в центральное время происходили насыщенные и содержательные математические разговоры?
Обеспечьте учащихся подмостками, которые открывают возможности для разговоров по математике.Если возможно, используйте такие вспомогательные средства, как карточки для разговоров по математике, направляющие вопросы и рамки предложений, чтобы предотвратить тишину или выключить обсуждение задач.
Ищете математические центры, соответствующие стандартам? Нажмите на свой уровень обучения ниже:
СОВЕТ № 4: Сохраняйте привычный распорядок дня, измените навыки
Это одна из важнейших составляющих независимости ваших детей. Как только я выучил это, время математического центра стало намного проще для меня и моих детей. Я начал использовать те же игры и упражнения, но изменил математические навыки.Вот и все. Простой. Раньше у меня был широкий выбор типов игр и занятий. Не поймите меня неправильно, все это были хорошие занятия, но мои ученики всегда перебивали меня во время моей небольшой группы, или я мог слышать замешательство за центральными столами (уши учителя потрясающие, не так ли?).
Но им не скучно? Нет. Позвольте мне пояснить. Я не говорю, что нужно использовать только один тип игры, и все. Вы можете переключить его. Но просто убедитесь, что ваши дети хорошо знакомы с видом деятельности.Эта стратегия работает, потому что дети настолько знакомы с рутиной игры, что теперь они могут сосредоточиться на математике в игре, а не на том, как играть в игру. В конце концов, причина, по которой мы хотим, чтобы они занимались этими задачами, заключается в том, чтобы укрепить свои математические знания.
Вот 3 основных типа игр, которые я использую:
ИГРА №1: Переверни и сопоставь
Иногда самая простая игра может быть самой интересной. В этой игре у учащихся есть два набора карточек. Один набор карт открыт, а другой — рубашкой вверх.Студенты по очереди переворачивают игровые карты и пытаются найти подходящую пару. Эта игра также включает в себя карточки разговоров по математике для обсуждения.
Совет учителя — Чтобы разделить задачи для некоторых из ваших учеников, вы можете держать оба набора карточек лицевой стороной вверх, чтобы облегчить задачу. Я также рекомендую скопировать каждый набор на карточках разного цвета.
ИГРА №2: Без лица
Дети ОБОЖАЮТ эту игру! Это игра для двоих. У каждого ученика есть свой набор игровых карточек.Студенты должны одновременно считать и переворачивать свои карточки. Они сканируют игровое поле и пытаются найти правильное место для размещения игровой карты. Студент, который кладет свою карту первым на правильное место, выигрывает матч.
Игра № 3: Финишная черта
Настольные игры классические. В этой игре учащиеся по очереди крутят спиннер и отвечают на самые разные вопросы. Дети должны правильно отвечать на вопросы, чтобы двигать свою игровую фишку.
СОВЕТ № 5: Требуйте использования листов для записи
Еще один способ убедиться, что ваши ученики не отвлекаются от задания, — это заставить их заполнить лист для записи. Это служит двум различным целям: (1) сделать студентов ответственными и (2) предоставить вам неформальную оценку.
СОВЕТ № 6: Предоставьте ключи для ответов
Еще одна причина, по которой дети обращаются за помощью, заключается в том, что они хотят знать, правильно ли они получили ответ.
Я знаю, что вы можете быть обеспокоены тем, что ваши дети могут попытаться обмануть, и это веский аргумент.Однако есть несколько способов обойти это в зависимости от деятельности математического центра.
Одним из решений может быть Game Master. Гейм-мастер — это ученик математического центра, который на самом деле не играет в игру. Его или ее работа — управлять станцией, проверяя ключ ответа и убеждаясь, что игра работает плавно.
Еще одно предложение — создать простую, но уникальную систему кодирования для ключа ответа, чтобы учащиеся могли самостоятельно проверять свои ответы.
СОВЕТ № 7: Дайте время для обмена
Закройте свои математические центры, предоставив учащимся время поделиться тем, что они сделали. Это помогает студентам стать более независимыми, потому что вы можете попросить их поделиться своим опытом. Это также хорошее время, чтобы задать вопросы и узнать, что они узнали.
Принимая во внимание все это, я создал Ready.Set.Play Math Games для основных математических навыков на уровне своего класса.Вы найдете все советы, которыми я поделился (ключи для ответов, карточки для разговоров по математике, листы для записей, инструкции к фотографиям), которые можно легко выполнить с помощью Ready.Set.Play Math Games.
Итак, если вы хотите помочь своим ученикам стать независимыми во время учебы в центре, нажмите на свой уровень обучения ниже, чтобы проверить Готово — Установить — Играть в математические игры. Игры отлично подходят для учеников начальной школы.
71Настройка управляемой математики — экономный в третьем классе
Я хочу поделиться с вами своими успехами в настройке управляемой математики.Этот метод работал у меня при обучении как младших, так и старших классов. Признаюсь … Я не занимаюсь управляемой математикой традиционным способом.
Когда я только начинал, я постоянно планировал, что будут делать мои ученики во время каждой ротации.
✔️Я готовил материалы.
✔️ Дифференциация.
✔️ Готовим больше.
✔️✔️✔️Подготовка. Подготовка. Подготовка.
И даже после того, как я сделал весь этот , управляемая математика никогда не работала гладко.
После всей этой подготовки я был все еще имел дело с учащимися, не выполняющими задания, отвлекающими внимание учителями или слишком большим количеством студентов в одном месте. Я решил, что с этим методом покончено.
Затем я внес одно базовое изменение в управляемую математику.
И это все изменило.
Я тоже помогу вам с математикой! Это будет безболезненно, обещаю
Прежде всего, знайте и верьте, что управляемая математика может работать в вашем классе. Не пугайтесь и не ошеломляйте. Ваши группы можно упростить, но при этом они остаются гибкими. Вы можете и сделать это без другого взрослого, помогающего в вашем классе.
Да — вы можете сделать это , даже если у вас есть этого класса .
«Революционное, потрясающее, глупое простое изменение, которое я сделал, изменившее ВСЕ»
🛑 Я перестал вращаться.
Кол-во вращения.
Вы знаете эти хитроумные графики, где группа А идет то туда, то сюда, то туда? Группа B начинается здесь.Группа C начинается там. Группа D работает там. Затем мы все вращаемся.
Да, я это остановил.
Вместо этого я разработал систему, которую назвал Flexible Guided Math. Все мои ученики работают на своих местах независимо (или на любом пустом столе в классе, на самом деле. Дело в том, чтобы разложить). Затем я перетаскиваю группы к своему столу.
☑️ Вот и все. Это так просто.
Я зову студентов к своему столу. Я не звоню в колокольчик и не заставляю всех вращаться. Я не установил время. Я могу работать в группе столько времени, сколько захочу!
У меня даже нет заданных групп. Я могу тянуть, кого хочу! 🎉
А это мощный ребята. Я передаю ответственность за обучение студентам.
Вместо того, чтобы сидеть на «станции» и работать над любой задачей, которую я поставил, они выбирают , над чем работать.
⚠️Конечно, есть рекомендации.(Я объясню это позже.)
Но дело в том, что учащимся предоставляется право выбора. Я не видел от этого ничего, кроме хороших результатов. Мой администратор даже однажды прокомментировал мне, оглядывая комнату: «Это может продолжаться, даже если вы выйдете из комнаты. Все ваши ученики знают, над чем они должны работать ».
Один важный ингредиент для успешной настройки гибкой управляемой математики
Это всего лишь одно.
График «Что нужно делать / может сделать».
Сейчас они бывают самых разных форм, но диаграмма «Сделать, можно сделать» — моя любимая из-за ее простоты. Но я видел, как другие учителя также добивались успеха с досками выбора / меню. Это действительно личное предпочтение. Я по натуре минималист, поэтому стараюсь делать вещи максимально простыми.
Это общий пример диаграммы привязки «Что нужно делать» / «Что можно сделать». Вы даже можете сделать индивидуальные для конкретных учеников, если вам нужно.Это отличный способ разделить ваши инструкции и ожидания.
Вы можете быть настолько подробными, насколько хотите. Вы можете разместить определенные центры или мероприятия, определенные технологии, которые будут использовать ваши ученики, все, что захотите!
План безболезненного лечения
Планирование этого стиля управляемой математики очень просто.
Если вы воспользуетесь моими модулями по управляемой математике для 1–5 классов, вы заметите, что есть план урока, страница практики и дополнительное задание на каждый день.
✔️✔️✔️ Итак, у вас есть урок для стола учителя (или даже математика для всей группы, если хотите), страница практики для обязательного занятия и дополнительное задание.
🤫Стол «Секрет учителя»
Помните — поскольку мои группы — это ГИБКИЕ групп, я могу постоянно вовлекать учащихся в них и из них.
Я использую информацию, которую я собираю в результате самостоятельной работы моих учеников по математике для всей группы, для создания своих групп. Это может быть что-то простое, например проблема с выходным билетом на стикере. (Регулирую ли я эти группы каждый день? Обычно нет. Но я всегда уверен, что буду улучшать их от модуля к разделу.) Во время преподавания я нацеливаю учеников на то, чтобы помочь им развить определенный навык.
Я использую целевые планы уроков, которые ориентированы на конкретную цель .🤫 Секрет стола учителя — порядок, в котором я тяну свои группы. 🤫
Обычно я начинаю с моей средней группы … ну знаете, дети, которые не соответствуют цели.Они вроде как понимают это, но не на 100% уверены, как и почему они решают проблему определенным образом. Обычно я обнаружил, что этой группе детей требуется немного дополнительной практики и руководства с моей стороны, прежде чем они будут готовы снова попробовать свою самостоятельную работу самостоятельно.
Следующая группа, которую я выберу, это мои хайлайеров . Обычно это очень кратко, поскольку они уже продемонстрировали мастерство владения навыком. Я использую это время быстрой проверки, чтобы убедиться, что они действительно понимают это и довольны поставленной задачей.К тому времени, когда я их тяну, они обычно заканчивают свою самостоятельную работу, и мы можем ее просмотреть. Убедившись, что они овладели этим навыком, я даю им дополнительное задание, чтобы продолжить работу.
Последняя группа, которую я отбираю, — это моя группа студентов, которые на самом деле борются с целью. Я тяну их в последнюю очередь, потому что мне нужно проводить больше всего времени, поддерживая их! Кроме того, к этому времени, если ученик из моей первой группы все еще испытывает трудности с чем-то, он, вероятно, обратился ко мне за поддержкой.Теперь я могу добавить их в свою последнюю группу и дать им еще одну дозу целевых инструкций.
Что я использую для обязательных / возможных занятий
В первую очередь — самостоятельная работа . Либо сегодняшняя страница практики из моих блоков управляемой математики , либо другая форма самостоятельной работы.
Ежедневная практика беглости речи
Существует так много разных способов, которыми учащиеся могут самостоятельно практиковать беглость речи во время занятий по управляемой математике. Если у вас есть устройства, студенты могут ежедневно публиковать свои факты на xtramath.org, а также используйте эти игры с магическим раскрытием , чтобы практиковать свои математические факты. Вы даже можете дать студентам простые самопроверяющиеся флеш-карты.
Один из моих любимых способов научить студентов практиковать свои факты — это простые страницы для беглости. Я распечатываю страницы с сайта math-drills.com и помещаю их в защитные пленки. Я распечатываю лист ответов на обратной стороне , чтобы студенты могли проверить свою работу.
Дополнительные услуги (центр)
Это центральные задания из моих модулей по управляемой математике , и есть по одному на каждый день!
Они идеально соответствуют уроку, который вы провели в тот день, и странице практики, которую ваши ученики делают для самостоятельной работы.
Модули управляемой математики включают в себя множество заданий, которые помогут вашим ученикам развлечься. Есть сортировки, игры в кости, спиннер, головоломки, настольные игры и многое другое.
Между прочим — эти мероприятия — еще один отличный способ к спирали пересматривать в течение всего года! Вы можете запретить учащимся заниматься различными видами деятельности. Подготовьте МНОЖЕСТВО в начале года и просто чередуйте их.
Практика цифровой математики
Если у вас есть доступ к устройствам для ваших учеников, им понравятся эти интерактивные цифровые уроки математики (1–5 классы).Они включают в себя несколько простых обучающих слайдов, чтобы помочь студентам понять урок, а также 10 практических задач. Слайды ясны и просты, поэтому учащиеся точно знают, как их решать, и им не нужно спрашивать, что им делать! Отлично подходит для самостоятельной работы!
🎉А Бонус? Что для вас означает гибкая управляемая математика? 🎉
Это в конечном итоге означает на ПУТЬ меньше подготовки каждую неделю!
У учащихся будет столько вариантов на выбор во время части «Можно сделать» в управляемой математике, что вряд ли будет слишком много повторений.
Просто время от времени меняйте центры, чтобы сохранять свежесть (и обзор по спирали)!
Еще кое-что, что я делаю, — продолжать становиться лучшим учителем
Мне нравится, когда в конце математического блока нужно время, чтобы поразмыслить над .На отражательном листе:
- Я записываю своих зеленых, желтых и красных учеников и делаю заметки об успеваемости в классе в целом.
- Если есть что-то, что, как я знаю, мне нужно провести по спирали, просматривая оставшуюся часть года, я отмечаю это здесь.
- Внизу страницы я делаю заметки о моем обучении. Если есть что-то, что мои дети изо всех сил пытались понять, возможно, мне нужно потратить некоторое время на изучение различных способов научить / сформулировать это.
- Кроме того, если есть что-то, что я обязательно хочу сделать по-другому в следующем году, я тоже пишу это здесь.
Это помогает мне улучшить мою педагогическую практику за лет. В следующем году я могу вытащить этот лист. (Этот раздел для размышлений идет в комплекте с учебными пособиями по математике на год и находится в пособии для учителя. См. Ссылки ниже для комплектов на год.)
🎉
Если вы готовы, возьмите все, что вам нужно для математических групп:105 Комментарии к табелю успеваемости, которые можно использовать и адаптировать
Практически каждый учитель согласен: комментарии к табелю успеваемости важны для понимания и дальнейших шагов для учеников и их семей. Но мало кто действительно хочет их написать.
Почему?
Потому что каждый инструктор знает, что работать в сжатые сроки для создания более 20 уникальных и подробных отчетов в конце года или семестра не совсем просто (или особенно весело). Это особенно актуально в эпоху дистанционного обучения.
И хотя никто в вашей школе не знает ваших учеников лучше вас, написание ценных комментариев в табеле успеваемости для каждого из них может быть огромной проблемой.
Вот почему мы создали список из 105 примеров комментариев в табелях успеваемости, которые помогут вам найти идеи, вдохновение и идеи при написании собственных табелей успеваемости.
105 комментариев в табеле успеваемости в этом списке помогут вам:
- Привить ученикам установку на рост
- Укрепить связи между школой и домом
- Напишите более сильные лиды и используйте более живой язык
- Выберите правильную формулировку при письме положительные и конструктивные комментарии в табеле успеваемости
Комментарии в табеле успеваемости, начавшие
Вы заметите, что комментарии в табеле успеваемости, приведенные ниже, могут служить трамплином для более полно разработанных.Но не волнуйтесь, используя их, вы сможете превратить некоторые из этих остроумных предложений в информативные и действенные следующие шаги!
Например, вы сможете взять замечание о чувстве числа 1-го класса, такое как «Ваш ребенок может складывать и вычитать числа до 20, используя различные манипуляции», и преобразовать его в:
Ваш ребенок может складывать и вычитайте числа до 20, используя различные манипуляторы. Это было очевидно, когда он работал самостоятельно, чтобы решить реальную проблему, добавляя игрушки в корзину для игрушек в классе.В качестве следующего шага они должны продолжать увеличивать числа, чтобы поощрять его навыки. Вы можете поддержать его, попросив сложить дома свои собственные груды игрушек.
Или воспользуйтесь комментарием по навыкам обучения, связанным с ответственностью, из раздела «Ваш ребенок может нести ответственность за свои действия как в классе, так и за его пределами» на номер:
Ваш ребенок может нести ответственность за свои действия как в классе, так и за его пределами. вне класса. Она часто проверяет свой распорядок дня и ежедневник, чтобы убедиться, что у нее есть все необходимые материалы для завершения работы дома перед отъездом.Во время перерыва в помещении ей нужно время, чтобы привести в порядок все, с чем она играла.
Заметили разницу?
По сравнению с однозначной или буквенной оценкой, комментарии в табеле успеваемости могут иметь еще большую ценность для ваших учащихся и их семей. Другими словами, число, буква или оценка обозначают , что , в то время как сопровождающий комментарий отражает , как .
В зависимости от возрастной группы или класса, который вы преподаете, может быть достаточно письма или оценки.Тем не менее, исследование в профессиональном журнале для преподавателей Phi Delta Kappan предлагает:
Комментарии, которые определяют, что учащиеся успели хорошо, какие улучшения им нужно внести и как их внести, при условии учета важных контекстных элементов, могут помочь учащиеся на пути к успеху в учебе и гарантируют, что все учатся на высшем уровне.
Навыки обучения (положительные комментарии)
- ________ уверенно, позитивно и является отличным примером для подражания для своих одноклассников.
- ________ часто одним из первых помогает и наставником других одноклассников. Он / она — ценная часть класса.
- ________ показал отличную способность ставить цели и быть настойчивым в их достижении.
- ________ заинтересован в собственном обучении, внимательно слушает и прилагает все усилия, чтобы не отвлекаться, которые могут прервать процесс обучения.
- ________ подотчетен и ответственен. Он / она принимает разумные решения, признает ошибки и прислушивается к возможностям для улучшения.
- ________ хорошо относится к одноклассникам и ценит разные точки зрения и опыт.
- ________ зрело управляет своими эмоциями и должным образом реагирует на отзывы.
- ________ всегда ищет способы помочь в классе.
- ________ является надежным и надежным, эффективно следует указаниям и выполняет свои обязательства перед собой и другими.
- ________ вдумчивый, проницательный и основательный в письменном и устном общении, а также имеет талант ясно выражать свои идеи.
- ________ хорошо работает с одноклассниками в групповой работе и часто берет на себя руководящую роль.
- ________ показывает позитивное отношение к одноклассникам в групповых проектах и мероприятиях, эффективно принимает и дает предложения и указания.
- ________ проявляет зрелость при решении проблем с одноклассниками и умеет хорошо общаться.
- ________ хорошо применяет то, что он / она изучает в классе, в реальных и реальных ситуациях.
- Было очень приятно иметь в моем классе энтузиазм, позитив и зрелость _______.
- ________ является энтузиастом класса и проявляет готовность учиться.
- ________ проявляет ответственное поведение, хорошо работает в группе и ценит старания одноклассников.
- ________ сосредоточен во время занятий в классе и охотно участвует в обсуждениях в классе.
- ________ уверенно и целеустремленно выполняет самостоятельную работу.
- ________ работает независимо и гордится хорошо выполненной работой.
- ________ сосредоточен на занятиях и охотно участвует в групповых обсуждениях.
- ________ очень добросовестен, проявляет отличные усилия и внимательность в повседневной работе.
- ________ демонстрирует готовность и сознательность в своей повседневной работе.
- ________ показывает сознательное усилие учиться.
- ________ проделала огромную работу, решая и преодолевая большие проблемы в этом году. Пожалуйста, продолжайте воспитывать и поощрять такое поведение в течение лета.
- ________ проявляет ответственность и следует указаниям, когда они даются.
- ________ точно и внимательно слушает и следует указаниям.
- ________ быстро и точно следует указаниям.
Навыки обучения (необходимо улучшить)
- ________ рекомендуется демонстрировать более ответственное отношение и поведение в классе.
- ________ необходимо вести себя более адекватно при общении с одноклассниками.
- ________ необходимо всегда обращать внимание на использование соответствующего языка
- ________ требует поощрения внимательно слушать во время группового общения.
- ________ необходимо внимательнее прислушиваться к указаниям во время уроков.
- ________ будет полезно проявить большее желание поделиться идеями в классе.
- ________ требует частых напоминаний, чтобы быть внимательным во время инструкций и уроков.
- ________ необходимо улучшить его / ее сотрудничество в настройках группы. Он / она должен работать над тем, чтобы выражать свои чувства и мнения и прислушиваться к другим.
- ________ необходимо улучшить свою работу с другими. Он / она должен убедиться, что принимает на себя часть работы при участии в групповом задании.
- ________ необходимо улучшить свою независимую работу, и обязательно обращайтесь за помощью только тогда, когда она необходима.
- ________ часто изо всех сил пытается сосредоточиться на уроке, что вредит его / ее способности хорошо заниматься классной деятельностью и заданиями.
- ________ рекомендуется разумно использовать время для завершения задач в требуемое время.
- ________ рекомендуется более ответственно подходить к выполнению задач без регулярных напоминаний.
- ________ должен показать качеством работы и использованием учебного времени, что он / она должным образом вовлечены в процесс обучения.
- ________ постоянно нуждается в напоминаниях, чтобы сосредоточиться на управлении временем.
- ________ необходимо более строго соблюдать правила класса в течение всего учебного дня.
Математика (общие комментарии)
- ________ испытывает значительные трудности с математикой. Я рекомендую ему поработать над изучением ________ и ________. Эта дополнительная практика поможет ему / ей почувствовать себя более расслабленным при выполнении математики в классе. Пожалуйста, свяжитесь со мной, если вам понадобятся материалы для его начала.
- ________ хорошо разбирается во всех математических концепциях, преподаваемых до сих пор в этом году. Он / она продолжает выполнять отличные задания и особенно любит практические занятия по математике.
- ________ положительно относится к математике, но по-прежнему испытывает трудности в нескольких ключевых областях. Он должен заниматься дома каждый вечер. Особого внимания требуют ________ и ________.
- ________ демонстрирует хорошее понимание всех изучаемых математических концепций и общается с ясностью и хорошим обоснованием рассуждений.
- ________ необходимо поработать над увеличением его / ее скорости в математических фактах. Он / она должен продолжать ежедневную практику с упором на сложение, вычитание, умножение и деление.
- ________, кажется, нуждается в постоянном поощрении по математике. Он / она продолжает бороться с базовыми математическими концепциями для своего класса.
- ________ испытывает трудности в некоторых областях математики. Области, нуждающиеся в дополнительной работе: ________. Работа над этими проблемными областями каждый вечер поможет улучшить его / ее результаты обучения.
- ________ не успевает по математике. Он / она могли бы извлечь пользу из практики таблицы умножения, а также должны продолжать практиковать процесс деления в столбик.
- ________ легко отвлекается на уроках математики, а проблемы с поведением мешают его обучению. Мы будем работать над более сложными предметами, и ему / ей будет сложно, если он / она не будет уделять внимание в классе.
- ________ не справляется с тестами по математике. Он / она хорошо справляется с заданиями, но, похоже, не сохраняет информацию для тестов.Я всегда предупреждаю вас за неделю до экзаменов, поэтому, пожалуйста, убедитесь, что ________ учится и должным образом готовится к ним по мере их приближения.
Сложение и вычитание
- ________ может вычислить факты сложения и вычитания до 18 с уверенностью и точностью.
- ________ становится более способным вычислять факты сложения и вычитания до 18 с уверенностью и точностью.
- ________ требует больше времени и практики в вычислении фактов сложения и вычитания до 18
- ________ необходимо приложить больше усилий для обучения вычислению фактов сложения и вычитания до 18.
Счетчик пропусков
- ________ может пропускать счет вперед и назад по двойкам, пятеркам, десяткам и сотням для завершения коротких шаблонов.
- ________ учится пропускать счет вперед и назад на двоек, пятерок, десятков и сотен для завершения коротких шаблонов.
- ________ требуется практика с пропуском счета вперед и назад по двойкам, пятеркам, десяткам и сотням для выполнения коротких шаблонов.
- ________ требует значительной практики с пропуском прямого и обратного счета на двоек, пятерок, десятков и сотен для завершения коротких шаблонов.
Разрядное значение
- ________ может продемонстрировать концепцию разрядного значения, чтобы придать значение числам от нуля до 1000, идентифицируя единицы, десятки и сотни.
- ________ развивает понимание концепций разряда, чтобы придать значение числам ноль, идентифицирующим единицам, десяткам и сотням.
- ________ требует больше времени и практики, чтобы продемонстрировать концепцию числового значения, чтобы придать значение числам от 0 до 1000, идентифицируя единицы, десятки и сотни.
Сравнение чисел
- ________ может сравнивать числа с 1000, используя такие термины, как большее или меньшее, наибольшее или наименьшее.
- ________ учится сравнивать числа с 1000, используя такие термины, как большее или меньшее, наибольшее или наименьшее.
- ________ требуется поддержка для сравнения чисел с 1000 с использованием таких терминов, как большее или меньшее, наибольшее или наименьшее.
- ________ демонстрирует ограниченное понимание при сравнении чисел с 1000 с использованием таких терминов, как большее или меньшее, наибольшее или наименьшее.
Сложение с перегруппировкой
- ________ может продемонстрировать и объяснить процесс сложения целых чисел до 100, с перегруппировкой и без нее.
- ________ требуется постоянная поддержка для демонстрации и объяснения процесса сложения целых чисел до 100 с перегруппировкой и без нее.
- ________ требует значительного внимания и индивидуальной инструкции, чтобы продемонстрировать и объяснить процесс сложения целых чисел до 100 с перегруппировкой и без нее.
Задачи со словами (математика)
- ________ может решать задачи со словами, используя одно- и двузначное сложение, показывая свою работу и составляя ответ в виде полного предложения.
- ________ становится все более уверенным в своей способности решать задачи со словами, используя одно- и двузначное сложение, показывая свою работу и написание ответа в виде полного предложения.
По мере того, как мы переходим к языку и грамотности, следующие разделы включают комментарии в стартовой табеле успеваемости, которые касаются навыков чтения, письма, устного общения и критического мышления.
Язык (общий)
- ________ (понимание, правописание, чтение) значительно улучшилось, но ему / ей по-прежнему требуется дополнительная работа (понимание, орфография, чтение). Свяжитесь со мной, если вам понадобятся дополнительные учебные материалы для практики дома.
- ________ уделяет внимание своей повседневной писательской работе и часто выходит за рамки минимальных требований для выполнения заданий.
- ________ проблемы с почерком.Я считаю, что он / она может хорошо составлять буквы, но ему нужно замедлиться и занять немного больше времени. Более аккуратный почерк улучшит его / ее школьную работу в целом.
- ________ прилагает все усилия, чтобы почерк был разборчивым. Он умеет печатать по линиям, использовать хороший интервал и правильно формировать буквы.
- ________ необходимо сосредоточить внимание на ее правописании. Необходимы дополнительные улучшения в областях (диктовка, еженедельные проверки орфографии, структура предложений). Ежедневные занятия дома помогут улучшить его / ее результаты.
- ________ показывает способность быстро использовать правила орфографии, пунктуации и грамматики, которые были недавно изучены. Он / она может быстро осваивать новые навыки и стремится применить их в своем письме.
- ________ имеет значительные трудности с чтением, особенно с беглостью и пониманием.
- ________ хорошо говорит перед классом, но требует улучшения письменной речи. У него проблемы с (диктовкой, правильным копированием слов, написанием рассказов, построением логических последовательностей).В этой области необходима дальнейшая практика.
- ________ продолжает добиваться отличных успехов в правописании и чтении. Он / она усердно работает, чтобы представить работы без грамматических ошибок.
- ________ плохо запоминает ранее обсуждавшиеся навыки письма и часто делает ошибки с пунктуацией, грамматикой и общей структурой предложения. Необходимо улучшить базовые навыки письма.
Чтение ответов
- ________ может предлагать прямые ответы на свои чтения и поддерживает идеи с помощью веских аргументов и конкретных примеров.
- ________ учится предлагать более прямые ответы на свой опыт чтения, подкрепленные причинами, примерами и деталями.
- ________ нуждается в частой поддержке, чтобы предлагать прямые ответы на его / ее опыт чтения, подкрепленные причинами, примерами и деталями.
Понимание прочитанного
- ________ показывает хорошие способности при прохождении тестов на понимание прочитанного.
- ________ будет полезно попрактиковаться в чтении вслух и обсуждении содержания.
- ________ последовательно демонстрирует понимание коротких устных текстов, отвечая на вопросы и объясняя описанные события.
- ________ постоянно самостоятельно читает материал на уровне класса.
- ________ использует хорошие навыки редактирования и правильно расставляет заглавные буквы, кавычки, вопросительные знаки, апострофы, запятые и точки.
- ________ хорошо справляется с разбивкой рассказа на параграфы.
- ________ определяет различные формы письма и выявляет важные идеи посредством разработки проницательных вопросов и ответов.
- ________ может анализировать действия персонажей, сюжеты рассказов и демонстрирует высокую беглость чтения.
Журнал ответов
- ________ использует правильное написание, грамматику и пунктуацию при написании простых предложений.
- ________ рекомендуется проявлять повышенное внимание к использованию правильного орфографии, грамматики и пунктуации с общими навыками письма.
- ________ требует больше времени и практики в использовании правильного орфографии, грамматики и пунктуации с общими навыками письма.
- ________ требуется значительная помощь для правильного написания, грамматики и пунктуации при написании простых предложений.
Ведение записей
- ________ показывает отличное понимание ведения записей на лекциях и чтениях при подготовке к тестам и заданиям.
- ________ требуется постоянная поддержка для развития понимания ведения заметок из лекций и чтений при подготовке к тестам.
Дистанционное обучение
- ________ был очень заинтересован и сосредоточен во время дистанционного обучения и участвовал в обсуждениях в классе.
- ________ оставался мотивированным к выполнению заданий во время дистанционного обучения и вовремя сдавал все необходимые материалы.
- ________ нуждались в дополнительных подсказках, чтобы оставаться вовлеченными во время онлайн-уроков, но при необходимости участвовали в обсуждениях.
- ________ смоделировал хорошее онлайн-обучение для других студентов.
- ________ мешал онлайн-обучению и не участвовал в обсуждениях в классе.
- ________ хорошо справлялся с техническими проблемами и всегда был готов.
- Хотя он / она не всегда мог получить доступ к устройству, _________ постоянно выполнял онлайн-задания и задавал вдумчивые вопросы.
- ________ следует задавать больше вопросов во время онлайн-обсуждений, чтобы в дальнейшем избежать путаницы.
- ________ посещал онлайн-уроки нечасто, а задания не всегда выполнялись.
- ________ хорошо работали самостоятельно и в группе во время дистанционного обучения.
- ________ отлично справляется с дистанционным обучением самостоятельно, но с трудом взаимодействует со своими одноклассниками во время групповых занятий или дискуссий в классе.
- ________ суперзвезда технологий! Он / она редко нуждался в помощи и даже помогал другим одноклассникам устранять неполадки.
- ________ задает хорошие вопросы и всегда активно обращается, когда ему / ей нужна помощь с заданием или уроком.
Советы учителям по написанию более эффективных комментариев к табелям успеваемости
Где-то примерно на полпути к вашему крайнему сроку для табелей успеваемости вы делаете все возможное, чтобы в конце каждой недели использовать время для размышлений и записи заметок — об успеваемости ваших учеников и учебной неделе.
Каковы их сильные и слабые стороны? Как развиваются их навыки общения с одноклассниками? Как их участие в классе — они с энтузиазмом учатся? Продемонстрировали ли они значительные улучшения в одной конкретной предметной области? Выполняются ли домашние задания? Возникли ли новые проблемы, влияющие на обучение?
Даже несколько минут записи заметок в недели, предшествующие крайним срокам в табеле успеваемости, помогут снять стресс, когда придет время писать свои окончательные комментарии.
Кроме того, наличие датированного журнала информации, детализированной в течение учебного года, поможет вам вспомнить, как учащиеся успевают в течение каждой недели, что может быть ценной информацией во время конференции родителей с учителем.
Это также поможет заинтересовать и успокоить родителей, которые хотят получить актуальные и подробные комментарии об успеваемости своего ребенка в школе.
Используйте Prodigy для написания содержательных табелей успеваемости с минимумом хлопот. Prodigy Math Game — это увлекательное математическое приключение для студентов, в котором успех зависит от правильных ответов на вопросы по адаптивной математике.
Во время игры учащиеся узнают:
- Какие навыки практикуют студенты
- Как далеко они продвинулись по учебной программе
- Что они освоили и где им нужна дополнительная поддержка
Используйте один из восьми отчетов Prodigy для отслеживания успеваемости студентов в течение года. Когда придет время писать комментарии к табелю успеваемости, у вас будут подробные отчеты обо всех достижениях ваших учеников.
Только начинаете работать с Prodigy? Без проблем! Когда учащиеся впервые исследуют мир Prodigy Math Game, они начнут сдавать тест на определение уровня, даже не подозревая об этом.Когда они закончат, у вас будет снимок их уровня обучения, того, что они знают, и конкретных навыков, над которыми им еще нужно работать.
Зарегистрируйте бесплатную учетную запись учителя сегодня, чтобы начать!
Зарегистрируйтесь сейчасХотя каждая табель успеваемости не может быть ярко-позитивной, старайтесь писать в обнадеживающем и информативном тоне. Когда вы пишете конструктивные комментарии в табеле успеваемости, используйте ободряющую лексику, в которой основное внимание уделяется возможностям ученика для совершенствования.
Например, вместо того, чтобы описывать ученика, который пытается слушать, как «плохого слушателя», отметьте, что ученику «было бы полезно слушать более внимательно.
Если возможно, сформулируйте отрицательный комментарий относительно того, что учащиеся делают хорошо, и подумайте, как эта более успешная характеристика может помочь им повысить успеваемость в других областях.
Добавьте в свой табель успеваемости положительные комментарии, а затем укажите области, требующие большего внимания.
Выбор правильного формата для представления информации упростит весь процесс, в результате чего получится более четкий и организованный конечный продукт.
Если вам неясен формат табелей успеваемости в вашей школе, запросите образцы или проконсультируйтесь с другими учителями или сотрудниками, чтобы уточнить это.
Открытость и честность в отношении успеваемости ученика требует такта и внимательности в отношении того, как вы выражаете эти комментарии. Будьте прозрачны и помните, что ваша цель — улучшить учебный опыт ваших учеников.
Открытость и честность являются ключом к обеспечению наилучшего качества обслуживания. Если возможно, обсудите, какие стратегии вмешательства вы можете использовать, чтобы улучшить результаты обучения учащегося.
Как отмечает учительница начальных классов Донна Донахью в своей книге Руководство для начинающих учителей начальной школы: как нанять и оставаться воодушевленными:
Если возникнет проблема, большинство родителей будут благодарны вам за то, что вы им рассказали, и захотят вам помочь исправьте это как можно скорее.Многие проблемы, которые проявляются в школе, также являются проблемами, замеченными дома, поэтому ваши комментарии не удивят родителей. В идеале, в какой-то момент до получения отчета о проделанной работе родители уже обсудили с вами проблему.
Если вы застряли при заполнении комментариев для определенного учащегося, перейдите к другим учащимся и вернитесь к нему позже. Скорее всего, у вас будет больше проблем с заполнением комментариев для студентов, у которых есть несколько областей, требующих дальнейшего улучшения и внимания.
Не стесняйтесь двигаться дальше и возвращаться к этим студентам периодически или по мере того, как вы найдете правильный язык, чтобы выразить свои мысли.
Хотя каждый комментарий в табеле успеваемости в конечном итоге касается вашего ученика, подумайте как можно больше о родителях или опекунах ваших учеников и внесите предложения по их участию.
На самом деле, если вы можете, постоянно информируйте родителей. Это поможет убедиться, что ваши комментарии не застигнут их врасплох.
Когда вы отмечаете сильные и слабые стороны своих учеников, постарайтесь включить практические идеи о том, как родители могут вовлекать и поддерживать своего ребенка дома.Если возможно, укажите, как вы используете дифференцированное обучение для поддержки данного учащегося.
Примеры простых советов для родителей:
- «Поощряйте ребенка к чтению. Это не обязательно должно быть в одиночестве. Выделите время перед сном для совместного чтения, это поможет сделать это менее утомительным. »
- «При необходимости помогите своему ребенку с домашними заданиями. Я и другие родители, которые также выполняют домашние задания для своего ребенка, — отличные ресурсы для начала.«
- » Убедитесь, что ваш ребенок выполнил домашнее задание, создав вместе с семьей распорядок домашнего задания, в котором такие стимулы, как телевизор или компьютерное время, приходят после домашнего задания. »
- « Помогите вашему ребенку с организационными навыками дома. Если комната в вашем доме могла бы быть опрятнее, попробуйте использовать это как возможность отсортировать такие вещи, как игрушки, посуда и утварь. «
- » Помогите своему ребенку подготовиться к тестам по математике, сосредоточив свои навыки на сложении и вычитании. Если им не нравится учиться по традиционным рабочим листам, попробуйте цифровой игровой инструмент обучения, который поможет им увлечься процессом.
Как пишет в своей книге «Стратегии , которые работают» Энн Гоудвис, преподаватель средней школы и эксперт по пониманию речи:
, важно, чтобы вы включили родителей в свой комментарий, чтобы они знали, что образование ребенка — это совместная миссия. должны звучать твердо, чтобы родители знали, что вам нужна их помощь, и что вы не позволите их ребенку продолжать ненадлежащее поведение.
Маловероятно, что ваши ученики или родители будут сравнивать комментарии своих табелей успеваемости, но все же рекомендуется стремитесь к тому, чтобы для каждого учащегося были представлены уникальные комментарии, отражающие каждый индивидуальный результат обучения.
Табель успеваемости — возможно, самый загруженный период в году, и понятно, что вы хотите просто покончить с этим.
Несмотря на это, вы должны дважды проверить все свои комментарии, прежде чем печатать и раздавать их. Все ваше общение с родителями является отражением вас как учителя и должно отражать заботу и внимание, которые вы проявляете к своим ученикам в классе.
Воспользуйтесь родительским порталом или электронной почтой вашей школы, чтобы сообщить родителям (при необходимости), что приближается время табеля успеваемости.
Это поможет родителям подготовиться, а также гарантирует, что все важные вопросы, которые могут у них возникнуть, будут рассмотрены до того, как будут доставлены итоговые табели успеваемости.
Записывайте и используйте анекдоты в классе в своих оценках. Независимо от того, насколько вы вовлечены в успеваемость своих учеников, все равно может быть сложно привести конкретные примеры, связанные с их успеваемостью, если вы не записали их в процессе.
Когда вы замечаете положительный или отрицательный навык, способность, силу или слабость в классном задании или задании, обязательно запишите это, чтобы вы могли сослаться на него в комментариях к табелю успеваемости.Точно так же подумайте о том, чтобы отмечать образец работы студента каждую неделю или две.
Чтобы упростить доступ, храните текущие файлы этой работы в личной папке или используйте цифровой инструмент, например Google Doc.
Практика сэкономит время и поможет предотвратить стресс в последнюю минуту. Такие стратегии, как прямое наблюдение и ведение заметок (как можно скорее), гораздо более надежны, чем попытки вспомнить информацию и поведение за несколько недель или месяцев до этого.
Ключевые моменты для комментариев в табеле успеваемости в конце года
Комментарии в табеле успеваемости должны быть нацелены на предоставление учащимся и родителям обратной связи, которая является персонализированной, подробной, и значимой .
Написание комментариев к табелю успеваемости не должно вызывать стресса. Используйте эти стратегии для создания более живых и значимых оценок.Эффективные комментарии в табеле успеваемости подчеркивают и обсуждают:
- Конкретные заметные сильные стороны, которые учащийся продемонстрировал и должен стараться продолжать демонстрировать
- Конкретные элементы знаний, навыков и других результатов, признанных в учебной программе, которые являются наиболее важные для успеваемости или развития учащегося в период оценивания
- Основные следующие шаги для улучшения, которые будут: определять наиболее важные потребности учащегося в обучении, предлагать учащимся следующие шаги и предлагать конкретные рекомендации о том, как родители и опекуны могут помочь учащимся учебные привычки и навыки учащегося (или развитие этих привычек и навыков)
Эффективные комментарии в табеле успеваемости персонализируются — настраиваются для каждого отдельного учащегося — и обсуждаются:
- Учебные предпочтения учащегося, его готовность учиться и интересы
- Подробное свидетельство обучения или повышения квалификации красный от наблюдений в классе и / или заданий учащихся
Эффективные комментарии в табеле успеваемости выражаются ясной и простой формулировкой, используя:
- Ободряющий и / или позитивный тон
- Язык, который легко понять для как ученики, так и родители, в отличие от образовательного жаргона, используемого в учебной программе.Но для занятых учителей может быть сложно просто не отставать … Прозрачность и справедливость являются ключом к управлению любым взаимодействием между домом и школой ».
Персонализированные комментарии в табеле успеваемости, которые являются ясными, точными и значимыми, необходимы для информирования учащихся и их родители о том, чему ученики научились, в чем их сильные стороны и как они могут эффективно прогрессировать
Несмотря на давление и сроки написания табелей успеваемости, может быть полезно помнить об этих ключевых целях.
Вдохновляйтесь примерами комментариев в табеле успеваемости — и стратегиями достижения успеха — выше, чтобы обеспечить точность, ясность и смысл в комментариях к табелю успеваемости.
Когда приходит время раздавать табели успеваемости, вы можете делать это с полной уверенностью, что вы сами — и каждый из ваших учеников — делаете то, чего заслуживает ваш упорный труд.
Собирайте мнения учащихся о Prodigy
Создайте или войдите в свою бесплатную учетную запись учителя на Prodigy — ориентированной на стандарты игровой платформе обучения, которая оценивает успеваемость и успеваемость учащихся во время игры.Используйте Prodigy, чтобы мотивировать учащихся к обучению, контролировать вопросы, на которые они отвечают во время игры, и собирать информацию об обучении учащихся в течение всего года.
Зарегистрируйте бесплатную учетную запись учителя сегодня!Использование технологий для адаптации уроков к каждому учащемуся
Джоэл Роуз, бывший учитель, и Крис Раш, эксперт по технологиям и дизайну, являются мозгами компании Teach to One 360, базирующейся в Нью-Йорке. Когда г-н Роуз впервые начал преподавать в пятом классе в Хьюстоне в 1990-х годах, он был ошеломлен количеством учеников, чьи математические навыки отставали на два или даже три класса.«Некоторые ученики достигли уровня второго класса, другие — восьмого класса, а другие — промежуточного звена», — сказал он.
Эта универсальная система не работает, сказал он, добавив: «Она сильно устарела».
Итак, в 2009 году, работая на канцлера школ Нью-Йорка, г-н Роуз сотрудничал с г-ном Рашем, чтобы создать School of One (позже переименованную в Teach to One 360), технологическую математическую программу для учащихся с пятого по 12.
Вот как это работает: учащиеся проходят 90-минутный тест MAP, который представляет собой стандартизированный тест для оценки математических навыков , и 60-минутный диагностический тест для определения пробелов и сильных сторон.Затем программа использует алгоритмы и машинное обучение для определения проблемных областей и сильных сторон и создает индивидуальный ежедневный урок или «плейлист».
Он также выбирает модальность или метод обучения. Некоторые могут получить урок в традиционном классе под руководством учителя; другие будут работать в небольших группах сверстников, сотрудничая со студентами аналогичного уровня навыков; а другие будут работать независимо, используя интерактивные онлайн-видео, игры и математические программы. Каждому ученику назначают по крайней мере два разных режима в день, и команда, по крайней мере, из четырех учителей математики наблюдает за программой.
В конце дня ученики проходят тест из пяти вопросов, и алгоритм использует результаты для определения уроков следующего дня.
В качестве пилотного проекта программа была развернута среди 1500 учеников в трех государственных школах — по одной в Бронксе, Манхэттене и Бруклине. В 2011 году г-н Роуз выделил программу в некоммерческую фирму New Classrooms и переименовал программу в Teach To One.
Советы по преподаванию комбинированных классов / многоуровневых классов
Если вы преподаете в раздельном классе (многоуровневом или комбинированном классе) и вам нужен совет по организации и организации работы в классе, вы попали в нужное место! Вы найдете практические советы от учителей, которые преподавали в многоуровневых классах и комбинированных классах на всех уровнях обучения.
Советы учителей общеобразовательных школ
Я пригласила учителя-блоггера Мэри Мюллер из Guided-Math, чтобы рассказать больше о своем опыте преподавания в раздельных классах. Спасибо, Мэри, за подсказки!
Вы только что узнали, что преподаете в раздельном / комбинированном / разновозрастном классе? Вы находитесь в состоянии паники, пытаясь понять, как вы собираетесь справляться с двумя (а иногда и более) уровнями обучения одновременно?
Десять лет назад моя педагогическая карьера началась в раздельном классе в очень большом школьном округе в Иллинойсе.Во-первых, не могу поверить, что я всего десять лет писал! Во-вторых, теперь, когда я считаю, я не могу поверить, что семь из этих лет я провел в комбинированных классах! Все эти вопросы и моменты паники пронеслись в моей голове, когда я узнал о моем первом назначении. Тогда я и представить себе не мог, что первый год, разделенный на 1/2, поставит меня на путь разделения классов и поможет положительно сформировать то, кем я являюсь сегодня как учитель.
Вначале я рассматривал комбинированное обучение как долгожданный вызов.Это был вызов, который я не собирался терпеть. Я всегда смотрел на то, что делал, и пытался понять, как я могу улучшить структуру как для моих учеников, так и для меня.
За годы обучения, разделенного на 1/2, 2/3, 3/4 группы и три года в 4-м классе, я понял, что разделенное обучение ничем не отличается от обычного класса. Я обнаружил, что не изменил способ преподавания или структуру дня в раздельном классе по сравнению с обычным классом.
Вот некоторые вещи, о которых следует подумать при планировании комбинированного класса.
- Поговорите со своим администратором, чтобы узнать, что от вас требуется. Вы должны преподавать по двум отдельным учебным программам? Какие предметы можно сочетать? Как товарищи по команде могут вас поддержать?
- Думайте о своем классе как о диапазоне способностей, а не о двух разных уровнях обучения. Реальность такова, что у обычных классов может быть только большой разброс способностей, чем у комбинированных классов.
- Я рекомендую сбалансированный формат грамотности. Преподавайте уроки чтения и письма всей группой, а затем разбивайтесь на небольшие группы для чтения с гидом или индивидуальных конференций.Здесь вы сможете удовлетворить потребности своих учеников.
- Обычно вам придется преподавать по двум отдельным учебным программам по математике. Я настоятельно рекомендую вам взглянуть на формат управляемой математики. Это решит, как преподавать две программы математики, и даст вам возможность индивидуализировать обучение математике.
- Подготовьтесь к началу учебного года с информацией для родителей. Когда эти списки классов увеличатся, у вас обязательно появятся вопросы от родителей. Если вы будете готовы показать им, как вы собираетесь эффективно справиться с двумя оценками, их страхи уменьшатся.Создайте брошюру или информационный бюллетень с указанием вашего расписания обучения, учебной программы, которую вы собираетесь охватить, и подробностей о том, как вы собираетесь удовлетворить потребности своих студентов.
- Оставайся позитивным !! Помните, что это будет отличный опыт не только для студентов, но и для вас самих!
Удачи вам в обучении в комбинированном классе! Я знаю, что у вас все получится и у вас все получится! Чтобы получить дополнительную информацию и узнать больше о том, как я структурирую свой класс по математике или разновозрастному классу, посетите мой веб-сайт Guided-Math.
Вопросы о разделенных классах и общих классах
Следующие вопросы были заданы мне в рамках серии сообщений в блоге «Спроси Анжелу о чем угодно». Вы можете отправить любой вопрос, связанный с преподаванием, анонимно, чтобы сохранить конфиденциальность и конфиденциальность учащихся. Я включил два вопроса ниже здесь, на этой странице, а не в столбец, чтобы учителям комбинированных классов было легче находить ответы в одном месте.
Я преподаю в 2/3 классах.Я слышал, что один уровень назывался юниорами, а другой — старшими. Мое чутье подсказывает мне не начинать первый день, говоря, что я второй или третий, но неизбежно ли это? Как лучше всего управлять классом, чтобы создать команду, соблюдая при этом свой класс? Я не хочу, чтобы кто-то из моих третьеклассников чувствовал, что они все еще второклассники.
-ДжейнПривет, Джейн! Бывают моменты, когда вам нужно будет ссылаться на них по уровням обучения, и тогда лично я бы назвал их второклассниками и третьеклассниками.Но вы также можете позволить каждому классу выбрать себе имя, которое отражает их уникальную идентичность как класса внутри класса. Это может быть часть вашей первой недели школьных занятий, как некоторые учителя делают с группами чтения. Я думаю, что это был бы хороший способ создать чувство общности и дать детям право владеть классом. Они также могут создать имя класса, чтобы иметь единую связную идентичность. Например, весь ваш класс может состоять из китов, второклассники могут быть косатками, а третьеклассники — белухами.Расскажите детям о своей дилемме, как их называть, и попросите их мнение! Бьюсь об заклад, они придумают что-нибудь получше, чем мы могли придумать.
Я подал заявление о приеме на работу в комбинированном классе 4/5, и у меня есть хорошие шансы пройти собеседование. У меня нет опыта работы с многоуровневыми комнатами, я даже не знаю, какие вопросы задавать, и, хотя я вижу, как книга Cornerstone может помочь в таком классе, есть ли что-нибудь, что в вашей книге не упоминается, чтобы помочь мне организовать этот тип комнаты?
-J.Я могу представить, что ученики 4 и 5 классов будут вместе работать над множеством заданий; вы сможете дифференцировать свои инструкции и занятия по уровню способностей, а не только по классу. Судя по тому, что я вижу в последних образовательных тенденциях, наверное, так бы и хотелось директору. Если бы вы учили так, то, вероятно, было бы полезно — при подготовке к собеседованию — придумать несколько конкретных примеров того, как вы бы это сделали. Что касается организации, вам может потребоваться хранить некоторые вещи отдельно (возможно, разные корзины, чтобы они могли сдавать свои бумаги и т. Д.), но по большей части я не думаю, что разделение классов сильно повлияет на планировку комнаты.
Управляемая математика: независимая практика — простое обучение
Давайте поговорим о НЕЗАВИСИМОЙ ПРАКТИКЕ во время управляемой математической ротации сегодня!
После того, как мои ученики встретятся со мной в Teacher Feature на уроке в небольшой группе, они перейдут к следующему раунду, который называется Workbook Nook. Это ротация, когда они работают над самостоятельным заданием на основе урока, который я только что провел в небольших группах.Почти все мои задания, которые студенты выполняют во время Workbook Nook, — это задания с интерактивной записной книжкой. Мои студенты ОБОЖАЮТ выполнять задания с интерактивной записной книжкой, потому что они не просто заполняют скучный рабочий лист. Они активны, пока работают. Они режут, склеивают, раскрашивают (отлично подходят для мелкой моторики) и думают. Они полностью увлечены и всегда говорят, как им весело в Workbook Nook. В конце урока в небольшой группе я даю инструкции о том, что от них ожидается во время Workbook Nook.Я даю им их активность, они ходят на станцию математических манипуляторов, чтобы получить необходимые им материалы, и они могут пойти куда угодно в комнате, где хотели бы работать.
ГЛАВНАЯ ПРИЧИНА , что управляемая математика так гладко работает в моем классе, связана с одной важной вещью — СООТВЕТСТВИЕ ! Моя независимая деятельность последовательна, поэтому они всегда знают, чего ожидать и как этого добиться. Моя работа в малых группах — СОГЛАСОВАННО . Они всегда знают, чего ожидать во время урока, потому что мои ожидания и уроки СООТВЕТСТВУЮТ .Мне больше не нужно пересматривать направления к середине октября, потому что они понимают и знают, что ожидается и что им нужно сделать, потому что все, что они делают, — это СОГЛАСОВАННО .
Я получаю ВСЕ ИХ ВРЕМЯ один вопрос: как исправить всю их работу? Взгляните на маленькую картинку в правом нижнем углу вверху… видите ли вы, что записные книжки сложены стопкой и открываются на страницу, которую они только что сделали? Вот и ответ! Когда мои ученики заканчивают самостоятельную работу, математическую станцию или математические журналы, они складывают их в стопку, открытую на странице, которую они только что закончили.У меня уходит меньше десяти минут, чтобы проверить всю их работу, потому что каждая книга уже открыта на странице, и они сложены стопкой. Это экономит мне часы времени каждую неделю!
Итак … вкратце, вот как я управляю самостоятельной работой моих учеников во время обучения по управляемой математике! Если вы хотите вернуться к моему основному посту, чтобы прочитать остальные части статьи «Начни свою работу с управляемой математикой», нажмите здесь, чтобы вернуться к моему основному посту и прочитать о следующем компоненте управляемой математики!
Если вам интересно узнать, как реализовать управляемую математику, используя пошаговый подход, я создал онлайн-семинар по управляемой математике для профессионального развития под названием «Управляемая математика, которая работает».
Управляемая математика, которая работает — это онлайн-семинар по профессиональному развитию, который я создал для учителей начальных классов в 1-5 классах! Этот семинар по профессиональному развитию был настоящим любовным трудом, на развитие которого у меня ушел год, чтобы убедиться, что я усвоил все ИЗУЧЕННЫЕ УРОКИ и ошибки, которые я сделал на этом пути, и помочь ВАМ ИЗБЕЖАТЬ тех же ошибок, что и я, когда я впервые реализовал структуру управляемой математики в своем классе и почувствовал себя успешным, как только запустил механизмы управляемой математики!
Управляемая математика, которая работает предоставляет вам четкую и действенную ДОРОЖНУЮ КАРТУ, которая поможет легко и эффективно подготовить и использовать управляемую математику в вашем классе! Я учу вас ВСЕМУ, что я сделал в своем собственном классе, чтобы получить спокойный, организованный, упорядоченный и свободный от хаоса математический блок, где вы начнете видеть успехи своих учеников в математике СРАЗУ!
Вот краткое описание Управляемая математика, которая работает…
Этот семинар профессионального развития включает:
- 5 учебных модулей, которые содержат 24 видеоурока
- 5 часов обучения, которые могут быть использованы для удовлетворения ваших требований профессионального развития
- загружаемые рабочие тетради в формате PDF для каждого модуля
- ТОННЫ и ТОННЫ замечательных БОНУСОВ в бонусном модуле курса (БОЛЕЕ 40 долларов США только в виде БОНУСОВ)
Этот семинар по профессиональному развитию можно провести не выходя из собственного дома (допустимы пижамы), или ваш школьный округ может приобрести лицензии для своих учителей через нашу программу лицензирования школьного округа.



 .. дм2
.. дм2 4 класс
4 класс 4 класс
4 класс 4 класс
4 класс 4 класс
4 класс





 Спасибо!
Спасибо! мне
мне