Петерсон математика 4 класс 1 часть решебник ответы гдз: ГДЗ часть 2 Урок 16 математика 4 класс ПетерсонГ

Содержание

ГДЗ по Математике 4 класса

ГДЗ по математике для 4 класса Петерсона – это онлайн-решебник с готовыми домашними заданиями: решенными задачам и примерам из учебника по арифметике, составленного авторитетным российским математиком Петерсоном Л.Г. Он рекомендован Минобразования РФ для большинства российских средних школ.

Структура ГДЗ по учебнику математики четвертого класса от Петерсона

В четвертом классе ученики рассматривают измерение углов, части числа, доли и проценты, дроби и смешанные числа. Готовые домашние задания по учебнику Петерсона помогают школьникам постичь углубленную программу изучения арифметики, подготовить почву для усвоения правил геометрии, алгебры, физики и химии.

ГДЗ по математике 4 класса Петерсона, составленные на основе учебника 2013 года, включают в себя примеры и задачи на такие темы:

решение двойных неравенств
оценка суммы, разности, произведения, частного
деление на двузначное и трехзначное число
оценка площади и приближенное вычисление площадей
доли и сравнение долей¸ проценты
дроби, сравнение дробей и нахождение части числа;
площадь прямоугольного треугольника;
правильные и неправильные дроби, сложение и вычитание дробей;
шкалы, числовой луч, координаты на луче;
скорость сближения и скорость удаления, встречное движение;
действия над составными именованными величинами;
сравнение углов, развернутый угол, смежные углы;
круговые, столбчатые и линейные диаграммы;
координаты на плоскости и точки на осях координат.

Учебник Петерсона нацелен на углубленное и опережающее изучение арифметики. Оттого готовые домашние задания – важный помощник для учеников и их родителей, которые чаще всего делают уроки вместе с младшими школьниками.

Готовое домашнее задание для 4 класса на сайте ГДЗ Путина предлагает детальные алгоритмы решений. Четвероклассник не просто списывает задания, но вникает в алгоритм их выполнения. Это позволяет отказаться от услуг репетиторов и дополнительных занятий.

Правильные решения от ГДЗ Путина по математике 4 класса к Петерсону

Среди многочисленных решений, которыми пестрит сеть готовые примеры и задачи ГДЗ от Путина по учебнику Петерсона обладают рядом достоинств:

по ним предлагается несколько вариантов решения;
ответы оформлены в соответствии с требованиями Министерства образования РФ;
материалы доступны в режиме 24/7, бесплатно и без регистрации.

Задачи и примеры из решебника – верное подспорье для учеников и их родителей. Их можно открыть круглосуточно с телефона, планшета, компьютера. Детальные решения позволяют усвоить сложные темы и разобрать домашнюю работу без помощи репетиторов.

Родители могут в любой момент сверить решение школьника с вариантами сайта ГДЗ от Путина, найти ошибки и объяснить ребенку причины неточностей.

ГДЗ Математика 4 класс Петерсон

Зачем нужен предмет математика

Некоторые ученики считают, что данный предмет совершенно бесполезен. Но на самом деле это не так. Как говорится, математика – царица наук. Так и есть. Во-первых, данный предмет сдают на экзаменах после девятого и одиннадцатого класса. Во-вторых, это предмет, который помогает работать мозгам. И, наконец, в-третьих, знания, которые приобретает школьник на данном уроке, понадобятся ему в течение всей жизни.

Как школьнику заниматься математикой

Первое место, где ученик изучает любую науку – это школа. После нее – колледж и университет. Но базовые знания любой человек получает именно во время обучения в своем самом первом учебном учреждении. Впрочем, помимо этого, ребенок также может заниматься с профессиональным репетитором. Его услуги зачастую требуются тому, кто с трудом изучает общий курс точных наук. Но этот способ, пусть даже проверенный временем, имеет серьезные недостатки — он занимает очень много дополнительного времени. Таким образом, ученик либо отнимает время от работы с другими предметами, либо остается без полноценного отдыха, что в таком возрасте очень важно. Есть и другой способ улучшения знаний и повышения текущей успеваемости – занятия с

«Математика 4 класс Учебник Петерсон Перспектива Ювента».

Зачем нужен онлайн-решебник

Данный способ улучшения качества знаний сейчас очень популярен. Многие ученики работают с такой страницей. Но не все взрослые признают её стоящей. Им кажется, что Готовое Домашнее Задание используют только двоечники, которые не могут ничего сделать сами. Но это не так. Онлайн-решебник может помочь:

Правильно выполнить домашнее задание;
Подробнее изучить тему, которую не понимаешь;
Немного опередить программу.

И всё это совершенно бесплатно!

Только ученик — с помощью родителей, конечно, должен понять: решебник это не шпаргалка, из которой списывают домашнее задание, как из тетради одноклассника. Это — надежный виртуальный репетитор, который дает отличные советы. Но выполнять домашнее задание ученик должен самостоятельно.

Что включено в пособие

Темы упражнений соответствуют порядку изложения материала в основном учебнике математике для четвертого класса:

Построение точек по их координатам.
Транспортир измерение углов.
Круговые диаграммы.

Издание полностью адаптировано на возраст младшей школы. Включены даже задания, увлекательные для любого ребенка — например, «Морской бой».

Екстра гдз математика 4 клас л.г.петерсон

Скачать екстра гдз математика 4 клас л.г.петерсон doc

ГДЗ 4 класс Математика Петерсон. Описание решебника.

автор: Петерсон Л.Г.. ГДЗ БОТ содержит верные ответы с несколькими вариантами решения по Математике за 4 класс, автор издания: Петерсон Л.Г.. часть 1, часть 2, часть 3 С нами учебный процесс станет лучше!

Рекомендуемые решебники. рабочая тетрадь Петерсон Л.Г., Бином. самостоятельные и контрольные работы Петерсон Л.Г., Ювента. Петерсон Л.Г, Ювента. Ответы к части 1. Страницы учебника. 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 ГДЗ: Онлайн готовые домашние задания по математике ФГОС за 4 класс, автор Петерсон Л.Г., спиши решения и ответы на omk-avto.ru ГДЗ к самостоятельным и контрольным работам по математике за 4 класс Петерсон Л.Г.

(Учусь учиться) можно скачать здесь. ГДЗ к учебнику по математике за 4 класс Петерсон Л.Г. (Перспектива) можно скачать здесь. ГДЗ: Онлайн готовые домашние задания по математике ФГОС за 4 класс, автор Петерсон Л.Г., спиши решения и ответы на omk-avto.

ru Часть 1. Страницы учебника. ГОТОВЫЕ ДОМАШНИЕ ЗАДАНИЯ (ГДЗ): ГДЗ ПО МАТЕМАТИКЕ: Гдз по математике — учебник Математика.

4 класс. Петерсон Л.Г. (в 3-х частях — Москва: Ювента, год). 4 класс. Петерсон Л.Г.) Решебники. ГДЗ для 4 класса. ГДЗ по математике за 4 класс. Учебные материалы. Рефераты, курсовые и дипломные работы. Петерсон Л.Г. ГДЗ к учебнику математике за 4 класс. АВТОР: Петерсон Л.Г., Мы добавили новые ответы к учебнику по математике за четвертый класс авторов Петерсон Л.Г. года издания. Это ГДЗ по математике поможет с решением почти всех упражнений по математике за 4 класс. Ответы. Ответы на задания по математике за четвертый класс к учебнику Петерсон Л.Г.

Математика 4 класс. Учебник. Петерсон. 1, 2, 3. Перспектива. Сборник поделен на три части, которые в целом включают в себя восемьдесят девять уроков. Все ответы в ГДЗ по математике 4 класс тщательно проработаны и приведены в очень доступной форме. В конце пособия даны задания для повторения пройденного материала.

Почему им стоит воспользоваться.

ГДЗ по Математике 4 класс Петерсон Л.Г ФГОС. Показать решебники. Классы. 1 2 3 4 5 6 7 8 9 10 Материалы ГДЗ Л.Г. Петерсона с верными ответами активно используются прогрессивными педагогами для создания авторских рабочих программ по математике. Разделение заданий и примеров по сложности упрощает его применение в разнородных коллективах. Пособие адресовано детям, их родителям, а также школьным учителям и репетиторам по математике для систематического использования.

© «omk-avto.ru» [email protected]. Математика 4 класс. Учебник. Петерсон. 1, 2, 3. Перспектива. Сборник поделен на три части, которые в целом включают в себя восемьдесят девять уроков. Все ответы в ГДЗ по математике 4 класс тщательно проработаны и приведены в очень доступной форме. В конце пособия даны задания для повторения пройденного материала. Почему им стоит воспользоваться. Решебники за 4 класс > Математика > Л.Г.

Петерсон. Решебник (ГДЗ) Математика 4 класс Л. Г. Петерсон ( год) Часть 1. Авторы: Л.Г. Петерсон. Год: |. Класс: 4 |. Предмет: Математика |. Поделиться с друзьями. 0. Похожие ГДЗ (2) +. Математика 4 класс Л.Г. Петерсон ( год) Часть 2. Математика 4 класс Л.Г. Петерсон ( год) Часть 3. Учебник: Математика 4 класс Л.Г. Петерсон ( год) Часть 1. Урок 1. Решение неравенства№

fb2, doc, txt, doc

Похожее:

Додавання і віднімання чисел у межах 20 1 клас

Гдз хімія 8 клас практична робота 1

Презентація економія води

Усі уроки геометрії 9 клас бабенко гдз

Історія хвороби хірургія рана

Контрольна робота амінокислоти білки

Презентація роль класного керівника у формуванні учнівського колективу

ГДЗ, Ответы по Математике 4 класс Петерсон. Все решебники тут GDZ-na5.info

Готовые Домашние Задания, Решебник по Математике 4 класс Петерсон

ГДЗ: 4 класс.

Математика.

Петерсон Л.Г. 2016 г.

Здравствуй, дорогой школьник! Ты уже учишься в четвёртом классе — самое время осваивать математику: если ты запустишь её на первых порах обучения, то потом понять этот предмет будет очень сложно. Ведь математика — точная наука, весь материал школьной программы по этому предмету связан между собой!

А понять математику тебе поможет наш решебник, который называется «Готовые домашние задания по Математике для четвёртого класса». На его страницах ты найдёшь решения и ответы ко всем задачам учебника, если чего-то не понял на уроке. С этим решебником ты освоишь математику быстро и легко!

Ответы к домашним заданиям по Математике 4 класс. Петерсон Л.Г.

Уроки на повторение.

Часть 1.

Урок-01.
Урок-02.
Урок-03.
Урок-04.
Урок-05.
Урок-06.
Урок-07.
Урок-08.
Урок-09.
Урок-10.
Урок-11.
Урок-12.
Урок-13.
Урок-14.
Урок-15.
Урок-16.
Урок-17.
Урок-18.
Урок-19.
Урок-20.
Урок-21.
Урок-22.
Урок-23.
Урок-24.
Урок-25.
Урок-26.
Урок-27.
Урок-28.
Урок-29.

Урок-30.
Урок-31.
Урок-32.

Часть 2.

Урок-28.
Урок-29.
Урок-30.
Урок-31.
Урок-32.
Урок-33.
Урок-34.
Урок-35.
Урок-36.

Часть 3.

Урок-20.
Урок-21.

Страница не найдена

Новости

21 фев

В Барнауле оперативные службы проводят проверку в связи с поступлением сообщений о минировании ряда школ.

20 фев

Министр образования Подмосковья Ирина Каклюгина отметила, что итоговое собеседование по русскому языку успешно прошли 99,5% девятиклассников Подмосковья. В регионе уже опубликовали результаты.

19 фев

Из-за сильных морозов в школах некоторых городов и посёлков Мурманской области отменены школьные занятия.

19 фев

Министр образования Подмосковья Ирина Каклюгина рассказала, что регион присоединился к всероссийской акции «100 баллов для Победы». Мероприятие прошло на базе Красногорского колледжа.

18 фев

Во всех возрастных группах жителей Москвы наблюдается спад заболеваемости коронавирусной инфекцией. Об этом сообщила заместитель столичного мэра по вопросам социального развития Анастасия Ракова.

18 фев

Во Владивостоке 26 классов в десяти муниципальных школах перешли на дистанционное обучение из-за коронавируса.

17 фев

В Московской области стартовала всероссийская акция «Единый день сдачи ЕГЭ родителями», она продолжится в марте и апреле.

▶▷▶ гдз математика 4 класс учебник 3 часть петерсон

Интерфейс	Русский/Английский
Тип лицензия	Free
Кол-во просмотров	257
Кол-во загрузок	132 раз
Обновление:	16-01-2019

гдз математика 4 класс учебник 3 часть петерсон — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Want more to discover? Make Yahoo Your Home Page See breaking news more every time you open your browser Add it now No Thanks Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download ГДЗ (решебник) по математике 4 класс Петерсон часть 1, 2, 3 reshatorcom/ 4 -klass/matematika/peterson Cached ГДЗ по математике 4 класс Петерсон часть 1, 2, 3 Ответы из решебника к учебнику ГДЗ, решебник по математике 4 класс Петерсон часть 1, 2, 3 gdz-fiveru/gdz/ 4 _class/mathematics/peterson Cached На этой странице размещены все ГДЗ к учебнику по математике за 4 класс автора ЛГ Петерсон 2013 года издания часть 1, 2, 3 ГДЗ по математике 4 класс Петерсон 1, 2, 3 часть ответы yagdzcom 1- 4 класс Математика ГДЗ решебник к учебнику по математике 4 класс Петерсон Часть 1, 2, 3 ФГОС 2016 » Математика ГДЗ (решебник) по математике 4 класс Петерсон reshebame/gdz/matematika/ 4 -klass/peterson Cached Материалы ГДЗ по математике к учебнику Петерсон в 3 -х частях 2014 года издания помогут 4 -классникам уточнить правильность выполнения заданий Решебник задач и ГДЗ по Математике 4 класс Петерсон ЛГ gdzputinanet/ 4 -klass-matematika-peterson Cached ГДЗ по Математике 4 класс автор: Петерсон ЛГ Математика в четвёртом классе становиться наиболее сложной Увеличивается количество задаваемого материала на дом ГДЗ по математике 4 класс Петерсон часть 1, 2, 3 онлайн gdz-onlinecom/ 4 -klass/matematika/peterson Cached ГДЗ к учебнику по математике за 4 класс Петерсон часть 1, 2, 3 онлайн ГДЗ Математика 3 класс учебник: часть 1, часть 2, часть 3 uchebenet … Математика Ответы для гдз по учебнику Математика 3 класс учебник : часть 1, часть 2, часть 3 2013 год от автора Петерсон издательства Ювента ГДЗ по математике за 4 класс часть 1, часть 2, часть 3 onlinegdzapp/ 4 -klass/matematika/peterson Cached Здесь вы найдете учебник по Математике 4 класса Часть 1, 2, 3 , авторы: Петерсон ЛГ, от издательства Ювента 2014 ГДЗ решебник Математика 4 класс Учебник Петерсон Л Г otlgdzonline 4 КЛАСС ГДЗ Математика 4 класс Учебник Петерсон Л Г Учебник по математике для 3 класса разработан в 3 частях и содержит логические задания, которые тренируют у детей мышление, память и навыки счета Решебник (ГДЗ) по математике 4 класс 1,2,3 часть Петерсон megareshebaru/index/02/0-472 Cached ГДЗ по Математике (1, 2, 3 часть ) за 4 класс автора Петерсон ЛГ, 2015 год, поможет родителям Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 54,500 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™

решебник Петерсон ЛГ

2015 год
2
которые тренируют у детей мышление

гдз математика 4 класс учебник 3 часть петерсон — Поиск в Google Специальные ссылки Перейти к основному контенту Справка по использованию специальных возможностей Оставить отзыв о специальных возможностях Нажмите здесь , если переадресация не будет выполнена в течение нескольких секунд Войти Удалить Пожаловаться на неприемлемые подсказки Режимы поиска Все Картинки Новости Видео Покупки Ещё Карты Книги Авиабилеты Финансы Настройки Настройки поиска Языки (Languages) Включить Безопасный поиск Расширенный поиск Ваши данные в Поиске История Поиск в справке Инструменты Результатов: примерно 28 (0,49 сек) Looking for results in English? Change to English Оставить русский Изменить язык Результаты поиска Все результаты Решебник (ГДЗ) по математике 4 класс 1,2,3 часть Петерсон › ГДЗ › 4 класс › Математика › Петерсон ЛГ Сохраненная копия Похожие ГДЗ по Математике (1, 2, 3 часть ) за 4 класс автора Петерсон ЛГ, 2015 год, поможет ГДЗ Рабочая тетрадь математика 4 класс Петерсон ЛГ Решебник (ГДЗ) Математика 4 класс 1, 2, 3 часть Петерсон Л Г gdzometrby/book337 Сохраненная копия Ответы к учебнику по математике для 4 класса Петерсон ‎ Часть 2 · ‎ Часть 1 · ‎ Часть 3 · ‎ Задачи на повторение Часть 2 — Решебник (ГДЗ) Математика 4 класс 1, 2, 3 часть gdzometrby/book608page4660 Сохраненная копия Ответы к учебнику по математике для 4 класса Петерсон ГДЗ по Математике за 4 класс Петерсон ЛГ Части 1,2 и 3 Решебник › ГДЗ › 4 класс › Математика › Петерсон ЛГ Сохраненная копия ГДЗ : Спиши готовые домашние задания по математике за 4 класс , решебник Петерсон ЛГ, ФГОС, часть 1, часть 2, часть 3 онлайн ответы на GDZ RU Математика 4 класс рабочая тетрадь Автор: Петерсон ЛГ издательство: ГДЗ (решебник) по математике 4 класс Петерсон часть 1, 2, 3 reshatorru/4-klass/matematika/peterson/ Сохраненная копия Предлагаем вашему вниманию гдз по математике 4 класс Петерсона Примеры решены по алгоритмам, Часть 1 ( учебник ) Урок 1 Нахождение части , которую одно число составляет от другого 1 2 3 4 5 6 7 8 9 10 11 12 Урок 3 ГДЗ по математике для 4 класса Петерсон ЛГ Перспектива Сохраненная копия Три части учебника по математике в 4 классе , как же успеть их Поэтому Петерсон ЛГ опубликовал свой замечательный решебник Все ГДЗ в Содержание сборника ответов расписано по урокам и разделено на 1,2 и 3 части ГДЗ по математике 4 класс Петерсон Сохраненная копия Ответы на задания учебника математики 4 класса в 3 -х частях автора Ответы по математике 4 класс Петерсон : Часть 1: Выберите номер урока: ГДЗ решебник по математике 4 класс Петерсон — Ботанам нет › Решебники › 4 класс › Математика Сохраненная копия ГДЗ по математике за 4 класс автора Петерсон ЛГ 2010-2014 года издания Учебник по математики состоит из трёх частей: первый раздел имеет 32 Решебник по Математике за 4 класс Петерсон ЛГ часть 1, 2, 3 на Сохраненная копия часть 2, часть 3 Автора: Петерсон ЛГ Издательство: Ювента Полные и подробные ответы к упражнениям на Гитем Решебник ( ГДЗ ) по Математике за 4 класс Петерсон ЛГ часть 1, 2, 3 Часть 1 страницы учебника 1 2 3 4 ГДЗ, Ответы по Математике 4 класс Петерсон ЛГ 2016 г | Более Сохраненная копия 25 дек 2014 г — Готовые Домашние Задания , Решебник по Математике 4 класс ты найдёшь решения и ответы ко всем задачам учебника , если ГДЗ по математике для 4 класса Петерсон ЛГ 1, 2, 3 часть › Математика › 4 класс Сохраненная копия Решебник к учебнику по математике для 4 класса общеобразовательных школ и гимназий, автор Петерсон ЛГ, 1 2 3 части Решебник (гдз) по Математике для 4 класса Петерсон ЛГ Сохраненная копия ГДЗ к рабочей тетради по математике за 4 класс Петерсон ЛГ можно скачать здесь Часть 1 страницы учебника 1 2 3 Часть 3 страницы учебника Математика 4 класс Петерсон › Учебники › Математика 4 класс Петерсон Сохраненная копия Учебники ; Математика 4 класс Петерсон Нахождение части числа 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 · 11 Нахождение числа по его части 1 · 2 · 3 · 4 · 5 · 6 ГДЗ по математике 4 класс Петерсон Часть 1, 2, 3 › Математика › 4 класс Сохраненная копия Похожие ГДЗ математика 4 класс часть 1, 2, 3 Петерсон Ювента интерес как основу развития способностей четвероклассников учебники математики из цикла ГДЗ ЛОЛ за 4 класс по Математике Петерсон ЛГ ФГОС Сохраненная копия Выполнения задания за 4 класс по Математике Петерсон ЛГ часть 1, 2, 3 , от издательства: Ювента 2014 ФГОС, не простое занятие Поэтому ГДЗ Решебник (ГДЗ) Математика, 4 класс 1, 2, 3 часть (Петерсон ЛГ Сохраненная копия Решебник ( ГДЗ ) для Математика , 4 класс 1, 2, 3 часть ( Петерсон ЛГ) 2010 ГДЗ по математике 4 класс Петерсон 1, 2, 3 часть учебник › 1-4 классы › Математика Сохраненная копия ГДЗ готовые домашние задания учебника по математике 4 класс Петерсон 1 ,2 и 3 часть ФГОС от Путина Решебник ( ответы на вопросы и задания) ▷ гдз по математике рабочая тетрадь 4 класс 2 часть петерсон wwwzstelceu//gdz-po-matematike-rabochaia-tetrad-4-klass-2-chast-petersonxml Сохраненная копия 8 нояб 2018 г — авторы учебника : Петерсон ЛГ на 2017-2018 год Часть 3 Страницы тетради Читать ещё ГДЗ 4 класс Математика рабочая тетрадь решебник по математике 4 класс петерсон рабочая тетрадь часть 3 immanuelenglishcom//reshebnik-po-matematike-4-klass-peterson-rabochaia-tetrad- Сохраненная копия решебник по математике 4 класс петерсон рабочая тетрадь часть 3 — Все результаты ГДЗ по математике за 4 класс рабочая тетрадь Петерсон — GDZru гдз по математике 4 класс автор Петерсон Л Г 2016 и 2013 год 1,2 Сохраненная копия 28 нояб 2017 г — гдз Петерсон Л Г 4 класс 1,2 и 3 часть математика ( учебник ) ГДЗ по математике для учебника первая, вторая и третья часть автора ГДЗ решебник по математике 1 класс Петерсон — 1, 2, 3 часть | В helpzaochnikuru/gdz-reshebnik-po-matematike-1-klass-peterson/ Сохраненная копия Похожие 7 июн 2016 г — Удобный решебник по математике за 1 класс в трёх частях (1, 2, 3 части ) поможет ученикам быстро списать решения нужных задач — к Картинки по запросу гдз математика 4 класс учебник 3 часть петерсон «id»:»VElp0ffGIRTqSM:»,»ml»:»600″:»bh»:90,»bw»:69,»oh»:947,»ou»:» «,»ow»:700,»pt»:»gdzlolbiz/gdzimg/4klass/matematika/peterson-tetra»,»rh»:»gdzlolbiz»,»rid»:»X2_o0PYDZ1gn5M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ ЛОЛ»,»th»:97,»tu»:» \u003dtbn:ANd9GcSK05L_CK5ATR-e2uHJwGILttFsWUIT__GhkRPvuruMaENnO2GPvJh2G6Q»,»tw»:72 «id»:»Hmgohe7KR8ae4M:»,»ml»:»600″:»bh»:90,»bw»:69,»oh»:947,»ou»:» «,»ow»:700,»pt»:»gdzlolbiz/gdzimg/4klass/matematika/peterson-tetra»,»rh»:»gdzlolbiz»,»rid»:»X2_o0PYDZ1gn5M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ ЛОЛ»,»th»:97,»tu»:» \u003dtbn:ANd9GcS7GZ7FQMAE7uTWd7P3X_KXD_OHZX17m_cO1kGP4WffS989tcuvyxmGoA»,»tw»:72 «id»:»XevCcJW1VYReqM:»,»ml»:»600″:»bh»:90,»bw»:61,»oh»:792,»ou»:» «,»ow»:525,»pt»:»ipinimgcom/736x/35/f1/c5/35f1c50586564267f526ad3″,»rh»:»pinterestcom»,»rid»:»nORmMQVRC1312M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Pinterest»,»th»:102,»tu»:» \u003dtbn:ANd9GcSkHuirjnivPWUgqkCePNEOsNQxkFjL3chMctsiVe6f6iqZwDX45LMcig»,»tw»:67 «id»:»Yq4mAKGuFQzxDM:»,»ml»:»600″:»bh»:90,»bw»:69,»oh»:947,»ou»:» «,»ow»:700,»pt»:»gdzlolbiz/gdzimg/4klass/matematika/peterson-tetra»,»rh»:»gdzlolbiz»,»rid»:»X2_o0PYDZ1gn5M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ ЛОЛ»,»th»:97,»tu»:» \u003dtbn:ANd9GcQfbcW7wpwwq2PXL3ljE9AmRq-z5zlhXf2aof1LqzdWrsDppKCu5cWFltI»,»tw»:72 «id»:»Hj4trWRIAWlXsM:»,»ml»:»600″:»bh»:90,»bw»:69,»oh»:947,»ou»:» «,»ow»:700,»pt»:»gdzlolbiz/gdzimg/4klass/matematika/peterson-tetra»,»rh»:»gdzlolbiz»,»rid»:»X2_o0PYDZ1gn5M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ ЛОЛ»,»th»:97,»tu»:» \u003dtbn:ANd9GcRkdPR-2O-uBODVCpDHvnot74bknXXEwHUxTn4DlSi2nx67vu_QRV4UBQ»,»tw»:72 «cl»:3,»id»:»pMSve_eUJO3ZxM:»,»ml»:»600″:»bh»:90,»bw»:48,»oh»:2529,»ou»:» «,»ow»:1312,»pt»:»reshatorru/otvety/4-klass-peterson/h2-2-9png»,»rh»:»reshatorru»,»rid»:»HIw-cOwF7lMhqM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:116,»tu»:» \u003dtbn:ANd9GcSeq57SCvsROMugTB1oa8PxzIDb4SM9TKiBBBHu_Av7ZthxzUifOqa3Kp0″,»tw»:60 «id»:»UT7HBsjYvR7i_M:»,»ml»:»600″:»bh»:90,»bw»:45,»oh»:3968,»ou»:» «,»ow»:1940,»pt»:»reshatorru/otvety/4-klass-peterson/h2-2-10png»,»rh»:»reshatorru»,»rid»:»HIw-cOwF7lMhqM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Решатор»,»th»:120,»tu»:» \u003dtbn:ANd9GcSOc2O3hpLHiLxV7XFwlAvUr5jmNZtbaKunr2ZjzQjkTudUwYNyhmTNfvI»,»tw»:58 «cl»:3,»ct»:3,»id»:»DdVPKYazYoenyM:»,»ml»:»600″:»bh»:90,»bw»:71,»oh»:947,»ou»:» «,»ow»:700,»pt»:»gdzlolbiz/gdzimg/4klass/matematika/peterson-tetra»,»rh»:»gdzlolbiz»,»rid»:»X2_o0PYDZ1gn5M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ ЛОЛ»,»th»:97,»tu»:» \u003dtbn:ANd9GcRCx75itgv6IKhU0Yl6XB96KjluljHOE_fS7zJWKYv74GgVVpRyZotUOA»,»tw»:72 «id»:»k87e6JaXRf2fTM:»,»ml»:»600″:»bh»:90,»bw»:67,»oh»:947,»ou»:» «,»ow»:700,»pt»:»gdzlolbiz/gdzimg/4klass/matematika/peterson-tetra»,»rh»:»gdzlolbiz»,»rid»:»X2_o0PYDZ1gn5M»,»rt»:0,»ru»:» «,»sc»:1,»st»:»ГДЗ ЛОЛ»,»th»:97,»tu»:» \u003dtbn:ANd9GcTYQzKZLhEU0mFgogrhZgdbZDyq0r5x-qnQ6XQLvKdqP8VAjDYksTqBz78″,»tw»:72 Другие картинки по запросу «гдз математика 4 класс учебник 3 часть петерсон» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Страница 53 Задание 11 – Математика 4 класс (Моро) Часть 1 ▶ 6:00 27 окт 2015 г — Добавлено пользователем UrokiTV Страница 53 Задание 11 – Математика 4 класс (Моро) Часть 1 UrokiTV 52 Задание 259 – Математика 4 класс Моро – Учебник Часть 1 Урок ГДЗ по русскому языку 4 класс Бунеев, Бунеева, Пронина 1, 2 часть Сохраненная копия ГДЗ по русскому языку за 4 класс Бунеев Ответы и решебник к учебнику часть 1, 2 Часть 1 Часть 1 (Упражнение с 1 по 173) 1 2 3 4 5 6 Вспоминаем ГДЗ решебник по английскому языку 4 класс сборник упражнений › 1-4 класс › Английский язык Сохраненная копия Рейтинг: 3,6 — ‎551 голос Предлагаются ответы на сборник упражнений по английскому языку, авторами которого являются ГДЗ по английскому языку 4 класс Быкова, Поспелова 1 Звезда 2 Звезды 3 Звезды 4 Звезды 5 Звезд ГДЗ решебник рабочая тетрадь по информатике 7 класс Босова ФГОС · ГДЗ решебник к контурным Задание 1 — ГДЗ Математика 4 класс 1, 2, 3 часть Петерсон Л Г Задание 1 — ГДЗ Математика 4 класс 1, 2, 3 часть Бесплатные учебники — Скачать учебник бесплатно — Бесплатные учебники Образование Детей, Математика 4 класс Учебник в 3 частях — Петерсон ЛГ 11klasovru › Математика Сохраненная копия Учебник является частью непрерывного курса математики «Учусь учиться» для Математика 4 класс Учебник в 3 частях — Петерсон ЛГ cкачать в PDF Учебник 1 Часть — Петерсон ЛГ 2018 Готовые домашние задания ГДЗ по математике 4 класс Петерсон часть 1, 2, 3 — решебник gdz-onlinecom/4-klass/matematika/peterson/ Сохраненная копия ГДЗ к учебнику по математике за 4 класс Петерсон часть 1, 2, 3 онлайн математике 4 класс Петерсон часть 1, 2, 3 онлайн Часть 1 ( учебник ) Урок 1 Математика — Школьные Знанияcom Сохраненная копия Похожие Математика ; 5 б; 5 минут назад Выразить в см Побудуй відрізок, довжина якого у 3 рази менша, ніж периметр такого прямокутника Ответь Решить уравнение (x+2)^ 4 /|sin2x|=1/sin2x iosiffinikov Математика ; 5 б; 2 часа назад Пояснения к фильтрации результатов Мы скрыли некоторые результаты, которые очень похожи на уже представленные выше (37) Показать скрытые результаты В ответ на официальный запрос мы удалили некоторые результаты (1) с этой страницы Вы можете ознакомиться с запросом на сайте LumenDatabaseorg В ответ на жалобу, поданную в соответствии с Законом США «Об авторском праве в цифровую эпоху», мы удалили некоторые результаты (1) с этой страницы Вы можете ознакомиться с жалобой на сайте LumenDatabaseorg Вместе с гдз математика 4 класс учебник 3 часть петерсон часто ищут гдз по математике 4 класс петерсон 2015 гдз по математике 4 класс петерсон рабочая тетрадь 1 часть петерсон 4 класс учебник петерсон математика 2 класс решебник по математике петерсон 4 класс гдз путина математика петерсон четвёртый класс часть первая петерсон гдз по математике 4 кл ч 3 математика петерсон ответы 4 класс 2 часть Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Покупки Документы Blogger Hangouts Google Keep Jamboard Подборки Другие сервисы Google

Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Знатоки Коллекции Музыка Переводчик Диск Почта Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Решебник задач и ГДЗ по Математике 4 класс Петерсон gdzputinanet › 4-klass-matematika-peterson Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Математика в четвёртом классе становиться наиболее сложной С помощью именно этого ГДЗ по математике 4 класс автор: ЛГ Петерсон ученик сможет преодолеть все сложности, подстерегающие его при Часть 3 страницы учебника 67 68 69 70 71 72 73 74 75 76 Читать ещё Математика в четвёртом классе становиться наиболее сложной Увеличивается количество задаваемого материала на дом С помощью именно этого ГДЗ по математике 4 класс автор: ЛГ Петерсон ученик сможет преодолеть все сложности, подстерегающие его при выполнении домашнего задания Этот решебник состоит из трёх частей Часть 3 страницы учебника 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 42 43 44 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 © gdzputinanet 2019 admin@gdzputinanet Скрыть 2 ГДЗ по математике за 4 класс Петерсон GDZplusru › 4-klass/matematika/peterson/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте Подробный разбор задач из учебника по математике за 4 класс Петерсон часть 1, 2 и 3 Бесплатные ответы к номерам онлайн Ответы и решения к учебнику части 1, 2 и 3 онлайн 1 2 3 4 5 6 7 8 9 10 Читать ещё Подробный разбор задач из учебника по математике за 4 класс Петерсон часть 1, 2 и 3 Бесплатные ответы к номерам онлайн Ответы и решения к учебнику части 1, 2 и 3 онлайн Петерсон Ювента, 2015 Часть 1 Часть 1 (Уроки с 1 по 32) Урок 1 Решение неравенства: 1 2 3 4 5 6 7 8 9 10 11 12 13 Урок 2 Множество решений: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Урок 3 Знаки и 3 4 5 6 7 8 9 10 11 12 13 14 15 Урок 4 Двойное неравенство: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Урок 5 Двойное неравенство 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Урок 5 Правильные и неправильные дроби Скрыть 3 ГДЗ по математике 4 класс Петерсон 1, 2, 3 часть ответы YaGDZcom › 1-4-klass/matematika…4…peterson…3-chast/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте ГДЗ решебник к учебнику по математике 4 класс Петерсон Часть 1, 2, 3 ФГОС 2016 Ответы и решения на задания на сайте ЯГДЗ из учебника 4 класс Петерсон позволят вам проверить правильность 4 ГДЗ по математике 4 класс Петерсон часть gdz-fiveru › Решебники › 4 класс › Математика › Петерсон Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте На этой странице размещены все ГДЗ к учебнику по математике за 4 класс автора ЛГ Петерсон 2013 года издания часть 1, 2, 3 Все задания данного решебника подробно рассмотрены и решены авторами, ученикам остается только Часть 3 Урок 2: 1 2 3 4 5 6 7 8 Читать ещё На этой странице размещены все ГДЗ к учебнику по математике за 4 класс автора ЛГ Петерсон 2013 года издания часть 1, 2, 3 Все задания данного решебника подробно рассмотрены и решены авторами, ученикам остается только списывать и забыть о домашних заданиях ! Однако сайт «GDZ-FIVERU» рекомендует списывать каждое задание с пониманием, чтобы при попадании похожих заданий и задач ученики сами смогли их решить Часть 1 Часть 3 : Урок 1: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 Урок 2: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Скрыть 5 ГДЗ по математике за 4 класс часть 1, 2, 3 Петерсон onlinegdzapp › 4-klass/matematika/peterson Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Здесь вы найдете учебник по Математике 4 класса Часть 1, 2, 3 , авторы: Петерсон ЛГ, от издательства Ювента 2014 ГДЗ содержит все ответы на вопросы и поможет Вам правильно выполнить домашнее задание ГДЗ к рабочей тетради по математике за 4 класс Петерсон Читать ещё Здесь вы найдете учебник по Математике 4 класса Часть 1, 2, 3 , авторы: Петерсон ЛГ, от издательства Ювента 2014 ГДЗ содержит все ответы на вопросы и поможет Вам правильно выполнить домашнее задание ГДЗ к рабочей тетради по математике за 4 класс Петерсон ЛГ можно скачать здесь ГДЗ к самостоятельным и контрольным работам по математике за 4 класс Петерсон ЛГ можно скачать здесь Часть 1 страницы учебника 1 2 3 4 5 6 Скрыть 6 ГДЗ по Математике за 4 класс : Петерсон ЛГ Части 1,2 и 3 GDZru › class-4/matematika/peterson-4/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробнее о сайте ГДЗ : Спиши готовые домашние задания по математике за 4 класс , решебник Петерсон ЛГ, ФГОС, часть 1, часть 2, часть 3 ГДЗ по математике для 4 класса Петерсона ЛГ заменит любого репетитор С помощью данного пособия в 3 частях В третьей выполнены задания по круговым диаграммам и координатам на Читать ещё ГДЗ : Спиши готовые домашние задания по математике за 4 класс , решебник Петерсон ЛГ, ФГОС, часть 1, часть 2, часть 3 онлайн ответы на GDZRU ГДЗ по математике для 4 класса Петерсона ЛГ заменит любого репетитор С помощью данного пособия в 3 частях школьник без сторонней помощи справится с примерами и задачами В сборнике ответов приводятся упражнения для тренировки теоретических знаний об оценке суммы и разности, площади треугольника Вторая часть содержит ответы по темам дроби, шкалы, движение В третьей выполнены задания по круговым диаграммам и координатам на плоскости Скрыть 7 ГДЗ от Путина по математике 4 класс Петерсон 3 части Gdz-Putinacc › 1-4 класс › Математика › peterson-3-chastihtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте На нашем учебном ресурсе вы найдете ответы по математике для 4 класса Петерсон 3 части Данный учебник включает в себя массу примеров и задач повышенной сложности, безошибочно выполнить которые четверокласснику 1 2 3 4 5 6 7 8 9 10 Читать ещё На нашем учебном ресурсе вы найдете ответы по математике для 4 класса Петерсон 3 части Данный учебник включает в себя массу примеров и задач повышенной сл Данный учебник включает в себя массу примеров и задач повышенной сложности, безошибочно выполнить которые четверокласснику помогут электронные ГДЗ Часть 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Задачи на повторение Скрыть 8 Учебник Математика 4 класс ЛГ Петерсон 2013 Часть 3 vklasseonline › 4…matematika…peterson-2013-chast-3 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Учебники за 4 класс Математика ЛГ Петерсон Учебник Математика 4 класс ЛГ Петерсон (2013 год) Часть 3 Математика 4 класс ЛГ Петерсон (2013 год) Часть 1 Читать ещё Учебники за 4 класс Математика ЛГ Петерсон Учебник Математика 4 класс ЛГ Петерсон (2013 год) Часть 3 Авторы: ЛГ Петерсон Год: 2013 | Класс: 4 | Предмет: Математика | Похожие учебники (2) + Математика 4 класс ЛГ Петерсон (2013 год) Часть 1 Математика 4 класс ЛГ Петерсон (2013 год) Часть 2 Решебник: Математика 4 класс ЛГ Петерсон (2013 год) Часть 3 Читать онлайн Скачать учебник Скрыть 9 ГДЗ по Математике за 4 класс рабочая тетрадь Петерсон MegaReshebaru › gdz/matematika/4-klass…peterson Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Подробный решебник ( ГДЗ ) по Математике для 4 класса рабочая тетрадь, часть 1, 2, 3 Авторы учебника : Петерсон ЛГ 66 67 68 69 70 71 72 73 74 75 Читать ещё Подробный решебник ( ГДЗ ) по Математике для 4 класса рабочая тетрадь, часть 1, 2, 3 Авторы учебника : Петерсон ЛГ Рекомендуемые решебники ГДЗ учебник математика 4 класс Петерсон ЛГ ГДЗ Самостоятельные и контрольные работы математика 4 класс Петерсон ЛГ Часть 1 Страницы тетради 66 67 68 69 70 71 72 73 74 75 76 77 78 79 Часть 3 Страницы тетради 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 © 2019 «megareshebaru» [email protected] Скрыть 10 ГДЗ по математике 4 класс Петерсон gdzmaniacom › …83-matematika-4-klass-petersonhtml Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте ГДЗ ( готовые домашние задания ) и решебник по математике за 4 класс ( учебник в 3-х частях), авторы: Петерсон ЛГ автор: Петерсон ЛГ (1, 2, 3 часть ) Мы предлагаем вам решебник к учебному предмету математика за 4 класс начальной Выберите номер урока: 1 2 3 4 5 6 7 Читать ещё ГДЗ ( готовые домашние задания ) и решебник по математике за 4 класс ( учебник в 3-х частях), авторы: Петерсон ЛГ автор: Петерсон ЛГ (1, 2, 3 часть ) Мы предлагаем вам решебник к учебному предмету математика за 4 класс начальной школы автора Петерсон С этими готовыми ответами и решениями на все задания (1,2, 3 части ) вам будет легче проверить безошибочность выполнения домашнего и школьного задания, или наверстать пропущенное по болезни Cмотреть тут: рабочая тетрадь ( Петерсон ЛГ) Ответы по математике 4 класс Петерсон : Часть 1 Выберите номер урока: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Задачи на повторение Скрыть Школьные учебники В наличии! / labirintru Лабиринт Пресс Акции Главные книги года Подарочные книги labirintru › учебники Не подходит по запросу Спам или мошенничество Мешает видеть результаты Информация о сайте реклама Учебники 3 класс Почти 20 000 видов Доставка Контактная информация +7 (495) 745-95-25 пн-пт круглосуточно Магазин на Маркете 18+ Вместе с « гдз математика 4 класс учебник 3 часть петерсон » ищут: гдз русский язык 4 класс учебник гдз математика 4 класс рабочая тетрадь гдз математика 4 класс рудницкая юдачева 1 часть учебник гдз математика 4 класс башмаков нефедова 1 часть учебник ответы гдз математика 4 класс истомина 1 часть учебник гдз математика 4 класс рабочая тетрадь 1 часть волкова гдз математика 4 класс тетрадь гдз математика 4 класс чекин 1 часть учебник гдз по русскому языку 4 класс канакина горецкий 1 часть ответы 1 2 3 4 5 дальше Браузер Предложит замену неверному адресу сайта 0+ Скачать Будьте в Плюсе

ГДЗ: Математика 4 класс Петерсон

Математика 4 класс

Тип: Учебник

Авторы: Петерсон

Издательство: Ювента

МАТЕМАТИКА ОСНОВА СОВРЕМЕННОГО ОБЩЕСТВА

С каждым годом, десятилетием, столетием мир меняется. От необразованности мы перешли к обязательному среднему образованию всех детей. Теперь каждому доступно изучение всех дисциплин от астрономии до географии и физики. Каждый член общества обязан обладать необходимым минимумом знаний по каждому предмету. Развитие цивилизации пошло по пути развития технологий. Каждое новое открытие в науке это новое изобретение для современного общества.

ДЛЯ ЧЕГО НАМ УЧИТЬ МАТЕМАТИКУ

В обществе развитых технологий и всеобщего распространения электронных гаджетов знание математики необходимо для:

Понимания базовых принципов работы.
Изучение языков программирования.
Освоения новых профессий и совершенствования полученных знаний.

Людям, не имеющим отношения к технологиям, достаточно знать лишь базовые принципы работы техники основанные на математике. Однако в мире поголовного увлечения компьютерной техникой все больше приобретает популярность профессия программиста. Языки программирования техники основаны на математических алгоритмах, их знание и понимание необходимо для успешного обучения по профессии.

ПРОГРАММА ДЛЯ ЧЕТВЕРОКЛАССНИКОВ

К четвёртому году обучения в школе математика заметно усложнится. Помимо повторения уже изученного материала добавятся темы:

по арифметическим действиям с поиском неизвестного числа.
измерение мер и величин.
понятие о натуральных числах.
введение в геометрию и различные действия с двузначными числами (сложение, вычитание, умножение и деление).

«Царица наук» далеко не всем школьникам даётся легко, особенно такие темы, как поиск неизвестного, некоторые действия с двузначными числами или новые термины. «Математика 4 класс Учебник Петерсон Перспектива» содержит все необходимые четверокласснику материалы и соответствует всем стандартам образования (ФГОС). Издательство Ювента.

РОДИТЕЛЯМ В ПОМОЩЬ

Грамотно организовать помощь ребёнку с выполнением домашних заданий поможет «ГДЗ по Математике 4 класс Петерсон». В этом пособии содержатся подробные описания решения задач и примеров, развёрнутые ответы и пояснения автора. Всё это поможет проверять правильность не только решения, но и выполнения всего задания. Эта книга сильно выручит, если школьник не мог присутствовать на занятиях в школе по уважительным причинам. Можно выполнять домашнюю работу вместе с ребёнком, проверяя и объясняя материал.

% PDF-1.3 % 1218 0 объект> endobj xref 1218 93 0000000016 00000 н. 0000004884 00000 н. 0000005069 00000 н. 0000005105 00000 н. 0000005473 00000 п. 0000005600 00000 н. 0000005727 00000 н. 0000005859 00000 н. 0000005988 00000 н. 0000006120 00000 н. 0000006252 00000 н. 0000006377 00000 н. 0000006504 00000 н. 0000006631 00000 н. 0000006758 00000 н. 0000006885 00000 н. 0000007012 00000 н. 0000007139 00000 н. 0000007266 00000 н. 0000007394 00000 н. 0000007522 00000 н. 0000007655 00000 н. 0000007786 00000 н. 0000007913 00000 п. 0000008045 00000 н. 0000008171 00000 п. 0000008302 00000 н. 0000008428 00000 н. 0000008554 00000 н. 0000008742 00000 н. 0000009235 00000 н. 0000009525 00000 н. 0000009595 00000 н. 0000010368 00000 п. 0000011143 00000 п. 0000011402 00000 п. 0000012015 00000 п. 0000012993 00000 п. 0000013096 00000 п. 0000015266 00000 п. 0000015532 00000 п. 0000015787 00000 п. 0000016137 00000 п. 0000016278 00000 п. 0000016867 00000 п. 0000017039 00000 п. 0000024353 00000 п. 0000024851 00000 п. 0000025283 00000 п. 0000025680 00000 п. 0000026412 00000 п. 0000026617 00000 п. 0000026941 00000 п. 0000027014 00000 п. 0000027487 00000 н. 0000027695 00000 п. 0000030087 00000 п. 0000030520 00000 п. 0000031238 00000 п. 0000031458 00000 п. 0000031778 00000 п. 0000031869 00000 п. 0000032456 00000 п. 0000032691 00000 п. 0000032955 00000 п. 0000033219 00000 п. 0000051948 00000 п. 0000069472 00000 п. 0000077291 00000 п. 0000081711 00000 п. 0000081771 00000 п. 0000081859 00000 п. 0000081946 00000 п. 0000082086 00000 п. 0000082291 00000 п. 0000082411 00000 п. 0000082517 00000 п. 0000082690 00000 н. 0000082788 00000 н. 51E / v2 ~ 熡 #] 5 | y 틏 nw-bG_o s == a [‘ ߼? XfvD [ݻ K $ nr Wo} 0fr jel_? | K3? O3ϼwj {~ kG? GcGOOꕗ ~] op> g! ٣oI8_6o> Rhk7 ;; Sch $ F! Oq1jk [: {Ю } `srN & R’OqOǦ»Nɓ: 6k> s |.K`ƑBfU | т L5ˆ1 0 (

Вода | Полный текст бесплатно | Пространственное распределение интегрированного снижения содержания нитратов в ненасыщенной зоне и подземных водах в Германии

1. Введение

Вмешательство человека в естественный цикл азота (N) имеет серьезные экологические последствия Реактивный азот является макроэлементом, необходимым для роста растений, но он также оказывает негативное влияние на здоровье человека, участвует в глобальном потеплении и отрицательно влияет на наземные и водные экосистемы [1].Таким образом, существует острая необходимость в устойчивом комплексном управлении азотом на всех уровнях, от полевых участков до глобального масштаба [2,3]. Европейская комиссия считает загрязнение водных систем серьезной проблемой. В общей сложности 25% подземных водных объектов в ЕС имеют плохой химический статус, при этом 18% в основном подвержены загрязнению нитратами [4].

Рамочная директива ЕС по водным ресурсам 2000/60 / EC (WFD) была внедрена с целью поддержания или восстановления «хорошего состояния» водных объектов.Ключом к достижению этой цели являются эффективные стратегии сокращения поступления азота в грунтовые и поверхностные воды. Согласно Fuchs et al. [5], 80% нагрузки N в поверхностных водах Германии происходит из антропогенных источников, при этом сельское хозяйство является самым большим фактором. На сельскохозяйственный сектор приходится почти 90% выщелачивания нитратов в водные системы [6]. Поскольку поступления в основном являются результатом диффузных излишков азота, необходимы первоначальные меры по сокращению или оптимизации использования удобрений. Загрязнение подземных водных объектов нитратами в значительной степени зависит от свойств недр.Эти свойства необходимо принимать во внимание, чтобы иметь возможность решить, где и в какой степени требуются меры по смягчению воздействия для достижения хорошего состояния воды. Зейтцингер и др.

[7] утверждает, что около 46% азота, вновь зафиксированного в результате технического синтеза аммиака, удаляется в результате биогеохимических процессов круговорота в земных почвах в глобальном масштабе. Это соответствует аналогичной степени удаления 40% по оценкам для Европы [8]. В исследовании, проведенном для федеральной земли Северный Рейн-Вестфалия Германии, средний уровень денитрификации около 45% для мобильного избытка азота в почвах был выведен Wendland et al.[9] и Kuhr et al. [10] определили диапазон снижения нагрузки N от 20% до 80%. Более того, подземные водные объекты могут обладать значительной способностью к восстановлению нитратов, но она может широко варьироваться в пространстве, и от 0% до 100% нагрузки N могут быть удалены в водоносных горизонтах [7,11]. Для Дании были заявлены средние темпы сокращения подземных вод в 63% [12]. Для федеральных земель Мекленбург-Передняя Померания и водосбора на севере Саксонии-Ангальт (оба в Германии) сообщалось, что 80% входящей нагрузки N было удалено из водоносных горизонтов [13,14].

Средняя скорость снижения нагрузки N 46% и максимальные значения выше 80% в некоторых болотных регионах были смоделированы для водосбора большой реки Везер в Германии [15]. Темпы снижения содержания нитратов в грунтовых водах от 65 до 83% были измерены для различных систем пахотных земель в восточном Китае [16]. Хойберг [12] проанализировал исследования в различных масштабах (от местного до национального), посвященные снижению содержания нитратов в подземных водах в бассейне Балтийского моря, и пришел к выводу, что пространственные различия могут быть значительными в большинстве стран.Исследования показали, что информация о неоднородном распределении снижения содержания нитратов в почвах и водоносных горизонтах, основанная на согласованных подходах с высоким пространственным разрешением, необходима для существенного улучшения оценки судьбы нагрузок N в подземных водных объектах в национальном масштабе. в первую очередь регулируется процессами денитрификации. Ноулз [17] описывает денитрификацию как процесс микробного восстановления оксидов азота до молекулярного азота в качестве конечного продукта (NO ₃ ^— → NO ₂ ^— → NO → N ₂ O → N ₂ ).

Денитрификация зависит от преобладающих биогеохимических условий водоносного горизонта и происходит только в анаэробных условиях, когда доступны доноры электронов [7,18]. Кроме того, время пребывания грунтовых вод влияет на денитрификацию [7]. В целом, различают гетеротрофную и автотрофную денитрификацию в зависимости от типа денитрифицирующих бактерий [18,19]. При гетеротрофной денитрификации бактерии используют органический углерод в качестве донора электронов, тогда как при автотрофной денитрификации они получают электроны в результате окисления неорганических частиц, например.г., сульфид железа (пирит, FeS ₂) [18,20]. Оба процесса были выявлены в нескольких исследованиях разложения нитратов в подземных водах [21,22,23,24]. Другие исследования показали, что концентрация нитратов в подземных водах сильно зависит от гидрогеологических условий и преобладающих окислительно-восстановительных условий [25,26]. Из-за сложности условий окружающей среды, которые способствуют процессам деградации, и сложности их измерения в полевых условиях, моделируются являются полезными инструментами для оценки степени снижения содержания нитратов в различных масштабах [27].

В различных исследованиях моделировалась и анализировалась денитрификация в масштабе водосбора [15,28,29,30,31,32]. Wriedt и Rode [14] успешно смоделировали процессы переноса и оборота нитратов в небольшом водосборе низменности, используя модель, основанную на процессах, которая учитывает подробные геохимические реакции для описания денитрификации. В исследованиях в более крупных масштабах, например, на региональном или национальном уровне, необходимо упрощенное представление процессов восстановления нитратов из-за ограниченной доступности данных и пространственного разрешения.Wendland et al. [9] и Kunkel et al. [13] объединили несколько моделей (GROWA – DENUZ – WEKU) для оценки денитрификации в почвах на уровне федеральных земель, в зависимости от типа почвы и времени пребывания перколяционной воды в соответствии с кинетикой Михаэлиса – Ментен, а также денитрификации. при транспортировке грунтовыми водами первого порядка. Hirt et al. [15] использовали тот же подход и соединили свою цепочку моделей с моделью выбросов биогенных веществ (MONERIS) для моделирования нагрузки азота в поверхностных водах.

В общенациональных исследованиях для Германии использовались упрощенные экспоненциальные функции, зависящие от скорости фильтрации воды и гидрогеологических условий, для описания снижения нагрузки N [33,34]. Эти функции были получены путем сравнения концентрации нитратов в фильтрационной воде и грунтовых водах для различных типов пород [34]. Были учтены данные о концентрациях с 217 участков мониторинга подземных вод и выделено четыре типа гидрогеологических пород. Что касается крупномасштабной проблемы и неоднородных ландшафтов в Германии, улучшенное приближение фактических темпов снижения содержания нитратов может быть достигнуто за счет более полного представления распределения концентрации нитратов в грунтовых водах и более сильной дифференциации гидрогеологических условий. .Посредством выполнения Директивы ЕС по нитратам и Рамочной директивы ЕС по водным ресурсам государства-члены ЕС обязались регулярно отчитываться о выполнении рекомендаций, что требует общенациональной согласованной оценки состояния качества воды.

Национальные оценки качества подземных вод и снижения содержания нитратов могут способствовать дальнейшим исследованиям, таким как национальные оценки поступления биогенных веществ в поверхностные воды [33]. Из-за ограничений моделирования сложных процессов снижения содержания нитратов в крупном масштабе (на национальном уровне) это исследование сочетает общенациональные наборы данных с упрощенным концептуальным подходом для получения темпов снижения содержания нитратов в ненасыщенной зоне и в грунтовом водном объекте.Цели настоящего исследования: (1) определить нагрузку поступления нитрат-азота в ненасыщенную зону и в грунтовые воды; (2) для количественной оценки темпов сокращения, описывающих комплексное сокращение нитратов в ненасыщенной зоне и грунтовом водном объекте; и (3) проанализировать взаимосвязь между гидрогеологическими условиями и результирующими темпами сокращения.

2. Материалы и методы

Это исследование посвящено регионализации Германии с пространственным разрешением 1 км × 1 км размером сетки [35], что в общей сложности составляет примерно 360 000 ячеек сетки.

Все данные, использованные в исследовании, обрабатывались в географической информационной системе ArcGIS (v. 10.4). Все анализы настоящего исследования, касающиеся возможных взаимосвязей между восстановлением нитратов и гидрогеологическими параметрами, были выполнены с использованием R (v. 3.4.1). На рисунке 1 показаны смоделированные пути потока воды и азота в нашей модели. Азот (N) поступает в почву в различных реактивных формах азота: в виде минерального азота (нитрат, аммоний) и органического азота. В типичных почвенно-климатических условиях Германии только нитрат-азот (NO ₃ -N) в количественных количествах замещается фильтрационной водой.Концентрации аммония и органического азота в почвенном растворе ниже корневой зоны обычно очень низкие. Поэтому для упрощения оправдано предположение NO ₃ -N для всей нагрузки N в просачивающейся воде (NO ₃ -N нагрузки). На основе излишка азота в гидросфере различных видов землепользования (сельскохозяйственных и городских территорий, а также лесов; N_surplus _{a, f, u}) потенциальная входная нагрузка NO ₃ -N в ненасыщенную зону (NO ₃ -N_load _{input_uz}) получено из предыдущего исследования [36].

Он переносится через ненасыщенную зону с фильтрационной водой (Q _sw), в зависимости от скорости фильтрации воды [37]. Из-за слияния и дренажа плиток (Q _i _{, d}) некоторая часть просачивающейся воды и, следовательно, также часть нагрузки NO ₃ -N (NO ₃ -N_load _i _{, d}) не доходит до грунтовых вод. Оставшаяся доля представляет собой данное пополнение подземных вод (Q _gw) [38] и расчетную входную нагрузку NO ₃ -N, переносимую через ненасыщенную зону в грунтовые воды Q _gw (NO ₃ -N_load _{input_gw}).Для подземного водного объекта карта концентрации нитратов в подземных водах (c (NO ₃) _gw) взята из предыдущего исследования [26]. Учитывая пополнение подземных вод Q _гВт, можно рассчитать нагрузку NO ₃ -N в грунтовых водах (NO ₃ -N_load _гВт). Чтобы описать процессы восстановления в ненасыщенной зоне и в подземном водном объекте, интегрированное восстановление нитратов, степень снижения нагрузки NO ₃ -N (NO ₃ -N_red), определяется как отношение NO ₃ -N_load _gw до NO ₃ -N_load _{input_uz}.

Параметры и расчеты подробно описаны в следующих разделах.

2.1. Входная нагрузка азота

Избыток азота в гидросфере определяется как излишек поверхностного азота, уменьшенный за счет газообразных потерь азота во время и после внесения органических и минеральных удобрений. Избыток азота в гидросфере описывает количество азота, потенциально перемещаемого в гидросферу; он используется как ключевой показатель, характеризующий возможное загрязнение воды нитратами из сельскохозяйственных систем. Годовые балансы азота и профицит азота в гидросфере для используемых сельскохозяйственных угодий (UAA) были рассчитаны на основе административных единиц (районных областей) [36].Средний избыток азота в гидросфере в Германии в период 2007–2016 гг. Был рассчитан как 56 кг N га ⁻¹ a ⁻¹ UAA, в диапазоне от 13 до 146 кг N га ⁻¹ a ⁻¹ UAA для районы. Поскольку эти значения относятся только к входам с сельскохозяйственных земель (пахотные земли, луга и специальные культуры), для остальных площадей были приняты постоянные значения излишка азота.

Лесам и природным территориям присвоено 5 кг N га ^–1 и ^–1, а городской земле — 18 кг N га ^–1 и ^–1; для специальных культур на сельскохозяйственных землях избыток азота был умножен на коэффициент 1.5. Пространственное распределение пяти типов землепользования было дано моделью земного покрова [39], а их пропорции площадей были присвоены ячейкам сетки. Взвешенный по площади и специфический для землепользования излишек азота в гидросфере был рассчитан в соответствии с Knoll et al. [26] и считается эквивалентным входной нагрузке NO ₃ -N в ненасыщенную зону (NO ₃ -N_load _{input_uz}):

NO ₃ -N_load _{input_uz} = Nsurplus _a w _a + Nsurplus _u w _u + Nsurplus _f w _f + Nsurplus _s w _s

(1)

NO ₃ -N_load _{input_uz} = NO ₃ -N Входная нагрузка в ненасыщенную зону (кг N га ⁻¹ a ⁻¹)
Nsurplus _a = гидросферная N- urplus пашни (кг N га ⁻¹ a ⁻¹) [36]
Nsurplus _u = N-излишки городских земель = 18 (кг N га ⁻¹ a ⁻¹)
Избыток N _f = Излишек N леса = 5 (кг N га ⁻¹ a ⁻¹)
Избыток N _с = Излишек N специальных культур = Излишек _a × 1. 5 (кг Н га ⁻¹ a ⁻¹)
w _{a, u, f, s} = весовой коэффициент площади (-) с ∑w _i = 1.

Большая часть груз NO ₃ -N транспортируется с фильтрационной водой через слитки или стоки (Q _{i, d}) в поверхностные воды (NO ₃ -N_load _{i, d}), так что транспортируется только оставшийся груз через ненасыщенную зону в грунтовые воды (NO ₃ -N_load _{input_gw}). Например, Kunkel et al.[13] сообщили, что в федеральной земле Мекленбург-Передняя Померания около 35% нагрузки N транспортируется через дренажные системы в поверхностные воды без какого-либо существенного снижения содержания нитратов. Соотношение подпитки подземных вод Q _gw [38] и скорости просачивания Q _sw [37] использовалось здесь в качестве косвенного показателя для оценки доли перетока и, следовательно, входной нагрузки NO ₃ -N на грунтовые воды через ненасыщенная зона:

NO ₃ -N_load _{input_gw} = (Q _gw / Q _sw) × NO ₃ -N_load _{input_uz}

(2)

NO ₃ -N_load _{input_gw} = NO ₃ -N входная нагрузка на грунтовые воды (кг N га ⁻¹ a ⁻¹)
NO ₃ -N_load _{input_uz} = NO ₃ -N входная нагрузка в ненасыщенную зону (кг N га ⁻¹ a ⁻¹)
Q _gw = среднегодовая скорость пополнения подземных вод (мм a ⁻¹) [ 38]
Q _sw = средний годовой расход фильтрационной воды (мм a ⁻¹) [37]

Из-за различий в способах оценки скорости фильтрации фильтрационной воды [37] и скорости пополнения подземных вод [38], может случиться, что скорость фильтрации воды будет ниже, чем скорость пополнения подземных вод, особенно в некоторых низменных районах.

В этом случае нормы считаются эквивалентными (Q _gw / Q _sw = 1), поскольку скорость пополнения подземных вод может быть только такой же высокой, как и скорость фильтрации фильтрационной воды.

2.2. Азотная нагрузка нитратов подземных вод

В исследовании Knoll et al. [26], сеточная карта концентраций нитратов в подземных водах в Германии размером 1 км × 1 км была рассчитана с использованием подхода, основанного на данных, на основе измеренных концентраций за период с 2009 по 2018 год. Применяя метод машинного обучения «случайного леса», Карта концентрации нитратов в подземных водах была смоделирована с использованием нескольких пространственных предикторов, таких как землепользование, гидрогеология и окислительно-восстановительные условия по всей Германии.Эти прогнозы применяются в данном исследовании, поскольку они обеспечивают хорошее допущение для общенациональных оценок нагрузки грунтовых вод NO ₃ -N. Для расчета нагрузки грунтовых вод используется скорость пополнения запасов грунтовых вод как приблизительное значение объемного расхода грунтовых вод.

С учетом перехода от нитратного к нитратно-азотному на гектар нагрузка грунтовых вод NO ₃ -N рассчитывается следующим образом:

NO ₃ -N_load _gw = (c _gw × Q _gw) / 443

(3)

NO ₃ -N_load _gw = грунтовые воды NO ₃ -N нагрузка (кг N га ⁻¹ a ⁻¹)
c _gw = концентрация нитратов в грунтовых водах (мг NO ₃ L ⁻¹) [26]
Q _gw = среднегодовая скорость пополнения подземных вод (мм a ⁻¹) [38]
= коэффициент преобразования единицы нитратного азота в нитратный на гектар
(атомные массы: N = 14, O = 16)

2.3. Уменьшение содержания нитратов

Принимая во внимание пространственное разрешение и размер исследуемой территории, разработан простой подход для оценки комплексного уменьшения содержания нитратов в ненасыщенной зоне и в грунтовом водоеме.

Такой подход уместен, поскольку данные для подтверждения процессов восстановления в ненасыщенной зоне очень ограничены. Поскольку как начальное значение (входная нагрузка NO ₃ -N), так и результирующее значение (нагрузка грунтовых вод NO ₃ -N) доступны из предыдущих исследований [26,36], все возможные процессы естественной деградации принимаются во внимание, когда определение восстановления нитратов.Интегрированное сокращение нитратов, снижение нагрузки NO ₃ -N, количественно определяется как отношение нагрузки грунтовых вод NO ₃ -N к входной нагрузке NO ₃ -N на грунтовые воды:

NO ₃ -N_red = (1 — (NO ₃ -N_load _gw / NO ₃ -N_load _{input_gw})) × 100

(4)

NO ₃ -N_red = снижение содержания нитратов (%)
NO ₃ -N_load _gw = грунтовые воды NO ₃ -N нагрузка (кг Н га ⁻¹ a ⁻¹ )
NO ₃ -N_load _{input_gw} = NO ₃ -N входная нагрузка на грунтовые воды (кг N га ⁻¹ a ⁻¹)

2.

4. Гидрогеологические условия На гидрогеологической карте Германии (HUEK200 [40]) гидрогеология верхнего водоносного горизонта описывается атрибутами «тип водоносного горизонта», «консолидация», «тип породы», «геохимический тип породы» и «Проводимость». Эти пять атрибутов связаны с ячейками сетки с помощью инструмента надстройки ArcGIS «Пространственное соединение — наибольшее перекрытие», который присваивает атрибутам доминирующую область, перекрывающуюся с соответствующей ячейкой сетки. В качестве дополнительного гидрогеологического параметра используются окислительно-восстановительные условия, моделированные Knoll et al.[26], который имеет четыре окислительно-восстановительных класса, а именно «сильный анаэробный», «анаэробный», «средний» и «аэробный», на основе концентраций кислорода и железа в грунтовых водах (конкретные пределы показаны в таблице 1).

3. Результаты

Для расчета входных нагрузок NO ₃ -N на грунтовые воды, оценивается отношение Q _gw к Q _sw (Рисунок 2).

Скорость фильтрации воды обычно выше, чем скорость пополнения подземных вод, и разница между ними больше в консолидированных водоносных горизонтах по сравнению с рыхлыми водоносными горизонтами.Таким образом, соотношение Q _gw / Q _sw для консолидированных водоносных горизонтов также значительно ниже, чем для неконсолидированных водоносных горизонтов. Это, вероятно, может быть связано с морфологическими особенностями горных регионов и связанной с ними более высокой глубиной уровня грунтовых вод, что приводит к большей подверженности слияниям. Сельскохозяйственные территории часто осушаются, что также приводит к снижению значений Q _gw / Q _sw; однако это обычно имеет место в менее горных районах и низинах.Средняя скорость фильтрации воды для Германии составляет около 287 мм, ^–1 [37], а средняя скорость пополнения подземных вод составляет 125 мм, ^–1 [38]. Следовательно, принимая во внимание допущения для уравнения (2), более 50% фильтрующей воды достигает поверхностных вод через слияния или дренаж.

Входные нагрузки NO ₃ -N, рассчитанные в соответствии с уравнением (2), показаны на рисунке 3a. Средняя входная нагрузка NO ₃ -N в ненасыщенную зону (N_load _{input_uz}) составляет около 36 кг N га ^-1 и ^-1.С учетом пропорционального сокращения за счет слияния и дренажа, среднее значение NO ₃ -N_load _{input_gw} составляет всего около 17 кг N га ^-1 a ^-1. Интенсивно управляемые сельскохозяйственные системы очевидны на севере, северо-западе и юго-востоке Германии, а также в некоторых предпочтительных регионах, в основном в низинах (рис. 3а). Самые высокие нагрузки в этих регионах превышают 40 кг N га ^–1 и ^–1. На Рисунке 3b показаны нагрузки NO ₃ -N в грунтовых водах, полученные в соответствии с уравнением (3).Следует еще раз отметить, что это нагрузки NO ₃ -N, а не концентрации нитратов в подземных водах, и поэтому их нельзя связать с предельным значением 50 мг NO ₃ L ^-1.

Уже очевидно, что NO ₃ -N_load _gw (среднее значение 6 кг N га ⁻¹ a ⁻¹) в большинстве случаев существенно ниже, чем NO ₃ -N_load _{input_gw} (среднее значение 17 кг N га ⁻¹ a ⁻¹). Пространственное распределение высокого NO ₃ -N_load _gw пространственно не коррелирует с высоким NO ₃ -N_load _{input_gw}.Таким образом, для Германии годовой вклад NO ₃ -N в ненасыщенную зону (NO ₃ -N_load _{input_uz}) составляет 1196 кт N a ⁻¹. NO ₃ -N_load _{input_gw} составляет 580 kt N a ^-1, из которых 236 kt N a ^-1 выбрасываются из грунтовых вод (NO ₃ -N_load _gw) на поверхность. воды. Таким образом, разница в 344 кт N a ^-1 связана с уменьшением нагрузки NO ₃ -N (NO ₃ -N_red) в ненасыщенной зоне и в подземном водном объекте.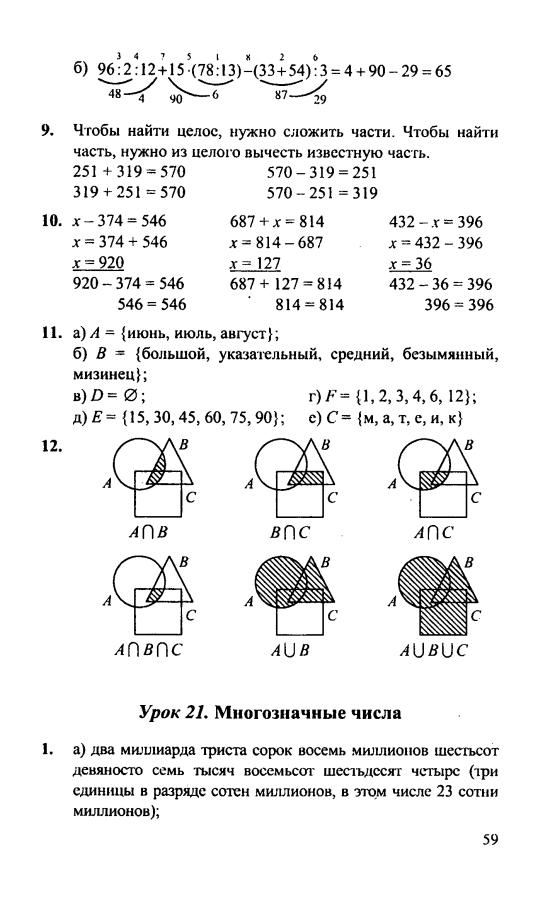

На рисунке 3 показано, что нагрузки NO ₃ -N в подземном водном объекте существенно уменьшены по сравнению с входными нагрузками NO ₃ -N. Снижение нагрузок NO ₃ -N было количественно определено на основе уравнения (4), где был рассчитан процент удаленной нагрузки NO ₃ -N. Пространственное распределение степени сокращения (%) показано на Рисунке 4. Наблюдается резкий контраст между севером и югом с высокими темпами сокращения, достигающими 100% на Северогерманской равнине и низким или нулевым снижением в центральной и южной Германии.В некоторых регионах, преимущественно в горных районах, но также, например, в регионах Гест на севере Германии, показатели сокращения равны нулю или ниже. Исключая районы, на которых отсутствует восстановление NO ₃ -N, средняя скорость восстановления от поступления NO ₃ -N через ненасыщенную зону и подземный водный объект составляет 57%. Скорость снижения содержания нитратов была дополнительно проанализирована с учетом их доминирующих гидрогеологических характеристик.

В таблице 1 приведены средние значения и стандартные отклонения для снижения нагрузки NO ₃ -N для атрибутов «типы водоносных горизонтов», «консолидация», «тип породы», «геохимический тип породы», «проводимость» и «Окислительно-восстановительные условия».Различия между характеристиками в пределах гидрогеологических объектов были статистически проанализированы с использованием апостериорного теста (Tukey HSD) (см. Таблицы S1 – S6 в дополнительных материалах). Очевидно, что пористые рыхлые водоносные горизонты, как правило, имеют значительно более высокие темпы сокращения (> 70%), чем консолидированные, трещиноватые и карстифицированные водоносные горизонты со скоростями сокращения ниже среднего (32,8–36,1%) (Рисунок 5a). Поскольку пористые водоносные горизонты преимущественно имеют осадочное происхождение, это различие в снижении нагрузки NO ₃ -N также проявляется в типе породы, причем для осадочных пород наблюдаются значительно более высокие скорости восстановления, чем для метаморфических и магматических пород.

Если посмотреть на геохимический тип породы, «силикатные» породы обычно имеют значительно более высокий потенциал снижения нагрузки NO ₃ -N; «Антропогенные» и «сульфатные / галитовые» породы показывают самый высокий и самый низкий уровень сокращения, соответственно. Однако оба класса встречаются редко, с долей снижения нагрузки ₃ -N 77,6% обнаружены для высокой проводимости, а также для перекрывающегося класса от средней до умеренной с 73,9%. Однако средние значения электропроводности показывают только скорость снижения нагрузки NO ₃ -N ниже среднего значения 42.6%, а для умеренной проводимости даже ниже. Наименьшие средние значения снижения нагрузки NO ₃ -N (28,5%) наблюдаются для класса «очень низкий», но как класс «очень низкий», так и класс «от очень высокого до высокого» встречаются редко, с долей, показанной на Рисунке 5b. ).

4. Обсуждение

Насколько нам известно, это исследование впервые представляет концептуальный экономичный подход к моделированию для оценки пространственного распределения с высоким разрешением (1 км) интегрированного снижения содержания нитратов в ненасыщенной зоне и в пределах подземного водного объекта в больших масштабах, применявшихся здесь для Германии.

Предыдущие исследования потоков N в Германии показали, что значительная часть нагрузок N в поверхностных водах происходит из грунтовых вод. Однако порядок величины темпа снижения нагрузки N во время перекачки грунтовых вод остается главным неизвестным [41]. Хотя представленный здесь подход упрощен, результаты обеспечивают ценное приближение для оценки потенциальных потерь азотных нагрузок через путь грунтовых вод. Невозможно оценить неопределенности, связанные с подходом, из-за сделанных предположений.Для излишка азота в гидросфере на сельскохозяйственных угодьях указаны погрешности ± 10 кг N га ^–1 и ^–1 [36]. Большие погрешности обнаружены также для концентраций нитратов в подземных водах с интервалами прогноза 53 мг л ^-1 и средней абсолютной ошибкой 12,7 мг л ^-1 [26]. Для оценок избытка азота на несельскохозяйственных территориях, скорости фильтрации и пополнения подземных вод не существует анализа неопределенностей. Можно утверждать, что обе входные переменные NO ₃ -N_load _{input_gw} и NO ₃ -N_load _gw технически хорошо установлены и задокументированы.

Поэтому они предоставляют наилучшие доступные и современные наборы данных по Германии. Если принять, что оценки NO ₃ -N_load _{input_gw} и NO ₃ -N_load _gw являются надежными, и можно сделать вывод, что результаты уравнения (4) также надежны в пределах общие неопределенности подхода, которые, однако, не могут быть определены количественно. Для проверки достоверности результатов можно применить метод N ₂ / Ar.Отношение N ₂ / Ar используется для расчета концентрации избытка N ₂ в грунтовых водах, которая может использоваться для определения скорости денитрификации. Поскольку соответствующие общенациональные программы измерения еще не созданы, валидация представленного здесь подхода в настоящее время не может быть проведена с помощью метода N ₂ / Ar, но предлагает большой потенциал для дальнейших исследований. Концептуальный подход к оценке нитратов сокращение на путях его переноса от источника через подземный водный объект включает множество процессов.

В исследованиях, посвященных этой теме [13,15], обычно проводится различие между сокращением ненасыщенной зоны и грунтовых вод. Однако для ненасыщенной зоны можно предположить небольшое снижение концентрации нитратов или консервативный перенос [42,43]. Возможность подтверждения восстановления нитратов в ненасыщенной зоне ограничена очень небольшим количеством измеренных концентраций нитратов в просачивающейся воде [44]. Поскольку данные о концентрации нитратов в грунтовых водах доступны с гораздо более высокой плотностью, чем измеренные значения концентрации нитратов в фильтрационной воде, Wendland et al.[9] сравнили смоделированные концентрации нитратов в фильтрационной воде с наблюдаемыми концентрациями нитратов в грунтовых водах и обнаружили хорошее согласие. Однако они отмечают, что в регионах с повышенной способностью к денитрификации измеренные концентрации подземных вод значительно ниже, чем смоделированные концентрации фильтрационной воды. В настоящем исследовании это было сделано наоборот, где концентрация нитратов в грунтовых водах использовалась в качестве исходных данных для определения общего снижения содержания нитратов.

Этот подход обеспечивает простой, единообразный и надежный метод количественной оценки снижения нитратов в зависимости от существующих общенациональных наборов данных. Снижение содержания нитратов для Германии в настоящем исследовании колеблется от 0% до 100%, что также имело место в исследовании Зейтцингер и др. [7]. Сравнивая общее среднее интегрированное сокращение нитратов на 57%, рассчитанное для Германии, с другими исследованиями, показывающими аналогичные размеры, по всей Германии, однако, наблюдается очень неоднородное пространственное распределение снижения нитратов.Например, если посмотреть на федеральную землю Мекленбург-Передняя Померания с ее широко распространенными ледниковыми образованиями позднего плейстоцена, было рассчитано среднее интегрированное сокращение нитратов примерно на 89%, в то время как Kunkel et al. [13] оценивает, что около 40% поступающего азота денитрифицировано в почве, и 85% нагрузки азота, переносимой через грунтовые воды, удаляется в водоносный горизонт.

Исходя из этого, можно вывести интегральный коэффициент сокращения для пути переноса из почвы в грунтовые воды и внутри подземного водоема около 74%, что находится в том же диапазоне, что и скорости сокращения, определенные в настоящем исследовании.Для водосбора Везер было рассчитано среднее снижение нагрузки NO ₃ -N примерно на 46%, что в точности совпадает с указанным в Hirt et al. [15]. Водосборный бассейн Везер охватывает типичные гидрогеологические характеристики, встречающиеся в Германии, от центральногерманских возвышенностей до Северо-Германской равнины. Согласно Fuchs et al. [41], среднее поступление азота в поверхностные воды Германии с 2006 по 2011 год по грунтовым водам составило 283 кт N, что соответствует оценкам в 236 кт N, оцененным в этом исследовании.На этом этапе необходимо учитывать, что эти нагрузки могут быть дополнительно уменьшены за счет способности прибрежной зоны по снижению содержания нитратов при входе в поверхностные воды. Хилл [45] проанализировал исследования последних десятилетий, посвященные удалению нитратов в прибрежной зоне, и обнаружил значительные различия в способности восстановления в зависимости от гидрогеологических свойств.

В то время как Häußermann et al. [36] сообщают о максимальных значениях избытка азота до 162 кг N га ⁻¹ a ⁻¹ (среднее значение 77 кг N га ⁻¹ a ⁻¹), значения взвешенных по площади Внесение азота в гидросферу для конкретных землепользований значительно ниже.Это отражает влияние на входные нагрузки NO ₃ -N территорий с меньшим антропогенным контролем, таких как естественные или лесные земли. Для примерно 12% территории Германии сокращение не было рассчитано, что связано с простотой нашего подхода. Когда входы азота недооценены или нагрузка на грунтовые воды переоценена, результат будет меньше нуля. Более пристальный взгляд на регионы, где «нет сокращения», показывает, что это в основном касается лесных массивов или естественной растительности, т.е.г., Альпы или Шварцвальд. В любом случае, эти территории не имеют отношения к антропогенному загрязнению воды. Пространственное распределение темпов снижения содержания нитратов очень хорошо отражает пространственную гидрогеологическую структуру Германии.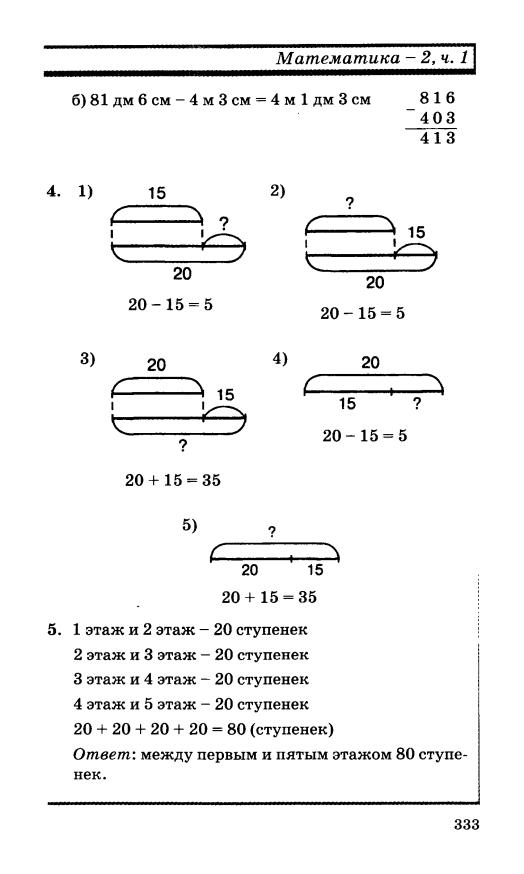

Rivas et al. [31] пришли к выводу, что факторы «текстура почвы», «класс дренажа», «материал водоносного горизонта» и «типы горных пород» влияют на потенциал денитрификации подземных вод. Они обнаружили, что хорошо дренированные почвы и породы не подходят для процессов денитрификации.Однако, в отличие от Rivas et al. [31], проводимости в этом исследовании не показывают явного влияния на восстановление нитратов. Настоящее исследование также показывает, что для Германии параметры «тип водоносного горизонта», «уплотнение» и, в частности, «окислительно-восстановительные условия» существенно влияют на интенсивность восстановления нитратов. Подземные водные объекты с анаэробными условиями показывают отчетливое влияние на восстановление нитратов, чего и следовало ожидать, поскольку анаэробные условия благоприятствуют процессам денитрификации [18].Рыхлые пористые водоносные горизонты, расположенные на Северо-Германской равнине, характеризуются в значительной степени замкнутыми водоносными горизонтами, низкой скоростью потока, длительным временем пребывания грунтовых вод и, из-за толстого покрова слоев тилла, сильно анаэробными условиями [26,46,47].

В результате на Северо-Германской равнине преобладают высокие темпы восстановления нитратов. Центрально-германские возвышенности в основном образованы трещиноватыми или закарстифицированными консолидированными водоносными горизонтами с преимущественно аэробными или промежуточными окислительно-восстановительными условиями, которые не подходят для процессов денитрификации и, таким образом, приводят к низким темпам восстановления по сравнению с четвертичными отложениями [48].Альпийский край на юге Германии показывает довольно неоднородное распределение по восстановлению нитратов. Южная часть, в основном характеризующаяся ледниковыми отложениями позднего плейстоцена, имеет более высокие темпы восстановления. Дальше к северу находятся месторождения четвертичного флювиатового гравия с высокой проводимостью и, в отличие от поровых водоносных горизонтов на севере Германии, восстановление нитратов очень низкое или отсутствует, что, однако, согласуется с результатами для хорошо дренированных пород [31].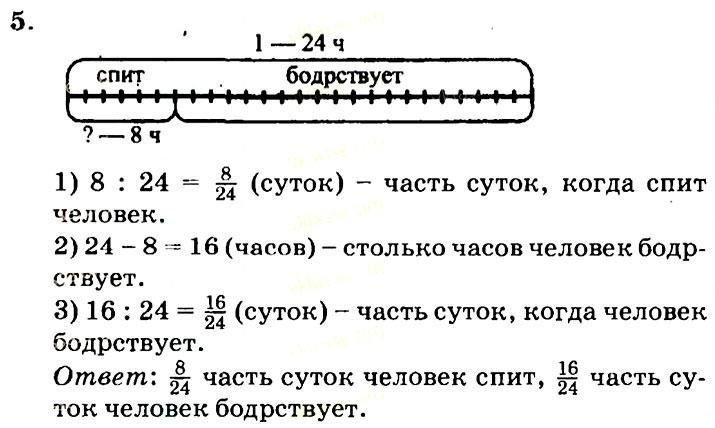

Третичные осадочные отложения на северных склонах Альп имеют местами толстые лёссовые покровы, которые снова приводят к более высоким темпам восстановления нитратов в этой области.При обсуждении стратегий управления подземными водными объектами, которые не соответствуют «хорошему статусу» согласно Рамочной директиве по водным ресурсам в отношении концентрации нитратов, необходимо учитывать пространственное распределение естественного снижения содержания нитратов. Меры по смягчению в основном предназначены для уменьшения избытка азота, в основном за счет ограничений на использование удобрений. В соответствии с Постановлением о подземных водах [49], подземные водные объекты должны оцениваться полностью в соответствии с принципом предосторожности.В контексте нынешней редакции Постановления о внесении удобрений все большую актуальность приобретает вопрос о внутренней дифференциации между чувствительными к нитратам участками, что требует 20% -ного сокращения внесения азотных удобрений. Для планирования и разработки мер по смягчению воздействия, информация о входной нагрузке NO ₃ -N, концентрациях нитратов в грунтовых водах или нагрузке в грунтовых водах NO ₃ -N, а также о снижении нагрузки NO ₃ -N, количественно выраженной в настоящем исследование, может быть применено для определения сокращения внесения азотных удобрений, необходимого для достижения предела содержания нитратов в грунтовых водах (50 мг NO ₃ л ^-1).

Рассматривая потенциальные темпы снижения содержания нитратов, наконец, следует также учитывать, что процессы денитрификации не являются неисчерпаемыми [21,50]. Специалисты по управлению водными ресурсами в Германии регулярно обращают внимание на отсутствие знаний о способности денитрификации в ненасыщенной зоне и в грунтовых водах в регионах Германии [51], а также на то, можно ли ожидать аналогичных темпов сокращения подземных нитратов в долгосрочной перспективе [52] ].

Произошла ошибка при настройке вашего пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера для приема файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:

В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или уточнить у системного администратора.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файлах cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.