Решебник и ГДЗ по Физике за 10‐11 класс Электродинамика, авторы Мякишев Г.Я., Синяков А.З. Углубленный уровень
Глава-1
Вопросы. Параграфы
1 2 3 4 5 7 8 9 10 11 12 13 14 15 17 18 19 20 21 25 27Упражнение 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Упражнение 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20Упражнение 3
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20Упражнение 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20Глава-2
Параграфы»> Вопросы. Параграфы 1 2 3 4 5 7 9 11 13 15 16 17Упражнение 5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25Упражнение 6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25Глава-3
Параграфы»> Вопросы. Параграфы 1 2 3 4 5 7 8 10 11 12 13 14Упражнение 7
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23Глава-4
Параграфы»> Вопросы. Параграфы 1 2 3 4 5 6 7 8 9 10Упражнение 8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22Глава-5
Параграфы»> Вопросы. Параграфы 1 2 4 5 6 7 8Упражнение 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Глава-6
Параграфы»> Вопросы. Параграфы 1 2 3 4 5Поиск материала «Физика, 11 класс, Жилко В.В., Маркович Л.Г., 2009» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Физика. 11 класс | Скачать | Учебники.by
Учебное пособие для 11 класса учреждений общего среднего образования с русским языком обучения (с электронным приложением для повышенного уровня). Пособие выпущено издательством «Народная асвета». Допущено Министерством образования Республики Беларусь. Все права защищены.
 Воспроизведение материалов сайта, в том числе материалов для скачивания и изображений обложек пособий, с целью извлечения прибыли (в коммерческих или рекламных целях) без разрешения правообладателей ЗАПРЕЩЕНО.
Воспроизведение материалов сайта, в том числе материалов для скачивания и изображений обложек пособий, с целью извлечения прибыли (в коммерческих или рекламных целях) без разрешения правообладателей ЗАПРЕЩЕНО.uchebniki.by
- Физика. 11 класс — Жилко В.В., Маркович Л.Г.
11 класс — Жилко В.В., Маркович Л.Г. Учебное пособие для 11 класса учреждений, обеспечивающих получение общего среднего образования, с русским языком обучения с 12-летним сроком обучения (базовый и повышенный уровни). Рубрика: Физика / 11 класс. Автор: Жилко В.В., Маркович Л.Г. Год: 2008.
11klasov.net
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.
 ru
ru - Учебное пособие для 11 класса | Жилко, В. В.
Ж72 Физика : учеб. пособие для 11-го кл. учреждений общ. сред. образования с рус. яз. обучения / В. В. Жилко, Л. Г. Маркович. — 2-е изд., пересмотр. и доп. — Минск : Народная асвета, 2014. —
В 11-м классе вы будете изучать физику колебаний и волно-вых процессов, а также оптику. Вам предстоит познакомиться с интересными явлениями и законами квантовой физики, физики микромира (атома, ядра, элементарных частиц), основами спе-циальной теории относительности, которая в свое время «пере-вернула мир».
www.aversev.by
- Фізіка. 11 клас | Скачать | Учебники.by
Вучэбны дапаможнік для 11 класа ўстаноў агульнай сярэдняй адукацыі з беларускай мовай навучання (з электронным дадаткам для павышанага ўзроўню). Дапаможнік выпушчаны выдавецтвам «Народная асвета». Дапушчана Міністэрствам адукацыі Рэспублікі Беларусь.
 Все права защищены. Воспроизведение материалов сайта, в том числе материалов для скачивания и изображений обложек пособий, с целью извлечения прибыли (в коммерческих или рекламных целях) без разрешения правообладателей ЗАПРЕЩЕНО.
Все права защищены. Воспроизведение материалов сайта, в том числе материалов для скачивания и изображений обложек пособий, с целью извлечения прибыли (в коммерческих или рекламных целях) без разрешения правообладателей ЗАПРЕЩЕНО.uchebniki.by
- Скачать | Физика. 11 класс
Скачать учебник (9.98 Mb). Авторы: Жилко В. В., Маркович Л. Г., Сокольский А. А. Предмет: Физика. Группа
Скачать учебник (9.98 Mb). Описание. Учебное пособие для 11 класса учреждений общего среднего образования с русским языком обучения (с электронным приложением для повышенного уровня). Пособие выпущено издательством «Народная асвета».
www.aversev.by
- Физика. 11 класс — Жилко В.В., Маркович Л.Г.
11 класс — Жилко В.В., Маркович Л.Г. Учебное пособие для 11 класса общеобразовательных учреждений с русским языком обучения.
 Рубрика: Физика / 11 класс. Автор: Жилко В.В., Маркович Л.Г. Год: 2009, 2014.
Рубрика: Физика / 11 класс. Автор: Жилко В.В., Маркович Л.Г. Год: 2009, 2014.11klasov.net
- Учебник Физика 11 класс Жилко Маркович
Данные книги можно бесплатно скачать для ознакомления, а также читать онлайн с компьютера или планшета (смартфона, телефона).
в. в. Жилко Л. Г. Маркович ФИЗИКА Учебное пособие для 11 класса общеобразовательных учреждений с русским языком обучения с 12-летним сроком обучения (базовый и повышенный уровни) Допущено Министерством образования Республики Беларусь 2-е издание, исправленное Минск «Народная асвета» 2008 IK 53(075.3=161.1) 5К 22.3Я721 Ж72 Рецензенты: канд. физ.-мат. наук, доц. БИТУ
uchebnik-skachatj-besplatno.com
- Физика. 11 класс | 10–11 классы | Каталог | Учебники.by
Авторы: Жилко В.
 В., Маркович Л. Г., Сокольский А. А. Предмет: Физика. Группа: Учебники (учебные пособия). Класс
В., Маркович Л. Г., Сокольский А. А. Предмет: Физика. Группа: Учебники (учебные пособия). КлассУчебное пособие для 11 класса учреждений общего среднего образования с русским языком обучения (с электронным приложением для повышенного уровня). Рeцeнзенты: кафедра физики и методики преподавания физики учреждения образования «Белорусский государственный педагогический университет имени Максима Танка» (кандидат физико-математических наук, доцент О. Н. Белая)
uchebniki.by
- Физика 11 класс
В. В. Жилко Л. Г. Маркович А. А. Сокольский. ФИЗИКА. Учебное пособие для 11 класса учреждений общего среднего образования. с русским языком обучения (с электронным приложением для повышенного уровня). Допущено Министерством образования.
Как писал Н. П. Третьяков в учебнике «Курс физики»: «В старших классах школы ученикам пора не только наблюдать и констатировать наблюдаемое, но и учиться применять общие положения к решению частных вопросов, пользуясь доступными им средствами математики.

oplk.ucoz.com
- Сборник задач по физике 10-11 класс жилко маркович
10—11 классы : пособие для учащихся учреждений общ. сред. образования / В. В. Жилко, Л. Г. Маркович. — 6-е изд. — Минск : Аверсэв, 2017.
Сборник вопросов и задач по физике составлен в соответствии с учебными программами по физике для 10—11 х классов и содер жит более 1400 задач по всем разделам учебного материала. Поря док следования глав выдержан в соответствии с программой, при чем для удобства пользования сборником все задачи имеют сквозную нумерацию.
100ballnik.com
- Физика. 11 класс Жилко В.В., Маркович Л.Г.
Учебное пособие для 11 класса учреждений, обеспечивающих получение общего среднего образования, с русским языком обучения с 12-летним сроком обучения (базовый и повышенный уровни).
 Формат: pdf. Размер: 66 Мб. Смотреть, скачать: drive.google ; Rghost. СОДЕРЖАНИЕ От авторов 3 Механика Повторительно-обобщающий курс Глава 1. Кинематика 5 § 1. Кинематика прямолинейного движения. Равномерное движение — § 2. Прямолинейное равноускоренное движение 13 § 3. Движение тела, брошенного горизонтально и под углом к горизонту 19 § 4…
Формат: pdf. Размер: 66 Мб. Смотреть, скачать: drive.google ; Rghost. СОДЕРЖАНИЕ От авторов 3 Механика Повторительно-обобщающий курс Глава 1. Кинематика 5 § 1. Кинематика прямолинейного движения. Равномерное движение — § 2. Прямолинейное равноускоренное движение 13 § 3. Движение тела, брошенного горизонтально и под углом к горизонту 19 § 4…to.alleng.org
- Физика. 11 класс. Жилко В.В., Маркович Л.Г.
Трансформатор 60 Упражнение 9 64 § 10. Производство, передача и потребление электрической энергии. Экологические проблемы производства и передачи электрической энергии 65 § 11. Электромагнитные волны и их свойства. Шкала электромагнитных волн 70 Упражнение 10 78 Самое важное в главе 2 — Глава 3. Оптика § 12. Электромагнитная природа света. Скорость света 80 Упражнение 11 86 § 13. Интерференция света — Упражнение 12 93 § 14. Принцип Гюйгенса — Френеля.
to.
 alleng.org
alleng.org - Учебник по физике 11 класс Жилко Маркович читать онлайн
Выберите нужную страницу с уроками, заданиями (задачами) и упражнениями из учебника по физике за 11 класс — Жилко Маркович. Онлайн книгу удобно смотреть (читать) с компьютера и смартфона. Электронное учебное пособие подходит к разным годам: от 2011-2012-2013 до 2015-2016-2017 года — создано по стандартам ФГОС.
На сайте можно читать, смотреть онлайн и скачать учебники и рабочие тетради по всем предметам за любой класс.
uchebnik-tetrad.com
- Жилко В.В. Физика 11 класс
TeachPro-2009 Мультимедийный учебник «Физика 11 класс» разработан в соответствии с действующей Программой общеобразовательных учреждений, рекомендованной Ученым советом Института общего среднего образования Российской Академии образования, и содержит учебный курс за одиннадцатый класс общеобразовательной школы в объеме 30 лекций и 38 типовых задач.
 rn.
rn.Издание содержит решения задач с подробными объяснениями к учебнику: В. В. Жилко, Л. Г. Маркович «Физика.
www.studmed.ru
- Учебник по физике 11 класс скачать бесплатно
Многие открытия, без которых было бы невозможно существование целых отраслей современной промышленности, помогли значительно продвинуться человечеству и облегчают бытовую жизнь. Школьная программа поведает ученикам множество терминов и законов, поэтому важно иметь возможность скачать учебник по физике 11 класс, что сделает учебный процесс гораздо легче и понятнее.
11klasov.net
- Физика. 11 класс | УМК: компоненты для учащихся | Каталог
Вучэбны дапаможнік для 11 класа ўстаноў агульнай сярэдняй адукацыі з беларускай мовай навучання (з электронным дадаткам для павышанага ўзроўню).Подробнее. Тетрадь для лабораторных работ по физике для 11 класса.
 Авторы: Жилко В. В., Маркович Л. Г., Егорова Л. П.
Авторы: Жилко В. В., Маркович Л. Г., Егорова Л. П.11 класс. Тетрадь подготовлена в полном соответствии с учебными программами по физике для базового и повышенного уровней и является неотъемлемой частью учебно-методического комплекса, обеспечивающего изучение физики в школе.Подробнее.
uchebniki.by
- Абитуриентам и школьникам. Физика. 11 класс.
Москва: Просвещение, 2008. — 399 с. Учебник по физике для 11 классов общеобразовательных учреждений — базовый и профильный уровни. Значительная часть курса XI класса посвящена современной физике — физике XX века.
— 416 с. Учебник предназначен учащимся 11 классов общеобразовательных учреждений и является продолжением учебника «Физика. 10 класс» того же автора. Он завершает курс физики и соответствует требованиям минимума содержания образования.
www.studmed.ru
- Решебник по физике 11 класс Жилко, Маркович
Решебник, готовые домашние задания (ГДЗ) по физике для учащихся 11 класса, авторов Жилко В.
 В., Маркович Л.Г.
В., Маркович Л.Г.Упражнение 1 Упражнение 2 Упражнение 3 Упражнение 4 Упражнение 5 Упражнение 6 Упражнение 7 Упражнение 8 Упражнение 9 Упражнение 10 Упражнение 11 Упражнение 12 Упражнение 13 Упражнение 14 Упражнение 15 Упражнение 16 Упражнение 17 Упражнение 18 Упражнение 19 Упражнение 20 Упражнение 21 Упражнение 22 Упражнение 23 Упражнение 24 Лабораторные работы.
gdz.wiki
- Гдз и решебник Физика 11 класс Жилко, Маркович — Учебник
При создании этого замечательного «ГДЗ по физике за 11 класс Жилко, Маркович (Народная асвета)» авторы использовали современную методику обучения. Книга полностью соответствует всем образовательным стандартам и нынешней учебной программе.
Однако по своему содержанию «ГДЗ по физике за 11 класс Жилко В. В., Маркович Л. Г. (Народная асвета)» и основная книга разные. Если в учебнике лишь поверхностно объясняются темы, то в сборнике ребята найдут и ключи к упражнениям, и подробные верные ответы.

spishi.ltd
- Решебник по Физике 11 класс — Жилко (2021) | Супер Решеба
Физика 11 класс. Решебник. Предмет. Физика. Авторы. Жилко В. В., Маркович Л. Г., Сокольский, А. А.
superresheba.by
- Учебники по физике 11 класс скачать в pdf на 1-1klasses
Самые актуальные учебники по физике за 11 класс скачать в pdf бесплатно на нашем образовательном портале. Также можно скачать учебные тетради и другую учебную литературу.
textbooks1-11.ru
- Физика. 11 класс — Жилко В.В., Маркович Л.Г.. Бесплатные PDF…
11 класс — Жилко В.В., Маркович Л.Г. Cdnpdf.com — учебники, журналы, книги со всего мира — читать и скачать.
 Ежедневное обновление бесплатных версий. 11 класс — Жилко В.В., Маркович Л.Г. Учебное пособие для 11 класса общеобразовательных учреждений с русским языком обучения.
Ежедневное обновление бесплатных версий. 11 класс — Жилко В.В., Маркович Л.Г. Учебное пособие для 11 класса общеобразовательных учреждений с русским языком обучения.cdnpdf.com
- Физика. 11 класс — Жилко В.В., Маркович Л.Г.. Бесплатные PDF…
11 класс — Жилко В.В., Маркович Л.Г. Cdnpdf.com — учебники, журналы, книги со всего мира — читать и скачать. Ежедневное обновление бесплатных версий. 11 класс — Жилко В.В., Маркович Л.Г. Учебное пособие для 11 класса учреждений, обеспечивающих получение общего среднего образования, с русским языком обучения с 12-летним сроком обучения (базовый и повышенный уровни).
cdnpdf.com
- Решебник по физике за 11 класс Жилко, ГДЗ 2021
Решебник по физике для 11 класса — Жилко.
 Авторы. Жилко В. В., Маркович Л. Г., Сокольский А. А. Год учебника. 2021. Издательство. Народная асвета. Физика – достаточно сложный предмет, тем более в 11 классе. У многих школьников возникают трудности с ее пониманием. Если вы столкнулись с подобной проблемой, не стоит опускать руки. Решебник по физике станет отличным помощником, благодаря которому вы сможете проверить, правильно ли выполнены домашние задания, восполнить пробелы в знаниях и подготовиться к выпускному экзамену.
Авторы. Жилко В. В., Маркович Л. Г., Сокольский А. А. Год учебника. 2021. Издательство. Народная асвета. Физика – достаточно сложный предмет, тем более в 11 классе. У многих школьников возникают трудности с ее пониманием. Если вы столкнулись с подобной проблемой, не стоит опускать руки. Решебник по физике станет отличным помощником, благодаря которому вы сможете проверить, правильно ли выполнены домашние задания, восполнить пробелы в знаниях и подготовиться к выпускному экзамену.resheba.top
- ГДЗ по Физике за 11 класс Жилко В.В., Маркович Л.Г.
авторы: Жилко В.В., Маркович Л.Г., Сокольский А.А.. Издательство: Народная асвета 2014-2021 год. Если вы хотите знать физику «на зубок» и никогда не иметь с ее изучением проблем, предлагаем сайт с готовыми домашними заданиями. «ГДЗ по физике за 11 класс к учебнику Жилко» соответствует всем правилам и строгим требованиям Федерального компонента государственного образовательного стандарта, а также прилагающемуся к нему учебнику.

megaresheba.net
- ГДЗ решебник по физике 11 класс Жилко, Маркович, Егорова…
«ГДЗ по физике 11 класс тетрадь для лабораторных работ Жилко, Маркович (Просвещение)» – современный онлайн-ресурс, помогающий школьникам познавать мир. Предмет дает ребятам полное представление о сущности природных явлений, физических законов.
«ГДЗ по физике 11 класс тетрадь для лабораторных работ В.В. Жилко, Л.Г. Маркович (Просвещение)» включает в себя выполненные исследования по программе с подробными пояснениями. Каждая работа имеет название. Номера заданий также подписаны.
spishi.ltd
- Физика 11 класс. Школьный курс физики
Глава 11. Физика атомного ядра. Элементарные частицы. § 64. Методы регистрации заряженных частиц.
Источник: По материалам учебника «Физика.
 11 класс» Г.Я. Мякишев, М.А. Петорва.
11 класс» Г.Я. Мякишев, М.А. Петорва.xn—-7sbbfb7a7aej.xn--p1ai
- Курс: Физика. 11 класс
Глава 6. Физика атома. Еще, быть может, каждый атом — Вселенная, где сто планет; Там все, что здесь, в объеме сжатом, Но также то, чего здесь нет.
Глава 7. Ядерная физика и элементарные частицы. Быть может, эти электроны — Миры, где пять материков, Искусства, знанья, войны, троны.
profil.adu.by
- Физика 11 класс Мякишев, Буховцев, Чаругин
Сила Лоренца 17 § 7. Магнитные свойства вещества 20 Упражнение 1 26 Краткие итоги главы 1 — Глава 2. Электромагнитная индукция 27 § 8. Открытие электромагнитной индукции — § 9. Магнитный поток 30 § 10. Направление индукционного тока. Правило Ленца 31 § 11.
Относительность одновременности 230 § 78. Основные следствия из постулатов теории относительности 232 § 79.
 Элементы релятивистской динамики 235 Упражнение 11 238 Краткие итоги главы 9 — Глава 10. Излучение и спектры 239 § 80. Виды излучений.
Элементы релятивистской динамики 235 Упражнение 11 238 Краткие итоги главы 9 — Глава 10. Излучение и спектры 239 § 80. Виды излучений.znayka.win
- ГДЗ Жилко 11 класс по Физике на Мегарешебе
ГДЗ к учебнику по физике за 11 класс Жилко — кладезь ценной информации. Ребята продолжают изучать физику. За все время у них скопился ценный багаж знаний, но им еще предстоит усовершенствовать свои навыки и умения.
ГДЗ-портал по физике за 11 класс под авторством Жилко, Марковича и Сокольского имеется в двух вариантах – обычное бумажное издание и онлайн. Каждой работе в пособии присвоен номер. Таким образом ,им можно воспользоваться не только дома, но и на уроке, чтобы проверить свои ответы.
megaresheba.com
- ГДЗ к лабораторным работам по физике 11 класс, Жилко
Решебник к лабораторным работам по физике за 11 класс.
 Авторы. Жилко В. В., Маркович Л. Г., Егорова Л. П. Год учебника. 2021. В 11 классе курс физики усложняется настолько, что даже у школьников с хорошей успеваемостью могут возникать трудности. Для понимания этого предмета необходим математический склад ума и хорошие аналитические способности. К сожалению, не все подростки обладают этими качествами. Но это не значит, что их проблема с непониманием физики неразрешима.
Авторы. Жилко В. В., Маркович Л. Г., Егорова Л. П. Год учебника. 2021. В 11 классе курс физики усложняется настолько, что даже у школьников с хорошей успеваемостью могут возникать трудности. Для понимания этого предмета необходим математический склад ума и хорошие аналитические способности. К сожалению, не все подростки обладают этими качествами. Но это не значит, что их проблема с непониманием физики неразрешима.resheba.top
- Решебник по Физике 11 класс | Супер Решеба
Решебник по Физике 11 класс. Готовые лабораторные работы по Физике. Физика. В. В. Жилко, Л. Г. Маркович, Л. П. Егорова. 2021 год. Решебник по Физике.
superresheba.by
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Физика, 11 класс, Жилко В. В., Маркович Л.Г., 2009»
В., Маркович Л.Г., 2009»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 18 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
учебники, ГДЗ, учебные пособия, справочная литература
Математика
Биология
Литература
Русский язык
География
Физика
Химия
История
Английский
Информатика
География
Информатика
учебникиГДЗтесты и ГИАсправочникидля учителя
- Демонстрационные задачи по школьному курсу физики для учащихся 10-11 классов, Нагорнов Ю.С., 2012
- Домашний эксперимент по физике, 7-11 класс, Ковтунович М.Г., 2007
- Иллюстрировынный Атлас по физике. 11 класс. Касьянов В.А. 2010
- Интегрированные уроки физики, 7-11 класс, Горлова Л.А., 2010
- Магнитные явления, Пособие по физике, 9-11 класс, Коршунова Л.
 Н., 2005
Н., 2005 - Опорные конспекты и разноуровневые задания, физика, 11 класс, Марон Е.А., 2013
- Физика для школьников старших классов и поступающих в ВУЗы, Яворский Б.М., Детлаф А.А., 2005
- Физика, 10-11 класс, Поурочное планирование, Шилов В.Ф., 2013
- Физика, 10-11 класс, Часть 1, Козел С.М., 2010
- Физика, 10-11 класс, Часть 2, Козел С.М., 2010
- Физика, 11 класс, Базовый и профильный уровни, Тихомирова С.А., Яворский Б.М., 2012
- Физика, 11 класс, Базовый уровень, Касьянов В.А., 2012
- Физика, 11 класс, Буховцев Б.Б., Мякишев Г.Я., Чаругин В.М., 2008
- Физика, 11 класс, Генденштейн Л.Э., Дик Ю.И., 2014
- Физика, 11 класс, Жилко В.В., Маркович Л.Г., 2008
- Физика, 11 класс, Жилко В.В., Маркович Л.Г., 2009
- Физика, 11 класс, Жилко В.В., Маркович Л.Г., 2014
- Физика, 11 класс, Марон А.Е., Мякишев Г.Я., 1992
- Физика, 11 класс, Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М., 2014
- Физика, 11 класс, Профильный уровень, Громов С.
 В., Шаронова Н.В., 2006
В., Шаронова Н.В., 2006 - Физика, 11 класс, Профильный уровень, Касьянов В.А., 2011
- Физика, 11 класс, Профильный уровень, Пинский А.А., Кабардин О.Ф., 2011
- Физика, 11 класс, Уровень стандарта, Коршак Е.В., Ляшенко А.И., Савченко В.Ф., 2011
- Физика, 11 класс, учебник для общеобразовательных организаций, базовый и профильный уровни, Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М., Парфентьева Н.А., 2014
- Физика, 11 класс, Учебник, Касьянов В.А., 2004
- Физика, 11 класс, Учимся решать задачи, Лукьянова А.В., 2011
- Физика, 11 класс, Часть 1, Генденштейн Л.Э., Дик Ю.И., 2010
- Физика, 11 класс, Часть 1, Генденштейн Л.Э., Дик Ю.И., 2012
- Физика, 11 класс, Электродинамика и квантовая физика, Анциферов Л.И., 2004
- Физика, базовый уровень, 11 класс, учебник, Касьянов В.А., 2014
- Физика, базовый уровень, 11 класс, учебник, Пурышева Н.С., Важеевская Н.Е., Исаев Д.А., Чаругин В.М., 2014
- Физика, Все законы и формулы в таблицах, 7-11 класс, Моркотун, 2007
- Физика, Задачник, 10-11 класс, пособие для общеобразовательных учреждений, Рымкевич А.
 П., 2013
П., 2013 - Физика, Колебания и волны, 11 класс, Мякишев Г.Я., Синяков А.З., 2002
- Физика, Опорные конспекты и дифференцированные задачи, 11 класс, Куперштейн Ю.С., 2004
- Физика, Оптика, Квантовая физика, 11 класс, Мякишев Г.Я., Синяков А.З., 2002
- Физика, Оптика, Тепловые явления, Строение и свойства вещества, Строение Вселенной, 11 класс, Громов С.В., Шаронова Н.В., Левитан Е.П., 2006
- Физика, учебник, 11 класс, Мякишев Г.Я., Буховцев Б.Б., 1993
- Физика, Электродинамика, 10-11 класс, Мякишев Г.Я., Синяков А.З., Слободсков Б.А., 2005
- Физика. 11 класс. Учебник. Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. 2010
- Физика. Колебания и волны. 11 класс. Профильный уровень. Мякишев Г.Я., Синяков А.З. 2010
- Физика. Оптика. Квантовая природа света. 11 класс. Ромашкевич А.И. 2009
- Физика. Электродинамика. 10-11 класс. Мякишев Г.Я., Синяков А.З., Слободсков Б.А. 2010
- Solutions to Irodov s problems in general physics — Решения — Vol.
 1. — Иродов И.Е.
1. — Иродов И.Е. - Solutions to Irodov s problems in general physics — Решения — Vol.2. — Иродов И.Е.
- Все решения задач — Сборник задач по общему курсу физики — Волькенштейн В.С.
- Все решения к сборнику задач Волькенштейн Т1 — Изергина Е.Н., Петров Н.И.
- Все решения к сборнику задач Волькенштейн Т2 — Изергина Е.Н., Петров Н.И.
- Все решения к Сборнику задач по общему курсу физики, Волькенштейн В.С., Книга 1, Изергина Е.Н., Петров Н.И., 1999
- ГДЗ — Физика — Задачник — 10 — 11 класс — Рымкевич А.П.
- ГДЗ по физике для 10-11 классов 2012 к «Физика. Задачник. 10-11 класс. Пособие для общеобразовательных учреждений, Рымкевич А.П., 2011»
- ГДЗ по физике для 10-11 классов к «Задачник. Физика. 10-11 класс. Пособие для общеобразовательных учебных заведений, Рымкевич А.П., 2001»
- ГДЗ по физике для 10-11 классов к «Сборник задач по физике для 10-11 классов общеобразовательных учреждений, Степанов Г.Н., 2000»
- ГДЗ по физике для 10-11 классов к «Физика.
 Задачник. 10-11 класс, Рымкевич А.П., 2006»
Задачник. 10-11 класс, Рымкевич А.П., 2006» - ГДЗ по физике для 10-11 классов к «Физика. Задачник. 10-11 класс. Пособие для общеобразовательных учебных заведений, Рымкевич А.П., 2003»
- ГДЗ по физике для 11 класса к «Физика. 11 класс: Учебник для общеобразовательных учебных заведений, Касьянов В.А., 2002»
- ГДЗ по физике для 11 класса к «Физика. 11 класс: Учебник для общеобразовательных учебных заведений, Мякишев Г.Я, Буховцев Б.Б., 2003»
- ГДЗ по физике для 11 класса к «Физика: Оптика. Тепловые явления. Строение и свойства вещества: Учебник для 11 класса общеобразовательных учреждений, Громов, Шаронова, 2002»
- ГДЗ по физике, 10-11 класс, 2012, к задачнику по физике за 10-11 класс, Рымкевич А.П.
- ГДЗ по физике, 11 класс, 2015, к учебнику по физике за 10-11 классы, Рымкевич А.П.
- ГДЗ по физике, 11 класс, 2015, к учебнику по физике за 11 класс, Мякишев Г.Я., Буховцев Б.Б.
- ГДЗ по физике, 11 класс, 2015, к учебнику по физике за 11 классы, Касьянов В.
 А.
А. - ГДЗ по физике, 11 класс, Касьянов В.А., Атаманская М.С., Богатин А.С., 2006, к учебнику по физике за 11 класс, Касьянов В.А.
- ГДЗ по физике, Игнашов И.А., 2000, к задачнику по теоретической механике, Мещерский И.В.
- ГДЗ по физике, Козлова З.П., Паншина А.В., Розенблат Г.М., 2007, к задачнику по теоретической механике, Мещерский И.В.
- ГДЗ по физике, Козлова З.П., Паншина А.В., Розенблат Г.М., 2009, к задачнику по теоретической механике, Мещерский И.В.
- ГДЗ по физике, Паншина А.В., Чуркин В.М., 2012, к задачнику по теоретической механике, Мещерский И.В.
- ГДЗ по физике, Чуркин В.М., 2010, к задачнику по теоретической механике, Мещерский И.В.
- ГДЗ по физике. 11 класс. К учебнику по физике за 11 класс. Мякишев Г.Я., Буховцев Б.Б. 2000
- ГДЗ по физике. 11 класс. Парфентьева Н.А. К учебнику по физике за 11 класс. Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. 2011
- Готовые домашние задания по физике — 10-11 класс — К задачнику Физика — 10 11 класс — Рымкевич А.
 П.
П. - Готовые домашние задания по физике — 10-11 класс — К сборнику задач по физике — 10-11 класс — Степанов Г.Н.
- Готовые домашние задания по физике — 11 класс — К учебнику Физика — 11 класс — Касьянов В.А.
- Готовые домашние задания по физике — 11 класс — К учебнику Физика: Оптика. Тепловые явления. Строение и свойства вещества — 11 класс — Громов С.В.
- Готовые домашние задания по физике, 11 класс, к учебнику по физике, Мякишев, Буховцев
- Готовые домашние задания по физике, 11 класс, К учебнику Физика, 11 класс, Мякишев, Буховцев
- Домашняя работа по физике, 11 класс, Тихонин Ф.Ф., 2012, к учебнику по физике за 11 класс, Мякишев Г.Я., Буховцев Б.Б., 2011
- Решебник задач по физике — Фомина М.В.
- Решебник по физике за 11 класс — К учебнику Физика — 11 класс — Касьянов В.А.
- Решебник по физике, 11 класс, Парфентьева Н.А., К учебнику по физике для 11 класса, Мякишев Г. Я., Буховцев Б. Б., Чаругин В.М., 2011
- Решебник. Теоретическая механика.
 Кирсанов М.Н., 2002
Кирсанов М.Н., 2002 - Решение задач по физике из задачника по общей физике — Иродов И.Е.
- Сборник задач по курсу физики с решениями, Трофимова, Павлова
- Сборник задач по физике 10-11 класс — Решение задач — Рымкевич А.П.
- Сборник задач по физике 10-11 класс — Решение задач — Электродинамика — Квантовая физика — Рымкевич А.П.
- Сборник задач по физике с решениями и ответами — Механика — Долгов А.Н., Протасов В.П., Соболев Б.Н. — 9 класс — 11 класс — 2000
- Сборник задач по физике с решениями и ответами — Молекулярная физика и термодинамика — Долгов А.Н., Протасов В.П., Соболев Б.Н. — 9 класс — 11 класс — 2000
- Сборник задач по физике с решениями и ответами — Электричество и оптика — Долгов А.Н., Протасов В.П., Соболев Б.Н. — 9 класс — 11 класс — 2000
- Теоретическая механика в решениях задач из сборника Мещерского И.В., Кинематика, Чуркин В.М., 2010
- Физика 10 класс: Решение задач из учебного пособия Рымкевича А.П. «Сборник задач по физике — 10-11 класс» — Механика.
 Молекулярная физика. Термодинамика.
Молекулярная физика. Термодинамика. - Физика 11 класс: Решение задач из учебного пособия Рымкевича А.П. «Сборник задач по физике — 10-11 класс» — Электродинамика, Квантовая физика
- Физика, Решения задач с подробными объяснениями, 11 класс, Сенчук Е.В., 2010, к учебнику по физике для 11 класса, Жилко В.В., Маркович Л.Г., 2010
- Физика, Решения задач, Трофимова Т.И., Фирсов А.В., 2008
- Физика. 10-11 классы Подробный разбор заданий из задачника А.П. Рымкевича — Борисов С.Н.
- Алгоритмы решения задач по механике в средней школе — Гутман В.И., Мощанский В.Н.
- ВПР 2017, Физика, 11 класс, Описание, Образец, Ответы, Проект
- ГИА 2012, Физика, 11 класс, Диагностическая работа №1, 2011
- Задачи по физике — Пособие для учащихся 9-11 классов — Гомонова А.И., Плетюшкин В.А., Погожев В.А.
- Задачи по физике и методы их решения — учебное пособие — Балаш В.А. — 1983
- Задачи по физике с анализом их решения — Савченко Н.Е. — 2000
- Задачник-практикум по элементарной физике, Архангельский A.
 C., Скворцова И.Л., Юшина М.Я., 2004
C., Скворцова И.Л., Юшина М.Я., 2004 - Колебания и волны. Пособие по решению задач — Коршунова Л.Н.
- Контрольные и проверочные работы по физике, 10-11 класс, Самойленко П.И., Сергеев А.В., 2005
- Контрольные и проверочные работы по физике, 7 -11 класс, Кабардин О.Ф., Кабардина С.И., Орлов В.А., 1997
- Методика решения задач по физике — Кобушкин В.К.
- Общая физика в задачах и решениях — Мурзов В.И., Коненко А.Ф., Филиппова Л.Г.
- Опорные конспекты и разноуровневые задания, физика, 11 класс, Марон Е.А., 2013
- Ответы на экзаменационные вопросы по физике — 11 класс
- Пособие для самостоятельного обучения решению задач по физике в ВУЗе — Мелёшина А.М., Зотова И.К., Фосс М.А.
- Решение задач по физике — 7-11 класс — Справочник школьника — 1997
- Решение задач по физике — Кириллов В.М., Давыдов В.А., Задерновский А.А., Зубов В.Е., Сафронов А.Н.
- Решение задач по физике — Савченко Н.Е.
- Решение задач по физике — часть 1 — Парфентьева Н.
 , Фомина М.
, Фомина М. - Решение задач по физике — часть 2 — Парфентьева Н., Фомина М.
- Сборник задач и упражнений по физике, 10-11 класс, Гладкова Р.А., Косоруков А.Л., 2007
- Сборник задач по физике для 9 — 11 классов — Степанова Г.Н.
- Сборник задач по физике для поступающих в ВУЗ, Горбунов А.К., Панаиотти Э.Д., 2005
- Сборник задач по физике с решениями и ответами, 9-11 класс, Часть 1, Долгов А.Н., Протасов В.П., Соболев Б.Н., 2000
- Сборник задач по физике с решениями и ответами, 9-11 класс, Часть 2, Долгов А.Н., Протасов В.П., Соболев Б.Н., 2001
- Сборник задач по физике с решениями и ответами, 9-11 класс, Часть 3, Долгов А.Н., Протасов В.П., Соболев Б.Н., 2001
- Сборник задач по физике с решениями и ответами, Механика, 9-11 класс, Долгов А.Н., 2000
- Сборник задач по физике, 10-11 класс, Демкович В.П., Демкович Л.П., 2001
- Сборник задач по физике, 10-11 класс, Парфентьева Н.А., 2010
- Сборник задач по физике, 10-11 классы, Громцева О.
 И., 2015
И., 2015 - Сборник задач по физике, 9-11 класс, Степанова Г.Н., 1997
- Сборник контрольных работ по физике для учащихся заочной формы обучения, 11 класс, Коваленкова О.В., Лобач Д.И., Малашонок В.А., Развина Т.И., Ракина Н.Н., 2004
- Справочное пособие для контроля верности выполнения заданий к Сборнику разноуровневых заданий для государственной итоговой аттестации по физике — Пискунов С.
- Тематические контрольные и самостоятельные работы по физике, 11 класс, Громцева О.И., 2012
- Тематические контрольные и самостоятельные работы по физике, 11 класс, Громцева О.И., 2012
- Тематические контрольные и самостоятельные работы по физике, 11 класс, Громцева, 2012
- Тренировочная работа по физике, 4 мая 2012, 3-4 Варианты, 11 класс
- Тренировочная работа № 1 по Физике, Вариант 3, 11 класс, 2012
- Физика — Вопросы и ответы — Задачи и решения — Часть 1 — Механика — Трубецкова С.В. — 2003
- Физика — Вопросы и ответы — Задачи и решения — Часть 2 — Основы молекулярной физики и термодинамики — Трубецкова С.
 В. — 2004
В. — 2004 - Физика — Вопросы и ответы — Задачи и решения — Часть 3 — Электричество и магнетизм — Трубецкова С.В. — 2004
- Физика — Вопросы и ответы — Задачи и решения — Часть 4 — Колебания и волны. Геометрическая и волновая оптика — Трубецкова С.В. — 2005
- Физика — Задачник — 10-11 классы — Рымкевич А.П. — 2006
- Физика — Теория и методы решения конкурсных задач — Колесников В.А.
- Физика — Экзаменационные билеты с ответами — 11 класс — Профильный уровень
- Физика в задачах — Экзаменационные задачи с решениями — Меледин Г.Ф.
- Физика на вступительных экзаменах в ВУЗы — Конкурсные задачи и их решения — Жилко В.В. — 2002
- Физика, 10-11 класс, Конструктор самостоятельных и контрольных работ, Андрюшечкин С.М., Слухаевский А.С., 2010
- Физика, 10-11 класс, Контроль знаний, Заботин В.А., Комиссаров В.Н., 2008
- Физика, 10-11 класс, Сборник задач и заданий с ответами и решениями, Козел С.М., Коровин В.А., Орлов В.А., 2001
- Физика, 11 класс, Базовый уровень, Рабочая тетрадь, Пурышева Н.
 С., Важеевская Н.Е., Исаев Д.А., Чаругин В.М., 2016
С., Важеевская Н.Е., Исаев Д.А., Чаругин В.М., 2016 - Физика, 11 класс, Диагностическая работа, Спецификация, Инженерный класс, 2016
- Физика, 11 класс, дидактические материалы к учебникам Касьянова В.А., Марон А.Е., Марон Е.А., 2014
- Физика, 11 класс, Дидактические материалы, Марон А.Е., 2007
- Физика, 11 класс, Задачник, Часть 2, Генденштейн Л.Э., Кирик Л.А., 2012
- Физика, 11 класс, Задачник, Часть 2, Генденштейн Л.Э., Кирик Л.А., Гельфгат И.М., 2010
- Физика, 11 класс, Контрольно-измерительные материалы, Зорин Н.И., 2014
- Физика, 11 класс, Контрольные работы
- Физика, 11 класс, Краевая диагностическая работа, 2011
- Физика, 11 класс, Краевая диагностическая работа, 2012
- Физика, 11 класс, Лабораторные работы, Контрольные задания, Губанов В.В., 2012
- Физика, 11 класс, Ответы на экзаменационные билеты, Соколова С.А., Московских Н.Б., 2009
- Физика, 11 класс, Профильный уровень, Тетрадь для лабораторных работ, Касьянов В.
 А., Коровин В.А., 2012
А., Коровин В.А., 2012 - Физика, 11 класс, Профильный уровень, Тетрадь для лабораторных работ, Касьянов В.А., Коровин В.А., 2014
- Физика, 11 класс, Разноуровневые самостоятельные и контрольные работы, Кирик Л.А., 2009
- Физика, 11 класс, самостоятельные работы, учебное пособие для учащихся общеобразовательных организаций (базовый и углублённый уровни), Генденштейн Л.Э., Кошкина А.В., Орлов В.А., 2014
- Физика, 11 класс, Тестовые задания, Рабочая тетрадь, Зорин Н.И., 2008
- Физика, 11 класс, Тестовые задания, Рабочая тетрадь, Зорин Н.И., 2008
- Физика, 11 класс, тесты в 2 частях, Сычев Ю.Н., 2012
- Физика, 11 класс, Тесты, Часть 1, Сычёв Ю.Н., 2012
- Физика, 11 класс, Тетрадь для лабораторных работ, Парфентьева Н.А., 2012
- Физика, 11 класс, Шпаргалки
- Физика, 11 класс, ЭДС, Закон Ома для полной цепи, Проверочная работа №1, Алексеева Е.В., 2012
- Физика, задачник, 10 11 класс, пособие для общеобразовательных учреждений, Рымкевич А.
 П., 2013
П., 2013 - Физика, Задачник, 10-11 класс, Гольдфарб Н.И., 2012
- Физика, задачник, 11 класс, Генденштейн Л.Э., Кошкина А.В., Левиев Г.И., 2014
- Физика, Задачник, 9-11 класс, Рымкевич А.П., 1990
- Физика, Конструктор самостоятельных и контрольных работ, 10-11 класс, Андрюшечкин С.М., Слухаевский А.С., 2010
- Физика, Контроль знаний, 10-11 класс, Заботин В.А., Комиссаров В.Н., 2008
- Физика, Контрольные работы, 10-11 класс, Куперштейн Ю.С., Марон Е.А., 2001
- Физика, Критерии оценивания заданий с развернутым ответом, 4 варианта, 11 класс, 2012
- Физика. 11 класс. Контрольные работы в новом формате. Годова И.В. 2011
- Физика. Задачник — 9-11 класс — Кабардин О.Ф., Орлов В.А., Зильберман А.Р.
- Физика. Ответы на экзаменационные билеты. 11 класс. Соколова С.А., Московских Н.Б. 2009
- Физика. Примеры решения задач, теория — Гомонова А.И.
- Экзаменационные вопросы и задачи — Физика — 11 класс
- Экзаменационные вопросы с ответами — Физика — 11 класс
- Физика — Учебно-справочное пособие для старшеклассников и абитуриентов — Черноуцан А.

- Физика в определениях, таблицах и схемах, 7-11 класс, Справочное пособие, Крот Ю.Е., 2004
- Физика в таблицах, 7-11 класс, Справочное пособие, Орлов В.А., 2008
- Физика, Все законы и формулы в таблицах, 7-11 класс, Моркотун В.Л., 2007
- Поурочные и календарные планы по физике — 11 класс
- Программа элективного курса, Методы решения задач по физике, 10-11 класс, 68 часов
- Программы для общеобразовательных учреждений, Физика, Астрономия, 7-11 класс, Коровин В.А., Орлов В.А., 2010
- Рабочие программы по физике, 7-11 класс, Выпуск 2, Корневич М.Л., 2012
- Рабочие программы по физике, 7-11 класс, Корневич М.Л., 2012
- Физика, 10-11 класс, Методические рекомендации, Кабардин О.Ф., Орлов В.А., 2004
- Физика, 10-11 класс, Методические рекомендации, Тулькибаева Н.Н., Пушкарев А.Э., 2004
- Физика, 10-11 класс, Методические рекомендации, Шаронова Н.В., 2004
- Физика, 10-11 класс, Рабочая программа
- Физика, 11 класс, Календарно-тематическое планирование, 2 часа в неделю, 70 часов, Мякишев Г.
 Я.
Я. - Физика, 11 класс, Поурочное планирование, Базовый уровень, 70 часов, Мякишев Г.Я., 2005
- Физика, 11 класс, Поурочное планирование, Профильный уровень, 175 часов, Касьянов В.А., 2004
- Физика, 11 класс, Поурочные планы к учебникам Мякишева Г.Я., Касьянова В.А., 2011
- Физика, 11 класс, Рабочая программа, 2 часа в неделю, Катербарг Т.О., 2010
- Физика, 11 класс, Рабочая программа, 2 часа в неделю, Катербарг Т.О., 2011
- Физика, 11 класс, Рабочая программа, 2 часа в неделю, Катербарг, 2011
- Физика, 11 класс, Рабочая программа, 3 часа в неделю, Катербарг Т.О., 2010
- Физика, 7-11 класс, Методичка, Комплект проверочных работ, Алексеева Е.В., 2012
- Физика, Поурочное планирование, 10-11 класс, 4 часа в неделю
- Физика, Таблично-графическая схема календарно-тематического плана, 11 класс
- Физика, Тематическое планирование изучения учебного материала, 10-11 класс
Напишите нам
РешенияNCERT для класса 11, физика, глава 3, движение по прямой линии
Решения NCERT для класса 11, физика, глава 3, движение по прямой являются частью решений NCERT для физики, класс 11. Здесь мы дали решения NCERT для класса 11 Physics Chapter 3 Motion in the Straight Line.
Здесь мы дали решения NCERT для класса 11 Physics Chapter 3 Motion in the Straight Line.
Темы и подтемы в NCERT Solutions for Class 11 Physics Chapter 3 Движение по прямой линии :
| Название раздела | Название темы |
| 3 | Движение по прямой |
| 3.1 | Введение |
| 3.2 | Положение, длина пути и смещение |
| 3,3 | Средняя скорость и средняя скорость |
| 3,4 | Мгновенная скорость и скорость |
| 3,5 | Ускорение |
| 3,6 | Кинематические уравнения равноускоренного движения |
| 3,7 | Относительная скорость |
NCERT Solutions Class 11 PhysicsPhysics Sample Papers
ВОПРОСЫ ИЗ УЧЕБНИКА
Вопрос 3. 1. В каком из следующих примеров движения можно считать тело приблизительно точечным объектом.
1. В каком из следующих примеров движения можно считать тело приблизительно точечным объектом.
(a) Железнодорожный вагон, движущийся без рывков между двумя станциями.
(b) Обезьяна, сидящая верхом на человеке, плавно едет на велосипеде по круговой дорожке.
(c) Вращающийся мяч для крикета, который резко поворачивается при ударе о землю.
(d) Переворачивающийся стакан, соскользнувший с края стола.
Ответ: (a) Вагон движется без рывков между двумя станциями, поэтому расстояние
между двумя станциями считается большим по сравнению с размером поезда. Поэтому поезд рассматривается как точечный объект.
(b) Обезьяну можно рассматривать как точечный объект, поскольку значение расстояния, пройденного на
круговой трассе, намного больше.
(c) Так как вращение мяча не является плавным, то расстояние, пройденное мячом за разумное время, невелико. Поэтому мяч нельзя рассматривать как точечный объект.
Поэтому мяч нельзя рассматривать как точечный объект.
(d) Опять же, кувыркающийся стакан, соскользнувший с края стола, не может рассматриваться как точечный объект, потому что пройденное расстояние ненамного больше.
Вопрос 3. 2. Графики положение-время (x -1) для двух детей A и B, возвращающихся из школы O в свои дома P и Q соответственно, показаны на рис. Выберите правильные записи в скобках ниже:
(a) (A/B) живет ближе к школе, чем (B/A).
(b) (A/B) начинается в школе раньше, чем (B/A).
(c) (A/B) ходит быстрее, чем (B/A).
(d) A и B возвращаются домой в (одно и то же/разное) время.
(e) (A/B) обгон (B/A) на дороге (один/два раза).
Ответ: (a) A живет ближе к школе, чем B, потому что B должен преодолевать большее расстояние [OP < OQ],
(b) A отправляется в школу раньше, чем B, потому что t = 0 для A, но для B t имеет некоторое конечное время.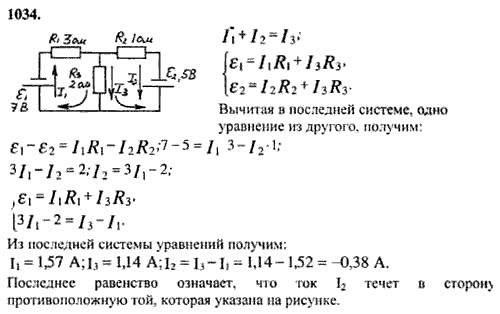
(c) Так как наклон B больше, чем у A, то B идет быстрее, чем A.
(d) A и B достигают дома в одно и то же время.
(e) В точке пересечения (т. е. X) B один раз обгоняет A на дорогах.
Дополнительные ресурсы для CBSE Class 11
- Решения NCERT
- Решения NCERT, класс 11, математика
- Решения NCERT, класс 11, физика
- Решения NCERT, класс 11, химический состав
- Решения NCERT, класс 11, биология
- Решения NCERT, класс 11, хинди
- Решения NCERT, класс 11, английский язык
- NCERT Solutions, класс 11, бизнес-исследования
- Решения NCERT, класс 11, бухгалтерский учет
- Решения NCERT, класс 11, психология
- Решения NCERT, класс 11, предпринимательство
- NCERT Solutions Class 11 Индийское экономическое развитие
- Решения NCERT, класс 11, информатика
Вопрос 3. 3. Женщина выходит из дома в 9.00, идет со скоростью 5 км ч -1 по прямой дороге до своего офиса 2,5 км, находится в офисе до 17:00 и возвращается домой на автомобиле со скоростью 2,5 км ч -1 . Выберите подходящие масштабы и постройте график x-t ее движения.
Выберите подходящие масштабы и постройте график x-t ее движения.
Ответ: Расстояние, пройденное пешком = 2,5 км.
Скорость при ходьбе = 5 км/ч
Время, затрачиваемое на то, чтобы добраться до офиса при ходьбе = (2,5/5) h=1/2 ч , х = 0
и в t = 9:30, x = 2,5 км.
OA представляет собой x-t график движения, когда женщина идет от дома до офиса пешком. Ее пребывание в офисе с 9:30 до 17:00 представлено на графике прямой линией АВ.
Теперь время, необходимое для возвращения домой на автомобиле = 2,5/5 ч = 1/10 ч = 6 минут
Итак, в t = 17:06, x = 0
Это движение представлено прямой линией BC на графике. При построении графика x-t были выбраны следующие масштабы:
По оси времени одно деление равно 1 часу.
Одно деление по положительной оси равно 0,5 км.
Вопрос 3. 4. Пьяный, идущий по узкому переулку, делает 5 шагов вперед и 3 шага назад, затем снова 5 шагов вперед и 3 шага назад и так далее. Каждый шаг имеет длину 1 м и требует 1 с. Постройте график x-t его движения. Определить графически и иначе, за какое время пьяница упадет в яму на расстоянии 13 м от старта.
Постройте график x-t его движения. Определить графически и иначе, за какое время пьяница упадет в яму на расстоянии 13 м от старта.
Ответ: Поскольку человек неуклонно движется вперед с течением времени, следующий график будет представлять его движение, пока он не пройдет 13 м. За 5 с он проходит расстояние 5 м, а затем за следующие 3 с возвращается на 3 м.
Таким образом, за 8 с он проходит только 2 м, как показано на графике, он упадет в яму за 37 с.
Как указывалось ранее, человек проходит 2 м за 8 с, значит, он пройдет 8 м за 32 с. Но в конце за 5 с он проедет еще 5 м, т. е. 32 с + 5 с = 37 с, он пройдет 8 м + 5 м = 13 м. Таким образом, он попадет в яму на 37-й секунде.
Вопрос 3. 5. Реактивный самолет, летящий со скоростью 500 км ч-1, выбрасывает продукты сгорания со скоростью 1500 км ч -1 относительно реактивного самолета. Какова скорость последнего относительно наблюдателя на земле?
Ответ: Скорость реактивного самолета относительно наблюдателя на земле = 500 км/ч.
Если Vj и v0 представляют скорости струи и наблюдателя соответственно, то vj – vo = 500 км ч -1
Аналогично, если vc представляет скорость продуктов сгорания относительно плоскости струи, тогда vc – vg = -1500 км /h
Знак минус указывает на то, что продукты сгорания движутся в направлении, противоположном направлению струи.
Скорость продуктов сгорания в.р.т. наблюдатель
= vc – u0 = (vc – vj) + (vj – v0) = (-1500 + 500) км ч -1 = -1000 км ч -1 .
Вопрос 3. 6. Автомобиль, движущийся по прямому шоссе со скоростью 126 км ч -1 , остановился на расстоянии 200 м. Каково замедление автомобиля (предполагается равномерным) и сколько времени требуется, чтобы автомобиль остановился?
Ответ:
Вопрос 3. 7. Два поезда А и В длиной по 400 м каждый движутся по двум параллельным путям с равномерной скоростью 71 км ч -1 в одном направлении, при этом А впереди B. Водитель B решает обогнать A и ускоряется на 1 мс -1 . Если через 50 с охранник B просто пронесется мимо водителя A, каково было исходное расстояние между ними?
Водитель B решает обогнать A и ускоряется на 1 мс -1 . Если через 50 с охранник B просто пронесется мимо водителя A, каково было исходное расстояние между ними?
Ответ: Здесь длина поезда A = длина поезда B = l = 400 м. Так как скорость обоих поездов u = 72 км ч -1 = 20 мс -1 в одном направлении, следовательно, их относительная скорость u BA = 0,
Пусть начальное расстояние между двумя поездами равно S, тогда поезд B проходит расстояние (S + 11) = (S + 800) м за время t = 50 с при равномерном ускорении a = 1 м/с 2 .
и начальное расстояние между охранником поезда В и машинистом поезда А = 450 + 800 = 1250 м.
Вопрос 3. 8. По двухполосной дороге автомобиль А едет со скоростью 36 км ч -1 . Две машины В и С приближаются к машине А навстречу друг другу со скоростью 54 км ч -1 каждая. В некоторый момент, когда расстояние АВ равно АС, а оба равны 1 км, В решает обогнать А раньше, чем это сделает С. Какое минимальное ускорение необходимо автомобилю B, чтобы избежать аварии?
Какое минимальное ускорение необходимо автомобилю B, чтобы избежать аварии?
Ответ:
Вопрос 3. 9. Два города A и B связаны регулярным автобусным сообщением, автобус отправляется в любом направлении каждые T минут. Человек, едущий на велосипеде со скоростью 20 км ч -1 в направлении от А до В, замечает, что автобус проходит мимо него каждые 18 мин в направлении его движения и каждые 6 мин в обратном направлении. Каков период T движения автобусов и с какой скоростью (считается постоянной) автобусы курсируют по дороге?
Ответ: Пусть vb будет скоростью каждого автобуса. Пусть vc — скорость велосипедиста.
Относительная скорость автобусов, следующих по направлению движения велосипедиста, vb – vc .
Автобусы, играющие по ходу движения велосипедиста, проезжают мимо него каждые
18 минут, т.е. 18/20 ч.
Вопрос 3. 10. Игрок бросает мяч вверх с начальной скоростью 29,4 мс -1 .
а) Каково направление ускорения при движении мяча вверх?
(б) Каковы скорость и ускорение мяча в высшей точке его движения?
(c) Выберите x = 0 м и t = 0 с, чтобы они были местоположением и временем мяча в его высшей точке, направление вертикально вниз должно быть положительным направлением оси x, и укажите знаки положения , скорость и ускорение мяча при его движении вверх и вниз.
(d) На какую высоту поднимается мяч и через какое время мяч возвращается в руки игрока? (Возьмите г = 90,8 м с -2 и сопротивлением воздуха пренебречь).
Ответ: (a) Направление ускорения при движении мяча вверх вертикально вниз.
(b) В высшей точке скорость мяча равна нулю, но ускорение (g = 9,8 мс -2 ) направлено вертикально вниз.
(c) Если принять высшую точку движения мяча за x = 0, t = 0, а вертикальное направление вниз принять за +ve направление оси x, то
(i) во время движения мяча вверх до достижения положения высшей точки (а также перемещение) x = +ve, скорость v = -ve и ускорение a = g = +ve.
(ii) при движении мяча вниз после достижения высшей точки x, v и a = g все три величины положительны.
(d) Во время восходящего движения
Вопрос 3. 11. Внимательно прочтите каждое приведенное ниже утверждение и объясните с указанием причин и примеров, верно оно или нет; Частица в одномерном движении
(а) с нулевой скоростью в данный момент времени может иметь в этот момент ненулевое ускорение.
(b) с, нулевая скорость может иметь ненулевую скорость.
(c) при постоянной скорости должно быть нулевое ускорение,
(d) при положительном значении ускорения должно быть ускорение.
Ответ: (а) Верно. Рассмотрим подброшенный вверх мяч. В высшей точке скорость равна нулю, но ускорение не равно нулю.
(б) Ложь. Если частица имеет ненулевую скорость, она должна иметь скорость.
(с) Верно. Если частица мгновенно отскакивает с той же скоростью, это подразумевает бесконечное ускорение, которое физически невозможно.
(г) Ложь. Истинно, только если выбранное направление положения совпадает с направлением движения.
Вопрос 3. 12. Мяч падает с высоты 90 м на пол. При каждом столкновении с полом мяч теряет одну десятую своей скорости. Постройте график зависимости скорости его движения между t = 0 и 12 с.
Ответ:
Вопрос 3. 13. Объясните ясно, на примерах, различие между:
длина пути, пройденного частицей за тот же интервал;
(b) Величина средней скорости за интервал времени и средняя скорость за тот же интервал . (Средняя скорость частицы за интервал времени определяется как общая длина пути, деленная на интервал времени). Покажите как в (а), так и в (б), что вторая величина либо больше, либо равна первой. Когда верен знак равенства? [Для простоты рассмотрим только одномерное движение],
Ответ: (а) Предположим, что частица движется из точки А в В по прямому пути и возвращается в А по тому же пути. Величина смещения частицы равна нулю, потому что частица вернулась в исходное положение. Общая длина пути, пройденного частицей, равна AB + BA = AB + AB = 2 AB. Таким образом, вторая величина больше первой,
Величина смещения частицы равна нулю, потому что частица вернулась в исходное положение. Общая длина пути, пройденного частицей, равна AB + BA = AB + AB = 2 AB. Таким образом, вторая величина больше первой,
(b) Предположим, что в приведенном выше примере частице требуется время t, чтобы пройти весь путь. Тогда величина средней скорости частицы за интервал времени t равна = Величина смещения / интервал времени = 0/t = 0
. В то время как средняя скорость частицы за тот же интервал времени равна = Общая длина пути /Time-interval= 2 AB /t
Опять же, вторая величина (средняя скорость) больше первой (величина средней скорости).
Примечание: В обоих приведенных выше случаях две величины равны, если частица движется из одной точки в другую по прямолинейному пути только в одном и том же направлении.
Вопрос 3.14. Человек идет по прямой дороге от своего дома до рынка, находящегося на расстоянии 2,5 км, со скоростью 5 км ч -1 . Обнаружив рынок закрытым, он мгновенно разворачивается и идет домой со скоростью 7,5 км ч -1 Чему равна (а) величина средней скорости и (б) средняя скорость человека за интервал времени (i) от 0 до 30 мин. (ii) от 0 до 50 мин. (iii) от 0 до 40 мин? [Примечание: из этого упражнения вы поймете, почему среднюю скорость лучше определять как общую длину пути, деленную на время, а не как величину средней скорости. Вам не хочется говорить уставшему человеку по возвращении домой, что его средняя скорость равна нулю!]
Обнаружив рынок закрытым, он мгновенно разворачивается и идет домой со скоростью 7,5 км ч -1 Чему равна (а) величина средней скорости и (б) средняя скорость человека за интервал времени (i) от 0 до 30 мин. (ii) от 0 до 50 мин. (iii) от 0 до 40 мин? [Примечание: из этого упражнения вы поймете, почему среднюю скорость лучше определять как общую длину пути, деленную на время, а не как величину средней скорости. Вам не хочется говорить уставшему человеку по возвращении домой, что его средняя скорость равна нулю!]
Ответ:
Вопрос 3. 15. В упражнениях 3.13 и 3.14 мы тщательно различали среднюю скорость и величину средней скорости. Нет необходимости в таком различии, когда мы рассматриваем мгновенную скорость и модуль скорости. Мгновенная скорость всегда равна величине мгновенной скорости. Почему?
Ответ: Мгновенная скорость — это скорость частицы в конкретный момент времени. В этом случае небольшого интервала времени величина смещения фактически равна расстоянию, пройденному частицей за тот же интервал времени. Следовательно, нет различия между мгновенной скоростью и скоростью.
Следовательно, нет различия между мгновенной скоростью и скоростью.
Вопрос 3. 16. Внимательно рассмотрите графики (a)–(d) рис. и укажите с указанием причин, какие из них никак не могут представлять одномерное движение частицы.
Ответ: Ни один из четырех графиков не представляет возможное одномерное движение. На графиках (а) и (б) движения определенно двумерны. График (а) представляет две позиции одновременно, что невозможно.
На графике (б) одновременно видно противоположное движение.
График (в) некорректен, так как показывает, что в некоторый момент времени частица имеет отрицательную скорость. Скорость всегда положительна.
На графике (d) длина пути показана как увеличивающейся, так и уменьшающейся. Длина пути никогда не уменьшается.
Вопрос 3. 17. На рисунке показан график x-t одномерного движения частицы.
Правильно ли из графика сказать, что частица движется по прямой при t < 0 и по параболе при t > 0? Если нет, предложите подходящий физический контекст для этого графика.
Ответ: Неправильно говорить, что частица движется по прямой при t < 0 (т. е. -ve) и по параболической траектории при t > 0 (т. е. + ve)
, потому что график x-t не может показать путь частицы.
Для графа подходящим физическим контекстом может быть частица, брошенная с вершины башни в момент времени t =0.
Вопрос 3. 18. Полицейский фургон, движущийся по шоссе со скоростью 30 км ч -1 , стреляет пулей в машину угонщика, мчащуюся в том же направлении со скоростью 192 км ч -1 . Если начальная скорость пули 150 мс -1 , с какой скоростью пуля попадет в машину вора? (Примечание: Добейтесь той скорости, которая необходима для повреждения машины вора).
Ответ:
Вопрос 3. 19. Предложите подходящую физическую ситуацию для каждого из следующих графиков:
Ответ: (a) Наносится удар по мячу, покоящемуся на гладком полу. Он отскакивает от стены с уменьшенной скоростью и движется к противоположной стене, которая его останавливает.
Он отскакивает от стены с уменьшенной скоростью и движется к противоположной стене, которая его останавливает.
(б) График показывает, что скорость меняется снова и снова с течением времени и каждый раз теряет некоторую скорость. Следовательно, это может представлять собой такую физическую ситуацию, как мяч, свободно падающий (после того, как его подбросили вверх), при ударе о землю отскакивает с уменьшенной скоростью после каждого удара о землю.
(c) Равномерно движущийся мяч для крикета повернулся назад в результате удара по нему битой в течение очень короткого промежутка времени.
Вопрос 3. 20. На рисунке показан график x-t частицы, совершающей одномерное простое гармоническое движение. (Вы узнаете об этом движении более подробно в главе 14). Укажите знаки переменных положения, скорости и ускорения частицы в моменты времени t = 0,3 с, 1,2 с, – 1,2 с.
Ответ: На графике x-t на рис., показывающем простое гармоническое движение частицы, знаки положения, скорости и ускорения указаны ниже.
В S.H.M., ускорение, a – x или a = – kx.
(i) При t = 0,3 с x < 0, т. е. x находится в -ve направлении. Более того, поскольку x со временем становится все более отрицательным, это показывает, что v также равно – ve (т. е. v < 0). Однако a = -kx будет +ve (a > 0).
(ii) При t = 1,2 с, x > 0, v > 0 и a < 0.
(iii) При t = -1,2 с, x < 0, но здесь с увеличением времени t значение x становится меньше отрицательный.
Это означает, что v равно +ve (т. е. v > 0). Снова a = – kx будет положительным (т. е. a > 0).
Вопрос 3. 21. На рисунке показан график x-t частицы в одномерном движении. Показаны три различных равных интервала времени. В каком интервале средняя скорость наибольшая, а в каком наименьшая? Укажите знак средней скорости для каждого интервала.
Ответ: Больше в 3, наименьшее в 2; v > 0 в 1 и 2, v < 0 в интервале 3.
Вопрос 3. 22. На рисунке приведен график зависимости скорости частицы, движущейся в постоянном направлении. Показаны три равных интервала времени. В каком интервале среднее ускорение наибольшее по величине? В каком интервале средняя скорость наибольшая? Выбрав положительное направление как постоянное направление движения, задайте знаки v и a на трех интервалах. Каковы ускорения в точках A, B, C и D?
Показаны три равных интервала времени. В каком интервале среднее ускорение наибольшее по величине? В каком интервале средняя скорость наибольшая? Выбрав положительное направление как постоянное направление движения, задайте знаки v и a на трех интервалах. Каковы ускорения в точках A, B, C и D?
Ответ: Ускорение максимально по величине на интервале 2, так как изменение скорости за то же время максимально на этом интервале.
Средняя скорость максимальна на интервале 3 (пик D максимален на оси скорости).
Знак v и a в трех интервалах:
v > 0 в 1, 2 и 3; a > 0 в 1
a < 0 в 2, a=0 в 3.
ускорение равно нулю в точках A, B, C и D.
Вопрос 3. 1 м с-2 по прямой дороге в течение 10 с, а затем движется с постоянной скоростью. Постройте расстояние, пройденное транспортным средством за n-ю секунду (n=1,2,3……..) в зависимости от n. каким, по-вашему, будет этот график при ускоренном движении: прямой линией или параболой?
Ответ:
Вопрос 3. 24. Мальчик, стоящий на стационарном подъемнике (открытом сверху), бросает мяч вверх с максимально возможной начальной скоростью, равной 49 м с -1 . Через сколько времени мяч вернется в его руки? Если лифт начнет двигаться вверх с равномерной скоростью 5 м с -1 и мальчик снова подбросит мяч вверх с максимально возможной скоростью, через сколько времени мяч вернется к нему в руки?
24. Мальчик, стоящий на стационарном подъемнике (открытом сверху), бросает мяч вверх с максимально возможной начальной скоростью, равной 49 м с -1 . Через сколько времени мяч вернется в его руки? Если лифт начнет двигаться вверх с равномерной скоростью 5 м с -1 и мальчик снова подбросит мяч вверх с максимально возможной скоростью, через сколько времени мяч вернется к нему в руки?
Ответ: Когда лифт покоится или движется вертикально вверх или вниз с постоянной скоростью, мы можем применить три простых кинетических уравнения движения, предполагая, что a = ± g (в зависимости от обстоятельств). В данном случае u = 49 мс -1 (вверх) a = g = 9,8 мс -2 (вниз)
Если мяч возвращается в руки мальчика через время t, то перемещение мяча относительно мальчика
равно нулю, т.е. = 0. Отсюда, используя уравнение s = ut + 1/2 при 2, имеем
Вопрос 3. 25. На длинной горизонтально движущейся ленте (рис. ) ребенок бегает туда-сюда со скоростью n 9 км ч -1 (относительно ленты) между отцом и матерью, расположенными в 50 а часть на движущейся ленте. Лента движется со скоростью 4 км ч -1 .
) ребенок бегает туда-сюда со скоростью n 9 км ч -1 (относительно ленты) между отцом и матерью, расположенными в 50 а часть на движущейся ленте. Лента движется со скоростью 4 км ч -1 .
(a) Скорость ребенка, бегущего в направлении движения ремня, для наблюдения за стационарной платформой снаружи?
(b) Скорость ребенка, бегущего против направления движения ремня?
(c) Время, потраченное ребенком в пунктах (a) и (b)?
Какой из ответов изменится, если один из родителей увидит движение?
Ответ: Скорость ребенка относительно ремня = 9 км ч -1 Скорость ремня = 4 км ч -1
(a) Когда ребенок бежит в направлении движения ремня, затем скорость ребенка w.r.t. стационарный наблюдатель = (9 + 4) км ч -1 = 13 км ч -1 .
(b) Когда ребенок бежит против направления движения ремня, тогда скорость ребенка относительно неподвижный наблюдатель = (9– 4) км ч -1 = 5 км ч -1
(c) Скорость ребенка w. r.t. любой из родителей = 9 км ч -1
r.t. любой из родителей = 9 км ч -1
Расстояние, которое нужно пройти = 50 м = 0,05 км 0,05 км
Время = 0,05 км/9 км ч -1 = 0,0056 ч = 20 с
Если движение просматривается одним из родителей, то ответы на вопросы (а) и (б) меняются, а ответ на вопрос (в) остается неизменным.
Вопрос 3. 26. С края обрыва высотой 200 м одновременно брошены два камня с начальными скоростями 15 мс -1 и 30 мс -1 . Убедитесь, что график, показанный на рис., правильно представляет изменение во времени относительного положения второго камня по отношению к первому. Сопротивлением воздуха пренебречь и считать, что камни не отскакивают после удара о землю. Возьмем g = 10 мс -2 . Приведите уравнения для линейной и криволинейной частей графика.
Ответ: Для первого камня
x (0) = 200 м, v (0) = 15 мс -1 , a = -10 мс -2
x 1 (t) = x (0) + v (0) t + 1/2 a t 2
x 1 (t) = 200 + 15t – 5t 2
При первом камне ударяется о землю, x 1 (t) = 0
– 5t 2 + 15t+ 200 = 0 При упрощении t = 8 с
Для второго камня x (0) = 200 м, v (0) = 30 мс -1 , a = -10 мс -2
x 1 (t) = 200 + 30t – 5t 2
Когда этот камень упадет на землю, x 1 (t) = 0 . -. -5т 2 + 30t + 200 = 0
-. -5т 2 + 30t + 200 = 0
Относительное положение второго камня относительно сначала определяется как x 2 (t) – x 1 (t) = 15t
. Поскольку между x 2 (t) – x 1 (t) и t существует линейная зависимость, является прямой линией.
Для максимального расстояния t = 8 с Таким образом, максимальное расстояние составляет 120 м.
Через 8 секунд только второй камень будет двигаться. Итак, график соответствует квадратному уравнению.
Вопрос 3. 27. График зависимости скорости частицы, движущейся в фиксированном направлении, показан на рис. Найдите расстояние, пройденное частицей между
(а) t = от 0 до 10 с. б) t = от 2 до 6 с.
Какова средняя скорость частицы на интервалах (а) и (б)?
Ответ:
Вопрос 3. 28. График скорость-время частицы в одномерном движении показан ниже. Какие из следующих формул верны для описания движения частицы на интервале времени от t 1 до t 2 ?
Ответ: (в), (г), (е).
Как видно из формы v-t графика, ускорение частицы неравномерно между временными интервалами t 1 и t 2 . (поскольку данный v-t график непрямой). Уравнения (a), (b) и (e) представляют равномерное ускорение.
Мы надеемся, что решения NCERT для класса 11, физика, глава 3 «Движение по прямой линии», помогут вам. Если у вас есть какие-либо вопросы относительно решений NCERT для класса 11, физика, глава 3, движение по прямой, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
Решения NCERT для 11 класса, физика, глава 3 — Движение по прямой [Последнее издание]
Решения NCERT для 11 класса, физика, глава 3, прямолинейное движение Упражнения
Упражнения | Q 1
В каком из следующих примеров движения тело можно считать приближенно точечным объектом:
(а) железнодорожный вагон, движущийся без рывков между двумя станциями.
(b) обезьяна, сидящая верхом на человеке, который плавно едет на велосипеде по круговой дорожке.
(c) вращающийся мяч для крикета, который резко поворачивается при ударе о землю.
(d) переворачивающийся стакан, соскользнувший с края стола.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | вопрос 2 |
Графики положение-время ( x-t ) для двух детей A и B, возвращающихся из школы O в свои дома P и Q соответственно, показаны на рисунке Выберите правильные значения в скобках ниже;
(a) (A/B) живет ближе к школе, чем (B/A)
(b) (A/B) выходит из школы раньше, чем (B/A)
(c) (A/B) идет быстрее, чем (B/A)
(d) A и B приходят домой в (одинаковое/разное) время
(e) (A/B) обгоняет (B/A) на дороге (один/два раза).
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 3 | Страница 56
Женщина выходит из дома в 9.00, идет со скоростью 5 км ч –1 по прямой дороге до своего офиса на расстоянии 2,5 км, остается в офисе до 17:00 и возвращается домой на автомобиле со скоростью 25 км ч –1 . Выберите подходящие масштабы и постройте график ее движения x — t .
Выберите подходящие масштабы и постройте график ее движения x — t .
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 4 | Страница 56
Пьяный, идущий по узкому переулку, делает 5 шагов вперед и 3 шага назад, затем снова 5 шагов вперед и 3 шага назад и так далее. Каждый шаг имеет длину 1 м и требует 1 с. Постройте x — t график его движения. Определить графически и иначе, за какое время пьяница упадет в яму на расстоянии 13 м от старта.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 5 | Страница 56
Реактивный самолет, летящий со скоростью 500 км ч –1 выбрасывает продукты сгорания со скоростью 1500 км ч –1 относительно реактивного самолета. Какова скорость последнего относительно наблюдателя на земле?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 6 |
Автомобиль, движущийся по прямому шоссе со скоростью 126 км/ч –1 , останавливается на расстоянии 200 м. Каково замедление автомобиля (предполагается равномерным) и за какое время автомобиль останавливается
Каково замедление автомобиля (предполагается равномерным) и за какое время автомобиль останавливается
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 7 | Страница 56
Два поезда А и В длиной по 400 м каждый движутся по двум параллельным путям с равномерной скоростью 72 км ч –1 в одном направлении, при этом А впереди В. Водитель В решает совершить обгон A и ускоряется на 1 м/с 2 . Если через 50 с охранник B просто пронесется мимо водителя A, каково было исходное расстояние между ними?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 8 | Страница 56
Автомобиль А движется по двухполосной дороге со скоростью 36 км ч –1 . Две машины В и С приближаются к машине А навстречу друг другу со скоростью 54 км ч –1 каждая. В некоторый момент, когда расстояние АВ равно АС, а оба равны 1 км, В решает обогнать А раньше, чем это сделает С. Какое минимальное ускорение необходимо автомобилю B, чтобы избежать аварии?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 9 | Страница 56
Два города A и B связаны регулярным автобусным сообщением, автобус отправляется в любом направлении каждые 906:50 T 90 651 минут. Человек, едущий на велосипеде со скоростью 20 км ч –1 в направлении от А до В, замечает, что автобус проходит мимо него каждые 18 минут в направлении его движения и каждые 6 минут в противоположном направлении. Каков период T движения автобусов и с какой скоростью (считается постоянной) автобусы курсируют по дороге?
Человек, едущий на велосипеде со скоростью 20 км ч –1 в направлении от А до В, замечает, что автобус проходит мимо него каждые 18 минут в направлении его движения и каждые 6 минут в противоположном направлении. Каков период T движения автобусов и с какой скоростью (считается постоянной) автобусы курсируют по дороге?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 10 |
Игрок бросает мяч вверх с начальной скоростью 29,4 м с –1 .
а) Каково направление ускорения при движении мяча вверх?
(б) Каковы скорость и ускорение мяча в высшей точке его движения?
(c) Выберите x = 0 м и t = 0 с в качестве местоположения и времени нахождения мяча в его высшей точке, вертикальное направление вниз в качестве положительного направления оси x и укажите знаки положения, скорости и ускорения мяча при его движении вверх и вниз.
(d) На какую высоту поднимается мяч и через какое время мяч возвращается в руки игрока? (Возьмем г = 9,8 м с –2 и пренебрежем сопротивлением воздуха).
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 11.1 | Page 57
Внимательно прочтите каждое утверждение ниже и объясните с указанием причин и примеров, верно оно или нет;
Частица в одномерном движении с нулевой скоростью в данный момент может иметь ненулевое ускорение в этот момент
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 11.2 | Page 57
Внимательно прочтите каждое утверждение ниже и объясните с указанием причин и примеров, верно оно или нет;
Частица в одномерном движении с нулевой скоростью может иметь ненулевую скорость,
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 11.3 | Page 57
Внимательно прочтите каждое утверждение ниже и объясните с указанием причин и примеров, верно оно или нет;
Частица, движущаяся в одном направлении с постоянной скоростью, должна иметь нулевое ускорение
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 11.4 | Page 57
Внимательно прочтите каждое утверждение ниже и объясните с указанием причин и примеров, верно оно или нет;
Частица в одномерном движении с положительным значением ускорения должна ускоряться.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 12 |
Мяч падает с высоты 90 м на пол. При каждом столкновении с полом мяч теряет одну десятую своей скорости. Постройте график зависимости скорости его движения между t = от 0 до 12 с.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 3.13 |
Четко объясните на примерах различие между:
- Величиной смещения (иногда называемого расстоянием) за интервал времени и общей длиной пути, пройденного частицей за тот же интервал.
Величина средней скорости за интервал времени и средняя скорость за тот же интервал. [Средняя скорость частицы за интервал времени определяется как общая длина пути, деленная на интервал времени]. Покажите как в (а), так и в (б), что вторая величина либо больше, либо равна первой.
Когда верен знак равенства? [Для простоты рассмотрим только одномерное движение].
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 14 | Страница 57
Человек идет по прямой дороге от своего дома до рынка на расстоянии 2,5 км со скоростью 5 км ч –1 . Обнаружив рынок закрытым, он мгновенно разворачивается и идет домой со скоростью 7,5 км ч –1 . Чему равна
Обнаружив рынок закрытым, он мгновенно разворачивается и идет домой со скоростью 7,5 км ч –1 . Чему равна
(а) величина средней скорости и
(б) средняя скорость человека за интервал времени (i) от 0 до 30 мин, (ii) от 0 до 50 мин, (iii) от 0 до 40 минут? [Примечание: из этого упражнения вы поймете, почему среднюю скорость лучше определять как общую длину пути, деленную на время, а не как величину средней скорости. Вы же не хотите говорить уставшему человеку по возвращении домой, что его средняя скорость равна нулю!]
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 15 |
В упражнениях 3.13 и 3.14 мы тщательно провели различие между средней скоростью и величиной средней скорости. Нет необходимости в таком различии, когда мы рассматриваем мгновенную скорость и модуль скорости. Мгновенная скорость всегда равна величине мгновенной скорости. Почему?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 16 | Страница 57
Посмотрите на графики с (a) по (d) Внимательно изобразите и объясните с указанием причин, какие из них не может представить одномерное движение частицы.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 17 | Страница 58
На рисунке показан график x-t одномерного движения частицы. Правильно ли по графику сказать, что частица движется по прямой при t < 0 и по параболе при t > 0? Если нет, предложите подходящий физический контекст для этого графика.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 18 | Страница 58
Полицейский фургон, движущийся по шоссе со скоростью 30 км ч –1 выстреливает пулей в машину угонщика, мчащуюся в том же направлении со скоростью 192 км ч –1 . Если начальная скорость пули 150 м с –1 , с какой скоростью пуля попадет в машину угонщика? (Примечание: добейтесь той скорости, которая необходима для повреждения автомобиля вора).
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 19.1 | Страница 58
Предложите подходящую физическую ситуацию для каждого из следующих графиков
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 19. 2 | Страница 58
2 | Страница 58
Предложите подходящую физическую ситуацию для каждого из следующих графиков:
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 19.3 | Страница 58
Предложите подходящую физическую ситуацию для каждого из следующих графиков:
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 20 | Страница 58
На рисунке показан график x-t частицы, совершающей одномерное простое гармоническое движение. Укажите знаки переменных положения, скорости и ускорения частицы при t = 0,3 с, 1,2 с, – 1,2 с.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 21 | Страница 58
На рисунке показан график x-t частицы в одномерном движении. Показаны три различных равных интервала времени. В каком интервале средняя скорость наибольшая, а в каком наименьшая? Укажите знак средней скорости для каждого интервала.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 22 | Страница 59
На рисунке показан график зависимости скорости от времени частицы, движущейся в постоянном направлении. Показаны три равных интервала времени. В каком интервале среднее ускорение наибольшее по величине? В каком интервале средняя скорость наибольшая? Выбрав положительное направление в качестве постоянного направления движения, задайте знаки v и a в трех интервалах. Чему равны ускорения в точках А, В, С и D?
Показаны три равных интервала времени. В каком интервале среднее ускорение наибольшее по величине? В каком интервале средняя скорость наибольшая? Выбрав положительное направление в качестве постоянного направления движения, задайте знаки v и a в трех интервалах. Чему равны ускорения в точках А, В, С и D?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 23 |
Трехколесный транспорт трогается с места, равномерно ускоряется за 1 м с –2 на прямой дороге в течение 10 с, а затем движется с постоянной скоростью. Постройте расстояние, пройденное транспортным средством за n th секунды (n = 1,2,3….), в зависимости от n. Каким, по-вашему, будет этот график при ускоренном движении: прямой линией или параболой?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 24 | Страница 59
Мальчик, стоящий на стационарном подъемнике (открытом сверху), бросает мяч вверх с максимально возможной начальной скоростью, равной 49 м/с.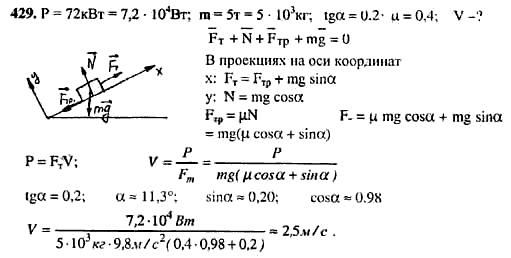 Через сколько времени мяч вернется в его руки? Если лифт начнет двигаться вверх с равномерной скоростью 5 м/с и мальчик снова подбросит мяч вверх с максимально возможной скоростью, через какое время мяч вернется к нему в руки?
Через сколько времени мяч вернется в его руки? Если лифт начнет двигаться вверх с равномерной скоростью 5 м/с и мальчик снова подбросит мяч вверх с максимально возможной скоростью, через какое время мяч вернется к нему в руки?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 25 | Страница 59
На длинной горизонтально движущейся ленте (рис. 3.26) ребенок бегает туда-сюда со скоростью 9км ч –1 (относительно ленты) между отцом и матерью, находящимися на расстоянии 50 м друг от друга на движущейся ленте. Лента движется со скоростью 4 км ч –1 . Какова
(а) скорость ребенка, бегущего в направлении движения ремня, для наблюдателя на стационарной платформе снаружи?.
(b) скорость ребенка, бегущего против направления движения ремня ?
(c) время, потраченное ребенком в пунктах (a) и (b) ?
Какой из ответов изменится, если движение увидит один из родителей?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 26 |
С края обрыва высотой 200 м одновременно брошены два камня с начальными скоростями 15 м/с и 30 м/с. Убедитесь, что график, показанный на рис. 3.27, правильно представляет изменение во времени относительного положения второго камня по отношению к первому. Сопротивлением воздуха пренебречь и считать, что камни не отскакивают после удара о землю. Возьмем г = 10 м/с 2 . Приведите уравнения для линейной и криволинейной частей графика.
Убедитесь, что график, показанный на рис. 3.27, правильно представляет изменение во времени относительного положения второго камня по отношению к первому. Сопротивлением воздуха пренебречь и считать, что камни не отскакивают после удара о землю. Возьмем г = 10 м/с 2 . Приведите уравнения для линейной и криволинейной частей графика.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 27 |
График зависимости скорости частицы, движущейся в фиксированном направлении, показан на рис. 3.28. Получите расстояние, пройденное частицей между (а) t = от 0 до 10 с, (б) t = от 2 до 6 с.
Какова средняя скорость частицы на отрезках (а) и (б)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 28 | Страница 60
График зависимости скорости частицы в одномерном движении показан на рисунке 9.0003
Какие из следующих формул верны для описания движения частицы в интервале времени от t 2 до t 1 ?
(a) x ( T 2 ) = x ( T 1 ) + V ( T 71550+ V ( T 777777778). 1 ) + (1/2) a ( т 2 –т 1 ) 2
1 ) + (1/2) a ( т 2 –т 1 ) 2
(b) v ( t 2 ) = v ( t 1 ) + a ( t 2 –t 1 )
(c) v Average = ( x ( t 2 ) – x ( t 1 )) / ( t 2 – т 1 )
(г) a Average = ( v ( t 2 ) – v ( t 1 )) / ( t 2 – t 1 )
(e) x ( t 2 ) = x ( t 1 ) + v Average (t 2 – t 1 ) + (1/2) a Среднее (t 2 – t 1 ) 2
(f) x ( t 2 ) – x ( t 1 ) = area under показана кривая v–t , ограниченная осью t и показанной пунктирной линией.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Q 29
Заполните пропуски подходящим преобразованием единиц
1 м =….. ly
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнения | Вопрос 30
Укажите количество значащих цифр в следующем:
2,64 × 10 24 кг
ПОКАЗАТЬ РЕШЕНИЕ
Решения NCERT для 11 класса Физика Глава 3 Движение по прямой линии
1 Решения по физике
9000 Физика Глава 3 Движение по прямой линии включает все важные темы с подробным объяснением, цель которого помочь учащимся лучше понять концепции. Учащиеся, которые готовятся к экзаменам по физике в 11 классе, должны пройти NCERT Solutions for 9.0005 11 класс Физика Глава 3 Движение по прямой . Просмотр решений, представленных на этой странице, поможет вам узнать, как подходить и решать проблемы.
Учащиеся также могут найти вводный текст NCERT, упражнения и вопросы в конце главы. Также работа над Класс 11 Физика Физика Глава 3 Движение по прямой линии Решения NCERT будут наиболее полезными для учащихся, чтобы вовремя решать свои домашние задания и задания. Учащиеся также могут загрузить NCERT Solutions для класса 11 Physics Physics Chapter 3 Motion in the Straight Line PDF для доступа к ним даже в автономном режиме.
Учащиеся также могут загрузить NCERT Solutions для класса 11 Physics Physics Chapter 3 Motion in the Straight Line PDF для доступа к ним даже в автономном режиме.
Решения NCERT для 11 класса Физика Глава 3 Физика Движение по прямой линии было решено опытными учителями CBSETuts.com. Все решения, представленные на этой странице, решаются на основе CBSE Syllabus и руководств NCERT.
NCERT Упражнения
Вопрос 1.
В каком из следующих примеров движения можно считать тело приближенно точечным объектом:
(а) железнодорожный вагон, движущийся без рывков между двумя станциями.
(b) обезьяна, сидящая верхом на человеке, плавно едет на велосипеде по круговой дорожке.
(c) вращающийся мяч для крикета, который резко поворачивается при ударе о землю.
(d) переворачивающийся стакан, соскользнувший с края стола.
Ответ:
(a) Вагон можно считать точечным объектом, поскольку расстояние между двумя станциями очень велико по сравнению с размером железнодорожного вагона.
(b) Обезьяну можно рассматривать как точечный объект, если велосипедист описывает круговую дорожку очень большого радиуса, поскольку в этом случае расстояние, пройденное велосипедистом, достаточно велико по сравнению с размером обезьяны. Обезьяну нельзя рассматривать как точечный объект, если велосипедист описывает круговую дорожку малого радиуса, поскольку в этом случае расстояние, пройденное велосипедистом, не очень велико по сравнению с размером обезьяны.
(c) Вращающийся крикетный мяч нельзя рассматривать как точечный объект, поскольку размер вращающегося крикетного мяча весьма ощутим по сравнению с расстоянием, на которое мяч может повернуться при ударе о землю.
(d) Стакан, соскальзывающий с края стола, не может рассматриваться как точечный объект, потому что размер стакана не является незначительным по сравнению с высотой стола.
Вопрос 2.
Графики положение-время (x-t) для двух детей A и B, возвращающихся из школы O в свои дома P и Q соответственно, показаны на рисунке. Выберите правильные записи в скобках ниже:
Выберите правильные записи в скобках ниже:
(a) (A/B) живет ближе к школе, чем (B/A)
(b) (A/B) выходит из школы раньше, чем (B/A)
(c) (A/B) идет быстрее, чем (B/A)
(d) A и B добираются до дома в (одно и то же/разное) время
(e) (A/B) обгоняет (B/A) по дороге (один/два раза).
Ответ:
(a) Из графика видно, что OQ > OP, поэтому A живет ближе к школе, чем B. от начала координат, поэтому x = 0, t = 0 для A, в то время как график (x-t) B начинается с C, который показывает, что B начинается позже, чем A, после временного интервала OC. Значит, А начинает ходить в школу (О) раньше, чем Б.
(c) Скорость представлена наклоном или крутизной графика (x-t). Чем круче график, тем больше будет скорость, тем быстрее будет ребенок с более крутым графиком. Поскольку график (x-t) B круче, чем график (x-t) A, мы заключаем, что B ходит быстрее, чем
(d) . Соответственно P и Q значение t из A и B одинаковы, т. е. OE. Таким образом, и A, и B достигают дома в одно и то же время.
е. OE. Таким образом, и A, и B достигают дома в одно и то же время.
(e) Так как графики (x-t) для A и B пересекаются друг с другом в одной точке, т.е. D и B стартуют из школы позже, то B обгоняет A на дороге только один раз.
Вопрос 3.
Женщина выходит из дома в 9.00, идет со скоростью 5 км ч -1 по прямой дороге до своего офиса 2,5 км, находится в офисе до 17.00 , и возвращается домой на автомобиле со скоростью 25 км ч -1 . Выберите подходящие масштабы и постройте (x-t) график ее движения.
Ответ:
Из дома в офис: Время, когда она уходит из дома в офис 9 утра.
скорость = 5 км ч -1 ; расстояние = 2,5 км
Следовательно, время, затраченное на то, чтобы добраться до офиса,
Таким образом, время, в которое она доберется до своего офиса = 9:30 утра.
С 9:30 до 17:00 она остается в своем офисе, т.е. на расстоянии 2,5 км от своего
Из офиса в дом: Время, когда она покидает свой офис = 17:00.
Скорость = 25 км ч -1 , расстояние = 2,5 км
Следовательно, время, необходимое для достижения дома,
Следовательно, время, в которое она достигает своего дома = 17:06.
Следовательно, (x-t) график ее движения будет таким, как показано на рисунке.
Вопрос 4.
Пьяный человек, идущий по узкой улочке, делает 5 шагов вперед и 3 шага назад, затем снова 5 шагов вперед и 3 шага назад и так далее. Каждый шаг имеет длину 1 м и требует 1 с. Постройте график x-t его движения. Определить графически и иначе, за какое время пьяница упадет в яму на расстоянии 13 м от старта.
Ответ:
График x-t пьяницы показан на рисунке.
Длина каждого шага = 1 м, время, необходимое для каждого шага = 1 с.
∴ Время, необходимое для перемещения на 5 шагов = 5 с.
5 шагов (т.е. 5 м) вперед и 3 шага (т.е. 3 м) назад означает, что чистая дистанция, пройденная им за первые 8 шагов, т.е. за 8 с = 5м-3м = 2 м.
Расстояние, пройденное им за первые 16 шагов или 16с = 2 + 2 = 4м.
Расстояние, пройденное пьяницей за первые 24 шага, т. е. 24 шага = 2 + 2 + 2 = 6 м, а расстояние, пройденное за 32 шага
, т. е. 32 сек = 8 м.
∴ Расстояние, пройденное за первые 37 шагов = 8 + 5 = 13 м.
Расстояние от ямы до старта = 13 м.
Общее время, затраченное пьяницей на то, чтобы упасть в яму = 37 с.
Так как 1 шаг требует 1 с времени, мы приходим к тому же результату из показанного графика.
Вопрос 5.
Реактивный самолет, летящий со скоростью 500 км ч -1 , выбрасывает продукты сгорания со скоростью 1500 км ч -1 относительно реактивного самолета. Какова скорость последнего относительно наблюдателя на земле?
Ответ:
Пусть υ j , υ g и υ o – скорости струи, выбрасываемых газов, т.е. продуктов сгорания, и скорости наблюдателя на земле соответственно.
Пусть струя движется вправо (+ve направление).
.’. Выбрасываемые газы будут двигаться влево (направление -ve).
Согласно утверждению
υ j = 500 км ч -1
Поскольку наблюдатель находится на земле, т.е. в состоянии покоя
.’. υ o = 0
Теперь относительная скорость самолета относительно наблюдатель
υ j -υ o = 500 – 0 = 500 км ч -1 …(1)
Относительная скорость продуктов сгорания отн. реактивный самолет
υ с – υ j = 1500 км ч -1 (дано) …(2)
-ве знак указывает на то, что продукты сгорания движутся в направлении, противоположном направлению струи.
.’. Складывая уравнения (1) и (2), получаем скорость продуктов сгорания м.с. наблюдатель на земле, т.е.
(υ j – υ o ) + (υ g – υ j ) = υ г -υ o = 500 + (-1500)
или υ г – v 0 = -1000 км ч -1
-ve знак показывает, что относительная скорость выбрасываемых газов с.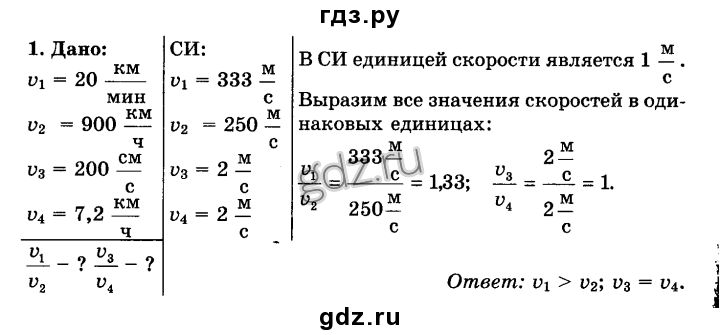 наблюдатель направлен влево, т.е. -в направлении, т.е. в направлении, противоположном движению реактивной плоскости.
наблюдатель направлен влево, т.е. -в направлении, т.е. в направлении, противоположном движению реактивной плоскости.
Вопрос 6.
Автомобиль, движущийся по прямому шоссе со скоростью 126 км ч -1 , остановился на расстоянии 200 м. Каково замедление автомобиля (предполагается равномерным) и сколько времени требуется, чтобы автомобиль остановился?
Ответ:
что называется замедлением, т.е. автомобиль равномерно замедлен на a = 3,06 м с -2 .
Вопрос 7.
Два поезда А и В длиной по 400 м каждый движутся по двум параллельным путям с равномерной скоростью 72 км/ч -1 в одном направлении, причем А впереди 6. Машинист В решает обогнать А и ускоряется на 1 м с -2 . Если через 50 с охранник B просто пронесется мимо водителя A, каково было исходное расстояние между ними?
Ответ:
Для поезда A:u A = 72 км ч -1 = 20 м с -1
t = 50 с; A = 0
S A = U A T
или S A = 20 x 50 = 1000 м
для поезда B: U B = 72 км ч -1 = 20 млн.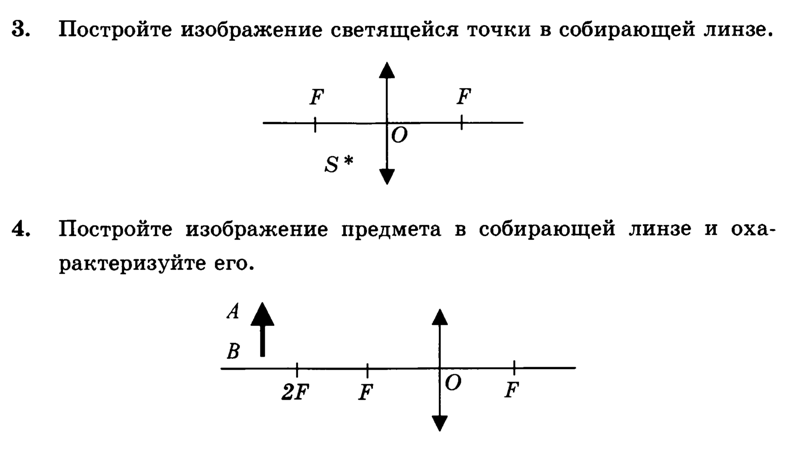 -1
-1
t = 50 с; а = 1 м с -2
.’. S B = u B t +\( \frac { 1}{ 2 } \) at 2
или S B = 20 x 50 + \( \frac { 1}{ 2} \) 1 х (50) 2 = 2250 м
Пусть исходное расстояние между двумя поездами равно S.
S =S B -S A
или S = 2250 – 1000 = 1250 м
0 Вопрос 8.1 a9050 двухполосная дорога, автомобиль А едет со скоростью 36 км ч -1 . Две машины B и C приближаются к машине A в противоположных направлениях со скоростью 54 км ч -1 В некоторый момент, когда расстояние AB равно AC, оба равны 1 км, B решает обогнать A раньше, чем C. Какое минимальное ускорение необходимо автомобилю B, чтобы избежать аварии?
Ответ:
Скорость автомобиля A = 36 км ч -1 = 10 м с -1 ;
Скорость автомобиля B или C = 54 км ч -1 = 15 м с _I ;
Относительная скорость B w. r.t. А = 15 -10 = 5 м с -1 ;
r.t. А = 15 -10 = 5 м с -1 ;
Относительная скорость C w.r.t. А = 15 + 10 = 25 мс -1 ;
As, AB = AC = 1 км = 1000 м
Время, доступное B или C для пересечения A
\( \frac { 1000}{ 2} \) =40 с
Если автомобиль B ускоряется с ускорением a, чтобы пересечь A до того, как это сделает автомобиль C, то u = 5 м sty t = 40 с, S = 1000 м, a = ?
Используя, S = ut + \( \frac { 1}{ 2 } \)at , мы имеем
1000 = 5 x 40 + \( \frac { 1}{ 2 } \) ax 40 2 2
или 1000-200 = 800 а или а = 1 мс -2
Вопрос 9.
Два города А и В соединены регулярным автобусным сообщением, причем автобус отправляется в обоих направлениях через каждую Т. Человек, едущий на велосипеде со скоростью 20 км ч -1 в направлении от А до В замечает, что автобус проходит мимо него каждые 18 мин в направлении его движения и каждые 6 мин в обратном направлении. Каков период T движения автобусов и с какой скоростью (считается постоянной) автобусы курсируют по дороге?
Ответ:
Пусть скорость каждого автобуса = υ b км ч _1 и скорость велосипедиста = υ c = 20 км ч -1
4 Относительная скорость автобусы, курсирующие по направлению движения велосипедиста, т. е. из А в В = υ b — υ c = (υ b -20) км ч -1 .
е. из А в В = υ b — υ c = (υ b -20) км ч -1 .
Вопрос 10.
Игрок бросает мяч вверх с начальной скоростью 29.4 мс -1 .
(а) Каково направление ускорения при движении мяча вверх?
(б) Каковы скорость и ускорение мяча в высшей точке его движения?
(c) Выберите x = 0 м и t = 0 с, чтобы они были положением и временем мяча в его высшей точке, направление вертикально вниз должно быть положительным направлением оси x, и укажите знаки положения, скорости и ускорение мяча при его движении вверх и вниз.
(d) На какую высоту поднимается мяч и через какое время мяч возвращается в руку игрока?
(Примите g = 9,8 мс -2 и пренебрегите сопротивлением воздуха).
Ответ:
(a) Поскольку мяч движется под действием силы тяжести, направление ускорения силы тяжести всегда вертикально вниз.
(b) Когда мяч находится в высшей точке своего движения, его скорость становится равной нулю, а ускорение равно ускорению свободного падения = 9,8 м с -2 в вертикальном направлении вниз.
(в) Когда в качестве местоположения для x = 0 и t = 0 выбрана самая высокая точка, а вертикальное направление вниз является положительным направлением оси x.
При движении вверх , знак положения отрицательный, знак скорости отрицательный, а знак ускорения положительный, т.е. υ< 0, a > 0.
При движении вниз , знак положения положительный, знак скорости положителен и знак ускорения тоже положителен, т. е. υ > 0, a > 0,
(d) Пусть t = время, за которое мяч достигает высшей точки.
H = высота самой высокой точки от земли.
∴ Начальная скорость, it = -29,4 м с _1 ,
a = g = 9,8 м с -2 ,
Конечная скорость υ = 0, S = H= ?, t = ?
Используя соотношение υ 2 -u 2 = 2aS, получаем
0 2 – (-29,4) 2 = 2 x 9,8H
где знак -ve показывает, что расстояние пройдено за восходящее направление.
Используя уравнение v = u + at, получаем
Также мы знаем, что когда объект движется только под действием силы тяжести, время подъема всегда равно времени спуска.
.’. Общее время, через которое мяч возвращается в руку игрока = 2t = 2 x 3 = 6 с.
Вопрос 11.
Внимательно прочитайте каждое приведенное ниже утверждение и укажите причины и примеры, верно оно или нет; Частица в одномерном движении
(а) с нулевой скоростью в данный момент может иметь ненулевое ускорение в этот момент
(b) с нулевой скоростью может иметь ненулевую скорость,
(c) с постоянной скоростью должно иметь нулевое ускорение,
(d) с положительным значением ускорения должно ускоряться.
Ответ:
(а) Верно , когда тело брошено в пространстве вертикально вверх, то в высшей точке тело имеет нулевую скорость, но имеет ускорение вниз, равное ускорению свободного падения.
(b) Ложь , потому что скорость — это скорость тела в заданном направлении. Когда скорость равна нулю, модуль скорости тела равен нулю, следовательно, скорость равна нулю.
Когда скорость равна нулю, модуль скорости тела равен нулю, следовательно, скорость равна нулю.
(c) Верно , когда частица движется по прямой с постоянной скоростью, ее скорость остается постоянной во времени.
Следовательно, ускорение (изменение скорости/времени) равно нулю.
(d) Утверждение зависит от выбора момента времени, взятого за начало отсчета, когда
тело движется прямолинейно с положительным ускорением. Скорость тела в момент времени t равна
υ= u + at
Данное утверждение неверно, если а положительно, а и отрицательно, в момент времени, взятый за начало отсчета. Тогда за все времена до Лайма, для которых y обращается в нуль, происходит замедление частицы, т.е. скорость частицы продолжает уменьшаться со временем. Это происходит, когда тело проецируется вертикально вверх. Однако данное утверждение верно, если и положительно, а положительно в момент времени, взятый за начало отсчета. Это так, когда тело падает вертикально вниз.
Это так, когда тело падает вертикально вниз.
Вопрос 12.
Мяч падает с высоты 90 м на пол. При каждом столкновении с полом мяч теряет одну десятую своей скорости. Постройте график скорости от времени его движения между t = 0 и 12 с.
Ответ:
При вертикальном движении мяча вниз с высоты 90 м имеем
Вопрос 13. ) за интервал времени и общую длину пути, пройденного частицей за тот же интервал.
(b) величина средней скорости за интервал времени и средняя скорость за тот же интервал. [Средняя скорость частицы за интервал времени определяется как общая длина пути, деленная на интервал времени]. Покажите в
(а) и (б), что вторая величина либо больше, либо равна первой. Когда верен знак равенства? [Для простоты рассмотрим только одномерное движение].
Ответ:
(а) Величина смещения движущейся частицы за данное время есть кратчайшее расстояние между начальным и конечным положениями частицы за это время, тогда как полная длина пути, пройденного частицей — реальный путь, пройденный частицей за заданное время. Если частица проходит путь от А до В и от В до С за время t, как показано на рисунке, то
Если частица проходит путь от А до В и от В до С за время t, как показано на рисунке, то
Величина смещения = расстояние AC. Общая длина пути = расстояние AB + расстояние BC. Сверху мы видим, что общая длина пути (AB + BC) больше, чем величина смещения (AC).
Если имеет место движение частицы в одном измерении, т.е. по прямой линии, то величина смещения становится равной полной длине пути, пройденного частицей за данное время.
(б) Величина средней скорости
Так как (AB + BC)> AC, то средняя скорость больше, чем величина средней скорости. Если частица движется прямолинейно, то за данное время величина смещения равна всей длине пути, пройденного частицей за это время, поэтому средняя скорость равна модулю средней скорости.
Вопрос 14.
Человек идет по прямой дороге от своего дома до рынка в 2,5 км со скоростью 5 км ч -1 . Обнаружив рынок закрытым, он мгновенно разворачивается и идет обратно со скоростью 7,5 км ч -1 . Чему равна
Чему равна
(а) величина средней скорости и
(б) средняя скорость человека за интервал времени (1) от 0 до 30 мин, (2) от 0 до 50 мин, (3) от 0 до 40 мин ?
Ответ:
Здесь расстояние рынка от дома человека,
S = 2,5 км
Скорость человека на пути от дома до рынка,
υ 1 = 5 км ч -1
(1) За интервал времени от 0 до 30 мин:
За это время мужчина преодолевает расстояние от дома до рынка.
Следовательно, водоизмещение = 2,5 км; и
пройденное расстояние = 2,5 км
Теперь затраченное время = 30 мин = 0,5 ч
Следовательно, модуль средней скорости
(2) За интервал времени от 0 до 50 мин:
В этот промежуток времени мужчина возвращается домой.
Вопрос 15.
В вопросах 13 и 14 мы тщательно различали среднюю скорость и величину средней скорости. Нет необходимости в таком различии, когда мы рассматриваем мгновенную скорость и модуль скорости. Мгновенная скорость всегда равна величине мгновенной скорости. Почему?
Мгновенная скорость всегда равна величине мгновенной скорости. Почему?
Ответ:
Мгновенная скорость определяется как скорость объекта в конкретный момент времени.
Мгновенная скорость определяется как предельное значение средней скорости. Таким образом, когда интервал времени очень мал, величина смещения фактически равна расстоянию, пройденному объектом за тот же небольшой интервал времени. Таким образом, и мгновенная скорость, и мгновенная скорость в этом случае равны. Это можно понять из следующего:
Рассмотрим небольшое смещение во времени В промежутке времени между t и t + Δt
Вопрос 16.
Внимательно посмотрите на графики (a)–(d) и объясните, какие из них не могут представлять одномерное движение частицы.
Ответ:
(a) Линия, проведенная в данный момент времени параллельно оси положения, разрежет график в двух точках, что означает, что в данный момент времени частица будет иметь два положения, что невозможно. . Следовательно, график (а) невозможен, т. е. не представляет одномерное движение.
. Следовательно, график (а) невозможен, т. е. не представляет одномерное движение.
(b) Этот график не отображает одномерное движение, потому что в данный момент времени у частицы будет два значения скорости в положительном и отрицательном направлениях, что невозможно при одномерном движении.
(c) Это график между скоростью и временем, и он не представляет одномерное движение, так как этот график говорит о том, что скорость частицы может быть отрицательной, но скорость никогда не может быть отрицательной.
(d) Это не представляет одномерное движение, так как этот график показывает, что общая длина пути уменьшается через определенное время, но общая длина пути движущейся частицы никогда не может уменьшаться со временем.
Вопрос 17.
На рисунке показан график (x-t) одномерного движения частицы. Правильно ли по графику сказать, что частица движется по прямой при t < 0 и по параболе при t > 0? Если нет, предложите подходящий физический контекст для этого графика.
Ответ:
Нет, неверно говорить, что частица движется по прямой линии при t < 0 и по параболической траектории при t > 0, так как график x-t не показывает траекторию пути частица. График показывает, что в момент времени t = 0, x = 0
Контекст : Подходящим контекстом является падение тела с вышки, т.е. свободное падение тела, т.е. x = 0 при t = 0
Вопрос 18.
Полицейский фургон, движущийся по шоссе со скоростью 30 км h -1 выстреливает пулей в машину угонщика, мчащуюся в том же направлении со скоростью 192 км h -1 . Если начальная скорость пули равна 150 м, с какой скоростью пуля попадет в машину угонщика? ( Примечание: Достигните той скорости, которая необходима для повреждения автомобиля вора).
Ответ:
Начальная скорость пули, υ B = 150 м с -1 = 540 км ч -1
Скорость полицейского фургона, υ P — 9,063 ч 4,0 30 км
Скорость автомобиля угонщика, υ T = 192 км/ч -1
Так как пуля разделяет скорость полицейского фургона, то ее эффективная скорость
V B = υ B + υ P = 540 + 30 = 570 км ч _1
Скорость пули относительно машины угонщика, движущейся в том же направлении
V BT = V B – υ T = 570 -192 = 378 км ч 1
Вопрос 19.
Предложите подходящую физическую ситуацию, показанную на следующем рисунке.
Ответ:
Рис. (a) : График (x-t) показывает, что первоначально x равно 0, достигает определенного значения x, снова x становится равным нулю, а затем x увеличивается в противоположном направлении, пока снова не достигнет постоянный x (т.е. останавливается). Таким образом, он может представлять физическую ситуацию, например, когда мяч (первоначально находящийся в покое) после удара ногой отскакивает от стены с уменьшенной скоростью, затем движется к противоположной стене и затем останавливается.
Рис. (б): Из графика (υ-t) следует, что скорость снова и снова меняет знак с течением времени и каждый раз теряет некоторую скорость. Следовательно, это может представлять собой физическую ситуацию, такую как мяч, свободно падающий (после того, как его подбросили вверх), при ударе о землю отскакивает с уменьшенной скоростью после каждого удара о землю.
Рис. (c) : График (a-t) показывает, что тело ускоряется только на короткое время. Следовательно, это может представлять физическую ситуацию, например, мяч, движущийся с постоянной скоростью, ударяется битой в течение очень короткого промежутка времени.
Вопрос 20.
На рисунке показан график x-t частицы, совершающей одномерное простое гармоническое движение. Укажите знаки переменных положения, скорости и ускорения частицы в моменты времени t = 0,3 с, 1,2 с, -1,2 с.
Ответ:
Мы знаем, что в С.Х.М. ускорение а определяется соотношением
а = -ω 2 х ………. (1)
, где ω — угловая частота, постоянная. Также скорость определяется выражением
υ= \( \cfrac { dx}{dt} \) …………(2)
- В момент времени t = 0,3 с x отрицательно, наклон графика (x-t) отрицателен, поэтому положение и скорость отрицательны, но ускорение положительно в соответствии с уравнением (1).
- В момент времени t = 1,2 с x положительно, наклон графика (x-t) также положителен, следовательно, положение и скорость положительны, но согласно уравнению (1) ускорение отрицательно.

- Во время t = -1,2 с, x отрицательно, наклон графика (x-t) также отрицателен. Но поскольку и x, и t отрицательны, следовательно, согласно уравнению (2), скорость положительна. Поскольку положение отрицательно, то согласно уравнению (1) ускорение положительно.
Вопрос 21.
На рисунке показан график (x-t) движения частицы в одном измерении. Показаны три различных равных интервала времени. В каком интервале средняя скорость наибольшая, а в каком наименьшая? Укажите знак средней скорости для каждого интервала.
Ответ:
Мы знаем, что средняя скорость за небольшой промежуток времени равна наклону графика (x-t) за этот промежуток времени. Средняя скорость наибольшая на интервале 3, потому что уклон наибольший, а средняя скорость наименьшая на интервале 2, потому что уклон там наименьший. скорость отрицательна в интервале 3, потому что наклон (xt) отрицателен.
Вопрос 22.
На рисунке приведен график зависимости скорости частицы от времени при одномерном движении вдоль постоянного направления. Показаны три равных интервала времени. В каком интервале среднее ускорение наибольшее по величине? В каком интервале средняя скорость наибольшая? Выбрав положительное направление как постоянное направление движения, задайте знаки v и a на трех интервалах. Чему равны ускорения в точках А, В, С и D?
Показаны три равных интервала времени. В каком интервале среднее ускорение наибольшее по величине? В каком интервале средняя скорость наибольшая? Выбрав положительное направление как постоянное направление движения, задайте знаки v и a на трех интервалах. Чему равны ускорения в точках А, В, С и D?
Ответ:
(1) Величина среднего ускорения определяется как
, т.е. среднее ускорение за небольшой интервал времени равно наклону графика (v-t) в этом интервале времени.
Поскольку наклон графика (υ-t) максимален на интервале 2 по сравнению с интервалами 1 и 3, следовательно, величина среднего ускорения наибольшая на интервале 2.
(2) Средняя скорость наибольшая на интервале 3 так как пик D находится на максимуме на оси скорости.
(3) υ > 0 э. положительный во всех трех интервалах.
(4) Наклон положителен в интервалах 1 и 3, поэтому V e. ускорение положительно на этих интервалах, а наклон отрицателен на интервале 2, поэтому ускорение на нем отрицательно. Итак, а > 0, т. е. положительно на интервалах 1 и 3. и а < 0, т. е. отрицательно на интервале 2.
Итак, а > 0, т. е. положительно на интервалах 1 и 3. и а < 0, т. е. отрицательно на интервале 2.
(5) Поскольку наклон равен нулю в точках А, В, С и D, ускорение равно нулю во всех четырех точки.
Вопрос 23.
Трехколесный автомобиль трогается с места, равномерно ускоряется за 1 м с -2 по прямой дороге в течение 10 с, а затем движется с постоянной скоростью. Постройте расстояние, пройденное транспортным средством за n -ю -ю секунду (n = 1, 2, 3..), в зависимости от того, каким, по вашему мнению, будет этот график при ускоренном движении: прямой линией или параболой?
Ответ:
Начальная скорость, u = 0, a = 1 мс -2 , t = 10 с. Затем
Ниже приведена таблица для расстояния S n th ездил в n th второй.
| н(ы) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
в(м) | 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | 6,5 | 7,5 | 8,5 | 9,5 |
Поскольку уравнение, описывающее связь между D„ и n, имеет вторую степень, то график движения транспортного средства от начала движения до 10 -й -й секунды должен представлять собой параболу. Скорость автомобиля в конце 10 th секунды равна v = 0 + 1 x 10 = 10 м с’ 1 , и он будет двигаться с этой скоростью через 10 секунд. Таким образом, график будет представлять собой прямую линию, наклоненную к оси времени при равноускоренном движении. График зависимости расстояния, пройденного трехколесным транспортным средством, от времени показан на графике.
Скорость автомобиля в конце 10 th секунды равна v = 0 + 1 x 10 = 10 м с’ 1 , и он будет двигаться с этой скоростью через 10 секунд. Таким образом, график будет представлять собой прямую линию, наклоненную к оси времени при равноускоренном движении. График зависимости расстояния, пройденного трехколесным транспортным средством, от времени показан на графике.
Вопрос 24.
Мальчик, стоящий на стационарном подъемнике (открытом сверху), бросает мяч вверх с максимально возможной начальной скоростью, равной 49 м с -1 . Через сколько времени мяч вернется в его руки? Если лифт начнет двигаться вверх с равномерной скоростью 5 м с -1 и мальчик снова подбросит мяч вверх с максимально возможной скоростью, через какое время мяч вернется к нему в руки?
Ответ:
Принимая вертикальное направление вверх за положительное направление оси x.
Когда лифт неподвижен, рассмотрим движение мяча, идущего вертикально вверх и опускающегося в руки мальчика, имеем u = 49 м с -1 ,
a = -9,8 м с -2 , t = ? , x-x 0 = S = 0
As, S = ut+\( \cfrac {1}{2} \) at 2 2
0 = 49t+\( \cfrac {1}{2} \) (- 9. 8) t 2
8) t 2
или 49f = 4,91 2 или f = 49/4,9 = 10 секунд Когда лифт начинает двигаться вверх с постоянной скоростью 5 м с -1 , относительная скорость не меняется. мяч по отношению к мальчику, т. е. остается 49м с’ 1 . Следовательно, даже в этом случае мяч вернется в руку мальчика через 10 секунд.
Вопрос 25.
На длинной горизонтально движущейся ленте (показана на рисунке) ребенок бегает туда-сюда со скоростью 9 км ч -1 (относительно ленты) между отцом и матерью, находящимися 50 м друг от друга на движущейся ленте. Лента движется со скоростью 4 км ч -1 . Какова
(а) скорость ребенка, бегущего в направлении движения ремня, для наблюдателя на стационарной платформе снаружи?
(б) скорость ребенка, бегущего против направления движения ремня?
(c) время, потраченное ребенком в пунктах (a) и (b)?
Какой из ответов изменится, если движение увидит один из родителей?
Ответ:
Будем считать слева направо положительное направление оси x.
(а) Здесь скорость ленты, υ B = + 4 км ч -1 ; Скорость ребенка w.r.t. ремень,
υc = + 9 км ч -1 = 5/2 м с -1
Скорость ребенка в.р.т. неподвижный наблюдатель,
? 1 ; υ c = -9 км ч -1
Скорость ребенка в.р.т. неподвижный наблюдатель,
? направление движения ремня.
(c) Расстояние между родителями, S = 50 м. Так как родители и ребенок находятся на одном поясе, скорость ребенка, наблюдаемая неподвижным наблюдателем в любом направлении (либо от матери к отцу, либо от отца к матери), будет равна 9 км
ч -1 .
Время, затраченное ребенком в случаях (a) и (b), равно
Если движение наблюдает один из родителей, ответ на случай (a) или случай (b) будет изменен. Это так, потому что скорость ребенка w.r.t. либо мама либо папа 9км ч 1 . Но ответ (c) остается неизменным из-за того, что родители и ребенок находятся на одном и том же ремне и поэтому все в равной степени подвержены влиянию движения ремня.
Вопрос 26.
С края обрыва высотой 200 м одновременно брошены два камня с начальными скоростями
15 м с -1 и 30 м с -1 . Убедитесь, что график, показанный на рисунке, правильно отображает изменение во времени относительного положения второго камня по отношению к первому. Сопротивлением воздуха пренебречь и считать, что камни не отскакивают после удара о землю.
Принять g = 10 м с -2 . Приведите уравнения для линейной и криволинейной частей графика.
Ответ:
Взяв вертикальное движение первого камня вверх за время f, получим
x 0 = 200 м, u = 15 м/с; a = -10 м/с 2 , t = t;x = x 1
As, x = x 0 +ut + \( \cfrac {1}{2} \) at 2
∴ X 1 = 200 + 151 + \( \cfrac {1}{2} \) (-10) t 2
или X 1 = 200 + 15 t -5 t 2 ..(1)
Взяв вертикальное движение второго камня вверх за время f, имеем
x 0 = 200 м, u = 30 м с _1 , = -10 м с -2 , t=t,x= x 2 1
Тогда x 2 = 200 + 30t \( \cfrac {1}{2} \) x 10t 2
= 200 +30 t-5t 2 …(2)
Когда первый камень упадет на землю, x 1 = 0,
поэтому t 2 – 3t – 40 = 0
или (t – 8) (t + 5) = 0 Либо t = 8 с, либо -5 с
Так как t = 0 соответствует моменту, когда камень был брошен. Следовательно, отрицательное время не имеет значения в этом случае.
Следовательно, отрицательное время не имеет значения в этом случае.
Итак, t = 8 с. Когда второй камень падает на землю, x 2 = 0, поэтому
0 = 200 + 30t – 5f 2
или t 2 -6t – 40 = 0
или (t – 10) (t + 4) = 0
Следовательно, либо t = 10 с, либо t = -4 с
Так как t = -4 с бессмысленно, то t = 10 с Относительное положение второго камня относительно сначала
= x 2 -x 1 = 15t …(3)
Из (1) и (2)
Так как (x 2 – x 1 ) и t связаны линейно, то график представляет собой прямую линию до t = 8 с. Для максимального эшелонирования t = 8 с, поэтому максимальное эшелонирование = 15 x 8 = 120 м через 8 с. Только второй камень будет двигаться в течение 2 секунд, поэтому график соответствует квадратному уравнению x 2 = 200 + 30t -5t 2 для интервала времени от 8 до 10 секунд.
Вопрос 27.
График зависимости скорости частицы от времени, движущейся в фиксированном направлении, показан на рисунке. Найдите расстояние, пройденное частицей между
Найдите расстояние, пройденное частицей между
(а) t = от 0 до 10 с,
(б) t = от 2 до 6 с.
Какова средняя скорость частицы на промежутках (а) и (б)?
Ответ:
(a) Пусть S будет расстоянием, пройденным частицей между t = 0 и t = 10 с. Тогда
S = площадь под (v-t) графиком = площадь треугольника, основание которого равно 10 (с), а высота равна 12 (м с -1 )
Вопрос 28. движения частицы в одном измерении показано на рисунке. Какая из следующих формул верна для описания движения частицы на интервале времени t 1 – t 2 :
(а) x(t 2 ) = x(t 1 ) + v(t 1 )(t 2 ) + (1 8 – t 1 /2)a (t 2 -t 1 ) 2
(b) v(t 2 ) = v(t 1 ) + a(t 2 -t 1 8)
(c) v среднее = (x(t 2 ) – x(t 1 ))/(t 2 -t 1 )
(d) среднее = M(t 2 ) – v(t 1 ))/(t 2 – t 1 )
(e) x(t 2 ) = x(t 1 ) +v среднее (t 2 -t 1 )+ (1/2) o среднее
(f) x(t 2 ) – x(t 1 ) = площадь под кривой v-t, ограниченная осью t и показанной пунктирной линией.



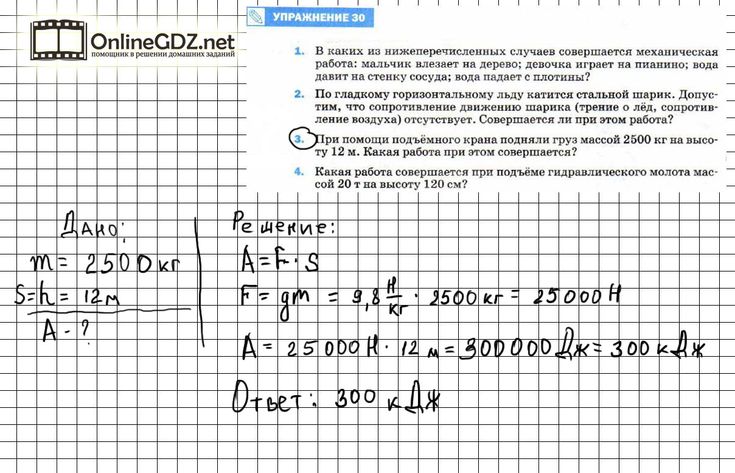 Воспроизведение материалов сайта, в том числе материалов для скачивания и изображений обложек пособий, с целью извлечения прибыли (в коммерческих или рекламных целях) без разрешения правообладателей ЗАПРЕЩЕНО.
Воспроизведение материалов сайта, в том числе материалов для скачивания и изображений обложек пособий, с целью извлечения прибыли (в коммерческих или рекламных целях) без разрешения правообладателей ЗАПРЕЩЕНО. ru
ru Все права защищены. Воспроизведение материалов сайта, в том числе материалов для скачивания и изображений обложек пособий, с целью извлечения прибыли (в коммерческих или рекламных целях) без разрешения правообладателей ЗАПРЕЩЕНО.
Все права защищены. Воспроизведение материалов сайта, в том числе материалов для скачивания и изображений обложек пособий, с целью извлечения прибыли (в коммерческих или рекламных целях) без разрешения правообладателей ЗАПРЕЩЕНО. Рубрика: Физика / 11 класс. Автор: Жилко В.В., Маркович Л.Г. Год: 2009, 2014.
Рубрика: Физика / 11 класс. Автор: Жилко В.В., Маркович Л.Г. Год: 2009, 2014. В., Маркович Л. Г., Сокольский А. А. Предмет: Физика. Группа: Учебники (учебные пособия). Класс
В., Маркович Л. Г., Сокольский А. А. Предмет: Физика. Группа: Учебники (учебные пособия). Класс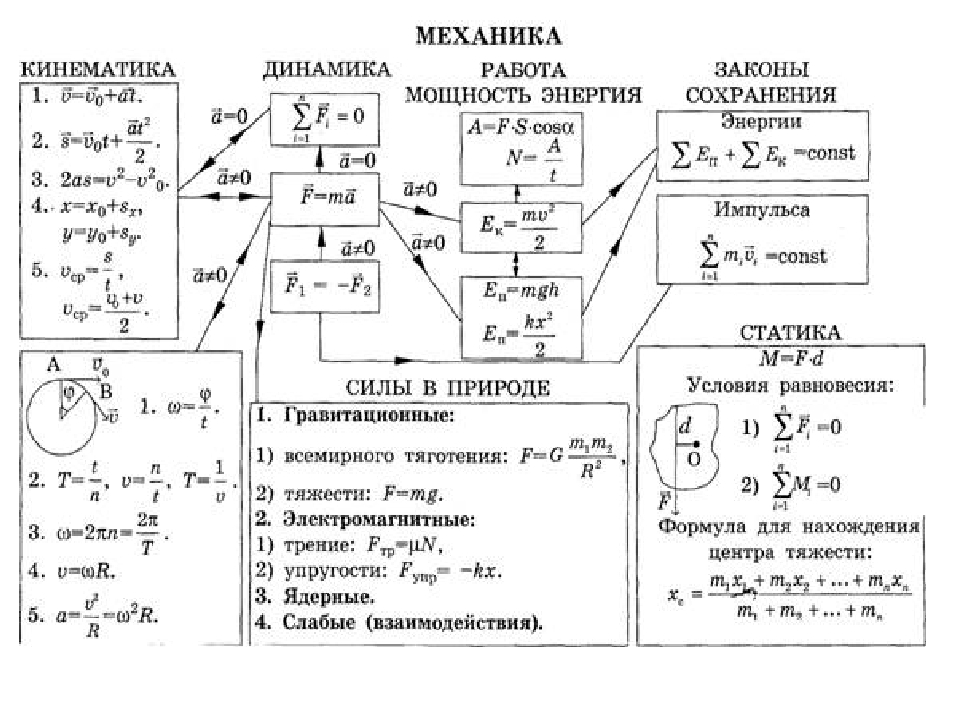
 Формат: pdf. Размер: 66 Мб. Смотреть, скачать: drive.google ; Rghost. СОДЕРЖАНИЕ От авторов 3 Механика Повторительно-обобщающий курс Глава 1. Кинематика 5 § 1. Кинематика прямолинейного движения. Равномерное движение — § 2. Прямолинейное равноускоренное движение 13 § 3. Движение тела, брошенного горизонтально и под углом к горизонту 19 § 4…
Формат: pdf. Размер: 66 Мб. Смотреть, скачать: drive.google ; Rghost. СОДЕРЖАНИЕ От авторов 3 Механика Повторительно-обобщающий курс Глава 1. Кинематика 5 § 1. Кинематика прямолинейного движения. Равномерное движение — § 2. Прямолинейное равноускоренное движение 13 § 3. Движение тела, брошенного горизонтально и под углом к горизонту 19 § 4… alleng.org
alleng.org rn.
rn. Авторы: Жилко В. В., Маркович Л. Г., Егорова Л. П.
Авторы: Жилко В. В., Маркович Л. Г., Егорова Л. П.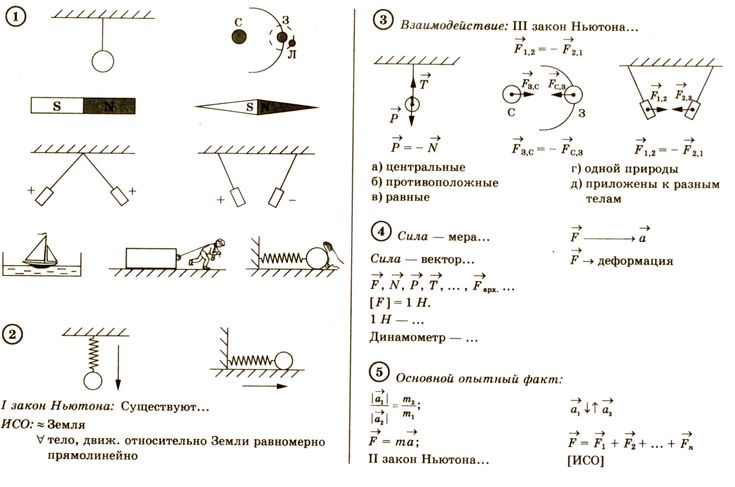 В., Маркович Л.Г.
В., Маркович Л.Г.
 Ежедневное обновление бесплатных версий. 11 класс — Жилко В.В., Маркович Л.Г. Учебное пособие для 11 класса общеобразовательных учреждений с русским языком обучения.
Ежедневное обновление бесплатных версий. 11 класс — Жилко В.В., Маркович Л.Г. Учебное пособие для 11 класса общеобразовательных учреждений с русским языком обучения. Авторы. Жилко В. В., Маркович Л. Г., Сокольский А. А. Год учебника. 2021. Издательство. Народная асвета. Физика – достаточно сложный предмет, тем более в 11 классе. У многих школьников возникают трудности с ее пониманием. Если вы столкнулись с подобной проблемой, не стоит опускать руки. Решебник по физике станет отличным помощником, благодаря которому вы сможете проверить, правильно ли выполнены домашние задания, восполнить пробелы в знаниях и подготовиться к выпускному экзамену.
Авторы. Жилко В. В., Маркович Л. Г., Сокольский А. А. Год учебника. 2021. Издательство. Народная асвета. Физика – достаточно сложный предмет, тем более в 11 классе. У многих школьников возникают трудности с ее пониманием. Если вы столкнулись с подобной проблемой, не стоит опускать руки. Решебник по физике станет отличным помощником, благодаря которому вы сможете проверить, правильно ли выполнены домашние задания, восполнить пробелы в знаниях и подготовиться к выпускному экзамену.
 11 класс» Г.Я. Мякишев, М.А. Петорва.
11 класс» Г.Я. Мякишев, М.А. Петорва. Элементы релятивистской динамики 235 Упражнение 11 238 Краткие итоги главы 9 — Глава 10. Излучение и спектры 239 § 80. Виды излучений.
Элементы релятивистской динамики 235 Упражнение 11 238 Краткие итоги главы 9 — Глава 10. Излучение и спектры 239 § 80. Виды излучений. Авторы. Жилко В. В., Маркович Л. Г., Егорова Л. П. Год учебника. 2021. В 11 классе курс физики усложняется настолько, что даже у школьников с хорошей успеваемостью могут возникать трудности. Для понимания этого предмета необходим математический склад ума и хорошие аналитические способности. К сожалению, не все подростки обладают этими качествами. Но это не значит, что их проблема с непониманием физики неразрешима.
Авторы. Жилко В. В., Маркович Л. Г., Егорова Л. П. Год учебника. 2021. В 11 классе курс физики усложняется настолько, что даже у школьников с хорошей успеваемостью могут возникать трудности. Для понимания этого предмета необходим математический склад ума и хорошие аналитические способности. К сожалению, не все подростки обладают этими качествами. Но это не значит, что их проблема с непониманием физики неразрешима. Н., 2005
Н., 2005 В., Шаронова Н.В., 2006
В., Шаронова Н.В., 2006 П., 2013
П., 2013.jpg) 1. — Иродов И.Е.
1. — Иродов И.Е. Задачник. 10-11 класс, Рымкевич А.П., 2006»
Задачник. 10-11 класс, Рымкевич А.П., 2006» А.
А. П.
П. Кирсанов М.Н., 2002
Кирсанов М.Н., 2002 Молекулярная физика. Термодинамика.
Молекулярная физика. Термодинамика.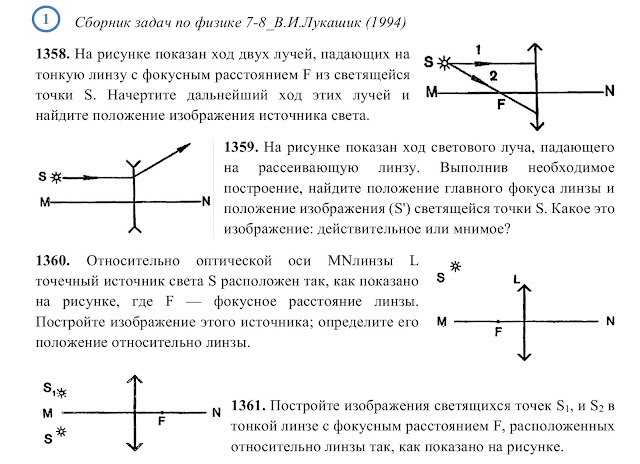 C., Скворцова И.Л., Юшина М.Я., 2004
C., Скворцова И.Л., Юшина М.Я., 2004 , Фомина М.
, Фомина М.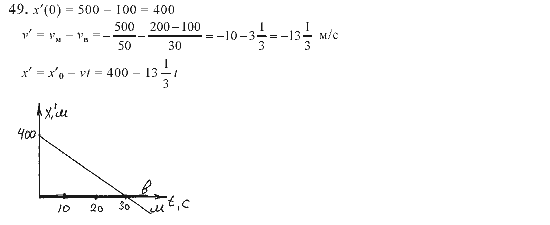 И., 2015
И., 2015 В. — 2004
В. — 2004 С., Важеевская Н.Е., Исаев Д.А., Чаругин В.М., 2016
С., Важеевская Н.Е., Исаев Д.А., Чаругин В.М., 2016 А., Коровин В.А., 2012
А., Коровин В.А., 2012 П., 2013
П., 2013
 Я.
Я.