11 класс задания по математике: Олимпиада по математике 11 класс, задания, уравнения, задачи с ответами

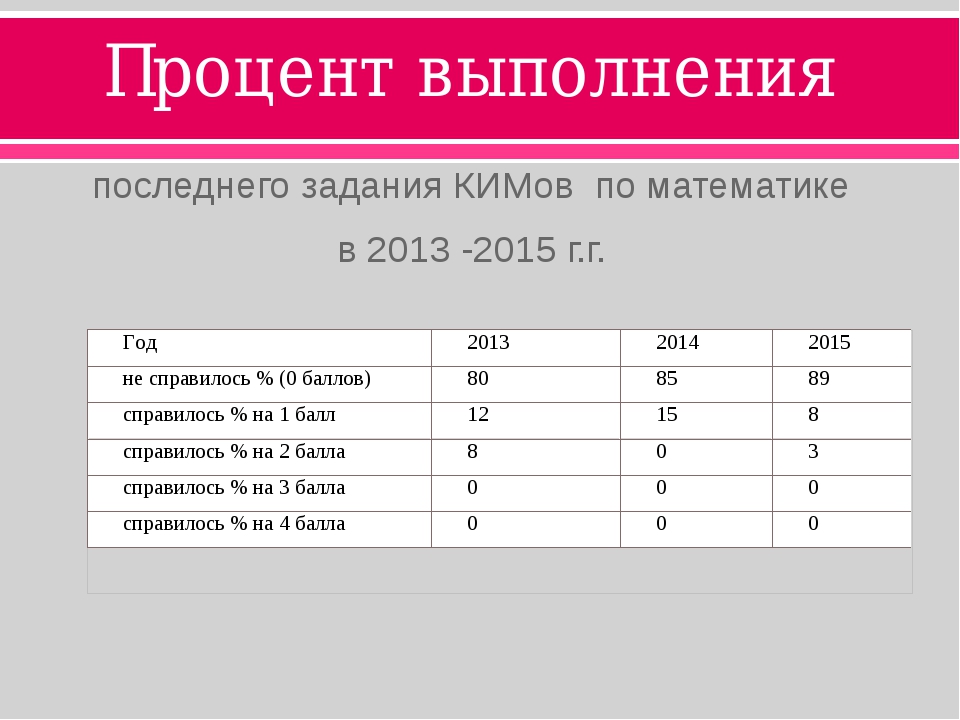
Олимпиада по математике 11 класс, задания, уравнения, задачи с ответами

Курс математики в выпускном классе посвящен изучению степеней и корней, знакомству с показательной и логарифмической функцией, интегралами и элементами математической статистикой. Отдельное внимание в 11 классе посвящено повторению изученного за весь курс математики и подготовке к грядущему экзамену.

В связи с этим, для учеников 11 класса особенно важно участие в олимпиадах по математике и дополнительные занятия, посвященные решению заданий различной сложности.

На этой странице собраны задания для подготовки к олимпиаде по математике для 11 класса. Представлены уравнения, задачи и математические загадки с ответами и решениями. Этот материал может быть использован учителями или репетиторами для повышения уровня знания учеников.

Уравнения

1. Решите уравнение: = 3

2. Решите уравнение: ( − 8)² = ( + 9)²

3. Решите уравнение: log2 (5 + ) = log2 (1 − ) + 1

4.

Решите уравнение: log5 ( + ) = log5 ( + 9)

5. Решите уравнение: log2 (4 − ) = 7

6. Решите уравнение: − + 72 = 0

7. Решите уравнение: ( + 7)² = ( − 1)²

8. Решите уравнение: ( − 8)² = ( − 2)²

9. Решите уравнение: ( − 6)² = −

10. Решите уравнение: + 9 = ( + 9)²

Задачи

Задача №1
Докажите, что уравнение  xy = 2006 (x + y) имеет решения в целых числах.

Задача №2
Докажите, что если α, β, γ — углы произвольного треугольника, то справедливо тождество cos2α + cos2β + cos2γ + 2 cosα cosβ cosγ = 1.

Задача №3
Три шара радиуса R касаются друг друга и плоскости α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных  шаров. Определите высоту «горки» из четырех шаров.

Задача №4

Докажите неравенство  −< 1/6 на луче [1/4; + ∞).

Задача №5
В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.

Математические загадки

Загадка №1

Сколько лет человеку, если в 2012 году его возраст оказался равным сумме цифр года его рождения.

Загадка №2

Двадцать одна девочка и двадцать один мальчик принимали участие в математическом конкурсе. Каждый участник решил не более шести задач. Для любых девочки и мальчика найдётся хотя бы одна задача, решённая обоими. Докажите, что была задача, которую решили не менее трёх девочек и не менее трёх мальчиков.

Загадка №3

Существует ли многогранник с нечетным числом граней, каждая из которых есть многоугольник с нечетным числом сторон?

Загадка №4

В каждую клетку квадратной таблицы 25 x 25 вписано произвольным образом одно из чисел 1 или -1. Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце. Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке. Докажите, что сумма 50 написанных произведений не может оказаться равной нулю.

Загадка №5

Сумма цифр в десятичной записи натурального числа n равна 100, а сумма цифр числа 44n равна 800.

Чему равна сумма цифр числа 3n?

Ответы к уравнениям

Уравнение	№ 1	№ 2	№ 3	№ 4	№ 5
Ответ	6	8,5 ∈ [8;9)	− 0,25	1,8	-124

Уравнение	№ 6	№ 7	№ 8	№ 9	№ 10
Ответ	9; 8	-1,5	1	-6	-4

Ответы к задачам

Задача 1
Преобразуем уравнение к следующему виду: (x – 2006)(y − 2006) = 20062. Уравнение имеет решения, например, x = y = 4012.

Задача 2
Преобразуем выражение в левой части равенства, учитывая, что α + β + γ = π, и применяя формулы: cos² x = (1 + cos 2x)/2, cos x = − cos (π − x), cos x + cos y = (2cos((x + y)/2)) cos((x − y)/2), получим справедливое тождество

.

Задача 3
Пусть четыре шара радиуса R c центрами A, B, C, D касаются друг друга и первые три из них – плоскости a в точках A1, B1, C1 . Тогда точки A, B, C, D являются вершинами правильной пирамиды с ребром 2R. Вершина D этой пирамиды проектируется в центр основания О.

Высота «горки» из четырех шаров равна сумме OD + 2R = 2R  + 1

Задача 4
Пусть =  −. Тогда   =  − и с помощью метода интервалов получаем, что  < 0 при всех  >2/9. Но 1/4>2/9, следовательно, функция  убывает на луче [1/4; +∞]. Это значит, что  − < 1/16 − 3/64 = 1/64 < 1/64.

Задача 5
Окружим каждый квадрат полоской шириной 1/2. Образующие фигуры тоже квадраты со стороной 1 + 2 x 1/2 = 2, имеют площадь равную 4. Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500. Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям. Круг радиуса  с центром в этой точке не имеет общих точек  ни с одним из квадратов

.

Ответ: 175 центов

Ответы на загадки

Загадка 1

1 вар. Человек родился в 19mn году, тогда

          2012 − 19mn= 1 + 9 + m + n

          2012 − 1900 − m − n = 10 + m + n

          102 = 11m + 2n

m = 8, n = 7, значит 1987 год, ему 25 лет.

2 вар. Человек родился в 200n году, тогда

          2012 − 200n = 2 + n

          2012 − 2000 − n = 2 + n

          12 − 2 = 2n

n = 5, значит 2005 год, ему 7 лет.

Загадка 2
Предположим, что нашлась задача, которую решили не более двух девочек или не более двух мальчиков.

Будем считать задачу «красной», если её решили не более двух девочек и «чёрной» в противоположном случае (тогда её решили не более двух мальчиков).

Представим шахматную доску с 21-й строкой, каждая из которых соответствует девочке, и 21-м столбцом, каждый из которых соответствует мальчику.

Тогда каждая клетка соответствует паре «мальчик–девочка». Каждую клетку покрасим в цвет какой-нибудь задачи, которую решили и мальчик-строка и девочка-столбец.

По принципу Дирихле в каком-нибудь столбце найдётся 11 чёрных клеток, или в какой-нибудь строке найдутся 11 красных клеток (потому что иначе получится, что всего клеток не более чем 21 × 10 + 21 × 10 < 21²).

Рассмотрим, например, девочку-строку, содержащую хотя бы 11 чёрных клеток.

Каждой из этих клеток соответствует задача, решённая максимум двумя мальчиками.

Тогда мы можем указать не менее 6 различных задач, решённых этой девочкой.

В силу первого условия никаких других задач девочка не решала, но тогда максимум 12 мальчиков имеют общие решённые задачи с этой девочкой, что противоречит второму условию.

Точно также разбирается случай, если в каком-нибудь столбце найдутся 11 красных клеток.

Загадка 3

Пусть такой многогранник существует. Обозначим за 1, 2, …, число ребер на гранях, тогда 1 + 2 + … – удвоенная сумма всех ребер многогранника, она – четная. А в левой части стоит нечетная сумма слагаемых, каждое из которых – нечетно. Получили противоречие. Значит, такого многогранника не существует

Загадка 4
Найдем произведение всех 25 чисел, записанных под каждым столбцом и всех 25 чисел, записанных справа от строчек. Так как в этом произведении каждое из чисел квадратной таблицы входит по два раза, то произведение этих 50 произведений, в каждом из которых стоит по 25 множителей, будет положительным, т. е. равно 1. А так как произведение 50 чисел положительно, то отрицательных сомножителей будет четное число (2, 4, …, 50). Сумма же 50 произведений может быть нулем лишь в случае, когда 25 слагаемых равно 1, а 25 слагаемых равно — 1, т. е. слагаемых с — 1 должно быть нечетное число. А это значит, что сумма 50 написанных произведений не может равняться нулю.

Загадка 5
Заметим, что 44n есть сумма 4 экземпляров числа n и 4 экземпляров числа 10n.

Если складывать эти числа поразрядно, то в каждом разряде окажется сумма учетверённой цифры из этого же разряда числа n и учетверённой цифры из следующего разряда.

Если при этом не происходит никаких переносов, то каждая цифра числа n складывается 8 раз, и сумма цифр во всех разрядах оказывается равной 800. При переносах же сумма цифр, очевидно, уменьшается (так как из одного разряда вычитается 10, а к другому прибавляется только 1). Поэтому в ситуации условия задачи переносов не происходит. Это означает, в частности, что любая цифра числа n не превосходит 2. Тогда при умножении n на 3 просто умножается на 3 каждая его цифра, а, значит, и сумма цифр. Поэтому сумма цифр числа 3n равна 300.

Другие классы

Обновлено: 26/02/2015 , автор: Валерия Токарева

Демонстрационные варианты (демоверсии) ЕГЭ по математике

Демонстрационные варианты ЕГЭ по математике для 11 класса за 2002-2009 годы

включали в себя три раздела: А (задачи с выбором ответа из нескольких предложенных), В (задачи с кратким ответом) и С (задания, для выполнения которых требовалось привести полное решение задачи).

В 2010 году из демонстрационного варианта ЕГЭ по математике были исключены задачи с выбором ответа, ранее составлявшие раздел А. Таким образом, демонстрационный вариант ЕГЭ стал состоять уже только из двух разделов В и С.

Демонстрационный вариант ЕГЭ 2011 года почти полностью совпадал с демонстрационным вариантом ЕГЭ 2010 года: были изменены лишь задания C1 и C5.

В 2014 году в демонстрационном варианте ЕГЭ по математике тематических изменений по сравнению с предыдущим годом не было: задачи В3, В9, В14, С2 и С4 были заменены на другие задачи той же тематики. Кроме того, было добавлено задание базового уровня сложности с кратким ответом, проверяющее практические навыки применения математики в повседневной жизни и изменен порядок заданий.

В 2015 году в порядке проведения ЕГЭ по математике произошли серьезные изменения: было решено проводить два отдельных экзамена – базового уровня и профильного уровня.

В связи с этим в 2015 году было представлено 2 демонстрационных варианта: новая модель демонстрационного варианта для ЕГЭ базового уровня и модернизированная модель демонстрационного варианта 2014 года для проведения ЕГЭ профильного уровня.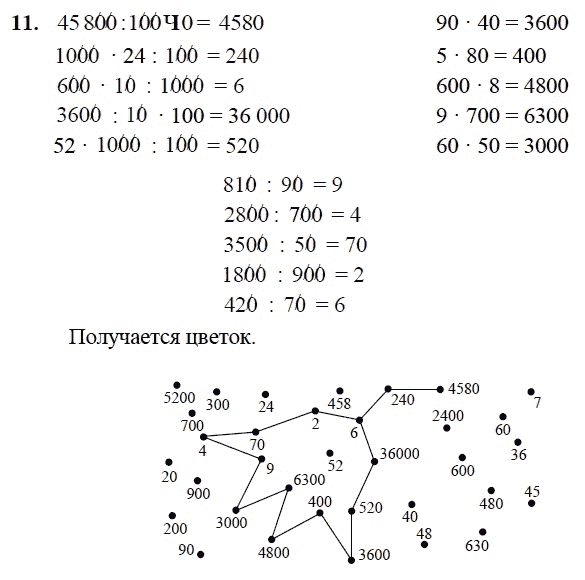

Демонстрационный вариант для ЕГЭ базового уровня содержал только задания базового уровня сложности с кратким ответом (20 заданий). В демонстрационном варианте было представлено по несколько примеров заданий на каждую позицию экзаменационной работы. В реальных вариантах экзаменационной работы на каждую позицию было предложено только одно задание.

Демонстрационный вариант профильного экзамена 2015 года разработан на основе демонстрационного варианта ЕГЭ по математике 2014 года со следующими изменениями:

• Вариант стал состоять из двух частей (часть 1 — задания с кратким ответом, часть 2 — задания с кратким ответом и задания с развернутым ответом).
• Нумерация заданий стала сквозной по всему варианту без буквенных обозначений В, С.
• Во второй части добавлено 1 задание высокого уровня сложности с развёрнутым ответом, проверяющее практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей.
• Из первой части исключено 1 задание базового уровня сложности.
• Произведены несущественные изменения формы и тематики заданий 16 и 17

В демонстрационном варианте ЕГЭ по математике базового уровня 2016 года изменений не было .

В демонстрационном варианте ЕГЭ по математике профильного уровня 2016 года произошли следующие изменения:

• Из первой части варианта были исключены два задания: задание практического содержания базового уровня сложности и задание по стереометрии повышенного уровня сложности.
• Максимальный первичный балл за выполнение всей работы был уменьшен с 34 до 32 баллов.

В демонстрационных вариантах ЕГЭ по математике 2017 — 2021 годов как базового уровня, так и профильного уровня, по сравнению с демонстрационными вариантами ЕГЭ по математике 2016 года изменений не было.

МБОУ «Лицей №23» — Поздравление выпускникам

♦ Внимание! Годовая промежуточная аттестация в 1- 8, 9,10-х классах. Сроки с 26.04 — 14.05.21г. (подробнее)

♦Внимание! С 21 апреля по 25 мая 2021 года ОФ «Талант и успех» проводит пригласительный школьный этап всероссийской олимпиады школьников в дистанционном формате для обучающихся 3-10 классов по 6 предметам! (подробнее)

♦ 24 апреля 2021 года в Кемерово, как и во всех населенных пунктах регионов страны, пройдет Всероссийский субботник (подробнее)

♦ Внимание! Акция Российского Красного Креста «С ЧИСТОГО ЛИСТА». Сдай макулатуру — протяни руку помощи! (подробнее)

♦ РСКШ 17.04.21 (подробнее)

♦ Внимание! Конкурс! «Школьная столовая. Одобрено! Дети!» с 15-30 апреля номинация «Лучшая презентация о моей школьной столовой» 1-4 кл. номинация «Лучший видеоролик о моей школьной столовой» 5-11кл (подробнее)

 (подробнее)

♦ 9 апреля в Лицее № 23 состоялась Секция «Физика, техника и инженерное дело» XXII городской  НПК школьников  «ИНТЕЛЛЕКТУАЛ» (подробнее)

♦ Внимание! Старт набора учащихся 4-5 классов на обучение в 2021-2022 учебном году в ЦДНИТТ при КузГТУ «УникУм» (подробнее)

♦ 6 апреля ученики 9 «А» и 9 «Б» классов в рамках профориентационной работы посетили профориентационные пробы в КузГТУ им.Т.Ф.Горбачева (подробнее)

♦ В Центре детского научного и инженерно-технического творчества при КузГТУ «УникУм» начался прием заявлений учащихся 4-5 классов на обучение в 2021-2022 учебном году по направлениям: — Робототехника,- Интеллектуальная электромеханика,- Искусственный интеллект. Занятия в ЦДНИТТ при КузГТУ «УникУм» БЕСПЛАТНЫЕ (подробнее)

♦ 2 апреля в рамках Всемирного дня распространения информации об аутизме в Кузбассе прошел инклюзивный фестиваль «#ЛюдиКакЛюди» (подробнее)

♦ В лицее продолжается подготовка к празднованию 300—летия Кузбасса.  #Кузбасс300 (подробнее)

♦#городаменяютсядлянас  #формированиекомфортнойгородскойсреды (подробнее)

♦ РСКШ 27.03.21 (подробнее)

♦ 27 марта 2021 года по инициативе Всемирного фонда дикой природы (WWF) прошла самая массовая на планете природоохранная акция Час Земли. В этот день люди по всему миру выключат свет на один час с 20.30 по 21.30 по местному времени, чтобы привлечь внимание жителей планеты к проблемам охраны окружающей среды, изменения климата, загрязнения природы и сбережения ресурсов Земли. Будет отключена подсветка таких известных зданий и сооружений, как Московский Кремль, Эйфелева башня, Биг Бен, Римский Колизей и сотен других.

♦ Внимание! Всероссийская Неделя финансовой грамотности для детей и молодежи 22-28 марта 2021г (подробнее)

♦ Группа компаний «Просвещение» с 22 по 26 марта 2021 года проводит масштабное онлайн-мероприятие для учителей: «Предметная неделя: традиции, новации, компетенции». Предметная неделя предназначена для учителей (подробнее)

♦  21 марта ученики 10 «Б» класса, химико-биологического профиля и классный руководитель Качаева Л.А. посетили День открытых дверей КемГУ (подробнее) 

♦ РСКШ 20.03.21 (подробнее) 

♦ 18 марта учителя лицея Лобикова С.Н, Карманова Н.В., Альберт Е. А. совместно  с кафедрой начального образования  КРИПиКРО провели областной вебинар «Модели  и технологии оценивания личностных, предметных и метапредметных результатов освоения ООП НОО»  (подробнее)

♦ В последний день недели «Профориентации» 10в класс рассказал о профессии программист, 10б о профессии товаровед, 7а о профессии сити-фермер (подробнее)

♦ Внимание! Детские технопарки «Кванториум» при поддержке ПАО «Ростелеком» 16 марта – 24 апреля 2021 года запускают бесплатный образовательный проект «DigitaLogia», направленный на повышение цифровой грамотности школьников и их знакомство с самыми современными технологиями (подробнее)

♦ 18 марта о профессии шахтера рассказал 10 а класс, о профессии агронома 9а, 8а класс представил профессию техник по защите информации. 6б рассказал о профессии геодезист (подробнее)

♦ В третий профориентационный день 5б класс представил профессию фармацевт, 5в рассказал о профессии блогер, 6а изучил и представил профессию нотариус (подробнее)

♦ 17 марта 2021г. в рамках «Недели профориентации» в Лицее состоялась встреча выпускников с Ивановым Константином Станиславовичем, кандидатом физ. – мат. наук, доцентом кафедры ЮНЕСКО по ИВТ института фундаментальных наук КемГУ (подробнее)

♦ 17 марта в рамках «Недели профориентации»  7 «А» класс принял участие в тренинге «Блогер в теме» (подробнее)

♦ 21 марта в 11:00  КемГУ приглашает на день открытых (подробнее)

♦ 20.03.2021 в 11:00 состоится День открытых дверей Строительного института КузГТУ (подробнее)

♦ 16 марта учащиеся лицея слушали лекцию по защите прав потребителей Регионального центра финансовой грамотности Кузбасса в рамках Всемирного дня прав потребителей (подробнее)

♦ 16 марта в лицее прошел 2 день недели «Профориентации». Учащиеся 5а класса рассказали лицеистам о  профессии финансист, 11а о профессии адвокат, 11в представил профессию вирусолог (подробнее)

♦ 15 марта  в Лицее началась неделя «Профориентационной работы»,  запланированной на период с 15 по 20 марта (подробнее)

♦ 15 марта в рамках недели «Профориентации» в 10в классе прошел интерактивный квиз «Знатоки Экономики». В данном проекте Учащиеся приобретают знания по экономике и учатся использовать их в повседневной жизни (подробнее)

♦ РСКШ 13.03.21 (подробнее)

♦ 12 марта в МБОУ «Лицей №23»  продолжила работу школьная  научно-практическая конференция «Королевские чтения», первый этап которой прошел ранее и был ориентирован на учащихся начальной школы (подробнее)

♦ Уважаемые лицеисты 2-11 классов, приглашаем к активному участию в региональном конкурсе мультимедийных презентаций «Алексей Архипович Леонов –космонавт-легенда» (подробнее)

♦ 21 марта 2021г. В 11:00 по адресу: г. Кемерово, ул. Красная, 6 (главный корпус) состоится день открытых дверей КемГУ. Подробности на сайте: https://kemsu.ru/

♦ Приглашаем вас посетить открытый мастер-класс по созданию компьютерных игр в среде визуального программирования Scratch. На мастер-классе вы научитесь создавать компьютерные игры, комиксы, анимацию и освоите основы событийно-ориентированного программирования. Начало в 14.30, ссылка на подключение https://ozhedal.clickmeeting.com/gamecreators

♦ Уважаемые лицеисты! КемГУ и Центр детского научного творчества «Интеллектуал КемГУ» Благотворительного фонда Андрея Мельниченко объявляют дополнительный набор учащихся школ 6−10-х классов города Кемерово по направлениям подготовки:«Пропедевтика»  (подробнее)

♦ 5 марта в МБОУ «Лицей №23» состоялся концерт, посвященный празднику 8 марта. Ребята адресовали теплые слова своим любимым педагогам (подробнее)

♦ Обучающийся лицея, ученик 11б класса Леонид Ким успешно освоил научно – технологическую образовательную программу «Большие вызовы» по направлению «Космические технологии» в образовательном центре «Сириус» (г. Сочи) (подробнее)

♦ 7 марта в 15:00 ч. в Виртуальном концертном зале Государственной научной библиотеки Кузбасса им.В.Д.Федорова в сопровождении концерта-трансляции Академического симфонического оркестра Московской государственной филармонии «Увертюры и вальсы Штрауса» состоится Бал Штрауса в честь Международного женского дня (подробнее)

♦ РСКШ 6.03.21 (подробнее)

♦ Полиция Кузбасса рекомендует НЕ ДАЙ СЕБЯ ОБМАНУТЬ! (подробнее)

♦ 27 февраля прошли городские соревнования по Спидкубингу (подробнее)

♦ 27,28 февраля начался районный этап Кузбасской спортивной лиги по волейболу. Команда МБОУ «Лицей N23»провела победные игры с СОШ N28,55. Товарищеские встречи продлятся до 14 марта. Пожелаем удачи нашей команде! (подробнее)

♦ 27 февраля 2021 года на базе МБОУ ДО «Городской центр детского (юношеского) технического творчества города Кемерово», по адресу г. Кемерово, б-р Строителей, 31А проведены  городские соревнования по робототехнике  в рамках региональных соревнований «Кузбасская спортивная школьная лига» (подробнее)

♦  РСКШ 27.02.21 (подробнее)

♦ 27.02.2021 в 12:00 состоится День открытых дверей Института информационных технологий, машиностроения и автотранспорта КузГТУ (ИИТМА) (подробнее)

♦ 24 февраля в лицее прошли профилактические беседы о безопасности дорожного движения. Беседу провел инспектор ГИБДД Руслан Александрович Райфекершт (подробнее)

♦ 24 февраля в лицее состоялась встреча учеников 11 «А» и 11 «Б» классов с Григорьевым А. В., зав. кафедрой электропривода и автоматизации, к.т.н., доцент КузГТУ (подробнее)

♦ С 5 по 9 апреля 2021г. в ФГБОУВО «Кузбасский государственный технический университет имени Т. Ф. Горбачёва» будут проводиться  профессиональные пробы для обучающихся 9-х классов (подробнее)

♦ 27 марта 2021 года (суббота) по инициативе Всемирного фонда дикой природы (WW. F) пройдет самая массовая на планете природоохранная акция Час Земли (подробнее)

♦ Приглашаем ребят 8, 9 и 10 классов принять участие в бесплатной онлайн-выставке «Навигатор поступления» 2021, который состоится 21.02 в 12:00 по московскому времени (подробнее)

♦ 27.02.2021 МБОУДО «ЦТ Заводского района» проводит городской турнир по спидкубингу (сборка Кубика-Рубика на время). Соревнование проводится по следующим направлениям (дисциплинам): 2x2x2; 3x3x3, 4х4х4, Pyraminx, Megaminx. от 7 до 16 лет (подробнее)

♦ 18 февраля состоялась научно-практическая конференция «Королёвские чтения» в начальной школе (подробнее)

♦ С 13 февраля лицее стартовала «Школьная волейбольная лига Кузбасса». Сборная команда юноши Лицея 23, провели две игры с командами школы 48 со счётом 2:0 и с гимназией 25 со счётом 0:2. Игры продолжаются. Желаем нашей команде успехов в соревнованиях! (подробнее)

♦ 16. 02.21 прошли соревнования по лыжным гонкам муниципального этапа региональных соревнований «Кузбасса спортивная школьная лига» среди школьников 1-4 классов. В составе были учащиеся 4 девочки Муренцова Екатерина, Тифус Алиса, Зайцева Катерина, Зимина Вероника. И 4 мальчика Риммер Александр, Ларионов Роман, Конгуров Матвей, Сорочинский Артём. Поздравляем с 3 местом (подробнее)

♦ РСКШ 13.02.21 (подробнее)

♦ #ДобраяСуббота (подробнее)

♦ 8 февраля в День российской  науки  ученики 10Б класса, химико-биологического профиля посетили Институт экологии человека СО РАН и ОНФ (подробнее)

♦ В рамках дней науки в Кемерово прошел детский научный фестиваль «НИТКА» (подробнее)

Олимпиадные задания по математике 10-11 класс

Просмотр содержимого документа
«10 и 11 классы »

Просмотр содержимого документа
«10 класс решение»

10 класс

Решения

1. Решение.

, т.к. первое слагаемое – это произведение трех последовательных натуральных чисел, т.е. оно кратно 3, а второе слагаемое содержит множитель 3, значит и вся сумма кратна 3.

1. Решение.

Проведем BK параллельно CD. Заметим KD || BC, KB || DC, следовательно, KBCD параллелограмм и KD = BC =. AD – секущая параллельных прямых BK и CD, следовательно AKB =ADC = 30°.

Далее найдем длину отрезка AK = AD – KD = . Боковую сторону AB теперь можно найти по теореме синусов для треугольника ABK: . При этом ABK = 180° – AKB – BKA = 180° – 30°– 15° = 135°.

И sin 135° = . Теперь можно найти AB, она получается равной 1.

Ответ: 1.

1. Ответ: на семь слагаемых.

Решение. Приведём пример разбиения числа 96 на семь слагаемых:

9 6 = 2 + 5 + 7 + 11 + 13 + 17 + 41.

Если слагаемых больше, то среди них не менее восьми нечётных (если их семь, то сумма нечётна). Заменим каждое из них на наименьший простой сомножитель. При этом сумма не увеличится, и все слагаемые будут различны. Но сумма восьми наименьших нечётных простых чисел равна 98.

1. Решение.

Имя	Белое платье	Красное платье	Голубое платье	Туфли
Тамара	—	+	—	Красные
Лида	+	—		Голубые
Валя			+	Белые

Ответ: у Тамары были красные туфли и платье, у Вали – белые туфли и голубое платье, у Лиды – белое платье и голубые туфли.

1. Ответ: х = 95, у = 0, z = 94 или х = 31, у = 2, z = 32.

Решение. Вычтя из второго уравнения первое, получим (х — z)(1 — у) = 1.

По условию, х, у, z целые, тогда возможны два случая:

1) х– z = 1, 1 – у = 1, т. е. у = 0. Подставив значение у в систему, получим: z =94, x=95.

2) х –z = -1, 1 – у = — 1, т. е. z = х +1, у = 2. Подставим найденные значения у и z в первое уравнение, получим 2х + х +1 = 94, х = 31. Отсюда z = 32 .

Просмотр содержимого документа
«11 класс решение»

11 класс

Решение

1. Ответ. в 17.00.

Решение. Расстояние между Мишей и Колей и их скорости не меняются, а скорости Васи и Пети равны. Вася встретил Колю через 2 часа после Миши, значит, Петя встретят Колю тоже через 2 часа после Миши, т. е. в 17.00.

1. Ответ. 17.

Решение. Так как из 18 шаров найдется хотя бы один синий, то красных не более 17, а из любых 10 шаров найдется хотя бы один красный, то есть синих не более 9. Так как всех шаров 26, то синих – 9, а красных – 17.

1. Ответ. 70 кг

Решение. 5 процентов от 30 кг — = 1,5 кг соли в 30кг морской воды,

Х л добавили, стало (х+30)л. Х+30-100 процентов, 1,5 -1,5 процентов, тогда х=70

1. Ответ: , k꞊1+5t, t.

Решение. tgx ctgx ꞊ sin5x

, k, n

Найдем теперь такие k, при которых ꞊. Это уравнение перепишем в виде 5n-4k꞊1.Частное решение последнего уравнения

n0꞊1, k0꞊1,тогда k꞊1+5t, t. Итак, k, t

1. Ответ:

Решение. Обозначим длину отрезка AB за 1, тогда SA=2. Найдём прежде всего длины отрезков BD и SD. Пусть BD=x. Тогда, применяя теорему Пифагора к треугольникам ABD и ASD, получаем AD²=1–x² = 4 – (2–x)², BD=x=1/2. Далее в треугольнике BMD BM꞊и, для того чтобы воспользоваться теоремой косинусов, достаточно найти косинус угла MBD. Но из прямоугольного треугольника SBM получаем: cos SBM ꞊

DM ² ꞊꞊, DM ꞊

Открытая региональная межвузовская олимпиада (ОРМО) — Сайт для абитуриента ТУСУР

Открытая региональная межвузовская олимпиада, проводимая вузами Томской области ОРМО – № 67 в перечне олимпиад школьников на 2020/2021 учебный год.

Основными целями и задачами олимпиады являются выявление и развитие у школьников творческих способностей и интереса к научной деятельности, создание условий для интеллектуального развития, поддержки одаренных детей, в том числе содействие им в профессиональной ориентации и продолжении образования, распространение и популяризация научных знаний. Одновременно олимпиада является составной частью общей концепции привлечения в вузы талантливой молодёжи и сочетается с проведением научных и общеобразовательных конкурсов, развитием и поддержкой проектной, творческой и волонтёрской деятельности школьников.

Предметы, дающие особые права при поступлении: русский язык, история, география, физика, математика, литература.

Предметы, дающие дополнительные баллы в портфолио: обществознание.

Вузы-организаторы ОРМО

Образовательное учреждение может участвовать в качестве площадки проведения. Для участия
необходимо заполнить заявку и отправить на электронную почту [email protected].

Сроки регистрации на 1-й тур: с 1 ноября 2020 г. до окончания олимпиады.

График проведения ОРМО в 2020/2021 учебном году

1. Отборочный этап, 8 – 11-е классы (очное участие): 20 ноября – 20 декабря 2020 г.
   Отборочный этап, 8 – 11-е классы (дистанционное участие): 20 ноября 2020 г. – 10 января 2021 г.
   Для участия в олимпиадах дистанционно каждому обучающемуся необходимо пройти индивидуальную регистрацию на сайте olymp.tsu.ru. Время проведения местное.
2. Заключительный этап, 8 – 11-е классы: февраль – март 2021 г.

В заключительном этапе участвуют победители и призёры отборочного этапа 2020/2021 г., а также призёры и победители (8 – 10-е классы) заключительного этапа олимпиады 2019/2020.

График заключительного этапа Открытой региональной межвузовской олимпиады (ОРМО)

Проведение по трём вариантам:

• Площадки вузов (очно). Проведение в воскресные дни с 28 февраля по 21 марта. Расписание найдёте в таблице ниже.
• Площадки образовательных организаций среднего образования (школы, лицеи, гимназии – очно) с 11 по 14 марта. Пункты проведения
• С применением дистанционных технологий (прокторинг). Инструкции будут опубликованы на сайте до 10 марта. Расписание найдёте в таблице ниже. 

Расписание (площадки вузов)

Расписание заключительного этапа ОРМО в ЗАТО «Северск»

Предмет	Дата	Время (местное регионов)	Место проведения
Русский язык	7 марта 2021 г. (воскресенье)	10:00	МБОУ «СОШ № 89»
Литература, физика, обществознание*	14 марта 2021 г. (воскресенье)	10:00	МБОУ «СОШ № 89»
История, математика	21 марта 2021 г. (воскресенье)	10:00	МБОУ «СОШ № 89»

На олимпиаду необходимо принести

1. Согласие на обработку персональных данных
2. Документ, удостоверяющий личность
3. Чёрную гелевую ручку
4. Справку из школы

Расписание проведения олимпиады ОРМО с применением дистанционных технологий, обеспечивающих в режиме реального времени посредством видео-конференц-связи идентификацию личности участников и контроль соблюдения условий и требований по проведению олимпиады

Дата	Предмет	Время московское
27 марта 2021г. (суббота)	Обществознание*, издательское дело*	10:00
28 марта 2021г. (воскресенье)	География	10:00
3 апреля 2021 г. (суббота)	Литература, физика	10:00
4 апреля 2021 г. (воскресенье)	Русский язык	10:00
10 апреля 2021 г. (суббота)	История	10:00
11 апреля 2021 г. (воскресенье)	Математика	10:00

Для участия в олимпиаде обязательно наличие

1. Высокой скорости интернета
2. Последней версия Zoom
3. Персонального компьютера или ноутбука с веб-камерой. Более подробные требования будут опубликованы в инструкции дистанционного проведения

На олимпиаду необходимо будет принести

1. Документ, удостоверяющий личность (паспорт, свидетельствово о рождении)
2. Заполненное согласие на обработку персональных данных (для несовершеннолетних заполнить заранее, для совершеннолетних заполнить можно в день проведения олимпиады на площадке)
3. Справку из образовательного учреждения для 11-го класса (что вы являетесь обучающимся в школе). Справка может быть одна на нескольких обучающихся из одного образовательного учреждения
4. Чёрную гелевую ручку

Положение об олимпиаде

Положение об олимпиаде

Методическая помощь

Тренировочные сессии-вебинары по предметам

Олимпиадные задания прошлых лет

Задания и ответы олимпиады 2018/2019 учебный год

Задания и ответы по географии

Задания и ответы по истории

Задания и ответы по литературе

Задания и ответы по математике

Задания и ответы по русскому языку

Задания и ответы по физике

Задания и ответы олимпиады 2017/2018 учебный год

Задания и ответы по географии

• Задания по географии 1 этап 8-9,10,11кл 1 вариант
• Задания по географии 1 этап 8-9,10,11кл 2 вариант
• Задания по географии 1 этап 8-9,10,11кл 3 вариант
• Задания по географии 1 этап 8-9,10,11кл 4 вариант
• Задания по географии 2 этап 8-9кл 1 вариант
• Задания по географии 2 этап 8-9кл 2 вариант
• Задания по географии 2 этап 10кл 1 вариант
• Задания по географии 2 этап 10кл 2 вариант
• Задания по географии 2 этап 11кл 1 вариант
• Задания по географии 2 этап 11кл 2 вариант
• Ответы по географии 1 этап 8-11 кл
• Ответы по географии 2 этап 8-9кл 1,2 вариант
• Ответы по географии 2 этап 10кл 1,2 вариант
• Ответы по географии 2 этап 11кл 1,2 вариант

Задания и ответы по истории

Задания и ответы по литературе

Задания и ответы по математике

Задания и ответы по русскому языку

Задания и ответы по физике

• Задания по физике 1 этап 8кл 1 вариант
• Задания по физике 1 этап 8кл 2 вариант
• Задания по физике 1 этап 8кл 3 вариант
• Задания по физике 1 этап 9кл 1 вариант
• Задания по физике 1 этап 9кл 2 вариант
• Задания по физике 1 этап 9кл 3 вариант
• Задания по физике 1 этап 10кл 1 вариант
• Задания по физике 1 этап 10кл 2 вариант
• Задания по физике 1 этап 10кл 3 вариант
• Задания по физике 1 этап 11кл 1 вариант
• Задания по физике 1 этап 11кл 2 вариант
• Задания по физике 1 этап 11кл 3 вариант
• Задания по физике 2 этап 8кл 1 вариант
• Задания по физике 2 этап 8кл 2 вариант
• Задания по физике 2 этап 9кл 1 вариант
• Задания по физике 2 этап 9кл 2 вариант
• Задания по физике 2 этап 10кл 1 вариант
• Задания по физике 2 этап 10кл 2 вариант
• Задания по физике 2 этап 11кл 1 вариант
• Задания по физике 2 этап 11кл 2 вариант
• Ответы по физике 1 этап 8кл 1,2,3 варианты
• Ответы по физике 1 этап 9кл 1,2,3 варианты
• Ответы по физике 1 этап 10кл 1,2,3 варианты
• Ответы по физике 1 этап 11кл 1,2,3 варианты
• Ответы по физике 2 этап 8кл 1,2 вариант
• Ответы по физике 2 этап 9кл 1,2 вариант
• Ответы по физике 2 этап 10кл 1,2 вариант
• Ответы по физике 2 этап 11кл 1,2 вариант

Ответственное лицо за проведение олимпиады

Любовь Вячеславовна Радишевская

ЕГЭ математика (профильный уровень)

Единый государственный экзамен (ЕГЭ) — это форма государственной итоговой аттестации (ГИА) по образовательным программам среднего общего образования.

При проведении ЕГЭ используются контрольные измерительные материалы (КИМ), представляющие собой комплексы заданий стандартизированной формы, а также специальные бланки для оформления ответов на задания.

ЕГЭ по математике является обязательным экзаменом для всех учащихся, заканчивающих 11 класс. Школьники могут выбрать базовый или профильный уровень экзамена. Профильный ЕГЭ нужен тем учащимся, которым при поступлении в ВУЗ понадобятся результаты ЕГЭ по математике, остальным подойдет базовый ЕГЭ по математике.

Профильный ЕГЭ по математике длится 235 мин и состоит из 12 заданий с кратким ответом, которым является целое число, или конечная десятичная дробь, или последовательность цифр и 7 заданий второй части к которым нужно привести полные решения.

Дальневосточный центр математики предлагает учащимся 10-х и 11-х классов пройти программу подготовки к профильному ЕГЭ по математике. Наш центр реализуются две программы подготовки к профильному ЕГЭ по математике:

• профильный уровень,
• ЕГЭ по математике 70+.

Первая программа подойдет для большинства школьников и позволит при должном уровне упорства набрать не менее 60 баллов. Данная программа предусматривает развитие общематематической грамотности, совершенствование навыков быстрого счета и развитие уверенности при решении тестовых задач. Основной акцент в данной программе сделан на подготовку к решению первых 12 заданий профильного экзамена. Кроме того, будут рассматриваться задачи 13, 15 и 17 из второй части, как наиболее простые из второй части экзамена.

Вторая программа подойдет для тех школьников, кто уже уверенно справляется с первыми 12 заданиями профильного экзамена. Для зачисления на курс учащиеся должны сдать входной тест не менее чем на 62 балла. Упор в данной программе сделан на подготовку к решению задач второй части профильного ЕГЭ.

Занятие длится 80 минут. На занятии учащиеся разбирают теоретический и практический материал, и большую часть времени решают задачи самостоятельно, закрепляя полученные знания.

Математика

Всесибирская открытая олимпиада школьников по математике — олимпиада 2 уровня, входящая в Перечень РСОШ. Олимпиада проводится в 3 этапа: отборочный очный, отборочный заочный и заключительный.

Очный

отборочный этап:

4 октября 2020 г.

Регистрация на очный этап:
22 сентября – 3 октября 2020 г.

Заочный отборочный этап:

25 декабря 2020 – 15 января 2021 г.

Регистрация на заочный этап:
1 декабря 2020 – 15 января 2021 г.

Заключительный

этап:

21 февраля

Регистрация на заключительный этап:
8 февраля — 18 февраля 2021 г.

Как участвовать?

Олимпиада по математике проходит в 3 этапа:

• два отборочных этапа – очный и заочный.
• заключительный этап.

На этой странице размещены полные пошаговые инструкции как принять участие на любом из этапов олимпиады.

Обратите внимание!

Чтобы принять участие в олимпиаде, необходимо зарегистрироваться в Личном кабинете, заполнить анкету и подать заявку на участие.

Олимпиада 2020-2021 уч.г.

Очный отборочный этап

• 4.10Очный этап
• 12.11Предварительные результаты по всем площадкам (проверено 90% работ)
• 30.11Окончательные итоги очного отборочного этапа (объявление победителей и призёров).

Заочный отборочный этап

Заключительный этап

 

• 2.2 Список включает в себя победителей и призеров заключительного этапа 2019-20 и очного отборочного этапа 2020-21.
• 3.2Рассылка приглашений победителям и призерам Заключительного этапа Всесибирской олимпиады 2019-2020 учебного года, с инструкцией
• 4-14. 2Размещение площадок проведения в городах
• 8.2Начало регистрации
• 15.2
• 15.2Итоговый список приглашенных. Внимание! Регистрация открыта для ID и класса, указанных в списке.
• 18.2Завершение регистрации: заявки на участие принимаются до 23:59 по московскому времени 19 февраля включительно
• 21.2Заключительный этап в 10.00 по местному времени на площадках. Регистрация на местах начинается за 40 минут. Продолжительность этапа — 4 часа. 
• 3.3Предварительные результаты (работы площадок Новосибирск, Саратов, Магнитогорск).
• 3.3Новосибирск. Очная апелляция. 15:00 — 7-8 класс. 16:00 — 9 класс. С 17:00-17:30 после 9 классов  — 10 класс.  Адрес: Ляпунова, 3. СУНЦ НГУ, 458 ауд. С собой иметь паспорт (свидетельство о рождении — до 14 лет).
• 4.3Новосибирск. Очная апелляция.  16:00 — 11 класс. Адрес: Ляпунова, 3. СУНЦ НГУ, 357 ауд. С собой паспорт.
• 10.3Саратов. Очная апелляция. 16:00 — все классы. Адрес: ул. Астраханская, 88, корпус 9, ауд. 319. Саратовский государственный университет. С собой паспорт (свидетельство о рождении — до 14 лет).
• 11.3Курган. Очная апелляция. 14:00 — все классы. Адрес: ул. Томина, 53, кабинет 301. Центр дополнительного математического образования. С собой паспорт (свидетельство о рождении — до 14 лет).
• 15-19.3Щелково. Онлайн апелляция. Связаться с жюри с 15 марта по 19 марта по почте [email protected] или написать сообщение в смс (лучше whatsapp) +79672134555 с указанием фамилии, имени, номера задач.
• 15-19.3Щелково Очная апелляция. 10:00 — для тех, кто может приехать. Адрес: Московской область, Щелково. Ул. Институтская стр. 37а. С собой паспорт (свидетельство о рождении — до 14 лет).
• 24.3Предварительные результаты (проверено 90% работ)
• 24.3Заочная апелляция. Заявки принимаются до 26 марта включительно (до 23:59 по новосибирскому времени).

Задания и решения

2020-2021 гг.

Заключительный этап

Очный отборочный этап

Заочый отборочный этап

Архив заданий прошлых лет

Очный отборочный этап

Задания за 2019—2020 гг.

Задания за 2018—2019 гг.

Задания за 2017—2018 гг.

Задания за 2016—2017 гг.

Задания за 2015—2016 гг.

Задания за 2014—2015 гг.

Задания за 2013—2014 гг.

Задания за 2012—2013 гг.

Задания за 2011—2012 гг.

Задания за 2010—2011 гг.

Задания за 2009—2010 гг.

Задания за 2008—2009 гг.

Задания за 2007—2008 гг.

Заочный отборочный этап

Задания за 2019—2020 гг.

Задания за 2018—2019 гг.

Задания за 2017—2018 гг.

Задания за 2016—2017 гг.

Задания за 2015—2016 гг.

Задания за 2014—2015 гг.

Задания за 2013—2014 гг.

Задания за 2012—2013 гг.

Задания за 2011—2012 гг.

Задания за 2010—2011 гг.

Задания за 2009—2010 гг.

Задания за 2008—2009 гг.

Задания за 2007—2008 гг.

Задания за 2006—2007 гг.

Заключительный этап

Задания за 2019—2020 гг.

Задания за 2018—2019 гг.

Задания за 2017—2018 гг.

Задания за 2016—2017 гг.

Задания за 2015—2016 гг.

Задания за 2014—2015 гг.

Задания за 2013—2014 гг.

Задания за 2012—2013 гг.

Задания за 2011—2012 гг.

Задания за 2010—2011 гг.

Задания за 2009—2010 гг.

Задания за 2008—2009 гг.

Задания за 2007—2008 гг.

Математика в 11 классе

Добро пожаловать в 11 класс по математике!

Covid-19 привел мир к феноменальному переходу.

За электронным обучением будущее уже сегодня.

Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!

Мы образовательный сайт ask-math.com, и у нас есть хорошие учебные материалы. Этот год важен, так как студентам необходимо решить, в каком направлении они будут строить свою карьеру. Учебная программа 11 класса по математике охватывает знания по темам, которые входят в математику.Поскольку мы знаем, что у курса нет ограничений, и если все обучение разделено на разные потоки, то определенно ограничение этих потоков для конкретного класса в соответствии с возможностями студентов является обязательным. Таким образом, программа 11-го класса необходима для того, чтобы учащиеся познакомились с темами, и они должны изучать 11-й стандарт, чтобы база 12-го стандарта была прочной. В Индии. 12-й стандартный процент имеет большое значение в жизни, и прием в старшие классы зависит от этого процента и знаний, и изучение 12-го стандарта может повлиять на знание базы 11-го класса.Так что очень важно знать темы, затронутые 11-м. Ask-math.com организовал все темы, включенные в 11-й класс. Чтобы изучить эти темы шаг за шагом, щелкните ссылки внизу этой страницы. Вот список всех тем, изучаемых учениками 11-го класса по математике. Наборов: Понятие набора является базовым во всех разделах математики. Это оказалось особенно важным при формировании отношений и функций.
Отношения и функции: В математике мы сталкиваемся с такими отношениями, как i) линия l параллельна строке m ii) число m меньше числа n.Во всем этом мы замечаем, что отношение включает пары объектов в определенном порядке. Этот раздел посвящен изучению отношений и функций в математике.
Математическая индукция: Процесс рассуждения от общего к частному и другого известен как процесс индукции. В алгебре или других дисциплинах математики есть определенные результаты или утверждения, которые сформулированы в терминах n, где n — положительное целое число. Чтобы доказать такие утверждения, мы используем особую технику, известную как «Принцип математической индукции».
Логарифмы: Это особый процесс, который сокращает объем работы, связанной с умножением и делением больших чисел.
Комплексные числа: Комплексное число — это число в форме a + ib, где a и b — действительные числа, а i — мнимая единица, имеющая свойство i ² = -1
Линейные неравенства: 13x <250 такие уравнения называются линейными неравенствами. Изучение неравенств очень полезно при решении задач в области науки, математики, статистики, задач оптимизации, экономики, психологии и т. Д.
Квадратные уравнения: В этом разделе ask-math предоставляет вам квадратные уравнения с действительными коэффициентами, но с отрицательным дискриминантом.
Последовательности и серии: В этом разделе ask-math рассматриваются все типы последовательностей, такие как арифметическая прогрессия (A.P), геометрическая прогрессия (G.P) и гармоническая прогрессия.
Тригонометрические функции: В этом разделе ask-math предоставляет круговую функцию и их свойства. Например, преобразование углов из радиан в градусы, знаки тригонометрических функций, область определения и диапазон тригонометрических функций, сумма и разность углов и т. Д.
Декартова система прямоугольных координат: В этом разделе представлены формула расстояния, формула сечения, площадь треугольника с использованием координат, параметрическое уравнение линии и т. Д.
Прямая линия и семейство прямых: В этом разделе мы должен вывести различные формы уравнения прямой, включая прямые, параллельные осям, и наклонные.

Наборы:
•

Наборы
• Декартово произведение наборов

Функции:
•

Круговая функция
• Составные функции
• Вычисление функции обратного косинуса
• Вычисление функции обратного синуса
• Четная и нечетная функция в тригонометрии

График функций:
•

График рациональной функции
• График тригонометрической функции
• График y = sin (bx)
• График y = cos (bx)
• График рациональных функций с отверстиями
• Перехват рациональной функции
• Обратный касательная функция
• Функция один к одному
• Функция на
• Периодическая функция в тригонометрии
• Тригонометрические функции в разных квадрантах

Математическая индукция:
•

Докажите математической индукцией

Логарифм:
•

Общий и натуральный логарифм
• Правила для логарифмы
• Вычисление логарифма
• Изменение логарифма основания
• Применение логарифма

Comp lex Числа:
•

Комплексные числа
• Сложение комплексных чисел
• Вычитание комплексных чисел
• Полярная форма комплексных чисел
• Комплексные корни квадратного уравнения
• Сопряженное комплексное число
• Деление комплексных чисел
• Модуль комплексного число
• Умножение комплексных чисел
• Выполнение операций с комплексными числами

Квадратичные функции:
•

Введение квадратного уравнения
• Иррациональные корни квадратного уравнения
• Природа корней квадратного уравнения
• Квадратные уравнения с действительными коэффициентами
• Показать это квадратное уравнение не может иметь более двух корней
• Квадратные уравнения с комплексными коэффициентами

• Линейные неравенства:
•

Графическое отображение линейного неравенства
• Графическое отображение систем линейных неравенств
• Линейные неравенства
• Решение двухшаговых линейных неравенств
• Решение линейных уравнений в алгебре неравенств
• Решение одношаговых уравнений и неравенств
• Системные линейные неравенства в текстовых задачах
• Система линейных неравенств

Последовательность и серия
• Серия

и последовательности
• Что такое арифметические средства
• Арифметическая прогрессия
• Найти термины арифметическая прогрессия
• Свойства арифметической последовательности
• Сумма арифметической прогрессии
• Геометрическая прогрессия
• Свойства геометрической прогрессии
• Найдите общее отношение, когда дана сумма n членов геометрической прогрессии
• Общий член геометрической прогрессии
• Задача геометрической прогрессии
• Выбор членов в геометрической прогрессии
• Решенные суммы в геометрической прогрессии
• Сумма гео метрическая прогрессия
• Сумма бесконечной геометрической прогрессии
• Связь между геометрическим и средним арифметическим по математике в 11 классе

Дом

Covid-19 повлиял на физическое взаимодействие между людьми.

Не позволяйте этому влиять на ваше обучение.

Учебная программа по математике для 11 класса — Spirit of Math Schools Inc.

Учебная программа по математике для 11 класса — Spirit of Math Schools Inc.

ПРЕДУПРЕЖДЕНИЕ О COVID-19: все наши очные занятия проводятся ОНЛАЙН до дальнейшего уведомления.

Search Spirit of Math Schools Inc.

11-й класс — последний год окончания курса «Дух математики». Уровень сложности эквивалентен первому или второму курсу математики в университете. В 11 классе учащиеся изучают математические дисциплины, включая пределы, производные, неявное и частное дифференцирование, интегралы и многое другое. Студенты также работают над независимыми заданиями, охватывающими функции, логарифмы, алгебраические уравнения, геометрию, последовательности и многое другое. Общая учебная программа готовит студентов с глубоким пониманием математики, а также сильным независимым мышлением и навыками управления временем.Совместная групповая работа и решение проблем по-прежнему являются ключевыми компонентами учебной программы 11-х классов. В целом, еженедельные двухчасовые занятия наполнены новыми полезными знаниями для успешных учеников.

Вот что мы изучаем в одиннадцатом классе:

• Ментальная арифметика: в 11 классе учащиеся продолжают практиковать свои умственные навыки вычисления

• 11-й класс специализируется на математическом анализе. Преподаваемый материал сопоставим с учебным курсом первого года обучения математике в университете.Охваченные темы включают:
• Пределы
• Производные правила
• 2 ^nd и 3 ^{rd производные на} градусов
• Производные логарифмических, экспоненциальных и тригонометрических функций
• Неявное дифференцирование
• Частичная дифференциация
• Максимум-минимум задач
• Скорость изменения проблем
• Эскиз кривой
• Интегральные устройства и приложения

• Наборы задач на основе следующих тем:
• Функции
• Логарифмы
• Алгебраические уравнения
• Последовательности и серии
• Geometry Mania: сложные задачи, основанные на различных концепциях в 2- и 3-мерной геометрии

• Сравнение и обсуждение решений домашнего задания с самостоятельными заданиями и основной работой
• Развитие коммуникативных и социальных навыков
• Обучение обмену идеями о совместном решении проблем
• Развитие критического мышления и навыков принятия решений

Оценки доступны в Интернете, и родители получают три табеля успеваемости каждый год.Наши студенты продемонстрируют свое понимание через:

• Тесты на основе наборов задач (на уроках 6, 11, 18 и 27)
• Шесть модульных тестов (на уроках 8, 16, 22, 25, 31 и 37)
• Итоговый комплексный экзамен

Что говорят наши родители и выпускники

Найдите ближайший к вам университетский городок

Имя магазина-заполнителя.

Адрес-заполнитель.

Заполнитель веб-сайта.

Заполнитель электронной почты.

Телефонный заполнитель.

Заполнитель факса.

Заполнитель описания.

Получить направление Просмотр улиц

Название магазина-заполнителя

Заполнитель для адреса

Посетите кампус, страница

Посетите кампус, страница

Заполнитель веб-сайта

Электронная почта

Телефон

Телефон

Телефонный заполнитель

Факс

В этом кампусе

Заполнитель описания

Внешний URL-адрес

Заполнитель Ext

Получить направление Просмотр улиц

Spirit of Math — инновационный лидер в области внешкольного математического образования для высокопроизводительный студенты.

Контактная информация

1446 Don Mills Road, Suite 101, Торонто, ON M3B 3N3
416-223-1985 х 110
[email protected]

×

Amazon.com: Упражнения по общей математике с ответами (934 набора), 424 стр.

Этот учебный материал состоит из 934 заданий или упражнений по общей математике. Он предоставляет учащимся набор общих математических вопросов для практики и развивает их понимание концепций и методов, взятых из чисел и алгебры, тригонометрии и геометрии мира, последовательностей, финансов, сетей, а также математики и статистики решений для решения прикладных задач. .

Подходит для:
• Ежедневных обсуждений в классе
• Классных занятий
• Занятия на дому
• Репетиторства
• Рецензента

Другие функции:
• Включает цветные и подробные рисунки, диаграммы и диаграммы.
• Легко печатать материалы на бумаге стандартного размера Letter (21,59 x 27,94 см).

Темы:

I. Функции и графики

A. Оценить функции
B.Выполняйте сложение, вычитание, умножение, деление и композицию функций
C. Представляйте реальные жизненные ситуации, используя рациональные функции
D. Различайте рациональные функции, рациональные уравнения и неравенства
E. Представляет рациональную функцию через таблицу значений, график и уравнение.
F. Найдите нули, точки пересечения, асимптоты рациональных функций
G. Решает задачи, связанные с рациональными функциями, уравнениями и неравенствами.
H.Определите обратную функцию взаимно однозначной
I. Представляет обратную функцию через таблицу значений, график и уравнение.
J. Найдите область определения и диапазон обратных функций
K. Решать задачи с обратными функциями
L. Представляйте реальные ситуации с помощью экспоненциальных функций
М. Различают экспоненциальные функции, экспоненциальные уравнения и неравенства
Н. Решает экспоненциальные уравнения и неравенства
О. Найдите область определения и диапазон экспоненциальных функций
P.Определяет точки пересечения, нули и асимптоты экспоненциальной функции
Q. Решать задачи, связанные с экспоненциальными функциями, уравнениями и неравенствами
R. Представляет логарифмическую функцию через таблицу значений, график и уравнение.
S. Определяет точки пересечения, нули и асимптоты логарифмической функции
T. Решает задачи, связанные с логарифмическими функциями, уравнениями и неравенствами

II. Основы бизнес-математики

U.Различайте простые и сложные проценты: вычисляет проценты, стоимость погашения, будущую стоимость и приведенную стоимость в простых процентах
V. и среда сложных процентов
W. Проиллюстрируйте простые и общие аннуитеты
X. Находит будущую стоимость и текущую стоимость как простых, так и общих аннуитетов.
Y. Рассчитывает текущую стоимость и период отсрочки отсроченного аннуитета
Z. Проиллюстрируйте акции и облигации
AA. Примеры коммерческих и потребительских кредитов

III.Логика

BB. Проиллюстрируйте предложение
CC. Символизируйте предложение
DD. Различайте простые и сложные предложения
EE. Определение истинности предложений
FF. Иллюстрирует различные формы условных предложений
GG. Иллюстрирует различные типы тавтологий и заблуждений: устанавливает обоснованность и ложность реальных аргументов с помощью логических суждений, силлогизмов,
HH. и заблуждения.
II. Иллюстрирует различные методы доказательства (прямые и косвенные) и опровержения (косвенные и контрпримеры).

(PDF) УРОКИ ПО МАТЕМАТИКЕ 11 КЛАССА С ИСПОЛЬЗОВАНИЕМ ПРИЛОЖЕНИЙ ГРАФИЧЕСКОГО КАЛЬКУЛЯТОРА

ЛЮДИ: Международный журнал социальных наук

ISSN 2454-5899

Доступно в Интернете по адресу: http: // grdspublishing.org /

В классе также было наложено, что каждый раз при группировании конкретные роли

назначались каждому члену группы. По этой причине каждый учащийся нес ответственность перед своим

. Например, в Уроке 2 наблюдатель написал: «Каждая группа разделяет задачи на

групповых действий, например, кто-то построит таблицу значений в приложении, кто-то напишет ее на картоне

, кто-то подготовит таблицу. Декартова плоскость, а остальные построят график.

Таким образом, каждая группа выполнила задачу раньше срока, и каждый член выполнил свои

обязанности в своей группе. Кроме того, на правом фото на Рисунке 1 изображена ответственность студентов

за свои обязанности. Видно, что менеджер по материалам обращался с мобильным устройством так, что

, что секретарь мог писать ответы удобным способом. Это помогло группе

легко облегчить выполнение заданий или поручений.

Более того, было также замечено, что студенты, у которых были смартфоны / планшеты, были очень любезны

, чтобы одалживать свои гаджеты другим одноклассникам. В некоторых случаях, когда у группы было достаточно

смартфонов, они позволяли другим группам одалживать некоторые из них, особенно когда эта группа

не удовлетворяла требованиям соотношения 1: 2 или 1: 3 с гаджетами.

3.2.2 Поведение ученика учителю

На протяжении всего курса поведение на уроках, внимательное слушание и следование инструкциям

всегда проявлялись учениками во время взаимодействия с учителем.Это

было основано на заметках наблюдателя, который написал: «Студенты хорошо взаимодействуют со своим учителем

, внимательно слушая и следуя его инструкциям». Когда учитель

разговаривал с классом, все ученики внимательно слушали, за исключением тех случаев, когда они немного отвлекались.

Кроме того, ученики следовали инструкциям учителя, особенно когда использовать графический калькулятор

приложений и вернуть все использованные материалы.

Наблюдатели также указали, что всякий раз, когда учитель задавал вопросы, ученики поднимали руки

, чтобы ответить и быть вызванными. В некоторых случаях они отвечали хором, но, насколько это было возможно, ответы на

вопросов и объяснение своей работы выполнялись поднятием рук. Кроме того, студенты

также поднимали руки, когда у них были какие-то неправильные представления или путаница по темам. Учитель позволил

другим ученикам дать разъяснения, но если это повлекло за собой более глубокие объяснения, учитель был тем

, который разъяснял эти заблуждения.

3.2.3 Поведение учеников в графических калькуляторах

Поскольку графические калькуляторы были новы для большинства студентов в первый день внедрения

, наблюдатель в своих заметках процитировал: «Студентам нравятся приложения с тех пор, как it

лет Рабочие листы по математике Cazoom Grade Основные математические уравнения алгебры Решая квадратичные My

Амеди Марго 27 января 2021 г.Они больше заинтересованы в развлечениях, поэтому лучше, если учитель научит их писать буквы в увлекательной игровой форме. Учителя могли заметить, что когда детям просто говорят, что им делать, они могут делать это не сразу из-за отсутствия интереса.

Существует много видов рабочих листов, предназначенных для помощи в обучении. Цветные страницы очень нравятся детям. Рабочие листы также учат лучшим способам чтения и написания текста. Это также заставляет детей улавливать звучание букв, и они могут легко научиться писать иероглифы в более поздние годы.Рабочие листы составлены в соответствии с возрастными группами, и учителя пытаются найти наилучшие средства для создания вариантов, подходящих для детей.

Маленький ребенок может не уметь писать или читать больше, чем несколько слов. Рабочие листы следует создавать с учетом этих факторов. Когда вы покупаете рабочие листы для своих детей, поищите, как объясняется их концепция. Это графическое изображение или просто набор слов? Рабочий лист с рисунками привлечет внимание ребенка больше, чем просто комбинация слов.

Рабочие листы, которые являются типами бесплатных ресурсов для учителей, также помогают в создании головоломки, которая будет иметь большое значение для того, чтобы ваши ученики освежили свой ум. Вы можете выбрать более простую головоломку для младших школьников и создать лист, содержащий сложную головоломку для продвинутых студентов, поскольку их уровень рассуждений не совпадает.

Задания по математике перед алгеброй

10 апреля 2021 г.

Задания по английскому языку для 6-х классов

10 апреля 2021 г.

Задания по математике в начальной школе

10 апреля 2021 г. , 2021

Есть много родителей, которые используют рабочие листы для письма для обучения детей схемам письма еще до того, как они пойдут в школу.Доступно множество вариантов, и в наши дни распространены даже онлайн-варианты. Это подготовит ваших детей к поступлению в среднюю школу. Онлайн-средства просты для родителей и учителей, а также интересны детям, чтобы они заинтересовались их идеями о письме.

Их очень много. Вы можете позволить своим детям учиться онлайн. Благодаря этому ваши дети будут готовы к школе. Эти онлайн-материалы легко загрузить и распечатать для использования.И что хорошо в том, что вы можете создавать столько копий, сколько захотите, пока ваш ребенок не научится писать и не овладеет им. Есть также учителя, которые используют такие методы, чтобы преподавать в более оживленной манере. Идея состоит в том, чтобы заинтересовать детей, потому что без их внимания трудно заставить их усвоить то, чему вы пытаетесь научить.

Фотографии основных заданий по математике 11-го класса

Оставьте свой ответ на учебные листы по математике Cazoom Grade Essential Math Алгебраные уравнения Решение квадратичных уравнений My

Переключено на планирование 11 класса

и сэкономьте время давая своим детям отличную академическую подготовку! Switched-On Schoolhouse от Alpha Omega Publishers предоставляет домашним школьникам увлекательную и гибкую основную учебную программу, которая представлена ​​в интерактивной учебной среде с богатым набором средств массовой информации.Этот набор из 4 предметов охватывает историю и географию, языковое искусство, математику и естественные науки в течение одного учебного года. На уроках представлены видеоролики, анимационные ролики, интерактивные графики и обучающие игры, а также викторины и тесты. Ресурсы учителя включают автоматическое планирование уроков и выставление оценок, настраиваемые параметры ведения записей и множество гибких вариантов учебной программы.

Темы для одиннадцатого класса включают:

История и география: история Америки, включая Американскую республику, гражданские и революционные войны, промышленную революцию, мировые войны и многое другое.
Language Arts: English III, который охватывает поэзию, научную литературу, американскую драму, американский роман и развитие исследовательских навыков.
Математика: Алгебра II, включая функции, линейные уравнения, алгебраические дроби, квадратичные отношения, экспоненциальные функции и многое другое.
Наука: химия, которая охватывает элементы, смеси, соединения, атомную структуру, химические реакции, химию углерода и многое другое.

Характеристики включаемого здания школы:

Возможность сохранять проекты на свой компьютер и загружать их в базу данных SOS по завершении
Автоматическая оценка 80-95% работы учащихся (эссе, оцениваемые родителями, абзацы и проекты)
Множественные отчеты, от форматных табелей успеваемости и стенограмм до быстрых ежедневные отчеты о деятельности
Настраиваемое расписание и простое перепланирование.
Функция преобразования текста в речь, чтобы студенты могли читать, одновременно слушая текст; для многих аудио / видео файлов также доступны письменные стенограммы
Возможность создания собственного курса или задания
Альтернативные викторины и тесты
Журналы чтения и активности для отслеживания занятий и чтения книг
Отслеживание посещаемости
Возможности печати для школьных заданий, выполненных вне компьютера -просто введите их ответы в SOS, когда будете дома!

11–12 классы Математика A Level — Сингапур — FutureSchool

. Ньютона Статистика Экзамен

1	Учебный план	Учебный план — 11–12 классы A Уровень
Цель: По завершении формирующей оценки курса создается индивидуальный учебный план, определяющий уроки, требующие пересмотра.
2	Графические полиномы	Построение графиков комплексных многочленов: квадраты без действительных корней
Задача: По завершении урока ученик сможет определить, имеет ли квадратный корень действительный или комплексный корень, а затем построить график.
3	Графические полиномы	Общее уравнение круга: определите и изобразите уравнение
Задача: По завершении урока учащийся сможет решать эти типы задач.Работа с кругами также поможет студенту в теме геометрии круга, которая проверяет навыки студента в логике и рассуждении.
4	Графические кубические кривые	Графические кубические кривые
Задача: По завершении этого урока учащийся сможет построить график кубики с учетом его уравнения или вывести уравнение кубического элемента с учетом его графика или другой соответствующей информации.
5	Уравнения абсолютных значений	Уравнения абсолютных значений
Цель: По завершении этого урока учащийся сможет использовать графики с функцией абсолютного значения.Учащийся сможет построить график функции с учетом ее уравнения и уметь находить пересечение абсолютного значения функции
6	Rect. Hyperbola	Прямоугольная гипербола.
Задача: По завершении урока учащийся сможет проанализировать и построить график прямоугольной гиперболы и описать ее важные особенности.
7	Экспоненциальная функция	Показательная функция.
Задача: По завершении урока ученик сможет построить график любого уравнения в форме y, равного a в степени x, где a — любое положительное вещественное число, кроме 1.
8	Функции журнала	Логарифмические функции.
Цель: По завершении этого урока ученик сможет определять основные логарифмические функции и описывать отношения между логарифмами и показателями, включая логарифмические функции графиков.Студент поймет связь между логаритом
9	Конические секции	Введение в конические сечения и их общее уравнение
Задача: По завершении урока ученик определит коническое сечение по коэффициентам уравнения.
10	Конические секции	Парабола x. = 4 дня
Цель: По завершении урока ученик определит фокус и направляющую для параболы, представленной в стандартной форме.
11	Конические секции	Круги
Задача: По завершении урока ученик определит радиус круга, заданный в стандартной форме.
12	Конические секции	Эллипсы
Цель: По завершении урока ученик определит фокус, вершины и оси эллипса.
13	Конические секции	Гипербола
Цель: По завершении урока ученик определит фокус, вершины, оси и асимптоты гиперболы.
14	Функции	Определение, область применения и диапазон
Цель: По завершении этого урока учащийся сможет выбирать функции из отношений, ссылаясь на домен и диапазон.
15	Функции	Обозначения и оценки
Цель: По завершении урока учащийся научится понимать различные обозначения функций.
16	Функции	Подробнее о домене и диапазоне
Цель: По завершении урока учащийся сможет описать область и диапазон, используя соответствующую систему обозначений.
17	Функции	Область и диапазон графических представлений
Цель: По завершении урока учащийся сможет описать предметную область и диапазон, используя соответствующие обозначения набора из графических представлений.
18	Функции	Вычисление и построение графиков кусочных функций
Задача: По завершении урока учащийся сможет оценивать и наносить на график кусочные функции.
19	Функции	Комбинации функций
Цель: По завершении урока учащийся сможет выполнять операции с функциями, работая со своими доменами.
20	Функции	Функциональный состав
Цель: По завершении урока учащийся поймет состав функций или функцию функции.
21	Функции	Обратные функции
Задача: По завершении урока ученик сможет находить обратные функции, правильно использовать обозначения и использовать тест горизонтальной линии.
22	Функции	Рациональные функции Часть 1
Цель: По завершении урока учащийся сможет работать с разделением функций и интерпретировать это на плоскости координатных чисел, показывая вертикальные и горизонтальные асимптоты.
23	Функции	Рациональные функции, часть 2
Цель: По завершении урока учащийся сможет использовать степень многочленов и деление многочленов, чтобы помочь построить график рациональных функций на плоскости координатных чисел, показывая вертикальные, горизонтальные и наклонные асимптоты.
24	Функции	Параметрические уравнения (этап 2)
Цель: По завершении урока учащийся сможет исключить параметр из набора уравнений и определить соответствующие ограничения для области определения и диапазона.
25	Функции	Сложение полиномов и т. Д. При объединении и упрощении функций (этап 2)
Задача: По завершении урока ученик получит несколько методов понимания и построения графиков с использованием алгебры.
26	Функции	Параметрические функции (этап 2)
Цель: По завершении урока ученик поймет некоторые стандартные параметрические формы, использующие тригонометрические тождества, оценит красоту графиков, которые могут быть созданы, и приложение для метательного движения.
27	Алгебра-неравенства	Устранение неравенств.
Задача: По завершении урока ученик научится понимать знаки «больше» и «меньше» и сможет выполнять простые неравенства.
28	Алгебраические дроби-двучлены	Сокращение биномиальных множителей в алгебраических дробях.
Цель: По завершении урока учащийся должен уметь разложить биномы на множители, чтобы упростить дроби.
29	Абсолютное значение или модуль	Упрощение абсолютных значений
Цель: По завершении урока учащийся сможет упрощать выражения, содержащие абсолютные значения или модуль действительных чисел.
30	Абсолютное значение или модуль	Решение для переменной
Цель: По завершении урока учащийся сможет решать уравнения, содержащие одно абсолютное значение.
31	Абсолютное значение или модуль	Решение неравенств и построение графиков
Задача: По завершении урока учащийся сможет решить неравенства, связанные с одним абсолютным значением.
32	Координатные геометрические неравенства	Неравенства на числовой плоскости.
Задача: По завершении урока учащийся сможет вывести выражение для неравенства с учетом его графика. Студент также сможет решать некоторые задачи, используя неравенства.
33	Переводы	Преобразования — отражения
Цель: По завершении урока ученик сможет сделать предварительный образ и, используя соответствующие приемы, точно показать его изображение после отражения.
34	Геометрические преобразования	Преобразования геометрии без матриц: отражение (этап 2)
Цель: По завершении этого урока учащийся будет использовать и понимать язык, используемый в геометрических преобразованиях и выполнять отражения в числовой плоскости.
35	Геометрические преобразования	Преобразования геометрии без матриц: трансляция (этап 2)
Задача: По завершении этого урока ученик выполнит переводы в числовой плоскости.
36	Геометрические преобразования	Преобразования геометрии без матриц: вращение (этап 2)
Цель: По завершении этого урока ученик будет выполнять и строить вращения.
37	Геометрические преобразования	Преобразования геометрии без матриц: расширение или расширение (этап 2)
Цель: По завершении этого урока ученик выполнит неконгруэнтное преобразование расширения или увеличения и вычислит масштабный коэффициент.
38	Геометрические преобразования	Определение и концепция комбинированных преобразований, приводящих к эквивалентному одиночному преобразованию.
Цель: По завершении этого урока ученик будет комбинировать отражения и трансформации скольжения для получения единичных изометрических трансформаций.
39	Логарифмы и журналы	Уравнения типа log x с основанием 3 = 4.
Цель: По завершении урока учащийся будет лучше понимать определение логарифма и то, как его использовать для поиска неизвестной переменной, которая в данном случае является числом, от которого эволюционирует логарифм.
40	Логарифмы и журналы	Уравнения типа log 32 с основанием x = 5.
Цель: По завершении урока учащийся будет лучше понимать определение логарифма и то, как его использовать для поиска неизвестной переменной, которая в данном случае является базой, из которой произошло число.
41	Законы логарифмов-логарифмов	Законы логарифмов.
Задача: По завершении урока ученик будет знаком с 5 законами логарифмирования.
42	Расширение логарифмов и логарифмов	Использование логарифмических законов для расширения логарифмических выражений.
Задача: По завершении урока учащийся сможет использовать логарифмические законы для расширения логарифмических выражений.
43	Логарифм-логарифмические законы, упрощающие	Использование логарифмических законов для упрощения выражений, содержащих логарифмы.
Цель: По завершении урока ученик сможет упростить логарифмические выражения, используя законы логарифма.
44	Логарифмы-Логарифм чисел	Использование законов журнала для нахождения логарифмов чисел.
Цель: По завершении урока учащийся будет лучше понимать использование законов журнала и сможет выполнять больше приложений с числовыми примерами.
45	Логарифмы и журналы	Уравнения с логарифмами.
Цель: По завершении урока учащийся сможет решать уравнения с логарифмическими членами.
46	Логарифмы для решения уравнений	Использование логарифмов для решения уравнений.
Цель: По завершении урока учащийся сможет использовать логарифмы для решения индексных уравнений с помощью калькулятора.
47	Базовая формула изменения логарифмов	Изменение базовой формулы
Задача: По завершении урока ученик увидит изменение базовой формулы для логарифмов и сможет использовать ее для замены логарифма одного основания на другое.
48	Логарифм-график-логарифм	График логарифмической кривой
Задача: По завершении урока учащийся сможет построить логарифмическую кривую с заданным основанием и знать общие свойства кривых каротажа.
49	Логарифм-логарифмические кривые	Работа с кривыми каротажа.
Задача: По завершении урока учащийся сможет решать задачи с кривыми каротажа
50	Последовательности и серии	Общие последовательности.
Задача: По завершении урока учащийся сможет составить формулу из заданного числового шаблона, а затем найти конкретные члены этой последовательности, используя формулу.
51	Последовательности и серии	Нахождение Tn по Sn.
Задача: По завершении урока ученик поймет, что сумма n членов ряда минус сумма n минус один член даст n-й семестр.
52	Арифметическая прогрессия	Арифметическая прогрессия
Цель: По завершении урока ученик сможет проверить, является ли данная последовательность арифметической прогрессией или нет, и сможет найти формулу для n-го члена, найти любой термин в AP и решить проблемы, связанные с эти концепции.
53	Арифметическая прогрессия	Определение позиции термина в A.С.
Цель: По завершении урока ученик сможет решить множество задач, связанных с нахождением членов арифметической прогрессии.
54	Арифметическая прогрессия	Дайте два члена A.P., найдите последовательность.
Задача: По завершении урока ученик сможет найти любой член арифметической прогрессии, если ему даны два члена
55	Арифметическая прогрессия	Средние арифметические
Задача: По завершении урока ученик сможет произвести арифметическую прогрессию между двумя заданными терминами.Это может включать поиск одного, двух или даже большего количества средних арифметических.
56	Арифметическая прогрессия	Сумма n членов A.P.
Цель: По завершении урока ученик поймет формулы для суммы арифметической прогрессии и научится их использовать при решении задач.
57	Геометрическая прогрессия	Геометрическая прогрессия.
Цель: По завершении урока ученик сможет проверить, является ли данная последовательность геометрической прогрессией или нет, и сможет найти формулу для n-го термина, найти любой термин в G.П. и решать проблемы, связанные с этими понятиями.
58	Геометрическая прогрессия	Определение позиции термина в G.P.
Задача: По завершении урока ученик поймет, как находить термины в геометрической прогрессии и как применять к ним различные типы задач.
59	Геометрическая прогрессия	Даны два члена G.P., найдите последовательность.
Цель: По завершении этого урока ученик сможет решить все задачи, связанные с нахождением общего отношения геометрической прогрессии.
60	Последовательности и ряды — геометрические средства	Средние геометрические.
Задача: По завершении урока ученик сможет провести геометрическую прогрессию между двумя заданными семестрами. Это может включать поиск одного, двух или даже большего числа геометрических средних.
61	Последовательности и сумма серий gp	Сумма n членов G.P.
Задача: по завершении урока ученик поймет формулы и научится их использовать для решения задач в суммировании геометрической прогрессии (G.П).
62	Последовательности и обозначение серий-сигма	Сигма-нотация
Цель: По завершении проекта G.P. На уроке учащийся познакомится с сигма-обозначением и принципом его действия.
63	Последовательности и серия-сумма-бесконечность	Ограничение суммы до бесконечности.
Цель: По завершении урока ученик выучит формулу предельной суммы G.П., условия его существования и способы его применения к конкретным задачам.
64	Последовательности и серии	Приложения арифметических последовательностей
Задача: По завершении урока ученик будет способен решать задачи, связанные с практическими ситуациями с арифметическими рядами.
65	Статистическая вероятность	Вероятность простых событий
Задача: По завершении урока ученик сможет понять вероятность простых событий.
66	Статистическая вероятность	Игра в кости
Задача: По завершении урока ученик сможет определить вероятность получения определенных результатов при одновременном броске двух кубиков.
67	Статистическая вероятность	Экспериментальная вероятность
Цель: По завершении этого урока учащийся сможет найти вероятности в экспериментальном исследовании.
68	Статистическая вероятность	Древовидные диаграммы — вне зависимости от предыдущих результатов
Цель: По завершении урока учащийся будет уверенно рисовать древовидные диаграммы для перечисления результатов многоэтапной вероятностной задачи, а затем находить вероятности определенных событий, не зависящих от предыдущих результатов.
69	Статистическая вероятность	Древовидные диаграммы — в зависимости от предыдущих результатов
Цель: По завершении урока ученик будет уверенно рисовать древовидные диаграммы, чтобы перечислить результаты других многоэтапных вероятностных задач, а затем находить вероятности определенных событий в зависимости от предыдущих результатов.
70	Статистическая вероятность	Дополнительный результат ..
Задача: По завершении урока учащийся сможет определить вероятность определенных результатов, когда задействовано дополнительное событие.
71	Статистическая вероятность	P [A или B] Когда A и B являются взаимоисключающими, а НЕ взаимоисключающими
Задача: По завершении этого урока учащийся сможет различать взаимоисключающие и не исключающие друг друга события и находить вероятности того и другого.
72	Статистическая вероятность	Биномиальная теорема — треугольник Паскаля
Цель: По завершении этого урока ученик будет использовать треугольник Паскаля и биномиальную теорему, чтобы написать разложение биномиальных выражений в целых степенях.
73	Статистическая вероятность	Биномиальные вероятности с использованием биномиальной теоремы
Цель: По завершении урока учащийся сможет решать определенные типы вероятностных вопросов, используя биномиальную теорему
74	Статистическая вероятность	Методы подсчета и упорядоченные выборки — перестановки
Задача: По завершении этого урока учащийся научится использовать некоторые новые методы счета, используемые для решения вероятностей.
75	Тригонометрические-точные соотношения	Тригонометрические соотношения 30, 45 и 60 — точные соотношения.
Задача: По завершении урока ученик сможет найти точные соотношения синуса, косинуса и тангенса для углов 30, 45 и 60.
76	Правило тригонометрии-косинуса	Правило косинуса для поиска неизвестной стороны. [Случай 1 SAS].
Цель: По завершении урока ученик сможет использовать правило косинуса, чтобы найти длину неизвестной стороны треугольника, зная 2 стороны и включенный угол.
77	Правило тригонометрии-косинуса	Правило косинуса для нахождения неизвестного угла. [Случай 2 SSS].
Цель: По завершении урока ученик сможет найти размер неизвестного угла треугольника, используя правило косинуса, учитывая длины трех сторон.
78	Тригонометрия-правило синуса	Правило синуса для поиска неизвестной стороны. Дело 1.
Цель: По завершении урока ученик сможет использовать правило синуса, чтобы найти длину определенной стороны, когда ученику даны размеры двух углов и одной из сторон.
79	Тригонометрия-правило синуса	Правило синуса для поиска неизвестного угла. Дело 2.
Цель: По завершении урока учащийся сможет использовать правило синуса, чтобы найти неизвестный угол, если у него есть две стороны и угол без включения.
80	Тригонометрические области	Формула площади
Цель: По завершении урока учащийся сможет использовать формулу синуса для определения площади треугольника с учетом двух сторон и включенного угла.
81	Тригонометрические отношения	Обратные отношения.
Цель: По завершении урока ученик сможет определить и использовать тригонометрические соотношения синуса, косинуса и тангенса, то есть косеканс, секанс и котангенс.
82	Дополнительные углы триггера	Дополнительные угловые результаты.
Цель: По завершении урока ученик поймет, как установить дополнительные угловые результаты для соотношений синуса и косинуса, а затем как использовать эти результаты для решения тригонометрических уравнений.
83	Идентификаторы триггеров	Тригонометрические идентификаторы
Задача: По завершении урока учащийся сможет упростить тригонометрические выражения и решить тригонометрические уравнения, используя знание тригонометрических тождеств.
84	Триггер большие углы	Углы любой величины
Цель: По завершении урока ученик сможет найти тригонометрические значения углов любой величины, назначив углы четырем квадрантам круга.
85	Триггер большие углы	Тригонометрические отношения 0 °, 90 °, 180 °, 270 ° и 360 °
Цель: По завершении урока ученик научится находить тригонометрические отношения 0, 90, 180, 270 и 360 градусов.
86	График синус	График тригонометрических соотношений — I Синусоидальная кривая.
Цель: По завершении урока ученик узнает и начертит синусоидальную кривую, исследуя изменения амплитуды и периода.
87	График косинус	График тригонометрических соотношений — II Косинусная кривая.
Цель: По завершении урока ученик научится распознавать и рисовать косинусную кривую, исследуя изменения амплитуды и периода.
88	Графики кривой загара	График тригонометрических отношений — III Касательная кривая.
Цель: По завершении урока ученик научится распознавать и рисовать кривую загара.
89	График обратных чисел	Построение тригонометрических соотношений — IV Обратные соотношения.
Цель: По завершении урока ученик научится распознавать и рисовать кривые взаимных отношений: cosec, sec и cot.
90	Триггер большие углы	Использование одного соотношения для поиска другого.
Цель: По завершении урока учащийся найдет другие триггерные соотношения для одного триггерного соотношения и сможет работать с углами любой величины.
91	Триггерные уравнения	Решение тригонометрических уравнений — тип I.
Цель: По завершении урока ученик будет решать простые триггерные уравнения с ограниченными областями.
92	Триггерные уравнения	Решение тригонометрических уравнений — Тип II.
Задача: По завершении урока ученик решит тригонометрические уравнения с кратными тета и ограниченными областями.
93	Триггерные уравнения	Решение тригонометрических уравнений — Тип III.
Задача: По завершении урока ученик решит тригонометрические уравнения с двумя тригонометрическими отношениями и ограниченными областями.
94	Тригонометрия	Sin (A + B) и т. Д. Тождества суммы и разности (этап 2)
Цель: По завершении урока ученик будет использовать контрольные треугольники для 30, 45 и 60 градусов с суммой и разностью углов, чтобы найти дополнительные точные значения тригонометрических соотношений.
95	Тригонометрия	Формулы двойного угла (этап 2)
Задача: По завершении урока ученик выведет и использует триггерные тождества двойного угла.
96	Тригонометрия	Идентификаторы половинного угла (этап 2)
Задача: По завершении урока ученик выведет и использует формулы уменьшения мощности и триггерные тождества половинного угла.
97	Тригонометрия	т Формулы (этап 2)
Задача: По завершении урока ученик решит тригонометрические уравнения с заменой t.
98	Равномерное движение	Равномерное движение с равными расстояниями
Цель: По завершении урока ученик будет использовать индексированные переменные для расчета скорости, равных расстояний и времени.
99	Равномерное движение	Равномерное движение с добавлением расстояний
Цель: По завершении урока ученик будет использовать индексированные переменные для расчета скорости, добавляя расстояния к общему расстоянию и времени.
100	Равномерное движение	Равномерное движение с неравными расстояниями
Цель: По завершении урока ученик будет использовать индексированные переменные для расчета скорости, неравных расстояний и времени.
101	Равномерное движение	Равномерное движение всех типов
Цель: По завершении урока ученик будет использовать все типы индексированных переменных для вычислений, чтобы определить скорость, расстояние и время.
102	Движение при ускорении	Движение под действием силы тяжести — объекты в вертикальном движении
Цель: По завершении урока ученик будет преобразовывать коэффициенты и использовать уравнения движения, которые включают равномерное ускорение.
103	Движение при ускорении	Представляем начальную скорость
Цель: По завершении урока ученик будет использовать уравнения движения, которые включают равномерное ускорение и начальную скорость.
104	Исчисление	Пределы
Задача: По завершении урока ученик сможет решать задачи, используя правило предельной суммы.
105	Исчисление = 1-й принт	Отличие от первых принципов.
Цель: По завершении урока учащийся сможет применить формулу первых принципов (исчисление), чтобы найти градиент касательной в любой точке непрерывной кривой.
106	Исчисление = 1-й принт	Дифференцирование y = x в степени n.
Задача: По завершении урока «Исчисление» ученик сможет различать несколько выражений, в которых x возведен в степень n.
107	Дифференциальное исчисление, целое	Значение dy над dx — уравнения касательных и нормалей.
Цель: По завершении урока математического анализа ученик сможет применить навыки дифференцирования и алгебры, чтобы найти уравнение касательной и нормали к точке на кривой.
108	Дифференциальное исчисление, целое	Функция правила функции, правила произведения, правила частного.
Цель: По завершении урока «Исчисление» учащийся поймет, как использовать правило цепочки, правило произведения и правило частного.
109	Дифференциальное исчисление, целое	Возрастающие, убывающие и стационарные функции.
Цель: По завершении урока учащийся поймет, как находить первую производную различных функций и использовать ее в различных ситуациях для определения возрастающих, убывающих и стационарных функций.
110	Исчисление	Первая производная — точки поворота и построение кривых
Цель: По завершении урока «Исчисление» учащийся сможет использовать первую производную, чтобы найти и определить характер стационарных точек на кривой.
111	Исчисление-2-я производная	Вторая производная — вогнутость.
Цель: По завершении урока математического анализа учащийся сможет найти вторую производную и использовать ее, чтобы найти область, в которой кривая вогнута вверх или вниз, а также любые точки перегиба.
112	Исчисление — построение кривых	Набросок кривой
Цель: По завершении урока математического анализа учащийся сможет использовать первую и вторую производные, чтобы найти точки поворота кривой, определить максимумы и минимумы, а также вогнутость, а затем использовать эту информацию для построения кривой.
113	Исчисление — минимумы максимума	Практическое применение максимумов и минимумов
Задача: По завершении урока учащийся сможет применить исчисление к набору простых задач на максимумы или минимумы.
114	Исчисление — Интеграция	Интеграция — антидифференциация, примитивная функция
Цель: По завершении урока «Исчисление» учащийся сможет использовать правила интегрирования для поиска примитивов некоторых простых функций.
115	Исчисление — Область вычислений	Расчет площади
Цель: По завершении урока «Исчисление» ученик сможет выбрать подходящую формулу для вычисления площади, изменить форму выражения в соответствии с формулой и использовать правильные пределы в формуле для оценки площади.
116	Исчисление — Объемы вычислений	Расчет объемов вращения
Цель: По завершении урока математического анализа ученик будет знать, как выбрать подходящую формулу объема, изменить форму выражения в соответствии с формулой и затем вычислить результат с заданной точностью.
117	Исчисление — правила трапеции и Симпсона	Правило трапеции и правило Симпсона
Цель: По завершении урока «Исчисление» учащийся научится рассчитывать подинтервалы, создавать таблицу значений, а затем применять правило трапеции или правило Симпсона для аппроксимации площади под кривой.
118	Векторы	Векторы
Цель: По завершении урока ученик сможет представить вектор в матричной и схематической форме, а также сложить два вектора с помощью матриц и / или диаграммы.
119	Одновременные уравнения	Количество решений (2 этап)
Задача: По завершении урока урока ученик определит совместные уравнения, которые являются непротиворечивыми, несовместимыми или одинаковыми.
120	Векторы	Сложение 2 векторов в 2 и 3D (стадия 2)
Задача: По завершении урока учащийся поймет и использует формы компонентов для векторного разрешения.
121	Линейные системы	Оптимальные решения (этап 2) — Векторы
Цель: По завершении урока учащийся поймет процесс линейного программирования для поиска оптимальных решений.
122	Приблизительные корни	Методы аппроксимации корней
Цель: По завершении урока ученик сможет находить приближенные корни полиномиальных уравнений, используя полуинтервальный метод. Студент сможет применить это правило несколько раз в одном вопросе.
123	Приблизительно	Метод приближения Ньютона
Цель: По завершении урока учащийся сможет использовать метод Ньютона для нахождения приближенных корней полиномиальных уравнений и уметь применять этот метод более чем один раз.
124	Логика	Индуктивные и дедуктивные рассуждения
Цель: По завершении этого урока ученик поймет и будет использовать термины гипотеза, заключение, индуктивный и дедуктивный.
125	Логика	Определение и использование примеров счетчиков
Задача: По завершении этого урока учащийся сможет создавать контрпримеры к утверждениям.
126	Логика	Косвенные доказательства
Задача: По завершении урока учащийся сможет использовать косвенные доказательства, предполагая противоположное доказываемому утверждению.
127	Логика	Математическая индукция
Цель: По завершении урока ученик сможет выполнить процесс математической индукции для простых рядов.
128	Логарифмы — комплексные числа	Мнимые числа и стандартная форма
Задача: По завершении урока ученик будет использовать форму a + bi комплексных чисел для сложения и вычитания.
129	Логарифмы — комплексные числа	Комплексные числа — умножение и деление
Задача: По завершении урока ученик будет использовать форму a + bi комплексных чисел для умножения и деления.
130	Логарифмы — комплексные числа	Построение комплексного числа и графического представления
Задача: По завершении урока учащийся будет использовать диаграмму аргандов для сложения и вычитания комплексных чисел.
131	Логарифмы — комплексные числа	Абсолютное значение
Цель: По завершении урока ученик будет использовать абсолютное значение или модуль комплексных чисел
132	Логарифмы — комплексные числа	Тригонометрическая форма комплексного числа
Задача: По завершении урока ученик напишет комплексные числа в тригонометрической или полярной форме.Это также может быть известно как модная форма.
133	Логарифмы — комплексные числа	Умножение и деление комплексных чисел в триггерной форме (этап 2)
Задача: По завершении урока ученик будет использовать тригонометрическую форму комплексных чисел для умножения и деления.
134	Логарифмы — комплексные числа	Теорема ДеМуавра (этап 2)
Цель: По завершении урока ученик будет использовать теорему ДеМуавра, чтобы найти степени комплексных чисел в триггерной форме.
135	Логарифмы — комплексные числа	Корень n-й степени из действительных и комплексных чисел (этап 2)
Цель: По завершении урока ученик будет использовать теорему ДеМуавра, чтобы найти корни комплексных чисел в триггерной форме.
136	Логарифмы — комплексные числа	Основная теорема алгебры (этап 2)
Цель: По завершении урока ученик узнает и использует основную теорему алгебры, чтобы найти множители для многочленов с действительными коэффициентами над полем комплексных чисел.
137	Статистика — сгруппированные данные	Расчет среднего, режима и медианы на основе сгруппированных данных
Задача: По завершении урока учащийся сможет определять центры классов, получать подсчеты частоты и определять средние и модовые значения.
138	Статистика с помощью калькулятора	Статистика и студенческий калькулятор
Задача: По завершении урока учащийся сможет использовать научный калькулятор в режиме статистики для вычисления ответов на статистические задачи.
139	Статистика — Дальность и разброс	Дальность как мера рассеивания
Задача: По завершении урока ученик сможет определять диапазон и использовать его при принятии решений.
140	— Распространение	Меры распространения
Цель: По завершении урока учащийся сможет найти стандартное отклонение, используя набор данных или таблицу частотного распределения и калькулятор.
141	Статистика — стандартное отклонение	Приложения стандартного отклонения
Цель: По завершении урока ученик сможет использовать стандартное отклонение как меру отклонения от среднего.
142	Статистика — стандартное отклонение	Нормальное распределение
Цель: По завершении урока учащийся сможет использовать стандартное отклонение нормального распределения, чтобы найти процентное соотношение баллов в пределах диапазона.
143	Статистика — Межквартильный размах	Меры разброса: межквартильный размах
Задача: По завершении урока учащийся сможет найти верхний и нижний квартили и межквартильный размах
144	Статистика	Делянки стеблей и листьев, а также делянки коробок и усов
Задача: По завершении урока учащийся будет ознакомлен со статистической лексикой, включая квартили, режим, медианное значение, диапазон и представление этой информации на графике прямоугольников и усов.
145	Экзамен	— 11–12 классы A Уровень
Цель: Экзамен

.