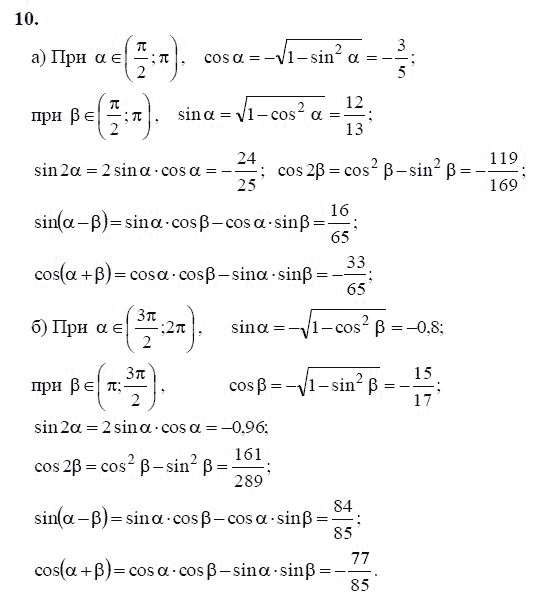Задачи по алгебре 10 класс с решением и ответами: 10 класс, задачи по алгебре и геометрии на разные темы, онлайн

Задачи повышенной сложности по математике 10

Задачи повышенной сложности по математике 10 — 11 класс с решением и ответами.

Задача 1.

Найдите все простые числа p и q такие, что p + q = (p – q)³.

Решение:

Ответ: p = 5, q = 3.
Пусть p – q = n, тогда p + q = n³.

Отсюда  .

Среди трех последовательных целых чисел одно делится на 3, поэтому q делится на 3. Среди простых чисел только 3 делится на 3. Значит, q = 3. Это значение q получается при n = 2.

Задача 2.

Приведенный квадратный трехчлен f(x) имеет 2 различных корня.
Может ли так оказаться, что уравнение f(f(x)) = 0 имеет 3 различных корня, а уравнение f(f(f(x))) = 0 — 7 различных корней?

Решение:

Ответ: Нет.
Из условия следует, что f(x) = (x – a)(x – b), где a ≠ b.
Пусть искомый многочлен f(x) существует.
Тогда, очевидно f(f(x)) = (x – t₁)²(x – t₂)(x – t₃).
Заметим, что t₁, t₂, t₃ — корни уравнений f(x) = a и f(x) = b, при этом корни этих уравнений не совпадают, поэтому можно считать, что уравнение f(x) = a имеет один корень x = t₁.
Рассмотрим уравнение f(f(f(x))) = 0. Его решения, очевидно, являются решениями уравнений f(f(x)) = a и f(f(x)) = b. Но уравнение f(f(x)) = a равносильно уравнению f(x) = t₁ и имеет не более двух корней, а уравнение f(f(x)) = b — не более четырех корней (как уравнение четвертой степени).
То есть уравнение f(f(f(x))) = 0 имеет не более 6 корней.

Задача 3.

Пусть AD — биссектриса треугольника ABC, и прямая l касается окружностей, описанных около треугольников ADB и ADC в точках M и N соответственно.
Докажите, что окружность, проходящая через середины отрезков BD, DC и MN, касается прямой l.

Решение:

Решение 1.
Обозначим центры окружностей, описанных около треугольников ADB и ADC через O₁ и O₂, а середины отрезков BD, DC, MN, DO₂ и O₁O₂ — через A₁, A₂, K, E и O соответственно (см. рис.). Пусть  ∠ BAD =  ∠ CAD =  α . Тогда  ∠ A₁O₁D =  ∠ A₂O₂D =  α  (так как половина центрального угла равна вписанному, опирающемуся на ту же дугу). Отрезок OK — средняя линия трапеции (или прямоугольника) O₁MNO₂, следовательно, OK ⊥ l, и  . Заметим, что точки E, O и A₂ лежат на одной прямой, так как  ∠ OEO₂ +  ∠ O₂EA₂ =  ∠ O₁DO₂ +  ∠ O₂EA₂ =  ∠ O₁AO₂ + (180° –  ∠ DO₂C) = 2 α  + (180° – 2 α ) = 180°, т.е. OK = OE + EA₂ = OA₂. Аналогично доказывается, что OA₁ = OK. Значит, точки A₁, A₂ и K лежат на окружности с центром O, а так как OK ⊥ l, то эта окружность касается прямой l.

Случай, когда вместо прямой l рассматривает-ся прямая l₁, разбирается аналогично.

Решение 2.
Пусть радиусы окружностей, описанных около треугольников ADB и ADC равны R₁ и R₂. Если эти радиусы различны, то прямая l пересекает линию центров O₁O₂ в точке O (см. рис.). Пусть OD пересекает окружности в точках B′ и C′, и OA пересекает  ω  в точке A′. При гомотетии H с центром O и коэффициентом   точки C′, D и A переходят в точки D, B′ и A′ соответственно, следовательно,  ∠ DAC′ =  ∠ B′A′D. С другой стороны,  ∠ B′A′D =  ∠ B′AD, поэтому  ∠ B′AD =  ∠ C′AD. А это означает, что точки B′ и C′ совпадают с точками B и C, так как в противном случае один из углов BAD и CAD был бы меньше  α , а другой — больше  α  ( α  =  ∠ B′AD =  ∠ C′AD).

Рассмотрим гомотетию H₁ с центром O, переводящую  ω ₂ в окружность  ω , проходящую через точку E — середину отрезка MN. Из того, что l проходит через точку O и  ω ₂ касается l, следует, что  ω  касается l в точке E. Кроме того, из гомотетичности треугольников ONC и OMD (гомотетия H) следует, что NC || MD. Кроме того, H₁(C) = C₁, где EC₁ || NC. Поэтому EC₁ — средняя линия трапеции CNMD, т. е. гомотетия H₁ переводит точку C в середину DC. Аналогично, она переводит D в середину отрезка BD. Значит,  ω  проходит через середины отрезков BD и DC.

Если же R₁ = R₂, то вместо гомотетии следует рассмотреть параллельный перенос на вектор  .

Решение 3.
Пусть R₁ ≠ R₂. Проведем перпендикуляр SO к плоскости  π , содержащей окружности  ω ₁ и  ω ₂ (см. обозначения в предыдущем решении). Нетрудно понять, что пересечение (наклонного) конуса с вершиной S и основанием  ω ₁ и прямого кругового цилиндра с основанием  ω ₂ является окружность, равная  ω ₂ и лежащая в плоскости  π ₁ ||  π . Глядя на рис., заключаем, что ортогональной проекцией на плоскость  π  пересечения конуса и плоскости, равноудаленной от  π  и  π ₁ является окружность, проходящая через середины отрезков BD, DC и MN и касающаяся прямой MN.

В случае R₁ = R₂ вместо конуса следует рассмотреть (наклонный) цилиндр с основанием  ω ₁.

Задача 4.

Дана последовательность x_k такая, что x₁ = 1, x_n + 1 = n sin x_n + 1.
Докажите, что последовательность непериодична.

Решение:

Предположим, что она периодична и длина периода равна T, тогда x_m + T = x_m и x_{m + T + 1} = x_m + 1 при m ≥ m₀.
Если при некотором m ≥ m₀  sin x_m ≠ 0, то x_{m + T + 1} = (m + T) sin x_m + T + 1 = (m + T) sin x_m + 1 ≠ m sin x_m + 1 = x_m + 1.
А если  sin x_m = 0, то x_m + 1 = 1, и  sin x_m + 1 =  sin 1 ≠ 0, так что предыдущее рассуждение применимо к x_m + 1.
Таким образом получаем противоречие.

Задача 5.

Докажите, что если у тетраэдра два отрезка, идущие из вершин некоторого ребра, в центры вписанных окружностей противолежащих граней, пересекаются, то отрезки, выпущенные из вершин скрещивающегося с ним ребра в центры вписанных окружностей двух других граней, также пересекаются.

Решение:

Пусть A₁ — центр вписанной окружности  ∆ SBC, B₁ — центр вписанной окружности  ∆ SAC, AA₁ пересекается с   A, A₁, B₁, B лежат в одной плоскости, значит прямые AB₁ и BA₁ пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то  . Но тогда AC • BS = BC • AS, отсюда  , следовательно биссектрисы углов S в  ∆ ASB и C в  ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей  ∆ ASB и  ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются.

Задача 6.

На плоскости дано бесконечное множество точек S, при этом в любом квадрате 1 × 1 лежит конечное число точек из множества S. Докажите, что найдутся две разные точки A и B из S такие, что для любой другой точки X из S выполняется: |XA|,\;|XB| ≥ 0,999|AB|.

Решение:

Докажем утверждение задачи от противного.
Можно предположить, что для любых двух разных точек A и B из S найдется отличная от них точка X из S такая, что либо XA  Переформулируем вышеприведенное утверждение: для любого отрезка I с концами в S и длиной l найдется отрезок I′ с концами в S длины не более 0,999l, один из концов которого совпадает с некоторым концом I.
Или, иначе говоря, I′ пересекает I.
Возьмем теперь первый отрезок I₁ длины l и будем брать отрезки I₂, I₃, …так, что I_k + 1 пересекается с I_k и |I_k + 1| _k|.
Все эти отрезки имеют концы в S. Ломаная не короче отрезка, соединяющего ее концы, поэтому расстояние от любого конца I_k до любого конца I₁ не превосходит

Следовательно, в квадрате 2000l × 2000l с центром в любом из концов I₁ лежит бесконечное число точек S.
Но из условия следует конечность их числа в любом квадрате.

Полученное противоречие завершает доказательство.

Задача 7.

Докажите, что в любом множестве, состоящем из 117 попарно различных трехзначных чисел, можно выбрать 4 попарно непересекающихся подмножества, суммы чисел в которых равны.

Решение:

Лемма.
Из любых 61 различных трехзначных чисел можно выбрать две непересекающиеся пары чисел, суммы в которых равны.
Доказательство:
Из 61 числа можно образовать   пар чисел, сумма чисел в каждой паре лежит между 200 и 2000, следовательно, у каких-то двух пар суммы совпадают.
Пары, для которых совпадают суммы, очевидно, не могут пересекаться, ибо если x + y = x + z, то y = z и пары совпадают.
Лемма доказана.
Выберем пару пар чисел с равными суммами 15 раз (каждый раз будем исключать из рассматриваемого набора 4 взятых числа, перед последующим выбором чисел останется как раз 61 число).
Если не все 15 сумм были различны, то мы нашли 4 искомых множества — это 4 пары чисел, у которых совпадают суммы.
Если все 15 сумм различны, то составим два множества пар N₁ и N₂ таким образом: из двух пар с равными суммами первую включим в N₁, вторую — в N₂. Рассмотрим первое множество пар. У него есть 2¹⁵ подмножеств.
Сумма всех чисел во всех парах любого подмножества не превосходит 30,000 тысяч (чисел не больше 30, каждое меньше тысячи).
Но 2¹⁵  30\,000, следовательно, есть два подмножества, для которых суммы чисел, входящих во все их пары совпадают.
Выбросив из этих подмножеств их пересечение, получим непересекающиеся подмножества M₁ и M₂ с тем же условием.
Теперь в N₂ возьмем подмножества пар, соответствовавших парам из множеств M₁ и M₂ — M₃ и M₄.
Множества чисел, входящих в пары M₁, M₂, M₃, M₄ — искомые.
Комментарий: Из аналогичных соображений выбирая не только пары, но также тройки и четверки, можно показать, что четыре непересекающиеся подмножества с равными суммами можно выбрать среди любых 97 трехзначных чисел.

Олимпиадные задания (математика) – Олимпиада школьников «Высшая проба» – Национальный исследовательский университет «Высшая школа экономики»

2022/2023 учебный год

 

Задания	Решения и критерии
7 класс	Критерии и решения
8 класс	Критерии и решения
9 класс	Критерии и решения
10 класс	Критерии и решения
11 класс	Критерии и решения

2021/2022 учебный год

Для младших классов (7-8): максимальная оценка за всю работу — 100 баллов. Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100. 

Для старших классов (9-11): итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.

Полученнные баллы по каждой задаче направлены участникам на указанный при регистрации электронный адрес. Если вы не получили письмо, проверьте спам и напишите на [email protected]

Задания	Решения и критерии
7 класс	Решения и критерии
8 класс	Решения и критерии
9-10 классы	Решения и критерии
11 класс	Решения и критерии

2020/2021 учебный год

Для младших классов: максимальная оценка за всю работу — 100 баллов. Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100. 

Для старших классов: итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.

Задания	Решения и критерии
7 класс	Решения
8 класс	Решения
9 класс 10 класс	Решения
11 класс	Решения

2019/2020 учебный год

Задания	Решения и критерии
7 класс	7-8 классы решения и критерии
8 класс
9-10 классы	9-10 классы решения и критерии
11 класс	11 класс решения и критерии
Система пересчета знаков в баллы

Для младших классов: максимальная оценка за всю работу — 100 баллов. Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100. 

Для старших классов: итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.

2018/2019 учебный год

Задания	Решения и критерии
7 класc	Решения и критерии
8 класс	Решения и критерии
9 класс	Решения и критерии
10 класс	Решения и критерии
11 класс	Решения и критерии

2017/2018 учебный год

 Перевод оценок в баллы

Задания	Решения и критерии
7 класс	Решения и критерии
8 класс	Решения и критерии
9 класс	Решения и критерии
10 класс	Решения и критерии
11 класс	Решения и критерии

2016/2017 учебный год

 Перевод оценок в баллы

Задания	Решения и критерии
7 класс	7 классы
8 класс	8 классы
9 класс	9 классы
10 класс	10 классы
11 класс	11 классы

2015/2016 учебный год

 Перевод оценок в баллы

Задания	Решения и критерии
7 класс	7 класс
8 класс	8 класс
9 класс	9 класс
10 класс	10 класс
11 класс	11 класс

2014/2015 учебный год

 Перевод оценок в баллы

Задания	Решения и критерии
7 класс	7 класс
8 класс	8 класс
9 класс	9 класс
10 класс	10 класс
11 класс	11 класс Видеоразбор заданий

2013/2014 учебный год

 Задания и ответы отборочного этапа

Задания	Решения и критерии
7 класс	Решения и критерии оценки
8 класс	Решения и критерии оценки
9 класс	Решения и критерии оценки
10 класс	Решения и критерии оценки
11 класс	Решения и критерии оценки
Баллы по задачам

2012/2013 учебный год

 Задания 8 класс (задачи 1 и 2 имеют вес 16 баллов, остальные — 17 баллов)  Задания 9 класс (все задачи имеют равный вес (кроме 4): 17 баллов, задача 4 — 15 баллов)  Задания 10 класс (все задачи имеют равный вес (кроме 2): 17 баллов, задача 2 — 15 баллов)  Задания 11 класс (все задачи имеют равный вес (кроме 3): 17 баллов, задача 3 — 15 баллов)

2011/2012 учебный год

 9 класс  10 класс  11 класс

Рабочий лист с задачами по алгебре для 10 класса

(1) Решить (1/3) (x + y −5) = y − z = 2x −11 = 9−(x +2z)

Решение

(2) В школу принимают сто пятьдесят учеников. Они распределяются по трем секциям A, B и C. Если 6 студентов переводятся из секции A в секцию C, в секциях будет равное количество студентов. Если количество учащихся секции С в 4 раза превышает количество учащихся секции А на количество учащихся секции Б, найти количество учащихся в трех секциях. Решение

(3)  В трехзначном числе, когда цифры десятков и сотен переставлены местами, новое число в 54 раза больше исходного числа более чем в три раза. Если к номеру добавить 198, цифры меняются местами. Цифра десятков превышает цифру сотен в два раза, так как цифра десятков превышает цифру единиц. Найдите исходное число.

Решение

(4)  Найдите наименьшее общее кратное xy(k ²  +1)+k(x ²  + y ² ) и xy(k ²  -1)+k(x ²  -y ² )       Решение

(5)  Найти НОД следующего по алгоритму деления 7x ² + 23x + 7 , x ³  + 3x ²  + 3x + 1 , x ²  + 2x + 1

Решение

(6) 0 Приведите заданные выражения Rational к наименьшей форме 90 03 (x ^3a  — 8)/(x ^2a  + 2x ^a  + 4)        Решение

(ii)  (10x ³  — 25x ²  + 4x — 10)/(-4 — 10x ² )        Решение

(7)  Simplify 

2

3

3 3

(8) Арул, Рави и Работая вместе, Рам может очистить магазин за 6 часов. Работая в одиночку, Рави тратит на уборку магазина в два раза больше времени, чем Арул. Раму нужно в три раза больше времени, чем Арулу. Сколько времени потребуется каждому, если они будут работать в одиночку? Решение

(9)  Найти квадратный корень из 289x ⁴  -612x ³  + 970x ²  −684x + 361.                Решение

(10)  Решите √(y + 1) + √(2y −5) = 3         часа ( 6        Часов на

1 9000) идти 36 км вверх по реке, чем вниз по реке. Какова скорость лодки в стоячей воде, если скорость течения 4 км/ч?

Решение

(12)  Можно ли спроектировать прямоугольный парк с периметром 320 м и площадью 4800 м ²  ? Если да, то найдите его длину и ширину. Решение

(13)  В t минут после 14:00 время, необходимое до 15:00, на 3 минуты меньше, чем t ² /4. Найдите т. Решение

(14)  Количество мест в ряду равно общему количеству рядов в зале. Общее количество мест в зале увеличится на 375, если количество рядов увеличить вдвое, а количество мест в каждом ряду уменьшить на 5. Найдите количество рядов в зале в начале    Решение

(15)  Если a и b — корни многочлена f(x) = x ²  −2x + 3, найдите полином, корни которого равны

(i) α + 2, β + 2                  Решение

(ii)  (α — 1)/(α + 1), (β — 1)/ (β + 1)          Решение

(16)  Если –4 является корнем уравнения x ²  + px −4 = 0 и если уравнение x ²  + px +q = 0 имеет одинаковые корни, найдите значения p и q. Решение

(17)  Два фермера Сентил и Рави выращивают три сорта зерновых, а именно рис, пшеницу и раги. Если продажа (в ₹) трех сортов зерна обоими фермерами в апреле задается матрицей.

, а распродажа в мае (в ₹) ровно в два раза больше, чем распродажа в апреле для каждого сорта.

(i) Каков средний объем продаж в апреле и мае.

(ii) Если объем продаж продолжает увеличиваться таким же образом в последующие месяцы, каким будет объем продаж в августе? Solution

(18)  

Solution

(19) Given 

Solution

(20)  

Solution

Если вам нужны какие-либо другие материалы в Google, пожалуйста, используйте математику, указанную выше, пользовательский поиск здесь.

Пожалуйста, отправьте ваш отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

15 вопросов по алгебре и практических задач для учащихся средней школы

Вопросы по алгебре предполагают использование букв или символов для представления неизвестных значений или значений, которые могут изменяться. Здесь вы найдете 15 вопросов по алгебре, чтобы проверить свои знания и показать вам различные способы использования алгебры для решения задачи на поиск неизвестного значения или для обобщения.

Контрольные работы по математике на конец года для 4 и 5 классов

Оцените успеваемость по математике к концу 4 и 5 классов или подготовьтесь к контрольным работам штата с помощью этого пакета контрольных работ по математике

Алгебра в средней школе

Существует множество тем и техники в рамках алгебры. В средней школе мы учимся писать и обрабатывать основные алгебраические выражения и линейные уравнения. Позже мы развиваем эти методы, чтобы позволить нам иметь дело с более сложными полиномами и математическими задачами, например, с квадратными уравнениями или системой уравнений, поэтому важно создать прочную основу.

Как решать алгебраические уравнения

Когда вам предлагают решить алгебраическую задачу, важно установить, что вас просят сделать, особенно если это тест по математике. Вот некоторые из ключевых терминов вместе с тем, что они означают:

• Решите уравнение – узнайте значение неизвестного
• Подставить — поместите полученные значения в алгебраическое выражение
• Коэффициенты – сумма, на которую умножается слагаемое. Например, в выражении 4с+2 4 — это коэффициент.
• Константы – значения, которые не являются переменными и остаются неизменными. Например, для 4c + 2 константой является 2.
• Биномиальное — биномиальное или биномиальное выражение состоит из двух частей, как в нашем примере 4c + 2.
• Упростить — собрать вместе похожие термины, чтобы выражение или уравнение выглядело проще
• Развернуть — умножить выражения в скобках
• Факторизация – заключено в скобки
• Через x – переписать уравнение в виде x =…. .

Помните, что при работе с алгеброй мы все равно должны применять порядок операций PEMDAS. т. е. скобки, показатели степени (степени, квадратные корни), умножение, деление, сложение, вычитание.

При работе с алгебраическими выражениями и уравнениями мы должны тщательно продумать, какие операции следует выполнять в первую очередь.

Алгебра в начальной школе

Учащиеся уже в детском саду начинают решать задачи с алгебраическим мышлением. Алгебраическое мышление начинается с того, что учащиеся понимают свойства операций, отношения между ними и состав чисел.

Они начинают связывать конкретные модели с абстрактными выражениями и уравнениями и продолжают эту работу в начальной школе. Они также рассматривают шаблоны и порядок операций, которые будут способствовать их пониманию алгебры в последующие годы.

Это гибкое понимание состава и представления чисел, а также операций настраивает их на более сложные и абстрактные уравнения, когда они переходят в среднюю школу.

Алгебра в средней школе

Идеи написания и упрощения выражений, решения уравнений и подстановок вводятся в начальной школе. Вот несколько примеров вопросов по алгебре для начального уровня:

Практические вопросы по алгебре для средней школы

2 плитки шоколада будут стоить 2 партии с или 2 цента, а 2 напитка будут стоить 2 партии d или 2 пенса.

Нам нужно собрать вместе подобные члены, поэтому 4m + 2m = 6m и 5 – 1 = 4 (следите за отрицательным).

В средней школе мы изучаем различные методы алгебры, чтобы отвечать на вопросы по алгебре и практиковаться в решении задач по алгебре. К ним относятся:

• Упрощение алгебраических выражений
• Расширяющие скобки и факторинг
• Составление алгебраических уравнений из текстовых задач
• Решение алгебраических уравнений и неравенств
• Подстановка в выражения
• Изменение субъекта уравнения
• Работа с реальными графиками и линейными графиками
• Последовательности

Слайд, помогающий учащимся разобраться с уравнением прямой из онлайн-интервенции Third Space Learning.

Вопросы по алгебре для средней школы: базовая алгебра

12a+5b

В этом вопросе n равно 7, поэтому мы можем подставить 7 в формулу.

 

Стоимость = 20 фунтов стерлингов + 4 × 7

Стоимость = 48 фунтов стерлингов

4x и 6x

4 и x-6

2 и 2x-3

3 2x 3 и 9

x 3x и 9 Есть два способа попытки ответить на этот вопрос. Мы знаем, что площадь прямоугольника = длина × ширина, поэтому мы можем перемножить каждую пару, чтобы узнать, какая пара дает 4x − 6,9.2 — 6х\\ \end{выровнено}

 

В качестве альтернативы, если мы разложим 4x − 6, мы получим 2(2x − 3), что означает, что стороны могут быть равны 2 и 2x − 3.

C=\frac{5(F-32)}{9}

C=\frac{5F-32}{9}

C=\frac{5F}{9}-32

C=5F-\frac{32}{9}

\begin{align} F&=\frac{9C}{5}+32 \hspace{3cm} &\text{вычесть 32}\\\\ F-32&=\frac{9C}{5} &\text{умножить на 5}\\\\ 5(F-32)&=9C &\text{разделить на 9}\\\\ \frac{5(F-32)}{9}&=C \end{выровнено} 9{\ круг} .

Чтобы решить это, нам нужно написать уравнение.

 

Пусть сейчас возраст Джейми равен x . Тогда возраст отца Джейми в 4 раза больше.

 

Через 14 лет возраст Джейми будет x + 14, а возраст отца Джейми будет 4x + 14 .

 

Поскольку мы знаем, что возраст отца Джейми будет в два раза больше возраста Джейми, мы можем записать

 

4x+14=2(x+14)

 

Теперь у нас есть уравнение, которое мы можем решить.

 

\begin{выровнено} 4x+14&=2(x+14) \hspace{3cm} &\text{раскрыть скобки}\\ 4x+14&=2x+28 \hspace{3cm} &\text{вычесть 2x}\\ 2x+14&=28\hspace{3cm} &\text{вычесть 14}\\ 2x&=14 \hspace{3cm} &\text{раскрыть скобки}\\ х&=7 \hпробел{3см} \end{выровнено}

 

Сейчас Джейми 7 лет, то есть его отцу 28 лет. Сумма их возрастов равна 35 .

Примечание: когда алгебраические уравнения содержат знаменатели с обеих сторон, мы можем использовать метод перекрестного умножения, чтобы найти ответ. Например, со следующими выражениями:

\frac{a}{b} = \frac{c}{d}

Тогда это может стать

ad = bc

И так далее.

Вопросы по алгебре для средней школы: графики

y=2x-1

y=2x+1

y=4x-2

y=2x+5

В точке (2, 5), x равно 2, а y равно 5. Мы можем проверить, какое уравнение работает, если подставить следующие значения:

 

\begin{выровнено} y&=2x−1 \quad \quad \quad 5=2×2−1 \quad \quad \text{False}\\ y&=2x+1 \quad \quad 5=2×2+1 \quad \quad \text{True}\\ y&=4x−2 \quad \quad \quad 5=4×2−2 \quad \quad \text{False}\\ y&=2x+5 \quad \quad 5=2×2+5 \quad \quad \text{False} \end{выровнено}

Ищете другие вопросы по алгебре и математике?

Попробуйте эти:

• 15 вопросов на соотношение
• 15 вопросов о вероятности
• 15 вопросов по тригонометрии
• 15 одновременных вопросов уравнения
• 15 вопросов по диаграмме Венна
• Вопросы на длинное деление

Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.